question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Why test case has leading zero?
|
why-test-case-has-leading-zero-by-k48723-3prs
|
In constraints, said that would not contain leading zeros.\n\nnum consists of only digits and does not contain leading zeros.\n\nHowever, when I submit my answe
|
k487237
|
NORMAL
|
2022-04-12T14:47:35.125730+00:00
|
2022-04-12T14:47:35.125784+00:00
| 94 | false |
In constraints, said that would not contain leading zeros.\n```\nnum consists of only digits and does not contain leading zeros.\n```\nHowever, when I submit my answer, show my answer is `Memory Limit Exceeded`\nAnd I look the Input, there have leading zero in input.\n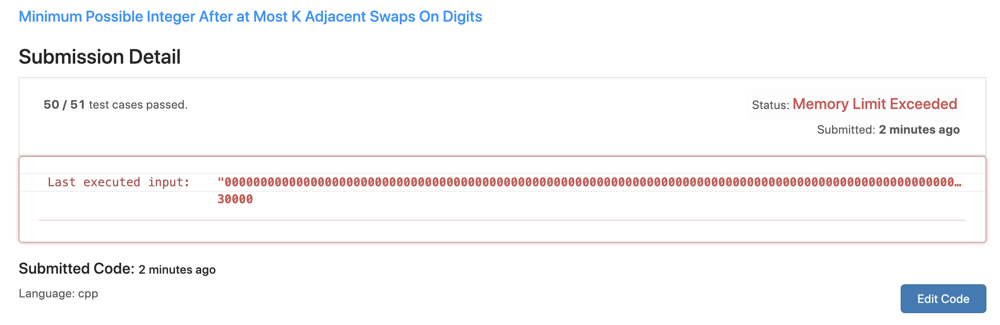\n\n\n
| 1 | 0 |
[]
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
C++ O(n^2) Simple Bruteforce (91.77/95.88)
|
c-on2-simple-bruteforce-91779588-by-ahol-oleg
|
\nclass Solution {\npublic:\n string minInteger(string num, int k) {\n int n = num.length();\n string ans(n,\'-\');\n int i = 0;\n
|
aholtzman
|
NORMAL
|
2021-12-16T20:33:00.498545+00:00
|
2021-12-19T18:57:22.709722+00:00
| 283 | false |
```\nclass Solution {\npublic:\n string minInteger(string num, int k) {\n int n = num.length();\n string ans(n,\'-\');\n int i = 0;\n int first = \'0\';\n int start = 0;\n int end = n-1;\n bool found = true;\n while (found == true)\n {\n found = false;\n for (char d = first; d<=\'9\' && k>0 && !found; d++)\n {\n int j, l;\n for (j = start, l=0; j<=end && k>=l; j++)\n {\n if (num[j] == d)\n {\n found = true;\n // cout << d << endl;\n ans[i++] = d;\n num[j] = \'-\';\n k -= l;\n if (d != first)\n break;\n }\n else if (num[j] != \'-\') l++;\n }\n if (j>end && d== first) first++;\n while (end >= start && num[end] == \'-\') end--;\n while (start <= end && num[start] == \'-\') start++;\n }\n }\n int j=start;\n while (i<n)\n {\n if (num[j] == \'-\')\n {\n j++;\n continue;\n }\n ans[i++] = num[j++];\n }\n return ans;\n }\n};\n```
| 1 | 1 |
[]
| 1 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
C++ O(nlogn) with segment tree
|
c-onlogn-with-segment-tree-by-yinyueemo-292v
|
\nstruct Node {\n int l, r;\n int v;\n Node() {\n v = 0;\n };\n};\n\n\nclass Solution {\npublic:\n vector<Node> tree;\n void build(int
|
yinyueemo
|
NORMAL
|
2021-05-30T06:24:43.671759+00:00
|
2021-05-30T06:24:43.671785+00:00
| 710 | false |
```\nstruct Node {\n int l, r;\n int v;\n Node() {\n v = 0;\n };\n};\n\n\nclass Solution {\npublic:\n vector<Node> tree;\n void build(int l, int r, int p) {\n tree[p].l = l;\n tree[p].r = r;\n if (l != r) {\n int mid = (l + r) >> 1;\n build(l, mid, 2 * p);\n build(mid+1, r, 2 * p + 1);\n }\n }\n void insert(int x, int p) {\n tree[p].v--;\n if (tree[p].l != tree[p].r) {\n int mid = (tree[p].l + tree[p].r) >> 1;\n if (x <= mid) insert(x, 2*p);\n else insert(x, 2*p+1);\n }\n }\n int query(int l, int r, int p) {\n if (tree[p].l == l && tree[p].r == r) return tree[p].v;\n else {\n int mid = (tree[p].l + tree[p].r) >> 1;\n if (r <= mid) return query(l, r, 2*p);\n else if (l >= mid+1) return query(l, r, 2*p + 1);\n else return query(l, mid, 2*p) + query(mid+1, r, 2*p + 1);\n }\n }\n \n string minInteger(string num, int k) {\n string result;\n \n vector<int> offset(num.size(), 0);\n vector<deque<int>> pos(10);\n for (int i = 0; i < num.size(); i++) pos[num[i]-\'0\'].push_back(i);\n \n tree = vector<Node>(4 * num.size() + 10);\n build(0, num.size() - 1, 1);\n \n int i = 0;\n while(true) {\n while (i < num.size() && offset[i] < 0) i++;\n if (i >= num.size()) break;\n \n int cp = i;\n if (cp - 1 >= 0) cp += query(0, cp - 1, 1);\n \n for (int p = 0; p <= 9; p++) {\n if (pos[p].size() > 0) {\n \n int fp = pos[p].front();\n if (fp - 1 >= 0) fp += query(0, fp - 1, 1);\n \n if (fp - cp <= k) {\n k -= fp - cp;\n offset[pos[p].front()] = -1;\n insert(pos[p].front(), 1);\n \n pos[p].pop_front();\n result += char(\'0\' + p);\n break;\n }\n }\n }\n }\n return result;\n }\n};\n```
| 1 | 0 |
[]
| 1 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
[Java] Brute Force via Bubble Sort
|
java-brute-force-via-bubble-sort-by-shen-hyp0
|
In short, the idea is to bubble up the smallest element so far (need to consider k swaps constraint)\n\n\tpublic class Solution1505 {\n\t\tpublic static void ma
|
shentianjie466357304
|
NORMAL
|
2021-03-04T01:40:34.073903+00:00
|
2021-03-04T01:41:38.588833+00:00
| 251 | false |
In short, the idea is to bubble up the smallest element so far (need to consider k swaps constraint)\n\n\tpublic class Solution1505 {\n\t\tpublic static void main(String[] args) {\n\t\t\tString num = "9438957234785635408";\n\t\t\tint k = 23;\n\n\t\t\tSolution1505 solution1505 = new Solution1505();\n\n\t\t\tSystem.out.println(solution1505.minInteger(num, k));\n\n\n\t\t}\n\n\t\tpublic String minInteger(String num, int k) {\n\t\t\tStringBuilder sb = new StringBuilder();\n\t\t\tchar[] input = num.toCharArray();\n\n\t\t\tint idx = 0;\n\n\t\t\twhile (idx < input.length && k > 0)\n\t\t\t{\n\t\t\t\tint minValue = input[idx] - \'0\';\n\t\t\t\tint minIndex = idx;\n\n\t\t\t\tint j = idx + 1;\n\n\t\t\t\tint tempK = k;\n\t\t\t\twhile (j < input.length && tempK > 0)\n\t\t\t\t{\n\t\t\t\t\tint curValue = input[j] - \'0\';\n\t\t\t\t\tif (curValue < minValue) {\n\t\t\t\t\t\tminValue = curValue;\n\t\t\t\t\t\tminIndex = j;\n\t\t\t\t\t}\n\t\t\t\t\tj++;\n\t\t\t\t\ttempK--;\n\t\t\t\t}\n\n\t\t\t\tsb.append(input[minIndex]);\n\n\t\t\t\tfor (int i = minIndex; i > idx; --i)\n\t\t\t\t{\n\t\t\t\t\tswap(input, i, i - 1);\n\t\t\t\t\tk--;\n\t\t\t\t}\n\n\t\t\t\tidx++;\n\t\t\t}\n\n\t\t\tfor (int i = idx; i < input.length; ++i)\n\t\t\t{\n\t\t\t\tsb.append(input[i]);\n\t\t\t}\n\n\t\t\treturn sb.toString();\n\n\t\t}\n\n\t\tprivate void swap(char[] input, int i, int j)\n\t\t{\n\t\t\tchar temp = input[i];\n\n\t\t\tinput[i] = input[j];\n\n\t\t\tinput[j] = temp;\n\t\t}\n\t}\n
| 1 | 0 |
[]
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Python3 - O(n^2) and O(n*log(n))
|
python3-on2-and-onlogn-by-yunqu-a4qj
|
Solution 1: The straightfoward O(n^2) solution will use a similar technique as the bubble sort; this will be TLE.\npython\nclass Solution:\n def minInteger(s
|
yunqu
|
NORMAL
|
2021-03-01T03:35:12.601900+00:00
|
2021-03-01T03:41:47.085685+00:00
| 325 | false |
**Solution 1**: The straightfoward O(n^2) solution will use a similar technique as the bubble sort; this will be TLE.\n```python\nclass Solution:\n def minInteger(self, num: str, k: int) -> str:\n """O(n^2) TLE"""\n i, size = 0, len(num)\n while k > 0 and i < size:\n mini = num[i]\n j_mini = i\n for j in range(i,min(i+k+1,size)):\n if num[j]<mini:\n mini = num[j]\n j_mini = j\n k -= (j_mini - i)\n num = num[:i] + mini + num[i:j_mini] + num[j_mini+1:]\n i += 1\n return num\n```\n**Solution 2**: The trickiest part is to convert this problem into a prefix sum problem. We will need to find the cost to move a digit up front. Consider the following case:\n* 6,5,4,3,2,1 - the move of 1 to the front will be 5, which is its index (5), straightfoward.\n* 5,1,0,4,3,2 - the move of 2 to the front will be 3, why? Because by the time we start to move 2, the digits 0 and 1 are already upfront by previous operations. Remember, you never want the digit 2 to be in front of digits 0 and 1. Since we have already moved those 2 digits, we need to exclude that cost (2) from its index (5). So the actual cost of moving 2 upfront, is 5-2 =3. How do we get the cost number 2? We can use an array (BIT) to store a 1 for each already moved position, and do a prefix sum up to the current index (5). \n\nWe break out from the loop either we run out of budget k, or we have sorted the string fully. Finally, if we have some leftover in the original string (digits that we have not moved because of shortage of k), we need to append the unused digits to our construted answer.\n\n```python\nclass BIT:\n def __init__(self, n):\n self.bit = [0]*(n+1)\n \n def update(self, index, value):\n index += 1\n while index < len(self.bit):\n self.bit[index] += value\n index += index & -index\n \n def query(self, index):\n index += 1\n value = 0\n while index > 0:\n value += self.bit[index]\n index -= index & -index\n return value\n\nclass Solution:\n def minInteger(self, num: str, k: int) -> str:\n # Fenwick tree\n n = len(num)\n tree = BIT(n)\n queues = defaultdict(lambda:deque([]))\n for i,j in enumerate(num):\n queues[int(j)].append(i)\n used = set()\n ans = \'\'\n while k > 0 and len(ans) < n:\n for digit in range(10):\n if digit not in queues:\n continue\n i = queues[digit][0]\n cost = i - tree.query(i-1)\n if cost > k:\n continue\n queues[digit].popleft()\n if not queues[digit]:\n del queues[digit]\n k -= cost\n tree.update(i,1)\n used.add(i)\n ans += num[i]\n break\n \n for i,j in enumerate(num):\n if i not in used:\n ans += j\n return ans\n```
| 1 | 0 |
[]
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Java Solution
|
java-solution-by-balenduteterbay-cier
|
java\n\nclass Solution {\n public String minInteger(String num, int k) {\n char[] ca = num.toCharArray();\n helper(ca, 0, k);\n return n
|
balenduteterbay
|
NORMAL
|
2020-12-19T09:33:27.987828+00:00
|
2020-12-19T09:33:27.987866+00:00
| 340 | false |
java\n```\nclass Solution {\n public String minInteger(String num, int k) {\n char[] ca = num.toCharArray();\n helper(ca, 0, k);\n return new String(ca);\n }\n \n public void helper(char[] ca, int I, int k) {\n if(k==0 || I==ca.length)\n return ;\n int min=ca[I], minindex=I;\n for(int i=I+1;i<Math.min( I+k+1, ca.length);i++) {\n \n if(ca[i]<min) {\n min=ca[i];\n minindex=i;\n }\n }\n char temp=ca[minindex];\n \n for(int i=minindex;i>I;i--) {\n ca[i]=ca[i-1];\n }\n ca[I]=temp;\n helper(ca, I+1, k-(minindex-I));\n }\n}\n```
| 1 | 0 |
[]
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
[C++] Fenwick tree O(n log n)
|
c-fenwick-tree-on-log-n-by-aleksey12345-nyj8
|
\nclass FenwickTree\n{\n public:\n explicit FenwickTree(int size)\n : arr(size + 1, 0)\n {\n }\n \n int get(int index)\n {\n ++i
|
aleksey12345
|
NORMAL
|
2020-08-19T17:40:31.283384+00:00
|
2020-08-19T17:40:31.283435+00:00
| 340 | false |
```\nclass FenwickTree\n{\n public:\n explicit FenwickTree(int size)\n : arr(size + 1, 0)\n {\n }\n \n int get(int index)\n {\n ++index;\n int value = 0;\n \n while (index)\n {\n value += arr[index];\n index -= index & (-index);\n }\n \n return value;\n }\n \n void set(int index)\n {\n ++index;\n \n while (index < arr.size())\n {\n ++arr[index];\n index += index & (-index);\n }\n }\n \nprivate:\n vector<int> arr;\n};\n\nclass Solution {\npublic:\n \n string minInteger(string num, int k) \n {\n vector<deque<int>> indexes(10, deque<int>());\n string result;\n FenwickTree tree(num.size());\n \n for (int i = 0; i < num.size(); ++i)\n indexes[num[i] - \'0\'].push_back(i);\n \n for (int i = 0; i < num.size(); ++i)\n {\n auto digit = num[i] - \'0\';\n \n if (indexes[digit].empty() || indexes[digit].front() != i)\n continue;\n \n indexes[digit].pop_front();\n \n for (int d = 0; d < digit; ++d)\n {\n if (!indexes[d].empty() && indexes[d].front() - i - \n tree.get(indexes[d].front()) + tree.get(i) <= k)\n {\n k -= indexes[d].front() - i - \n tree.get(indexes[d].front()) + tree.get(i);\n \n tree.set(indexes[d].front());\n \n indexes[d].pop_front();\n result += (char)(d-- + \'0\');\n }\n }\n \n result += num[i];\n }\n \n return result;\n }\n};\n```
| 1 | 0 |
[]
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Java Solution. Complexity O(k * n)
|
java-solution-complexity-ok-n-by-rutvikb-483l
|
\nclass Solution {\n public String minInteger(String num, int swaps) {\n char[] arr = num.toCharArray();\n arr = minArray(arr, arr.length, swap
|
rutvikbk
|
NORMAL
|
2020-07-07T17:20:02.154109+00:00
|
2020-07-07T17:20:02.154159+00:00
| 138 | false |
```\nclass Solution {\n public String minInteger(String num, int swaps) {\n char[] arr = num.toCharArray();\n arr = minArray(arr, arr.length, swaps); \n return new String(arr);\n }\n char[] minArray(char[] arr, int length, int swaps) { \n if (swaps == 0) \n return arr; \n for (int i = 0; i < length; i++) { \n int min_index = 0, min = Integer.MAX_VALUE;\n int limit = (swaps+i) > length-1 ? length-1 : swaps + i; \n for (int j = i; j <= limit; j++) {\n if (arr[j] < min) { \n min = arr[j]; \n min_index = j; \n }\n }\n swaps -= (min_index - i); \n arr = swapMin(arr, i, min_index); \n if (swaps == 0) \n break; \n }\n return arr;\n } \n char[] swapMin(char[] arr, int target, int current) { \n char temp = \'0\'; \n for (int i = current; i > target; i--) { \n temp = arr[i - 1]; \n arr[i - 1] = arr[i]; \n arr[i] = temp; \n }\n return arr;\n } \n}\n```
| 1 | 1 |
[]
| 1 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
[Python] O(NogN) BIT/FenwickTree solution
|
python-onogn-bitfenwicktree-solution-by-dkq0u
|
BIT : to get number of elements shifted before processing index\nind : to store occurence of digit\n\nclass Solution:\n def minInteger(self, num: str, k:
|
vaibhavd143
|
NORMAL
|
2020-07-06T19:49:47.232183+00:00
|
2020-07-06T19:49:47.232231+00:00
| 158 | false |
`BIT` : to get number of elements shifted before processing index\n`ind` : to store occurence of digit\n```\nclass Solution:\n def minInteger(self, num: str, k: int) -> str:\n def update(ind,bit):\n ind=ind+1\n while ind<len(bit):\n bit[ind]+=1\n ind += (ind&-ind)\n \n def getSum(ind,bit):\n ind+=1\n res=0\n while ind>0:\n res+=bit[ind]\n ind-=(ind&-ind)\n return res\n \n bit = [0]*(1+len(num))\n \n ind = {i:deque([]) for i in range(10)}\n for i,n in enumerate(num):\n ind[int(n)].append(i)\n res = []\n for i in range(len(num)):\n for dig in range(10):\n if ind[dig]:\n pos = ind[dig][0]\n dist = pos-getSum(pos,bit)\n if dist<=k:\n k-=dist\n res.append(str(dig))\n ind[dig].popleft()\n update(pos,bit)\n break\n \n return \'\'.join(res)\n```
| 1 | 0 |
['Binary Indexed Tree']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
[C++] O(N) Count the used index
|
c-on-count-the-used-index-by-zakyking-wv7f
|
The ituition of the problem is to collect the smallest reachable number iteratively.\nObviously, Greedy method will be used by looping from 0 to 9, and check if
|
zakyking
|
NORMAL
|
2020-07-06T19:49:04.327888+00:00
|
2020-07-07T02:31:46.798211+00:00
| 255 | false |
The ituition of the problem is to collect the smallest reachable number iteratively.\nObviously, Greedy method will be used by looping from 0 to 9, and check if any index reachable.\n\nThere are several ways to check if the index is reachable.\nThe straightfoward way is to loop and find number within K, by recording if the index is used. This will be O(N\\*N) and TLE.\nThis can also be implemented by the elegant Fenwick tree. By updating/querying the used count before the index in O(logN), this solution will be accepted in O(NlogN)\n\n\nHere I proposed the alternative solution of O(N). \n\nWhen we look into the chosing history of one number, the used count before the index is increasing.\nTherefore we can record the used count before the next candidate (smallest index) of number 0-9.\nWe update all the other 9 skipped counts after chosing a number. We will find the next candidate index and update the skip count for the chosen number.\n \n[main variables]\n \\- Used[i] : to check if the num[i] is used\n \\- NextIndex[n] : next index of specific number n\n \\- Skipped[n] : total skipped count before next candidate NextIndex[n]\n\n```\nclass Solution {\nprivate:\n int N;\n void Update(string& num, vector<int>& NextIndex, vector<int>& Skipped, vector<bool>& Used, int n) {\n int idx = NextIndex[n];\n \n // update the Skipped arrays except n\n for (int i = 0; i < 10; i++) {\n if (NextIndex[i] > idx)\n Skipped[i]++;\n }\n Used[idx] = true;\n NextIndex[n] = -1;\n \n // update the Skipped array of n\n for (int i = idx; i < N; i++) {\n if (Used[i])\n Skipped[n]++;\n else if (num[i] == n + \'0\') {\n NextIndex[n] = i;\n break;\n }\n }\n }\n\npublic:\n string minInteger(string num, int k) {\n N = num.size();\n vector<bool> Used(N, false);\n vector<int> NextIndex(10, -1);\n vector<int> Skipped(10, 0);\n \n for (int i = 0; i < N; i++) {\n if (NextIndex[num[i] - \'0\'] == -1)\n NextIndex[num[i] - \'0\'] = i;\n }\n \n string result;\n int i = 0;\n while (i < N && k) {\n if (Used[i]) {\n i++;\n continue;\n }\n\n // choose the reachable smallest number to swap\n int n = 0;\n for (; n < 10; n++) {\n if (NextIndex[n] == -1)\n continue;\n \n if (NextIndex[n] - Skipped[n] <= k) {\n k -= (NextIndex[n] - Skipped[n]);\n break;\n }\n }\n \n if (n == 10) { // no swap\n n = num[i] - \'0\';\n i++;\n }\n\n result.push_back(n + \'0\');\n Update(num, NextIndex, Skipped, Used, n);\n }\n \n for (; i < N; i++) {\n if (!Used[i])\n result.push_back(num[i]);\n }\n return result;\n }\n};\n\n```
| 1 | 0 |
[]
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
[C++] O(n log n) Fenwick Tree Solution Inspired By @awice
|
c-on-log-n-fenwick-tree-solution-inspire-88m6
|
You can watch his full explanation starting at 33:47: https://www.youtube.com/watch?v=pO_TtGTe6GQ\n\nclass FenwickTree {\nprivate:\n vector<int> arr; \n\npub
|
blackspinner
|
NORMAL
|
2020-07-06T02:52:13.556329+00:00
|
2020-07-06T02:53:00.108047+00:00
| 156 | false |
You can watch his full explanation starting at 33:47: https://www.youtube.com/watch?v=pO_TtGTe6GQ\n```\nclass FenwickTree {\nprivate:\n vector<int> arr; \n\npublic:\n FenwickTree(int n) {\n n++;\n arr = vector<int>(n, 0);\n }\n \n void add(int index, const int num) {\n index++;\n while (index < static_cast<int>(arr.size())) {\n arr[index] += num;\n index += (~index + 1) & index; \n }\n }\n \n int getPrefixSum(int index) const {\n int sum = 0;\n index++;\n while (index > 0) {\n sum += arr[index];\n index -= (~index + 1) & index; \n }\n return sum;\n }\n};\n\nclass Solution {\npublic:\n string minInteger(string num, int k) {\n int n = num.length();\n FenwickTree tree(n);\n vector<int> numArr(n);\n for (int i = 0; i < n; i++) {\n numArr[i] = num[i] - \'0\';\n }\n unordered_map<int,vector<int>> indexMap;\n for (int i = 0; i < n; i++) {\n if (indexMap.count(numArr[i]) == 0) {\n indexMap[numArr[i]] = {i};\n }\n else {\n indexMap[numArr[i]].push_back(i);\n }\n }\n for (int i = 0; i < 10; i++) {\n if (indexMap.count(i) != 0) {\n reverse(indexMap[i].begin(), indexMap[i].end());\n }\n }\n string res = "";\n while (k > 0) {\n int i;\n for (i = 0; i < 10; i++) {\n if (indexMap.count(i) == 0) {\n continue;\n }\n int leftMostIndex = indexMap[i].back();\n int usedIndices = tree.getPrefixSum(leftMostIndex);\n int rank = leftMostIndex - usedIndices;\n if (rank <= k) {\n k -= rank;\n res.push_back(i + \'0\');\n indexMap[i].pop_back();\n if (indexMap[i].empty()) {\n indexMap.erase(i);\n }\n tree.add(leftMostIndex, 1);\n break;\n }\n }\n if (i == 10) {\n break;\n }\n }\n vector<vector<int>> remaining;\n for (auto& [digit,row] : indexMap) {\n for (int i : row) {\n remaining.push_back({i,digit});\n }\n }\n sort(remaining.begin(), remaining.end(), \n [](const vector<int>& a, const vector<int>& b) -> bool\n { \n return a[0] < b[0]; \n });\n for (vector<int>& entry : remaining) {\n res.push_back(entry[1] + \'0\');\n }\n return res;\n }\n};\n```\nHaven\'t write C++ in a while. So please forgive me if there are any stylistic issues...
| 1 | 0 |
[]
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
[C++} O(NlogN) Solution Faster Than 100% soln
|
c-onlogn-solution-faster-than-100-soln-b-3s04
|
Well Idea is to reduce the simple n^2 solution using Binary Indexed Tree. In O(n^2) solution we check for all non selected indices but only ten digits are possi
|
abhutani06
|
NORMAL
|
2020-07-05T09:13:11.671710+00:00
|
2020-07-06T10:58:21.467526+00:00
| 127 | false |
Well Idea is to reduce the simple n^2 solution using Binary Indexed Tree. In O(n^2) solution we check for all non selected indices but only ten digits are possible from \'0\' to \'9\' well we can maintain a queue for each digit from \'0\' to \'9\' that consists first occurance of the the digit at the front. We can use BIT to find how many indices before the current indices have been moved in front of our answer by that amount we have to shift to find the cost of swapping current index to the ith position. Rest can be done same as the n^2 soln.\n\n\n\n\n\n```\ntypedef int ll;\nclass Solution {\n vector<ll>bit;\npublic:\n \n void update(ll x,ll n)\n {\n while(x<=n)\n {\n bit[x]+=1;\n x+=(x&(-x));\n }\n }\n ll query(ll x)\n {\n ll ans=0;\n while(x>0)\n {\n ans+=bit[x];\n x-=(x&(-x));\n }\n return ans;\n }\n string minInteger(string num, int k) {\n ll n=num.size();\n for(ll i=0;i<=n+1;i++)\n {\n bit.push_back(0);\n }\n \n \n string ans="";\n vector< queue<ll> > v(10);\n for(ll i=0;i<n;i++)\n {\n ll x=num[i]-\'0\';\n v[x].push(i);\n }\n for(ll i=0;i<n;i++)\n {\n ll pos=-1;\n ll dig=\'a\';\n ll cnt=i;\n ll hh=0;\n for(ll j=9;j>=0;j--)\n {\n \n ll ch=j+\'0\';\n if((!v[j].empty())&&ch<dig)\n {\n ll pp=v[j].front();\n ll ind=query(pp+1);\n ll val=pp-i+cnt-ind;\n \n if(val<=k)\n {\n pos=pp;\n dig=ch;\n hh=val;\n }\n }\n }\n if(pos!=-1)\n {\n update(pos+1,n);\n v[dig-\'0\'].pop();\n ans+=dig;\n k=k-hh;\n //cout<<(char)dig<<" "<<k<< " "<<pos<<endl;\n }\n }\n return ans;\n }\n};\n```
| 1 | 1 |
[]
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
java n^2 solution / nlogn segment tree solution/ nlogn BIT solution
|
java-n2-solution-nlogn-segment-tree-solu-r7l4
|
BIT\n\nclass Solution {\n public String minInteger(String s, int k) {\n int arr[]=new int[s.length()];\n Arrays.fill(arr,1);\n Fenwick f
|
66brother
|
NORMAL
|
2020-07-05T08:32:16.290684+00:00
|
2020-11-11T23:39:42.711676+00:00
| 127 | false |
BIT\n```\nclass Solution {\n public String minInteger(String s, int k) {\n int arr[]=new int[s.length()];\n Arrays.fill(arr,1);\n Fenwick fe=new Fenwick(arr);\n StringBuilder res=new StringBuilder();\n Queue<Integer>q[]=new LinkedList[10];\n for(int i=0;i<q.length;i++){\n q[i]=new LinkedList<>();\n }\n \n for(int i=0;i<s.length();i++){\n char c=s.charAt(i);\n q[c-\'0\'].add(i);\n }\n \n \n \n while(k>0){\n boolean good=false;\n for(int i=0;i<10;i++){\n if(q[i].size()==0)continue;\n \n int index=q[i].peek();\n int less=fe.sumRange(0,index-1);//how many elements remain less than it \n if(k>=less){\n good=true;\n q[i].poll();\n k-=less;\n res.append(i+"");\n fe.update(index,-1);\n break;\n }\n }\n \n if(!good)break;\n }\n \n \n \n \n \n \n List<int[]>A=new ArrayList<>();\n for(int i=0;i<q.length;i++){\n while(q[i].size()>0){\n A.add(new int[]{i,q[i].poll()});\n }\n }\n \n Collections.sort(A,(a,b)->{\n return a[1]-b[1];\n });\n \n for(int i=0;i<A.size();i++){\n res.append(A.get(i)[0]+"");\n }\n \n return res.toString();\n }\n \n \n class Fenwick {\n int tree[];//1-index based\n int A[];\n int arr[];\n public Fenwick(int[] A) {\n this.A=A;\n arr=new int[A.length];\n tree=new int[A.length+1];\n int sum=0;\n for(int i=0;i<A.length;i++){\n update(i,A[i]);\n }\n }\n\n public void update(int i, int val) {\n arr[i]+=val;\n i++;\n while(i<tree.length){\n tree[i]+=val;\n i+=(i&-i);\n }\n \n }\n\n public int sumRange(int i, int j) {\n \n return pre(j+1)-pre(i);\n }\n\n public int pre(int i){\n int sum=0;\n while(i>0){\n sum+=tree[i];\n i-=(i&-i);\n }\n return sum;\n }\n }\n}\n```\n\nn^2 solution\n```\nclass Solution {\n public String minInteger(String s, int k) {\n char A[]=s.toCharArray();\n for(int i=0;i<A.length;i++){\n char min=A[i];\n int j=i+1;\n int copyk=k;\n int index=-1;\n while(copyk>0&&j<A.length){\n if(A[j]<min){\n min=A[j];\n index=j;\n }\n copyk--;j++;\n }\n if(index==-1||min==A[i])continue;\n for(j=index;j>i;j--){\n swap(A,j,j-1);\n }\n k-=(index-i);\n if(k==0)break;\n }\n StringBuilder str=new StringBuilder();\n for(char c:A)str.append(c+"");\n return str.toString();\n }\n \n public void swap(char A[],int i,int j){\n char temp=A[i];\n A[i]=A[j];\n A[j]=temp;\n }\n}\n```\n\n\nsegment tree nlogn\n\n```\nclass Solution {\n public String minInteger(String s, int k) {\n Seg seg=new Seg(0,s.length()-1);\n StringBuilder str=new StringBuilder();\n Queue<Integer>A[]=new LinkedList[10];\n for(int i=0;i<10;i++)A[i]=new LinkedList<>();\n for(int i=0;i<s.length();i++){\n char c=s.charAt(i);\n A[c-\'0\'].add(i);\n }\n \n while(k>0){\n int i=Integer.MAX_VALUE;\n for(int j=0;j<10;j++){\n if(A[j].size()==0)continue;\n i=Math.min(i,A[j].peek());\n }\n if(i==Integer.MAX_VALUE)break;\n char cur=s.charAt(i);\n boolean found=false;\n for(int j=0;j<10;j++){\n char next=(char)(j+\'0\');\n if(next>=cur)break;\n if(A[j].size()==0)continue;//nothing can take out\n int index=A[j].peek();\n int cnt=seg.query(i+1,index);\n if(cnt<=k){//smallest\n found=true;\n A[j].poll();\n k-=cnt;\n str.append(next);\n seg.update(index);\n break;\n }\n }\n if(!found){\n A[cur-\'0\'].poll();\n str.append(""+cur);\n }\n }\n for(int i=0;i<s.length();i++){\n char c=s.charAt(i);\n if(A[c-\'0\'].size()==0)continue;\n if(A[c-\'0\'].peek()!=i)continue;\n str.append(""+c);A[c-\'0\'].poll();\n }\n return str.toString();\n }\n \n class Seg{\n int l,r;\n Seg left,right;\n int cnt;\n public Seg(int l,int r){\n this.l=l;this.r=r;\n if(l!=r){\n int mid=l+(r-l)/2;\n left=new Seg(l,mid);\n right=new Seg(mid+1,r);\n cnt=(r-l)+1;\n }else{\n cnt=1;\n }\n \n }\n \n public int query(int s,int e){\n if(l==s&&e==r){\n return cnt;\n }\n int mid=l+(r-l)/2;\n int res=0;\n if(e<=mid){\n res+=left.query(s,e);\n }\n else if(s>=mid+1){\n res+=right.query(s,e);\n }else{\n res+=left.query(s,mid)+right.query(mid+1,e);\n }\n return res;\n \n }\n \n public void update(int index){\n this.cnt--;\n if(l==r&&l==index){\n return;\n }\n int mid=l+(r-l)/2;\n if(index<=mid){\n left.update(index);\n }else{\n right.update(index);\n }\n }\n }\n}\n```
| 1 | 1 |
[]
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
[C++] greedy with index preprocessing
|
c-greedy-with-index-preprocessing-by-phi-irpt
|
\nclass Solution {\npublic:\n string minInteger(string num, int k) {\n std::vector<std::vector<int>> digit_to_inds(10);\n std::vector<int> void
|
phi9t
|
NORMAL
|
2020-07-05T07:53:07.293711+00:00
|
2020-07-05T07:53:07.293760+00:00
| 174 | false |
```\nclass Solution {\npublic:\n string minInteger(string num, int k) {\n std::vector<std::vector<int>> digit_to_inds(10);\n std::vector<int> voids; // locations that are empty, no price to pay\n for (int i = num.size() - 1; i >= 0; --i) {\n digit_to_inds[static_cast<int>(num[i] - \'0\')].push_back(i);\n } \n constexpr char VOID_MARK = \'X\';\n int reserved = k;\n std::vector<int> res;\n while ((reserved > 0) && (res.size() < num.size())) {\n for (int d = 0; d <= 9; ++d) {\n auto &inds = digit_to_inds[d];\n if (inds.empty()) {\n continue;\n }\n const int i = inds.back(); // smallest index for `d`\n // There were `j` elements prior to the index `i`\n // removed from `num`. There\'s no need to swap with them.\n const int j = std::distance(\n voids.begin(), \n std::lower_bound(voids.begin(), voids.end(), i)\n );\n\t\t\t\t// Number of swap ops needed to bubble this to top.\n const int price = i - 0 - j;\n if (price > reserved) {\n continue;\n }\n // Housekeeping.\n reserved -= price;\n res.push_back(d);\n voids.insert(voids.begin() + j, i); \n num[i] = VOID_MARK;\n inds.pop_back();\n break;\n }\n }\n\t\t// Results come from the elements pushed to `res`, \n\t\t// as well as the remaining ones in `num`.\n std::stringstream ss;\n for (int d : res) {\n ss << d;\n }\n for (char ch : num) {\n if (ch != VOID_MARK) {\n ss << ch;\n }\n }\n return ss.str();\n }\n};\n```
| 1 | 0 |
[]
| 1 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Java,Binary Indexed Tree,O(nlogn),17ms
|
javabinary-indexed-treeonlogn17ms-by-tbl-l6qk
|
idea : Every turn we find the smallest number that we can move to the head of the left string, it will make the answer minimum. We can calculate how many chara
|
tblade-caohui
|
NORMAL
|
2020-07-05T06:25:59.024146+00:00
|
2020-07-05T06:27:55.059087+00:00
| 100 | false |
idea : Every turn we find the smallest number that we can move to the head of the left string, it will make the answer minimum. We can calculate how many characters in the left string before the most left index of current number, if it is less than or equal to k, then we can move a current number of most left index to the head of the left string.Using data struct like BIT or segment Tree will solve this problem.\n```\nclass Solution {\n int[] C;\n int lowbit(int x) {\n return x & (-x);\n }\n void add(int x, int k) {\n while(k < C.length) {\n C[k] += x;\n k += lowbit(k);\n }\n }\n int getSum(int r) {\n int res = 0;\n while(r > 0) {\n res += C[r];\n r ^= lowbit(r);\n }\n return res;\n }\n public String minInteger(String num, int k) {\n int n = num.length();\n C = new int [n + 1];\n for(int i = 1; i < C.length; ++i) add(1,i);\n StringBuilder ans = new StringBuilder();\n ArrayList<Integer>[] arr = new ArrayList[10];\n for(int i = 0; i < num.length(); i++) {\n int x = num.charAt(i) - \'0\';\n if(arr[x] == null) arr[x] = new ArrayList<>();\n arr[x].add(i + 1);\n }\n int[] pos = new int[10];\n for(int i = 0; i < n; i++ ){\n for(int j = 0; j <= 9; j++) {\n if(arr[j] == null || pos[j] >= arr[j].size()) continue;\n int top = arr[j].get(pos[j]);\n int p = getSum(top - 1);\n if(p <= k) {\n ans.append((char)(\'0\' + j));\n k -= p;\n add(-1,top);\n pos[j]++;\n break;\n }\n }\n }\n return ans.toString();\n }\n}
| 1 | 0 |
[]
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Python (NlogN) using Binary Index Tree
|
python-nlogn-using-binary-index-tree-by-2qrqs
|
Well.. the average performance should be NlogN, but it is hard to prove whether the worst case still holds. Anyway, I still share my solution.\n\n\nfrom heapq i
|
pze168
|
NORMAL
|
2020-07-05T05:14:02.727597+00:00
|
2020-07-05T05:15:29.606345+00:00
| 218 | false |
Well.. the average performance should be NlogN, but it is hard to prove whether the worst case still holds. Anyway, I still share my solution.\n\n```\nfrom heapq import heapify, heappop, heappush\n\ndef getsum(tree, i): \n s = 0\n i += 1\n while i > 0: \n s += tree[i] \n i -= i & (-i) \n return s \n \n# modify the value from the original one,\n# v is diff/increment.\ndef update(tree, i ,v): \n i += 1\n while i < len(tree): \n tree[i] += v \n i += i & (-i)\n \ndef construct(arr): \n tree = [0] * (len(arr) + 1) \n \n for i in range(len(arr)): \n update(tree, i, arr[i]) \n\n return tree \n\nclass Solution:\n def minInteger(self, num: str, k: int) -> str:\n pq = []\n ans = []\n \n # the input array looks like [0, 1,1,1,1,...]\n tree = construct([0] + [1] * len(num))\n \n\n used = set()\n # a heap to store un-unsed indices\n wait_queue = list(range(len(num)))\n heapify(wait_queue)\n \n \n while k > 0:\n # getsum(tree, idx) is to get the actual index of an element whose original index\n # is idx.\n while len(wait_queue) > 0 and getsum(tree, wait_queue[0]) <= len(ans) + k: \n idx = heappop(wait_queue)\n heappush(pq, (num[idx], idx))\n \n if len(pq) == 0:\n break\n ch, i = heappop(pq)\n \n \n cost = getsum(tree, i) - len(ans)\n if cost > k:\n heappush(wait_queue, i)\n continue\n \n k -= cost\n \n # move the one from i and add to zero.\n update(tree, i + 1, -1)\n update(tree, 0, 1) \n \n \n ans.append(ch)\n used.add(i)\n \n for i, ch in enumerate(num):\n if i not in used:\n ans.append(ch)\n \n return "".join(ans)\n \n \n \n```
| 1 | 0 |
[]
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
[Python] O(N log N) 316ms Greedy Solution, finished 5 min after contest end 😭
|
python-on-log-n-316ms-greedy-solution-fi-s93c
|
Probably being distracted by the Independence Day fireworks, I finished coding this O(N log N) solution 5 min after the end of the weekly contest \uD83D\uDE2D\n
|
wwssyy5511
|
NORMAL
|
2020-07-05T04:10:03.509475+00:00
|
2020-07-05T04:34:14.104620+00:00
| 529 | false |
Probably being distracted by the Independence Day fireworks, I finished coding this O(N log N) solution 5 min after the end of the weekly contest \uD83D\uDE2D\n\n\n**O(N log N)** Solution\n```\nclass Solution:\n def minInteger(self, num: str, k: int) -> str:\n ind = [[] for _ in range(10)]\n for i in range(len(num)-1, -1, -1):\n ind[int(num[i])].append(i)\n i = 0\n res = []\n picked = []\n moveright = {}\n for i in range(len(num) - 1):\n for _ in range(10):\n if ind[_]:\n if _ not in moveright:\n moveright[_] = len(picked) - bisect.bisect(picked, ind[_][-1])\n if ind[_][-1] + moveright[_] - i <= k:\n k -= ind[_][-1] + moveright[_] - i\n insort(picked, ind[_][-1])\n res.append(str(_))\n ind[_].pop()\n moveright.pop(_)\n break\n if k == 0:\n break\n unpicked = []\n pickedset = set(picked)\n for i in range(len(num)):\n if i not in pickedset:\n unpicked.append(i)\n return "".join(res) + "".join([num[j] for j in unpicked])\n```\n\n------------------------------------\nDuring the contest I figured out two \uFF2F(N^2) solutions (the first one is actually O(10\\*N^2)), but both of them result in TLE.\n\nI see some other posts in which their O(N^2) solutions pass the OJ. Is it because my way is recursive? Does `newstr = "a" + oldstr_of_length_N` takes O(1) or O(N) time in Python? But anyway my solutions are O(N^2)\n**O(10\\*N^2)** Solution\n```\nclass Solution:\n def minInteger(self, num: str, k: int) -> str:\n if len(num) == 1 or k == 0:\n return num\n for i in range(10):\n for j in range(min(k+1, len(num))):\n if num[j] == str(i):\n return num[j] + self.minInteger(num[:j] + num[j+1:], k - j)\n```\n**O(N^2)** Solution\n```\nclass Solution:\n def minInteger(self, num: str, k: int) -> str:\n if len(num) == 1 or k == 0:\n return num\n m = 10\n for j in range(min(k+1, len(num))):\n if num[j] == "0":\n return num[j] + self.minInteger(num[:j] + num[j+1:], k - j)\n if int(num[j]) < m:\n m = int(num[j])\n i = j\n return num[i] + self.minInteger(num[:i] + num[i+1:], k - i)\n```
| 1 | 0 |
[]
| 2 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Explained | Clean Code | Fenwick | 7ms
|
explained-clean-code-fenwick-7ms-by-ivan-7ha9
|
IntuitionTo minimize a number, place the smallest digits as early as possible, using a greedy approach where each adjacent swap costs 1 move from our budget of
|
ivangnilomedov
|
NORMAL
|
2025-03-23T09:42:42.050272+00:00
|
2025-03-23T09:42:42.050272+00:00
| 4 | false |
# Intuition
To minimize a number, place the smallest digits as early as possible, using a greedy approach where each adjacent swap costs 1 move from our budget of k swaps.
# Approach
1. **Build Digit Lookup Structure**: Create linked lists for each digit (0-9) to find all occurrences in the input.
2. **Fenwick Tree for Position Tracking**: to track how positions shift when we move digits forward, since moving one digit affects the relative positions of all subsequent digits.
3. **Greedy Selection**: For each position:
- Try digits 0-9 in ascending order
- For each digit, find its first occurrence that can be moved to the current position within our remaining swap budget
- Choose the smallest such digit, update remaining swaps, and adjust position offsets for all affected digits
4. **Position Shift Management**: The critical insight is maintaining index of each digit as we move elements around. When we bring a digit forward, all digits in between shift backward by 1 position.
# Complexity
- Time complexity: **O(n log n)**
# Code
```cpp []
class Solution {
public:
string minInteger(const string& num, int k) {
const int L = num.length();
// Maps each digit (0-9) to the next occurrence index
vector<int> dig2idx(kDigitsSize, L);
// For each index, stores the next equal digit's index
vector<int> idx2nxeq(L, L);
for (int i = L - 1; i >= 0; --i) {
int d = num[i] - kDigitsBeg;
idx2nxeq[i] = dig2idx[d];
dig2idx[d] = i;
}
// Fenwick Tree (Binary Indexed Tree) : dynamic prefix sums
struct PrefixStats {
vector<int> subtract;
int overall_acc = 0;
PrefixStats(int L) : subtract(L + 1) {}
void inc_prefix(int end_excl, int delta) {
if (end_excl == 0) return;
overall_acc += delta;
const int N = subtract.size();
for (int i = end_excl; i < N; i += i & (-i))
subtract[i] += delta;
}
int get(int idx) {
int sum = overall_acc;
for (int i = idx; i > 0; i -= i & (-i))
sum -= subtract[i];
return sum;
}
};
// Tracks the position offsets as digits are moved
PrefixStats idx2offset(L); // Whatever style preferrable: idx_to_offset / offset_by_idx etc...
// Greedy algorithm: For each position in the result,
// find the smallest digit that can be moved there with ≤ k swaps
vector<int> idx_2_res_pos(L, -1);
for (int i = 0; i < L; ++i) {
int best_idx = -1, need_swaps = k + 1;
for (int d = 0; d < kDigitsSize; ++d) { // Try each digit from 0-9 (greedy)
int eff_idx = k + i + 1; // Unreachable
while (dig2idx[d] < L) { // Skip illegal positions for d
eff_idx = dig2idx[d] + idx2offset.get(dig2idx[d]);
if (eff_idx < i || idx_2_res_pos[dig2idx[d]] > -1) {
dig2idx[d] = idx2nxeq[dig2idx[d]];
continue;
} else {
break;
}
}
if (dig2idx[d] == L) continue; // No valid occurrence of this digit
need_swaps = eff_idx - i;
if (need_swaps <= k) {
best_idx = dig2idx[d];
break;
}
}
// assert(best_idx > -1);
idx_2_res_pos[best_idx] = i; // Bind position in result
k -= need_swaps;
idx2offset.inc_prefix(best_idx, 1); // Update offset for shifted values
}
string res(L, '\0');
for (int i = 0; i < L; ++i) { // Construct the final result string
// assert(idx_2_res_pos[i] > -1);
// assert(res[idx_2_res_pos[i]] == '\0');
res[idx_2_res_pos[i]] = num[i];
}
return res;
}
private:
static constexpr char kDigitsBeg = '0';
static constexpr char kDigitsSize = '9' - kDigitsBeg + 1;
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
py3 82%beats
|
py3-82beats-by-fareedbaba-xhke
|
IntuitionGiven a string num representing the digits of a large integer and an integer k, you can swap any two adjacent digits at most k times. The goal is to re
|
fareedbaba
|
NORMAL
|
2025-02-23T10:27:09.418857+00:00
|
2025-02-23T10:27:09.418857+00:00
| 12 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Given a string num representing the digits of a large integer and an integer k, you can swap any two adjacent digits at most k times. The goal is to return the smallest possible integer that can be formed.
# Approach
<!-- Describe your approach to solving the problem. -->
1️⃣ If k is large enough, simply sort the digits.
2️⃣ Use a greedy approach to find the smallest leading digit that can be moved within k swaps.
3️⃣ Efficiently track digit positions using a Fenwick Tree / BIT or Segment Tree to optimize swaps.
# Performance:
✅ Beats 82% in runtime
✅ Memory optimized
# Code
```python3 []
class Solution:
def minInteger(self, num: str, k: int) -> str:
if k <= 0: return num
n = len(num)
if k >= n*(n-1)//2:
return "".join(sorted(list(num)))
# for each number, find the first index
for i in range(10):
ind = num.find(str(i))
if 0 <= ind <= k:
return str(num[ind]) + self.minInteger(num[0:ind] + num[ind+1:], k-ind)
```
| 0 | 0 |
['Python3']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
1505. Minimum Possible Integer After at Most K Adjacent Swaps On Digits
|
1505-minimum-possible-integer-after-at-m-82gf
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
G8xd0QPqTy
|
NORMAL
|
2025-01-13T05:41:40.935828+00:00
|
2025-01-13T05:41:40.935828+00:00
| 10 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
string minInteger(string num, int k) {
int n = num.size();
vector<vector<int>> pos(10);
for (int i = 0; i < n; ++i) pos[num[i] - '0'].push_back(i);
vector<bool> used(n, false);
string result;
vector<int> bit(n + 1, 0);
auto add = [&](int idx, int val) {
for (++idx; idx <= n; idx += idx & -idx) bit[idx] += val;
};
auto sum = [&](int idx) {
int s = 0;
for (++idx; idx > 0; idx -= idx & -idx) s += bit[idx];
return s;
};
for (int i = 0; i < n && k > 0; ++i) {
for (int d = 0; d <= 9; ++d) {
if (!pos[d].empty()) {
int idx = pos[d].front();
int shift = idx - sum(idx - 1);
if (shift <= k) {
k -= shift;
used[idx] = true;
result += '0' + d;
pos[d].erase(pos[d].begin());
add(idx, 1);
break;
}
}
}
}
for (int i = 0; i < n; ++i) {
if (!used[i]) result += num[i];
}
return result;
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Backtracking approach ( TLE)
|
backtracking-approach-tle-by-anushakanda-v9ri
|
Code
|
anushakandagal
|
NORMAL
|
2024-12-29T06:30:06.948433+00:00
|
2024-12-29T06:30:06.948433+00:00
| 11 | false |
# Code
```java []
class Solution {
String minNum = "";
public String minInteger(String num, int k) {
minNum = num;
char[] array = num.toCharArray();
findNum(array , k);
return minNum;
}
public void findNum(char[] array , int k){
String num = new String(array);
if(minNum.compareTo(num) > 0)
minNum = num;
if(k == 0) return;
for(int i = 0; i < array.length-1; i++){
if(array[i] > array[i+1]){
char temp = array[i];
array[i] = array[i+1];
array[i+1] = temp;
findNum(array , k-1);
temp = array[i];
array[i] = array[i+1];
array[i+1] = temp;
}
}
}
}
```
| 0 | 0 |
['Backtracking', 'Recursion', 'Java']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
For every position i , replace it with smallest element found within k window size. ACCEPTED!!
|
for-every-position-i-with-smallest-eleme-y7gc
|
Intuition
For every position i , replace it with smallest element found within k window size.
Fill ith position by bringing smallest element till ith position u
|
anushakandagal
|
NORMAL
|
2024-12-29T06:20:36.532247+00:00
|
2024-12-29T06:23:11.387883+00:00
| 8 | false |
# Intuition
- For every position i , replace it with smallest element found within k window size.
- Fill ith position by bringing smallest element till ith position using bubble sort technique and decrease k with each swap.
# Complexity
- Time complexity: O(N^2)
- Space complexity: O(N)
# Code
```java []
class Solution {
public String minInteger(String num, int k) {
char[] array = num.toCharArray();
return findNum(array , k);
}
public String findNum(char[] array , int k){
for(int i = 0; i < array.length-1; i++){
int minIndex = i;
char min = array[i];
int j = i+1;
while(j <= i+k && j < array.length){
if(array[j] < min){
min = array[j];
minIndex = j;
}
j++;
}
//bubble swap
for(j = minIndex; j >= i+1; j--)
array[j] = array[j-1];
array[i] = min;
k = k- ( minIndex -i);
if(k <= 0) break;
}
return new String(array);
}
}
```
| 0 | 0 |
['Greedy', 'Java']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
find the min value in k region
|
find-the-min-value-in-k-region-by-linda2-r8ba
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
linda2024
|
NORMAL
|
2024-12-17T00:26:47.515817+00:00
|
2024-12-17T00:26:47.515817+00:00
| 5 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```csharp []\npublic class Solution {\n public string MinInteger(string num, int k) {\n \t\t\tStringBuilder sb = new StringBuilder(num);\n\t\t\tint len = num.Length;\n\n\t\t\tfor (int i = 0; i < len && k > 0; i++)\n\t\t\t{\n\t\t\t\tint minIdx = i;\n\t\t\t\tint upLimit = Math.Min(len, i + k + 1);\n\t\t\t\tfor (int j = i + 1; j < upLimit; j++)\n\t\t\t\t{\n\t\t\t\t\tif (sb[j] < sb[minIdx])\n\t\t\t\t\t\tminIdx = j;\n\t\t\t\t}\n\n\t\t\t\tif (minIdx != i)\n\t\t\t\t{\n\t\t\t\t\tint diff = minIdx - i;\n\t\t\t\t\tif (diff <= k)\n\t\t\t\t\t{\n\t\t\t\t\t\tchar minC = sb[minIdx];\n\t\t\t\t\t\tsb.Remove(minIdx, 1);\n\t\t\t\t\t\tsb.Insert(i, minC);\n\t\t\t\t\t\tk -= diff;\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t}\n\n\t\t\treturn sb.ToString();\n }\n}\n```
| 0 | 0 |
['C#']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
The greedy **non Segment-Tree** solution you have been searching for
|
the-greedy-non-segment-tree-solution-you-ua5i
|
Intuition\nWe need to place the numerically smallest digit at the most significant place(i.e leftmost place).\n# Approach\nWe find the smallest digit in the rig
|
pramodhv_28
|
NORMAL
|
2024-11-11T09:31:30.236064+00:00
|
2024-11-11T09:31:30.236100+00:00
| 7 | false |
# Intuition\nWe need to place the numerically smallest digit at the most significant place(i.e leftmost place).\n# Approach\nWe find the smallest digit in the right from i and perform x operations such that x <= k.\nAfter which we subtract x from k, \nIn 4321, we perform 3 operations to bring 1 from num[3] to nums[0].Now k becomes 4-3=1. \nThe string becomes 1432.\nNext we can\'t bring 2 from num[3] to num[1] as 3-1=2 > 1.\nHence we see the next eligible option(i.e 3 from num[2] to num[1]).\n\n# Complexity\n- Time complexity:\nO(n^2)\n\n- Space complexity:\nO(1) for variables and swapping + O(sorting)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n string minInteger(string num, int k) {\n int n = num.length();\n if(k > n*(n+1)/2){\n sort(num.begin(),num.end());\n return num;\n }\n for(int i=0;i<n-1 && k>0;i++){\n int curPos = i;\n for(int j=i+1;j<n;j++){\n if(j-i > k)\n break;\n if(num[j] < num[curPos])\n curPos = j;\n }\n for(int j=curPos;j>i;j--)\n swap(num[j],num[j-1]);\n k-=(curPos-i);\n }\n return num;\n }\n};\n```
| 0 | 0 |
['String', 'Greedy', 'Sliding Window', 'C++']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits- JavaSolution
|
minimum-possible-integer-after-at-most-k-ki16
|
\n\n# Code\njava []\nclass Solution {\n public String minInteger(String num, int k) {\n //pqs stores the location of each digit.\n List<Queue<I
|
himashusharma
|
NORMAL
|
2024-10-04T07:54:26.443740+00:00
|
2024-10-04T07:54:26.443773+00:00
| 16 | false |
\n\n# Code\n```java []\nclass Solution {\n public String minInteger(String num, int k) {\n //pqs stores the location of each digit.\n List<Queue<Integer>> pqs = new ArrayList<>();\n for (int i = 0; i <= 9; ++i) {\n pqs.add(new LinkedList<>());\n }\n\n for (int i = 0; i < num.length(); ++i) {\n pqs.get(num.charAt(i) - \'0\').add(i);\n }\n String ans = "";\n SegmentTree seg = new SegmentTree(num.length());\n\n for (int i = 0; i < num.length(); ++i) {\n // At each location, try to place 0....9\n for (int digit = 0; digit <= 9; ++digit) {\n // is there any occurrence of digit left?\n if (pqs.get(digit).size() != 0) {\n // yes, there is a occurrence of digit at pos\n Integer pos = pqs.get(digit).peek();\n\t\t\t\t\t// Since few numbers already shifted to left, this `pos` might be outdated.\n // we try to find how many number already got shifted that were to the left of pos.\n int shift = seg.getCountLessThan(pos);\n // (pos - shift) is number of steps to make digit move from pos to i.\n if (pos - shift <= k) {\n k -= pos - shift;\n seg.add(pos); // Add pos to our segment tree.\n pqs.get(digit).remove();\n ans += digit;\n break;\n }\n }\n }\n }\n return ans;\n }\n\n class SegmentTree {\n int[] nodes;\n int n;\n\n public SegmentTree(int max) {\n nodes = new int[4 * (max)];\n n = max;\n }\n\n public void add(int num) {\n addUtil(num, 0, n, 0);\n }\n\n private void addUtil(int num, int l, int r, int node) {\n if (num < l || num > r) {\n return;\n }\n if (l == r) {\n nodes[node]++;\n return;\n }\n int mid = (l + r) / 2;\n addUtil(num, l, mid, 2 * node + 1);\n addUtil(num, mid + 1, r, 2 * node + 2);\n nodes[node] = nodes[2 * node + 1] + nodes[2 * node + 2];\n }\n\n // Essentialy it tells count of numbers < num.\n public int getCountLessThan(int num) {\n return getUtil(0, num, 0, n, 0);\n }\n\n private int getUtil(int ql, int qr, int l, int r, int node) {\n if (qr < l || ql > r) return 0;\n if (ql <= l && qr >= r) {\n return nodes[node];\n }\n\n int mid = (l + r) / 2;\n return getUtil(ql, qr, l, mid, 2 * node + 1) + getUtil(ql, qr, mid + 1, r, 2 * node + 2);\n }\n }\n\n}\n```
| 0 | 0 |
['String', 'Greedy', 'Binary Indexed Tree', 'Segment Tree', 'Java']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
1505. Minimum Possible Integer After at Most K Adjacent Swaps On Digits.cpp
|
1505-minimum-possible-integer-after-at-m-0q4t
|
Code\n\nclass Solution {\npublic:\n string minInteger(string num, int k) {\n int n = num.size();\n if(k > n*(n+1)/2)\n {\n so
|
202021ganesh
|
NORMAL
|
2024-09-30T12:27:07.807980+00:00
|
2024-09-30T12:27:07.808020+00:00
| 1 | false |
**Code**\n```\nclass Solution {\npublic:\n string minInteger(string num, int k) {\n int n = num.size();\n if(k > n*(n+1)/2)\n {\n sort(num.begin(), num.end());\n }\n for(int i=0;i<n && k >0;i++)\n {\n int pos = i;\n for(int j=i+1;j<n;j++)\n {\n if(j-i > k)\n break;\n if(num[j] < num[pos])\n pos = j;\n }\n while(pos > i)\n {\n swap(num[pos], num[pos-1]);\n pos--;\n k--;\n }\n }\n return num;\n }\n};\n```
| 0 | 0 |
['C']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Simplest Solution (code commented)
|
simplest-solution-code-commented-by-vidy-4h9i
|
Code\ncpp []\nclass Solution {\npublic:\n string minInteger(string num, int k) {\n // idea: find the min num that is within\n // k and bring th
|
vidyatheerthan
|
NORMAL
|
2024-09-16T03:34:26.620512+00:00
|
2024-09-16T03:34:26.620549+00:00
| 11 | false |
# Code\n```cpp []\nclass Solution {\npublic:\n string minInteger(string num, int k) {\n // idea: find the min num that is within\n // k and bring them forward 1 at a time\n // then start next search after previously\n // placed min num.\n // eg: 4321\n // 1st itr => 1432 (offset=0)\n // 2nd ite => 1342 (offset=1)\n int n = num.length();\n int offset = 0; // used to offset from already found min nums\n while(k) {\n int minIndex = offset; // start right after previous found min num\n for (int i=offset; i<=offset+k && i<n; i++) {\n if (num[i]-\'0\' < num[minIndex]-\'0\') {\n minIndex = i; // this is the min we could find within \'k\' items\n }\n }\n char c = num[minIndex]; // save min\n num.erase(num.begin() + minIndex); // erase the min\n num.insert(num.begin() + offset, c); // insert min in front after offset\n k -= minIndex-offset; // reduce k : minIndex times\n offset++; // move offset to next front position\n if (offset >= n) {\n break; // we have completed iterating through nums\n }\n }\n return num;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
O(N) python with explanation
|
on-python-with-explanation-by-swarbrickj-iie3
|
Approach\nWe need to bring the small numbers to the front to make the start of the string sorted low->high. It\'s tough to keep track of how far each number nee
|
swarbrickjones
|
NORMAL
|
2024-09-15T22:01:17.921102+00:00
|
2024-09-15T22:01:17.921123+00:00
| 19 | false |
# Approach\nWe need to bring the small numbers to the front to make the start of the string sorted low->high. It\'s tough to keep track of how far each number needs to move to get to sorted position, as this changes over time. The trick: first scan for 0s going left to right, then move them to the front (or rather the end of the starting 0s). Then regenerate the list without the 0s in it and move the 1s to the front etc. To keep track of how far a 0 (say) has to move to reach the back of the starting 0s, just count how many non-0s there were before it.\n\nAt some point we might not be able to move any of the current digit we\'re looking at to the start with the moves remaining. That\'s fine, just delete the ones we moved and go on to the next digit (but make sure never to move a higher digit to the start if it will go over a lower digit)\n\nUnfortunately we aren\'t _quite_ finished - there could still be some moves left over (e.g. 3231 k=2 will end at 2331 with 1 move remaining). In this case the start of the list will be sorted, just look for the first unsorted character (in this case 1) and move it back as far as possible. \n\n# Complexity\n- Time complexity: O(10xN)\n\n- Space complexity: O(N)\n\n# Code\n```python3 []\nclass Solution:\n def minInteger(self, num: str, k: int) -> str:\n nums = [int(c) for c in num]\n moves_remaining = k\n\n start = []\n for digit in range(10):\n non_digits = 0 \n min_seen = 10 # minimum integer seen this round \n new_nums = [] # not deleted from this round\n for idx, num in enumerate(nums):\n if num == digit:\n if ((non_digits <= moves_remaining) \n # edge case if we have to break here\n and (digit <= min_seen)): \n start.append(num)\n moves_remaining -= non_digits\n else:\n new_nums.append(num)\n else:\n min_seen = min(min_seen, num)\n non_digits += 1\n new_nums.append(num)\n \n nums = new_nums\n\n # we can\'t get the number we need to move to the start\n # just look along nums for an unsorted digit, and move it\n \n nums = start + nums\n\n if moves_remaining > 0:\n current = -1\n for idx, num in enumerate(nums):\n if num < current:\n target_idx = idx - moves_remaining\n nums = (\n nums[:target_idx] \n + [num]\n + nums[target_idx: idx]\n + nums[idx + 1:]\n )\n break\n current = num\n return "".join(str(x) for x in nums)\n \n \n\n\n```
| 0 | 0 |
['Python3']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
👍Runtime 57 ms Beats 100.00%
|
runtime-57-ms-beats-10000-by-pvt2024-lmvk
|
Code\n\ntype SegmentTree struct {\n\tnodes []int\n\tn int\n}\n\nfunc NewSegmentTree(max int) *SegmentTree {\n\treturn &SegmentTree{nodes: make([]int, 4*max)
|
pvt2024
|
NORMAL
|
2024-06-30T03:01:48.968648+00:00
|
2024-06-30T03:01:48.968678+00:00
| 7 | false |
# Code\n```\ntype SegmentTree struct {\n\tnodes []int\n\tn int\n}\n\nfunc NewSegmentTree(max int) *SegmentTree {\n\treturn &SegmentTree{nodes: make([]int, 4*max), n: max}\n}\n\nfunc (st *SegmentTree) add(num, l, r, node int) {\n\tif num < l || num > r {\n\t\treturn\n\t}\n\tif l == r {\n\t\tst.nodes[node]++\n\t\treturn\n\t}\n\tmid := (l + r) / 2\n\tst.add(num, l, mid, 2*node+1)\n\tst.add(num, mid+1, r, 2*node+2)\n\tst.nodes[node] = st.nodes[2*node+1] + st.nodes[2*node+2]\n}\n\nfunc (st *SegmentTree) Add(num int) {\n\tst.add(num, 0, st.n, 0)\n}\n\nfunc (st *SegmentTree) getUtil(ql, qr, l, r, node int) int {\n\tif qr < l || ql > r {\n\t\treturn 0\n\t}\n\tif ql <= l && qr >= r {\n\t\treturn st.nodes[node]\n\t}\n\tmid := (l + r) / 2\n\treturn st.getUtil(ql, qr, l, mid, 2*node+1) + st.getUtil(ql, qr, mid+1, r, 2*node+2)\n}\n\nfunc (st *SegmentTree) GetCountLessThan(num int) int {\n\treturn st.getUtil(0, num, 0, st.n, 0)\n}\n\nfunc minInteger(num string, k int) string {\n\tn := len(num)\n\tpqs := make([][]int, 10)\n\tfor i := 0; i < 10; i++ {\n\t\tpqs[i] = []int{}\n\t}\n\tfor i := 0; i < n; i++ {\n\t\tpqs[num[i]-\'0\'] = append(pqs[num[i]-\'0\'], i)\n\t}\n\tans := []byte{}\n\tseg := NewSegmentTree(n)\n\tfor i := 0; i < n; i++ {\n\t\tfor digit := 0; digit <= 9; digit++ {\n\t\t\tif len(pqs[digit]) != 0 {\n\t\t\t\tpos := pqs[digit][0]\n\t\t\t\tshift := seg.GetCountLessThan(pos)\n\t\t\t\tif pos-shift <= k {\n\t\t\t\t\tk -= pos - shift\n\t\t\t\t\tseg.Add(pos)\n\t\t\t\t\tpqs[digit] = pqs[digit][1:]\n\t\t\t\t\tans = append(ans, byte(\'0\'+digit))\n\t\t\t\t\tbreak\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t}\n\treturn string(ans)\n}\n```
| 0 | 0 |
['Go']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Using Walk on Segment Tree
|
using-walk-on-segment-tree-by-theabbie-hm9p
|
\nfrom collections import defaultdict\nfrom sortedcontainers import SortedList\n\nclass SegTree:\n def __init__(self, n):\n self.ctr = defaultdict(int
|
theabbie
|
NORMAL
|
2024-05-21T15:40:01.613970+00:00
|
2024-05-21T15:40:01.614004+00:00
| 11 | false |
```\nfrom collections import defaultdict\nfrom sortedcontainers import SortedList\n\nclass SegTree:\n def __init__(self, n):\n self.ctr = defaultdict(int)\n self.init = (float(\'inf\'), n)\n self.vals = defaultdict(lambda: self.init)\n \n def update(self, i, v, x, y, k = 1):\n if x + 1 == y:\n self.ctr[k] = 0 if v == -1 else 1\n self.vals[k] = (float(\'inf\'), i) if v == -1 else (v, i)\n return\n mid = (x + y) // 2\n if i < mid:\n self.update(i, v, x, mid, 2 * k)\n else:\n self.update(i, v, mid, y, 2 * k + 1)\n self.ctr[k] = self.ctr[2 * k] + self.ctr[2 * k + 1]\n self.vals[k] = min(self.vals[2 * k], self.vals[2 * k + 1])\n \n def getMin(self, p, x, y, k = 1):\n if p == 0:\n return self.init\n if x + 1 == y:\n return self.vals[k]\n mid = (x + y) // 2\n res = self.init\n if p >= self.ctr[2 * k]:\n res = min(res, self.vals[2 * k], self.getMin(p - self.ctr[2 * k], mid, y, 2 * k + 1))\n else:\n res = min(res, self.getMin(p, x, mid, 2 * k))\n return res\n\nclass Solution:\n def minInteger(self, num: str, k: int) -> str:\n n = len(num)\n segtree = SegTree(n)\n for i in range(n):\n segtree.update(i, int(num[i]), 0, n)\n w = k + 1\n res = []\n bst = SortedList()\n while len(res) < n:\n val, j = segtree.getMin(min(w, n), 0, n)\n res.append(num[j])\n pos = j - bst.bisect_right(j - 1)\n bst.add(j)\n w -= pos\n segtree.update(j, -1, 0, n)\n return "".join(res)\n```
| 0 | 0 |
['Python']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Direct Simulation
|
direct-simulation-by-theabbie-ltnp
|
\nclass Solution:\n def minInteger(self, num: str, k: int) -> str:\n n = len(num)\n w = k + 1\n res = []\n while num and w:\n
|
theabbie
|
NORMAL
|
2024-05-21T03:59:33.004988+00:00
|
2024-05-21T03:59:33.005008+00:00
| 3 | false |
```\nclass Solution:\n def minInteger(self, num: str, k: int) -> str:\n n = len(num)\n w = k + 1\n res = []\n while num and w:\n s = num[:w]\n j = s.index(min(s))\n res.append(s[j])\n w -= j\n num = num[:j] + num[j+1:]\n return "".join(res)\n```
| 0 | 0 |
['Python']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Brute force
|
brute-force-by-maxorgus-wmip
|
Did not expect this to pass\n\n# Code\n\nclass Solution:\n def minInteger(self, num: str, k: int) -> str:\n n = len(num)\n if k >= n*(n-1) // 2
|
MaxOrgus
|
NORMAL
|
2024-05-08T02:38:18.694400+00:00
|
2024-05-08T02:38:18.694429+00:00
| 37 | false |
Did not expect this to pass\n\n# Code\n```\nclass Solution:\n def minInteger(self, num: str, k: int) -> str:\n n = len(num)\n if k >= n*(n-1) // 2:return \'\'.join(sorted(num))\n res = \'\'\n i = 0\n while k > 0:\n if len(res) == n:\n break\n mi = min(num[:k+1])\n j = num.index(mi)\n if j <= k:\n res += mi\n k -= j\n num = num[:j]+num[j+1:]\n else:\n res += num\n return res\n if num:\n res += num\n return res\n\n \n```
| 0 | 0 |
['Python3']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Fenwick Tree solution
|
fenwick-tree-solution-by-dagmarc-g5qe
|
\n# Code\n\npackage main\n\nimport (\n\t"container/list"\n)\n\ntype FenwickTree struct {\n\tsize int // n: length of the array\n\tbitTree []int // bit: sto
|
DagmarC
|
NORMAL
|
2024-04-15T13:24:52.633780+00:00
|
2024-04-15T13:24:52.633800+00:00
| 11 | false |
\n# Code\n```\npackage main\n\nimport (\n\t"container/list"\n)\n\ntype FenwickTree struct {\n\tsize int // n: length of the array\n\tbitTree []int // bit: store the sum of range\n}\n\n// The NewFenwickTree function initializes a Fenwick tree data structure with the given array.\nfunc NewFenwickTree(n int) *FenwickTree {\n\tft := FenwickTree{\n\t\tsize: n + 1,\n\t\tbitTree: make([]int, n+1),\n\t}\n\treturn &ft\n}\n\n// This `CountElementsLeft` method in the `FenwickTree` struct is used to calculate the number of elements already shifted in\n// the num located left from the index `i`.\nfunc (ft *FenwickTree) CountElementsLeft(i int) int {\n\tsum := 0\n\tfor i > 0 {\n\t\tsum += ft.bitTree[i]\n\t\ti -= (i & -i) // flip the last set bit\n\t}\n\treturn sum\n}\n\n// The `Add` method in the `FenwickTree` struct is used to update the Fenwick tree by adding a value to\n// a specific index `i` and propagating the changes through the tree structure. Here is a breakdown of\n// what the method does:\nfunc (ft *FenwickTree) Add(i, inc int) {\n\tfor i < ft.size {\n\t\tft.bitTree[i] += inc\n\t\ti += (i & -i) // add last set bit\n\t}\n}\n\nfunc minInteger(num string, k int) string {\n\tn := len(num)\n\t// Map of digits [0-9] and list of positions to the each digit\n\tpositions := make([]*list.List, 10)\n\t// Init Linked list for each digit\n\tfor i := 0; i <= 9; i++ {\n\t\tpositions[i] = list.New()\n\t}\n\t// Go through num and save each position corresponding to digit\n\tfor i := 0; i < n; i++ {\n\t\td := num[i] - \'0\'\n\t\tpositions[d].PushBack(i + 1) // indexing starts from 1 in Binary Indexed Tree\n\t}\n\tft := NewFenwickTree(n)\n\tanswer := make([]byte, 0, n)\n\tfor i := 0; i < n; i++ {\n\t\tfor d := 0; d <= 9; d++ {\n\t\t\tposEl := positions[d].Front()\n\t\t\tif posEl != nil {\n\t\t\t\tposition := posEl.Value.(int)\n\t\t\t\tleftShifts := ft.CountElementsLeft(position)\n\t\t\t\tif position-1-leftShifts <= k {\n\t\t\t\t\tanswer = append(answer, byte(d+\'0\'))\n\t\t\t\t\tft.Add(position, 1)\n\t\t\t\t\tk -= (position - 1 - leftShifts)\n\t\t\t\t\tpositions[d].Remove(posEl)\n\t\t\t\t\tbreak // element added, jump to the next iteration\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t}\n\treturn string(answer)\n}\n\n```
| 0 | 0 |
['Binary Indexed Tree', 'Go']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Python BinaryIndexedTree detailed solution | Time O(n*log(n)) | Space O(n)
|
python-binaryindexedtree-detailed-soluti-csnt
|
https://leetcode.ca/2020-01-13-1505-Minimum-Possible-Integer-After-at-Most-K-Adjacent-Swaps-On-Digits/\n\n# Intuition\n\nI highly recommend you to read this (ht
|
qodewerty
|
NORMAL
|
2024-03-31T20:53:25.086989+00:00
|
2024-03-31T20:53:25.087020+00:00
| 36 | false |
* https://leetcode.ca/2020-01-13-1505-Minimum-Possible-Integer-After-at-Most-K-Adjacent-Swaps-On-Digits/\n\n# Intuition\n\nI highly recommend you to read this (https://leetcode.com/problems/minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits/solutions/720548/o-n-logn-detailed-explanation/) well explained approach before reading further.\n\nWe are given a string of length `n`, and we want to construct a new string `res` of length `n`.\n\nWe start contructing `res` from index `0` to `n` placing on small digit at a time.\n\nfor each index `i` we check for digits starting `0` to `9` for which smallest digit we can place at `i` using the available number of swaps. So, basically if we can do `k` swaps, and the index of a digit is `j` in original string, we can use the digit if distance `dist` required to move the digit to `i` from `j` is less than `k`.\n\nTo calculate the `dist` we use `BITree`. Formula:\n\n* `dist = biTree.query(n-1) - biTree.query(j) + j - i`\n\n## Formula explained\n\nThe above formula is the most important logic in our algorithm. Let\'s see what does it mean.\n\n* `biTree.query(n-1)` = total no. of digits placed in `res`\n* `biTree.query(j)` = total no. of digits before `j` in original string that is placed in `res`.\n\nWe want the above two information to figure out how many new elements has been inserted before `num[j]` because each new element will shift the `num[j]` position by 1.\n\n* Shift: `shift = biTree.query(n-1) - biTree.query(j)`\n* New effective position: `newPos = j + shift`\n* Distance from `i`: `dist = newPos - i`\n\nPutting the values we get:\n* `dist = biTree.query(n-1) - biTree.query(j) + j - i`\n\n## Quick word on why using BITree\n\nIf you know about prefix sum array and how we use it to get range sum between indexes, think about updating a value in the orignal array. When we do that we will need to re-calculate our prefix sum, and the conventional approach will have $O(n)$ time complexity.\n\nThis is where BITree or Segment tree step in to reduct the time complexity to $O(n*log(n))$.\n\n# Complexity\n- Time complexity: $O(n * log(n))$\n- Space complexity: $O(n)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass BITree:\n def __init__(self, n):\n self.size = n\n self.nums = [0] * (n + 1)\n\n def update(self, i, val):\n i += 1\n while i <= self.size:\n self.nums[i] += val\n i += i & -i\n\n def query(self, i):\n i += 1\n res = 0\n while i:\n res += self.nums[i]\n i -= i & -i\n return res \n\n\nclass Solution:\n def minInteger(self, num: str, k: int) -> str:\n pos = defaultdict(deque)\n for i, digit in enumerate(num):\n pos[digit].append(i)\n \n res = []\n n = len(num)\n biTree = BITree(n)\n for i in range(n):\n for d in range(10):\n digit = str(d)\n q = pos[digit]\n if q:\n j = q[0]\n dist = biTree.query(n-1) - biTree.query(j) + j - i\n if dist <= k:\n k -= dist\n q.popleft()\n res.append(digit)\n biTree.update(j, 1)\n break\n return "".join(res)\n```
| 0 | 0 |
['Python3']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Python 3: FT 75: TC O(n*10*log(n)), SC O(n): Fenwick Tree and Adjusted Indices
|
python-3-ft-75-tc-on10logn-sc-on-fenwick-dxaa
|
Intuition\n\nThis is a tough one.\n\nWhat I realized is this:\n to minimize a number, you want to minimize the first digit\n that\'s because for any two numbers
|
biggestchungus
|
NORMAL
|
2024-03-17T06:16:00.895474+00:00
|
2024-03-17T06:16:00.895510+00:00
| 10 | false |
# Intuition\n\nThis is a tough one.\n\nWhat I realized is this:\n* to minimize a number, you want to minimize the first digit\n* that\'s because for any two numbers with prefixes p and p\' of the same length, if p < p\', then the first number is smaller\n* this is due to each digit being 10x larger than the next, so any reduction of an earlier digit is more influential than decrementing any combination of later digits\n\nThis means\n* for the first digit, we want to take the lowest one within `k` indices and swap it into the first index (`i=0`)\n* swap into the first index\n* then continue with the second digit: among all untaken digits, take the lowest one within `k` of `i=1`\n* then take the one within `k` of the third slot, `i=2`\n\n## Nominal Indices\n\nThese are the original indices in `num`. Nothing special.\n\nIf we swap a number into index `i`, the relative order of the remaining numbers doesn\'t change.\n\n## Adjusted Indices\n\nBut when we swap a number at index `j` into the next output index `i`, the "distance" of indices to i+1 changes:\n* the distance of nominal indices `...j` doesn\'t change: we basically insert a new number at `i` which increases distance, but then at the next iteration, we look at `i+1` so the distance decreases by one\n* for nominal indices `j+1..` though, we effectively removed `j` and inserted it at `i`, no change yet. But at the next iteration, `i+1`, the distance to later `j` decreases one.\n\nSo relative to the next "slot"/output index to pick a digit for, the offset changes by -1.\n\nHere\'s an illustration where 5 is the minimum index we can move into position with `k==4`\n```\n.....987654321 ; k ==4\n i\n 012345678 # distance to i before the swap\n\nNext iteration, i += 1\n\n.....598764321\n i\n 01234567 # distance to i before the next swap\n```\n\nThe distances/"adjusted indices" before the `5` didn\'t change from one iteration to the next. But the digits after the \'5\' got one position closer.\n\n## An Algorithm Emerges\n\nSo what we can do is\n* get a `deque` of all the indices for each digit\n* and also record offsets: when we take the digit at nominal index `i` for the output, we decrement all those indices by 1. See the Approach for a `log(n)` way to get this\n\nThen for each next output digit:\n* find the minimum digit within `k` (adjusted index `<= k`)\n* take that digit, at nominal index `i` and adjusted index `i+o`, and\n * record we took `i`\n * decrement `k` by `i+o`\n * decrement the offset for indices `i+1..` by 1\n\nRepeat this until\n* `k==0`: all untaken digits are still in the same relative order as they were in `num`, so we dump all untaken digits in order to `out`\n* or `out` has all the digits, in which case we\'re done\n * we\'d counter this if `num` is already sorted and `k > 0`\n\n# Approach\n\nBesides the insight about adjusted indices / decreasing the offset of `i+1..N` by 1, the hard part is *how* we do this efficiently.\n\nBrute force would be `O(n)`, leading to an `O(n^2)` algorithm and likely TLE since `n` can be 3e4.\n\nWe need a faster way to change all values associated with `i+1..N` by a constant.\n\nThis is equivalent to updating the cumulative sum over `N` elements in faster than `O(N)`; the offset is the cumulative sum of `-1` offsets applied at all `i+1` when we pick the digit at nominal index `i`\n\n## Fast Cumulative Sum Updates: Fenwick Tree\n\nA Fenwick tree is the easiest way in an interview to support getting and updating the cumulative sum of `n` elements.\n\n**You should probably know Fenwick trees in the current hiring environment.**\n\nThe idea is kind of hard to explain, but suppose I want to get the cumulative sum of elements `1..m` (1-indexed, it makes the math easier).\n\nIt turns out we can do this with a binary expansion! Let\'s look at the bits of `m`: e.g. `100011001_2`.\n\nWe could get a decent approximation if we know the sum of the first `100000000_2` elements, in that we\'d get the sum over more than half of them.\n\nThen if we knew the sum of of elements in `(100000000_2, 100010000_2] then we\'d get at least halfway closer still to summing over all the digits.\n\nThen we\'d repeat. We can see that we\'re getting another digit each time, so this will take `log(n)` time.\n\nThis looks really hard to do. It is hard to figure it out, but once you realize the pattern and memorize the code, it becomes easy.\n\nWe see that we need sums of ranges of the form `(m-lsb(m), m]`. We can store that sum at index `m` in the Fenwick "tree" (really a `list`. Hence the LSB stuff in the code. So we iterate `m -= lsb(m)` and add its contents to the answer. Repeat until `m == 0`.\n\nFor updating a sum by changing the value at `m`:\n* clearly m is in `(m-lsb(m), m]`, so update the value at `m`\n* this is tricky, but let `m\' = m + lsb(m)`. Then `m` is in `(m\'-lsb(m), m\']` as well\n * this is because m is less than m+lsb(m), clearly\n * and if we take m+lsb(m), *that* number\'s lsb is at least `2*lsb(m)`. So if you then subtract `lsb(m\')` for `m\'`\'s Fenwick tree node, then you\'ll find that the lower bound is below `m`. Therefore `m` is in that interval\n* repeat this iterative "add the lsb, then update that node" loop until `m\'` is out of range\n\n## Other Misc Items\n\nTo find the min digit, I just iterate over all 10 digits and take the least. There might be a marginally faster way to do a clever min heap with changing priorities in Python. For an O(1) improvement I didn\'t bother.\n\nTo make interacting with the Fenwick tree easier, especially because we want to work with 0-based indexs in the code but Fenwick trees use 1-based indexing, I added `incrOffset` and `getOffset` methods to encapsulate those operations.\n\nThis is analogous to how you *could* do union find without having literal `union` and `find` helper methods, but it would be really annoying.\n\n## Alternatives to Fenwick Trees\n\nIf you really don\'t want to learn Fenwick trees there are a few other alternatives, but IMO worse.\n\n### Use the `sortedcontainers` Package\n\nYou could probably use something like the `SortedList` or `SortedDict` for this, but you\'d have to be very clever about how to make the keys work and decrement positions.\n\nYou\'ll also depend on the OA environment / phone interview environment or your interviewer allowing you to use third-party packages (hit or miss).\n\n### Segment Tree\n\nYou can update the offsets for a range of nominal indices conceptually very easily using a segment tree. You\'d literally by changing the offset for a whole range.\n\nUpside: a bit more clear than using a Fenwick tree and get the cumulative sum of -1 values at each taken `i`.\n\nDownsides:\n* takes twice as much memory, you need to store `2n` nodes at least, maybe a few more to handle edge cases?\n* updates are more complicated\n * each node in the tree has two leaves so you have to wrangle with bisecting\n * each node represents a different range of indices so you have to deal with that, either with auxiliary entries to store the ranges (takes up even more space) or passing in the range to each node when updating in the recursive calls (adds boilerplate and bug risks)\n * to efficiently update ranges you need to implement lazy range updates, which of course adds even more potential for bugs\n\n**In general: Fenwick trees are a lot easier to write in an interview than a segment tree IMO.**\n\n# Complexity\n* Time complexity: `O(n*10*log(n))`\n * `n` part comes from iterating over all `n` digits in the worst case\n * `10` comes from iterating over all digits `0..9` as candidates\n * NOTE: technically constants don\'t belong in big-O notation... but it\'s here to help illustrate what the algorithm is doing\n * `log(n)` because for each digit, we do `log(n)` operations with the Fenwick tree to get the index offset\n* Space complexity: `O(n)`: we have `N` entries in the `idxs` and `f` (Fenwick "tree"/list) structures\n\n# Code\n```\nclass Solution:\n def minInteger(self, num: str, k: int) -> str:\n # prior idea: kind of worked, but not quite:\n # move as many 1s to front as possible, then 2s, etc.\n # but it gets stuck if we can\'t move things to the front\n\n\n # idea: what digit do we take next?\n # the smallest one possible!\n\n # suppose we have digits d0, d1, .. d{r-1} labeled by their distance from the current front\n # we\'ll take the best digit within k, then reduce k by the label of the one we took\n\n # how do we update labels?\n # if we take di, then i+1..r-1 are all decremented by one because they get one closer\n # to the next position we swap into\n\n # segment or fenwick tree? we can record the original indices of each digit\n # and in log(N) get the cumulative offset that accounts for swaps made thus far\n \n # then for each digit, we\'d find the best/only in 0..9 we can move, move it by i-o(i), then decrement k\n # do this while k, then take all the remaining digits\n\n N = len(num)\n\n # Fenwick tree for cumulative offsets\n f = [0]*(N+1)\n\n def incrOffset(i: int, by: int) -> None:\n """modifies the cumulative offset of i.. by `by`"""\n i += 1\n while i <= N:\n f[i] += by\n i += i & (-i)\n\n def getOffset(i: int) -> int:\n i += 1\n ans = 0\n while i:\n ans += f[i]\n i &= i-1\n return ans\n\n # record nominal indices of all digits, use a deque for easy pop left\n # to improve speed: use a list, and also store a pointer to the next index\n idxs = [deque() for d in range(10)]\n for i, d in enumerate(num): idxs[int(d)].append(i)\n\n taken = [False]*N # nominal indices we\'ve taken thus far\n\n out = [] # digits we\'ve taken already\n while k and len(out) < N:\n # TODO: we can optimize away duplicate getOffset calls at the cost of illegibility\n\n # find the lowest digit we can take next: it must be within k swaps\n # "within k" meaning it\'s *adjusted* index to account for earlier numbers swapped out\n m = min(d for d, iq in enumerate(idxs) if iq and iq[0]+getOffset(iq[0]) <= k)\n\n # take m:\n # add to output (ofc), mark as taken\n # and since we moved the number at index i, all nums at i+1 are\n # one closer to the front of the untaken numbers\n out.append(m)\n i = idxs[m].popleft()\n taken[i] = True\n k -= i + getOffset(i)\n # when we take the digit at i, digits at higher nominal indices\n # move 1 closer to the next digit to take\n incrOffset(i+1, by=-1)\n\n if len(out) < N:\n # out of swaps: take remaining numbers in their original order;\n # we didn\'t change the relative order of untaken numbers\n out.extend(num[i] for i in range(N) if not taken[i])\n\n return \'\'.join(map(str, out))\n```
| 0 | 0 |
['Python3']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
segment tree+lazy propagation solution
|
segment-treelazy-propagation-solution-by-qh1j
|
\n\n# Code\n\nclass Solution {\npublic:\nvector<int>seg,lazy;\nint query(int ind,int low,int high,int i){\n if(lazy[ind]!=0){\n seg[ind]+=(high-low+1)
|
Saiteja6
|
NORMAL
|
2024-01-29T12:56:56.219873+00:00
|
2024-01-29T12:56:56.219900+00:00
| 58 | false |
\n\n# Code\n```\nclass Solution {\npublic:\nvector<int>seg,lazy;\nint query(int ind,int low,int high,int i){\n if(lazy[ind]!=0){\n seg[ind]+=(high-low+1)*lazy[ind];\n if(low!=high){\n lazy[2*ind+1]+=lazy[ind];\n lazy[2*ind+2]+=lazy[ind];\n }\n lazy[ind]=0;\n }\n if(low==high)return seg[ind];\n int mid=(low+high)/2;\n if(i<=mid)return query(2*ind+1,low,mid,i);\n return query(2*ind+2,mid+1,high,i);\n}\nvoid update(int ind,int low,int high,int l,int r){\n if(lazy[ind]!=0){\n seg[ind]+=(high-low+1)*lazy[ind];\n if(low!=high){\n lazy[2*ind+1]+=lazy[ind];\n lazy[2*ind+2]+=lazy[ind];\n }\n lazy[ind]=0;\n }\n if(high<l||low>r)return;\n if(low>=l&&high<=r){\n seg[ind]+=(high-low+1);\n if(low!=high){\n lazy[2*ind+1]+=1;\n lazy[2*ind+2]+=1;\n }\n return;\n }\n int mid=(low+high)/2;\n update(2*ind+1,low,mid,l,r);\n update(2*ind+2,mid+1,high,l,r);\n}\n string minInteger(string num, int k) {\n vector<int>adjls[10];\n int n=num.size();\n seg.resize(4*n,0);\n lazy.resize(4*n,0);\n for(int i=n-1;i>=0;i--){\n adjls[num[i]-48].push_back(i);\n } \n \n vector<bool>a(n,false);\n string res; \n for(int i=0;i<n;i++){\n if(a[i])continue;\n if(k<=0){\n res+=num[i];\n continue;\n }\n bool flag=true;\n int l=num[i]-\'0\';\n for(int j=0;j<l;j++){\n if(adjls[j].empty())continue;\n int p=adjls[j].back();\n int q=query(0,0,n-1,p);\n int r=query(0,0,n-1,i);\n int swaps=p-i-q+r;\n if(swaps<=k){\n k-=swaps;\n res+=j+\'0\';\n a[p]=true;\n adjls[j].pop_back();\n flag=false;\n update(0,0,n-1,p,n-1);\n i--;\n break;\n }\n }\n if(flag)res+=num[i],a[i]=true,adjls[l].pop_back();\n }\n cout<<k;\n return res;\n }\n};\n```
| 0 | 0 |
['Segment Tree', 'C++']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Go - 100% Runtime & Memory
|
go-100-runtime-memory-by-frankdizzle-dtkn
|
Intuition\nStarting from the first digit and iterating forwards, swap in the lowest digit possible.\n\n# Approach\nBuild the solution in a new array of bytes.\n
|
frankdizzle
|
NORMAL
|
2024-01-10T20:42:16.929038+00:00
|
2024-01-10T20:42:16.929078+00:00
| 6 | false |
# Intuition\nStarting from the first digit and iterating forwards, swap in the lowest digit possible.\n\n# Approach\nBuild the solution in a new array of bytes.\n\n# Complexity\n- Time complexity:\n$$O(n^2)$$ is an upper bound\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nfunc minInteger(num string, k int) string {\n bytes := ([]byte)(num)\n res := make([]byte, len(num))\n targetIndex := 0\n swaps := k\n for swaps > 0 && targetIndex <= len(bytes) - 1 {\n rangeEnd := min(targetIndex + swaps, len(bytes)-1)\n target := bytes[targetIndex]\n b, index := findMinDigit(bytes[targetIndex:rangeEnd + 1], target)\n if index > -1 {\n index += targetIndex\n res[targetIndex] = b\n copy(bytes[targetIndex+1:index+1], bytes[targetIndex:index])\n // perform all swaps \n swaps -= index-targetIndex \n } else {\n // no swap\n res[targetIndex] = bytes[targetIndex]\n }\n targetIndex++\n }\n copy(res[targetIndex:], bytes[targetIndex:])\n return string(res)\n}\n\nfunc min(a, b int) int {\n if a < b {\n return a\n }\n return b\n}\n\n// will return index -1 if none found\nfunc findMinDigit(arr []byte, threshold byte) (b byte, index int) {\n b = threshold\n index = -1\n for i, ch := range arr {\n if ch < b {\n index = i\n b = ch\n }\n }\n return b, index\n}\n```
| 0 | 0 |
['Go']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
C++ Simple Segment Tree and Fenwick Tree O(n*log n)
|
c-simple-segment-tree-and-fenwick-tree-o-aezh
|
Code\n\nclass Solution {\n using Indices = std::vector<int>;\n\n static constexpr int kMaxIndex = 3 * 1e4;\n\n struct BIT{\n explicit BIT(int n)
|
nnuttertools
|
NORMAL
|
2023-12-31T02:18:44.389622+00:00
|
2023-12-31T02:18:44.389638+00:00
| 45 | false |
# Code\n```\nclass Solution {\n using Indices = std::vector<int>;\n\n static constexpr int kMaxIndex = 3 * 1e4;\n\n struct BIT{\n explicit BIT(int n) : n(n), t(n + 1, 0) {}\n\n void update(int i, int v) noexcept {\n for(++i; i < n; i += i & (-i)) {\n t[i] += v;\n }\n }\n\n auto query(int i) const noexcept {\n int counter{0};\n for(++i; i > 0; i -= i & (-i)) {\n counter += t[i];\n }\n return counter;\n }\n\n private:\n int n;\n std::vector<int> t;\n };\n\n\n\npublic:\n string minInteger(string num, int k) {\n const int n = num.size();\n BIT tree(n);\n \n std::array<Indices, 10> digit2index;\n for(int i = 0; i < n; ++i) {\n digit2index[num[i] - \'0\'].push_back(i);\n }\n std::ranges::for_each(digit2index, [](auto& indices){\n std::ranges::sort(indices, std::ranges::greater{});\n });\n\n std::string result;\n result.reserve(n);\n std::array<bool, kMaxIndex> used_indices;\n used_indices.fill(false);\n \n for(int i = 0; i < n && k > 0; ++i) {\n for(int digit = 0; digit <= 9; ++digit) {\n if(digit2index[digit].empty()) {\n continue;\n }\n const auto idx = digit2index[digit].back();\n const auto processed_before = tree.query(idx - 1);\n const auto swaps = idx - processed_before;\n if(swaps > k) {\n continue;\n }\n\n digit2index[digit].pop_back();\n tree.update(idx, 1);\n used_indices[idx] = true;\n k -= swaps;\n\n result += digit + \'0\';\n break;\n }\n }\n\n for(int i = 0; i < n; ++i) {\n if(used_indices[i]) {\n continue;\n }\n result += num[i];\n }\n\n return result;\n }\n};\n```\n\n## Segment Tree\n```\n\n struct SegmentTree{\n explicit SegmentTree(int n) : n(n), t(2*n + 2, 0) {}\n\n void update(int i, int v) noexcept {\n for(t[i += n] = v; i > 0; i >>= 1) {\n t[i >> 1] = t[i] + t[i ^ 1];\n }\n }\n\n auto query(int i) const noexcept {\n int res{0};\n int l{0}, r{i};\n for(l += n, r += n; l <= r; l >>= 1, r >>= 1) {\n if(l & 1) res += t[l++];\n if(!(r & 1)) res += t[r--];\n }\n return res;\n }\n\n private:\n int n;\n std::vector<int> t;\n };\n```
| 0 | 0 |
['C++']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Solution using Fenwick Tree
|
solution-using-fenwick-tree-by-isheoran-hw8x
|
Complexity\n- Time complexity:\nO(n*log(n))\n\n- Space complexity:\nO(n) \n\n# Code\n\n\nclass BIT {\n vector<int>tree;\n int n;\npublic:\n BIT(){}\n\n
|
isheoran
|
NORMAL
|
2023-11-18T13:26:04.153923+00:00
|
2023-11-18T13:26:04.153952+00:00
| 21 | false |
# Complexity\n- Time complexity:\n$$O(n*log(n))$$\n\n- Space complexity:\n$$O(n)$$ \n\n# Code\n```\n\nclass BIT {\n vector<int>tree;\n int n;\npublic:\n BIT(){}\n\n BIT(int n) {\n tree.resize(n);\n this->n = n;\n }\n\n void add(int i,int val) {\n while(i < n) {\n tree[i] += val;\n i |= i+1;\n }\n }\n\n int sum(int i) {\n int res = 0;\n while(i >= 0) {\n res += tree[i];\n i = (i&(i+1))-1;\n }\n\n return res;\n }\n};\n\nclass Solution {\npublic:\n string minInteger(string num, int k) {\n int n = num.size();\n BIT tr(n);\n\n vector<int>idx[10];\n\n for(int i=n-1;i>=0;i--) {\n tr.add(i,1);\n\n idx[num[i]-\'0\'].push_back(i);\n }\n\n string ans = num;\n\n for(int i=0;i<n;i++) {\n for(int d=0;d<10;d++) {\n if(idx[d].empty() or tr.sum(idx[d].back()) > k+1) continue;\n ans[i] = \'0\'+d;\n k -= tr.sum(idx[d].back())-1;\n tr.add(idx[d].back(),-1);\n idx[d].pop_back(); \n break;\n }\n }\n\n return ans;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Very Easy C++: Solution: Beats 94%
|
very-easy-c-solution-beats-94-by-raj_y-bjg2
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
raj_y
|
NORMAL
|
2023-09-04T22:32:48.268130+00:00
|
2023-09-04T22:32:48.268148+00:00
| 58 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\n- O(3*n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n string minInteger(string s, int k) {\n int n=s.size();\n vector<int> prefix(n,0),prefix1(n,0),visited(n,0);\n string ans="";\n int cnt;\n bool tp=false;\n int current=n;\n for(int i=0;i<9;i++){\n cnt=0;\n for(int j=0;j<n;j++){\n if(current<j)break;\n if(s[j]==(i+\'0\')){\n if((j-prefix1[j]-cnt)<=k){\n prefix[j]++;\n // cout<<prefix1[j]<<" "<<i<<" "<<cnt<<endl;\n k-=(j-prefix1[j]-cnt);\n ans+=s[j];\n visited[j]=1;\n cnt++;\n // cout<<k<<" "<<i<<endl;\n }\n else{\n // tp=true;\n current=j;\n break;\n }\n // else{\n\n // }\n }\n }\n // if(tp)break;\n prefix1=prefix;\n for(int j=1;j<n;j++){\n prefix1[j]+=prefix1[j-1];\n }\n }\n cout<<k<<" ";\n for(int i=0;i<n;i++){\n if(!visited[i]){\n ans+=s[i];\n }\n }\n cout<<ans<<endl;\n for(int i=0;i<n-1;i++){\n if(ans[i]>ans[i+1]){\n current=i+1;\n break;\n }\n }\n // cout<<current<<" ";\n while(current!=n && current>0 && k>0){\n swap(ans[current],ans[current-1]);\n current--;\n k--;\n }\n return ans;\n \n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
BIT|| COMMENTED |||QUEUE
|
bit-commented-queue-by-aasmaan_vs_aasmaa-9b4e
|
*Binary Indexed Tree (BIT):\n\nPurpose: The Binary Indexed Tree, also known as a Fenwick Tree, is used to efficiently perform prefix sum queries and updates. It
|
Aasmaan_Vs_Aasmaan
|
NORMAL
|
2023-09-04T16:12:14.374532+00:00
|
2023-09-04T16:12:14.374550+00:00
| 14 | false |
****Binary Indexed Tree (BIT):\n****\nPurpose: The Binary Indexed Tree, also known as a Fenwick Tree, is used to efficiently perform prefix sum queries and updates. It helps keep track of the number of digits that have been removed from the original string, which is essential for selecting and processing digits during the optimization process.\nHow It\'s Used:\nThe BIT is initialized with a size of \'n+1,\' where \'n\' is the number of elements (positions in the string).\nThe update method is used to increment the value at a specific index (position) by a given delta (usually 1). This operation marks that a digit has been removed from the original string.\nThe query method is used to efficiently compute the prefix sum up to a specific index. It helps determine how many digits have been removed from positions preceding a given position.\nQueues (qs - Vector of Queues):\n**\nPurpose: Queues **are used to keep track of the positions of each digit in the original string. Each queue corresponds to a digit from 0 to 9, and it stores the positions of that digit in the string.\nHow They\'re Used:\nDuring the initialization of qs, each digit\'s queue is populated with its respective positions in the original string.\nThe queues are used to efficiently select and process digits during the process of minimizing the integer:\nDigits that can be moved to the left-hand side (i.e., smaller digits that have sufficient available swaps) are selected from their respective queues and added to the result.\nPositions of processed digits are marked as "removed" in the BIT using the update method.\nThis process continues until \'k\' swaps are exhausted or no more valid swaps are possible.\n\n# Code\n```\nclass BIT {\npublic:\n int n; // Number of elements\n vector<int> nodes; // Binary Indexed Tree (Fenwick Tree)\n\n BIT(int n) {\n this->n = n;\n nodes = vector<int>(n + 1); // Initialize the BIT with size (n + 1)\n }\n\n // Function to update a value at index \'i\' by adding \'delta\'\n void update(int i, int delta) {\n ++i; // Increment \'i\' to convert 0-based indexing to 1-based indexing\n while (i <= n) {\n nodes[i] += delta; // Update the BIT node at index \'i\' by adding \'delta\'\n i += (i & -i); // Move to the parent node (next node with a higher significant bit)\n }\n }\n\n // Function to query the prefix sum up to index \'i\'\n int query(int i) {\n ++i; // Increment \'i\' to convert 0-based indexing to 1-based indexing\n int sum = 0;\n while (i > 0) {\n sum += nodes[i]; // Accumulate the sum from the current node\n i -= (i & -i); // Move to the previous node (next node with a lower significant bit)\n }\n return sum;\n }\n};\n\nclass Solution {\npublic:\n string minInteger(string num, int k) {\n vector<queue<int>> qs(10); // An array of queues to store positions of each digit\n int n = num.size();\n\n // Populate queues with the positions of each digit\n for (int i = 0; i < n; ++i) {\n qs[num[i] - \'0\'].push(i);\n }\n\n string lhs; // Left-hand side of the result string\n vector<bool> removed(n, false); // Indicates if a digit has been removed from the original string\n BIT* tree = new BIT(n); // Create a Binary Indexed Tree (BIT) to track removed digits\n\n while (k > 0) {\n bool found = false;\n for (int d = 0; d <= 9; ++d) {\n if (!qs[d].empty()) {\n int pos = qs[d].front(); // Get the position of the current digit\n int shifted = tree->query(pos - 1); // Query the BIT to find the number of removed digits before pos\n if (pos - shifted <= k) {\n k -= pos - shifted; // Update remaining swaps\n tree->update(pos, 1); // Mark the current digit as removed in the BIT\n qs[d].pop(); // Remove the position from the queue\n lhs += (\'0\' + d); // Append the digit to the left-hand side\n removed[pos] = true; // Mark the digit as removed\n found = true;\n break;\n }\n }\n }\n if (!found) break; // If no valid swap is possible, exit the loop\n }\n\n string rhs; // Right-hand side of the result string\n for (int i = 0; i < n; ++i) {\n if (!removed[i]) {\n rhs += num[i]; // Append the remaining digits to the right-hand side\n }\n }\n\n return lhs + rhs; // Concatenate the left-hand and right-hand sides to form the final result\n }\n};\n\n```
| 0 | 0 |
['C++']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
commented +segment tree+queue
|
commented-segment-treequeue-by-aasmaan_v-1olv
|
see this for best explanation\nhttps://leetcode.com/problems/minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits/solutions/720548/o-n-logn-detaile
|
Aasmaan_Vs_Aasmaan
|
NORMAL
|
2023-09-04T15:59:02.885021+00:00
|
2023-09-04T16:00:18.879554+00:00
| 16 | false |
see this for best explanation\nhttps://leetcode.com/problems/minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits/solutions/720548/o-n-logn-detailed-explanation/\n\nwhy\n\n1. **Segment Tree (`SegTree`):**\n - **Purpose:** The segment tree is used to keep track of which digits have been removed from the original string during the process of minimizing the integer.\n - **How It\'s Used:**\n - The segment tree maintains information about the positions of removed digits, allowing quick queries to find the count of removed digits before a given position.\n - The `update` method is used to mark a position as "removed" in the segment tree when a digit is moved to the left-hand side of the result.\n - The `queryLessThan` method is used to find the count of removed digits before a specified position.\n\n\nwhy\n2. **Queues (`qs` - Vector of Queues):**\n - **Purpose:** Queues are used to keep track of the positions of each digit in the original string. Each queue corresponds to a digit from 0 to 9, and it stores the positions of that digit in the string.\n - **How They\'re Used:**\n - During the initialization of `qs`, each digit\'s queue is populated with its respective positions in the original string.\n - The queues are used to efficiently select and process digits during the process of minimizing the integer:\n - Digits that can be moved to the left-hand side (i.e., smaller digits that have sufficient available swaps) are selected from their respective queues and added to the result.\n - Positions of processed digits are marked as "removed" in the segment tree.\n - This process continues until \'k\' swaps are exhausted or no more valid swaps are possible.\n\nIn summary, the segment tree is employed to keep track of removed digits and efficiently answer queries about the number of removed digits before a given position. The queues are used to manage the positions of digits in the original string and facilitate the selection and processing of digits during the optimization process. Together, these data structures enable an efficient solution to the problem of minimizing the integer while respecting the swap limit \'k\'.\n\n# Code\n```\nclass SegTree {\npublic:\n vector<int> nodes; // Array representing the segment tree\n int n; // Number of elements in the original array\n\n SegTree(int n) {\n this->n = n;\n nodes = vector<int>(this->n << 2); // Initialize the segment tree with size 4 * n\n }\n\n // Function to update a node in the segment tree\n void update(int treeIdx, int l, int r, int ql, int val) {\n if (ql < l || ql > r) {\n return; // If the query index is out of the current segment, return\n }\n\n if (l == r) {\n nodes[treeIdx] += val; // If the segment has only one element, update it and return\n return;\n }\n\n int mid = (l + r) >> 1; // Calculate the middle index of the segment\n\n if (ql <= mid) {\n update((treeIdx << 1) | 1, l, mid, ql, val); // Recursively update the left subtree\n } else {\n update((treeIdx << 1) + 2, mid + 1, r, ql, val); // Recursively update the right subtree\n }\n\n nodes[treeIdx] = nodes[(treeIdx << 1) | 1] + nodes[(treeIdx << 1) + 2]; // Update the current node based on child nodes\n }\n\n // Function to increase the value at a specific index in the segment tree\n void increase(int ql) {\n update(0, 0, n - 1, ql, 1); // Start the update process from the root of the segment tree\n }\n\n // Function to query the sum of elements in a specific range [ql, qr] in the segment tree\n int query(int treeIdx, int l, int r, int ql, int qr) {\n if (l > qr || r < ql) {\n return 0; // If the current segment is completely outside the query range, return 0\n }\n\n if (ql <= l && r <= qr) {\n return nodes[treeIdx]; // If the current segment is completely inside the query range, return its value\n }\n\n int mid = (l + r) >> 1; // Calculate the middle index of the segment\n\n if (qr <= mid) {\n return query((treeIdx << 1) | 1, l, mid, ql, qr); // Recursively query the left subtree\n } else if (ql > mid) {\n return query((treeIdx << 1) + 2, mid + 1, r, ql, qr); // Recursively query the right subtree\n }\n\n // If the query range partially overlaps with both left and right subtrees\n int leftRes = query((treeIdx << 1) | 1, l, mid, ql, mid); // Query the left subtree\n int rightRes = query((treeIdx << 1) + 2, mid + 1, r, mid + 1, qr); // Query the right subtree\n\n return leftRes + rightRes; // Return the sum of results from both subtrees\n }\n\n // Function to query the sum of elements less than a given value qnum in the segment tree\n int queryLessThan(int qnum) {\n return query(0, 0, n - 1, 0, qnum - 1); // Start the query from the root with the specified query range\n }\n};\n\nclass Solution {\npublic:\n string minInteger(string num, int k) {\n vector<queue<int>> qs(10); // An array of queues to store positions of each digit\n int n = num.size();\n\n // Populate queues with the positions of each digit\n for (int i = 0; i < n; ++i) {\n qs[num[i] - \'0\'].push(i);\n }\n\n string lhs; // Left-hand side of the result string\n vector<bool> removed(n, false); // Indicates if a digit has been removed from the original string\n SegTree* tree = new SegTree(n); // Create a segment tree to track removed digits\n\n while (k > 0) {\n bool found = false;\n for (int d = 0; d <= 9; ++d) {\n if (!qs[d].empty()) {\n int pos = qs[d].front(); // Get the position of the current digit\n int shifted = tree->queryLessThan(pos); // Query the segment tree to find the number of removed digits before pos\n if (pos - shifted <= k) {\n k -= pos - shifted; // Update remaining swaps\n tree->increase(pos); // Mark the current digit as removed in the segment tree\n qs[d].pop(); // Remove the position from the queue\n lhs += (\'0\' + d); // Append the digit to the left-hand side\n removed[pos] = true; // Mark the digit as removed\n found = true;\n break;\n }\n }\n }\n if (!found) break; // If no valid swap is possible, exit the loop\n }\n\n string rhs; // Right-hand side of the result string\n for (int i = 0; i < n; ++i) {\n if (!removed[i]) {\n rhs += num[i]; // Append the remaining digits to the right-hand side\n }\n }\n\n return lhs + rhs; // Concatenate the left-hand and right-hand sides to form the final result\n }\n};\n\n```
| 0 | 0 |
['C++']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Easy Java solution
|
easy-java-solution-by-thomasshelbyobe-2bik
|
Intuition\nGet the minimum in window of size k that starts from i+1. bring that minimum to front and decerease k accordingly.\n\n# Approach\n Describe your appr
|
ThomasShelbyOBE
|
NORMAL
|
2023-07-16T16:47:12.522515+00:00
|
2023-07-16T16:47:12.522547+00:00
| 138 | false |
# Intuition\nGet the minimum in window of size k that starts from i+1. bring that minimum to front and decerease k accordingly.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public String minInteger(String num, int k) {\n int n = num.length();\n char[] arr = num.toCharArray();\n for(int i=0; i<n; i++){\n if(k<=0){\n break;\n }\n char minChar = arr[i];\n int minCharIndex = -1;\n // System.out.println(i+" "+minChar+" "+ minCharIndex+" "+new String(arr));\n //for each index get index of min in window of k;\n for(int j=i+1; j<Math.min(i+k+1, n); j++){\n // System.out.println(minChar+" "+ arr[j]);\n if(minChar > arr[j]){\n minChar = arr[j];\n minCharIndex = j;\n }\n }\n if(minCharIndex == -1){\n continue;\n }\n while(minCharIndex > i){\n swap(arr, minCharIndex);\n k--;\n minCharIndex--;\n }\n // System.out.println(new String(arr));\n // System.out.println();\n }\n return new String(arr);\n }\n private void swap(char[] arr, int i){\n char temp = arr[i];\n arr[i] = arr[i-1];\n arr[i-1] = temp;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
simple segment tree solution || C++
|
simple-segment-tree-solution-c-by-__a__j-a0gu
|
\n# Code\n\nclass Solution {\npublic:\n\n void build(int nl, int nr, int tidx, vector<int> &nums, vector<pair<int, int>> &tree) {\n if(nl == nr) {\n
|
__a__j
|
NORMAL
|
2023-06-08T04:59:11.555337+00:00
|
2023-06-08T04:59:11.555405+00:00
| 77 | false |
\n# Code\n```\nclass Solution {\npublic:\n\n void build(int nl, int nr, int tidx, vector<int> &nums, vector<pair<int, int>> &tree) {\n if(nl == nr) {\n tree[tidx] = {nums[nl], nl};\n return;\n }\n int mid = (nl+nr)/2;\n\n build(nl, mid, 2*tidx+1, nums, tree);\n build(mid+1, nr, 2*tidx+2, nums, tree);\n\n if(tree[2*tidx+1].first < tree[2*tidx+2].first) {\n tree[tidx] = tree[2*tidx+1];\n } else if(tree[2*tidx+1].first > tree[2*tidx+2].first) {\n tree[tidx] = tree[2*tidx+2];\n } else {\n if(tree[2*tidx+1].second < tree[2*tidx+2].second) {\n tree[tidx] = tree[2*tidx+1];\n } else {\n tree[tidx] = tree[2*tidx+2]; \n }\n }\n }\n\n void update(int nl, int nr, int tidx, int idx, vector<pair<int, int>> &tree) {\n if(nl == nr) {\n tree[tidx] = {INT_MAX, INT_MAX};\n return; \n }\n\n int mid = (nl+nr)/2;\n\n if(idx <= mid) {\n update(nl, mid, 2*tidx+1, idx, tree);\n } else {\n update(mid+1, nr, 2*tidx+2, idx, tree); \n }\n\n if(tree[2*tidx+1].first < tree[2*tidx+2].first) {\n tree[tidx] = tree[2*tidx+1];\n } else if(tree[2*tidx+1].first > tree[2*tidx+2].first) {\n tree[tidx] = tree[2*tidx+2];\n } else {\n if(tree[2*tidx+1].second < tree[2*tidx+2].second) {\n tree[tidx] = tree[2*tidx+1];\n } else {\n tree[tidx] = tree[2*tidx+2]; \n }\n }\n }\n\n pair<int, int> query(int nl, int nr, int tidx, int l, int r, vector<pair<int, int>> &tree) {\n if(nl > r or nr < l) return {INT_MAX, INT_MAX};\n if(nl >= l and nr <= r) return tree[tidx];\n\n int mid = (nl+nr)/2;\n\n pair<int, int> left = query(nl, mid, 2*tidx+1, l, r, tree);\n pair<int, int> right = query(mid+1, nr, 2*tidx+2, l, r, tree);\n\n if(left.first < right.first) {\n return left;\n } else if(left.first > right.first) {\n return right; \n } else {\n if(left.second < right.second) {\n return left;\n } \n }\n\n return right;\n }\n\n void build2(int nl, int nr, int tidx, vector<int> &tree) {\n if(nl == nr) {\n tree[tidx] = 1;\n return; \n }\n\n int mid = (nl+nr)/2; \n build2(nl, mid, 2*tidx+1, tree);\n build2(mid+1, nr, 2*tidx+2, tree);\n\n tree[tidx] = tree[2*tidx+1] + tree[2*tidx+2];\n }\n\n void update2(int nl, int nr, int tidx, int idx, vector<int> &tree) {\n if(nl == nr) {\n tree[tidx] = 0; \n return; \n }\n int mid = (nl+nr)/2; \n\n if(idx <= mid){\n update2(nl, mid, 2*tidx+1, idx, tree);\n } else {\n update2(mid+1, nr, 2*tidx+2, idx, tree);\n }\n\n tree[tidx] = tree[2*tidx+1] + tree[2*tidx+2];\n }\n\n int query2(int nl, int nr, int tidx, int l, int r, vector<int> &tree) {\n if(nl > r or nr < l) return 0;\n if(nl >= l and nr <= r) return tree[tidx];\n\n int mid = (nl+nr)/2;\n int left = query2(nl, mid, 2*tidx+1, l, r, tree);\n int right = query2(mid+1, nr, 2*tidx+2, l, r, tree);\n\n return left + right;\n } \n\n int getIdx(int n, int k, vector<int> &tree, int i) {\n int lo = 0, hi = n-1;\n int idx = -1; \n while(lo <= hi) {\n int mid = (lo+hi)/2; \n \n int sum = query2(0, n-1, 0, 0, mid, tree); \n // if(i == 1) {\n // cout<<mid<<" "<<sum<<" "<<lo<<" "<<hi<<" "<<k<<endl;\n // }\n \n if(sum-1 > k) {\n hi=mid-1; \n } else {\n idx=mid;\n lo=mid+1;\n }\n }\n\n return idx; \n }\n\n string minInteger(string num, int k) {\n int n = num.size();\n\n vector<int> nums(n);\n for(int i = 0; i < n; i++) {\n nums[i] = num[i]-\'0\'; \n }\n\n vector<pair<int, int>> tree1(4*n+1, {0, 0});\n build(0,n-1,0, nums, tree1);\n vector<int> tree2(4*n+1, 1); \n build2(0, n-1, 0, tree2); \n\n string ans = num;\n\n int i = 0; \n vector<bool> vis(n,false);\n while(k > 0 and i < n) {\n \n int idx = getIdx(n, k, tree2, i); \n pair<int, int> mini = query(0, n-1, 0, 0, idx, tree1);\n\n int valIdx = mini.second;\n int val = mini.first;\n // cout<<valIdx<<endl;\n int temp = query2(0, n-1, 0, valIdx, n-1, tree2); \n int numberOfZeroes = n-valIdx-temp; \n \n int realIdx = numberOfZeroes + valIdx;\n\n int reqOp = abs(i-realIdx); \n if(k >= reqOp) {\n k -= reqOp;\n ans[i] = num[valIdx];\n } else {\n break;\n }\n\n update2(0, n-1, 0, valIdx, tree2);\n update(0, n-1, 0, valIdx, tree1);\n\n vis[valIdx] = true; \n i++; \n }\n\n for(int j = 0; j < n; j++) {\n if(not vis[j]) {\n ans[i++] = num[j];\n }\n }\n return ans; \n\n } \n};\n```
| 0 | 0 |
['Segment Tree', 'C++']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Python (Simple BIT)
|
python-simple-bit-by-rnotappl-r0ss
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
rnotappl
|
NORMAL
|
2023-04-08T08:41:17.707439+00:00
|
2023-04-08T08:41:17.707481+00:00
| 139 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass BIT:\n def __init__(self,n):\n self.ans = [0]*(n+1)\n\n def query(self,i):\n res = 0\n while i > 0:\n res += self.ans[i]\n i -= i&-i\n return res\n\n def update(self,i,val):\n while i < len(self.ans):\n self.ans[i] += val\n i += i&-i\n\nclass Solution:\n def minInteger(self, num, k):\n n, dict1, res = len(num), defaultdict(deque), ""\n\n for i,x in enumerate(num):\n dict1[x].append(i)\n\n result = BIT(n)\n\n for i in range(n):\n result.update(i+1,1)\n\n for i in range(n):\n for v in "0123456789":\n if dict1[v]:\n idx = dict1[v][0]\n cnt = result.query(idx)\n if cnt <= k:\n dict1[v].popleft()\n k -= cnt\n res += v\n result.update(idx+1,-1)\n break\n\n return res\n\n\n \n\n\n \n```
| 0 | 0 |
['Python3']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
c++ segment tree with 46ms runtime
|
c-segment-tree-with-46ms-runtime-by-idvj-mgts
|
\nclass Solution {\npublic:\n string ans;\n int tree[12*10001],lazy[12*10001],count;\n void Lazy(int id)\n {\n tree[id*2]+=lazy[id];\n
|
idvjojo123
|
NORMAL
|
2023-03-10T17:36:43.168726+00:00
|
2023-03-10T17:36:43.168759+00:00
| 43 | false |
```\nclass Solution {\npublic:\n string ans;\n int tree[12*10001],lazy[12*10001],count;\n void Lazy(int id)\n {\n tree[id*2]+=lazy[id];\n lazy[id*2]+=lazy[id];\n tree[id*2+1]+=lazy[id];\n lazy[id*2+1]+=lazy[id];\n lazy[id]=0;\n }\n void update(int id,int l,int r,int x,int y)\n {\n if(l>y||r<x) return;\n if(l>=x&&r<=y)\n {\n tree[id]++;\n lazy[id]++;\n return;\n }\n int mid=(l+r)/2;\n Lazy(id);\n update(id*2,l,mid,x,y);\n update(id*2+1,mid+1,r,x,y);\n tree[id]++;\n }\n int query(int id,int l,int r,int x)\n {\n if(l>x||r<x) return 0;\n if(l==r) return tree[id];\n int mid=(l+r)/2;\n Lazy(id);\n return query(id*2,l,mid,x)+query(id*2+1,mid+1,r,x);\n }\n string minInteger(string & num, int k) {\n vector<queue<int>> A(10);\n vector<int> kt(num.size(),0);\n for(int i=0;i<=num.size()-1;i++)\n A[int(num[i])-\'0\'].push(i);\n for(int i=0;i<=num.size()-1;i++)\n {\n if(k==0) break;\n for(int j=0;j<=9;j++)\n {\n if(A[j].empty()!=0) continue;\n count=A[j].front()+query(1,0,num.size()-1,A[j].front())-i;\n if(count<=k)\n {\n kt[A[j].front()]=1;\n ans+=num[A[j].front()];\n k=k-count;\n update(1,0,num.size()-1,0,A[j].front());\n A[j].pop();\n break;\n }\n }\n }\n for(int i=0;i<=num.size()-1;i++)\n {\n if(kt[i]==0) ans+=num[i];\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['Queue', 'C']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Just a runnable solution
|
just-a-runnable-solution-by-ssrlive-nh6h
|
Code\n\nimpl Solution {\n pub fn min_integer(num: String, k: i32) -> String {\n let mut k = k as usize;\n let num = num.into_bytes();\n
|
ssrlive
|
NORMAL
|
2023-02-09T04:05:58.861774+00:00
|
2023-02-09T04:11:23.949995+00:00
| 18 | false |
# Code\n```\nimpl Solution {\n pub fn min_integer(num: String, k: i32) -> String {\n let mut k = k as usize;\n let num = num.into_bytes();\n let n = num.len();\n let mut res = Vec::with_capacity(n);\n let mut q = vec![n; 10];\n for (i, &item) in num.iter().enumerate() {\n let d = (item - b\'0\') as usize;\n if q[d] == n {\n q[d] = i;\n }\n }\n let mut used = vec![false; n];\n let mut q_used = vec![0; 10];\n for _ in 0..n {\n for d in 0..10_usize {\n if q[d] == n {\n continue;\n }\n let c = q[d] - q_used[d];\n if c <= k {\n k -= c;\n res.push(b\'0\' + d as u8);\n used[q[d]] = true;\n for d1 in 0..10_usize {\n if q[d1] > q[d] {\n q_used[d1] += 1;\n }\n }\n while q[d] < n {\n if used[q[d]] {\n q_used[d] += 1;\n }\n q[d] += 1;\n let &c = num.get(q[d]).unwrap_or(&0_u8);\n if c == b\'0\' + d as u8 {\n break;\n }\n }\n break;\n }\n }\n }\n String::from_utf8(res).unwrap()\n }\n}\n```
| 0 | 0 |
['Rust']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
O(NlogN), a SortedList and 10 queues
|
onlogn-a-sortedlist-and-10-queues-by-kaa-u04c
|
Intuition\nIterating from the left, we want to find the smallest reacheable digit and put it on each place.\n\n# Approach\nWe keep 10 queues, containing sequenc
|
kaathewise
|
NORMAL
|
2023-01-17T15:44:27.524674+00:00
|
2023-01-17T15:44:27.524701+00:00
| 126 | false |
# Intuition\nIterating from the left, we want to find the smallest reacheable digit and put it on each place.\n\n# Approach\nWe keep 10 queues, containing sequences of indices for each digit. At each step we pick the smallest digit that is not further than `k` steps away. After that we remove it from its queue, and reduce `k` by the number of steps used.\n\nThe question, then, rises, how to recalculate the correct indices and distances after a digit is removed from its place. Of course, we don\'t want to modify the queues, that would be too slow. But, it can be seen that the correction to every index is simply the number of used indices to the left of it, which we can calculate efficiently with `SortedList`.\n\n# Complexity\n- Time complexity: $$O(nlogn)$$, dominated by `SortedList` operations, at most `n` inserts and `n` bisections. Technically, `SortedList` has larger [time complexity](https://grantjenks.com/docs/sortedcontainers/performance-scale.html), but in practice it is fast.\n\n- Space complexity: $$O(n)$$, one `SortedList` and 10 queues each\n\n# Code\n```\nfrom collections import deque\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def minInteger(self, num: str, k: int) -> str:\n N = len(num)\n lists = [deque() for _ in range(10)]\n for i,c in enumerate(num):\n lists[int(c)].append(i)\n res = []\n used = SortedList()\n unused = set(range(N))\n while k and len(res) < N:\n for d in range(10):\n if not lists[d]:\n continue\n i = lists[d][0]\n i -= used.bisect_left(i)\n if i <= k:\n k -= i\n i = lists[d].popleft()\n used.add(i)\n unused.remove(i)\n res.append(i)\n break\n res.extend(unused)\n return \'\'.join(num[x] for x in res)\n\n```
| 0 | 0 |
['Python3']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Dart solution, O(n^2), LinkedList
|
dart-solution-on2-linkedlist-by-yakiv_ga-litb
|
Intuition\nWhen swapping (similar to bubble sort) numbers in a string - we should start minimising number from the left side by swapping every digit with the lo
|
yakiv_galkin
|
NORMAL
|
2022-12-12T09:07:58.498765+00:00
|
2022-12-12T09:07:58.498812+00:00
| 40 | false |
# Intuition\nWhen swapping (similar to bubble sort) numbers in a string - we should start minimising number from the left side by swapping every digit with the lowest possible number from the remaining ight side within the K limit.\n\n\n# Approach\n\nWhile the idea is prerry simple I faced timeout error on submission when result was kept in the array (List<int>) and swapping was perfomed by internal cycle.\nReplacing array with the LinkedList (where swap costs O(1) instead of O(N) ) helped to submit solution within the Leetcode time limits.\n\n# Complexity\n- Time complexity:\nO(N*N)\n\n- Space complexity:\nO(N) for the linked list\n\n# Code\n```\n\nimport \'dart:collection\';\n\nclass IntEntry extends LinkedListEntry<IntEntry> {\n int val;\n IntEntry(this.val);\n}\n\nclass Solution {\n static int zeroCode = \'0\'.codeUnitAt(0);\n\n String minInteger(String num, int k) {\n int L = num.length;\n if (L == 0) return "";\n\n final List<int> arr = num.codeUnits.map((e) => e - zeroCode).toList();\n final LinkedList<IntEntry> lst = LinkedList<IntEntry>();\n lst.addAll(arr.map((e) => IntEntry(e)));\n\n int i = 0;\n int r = k;\n\n IntEntry next = lst.first;\n while (next.next != null && r > 0) {\n int swapLess = 0;\n var minIdx = 0;\n var minPtr = next;\n\n var findMinIdx = 1;\n var findMinPtr = next.next;\n\n for (;\n findMinPtr != null && findMinIdx <= r;\n findMinPtr = findMinPtr.next, findMinIdx++)\n if (findMinPtr.val < minPtr.val) {\n minPtr = findMinPtr;\n minIdx = findMinIdx;\n }\n\n if (minPtr != next) {\n r -= minIdx;\n minPtr.unlink();\n next.insertBefore(minPtr);\n } else\n next = next.next!;\n }\n\n final ret = StringBuffer();\n lst.forEach((entry) {\n ret.write(entry.val);\n });\n return ret.toString();\n }\n}\n```
| 0 | 0 |
['Dart']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
O(nlogn) sliding window and AVL tree
|
onlogn-sliding-window-and-avl-tree-by-ma-kaq5
|
\n from sortedcontainers import SortedList\n\n n = len(num)\n window = SortedList() # sliding window of size k + 1, store (value, index) o
|
mathorlee
|
NORMAL
|
2022-11-27T00:57:08.438280+00:00
|
2022-11-27T00:57:54.166330+00:00
| 69 | false |
```\n from sortedcontainers import SortedList\n\n n = len(num)\n window = SortedList() # sliding window of size k + 1, store (value, index) of num\n remains = SortedList(range(n)) # remained remains\n pops = [] # popped indices\n\n while k > 0:\n # add to keep window size to k + 1\n while len(window) < k + 1 and len(window) < len(remains):\n _ = remains[len(window)]\n window.add((num[_], _))\n\n # empty window, break\n if not window:\n break\n\n # pop minimum value\n index = window.pop(0)[1]\n k -= remains.bisect_left(index)\n remains.remove(index)\n pops.append(index)\n\n # remove to keep window size to k + 1\n for _ in remains[k + 1: len(window)]:\n window.remove((num[_], _))\n\n s0 = set(pops)\n return "".join(num[j] for j in pops) + "".join(num[j] for j in range(n) if j not in s0)\n```
| 0 | 0 |
['Sliding Window']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
segment tree + BIT || CPP
|
segment-tree-bit-cpp-by-vvd4-bdpr
|
\nclass Solution {\npublic:\n \n int Do(int a,int b,string &s){\n if(a==s.size())return b;\n if(b==s.size())return a;\n if(s[a]<=s[b]
|
vvd4
|
NORMAL
|
2022-09-22T16:30:39.607305+00:00
|
2022-09-22T16:30:39.607351+00:00
| 34 | false |
```\nclass Solution {\npublic:\n \n int Do(int a,int b,string &s){\n if(a==s.size())return b;\n if(b==s.size())return a;\n if(s[a]<=s[b])return a;\n return b;\n }\n \n void build(vector<int> &seg,int si,int sl,int sr,string &s){\n if(sl==sr){\n seg[si]=sl;\n return;\n }\n \n int mid=(sl+sr)/2;\n build(seg,2*si,sl,mid,s);\n build(seg,2*si+1,mid+1,sr,s);\n seg[si]=Do(\n seg[si*2],\n seg[si*2+1],\n s\n );\n \n }\n \n \n int Q(vector<int> &seg,int si,int sl,int sr,int l,int r,string &s){\n if(l>r)return s.size();\n if(sl==l and sr==r)return seg[si];\n int mid=(sl+sr)/2;\n return Do(\n Q(seg,si*2,sl,mid,l,min(mid,r),s),\n Q(seg,si*2+1,mid+1,sr,max(l,mid+1),r,s),\n s\n );\n }\n \n void update(vector<int> &seg,int si,int sl,int sr,int ind,char val,string &s){\n if(sl==sr){\n s[ind]=val;\n seg[si]=sl;\n return ;\n }\n \n int mid=(sl+sr)/2;\n if(ind<=mid)update(seg,si*2,sl,mid,ind,val,s);\n else update(seg,si*2+1,mid+1,sr,ind,val,s);\n seg[si]=Do(seg[si*2],seg[si*2+1],s);\n }\n \n int sum(int ind,vector<int> &BIT){\n if(ind<0)return 0;\n return BIT[ind]+sum((ind&(ind+1))-1,BIT);\n }\n \n void updateBIT(int ind,vector<int> &BIT,int val){\n if(ind>=BIT.size())return;\n BIT[ind]+=val;\n updateBIT(ind|(ind+1),BIT,val);\n }\n \n int DO(int k,vector<int> &BIT){\n int l=0,r=BIT.size()-1;\n int ans;\n while(l<=r){\n int mid=(l+r)/2;\n if(sum(mid,BIT)<=k)ans=mid,l=mid+1;\n else r=mid-1;\n }\n return ans;\n }\n \n \n string minInteger(string num, int k) {\n int n=num.size();\n vector<int> seg(4*n);\n build(seg,1,0,n-1,num);\n vector<int> BIT(n);\n for(int i=0;i<n;i++)updateBIT(i,BIT,1);\n \n string ans;\n vector<int> vis(n,0);\n for(int i=0;i<n;i++){\n int ind=DO(k+1,BIT);\n int aind=Q(seg,1,0,n-1,0,ind,num);\n ans+=num[aind];\n update(seg,1,0,n-1,aind,(\'9\'+1),num);\n int sumi=sum(aind,BIT);\n k-=sumi;\n k++;\n updateBIT(aind,BIT,-1);\n \n }\n return ans;\n \n }\n};\n```
| 0 | 0 |
[]
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
C++ Segment Tree | O(NlogN) | Cleanest Code
|
c-segment-tree-onlogn-cleanest-code-by-g-d3in
|
\nclass SegTree {\npublic:\n vector<int> nodes;\n int n;\n\n //constructor\n SegTree(int n) {\n this->n = n;\n nodes = vector<int>(thi
|
GeekyBits
|
NORMAL
|
2022-09-13T12:36:12.656712+00:00
|
2022-09-13T16:54:22.628296+00:00
| 56 | false |
```\nclass SegTree {\npublic:\n vector<int> nodes;\n int n;\n\n //constructor\n SegTree(int n) {\n this->n = n;\n nodes = vector<int>(this->n << 2);\n }\n\n void update(int ss, int se, int ql, int idx, int val) {\n //update[ql,ql]\n if (ql<ss or ql>se) {\n return;\n }\n if (ss == se) {\n nodes[idx] += val;\n return;\n }\n int mid = (ss + se) >> 1;\n update(ss, mid, ql, 2 * idx + 1, val);\n update(mid + 1, se, ql, 2 * idx + 2, val);\n nodes[idx] = nodes[2 * idx + 1] + nodes[2 * idx + 2];\n }\n\n int query(int ss, int se, int ql, int qr, int idx) {\n //ql aur qr ke beech me answer nikal\n if (ql > se or qr < ss) {\n return 0;\n }\n if (ql <= ss and se <= qr) {\n return nodes[idx];\n }\n int mid = (ss + se) >> 1;\n int lt = query(ss, mid, ql, qr, 2 * idx + 1);\n int rt = query(mid + 1, se, ql, qr, 2 * idx + 2);\n return lt + rt;\n }\n int querylessthan(int pos) {\n return query(0, n - 1, 0, pos - 1, 0); //query left is 0 and query right is pos-1\n }\n void increase(int pos) {\n update(0, n - 1, pos, 0, 1);\n }\n};\nclass Solution {\npublic:\n string minInteger(string num, int k) {\n string ans = "";\n int n = num.size();\n SegTree* tree = new SegTree(n);\n vector<queue<int>> qs(10);\n for (int i = 0; i < n; i++) {\n qs[num[i] - \'0\'].push(i); //pushing back the positions for each digit from 0 to 9\n }\n for (int i = 0; i < n; i++) {\n for (int d = 0; d <= 9; d++) {\n if (qs[d].empty() == false) {\n int pos = qs[d].front();\n \n\n /*Explanation\n Since few numbers already shifted to left, this `pos` might be outdated,so we try to find how many numbers already got shifted that were to the left of pos.\n int shifted = seg.getCountLessThan(pos);\n (pos - shift) is number of steps to make digit d move from pos to i.\n\n */\n\t\t\t\t\t/*how many digits infront of this position "pos" has been moved to the right position*/\n if (pos - shifted <= k) {\n k -= (pos - shifted);\n tree->increase(pos);\n qs[d].pop();\n ans += d + \'0\';\n break;\n }\n }\n }\n }\n return ans;\n }\n};\n```
| 0 | 0 |
[]
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
[C++, O(nlogn)] Segment Tree
|
c-onlogn-segment-tree-by-arpitpandey992-ih65
|
\nclass Solution {\n class SegTree {\n vector<int> st;\n int siz;\n\n void upd(int i, int k) {\n i += siz;\n st[i]
|
arpitpandey992
|
NORMAL
|
2022-09-06T10:16:50.527968+00:00
|
2022-09-06T10:16:50.528001+00:00
| 49 | false |
```\nclass Solution {\n class SegTree {\n vector<int> st;\n int siz;\n\n void upd(int i, int k) {\n i += siz;\n st[i]+= k;\n i /= 2;\n while (i > 0) {\n st[i] = st[i * 2] + st[i * 2 + 1];\n i /= 2;\n }\n }\n int qry(int l, int r) {\n l += siz;\n r += siz;\n int ans = 0;\n while (l <= r) {\n if (l % 2 == 1) ans += st[l++];\n if (r % 2 == 0) ans += st[r--];\n l /= 2;\n r /= 2;\n }\n return ans;\n }\n\n public:\n SegTree(int n) {\n n++;\n siz = 1 << int(ceil(log2(n)));\n st.resize(siz * 2, 0);\n }\n int query(int i) { // elements shifted from 0 to i -> prefix sum from 0 to i\n return qry(0, i);\n }\n void update(int i) { // shift ith element to first position -> add 1 to 0 to i\n upd(0, 1);\n upd(i + 1, -1);\n }\n };\n\n public:\n string minInteger(string s, int k) {\n int n = s.size();\n vector<vector<int>> pos(10);\n for (int i = 0; i < n; i++)\n pos[s[i] - \'0\'].push_back(i);\n for (int dig = 0; dig < 10; dig++)\n reverse(pos[dig].begin(), pos[dig].end());\n SegTree st(n);\n string ans;\n int i = 0;\n while (k > 0 && i < n) {\n for (int dig = 0; dig < 10; dig++) {\n if (pos[dig].empty()) continue;\n int p = pos[dig].back();\n int actual = p + st.query(p);\n if (actual <= i + k) {\n pos[dig].pop_back();\n ans += to_string(dig);\n st.update(p);\n k -= actual - i;\n break;\n }\n }\n i++;\n }\n vector<pair<int, int>> v;\n for (int dig = 0; dig < 10; dig++) {\n while (pos[dig].size()) {\n v.push_back({pos[dig].back(), dig});\n pos[dig].pop_back();\n }\n }\n sort(v.begin(), v.end());\n for (auto &[p, d] : v)\n ans += to_string(d);\n\n return ans;\n }\n};\n```
| 0 | 0 |
[]
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Python Code
|
python-code-by-athenalei-arz9
|
\nclass Solution:\n def minInteger(self, num: str, k: int) -> str:\n n = len(num)\n num = list(num)\n BIT = [0] *(n+1)\n counter
|
athenalei
|
NORMAL
|
2022-08-21T17:16:41.177650+00:00
|
2022-08-21T17:17:21.039172+00:00
| 64 | false |
```\nclass Solution:\n def minInteger(self, num: str, k: int) -> str:\n n = len(num)\n num = list(num)\n BIT = [0] *(n+1)\n counter = defaultdict(deque)\n for idx, val in enumerate(num):\n counter[val].append(idx)\n def update(i,x):\n while i< len(BIT):\n BIT[i] +=x\n i += i & -i\n def query(i):\n res = 0\n while i>0:\n res +=BIT[i]\n i -= i&-i\n return res\n ans = []\n used = [False]*n\n while k>0 and len(ans)<n:\n for d in list(\'0123456789\'):\n if not counter[d]:\n continue\n index = counter[d][0]\n offset = query(index)\n if index - offset >k:\n continue\n if index - offset <=k:\n k -= index-offset\n ans.append(d)\n counter[d].popleft()\n update (index+1, 1)\n used[index] = True\n break\n for i in range(n):\n if not used[i]:\n ans +=num[i]\n return \'\'.join(ans)\n```
| 0 | 0 |
[]
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Java | O(nlogn) 30ms | Check Pos By Pos NOT Digit by Digit
|
java-onlogn-30ms-check-pos-by-pos-not-di-2kvw
|
Wrong Strategy\nInitially I tried to arrange all the 0s first, then 1s, 2s ..., but that strategy is flawed when there are multiple identical numbers together l
|
Student2091
|
NORMAL
|
2022-08-08T21:07:47.418323+00:00
|
2022-08-08T21:14:45.381263+00:00
| 281 | false |
#### Wrong Strategy\nInitially I tried to arrange all the 0s first, then 1s, 2s ..., but that strategy is flawed when there are multiple identical numbers together like "235288888...1" It is because when we are looking at number 1, we conclude that the last 1 can\'t be moved to the head of whatever current is, so we skipped it, but then when we get to 8, due to it being .. 88888 .. , we incur 0 cost to add them, then 1 becomes doable to switch to the current head when previously we\'ve concluded that it can\'t be done - **ERROR (44/50 testcase passed)**. This only works if there is no adjcent identical characters and run in `O(10N)`\n\n#### Correct Strategy\nSo then, I decided to check position by position, for each position, I need the best digit, but for this approach, we\'ve got a problem to deal with. How do we know how many elements to the **right** of the current digit has been swapped? We care only care about those to the **right** because it pushes the current digit to the right when they pass it. In the **Wrong Strategy** section, I dealt with this by just simple suffix sum update, one update takes `O(N)` and for 10 times, in total, `O(10N)`. That approach is not possible here because the outer loop is now position, so we need a Binary Index Tree, making the whole problem solvable in `O(NlogN)`.\n\nI am using a queue to keep track of the index of the first number that hasn\'t been used. It can be shown that the first index is always the better choice.\n\n```Java\n// Time O(NlogN) [30ms submitted once]\n// Space O(N)\nclass Solution {\n public String minInteger(String num, int k) {\n StringBuilder sb = new StringBuilder();\n char[] A = num.toCharArray();\n int[] bit = new int[A.length+2];\n Queue<Integer>[] queue = new ArrayDeque[10];\n Arrays.setAll(queue, o -> new ArrayDeque<>());\n for (int i = 0; i < A.length; i++){ // track indexes for each digit\n queue[A[i]-\'0\'].offer(i);\n }\n for (int i = 0; i < A.length; i++){ // solve for each position\n for (int j = 0; j < 10; j++){ // from the best to worst\n if (!queue[j].isEmpty()){\n int cost = queue[j].peek() - i + (i - sum(bit, queue[j].peek())); // cost needed to move to the head.\n if (cost <= k){\n k -= cost;\n sb.append(j);\n add(bit, queue[j].poll(), 1);\n break;\n }\n }\n }\n }\n return sb.toString();\n }\n\n private void add(int[] bit, int idx, int inc){\n for (++idx; idx < bit.length; idx += idx & -idx){\n bit[idx]+=inc;\n }\n }\n\n private int sum(int[] bit, int idx){\n int ans = 0;\n for (++idx; idx > 0; idx -= idx & -idx){\n ans += bit[idx];\n }\n return ans;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
MY INTUITIVE JAVA SOLUTION
|
my-intuitive-java-solution-by-divyaratho-i7d4
|
\nclass Solution {\n public String minInteger(String s, int k) {\n int length = s.length();\n int[] num = new int[length];\n int i = 0;\
|
DivyaRathod3D
|
NORMAL
|
2022-08-08T09:19:05.567315+00:00
|
2022-08-08T09:19:05.567353+00:00
| 128 | false |
```\nclass Solution {\n public String minInteger(String s, int k) {\n int length = s.length();\n int[] num = new int[length];\n int i = 0;\n for(char ch : s.toCharArray()) \n num[i++] = Integer.parseInt(String.valueOf(ch));\n \n\t\tfor (i = 0; i < length && k > 0; i++){\n\t\t\tint minIndex = 0, min = Integer.MAX_VALUE;\n\n\t\t\tint limit = (k + i) > length - 1 ? length - 1 : k + i;\n\n\t\t\tfor(int j = i; j <= limit; j++){\n\t\t\t\tif (num[j] < min){\n\t\t\t\t\tmin = num[j];\n\t\t\t\t\tminIndex = j;\n\t\t\t\t}\n\t\t\t}\n\n\t\t\tk -= (minIndex - i);\n\t\t\tfor(int idx = minIndex; idx > i; idx--) {\n\t\t\t\tint temp = num[idx - 1];\n\t\t\t\tnum[idx - 1] = num[idx];\n\t\t\t\tnum[idx] = temp;\n\t\t\t}\n\t\t}\n StringBuilder ans = new StringBuilder("");\n for(int n : num) ans.append(n);\n\t\treturn ans.toString();\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
Python Fenwick Tree solution
|
python-fenwick-tree-solution-by-liulaoye-ouj9
|
\nclass Solution:\n def minInteger(self, num: str, k: int) -> str:\n n = len(num)\n tr = [0 for i in range(n+1)]\n def add(ind,d):\n
|
liulaoye135
|
NORMAL
|
2022-06-02T05:06:51.629339+00:00
|
2022-06-02T05:06:51.629381+00:00
| 147 | false |
```\nclass Solution:\n def minInteger(self, num: str, k: int) -> str:\n n = len(num)\n tr = [0 for i in range(n+1)]\n def add(ind,d):\n while ind<=n:\n tr[ind] += d\n ind += -ind&ind\n def query(ind):\n res = 0\n while ind:\n res += tr[ind]\n ind -= -ind&ind\n return res\n \n pm = [[]for i in range(10)]\n for i in range(n-1,-1,-1):\n pm[ord(num[i]) - ord(\'0\')].append(i)\n ans = ""\n for i in range(n):\n for j in range(10):\n if pm[j]:\n cnt = query(n) - query(pm[j][-1]+1)\n if pm[j][-1] - i + cnt <= k:\n k -= pm[j][-1] - i + cnt\n ans += str(j)\n add(pm[j][-1]+1,1)\n pm[j].pop()\n break\n return ans\n```
| 0 | 0 |
['Tree']
| 0 |
minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
|
[C++] Segment Tree | Greedy | O(nlogn) Time
|
c-segment-tree-greedy-onlogn-time-by-mek-lxoe
|
\n/* \n Time: O(nlogn)\n Space: O(n)\n Tag: Segment Tree, Greedy (put the possible feasible smallest index in place of cur index), Queue\n Difficult
|
meKabhi
|
NORMAL
|
2022-05-30T19:53:29.962990+00:00
|
2022-05-30T19:53:29.963017+00:00
| 564 | false |
```\n/* \n Time: O(nlogn)\n Space: O(n)\n Tag: Segment Tree, Greedy (put the possible feasible smallest index in place of cur index), Queue\n Difficulty: H (Both Logic and Implementation)\n*/\n\nclass SegmentTree {\n vector<int> tree;\n\npublic:\n SegmentTree(int size) {\n tree.resize(4 * size + 1, 0);\n }\n\n void printTree() {\n for (int num : tree) cout << num << "";\n cout << endl;\n }\n\n void updateTree(int lo, int hi, int index, int upd) {\n if (upd < lo || upd > hi) return;\n if (lo == hi) {\n tree[index]++;\n return;\n }\n int mid = lo + (hi - lo) / 2;\n updateTree(lo, mid, 2 * index, upd);\n updateTree(mid + 1, hi, 2 * index + 1, upd);\n tree[index] = tree[2 * index] + tree[2 * index + 1];\n }\n\n int queryTree(int lo, int hi, int index, int qs, int qe) {\n if (qe < lo || qs > hi) return 0;\n if (qe >= hi && qs <= lo) return tree[index];\n\n int mid = lo + (hi - lo) / 2;\n\n int left = queryTree(lo, mid, 2 * index, qs, qe);\n int right = queryTree(mid + 1, hi, 2 * index + 1, qs, qe);\n return left + right;\n }\n};\n\nclass Solution {\npublic:\n string minInteger(string num, int k) {\n queue<int> pos[10];\n for (int i = 0; i < num.length(); i++) {\n pos[num[i] - \'0\'].push(i);\n }\n string res = "";\n SegmentTree *seg = new SegmentTree((int)num.length());\n for (int i = 0; i < num.length(); i++) {\n if (num[i] == \'-\') continue;\n int digit = num[i] - \'0\';\n\n bool swapped = false;\n for (int j = 0; j < digit; j++) {\n if (pos[j].size() > 0) {\n int curNumIndex = pos[j].front();\n int shifts = seg->queryTree(0, num.length() - 1, 1, i, pos[j].front());\n\n if (curNumIndex - i - shifts <= k) {\n seg->updateTree(0, num.length() - 1, 1, curNumIndex);\n k -= curNumIndex - i - shifts;\n pos[j].pop();\n res += num[curNumIndex];\n num[curNumIndex] = \'-\';\n swapped = true;\n i--;\n break;\n }\n }\n }\n if (!swapped) {\n res += num[i];\n pos[digit].pop();\n }\n }\n return res;\n }\n};\n```
| 0 | 0 |
['Greedy', 'Tree', 'Queue', 'C', 'C++']
| 0 |
stone-game-v
|
[Java] O(n^3), O(n^2 log n) and O(n^2) with explanation
|
java-on3-on2-log-n-and-on2-with-explanat-3ic1
|
O(n^3)\n\nBasic approach\ndp[i][j]: max score you can obtain from stones[i..j]\nsum[i][j]: sum of stoneValues[i..j]\nTry all possible k i.e. k goes from i to j-
|
shk10
|
NORMAL
|
2020-10-26T23:14:46.177330+00:00
|
2020-10-26T23:27:12.930447+00:00
| 6,444 | false |
**O(n^3)**\n\n**Basic approach**\ndp[i][j]: max score you can obtain from stones[i..j]\nsum[i][j]: sum of stoneValues[i..j]\nTry all possible k i.e. k goes from i to j-1:\nwe have 2 choices for score: **sum[i][k] + dp[i][k]** and **sum[k+1][j] + dp[k+1][j]**\nbut we can only pick the side where sum is smaller or either of them when both sides are equal.\nTake the maximum score from all of these choices and we have computed dp[i][j].\nIn all my codes, I am building the dp table bottom-up i.e. dp[0][1], dp[1][2] gets calculated before dp[0][2].\n\n```\nclass Solution {\n public int stoneGameV(int[] stoneValue) {\n int n = stoneValue.length;\n int[] pre = new int[n+1];\n for(int i = 1; i <= n; i++) {\n pre[i] = pre[i-1] + stoneValue[i-1];\n }\n int[][] dp = new int[n][n];\n for(int l = 1; l < n; l++) {\n for(int i = 0; i < n-l; i++) {\n int j = i+l, res = 0;\n for(int k = i; k < j; k++) {\n int left = pre[k+1] - pre[i], right = pre[j+1] - pre[k+1];\n if(left < right) {\n res = Math.max(res, left + dp[i][k]);\n } else if(left > right) {\n res = Math.max(res, right + dp[k+1][j]);\n } else {\n res = Math.max(res, left + dp[i][k]);\n res = Math.max(res, right + dp[k+1][j]);\n }\n }\n dp[i][j] = res;\n }\n }\n return dp[0][n-1];\n }\n}\n```\n\n**O(n^2 log n)**\n\n**Optimization**\nAs k goes from i to j in stones[i..j], sum of left part sum[i][k] increases continuously and it remains a valid subarray for our consideration for calculating dp[i][j] until the point when it becomes greater than right half. From that point onwards, all the right ones are valid subarrays for consideration. We can find this critical k (= **k\'**) using binary search. Forget about boundary cases and equal halves etc for now, just try to understand the general idea.\n\ndp[i][j] = max( max(sum[i][k] + dp[i][k]) for k: i to **k\'**, max(sum[k][j] + dp[k][j]) for k: **k\'**+1 to j )\n(refer to the code for exact condition for all cases)\n\nIf we have to calculate first and second terms in above by iterating from k: i to **k\'** or k: **k\'**+1 to j, then it\'d take O(n) time and we are back to first solution. What we can instead do is maintain 2 more arrays defined as:\nleft[i][j] = max( sum[i][k] + dp[i][k] for k: i to j )\nright[i][j] = max( sum[k][j] + dp[k][j] for k: i to j )\n\nand use them to redefine dp[i][j] = max( left[i][**k\'**], right[**k\'**+1][j] )\n\nNote that left and right arrays can also be calculated along with dp table so they don\'t increase our worst case time complexity.\n\nleft[i][j] = max( left[i][j-1], sum[i][j] + dp[i][j] )\nright[i][j] = max( right[i+1][j], sum[i][j] + dp[i][j] )\n\nWith these ideas in mind and taking care of boundary cases like **k\'** == i or **k\'** == j and equal halves etc, we have our solution ready.\n\n```\nclass Solution {\n // returns first index where sum of left half >= sum of right half\n private int search(int[] pre, int l, int r) {\n int sum = pre[r+1] - pre[l], L = l;\n while(l < r) {\n int m = l + ((r - l) >> 1);\n if(((pre[m+1] - pre[L]) << 1) >= sum) {\n r = m;\n } else {\n l = m + 1;\n }\n }\n return l;\n }\n public int stoneGameV(int[] stoneValue) {\n int n = stoneValue.length;\n int[] pre = new int[n+1];\n for(int i = 1; i <= n; i++) {\n pre[i] = pre[i-1] + stoneValue[i-1];\n }\n int[][] dp = new int[n][n], left = new int[n][n], right = new int[n][n];\n for(int i = 0; i < n; i++) {\n left[i][i] = right[i][i] = stoneValue[i];\n }\n for(int l = 1; l < n; l++) {\n for(int i = 0; i < n-l; i++) {\n int j = i+l, k = search(pre, i, j);\n int sum = pre[j+1] - pre[i], leftHalf = pre[k+1] - pre[i];\n if((leftHalf << 1) == sum) { // equal parts\n dp[i][j] = Math.max(left[i][k], right[k+1][j]);\n } else { // left half > right half\n dp[i][j] = Math.max(k == i ? 0 : left[i][k-1], k == j ? 0 : right[k+1][j]);\n }\n left[i][j] = Math.max(left[i][j-1], sum + dp[i][j]);\n right[i][j] = Math.max(right[i+1][j], sum + dp[i][j]);\n }\n }\n return dp[0][n-1];\n }\n}\n```\n\n**O(n^2)**\n\n**Optimization**\nWe can optimize the previous solution even further by getting rid of the binary search step needed to find the critical k (= **k\'**) of stones[i..j].\nBinary search is great when we need the answer for arbitrary i and j but why not calculate dp[i][j] in such an order where we could leverage the **k\'** information from previous i and j.\n\nSuppose we know the **k\'** for stones[i..j], what do we know about **k\'** for stones[i..j+1]? It is either the same or it got shifted a few places to the right.\nAnd so if we calculate dp values in the order: dp[i][i], dp[i][i+1], dp[i][i+2], ..., dp[i][j], we can essentially keep track of **k\'** as we go within that same linear time bound.\n\nUsing this idea, we implement the final solution. Couple of pointers about my code:\n* mid: represents **k\'** or first index such that left half >= right half\n* with i < j, max[i][j] represents left[i][j] of previous solution i.e. max(dp[i][i], dp[i][i+1], dp[i][i+2] .. dp[i][j]) and max[j][i] represents right[i][j] of previous solution i.e. max(dp[i][j], dp[i+1][j], dp[i+2][j] .. dp[j][j]). We could have used two different arrays left and right just like previous solution but this trick saves space.\n* I am traversing in the order: dp[j][j], dp[j-1,j], dp[j-2, j], .., dp[i][j] instead of the above mentioned order but the idea remains same.\n\n```\nclass Solution {\n public int stoneGameV(int[] stoneValue) {\n int n = stoneValue.length;\n int[][] dp = new int[n][n], max = new int[n][n];\n for(int i = 0; i < n; i++) {\n max[i][i] = stoneValue[i];\n }\n for(int j = 1; j < n; j++) {\n int mid = j, sum = stoneValue[j], rightHalf = 0;\n for(int i = j-1; i >= 0; i--) {\n sum += stoneValue[i];\n while((rightHalf + stoneValue[mid]) * 2 <= sum) {\n rightHalf += stoneValue[mid--];\n }\n dp[i][j] = rightHalf * 2 == sum ? max[i][mid] : (mid == i ? 0 : max[i][mid - 1]);\n dp[i][j] = Math.max(dp[i][j], mid == j ? 0 : max[j][mid + 1]);\n max[i][j] = Math.max(max[i][j - 1], dp[i][j] + sum);\n max[j][i] = Math.max(max[j][i + 1], dp[i][j] + sum);\n }\n }\n return dp[0][n-1];\n }\n}\n```
| 167 | 2 |
['Binary Search', 'Dynamic Programming', 'Java']
| 13 |
stone-game-v
|
[C++] Prefix Sum + DP (Memoization)
|
c-prefix-sum-dp-memoization-by-phoenixdd-17xr
|
[UPDATE] \nNew test cases added, forcing the solution to be O(n^2). Please consider looking at other solutions, I\'ll update this post once I find time to do so
|
phoenixdd
|
NORMAL
|
2020-08-23T04:01:07.108510+00:00
|
2021-05-15T23:35:07.175634+00:00
| 7,848 | false |
**[UPDATE]** \nNew test cases added, forcing the solution to be `O(n^2)`. Please consider looking at other solutions, I\'ll update this post once I find time to do so.\n**Observation**\n1. We can simply do what\'s stated in the question and try all the possible partitions.\n1. If the sum of left row is less recur on the left row.\n1. If the sum of right row is less recur on the right row.\n1. If the sum of both rows are equal we try recuring on both the partitions and chose the one with maximum result.\n1. Now simply repeat the steps for the new row\n1. Do this until there is only 1 stone left.\n1. We can see that there are recalculations of selected row when we perform the previous 3 steps. Thus we memoize on the row represented by `i,j` i.e row start and row end.\n\n**Solution**\n\n```c++\nclass Solution {\npublic:\n vector<int> prefixSum;\t\t\t//Stores prefixSums\n vector<vector<int>> memo;\n int dp(vector<int>& stoneValue,int i,int j)\n {\n if(i==j)\n return 0;\n if(memo[i][j]!=-1)\n return memo[i][j];\n memo[i][j]=0;\n for(int p=i+1;p<=j;p++)\t\t//Try each partition.\n {\n\t\t\tint l=prefixSum[p]-prefixSum[i],r=prefixSum[j+1]-prefixSum[p];\n\t\t\tif(l<r)\t\t//Left part is smaller\n memo[i][j]=max(memo[i][j],l+dp(stoneValue,i,p-1));\n else if(l>r)\t//Right part is smaller\n memo[i][j]=max(memo[i][j],r+dp(stoneValue,p,j));\n else\t//Both parts are equal\n memo[i][j]=max(memo[i][j],l+max(dp(stoneValue,p,j),dp(stoneValue,i,p-1)));\n }\n return memo[i][j];\n }\n int stoneGameV(vector<int>& stoneValue)\n {\n memo.resize(stoneValue.size(),vector<int>(stoneValue.size(),-1));\n prefixSum.resize(stoneValue.size()+1,0);\n for(int i=0;i<stoneValue.size();i++)\t\t//Create prefix Sums\n prefixSum[i+1]=prefixSum[i]+stoneValue[i];\n return dp(stoneValue,0,stoneValue.size()-1);\n }\n};\n```\n\n**Complexity**\nTime: `O(n^3)`\nSpace: `O(n^2)`
| 74 | 13 |
[]
| 11 |
stone-game-v
|
[Java] Detailed Explanation - Easy Understand DFS + Memo - Top-Down DP
|
java-detailed-explanation-easy-understan-bj02
|
Key Notes:\n- Classic DP problem\n- Top-Down (DFS + Memo) is easy to understand\n- Try split array at every possible point:\n\t- get left sum and right sum, cho
|
frankkkkk
|
NORMAL
|
2020-08-23T04:00:43.118102+00:00
|
2020-08-23T04:00:43.118160+00:00
| 3,413 | false |
**Key Notes:**\n- Classic DP problem\n- Top-Down (DFS + Memo) is **easy to understand**\n- Try split array at every possible point:\n\t- get left sum and right sum, choose the smaller one and keep searching\n\t- to save some time, we can pre-compute a **prefix array** to quick calculate sum\n\t- if left == right: try both ways\n\t- stop searching when only one element left, which means **pointer l == r**\n- Cache searched result in dp by using state: pointer l and r\n\n```java\npublic int stoneGameV(int[] stoneValue) {\n \n\tint N = stoneValue.length;\n\n\t// cache prefix\n\tint[] prefix = new int[N + 1];\n\tfor (int i = 0; i < N; ++i) {\n\t\tprefix[i + 1] = prefix[i] + stoneValue[i];\n\t}\n\n\treturn helper(stoneValue, 0, N - 1, prefix, new Integer[N][N]);\n}\n\nprivate int helper(int[] stoneValue, int l, int r, int[] prefix, Integer[][] dp) {\n\n\tif (l == r) return 0;\n\tif (l + 1 == r) return Math.min(stoneValue[l], stoneValue[r]);\n\n\tif (dp[l][r] != null) return dp[l][r];\n\n\tint res = 0;\n\n\t// left: [l, i], right: [i + 1, r]\n\tfor (int i = l; i < r; ++i) {\n\n\t\tint left = prefix[i + 1] - prefix[l];\n\t\tint right = prefix[r + 1] - prefix[i + 1];\n\n\t\tif (left > right) { // go right\n\t\t\tres = Math.max(res, right + helper(stoneValue, i + 1, r, prefix, dp));\n\t\t} else if (left < right) { // go left\n\t\t\tres = Math.max(res, left + helper(stoneValue, l, i, prefix, dp));\n\t\t} else { // left == right: go whatever max\n\t\t\tres = Math.max(res, Math.max(helper(stoneValue, l, i, prefix, dp),\n\t\t\t\t\t\t\t\t\t\t helper(stoneValue, i + 1, r, prefix, dp)) \n\t\t\t\t\t\t\t\t\t\t + left);\n\t\t}\n\n\t}\n\n\treturn dp[l][r] = res;\n}\n```\n
| 46 | 5 |
[]
| 4 |
stone-game-v
|
[Python] DP
|
python-dp-by-lee215-fhar
|
Update 2020/09/01:\nSeems new test cases added and enforce it to be O(N^2).\nThis solution is TLE now.\n\n## Intuition\nWe have done stone games many times.\nJu
|
lee215
|
NORMAL
|
2020-08-23T04:02:45.226779+00:00
|
2020-09-02T14:34:26.130979+00:00
| 6,140 | false |
**Update 2020/09/01:**\nSeems new test cases added and enforce it to be O(N^2).\nThis solution is TLE now.\n\n## **Intuition**\nWe have done stone games many times.\nJust dp it.\n<br>\n\n## **Complexity**\nTime `O(N^3)`\nSpace `O(N^2)`\n<br>\n\n\n**Python:**\n```py\n def stoneGameV(self, A):\n n = len(A)\n prefix = [0] * (n + 1)\n for i, a in enumerate(A):\n prefix[i + 1] = prefix[i] + A[i]\n\n @functools.lru_cache(None)\n def dp(i, j):\n if i == j: return 0\n res = 0\n for m in range(i, j):\n left = prefix[m + 1] - prefix[i]\n right = prefix[j + 1] - prefix[m + 1]\n if left <= right:\n res = max(res, dp(i, m) + left)\n if left >= right:\n res = max(res, dp(m + 1, j) + right)\n return res\n return dp(0, n - 1)\n```\n
| 44 | 8 |
[]
| 22 |
stone-game-v
|
[C++] O(n^2log(n)) solution and why top-down approach is faster
|
c-on2logn-solution-and-why-top-down-appr-lkra
|
I get my O(n^3) solution TLE in the contest and I passed my O(n^2log(n)) solution at 1:32 (so sad....). I managed to make my O(n^3) solution accepted at last :)
|
chenhao4
|
NORMAL
|
2020-08-23T04:18:12.181690+00:00
|
2020-08-23T07:19:23.213541+00:00
| 2,628 | false |
I get my O(n^3) solution TLE in the contest and I passed my O(n^2log(n)) solution at 1:32 (so sad....). I managed to make my O(n^3) solution accepted at last :)\n\nConsider the initialized state of this problem and we have an interval [1, N] to solve. For all the possible ways to split this interval, we will always ignore the sub interval with bigger sum. it means we pruning these state and will never touch them again. As the time limit is tight for O(n^3) solution, it makes huge difference for the result..... Don\'t like it. :(\n\nO(n^2log(n)) solution\nExplanation:\nDefinitions:\n* f[i][j]: the maximum score we can get from interval [i, j]\n* sum[i][j]: the sum of stoneValue[i] to stoneValue[j]\n* lf[m][n]: the maximum value for all f[i][j] + sum[i][j] where i == m and j in range [m, n]\n* rf[m][n]: the maximum value for all f[i][j] + sum[i][j] where j == n and i in range [m, n]\n\nConsider the following DP equation:\n* f[i][j] = max(sum[i][m] + f[i][m]) if sum[i][m] < sum[m+1][j] for all m from i to j - 1 \n* f[i][j] = max(sum[m+1][j] + f[m+1][j]) if sum[i][m] > sum[m+1][j] for all m from i to j - 1 \n* f[i][j] = max(sum[i][m] + f[i][m], sum[m+1][j] + f[m+1][j]) if sum[i][m] < sum[m+1][j] for all m from i to j - 1\n\nWe can find the maximum m from i to j - 1 using binary search with O(log(n)) which keeps sum[i][m - 1] <= sum[m+1][j], then we get:\n* For f[i][j]\n * if sum[i][m] == sum[m+1][j]: f[i][j] = max(lf[i][m], rf[m+1][j])\n * if sum[i][m] < sum[m+1][j]: f[i][j] = max(lf[i][m], rf[m+2][j])\n* lf[i][j] = max(lf[i][j-1], f[i][j] + sum[i][j])\n* rf[i][j] = max(rf[i+1][j], f[i][j] + sum[i][j])\n\n```\nclass Solution {\n public:\n int getsum(vector<int>& sum, int l, int r) {\n if (l > r) return 0;\n if (l == 0) return sum[r];\n return sum[r] - sum[l - 1];\n }\n int stoneGameV(vector<int>& stoneValue) {\n int n = stoneValue.size();\n vector<int> sum(n, 0);\n for (int i = 0; i < n; ++i) {\n if (i > 0) sum[i] += sum[i - 1];\n sum[i] += stoneValue[i];\n }\n vector<vector<int>> f = vector<vector<int>>(n, vector<int>(n, 0));\n vector<vector<int>> lf = vector<vector<int>>(n, vector<int>(n, 0));\n vector<vector<int>> rf = vector<vector<int>>(n, vector<int>(n, 0));\n\n for (int i = 0; i < n; ++i) {\n lf[i][i] = rf[i][i] = stoneValue[i];\n }\n\n for (int i = n - 1; i >= 0; --i) {\n for (int j = i + 1; j < n; ++j) {\n int segsum = getsum(sum, i, j);\n int l = i - 1, r = j;\n while (l < r - 1) {\n int mid = (l + r) / 2;\n int left = getsum(sum, i, mid);\n if (left * 2 <= segsum) {\n l = mid;\n } else {\n r = mid;\n }\n }\n if (l >= i) f[i][j] = max(f[i][j], lf[i][l]);\n int rst = l;\n if (getsum(sum, i, l) * 2 < segsum) {\n rst += 2;\n } else {\n rst += 1;\n }\n if (rst <= j)\n f[i][j] = max(f[i][j], rf[rst][j]);\n lf[i][j] = max(lf[i][max(i, j - 1)], f[i][j] + segsum);\n rf[i][j] = max(rf[max(0, i + 1)][j], f[i][j] + segsum);\n }\n }\n return f[0][n - 1];\n }\n};\n\n```\n\nO(n^3) accepted solution\n```\nclass Solution {\npublic:\n int f[550][550];\n int sum[550];\n int stoneGameV(vector<int>& stoneValue) {\n int n = stoneValue.size();\n for (int i = 0; i < n; ++i) {\n sum[i + 1] = sum[i] + stoneValue[i];\n }\n \n for (int i = 1; i <= n; ++i) {\n f[i][i] = 0;\n }\n for (int i = n; i > 0; --i) {\n for (int j = i + 1; j <= n; ++j) {\n for (int m = i; m < j; ++m) {\n int left = sum[m] - sum[i - 1];\n int right = sum[j] - sum[m];\n if (left > right) {\n f[i][j] = max(f[i][j], right + f[m + 1][j]);\n } else if (left < right) {\n f[i][j] = max(f[i][j], left + f[i][m]);\n } else {\n f[i][j] = max(f[i][j], right + f[m + 1][j]);\n f[i][j] = max(f[i][j], left + f[i][m]);\n }\n }\n }\n }\n return f[1][n];\n }\n};\n```\n\nO(n^3) TLE solution\n```\nclass Solution {\npublic:\n int getsum(vector<int> &sum, int l, int r) {\n if (l == 0) return sum[r];\n return sum[r] - sum[l - 1];\n }\n int stoneGameV(vector<int>& stoneValue) {\n int n = stoneValue.size();\n vector<int> sum(n, 0);\n for (int i = 0; i < n; ++i) {\n if (i > 0) sum[i] += sum[i - 1];\n sum[i] += stoneValue[i];\n }\n vector<vector<int>> f = vector<vector<int>>(n, vector<int>(n, 0));\n for (int i = n - 1; i >= 0; --i) {\n for (int j = i + 1; j < n; ++j) {\n for (int m = i; m < j; ++m) {\n int left = getsum(sum, i, m);\n int right = getsum(sum, m + 1, j);\n if (left > right) {\n f[i][j] = max(f[i][j], right + f[m + 1][j]);\n } else if (left < right) {\n f[i][j] = max(f[i][j], left + f[i][m]);\n } else {\n f[i][j] = max(f[i][j], right + f[m + 1][j]);\n f[i][j] = max(f[i][j], left + f[i][m]);\n }\n }\n }\n }\n return f[0][n - 1];\n }\n};\n```
| 34 | 1 |
[]
| 9 |
stone-game-v
|
[C++] O(N^2) DP
|
c-on2-dp-by-lee0560-euhr
|
In the intuitive O(N^3) DP, to calculate the maximum score h[i][j], we need to iterate through any k that i <= k < j. But if we examine the relationship amon
|
lee0560
|
NORMAL
|
2020-08-23T09:36:01.028088+00:00
|
2020-08-23T09:36:01.028123+00:00
| 2,706 | false |
In the intuitive O(N^3) DP, to calculate the maximum score h[i][j], we need to iterate through any k that i <= k < j. But if we examine the relationship among h[i][j], h[i][j+1] and h[i-1][j], it\'s possible to derive an optimized O(N^2) solution.\n\nLet\'s split the candidates of h[i][j] into 2 groups, depending on whether picking the left or right row:\n1) picking the left row [i,k], score = sum(stoneValue[i], ..., stoneValue[k]) + h[i][k], iff sum(stoneValue[i], ..., stoneValue[k]) <= sum(stoneValue[k+1],..., stoneValue[j])\n2) picking the right row [k+1,j], score = sum(stoneValue[k+1],..., stoneValue[j]) + h[k+1][j], iff sum(stoneValue[k+1],..., stoneValue[j]) <= sum(stoneValue[i],..., stoneValue[k])\n\nNow, what if we need to calculate h[i][j+1]? The left row candidates for h[i][j] are also candidates for h[i][j+1], since sum(stoneValue[i], ..., stoneValue[k]) <= sum(stoneValue[k+1],..., stoneValue[j]) and stoneValue[j+1] > 0. \n\nSo when we calculate all of h[i][i], h[i][i+1],...h[i][n], each left row candidate with score = sum(stoneValue[i], ..., stoneValue[k]) + h[i][k] (i <= k < n) only needs to calculate once. \n\nThe same trick also holds when we need to calculate h[i-1][j]. The right row candidates for h[i][j] are also candidates for h[i-1][j].\n\nSo when we calculate all of h[j][j], h[j-1][j], ... h[1][j], each right row candidate with score = sum(stoneValue[k+1],..., stoneValue[j]) + h[k+1][j] (1 <= k < j) only needs to calculate once. \n\nTo keep the calculation of both left row and right row candidates in order respectively, the first loop should iterate through the row length from 1 to n, then the second loop simply enumates all possible rows with that length.\n\nTime: O(N^2)\nSpace: O(N^2)\n\nclass Solution {\npublic:\n int f[502], g[502], h[502][502];\n int x[502], y[502];\n int s[502];\n \n int stoneGameV(vector<int>& stoneValue) {\n vector<int>& a = stoneValue;\n int n = a.size();\n s[0] = 0;\n for (int i=0; i<n; i++) s[i+1] = s[i] + a[i];\n \n for (int i=1; i<=n; i++) {\n f[i] = g[i] = 0;\n x[i] = i;\n y[i] = i-1;\n }\n \n for (int len=2; len<=n; len++) {\n for (int i=1, j; (j = i+len-1) <= n; i++) {\n int half = (s[j] - s[i-1]) >> 1;\n\n int& k = x[i];\n int& t = f[i]; \n int delta;\n while (k < j && (delta = s[k] - s[i-1]) <= half) {\n t = max(t, delta + h[i][k++]);\n }\n \n int& k2 = y[j];\n int& t2 = g[j];\n while (k2 >= i && (delta = (s[j] - s[k2])) <= half) {\n t2 = max(t2, delta + h[k2+1][j]);\n k2--;\n }\n \n h[i][j] = max(t, t2);\n }\n }\n \n return h[1][n];\n } \n};
| 33 | 0 |
[]
| 5 |
stone-game-v
|
Why my C++ O(n^3) solution will TLE
|
why-my-c-on3-solution-will-tle-by-szzzwn-v8ga
|
Code as follows:\n\n\nclass Solution {\npublic:\n int stoneGameV(vector<int>& s) {\n int n = s.size();\n vector<int> prefix(n);\n prefix
|
szzzwno123
|
NORMAL
|
2020-08-23T04:04:34.537312+00:00
|
2020-08-23T04:25:57.028205+00:00
| 2,149 | false |
Code as follows:\n\n```\nclass Solution {\npublic:\n int stoneGameV(vector<int>& s) {\n int n = s.size();\n vector<int> prefix(n);\n prefix[0] = s[0];\n \n for (int i = 1; i < n; i++)\n prefix[i] = prefix[i - 1] + s[i];\n \n vector<vector<int>> dp(n, vector<int>(n));\n \n for (int i = 0; i < n - 1; i++)\n dp[i][i + 1] = min(s[i], s[i + 1]); \n \n for (int len = 3; len <= n; len++)\n for (int i = 0; i <= n - len; i++){\n int j = i + len - 1;\n \n for (int k = i; k < j; k++){\n // s[i ~ k] and s[k + 1 ~ j]\n int s1 = i == 0 ? prefix[k] : prefix[k] - prefix[i - 1];\n int s2 = prefix[j] - prefix[k];\n if (s1 == s2)\n dp[i][j] = max(dp[i][j], s1 + max(dp[i][k], dp[k + 1][j]));\n else if (s1 < s2)\n dp[i][j] = max(dp[i][j], s1 + dp[i][k]);\n else\n dp[i][j] = max(dp[i][j], s2 + dp[k + 1][j]);\n }\n }\n \n return dp[0][n - 1];\n }\n};\n```\nUpdate: Even after changing\n```\nvector<vector<int>> dp(n, vector<int>(n));\n```\nto \n```\nint dp[505][505];\n```\ncode still TLE. This is a really funny contest...
| 28 | 2 |
[]
| 21 |
stone-game-v
|
Java Top-down DP
|
java-top-down-dp-by-hobiter-00y7
|
dp[fr][to] is the max points that you can gain if you pick sub array from fr to to;\nCache the result to avoid duplicate calculation\n\n\nclass Solution {\n
|
hobiter
|
NORMAL
|
2020-08-23T04:01:56.038524+00:00
|
2020-08-23T04:01:56.038574+00:00
| 1,151 | false |
dp[fr][to] is the max points that you can gain if you pick sub array from fr to to;\nCache the result to avoid duplicate calculation\n\n```\nclass Solution {\n int[][] dp;\n int[] acc;\n public int stoneGameV(int[] ss) {\n int m = ss.length;\n dp = new int[m][m];\n acc = new int[m + 1];\n for (int i = 0; i < m; i++) acc[i + 1] = acc[i] + ss[i];\n return dfs(0, m - 1);\n }\n \n private int dfs(int fr, int to) {\n if (fr == to) return 0;\n if (dp[fr][to] > 0) return dp[fr][to];\n for (int d = fr + 1; d <= to; d++) {\n int first = acc[d] - acc[fr], second = acc[to + 1] - acc[d];\n if (first == second) dp[fr][to] = Math.max(dp[fr][to], first + Math.max(dfs(fr, d - 1), dfs(d, to)));\n else if (first > second) dp[fr][to] = Math.max(dp[fr][to], second + dfs(d, to));\n else dp[fr][to] = Math.max(dp[fr][to], first + dfs(fr, d - 1));\n }\n return dp[fr][to];\n }\n}\n```\n
| 24 | 1 |
[]
| 3 |
stone-game-v
|
Please do not assume monotonicity like stoneGameV(A) ≥ stoneGameV(A[:-1])
|
please-do-not-assume-monotonicity-like-s-4bda
|
I read a few posts and some of the "fast" DP solutions implicitly assumed that the result is non-decreasing as the list goes longer and longer. This is not true
|
3abc
|
NORMAL
|
2020-10-11T05:49:44.785289+00:00
|
2020-10-11T07:40:28.847665+00:00
| 460 | false |
I read a few posts and some of the "fast" DP solutions implicitly assumed that the result is non-decreasing as the list goes longer and longer. This is not true. The simpliest counter example being `[1,3,2,2,1]`, we have:\n\n`stoneGameV([1,3,2,2]) = 6` and `stoneGameV([1,3,2,2,1]) = 5`.\n\n(To achieve the max for `[1,3,2,2]` cut in the middle and proceed with the right half, adding a `1` to the right simply breaks that.) \n\nAs a result, do not assume cutting to make the left and right sum as equal as possible is the optimal play. Some of the best solutions are simply wrong for this reason. Take the fastest Python3 solution for example, here\'s the code:\n\n```\nclass Solution:\n def stoneGameV(self, stoneValue: List[int]) -> int:\n presum = [0] + list(accumulate(stoneValue))\n\n def subsum(start, end):\n return presum[end] - presum[start]\n \n def med(start, end):\n # max_k {subsum(start, k) <= subsum(k, end)}\n return bisect.bisect(presum, (presum[start] + presum[end]) // 2) - 1\n\n @lru_cache(None)\n def DP(start, end):\n if start + 1 == end:\n return 0\n elif start + 2 == end:\n return min(stoneValue[start], stoneValue[start + 1])\n\n Lmed, Rmed = med(start, end - 1), med(start + 1, end) + 1\n ret = 0\n for i in range(\n max(start + 1, Lmed),\n min(end, Rmed + 1),\n ):\n # split to [start, i), [i, end)\n Lsum, Rsum = subsum(start, i), subsum(i, end)\n if Lsum < Rsum:\n newval = Lsum + DP(start, i)\n elif Lsum > Rsum:\n newval = Rsum + DP(i, end)\n else:\n newval = Lsum + max(DP(start, i), DP(i, end))\n\n ret = max(newval, ret)\n return ret\n\n return DP(0, len(stoneValue))\n```\n\nA simple counter example for it would be `[1,99,1,99,50,50,50,50,1,401,1]`. The best cut is actually at `[1,99,1,99,50,50,50,50]` but it only checks `[1,99,1,99,50,50,50,50,1]` and cuts to its right. As a result it got 702 while the correct answer is 750. Unfortunately this solution passes all 131 test case.
| 20 | 0 |
[]
| 5 |
stone-game-v
|
[Python / Golang] Simple DP Solution with a Trick for Python
|
python-golang-simple-dp-solution-with-a-i6jx5
|
Idea\nThe idea is straight forward. we just try out all the possibilities to find the answer. Naive brute force solution will lead to O(n!) complexity, so we ne
|
yanrucheng
|
NORMAL
|
2020-08-23T04:01:31.985745+00:00
|
2020-08-23T04:08:24.284720+00:00
| 1,509 | false |
**Idea**\nThe idea is straight forward. we just try out all the possibilities to find the answer. Naive brute force solution will lead to O(n!) complexity, so we need to store the interim results to improve the complexity to O(n^3).\n\n**A trick for slower languages**\nSince I got TLE for the O(n^3) solution in Python. I add a shortcut for a special case when all the elements within a specific range are the same. In this special case, we can get the results in O(logn) complexity.\n\n**Complexity**\nTime: O(n^3)\nSpace: O(n^2)\n\nPlease do not downvote unless you find it necessary. Please bro.\n\n**Python**\n```\nfrom functools import lru_cache\nclass Solution:\n def stoneGameV(self, stoneValue: List[int]) -> int:\n presum = [0]\n for s in stoneValue:\n presum += presum[-1] + s,\n \n def sm(i, j):\n return presum[j + 1] - presum[i]\n \n @lru_cache(None)\n def helper(i, j):\n if i == j: return 0\n \n if all(stoneValue[k] == stoneValue[j] for k in range(i, j)):\n cnt = 0\n l = j - i + 1\n while l > 1:\n l //= 2\n cnt += l\n return cnt * stoneValue[j] \n \n res = 0\n for k in range(i, j):\n if sm(i, k) < sm(k + 1, j):\n score = helper(i, k) + sm(i, k)\n elif sm(i, k) > sm(k + 1, j):\n score = sm(k + 1, j) + helper(k + 1, j)\n else: \n score = max(helper(i, k) + sm(i, k), sm(k + 1, j) + helper(k + 1, j))\n res = max(res, score)\n return res \n \n return helper(0, len(stoneValue) - 1)\n```\n\n\n**Golang**\n```\nfunc stoneGameV(stoneValue []int) int {\n n := len(stoneValue)\n memo := make([][]int, n)\n for i := range memo {\n memo[i] = make([]int, n)\n }\n presum := make([]int, n + 1)\n for i := 1; i <= n; i++ {\n presum[i] = presum[i - 1] + stoneValue[i - 1]\n }\n sum := func(i, j int) int {return presum[j + 1] - presum[i]}\n \n \n for l := 2; l <= n; l++ { // l mean length\n for i := 0; i < n - l + 1; i++ {\n j := i + l - 1\n score := 0\n for k := i; k < j; k++ {\n switch {\n case sum(i, k) > sum(k + 1, j):\n score = max(score, memo[k + 1][j] + sum(k + 1, j))\n case sum(i, k) < sum(k + 1, j):\n score = max(score, memo[i][k] + sum(i, k))\n default:\n tmp := max(memo[i][k] + sum(i, k), memo[k + 1][j] + sum(k + 1, j))\n score = max(score, tmp)\n }\n }\n memo[i][j] = score\n }\n }\n return memo[0][n - 1]\n}\n\nfunc max(i, j int) int {\n if i < j {\n return j\n }\n return i\n}\n```
| 20 | 6 |
['Go', 'Python3']
| 3 |
stone-game-v
|
[C++] O(n^2)-Time DP Solution: No Binary Search Needed
|
c-on2-time-dp-solution-no-binary-search-2h0qb
|
Let a[1..n] denote the values of stones, s(i, j) denote the sum a[i]+a[i+1]+...+a[j], and D(i, j) denote the maximum score of a[i..j]. We first calculate D(1, 1
|
xavier13540
|
NORMAL
|
2020-08-23T17:01:34.189572+00:00
|
2020-08-23T17:10:06.876255+00:00
| 1,353 | false |
Let *a[1..n]* denote the values of stones, *s(i, j)* denote the sum *a[i]+a[i+1]+...+a[j]*, and *D(i, j)* denote the maximum score of *a[i..j]*. We first calculate *D(1, 1), D(2, 2), ..., D(n, n)*, then calculate *D(1, 2), D(2, 3), ..., D(n-1, n)*, then calculate *D(1, 3), D(2, 4), ..., D(n-2, n)*, and so on. Note that the answer is given by *D(1, n)*.\n\nWe introduce *K(i, j)* for all *1 \u2264 i \u2264 j \u2264 n*, defined by the smallest index *k* such that *2s(i, k) \u2265 s(i, j)*. The recursive relation of *D* is thereby given by\n\n*D(i, j) =*\n* *max{ max{ s(i, k)+D(i, k): i \u2264 k \u2264 K(i, j) }, max{ s(k+1, j)+D(k+1, j): K(i, j) \u2264 k \u2264 j-1 } }*, if *2s(i, K(i, j)) = s(i, j)*,\n* *max{ max{ s(i, k)+D(i, k): i \u2264 k \u2264 K(i, j)-1 }, max{ s(k+1, j)+D(k+1, j): K(i, j) \u2264 k \u2264 j-1 } }*, if *2s(i, K(i, j)) > s(i, j)*.\n\nIf we have found all *K(i, j)*\'s, the answer *D(1, n)* can be figured out within *O(n\xB2)*-time, since all we need is the auxiliary *Q(i, j) := max{ s(i, k)+D(i, k): min{i, j} \u2264 k \u2264 max{i, j} }*, which can be calculated together with *D*. As *a[i] > 0*, one can obtain an *O(n\xB2* log *n)*-time algorithm with binary search.\n\nBut observe that *K(i, j) \u2264 K(i, j+1) \u2264 K(i+1, j+1)* and that *K(i, i) = i*. If we\'ve found *K(1, i), K(2, i+1), ..., K(n-i+1, n)*, then *K(1, i+1), K(2, i+2), ..., K(n-i, n)* can be figured out in *O(n)*-time with a simple linear-time search since\n\n*1 \u2264 K(1, i) \u2264 K(1, i+1) \u2264 K(2, i+1) \u2264 K(2, i+2) \u2264 K(3, i+2) \u2264 ... \u2264 K(n-i, n-1) \u2264 K(n-i, n) \u2264 K(n-i+1, n) \u2264 n.*\n\nTherefore, all *K(i, j)*\'s can be found in *O(n\xB2)*, and thus the total time complexity is also *O(n\xB2)*.\n\nThe following shows my C++ AC code. *D, K, Q* are replaced by `dp`, `mid`, and `rmq`.\n\n```\nclass Solution{\npublic:\n int stoneGameV(vector<int> const &stoneValue) const{\n int n = stoneValue.size();\n vector<int> s(n+1);\n partial_sum(stoneValue.cbegin(), stoneValue.cend(), s.begin()+1);\n auto idx = [n](int i, int j){\n return (i-1)*n+(j-1);\n };\n vector<int> dp(n*n), rmq(n*n), mid(n*n);\n for(int i=1; i<=n; ++i){\n dp[idx(i, i)] = 0;\n rmq[idx(i, i)] = s[i]-s[i-1];\n mid[idx(i, i)] = i;\n }\n for(int i=1; i<=n-1; ++i){\n for(int j=1; j+i<=n; ++j){\n int &k = mid[idx(j, j+i)];\n k = mid[idx(j, j+i-1)];\n while(2*(s[k]-s[j-1]) < s[j+i]-s[j-1]){\n ++k;\n }\n int &x = dp[idx(j, j+i)];\n if(k < j+i){\n x = max(x, rmq[idx(j+i, k+1)]);\n }\n if(2*(s[k]-s[j-1]) == s[j+i]-s[j-1]){\n x = max(x, rmq[idx(j, k)]);\n }else if(k > j){\n x = max(x, rmq[idx(j, k-1)]);\n }\n rmq[idx(j, j+i)] = max(rmq[idx(j, j+i-1)], s[j+i]-s[j-1]+x);\n rmq[idx(j+i, j)] = max(rmq[idx(j+i, j+1)], s[j+i]-s[j-1]+x);\n }\n }\n return dp[idx(1, n)];\n }\n};\n```
| 19 | 1 |
[]
| 3 |
stone-game-v
|
Some test cases that refuse plausible assumptions
|
some-test-cases-that-refuse-plausible-as-mljt
|
Some may wonder if we can turn typical O(n^3) dynamic programming algorithm (can be seen in many other posts) into O(n^2), by some strong assumptions. Here are
|
szp14
|
NORMAL
|
2020-08-23T09:37:36.222828+00:00
|
2021-06-13T01:30:50.573080+00:00
| 456 | false |
Some may wonder if we can turn typical O(n^3) dynamic programming algorithm (can be seen in many other posts) into O(n^2), by some strong assumptions. Here are some assumptions seeming to be correct but in fact wrong:\n\n1. If array **A** is a subarray of **B**, then Alice\'s score over **B** can\'t be lower than that over **A**\n\n\tcounterexample:\n\t\n\tA=[2,10,2,4,4,5], result is 18\n\tB=[2,10,2,4,4,5,4], result is 17\n\tThis fact tells us shorter array may not have lower score.\n2. We only need to consider splits that cut an array as balanced as possible, that is, if we can find an index **k**, such that ```sum(A[0]...A[k]) <= sum(A[k+1]...A[n-1])``` and ```sum(A[0]...A[k+1]) >= sum(A[k+2]...A[n-1])```, the optimal split must be either **k** or **k+1**\n\n\tcounterexample:\n\t\n\t[98, 77, 24, 49, 6, 12, 2, 44, 51, 96]\n\tThe most balanced split is \n\t[98, 77, 24][49, 6, 12, 2, 44, 51, 96], left part sum 199, right part sum 260\n\t[98, 77, 24, 49][6, 12, 2, 44, 51, 96], left part sum 248, right part sum 211\n\tHowever, the optimal result of this example is\n\t[98, 77, 24, 49, 6, 12, 2, 44, 51, 96]->[98, 77, 24, 49, 6, 12, 2][44, 51, 96] -> [44, 51, 96]->[44, 51][96] -> [44, 51] -> [44][51] ->[44], get 191+95+44=330 score, which doesn\'t cut the array in the most balanced way
| 15 | 0 |
[]
| 4 |
stone-game-v
|
C++/Python partial_sum + DFS
|
cpython-partial_sum-dfs-by-votrubac-d48p
|
This is similar to other DP problems when you find the best split point k for a range [i, j]. To avoid recomputation, we memoise the best answer in dp[i][j].\n\
|
votrubac
|
NORMAL
|
2020-08-23T04:01:47.062178+00:00
|
2020-08-23T05:09:43.637461+00:00
| 1,763 | false |
This is similar to other DP problems when you find the best split point `k` for a range `[i, j]`. To avoid recomputation, we memoise the best answer in `dp[i][j]`.\n\nTo speed things up, we first convert our array into a prefix sum array, so that we can easily get the sum of interval `[i, j]` as `v[j] - v[i - 1]`. \n\n**C++**\n```cpp\nint dp[501][501] = {};\nint dfs(vector<int>& v, int i, int j) {\n if (!dp[i][j]) \n for (int k = i; k < j; ++k) {\n int left = v[k] - (i > 0 ? v[i - 1] : 0), right = v[j] - v[k];\n if (left <= right)\n dp[i][j] = max(dp[i][j], left + dfs(v, i, k));\n if (left >= right)\n dp[i][j] = max(dp[i][j], right + dfs(v, k + 1, j));\n }\n return dp[i][j]; \n}\nint stoneGameV(vector<int>& v) {\n partial_sum(begin(v), end(v), begin(v));\n return dfs(v, 0, v.size() - 1);\n}\n```\n**Python**\nWe add a sentinel value to the prefix sum array to avoid `i > 0` check.\n\n```python\ndef stoneGameV(self, v: List[int]) -> int:\n\t@lru_cache(None)\n\tdef dfs(i: int, j: int) -> int:\n\t\tres = 0\n\t\tfor k in range(i, j):\n\t\t\tif v[k] - v[i - 1] <= v[j] - v[k]:\n\t\t\t\tres = max(res, v[k] - v[i - 1] + dfs(i, k))\n\t\t\tif v[k] - v[i - 1] >= v[j] - v[k]:\n\t\t\t\tres = max(res, v[j] - v[k] + dfs(k + 1, j))\n\t\treturn res\n\tv = [0] + list(itertools.accumulate(v))\n\treturn dfs(1, len(v) - 1) \n```\n**Complexity Analysis**\n- Time: O(n ^ 3). For each combination of `i` and `j`, we perform `j - i` operations.\n- Memory: O(n ^ 2) for the memoisation.
| 15 | 0 |
[]
| 4 |
stone-game-v
|
Java | TopDown DP | Prefix Sum | Optimized: pruning recursion using sum of geometric sequence
|
java-topdown-dp-prefix-sum-optimized-pru-ix0f
|
Look for this key pruning idea to speed up recursion: if(2 x Math.min(l,r)<max) continue; (the DP works without it but is much slower).\nNo need to consider an
|
prezes
|
NORMAL
|
2021-06-01T23:27:41.785021+00:00
|
2021-08-02T04:25:50.410187+00:00
| 449 | false |
Look for this key pruning idea to speed up recursion: if(2 x Math.min(l,r)<max) continue; (the DP works without it but is much slower).\nNo need to consider any branches with the sum smaller than the max score known so far, as for a given subset of stones with sum of values equal a, the total score cannot be bigger than 2a, by the rules of the game: in each turn the sum of stone values gets reduced by half or more. The total score\'s upper bound can be calculated as a sum of the geometric sequence:\nscore = a + a/2 + a/4 + a/8 + a/16 + ... = a x (1 + 1/2 + 1/4 + 1/8 + 1/16 + ...) = 2 x a\n\n\n```\nclass Solution {\n public int stoneGameV(int[] stoneValue) {\n int n= stoneValue.length;\n int[] ps= new int[n];\n ps[0]= stoneValue[0];\n for(int i=1; i<n; i++) ps[i]= ps[i-1]+stoneValue[i];\n return gameDP(ps, 0, n-1, new Integer[n][n]);\n }\n\n private int gameDP(int[] ps, int i, int j, Integer[][] dp){\n if(i==j) return 0;\n if(dp[i][j]!=null) return dp[i][j];\n int max= 0;\n // k is the first stone in the right part\n for(int k= i+1; k<=j; k++){\n int l= ps[k-1]-(i==0?0:ps[i-1]);\n int r= ps[j]-ps[k-1];\n // key branch pruning idea to speed up recursion\n if(2*Math.min(l,r)<max) continue;\n if(l<=r) max= Math.max(max, l + gameDP(ps, i, k-1, dp));\n if(l>=r) max= Math.max(max, r + gameDP(ps, k, j, dp));\n }\n return dp[i][j]= max;\n }\n}
| 9 | 0 |
[]
| 3 |
stone-game-v
|
Optimal Strategy for Stone Game: Maximizing Alice's Score with Memoization
|
optimal-strategy-for-stone-game-maximizi-g5yc
|
Intuition\n Describe your first thoughts on how to solve this problem. \nTo solve this problem, we can use dynamic programming. We can create a memoization tabl
|
Ratan_md
|
NORMAL
|
2023-08-03T03:07:28.349617+00:00
|
2023-08-03T03:07:28.349640+00:00
| 327 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo solve this problem, we can use dynamic programming. We can create a memoization table to keep track of the maximum scores Alice can obtain for each subproblem. The subproblem can be defined as the range of stones from index i to j.\n\nThe approach can be summarized as follows:\n\n1. Initialize a memoization table to store the maximum score Alice can obtain for each subproblem.\n2. Create a helper function that calculates the maximum score Alice can obtain for a given range of stones (i.e., from index i to j).\n3. In the helper function, check the base case when there\'s only one stone left in the range (i.e., i == j), and return its value as the score.\n4. If there are more than one stone, calculate the score for each possible division of the current range into two non-empty rows (i.e., left row and right row). To do this, iterate through all possible split points from i to j-1 and recursively calculate the maximum scores for the resulting left and right ranges.\n5. For each split point, update the maximum score Alice can obtain by comparing the scores of the two rows and taking the maximum.\n6. Return the maximum score for the current range.\n\nBy following the above approach, we can efficiently calculate the maximum score Alice can obtain by dividing the problem into smaller subproblems and reusing the already calculated results using memoization.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe given code implements a solution to the problem using dynamic programming and memoization. The main function `stoneGameV` takes an array `a` representing the values of the stones. It calculates the prefix sum of the array to facilitate quick range sum queries. It then initializes a memoization table `memo` and calls the `stoneGameHelper` function to find the maximum score Alice can obtain.\n\nThe `stoneGameHelper` function is a recursive helper function that calculates the maximum score for a given range of stones defined by the `left` and `right` indices. It uses the memoization table to store and reuse the results of subproblems to avoid redundant calculations.\n\nIn the `stoneGameHelper` function, it first checks the base case when there\'s only one stone in the range, and in that case, it returns 0. If the result for the current range is already present in the memoization table, it returns the stored value directly.\n\nOtherwise, it iterates through all possible split points from `left` to `right-1`, and for each split point `i`, it calculates the scores of the left and right rows based on the prefix sum array. Then, it compares the scores and updates the result with the maximum value considering the two rows.\n\nIf the left and right rows have equal scores, it considers both divisions and takes the maximum score among them.\n\nFinally, the calculated result is stored in the memoization table, and the function returns the result.\n\nOverall, this solution effectively solves the problem by breaking it into smaller subproblems and using memoization to avoid redundant calculations, making it efficient for larger input sizes.# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n^2)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n^2)\n# Code\n```\nclass Solution {\npublic:\n int stoneGameV(vector<int>& a) {\n int n = a.size();\n if (n == 1)\n return 0;\n \n // Calculate the prefix sum of the array for quick range sum queries.\n vector<int> prefixSum(n + 1, 0);\n for (int i = 0; i < n; ++i) {\n prefixSum[i + 1] = prefixSum[i] + a[i];\n }\n \n // Initialize the memoization table to store the results of subproblems.\n vector<vector<int>> memo(n, vector<int>(n, -1));\n \n return stoneGameHelper(a, prefixSum, memo, 0, n - 1);\n }\n \n int stoneGameHelper(vector<int>& a, vector<int>& prefixSum, vector<vector<int>>& memo, int left, int right) {\n if (left == right)\n return 0;\n \n if (memo[left][right] != -1)\n return memo[left][right];\n \n int result = 0;\n for (int i = left; i < right; ++i) {\n int leftSum = prefixSum[i + 1] - prefixSum[left];\n int rightSum = prefixSum[right + 1] - prefixSum[i + 1];\n \n if (leftSum < rightSum) {\n result = max(result, leftSum + stoneGameHelper(a, prefixSum, memo, left, i));\n } else if (leftSum > rightSum) {\n result = max(result, rightSum + stoneGameHelper(a, prefixSum, memo, i + 1, right));\n } else {\n // If leftSum and rightSum are equal, consider both divisions.\n result = max(result, leftSum + max(\n stoneGameHelper(a, prefixSum, memo, left, i),\n stoneGameHelper(a, prefixSum, memo, i + 1, right)\n ));\n }\n }\n \n memo[left][right] = result;\n return result;\n }\n};\n\n```
| 8 | 0 |
['C++']
| 7 |
stone-game-v
|
💥💥Beats 100% on runtime and memory [EXPLAINED]
|
beats-100-on-runtime-and-memory-explaine-th3p
|
\n\n\n\n# Intuition\nThe goal is to maximize Alice\'s score by strategically splitting the stones into two non-empty parts, ensuring she always benefits from th
|
r9n
|
NORMAL
|
2024-09-26T21:05:24.715310+00:00
|
2024-09-26T21:06:58.727602+00:00
| 75 | false |
\n\n\n\n# Intuition\nThe goal is to maximize Alice\'s score by strategically splitting the stones into two non-empty parts, ensuring she always benefits from the remaining stones after Bob discards the higher-value part.\n\n# Approach\nEvaluate all possible splits of the stones, calculating the scores recursively while storing results to avoid redundant calculations.\n\n# Complexity\n- Time complexity:\nO(n\xB3) due to nested loops iterating through all possible pairs and splits.\n\n- Space complexity:\nO(n\xB2) for storing the maximum scores of subarrays in a 2D array.\n\n# Code\n```csharp []\npublic class Solution {\n public int StoneGameV(int[] stoneValue) {\n int n = stoneValue.Length;\n int[,] dp = new int[n, n]; // dp[i, j] = max score for stones from index i to j\n int[] prefixSum = new int[n + 1];\n\n // Calculate prefix sums for quick range sum queries\n for (int i = 0; i < n; i++) {\n prefixSum[i + 1] = prefixSum[i] + stoneValue[i];\n }\n\n // Fill dp array\n for (int length = 2; length <= n; length++) {\n for (int i = 0; i <= n - length; i++) {\n int j = i + length - 1; // right boundary\n for (int k = i; k < j; k++) {\n int leftSum = prefixSum[k + 1] - prefixSum[i]; // Sum of left part\n int rightSum = prefixSum[j + 1] - prefixSum[k + 1]; // Sum of right part\n if (leftSum < rightSum) {\n dp[i, j] = Math.Max(dp[i, j], dp[i, k] + leftSum);\n } else if (leftSum > rightSum) {\n dp[i, j] = Math.Max(dp[i, j], dp[k + 1, j] + rightSum);\n } else {\n dp[i, j] = Math.Max(dp[i, j], Math.Max(dp[i, k] + leftSum, dp[k + 1, j] + rightSum));\n }\n }\n }\n }\n\n return dp[0, n - 1]; // Result for the entire range\n }\n}\n\n```
| 7 | 0 |
['C#']
| 0 |
stone-game-v
|
[Python] 350ms - beats 98%
|
python-350ms-beats-98-by-wdhiuq-voiz
|
Intuition\nMemoized solution can take advantage of some constraints to shrink search space. \n\n# Approach\nWhen considering a subproblem (solution for contiguo
|
wdhiuq
|
NORMAL
|
2022-12-18T00:06:58.300216+00:00
|
2022-12-18T21:03:11.195910+00:00
| 530 | false |
# Intuition\nMemoized solution can take advantage of some constraints to shrink search space. \n\n# Approach\nWhen considering a subproblem (solution for contiguos sublist of the original list) there is no need to check all possible divisions of the sublist, since there is an upper bound on the value of the solution. Specifically the solution cannot exceed sum of values of stones in the sublist minus 1 (think sum of geometric progression with ratio 1/2). Based on this, if the sublist is divided into two parts with boundary too far from the median (such that the bound mentioned above implies that solution for this divison cannot beat the best solution discovered so far), then search can be safely stopped. We start search by dividing in two parts with equal sums (or the closest possible) and expand search by moving index of the boundary between left and right part of the sublist, first - the one to the left and then - the one to the right until we are stopped by the constraint mentioned above.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom itertools import accumulate\nfrom bisect import bisect_left\nfrom functools import cache\n\nclass Solution:\n def stoneGameV(self, stoneValue: List[int]) -> int:\n\n sv = [0, *accumulate(stoneValue)]\n\n @cache\n def helper(fro, to):\n if to - fro == 1:\n return 0\n\n mid = bisect_left(sv, (sv[to] + sv[fro]) // 2)\n\n dist = res = 0\n explore_more = True\n while explore_more:\n explore_more = False\n for i in [mid - dist, mid + dist]: \n if fro < i <= to:\n left, right = sv[i] - sv[fro], sv[to] - sv[i]\n if res // 2 <= left <= right:\n res = max(res, left + helper(fro, i))\n explore_more = True\n if left >= right >= res // 2:\n res = max(res, right + helper(i, to))\n explore_more = True\n dist += 1\n return res\n\n return helper(0, len(stoneValue))\n```
| 6 | 0 |
['Python3']
| 0 |
stone-game-v
|
Python O(n^2) optimized solution. O(n^3) cannot pass.
|
python-on2-optimized-solution-on3-cannot-edfb
|
Python is slow sometimes!\n\nTraditional DP: \n\nfor i in (0, length): \n\tfor j in (0, length): \n\t\tfor k in (i, j): \n\t\t\tdp[i][j] = dp[i][k] + s[i][k]] o
|
pureme
|
NORMAL
|
2021-10-05T17:33:51.862093+00:00
|
2021-10-05T17:39:58.543435+00:00
| 820 | false |
Python is slow sometimes!\n\nTraditional DP: \n```\nfor i in (0, length): \n\tfor j in (0, length): \n\t\tfor k in (i, j): \n\t\t\tdp[i][j] = dp[i][k] + s[i][k]] or dp[k+1][j] + s[k+1][j]\n```\n\nThe hardest thing for us to optimize the O(n^3) is finding a way to reduce the innest loop for k in (i, j), but it\'s not sorted and no way to find which one is best, totaly irregular?\n**However**, the lowest bound and hight bound of the cut index in (i, j) comes from the best cut in (i+1, j) and (i, j-1), **BECAUSE**\n\n**`best_cut[i][j-1] - 1 <= best_cut[i][j] <= best_cut[i+1][j] + 1`** \n\nYou can prove it by yourself.\n\nAdd a best cut array to optimize the O(n^3) solution, to make it **ALMOST O(n^2)**, the number of k from bestcut[i][j-1] to bestcut[i+1][j] is ***almost a constant value averagly*** (depends on the values in list).\n\n\n```\nclass Solution:\n def stoneGameV(self, stoneValue: List[int]) -> int:\n length = len(stoneValue)\n if length == 1:\n return 0\n \n\t\t# Calculate sum\n s = [0 for _ in range(length)]\n s[0] = stoneValue[0]\n for i in range(1, length):\n s[i] = s[i-1] + stoneValue[i]\n\t\t\n\t\t# dp for best value, best_cut for where is the cut in (i, j), i, j inclusive\n dp = [[0 for _ in range(length)] for _ in range(length)]\n best_cut = [[0 for _ in range(length)] for _ in range(length)]\n \n for i in range(0, length-1):\n dp[i][i+1] = min(stoneValue[i], stoneValue[i+1])\n best_cut[i][i+1] = i\n \n for t in range(2, length):\n for i in range(0, length-t):\n tmp_dp = 0\n tmp_cut = 0\n left_bound = best_cut[i][i+t-1]\n if left_bound > i:\n left_bound -= 1\n right_bound = best_cut[i+1][i+t]\n if right_bound < i+t-1:\n right_bound += 1\n \n for k in range(left_bound, 1+right_bound):\n s1 = s[k] - s[i-1] if i > 0 else s[k]\n s2 = s[i+t] - s[k]\n if s1 < s2:\n tmp = s1 + dp[i][k]\n if tmp > tmp_dp:\n tmp_dp = tmp\n tmp_cut = k\n elif s1 > s2:\n tmp = s2 + dp[k+1][i+t]\n if tmp > tmp_dp:\n tmp_dp = tmp\n tmp_cut = k\n else:\n tmp1 = s1 + dp[i][k]\n tmp2 = s2 + dp[k+1][i+t]\n if tmp1 > tmp_dp:\n tmp_dp = tmp1\n tmp_cut = k\n if tmp2 > tmp_dp:\n tmp_dp = tmp2\n tmp_cut = k\n \n dp[i][i+t] = tmp_dp\n best_cut[i][i+t] = tmp_cut\n \n return dp[0][length-1]\n```
| 6 | 0 |
['Dynamic Programming', 'Python3']
| 2 |
stone-game-v
|
Is this question not meant for python?
|
is-this-question-not-meant-for-python-by-xgss
|
\nI have submitted most optimized code but even that one gives TLE in python.\n
|
shreyashnahar0
|
NORMAL
|
2021-05-19T06:29:28.531936+00:00
|
2021-05-19T06:31:49.262945+00:00
| 195 | false |
```\nI have submitted most optimized code but even that one gives TLE in python.\n```
| 5 | 0 |
[]
| 0 |
stone-game-v
|
JAVA Solution USING MCM (matrix chain multiplication) and prefix sum
|
java-solution-using-mcm-matrix-chain-mul-2y8l
|
\'\'\' \nclass Solution {\n public int stoneGameV(int[] s) {\n \n int pre[]=new int[s.length];\n pre[0]=s[0];\n\t\t// calculate prefix s
|
abhishekbabbar1989
|
NORMAL
|
2021-03-30T09:50:49.940167+00:00
|
2021-03-30T09:54:50.459296+00:00
| 353 | false |
\'\'\' \nclass Solution {\n public int stoneGameV(int[] s) {\n \n int pre[]=new int[s.length];\n pre[0]=s[0];\n\t\t// calculate prefix sum\n for(int i=1;i<s.length;i++)\n {\n pre[i]=pre[i-1]+s[i];\n }\n \n int dp[][]=new int[501][501];\n for(int i=0;i<dp.length;i++)\n Arrays.fill(dp[i],-1);\n \n return solve(s,pre,0,s.length-1,dp);\n \n \n }\n \n public int solve(int a[],int pre[],int i,int j,int dp[][])\n {\n // if only one element left, we dont have any options\n if(i>=j)\n return 0;\n \n if(dp[i][j]!=-1)\n return dp[i][j];\n \n\t\t\n int ans=0; // global ans\n for(int k=i;k<j;k++)\n {\n int op1=0,op2=0;\n // i-k , k+1,j\n int temp=0;\n \n op1= i==0?pre[k]: pre[k]-pre[i-1]; \n op2= pre[j]-pre[k];\n \n if(op1<op2) // take minimum of two options\n {\n temp=op1+solve(a,pre,i,k,dp);\n }\n else if(op2<op1)\n {\n temp=op2+solve(a,pre,k+1,j,dp);\n }\n else\n {\n\t\t\t // if both are equal then explore both options and choose best one\n temp=Math.max(op1+solve(a,pre,i,k,dp),op2+solve(a,pre,k+1,j,dp)); \n }\n \n\t\t\t// update global ans\n ans=Math.max(ans,temp);\n }\n \n return dp[i][j]=ans;\n \n \n }\n \n}\n\'\'\'
| 5 | 0 |
[]
| 1 |
stone-game-v
|
python top down dp with thinking process
|
python-top-down-dp-with-thinking-process-4l1q
|
The first time Alice is picking, she needs to decide a cut point s.t. she get max score. The first intuision is we go through each potential cut point and find
|
ytb_algorithm
|
NORMAL
|
2021-01-19T02:31:38.202307+00:00
|
2021-01-19T02:31:38.202338+00:00
| 709 | false |
The first time Alice is picking, she needs to decide a cut point s.t. she get max score. The first intuision is we go through each potential cut point and find the most optimized score. The following is the code. \n```\nclass Solution:\n def stoneGameV(self, stoneValue: List[int]) -> int:\n def dfs(start, end):\n if start >= end:\n return 0\n max_score = 0\n # divides the array into [start,cut] and \n # [cur+1, end]\n for cut in range(start, end):\n sum1 = partial_sum[start][cut]\n sum2 = partial_sum[cut+1][end]\n # remaing part is [cut+1, end]\n if sum1 > sum2:\n score = sum2+dfs(cut+1, end)\n # remaining part is [start, cut]\n elif sum1 < sum2:\n score = sum1+dfs(start, cut)\n # two rows are equal\n else:\n score = sum1+max(dfs(start, cut), dfs(cut+1, end))\n max_score = max(score, max_score)\n return max_score\n \n \n def getPartialSum():\n for i in range(n):\n partial_sum[i][i] = stoneValue[i]\n for i in range(n):\n for j in range(i+1, n):\n partial_sum[i][j] = partial_sum[i][j-1]+stoneValue[j]\n \n \n n = len(stoneValue)\n partial_sum = [[0]*n for _ in range(n)]\n getPartialSum()\n return dfs(0, n-1)\n\n```\nGot TLE (Maybe it\'s python. I found lots of similar solution by C++ or Java get passed). Need some optimization. The bottleneck is in the traverse of all the possible cut points, which cause the time complexity to be O(n^3). We need to do something about that. During thinking, I recall a similar speedup process in a question of throwing an egg from a building and to find the highest level that the egg won\'t be broken (lc 887). In a word, the big direction is to apply binary search or linear search to find the cut point. However, this is exactly where I was stuck since there is no sorted property for the scores Alice can get for all the cut points. Which means, if Alice pick k or k+1, the relationship between scores(k) and scores(k+1) is not certain. \nThen I looked for help in the discussion section. And this one is perfect: https://leetcode.com/problems/stone-game-v/discuss/911676/Java-O(n3)-O(n2-log-n)-and-O(n2)-with-explanation. It shows that my intuition is right, but I really need some further thinking. \nThere is one missing sorted array, which is the array of previous sum of the scores (score represents number of stones, which is non-negative). And this is the place where we should apply binary search or linear search. However, how this relates to finding the optimized cut point? It turns out we need two extra arrays (left and right), recording calculated max scores of left part and right part. For example, left[i][j] records max scores of left part with cut points in the range of [i, j]. So if we use dfs(i, j) to represents the max scores Alice can get from i to j. left[i][j] = max(dfs(i, cut), i<=cut<j) and similarly, right[i][j]=max(dfs(cut, j) i<=cut<j). With the two arrays, we are ready to calculate dfs(i, j):\n1. We first find smallest point c s.t. sum from i to c (sum1) is larger than or equal to sum from c+1 to end (sum2).\n2. We may have three situations: \n\t* \tsum1 < sum2. That is to say, no matter how we cut, the remaining will always be the left part of the cut. So dfs(i,j)=left(i,j-1) (we need at least one pile of stones allocated to the right part)\n\t* \tsum1 = sum2. If we cut before c, remaining will be the left part. If we cut after c, it will be the right part. If we cut at c, both parts can be the remaining. Thus, dfs(i,j) = max(left(i, c), right(c+1, j))\n\t* \tsum1 > sum2. If we cut after c, remaining will be the right part. And since c is the first idx s.t. sum1>sum2, if we cut before c, remaining will be left part. Thus dfs(i,j) = max(left(i, c-1), right(c+1,j)). \n\nThe code is in below (only O(n) solution is presented)\n```\nclass Solution:\n def stoneGameV(self, stoneValue: List[int]) -> int:\n def getPartialSum():\n for i in range(n):\n partial_sum[i][i] = stoneValue[i]\n for i in range(n):\n for j in range(i+1, n):\n partial_sum[i][j] = partial_sum[i][j-1]+stoneValue[j]\n \n # (O(n) search) \n def preCalCutIdx():\n # based on the fact that cut index is increasing with k for \n # partial_sum[start][k]\n for i in range(n-1):\n cp = i\n cut_index[i][i+1] = i\n for j in range(i+2, n):\n while cp < j-1 and partial_sum[i][cp] < partial_sum[cp+1][j]:\n cp += 1 \n cut_index[i][j] = cp\n\t\t\n\t\t\t\n @lru_cache(None)\n def dfs(start, end):\n if start >= end:\n return 0\n max_score = 0\n # find first cut s.t. left sum >= right sum \n cut = cut_index[start][end]\n # we can\'t find cut s.t. left sum >= right sum\n if cut == -1:\n cut = end-1\n sum1 = partial_sum[start][cut]\n sum2 = partial_sum[cut+1][end]\n if sum1 < sum2:\n # calcuate left[start][cut] if not yet\n dfs(start, cut)\n # the remaining will be the left part for sure, no \n # matter where the cut is. \n max_score = left[start][cut]\n elif sum1 == sum2:\n dfs(start, cut)\n dfs(cut+1, end)\n # if real cut in the range of [cut+1, end], remaining will be the right part\n # if real cut in the range of [0, cut], remaing will be the left part\n # if real cut is cut, either can be the remaining. \n max_score = max(left[start][cut], right[cut+1][end])\n else:\n dfs(cut+1, end)\n # we are selecting the cut in the range of [cut, end] having \n # the max score. For cut in that range, the remaining is \n # the right part of the cut for sure. \n max_score = right[cut+1][end]\n if cut > start:\n dfs(start, cut-1)\n # we are selecting the cut in the range of [0, cut] having \n # the max score. The remaining is the left part for sure. \n max_score = max(max_score, left[start][cut-1])\n dfs(start, end-1)\n dfs(start+1, end)\n # updating left and right arrays. \n left[start][end] = max(left[start][end-1], partial_sum[start][end]+max_score)\n right[start][end] = max(right[start+1][end], partial_sum[start][end]+max_score)\n return max_score\n \n n = len(stoneValue)\n partial_sum = [[0]*n for _ in range(n)]\n cut_index = [[-1]*n for _ in range(n)]\n # left[i][j]: cut in the range of [i, j], max score of left part\n # right[i][j]: cut in the range of [i, j], max score of right part\n left = [[0]*n for _ in range(n)]\n right = [[0]*n for _ in range(n)]\n for i in range(n):\n left[i][i] = stoneValue[i]\n right[i][i] = stoneValue[i]\n getPartialSum()\n # for partial_sum[i][j], find cut index between i and j \n # s.t partial_sum[i][cut_index] >= partial_sum[cut_index+1][j] or \n # cut_index = j-1 if not exist. \n preCalCutIdx()\n return dfs(0, n-1)\n```\n
| 5 | 1 |
['Dynamic Programming', 'Binary Tree', 'Python3']
| 0 |
stone-game-v
|
[Python3] Game Theory + DP + Prefix Sum - Simple Solution
|
python3-game-theory-dp-prefix-sum-simple-p6r0
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
dolong2110
|
NORMAL
|
2024-09-10T12:24:14.903353+00:00
|
2024-09-10T14:03:50.661535+00:00
| 142 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n##### 1. O(N^3)\n```python3 []\nclass Solution:\n def stoneGameV(self, stoneValue: List[int]) -> int:\n ps = [0] + list(accumulate(stoneValue))\n @cache\n def dp(l: int, r: int) -> int:\n if l == r: return 0\n res = 0\n for i in range(l + 1, r + 1):\n left_sum, right_sum = ps[i] - ps[l], ps[r + 1] - ps[i]\n if left_sum > right_sum: res = max(res, dp(i, r) + right_sum)\n elif left_sum < right_sum: res = max(res, dp(l, i - 1) + left_sum)\n else: res = max(res, dp(l, i - 1) + left_sum, dp(i, r) + right_sum)\n return res\n \n return dp(0, len(stoneValue) - 1)\n```\n# Complexity\n- Time complexity: $$O(N^3)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->
| 4 | 0 |
['Array', 'Math', 'Dynamic Programming', 'Prefix Sum', 'Python3']
| 1 |
stone-game-v
|
Cpp || dynamic programming || memoisation
|
cpp-dynamic-programming-memoisation-by-s-fwoz
|
Intuition\n Describe your first thoughts on how to solve this problem. \nAs problem gives us option to choose which part to throw , this gives the intuition tha
|
shankar999
|
NORMAL
|
2023-05-26T09:22:52.790741+00:00
|
2023-05-26T09:23:47.889365+00:00
| 991 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs problem gives us option to choose which part to throw , this gives the intuition that we try all the possibilities and hence dp can be used to memoise those states. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1) first calculate the prefix sum of the given vector (stoneValue) .\n2) then divide the stoneValue vector at each index i , such that\n the left part is from start ..... i \n the right part is from i+1 ...... end \n \n ```\n for(int i=start;i<=end;i++)\n{ \n leftSum = pref[i]-pref[start-1] (when start>0)\n pref[i] (when start==0)\n \n rightSum=pref[end]-pref[i]\n\n //next function calls depending upon leftSum and rightSum\n}\n \n```\n\n3) if leftSum is greater then we add remaining part (rightSum) to the score and make next call with start=i+1 and end=end\n4) if rightSum is greater then we add remaining part (leftSum) to the score and make next call with start=start and end=i\n5) if leftSum is equal to rightSum then add this value(rightSum or leftSum as both are equal ) to score and make two calls \n i) first one with start=start and end=i\n ii) second one with start=i+1 and end =end \n6) base case is when single element is remaining .\n\n \n\n# Code\n```\nclass Solution {\npublic:\n\n int dp[501][501];\n\n int solve(int start,int end,vector<int>&stoneValue,vector<int>&pref)\n {\n if(end==start) return 0;\n if(end<start)return 0;\n \n if(dp[start][end]!=-1)return dp[start][end];\n\n int score=0; \n for(int i=start;i<=end;i++)\n {\n int lf=(start==0)?pref[i]:pref[i]-pref[start-1]; //leftSum\n int rf=pref[end]-pref[i]; //rightSum\n \n \n if(lf>rf)\n {\n int val=rf+solve(i+1,end,stoneValue,pref);\n score=max(score,val);\n }\n else if(rf>lf)\n {\n int val=lf+solve(start,i,stoneValue,pref);\n score=max(score,val);\n }\n else{\n int val1=lf+solve(start,i,stoneValue,pref);\n int val2=rf+solve(i+1,end,stoneValue,pref);\n int mx=max(val1,val2);\n score=max(score,mx);\n }\n }\n\n return dp[start][end]=score;\n }\n\n int stoneGameV(vector<int>& stoneValue) {\n \n memset(dp,-1,sizeof(dp));\n\n vector<int>pref(stoneValue.size()+1,0);\n pref[0]=stoneValue[0];\n\n for(int i=1;i<stoneValue.size();i++)\n {\n pref[i]=pref[i-1]+stoneValue[i];\n }\n\n return solve(0,(int)stoneValue.size()-1,stoneValue,pref);\n \n }\n};\n```
| 4 | 0 |
['C++']
| 0 |
stone-game-v
|
C++ (Recursion to DP) Intitutive Way
|
c-recursion-to-dp-intitutive-way-by-vfor-tg1r
|
```\nclass Solution {\npublic:\n //map,int>mp;\n //I got tle using map\n \n int memo[501][501];\n int score(vector&nums,int st,int end)\n {\n
|
vforvibhu
|
NORMAL
|
2020-10-26T07:52:20.233968+00:00
|
2020-10-26T07:52:20.234012+00:00
| 570 | false |
```\nclass Solution {\npublic:\n //map<pair<int,int>,int>mp;\n //I got tle using map\n \n int memo[501][501];\n int score(vector<int>&nums,int st,int end)\n {\n if(st>=end)return 0;\n int ans=0;\n //if(mp.find({st,end})!=mp.end())return mp[{st,end}];\n if(memo[st][end]!=-1)return memo[st][end];\n for(int i=st;i<end;i++)\n {\n // Breek it in [st,i] and [i+1,end] ...both should be non -empty\n int lSum,rSum;\n if(st==0)\n {\n lSum=nums[i];\n }\n else\n lSum=nums[i]-nums[st-1]; // st to i\n rSum=nums[end]-nums[i]; // i+1 to end\n \n if(lSum>rSum)\n {\n ans=max(ans,rSum+score(nums,i+1,end));\n }\n else if(lSum==rSum)\n {\n ans=max(ans,max(lSum+score(nums,st,i),rSum+score(nums,i+1,end)));\n }\n else\n {\n ans=max(ans,lSum+score(nums,st,i));\n }\n }\n // return mp[{st,end}]= ans;\n return memo[st][end]=ans;\n }\n \n //?????????? Recursive Code ?????????\n \n// int score(vector<int>&nums,int st,int end)\n// {\n// if(st>=end)return 0;\n// int ans=0;\n// for(int i=st;i<end;i++)\n// {\n// int lSum,rSum;\n// if(st==0)\n// {\n// lSum=nums[i];\n// }\n// else\n// lSum=nums[i]-nums[st-1]; // st to i\n// rSum=nums[end]-nums[i]; // i+1 to end\n \n// if(lSum>rSum)\n// {\n// ans=max(ans,rSum+score(nums,i+1,end));\n// }\n// else if(lSum==rSum)\n// {\n// ans=max(ans,max(lSum+score(nums,st,i),rSum+score(nums,i+1,end)));\n// }\n// else\n// {\n// ans=max(ans,lSum+score(nums,st,i));\n// }\n// }\n// return ans;\n// }\n \n \n int stoneGameV(vector<int>& stoneValue) {\n int n=stoneValue.size();\n vector<int>freq(n,0);\n freq[0]=stoneValue[0];\n memset(memo,-1,sizeof(memo));\n for(int i=1;i<n;i++)\n {\n freq[i]+=stoneValue[i]+freq[i-1]; // It\'s good to have prefix array to calculate rangeSum in o(1)after one time implementation ,will use in recursive function\n }\n return score(freq,0,n-1);\n }\n};
| 4 | 0 |
['Dynamic Programming', 'Recursion', 'Memoization', 'C', 'C++']
| 0 |
stone-game-v
|
O(N^2) A (hopefully) confusion-free, intuitive explanation
|
on2-a-hopefully-confusion-free-intuitive-k7mr
|
Intuitive brute force\nIt is quite simple to com up with O(N^3) solution. Say we have input array size 8, [1,7,3,5,2,9,4,7], we can just try to "cut" the line a
|
XavierWantMoreMoney
|
NORMAL
|
2022-02-08T08:13:49.821704+00:00
|
2022-02-08T08:13:49.821761+00:00
| 261 | false |
### Intuitive brute force\nIt is quite simple to com up with O(N^3) solution. Say we have input array size 8, `[1,7,3,5,2,9,4,7]`, we can just try to "cut" the line at all the possible places\n\n```\n[1, | 7,3,5,2,9,4,7]\n[1,7, | 3,5,2,9,4,7]\n[1,7,3, | 5,2,9,4,7]\n...\n```\nFor each cut, we calculate which half is bigger, and we dump the bigger one and keep the smaller one. If equal, we need to continue on both half. This tells us we need **prefix sum** to easily get which half is bigger.\n\nAlso since for each cut we will divide the problem into smaller question (for example for our case, after we, say, cut between 3rd and 4th number, we will need to check how many scores can `[1,7,3]` gives us). This **natually lead us to DP**.\n\nSay we have a N x N array `resTable` (this will be our "DP" table), where N is the size of input array. \n\nThe meaning of `resTable` is `resTable[i][j] = if the input array is only from ith element to jth element, what max score can Alice get from it`. Note that the final answer we want is `resTable[0][inputarray.size() - 1]`\n\nLet\'s say we cut the line at the right side of `k`th element. \n\n```\n[1,2,5,7 | (cut) 8,9,4]\n7 is the kth element\n```\n\nAlso, I will use `sum[i to j]` to represent the sum of input array from ith element to jth element (`sum[i to j] = inputarray[i] + inputarray[i + 1] + ... + inputarray[j]`)\n\nthen \n```\nfor each k between i and j\n\tif (leftHalf is smaller) resTable[i][j] = sum[i to k] + resTable[i][k] (recall `k` is where we cut the line)\n\telse if (rightHalf is smaller) resTable[i][j] = sum[k + 1 to j] + resTable[k + 1][j]\n```\n\nWe have a N x N `resTable` (aka the DP table) and for each element in `resTable[i][j]`, we need to iterate through `i` and `j` to that find THE `k`th element so it gives us the best score. So the time complexity is `O(N x N) x O(N) = O(N^3)`\n\n### Optimize to O(N^2)\nWhile hand writing some examples, it occurs to me that if I cut the line from left to right, at some point, left half will always be bigger than right half as we move our cut to right.\n\nFor example\n`[1,2,3,4,5,6,7]`, after I cut at the right side of 5 `[1, 2, 3, 4, 5 | 6, 7]`, left half will always be bigger than right side. What this tells us is that once we find this "flip point", all the cuts we made on the left side of this flip point will result in right half being dumped, while all the cuts we made on the right side of this flip point will result in left half being dumped. \n\nFurther, I think we can give this "flip point" a more intuitive name: **"bad luck number"**\n\nWhy? Because if the left half includes this bad luck number, then left half will be dumped (because left half now is bigger than right half). Similarly, if right half includes this bad luck number, then right half will be dumped (because this time, right half is bigger than left half). Whicever half includes this number will be dumped, this number brings bad luck to us. (There is one exception though. When left half and right half are equal, it is "ok" for left half to include this bad luck number, but still, i think this name can help you understand the main idea of this method).\n\n`[3, 6, 5, 2]` -> 6 is the bad luck number, if left half keeps it, then left half becomes 9 (3 + 6) which is bigger than right half (5 + 2), left half got dumped. On the other hand, if right half keeps 6, then left half is 3, right half is 6 + 5 + 2, right half is bigger, dumped\n`[10,1,2,3]` -> 10 is the bad luck number, if left half keeps it, left half will be 10 and right half will be 6, and left half will be dumped. But of course in this case, left half has to keep 10 becasue Alice cannot cut an empty row out.\n`\'[3,6,5,4]` -> 6 is the bad luck number now, but since left half and right half are equal, so it is ok for left half to include this bad luck number. If you feel bad luck number is hard to understand for "left == right" case, don\'t think about it too hard, we will cover this "edge case" later.\n\nWith this idea, I was wondering if finding all back luck number (or bad luck index, to be more precise) for each `i to j` subarray can be helpful?\n\nWhat this bad luck number tells us is that \n- if you make a cut left to this bad luck number, it is guaranteed the best score comes from left half (and safe to dump right half)\n- if you make a cut right to this bad luck number, it is guaranteed the best score comes from right half (and safe to dump left half)\n\nOr more intuitively:\n\n```\nresTable[i][j] = max(\n\tthe best score Alice can get if she made a cut LEFT to bad luck number,\n\tthe best score Alice can get if she made a cut RIGHT to bad luck number,\n);\n(let\'s not consider lefthalf == righthalf case just yet)\n```\n\nYou might think: even though Alice can make a cut LEFT to bad luck number, she still needs to cut the line on the left at all possible positions, this is still O(N^3) right?\n\nWell, you are right, she still needs to try all possible positions to the left of bad luck number, BUT can we have an extra data strcture so that it can give us `the best score Alice can get if she made a cut LEFT to bad luck number` in constant time??\n\nBasically we want a `leftBest` and `rightBest`, so that\n\n`leftBest[i][j] = the best score Alice can get if she made a cut in range of [i, j] and only keep the LEFT half and dump the RIGHT half`\n`rightBest[i][j] = the best score Alice can get if she made a cut in range of [i, j] and only keep the RIGHT half, dump the LEFT half`\n\nThen suddenly our `resTable[i][j]` becomes\n```\nresTable[i][j] = max(\n\tleftBest[i][bad luck number index - 1],\n\trightBest[bad luck number index + 1][j],\n)\n```\n\nAt here, if `leftHalf == rightHalf`, then we only have a slightly different equation:\n\n```\nresTable[i][j] = max(\n\tleftBest[i][bad luck number index], // because including bad luck number only makes left half and right half equal, no one gets dumped yet, so we still include it in left half.\n\trightBest[bad luck number index + 1][j], // yes, rightBest equation remains the same\n)\n```\n\nNote that thanks to bad luck number, if we cut on left side of bad luck number, it is always safe to assume we can dump right half and keep the left half! And similarly, if we cut on the right side of bad luck number, it is also safe to dump the left half and keep the right half!\n\nSo we only have one question now, how do we update `leftBest` and `rightBest`? Well it is actually simple:\n\n```\nleftBest[i][j] = max(\n\tleftBest[i][j - 1], // the best score we can get from i to j - 1\n\tsum[i to j] + resTable[i][j] // or maybe after including the jth element, we can have a higher score?\n)\n```\n\nIf you are wondering why we are not adding `leftBest[i + 1][j]` to the comparison... This is because what `leftBest[i + 1][j]` means is if we cut between `i + 1 to j`, what best score can we get. Let\'s say we cut at k, then `i + 1 to k` will be kept and the right half will be dumped. `i + 1 to k` DOES NOT INCLUDE `i`, while you are calculating `leftBest[i][j]` here - you have to include `i`, so `leftBest[i + 1][j]` should not be considered.\n\n`rightBest` will be similar.\n\n```\nrightBest[i][j] = max(\n\trightBest[i + 1][j], // the best score we can get from i + 1 to j\n\tsum[i to j] + resTable[i][j] // or maybe after including the ith element, we can have a higher score?\n)\n```\n\nNow we have everything we need to get to this O(N^2) answer\n1. for all `i` and `j` where `0 <= i <= j <= input array size - 1`, find its bad luck number (O(N^2))\n2. convert input array to prefix sum format so it is easier for us to calculate `sum[i to j]` (linear)\n3. initialize `resTable[i][i]`, initialize `leftBest and rightBest` (linear)\n4. traverse `resTable` **bottom up**, row by row (O(N^2))\n\nCode in C++:\n```\nclass Solution {\npublic:\n struct BadLuck {\n int index;\n bool halfEqual;\n };\n int stoneGameV(vector<int>& stoneValue) {\n if (stoneValue.size() == 1) return 0;\n \n vector<vector<int>> resTable(stoneValue.size(), vector<int>(stoneValue.size()));\n // initailize res table (DP table)\n for (int row = 0; row < stoneValue.size(); ++row) {\n resTable[row][row] = stoneValue[row];\n if (row + 1 < stoneValue.size()) resTable[row][row + 1] = min(stoneValue[row], stoneValue[row + 1]);\n }\n \n // find all subarray\'s badluck\n vector<vector<BadLuck>> badlucks(stoneValue.size(), vector<BadLuck>(stoneValue.size()));\n for (int row = 0; row < stoneValue.size() - 2; ++row) {\n int left = row; // points to the first num so that leftSum >= rightSum\n \n int leftSum = stoneValue[left];\n int rightSum = 0;\n \n if (stoneValue[left] < stoneValue[left + 1]) {\n ++left;\n leftSum += stoneValue[left];\n } else {\n rightSum = stoneValue[left + 1];\n }\n \n badlucks[row][row + 1] = {left, stoneValue[left] == stoneValue[left + 1]};\n \n for (int right = row + 2; right < stoneValue.size(); ++right) {\n rightSum += stoneValue[right];\n if (leftSum > rightSum) {\n badlucks[row][right] = {left, false};\n } else if (leftSum == rightSum) {\n badlucks[row][right] = {left, true};\n } else {\n while (left <= right and leftSum < rightSum) {\n ++left;\n leftSum += stoneValue[left];\n rightSum -= stoneValue[left];\n }\n badlucks[row][right] = {left, leftSum == rightSum};\n }\n }\n }\n \n // initialize leftBest and rightBest\n vector<vector<int>> leftBest(stoneValue.size(), vector<int>(stoneValue.size()));\n vector<vector<int>> rightBest(stoneValue.size(), vector<int>(stoneValue.size()));\n\n for (int row = 0; row < stoneValue.size(); ++row) {\n leftBest[row][row] = stoneValue[row];\n rightBest[row][row] = stoneValue[row];\n if (row + 1 < stoneValue.size()) {\n leftBest[row][row + 1] = stoneValue[row] + stoneValue[row + 1] + resTable[row][row + 1];\n rightBest[row][row + 1] = leftBest[row][row + 1];\n }\n }\n \n // convert stoneValue to prefix sum\n for (int i = 1; i < stoneValue.size(); ++i) {\n stoneValue[i] += stoneValue[i - 1];\n }\n \n // fill resTable and leftBest and rightBest\n for (int row = stoneValue.size() - 3; row >= 0; --row) {\n for (int col = row + 2; col < stoneValue.size(); ++col) {\n auto badluck = badlucks[row][col];\n int badluckIndex = badluck.index;\n \n // if left half remians, what is the best score we can get from it if we cut a line in it\n int leftBestScore = 0;\n if (badluck.halfEqual) leftBestScore = leftBest[row][badluckIndex];\n else if (badluckIndex > 0) leftBestScore = leftBest[row][badluckIndex - 1];\n \n // if right half remians, what is the best score we can get from it if we cut a line in it\n int rightBestScore = 0;\n if (badluckIndex + 1 < stoneValue.size()) rightBestScore = rightBest[badluckIndex + 1][col];\n \n resTable[row][col] = max(leftBestScore, rightBestScore);\n \n leftBest[row][col] = max(\n leftBest[row][col - 1], \n (stoneValue[col] - (row > 0 ? stoneValue[row - 1] : 0)) + resTable[row][col]\n );\n rightBest[row][col] = max(\n rightBest[row + 1][col], \n (stoneValue[col] - (row > 0 ? stoneValue[row - 1] : 0)) + resTable[row][col]\n );\n }\n }\n \n return resTable[0][stoneValue.size() - 1];\n }\n};\n```\n\nHope this helps\n\n
| 3 | 0 |
['C']
| 1 |
stone-game-v
|
python3 O(N^2) beats 98%
|
python3-on2-beats-98-by-miao_txy-nne6
|
idx is the first point in [l, r]\nwhere sum([l, idx]) > sum([idx + 1, r])\n\n\tfrom functools import lru_cache\n\timport itertools\n\n\n\tclass Solution:\n\t\td
|
miao_txy
|
NORMAL
|
2020-08-26T11:49:04.312771+00:00
|
2020-08-26T11:51:00.910100+00:00
| 440 | false |
idx is the first point in [l, r]\nwhere sum([l, idx]) > sum([idx + 1, r])\n\n\tfrom functools import lru_cache\n\timport itertools\n\n\n\tclass Solution:\n\t\tdef stoneGameV(self, A) -> int:\n\n\t\t\tpre = [0] + list(itertools.accumulate(A))\n\n\t\t\tn = len(A)\n\t\t\tidx = [[0] * n for _ in range(n)]\n\t\t\tfor i in range(n):\n\t\t\t\tidx[i][i] = i\n\t\t\t\tif i < n - 1:\n\t\t\t\t\tidx[i][i + 1] = i\n\t\t\tfor i in range(n - 2):\n\t\t\t\tfor j in range(i + 2, n):\n\t\t\t\t\ttmp = idx[i][j - 1]\n\t\t\t\t\twhile pre[tmp + 1] - pre[i] < pre[j + 1] - pre[tmp + 1]:\n\t\t\t\t\t\ttmp += 1\n\t\t\t\t\tidx[i][j] = tmp\n\n\t\t\t@lru_cache(None)\n\t\t\tdef maxL(i, j):\n\t\t\t\tif i == j: return A[i]\n\t\t\t\treturn max(maxL(i, j - 1), pre[j + 1] - pre[i] + dp(i, j))\n\n\t\t\t@lru_cache(None)\n\t\t\tdef maxR(i, j):\n\t\t\t\tif i == j: return A[i]\n\t\t\t\treturn max(maxR(i + 1, j), pre[j + 1] - pre[i] + dp(i, j))\n\n\t\t\t@lru_cache(None)\n\t\t\tdef dp(i, j):\n\t\t\t\tif i + 1 == j: return min(A[i], A[j])\n\t\t\t\tmid = idx[i][j]\n\t\t\t\tres = 0\n\t\t\t\tif mid > i: res = max(res, maxL(i, mid - 1))\n\t\t\t\tif mid < j: res = max(res, maxR(mid + 1, j))\n\t\t\t\tif pre[j + 1] - pre[mid + 1] == pre[mid + 1] - pre[i]:\n\t\t\t\t\tres = max(res, maxL(i, mid), maxR(mid + 1, j))\n\t\t\t\treturn res\n\n\t\t\treturn dp(0, n - 1)
| 3 | 0 |
[]
| 2 |
stone-game-v
|
Simple DP solution
|
simple-dp-solution-by-leoooooo-nqxv
|
\npublic class Solution\n{\n public int StoneGameV(int[] stoneValue)\n {\n int[] presum = new int[stoneValue.Length + 1];\n for (int i = 0;
|
leoooooo
|
NORMAL
|
2020-08-23T04:22:13.546938+00:00
|
2020-08-23T04:29:47.014426+00:00
| 360 | false |
```\npublic class Solution\n{\n public int StoneGameV(int[] stoneValue)\n {\n int[] presum = new int[stoneValue.Length + 1];\n for (int i = 0; i < stoneValue.Length; i++)\n {\n presum[i + 1] = presum[i] + stoneValue[i];\n }\n return DFS(presum, 0, stoneValue.Length, new int[presum.Length, presum.Length]);\n }\n\n private int DFS(int[] presum, int start, int end, int[,] memo)\n {\n if (start == end)\n return 0;\n if (memo[start, end] > 0)\n return memo[start, end];\n int max = 0;\n int cur = 0;\n for (int mid = start + 1; mid < end; mid++)\n {\n int left = presum[mid] - presum[start];\n int right = presum[end] - presum[mid];\n if (right > left)\n cur = left + DFS(presum, start, mid, memo);\n else if (right < left)\n cur = right + DFS(presum, mid, end, memo);\n else\n cur = Math.Max(right + DFS(presum, mid, end, memo), left + DFS(presum, start, mid, memo));\n max = Math.Max(max, cur);\n }\n memo[start, end] = max;\n return max;\n }\n}\n```
| 3 | 0 |
[]
| 1 |
stone-game-v
|
Why TLE on O(n^3)? DP Merging intervals. C++
|
why-tle-on-on3-dp-merging-intervals-c-by-ah42
|
Time Limit Exceeded on 131th test case. During contest I was hitting TLE continuously.\nBut copying and pasting the larger test cases in custom input was work
|
mr_robot11
|
NORMAL
|
2020-08-23T04:16:42.318469+00:00
|
2020-08-23T04:31:15.254681+00:00
| 332 | false |
Time Limit Exceeded on 131th test case. During contest I was hitting TLE continuously.\nBut copying and pasting the larger test cases in custom input was working fine.\n```\nWhy there was no TLE when I was running the same test case using custom input? \n```\n\n```\nIn the discussion everyone\'s solution is O(n^3) time comlexity, but why my O(n^3) is TLE? \nIs this not O(n^3) or is there anything I am missing?\n```\nThanks for your help in advance :)\n\nHere is my C++ solution:\n\n```\nclass Solution {\npublic:\n Solution()\n { ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0); }\n \n int stoneGameV(vector<int>& a) {\n \n int n=a.size(); if(n<=1) return 0;\n vector<int> pre(n,0); pre[0]=a[0];\n for(int i=1;i<n;i++) pre[i]=pre[i-1]+a[i];\n \n vector<vector<int> > dp(n, vector<int> (n,0));\n for(int j=1;j<n;j++)\n {\n for(int i=j-1;i>=0;i--)\n {\n int temp=0;\n for(int k=i;k<j;k++)\n {\n int a1=pre[k]-(i-1>=0?pre[i-1]:0);\n int a2=pre[j]-pre[k];\n \n if(a1>a2) temp=max(temp,a2+dp[k+1][j]);\n if(a1<a2) temp=max(temp,a1+dp[i][k]);\n if(a1==a2) temp=max({temp,a1+dp[i][k],a2+dp[k+1][j] });\n }\n dp[i][j]=temp;\n }\n }\n return dp[0][n-1];\n }\n};\n```
| 3 | 0 |
[]
| 0 |
stone-game-v
|
[Python3] top-down dp
|
python3-top-down-dp-by-ye15-nrjy
|
\n\nclass Solution:\n def stoneGameV(self, stoneValue: List[int]) -> int:\n # prefix sum \n prefix = [0]\n for x in stoneValue: prefix.a
|
ye15
|
NORMAL
|
2020-08-23T04:04:33.492789+00:00
|
2020-08-23T23:58:03.141134+00:00
| 370 | false |
\n```\nclass Solution:\n def stoneGameV(self, stoneValue: List[int]) -> int:\n # prefix sum \n prefix = [0]\n for x in stoneValue: prefix.append(prefix[-1] + x)\n \n @lru_cache(None)\n def fn(lo, hi):\n """Return the score of arranging values from lo (inclusive) to hi (exclusive). """\n if lo+1 == hi: return 0 \n val = 0\n for mid in range(lo+1, hi): \n lower = prefix[mid] - prefix[lo]\n upper = prefix[hi] - prefix[mid]\n if lower < upper: val = max(val, lower + fn(lo, mid))\n elif lower > upper: val = max(val, upper + fn(mid, hi))\n else: val = max(val, lower + max(fn(lo, mid), fn(mid, hi)))\n return val \n \n return fn(0, len(stoneValue))\n```
| 3 | 2 |
['Python3']
| 2 |
stone-game-v
|
Java | Memoization | DP | Beats 80%
|
java-memoization-dp-beats-80-by-nishant7-7lev
|
java\nclass Solution {\n Integer[][] dp;\n public int stoneGameV(int[] stoneValue) {\n dp = new Integer[stoneValue.length][stoneValue.length];\n
|
nishant7372
|
NORMAL
|
2023-07-15T09:11:04.677184+00:00
|
2023-07-15T09:11:04.677246+00:00
| 180 | false |
``` java\nclass Solution {\n Integer[][] dp;\n public int stoneGameV(int[] stoneValue) {\n dp = new Integer[stoneValue.length][stoneValue.length];\n int total = 0;\n for(int x:stoneValue){\n total+=x;\n }\n return solve(stoneValue,0,stoneValue.length-1,total);\n }\n\n private int solve(int[] stones,int i,int j,int total){\n if(i>=j){\n return 0;\n }\n if(dp[i][j]!=null){\n return dp[i][j];\n }\n int sum=0, result=0;\n for(int k=i;k<=j;k++){\n sum+=stones[k];\n int max = 0;\n if(2*sum<total){\n max = sum+solve(stones,i,k,sum);\n }\n else if(2*sum>total){\n max = total-sum + solve(stones,k+1,j,total-sum);\n }\n else{\n max = Math.max(sum+solve(stones,i,k,sum), total-sum+solve(stones,k+1,j,total-sum));\n }\n result = Math.max(max,result);\n }\n return dp[i][j] = result;\n }\n}\n```
| 2 | 0 |
['Memoization', 'Java']
| 0 |
stone-game-v
|
C++ Memoization
|
c-memoization-by-rajatrajoria-mtld
|
\nclass Solution \n{\npublic:\n \n int fn(vector<int> &nums, int l, int r, int total, vector<vector<int>> &dp)\n {\n if(l>=r) // Game
|
rajatrajoria
|
NORMAL
|
2022-07-29T13:04:54.204952+00:00
|
2022-07-29T13:04:54.205015+00:00
| 286 | false |
```\nclass Solution \n{\npublic:\n \n int fn(vector<int> &nums, int l, int r, int total, vector<vector<int>> &dp)\n {\n if(l>=r) // Game ends here.\n return 0;\n if(dp[l][r]!=-1) // This state was already precomputed.\n return dp[l][r];\n \n int sum = 0, ans = INT_MIN;\n for(int i=l;i<=r;i++)\n {\n sum+=nums[i];\n int leftsum = total - sum;\n \n if(sum < leftsum) // left half sum < right half sum\n ans = max(ans,sum + fn(nums,l,i,sum,dp));\n else if(sum > leftsum) // right half sum < left half sum\n ans = max(ans,leftsum + fn(nums,i+1,r,leftsum,dp));\n else // both sums are equal, so we can break them in any direction possible\n ans = max({ans, sum + fn(nums,l,i,sum,dp) , leftsum + fn(nums,i+1,r,leftsum,dp)});\n }\n return dp[l][r] = ans;\n }\n \n int stoneGameV(vector<int>& stoneValue) \n {\n int l = 0, r = stoneValue.size()-1, total = 0;\n vector<vector<int>> dp(stoneValue.size(), vector<int>(stoneValue.size(),-1));\n for(auto &e: stoneValue)\n total+=e;\n return fn(stoneValue, l, r, total,dp);\n \n }\n};\n```
| 2 | 0 |
['Dynamic Programming', 'Memoization', 'C', 'C++']
| 0 |
stone-game-v
|
C++ || EASY TO UNDERSTAND || Memoization || DP
|
c-easy-to-understand-memoization-dp-by-a-a199
|
\nclass Solution {\npublic:\n int fun(vector<int> &v,int l,int r,vector<vector<int> > &dp)\n {\n if(dp[l][r]!=-1)\n return dp[l][r];\n
|
aarindey
|
NORMAL
|
2022-04-12T19:30:59.091871+00:00
|
2022-04-12T19:30:59.091911+00:00
| 160 | false |
```\nclass Solution {\npublic:\n int fun(vector<int> &v,int l,int r,vector<vector<int> > &dp)\n {\n if(dp[l][r]!=-1)\n return dp[l][r];\n int total=accumulate(v.begin()+l,v.begin()+r+1,0);\n int sum=0,res=0; \n if(l>=r)\n return 0;\n for(int i=l;i<r;i++)\n {\n sum+=v[i];\n total-=v[i];\n if(sum<total)\n {\n res=max(res,sum+fun(v,l,i,dp)); \n }\n else if(sum>total)\n {\n res=max(res,total+fun(v,i+1,r,dp));\n }\n else\n {\n res=max(res,sum+max(fun(v,l,i,dp),fun(v,i+1,r,dp)));\n }\n }\n return dp[l][r]=res;\n }\n int stoneGameV(vector<int>& stoneValue) { \n int n=stoneValue.size();\n vector<vector<int>> dp(n,vector<int>(n,-1));\n return fun(stoneValue,0,n-1,dp);\n }\n};\n```\n**Please upvote to motivate me in my quest of documenting all leetcode solutions(to help the community). HAPPY CODING:)\nAny suggestions and improvements are always welcome**
| 2 | 0 |
[]
| 0 |
stone-game-v
|
Java Simple and easy DP - memoization solution,, clean code with comments
|
java-simple-and-easy-dp-memoization-solu-0hiz
|
PLEASE UPVOTE IF YOU LIKE THIS SOLUTION\n\n\n\nclass Solution {\n Integer[][] cache;\n \n public int stoneGameV(int[] stoneValue) {\n int n = st
|
satyaDcoder
|
NORMAL
|
2021-06-18T03:51:18.912888+00:00
|
2021-06-18T03:51:18.912920+00:00
| 317 | false |
**PLEASE UPVOTE IF YOU LIKE THIS SOLUTION**\n\n\n```\nclass Solution {\n Integer[][] cache;\n \n public int stoneGameV(int[] stoneValue) {\n int n = stoneValue.length;\n \n cache = new Integer[n + 1][n + 1];\n \n //cumlative sum of stone values\n int[] prefixSum = new int[n + 1];\n for(int i = 0; i < n; i++){\n prefixSum[i + 1] = prefixSum[i] + stoneValue[i];\n }\n\n return getAliceStore(prefixSum, 1, n);\n }\n \n private int getAliceStore(int[] prefixSum , int l, int r){\n if(l == r) return 0;\n \n //reterive from cache \n if(cache[l][r] != null) return cache[l][r];\n \n int maxScore = Integer.MIN_VALUE;\n for(int i = l; i <= r - 1; i++){\n int left = prefixSum[i] - prefixSum[l - 1];\n int right = prefixSum[r] - prefixSum[i];\n \n if(left > right){\n //As right is smaller than left, Bob will select smaller sub row\n maxScore = Math.max(maxScore, right + getAliceStore(prefixSum, i + 1, r));\n \n }else if(left < right){\n //As left is smaller than right, Bob will select smaller sub row\n maxScore = Math.max(maxScore, left + getAliceStore(prefixSum, l, i));\n \n }else if(left == right){\n //lets Alice decide which row will be thrown away. \n maxScore = Math.max(maxScore, left + getAliceStore(prefixSum, l, i));\n maxScore = Math.max(maxScore, right + getAliceStore(prefixSum, i + 1, r));\n }\n }\n \n //save in cache \n return cache[l][r] = maxScore;\n }\n}\n```
| 2 | 0 |
['Dynamic Programming', 'Memoization', 'Java']
| 1 |
stone-game-v
|
C++ MCM solution, easy to understand.
|
c-mcm-solution-easy-to-understand-by-sha-d6hz
|
\n\t class Solution {\npublic:\n vector<int> pre;\n vector<vector<int>> dp;\n int helper(vector<int>&arr,int i,int j){\n if(i>=j){ // base case
|
shakiralam2017
|
NORMAL
|
2021-03-30T11:53:20.972660+00:00
|
2021-04-04T14:40:30.630008+00:00
| 266 | false |
```\n\t class Solution {\npublic:\n vector<int> pre;\n vector<vector<int>> dp;\n int helper(vector<int>&arr,int i,int j){\n if(i>=j){ // base case , element should be atleat one to divide the array.\n return 0;\n }\n if(dp[i][j] != -1){\n return dp[i][j];\n }\n int ans = INT_MIN/2;\n for(int k=i;k<j;k++){ // running loop to divide the array at each each position.\n int t1 = 0;\n int t2 = 0;\n int sum1 = (pre[j]-pre[k+1]+arr[k+1]); // sum of elements of second partition array.\n int sum2 = (pre[k]-pre[i]+arr[i]); // sum of elements of first partition array.\n if(sum1>=sum2){ // According to question, we will throw the greater sum array and keep score of less sum array.\n t1 = helper(arr,i,k);\n ans = max(ans,sum2+t1);\n }\n if(sum1<=sum2){ // same here above.\n t2 = helper(arr,k+1,j);\n ans = max(ans,sum1+t2);\n }\n }\n return dp[i][j] = ans;\n }\n int stoneGameV(vector<int>& arr) {\n int n = arr.size();\n dp.assign(n,vector<int>(n,-1));\n pre.assign(n,0);\n pre[0] = arr[0];\n for(int i=1;i<n;i++){\n pre[i] = pre[i-1]+arr[i];\n }\n return helper(arr,0,n-1);\n }\n};\n```
| 2 | 0 |
[]
| 0 |
stone-game-v
|
C++. Simple, DP + recursion, O(n^3), Straightforward, Easy to understand
|
c-simple-dp-recursion-on3-straightforwar-7t4n
|
pref is used to store prefix sum of the array.\n dp[i][j] is used to store answer for subarray {i, i+1, i+2,....., j-1, j}\n\n\nclass Solution {\npublic:\n
|
zeddie
|
NORMAL
|
2020-11-06T11:15:21.740578+00:00
|
2020-12-07T06:47:29.326127+00:00
| 264 | false |
<strong> pref </strong> is used to store prefix sum of the array.\n<strong> dp[i][j]</strong> is used to store answer for subarray {i, i+1, i+2,....., j-1, j}\n\n```\nclass Solution {\npublic:\n vector< vector<long> > dp;\n vector< long> pref;\n \n int helper(int i, int j, vector<int> &val) {\n if(i>j) return 0;\n if(dp[i][j]!=-1) return dp[i][j];\n \n long l=0, r= pref[j+1]-pref[i];\n long ans=0;\n for(int s=i; s<j; ++s){\n l+=val[s];\n r-=val[s];\n \n if(l==r) ans = max( ans, l+ max(helper(i, s, val), helper(s+1, j, val)));\n else if(l<r) ans= max(ans, l+ helper(i,s, val));\n else ans= max(ans, r+ helper(s+1, j, val));\n }\n \n return dp[i][j]=ans;\n }\n int stoneGameV(vector<int>& val) {\n int n=val.size();\n dp.assign(501, vector<long > (501, -1));\n pref.assign(501,0);\n \n for(int i=0; i<n; ++i) pref[i+1]= pref[i]+ val[i];\n return helper(0, n-1, val);\n }\n};\n```
| 2 | 0 |
[]
| 1 |
stone-game-v
|
memoization c++ solutions
|
memoization-c-solutions-by-atulkumar1-pdj6
|
\n \n int solve(vector<int>& a,int s,int e, vector<vector<int>>&dp)\n {\n if(s>e)\n {\n return 0; \n }\n \n
|
ATulKumaR1
|
NORMAL
|
2020-08-23T05:39:23.603669+00:00
|
2020-08-23T05:39:23.603700+00:00
| 91 | false |
```\n \n int solve(vector<int>& a,int s,int e, vector<vector<int>>&dp)\n {\n if(s>e)\n {\n return 0; \n }\n \n if(dp[s][e]!=-1)\n {\n return dp[s][e]; \n }\n \n int i,j,k,l; \n int sum=0;\n int ans=0; \n \n for(i=s;i<=e;i++)\n {\n sum+=a[i]; \n }\n \n k=0; \n \n for(j=s;j<=e;j++)\n {\n k+=a[j]; \n l=sum-k; \n if(k>l)\n {\n ans=max(ans,l+solve(a,j+1,e,dp));\n }\n else if(k<l)\n {\n ans=max(ans,k+solve(a,s,j,dp));\n }\n else\n {\n \n ans=max(ans,k+solve(a,s,j,dp));\n ans=max(ans,l+solve(a,j+1,e,dp));\n }\n } \n \n dp[s][e]=ans; \n \n return ans; \n }\n int stoneGameV(vector<int>& s) {\n \n if(s.size()<=1)\n {\n return 0;\n }\n \n int n=s.size(); \n vector<vector<int>>dp(n+1,vector<int>(n+1,-1)); \n \n int ans=solve(s,0,s.size()-1,dp); \n return ans; \n \n }\n\t```\n};\n```
| 2 | 0 |
[]
| 0 |
stone-game-v
|
[Java] DFS + dp memo
|
java-dfs-dp-memo-by-marvinbai-idd7
|
\nclass Solution {\n public int stoneGameV(int[] sv) {\n int n = sv.length;\n int[][] dp = new int[n + 1][n + 1];\n int[] sum = new int[
|
marvinbai
|
NORMAL
|
2020-08-23T04:11:57.546449+00:00
|
2020-08-23T04:19:59.254265+00:00
| 217 | false |
```\nclass Solution {\n public int stoneGameV(int[] sv) {\n int n = sv.length;\n int[][] dp = new int[n + 1][n + 1];\n int[] sum = new int[n + 1];\n for(int i = 1; i <= n; i++) {\n sum[i] = sv[i - 1] + sum[i - 1];\n } \n return dfs(sv, 1, n, dp, sum);\n }\n \n private int dfs(int[] sv, int i, int j, int[][] dp, int[] sum) {\n if(dp[i][j] != 0) return dp[i][j];\n if(i == j) return 0;\n if(j - i == 1) return Math.min(sv[i - 1], sv[j - 1]);\n int res = 0;\n for(int k = i; k < j; k++) {\n int ans = 0;\n int sum_l = sum[k] - sum[i - 1]; // i-th ... k-th\n int sum_r = sum[j] - sum[k]; // (k+1)-th ... j-th\n if(sum_l > sum_r) {\n ans = sum_r + dfs(sv, k + 1, j, dp, sum);\n } else if(sum_l < sum_r) {\n ans = sum_l + dfs(sv, i, k, dp, sum);\n } else {\n ans = Math.max(sum_r + dfs(sv, k + 1, j, dp, sum),\n sum_l + dfs(sv, i, k, dp, sum));\n }\n res = Math.max(res, ans);\n }\n dp[i][j] = res;\n return res;\n }\n}\n```
| 2 | 0 |
[]
| 0 |
stone-game-v
|
[C++] Top Down DP + prefix sum solution.
|
c-top-down-dp-prefix-sum-solution-by-che-ee0f
|
\ndp[i][j] represent the maximum value from i to j. We try to spilt the array to two part left and right, There are 3 situation we need to cosider: \n1. if the
|
chejianchao
|
NORMAL
|
2020-08-23T04:07:50.980553+00:00
|
2020-08-23T04:11:38.277957+00:00
| 148 | false |
\ndp[i][j] represent the maximum value from i to j. We try to spilt the array to two part `left` and `right`, There are 3 situation we need to cosider: \n1. if the sum of `left` is less than `right` part, then we do dfs(l, i); \n2. if the sum of `left` is greater than `right` part, then we do dfs(l, i + 1, r); \n3. if the sum of `left` is equal `right` part, then we do both of `1` and `2` \nwe can get the sum of the left and right part in O(1) by using prefix sum. \nWhen we do this calculation, we keep th maximum result and store it into dp at the end. \n```\nclass Solution {\npublic:\n int dp[501][501];\n int dfs(vector<int>& sv, int l, int r) {\n if(l >= r) return 0;\n if(dp[l][r] >= 0) return dp[l][r];\n int res = 0;\n for(int i = l; i <r ; ++i) {\n int lv = sv[i] - (l > 0 ? sv[l - 1] : 0);\n int rv = sv[r] - sv[i];\n if(lv > rv) res = max(res, dfs(sv, i + 1, r) + rv);\n else if(lv < rv) res = max(res, dfs(sv, l, i) + lv);\n else {\n res = max({res, dfs(sv, i + 1, r) + rv, dfs(sv, l, i) + lv});\n }\n \n }\n return dp[l][r] = res;\n }\n int stoneGameV(vector<int>& stoneValue) {\n memset(dp, -1, sizeof(dp));\n if(stoneValue.size() == 1) return 0;\n for(int i = 1; i < stoneValue.size(); ++i) stoneValue[i] += stoneValue[i - 1];\n return dfs(stoneValue, 0, stoneValue.size() - 1);\n }\n};\n```
| 2 | 0 |
[]
| 0 |
stone-game-v
|
Python, elegant memoization
|
python-elegant-memoization-by-warmr0bot-eyj8
|
\nfrom functools import lru_cache\nclass Solution:\n def stoneGameV(self, stoneValue: List[int]) -> int:\n prefix = [0]\n for i in range(len(st
|
warmr0bot
|
NORMAL
|
2020-08-23T04:02:50.189289+00:00
|
2020-08-23T04:05:22.584943+00:00
| 456 | false |
```\nfrom functools import lru_cache\nclass Solution:\n def stoneGameV(self, stoneValue: List[int]) -> int:\n prefix = [0]\n for i in range(len(stoneValue)):\n prefix += [prefix[-1] + stoneValue[i]]\n print(prefix)\n \n @lru_cache(None)\n def dfs(left=0, right=len(prefix)-1):\n if right - left == 1: return 0\n \n maxval = -1\n for i in range(left+1, right):\n leftsum = prefix[i] - prefix[left]\n rightsum = prefix[right] - prefix[i]\n \n if leftsum > rightsum:\n maxval = max(maxval, rightsum + dfs(i, right))\n elif rightsum > leftsum:\n maxval = max(maxval, leftsum + dfs(left, i))\n else:\n maxval = leftsum + max(dfs(left, i), dfs(i, right))\n \n return maxval\n \n return dfs()\n```
| 2 | 0 |
['Memoization', 'Python']
| 0 |
stone-game-v
|
Python DFS + Memo
|
python-dfs-memo-by-tomzy-bshx
|
\nclass Solution:\n def stoneGameV(self, stoneValue: List[int]) -> int:\n n = len(stoneValue)\n pre = [0]\n for i in range(n):\n
|
tomzy
|
NORMAL
|
2020-08-23T04:02:36.749536+00:00
|
2020-08-23T04:27:00.863765+00:00
| 538 | false |
```\nclass Solution:\n def stoneGameV(self, stoneValue: List[int]) -> int:\n n = len(stoneValue)\n pre = [0]\n for i in range(n):\n pre.append(stoneValue[i] + pre[-1])\n @lru_cache(None)\n def dfs(l, r):\n if r <= l:\n return 0\n res = 0\n for i in range(l, r):\n # [l, i] [i + 1, r]\n left = pre[i + 1] - pre[l]\n right = pre[r + 1] - pre[i + 1]\n if right > left:\n res = max(res, dfs(l, i) + left)\n elif left > right:\n res = max(res, dfs(i + 1, r) + right)\n else:\n res = max(res, dfs(l, i) + left)\n res = max(res, dfs(i + 1, r) + right)\n return res\n return dfs(0, n - 1)\n```
| 2 | 0 |
['Depth-First Search', 'Memoization', 'Python', 'Python3']
| 1 |
stone-game-v
|
Simple Java memoization solution
|
simple-java-memoization-solution-by-hee_-qs7z
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
hee_maan_shee
|
NORMAL
|
2025-03-23T19:43:09.282047+00:00
|
2025-03-23T19:43:09.282047+00:00
| 8 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int stoneGameV(int[] stones) {
int n = stones.length;
int[] preSum = new int[n];
preSum[0] = stones[0];
for(int i=1; i<n; i++){
preSum[i] = preSum[i-1] + stones[i];
}
int[][] dp = new int[n][n];
for(int[] row : dp){
Arrays.fill(row, -1);
}
return solve(0, n-1, dp, preSum, stones);
}
private int solve(int start, int end, int[][] dp, int[] preSum, int[] stones){
if(end-start+1 == 1) return 0;
if(start + 1 == end) return Math.min(stones[start], stones[end]);
if(dp[start][end] != -1) return dp[start][end];
int maxi = 0;
for(int i=start; i<end; i++){
int leftSum = preSum[i] - (start-1 >= 0 ? preSum[start-1] : 0);
int rightSum = preSum[end] - preSum[i];
if(leftSum > rightSum){
//considering right sum
maxi = Math.max(maxi, rightSum + solve(i+1, end, dp, preSum, stones));
}else if(leftSum < rightSum){
//considering left sum
maxi = Math.max(maxi, leftSum + solve(start, i, dp, preSum, stones));
}else{
maxi = Math.max(maxi, rightSum + solve(i+1, end, dp, preSum, stones));
maxi = Math.max(maxi, leftSum + solve(start, i, dp, preSum, stones));
}
}
return dp[start][end] = maxi;
}
}
```
| 1 | 0 |
['Dynamic Programming', 'Java']
| 0 |
stone-game-v
|
Easy to Understand || Memoization || DP (Top Down)
|
easy-to-understand-memoization-dp-top-do-krva
|
Intuition\nThe problem at hand requires finding the maximum score a player can achieve given a series of stone piles where the player can choose to split the ar
|
tinku_tries
|
NORMAL
|
2024-06-03T04:43:18.755492+00:00
|
2024-06-03T04:43:18.755511+00:00
| 344 | false |
# Intuition\nThe problem at hand requires finding the maximum score a player can achieve given a series of stone piles where the player can choose to split the array into two parts. The score is determined by the sum of stones in the smaller segment. To solve this, we can use dynamic programming to efficiently compute the maximum score by storing intermediate results.\n\n# Approach\n1. **Prefix Sum Array**: Calculate the prefix sum array for quick calculation of segment sums.\n2. **Dynamic Programming**: Use a 2D `dp` array where `dp[st][end]` represents the maximum score the player can achieve from the segment of the array starting at `st` and ending at `end`.\n3. **Recursive Function**: Define a recursive function `f` to compute the maximum score for a given segment. The function will:\n - Use the prefix sum array to determine the sum of the left and right segments.\n - Recursively call itself to compute the maximum score for the next possible segments.\n - Store and reuse intermediate results to avoid redundant calculations.\n\n# Complexity\n- **Time complexity**: The time complexity is \\(O(n^3)\\) because for each pair `(st, end)` we might iterate through all possible split points.\n- **Space complexity**: The space complexity is \\(O(n^2)\\) for storing the `dp` array and the prefix sum array.\n# Beats\n\n\n# Code\n```cpp\nclass Solution {\npublic:\n // Declare the dp array to store the results of subproblems\n vector<vector<int>> dp;\n\n // Function to calculate the maximum score for the segment from st to end\n int f(vector<int>& pref_sum, int st, int end) {\n // Base case: if the start index is greater than or equal to the end index, return 0\n if (st >= end) return 0;\n \n // If the result for this subproblem is already calculated, return it\n if (dp[st][end] != -1) return dp[st][end];\n \n // Initialize the score to 0\n int score = 0;\n \n // Iterate through all possible split points\n for (int i = st; i <= end; i++) {\n // Calculate the left segment sum\n int lf = (st == 0) ? pref_sum[i] : pref_sum[i] - pref_sum[st-1];\n // Calculate the right segment sum\n int rt = pref_sum[end] - pref_sum[i];\n \n // If the left segment sum is greater than the right, maximize score using the right segment\n if (lf > rt) \n score = max(score, rt + f(pref_sum, i + 1, end));\n // If the right segment sum is greater than the left, maximize score using the left segment\n else if (lf < rt) \n score = max(score, lf + f(pref_sum, st, i));\n // If both segments are equal, maximize score using both possible segments\n else \n score = max({score, rt + f(pref_sum, i + 1, end), lf + f(pref_sum, st, i)});\n }\n // Store the result in the dp array and return it\n return dp[st][end] = score;\n }\n \n // Main function to calculate the maximum score for the entire array\n int stoneGameV(vector<int>& v) {\n int n = v.size(); // Get the size of the array\n dp.clear(); // Clear the dp array\n dp.resize(n + 1, vector<int>(n + 1, -1)); // Resize the dp array and initialize it with -1\n \n // Create the prefix sum array\n vector<int> pref_sum(n + 1, 0);\n pref_sum[0] = v[0];\n for (int i = 1; i < n; i++) \n pref_sum[i] = v[i] + pref_sum[i-1];\n \n // Call the recursive function and return the result\n return f(pref_sum, 0, n - 1);\n }\n};\n\n```\n\nThis solution leverages dynamic programming and prefix sums to efficiently compute the maximum score in the stone game, ensuring that we minimize redundant calculations and achieve optimal performance for larger inputs.
| 1 | 0 |
['Array', 'Math', 'Dynamic Programming', 'Game Theory', 'C++']
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.