question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
find-n-unique-integers-sum-up-to-zero
|
Easy and Simple Solution in Java, C++ and Python ||0ms Runtime in Java and C++||
|
easy-and-simple-solution-in-java-c-and-p-c0jp
|
Java []\nclass Solution {\n public int[] sumZero(int n) {\n int ans[] = new int[n];\n for(int i=0;i<n;i++)\n {\n ans[i] = i*2
|
_veer_singh04_
|
NORMAL
|
2023-07-05T17:44:59.266660+00:00
|
2023-07-05T17:57:20.961140+00:00
| 670 | false |
```Java []\nclass Solution {\n public int[] sumZero(int n) {\n int ans[] = new int[n];\n for(int i=0;i<n;i++)\n {\n ans[i] = i*2 -n+1;\n }\n return ans;\n }\n}\n```\n```python []\nclass Solution(object):\n def sumZero(self, n):\n return [i*2-n+1 for i in range(0,n)]\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> sumZero(int n) {\n vector <int> ans;\n for (int i=0; i<n; i++)\n {\n ans.push_back(i*2-n+1);\n }\n return ans;\n }\n};\n```\n
| 4 | 0 |
['Array', 'Math', 'Python', 'C++', 'Java']
| 1 |
find-n-unique-integers-sum-up-to-zero
|
Python Solution, simple and easy to follow
|
python-solution-simple-and-easy-to-follo-006f
|
\ndef uniqueSum(n):\n result = []\n\n for i in range(n):\n result.append(i*2 - n + 1)\n return result\n
|
vikingdev
|
NORMAL
|
2022-09-13T15:18:32.341774+00:00
|
2022-09-13T15:18:32.349839+00:00
| 551 | false |
```\ndef uniqueSum(n):\n result = []\n\n for i in range(n):\n result.append(i*2 - n + 1)\n return result\n```
| 4 | 0 |
['Array', 'Python', 'Python3']
| 1 |
find-n-unique-integers-sum-up-to-zero
|
Beginner Friendly JAVA easy solution with comments || 0 ms 100% fast
|
beginner-friendly-java-easy-solution-wit-j2w2
|
100% Fastest JAVA SOLUTION\nREAD the comments along the steps...........feel free to comment any query\n\nDon\'T forget to UPVOTE....it means a lot and encourag
|
satish2203
|
NORMAL
|
2022-01-22T17:46:15.825811+00:00
|
2022-01-22T17:46:15.825839+00:00
| 222 | false |
**100% Fastest JAVA SOLUTION**\n**READ the comments along the steps...........feel free to comment any query**\n\n**Don\'T forget to UPVOTE....it means a lot and encourage to post more**\n\n```\n public int[] sumZero(int n) {\n \n int arr[]=new int[n]; // create a array of given size\n int pos=1; // for filling positive numbers\n int neg=1; // for filling negative numbers\n \n if(n%2==0) // --------> If n is even \n {\n for(int i=0;i<n/2;i++) // divide array into two parts\n {\n arr[i] = pos++; // fill half of array with positive\n arr[i+n/2] = -(neg++); // fill another half with same number but negative so total sum is zero\n }\n }\n else // if n is odd\n {\n arr[0]=0; // add 0 to first index.....now remaining size is again even...repeat // above steps\n for(int i=1;i<=n/2;i++)\n {\n arr[i] = pos++; \n arr[i+n/2] = -(neg++);\n }\n \n }\n \n return arr; // return the array\n \n // Runtime: 0 ms, faster than 100.00% of Java online submissions\n \n //PLEASE UPVOTE......\n \n```
| 4 | 0 |
['Java']
| 1 |
find-n-unique-integers-sum-up-to-zero
|
Python 3 simple solution
|
python-3-simple-solution-by-derek-y-qqt6
|
```\nclass Solution:\n def sumZero(self, n: int) -> List[int]:\n res = [0] if n % 2 else []\n for i in range(1, n // 2 + 1):\n res.a
|
derek-y
|
NORMAL
|
2021-11-26T16:46:35.345531+00:00
|
2021-11-26T16:46:35.345562+00:00
| 420 | false |
```\nclass Solution:\n def sumZero(self, n: int) -> List[int]:\n res = [0] if n % 2 else []\n for i in range(1, n // 2 + 1):\n res.append(i)\n res.append(-i)\n return res
| 4 | 1 |
['Python', 'Python3']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
Very easy JAVA Solution. Runtime: 0 ms, faster than 100.00%
|
very-easy-java-solution-runtime-0-ms-fas-4j46
|
\nclass Solution\n{\n public int[] sumZero(int n)\n {\n int arr[] = new int[n];\n if(n%2==0)\n {\n for(int i=0, val=1; i<n
|
ghosharindam195
|
NORMAL
|
2021-02-17T06:26:31.515784+00:00
|
2021-02-17T06:26:31.515811+00:00
| 364 | false |
```\nclass Solution\n{\n public int[] sumZero(int n)\n {\n int arr[] = new int[n];\n if(n%2==0)\n {\n for(int i=0, val=1; i<n; i+=2,val++)\n {\n arr[i]=val;\n arr[i+1]=-val;\n }\n }\n else\n {\n arr[0]=0;\n for(int i=1, val=1; i<n; i+=2,val++)\n {\n arr[i]=val;\n arr[i+1]=-val;\n }\n }\n return arr;\n \n }\n}\n```
| 4 | 1 |
['Java']
| 1 |
find-n-unique-integers-sum-up-to-zero
|
C++ Super Easy Solution, 0ms faster than 100%
|
c-super-easy-solution-0ms-faster-than-10-oa8r
|
\nclass Solution {\npublic:\n vector<int> sumZero(int n) {\n vector<int> res(n);\n int a = 1;\n for (int i = 0; i < n; i+=2) {\n
|
yehudisk
|
NORMAL
|
2020-12-17T15:38:26.276634+00:00
|
2020-12-17T15:38:26.276675+00:00
| 267 | false |
```\nclass Solution {\npublic:\n vector<int> sumZero(int n) {\n vector<int> res(n);\n int a = 1;\n for (int i = 0; i < n; i+=2) {\n if (i == n-1) {\n res[i] = 0;\n return res;\n }\n \n res[i] = a;\n res[i+1] = -a;\n a++;\n }\n return res;\n }\n};\n```\n**Like it? please upvote...**
| 4 | 1 |
['C']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
Python Solution
|
python-solution-by-rachitsxn292-zac0
|
\nclass Solution(object):\n def sumZero(self, n):\n return range(1-n, n, 2)\n
|
rachitsxn292
|
NORMAL
|
2020-04-01T21:24:21.272793+00:00
|
2020-04-01T21:24:21.272845+00:00
| 360 | false |
```\nclass Solution(object):\n def sumZero(self, n):\n return range(1-n, n, 2)\n```
| 4 | 0 |
['Python']
| 1 |
find-n-unique-integers-sum-up-to-zero
|
Easy Python Solution
|
easy-python-solution-by-ignasialemany-vltj
|
\timport random\n\tclass Solution:\n\t\tdef sumZero(self, n: int) -> List[int]:\n\t\t\tanswer = []\n\t\t\tanswer = random.sample(range(1,1000),n-1)\n\t\t\tanswe
|
ignasialemany
|
NORMAL
|
2020-01-26T08:18:08.786758+00:00
|
2020-01-26T08:18:08.786795+00:00
| 355 | false |
\timport random\n\tclass Solution:\n\t\tdef sumZero(self, n: int) -> List[int]:\n\t\t\tanswer = []\n\t\t\tanswer = random.sample(range(1,1000),n-1)\n\t\t\tanswer.append(-sum(answer))\n\t\t\treturn answer
| 4 | 0 |
[]
| 2 |
find-n-unique-integers-sum-up-to-zero
|
[JAVA] simple solution
|
java-simple-solution-by-nandathantsin-ye0k
|
\nclass Solution {\n public int[] sumZero(int n) {\n int[] res = new int[n];\n for(int i=0;i<n/2;i++){\n res[i]=-1*(i+1);\n
|
nandathantsin
|
NORMAL
|
2019-12-29T04:04:34.777917+00:00
|
2019-12-29T04:04:34.777954+00:00
| 806 | false |
```\nclass Solution {\n public int[] sumZero(int n) {\n int[] res = new int[n];\n for(int i=0;i<n/2;i++){\n res[i]=-1*(i+1);\n res[n-i-1]=(i+1);\n }\n return res;\n }\n}\n```
| 4 | 1 |
['Java']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
Beats 100% || JAVA||
|
beats-100-java-by-novasynapse17-3ifr
|
Intuition\nOnly thought was to add positive and negative numbers to sum up zero but wait there are two cases (odd and even)\n\n# Approach\nMade two seperate cas
|
theDummy
|
NORMAL
|
2024-09-05T08:53:31.793147+00:00
|
2024-09-05T08:53:31.793180+00:00
| 396 | false |
# Intuition\nOnly thought was to add positive and negative numbers to sum up zero but wait there are two cases (odd and even)\n\n# Approach\nMade two seperate cases for odd and even \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int[] sumZero(int n) {\n int[] ansArray=new int[n];\n if(n%2==0){ \n for(int c=0;c<n/2;c++){\n ansArray[c]=c+1;\n ansArray[n/2+c]=-( ansArray[c]);\n }\n }\n else{\n ansArray[n/2]=0;\n for(int c=0;c<n/2;c++){\n ansArray[c]=c+1;\n ansArray[n/2+c]=-( ansArray[c]);\n }\n\n }\n return ansArray;\n }\n}\n```
| 3 | 0 |
['Java']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
Brute force approach || Easy Solution || 100% runtime
|
brute-force-approach-easy-solution-100-r-fsi1
|
Intuition\nIf n is odd then only add zero at last and if n is even then don\'t add zero in the array and return it and first add 1 and -1 pair, 2 and -2 pair, 3
|
Sushant_3999
|
NORMAL
|
2024-08-13T17:51:55.773662+00:00
|
2024-08-13T17:51:55.773679+00:00
| 394 | false |
# Intuition\nIf n is odd then only add zero at last and if n is even then don\'t add zero in the array and return it and first add 1 and -1 pair, 2 and -2 pair, 3 and -3 pair and so on until n-1 times.\n\n# Approach\n1. Create a array sumArr with n size.\n2. create a for() loop with (i=0; i<n ; i++):\ni.check if(n%2==1 && i==n-1), yes then set last element as 0.\nii.set sumArr[i++] = -1*(num); and set sumArr[i] = num++;\n3. After processing the elements in array, return the array.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n). Because array creates in function.\n\n# Code\n```\nclass Solution {\n public int[] sumZero(int n) {\n int[] sumArr = new int[n];\n int num = 1;\n for(int i=0; i<n; i++){\n if(n%2==1 && i==n-1){\n sumArr[n-1] = 0;\n break;\n }\n sumArr[i++] = -1*(num);\n sumArr[i] = num++;\n }\n return sumArr;\n }\n}\n```
| 3 | 0 |
['Java']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
Easy | O(n) | Java |
|
easy-on-java-by-suraj_ph116-amd4
|
Intuition\nIf n is odd add 0 to the resultant array.\n\n# Approach\nMaintain the symmetry of integers i.e. resultant array must contain +ve as well as -ve value
|
suraj_ph116
|
NORMAL
|
2024-03-19T16:58:30.812416+00:00
|
2024-03-19T16:58:30.812452+00:00
| 261 | false |
# Intuition\nIf n is odd add 0 to the resultant array.\n\n# Approach\nMaintain the symmetry of integers i.e. resultant array must contain +ve as well as -ve value of the number that is being inserted.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution {\n public int[] sumZero(int n) {\n int[] arr = new int[n];\n\n if (n == 1) {\n arr[0] = 0;\n return arr;\n }\n\n if (n % 2 != 0) {\n arr[0] = 0;\n for (int j = 1; j < n; j = j + 2) {\n arr[j] = j;\n arr[j + 1] = -j;\n }\n } else {\n for (int j = 0; j < n; j = j=j+2) {\n arr[j] = j+1;\n arr[j + 1] = -(j+1);\n }\n }\n return arr;\n }\n}\n```
| 3 | 0 |
['Java']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
very simple solution 💯|| interesting
|
very-simple-solution-interesting-by-moha-m1kr
|
Intuition\n- simple solution\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n- unique elements \uD83D\uDE02\n Describe your approac
|
Mohanraj04
|
NORMAL
|
2023-12-06T10:06:30.666336+00:00
|
2023-12-06T10:06:30.666369+00:00
| 457 | false |
# Intuition\n- simple solution\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- unique elements \uD83D\uDE02\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] sumZero(int n) {\n int arr[] = new int[n];\n int sum=0;\n for(int i =0;i<n-1;i++){\n arr[i]=i+1;\n sum = sum +arr[i];\n }\n arr[n-1]=(-(sum));\n\n \n return arr;\n }\n}\n```
| 3 | 0 |
['Java']
| 1 |
find-n-unique-integers-sum-up-to-zero
|
Beats 100.00%of users with C++ || Easy To Understand
|
beats-10000of-users-with-c-easy-to-under-vhtk
|
\n\n# Approach : \n\n1. Check if n is equal to 1.\n- If yes, return a vector containing [0].\n- This handles the special case where the sequence length is 1.\n
|
VenkateshMundra
|
NORMAL
|
2023-10-21T13:30:03.690980+00:00
|
2023-10-21T13:31:42.338664+00:00
| 42 | false |
\n\n# Approach : \n\n1. Check if **n** is equal to 1.\n- If yes, return a vector containing [0].\n- This handles the special case where the sequence length is 1.\n\n2. Check if **n** is even (e.g., 2, 4, 6, etc.).\n- If **n** is even, we want to generate a sequence with both negative and positive numbers.\n- Initialize a loop to generate negative numbers from -n/2 to -1 and add them to the **answer** vector.\n- Then, use another loop to generate positive numbers from 1 to n/2 and add them to the **answer** vector.\n\n3. If **n** is odd (e.g., 3, 5, 7, etc.), we want to ensure that 0 is included in the sequence.\n- Initialize two variables, **start** and **end**, to -n/2 and n/2, respectively.\n- Use a loop that continues as long as **start** is less than or equal to end.\n- Inside the loop, add the value of **start** to the answer vector and increment **start** by 1 in each iteration.\n\n4. Return the **answer** vector, which contains the sequence of integers that sum up to zero and has a length of **n**.\n\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> sumZero(int n) {\n vector<int>answer;\n\n if(n==1){\n answer.push_back(0);\n return answer;\n }\n\n if(n%2==0){\n for(int i=-n/2;i<0;i++){\n answer.push_back(i);\n }\n for(int i=1;i<=n/2;i++){\n answer.push_back(i);\n }\n }\n else{\n int start=-n/2;\n int end=n/2;\n\n while(start<=end){\n answer.push_back(start);\n start++;\n }\n }\n return answer;\n }\n};\n```
| 3 | 0 |
['C++']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
Beats 100.00% runtime and 99.31% memory
|
beats-10000-runtime-and-9931-memory-by-c-7x2z
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
chaitanyanitin59
|
NORMAL
|
2023-09-15T06:04:27.524476+00:00
|
2023-09-15T06:04:27.524508+00:00
| 238 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] sumZero(int n) {\n int[] array = new int[n];\n\t\tfor(int i=1;i<n;i+=2) {\n\t\t\tarray[i-1]=i;\n\t\t\tarray[i]=-i;\n\t\t}\n return array;\n }\n}\n```
| 3 | 0 |
['Java']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
Python || C++ || Java || Easy and Neat Solution (0 ms runtime)
|
python-c-java-easy-and-neat-solution-0-m-48gi
|
Code\nPython []\nclass Solution(object):\n def sumZero(self, n):\n return [i*2-n+1 for i in range(0,n)]\n \n\nJava []\nclass Solution {\n pu
|
phalakbh
|
NORMAL
|
2023-07-05T17:59:58.147685+00:00
|
2023-07-05T17:59:58.147713+00:00
| 635 | false |
# Code\n```Python []\nclass Solution(object):\n def sumZero(self, n):\n return [i*2-n+1 for i in range(0,n)]\n \n```\n```Java []\nclass Solution {\n public int[] sumZero(int n) {\n int ans[] = new int[n];\n for(int i=0;i<n;i++)\n {\n ans[i] = i*2 -n+1;\n }\n return ans;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> sumZero(int n) {\n vector <int> ans;\n for (int i=0; i<n; i++)\n {\n ans.push_back(i*2-n+1);\n }\n return ans;\n }\n};\n```\n
| 3 | 0 |
['Array', 'Math', 'Python', 'C++', 'Java']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
Simplest Java Solution - based on intuition rather then series operations - O(n).
|
simplest-java-solution-based-on-intuitio-hlu8
|
Intuition\nIn order to make an array sum 0, the array will def have complementary pairs that add upto 0: \n- (0), (-1,1), (-2, 2)...(-n,n) etc.\n\nNow if the si
|
pateltrushit1710
|
NORMAL
|
2023-06-02T06:20:07.428372+00:00
|
2023-06-07T04:20:59.034715+00:00
| 404 | false |
# Intuition\nIn order to make an array sum 0, the array will def have complementary pairs that add upto 0: \n- (0), (-1,1), (-2, 2)...(-n,n) etc.\n\nNow if the size of the array is n, then we start filling the ends of array with the negative pairs starting from n and then decrement by 1:\n- Even n: -n, -(n-1), ..., -1, 1, ..., n-1, n\n- Odd n: -n, -(n-1), ..., 0, ..., n-1, n\n\nIn this way addition of each and every pair will always result into 0.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n##### Case 1: n = odd\n example n = 5\n initial array arr[5] = [0, 0, 0, 0, 0]\n\n iteration 1:\n i = 0, j = 4 ( i < j )\n ans[0] = 5;\n i += 1;\n ans[4] = -5;\n j -= 1;\n n -= 1;\n ans = [-5, 0, 0, 0, 5], n = 4\n\n iteration 2:\n i = 1, j = 3 ( i < j )\n ans[1] = 4;\n i += 1;\n ans[3] = -4;\n j -= 1;\n n -= 1;\n ans = [-5, -4, 0, 4, 5], n = 3\n\n iteration 3:\n i = 2, j = 2 (i is not less then j)\n end while\n final ans = [-5, -4, 0, 4, 5], n = 3\n\n##### Case 2: n = even\n example n = 4\n initial array arr[4] = [0, 0, 0, 0]\n\n iteration 1:\n i = 0, j = 3 ( i < j )\n ans[0] = 4;\n i += 1;\n ans[3] = -4;\n j -= 1;\n n -= 1;\n ans = [-4, 0, 0, 4], n = 3\n\n iteration 2:\n i = 1, j = 2 ( i < j )\n ans[1] = 3;\n i += 1;\n ans[2] = -3;\n j -= 1;\n n -= 1;\n ans = [-4, -3, 3, 4], n = 2\n\n iteration 3:\n i = 2, j = 1 (i is not less then j)\n out of loop\n final ans = [-4, -3, 3, 4], n = 2\n\n\n\n# Approach\nWe create an araay of length n ```int[] ans = new int[n];```\n\nStep 1: To iterate the array from both the ends we use a while loop with condition ```i < j``` and ```i = 0``` and ```j = n-1```.\nStep 2: Put the values ```-n``` and ```n``` into ```ans[i]``` and ```ans[j]```.\nStep 3: Decrement ```n``` by 1.\n > **Hit me up at [email protected] for any doubts.**\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] sumZero(int n) {\n int[] ans = new int[n];\n int i = 0 , j = n - 1;\n while(i < j){\n ans[i++] = n;\n ans[j--] = -n;\n n--;\n }\n return ans;\n }\n}\n```
| 3 | 0 |
['Java']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
Java | Easy Solution | 0 ms - 100% beats
|
java-easy-solution-0-ms-100-beats-by-ako-71i9
|
Approach\n\n1. The sumZero method takes an integer n as input and returns an array of n unique integers.\n2. Initialize an integer array res of size n to store
|
akobirswe
|
NORMAL
|
2023-05-30T04:27:16.160925+00:00
|
2023-05-30T04:27:16.160974+00:00
| 252 | false |
# Approach\n\n1. The `sumZero` method takes an integer `n` as input and returns an array of `n` unique integers.\n2. Initialize an integer array `res` of size `n` to store the resulting array.\n3. Iterate from `i = 0` to `n/2 - 1`. This iteration covers half of the array because for each positive number generated, its negative counterpart will also be included.\n4. Inside the loop, assign `i + 1` to `res[i]` to populate the first half of the array with increasing positive integers starting from 1.\n5. Assign the negation of `(i + 1)` to `res[i + n/2]` to populate the second half of the array with corresponding negative integers.\n - By adding `n/2` to the index, you ensure that the negative integers are stored in the latter half of the array.\n6. After completing the loop, the array `res` will contain `n` unique integers that sum up to zero.\n7. Return the resulting array `res` as the output.\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n# Code\n```\nclass Solution {\n public int[] sumZero(int n) {\n int[] res = new int[n];\n for(int i = 0; i < n/2; i++){\n res[i]= i+1;\n res[i + n/2] = -(i+1);\n }\n return res;\n }\n}\n```
| 3 | 0 |
['Array', 'Math', 'Java']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
PHP and Python solution
|
php-and-python-solution-by-__bakhtiyorof-tmkq
|
Intuition\narray[ i ] = i * 2 - n + 1\n\n- Space complexity:\n Add your space complexity here, e.g. O(n) \n\n# Code\nPHP\n\nclass Solution {\n\n /**\n *
|
__bakhtiyoroff__
|
NORMAL
|
2023-04-17T21:25:19.456761+00:00
|
2023-04-17T21:26:10.775345+00:00
| 753 | false |
# Intuition\narray[ i ] = i * 2 - n + 1\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\nPHP\n```\nclass Solution {\n\n /**\n * @param Integer $n\n * @return Integer[]\n */\n function sumZero($n) {\n $array= array();\n for ($i = 0; $i < $n; $i++){\n array_push($array, $i * 2 - $n + 1);\n }\n return $array;\n }\n}\n```\n\nPython\n``` \nclass Solution:\n def sumZero(self, n: int) -> List[int]:\n array = [ int(i * 2 - n + 1) for i in range(n)]\n return array\n```
| 3 | 0 |
['PHP', 'Python3']
| 1 |
find-n-unique-integers-sum-up-to-zero
|
5 Lines | Easy Java Solution | Beats 100% | 0 ms
|
5-lines-easy-java-solution-beats-100-0-m-jg4b
|
Code\nAlso beats 86.68% in terms of memory at the time of submission.\n\nclass Solution {\n public int[] sumZero(int n) {\n int[] answer = new int[n];
|
KevinKwan
|
NORMAL
|
2023-01-11T01:52:50.692384+00:00
|
2023-01-18T04:33:15.439777+00:00
| 1,133 | false |
# Code\nAlso beats 86.68% in terms of memory at the time of submission.\n```\nclass Solution {\n public int[] sumZero(int n) {\n int[] answer = new int[n];\n for (int i = 1; i<n; i+=2) {\n answer[i-1]=i;\n answer[i]=-i;\n }\n return answer;\n }\n}\n```
| 3 | 0 |
['Java']
| 2 |
find-n-unique-integers-sum-up-to-zero
|
Q1304 Accepted C++ ✅ 100% Fastest Sol | Simple & Easiest
|
q1304-accepted-c-100-fastest-sol-simple-anq7u
|
CRUX\n1) We need to return a vector whose sum is equal to 0.\n2) So there are 2 options either odd or even number.\n3) If odd, 5 then index would be 0,1,2,3,4 t
|
adityasrathore
|
NORMAL
|
2023-01-06T20:01:53.172731+00:00
|
2023-01-06T20:01:53.172764+00:00
| 730 | false |
CRUX\n1) We need to return a vector whose sum is equal to 0.\n2) So there are 2 options either odd or even number.\n3) If odd, 5 then index would be 0,1,2,3,4 thus middle would be zero and right side would be positive and left side would be negative of same number.\n4) Similary for even, 4 index would be same 0,1,2,3 and we can omit insertion of 0.\n5) I have mapped the corresponding index to the random numbers toward left and right with additive inverse.\n```\nclass Solution {\npublic:\n vector<int> sumZero(int n) {\n vector<int> v(n,0);\n if(n%2==1){\n for(int i=n/2+1;i<n;i++){\n v[i]=i;\n v[n-i-1]=-1*i; // n=5 [-4,-3,0,3,4]\n }\n }\n else{\n for(int i=n/2;i<n;i++){\n v[i]=i;\n v[n-i-1]=-1*i; // n=4 [-3,-2,2,3]\n }\n }\n return v;\n }\n};\n```
| 3 | 0 |
['C']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
c++ | easy understanding | 100% | 0ms
|
c-easy-understanding-100-0ms-by-nehagupt-zxnr
|
\nclass Solution {\npublic:\n vector<int> sumZero(int n) {\n vector<int>ans;\n for(int i=1;i<=n/2;i++)\n {\n ans.push_back(i)
|
NehaGupta_09
|
NORMAL
|
2022-09-30T05:55:01.128280+00:00
|
2022-09-30T05:55:01.128322+00:00
| 410 | false |
```\nclass Solution {\npublic:\n vector<int> sumZero(int n) {\n vector<int>ans;\n for(int i=1;i<=n/2;i++)\n {\n ans.push_back(i);\n ans.push_back(i*-1);\n }\n if(n%2!=0)\n {\n ans.push_back(0);\n }\n return ans;\n }\n};\n```
| 3 | 0 |
['C', 'C++']
| 2 |
find-n-unique-integers-sum-up-to-zero
|
Easiest solution in Java
|
easiest-solution-in-java-by-silvan8124-f3nz
|
One of the easiest solutions\n\nclass Solution {\n public int[] sumZero(int n) {\n int [] result = new int[n];\n int sum = 0;\n \n
|
silvan8124
|
NORMAL
|
2022-09-23T17:36:17.663876+00:00
|
2022-09-23T17:36:17.663904+00:00
| 180 | false |
One of the easiest solutions\n\nclass Solution {\n public int[] sumZero(int n) {\n int [] result = new int[n];\n int sum = 0;\n \n for(int i = 1 ; i < n ; i++) {\n result[i] = i;\n sum += i;\n }\n \n result[0] = -sum;\n \n return result;\n }\n}
| 3 | 0 |
['Array']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
Python Easy Solution in 5 lines
|
python-easy-solution-in-5-lines-by-pulki-seug
|
\nclass Solution:\n def sumZero(self, n: int) -> List[int]:\n a=[]\n if n%2!=0:\n a.append(0)\n for i in range(1,n,2):\n
|
pulkit_uppal
|
NORMAL
|
2022-09-20T04:31:22.357026+00:00
|
2022-09-20T04:33:47.222916+00:00
| 939 | false |
```\nclass Solution:\n def sumZero(self, n: int) -> List[int]:\n a=[]\n if n%2!=0:\n a.append(0)\n for i in range(1,n,2):\n a.append(i)\n a.append(i*(-1))\n return a\n \n \n \n ```
| 3 | 0 |
['Python']
| 1 |
find-n-unique-integers-sum-up-to-zero
|
JS | One-liner | faster than 81.31%
|
js-one-liner-faster-than-8131-by-diff64-12iz
|
\nvar sumZero = (n) => (arr = new Int32Array(n).map((el, idx) => idx), arr[0] = -n * (n-1) / 2, arr)\n
|
Diff64
|
NORMAL
|
2022-08-16T22:01:46.650767+00:00
|
2022-11-08T19:40:31.528826+00:00
| 374 | false |
```\nvar sumZero = (n) => (arr = new Int32Array(n).map((el, idx) => idx), arr[0] = -n * (n-1) / 2, arr)\n```
| 3 | 0 |
['JavaScript']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
My Javascript Answer
|
my-javascript-answer-by-parkryan0128-50qz
|
easy javascript answer\n\n\nvar sumZero = function(n) {\n let arr = []\n let sum = 0\n for (let i=1; i < n; i++) {\n arr.push(i)\n sum =
|
parkryan0128
|
NORMAL
|
2022-06-12T00:35:54.409336+00:00
|
2022-06-12T00:35:54.409366+00:00
| 355 | false |
easy javascript answer\n\n```\nvar sumZero = function(n) {\n let arr = []\n let sum = 0\n for (let i=1; i < n; i++) {\n arr.push(i)\n sum = sum + i\n }\n arr.push(-sum)\n return arr\n};\n```
| 3 | 0 |
['JavaScript']
| 1 |
find-n-unique-integers-sum-up-to-zero
|
Simple Java Approach: 0ms
|
simple-java-approach-0ms-by-bazinga18-1gpm
|
Pair up the indices, in the first loop populate 0th and 1st index, then 2nd and 3rd index and so on...\nThis way you can uniquely populate even number of indice
|
bazinga18_
|
NORMAL
|
2022-04-09T01:01:39.018228+00:00
|
2022-04-09T01:01:39.018265+00:00
| 115 | false |
Pair up the indices, in the first loop populate 0th and 1st index, then 2nd and 3rd index and so on...\nThis way you can uniquely populate even number of indices.\nIf n is odd, then we would just populate the (n - 1) even bits using the same approach explained above and leave the last element as 0.\n\nFor example:\nIf even: add 1, -1, 3, -3 .. till n\nIf odd: add 1, -1, 3, -3 .. till (n - 1) + add additional 0 for nth element\n\n```\npublic int[] sumZero(int n) {\n\n if(n == 1)\n return new int[]{0};\n\n int[] result = new int[n];\n\n for(int i = 0; i < n-1; i+=2) {\n result[i] = i + 1;\n result[i+1] = (i + 1) * -1;\n }\n return result; \n}\n```
| 3 | 0 |
['Java']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
Python - Pretty Easy
|
python-pretty-easy-by-siddheshsagar-ul9u
|
\ndef sumZero(self, n: int) -> List[int]:\n ans = [] \n i = 1 \n if n % 2 == 0:\n j = 0\n else:\n j = 1\n
|
SiddheshSagar
|
NORMAL
|
2022-03-24T03:10:32.652419+00:00
|
2022-07-31T19:14:15.255482+00:00
| 413 | false |
```\ndef sumZero(self, n: int) -> List[int]:\n ans = [] \n i = 1 \n if n % 2 == 0:\n j = 0\n else:\n j = 1\n ans.append(0)\n while j < n:\n ans.append(i)\n ans.append(-i)\n i += 1\n j += 2\n return ans\n```
| 3 | 0 |
['Python', 'Python3']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
[ Java ] Simple solution with explanation beats 100% O(n)
|
java-simple-solution-with-explanation-be-wgmz
|
Approach: \n\n1. Case 1 : n is even => return array in range [-n/2,n/2] but exclude 0.\n\tEg : n=8 return {-4,-3,-2,-1, 1, 2, 3, 4}\n2. Case 2 : n is odd => ret
|
KapProDes
|
NORMAL
|
2021-12-10T10:35:51.623754+00:00
|
2021-12-10T10:35:51.623792+00:00
| 154 | false |
__Approach__: \n\n1. __Case 1__ : n is even => return array in range [-n/2,n/2] but exclude 0.\n\tEg : n=8 return {-4,-3,-2,-1, 1, 2, 3, 4}\n2. __Case 2__ : n is odd => return array in range [-n/2,n/2] including 0.\n\tEg : n=7 return {-3,-2,-1, 0, 1, 2, 3}\n\n__Code__ :\n\n```\nclass Solution {\n public int[] sumZero(int n) {\n int nums[] = new int[n];\n int j = 0;\n //Case 1 : n is even\n if(n%2==0){\n for(int i=-n/2;i<=n/2;i++){\n if(i==0){\n continue;\n }\n nums[j] = i;\n j++;\n }\n }\n //Case : n is odd \n else{\n for(int i=-n/2;i<=n/2;i++){\n nums[j] = i;\n j++;\n }\n }\n return nums;\n }\n}\n```
| 3 | 0 |
['Java']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
Rust one liner
|
rust-one-liner-by-bigmih-1ijn
|
\nimpl Solution {\n pub fn sum_zero(n: i32) -> Vec<i32> {\n (1..n).chain(std::iter::once(-n * (n - 1) / 2)).collect()\n }\n}\n
|
BigMih
|
NORMAL
|
2021-08-06T11:28:39.420264+00:00
|
2021-08-06T11:28:39.420306+00:00
| 71 | false |
```\nimpl Solution {\n pub fn sum_zero(n: i32) -> Vec<i32> {\n (1..n).chain(std::iter::once(-n * (n - 1) / 2)).collect()\n }\n}\n```
| 3 | 0 |
['Rust']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
[Java] fill up to n-1 and last index put negative of the sum
|
java-fill-up-to-n-1-and-last-index-put-n-bn0x
|
\nclass Solution {\n public int[] sumZero(int n) {\n if (n == 1) return new int[]{0};\n \n int[] arr = new int[n];\n int sum = 0;
|
vinsinin
|
NORMAL
|
2021-03-02T01:38:26.503257+00:00
|
2021-03-02T01:38:26.503299+00:00
| 144 | false |
```\nclass Solution {\n public int[] sumZero(int n) {\n if (n == 1) return new int[]{0};\n \n int[] arr = new int[n];\n int sum = 0;\n for (int i = 0;i<n-1;i++){\n arr[i] = i+1;\n sum += arr[i];\n }\n arr[n-1] = -sum;\n return arr;\n }\n}\n```
| 3 | 1 |
['Java']
| 3 |
find-n-unique-integers-sum-up-to-zero
|
Java 0ms, O(n) with comments
|
java-0ms-on-with-comments-by-denz1994-9k5a
|
\nclass Solution {\n public int[] sumZero(int n) {\n int[] retArr = new int[n];\n int arrVal = 0;\n \n // Set the leftmost and ri
|
denz1994
|
NORMAL
|
2020-10-28T02:38:08.628565+00:00
|
2020-10-28T02:38:20.869441+00:00
| 202 | false |
```\nclass Solution {\n public int[] sumZero(int n) {\n int[] retArr = new int[n];\n int arrVal = 0;\n \n // Set the leftmost and rightmost elements and traverse the array towards the middle \n // Array should be set so... anyRightHalfElement = abs(anyLeftHalfElement)\n for(int i =0;i<n/2;i++){\n arrVal = n-i;\n \n // Set leftmost value of array\n retArr[i]=-1*arrVal;\n \n // Set rightMost value of array\n retArr[n-1-i]=arrVal;\n }\n return retArr;\n }\n}\n```
| 3 | 0 |
['Java']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
Python - Faster than 100%
|
python-faster-than-100-by-juanrodriguez-9r39
|
Basically if n is even skip the zero.\n\n\nclass Solution:\n def sumZero(self, n: int) -> List[int]:\n mid = n // 2\n if (n & 1): return [num f
|
juanrodriguez
|
NORMAL
|
2020-10-24T01:32:00.779438+00:00
|
2020-10-24T01:32:00.779470+00:00
| 503 | false |
Basically if n is even skip the zero.\n\n```\nclass Solution:\n def sumZero(self, n: int) -> List[int]:\n mid = n // 2\n if (n & 1): return [num for num in range(-mid, mid + 1)]\n else: return [num for num in range(-mid, mid + 1) if num != 0]\n```
| 3 | 0 |
['Python', 'Python3']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
Simple Java Solution beats 100%
|
simple-java-solution-beats-100-by-idiotp-e9nj
|
Initializes an array matching this pattern\n\nn = 1, [0]\nn = 2, [1, -1]\nn = 3, [1, -1, 0]\nn = 4, [1, -1, 2, -2]\nn = 5, [1, -1, 2, -2, 0]\nn = 6, [1, -1, 2,
|
idiotplayer
|
NORMAL
|
2020-07-29T06:44:38.371160+00:00
|
2020-07-29T06:44:38.371201+00:00
| 111 | false |
Initializes an array matching this pattern\n```\nn = 1, [0]\nn = 2, [1, -1]\nn = 3, [1, -1, 0]\nn = 4, [1, -1, 2, -2]\nn = 5, [1, -1, 2, -2, 0]\nn = 6, [1, -1, 2, -2, 3, -3]\n```\n```\npublic int[] sumZero(int n) {\n int[] result = new int[n];\n \n for (int i=1, j=0; i<=n/2; i++) {\n result[j++] = i;\n result[j++] = i*(-1);\n }\n return result; \n}\n```
| 3 | 0 |
[]
| 0 |
find-n-unique-integers-sum-up-to-zero
|
Python: solution
|
python-solution-by-onysuke-ydnf
|
Runtime: 32 ms, faster than 69.06% of Python3 online submissions for Find N Unique Integers Sum up to Zero.\nMemory Usage: 13.9 MB, less than 100.00% of Python3
|
onysuke
|
NORMAL
|
2020-05-06T00:18:40.597271+00:00
|
2020-05-06T00:18:40.597303+00:00
| 552 | false |
Runtime: 32 ms, faster than 69.06% of Python3 online submissions for Find N Unique Integers Sum up to Zero.\nMemory Usage: 13.9 MB, less than 100.00% of Python3 online submissions for Find N Unique Integers Sum up to Zero.\n\n```\nclass Solution:\n def sumZero(self, n: int) -> List[int]:\n ans = []\n ans.extend([x for x in range(1, n // 2 + 1)])\n ans.extend([-x for x in range(1, n // 2 + 1)])\n if len(ans) != n:\n ans.append(0)\n return ans\n```
| 3 | 0 |
[]
| 0 |
find-n-unique-integers-sum-up-to-zero
|
javascript o(n) 100%/100% w/ very detailed explanation
|
javascript-on-100100-w-very-detailed-exp-8mgj
|
explanation:\nIn brief, we want to fill the result array with a sequence as follows: 0, -1, 1, -2, 2, -3, 3, ...\n\nThis will work for any odd number and is ver
|
carti
|
NORMAL
|
2020-04-10T23:00:20.576120+00:00
|
2020-04-10T23:06:18.793701+00:00
| 248 | false |
**explanation:**\nIn brief, we want to fill the result array with a sequence as follows: `0, -1, 1, -2, 2, -3, 3, ...`\n\nThis will work for any *odd* number and is very easy to generate, as seen in the code below. Example, for `n = 1`, result would be `[0]`. This sums to 0 obviously. For` n = 3`, result would be `[0,-1,1]`, and this sums to 0. So on, and so on.\n\nFor *even* numbers, it gets somewhat tricky. Take an example of `n = 4` following the same sequence. The result would be `0, -1, 1, -2` and this would sum to -2. For ` n = 6`, it would generate `[0, -1, 1, -2, 2, -3]` this would sum to -3.\n\nHowever, there is a pattern. For even numbers, with this sequence, the last number is always the sum. Therefore, we could just increment the the second to last number by the last number, and it would always work. This ensures uniqueness, since the sequence is always ascending, and anything added to the biggest number is guaranteed to NOT have been seen before.\n\nTaking the example above for `n = 4`, it generates `[0, -1, 1, -2]` and this sums to -2. Take the second to last index, and the number is `1`. Subtract the LAST number from this: `1 -- 2 = 3` so result array would be `[0, -1, 3, -2]`. This is both unique, and sums to 0.\n\n**solution:**\n```\n/**\n * @param {number} n\n * @return {number[]}\n */\nconst sumZero = (n) => {\n // result (start with single 0)\n let res = [0];\n\n // negative and positive pointer\n let neg = -1;\n let pos = 1;\n\n // iterate n - 1 times\n for (let i = 0, j = 0; i < n - 1; i++) {\n // i is even, use neg, i is odd, use pos\n if (i % 2 === 0) {\n // push neg to array, and decrement neg\n res.push(neg--);\n } else {\n // push pos to array, and increment pos\n res.push(pos++);\n }\n }\n\n // if n was even, we need to subtract the last number to the second to last\n if (n % 2 === 0) res[n - 2] -= res[n - 1];\n\n return res;\n};\n\n```\n\nnote: There are hacks to make this syntactically shorter, but logic remains the same.
| 3 | 0 |
['JavaScript']
| 1 |
find-n-unique-integers-sum-up-to-zero
|
Extremely Simple Logic (beats 100%)
|
extremely-simple-logic-beats-100-by-nsai-t9d3
|
You just need to add the index values in the result array and keep track of the sum of the values.\nInsert the last value of the result array as the negative of
|
nsai
|
NORMAL
|
2020-03-04T15:18:06.624997+00:00
|
2020-03-11T09:12:44.258330+00:00
| 259 | false |
You just need to add the index values in the result array and keep track of the sum of the values.\nInsert the last value of the result array as the negative of the sum so far. This will give unique values with sum of the values equaling zero.\n```\nclass Solution {\n public int[] sumZero(int n) {\n int res[] = new int[n];\n int sum = 0;\n for(int i = 0;i<res.length-1;i++)\n {\n res[i] = i;\n sum = sum + res[i];\n }\n res[n-1] = -sum;\n return res;\n }\n}\n```
| 3 | 0 |
['Java']
| 2 |
find-n-unique-integers-sum-up-to-zero
|
One Line Solution
|
one-line-solution-by-fallenranger-20z4
|
Logic :\nIf n is odd:\neg: n = 5 \n1, 2, 0, -2, -1\n\nIf n is even:\neg: n = 4\n1, 2, -2, -1\n\nSo if n is odd, array will have 0 in middle and half mirror arra
|
fallenranger
|
NORMAL
|
2019-12-29T05:31:45.578729+00:00
|
2019-12-29T05:35:27.981151+00:00
| 298 | false |
Logic :\nIf n is odd:\neg: n = 5 \n1, 2, 0, -2, -1\n\nIf n is even:\neg: n = 4\n1, 2, -2, -1\n\nSo if n is odd, array will have 0 in middle and half mirror arrays around 0.\nIf n is even, array will just have two mirror half arrays.\n``` list(range(1,n//2+1))``` will create mirror & negative array of ```list(range(-(n//2),0))```\n\n```\nclass Solution:\n def sumZero(self, n: int) -> List[int]:\n return list(range(1,n//2+1))+[0]*(n&1)+list(range(-(n//2),0))\n```
| 3 | 1 |
['Python', 'Python3']
| 1 |
find-n-unique-integers-sum-up-to-zero
|
[Java/Python/C++] Simple solution to create symmetric array with sum 0 - Explained
|
javapythonc-simple-solution-to-create-sy-1k95
|
Explaination\n\n - Insert 0 in the middle if odd length is required\n - Keep adding +ve and -ve nos on the right and left of same magnitude to maintain the sum
|
sankalpdayal5
|
NORMAL
|
2019-12-29T04:07:10.083289+00:00
|
2019-12-29T13:05:58.355264+00:00
| 451 | false |
**Explaination**\n\n - Insert `0` in the middle if `odd length` is required\n - Keep adding `+ve` and `-ve` nos on the `right` and `left` of *same magnitude* to maintain the sum as `0`\n\n\n\n**Java -**\n```\nclass Solution {\n public int[] sumZero(int n) {\n int[] res = new int[n];\n \n // If odd sized array, add 0 in the middle\n if (n%2 == 1)\n res[n/2] = 0;\n \n // Add +ve and -ve integers on the right and left of the array\n for (int i=0; i<n/2; i++){\n res[i] = i+1;\n res[n-i-1] = -i-1;\n }\n \n return res;\n }\n}\n```\n\n**Python -**\n```\nclass Solution:\n def sumZero(self, n: int) -> List[int]:\n res = []\n \n # // If odd sized array, add 0 in the middle\n if n%2 == 1:\n res.append(0)\n n -= 1\n \n # // Add +ve and -ve integers on the right and left of the array\n for i in range(1, n//2 + 1):\n res = [-i] + res + [i]\n \n return res\n```\t\t\n\n**C++ -**\nNote - To make it symmetric, use list.\nVector only allows addition at the end of the vector. So it will be alternating values.\n```\nclass Solution {\npublic:\n vector<int> sumZero(int n) {\n vector<int> res;\n\t\t\n // If odd sized array, add 0 to the vector\n if (n % 2) res.push_back(0);\n \n // Add +ve and -ve integers alternately to the vector\n for (int i = 1; i <= n / 2; ++i) {\n\t\t\tres.push_back(i);\n\t\t\tres.push_back(-i);\n\t\t}\n\t\t\n\t\treturn res;\n }\n};\n```\n\n
| 3 | 2 |
[]
| 1 |
find-n-unique-integers-sum-up-to-zero
|
Python 3 O(N/2) with explanation
|
python-3-on2-with-explanation-by-strawbe-6gnq
|
The idea is this. If you have an even number of elements to append, you can just keep adding any arbitrary element and its inverse (e.g., 5 and -5) until you ha
|
strawberrykiwi
|
NORMAL
|
2019-12-29T04:02:29.874022+00:00
|
2019-12-29T04:02:29.874063+00:00
| 532 | false |
The idea is this. If you have an even number of elements to append, you can just keep adding any arbitrary element and its inverse (e.g., 5 and -5) until you have appended enough. If you have an odd, just append 0, then do what you\'d do for an even.\n\n```\nclass Solution:\n def sumZero(self, n: int) -> List[int]:\n res = []\n \n if n%2 == 1:\n res.append(0)\n n -= 1\n \n while n > 0:\n res.append(n)\n res.append(-n)\n n -= 2\n \n return res\n```
| 3 | 0 |
[]
| 0 |
find-n-unique-integers-sum-up-to-zero
|
Generate an Array with Sum Zero || Beats 100%
|
generate-an-array-with-sum-zero-beats-10-59fq
|
IntuitionTo create an array of size n where the sum of all elements is zero, we can leverage the property of symmetric pairs. If n is even, we can use numbers l
|
lokeshthakur8954
|
NORMAL
|
2025-03-23T07:50:26.377582+00:00
|
2025-03-23T07:50:26.377582+00:00
| 70 | false |
# Intuition
To create an array of size n where the sum of all elements is zero, we can leverage the property of symmetric pairs. If n is even, we can use numbers like (-x, x). If n is odd, we include an extra 0 in the middle.
# Approach
Initialize an array of size n.
If n is 1, return [0] directly.
Fill the first half of the array with negative numbers from -n/2 to -1.
If n is odd, place 0 in the middle.
Fill the remaining positions with positive numbers from 1 to n/2.
Return the array.
# Complexity
- Time complexity:
$$O(n)$$
We iterate over n elements once.
- Space complexity:
$$O(1)$$
We use only the output array.
# Code
```java []
class Solution {
public int[] sumZero(int n) {
// If n is 1, the only possible array is [0]
if(n == 1){
return new int[]{0};
}
int arr[] = new int[n]; // Initialize an array of size n
int i = 0, num = (n / 2) * (-1), j = 1; // Start from the smallest negative number
// Fill the first half of the array with negative numbers
for(; j <= n / 2; j++){
arr[i] = num; // Assign the current negative number
num++; // Increment to move towards zero
i++; // Move to the next index
}
num = 1; // Reset num for positive numbers
// If n is odd, add 0 in the middle
if(n % 2 != 0){
arr[i] = 0;
i++; // Move to the next index
j++; // Increment j since we added an extra element
}
// Fill the second half with positive numbers
for(; j <= n; j++){
arr[i] = num; // Assign the positive number
num++; // Increment to move away from zero
i++; // Move to the next index
}
return arr; // Return the final array
}
}
```
| 2 | 0 |
['Java']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
0ms solution beats 100 percent easy to understand just try to dry run it then you will find it easy.
|
0ms-solution-beats-100-percent-easy-to-u-vbd3
|
IntuitionApproachComplexity
Time complexity:
O(n)
Space complexity:
0(n)
Code
|
anshgupta1234
|
NORMAL
|
2025-02-05T15:14:38.951250+00:00
|
2025-02-05T15:14:38.951250+00:00
| 344 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
O(n)
- Space complexity:
0(n)
# Code
```java []
class Solution {
public int[] sumZero(int n) {
int[] arr=new int[n];
int q=n/2;
int count=1;
if(n%2!=0){
for(int i=0;i<arr.length;i++){
arr[i]= -q+i;
}
return arr;
}
if(n%2==0){
for(int i=0;i<arr.length;i++){
arr[i]=-q+i;
if(i>=q){
arr[i]=count++;
}
}
return arr;
}
return arr;
}
}
```
| 2 | 0 |
['Java']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
Видео-анализ за 5 минут || Video analysis in 5 minutes
|
video-analiz-za-5-minut-video-analysis-i-d2dd
|
Разбор задачи на ютуб
Спасибо за подписки!!
ApproachЕсли n не равны 1 или 2 то создаем переменную, которая будет хранить сумму всех добавленных чисел
int sum=0;
|
Alexandre_gtg_133
|
NORMAL
|
2025-01-31T19:32:35.520167+00:00
|
2025-01-31T19:32:35.520167+00:00
| 63 | false |
# Разбор задачи на ютуб
https://youtu.be/_9qiFSiSvWM
Спасибо за подписки!!

# Approach
Если **n** не равны **1** или **2** то создаем переменную, которая будет хранить сумму всех добавленных чисел
**int sum=0;**
Создадим итоговый массив
**vector<int> ans;**
В цикле будем добавлять в наш массив **i** ,**n-1** раз и параллельно считать общую сумму элементов
**for(int i=0;i<n-1;++i){
ans.push_back(i);
sum+=ans[i];
}**
Добавляем в массив переменную **sum** но со знаком минус(чтобы уравнять остальные элементы)
**ans.push_back(-sum);**
Возвращаем итоговый массив
**return ans;**
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(n)
# Code
```cpp []
class Solution {
public:
vector<int> sumZero(int n) {
if(n==1){
return {0};
}
if(n==2){
return {-1,1};
}
int sum=0;
vector<int> ans;
for(int i=0;i<n-1;++i){
ans.push_back(i);
sum+=ans[i];
}
ans.push_back(-sum);
return ans;
}
};
```
| 2 | 0 |
['C++']
| 1 |
find-n-unique-integers-sum-up-to-zero
|
Easy CPP Solution | Beats 100% of the solutions
|
easy-cpp-solution-beats-100-of-the-solut-d0fv
|
IntuitionApproachComplexity
Time complexity:
O(n)
Space complexity:
O(n)
Code
|
VaibhaviShah25
|
NORMAL
|
2025-01-16T18:52:18.692267+00:00
|
2025-01-16T18:52:18.692267+00:00
| 197 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(n)
# Code
```cpp []
class Solution {
public:
vector<int> sumZero(int n) {
int sum = 0;
if(n == 1) return {0};
if (n == 2) return {-1,1};
vector<int> res;
for(int i=0; i<n-1; i++){
res.push_back(i);
sum += i;
}
res.push_back(-sum);
return res;
}
};
```
| 2 | 0 |
['Array', 'Math', 'C++']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
Zero-Sum Game: Crafting a Balanced Array Using Python
|
zero-sum-game-crafting-a-balanced-array-4pce4
|
Intuition\nThe goal is to create an array of integers where the sum of the elements is zero. A simple way to achieve this is to generate a sequence of numbers a
|
Krishnaa2004
|
NORMAL
|
2024-09-06T13:19:34.827341+00:00
|
2024-09-06T13:19:34.827366+00:00
| 213 | false |
# Intuition\nThe goal is to create an array of integers where the sum of the elements is zero. A simple way to achieve this is to generate a sequence of numbers and adjust the last element to balance the sum to zero.\n\n# Approach\n1. Generate a sequence of numbers from 1 to \\( n-1 \\).\n2. The sum of these numbers can be calculated using the formula for the sum of an arithmetic series: sum = n * (n - 1) // 2\n3. Append the negative of this sum as the last element to ensure that the total sum of the array is zero.\n4. Return the resulting array.\n\n# Complexity\n- **Time complexity:** \\( O(n) \\), where \\( n \\) is the number of elements. This accounts for the creation of the list and the final computation.\n- **Space complexity:** \\( O(n) \\), as the space required grows linearly with the size of the input.\n\n# Code\n```python\nclass Solution:\n def sumZero(self, n: int) -> List[int]:\n arr = [x for x in range(1, n)]\n arr.append(-1 * (n * (n - 1)) // 2)\n return arr\n```\n
| 2 | 0 |
['Python3']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
Beginner Level Approach Using One Loop
|
beginner-level-approach-using-one-loop-b-faav
|
\n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time complexity:\n Add your time complexity here, e.g. O(n) \n\n- Space comp
|
Akhil1489
|
NORMAL
|
2024-07-11T07:05:07.635867+00:00
|
2024-07-11T07:05:07.635883+00:00
| 139 | false |
\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {number} n\n * @return {number[]}\n */\nvar sumZero = function(n) { \n\n let arr = []\n\n for(let i = 0 ;i < n/2 ; i++){\n if(n%2 ==0){\n arr.push(i+1,-(i+1))\n } else {\n if(i == 0){\n arr.push(i)\n } else {\n arr.push(i,-(i))\n }\n }\n }\n\n return arr\n};\n```
| 2 | 0 |
['JavaScript']
| 1 |
find-n-unique-integers-sum-up-to-zero
|
Python3 || Easy and Optimized Approach... ✌
|
python3-easy-and-optimized-approach-by-h-w1kd
|
Explanation:\n1. Initialization: Initialize an empty list res to store the result.\n2. Generate Pairs: Loop from 1 to n//2 (integer division) and add pairs of i
|
hanishb81
|
NORMAL
|
2024-05-15T14:36:58.944871+00:00
|
2024-05-15T14:36:58.944902+00:00
| 281 | false |
### Explanation:\n1. **Initialization**: Initialize an empty list `res` to store the result.\n2. **Generate Pairs**: Loop from `1` to `n//2` (integer division) and add pairs of integers `(i, -i)` to the list. This ensures that each pair sums to zero.\n3. **Handle Odd n**: If `n` is odd, append `0` to the list. This is necessary because the loop generates `n//2` pairs, which sum to zero, and we need an extra `0` to balance the sum when `n` is odd.\n4. **Return the Result**: The list `res` now contains `n` unique integers that sum to zero.\n\n### Example:\nFor `n = 5`:\n- The loop will add `1, -1`, `2, -2` to the list.\n- Since `5` is odd, we append `0` to the list.\n- Result: `[1, -1, 2, -2, 0]`\n\nFor `n = 3`:\n- The loop will add `1, -1` to the list.\n- Since `3` is odd, we append `0` to the list.\n- Result: `[1, -1, 0]`\n\nFor `n = 1`:\n- The loop doesn\'t run because `n//2` is `0`.\n- Since `1` is odd, we append `0` to the list.\n- Result: `[0]`\n\n### Efficiency:\n- **Time Complexity**: O(n), as we are looping through `n//2` elements and adding to the list.\n- **Space Complexity**: O(n), as we store the result in a list of size `n`.\n\n\n# Code\n```\nclass Solution(object):\n def sumZero(self, n):\n res = []\n for i in range(1, n//2 + 1):\n res.append(i)\n res.append(-i)\n if n % 2 != 0:\n res.append(0)\n return res\n\n```\n\n\n\n
| 2 | 0 |
['Python3']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
Code by a Newbie(beats 100%)
|
code-by-a-newbiebeats-100-by-harshith_gr-q6ze
|
\n\n# Code\n\nclass Solution {\n public int[] sumZero(int n) {\n int a[]=new int[n];\n int c=1;\n int sum=0;\n for(int i=0;i<n-1;
|
harshith_griet
|
NORMAL
|
2024-04-27T11:04:44.310411+00:00
|
2024-04-27T11:04:44.310435+00:00
| 211 | false |
\n\n# Code\n```\nclass Solution {\n public int[] sumZero(int n) {\n int a[]=new int[n];\n int c=1;\n int sum=0;\n for(int i=0;i<n-1;i++)\n {\n sum+=c;\n a[i]=c;\n c++;\n }\n a[n-1]=-1*sum;\n return a; \n }\n}\n```
| 2 | 0 |
['Java']
| 3 |
find-n-unique-integers-sum-up-to-zero
|
Easy Soln || C++ || Beat 100%🔥🔥
|
easy-soln-c-beat-100-by-vishalkumar00-v3t1
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
vishalkumar00
|
NORMAL
|
2024-03-20T07:57:12.837065+00:00
|
2024-03-20T07:57:12.837103+00:00
| 346 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> sumZero(int n) {\n vector<int>ans;\n for(int i=1;i<=n/2;i++){\n ans.push_back(-i);\n ans.push_back(i);\n }\n if(n&1!=0){\n ans.push_back(0);\n }\n return ans;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
Easy java sol (100% beat): Dont copy - paste please : first understand then write code
|
easy-java-sol-100-beat-dont-copy-paste-p-4cl1
|
\n\n# Code\n\nclass Solution {\n public int[] sumZero(int n) {\n int[] arr = new int[n];\n \n if(n%2!=0){\n arr[0]=0;\n }
|
rushikesh3010
|
NORMAL
|
2024-01-11T16:07:28.935374+00:00
|
2024-01-11T16:07:28.935411+00:00
| 73 | false |
\n\n# Code\n```\nclass Solution {\n public int[] sumZero(int n) {\n int[] arr = new int[n];\n \n if(n%2!=0){\n arr[0]=0;\n }\n for(int i=0;i<n-1;i+=2){\n arr[i]=1+i;\n arr[i+1]=-(i+1);\n }\n\n return arr;\n \n }\n}\n```\n\n\n
| 2 | 0 |
['Java']
| 1 |
find-n-unique-integers-sum-up-to-zero
|
veryyyyyyy easyyyyyyyy lollllllllllllllllll
|
veryyyyyyy-easyyyyyyyy-lolllllllllllllll-pkmy
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
ramuyadav90597
|
NORMAL
|
2023-12-17T14:03:56.218942+00:00
|
2023-12-17T14:03:56.218970+00:00
| 251 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] sumZero(int n) {\n if(n==1){\n int a [] = {0};\n return a;\n }\n\n int a [] = new int[n];\n int j=0;\n if(n%2==0){\n for(int i=(-n/2);i<=-1;i++){\n a[j]=i;\n j++;\n a[j]=Math.abs(i);\n j++;\n }\n return a;\n }\n else{\n for(int i=(-n/2);i<=-1;i++){\n a[j]=i;\n j++;\n a[j]=Math.abs(i);\n j++;\n }\n a[j]=0;\n return a;\n }\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
JAVA SOLUTION : simple and easy
|
java-solution-simple-and-easy-by-jyothii-4fb9
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
jyothii_20
|
NORMAL
|
2023-10-05T17:17:32.486571+00:00
|
2023-10-05T17:17:32.486605+00:00
| 124 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:0 ms\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] sumZero(int n) {\n int i;\n \n int[] arr= new int[n];\n if(n%2 != 0){\n arr[n-1] = 0;\n }\n for(i=0;i<n-1;i=i+2){\n arr[i] = 1+i;\n arr[i+1] = -(i+1);\n }\n \n return arr;\n\n\n \n\n }\n}\n```
| 2 | 0 |
['Java']
| 1 |
find-n-unique-integers-sum-up-to-zero
|
JS Very Easy Solution||Easy to Understand
|
js-very-easy-solutioneasy-to-understand-m7v52
|
javascript []\n\n/**\n * @param {number} n\n * @return {number[]}\n */\nvar sumZero = function(n) {\n let mid = Math.floor(n/2);\n let arr=[]\n for(let
|
unaisek
|
NORMAL
|
2023-09-18T05:18:35.076118+00:00
|
2023-09-18T05:18:35.076138+00:00
| 82 | false |
```javascript []\n\n/**\n * @param {number} n\n * @return {number[]}\n */\nvar sumZero = function(n) {\n let mid = Math.floor(n/2);\n let arr=[]\n for(let i =1;i<=mid;i++){\n arr.push(i,-i);\n }\n if(n%2 == 1){\n arr.push(0)\n }\n return arr\n};\n```
| 2 | 0 |
['JavaScript']
| 1 |
find-n-unique-integers-sum-up-to-zero
|
Simple & Easy Code || JAVA || Beats 100% || Runtime 0ms
|
simple-easy-code-java-beats-100-runtime-24k4f
|
Intuition\nWe have to return an array in output whose elements make the sum of 0. \n Describe your first thoughts on how to solve this problem. \n\n# Approach\n
|
rajswapnil50
|
NORMAL
|
2023-09-06T18:50:23.762304+00:00
|
2023-09-06T18:50:23.762327+00:00
| 30 | false |
# Intuition\nWe have to return an array in output whose elements make the sum of 0. \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nFirstly take an array where you can store the numbers. Now, as we have to output an array in which on adding up all the elements in array give the `sum = 0`. So we have to just return a random array which gives the sum of 0. \nIsme doo conditions baan rhi hain...\n`1.` Agar array ka length even digits ka banaya jaaye toh fir toh aap directly numbers input krrwaao and uske adjacent (i+2) prr uss number ka negetive input krrdo so that Sum and kreenge toh 0 aayega.\n`Example : [1,-1,2,-2,4,-4]`\n\n`2.` Agar array odd length ka hai then, usme n-1 position waala array(if loop starting from i =0) matlab array ka last element ko 0 declare krrdo starting me hi so that fir ek position odd length me 0 hoogai toh waps wahi even length me jaise kiya tha waisa hi hoojayega ek number input and then uska negetive input.\n`Example : [1,-1,2,-2,0]`\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity : 0(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n```\nclass Solution {\n public int[] sumZero(int n) {\n int [] arr = new int[n];\n if(n%2 !=0){\n arr[n-1]=0;\n for(int i = 0; i<n-1; i+=2){\n arr[i] = i+1;\n arr[i+1] =(i+1)*(-1);\n }\n }else{\n for(int i =0; i<n-1; i+=2){\n arr[i] = i+1;\n arr[i+1] = (i+1)*(-1);\n }\n }\n return arr;\n }\n} \n```
| 2 | 0 |
['Array', 'Math', 'Java']
| 1 |
find-n-unique-integers-sum-up-to-zero
|
Two pointers Approach
|
two-pointers-approach-by-tausif_02-lrkx
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
tausif_02
|
NORMAL
|
2023-07-30T19:36:23.305504+00:00
|
2023-07-30T19:36:23.305525+00:00
| 184 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] sumZero(int n) {\n int []ans = new int[n];\n int left=0;\n int right=n-1;\n int start=1;\n while(left<right)\n {\n ans[left++]=start;\n ans[right--]=-start;\n start++;\n }\n return ans;\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
java two pointer approach
|
java-two-pointer-approach-by-rsnishank-yt66
|
Intuition \n Describe your first thoughts on\nbasic two pointer approach how to solve this problem. \n\n# Approach\n Describe your approach to solving the probl
|
rsnishank
|
NORMAL
|
2023-07-29T08:29:34.312494+00:00
|
2023-07-29T08:29:34.312525+00:00
| 247 | false |
# Intuition \n<!-- Describe your first thoughts on\nbasic two pointer approach how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] sumZero(int n) {\n int arr[]=new int [n];\n if(n%2!=0)\n arr[n/2]=0;\n int start=0;\n int end=n-1;\n int val=1;\n while(start<end){\n arr[start]=val;\n arr[end]=-val;\n start++;\n end--;\n val++;\n }\n \n return arr;\n}\n}\n\'\'\'
| 2 | 0 |
['Java']
| 1 |
find-n-unique-integers-sum-up-to-zero
|
Find N Unique Integers Sum up to Zero 👨🏻💻👨🏻💻 || Java solution code🔥🔥🔥...
|
find-n-unique-integers-sum-up-to-zero-ja-epds
|
Code\n\nclass Solution {\n public int[] sumZero(int n) {\n int[] arr = new int[n];\n int sum = 0;\n \n for(int i=0; i<n; i++){\n
|
Jayakumar__S
|
NORMAL
|
2023-06-30T13:28:28.785913+00:00
|
2023-06-30T13:28:28.785935+00:00
| 698 | false |
# Code\n```\nclass Solution {\n public int[] sumZero(int n) {\n int[] arr = new int[n];\n int sum = 0;\n \n for(int i=0; i<n; i++){\n if(i == n-1){\n arr[i] = sum * (-1);\n }\n else{\n arr[i] = i+1;\n sum+= i+1;\n }\n }\n return arr;\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
find-n-unique-integers-sum-up-to-zero
|
Beginners friendly
|
beginners-friendly-by-bhaskarkumar07-iz0t
|
\n\n# Approach\n Describe your approach to solving the problem. \n there are 2 cases when n is odd \n and when n is even \n in odd one element must be
|
bhaskarkumar07
|
NORMAL
|
2023-05-21T12:49:20.551109+00:00
|
2023-05-21T12:49:20.551156+00:00
| 908 | false |
\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n there are 2 cases when n is odd \n and when n is even \n in odd one element must be 0;\n and in even there should be no zero. it will work as simple \n just observe the example testcase\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] sumZero(int n) {\n int[] res= new int[n];\n if(n%2==1) {\n res[n-1]=0;\n for(int i=0;i<n-1;i+=2){\n res[i]=i+1;\n res[i+1]=-(i+1);\n }\n }else{\n for(int i=0;i<n;i+=2){\n res[i]=i+1;\n res[i+1]=-(i+1);\n }\n }\n\n return res;\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
maximum-size-of-a-set-after-removals
|
Easy to understand | C++ | Sets
|
easy-to-understand-c-sets-by-amaan2510-8u1d
|
Approach\n Describe your approach to solving the problem. \n1. Calculate the number of unique elements in nums1 and nums2 by storing their elements in sets s1 a
|
amaan2510
|
NORMAL
|
2024-01-07T04:15:58.288973+00:00
|
2024-01-07T04:15:58.288992+00:00
| 2,121 | false |
# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Calculate the number of unique elements in nums1 and nums2 by storing their elements in sets s1 and s2.\n2. Also calculate total unique elements in both arrays in set s.\n3. The answer is minimum of:\n a. size of s\n b. sum of number of unique elements provided by both arrays, which is min(n/2, s1.size) + min(n/2, s2.size)\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n set<int> s1, s2, s;\n int n = nums1.size();\n for (int x : nums1) {\n s1.insert(x);\n s.insert(x);\n }\n for (int x : nums2) {\n s2.insert(x);\n s.insert(x);\n }\n int ans = min(min(n/2, (int)s1.size()) + min(n/2, (int)s2.size()),(int) s.size());\n \n return ans;\n }\n};\n```
| 25 | 2 |
['C++']
| 2 |
maximum-size-of-a-set-after-removals
|
Easy Video Explanation with Proofs 🔥 || Set Intersection 🔥
|
easy-video-explanation-with-proofs-set-i-pvt1
|
Intuition\n Describe your first thoughts on how to solve this problem. \nTry to use set and basic of math is required. Try to dry run few scenarios for better u
|
ayushnemmaniwar12
|
NORMAL
|
2024-01-07T06:05:48.774490+00:00
|
2024-01-07T06:05:48.774519+00:00
| 2,107 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTry to use set and basic of math is required. Try to dry run few scenarios for better understanding\n\n# ***Easy Video Explanation***\n\nhttps://youtu.be/crNIGc4zb8s\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBasic\nThe code determines the maximum size of a set formed by merging two sets. It considers the size of the first set, and then iterates through the second set, incrementing the size based on elements not present in the first set, up to half the size of the second set.\n\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(N*log(N))\n \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(N)\n \n\n# Code\n\n\n```C++ []\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& v1, vector<int>& v2) {\n set<int>s1;\n set<int>s2;\n for(auto i:v1)\n s1.insert(i);\n for(auto i:v2)\n s2.insert(i);\n int n=v1.size(),m=v2.size();\n int x=s1.size(),y=s2.size();\n int ans=min(n/2,x);\n int rem=x-ans;\n int c=0;\n for(auto i:s2) {\n if(s1.find(i)==s1.end()) {\n c++;\n } else if(rem>0) {\n c++;\n rem--;\n }\n if(c>=m/2)\n break;\n }\n return ans+c;\n }\n};\n```\n```python []\nclass Solution:\n def maximumSetSize(self, v1, v2):\n s1 = set(v1)\n s2 = set(v2)\n n, m = len(v1), len(v2)\n x, y = len(s1), len(s2)\n ans = min(n // 2, x)\n rem = x - ans\n c = 0\n for i in s2:\n if i not in s1:\n c += 1\n elif rem > 0:\n c += 1\n rem -= 1\n if c >= m // 2:\n break\n return ans + c\n\n```\n```Java []\nimport java.util.HashSet;\nimport java.util.Set;\n\nclass Solution {\n public int maximumSetSize(int[] v1, int[] v2) {\n Set<Integer> s1 = new HashSet<>();\n Set<Integer> s2 = new HashSet<>();\n for (int i : v1)\n s1.add(i);\n for (int i : v2)\n s2.add(i);\n int n = v1.length, m = v2.length;\n int x = s1.size(), y = s2.size();\n int ans = Math.min(n / 2, x);\n int rem = x - ans;\n int c = 0;\n for (int i : s2) {\n if (!s1.contains(i)) {\n c++;\n } else if (rem > 0) {\n c++;\n rem--;\n }\n if (c >= m / 2)\n break;\n }\n return ans + c;\n }\n}\n\n\n```\n\n# ***If you like the solution Please Upvote and subscribe to my youtube channel***\n***It Motivates me to record more videos***\n\n*Thank you* \uD83D\uDE00
| 22 | 0 |
['Math', 'Ordered Set', 'C++', 'Java', 'Python3']
| 2 |
maximum-size-of-a-set-after-removals
|
Java HashSet O(N)
|
java-hashset-on-by-hobiter-veea
|
See comments for details\n\n- Time complexity:\n Add your time complexity here, e.g. O(n) \nO(N)\n- Space complexity:\n Add your space complexity here, e.g. O(n
|
hobiter
|
NORMAL
|
2024-01-07T08:31:26.194391+00:00
|
2024-01-07T08:33:12.519197+00:00
| 708 | false |
See comments for details\n\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n# Code\n```\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) {\n Set<Integer> set1 = toSet(nums1), set2 = toSet(nums2);\n int common = 0, m1 = set1.size(), m2 = set2.size(), n = nums1.length;\n for (int num : set1) {\n if (set2.contains(num)) common++;\n }\n int uniq1 = m1 - common, uniq2 = m2 - common;\n // uniq is enough in both sets;\n if (uniq1 >= n / 2 && uniq2 >= n / 2) return n;\n // uniq is not enough in either sets;\n // try to divide common in set 1 or set 2, greedy;\n if (uniq1 < n / 2 && uniq2 < n / 2) return Math.min(n, uniq1 + uniq2 + common);\n // if only set 2 has enough unique\n // put all common in set 1;\n if (uniq1 < n / 2) return Math.min(n / 2, uniq1 + common) + n/2;\n // if only set 1 has enough unique\n // put all common in set 2;\n return Math.min(n / 2, uniq2 + common) + n/2;\n }\n\n private Set<Integer> toSet(int[] arr) {\n Set<Integer> set = new HashSet();\n for (int num : arr) set.add(num);\n return set;\n }\n}\n```
| 12 | 0 |
['Java']
| 3 |
maximum-size-of-a-set-after-removals
|
Simple set operations, symmetric difference
|
simple-set-operations-symmetric-differen-u57d
|
\n\n# Code\npython\nclass Solution:\n def maximumSetSize(self, nums1: List[int], nums2: List[int]) -> int:\n s1 = set(nums1)\n s2 = set(nums2)\
|
cpacc1
|
NORMAL
|
2024-01-07T04:05:27.389163+00:00
|
2024-01-07T04:06:30.536247+00:00
| 1,295 | false |
\n\n# Code\n```python\nclass Solution:\n def maximumSetSize(self, nums1: List[int], nums2: List[int]) -> int:\n s1 = set(nums1)\n s2 = set(nums2)\n n = len(nums1)\n inter = s1.intersection(s2)\n ex1 = min(len(s1) - len(inter) , n//2)\n ex2 = min(len(s2) - len(inter) , n//2)\n return (min(ex1 + ex2 + len(inter) , n))\n```
| 11 | 1 |
['Python3']
| 7 |
maximum-size-of-a-set-after-removals
|
Python: 5 lines Venn diagram for two sets. Few set operations
|
python-5-lines-venn-diagram-for-two-sets-sqcf
|
Intuition\nIt is clear that duplicate numbers in nums1 and nums2 do not matter. So you can conver them into two sets.\n\nNow some values can overlap so you have
|
salvadordali
|
NORMAL
|
2024-01-07T04:29:56.596606+00:00
|
2024-01-07T04:29:56.596626+00:00
| 524 | false |
# Intuition\nIt is clear that duplicate numbers in nums1 and nums2 do not matter. So you can conver them into two sets.\n\nNow some values can overlap so you have the following Venn diagram.\n\n![clip_image007\\[1\\].gif](https://assets.leetcode.com/users/images/dafda736-394e-4135-9049-82583da52613_1704601596.873948.gif)\n\nSo you calculate intersection of both sets (in fact you need only number of them).\n\nNow count the maximum number of elements you can take only from set one: `v1` value. Same for set two. And then check if you can combine them and take the intersection (limiting by total number you can take)\n\n\n# Complexity\n- Time complexity: $O(n)$\n- Space complexity: $O(n)$\n\n# Code\n```\nclass Solution:\n def maximumSetSize(self, nums1: List[int], nums2: List[int]) -> int:\n n, nums1, nums2 = len(nums1) // 2, set(nums1), set(nums2)\n len_both = len(nums1 & nums2)\n\n v1 = min(len(nums1) - len_both, n)\n v2 = min(len(nums2) - len_both, n)\n return min(v1 + v2 + len_both, n * 2)\n```
| 10 | 0 |
['Python3']
| 5 |
maximum-size-of-a-set-after-removals
|
Video Explanation
|
video-explanation-by-codingmohan-q9wa
|
Explanation\n\nClick here for the video\n\n# Code\n\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n int n
|
codingmohan
|
NORMAL
|
2024-01-07T04:07:42.084134+00:00
|
2024-01-07T04:07:42.084153+00:00
| 505 | false |
# Explanation\n\n[Click here for the video](https://youtu.be/63dNVenHJ_c)\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size();\n unordered_map<int, int> m1, m2;\n \n for (auto i : nums1) m1[i] ++;\n for (auto i : nums2) m2[i] ++;\n \n int only_in_1 = 0;\n int only_in_2 = 0;\n int both = 0;\n \n for (auto i : m1) \n if (m2.find(i.first) != m2.end()) both ++;\n else only_in_1 ++;\n \n for (auto i : m2) \n if (m1.find(i.first) == m1.end()) only_in_2 ++;\n \n only_in_1 = min (only_in_1, n/2);\n only_in_2 = min (only_in_2, n/2);\n \n if (only_in_1 < n/2) {\n int req = n/2 - only_in_1;\n int has = min (req, both);\n \n both -= has;\n only_in_1 += has;\n }\n if (only_in_2 < n/2) {\n int req = n/2 - only_in_2;\n int has = min (req, both);\n \n both -= has;\n only_in_2 += has;\n }\n \n return (only_in_1 + only_in_2);\n }\n};\n```
| 7 | 0 |
['C++']
| 2 |
maximum-size-of-a-set-after-removals
|
C++ | Easy beginner friendly sol | Deatailed explanation with comment | Set
|
c-easy-beginner-friendly-sol-deatailed-e-nznn
|
# Intuition \n\n\n\n\n\n# Complexity\n- Time complexity: O(n) [Insert operation in unordered set takes O(1) time on avg.]\n\n\n- Space complexity: O(n) [To s
|
abhik2003
|
NORMAL
|
2024-01-07T04:04:20.038713+00:00
|
2024-01-07T04:56:19.946476+00:00
| 514 | false |
<!-- # Intuition -->\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n<!-- # Approach -->\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$ [Insert operation in unordered set takes $$O(1)$$ time on avg.]\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$ [To store elements in set]\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n unordered_set<int> s1, s2, u;\n //s1 = set(nums1) and s2 = set(nums2)\n //u= s1 union s2\n\n int n = nums1.size() / 2; // number of elements to be choosen from each array\n for(auto x:nums1){\n s1.insert(x);\n u.insert(x);\n }\n for(auto x:nums2){\n s2.insert(x);\n u.insert(x);\n }\n int common = s1.size() + s2.size() - u.size(); // size of s1 intersection s2\n int n1 = s1.size();\n int n2 = s2.size();\n\n int ans = 0;\n ans += min(n, n1-common); // take all elements from s1-s2 [maximum n elements]\n ans += min(n, n2-common); // take all elements from s2-s1\n ans += common; // now take common elements\n ans = min(ans, n * 2); // if nukber of elements taken are more than 2*n make the answer 2*n\n return ans;\n }\n};\n```
| 6 | 0 |
['C++']
| 1 |
maximum-size-of-a-set-after-removals
|
Set || Easy
|
set-easy-by-aayush0606-sb9c
|
Code\n\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& A, vector<int>& B) {\n int n=A.size();\n unordered_set<int>s1(A.begin(),A.e
|
Aayush0606
|
NORMAL
|
2024-01-07T04:00:52.982094+00:00
|
2024-01-07T04:37:15.936213+00:00
| 1,037 | false |
# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& A, vector<int>& B) {\n int n=A.size();\n unordered_set<int>s1(A.begin(),A.end());\n unordered_set<int>s2(B.begin(),B.end());\n int i=0,j=0;\n unordered_set<int>st;\n // Add all unique elements first\n\n for(auto&it:s1){\n if(i==n/2) break;\n if(s2.find(it)==s2.end()) {\n st.insert(it);\n i++;\n }\n }\n for(auto&it:s2){\n if(j==n/2) break;\n if(s1.find(it)==s1.end()) {\n st.insert(it);\n j++;\n }\n }\n\n //If we still have some elements left, add duplicates\n\n if(i<n/2){\n for(auto&it:s1){\n if(i==n/2) break;\n if(s2.find(it)!=s2.end()) {\n st.insert(it);\n // to add it in different n/2 set from s2\n s2.erase(it);\n i++;\n }\n }\n }\n if(j<n/2){\n for(auto&it:s2){\n if(j==n/2) break;\n if(s1.find(it)!=s1.end()) {\n st.insert(it);\n j++;\n }\n }\n }\n return st.size();\n }\n};\n```
| 6 | 0 |
['Math', 'Greedy', 'Simulation', 'Ordered Set', 'C++']
| 1 |
maximum-size-of-a-set-after-removals
|
Java solution using HashSet
|
java-solution-using-hashset-by-hrishi_ch-yetx
|
Code\n\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) {\n Set<Integer> s1 = new HashSet(); \n Set<Integer> s2 = new Ha
|
hrishi_chavan
|
NORMAL
|
2024-01-07T04:27:51.165884+00:00
|
2024-01-08T04:22:49.392416+00:00
| 326 | false |
# Code\n```\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) {\n Set<Integer> s1 = new HashSet(); \n Set<Integer> s2 = new HashSet();\n Set<Integer> s3 = new HashSet(); \n \n for (int num: nums1){\n s1.add(num);\n s3.add(num);\n } \n for (int num: nums2) {\n s2.add(num);\n s3.add(num);\n } \n \n return Math.min(Math.min(s1.size(), nums1.length/2) + \n Math.min(s2.size(), nums2.length/2), s3.size()); \n }\n}\n```
| 5 | 0 |
['Java']
| 4 |
maximum-size-of-a-set-after-removals
|
a few solutions
|
a-few-solutions-by-claytonjwong-xvwb
|
Synopsis:\n\nIt is more simple to include values than exclude values!\n\nGame Plan: \n1. Let N be the cardinality of the input array A and let threshold T be N
|
claytonjwong
|
NORMAL
|
2024-01-16T16:37:00.271717+00:00
|
2024-01-17T14:09:49.710054+00:00
| 81 | false |
**Synopsis:**\n\nIt is more simple to *include* values than *exclude* values!\n\n**Game Plan:** \n1. Let `N` be the cardinality of the input array `A` and let threshold `T` be `N / 2`\n2. Let `A` and `B` be sets from input arrays `A` and `B` correspondingly\n3. Further reduce `A` and `B` as **mutually exclusive** sets, ie. all values in `A` *not* in `B` and vice versa all values in `B` *not* in `A`, and let `C` be the **mutually exclusive** set of common values within the set intersection of `A` and `B`\n4. We can take up to threshold `T` of each mutually exclusive set `A` and `B` separately and distinctly; and we can also "fill in the potential leftover space available" in `A` inclusive-or `B` with common values `C` (\u2B50\uFE0F Note: \uD83D\uDC40 see **Supplemental** \uD83C\uDF5E "breadcrumbs" below for iterative details for how we arrived "here" \uD83C\uDFAF)\n\n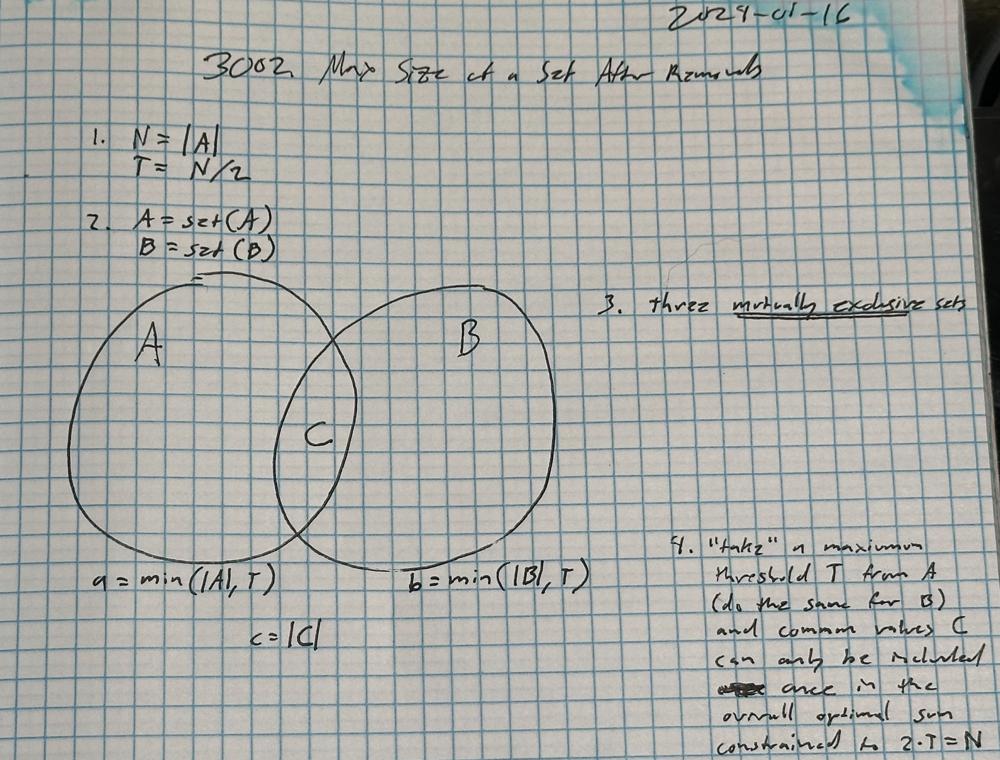\n\n*Kotlin*\n```\ntypealias VI = IntArray\nclass Solution {\n fun maximumSetSize(A_: VI, B_: VI): Int {\n var N = A_.size\n var T = N / 2\n var A = A_.toSet()\n var B = B_.toSet()\n var C = A.intersect(B)\n var a = Math.min(A.filter{ !C.contains(it) }.size, T)\n var b = Math.min(B.filter{ !C.contains(it) }.size, T)\n var c = C.size\n return Math.min(a + b + c, N)\n }\n}\n```\n\n*Javascript*\n```\nlet maximumSetSize = (A, B, C = null) => {\n let N = A.length,\n T = Math.floor(N / 2);\n A = new Set(A);\n B = new Set(B);\n C = new Set([...A].filter(x => B.has(x)));\n [A, B] = [new Set([...A].filter(x => !B.has(x))), new Set([...B].filter(x => !A.has(x)))];\n let a = Math.min(A.size, T),\n b = Math.min(B.size, T),\n c = C.size;\n return Math.min(a + b + c, N);\n};\n```\n\n*Python3*\n```\nclass Solution:\n def maximumSetSize(self, A: List[int], B: List[int]) -> int:\n N = len(A)\n T = N // 2\n A = set(A)\n B = set(B)\n A, B, C = A - B, B - A, A & B\n a, b, c = min(len(A), T), min(len(B), T), len(C)\n return min(a + b + c, N)\n```\n\n*Rust*\n```\nuse std::cmp::min;\nuse std::collections::HashSet;\ntype VI = Vec<i32>;\ntype Set = HashSet<i32>;\nimpl Solution {\n pub fn maximum_set_size(mut A: VI, mut B: VI) -> i32 {\n let N = A.len();\n let T = N / 2;\n let mut A = A.drain(..).collect::<Set>();\n let mut B = B.drain(..).collect::<Set>();\n let mut C = Set::new();\n for x in A.clone() {\n if B.contains(&x) {\n C.insert(x);\n }\n }\n for same in &C {\n A.remove(same);\n B.remove(same);\n }\n let a = min(A.len(), T);\n let b = min(B.len(), T);\n let c = C.len();\n min(a + b + c, N) as i32\n }\n}\n```\n\n*C++*\n```\nclass Solution {\npublic:\n using VI = vector<int>;\n using Set = set<int>;\n int maximumSetSize(VI& A_, VI& B_, Set C = {}) {\n auto N = A_.size(),\n T = N / 2;\n Set A{ A_.begin(), A_.end() },\n B{ B_.begin(), B_.end() };\n set_intersection(A.begin(), A.end(), B.begin(), B.end(), inserter(C, C.end()));\n erase_if(A, [&](auto x) { return C.find(x) != C.end(); });\n erase_if(B, [&](auto x) { return C.find(x) != C.end(); });\n auto a = min(A.size(), T),\n b = min(B.size(), T),\n c = C.size();\n return min(a + b + c, N);\n }\n};\n```\n\n---\n\n**Supplemental:** \uD83C\uDF5E Breadcrumbs for how we arrived "here." -- I had a hard time on this question until I looked at hint #1, ie. it is more simple to create a set by adding half rather than removing half.\n\n```\n# 9:03am -\n\n# we must remove half of A\n# " " " " " " B\n\n# return A + B\n\n# goal is to maximumize the cardinal of the set A + B\n\n# question: how to maximumize the set A + B\n\n# different values in A and B increases the size of the set\n# same values " " "decreases" <-- stays same, not really decreaseing, but certainly not increasing!\n\n# continuously remove the same value between A and B such that one of those same values will remain\n# ie. use a heap to track maximum counts of values between A and B\n\n# ok that sounds good, let\'s see what happens\n\n# 9:07am - implementation begins\n\n\n# 9:10am - hold up, actually I\'m not exactly certain how to choose here, I kinda understand high-level strategy\n# but need to come up with some pseduocode to iron out the details...\n\n# lets look at a concrete example:\n\n# ex1:\n\n# A = [1,1,2,2]\n# B = [1,1,1,1]\n# X X\n\n# ex2:\n\n# [1,2,3,4,5,6]\n# [2,2,2,3,3,3]\n# X X X\n\n# ex3:\n\n# [1,1,2,2,3,3]\n# [4,4,5,5,6,6]\n# X X X\n\n# question: can we perform validation of a guess in linear time? I dunno\n\n# here\'s the deal:\n\n# from A\'s perspective, it is optimal to remove everything that exists in B (ie. the overlapping intersection between A and B)\n# otherwise if nothing overlaps, then remove most frequent value?\n\n# actually maybe I\'m overthinking this?\n\n# almost always when I miss problems it is because I make things too complicated\n\n# so KISS == keep it super simple\n\n# what if we just greedily remove most frequent values from A and B, then take the union of that as the best answer?]\\\n# ya that seems more simple, right?\n\n# 9:18am - implementation begins\n# 9:21am - implementation ends\n\n# class Solution:\n# def maximumSetSize(self, A: List[int], B: List[int]) -> int:\n# def f(A):\n# N = len(A)\n# q = [(-cnt, x) for x, cnt in Counter(A).items()]; heapify(q)\n# while N // 2 < len(q):\n# heappop(q)\n# return set(x for _, x in q)\n# return len(f(A) | f(B))\n \n# 9:22am - wrong answer\n\n# Submission Detail\n# 316 / 969 test cases passed.\n# Status: Wrong Answer\n# Submitted: 0 minutes ago\n# Input:\n# [9,8,4,7]\n# [5,5,9,5]\n# Output:\n# 3\n# Expected:\n# 4\n\n# ok ya, so we\'re not taking into account the hollistic set union between A+B, good try though, it is super simple!\n\n# I suppose we would always want to greedily consume all values in common amoungst each array A, B *separately*\n# then greedily consume all values in common amoungst each array A, B *together*\n# finally we must remove values that would have been helpful to include in the answer, but we cannot afford to do so, since\n# we must remove half of the values\n# ok so that\'s where the inversion comes from, right?\n\n\n# 9:34am - ok let\'s take a break, I think I\'m on the right track:\n\n# from A\'s perspective:\n# * remove cnt-1 values for each x in common with itself (leaving just 1 of each x)\n# * completely remove all instances of the value x which exist in B\n# * aribtrarily remove remaining values x,y,z which do not exist in B\n\n# from B\'s perspective: same deal\n# * remove cnt-1 values for each x in common with itself (leaving just 1 of each x)\n# * completely remove all instances of the value x which exist in A\n# * aribtrarily remove remaining values x,y,z which do not exist in A\n\n# 9:38am - alright whatever, now that it is written out verbosely might as well implement it...\n# 9:46am - well that\'s correct for example 1 and example 3, but fails for example 2\n\n# class Solution:\n# def maximumSetSize(self, A: List[int], B: List[int]) -> int:\n# N = len(A)\n# T = N // 2\n# same = lambda A: sum(cnt - 1 for cnt in Counter(A).values())\n# def f(A, B):\n# take = same(A)\n# if T <= take:\n# return set(A)\n# take += len(set(A) & set(B))\n# if T <= take:\n# return set(A) - set(B)\n# need = T - take\n# return set(list(A)[:need])\n# return len(f(A, B) | f(B, A))\n\n# Wrong Answer\n# Runtime: 75 ms\n# Your input\n# [1,2,1,2]\n# [1,1,1,1]\n# [1,2,3,4,5,6]\n# [2,3,2,3,2,3]\n# [1,1,2,2,3,3]\n# [4,4,5,5,6,6]\n# Output\n# 2\n# 3\n# 6\n# Expected\n# 2\n# 5\n# 6\n\n# 9:47am - let\'s take a break for real\'s...\n\n# question: how to remove same values optimally? right? keeping the different values if we can, since that makes the set bigger\n\n# key hint 1: that I missed, but almost got... LOL\n\n# Removing n / 2 elements from each array is the same as keeping n / 2 elements in each array.\n\n# game plan: sort A and B, then use i and j to cherry pick unseen values?\n# hold up, how to only take N/2 each? let\'s come back tomorrow fresh...\n\n# class Solution:\n# def maximumSetSize(self, A: List[int], B: List[int]) -> int:\n# N = len(A)\n# A.sort()\n# B.sort()\n# seen = set()\n# i, j = 0, 0\n# while i < N or j < N:\n# while i < N and A[i] in seen:\n# i += 1\n# if i < N:\n# seen.add(A[i])\n# return len(seen)\n\n# 8:33am - \n# 8:52am - AC in ~19 minutes\n\n# greedily take values in A that are not in B\n# " " " " in B that are not in A\n\n# take up to threshold T=N/2 of all values in A that are not in B\n# " " " " " " B A\n\n# if they exist, then the leftovers are each array\'s unused values in A and/or B\n\n# leftovers = min(T - min(T, len(A)), T - min(T, len(B)))\n\n# class Solution:\n# def maximumSetSize(self, A: List[int], B: List[int]) -> int:\n# N = len(A)\n# T = N // 2\n# A = set(A)\n# B = set(B)\n# C = A & B\n# f = lambda A, B: set(x for x in A if x not in B)\n# A, B = f(A, B), f(B, A)\n# extra_A = max(0, T - len(A))\n# extra_B = max(0, T - len(B))\n# same = len(C)\n# have = 0\n# take = min(same, extra_A); same -= take; have += take\n# take = min(same, extra_B); same -= take; have += take\n# return min(len(A), T) + min(len(B), T) + have\n\n# class Solution:\n# def maximumSetSize(self, A: List[int], B: List[int]) -> int:\n# N = len(A)\n# T = N // 2\n# A = set(A)\n# B = set(B)\n# A, B, C = A - B, B - A, A & B\n# have = 0\n# same = len(C)\n# give = lambda A: max(0, T - len(A))\n# take = min(same, give(A)); same -= take; have += take\n# take = min(same, give(B)); same -= take; have += take\n# return min(len(A), T) + min(len(B), T) + have\n\nclass Solution:\n def maximumSetSize(self, A: List[int], B: List[int]) -> int:\n N = len(A)\n T = N // 2\n A = set(A)\n B = set(B)\n A, B, C = A - B, B - A, A & B\n a, b, c = min(len(A), T), min(len(B), T), len(C)\n return min(a + b + c, N)\n```
| 4 | 0 |
[]
| 2 |
maximum-size-of-a-set-after-removals
|
Easy C++ Solution ✅✅
|
easy-c-solution-by-abhi242-smd3
|
Code\n\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n unordered_set<int> s;\n int n1=nums1.size();
|
Abhi242
|
NORMAL
|
2024-01-07T05:17:31.750917+00:00
|
2024-01-07T05:17:31.750945+00:00
| 309 | false |
# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n unordered_set<int> s;\n int n1=nums1.size();\n int n2=nums2.size();\n for(int i=0;i<n1;i++){\n s.insert(nums1[i]);\n }\n int use1=s.size();\n s.clear();\n for(int i=0;i<n2;i++){\n s.insert(nums2[i]);\n }\n int use2=s.size();\n s.clear();\n for(int i=0;i<n1;i++){\n s.insert(nums1[i]);\n }\n for(int i=0;i<n2;i++){\n s.insert(nums2[i]);\n }\n int use3=s.size();\n return min(use3,min(n1/2,use1)+min(n2/2,use2));\n \n }\n};\n```
| 4 | 0 |
['C++']
| 0 |
maximum-size-of-a-set-after-removals
|
SET -Union-Intersection
|
set-union-intersection-by-satyam_9911-0lvg
|
Intuition\n ans will not exceed n/2 (unique elements from nums1) + n/2(unique elements from nums2) = n. \n If there are more than n/2 unique elements from nums
|
satyam_9911
|
NORMAL
|
2024-01-07T04:41:58.286142+00:00
|
2024-01-07T14:13:21.088065+00:00
| 156 | false |
# Intuition\n* ans will not exceed n/2 (unique elements from nums1) + n/2(unique elements from nums2) = `n`. \n* If there are more than n/2 unique elements from nums1 , then we can easily delete `n/2` elements and make the uniqueness factor from nums1 to `n/2`. \n* Similarly for `nums2`. \n\n* `ans = min(n , min(n/2 , s1.size()-common) + min(n/2 , s2.size() - common) + common)`. \n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n \n int n = nums1.size();\n set<int>Union; \n set<int> s1(nums1.begin() , nums1.end()); \n set<int> s2(nums2.begin() , nums2.end()); \n for(int num : nums1)Union.insert(num); \n for(int num : nums2)Union.insert(num);\n int common = s1.size() + s2.size() - Union.size(); \n int ans = 0; \n ans+= min(n/2 , (int)s1.size() - common); \n ans+= min(n/2 , (int)s2.size() - common); \n ans+=common; \n return min(n , ans); \n }\n};\n```
| 4 | 0 |
['Hash Table', 'Math', 'Union Find', 'Ordered Set', 'C++']
| 1 |
maximum-size-of-a-set-after-removals
|
CONDITION BASED || C++
|
condition-based-c-by-this_is_4503-hpa3
|
Code\n\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n unordered_map<int,int> mp1,mp2;\n unordered_
|
SatyamJha03
|
NORMAL
|
2024-01-07T04:16:05.761503+00:00
|
2024-01-07T04:16:05.761525+00:00
| 1,631 | false |
# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n unordered_map<int,int> mp1,mp2;\n unordered_set<int> s;\n for(auto &i: nums1){\n mp1[i]++;\n }\n for(auto &i: nums2){\n mp2[i]++;\n }\n int a = 0, b = 0,c=0,n=nums1.size(),x;\n for(auto &i: mp1){\n a += (i.second-1);\n }for(auto &i: mp2){\n b += (i.second-1);\n }for(auto &i: mp1){\n if(mp2.count(i.first)){\n c++;\n }\n }\n if(a==0&&b==0&&c==0)return min(n,2*n-c);\n if(a>=n/2&&b>=n/2){\n return 2*n-a-b-c;\n }else if(a>=n/2 && b<n/2){\n if(b+c>=n/2)return 2*n-a-b-c;\n else return 2*n-a-n/2;\n }else if(a<n/2 && b>=n/2){\n if(a+c>=n/2)return 2*n-a-b-c;\n else return 2*n-b-n/2;\n }\n if(a+b+c>=n)return 2*n-a-b-c;\n if(a<=n/2){\n x = n/2-a;\n a += min(x,c);\n c = min(0,c-x);\n }\n if(b<=n/2&&c>0){\n x = n/2-b;\n b += min(x,c);\n c = min(0,c-x);\n }\n return min(2*n-a-b-c,n);\n }\n};\n```
| 4 | 0 |
['C++']
| 1 |
maximum-size-of-a-set-after-removals
|
✅✅ Explanation with Proofs 💯 || C++ || ✅Clean Code ||
|
explanation-with-proofs-c-clean-code-by-dkegs
|
Intuition:\nThe problem seems to involve finding the maximum possible size of a set that can be formed using elements from two given arrays (nums1 and nums2). T
|
arslanarsal
|
NORMAL
|
2024-01-20T14:26:58.680715+00:00
|
2024-01-20T14:26:58.680753+00:00
| 130 | false |
# Intuition:\nThe problem seems to involve finding the maximum possible size of a set that can be formed using elements from two given arrays (`nums1` and `nums2`). The intuition might involve using sets to represent unique elements in each array and finding the common elements between them.\n\n# Approach:\n1. Create two sets, `s1` and `s2`, to store unique elements from `nums1` and `nums2`, respectively.\n2. Create a third set, `common`, to store common elements between `s1` and `s2`.\n3. Iterate through `nums1` and insert each element into `s1`.\n4. Iterate through `nums2`, insert each element into `s2`, and check if it is common with `s1`. If common, insert it into the `common` set.\n5. Calculate the sizes of sets `s1`, `s2`, and `common` (denoted as `n1`, `n2`, and `c`).\n6. Return the minimum of the following three values:\n - The total size of `nums1` (`n`).\n - The minimum of (`n1 - c`) and (`n / 2`).\n - The minimum of (`n2 - c`) and (`n / 2`).\n - The size of the `common` set (`c`).\n# Complexity:\n- **Time Complexity:** The time complexity is O(n), where n is the total number of elements in both `nums1` and `nums2`. The code iterates through both arrays once to build the sets.\n \n- **Space Complexity:** The space complexity is O(n), where n is the total number of elements in both `nums1` and `nums2`. The sets `s1`, `s2`, and `common` can grow linearly with the input size.\n\n# Code:\n```cpp\nclass Solution\n{\npublic:\n int maximumSetSize(vector<int> &nums1, vector<int> &nums2)\n {\n int n = nums1.size();\n unordered_set<int> s1, s2, common;\n\n // Insert elements from nums1 into s1\n for (auto &&i : nums1)\n {\n s1.insert(i);\n }\n\n // Insert elements from nums2 into s2 and check for common elements\n for (auto &&i : nums2)\n {\n s2.insert(i);\n if (s1.find(i) != s1.end())\n {\n common.insert(i);\n }\n }\n\n int n1 = s1.size(), n2 = s2.size(), c = common.size();\n\n // Return the minimum of three values\n return min(n, min(n1 - c, n / 2) + min(n2 - c, n / 2) + c);\n }\n};\n```
| 3 | 0 |
['Array', 'Hash Table', 'Greedy', 'C++']
| 2 |
maximum-size-of-a-set-after-removals
|
[Python3] sets
|
python3-sets-by-awice-c7rg
|
Let N be the number of items we have to pick from each array.\n\nUse sets. Among the elements that only occur in $A$ (ie. $A-B$), we pick them first, to a maxi
|
awice
|
NORMAL
|
2024-01-07T05:41:51.694999+00:00
|
2024-01-07T05:41:51.695023+00:00
| 139 | false |
Let N be the number of items we have to pick from each array.\n\nUse sets. Among the elements that only occur in $A$ (ie. $A-B$), we pick them first, to a maximum of $N$ elements. Similarly for $B$.\n\nNow you have $2 N - \\text{onlyA} - \\text{onlyB}$ picks remaining, and you can pick from $A \\cap B$.\n\n# Code\n```\nclass Solution:\n def maximumSetSize(self, A: List[int], B: List[int]) -> int:\n N = len(A) // 2\n A = set(A)\n B = set(B)\n onlyA = min(len(A - B), N)\n onlyB = min(len(B - A), N)\n both = min(len(A & B), 2 * N - onlyA - onlyB)\n return onlyA + onlyB + both\n```
| 3 | 0 |
['Python3']
| 0 |
maximum-size-of-a-set-after-removals
|
Java solution
|
java-solution-by-charlie-tej-123-q58a
|
\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) {\n int i,j,n=nums1.length;\n Set<Integer> set1=new HashSet<>();\n
|
charlie-tej-123
|
NORMAL
|
2024-01-07T04:33:18.294935+00:00
|
2024-01-07T04:33:18.294958+00:00
| 604 | false |
```\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) {\n int i,j,n=nums1.length;\n Set<Integer> set1=new HashSet<>();\n Set<Integer> set2=new HashSet<>();\n Set<Integer> set3=new HashSet<>();\n for(int x:nums1)\n {\n set1.add(x);\n set3.add(x);\n }\n for(int x:nums2)\n {\n set2.add(x);\n set3.add(x);\n }\n int common=set1.size()+set2.size()-set3.size();\n int n1=set1.size(),n2=set2.size();\n int ans=Math.min(n/2,n1-common);\n ans+=Math.min(n/2,n2-common);\n ans+=common;\n ans=Math.min(n,ans);\n return ans;\n }\n}\n```
| 3 | 0 |
['Java']
| 1 |
maximum-size-of-a-set-after-removals
|
Simple HashMaps and Set Solution
|
simple-hashmaps-and-set-solution-by-gupt-r0u1
|
\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) {\n HashMap<Integer,Integer> map1=new HashMap<>();\n int n=nums1.lengt
|
guptasheenam1510
|
NORMAL
|
2024-01-07T04:03:23.172343+00:00
|
2024-01-09T14:42:29.666279+00:00
| 483 | false |
```\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) {\n HashMap<Integer,Integer> map1=new HashMap<>();\n int n=nums1.length;\n HashMap<Integer,Integer> map2=new HashMap<>();\n Set set=new HashSet<>();\n int ans=0;\n for(int i=0;i<nums1.length;i++)\n {\n map1.put(nums1[i],map1.getOrDefault(nums1[i],0)+1);\n set.add(nums1[i]);\n }\n for(int i=0;i<nums2.length;i++)\n {\n map2.put(nums2[i],map2.getOrDefault(nums2[i],0)+1);\n set.add(nums2[i]);\n }\n if(map1.size()>=n/2) ans+=n/2;\n else ans+=map1.size();\n if(map2.size()>=n/2) ans+=n/2;\n else ans+=map2.size();\n if(set.size()>=ans)\n return ans;\n return set.size();\n }\n}\n```\n\n\n
| 3 | 0 |
['Java']
| 3 |
maximum-size-of-a-set-after-removals
|
Python Simple Solution (sets) (accepted)
|
python-simple-solution-sets-accepted-by-akxn8
|
Code\n\nimport collections\nclass Solution:\n def maximumSetSize(self, nums1: List[int], nums2: List[int]) -> int:\n max_len = len(nums1) // 2\n
|
nithil
|
NORMAL
|
2024-01-07T04:03:02.757547+00:00
|
2024-01-07T04:03:02.757577+00:00
| 446 | false |
# Code\n```\nimport collections\nclass Solution:\n def maximumSetSize(self, nums1: List[int], nums2: List[int]) -> int:\n max_len = len(nums1) // 2\n nums1_set = set(nums1)\n nums2_set = set(nums2)\n \n if len(nums1_set) <= max_len and len(nums2_set) <= max_len:\n return len(nums1_set.union(nums2_set))\n \n num1_added = set()\n\n for num in nums1_set:\n if num not in nums2_set and len(num1_added) < max_len:\n num1_added.add(num)\n \n num2_added = set()\n \n for num in nums2_set:\n if num not in nums1_set and len(num2_added) < max_len:\n num2_added.add(num)\n \n for i in nums1_set:\n if len(num1_added) < max_len and i not in num1_added:\n num1_added.add(i)\n \n for i in nums2_set:\n if len(num2_added) < max_len and i not in num1_added and i not in num2_added:\n num2_added.add(i)\n \n return len(num1_added.union(num2_added))\n \n \n \n \n \n```
| 3 | 0 |
['Python3']
| 1 |
maximum-size-of-a-set-after-removals
|
✅ 97% beats || Python3 || Set
|
97-beats-python3-set-by-lutfullo_m-p9wr
|
\n\n\n\n# Intuition\nTo solve this problem, we can use a greedy approach. We aim to maximize the size of the set s after removing elements from nums1 and nums2.
|
lutfullo_m
|
NORMAL
|
2024-05-26T12:40:13.802447+00:00
|
2024-05-26T12:40:13.802468+00:00
| 90 | false |
\n\n\n\n# Intuition\nTo solve this problem, we can use a greedy approach. We aim to maximize the size of the set `s` after removing elements from `nums1` and `nums2`. We can achieve this by removing elements that appear the most in both arrays. Additionally, we may need to remove elements from one array to balance the removals between the two arrays.\n\n# Approach\n1. Initialize variables `length`, `n1`, and `n2`. `length` represents half the length of the input arrays, while `n1` and `n2` are sets of unique elements from `nums1` and `nums2`, respectively.\n2. Calculate the number of elements common to both `n1` and `n2` and store it in `inter_num`.\n3. Calculate the difference between the lengths of `n1` and `n2` and `length`, representing the excess elements in each array.\n4. Determine the maximum possible difference between the lengths of `n1` and `n2` and `length`, or the number of elements common to both arrays. Store this maximum difference in `max_diff`.\n5. Return the sum of the lengths of `n1` and `n2` minus `max_diff`, which represents the maximum possible size of the set `s`.\n\n# Complexity\n- Time complexity: O(n), where `n` is the total number of elements in both `nums1` and `nums2`. Calculating the set intersection and differences takes linear time.\n- Space complexity: O(n), where `n` is the total number of elements in both `nums1` and `nums2`. The space complexity is dominated by the sets `n1` and `n2`, which store unique elements from the input arrays.\n\n\n# Code\n```\nclass Solution:\n def maximumSetSize(self, nums1: list[int], nums2: list[int]) -> int:\n length, n1, n2 = len(nums1) // 2, set(nums1), set(nums2)\n inter_num = len(n1.intersection(n2))\n diff = 0\n\n diff += len(n1) - length if len(n1) >= length else 0\n diff += len(n2) - length if len(n2) >= length else 0\n\n max_diff=max(diff,inter_num)\n\n return (len(n1)+len(n2))-max_diff\n\n\n\n\n```\n\n\n\n
| 2 | 0 |
['Python3']
| 0 |
maximum-size-of-a-set-after-removals
|
100% Solution using HashSet O(n+m)
|
100-solution-using-hashset-onm-by-thanus-xmtc
|
Complexity\n- Time complexity: O(n+m)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n+m)\n Add your space complexity here, e.g. O(n) \n\n
|
thanushasm25
|
NORMAL
|
2024-01-19T06:28:44.779513+00:00
|
2024-01-19T06:28:44.779536+00:00
| 306 | false |
# Complexity\n- Time complexity: $$O(n+m)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n+m)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) {\n Set<Integer> set1 = new HashSet<>();\n Set<Integer> set2 = new HashSet<>();\n Set<Integer> set3 = new HashSet<>();\n int ans=0;\n for(int i:nums1){\n set1.add(i);\n set3.add(i);\n }\n if(set1.size()>nums1.length/2)\n ans=nums1.length/2;\n else\n ans=set1.size();\n for(int i:nums2){\n set2.add(i);\n set3.add(i);\n } \n if(set2.size()>nums2.length/2)\n ans+=nums2.length/2;\n else\n ans+=set2.size(); \n return ans>set3.size() ? set3.size() : ans; \n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
maximum-size-of-a-set-after-removals
|
🔥Greedy💯 || ✅Clean Code
|
greedy-clean-code-by-adish_21-da61
|
Complexity\n\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n\n# Code\n## Please Upvote if it helps\uD83E\uDD17\n\nclass Solution {\npublic:\n int
|
aDish_21
|
NORMAL
|
2024-01-11T18:30:59.626309+00:00
|
2024-01-11T18:30:59.626372+00:00
| 200 | false |
# Complexity\n```\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n```\n\n# Code\n## Please Upvote if it helps\uD83E\uDD17\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size(), ans = 0, count = 0;\n unordered_set<int> st1(nums1.begin(), nums1.end());\n unordered_set<int> st2(nums2.begin(), nums2.end());\n for(auto x : st1){\n if(!st2.contains(x)){\n count++;\n ans++;\n }\n if(count == n / 2)\n break;\n }\n count = 0;\n for(auto x : st2){\n if(!st1.contains(x)){\n count++;\n ans++;\n }\n if(count == n / 2)\n break;\n }\n count = 0;\n if(ans != n){\n for(auto x : st1){\n if(st2.contains(x))\n count++;\n }\n ans += min(n - ans, count);\n }\n return ans;\n }\n};\n```
| 2 | 0 |
['Array', 'Greedy', 'Ordered Set', 'C++']
| 0 |
maximum-size-of-a-set-after-removals
|
Java Most Easy Solution
|
java-most-easy-solution-by-vedantzope9-qyw1
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
vedantzope9
|
NORMAL
|
2024-01-08T02:57:17.838909+00:00
|
2024-01-08T02:57:17.838942+00:00
| 20 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) \n {\n int n=nums1.length;\n\n Set<Integer>set1=new HashSet<>();\n Set<Integer>set=new HashSet<>();\n\n for(int num : nums1)\n {\n set.add(num);\n set1.add(num);\n }\n int n1=set1.size();\n set1.clear();\n\n for(int num : nums2)\n {\n set.add(num);\n set1.add(num);\n }\n int n2=set1.size();\n int n3=set.size();\n\n int common=n1+n2-n3;\n\n int ans=Math.min(n/2 , n1-common);\n ans=ans+ Math.min(n/2 , n2-common);\n ans=ans+common;\n\n return Math.min(ans,n);\n }\n}\n```
| 2 | 0 |
['Ordered Set', 'Java']
| 0 |
maximum-size-of-a-set-after-removals
|
💡Most Optimized and Intuitive Code💡
|
most-optimized-and-intuitive-code-by-nis-o94b
|
Code\n\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n unordered_set<int>s1,s2,combined;\n int n =
|
nishant101
|
NORMAL
|
2024-01-07T05:23:28.209684+00:00
|
2024-01-07T05:23:28.209715+00:00
| 176 | false |
# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n unordered_set<int>s1,s2,combined;\n int n = nums1.size();\n for(auto it : nums1) s1.insert(it);\n for(auto it : nums2) s2.insert(it);\n for(auto it : s1) combined.insert(it);\n for(auto it : s2) combined.insert(it);\n int a,b; // a,b = maximum no. of elements from first and second set \n \n if(s1.size()< n/2) a = s1.size(); // if the size of set is less than the maximum elements we can take\n else a = n/2; // else take all n/2 elements i.e. atleast n/2 elements are distinct\n \n if(s2.size() < n/2) b = s2.size();\n else b = n/2;\n int combined_size = combined.size();\n \n return min(combined_size,a+b); \n // min - as from a+b same elements from both the sets could be calculated\n // ans.size() to consider the possibility of repeated elements in both the sets\n }\n};\n```\n# Kindly Upvote If you like the code \uD83D\uDE0A
| 2 | 0 |
['C++']
| 0 |
maximum-size-of-a-set-after-removals
|
Simple and Easy Casework
|
simple-and-easy-casework-by-manmeet8287-vvb5
|
Intuition\nThere can be 2 types of elements in each set,\n\n1. Which are common in both the arrays\n2. Which are distinct in both the arrays\n\n\nNow, suppose t
|
Manmeet8287
|
NORMAL
|
2024-01-07T05:16:39.505732+00:00
|
2024-01-07T05:16:39.505760+00:00
| 60 | false |
# Intuition\nThere can be 2 types of elements in each set,\n```\n1. Which are common in both the arrays\n2. Which are distinct in both the arrays\n```\n\nNow, suppose there are **x** elements in set A which are distinct and **y** elements in set B which are distinct and **m** elements arre common in both of them.\nThere can be atmax **4** possible cases:\n\n1. `x>=n/2 and y>=n/2`\n We can pick only distinct elements from the both the set and **answer=n**.\n2. `x>=n/2 and y<n/2 `\n We can keep distinct elements in set 1 and common elements + y in set 2. In this way, the **answer= n/2+min(n/2,y+m);**\n3. `x<n/2 and y>=n/2`\n We can keep distinct elements in set 2 and common elements + x in set 1.Then, **answer=n/2+min(n/2,x+m)**;\n4. `x<n/2 and y<n/2`\nWe keep distinct elements of both the elements in combination with the common elements. Then **answer=min(n,x+y+m)**;\n# Approach\nWe will copy all the elements of nums1 and nums2 in 2 sets, in order to have only distinct elements.Then we we will iterate through set1 and check if this particular element is present in set2, simply push it in common and erase from second. Also, then we will iterate through common elements and remove this element from set 1 as well and then we will do the casework which i discussed above.\n\n# Complexity\n- Time complexity:\nSince, we are using only set to erase and insert elements.\n**TC- O(nlogn)**\n\n- Space complexity:\nWe are using 3 distinct sets which will store atmost 2*n elements when all of them are distinct. Hence, **SC=O(2n)**\n\n# Code\n```\n#define all(v) v.begin(),v.end()\n\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n int n=nums1.size();\n set<int> st1(all(nums1));\n set<int> st2(all(nums2));\n set<int> common;\n for(auto &it:st1)\n {\n if(st2.count(it))\n {\n common.insert(it);\n st2.erase(it);\n }\n }\n for(auto &it:common) st1.erase(it);\n int siz1=st1.size(),siz2=st2.size(),m=common.size();\n if(siz1>=n/2 and siz2>=n/2) return n;\n else if(siz1>=n/2)\n {\n int sec=min(siz2+m,n/2);\n return n/2+sec;\n }\n else if(siz2>=n/2)\n {\n int sec=min(siz1+m,n/2);\n return n/2+sec;\n }\n else\n {\n int ans=min(siz1+siz2+m,n);\n return ans;\n }\n }\n};\n```
| 2 | 0 |
['Math', 'C++']
| 1 |
maximum-size-of-a-set-after-removals
|
3 sets - Java O(N) | O(N)
|
3-sets-java-on-on-by-wangcai20-1dm0
|
Intuition\n Describe your first thoughts on how to solve this problem. \nPure logic, we first should pick non-overlap unique numbers from nums1 up to n/2 as wel
|
wangcai20
|
NORMAL
|
2024-04-29T01:52:05.352869+00:00
|
2024-04-29T01:52:05.352895+00:00
| 32 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nPure logic, we first should pick non-overlap unique numbers from `nums1` up to `n/2` as well as non-overlap unique numbers from `nums2` up to `n/2`. We can see these numbers is safe to pick without affecting the rest.\n\nThen we can add the `overlap` on top of picked numbers as long as if the total number is less than `nums1` size.\n\nUse 3 sets to track:\n* `set1` - unique numbers from `nums1`\n* `set2` - unique numbers from `nums2`\n* `overlap` - overlap of `set1 and set2`\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) {\n // each set can contribute 0..n/2 unique numbers after removal\n // first pick unique non-overlap up to n/2 on each set, then add overlap, max by n\n Set<Integer> set1 = new HashSet<>(), set2 = new HashSet<>(), overlap = new HashSet<>();\n for (int val:nums1) set1.add(val);\n for (int val:nums2) set2.add(val);\n for (int val:set1) \n if (set2.contains(val)) \n overlap.add(val);\n for (int val:overlap) {\n set1.remove(val);\n set2.remove(val);\n }\n int cnt = 0, len = nums1.length;\n cnt += Math.min(set1.size(), len/2);\n cnt += Math.min(set2.size(), len/2);\n cnt = Math.min(cnt + overlap.size(),len);\n return cnt;\n }\n}\n```
| 1 | 0 |
['Java']
| 1 |
maximum-size-of-a-set-after-removals
|
Greedy Approach | Simple Solution | C++
|
greedy-approach-simple-solution-c-by-sam-eec2
|
Intuition\nThe value can be seperated into unique and common.\n\n# Approach\nGreedy approach of counting unique and common values.\n\n# Complexity\n- Time compl
|
sameerahmed56
|
NORMAL
|
2024-03-23T10:52:30.887727+00:00
|
2024-03-23T10:52:30.887750+00:00
| 287 | false |
# Intuition\nThe value can be seperated into unique and common.\n\n# Approach\nGreedy approach of counting unique and common values.\n\n# Complexity\n- Time complexity:\n- O(N)\n\n- Space complexity:\n- O(N)\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n int m = nums1.size()/2;\n unordered_map<int,int> mp1,mp2;\n \n for(auto &i: nums1){\n mp1[i]++;\n }\n for(auto &i: nums2){\n mp2[i]++;\n }\n int u1 =0, u2 =0, cm = 0;\n // Counting all unique values in nums1 that is not in nums2\n // Also counting commong values of in nums1 and nums2 \n for(auto &i: mp1){\n if(mp2.find(i.first) == mp2.end()) u1++;\n else cm++; \n }\n // Counting all unique values in nums2 that is not in nums1\n for(auto &i: mp2){\n if(mp1.find(i.first) == mp1.end()) u2++;\n }\n // The max values of common from after getting all the unique values\n int left1 = max(0,min(m-u1,cm)), left2 = max(0,min(m-u2,cm));\n // The answer would be sum of unique values and commong values \n return min(m,u1) + min(m,u2) + min(left1+left2,cm); \n }\n};\n```
| 1 | 0 |
['Greedy', 'Counting', 'C++']
| 0 |
maximum-size-of-a-set-after-removals
|
Intuition Based Solution || Diff to understand || Clean Code
|
intuition-based-solution-diff-to-underst-og73
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nBrute Force approach.\n
|
Marlboro_Man_10
|
NORMAL
|
2024-03-10T01:16:03.245297+00:00
|
2024-03-10T01:16:03.245336+00:00
| 13 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBrute Force approach.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->O(NlogN)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n int n= nums1.size();\n set<int> nums11;\n\n for(int i:nums1) nums11.insert(i);\n\n set<int> nums22;\n\n for(int i: nums2) nums22.insert(i);\n \n \n nums1.clear();\n nums2.clear();\n\n for(auto it: nums11) nums1.push_back(it);\n for(auto it: nums22) nums2.push_back(it);\n\n sort(nums1.begin(),nums1.end());\n sort(nums2.begin(),nums2.end());\n\n int i=0,j=0;\n int count=0;\n\n while(i<nums1.size() && j<nums2.size()){\n if(nums1[i]==nums2[j]) {\n count++;\n i++;\n j++;\n }\n\n else if(nums1[i]>nums2[j]) j++;\n else i++;\n }\n int one,two;\n \n if(nums1.size()>=nums2.size()){\n one = nums1.size()-count;\n if(one>n/2) one =n/2;\n two = nums2.size();\n \n\n }\n else {\n one = nums1.size();\n \n two = nums2.size()-count;\n if(two>n/2) two =n/2;\n }\n\n return one+two>n ? n : one + two;\n\n }\n};\n```
| 1 | 0 |
['Sorting', 'Ordered Set', 'C++']
| 0 |
maximum-size-of-a-set-after-removals
|
Simple with sets
|
simple-with-sets-by-kiujpl-jodf
|
Intuition\nGreedy algorithm: first pick unique elements from each list, then pick common elements.\n\n# Approach\n\nLet A be the (unique) elements that are only
|
kiujpl
|
NORMAL
|
2024-02-01T13:13:32.787753+00:00
|
2024-02-01T13:13:32.787775+00:00
| 6 | false |
# Intuition\nGreedy algorithm: first pick unique elements from each list, then pick common elements.\n\n# Approach\n\nLet A be the (unique) elements that are only in nums1, let B be the (unique) elements that are only in nums2, and let C be the (unique) elements that are in both.\n\nFirst pick `a = min(n/2, len(A))` elements from A and `b = min(n/2, len(B))` elements from B, which will be unique.\nThen pick `c = min(len(C), n-(a+b))` elements from C since we can pick `n/2-a` common elements from nums1 and `n/2-b` common elements from nums2, but at most `len(C)` common elements overall.\nThe answer is a + b + c.\n\nExample 1: A = [2], B = [], C = [1], n = 4.\n a = 1, b = 0, c = 1 -> return 2.\n\nExample 2: A = [1,4,5,6], B = [], C = [2,3], n = 6.\n a = 3, b = 0, c = 2 -> return 5.\n\nExample 3: A = [1,2,3], B = [4,5,6], C = [], n = 6.\n a = 3, b = 3, c = 0 -> return 6.\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n int maximumSetSize(List<int> nums1, List<int> nums2) {\n final set1 = Set<int>.from(nums1);\n final set2 = Set<int>.from(nums2);\n final A = set1.difference(set2);\n final B = set2.difference(set1);\n final C = set1.intersection(set2);\n final n = nums1.length;\n final a = min(A.length, n~/2);\n final b = min(B.length, n~/2);\n final c = min(C.length, n-(a+b));\n return a + b + c;\n }\n}\n```
| 1 | 0 |
['Dart']
| 0 |
maximum-size-of-a-set-after-removals
|
C++ map greedy observation
|
c-map-greedy-observation-by-uchihaxmadar-cka3
|
Intuition\n- The frequency of a number in an array is irrelevant; it will contribute at most once to the final count, whether it appears in one array or both.\n
|
uchihaXmadara
|
NORMAL
|
2024-01-08T21:25:18.243499+00:00
|
2024-01-08T21:30:54.550764+00:00
| 131 | false |
# Intuition\n- The frequency of a number in an array is irrelevant; it will contribute at most once to the final count, whether it appears in one array or both.\n\n- It\'s unnecessary to strictly select n/2 numbers from both arrays. For example, consider nums1: [1, 2, 4, 4, 4, 4, 4, 4], nums2: [1, 2, 3, 4, 5, 6, 7, 8]. If we select distinct elements from nums1, such as [1, 2], which is less than n/2 = 4, we can include the numbers common to both arrays: [1, 2, 4]. Similarly, for nums2: [3, 5, 6, 7], resulting in the set [1, 2, 4, 5, 6, 7]. Even if nums1 had [1, 2, 4, 4], the final set would remain the same. This is because having fewer distinct elements than n/2 implies the presence of repeating numbers. Including repeating numbers won\'t affect the final set, as it is ensured to have distinct values.\n\n\n# Approach\n- For nums1 count dinstinct numbers that are not present in nums2.\n- If these distinct numbers are less than n/2, count distinct numbers that are present in both.\n- Similarly, for nums2, ensuring that common numbers already taken from nums1 are not considered again.\n\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size();\n map<int, int> f1, f2;\n for(auto &e:nums1) f1[e]++;\n for(auto &e:nums2) f2[e]++;\n int ans = 0;\n int ct = 0;\n for(auto &[e, v]:f1) {\n if(ct == n/2) break;\n if(f2.find(e)==f2.end()) ct++;\n }\n for(auto &[e, v]:f1) {\n if(f2.find(e) == f2.end()) continue;\n if(ct == n/2) break;\n ct++;\n f2[e] = INT_MAX;\n }\n ans += ct;\n\n ct = 0;\n for(auto &[e, v]:f2) {\n if(ct == n/2) break;\n if(f1.find(e)==f1.end()) ct++;\n }\n for(auto &[e, v]:f2) {\n if(f1.find(e)==f1.end() || f2[e]==INT_MAX) continue; // if it\'s already counted in nums1\n if(ct == n/2) break;\n ct++;\n }\n return ans+ct;\n }\n};\n```
| 1 | 0 |
['Hash Table', 'Greedy', 'C++']
| 0 |
maximum-size-of-a-set-after-removals
|
Easy Sorting + Hashmaps
|
easy-sorting-hashmaps-by-piyuxh_01-1a65
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Piyuxh_01
|
NORMAL
|
2024-01-08T15:11:31.782272+00:00
|
2024-01-08T15:11:31.782302+00:00
| 8 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size();\n sort(begin(nums1),end(nums1));\n sort(begin(nums2),end(nums2));\n int r1 = 0, r2 = 0;\n for(int i=1;i<n;i++){\n if(r1 == n/2) break;\n if(nums1[i] == nums1[i-1]){\n nums1[i-1] = 0;\n r1++;\n }\n }\n for(int i=1;i<n;i++){\n if(r2 == n/2) break;\n if(nums2[i] == nums2[i-1]){\n nums2[i-1] = 0;\n r2++;\n }\n }\n unordered_map<int,int> mp;\n for(auto i:nums1){\n if(i != 0) mp[i]++;\n }\n for(auto i:nums2){\n if(i != 0) mp[i]++;\n }\n if(r1 >= n/2 and r2 >= n/2) return mp.size();\n int req1 = n/2 - r1;\n int req2 = n/2 - r2;\n req1 = max(req1,0);\n req2 = max(req2,0);\n cout<<req1 <<" "<<req2<<endl;\n if(req1 > 0){\n for(auto i:nums1){\n if(req1 == 0) break;\n if(i != 0){\n if(mp[i] > 1){\n req1--;\n mp[i]--;\n }\n }\n }\n }\n if(req2 > 0){\n for(auto i:nums2){\n if(req2 == 0) break;\n if(i != 0){\n if(mp[i] > 1){\n req2--;\n mp[i]--;\n }\n }\n }\n }\n cout<<req1<<" "<<req2<<endl;\n int ans = mp.size();\n ans -= (req1 + req2);\n return ans;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
maximum-size-of-a-set-after-removals
|
C++ Most Optimal and Concise Solution with Comments and Explanation!
|
c-most-optimal-and-concise-solution-with-huix
|
Please upvote if you found this helpful!\n\n# Code\n\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n // se
|
Ningck
|
NORMAL
|
2024-01-07T18:48:48.379206+00:00
|
2024-01-07T18:53:15.929380+00:00
| 4 | false |
Please upvote if you found this helpful!\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n // set1 is the number of unique elements that will be remaining after removal in nums1 (max size will be n/2)\n // set2 is the number of unique elements that will be remaining after removal in nums2 (max size will be n/2)\n // both is the number of elements that overlap in nums1 & nums2\n int set1 = 0, set2 = 0, both = 0, n = nums1.size();\n unordered_set<int> allNums1, allNums2;\n for (int num: nums1) allNums1.insert(num);\n for (int num: nums2) allNums2.insert(num);\n\n // greedily add all unique nums in nums1 to set1\n // and add all of the overlap to both\n for (int num: allNums1) {\n if (allNums2.find(num) == allNums2.end()) ++set1;\n else ++both;\n }\n set1 = std::min(set1, n/2); // you can only have at most n/2\n\n // greedily add all unique nums in nums2 to set2\n for (int num: allNums2) {\n if (allNums1.find(num) == allNums1.end()) ++set2;\n }\n set2 = std::min(set2, n/2); // you can only have at most n/2\n\n // add as many of "both" to set1 to get it as high as n/2\n if (set1 < n/2) {\n int need = n/2 - set1;\n int use = std::min(need, both);\n set1 += use;\n both -= use;\n }\n\n // add as many of "both" to set2 to get it as high as n/2\n if (set2 < n/2) {\n int need = n/2 - set2;\n int use = std::min(need, both);\n set2 += use;\n both -= use;\n }\n\n return set1 + set2;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
maximum-size-of-a-set-after-removals
|
C ++ solution . TC -- > O(n)
|
c-solution-tc-on-by-blueberryy-b7l7
|
Intuition\n Describe your first thoughts on how to solve this problem. \nPick unique elements from both arrays and then go for common elements if needed .\n\n#
|
blueberryy
|
NORMAL
|
2024-01-07T13:58:15.275439+00:00
|
2024-01-07T13:58:15.275471+00:00
| 29 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nPick unique elements from both arrays and then go for common elements if needed .\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size();\n unordered_map<int,int>mp;\n unordered_set<int>st(nums1.begin(), nums1.end());\n unordered_set<int>st2(nums2.begin(), nums2.end());\n for(auto it : st){\n mp[it]++;\n }\n for(auto it : st2){\n mp[it]++;\n }\n int nn = n / 2, mm = nn;\n unordered_set<int>ans;\n int common = 0;\n for(auto it : mp){\n if(it.second == 2) common ++;\n }\n for(auto it : st){\n if(mp[it] == 1 && nn > 0){\n ans.insert(it);\n nn --;\n }\n }\n for(auto it : st2){\n if(mp[it] == 1 && mm > 0){\n ans.insert(it);\n mm --;\n }\n }\n return ans.size() + min(common, mm + nn);\n \n }\n};\n```
| 1 | 0 |
['C++']
| 1 |
maximum-size-of-a-set-after-removals
|
C++ Implementation using Set
|
c-implementation-using-set-by-ayushnauti-o91i
|
\n\n# Code\n\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n vector<int>v,v1;\n sort(nums1.begin(),
|
ayushnautiyal1110
|
NORMAL
|
2024-01-07T09:47:15.174395+00:00
|
2024-01-07T09:47:15.174423+00:00
| 26 | false |
\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n vector<int>v,v1;\n sort(nums1.begin(),nums1.end());\n \n sort(nums2.begin(),nums2.end());\n for(auto x:nums1){\n if(v.empty()){\n v.push_back(x);\n }\n else if(v.back()!=x){\n v.push_back(x);\n }\n }\n for(auto x:nums2){\n if(v1.empty()){\n v1.push_back(x);\n }\n else if(v1.back()!=x){\n v1.push_back(x);\n }\n }\n \n set<int>st(nums1.begin(),nums1.end());\n set<int>st2(nums2.begin(),nums2.end());\n int i=0,j=0,n=nums1.size()/2,m=nums2.size()/2;\n set<int>s;\n \n for(auto x:v)\n {\n if(st2.find(x)==st2.end()){\n i++;\n s.insert(x);\n st.erase(x);\n }\n if(i==n)\n {\n break;\n }\n }\n for(auto x:v1)\n {\n if(st.find(x)==st.end()){\n j++;\n // cout<<x<<" ";\n s.insert(x);\n st2.erase(x);\n }\n if(j==m){\n break;\n }\n }\n // cout<<i<<" "<<j<<endl;\n while(i<n && j<m && st.size() && st2.size()){\n if(*st.begin()==*st2.begin()){\n if(n-i>m-j){\n i++;\n s.insert(*st.begin());\n st.erase(*st.begin());\n st2.erase(*st2.begin());\n }\n else{\n j++;\n s.insert(*st.begin());\n st.erase(*st.begin());\n st2.erase(*st2.begin());\n }\n }\n else{\n \n }\n }\n while(i<n && st.size()){\n \n if(s.find(*st.begin())==s.end())\n i++,s.insert(*st.begin()), st.erase(*st.begin());\n else\n st.erase(*st.begin());\n }\n while(j<m && st2.size()){\n \n if(s.find(*st2.begin())==s.end())\n j++,s.insert(*st2.begin()), st2.erase(*st2.begin());\n else\n st2.erase(*st2.begin());\n }\n return i+j;\n }\n};\n```
| 1 | 0 |
['Hash Table', 'C++']
| 0 |
maximum-size-of-a-set-after-removals
|
C++ | Intuitive solution
|
c-intuitive-solution-by-sahan_18-bxsu
|
Intuition\nVenn Diagram\n\n# Approach\nCalculate no. of same and different elements\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\n Add your
|
sahan_18
|
NORMAL
|
2024-01-07T06:51:14.930005+00:00
|
2024-01-07T06:51:14.930052+00:00
| 12 | false |
# Intuition\nVenn Diagram\n\n# Approach\nCalculate no. of same and different elements\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size();\n set<int> st1, st2;\n for(auto x : nums1) st1.insert(x);\n for(auto x : nums2) st2.insert(x);\n\n int same = 0;\n unordered_map<int, int> mp;\n for(auto it : st1) {\n if(st2.find(it) != st2.end()) {\n mp[it]++;\n same++;\n }\n }\n\n int left = n - same;\n if(left <= 0) return same;\n\n int d1 = 0, d2 = 0;\n for(auto it : st1) {\n if(mp.find(it) == mp.end()) d1++;\n }\n for(auto it : st2) {\n if(mp.find(it) == mp.end()) d2++;\n }\n\n int p1 = min(d1, n / 2);\n int p2 = min(d2, n / 2);\n\n if(p1 >= n / 2 && p2 >= n / 2) {\n return (p1 + p2);\n } else if (p1 >= n / 2) {\n return (p1 + p2 + min(same, (n / 2) - p2));\n } else if (p2 >= n / 2) {\n return (p1 + p2 + min(same, (n / 2) - p1));\n }\n return (p1 + p2 + min(same, n - (p1 + p2)));\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
maximum-size-of-a-set-after-removals
|
Easy to understand with approach and by using map
|
easy-to-understand-with-approach-and-by-mdxlu
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n1-Determine Target Size count1 and count2 which is nums1.size()/2.\n\n2-C
|
84SiddhantGupta
|
NORMAL
|
2024-01-07T06:02:04.107015+00:00
|
2024-01-07T06:02:04.107046+00:00
| 38 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n**1-Determine Target Size count1 and count2 which is nums1.size()/2.**\n\n**2-Count Occurrences of elements in nums1 and nums2**\n\n**3-Prioritize Arrays: which is having more unique elements.**\nCheck if the size of mp1 is greater than or equal to the size of mp2.\n\n4-**Create a set (st) to store unique elements**.\n\n5-**Iterate through nums1 and insert unique elements into the set until the target size (count1) is reached.**\n**Exclude elements already present in st and those found in nums2 (mp2)**.\n\n6-**If the target size (count1) is not reached then(count2 += count1), add remaining unique elements from nums2 to the set according to count2**.\n\n7-**Repeat steps 4-6 with the roles of nums1 and nums2 swapped**.\n\n**Return the size of the final set obtained from the array with more unique elements.**\n\n\n# Complexity\n- Time complexity: O(m + n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(min(m, n))\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n int count1 = nums1.size()/2;\n int count2 = nums2.size()/2;\n unordered_map<int,int>mp2;\n for(int i =0;i<nums2.size();i++) mp2[nums2[i]]++;\n unordered_map<int,int>mp1;\n for(int i =0;i<nums1.size();i++) mp1[nums1[i]]++;\n \n if(mp1.size()>=mp2.size()){\n set<int> st;\n for(int i = 0;i<nums1.size();i++){\n if(st.find(nums1[i])==st.end() && count1>0 && mp2.find(nums1[i])==mp2.end()){\n st.insert(nums1[i]); \n count1--;\n }\n }\n if(count1 != 0) count2 += count1;\n for(int i = 0;i<nums2.size();i++){\n if(st.find(nums2[i])==st.end() && count2>0){\n st.insert(nums2[i]);\n count2--;\n }\n }\n return st.size();\n }\n else{\n set<int> st;\n for(int i = 0;i<nums2.size();i++){\n if(st.find(nums2[i])==st.end() && count2>0 && mp1.find(nums2[i])==mp1.end()){\n st.insert(nums2[i]);\n count2--;\n }\n }\n if(count2 != 0) count1 += count2;\n for(int i = 0;i<nums1.size();i++){\n if(st.find(nums1[i])==st.end() && count1>0){\n st.insert(nums1[i]);\n count1--;\n }\n }\n for(auto it: st){\n cout<<it<<" ";\n }\n return st.size();\n }\n \n }\n};\n```
| 1 | 0 |
['Ordered Set', 'C++']
| 0 |
maximum-size-of-a-set-after-removals
|
JavaScript set and logic operations
|
javascript-set-and-logic-operations-by-t-jva2
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThis solution was inspired by @blackbrain2009\n\n\n# Approach\n Describe your approach
|
Tayomide
|
NORMAL
|
2024-01-07T04:38:44.961562+00:00
|
2024-01-07T04:45:20.876509+00:00
| 127 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis solution was inspired by [@blackbrain2009](https://leetcode.com/problems/maximum-size-of-a-set-after-removals/solutions/4520698/hash-table-math-t-o-n)\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nStep 1: You get the unique numbers of each array\nStep 2: You get the number of unique elements that appear in both arrays\nStep 3: You get the unique elements that do not appear in the other array and cap how many you can get to half the length, then you add the unique elements that appear in both arrays. If the answer is more than the needed length you return the full length of the array\n\n# Complexity\n- Time complexity: $$O(m + n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(m + n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {number[]} nums1\n * @param {number[]} nums2\n * @return {number}\n */\nvar maximumSetSize = function(nums1, nums2) {\n const d1 = new Set(nums1), d2 = new Set(nums2);\n\n let len1 = d1.size, len2 = d2.size, eq = 0;\n\n for (const key of d1) {\n if (d2.has(key)) eq++;\n }\n\n const halfLength = nums1.length / 2;\n \n return Math.min(Math.min(len2 - eq, halfLength) + Math.min(len1 - eq, halfLength) + eq, halfLength*2)\n};\n```
| 1 | 0 |
['JavaScript']
| 1 |
maximum-size-of-a-set-after-removals
|
[JavaScript] 10037. Maximum Size of a Set After Removals
|
javascript-10037-maximum-size-of-a-set-a-pi8t
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
pgmreddy
|
NORMAL
|
2024-01-07T04:28:45.568269+00:00
|
2024-01-07T04:30:28.915757+00:00
| 66 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n---\n\n```\nvar maximumSetSize = function (a, b) {\n function tryTrimToHalf(set1, set2, n) {\n for (const e of set1)\n if (set1.size > n / 2)\n if (set2.has(e)) {\n set1.delete(e)\n }\n }\n function trimBothToHalf_andMerge(set1, set2, n) {\n const a = [...set1].slice(0, n / 2)\n const b = [...set2].slice(0, n / 2)\n const merged = [...a, ...b]\n return merged\n }\n const n = a.length\n const set1 = new Set([...a])\n const set2 = new Set([...b])\n tryTrimToHalf(set1, set2, n)\n tryTrimToHalf(set2, set1, n)\n const merged = trimBothToHalf_andMerge(set2, set1, n)\n const set = new Set(merged)\n return set.size <= n ? set.size : n\n}\n```\n\n---\n\nWeekly Contest 379\n\n- Q1 answer - https://leetcode.com/problems/maximum-area-of-longest-diagonal-rectangle/solutions/4520901/javascript-10035-maximum-area-of-longest-diagonal-rectangle/\n\n---\n
| 1 | 0 |
['JavaScript']
| 1 |
maximum-size-of-a-set-after-removals
|
Simple solution using set operations
|
simple-solution-using-set-operations-by-8yz8u
|
Code\n\nclass Solution:\n def maximumSetSize(self, nums1: List[int], nums2: List[int]) -> int:\n s1, s2, n = set(nums1), set(nums2), len(nums1)\n
|
ajmalhassan
|
NORMAL
|
2024-01-07T04:28:40.063769+00:00
|
2024-01-07T04:28:40.063802+00:00
| 16 | false |
# Code\n```\nclass Solution:\n def maximumSetSize(self, nums1: List[int], nums2: List[int]) -> int:\n s1, s2, n = set(nums1), set(nums2), len(nums1)\n return min(\n min(len(s1 - s2), n // 2) # Numbers in s1 but not in s2, limited to n/2 as we have to pick max of n/2\n + min(len(s2 - s1), n // 2) # Numbers in s2 but not in s1, limited to n/2 as we have to pick max of n/2\n + len(s1.intersection(s2)), # Common numbers in both sets\n n # The maximum result should not exceed n\n )\n```
| 1 | 0 |
['Python3']
| 0 |
maximum-size-of-a-set-after-removals
|
Easy C++✅✅ solution using 'unordered_set'
|
easy-c-solution-using-unordered_set-by-a-efzx
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Abbas_R
|
NORMAL
|
2024-01-07T04:22:46.539740+00:00
|
2024-01-07T04:22:46.539764+00:00
| 35 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n unordered_set<int>s1,s2,s;\n for(auto v:nums1){\n s1.insert(v);\n }\n for(auto v:nums2){\n s2.insert(v);\n }\n int n = nums1.size()/2;\n vector<int>a,b;\n for(auto v:s1){\n a.push_back(v);\n }\n for(auto v:s2){\n b.push_back(v);\n }\n for(auto v : a){\n if(s1.size()<=n)break;\n if(s2.find(v)!=s2.end()){\n s1.erase(v);\n }\n }\n for(auto v : b){\n if(s2.size()<=n)break;\n if(s1.find(v)!=s1.end()){\n s2.erase(v);\n }\n }\n while(s1.size()>n){\n s1.erase(s1.begin());\n }\n while(s2.size()>n){\n s2.erase(s2.begin());\n }\n for(auto v:s1){\n s.insert(v);\n }\n for(auto v:s2){\n s.insert(v);\n }\n return s.size();\n }\n};\n```
| 1 | 0 |
['Ordered Set', 'C++']
| 0 |
maximum-size-of-a-set-after-removals
|
[Python 🐍] Sets Unique in nums1 PLUS Unique in nums2 PLUS Shared nums1 nums2
|
python-sets-unique-in-nums1-plus-unique-od9wb
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
xmky
|
NORMAL
|
2024-01-07T04:21:34.607502+00:00
|
2024-01-08T02:48:09.817331+00:00
| 179 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumSetSize(self, nums1: List[int], nums2: List[int]) -> int:\n N = len(nums1)\n\n s1 = set(nums1)\n s2 = set(nums2)\n \n u1 = s1 -s2\n u2 = s2 - s1\n\n shared = s1 & s2\n\n return min( min(len(u1), N//2) + min(len(u2), N//2) + len(shared), N )\n\n\n```
| 1 | 0 |
['Python3']
| 1 |
maximum-size-of-a-set-after-removals
|
Brute Force
|
brute-force-by-prithvinadagouda-gevs
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nDONT LOOK AT THE SIZE ITS UNDERSTANTABLE\n\n# Complexity\n- Time complexi
|
PrithviNadagouda
|
NORMAL
|
2024-01-07T04:11:16.072851+00:00
|
2024-01-07T04:11:16.072891+00:00
| 490 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nDONT LOOK AT THE SIZE ITS UNDERSTANTABLE\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n map<int,int>mp1;\n map<int,int>mp2;\n int k1=nums1.size()/2;\n int k2=nums2.size()/2;\n for(auto x:nums1){\n mp1[x]++;\n }\n for(auto x:nums2){\n mp2[x]++;\n }\n for(auto &x:mp1){\n if(k1<=0) break;\n while(x.second>1 and k1>0){\n x.second--;\n k1--;\n }\n }\n for(auto &x:mp2){\n if(k2<=0) break;\n while(x.second>1 and k2>0){\n x.second--;\n k2--;\n }\n }\n if(k1==0 and k2==0){\n set<int>st;\n for(auto x:mp1){\n st.insert(x.first);\n }\n for(auto x:mp2){\n st.insert(x.first);\n }\n return st.size();\n }\n if(k1>0 and k2==0){\n for(auto &x:mp1){\n if(k1<=0) break;\n if(mp2.find(x.first)!=mp2.end()){\n mp1[x.first]--;\n k1--;\n }\n }\n \n set<int>st;\n for(auto x:mp1){\n st.insert(x.first);\n }\n for(auto x:mp2){\n st.insert(x.first);\n }\n return st.size()-k1;\n }\n if(k1==0 and k2>0){\n for(auto &x:mp2){\n if(k2<=0) break;\n if(mp1.find(x.first)!=mp1.end()){\n mp2[x.first]--;\n k2--;\n }\n }\n \n set<int>st;\n for(auto x:mp1){\n st.insert(x.first);\n }\n for(auto x:mp2){\n st.insert(x.first);\n }\n return st.size()-k2;\n }\n if(k1>0 and k2>0){\n for(auto &x:mp1){\n if(k1<=0) break;\n if(mp2.find(x.first)!=mp2.end()){\n mp1[x.first]--;\n k1--;\n }\n }\n for(auto &x:mp2){\n if(k2<=0) break;\n if(mp1.find(x.first)!=mp1.end()){\n mp2[x.first]--;\n k2--;\n }\n }\n set<int>st;\n for(auto x:mp1){\n st.insert(x.first);\n }\n for(auto x:mp2){\n st.insert(x.first);\n }\n if((st.size()-k2-k1)>nums1.size()){\n return nums1.size();\n }\n return st.size()-k2-k1;\n }\n return -1;\n }\n};\n```
| 1 | 0 |
['Ordered Map', 'C++']
| 2 |
maximum-size-of-a-set-after-removals
|
Brute Force Python Sol.
|
brute-force-python-sol-by-r34per-twri
|
Code\n\nclass Solution:\n def maximumSetSize(self, nums1: List[int], nums2: List[int]) -> int:\n cnt1=Counter(nums1)\n cnt2=Counter(nums2)\n
|
R34PER
|
NORMAL
|
2024-01-07T04:08:08.721502+00:00
|
2024-01-07T04:08:08.721591+00:00
| 125 | false |
# Code\n```\nclass Solution:\n def maximumSetSize(self, nums1: List[int], nums2: List[int]) -> int:\n cnt1=Counter(nums1)\n cnt2=Counter(nums2)\n \n target=len(nums1)//2\n temp=set()\n \n c1,c2=0,0\n for key,val in cnt1.items():\n if c1>=target:\n break\n if key not in cnt2:\n c1+=1\n temp.add(key)\n \n for key,val in cnt2.items():\n if c2>=target:\n break\n if key not in cnt1:\n c2+=1\n temp.add(key)\n \n if c1>c2:\n for key,val in cnt1.items():\n if c1>=target:\n break\n if key not in temp:\n temp.add(key)\n c1+=1\n \n for key,val in cnt2.items():\n if c2>=target:\n break\n if key not in temp:\n temp.add(key)\n c2+=1\n \n else:\n for key,val in cnt2.items():\n if c2>=target:\n break\n if key not in temp:\n temp.add(key)\n c2+=1\n \n for key,val in cnt1.items():\n if c1>=target:\n break\n if key not in temp:\n temp.add(key)\n c1+=1\n \n print(c1,c2)\n print(temp)\n return len(temp)\n \n \n \n \n \n \n \n \n \n \n \n \n \n \n```
| 1 | 0 |
['Python3']
| 1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.