question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
maximum-size-of-a-set-after-removals
|
Set + math O(t):n
|
set-math-t-on-by-blackbrain2009-0f9q
|
I inspired Tayomide for solution, it pleasantly surprised me.IntuitionApproachComplexity
Time complexity: O(n)
Space complexity: O(n)
Code
|
blackbrain2009
|
NORMAL
|
2024-01-07T04:02:00.881639+00:00
|
2025-03-31T20:09:11.492703+00:00
| 97 | false |
I inspired [Tayomide](https://leetcode.com/Tayomide/) for [solution](https://leetcode.com/problems/maximum-size-of-a-set-after-removals/solutions/4520968/javascript-set-and-logic-operations/), it pleasantly surprised me.
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(n)
- Space complexity: O(n)
# Code
```
var maximumSetSize = function (nums1, nums2) {
const d1 = new Set(nums1),
d2 = new Set(nums2);
let eq = 0;
for (const element of d1) if (d2.has(element)) eq++;
let [len1, len2] =
d1.size < d2.size ? [d1.size, d2.size] : [d2.size, d1.size];
const halfLength = nums1.length / 2;
return (
Math.min(
len2 - Math.max(0, eq - Math.max(0, len1 - halfLength)),
halfLength
) + Math.min(len1, halfLength)
);
};
```
| 1 | 0 |
['Math', 'JavaScript']
| 0 |
maximum-size-of-a-set-after-removals
|
JAVA COMMENTED SOLUTION INTUTIVE PRIORITY QUEUE BASED SOLUTION
|
java-commented-solution-intutive-priorit-i2r0
|
\n\n\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) {\n // Frequency map for nums1 and nums2\n HashMap<Integer, Intege
|
Sai_Govind_2024
|
NORMAL
|
2024-01-07T04:01:47.262767+00:00
|
2024-01-07T04:46:45.945498+00:00
| 350 | false |
```\n\n\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) {\n // Frequency map for nums1 and nums2\n HashMap<Integer, Integer> frequencyMap1 = new HashMap<>();\n HashMap<Integer, Integer> frequencyMap2 = new HashMap<>();\n\n // Counting frequency for nums1\n for (int num : nums1) {\n frequencyMap1.put(num, frequencyMap1.getOrDefault(num, 0) + 1);\n }\n \n // Counting frequency for nums2\n for (int num : nums2) {\n frequencyMap2.put(num, frequencyMap2.getOrDefault(num, 0) + 1);\n }\n\n // Priority queue for nums1 based on frequency and secondary sorting on nums2 frequency\n PriorityQueue<Integer> pq1 = new PriorityQueue<>((a, b) -> {\n if (frequencyMap1.get(a).equals(frequencyMap1.get(b))) {\n return frequencyMap2.getOrDefault(b, 0) - frequencyMap2.getOrDefault(a, 0);\n } else {\n return frequencyMap1.get(b) - frequencyMap1.get(a);\n }\n });\n\n // Adding keys from frequencyMap1 to pq1\n for (int key : frequencyMap1.keySet()) {\n pq1.add(key);\n }\n\n // Reduce frequencyMap1 to half of its original size\n int size1 = nums1.length / 2;\n while (size1-- > 0) {\n int top = pq1.poll();\n if (frequencyMap1.get(top) == 1) {\n frequencyMap1.remove(top);\n } else {\n frequencyMap1.put(top, frequencyMap1.get(top) - 1);\n pq1.add(top);\n }\n }\n\n // Priority queue for nums2 based on frequency and secondary sorting on nums1 frequency\n PriorityQueue<Integer> pq2 = new PriorityQueue<>((a, b) -> {\n if (frequencyMap2.get(a).equals(frequencyMap2.get(b))) {\n return frequencyMap1.getOrDefault(b, 0) - frequencyMap1.getOrDefault(a, 0);\n } else {\n return frequencyMap2.get(b) - frequencyMap2.get(a);\n }\n });\n\n // Adding keys from frequencyMap2 to pq2\n for (int key : frequencyMap2.keySet()) {\n pq2.add(key);\n }\n\n // Reduce frequencyMap2 to half of its original size\n int size2 = nums1.length / 2;\n while (size2-- > 0) {\n int top = pq2.poll();\n if (frequencyMap2.get(top) == 1) {\n frequencyMap2.remove(top);\n } else {\n frequencyMap2.put(top, frequencyMap2.get(top) - 1);\n pq2.add(top);\n }\n }\n\n // Combining unique keys from both maps\n HashSet<Integer> uniqueKeys = new HashSet<>(frequencyMap1.keySet());\n uniqueKeys.addAll(frequencyMap2.keySet());\n\n // Returning the size of unique keys\n return uniqueKeys.size();\n }\n}\n```\n
| 1 | 0 |
['Hash Table', 'Greedy', 'C', 'Heap (Priority Queue)', 'Java']
| 0 |
maximum-size-of-a-set-after-removals
|
Super Easy and Fast solution C#
|
super-easy-and-fast-solution-c-by-bogdan-ub2s
|
Complexity
Time complexity: O(N)
Space complexity: O(N)
Code
|
bogdanonline444
|
NORMAL
|
2025-03-27T12:17:34.640693+00:00
|
2025-03-27T12:17:34.640693+00:00
| 2 | false |
# Complexity
- Time complexity: O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(N)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```csharp []
public class Solution {
public int MaximumSetSize(int[] nums1, int[] nums2) {
int n = nums1.Length;
HashSet<int> arr1 = new HashSet<int>(nums1);
HashSet<int> arr2 = new HashSet<int>(nums2);
int count1 = arr1.Count;
int count2 = arr2.Count;
foreach(int num in arr1)
{
if(!arr2.Contains(num))
{
arr1.Remove(num);
}
}
int removed = arr1.Count;
return Math.Min(count1 + count2 - removed, Math.Min(n / 2, count1) + Math.Min(n / 2, count2));
}
}
```

| 0 | 0 |
['Array', 'Hash Table', 'C#']
| 0 |
maximum-size-of-a-set-after-removals
|
first one solved
|
first-one-solved-by-abbass_tabikh-koed
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Abbass_Tabikh
|
NORMAL
|
2025-03-09T14:48:03.461417+00:00
|
2025-03-09T14:48:03.461417+00:00
| 4 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```csharp []
public class Solution {
public int MaximumSetSize(int[] nums1, int[] nums2) {
var unique = new HashSet<int>();
var common = new HashSet<int>();
int halfMax = nums1.Length / 2;
int uniqueCount = 0;
// Process the first array
for (int i = 0; i < nums1.Length; i++) {
if (uniqueCount == halfMax)
break;
// If already exists in either set, skip
if (unique.Contains(nums1[i]) || common.Contains(nums1[i]))
continue;
// If the element is in the second array, add to common set
if (nums2.Contains(nums1[i])) {
common.Add(nums1[i]);
} else {
// Otherwise, add to unique set and increment the count
unique.Add(nums1[i]);
uniqueCount++;
}
}
// Reset unique count for the second array processing
uniqueCount = 0;
// Process the second array
for (int i = 0; i < nums2.Length; i++) {
if (uniqueCount == halfMax)
break;
// If already in common set, skip
if (common.Contains(nums2[i]))
continue;
// If not in unique set, add to unique set and increment the count
if (!unique.Contains(nums2[i])) {
unique.Add(nums2[i]);
uniqueCount++;
}
}
// Calculate the total count of unique and common elements
int totalCount = unique.Count + common.Count;
// Return the minimum of totalCount and halfMax * 2
return totalCount >= (halfMax * 2) ? halfMax * 2 : totalCount;
}
}
```
| 0 | 0 |
['C#']
| 0 |
maximum-size-of-a-set-after-removals
|
Easy CPP Solution
|
easy-cpp-solution-by-rdbhalekar_2907-pdro
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Rdbhalekar_2907
|
NORMAL
|
2025-03-06T06:30:26.961095+00:00
|
2025-03-06T06:30:26.961095+00:00
| 0 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(N)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(N)
# Code
```cpp []
class Solution {
public:
int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {
unordered_set<int> s1,s2,c;
for(int i=0;i<nums1.size();i++)
{
s1.insert(nums1[i]);
}
for(int i=0;i<nums2.size();i++)
{
s2.insert(nums2[i]);
if(s1.find(nums2[i]) != s1.end())
{
c.insert(nums2[i]);
}
}
int n1 = s1.size();
int n2 = s2.size();
int n = nums1.size();
int c1 = c.size();
return min(min(n1-c1,n/2) + min(n2-c1,n/2)+c1,n);
}
};
```
| 0 | 0 |
['C++']
| 0 |
maximum-size-of-a-set-after-removals
|
Easy CPP Solution
|
easy-cpp-solution-by-rdbhalekar_2907-ntvn
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Rdbhalekar_2907
|
NORMAL
|
2025-03-06T06:30:25.157019+00:00
|
2025-03-06T06:30:25.157019+00:00
| 2 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(N)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(N)
# Code
```cpp []
class Solution {
public:
int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {
unordered_set<int> s1,s2,c;
for(int i=0;i<nums1.size();i++)
{
s1.insert(nums1[i]);
}
for(int i=0;i<nums2.size();i++)
{
s2.insert(nums2[i]);
if(s1.find(nums2[i]) != s1.end())
{
c.insert(nums2[i]);
}
}
int n1 = s1.size();
int n2 = s2.size();
int n = nums1.size();
int c1 = c.size();
return min(min(n1-c1,n/2) + min(n2-c1,n/2)+c1,n);
}
};
```
| 0 | 0 |
['C++']
| 0 |
maximum-size-of-a-set-after-removals
|
Easy hash table
|
easy-hash-table-by-minh_hung-kopt
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
minh_hung
|
NORMAL
|
2025-03-05T22:55:12.574947+00:00
|
2025-03-05T22:55:12.574947+00:00
| 2 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def maximumSetSize(self, nums1: List[int], nums2: List[int]) -> int:
n = len(nums1)
c1 = set(nums1)
c2 = set(nums2)
common = set()
for k in c1:
if k in c2:
common.add(k)
l1 = max(n//2 - (len(nums1) - len(c1)), 0)
l2 = max(n//2 - (len(nums2) - len(c2)), 0)
total = len(c1) + len(c2) - len(common)
miss = max(l1 + l2 - len(common), 0)
print(l1,l2,total,miss)
return total - miss
```
| 0 | 0 |
['Python3']
| 0 |
maximum-size-of-a-set-after-removals
|
C++ Simple Hash Based Solution With Step-Wise Comments
|
c-simple-hash-based-solution-with-step-w-dmlg
|
IntuitionTry removing elems having freq>1 and than target common elements.Common elems remove from both and than later distribute to map which can accomodate it
|
SJ4u
|
NORMAL
|
2025-02-22T11:18:08.262478+00:00
|
2025-02-22T11:18:08.262478+00:00
| 3 | false |
# Intuition
Try removing elems having freq>1 and than target common elements.
Common elems remove from both and than later distribute to map which can accomodate it (i.e. removal has become negative).
# Complexity
- Time complexity: $$O(n)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(n)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
// Function to collect frequency of elements in a map
void collectFrequency(const vector<int>& nums, unordered_map<int, int>& freqMap) {
for (int num : nums) {
freqMap[num]++;
}
}
// Function to trim repeated elements until a limit 'n' is reached
int trimRepeatedElements(unordered_map<int, int>& freqMap, int n) {
for (auto& [key, count] : freqMap) {
if (count > 1) {
if (n <= 0) break;
int reduction = min(n, count - 1);
freqMap[key] -= reduction;
n -= reduction;
}
}
return n;
}
// Function to handle common elements between both sets
void handleCommonElements(unordered_map<int, int>& freqMap1, unordered_map<int, int>& freqMap2, int& n1, int& n2) {
vector<int> commonElements;
// Identify common elements
for (const auto& [key, _] : freqMap1) {
if (freqMap2.count(key)) {
commonElements.push_back(key);
n1 -= freqMap1[key];
n2 -= freqMap2[key];
}
}
// Remove common elements from both maps
for (int key : commonElements) {
freqMap1.erase(key);
freqMap2.erase(key);
}
int idx = 0;
// Adjust remaining n1 and n2 by reintroducing common elements if necessary
while (n1 < 0 && idx < commonElements.size()) {
freqMap1[commonElements[idx]]++;
idx++;
n1++;
}
while (n2 < 0 && idx < commonElements.size()) {
freqMap2[commonElements[idx]]++;
idx++;
n2++;
}
}
// Function to trim extra elements from a frequency map
void trimExtraElements(unordered_map<int, int>& freqMap, int& n) {
while (n > 0 && !freqMap.empty()) {
auto it = freqMap.begin();
freqMap.erase(it);
n--;
}
}
// Main function to determine the maximum set size
int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {
unordered_map<int, int> freqMap1, freqMap2, finalFreqMap;
int n1 = nums1.size() / 2;
int n2 = n1;
// Step 1: Collect frequencies of elements
collectFrequency(nums1, freqMap1);
collectFrequency(nums2, freqMap2);
// Step 2: Trim repeated elements
n1 = trimRepeatedElements(freqMap1, n1);
n2 = trimRepeatedElements(freqMap2, n2);
// Step 3: Handle common elements
if (n1 > 0 || n2 > 0) {
handleCommonElements(freqMap1, freqMap2, n1, n2);
}
// Step 4: Trim extra elements if necessary
if (n1 > 0) trimExtraElements(freqMap1, n1);
if (n2 > 0) trimExtraElements(freqMap2, n2);
// Step 5: Merge both frequency maps into final map
for (const auto& [key, count] : freqMap1) {
if (count > 0) finalFreqMap[key] += count;
}
for (const auto& [key, count] : freqMap2) {
if (count > 0) finalFreqMap[key] += count;
}
return finalFreqMap.size();
}
};
```
| 0 | 0 |
['C++']
| 0 |
maximum-size-of-a-set-after-removals
|
Easy solution C++
|
easy-solution-c-by-trivedi_anshul-e9f5
|
IntuitionA set contains unique entries.1)So, why don't we first remove all the duplicate entries, keeping at least only one entry of that element.Now, if the re
|
Trivedi_Anshul
|
NORMAL
|
2025-02-21T05:49:27.742455+00:00
|
2025-02-21T05:49:27.742455+00:00
| 2 | false |
# Intuition
A set contains unique entries.
1)So, why don't we first remove all the duplicate entries, keeping at least only one entry of that element.
Now, if the required size (n) is achieved, the job is done.
2)Otherwise, we still need to remove elements from the arrays(either from one or from the other or from both of them). For that matter, why don't we remove all the entries that are duplicate in these arrays, first keeping the at least one of the duplicate entry in one of the array.
3)Now, even after doing the 2nd operation, still the required size is not achieved, then we are left with no option other than to remove the unqiue entry, from either of the array.
Now, since all the duplicate entries that are present in the entire combnation considering 1 and 2 together, are removed, we are left with only unique elements.
So, now remove the unique entries up until our target is achieved.
# Approach
1)First, we put both the array elements in a set and in map mpp1 and mpp2.
2)Now we check, that weather first removing duplicate entries does our task or not.
For that operation, we remove all the values of a no. up until the value for that particular key is just 1.
And if p1 has reached n/2 we break out of mpp1, loop
Same we do for p2
3) We check, weather after adding count, gives the required size or not.
4)If it still does not, then we we have to remove some element from the set.
This is done, by finding out the required elements by sub the current total from the original set size.
# Complexity
- Time complexity:
O(N)
- Space complexity:
O(N+M)
# Code
```cpp []
class Solution {
public:
int maximumSetSize(vector<int>& nums1, vector<int>& nums2)
{
unordered_set<int>st;
unordered_set<int>mpp1, mpp2;
int n = nums1.size();
for(int i = 0; i<n; ++i)
{
st.insert(nums1[i]);
st.insert(nums2[i]);
mpp1.insert(nums1[i]);
mpp2.insert(nums2[i]);
}
int p1 = 0, p2 = 0;
int m = n/2;
int r1 = n - mpp1.size();
int r2 = n - mpp2.size();
if(r1 > m)
{
p1 = m;
}
else
{
p1 = r1;
}
if(r2 > m)
{
p2 = m;
}
else
{
p2 = r2;
}
if(p1 + p2 == n)
{
int s = st.size();
st.clear();
mpp1.clear();
mpp2.clear();
return s;
}
else
{
int o = st.size();
int sub = 0;
int s = 0;
for(auto it: st)
{
if(mpp1.find(it) != mpp1.end() && mpp2.find(it) != mpp2.end())
{
s++;
}
}
st.clear();
mpp1.clear();
mpp2.clear();
int val = p1 + p2;
if(val + s < n)
{
sub = n - (val + s);
}
return o - sub;
}
};
```
| 0 | 0 |
['C++']
| 0 |
maximum-size-of-a-set-after-removals
|
It's a math question
|
its-a-math-question-by-linda2024-c1kh
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
linda2024
|
NORMAL
|
2025-02-10T19:56:47.890321+00:00
|
2025-02-10T19:56:47.890321+00:00
| 4 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
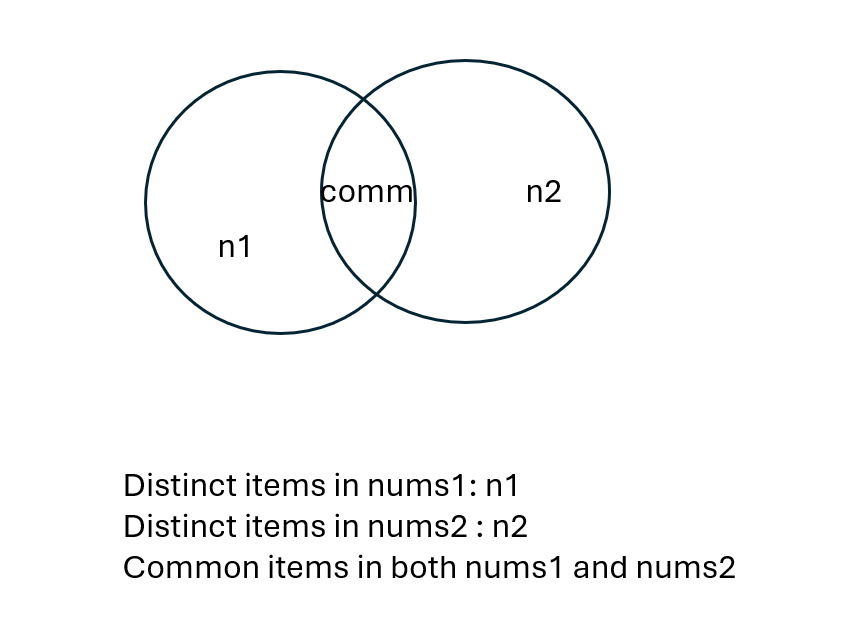
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```csharp []
public class Solution {
public int MaximumSetSize(int[] nums1, int[] nums2) {
int len1 = nums1.Length, len2 = nums2.Length;
HashSet<int> dist1 = new HashSet<int>(nums1), dist2 = new HashSet<int>(nums2);
int comm = 0;
foreach(int n in dist2)
{
if(dist1.Contains(n))
comm++;
}
int only1 = dist1.Count-comm, only2 = dist2.Count-comm;
int res = Math.Min(len1/2, only1) + Math.Min(len2/2, only2);
int rest = Math.Min(len1/2+len2/2-res, comm);
return res+rest;
}
}
```
| 0 | 0 |
['C#']
| 0 |
maximum-size-of-a-set-after-removals
|
Maximum size of a Set After Removals
|
maximum-size-of-a-set-after-removals-by-b8f39
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Naeem_ABD
|
NORMAL
|
2025-01-13T18:52:32.560521+00:00
|
2025-01-13T18:52:32.560521+00:00
| 7 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def maximumSetSize(self, nums1: List[int], nums2: List[int]) -> int:
target = len(nums1) // 2
unique1, unique2 = set(nums1), set(nums2)
present_in_both = unique1 & unique2
# Calculate initial removals
removals1 = len(nums1) - len(unique1)
removals2 = len(nums2) - len(unique2)
# Remove elements from unique1 until target is met
while removals1 < target:
if present_in_both:
n = present_in_both.pop()
unique1.remove(n)
else:
unique1.pop()
removals1 += 1
# Remove elements from unique2 until target is met
while removals2 < target:
if present_in_both:
n = present_in_both.pop()
unique2.remove(n)
else:
unique2.pop()
removals2 += 1
# Combine remaining elements
unique1.update(unique2)
return len(unique1)
```
| 0 | 0 |
['Python3']
| 0 |
maximum-size-of-a-set-after-removals
|
Simple logical thinking
|
simple-logical-thinking-by-vaibhavt19-fpu2
|
IntuitionApproachComplexity
Time complexity: O(n)
Space complexity:O(n)
Code
|
Vaibhavt19
|
NORMAL
|
2025-01-04T17:57:03.416459+00:00
|
2025-01-04T17:57:03.416459+00:00
| 6 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(n)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int maximumSetSize(int[] nums1, int[] nums2) {
HashMap<Integer,Integer> map=new HashMap<>();
int distinctUniqueToArray1=0, distinctUniqueToArray2=0,distinctCommonToBoth=0;
/*
We will mark all those numbers unique to Array1 with value 1 in the map
We will mark all those numbers unique to Array2 with value 2 in the map
We will mark all those numbers common to both Array1 and Array2 with value 3 in the map
*/
for(int i=0;i<nums1.length;i++)
{
if(!map.containsKey(nums1[i]))
{
map.put(nums1[i],1);
distinctUniqueToArray1++;
}
}
for(int i=0;i<nums2.length;i++)
{
if(!map.containsKey(nums2[i]))
{
map.put(nums2[i],2);
distinctUniqueToArray2++;
}
else
{
int j=map.get(nums2[i]);
if(j==1)
{
distinctUniqueToArray1--;
map.put(nums2[i],3);
distinctCommonToBoth++;
}
}
}
int k=Math.min(nums1.length/2,distinctUniqueToArray1); //no of choices filled out of a total n/2 from Array 1 taking elements present only in Array1
int K=Math.max(0,nums1.length/2-k);// no of choices left to be made from Array1
int m=Math.min(nums1.length/2,distinctUniqueToArray2);//no of choices filled out of a total n/2 from Array2 taking elements present only in Array2
int M=Math.max(0,nums1.length/2-m);// no of choices left to be made from Array1
return k+m+Math.min(distinctCommonToBoth,K+M);
}
}
```
| 0 | 0 |
['Java']
| 0 |
maximum-size-of-a-set-after-removals
|
Big And Small
|
big-and-small-by-tonitannoury01-t6bv
|
IntuitionApproachComplexity
Time complexity:
O(n)
Space complexity:
Code
|
tonitannoury01
|
NORMAL
|
2024-12-27T19:49:03.721123+00:00
|
2024-12-27T19:49:03.721123+00:00
| 2 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
O(n)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```javascript []
/**
* @param {number[]} nums1
* @param {number[]} nums2
* @return {number}
*/
var maximumSetSize = function (nums1, nums2) {
let s1 = new Set(nums1);
let s2 = new Set(nums2);
let n = nums1.length;
let r1 = n - s1.size;
let r2 = n - s2.size;
let sf1 = Math.max(0, n / 2 - r1);
let sf2 = Math.max(0, n / 2 - r2);
let smaller;
let bigger;
let remFromBig;
let remFromSmall;
if (s1.size > s2.size) {
smaller = s2;
bigger = s1;
remFromBig = sf1;
remFromSmall = sf2;
} else {
smaller = s1;
bigger = s2;
remFromBig = sf2;
remFromSmall = sf1;
}
for (let s of smaller) {
if (!remFromBig) {
break;
}
if (bigger.has(s)) {
bigger.delete(s);
remFromBig--;
}
}
for (let b of bigger) {
if (!remFromSmall) {
break;
}
if (smaller.has(b)) {
smaller.delete(b);
remFromSmall--;
}
}
for (let s of smaller) {
bigger.add(s);
}
return bigger.size - remFromBig - remFromSmall;
};
```
| 0 | 0 |
['JavaScript']
| 0 |
maximum-size-of-a-set-after-removals
|
Hash Map Solution CPP 0(n)
|
hash-map-solution-cpp-0n-by-saga_9-evok
|
Intuition-> First keep them in hash map respectively, to make search in constant time,
-> Now we will get the common element count and two variable for unique e
|
saga_9
|
NORMAL
|
2024-12-24T08:04:20.700670+00:00
|
2024-12-24T08:04:20.700670+00:00
| 3 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
-> First keep them in hash map respectively, to make search in constant time,
-> Now we will get the common element count and two variable for unique element count from repective array against other array.
# Approach
<!-- Describe your approach to solving the problem. -->
-> Now count the elements for **ucount** as unique element that is present in array1 and common element from both array in **ccount**.
-> Now count the unique element from the array 2 against array 1.
-> Now the main logic, we will the count of the elememt to exact half of the arrat size if count value is greater than half, the reason we are doing because we need to take only half from the both array.
e.g. [1,2,3,4] and [5,6,7,8]
ucount1 = 4; half of it -> 2
ucount2 = 4; half of it -> 2;
->Now adding them will give the answer and obviously ccount will be zero.
-> Now we have ccount > 0 and other count varaible are also > 0 then we need to add all of it and check if we are not exceeding the actual array size, if yes return 'n'(the size of the array).
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(n)$$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(n)$$
# Code
```cpp []
class Solution {
public:
int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {
int n = nums1.size();
unordered_map<int,int> mp1;
unordered_map<int,int> mp2;
int ucount1 = 0;
int ucount2 = 0;
int ccount = 0;
for(auto x: nums1) {
mp1[x]++;
}
for(auto x: nums2) {
mp2[x]++;
}
for(auto x: mp1){
if(mp2.find(x.first) == mp2.end()){
ucount1++;
}else{
ccount++;
}
}
for(auto x: mp2) {
if(mp1.find(x.first) == mp1.end()) {
ucount2++;
}
}
if(ucount1 > n/2){
ucount1 = n/2;
}
if(ucount2 > n/2){
ucount2 = n/2;
}
if(ucount1 + ccount + ucount2 > n){
return n;
}
return ucount1 + ccount + ucount2;
}
};
```
| 0 | 0 |
['C++']
| 0 |
maximum-size-of-a-set-after-removals
|
Hash Map Solution CPP 0(n)
|
hash-map-solution-cpp-0n-by-saga_9-w5mw
|
Intuition-> First keep them in hash map respectively, to make search in constant time,
-> Now we will get the common element count and two variable for unique e
|
saga_9
|
NORMAL
|
2024-12-24T08:04:18.050172+00:00
|
2024-12-24T08:04:18.050172+00:00
| 3 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
-> First keep them in hash map respectively, to make search in constant time,
-> Now we will get the common element count and two variable for unique element count from repective array against other array.
# Approach
<!-- Describe your approach to solving the problem. -->
-> Now count the elements for **ucount** as unique element that is present in array1 and common element from both array in **ccount**.
-> Now count the unique element from the array 2 against array 1.
-> Now the main logic, we will the count of the elememt to exact half of the arrat size if count value is greater than half, the reason we are doing because we need to take only half from the both array.
e.g. [1,2,3,4] and [5,6,7,8]
ucount1 = 4; half of it -> 2
ucount2 = 4; half of it -> 2;
->Now adding them will give the answer and obviously ccount will be zero.
-> Now we have ccount > 0 and other count varaible are also > 0 then we need to add all of it and check if we are not exceeding the actual array size, if yes return 'n'(the size of the array).
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(n)$$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(n)$$
# Code
```cpp []
class Solution {
public:
int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {
int n = nums1.size();
unordered_map<int,int> mp1;
unordered_map<int,int> mp2;
int ucount1 = 0;
int ucount2 = 0;
int ccount = 0;
for(auto x: nums1) {
mp1[x]++;
}
for(auto x: nums2) {
mp2[x]++;
}
for(auto x: mp1){
if(mp2.find(x.first) == mp2.end()){
ucount1++;
}else{
ccount++;
}
}
for(auto x: mp2) {
if(mp1.find(x.first) == mp1.end()) {
ucount2++;
}
}
if(ucount1 > n/2){
ucount1 = n/2;
}
if(ucount2 > n/2){
ucount2 = n/2;
}
if(ucount1 + ccount + ucount2 > n){
return n;
}
return ucount1 + ccount + ucount2;
}
};
```
| 0 | 0 |
['C++']
| 0 |
maximum-size-of-a-set-after-removals
|
Using sets, 100% speed
|
using-sets-100-speed-by-evgenysh-02h5
|
\n\n# Code\npython3 []\nclass Solution:\n def maximumSetSize(self, nums1: List[int], nums2: List[int]) -> int:\n target = len(nums1) // 2\n uni
|
evgenysh
|
NORMAL
|
2024-10-19T22:50:28.507975+00:00
|
2024-10-19T22:50:28.507992+00:00
| 7 | false |
\n\n# Code\n```python3 []\nclass Solution:\n def maximumSetSize(self, nums1: List[int], nums2: List[int]) -> int:\n target = len(nums1) // 2\n unique1, unique2 = set(nums1), set(nums2)\n present_in_both = unique1 & unique2\n\n # Calculate initial removals\n removals1 = len(nums1) - len(unique1)\n removals2 = len(nums2) - len(unique2)\n\n # Remove elements from unique1 until target is met\n while removals1 < target:\n if present_in_both:\n n = present_in_both.pop()\n unique1.remove(n)\n else:\n unique1.pop()\n removals1 += 1\n\n # Remove elements from unique2 until target is met\n while removals2 < target:\n if present_in_both:\n n = present_in_both.pop()\n unique2.remove(n)\n else:\n unique2.pop()\n removals2 += 1\n\n # Combine remaining elements\n unique1.update(unique2)\n\n return len(unique1)\n```
| 0 | 0 |
['Python3']
| 0 |
maximum-size-of-a-set-after-removals
|
Using only hashset O(N)
|
using-only-hashset-on-by-happy_coderr-x637
|
Intuition\nTo maximize the set we need to pick most unique elements\n\n# Approach\n1. Get unique elements of num1 in set1 which are not there in set2\n2. Get un
|
happy_coderr
|
NORMAL
|
2024-10-15T19:16:42.741466+00:00
|
2024-10-15T19:23:10.679931+00:00
| 0 | false |
# Intuition\nTo maximize the set we need to pick most unique elements\n\n# Approach\n1. Get unique elements of num1 in set1 which are not there in set2\n2. Get unique elements of num2 in set2 which are not there in set1\n3. Get common elemenets which are available in both set1 and set2\n4. Not we can pick elements from set1, set2, and common such that the size doesn\'t exceed n.\n\n# Complexity\n- Time complexity:\nO(n)\n- Space complexity:\no(n)\n\n# Code\n```java []\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) {\n Set<Integer> set1 = new HashSet<>();\n Set<Integer> set2 = new HashSet<>();\n\n for (int num : nums1) {\n set1.add(num);\n }\n int common = 0;\n for (int num : nums2) {\n set2.add(num);\n if (set1.contains(num)) {\n common++;\n }\n set1.remove(num);\n }\n for (int num : nums1) {\n set2.remove(num);\n }\n\n // 1 2 3 4\n int n = nums1.length;\n int left = (set1.size() <= n / 2) ? set1.size() : n / 2;\n int right = (set2.size() <= n / 2) ? set2.size() : n / 2;\n //System.out.println(set1.size() +":"+ set2.size()+ ":"+ common);\n int result = left + right + common;\n if(result <= n){\n return result;\n }\n return n;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximum-size-of-a-set-after-removals
|
solving this by good approach for beginner easily to understand using set in java script
|
solving-this-by-good-approach-for-beginn-bw2m
|
Intuition\nThe function maximumSetSize aims to determine the maximum size of a set formed from two input arrays, nums1 and nums2, with certain constraints. The
|
adii-the-billionaire
|
NORMAL
|
2024-10-08T14:09:19.932431+00:00
|
2024-10-08T14:09:19.932464+00:00
| 6 | false |
# Intuition\nThe function maximumSetSize aims to determine the maximum size of a set formed from two input arrays, nums1 and nums2, with certain constraints. The constraints are based on the number of common elements between the two sets created from the input arrays. The idea is to maximize the size of a new set while adhering to the following conditions:\n\nThe total size of the new set cannot exceed half of the size of nums1.\nThe size of the new set also takes into account the unique elements from both sets while considering the common elements Describe your first thoughts on how to solve this problem.\n\n# Approach\nSet Creation: Convert both input arrays into sets (s1 and s2) to eliminate duplicates.\nCommon Elements: Iterate through one set and check for common elements in the other set. Store these common elements in a new set called common.\nCalculate Sizes:\nDetermine the size of the original arrays, the unique sizes of both sets, and the size of the common elements.\nReturn the Result: Calculate the maximum possible size of the new set using the formula:\nresult=min(n,min(n/2,n1\u2212c)+min(n/2,n2\u2212c)+c)\nHere, n is the length of nums1, n1 and n2 are the sizes of the unique sets, and c is the count of common elements.\n\n\n\n# Complexity\n- Time complexity:\nCreating sets from nums1 and nums2 takes O(n1 + n2), where n1 is the length of nums1 and n2 is the length of nums2.\nThe loop to find common elements iterates through s1 (size n1), and checking membership in s2 is O(1) on average. Thus, this part also takes O(n1).\nOverall, the time complexity is O(n1 + n2).\n\n- Space complexity:\nThe space complexity is determined by the space required to store the sets s1, s2, and common.\nThe maximum space used is proportional to the unique elements in both arrays, which is O(n1 + n2) in the worst case (if all elements are unique).\nTherefore, the space complexity is also O(n1 + n2).\n\n# Code\n```javascript []\n/**\n * @param {number[]} nums1\n * @param {number[]} nums2\n * @return {number}\n */\nvar maximumSetSize = function (nums1, nums2) {\n\tlet s1 = new Set(nums1);\n\tlet s2 = new Set(nums2);\n\tlet common = new Set();\n\t//now checking the common elements from the two set\n\tfor (let val of s1) {\n\t\tif (s2.has(val)) {\n\t\t\tcommon.add(val);\n\t\t}\n\t}\n\tlet n = nums1.length;\n\tlet n1 = s1.size;\n\tlet n2 = s2.size;\n\tlet c = common.size;\n\treturn Math.min(n, Math.min(n / 2, n1 - c) + Math.min(n / 2, n2 - c) + c);\n};\n```
| 0 | 0 |
['JavaScript']
| 1 |
maximum-size-of-a-set-after-removals
|
Easy Solution using HashSet in Java
|
easy-solution-using-hashset-in-java-by-k-zlvk
|
Intuition\n Describe your first thoughts on how to solve this problem. \nWe neet to maximise the size of the final set , so we need unique elements because is r
|
kakuruhela2511
|
NORMAL
|
2024-09-24T12:43:43.775592+00:00
|
2024-09-24T12:43:43.775626+00:00
| 8 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe neet to maximise the size of the final set , so we need unique elements because is repeated elements are there they are added once and will not increase the size of final set.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTake set1 (Store unique elements of first array)\nTake set2 (Store unique elements of second array)\nTake set3 (Store unique elements from both the array)\n\nGet the common element using (set1.size()+set2.size()-set3.size())\n\nNow from set1 we need to take n/2 elements apart from common\nSimilarly from set2 we need to take n/2 elements apart from common\nNow add common element once.\n\nTill now we will get a answer but there are chances that value can be greater than n , so we use ans=Math.min(ans,n) becuause if n/2 ele is removed from first array and n/2 element is removed from second array then final set will contain max n element.\n\nWe return our final answer.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```java []\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) {\n int n=nums1.length;\n Set<Integer> set1=new HashSet<>();\n Set<Integer> set2=new HashSet<>();\n Set<Integer> set3=new HashSet<>();\n\n for(int ele:nums1)\n {\n set1.add(ele);\n set3.add(ele);\n } \n \n for(int ele:nums2)\n {\n set2.add(ele);\n set3.add(ele);\n }\n\n int common=set1.size()+set2.size()-set3.size();\n int n1=set1.size();\n int n2=set2.size();\n int ans=Math.min(n/2,n1-common);\n ans+=Math.min(n/2,n2-common);\n ans+=common;\n ans=Math.min(ans,n);\n return ans;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximum-size-of-a-set-after-removals
|
Simple || Straightforward
|
simple-straightforward-by-abhi5114-51el
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Abhi5114
|
NORMAL
|
2024-09-09T10:12:59.670257+00:00
|
2024-09-09T10:15:14.191603+00:00
| 0 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) {\n int n = nums1.length;\n HashMap<Integer, Integer> hm1 = new HashMap<>();\n HashMap<Integer, Integer> hm2 = new HashMap<>();\n int cnt1 = 0, cnt2 = 0;\n for (int i : nums1) {\n if (hm1.containsKey(i))\n cnt1++;\n hm1.put(i, hm1.getOrDefault(i, 0) + 1);\n\n }\n for (int i : nums2) {\n if (hm2.containsKey(i))\n cnt2++;\n hm2.put(i, hm2.getOrDefault(i, 0) + 1);\n }\n int r1 = hm1.size(), r2 = hm2.size();\n int common=findCommon(nums1,nums2);\n\n\n if (cnt1 < n / 2) {\n int remove =n / 2 - cnt1;\n if(remove<=common)\n common=common-remove;\n else\n common=0;\n r1 = r1 - remove;\n }\n if (cnt2 < n / 2) {\n int remove =n / 2 - cnt2;\n if(remove>=common){\n r2=r2-(remove);\n common=0;\n }\n \n }\n return r1 + r2 - common ;\n\n }\n public int findCommon(int nums1[],int nums2[])\n {\n Set<Integer> set1 = new HashSet<>();\n for (int num : nums1) {\n set1.add(num);\n }\n \n // Use another HashSet to store common elements\n Set<Integer> common = new HashSet<>();\n for (int num : nums2) {\n if (set1.contains(num)) {\n common.add(num);\n }\n }\n \n // Return the number of common elements\n return common.size();\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximum-size-of-a-set-after-removals
|
Easy Set Solution
|
easy-set-solution-by-kvivekcodes-hn86
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
kvivekcodes
|
NORMAL
|
2024-08-21T03:42:55.896053+00:00
|
2024-08-21T03:42:55.896085+00:00
| 4 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size();\n set<int> st1, st2, st;\n for(auto it: nums1) st1.insert(it);\n for(auto it: nums2) st2.insert(it);\n\n for(auto it: nums1){\n if(st2.count(it)) st.insert(it);\n }\n\n while(st1.size() > n/2 && !st.empty()){\n auto it = *st.begin();\n st1.erase(it);\n st.erase(st.begin());\n }\n while(st2.size() > n/2 && !st.empty()){\n auto it = *st.begin();\n st2.erase(it);\n st.erase(st.begin());\n }\n\n if(!st.empty()){\n return st1.size() + st2.size() - st.size();\n }\n return min(n/2, (int)st1.size()) + min(n/2, (int)st2.size());\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximum-size-of-a-set-after-removals
|
HASH SET
|
hash-set-by-shahsb-brhz
|
Key Observation\n1) The final answer will not exceed N. Where N = (n/2) + (n/2) (unique elements of nums1 & nums2).\n2) Common items from s1 & s2 would be consi
|
shahsb
|
NORMAL
|
2024-08-18T09:10:24.024937+00:00
|
2024-08-18T09:28:29.537918+00:00
| 2 | false |
# Key Observation\n1) The final answer will not exceed N. Where `N = (n/2) + (n/2)` (unique elements of nums1 & nums2).\n2) Common items from s1 & s2 would be considered only once.\n3) If we have more than `n/2` unique elements in both s1 & s2, we can easily discard them.\n4) Imporatant observation is that we have to return size at the end and hence no need to maintain numbers & calculate result from it.\n# Intuition\n1) **Step-1:** Calculate the number of unique elements in nums1 and nums2.\n2) **Step-2:** Identify the common unique elements between the two arrays.\n3) **Step-3:** Adjust the number of unique elements in each array to ensure that the total does not exceed n.\n# Complexity\n+ **TIME:** O(N)\n+ **SPACE:** O(N)\n# CODE:\n```\nclass Solution {\npublic:\n // SOL-1: HASH SET -- TC: O(N), SC: O(N).\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) \n {\n int n = nums1.size();\n\t\t// Step-1: Calculate unique elements in nums1 & nums2 -- O(N).\n unordered_set<int> s1(nums1.begin(), nums1.end());\n unordered_set<int> s2(nums2.begin(), nums2.end());\n \n // Step-2: Calculate the number of common elements -- O(N).\n int common = 0;\n for ( int num : s1 )\n if ( s2.count(num) )\n common++;\n \n // Step-3: Calculate the answer -- O(1).\n int ans = 0;\n ans += min(n / 2, static_cast<int>(s1.size()) - common);\n ans += min(n / 2, static_cast<int>(s2.size()) - common);\n ans += common;\n \n return min(n, ans);\n }\n};\n```
| 0 | 0 |
['C']
| 0 |
maximum-size-of-a-set-after-removals
|
Simple Java Set Solution: Beats 89%
|
simple-java-set-solution-beats-89-by-gav-tywx
|
Intuition\n Describe your first thoughts on how to solve this problem. \nIn order to maximize set size, you want to remove duplicates first before having to rem
|
gavgustin3
|
NORMAL
|
2024-08-15T05:23:56.819532+00:00
|
2024-08-15T05:23:56.819573+00:00
| 4 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIn order to maximize set size, you want to remove duplicates first before having to remove numbers that only appear once.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCalculate how many numbers you need to remove from both arrays. Store all seen numbers in a set. So, if the set contains a number, that means it\'s a duplicate and can reduce the amount of numbers to remove from the respective array (n1R or n2R).\n\nLogic behind Math.max() in return statement:\n If there are more shared values between the two array sets than there are elements needed to be removed from each set (ie same > n1R + n2R), then the total set will be limited by how many shared values there are. \n\nEx: nums1 set {1, 2, 3} with n1R = 1 (original size 3) and nums2 set {2, 3, 4} (original size 3) with n2R = 0. There are 2 values that are the same and only 1 element that needs to be removed. So, you can take care of the last element needed to be removed from nums1 by removing one of the shared values, like 2, creating a set of {1, 3}. But, because nums1 set and nums2 set still share the value of 3, the combined set will be {1, 3, 4}. This set is the same size of 3 + 3 - Math.max(2, 1 + 0)\nWhich is the equation n1.size() + n2.size() - Math.max(same, n1R + n2R)\n\nThe same logic can be applied with the opposite situtation, where there are more elements needed to be removed than shared values\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(nums1.length + nums2.length)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(nums1.length + nums2.length)\n\n# Code\n```\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) {\n Set<Integer> n1 = new HashSet<>();\n int n1R = nums1.length / 2;\n\n Set<Integer> n2 = new HashSet<>();\n int n2R = nums2.length / 2;\n\n for (int i : nums1) {\n if (n1.contains(i)) {\n if (n1R > 0) {\n n1R--;\n } \n } else {\n n1.add(i);\n }\n }\n\n for (int i : nums2) {\n if (n2.contains(i)) {\n if (n2R > 0) {\n n2R--;\n }\n } else {\n n2.add(i);\n }\n }\n\n int same = 0;\n for (int i : n1) {\n if (n2.contains(i)) {\n same++;\n }\n }\n\n return n1.size() + n2.size() - Math.max(same, n1R + n2R);\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximum-size-of-a-set-after-removals
|
Easy CPP Solution
|
easy-cpp-solution-by-clary_shadowhunters-mo2g
|
\n\n# Code\n\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) \n {\n set<int>st1(nums1.begin(),nums1.end());
|
Clary_ShadowHunters
|
NORMAL
|
2024-08-13T17:59:44.335804+00:00
|
2024-08-13T17:59:44.335847+00:00
| 0 | false |
\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) \n {\n set<int>st1(nums1.begin(),nums1.end());\n set<int>st2(nums2.begin(),nums2.end());\n int ans1=0;\n int n=nums1.size();\n for (auto it:nums1)\n {\n if (st1.find(it)!=st1.end() && st2.find(it)==st2.end())\n {\n ans1++;\n st1.erase(it);\n st2.erase(it);\n }\n }\n if (ans1>n/2) ans1=n/2;\n int ans2=0;\n for (auto it:nums2)\n {\n if (st2.find(it)!=st2.end() && st1.find(it)==st1.end())\n {\n ans2++;\n st2.erase(it);\n st1.erase(it);\n }\n }\n if (ans2>n/2) ans2=n/2;\n if (ans1+ans2==n) return n;\n int sz=st1.size();\n return min(ans1+ans2+sz,n);\n\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximum-size-of-a-set-after-removals
|
Set || Super Simple || C++
|
set-super-simple-c-by-lotus18-t5r9
|
Code\n\nclass Solution \n{\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) \n {\n set<int> st1, st2;\n int c1=nums1.si
|
lotus18
|
NORMAL
|
2024-08-13T17:51:03.537073+00:00
|
2024-08-13T17:51:03.537104+00:00
| 1 | false |
# Code\n```\nclass Solution \n{\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) \n {\n set<int> st1, st2;\n int c1=nums1.size()/2, c2=nums2.size()/2;\n for(auto it: nums1)\n {\n if(c1>0 && st1.find(it)!=st1.end()) c1--;\n st1.insert(it);\n }\n for(auto it: nums2)\n {\n if(c2>0 && st2.find(it)!=st2.end()) c2--;\n st2.insert(it);\n }\n set<int> st;\n for(auto it: st1) st.insert(it);\n for(auto it: st2) st.insert(it);\n int ans=st.size();\n set<int> newst1=st1;\n if(c1)\n {\n for(auto it: st1)\n {\n if(st2.find(it)!=st2.end()) \n {\n c1--;\n newst1.erase(it);\n if(c1==0) break;\n }\n }\n }\n if(c2)\n {\n for(auto it: st2)\n {\n if(newst1.find(it)!=newst1.end()) \n {\n c2--;\n if(c2==0) break;\n }\n }\n }\n if(c1) ans-=c1;\n if(c2) ans-=c2;\n return ans;\n }\n};\n\n```
| 0 | 0 |
['C++']
| 0 |
maximum-size-of-a-set-after-removals
|
JavaScript Greedy O(n)
|
javascript-greedy-on-by-lilongxue-n47n
|
Intuition\nUse the greedy approach. Of course, we should remove duplicates first.\n# Approach\nFor each set:\n 1. Remove all local duplicate elements until hal
|
lilongxue
|
NORMAL
|
2024-08-01T10:40:15.331528+00:00
|
2024-08-01T10:40:15.331546+00:00
| 5 | false |
# Intuition\nUse the greedy approach. Of course, we should remove duplicates first.\n# Approach\nFor each set:\n 1. Remove all local duplicate elements until half are left\n 2. If there are more than half left, remove elements that are also in the other set, until half are left\n 3. If there are still more than half left, remove any elements until half are left\n# Complexity\n- Time complexity:\nO(n)\n- Space complexity:\nO(n)\n# Code\n```\n/**\n * @param {number[]} nums1\n * @param {number[]} nums2\n * @return {number}\n */\nvar maximumSetSize = function(nums1, nums2) {\n const len = nums1.length, half = len >> 1\n function toFreqs(nums) {\n const map = new Map()\n for (const val of nums)\n map.set(val, 1 + (map.get(val) ?? 0))\n\n return map\n }\n\n function removeDuplicates(freqs, limit) {\n let result = 0\n for (const [val, freq] of freqs.entries()) {\n const needToRemove = freq - 1\n if (needToRemove > 0) {\n if (limit > needToRemove) {\n limit -= needToRemove\n freqs.set(val, 1)\n result += needToRemove\n } else {\n freqs.set(val, freq - limit)\n result += limit\n break\n }\n }\n }\n\n return result\n }\n\n\n const freqsA = toFreqs(nums1), freqsB = toFreqs(nums2)\n let rmgA = half - removeDuplicates(freqsA, half)\n let rmgB = half - removeDuplicates(freqsB, half)\n\n if (rmgA > 0) {\n for (const val of freqsA.keys()) {\n if (freqsB.get(val) > 0) {\n freqsA.set(val, 0)\n rmgA--\n if (rmgA === 0)\n break\n }\n }\n }\n if (rmgB > 0) {\n for (const val of freqsB.keys()) {\n if (freqsA.get(val) > 0) {\n freqsB.set(val, 0)\n rmgB--\n if (rmgB === 0)\n break\n }\n }\n }\n\n\n if (rmgA > 0) {\n for (const [val, freq] of freqsA.entries()) {\n if (freq !== 0) {\n freqsA.set(val, 0)\n rmgA--\n if (rmgA === 0)\n break\n }\n }\n }\n\n if (rmgB > 0) {\n for (const [val, freq] of freqsB.entries()) {\n if (freq !== 0) {\n freqsB.set(val, 0)\n rmgB--\n if (rmgB === 0)\n break\n }\n }\n }\n\n\n const set = new Set()\n for (const [val, freq] of freqsA) {\n if (freq) set.add(val)\n }\n for (const [val, freq] of freqsB) {\n if (freq) set.add(val)\n }\n\n\n return set.size\n};\n```
| 0 | 0 |
['JavaScript']
| 0 |
maximum-size-of-a-set-after-removals
|
Easy C++ using sets
|
easy-c-using-sets-by-0xsupra-2gwn
|
Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n)\n Add your space complexity here, e.g. O(n) \n\n# Co
|
0xsupra
|
NORMAL
|
2024-07-27T21:22:16.104638+00:00
|
2024-07-27T21:22:16.104659+00:00
| 6 | false |
# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& A, vector<int>& B) {\n int n = A.size();\n\n unordered_set<int> set1(A.begin(), A.end());\n unordered_set<int> set2(B.begin(), B.end());\n unordered_set<int> set;\n\n for(int i : A) set.insert(i);\n for(int i : B) set.insert(i);\n \n int max_s1 = min(n/2, (int)set1.size());\n int max_s2 = min(n/2, (int)set2.size());\n return min((int)set.size(), max_s1 + max_s2);\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximum-size-of-a-set-after-removals
|
Beats 100%💯 Easy to understand c++
|
beats-100-easy-to-understand-c-by-gokuuu-0jlq
|
\n\n# Approach\nUse Hashmaps to store freq of both arrays.Add unique elements of both arrays in the set.If space left add duplicate elements:)\n\n# Complexity\n
|
Gokuuu
|
NORMAL
|
2024-07-19T04:53:12.416105+00:00
|
2024-07-19T04:53:12.416121+00:00
| 3 | false |
\n\n# Approach\nUse Hashmaps to store freq of both arrays.Add unique elements of both arrays in the set.If space left add duplicate elements:)\n\n# Complexity\n- Time complexity:\nO(N1+N2)\n\n- Space complexity:\nO(N1+N2)\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n unordered_set<int>res;\n unordered_map<int, int> f1;\n unordered_map<int, int> f2;\n \n for (auto it : nums1) {\n f1[it]++;\n }\n for (auto it : nums2) {\n f2[it]++;\n }\n int td2=nums2.size()/2;\n int td1=td2;\n for(auto it:nums2)\n {\n if(f1[it]==0 && td2!=0 && res.find(it)==res.end())\n {\n res.insert(it);\n td2--;\n }\n }\n for(auto it:nums1)\n {\n if(f2[it]==0 && td1!=0 && res.find(it)==res.end())\n {\n res.insert(it);\n td1--;\n }\n }\n while(td1!=0)\n {\n for(auto it:nums1)\n {\n if(f2[it]>0 && td1!=0 && res.find(it)==res.end())\n {\n res.insert(it);\n td1--;\n }\n if(td1==0)\n break;\n }\n break;\n }\n while(td2!=0)\n {\n for(auto it:nums2)\n {\n if(f1[it]>0 && td2!=0 && res.find(it)==res.end())\n {\n res.insert(it);\n td2--;\n }\n if(td2==0)\n break;\n }\n break;\n }\n return res.size();\n }\n};\n\n```
| 0 | 0 |
['C++']
| 0 |
maximum-size-of-a-set-after-removals
|
Easy Java Solution || HashSet
|
easy-java-solution-hashset-by-mnnit1prak-haeq
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
mnnit_prakharg
|
NORMAL
|
2024-07-16T15:26:11.046242+00:00
|
2024-07-16T15:26:11.046278+00:00
| 7 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport java.util.*;\nimport java.io.*;\nclass Solution {\n public int maximumSetSize(int[] arr1, int[] arr2) {\n int n = arr1.length;\n HashSet<Integer> set1 = new HashSet<>();\n for(int i = 0; i < n; i++) set1.add(arr1[i]);\n HashSet<Integer> set2 = new HashSet<>();\n for(int i = 0; i < n; i++) set2.add(arr2[i]);\n HashSet<Integer> set3 = new HashSet<>();\n Iterator<Integer> it = set1.iterator();\n while(it.hasNext()){\n int x = it.next();\n if(set2.contains(x)) set3.add(x);\n }\n int ans1 = set1.size() - set3.size(), ans2 = set2.size() - set3.size();\n int dis1 = Math.min(ans1, n / 2), dis2 = Math.min(ans2, n / 2);\n int req = n - dis1 - dis2;\n return dis1 + dis2 + Math.min(req, set3.size());\n }\n}\n```
| 0 | 0 |
['Hash Table', 'Greedy', 'Java']
| 0 |
maximum-size-of-a-set-after-removals
|
[C++] Greedy, Hash Tables
|
c-greedy-hash-tables-by-amanmehara-n0kx
|
Complexity\n- Time complexity: O(n)\n- Space complexity: O(n)\n\n# Code\n\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nu
|
amanmehara
|
NORMAL
|
2024-07-04T02:51:27.885923+00:00
|
2024-07-04T02:51:27.885959+00:00
| 3 | false |
# Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size();\n unordered_set<int> s1, s2, join;\n for (const auto& num : nums1) {\n s1.insert(num);\n join.insert(num);\n }\n for (const auto& num : nums2) {\n s2.insert(num);\n join.insert(num);\n }\n int unique1 = s1.size(), unique2 = s2.size(), unique_join = join.size();\n return min(unique_join, min(unique1, n / 2) + min(unique2, n / 2));\n }\n};\n```
| 0 | 0 |
['Array', 'Hash Table', 'Greedy', 'C++']
| 0 |
maximum-size-of-a-set-after-removals
|
Simple Java Solution!!!
|
simple-java-solution-by-shankarreddy1503-6zb4
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
shankarreddy1503
|
NORMAL
|
2024-06-07T05:40:41.498388+00:00
|
2024-06-07T05:40:41.498416+00:00
| 17 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) {\n // Map<Integer,Integer> map1=new HashMap<>();\n // Map<Integer,Integer> map2=new HashMap<>();\n // for(int i:nums1){\n // map1.put(i,map1.getOrDefault(i,0)+1);\n // }\n // for(int i:nums2){\n // map2.put(i,map2.getOrDefault(i,0)+1);\n // }\n // for(int i:nums1){\n // if(map2.containsKey(i)){\n // map2.put(i,map2.get(i,0)-1);\n // map1.put(i,map1.get(i,0)-1);\n // if(map1.get(i)==0){\n // map1.remove(i);\n // }\n // if(map2.get(i)==0){\n // map2.remove(i);\n // }\n // }\n // }\n int n=nums1.length;\n Set<Integer> set1=new HashSet<>();\n Set<Integer> set2=new HashSet<>();\n Set<Integer> com=new HashSet<>();\n for(int i:nums1){\n set1.add(i);\n }\n for(int i:nums2){\n set2.add(i);\n }\n for(int i:set1){\n if(set2.contains(i)){\n com.add(i);\n }\n }\n int n1=set1.size(),n2=set2.size(),c=com.size();\n return Math.min(n,Math.min(n1-c,n/2)+Math.min(n2-c,n/2)+c);\n\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximum-size-of-a-set-after-removals
|
Finally Got it
|
finally-got-it-by-brianh27-ljqb
|
I first wen through each list. We may use greedy since we just need 1 occurence of an item for it to count.\nSo I start with 2 variables.\nThen I went through e
|
brianh27
|
NORMAL
|
2024-06-03T04:50:12.592665+00:00
|
2024-06-03T04:50:12.592684+00:00
| 13 | false |
I first wen through each list. We may use greedy since we just need 1 occurence of an item for it to count.\nSo I start with 2 variables.\nThen I went through each list to get rid of the numbers that occur more than once in each individual list. This is a guarenteed thinning.\n(Also I stored the occurences of both lists combined in a dictionary for O(1) access)\nThen I iterated through each list and if the occurence of that item occurs more in both lists, that would be redudant, thus we can remove it.\nThen after all of this is done, the last case scenario would be removing actual items from the set. We must remove at least n/2, so we subtract the items we\'ve already removed from n/2 for both variables, then subtract that from the total number of unique items from both lists. \n\n# Code\n```\nclass Solution:\n def maximumSetSize(self, nums1: List[int], nums2: List[int]) -> int:\n from collections import Counter\n d={}\n for a in Counter(nums1+nums2).most_common():\n d[a[0]]=a[1]\n n=int(len(nums1)/2)\n de=0\n un1=Counter(nums1).most_common()\n for a in un1:\n if (a[1]-1)+de>=n:\n d[a[0]]-=(n-de)\n de=False\n break\n d[a[0]]-=(a[1]-1)\n de+=(a[1]-1)\n \n if (a[1]-1)==0:\n \n break\n \n de1=0\n un2=Counter(nums2).most_common()\n for a in un2:\n if (a[1]-1)+de1>=n:\n d[a[0]]-=(n-de1)\n de1=False\n break\n d[a[0]]-=(a[1]-1)\n de1+=(a[1]-1)\n \n if (a[1]-1)==0:\n \n break\n #print(de,de1)\n if type(de)==int:\n\n for a in un1:\n if d[a[0]]>1:\n d[a[0]]-=1\n de+=1\n if de>=n:\n de=False\n break\n \n if type(de1)==int:\n for a in un2:\n if d[a[0]]>1:\n d[a[0]]-=1\n de1+=1\n if de1>=n:\n de1=False\n break\n \n diff=0\n if type(de)==int:\n diff+=(n-de)\n \n if type(de1)==int:\n diff+=(n-de1)\n return len(list(d.keys()))-diff\n \n \n \n```
| 0 | 0 |
['Python3']
| 0 |
maximum-size-of-a-set-after-removals
|
Easy C++ only Maps Solution| TC: O(n) | SC: O(n)
|
easy-c-only-maps-solution-tc-on-sc-on-by-yvew
|
Approach\n1. feed all the elements from nums1 to map1 (m1)\n2. feed all the elements from nums2 to map2 (m2)\n3. iterate over the m1 and take unique elements on
|
the_shridhar
|
NORMAL
|
2024-05-18T14:29:27.678350+00:00
|
2024-05-18T14:29:27.678389+00:00
| 9 | false |
# Approach\n1. feed all the elements from `nums1` to `map1 (m1)`\n2. feed all the elements from `nums2` to `map2 (m2)`\n3. iterate over the `m1` and take unique elements only, while iterating your are taking only `<=n/2` elements and delete them from map if taken. Maintain a count how much elements you took (lets say `taken1`)\n4. same process for map 2 (`m2`). Maintain a count how much elements you took (lets say `taken2`)\n5. now after this you have left only elements which are common and present in both m1 and m2\n6. iterate over `m1` again and take (`n/2-taken1`) elements and repeat same for `m2`, if taken erase them from another map since they are common and should be taken only once\n(can use`unordered_map` also)\n# Complexity\n- Time complexity:\nO(n)\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size();\n map<int,int> m1;\n map<int,int> m2;\n\n for(int i = 0; i<n; i++)\n {\n m1[nums1[i]]++;\n m2[nums2[i]]++;\n }\n\n int taken1 = 0;\n map<int,int> m;\n for(auto it: m1)\n {\n if(taken1<n/2 && !m2.count(it.first))\n {\n cout<<it.first<<", ";\n m[it.first]++;\n taken1++;\n m1[it.first] = 0;\n }\n else if(taken1>=n/2) break;\n }\n int taken2 = 0;\n cout<<endl;\n for(auto it: m2)\n {\n if(taken2<n/2 && !m1.count(it.first))\n {\n cout<<it.first<<", ";\n m[it.first]++;\n taken2++;\n m2[it.first] = 0;\n }\n else if(taken2>=n/2) break;\n }\n\n for(auto it: m1)\n {\n if(taken1<n/2 && it.second > 0)\n {\n m[it.first]++;\n taken1++;\n m2.erase(it.first);\n }\n else if(taken1>=n/2) break;\n }\n for(auto it: m2)\n {\n if(taken2<n/2 && it.second>0)\n {\n m[it.first]++;\n taken2++;\n m1.erase(it.first);\n }\n else if(taken2>=n/2) break;\n }\n return m.size();\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximum-size-of-a-set-after-removals
|
Simple Java Solution
|
simple-java-solution-by-sakshikishore-o3di
|
Code\n\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) {\n HashMap<Integer,Integer> h1=new HashMap<Integer,Integer>();\n
|
sakshikishore
|
NORMAL
|
2024-05-17T06:36:19.783087+00:00
|
2024-05-17T06:36:19.783116+00:00
| 9 | false |
# Code\n```\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) {\n HashMap<Integer,Integer> h1=new HashMap<Integer,Integer>();\n HashMap<Integer,Integer> h2=new HashMap<Integer,Integer>();\n int count1=0,count2=0;\n for(int i=0;i<nums1.length;i++)\n {\n if(!h1.containsKey(nums1[i]))\n {\n h1.put(nums1[i],1);\n }\n else\n {\n if(count1<nums1.length/2)\n {\n count1++;\n }\n else\n {\n h1.put(nums1[i],h1.get(nums1[i])+1);\n }\n }\n }\n for(int i=0;i<nums2.length;i++)\n {\n if(!h2.containsKey(nums2[i]))\n {\n h2.put(nums2[i],1);\n }\n else\n {\n if(count2<nums2.length/2)\n {\n count2++;\n }\n else\n {\n h2.put(nums2[i],h2.get(nums2[i])+1);\n }\n }\n }\n if(count1==nums1.length/2 && count2==nums2.length/2)\n {\n HashSet<Integer> hset=new HashSet<Integer>();\n for(Map.Entry<Integer,Integer> entry:h1.entrySet())\n {\n hset.add(entry.getKey());\n }\n for(Map.Entry<Integer,Integer> entry:h2.entrySet())\n {\n hset.add(entry.getKey());\n }\n\n return hset.size();\n }\n else if(count1==nums1.length/2)\n {\n HashSet<Integer> hset=new HashSet<Integer>();\n for(Map.Entry<Integer,Integer> entry:h1.entrySet())\n {\n hset.add(entry.getKey());\n }\n for(Map.Entry<Integer,Integer> entry:h2.entrySet())\n {\n int p=entry.getKey();\n if(hset.contains(p))\n {\n if(count2<nums2.length/2)\n {\n count2++;\n }\n }\n else\n {\n hset.add(p);\n }\n }\n \n return hset.size()-((nums2.length/2)-count2);\n\n }\n else if(count2==nums2.length/2)\n {\n HashSet<Integer> hset=new HashSet<Integer>();\n for(Map.Entry<Integer,Integer> entry:h2.entrySet())\n {\n hset.add(entry.getKey());\n }\n for(Map.Entry<Integer,Integer> entry:h1.entrySet())\n {\n int p=entry.getKey();\n if(hset.contains(p))\n {\n if(count1<nums1.length/2)\n {\n count1++;\n }\n }\n else\n {\n hset.add(p);\n }\n }\n \n return hset.size()-((nums1.length/2)-count1);\n\n }\n else\n {\n HashSet<Integer> hset=new HashSet<Integer>();\n for(Map.Entry<Integer,Integer> entry:h1.entrySet())\n {\n int p=entry.getKey();\n if(h2.containsKey(p))\n {\n if(count1<nums1.length/2)\n {\n count1++;\n }\n else\n {\n hset.add(p);\n }\n }\n else\n {\n hset.add(p);\n }\n }\n\n for(Map.Entry<Integer,Integer> entry:h2.entrySet())\n {\n int p=entry.getKey();\n if(hset.contains(p))\n {\n if(count2<nums2.length/2)\n {\n count2++;\n }\n else\n {\n hset.add(p);\n }\n }\n else\n {\n hset.add(p);\n }\n }\n\n return hset.size()-((nums1.length/2)-count1)-((nums2.length/2)-count2);\n }\n \n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximum-size-of-a-set-after-removals
|
Done 🎯|| C++ ✅
|
done-c-by-ajitpal0821-uu83
|
Intuition\n Describe your first thoughts on how to solve this problem. \n- Find unique in arr1\n- Find common in both\n- Find unique in arr2\n- Common in both b
|
ajitpal0821
|
NORMAL
|
2024-05-09T11:41:18.057763+00:00
|
2024-05-09T11:41:18.057794+00:00
| 9 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- Find unique in arr1\n- Find common in both\n- Find unique in arr2\n- Common in both but not repeated\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n int cnt = 0;\n int n = nums1.size();\n int m = nums2.size();\n map<int, int> mp1, mp2;\n for (auto it : nums1)\n mp1[it]++;\n\n for (auto it : nums2)\n mp2[it]++;\n\n \n for (auto it : mp1) {\n if (cnt == (n / 2)) /// unique elem in arr1\n break;\n if (mp2.find(it.first) == mp2.end())\n cnt++;\n }\n\n for (auto it : mp1) {\n if (mp2.find(it.first) == mp2.end())\n continue;\n if (cnt == (n / 2)) /// common elem in arr1 && arr2\n break;\n\n cnt++;\n mp2[it.first] = INT_MAX;\n }\n int ans=cnt;\n cnt=0;\n for(auto it:mp2){\n if(mp1.find(it.first)==mp1.end()) //uniq in arr2\n cnt++;\n\n if(cnt==(n/2))\n break;\n }\n\n for(auto it:mp2){ /// common but not repeated\n if(mp1.find(it.first)==mp1.end() || mp2[it.first]==INT_MAX)\n continue;\n\n if(cnt==(n/2))\n break;\n\n cnt++;\n }\n return cnt+ans;\n }\n};\n```
| 0 | 0 |
['Array', 'Hash Table', 'Greedy', 'C++']
| 0 |
maximum-size-of-a-set-after-removals
|
C++ maps
|
c-maps-by-user5976fh-fpor
|
\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n unordered_map<int, int> m1, m2;\n for (int i = 0;
|
user5976fh
|
NORMAL
|
2024-05-08T03:38:32.719442+00:00
|
2024-05-08T03:38:32.719510+00:00
| 0 | false |
```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n unordered_map<int, int> m1, m2;\n for (int i = 0; i < nums1.size(); ++i)\n ++m1[nums1[i]], ++m2[nums2[i]];\n int n1 = nums1.size() / 2, n2 = n1;\n for (auto& [f, s] : m1) n1 -= s - 1;\n for (auto& [f, s] : m2) n2 -= s - 1;\n int ans = 0;\n for (auto& [f,s] : m1){\n if (m2.count(f)){\n m2.erase(f);\n if (n1 > 0) --n1;\n else --n2;\n }\n ++ans;\n }\n return ans + m2.size() - max(0, n1) - max(0, n2);\n }\n};\n```
| 0 | 0 |
[]
| 0 |
maximum-size-of-a-set-after-removals
|
Simple
|
simple-by-sdg9670-ibov
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
sdg9670
|
NORMAL
|
2024-04-29T13:13:57.348845+00:00
|
2024-04-29T13:14:40.618372+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(2n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfunction maximumSetSize(nums1: number[], nums2: number[]): number {\n const target = nums1.length / 2\n const set1 = new Set(nums1)\n const set2 = new Set(nums2)\n let intersection = 0\n\n // count intersection nums\n set1.forEach(n => {\n if(set2.has(n)) intersection ++\n })\n\n // difference nums\n const count1 = Math.min(set1.size - intersection, target)\n const count2 = Math.min(set2.size - intersection, target)\n \n // intersection\n const commonCount = Math.min((target - count1) + (target - count2), intersection)\n\n return count1 + count2 + commonCount;\n};\n```
| 0 | 0 |
['TypeScript']
| 0 |
maximum-size-of-a-set-after-removals
|
3 Set solution
|
3-set-solution-by-sanyamgoyal401-jh38
|
Code\n\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size();\n set<int> s1;\n
|
SanyamGoyal401
|
NORMAL
|
2024-04-19T17:47:18.619481+00:00
|
2024-04-19T17:47:18.619497+00:00
| 1 | false |
# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size();\n set<int> s1;\n set<int> s2;\n set<int> s3;\n for(int i=0; i<n; i++){\n s1.insert(nums1[i]);\n s2.insert(nums2[i]);\n }\n\n merge(s1.begin(), s1.end(), s2.begin(), s2.end(), inserter(s3, s3.begin()));\n int x = s1.size();\n int y = s2.size();\n int z = s3.size();\n\n int intersection = x + y - z;\n int a = max(0, x-intersection);\n int b = max(0, y-intersection);\n\n int i = min(a, n/2);\n int j = min(b, n/2);\n int k = min(intersection, n-(i+j));\n return i + j + k;\n }\n};\n```
| 0 | 0 |
['Ordered Set', 'C++']
| 0 |
maximum-size-of-a-set-after-removals
|
One Liner Easy Solution || Python3
|
one-liner-easy-solution-python3-by-yangz-mmrl
|
One Liner Very Easy Solution\n\n\nclass Solution:\n def maximumSetSize(self, nums1: List[int], nums2: List[int]) -> int:\n return min(len(set(nums1 +
|
YangZen09
|
NORMAL
|
2024-04-09T21:14:48.200742+00:00
|
2024-04-09T21:14:48.200772+00:00
| 7 | false |
*One Liner Very Easy Solution*\n\n```\nclass Solution:\n def maximumSetSize(self, nums1: List[int], nums2: List[int]) -> int:\n return min(len(set(nums1 + nums2)), min(len(set(nums1)), len(nums1) // 2) + min(len(set(nums2)), len(nums2) // 2))\n```
| 0 | 0 |
['Math', 'Ordered Set', 'Python3']
| 0 |
maximum-size-of-a-set-after-removals
|
✅🔥Easy & simple C++ solution with line by line explanation🔥✅
|
easy-simple-c-solution-with-line-by-line-lgwf
|
Intuition\nNeed to remove n/2 elements from both nums1 and nums2 such that when we combine both then the elements will be maximum.\n\n---\n\n# Approach\n- First
|
Anshmishra
|
NORMAL
|
2024-03-15T16:37:52.505317+00:00
|
2024-03-15T16:37:52.505350+00:00
| 20 | false |
# Intuition\nNeed to remove n/2 elements from both nums1 and nums2 such that when we combine both then the elements will be maximum.\n\n---\n\n# Approach\n- First make a set and store the elements of num1 in the set and take its size.\n- Then clear that set and perform same thing with nums2.\n- Then again clear the set and now store both nums1 and nums2 in the set and store in another variable as size3.\n- Now take the min of size3, min(n/2, size1)+min(n/2, size2).\n\n---\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n---\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n unordered_set<int> s;\n int n = nums1.size();\n for(int i = 0 ; i < n ; i++) s.insert(nums1[i]);\n int size1 = s.size();\n s.clear();\n for(int i = 0 ; i < n ; i++) s.insert(nums2[i]);\n int size2 = s.size();\n s.clear();\n for(int i = 0 ; i < n ; i++){\n s.insert(nums1[i]);\n s.insert(nums2[i]);\n }\n int size3 = s.size();\n return min(size3, min(n/2, size1)+min(n/2, size2));\n }\n};\n```
| 0 | 0 |
['Array', 'Hash Table', 'Greedy', 'C', 'C++']
| 0 |
maximum-size-of-a-set-after-removals
|
scala solution
|
scala-solution-by-vititov-rfzh
|
\nobject Solution {\n def maximumSetSize(nums1: Array[Int], nums2: Array[Int]): Int = {\n val (set1,set2,n) = (nums1.to(Set), nums2.to(Set),nums1.size)\n
|
vititov
|
NORMAL
|
2024-03-10T15:23:29.868826+00:00
|
2024-03-10T15:36:37.288149+00:00
| 2 | false |
```\nobject Solution {\n def maximumSetSize(nums1: Array[Int], nums2: Array[Int]): Int = {\n val (set1,set2,n) = (nums1.to(Set), nums2.to(Set),nums1.size)\n val both = set1.count(set2.contains(_))\n ((set1.size - both).min(n>>1) + (set2.size - both).min(n>>1) + both) min n\n }\n}}```
| 0 | 0 |
['Scala']
| 0 |
maximum-size-of-a-set-after-removals
|
C++ Solution
|
c-solution-by-rattanankit2004-f9yp
|
Intuition\n Describe your first thoughts on how to solve this problem. \nUsing Sets\n# Approach\n Describe your approach to solving the problem. \n\n# Complexit
|
rattanankit2004
|
NORMAL
|
2024-03-10T04:42:24.942712+00:00
|
2024-03-10T04:42:24.942745+00:00
| 3 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUsing Sets\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n set<int>s1; set<int>s2;\n for(auto i : nums1){\n s1.insert(i);\n }\n for(auto i : nums2){\n s2.insert(i);\n }\n int n = nums1.size();\n int t1, t2 = 0;\n if(n/2 > s1.size()) {\n t1 = s1.size();\n }else{\n t1 = n/2;\n }\n if(n/2 > s2.size()) {\n t2 = s2.size();\n }else{\n t2 = n/2;\n } \n\n for(auto i : s2){\n s1.insert(i);\n } \n int temp = t1+t2;\n if(s1.size() > temp) return temp;\n return s1.size();\n \n \n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximum-size-of-a-set-after-removals
|
Greedy | Beats 81% | Using 2 Hash Tables
|
greedy-beats-81-using-2-hash-tables-by-d-obvt
|
Submission Screenshot\n\n\n\n\n# Code\ncpp\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n unordered_map<i
|
darshdattu
|
NORMAL
|
2024-03-09T05:57:39.631437+00:00
|
2024-03-09T05:57:39.631467+00:00
| 9 | false |
# Submission Screenshot\n\n\n\n\n# Code\n```cpp\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n unordered_map<int, int> mp1;\n unordered_map<int, int> mp2;\n // Make frequency maps for both arrays.\n for(int i=0; i<nums1.size(); i++) mp1[nums1[i]]++;\n for(int i=0; i<nums2.size(); i++) mp2[nums2[i]]++;\n int toDelete1 = nums1.size()/2, toDelete2 = nums2.size()/2;\n // Remove as many duplicates as possible\n for(auto i=mp1.begin(); i!=mp1.end(); i++) {\n if(i->second > 1) {\n toDelete1 -= (i->second - 1);\n i->second = 1;\n }\n }\n for(auto i=mp2.begin(); i!=mp2.end(); i++) {\n if(i->second > 1) {\n toDelete2 -= (i->second - 1);\n i->second = 1;\n }\n }\n // If removing duplicates satisfies the number of removals expected than return\n if(toDelete1<=0 && toDelete2<=0){\n mp1.insert(mp2.begin(), mp2.end());\n return mp1.size();\n }\n // If not, merge the maps. And again do the same thing i.e, remove duplicates.\n for(auto i=mp2.begin(); i!=mp2.end(); i++) mp1[i->first]++;\n if(toDelete1<=0 || toDelete2<=0) toDelete1 = max(toDelete1, toDelete2);\n else toDelete1 = toDelete1 + toDelete2;\n for(auto i=mp1.begin(); i!=mp1.end(); i++) {\n if(i->second > 1) {\n toDelete1 = toDelete1 - 1;\n i->second = 1;\n }\n }\n // If removing duplicates from mergind, satisfies the removal condition then return\n if(toDelete1<=0) return mp1.size();\n // Else,...\n return mp1.size()-toDelete1;\n }\n};\n```
| 0 | 0 |
['Array', 'Hash Table', 'Greedy', 'C++']
| 0 |
maximum-size-of-a-set-after-removals
|
MaximumSetSize
|
maximumsetsize-by-santhosh106-gl5s
|
Intuition\nThink of time Complexity while wirte the code. \n\n# Approach\nUse Greedy Approach to solve the problem.\n# Complexity\n- Time complexity:\nO(n)\n\n-
|
santhosh106
|
NORMAL
|
2024-02-25T09:57:14.344615+00:00
|
2024-02-25T09:57:14.344646+00:00
| 5 | false |
# Intuition\nThink of time Complexity while wirte the code. \n\n# Approach\nUse Greedy Approach to solve the problem.\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n# Code\n```\n/**\n * @param {number[]} nums1\n * @param {number[]} nums2\n * @return {number}\n */\nvar maximumSetSize = function (nums1, nums2) {\n const set1 = new Set(nums1)\n const set2 = new Set(nums2)\n\n\n let overlap = 0\n for (const n of set1) if (set2.has(n)) overlap++\n\n const half = nums1.length / 2\n\n return Math.min(\n\n Math.min(set2.size - overlap, half)\n + Math.min(set1.size - overlap, half)\n + overlap,\n\n half * 2\n\n )\n};
| 0 | 0 |
['JavaScript']
| 0 |
maximum-size-of-a-set-after-removals
|
👍Runtime 851 ms Beats 100.00% of users with Scala
|
runtime-851-ms-beats-10000-of-users-with-rpxb
|
Code\n\nimport scala.collection.mutable.HashSet\n\nobject Solution {\n def maximumSetSize(nums1: Array[Int], nums2: Array[Int]): Int = {\n val set1 =
|
pvt2024
|
NORMAL
|
2024-02-25T07:24:57.255757+00:00
|
2024-02-25T07:24:57.255798+00:00
| 6 | false |
# Code\n```\nimport scala.collection.mutable.HashSet\n\nobject Solution {\n def maximumSetSize(nums1: Array[Int], nums2: Array[Int]): Int = {\n val set1 = HashSet[Int]()\n val set2 = HashSet[Int]()\n val set3 = HashSet[Int]()\n \n nums1.foreach(x => {\n set1.add(x)\n set3.add(x)\n })\n \n nums2.foreach(x => {\n set2.add(x)\n set3.add(x)\n })\n \n val common = set1.size + set2.size - set3.size\n val n1 = set1.size\n val n2 = set2.size\n \n var ans = math.min(nums1.length / 2, n1 - common)\n ans += math.min(nums1.length / 2, n2 - common)\n ans += common\n ans = math.min(nums1.length, ans)\n \n ans\n }\n}\n```
| 0 | 0 |
['Scala']
| 0 |
maximum-size-of-a-set-after-removals
|
Java | Simplistic Set
|
java-simplistic-set-by-baljitdhanjal-dyy5
|
\n\n# Code\n\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) {\n Set<Integer> sA = Arrays.stream(nums1).boxed().collect(Collec
|
baljitdhanjal
|
NORMAL
|
2024-02-22T20:18:11.055267+00:00
|
2024-02-22T20:18:11.055303+00:00
| 14 | false |
\n\n# Code\n```\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) {\n Set<Integer> sA = Arrays.stream(nums1).boxed().collect(Collectors.toCollection(HashSet::new));\n Set<Integer> sB = Arrays.stream(nums2).boxed().collect(Collectors.toCollection(HashSet::new));\n\n int sizeA = nums1.length / 2;\n int sizeB = nums2.length / 2;\n\n if (sizeA <= sA.size() && sizeB <= sB.size()) {\n sA.addAll(sB);\n return Math.min(sizeA + sizeB, sA.size());\n } else {\n if (sizeA > sA.size()) {\n for (int k : sA) {\n sB.remove(k);\n }\n }\n\n if (sizeB > sB.size()) {\n for (int k : sB) {\n sA.remove(k);\n }\n }\n }\n\n return Math.min(sA.size(), sizeA) + Math.min(sB.size(), sizeB);\n }\n}\n\n```
| 0 | 0 |
['Java']
| 0 |
maximum-size-of-a-set-after-removals
|
Easy Java
|
easy-java-by-lakshyasaharan1997-2dl0
|
Code\n\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) { \n Map<Integer,Integer> mp1 = new HashMap<>(); \n
|
lakshyasaharan1997
|
NORMAL
|
2024-02-20T18:36:55.049098+00:00
|
2024-02-20T18:36:55.049135+00:00
| 16 | false |
# Code\n```\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) { \n Map<Integer,Integer> mp1 = new HashMap<>(); \n Map<Integer,Integer> mp2 = new HashMap<>();\n for(int i=0; i<nums1.length; i++){\n if(!mp1.containsKey(nums1[i])){\n mp1.put(nums1[i],1);\n }else{\n mp1.put(nums1[i],mp1.get(nums1[i])+1);\n } \n if(!mp2.containsKey(nums2[i])){\n mp2.put(nums2[i],1);\n }else{\n mp2.put(nums2[i],mp2.get(nums2[i])+1);\n }\n } \n Set<Integer> res = new HashSet<>();\n int cnt = 0;\n for (Map.Entry<Integer, Integer> entry : mp1.entrySet()) {\n int currElem = entry.getKey();\n if(!mp2.containsKey(currElem)){\n res.add(currElem);\n cnt++;\n }\n if(cnt==nums1.length/2)\n break;\n \n }\n if(cnt<nums1.length/2){\n for (Map.Entry<Integer, Integer> entry : mp1.entrySet()) {\n if(!res.contains(entry.getKey())){\n res.add(entry.getKey());\n cnt++;\n }\n if(cnt==nums1.length/2)\n break;\n } \n }\n cnt = 0;\n for (Map.Entry<Integer, Integer> entry : mp2.entrySet()) {\n if(!res.contains(entry.getKey())){\n res.add(entry.getKey());\n cnt++;\n }\n if(cnt==nums1.length/2)\n break;\n }\n return res.size();\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximum-size-of-a-set-after-removals
|
Set || Beat 100% || C++
|
set-beat-100-c-by-jacklee13520-6ze3
|
\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) \n {\n unordered_set<int> s1,s2;\n for(auto n:nums1
|
jacklee13520
|
NORMAL
|
2024-02-20T14:24:45.647789+00:00
|
2024-02-20T14:24:45.647815+00:00
| 2 | false |
```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) \n {\n unordered_set<int> s1,s2;\n for(auto n:nums1)\n {\n s1.insert(n);\n }\n for(auto n:nums2)\n {\n s2.insert(n);\n }\n \n // count the overlap\n int overlap = 0;\n for(auto n:s1)\n {\n if(s2.find(n) != s2.end())\n {\n overlap++;\n }\n }\n \n return min(\n min(s1.size(),nums1.size()/2)\n + min(s2.size(),nums2.size()/2),\n s1.size() + s2.size() - overlap\n );\n }\n};\n```
| 0 | 0 |
[]
| 0 |
maximum-size-of-a-set-after-removals
|
🚩 1-liner ^^
|
1-liner-by-andrii_khlevniuk-kbd8
|
\n\n\ndef maximumSetSize(self, x, y):\n\treturn min(len(set(x+y)), min(len(set(x)), len(x)//2) + min(len(set(y)), len(y)//2))\n
|
andrii_khlevniuk
|
NORMAL
|
2024-02-20T13:19:31.628729+00:00
|
2024-02-20T16:58:01.209651+00:00
| 46 | false |
\n\n```\ndef maximumSetSize(self, x, y):\n\treturn min(len(set(x+y)), min(len(set(x)), len(x)//2) + min(len(set(y)), len(y)//2))\n```
| 0 | 0 |
['Python', 'Python3']
| 0 |
maximum-size-of-a-set-after-removals
|
Beginners friendly
|
beginners-friendly-by-magagical_star-zp3h
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Magagical_star
|
NORMAL
|
2024-02-17T13:46:33.137687+00:00
|
2024-02-17T13:46:33.137732+00:00
| 11 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2)\n {\n int y = nums1.size(),x=nums2.size();\n sort(nums1.begin(),nums1.end());\n nums1.erase(unique(nums1.begin(),nums1.end()),nums1.end());\n sort(nums2.begin(),nums2.end());\n nums2.erase(unique(nums2.begin(),nums2.end()),nums2.end());\n int n1 = nums1.size(), n2 = nums2.size();\n int rem1 = y-n1;int rem2 = x-n2,cnt=0;\n unordered_map<int,int>mp;\n for(int i=0;i<n1;i++)\n mp[nums1[i]]++;\n for(int i=0;i<n2;i++)\n {\n if(mp.find(nums2[i]) != mp.end())\n cnt++;\n }\n if(rem2>y/2)\n rem2=y/2;\n if(rem1>y/2)\n rem1 = y/2;\n if(rem1+rem2+cnt>=y)\n return n1+n2-cnt;\n \n return n1+n2-cnt-(y-(rem1+rem2+cnt));\n \n\n }\n};\n```
| 0 | 0 |
['Greedy', 'Sorting', 'C++']
| 0 |
maximum-size-of-a-set-after-removals
|
Pythonic Mathematical Solution :)
|
pythonic-mathematical-solution-by-elucid-yekr
|
Intuition\n\nThe first intuition that came to mind when solving this problem was to determine the unique contribution of each list to the length of the maximum
|
elucidativemind
|
NORMAL
|
2024-02-15T13:15:23.111097+00:00
|
2024-02-15T13:15:23.111132+00:00
| 35 | false |
# Intuition\n\nThe first intuition that came to mind when solving this problem was to determine the unique contribution of each list to the length of the maximum set. By finding the intersecting elements among the lists and converting each list into a hash set, we can identify the unique contribution of each list.\n\n# Approach\n\nTo find the unique contribution of two lists:\n\n1. Convert both `nums1` and `nums2` into sets.\n2. Find the intersection of the sets to identify the common elements.\n3. Calculate the lengths of unique elements in each set.\n4. Determine the maximum size of the set considering the unique contributions and the intersection by remembering that the bottleneck/the max bound of the solution could be "n".\n\n# Complexity Analysis\n\n- Time complexity: \\(O(n)\\), where \\(n\\) is the total number of elements in both lists.\n- Space complexity: \\(O(n)\\), where \\(n\\) is the total number of unique elements in both lists.\n\n# Code\n\n```python\nclass Solution(object):\n def maximumSetSize(self, nums1, nums2):\n halflength = len(nums1) // 2\n x1 = set(nums1)\n x2 = set(nums2)\n inter = x1.intersection(x2)\n unix1 = len(x1 - inter)\n unix2 = len(x2 - inter)\n intermediate = min(halflength, unix1) + min(halflength, unix2) \n if intermediate < 2 * halflength:\n return min(intermediate + len(inter), 2 * halflength)\n return intermediate\n
| 0 | 0 |
['Math', 'Python']
| 0 |
maximum-size-of-a-set-after-removals
|
BEAT 96.42% | Shortest, Easiest & Well Explained | To the Point & Beginners Friendly Approach(❤️ω❤️)
|
beat-9642-shortest-easiest-well-explaine-642g
|
\n\n# Welcome to My Coding Family\u30FE(\u2267 \u25BD \u2266)\u309D\nThis is my shortest, easiest & to the point approach. This solution mainly aims for purely
|
Nitansh_Koshta
|
NORMAL
|
2024-02-15T12:25:21.645116+00:00
|
2024-02-15T12:25:21.645143+00:00
| 8 | false |
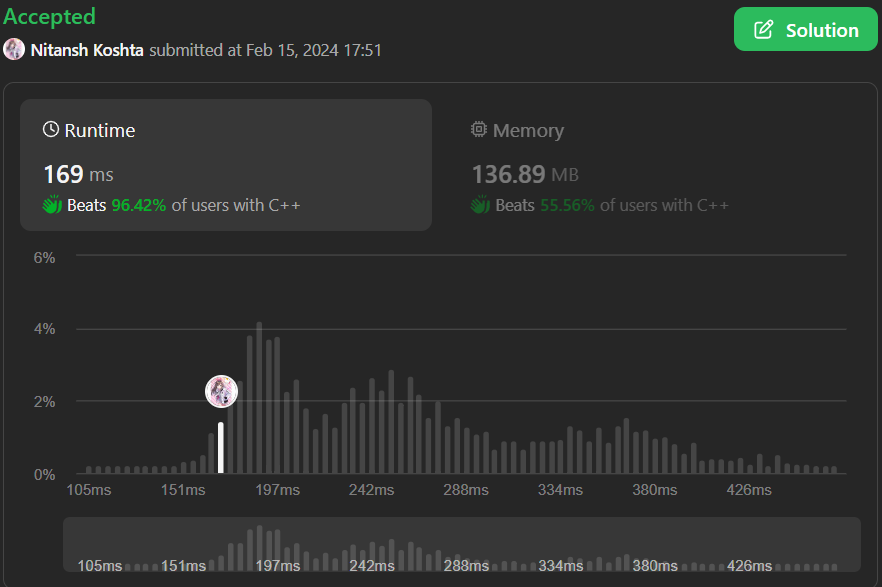\n\n# Welcome to My Coding Family\u30FE(\u2267 \u25BD \u2266)\u309D\n*This is my shortest, easiest & to the point approach. This solution mainly aims for purely beginners so if you\'re new here then too you\'ll be very easily be able to understand my this code. If you like my code then make sure to UpVOTE me. Let\'s start^_~*\n\n**The code is given below(p\u2267w\u2266q)**\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& v1, vector<int>& v2) {\n unordered_set<int>st1,st2,comm;\n for(auto i:v1)st1.insert(i);\n for(auto i:v2){\n if(st1.find(i)!=st1.end()){st2.insert(i);comm.insert(i);}\n else st2.insert(i);\n }\n return min(v1.size(),min(st1.size()-comm.size(),v1.size()/2)+min(st2.size()-comm.size(),v1.size()/2)+comm.size());\n\n// if my code helped you then please UpVOTE me, an UpVOTE encourages me to bring some more exciting codes for my coding family. Thank You o((>\u03C9< ))o\n }\n};\n```\n\n\n
| 0 | 0 |
['C++']
| 0 |
maximum-size-of-a-set-after-removals
|
Easy To Understand Java Code
|
easy-to-understand-java-code-by-harshitm-etpu
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
harshitmittal8090
|
NORMAL
|
2024-02-11T14:07:14.617133+00:00
|
2024-02-11T14:07:14.617161+00:00
| 24 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n O(n)\n\n- Space complexity:\n O(n)\n\n# Code\n```\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2){\n\n HashSet<Integer> set = new HashSet<>();\n HashSet<Integer> set1 = new HashSet<>();\n int numsl = nums1.length/2;\n int nums1l = nums2.length/2;\n\n for(int i : nums1){\n\n if(!set.contains(i)) set.add(i);\n\n else if(numsl > 0) numsl--;\n\n }\n\n for(int i : nums2){\n \n if(numsl > 0 && set.contains(i)){\n\n set.remove(i);\n numsl--; \n\n } \n if(!set1.contains(i)) set1.add(i);\n\n else if(nums1l > 0) nums1l--;\n \n\n }\n\n set.stream().forEach(i -> {\n if(set1.contains(i)) set1.remove(i);\n });\n\n \n\n int res = set.size() > nums1.length/2 ? nums1.length/2 : set.size();\n int res2 = set1.size() > nums2.length/2 ? nums2.length/2 : set1.size();\n \n return res + res2; \n \n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximum-size-of-a-set-after-removals
|
[C++] a method using set
|
c-a-method-using-set-by-hirofumitsuda-leqy
|
Intuition\n Describe your first thoughts on how to solve this problem. \nTake components in the following way:\n- take components included either of two vectors
|
HirofumiTsuda
|
NORMAL
|
2024-02-11T08:38:36.212077+00:00
|
2024-02-11T08:38:36.212105+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTake components in the following way:\n- take components included either of two vectors first\n- then take ones appearing in the two vectors\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe problem can be interpretd as "By extracting at most n/2 elements from each vector, calculate the maximum number of kinds of components created using the exctracted components". It means only numbers are important and the amount of each numbers appearing in each vector does not play an important role.\n\nAs shown in my solution, numbers are separated into the two types:\n- one contained in either of the two vectors\n- one contained in the both\n\nThen the results could be obtained.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(nlogn), where n is the number of components.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(nlogn) since sets are used.\n\n# Code\n```\nstruct Info {\n int only;\n int common;\n};\n\nclass Solution {\npublic:\n std::set<int> get_set(const vector<int>& v) const {\n std::set<int> s;\n for(const int n : v){\n s.insert(n);\n }\n return std::move(s);\n }\n Info get_info(const std::set<int>& target, const std::set<int>& compare) const {\n int only = 0;\n int common = 0;\n for(const int n : target){\n if(compare.count(n) > 0){\n common++;\n }else{\n only++;\n }\n }\n return std::move(\n Info(only, common)\n );\n }\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size();\n int count = 0;\n std::set<int> s1, s2;\n s1 = get_set(nums1);\n s2 = get_set(nums2);\n Info i1 = get_info(s1, s2);\n Info i2 = get_info(s2, s1);\n int common = i1.common;\n int only1 = std::min(i1.only, n/2);\n int only2 = std::min(i2.only, n/2);\n int common_n = std::min(std::max(n - only1 - only2, 0), common);\n return only1 + only2 + common_n;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximum-size-of-a-set-after-removals
|
100% Solution using Set Data Structure
|
100-solution-using-set-data-structure-by-imuu
|
\n# Complexity\n- Time complexity:\nO(n+m)\n\n- Space complexity:\nO(n+m)\n\n# Code\n\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2)
|
Sourav4676
|
NORMAL
|
2024-02-10T17:01:08.011307+00:00
|
2024-02-10T17:01:08.011331+00:00
| 12 | false |
\n# Complexity\n- Time complexity:\nO(n+m)\n\n- Space complexity:\nO(n+m)\n\n# Code\n```\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) {\n Set<Integer> set1 = new HashSet<>();\n Set<Integer> set2 = new HashSet<>();\n Set<Integer> set3 = new HashSet<>();\n int ans=0;\n for(int i:nums1){\n set1.add(i);\n set3.add(i);\n }\n if(set1.size()>nums1.length/2)\n ans=nums1.length/2;\n else\n ans=set1.size();\n for(int i:nums2){\n set2.add(i);\n set3.add(i);\n } \n if(set2.size()>nums2.length/2)\n ans+=nums2.length/2;\n else\n ans+=set2.size(); \n return ans>set3.size() ? set3.size() : ans; \n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximum-size-of-a-set-after-removals
|
Easy Java Solution || Simple Freq Check || Beats 100% ✅✅
|
easy-java-solution-simple-freq-check-bea-5l07
|
Complexity\n- Time complexity:O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(n)\n Add your space complexity here, e.g. O(n) \n\n# Code
|
vritant-goyal
|
NORMAL
|
2024-02-07T06:07:10.295508+00:00
|
2024-02-07T06:08:15.440033+00:00
| 16 | false |
# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int maximumSetSize(int[] nums1, int[] nums2) {\n HashSet<Integer>st=new HashSet<>();\n int n1=nums1.length;\n int n2=nums2.length;\n for(int i=0;i<nums1.length;i++){\n st.add(nums1[i]);\n }\n int size1=st.size();\n st.clear();\n\n for(int i=0;i<nums2.length;i++){\n st.add(nums2[i]);\n }\n int size2=st.size();\n st.clear();\n\n for(int i=0;i<nums1.length;i++){\n st.add(nums1[i]);\n }\n for(int i=0;i<nums2.length;i++){\n st.add(nums2[i]);\n }\n int size3=st.size();\n\n\n return Math.min(size3,Math.min(n1/2,size1)+Math.min(n2/2,size2));\n }\n}\n```
| 0 | 0 |
['Array', 'Greedy', 'Java']
| 0 |
maximum-size-of-a-set-after-removals
|
Simplest Code|Greedy|C++
|
simplest-codegreedyc-by-himanshu_0408-4ibt
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
himanshu_0408
|
NORMAL
|
2024-02-07T03:17:40.810341+00:00
|
2024-02-07T03:17:40.810374+00:00
| 9 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n);\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {\n set<int>s1,s2,s;\n int n=nums1.size();\n for(int i=0;i<n;i++){\n s1.insert(nums1[i]);\n s2.insert(nums2[i]);\n }\n for(int it:s1) if(s2.find(it)!=s2.end()&&s2.size()>n/2) s2.erase(it);\n for(int it:s2) if(s1.find(it)!=s1.end()&&s1.size()>n/2) s1.erase(it);\n \n if(s1.size()<=n/2&&s2.size()<=n/2){\n for(int it:s1) s.insert(it);\n for(int it:s2) s.insert(it);\n return s.size();\n }\n else if(s1.size()>n/2&&s2.size()<=n/2) return s2.size()+n/2;\n else if(s1.size()<=n/2&&s2.size()>n/2) return s1.size()+n/2;\n else return n;\n return 0;\n }\n};\n```
| 0 | 0 |
['Greedy', 'C++']
| 0 |
maximum-number-of-non-overlapping-palindrome-substrings
|
[C++, Java, Python3] Palindromic Substrings + Non-overlapping Intervals
|
c-java-python3-palindromic-substrings-no-r0a6
|
\nExplanation\nThis question is a combination of Palindromic Substring and Non-overlapping intervals\nhttps://leetcode.com/problems/palindromic-substrings/\nhtt
|
tojuna
|
NORMAL
|
2022-11-13T04:00:54.217031+00:00
|
2022-11-13T06:43:26.238568+00:00
| 7,600 | false |
\n**Explanation**\nThis question is a combination of Palindromic Substring and Non-overlapping intervals\nhttps://leetcode.com/problems/palindromic-substrings/\nhttps://leetcode.com/problems/non-overlapping-intervals/\n* First find all palindromic substrings with length >= k in O(n*k) and store their start and end in an `intervals` list\n\n* Then find minumum number of intervals you need to remove to make the `intervals` array non overlapping in O(n) (`intervals` is already added in sorted order.)\n\n**Solution1:**\n<iframe src="https://leetcode.com/playground/FZexChvv/shared" frameBorder="0" width="1000" height="510"></iframe>\n\n*Time complexity = O(nk)*\n\n**Solution2:**\nNo need to find non overlapping intervals just record the end of the last found palindromic substring. \n\n<iframe src="https://leetcode.com/playground/V2R8VVPx/shared" frameBorder="0" width="1000" height="345"></iframe>\n\n*Time complexity = O(nk)*
| 115 | 2 |
['C++', 'Java', 'Python3']
| 17 |
maximum-number-of-non-overlapping-palindrome-substrings
|
DP + Greedy
|
dp-greedy-by-votrubac-tywh
|
We precompute a 2d array pal that tells us whether a string between i and j is a palindrome (pal[i][j] == true).\n\nThis is the same DP approach as for 647. Pal
|
votrubac
|
NORMAL
|
2022-11-13T04:03:42.478390+00:00
|
2022-11-15T09:11:47.691363+00:00
| 4,754 | false |
We precompute a 2d array `pal` that tells us whether a string between `i` and `j` is a palindrome (`pal[i][j] == true`).\n\nThis is the same DP approach as for [647. Palindromic Substrings](https://leetcode.com/problems/palindromic-substrings/).\n\nThen, we use DP to find maximum number of splits.\n\n**Important Optimization**\nWe only need to check palindromes of size `k` and `k + 1`. \n\nThis is because if `[i - 1..i + k]` is a palindrome (with size `k + 2`), then `[i..i + k - 1]` is also a palindome (with size `k`).\n\nWith this realization, we can greedily find the maximum number of splits (no \nneed to use DP).\n \n ## Greedy Solution\n **C++**\n ```cpp\n bool pal[2002][2002] = {};\nint maxPalindromes(string s, int k) {\n if (k == 1)\n return s.size();\n for (int len = 1; len <= k + 1; ++len)\n for (int i = 0, j = i + len - 1; j < s.size(); ++i, ++j)\n pal[i][j] = (len < 3 ? true : pal[i + 1][j - 1]) && (s[i] == s[j]);\n int i = 0, res = 0;\n for (int i = 0; i + k <= s.size(); ++i) {\n res += pal[i][i + k - 1] || pal[i][i + k];\n i += pal[i][i + k - 1] ? k - 1 : pal[i][i + k] ? k : 0;\n }\n return res;\n}\n ```\n \n ## DP Solution\n**C++**\n```cpp\nint dp[2001] = {};\nbool pal[2001][2001] = {};\nint dfs(int i, int k, string &s) {\n if (i + k > s.size())\n return 0;\n if (!dp[i]) {\n dp[i] = 1 + dfs(i + 1, k, s);\n if (pal[i][i + k - 1])\n dp[i] = max(dp[i], 2 + dfs(i + k, k, s));\n if (i + k < s.size() && pal[i][i + k])\n dp[i] = max(dp[i], 2 + dfs(i + k + 1, k, s));\n }\n return dp[i] - 1;\n}\nint maxPalindromes(string s, int k) {\n if (k == 1)\n return s.size();\n for (int len = 1; len <= k + 1; ++len)\n for (int i = 0, j = i + len - 1; j < s.size(); ++i, ++j)\n pal[i][j] = (len < 3 ? true : pal[i + 1][j - 1]) && (s[i] == s[j]); \n return dfs(0, k, s);\n}\n```
| 60 | 1 |
['C']
| 9 |
maximum-number-of-non-overlapping-palindrome-substrings
|
Simplest Solution | NO DP + ( why only k+1 )
|
simplest-solution-no-dp-why-only-k1-by-h-rtkn
|
Too much Simple\n\n Main catch here was to avoid picking a palindromic substring with size greater than k+1 because if there exist a palindromic substring with
|
HarshitMaurya
|
NORMAL
|
2022-11-13T14:14:54.690786+00:00
|
2022-11-14T11:14:58.881883+00:00
| 1,861 | false |
# Too much Simple\n\n* Main catch here was to avoid picking a palindromic substring with size greater than k+1 because if there exist a palindromic substring with size greater than k+1 then it would definitely contain a palindromic substring with size at least k ( It was just basic observation ) And we are trying to minimize the length of the palindromic string ( with size >= k ) to maximize our answer.\n\nSuppose,\nstring =` abaczbzccc` & `k = 3`\n\nWithout break condition, answer would have been 2 `( aba, czbzc )`\nWith break condition, answer would be 3 `( aba, zbz, ccc )`\n\n* Now observe the difference, instead of picking \'czbzc\' we pick \'zbz\' which allowed us to further pick \'ccc\' as well. I hope it clarifies your doubt.\n```\nclass Solution {\n public int maxPalindromes(String s, int k) {\n int ans = 0;\n for (int i = 0; i < s.length(); i++) {\n for (int j = i; j < s.length(); j++) {\n int len = (j - i) + 1;\n if (len > k + 1) break; // this is the key \n if (len >= k && isPalindrome(s, i, j)) {\n ans++; i = j; break;\n }\n }\n }\n return ans;\n }\n\n boolean isPalindrome(String s, int l, int r) {\n while (l < r) {\n if (s.charAt(l++) != s.charAt(r--)) return false;\n }\n return true;\n }\n}\n\n\n```\n\ncredit : @_aka5h
| 37 | 0 |
['Greedy', 'C', 'Java']
| 8 |
maximum-number-of-non-overlapping-palindrome-substrings
|
✅ [Python/C++] recursive & iterative DP solutions (explained)
|
pythonc-recursive-iterative-dp-solutions-00eg
|
\u2705 IF YOU LIKE THIS SOLUTION, PLEASE UPVOTE.\n*\nThis solution employs a Dynamic Programming* approach to explore all possible non-overlapping palindromes.
|
stanislav-iablokov
|
NORMAL
|
2022-11-13T05:23:09.622814+00:00
|
2022-11-15T08:31:33.399812+00:00
| 1,316 | false |
**\u2705 IF YOU LIKE THIS SOLUTION, PLEASE UPVOTE.**\n****\nThis solution employs a *Dynamic Programming* approach to explore all possible non-overlapping palindromes. Time complexity is linear: **O(nk)**. Space complexity is linear: **O(n)**.\n\n**Comment.** If one palindrome is a substring of another palidrome then considering the second one will not increase the total number of non-overlapping palindromes. Thus, we only need to consider the minimally allowed palindromes of even and odd lengths (i.e., of `k` and `k+1`).\n\n**Python #1.** Recursive solution.\n```\nclass Solution:\n def maxPalindromes(self, s: str, k: int) -> int:\n \n def pal(i, j): # [a] if you dare to solve hard problems then you\n if j > len(s) : return False # probably know many ways to test palindromes;\n return s[i:j] == s[i:j][::-1] # this one is for clarity, not for speed\n \n @lru_cache(None) # [b] this recursive function finds the maximal\n def dfs(i): # number of non-overlapping palindroms in\n if i + k > len(s) : return 0 # the string \'s\' if we start at position \'i\';\n m = dfs(i+1) # [c] we consider cases when there is a palindrome \n if pal(i,i+k) : m = max(m, 1 + dfs(i+k)) # of length k/k+1 at the i-th position or when\n if pal(i,i+k+1) : m = max(m, 1 + dfs(i+k+1)) # there is no such palindrome (and we take the\n return m # number of palindromes for the i+1-th position)\n \n return dfs(0)\n```\n\n**Python #2.** Iterative solution.\n```\nclass Solution:\n def maxPalindromes(self, s: str, k: int) -> int:\n \n def pal(i, j):\n if i < 0 : return False\n return s[i:j] == s[i:j][::-1]\n \n dp = [0] * (len(s)+1)\n \n for i in range(k, len(s)+1):\n dp[i] = dp[i-1]\n if pal(i-k,i) : dp[i] = max(dp[i], 1 + dp[i-k])\n if pal(i-k-1,i) : dp[i] = max(dp[i], 1 + dp[i-k-1])\n \n return dp[-1]\n```\n\nThis solution in other languages.\n\n<iframe src="https://leetcode.com/playground/D3xsirVa/shared" frameBorder="0" width="800" height="700"></iframe>
| 30 | 2 |
[]
| 5 |
maximum-number-of-non-overlapping-palindrome-substrings
|
[Python3] DP with Explanations | Only Check Substrings of Length k and k + 1
|
python3-dp-with-explanations-only-check-y3wgr
|
Observation\nGiven the constraints, a solution with quadratic time complexity suffices for this problem. The key to this problem is to note that, if a given pal
|
xil899
|
NORMAL
|
2022-11-13T04:01:59.527569+00:00
|
2022-11-13T04:30:17.179494+00:00
| 1,809 | false |
**Observation**\nGiven the constraints, a solution with quadratic time complexity suffices for this problem. The key to this problem is to note that, if a given palindromic substring has length greater or equal to `k + 2`, then we can always remove the first and last character of the substring without losing the optimality. As such, we only need to check if a substring is a palindrome that has length `k` or `k + 1`.\n \n**Implementation**\nWe define a `dp` array where `dp[i]` represents the maximum number of substrings in the first `i` characters. For each possible `i`, we check whether the substring with length `k` or `k + 1` ending at the `i`-th character (1-indexed) is a valid palindrome, and update the value of `dp[i]`.\n \n**Complexity**\nTime Complexity: `O(nk)`\nSpace Complexity: `O(n)`, for the use of `dp`\n \n**Solution**\n```\nclass Solution:\n def maxPalindromes(self, s: str, k: int) -> int:\n n = len(s)\n dp = [0] * (n + 1)\n for i in range(k, n + 1):\n dp[i] = dp[i - 1]\n for length in range(k, k + 2):\n j = i - length\n if j < 0:\n break\n if self.isPalindrome(s, j, i):\n dp[i] = max(dp[i], 1 + dp[j])\n return dp[-1]\n \n \n def isPalindrome(self, s, j, i):\n left, right = j, i - 1\n while left < right:\n if s[left] != s[right]:\n return False\n left += 1\n right -= 1\n return True\n```\n \n **Follow-up (open question)** Can we improve the time complexity from `O(nk)` to `O(n)` by using the Manacher\'s algorithm?
| 19 | 5 |
['Dynamic Programming', 'Python3']
| 6 |
maximum-number-of-non-overlapping-palindrome-substrings
|
[Java/C++] Simple DP
|
javac-simple-dp-by-virendra115-9ci8
|
Only check substrings of length k and k + 1\n\nJava\njava\nclass Solution {\n public int maxPalindromes(String s, int k) {\n int ans = 0, n = s.length
|
virendra115
|
NORMAL
|
2022-11-13T04:00:43.417030+00:00
|
2022-11-13T04:16:10.339516+00:00
| 1,568 | false |
Only check substrings of length k and k + 1\n\n**Java**\n```java\nclass Solution {\n public int maxPalindromes(String s, int k) {\n int ans = 0, n = s.length();\n int[] dp = new int[n + 1];\n for (int i = k - 1; i < n; i++) {\n dp[i + 1] = dp[i];\n if (helper(s, i-k+1, i)) dp[i + 1] = Math.max(dp[i + 1], 1 + dp[i - k + 1]);\n if (i-k>=0 && helper(s,i-k,i)) dp[i + 1] = Math.max(dp[i + 1], 1 + dp[i - k]);\n }\n return dp[n];\n }\n boolean helper(String s, int l, int r) {\n while (l < r) {\n if (s.charAt(l) != s.charAt(r)) return false;\n l++; r--;\n }\n return true;\n }\n}\n```\n**C++**\n```\nclass Solution {\npublic:\n bool helper(string s, int l, int r) {\n while (l < r) {\n if (s[l] != s[r]) return false;\n l++; r--;\n }\n return true;\n }\n int maxPalindromes(string s, int k) {\n int ans = 0, n = s.length();\n vector<int> dp(n + 1,0);\n for (int i = k - 1; i < n; i++) {\n dp[i + 1] = dp[i];\n if (helper(s, i-k+1, i)) dp[i + 1] = max(dp[i + 1], 1 + dp[i - k + 1]);\n if (i-k>=0 && helper(s,i-k,i)) dp[i + 1] = max(dp[i + 1], 1 + dp[i - k]);\n }\n return dp[n];\n }\n};\n```
| 17 | 4 |
[]
| 5 |
maximum-number-of-non-overlapping-palindrome-substrings
|
DP + Max Meetings in a Room | C + +
|
dp-max-meetings-in-a-room-c-by-megamind-dcdg
|
\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n The problem can be broken into
|
megamind_
|
NORMAL
|
2022-11-13T04:01:37.661094+00:00
|
2022-11-13T04:11:41.223426+00:00
| 1,215 | false |
\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n The problem can be broken into two parts:-\n\n - Finding all the start and end indices of palindromes in the string such that length of palindrome is k . *(This can be done in O(n x n) using DP similar to finding max length palindrome)*\n\n - Now among all these start and end indices , select maximum non overlapping indices. \n *(This can be done in O(n log n) by a greedy approach) (this part is exactly same as maximum meetings in a single room problem )* \n\n\n# Complexity\n- Time complexity: O(n*n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n*n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n int n = s.size();\n vector<pair<int,int>> vec; //**** vector to store start & end indices of all valid palindromes\n vector<vector<int>> dp(n,vector<int>(n,0));\n for(int i =0;i<n;i++){\n dp[i][i] = 1;\n if(k==1)\n vec.push_back({i,i});\n }\n \n \n for(int j = 1;j<= n;j++){ //***** dp approach to find what are the start and end indices of palindromes\n for(int i=0;i<n;i++){\n if(i+j>=n)break;\n if(s[i]==s[i+j]){\n if(i+1 <= i+j-1)\n dp[i][i+j] =dp[i+1][i+j-1];\n \n else{\n dp[i][i+j] = 1;\n } \n } \n if(dp[i][i+j]==1 && j>= k-1) //** push in vec only if size of pal is >= k\n vec.push_back({i+j,i}); \n }\n }\n \n int res = 0; //**** from the given palindrome indices select maximum number of non - overlapping\n sort(vec.begin(),vec.end());\n int end = -1;\n for(pair<int,int> &p:vec){ //*** this is a greedy way to find (same as maximum meetings in a room )\n if(p.second>end){\n end = p.first;\n res++;\n } \n }\n \n \n return res;\n```
| 14 | 2 |
['C++']
| 2 |
maximum-number-of-non-overlapping-palindrome-substrings
|
[Python] DP Solution
|
python-dp-solution-by-lee215-u56q
|
Explanation\ndp[i] means the result for prefix string to s[i].\ndp[i] = dp[i-1], means s[i] is not used in palindrome substrings.\nThen we check substring with
|
lee215
|
NORMAL
|
2022-11-13T04:57:48.210728+00:00
|
2022-11-13T04:57:48.210764+00:00
| 951 | false |
# **Explanation**\n`dp[i]` means the result for prefix string to `s[i]`.\n`dp[i] = dp[i-1]`, means `s[i]` is not used in palindrome substrings.\nThen we check substring with the `k` last characters,\nwith `s[i-k+1], s[i-k+2] ... s[i]`,\nif it\'s palindrome we have `dp[i] = dp[i - k] + 1`\n\nIf the above string is not palindrome,\nwe continue to check substring with the `k + 1` last characters,\nif it\'s palindrome we have `dp[i] = dp[i - k - 1] + 1`.\n\nNote that we don\'t need to check string with length bigger than `k + 1`,\nwe only need to greedily check string with length `k` and `k + 1`.\n<br>\n\n# **Complexity**\nTime `O(n^2)`, can be improved to `O(n)` with Manacher\nSpace `O(n)`\n<br>\n\n**Python**\n```py\n def maxPalindromes(self, s: str, k: int) -> int:\n n = len(s)\n dp = [0] * n\n for i in range(k - 1, n):\n dp[i] = dp[i - 1]\n if dp[i] <= dp[i-k] and s[i-k+1:i+1] == s[i-k+1:i+1][::-1]:\n dp[i] = dp[i - k] + 1\n elif i - k >= 0 and dp[i] <= dp[i-k-1] and s[i-k:i+1] == s[i-k:i+1][::-1]:\n dp[i] = dp[i - k - 1] + 1\n return dp[n - 1]\n```\n
| 11 | 0 |
[]
| 2 |
maximum-number-of-non-overlapping-palindrome-substrings
|
C++ - Both DP + Greedy Solution Explained - Clean Code
|
c-both-dp-greedy-solution-explained-clea-wn2n
|
Intuition\nThis question is going to mess with TLE if you don\'t memoize it properly.\nIt\'s very similar to Palindrome Paritioning, but requires condition of m
|
geekykant
|
NORMAL
|
2022-11-13T05:12:09.493935+00:00
|
2022-11-13T06:20:56.239749+00:00
| 836 | false |
**Intuition**\nThis question is going to mess with TLE if you don\'t memoize it properly.\nIt\'s very similar to [Palindrome Paritioning](https://leetcode.com/problems/palindrome-partitioning/), but requires condition of minLength `K`.\n\n**Method 1: DP Solution**\n```cpp\nint minLen;\nvector<vector<bool>> dp;\nunordered_map<int, int> mp;\n\nint solve(string& s, int pos){\n int n = s.size();\n if(pos >= n) return 0;\n if(mp.count(pos)) return mp[pos];\n\n int dontTake = solve(s, pos+1);\n int take = INT_MIN;\n\n for(int j=pos+minLen-1; j < n; j++){\n if(dp[pos][j])\n take = max(take, 1 + solve(s, j+1));\n }\n return mp[pos] = max(take, dontTake);\n}\n\nint maxPalindromes(string s, int minLen) {\n this->minLen = minLen;\n int n = s.size();\n dp.resize(n, vector<bool>(n, false));\n\n // Creates DP array with s[i -> j] true if palindrome, else false\n for(int len=1; len <= n; len++){\n for(int i=0; i <= n-len; i++){\n int j = i+len-1;\n dp[i][j] = (len <= 2 ? true : dp[i+1][j-1]) && s[i] == s[j];\n }\n }\n return solve(s, 0);\n}\n```\n\n\n**Method 2: Greedy Solution**\n(Inspired from [@xil899 solution](https://leetcode.com/problems/maximum-number-of-non-overlapping-palindrome-substrings/discuss/2808845/Python3-DP-with-Explanations-or-Only-Check-Substrings-of-Length-k-and-k-%2B-1))\n\nSuppose we have strings - \n* "aa", K length, its a palindrome\n* "aba", we could also check K+1 incase odd length\n\nShould we check K+2?\n* "ab", not a palindrome\n* "abb", not a palindrome\n* "abba", suppose if it\'s a palindrome, even if we remove the first and last chars,\nit will be "<s>a</s>bb<s>a</s>" -> "bb", which is a palindrome of len = K.\n\nOtherwise, think like this, we could include this K+2.\nBut isn\'t it same as moving to `idx+1` and taking K len substring -> "bb",\nwhich will anyway happen in the loop. \n\nHence checking `len = K+2` can be avoided.\n\n```cpp\nint maxPalindromes(string s, int minLen) {\n int n = s.size();\n vector<vector<bool>> dp(n, vector<bool>(n, false));\n for(int len=1; len <= n; len++){\n for(int i=0; i <= n-len; i++){\n int j = i+len-1;\n dp[i][j] = (len <= 2 ? true : dp[i+1][j-1]) && s[i] == s[j];\n }\n }\n\n int res = 0, i = 0;\n while(i < n){\n\t\t// check K len substring\n if(i+minLen-1 < n && dp[i][i+minLen-1]){\n res++;\n i += minLen;\n }\n\t\t// check K+1 len substring\n else if(i+minLen < n && dp[i][i+minLen]){\n res++;\n i = i+minLen+1;\n }\n else\n i++;\n }\n return res;\n}\n```\n**Upvote and let\'s learn together!**
| 8 | 0 |
['Dynamic Programming', 'C']
| 2 |
maximum-number-of-non-overlapping-palindrome-substrings
|
Java Greedy Approach
|
java-greedy-approach-by-zadeluca-c0g5
|
\nclass Solution {\n public int maxPalindromes(String s, int k) {\n int count = 0;\n int idx = 0;\n \n // greedily check for pali
|
zadeluca
|
NORMAL
|
2022-11-13T04:00:49.222842+00:00
|
2022-11-13T04:00:49.222893+00:00
| 800 | false |
```\nclass Solution {\n public int maxPalindromes(String s, int k) {\n int count = 0;\n int idx = 0;\n \n // greedily check for palindromes of length k or k + 1\n while (idx <= s.length() - k) {\n if (isPalindrome(s, idx, idx + k - 1)) {\n count++;\n idx += k;\n } else if (idx < s.length() - k && isPalindrome(s, idx, idx + k)) {\n count++;\n idx += k + 1;\n } else {\n idx++;\n }\n }\n return count;\n }\n \n private boolean isPalindrome(String s, int left, int right) {\n while (left < right) {\n if (s.charAt(left) != s.charAt(right)) {\n return false;\n }\n left++;\n right--;\n }\n return true;\n }\n}\n```
| 8 | 0 |
['Greedy', 'Java']
| 3 |
maximum-number-of-non-overlapping-palindrome-substrings
|
[C++ ] Without using dp and palindrome function.
|
c-without-using-dp-and-palindrome-functi-5pn0
|
\nclass Solution {\npublic:\n int maxPalindromes(string s, int k) {\n int n = s.size();\n int count = 0;\n for(int i=0;i<n;i++){\n
|
iamronnie847
|
NORMAL
|
2022-11-13T07:44:17.927694+00:00
|
2022-11-13T18:38:00.068375+00:00
| 281 | false |
```\nclass Solution {\npublic:\n int maxPalindromes(string s, int k) {\n int n = s.size();\n int count = 0;\n for(int i=0;i<n;i++){\n string str = "",str1="";\n for(int j=i;j<n;j++){\n str += s[j];\n str1 = s[j] + str1;\n if(str.size()>=k && str==str1)\n {\n count++;\n i = j;\n break;\n }\n if(str.size()>k)\n break;\n }\n }\n return count;\n }\n};\n```
| 7 | 0 |
['String', 'C']
| 2 |
maximum-number-of-non-overlapping-palindrome-substrings
|
c++ solution using memoization
|
c-solution-using-memoization-by-dilipsut-teto
|
\nclass Solution {\npublic:\n int k;\n int n;\n int p[2001][2001];\n int memo[3000];\n int f(int idx)\n {\n if(idx>=n)\n {\n
|
dilipsuthar17
|
NORMAL
|
2022-11-13T06:24:01.871934+00:00
|
2022-12-01T04:44:58.164806+00:00
| 1,355 | false |
```\nclass Solution {\npublic:\n int k;\n int n;\n int p[2001][2001];\n int memo[3000];\n int f(int idx)\n {\n if(idx>=n)\n {\n return 0;\n }\n if(memo[idx]!=-1)\n {\n return memo[idx];\n }\n int ans=0;\n for(int i=idx;i<n;i++)\n {\n if((i-idx+1>=k)&&p[idx][i])\n {\n ans=max(ans,1+f(i+1));\n }\n }\n ans=max(ans,f(idx+1));\n return memo[idx]=ans;\n }\n int maxPalindromes(string s, int K) \n {\n k=K;\n memset(p,0,sizeof(p));\n memset(memo,-1,sizeof(memo));\n\n n=s.size();\n for(int gap=0;gap<n;gap++)\n {\n for(int i=0,j=gap;j<n;i++,j++)\n {\n if(gap==0)\n {\n p[i][j]=1;\n }\n else if(gap==1)\n {\n p[i][j]=(s[i]==s[j]);\n }\n else\n {\n if(s[i]==s[j]&&p[i+1][j-1])\n {\n p[i][j]=1;\n }\n }\n \n }\n } \n return f(0);\n }\n};\n```
| 7 | 0 |
['Dynamic Programming', 'Memoization', 'C']
| 1 |
maximum-number-of-non-overlapping-palindrome-substrings
|
Java | 1 dimension DP | Explained
|
java-1-dimension-dp-explained-by-nadaral-3y8o
|
Intuition\ndp[i] means the amount of palindomres found up to index i (exclusive).\n\nWe will iterate over the string s and at every iteration the i index will r
|
nadaralp
|
NORMAL
|
2022-11-13T16:02:08.678026+00:00
|
2022-11-13T16:06:47.985217+00:00
| 687 | false |
# Intuition\n`dp[i]` means the amount of palindomres found up to index `i` (exclusive).\n\nWe will iterate over the string `s` and at every iteration the `i` index will represent the center of a palindrome.\n\nWe will try expanding from that center to the left and right, and if we are holding equality `A[left] == A[right]` it means we still have a palindrome, therefore we can update `dp[right + 1] = max(1 + dp[left], dp[right + 1])`.\nThis is because we found a new palindrome that ended at index `right`, and because our dp is excluding the last index, we add +1.\n\nWe must also check for even palindrome, therefore run the checks when we have a center of 2 indexes.\n\nOdd palindrome: `left` and `right` start at the same index. i.e. left = i-j. right = i+j (assume j=0 in the beginning)\nEven palindrome: `left` and `right` must have 1 index difference. either left-1 or right+1.\n\n\n\n# Code\n```\nclass Solution {\n public int maxPalindromes(String s, int k) {\n int n = s.length();\n int[] dp = new int[n + 1];\n\n // Base case (redundant, but for clarity)\n dp[0] = 0;\n\n // Odd palindrome (center of 1 index)\n for (int i = 0; i < n; i++) {\n dp[i + 1] = Math.max(dp[i], dp[i + 1]);\n for (int j = 0; j < n; j++) {\n int left = i - j;\n int right = i + j;\n if (left < 0 || right >= n) break;\n if (s.charAt(left) != s.charAt(right)) break;\n\n if (right - left + 1 >= k) {\n dp[right + 1] = Math.max(dp[right + 1], dp[left] + 1);\n }\n\n }\n\n // Even palindrome (center of 2 indexes)\n for (int j = 0; j < n; j++) {\n int left = i - j - 1;\n int right = i + j;\n if (left < 0 || right >= n) break;\n if (s.charAt(left) != s.charAt(right)) break;\n\n if (right - left + 1 >= k) {\n dp[right + 1] = Math.max(dp[right + 1], dp[left] + 1);\n }\n }\n }\n\n // for (int a : dp) System.out.print(a + " ");\n return dp[n];\n }\n}\n```
| 6 | 0 |
['Java']
| 0 |
maximum-number-of-non-overlapping-palindrome-substrings
|
Simple Longest Palindromic Substring | Brute Force | C++
|
simple-longest-palindromic-substring-bru-qqk8
|
\n Describe your first thoughts on how to solve this problem. \nJust find longest palindromic substring greedly in every substring>=K\n\n# Code\n\nclass Solutio
|
rajat7k
|
NORMAL
|
2022-11-13T04:22:55.915280+00:00
|
2022-11-13T04:22:55.915340+00:00
| 1,069 | false |
\n<!-- Describe your first thoughts on how to solve this problem. -->\nJust find longest palindromic substring greedly in every substring>=K\n\n# Code\n```\nclass Solution {\npublic:\n \n int longestPalSubstr(string str)\n{\n int n = str.size();\n if (n < 2)\n return n;\n int maxLength = 1, start = 0;\n int low, high;\n for (int i = 0; i < n; i++) {\n low = i - 1;\n high = i + 1;\n while (high < n\n && str[high] == str[i])\n high++;\n \n while (low >= 0\n && str[low] == str[i])\n low--;\n \n while (low >= 0 && high < n\n && str[low] == str[high]) {\n low--;\n high++;\n }\n \n int length = high - low - 1;\n if (maxLength < length) {\n maxLength = length;\n start = low + 1;\n }\n }\n return maxLength;\n}\n \n int maxPalindromes(string s, int k) {\n int ans=0;\n string st="";\n int n=s.size();\n for(int i=0;i<n;i++){\n st.push_back(s[i]);\n if(st.size()>=k){\n if(longestPalSubstr(st)>=k){\n st="";\n ans+=1;\n }\n }\n }\n return ans;\n }\n};\n```
| 6 | 0 |
['Dynamic Programming', 'Greedy', 'C++']
| 1 |
maximum-number-of-non-overlapping-palindrome-substrings
|
Java O(N) Solution | DP + Manacher's algorithm
|
java-on-solution-dp-manachers-algorithm-cf7gg
|
I implemented two different solution during the contest and even the brute force approach can pass all the test cases.\nThus, I guess this problem shouldn\'t be
|
hdchen
|
NORMAL
|
2022-11-13T04:10:47.619315+00:00
|
2022-11-14T08:02:41.135641+00:00
| 595 | false |
I implemented two different solution during the contest and even the brute force approach can pass all the test cases.\nThus, I guess this problem shouldn\'t be labeled as hard.\n\n#### Algorithm\n* dp[i] means the maximum number of non-overlapping palindrome substrings from cs[i...n-1]\n* Use brute-force or manacher\'s algorithm to find out the palindrome substring that fulfills the requirement and build up the dp array by bottom-up approach.\n```\nclass Solution {\n public int maxPalindromes(String s, int min) {\n char[] cs = s.toCharArray();\n int n = cs.length;\n int[] odd = new int[n], even = new int[n], dp = new int[n + 1];\n for (int i = 0, l = 0, r = -1; i < n; ++i) {\n int k = i > r ? 1 : Math.min(odd[l + r - i], r - i + 1);\n while (0 <= i - k && i + k < n && cs[i - k] == cs[i + k]) k++;\n odd[i] = k--;\n if (r < i + k) {\n r = i + k;\n l = i - k;\n }\n }\n for (int i = 0, l = 0, r = -1; i < n; ++i) {\n int k = i > r ? 0 : Math.min(even[l + r - i + 1], r - i + 1);\n while (0 <= i - k - 1 && i + k < n && cs[i - k - 1] == cs[i + k]) k++;\n even[i] = k--;\n if (r < i + k) {\n r = i + k;\n l = i - k - 1;\n }\n } \n for (int i = n - 1; 0 <= i; --i) {\n int diff = odd[i] * 2 - 1 - min;\n if (0 <= diff) {\n diff /= 2; \n dp[i - odd[i] + 1 + diff] = Math.max(dp[i - odd[i] + 1 + diff], 1 + dp[i + odd[i] - diff]);\n }\n diff = even[i] * 2 - min;\n if (0 <= diff) {\n diff /= 2;\n dp[i - even[i] + diff] = Math.max(dp[i - even[i] + diff], 1 + dp[i + even[i] - diff]);\n }\n dp[i] = Math.max(dp[i], dp[i + 1]);\n }\n return dp[0];\n }\n}\n```\n\n#### O(N^2) Edition\n```\nclass Solution {\n public int maxPalindromes(String s, int k) {\n char[] cs = s.toCharArray();\n int n = cs.length;\n int[] dp = new int[n + 1];\n for (int i = n - 1; 0 <= i; --i) {\n int l = i, r = i;\n while (0 <= l - 1 && r + 1 < n && cs[l - 1] == cs[r + 1] && r - l + 1 < k) {\n l--;\n r++;\n }\n if (r - l + 1 >= k) dp[l] = Math.max(dp[l], 1 + dp[r + 1]);\n if (0 != i && cs[i - 1] == cs[i]) {\n l = i - 1;\n r = i;\n while (0 <= l - 1 && r + 1 < n && cs[l - 1] == cs[r + 1] && r - l + 1 < k) {\n l--;\n r++;\n }\n if (r - l + 1 >= k) dp[l] = Math.max(dp[l], 1 + dp[r + 1]);\n }\n dp[i] = Math.max(dp[i], dp[i + 1]);\n }\n return dp[0];\n }\n}\n```
| 6 | 0 |
['Dynamic Programming', 'Java']
| 0 |
maximum-number-of-non-overlapping-palindrome-substrings
|
Simple C++ solution: No DP
|
simple-c-solution-no-dp-by-jenish_09-nos4
|
\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nHere we observe that if any stri
|
jenish_09
|
NORMAL
|
2022-11-18T16:17:40.946179+00:00
|
2022-11-18T16:17:40.946225+00:00
| 138 | false |
\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHere we observe that if any string which size is k+2 and string is palindrome then substring of that string whose size k is also palidrome so we check for substring whose size is k or k+1.\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n bool cal(string str)\n\t{\n\t\tstring tmp=str;\n\t\treverse(str.begin(),str.end()); \n\t\treturn str==tmp;\n\t}\n int maxPalindromes(string s, int k) {\n \n int n=s.size();\n\t\tstring str="";\n\t\tint ans=0;\n\t\tfor(int i=0;i<n;i++)\n\t\t{\n\t\t\tstr+=s[i];\n\t\t\tif(str.size()==k)\n\t\t\t{\n\t\t\t\tbool flag=cal(str);\n\t\t\t\tif(flag)\n\t\t\t\t{\n\t\t\t\t\tstr="";\n\t\t\t\t\tans++;\n\t\t\t\t}\n\t\t\t}\n\t\t\telse if(str.size()==k+1)\n\t\t\t{\n\t\t\t\tbool flag=cal(str);\n\t\t\t\tif(flag)\n\t\t\t\t{\n\t\t\t\t\tstr="";\n\t\t\t\t\tans++;\n\t\t\t\t}\n\t\t\t\telse\n\t\t\t\t{\n\t\t\t\t\tstr.erase(str.begin());\n\t\t\t\t\tflag=cal(str);\n\t\t\t\t\tif(flag)\n\t\t\t\t\t{\n\t\t\t\t\t\tstr="";\n\t\t\t\t\t\tans++;\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t\treturn ans;\n }\n};\n```
| 5 | 0 |
['C++']
| 0 |
maximum-number-of-non-overlapping-palindrome-substrings
|
C++ || DP + Binary Search
|
c-dp-binary-search-by-puneet801-jgsf
|
\nclass Solution {\npublic:\n bool isPal(string &s,int i, int j){\n while(i < j){\n if(s[i++] != s[j--]){\n return false;\n
|
puneet801
|
NORMAL
|
2022-11-13T04:00:50.409431+00:00
|
2022-11-13T04:04:05.243170+00:00
| 483 | false |
```\nclass Solution {\npublic:\n bool isPal(string &s,int i, int j){\n while(i < j){\n if(s[i++] != s[j--]){\n return false;\n }\n }\n return true;\n }\n\t// Simple pick/notpick dp function\n int solve(int i, vector<pair<int,int>>&arr,vector<int>&dp){\n if(i == arr.size()){\n return 0;\n }\n if(dp[i] != -1){\n return dp[i];\n }\n int no = solve(i + 1, arr,dp);\n int yes = 0;\n\t\t//if you pick the ith element and consider it a candidate for a palindrome substring, find the next index in the array which has a possible palindrome and is non-overlapping\n int lower = lower_bound(arr.begin(),arr.end(),make_pair(arr[i].second,0)) - arr.begin();\n if(lower < arr.size() && arr[lower].first == arr[i].second){\n lower++;\n }\n yes = 1+ solve(lower, arr,dp);\n return dp[i] = max(yes,no);\n }\n int maxPalindromes(string s, int k) {\n vector<pair<int,int>>temp;\n int n = s.size();\n int cnt = 0;\n for(int i=0;i<n;i++){\n for(int j=i;j<n;j++){\n if(j - i + 1 >= k && isPal(s,i,j)){ //pair the shortest palindrome starting from i and ending with j \n temp.push_back({i,j});\n break;\n }\n }\n }\n int sz = temp.size();\n vector<int>dp(sz,-1);\n return solve(0,temp,dp);\n }\n};\n```
| 5 | 0 |
['C', 'Binary Tree']
| 3 |
maximum-number-of-non-overlapping-palindrome-substrings
|
Python3 | Memoization
|
python3-memoization-by-dr_negative-p435
|
\nclass Solution:\n def maxPalindromes(self, s: str, k: int) -> int:\n n=len(s)\n def checkIfPalindrome(i,j):\n while i<j:\n
|
dr_negative
|
NORMAL
|
2022-11-20T10:40:02.568575+00:00
|
2022-11-20T10:40:02.568616+00:00
| 358 | false |
```\nclass Solution:\n def maxPalindromes(self, s: str, k: int) -> int:\n n=len(s)\n def checkIfPalindrome(i,j):\n while i<j:\n if s[i]!=s[j]:\n return False\n i+=1\n j-=1\n return True\n @lru_cache(2000)\n def dp(i,j):\n if i>=n or j>=n or (j-i)>k+1:\n return 0\n if s[i]==s[j]:\n if checkIfPalindrome(i,j):\n return 1+dp(j+1,j+k)\n return max(dp(i,j+1),dp(i+1,j+1))\n return dp(0,k-1)\n \n \n```
| 4 | 0 |
['Dynamic Programming', 'Memoization', 'Python3']
| 1 |
maximum-number-of-non-overlapping-palindrome-substrings
|
Simplest Greedy Python Solution | O(1) Space | O(n*k) Time
|
simplest-greedy-python-solution-o1-space-p2nk
|
Intuition\nIf there is a substring of size k + 2 which is a palindrome, then for sure there is a substring of size k which is a palindrome. Similarly, if there
|
deepaklaksman
|
NORMAL
|
2022-11-14T16:31:12.378417+00:00
|
2022-11-14T16:31:12.378457+00:00
| 343 | false |
# Intuition\nIf there is a substring of size k + 2 which is a palindrome, then for sure there is a substring of size k which is a palindrome. Similarly, if there is a substring of size k + 3 which is a palindrome, then there is a substring of size k + 1 which is a palindrome.\n\n# Approach\nSo we can **greedily** start from 0th index and check for a substring of size k which is a palindrome, if not then size k + 1. *Then our new start index is either k or k + 1 based on which is a palindrome* and we can proceed similarly. *If both are not a palindrome then for sure we can\'t find any palindrome starting from that index*, so we move to next index.\n\n# Complexity\n- Time complexity:\n **O(nk)**\n O(n) for traversing the string and a factor of **"k" on each index** for checking whether s[i to i + k] its a palindrome or not by using the valid function.\n\n- Space complexity:\n **O(1)**\n\n# Code\n```\nclass Solution:\n \n def maxPalindromes(self, s: str, k: int) -> int:\n n = len(s)\n # function to check whether substring is a palindrome\n def valid(i, j):\n # if end index is greater then length of string\n if j > len(s):\n return False\n if s[i : j] == s[i : j][::-1]:\n return True\n return False\n maxSubstrings = 0\n start = 0\n while start < n:\n if valid(start, start + k):\n maxSubstrings += 1\n start += k\n elif valid(start, start + k + 1):\n maxSubstrings += 1\n start += k + 1\n else:\n # when there is no palindrome starting at that particular index \n start += 1\n return maxSubstrings\n```
| 4 | 0 |
['Greedy', 'Python', 'Python3']
| 3 |
maximum-number-of-non-overlapping-palindrome-substrings
|
✅ C++ || recursion || memoization || dynamic programming
|
c-recursion-memoization-dynamic-programm-2u3o
|
Approach:- Checking each possibility through recursion,and doing memoization after that.\n\n\u2705 C++ || recursion || memoization || dynamic programming\nclas
|
niraj_1
|
NORMAL
|
2022-11-13T14:41:58.161339+00:00
|
2022-11-13T14:41:58.161363+00:00
| 270 | false |
**Approach:- Checking each possibility through recursion,and doing memoization after that.**\n```\n\u2705 C++ || recursion || memoization || dynamic programming\nclass Solution {\npublic:\n int dp[2001][2001];\n bool isPal(string &s,int i,int j){\n while(i<j){\n if(s[i++]!=s[j--])return false;\n }\n return true;\n }\n int solve(int i,int j,string &s,int k){\n if(j>=s.size() || i>=s.size())return 0;\n if(dp[i][j]!=-1)return dp[i][j];\n if(isPal(s,i,j)){\n return dp[i][j]=max(solve(i,j+1,s,k),max(solve(j+1,j+k,s,k)+1,solve(i+1,j+1,s,k)));\n }\n return dp[i][j]=max(solve(i+1,j+1,s,k),solve(i,j+1,s,k));\n }\n int maxPalindromes(string s, int k) {\n int n=s.size();\n if(k==1)return n;\n memset(dp,-1,sizeof(dp));\n return solve(0,k-1,s,k);\n }\n};\n```
| 4 | 0 |
['Dynamic Programming', 'Recursion', 'Memoization', 'C', 'C++']
| 0 |
maximum-number-of-non-overlapping-palindrome-substrings
|
C++ || Dynamic Programming || Memoization || Explained with comments
|
c-dynamic-programming-memoization-explai-0krw
|
\nclass Solution {\n vector<vector<bool>> is; // this 2-D vector is used to check whether substring from i to j is palindrome or not.\n int n;\n vector
|
sarthu858
|
NORMAL
|
2022-11-13T06:00:03.704488+00:00
|
2022-11-13T08:25:11.409625+00:00
| 739 | false |
```\nclass Solution {\n vector<vector<bool>> is; // this 2-D vector is used to check whether substring from i to j is palindrome or not.\n int n;\n vector<int> dp;\n int solve(string& s, int i, int k) {\n // if we are at end of string we have 0 ans\n if(i >= n) return 0;\n \n // Using memoization.\n int &ans = dp[i];\n if(ans != -1) return ans;\n \n ans = 0;\n // from i we will chech each substring.\n for(int j = i; j < n; j++) {\n // if substring from i to j if palindrome and its size if >= k, then 1 count will add to ans otherwise, it will consider as gap and next substring or gap will calculated from j + 1.\n ans = max(ans, (is[i][j] && (j - i + 1 >= k)) + solve(s, j + 1, k));\n }\n return ans;\n }\npublic:\n int maxPalindromes(string s, int k) {\n n = s.size();\n \n is = vector<vector<bool>>(n, vector<bool>(n, false)); // let all substring be false;\n \n // precomputing palindromes using longest palindromic substring concept.\n for(int g = 0; g < n; g++) { // for each gap between i & j.\n int j = g;\n for(int i = 0; j < n; i++, j++) {\n // if gap is 0 then only one char is there and it is palindome.\n if(g == 0) is[i][j] = true;\n \n // if gap is 1, then if both are equal then it is palindrome. \n else if(g == 1) {\n if(s[i] == s[j]) is[i][j] = true;\n }\n \n // if gap is > 1, then if s[i] and s[j] are equal, and its inner substring is palindrome then it is also palindrome.\n // ie. if substr from i + 1 to j - 1 is palindrome and i & j are equal.\n else {\n if(s[i] == s[j] && is[i + 1][j - 1]) is[i][j] = true;\n }\n }\n }\n \n // Initialising DP\n dp = vector<int>(n + 1, -1);\n \n return solve(s, 0, k);\n }\n};\n```\n\nPlease **upvote** if you find it helpful!
| 4 | 0 |
['Dynamic Programming', 'Memoization', 'C']
| 1 |
maximum-number-of-non-overlapping-palindrome-substrings
|
Easy DP solution using Java
|
easy-dp-solution-using-java-by-devkd-d2nj
|
Intuition\n Describe your first thoughts on how to solve this problem. \nAs it is a maximum/minimum type of problem with n number of solutions possible its tell
|
DevKD
|
NORMAL
|
2022-11-13T04:06:02.612540+00:00
|
2022-11-13T04:06:02.612570+00:00
| 371 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs it is a maximum/minimum type of problem with n number of solutions possible its tell us we need to use recursion and to optimize it we use dp.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe need to check from an given index how many strings of length k are there which are plaindrome, then we given function calls for the plaindromic strings from index j+1 given palindromic string is from index i to index j. Later we also give the function call of i+1 for skipping the current character. \nWe need to include a check that if alll charcters in a string are same then we can directly return maximum number of possible non-overlapping substrings is length of string/k.\n\n# Complexity\n- Time complexity: O(length(s))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(length(s))\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int maxPalindromes(String s, int k) {\n //To check if all the chaarcter in string are same\n HashSet<Character> set=new HashSet<Character>();\n for(int i=0;i<s.length();i++){\n set.add(s.charAt(i));\n }\n //If all characters are same we can have maximum answer\n if(set.size()==1){\n return s.length()/k;\n }\n //Initialize a dp of size 2001\n int[] dp=new int[2001];\n //Fill the dp by -1 indicating value not calculated yet\n Arrays.fill(dp,-1);\n return helper(s,dp,0,k);\n }\n public int helper(String s,int[] dp,int i,int k){\n //If starting index greater then length of string return 0\n if(i>=s.length()){\n return 0;\n }\n int ans=0;\n //If value calculated before then directly return it\n if(dp[i]!=-1){\n return dp[i];\n }\n for(int j=i+k-1;j<s.length();j++){\n //Check if a given substring from index i to j is a palindrome\n boolean palindrome=pal(s,i,j,k);\n //If palindrome give function call from index j+1\n if(palindrome){\n ans=Math.max(ans,1+helper(s,dp,j+1,k));\n }\n }\n //If we skip the current charcter then giving function call for index i+1\n ans=Math.max(ans,helper(s,dp,i+1,k));\n //Storing the maximum of all in ans and storing in dp array\n dp[i]=ans;\n return ans;\n }\n public boolean pal(String s,int a,int b,int k){\n //If lastIndex greater than length of string return false\n if(b>=s.length()){\n return false;\n }\n int freq=0;\n int length=b-a+1;\n //Check if string is palindrome, if palindrome return true else return false\n for(int j=a;j<a+length/2;j++){\n if(s.charAt(j)!=s.charAt(b-freq)){\n return false;\n }\n ++freq;\n }\n return true;\n }\n}\n```
| 4 | 0 |
['Dynamic Programming', 'Java']
| 1 |
maximum-number-of-non-overlapping-palindrome-substrings
|
Beautiful Code: Optimizing Palindrome Substring Count with Memoization
|
beautiful-code-optimizing-palindrome-sub-d92n
|
\n# Intuition\nNote: here curr substring means (start - end),i wrote code so that it can be understood by everyone just by reading it\n\nThere are three action
|
whoisslimshady
|
NORMAL
|
2023-06-27T13:06:07.704532+00:00
|
2023-06-27T13:06:07.704565+00:00
| 79 | false |
\n# Intuition\nNote: here curr substring means (start - end),i wrote code so that it can be understood by everyone just by reading it\n\nThere are three action we can take at any possible moment \n1. curr substring as ans and increase the count make curr substring empty \n2. add char in curr substring and recurive on that\n3. make curr substrig empty and check for substring after than curr substring\n\n\noption 1 is only possible when curr substring is palindrome \n\n\n# Complexity\n- Time complexity: \n-The solve function is called recursively. In the worst case, it can be called for each substring of s, starting from every position start and ending at every position end. This results in a total of O(N^2) recursive calls, where N is the length of the string s.\nFor each recursive call, the function checks if the result is already present in the dp array in constant time, resulting in a time complexity of O(1) for the memoization lookup.\nIf the result is not already present in the dp array, the function performs some operations:\nChecking if the substring is a palindrome takes O(k) time, where k is the length of the substring being checked.\nThe function makes recursive calls based on different conditions, resulting in a total of O(1) recursive calls.\nthe time complexity of the solution can be expressed as O(N^2 * k), where N is the length of the string s and k is the maximum length of a palindrome substring to be considered.\n\n\n- Space complexity:\nO(n*n) here n is size of the string s \n# Code\n```\nclass Solution {\npublic:\n\n bool palindrome(string &s,int i,int j,int k){ \n while(i<j) if(s[i++]!=s[j--]) return false;\n return true;\n }\n int solve(vector<vector<int>>&dp,string &s,int start, int end,int ans,int k ){\n if(start >= s.size() || end>=s.size()) return 0;\n if(dp[start][end]!=-1) return dp[start][end];\n\n int count =0,notCount =0,slideWindow=0; \n if(palindrome(s,start,end,k)){\n count = 1 + solve(dp,s,end+1, end+k,ans+1,k);\n notCount = 0 + solve(dp,s,start, end+1,ans, k);\n slideWindow = 0 + solve(dp,s,start+1,end+1,ans, k);\n return dp[start][end] = max(count,max(notCount,slideWindow));\n }\n\n notCount = solve(dp,s,start, end+1,ans,k);\n slideWindow = solve(dp,s,start+1,end+1,ans,k);\n return dp[start][end] = max(notCount,slideWindow);\n \n }\n int maxPalindromes(string s, int k) {\n vector<vector<int>>dp(s.size()+1,vector<int>(s.size()+1,-1));\n if(k==1) return s.size();\n return solve(dp,s,0,k-1,0,k);\n }\n};\n```
| 3 | 0 |
['Dynamic Programming', 'Recursion', 'Memoization', 'C++']
| 0 |
maximum-number-of-non-overlapping-palindrome-substrings
|
Easiest(2d-DP and 1d-DP)
|
easiest2d-dp-and-1d-dp-by-piyush9818-v7gp
|
```\n\t//2d dp if number is pal or not \n\tint ispal[2001][2001]={0};\n\t//1d dp for for optimizing recursion\n int dp[2001];\n int n;//length of string\n
|
piyush9818
|
NORMAL
|
2022-11-16T10:40:40.385950+00:00
|
2022-11-16T10:40:40.385989+00:00
| 524 | false |
```\n\t//2d dp if number is pal or not \n\tint ispal[2001][2001]={0};\n\t//1d dp for for optimizing recursion\n int dp[2001];\n int n;//length of string\n int fun(int index,int k)\n {\n if(index>=n)\n return 0;\n if(dp[index]!=-1)\n return dp[index];\n int ans=0;\n for(int i=index+k-1;i<n;i++)\n ans=max(ans,fun(i+1,k)+ispal[index][i]);\n ans=max(ans,fun(index+1,k));\n return dp[index]=ans;\n }\n int maxPalindromes(string s, int k) {\n n=s.length();\n\t\t//now just read carefully this part enter value of substring as 1 if palindrome and 0 if not\n\t\t//like eg abaccddb then ispal[0][2]=1 because aba is a palindrome.\n for(int i=0;i<n;i++)\n {\n dp[i]=-1;\n ispal[i][i]=1;\n if(i+1<n&&s[i]==s[i+1])\n pal[i][i+1]=1;\n }\n int gap=2;\n while(gap<n)\n {\n for(int i=0;i+gap<n;i++)\n {\n if(s[i]==s[i+gap]&&ispal[i+1][i+gap-1])\n ispal[i][i+gap]=1;\n }\n gap++;\n }\n\t\t//ispal created now just return ans\n return fun(0,k);\n }\n
| 3 | 0 |
['Dynamic Programming', 'Recursion']
| 1 |
maximum-number-of-non-overlapping-palindrome-substrings
|
✅ [Python] Very simple solution - O(n) || no DP
|
python-very-simple-solution-on-no-dp-by-5cw4c
|
Intuition\nSimilar to 647 https://leetcode.com/problems/palindromic-substrings/\nJust need to add the constraint - non-overlapping\n\n## Approach\nExpand from c
|
Meerka_
|
NORMAL
|
2022-11-13T18:12:47.877015+00:00
|
2022-11-13T18:13:17.290868+00:00
| 188 | false |
## Intuition\nSimilar to 647 https://leetcode.com/problems/palindromic-substrings/\nJust need to add the constraint - non-overlapping\n\n## Approach\nExpand from centers to make the time complexity O(N), space complexity O(1)\nOnly count the palindrome with shortest length (>=k)\nKeep track of the last end position to avoid overlapping\n\n## Code\n```\nclass Solution:\n def maxPalindromes(self, s: str, k: int) -> int:\n res = 0\n lastp = -1\n\n def helper(l, r):\n nonlocal lastp, res\n while l >= 0 and r < len(s) and s[l] == s[r] and l > lastp:\n if r-l+1 >= k:\n res += 1\n lastp = r\n break # find the shortest palindrome\n else:\n l -= 1\n r += 1\n \n for i in range(len(s)):\n helper(i, i) # odd length\n helper(i, i+1) # even length\n return res \n```
| 3 | 0 |
['Python3']
| 0 |
maximum-number-of-non-overlapping-palindrome-substrings
|
Dp solution. O(n^2) approach.
|
dp-solution-on2-approach-by-goyaltushar0-rm7c
|
Intuition\n Describe your first thoughts on how to solve this problem. \nFirst approach which hit our mind is to find all palindrome substrings starting from an
|
goyaltushar09
|
NORMAL
|
2022-11-13T05:54:10.845051+00:00
|
2022-11-13T06:03:41.775792+00:00
| 126 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst approach which hit our mind is to find all palindrome substrings starting from an index.\n\nThen calculate maximum no. of partition, we can get considering each possible substrings for an index.\n\neg: `[abababcdc]` , `k = 3`\npossible palindrome substring for index:\n0 : `a` , `aba` , `ababa`\n1 : `b` , `bab` , `babab`\n2 : `a` , `aba `\n3 : `b` , `bab `\n4 : `a`\n5 : `b`\n6 : `c`, `cdc`\n7 : `d`\n8 : `c`\n\ns = `[abababcdc]`\nstarting at index 8, maximum possible palidrome substring partioning of size>=3 : 0,\nstarting at index 7, maximum possible palidrome substring partioning of size>=3 : 0, \nstarting at index 6, maximum possible palidrome substring partioning of size>=3 : 1 (**cdc**)\nstarting at index 5 : 1 (.**cdc**), \nstarting at index 4 : 1 (..**cdc**),\nstarting at index 3 : 2 (**bab** **cdc**),\nstarting at index 2 : 2 (**aba** b **cdc**),\nstarting at index 1 : 2 (**babab** **cdc**) or (**bab** ab **cac**) \nstarting at index 0 : 3 max (**ababa** b **cdc**) and (**aba** **bab** **cac**) \n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nAbove solution will give TLE $$O(n)^3$$.\nSo to calculate possible palindrome substring we will use a property that :\n\n```\nfor a substring s( i , j ) to be palindrome,\ns( i+1 , j-1 ) must be palindrome. \n```\n\nin above example `abababcdc`\nsustring bab is palindrome because **a** is palindrome.\n\n---\n\n\nTake a 2-d array (**pd**) to maintain length of palindromes starting at index i and a dp array to store count of **maximum number of palindrome substring partitioning possible starting from ith index.**\n\nIn above example dp array will be like : `3 2 2 2 1 1 1 0 0`\nand **pd** 2-d array be like:\npd[0] = `0 1 3 5`,\npd[1] = `0 1 3 5`,\npd[2] = `0 1 3`,\npd[3] = `0 1 3`,\npd[4] = `0 1`,\npd[5] = `0 1`, ... so on.\n\nSo for index i, calculate palindrome substrings by considering length (len) of palindromic substrings starting at index i+1 . Then check whether s[i]==s[ i + len + 1 ] , if yes , then push len+2 to pd[i].\nCalculate dp[i] = max(dp[i] , 1 + dp[i+len+2])\ndp[i+len+2] is taken because we considered one substring (i,i+len+1) so, rest are to be chosen from s(i+len+1 + 1 , n);\n\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n# Code\n```\nclass Solution {\npublic:\n int maxPalindromes(string s, int k) {\n int n = s.length();\n if(k==1)return n;\n\n vector<vector<int>>pd(n+1);\n vector<int> dp(n+1,0);\n for(int i =0 ;i<=n; i++){\n pd[i].push_back(0);\n pd[i].push_back(1); \n } \n\n for(int i = n-2 ; i>=0 ;i--){ \n for(auto len : pd[i+1]){ \n int toCheck = i+len+1;\n if(toCheck<n){\n if(s[toCheck]==s[i]){ \n pd[i].push_back(len+2);\n if(len+2>=k)\n dp[i] = max(dp[i] , 1+dp[toCheck+1]);\n }\n } \n }\n \n dp[i] = max(dp[i] , dp[i+1]);\n } \n return dp[0];\n }\n};\n```
| 3 | 0 |
['Dynamic Programming', 'C++']
| 1 |
maximum-number-of-non-overlapping-palindrome-substrings
|
C++ | DP | Recursion | memoization | Easy to Understand | O(n*n)
|
c-dp-recursion-memoization-easy-to-under-oqcj
|
Approach\n\nLet us first get all the palindromic substring, to do this:\n\n1. Lets say we are checking palindromic substrings of length n, for index i to j, the
|
DevChoganwala
|
NORMAL
|
2022-11-13T04:16:37.621698+00:00
|
2022-11-13T04:16:37.621737+00:00
| 396 | false |
## Approach\n<hr>\nLet us first get all the palindromic substring, to do this:\n\n1. Lets say we are checking palindromic substrings of length `n`, for index `i` to `j`, then, if `s[i] == s[j]` && `isPalindrome[i+1][j-1]`, we can set `isPalindrome[i][j] = 1`\n\nWe are essentially checking palindromes of length `n-2`, we can construct isPalindome in a bottom up manner\n\nBase case:\n`isPalindrome[i][i] = 1`\n`if s[i] == s[i+1] isPalindrome[i][i+1] = 1`\n\nNow that we have all the palindromic substrings, we can think of a recursive way to solve this problem. Consider the following recursive problem:\n1. If we are at an index `i`, include a palindromic substring of `length >= k` ending at `j` and go to index `j+1`\n2. Skip index `i`\n\nBase case:\nif index `i == n`, return `0`\n\nLets keep a variable `ans` initialized to `0`\ncase 1:\n```cpp\nfor(int j = i+k-1;j<n;j++){\n if(pal[i][j]){\n ans = max(ans, 1 + recurse(j+1));\n }\n}\n```\ncase 2:\n```cpp\nans = max(ans, recurse(i+1));\n```\n\nFinally we can memoize this recursion since there are repeating subproblems.\n\n## Code\n<hr>\n\n```cpp\nint dp[2001];\nint recurse(int i, vector<vector<bool>>& pal, int k, int n){\n if(dp[i] != -1) return dp[i];\n if(i == n) return dp[i] = 0;\n int ans = 0;\n for(int j = i+k-1;j<n;j++){\n if(pal[i][j]){\n ans = max(ans, 1 + recurse(j+1, pal, k, n));\n }\n }\n ans = max(ans, recurse(i+1, pal, k, n));\n return dp[i] = ans;\n}\n\nint maxPalindromes(string s, int k) {\n int n = s.length();\n string curr;\n for(int i = 0;i<2001;i++) dp[i] = -1;\n vector<vector<bool>> pal(n, vector<bool>(n, 0));\n for(int i = 0;i<n;i++) pal[i][i] = 1;\n for(int i = 0;i<n-1;i++){\n if(s[i] == s[i+1]) pal[i][i+1] = 1;\n }\n for(int i = 3;i<=n;i++){\n for(int j = 0;j<n-(i-1);j++){\n if(s[j] == s[j + i-1] && pal[j+1][j+i-2]){\n pal[j][j+i-1] = 1;\n }\n }\n }\n return recurse(0, pal, k, n);\n}\n```\n\nTime: `O(n*n)`\nSpace: `O(n*n)`\n
| 3 | 0 |
['Dynamic Programming', 'Recursion', 'Memoization', 'C']
| 2 |
maximum-number-of-non-overlapping-palindrome-substrings
|
DP Solution
|
dp-solution-by-roboto7o32oo3-tkj6
|
Code\n\nclass Solution {\npublic:\n \n vector<vector<bool>> isPalindrome(string& s){\n int n = s.size();\n vector<vector<bool>> dp(n, vector
|
roboto7o32oo3
|
NORMAL
|
2022-11-13T04:01:33.282206+00:00
|
2022-11-13T04:12:59.457639+00:00
| 1,645 | false |
# Code\n```\nclass Solution {\npublic:\n \n vector<vector<bool>> isPalindrome(string& s){\n int n = s.size();\n vector<vector<bool>> dp(n, vector<bool>(n, false));\n \n for(int i=0; i<n; i++){\n dp[i][i] = true;\n }\n \n for(int i=0; i<n-1; i++){\n if(s[i] == s[i+1]){\n dp[i][i+1] = true;\n }\n }\n \n int k = 2;\n \n while(k < n){\n int i=0;\n int j=k;\n \n while(j<n){\n if(s[i] == s[j] and dp[i+1][j-1]){\n dp[i][j] = true;\n }\n \n i++;\n j++;\n }\n \n k++;\n }\n \n return dp;\n }\n \n int maxPalindromes(string s, int k) {\n // get the dp table for palindrome\n vector<vector<bool>> isPalin = isPalindrome(s);\n vector<int> memo(s.size()+1, -1);\n \n function<int(int)> solve = [&](int i) {\n // base cases\n if(i >= s.size()) return 0;\n if(memo[i] != -1) return memo[i];\n \n // skip the current index\n int result = solve(i+1);\n \n // consider segments having length greater than or equal to k\n for(int j=i+k; j<=s.size(); j++) {\n if(isPalin[i][j-1]) result = max(result, solve(j)+1);\n }\n \n return memo[i] = result;\n };\n \n return solve(0);\n }\n};\n```
| 3 | 0 |
['Dynamic Programming', 'C++']
| 2 |
maximum-number-of-non-overlapping-palindrome-substrings
|
Easy Java Solution
|
easy-java-solution-by-sumitk7970-d9sr
|
\nclass Solution {\n int start = 0;\n int count = 0;\n \n public int maxPalindromes(String s, int k) {\n for(int i=0; i<s.length(); i++) {\n
|
Sumitk7970
|
NORMAL
|
2022-11-13T04:01:16.314452+00:00
|
2022-11-13T04:01:16.314512+00:00
| 1,011 | false |
```\nclass Solution {\n int start = 0;\n int count = 0;\n \n public int maxPalindromes(String s, int k) {\n for(int i=0; i<s.length(); i++) {\n helper(s, i, i, k);\n helper(s, i, i+1, k);\n }\n \n return count;\n }\n \n void helper(String s, int i, int j, int k) {\n while(i >= start && j < s.length()) {\n if(s.charAt(i) != s.charAt(j)) break;\n if(j-i+1 >= k) {\n count++;\n start = j+1;\n break;\n }\n i--;\n j++;\n }\n }\n}\n```
| 3 | 0 |
['Java']
| 1 |
maximum-number-of-non-overlapping-palindrome-substrings
|
Solution using dp
|
solution-using-dp-by-rohit_1610-mmig
|
\n\n<!-- # Complexity\n- Time complexity:\n Add your time complexity here, e.g. O(n) \n- Space complexity:\nAdd your space complexity here, e.g. O(n) \n\n# Code
|
rohit_1610
|
NORMAL
|
2024-07-07T12:02:19.327819+00:00
|
2024-07-07T12:02:19.327880+00:00
| 51 | false |
\n\n<!-- # Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ \n- Space complexity:\nAdd your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n bool check(int i, int j, string &s, vector<vector<int>> &palindrome) {\n if (palindrome[i][j] != -1) {\n return palindrome[i][j];\n }\n while (i < j) {\n if (s[i] != s[j]) {\n palindrome[i][j] = 0;\n return false;\n }\n i++;\n j--;\n }\n palindrome[i][j] = 1;\n return true;\n }\n\n int maxPalindromes(string s, int k) {\n int n = s.size();\n if(k==1)return n;\n vector<int> dp(n + 1, 0);\n vector<vector<int>> palindrome(n, vector<int>(n, -1));\n\n for (int ind = n - 1; ind >= 0; ind--) {\n int ntake=dp[ind+1];\n int take=0;\n for (int i = ind; i < n; i++) {\n if ((i - ind + 1) >= k && check(ind, i, s, palindrome)) {\n take = max(take, 1 + dp[i + 1]);\n }\n }\n dp[ind] = max(take, ntake);\n }\n return dp[0];\n }\n};\n\n```
| 2 | 0 |
['C++']
| 0 |
maximum-number-of-non-overlapping-palindrome-substrings
|
Java/C++ Clean Easy Solution || With Detail Description
|
javac-clean-easy-solution-with-detail-de-4qxe
|
Complexity\n- Time complexity:O(n*k)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(n)\n Add your space complexity here, e.g. O(n) \n\n# Co
|
Shree_Govind_Jee
|
NORMAL
|
2024-07-02T15:28:16.460271+00:00
|
2024-07-02T15:28:16.460297+00:00
| 112 | false |
# Complexity\n- Time complexity:$$O(n*k)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n\n private boolean isPalindrom(String str, int start, int end) {\n while (start < end) {\n if (str.charAt(start) != str.charAt(end)) {\n return false;\n }\n start++;\n end--;\n }\n return true;\n }\n\n public int maxPalindromes(String s, int k) {\n int[] dp = new int[s.length() + 1];\n for (int i = k - 1; i < s.length(); i++) { // k-1 bcz the index start from 0\n dp[i + 1] = dp[i];\n\n // if s.substr(i-k+1, i) is palindrom\n // then count it\n if (isPalindrom(s, i - k + 1, i)) {\n dp[i + 1] = Math.max(dp[i + 1], 1 + dp[i - k + 1]);\n }\n\n if (i - k >= 0 && isPalindrom(s, i - k, i)) {\n dp[i + 1] = Math.max(dp[i + 1], 1 + dp[i - k]);\n }\n }\n return dp[s.length()];\n }\n}\n```
| 2 | 0 |
['String', 'Dynamic Programming', 'Greedy', 'Recursion', 'Memoization', 'Java']
| 0 |
maximum-number-of-non-overlapping-palindrome-substrings
|
Be Greedy
|
be-greedy-by-cs22m020-ywf7
|
Intuition\n Describe your first thoughts on how to solve this problem. \nStart at i:\nif : i to i+k-1 is a pallindrome i=i+k\nelse if : i to i+k is a pallindrom
|
cs22m020
|
NORMAL
|
2023-10-08T10:35:36.943504+00:00
|
2023-10-08T10:35:36.943522+00:00
| 101 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nStart at i:\nif : i to i+k-1 is a pallindrome i=i+k\nelse if : i to i+k is a pallindrome i=i+k+1;\nelse : i=i+1\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n*k)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution {\npublic:\n int check(int i, int j, string& s){\n while(i<=j){\n if(s[i]!=s[j]){\n return false;\n }\n i++;\n j--;\n }\n return true;\n }\n \n int maxPalindromes(string s, int k) {\n int count=0;\n int i=0;\n int n=s.length();\n while(i+k<=n){\n if(check(i,i+k-1,s)){\n count+=1;\n i+=k;\n }else if(i+k<n && check(i,i+k,s)){\n count+=1;\n i+=k+1;\n }else{\n i++;\n }\n }\n return count;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
maximum-number-of-non-overlapping-palindrome-substrings
|
C++ | Sliding Window Approach | Easy to Understand
|
c-sliding-window-approach-easy-to-unders-q7n6
|
\n# Code\n\nclass Solution {\n bool isPalindrome(string s, int i, int j){\n while(i<j){\n if(s[i++]!=s[j--]){\n return false
|
PulkitAgga01
|
NORMAL
|
2023-03-19T17:03:53.952990+00:00
|
2023-03-19T17:03:53.953040+00:00
| 353 | false |
\n# Code\n```\nclass Solution {\n bool isPalindrome(string s, int i, int j){\n while(i<j){\n if(s[i++]!=s[j--]){\n return false;\n }\n }\n return true;\n }\npublic:\n int maxPalindromes(string s, int k) {\n int ans = 0;\n for(int i=0; i<s.length(); i++){\n for(int j=i; j<s.length(); j++){\n int len= j-i+1;\n if(len>k+1){\n break;\n }\n if(len>=k and isPalindrome(s, i, j)){\n ans++; \n i=j;\n break;\n }\n }\n }\n return ans;\n }\n};\n```
| 2 | 0 |
['Sliding Window', 'C++']
| 3 |
maximum-number-of-non-overlapping-palindrome-substrings
|
Easy to understand solution in java using center expansion technique in O(n)
|
easy-to-understand-solution-in-java-usin-x9ua
|
\n# Approach\nUsing each element of the array as center keep on building the pallindrome as soon as it reaches the min length criteria just stop the operation a
|
sarja830
|
NORMAL
|
2023-02-09T23:12:56.966540+00:00
|
2024-01-23T12:23:43.822892+00:00
| 410 | false |
\n# Approach\nUsing each element of the array as center keep on building the pallindrome as soon as it reaches the min length criteria just stop the operation and return index next to it because it is already used in the pallindrome once and we dont want overlapping pallindromes. \nMaintain a used array to track whether the character is used or not. if not used then only take it in the next pallindrome to be considered.\n<!-- Describe your approach to solving the problem. -->\n\n\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n\n[can be decreased to O(1) with the help of a pointer which points to the last location of the last counted pallindrome. initialize the pointer to -1]\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n \n int k;\n boolean[] used;\n public int maxPalindromes(String s, int k) {\n this.k=k;\n used= new boolean[s.length()];\n Arrays.fill(used,false);\n if(k==1) return s.length();\n int res=0;\n int i=0;\n while(i<s.length())\n {\n int oddLength = centerExpansion(i,i,s);\n int evenLength = centerExpansion(i,i+1,s);\n if(oddLength==i && evenLength==i) \n {\n i++;\n }\n else if( oddLength==i || evenLength==i)\n {\n i=oddLength==i?evenLength:oddLength;\n used[i]=true;\n res=res+1;\n i=i+1;\n }\n else \n {\n i=Math.min(oddLength,evenLength);\n used[i]=true;\n i=i+1;\n res=res+1;\n }\n }\n return res;\n }\n int centerExpansion(int l, int r, String s)\n {\n int count=0;\n int ol=l;\n while(l>=0 && r<s.length())\n {\n if(s.charAt(l)==s.charAt(r))\n {\n if(r-l+1>=k && !used[l]) {\n \n return r;\n }\n }\n else\n {\n return ol;\n }\n r++;\n l--;\n }\n return ol;\n } \n}\n```
| 2 | 0 |
['Java']
| 2 |
maximum-number-of-non-overlapping-palindrome-substrings
|
✅ [C++] || DP + Greedy || Most intuitive solution || easy to understand
|
c-dp-greedy-most-intuitive-solution-easy-w0vz
|
You can check for each index j what all are the index i for which i-j is a palindrome and store it in a map (O(n^2)). Now using top down, check for each index i
|
iamvaibhav070101
|
NORMAL
|
2022-11-16T20:05:07.984771+00:00
|
2022-11-16T20:05:34.226283+00:00
| 186 | false |
You can check for each index ```j``` what all are the index ```i``` for which ```i-j``` is a palindrome and store it in a map ```(O(n^2))```. Now using top down, check for each index ```i``` what can be a possible selection of ```j``` using the map, and call again recursively on ```j-1``` (Note that if ```j-1<0``` then you need to return ```0```). You also need to consider the case where you can\'t or you don\'t use the character at place ```i```. \n\n```\nclass Solution {\npublic:\n vector<vector<int>> dp;\n unordered_map<int,vector<int>> mp;\n vector<int> mem;\n \n bool isPal(int i, int j, string &s){\n if(i==j){\n return dp[i][j] = 1;\n }\n if(i==j-1){\n return dp[i][j] = s[i]==s[j];\n }\n if(dp[i][j]!=-1){\n return dp[i][j];\n }\n if(s[i]==s[j]){\n return dp[i][j] = isPal(i+1,j-1,s);\n }\n return dp[i][j] = 0;\n }\n \n int solve(int i, string &s){\n if(i<0){\n return 0;\n }\n if(mem[i]!=-1){\n return mem[i];\n }\n if(mp.count(i)){\n int ans = 0;\n for(int j : mp[i]){\n ans = max(ans,solve(j-1,s)+1);\n }\n ans = max(ans,solve(i-1,s));\n return mem[i] = ans;\n }else{\n return mem[i] = solve(i-1,s);\n }\n }\n int maxPalindromes(string s, int k) {\n int n = s.length();\n dp.resize(n+1, vector<int>(n+1,-1));\n mp.clear();\n for(int i = 0; i<n; i++){\n for(int j = i; j<n; j++){\n if(isPal(i,j,s) && j-i+1>=k){\n mp[j].push_back(i);\n }\n }\n }\n mem.resize(n,-1);\n return solve(n-1,s);\n }\n};\n```
| 2 | 0 |
['Dynamic Programming', 'Greedy', 'C']
| 0 |
maximum-number-of-non-overlapping-palindrome-substrings
|
Detailed Explanation ✅ - Dynamic Programming Solution O(N*N)
|
detailed-explanation-dynamic-programming-yce4
|
Intuition\nI found out the find maximum number of valid substrings in every interval \n[i,n-1], where i vary from (0 to n-1)\nand dp[0] is the answer\n\n# Appro
|
bhavya_kawatra13
|
NORMAL
|
2022-11-14T12:08:29.507913+00:00
|
2022-11-14T15:14:45.594673+00:00
| 479 | false |
# Intuition\nI found out the find maximum number of valid substrings in every interval \n[i,n-1], where i vary from (0 to n-1)\nand dp[0] is the answer\n\n# Approach\nWe iterated over the string and for each character \'i\', we stored the result of \'maximum number of valid substrings it can make in range i to n-1\' in dp[i];\n\nTo do that,\n\nfor evry i I iterated over the remaining portion of string using pointer j\ni.e from i to n-1 \n\nand I checked whether i to j is palindrom or not?\n\nIf it is palindrom then I added dp[j+1] to answer and added 1 to it additionally..\n(((added 1 beacause we have i to j as palindromic and then added maximum valid string in range j+1 to n-1 i.e. dp[j+1])))\n.\nif(it is not palindromic) then we just add the reult of dp[j+1];\n```\ntransition is : \n if(substring(i to j) is palindrome)\n dp[i]=max(dp[i],dp[j+1]**+1**);\n else\n dp[i]=max(dp[i],dp[j+1]);\n```\n\nTo reduce time complexity to O(N*N):\nWe precalculated whether a string in range i to j is palindromic or not\n\n# Complexity\n\n- Time complexity: O(N*N)\n\n\n- Space complexity: O(N*N)\n\n# Code\n```\nclass Solution {\npublic:\n int maxPalindromes(string a, int k) {\n int n=a.size();\n // p[i][j] -> true if string in i to j is palindromic\n vector<vector<bool>>p(n+5,vector<bool>(n+5,false));\n for(int i=n-1;i>=0;i--){\n for(int j=i;j<n;j++){\n if(i==j)\n p[i][j]=true;\n else if(a[i]==a[j]&&(j-i==1||p[i+1][j-1]))\n p[i][j]=true;\n }\n }\n // dp[i] -> maximum number of valid substrings in range i to n-1\n vector<int>dp(n+5,0);\n for(int i=n-1;i>=0;i--){\n for(int j=i;j<n;j++){\n int len=j-i+1;\n dp[i]=max(dp[i],dp[j+1]+(len>=k?p[i][j]:0));\n }\n }\n return dp[0];\n }\n};\n\n```
| 2 | 0 |
['Dynamic Programming', 'C++']
| 0 |
maximum-number-of-non-overlapping-palindrome-substrings
|
O(n) solution with Manacher's algorithm + checking the shortest palindrome of any given center
|
on-solution-with-manachers-algorithm-che-1p2t
|
Intuition\nManacher\'s algorithm computes the longest palindrome of all possible centers in linear time. Combined with the fact that the shortest palindrome tha
|
chuan-chih
|
NORMAL
|
2022-11-13T07:45:09.499880+00:00
|
2022-11-13T07:45:09.499945+00:00
| 254 | false |
# Intuition\n[Manacher\'s algorithm](https://en.wikipedia.org/wiki/Longest_palindromic_substring#Manacher\'s_algorithm) computes the longest palindrome of all possible centers in linear time. Combined with the fact that the shortest palindrome that starts later and ends earlier is always preferred since the answer up to an index increases monotonically, we get O(n) solution.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Call `manacher(s)`\n2. Go through the returned list. For centers whose palindromes can be at least `k` characters long, update the last neighbor of end index `i + length // 2`.\n3. Construct `dp`, padded to make sure that index `-1` refers to the answer up to an empty string (zero), one index at a time by taking the `max()` between the prior index and `1 + dp[last_neighbor]` if applicable.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\ndef manacher(s):\n t = \'#\'.join(\'^\' + s + \'\n```)\n p = [0] * len(t)\n c = r = 0\n for i in range(2, len(t) - 2):\n p[i] = int(r > i) and min(r - i, p[2 * c - i])\n while t[i + p[i] + 1] == t[i - p[i] - 1]:\n p[i] += 1\n if i + p[i] > r:\n c, r = i, i + p[i]\n return p\n\nclass Solution:\n def maxPalindromes(self, s: str, k: int) -> int:\n p = manacher(s)[2:-2]\n n = len(s)\n dp = [0] * (n + 1)\n adj = [-math.inf] * n\n for j in range(len(p)):\n i = j // 2\n if not j % 2:\n length = k + (not k % 2)\n if length <= p[j]:\n adj[i + length // 2] = max(adj[i + length // 2], i - length // 2 - 1)\n else:\n length = k + k % 2\n if length <= p[j]:\n adj[i + length // 2] = max(adj[i + length // 2], i - length // 2)\n for i in range(n):\n dp[i] = max(dp[i - 1], 1 + dp[adj[i]] if adj[i] > -math.inf else 0)\n return dp[n - 1]\n \n \n```
| 2 | 0 |
['Python3']
| 0 |
maximum-number-of-non-overlapping-palindrome-substrings
|
[JavaScript] Simple and fast brute force 😀
|
javascript-simple-and-fast-brute-force-b-9eh8
|
If there is a palindrome string of length N where N > k + 1, the string can be always "trimmed" to a substring of length k or k + 1. E.g. for k = 3, abcddcba =>
|
m12s44
|
NORMAL
|
2022-11-13T05:54:14.527606+00:00
|
2022-11-13T05:54:14.527649+00:00
| 94 | false |
1. If there is a palindrome string of length N where N > k + 1, the string can be always "trimmed" to a substring of length k or k + 1. E.g. for k = 3, ab**cddc**ba =>cddc; or abc**ded**cba => ded\n2. As far as we need to find a maximum number of substrings in an optimal selection we can ignore all palindromes longer than k + 1, due to the fact that all longer palindromes will have their "shorter" version of length k or k + 1.\n3. So, starting from the very first chat of string, check all string of length k and k + 1 if it\'s a palindrome. If so, skip next k/k+1 chars.\n\n\n```\n/**\n * @param {string} s\n * @param {number} k\n * @return {number}\n */\nvar maxPalindromes = function(s, k) {\n let ans = 0 \n\t\n const isPalindrome = (str) => {\n let start = 0\n let end = str.length - 1\n while (start < end) {\n if (str[start] !== str[end]) return false\n start++\n end--\n }\n return true\n }\n \n let len = s.length\n let i = 0\n \n while (i + k <= len) {\n let step = 1\n if (isPalindrome(s.substring(i, i + k) )) {\n ans++\n step = k\n } else if (i + k + 1 <= len) {\n if (isPalindrome(s.substring(i, i + k + 1))) {\n ans++\n step = k + 1\n } \n }\n i += step\n }\n return ans\n};
| 2 | 0 |
['JavaScript']
| 0 |
maximum-number-of-non-overlapping-palindrome-substrings
|
[Python3] greedy - only check length k and k + 1
|
python3-greedy-only-check-length-k-and-k-b57v
|
\nclass Solution:\n def maxPalindromes(self, s: str, k: int) -> int:\n ans = 0\n l = 0\n while l<len(s):\n cdd1 = s[l:l+k]\n
|
nxiayu
|
NORMAL
|
2022-11-13T05:03:53.424661+00:00
|
2022-11-13T05:05:35.296517+00:00
| 336 | false |
```\nclass Solution:\n def maxPalindromes(self, s: str, k: int) -> int:\n ans = 0\n l = 0\n while l<len(s):\n cdd1 = s[l:l+k]\n if len(cdd1)>=k and cdd1 == cdd1[::-1]:\n ans += 1\n l = l+k\n continue\n cdd2 = s[l:l+k+1]\n if len(cdd2)>=k and cdd2 == cdd2[::-1]:\n ans += 1\n l = l+k+1\n continue\n l += 1\n return ans\n\n```
| 2 | 0 |
['Greedy', 'Python', 'Python3']
| 0 |
maximum-number-of-non-overlapping-palindrome-substrings
|
Longest Palindromic Substring || Easy to Understand || Java || Expanding around a fixed pivot
|
longest-palindromic-substring-easy-to-un-b2qd
|
The intution of the problem can be very well driven from the idea of the Longest Palindromic Substring problem.\n\nLets first review the code for the longest pa
|
Utkarsh_09
|
NORMAL
|
2022-11-13T04:19:31.159805+00:00
|
2022-11-13T04:27:17.480490+00:00
| 375 | false |
The **intution of the problem can be very well driven from the idea** of the [Longest Palindromic Substring](http://leetcode.com/problems/longest-palindromic-substring/) problem.\n\nLets first review the code for the longest palindromic substring:\n```\nclass Solution {\n public int expand(int left, int right, String s)\n {\n\t // Expading the boundaries around the fixed pivot\n while(left>=0 && right<s.length() && s.charAt(left)==s.charAt(right))\n {\n left--;\n right++;\n }\n return right-left-1;\n }\n public String longestPalindrome(String s) {\n int left = 0;\n int right = 0;\n \n for(int i = 0;i<s.length();i++)\n {\n int len1 = expand(i,i,s); // For the substring having the length odd\n int len2 = expand(i,i+1,s); // For the substring having the length even\n \n int len = Math.max(len1,len2);\n if(len>(right-left))\n {\n left = i-(len-1)/2;\n right = i+ (len)/2;\n }\n }\n \n return s.substring(left,right+1);\n }\n}\n```\n\nThe idea for this problem is very much similar. All we need to **consider the following constraints**: \n```\n1 - Palindromic Substrings should be non overlapping (i.e the right boundary of previous palindromic substring should be less than the left boundary of current palindromic substring).\n\n2 - The length of the palindromic substring should be >= k.\n\n```\n\nThe implementation for the above algorithmic intuition is described in the code given below.\n```\nclass Solution {\n public boolean getLen(int[] Ar, String s, int left, int k)\n {\n\t // Expanding the boundaries around fixed pivot with given constraints\n while(Ar[0]>=left && Ar[1]<s.length() && s.charAt(Ar[0])==s.charAt(Ar[1]))\n {\n \n if((Ar[1]-Ar[0]+1)>=k)\n return true;\n Ar[0]--;\n Ar[1]++;\n }\n return false;\n }\n public int maxPalindromes(String s, int k) {\n \n int left = 0;\n int[] Ar = new int[2];\n int cnt = 0;\n //0-> Left\n //1-> Right\n for(int right = 0;right<s.length();right++)\n {\n boolean isPossible = false;\n Ar[0] = right;\n Ar[1] = right;\n isPossible = getLen(Ar,s,left,k); // For odd length substring\n if(isPossible)\n {\n left = Ar[1]+1;\n cnt++;\n }\n else\n {\n Ar[0] = right;\n Ar[1] = right+1;\n isPossible = getLen(Ar,s,left,k); // For substring of even length\n if(isPossible)\n {\n left = Ar[1]+1;\n cnt++;\n }\n }\n }\n \n return cnt;\n }\n}\n```\n\n```\nThe dry for the sample test just for better understanding of the algorithm:\n\ns = "abaccdbbd", k = 3\n\n```\n\n\n\n\n**Palindromic Substring Count** : 2\n\nHope this helps. Have an awesome day folks \uD83D\uDE0A\n\n
| 2 | 1 |
['Java']
| 0 |
maximum-number-of-non-overlapping-palindrome-substrings
|
Java Solution
|
java-solution-by-solved-8fz1
|
\nclass Solution {\n public int maxPalindromes(String s, int k) {\n int result = 0;\n for (int i = 0; i < s.length(); i++) {\n if (i
|
solved
|
NORMAL
|
2022-11-13T04:01:27.187588+00:00
|
2022-11-13T04:01:27.187629+00:00
| 336 | false |
```\nclass Solution {\n public int maxPalindromes(String s, int k) {\n int result = 0;\n for (int i = 0; i < s.length(); i++) {\n if (isPalindrome(s, i, i + k - 1)) {\n result++;\n i = i + k - 1;\n } else if (isPalindrome(s, i, i + k)) {\n result++;\n i = i + k;\n }\n }\n return result;\n }\n public boolean isPalindrome(String s, int startIndex, int endIndex) {\n if (endIndex >= s.length()) {\n return false;\n }\n while (startIndex <= endIndex) {\n char startChar = s.charAt(startIndex);\n char endChar = s.charAt(endIndex);\n if (startChar != endChar) {\n return false;\n }\n startIndex++;\n endIndex--;\n }\n return true;\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
maximum-number-of-non-overlapping-palindrome-substrings
|
Palindrome Matrix pre-computation + 1D memoization DP
|
palindrome-matrix-pre-computation-1d-mem-ojju
|
Code
|
vats_lc
|
NORMAL
|
2024-12-27T08:02:50.098058+00:00
|
2024-12-27T08:02:50.098058+00:00
| 46 | false |
# Code
```cpp []
class Solution {
public:
int getAns(int i, int n, vector<vector<int>>& palin, int& k,
vector<int>& dp) {
if (i == n)
return 0;
if (dp[i] != -1)
return dp[i];
int nt = getAns(i + 1, n, palin, k, dp), ans = 0;
for (int j = i + k - 1; j < n; j++)
if (palin[i][j])
ans = max(ans, 1 + getAns(j + 1, n, palin, k, dp));
return dp[i] = max(ans, nt);
}
int maxPalindromes(string s, int k) {
int n = s.size();
vector<vector<int>> palin(n, vector<int>(n, 0));
for (int i = 0; i < n; i++)
palin[i][i] = 1;
for (int i = 0; i < n - 1; i++)
palin[i][i + 1] = (s[i] == s[i + 1]);
for (int len = 3; len <= n; len++)
for (int i = 0; i + len - 1 < n; i++) {
int j = i + len - 1;
palin[i][j] = (s[i] == s[j]) && palin[i + 1][j - 1];
}
vector<int> dp(n, -1);
return getAns(0, n, palin, k, dp);
}
};
```
| 1 | 0 |
['C++']
| 0 |
maximum-number-of-non-overlapping-palindrome-substrings
|
Crystal clear javascript code, not using GPT !
|
crystal-clear-javascript-code-not-using-tnc5f
|
Made a repo with all my DSA solutions, you should check it out \nhttps://github.com/Abhaydutt2003/DataStructureAndAlgoPractice/tree/master/src/Strings\n\n\n\n#
|
AbhayDutt
|
NORMAL
|
2024-05-27T04:35:19.690465+00:00
|
2024-05-27T04:35:19.690509+00:00
| 13 | false |
Made a repo with all my DSA solutions, you should check it out \nhttps://github.com/Abhaydutt2003/DataStructureAndAlgoPractice/tree/master/src/Strings\n\n\n\n# Code\n```\n/**\n * @param {string} s\n * @param {number} k\n * @return {number}\n */\nvar maxPalindromes = function (s, k){\n let dpPal = new Array(s.length+1).fill().map(()=>{\n return new Array(s.length+1).fill(false);\n });\n let generateAllPalindromes = ()=>{\n //all one length substrings\n for(let i = 0;i<s.length;i++){\n dpPal[i][i] = true;\n }\n //will take care of 2 length 2 because of odd even length scenarios\n for(let i = 0;i<s.length-1;i++){\n if(s[i] === s[i+1])dpPal[i][i+1] = true;\n }\n //start to fill all the remaning substrings\n for(let k = 2;k<s.length;k++){\n let i = 0,j = k;\n while(j<s.length){\n if(s[i] === s[j] && dpPal[i+1][j-1])dpPal[i][j] = true;\n i++;j++;\n }\n }\n }\n generateAllPalindromes();\n let memo = new Map();\n\n let getAns = (start)=>{\n if(start>=s.length)return 0;\n if(memo.has(start))return memo.get(start);\n let answer = 0;\n for(let i = start;i<s.length;i++){\n let smallAns = getAns(i+1);\n if(i-start+1 >=k && dpPal[start][i] == true)smallAns++;\n answer = Math.max(answer,smallAns);\n }\n memo.set(start,answer);\n return answer;\n }\n return getAns(0);\n}\n```
| 1 | 0 |
['JavaScript']
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.