question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
count-substrings-with-k-frequency-characters-i
|
Easy to understand solution in Java using sliding window.
|
easy-to-understand-solution-in-java-usin-1c6t
|
ApproachWe maintain two pointers, left and right, to represent the sliding window's boundaries. left starts at 0, and right moves from 0 to the end of the strin
|
Khamdam
|
NORMAL
|
2025-02-14T16:43:42.334586+00:00
|
2025-02-14T16:43:42.334586+00:00
| 1 | false |
# Approach
We maintain two pointers, left and right, to represent the sliding window's boundaries. left starts at 0, and right moves from 0 to the end of the string.
We use a HashMap freq to track the frequency of characters in the current window. As right moves to the next character, we update the frequency of that character in the map.
**The key idea is that a window is valid if at least one character in the window appears at least k times. We use the helper function isValidWindow() to check if the window is valid based on the frequencies in the freq map.**
**For each valid window (when isValidWindow() returns true), all substrings from left to right, left to right+1, ..., left to n-1 are valid. We add (n - right) to the count of valid substrings because all those substrings starting from left and ending at positions right to n-1 are valid.**
After counting valid substrings, we move the left pointer forward to explore new possible windows, decreasing the frequency of the character at left.
This process continues until right reaches the end of the string. Finally, the count will store the total number of valid substrings.
- Time complexity:
O(n)
- Space complexity:
O(1)
# Code
```java []
class Solution {
public int numberOfSubstrings(String s, int k) {
int n = s.length();
if (n < k) {
return 0;
}
Map<Character, Integer> freq = new HashMap<>();
int left = 0;
int count = 0;
for (int right = 0; right < n; right++) {
char rightChar = s.charAt(right);
freq.put(rightChar, freq.getOrDefault(rightChar, 0) + 1);
while (isValidWindow(freq, k)) {
count += (n - right);
char leftChar = s.charAt(left);
freq.put(leftChar, freq.get(leftChar) - 1);
if (freq.get(leftChar) == 0) {
freq.remove(leftChar);
}
left++;
}
}
return count;
}
private boolean isValidWindow(Map<Character, Integer> freq, int k) {
for (int count : freq.values()) {
if (count >= k) {
return true;
}
}
return false;
}
}
```
| 0 | 0 |
['Java']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Python3 solution | explained | sliding window
|
python3-solution-explained-sliding-windo-mez4
|
IntuitionSliding windowApproachConstruct a frequency hashmap to maintain the numbers for each letter. The number of elements in the dictionary will always be 26
|
FlorinnC1
|
NORMAL
|
2025-02-13T20:42:20.584202+00:00
|
2025-02-13T20:42:20.584202+00:00
| 6 | false |
# Intuition
Sliding window
# Approach
Construct a frequency hashmap to maintain the numbers for each letter. The number of elements in the dictionary will always be 26 at maximum. We will get the number of numbers wich have freq >= k at every iteration and based on that add it to the count. We always only need 1 element with freq >= k when counting, so we will leverage that.
# Complexity
- Time complexity:
O(n) | n = len(s) * 26
- Space complexity:
O(1) since we use only the dictionary with 26 max keys
# Code
```python3 []
class Solution:
def numberOfSubstrings(self, s: str, k: int) -> int:
j = 0
d = defaultdict(lambda: 0)
count = 0
for i in range(len(s)):
d[s[i]] += 1
k_elements = 0
for _, element in enumerate(d):
if d[element] >= k:
k_elements += 1
if k_elements > 0:
count += j + 1
# if it's only 1 element with freq == k and d[s[j]] < k it means s[j] is not that element and we can delete it
# if it's only 1 element with freq == k and d[s[j]] > k it means s[j] is that element and we can delete since it's still >= k as freq
while j < i and (k_elements >= 2 or k_elements == 1 and d[s[j]] != k):
d[s[j]] -= 1
if d[s[j]] == k - 1:
k_elements -= 1
count += 1
j += 1
return count
```
| 0 | 0 |
['Sliding Window', 'Python3']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Simple sliding window solution 😊
|
simple-sliding-window-solution-by-harshl-1hpg
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
harshlage
|
NORMAL
|
2025-01-25T11:16:45.380304+00:00
|
2025-01-25T11:16:45.380304+00:00
| 4 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int numberOfSubstrings(string s, int k) {
int i = 0;
int j = 0;
unordered_map<char,int>mp;
int ans = 0;
int n = s.size() - 1;
while(i < s.size() && j < s.size()){
mp[s[j]]++;
if(mp[s[j]] == k){
while(mp[s[j]] == k){
ans += n - j + 1;
mp[s[i]]--;
i++;
}
}
j++;
}
return ans;
}
};
```
| 0 | 0 |
['C++']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Count Substrings in one pass.
|
count-substrings-in-one-pass-by-rishiins-wy4f
|
IntuitionApproachOur aim is to count the number of substrings where no character appears at least (k) times. It starts by calculating the total number of substr
|
RishiINSANE
|
NORMAL
|
2025-01-25T08:29:54.752737+00:00
|
2025-01-25T08:29:54.752737+00:00
| 2 | false |
# Intuition
# Approach
Our aim is to count the number of substrings where no character appears at least \(k\) times. It starts by calculating the total number of substrings in the string using the formula `(n * (n + 1)) / 2`, where \(n\) is the string length. Then, it uses a sliding window technique with two pointers, \(i\) and \(j\), to go through the string. As we move the right pointer \(j\), we track the frequency of characters in the window. If any character reaches \(k\) occurrences, we move the left pointer \(i\) to shrink the window until the condition is violated. For each valid window, we subtract the number of substrings ending at \(j\) but starting within the window from the total. This ensures that only substrings where no character appears \(k\) or more times are counted.
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(1)
# Code
```cpp []
class Solution {
public:
int numberOfSubstrings(string s, int k) {
int n = s.size();
int totalSubs = (n * (n + 1)) / 2;
unordered_map<char, int> mpp;
int i = 0, j = 0;
while (j < n) {
mpp[s[j]]++;
while (mpp[s[j]] >= k) {
mpp[s[i]]--;
i++;
}
totalSubs -= j - i + 1;
j++;
}
return totalSubs;
}
};
```
| 0 | 0 |
['C++']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Simple Greedy & Sliding Window
|
simple-greedy-sliding-window-by-eskandar-rfxx
|
Complexity
Time complexity:
O(n)
Space complexity:
O(1)Code
|
Eskandar1
|
NORMAL
|
2025-01-23T20:55:44.773103+00:00
|
2025-01-23T21:10:17.542648+00:00
| 6 | false |
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(n)
---
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(1)
---
# Code
```cpp []
class Solution {
public:
int numberOfSubstrings(string s, int k) {
int frq[26]={0};
int l=0, r=0, n=s.size(), ans=0;
while(r<n){
frq[s[r]-'a']++;
while(frq[s[r]-'a']==k){
ans +=n-r;
frq[s[l]-'a']--;
l++;
}
r++;
}
return ans;
}
};
```
```java []
class Solution {
public int numberOfSubstrings(String s, int k) {
int[] frq = new int[26];
int l=0, r=0, n=s.length(), ans=0;
while(r<n){
frq[s.charAt(r)-'a']++;
while(frq[s.charAt(r)-'a']==k){
ans +=n-r;
frq[s.charAt(l)-'a']--;
l++;
}
r++;
}
return ans;
}
}
```
| 0 | 0 |
['Hash Table', 'String', 'Greedy', 'Sliding Window', 'C++', 'Java']
| 0 |
count-substrings-with-k-frequency-characters-i
|
📌📌Easy to understand solution📌📌 | Beginner-friendly✅✅
|
easy-to-understand-solution-beginner-fri-2mke
|
Complexity
Time complexity: O(n)
Space complexity: O(26)
Code
|
Sankar_Madhavan
|
NORMAL
|
2025-01-20T16:53:08.986371+00:00
|
2025-01-20T16:53:08.986371+00:00
| 4 | false |
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(26)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int numberOfSubstrings(string s, int k) {
int n = s.length();
unordered_map<char, int> mp;
int l = 0, r = 0, ans = 0;
while (r < n) {
mp[s[r]]++;
while (mp[s[r]] >= k) {
mp[s[l]]--;
l++;
}
ans+=(r-l+1);
r++;
}
return n * (n+1) / 2 - ans;
}
};
```
| 0 | 0 |
['Sliding Window', 'C++']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Simple Brute Force Solution
|
simple-brute-force-solution-by-shaik_far-xklm
|
IntuitionIf any character frequency is equal to K then increment the count.Twist if as soon as we find character frequency equal to k then if any other characte
|
shaik_farhaan1
|
NORMAL
|
2025-01-19T11:48:56.613066+00:00
|
2025-01-19T11:48:56.613066+00:00
| 5 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
If any character frequency is equal to K then increment the count.Twist if as soon as we find character frequency equal to k then if any other characters are left then that cnt of the substring including that characters must also be added.
I used (total length - whereever my j is standing) to find the cnt.
Don't worry let's understand with an example.
# Approach
<!-- Describe your approach to solving the problem. -->
Why I have used the BruteForce bcz see the constraints.
O(n ^ n)
if n == 3000 O(3000 * 3000) = 9,000,000.IT CAN run within 1sec so.
Example : S = "a b a c b" K = 2
First iteration
cnt = 0;
i = 0;
j = 0;
hash[j]++
//Taking an array for visualization
[1,0,0]
[a,b,c]
i = 0;
j = 1;
[1,1,0]
[a,b,c]
j = 2
[2,1,0]
[a,b,c]
*
Now you can see 'j' got a character which has a frequency equal to k
now if we increment the count then count will be only 1
also when i = 0 and j = 3 the freq of c will increase but
but the freq of a is yet equal to two the j has not yet reached n so including 'c' as well there is a substring*
"aba" is a substring
"abac" is also a substring so
**once I get the char which has frequency equal to two then
totallength - index will get me the remaining frequencies as well.**
Make sure to do a dry runn.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(n^2)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(26) For the alphabets
# Code
```java []
class Solution {
public int numberOfSubstrings(String s, int k) {
int n = s.length();
int cnt = 0;
for(int i = 0 ; i < n ; i++){
int hash[] = new int[26];
for(int j = i ; j < n ; j++){
hash[s.charAt(j) -'a']++;
if(hash[s.charAt(j) - 'a'] == k){
cnt += n - j;
break;
}
}
}
return cnt;
}
}
```
| 0 | 0 |
['Sliding Window', 'Java']
| 0 |
count-substrings-with-k-frequency-characters-i
|
C++ Sliding Window, ( 100.00% | 87.57%)
|
c-sliding-window-10000-8757-by-lckharry-sc5l
|
IntuitionApproachComplexity
Time complexity:O(n)
Space complexity:O(1)
Code
|
LCKharry
|
NORMAL
|
2025-01-15T08:32:23.294641+00:00
|
2025-01-15T08:32:23.294641+00:00
| 5 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:$$O(n)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:$$O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int numberOfSubstrings(string s, int k) {
vector<int> freq(26, 0);
int result = 0;
int i = 0; int n = s.size();
int j = 0;
while(i<n && j<n){
while(j<n){
freq[s[j]-'a']++;
if(freq[s[j]-'a']>=k) break;
j++;
}
if(j==n) break;
int start = i;
while(start<=j && freq[s[j]-'a']>=k){
freq[s[start]-'a']--;
start++;
}
result+=(start-i)*(n-j);
i = start;
j++;
}
return result;
}
};
```
| 0 | 0 |
['Sliding Window', 'C++']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Slide Window
|
slide-window-by-linda2024-bpn2
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
linda2024
|
NORMAL
|
2025-01-13T21:18:38.347194+00:00
|
2025-01-13T21:18:38.347194+00:00
| 4 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```csharp []
public class Solution {
public int NumberOfSubstrings(string s, int k) {
// slide window:
int[] sample = new int[26];
int start = 0, len = s.Length, res = 0;
if(len < k)
return res;
for(int i = 0; i < len; i++)
{
if(++sample[s[i]-'a'] == k)
{
int pre = start, tail = len-i;
while(pre < len && s[pre] != s[i])
{
sample[s[pre++]-'a']--;
}
sample[s[i] -'a']--;
pre++;
int preCnt = pre-start;
res += preCnt*tail;
start = pre;
}
}
return res;
}
}
```
| 0 | 0 |
['C#']
| 0 |
count-substrings-with-k-frequency-characters-i
|
C++, sliding window, O(n) && O(1)
|
c-sliding-window-on-o1-by-viktor_komarov-2vmr
|
Complexity
Time complexity:
O(n)
Space complexity:
O(1)
Code
|
viktor_komarov
|
NORMAL
|
2025-01-12T09:25:00.423369+00:00
|
2025-01-12T09:25:00.423369+00:00
| 4 | false |
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(1)
# Code
```cpp []
class Solution {
public:
int numberOfSubstrings(string s, int k) {
array<int, 26> counts = {0};
int total = 0;
size_t left = 0;
for (size_t right = 0; right < s.size(); ++right) {
++counts[s[right]-'a'];
while(atLeastK(counts, k)) {
total += (s.size()-right);
--counts[s[left]-'a'];
++left;
}
}
return total;
}
int atLeastK(array<int, 26>& counts, int k) {
for (size_t i = 0; i < 26; ++i) {
if (counts[i] >= k) {
return true;
}
}
return false;
}
};
```
| 0 | 0 |
['C++']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Simple | Intuitive
|
simple-intuitive-by-richardleee-46br
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
RichardLeee
|
NORMAL
|
2025-01-11T11:25:43.509411+00:00
|
2025-01-11T11:25:43.509411+00:00
| 3 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int numberOfSubstrings(String s, int k) {
int n = s.length();
int l = 0;
int res = 0;
int[] cnt = new int[26];
for (int r = 0; r < n; r++) {
cnt[s.charAt(r) - 'a']++;
while (l <= r && cnt[s.charAt(r) - 'a'] >= k) {
res += (n - r);
cnt[s.charAt(l) - 'a']--;
l++;
}
}
return res;
}
}
```
| 0 | 0 |
['Java']
| 0 |
count-substrings-with-k-frequency-characters-i
|
o[n] solution in c++
|
on-solution-in-c-by-ansh0111-gnv6
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
ansh0111
|
NORMAL
|
2025-01-04T07:34:52.267905+00:00
|
2025-01-04T07:34:52.267905+00:00
| 4 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int numberOfSubstrings(string s, int k) {
int i=0;
int j=0;
int ans=0;
unordered_map<char,int> mp;
int n=s.length();
while(j<n)
{
char x=s[j];
mp[x]++;
while(mp[x]>=k)
{
ans+=n-j;
mp[s[i]]--;
i++;
}
j++;
}
return ans;
}
};
```
| 0 | 0 |
['C++']
| 0 |
count-substrings-with-k-frequency-characters-i
|
3325. Count Substrings With K-Frequency Characters I
|
3325-count-substrings-with-k-frequency-c-zusl
|
IntuitionOnce we are confirmed that a character repeats k times, we no longer need to keep traversing through the array.Code
|
priyam_saha17
|
NORMAL
|
2024-12-29T01:17:27.767671+00:00
|
2024-12-29T01:17:27.767671+00:00
| 7 | false |
# Intuition
Once we are confirmed that a character repeats k times, we no longer need to keep traversing through the array.
# Code
```python3 []
class Solution:
def numberOfSubstrings(self, s: str, k: int) -> int:
ans = 0
for i in range(0, len(s)):
freq = [0]*26
for j in range(i, len(s)):
freq[ord(s[j])-97]+=1
if max(freq)>=k:
ans+=1
break
ans += len(s) -j -1
return ans
```
| 0 | 0 |
['Python3']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Sliding window| Optimal Approach| Beginner Friendly
|
sliding-window-optimal-approach-beginner-5wxg
|
\n\n# Code\ncpp []\nclass Solution {\npublic:\n int numberOfSubstrings(string s, int k) {\n //abcde k=1\n int i,j=0;\n int n=s.size();\n
|
ashishabhishek2019
|
NORMAL
|
2024-12-08T16:15:48.232179+00:00
|
2024-12-08T16:15:48.232203+00:00
| 6 | false |
\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int numberOfSubstrings(string s, int k) {\n //abcde k=1\n int i,j=0;\n int n=s.size();\n \n map<char,int>mp;\n int cnt=0;\n // just as soon as a frequency gets to k you can count all substring by simple math because all substrings ending at any index from here on will have this freq ==k\n while(j<n){\n \n mp[s[j]]++;\n while(mp[s[j]]==k){\n cnt+=(n-j);\n \n \n \n mp[s[i++]]--; \n }\n j++;\n \n }\n return cnt;\n \n }\n};\n```
| 0 | 0 |
['Hash Table', 'String', 'Sliding Window', 'C++']
| 0 |
count-substrings-with-k-frequency-characters-i
|
python Solution || Sliding window
|
python-solution-sliding-window-by-nitish-6b53
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Nitishk25
|
NORMAL
|
2024-12-02T09:56:38.139415+00:00
|
2024-12-02T09:56:38.139439+00:00
| 5 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def numberOfSubstrings(self, s: str, k: int) -> int:\n cnt =0\n left =0\n mp={}\n for right in range(len(s)):\n mp[s[right]]=mp.get(s[right],0)+1\n while mp[s[right]]>=k:\n mp[s[left]]-=1\n cnt += len(s)-right\n left+=1\n return cnt\n \n```
| 0 | 0 |
['Python3']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Sliding window || C++ Solution
|
sliding-window-c-solution-by-nitishk25-e8b8
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Nitishk25
|
NORMAL
|
2024-12-02T08:15:47.481758+00:00
|
2024-12-02T08:15:47.481798+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int numberOfSubstrings(string s, int k) {\n int cnt = 0; int left = 0;\n unordered_map<char,int>mp;\n for (int right = 0; right < s.size(); right++) {\n mp[s[right]]++;\n while (mp[s[right]]>=k){\n mp[s[left]]--;\n cnt+=s.size()-right; //Number of substrings starting from left index.\n left++;\n }\n }\n return cnt;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Copied solution
|
copied-solution-by-sachinab-pphx
|
\n# Code\njava []\nclass Solution {\n public int numberOfSubstrings(String s, int k) {\n int n = s.length(), res = n*(n+1)/2;\n int[] count = n
|
sachinab
|
NORMAL
|
2024-11-29T13:43:49.773966+00:00
|
2024-11-29T13:43:49.774000+00:00
| 2 | false |
\n# Code\n```java []\nclass Solution {\n public int numberOfSubstrings(String s, int k) {\n int n = s.length(), res = n*(n+1)/2;\n int[] count = new int[26];\n\n for(int i=0, j=0; j<n; j++){\n char c = s.charAt(j);\n count[c-\'a\']++;\n\n while(count[c-\'a\']>=k){\n char lc = s.charAt(i);\n count[lc-\'a\']--;\n i++;\n }\n res-= (j-i+1);\n }\n\n return res;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Count Substrings with K-Frequency
|
count-substrings-with-k-frequency-by-suy-veba
|
Intuition\n Describe your first thoughts on how to solve this problem. \nFirstly I thought of using the sliding window approach as there is k.\n# Approach\n Des
|
ranges
|
NORMAL
|
2024-11-27T16:18:03.949652+00:00
|
2024-11-27T16:18:03.949681+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirstly I thought of using the sliding window approach as there is k.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSliding Window:\n\nWe use two pointers, i and j, to represent the sliding window. i is the start of the window, and j is the end of the window.\n\nAs we expand the window by moving j, we keep track of the frequency of characters within the window using a hash map (freq).\n\nFrequency Map:\n\nThe hash map (freq) stores the frequency of each character in the current window.\n\nExpand and Contract the Window:\n\nFor each character s[j], we increment its frequency in the hash map.\n\nIf the frequency of s[j] is greater than or equal to k, it means we have found a valid substring.\n\nWe then contract the window by moving i and decrementing the frequency of s[i] until the frequency of s[j] is less than k.\n\nCount Valid Substrings:\n\nFor each valid window, we add n - j to the count because all substrings starting from i to j and ending at any position from j to n-1 are valid.\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int numberOfSubstrings(string s, int k) {\n int n = s.size();\n int count = 0;\n unordered_map<char, int> freq;\n \n for(int i=0, j=0; j<n; j++ ){\n freq[s[j]]++;\n while(freq[s[j]] >= k){\n count += n-j;\n freq[s[i]]--;\n i++;\n }\n }\n return count;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Easy C++ solution -- O(n) -- Sliding window
|
easy-c-solution-on-sliding-window-by-shu-f4v9
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
shubhamkmt
|
NORMAL
|
2024-11-27T15:44:49.852820+00:00
|
2024-11-27T15:44:49.852863+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int numberOfSubstrings(string s, int k) {\n int left = 0, right = 0;\n vector<int> check(26, 0);\n\n int ans = 0;\n while(right < s.size()){\n check[s[right]-\'a\']++;\n while(check[s[right]-\'a\'] >= k && left <= right){\n ans += s.size() - right;\n check[s[left]-\'a\']--;\n left++;\n }\n right++;\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Easy solution
|
easy-solution-by-_jyoti_geek-7wwv
|
Code\njava []\nclass Solution {\n public int numberOfSubstrings(String s, int k) {\n int n = s.length();\n HashMap<Character, Integer> map = ne
|
_jyoti_geek
|
NORMAL
|
2024-11-22T15:40:54.526684+00:00
|
2024-11-22T15:40:54.526715+00:00
| 2 | false |
# Code\n```java []\nclass Solution {\n public int numberOfSubstrings(String s, int k) {\n int n = s.length();\n HashMap<Character, Integer> map = new HashMap<>();\n\n int i = 0, j = 0;\n int ct = 0;\n while (i < n) {\n char ch = s.charAt(i);\n map.put(ch, map.getOrDefault(ch, 0) + 1);\n\n while (map.containsKey(ch) && map.get(ch) >= k) {\n if (map.get(ch) >= k) {\n ct += n - i;\n }\n map.put(s.charAt(j), map.get(s.charAt(j)) - 1);\n if (map.get(s.charAt(j)) == 0) {\n map.remove(s.charAt(j));\n }\n j++;\n }\n i++;\n }\n return ct;\n }\n}\n```
| 0 | 0 |
['Hash Table', 'String', 'Sliding Window', 'Java']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Count Substrings With K-Frequency Characters I | Java | 100%
|
count-substrings-with-k-frequency-charac-vrtn
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Ajay-Ganapathy
|
NORMAL
|
2024-11-21T14:41:14.251015+00:00
|
2024-11-21T14:41:14.251041+00:00
| 3 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int numberOfSubstrings(String s, int k) {\n int l = 0 ;\n int ans = 0 ;\n int r = 0 ;\n int n = s.length();\n\n int freq[] = new int[26];\n\n while(l <= r && r < s.length()){\n freq[s.charAt(r) - \'a\']++;\n \n while(freq[s.charAt(r) - \'a\'] == k){\n ans+= (s.length()-r);\n \n freq[s.charAt(l) - \'a\']--;\n l++;\n \n }\n r++;\n \n } \n\n return ans;\n }\n}\n```
| 0 | 0 |
['Hash Table', 'Sliding Window', 'Java']
| 0 |
count-substrings-with-k-frequency-characters-i
|
C++ solution
|
c-solution-by-nguyenchiemminhvu-smis
|
\nstatic bool fast = []()\n{\n std::cin.tie(0)->sync_with_stdio(false);\n return true;\n}();\n\nclass Solution\n{\npublic:\n int numberOfSubstrings(con
|
nguyenchiemminhvu
|
NORMAL
|
2024-11-18T06:13:03.527528+00:00
|
2024-11-18T06:13:03.527553+00:00
| 0 | false |
```\nstatic bool fast = []()\n{\n std::cin.tie(0)->sync_with_stdio(false);\n return true;\n}();\n\nclass Solution\n{\npublic:\n int numberOfSubstrings(const string& s, int k)\n {\n int res = 0;\n\n int left = 0;\n int right = 0;\n std::unordered_map<char, int> freq;\n int count_at_least = 0;\n while (right < s.length())\n {\n freq[s[right]]++;\n\n if (freq[s[right]] >= k)\n {\n count_at_least++;\n }\n\n while (left <= right && count_at_least > 0)\n {\n res += s.length() - right;\n\n int f_before = freq[s[left]];\n freq[s[left]]--;\n if (f_before >= k && freq[s[left]] < k)\n {\n count_at_least--;\n }\n left++;\n }\n\n right++;\n }\n\n return res;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Simple Sliding Window C++
|
simple-sliding-window-c-by-ken_14-2pk0
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
ken_14
|
NORMAL
|
2024-11-17T14:28:58.136777+00:00
|
2024-11-17T14:28:58.136802+00:00
| 4 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int numberOfSubstrings(string s, int k) \n {\n int ct = 0;\n \n unordered_map<char,int>mp;\n \n int i = 0, j = 0;\n \n while(j<(int)s.size())\n {\n mp[s[j]]++;\n \n while(1)\n {\n bool ck = false;\n for(auto ele:mp)\n {\n if(ele.second>=k)\n {\n ct += ((int)s.size()-j);\n mp[s[i]]--;\n // cout<<i<<" "<<j<<"\\n";\n i++;\n ck = true;\n break;\n }\n }\n if(!ck){\n break;\n }\n \n }\n \n j++;\n \n }\n \n return ct;\n }\n};\n```
| 0 | 0 |
['Sliding Window', 'C++']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Slide Window
|
slide-window-by-hityxh2018-rv1m
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
hityxh2018
|
NORMAL
|
2024-11-13T13:18:10.100613+00:00
|
2024-11-13T13:18:10.100649+00:00
| 0 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int numberOfSubstrings(String s, int k) {\n int n = s.length();\n if (k == 1) {\n return n * (n + 1) >> 1;\n }\n\n int ans = 0;\n Map<Character, Integer> map = new HashMap<>();\n char c = \'\\0\';\n int val = 0;\n int prefix, suffix;\n for (int i = 0, j = 0; i < n - 1; ++i) {\n boolean isMatch = false;\n while (j < n) {\n c = s.charAt(j);\n val = map.getOrDefault(c, 0) + 1;\n map.put(c, val);\n j += 1;\n\n if (val == k) {\n isMatch = true;\n break;\n }\n }\n\n if (!isMatch) {\n break;\n }\n\n suffix = n - j;\n \n prefix = 0;\n while (i < j) {\n c = s.charAt(i);\n val = map.get(c);\n val -= 1;\n if (val == 0) {\n map.remove(c);\n } else {\n map.put(c, val);\n\n if (val == k - 1) {\n break;\n }\n }\n\n prefix += 1;\n i += 1;\n }\n\n ans += (prefix + 1) * (suffix + 1);\n }\n\n return ans;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Sliding Window 100 beats
|
sliding-window-100-beats-by-pk1698629-p2hd
|
Intuition\nSo we will bw doing this problem bu using sliding window approach\n\n\n# Approach\n\nwe have to run a for loop by expanding the right \nnow\nwe just
|
pk1698629
|
NORMAL
|
2024-11-12T12:54:51.779274+00:00
|
2024-11-12T12:54:51.779298+00:00
| 1 | false |
# Intuition\nSo we will bw doing this problem bu using sliding window approach\n\n\n# Approach\n\nwe have to run a for loop by expanding the right \nnow\nwe just have to see the point where we are having an alphabet with frequency of k and then we have to count the possibilities of substrings by subtracting the index(at where we found the frequency as k) from total size;\n\nAnd then we have to just remove the frequency of (the left most character by one and have to move the left by one (shrinking the window from left side))\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int numberOfSubstrings(string s, int k) {\n unordered_map <char, int> m;\n int count=0;\n int left=0;\n for (int right =0; right<s.size(); right++){\n m[s[right]]++;\n while(m[s[right]]>=k){\n count += (s.size()-right);\n m[s[left]]--;\n left++;\n }\n\n }\n return count;\n }\n\n};\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n// int maxi=0,count=0;\n// for (int i=0; i<s.size();i++){\n// // int count=0;\n// unordered_map<char,int> m;\n// for (int j=i; j<s.size();j++){\n// m[s[j]]++;\n// }\n// for (auto i: m){\n// if (i.second>=k){\n// count+=1;\n// break;\n// }\n// }\n// //maxi = max(maxi,count);\n// }\n// return count;\n// }\n// };\n```
| 0 | 0 |
['Two Pointers', 'Sliding Window', 'C++']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Two pointers easy c++ code
|
two-pointers-easy-c-code-by-ziang142019-mk2b
|
\n# Code\ncpp []\n#define FOR(i,a,b) for(int i = a; i < b.size(); i++)\n#define F0(i,b) for(int i = 0; i< b.size(); i++)\n#define BE(a) a.begin(),
|
ziang142019
|
NORMAL
|
2024-11-11T19:11:25.538211+00:00
|
2024-11-11T19:11:25.538253+00:00
| 1 | false |
\n# Code\n```cpp []\n#define FOR(i,a,b) for(int i = a; i < b.size(); i++)\n#define F0(i,b) for(int i = 0; i< b.size(); i++)\n#define BE(a) a.begin(), a.end()\n#define __S(a) a.size()\n\ntypedef long long ll;\ntypedef vector<int> vi;\ntypedef vector<vector<int>> vvi;\ntypedef vector <long long> vl;\ntypedef vector<vector<long long>> vvl;\n\n\n\nclass Solution {\npublic:\n int numberOfSubstrings(string s, int k) {\n // when one number reaches k, every thing outside is doable => only check inside\n // two pointers?\n\n int ans{};\n map <char,int> mp;\n\n for (int l = 0, r = 0; r < __S(s); ++r){\n mp[s[r]]++;\n if (mp[s[r]] < k) continue;\n\n // reducing \n for (;l <= r && mp[s[r]] >= k; ++l){\n ans+= __S(s) - r;\n mp[s[l]]--;\n }\n //cout << ans << " ";\n }\n return ans;\n \n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Sliding window in js, Beats 73.31% in runtime
|
sliding-window-in-js-beats-7331-in-runti-qdy1
|
Intuition\n Describe your first thoughts on how to solve this problem. \nsliding window\n\n# Approach\n Describe your approach to solving the problem. \nif we a
|
masha-nv
|
NORMAL
|
2024-11-08T13:11:48.217761+00:00
|
2024-11-08T13:13:29.952841+00:00
| 4 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nsliding window\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nif we are on our left and right pointers such that number of any char is equal to k, we need to add to our final count that substring and all left and right substrings, record that we have counted all substrings for the given left and right positions, so we dont double count same substrings. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nit is a constant time\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nconstant for keep a set, and a map\n\n\n\n\n# Code\n```javascript []\n/**\n * @param {string} s\n * @param {number} k\n * @return {number}\n dababck; k=2\n map : {d: 0, a: 1, b: 2}\n */\nvar numberOfSubstrings = function(s, k) {\n let cnt = 0;\n const map = new Map();\n let l = 0, r = 0;\n const seen = new Set()\n \n\n while (r < s.length) {\n map.set(s[r], (map.get(s[r])??0)+1);\n\n while (map.get(s[r]) === k) {\n if (!seen.has(`${l}->${r}`)) {\n cnt += 1\n cnt += s.length - r - 1;\n }\n seen.add(`${l}->${r}`)\n map.set(s[l], map.get(s[l])-1)\n l++;\n }\n r++;\n }\n\n return cnt;\n};\n```
| 0 | 0 |
['JavaScript']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Aditya Verma | Sliding Window Pattern | C++
|
aditya-verma-sliding-window-pattern-c-by-6cw3
|
\n\n\n\n\n## Aditya Verma - Variable Sized Sliding Window Approach\n\n## Complexity\n- Time complexity: O(N)\n Add your time complexity here, e.g. O(n) \n\n\n-
|
konarksharmaa
|
NORMAL
|
2024-11-05T12:35:36.737926+00:00
|
2024-11-05T12:35:36.737963+00:00
| 1 | false |
\n\n\n\n\n## Aditya Verma - Variable Sized Sliding Window Approach\n\n## Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n## Code\n```cpp []\nclass Solution {\npublic:\n int numberOfSubstrings(string s, int k) {\n unordered_map<char,int> mp;\n int i=0,j=0;\n int ans=0;\n while(j < s.size()){\n mp[s[j]]++;\n if(mp[s[j]] < k) j++;\n else if(mp[s[j]] >= k){\n while(mp[s[j]] >= k){\n // Remove calculations for i\n mp[s[i]]--;\n if(mp[s[i]] == 0) mp.erase(s[i]);\n i++;\n // Calculate ans\n ans += s.size() - j;\n }\n j++;\n }\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['Sliding Window', 'C++']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Super Simple || C++
|
super-simple-c-by-lotus18-syim
|
Code\ncpp []\nclass Solution \n{\npublic:\n int numberOfSubstrings(string s, int k) \n {\n int n=s.size(), cnt=0;\n for(int x=0; x<n; x++)\n
|
lotus18
|
NORMAL
|
2024-11-05T07:27:22.548086+00:00
|
2024-11-05T07:27:22.548118+00:00
| 1 | false |
# Code\n```cpp []\nclass Solution \n{\npublic:\n int numberOfSubstrings(string s, int k) \n {\n int n=s.size(), cnt=0;\n for(int x=0; x<n; x++)\n {\n map<char,int> m;\n int flag=0;\n for(int y=x; y<n; y++)\n {\n m[s[y]]++;\n if(m[s[y]]==k) flag=1;\n if(flag) cnt++;\n }\n }\n return cnt;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Intuitive Sliding Window Solution in C++
|
intuitive-sliding-window-solution-in-c-b-j3wo
|
---\n\n# Solution Explanation\n\n## Problem\nGiven a string s and an integer k, we need to count the number of substrings where any character appears at least k
|
_jayesh
|
NORMAL
|
2024-11-02T17:52:24.044328+00:00
|
2024-11-02T17:52:24.044365+00:00
| 4 | false |
---\n\n# Solution Explanation\n\n## Problem\nGiven a string `s` and an integer `k`, we need to count the number of substrings where any character appears at least `k` times. This problem is solved by iterating over possible substrings and using a sliding window approach to efficiently count the substrings that satisfy this condition.\n\n## Approach\nWe use a **sliding window** technique to maintain a window `[start, end]` where:\n- `start` and `end` are pointers defining the current substring.\n- A `count` array of size 26 keeps track of character frequencies within the window.\n\n### Steps:\n1. **Expand the Window**:\n - For each character at `end`, increment its count in `count`.\n - Check if any character in the window meets or exceeds the required frequency `k`.\n\n2. **Shrink the Window**:\n - If any character\u2019s frequency is `\u2265 k`, start shrinking the window from the left by incrementing `start` and decrementing the count of characters as we slide out of the window.\n - Each time the window meets the criteria, every substring starting from `start` to the end of the string will also meet the criteria. Therefore, add `(n - end)` to the result for all these substrings.\n\n3. **Repeat** until `end` reaches the end of the string.\n\n### Complexity Analysis\n- **Time Complexity**: \\( O(n) \\) \u2014 We traverse the string once with `end`, and within the loop, `start` can also move at most `n` steps.\n- **Space Complexity**: \\( O(1) \\) \u2014 We use a fixed-size `count` array of length 26.\n\n## Code\n\n```cpp\nclass Solution {\npublic:\n int numberOfSubstrings(string s, int k) {\n vector<int> count(26, 0);\n int n = s.length();\n int start = 0;\n int result = 0;\n\n for (int end = 0; end < n; end++) {\n count[s[end] - \'a\']++;\n int maxFrequency = *max_element(begin(count), end(count));\n\n // While there is a character in the current window with a frequency >= k\n while (maxFrequency >= k && start <= end) {\n count[s[start] - \'a\']--; // Slide the window from the left\n start++;\n maxFrequency = *max_element(begin(count), end(count)); // Recompute max frequency\n \n // Every substring from start to end meets the condition\n result += (n - end);\n }\n }\n return result;\n }\n};\n```\n\n## Explanation of Key Lines\n\n- `count[s[end] - \'a\']++`: Tracks the frequency of the character at `end` in the current window.\n- `int maxFrequency = *max_element(begin(count), end(count));`: Checks the maximum character frequency in the current window.\n- `while (maxFrequency >= k && start <= end)`: Shrinks the window from the left if any character frequency reaches `k`.\n- `result += (n - end);`: Adds all valid substrings from `start` to the end of the string to the result.\n\nThis approach efficiently counts all substrings meeting the criteria without needing to explore each substring individually.
| 0 | 0 |
['Two Pointers', 'String', 'Sliding Window', 'C++']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Sliding Window | Beats 100% | Frequency Array
|
sliding-window-beats-100-frequency-array-muky
|
Intuition\nWe can see from the problem that if we find a string that satisfies the condition, we can keep adding each character left in the whole string and it
|
nuggetcrab
|
NORMAL
|
2024-10-30T17:05:59.094302+00:00
|
2024-10-30T17:05:59.094335+00:00
| 3 | false |
# Intuition\nWe can see from the problem that if we find a string that satisfies the condition, we can keep adding each character left in the whole string and it would still satisfy this condition. We know that we should then find every first occurence that satisfies the condition, and then add the amount of characters after its end state.\n\n# Approach\nWe initialize a freq array to keep track of the frequency of characters in the string. When we uncounter a substring that satisfies the condition, we add the amount of characters after the right pointer. Because we then know we have account for every possible string that starts at the left pointer, we increment it by one.\n\nWe make sure to track the prequencies upon the movement of the pointers.\n\nNote - I check if the right is within the range whenever I check, because it will always attempt to reach out of the array.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```java []\nclass Solution {\n public int numberOfSubstrings(String s, int k) {\n int[] freq = new int[26];\n\n int left = 0;\n int right = 0;\n\n char[] chars = s.toCharArray();\n\n freq[chars[0] - \'a\'] = 1;\n\n int sum = 0;\n\n while(right != s.length()) {\n if(freq[chars[right] - \'a\'] < k) {\n right++;\n if(right < s.length()) {\n freq[chars[right] - \'a\']++;\n }\n } else {\n freq[chars[left] - \'a\']--;\n sum += s.length() - right;\n left++;\n }\n }\n\n return sum;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
count-substrings-with-k-frequency-characters-i
|
My Solution Java Simple
|
my-solution-java-simple-by-user5475a-hmld
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
user5475a
|
NORMAL
|
2024-10-29T17:26:25.837905+00:00
|
2024-10-29T17:26:25.837935+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int numberOfSubstrings(String s, int k) {\n\n int incr =0;\n for(int i=0;i<s.length();i++)\n {\n int count[] = new int[26];\n for(int j=i;j<s.length();j++)\n {\n \n count[s.charAt(j)-\'a\']++;\n if(count[s.charAt(j)-\'a\']==k){\n incr=incr+(s.length()-j);\n break;\n }\n }\n }\n return incr;\n }\n boolean check(String str,int k)\n { \n \n for(int i=0;i<str.length();i++)\n {\n \n return true;\n }\n return false;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
count-substrings-with-k-frequency-characters-i
|
sliding window technique
|
sliding-window-technique-by-owenwu4-c8f3
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
owenwu4
|
NORMAL
|
2024-10-28T00:18:23.840238+00:00
|
2024-10-28T00:18:23.840265+00:00
| 9 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def numberOfSubstrings(self, s: str, k: int) -> int:\n l = 0\n res = 0\n d = defaultdict(int)\n maxvalues = 0\n for l in range(len(s)):\n d.clear()\n maxvalues = 0\n for r in range(l, len(s)):\n d[s[r]] += 1\n maxvalues = max(maxvalues, d[s[r]])\n if maxvalues >= k:\n res += 1\n return res\n \n```
| 0 | 0 |
['Python3']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Simple C++ Approach and Solution | Weekly Contest 420 | Question 2
|
simple-c-approach-and-solution-weekly-co-xuaz
|
Intuition\n Describe your first thoughts on how to solve this problem. \n1. Fix the left index of the substring.\n2. For the fixed left index, find the first ri
|
ak0012916
|
NORMAL
|
2024-10-27T04:26:12.317859+00:00
|
2024-10-27T04:26:12.317880+00:00
| 5 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1. Fix the left index of the substring.\n2. For the fixed left index, find the first right index for which substring `s[left..right]` satisfies the condition.\n3. Every substring that starts at left and ends after right satisfies the condition.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. if `k == 1`, then all substrings are valid because every character appears at least once.\n2. if `k >=2`, then we try to check all the substring using sliding window concept.\n3. iterate the loop from left to end of string.\n4. we increment the frequency of character during iterating the string. `mp[s[right]]++;`.\n5. we check the condition `if(mp[s[right]] == k)` whether it satisfy or not.\n6. if it satisfy then every substring that starts at left and ends after right satisfies the condition.\n7. at last, return `count`.\n# Complexity\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int numberOfSubstrings(string s, int k) {\n \n int count = 0;\n int n = s.length();\n if(k == 1) return n*(n+1)/2;\n for(int left = 0; left < n; left++){\n unordered_map<char, int> mp;\n for(int right = left; right < n; right++){\n mp[s[right]]++;\n if(mp[s[right]] == k){\n count += (n - right);\n break;\n }\n }\n }\n return count;\n }\n};\n```
| 0 | 0 |
['Hash Table', 'String', 'Sliding Window', 'C++']
| 0 |
count-substrings-with-k-frequency-characters-i
|
C++ solution using sliding window way
|
c-solution-using-sliding-window-way-by-l-kc7y
|
\n\n# Code\ncpp []\nclass Solution {\npublic:\n int numberOfSubstrings(string s, int k) {\n\n int res = 0;\n int count_larger_k = 0;\n u
|
lcq_dev
|
NORMAL
|
2024-10-26T06:55:21.228925+00:00
|
2024-10-26T06:55:21.228962+00:00
| 1 | false |
\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int numberOfSubstrings(string s, int k) {\n\n int res = 0;\n int count_larger_k = 0;\n unordered_map<char, int> char2Int;\n int i = 0;\n \n\n for(int j = 0; j < s.size();j ++) {\n char cur_char = s[j];\n char2Int[cur_char] += 1;\n if(char2Int[cur_char] == k) {\n count_larger_k += 1;\n }\n\n while(count_larger_k != 0) {\n res += s.size() - j;\n\n char2Int[s[i]] -= 1;\n if(char2Int[s[i]] == k-1) {\n count_larger_k -= 1;\n }\n i++;\n \n }\n }\n\n return res;\n \n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Simple and Easy JAVA Solution , Beats 100% using Sliding Window approach
|
simple-and-easy-java-solution-beats-100-al097
|
Intuition\n\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Tim
|
Triyaambak
|
NORMAL
|
2024-10-25T19:53:39.172121+00:00
|
2024-10-25T19:53:39.172155+00:00
| 2 | false |
# Intuition\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int numberOfSubstrings(String s, int k) {\n int map[] = new int[26];\n int left = 0;\n int right = 0;\n int n = s.length();\n int count = 0;\n int ans = 0;\n \n while(right < n){\n int rtCh = s.charAt(right) - \'a\';\n if(++map[rtCh] >= k)\n count++;\n \n while(left <= right && count == 1){\n ans += n - right;\n int lftCh = s.charAt(left) - \'a\';\n if(map[lftCh]-- >= k)\n count--;\n left++;\n }\n\n right++;\n }\n\n return ans;\n }\n}\n```
| 0 | 0 |
['Sliding Window', 'Java']
| 0 |
count-substrings-with-k-frequency-characters-i
|
scala sliding window
|
scala-sliding-window-by-vititov-lvkg
|
scala []\nobject Solution {\n def numberOfSubstrings(s: String, k: Int): Int = {\n def f(l0: Int, l1: Int, r: Int, aMap: Map[Char,Int], acc: Int): Int =\n
|
vititov
|
NORMAL
|
2024-10-25T19:41:00.363907+00:00
|
2024-10-25T19:41:00.363931+00:00
| 1 | false |
```scala []\nobject Solution {\n def numberOfSubstrings(s: String, k: Int): Int = {\n def f(l0: Int, l1: Int, r: Int, aMap: Map[Char,Int], acc: Int): Int =\n if(aMap.values.maxOption.getOrElse(0)>=k) g(l0,l1,r,aMap,acc)\n else if(r >= s.length) acc\n else f(l0,l1,r+1,aMap+(s(r) -> (aMap(s(r))+1)),acc)\n def g(l0: Int, l1: Int, r: Int, aMap: Map[Char,Int], acc: Int): Int =\n if(aMap.values.maxOption.getOrElse(0)<k) f(l1,l1,r,aMap,acc + (s.length-r+1)*(l1-l0))\n else g(l0,l1+1,r,aMap+(s(l1) -> (aMap(s(l1))-1)),acc)\n f(0,0,0,Map().withDefaultValue(0),0)\n }\n}\n```
| 0 | 0 |
['Hash Table', 'String', 'Sliding Window', 'Scala']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Easy solution using hashtable || GOLANG || CPP
|
easy-solution-using-hashtable-golang-cpp-3oun
|
Intuition\nThe problem requires counting the number of substrings where each character appears at least k times. We iterate over each starting index of the subs
|
sonuola
|
NORMAL
|
2024-10-25T16:18:51.612084+00:00
|
2024-10-25T16:18:51.612110+00:00
| 7 | false |
# Intuition\nThe problem requires counting the number of substrings where each character appears at least k times. We iterate over each starting index of the substring, expanding from that point and using an array to keep track of character counts. Once a substring meets the condition, all following substrings starting from this position will also meet it, allowing us to increment the count.\n\n# Approach\n1. Loop through each starting index: For each starting point i, use another loop to expand the substring from i to n.\n2. Track Character Counts: Use an array arr to store the frequency of each character as the substring grows.\n3. Check Condition: For each substring, check if any character reaches k occurrences:\n* If so, mark found to 1, indicating that all further substrings starting at i will meet the requirement.\n* Increment ans to count valid substrings.\n\n# Complexity\n- Time complexity:\nO(n^2)\n\n- Space complexity:\nO(1)\n\n# Code\n```golang []\nfunc numberOfSubstrings(s string, k int) int {\n\n n := len(s);\n ans := 0;\n for i := 0 ; i < n ; i++ {\n var arr[26] int;\n found := 0;\n for j := i ; j < n ; j++ {\n if found == 1 {\n ans++;\n } else {\n if arr[s[j] - \'a\'] == k-1 {\n ans++;\n found = 1;\n }\n arr[s[j] - \'a\']++;\n }\n }\n }\n return ans;\n}\n```\n```cpp []\nclass Solution {\npublic:\n int numberOfSubstrings(string s, int k) {\n int n = s.size();\n int ans = 0;\n for(int i = 0 ; i < n ; i++) {\n vector<int>v(26,0);\n int found = 0;\n for(int j = i ; j < n ; j++) {\n if(found) {\n ans++;\n } else {\n if(v[s[j] - \'a\'] == k-1) {\n found = 1; \n ans++;\n }\n v[s[j] - \'a\']++;\n }\n }\n }\n return ans;\n }\n};\n```\n\n
| 0 | 0 |
['Hash Table', 'C++', 'Go']
| 0 |
count-substrings-with-k-frequency-characters-i
|
MAP || AVS
|
map-avs-by-vishal1431-ex0e
|
\n# Code\ncpp []\nclass Solution {\npublic:\n int numberOfSubstrings(string s, int k) {\n int ans = 0;\n for (int i = 0; i < s.size(); i++) {\n
|
Vishal1431
|
NORMAL
|
2024-10-24T19:02:12.631917+00:00
|
2024-10-24T19:02:12.631962+00:00
| 0 | false |
\n# Code\n```cpp []\nclass Solution {\npublic:\n int numberOfSubstrings(string s, int k) {\n int ans = 0;\n for (int i = 0; i < s.size(); i++) {\n map<char, int> m;\n int check = 0;\n for (int j = i; j < s.size(); j++) {\n m[s[j]]++;\n if (m[s[j]] == k)check++;\n if (check)ans++;\n }\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['Hash Table', 'C++']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Simple Sliding Window solution
|
simple-sliding-window-solution-by-vikash-sgmn
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
vikash_kumar_dsa2
|
NORMAL
|
2024-10-24T18:00:19.932594+00:00
|
2024-10-24T18:00:19.932620+00:00
| 13 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int numberOfSubstrings(string s, int k) {\n int n = s.length();\n int res = n*(n+1)/2;\n unordered_map<char, int> count;\n for(int i = 0,j = 0;j<n;j++){\n count[s[j]]++;\n while(count[s[j]] >= k){\n --count[s[i++]];\n }\n res -= (j-i+1);\n }\n return res;\n }\n};\n```
| 0 | 0 |
['Hash Table', 'Sliding Window', 'C++']
| 0 |
count-substrings-with-k-frequency-characters-i
|
[scala] - sliding window, no index, foldLeft, recursion
|
scala-sliding-window-no-index-foldleft-r-p71r
|
I am deeply concerned by the amount of attention given to Scala. Please upvote and submit your solutions.\n\n# Code\nscala\nobject Solution {\n import scala.co
|
nikiforo
|
NORMAL
|
2024-10-24T16:14:17.070122+00:00
|
2024-10-24T16:15:47.235261+00:00
| 2 | false |
I am deeply concerned by the amount of attention given to Scala. Please upvote and submit your solutions.\n\n# Code\n```scala\nobject Solution {\n import scala.collection.immutable.Queue\n\n def numberOfSubstrings(s: String, k: Int): Int =\n s.foldLeft(Queue.empty[Char], Map.empty[Char, Int], 0) { case ((queue, map, acc), c) =>\n val (nQueue, nMap) = (queue :+ c, map.updated(c, map.getOrElse(c, 0) + 1))\n (nQueue, nMap, go(nQueue, nMap, k) + acc)\n }._3\n\n private def go(q: Queue[Char], map: Map[Char, Int], k: Int): Int =\n if (map.exists(_._2 >= k)) 1 + go(q.tail, map.updated(q.head, map(q.head) - 1), k) else 0\n}\n```
| 0 | 0 |
['Scala']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Variable Sized Sliding Window Solution
|
variable-sized-sliding-window-solution-b-ljjh
|
Intuition: Find total of all substring and subtract it with total of unfit Substrings\n Describe your first thoughts on how to solve this problem. \n\n# Approac
|
ALOK_SRIVASTAVA
|
NORMAL
|
2024-10-24T15:31:12.697760+00:00
|
2024-10-24T15:31:12.697793+00:00
| 5 | false |
# Intuition: Find total of all substring and subtract it with total of unfit Substrings\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach: Approached the Problem using Sliding Window\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: 0(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: 0(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n\n int find(String str, int k){\n \n int freqArr[] = new int[26];\n int unfitSubstring = 0;\n int start = 0;\n\n for(int end = 0 ; end < str.length() ; end++){\n\n int asciiValue = str.charAt(end) - 97;\n freqArr[asciiValue]++;\n\n while(start <= end && freqArr[asciiValue] >= k) {\n \n int val = str.charAt(start) - 97;\n freqArr[val]--;\n start++;\n \n }\n\n unfitSubstring += (end-start) + 1;\n\n }\n\n return unfitSubstring;\n\n }\n\n public int numberOfSubstrings(String s, int k) {\n \n int length = s.length();\n int totalSubstrings = length * (length + 1) / 2;\n\n return totalSubstrings - find(s, k);\n \n }\n}\n```
| 0 | 0 |
['Hash Table', 'Sliding Window', 'Java']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Sliding Window
|
sliding-window-by-a90100-luju
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
a90100
|
NORMAL
|
2024-10-24T13:20:21.147022+00:00
|
2024-10-24T13:25:55.871235+00:00
| 4 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(26 * n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(c)\uFF0Cc is the types of English letters in a string s.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```javascript []\n/**\n * @param {string} s\n * @param {number} k\n * @return {number}\n */\nvar numberOfSubstrings = function(s, k) {\n let times = 0;\n const charMap = new Map();\n let l = 0;\n\n for (let i = 0; i < s.length; i++) {\n charMap.set(s[i], (charMap.get(s[i]) || 0) + 1);\n while (Math.max(...Array.from(charMap.values())) >= k) {\n times += s.length - i;\n charMap.set(s[l], charMap.get(s[l]) - 1);\n l++;\n }\n }\n\n return times;\n};\n```
| 0 | 0 |
['JavaScript']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Intuition from brute force to O(N) for all kinds of arrays
|
intuition-from-brute-force-to-on-for-all-6coj
|
Brute Force\nTime = O(N^2)\nSpace = O(26) for chars, O(N) for ints.\n\n##### Two Pointer 1\n\n1. Iterate over string while storing counts.\n2. While count of ch
|
antrixm
|
NORMAL
|
2024-10-24T13:06:03.798300+00:00
|
2024-10-24T13:09:13.961445+00:00
| 17 | false |
##### Brute Force\nTime = O(N^2)\nSpace = O(26) for chars, O(N) for ints.\n\n##### Two Pointer 1\n\n1. Iterate over string while storing counts.\n2. While count of char == k, iterate while removing elements from left.\n3. For each such iteration, ans += n - r, since if for an index r the count is >=k, the condition will be true for all i > r.\n4. Return ans. \n\nTime: O(N)\nSpace = O(26) for chars, O(N) for ints.\n\n\n##### Two Pointer 2 (most optimal)\n\n1. Count total subarrays possible = n*(n+1)//2\n2. Instead of counting for freq >=k, count subarrays with freq of all characters < k.\n3. Remove these subarrays fro total possible subarrays.\n4. This will give subarrays where frequencey of atleast a single character is >= k.\n\nTime: O(N)\nSpace = O(26) for chars, O(N) for ints.\n
| 0 | 0 |
['Array', 'Two Pointers', 'Python3']
| 0 |
count-substrings-with-k-frequency-characters-i
|
java solution using sliding window and hashmap
|
java-solution-using-sliding-window-and-h-7dzj
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
TanmayYadav
|
NORMAL
|
2024-10-24T12:32:05.951432+00:00
|
2024-10-24T12:32:05.951464+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int numberOfSubstrings(String s, int k) {\n int i=0;int ans=0;int n =s.length();\n HashMap<Character,Integer> map=new HashMap<>();\n for(int j=0;j<s.length();j++) {\n char ch =s.charAt(j);\n map.put(ch,map.getOrDefault(ch,0)+1);\n if(map.get(ch)>=k) {\n while(i<=j && map.get(ch)>=k ) {\n map.put(s.charAt(i),map.get(s.charAt(i))-1);\n i++;\n ans+= n-j;\n }\n }\n\n }\n\n return ans;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Java beats 100%
|
java-beats-100-by-lee216-2jbj
|
\n\n# Complexity\n- Time complexity:\nO(n)\n\n\n# Code\njava []\nclass Solution {\n public int numberOfSubstrings(String s, int k) {\n int l = 0, r =
|
lee216
|
NORMAL
|
2024-10-24T02:13:36.626675+00:00
|
2024-10-24T02:13:36.626735+00:00
| 6 | false |
\n\n# Complexity\n- Time complexity:\nO(n)\n\n\n# Code\n```java []\nclass Solution {\n public int numberOfSubstrings(String s, int k) {\n int l = 0, r = 0, len = s.length(), res = 0;\n int freq[] = new int[26];\n while(r != len && l != len) {\n freq[s.charAt(r) - \'a\']++;\n while(freq[s.charAt(r) - \'a\'] == k && l != len) {\n res += len - r;\n freq[s.charAt(l++) - \'a\']--;\n }\n r++;\n }\n return res;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
count-substrings-with-k-frequency-characters-i
|
[Accepted] Swift
|
accepted-swift-by-vasilisiniak-pjnu
|
\nclass Solution {\n func numberOfSubstrings(_ s: String, _ k: Int) -> Int {\n \n let s = Array(s)\n var ch = [s[0]: 1]\n var r =
|
vasilisiniak
|
NORMAL
|
2024-10-23T20:28:57.287710+00:00
|
2024-10-23T20:28:57.287738+00:00
| 1 | false |
```\nclass Solution {\n func numberOfSubstrings(_ s: String, _ k: Int) -> Int {\n \n let s = Array(s)\n var ch = [s[0]: 1]\n var r = 0\n var res = 0\n\n for l in 0...s.count - k {\n if l > 0 {\n ch[s[l - 1]] = (ch[s[l - 1]]! > 0) ? (ch[s[l - 1]]! - 1) : nil\n }\n if ch.values.max()! < k {\n while r < s.count {\n r += 1\n guard r < s.count else { break }\n ch[s[r], default: 0] += 1\n guard ch[s[r]]! != k else { break }\n }\n }\n guard r < s.count else { break }\n res += s.count - r\n }\n\n return res\n }\n}\n```
| 0 | 0 |
['Swift']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Java contest SOULTION beats 73%
|
java-contest-soultion-beats-73-by-qlob-h37t
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Qlob
|
NORMAL
|
2024-10-23T17:34:11.958347+00:00
|
2024-10-23T17:34:11.958384+00:00
| 4 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int numberOfSubstrings(String s, int k) {\n int n = s.length();\n int count = 0; \n int left = 0, right = 0; \n HashMap<Character, Integer> freqMap = new HashMap<>(); \n while (right < n) { \n char rightChar = s.charAt(right);\n freqMap.put(rightChar, freqMap.getOrDefault(rightChar, 0) + 1);\n \n while (validSubstring(freqMap, k)) {\n \n count += (n - right); \n \n \n char leftChar = s.charAt(left);\n freqMap.put(leftChar, freqMap.get(leftChar) - 1);\n if (freqMap.get(leftChar) == 0) {\n freqMap.remove(leftChar);\n }\n left++;\n }\n \n \n right++;\n }\n \n return count;\n }\n private boolean validSubstring(HashMap<Character, Integer> freqMap, int k) {\n for (int freq : freqMap.values()) {\n if (freq >= k) {\n return true;\n }\n }\n return false;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
count-substrings-with-k-frequency-characters-i
|
That's Easy
|
thats-easy-by-y_v_singh-9d38
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nJust follow the provide
|
Y_V_Singh
|
NORMAL
|
2024-10-23T17:26:59.541600+00:00
|
2024-10-23T17:26:59.541633+00:00
| 4 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nJust follow the provided hint\nThen hit the brute force\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nJAT\nclass Solution {\n public int numberOfSubstrings(String s, int k) {\n int n=s.length();\n if(k==1)\n return (n*(n+1))/2;\n int ct=0;\n for(int i=0;i<n;i++)\n {\n HashMap<Character,Integer> mp=new HashMap<>();\n //lt.add(s.charAt(i));\n for(int j=i;j<n;j++)\n {\n char ch=s.charAt(j);\n if(mp.containsKey(ch))\n mp.put(ch,mp.get(ch)+1);\n else\n mp.put(ch,1);\n if(mp.get(ch)==k)\n {\n ct+=n-j;\n break;\n }\n }\n }\n return ct;\n }\n}\n```
| 0 | 0 |
['Hash Table', 'String', 'Sliding Window', 'Java']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Intuitive Optimised Brute Force
|
intuitive-optimised-brute-force-by-vatad-yeyc
|
Intuition\n- Optimised Brute Force.\n\n# Approach\n- Started generating substring from index 0.\n- Stopped generating substring oncce any char freq = k\n- Added
|
vatadya
|
NORMAL
|
2024-10-23T12:53:49.480101+00:00
|
2024-10-23T12:53:49.480138+00:00
| 2 | false |
# Intuition\n- Optimised Brute Force.\n\n# Approach\n- Started generating substring from index 0.\n- Stopped generating substring oncce any char freq = k\n- Added remaing length of substring from that char to final result\n\n# Complexity\n- Time complexity:O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int numberOfSubstrings(String s, int k) {\n int[] freq = new int[26];\n Arrays.fill(freq,0);\n \n int result = 0;\n for(int i=0;i<s.length();i++) {\n Arrays.fill(freq,0);\n for(int j=i; j<s.length(); j++){\n freq[s.charAt(j)-\'a\']++;\n if(freq[s.charAt(j)-\'a\']>=k){\n result += s.length()-j;\n break;\n }\n } \n }\n \n return result;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Python Solution (7 ms) Beats 95%🔥🔥🔥
|
python-solution-7-ms-beats-95-by-abhigun-hsyo
|
Time Complexity: O(n)\n\n class Solution:\n def numberOfSubstrings(self, s: str, k: int) -> int:\n n = len(s)\n char_count = [0]
|
abhigunjal
|
NORMAL
|
2024-10-23T08:50:17.335839+00:00
|
2024-10-23T08:50:17.335877+00:00
| 15 | false |
**Time Complexity:** O(n)\n\n class Solution:\n def numberOfSubstrings(self, s: str, k: int) -> int:\n n = len(s)\n char_count = [0] * 26\n left = 0\n result = 0\n valid = 0 # Number of characters that have frequency >= k\n\n for right in range(n):\n # Update the count for the current character\n char_count[ord(s[right]) - ord(\'a\')] += 1\n\n # Check if the current character reaches the count >= k\n if char_count[ord(s[right]) - ord(\'a\')] == k:\n valid += 1\n \n # Shrink the window when it\'s no longer valid\n while valid > 0: # At least one character has count >= k\n # Count all substrings ending at the current \'right\'\n result += n - right\n \n # Move left pointer to reduce window size\n char_count[ord(s[left]) - ord(\'a\')] -= 1\n\n # If the count of the left character falls below k, reduce valid count\n if char_count[ord(s[left]) - ord(\'a\')] == k - 1:\n valid -= 1\n left += 1\n\n return result
| 0 | 0 |
['Python3']
| 0 |
count-substrings-with-k-frequency-characters-i
|
count substrings with k frequency characters using javascript
|
count-substrings-with-k-frequency-charac-13ky
|
Intuition\nGiven a string s and an integer k, return the total number of \nsubstrings of s where at least one character appears at least k times.\n\n# Approach\
|
lucifer_300
|
NORMAL
|
2024-10-23T03:57:08.229470+00:00
|
2024-10-23T03:57:08.229504+00:00
| 4 | false |
# Intuition\nGiven a string s and an integer k, return the total number of \nsubstrings of s where at least one character appears at least k times.\n\n# Approach\nrun nested loop to generate all possible substrings and then store them in hashmap on every iteration.\n\nif the count of the any character in substring equals or exceeds "k" frequency, then update counter.\n\nfinally return the counter value\n\n# Complexity\n- Time complexity:\nO(N2)\n\n- Space complexity:\nO(N)\n\n# Code\n```javascript []\n/**\n * @param {string} s\n * @param {number} k\n * @return {number}\n */\nvar numberOfSubstrings = function(s, k) {\n \n let count = 0;\n \n for(let i=0;i<s.length;i++) {\n let obj = new Map();\n for(let j=i;j<s.length;j++) {\n obj.set(s[j], (obj.get(s[j]) || 0) +1);\n for (let value of obj.values()) {\n if(value >= k) {\n count ++;\n break;\n }\n }\n }\n \n }\n\n return count;\n};\n```
| 0 | 0 |
['JavaScript']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Python (Simple Sliding Window)
|
python-simple-sliding-window-by-rnotappl-h25f
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
rnotappl
|
NORMAL
|
2024-10-22T19:21:58.988625+00:00
|
2024-10-22T19:21:58.988657+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def numberOfSubstrings(self, s, k):\n n, left, count, dict1 = len(s), 0, 0, defaultdict(int)\n\n for right in range(n):\n dict1[s[right]] += 1 \n\n while dict1[s[right]] >= k:\n dict1[s[left]] -= 1 \n\n if dict1[s[left]] == 0:\n del dict1[s[left]]\n\n left += 1 \n\n count += right - left + 1 \n\n return n*(n+1)//2 - count \n```
| 0 | 0 |
['Python3']
| 0 |
count-substrings-with-k-frequency-characters-i
|
two pointers
|
two-pointers-by-user5285zn-0ei8
|
We just keep a tight sliding window that contains a string that has just one character $k$ times.\n\nrust []\nimpl Solution {\n pub fn number_of_substrings(s
|
user5285Zn
|
NORMAL
|
2024-10-22T15:31:26.096511+00:00
|
2024-10-22T15:31:26.096536+00:00
| 6 | false |
We just keep a tight sliding window that contains a string that has just one character $k$ times.\n\n```rust []\nimpl Solution {\n pub fn number_of_substrings(s: String, k: i32) -> i32 {\n let s = s.chars().collect::<Vec<char>>();\n let mut total = 0;\n let mut i = 0;\n let mut a = vec![0; 26];\n let mut valid = 0;\n for &x in &s {\n a[x as usize - \'a\' as usize] += 1;\n if a[x as usize - \'a\' as usize] == k {valid += 1;}\n if valid == 0 {continue}\n \n while valid > 0 {\n let y = s[i];\n a[y as usize - \'a\' as usize] -= 1;\n if a[y as usize - \'a\' as usize] == k - 1 {\n valid -= 1;\n }\n i += 1;\n }\n i -= 1;\n let y = s[i];\n a[y as usize - \'a\' as usize] += 1;\n valid = 1;\n total += i as i32 + 1;\n }\n total\n }\n}\n```
| 0 | 0 |
['Rust']
| 0 |
count-substrings-with-k-frequency-characters-i
|
Fast, Readable Solution - Sliding window
|
fast-readable-solution-sliding-window-by-oi36
|
Intuition\nThe intuition behind the solution to count substrings that contain at least one character appearing at least k times revolves around the concept of m
|
chandroos
|
NORMAL
|
2024-10-22T14:22:24.228779+00:00
|
2024-10-22T14:31:50.346346+00:00
| 3 | false |
# Intuition\nThe intuition behind the solution to count substrings that contain at least one character appearing at least `k` times revolves around the concept of maintaining a dynamic window (or substring) and efficiently checking conditions as we expand and contract this window. Here\u2019s a breakdown of the key intuitive elements:\n\n### 1. **Sliding Window Technique**:\n - The sliding window technique allows us to explore substrings without generating all possible combinations explicitly. Instead of checking every possible substring, we maintain a window defined by two pointers (`left` and `right`).\n - As we move the `right` pointer to expand the window, we include new characters and update our character count. This allows us to dynamically adjust our view of the substring.\n\n### 2. **Dynamic Character Count**:\n - By using a `HashMap` to keep track of character frequencies, we can quickly determine how many times each character appears in the current substring.\n - This dynamic counting is crucial because it allows us to check the condition (at least one character appearing `k` times) efficiently without needing to recount characters from scratch for every substring.\n\n### 3. **Condition Checking**:\n - The inner loop checks if the current substring meets the condition of having at least one character with `k` occurrences. If it does, we can count all valid substrings that can be formed from the current `left` to `right` position.\n - This is based on the observation that if a substring is valid (i.e., it contains a character with at least `k` occurrences), then all extensions of this substring (by moving `right` further) will also be valid until the condition is violated.\n\n### 4. **Counting Valid Substrings**:\n - When we find a valid substring, we count all possible substrings that can be formed from the current `left` to `right` position. This is efficient because it leverages the fact that once a valid substring is found, all subsequent substrings that start from the same `left` and end at `right`, `right + 1`, etc., are also valid.\n - This counting mechanism avoids the need for nested loops, which would be computationally expensive.\n\n### 5. **Adjusting the Window**:\n - After counting valid substrings, we increment the `left` pointer to explore new potential substrings. This adjustment is crucial because it allows us to maintain the condition while exploring different starting points for substrings.\n - By decrementing the count of the character at the `left` index, we can check if the condition still holds. If it doesn\u2019t, we continue adjusting the `left` pointer until we find a valid substring again.\n\n### Conclusion\nThe intuition behind this solution is to leverage the sliding window technique combined with dynamic character counting to efficiently explore and count valid substrings. By maintaining a balance between expanding and contracting the window, we can ensure that we consider all possible substrings while adhering to the specified condition, resulting in an optimal and elegant solution.\n\n# Approach\nLet\'s break down how the code ensures that all substrings are considered while counting those that contain at least one character appearing at least `k` times.\n\n### Code Breakdown\n\n1. **Initialization**:\n - We initialize a `HashMap<Character, Integer> charCount` to keep track of the frequency of each character in the current substring.\n - We also initialize two pointers: `left` (starting point of the substring) and `right` (ending point of the substring).\n\n2. **Outer Loop**:\n - The outer loop iterates through the string with the `right` pointer, which expands the current substring by including the character at the `right` index.\n - For each character added to the substring, we update its count in the `charCount` map.\n\n3. **Inner While Loop**:\n - The inner `while` loop checks if the current substring (from `left` to `right`) contains at least one character that appears `k` times by calling the `occurs` method.\n - If the condition is met, it means we have found a valid substring.\n\n4. **Counting Valid Substrings**:\n - When the condition is satisfied, we count all possible substrings that can be formed from the current `left` to `right` position. This is done using the expression `count += s.length() - right;`.\n - This expression counts all substrings that start from `left` and end anywhere from `right` to the end of the string. For example, if `right` is at index 3, and the string length is 5, it counts substrings: `s[left..3]`, `s[left..4]`, and `s[left..5]`.\n\n5. **Adjusting the Left Pointer**:\n - After counting, we need to check if we can still maintain the condition of having at least one character appearing `k` times while moving the `left` pointer to the right.\n - We decrement the count of the character at the `left` index in the `charCount` map. If the count of that character drops to zero, we remove it from the map.\n - The `left` pointer is then incremented to explore the next potential substring.\n\n6. **Continuing the Process**:\n - The outer loop continues to expand the substring by moving the `right` pointer until all characters in the string have been processed.\n - The inner loop ensures that we only count valid substrings while maintaining the condition of at least one character appearing `k` times.\n\n### Ensuring All Substrings Are Considered\n\n- **Comprehensive Coverage**: By using the two-pointer technique, we systematically explore all possible substrings. The `right` pointer expands the substring, while the `left` pointer contracts it when necessary. This guarantees that every possible starting point (`left`) and ending point (`right`) combination is considered.\n \n- **Counting Mechanism**: The counting mechanism (`count += s.length() - right;`) ensures that for every valid substring found, all possible extensions of that substring are counted. This means that if a valid substring is found at a certain `right` position, all substrings starting from `left` to `right`, `left` to `right + 1`, and so on, are included in the count.\n\n- **Dynamic Adjustment**: The dynamic adjustment of the `left` pointer allows the algorithm to explore new substrings while ensuring that the condition of having at least one character appearing `k` times is maintained. This means that as we move through the string, we are continuously checking and counting valid substrings without missing any.\n\n### Conclusion\n\nOverall, the combination of the sliding window technique, the frequency count of characters, and the systematic counting of valid substrings ensures that all possible substrings are considered while adhering to the specified condition. This results in an efficient and comprehensive solution to the problem.\n# Complexity\n- Time complexity:\n - The overall approach is efficient because it processes each character in the string a limited number of times (once when added and once when removed), leading to a linear time complexity of O(n), where n is the length of the string.\n - This efficiency is achieved by avoiding the need to generate all substrings explicitly and instead focusing on maintaining a valid window of characters.\n\n- Space complexity:\n- O(m), where m is the number of unique characters in the string.\nIn practical scenarios with a limited character set, this can be treated as O(1). However, in the general case, it is O(m).\n\nLet\'s analyze it step by step:\n1. Character Count Storage:\nThe solution uses a HashMap<Character, Integer> to keep track of the frequency of characters in the current substring.\nIn the worst case, if all characters in the string are unique, the HashMap will store an entry for each character. Therefore, the space required for the HashMap is O(m), where m is the number of unique characters in the string.\n2. Input String:\nThe input string s itself takes O(n) space, where n is the length of the string. However, this space is typically not counted in the space complexity analysis of the algorithm itself, as it is part of the input.\n3. Other Variables:\nThe algorithm uses a few integer variables (count, left, right) and a constant amount of additional space for the loop control and function calls. This contributes O(1) to the space complexity.\n\n# Code\n```java []\n\nclass Solution {\n\n public int numberOfSubstrings(String s, int k) {\n return countSubstrings(s, k);\n }\n\n private int countSubstrings(String s, int k) {\n int count = 0;\n HashMap<Character, Integer> charCount = new HashMap<>();\n int left = 0;\n\n for (int right = 0; right < s.length(); right++) {\n charCount.put(s.charAt(right), charCount.getOrDefault(s.charAt(right), 0) + 1);\n\n while (occurs(charCount, k)) {\n count += s.length() - right; \n charCount.put(s.charAt(left), charCount.get(s.charAt(left)) - 1);\n if (charCount.get(s.charAt(left)) == 0) {\n charCount.remove(s.charAt(left));\n }\n left++;\n }\n }\n\n return count;\n }\n\n private boolean occurs(HashMap<Character, Integer> charCount, int k) {\n for (int count : charCount.values()) {\n if (count >= k) {\n return true;\n }\n }\n return false;\n }\n}\n```
| 0 | 0 |
['Sliding Window', 'Java']
| 0 |
count-substrings-with-k-frequency-characters-i
|
C++ Sliding Window Solution
|
c-sliding-window-solution-by-baxi_darsh-jfzh
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Baxi_Darsh
|
NORMAL
|
2024-10-22T13:11:50.981695+00:00
|
2024-10-22T13:11:50.981736+00:00
| 16 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(26)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int f(vector<int>&v,int k){\n int c=0;\n for(int i=0;i<26;i++){\n if(v[i]>=k)c++;\n }\n return c>=1;\n }\n\n int numberOfSubstrings(string s, int k) {\n vector<int>v(26);\n int ans=0;\n int j=0;\n int n=s.size();\n for(int i=0;i<s.size();i++){\n v[s[i]-\'a\']++;\n while(j<=i && f(v,k)){\n ans+=(n-i);\n v[s[j]-\'a\']--;\n j++;\n }\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['Sliding Window', 'C++']
| 0 |
count-subarrays-with-median-k
|
Balance
|
balance-by-votrubac-5j4w
|
A subarray has a median k if:\n- It includes k\n- Count n[i] < k is equal to count n[i] > k (odd-size subarrays).\n- Count n[i] < k is one less than count n[i]
|
votrubac
|
NORMAL
|
2022-11-27T04:00:48.933669+00:00
|
2022-11-27T05:23:16.133064+00:00
| 7,858 | false |
A subarray has a median `k` if:\n- It includes `k`\n- Count `n[i] < k` is equal to count `n[i] > k` (odd-size subarrays).\n- Count `n[i] < k` is one less than count `n[i] > k` (even-size subarrays).\n \nOr, in other words, the balance between the count of smaller and larger elements is zero or one.\n \nSince integers are distinct, we have only one `k` element in the array. So, we find it first.\n \nThen, we go right from `k`, tracking the ballance and counting balances using a hash map.\n \nFinally, we go left from `k`, tracking the balance, and counting complimentary balances in the hash map.\n \n> Say the ballance is `-3` (more smaller elements). We look for value `3` and `4` in the hash map to count valid subarrays.\n> This is how our balances look for `[7, 1, 3, 4, 2, 5 ,6], 4`, resulting in 5 valid subarrays.\n \n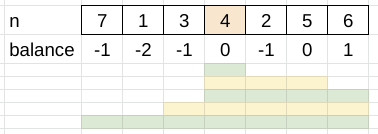\n\n \n**C++**\n```cpp\nint countSubarrays(vector<int>& n, int k) {\n unordered_map<int, int> cnt;\n int p = find(begin(n), end(n), k) - begin(n), res = 0;\n for(int i = p, bal = 0; i < n.size(); ++i) {\n bal += n[i] == k ? 0 : n[i] < k ? -1 : 1;\n ++cnt[bal];\n }\n for(int i = p, bal = 0; i >= 0; --i) {\n bal += n[i] == k ? 0 : n[i] < k ? -1 : 1;\n res += cnt[-bal] + cnt[-bal + 1];\n }\n return res;\n}\n```
| 195 | 1 |
['C']
| 31 |
count-subarrays-with-median-k
|
🔥Python3🔥 Hashmap counting Explained O(n)
|
python3-hashmap-counting-explained-on-by-68tc
|
Intuition\n - We are looking for subarrays that contain k.\n - Elements are unique (from 1 to n).\n - Since the subarray has to contain k, and there is only one
|
MeidaChen
|
NORMAL
|
2022-11-27T04:40:54.205153+00:00
|
2024-01-04T19:17:20.515255+00:00
| 2,812 | false |
**Intuition**\n - We are looking for subarrays that contain ```k```.\n - Elements are unique (from 1 to n).\n - Since the subarray has to contain ```k```, and there is only one ```k```, we can start from ```k``` to build the subarrays.\n\nWhat makes a valid subarray (i.e., k as the median)?\n - the number of elements larger than k == the number of elements smaller than k (odd length)\n - the number of elements larger than k + 1 == the number of elements smaller than k (even length)\n => large == small or large == small+1\n\n**Algorithm**\nWe can check the elements before ```k``` and after ```k```, and count the number of elements larger/smaller than ```k```.\n - let\'s use ```l1``` and ```s1``` denoting the number of elements larger and smaller than k, **Before ```k```**.\n - and ```l2```, ```s2``` denoting the number of elements larger and smaller than k, **After ```k```**.\n => The above equation becomes: \n - ```l1 + l2 == s1 + s2``` => ```l1 - s1 == s2 - l2```\n - ```l1 + l2 == s1 + s2 + 1``` => ```l1 - s1 == s2 - l2 + 1```\n\nNow we can use a hash map to count the frequency of ```l1 - s1``` for the subarray before ```k``` (and contains ```k```).\nThen, check if ```s2 - l2``` and ```s2 - l2 + 1``` in the hash map for the subarray after ```k``` (and contains ```k```) to compute the result.\n\n**TC** O(n), since we only go through the elements before ```k``` and after ```k``` once.\n\n```python\nclass Solution:\n def countSubarrays(self, nums: List[int], k: int) -> int:\n # Find the index of k in nums\n index = nums.index(k)\n \n # l (larger) is count of element>k\n # s (smaller) is count of element<k\n res = l1 = s1 = 0\n before = defaultdict(int)\n \n # run from index-1 to 0 (before index)\n for i in reversed(range(index)):\n # Increase l or s, and increase the differece in \'before\'\n if nums[i] > k: l1 += 1\n else: s1 += 1\n before[(l1-s1)] += 1\n \n # If the number of larger element and smaller element are the same,\n # we find a valid subarray which is nums[i:index+1], so increase res.\n if l1-s1==1 or l1-s1==0: res += 1\n\n l2 = s2 = 0\n for i in range(index+1,len(nums)):\n if nums[i] > k: l2 += 1\n else: s2 += 1\n \n # we need the number of larger elements and smaller elements to be the same in a subarray,\n # l1 + l2 == s1 + s2 or l1 + l2 + 1 == s1 + s2\n # => l1 - s1 == s2 - l2 or l1 - s1 == s2 - l2 + 1\n # so we need to check if s2-l2 or s2-l2+1 exist in before\n res += before[s2-l2] + before[s2-l2+1]\n \n if l2-s2==1 or l2-s2==0: res += 1\n \n return res+1\n```\n\n**Upvote** if you like this post.\n\n**Connect with me on [LinkedIn](https://www.linkedin.com/in/meida-chen-938a265b/)** if you\'d like to discuss other related topics\n\n\uD83C\uDF1F If you are interested in **Machine Learning** || **Deep Learning** || **Computer Vision** || **Computer Graphics** related projects and topics, check out my **[YouTube Channel](https://www.youtube.com/@meidachen8489)**! Subscribe for regular updates and be part of our growing community.
| 64 | 0 |
[]
| 6 |
count-subarrays-with-median-k
|
[Java/Python 3/C++] 1 pass O(n) codes: Count the prefix sum of the balance of (greater - samller).
|
javapython-3c-1-pass-on-codes-count-the-8g756
|
Key observation: Within any subarray, the # of elements greater than median - the # of those less than median = 0 or 1.In order to guarantee the median k to pre
|
rock
|
NORMAL
|
2022-11-27T04:00:51.228678+00:00
|
2025-04-05T17:08:02.373342+00:00
| 4,447 | false |
**Key observation:** Within any subarray, the # of elements greater than median - the # of those less than median `= 0` or `1`.
In order to guarantee the median `k` to present in subarrays, we ONLY save into HashMap/dict the frequencies of the running balances BEFORE finding the median `k`. e.g.,
`nums = [7, 1, 3, 4, 2, 5, 6], k = 4`
running balance:
`bals = [1, 0,-1,-1,-2,-1, 0]`
At index:
-1: running balance = 0 Note: -1 is a virtual index for dummy value 0.
0: running balance = 1
1: running balance = 0
2: running balance = -1
3: running balance = -1, median k found! stop saving the frequencies into HashMap/dict; begin to count the # of subarrays and there is a `-1` at index `2`, and `-1 - (-1) = 0`, a subarry with median `k` is found, and it is `[4]`.
4: running balance = -2, no subarray ending here meets the requirement.
5: running balance = -1, there is one `-1`s at index `2`, and the corresponding subarrays is from index `3` to `5`: `[4,2,5]`. Note: though `(-1 -1) == -2` at index `4`, it is not what we need, because the subarray from index `5` to index `5`, `[5]`, does not include median at index `3`.
6: running balance = 0, there are a `0` at index `1` and dummy value of `0` at index `-1`: `[3,4,2,5,6]` & `[7,1,3,4,2,5,6]`, and a `0 - 1 == -1`s at index `2`: `[4,2,5,6]`.
We have to use the running balance after median to minus the running balance before the median. Otherwise, we could NOT make sure the median is in the subarray.
----
Based on the above, we implement the algorithm as follows:
1. Use a HashMap/dict to count the frequencies of the prefix sum of the running balance (bigger ones - smaller ones);
2. If `k` is the median of a subarray, it must present in the subarray. Therefore, before finding the median, no subarray ending at current element meets the problem requirement;
3. After finding `k`during traversal, no need to count the frequencies any more in the HashMap/dict. If `number of bigger ones == number of the smaller (or + 1)`, that is, `the difference between prefix sum of balances (bigger - smaller) is 0 or 1`, then `k`is the median of the subarray ending at current element;
4. Use the difference of prefix sums to get the count of the required number of subarrays.
----
```java
public int countSubarrays(int[] nums, int k) {
Map<Integer, Integer> prefixSumOfBalance = new HashMap<>();
prefixSumOfBalance.put(0, 1); // Dummy value of 0's frequency is 1.
int ans = 0, runningBalance = 0;
boolean found = false;
for (int num : nums) {
if (num < k) {
--runningBalance;
}else if (num > k) {
++runningBalance;
}else {
found = true;
}
if (found) {
ans += prefixSumOfBalance.getOrDefault(runningBalance, 0) + prefixSumOfBalance.getOrDefault(runningBalance - 1, 0);
}else {
// prefixSumOfBalance.merge(runningBalance, 1, Integer::sum); // Similar to the following statement, but it is shorter.
prefixSumOfBalance.put(runningBalance, prefixSumOfBalance.getOrDefault(runningBalance, 0) + 1);
}
}
return ans;
}
```
```python
def countSubarrays(self, nums: List[int], k: int) -> int:
prefix_sum_of_balance = Counter([0]) # Dummy value of 0's frequency is 1.
running_balance = ans = 0
found = False
for num in nums:
if num < k:
running_balance -= 1
elif num > k:
running_balance += 1
else:
found = True
if found:
ans += prefix_sum_of_balance[running_balance] + prefix_sum_of_balance[running_balance - 1]
else:
prefix_sum_of_balance[running_balance] += 1
return ans
```
Credit to **@Sung-Lin** for his code and explanation.
```cpp
/*
[ 7, 1, 3, 4, 2, 5, 6], 4
bal 1, 0, -1, -1, -2, -1, 0
|<- cnt ->|
ans 1. 0. 1. 2+1
-1 [4]
-1 [4,2,5]
0 [3,4,2,5,6]
0 [7,1,3,4,2,5,6]
-1 [4,2,5,6]
cnt (prefix)
1: 1 (idx 0)
0: 2 (idx -1, 1)
-1: 1 (idx 2)
e.g. 4(idx 3) -> -1
=> find 3(idx 2) -> -1 => idx 2+1(=3) ~ idx 3 => balance == -1 - -1 == 0
curBalance - x == 0 or 1
=> x == curBalance or x == curBalance - 1
*/
class Solution {
public:
int countSubarrays(vector<int>& nums, int k) {
int n = (int) nums.size();
unordered_map<int, int> cnt; // prefix
cnt[0] = 1; // can be think as the prefix on index -1
bool includeK = false;
int balance = 0;
int ans = 0;
for (int i = 0; i < n; i++) {
if (nums[i] < k)
balance--;
else if (nums[i] > k)
balance++;
else // num[i] == k
includeK = true;
if (includeK) {
// find x in prefix hashmap
// greater - smaller == 0 or 1
// => prefix[i] - prefix[x] == 0 or 1
// => curBalance - prefix[x] == 0 or curBalance - prefix[x] == 1
// => prefix[x] == curBalance or prefix[x] == curBalance - 1
ans += cnt[balance] + cnt[balance - 1];
}
else
cnt[balance]++;
}
return ans;
}
};
```
**Analysis:**
Time & space: `O(n)`, where `n = nums.length`.
| 55 | 0 |
['Array', 'Hash Table', 'C', 'Prefix Sum', 'C++', 'Java', 'Python3']
| 7 |
count-subarrays-with-median-k
|
Simple Map !!
|
simple-map-by-megamind-2wwf
|
\n# Approach\n Describe your approach to solving the problem. \nSince we need to find the median and it depends only on the number of numbers less than k or gre
|
megamind_
|
NORMAL
|
2022-11-27T04:01:42.024671+00:00
|
2022-11-27T06:27:06.286612+00:00
| 2,543 | false |
\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSince we need to find the median and it depends only on the number of numbers less than k or greater than k. So we can change the array to 1 and -1 where nums[i]>k and nums[i]<k respectively. Now ,in order to get median ,we must include k in our subarray. So , starting form k (taking sum of elemnts), we will go left to find out the number of greater and smaller elements present till every index and store it in a hashmap.\n eg. 3 2 1 4 5 k=4 -> -1 -1 -1 0 1\nNow going left from k summation wd be -3 -2 -1 0 1;\n\nNow we will go right taking sum from position of k to find the possible subarrays. If we have seen and entry in map (such that key i map + sum = 0 or 1 ) this means we found a possible subarray.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfor(int i =0;i<nums.size();i++){ //*** changing array to 0 1 and -1\n if(nums[i]>k)\n {\n nums[i]= 1;\n }\n else if(nums[i]<k){\n nums[i]= -1;\n }\n else{\n nums[i]=0;\n }\n }\n \n int res = 0;\n int in = -1;\n for(int i =0;i<nums.size();i++){\n if(nums[i]==0){\n in = i; //*** index of k in array \n break;\n }\n }\n \n int sum = 0;\n unordered_map<int,int> hm;\n for(int i = in;i>=0;i--){ //*** going left \n sum += nums[i];\n hm[sum]++;\n }\n sum = 0;\n for(int i = in;i<nums.size();i++){ //*** going right \n sum += nums[i];\n int f = -1*sum;\n if(hm.count(f)!=0){\n res += (hm[f]);\n }\n f+=1;\n if(hm.count(f)!=0){\n res += (hm[f]);\n }\n }\n \n return res; \n```
| 31 | 0 |
['C++']
| 5 |
count-subarrays-with-median-k
|
Python 3 ||| 7 lines, w/ example || T/S: 62% / 99%
|
python-3-7-lines-w-example-ts-62-99-by-s-7g3p
|
https://leetcode.com/problems/count-subarrays-with-median-k/submissions/1277527921/I could be wrong, but I think that time complexity is O(N) and space complexi
|
Spaulding_
|
NORMAL
|
2022-11-27T18:37:44.719704+00:00
|
2025-04-02T17:45:38.147863+00:00
| 542 | false |
```
class Solution:
def countSubarrays(self, nums: List[int], k: int) -> int:
d, iMed = defaultdict(int), nums.index(k) # Ex: [3, 2, 1, 4, 5] k = 4
ans, diff, d[0] = 0, 0, 1
# i n diff ans d
for i, n in enumerate(nums): # –––– –––– –––– –––– ––––
# 0 3 -1 0 {0: 1, -1: 1}
diff+= (n>k) - (n<k) # 1 2 -2 0 {0: 1, -1: 1, -2: 1}
# 2 1 -3 0 {0: 1, -1: 1, -2: 1, -3: 1}
if i < iMed: d[diff]+= 1 # 3 4 -3 1 {0: 1, -1: 1, -2: 1, -3: 1, -4: 0}
# 4 5 -2 3 {0: 1, -1: 1, -2: 1, -3: 1, -4: 0}
else: ans += (d[diff] + d[diff-1]) # |
# return 3
return ans
```
[https://leetcode.com/problems/count-subarrays-with-median-k/submissions/1277527921/](https://leetcode.com/problems/count-subarrays-with-median-k/submissions/1277527921/)
I could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*) *N* ~ `len(nums)`
| 17 | 0 |
['Python3']
| 0 |
count-subarrays-with-median-k
|
✅ C++ || Using Map || Easy Solution
|
c-using-map-easy-solution-by-indresh149-ncvc
|
\n\nclass Solution {\npublic:\n int segments(int n, vector<int> p, int m)\n {\n map<int, int> c;\n c[0] = 1;\n bool has = false;\n int sum = 0
|
indresh149
|
NORMAL
|
2022-11-27T04:08:21.602213+00:00
|
2022-11-27T04:08:21.602258+00:00
| 2,094 | false |
\n```\nclass Solution {\npublic:\n int segments(int n, vector<int> p, int m)\n {\n map<int, int> c;\n c[0] = 1;\n bool has = false;\n int sum = 0;\n long long ans = 0;\n for (int r = 0; r < n; r++) {\n \n // If element is less than m\n if (p[r] < m)\n sum--;\n \n // If element greater than m\n else if (p[r] > m)\n sum++;\n \n // If m is found\n if (p[r] == m)\n has = true;\n \n // Count the answer\n if (has)\n ans += c[sum] + c[sum - 1];\n \n // Increment sum\n else\n c[sum]++;\n }\n \n return ans;\n}\n int countSubarrays(vector<int>& nums, int k) {\n int res = segments(nums.size(),nums,k);\n \n return res;\n }\n};\n```\n**Please upvote if it was helpful for you, thank you!**
| 15 | 1 |
['C']
| 2 |
count-subarrays-with-median-k
|
Easy map solution
|
easy-map-solution-by-sumitk7970-q4xy
|
Approach:\nFor a number to be median of an array, it must be included in the array and the count of numbers greater than it should be either equal to or 1 more
|
Sumitk7970
|
NORMAL
|
2022-11-27T04:03:21.354108+00:00
|
2022-11-27T18:33:34.449449+00:00
| 1,820 | false |
**Approach:**\nFor a number to be median of an array, it must be included in the array and the count of numbers greater than it should be either equal to or 1 more than the count of numbers less than it.\n\n**C++ Code:**\n```\nclass Solution {\npublic:\n int countSubarrays(vector<int>& nums, int k) {\n unordered_map<int, int> m;\n int n = nums.size();\n int less = 0, great = 0;\n int pivot = -1;\n for(int i=0; i<n; ++i) {\n if(nums[i] == k) {\n pivot = i;\n break;\n }\n }\n \n for(int i=pivot; i<n; ++i) {\n if(nums[i] > k) great++;\n else if(nums[i] < k) less++;\n int key = great-less;\n if(m.find(key) != m.end()) m[key]++;\n else m.insert({key, 1});\n }\n \n int count = 0;\n less=great=0;\n for(int i=pivot; i>=0; --i) {\n if(nums[i] > k) great++;\n else if(nums[i] < k) less++;\n int key = less-great;\n if(m.find(key) != m.end()) count += m[key];\n if(m.find(key+1) != m.end()) count += m[key+1];\n }\n \n return count;\n }\n};\n```\n\n**Java Code:**\n```\nclass Solution {\n public int countSubarrays(int[] nums, int k) {\n Map<Integer, Integer> map = new HashMap<>();\n int n = nums.length;\n int less = 0, great = 0;\n int pivot = -1;\n for(int i=0; i<n; ++i) {\n if(nums[i] == k) {\n pivot = i;\n break;\n }\n }\n \n for(int i=pivot; i<n; ++i) {\n if(nums[i] > k) great++;\n else if(nums[i] < k) less++;\n map.put(great-less, map.getOrDefault(great-less, 0)+1);\n }\n \n int count = 0;\n less=great=0;\n for(int i=pivot; i>=0; --i) {\n if(nums[i] > k) great++;\n else if(nums[i] < k) less++;\n int key = less-great;\n count += map.getOrDefault(key, 0) + map.getOrDefault(key+1, 0);\n }\n \n return count;\n }\n}
| 11 | 0 |
['C', 'Java']
| 1 |
count-subarrays-with-median-k
|
C++ | Counting | O(n) | Detailed Explaination
|
c-counting-on-detailed-explaination-by-u-79gx
|
Approach\n\nThe goal is to find the number of subarrays that have a median equal to $k$.\n\nLet center be the index of value $k$ (nums[center] == k), obviously
|
uier890305
|
NORMAL
|
2022-11-27T04:02:58.298473+00:00
|
2022-11-27T19:22:54.344982+00:00
| 1,079 | false |
# Approach\n\nThe goal is to find the number of subarrays that have a median equal to $k$.\n\nLet `center` be the index of value $k$ (`nums[center] == k`), obviously `nums[center]` itself is a valid subarray, and let\'s expand the subarray to the left and right.\n\n- The key to have a median $= k$ is balancing the number of elements less than $k$ and greater than $k$.\n- Since the integers in `nums` are distinct, except `nums[center]`, `nums[i]` is eithor `< k` or `> k`.\n- Let\'s assign the elements a score:\n - $< k$ scores $-1$\n - $> k$ scores $1$\n - $= k$ scores $0$\n- A valid subarray should have total score $0$ or $1$\n\nConsidering the following 3 scenario with an example `nums = [4, 2, 3, 5, 1]`:\n\n1. the subarrays are end with `center`, such as `[4, 2, 3]`.\n2. the subarrays are begin with `center`, such as `[3, 5]` and `[3, 5, 1]`.\n3. the subarrays are across `center`, such as `[4, 2, 3, 5, 1]`.\n\nand let\'s see how to compute the answer with these three scenario\n\n\n# Code\n\n```\nclass Solution {\npublic:\n int countSubarrays(vector<int>& nums, int k) {\n int n = nums.size();\n int center = -1;\n for ( int i=0; i<n; ++i )\n if ( nums[i] == k ) center = i;\n // k not found in nums\n if ( center == -1 ) return 0;\n\n // init with 1 because nums[center] is an answer\n int ans = 1;\n // store the number of scores at the left, used for scenario 3\n unordered_map<int,int> cnt_l;\n for ( int i=center-1, sum=0; i>=0; --i ) {\n // sum is the accumulate score from center-1 to the left\n sum += (nums[i] < k) ? -1 : 1;\n // scenario 1: end with `center`\n if ( sum == 0 || sum == 1 ) ans++;\n // update the counter of this score\n cnt_l[sum]++;\n }\n for ( int i=center+1, sum=0; i<n; ++i ) {\n // sum is the accumulate score from center+1 to the right\n sum += (nums[i] < k) ? -1 : 1;\n // scenario 2: start with `center`\n if ( sum == 0 || sum == 1 ) ans++;\n // scenario 3: across `center`\n ans += cnt_l[-sum] + cnt_l[1-sum];\n }\n return ans;\n }\n};\n```
| 11 | 0 |
['C++']
| 2 |
count-subarrays-with-median-k
|
Java Solution With Detailed Explanation
|
java-solution-with-detailed-explanation-ysgrb
|
\n# Background:\nIf K is the median of a sub array, then the subarray must contain K \n\nNow let\u2019s compute the SUM OF SUBARRAY as follows, for each element
|
profchi
|
NORMAL
|
2022-11-27T04:02:02.271053+00:00
|
2022-11-27T04:02:02.271095+00:00
| 865 | false |
\n# Background:\nIf K is the median of a sub array, then the subarray must contain K \n\nNow let\u2019s compute the SUM OF SUBARRAY as follows, for each element in the subarray greater than K, add one to the sum. For each element in the subarray less than K, subtract one from the sum.\nFor example suppose K = 4 and we have a subarray [3, 4, 1, 5, 6]\nSUM OF SUBARRAY [3, 4, 1, 5, 6] -> [-1,0,-1,1,1] -> -1 + 0 + -1 + 1 + 1 = 0\nNotice that for K to be the median of a subarray, the SUM OF SUBARRAY should be 0 for odd length and 1 for even length\n\n# Solution:\nFirst find the index of K, for simplicity, let\u2019s call that k\n\nThen for elements to the right, k <= r <= n - 1, compute the SUM OF SUBARRAY (k, r) on a rolling basis, and store the frequency of each unique sum using a frequency map\n\nNext iterate backwards from k to 0, k >= l >= 0. During the iteration compute the SUM OF SUBARRAY (l, k) on a rolling basis. For each index, we want to compute the number of subarrays where the median is k that starts at that index l. Since the subarrays must contain the index k and the SUM OF SUBARRAY must be either 1 or 0. We can easily find the number of subarrays that has k as median starting as l by finding the frequency map created for the elements to the right and finding the frequency of the values ( 0 - SUM OF SUBARRAY ( l , k) ) and ( 1 - SUM OF SUBARRAY ( l , k) ). \n\n\nPlease upvote if you like the solution :)\n\n# Code \n\n```\nclass Solution {\n public int countSubarrays(int[] nums, int k) {\n int idx = 0;\n \n for (int i = 0; i < nums.length; ++i){\n if (nums[i] == k){\n idx = i;\n break;\n }\n }\n \n Map<Integer, Integer> map = new HashMap<>();\n \n int sum = 0;\n \n for (int i = idx; i < nums.length; ++i){\n sum += nums[i] == k ? 0 : nums[i] > k ? 1 : -1;\n \n map.put(sum, map.getOrDefault(sum, 0) + 1);\n }\n \n long result = 0;\n sum = 0;\n \n for (int i = idx; i >= 0; --i){\n sum += nums[i] == k ? 0 : nums[i] > k ? 1 : -1;\n \n result += map.getOrDefault(0 - sum , 0);\n result += map.getOrDefault(1 - sum , 0);\n }\n \n return (int) result;\n }\n}\n```
| 9 | 0 |
['Java']
| 1 |
count-subarrays-with-median-k
|
[Python3] freq table
|
python3-freq-table-by-ye15-89zy
|
Please pull this commit for solutions of weekly 321. \n\nIntuition\nThe subarray whose median is k has to include k itself. So we construct our subarrays starti
|
ye15
|
NORMAL
|
2022-11-27T04:04:15.979910+00:00
|
2022-11-27T05:09:36.803205+00:00
| 1,223 | false |
Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/e728a9f475e5742bea7cf67ac2d1a98ab99fb206) for solutions of weekly 321. \n\n**Intuition**\nThe subarray whose median is `k` has to include `k` itself. So we construct our subarrays starting from where `k` is located. \nWe find the index of `k` (say `idx`). Then, we first move to the left and write down the difference of counts larger than k and smaller than `k`. \nLater, we move to the right and calculate the same difference. Here, we can calculate the number of subarrays with median equal to `k` ending at the current index via `freq[-diff]`. \n**Implementation**\n```\nclass Solution:\n def countSubarrays(self, nums: List[int], k: int) -> int:\n idx = nums.index(k)\n freq = Counter()\n prefix = 0\n for i in reversed(range(idx+1)): \n prefix += int(nums[i] > k) - int(nums[i] < k)\n freq[prefix] += 1\n ans = prefix = 0 \n for i in range(idx, len(nums)): \n prefix += int(nums[i] > k) - int(nums[i] < k)\n ans += freq[-prefix] + freq[-prefix+1]\n return ans \n```\n**Complexity**\nTime O(N)\nSpace O(N)\n\nAlternative implementation inspired by @rock\n```\nclass Solution:\n def countSubarrays(self, nums: List[int], k: int) -> int:\n freq = Counter({0 : 1})\n ans = diff = found = 0\n for x in nums: \n if x < k: diff -= 1\n elif x > k: diff += 1\n else: found = 1\n if found: ans += freq[diff] + freq[diff-1]\n else: freq[diff] += 1\n return ans \n```
| 8 | 0 |
['Python3']
| 0 |
count-subarrays-with-median-k
|
✅C++ || Hash Table
|
c-hash-table-by-chiikuu-ywn8
|
Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n)\n Add your space complexity here, e.g. O(n) \n\n# Co
|
CHIIKUU
|
NORMAL
|
2023-03-18T11:16:02.241074+00:00
|
2023-03-18T11:16:02.241120+00:00
| 580 | false |
# Complexity\n- Time complexity: **O(n)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(n)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long help(int n,vector<int> v,int k){\n long long ans=0;\n long long crr=0;\n map<long long,long long>m;\n m[0]=1;\n long long sum=0;\n for(int i=0;i<n;i++){\n if(v[i]<k){\n sum--;\n crr -= m[sum];\n }\n else {\n crr += m[sum];\n sum++;\n }\n ans+=crr;\n m[sum]++;\n }\n return ans;\n }\n int countSubarrays(vector<int>& v, int k) {\n int n=v.size();\n return help(n,v,k) - help(n,v,k+1);\n }\n};\n```\n\n
| 6 | 0 |
['Array', 'Hash Table', 'C++']
| 0 |
count-subarrays-with-median-k
|
Short & Concise | C++
|
short-concise-c-by-tusharbhart-phxt
|
\nclass Solution {\npublic:\n int countSubarrays(vector<int>& nums, int k) {\n unordered_map<int, int> m;\n m[0] = 1;\n int found = 0, a
|
TusharBhart
|
NORMAL
|
2022-11-27T12:58:27.443983+00:00
|
2022-11-27T12:58:27.444021+00:00
| 613 | false |
```\nclass Solution {\npublic:\n int countSubarrays(vector<int>& nums, int k) {\n unordered_map<int, int> m;\n m[0] = 1;\n int found = 0, ans = 0, s = 0;\n \n for(int i : nums) {\n if(i == k) found = 1;\n else s += i < k ? -1 : 1;\n\n if(found) ans += m[s - 1] + m[s];\n else m[s]++; \n }\n return ans;\n }\n};\n\n```
| 5 | 0 |
['Hash Table', 'Prefix Sum', 'C++']
| 3 |
count-subarrays-with-median-k
|
C++ ✅✅| Easy Solution | Using Unordered Map 🔥|
|
c-easy-solution-using-unordered-map-by-k-bc5e
|
Code\n\nclass Solution {\npublic:\n int countSubarrays(vector<int>& nums, int k) {\n int n=nums.size();\n unordered_map<int, int> mp;\n
|
kunal0612
|
NORMAL
|
2022-11-27T05:19:12.557483+00:00
|
2022-11-27T05:19:12.557526+00:00
| 768 | false |
# Code\n```\nclass Solution {\npublic:\n int countSubarrays(vector<int>& nums, int k) {\n int n=nums.size();\n unordered_map<int, int> mp;\n mp[0] = 1;\n bool flag = false;\n int sum = 0;\n long long ans = 0;\n for (int i = 0; i < n; i++){\n if (nums[i] < k){\n sum--;\n }\n else if(nums[i]>k){\n sum++;\n }\n if (nums[i] == k){\n flag=true;\n }\n if (flag){\n ans += mp[sum] + mp[sum - 1];\n }\n else{\n mp[sum]++;\n }\n }\n return ans;\n }\n};\n```
| 5 | 0 |
['C++']
| 0 |
count-subarrays-with-median-k
|
Number of subarrays with sum k | Breaks to standard Problem
|
number-of-subarrays-with-sum-k-breaks-to-pvtr
|
if median is k then u need equal number of elements on both sides ? \nthen ->\nfor every index i count the numbers greater than and less than k then store the d
|
njcoder
|
NORMAL
|
2022-11-27T04:18:38.123449+00:00
|
2022-11-27T04:26:30.732826+00:00
| 830 | false |
**if median is k then u** need equal number of elements on both sides ? \nthen ->\n**for every index i cou**nt the numbers greater than and less than k then store the difference (diff)\nthen search for diff and diff-1 why ?\ndiff case : suppose \ncntl = number of elements less than k \ncntr = number of elements greater than k \n\n**assume at i : cntl = 3, cntr = 7 , diff = -4**\nthis difference can help if u search for this diff the all subarrys u can count why ?\ncurrent cntl = 3, cntr = 7 , diff = -4\nthen search for diff = -4 , if u get 3 suppose then there are 3 subaarys with median as k why ?\n3 7 -> diff = -4 , \n2 6 -> diff = -4 , the subaary between this have cntl = 1 ,cntr = 1 \n1 5 -> diff = -4 , the subaary between this have cntl = 2 ,cntr = 2\nso u can see that if we search for this diff we always get cntl == cntr \nnow u can understand the code and think for even number of elements and do solve the pre requisite problem which is the heading itself \n\n\n \n```\nint countSubarrays(vector<int>& nums, int k) {\n int n = nums.size();\n \n bool is = false;\n \n unordered_map<int,int> um;\n \n int cntl = 0, cntg = 0;\n um[0]++;\n int ans = 0;\n for(int i=0;i<n;i++){\n if(nums[i] == k){\n is = true;\n }\n \n if(nums[i] > k){\n cntg++;\n }else{\n cntl++;\n }\n \n int diff = cntl - cntg;\n \n if(is == true){\n if(um.find(diff) != um.end()){\n ans += um[diff];\n }\n if(um.find(diff-1) != um.end()){\n ans += um[diff-1];\n }\n }\n if(is == false)\n um[diff]++;\n }\n \n return ans;\n \n }
| 5 | 1 |
[]
| 2 |
count-subarrays-with-median-k
|
C++ || sub array sum || easy || trick
|
c-sub-array-sum-easy-trick-by-nishu_1234-gjv8
|
Trick - turn every larger element to -1\nevery smaller element to 1\nevery equal element to some larger value (I have used 1e5 * 2)\n\nthen answer will be subse
|
nishu_1234567
|
NORMAL
|
2022-11-27T04:03:52.591217+00:00
|
2022-11-27T04:04:54.562670+00:00
| 909 | false |
Trick - turn every larger element to -1\nevery smaller element to 1\nevery equal element to some larger value (I have used 1e5 * 2)\n\nthen answer will be subset sum (1e5 * 2 ) + subset sum(1e5 * 2 - 1) [ for even sized sub array]\n```\nclass Solution {\npublic:\n int countSubarrays(vector<int>& nums, int k) {\n int ans = 0;\n int f = 0;\n \n int n = nums.size();\n \n \n for(int i=0;i<n;i++)\n {\n if(nums[i] == k) nums[i] = 1e5 + 1e5;\n else if(nums[i] > k) nums[i] = -1;\n else nums[i] = 1;\n }\n \n unordered_map<int,int> mp;\n k = 1e5 + 1e5;\n int sum =0;\n for(auto i:nums){\n sum+=i;\n \n if(sum==k) ans++;\n if(mp.find(sum - k)!= mp.end()) \n {\n ans+= mp[sum - k];\n }\n \n if(sum == k-1) ans++;\n if(mp.find(sum - (k-1))!= mp.end())\n {\n ans+= mp[sum - (k-1)];\n }\n \n mp[sum]++;\n }\n \n return ans;\n \n }\n};
| 5 | 0 |
['C']
| 2 |
count-subarrays-with-median-k
|
Similar to Subarray sum equal to k || Simple Solution || O(N)
|
similar-to-subarray-sum-equal-to-k-simpl-2rtd
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nThis question is similar to Subarray sum equal to k.\n\nHere what we want
|
Krishna_Morker
|
NORMAL
|
2024-08-26T13:21:20.521077+00:00
|
2024-08-26T13:21:20.521098+00:00
| 245 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis question is similar to Subarray sum equal to k.\n\nHere what we want is that k should be median. so for odd number of length of array we want that same number of eleement less then k and more then k should be present. so whatt we will do , we will make nums[i]<k as -1 and nums[i]>k as 1 now the question is reduced to get subarray sum equal to k.\n\nBut there would be one problem that here we will count extra subarray in which k is not included . but we want only those in which k is include so we will cosider nums[i]<k as -1 , nums[i]==k as n(size of array) and nums[i]>k as 1. SO now it is reduced to subarray sum equal to n . But now by this we will get all odd length subarray. So for even length we want just sum n+1. because we can just include one greater element in odd length. \nDRY RUN FOR TEST CASE YOU WILL GET IT || \n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int countSubarrays(vector<int>& nums, int k) {\n int n=nums.size();\n\n vector<int> v(n,0);\n\n for(int i=0;i<n;i++){\n if(nums[i]<k){\n v[i]=-1;\n }else v[i]=1;\n\n if(nums[i]==k)v[i]=n;\n }\n\n unordered_map<int,int> mp;\n mp[0]=1;\n int sum=0,ans=0;\n for(int i=0;i<n;i++){\n sum+=v[i];\n if(mp.find(sum-(n))!=mp.end()){\n ans+=mp[sum-(n)];\n }\n if(mp.find(sum-(n+1))!=mp.end()){\n ans+=mp[sum-(n+1)];\n }\n\n mp[sum]+=1;\n \n }\n \n return ans;\n }\n};\n```
| 4 | 0 |
['C++']
| 2 |
count-subarrays-with-median-k
|
[Python] O(n) Picture / Video Solution
|
python-on-picture-video-solution-by-chea-fgms
|
You can watch the video solution.\n\n# Conditions for valid subarray\n\n\n\n\nThe condition for a valid subarray:\n Must include K\n Difference in counts:\n\t F
|
cheatcode-ninja
|
NORMAL
|
2022-12-01T17:09:43.537379+00:00
|
2022-12-01T17:26:54.963299+00:00
| 499 | false |
You can watch the [video](https://youtu.be/oLEKpPXUgm4) solution.\n\n# Conditions for valid subarray\n\n\n\n\nThe condition for a valid subarray:\n* Must include `K`\n* Difference in counts:\n\t* For **Odd length** subarray, ```no. of elements smaller than K = no. of elements greater than K ```\n\t* For **Even length** subarray, ```(no. of elements smaller than K) + 1 = no. of elements greater than K ```\n\n # Valid Subarrays\n\n\n\n# Counting pairs using our conditions\n\n\n\n\nSince we are dealing only with the difference between the count of **smaller** elements & **greater** elements, we can just store the difference between them for each index in our array starting from the **Median K**.\n\n```\nbal += 1 if num > k else (-1 if num < k else 0)\n```\n\nWe just have to do it for any one side ( let\'s assume right) from **Median K**. \n\n\n\n\nWe can store it in a HashMap where the key would be the `difference ( balance) ` and the value would be its `count`.\n\nWe now, have to go just left and using our conditions find pairs for both odd & even length.\n\nWhile going left, we have to calculate our `balance` on the fly, \n* for the odd length subarrays, we have to try to pair it with `cnt[-bal]`\n* for the even length subarrays, we have to try to pair it with `cnt[-bal + 1]`.\n\n\n# Time & Space Complexity\n\n`Time: O(n)` We are only going through the elements only once.\n\n`Space: O(n)` We are using a HashMap.\n\nIf you thought this was helpful, please upvote, like the video and subscribe to the channel.\n\nCheers.\n\n\n```\nclass Solution:\n def countSubarrays(self, nums: List[int], k: int) -> int:\n n = len(nums)\n pos = nums.index(k)\n \n cnt = defaultdict(int)\n \n bal=0\n for i in range(pos, n):\n num = nums[i]\n \n bal += 1 if num > k else (-1 if num < k else 0)\n cnt[bal] += 1\n \n res=0\n bal=0\n for i in reversed(range(pos+1)):\n num = nums[i]\n \n bal += 1 if num > k else (-1 if num < k else 0)\n \n res += cnt[-bal] # ODD\n res += cnt[-bal + 1] # EVEN\n \n return res\n\t
| 4 | 0 |
['Python', 'Python3']
| 0 |
count-subarrays-with-median-k
|
Very easy✅ || Beginner friendly C++ solution using MAP || beats 💯
|
very-easy-beginner-friendly-c-solution-u-lgpg
|
```\nint countSubarrays(vector& p, int m) {\n map c;\n c[0] = 1;\n bool flag = false;\n int sum = 0;\n int n=p.size();\n long long ans = 0;\n
|
SuMiT_P13
|
NORMAL
|
2022-11-27T04:42:14.977395+00:00
|
2022-11-27T04:43:51.897440+00:00
| 736 | false |
```\nint countSubarrays(vector<int>& p, int m) {\n map<int, int> c;\n c[0] = 1;\n bool flag = false;\n int sum = 0;\n int n=p.size();\n long long ans = 0;\n for (int i = 0; i < n; i++) {\n \n \n if (p[i] < m)\n sum--;\n else if (p[i] > m)\n sum++;\n if (p[i] == m)\n flag = true;\n \n \n if (flag)\n ans += c[sum] + c[sum - 1];\n else\n c[sum]++;\n }\n \n return ans;\n }\n\t\n\t//Upvote if u got the solution
| 4 | 0 |
['C']
| 3 |
count-subarrays-with-median-k
|
Python || prefix sum || O(n)
|
python-prefix-sum-on-by-hanna9221-cii2
|
First we transform nums into an array of -1, 0, 1: \nn < k to -1, n == k to 0, n > k to 1.\nFor example, nums = [5,1,3,4,2], k = 4 -> arr = [1,-1,-1,0,-1]\n\nFo
|
hanna9221
|
NORMAL
|
2022-11-27T04:03:24.671301+00:00
|
2022-11-27T04:16:05.487002+00:00
| 1,991 | false |
First we transform `nums` into an array of -1, 0, 1: \nn < k to -1, n == k to 0, n > k to 1.\nFor example, `nums` = [5,1,3,4,2], k = 4 -> arr = [1,-1,-1,0,-1]\n\nFor a subarray with sum equals to 0, number of {n: n < k} = number of {n: n > k}.\nFor a subarray with sum equals to 1, number of {n: n < k} = number of {n: n > k} - 1.\nEvery subarray containing 0 and with sum equals to 0(odd length) or 1(even length) counts.\n\n```\nclass Solution:\n def countSubarrays(self, nums: List[int], k: int) -> int:\n arr = []\n for n in nums:\n if n < k:\n arr.append(-1)\n elif n > k:\n arr.append(1)\n else:\n arr.append(0)\n \n book_pre = Counter()\n book_pre[0] = 1\n agg = 0\n check = False\n ans = 0\n for a in arr:\n if a == 0:\n check = True\n agg += a\n if check:\n ans += book_pre[agg] + book_pre[agg-1]\n else:\n book_pre[agg] += 1\n return ans
| 4 | 0 |
['Python3']
| 1 |
count-subarrays-with-median-k
|
Java || PrefixSum of -1, 0,1 || Total - left - right || Commented
|
java-prefixsum-of-1-01-total-left-right-hu5nm
|
find index of k, and convert array into -1, 0, 1\n2. calculate the prefix Sum\n3. calculate three range: total [0, n - 1] - left[0, idxK - 1] - right[idxK + 1
|
cooper--
|
NORMAL
|
2022-11-27T04:02:03.235197+00:00
|
2022-11-27T04:02:44.692847+00:00
| 1,644 | false |
1. find index of k, and convert array into -1, 0, 1\n2. calculate the prefix Sum\n3. calculate three range: total [0, n - 1] - left[0, idxK - 1] - right[idxK + 1]; ( exclude case without `k`)\n```\nclass Solution {\n public int countSubarrays(int[] nums, int k) {\n // 1. find index of k, and convert array into -1, 0, 1\n int idxK = -1;\n for (int i = 0; i < nums.length; i++) {\n if (nums[i] < k) nums[i] = -1;\n else if (nums[i] > k) nums[i] = 1;\n else {\n idxK = i;\n nums[i] = 0;\n }\n }\n // 2. calculate the prefix Sum\n int[] prefixSum = new int[nums.length + 1];\n \n for (int i = 1; i < prefixSum.length; i++) prefixSum[i] = prefixSum[i - 1] + nums[i - 1];\n \n // 3. calculate three range: total [0, n - 1] - left[0, idxK - 1] - right[idxK + 1];\n int left = helper(0, idxK, prefixSum);\n int right = helper(idxK + 1, nums.length, prefixSum);\n int total = helper( 0, nums.length, prefixSum);\n \n return total - left - right;\n }\n \n // calculate current interval, subarray sum = 0 and 1;\n private int helper(int l, int r, int[] prefixSum) {\n Map<Integer, Integer> counter = new HashMap<>();\n \n int ans = 0;\n for (int i = l; i <= r; i++) {\n int currSum = prefixSum[i];\n \n if (counter.containsKey(currSum)) {\n ans += counter.get(currSum);\n }\n \n if (counter.containsKey(currSum - 1)) {\n ans += counter.get(currSum - 1);\n }\n \n counter.put(currSum, counter.getOrDefault(currSum, 0) + 1);\n }\n\n return ans;\n }\n}\n```
| 4 | 1 |
['Prefix Sum', 'Java']
| 0 |
count-subarrays-with-median-k
|
C++ | Easy
|
c-easy-by-pradeep-hjhf
|
Intution : \n# First find the index of the element k \t\t \n# \nNow create left array to store the number which may be the part of the left and tells th
|
pradeep_
|
NORMAL
|
2022-11-27T04:01:33.484529+00:00
|
2022-11-27T04:16:15.536431+00:00
| 566 | false |
# **Intution : **\n# First find the index of the element k \t\t \n# \nNow create left array to store the number which may be the part of the left and tells the position of number \'k\' from the increment for the number which are less than \'k\' and decrement for the number which are greater than \'k\' \nIf contribute towards the left part then increment by 1 and if contribute towards the right part then decrement by 1\n\nNow create right array to store the number which may be the part of the right and tells the position of number \'k\' from the increment for the number which are greater than \'k\' and for the number which are less than \'k\' \t\t\t \t\t\t \nIf contribute towards the left part then decrement by 1 and if contribute towards the right part then increment by 1\n\nSort both the left and right array \t\t \t\t \n\nAfter sorting the subarray \nLet there are \'x\' element in right \nthen for the MEDIAN to be \'k\' there should be \'x\' or \'x-1\'element in left \n\nFor example array = [3, 4, 5, 6, 7] \nHere for element \'5\' to be MEDIAN, there are 2 element in the right and 2 element in the left \narray = [3, 4, 5, 6, 7, 8] \nHere for element \'5\' to be MEDIAN, there are 3 element in the right and 2 element in the left \n\n\nFor each element \'x\' in right array \nfind how many element are there in left array which are equal to \'x\' + how many element are there in left array which are equal to \'x-1\' \n\nApply Binary Search to find in O(logn) for each element \n\n**Code**\n```\nclass Solution {\npublic:\n int countSubarrays(vector<int>& nums, int k) {\n \n int id = 0;\n for(int i=0; i<nums.size(); i++){\n if(nums[i] == k ) {\n id = i;\n break;\n }\n }\n \n vector<int>left , right;\n left.push_back(0);\n right.push_back(0);\n \n int ct = 0;\n for(int i = id-1; i>=0; i--){\n if(nums[i] < k) ct++;\n else ct--;\n \n left.push_back(ct);\n }\n \n ct = 0;\n for(int i = id+1; i<nums.size(); i++){\n if(nums[i] > k) ct++;\n else ct--;\n \n right.push_back(ct);\n }\n \n sort(left.begin() , left.end());\n sort(right.begin() , right.end());\n\n int ans = 0;\n for(auto i : right){\n vector<int>::iterator lower, upper;\n lower = lower_bound(left.begin(), left.end() , i);\n upper = upper_bound(left.begin(), left.end() , i); \n ans += upper - lower;\n \n \n lower = lower_bound(left.begin(), left.end() , i-1);\n upper = upper_bound(left.begin(), left.end() , i-1); \n ans += upper - lower;\n }\n return ans; \n }\n \n};\n```\n\n\n\n**Code with explanations**\n```\nclass Solution {\npublic:\n int countSubarrays(vector<int>& nums, int k) {\n \n //First find the index of the element k\n int id = 0;\n for(int i=0; i<nums.size(); i++){\n if(nums[i] == k ) {\n id = i;\n break;\n }\n }\n \n // Now create left array to store the number which may be the part of the left subarray \n // and tells the postion of number \'k\' from the left\n // increment for the number which are less than \'k\' and decrement for the number which are greater than \'k\'\n // Now create right array to store the number which may be the part of the right subarray \n // and tells the postion of number \'k\' from the right \n // increment for the number which are greater than \'k\' and decrement for the number which are less than \'k\' \n \n vector<int>left , right;\n left.push_back(0);\n right.push_back(0);\n \n int ct = 0;\n for(int i = id-1; i>=0; i--){\n if(nums[i] < k) ct++;\n else ct--;\n \n left.push_back(ct);\n }\n \n ct = 0;\n for(int i = id+1; i<nums.size(); i++){\n if(nums[i] > k) ct++;\n else ct--;\n \n right.push_back(ct);\n }\n \n //Sort both the left and right array\n sort(left.begin() , left.end());\n sort(right.begin() , right.end());\n\n// After sorting the subarray \n// Let there are \'x\' element in right\n// then for the MEDIAN to be \'k\' there should be \'x\' or \'x-1\'element in left\n \n// For example array = [3, 4, 5, 6, 7]\n// Here for element \'5\' to be MEDIAN, there are 2 element in the right and 2 element in the left\n \n// array = [3, 4, 5, 6, 7, 8] \n// Here for element \'5\' to be MEDIAN, there are 3 element in the right and 2 element in the left\n \n \n \n // For each element \'x\' in right array \n // find how many element are there in left array which are equal to \'x\'\n // + how many element are there in left array which are equal to \'x-1\'\n // Apply Binary Search to find in O(logn) for each element \n int ans = 0;\n for(auto i : right){\n vector<int>::iterator lower, upper;\n lower = lower_bound(left.begin(), left.end() , i);\n upper = upper_bound(left.begin(), left.end() , i); \n ans += upper - lower; \n \n lower = lower_bound(left.begin(), left.end() , i-1);\n upper = upper_bound(left.begin(), left.end() , i-1); \n ans += upper - lower;\n }\n return ans; \n }\n \n};\n```\n\n\n
| 4 | 0 |
['Binary Search']
| 0 |
count-subarrays-with-median-k
|
C++ solution using HashMap
|
c-solution-using-hashmap-by-sachin_kumar-d17l
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Sachin_Kumar_Sharma
|
NORMAL
|
2024-04-14T06:49:17.998974+00:00
|
2024-04-14T06:49:17.999027+00:00
| 21 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int countSubarrays(vector<int>& nums, int k) {\n int i,n=nums.size(),ind=-1,ans=0;;\n\n unordered_map<int,int> mp;\n\n\n for(i=0;i<n;i++){\n if(nums[i]==k) ind=i;\n }\n\n if(ind==-1) return -1;\n mp[0]++;\n int diff=0;\n\n for(i=ind+1;i<n;i++){\n if(nums[i]>k) diff++;\n else if(nums[i]<k) diff--;\n mp[diff]++;\n }\n diff=0;\n\n for(i=ind;i>=0;i--){\n if(nums[i]>k) diff++;\n else if(nums[i]<k) diff--;\n // mp[diff]++;\n\n ans+=mp[-diff];\n ans+=mp[1-diff];\n }\n return ans;\n }\n};\n```
| 3 | 0 |
['C++']
| 0 |
count-subarrays-with-median-k
|
C++ | prefix sum | O(N) | explanation
|
c-prefix-sum-on-explanation-by-milochen-igg1
|
\nIn the following source code, \ncountSol(vk,q,0) will figure out all possible odd size subarray.\ncountSol(vk,q,-1) will fiture out all possible even size sub
|
milochen
|
NORMAL
|
2022-11-27T14:47:55.526998+00:00
|
2022-11-27T14:54:40.729164+00:00
| 1,058 | false |
\nIn the following source code, \ncountSol(vk,q,0) will figure out all possible odd size subarray.\ncountSol(vk,q,-1) will fiture out all possible even size subarray.\nFor example, \nInput: nums = [3,2,1,4,5], k = 4\nOutput: 3\nThe subarrays that have a median equal to 4 are: [4], [4,5] and [1,4,5].\nThe cases [4] & [1,4,5] are counted up in countSol(vk,q,0).\nThe case [4,5] is counted up in countSol(vk,q,-1). \n\n\n```C++\nclass Solution {\npublic:\n int countSubarrays(vector<int>& nums, int k) {\n int n = nums.size(), q=0;//q will be index of k in nums\n vector<int> vk = vector<int>(n,0); \n for(int i = 0; i<n; i++) if((nums[i]-k)!=0) vk[i] = abs(nums[i]-k)/(nums[i]-k); //e.g. [3,2,1,4,5], k = 4, then let vk\' = [-1,-1,-1,0,1]\n for(int i = 1; i<n; i++) vk[i] = vk[i-1] + vk[i]; //let vk be the prefix sum of vk\'. \n for(int i = 0;i<n;i++) if(nums[i] == k) q = i;\n return countSol(vk,q,0) + countSol(vk,q,-1);\n }\n\t\n int countSol(vector<int>&vk, int &q, int added) {\n int n = vk.size(), ans=0;\n unordered_map<int,vector<int>> mpL, mpR;\n for(int L = 0; L<=q;L++) mpL[getSum(L,q,vk)+added].push_back(L); \n for(int R = q;R<n;R++) mpR[getSum(q,R,vk)].push_back(R);\n for(auto& [sum,idxs]:mpL) ans+=idxs.size() * mpR[sum*-1].size();\n return ans;\n }\n\n int getSum(int L, int R, vector<int> &vk) {//return sum of vk\'[L..R]\n int vk_R = vk[R], vk_L_1 = (L==0)?0:vk[L-1];\n return vk_R-vk_L_1;\n }\n\t\n};\n```\n\nTime complexity O(N)
| 3 | 0 |
['C', 'Prefix Sum']
| 0 |
count-subarrays-with-median-k
|
✅ [Python] Multiply diff counts around median | O(n) Solution w/ Explanation
|
python-multiply-diff-counts-around-media-ydat
|
Intuition\nBrute Force - O(n^3)\nYou should always start by coming up with the brute force solution. In this case, we can check every possible subarray, count t
|
takanuva15
|
NORMAL
|
2022-11-27T04:01:57.236402+00:00
|
2022-11-27T13:41:17.651601+00:00
| 401 | false |
# Intuition\n**Brute Force - O(n^3)**\nYou should always start by coming up with the brute force solution. In this case, we can check every possible subarray, count the number of elements above/below the median, and check that the median exists in the subarray. As long as there are the same number of elements above/below, or there is 1 more above than below, then the subarray is accepted.\n\n\nEx: [1,2,3,4], k=2\n[1] - no\n[1,2] - no\n[1,2,3] - yes (1 below, 1 above)\n[1,2,3,4] - yes (1 below, 2 above)\n[2] - yes\n[2,3] - yes (0 below, 1 above)\n[2,3,4] - no\n...other subarrays do not contain 3 so they would be invalid.\n\n\n---\n\n\n\n**Optimization to O(n^2)**\nSince the size of nums can be very large (up to 10^5), it\'s clear we need a solution with O(n) time. It\'s also clear that any subarray that doesn\'t contain k is useless, so our 1st potential approach could be to find where k is in nums. After that, perhaps we can use some sort of left and right pointer, expand the subarray being considered around k, and verify the total number of above elements is equal to (or 1 more greater) than the number of below elements being considered. \n\nNote: The left pointer will consider elements to the left of the median, and the right pointer for elements to the right of the median\n\n\nEx: [1,2,3,4,5], k=3\nl=1,r=3 yes\nl=1,r=4 yes\nl=0,r=3 no\nl=0,r=4 yes\n(There is also the subarray of just [3], which we can manually add to the 4 above for a total of 5)\n\n\nWhile this makes sense, this still requires us to consider every possible combination of left pointer and right pointer so that we cover all possible subarrays that contain the median. This results in O(n^2) runtime - still a little slow.\n\n\n# Approach\n**Optimization to O(n)**\nThe realization we need to make to reach O(n) time is the fact that we are going to see the same differences between above/below on the left side and right side of the median. And, we might see those same differences multiple times.\n\nExample: Let med = index of the median.\nSuppose at some l < med, we have 3 above and 1 below, then the diff is -2 total (below - above). In order to set k as the median with these 4 elements on the left (3 above/1 below) we need to know all the subarrays to the right of med which can "balance out" the missing 2 below from the left side. \n\nIf we calculate the diffs of the above/below counts for all r, where med < r < n, then we would know instantly whether there are any subarrays to the right which have a diff of 2 (ie 2 more below than above). That\'s all we need to balance out our left side.\n\nThe only hitch here is if we have a diff of -2 occurring multiple times on the left side. In that case, every one of those will need a diff of 2 on the right side. And if there were multiple diffs of 2 occurring on the right side, then every one those is a valid r to pick for completing the subarray. To handle this, we can do a standard multiplication to add all possible combinations of left side and right matching diffs.\n\nNote: To accommodate the fact that even arrays need 1 more above than below, we also multiply by -diff - 1 on the right side, which represents the diffs that would have one extra above to add to our total subarray.\n\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n\n- `diff` represents the difference between the number of above/below elements (ie below - above)\n- We initialize `res` with the left/right diffs of 0 since that represents subarrays that use elements only on the left/right side of the median. (Likewise for -1, where we have one extra above than below only on one side.)\n\n```\nclass Solution:\n def countSubarrays(self, nums: List[int], k: int) -> int:\n n = len(nums)\n med_i = nums.index(k)\n\n left_of_med_diff_counts = collections.defaultdict(int)\n diff = 0\n for l in range(med_i - 1, -1, -1):\n diff += 1 if nums[l] < k else -1\n left_of_med_diff_counts[diff] += 1\n\n right_of_med_diff_counts = collections.defaultdict(int)\n diff = 0\n for r in range(med_i + 1, n):\n diff += 1 if nums[r] < k else -1\n right_of_med_diff_counts[diff] += 1\n\n res = left_of_med_diff_counts[0] + right_of_med_diff_counts[0] \\\n + left_of_med_diff_counts[-1] + right_of_med_diff_counts[-1] + 1\n for diff, total in left_of_med_diff_counts.items():\n res += (total * right_of_med_diff_counts[-diff]) + (total * right_of_med_diff_counts[-diff - 1])\n return res\n```\n\nI hope that was helpful! (Please upvote if so)
| 3 | 0 |
['Python3']
| 1 |
count-subarrays-with-median-k
|
[Javascript] Count Left & Right Balance
|
javascript-count-left-right-balance-by-a-aaiz
|
Solution: Count Left & Right Balance\n\nFor a subarray to have median of k:\n 1. The subarray must contain k.\n 2. k must be the middle element (if odd) or lo
|
anna-hcj
|
NORMAL
|
2022-11-27T04:00:53.965300+00:00
|
2022-11-27T04:00:53.965341+00:00
| 386 | false |
**Solution: Count Left & Right Balance**\n\nFor a subarray to have median of `k`:\n 1. The subarray must contain `k`.\n 2. `k` must be the middle element (if odd) or lower mid element (if even).\n\nCreate subarrays revolving around `nums[i] = k`.\n\nHow do we find whether `k` is the mid/lower mid element?\n* Starting from `k`, count the "balance" on the left and right of `k`.\n\t* If `nums[i] < k`, add `-1` to the balance.\n\t* If `nums[i] > k`, add `1` to the balance.\n* If `k` is the mid element, the left balance + right balance = `0`.\n* If `k` is the lower mid element, left balance + right balance = `1`.\n\nStore the count of left balances in a hashmap.\nGo through each right balance,\n `Balance = 0`: Count the number of left balances that are equal to (`-right balance`)\n `Balance = 1`: Count the number of left balances that are equal to (`-right balance + 1`)\n\nTime Complexity: `O(n)`\nSpace Complexity: `O(n)`\n```\nvar countSubarrays = function(nums, k) {\n let n = nums.length, kIndex = nums.indexOf(k);\n let map = new Map(), leftBalance = 0;\n map.set(0, 1);\n for (let i = kIndex - 1; i >= 0; i--) {\n leftBalance += nums[i] > k ? 1 : -1;\n map.set(leftBalance, (map.get(leftBalance) || 0) + 1);\n }\n \n let rightBalance = 0, ans = 0;\n for (let j = kIndex; j < n; j++) {\n if (nums[j] !== k) rightBalance += nums[j] > k ? 1 : -1;\n let oddComplement = -rightBalance; // k = mid\n let evenComplement = -rightBalance + 1; // k = lower mid\n ans += (map.get(oddComplement) || 0);\n ans += (map.get(evenComplement) || 0);\n }\n return ans;\n};\n```
| 3 | 0 |
['JavaScript']
| 2 |
count-subarrays-with-median-k
|
2 Sum || Prefix & Suffix || O(N)
|
2-sum-prefix-suffix-on-by-dragonzz-398v
|
Intuition\nWe can reduce this problem to a 2Sum after pre-processing \n\n# Approach\n\nlet idx be the index of k in nums\n1. find the prefix array where pre[i]=
|
dragonzz
|
NORMAL
|
2022-11-27T04:00:52.305254+00:00
|
2022-11-27T04:06:52.795597+00:00
| 668 | false |
# Intuition\nWe can reduce this problem to a 2Sum after pre-processing \n\n# Approach\n\nlet idx be the index of k in nums\n1. find the prefix array where pre[i]= # of element > k - # of element < k in num[i:idx]\n2. find the suffix array where suf[i]= # of element > k - # of element < k in num[idx:i]\n\nif pre[i] + suf[j] = 0, for subarray nums[i:j+1], we have # of element > k = # of element < k ==> k is the median (for odd cases)\n\nsimilarly, if pre[i] + suf[j] = 1, for subarray nums[i:j+1], we have # of element > k = 1 + # of element < k ==> k is the median (for even cases)\n\nthen, we just need to find all (i,j) pair where pre[i] + suf[j] = 0 or 1\nthis becomes a 2Sum problem\n\n# Complexity\nO(N)\n\n# Code\n\n\n```\n def countSubarrays(self, nums: List[int], k: int) -> int:\n pre = defaultdict(int)\n suf = defaultdict(int)\n n = len(nums)\n idx = nums.index(k)\n\n cur = 0 # bigger - smaller\n for i in range(idx)[::-1]:\n cur += 1 if nums[i] > k else - 1\n pre[cur] += 1\n\n cur = 0 # smaller - bigger\n for i in range(idx + 1, n):\n cur += 1 if nums[i] < k else - 1\n suf[cur] += 1\n\n res = 1 + pre[0] + suf[0] + pre[1] + suf[-1]\n for k, v in pre.items():\n res += v * (suf[k]) + v * (suf[k - 1])\n\n return res\n```
| 3 | 0 |
['Python3']
| 1 |
count-subarrays-with-median-k
|
o(N)
|
on-by-12345556-5y2c
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
12345556
|
NORMAL
|
2023-07-23T18:53:34.886916+00:00
|
2023-07-23T18:53:34.886969+00:00
| 83 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int countSubarrays(vector<int>& a, int k) {\n long long ans=0;\n int n=a.size();\n int pf[n];\n for(int i=0;i<n;i++)\n {\n if(a[i]>k)\n {\n pf[i]=1;\n }\n else if(a[i]==k)\n {\n pf[i]=0;\n }\n else{\n pf[i]=-1;\n }\n }\n map<int,int> mp;\n int sum=0;\n mp[0]=1;\n bool f=false;\n for(int i=0;i<n;i++)\n {\n sum+=pf[i];\n if(pf[i]==0||f)\n {\n f=true;\n ans+=mp[sum]+mp[sum-1];\n }\n else{\n mp[sum]++;\n }\n }\n return ans;\n \n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
count-subarrays-with-median-k
|
C++|| Easy Map Solution Using Simple Balance
|
c-easy-map-solution-using-simple-balance-hmod
|
\nclass Solution {\npublic:\n int countSubarrays(vector<int>& nums, int k) {\n map<int,int> mp;\n int cnt=0;// no of elements\n int i=0,n=n
|
Arko-816
|
NORMAL
|
2022-12-29T05:43:46.559355+00:00
|
2022-12-29T06:24:14.413416+00:00
| 218 | false |
```\nclass Solution {\npublic:\n int countSubarrays(vector<int>& nums, int k) {\n map<int,int> mp;\n int cnt=0;// no of elements\n int i=0,n=nums.size();\n bool found=false;\n mp[0]=1;\n int ans=0;\n while(i<n)\n {\n if(nums[i]<k)//elements left of k we decrease cnt\n cnt--;\n else if(nums[i]>k)// elements right of k we increase cnt\n cnt++;\n else\n found=true;\n if(found)\n {\n ans+=mp[cnt]+mp[cnt-1];//if odd no of elements then no of elements right of k is equal to no of elements to left of k \n\t\t\t\t//basically left count is equal to right cnt\n\t\t\t} //if even no of elements then no of elements left is 1 less than no of elements to right \n else\n mp[cnt]++;\n i++;\n }\n return ans;\n }\n};\n```
| 2 | 0 |
[]
| 0 |
count-subarrays-with-median-k
|
[C++] Transform the input array and use the approach of Target sum problem
|
c-transform-the-input-array-and-use-the-08n3y
|
Steps:\n1) First transform the input array -> set the nums[i] == k to 0; nums[i] < k to -1; nums[i] > k to 1\n So for example: nums = [3,2,1,4,5], k = 4; nu
|
samore65
|
NORMAL
|
2022-11-27T19:31:12.833632+00:00
|
2022-11-27T19:35:28.699376+00:00
| 276 | false |
Steps:\n1) First transform the input array -> set the nums[i] == k to 0; nums[i] < k to -1; nums[i] > k to 1\n So for example: nums = [3,2,1,4,5], k = 4; nums -> [-1,-1,-1,0,1]\n2) Start a cummulative sum of the transformed input array, from the k value element and store the cummulative sum\'s freq in a map\n\t mp[0]=1, mp[1]=1;\n3) Start the target sum approach from index of k value all the way to zero index. For finding the target sum we start with cummulative sum of the transformed array and find the match for the targets in the map already store in step 2. Also, there will be two targets to look for, namely target = 0 and target = 1. The reason for value 0 is we are looking for an odd size subarray whose median is k, hence we need to have equal number of values less than and greater than k along with the k element. The reason for value 1 is that we are looking here for even size subarray and the median will be on the left most element after we partition this subarray into two equal parts.\n\t\ttarget = 0 - sum;\n\t\ttarget2 = 1 - sum;\n\t\tThe counts in the frequency map to these values will give us subarrays with required property as decribed in the problem and will always have the k element a part of the subarray.\n\t\t\n```cpp\nclass Solution {\npublic:\n int countSubarrays(vector<int>& nums, int k) {\n int n = nums.size();\n unordered_map<int,int> mp;\n \n int pivot = -1;\n for(int i = 0; i < n; i++)\n {\n if (nums[i] == k)\n {\n pivot = i;\n break;\n }\n }\n \n int sum = 0;\n for(int i = pivot; i < n; i++)\n {\n if (nums[i] == k) sum += 0;\n else if (nums[i] < k) sum -= 1;\n else sum += 1;\n \n mp[sum]++;\n }\n \n sum = 0; \n int ans = 0;\n for(int i = pivot; i >= 0; i--)\n {\n if (nums[i] == k) sum += 0;\n else if (nums[i] < k) sum -= 1;\n else sum += 1;\n \n int target = 0 - sum;\n if (mp[target]) ans += mp[target];\n int target2 = 1 - sum;\n if (mp[target2]) ans += mp[target2];\n }\n \n return ans;\n }\n};\n```\n\n**Please up vote or provide your comments/suggestions for improvements**
| 2 | 0 |
['C']
| 0 |
count-subarrays-with-median-k
|
Prefix for greater and lesser elements (Balancing)
|
prefix-for-greater-and-lesser-elements-b-8tcv
|
\n Find the index of k which is pivot\n compute the prefix sum for greater and lesser elements of k (count of greater and lesser elements than k)\n First check
|
NaveenprasanthSA
|
NORMAL
|
2022-11-27T10:53:45.462070+00:00
|
2022-11-27T11:01:17.132045+00:00
| 443 | false |
\n* Find the index of k which is pivot\n* compute the prefix sum for greater and lesser elements of k (count of greater and lesser elements than k)\n* First check the right side of the pivot\n* If the difference number of greater and lesser elements is equal or 1 , we can consider that subarray will have the median as k\n* Now check the left portion of the pivot\n* Here we need to check the balance, so keep the combination of differences in a map while computing right portion\n* While checking left portion, check the difference combo is present in the map and add to the result if present. \n\n\n\n\n\t\tclass Solution:\n\t\t\tdef countSubarrays(self, a: List[int], k: int) -> int:\n\n\t\t\t\tn = len(a)\n\t\t\t\tif k not in a: return 0\n\t\t\t\tpvt = a.index(k)\n\n\t\t\t\tgreat = [0]*n\n\t\t\t\tless = [0]*n \n\n\t\t\t\tfor i in range(pvt-1,-1,-1):\n\t\t\t\t\tgreat[i] = great[i+1]\n\t\t\t\t\tless[i] = less[i+1] \n\t\t\t\t\tif a[i]>k: great[i] += 1 \n\t\t\t\t\telse: less[i] += 1 \n\n\t\t\t\tfor i in range(pvt+1,n):\n\t\t\t\t\tgreat[i] = great[i-1]\n\t\t\t\t\tless[i] = less[i-1] \n\t\t\t\t\tif a[i]>k: great[i] += 1 \n\t\t\t\t\telse: less[i] += 1 \n\n\n\t\t\t\tprint(great)\n\t\t\t\tprint(less)\n\n\t\t\t\tres = 0\n\t\t\t\tdiff = defaultdict(int)\n\t\t\t\tdiff[0] = 1\n\n\t\t\t\tfor i in range(pvt+1,n):\n\t\t\t\t\tif 0 <= great[i] - less[i] <= 1: res+=1\n\t\t\t\t\tdiff[great[i]-less[i]]+=1\n\n\t\t\t\tfor i in range(pvt):\n\t\t\t\t\tif less[i]-great[i] in diff or less[i]-great[i]+1 in diff:\n\t\t\t\t\t\tres+=(diff[less[i]-great[i]]+diff[less[i]-great[i]+1])\n\n\t\t\t\treturn res+1\n\n\n\n
| 2 | 0 |
['Python']
| 1 |
count-subarrays-with-median-k
|
Explanation
|
explanation-by-iyershridhar-5qh5
|
Tricky Subarray counting !!!!!\n\n\n\n\n\n\nclass Solution {\npublic:\n int subarray(vector<int> &arr , int k , int index){\n map<int , int> mp;\n
|
iyershridhar
|
NORMAL
|
2022-11-27T05:52:21.906825+00:00
|
2022-11-27T05:52:45.964381+00:00
| 180 | false |
# Tricky Subarray counting !!!!!\n\n\n\n\n\n```\nclass Solution {\npublic:\n int subarray(vector<int> &arr , int k , int index){\n map<int , int> mp;\n mp[0] = 1;\n int cnt = 0;\n int sm = 0;\n \n for (int i = 0 ; i < arr.size() ; i++){\n sm += arr[i];\n \n if (i >= index and mp.find(sm - k) != mp.end()){\n cnt += mp[sm-k];\n }\n \n if (i < index){\n mp[sm] += 1;\n }\n }\n return cnt;\n }\n \n \n int countSubarrays(vector<int>& nums, int k) {\n vector<int> arr;\n int index = -1;\n for (int i = 0 ; i < nums.size() ; i++){\n int val = 0;\n if (nums[i] > k) val = 1;\n if (nums[i] < k) val = -1;\n if (nums[i] == k) {index = i ; val = 0;}\n arr.push_back(val);\n }\n \n if (index == -1) return 0;\n return subarray(arr , 0, index ) + subarray(arr , 1 , index);\n }\n};\n```
| 2 | 0 |
['Prefix Sum']
| 0 |
count-subarrays-with-median-k
|
[C++] Count the left side and Check the right side
|
c-count-the-left-side-and-check-the-righ-c2or
|
Idea\nLet large be the count of larger numbers and small be the count of smaller numbers. \nCalculate the difference (= large - small) of both side.\nNow assume
|
Jason0704
|
NORMAL
|
2022-11-27T04:07:30.341643+00:00
|
2022-11-27T14:10:03.982928+00:00
| 391 | false |
**Idea**\nLet `large` be the count of larger numbers and `small` be the count of smaller numbers. \nCalculate the `difference` (= large - small) of both side.\nNow assume at the index i, we have difference = 2, which means we have 2 more "largers" than "smallers".\nSo what we only need to do, is to find the count of difference = -2 (2 more "smallers") and difference = -1 (1 more "smaller") and add them to the result.\n\n**C++**\n```\nclass Solution {\npublic:\n int countSubarrays(vector<int>& nums, int k) {\n int n = nums.size();\n int kpos;\n int res = 0;\n \n //Find the index of k \n for(int i = 0, cnt = 0; i < n; i++){\n if(nums[i] == k) kpos = i;\n }\n \n //Left side of k (including k)\n unordered_map<int, int> m;\n for(int i = kpos, large = 0, small = 0; i >= 0; i--){\n if(nums[i] > k) large++;\n if(nums[i] < k) small++;\n m[large - small]++;\n }\n \n //Right side of k (including k)\n for(int i = kpos, large = 0, small = 0; i < n; i++){\n if(nums[i] > k) large++;\n if(nums[i] < k) small++;\n int d = large - small; //e.g. If d = 2, then we need m[-2] and also m[-1]\n res += m[-d];\n res += m[-(d - 1)];\n }\n return res;\n }\n};\n```
| 2 | 0 |
['C']
| 0 |
count-subarrays-with-median-k
|
[Python3] Counting O(N) With Explanations
|
python3-counting-on-with-explanations-by-1vvd
|
Hint1: We record 1 if num > k; -1 if num < k, and 0 if num == k.\n\nHint2: Let pos denote the index of k in nums, where k is the median. Then the problem is equ
|
xil899
|
NORMAL
|
2022-11-27T04:01:16.531939+00:00
|
2022-11-27T21:12:44.825562+00:00
| 426 | false |
**Hint1:** We record 1 if `num > k`; -1 if `num < k`, and 0 if `num == k`.\n\n**Hint2:** Let `pos` denote the index of `k` in `nums`, where `k` is the median. Then the problem is equivalent to:\n1. `pos` is in the indices of the subarray;\n2. the sum of the subarray is either `0` or `1`.\n\n**Hint3:** Let `c_i` be the # of `num > k` - the # of `num < k` for `num` in `nums[pos..i]`. We count the frequencies of `c_i` using a hashmap `cnt`. Then, let `c_i` be the # of `num < k` - the # of `num > k` for `num` in `nums[i..pos]`.\nNow for each `i`,\n* `cnt[c_i]` is the number of valid subarrays with odd length in **Hint 2**\n* `cnt[c_i + 1]` is the number valid subarrays with even length in **Hint 2**\n\nWe can sum them up to get the final `ans`.\n\n**Complexity**\nTime Complexity: `O(n)`\nSpace Complexity: `O(n)`\n \n**Solution (credit to @endlesscheng)**\n```\nclass Solution:\n def countSubarrays(self, nums: List[int], k: int) -> int:\n\t\tpos = nums.index(k)\n cnt = defaultdict(int)\n cnt[0] = 1\n c = 0\n for i in range(pos + 1, len(nums)):\n c += 1 if nums[i] > k else -1\n cnt[c] += 1\n\n ans = cnt[0] + cnt[1]\n c = 0\n for i in range(pos - 1, -1, -1):\n c += 1 if nums[i] < k else -1\n ans += cnt[c] + cnt[c + 1]\n return ans\n```
| 2 | 0 |
['Python', 'Python3']
| 0 |
count-subarrays-with-median-k
|
[C++] Prefix Sum, Count, O(n), short
|
c-prefix-sum-count-on-short-by-kevin1010-0yfv
|
First, find the index of k. \n\nConstruct 2 prefix sum, the sum equals to the number of integers larger than k minus the number of integers less than k.\n\nThe
|
kevin1010607
|
NORMAL
|
2022-11-27T04:00:51.764581+00:00
|
2022-11-27T04:00:51.764628+00:00
| 593 | false |
First, find the index of `k`. \n\nConstruct 2 prefix sum, the sum equals to the number of integers larger than `k` minus the number of integers less than `k`.\n\nThe first prefix sum `L` is from the index of `k` to `0`.\nThe second prefix sum `R` is from the index of `k` to `n-1`.\nFor example: `nums = [3,2,1,4,5]`, `k = 4`.\n`L = [0,-1,-2,-3]`, `R = [0,1]`\n\nNow the problem is transformed to find the number of pairs whose sum equals to 0 or 1, 0 is the odd case, 1 is the even case, where the pair is constructed by one from `L`, one from `R`.\n\nSo we can use an unordered_map to count the numbers in the `L`, and iterate `R` to get the total number of pairs.\n\n```\nclass Solution {\npublic:\n int countSubarrays(vector<int>& A, int k) {\n int n = A.size(), idx, res = 0;\n for(int i = 0; i < n; i++)\n if(A[i] == k) {idx = i; break;}\n vector<int> L(idx+1), R(n-idx);\n for(int i = 1; i < idx+1; i++)\n L[i] = L[i-1]+(A[idx-i]>k)-(A[idx-i]<k);\n for(int i = 1; i < n-idx; i++)\n R[i] = R[i-1]+(A[idx+i]>k)-(A[idx+i]<k);\n unordered_map<int, int> m;\n for(auto i : L) m[i]++;\n for(auto i : R){\n if(m.count(1-i)) res += m[1-i];\n if(m.count(-i)) res += m[-i];\n }\n return res;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
count-subarrays-with-median-k
|
✅Beginner Friendly 🔥|| Step By Steps Solution ✅ || HashMap Approach ✅🔥
|
beginner-friendly-step-by-steps-solution-lt1t
|
Code
|
rajput11dynamic
|
NORMAL
|
2025-01-16T18:43:09.295009+00:00
|
2025-01-16T18:43:09.295009+00:00
| 106 | false |

# Code
```java []
class Solution {
public int countSubarrays(int[] nums, int k) {
Map<Integer, Integer> map = new HashMap<>();
map.put(0, 1);
int c = 0, i = 0;
boolean found = false;
for (int num : nums) {
if (num < k) --i;
else if (num > k) ++i;
else found = true;
if (found) c += map.getOrDefault(i,0)+map.getOrDefault(i-1,0);
else map.put(i, map.getOrDefault(i, 0) + 1);
}
return c;
}
}
```
| 1 | 1 |
['Java']
| 0 |
count-subarrays-with-median-k
|
clean code...using subarray sum equal k logic...without finding index of k
|
clean-codeusing-subarray-sum-equal-k-log-xcue
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
niteshsaxena03
|
NORMAL
|
2025-01-02T15:34:08.839953+00:00
|
2025-01-02T15:34:08.839953+00:00
| 66 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
private:
int countSubarraySumEqualK(vector<int>& temp, int k) {
int prefixSum = 0;
int ans = 0;
map<int, int> countPrefixSum;
for (auto& i : temp) {
prefixSum += i;
if (prefixSum == k)
ans++;
if (countPrefixSum.find(prefixSum - k) != countPrefixSum.end())
ans += countPrefixSum[prefixSum - k];
countPrefixSum[prefixSum]++;
}
return ans;
}
public:
int countSubarrays(vector<int>& nums, int k) {
int n=nums.size();
vector<int> temp = nums;
for (auto& i : temp) {
if (i == k)
i = n;
else if (i < k)
i = -1;
else
i = 1;
}
// for(auto &i:temp)cout<<i<<" ";
int ans1 = countSubarraySumEqualK(temp, n);
int ans2 = countSubarraySumEqualK(temp, n+1);
// cout<<ans1<<" "<<ans2;
return ans1 + ans2;
}
};
```
| 1 | 0 |
['C++']
| 0 |
count-subarrays-with-median-k
|
[Java] Easy 100% solution
|
java-easy-100-solution-by-ytchouar-4x72
|
java\nclass Solution {\n public int countSubarrays(final int[] nums, final int k) {\n final int n = nums.length;\n final int[] counts = new int
|
YTchouar
|
NORMAL
|
2024-11-04T04:58:13.298727+00:00
|
2024-11-04T04:58:13.298764+00:00
| 78 | false |
```java\nclass Solution {\n public int countSubarrays(final int[] nums, final int k) {\n final int n = nums.length;\n final int[] counts = new int[n * 2 + 1];\n\n int count = 0, result = 1, pos = 0;\n\n for(int i = 0; i < n; ++i)\n if(nums[i] == k)\n pos = i;\n\n for(int i = pos + 1; i < n; ++i) {\n count += nums[i] > k ? 1 : -1;\n\n if(count == 0 || count == 1)\n result++;\n\n counts[count + n]++;\n }\n\n count = 0;\n\n for(int i = pos - 1; i >= 0; --i) {\n count += nums[i] > k ? 1 : -1;\n\n if(count == 0 || count == 1)\n result++;\n\n result += counts[-count + n] + counts[-count + 1 + n];\n }\n\n return result;\n }\n}\n```
| 1 | 0 |
['Java']
| 0 |
count-subarrays-with-median-k
|
Easy java solution with intuition , approach and description
|
easy-java-solution-with-intuition-approa-6o8l
|
Intuition and Approach\n\nThe problem requires counting the number of subarrays where the median equals a given integer k. A median is the middle element in a s
|
workwithracian
|
NORMAL
|
2024-07-01T09:14:54.339143+00:00
|
2024-07-01T09:14:54.339178+00:00
| 23 | false |
### Intuition and Approach\n\nThe problem requires counting the number of subarrays where the median equals a given integer `k`. A median is the middle element in a sorted array, so the goal is to identify subarrays where `k` is the middle element.\n\nThe approach is based on prefix sums and the idea of balancing counts of elements greater than and less than `k`. Here\'s a detailed explanation:\n\n1. **Prefix Sum Transformation**:\n - Convert each element in the array:\n - Increment the prefix sum if the element is greater than `k`.\n - Decrement the prefix sum if the element is less than `k`.\n - Keep the prefix sum unchanged if the element equals `k`.\n - This transformation helps track the balance of elements greater than and less than `k` up to any point in the array.\n\n2. **Counting Subarrays**:\n - Use a map to store counts of prefix sums.\n - If a subarray has `k` as its median, the number of elements greater than `k` on the left should be equal to or one more than the number of elements less than `k` on the left.\n - The map helps check how many times a particular prefix sum has occurred, indicating possible starting points for valid subarrays.\n\n3. **Handling Special Cases**:\n - Initialize the map with `mp.put(0, 1)` to account for the case where the subarray starts from the beginning.\n - Once `k` is encountered (`go` becomes true), check the prefix sum and update the result count accordingly.\n\n### Complexity Analysis\n\n- **Time Complexity**: `O(n)`\n - The algorithm processes each element in the array exactly once.\n - Map operations (get and put) are on average O(1), leading to an overall time complexity of O(n).\n- **Space Complexity**: `O(n)`\n - The space complexity is due to the map storing prefix sums, which in the worst case can be equal to the number of elements in the array.\n\n\n### Code\njava\n```\nclass Solution {\n public int countSubarrays(int[] nums, int k) {\n Map<Integer, Integer> mp = new HashMap<>();\n int sum = 0, ans = 0;\n boolean go = false;\n mp.put(0,1);\n\n for(int n : nums){\n if(n>k){\n ++sum;\n }\n else if(n<k){\n --sum;\n }\n if(n==k){\n go = true;\n }\n if(go){\n ans += mp.getOrDefault(sum,0)+mp.getOrDefault(sum-1,0);\n }\n else{\n mp.put(sum, mp.getOrDefault(sum,0)+1);\n }\n \n }\n return ans;\n }\n}\n\n```\n\n### Dry Run\n\nLet\'s dry run the algorithm with an example:\n\n**Example**: `nums = [3, 2, 1, 4, 5]`, `k = 4`\n\n1. **Initial State**:\n - `sum = 0`, `ans = 0`, `go = false`\n - `mp = {0: 1}`\n\n2. **Iteration**:\n\n - **First Element (3)**:\n - `3 < 4`, so `sum = -1`\n - `go = false`\n - Update map: `mp = {0: 1, -1: 1}`\n\n - **Second Element (2)**:\n - `2 < 4`, so `sum = -2`\n - `go = false`\n - Update map: `mp = {0: 1, -1: 1, -2: 1}`\n\n - **Third Element (1)**:\n - `1 < 4`, so `sum = -3`\n - `go = false`\n - Update map: `mp = {0: 1, -1: 1, -2: 1, -3: 1}`\n\n - **Fourth Element (4)**:\n - `4 == 4`, so `sum remains -3`\n - `go = true`\n - Update `ans`: `ans = mp.getOrDefault(-3, 0) + mp.getOrDefault(-4, 0) = 1 + 0 = 1`\n - No map update as `go` is true\n\n - **Fifth Element (5)**:\n - `5 > 4`, so `sum = -2`\n - `go = true`\n - Update `ans`: `ans = ans + mp.getOrDefault(-2, 0) + mp.getOrDefault(-3, 0) = 1 + 1 + 1 = 3`\n\n3. **Result**:\n - `ans = 3`\n\nThe algorithm correctly identifies three subarrays with median 4:\n- Subarray `[4]`\n- Subarray `[4, 5]`\n- Subarray `[2, 1, 4, 5]`\n\n\n
| 1 | 0 |
['Python', 'C++', 'Java']
| 0 |
count-subarrays-with-median-k
|
C++ || Beginner Friendly || Full explanation || Easy
|
c-beginner-friendly-full-explanation-eas-i9us
|
\n class Solution {\npublic:\n int countSubarrays(vector<int>& nums, int k) {\n //valid subarrays will be starting from 0 to i where i being the index
|
1821_sank
|
NORMAL
|
2023-09-21T09:05:49.937914+00:00
|
2023-09-21T09:05:49.937963+00:00
| 610 | false |
```\n class Solution {\npublic:\n int countSubarrays(vector<int>& nums, int k) {\n //valid subarrays will be starting from 0 to i where i being the index of k and ending at i to n\n //suppose i foudn a valid subarray between s and e\n //numbers greater than k between s to i be g1\n //number smaller than k be s1\n //from i to end \n //number greater than k be g2 and less than be s2\n // from given we know (g1+g2)-(s1+s2)=0 0r 1\n //----> (g1-s1)+(g2-s2)==0 o1 1\n //in first for loop we are calucalting g2-s2 at every index\n \n int n=nums.size();\n int ind=-1;\n for(int i=0;i<n;i++)\n {\n if(nums[i]==k)\n {\n ind=i;\n }\n }\n if(ind==-1)\n {\n return -1;\n }\n unordered_map<int,int>map;\n int diff=0;\n map[0]++;\n for(int i=ind+1;i<n;i++){\n if(nums[i]>k)\n {\n diff++;\n }\n \n else if(nums[i]<k) \n {\n diff--;\n }\n map[diff]++;\n }\n diff=0;\n int ans=0;\n //finding complement for the (g1-s1)\n //we have already counted g2-s2\n for(int i=ind;i>=0;i--)\n {\n if(nums[i]>k)\n {\n diff++;\n }\n else if(nums[i]<k) \n {\n diff--;\n }\n ans+=map[0-diff];\n ans+=map[1-diff];\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['C', 'Prefix Sum']
| 0 |
count-subarrays-with-median-k
|
C++ | Hints Solution | With Comments
|
c-hints-solution-with-comments-by-ama29n-w8gy
|
\nclass Solution {\npublic:\n int countSubarrays(vector<int>& nums, int k) {\n int n = nums.size();\n for(auto& it : nums) {\n it =
|
ama29n
|
NORMAL
|
2023-02-24T15:13:39.528442+00:00
|
2023-02-24T15:13:39.528473+00:00
| 107 | false |
```\nclass Solution {\npublic:\n int countSubarrays(vector<int>& nums, int k) {\n int n = nums.size();\n for(auto& it : nums) {\n it = it == k ? 0 : it > k ? 1 : -1;\n }\n int idx;\n for(auto i = 0; i < n; i++) {\n if(nums[i] == 0) {\n idx = i; break;\n }\n }\n unordered_map<int, int> map;\n int sum = 0;\n for(int i = idx; i >= 0; i--) { // going left\n sum += nums[i];\n map[sum]++;\n }\n sum = 0;\n int ans = 0;\n for(int i = idx; i < n; i++) { // going right\n sum += nums[i];\n ans += map[-sum]; // if subarray is odd\n ans += map[-(sum - 1)]; // if subarray is even, median is left middle element\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['Hash Table', 'Prefix Sum']
| 0 |
count-subarrays-with-median-k
|
Python | Counter | O(n)
|
python-counter-on-by-aryonbe-nk2f
|
Code\n\nfrom collections import Counter\nclass Solution:\n def countSubarrays(self, nums: List[int], k: int) -> int:\n n = len(nums)\n i = nums
|
aryonbe
|
NORMAL
|
2022-12-19T08:45:06.085055+00:00
|
2022-12-19T08:45:06.085097+00:00
| 71 | false |
# Code\n```\nfrom collections import Counter\nclass Solution:\n def countSubarrays(self, nums: List[int], k: int) -> int:\n n = len(nums)\n i = nums.index(k)\n lcounter = Counter()\n cursum = 0\n lcounter[0] = 1\n for j in range(i-1,-1,-1):\n cursum += -1 if nums[j] < k else 1\n lcounter[cursum] += 1\n res = lcounter[0] + lcounter[1]\n cursum = 0\n for j in range(i+1,n):\n cursum += 1 if nums[j] > k else -1\n res += lcounter[-cursum] + lcounter[-cursum+1]\n return res \n```
| 1 | 0 |
['Python3']
| 0 |
count-subarrays-with-median-k
|
Java || Easy Solution || Using HashMap
|
java-easy-solution-using-hashmap-by-maaw-2j30
|
\nclass Solution {\n public int countSubarrays(int[] arr, int k) {\n HashMap<Integer , Integer> map = new HashMap<>();\n int index = -1;\n
|
MaawanAhmad
|
NORMAL
|
2022-12-08T13:47:51.520292+00:00
|
2022-12-08T13:47:51.520325+00:00
| 60 | false |
```\nclass Solution {\n public int countSubarrays(int[] arr, int k) {\n HashMap<Integer , Integer> map = new HashMap<>();\n int index = -1;\n for(int i = 0 ; i < arr.length ; i++){\n if(arr[i] == k){\n index = i;\n break;\n }\n }\n // System.out.println("");\n int ans = 0;\n int bal = 0;\n for(int i = index + 1 ; i < arr.length ; i++){\n if(arr[i] > k){\n bal++;\n }else{\n bal--;\n }\n if(bal == 0 || bal == 1) ans++;\n insertInMap(map , bal);\n }\n bal = 0;\n for(int i = index - 1 ; i >= 0 ; i--){\n if(arr[i] > k){\n bal++;\n }else{\n bal--;\n }\n if(bal == 0 || bal == 1) ans++;\n if(map.containsKey(0 - bal)){\n ans += map.get(0 - bal);\n }\n if(map.containsKey(1 - bal)){\n ans += map.get(1 - bal);\n }\n }\n return ans+1;\n }\n private void insertInMap(HashMap<Integer , Integer> map , int ele){\n if(!map.containsKey(ele)){\n map.put(ele , 0);\n }\n map.put(ele , map.get(ele) + 1);\n }\n}\n```
| 1 | 0 |
[]
| 1 |
count-subarrays-with-median-k
|
C++| MAP | O(N)
|
c-map-on-by-kumarabhi98-vjnp
|
\nclass Solution {\npublic:\n int countSubarrays(vector<int>& nums, int k) {\n unordered_map<int,int> mp; mp[0]++;\n int sum = 0, in = 0, re =
|
kumarabhi98
|
NORMAL
|
2022-11-27T09:54:38.419623+00:00
|
2022-11-27T09:54:38.419668+00:00
| 30 | false |
```\nclass Solution {\npublic:\n int countSubarrays(vector<int>& nums, int k) {\n unordered_map<int,int> mp; mp[0]++;\n int sum = 0, in = 0, re = 0;\n while(in<nums.size() && nums[in]!=k) in++;\n for(int i = in-1; i>=0;i--) {\n if(nums[i]>k) sum++; else sum--;\n mp[sum]++;\n }\n re = mp[0]+mp[1];\n sum = 0;\n for(int i = in+1; i<nums.size();++i){\n if(nums[i]>k) sum++; else sum--;\n re+=mp[-sum]+mp[-(sum-1)];\n }\n return re;\n }\n};\n```
| 1 | 0 |
['C']
| 0 |
count-subarrays-with-median-k
|
✅Using HashMap || Easy C++ Solution
|
using-hashmap-easy-c-solution-by-ramkish-l5j5
|
Please upvote if you like.\nApproach\n\nLogic is that k would be median of a subarray if the count of smaller and greater value on the left side is 1 more than
|
ramkishanteli2
|
NORMAL
|
2022-11-27T07:00:22.450536+00:00
|
2022-11-27T07:00:22.450575+00:00
| 70 | false |
**Please upvote if you like.**\n**Approach**\n\nLogic is that k would be median of a subarray if the count of smaller and greater value on the left side is 1 more than the count of smaller and greater value on the right side.\n\n\nWe find the count of the smaller and greater value then the median k on the right side and we store the counting in the HashMap.\nThen again we find the counting of smaller and greater value on the left side and we check that if the -cnt and -cnt+1 exists on the right hand side then we add that in our answer.\n\n\n```\nclass Solution {\npublic:\n int countSubarrays(vector<int>& nums, int k) {\n int pos;\n int n = nums.size();\n int ans = 0;\n for(int i = 0;i < n;i++){\n if(nums[i] == k){\n pos = i;\n break;\n }\n }\n unordered_map<int,int>mp;\n int cnt = 0;\n for(int i = pos;i < n;i++){\n cnt += nums[i] == k ? 0 : nums[i] < k ? -1 : 1;\n mp[cnt]++;\n }\n for(int i = pos,cnt = 0;i >= 0;i--){\n cnt += nums[i] == k ? 0 : nums[i] < k ? -1 : 1;\n ans += mp[-cnt] + mp[-cnt+1];\n }\n return ans;\n }\n};\n```\n
| 1 | 0 |
[]
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.