question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
mirror-reflection
|
[C++] Minimalist/Golfed Solution Explained, 100% Time, 100% Space
|
c-minimalistgolfed-solution-explained-10-05sf
|
This was not actually too much fun per se - you either figure out the trick of repeating the space above (as brilliantly explained by codedayday here) or you en
|
ajna
|
NORMAL
|
2020-11-17T23:33:29.268594+00:00
|
2020-11-17T23:33:29.268636+00:00
| 517 | false |
This was not actually too much fun per se - you either figure out the trick of repeating the space above (as brilliantly explained by [codedayday](https://leetcode.com/codedayday) [here](https://leetcode.com/problems/mirror-reflection/discuss/939143/C%2B%2B-Geometry-mirror-game)) or you end up hitting a wall - or possibly writing over-complicated code with several cases.\n\nAnd while I will not even try to even repeat that brilliant explanation, I just decided to golf it a bit.\n\nBasically we know that we cannot have a reliable solution with `q * reflections == p * repetitions` [check the pic in the link above] and the first corner to be hit depends on the combination of `p` and `q` being even or odd.\n\nFurther more, we know that when both `p` and `q` are even, since that would hit our entrance point (which has no mirrors) - check the math or, even better, with some pen and paper to confirm it, because I am afraid no explanation of mine could match some good grinding process on your own, but if that would help a bit, consider this quick table of mine that gives which mirror would be hit, depending on the parity of our 2 variables (with `3` being an ideal mirror at our entry point):\n\n```cpp\n// qe = q even, qo = q odd\n// pe = p even, po = p odd\n qe qo\npe 3 2\npo 0 1\n```\n\nWe need to proceed and reduce the problem to one in which we reduce the problem to a situation in which we get at least one of them to be odd - that equates to repeating the problem, having our light bounce over and over again until one corner which is not the bottom left gets hit.\n\nAt that point, we have the following possible scenarios:\n* `p` is even => we hit mirror `2`;\n* `q` is even => we hit mirror `0`;\n* both `q` and `p` are odd => we hit mirror `1`.\n\nWe can compress this logic a bit and have the fancy return statement I wrote down below.\n\nThe code:\n\n```cpp\nclass Solution {\npublic:\n int mirrorReflection(int p, int q) {\n // reducing p and q if/while both even\n while (p % 2 == 0 && q % 2 == 0) p >>= 1, q >>= 1;\n return p % 2 ? q % 2 : 2;\n }\n};\n```
| 5 | 0 |
['Math', 'Geometry', 'C', 'C++']
| 0 |
mirror-reflection
|
Mirror Reflection
|
mirror-reflection-by-orthonormalize-8o8q
|
\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n while (not((p%2)or(q%2))):\n (p,q) = (p//2,q//2)\n return(1
|
orthonormalize
|
NORMAL
|
2020-11-17T11:03:34.245005+00:00
|
2020-11-18T11:03:25.573286+00:00
| 479 | false |
```\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n while (not((p%2)or(q%2))):\n (p,q) = (p//2,q//2)\n return(1+(q%2)-(p%2))\n```\n\nDuring each horizontal traversal (from left to right or from right to left), the fraction of the box covered vertically is (q/p). To reach a receptor, we require the sum of these vertical fractions to reach an integer at the same time that we reach a horizontal edge. The first time this will happen is when the total vertical distance travelled equals the box length multiplied by the smallest positive integer multiple of (q/p) that is itself an integer.\n\nSo the problem boils down to expressing (q/p) as a reduced fraction. Further, since we only care about even vs odd, we only need to reduce the fraction by mutual multiples of 2.\n \n The destination receptor will depend on the even-odd parity of the reduced p and q as follows: (Even p and odd q => receptor 2, Odd p and odd q => receptor 1, Odd p and even q => receptor 0).
| 5 | 0 |
['Python3']
| 3 |
mirror-reflection
|
Mirror Reflection || c++14 || Easy to understand
|
mirror-reflection-c14-easy-to-understand-g41q
|
box cordinates are used as base condition\n(0,0) (P,0) (0,Q) (P,Q)\n\n\nclass Solution {\npublic:\n int mirrorReflection(int p, int q) {\n bool up=tru
|
chandr_a0056
|
NORMAL
|
2020-11-17T10:50:14.950343+00:00
|
2020-11-17T10:50:14.950425+00:00
| 316 | false |
**box cordinates are used as base condition\n(0,0) (P,0) (0,Q) (P,Q)**\n\n```\nclass Solution {\npublic:\n int mirrorReflection(int p, int q) {\n bool up=true,down =false;\n int x=0,y=0;\n if(q==0)\n return 0;\n else if(p==q)\n return 1;\n else\n {\n for(int i=0;i<1000;i++)\n {\n\t\t\t// for going up \n if(up==true)\n {\n if(i%2==0)\n x = x+p,y=y+q;\n else\n x = x-p,y=y+q;\n // y goes out the box but x never go out of the box\n\t\t\t\t\t// so we have to keep y inside the box \n if(y>p)\n {\n y = 2*p -y;\n down =true;\n up = false;\n }\n }\n\t\t\t\t// for going down\n else if(down==true)\n {\n if(i%2==0)\n x = x+p,y=y-q;\n else\n x = x-p,y=y-q;\n \n if(y<0)\n {\n y =(-1)*y;\n up =true;\n down = false;\n }\n }\n cout<<x<<" "<<y<<" "<<up<<" "<<down<<endl;\n if(x==0&&y==p)\n return 2;\n else if(x==p&&y==0)\n return 0;\n else if(x==p&&y==p)\n return 1;\n \n }\n }\n return 1;\n }\n};\n```
| 5 | 0 |
[]
| 0 |
mirror-reflection
|
Finding the LCM and checking the bounce frequncy and the top refraction count (C++, 100%)
|
finding-the-lcm-and-checking-the-bounce-4os3a
|
Idea: If you know how many times it will bounce off the left and right wall, you will know which side it ended on. If you know how many time it bounced off the
|
le_li_mao
|
NORMAL
|
2019-04-24T20:17:22.730124+00:00
|
2019-04-24T20:17:22.730151+00:00
| 206 | false |
**Idea: If you know how many times it will bounce off the left and right wall, you will know which side it ended on. If you know how many time it bounced off the top and bottom wall you will know it will ended up on top or bottom.**\n\nHow to know the number of bounces? \n\nYou know the meeting point will be at a height with proportional to p and also q because the height of the beam will increment by q every time a ray hits the left or right wall. It will be proportional to P because the height of the recepter are either P or 0 (which means %P==0). Based on this, you can calculate the LCM (least common multiple) to find out the total y direction distance traveled by the ray. \n\nDividing the y distance by q and minus 1 will give you the number of bounces off of the right and left wall while dividing y distance by the p and minus 1 will give the number of bounce off of the top and bottom. \n\t\t\t\t\t\nBased on the number of bounce, you know that odd number of bounce off the left and right wall will mean recepter 2. Odd number of top and bottom bounces will give recepter 0. Which leaves the recepter 1 when both the top/bottom and left/right bounce count are even.\n\nHere is the code\nI used the Euclid algorithim to find the gcd to find the lcm\n\nIf you guys find the explaination useful please feel free to upvote it as it encourages me to do more stuff like this. \nIf you have any question feel free to ask below and I will try to answer as soon as possible.\n``` \nclass Solution {\npublic:\n int mirrorReflection(int p, int q) {\n if(q==0)return 0;\n int lcm = p*q/gcd(p,q);\n if((lcm/q)%2==0)return 2;\n else{\n if((lcm/p)%2==0)return 0;\n else return 1;\n }\n return 0;\n }\n int gcd(int a, int b){\n if(b==0)return a;\n return gcd(b,a%b);\n }\n};\n```
| 5 | 0 |
[]
| 1 |
mirror-reflection
|
✅Short || C++ || Java || PYTHON || Explained Solution✔️ || Beginner Friendly ||🔥 🔥 BY MR CODER
|
short-c-java-python-explained-solution-b-s1jy
|
Please UPVOTE if you LIKE!!\nWatch this video \uD83E\uDC83 for the better explanation of the code.\n\nhttps://www.youtube.com/watch?v=gcRdVnBLGbQ&t=145s\n\n\nAl
|
mrcoderrm
|
NORMAL
|
2022-08-19T20:50:07.745296+00:00
|
2022-09-12T19:25:31.971149+00:00
| 129 | false |
**Please UPVOTE if you LIKE!!**\n**Watch this video \uD83E\uDC83 for the better explanation of the code.**\n\nhttps://www.youtube.com/watch?v=gcRdVnBLGbQ&t=145s\n\n\n**Also you can SUBSCRIBE \uD83E\uDC81 \uD83E\uDC81 \uD83E\uDC81 this channel for the daily leetcode challange solution.**\n\nhttps://t.me/dsacoder \u2B05\u2B05 **Telegram link** to discuss leetcode daily questions and other dsa problems\n\n**C++**\n```\n\nclass Solution {\npublic:\n \n int gcd(int a, int b) {\n while(b) {\n a = a % b;\n swap(a, b);\n }\n return a;\n }\n \n int mirrorReflection(int p, int q) {\n int lcm = (p*q)/gcd(p, q); // calculating lcm using gcd\n int m = lcm/p;\n int n = lcm/q;\n if(m%2==0 && n%2==1) return 0;\n if(m%2==1 && n%2==1) return 1;\n if(m%2==1 && n%2==0) return 2;\n return -1;\n }\n};\n```\n**JAVA**\n```\nclass Solution {\n public int mirrorReflection(int p, int q) {\n int incident = q; \n int reflect = p;\n \n while(incident%2 == 0 && reflect%2 == 0){\n incident /= 2;\n reflect /=2;\n }\n \n if(incident%2 == 0 && reflect%2 != 0) return 0;\n if(incident%2 == 1 && reflect%2 == 0) return 2;\n if(incident%2 == 1 && reflect%2 != 0) return 1; \n \n return Integer.MIN_VALUE;\n }\n}\n```\n**PYTHON**\n```\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n\n L = lcm(p,q)\n\n if (L//q)%2 == 0:\n return 2\n\n return (L//p)%2\n```\n**Please do UPVOTE to motivate me to solve more daily challenges like this !!**
| 4 | 0 |
[]
| 0 |
mirror-reflection
|
C# Solution | Easy to understand, Simulation, With comments
|
c-solution-easy-to-understand-simulation-gkyq
|
C#\npublic class Solution {\n public int MirrorReflection(int p, int q) {\n int height = q;\n bool moveLeft = true, goingUp = true;\n wh
|
tonytroeff
|
NORMAL
|
2022-08-04T11:20:24.431430+00:00
|
2022-08-04T11:20:24.431464+00:00
| 93 | false |
```C#\npublic class Solution {\n public int MirrorReflection(int p, int q) {\n int height = q;\n bool moveLeft = true, goingUp = true;\n while (height != 0 && height != p) {\n\t\t // If we are going up, we should add the amount of `q` to the height. If we are going down, we should subtract it.\n int multiplier = goingUp ? 1 : -1;\n height += multiplier * q;\n\t\t\t\n if (height > p) { height = 2 * p - height; goingUp = false; } // If the laser beam crossed the upper side of the square\n else if (height < 0) { height *= -1; goingUp = true; } // If the laser beam crossed the bottom side of the square\n \n\t\t\t// Change the directions. If the laser beam was going to the left, it will bounce from the left side of the square and will start moving to the right on the next iteration of the loop.\n moveLeft = !moveLeft;\n }\n \n\t\t// If we were going down, we have reached the bottom-right corner.\n if (!goingUp) return 0;\n\t\t\n\t\t// If we were moving to the right, after the directions is chaged, `moveLeft` will equal true. In this case we have reached to upper-right corner.\n if (moveLeft) return 1;\n \n\t\t// If we were moving to the left, after the directions is chaged, `moveLeft` will equal false. In this case we have reached to upper-left corner.\n\t\treturn 2;\n }\n}\n```
| 4 | 0 |
['Math', 'Geometry', 'Simulation']
| 1 |
mirror-reflection
|
Faster than 100%😍🎆 python users || Easy Python Solution🤑 || GCD ,LCM Solution😎
|
faster-than-100-python-users-easy-python-94iz
|
\n\n\n\n\n\n\n\n\n\n\n\nWe just have to find m&n which satisfy the given equation m * p = n * q, where\nm = the number of room extension \nn = the number q exte
|
ChinnaTheProgrammer
|
NORMAL
|
2022-08-04T09:20:30.047648+00:00
|
2022-08-04T09:49:18.359006+00:00
| 200 | false |
\n\n\n\n\n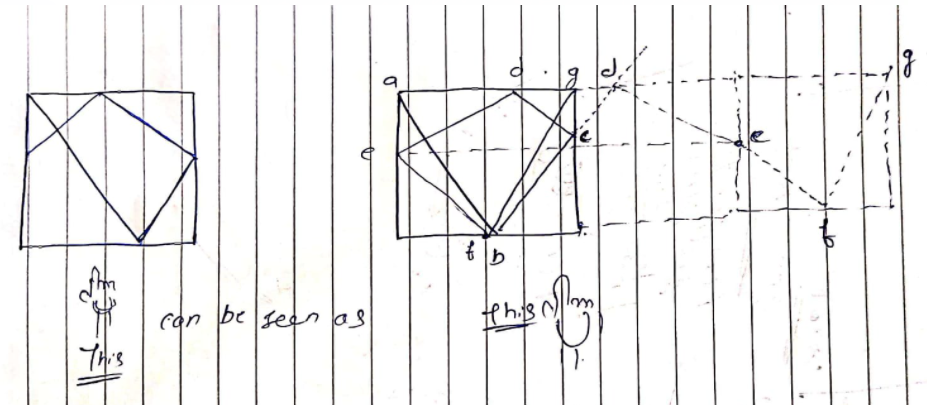\n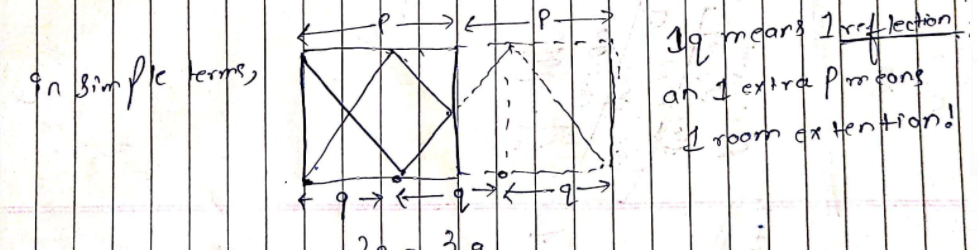\n\n\n\n\n\nWe just have to find m&n which satisfy the given equation m * p = n * q, where\nm = the number of room extension \nn = the number q extentions or the number of reflection\n\nIf the number of light reflection is odd (which means n is even), it means the corner is on west side so out answer can only be 2 in that case.\nOtherwise, the corner is on the right-hand side. The possible corners are 0 and 1.\nSo if n is odd, \nIf the number of total room extension (+the room itself) is even , it means the corner is 0. Otherwise, the corner is 1.\nNow in order to find m and n, we have to find the LCM of p &q and as we know,\nx*y=lcm(x,y)*gcd(x,y)\nso lcm=gdc//x*y\nhence, m=lcm//p || n=lcm//q\n\n**CODE**\n\n```\nclass Solution(object):\n def gcd(self,a,b):\n if a == 0:\n return b\n return self.gcd(b % a, a)\n def lcm(self,a,b):\n return (a / self.gcd(a,b))* b\n def mirrorReflection(self, p,q):\n \n lcm=self.lcm(p,q)\n m=lcm//p\n n=lcm//q\n if n%2==0:\n return 2\n if m%2==0:\n return 0\n return 1\n \n \n# basically you can just ignore the north wall and imagine the mirrors \n# as two parallel mirrors with just extending east and west walls and the end points of east walls are made of 0 reflector then 1 reflector the oth the 1th and so onn....\n# eventually we gotta find the point where m*p=n*q\n# and we can find m and n by lcm of p and q \n# now the consept is simple .....\n# if number of extensions of q(ie n) is even that means the end reflection must have happened on west wall ie. reflector 2 else \n# else there are two possibility reflector 1 or 0 which depends on the value of m(ie. the full fledged square extentions) if its even or odd\n```\n
| 4 | 0 |
['Python', 'Python3']
| 0 |
mirror-reflection
|
3-line Java solution beats 100% | Based on induction and not geometry/simulation
|
3-line-java-solution-beats-100-based-on-u8a87
|
Disclaimer: This approach might not be ideal in an interview setting, but nonetheless I liked solving this problem in this manner so thought of sharing it!\nIni
|
vanradius
|
NORMAL
|
2022-08-04T03:37:04.898786+00:00
|
2022-08-08T03:44:52.330718+00:00
| 247 | false |
**Disclaimer:** This approach might not be ideal in an interview setting, but nonetheless I liked solving this problem in this manner so thought of sharing it!\nInitially, I started thinking about this problem through geometry but was having a hard time generalizing the solution. But then I started to look for patterns for different combinations.\nThe first thing I noticed, for all odd p, the rays intersecting would alternate between 1 and 0. They will never reach 2 since for a ray to reach 2, q would be a non-integer. For example, p = 3, q needs to be 1.5 for the ray to reach 2.\nSo, if p is odd, for q (1...n) -> mirror reflected will be (1,0,1...0,1). This can easily be generalized as q % 2, since mirror reflected will be 1 when q is odd, and 0 when q is even.\nNow, the tricky part comes in when p is even. When I started comparing results for even p, I realized, that if p is a power of 2, the mirror reflected will always be 2 except for when q == p, and then mirror reflected is 1.\nHowever, this wasn\'t good enough for other even p. After digging deeper, I realized whenever q is odd, the reflected mirror is always 2, which makes sense since if you trying visualizing by stacking the box over itself eventually the ray will always end up at 2 for every odd q. Check out some of the other posts for the picture.\nThe real problem was when q is even. After going deeper, I realized, when p and q are both even, they follow the same pattern as the mirrors with half p, half q. Example:\n\np = 3\n**q = 1 -> 1\nq = 2 -> 0\nq = 3 -> 1**\n\np = 6\nq = 1 -> 2\n**q = 2 -> 1**\nq = 3 -> 2\n**q = 4 -> 0**\nq = 5 -> 2\n**q = 6 -> 1**\n\n-----------------\n\np = 2\n**q = 1 -> 2\nq = 2 -> 1**\n\np = 4\nq = 1 -> 2\n**q = 2 -> 2**\nq = 3 -> 2\n**q = 4 -> 1**\n\np = 8\nq = 1 -> 2\n**q = 2 -> 2**\nq = 3 -> 2\n**q = 4 -> 2**\nq = 5 -> 2\n**q = 6 -> 2**\nq = 7 -> 2\n**q = 8 -> 1**\n\n-----------------\n\np = 5\n**q = 1 -> 1\nq = 2 -> 0\nq = 3 -> 1\nq = 4 -> 0\nq = 5 -> 1**\n\np = 10\nq = 1 -> 2\n**q = 2 -> 1**\nq = 3 -> 2\n**q = 4 -> 0**\nq = 5 -> 2\n**q = 6 -> 1**\nq = 7 -> 2\n**q = 8 -> 0**\nq = 9 -> 2\n**q = 10 -> 1**\n\nAgain, this pattern might be difficult to find and also to calculate the answers yourself most likely would be impossible. I was able to do it only by running the code with the test cases and checking the expected results. So, not really possible in an interview or a contest.\nIn the end, the logic can be broken down to -\n```\np is odd\n\treturn q % 2;\np is even \n\tq is odd\n\t\treturn 2;\n\telse q is even\n\t\tmirrorReflection(p/2, q/2)\n```\n\nHere is the condensed code -\n\n**Recursion**\n```\n public int mirrorReflection(int p, int q) {\n if (p % 2 == 1) return q % 2; // odd p\n if (q % 2 == 1) return 2; // even p and odd q\n return mirrorReflection(p/2, q/2); // even p and q\n }\n```\n\n**Without Recursion**\n```\n\tpublic int mirrorReflection(int p, int q) {\n while (p % 2 == 0 && q % 2 == 0) { p /= 2; q /= 2; } // Recursion in the last step converted to a while loop\n return p % 2 == 1 ? q % 2 : 2; // First 2 conditions of the previous code\n }\n```
| 4 | 0 |
['Math', 'Recursion']
| 0 |
mirror-reflection
|
Can see why people hate this question
|
can-see-why-people-hate-this-question-by-zxey
|
\nfrom decimal import Decimal\nclass Solution(object):\n def isCloseNuff(self, location, receptor):\n return abs(location[0] - receptor[0]) < 0.0001 a
|
feng3245
|
NORMAL
|
2022-08-04T03:34:26.603164+00:00
|
2022-08-04T03:34:26.603198+00:00
| 257 | false |
```\nfrom decimal import Decimal\nclass Solution(object):\n def isCloseNuff(self, location, receptor):\n return abs(location[0] - receptor[0]) < 0.0001 and abs(location[1] - receptor[1]) < 0.0001\n def movingDown(self, trajectory):\n return trajectory[0] < 0\n def movingUp(self, trajectory):\n return trajectory[0] > 0\n def bounce(self, currentLocation, trajectory, p):\n # if right wall bounce up IE negative x\n # if top wall bounce down IE negative x and y\n # if left wall bounce right down negative y and pos x\n # if bottom wall bounce up right IE positive x and y\n currentTrajectory = trajectory\n nextWall = None\n #x direction should reverse on x walls\n upperLeft = (p, 0)\n lowerLeft = (0, 0)\n lowerRight = (0, p)\n upperRight = (p, p)\n \n if currentLocation[1] == p or currentLocation[1] == 0:\n currentTrajectory = (currentTrajectory[0], currentTrajectory[1]*-1)\n\n if currentLocation[0] == p or currentLocation[0] == 0:\n currentTrajectory = (currentTrajectory[0]*-1, currentTrajectory[1])\n\n \n if currentLocation[1] == p: \n if self.movingUp(currentTrajectory):\n nextWall = upperLeft\n else:\n nextWall = lowerLeft\n if currentLocation[1] == 0:\n if self.movingDown(currentTrajectory):\n nextWall = lowerRight\n else:\n nextWall = upperRight\n #y direction reverses on y walls \n if currentLocation[0] == p:\n if currentTrajectory[1] < 0:\n nextWall = lowerLeft\n else:\n nextWall = lowerRight\n if currentLocation[0] == 0:\n if currentTrajectory[1] > 0:\n nextWall = upperRight\n else:\n nextWall = upperLeft\n distance = min((nextWall[0] - currentLocation[0])/currentTrajectory[0], (nextWall[1] - currentLocation[1])/currentTrajectory[1])\n newY = currentLocation[0] + currentTrajectory[0] * distance\n if (nextWall[0] - currentLocation[0])/currentTrajectory[0] < (nextWall[1] - currentLocation[1])/currentTrajectory[1]:\n newY = Decimal(nextWall[0])\n newX = currentLocation[1] + currentTrajectory[1] * distance\n if (nextWall[0] - currentLocation[0])/currentTrajectory[0] > (nextWall[1] - currentLocation[1])/currentTrajectory[1]:\n newX = Decimal(nextWall[1])\n return currentTrajectory, (newY, newX)\n def mirrorReflection(self, p, q):\n """\n :type p: int\n :type q: int\n :rtype: int\n """\n receptors = [(0,p), (p, p), (p, 0)]\n currentLocation = (q, p)\n trajectory = (q/(p*Decimal(1.0)), Decimal(1.0))\n while not any([self.isCloseNuff(currentLocation, receptor) for receptor in receptors]):\n trajectory, currentLocation = self.bounce(currentLocation, trajectory, p)\n return [i for i,receptor in enumerate(receptors) if self.isCloseNuff(currentLocation, receptor)][0]\n```\n\nRounding error was driving me nuts
| 4 | 0 |
['Python']
| 0 |
mirror-reflection
|
C++ || Easy || Maths || Geometry || Explaination
|
c-easy-maths-geometry-explaination-by-ya-euh7
|
Approach to solve this question:-\n 1) The given question is based on Geometry and Math. Requirement is to think the approach using pen and paper which makes t
|
yashgaherwar2002
|
NORMAL
|
2022-08-04T02:34:53.769838+00:00
|
2022-08-07T11:23:05.218830+00:00
| 231 | false |
Approach to solve this question:-\n 1) The given question is based on Geometry and Math. Requirement is to think the approach using pen and paper which makes the question very easy and clear.\n 2) Here we need to consider extension and reflection and need to derive the the equation that is:-\n p * extension = q * reflection\n 3) After getting this equation the question become quite simple.\n 4) We need to run a loop until anyone of reflection and extension becomes odd.\n 5) At last need to check the below conditions:-\n --> If Reflection is odd and extension is even then the receptor is 0;\n\t\t\t--> If Reflection is even and extension is odd then the receptor is 2;\n\t\t\t--> If Reflection is odd and extension is odd then the receptor is 1;\n\t\t\t--> Else remaining all condition will not reach to receptor and hence return -1;\n\t\t\t\n\t\t\tNote:- Try to solve the eg. by considering p=3 and q=2. It will give the proper idea about how the equation is generated. And sample test cases are too imp.\n\t\t\t :- It can also be solved using gcd function but for proper logic building first try to think it mathematically by creating equation.\n\t\t\t\n\t\t\t\nclass Solution {\npublic:\n \n // Geometry and Math Approach\n \n int mirrorReflection(int p, int q) {\n int ext=q;\n int ref=p;\n \n while(ref%2==0 && ext%2==0){\n ref=ref/2;\n ext=ext/2;\n }\n \n if(ref%2==1 && ext%2==0){\n return 0;\n }\n else if(ref%2==0 && ext%2==1){\n return 2;\n }\n else if(ref%2==1 && ext%2==1){\n return 1;\n }\n else{\n return -1; \n }\n }\n};
| 4 | 0 |
['Math', 'Geometry', 'C++']
| 1 |
mirror-reflection
|
[PHP] Easy solution with explanations and pictures!
|
php-easy-solution-with-explanations-and-m7j8n
|
Hello! This solution in two steps.\n\nStep 1. We are looking for the point where the line will be in the corner. Looking for n and m so that q * n = p * m is co
|
rozinko
|
NORMAL
|
2020-11-17T22:37:33.989686+00:00
|
2020-11-17T22:38:27.396138+00:00
| 131 | false |
**Hello! This solution in two steps.**\n\n**Step 1.** We are looking for the point where the line will be in the corner. Looking for `n` and `m` so that `q * n = p * m` is correct.\n\n**Step 2.** Return the result based on the values of `n` and `m`.\n\n**if `n` is even, then result will be 2.**\n\n\n**if `n` is odd and `m` is odd, then result will be 1.**\n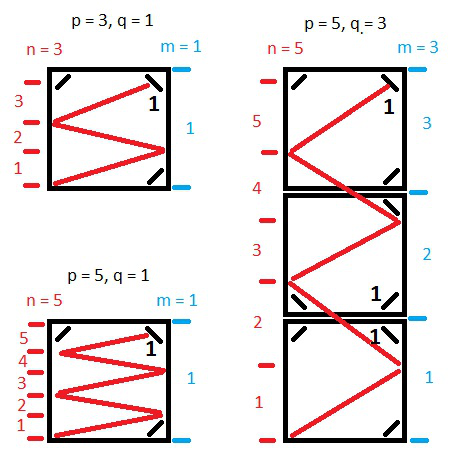\n\n**if `n` is odd and `m` is even, then result will be 0.**\n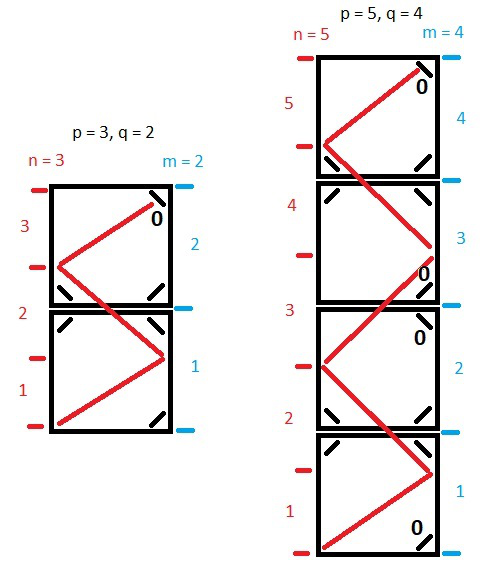\n\n**And code:**\n```\nfunction mirrorReflection($p, $q)\n {\n $n = $m = 1;\n while ($q * $n != $p * $m) {\n $n++;\n if ($p * $m < $q * $n) $m++;\n }\n return $n % 2 ? $m % 2 : 2;\n }\n```\n\nIf you like this solution and explanations, please **Upvote**!
| 4 | 0 |
['PHP']
| 0 |
mirror-reflection
|
[Java] Simultation of the ray | Explained | Intuition | Diagram
|
java-simultation-of-the-ray-explained-in-d9b8
|
Intution: A ray will have direction before and after touching each side of the mirror, Right. So. What I am using here is the ray\'s direction after touching ho
|
a_lone_wolf
|
NORMAL
|
2020-11-17T17:54:51.508666+00:00
|
2020-11-18T05:13:45.892335+00:00
| 456 | false |
Intution: A ray will have direction before and after touching each side of the mirror, Right. So. What I am using here is the ray\'s direction after touching horizontal sides and to check whether r == 0 that means whether there is all q\'s which gets completed, and on that basis which receptor is it going to touch. I know it is still not explanatory.\n\nLet me explain it using diagrams now:-\n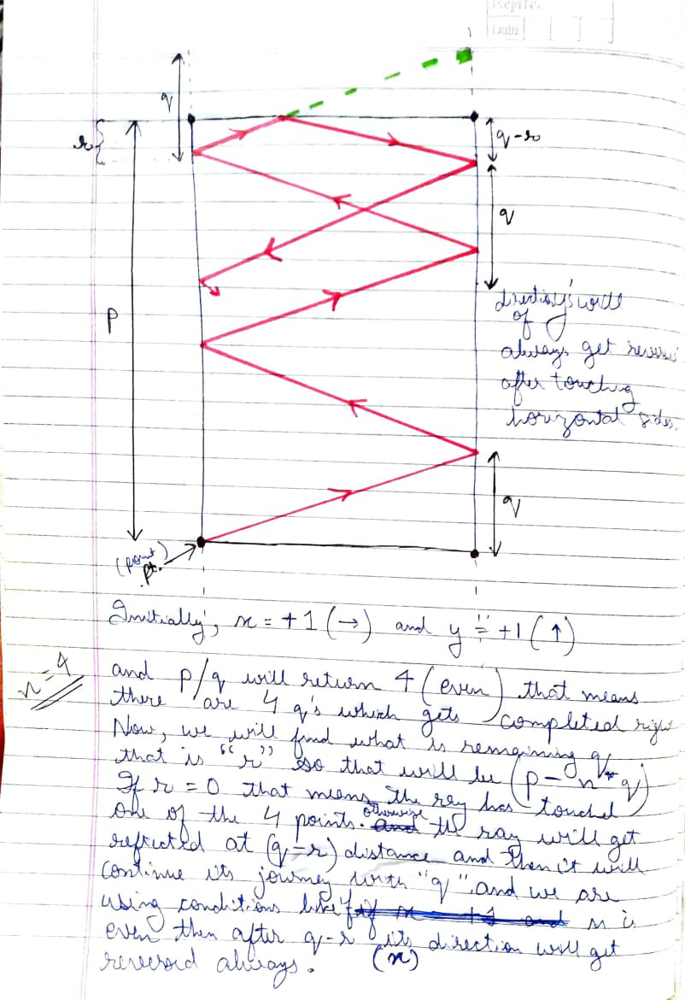\n\n\n\n```\nclass Solution {\n public int mirrorReflection(int p, int q) {\n int xdir = 1;\n int ydir = 1;\n \n double dp = p;\n \n while(true){\n int n = (int)dp/q;\n double r = dp - n*q;\n\n if(r == 0){\n if(ydir == 1){\n if(xdir == 1)\n return n % 2 == 0? 2 : 1;\n else if(xdir == -1)\n return n % 2 == 0? 1 : 2;\n }\n else{\n if((xdir == -1 && n % 2 == 0) || (xdir == 1 && n % 2 != 0)){\n return 0;\n }\n }\n }\n \n dp = p - (q-r);\n \n if(n % 2 == 0){\n xdir *= -1;\n }\n \n ydir *= -1;\n }\n }\n}\n```\nPlease upvote if you like it :)
| 4 | 2 |
[]
| 1 |
mirror-reflection
|
INTUITIVE SoLution with explanation...
|
intuitive-solution-with-explanation-by-r-pm52
|
This approach works because of the given constraint i.e. 0<=q<=p. So each time we move q distance vertically,we are definately going to hit on the alternate sid
|
rakesh_yadav
|
NORMAL
|
2020-11-17T10:34:39.360200+00:00
|
2020-11-17T19:06:38.752938+00:00
| 281 | false |
This approach works because of the given constraint i.e. **0<=q<=p**. So each time we move q distance vertically,we are definately going to hit on the alternate side i.e. left side if currently on right side and vice versa.\nIf vertical distance equal to 0 or p when we hit any side, we will be at any of the receipters.\n```\nclass Solution {\n public int mirrorReflection(int p, int q) {\n int vertical=0; //Vertical distance\n boolean isRight=true; //Side we are on currently i.e. left/right\n\t\tboolean up=true; //Are we moving up or down currently\n while(true){\n if(up)\n vertical+=q; //if moving up increment vertical distance\n else\n vertical-=q; //if moving down decrement vertical distance\n if(vertical==0) \n return 0;\n else if(vertical==p){\n if(isRight)\n return 1;\n else\n return 2;\n }\n else if(vertical>p){ //if we go higher than box\n up=false; //move down \n vertical=2*p-vertical; //update the moved distance \n }\n else if(vertical<0){ //if we go below the box\n up=true; //move up\n vertical=-vertical; //update distance moved\n }\n isRight=!isRight; //change side each time\n }\n }\n}\n```
| 4 | 0 |
[]
| 0 |
mirror-reflection
|
C++ Solutions 0 ms(with Image Explain)
|
c-solutions-0-mswith-image-explain-by-sh-f2bd
|
Mirror Imaging can be like this:\n\n\nignore horizontal coordinate so we can see this answer like this:\n\n\n2 -> (horizontal, kp), k is odd\n1 -> (horizontal,
|
shi-zhe
|
NORMAL
|
2018-07-05T07:16:43.645564+00:00
|
2018-09-30T03:17:33.278979+00:00
| 494 | false |
Mirror Imaging can be like this:\n\n\nignore horizontal coordinate so we can see this answer like this:\n\n\n2 -> (horizontal, kp), k is odd\n1 -> (horizontal, kp), k is odd\n0 -> (horizontal, kp), k is even\n\nthen we use q to check the receptors is at right or left\n2 -> (horizontal, nq), n is even\n1 -> (horizontal, nq), n is odd\n0 -> (horizontal, nq), n is odd\n\ngetting (kp=nq) by using lcm, getting lcm by using gcd, apparently, we get the answer.\n\n```\nclass Solution {\npublic:\n int mirrorReflection(int p, int q) {\n int lcm = p * q / gcd(q, p);\n int k = lcm / p;\n int n = lcm / q;\n return (k & 0b1) ? (n & 0b1 ? 1 : 2) : (n & 0b1 ? 0 : -1);\n }\n int gcd(int a, int b){\n if(b)while((b %= a) && (a %= b));\n return a + b;\n } \n};\n```
| 4 | 0 |
[]
| 0 |
mirror-reflection
|
✅Short || C++ || Java || PYTHON || Explained Solution✔️ || Beginner Friendly ||🔥 🔥 BY MR CODER
|
short-c-java-python-explained-solution-b-qdcx
|
Please UPVOTE if you LIKE!!\nWatch this video \uD83E\uDC83 for the better explanation of the code.\n\nhttps://www.youtube.com/watch?v=gcRdVnBLGbQ&t=145s\n\n\nAl
|
mrcoderrm
|
NORMAL
|
2022-09-12T19:25:53.697832+00:00
|
2022-09-12T19:25:53.697946+00:00
| 82 | false |
**Please UPVOTE if you LIKE!!**\n**Watch this video \uD83E\uDC83 for the better explanation of the code.**\n\nhttps://www.youtube.com/watch?v=gcRdVnBLGbQ&t=145s\n\n\n**Also you can SUBSCRIBE \uD83E\uDC81 \uD83E\uDC81 \uD83E\uDC81 this channel for the daily leetcode challange solution.**\n\nhttps://t.me/dsacoder \u2B05\u2B05 **Telegram link** to discuss leetcode daily questions and other dsa problems\n\n**C++**\n```\n\nclass Solution {\npublic:\n \n int gcd(int a, int b) {\n while(b) {\n a = a % b;\n swap(a, b);\n }\n return a;\n }\n \n int mirrorReflection(int p, int q) {\n int lcm = (p*q)/gcd(p, q); // calculating lcm using gcd\n int m = lcm/p;\n int n = lcm/q;\n if(m%2==0 && n%2==1) return 0;\n if(m%2==1 && n%2==1) return 1;\n if(m%2==1 && n%2==0) return 2;\n return -1;\n }\n};\n```\n**JAVA**\n```\nclass Solution {\n public int mirrorReflection(int p, int q) {\n int incident = q; \n int reflect = p;\n \n while(incident%2 == 0 && reflect%2 == 0){\n incident /= 2;\n reflect /=2;\n }\n \n if(incident%2 == 0 && reflect%2 != 0) return 0;\n if(incident%2 == 1 && reflect%2 == 0) return 2;\n if(incident%2 == 1 && reflect%2 != 0) return 1; \n \n return Integer.MIN_VALUE;\n }\n}\n```\n**PYTHON**\n```\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n\n L = lcm(p,q)\n\n if (L//q)%2 == 0:\n return 2\n\n return (L//p)%2\n```\n**Please do UPVOTE to motivate me to solve more daily challenges like this !!**
| 3 | 0 |
[]
| 0 |
mirror-reflection
|
Java Easiest Solution || 0Ms Runtime Faster Than 100% online submission || Liner Code
|
java-easiest-solution-0ms-runtime-faster-3gjo
|
\nclass Solution {\n public int mirrorReflection(int p, int q) {\n int extens = q; \n int reflect = p;\n \n while(extens%2 == 0 &
|
Hemang_Jiwnani
|
NORMAL
|
2022-08-07T08:12:02.231461+00:00
|
2022-08-07T08:12:02.231508+00:00
| 117 | false |
```\nclass Solution {\n public int mirrorReflection(int p, int q) {\n int extens = q; \n int reflect = p;\n \n while(extens%2 == 0 && reflect%2 == 0){\n extens /= 2;\n reflect /=2;\n }\n \n if(extens%2 == 0 && reflect%2 != 0) return 0;\n if(extens%2 == 1 && reflect%2 == 0) return 2;\n if(extens%2 == 1 && reflect%2 != 0) return 1; \n \n return Integer.MIN_VALUE;\n }\n}\n```
| 3 | 0 |
['Java']
| 0 |
mirror-reflection
|
[C++] Very very very easy to understand with detailed examples and pictures
|
c-very-very-very-easy-to-understand-with-537i
|
I was Inspired by : https://leetcode.com/problems/mirror-reflection/discuss/146336/Java-solution-with-an-easy-to-understand-explanation\n\n\n\n\nIn the example1
|
franky50616
|
NORMAL
|
2022-08-05T11:18:49.666375+00:00
|
2022-08-05T11:20:45.490497+00:00
| 201 | false |
I was Inspired by : https://leetcode.com/problems/mirror-reflection/discuss/146336/Java-solution-with-an-easy-to-understand-explanation\n\n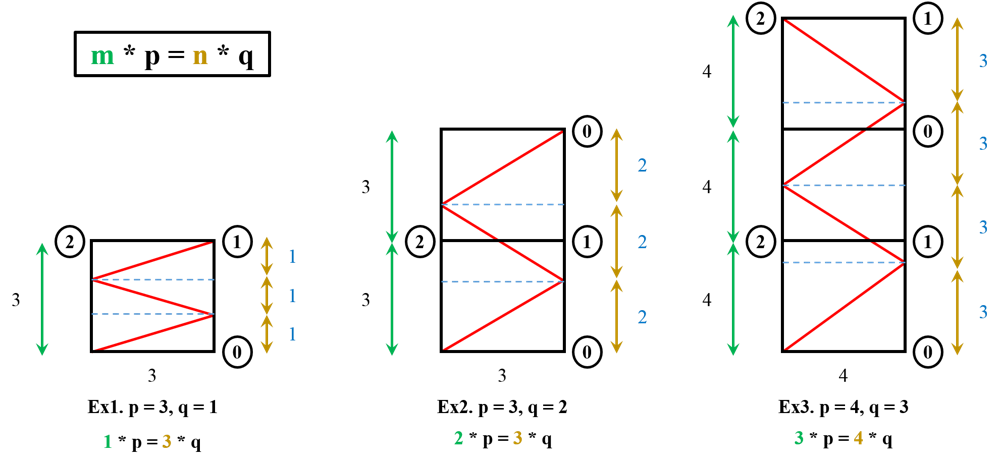\n\n\nIn the example1 (p=3, q=1), after <strong>three times</strong>, the laser ray(red line) went to the receptor1. \nIn the example2 (p=3, q=2), after <strong>three times</strong> transmitted, the laser ray(red line) went to the receptor0. But it also need <strong>one original room</strong> and <strong>one flipped room</strong>.\nIn the example3 (p=4, q=3), after <strong>four times</strong> transmitted, the laser ray(red line) went to the receptor2. But it also need <strong>two original room</strong> and <strong>one flipped room</strong>. \n\nThe description of this problem tells us <strong>"The test cases are guaranteed so that the ray will meet a receptor eventually".</storng>\n\nFrom the above three examples, we can find some patterns.\nPattern1 : If the last room is the original room, then the top receptor would be either receptor2 or receptor1.\nPattern2 : If the last room is the filpped room, then the top receptor would be only receptor0.\nPattern3 : If the laser ray(red line) went odd times, than it would be finallly finished in the right side.\nPattern4 : If the laser ray(red line) went even times, than it would be finallly finished in the left side.\n\nAssume m is the number of rooms, and n is the number of laser ray(red line) transmitted.\nFrom the above four patterns, we can conclude to the below three conditions and results.\n1. if m is even, then return 0. (Pattern2)\n2. if m is odd and n is odd, then return 1. (Pattern1 + Pattern3)\n3. if m is odd and n is even, then return 2. (Pattern1 + Pattern4)\n\nSo our our goal would be very easy. We just need to find the m and n from both p and q.\nWe could simply find the <strong>least common mltiple (lcm)</strong> of p and q, and uses lcm/p and lcm/q to get m and n.\nThere is a formula ```p * q = least_common_mltiple * greatest_common_divisor```, so ```lcm = p * q / gcd```.\n\nThe C++ version code shows below\n```cpp\nclass Solution {\npublic:\n int mirrorReflection(int p, int q)\n {\n int lcm=least_common_multiple(p,q);\n \n int m=lcm/p;\n int n=lcm/q;\n \n if(m%2==0) return 0; //the last was the flipped room\n if(m%2==1 && n%2==1) return 1; //the last was the original room and the laser ray finished in the right side\n if(m%2==1 && n%2==0) return 2; //the last was the original room and the laser ray finished in the left side\n \n //dummy return\n return -1;\n }\n \n int least_common_multiple(int p, int q)\n {\n int gcd=greatest_common_divisor(p,q);\n return p*q/gcd;\n }\n \n int greatest_common_divisor(int p, int q)\n {\n /*\n gcd(16,12)=gcd(12,4)=gcd(4,0)\n gcd(5,4)=gcd(4,1)=gcd(1,0)\n */\n \n while(q!=0)\n {\n int tmp=p;\n p=q;\n q=tmp%q;\n }\n \n return p;\n }\n};\n```\n\nHope this can help everyone!
| 3 | 0 |
['C']
| 0 |
mirror-reflection
|
✅Super Fast GCD/LCM Java Solute in Solvent✅ with explanation
|
super-fast-gcdlcm-java-solute-in-solvent-tukp
|
Explanation: \nAt first I am finding the triangle\'s base and height for which the ideal tip of the triangle touches the corner of the extended box. Then, find
|
Lil_ToeTurtle
|
NORMAL
|
2022-08-04T18:18:42.639707+00:00
|
2022-08-04T18:26:54.877276+00:00
| 89 | false |
# Explanation: \nAt first I am finding the triangle\'s base and height for which the ideal tip of the triangle touches the corner of the extended box. Then, find the number of times the box will fit in the height and the base. \n# Now comes the important part:\nWe can see that for the tip of triangle in the even rows are always 0 and the odd rows, The corner alternates by 1 and 2\nSo for odd column it is 1 and for even it is 2\n\n# The reason for GCD and LCM:\nLCM of p and q is the height of the triangle. \nGCD is was because the timecomplexity to find the gcd is faster than finding lcm. Now, we know LCM*GCD = P*Q\nnow implementing the formula I calculated the LCM from GCD\n\n# The image of a sample Grid is:\n\n 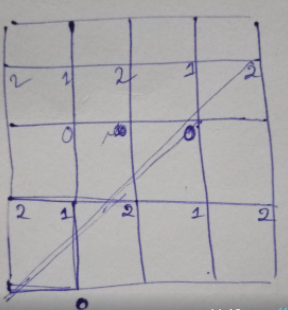\n\n\nThe CODE is -->\n```\nclass Solution { // 100% Faster - 0ms Solution\n int gcd(int n1,int n2){\n while(n1 != n2) \n if(n1 > n2) n1 -= n2;\n else n2 -= n1;\n return n1;\n }\n public int mirrorReflection(int p, int q) {\n int lcm=(p*q)/gcd(p,q);\n int height=lcm, base=(height*p)/q; // triangle\'s dimention\n int y=height/p, x=base/p; // number boxes needed to form the triangle\n \n if(y%2==0) return 0;\n else if(x%2==1) return 1;\n else return 2;\n }\n}\n```
| 3 | 0 |
['Java']
| 1 |
mirror-reflection
|
Naive and Mathmatical approach - both faster than 100%
|
naive-and-mathmatical-approach-both-fast-upiv
|
Naive Approach\nJust simulate the reflection using a loop until you reach a corner. Keep track of three things in each iteration:\n which wall the laser is hitt
|
sadmanrizwan
|
NORMAL
|
2022-08-04T07:41:19.538774+00:00
|
2022-08-04T07:41:19.538812+00:00
| 129 | false |
**Naive Approach**\nJust simulate the reflection using a loop until you reach a corner. Keep track of three things in each iteration:\n* which wall the laser is hitting (left / right)\n* which direction the laser is going (up / down)\n* height **h** of the hitting point\n\nThe loop will iterate **LCM(p, q)** times, which will be equal to **pq** if **p** and **q** both are prime numbers.\n```\nclass Solution {\npublic:\n int mirrorReflection(int p, int q) {\n int h = q;\n bool up = true, left = false;\n \n while(true) {\n if(h == 0 && !left) return 0;\n if(h == p) return left ? 2 : 1;\n \n if(up) {\n int x = h + q;\n if(x > p) x = p - (x - p), up = false;\n h = x;\n }\n else {\n int x = h - q;\n if(x < 0) x = -x, up = true;\n h = x;\n }\n \n left = !left;\n }\n \n return 0;\n }\n};\n```\n\n**Mathmatical Approach**\nTotal height / vertical distance the laser covers until it reaches a corner is equal to **x = LCM(p, q)**. \nHitting points on the left wall are **2q, 4q, 6q....**\nHitting points on the right wall are **q, 3q, 5q, 7q...**\n\nSo, if **x = y * q** where **y** is an even number, it hits the corner on the left wall.\nOtherwise, it hits one of the corners on the right wall. Now how can we find out which corner it hits on the right wall?\n\nWe can write **x = z * p**, since **x** is a multiple of **p** too.\nIt is easy to see that the laser will hit the bottom corner if **z** is even, otherwise it will hit the top corner.\n```\nclass Solution {\npublic:\n int gcd(int a, int b) {\n return b ? gcd(b, a % b) : a;\n }\n \n int lcm(int a, int b) {\n return (a * b) / gcd(a, b);\n }\n \n int mirrorReflection(int p, int q) {\n int x = lcm(p, q);\n int y = x / q;\n int z = x / p;\n \n if(y & 1) return (z & 1) ? 1 : 0;\n return 2;\n }\n};\n```
| 3 | 0 |
[]
| 0 |
mirror-reflection
|
Java | Easy | 100% faster | GCD
|
java-easy-100-faster-gcd-by-tauhait-h6ny
|
\n\tpublic int mirrorReflection(int p, int q) {\n int m = 1, n = 1;\n int gcd = gcd(p,q);\n p /= gcd;\n q /= gcd;\n while (p*
|
tauhait
|
NORMAL
|
2022-08-04T05:57:31.104467+00:00
|
2022-08-04T05:57:58.250711+00:00
| 172 | false |
```\n\tpublic int mirrorReflection(int p, int q) {\n int m = 1, n = 1;\n int gcd = gcd(p,q);\n p /= gcd;\n q /= gcd;\n while (p*m != q*n){\n n++;\n m = (q*n)/p;\n }\n //p*m == q*n\n\n if(n % 2 == 0) return 2;\n else if(m % 2 == 1) return 1;\n else return 0;\n }\n private int gcd(int p, int q){\n if(q == 0) return p;\n return gcd(q, p % q);\n }\n```\nFor visual understanding \nRef: https://www.youtube.com/watch?v=TEh0Fcu5Nok\n
| 3 | 0 |
['Java']
| 0 |
mirror-reflection
|
JAVA ll EASY-TO-UNDERSTAND SOLUTION
|
java-ll-easy-to-understand-solution-by-s-ig9v
|
class Solution {\n public int mirrorReflection(int p, int q) {\n \n while(q % 2 == 0 && p % 2 == 0){\n q /=2;\n p /= 2;\n
|
Samirtaa
|
NORMAL
|
2022-08-04T05:40:33.593824+00:00
|
2022-08-04T05:40:33.593886+00:00
| 56 | false |
class Solution {\n public int mirrorReflection(int p, int q) {\n \n while(q % 2 == 0 && p % 2 == 0){\n q /=2;\n p /= 2;\n }\n \n //using our observations here\n if(q % 2 == 0 && p % 2 != 0){\n return 0;\n }\n if(q % 2 != 0 && p % 2 == 0){\n return 2;\n }\n if(q % 2 != 0 && p % 2 != 0){\n return 1;\n }\n return -1;\n }\n}
| 3 | 0 |
['Math', 'Java']
| 0 |
mirror-reflection
|
[JAVA] 6 liner 0ms, 100 % faster solution
|
java-6-liner-0ms-100-faster-solution-by-s7mfc
|
\nclass Solution {\n public int mirrorReflection(int p, int q) {\n while(p % 2 == 0 && q % 2 == 0) {\n p /= 2;\n q /= 2;\n }\n
|
Jugantar2020
|
NORMAL
|
2022-08-04T05:27:50.949824+00:00
|
2022-08-04T05:27:50.949852+00:00
| 184 | false |
```\nclass Solution {\n public int mirrorReflection(int p, int q) {\n while(p % 2 == 0 && q % 2 == 0) {\n p /= 2;\n q /= 2;\n }\n if(p % 2 == 0) return 2;\n else if(q % 2 == 0) return 0;\n else return 1;\n }\n}\n```\n# PLEASE UPVOTE IF IT WAS HELPFULL
| 3 | 0 |
['Math', 'Geometry', 'Java']
| 0 |
mirror-reflection
|
C++ || Explained || Easiest
|
c-explained-easiest-by-kanupriya_11-0cb0
|
Explained each and every step using comments!!\n~ Kindly upvote if you got some help :)\n\n\nclass Solution {\npublic:\n int mirrorReflection(int p, int q) {
|
kanupriya_11
|
NORMAL
|
2022-08-04T05:03:03.188396+00:00
|
2022-08-04T05:03:03.188437+00:00
| 233 | false |
**Explained each and every step using comments!!**\n*~ Kindly upvote if you got some help :)*\n\n```\nclass Solution {\npublic:\n int mirrorReflection(int p, int q) {\n int g = gcd(p,q); //taking gcd because the value of p and q may have some common factors "MOST IMPO STEP"\n p=p/g;\n q=q/g;\n \n if(p==q) //if both are equal then return 1 : as it would be 45degree when both have same value\n return 1;\n \n if(p%2==0) //if p is even then return 2\n {\n return 2;\n }\n else \n {\n if(q%2==0) //if p is odd and q is even\n return 0;\n else //if p is odd and q is also odd\n return 1;\n }\n }\n};\n```
| 3 | 0 |
['Math', 'C', 'C++']
| 0 |
mirror-reflection
|
[Java/JavaScript/Python] solution
|
javajavascriptpython-solution-by-himansh-w9yq
|
Java\n\nclass Solution {\n public int mirrorReflection(int p, int q) {\n while(p % 2 == 0 && q % 2 == 0){\n p /= 2;\n q /= 2;\n
|
HimanshuBhoir
|
NORMAL
|
2022-08-04T01:00:00.492082+00:00
|
2022-08-04T01:14:28.431732+00:00
| 131 | false |
**Java**\n```\nclass Solution {\n public int mirrorReflection(int p, int q) {\n while(p % 2 == 0 && q % 2 == 0){\n p /= 2;\n q /= 2;\n }\n if(p % 2 == 0 && q % 2 == 1) return 2;\n else if(p % 2 == 1 && q % 2 == 1) return 1;\n else return 0;\n }\n}\n```\n**JavaScript**\n```\nvar mirrorReflection = function(p, q) {\n while(p % 2 == 0 && q % 2 == 0){\n p /= 2\n q /= 2\n }\n if(p % 2 == 0 && q % 2 == 1) return 2\n else if(p % 2 == 1 && q % 2 == 1) return 1\n else return 0\n};\n```\n**Python**\n```\nclass Solution(object):\n def mirrorReflection(self, p, q):\n while p % 2 == 0 and q % 2 == 0:\n p /= 2\n q /= 2\n if p % 2 == 0 and q % 2 == 1: return 2\n elif p % 2 == 1 and q % 2 == 1: return 1\n else: return 0\n```
| 3 | 2 |
['Python', 'Java', 'JavaScript']
| 0 |
mirror-reflection
|
Easy C++ Solution || even and odd
|
easy-c-solution-even-and-odd-by-jahnavim-4udf
|
\n int mirrorReflection(int p, int q) { \n //If p and q are even ,divide both p,q by 2 until at least one becomes odd.\n while(p%2==0 && q%2==0)\n
|
jahnavimahara
|
NORMAL
|
2022-08-04T00:29:36.103507+00:00
|
2022-08-04T00:29:36.103549+00:00
| 66 | false |
```\n int mirrorReflection(int p, int q) { \n //If p and q are even ,divide both p,q by 2 until at least one becomes odd.\n while(p%2==0 && q%2==0)\n {\n p/=2;\n q/=2;\n }\n\n if(p%2!=0 && q%2==0)\n return 0;\n\n if(p%2==0 && q%2!=0)\n return 2;\n return 1;\n }\n```\n
| 3 | 0 |
['Math']
| 0 |
mirror-reflection
|
Java Solution
|
java-solution-by-solved-k8vh
|
\nclass Solution {\n public int mirrorReflection(int p, int q) {\n while (p % 2 == 0 && q % 2 == 0) {\n p /= 2;\n q /= 2;\n
|
solved
|
NORMAL
|
2022-08-04T00:02:40.010248+00:00
|
2022-08-04T00:02:40.010275+00:00
| 283 | false |
```\nclass Solution {\n public int mirrorReflection(int p, int q) {\n while (p % 2 == 0 && q % 2 == 0) {\n p /= 2;\n q /= 2;\n }\n if (p % 2 == 0) {\n return 2;\n } else if (q % 2 == 0) {\n return 0;\n } else {\n return 1;\n }\n }\n}\n```
| 3 | 1 |
['Java']
| 0 |
mirror-reflection
|
C++ quick solution with explanation
|
c-quick-solution-with-explanation-by-cha-31yf
|
`\nclass Solution {\npublic:\n int mirrorReflection(int p, int q) {\n // We should try to avoid complex reflection calculation. Instead just assume th
|
chase1991
|
NORMAL
|
2021-01-24T00:55:52.543759+00:00
|
2021-01-24T00:55:52.543789+00:00
| 294 | false |
```\nclass Solution {\npublic:\n int mirrorReflection(int p, int q) {\n // We should try to avoid complex reflection calculation. Instead just assume there is no north boundary and \n // the layser can reflect all the way to the infinite north. Then from the knowledge of physics, it is easy\n // to know when we reach the receptor, we must have reflect for N times and (q*N) can be divided by p.\n // And it is also obvious if N is even number then we reach the receptor 2. Otherwise, we can calculate how many\n // mirrors we have gone through. If the number is odd, then we reach the receptor 1, else receptor 0.\n int ref = 1;\n while ((q * ref) % p != 0)\n {\n ++ref;\n }\n \n // To reach 2, ref must be even;\n // to reach 1, ref must be odd and mod must be odd;\n // to reach 0, ref must be odd and mod must be even.\n int mod = (q * ref) / p;\n if (ref % 2 == 0)\n {\n return 2;\n }\n \n return mod % 2 == 1 ? 1 : 0;\n }\n};\n``
| 3 | 0 |
[]
| 0 |
mirror-reflection
|
C++ | mapping 4 mirrors into 2 mirrors | beats 94%
|
c-mapping-4-mirrors-into-2-mirrors-beats-8ln5
|
\nclass Solution {\npublic:\n enum {NE, NW, SW, SE};\n int mirrorReflection(int p, int q) {\n string s[] = {"NE", "NW", "SW", "SE"};\n if(no
|
sanganak_abhiyanta
|
NORMAL
|
2020-11-17T21:35:28.358578+00:00
|
2020-11-17T21:35:28.358609+00:00
| 104 | false |
```\nclass Solution {\npublic:\n enum {NE, NW, SW, SE};\n int mirrorReflection(int p, int q) {\n string s[] = {"NE", "NW", "SW", "SE"};\n if(not q) return 0;\n if(q == p) return 1;\n int direction = NE;\n int stepY = q;\n while(q) {\n // cout<<q<<" "<<s[direction]<<endl;\n if((q + stepY) <= p) {\n switch(direction){\n case NE: direction = NW; break;\n case NW: direction = NE; break;\n case SE: direction = SW; break;\n case SW: direction = SE; break;\n }\n }\n else{\n switch(direction){\n case NE: direction = SW; break;\n case NW: direction = SE; break;\n case SE: direction = NW; break;\n case SW: direction = NE; break;\n }\n }\n q += stepY;\n q = q % p;\n }\n // cout<<"final "<<q<<" "<<s[direction]<<endl;\n if(direction == NE) return 1;\n if(direction == NW) return 2;\n if(direction == SE) return 0;\n return -1;\n }\n};\n```\n\n### Theory\n```\nNW--NE\n| |\nSW--SE\n```\n\nI am considering reflection only along vertical mirrors. (*Reflections along horizontal mirrors can be extended as reflection along vertical mirrors.)*\n\nFinding solution requires checking two components.\n1. Check if ray reaches one of the receptors 2, 1, or 0. Or say one of the coordinates {x, y} = {p,p}, {0, p} or {0, 0}.\n\t- with every reflection y coordinate will change to (y+q). We can percieve it as virtual point on vertical mirrors if (y+q) exceeds box side length \'p\'.\n\n2. Find the direction in which ray was moving before it hit one of the receptors:\n\t- If the reflection \'q\' coordinate is more than (p/2), then ray will be reflected from one of the horizontal mirrors before reaching opposite vertical mirror. So direction of ray will change twice - once at current vertical mirror and once at one of the horizontal mirrors. \n If the reflection \'q\' coordinate is less than or equal to (p/2), it will reach the opposite vertical mirror in one reflection.
| 3 | 0 |
[]
| 0 |
mirror-reflection
|
[Concept] Simulation, Easy to understand (with illustration)
|
concept-simulation-easy-to-understand-wi-ml6x
|
I\'ve come up with this trivial solution (not optimal), but quite easy to understand, so I\'d like to share with you guys.\n\nWith different directions, the ray
|
iamsuperwen
|
NORMAL
|
2020-11-17T16:44:02.643841+00:00
|
2020-11-17T17:25:23.806493+00:00
| 194 | false |
I\'ve come up with this trivial solution (not optimal), but quite easy to understand, so I\'d like to share with you guys.\n\nWith different directions, the ray meet different receptors.\n* d is the distance to go.\n* For every q, the ray meets the vertical mirror, so the horizontal direction *(right)* will change.\n* If d is negative, the ray meets the horizontal mirros, so the vertical direction *(up)* will change.\n* If the ray meet the bottom left coner, it will reflect to *receptor 1*.\n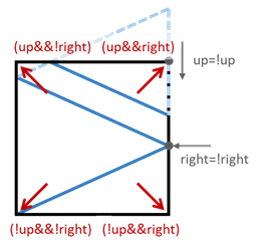\n\n\n\n```cpp\n int mirrorReflection(int p, int q) {\n int d=p;\n bool up=1, right=1;\n while(d){\n d-=q;\n if(d==0){\n if(!(right ^ up)) return 1;\n if(right && !up) return 0;\n if(!right && up) return 2;\n }\n right=!right;\n if(d<0){\n d+=p;\n up=!up;\n }\n }\n return -1;\n }\n```
| 3 | 0 |
['C']
| 0 |
mirror-reflection
|
Physics, Infinite Lattice, and Intuition
|
physics-infinite-lattice-and-intuition-b-1wwm
|
Don\'t let mirrors trick you. Break the mirrors and enter the "space" behind. -- Simple Fun Physics\n\nclass Solution:\n def mirrorReflection(self, p: int, q
|
phillipfeiding
|
NORMAL
|
2020-10-08T05:26:44.796940+00:00
|
2020-10-08T05:29:00.072822+00:00
| 176 | false |
> Don\'t let mirrors trick you. Break the mirrors and enter the "space" behind. -- Simple Fun Physics\n```\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n while p % 2 == 0 and q % 2 == 0:\n p = p // 2\n q = q // 2\n if p % 2 == 1 and q % 2 == 0:\n return 0\n elif p % 2 == 1 and q % 2 == 1:\n return 1\n else :\n return 2\n```\n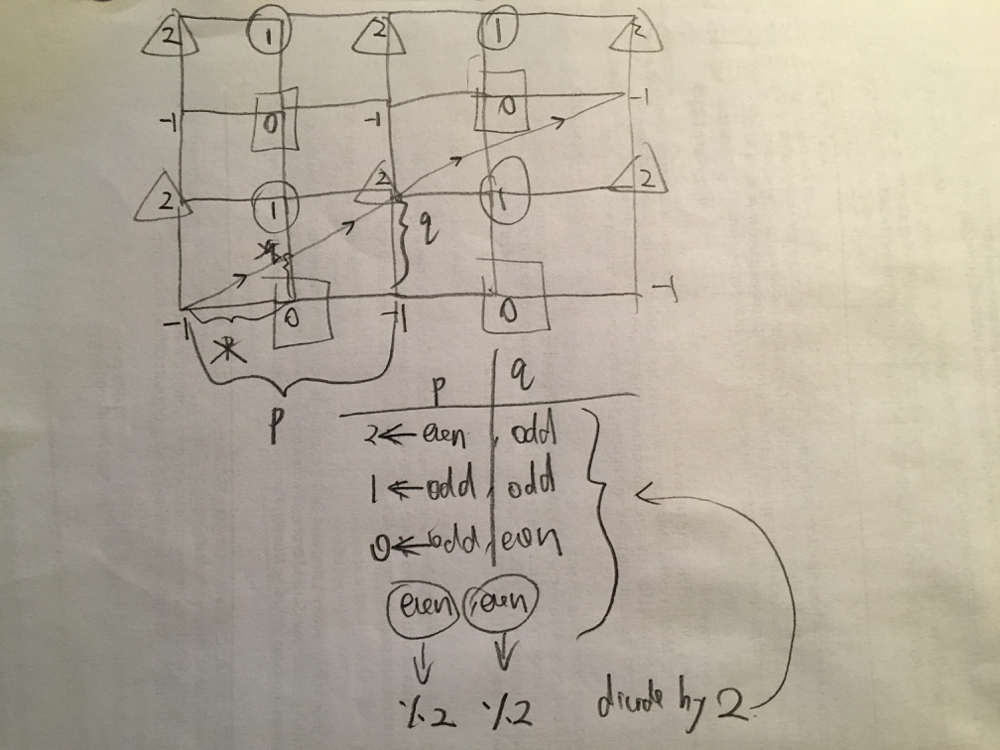\n\n
| 3 | 1 |
[]
| 1 |
mirror-reflection
|
Detailed explanation
|
detailed-explanation-by-lzl124631x-0wl2
|
Solution 1. Simulation\n\nThe equation of the ray is (y - y1) / ry = (x - x1) / rx.\n\nWe start from x = 0, y = 0 and rx = p, ry = q.\n\nAfter time t the ray wi
|
lzl124631x
|
NORMAL
|
2020-09-04T10:44:58.786241+00:00
|
2020-09-04T10:44:58.786278+00:00
| 275 | false |
## Solution 1. Simulation\n\nThe equation of the ray is `(y - y1) / ry = (x - x1) / rx`.\n\nWe start from `x = 0, y = 0` and `rx = p, ry = q`.\n\nAfter time `t` the ray will be at `(a, b) = (x + rx * t, y + ry * t)`. We want to find the smallest positive `t` which makes `(a, b)` be at `(0, p)`, `(p, 0)` or `(p, p)`.\n\nAt time `t`, if the ray lands on\n* the west edge, then `x + rx * t = 0` so `t = -x / rx`.\n* the south edge, then `y + ry * t = 0`, so `t = -y / ry`.\n* the east edge, then `x + rx * t = p`, so `t = (p - x) / rx`.\n* the north edge, then `y + ry * t = p`, so `t = (p - y) / ry`.\n\nWe can try the four edges, and the smallest positive time `t` is the time we should take because it takes us to the next landing edge.\n\n```cpp\n// OJ: https://leetcode.com/problems/mirror-reflection/\n// Author: github.com/lzl124631x\n// Time: O(P)\n// Space: O(1)\n// Ref: https://leetcode.com/problems/mirror-reflection/solution/\nclass Solution {\n double eps = 1e-6;\n bool equal(double x, double y) {\n return abs(x - y) < eps;\n }\npublic:\n int mirrorReflection(int p, int q) {\n double x = 0, y = 0, rx = p, ry = q;\n while (!(\n (equal(x, p) && (equal(y, 0) || equal(y, p))) // touches 0 or 1\n || (equal(x, 0) && equal(y, p)) // touches 2\n )) {\n double t = 1e9;\n if ((-x / rx) > eps) t = min(t, -x / rx); // try reaching west edge (set the new x to be 0)\n if ((-y / ry) > eps) t = min(t, -y / ry); // try reaching south edge (set the new y to be 0)\n if ((p - x) / rx > eps) t = min(t, (p - x) / rx); // try reaching east edge (set the new x to be p)\n if ((p - y) / ry > eps) t = min(t, (p - y) / ry); // try reaching north edge (set the new y to be p)\n x += rx * t; // we take the closest reacheable edge\n y += ry * t;\n if (equal(x, p) || equal(x, 0)) rx *= -1; // if touches west or east edge, flip rx\n else ry *= -1; // otherwise flip ry.\n }\n if (equal(x, p) && equal(y, p)) return 1;\n return equal(x, p) ? 0 : 2;\n }\n};\n```\n\n## Solution 2. Math\n\nInstead of bounceing back, just let the ray go straight. The first receptor the ray touches is at `(kp, kq)` where `k` is integer and `kq` is a multiple of `p`. So the goal is the find the smallest integer `k` for which `kq` is a multiple of `p`.\n\nThe mathematical answer is `k = p / gcd(p, q)`.\n\n`p /= k` and `q /= k` reduces `p` and `q` to the base cases where `p` and `q` are coprime. For example, `p = 9, q = 6` is reduced to `p = 3, q = 2`.\n\nThen `p` and `q` won\'t be both even otherwise they are not coprime.\n\nSo we just have 3 cases:\n\n`p` and `q` are\n1. odd, odd\n2. odd, even\n3. even, odd\n\nrespectively\n\nEach case has a fixed top-right value as shown in the figure below.\n\n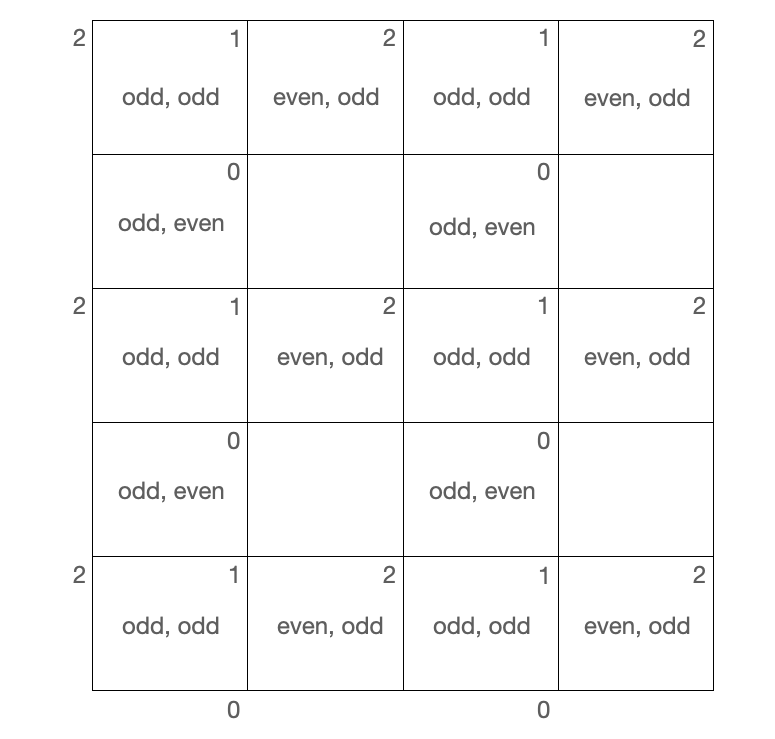\n\n\nSo the pattern is:\n* `p` is odd and `q` is odd the result is `1`.\n* `p` is odd and `q` is even, the result is `0`.\n* `p` is even and `q` is odd, the result is `2`.\n\n```cpp\n// OJ: https://leetcode.com/problems/mirror-reflection/\n// Author: github.com/lzl124631x\n// Time: O(logP)\n// Space: O(1)\n// Ref: https://leetcode.com/problems/mirror-reflection/solution/\nclass Solution {\n int gcd(int p, int q) {\n return q ? gcd(q, p % q) : p;\n }\npublic:\n int mirrorReflection(int p, int q) {\n int k = gcd(p, q);\n p /= k; p %= 2;\n q /= k; q %= 2;\n if (p == 1 && q == 1) return 1;\n return p == 1 ? 0 : 2;\n }\n};\n```\n\n# Solution 3.\n\nSimilar to Solution 2, but we don\'t need to compute the GCD. Simply keep dividing `p` and `q` by `2` until they are not both even. Then we use the parity of `p` and `q` to determine the result.\n\n```cpp\n// OJ: https://leetcode.com/problems/mirror-reflection/\n// Author: github.com/lzl124631x\n// Time: O(logP)\n// Space: O(1)\n// Ref: https://leetcode.com/problems/mirror-reflection/discuss/141765/Java-short-solution-with-a-sample-drawing\nclass Solution {\npublic:\n int mirrorReflection(int p, int q) {\n while (p % 2 == 0 && q % 2 == 0) p /= 2, q /= 2;\n if (p % 2 && q % 2) return 1;\n return p % 2 ? 0 : 2;\n }\n};\n```\n\nOr\n\n```cpp\n// OJ: https://leetcode.com/problems/mirror-reflection/\n// Author: github.com/lzl124631x\n// Time: O(logP)\n// Space: O(1)\nclass Solution {\npublic:\n int mirrorReflection(int p, int q) {\n while (p % 2 == 0 && q % 2 == 0) p /= 2, q /= 2;\n return 1 + (q & 1) - (p & 1);\n }\n};\n```
| 3 | 0 |
[]
| 0 |
mirror-reflection
|
可以不用求gcd呀
|
ke-yi-bu-yong-qiu-gcdya-by-taoxinzhi-9tmp
|
\u628A\u8FD9\u4E2A\u5C04\u7EBF\u65E0\u9650\u5EF6\u957F\uFF0C\u80AF\u5B9A\u4F1A\u5230\u8FBE\u67D0\u4E2A\u65B9\u5757\u7684\u53F3\u4E0A\u89D2\uFF08\u65B9\u5757\u4F
|
taoxinzhi
|
NORMAL
|
2018-11-14T07:23:50.218212+00:00
|
2018-11-14T07:23:50.218281+00:00
| 511 | false |
\u628A\u8FD9\u4E2A\u5C04\u7EBF\u65E0\u9650\u5EF6\u957F\uFF0C\u80AF\u5B9A\u4F1A\u5230\u8FBE\u67D0\u4E2A\u65B9\u5757\u7684\u53F3\u4E0A\u89D2\uFF08\u65B9\u5757\u4F60\u5728\u8349\u7A3F\u7EB8\u4E0A\u8865\u9F50\uFF09\u3002\u8FD9\u6837\uFF0C\u6C34\u5E73\u65B9\u5411\u5047\u8BBEx\u4E2A\u65B9\u5757\uFF0C\u5782\u76F4\u65B9\u5411\u5047\u8BBEy\u4E2A\u65B9\u5757\uFF0Cy/x = q/p\u3002\u5B83\u7ED9\u7684\u6570\u636Ep\u548Cq\u90FD\u662F\u6574\u6570\uFF0C\u5B9E\u9645\u6C34\u5E73\u6269\u5C55\u5230p\u4E2A\u65B9\u5757\uFF0C\u5782\u76F4\u6269\u5C55\u5230q\u4E2A\u65B9\u5757\u5C31\u6EE1\u8DB3\u4E86\u3002\u81EA\u5DF1\u770B\u4E00\u4E0B\u89C4\u5F8B\u3002x\u662F\u5947\u6570\uFF0Cy\u662F\u5947\u6570\u65F6\uFF0C\u53F3\u4E0A\u89D2\u662F1\uFF1Bx\u662F\u5947\u6570\uFF0Cy\u662F\u5076\u6570\u65F6\uFF0C\u53F3\u4E0A\u89D2\u662F0\uFF1Bx\u662F\u5076\u6570\uFF0Cy\u662F\u5947\u6570\u65F6\uFF0C\u53F3\u4E0A\u89D2\u662F2\uFF1Bx\u662F\u5076\u6570\uFF0Cy\u662F\u5076\u6570\uFF0C\u53F3\u4E0A\u89D2\u662F\u53D1\u5C04\u70B9\u3002\u6700\u540E\u4E00\u79CD\u60C5\u51B5\u628Ax\uFF0Cy\u540C\u65F6\u9664\u4EE52\u76F4\u5230\u67D0\u4E00\u65B9\u4E0D\u662F\u5076\u6570\u5C31\u884C\u4E86\u3002\n```\nint mirrorReflection(int p, int q) {\n while(p % 2 == 0 && q % 2 == 0) {\n p /= 2;\n q /= 2;\n }\n if (p % 2 == 0) {\n return 2;\n } else {\n if (q % 2 == 0) {\n return 0;\n } else {\n return 1;\n }\n }\n }\n```
| 3 | 0 |
[]
| 3 |
mirror-reflection
|
Easy Understand and short java AC solution
|
easy-understand-and-short-java-ac-soluti-ofs6
|
Try to imagine the laser can keep going up because that it is mirror symmetrical.\n\n\nclass Solution {\n public int mirrorReflection(int p, int q) {\n
|
woaishuati
|
NORMAL
|
2018-06-24T14:13:16.705626+00:00
|
2018-06-24T14:13:16.705626+00:00
| 431 | false |
Try to imagine the laser can keep going up because that it is mirror symmetrical.\n\n```\nclass Solution {\n public int mirrorReflection(int p, int q) {\n int sum = q;\n int times = 1;\n while (sum % p != 0) {\n sum += q;\n times++;\n }\n \n if (times % 2 == 0) {\n return 2;\n } else {\n if ((sum / p ) % 2 == 0) {\n return 0;\n } else {\n return 1;\n }\n }\n }\n}\n```
| 3 | 0 |
[]
| 1 |
mirror-reflection
|
Naive solution that simulate relfection
|
naive-solution-that-simulate-relfection-cxizj
|
\nclass Solution {\n public int mirrorReflection(int p, int q) {\n double slope = q * 1.0 / p, b = 0;\n double[] cur = new double[2];\n
|
cai41
|
NORMAL
|
2018-06-24T06:09:34.898714+00:00
|
2018-06-24T06:09:34.898714+00:00
| 327 | false |
```\nclass Solution {\n public int mirrorReflection(int p, int q) {\n double slope = q * 1.0 / p, b = 0;\n double[] cur = new double[2];\n while (true) {\n double[] next = getNext(cur, slope, b, p);\n if (near(next[0], p) && near(next[1], 0)) return 0;\n if (near(next[0], p) && near(next[1], p)) return 1;\n if (near(next[0], 0) && near(next[1], p)) return 2;\n slope = -(cur[1] - next[1]) / (cur[0] - next[0]);\n b = next[1] - slope * next[0];\n cur = next;\n }\n }\n \n private boolean near(double a, double b) {\n return Math.abs(a - b) < 0.000001;\n }\n \n // y = slope*x + b\n private double[] getNext(double[] current, double slope, double b, double p) {\n double[][] inter = new double[4][2];\n inter[0][1] = b;\n inter[1][0] = p;\n inter[1][1] = p * slope + b;\n inter[2][0] = (0 - b) / slope;\n inter[3][0] = (p - b) / slope;\n inter[3][1] = p;\n \n int i;\n for (i = 0; i < 4; i++) {\n if (current[0] == inter[i][0] || current[1] == inter[i][1]) continue;\n if (inter[i][0] >= 0 && inter[i][0] <= p && inter[i][1] >= 0 && inter[i][1] <= p) break;\n }\n return inter[i];\n }\n}\n```
| 3 | 0 |
[]
| 0 |
mirror-reflection
|
Java 100% Faster with Explanation
|
java-100-faster-with-explanation-by-lazy-tphi
|
\nclass Solution {\n public int mirrorReflection(int p, int q) {\n \n while(p%2 == 0 && q%2 == 0){ // if it\'s a bigger square, we can shrink it
|
lazyhack
|
NORMAL
|
2022-08-05T01:32:59.591834+00:00
|
2022-08-05T02:18:03.844155+00:00
| 34 | false |
```\nclass Solution {\n public int mirrorReflection(int p, int q) {\n \n while(p%2 == 0 && q%2 == 0){ // if it\'s a bigger square, we can shrink it into a small square like in the example\n p/=2;\n q/=2;\n }\n \n return 1 - p % 2 + q % 2;\n \n }\n}\n```
| 2 | 0 |
[]
| 0 |
mirror-reflection
|
[Java][eli5] Solution with illustrations
|
javaeli5-solution-with-illustrations-by-zlhcb
|
The problem is hard to visualize rather than a hard to code one so having a proper visual aid is going to make this super easy one. with that being said here\'s
|
udaykrishna5
|
NORMAL
|
2022-08-04T22:19:34.242424+00:00
|
2022-08-04T22:23:39.428403+00:00
| 30 | false |
The problem is hard to visualize rather than a hard to code one so having a proper visual aid is going to make this super easy one. with that being said here\'s how to approach this.\n\nwe are given a 4 walled square mirror room something like this, and are asked to find which corner the ray ends up at given `p` which is the length of the side of the room and `q` which is the length from corner to where light is incident at\n\n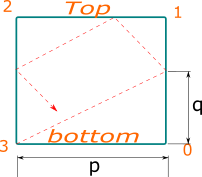\n\nIn this image the ray can internally reflect many times creating a very hard to work with, so we instead unfold the ray by opening the room like so to make it easier to reason with.\n\n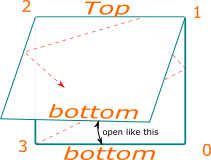\n\nAfter opening up the image it\'ll look something like this, and in the end we know that the ray will stop somewhere at the top ray hits a corner of the room so we\'ll have `n` number of `q`s on right and `m` number of `p` s on left.\n\n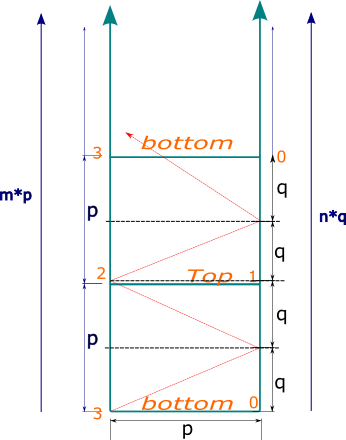\n\nso we can say that our search ends when `m*p=n*q`\n\nIf you are confused on why `q`s on the left are equal ? that\'s because angle of incidence is equal to angle of reflection and since both angles are the same and mirrors are parallel length of the segment is also the same. \n\n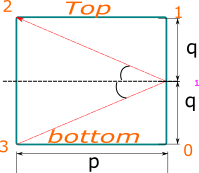\n\nBecause of every even reflection is going to make light rays get reflected in parallel to original light ray and will lead to alternate angles being same and this `q` length being same part will keep repeating. [[read up parallel postulates](https://en.wikipedia.org/wiki/Parallel_postulate)]\n\nNow that we are through with maths and physics let\'s figure out where the light ray will end up, we basically have to think if it\'ll endup at `top` or `bottom` and also figure out if its going to end up `right` or `left`\n\n\nFor top or bottom our folding will help us, if you notice if m is even, we\'ll have light end up at bottom since we know ray ends after `m*p` length. see how we open/unfold up the room to see how bottom becomes top alternatively.\n\nso **Even `m` would mean bottom and odd `m` would mean top.**\n\nNow for left and right, we can see that odd number of reflections will cause the light to end up at left and even will cause it to end up at right, but we don\'t know reflection count but we can know `n` and `n = number of reflections + 1` so it has opposite parity of `number of reflections`. see images below\n\nwe can now say that **if we have odd `n` we\'ll end up at right and even will endup at left**\n\n ||| \n\nBased on this let\'s make a table to say where the light ends up in terms of `top` `bottom` `left` and `right`.\n\n| m | n | Top/Bottom | Left/Right | Corner |\n|---|---|------------|------------|--------|\n| odd | odd | Top | Right | 1 |\n| odd | even | Top | Left | 2 |\n| even | odd | Bottom | Right | 0 |\n| even | even | Bottom | Left | 3 |\n\nNow let\'s use this logic to find out value of `m` and `n` for a given value of `p` and `q` such that `m*p=n*q`\n\n```java\nclass Solution {\n public int mirrorReflection(int p, int q) {\n // m*p=n*q\n int m=1,n=1;\n while(m*p != n*q){\n ++n; // if we don\'t place this above for some reason we get a time out next line\n m=n*q/p;\n }\n \n if(((m&1)!=0) && ((n&1)!=0)) return 1;\n else if(((m&1)!=0) && ((n&1)==0)) return 2;\n else if(((m&1)==0) && ((n&1)!=0)) return 0;\n else return 3; // ((m&1==0) && (n&1==0))\n }\n}\n```\n
| 2 | 0 |
['Java']
| 0 |
mirror-reflection
|
go. 0ms. Math. Easy and clean
|
go-0ms-math-easy-and-clean-by-sobik-ov3t
|
\nfunc gcd(a, b int) int {\n\tif a == 0 || a == b { return b }\n\tif b == 0 { return a }\n\tif a > b {\n\t\treturn gcd(a - b, b)\n\t} else {\n\t\treturn gcd(a,
|
sobik
|
NORMAL
|
2022-08-04T19:42:50.900796+00:00
|
2022-08-04T19:43:04.709745+00:00
| 56 | false |
```\nfunc gcd(a, b int) int {\n\tif a == 0 || a == b { return b }\n\tif b == 0 { return a }\n\tif a > b {\n\t\treturn gcd(a - b, b)\n\t} else {\n\t\treturn gcd(a, b - a)\n\t}\n}\n\nfunc lcm(a, b int) int {\n\treturn a*b / gcd(a, b)\n}\n\nfunc mirrorReflection(p int, q int) int {\n\tlcm := lcm(p, q)\n\tm := lcm / p\n\tn := lcm / q\n\treturn 1 + m % 2 - n % 2\n}\n```
| 2 | 0 |
['Math', 'Go']
| 0 |
mirror-reflection
|
100% Fast C++ Code
|
100-fast-c-code-by-amit_bhardwaj-ko85
|
\nclass Solution {\npublic:\nint mirrorReflection(int p, int q) {\nwhile(p%2==0 && q%2==0)\n p/=2,q/=2;\n\nif(p%2!=0 && q%2==0) return 0;\nelse if(p%2==0 && q%2
|
Amit_bhardwaj
|
NORMAL
|
2022-08-04T15:22:22.329164+00:00
|
2022-08-04T15:22:37.055412+00:00
| 73 | false |
```\nclass Solution {\npublic:\nint mirrorReflection(int p, int q) {\nwhile(p%2==0 && q%2==0)\n p/=2,q/=2;\n\nif(p%2!=0 && q%2==0) return 0;\nelse if(p%2==0 && q%2!=0)return 2;\nelse if(p%2!=0 && q%2!=0)return 1;\n return -1;\n}\n};\n```
| 2 | 0 |
['Geometry', 'C']
| 0 |
mirror-reflection
|
C++ || Fastest Solution || 1 line solution || Easy logic
|
c-fastest-solution-1-line-solution-easy-9x1wg
|
Iterative way\n\nclass Solution {\npublic:\n int mirrorReflection(int p, int q) {\n while (p % 2 == 0 && q % 2 == 0){ \n p/=2;\n
|
Shuvam_Barman
|
NORMAL
|
2022-08-04T14:52:02.472537+00:00
|
2022-08-04T14:59:15.075302+00:00
| 86 | false |
Iterative way\n```\nclass Solution {\npublic:\n int mirrorReflection(int p, int q) {\n while (p % 2 == 0 && q % 2 == 0){ \n p/=2;\n q/=2;\n }\n return 1 - p % 2 + q % 2;\n }\n};\n```\n1 line solution\n```\nclass Solution {\npublic:\n int mirrorReflection(int p, int q) {\n return 1 + q / gcd(p, q) % 2 - p / gcd(p, q) % 2;\n }\n};\n```\nPlease upvote if the solutions were helpful.
| 2 | 0 |
['C', 'Iterator']
| 0 |
mirror-reflection
|
6-lines solution + Explanation [C#]
|
6-lines-solution-explanation-c-by-andrei-9354
|
Explanation\nWe can present mirror square room as two parallel mirrors of endless length. The laser ray start from 0 point at the left mirrow and goes to q dist
|
Andrei_
|
NORMAL
|
2022-08-04T14:22:53.397621+00:00
|
2022-08-04T14:22:53.397664+00:00
| 35 | false |
##### Explanation\nWe can present mirror square room as two parallel mirrors of endless length. The laser ray start from `0` point at the left mirrow and goes to `q` distanse at the right mirrow, then to `2q` distance at the left mirrow, then to `3q` at the right, etc. The receptors in this presentation will be placed:\n* receptor 0 - at 0p, 2p, 4p, 6p, etc... distances at the **right** wall;\n* receptor 1 - at 1p, 3p, 5p, 7p, etc... distances at the **right** wall;\n* receptor 2 - at 1p, 3p, 5p, 7p, etc... distances at the **left** wall;\n\nThe code for such representation is below.\n```\npublic int MirrorReflection(int p, int q) {\n\tfor (var distance = q; true; distance += q) {\n\t\tif (distance % p == 0) // Check right wall\n\t\t\treturn (distance / p) % 2 == 1 ? 1 : 0;\n\n\t\tdistance += q;\n\t\tif (distance % p == 0 && (distance / p) % 2 == 1) // Check left wall\n\t\t\treturn 2;\n\t}\n}\n```\n\uD83D\uDC4D\uD83C\uDFFB Upvote if it helped you or you learnt something new.
| 2 | 0 |
[]
| 0 |
mirror-reflection
|
Usign GCD
|
usign-gcd-by-tmleyncodes-yk3g
|
\nclass Solution {\npublic:\n int mirrorReflection(int p, int q) {\n int k = __gcd(p, q);\n p = (p/k)%2; \n q = (q/k)%2;\n if(p &
|
tmleyncodes
|
NORMAL
|
2022-08-04T13:30:38.281043+00:00
|
2022-08-04T13:30:38.281080+00:00
| 32 | false |
```\nclass Solution {\npublic:\n int mirrorReflection(int p, int q) {\n int k = __gcd(p, q);\n p = (p/k)%2; \n q = (q/k)%2;\n if(p && q) return 1;\n return (q)?2:0;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
mirror-reflection
|
[Java] math solution beats 100%
|
java-math-solution-beats-100-by-olsh-jhgc
|
\nclass Solution {\n public int mirrorReflection(int p, int q) {\n int gcd = gcd(p,q);\n int lcd = p*q/gcd;\n \n if (lcd/p>=2 && l
|
olsh
|
NORMAL
|
2022-08-04T12:45:23.530173+00:00
|
2022-08-04T12:45:23.530217+00:00
| 51 | false |
```\nclass Solution {\n public int mirrorReflection(int p, int q) {\n int gcd = gcd(p,q);\n int lcd = p*q/gcd;\n \n if (lcd/p>=2 && lcd/p%2==0)return 0;\n else return (lcd/q)%2==0?2:1;\n }\n \n static int gcd(int p, int q) \n { \n while(p!=q){ \n if(p>q) p=p-q; \n else q=q-p; \n }\n return q;\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
mirror-reflection
|
Python | Java | Easy Solution using simple geometric observation | Commented code
|
python-java-easy-solution-using-simple-g-b0at
|
Please do upvote if it is helpful!!!!!!\n\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n \'\'\'\n Using simple geome
|
__Asrar
|
NORMAL
|
2022-08-04T07:14:57.889501+00:00
|
2022-08-04T07:32:11.670700+00:00
| 111 | false |
***Please do upvote if it is helpful!!!!!!***\n```\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n \'\'\'\n Using simple geometry and just by observing we can decide where\n will the ray hit. for example:\n p = 2, q = 1; the ray first meets 2nd receptor after it gets reflected\n for 1 time\n p = 3, q = 1; the ray first meets 1st receptor after it gets reflected\n for 2 times.\n From the given examples one can easly observe that\n 1:if p is even and q is odd, it\'ll surely hit 2nd receptor for the first\n time\n 2:if both p and q is odd, it\'ll surely hit 1st receptor for the first time\n \n \'\'\'\n # base case if both p and q are equal, it will always hit receptor 1,\n # irrespective of their nature\n if p == q: \n return 1\n \n while p % 2 == 0 and q % 2 == 0:\n p //= 2\n q //= 2\n \n if p % 2 == 1 and q % 2 == 0:\n return 0\n elif p % 2 == 1 and q % 2 == 1:\n return 1\n elif p % 2 == 0 and q % 2 == 1:\n return 2\n```\n**JAVA**\n```\nclass Solution {\n public int mirrorReflection(int p, int q) {\n if (p == q){\n return 1;\n } \n while(p % 2 == 0 && q % 2 == 0){\n p /= 2;\n q /= 2;\n }\n if (p % 2 == 1 && q % 2 == 0){\n return 0;\n }\n else if (p % 2 == 1 && q % 2 == 1){\n return 1;\n }\n else if (p % 2 == 0 && q % 2 == 1){\n return 2;\n }\n return 0;\n }\n}\n\n```
| 2 | 0 |
['Math', 'Geometry', 'Python', 'Python3']
| 0 |
mirror-reflection
|
Python Solution, Faster than 92% users DO CHECK OUT!
|
python-solution-faster-than-92-users-do-tmj2y
|
\tclass Solution:\n\t\tdef isEven(self,num):\n\t\t\treturn num&1==0\n\t\tdef mirrorReflection(self, p: int, q: int) -> int:\n\t\t\twhile self.isEven(p) and self
|
shambhavi_gupta
|
NORMAL
|
2022-08-04T06:07:56.952338+00:00
|
2022-08-04T06:07:56.952379+00:00
| 81 | false |
\tclass Solution:\n\t\tdef isEven(self,num):\n\t\t\treturn num&1==0\n\t\tdef mirrorReflection(self, p: int, q: int) -> int:\n\t\t\twhile self.isEven(p) and self.isEven(q):\n\t\t\t\tp>>=1\n\t\t\t\tq>>=1\n\t\t\tif self.isEven(p) and not self.isEven(q):\n\t\t\t\treturn 2\n\t\t\telif self.isEven(q) and not self.isEven(p):\n\t\t\t\treturn 0\n\t\t\telse:\n\t\t\t\treturn 1
| 2 | 0 |
['Python']
| 0 |
mirror-reflection
|
C++|0ms runtime| Faster than everyone on planet earth| Literally the best solution ever XD
|
c0ms-runtime-faster-than-everyone-on-pla-3bz8
|
So we extended the blocks vertically , and let the light reflect, the light will meet a corner on the lcm of p and q\n\n\nMy Code is as follows :\n"\'class Solu
|
shriganesh2019
|
NORMAL
|
2022-08-04T05:45:23.547894+00:00
|
2022-08-04T05:45:23.547933+00:00
| 46 | false |
So we extended the blocks vertically , and let the light reflect, the light will meet a corner on the lcm of p and q\n\n\nMy Code is as follows :\n"\'class Solution {\npublic:\n int gcd(int a, int b)\n {\n if(a==b && a!=0)\n return a;\n else if(a==0 || b==0)\n {\n return 1;\n }\n else {\n if(a>b)\n {\n swap(a, b);\n }\n return gcd(a , b - a);\n }\n }\n int mirrorReflection(int p, int q) {\n int ans = 0;\n int gcdi = gcd(p,q);\n int lcmi = p*q/gcdi;\n int ext = lcmi/p;\n if(ext%2==0)\n return 0;\n else{\n if((lcmi/q)%2==0)\n return 2;\n else{\n return 1;\n }\n }\n \n }\n};"\'
| 2 | 0 |
['Math', 'Geometry']
| 0 |
mirror-reflection
|
[Ruby] Simple and fast
|
ruby-simple-and-fast-by-kevin-shu-y3af
|
\n\n\ndef mirror_reflection(p, q)\n return 1 if p==q\n while p.even? and q.even?\n p = p/2\n q = q/2\n end\n return 0 if p.odd? and q.
|
kevin-shu
|
NORMAL
|
2022-08-04T05:30:21.711851+00:00
|
2022-08-04T05:30:42.014894+00:00
| 22 | false |
\n\n```\ndef mirror_reflection(p, q)\n return 1 if p==q\n while p.even? and q.even?\n p = p/2\n q = q/2\n end\n return 0 if p.odd? and q.even?\n return 1 if p.odd? and q.odd?\n return 2 if p.even? and q.odd?\nend\n```
| 2 | 0 |
[]
| 0 |
mirror-reflection
|
✔️ [ JavaScript ] 2 Solutions - Simple Math - Beats 100%
|
javascript-2-solutions-simple-math-beats-fqds
|
Solution 1: Using ext * p = ref * q equation ~ 90 ms\n\n\n// Time complexity: O(log (min(p,q))\n// Space complexity: O(1)\n\nvar mirrorReflection = function(p,
|
prashantkachare
|
NORMAL
|
2022-08-04T05:28:20.698359+00:00
|
2022-08-04T06:52:41.403408+00:00
| 133 | false |
**Solution 1: Using ext * p = ref * q equation ~ 90 ms**\n\n```\n// Time complexity: O(log (min(p,q))\n// Space complexity: O(1)\n\nvar mirrorReflection = function(p, q) {\n\tlet ext = q, ref = p;\n\t\n\twhile (ext % 2 == 0 && ref % 2 == 0) {\n\t\text /= 2;\n\t\tref /= 2;\n\t}\n\t\n\tif (ext % 2 == 0 && ref % 2 == 1) return 0;\n\tif (ext % 2 == 1 && ref % 2 == 1) return 1;\n\tif (ext % 2 == 1 && ref % 2 == 0) return 2;\n\t\n\treturn -1;\n};\n```\n\n**Solution 2: Using p/q ratio ~ 76 ms**\n\n```\n// Time complexity: O(log (min(p,q))\n// Space complexity: O(1)\n\nvar mirrorReflection = function(p, q) {\n\twhile (p % 2 == 0 && q % 2 == 0) { // p & q are both even, divide both by 2\n\t\tp = p / 2;\n\t\tq = q / 2;\n\t}\n\t\n\tif (p % 2 == 0) // p is even\n\t\treturn 2; \n\t\t\n\telse if (q % 2 == 0) // q is even\n\t\treturn 0;\n\t\t\n\telse return 1; // p & q are odd\n};\n```\n\n***Please upvote if you find this post useful. Happy Coding!***
| 2 | 0 |
['Math', 'JavaScript']
| 1 |
mirror-reflection
|
✔99.01% FASTER🐍PYTHON SIMPLE MATH🔥EXPLAINED.
|
9901-fasterpython-simple-mathexplained-b-4s35
|
Python Solution\uD83D\uDC0D\nNow picture this four mirror walls of a square and\nwe\'re given p; the length of each wall \uD83D\uDC49 \uD83D\uDC48and q; distanc
|
shubhamdraj
|
NORMAL
|
2022-08-04T04:29:37.699355+00:00
|
2022-08-04T15:23:41.310801+00:00
| 89 | false |
# Python Solution\uD83D\uDC0D\nNow picture this four mirror walls of a square and\nwe\'re given p; the length of each wall \uD83D\uDC49 \uD83D\uDC48and q; distance from 0th receptor to where the ray hit.\n**Examples:**\n- p = 2, q = 1; the ray first meets 2nd receptor after it gets reflected for 1 time\n- p = 3, q = 1; the ray first meets 1st receptor after it gets reflected for 2 times.\n\nFrom these we can **observe**:\n- if **p is even** and **q is odd**, it\'ll surely **hit 2nd receptor** for the first time\n- if **both p and q is odd**, it\'ll surely **hit 1st receptor** for the first time\n\n**Edge Cases:**\n- p = 4, q = 2; **if both are even**, the ray will **first** definitely meet **2nd receptor**, beacuse the ray gets reflected for q times.\n- p = 2, q = 2; **if both are same**, the ray **first** meets **1st receptor**.\n\n```\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n\t\t# same?\n if p == q: return 1\n\t\t\n # if both are even, we need to keep dividing them by 2, until q becomes 1, \n\t\t# then as we know p even and q is odd, so it first meets 2nd receptor e.g. -> 4, 2\n while p%2 == 0 and q%2 == 0:\n p = p // 2\n q = q // 2\n \n if p%2 == 0 and q%2 == 1: return 2\n elif p%2 == 1 and q%2 == 1: return 1\n elif p%2 == 1 and q%2 == 0: return 0\n```\n## Give it a **Upvote** If You Like My Explanation.\n### Have a Great Day/Night.
| 2 | 0 |
['Math', 'Python']
| 0 |
mirror-reflection
|
Python solution using directions
|
python-solution-using-directions-by-toor-2eqt
|
\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n if p == q:\n return 1\n \n height = q\n right
|
ToORu124124
|
NORMAL
|
2022-08-04T01:07:59.264007+00:00
|
2022-08-04T01:07:59.264048+00:00
| 275 | false |
```\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n if p == q:\n return 1\n \n height = q\n right, up = False, True\n while 1:\n if height + q == p:\n if right and up:\n return 1\n elif not right and up:\n return 2\n else:\n return 0\n elif height + q < p:\n height += q\n right = not right\n else:\n height += q\n height %= p\n right = not right\n up = not up\n```
| 2 | 0 |
['Python', 'Python3']
| 0 |
mirror-reflection
|
Python
|
python-by-danurag-409b
|
class Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n m = 1 # of room extension + 1\n n = 1 # of reflection + 1\n\n while m * p !=
|
Danurag
|
NORMAL
|
2022-08-04T00:11:27.909262+00:00
|
2022-08-04T00:11:27.909306+00:00
| 75 | false |
class Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n m = 1 # of room extension + 1\n n = 1 # of reflection + 1\n\n while m * p != n * q:\n n += 1\n m = n * q // p\n\n if m % 2 == 0 and n % 2 == 1:\n return 0\n if m % 2 == 1 and n % 2 == 1:\n return 1\n if m % 2 == 1 and n % 2 == 0:\n return 2\n\n
| 2 | 1 |
['Python']
| 1 |
mirror-reflection
|
easy to understand | short code | 3 cases
|
easy-to-understand-short-code-3-cases-by-39ia
|
```\nclass Solution {\npublic:\n int mirrorReflection(int p, int q) {\n while((p%2==0) && (q%2==0)){\n p/=2;\n q/=2;\n }\
|
aryatito
|
NORMAL
|
2021-12-19T08:03:26.079167+00:00
|
2021-12-19T08:03:26.079194+00:00
| 235 | false |
```\nclass Solution {\npublic:\n int mirrorReflection(int p, int q) {\n while((p%2==0) && (q%2==0)){\n p/=2;\n q/=2;\n }\n //both p qnd q can\'t be even\n if((p%2)==0 && (q%2)!=0) return 2;//p=even q=odd\n if((p%2)!=0 && (q%2)!=0) return 1;//p=odd q=odd\n return 0;//p=odd q=even\n }\n};
| 2 | 0 |
['C']
| 0 |
mirror-reflection
|
Java | Intuitive, 100% speed
|
java-intuitive-100-speed-by-auroboros33-082i
|
Thought I would post this because I built it pretty intuitively and people seemed to be complaining that this is hard to solve on the spot... Instead of getting
|
auroboros33
|
NORMAL
|
2021-04-20T21:00:06.077705+00:00
|
2021-04-20T21:01:24.928833+00:00
| 245 | false |
Thought I would post this because I built it pretty intuitively and people seemed to be complaining that this is hard to solve on the spot... Instead of getting into float point math, we can just always travel 1 left-to-right or right-to-left iteration. Then, if we are outside the bounds of the room, reflect our y coord back into it & record that we changed direction. If we\'re at a corner, it\'s solved.\n\nLooking at the solutions given by LeetCode, I\'d imagine there\'s also a simpler way to use this integer based approach but just solve with modulo math. I believe that would be simpler than all the presented solutions...\n\n```\nclass Solution {\n public int mirrorReflection(int p, int q) {\n int x = p;\n int y = q;\n \n int yDir = 1;\n \n while (true) {\n if (x == p && y == 0) {\n return 0;\n } else if (x == p && y == p) {\n return 1;\n } else if (x == 0 && y == p) {\n return 2;\n }\n \n x = p - x; // ping pong from wall to wall\n y = y + q * yDir;\n\t\t\t// fix y position to be within room, update direction if changed\n if (y > p) {\n y = p - (y - p);\n yDir = -1;\n } else if (y < 0) {\n y = -y;\n yDir = 1;\n }\n }\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
mirror-reflection
|
100% faster || 99.98 % space || 3 line code || Observations
|
100-faster-9998-space-3-line-code-observ-le2c
|
Just Extend squares(By Duplicating) and observe couple of examples\nYou will observe following-\n1. When number of q is even than you will observe that in every
|
aniketang
|
NORMAL
|
2021-01-15T05:38:51.683655+00:00
|
2021-01-16T04:07:48.576618+00:00
| 165 | false |
Just Extend squares(By Duplicating) and observe couple of examples\nYou will observe following-\n1. When number of q is even than you will observe that in every condition it will reaches receptor 2 (see by extending squares in vertical direction for better observation)\n2. When number of q is odd than we have 2 condition -\n i) if number of p is even than answer will be receptor 0\n ii) if number of p is odd than answer will be receptor 1\n for understanding Above 2 condition - when you extend squares in vertical direction than you will observe that 0 - 1 position keeps changing up - down.\n \nActually the equation will be\npx =qy \n\nfor getting x and y we can use while loop or better we can use lcm of P and Q\n\n****Comment for correction or doubt -\n\nint mirrorReflection(int p, int q) {\n \n if(((p)/__gcd(p,q))%2 == 0) return 2;\n if(((q)/__gcd(p,q))%2 == 0) return 0;\n else return 1;\n\n }
| 2 | 0 |
[]
| 0 |
mirror-reflection
|
Mirror Reflection | Simple Python
|
mirror-reflection-simple-python-by-iamhi-5nsy
|
\ndef mirrorReflection(self, p: int, q: int) -> int:\n \n while p%2==0 and q%2==0: #reducing to the lowest multiple of 2 form\n p, q =
|
iamhimmat
|
NORMAL
|
2020-11-17T22:57:32.732059+00:00
|
2020-11-17T22:57:32.732090+00:00
| 158 | false |
```\ndef mirrorReflection(self, p: int, q: int) -> int:\n \n while p%2==0 and q%2==0: #reducing to the lowest multiple of 2 form\n p, q = p//2, q//2\n \n if p%2==0 and q%2==1: #if p even and q odd\n return 2\n \n elif p%2==1 and q%2==0: #if p odd and q even\n return 0\n \n else: #if p odd and q odd\n return 1\n```
| 2 | 0 |
['Python', 'Python3']
| 0 |
mirror-reflection
|
[Python] Only consider y increasing...
|
python-only-consider-y-increasing-by-row-5j1f
|
\n\nApproach: (click to show)\nStart at x, y = (0, 0) where y is the height of the beam and x is the position.\nEach step, increase x by 1 and y by q.\n\nIncrea
|
rowe1227
|
NORMAL
|
2020-11-17T19:34:01.585818+00:00
|
2020-11-17T19:58:06.738040+00:00
| 88 | false |
<details>\n\n<summary><b>Approach: (click to show)</b></summary>\nStart at x, y = (0, 0) where y is the height of the beam and x is the position.\nEach step, increase x by 1 and y by q.\n\nIncreasing x by 1 means the beam traveled from one wall to the other.\n**When x is odd the beam is on the right wall, and when x is even the beam is on the left wall.**\n\nIncreasing y by q means that y will eventually pass the height of the box, but that\'s okay.\n**When y is evenly divisible by 2·p the beam must be on the bottom of the box.**\n**When y is evenly disivisible by p the beam must be on the top of the box (if it is not on the bottom of the box).**\n\nEach step we just check if the beam is at the top or bottom of the box.\nIf the beam is at the top, we look at x to see if it is on the left or the right (mirror 2 or mirror 1).\nIf it is at the bottom, it must be at mirror 0 because if it returned to the bottom left corner, there would be no solution.\n\n</details>\n\n<br>\n\n```python\ndef mirrorReflection(self, p: int, q: int) -> int:\n\n\tif not q: return 0\n\n\tx, y = 0, 0\n\twhile True:\n\t\tx, y = x + 1, y + q \n\t\tif not y % (2 * p):\n\t\t\treturn 0\n\t\telif not y % p:\n\t\t\treturn 1 if x&1 else 2\n```\n\n<details>\n\n<summary><b>One-liner: (click to show)</b></summary>\n\n```python\ndef mirrorReflection(self, p: int, q: int, x = 0, y = 0) -> int:\n\treturn self.mirrorReflection(p, q, x+1, y+q) if (not y or y%p) else 0 if (not y % (2 * p)) else 2 - (x&1)\n```\n\n</details>
| 2 | 0 |
[]
| 1 |
mirror-reflection
|
Simple JAVA simulation, 0ms
|
simple-java-simulation-0ms-by-vsavko-gjjp
|
Nothing too clever, trying all the smart math moves made my head hurt.\n\n\nclass Solution {\n public static int mirrorReflection(int p, int q) {\n\t\tboolea
|
vsavko
|
NORMAL
|
2020-11-17T15:30:55.412575+00:00
|
2020-11-17T15:30:55.412606+00:00
| 146 | false |
Nothing too clever, trying all the smart math moves made my head hurt.\n\n```\nclass Solution {\n public static int mirrorReflection(int p, int q) {\n\t\tboolean isLeft = true;\n\t\tboolean isUp = true;\n\t\tint YPos = 0;\n\t\twhile(true) {\n\t\t\tif(isUp) {\n\t\t\t\tif (YPos + q <= p) {\n\t\t\t\t\tYPos += q;\n\t\t\t\t}\n\t\t\t\telse{\n\t\t\t\t\tYPos = p - (q - (p - YPos));\n\t\t\t\t\tisUp = false;\n\t\t\t\t}\n\t\t\t}\n\t\t\telse {\n\t\t\t\tif (YPos - q >= 0) {\n\t\t\t\t\tYPos -= q;\n\t\t\t\t}\n\t\t\t\telse {\n\t\t\t\t\tYPos = q - YPos;\n\t\t\t\t\tisUp = true;\n\t\t\t\t}\n\t\t\t}\n\t\t\tisLeft = !isLeft;\n\t\t\tif(isLeft && YPos == p) return 2;\n\t\t\tif(!isLeft && YPos == p) return 1;\n\t\t\tif(!isLeft && YPos == 0) return 0;\n\t\t}\n }\n}\n```
| 2 | 0 |
[]
| 0 |
mirror-reflection
|
C++ || 1-liner || 2-liner || Bit-Manipulation || Easy
|
c-1-liner-2-liner-bit-manipulation-easy-1hf3c
|
2-Liner to understand the logic.\n\n int mirrorReflection(int p, int q) {\n while(p%2==0&&q%2==0)p>>=1,q>>=1;\n return 1+q%2-p%2;\n }\n\nInteg
|
saurav28_
|
NORMAL
|
2020-11-17T14:40:07.788320+00:00
|
2020-11-17T14:40:07.788351+00:00
| 158 | false |
2-Liner to understand the logic.\n```\n int mirrorReflection(int p, int q) {\n while(p%2==0&&q%2==0)p>>=1,q>>=1;\n return 1+q%2-p%2;\n }\n```\nIntegrated Solution\n1-Liner\n```\n int mirrorReflection(int p, int q) {\n\t return (p&-p)>(q&-q)?2:(p&-p)<(q&-q)?0:1;\n }\n```
| 2 | 1 |
['Math', 'Bit Manipulation', 'C', 'C++']
| 0 |
mirror-reflection
|
Java intuitive simulation, no math
|
java-intuitive-simulation-no-math-by-yun-nufu
|
```\nclass Solution {\n public int mirrorReflection(int p, int q) {\n // (x, y) start at (0,0)\n int x = 0, y = 0, dx = p, dy = q;\n //
|
yunsim
|
NORMAL
|
2020-06-08T08:00:10.890853+00:00
|
2020-06-08T08:00:10.890893+00:00
| 151 | false |
```\nclass Solution {\n public int mirrorReflection(int p, int q) {\n // (x, y) start at (0,0)\n int x = 0, y = 0, dx = p, dy = q;\n // while until hit the receptor \n while (x % p != 0 || y % p != 0 || (x == 0 && y == 0)) {\n\t\t // next coordinate on the mirrow will be (x + dx, y + dy)\n x += dx; \n y += dy;\n\t\t\t// everytime turn the direction of x\n dx = - dx;\n // if y go beyound the boundery, \n // find the symmetry position in the boundery and change direction\n if (y > p || y < 0) {\n dy = -dy;\n if (y > p) {\n y = 2 * p - y;\n }\n if (y < 0) {\n y = -y;\n }\n }\n }\n if (x == p && y == 0) return 0;\n if (x == 0 && y == p) return 2;\n return 1;\n }\n}
| 2 | 0 |
[]
| 1 |
mirror-reflection
|
Javascript 95%
|
javascript-95-by-franklioxygen-gb7u
|
\n/**\n * 858. Mirror Reflection\n * @param {number} p\n * @param {number} q\n * @return {number}\n */\nvar mirrorReflection = function (p, q) {\n while (p %
|
franklioxygen
|
NORMAL
|
2019-06-27T00:28:13.938415+00:00
|
2019-06-27T00:28:13.938452+00:00
| 294 | false |
```\n/**\n * 858. Mirror Reflection\n * @param {number} p\n * @param {number} q\n * @return {number}\n */\nvar mirrorReflection = function (p, q) {\n while (p % 2 == 0 && q % 2 == 0) {\n p /= 2;\n q /= 2;\n }\n if (p % 2 == 1 && q % 2 == 0) return 0;\n if (p % 2 == 1 && q % 2 == 1) return 1;\n else return 2;\n};\n```
| 2 | 0 |
[]
| 0 |
mirror-reflection
|
Python with some math
|
python-with-some-math-by-hexadecimal-ggzf
|
Since p and q are both integers, the ray will reach a point with integer coordinates eventually if there were no walls. That point is (lcm/q,lcm/p). If the x-co
|
hexadecimal
|
NORMAL
|
2018-06-24T03:01:38.144293+00:00
|
2018-06-24T03:01:38.144293+00:00
| 407 | false |
Since ```p``` and ```q``` are both integers, the ray will reach a point with integer coordinates eventually if there were no walls. That point is ```(lcm/q,lcm/p)```. If the x-coordinate is even, the correspoding receptor is ```2```. Otherwise, if the y-coordinate is even, the correspoding receptor is ```1```, if the y-coordinate is odd, the correspoding receptor is ```0```. If you flip the region by its eastern and northern boundary you will find this correspondence.\n```\nclass Solution:\n def mirrorReflection(self, p, q):\n """\n :type p: int\n :type q: int\n :rtype: int\n """\n def lcm(x, y):\n x,y=min(x,y),max(x,y)\n lcm=x*y\n while x>0:\n x,y=y%x,x\n \n return lcm//y\n \n f=lcm(p,q)\n m,n=f//p,f//q\n return 2 if n%2==0 else (1 if m%2 else 0)\n```
| 2 | 0 |
[]
| 1 |
mirror-reflection
|
Very easy using euclid method
|
very-easy-using-euclid-method-by-amekiky-l1cm
|
\nclass Solution {\npublic:\n int gcd(int a,int b){\n if (b==0) return a;\n return gcd(b,a%b);\n }\n int mirrorReflection(int p, int q) {
|
amekikyou
|
NORMAL
|
2018-06-24T03:00:39.209049+00:00
|
2018-06-24T03:00:39.209049+00:00
| 917 | false |
```\nclass Solution {\npublic:\n int gcd(int a,int b){\n if (b==0) return a;\n return gcd(b,a%b);\n }\n int mirrorReflection(int p, int q) {\n /*\n It can be expanded to this...\n ...\n |-0\n | |\n 2-1\n | |\n |-0\n | |\n 2-1\n | |\n |-0\n you just need to know ?q=kp (?,k belong to Z)\n */\n int vertlen=p*q/gcd(p,q);\n int box=vertlen/p;\n if (box%2==0) return 0;\n int reftime=vertlen/q;\n if (reftime%2==0) return 2;\n return 1;\n }\n};\n```\n
| 2 | 0 |
[]
| 2 |
mirror-reflection
|
LOg(N) solution | GCD & LCM
|
logn-solution-gcd-lcm-by-iitian_010u-y7j3
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
iitian_010u
|
NORMAL
|
2025-02-20T23:57:58.137983+00:00
|
2025-02-20T23:57:58.137983+00:00
| 31 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int gcd(int a,int b){
if(b==0)return a;
return gcd(b,a%b);
}
int mirrorReflection(int p, int q) {
int lcm = (p*q)/gcd(p,q);
int m = lcm/p, n = lcm/q;
if(m%2==0 && n%2==1)return 0;
if(m%2==1 && n%2==1)return 1;
if(m%2==1 && n%2==0)return 2;
return -1;
}
};
```
| 1 | 0 |
['C++']
| 0 |
mirror-reflection
|
Beats 99% || Easiest Java solution
|
beats-99-easiest-java-solution-by-shivan-ouwj
|
\n# Complexity\n- Time complexity: O(1)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n
|
Shivansu_7
|
NORMAL
|
2023-11-27T08:22:44.938982+00:00
|
2023-11-27T08:22:44.939010+00:00
| 86 | false |
\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int mirrorReflection(int p, int q) {\n while(p%2 == 0 && q%2 == 0) {\n p /= 2;\n q /= 2;\n }\n if(q%2 == 0 && p%2 != 0) \n return 0;\n \n if(q%2 != 0 && p%2 == 0)\n return 2;\n\n if(q%2 != 0 && p%2 !=0)\n return 1;\n\n return -1;\n }\n}\n```
| 1 | 0 |
['Java']
| 0 |
cracking-the-safe
|
DFS with Explanations
|
dfs-with-explanations-by-gracemeng-5gqw
|
In order to guarantee to open the box at last, the input password ought to contain all length-n combinations on digits [0..k-1] - there should be k^n combinatio
|
gracemeng
|
NORMAL
|
2018-07-23T23:16:25.318515+00:00
|
2018-10-23T05:31:59.737251+00:00
| 41,708 | false |
In order to guarantee to open the box at last, the input password ought to contain all length-n combinations on digits [0..k-1] - there should be `k^n` combinations in total. \n\nTo make the input password as short as possible, we\'d better make each possible length-n combination on digits [0..k-1] occurs **exactly once** as a substring of the password. The existence of such a password is proved by [De Bruijn sequence](https://en.wikipedia.org/wiki/De_Bruijn_sequence#Uses):\n\n*A de Bruijn sequence of order n on a size-k alphabet A is a cyclic sequence in which every possible length-n string on A occurs exactly once as a substring. It has length k^n, which is also the number of distinct substrings of length n on a size-k alphabet; de Bruijn sequences are therefore optimally short.*\n\nWe reuse last n-1 digits of the input-so-far password as below:\n```\ne.g., n = 2, k = 2\nall 2-length combinations on [0, 1]: \n00 (`00`110), \n 01 (0`01`10), \n 11 (00`11`0), \n 10 (001`10`)\n \nthe password is 00110\n```\n\nWe can utilize **DFS** to find the password:\n> **goal**: to find the shortest input password such that each possible n-length combination of digits [0..k-1] occurs exactly once as a substring.\n\n>**node**: current input password\n\n>**edge**: if the last n - 1 digits of `node1` can be transformed to `node2` by appending a digit from `0..k-1`, there will be an edge between `node1` and `node2` \n\n>**start node**: n repeated 0\'s\n**end node**: all n-length combinations among digits 0..k-1 are visited\n\n> **visitedComb**: all combinations that have been visited\n****\n```\n public String crackSafe(int n, int k) {\n // Initialize pwd to n repeated 0\'s as the start node of DFS.\n String strPwd = String.join("", Collections.nCopies(n, "0"));\n StringBuilder sbPwd = new StringBuilder(strPwd);\n \n Set<String> visitedComb = new HashSet<>();\n visitedComb.add(strPwd);\n \n int targetNumVisited = (int) Math.pow(k, n);\n \n crackSafeAfter(sbPwd, visitedComb, targetNumVisited, n, k);\n \n return sbPwd.toString();\n }\n \n private boolean crackSafeAfter(StringBuilder pwd, Set<String> visitedComb, int targetNumVisited, int n, int k) {\n // Base case: all n-length combinations among digits 0..k-1 are visited. \n if (visitedComb.size() == targetNumVisited) {\n return true;\n }\n \n String lastDigits = pwd.substring(pwd.length() - n + 1); // Last n-1 digits of pwd.\n for (char ch = \'0\'; ch < \'0\' + k; ch++) {\n String newComb = lastDigits + ch;\n if (!visitedComb.contains(newComb)) {\n visitedComb.add(newComb);\n pwd.append(ch);\n if (crackSafeAfter(pwd, visitedComb, targetNumVisited, n, k)) {\n return true;\n }\n visitedComb.remove(newComb);\n pwd.deleteCharAt(pwd.length() - 1);\n }\n }\n \n return false;\n }\n```\n\n**(\u4EBA \u2022\u0348\u1D17\u2022\u0348)** Thanks for voting!
| 506 | 7 |
[]
| 45 |
cracking-the-safe
|
Easy DFS
|
easy-dfs-by-1moretry-ct8g
|
This is kinda greedy approach.\nSo straight up we can tell that we have k^n combinations of the lock.\nSo the best way to generate the string is reusing last n-
|
1moretry
|
NORMAL
|
2017-12-24T04:15:18.923000+00:00
|
2018-10-15T15:41:27.248371+00:00
| 29,576 | false |
This is kinda greedy approach.\nSo straight up we can tell that we have k^n combinations of the lock.\nSo the best way to generate the string is reusing last n-1 digits of previous lock << I can't really prove this but I realized this after writing down some examples.\n\nHence, we'll use dfs to generate the string with goal is when our string contains all possible combinations.\n\n```java\nclass Solution {\n public String crackSafe(int n, int k) {\n StringBuilder sb = new StringBuilder();\n int total = (int) (Math.pow(k, n));\n for (int i = 0; i < n; i++) sb.append('0');\n\n Set<String> visited = new HashSet<>();\n visited.add(sb.toString());\n\n dfs(sb, total, visited, n, k);\n\n return sb.toString();\n }\n\n private boolean dfs(StringBuilder sb, int goal, Set<String> visited, int n, int k) {\n if (visited.size() == goal) return true;\n String prev = sb.substring(sb.length() - n + 1, sb.length());\n for (int i = 0; i < k; i++) {\n String next = prev + i;\n if (!visited.contains(next)) {\n visited.add(next);\n sb.append(i);\n if (dfs(sb, goal, visited, n, k)) return true;\n else {\n visited.remove(next);\n sb.delete(sb.length() - 1, sb.length());\n }\n }\n }\n return false;\n }\n\n}\n```
| 136 | 3 |
[]
| 28 |
cracking-the-safe
|
A Brainstorming Python Solution
|
a-brainstorming-python-solution-by-books-be1i
|
I tested the solution with all possible test cases, the result seems correct.\n\nAccepted Python Code\n\nclass Solution(object):\n def crackSafe(self, n, k):
|
bookshadow
|
NORMAL
|
2017-12-24T13:01:18.400000+00:00
|
2018-10-17T04:48:53.808771+00:00
| 8,903 | false |
I tested the solution with all possible test cases, the result seems correct.\n\n***Accepted Python Code***\n```\nclass Solution(object):\n def crackSafe(self, n, k):\n """\n :type n: int\n :type k: int\n :rtype: str\n """\n ans = "0" * (n - 1)\n visits = set()\n for x in range(k ** n):\n current = ans[-n+1:] if n > 1 else ''\n for y in range(k - 1, -1, -1):\n if current + str(y) not in visits:\n visits.add(current + str(y))\n ans += str(y)\n break\n return ans\n```\n***Test:***\n```\nimport collections\nso = Solution()\nfor n in range(1, 5):\n for k in range(1, 11):\n if k ** n > 4096: continue\n ans = so.crackSafe(n, k)\n vset = set(ans[x : x + n] for x in range(len(ans) - n + 1))\n print 'k =', k, ' n =', n\n print len(ans), len(vset), sorted(collections.Counter(ans).items()), '\\n'\n```\nSee also: http://bookshadow.com/weblog/2017/12/24/leetcode-open-the-lock/
| 54 | 4 |
[]
| 12 |
cracking-the-safe
|
Easiest Explanation and Shortest Code, Beat 100%
|
easiest-explanation-and-shortest-code-be-rwkh
|
Rewrite the description of the task in simple words:\na password is a combination of digits, such as 0,1,2.....k-1, and its length is n. \nIf we can enter digit
|
marcochang
|
NORMAL
|
2020-10-20T03:19:51.753700+00:00
|
2020-11-11T15:40:59.516850+00:00
| 4,162 | false |
Rewrite the description of the task in simple words:\na password is a combination of digits, such as 0,1,2.....k-1, and its length is n. \nIf we can enter digits of an arbitrary length, \n***find any minimal length of digits can unlock in one operation.***\n\nIt means \nif k=2 and n=3, \ndigits would be 0 and 1, and password may be any of 010, 000, 100, 001, 111, 110, 101, 011.\nAlthough we don\'t know which one is correct, \nwe can enter all combinations in one entering. If any one in combinations matches, unlock.\n***The number of all combinations is k^n***.\n\nWe can use all combinations\' suffixes and keep updating suffixes \nuntil the end because ***each suffix must be others\' prefix***.\nFor example, 0+10 --> 10+1, 1+01 --> 01+1 and so on.\n\nTherefore, \nwe can create a hashmap, keys of which are suffixes of combinations, and keep updating it\nbecause the same suffix in the same prefix can\'t appear twice.\nFor example, 11+0 and 11+1\n\nTime complexity: O(k^n)\nSpace complexity: O(k^n)\n**Code with clear comments as below**\n```\nclass Solution(object): # best 24 ms\n def crackSafe(self, n, k):\n # n: length of password\n # k: kinds of digits (0,1,2....)\n \n if n == 1: return "".join(str(i) for i in range(k))\n if k == 1: return "0" * n\n\n suffixMap = {}\n allCombination = "0" * (n-1)\n\n for _ in range(k**n):\n # get suffix\n suffix = allCombination[1-n:]\n # create suffix map, value is k - 1 or update previous value - 1\n suffixMap[suffix] = suffixMap.get(suffix, k) - 1\n # add new suffix\n allCombination += str(suffixMap[suffix])\n\n return allCombination\n```\n\n***If helpful, please upvote!! Thanks a lot!!***
| 46 | 1 |
[]
| 3 |
cracking-the-safe
|
Accepted Cheat 1-liner :-D
|
accepted-cheat-1-liner-d-by-stefanpochma-wwev
|
The judge doesn't check that I'm only using the allowed digits or even digits at all, so I just build a string with the correct length without repeating substri
|
stefanpochmann
|
NORMAL
|
2017-12-24T23:10:15.488000+00:00
|
2017-12-24T23:10:15.488000+00:00
| 6,403 | false |
The judge doesn't check that I'm only using the allowed digits or even digits at all, so I just build a string with the correct length without repeating substrings of length n. Currently it does get accepted (edit: not anymore, see reply below). And hey, if I'm cracking a safe, I might as well cheat.\n\nRuby:\n```\ndef crack_safe(n, k)\n [''].product(*%w(abcdefghij klmnop ABCDEF KLM).map(&:chars)[0, n]).join[0, k**n + n-1]\nend\n```\n\nPython:\n\n def crackSafe(self, n, k):\n chunks = itertools.product(*'abcdefghij klmnop ABCDEF KLM'.split()[:n])\n return ''.join(map(''.join, chunks))[:k**n + n-1]\n\nExplanation:\n\nLet's say n is 2. Then I concatenate these *pairs* of characters: "ak", "al", "am", ..., "jn", "jo", "jp". That is, all combinations of a letter from "abcdefghij" with a letter from "klmnop". So my result is "akalam...jnjojp". I just need to cut it off at the right length.\n\nBut how do I know there are no duplicate substrings of length 2? Well, those starting at *even* indexes are just "ak", "al", etc, all *different* combinations I used to build the string in the first place. I also can't have a substring at an *even* index matching a substring at an *odd* substring, since I use different alphabets ("abcdefghij" and "klmnop") for even and odd indices. Could two substrings at *odd* indices match? Heh, actually I just noticed that I forgot to think about this. But I think I just get all combinations of a letter from "klmnop" with a letter from "abcdefghij", just not in the normal order.\n\nWhen n is 1, 3 or 4, I do the same, except I concatenate singles or triples or quadruples.\n\nThe four alphabet sizes are btw minimized so they're just long enough for all cases.
| 41 | 12 |
[]
| 3 |
cracking-the-safe
|
C++, greedy loop from backward with explaination
|
c-greedy-loop-from-backward-with-explain-c7vw
|
Taking n = 2,k= 2 as example, we start with "00", let string prev = last n-1 digits (prev = '0'), and create an new string by appending a new digit from k-1 to
|
wenyi3
|
NORMAL
|
2017-12-26T20:48:49.599000+00:00
|
2017-12-26T20:48:49.599000+00:00
| 5,964 | false |
Taking n = 2,k= 2 as example, we start with "00", let string prev = last n-1 digits (prev = '0'), and create an new string by appending a new digit from k-1 to 0 respectively. in this case we first check string '01'.\nfor each string, we use an unordered_set to check if visited. if valid then we append another digit until the end.\n\n```\nstring crackSafe(int n, int k) {\n string ans = string(n, '0');\n unordered_set<string> visited;\n visited.insert(ans);\n \n for(int i = 0;i<pow(k,n);i++){\n string prev = ans.substr(ans.size()-n+1,n-1);\n for(int j = k-1;j>=0;j--){\n string now = prev + to_string(j);\n if(!visited.count(now)){\n visited.insert(now);\n ans += to_string(j);\n break;\n }\n }\n }\n return ans;\n }\n```
| 37 | 0 |
[]
| 15 |
cracking-the-safe
|
De Bruijn sequence C++
|
de-bruijn-sequence-c-by-plotcondor-g665
|
From wiki: De Bruijn sequence \n"a de Bruijn sequence of order n on a size-k alphabet A is a cyclic sequence in which every possible length-n string on A occurs
|
plotcondor
|
NORMAL
|
2017-12-24T04:30:18.852000+00:00
|
2018-09-22T18:47:22.058255+00:00
| 9,909 | false |
From wiki: [De Bruijn sequence](https://en.wikipedia.org/wiki/De_Bruijn_sequence) \n"a de Bruijn sequence of order n on a size-k alphabet A is a cyclic sequence in which every possible length-n string on A occurs exactly once as a substring".\n\nThe De Brujin sequence has length k^n. See the proof from the link.\n\n"The de Bruijn sequences can be constructed by taking a Hamiltonian path of an n-dimensional de Bruijn graph over k symbols (or equivalently, an Eulerian cycle of an (n \u2212 1)-dimensional de Bruijn graph)."\n\nUse Hierholzer's Algorithm to construct the Eulerian circuit.\nI read @dietpepsi 's post about this problem. \n\n```\nclass Solution {\n int n, k, v;\n vector<vector<bool> > visited;\n string sequence;\npublic:\n string crackSafe(int n, int k) {\n if (k == 1) return string(n, '0');\n this->n = n;\n this->k = k;\n v = 1;\n for (int i = 0; i < n -1; ++i) v *= k;\n visited.resize(v, vector<bool>(k, false));\n dfs(0);\n return sequence + sequence.substr(0, n - 1);\n }\n \n void dfs(int u) {\n for (int i = 0; i < k; ++i) {\n if (!visited[u][i]) {\n visited[u][i] = true;\n dfs((u * k + i) % v);\n sequence.push_back('0' + i);\n }\n }\n }\n};\n```
| 36 | 1 |
[]
| 8 |
cracking-the-safe
|
Python Eulerian Path (Eulerian Trail) Solution
|
python-eulerian-path-eulerian-trail-solu-lc4c
|
Intuition\nThe original problem can be formulated as finding the Eulerian Path in a finite connected graph. If you are not familiar with the concept of the Eule
|
Daniel513
|
NORMAL
|
2023-01-16T03:33:13.217065+00:00
|
2023-01-16T17:48:22.259510+00:00
| 1,108 | false |
# Intuition\nThe original problem can be formulated as finding the Eulerian Path in a finite connected graph. If you are not familiar with the concept of the Eulerian Path, please read [this Wikipedia page](https://en.wikipedia.org/wiki/Eulerian_path).\n\nLet\'s say the length of the correct password is `n`, and the possible digits are in the range `[0, k-1]`. If we enumerate all the possible permutations of length `n-1` and model them as vertices, then we get a graph. Let\'s use a concrete example, let\'s say `n = 3`, `k = 3`. Then if we draw all the permutations with length `2`, we get the following graph.\n\n\n\nNow we add one more digit to the end of these permutations. The available digits are in the range `[0, k-1]`. We model the added digit as an outgoing edge. Let\'s use the vertex `00` in the above graph as an example. After appending one more digit to this vertex, the graph will look like the following.\n \n\n\nThe formed length `n` permutations are `000, 001, 002`. These three permutations are all the permutations of length `n` with the prefix `00`. We do the same thing to all the other vertices, and then the graph will contain all the possible permutations of length `n` on a size-k alphabet. Each edge represents a distinct permutation. Since there is `k` to the power of `n` permutations, the number of edges in the graph will also be `k^n`. The suffixes of the permutations `000, 001, 002` are `00, 01, 02`. If we treat vertices in the graph as suffixes, then we can connect the vertex `00` to `02` to represent the transformation between two different vertices(suffixes).\n\n\n\nNow we connect all the vertices in this way. Then we get a connected graph. Each edge in the graph represents a permutation of length `n`. In the example we used, `n = 3`.\n\n\n\nLet\'s go back to the problem itself. It asks us to find the shortest length of unlocking the safe. Imagine that you are pressing the keyboard and entering a sequence of digits, trying to break the safe. The sequence of digits you used is the following:\n\n\n\nThe `n` is `3`, and `k` is in the range `[0, 2]`. The first password you tried is `002`, the second is `022`, the third is `221`, and so on. The suffixes of these passwords are `02`, `22`, `21`, and so on. In the graph, it equivalents to you starting from node `00`, passing through `02`, `22`, and arrived at node `21`. The path you have gone through is shown in the following graph.\n\n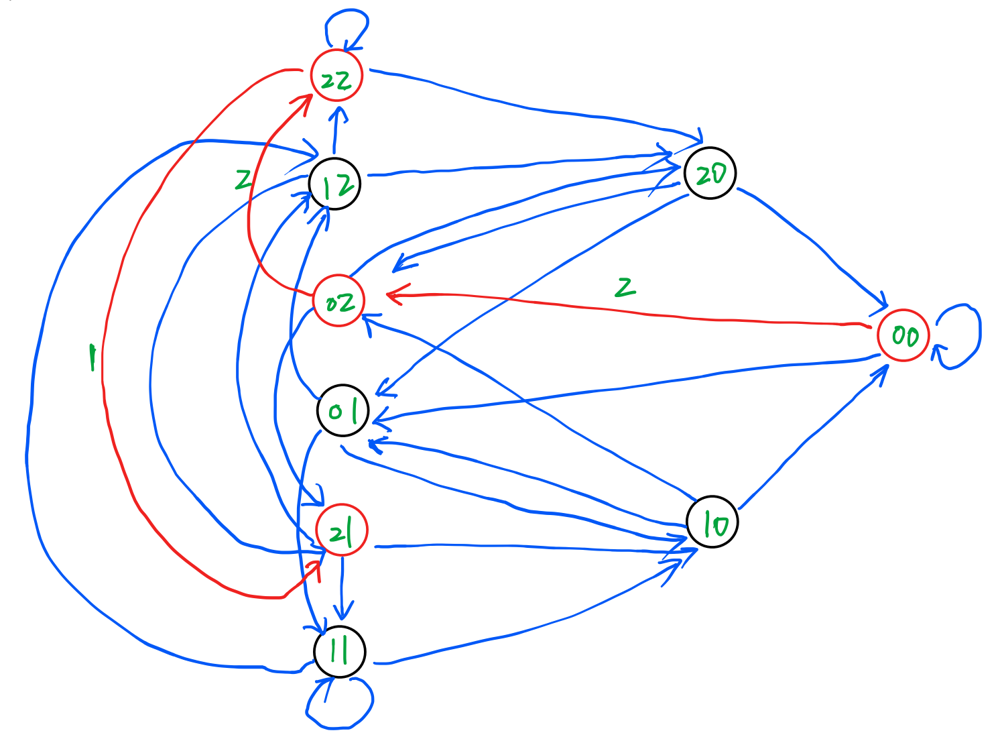\n\nIn fact, you can think of the sequence of digits that you just entered as a flattened graph. Every subsequence of length `n-1` (In this example, `n-1` is `2`.) is a vertex in the graph.\n\n\n\nNow the original problem has been completely transformed into a graph traversing problem. To make the sequence as short as possible, we just need to make sure that we traverse the above graph as short as possible. Also, since we also want to make sure the safe can be cracked in the end, we want to make sure we try each possible password of length `n` at least once. Each edge of the above graph represents a distinct password. All edges represent all possible passwords. So we want to traverse each edge at least once. Combining all these, ***we want to find a path in the graph that traverses each edge exactly once.*** If such a path exists, then we have found the shortest sequence of digits, which can surely crack the safe.\n\nThe definition of the Eulerian Path is exactly the same: it is a path in a finite graph that visits every edge exactly once. So the problem actually asks us to determine whether there is an Eulerian Path in the above graph. If so, then find it. The Eulerian Theorem tells us: \n\n* A connected graph has an Euler cycle if and only if every vertex has an even degree.\n\nIn the above graph, each vertex has `k` incoming edges and `k` outcoming edges. Therefore each vertex has `2k` connected edges, which means the above graph has an Euler cycle. The Euler cycle is also one kind of Eulerian path. Therefore we know there must be a path that covers each edge exactly once in the above graph. Now the question is: how to find it?\n\nThe solution we used is to start from node `00`. At each vertex, we choose the highest possible `k` edge. In the end, we surely go back to node `00,` and the path we have traversed is the answer. Why? How do we prove that we always got all the edge using the algorithm I described above?\n\nFirst, we can prove that we would never get stuck in any vertex except for the node where we start. In other words, we can prove that starting from any arbitrary vertex in the graph, we will surely be able to go back to this starting node. \n\nWe can use contradiction to prove this. Let\'s say the node below is where we get stuck, and this node is not the starting node. The incoming red edge is where the stuck occurred.\n\n\n\nWe are stuck at this node because all the outcoming edges have been used once. As a result, when we traverse into this node by the incoming red edge, there is no way for us to get out of this node. Since each node has the same number of incoming edges and outcoming edges, the number of used outcoming edges is `3`. That means we must also have used `3` incoming different edges before. However, we only have `3` incoming edges in total. That means we only used `2` incoming edges. This is a contradiction. Therefore we proved that we would never get stuck at any node in the middle. We can also prove that the only node we will get stuck in is the node where we started. We can use the same logic above to prove this. The difference between the starting node and the middle node is that we used the outcoming edge first in the starting node. However, for the other node, we used their incoming edge first.\n\nNow we have proved that we would only get stuck at the starting node after we have used all its outcoming and incoming edges. In other words, when the traversal ends, all edges of the starting node have been traversed. Now, if we can prove that all the edges of other nodes have been traversed, we are done. Not all kinds of traversals cover all edges of the graph. See the following example.\n\n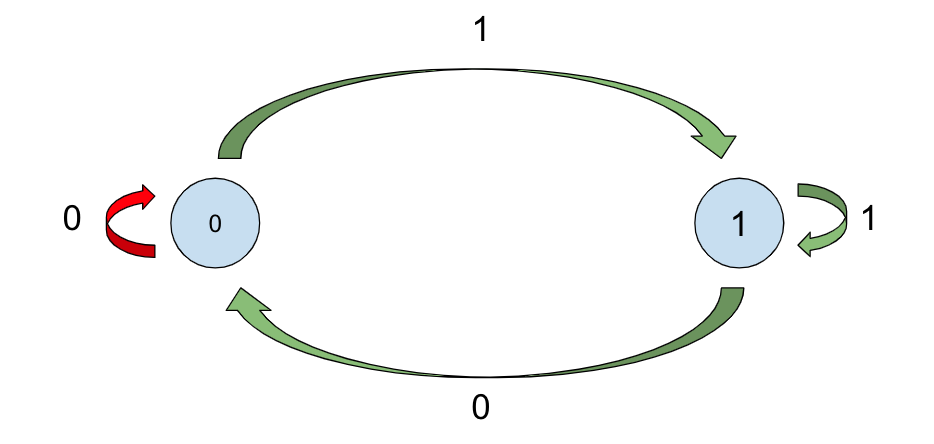\n\nIn this example, `n = 2` and `k = 2`. If the starting node is the vertex with value `1`, and the algorithm picks the edges from the highest value to the lowest value, then when the traversal ends, there is one edge that has not been traveled - the edge in red in the graph. How do we prove that the traversal used in our algorithm does cover all the edges?\n\nBelow is the graph of our previous example.\n\n\n\nTo remind you, the algorithm we used traverses the graph from the node `00`, and always pick the highest-value untraveled edge to go at each step. As we said before, when the algorithm ends, all the edges of the starting node are traversed. Now we go backward and look at the nodes `20` and `10`. When the algorithm goes from `20` or `10` to the node `00`, all the other edges of these two nodes must have been traversed. The reason is the edges connecting `20` or `10` to the node `00` have the lowest edge value, `0`. According to the algorithm, it means all the outcoming edges with higher values (`2`, `0`) have been traversed. Since one outcoming edge must be paired with one incoming edge, we know that when the algorithm picks the lowest-value outcoming edge, all the edges of this node must have been traversed. Thus, we can conclude that all the edges connected to nodes `20` and `10` have been covered.\n\nWe can go backward further and make the same conclusion for the nodes `22`, `12`, `02`, `01`, `21`, and `11`. Specifically, when the length of the password is `n`, starting from the starting node `0...0`, we can go `n-1` layers backward and make the same conclusion for all nodes in these `n-1` layers. The number of nodes in these layers is:\n\n`(k-1) + (k-1)*k + (k-1)*k^2 + ...... + (k-1)*k^(n-2)`\n\nWe can simplify this to:\n\n`k^(n-1) - 1`\n\nAdding the starting node, the number of nodes becomes:\n\n`k^(n-1)`\n\nTherefore, up until now, we have proved there are `k^(n-1)` nodes having all connected edges covered. The number of nodes in the graph is also `k^(n-1)`, since the number of permutations of length `n-1` is `k^(n-1)`. That proves all edges of all nodes in the graph have been traversed.\n\n# Code\n```\nclass Solution:\n def crackSafe(self, n: int, k: int) -> str:\n ava_edge = defaultdict(lambda: k-1)\n res = [\'0\'] * (n-1)\n suffix = \'\'.join(res)\n while ava_edge[suffix] >= 0:\n res.append(str(ava_edge[suffix]))\n ava_edge[suffix] -= 1\n suffix = \'\'.join(res[1-n:] if n > 1 else [])\n return \'\'.join(res)\n```\n\n
| 28 | 0 |
['Python3']
| 1 |
cracking-the-safe
|
Easy to understand Python DFS
|
easy-to-understand-python-dfs-by-albingr-zs9i
|
Starting from all 0\'s, then dfs traverse each possibility and backtrack if not possible. \n\ndef crackSafe(self, n, k):\n """\n :type n: int\n
|
albingrace
|
NORMAL
|
2018-10-24T04:18:53.754218+00:00
|
2018-10-24T04:18:53.754259+00:00
| 3,627 | false |
Starting from all 0\'s, then dfs traverse each possibility and backtrack if not possible. \n```\ndef crackSafe(self, n, k):\n """\n :type n: int\n :type k: int\n :rtype: str\n """\n def dfs(curr, counted, total):\n if len(counted)==total:\n return curr\n \n for i in range(k):\n tmp = curr[-(n-1):]+str(i) if n!=1 else str(i)\n if tmp not in counted:\n counted.add(tmp)\n res = dfs(curr+str(i), counted, total)\n if res:\n return res\n counted.remove(tmp)\n \n return dfs("0"*n, set(["0"*n]), k**n)\n```
| 28 | 1 |
[]
| 2 |
cracking-the-safe
|
Python Hierholzer's with inline explanations
|
python-hierholzers-with-inline-explanati-3f7c
|
``python\nfrom itertools import product\n\nclass Solution:\n def crackSafe(self, n: int, k: int) -> str:\n """\n The strategy to crack the safe
|
dcvan24
|
NORMAL
|
2019-10-24T17:53:19.929773+00:00
|
2019-10-24T18:00:58.432474+00:00
| 2,509 | false |
```python\nfrom itertools import product\n\nclass Solution:\n def crackSafe(self, n: int, k: int) -> str:\n """\n The strategy to crack the safe is to try all the code combinations. As \n the safe is designed in the way that it always reads the last `n` digits \n keyed in, there are opportunities that we can reuse the common digits \n shared between contiguous combinations and thus save certain key \n strokes. Herein, the problem asks for one working code sequence that has \n the minimum length and thus saves us the most key strokes. \n\n Obviously, given a safe with a k-digit pad and n-digit password length, \n to crack it with brute force, there are `k^n` combinations to try, so \n the worst case is that we key in every single combination and get a \n sequence with a length of `n * k^n`. But there are definitely certain \n common digits shared among the combinations, which we can leverage to \n shorten the sequence. The crux is the order to try all the combinations \n that exploits the common ground. \n\n If we think of every combination as a node in the graph, the common \n ground between the combinations is the edge between every pair of nodes, \n which allows a combination to be transformed to another by removing the \n first digit at the front and adding a new digit to the end. Our goal is \n to go over all the nodes in a single pass, since we don\'t want to try a\n combination twice to prolong the code sequence. Intuitively, we try to \n find an euler path from such graph. A known algorithm to find an euler \n path is Hierholzer\'s, which has been thoroughly introduced here: \n https://www.geeksforgeeks.org/hierholzers-algorithm-directed-graph/ \n \n """\n # generate all the possible combinations with the given `n` and `k`, \n # which are the nodes in the graph and the edges are implicitly created \n # if any pair of combinations have certain digit sequence in common\n perms = set(map(lambda x: \'\'.join(x), product(map(str, range(k)), repeat=n)))\n res = []\n \n # run DFS to traverse all the nodes in the graph and remove them once \n # they being visited. Removing a node also implicitly removes the \n # edge(s) to the combinations it can be transformed to\n def dfs(n):\n # stop when the graph is empty\n if not perms:\n return\n for d in map(str, range(k)):\n # transform the current combination to another by removing the \n # digit at the front and appending a digit to the end\n next_ = (n + d)[1:]\n # check if the new combination is still reachable, i.e. if it is \n # not yet visited and the edge to it still exists\n if next_ in perms:\n # if it is not yet visited, remove it from the graph and \n # visit it next\n perms.remove(next_)\n dfs(next_)\n # according to Hierholzer\'s, we can only add a node to an \n # euler path until it has no edges to other nodes. So we \n # visit the node first to remove all its edges to others \n # first and add the node to the path then\n res.append(d)\n \n # start with all digits set to 0\n start = \'0\' * n\n # remove the start from the graph\n perms.remove(start)\n \n # start the traversal\n dfs(start)\n \n # add the start to the end of the path to form the euler circuit\n return \'\'.join(res) + start
| 22 | 0 |
[]
| 5 |
cracking-the-safe
|
Python short with proof sketch.
|
python-short-with-proof-sketch-by-veryra-tuio
|
You look at a graph which\'s nodes are all possible strings of length n-1. Such a node represents the "recent memory" or state of the password input. If you th
|
veryrandomname
|
NORMAL
|
2020-12-13T10:36:57.289093+00:00
|
2021-01-05T22:34:16.612818+00:00
| 1,290 | false |
You look at a graph which\'s nodes are all possible strings of length n-1. Such a node represents the "recent memory" or state of the password input. If you then input a letter, this state plus the new letter is checked against the password. The edges of the graph are all the possible transitions between these states. Then observe that every node has exactly k incoming and k outgoing edges. Thus there exists an euler path in that graph. In this particular case you can find that euler path by starting at `"0" * (n - 1)` and using the edges corresponding to larger numbers first. Every node except the start node has an unused outgoing edge for every unused incoming edge, so you can only get stuck at `"0" * (n - 1)`.\nHow does one know that one does not get stuck at `"0" * (n - 1)` before enumerating all edges?\nSince you always pick the highest available edge first, you get to enumerate all the edges involving high numbers first. If you were to get stuck at `"0" * (n - 1)`, you would have already enumerated all edges of `"0" * (n - 1)` and all edges of the neighbors of `"0" * (n - 1)` and so on...\n\nHere\'s my code\n```\nclass Solution:\n def crackSafe(self, n: int, k: int) -> str:\n visited = set()\n s = \'0\'*(n-1)\n res = s\n while True:\n for i in range(k-1,-1,-1):\n if (s,i) not in visited:\n res += str(i)\n visited.add((s,i))\n s = (s+str(i))[1:]\n break\n else:\n return res\n```
| 18 | 0 |
[]
| 5 |
cracking-the-safe
|
[Java] Greedy DFS with explanation
|
java-greedy-dfs-with-explanation-by-curi-kicw
|
This one made me little crazy but I think this should be good enough for an interview. \n\nclass Solution {\n /**\n This problem is really hard for an int
|
curiousgeorge1976
|
NORMAL
|
2021-02-26T23:35:13.048352+00:00
|
2021-02-26T23:35:13.048386+00:00
| 1,171 | false |
This one made me little crazy but I think this should be good enough for an interview. \n```\nclass Solution {\n /**\n This problem is really hard for an interview. But companies who are notorious for asking these kind of questions getting this\n in the interview is a blessing. This is because those companies stack rank interviewers answer and you need to be in the elite\n group to get a hire. Now if you are asked an easy question, you will really need to ace it and throw it out of the park. Any\n mistake will work against you. You may think you have done well but in fact you have not. That is just my 2 cents.\n Now let\'s see what this question means if we do not have minimum length requirement. Does that make this question easy?\n It does because in that case it is a simple permutation problem. Steps:\n 1. Since you can place one of the k number at n places, simply generate all permuation, concatenate it and you are done (An interview\n is actually trying to find your strength and not demoralize you unless... you get it). At this time interviewer should be reasonably impressed\n and should be willing to help.\n 2. Now the question is while generating the concatenation (remember all n length suffix is matched), in the best case you can reuse n-1 suffix.\n Couple of important things;\n - If length restriction is not there we can always generate all k^n combination and done. Each combination is of length n. So string length = n * k^n\n - Optimal solution is to reuse last n-1 character everytime, so string length will be k^n + n-1.\n By this time I know that this is a graph problem. Thought of mapping each digit to a node but got stuck because transition from\n one node to other was not deterministic. I mean if I have node 0 and 1, how do I know how many edges between 0 and 1.\n \n So my next thought was to exactly do as I was thinking. Take any permutation and greedily try traversing all nodes.\n If we get stuck bracktrack. But how do I know I am stuck. It is easy. If I keep a visited set and at any point of time from one node\n I cannot go to another node I know I am stuck. But when to end? When I have k^n node in the set.\n \n Let\'s code this and see.\n **/ \n public String crackSafe(int n, int k) {\n // String is immutable, use StringBuilder\n StringBuilder result = new StringBuilder();\n // This is total number of permutation we need in the set\n int total = (int) (Math.pow(k, n));\n \n // This is just for fun and to prove that we can start with any permutation\n Random rand = new Random();\n for (int i = 0; i < n; i++) {\n result.append(rand.nextInt(k));\n }\n\n Set<String> visited = new HashSet<>();\n visited.add(result.toString());\n\n dfs(result, total, visited, n, k);\n\n return result.toString();\n }\n\n private boolean dfs(StringBuilder result, int target, Set<String> visited, int n, int k) {\n if (visited.size() == target) {\n // We are done, terminate all recursion\n return true;\n }\n String prev = result.substring(result.length() - n + 1, result.length());\n for (int i = 0; i < k; i++) {\n String next = prev + i;\n if (!visited.contains(next)) {\n visited.add(next);\n result.append(i);\n if (dfs(result, target, visited, n, k)) {\n // recursively terminate, we are done\n return true;\n }\n else {\n // We got stuck so this will not yield optimal path, go back\n // Try other path\n visited.remove(next);\n result.delete(result.length() - 1, result.length());\n }\n }\n }\n return false;\n }\n}\n```
| 15 | 1 |
[]
| 0 |
cracking-the-safe
|
Javascript Solution with comments and explanation
|
javascript-solution-with-comments-and-ex-z68b
|
To solve the problem we must generate a De Bruijn sequence which is the shortest sequence containing all possible combinations of a given set, for the current p
|
user0657y
|
NORMAL
|
2019-07-23T23:44:43.332543+00:00
|
2019-07-23T23:51:57.441567+00:00
| 998 | false |
To solve the problem we must generate a De Bruijn sequence which is the shortest sequence containing all possible combinations of a given set, for the current problem it would be every combination of length n containing numbers from 0 to k - 1. The idea is to start with the first full combination as the starting point for our sequence and traverse every node once (a Euler walk) using a depth first traversal and append the last element of adjacent combinations to the sequence. I have included some addition resources below to give more context.\n\nDe Bruijn Sequence:\nhttps://www.youtube.com/watch?v=iPLQgXUiU14\n\nEuler Walk:\nhttps://www.youtube.com/watch?v=TNYZZKrjCSk\n\nAdditional Resources:\nhttps://www.geeksforgeeks.org/de-bruijn-sequence-set-1/\n\n\n```\nconst crackSafe = (n, k) => {\n // If k and n equal 1 the only combination possible is 0.\n if (n === 1 && k === 1) return \'0\'\n \n // visited will keep track of all visited edges.\n const visited = new Set()\n \n // The De Bruijn Sequence that will be the output of the function.\n const seq = []\n \n // To generate a De Bruijn sequence we must traverse every combination of size n\n // containing the number from 0 to k - 1. We will start with the prefix of the \n // combination with all 0s. If n equals 3 and k is greater than 1 our prefix would be\n // 00 and the first combination, our starting edge would be 000.\n const prefix = \'0\'.repeat(n - 1)\n \n // We will perform a depth first traveral until we visit every edge (combination)\n // while adding the last element of a combination to the sequence.\n dfs(prefix, seq, visited, k)\n \n // We append the original prefix to the sequence as the a De Bruijn sequence \n // ends with the first combination. If we reverse the sequence it would still be \n // valid and in that case would start with the first combination instead.\n seq.push(prefix)\n \n // Join the array to return the sequence as a string.\n return seq.join(\'\')\n}\n\nconst dfs = (prefix, seq, visited, k) => {\n for (let i = 0; i < k; i++) {\n // Generate a new combination using all the numbers from 0 to k - 1\n // this will give us all the edges that are adjacent to the previous\n // combination.\n const combination = prefix + i.toString()\n \n // Check if the current combination has been visited we skip it.\n if (visited.has(combination)) continue\n \n // If the current combination hasn\'t been visited add it to the visited set\n // so we do no revisit it.\n visited.add(combination)\n \n // Create a new prefix using the current combination\n // and continue the depth first traversal.\n dfs(combination.slice(1), seq, visited, k)\n \n // Add the last element of the visited combination to the sequence.\n seq.push(i)\n }\n}\n
| 14 | 0 |
['Depth-First Search', 'JavaScript']
| 4 |
cracking-the-safe
|
De Bruijn Sequence | Euler's Path | Python
|
de-bruijn-sequence-eulers-path-python-by-pt58
|
The question asks us to find the De Bruijn sequence which is basically either an eulers path (visiting all edges once) or a hamiltonian path ( visiting all vert
|
veecos1
|
NORMAL
|
2021-07-05T21:24:25.861245+00:00
|
2021-07-05T21:26:42.861415+00:00
| 923 | false |
The question asks us to find the De Bruijn sequence which is basically either an eulers path (visiting all edges once) or a hamiltonian path ( visiting all vertexes once ). \n\nThe algorithm below finds the eulers path by enumerating all all edges as the different combinations one can enter into a lock. Lets look at this for n = 2 and k =2. Here we have two vertexes 0 and 1 and four edges 00, 01, 10, 11. We start with vertex and do a depth first search until we hit the starting node and then backtrack. When we backtrack as we come across any unvisited edges we do a depth first search on them as well. Hierholzer\'s algorithm is also related to this. The edges and the transitions can be described by the last digit and we record all them when backtracking\n\nNow in the case of 0, we visit 00, 01 reach vertex 1, visit 10, reach vertex 0. Realize we have already visited 00 and 01 here and start backtracking add 0 (for 10), visit 11, add 1 (for 11), add 1 for (for 01) and finally add 0 for (00). \n\nNow De Bruijn sequences are considered cyclic. For example*0*11*0* is used to denote 00 as they are the first and last characters and we consider them cyclic. The question however asks us to present this continously and hence we add the 0\'s to the end.\n\nHope this helps someone. I saw several videos on youtube, referred to the diagrams on wikipedia and went through geeks for geeks for this one.\n\nTime Complexity is O(V+E) = O(k^n)\nSpace Complexity is dominated by the call stack of DFS = O(k^n)\n\n```\n def crackSafe(self, n: int, k: int) -> str:\n # starting vertex\n # There are a total of k^(n-1) vertexes\n start_string = \'0\' * (n-1)\n result = []\n edges_seen = set()\n \n def dfs(node):\n nonlocal result\n for i in range(k):\n current_edge = node + str(i)\n if current_edge not in edges_seen:\n edges_seen.add(current_edge)\n # This actually does dfs for the current vertex\n # Because the current vertex is the edge value after \n # the first character\n dfs(current_edge[1:])\n result.append(str(i))\n \n dfs("0"*(n-1))\n result.extend([\'0\']*(n-1))\n \n return "".join(result)
| 12 | 0 |
[]
| 2 |
cracking-the-safe
|
hamiltonian cycle - explanation why it's applicable here and implementation. (python)
|
hamiltonian-cycle-explanation-why-its-ap-chc3
|
hamiltonian cycle - consists of node which needs to be visited only once forming a cycle. \n\nModel - \nwe have to find shortest string that contains all possib
|
asyncdevs
|
NORMAL
|
2021-04-26T08:49:17.441750+00:00
|
2021-09-13T11:35:53.305424+00:00
| 4,154 | false |
hamiltonian cycle - consists of node which needs to be visited only once forming a cycle. \n\nModel - \nwe have to find shortest string that contains all possible password as a substring.\n\nAssume we have two strings "0000" and "0001". then shortest string is "00001", if we consider strings as node then we can think of an edge from node1 to node2 as the minimum number of characters need to be added in node1 to make node2. in this case it is 1 and from node2 to node1, minimum weight is 4 since no suffix of node2 matches with the prefix of node1\nedge with **weight 1** is the best that we can get if two strings are different\nNow if we can model our problem such that every possible node is connected to another node with minimum weight exactly equals to **weight 1** then the answer will be finding any cycle which contains every node once, this will be the shortest superstring which contains all possible node, this is hamiltonian cycle. Now we need to find hamiltonian cycle with mimum weight since we made sure that every node is connected to another node only if the edge weight between them is 1, so all the various hamiltonian cycle will have the same weight. \n\nNow, how to model a directed graph as explained above such that edge weight of all (u, v) == 1\n\nsince the password length is n, and every digit is [0, k-1] we have k^n possible nodes, since every position there is k possible values. \nassume k = 2, n= 3 then there are 8 possible nodes\nif we cur at "000" then we take the n-1 suffix of the start and generate [001, 000] by adding ["0" and "1"] to "00", but since "000" is same as prev node we skip that, so \n\n"000" -> "001"\nnow the current is "001", we n-1 suffix of "001" which is "01" and try generating nodes ["010", "011"]\n\n"000" -> "001" -> "010"\n\t\t\t\t\t\t-> "011"\n\t\t\t\t\t\t\nnote generated node can pont to node which have been generated earlier in this enumeration. \n\nthe comeplete graph is shown below - \n\n\nsince the node generated have n-1 starting characters same as n-1 ending characters from the previous node, the edge weight will always be 1, so all the possible hamiltonian cycles(if present, from intution there should be hamiltonian cycle since every node suffix is prefix of another node, I don\'t have proper proof for it though) are having same weight. \n\nImplementation-\nsame as above, but instead of first generating the whole graph and find the hamiltonian cycle, we enumerate step by step with backtarcking. \n\n```\nclass Solution:\n def crackSafe(self, n: int, k: int) -> str:\n seen = set()\n startNode = "0"*n \n\t\t# base cases\n if n == 1:\n s = ""\n for i in range(k):\n s+= str(i)\n return s\n elif k == 1:\n return "0"*n\n\t\t\t\n\t\t\n def dfs(curNode, partialpath):\n if len(seen) == k**n and curNode == startNode:\n\t\t\t\t#if we have seen k^n nodes and the curNode traversed back to startNode\n return partialpath[:-1]\n if curNode in seen:\n\t\t\t\t# this will make cycle to avoid and backtrack\n return\n seen.add(curNode)\n suffix = curNode[1:]\n a = None\n for c in range(k):\n newNode = suffix+str(c)\n if newNode == curNode:\n\t\t\t\t\t# if the next node is same as prev node then skip it\n continue\n a = dfs(newNode, partialpath+[newNode])\n if a:\n return a\n\t\t\t# once we backtrack, remove the current node from seen, since this node can be visited again from another path\n seen.remove(curNode)\n \n password = dfs(startNode, [startNode])\n s= password[0]\n for p in range(1, len(password)):\n s += password[p][-1]\n return s\n```
| 12 | 0 |
[]
| 3 |
cracking-the-safe
|
DFS with Explanation, Clean Code
|
dfs-with-explanation-clean-code-by-yu_sh-pyg7
|
```\n// Graph Traversal Problem\n// Vertex: "00", "01", "10", "11" such numbers\n// Neighbors: for "00", the neighbors are "01", "00" (X self)\n//
|
yu_shuxin
|
NORMAL
|
2020-06-27T20:34:57.277989+00:00
|
2020-06-27T20:34:57.278035+00:00
| 1,228 | false |
```\n// Graph Traversal Problem\n// Vertex: "00", "01", "10", "11" such numbers\n// Neighbors: for "00", the neighbors are "01", "00" (X self)\n// for "01", the neighbors are "11", "10"\n// Neighbor\'s first n-1 digits are the same as cur node\'s last n-1 digits\n// This problem actually asks us to find a path which contains all the nodes (no cycle obviously)\n// All reachable nodes problem\n// So we can use depth first search \n// Base case is when we find such path (used up all nodes)\n// And we don\'t need to construct the whole graph at the beginning, we can get neighbors on the fly\n// Time Complexity: O(|V| + |E|) |V| = the number of nodes = k ^n |E| = k * k^n (every node has k neighbors)\n// Space: height of recursion tree: O(|V|) = k^n\n public String crackSafe(int n, int k) {\n if (n <= 0 || k <= 0) {\n return "";\n }\n Set<String> visited = new HashSet<>();\n String cur = "";\n for (int i = 0; i < n; i++) {\n cur += "0";\n }\n // start with "00"\n int total = (int) Math.pow(k, n);\n StringBuilder sb = new StringBuilder();\n visited.add(cur);\n sb.append(cur);\n dfs(n, k, total, sb, cur, visited);\n return sb.toString();\n }\n \n private boolean dfs(int n, int k, int total, StringBuilder sb, String cur, Set<String> visited) {\n if (visited.size() == total) {\n return true;\n }\n String str = cur.toString();\n String suffix = str.substring(1);\n for (int i = 0; i < k; i++) {\n char ch = (char)(i + \'0\');\n String nei = suffix + ch;\n if(!visited.contains(nei)) {\n visited.add(nei);\n sb.append(ch);\n if (dfs(n,k,total,sb,nei,visited)) {\n return true;\n }\n sb.deleteCharAt(sb.length()-1);\n visited.remove(nei);\n }\n }\n return false;\n }
| 12 | 0 |
[]
| 1 |
cracking-the-safe
|
💥TypeScript | Runtime and memory beats 100.00% [EXPLAINED]
|
typescript-runtime-and-memory-beats-1000-be2g
|
Intuition\nThe problem is about finding the shortest string that contains every possible sequence of n digits using a given set of digits. This is akin to creat
|
r9n
|
NORMAL
|
2024-09-04T17:28:14.867377+00:00
|
2024-09-04T17:28:14.867400+00:00
| 152 | false |
# Intuition\nThe problem is about finding the shortest string that contains every possible sequence of n digits using a given set of digits. This is akin to creating a "superstring" that includes every possible combination of length n as a substring.\n\n# Approach\nDe Bruijn Sequence: Use a special mathematical sequence called a De Bruijn sequence. It efficiently covers all possible combinations of length n using k digits.\n\nConstruct the Sequence: Build this sequence for the given n and k. For special cases like k = 1, handle them separately since all characters are the same.\n\nAdjust for Circular Nature: Append a prefix to ensure all sequences are included when considering rotations.\n\n# Complexity\n- Time complexity:\nO(k^n), where n is the length of the sequences and k is the number of possible digits. This is because generating a De Bruijn sequence requires processing all possible combinations.\n\n- Space complexity:\nO(k^n), used to store the sequence which covers all k^n possible combinations.\n\n# Code\n```typescript []\nfunction crackSafe(n: number, k: number): string {\n function buildDeBruijn(n: number, k: number): string {\n const sequence: number[] = [];\n const a: number[] = Array(k ** n).fill(0);\n const sequenceLength = k ** n;\n const generate = (t: number, p: number) => {\n if (t > n) {\n if (n % p === 0) {\n for (let j = 1; j <= p; j++) {\n sequence.push(a[j]);\n }\n }\n } else {\n a[t] = a[t - p];\n generate(t + 1, p);\n for (let j = a[t - p] + 1; j < k; j++) {\n a[t] = j;\n generate(t + 1, t);\n }\n }\n };\n generate(1, 1);\n return sequence.join(\'\');\n }\n\n if (k === 1) {\n // Special case when k = 1, every character must be \'0\'\n return \'0\'.repeat(n * k);\n }\n \n const deBruijn = buildDeBruijn(n, k);\n const result = deBruijn + deBruijn.slice(0, n - 1);\n return result;\n}\n\n\n\n```
| 10 | 0 |
['TypeScript']
| 0 |
cracking-the-safe
|
[C++] Interview Friendly Explanation & Approach [Detailed Explanation]
|
c-interview-friendly-explanation-approac-rxi8
|
\n/*\n https://leetcode.com/problems/cracking-the-safe/\n \n TC: O(n * k ^ n), \n there are total k^n combinations and for each combo it takes \
|
cryptx_
|
NORMAL
|
2023-06-21T06:15:01.861226+00:00
|
2023-06-21T06:18:45.853138+00:00
| 1,064 | false |
```\n/*\n https://leetcode.com/problems/cracking-the-safe/\n \n TC: O(n * k ^ n), \n there are total k^n combinations and for each combo it takes \n iterating the n length string\n SC: O(k ^ n)\n \n With n length and k chars, we can have k ^ n combinations. All these are\n possible passwords, the problems asks for the shortest length string which has all\n the possible string combos.\n \n Points to note:\n 1. Since we are talking of all possible combinations, that means there will be overlapping between\n strings and we can find strings that differ only at one position.\n E.g 110, 111, these differ at the last position\n \n Now to get the shortest length string, we need to find and arrange these overlapping strings in \n such a manner that each adjacent string only differs by the last char. Arranging the strings such that\n ith string\'s last n-1 chars are the prefix of i+1th string ensures max compression of strings. And with that\n suffix add each of the k chars one by one to get to other nodes (these k chars act like edges). So with that in\n mind we it is possible to have the final string of length:\n (n-1)(Initial string\'s n-1 chars) + k^n (diff string\'s differentiating char)\n\n E.g\n n = 2, k = 2\n Possible combos: 00, 01, 10, 11\n \n If they are arranged as described above (notice how each node has the n-1 chars from prev node as prefix):\n 00 -> 01 -> 11 -> 10\n \n To get 01: n-1 chars suffix[00] = 0 and edge=1 => 01\n To get 11: n-1 chars suffix[01] = 1 and edge=1 => 11\n To get 10: n-1 chars suffix[11] = 1 and edge=0 => 10\n \n 2. Now if we draw all the possible k edges from each of the nodes, we will notice that it can take us to different nodes, which can\n be different from the path shown above.\n E.g, On following edge = 0 after 2nd node 01, we get 10 and not 11. Now if we go to 10, then if we follow either 0 or 1 edge\n we will again go to a seen node\n 10 --0--> 00 \n 10 --1--> 01\n So this edge path would have been of no use since this would have only resulted in redundant ans string\n 00101...\n \n So the idea is to find the optimal path which can cover all the nodes only once ( To ensure the final string is shortest), \n which is nothing but a hamiltonian path (path such that all the nodes are visited only once).\n \n 3. We start with n length starting node comprising of 0s. Then we follow the rule of getting the next node by using the last n-1 chars and following\n one of the k edges. Then with this new node, we do dfs further till we are able to cover all the nodes. We do this with backtracking.\n \n*/\nclass Solution {\npublic:\n bool dfs(int n, int k, string& ans, \n unordered_set<string>& visited) {\n // base case, all the possible passwords (k^n combos) have been found\n // in the current hamiltonian path\n if(visited.size() == pow(k, n))\n return true;\n \n // take the last n-1 chars\n string suffix = ans.substr(ans.size() - (n-1), n-1);\n \n // now with this suffix=pwd[1:n-1], we try adding all the possible\n // k chars at the end to get the new node and perform dfs from there.\n // We only add the new node value for which it is possible to traverse further\n // and get the remaining nodes (hamiltonian path)\n \n // Add a dummy char at the end, this is the position where all the other k chars \n // will be placed\n string nextNode = suffix + \'0\';\n for(int i = 0; i < k; i++) {\n nextNode[n-1] = (i + \'0\');\n \n if(!visited.count(nextNode)) {\n visited.insert(nextNode);\n // ans = xxxxo, add the current char with the suffix which creates the new pwd node\n // ____ --> pwd 1 (current node)\n // ____ --> pwd 2 (next node)\n ans += (i + \'0\');\n \n // hamiltonian path found\n if(dfs(n, k, ans, visited))\n return true;\n\n visited.erase(nextNode);\n ans.pop_back();\n }\n }\n \n return false;\n }\n \n string crackSafe(int n, int k) {\n // tracks the visited password combinations\n unordered_set<string> visited;\n \n // shortest string that contains all the possible passwords\n // initial starting node is a n length str comprising of 0s\n string ans = string(n, \'0\');\n visited.insert(ans);\n \n dfs(n, k, ans, visited);\n return ans;\n }\n};\n```
| 9 | 0 |
['Backtracking', 'Depth-First Search', 'C', 'C++']
| 1 |
cracking-the-safe
|
DFS Javascript (heavily commented)
|
dfs-javascript-heavily-commented-by-sage-beux
|
\n\n/*\n\nit is important that we first traverese the last n-1th of string first before adding the char in the final combination.\n\nbecause if we add it to the
|
sage33
|
NORMAL
|
2019-12-13T12:23:15.649946+00:00
|
2019-12-13T12:23:15.649985+00:00
| 686 | false |
```\n\n/*\n\nit is important that we first traverese the last n-1th of string first before adding the char in the final combination.\n\nbecause if we add it to the combination before traversing all of n-1th string combination then we will stop prematurely\n\nit is also mentioned in the solution under the hierholzer approach.\n\nto prove it, try to add the char to the seq array and then run dfs on the n-1th string.\n\n*/\n\n\nvar crackSafe = function (n, k) {\n // If k and n equal 1 the only combination possible is 0.\n if (n === 1 && k === 1) return \'0\'\n \n // visited will keep track of all visited edges.\n const visited = new Set()\n \n // The De Bruijn Sequence that will be the output of the function.\n const seq = []\n \n // To generate a De Bruijn sequence we must traverse every combination of size n\n // containing the number from 0 to k - 1. We will start with the prefix of the \n // combination with all 0s. If n equals 3 and k is greater than 1 our prefix would be\n // 00 and the first combination, our starting edge would be 000.\n const prefix = \'0\'.repeat(n - 1)\n \n // We will perform a depth first traveral until we visit every edge (combination)\n // while adding the last element of a combination to the sequence.\n \n // this is bottom up backtracking\n // first visit all the edges completely before adding the node to the final solution\n dfs(prefix, seq, visited, k)\n \n // We append the original prefix to the sequence as the a De Bruijn sequence \n // ends with the first combination. If we reverse the sequence it would still be \n // valid and in that case would start with the first combination instead.\n seq.push(prefix)\n \n // Join the array to return the sequence as a string.\n return seq.join(\'\')\n}\n\nconst dfs = (prefix, seq, visited, k) => {\n for (let i = 0; i < k; i++) {\n // Generate a new combination using all the numbers from 0 to k - 1\n // this will give us all the edges that are adjacent to the previous\n // combination.\n const combination = prefix + i.toString()\n \n // Check if the current combination has been visited we skip it.\n if (visited.has(combination)) continue\n \n // If the current combination hasn\'t been visited add it to the visited set\n // so we do no revisit it.\n visited.add(combination)\n \n // Create a new prefix using the current combination\n // and continue the depth first traversal.\n dfs(combination.slice(1), seq, visited, k)\n \n // Add the last element of the visited combination to the sequence.\n seq.push(i)\n }\n}\n\n```
| 9 | 1 |
['JavaScript']
| 2 |
cracking-the-safe
|
Euler Path with Detailed Explanation | C++
|
euler-path-with-detailed-explanation-c-b-75x6
|
c++\nclass Solution {\npublic:\n /*\n Euler PATH (start != end) and Euler CIRCUIT (start == end)\n \n say the length of password is n, a
|
quminzhi
|
NORMAL
|
2022-09-08T17:11:52.511931+00:00
|
2022-09-08T17:11:52.511974+00:00
| 1,373 | false |
```c++\nclass Solution {\npublic:\n /*\n Euler PATH (start != end) and Euler CIRCUIT (start == end)\n \n say the length of password is n, and we have k different numbers\n \n theoritically, the min length is n^k + n - 1\n \n len = n\n -----------\n |--------| one state => \n |--------| other state\n \n \n we see string with length of n - 1 as a prefix (node) for new password, and the new digit we insert combined with prefix (i.e. a password string) is an edge.\n \n ex>\n (102)3\n 102 ------> 023\n \n for such DAG, the best way is to traverse all nodes in the graph and each edge will be covered once (Eulerian Circuit)\n \n the criteria for a eular graph:\n - for each node, indegree == outdegree (GREAT, id == od == k)\n - the graph is a strongly connected graph\n */\n unordered_set<string> hash;\n string ans;\n int k;\n \n void dfs(string u) {\n for (int i = 0; i < k; i++) {\n auto e = u + to_string(i);\n if (!hash.count(e)) {\n hash.insert(e);\n dfs(e.substr(1));\n ans += to_string(i);\n }\n }\n }\n \n string crackSafe(int n, int _k) {\n k = _k;\n string start(n - 1, \'0\');\n dfs(start);\n return ans + start;\n }\n};\n```
| 8 | 0 |
[]
| 5 |
cracking-the-safe
|
Suggestion to rephrase the Question
|
suggestion-to-rephrase-the-question-by-a-pamj
|
In Question, it is asking for Return any password of minimum length that is guaranteed to open the box at some point of entering it.\n\nSo, according to this Qu
|
akyadav7303
|
NORMAL
|
2021-04-23T20:07:31.943742+00:00
|
2021-04-23T20:11:46.164126+00:00
| 403 | false |
In Question, it is asking for ``` Return any password of minimum length that is guaranteed to open the box at some point of entering it.```\n\nSo, according to this Question my answer [It will not depend on k as it is always greater than 0] could always be like\nfor `n =2 answer could be 00`\nfor ` n=3 answer could be 000`\nfor `n=4 answer could be 0000`\n\nThey all are minimum length. I think author should rephrase the question with below information:\n``` Return any String of minimum length containing all possible answers of length n which guaranteed to open the box at some point of entering it.```\n\n
| 8 | 1 |
[]
| 1 |
cracking-the-safe
|
C++/Hierholzer's Algorithm/De Bruijn sequence/double 100%
|
chierholzers-algorithmde-bruijn-sequence-a771
|
First of all, I must say it\'s a De Bruijn sequence question. So if you need any background about De Bruijn sequence, please google it first.\nSo to generate a
|
sunnyleevip
|
NORMAL
|
2019-09-14T03:26:33.009789+00:00
|
2019-09-14T03:26:33.009850+00:00
| 768 | false |
First of all, I must say it\'s a De Bruijn sequence question. So if you need any background about De Bruijn sequence, please google it first.\nSo to generate a De Bruijn sequence, we need to get the Euler circuit for the graph for all n-1 possible strings. For an example, if n = 4, k = 2, the graph is as below, (pick it from [wiki](https://en.wikipedia.org/wiki/De_Bruijn_sequence)):\n\n\nSort all n-1 length possible strings in lexicographic order is as below:\n```\n\t000\n\t001\n\t010\n\t011\n\t100\n\t101\n\t110\n\t111\n```\n\nThose are the vertices and number them from 0, then you will get vertex 0 to 7. There are k edges comes out from each vertex.\nSo I create below "edges" vector to save all edges in above graph.\n```\n\t\tvector<vector<int>> edges(vertices, vector<int>(k, 0));\n int edges_cnt = vertices * k;\n \n for (int i = 0; i < vertices; ++i) {\n for (int j = 0; j < k; ++j) {\n edges[i][j] = 1;\n }\n }\n```\n\nTo get the Euler circuit for above graph, we use Hierholzer\'s Algorithm, the time complecity of which is O(edges_cnt).\nUse an answer string to save the ongoing path, and pointer end to control the end of thing, so no need to allocate memory again.\nWe can start at any vertex, so just start from 0.\nIn the end of each circle, we can get the next vertex by find out the last (n-1) bytes from answer string.\n\n**Full solution:**\n```\nclass Solution {\npublic:\n string crackSafe(int n, int k) {\n if (k == 1) return string(n, \'0\');\n \n int vertices = 1;\n for (int i = 1; i < n; ++i) {\n vertices *= k;\n }\n \n vector<vector<int>> edges(vertices, vector<int>(k, 0));\n int edges_cnt = vertices * k;\n \n for (int i = 0; i < vertices; ++i) {\n for (int j = 0; j < k; ++j) {\n edges[i][j] = 1;\n }\n }\n \n string answer(vertices * k + n - 1, \'0\');\n int end = n - 1;\n int cur_vertex = 0;\n vector<char> circuit;\n \n while (end < answer.size()) {\n int i;\n for (i = 0; i < k; ++i) {\n if (edges[cur_vertex][i] > 0) {\n edges[cur_vertex][i] = 0;\n --edges_cnt;\n break;\n }\n }\n \n if (i < k) {\n answer[end++] = i + \'0\';\n if (edges_cnt == 0) break;\n } else {\n circuit.push_back(answer[end - 1]);\n --end;\n }\n \n string next = answer.substr(end - n + 1, n - 1).c_str();\n cur_vertex = 0;\n for (int j = 0; j < next.size(); ++j) {\n cur_vertex = cur_vertex * k + next[j] - \'0\';\n }\n }\n \n for (int i = circuit.size() - 1; i >= 0; --i) answer[end++] = circuit[i];\n \n return answer;\n }\n};\n```
| 8 | 0 |
[]
| 1 |
cracking-the-safe
|
C++ dfs to find Eulerian Circle
|
c-dfs-to-find-eulerian-circle-by-yanchen-3u2a
|
\nclass Solution {\npublic:\n string crackSafe(int n, int k) {\n int len = (int) pow(k, n - 1);\n vector<vector<bool>> visited(len, vector<bool
|
yanchenw
|
NORMAL
|
2019-03-04T06:57:38.193423+00:00
|
2019-03-04T06:57:38.193462+00:00
| 1,008 | false |
```\nclass Solution {\npublic:\n string crackSafe(int n, int k) {\n int len = (int) pow(k, n - 1);\n vector<vector<bool>> visited(len, vector<bool>(k, false));\n \n string res = "";\n dfs(visited, res, len, k, 0);\n \n return res + string(n - 1, \'0\');\n }\n \n void dfs(vector<vector<bool>>& visited, string& res, int len, int k, int node) {\n for (int i = 0; i < k; i++) {\n if (!visited[node][i]) {\n visited[node][i] = true;\n dfs(visited, res, len, k, (node * k + i) % len);\n res += \'0\' + i;\n }\n }\n }\n};\n```
| 8 | 1 |
[]
| 1 |
cracking-the-safe
|
Fast Python Hierholzer's
|
fast-python-hierholzers-by-matt_cochrane-af1j
|
python\nfrom itertools import product\nfrom collections import defaultdict\n\nclass Solution:\n def crackSafe(self, n: int, k: int) -> str:\n if n ==
|
matt_cochrane1
|
NORMAL
|
2021-12-05T12:18:08.547193+00:00
|
2021-12-05T12:18:35.678186+00:00
| 960 | false |
```python\nfrom itertools import product\nfrom collections import defaultdict\n\nclass Solution:\n def crackSafe(self, n: int, k: int) -> str:\n if n == 1:\n return \'\'.join(map(str, range(k)))\n \n adjlist = defaultdict(list)\n\t\t# Use product to create the possible passwords\n for comb in product(range(k), repeat=n):\n\t\t\t# Each node has n-1 digits\n\t\t\t# Eg. if comb was 01001 (where n=4 and k=2)\n\t\t\t# We would add an edge from node 0100 to node 1001\n adjlist[tuple(comb[:-1])].append(tuple(comb[1:]))\n \n\t\t# Then we just use Hierholzer\'s to fine an Euler circuit.\n path = []\n def dfs(node):\n while adjlist[node]:\n dfs(adjlist[node].pop())\n path.append(node[0])\n \n\t\t# Want to start from the 0 node which has n-1 zeros.\n dfs(tuple([0]*(n-1)))\n \n # We only add the first digit of each node, so need to add n-2 extra zeros\n # at the end, for the missing digits of the first node.\n return \'\'.join(map(str, [*reversed(path), *([0]*(n-2))]))\n```
| 7 | 0 |
['Python']
| 2 |
cracking-the-safe
|
DFS Solution Java
|
dfs-solution-java-by-animesh_bote-amh9
|
\nclass Solution {\n public String crackSafe(int n, int k) {\n StringBuilder sb = new StringBuilder("");\n for(int i=0;i<n;i++) {\n
|
animesh_bote
|
NORMAL
|
2021-10-17T00:13:37.935272+00:00
|
2021-10-17T00:13:37.935305+00:00
| 673 | false |
```\nclass Solution {\n public String crackSafe(int n, int k) {\n StringBuilder sb = new StringBuilder("");\n for(int i=0;i<n;i++) {\n sb.append("0");\n }\n int total = (int)Math.pow(k,n);\n HashSet<String> visited = new HashSet<>();\n visited.add(sb.toString());\n if(crackTheSafe(sb, n, k, visited, total)) {\n return sb.toString();\n } \n return "-1";\n }\n \n public boolean crackTheSafe(StringBuilder sb, int n, int k, HashSet<String> visited, int total) {\n if(total == visited.size())\n return true;\n String lastDigits = sb.substring(sb.length() - (n-1)).toString();\n for(int i=0;i<k;i++) {\n Character ch = (char)(i+\'0\');\n String newStr = lastDigits + ch;\n if(!visited.contains(newStr)) {\n visited.add(newStr);\n sb.append(ch);\n if(crackTheSafe(sb, n, k, visited, total)) {\n return true;\n }\n visited.remove(newStr);\n sb.deleteCharAt(sb.length()-1);\n }\n }\n return false;\n }\n}\n```
| 7 | 0 |
[]
| 0 |
cracking-the-safe
|
C++ Hamiltonian path solution
|
c-hamiltonian-path-solution-by-jasperjoe-wjux
|
\tclass Solution {\n\tpublic:\n\t\tstring crackSafe(int n, int k) {\n\t\t\tunordered_map m;\n\t\t\tstring ans="";\n\t\t\tfor(int i=0;i<n-1;i++)\n\t\t\t{\n\t\t\t
|
jasperjoe
|
NORMAL
|
2020-04-11T14:38:56.215548+00:00
|
2020-04-11T14:38:56.215593+00:00
| 1,040 | false |
\tclass Solution {\n\tpublic:\n\t\tstring crackSafe(int n, int k) {\n\t\t\tunordered_map<string,int> m;\n\t\t\tstring ans="";\n\t\t\tfor(int i=0;i<n-1;i++)\n\t\t\t{\n\t\t\t\tans+=\'0\';\n\t\t\t}\n\n\t\t\tfor(int i=0;i<pow(k,n);i++)\n\t\t\t{\n\t\t\t\tstring temp=ans.substr(ans.size()-n+1,n-1);\n\t\t\t\tm[temp]=(m[temp]+1)%k;\n\t\t\t\tans+=(\'0\'+m[temp]);\n\t\t\t}\n\n\t\t\treturn ans;\n\t\t}\n\t};
| 7 | 0 |
['C++']
| 3 |
cracking-the-safe
|
Very simple and short C++ solution based on inverse Burrows - Wheeler transform
|
very-simple-and-short-c-solution-based-o-odte
|
Explanation and example available on wikipedia: Wikipedia\n\nC++\nclass Solution {\npublic:\n string crackSafe(int n, int k) {\n // Compute the length
|
kaspersky
|
NORMAL
|
2018-02-01T00:51:30.674000+00:00
|
2018-09-02T23:07:01.721948+00:00
| 1,544 | false |
Explanation and example available on wikipedia: [Wikipedia](https://en.wikipedia.org/wiki/De_Bruijn_sequence#Example_using_inverse_Burrows\u2014Wheeler_transform)\n\n```C++\nclass Solution {\npublic:\n string crackSafe(int n, int k) {\n // Compute the length. Total length will be s * k\n int s = 1;\n for (int i = 0; i < n - 1; ++i)\n s *= k;\n\n // Construct the permutation according to wiki\n std::vector<int> inds(s * k);\n for (int i = 0; i < k * s; ++i)\n inds[i] = i / s + (i % s) * k;\n\n std::string seq;\n for (int off = 0; off < s * k; ++off)\n {\n // Find cycles in the permutation\n int c = off, tmp = 0;\n while (inds[c] != -1)\n {\n seq.push_back(c / s + '0');\n tmp = inds[c];\n inds[c] = -1;\n c = tmp;\n }\n }\n\n // Need to append n - 1 more characters\n for (int i = 0; i < n - 1; ++i)\n seq.push_back(seq[i]);\n return seq;\n }\n};\n```
| 7 | 0 |
[]
| 0 |
cracking-the-safe
|
Deque solution with proof
|
deque-solution-with-proof-by-weirongwang-n025
|
/\n Represent the codes as nodes and the transitions between them as directed edges in a graph. \n For a pair of nodes A and B, A->B exists iff postfix(A, n-1)
|
weirongwang
|
NORMAL
|
2017-12-25T08:19:38.556000+00:00
|
2018-10-26T16:25:41.826828+00:00
| 1,849 | false |
/*\n Represent the codes as nodes and the transitions between them as directed edges in a graph. \n For a pair of nodes A and B, A->B exists iff postfix(A, n-1) == prefix(B, n-1). \n\nProve that there exists a path P, such that every node in the graph is in P, and only once. \nBy construction: \n 1) Represent the path P as a deque. Add an arbitrary node as the first node to P. \n 2) Peek the last node A from the path P. \n 2.1) If there exists A->B, and B is not in path P yet, add B at the tail of path P. \n (when there are multiple choices, arbitrarily take one.)\n This is the only case in this construction that a new node could be added into P. \n Therefore, every node is unique in P. \n 2.2) If no such node B exists, then there must exist an edge A->Head of path P. Why? \n There must exist k nodes in P, such that their prefix == postfix(A, n-1); \n and Except node A, there are at most k-1 nodes in the path that could have postfix(A, n-1), \n this discrepancy indicates that the head of the path, which is the only node in the path without \n an incoming edge, must have a prefix == postfix(A, n-1). \n In this case, remove the head of path P, and add it at the tail of path P. \n Repeat Step 2 until all nodes are in P. \n \n Why every node is eventually added to path P: \n Assume there is some nodes not in P yet. Recall the definition of edge, so there exists a path between every pair of nodes in the graph.Then there must exist a node E, such at there exist a path: tail of P ->...->A->E, where A is on P, and E is not. Given Step 2.2, node A will eventually become the tail of P, then E could be added at the next iteration.At least one such E will be added to P when we traverse through P once, so eventually every node is in P.\n*/\n\n```\npublic String crackSafe(int n, int k) {\n Deque<String> dq = new LinkedList<>();\n Set<String> mark = new HashSet<>(); \n\n int nbfCodes = 1;\n for (int i=0; i<n; i++)\n nbfCodes = nbfCodes*k; \n \n String code ="";\n for (int i=0; i<n; i++)\n code = code+"0";\n mark.add(code);\n dq.add(code);\n while (dq.size() < nbfCodes)\n {\n String tail = dq.getLast();\n String prefix = tail.substring(1);\n int i; \n for (i=0; i<k; i++)\n {\n String next = prefix + Integer.toString(i);\n if (!mark.contains(next))\n {\n mark.add(next);\n dq.addLast(next);\n break;\n }\n }\n if (i == k)\n {\n String head = dq.pollFirst();\n dq.addLast(head);\n }\n }\n String res = ""; \n String head = dq.poll();\n res = res+ head;\n while (!dq.isEmpty())\n {\n head = dq.poll();\n res = res + head.substring(n-1);\n }\n return res; \n }
| 7 | 0 |
[]
| 5 |
cracking-the-safe
|
[C++] Euler Path with video links to explain the solution
|
c-euler-path-with-video-links-to-explain-02oa
|
First of all.. questions like this are taking me back to when I was in school and used to be good at math. \nHad to watch 3 videos to understand this. \nhttps:/
|
onesuccess
|
NORMAL
|
2020-10-29T23:52:37.498631+00:00
|
2020-10-29T23:56:44.229711+00:00
| 768 | false |
First of all.. questions like this are taking me back to when I was in school and used to be good at math. \nHad to watch 3 videos to understand this. \nhttps://www.wikiwand.com/en/De_Bruijn_sequence#/overview\n\nhttps://www.youtube.com/watch?v=iPLQgXUiU14&feature=youtu.be&ab_channel=singingbanana\n\nhttps://www.youtube.com/watch?v=xR4sGgwtR2I&ab_channel=WilliamFiset\n\nhttps://www.youtube.com/watch?v=8MpoO2zA2l4&t=33s&ab_channel=WilliamFiset\n\n\nAnd finally for the solution we implement the euler path, but the solution contains edges, not vertices. \n\n```\nclass Solution {\npublic:\n\n unordered_map<string, vector<string>> g;\n unordered_map<string, int> out;\n \n vector<string> generateAllStrings(int n, int k) {\n vector<string> res;\n if (n == 0) {\n for (int i = 0; i < k; i ++) {\n string str = to_string(i);\n res.push_back(str);\n }\n // cout << n << " = " ;\n // for (auto &s: res) cout << s << " "; cout << endl;\n return res;\n }\n auto minus1 = generateAllStrings(n - 1, k);\n \n for (int i = 0; i < k; i ++) {\n \n for (auto &s: minus1) {\n string str = to_string(i);\n str += s;\n res.push_back(str);\n }\n }\n // cout << n << " = " ;\n // for (auto &s: res) cout << s << " "; cout << endl;\n return res;\n }\n\n void buildgraph(int n, int k) {\n for (auto &start: generateAllStrings(n, k)) {\n for (int i = 0; i < k; i ++) {\n string to = (start + to_string(i));\n to = to.substr(1); // to.pop_front\n g[start].push_back(to);\n out[start] ++;\n } \n }\n }\n \n string res = "";\n string dfs(string at) {\n cout << "here";\n if (out[at] == 0) return res;\n while (out[at]) {\n out[at] --;\n res += g[at][out[at]].back();\n dfs(g[at][out[at]]);\n }\n return res;\n }\n \n string crackSafe(int n, int k) {\n if (n == 1) {\n string res = "";\n for (int i = 0; i < k; i ++) res += to_string(i);\n return res;\n }\n // generate all combinations of length n - 1\n // 2 nodes are connected if adding a digit to the end of a node leads it to an other node with the same ending digits\n // for example: 000 --1--> 001\n // 000 --0--> 000 \n // each node has k outgoing edges\n // so start from 000 and you have k other edges in the graph\n // for each of the new nodes, we do the same thing\n \n // once the graph is built, we need to find a Euler path on it\n // each edge is visited once\n buildgraph(n - 2, k);\n // for (auto &i: g) { cout << i.first << " -> " ; for (auto &to: i.second) {cout << to << " ";} cout << endl;}\n string start(n - 1, \'0\');\n dfs(start);\n return start + res;\n }\n};\n```\n
| 6 | 0 |
[]
| 0 |
cracking-the-safe
|
Java-DFS, not a fast solution but easy to understand. With explanation.
|
java-dfs-not-a-fast-solution-but-easy-to-d8m9
|
The key point for solving this problem is confidence :-) I\'m serious.\n\nThe whole solution is based on an assumption: the length of result string must be n +
|
ch_z
|
NORMAL
|
2019-06-19T05:40:12.146969+00:00
|
2019-06-19T06:05:11.295432+00:00
| 1,371 | false |
The key point for solving this problem is confidence :-) I\'m serious.\n\nThe whole solution is based on an assumption: the length of result string must be n + k^n-1, which means every following substring takes n-1 characters of previous string as its first n-1 characters. For example: n=2, k=2, result="00110": "00"+"01"+"11"+"10".\n\nHowever sometimes simply add a random character after first n-1 characters may not form the correct result. For example: still n=2, k=2, "0010": "00"+"01"+"10", then we found that we cannot add any characters after "0010" to form "11"\n\nSo the problem becomes trying all possible results and find the one that has length of n+k^n-1, and that is the reason why I use DFS.\n\n(Note: In fact the assumption has been proved, it is called "De Bruijn sequence", but for people like me who does not know it, the only way is trying several combinations and believe in your intuition)\n\n```\nclass Solution {\n public String crackSafe(int n, int k) {\n Set<String> visited = new HashSet<String>();\n //*start from string "00.."\n String res = "";\n for(int j = 0; j < n; j++){\n res+=0;\n }\n //*calculate target length, which is k^n+n-1\n int total = 1;\n for(int i = 0; i < n; i++){\n total *= k;\n }\n total += n-1;\n //*run DFS\n res=DFS(res, n, k, visited, total);\n return res;\n }\n private String DFS(String res, int n, int k, Set<String> visited, int total){\n int len = res.length();\n visited.add(res.substring(len-n, len));\n for(int i = 0; i < k; i++){\n if(!visited.contains(res.substring(len-n+1, len)+i)){\n String tmp = DFS(res+i, n, k, visited, total);\n //*if length of result is less than total length, remove substring from visited and continue loop, else we are done! break the loop!\n if(tmp.length() == total){\n res = tmp;\n break;\n }\n visited.remove(res.substring(len-n+1, len)+i);\n }\n } \n return res;\n }\n}\n```\nsubstring() usually is not a good way to deal with a string, but in this problem the length is limited to 4. I believe this solution can be improved by using char array or string builder etc. to replace substring() method. But I\'m lazy :-)
| 6 | 0 |
['Depth-First Search', 'Java']
| 3 |
cracking-the-safe
|
Simple and Clean C++ DFS Solution
|
simple-and-clean-c-dfs-solution-by-wendy-s8vk
|
Brute force idea. try to append every number from 0 to k - 1. \nIf we got k^n pwd, then we done.\nUse a map to store which pwd has is visited and pruning. If we
|
wendy2003888
|
NORMAL
|
2018-08-11T21:24:18.039403+00:00
|
2018-10-06T18:57:12.140705+00:00
| 723 | false |
Brute force idea. try to append every number from 0 to k - 1. \nIf we got k^n pwd, then we done.\nUse a map to store which pwd has is visited and pruning. If we got same pwd after append a number, this sequence must not be shortest.\n\n```\nclass Solution {\n bool Gene(const int n, const int k, unordered_map<string, bool>&vis, string& ans) {\n if (vis.size() == pow(k, n)) {\n return true;\n }\n for (int i = 0; i < k; ++i) {\n ans += \'0\' + i;\n string pwd = ans.substr(ans.length() - n);\n if (vis.find(pwd) == vis.end()) {\n vis[pwd] = 1;\n if (Gene(n, k, vis, ans)) {\n return true;\n }\n vis.erase(pwd);\n }\n ans.pop_back();\n }\n return false;\n }\npublic:\n string crackSafe(int n, int k) {\n string ans = string(n, \'0\');\n unordered_map<string, bool>vis;\n vis[ans] = 1;\n Gene(n, k, vis, ans);\n return ans;\n }\n};\n```
| 6 | 0 |
[]
| 0 |
cracking-the-safe
|
753: Solution with step by step explanation
|
753-solution-with-step-by-step-explanati-rrtf
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n\nif n == 1:\n return \'\'.join(map(str, range(k)))\n\n\nIf n is 1, we
|
Marlen09
|
NORMAL
|
2023-10-23T08:04:23.410927+00:00
|
2023-10-23T08:04:23.410977+00:00
| 845 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\nif n == 1:\n return \'\'.join(map(str, range(k)))\n```\n\nIf n is 1, we simply return a string made of all numbers from 0 to k-1. This is because for n=1, every single digit is a possible password. We use map to convert numbers to strings and join to combine them into a single string.\n\n```\nseen = set()\nresult = []\n\nstart_node = "0" * (n - 1)\n```\nseen is a set that will store all the sequences we have seen (or visited) so far. This helps to avoid revisiting sequences.\nresult is the list that will store the final sequence to unlock the safe.\nstart_node is initialized to a string of n-1 zeros, which will be our starting point.\n\n```\nself.dfs(start_node, k, seen, result)\n```\nWe call the depth-first search (DFS) function starting from the start_node. The goal of this DFS is to find the Eulerian path in the de Bruijn graph. An Eulerian path visits every edge exactly once.\n\n```\ndef dfs(self, node, k, seen, result):\n for i in range(k):\n edge = node + str(i)\n\n if edge not in seen:\n seen.add(edge)\n self.dfs(edge[1:], k, seen, result)\n result.append(str(i))\n```\nFor each node in the graph (which is a string of length n-1), we try to extend it by one character (from 0 to k-1) to form an edge. If this edge has not been seen before, we add it to the seen set. Then, we recursively call the DFS function with the next node, which is the last n-1 characters of the edge. After we have explored all possible extensions from the current node, we add the current digit to our result.\n\n```\nreturn "".join(result) + start_node\n```\nWe convert the result list into a string and append the start_node to it. This is because our DFS would have traversed the graph in such a way that appending the start_node at the end ensures all n-length combinations appear in the sequence.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def crackSafe(self, n: int, k: int) -> str:\n if n == 1:\n return \'\'.join(map(str, range(k)))\n \n seen = set()\n result = []\n \n start_node = "0" * (n - 1)\n self.dfs(start_node, k, seen, result)\n \n return "".join(result) + start_node\n\n def dfs(self, node, k, seen, result):\n for i in range(k):\n edge = node + str(i)\n\n if edge not in seen:\n seen.add(edge)\n\n self.dfs(edge[1:], k, seen, result)\n result.append(str(i))\n\n```
| 5 | 0 |
['Depth-First Search', 'Eulerian Circuit', 'Python', 'Python3']
| 0 |
cracking-the-safe
|
Google Interview Ques|| Follow the linked video to understand the below Code
|
google-interview-ques-follow-the-linked-hg24p
|
Intuition\n Describe your first thoughts on how to solve this problem. \nTo Understand the code, follow this video:- \nhttps://youtu.be/VZvU1_oPjg0\n\n# Code\n\
|
Shubham_Raj22
|
NORMAL
|
2023-01-20T09:04:36.585243+00:00
|
2023-01-20T09:06:22.645380+00:00
| 327 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo Understand the code, follow this video:- \nhttps://youtu.be/VZvU1_oPjg0\n\n# Code\n```\nclass Solution {\npublic:\n unordered_set<string> seen;\n string ans;\n int k;\n\n void dfs(string u){\n for(int i=0;i<k;i++){\n auto e = u+to_string(i);\n if(!seen.count(e)){\n seen.insert(e);\n dfs(e.substr(1));\n ans+=to_string(i);\n }\n }\n }\n string crackSafe(int n, int _k) {\n \n k =_k;\n\n string start(n-1,\'0\');\n\n dfs(start);\n\n string res = ans+start;\n\n return res;\n\n }\n};\n```
| 5 | 0 |
['C++']
| 0 |
cracking-the-safe
|
C++ Solution
|
c-solution-by-tarruuuu-0q5t
|
\nclass Solution {\npublic:\n unordered_set<string> combinations;\n string output = "";\n \n bool traversal(string& curr, int num, int k, int n){\n
|
tarruuuu
|
NORMAL
|
2021-06-06T05:29:33.342032+00:00
|
2021-06-06T05:29:33.342084+00:00
| 1,118 | false |
```\nclass Solution {\npublic:\n unordered_set<string> combinations;\n string output = "";\n \n bool traversal(string& curr, int num, int k, int n){\n if(combinations.size() == num){\n output = curr;\n return true;\n }\n \n string s = curr.substr(curr.length()-n+1,n-1);\n \n for(int i=0;i<k;i++){\n string temp = s+to_string(i);\n curr+=to_string(i);\n if(combinations.find(temp)==combinations.end()){\n combinations.insert(temp);\n if(traversal(curr,num,k,n)) \n return true;\n \n combinations.erase(temp);\n }\n curr.pop_back();\n }\n return false;\n \n }\n \n string crackSafe(int n, int k) {\n string curr = "";\n for(int i=0;i<n;i++){\n curr+="0";\n } \n \n int num = pow(k,n);\n combinations.insert(curr);\n \n traversal(curr,num,k,n);\n return output;\n }\n};\n```
| 5 | 0 |
['C', 'C++']
| 1 |
cracking-the-safe
|
Euler Path with explanation in Java (solutions code)
|
euler-path-with-explanation-in-java-solu-tgh9
|
A good explanation: https://www.youtube.com/watch?v=iPLQgXUiU14\njava\n/**\n * Idea:\n * The primary idea rotates around finding overlapping sequence which will
|
sutirtho
|
NORMAL
|
2020-06-03T13:21:51.091564+00:00
|
2020-06-03T13:21:51.091611+00:00
| 441 | false |
A good explanation: https://www.youtube.com/watch?v=iPLQgXUiU14\n```java\n/**\n * Idea:\n * The primary idea rotates around finding overlapping sequence which will cover\n * all possible sequence of k digit number. For example if we know the combination\n * is of length 2, and we have 2 digits {1,2} to cover it then we want to come up \n * with a string which covers all combination of {1,2}, one such string will be \n * 11221 -> contains all sequence {11, 12, 21, 22}.\n * so we have graph which looks like this 11 ---2---> 12 ---1---> 21 (this one is incomplete)\n * this means from one node (11) we can append an edge value (2) to go to the next node (12) \n * (we are removing the first character in next node value) and so on.\n * Now to find the complete sequence, we need to find a euler cycle which covers all edges exactly \n * once. \n * For detailed explanation please refer: https://www.youtube.com/watch?v=iPLQgXUiU14\n * \n * To find a euler cycle we can use DFS where node + edge value can be kept in a visited set \n * to not visit the same edge again ... meaning if we already visited "11" + "2" (meaning we visited)\n * edge 2 of node "11" then we don\'t visit it again.\n * Time complexity: O(n * k^n ), because n length have k^n possibilities, we need to concatenate all possibilities\n * exactly once!\n * Space complexity: O(n * k^n) for visited set\n */\n \nclass Solution {\n Set<String> visited;\n StringBuilder sequence;\n public String crackSafe(int n, int k) {\n if (n == 1 && k == 1) {\n return "0";\n }\n \n visited = new HashSet<>();\n sequence = new StringBuilder();\n \n StringBuilder startingNode = new StringBuilder();\n // we start from 000... total of n-1 0s :: IMPORTANT\n for (int i = 0; i < n-1; i++) {\n startingNode.append("0");\n }\n \n dfs(startingNode.toString(), k);\n // We append the starting node at the end\n sequence.append(startingNode.toString());\n \n return sequence.toString();\n }\n \n private void dfs(String node, int k) {\n // For each edge, meaning each value of k\n for (int i = 0; i < k; i++) {\n String nodeEdgeCombo = node + Integer.toString(i);\n if (!this.visited.contains(nodeEdgeCombo)) {\n this.visited.add(nodeEdgeCombo);\n String nextNode = nodeEdgeCombo.substring(1); // remove the first character 11 ---2---> 12\n dfs(nextNode, k);\n this.sequence.append(Integer.toString(i));\n }\n }\n }\n}\n```
| 5 | 0 |
[]
| 0 |
cracking-the-safe
|
Python - Euler Path (99.47% Faster, ~15 Lines)
|
python-euler-path-9947-faster-15-lines-b-1183
|
Intriguing question! Approach for this code is to first create all possible strings of size n-1 using the K digits. Then we can initialize our path with [0] * n
|
user3088h
|
NORMAL
|
2020-02-08T00:47:13.544469+00:00
|
2020-02-08T01:08:15.386757+00:00
| 731 | false |
Intriguing question! Approach for this code is to first create all possible strings of size n-1 using the K digits. Then we can initialize our path with [0] * n-1. We can then traverse the graph to another node based on one of K edges such that tail of the current node + edge value matches the next node value i.e. next_node = tuple(current_node + edge)[1:]\n\n```\n def crackSafe(self, n: int, k: int) -> str:\n from itertools import product\n \n digits, G, res = range(k), {}, []\n nodes = list(product(digits, repeat=n-1))\n for node in nodes: \n G[node] = list(range(k))\n \n node = tuple([0] * (n-1))\n res.extend(node)\n while node in G and G[node]:\n edge = G[node].pop()\n res.extend([edge])\n node = tuple(node + (edge,))[1:]\n \n return "".join(str(ch) for ch in res)\n\t```
| 5 | 0 |
[]
| 0 |
cracking-the-safe
|
C++ || Small Code || De Bruijn Sequence
|
c-small-code-de-bruijn-sequence-by-rezn0-kfte
|
Intuition\n Describe your first thoughts on how to solve this problem. \nDe Bruijn Sequence construction using DFS traversal and eulerian path creation.\nEach n
|
rezn0v
|
NORMAL
|
2024-08-06T17:49:33.566502+00:00
|
2024-08-06T17:49:33.566528+00:00
| 692 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nDe Bruijn Sequence construction using DFS traversal and eulerian path creation.\nEach node is analogus to n-1 length prefix possible of the k characters and edges would be between nodes with one letter difference.\n\n\n# Complexity\n- Time complexity: O(k^n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\nprivate:\n void dfs(string prefix, string &res, unordered_set<string> &visit, int &k) {\n for(int i = 0; i < k; i++) {\n string temp = prefix + to_string(i);\n if(visit.find(temp) != visit.end()) continue;\n visit.insert(temp);\n dfs(temp.substr(1, prefix.size()), res, visit, k);\n res += to_string(i);\n }\n }\npublic:\n string crackSafe(int n, int k) {\n if(n == 1 && k == 1) return "0";\n unordered_set<string> visit;\n string res, prefix(n-1, \'0\');\n dfs(prefix, res, visit, k);\n res += prefix;\n return res;\n }\n};\n```
| 4 | 0 |
['C++']
| 1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.