question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
minimum-increments-for-target-multiples-in-an-array
|
JAVA DP SOLUTION
|
java-dp-solution-by-subhankar752-83mr
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Subhankar752
|
NORMAL
|
2025-02-04T17:37:20.878062+00:00
|
2025-02-04T17:37:20.878062+00:00
| 31 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
int numCount, targetCount;
int[] nums, target;
long[][] dp;
long[] lcmPrecomputed;
public int minimumIncrements(int[] nums, int[] target) {
this.nums = nums;
this.target = target;
this.numCount = nums.length;
this.targetCount = target.length;
this.dp = new long[numCount + 1][1 << targetCount + 1];
for (int i = 0; i < numCount + 1; i++) {
Arrays.fill(dp[i], -1);
}
lcmPrecomputed = new long[1 << targetCount];
precompute();
long ans = solve(0, 0);
return (int) ans;
}
public void precompute() {
int total = 1 << targetCount;
for (int i = 0; i < total; i++) {
lcmPrecomputed[i] = 1;
for (int j = 0; j < targetCount; j++) {
if ((i & (1 << j)) != 0) {
lcmPrecomputed[i] = findLCM(lcmPrecomputed[i], target[j]);
}
}
}
}
public long findLCM(long a, long b) {
return (a * b) / gcd(a, b);
}
public long gcd(long a, long b) {
if (b == 0) {
return a;
}
return gcd(b, a % b);
}
public long solve(int i, int mask) {
int fullMask = (1 << targetCount) - 1;
if (mask == fullMask) {
return 0;
}
if (i == numCount) {
return (long) 1e9;
}
if (dp[i][mask] != -1) {
return dp[i][mask];
}
long min = (long) 1e9;
// skip
min = Math.min(min, solve(i + 1, mask));
// take
int totalSubsets = 1 << targetCount;
for (int subset = 1; subset < totalSubsets; subset++) {
long subsetLCM = lcmPrecomputed[subset];
long nextMultiple = (long) (Math.ceil((nums[i] * 1.0) / subsetLCM) * subsetLCM);
min = Math.min(min, (nextMultiple - nums[i]) + solve(i + 1, mask | subset));
}
return dp[i][mask] = min;
}
}
```
| 1 | 0 |
['Dynamic Programming', 'Bitmask', 'Java']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Get the Intuition | Why DP Bitmask | 🏆
|
get-the-intuition-why-dp-bitmask-by-sour-xtlg
|
Intuition- Why use Bitmask ??=> We have to select any comination of elemnts from target set, we can do that by seecting the set bit position elements of mask.
=
|
souraman19
|
NORMAL
|
2025-02-03T10:49:00.388666+00:00
|
2025-02-03T10:49:00.388666+00:00
| 106 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
## - Why use Bitmask ??
=> We have to select any comination of elemnts from target set, we can do that by seecting the set bit position elements of mask.
=> Again we can do OR opearion in case of numbers easily and can select larger subset from small subsets. Example given below.
## - Why Use DP ??
=> Lets assume the elements we have [2,3,4]
=> We select combination of 2,3,4 by the mask 7 (1 1 1) which needed 10 opearions.
=> Again we have combination of 2 and 3 selected by mask 6 (1 1 0) which needed 3 opration.
=> Now by calculation we got that combination of 3 and 4 by mask 3 (0 1 1) we are getting this in 2 opearion. So with use of dp we can tell that the the total mask 6 OR 3 = 7 which gives all elements we can tell we can get them in lesser no of opearions that is 3 + 2 = 5, so will update this in corresponding dp array position.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Get the all possible subsets of the elements of nums array. To do this, use bitmasking. So, traverse from 1 to 2^n-1 where 2^n-1 means upper_limit of mask value, where n means the size of target array. Now calculate lcm of all elements and store in map, like mask as key and lcm value as value.
2. Now, create a dp array of size 2^n with each element value 1e9 or INT_MAX. It will store the minimum increment required of a number of nums to be multiple of the dp current element. Also make the dp[0] = 0, as no incremnt required as we are not selecting any element from target array, means our subset is empty.
3. Now we will process each element of nums one by one. First to make that element as the multiple of each lcm value from the map, the increment will be calculated and stored in a vector v.
4. After that a temporary dp vector is created for calculation purpose, initially make that vector equal to main dp vector. The iterate from index prev_musk = 0 to 2^n-1 where n is target array size. If the current element of dp is 1e9 means it has not processed till yet so continue. Otherwise, iterate through vector v, get the current mask and calculate total mask by doing or of prev_musk and current. Also calculate total increment req by adding dp[prev_musk] and current_incrment value, if sum value is lesser than value for the total mask of in dp_temp then update it in dp_temp. Note, while doing comparison we will use dp_temp here.
5. At the end of the outer loop, make the original dp vector equal to dp_temp here.
6. At last of the function return dp[2^n-1] or dp[upper_limit_mask] which indicates min increment needed so that all elements of target has at least one multiple in nums vector.
# Code
```cpp []
#define ll long long
class Solution {
public:
ll calLCM(ll a, ll b){
if(a == b) return a;
ll x = a, y = b;
while(a > 0 && b > 0){
if(a > b) a = a%b;
else b = b % a;
}
ll gcd;
if(a == 0) gcd = b;
else gcd = a;
return (x*y)/gcd;
}
int minimumIncrements(vector<int>& nums, vector<int>& target) {
ll n = target.size();
ll upper_limit_mask = (1 << n) - 1; //count of subsets, 1 to 2^n-1
unordered_map<ll, ll>mp; //for storing the lcm of numbers present in a subset
for(ll mask = 1; mask <= upper_limit_mask; mask++){
set<ll>st;
for(ll bit_slide_pos = 0; bit_slide_pos < n; bit_slide_pos++){
if((mask >> bit_slide_pos) & 1){
st.insert(target[bit_slide_pos]); //selecet the target vector element as current bit is set bit
}
}
ll lcm = 1;
for(auto it : st){
lcm = calLCM(lcm, it);
}
mp[mask] = lcm; //storing the lcm of all elements and store in the map
}
vector<ll>dp(upper_limit_mask + 1, 1e9);
dp[0] = 0; // if no elements present in subset then no increment needed for the opearation
for(auto it : nums){
vector<pair<ll, ll>>v; //for storing 'mask' and the 'increment needed' from the current element of nums to be the multiple of mask
for(auto itt: mp){
ll mask = itt.first;
ll lcm = itt.second;
ll r = it%lcm;
ll increment_req;
if(r == 0) increment_req = 0; //if the number is divided by lcm value then no inc req
else increment_req = lcm - r; //increment required to be multiple of lcm
v.push_back({mask, increment_req});
}
vector<ll>dp_temp = dp;
for(ll prev_mask = 0; prev_mask < dp_temp.size(); prev_mask++){
if(dp[prev_mask] == 1e9) continue; //if the the mask is not processed yet then it cant hell in further processing
for(auto it : v){
ll current_mask = it.first;
ll increment_current = it.second;
ll full_mask = prev_mask | current_mask; //getting full subset by doing or of both
ll total_increment = dp[prev_mask] + increment_current; //toal increment got
if(total_increment < dp_temp[full_mask]){
dp_temp[full_mask] = total_increment;
}
}
}
dp = dp_temp; //update the main dp
}
return dp[upper_limit_mask]; //return the value of full selected subset of elements of target
}
};
```
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(pow(|target|,2)*(|target| + log(avg(targetArrayElement))) + O(|nums| * (pow(|target|,2) + pow(|target|,2)*pow(|target|,2)))$$
where log(avg(targetArrayElement)) is avg TC for LCM cal
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(|target| + O(pow(|target|,2) + 3*O(pow(|target|,2))$$
| 1 | 0 |
['Array', 'Dynamic Programming', 'Bit Manipulation', 'Ordered Map', 'Ordered Set', 'Bitmask', 'C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Simple Bitmask + DP
|
simple-bitmask-dp-by-22147407-hqwa
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
22147407
|
NORMAL
|
2025-02-03T07:09:39.718378+00:00
|
2025-02-03T07:09:39.718378+00:00
| 40 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<vector<int>>dp;
int solve(vector<int>&nums,vector<int>&t,int i,int state){
if(state==(1<<t.size())-1)return 0;
if(i>=nums.size())return 1e6;
if(dp[i][state]!=-1)return dp[i][state];
int cur=nums[i];
int ans=1e6;
for(int x=0;x<t.size();x++){
if(state&(1<<x))continue;
int cost=0;
int newcur=0;
if(cur<t[x]){
newcur=t[x];
cost=t[x]-cur;
}else if(cur>t[x]) {
int rem=cur%t[x];
if(rem!=0)
cost=t[x]-rem;
newcur=cur+cost;
}else {
cost=0;
newcur=cur;
}
int curstate=state;
for(int x=0;x<t.size();x++){
if(state&(1<<x))continue;
if(newcur%t[x]==0){
curstate=curstate|(1<<x);
}
}
ans=min(ans,cost+solve(nums,t,i+1,curstate));
}
ans=min(ans,solve(nums,t,i+1,state));
return dp[i][state]= ans;
}
int minimumIncrements(vector<int>& nums, vector<int>& target) {
dp.resize(nums.size(),vector<int>(1<<target.size(),-1));
return solve(nums,target,0,0);
}
};
```
| 1 | 0 |
['Dynamic Programming', 'Recursion', 'Memoization', 'Bitmask', 'C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
✅✅ C++ || Easy Explanation with intuition || Bitmask || DP ✅✅
|
c-easy-explanation-with-intuition-bitmas-x5o9
|
IntuitionThis problem is nothing more than dp with bitmasking, the idea comes because we dont know greedily that which number is it optimal to change nums[i] to
|
ssugamlm10
|
NORMAL
|
2025-02-03T06:55:57.512784+00:00
|
2025-02-03T06:55:57.512784+00:00
| 99 | false |
# Intuition
This problem is nothing more than dp with bitmasking, the idea comes because we dont know greedily that which number is it optimal to change nums[i] to in order to make it a multiple of an element in target[j], or whether to leave it without making it a multiple since you have better options ahead!!! So, in such situations we go for brute force.
# Approach
Since length of target is at max 4, we can use a bitmask to track whether a multiple of target[j] is found or not in nums array.
1 => it has been found
0 => yet to find
So in the recursive procedure we iterate it over the nums array and try to change each element to a multiple of some or all elements of target array, we do not need to change it to LCM of few elements (for example LCM(4,3) = 12, now is it better to seperately change 2 numbers in nums[i] to multiples of 4 and 3 that takes at max 7 operations or one number in nums[i] to their LCM that might take upto 12 operations, but yeah in the code you always need to check when you change to a number that if the other number also divides it, in my code this line does the task :
```
if ((nums[i] + add) % target[k] == 0)
set |= (1 << k);
```
), okay now coming back, I have used set variable so that i can set the bit of all the numbers that are divisors of the altered nums[i], while I was trying to make it a multiple of target[j], then in the recursive call I can take it's OR with the existing mask.
Another condition is that we might want to just skip the current nums[i] and try to create multiples of numbers in the target array from the remaining elements in the nums array, this is achieved by :
```
ops = min(ops, f(i + 1, mask, nums, target));
```
# Complexity
- Time complexity:
O(n * 16)
- Space complexity:
O(n * 16)
# Code
```cpp []
class Solution {
public:
int n;
int len;
int dp[50001][17];
int f(int i, int mask, vector<int>& nums, vector<int>& target) {
// Use (1 << len) - 1 instead of pow(2, len) - 1
if (mask == (1 << len) - 1)
return 0;
if(i == n) return INT_MAX;
if(dp[i][mask] != -1) return dp[i][mask];
int ops = INT_MAX;
for (int j = 0; j < len; j++) {
if (((mask >> j) & 1) == 0) {
int add = 0;
if(nums[i] % target[j] != 0){
add = target[j] - (nums[i] % target[j]);
}
int set = 0;
for (int k = 0; k < len; k++) {
if ((nums[i] + add) % target[k] == 0)
set |= (1 << k);
}
int rec = f(i + 1, mask | set, nums, target);
if(rec != INT_MAX)
ops = min(ops, rec + add);
}
}
ops = min(ops, f(i + 1, mask, nums, target));
return dp[i][mask] = ops;
}
int minimumIncrements(vector<int>& nums, vector<int>& target) {
n = nums.size();
len = target.size();
memset(dp,-1,sizeof(dp));
return f(0, 0, nums, target);
}
};
```
| 1 | 0 |
['Dynamic Programming', 'Greedy', 'Recursion', 'Bitmask', 'C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
C++ DP Solution
|
c-dp-solution-by-retire-pf0a
|
Code
|
Retire
|
NORMAL
|
2025-02-03T01:26:51.932653+00:00
|
2025-02-03T01:26:51.932653+00:00
| 99 | false |
# Code
```cpp []
typedef long long ll;
class Solution {
public:
int minimumIncrements(vector<int>& nums, vector<int>& target) {
int m = nums.size();
int n = target.size();
vector<ll> record(1 << n);
for (int i = 0; i < (1 << n); i++) {
ll need = 1;
for (int j = 0; j < n; j++) {
if ((i >> j) & 1) need = lcm(need, target[j]);
}
record[i] = need;
}
vector<ll> f(1 << n, LLONG_MAX);
f[0] = 0;
for (auto &x: nums) {
for (int pre = (1 << n) - 1; pre >= 0; pre--) {
if (f[pre] == LLONG_MAX) continue;
for (int cur = (1 << n) - 1; cur >= 0; cur--) {
if (pre == cur) continue;
if (pre != (pre & cur)) continue;
ll target = 1ll * (x / record[pre ^ cur] + ((x % record[pre ^ cur]) != 0)) * record[pre ^ cur];
f[cur] = min(f[cur], f[pre] + target - x);
}
}
}
return f.back();
}
};
```
| 1 | 0 |
['Dynamic Programming', 'C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
C++ || 100% || 40ms & 50.13mb || Optimized DP & Bitmasking for Minimum Increments to Cover Multiples
|
c-100-40ms-5013mb-optimized-dp-bitmaskin-1qzu
|
IntuitionWe observe that incrementing a number in nums allows it to "cover" one or more targets if, after increments, it becomes a multiple of those targets. In
|
4fPYADGrHM
|
NORMAL
|
2025-02-02T17:47:56.589029+00:00
|
2025-02-02T17:47:56.589029+00:00
| 34 | false |
# Intuition
We observe that incrementing a number in `nums` allows it to "cover" one or more targets if, after increments, it becomes a multiple of those targets. In fact, if we take a subset of targets, we can require the number to be a multiple of the least common multiple (LCM) of that subset so it simultaneously covers all of them. Because we can only increment numbers, we must compute, for each number and for every (nonempty) target subset, the minimal cost to bring the number up to the next multiple of the corresponding LCM. Given the small size of `target` (at most 4) we can use a bitmask (with at most 16 states) to represent which targets have been covered so far and combine the candidates with a DP
# Approach
1. **Precomputation of LCMs:**
For every nonempty subset (represented by a bitmask) of the `target` array, calculate the LCM. We clamp the LCM to avoid overflow issues using a helper function.
2. **Per-Number Costs:**
For each number in `nums` iterate through each nonempty subset of targets. For each subset, compute the cost to increment the number so that it becomes a multiple of the subset’s LCM. Then, determine which targets this new candidate covers using a helper function.
3. **Dynamic Programming (DP):**
We use a fixed DP array of size 16 (since there are at most 4 targets) where `dp[mask]` stores the minimum cost required to cover the targets represented by `mask` For each number in `nums` we use a temporary fixed-size array (`best`) to keep track of the minimal cost to achieve each possible coverage by using that number. We then update the global DP state by merging the new coverage with the previous ones.
4. **Result:**
The answer is found in `dp[FULL_MASK]` where `FULL_MASK` means all targets are covered.
# Complexity
- **Time complexity:**
- Precomputing LCMs for up to 15 subsets: **O(2^b * b)** where b ≤ 4.
- Processing each number across at most 15 target subsets and merging DP states over 16 masks results in about O(n * 15 * 16) worst-case, which is effectively **O(n)**
- **Space complexity:**
- The DP and temporary arrays use fixed sizes (up to 16 integers), so the extra space is **O(1)** (ignoring input size).
# Code
```cpp []
#include <bits/stdc++.h>
using namespace std;
static const int MAX_INC_COST = 40000;
// Standard GCD.
long long gcdLL(long long a, long long b) {
while(b) {
long long temp = a % b;
a = b;
b = temp;
}
return a;
}
// Compute LCM but clamp to a given limit (to avoid overflow).
long long safeLCM(long long a, long long b, long long limit) {
long long g = gcdLL(a, b);
long long mul = a / g;
if (mul > limit / b) return limit; // clamp if too big
long long l = mul * b;
return (l > limit ? limit : l);
}
// Given x and L, return the minimal increments to get to a multiple of L.
int incrementCostToMultiple(int x, int L) {
int r = x % L;
return (r == 0 ? 0 : L - r);
}
// Given a new value x (after increment) and target array, return a bitmask
// of which elements in target divide x.
int coverageOf(int x, const vector<int>& target) {
int mask = 0;
for (int i = 0; i < target.size(); i++) {
if (x % target[i] == 0)
mask |= (1 << i);
}
return mask;
}
class Solution {
public:
int minimumIncrements(vector<int>& nums, vector<int>& target) {
int b = target.size();
int FULL_MASK = (1 << b) - 1;
// Precompute lcms for all nonempty subsets of target.
// There are at most 15 of these (b <= 4).
vector<long long> lcms(1 << b, 1);
for (int mask = 1; mask < (1 << b); mask++){
long long L = 1;
for (int i = 0; i < b; i++){
if (mask & (1 << i)){
L = safeLCM(L, target[i], 60000LL); // use a clamp value around 60000
}
}
lcms[mask] = L;
}
// We will use a DP array with 16 entries (since b<=4) where:
// DP[mask] = minimal total increments needed to cover target bits in mask.
// We use INF = a large number.
const int INF = INT_MAX;
int dp[16];
for (int i = 0; i < (1 << b); i++) {
dp[i] = INF;
}
dp[0] = 0;
// Process each number in nums.
for (int a : nums) {
// For the current number a, compute the minimal cost to achieve
// each coverage (bitmask) by incrementing it.
// There are at most 15 candidate subsets. Because b is small, we can
// keep these in a fixed array "best"; best[mask] is the minimum cost
// for a to produce coverage exactly equal to mask.
int best[16];
for (int i = 0; i < (1 << b); i++) {
best[i] = INF;
}
// Try every nonempty subset s of targets.
// For subset s, we require a candidate to be a multiple of lcms[s]
// so that it is automatically a multiple of every target in s.
for (int s = 1; s < (1 << b); s++) {
int L = (int) lcms[s]; // lcms[s] was clamped so it fits into int
int cost = incrementCostToMultiple(a, L);
if(cost > MAX_INC_COST) continue; // skip if cost is too high (should not happen)
int newVal = a + cost;
int cov = coverageOf(newVal, target);
// Save the best cost to achieve coverage cov using this a.
best[cov] = min(best[cov], cost);
}
// Combine DP from the previous numbers with the candidate offers from a.
int nextDP[16];
for (int i = 0; i < (1 << b); i++) {
nextDP[i] = dp[i]; // option to skip a.
}
for (int mask = 0; mask < (1 << b); mask++) {
if (dp[mask] == INF) continue;
for (int cov = 0; cov < (1 << b); cov++) {
if (best[cov] == INF) continue;
int newMask = mask | cov;
nextDP[newMask] = min(nextDP[newMask], dp[mask] + best[cov]);
}
}
// Update dp with nextDP.
for (int i = 0; i < (1 << b); i++)
dp[i] = nextDP[i];
}
return dp[FULL_MASK];
}
};
```
| 1 | 0 |
['Math', 'Dynamic Programming', 'Greedy', 'Bitmask', 'C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Easy Bitmask Solution | Python3 | Best Time Complexity | Beats 100% of Solutions
|
easy-bitmask-solution-python3-best-time-3nksc
|
ProblemThe problem requires us to ensure that each element in target has at least one multiple present in nums by incrementing elements of nums as needed. Our g
|
shreyvarshney1
|
NORMAL
|
2025-02-02T16:26:47.094143+00:00
|
2025-02-03T10:55:54.395962+00:00
| 87 | false |
## Problem
The problem requires us to ensure that each element in `target` has at least one multiple present in `nums` by incrementing elements of `nums` as needed. Our goal is to achieve this in the minimum number of operations.
### Key Observations:
1. If an element of `target` already has a multiple in `nums`, we do not need to change anything.
2. If no element of `target` has a multiple in `nums`, we need to increment some elements in `nums` until they become a multiple of at least one element in `target`.
3. The problem can be approached using a bitmask DP technique, where we track subsets of `target` elements that have at least one multiple in `nums`.
# Intuition
The problem requires finding the minimum number of increments needed in the `nums` array such that each element in the `target` array has at least one multiple in the modified `nums`. The key insight is to use dynamic programming (DP) with bitmasking to efficiently track the coverage of target elements while minimizing the increments.
# Approach
1. **Bitmask Representation**: Each bit in a bitmask represents whether a corresponding target element is covered. For example, a bitmask `0b11` (binary) for a target array of length 2 means both elements are covered.
2. **LCM Calculation**: For each subset of the target array, compute the Least Common Multiple (LCM). This LCM helps determine the smallest multiple of the subset that a number in `nums` can be incremented to.
3. **Dynamic Programming**: Use a DP dictionary where keys are bitmasks representing covered targets and values are the minimum cost to achieve that coverage. For each number in `nums`, generate all possible subsets of the `target` array, compute the required increments, and update the DP states to track the minimal cost for each coverage state.
# Complexity
- **Time Complexity**: The algorithm runs in \( O(n \cdot (2^m \cdot m + 4^m)) \), where \( n \) is the number of elements in `nums` and \( m \) is the number of elements in `target`. This is due to processing all subsets of `target` for each element in `nums` and combining DP states.
- **Space Complexity**: The space complexity is \( O(2^m) \), required to store the DP states for all possible coverage masks.
# Code Explanation
1. **Initialization**: Start with a DP dictionary initialized to `{0: 0}`, representing no targets covered with zero cost.
2. **Processing Each Number**: For each number in `nums`, generate all possible subsets of `target` elements. For each subset:
- Compute the LCM and determine the smallest multiple of this LCM greater than or equal to the current number.
- Calculate the cost to increment the number to this multiple and determine which targets are covered by this new value.
3. **Updating DP States**: Combine the current number's coverage options with existing DP states to form new coverage states, tracking the minimal cost for each state.
4. **Result Extraction**: After processing all numbers, the result is the minimal cost for the full coverage mask (all targets covered).
This approach efficiently explores all possible ways to cover the target elements using the numbers in `nums` while minimizing the total increments through dynamic programming and bitmasking.
## Edge Cases Considered
- `nums` already contains a multiple of all elements in `target` (answer should be `0`).
- `nums` has elements that need minimal increments to cover `target`.
- Large `target` values requiring significant increments.
- `nums` with redundant values that don’t contribute to a solution.
## Summary
- We use **bitmask DP** to track subsets of `target` covered.
- We efficiently determine the minimal increments required using **LCM-based calculations**.
- The approach balances feasibility and efficiency by using **subset enumeration with LCM calculations**, ensuring an optimal solution.
# Code
```python3 []
class Solution:
def minimumIncrements(self, nums: List[int], target: List[int]) -> int:
m = len(target)
n = len(nums)
full_mask = (1 << m) - 1
dp = {0: 0}
for num in nums:
options = defaultdict(lambda: float('inf'))
for subset_mask in range(0, 1 << m):
if subset_mask == 0:
x_i = num
covered_mask = 0
for t_idx in range(m):
t = target[t_idx]
if x_i % t == 0:
covered_mask |= (1 << t_idx)
if 0 < covered_mask:
options[covered_mask] = min(options[covered_mask], 0)
else:
options[covered_mask] = min(options[covered_mask], 0)
continue
subset = []
for j in range(m):
if subset_mask & (1 << j):
subset.append(target[j])
if not subset:
continue
current_lcm = subset[0]
for t in subset[1:]:
current_lcm = current_lcm * t // gcd(current_lcm, t)
x_i = ((num + current_lcm - 1) // current_lcm) * current_lcm
cost = x_i - num
covered_mask = 0
for t_idx in range(m):
t = target[t_idx]
if x_i % t == 0:
covered_mask |= (1 << t_idx)
if cost < options[covered_mask]:
options[covered_mask] = cost
new_dp = defaultdict(lambda: float('inf'))
for current_mask in dp:
current_cost = dp[current_mask]
for covered_mask in options:
new_mask = current_mask | covered_mask
new_cost = current_cost + options[covered_mask]
if new_cost < new_dp[new_mask]:
new_dp[new_mask] = new_cost
dp = {}
for mask in new_dp:
if new_dp[mask] < dp.get(mask, float('inf')):
dp[mask] = new_dp[mask]
return dp.get(full_mask, -1)
```
| 1 | 0 |
['Dynamic Programming', 'Bitmask', 'Python3']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
DP Bitmask Beat 100% Runtime and Memory
|
dp-bitmask-beat-100-runtime-and-memory-b-7thj
|
ApproachLet n be the size of nums, and t be the size of target. We use dynamic programming with two states dp[i][j], where 0≤i<n and 0≤j<2t, denoting the minimu
|
donbasta
|
NORMAL
|
2025-02-02T14:36:29.190006+00:00
|
2025-02-02T14:36:29.190006+00:00
| 82 | false |
# Approach
<!-- Describe your approach to solving the problem. -->
Let $n$ be the size of `nums`, and $t$ be the size of `target`. We use dynamic programming with two states $dp[i][j]$, where $0 \le i < n$ and $0 \le j < 2^t$, denoting the minimum number of increments so that each elements of `target` with indices in mask $j$ has at least a multiple in the elements of `nums` up to index $i$.
Now we handle the transition. When we want to calculate $dp[i][j]$, some submask $sm$ of $j$ has multiples already in $nums$ up to index $i-1$ using $dp[i - 1][sm]$ increments, and for the remaining elements, we increment $nums[i]$ to the closest multiple of each one of $target[x]$, where bit $x$ is on in submask $j \oplus sm$. This is basically the multiple of $\text{LCM}$ of each one of $target[x]$, where $x$ is the on bits in $j \oplus sm$, and we can precompute these $\text{LCM}$ values to make the computations quicker.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(n * 3^t) \sim O(81n)$$ in this case. ([reference](https://cp-algorithms.com/algebra/all-submasks.html))
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(n * 2^t) \sim O(16n)$$
# Code
```cpp []
class Solution {
public:
int minimumIncrements(vector<int>& nums, vector<int>& target) {
using ll = long long;
int n = nums.size();
int t = target.size();
ll dp[n][1 << t];
ll kpk[1 << t]; //stores LCM of elements of targets with indices in the mask
memset(dp, -1, sizeof(dp));
auto LCM = [&](ll x, ll y) -> ll {
return x * (y / __gcd(x, y));
};
kpk[0] = 1;
for (int i = 1; i < (1 << t); i++) {
for (int j = 0; j < t; j++) {
if ((i >> j) & 1) {
kpk[i] = LCM(kpk[i ^ (1 << j)], 1ll * target[j]);
break;
}
}
}
/// return the difference between b and the closest multiple of a not less than b,
/// basically outputs (a * ceil(a/b) - b)
auto F = [&](ll a, ll b) -> ll {
return a * ((b + a - 1) / a) - b;
};
const ll INF = 1e18;
for (int i = 0; i < n; i++) {
dp[i][0] = 0;
for (int j = 1; j < (1 << t); j++) {
ll tmp = INF;
if (i == 0) {
tmp = F(kpk[j], nums[i]);
} else {
for (int sm = j; sm > 0; sm = (sm - 1) & j) {
int need = j ^ sm;
if (dp[i - 1][sm] != -1) {
tmp = min(tmp, dp[i - 1][sm] + F(kpk[need], nums[i]));
}
}
tmp = min(tmp, dp[i - 1][0] + F(kpk[j], nums[i]));
}
dp[i][j] = tmp;
}
}
return dp[n - 1][(1 << t) - 1];
}
};
```
| 1 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Simple DP solution without LCM, O(1) space , beats 100%(Time & space)
|
dp-without-lcm-o1-space-by-saptak8837-cu3e
|
IntuitionTry to make each element in nums multiple of an element in targetApproachComplexity
Time complexity: O(n∗(2m))
Space complexity:O(1)
Code
|
saptak8837
|
NORMAL
|
2025-02-02T14:24:09.771121+00:00
|
2025-02-02T14:31:40.259064+00:00
| 97 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Try to make each element in nums multiple of an element in target
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: $$O(n*(2^m))$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:$$O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
class Solution {
public:
int minimumIncrements(vector<int>& nums, vector<int>& target) {
int mmask=0;
//mark factors of larger numbers in target as
//we only need to find cost for the highest multiple
for(int i=0;i<target.size();i++){
if(mmask&(1<<i))
continue;
for(int j=0;j<target.size();j++){
if(i!=j && target[i]%target[j]==0){
mmask|=(1<<j);
}
}
}
int n=nums.size();
int q=target.size();
vector<int>next(16,1e9);
int fullMask=(1<<q)-1;
next[fullMask]=0;
for(int i=n-1;i>=0;i--){
vector<int>curr(16,1e9);
for(int mask=mmask;mask<=fullMask;mask++){
curr[mask]=next[mask];
for(int j=0;j<q;j++){
//for each element in target if it is not marked find cost with current elemnt in nums
if((mask&(1<<j))==0){
int temp=target[j];
int cost=nums[i]%temp==0?0:temp-nums[i]%temp;
//if current element is made multiple the updated element
int newnum=nums[i]+cost;
int newmask=mask | (1<<j);
//if we find some numbers in target which are factor of newnum mark them
for(int k=0;k<target.size();k++){
if(k!=j && newnum%target[k]==0){
newmask|=(1<<k);
}
}
curr[mask]=min(curr[mask],cost+next[newmask]);
}
}
}
next=curr;
}
return next[mmask];
}
};
```
| 1 | 0 |
['Dynamic Programming', 'Bitmask', 'C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Ugly Q3 but basically try all the possible choices and calculate LCM
|
ugly-q3-but-basically-try-all-the-possib-s2r9
|
Code
|
nishsolvesalgo
|
NORMAL
|
2025-02-02T04:05:34.742052+00:00
|
2025-02-02T04:05:34.742052+00:00
| 203 | false |
# Code
```cpp []
class Solution {
public:
int minimumIncrements(vector<int>& nums, vector<int>& target) {
bool first = true, second = true, third = true, fourth = true;
for (int i = 0; i < target.size(); i++) {
if (i == 0) first = false;
if (i == 1) second = false;
if (i == 2) third = false;
if (i == 3) fourth = false;
}
static long long dp[2][2][2][2][50001];
memset(dp, -1, sizeof(dp));
auto recurse = [&](auto&& recurse, bool fir, bool sec, bool thi, bool four, int indx) -> long long {
if (fir && sec && thi && four) return 0;
if (indx == nums.size()) return 10000000LL;
if (dp[fir][sec][thi][four][indx] != -1) return dp[fir][sec][thi][four][indx];
long long minOpr = LLONG_MAX;
long long currEle = nums[indx];
for (int i = 0; i <= 15; i++) {
long long lcmm = 1;
if (i == 0) {
minOpr = min(minOpr, recurse(recurse, fir, sec, thi, four, indx + 1));
continue;
}
for (int j = 0; j < target.size(); j++) {
if (j == 0 && !fir && (i & (1 << j))) lcmm = lcm(lcmm, (long long)target[j]);
if (j == 1 && !sec && (i & (1 << j))) lcmm = lcm(lcmm, (long long)target[j]);
if (j == 2 && !thi && (i & (1 << j))) lcmm = lcm(lcmm, (long long)target[j]);
if (j == 3 && !four && (i & (1 << j))) lcmm = lcm(lcmm, (long long)target[j]);
}
bool newfir = fir || (i & (1 << 0));
bool newsec = sec || (i & (1 << 1));
bool newthi = thi || (i & (1 << 2));
bool newfour = four || (i & (1 << 3));
long long nxt = ((currEle + lcmm - 1) / lcmm) * lcmm;
minOpr = min(minOpr, (nxt - currEle) + recurse(recurse, newfir, newsec, newthi, newfour, indx + 1));
}
return dp[fir][sec][thi][four][indx] = minOpr;
};
return (int)recurse(recurse, first, second, third, fourth, 0);
}
};
```
| 1 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Bitmask DP keep track of satisfied target and greedily choose LCM
|
bitmask-dp-keep-track-of-satisfied-targe-002v
| null |
theabbie
|
NORMAL
|
2025-02-02T04:01:27.403095+00:00
|
2025-02-02T04:01:27.403095+00:00
| 330 | false |
```python3 []
import math
def gcd(a, b):
while b:
a, b = b, a % b
return a
def lcm(a, b):
return a * b // gcd(a, b)
class Solution:
def minimumIncrements(self, nums: List[int], target: List[int]) -> int:
k = len(target)
umask = (1 << k) - 1
n = len(nums)
v = []
for cmask in range(1, 1 << k):
l = 1
for j in range(k):
if cmask & (1 << j):
l = lcm(l, target[j])
v.append((cmask, l))
dp = [[float('inf')] * (1 << k) for _ in range(n + 1)]
dp[n][umask] = 0
for i in range(n - 1, -1, -1):
for mask in range(1 << k):
dp[i][mask] = dp[i + 1][mask]
val = nums[i]
for cmask, l in v:
new_mask = mask | cmask
cost = l * math.ceil(val / l) - val
dp[i][mask] = min(dp[i][mask], cost + dp[i + 1][new_mask])
return dp[0][0]
```
| 1 | 0 |
['Python3']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
C++ | DP + Bitmask
|
c-dp-bitmask-by-kena7-b9yb
|
Code
|
kenA7
|
NORMAL
|
2025-02-22T10:05:38.726086+00:00
|
2025-02-22T10:05:38.726086+00:00
| 9 | false |
# Code
```cpp []
class Solution {
public:
int dp[50001][16];
int minOps(int x, int mask, vector<int>&t)
{
long lcm=0;
for(int i=0;i<t.size();i++)
{
int bit=1&(mask>>i);
if(bit)
{
lcm=(lcm==0)?t[i]:(lcm*t[i])/__gcd(lcm,(long)t[i]);
}
}
if(lcm==0)
return 0;
if(lcm<x)
{
lcm=lcm*(x/lcm+(x%lcm!=0));
}
return lcm-x;
}
int find(int i,int mask, vector<int>&v,vector<int>&t)
{
if(mask==(1<<t.size())-1)
return 0;
if(i>=v.size())
return INT_MAX;
if(dp[i][mask]!=-1)
return dp[i][mask];
int res=INT_MAX;
for(int j=0;j<(1<<t.size());j++)
{
if((j&mask)==mask)
{
int op=minOps(v[i],j^mask,t);
int next=find(i+1,j,v,t);
if(next!=INT_MAX && op>=0)
res=min(res,op+next);
}
}
return dp[i][mask]=res;
}
int minimumIncrements(vector<int>& nums, vector<int>& target)
{
memset(dp,-1,sizeof(dp));
return find(0,0,nums,target);
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
C++ bit masks solution + lcm - DP
|
c-bit-masks-solution-lcm-dp-by-joelchaco-dh8u
|
IntuitionApproachComplexity
Time complexity:
O(N∗2N∗2M)
Space complexity:
O(N∗2M) can be improved to O(2M)
Code
|
joelchacon
|
NORMAL
|
2025-02-15T18:58:52.388348+00:00
|
2025-02-15T18:58:52.388348+00:00
| 7 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
- $$O(N*2^N*2^M)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
- $$O(N*2^M)$$ can be improved to $$O(2^M)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
long long lcm(long long a, long long b){
return a/__gcd(a,b)*b;
}
long long lcm_mask(vector<int> &target, long long mask){
long long _lcm = 1, m = target.size();
for(int j = 0; j < m; j++){
if( mask&(1LL<<j)){
_lcm = lcm(_lcm, target[j]);
}
}
return _lcm;
}
int solve(vector<int> &nums, vector<int> &target){
long long n = nums.size(), m = target.size();
vector<vector<long long> > dp(n+1, vector<long long > ((1<<m), INT_MAX));
long long targetMask = (1LL<<m)-1LL;
dp[0][0]=0;
vector<long long> lcm_values(1 << m);
for (long long i = 0; i < (1 << m); i++) {
lcm_values[i] = lcm_mask(target, i);
}
for(long long i = 1 ; i <= n; i++){
for(long long mask = 0; mask < (1<<m); mask++){
dp[i][mask] = dp[i-1][mask];
for (long long submask = mask; submask; submask = (submask - 1) & mask) {
long long lcm_val = lcm_values[submask];
long long rem = nums[i - 1] % lcm_val;
long long cost = (rem == 0) ? 0 : (lcm_val - rem);
if (dp[i - 1][mask ^ submask] != INT_MAX) {
dp[i][mask] = min(dp[i][mask], dp[i - 1][mask ^ submask] + cost);
}
}
}
}
// for(auto i:dp){
// for(auto j:i)cout << j << " ";
// cout <<endl;
// }
return dp[n][targetMask] == INT_MAX? -1 : dp[n][targetMask];
}
int minimumIncrements(vector<int>& nums, vector<int>& target) {
return solve(nums, target);
}
};
/*
dp[i][mask] --> min cost of considering item 1...i with <mask> targets
dp[i][mask] = min(dp[i-1][mask]+cost of adding i)
8 4 10 5 3 2
*
1 <= n <= 10^4
1 <= t <=4 !!!!
How many operations to make t items cool?
10, 5
00 01 10 11
0 5 10 10
8 0 2 2 2
4 0 2 2 2
7 0
4,7 4 4 6
dp[i][0000] --> min(dp[j!=i][mask-bit k])
* */
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Explained Clean Code | 27ms | DP + LCM + bitmask
|
explained-clean-code-27ms-dp-lcm-bitmask-7x4k
|
IntuitionUse Dynamic Programming with bitmasks to track which target numbers are covered by incrementing each number in nums, where "covered" means the incremen
|
ivangnilomedov
|
NORMAL
|
2025-02-14T13:55:09.826820+00:00
|
2025-02-14T13:55:09.826820+00:00
| 7 | false |
# Intuition
Use Dynamic Programming with bitmasks to track which target numbers are covered by incrementing each number in nums, where "covered" means the incremented number becomes a multiple of those target numbers.
# Approach
1. **Optimize Target Array**
- Remove duplicates.
2. **Precompute LCMs**
- Calculate LCM for each possible subset of target numbers using bitmasks.
- If a number is multiple of LCM, it is multiple of all numbers in that subset.
3. **DP State**
- `dp_mask2minc[mask]` = minimum operations needed to make some numbers in nums multiples of all numbers marked in mask.
- For each num in nums:
- Try using it to cover different subsets of remaining uncovered targets
- Calculate minimum increments needed to reach next multiple of subset is LCM
- Update DP state by combining with previous best solutions
- The `(num-1)/lcm + 1` formula efficiently finds how many times to multiply LCM to get next multiple after num.
# Complexity
- Time complexity: $$O(N * M * 3^N)$$
- N = target.size()
- M = nums.size()
- 3^N comes from analyzing all subsets of mask for each mask (approximately)
# Code
```cpp []
class Solution {
public:
int minimumIncrements(const vector<int>& nums, vector<int>& target) {
// Remove duplicates for optimization.
sort(target.begin(), target.end());
int tgte = 0;
for (int i = 1; i < target.size(); ++i) {
if (target[i] > target[tgte]) {
++tgte;
swap(target[i], target[tgte]);
}
}
target.resize(tgte + 1);
const int N = target.size();
const int kMaskEnd = 1 << N; // 2^N all possible subsets of target
// Precompute LCM for each subset of targets
// A number is multiple of LCM IFF it is multiple of all numbers in that subset
vector<long long> mask2lcm(kMaskEnd, 1);
for (int m = 1; m < kMaskEnd; ++m) {
long long lcm = 1;
for (int i = 0; i < N; ++i)
if ((m >> i) & 1)
lcm = ::lcm<long long>(lcm, target[i]);
mask2lcm[m] = lcm;
}
// dp_mask2minc[mask] = min operations needed to make some numbers
// in nums multiples of all numbers marked in mask
vector<long long> dp_mask2minc(kMaskEnd, kInf);
vector<long long> up_mask2minc(kMaskEnd, kInf); // tmp array for DP updates
dp_mask2minc[0] = up_mask2minc[0] = 0; // empty mask needs 0 operations
long long res = kInf;
for (int num : nums) { // For each number in nums, try to use it to cover some subset of target
for (int mask = 1; mask < kMaskEnd; ++mask) {
long long mask_minc = up_mask2minc[mask];
for (int subm = mask; subm; subm = (subm - 1) & mask) { // Trick to iterate through subsets of mask
long long lcm = mask2lcm[subm];
long long n = (num - 1) / lcm + 1;
mask_minc = min(
mask_minc,
dp_mask2minc[mask ^ subm]
// This will be minimal value in nums that is multiple of subm LCM and is GE num
+ n * lcm - num);
}
up_mask2minc[mask] = mask_minc;
}
dp_mask2minc = up_mask2minc;
res = min(res, dp_mask2minc.back()); // back() represents all targets covered
}
return res;
}
private:
static constexpr long long kInf = numeric_limits<long long>::max() / 4;
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
DP with bitmasking
|
dp-with-bitmasking-by-raikou_thunder-qdci
|
IntuitionApproachComplexity
Time complexity:O(256*n)
Space complexity:O(n*n)
Code
|
Raikou_Thunder
|
NORMAL
|
2025-02-13T15:16:10.158336+00:00
|
2025-02-13T15:16:10.158336+00:00
| 4 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->


# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:O(256*n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(n*n)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
#include <bits/stdc++.h>
using namespace std;
#define ll long long int
ll dp[50005][17], numCount, targetCount;
ll lcmPrecomputed[1 << 17]; // Fix: Use 1 << targetCount for all subsets
vector<int> nums, target;
ll computeLCM(ll x, ll y) {
return (x / __gcd(x, y)) * y; // Fix: Prevent overflow
}
void precomputeLCM() {
for (ll subset = 1; subset < (1 << targetCount); subset++) {
ll lcm = 1;
for (ll j = 0; j < targetCount; j++) {
if (subset & (1 << j)) {
lcm = computeLCM(lcm, target[j]);
}
}
lcmPrecomputed[subset] = lcm;
}
}
ll findMinOperations(ll i, ll mask) {
if (mask == (1 << targetCount) - 1) return 0;
if (i == numCount) return 1e9;
if (dp[i][mask] != -1) return dp[i][mask];
ll minOperations = findMinOperations(i + 1, mask); // Not taking nums[i]
for (ll subset = 1; subset < (1 << targetCount); subset++) {
ll subsetLCM = lcmPrecomputed[subset];
ll nextMultiple = ((nums[i] + subsetLCM - 1) / subsetLCM) * subsetLCM; // Fix: Use integer division
minOperations = min(minOperations, (nextMultiple - nums[i]) + findMinOperations(i + 1, mask | subset));
}
return dp[i][mask] = minOperations;
}
class Solution {
public:
int minimumIncrements(vector<int>& inputNums, vector<int>& inputTarget) {
nums = inputNums;
target = inputTarget;
numCount = nums.size();
targetCount = target.size();
memset(dp, -1, sizeof(dp));
memset(lcmPrecomputed, 0, sizeof(lcmPrecomputed));
precomputeLCM();
return findMinOperations(0, 0);
}
};
```
| 0 | 0 |
['Dynamic Programming', 'C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Using 2D DP and BitMask + LCM AND GCD in C++ (100% faster)
|
using-2d-dp-and-bitmask-lcm-and-gcd-in-c-ax1x
|
IntuitionApproachComplexity
Time complexity:
O(n*16*16)
Space complexity:
O(n*16)
Code
|
Balram_54321
|
NORMAL
|
2025-02-09T09:49:17.775988+00:00
|
2025-02-09T09:49:17.775988+00:00
| 12 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
- O(n\*16*16)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
- O(n*16)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
typedef long long ll;
int countNums, countTarget;
vector<int> nums, target;
vector<vector<ll>> dp;
vector<ll> lcmForSubset;
ll computeLcm(ll a , ll b){
return (a*b)/gcd(a,b);
}
void subsetLcm(){
for(int subset = 1;subset< (1<<countTarget); subset++){
ll lcm = 1;
for(int i=0;i<countTarget;i++){
if(subset&(1<<i)){
lcm = computeLcm(lcm, target[i]);
}
}
this->lcmForSubset[subset] = lcm;
}
}
ll solve(int n, int mask){
// base condition
if(mask+1==(1<<countTarget)) return 0;
if(n==0) return 1e9;
// general condition
if(dp[n][mask]!=-1) return dp[n][mask];
ll ans = 1e9;
ans = min(ans, solve(n-1, mask));
for(int subset=1;subset< (1<<countTarget);subset++){
ll cost = (ll)(ceil((double)nums[n-1]/lcmForSubset[subset])*lcmForSubset[subset]);
ans = min(ans, (cost-nums[n-1])+solve(n-1,mask|subset));
}
return dp[n][mask]=ans;
}
int minimumIncrements(vector<int>& nums, vector<int>& target) {
int n = nums.size();
this->countNums = nums.size();
this->countTarget = target.size();
this->nums = nums;
this->target = target;
this->dp = vector<vector<ll>>(countNums+1,vector<ll>(16, -1));
this->lcmForSubset = vector<ll>(16,1);
subsetLcm();
return (int)solve(n,0);
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
(01 DP) + Bitmasking Without LCM approach
|
01-dp-bitmasking-without-lcm-approach-by-vdrn
|
Code
|
spravinkumar9952
|
NORMAL
|
2025-02-08T12:33:48.642938+00:00
|
2025-02-08T12:33:48.642938+00:00
| 12 | false |
# Code
```cpp []
class Solution {
public:
int MX = 1e9;
int memo[50001][17];
int N;
int dfs(int ind, vector<int>& nums, vector<int>& target, int mask){
// Base case
if(ind >= nums.size()){
int targetMask = (1 << N)-1;
return mask == targetMask ? 0 : MX;
}
// Memo Case
if(memo[ind][mask] != -1){
return memo[ind][mask];
}
// Don't take
int may = dfs(ind+1, nums, target, mask);
for(int i = 0; i<target.size(); i++){
if( (mask & ( 1<<i)) == 0 ){
int mod = nums[ind] % target[i];
int inc = mod == 0 ? 0 : target[i] - mod ;
int newNumber = nums[ind] + inc;
int newMask = mask;
// Take all the smaller targets can be multiple of new number
for(int j = i; j<target.size(); j++){
if(newNumber % target[j] == 0 ){
newMask = newMask | (1 << j);
}
}
int ret = dfs(ind+1, nums, target, newMask);
if(ret == MX) continue;
may = min(may, inc + ret);
}
}
return memo[ind][mask]=may;
}
int minimumIncrements(vector<int>& nums, vector<int>& target) {
N = target.size();
memset(memo, -1, sizeof(memo));
sort(target.rbegin(), target.rend());
return dfs(0, nums, target, 0);
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Simple DP+Bitmasking
|
simple-dpbitmasking-by-catchme999-yqae
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
catchme999
|
NORMAL
|
2025-02-08T11:56:57.905012+00:00
|
2025-02-08T11:56:57.905012+00:00
| 16 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
from math import gcd, ceil
def compute_lcm(x, y):
return (x * y) // gcd(x, y)
def precompute_lcm(target):
target_count = len(target)
lcm_precomputed = [1] * (1 << target_count)
for subset in range(1, 1 << target_count):
lcm_precomputed[subset] = 1
for j in range(target_count):
if subset & (1 << j):
lcm_precomputed[subset] = compute_lcm(lcm_precomputed[subset], target[j])
return lcm_precomputed
class Solution:
def minimumIncrements(self, nums, target):
num_count, target_count = len(nums), len(target)
lcm_precomputed = precompute_lcm(target)
dp=[[-1 for _ in range(1<<len(target))] for _ in range(len(nums)+1)]
# @lru_cache(None)
def find_min_operations(i, mask):
if mask == (1 << target_count) - 1:
return 0
if i == num_count:
return int(1e9)
if(dp[i][mask]!=-1):
return dp[i][mask]
min_operations = find_min_operations(i + 1, mask)
for subset in range(1, 1 << target_count):
if(mask&subset==0):
subset_lcm = lcm_precomputed[subset]
next_multiple = ceil(nums[i] / subset_lcm) * subset_lcm
min_operations = min(min_operations, (next_multiple - nums[i]) + find_min_operations(i + 1, mask | subset))
dp[i][mask]=min_operations
return min_operations
return find_min_operations(0, 0)
```
| 0 | 0 |
['Python3']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Clean C++ solution O(N)
|
clean-c-solution-on-by-vishal_781-5umi
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
vishal_781
|
NORMAL
|
2025-02-08T08:42:21.949577+00:00
|
2025-02-08T08:42:21.949577+00:00
| 8 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
#define ll long long
ll lcm(ll a,ll b){
ll gc = __gcd(a,b);
gc = (a*(b/gc));
return gc;
}
int minimumIncrements(vector<int>& nums, vector<int>& target) {
int n = nums.size();
int m = target.size();
ll sz = (1<<m);
const ll inf = INT_MAX;
vector<vector<ll>> dp(n,vector<ll>(sz,inf));
dp[0][0] = 0;
for(ll i = 0;i<sz;i++){
ll lc = 0;
for(ll j =0;j<m;j++){
if(i&(1ll<<j)){
if(lc == 0){
lc = target[j];
}
else{
lc = lcm(lc,target[j]);
}
}
}
if(lc != 0){
ll k = (nums[0]+lc - 1)/lc;
k *= lc;
dp[0][i] = k - nums[0];
}
}
for(ll i = 1;i<n;i++){
for(ll mask =0;mask<sz;mask++){
dp[i][mask] = dp[i-1][mask];
// cout<<mask<<" ";
for(ll k = mask;k>0;k = (k-1)&mask){
ll lc = 0;
ll req = mask^k;
if(dp[i-1][req] == inf) continue;
for(ll j =0;j<m;j++){
if(k&(1ll<<j)){
if(lc == 0){
lc = target[j];
}
else{
lc = lcm(lc,target[j]);
}
}
}
if(lc != 0){
ll p = (nums[i]+lc - 1)/lc;
p *= lc;
dp[i][mask] = min(dp[i][mask],dp[i-1][req] + (p - nums[i]));
}
}
}
}
return dp[n-1][sz-1];
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
5D dp..
|
5d-dp-by-joshuadlima-mhiw
|
Intuition0 -> 16 we get all possibilities for 4 numbers so i use that as bruteforcewe will keep track of whether each number in target has been satisfied or not
|
joshuadlima
|
NORMAL
|
2025-02-07T14:56:22.535602+00:00
|
2025-02-07T14:56:22.535602+00:00
| 6 | false |
# Intuition
0 -> 16 we get all possibilities for 4 numbers so i use that as bruteforce
we will keep track of whether each number in target has been satisfied or not
rest is basic math
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
#define ll long long
class Solution {
public:
int dp[50010][2][2][2][2];
long long lcm(long long a, long long b) {return a * b / __gcd(a, b);}
int bruteforce(int ix, vector<int>& nums, vector<int>& target, vector<bool>& isDone) {
bool minE = *min_element(isDone.begin(), isDone.end());
if (ix == nums.size() && minE == 1)
return 0;
else if(ix == nums.size())
return INT_MAX;
if(dp[ix][isDone[0]][isDone[1]][isDone[2]][isDone[3]] == -1){
int ans = INT_MAX;
for(int cur = 0; cur < 16; cur++) {
int temp = cur, v0, v1, v2, v3;
v0 = temp % 2, temp /= 2;
v1 = temp % 2, temp /= 2;
v2 = temp % 2, temp /= 2;
v3 = temp % 2;
if((v0 && isDone[0]) || (v1 && isDone[1]) || (v2 && isDone[2]) || (v3 && isDone[3]))
continue;
int newVal = 1;
// update isDone
if(v0)
newVal = lcm(newVal, target[0]), isDone[0] = 1;
if(v1)
newVal = lcm(newVal, target[1]), isDone[1] = 1;
if(v2)
newVal = lcm(newVal, target[2]), isDone[2] = 1;
if(v3)
newVal = lcm(newVal, target[3]), isDone[3] = 1;
int aTemp = bruteforce(ix + 1, nums, target, isDone);
// undo isDone
if(v0)
isDone[0] = 0;
if(v1)
isDone[1] = 0;
if(v2)
isDone[2] = 0;
if(v3)
isDone[3] = 0;
if(aTemp != INT_MAX && newVal > 0) {
ans = min(ans, ((nums[ix] + newVal - 1) / newVal) * newVal - nums[ix] + aTemp);
}
}
dp[ix][isDone[0]][isDone[1]][isDone[2]][isDone[3]] = ans;
}
return dp[ix][isDone[0]][isDone[1]][isDone[2]][isDone[3]];
}
int minimumIncrements(vector<int>& nums, vector<int>& target) {
while (target.size() < 4)
target.push_back(1);
for(int i = 0; i <= nums.size(); i++)
for(int j = 0; j < 2; j++)
for(int k = 0; k < 2; k++)
for(int l = 0; l < 2; l++)
for(int m = 0; m < 2; m++)
dp[i][j][k][l][m] = -1;
vector<bool> isDone(4, 0);
return bruteforce(0, nums, target, isDone);
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Dp + Bitmasking (Simplified)
|
dp-bitmasking-simplified-by-vineeth0904-8k87
|
IntuitionApproachComplexity
Time complexity:
O(N * K * 2^k)
Space complexity:
Code
|
vineeth0904
|
NORMAL
|
2025-02-07T13:58:21.232846+00:00
|
2025-02-07T13:58:21.232846+00:00
| 6 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
O(N * K * 2^k)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int minimumIncrements(vector<int>& nums, vector<int>& target) {
int n = nums.size();
int k = target.size();
vector<vector<long long>>dp(n, vector<long long>(1 << k, 0));
for(int i = 1; i < (1 << k); i++){
long long init = 1;
long long itr = i, cnt = 0;
while(itr){
if(itr & 1){
init = lcm(init, target[k - cnt - 1]);
}
itr >>= 1;
cnt++;
}
dp[0][i] = (nums[0] / init) * init - nums[0];
dp[0][i] += (nums[0] % init) ? init : 0;
}
for(int i = 1; i < n; i++){
for(int j = 0; j < (1 << k); j++){
dp[i][j] = 1e18;
for(int l = 0; l < (1 << k); l++){
if(((j ^ l) | j) != j)continue;
long long init = 1;
long long itr = (j ^ l), cnt = 0;
while(itr){
if(itr & 1){
init = lcm(init, target[k - cnt - 1]);
}
itr >>=1 ;
cnt++;
}
long long tot = (nums[i] / init) * init - nums[i];
tot += (nums[i] % init) ? init : 0;
dp[i][j] = min(dp[i][j], tot + dp[i - 1][l]);
}
}
}
return dp[n - 1][(1 << k) - 1];
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
C++ Dynamic Programming + Bit-Masking
|
c-dynamic-programming-bit-masking-by-sj4-pnwz
|
Intuitionkeep most things pre-computedCode
|
SJ4u
|
NORMAL
|
2025-02-06T20:25:17.940085+00:00
|
2025-02-06T20:25:17.940085+00:00
| 10 | false |
# Intuition
keep most things pre-computed
# Code
```cpp []
#define ll long long
class Solution {
public:
vector<vector<int>> pairOf1 = {{0}, {1}, {2}, {3}};
vector<vector<int>> pairOf2 = {{0, 1}, {0, 2}, {0, 3},
{1, 2}, {1, 3}, {2, 3}};
vector<vector<int>> pairOf3 = {{0, 1, 2}, {0, 1, 3}, {0, 2, 3}, {1, 2, 3}};
vector<vector<int>> pairOf4 = {{0, 1, 2, 3}};
vector<vector<vector<int>>> pairOf = {pairOf1, pairOf2, pairOf3, pairOf4};
vector<int> req_mask = {1, 3, 7, 15};
ll dp[50001][17];
ll lcm_dp[17];
// Function to compute LCM of two numbers
ll compute_lcm(ll a, ll b) { return (a / __gcd(a, b)) * b; }
ll recurs(const vector<int>& nums, const vector<int>& target, int pos, int mask) {
if (mask == req_mask[target.size() - 1]) return 0;
if (pos >= nums.size()) return INT_MAX;
if (dp[pos][mask] != -1) return dp[pos][mask];
ll ans = INT_MAX, new_mask, deficit;
for (int i = 0; i < pairOf.size(); i++) {
if (target.size() < i + 1) break;
for (auto& x : pairOf[i]) {
if (x.back() >= target.size()) continue;
bool flag = false;
new_mask = mask;
int curr_mask = 0;
for (int y : x) {
if (!(mask & (1 << y))) flag = true;
new_mask |= (1 << y);
curr_mask |= (1 << y);
}
if (flag) {
ll lcm_ = lcm_dp[curr_mask];
deficit = (nums[pos] > lcm_) ?
(((nums[pos] / lcm_) + (nums[pos] % lcm_ ? 1 : 0)) * lcm_) - nums[pos]
: lcm_ - nums[pos];
ans = min(ans, deficit + recurs(nums, target, pos + 1, new_mask));
}
}
}
ans = min(ans, recurs(nums, target, pos + 1, mask));
return dp[pos][mask] = ans;
}
int minimumIncrements(vector<int>& nums, vector<int>& target) {
memset(dp, -1, sizeof(dp));
memset(lcm_dp, -1, sizeof(lcm_dp));
// **Precompute LCMs for all possible masks**
int n = target.size();
for (int mask = 1; mask < (1 << n); mask++) {
ll lcm_ = 1;
for (int i = 0; i < n; i++) {
if (mask & (1 << i)) {
lcm_ = compute_lcm(lcm_, target[i]);
}
}
lcm_dp[mask] = lcm_;
}
return recurs(nums, target, 0, 0);
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Dp + bitmask
|
dp-bitmask-by-maxorgus-efer
|
Try to increase every number to the nearest multiplication of each of the traget and check whether we have had all the multiplactions.Upper limit of number of t
|
MaxOrgus
|
NORMAL
|
2025-02-06T03:56:39.390723+00:00
|
2025-02-06T03:56:39.390723+00:00
| 10 | false |
Try to increase every number to the nearest multiplication of each of the traget and check whether we have had all the multiplactions.
Upper limit of number of targets 4 does not look typically bitmask -- it kinda too small.
# Code
```python3 []
class Solution:
def minimumIncrements(self, nums: List[int], target: List[int]) -> int:
T = len(target)
N = len(nums)
@cache
def dp(i,mask):
if mask == 2**T-1: return 0
if i == N:return inf
res = inf
a = nums[i]
for j in range(T):
res = min(res,dp(i+1,mask))
if (1 << j) & mask:continue
if a % target[j] == 0: newa = a
else: newa = a + target[j] - a%target[j]
newmask = mask
for k in range(T):
if newa % target[k] == 0: newmask = newmask | (1<<k)
res = min(res,newa-a+dp(i+1,newmask))
#print(i,mask,res)
return res
return dp(0,0)
```
| 0 | 0 |
['Dynamic Programming', 'Bitmask', 'Python3']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
My Solution
|
my-solution-by-hope_ma-q72v
| null |
hope_ma
|
NORMAL
|
2025-02-05T11:00:15.031384+00:00
|
2025-02-05T11:00:15.031384+00:00
| 12 | false |
```
/**
* Time Complexity: O(n * (3 ^ n_target))
* Space Complexity: O(2 ^ n_target)
* where `n` is the length of the vector `nums`
* `n_target` is the length of the vector `target`
*/
class Solution {
public:
int minimumIncrements(const vector<int> &nums, const vector<int> &target) {
constexpr int range = 2;
const int n = static_cast<int>(nums.size());
const int n_target = static_cast<int>(target.size());
const int layouts = 1 << n_target;
long long lcms[layouts];
lcms[0] = 1;
for (int offset = 0; offset < n_target; ++offset) {
for (int layout = 0; layout < (1 << offset); ++layout) {
lcms[layout | (1 << offset)] = lcm(target[offset], lcms[layout]);
}
}
long long dp[range][layouts];
memset(dp, 0, sizeof(dp));
int previous = 0;
int current = 1;
fill(dp[previous] + 1, dp[previous] + layouts, numeric_limits<long long>::max());
for (const int num : nums) {
for (int layout = 0; layout < layouts; ++layout) {
dp[current][layout] = dp[previous][layout];
for (int sublayout = layout; sublayout > 0; sublayout = (sublayout - 1) & layout) {
dp[current][layout] = min(dp[current][layout], plus(dp[previous][layout ^ sublayout], ops(num, lcms[sublayout])));
}
}
previous ^= 1;
current ^= 1;
memset(dp[current], 0, sizeof(dp[current]));
}
return dp[previous][layouts - 1];
}
private:
long long ops(const long long num, const long long lcm) {
return (lcm - (num % lcm)) % lcm;
}
long long plus(const long long lhs, const long long rhs) {
if (lhs == numeric_limits<long long>::max() || rhs == numeric_limits<long long>::max()) {
return numeric_limits<long long>::max();
}
return lhs + rhs;
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
DP Recursion Solution || O(n*4^k) || Easy to Understand
|
dp-recursion-solution-on4k-easy-to-under-zyvc
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
dnanper
|
NORMAL
|
2025-02-05T08:37:29.273492+00:00
|
2025-02-05T08:37:29.273492+00:00
| 9 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int n, m;
int minimumIncrements(vector<int>& nums, vector<int>& tar)
{
m = tar.size(); n = nums.size();
int k = 1 << m;
vector<long long> mp(k);
for (int mask = 1; mask < (1 << m); mask++)
{
vector<int> tmp;
for (int i = 0; i < m; i++)
{
if (mask & (1 << i))
{
tmp.push_back(tar[i]);
}
}
long long curLCM = tmp[0];
for (int i = 1; i < tmp.size(); i++)
{
curLCM = lcm(curLCM, tmp[i]);
}
mp[mask] = curLCM;
}
vector<vector<int>> dp(n+1, vector<int>(k+1, -1));
return solve(0, 0, mp, nums, dp);
}
private:
int solve(int i, int mask, vector<long long> &mp, vector<int> &nums, vector<vector<int>> &dp)
{
if (__builtin_popcount(mask) == m)
{
return 0;
}
if (i >= n)
{
return 1e9;
}
if (dp[i][mask] != -1) return dp[i][mask];
long long ans = solve(i+1, mask, mp, nums, dp);
for (int mk = 1; mk < mp.size(); mk++)
{
long long r = nums[i] % mp[mk];
long long plus = (r == 0) ? 0 : mp[mk] - r;
ans = min(ans, plus + solve(i+1, mask | mk, mp, nums, dp));
}
return dp[i][mask] = ans;
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Basic BitMask Application Solution | Beginner level Bit Mask
|
basic-bitmask-application-solution-begin-o8do
|
IntuitionBasic BitMask Dp Application
size of target is <<<< size of nums, generally a bit mask questionApproachwe will traverse on nums array and try to do ope
|
BOLTA7479
|
NORMAL
|
2025-02-05T04:17:18.249462+00:00
|
2025-02-05T04:22:44.173072+00:00
| 8 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Basic BitMask Dp Application
size of target is <<<< size of nums, generally a bit mask question
# Approach
<!-- Describe your approach to solving the problem. -->
we will traverse on nums array and try to do operations on it for a target whose multiple we have not obtained, after performing opertation, we will mark all the elemnts in target which were previously unmarked and is a divisor of this updated value .
Finally we will return the minimum ans;
We can also skip element of nums, so will also do a call for that ;
return the min of the above two recursive calls .
combination of mask(track of indices of target whose multples are already obtained) and index of nums defines unique state of evey recursive call , so we will memoize it in this way
dp[index][mask_value];
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(N* M *M) M is very small so its === O(N)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(N*2^M)
# Code
```cpp []
class Solution {
public:
int dp[50002][70];
int n,m,p;
int rec(int ind,int mask,vector<int>& nums,vector<int>&target) {
if(mask == p) return 0;
if(ind >= n) return 1e9;
if(dp[ind][mask] != -1) return dp[ind][mask];
//skip this index
int ans = 0;
int nskp = 1e9;
//take this and convert one of the index of target
for(int i = 0;i<m;i++) {
if(mask & (1<<i)) continue;
//convert his one
int divisor = target[i];
int dividend = nums[ind];
int remainder = dividend%divisor;
int rem = 0;
if(remainder) rem = divisor - remainder;
int newmask = mask;
int nval = nums[ind] + rem;
newmask |= (1<<i);
for(int j = 0;j<m;j++) if(!(mask&(1<<j))) if(nval%target[j] == 0) newmask |= (1<<j);
nskp = min(nskp,rem + rec(ind+1,newmask,nums,target));
}
int skp = rec(ind+1,mask,nums,target);
ans = min(skp,nskp);
return dp[ind][mask] = ans;
}
int minimumIncrements(vector<int>& nums, vector<int>& target) {
n = nums.size();
m = target.size();
p = int(pow(2,m)) - 1;
memset(dp,-1,sizeof(dp));
int ans = rec(0,0,nums,target);
return ans;
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
😃🚀Classic Striver Take not Take O(n) (DP+BITMASKING)🚀😃
|
classic-striver-take-not-take-on-dpbitma-pcf2
|
Complexity
Time complexity:
O(2x∗x∗logM) + O(n∗2x∗2x)=O(n)
LCM_Precomputation + solve()
Space complexity:
O(n)
Code
|
Dynamic_Dishank
|
NORMAL
|
2025-02-04T13:45:14.093239+00:00
|
2025-02-04T13:45:14.093239+00:00
| 24 | false |
# Complexity
- Time complexity:
$$O(2^x * x * logM)$$ + $$O(n * 2^x * 2^x)$$=$$O(n)$$
LCM_Precomputation + solve()
- Space complexity:
$$O(n)$$
# Code
```cpp []
// Generalising the idea of take not_take
// Since some of the elements in the arr will not be used at all
// And some will serve some subset of target
// How many subset are possible 2*2*2*2=16
// We can easily generate them via the bitmask representation
// 1011 means t0,t3 and t4 are already served
// dp[index][mask]: O(n*16)
// operations required for satisfying condition for index from 0 to i
// if the ith element in the arr serves subset lets say 1101 how many operations are req for the same
// LCM({t0,t1,t4}) make arr[i] then smallest multiple greater than or equal to LCM
// So its benificial to precompute the LCM of every subset possible
// LCM*GCD=a*b
// How (if(curr_LCM>=1e5) break;) helped overcome the overflow issue?
// Incase the curr_LCM just becomes 1e5 we break hence for that subset LCM[subset]=1e5
// In the (Best case: cost is as minimum as possible: arr[i]=1e4 (max_possible))
// curr_cost=1e5-1e4 >>> sum(all arr[i] with let say 1e4 operations each)
// Hence such LCM would never give me better ans
// O(2^x * x * logM) for the LCM precomputation
// O(n * 2^x * 2^x) for the solve()
// O(n) Final time complexity
class Solution {
public:
int n,x;
vector<int> arr,target,LCM;
vector<vector<int>> dp;
void precompute()
{
int total_subset=(1<<x);
LCM=vector<int>(total_subset,1);
for(int subset=1;subset<total_subset;subset++)
{
int curr_LCM=1;
for(int i=0;i<x;i++)
{
if(subset&(1<<i))
{
curr_LCM=(target[i]*curr_LCM)/__gcd(target[i],curr_LCM);
if(curr_LCM>=1e5) break;
}
}
LCM[subset]=curr_LCM;
}
}
int solve(int index,int mask)
{
if((mask+1)==(1<<x)) return 0;
if(index==n) return 1e9;
if(dp[index][mask]!=-1) return dp[index][mask];
int take=INT_MAX;
int not_take=solve(index+1,mask);
int total_subsets=(1<<x)-1;
for(int subset=1;subset<=total_subsets;subset++)
{
int lcm=LCM[subset];
int next_multiple=lcm*((arr[index]+lcm-1)/lcm);
int cost=next_multiple-arr[index];
take=min(take,cost+solve(index+1,subset|mask));
}
return dp[index][mask]=min(take,not_take);
}
int minimumIncrements(vector<int>& new_arr, vector<int>& new_target)
{
arr=new_arr;
target=new_target;
n=arr.size();
x=target.size();
precompute();
// for(auto itr:LCM) cout<<itr<<" ";
dp=vector<vector<int>> (n,vector<int> ((1<<x),-1));
return solve(0,0);
}
};
```
| 0 | 0 |
['Array', 'Dynamic Programming', 'Bit Manipulation', 'Number Theory', 'Bitmask', 'C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Solution DP + Bitmasking +number theory
|
solution-dp-bitmasking-number-theory-by-2v4kv
|
IntuitionWe need to ensure that each element in target (b[]) has at least one multiple in nums (a[]). The key observation is that instead of making individual e
|
Happymood
|
NORMAL
|
2025-02-04T09:42:13.624703+00:00
|
2025-02-04T09:42:13.624703+00:00
| 17 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
We need to ensure that each element in target (b[]) has at least one multiple in nums (a[]). The key observation is that instead of making individual elements in a[] multiples of b[], we can use Least Common Multiple (LCM) to handle subsets of b[] efficiently.
By iterating through subsets of b[], we can determine the optimal multiple for each number in a[], minimizing the number of increments required. Using bitmasking, we track which b[i] values have been satisfied while using dynamic programming (DP) to compute the minimal cost.
# Approach
<!-- Describe your approach to solving the problem. -->
Precompute LCM for all subsets of b[]
Since b[] is small (≤ 4 elements), there are at most 16 subsets (2^4).
We compute the LCM for each subset, so we can later check which multiple is most efficient.
Recursive DP with Bitmasking
Define dp[idx][mask], where:
idx represents the current index in a[].
mask is a bitmask indicating which elements of b[] have at least one multiple in a[].
Base case:
If idx == n, check if mask covers all b[i]. If yes, return 0, otherwise return a large penalty (500000).
Recursive step:
Option 1: Skip a[idx] and move to the next element.
Option 2: Modify a[idx] to be a multiple of some LCM subset of b[] and update mask accordingly.
Iterate through all valid subsets of b[] that are still missing and find the minimum increment cost.
Use Memoization (dp[][])
Store results of dp[idx][mask] to avoid redundant calculations.
Since b.size() ≤ 4, mask can take at most 16 values, keeping the state space manageable.
Return the minimal increments needed
Start the recursion from sol(0, 0, a, b), meaning:
Begin with the first element in a[].
No b[i] values have a multiple yet (mask = 0).
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
Precomputing LCM: There are at most 16 subsets, and each subset takes at most 4 operations → O(16 × 4) ≈ O(64).
DP Transitions:
dp[idx][mask] has at most N × 16 states.
Each state iterates over at most 16 subsets.
Total Complexity: O(N × 16 × 16) ≈ O(N × 256) ≈ O(N) (since b.size() is small).
- Space complexity:
DP table: O(N × 16) = O(N).
LCM array: O(16) = O(1).
# Code
```cpp []
#include <algorithm>
class Solution {
public:
int dp[50001][16];
long long lcm[16] = {};
int sol(int idx, int mask, vector<int>& a, vector<int>& b) {
if (idx == a.size()) {
int m = b.size();
if (mask == (1 << m) - 1) {
return 0;
}
return 500000;
}
if (dp[idx][mask] != -1)
return dp[idx][mask];
long long ans = sol(idx + 1, mask, a, b);
int m = b.size();
int state = (1 << m) - 1;
state = state ^ mask;
for (int subset = state; subset > 0; subset = (subset - 1) & state) {
int cost = (a[idx] + lcm[subset] - 1) / lcm[subset];
ans = min(ans,
cost * lcm[subset] - a[idx] + sol(idx + 1, subset|mask, a, b));
}
return dp[idx][mask] = ans;
}
int minimumIncrements(vector<int>& a, vector<int>& b) {
int n = a.size();
for (int i = 0; i < n; i++) {
for (int j = 0; j < 16; j++) {
dp[i][j] = -1;
}
}
int m = b.size();
int state = (1 << m) - 1;
for (int subset = state; subset > 0; subset = (subset - 1) & state) {
lcm[subset] = 1;
for (int i = 0; i < b.size(); i++) {
if (subset & (1 << i)) {
lcm[subset] =
1ll * lcm[subset] * b[i] / __gcd(lcm[subset], 1ll*b[i]);
}
}
}
return sol(0, 0, a, b);
}
};
```
| 0 | 0 |
['Dynamic Programming', 'Bit Manipulation', 'Number Theory', 'C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
C++ [NON DP] approach that beats 99%
|
c-non-dp-approach-that-beats-99-by-thezi-3wte
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
thezi
|
NORMAL
|
2025-02-03T19:46:06.770252+00:00
|
2025-02-03T19:46:06.770252+00:00
| 24 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
void permutations(vector<vector<int>> &result, unordered_set<int> &used, vector<int> &curr, vector<int> &nums){
int n = nums.size();
if (used.size() == n){
result.push_back(curr);
return;
}
for (int i = 0; i < n; i++){
if (used.contains(nums[i])){
continue;
}
curr.push_back(nums[i]);
used.insert(nums[i]);
permutations(result, used, curr, nums);
used.erase(nums[i]);
curr.pop_back();
}
}
int minimumIncrements(vector<int>& nums, vector<int>& targets) {
// IS a multiple... so N or 2*N... maybe divide?
// solve largest number then see if lesser follow suit (?)
sort(targets.begin(), targets.end(), greater<int>());
vector<int> unique_targets = {targets[0]};
for (int i = 1; i < targets.size(); i++){
int target = targets[i];
bool flag = false;
for (int &factor : unique_targets){
if (factor >= target && factor % target == 0){
flag = true;
break;
}
}
if (!flag){
unique_targets.push_back(target);
}
}
sort(unique_targets.begin(), unique_targets.end(), greater<int>());
// solve for one first then think...
// reduce targets to a unique
int global_total = INT_MAX;
vector<vector<int>> result;
vector<int> curr;
unordered_set<int> used;
permutations(result, used, curr, unique_targets);
sort(nums.begin(), nums.end(), std::greater<int>());
for (vector<int> &perm_target : result){
int total = 0;
unordered_set<int> solved;
unordered_set<int> marked_idx;
int n = nums.size();
for (int target : perm_target){
if (solved.contains(target)){
continue;
}
std::pair<int, int> p = {INT_MAX, 0};
auto &[diff, mark] = p;
for (int i = 0; i < nums.size(); i++){
int num = nums[i];
if (num > target){
if (num % target == 0) num = target;
else num %= (target);
}
int curr = target-num;
if (diff > curr && !marked_idx.contains(i)){
diff = curr;
mark = i;
}
}
int og = nums[mark];
int num = nums[mark];
if (num > target){
if (num % target == 0) num = target;
else num %= (target);
}
int curr = target-num;
og+= curr;
for (int t : unique_targets){
if (!solved.contains(t)){
if (og % t == 0){
solved.insert(t);
}
}
}
total += diff;
marked_idx.insert(mark);
}
global_total = min(global_total, total);
}
return global_total;
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Rust solution
|
rust-solution-by-abhineetraj1-scr7
|
IntuitionThe problem asks for the minimum number of increments needed to make the elements of nums divisible by all the corresponding elements in target. The k
|
abhineetraj1
|
NORMAL
|
2025-02-03T18:02:26.619483+00:00
|
2025-02-03T18:02:26.619483+00:00
| 8 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem asks for the minimum number of increments needed to make the elements of nums divisible by all the corresponding elements in target. The key insight is that for a given number x and a set of targets, the minimum increments needed to make x divisible by all targets is related to the Least Common Multiple (LCM) of those targets. If x is not divisible by the LCM, the cost is the difference between the LCM and the remainder when x is divided by the LCM.
# Approach
<!-- Describe your approach to solving the problem. -->
Calculate LCMs: Precompute the LCM for all possible subsets of the target array. We use bitmasking to represent each subset. lcm_arr[mask] stores the LCM of the subset represented by the mask.
Dynamic Programming: Use dynamic programming to find the minimum increments. dp[mask] stores the minimum increments needed to make the elements of nums divisible by the subset of target represented by mask.
Iterate and Update: Iterate through the nums array. For each number x in nums, iterate through all possible subsets (masks). Calculate the cost of making x divisible by the LCM of the current subset. Update the dp array accordingly. Specifically, if x is not divisible by the LCM of a subset, we find the remainder r. The cost will be lcm - r.
Result: The final answer is stored in dp[full_mask], where full_mask represents the set of all elements in target.
# Complexity
- Time complexity: O(m * 2<sup>m</sup> * n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(2<sup>m</sup>)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```rust []
use std::cmp::min;
impl Solution {
pub fn minimum_increments(nums: Vec<i32>, target: Vec<i32>) -> i32 {
let m = target.len();
let full_mask = (1 << m) - 1;
let mut lcm_arr = vec![0; 1 << m];
for mask in 1..(1 << m) {
let mut l = 1i64;
for j in 0..m {
if (mask & (1 << j)) != 0 {
l = Self::lcm(l, target[j] as i64);
}
}
lcm_arr[mask] = l;
}
let inf = i64::MAX / 2;
let mut dp = vec![inf; 1 << m];
dp[0] = 0;
for &x in &nums {
let mut new_dp = dp.clone();
for mask in 1..(1 << m) {
let l = lcm_arr[mask];
let r = x as i64 % l;
let cost = if r == 0 { 0 } else { l - r };
for old in 0..(1 << m) {
let new_mask = old | mask;
new_dp[new_mask] = min(new_dp[new_mask], dp[old] + cost);
}
}
dp = new_dp;
}
dp[full_mask] as i32
}
fn gcd(a: i64, b: i64) -> i64 {
if b == 0 {
a
} else {
Self::gcd(b, a % b)
}
}
fn lcm(a: i64, b: i64) -> i64 {
a / Self::gcd(a, b) * b
}
}
```
| 0 | 0 |
['Dynamic Programming', 'Greedy', 'Bit Manipulation', 'Rust']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
DP || bitmasking || C++.
|
dp-bitmasking-c-by-rishiinsane-f8s8
|
IntuitionApproachComplexity
Time complexity:
o(n)
Space complexity:
O(16) ~ O(1)
Code
|
RishiINSANE
|
NORMAL
|
2025-02-03T16:17:37.317550+00:00
|
2025-02-03T16:17:37.317550+00:00
| 19 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
o(n)
- Space complexity:
O(16) ~ O(1)
# Code
```cpp []
class Solution {
public:
int minimumIncrements(vector<int>& nums, vector<int>& target) {
int n = nums.size();
// DP array to store the minimum cost to cover target elements using bitmasking
vector<int> prev(16, 1e6);
prev[0] = 0;
for (int i = 0; i < n; i++) {
vector<int> next(16, 1e6);
//all possible bitmask states (0 to 15)
for (int j = 0; j < 16; j++) {
if (prev[j] == 1e6) //unreachable, skip
continue;
//subsets of target elements
for (int m = 0; m < 16; m++) {
int nm = j | m;
next[nm] = min(next[nm], prev[j] + cost(nums[i], target, m));
}
}
prev = next;
}
return prev[15];
}
int cost(int num, vector<int>& target, int mask) {
int inum = num;
int l = 1;
for (int i = 0; i < target.size(); i++) {
if (mask >> i & 1 ^ 1) //i-th bit in mask is not set - skip
continue;
l = lcm(l, target[i]);
if (l >= 1e5)
return 1e6;
}
int fnum = (num + l - 1) / l * l;
return fnum - inum;
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Brute Force with Number Theory and Partitions
|
brute-force-with-number-theory-and-parti-adeo
|
ApproachConsider all the partitions and divide into groups based on the lcms of a certain partition set.
Consider all permutations of the lcm set and find out t
|
math_pi
|
NORMAL
|
2025-02-03T16:12:43.596666+00:00
|
2025-02-03T16:12:43.596666+00:00
| 27 | false |
# Approach
Consider all the partitions and divide into groups based on the lcms of a certain partition set.
Consider all permutations of the lcm set and find out the minimum answer via brute force.
# Complexity
- Time complexity:
$$O(n)$$
- Space complexity:
$$O(n)$$
# Code
```cpp []
class Solution {
public:
vector<vector<int>> allPartitions;
vector<vector<vector<int>>> curPartition;
void findPartitions(int i, vector<int> &a) {
if(i == a.size()) {
curPartition.push_back(allPartitions);
return;
}
for(int j=0; j<allPartitions.size(); j++) {
allPartitions[j].push_back(a[i]);
findPartitions(i+1, a);
allPartitions[j].pop_back();
}
allPartitions.push_back({a[i]});
findPartitions(i+1, a);
allPartitions.pop_back();
}
long long lcm(int x, int y) {
return x*1ll*y/__gcd(x, y);
}
int minimumIncrements(vector<int>& nums, vector<int>& target) {
allPartitions.clear();
int n = nums.size();
int m = target.size();
findPartitions(0, target);
vector<vector<long long>> partitions;
vector<long long> all;
for(auto x: curPartition) {
for(auto y: x) {
long long g = 1;
for(auto z: y) {
g = lcm(g, z);
}
all.push_back(g);
}
sort(begin(all), end(all));
if(all.size() <= nums.size()) partitions.push_back(all);
all.clear();
}
// for(auto x: partitions) {
// for(auto y: x) cout << y << ' '; cout << '\n';
// }
vector<int> mark(n, 0);
long long res = 8e18;
for(auto x: partitions) {
do {
long long ans = 0;
for(auto y: x) {
long long cur = 1e18, num = -1;
for(int i=0; i<n; i++) {
if(mark[i]) continue;
long long req = ((nums[i]+y-1)/y)*y-nums[i];
if(req < cur) {
cur = req;
num = i;
}
}
if(cur < 0) {
cout << cur << '\n';
}
ans += cur;
mark[num] = 1;
}
if(ans >= 0) res = min(res, ans);
mark.assign(n, 0);
} while(next_permutation(begin(x), end(x)));
}
return res;
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
[Python] concise combinations + bit-DP
|
python-concise-combinations-bit-dp-by-kn-p7ig
| null |
knatti
|
NORMAL
|
2025-02-03T12:24:37.717140+00:00
|
2025-02-03T12:24:37.717140+00:00
| 27 | false |
```python3 []
class Solution:
def minimumIncrements(self, nums: List[int], target: List[int]) -> int:
N,T =len(nums), len(target)
multiples=defaultdict(list)
for mask in range(1,1<<T):
multiples[ lcm(*[n for i, n in enumerate(target) if (1<<i) &mask ])].append(mask)
@cache
def dp(i, mask):
if not mask: return 0
if i >= N: return float("inf")
#no increment
ret = dp(i+1,mask)
# increment
for m in multiples:
ret=min(ret, -nums[i] % m +dp(i+1,mask&reduce(and_,map(inv,multiples[m]))))
return ret
return dp(0,(1<<T)-1)
```
| 0 | 0 |
['Python3']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Simple Very Easy BIT MASK DP !! beats 100%
|
simple-very-easy-bit-mask-dp-beats-100-b-dopa
|
Complexity
Time complexity: O(1e7)
Space complexity: O(1e6)
Code
|
atulsoam5
|
NORMAL
|
2025-02-03T12:20:02.934689+00:00
|
2025-02-03T12:20:02.934689+00:00
| 14 | false |
# Complexity
- Time complexity: O(1e7)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1e6)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int minimumIncrements(vector<int>& nums, vector<int>& target) {
int n = nums.size(), m = target.size();
vector<vector<long long>> dp(n + 1, vector<long long>((1 << m), 1e8));
//~O(1e7) it passes
// target length is less than 20 biggest HINT ===> BIT MASK !!! :)
dp[0][0] = 0;
for (int i = 0; i < n; i++) {
for (int mask = 0; mask < (1 << m); mask++) {
dp[i + 1][mask] = min(dp[i + 1][mask], dp[i][mask]);
for (int bit = 0; bit < (1 << m); bit++) {
int temp = mask;
long long res = 0;
for (int j = 0; j < m; j++) {
if (bit & (1 << j)) {
if (!res) res = target[j];
else res = lcm(res, target[j]);
temp |= (1 << j);
}
}
if (res) {
long long c = (nums[i] + res - 1) / res;
long long d = c * res;
dp[i + 1][temp] = min(dp[i + 1][temp], dp[i][mask] + d - nums[i]);
}
}
}
}
return dp[n][(1 << m) - 1];
}
};
```
| 0 | 0 |
['Dynamic Programming', 'Bit Manipulation', 'Bitmask', 'C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
DP Bitmasking soln
|
dp-bitmasking-soln-by-prikshit2803-i0e2
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Prikshit2803
|
NORMAL
|
2025-02-03T10:58:38.922189+00:00
|
2025-02-03T10:58:38.922189+00:00
| 7 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int get_cost(int num,vector<int> &target,int mask){
int org_num = num;
int l=1;
for(int i=0;i<target.size();i++){
if(mask>>i & 1^1) continue;
l=lcm(l,target[i]);
if(l>=1e5)
return 1e6;
}
num = (num+l-1)/l * l;
return num-org_num;
}
int minimumIncrements(vector<int>& nums, vector<int>& target) {
const int NP=1e6;
vector<int> dp(16,NP);
dp[0]=0;
for(int i=0;i<nums.size();i++){
vector<int> ndp(16,NP);
for(int m=0;m<=15;m++){
if(dp[m]==NP) continue;
for(int mm=0;mm<=15;mm++){
int nm=m | mm;
ndp[nm]= min(ndp[nm],dp[m] + get_cost(nums[i],target,mm) );
}
}
dp=ndp;
}
return dp[15];
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
DP+BitMask+ BinarySearch (Beats 100% in Time and Space)
|
dpbitmask-binarysearch-beats-100-in-time-hono
|
IntuitionDP+BitMask + BinarySearchApproachAdded in commentsComplexity
Time complexity: O(N*log(N))
Space complexity: O(N)
Code
|
ekalavya_pc
|
NORMAL
|
2025-02-03T09:41:04.209820+00:00
|
2025-02-03T09:41:04.209820+00:00
| 29 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
DP+BitMask + BinarySearch
# Approach
<!-- Describe your approach to solving the problem. -->
Added in comments
# Complexity
- Time complexity: **O(N*log(N))**
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: **O(N)**
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int getNearestGreaterToCurrentVal(int curVal,int targetVal){
int lo=1,hi=1e4; // low and high multipliers to tagetVal
int nearestGreater;
while(lo<=hi){
int mid=(lo+hi)/2;
if(mid*targetVal>=curVal) nearestGreater=targetVal*mid,hi=mid-1;
else lo=mid+1;
}
return nearestGreater;
}
int dp[5*10001][16];
int solve(int i,int mask,vector<int>&nums,vector<int>&target){
if(i==nums.size()){
if(mask==(pow(2,target.size())-1)) return 0; // if all target values perfomrmed
return 1e5;
}
if(dp[i][mask]!=-1) return dp[i][mask];
int ans=solve(i+1,mask,nums,target); //case1: skip the current val
//case2: increment cuurent num( nums[i] ) to any targetvalue
for(int j=0;j<target.size();j++){
int newMask=mask;
if(!(newMask & (1<<j))){
int targetVal=target[j];
//if current val is greater than target then its not possible to convert currentVal
// to targetVal by incrementing ,hence get a multiple of targetVal nearest to currentVal
if(nums[i]>targetVal) targetVal=getNearestGreaterToCurrentVal(nums[i],targetVal);
//Mark all the target values which are divisors of targetVal as
//we are changing current val to targetVal
for(int k=0;k<target.size();k++){
if(targetVal%target[k]==0) newMask=newMask | (1<<k);
}
ans=min(ans,targetVal-nums[i]+solve(i+1,newMask,nums,target)); //compare case1 with Case 2
}
}
return dp[i][mask]=ans;
}
int minimumIncrements(vector<int>& nums, vector<int>& target) {
memset(dp,-1,sizeof(dp));
return solve(0,0,nums,target);
}
};
```
| 0 | 0 |
['Binary Search', 'Dynamic Programming', 'Bitmask', 'C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Sets + Binary Search + Generate Permutation
|
sets-binary-search-generate-permutation-j1pys
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
kizu
|
NORMAL
|
2025-02-03T07:54:40.374868+00:00
|
2025-02-03T07:54:40.374868+00:00
| 19 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
#define ll long long
#define is ==
#define isnt !=
int minimumIncrements(vector<int>& x, vector<int>& t) {
set <ll> s ;
ll cap = 3e4 ;
vector <ll> mpg (20010, 0) ;
vector <ll> u (20010, 0) ;
for (auto itr : x) mpg [itr] ++ ;
s.insert (-1e9) ;
s.insert (1e9) ;
for (int i = 1 ; i <= 10000 ; i ++) if (mpg [i]) s.insert (i) ;
ll ans = 1e18 ;
sort (t.begin (), t.end ()) ;
do {
ll ct = 0 ;
vector <ll> c, d ;
for (int i = 0 ; i < t.size () ; i ++) {
ll mn = 1e9, mni = -1, mnr = -1 ;
for (ll run = t [i] ; run <= cap ; run += t [i]) {
auto lb = s.lower_bound (run) ;
if (*lb > run) lb -- ;
ll v = run - *lb ;
if (run is *lb) mn = v, mni = *lb, mnr = run ;
else {
while (*lb isnt -1e9 and u [*lb] is mpg [*lb]) lb -- ;
if (*lb is -1e9) continue ;
v = run - *lb ;
if (v <= mn and u [*lb] isnt mpg [*lb]) mn = v, mni = *lb, mnr = run ;
}
}
mpg [mni] -- ;
mpg [mnr] ++ ;
u [mnr] = 1 ;
s.insert (mnr) ;
if (not mpg [mni]) s.erase (mni) ;
ct += mn ;
c.push_back (mni) ;
d.push_back (mnr) ;
}
ans = min (ans, ct) ;
for (auto itr : c) mpg [itr] ++, s.insert (itr) ;
for (auto itr : d) {
u [itr] = 0 ;
mpg [itr] -- ;
if (not mpg [itr]) s.erase (itr) ;
}
} while (next_permutation (t.begin (), t.end ())) ;
return ans ;
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Minimum Increments for Target Multiples in an Array ( Beats 100%)
|
minimum-increments-for-target-multiples-qly8h
|
Complexity
Time complexity: O(2^N)
Space complexity: O(N)
Code
|
Ansh1707
|
NORMAL
|
2025-02-02T17:52:13.717491+00:00
|
2025-02-02T17:52:13.717491+00:00
| 21 | false |
# Complexity
- Time complexity: O(2^N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(N)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python []
def gcd(a, b):
if b == 0:
return a
return gcd(b, a % b)
class Solution(object):
def minimumIncrements(self, nums, target):
"""
:type nums: List[int]
:type target: List[int]
:rtype: int
"""
n = len(nums)
t = len(target)
def LCM(x, y):
return x * (y // gcd(x, y))
kpk = [0] * (1 << t)
kpk[0] = 1
for i in range(1, 1 << t):
for j in range(t):
if (i >> j) & 1:
kpk[i] = LCM(kpk[i ^ (1 << j)], target[j])
break
def F(a, b):
return a * ((b + a - 1) // a) - b
INF = float('inf')
dp = [[-1] * (1 << t) for _ in range(n)]
for i in range(n):
dp[i][0] = 0
for j in range(1, 1 << t):
tmp = INF
if i == 0:
tmp = F(kpk[j], nums[i])
else:
sm = j
while sm > 0:
need = j ^ sm
if dp[i - 1][sm] != -1:
tmp = min(tmp, dp[i - 1][sm] + F(kpk[need], nums[i]))
sm = (sm - 1) & j
tmp = min(tmp, dp[i - 1][0] + F(kpk[j], nums[i]))
dp[i][j] = tmp
return dp[n - 1][(1 << t) - 1]
```
| 0 | 0 |
['Math', 'Dynamic Programming', 'Bit Manipulation', 'Bitmask', 'Python']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
C++ | Power set Solution | Easy | Self Understandable
|
c-power-set-solution-easy-self-understan-4p56
|
IntuitionWe can get the minimum answer by taking lcm of none, one or more number of elements and then computing the minimun required to achieve that particluar
|
adithya_u_bhat
|
NORMAL
|
2025-02-02T16:59:40.067828+00:00
|
2025-02-02T16:59:40.067828+00:00
| 27 | false |
# Intuition
We can get the minimum answer by taking lcm of none, one or more number of elements and then computing the minimun required to achieve that particluar set of elements
# Approach
Try all combinations and along with all the priority combinations (the order in which they modify the nums is determined by priority)
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
long long gcd(long long a, long long b)
{
if (b == 0)
return a;
return gcd(b, a % b);
}
int minimumIncrements(vector<int>& nums, vector<int>& target) {
long long n = target.size();
long long ans = INT_MAX;
for(long long power = 0;power<(1<<n);power++){
long long lcm = 1;
long long op=0;
vector<long long> v;
for(long long j=0;j<n;j++){
if(power&(1<<j)){
lcm = (lcm*target[j])/gcd(lcm,target[j]);
}
else{
v.push_back(target[j]);
}
}
if(lcm!=1){
v.push_back(lcm);
}
sort(v.begin(),v.end());
vector<int> temp=nums;
do {
long long op=0;
map<long long,long long> mp;
for(int j=0;j<v.size();j++){
long long val = 1e18;
long long ele = 0;
long long idx = -1;
for(int i=0;i<nums.size();i++){
if(mp.find(i)!=mp.end()){
if((nums[i]%v[j])==0){
ele=nums[i];
val=0;
idx=i;
}
}
else if(val>(long long)(v[j]*((nums[i]+v[j]-1)/v[j]))-nums[i]){
val = (long long)(v[j]*((nums[i]+v[j]-1)/v[j]))-nums[i];
ele = v[j]*((nums[i]+v[j]-1)/v[j]);
idx=i;
}
}
nums[idx]=ele;
mp[idx]=1;
op+=val;
}
ans = min(ans,op);
nums=temp;
} while (next_permutation(v.begin(), v.end()));
}
return ans;
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
quick solution in java
|
quick-solution-in-java-by-klueqjnom3-7dho
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
kLUeqJNoM3
|
NORMAL
|
2025-02-02T16:51:36.654776+00:00
|
2025-02-02T16:51:36.654776+00:00
| 37 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int minimumIncrements(int[] nums, int[] target) {
int[][] plorvexium = new int[][] { nums, target };
int m = target.length;
int fullMask = (1 << m) - 1;
int n = nums.length;
long INF = (long)1e18;
long[] dp = new long[1 << m];
for (int mask = 0; mask < (1 << m); mask++) {
dp[mask] = INF;
}
dp[0] = 0;
for (int x : nums) {
java.util.HashMap<Integer, Long> offers = new java.util.HashMap<>();
for (int j = 0; j < m; j++) {
int t = target[j];
int v = ((x + t - 1) / t) * t;
long cost = v - x;
int cov = 0;
for (int k = 0; k < m; k++) {
if (v % target[k] == 0) {
cov |= (1 << k);
}
}
offers.put(cov, Math.min(offers.getOrDefault(cov, INF), cost));
}
long[] newDP = dp.clone();
for (int mask = 0; mask < (1 << m); mask++) {
if (dp[mask] < INF) {
for (java.util.Map.Entry<Integer, Long> entry : offers.entrySet()) {
int offerMask = entry.getKey();
long cost = entry.getValue();
int newMask = mask | offerMask;
newDP[newMask] = Math.min(newDP[newMask], dp[mask] + cost);
}
}
}
dp = newDP;
}
return (int) dp[fullMask];
}
}
```
| 0 | 0 |
['Java']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
No DP/Bitmask | Bell Number | Store 4 lowest cost + Backtrack
|
bell-number-store-4-lowest-cost-backtrac-hevw
|
ApproachTargets may share or not share the same element in nums as min cost.
We group the targets such that only target in same group must share the same elemen
|
justinleung0204
|
NORMAL
|
2025-02-02T15:26:34.768027+00:00
|
2025-02-02T15:42:50.759492+00:00
| 40 | false |
# Approach
<!-- Describe your approach to solving the problem. -->
Targets may share or not share the same element in nums as min cost.
We group the targets such that only target in same group must share the same element in nums, by considering the lcm of each group.
For the grouping, see [Bell Number](https://en.wikipedia.org/wiki/Bell_number).
Since B(4)=15, we can brute force all groupings.
Each group is assigned to their top 4 lowest costs by brute force backtracking in O(4!).
# Complexity
- Time complexity: $$O(B(M)*(N+M!)) = O(N)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(M^2) = O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
, for $$M=len(target)$$
# Code
```python3 []
groupings = [
[],
[[[0]]],
[[[0,1]],[[0],[1]]],
[[[0,1,2]],[[0],[1,2]],[[1],[0,2]],[[2],[0,1]], [[0],[1],[2]]],
[
[[0,1,2,3]],
[[0],[1,2,3]],
[[1],[0,2,3]],
[[2],[0,1,3]],
[[3],[0,1,2]],
[[0,1],[2,3]],
[[0,2],[1,3]],
[[0,3],[1,2]],
[[0,1],[2],[3]],
[[0,2],[1],[3]],
[[0,3],[1],[2]],
[[1,2],[0],[3]],
[[1,3],[0],[2]],
[[2,3],[0],[1]],
[[0],[1],[2],[3]]
]
]
class Solution:
def minimumIncrements(self, nums: List[int], target: List[int]) -> int:
N = len(nums)
INF = 10**20
M = len(target)
def cal(groups): #indicies of grouping e.g. [[0,1],[2],[3]]
nonlocal N, INF,M
G = len(groups)
lcms = [1 for _ in range(G)] #lcm of each group
for j in range(G):
for i in groups[j]:
lcms[j] = lcm(cms[j], target[i])
#G lowest costs for each group
costs = [[] for _ in range(G)]
for i in range(N): #O(N)
for j in range(G):
mod = nums[i]%lcms[j]
if mod==0:
costs[j].append((0,i))
else:
costs[j].append((lcms[j] - mod,i))
costs[j].sort() #O(4log4)
while len(costs[j])>G:
costs[j].pop()
#now have G lowest costs for each group
res = INF
used = set()
def dfs(j,curCost): #O(4!), backtrack
if j==G:
nonlocal res
res = min(res,curCost)
return
for i in range(G):
if costs[j][i][1] in used:
continue
used.add(costs[j][i][1])
dfs(j+1, curCost + costs[j][i][0])
used.remove(costs[j][i][1])
dfs(0,0)
return res
ans = INF
for group in groupings[M]: #atmost 15 groupings
#groupings[M]: [[[0,1]],[[0],[1]]]
#group: [[0],[1]]
ans = min(ans,cal(group))
return ans
```
| 0 | 0 |
['Backtracking', 'Python3']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Dynamic Programming | C++ | Solution with explanation
|
dynamic-programming-c-solution-with-expl-pifa
|
Solution
Also on my blog: https://www.zerotoexpert.blog/p/leetcode-weekly-contest-435
In this problem, we should find the minimum increments to meet the conditi
|
a_ck
|
NORMAL
|
2025-02-02T13:00:47.525908+00:00
|
2025-02-02T13:00:47.525908+00:00
| 26 | false |
# Solution
- Also on my blog: https://www.zerotoexpert.blog/p/leetcode-weekly-contest-435
In this problem, we should find the minimum increments to meet the condition. The critical point is that we only can increase the element. By this restriction, we can calculate the minimum value to make nums[i] to be the multiple of targets[j].
However, we don’t know which number will be the multiple of which target. Also, one number can be the multiple of two different targets. We cannot consider all of these cases one by one.
Fortunately, we only have at most 4 targets. It means that if we calculate all the cases that nums[i] cover, it is at most 2^4 = 16. So, it is fast enough to iterate all cases for each index i of nums.
I precalculated the Least Common Multiple for each target combination to get the minimum increment faster. I record the state to find which targets are covered. If all targets are covered before iterating all nums, then return 0. If iterating all numbers finished before covering all targets, return an invalid value.
I also used memoization to skip the duplicated case.
# Code
```cpp []
class Solution {
public:
int n, m;
unordered_map<int, long long> mp;
int dp[50001][1<<4];
long long func(vector<int> & nums, vector<int> & target, int i, int state) {
if (state == (1<<m) - 1) {
return 0;
}
if (i == n) {
// not matched
return 1e9;
}
if (dp[i][state] != -1) return dp[i][state];
long long ans = 1e9;
for (int x = 0; x < (1 << m); ++x) {
long long l = mp[x];
long long diff = ((nums[i] + l-1) / l) * l - nums[i];
ans = min(ans, func(nums, target, i+1, state | x) + diff);
}
return dp[i][state] = ans;
}
int minimumIncrements(vector<int>& nums, vector<int>& target) {
n = (int)nums.size();
m = (int)target.size();
memset(dp, -1,sizeof(dp));
for (int x = 0; x < (1 << m); ++x) {
vector<long long> a;
for (int j = 0; j < m; ++j) {
if (x & (1 << j)) {
a.push_back(target[j]);
}
}
if (a.size() == 0) {
mp[x] = 1;
} else {
long long l = a[0];
for (int i = 1; i < a.size(); ++i) {
l = l * a[i] / gcd(l, a[i]);
}
mp[x] = l;
}
}
return func(nums, target, 0, 0);
}
};
```
| 0 | 0 |
['Dynamic Programming', 'C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Consider all cases(divide all, lcm all, 1/1/2, 1/rest, 2/2) w/ no index select duplications
|
consider-all-casesdivide-all-lcm-all-112-72oo
|
IntuitionGet minimum operations to achieve the goal, with given numbers (<= 4) and no index select duplications
Consider all cases(divide all, lcm all, 1/1/2, 1
|
townizm
|
NORMAL
|
2025-02-02T11:08:07.216313+00:00
|
2025-02-02T11:08:42.928855+00:00
| 30 | false |
# Intuition
Get minimum operations to achieve the goal, with given numbers (<= 4) and no index select duplications
Consider all cases(divide all, lcm all, 1/1/2, 1/rest, 2/2)
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def minimumIncrements(self, nums: List[int], target: List[int]) -> int:
def get_min_ops(*args):
l = len(args)
assert l <= 4, l
if len(nums) < l:
return inf
gains = [[] for _ in range(l)]
for j, arg in enumerate(args):
for i, num in enumerate(nums):
heapq.heappush(gains[j], (-(-num % arg), i))
while len(gains[j]) > l:
heapq.heappop(gains[j])
# Get results for all combinations
res = inf
dfs = [(0, 0, 0)]
while dfs:
i, curr, used = dfs.pop()
if i == len(gains):
res = min(res, curr)
continue
for gain, j in gains[i]:
if (1 << j) & used == 0:
dfs.append((i + 1, curr + (-gain), (1 << j) | used))
return res
res = min(get_min_ops(*target), get_min_ops(lcm(*target)))
# 1 / rest
if len(target) >= 3:
for j in range(len(target)):
res = min(res, get_min_ops(target[j], lcm(*[
target[i] for i in range(len(target))
if i != j])))
if len(target) == 4:
for i, j in combinations(list(range(4)), 2):
k, l = [idx for idx in range(4) if idx not in (i, j)]
ti, tj, tk, tl = target[i], target[j], target[k], target[l]
res = min(res,
get_min_ops(lcm(ti, tj), lcm(tk, tl)), # 2 / 2
get_min_ops(lcm(ti, tj), tk, tl), # 2 / 1 / 1
)
return res
```
| 0 | 0 |
['Python3']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
[Python] Top-Down DP + BitMask, Easy to understand with detailed explanation.
|
python-dp-bitmask-easy-to-understand-wit-y2b2
|
IntuitionIn the contest, I notice that:
For each number in nums, we want to try if it can be a multiple to any value in the target. In this sense, we want to us
|
casterkiller
|
NORMAL
|
2025-02-02T10:22:08.180222+00:00
|
2025-02-02T10:34:07.384703+00:00
| 38 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
In the contest, I notice that:
1. For each number in nums, we want to try if it can be a multiple to any value in the target. In this sense, we want to use DP, and a good way to mark the value in the target which have found a multiple in nums is bit mask.
2. Since a multiple can match several value in the target, we need to find LCM of these values and mark them in one go. For example, 10 can be a multiple of 2, 5 and 10 at the same time.
3. Since leetcode contest's python cache issue, we use cache_clear for DP function just in case.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Precalcute LCM for every possible mask.
2. DP function with two parameters, idx for current index of nums and mask for marking the values in target which has found its multiple.
3. Try every next mask which the values in next mask haven't been use yet (nxt & mask === 0), and get the minimum result to return. For the next mask, we try to find the LCM value forming from nums[idx] to satify all the values marked by next mask.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
1. Precalculate LCM: O(T * 2^T)
2. DP: O(N * 2^T * 2^T)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
1. Precalculate LCM: O(2^T)
2. DP: O(N * 2^T)
# Code
```python3 []
class Solution:
def minimumIncrements(self, nums: List[int], target: List[int]) -> int:
N = len(nums)
T = len(target)
FULL = (1 << T) - 1
lcm_lookup = [0] * (1 << T)
for mask in range(1 << T):
m = 1
for i in range(T):
if (1 << i) & mask:
m = lcm(m, target[i])
lcm_lookup[mask] = m
@cache
def cost(n, v):
return (v - (n % v)) % v
@cache
def go(idx, mask):
if mask == FULL:
return 0
if idx == N:
return inf
best = inf
# when nxt is 0, that means we skip nums[idx]
for nxt in range(FULL + 1):
if nxt & mask:
continue
best = min(best, cost(nums[idx], lcm_lookup[nxt]) + go(idx + 1, nxt | mask))
return best
r = go(0, 0)
go.cache_clear()
return r
```
| 0 | 0 |
['Dynamic Programming', 'Bit Manipulation', 'Bitmask', 'Python3']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Beats 100% in Time and 100% in Space
|
beats-100-in-time-and-100-in-space-by-ha-qb47
|
IntuitionAs we can see, bitmasking can be used so just brute force using bitmask DPComplexity
Time complexity:
Space complexity:
Code
|
harshkankhar1
|
NORMAL
|
2025-02-02T09:35:57.440390+00:00
|
2025-02-02T09:35:57.440390+00:00
| 41 | false |
# Intuition
As we can see, bitmasking can be used so just brute force using bitmask DP
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int minimumIncrements(vector<int>& nums, vector<int>& target) {
int m = target.size();
int n = nums.size();
set<int> to_remove;
set<int> t(target.begin(), target.end());
target.assign(t.begin(), t.end());
m = target.size();
for (int i = 0; i < m; i++) {
for (int j = i + 1; j < m; j++) {
if (target[j] % target[i] == 0) {
to_remove.insert(i);
}
}
}
vector<int> new_target;
for (int i = 0; i < m; i++) {
if (to_remove.find(i) == to_remove.end()) {
new_target.push_back(target[i]);
}
}
target = new_target;
m = target.size();
int mask_size = (1 << m);
vector<vector<int>> dp(mask_size, vector<int>(n + 1, 1e9));
dp[0][0] = 0;
for (int i = 0; i < n; i++) {
for (int mask = 0; mask < mask_size; mask++) {
if (dp[mask][i] == 1e9) continue;
dp[mask][i + 1] = min(dp[mask][i + 1], dp[mask][i]);
for (int j = 0; j < m; j++) {
if ((mask & (1 << j)) == 0) {
int sum = (nums[i] % target[j] == 0) ? 0 : (target[j] - (nums[i] % target[j]));
int new_val = nums[i] + sum;
int new_mask = mask;
for (int k = 0; k < m; k++) {
if (new_val % target[k] == 0) {
new_mask |= (1 << k);
}
}
dp[new_mask][i + 1] = min(dp[new_mask][i + 1], dp[mask][i] + sum);
}
}
}
}
return dp[mask_size - 1][n];
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
bitmask dp
|
bitmask-dp-by-ttn628826-00hg
|
Approach
LCM Calculation for Subsets:
We first precompute the LCM for every possible subset of the target array. A subset is represented by a bitmask, where e
|
ttn628826
|
NORMAL
|
2025-02-02T09:22:27.844992+00:00
|
2025-02-02T09:22:27.844992+00:00
| 23 | false |
# Approach
1. LCM Calculation for Subsets:
- We first precompute the LCM for every possible subset of the target array. A subset is represented by a bitmask, where each bit indicates whether an element from the target set is included in the subset.
- The __computeSubsetLCMs__ function computes the LCM for each subset by iterating over all possible masks (from $1$ to $2^k - 1$, where $k$ is the size of the target). For each $mask$, we calculate the LCM of the corresponding elements in the $target$ set.
1. Dynamic Programming Setup:
- We initialize a DP array ($dp$) where $dp[mask]$ represents the minimum cost to achieve the subset of the target represented by $mask$. Initially, the cost of the empty subset ($dp[0]$) is set to $0$, as no increments are needed for an empty subset.
- The array is initialized with $INT\_MAX$ for all other masks to signify that they are initially unreachable.
1. Processing Each Number in $nums$:
- For each number in $nums$, we calculate the "cost" for every subset (represented by a mask) in terms of how much we need to increment that number to fit the LCM of the subset.
- The __calculateMaskCosts__ function computes the cost of each mask when adding the current number from $nums$. The cost is determined by finding the $remainder$ when dividing the number by the subset's LCM and calculating how much more is needed to make the number a multiple of the LCM.
1. Updating the DP Array:
- We then update the DP array by considering all possible previous subsets (represented by $prevMask$) and updating the new subset ($newMask$) formed by including the current subset. We ensure that the DP array is updated in reverse order ($prevMask$ from $ub-1$ down to $0$) to prevent overwriting values that are still needed in the same iteration.
- The DP transition formula is:
$dp[newMask] = min(dp[newMask], dp[prevMask] + maskCost[mask]);$
- This ensures that the DP array always holds the minimum cost to achieve each subset configuration.
1. Returning the Result:
- After processing all numbers, the result is stored in $dp[fullmask]$, where $fullmask$ represents the mask of the full $target$ set. If the value is still $INT\_MAX$, it means it is not possible to achieve the target set, so we return $-1$.
# Complexity
- Time complexity: The time complexity of this solution is dominated by the operations on the DP array and the number of subsets:
- For each number in $nums$, we process all possible subsets ($2^k$ subsets) and update the DP array.
- Therefore, the overall time complexity is $O(n * 2^k * k)$, where $n$ is the number of elements in $nums$ and $k$ is the number of elements in $target$.
- Space complexity: The space complexity is $O(2^k)$, which is used to store the DP array and the precomputed LCMs for all subsets of the $target$.
# Code
```cpp []
class Solution {
// Function to calculate LCM (Least Common Multiple) of two numbers
long long lcm(long long a, long long b) {
return a / __gcd(a, b) * b; // LCM formula: a * b / GCD(a, b)
}
public:
int minimumIncrements(vector<int>& nums, vector<int>& target) {
int k = target.size(); // Size of the target vector
int ub = 1 << k; // Upper bound for the number of subsets (2^k)
// Step 1: Precompute the LCM for each subset of target
vector<long long> subsetLCM(ub, 1); // Vector to store LCM values for each subset
computeSubsetLCMs(target, k, ub, subsetLCM);
// Step 2: DP setup
vector<long long> dp(ub, INT_MAX); // DP array to store the minimum cost for each subset
dp[0] = 0; // Base case: No cost for the empty subset
// Step 3: Process each number in nums to compute the minimum increments
for (auto num : nums) {
vector<long long> maskCost(ub); // Array to store the cost for each mask
// Step 3.1: Calculate the cost of each mask when adding the current num
calculateMaskCosts(num, k, ub, subsetLCM, maskCost);
// Step 3.2: Update the DP array based on the current num
updateDP(dp, ub, maskCost);
}
// Step 4: Return the result: minimum cost to achieve the full target subset, or -1 if it's not possible
return dp[ub - 1] == INT_MAX ? -1 : dp[ub - 1];
}
private:
// Helper function to compute the LCM for each subset of the target
void computeSubsetLCMs(const vector<int>& target, int k, int ub, vector<long long>& subsetLCM) {
for (int mask = 1; mask < ub; mask++) { // Iterate over all possible subsets (from 1 to 2^k - 1)
long long lcmVal = 1;
for (int i = 0; i < k; i++) {
if (mask & (1 << i)) { // Check if the i-th element is in the subset (using bitmask)
// Compute the LCM for the current subset
lcmVal = lcm(lcmVal, target[i]);
}
}
subsetLCM[mask] = lcmVal; // Store the LCM of the subset corresponding to the mask
}
}
// Helper function to calculate the cost for each mask when adding the current num
void calculateMaskCosts(int num, int k, int ub, const vector<long long>& subsetLCM, vector<long long>& maskCost) {
for (int mask = 1; mask < ub; mask++) {
long long lcmVal = subsetLCM[mask];
long long remainder = num % lcmVal; // Remainder when num is divided by the LCM of the subset
maskCost[mask] = (lcmVal - remainder) % lcmVal; // Store the cost for this mask
}
}
// Helper function to update the DP array based on the current num
void updateDP(vector<long long>& dp, int ub, const vector<long long>& maskCost) {
for (int prevMask = ub - 1; prevMask >= 0; prevMask--) { // Traverse backwards to avoid overwriting current dp values
if (dp[prevMask] == INT_MAX) continue; // Skip if the previous state is unreachable
// Update the DP table by considering adding the current num to the subsets
for (int mask = 1; mask < ub; mask++) {
int newMask = prevMask | mask; // New mask formed by including the current subset
// Update the DP array if the new cost is better
dp[newMask] = min(dp[newMask], dp[prevMask] + maskCost[mask]);
}
}
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
dp
|
dp-by-titu02-bkog
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Titu02
|
NORMAL
|
2025-02-02T09:16:57.398757+00:00
|
2025-02-02T09:16:57.398757+00:00
| 14 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
#define ll int64_t
ll gcd(ll a,ll b) { if (b==0) return a; return gcd(b, a%b); }
ll lcm(ll a,ll b){ return (a/gcd(a,b))*b;}
int minimumIncrements(vector<int>& a, vector<int>& b) {
int n=a.size(),m=b.size();
vector<ll>sub(1<<m);
for(int i=0;i<(1<<m);i++){
ll curr=1;
for(int j=0;j<m;j++){
if(i&(1<<j)){
curr=lcm(curr,b[j]);
}
}
sub[i]=curr;
}
vector<ll>dp(1<<m,1e18);
dp[0]=0;
for(auto x : a){
vector<ll>ndp=dp;
for(int i=0;i<(1<<m);i++){
//cout<<sub[i]<<" ";
ll cost=(sub[i]-x%sub[i])%sub[i];
// cout<<cost<<' ';
ndp[i]=min(ndp[i],cost);
for(int j=0;j<(1<<m);j++){
int curr=j|(i);
ndp[curr]=min(ndp[curr],dp[j]+cost);
}
}
dp=ndp;
}
// for(int i=0;i<(1<<m);i++) cout<<dp[i]<<' ';
return dp[(1<<m)-1];
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Java Bitmask Dynamic Programming
|
java-bitmask-dynamic-programming-by-mot8-2izi
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
mot882000
|
NORMAL
|
2025-02-02T09:10:21.649030+00:00
|
2025-02-02T09:10:21.649030+00:00
| 46 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int minimumIncrements(int[] nums, int[] target) {
int k = 1 << target.length;
int n = nums.length;
long dp[][] = new long[n][k];
for(int i = 0; i < dp.length; i++) for(int j = 1; j < k; j++) dp[i][j] = Integer.MAX_VALUE;
for(int i = 0; i < n; i++) {
for(int j = 0; j < k; j++) {
long lcm = 1;
for(int a = 0; a < target.length; a++){
if ( (j & (1 << a)) != 0 ) {
lcm = lcm(lcm, target[a]);
}
}
long diff = 0;
if ( lcm >= nums[i]) {
diff = lcm -nums[i];
} else{
if ( nums[i] % lcm == 0 ) diff = 0;
else diff = lcm - ( nums[i] % lcm);
}
if ( i-1 >= 0 ) {
for(int a = 0; a < k; a ++) {
if ( (a & j) == 0 ) {
if ( dp[i-1][a] != Integer.MAX_VALUE) {
dp[i][j|a] = Math.min(dp[i][j|a], dp[i-1][a] + diff);
}
}
}
}
dp[i][j] = Math.min(dp[i][j], diff);
}
if (i-1 >= 0 ) for(int j = 0; j < k; j++) dp[i][j] = Math.min(dp[i][j], dp[i-1][j]);
}
return (int)dp[n-1][k-1];
}
private long gcd(long a, long b) {
if ( a < b ) {
long temp = a;
a = b;
b = temp;
}
while( b != 0 ){
long n = a % b;
a = b;
b = n;
}
return a;
}
private long lcm(long a, long b) {
long gcd = gcd(a, b);
return (long)(a/gcd)*(b/gcd)*gcd;
}
}
```
| 0 | 0 |
['Dynamic Programming', 'Bitmask', 'Java']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
New Idea of Grouping elements
|
new-idea-of-grouping-elements-by-ishan-2-u4f4
|
IntuitionSince size of target was small and greedy would not work was clearly visible, dp was an intutive approach.
Why greedy does not work ?
Suppose nums = [5
|
Ishan-23
|
NORMAL
|
2025-02-02T08:26:31.601802+00:00
|
2025-02-02T08:26:31.601802+00:00
| 40 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Since size of target was small and greedy would not work was clearly visible, dp was an intutive approach.
Why greedy does not work ?
Suppose `nums = [5,7] and target = [4]`
Then Choosing `5` was a bad idea.
# Approach
<!-- Describe your approach to solving the problem. -->
The idea was to gather element into groups and then use bitmask dp to solve the problem efficiently.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
`O(4*4*n)`
4*4 for grouping the elements and O(n) for dp.
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
4*4 for grouping the elements and O(n) for dp.
# Code
```cpp []
class Solution {
public:
vector<vector<long long>> groups;
void dfs(int i,vector<int>& t,vector<long long>& nt){
if(i == t.size()) {
groups.push_back(nt);
return;
}
for(int j = 0;j<nt.size();j++){
int p = nt[j];
nt[j] = lcm(nt[j],t[i]);
if(nt[j] > 1e9) {
nt[j] = p;
continue;
}
dfs(i+1,t,nt);
nt[j] = p;
}
nt.push_back(t[i]);
dfs(i+1,t,nt);
nt.pop_back();
}
int dp[50000][20];
int f(int i,int j,vector<int>& nums,vector<long long>& t){
if(i == nums.size()){
if(j == 0) return 0;
return 1e8;
}
if(dp[i][j] != -1) return dp[i][j];
int ans = f(i+1,j,nums,t);
for(int k=0;k<t.size();k++){
if(j & (1<<k)) {
int cost = 0;
if(nums[i]<= t[k]) cost = t[k]-nums[i];
else cost = ((nums[i]+t[k]-1)/t[k])*t[k] - nums[i];
ans = min(ans,cost + f(i+1,j^(1<<k),nums,t));
}
}
return dp[i][j] = ans;
}
int minimumIncrements(vector<int>& nums, vector<int>& t) {
sort(t.begin(),t.end());
t.erase(unique(t.begin(),t.end()),t.end());
int ans = INT_MAX;
vector<long long> nt;
dfs(0,t,nt);
for(auto i:groups){
int n = i.size();
// for(auto j:i) cout<<j<<" ";
// cout<<endl;
for(int i=0;i<nums.size();i++) for(int j=0;j<20;j++) dp[i][j] = -1;
ans = min(ans,f(0,(1<<n)-1,nums,i));
}
return ans;
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
JAVA SOLUTION
|
java-solution-by-ashuramajestic-o60e
|
IntuitionThe problem requires us to modify the given numbers array so that each number can contribute to forming all values in the goal array using the Least Co
|
ashuramajestic
|
NORMAL
|
2025-02-02T07:25:02.833777+00:00
|
2025-02-02T07:27:46.473261+00:00
| 51 | false |
## **Intuition**
The problem requires us to modify the given numbers array so that each number can contribute to forming all values in the goal array using the Least Common Multiple (LCM). Since modifying each number comes with a cost (the increment operation), our objective is to minimize this cost while ensuring that all elements in the goal array can be achieved as LCMs of some subset of modified numbers.
To efficiently solve this problem, we can use a **bitmask dynamic programming (DP) approach** to track the minimal cost required to cover different subsets of the goal array.
---
## **Approach**
1. **Generate all subsets of the goal array:**
- Since we need to ensure that numbers can form LCMs of any subset of `goal`, we precompute the LCMs of all possible subsets of `goal`.
- There are `2^m` subsets, where `m` is the length of `goal`, so we iterate through all bitmask representations of subsets and compute their LCM.
2. **Use Bitmask DP to track the minimum cost:**
- We define `dp[mask]` as the minimum cost required to cover the subset of `goal` represented by `mask`.
- Initialize `dp[0] = 0` (cost of covering nothing is zero), and set all other values to a large number (`Long.MAX_VALUE`).
3. **Process each number in `numbers`:**
- Try to use each number and determine the minimum cost to modify it to become a multiple of any subset’s LCM.
- Update the DP table to reflect new achievable subsets with the minimum cost.
4. **Return `dp[(1 << m) - 1]`,** which represents the minimum cost to cover all elements in `goal`.
---
## **Complexity Analysis**
- **Generating all subsets of goal:**
- There are `2^m` subsets, and for each subset, computing the LCM takes `O(m)`.
- Total complexity for this step: **`O(m * 2^m)`**.
- **Processing each number in numbers:**
- For each `num`, we iterate over all `2^m` subsets and update the DP table, which is of size `2^m`.
- This results in complexity **`O(n * 2^m)`**.
### **Overall Complexity:**
**`O(m * 2^m + n * 2^m) ≈ O(n * 2^m)`**,
where `n` is the number of elements in `numbers`, and `m` is the number of elements in `goal`.
Since `m` is small (≤ 10), `2^m` is manageable (~1024 in the worst case), making this approach feasible.
# Code
```java []
import java.io.*;
import java.util.*;
class Solution {
public int minimumIncrements(int[] numbers, int[] goal) {
int size = goal.length;
int totalSubsets = 1 << size;
List<Map.Entry<Integer, Long>> subsetDetails = new ArrayList<>();
// Generate all subsets of the goal array and compute their LCM
for (int bitmask = 0; bitmask < totalSubsets; bitmask++) {
List<Long> selectedElements = new ArrayList<>();
for (int i = 0; i < size; i++) {
if ((bitmask & (1 << i)) != 0) {
selectedElements.add((long) goal[i]);
}
}
long currentLcm = findLcmOfList(selectedElements);
subsetDetails.add(new AbstractMap.SimpleEntry<>(bitmask, currentLcm));
}
int completeMask = (1 << size) - 1; // Bitmask representing all goals covered
int dpLength = 1 << size;
long[] dpTable = new long[dpLength];
Arrays.fill(dpTable, Long.MAX_VALUE);
dpTable[0] = 0; // Base case: no goals covered requires 0 operations
// Process each number in numbers
for (int num : numbers) {
long[] tempDp = Arrays.copyOf(dpTable, dpLength); // Create a copy of the current DP table
for (Map.Entry<Integer, Long> subset : subsetDetails) {
int subsetBitmask = subset.getKey();
long subsetLcm = subset.getValue();
// Compute the cost to make num a multiple of the subset's LCM
long increment;
if (subsetBitmask == 0) {
increment = 0; // Empty subset requires no operations
} else {
if (num % subsetLcm == 0) {
increment = 0; // Already a multiple
} else {
increment = ((num / subsetLcm) + 1L) * subsetLcm - num; // Increment required
}
}
// Update the DP table for all bitmasks
for (int bitmask = 0; bitmask < dpLength; bitmask++) {
if (dpTable[bitmask] == Long.MAX_VALUE) {
continue; // Skip unreachable states
}
int newBitmask = bitmask | subsetBitmask; // Combine the current bitmask with the subset bitmask
long newCost = dpTable[bitmask] + increment; // Total cost to reach the new bitmask
if (newCost < tempDp[newBitmask]) {
tempDp[newBitmask] = newCost; // Update the DP table with the minimum cost
}
}
}
dpTable = tempDp; // Update the DP table for the next number
}
// The result is the minimum operations to cover all goals
return dpTable[completeMask] == Long.MAX_VALUE ? 0 : (int) dpTable[completeMask];
}
private long findLcmOfList(List<Long> values) {
if (values.isEmpty()) {
return 1;
}
long currentLcm = values.get(0);
for (int i = 1; i < values.size(); i++) {
currentLcm = calculateLcm(currentLcm, values.get(i));
}
return currentLcm;
}
private long calculateLcm(long x, long y) {
return x / calculateGcd(x, y) * y;
}
private long calculateGcd(long x, long y) {
while (y != 0) {
long temp = y;
y = x % y;
x = temp;
}
return x;
}
}
```
| 0 | 0 |
['Bit Manipulation', 'Bitmask', 'Java']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Dynamic Programming + Python
|
dynamic-programming-python-by-leaf_light-9oda
|
IntuitionDP + BitmaskingApproachDP + BitmaskingComplexity
Time complexity:
O(n∗2t)
Space complexity:
O(n∗2t)
Code
|
leaf_light
|
NORMAL
|
2025-02-02T07:01:37.614825+00:00
|
2025-02-02T07:01:37.614825+00:00
| 37 | false |
# Intuition
DP + Bitmasking
# Approach
DP + Bitmasking
# Complexity
- Time complexity:
$$O(n*2^t)$$
- Space complexity:
$$O(n*2^t)$$
# Code
```python3 []
class Solution:
def minimumIncrements(self, nums: List[int], target: List[int]) -> int:
t = len(nums)
p = len(target)
lcm_dt = {}
print(nums)
print(target)
for i in range(0,2**p):
lcm_dt[i] = calc(target, i)
print(lcm_dt)
dp = []
for i in range(0,t+1):
dp.append([])
for j in range(0, 2**p):
dp[i].append(0)
for i in range(1, 2**p):
dp[0][i] = 10**20
# print(dp)
result = 10**20
for i in range(0,t):
for j in range(0, 2**p):
dp[i+1][j] = 10**20
for k in range(0, 2**p):
if k & j == k:
dp[i+1][j] = min(dp[i+1][j], dp[i][j-k]
+ (lcm_dt[k]-(nums[i]%lcm_dt[k])))
if (nums[i]%lcm_dt[k]==0):
dp[i+1][j] = min(dp[i+1][j], dp[i][j-k])
for i in range(0, len(dp)):
print(dp[i])
print()
return dp[t][2**p-1]
def calc(target: List[int], i):
k = 0
result = 1
while i > 0:
# print(k, i)
if i%2 == 1:
result = lcm(result, target[k])
i = i//2
k = k+1
return result
def lcm(a, b):
if a==0 or b==0:
return 0
return (a*b)//gcd(a,b)
def gcd(a, b):
while b != 0:
temp = b
b = a%b
a = temp
return a
```
| 0 | 0 |
['Dynamic Programming', 'Bitmask', 'Python3']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Dp - Bit Masking - Easy to Understand - Beats 100%
|
dp-bit-masking-easy-to-understand-beats-bo5ar
|
Code
|
UCJTBKG5qL
|
NORMAL
|
2025-02-02T06:54:26.189782+00:00
|
2025-02-02T06:54:26.189782+00:00
| 28 | false |
# Code
```python3 []
class Solution:
def compute_lcm(self, a, b):
return (a*b)//math.gcd(a, b)
def minimumIncrements(self, nums: List[int], target: List[int]) -> int:
n = len(nums)
m = len(target)
if m == 0:
return 0
end = 1 << m
lcm = {}
for m in range(1, end):
temp = 1
for t in range(m):
if m & (1 << t) != 0:
temp = self.compute_lcm(temp, target[t])
lcm[m] = temp
# print(lcm)
costs = []
for num in nums:
cost = {}
for k, v in lcm.items():
cost[k] = 0 if num % v == 0 else v - (num%v)
costs.append(cost)
# print(costs)
dp = [float('inf')] * end
dp[0] = 0
i = 0
while i < len(nums):
v = nums[i]
dp_m = dp[:]
c = costs[i]
for cur_mask in range(end):
if dp[cur_mask] == float('inf'):
continue
else:
for k1, cost in c.items():
dp_m[cur_mask | k1] = min(dp_m[cur_mask | k1], dp[cur_mask] + cost)
dp = dp_m
i += 1
# print(dp)
return dp[-1]
```
| 0 | 0 |
['Python3']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
DP BRUTEFORCE || TOO EASY TO UNDERSTAND
|
dp-bruteforce-too-easy-to-understand-by-e5ouh
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
kungfupandaisbackagain
|
NORMAL
|
2025-02-02T06:45:38.788111+00:00
|
2025-02-02T06:46:07.302875+00:00
| 81 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int a = 1;
int b = 1;
int c = 1;
int d = 1;
int n;
vector<int> nums, t;
vector<vector<int>> ds;
int dp[50002][2][2][2][2];
int f(int indx, int da, int db, int dc, int dd) {
if (indx >= n) {
if (da & db & dc & dd == 1) {
return 0;
}
return 2e9;
}
auto& x = dp[indx][da][db][dc][dd];
if (x != -1) {
return x;
}
int ans = 1e9;
// cout << indx << " " << da << db << dc << dd << endl;
for (int i = 0; i < 4; i++) {
int curr = ds[indx][i];
int aa = 0;
int bb = 0;
int cc = 0;
int ddd = 0;
ans = min(ans, f(indx + 1, aa | da, bb | db, cc | dc, dd | ddd));
for (int j = 0; j < 4; j++) {
if ((curr + nums[indx]) % t[j] == 0) {
if (j == 0) {
aa = 1;
} else if (j == 1) {
bb = 1;
} else if (j == 2) {
cc = 1;
} else {
ddd = 1;
}
}
}
ans = min(ans,
curr + f(indx + 1, aa | da, bb | db, cc | dc, dd | ddd));
}
return x = ans;
}
int minimumIncrements(vector<int>& nums, vector<int>& t) {
n = nums.size();
this->nums = nums;
while (t.size() < 4) {
t.push_back(1);
}
this->t = t;
a = t[0];
b = t[1];
c = t[2];
d = t[3];
ds.assign(n, vector<int>(4, 0));
int indx = 0;
for (auto i : t) {
int indx2 = 0;
for (auto j : nums) {
if (j % i == 0) {
indx2++;
continue;
}
ds[indx2][indx] = (i - (j % i));
indx2++;
}
indx++;
}
memset(dp, -1, sizeof(dp));
return f(0, 0, 0, 0, 0);
}
};
```
| 0 | 0 |
['Dynamic Programming', 'C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
DP With Bitmasking
|
dp-with-bitmasking-by-arif2321-k8nl
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Arif2321
|
NORMAL
|
2025-02-02T05:55:59.490760+00:00
|
2025-02-02T05:55:59.490760+00:00
| 29 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int minimumIncrements(vector<int>& nums, vector<int>& target)
{
int n = nums.size();
int t = target.size();
vector<vector<int>> dp(n,vector<int>((1<<t),1e9));
auto subset = [&](int sub, int mask)
{
for(int i = 0; i < t; i++)
{
if(sub&(1<<i) && !(mask&(1<<i))) return 0;
}
return 1;
};
for(int i = 0; i < n; i++)
{
for(int mask = 0; mask < (1<<t); mask++)
{
if(i) dp[i][mask] = dp[i-1][mask];
if(mask == 0)
{
dp[i][mask] = 0;
// cout << dp[i][mask] << " ";
continue;
}
for(int submask = 1; submask < (1<<t); submask++)
{
if(!subset(submask,mask)) continue;
// cout << mask << ' ' << submask << endl;
int max_req = 0;
for(int j = 0; j < t; j++)
{
if(submask&(1<<j))
{
max_req = max(max_req,((nums[i]+target[j]-1)/(target[j]))*target[j] - nums[i]);
}
}
// cout << max_req << endl;
bool ispossible = 1;
for(int j = 0; j < t; j++)
{
if(submask&(1<<j) && (nums[i]+max_req)%target[j] != 0)
{
ispossible = 0;
}
}
if(ispossible)
{
dp[i][mask] = min(dp[i][mask],max_req + (i ? dp[i-1][mask^submask] : (mask^submask) == 0 ? 0 : (int)1e9));
}
}
// cout << dp[i][mask] << " ";
}
cout << endl;
}
return dp[n-1][(1<<t)-1];
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Approach explained | Easy to understand | C++ | DP with Bitmask
|
easy-to-understand-c-dp-with-bitmask-by-jsyf3
|
IntuitionSolve the DP for DP[i][mask]Approach
Each ith elment in nums can be taken or not taken to contribute to answer.
If it can be taken, it can contribute t
|
gamer37
|
NORMAL
|
2025-02-02T05:52:08.906726+00:00
|
2025-02-02T05:55:41.274684+00:00
| 51 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Solve the DP for DP[i][mask]
# Approach
<!-- Describe your approach to solving the problem. -->
- Each ith elment in nums can be taken or not taken to contribute to answer.
- If it can be taken, it can contribute to a subset of target. This subset of target is equivalent to LCM these target numbers.
- So, check the required amount of increment if current ith element has to contribute to a subset.
- This required amount of increment will be (Greater than equal multiple of LCM from nums[i]) - nums[i].
- Add this increment, and move forward to i+1 with mask as (previous mask | current mask of target elements)
**NOTE - You can fasten your code by precomputing the value of LCM for all subset of targets before. See Compute method below.**
# Complexity
- Time complexity:
O(N * 16 * 16)
- Space complexity:
O(N * 16)
# Code
```cpp []
#define ll long long int
ll dp[50005][17],n,m;
ll pre[17];
ll lcm(ll x, ll y)
{
return (x*y)/__gcd(x,y);
}
void Compute(vector<int>& target)
{
ll i,j;
for(i=1;i<(1<<m);i++)
{
pre[i]=1;
for(j=0;j<m;j++)
{
if(i & (1<<j))
pre[i]=lcm(pre[i],target[j]);
}
}
}
ll solve(ll i ,ll mask, vector<int>& nums, vector<int>& target)
{
if(mask==(1<<m)-1)
return 0;
else if(i==n)
return 1e9;
if(dp[i][mask]!=-1)
return dp[i][mask];
ll ans=1e9,lcm,j;
ans=min(ans,solve(i+1,mask,nums,target));
for(j=1;j<(1<<m);j++)
{
lcm = pre[j];
ll x = ((nums[i]+lcm-1)/lcm)*lcm;
ans=min(ans,x-nums[i]+solve(i+1,mask | j , nums,target));
}
return dp[i][mask]=ans;
}
class Solution {
public:
int minimumIncrements(vector<int>& nums, vector<int>& target) {
n=nums.size(),m=target.size();
memset(dp,-1,sizeof(dp));
memset(pre,0,sizeof(pre));
Compute(target);
return solve(0,0,nums,target);
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
C#
|
c-by-7qlcxgljt2-t4am
|
Actually I didn't solve this question, but I see nobody post their C# answer. So I copy from Leetcode.cn. Answer is from here, I translate Java code to C# versi
|
7qlcxGljt2
|
NORMAL
|
2025-02-02T05:43:30.025861+00:00
|
2025-02-02T05:43:30.025861+00:00
| 13 | false |
Actually I didn't solve this question, but I see nobody post their C# answer. So I copy from Leetcode.cn. Answer is from [here](https://leetcode.cn/problems/minimum-increments-for-target-multiples-in-an-array/solutions/3061806/zi-ji-zhuang-ya-dpji-yi-hua-sou-suo-di-t-aeaj), I translate Java code to C# version.
# Complexity
- Time complexity:
$$O(n3^{m})$$
- Space complexity:
$$O(n2^{m})$$
# Code
```csharp []
public class Solution {
public int MinimumIncrements(int[] nums, int[] target)
{
int n = nums.Length;
int m = target.Length;
// Preprocess all subsets LCM of target
long[] lcms = new long[1 << m];
Array.Fill(lcms, 1);
for (int i = 0; i < m; i++)
{
int bit = 1 << i;
for (int mask = 0; mask < bit; mask++)
{
lcms[bit | mask] = lcm(target[i], lcms[mask]);
}
}
long[,] memo = new long[n, 1 << m];
for (int i = 0; i < n; i++)
{
for (int j = 0; j < (1 << m); j++)
{
memo[i, j] = -1;
}
}
return (int)dfs(n - 1, (1 << m) - 1, nums, lcms, memo);
}
private long dfs(int i, int j, int[] nums, long[] lcms, long[,] memo)
{
if (j == 0)
{
return 0;
}
if (i < 0)
{ // don't left anything
return int.MaxValue / 2;
}
if (memo[i, j] != -1)
{
return memo[i, j];
}
long res = dfs(i - 1, j, nums, lcms, memo); // don't change nums[i]
for (int sub = j; sub > 0; sub = (sub - 1) & j)
{ // Enumerate all non-empty subsets of j
long l = lcms[sub];
res = Math.Min(res, dfs(i - 1, j ^ sub, nums, lcms, memo) + (l - nums[i] % l) % l);
}
return memo[i, j] = res;
}
private long lcm(long a, long b)
{
return a / gcd(a, b) * b;
}
private long gcd(long a, long b)
{
return b == 0 ? a : gcd(b, a % b);
}
}
```
| 0 | 0 |
['C#']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Minimum Increments for Target Multiples in an Array
|
minimum-increments-for-target-multiples-0bdz8
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
subhampujari1
|
NORMAL
|
2025-02-02T04:54:14.820467+00:00
|
2025-02-02T04:54:14.820467+00:00
| 75 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int minimumIncrements(int[] nums, int[] target) {
int[] plorvexium = target;
int m = target.length;
int fullMask = (1 << m) - 1;
long INF = (long) 1e18;
long[] dp = new long[1 << m];
for (int i = 0; i < dp.length; i++) {
dp[i] = INF;
}
dp[0] = 0; // Added missing semicolon here
for (int n : nums) {
long[] bestForMask = new long[1 << m];
for (int i = 0; i < bestForMask.length; i++) {
bestForMask[i] = INF;
}
for (int subset = 1; subset < (1 << m); subset++) {
long L = 1;
for (int j = 0; j < m; j++) {
if ((subset & (1 << j)) != 0) {
L = lcm(L, target[j]);
}
}
long multiplier = (n + L - 1) / L;
long m_val = multiplier * L;
long cost = m_val - n;
int achievedMask = 0;
for (int j = 0; j < m; j++) {
if (m_val % target[j] == 0) {
achievedMask |= (1 << j);
}
}
bestForMask[achievedMask] = Math.min(bestForMask[achievedMask], cost);
}
long[] newDP = new long[1 << m];
System.arraycopy(dp, 0, newDP, 0, dp.length);
for (int maskOption = 0; maskOption < (1 << m); maskOption++) {
if (bestForMask[maskOption] == INF) continue;
for (int oldMask = 0; oldMask < (1 << m); oldMask++) {
if (dp[oldMask] == INF) continue;
int newMask = oldMask | maskOption;
newDP[newMask] = Math.min(newDP[newMask], dp[oldMask] + bestForMask[maskOption]);
}
}
dp = newDP;
}
return dp[fullMask] >= INF ? -1 : (int) dp[fullMask];
}
private long gcd(long a, long b) {
while (b != 0) {
long temp = a % b;
a = b;
b = temp;
}
return a;
}
private long lcm(long a, long b) {
return a / gcd(a, b) * b;
}
}
```
| 0 | 0 |
['Java']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
DP + Bitmask + Precomputation | Easy To Understand | Clean Code
|
dp-bitmask-precomputation-easy-to-unders-s6mu
|
Code
|
braindroid
|
NORMAL
|
2025-02-02T04:41:55.369598+00:00
|
2025-02-02T04:41:55.369598+00:00
| 75 | false |
# Code
```cpp []
class Solution {
public:
vector<vector<long long>>sc;
vector<vector<long long>>dp;
int n;
int m;
long long solve(int i , int mask) {
if(i == n) {
if(mask == (1 << m) - 1) {
return 0;
}
return 1e9;
}
if(dp[i][mask] != -1) {
return dp[i][mask];
}
long long ans = 1e9;
for(int j = 0 ; j < (1 << m) ; j++) {
ans = min(ans,sc[i][j] + solve(i+1,(mask | j)));
}
return dp[i][mask] = ans;
}
int minimumIncrements(vector<int>& a, vector<int>& b) {
n = (int)a.size();
m = (int)b.size();
sc.resize(n+2,vector<long long>((1 << m) + 5,0LL));
dp.resize(n+2,vector<long long>((1 << m) + 5 ,-1));
for(int i = 0 ; i < n ; i++) {
for(int j = 1 ; j < (1 << m) ; j++) {
long long l = -1;
long long mv = 2e9;
for(int k = 0 ; k < m ; k++) {
if((j & (1 << k))) {
if(l == -1) {
l = b[k];
} else {
l = lcm(b[k],l);
}
}
}
if(l < a[i]) {
l = ((a[i] + l - 1) / l) * l;
}
mv = l - a[i];
sc[i][j] = mv;
}
}
return solve(0,0);
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
O(81 * n) bitmask dp solution
|
o81-n-bitmask-dp-solution-by-skuthuru-iis5
|
IntuitionThere's only up to 4 target elements, this leads to an intuition of some bitmask dp solution.ApproachThe idea is to do a bitmask dp where we have dp[in
|
skuthuru
|
NORMAL
|
2025-02-02T04:30:02.505860+00:00
|
2025-02-02T04:30:02.505860+00:00
| 58 | false |
# Intuition
There's only up to 4 target elements, this leads to an intuition of some bitmask dp solution.
# Approach
The idea is to do a bitmask dp where we have dp[index][mask] storing the current mask of target elements we have taken the lcm of at this current index in nums. Next we will transition on all the submasks to take out of this mask and use num[index] to fulfill the requirement as a multiple and add the number of operations to the dp. Some care is required to not overflow.
# Complexity
- Time complexity:
O(3^m * n) ~ O(81 * n)
- Space complexity:
O(2^m)
# Code
```cpp []
class Solution {
public:
using ll = long long;
ll INF = (ll) 1e18;
ll mult(ll a, ll b) {
if(a == 0 || b == 0) return 0;
return INF / a < b ? INF : a * b;
}
ll lcm(ll a, ll b) {
return mult(a / __gcd(a, b), b);
}
int minimumIncrements(vector<int>& nums, vector<int>& target) {
int n = target.size();
vector<ll> dp(1 << n, INF);
vector<ll> val(1 << n);
for(int i = 0; i < (1 << n); i++) {
ll l = 1;
for(int j = 0; j < n; j++) {
if(i & (1 << j)) {
l = lcm(l, target[j]);
if(l == INF) break;
}
}
val[i] = l;
}
dp[(1 << n) - 1] = 0;
for(int x : nums) {
vector<ll> ndp(dp);
for(int mask = 0; mask < (1 << n); mask++) {
for(int i = mask; i > 0; i = (i-1) & mask){
int submask = mask ^ i;
ndp[submask] = min(ndp[submask], dp[mask] + (val[i] - x % val[i]) % val[i]);
}
}
swap(dp, ndp);
}
return dp[0];
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
[JS] DFS over all reasonable solutions
|
js-dfs-over-all-reasonable-solutions-by-6q9d9
|
IntuitionThe solution will involve adjusting up to 4 different numbers in nums. It will always be possible to come up with a solution by finding the LCM of ever
|
michaelm12358
|
NORMAL
|
2025-02-02T04:17:33.015177+00:00
|
2025-02-02T04:17:33.015177+00:00
| 74 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The solution will involve adjusting up to 4 different numbers in nums. It will always be possible to come up with **a** solution by finding the LCM of everything in target, but that may not be the **best** solution.
We can pessimistically build a list of the 4 best options for the LCM of every permutation of target, where 'best' means the number we picked needs the smallest number of operations to be a multiple of the LCM.
Then, we simply brute force DFS over those lists, finding the smallest sum where we satisfy all targets.
The code could be simplified a lot, but I'll leave that as an exercise to the reader 😂
# Code
```javascript []
/**
* @param {number[]} nums
* @param {number[]} target
* @return {number}
*/
var minimumIncrements = function(nums, target) {
//we'll fill this with the lcm of all possible permutations of target
let lcms = new Array(2**target.length);
//we'll fill this with a list of the best 'num' to pick for that corresponding permutation
let combinationTopFours = new Array(lcms.length);
for(let i = 1; i < combinationTopFours.length; ++i) {
combinationTopFours[i] = [];
let factors = [];
for(let j = 0; j < target.length; ++j) {
if((i & (1<<j))) {
factors.push(target[j]);
}
}
let lcm = findlcm(factors);
lcms[i] = lcm;
}
for(let numIdx = 0; numIdx < nums.length; ++numIdx) {
let num = nums[numIdx];
for(let i = 1; i < combinationTopFours.length; ++i) {
let lcm = lcms[i];
let diff = Number((BigInt(lcm) - (BigInt(num) % BigInt(lcm))) % BigInt(lcm));
insertIntoCombination(combinationTopFours[i], numIdx, diff);
}
}
return dfs(0, [])
//brute force dfs, where the target is having all bits set to 1.
//i.e. for a target of [1,2,3,4], the mask would be 1111 -> 15
function dfs(mask, usedIndexes) {
if(mask === ((2**target.length)-1)) {
return 0;
}
let best = Infinity;
for(let i = 1; i < combinationTopFours.length; ++i) {
if((mask & i)) { continue; }
//just try everything lol.
let topFour = combinationTopFours[i];
for(let j = 0; j < topFour.length; ++j) {
let [diff, numsIdx] = topFour[j];
//if we already tried this num, we can't touch it again
if(usedIndexes.includes(numsIdx)) { continue; }
best = Math.min(best, diff + dfs(mask | i, [...usedIndexes, numsIdx]));
}
}
return best;
}
function insertIntoCombination(arr, idx, diff) {
if(arr.length < target.length) {
return arr.push([diff, idx]);
}
arr.sort((a, b) => a[0]-b[0]);
if(diff < arr.at(-1)[0]) {
arr[arr.length-1] = [diff, idx];
}
}
};
function gcd(a, b) {
if (!b) { return a; }
return gcd(b, a % b);
}
function findlcm(arr) {
let ans = arr[0];
for (let i = 1; i < arr.length; i++) {
ans = (arr[i] * ans) / gcd(arr[i], ans);
}
return ans;
}
```
| 0 | 0 |
['JavaScript']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
C++ double dfs
|
c-double-dfs-by-user5976fh-o90d
| null |
user5976fh
|
NORMAL
|
2025-02-02T04:16:13.850790+00:00
|
2025-02-02T04:16:13.850790+00:00
| 79 | false |
```cpp []
class Solution {
public:
vector<int> v, t;
vector<vector<int>> grouped;
long long dfs(int i){
if (i == t.size()) return getMin();
long long ans = LLONG_MAX;
if (!grouped.empty()){
for (int y = 0; y < grouped.size(); ++y){
grouped[y].push_back(t[i]);
ans = min(ans, dfs(i + 1));
grouped[y].pop_back();
}
}
grouped.push_back({t[i]});
ans = min(ans, dfs(i + 1));
grouped.pop_back();
return ans;
}
long long getMin(){
vector<vector<pair<long long, int>>> lowestCost4(grouped.size());
int g = 0;
for (auto& group : grouped){
long long l = 1, t = LLONG_MAX;
for (auto& n : group) l = lcm(n, l);
for (int i = 0; i < v.size(); ++i){
long long next = v[i] % l == 0 ? 0 : l - (v[i] % l);
lowestCost4[g].push_back({next, i});
if (lowestCost4[g].size() > 4){
sort(lowestCost4[g].begin(), lowestCost4[g].end());
lowestCost4[g].pop_back();
}
}
++g;
}
unordered_set<int> taken;
return dfs2(0, lowestCost4, taken);
}
long long dfs2(int i, vector<vector<pair<long long, int>>>& lc4, unordered_set<int>& taken){
if (i == lc4.size()) return 0;
long long ans = LLONG_MAX;
for (auto& [f,s] : lc4[i]){
if (!taken.count(s)){
taken.insert(s);
ans = min(ans, dfs2(i + 1, lc4, taken) + f);
taken.erase(s);
}
}
return ans;
}
int minimumIncrements(vector<int>& nums, vector<int>& target) {
v = nums;
sort(target.begin(), target.end());
for (auto& n : target) if (t.empty() || t.back() != n) t.push_back(n);
return dfs(0);
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
LEETCODE WEEKLY 435 | Q3 | EASY TO UNDERSTAND
|
leetcode-weekly-435-q3-easy-to-understan-8l02
|
IntuitionThe problem requires modifying elements in nums such that their least common multiple (LCM) covers all elements in target.
We need to increment numbers
|
prybruhta
|
NORMAL
|
2025-02-02T04:10:26.430469+00:00
|
2025-02-02T04:10:26.430469+00:00
| 139 | false |
# **Intuition**
The problem requires modifying elements in `nums` such that their **least common multiple (LCM)** covers all elements in `target`.
- We need to **increment numbers minimally** so that at least one subset of `nums` has an LCM equal to some subset of `target`.
- The approach revolves around **bitmasking** and **dynamic programming (DP)** to track valid LCMs efficiently.
---
# **Approach**
### **1. Precompute All LCM Combinations of `target`**
- Since `target` has at most `10` elements, we can generate all `2^m` subsets using **bitmasking**.
- Store the **LCM of each subset** in an array `mpp`.
### **2. Initialize DP**
- Use `dp[i]` where `i` represents a bitmask of `target` subsets.
- `dp[i]` stores the **minimum increments** required to make `nums` cover the subset represented by `i`.
### **3. Iterate Through `nums`**
- Compute the cost of adjusting each `nums[i]` to align with **each LCM subset**.
- Use another DP array `dp2` to update values based on previous states.
### **4. Compute Final Answer**
- The result is `dp[comb - 1]`, which holds the minimum increments required to cover all elements in `target`.
---
# **Complexity Analysis**
- **Time Complexity**:
- Precomputing LCM: **O(m × 2^m)**
- Iterating `nums`: **O(n × 2^m × 2^m)**
- **Overall: O(n × 2^m × m)** (manageable since `m ≤ 4`).
- **Space Complexity**:
- **O(2^m)** for `mpp` and `dp` arrays.
---
# **Code**
```cpp
class Solution {
public:
int minimumIncrements(vector<int>& nums, vector<int>& target) {
int n = nums.size();
int m = target.size();
int comb = pow(2, m);
// Precompute LCM for all subsets of target
vector<long long> mpp(comb, 1);
for (int i = 1; i < comb; i++) {
long long val = 1;
for (int j = 0; j < m; j++) {
if (i & (1 << j)) {
val = lcm(val, target[j]);
}
}
mpp[i] = val;
}
// Initialize DP
vector<long long> dp(comb, 1e18);
dp[0] = 0;
// Process each number in nums
for (auto num : nums) {
vector<long long> cost(comb, 1e18);
// Compute the cost to modify num for each subset of target
for (int i = 1; i < comb; i++) {
long long val = mpp[i];
long long mod = num % val;
long long amt = (mod == 0 ? 0 : val - mod);
cost[i] = amt;
}
// Update DP using previous states
vector<long long> dp2 = dp;
for (int i = 0; i < comb; i++) {
if (dp[i] == 1e18) continue;
for (int j = 1; j < comb; j++) {
int cur = i | j;
dp2[cur] = min(dp2[cur], dp[i] + cost[j]);
}
}
dp = dp2;
}
return dp[comb - 1];
}
};
| 0 | 0 |
['Dynamic Programming', 'Bit Manipulation', 'C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Python Hard
|
python-hard-by-lucasschnee-09wi
| null |
lucasschnee
|
NORMAL
|
2025-02-02T04:09:56.328334+00:00
|
2025-02-02T04:09:56.328334+00:00
| 79 | false |
```python3 []
class Solution:
def minimumIncrements(self, nums: List[int], target: List[int]) -> int:
'''
target.length <= 4
'''
nums.sort()
target.sort()
N = len(nums)
M = len(target)
INF = 10 ** 20
def get_min_multiple(x, y):
r = x % y
return x if r == 0 else x + (y - r)
@cache
def calc(index, mask):
if mask == (1 << M) - 1:
return 0
if index == N:
return INF
best = calc(index + 1, mask)
for i in range(M):
if (1 << i) & mask:
continue
new_mask = mask
m = get_min_multiple(nums[index], target[i])
cost = m - nums[index]
for i in range(M):
if m % target[i] == 0:
new_mask |= (1 << i)
best = min(best, calc(index + 1, new_mask) + cost)
return best
return calc(0, 0)
```
| 0 | 0 |
['Python3']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
Group by LCM
|
group-by-lcm-by-jianstanleya-grg6
|
IntuitionNotice how we can "match" each number in target individually or multiple at once using their LCM.ApproachWe iterate over all unique partitions of targe
|
jianstanleya
|
NORMAL
|
2025-02-02T04:05:57.759442+00:00
|
2025-02-02T04:06:43.881706+00:00
| 95 | false |
# Intuition
Notice how we can "match" each number in `target` individually or multiple at once using their LCM.
# Approach
We iterate over all unique partitions of `target`. For each subset in each partition, we find the best number to match with in `nums`. Each number should only be used once!
# Complexity
- Time complexity: fast enough
- Space complexity: small enough
# Code
```cpp []
#define LL long long
class Solution {
vector<int> _target;
int k = 0, n = 0;
LL result = 2e18;
public:
LL gcd(LL x, LL y) {
while(y > 0) {
LL t = y;
y = x % y;
x = t;
}
return x;
}
LL lcm(LL x, LL y) {
return x * y / gcd(x, y);
}
void recur(int curr, vector<int>& choices, vector<int>& nums) {
if(curr < k) {
for(int i = 0; i < k; ++i) {
choices.push_back(i);
recur(curr + 1, choices, nums);
choices.pop_back();
}
}else {
vector<LL> lcms;
for(int i = 0; i < k; ++i) {
LL t = 1;
for(int j = 0; j < k; ++j) {
if(choices[j] == i) {
t = lcm(t, _target[j]);
}
}
if(t > 1) lcms.push_back(t);
}
LL total = 0;
unordered_set<int> banned;
for(LL i : lcms) {
int cand = -1;
LL crem = 2e18;
for(int j = 0; j < n; ++j) {
if(!banned.count(j)) {
LL rem = (i - (LL)nums[j] % i) % i;
if(cand < 0 || rem < crem) {
cand = j;
crem = rem;
}
}
}
banned.insert(cand);
total += crem;
}
result = min(result, total);
}
}
int minimumIncrements(vector<int>& nums, vector<int>& target) {
n = nums.size();
k = target.size();
_target = target;
vector<int> choices;
recur(0, choices, nums);
return result;
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimum-increments-for-target-multiples-in-an-array
|
DP for Bitmasks
|
dp-for-bitmasks-by-whoawhoawhoa-gmz7
|
IntuitionGiven that target array length is 4 at maximum we can employ bitmasking here.ApproachFirst step - we find lcm map containing lcm for each combination o
|
whoawhoawhoa
|
NORMAL
|
2025-02-02T04:01:03.480000+00:00
|
2025-02-02T04:07:25.083615+00:00
| 164 | false |
# Intuition
Given that target array length is 4 at maximum we can employ bitmasking here.
# Approach
First step - we find lcm map containing lcm for each combination of numbers in target array.
Then we do Top-Down DP keeping the state of mask / index.
At each index our process is:
1. Try to keep `nums[ix]` to be the same and move on. **Caution**: need to handle the case of `nums[ix]` being a multiple of some numbers in target.
2. For each known mask pretend we want to change `nums[ix]` to cover numbers in target corresponding to the mask. **Caution**: we can be in situation where `nums[ix] > lcm[mask]` but we are only allowed to increment. In this case we need to find the next element bigger or equal to `nums[ix]` which is multiple of `lcm[mask]`.
# Complexity
`n = nums.length; m = target.length`
- Time complexity:
$$O(n * 2^m)$$
- Space complexity:
$$O(n * 2^m)$$
# Code
```java []
class Solution {
public int minimumIncrements(int[] nums, int[] target) {
Map<Integer, Integer> lcm = new HashMap<>();
for (int mask = 1; mask < (1 << target.length); mask++) {
List<Integer> l = new ArrayList<>();
for (int i = 0; i < (1 << target.length); i++) {
if ((mask & (1 << i)) != 0) {
l.add(target[i]);
}
}
lcm.put(mask, lcm(l));
}
Integer[][] dp = new Integer[nums.length][1 << target.length];
return find(dp, lcm, nums, 0, 0, target);
}
static int find(Integer[][] dp, Map<Integer, Integer> lcm, int[] nums, int ix, int mask, int[] target) {
if (Integer.bitCount(mask) == target.length) {
return 0;
}
if (ix == nums.length) {
return Integer.MAX_VALUE;
}
if (dp[ix][mask] != null) {
return dp[ix][mask];
}
int keep = mask;
for (int i = 0; i < target.length; i++) {
if (nums[ix] % target[i] == 0) {
keep |= (1 << i);
}
}
int res = find(dp, lcm, nums, ix + 1, keep, target);
for (Map.Entry<Integer, Integer> e : lcm.entrySet()) {
int change = e.getValue();
if (e.getValue() < nums[ix]) {
change = next(nums[ix], e.getValue());
}
int tmp = find(dp, lcm, nums, ix + 1, mask | e.getKey(), target);
if (tmp == Integer.MAX_VALUE) {
continue;
}
tmp += change - nums[ix];
res = Math.min(tmp, res);
}
return dp[ix][mask] = res;
}
static int next(int a, int b) {
return ((a / b) + 1) * b;
}
static int lcm(List<Integer> l) {
int res = l.get(0);
for (int i = 1; i < l.size(); i++) {
res = lcm(res, l.get(i));
}
return res;
}
static int lcm(int a, int b) {
return Math.abs(a * b) / gcd(a, b);
}
static int gcd(int a, int b) {
while (b != 0) {
int temp = b;
b = a % b;
a = temp;
}
return a;
}
}
```
| 0 | 0 |
['Math', 'Bit Manipulation', 'Bitmask', 'Java']
| 1 |
special-positions-in-a-binary-matrix
|
C++ 2 passes
|
c-2-passes-by-votrubac-4vhx
|
First pass, count number of ones in rows and cols. \n\nSecond pass, go through the matrix, and for each one (mat[i][j] == 1) check it it\'s alone in the corresp
|
votrubac
|
NORMAL
|
2020-09-13T04:02:31.690736+00:00
|
2020-09-14T18:10:33.178652+00:00
| 10,539 | false |
First pass, count number of ones in `rows` and `cols`. \n\nSecond pass, go through the matrix, and for each one (`mat[i][j] == 1`) check it it\'s alone in the corresponding row (`rows[i] == 1`) and column (`cols[j] == 1`).\n\nThis is a copycat question to [531. Lonely Pixel I](https://leetcode.com/problems/lonely-pixel-i/). I am wondering why that question is Medium, and this one - Easy? Does it mean that we getting better at this, as a community \uD83E\uDD14 ?\n\n**C++**\n\n```cpp\nint numSpecial(vector<vector<int>>& mat) {\n vector<int> rows(mat.size()), cols(mat[0].size());\n for (int i = 0; i < rows.size(); ++i)\n for (int j = 0; j < cols.size(); ++j) {\n if (mat[i][j])\n ++rows[i], ++cols[j];\n }\n int res = 0;\n for (int i = 0; i < rows.size(); ++i)\n for (int j = 0; j < cols.size(); ++j)\n if (mat[i][j] && rows[i] == 1 && cols[j] == 1)\n ++res;\n return res;\n}\n```
| 146 | 3 |
[]
| 17 |
special-positions-in-a-binary-matrix
|
✅Beats 100% - Explained with [ Video ] - Check Row and Column - C++/Java/Python/JS - Visualized
|
beats-100-explained-with-video-check-row-0jq6
|
\n\n# YouTube Video Explanation:\n\nhttps://youtu.be/GI7EWjkXLnY\n **If you want a video for this question please write in the comments** \n\n\uD83D\uDD25 Pleas
|
lancertech6
|
NORMAL
|
2023-12-13T02:14:41.735819+00:00
|
2023-12-13T02:49:23.658357+00:00
| 19,332 | false |
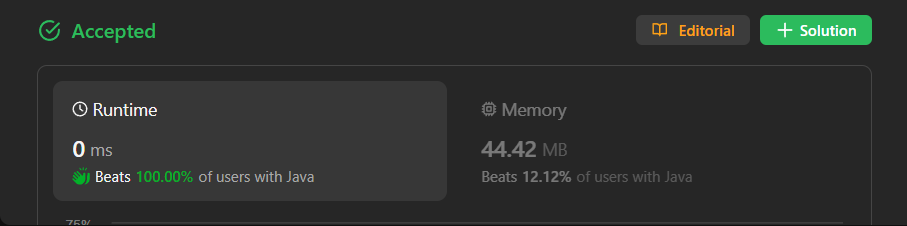\n\n# YouTube Video Explanation:\n\n[https://youtu.be/GI7EWjkXLnY](https://youtu.be/GI7EWjkXLnY)\n<!-- **If you want a video for this question please write in the comments** -->\n\n**\uD83D\uDD25 Please like, share, and subscribe to support our channel\'s mission of making complex concepts easy to understand.**\n\nSubscribe Link: https://www.youtube.com/@leetlogics/?sub_confirmation=1\n\n*Subscribe Goal: 800 Subscribers*\n*Current Subscribers: 754*\n\n---\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo find the special positions in the binary matrix, we need to iterate through each row and column and check if the current position (i, j) is special. A position is considered special if the element at that position is 1, and all other elements in its row and column are 0.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Iterate through each row of the matrix.\n2. For each row, check if there is exactly one element with the value 1. If found, remember its column index.\n3. After scanning the row, check the corresponding column for the remembered index. If the element is 1 and there are no other 1s in that column, it\'s a special position.\n4. Repeat this process for all rows.\n5. Count and return the number of special positions.\n\n# Complexity\n- Time Complexity: O(m * n), where m is the number of rows and n is the number of columns in the matrix.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space Complexity: O(1) as we use constant space.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int numSpecial(int[][] mat) {\n \n int specials = 0;\n\n for (int i = 0; i < mat.length; i++) {\n int index = checkRow(mat, i);\n if (index >= 0 && checkColumn(mat, i, index))\n specials++;\n }\n\n return specials;\n }\n\n private int checkRow(int[][] mat, int i) {\n int index = -1;\n for (int j = 0; j < mat[0].length; j++) {\n if (mat[i][j] == 1) {\n if (index >= 0)\n return -1;\n else\n index = j;\n }\n }\n return index;\n }\n\n private boolean checkColumn(int[][] mat, int i, int index) {\n for (int j = 0; j < mat.length; j++) {\n if (mat[j][index] == 1 && j != i)\n return false;\n }\n return true;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int numSpecial(std::vector<std::vector<int>>& mat) {\n int specials = 0;\n\n for (int i = 0; i < mat.size(); i++) {\n int index = checkRow(mat, i);\n if (index >= 0 && checkColumn(mat, i, index))\n specials++;\n }\n\n return specials;\n }\n\nprivate:\n int checkRow(std::vector<std::vector<int>>& mat, int i) {\n int index = -1;\n for (int j = 0; j < mat[0].size(); j++) {\n if (mat[i][j] == 1) {\n if (index >= 0)\n return -1;\n else\n index = j;\n }\n }\n return index;\n }\n\n bool checkColumn(std::vector<std::vector<int>>& mat, int i, int index) {\n for (int j = 0; j < mat.size(); j++) {\n if (mat[j][index] == 1 && j != i)\n return false;\n }\n return true;\n }\n};\n```\n```Python []\nclass Solution(object):\n def numSpecial(self, mat):\n specials = 0\n\n for i in range(len(mat)):\n index = self.checkRow(mat, i)\n if index >= 0 and self.checkColumn(mat, i, index):\n specials += 1\n\n return specials\n\n def checkRow(self, mat, i):\n index = -1\n for j in range(len(mat[0])):\n if mat[i][j] == 1:\n if index >= 0:\n return -1\n else:\n index = j\n return index\n\n def checkColumn(self, mat, i, index):\n for j in range(len(mat)):\n if mat[j][index] == 1 and j != i:\n return False\n return True\n \n```\n```JavaScript []\n/**\n * @param {number[][]} mat\n * @return {number}\n */\nvar numSpecial = function(mat) {\n let specials = 0;\n\n for (let i = 0; i < mat.length; i++) {\n let index = checkRow(mat, i);\n if (index >= 0 && checkColumn(mat, i, index))\n specials++;\n }\n\n return specials;\n\n function checkRow(mat, i) {\n let index = -1;\n for (let j = 0; j < mat[0].length; j++) {\n if (mat[i][j] === 1) {\n if (index >= 0)\n return -1;\n else\n index = j;\n }\n }\n return index;\n }\n\n function checkColumn(mat, i, index) {\n for (let j = 0; j < mat.length; j++) {\n if (mat[j][index] === 1 && j !== i)\n return false;\n }\n return true;\n }\n};\n```\n---\n\n
| 87 | 2 |
['Array', 'Matrix', 'Python', 'C++', 'Java', 'JavaScript']
| 9 |
special-positions-in-a-binary-matrix
|
Java Simple Loop
|
java-simple-loop-by-hobiter-u97k
|
\n public int numSpecial(int[][] mat) {\n int m = mat.length, n = mat[0].length, res = 0, col[] = new int[n], row[] = new int[m];\n for (int i
|
hobiter
|
NORMAL
|
2020-09-13T04:02:48.095117+00:00
|
2020-09-15T05:04:13.349551+00:00
| 5,651 | false |
```\n public int numSpecial(int[][] mat) {\n int m = mat.length, n = mat[0].length, res = 0, col[] = new int[n], row[] = new int[m];\n for (int i = 0; i < m; i++) \n for (int j = 0; j < n; j++) \n if (mat[i][j] == 1){\n col[j]++;\n row[i]++;\n } \n for (int i = 0; i < m; i++) \n for (int j = 0; j < n; j++) \n if (mat[i][j] == 1 && row[i] == 1 && col[j] == 1) res++;\n return res;\n }\n```
| 85 | 3 |
[]
| 9 |
special-positions-in-a-binary-matrix
|
【Video】Give me 5 minutes - How we think about a solution
|
video-give-me-5-minutes-how-we-think-abo-hrkz
|
Intuition\nCheck row and column direction.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/qTAh4HGfUHk\n\n\u25A0 Timeline of the video\n\n0:05 Explain algorithm
|
niits
|
NORMAL
|
2023-12-13T01:33:13.578775+00:00
|
2023-12-14T04:13:27.411387+00:00
| 8,080 | false |
# Intuition\nCheck row and column direction.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/qTAh4HGfUHk\n\n\u25A0 Timeline of the video\n\n`0:05` Explain algorithm of the first step\n`1:06` Explain algorithm of the second step\n`2:36` Coding\n`4:17` Time Complexity and Space Complexity\n`4:55` Step by step algorithm of my solution code\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,434\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n\u25A0 MVC(Most Valuable Comment) for me on youtube for the last 7 days\n\n\n\nThank you for your comment @bun_bun17! What you\'re saying is the greatest significance for my presence on YouTube.\n\nThanks everyone who left your comment and thanks everyone who watched videos!\n\n\n---\n\n# Approach\n## How we think about a solution\n\nThe phrase "special positions" implies that only one element in each row and each column has the value 1. Therefore, it seems appropriate to check all rows and columns for this condition.\n\n```\nInput: mat = [[1,0,0],[0,0,1],[1,0,0]]\n\n[1,0,0]\n[0,0,1]\n[1,0,0]\n```\n\nFirst of all, let\'s check row direction.\n```\n\u2192[1,0,0]\n\u2192[0,0,1]\n\u2192[1,0,0]\n```\n\nChecking each row individually, if the sum of elements in a row is 1, there is a potential for that row to have a special position. This is because if the sum is 0, it means there are no positions with a value of 1, and if the sum is 2, it implies there are two positions with a value of 1, which also does not qualify as a special position.\n\n---\n\n\u2B50\uFE0F Points\n\nFind rows with a sum of 1.\n\n---\n\nIn this case, all rows are a sum of 1.\n\n```\n\u2192[1,0,0] = 1\n\u2192[0,0,1] = 1\n\u2192[1,0,0] = 1\n```\nNext, let\'s check column direction. First of all, we need to know index of 1 in each row.\n\n```\n[1,0,0] = index 0 \n[0,0,1] = index 2\n[1,0,0] = index 0\n```\nThen, acutually we do the same thing. Calculate sum of each column.\n```\n \u2193 \u2193\n[1,0,0] = index 0 \n[0,0,1] = index 2\n[1,0,0] = index 0\n```\nIf sum of column is 1, that means we find one of special positions because we iterate the matrix in column direction based on index of possible position. In this case, column index 0 and 2.\n\n---\n\n\u2B50\uFE0F Points\n\nCheck columns based on index of possible position\n\n---\n\nIn the end, we know that only mat[1][2] is special position, because\n```\nsum of column index 0 is 2\nsum of column index 2 is 1\n```\n```\nOutput: 1\n```\n\nEasy!\uD83D\uDE04\nLet\'s see a real algorithm!\n\n---\n\n# Complexity\n- Time complexity: $$O(m * (n + m))$$\n\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n def get_column_sum(col_idx):\n return sum(row[col_idx] for row in mat)\n\n special = 0\n for row in mat:\n if sum(row) == 1:\n col_idx = row.index(1)\n special += get_column_sum(col_idx) == 1\n\n return special\n```\n```javascript []\nvar numSpecial = function(mat) {\n function getColumnSum(colIdx) {\n return mat.reduce((sum, row) => sum + row[colIdx], 0);\n }\n\n let special = 0;\n for (let row of mat) {\n if (row.reduce((acc, val) => acc + val, 0) === 1) {\n const colIdx = row.indexOf(1);\n special += getColumnSum(colIdx) === 1;\n }\n }\n\n return special; \n};\n```\n```java []\nclass Solution {\n public int numSpecial(int[][] mat) {\n int special = 0;\n\n for (int[] row : mat) {\n if (getRowSum(row) == 1) {\n int colIdx = getIndexOfOne(row);\n special += (getColumnSum(mat, colIdx) == 1) ? 1 : 0;\n }\n }\n\n return special; \n }\n\n private int getRowSum(int[] row) {\n int sum = 0;\n for (int num : row) {\n sum += num;\n }\n return sum;\n }\n\n private int getColumnSum(int[][] mat, int colIdx) {\n int sum = 0;\n for (int[] row : mat) {\n sum += row[colIdx];\n }\n return sum;\n }\n\n private int getIndexOfOne(int[] row) {\n for (int i = 0; i < row.length; i++) {\n if (row[i] == 1) {\n return i;\n }\n }\n return -1; // If 1 is not found, return -1 or handle accordingly\n } \n}\n```\n```C++ []\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n int special = 0;\n\n for (const auto& row : mat) {\n if (accumulate(row.begin(), row.end(), 0) == 1) {\n int colIdx = distance(row.begin(), find(row.begin(), row.end(), 1));\n special += getColumnSum(mat, colIdx) == 1;\n }\n }\n\n return special; \n }\n\nprivate:\n int getColumnSum(const vector<vector<int>>& mat, int colIdx) {\n int sum = 0;\n for (const auto& row : mat) {\n sum += row[colIdx];\n }\n return sum;\n }\n};\n```\n\n## Step by step algorithm\n\n1. **Initialize Variables:**\n - `special`: A counter to keep track of the number of special positions.\n\n```python\nspecial = 0\n```\n\n2. **Iterate Over Each Row:**\n - Loop through each row in the matrix `mat`.\n\n```python\nfor row in mat:\n```\n\n3. **Check Sum of Current Row:**\n - Check if the sum of elements in the current row is equal to 1.\n\n```python\nif sum(row) == 1:\n```\n\n4. **Find Column Index with Value 1:**\n - If the sum is 1, find the index of the element with value 1 in the current row. This assumes there is exactly one element with value 1 in the row.\n\n```python\ncol_idx = row.index(1)\n```\n\n5. **Calculate Column Sum:**\n - Use the `get_column_sum` function to calculate the sum of elements in the column with index `col_idx`.\n\n```python\ncol_sum = get_column_sum(col_idx)\n```\n\n - The `get_column_sum` function iterates through each row and accumulates the value in the specified column.\n\n```python\ndef get_column_sum(col_idx):\n return sum(row[col_idx] for row in mat)\n```\n\n6. **Check if Column Sum is 1:**\n - If the column sum is also equal to 1, it indicates that the element at the intersection of the identified row and column is the only \'1\' in its row and column. Increment the `special` counter.\n\n```python\nspecial += col_sum == 1\n```\n\n7. **Return the Result:**\n - The final result is the count of special positions.\n\n```python\nreturn special\n```\n\nIn summary, the algorithm iterates through each row, checks if the sum of elements in the row is 1, finds the corresponding column index with a value of 1, calculates the sum of elements in that column, and increments the `special` counter if both row and column sums are equal to 1. The final result is the count of special positions in the matrix.\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/difference-between-ones-and-zeros-in-row-and-column/solutions/4401811/video-give-me-5-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/swafoNFu99o\n\n\u25A0 Timeline of the video\n\n`0:06` Create number of 1 in each row and column\n`1:16` How to calculate numbers at each position \n`4:03` Coding\n`6:32` Time Complexity and Space Complexity\n`7:02` Explain zip(*grid)\n`8:15` Step by step algorithm of my solution code\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/maximum-product-of-two-elements-in-an-array/solutions/4392747/video-give-me-5-minutes-2-solutions-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/JV5Kuinx-m0\n\n\u25A0 Timeline of the video\n\n`0:05` Explain algorithm of Solution 1\n`3:18` Coding of solution 1\n`4:18` Time Complexity and Space Complexity of solution 1\n`4:29` Step by step algorithm of solution 1\n`4:36` Explain key points of Solution 2\n`5:25` Coding of Solution 2\n`6:50` Time Complexity and Space Complexity of Solution 2\n`7:03` Step by step algorithm with my stack solution code\n
| 62 | 0 |
['C++', 'Java', 'Python3', 'JavaScript']
| 7 |
special-positions-in-a-binary-matrix
|
✅☑[C++/Java/Python/JavaScript] || 2 Approaches || EXPLAINED🔥
|
cjavapythonjavascript-2-approaches-expla-73ag
|
PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n(Also explained in the code)\n\n#### Approach 1(Brute Force)\n1. It iterates through each element of the ma
|
MarkSPhilip31
|
NORMAL
|
2023-12-13T00:32:23.798285+00:00
|
2023-12-13T03:05:56.978491+00:00
| 9,028 | false |
# PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1(Brute Force)***\n1. It iterates through each element of the matrix, checking if it equals 1.\n1. For each element that equals 1, it checks the entire row and column to see if there are any other \'1\'s apart from the current row or column.\n1. If the element has no other \'1\'s in its row and column except for itself, it is considered "special," and the counter \'ans\' is incremented.\n1. Finally, the function returns the count of "special" elements found in the matrix.\n\n# Complexity\n- *Time complexity:*\n $$O(m.n.(m+n)))$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n // Function to count the number of "special" elements in the given matrix \'mat\'\n int numSpecial(vector<vector<int>>& mat) {\n int ans = 0; // Variable to store the count of "special" elements\n int m = mat.size(); // Number of rows in the matrix\n int n = mat[0].size(); // Number of columns in the matrix\n \n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 0) {\n continue; // If the element is 0, continue to the next iteration\n }\n \n bool good = true; // Flag to determine if the element is "special"\n \n // Checking the entire column for other \'1\'s except for the current row\n for (int r = 0; r < m; r++) {\n if (r != row && mat[r][col] == 1) {\n good = false; // If a \'1\' is found in the same column in another row, mark as not "special"\n break;\n }\n }\n \n // Checking the entire row for other \'1\'s except for the current column\n for (int c = 0; c < n; c++) {\n if (c != col && mat[row][c] == 1) {\n good = false; // If a \'1\' is found in the same row in another column, mark as not "special"\n break;\n }\n }\n \n if (good) {\n ans++; // If the element is "special," increment the count\n }\n }\n }\n \n return ans; // Return the count of "special" elements\n }\n};\n\n\n\n```\n```C []\n#include <stdio.h>\n\nint numSpecial(int** mat, int matSize, int* matColSize) {\n int ans = 0;\n int m = matSize; // Number of rows in the matrix\n int n = *matColSize; // Number of columns in the matrix\n\n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 0) {\n continue; // If the element is 0, continue to the next iteration\n }\n\n int good = 1; // Flag to determine if the element is "special"\n\n // Checking the entire column for other \'1\'s except for the current row\n for (int r = 0; r < m; r++) {\n if (r != row && mat[r][col] == 1) {\n good = 0; // If a \'1\' is found in the same column in another row, mark as not "special"\n break;\n }\n }\n\n // Checking the entire row for other \'1\'s except for the current column\n for (int c = 0; c < n; c++) {\n if (c != col && mat[row][c] == 1) {\n good = 0; // If a \'1\' is found in the same row in another column, mark as not "special"\n break;\n }\n }\n\n if (good) {\n ans++; // If the element is "special," increment the count\n }\n }\n }\n\n return ans; // Return the count of "special" elements\n}\n\n\n\n\n```\n```Java []\nclass Solution {\n public int numSpecial(int[][] mat) {\n int ans = 0;\n int m = mat.length;\n int n = mat[0].length;\n \n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 0) {\n continue;\n }\n \n boolean good = true;\n for (int r = 0; r < m; r++) {\n if (r != row && mat[r][col] == 1) {\n good = false;\n break;\n }\n }\n \n for (int c = 0; c < n; c++) {\n if (c != col && mat[row][c] == 1) {\n good = false;\n break;\n }\n }\n \n if (good) {\n ans++;\n }\n }\n }\n \n return ans;\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n ans = 0\n m = len(mat)\n n = len(mat[0])\n \n for row in range(m):\n for col in range(n):\n if mat[row][col] == 0:\n continue\n \n good = True\n for r in range(m):\n if r != row and mat[r][col] == 1:\n good = False\n break\n \n for c in range(n):\n if c != col and mat[row][c] == 1:\n good = False\n break\n \n if good:\n ans += 1\n \n return ans\n\n\n```\n```javascript []\nfunction numSpecial(mat) {\n let ans = 0;\n const m = mat.length; // Number of rows in the matrix\n const n = mat[0].length; // Number of columns in the matrix\n\n for (let row = 0; row < m; row++) {\n for (let col = 0; col < n; col++) {\n if (mat[row][col] === 0) {\n continue; // If the element is 0, continue to the next iteration\n }\n\n let good = true; // Flag to determine if the element is "special"\n\n // Checking the entire column for other \'1\'s except for the current row\n for (let r = 0; r < m; r++) {\n if (r !== row && mat[r][col] === 1) {\n good = false; // If a \'1\' is found in the same column in another row, mark as not "special"\n break;\n }\n }\n\n // Checking the entire row for other \'1\'s except for the current column\n for (let c = 0; c < n; c++) {\n if (c !== col && mat[row][c] === 1) {\n good = false; // If a \'1\' is found in the same row in another column, mark as not "special"\n break;\n }\n }\n\n if (good) {\n ans++; // If the element is "special," increment the count\n }\n }\n }\n\n return ans; // Return the count of "special" elements\n}\n\n\n```\n\n---\n\n#### ***Approach 2(Pre Count)***\n1. It first calculates the count of \'1\'s in each row and column and stores them in the rowCount and colCount vectors, respectively.\n1. Then, it iterates through each element of the matrix and checks if the element is \'1\' and if its corresponding row and column contain exactly one \'1\'. If so, it counts it as a "special" element.\n1. Finally, it returns the count of "special" elements found in the matrix.\n\n# Complexity\n- *Time complexity:*\n $$O(m.n)$$\n \n\n- *Space complexity:*\n $$O(m+n)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n // Function to count the number of "special" elements in the given matrix \'mat\'\n int numSpecial(vector<vector<int>>& mat) {\n int m = mat.size(); // Number of rows in the matrix\n int n = mat[0].size(); // Number of columns in the matrix\n\n // Vector to store counts of \'1\'s in each row and column\n vector<int> rowCount(m, 0); // Initialize row count vector with 0s\n vector<int> colCount(n, 0); // Initialize column count vector with 0s\n\n // Counting \'1\'s in each row and column\n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 1) {\n rowCount[row]++; // Increment row count when \'1\' is encountered in the row\n colCount[col]++; // Increment column count when \'1\' is encountered in the column\n }\n }\n }\n\n int ans = 0; // Variable to store the count of "special" elements\n\n // Checking for "special" elements\n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 1) { // If the element is \'1\'\n if (rowCount[row] == 1 && colCount[col] == 1) {\n // If the row and column containing this \'1\' have exactly one \'1\' (i.e., the element is "special")\n ans++; // Increment the count of "special" elements\n }\n }\n }\n }\n\n return ans; // Return the count of "special" elements\n }\n};\n\n\n```\n```C []\n#include <stdio.h>\n#include <stdlib.h>\n\nint numSpecial(int** mat, int matSize, int* matColSize) {\n int m = matSize; // Number of rows in the matrix\n int n = *matColSize; // Number of columns in the matrix\n\n // Array to store counts of \'1\'s in each row and column\n int* rowCount = (int*)calloc(m, sizeof(int)); // Initialize row count array with 0s\n int* colCount = (int*)calloc(n, sizeof(int)); // Initialize column count array with 0s\n\n // Counting \'1\'s in each row and column\n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 1) {\n rowCount[row]++; // Increment row count when \'1\' is encountered in the row\n colCount[col]++; // Increment column count when \'1\' is encountered in the column\n }\n }\n }\n\n int ans = 0; // Variable to store the count of "special" elements\n\n // Checking for "special" elements\n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 1) { // If the element is \'1\'\n if (rowCount[row] == 1 && colCount[col] == 1) {\n // If the row and column containing this \'1\' have exactly one \'1\' (i.e., the element is "special")\n ans++; // Increment the count of "special" elements\n }\n }\n }\n }\n\n free(rowCount);\n free(colCount);\n return ans; // Return the count of "special" elements\n}\n\n\n\n\n```\n```Java []\nclass Solution {\n public int numSpecial(int[][] mat) {\n int m = mat.length;\n int n = mat[0].length;\n int[] rowCount = new int[m];\n int[] colCount = new int[n];\n \n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 1) {\n rowCount[row]++;\n colCount[col]++;\n }\n }\n }\n \n int ans = 0;\n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (mat[row][col] == 1) {\n if (rowCount[row] == 1 && colCount[col] == 1) {\n ans++;\n }\n }\n }\n }\n \n return ans;\n }\n}\n\n\n```\n```python3 []\n\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n m = len(mat)\n n = len(mat[0])\n row_count = [0] * m\n col_count = [0] * n\n \n for row in range(m):\n for col in range(n):\n if mat[row][col] == 1:\n row_count[row] += 1\n col_count[col] += 1\n \n ans = 0\n for row in range(m):\n for col in range(n):\n if mat[row][col] == 1:\n if row_count[row] == 1 and col_count[col] == 1:\n ans += 1\n\n return ans\n\n```\n```javascript []\nfunction numSpecial(mat) {\n const m = mat.length; // Number of rows in the matrix\n const n = mat[0].length; // Number of columns in the matrix\n\n // Arrays to store counts of \'1\'s in each row and column\n const rowCount = new Array(m).fill(0); // Initialize row count array with 0s\n const colCount = new Array(n).fill(0); // Initialize column count array with 0s\n\n // Counting \'1\'s in each row and column\n for (let row = 0; row < m; row++) {\n for (let col = 0; col < n; col++) {\n if (mat[row][col] === 1) {\n rowCount[row]++; // Increment row count when \'1\' is encountered in the row\n colCount[col]++; // Increment column count when \'1\' is encountered in the column\n }\n }\n }\n\n let ans = 0; // Variable to store the count of "special" elements\n\n // Checking for "special" elements\n for (let row = 0; row < m; row++) {\n for (let col = 0; col < n; col++) {\n if (mat[row][col] === 1) { // If the element is \'1\'\n if (rowCount[row] === 1 && colCount[col] === 1) {\n // If the row and column containing this \'1\' have exactly one \'1\' (i.e., the element is "special")\n ans++; // Increment the count of "special" elements\n }\n }\n }\n }\n\n return ans; // Return the count of "special" elements\n}\n\n\n```\n\n---\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n---
| 48 | 3 |
['Array', 'C', 'Matrix', 'C++', 'Java', 'Python3', 'JavaScript']
| 6 |
special-positions-in-a-binary-matrix
|
[Python] Easy to Understand Solution
|
python-easy-to-understand-solution-by-ch-v4yj
|
\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n n = len(mat)\n m = len(mat[0])\n #taking transpose of matrix \n
|
chandreshwar
|
NORMAL
|
2020-09-13T04:02:09.314535+00:00
|
2020-09-13T04:02:09.314578+00:00
| 3,649 | false |
```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n n = len(mat)\n m = len(mat[0])\n #taking transpose of matrix \n lst = [[mat[j][i] for j in range(n)] for i in range(m)] \n res = 0\n for i in range(n):\n for j in range(m):\n #Checking if current element is 1 and sum of elements of current row and column is also 1\n if mat[i][j] == 1 and sum(mat[i]) == 1 and sum(lst[j]) == 1:\n res += 1\n return res\n```
| 42 | 6 |
[]
| 7 |
special-positions-in-a-binary-matrix
|
Python easy to understand 100% faster
|
python-easy-to-understand-100-faster-by-7rjfw
|
\n\ndef column(matrix, i):\n return [row[i] for row in matrix]\nclass Solution:\n \n def numSpecial(self, mat: List[List[int]]) -> int:\n c=
|
jatindscl
|
NORMAL
|
2020-09-13T04:13:34.761215+00:00
|
2020-09-13T04:13:34.761300+00:00
| 3,271 | false |
\n```\ndef column(matrix, i):\n return [row[i] for row in matrix]\nclass Solution:\n \n def numSpecial(self, mat: List[List[int]]) -> int:\n c=0\n for i in range(len(mat)):\n if(mat[i].count(1)==1):\n i=mat[i].index(1)\n col=column(mat,i)\n if(col.count(1)==1):\n c+=1\n \n return c \n \n \n \n```
| 27 | 1 |
['Python', 'Python3']
| 5 |
special-positions-in-a-binary-matrix
|
💯Faster✅💯 Lesser✅2 Methods🔥Brute Force🔥Hashing🔥Python🐍Java☕C++✅C📈
|
faster-lesser2-methodsbrute-forcehashing-ibmj
|
\uD83D\uDE80 Hi, I\'m Mohammed Raziullah Ansari, and I\'m excited to share 2 ways to solve this question with detailed explanation of each approach:\n\n# Proble
|
Mohammed_Raziullah_Ansari
|
NORMAL
|
2023-12-13T04:37:18.379851+00:00
|
2023-12-13T09:22:32.078007+00:00
| 2,793 | false |
# \uD83D\uDE80 Hi, I\'m [Mohammed Raziullah Ansari](https://leetcode.com/Mohammed_Raziullah_Ansari/), and I\'m excited to share 2 ways to solve this question with detailed explanation of each approach:\n\n# Problem Explaination: \nThe problem involves finding the number of special positions in a binary matrix. A special position is defined as a cell with a value of 1 and having all other cells in the same row and column as 0. The task is to determine the count of such special positions in the given binary matrix.\n\n# \uD83D\uDD0D Methods To Solve This Problem:\nI\'ll be covering two different methods to solve this problem:\n1. Brute Force\n2. Hashing\n\n# 1. Brute Force: \n- Iterate through each cell in the matrix.\n- For each cell with a value of 1, check if all other cells in its row and column are 0.\n# Complexity\n- \u23F1\uFE0F Time Complexity: `O(n^3)`, where n is the size of the matrix.\n\n- \uD83D\uDE80 Space Complexity: `O(1)` - no extra space used.\n\n# Code\n```Python []\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n count = 0\n for i in range(len(mat)):\n for j in range(len(mat[0])):\n if mat[i][j] == 1 and sum(mat[i]) == 1 and sum(row[j] for row in mat) == 1:\n count += 1\n return count\n```\n```Java []\nimport java.util.Arrays;\n\nclass Solution {\n public int numSpecial(int[][] mat) {\n int count = 0;\n for (int i = 0; i < mat.length; i++) {\n for (int j = 0; j < mat[0].length; j++) {\n int sumR = 0;\n int sumC = 0;\n if(mat[i][j]==1){\n for(int k=0;k<mat.length;k++){\n sumR+=mat[k][j];\n }\n for(int k=0;k<mat[0].length;k++){\n sumC+=mat[i][k];\n }\n }\n if(sumR+sumC==2) count++;\n }\n }\n return count;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n int count = 0;\n for (int i = 0; i < mat.size(); i++) {\n for (int j = 0; j < mat[0].size(); j++) {\n if (mat[i][j] == 1 && accumulate(mat[i].begin(), mat[i].end(), 0) == 1 &&\n accumulate(mat.begin(), mat.end(), 0, [j](int sum, const vector<int>& row) { return sum + row[j]; }) == 1) {\n count++;\n }\n }\n }\n return count;\n }\n};\n```\n# 2. Hashing:\n- Maintain two arrays, rowSum and colSum, to store the sum of each row and column, respectively.\n- Iterate through each cell in the matrix and update the corresponding rowSum and colSum.\n- For each cell with a value of 1, check if its row and column sums are both 1.\n# Complexity\n- \u23F1\uFE0F Time Complexity: `O(n^2)`, where n is the size of the matrix.\n- \n- \uD83D\uDE80 Space Complexity: `O(n)` - for the rowSum and colSum arrays.\n\n# Code\n```Python []\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n rowSum = [sum(row) for row in mat]\n colSum = [sum(row[j] for row in mat) for j in range(len(mat[0]))]\n count = 0\n for i in range(len(mat)):\n for j in range(len(mat[0])):\n if mat[i][j] == 1 and rowSum[i] == 1 and colSum[j] == 1:\n count += 1\n return count\n```\n```Java []\nclass Solution {\n public int numSpecial(int[][] mat) {\n int[] rowSum = new int[mat.length];\n int[] colSum = new int[mat[0].length];\n for (int i = 0; i < mat.length; i++) {\n for (int j = 0; j < mat[0].length; j++) {\n rowSum[i] += mat[i][j];\n colSum[j] += mat[i][j];\n }\n }\n int count = 0;\n for (int i = 0; i < mat.length; i++) {\n for (int j = 0; j < mat[0].length; j++) {\n if (mat[i][j] == 1 && rowSum[i] == 1 && colSum[j] == 1) {\n count++;\n }\n }\n }\n return count;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n vector<int> rowSum(mat.size(), 0);\n vector<int> colSum(mat[0].size(), 0);\n for (int i = 0; i < mat.size(); i++) {\n for (int j = 0; j < mat[0].size(); j++) {\n rowSum[i] += mat[i][j];\n colSum[j] += mat[i][j];\n }\n }\n int count = 0;\n for (int i = 0; i < mat.size(); i++) {\n for (int j = 0; j < mat[0].size(); j++) {\n if (mat[i][j] == 1 && rowSum[i] == 1 && colSum[j] == 1) {\n count++;\n }\n }\n }\n return count;\n }\n};\n```\n```C []\nint numSpecial(int** mat, int matSize, int* matColSize) {\n int* rowSum = (int*)malloc(matSize * sizeof(int));\n int* colSum = (int*)malloc((*matColSize) * sizeof(int));\n memset(rowSum, 0, matSize * sizeof(int));\n memset(colSum, 0, (*matColSize) * sizeof(int));\n\n for (int i = 0; i < matSize; i++) {\n for (int j = 0; j < *matColSize; j++) {\n rowSum[i] += mat[i][j];\n colSum[j] += mat[i][j];\n }\n }\n\n int count = 0;\n for (int i = 0; i < matSize; i++) {\n for (int j = 0; j < *matColSize; j++) {\n if (mat[i][j] == 1 && rowSum[i] == 1 && colSum[j] == 1) {\n count++;\n }\n }\n }\n\n free(rowSum);\n free(colSum);\n return count;\n}\n```\n# \uD83C\uDFC6Conclusion: \nIn this problem to find the number of special positions in a binary matrix, we discussed two distinct approaches: the Brute Force method and the Hashing method. and hashing will be a better approach compared to brute force.\n\n\n# \uD83D\uDCA1 I invite you to check out my profile for detailed explanations and code for each method. Happy coding and learning! \uD83D\uDCDA
| 24 | 0 |
['Array', 'Hash Table', 'C', 'Matrix', 'C++', 'Java', 'Python3']
| 4 |
special-positions-in-a-binary-matrix
|
[C++] SImple Approach Explained and Code and Complexity
|
c-simple-approach-explained-and-code-and-qmyy
|
This problem is very easy to think. Please do not go to code directly, take steps as hint and try to implement it yourself :)\nSteps:\n\t1. Get the sum of all t
|
rahulanandyadav2000
|
NORMAL
|
2020-09-13T04:17:16.649477+00:00
|
2020-09-13T04:17:16.649518+00:00
| 2,057 | false |
This problem is very easy to think. Please do not go to code directly, take steps as hint and try to implement it yourself :)\nSteps:\n\t1. Get the sum of all the rows\n\t2. Get the sum of all the coloumns\n\t3. Traverse the matrix and whenever encounter 1 check its row and col sum, if 1 then increment count by 1.\n\t4. Return count.\n\n\nComplexity Analysis\nTime : O(m*n)\nSpace: O(m+n+1)\n\n```\nclass Solution\n{\npublic:\n int numSpecial(vector<vector<int>> &mat)\n {\n int rows = mat.size(), col = mat[0].size();\n int rsum[rows];\n int csum[col];\n int i, j;\n //get sum of rows\n for (i = 0; i < rows; i++)\n {\n rsum[i] = 0;\n for (j = 0; j < col; j++)\n rsum[i] += mat[i][j];\n }\n //get sum of coloumns\n for (i = 0; i < col; i++)\n {\n csum[i] = 0;\n for (j = 0; j < rows; j++)\n csum[i] += mat[j][i];\n }\n //If value in mat is one with sum of that row and col =1 then add this to result\n int count = 0;\n for (i = 0; i < rows; i++)\n for (j = 0; j < col; j++)\n if (mat[i][j] == 1 && rsum[i] == 1 && csum[j] == 1)\n count++;\n return count;\n }\n};\n```\n\n\nHappy Coding :)
| 18 | 0 |
['C']
| 4 |
special-positions-in-a-binary-matrix
|
🚀🚀🚀EASY SOLUTiON EVER !!! || Java || C++ || Python || JS || C# || Ruby || Go 🚀🚀🚀 by PRODONiK
|
easy-solution-ever-java-c-python-js-c-ru-apwg
|
Intuition\nThe problem aims to find the number of special positions in a given matrix. A position is considered special if the element at that position is 1, an
|
prodonik
|
NORMAL
|
2023-12-13T00:19:20.588235+00:00
|
2023-12-13T01:38:46.842848+00:00
| 2,893 | false |
# Intuition\nThe problem aims to find the number of special positions in a given matrix. A position is considered special if the element at that position is 1, and there is no other 1 in the same row and the same column.\n\n# Approach\nThe `numSpecial` method iterates over each row in the matrix. For each element with the value 1 in the row, it increments the `ones_in_the_row` variable, indicating the number of 1s in that row. If it\'s the first 1 in the row (`ones_in_the_row == 1`), it marks the corresponding column as potentially special. If it\'s not the first 1 in the row (`ones_in_the_row > 1`), it marks both the current and the previously marked columns as non-special.\n\nThe `columns` array is used to keep track of the status of each column:\n- `0`: Not marked\n- `1`: Potentially special (first 1 in the row)\n- `2`: Not special (more than one 1 in the row)\n\nAfter processing all rows, the method counts the columns marked as potentially special and returns the result.\n\n# Complexity\n- Time complexity: O(m * n)\n The time complexity is linear in the size of the matrix, where `m` is the number of rows and `n` is the number of columns.\n\n- Space complexity: O(n)\n The space complexity is linear in the number of columns, as the `columns` array is used to keep track of the status of each column.\n\n# Code\n```Java []\nclass Solution {\n public int numSpecial (int[][] nums) {\n int result = 0;\n int [] columns = new int [nums[0].length];\n for (int i = 0; i < nums.length; i ++) {\n int ones_in_the_row = 0;\n int column = 0;\n for (int j = 0; j < nums[i].length; j ++) {\n if (nums[i][j] == 1) {\n ones_in_the_row ++;\n if (ones_in_the_row == 1) {\n columns[j] = columns[j] == 0 ? 1 : 2;\n column = j;\n }\n else {\n columns[column] = 2;\n columns[j] = 2;\n }\n }\n }\n\n }\n for (int column : columns) {\n result += (column == 1 ? 1 : 0);\n }\n return result;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int numSpecial(std::vector<std::vector<int>>& nums) {\n int result = 0;\n std::vector<int> columns(nums[0].size(), 0);\n\n for (int i = 0; i < nums.size(); ++i) {\n int ones_in_the_row = 0;\n int column = 0;\n\n for (int j = 0; j < nums[i].size(); ++j) {\n if (nums[i][j] == 1) {\n ones_in_the_row++;\n\n if (ones_in_the_row == 1) {\n columns[j] = columns[j] == 0 ? 1 : 2;\n column = j;\n } else {\n columns[column] = 2;\n columns[j] = 2;\n }\n }\n }\n }\n\n for (int column : columns) {\n result += (column == 1 ? 1 : 0);\n }\n\n return result;\n }\n};\n```\n```Python []\nclass Solution:\n def numSpecial(self, nums: List[List[int]]) -> int:\n result = 0\n columns = [0] * len(nums[0])\n\n for i in range(len(nums)):\n ones_in_the_row = 0\n column = 0\n\n for j in range(len(nums[i])):\n if nums[i][j] == 1:\n ones_in_the_row += 1\n\n if ones_in_the_row == 1:\n columns[j] = 1 if columns[j] == 0 else 2\n column = j\n else:\n columns[column] = 2\n columns[j] = 2\n\n result += sum(column == 1 for column in columns)\n return result\n```\n```JavaScript []\nclass Solution {\n numSpecial(nums) {\n let result = 0;\n const columns = new Array(nums[0].length).fill(0);\n\n for (let i = 0; i < nums.length; ++i) {\n let ones_in_the_row = 0;\n let column = 0;\n\n for (let j = 0; j < nums[i].length; ++j) {\n if (nums[i][j] === 1) {\n ones_in_the_row++;\n\n if (ones_in_the_row === 1) {\n columns[j] = columns[j] === 0 ? 1 : 2;\n column = j;\n } else {\n columns[column] = 2;\n columns[j] = 2;\n }\n }\n }\n }\n\n result += columns.filter(column => column === 1).length;\n return result;\n }\n}\n```\n```C# []\npublic class Solution {\n public int NumSpecial(int[][] nums) {\n int result = 0;\n int[] columns = new int[nums[0].Length];\n\n for (int i = 0; i < nums.Length; ++i) {\n int ones_in_the_row = 0;\n int column = 0;\n\n for (int j = 0; j < nums[i].Length; ++j) {\n if (nums[i][j] == 1) {\n ones_in_the_row++;\n\n if (ones_in_the_row == 1) {\n columns[j] = columns[j] == 0 ? 1 : 2;\n column = j;\n } else {\n columns[column] = 2;\n columns[j] = 2;\n }\n }\n }\n }\n\n result += Array.FindAll(columns, column => column == 1).Length;\n return result;\n }\n}\n```\n```Ruby []\nclass Solution\n def num_special(nums)\n result = 0\n columns = Array.new(nums[0].length, 0)\n\n (0...nums.length).each do |i|\n ones_in_the_row = 0\n column = 0\n\n (0...nums[i].length).each do |j|\n if nums[i][j] == 1\n ones_in_the_row += 1\n\n if ones_in_the_row == 1\n columns[j] = columns[j] == 0 ? 1 : 2\n column = j\n else\n columns[column] = 2\n columns[j] = 2\n end\n end\n end\n end\n\n result += columns.count { |column| column == 1 }\n result\n end\nend\n```\n```Go []\ntype Solution struct{}\n\nfunc (s *Solution) NumSpecial(nums [][]int) int {\n\tresult := 0\n\tcolumns := make([]int, len(nums[0]))\n\n\tfor i := 0; i < len(nums); i++ {\n\t\tones_in_the_row := 0\n\t\tcolumn := 0\n\n\t\tfor j := 0; j < len(nums[i]); j++ {\n\t\t\tif nums[i][j] == 1 {\n\t\t\t\tones_in_the_row++\n\n\t\t\t\tif ones_in_the_row == 1 {\n\t\t\t\t\tif columns[j] == 0 {\n\t\t\t\t\t\tcolumns[j] = 1\n\t\t\t\t\t} else {\n\t\t\t\t\t\tcolumns[j] = 2\n\t\t\t\t\t}\n\t\t\t\t\tcolumn = j\n\t\t\t\t} else {\n\t\t\t\t\tcolumns[column] = 2\n\t\t\t\t\tcolumns[j] = 2\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t}\n\n\tfor _, column := range columns {\n\t\tif column == 1 {\n\t\t\tresult++\n\t\t}\n\t}\n\n\treturn result\n}\n```\n\n
| 17 | 0 |
['C++', 'Java', 'Go', 'Python3', 'Ruby', 'JavaScript', 'C#']
| 4 |
special-positions-in-a-binary-matrix
|
Python | Readable Solution with Comments
|
python-readable-solution-with-comments-b-kshe
|
\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n \n res = 0\n rows = len(mat)\n cols = len(mat[0])\n
|
jgroszew
|
NORMAL
|
2022-01-08T19:18:36.048619+00:00
|
2022-01-08T19:18:36.048663+00:00
| 819 | false |
```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n \n res = 0\n rows = len(mat)\n cols = len(mat[0])\n \n rowtotals = []\n coltotals = []\n \n # Store the sum of each row\n for row in mat:\n rowtotals.append(sum(row))\n \n # Store the sum of each column\n for col in zip(*mat):\n coltotals.append(sum(col))\n \n # Check if current position is "1" and is the only "1" in that row and column\n for i in range(rows):\n for j in range(cols):\n if mat[i][j] == 1 and rowtotals[i] == 1 and coltotals[j] == 1:\n res += 1\n \n \n return res\n```
| 13 | 0 |
['Python']
| 1 |
special-positions-in-a-binary-matrix
|
🚀✅🚀 100% beats Users by TC || Java, C#, Python, Rust, C++, C, Ruby, Go|| 🔥🔥
|
100-beats-users-by-tc-java-c-python-rust-4e29
|
Intuition\nThe problem seems to be asking for the number of special positions in a binary matrix. A position is considered special if it contains a 1 and the su
|
ilxamovic
|
NORMAL
|
2023-12-13T04:18:42.500306+00:00
|
2023-12-13T04:19:32.614821+00:00
| 1,053 | false |
# Intuition\nThe problem seems to be asking for the number of special positions in a binary matrix. A position is considered special if it contains a 1 and the sum of elements in its row and column is 1.\n\n# Approach\nThe provided code iterates through each element of the matrix and checks if it is 1. If it is, it calculates the sum of elements in its row and column and checks if both sums are equal to 1. If they are, the position is considered special, and the result is incremented.\n\n# Complexity\n- Time complexity: O(m * n^2), where m is the number of rows and n is the number of columns in the matrix.\n- Space complexity: O(1) as no additional space is used.\n\n# Code\n```csharp []\npublic class Solution {\n public int NumSpecial(int[][] mat)\n {\n int result = 0;\n for (int i = 0; i < mat.Length; i++)\n {\n for (int j = 0; j < mat[i].Length; j++)\n {\n if (mat[i][j] == 1)\n {\n int sumx = 0;\n int sumy = 0;\n for (int m = 0; m < mat[i].Length; m++)\n {\n sumx += mat[i][m];\n }\n for (int k = 0; k < mat.Length; k++)\n {\n sumy += mat[k][j];\n }\n if (sumx == 1 && sumy == 1)\n {\n result++;\n }\n }\n }\n }\n return result;\n }\n}\n```\n``` Java []\npublic class Solution {\n public int numSpecial(int[][] mat) {\n int result = 0;\n\n // Arrays to store the sums of elements in each row and column\n int[] rowSums = new int[mat.length];\n int[] colSums = new int[mat[0].length];\n\n // Calculate the sums of elements in each row and column\n for (int i = 0; i < mat.length; i++) {\n for (int j = 0; j < mat[i].length; j++) {\n rowSums[i] += mat[i][j];\n colSums[j] += mat[i][j];\n }\n }\n\n // Check if each 1 is special using the precalculated sums\n for (int i = 0; i < mat.length; i++) {\n for (int j = 0; j < mat[i].length; j++) {\n if (mat[i][j] == 1 && rowSums[i] == 1 && colSums[j] == 1) {\n result++;\n }\n }\n }\n\n return result;\n }\n}\n```\n```Python []\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n result = 0\n\n # Lists to store the sums of elements in each row and column\n row_sums = [0] * len(mat)\n col_sums = [0] * len(mat[0])\n\n # Calculate the sums of elements in each row and column\n for i in range(len(mat)):\n for j in range(len(mat[i])):\n row_sums[i] += mat[i][j]\n col_sums[j] += mat[i][j]\n\n # Check if each 1 is special using the precalculated sums\n for i in range(len(mat)):\n for j in range(len(mat[i])):\n if mat[i][j] == 1 and row_sums[i] == 1 and col_sums[j] == 1:\n result += 1\n\n return result\n```\n``` Go []\nfunc numSpecial(mat [][]int) int {\n\tresult := 0\n\n\t// Slices to store the sums of elements in each row and column\n\trowSums := make([]int, len(mat))\n\tcolSums := make([]int, len(mat[0]))\n\n\t// Calculate the sums of elements in each row and column\n\tfor i := 0; i < len(mat); i++ {\n\t\tfor j := 0; j < len(mat[i]); j++ {\n\t\t\trowSums[i] += mat[i][j]\n\t\t\tcolSums[j] += mat[i][j]\n\t\t}\n\t}\n\n\t// Check if each 1 is special using the precalculated sums\n\tfor i := 0; i < len(mat); i++ {\n\t\tfor j := 0; j < len(mat[i]); j++ {\n\t\t\tif mat[i][j] == 1 && rowSums[i] == 1 && colSums[j] == 1 {\n\t\t\t\tresult++\n\t\t\t}\n\t\t}\n\t}\n\n\treturn result\n}\n```\n``` Rust []\nimpl Solution {\n pub fn num_special(mat: Vec<Vec<i32>>) -> i32 {\n let mut result = 0;\n\n // Vectors to store the sums of elements in each row and column\n let mut row_sums = vec![0; mat.len()];\n let mut col_sums = vec![0; mat[0].len()];\n\n // Calculate the sums of elements in each row and column\n for i in 0..mat.len() {\n for j in 0..mat[i].len() {\n row_sums[i] += mat[i][j];\n col_sums[j] += mat[i][j];\n }\n }\n\n // Check if each 1 is special using the precalculated sums\n for i in 0..mat.len() {\n for j in 0..mat[i].len() {\n if mat[i][j] == 1 && row_sums[i] == 1 && col_sums[j] == 1 {\n result += 1;\n }\n }\n }\n\n result\n }\n}\n```\n``` Ruby []\ndef num_special(mat)\n result = 0\n\n # Arrays to store the sums of elements in each row and column\n row_sums = Array.new(mat.length, 0)\n col_sums = Array.new(mat[0].length, 0)\n\n # Calculate the sums of elements in each row and column\n mat.each_with_index do |row, i|\n row.each_with_index do |value, j|\n row_sums[i] += value\n col_sums[j] += value\n end\n end\n\n # Check if each 1 is special using the precalculated sums\n mat.each_with_index do |row, i|\n row.each_with_index do |value, j|\n if value == 1 && row_sums[i] == 1 && col_sums[j] == 1\n result += 1\n end\n end\n end\n\n result\nend\n```\n```Cpp []\n#include <vector>\n\nclass Solution {\npublic:\n int numSpecial(std::vector<std::vector<int>>& mat) {\n int result = 0;\n\n // Vectors to store the sums of elements in each row and column\n std::vector<int> row_sums(mat.size(), 0);\n std::vector<int> col_sums(mat[0].size(), 0);\n\n // Calculate the sums of elements in each row and column\n for (int i = 0; i < mat.size(); i++) {\n for (int j = 0; j < mat[i].size(); j++) {\n row_sums[i] += mat[i][j];\n col_sums[j] += mat[i][j];\n }\n }\n\n // Check if each 1 is special using the precalculated sums\n for (int i = 0; i < mat.size(); i++) {\n for (int j = 0; j < mat[i].size(); j++) {\n if (mat[i][j] == 1 && row_sums[i] == 1 && col_sums[j] == 1) {\n result++;\n }\n }\n }\n\n return result;\n }\n};\n```\n```c []\n#include <stdlib.h>\n\nint numSpecial(int** mat, int matSize, int* matColSize) {\n int result = 0;\n\n // Arrays to store the sums of elements in each row and column\n int* rowSums = (int*)malloc(matSize * sizeof(int));\n int* colSums = (int*)malloc(matColSize[0] * sizeof(int));\n\n // Initialize rowSums and colSums to zeros\n for (int i = 0; i < matSize; i++) {\n rowSums[i] = 0;\n }\n for (int j = 0; j < matColSize[0]; j++) {\n colSums[j] = 0;\n }\n\n // Calculate the sums of elements in each row and column\n for (int i = 0; i < matSize; i++) {\n for (int j = 0; j < matColSize[0]; j++) {\n rowSums[i] += mat[i][j];\n colSums[j] += mat[i][j];\n }\n }\n\n // Check if each 1 is special using the precalculated sums\n for (int i = 0; i < matSize; i++) {\n for (int j = 0; j < matColSize[0]; j++) {\n if (mat[i][j] == 1 && rowSums[i] == 1 && colSums[j] == 1) {\n result++;\n }\n }\n }\n\n // Free allocated memory\n free(rowSums);\n free(colSums);\n\n return result;\n}\n```\n\n\n- Please upvote me !!!
| 10 | 0 |
['C', 'C++', 'Java', 'Go', 'Python3', 'Rust', 'Ruby', 'C#']
| 1 |
special-positions-in-a-binary-matrix
|
C++/Python one pass||0 ms Beats 100%
|
cpython-one-pass0-ms-beats-100-by-anwend-uz5s
|
Intuition\n Describe your first thoughts on how to solve this problem. \nCheck which rows & columns have exactly one 1!\n\nThe revised C++ code simplifies the l
|
anwendeng
|
NORMAL
|
2023-12-13T02:12:36.685440+00:00
|
2023-12-14T22:43:08.859049+00:00
| 3,000 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCheck which rows & columns have exactly one 1!\n\nThe revised C++ code simplifies the loop. The unnecessary copying for column vector is omitted which becomes a fast code, runs in 0 ms and beats 100%!\n\nPython code is in the same manner implemented which runs in 137ms & beats 100%.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBuild a function `check1` to locate the positions of 1\'s in a vector. This`check1` function is useful. The very crucual part is especially when `idx=check1(vect, sz).size()>1`; the columns `j` in `idx` cannot be special indices which can save redundant checking.\n```\n vector<int> check1(vector<int>& vect, int sz){\n vector<int> ans;\n for(int i=0; i<sz; i++){\n if (vect[i]==1) ans.push_back(i);\n }\n return ans;\n }\n```\nIt takes a reference to a vector of integers `vect` and an integer `sz` as parameters. The function iterates through the elements of vect and collects the indices where the value is equal to 1 into a new vector `ans`. \n\n```\n for(int i=0; i<m; i++){\n auto idx=check1(mat[i], n);\n int j;\n if (idx.size()==1 && col[(j=idx[0])]==0){\n col[j]=1;\n col_j.assign(m, 0);\n for(int k=i+1; k<m; k++)\n col_j[k]=mat[k][j];\n if (check1(col_j, m).size()==0){\n // cout<<"("<<i<<","<<j<<")";\n ans++;\n } \n }\n else{//cannot be special indices\n for(int j: idx)\n col[j]=1;\n }\n }\n return ans;\n\n```\nIt iterates through each row of the matrix (`mat`). For each row, it uses the `check1` function to find the indices of \'1\' in that row (`idx`). If there is exactly one \'1\' in the row and the corresponding column (`j`) has not been marked (`col[j] == 0`), it marks the column, copies the column into `col_j`, and checks if there is exactly one \'1\' in the column using `check1`. If true, it increments the ans counter.\n\nIf there is more than one \'1\' in the row, it marks all the corresponding columns in the `col` vector.\n\nLet\'s consider the testcase\n`[[0,0,0,0,0,1,0,0],[0,0,0,0,1,0,0,1],[0,0,0,0,1,0,0,0],[1,0,0,0,1,0,0,0],[0,0,1,1,0,0,0,0],[0,0,0,0,0,0,1,0]]`\nThe speical indices are `(0,5), (5,6)`. The process is as follows\n```\nrow0->idx=[5]:(0,5)\nrow1->idx=[4,7] \nrow2->idx=[4] \nrow3->idx=[0,4] \nrow4->idx=[2,3] \nrow5->idx=[6]:(5,6)\n\nans=2\n```\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(nm)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$O(m+n)$\n# Code\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n vector<int> check1(vector<int>& vect, int sz){\n vector<int> ans;\n for(int i=0; i<sz; i++){\n if (vect[i]==1) ans.push_back(i);\n }\n return ans;\n }\n int numSpecial(vector<vector<int>>& mat) {\n int m=mat.size(), n=mat[0].size(), ans=0;\n vector<bool> col(n, 0);// check or \n vector<int> col_j(m);\n for(int i=0; i<m; i++){\n auto idx=check1(mat[i], n);\n int j;\n if (idx.size()==1 && col[(j=idx[0])]==0){\n col[j]=1;\n col_j.assign(m, 0);\n \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 for(int k=i+1; k<m; k++)//Check if other 1 in remaining rows\n count_col1+=mat[k][j];\n if (count_col1==0){\n // cout<<"("<<i<<","<<j<<")\\n";\n ans++;\n } \n }\n else{//cannot be special indices\n for(int j: idx)\n col[j]=1;\n }\n }\n return ans;\n }\n};\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n# Revised C++ 0 ms Beats 100% \n```\n int numSpecial(vector<vector<int>>& mat) {\n int m=mat.size(), n=mat[0].size(), ans=0;\n vector<bool> col(n, 0);//already check or not\n for(int i=0; i<m; i++){\n auto idx=check1(mat[i], n);\n int j;\n if (idx.size()==1 && col[(j=idx[0])]==0){\n col[j]=1;\n int count_col1=0;\n for(int k=i+1; k<m; k++)//Check if other 1 in remaining rows\n count_col1+=mat[k][j];\n if (count_col1==0){\n // cout<<"("<<i<<","<<j<<")\\n";\n ans++;\n } \n }\n else{//cannot be special indices\n for(int j: idx)\n col[j]=1;\n }\n }\n return ans;\n }\n```\n# Python code runs in 137ms & beats 100%\n```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n def check1(row):\n ans=[]\n for i, x in enumerate(row):\n if x==1: \n ans.append(i)\n return ans\n m=len(mat)\n n=len(mat[0])\n ans=0\n col=[False]*n\n for row in mat:\n idx=check1(row)\n if len(idx)==1 and not col[j:=idx[0]]:\n col[j]=True\n count_col1=0\n for k in range(m):\n count_col1+=mat[k][j]\n if count_col1==1:\n ans+=1\n else:\n for j in idx:\n col[j]==True\n return ans\n```
| 10 | 0 |
['C', 'Matrix', 'Python3']
| 2 |
special-positions-in-a-binary-matrix
|
Java | Simple | Clean code
|
java-simple-clean-code-by-judgementdey-vts7
|
Complexity\n- Time complexity: O(m*n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(m+n)\n Add your space complexity here, e.g. O(n) \n\n
|
judgementdey
|
NORMAL
|
2023-12-13T01:42:04.886204+00:00
|
2023-12-13T01:42:04.886233+00:00
| 855 | false |
# Complexity\n- Time complexity: $$O(m*n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(m+n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int numSpecial(int[][] mat) {\n var m = mat.length;\n var n = mat[0].length;\n\n var rows = new int[m];\n var cols = new int[n];\n\n for (var i=0; i<m; i++) {\n for (var j=0; j<n; j++) {\n rows[i] += mat[i][j];\n cols[j] += mat[i][j];\n }\n }\n var ans = 0;\n\n for (var i=0; i<m; i++)\n for (var j=0; j<n; j++)\n if (mat[i][j] == 1 && rows[i] == 1 && cols[j] == 1)\n ans++;\n\n return ans;\n }\n}\n```\nIf you like my solution, please upvote it!
| 9 | 0 |
['Array', 'Matrix', 'Java']
| 1 |
special-positions-in-a-binary-matrix
|
🚀🚀 Beats 95% | Easy To Understand | Fully Explained 😎💖
|
beats-95-easy-to-understand-fully-explai-wc0a
|
Intuition\n- We want to find special positions in a binary matrix.\n- A position is special if the element at that position is 1 and all other elements in its r
|
The_Eternal_Soul
|
NORMAL
|
2023-12-13T02:34:32.139050+00:00
|
2023-12-13T02:34:32.139076+00:00
| 956 | false |
# Intuition\n- We want to find special positions in a binary matrix.\n- A position is special if the element at that position is 1 and all other elements in its row and column are 0.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Iterate through the matrix to find the positions where the element is 1.\n2. Store these positions in a map where the key is the row index and the value is the column index.\n3. For each position in the map, check the entire row and column to ensure that all other elements are 0.\n4. If a position satisfies the condition, increment the count of special positions.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- **Time complexity**:\n- The two nested loops iterate through the matrix, resulting in O(m * n) operations.\n- The final loop iterates through the map, resulting in additional O(m + n) operations.\n- Thus, the overall time complexity is O(m * n + m + n), which simplifies to O(m * n).\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- **Space complexity**:\n- We use a map to store positions, which can have at most m entries (number of rows).\n- The space complexity is O(m) for the map.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) \n {\n ios_base::sync_with_stdio(false);\n cin.tie(0);\n cout.tie(0);\n\n int ans = 0;\n int m = mat.size();\n int n = mat[0].size();\n unordered_map<int, int> mp; // Map to store positions where element is 1\n\n // Find positions where element is 1 and store in the map\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (mat[i][j] == 1)\n mp[i] = j;\n }\n }\n\n // Check each position in the map\n for (auto x : mp) {\n int i = x.first;\n int j = x.second;\n int temp = n - 1;\n int count = 0;\n\n // Check the entire row\n while (temp >= 0) {\n if (mat[i][temp] == 1)\n count++;\n temp--;\n }\n\n temp = m - 1;\n // Check the entire column\n while (temp >= 0) {\n if (mat[temp][j] == 1)\n count++;\n temp--;\n }\n\n if (count == 2)\n ans++; // If count is 2, the position is special\n }\n\n return ans;\n}\n\n};\n```\n\n
| 8 | 0 |
['Array', 'C', 'Matrix', 'Python', 'C++', 'Java', 'Python3', 'JavaScript']
| 1 |
special-positions-in-a-binary-matrix
|
[Python 3] One pass || 155ms || beats 99%
|
python-3-one-pass-155ms-beats-99-by-your-4qqw
|
python3 []\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n res = 0\n rows = [[] for _ in range(len(mat))]\n cols
|
yourick
|
NORMAL
|
2023-06-28T13:08:50.668536+00:00
|
2023-12-13T00:05:59.678439+00:00
| 784 | false |
```python3 []\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n res = 0\n rows = [[] for _ in range(len(mat))]\n cols = [0] * len(mat[0])\n \n for i in range(len(mat)):\n for j in range(len(mat[0])):\n if mat[i][j]:\n rows[i].append(j) \n cols[j] += 1\n\n for row in rows:\n if len(row) == 1 and cols[row[0]] == 1:\n res += 1\n\n return res\n```\n\n
| 8 | 0 |
['Matrix', 'Python', 'Python3']
| 0 |
special-positions-in-a-binary-matrix
|
C++ || Matrix || Short and Simple
|
c-matrix-short-and-simple-by-user3405ye-mcr2
|
Please upvote if you find the solution clean and concise.\nThank You!!\n\n\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n i
|
user3405Ye
|
NORMAL
|
2023-04-24T05:01:35.033878+00:00
|
2023-04-24T05:01:35.033926+00:00
| 746 | false |
Please upvote if you find the solution clean and concise.\n***Thank You!!***\n\n```\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n int m = mat.size(), n = mat[0].size(), res = 0;\n vector<int> rows(m), cols(n);\n for(int i=0;i<m;i++) {\n for(int j=0;j<n;j++) {\n rows[i] += mat[i][j];\n cols[j] += mat[i][j];\n }\n }\n for(int i=0;i<m;i++) {\n for(int j=0;j<n;j++) \n res += (rows[i] == 1 and cols[j] == 1 and mat[i][j]);\n }\n return res;\n }\n};\n```
| 8 | 0 |
['C', 'Matrix', 'C++']
| 0 |
special-positions-in-a-binary-matrix
|
a few solutions
|
a-few-solutions-by-claytonjwong-udea
|
Accumulate the sum of values for each ith row and jth column. Traverse each cell i, j of the input A and increment the count cnt if and only if A[i][j], row[i]
|
claytonjwong
|
NORMAL
|
2020-09-13T04:00:31.779041+00:00
|
2023-01-01T23:54:41.859548+00:00
| 763 | false |
Accumulate the sum of values for each `i`<sup>th</sup> row and `j`<sup>th</sup> column. Traverse each cell `i`, `j` of the input `A` and increment the count `cnt` if and only if `A[i][j]`, `row[i]`, and `col[j]` are all equal-to 1.\n\n---\n\n*Kotlin*\n```\nclass Solution {\n fun numSpecial(A: Array<IntArray>): Int {\n var cnt = 0\n var M = A.size\n var N = A[0].size\n var row = IntArray(M) { 0 }\n var col = IntArray(N) { 0 }\n for (i in 0 until M) {\n for (j in 0 until N) {\n if (A[i][j] == 1) {\n ++row[i]\n ++col[j]\n }\n }\n }\n for (i in 0 until M)\n for (j in 0 until N)\n if (A[i][j] == 1 && row[i] == 1 && col[j] == 1)\n ++cnt\n return cnt\n }\n}\n```\n\n*Javascript*\n```\nlet numSpecial = (A, cnt = 0) => {\n let M = A.length,\n N = A[0].length;\n let row = Array(M).fill(0),\n col = Array(N).fill(0);\n for (let i = 0; i < M; ++i)\n\t for (let j = 0; j < N; ++j)\n if (A[i][j])\n ++row[i],\n ++col[j];\n for (let i = 0; i < M; ++i)\n for (let j = 0; j < N; ++j)\n if (A[i][j] && row[i] == 1 && col[j] == 1)\n ++cnt;\n return cnt;\n};\n```\n\n*Python3*\n```\nclass Solution:\n def numSpecial(self, A: List[List[int]], cnt = 0) -> int:\n M = len(A)\n N = len(A[0])\n row = [0] * M\n col = [0] * N\n for i in range(M):\n for j in range(N):\n if A[i][j]:\n row[i] += 1\n col[j] += 1\n for i in range(M):\n for j in range(N):\n if A[i][j] and row[i] == 1 and col[j] == 1:\n cnt += 1\n return cnt\n```\n\n*C++*\n\n```\nclass Solution {\npublic:\n using VI = vector<int>;\n using VVI = vector<VI>;\n int numSpecial(VVI& A, int cnt = 0) {\n int M = A.size(),\n N = A[0].size();\n VI row(M),\n col(N);\n for (auto i{ 0 }; i < M; ++i)\n for (auto j{ 0 }; j < N; ++j)\n if (A[i][j])\n ++row[i],\n ++col[j];\n for (auto i{ 0 }; i < M; ++i)\n for (auto j{ 0 }; j < N; ++j)\n if (A[i][j] && row[i] == 1 && col[j] == 1)\n ++cnt;\n return cnt;\n }\n};\n```
| 8 | 1 |
[]
| 1 |
special-positions-in-a-binary-matrix
|
Go one pass 16 ms, 6.1 MB
|
go-one-pass-16-ms-61-mb-by-vashik-e2m4
|
\nfunc numSpecial(mat [][]int) int {\n rows, columns := len(mat),len(mat[0])\n specials := 0\n for i := 0; i < rows; i++ {\n checkCol := -1\n
|
vashik
|
NORMAL
|
2020-09-14T12:15:24.141329+00:00
|
2020-09-14T12:26:45.004033+00:00
| 401 | false |
```\nfunc numSpecial(mat [][]int) int {\n rows, columns := len(mat),len(mat[0])\n specials := 0\n for i := 0; i < rows; i++ {\n checkCol := -1\n for j := 0; j < columns; j++ {\n if mat[i][j] == 1 {\n if checkCol == -1 {\n checkCol = j\n } else {\n checkCol = -1\n break\n }\n }\n }\n if checkCol == -1 {\n continue\n }\n special := 1\n for k := 0; k < rows; k++ {\n if k == i {\n continue\n }\n if mat[k][checkCol] == 1 {\n special = 0\n\t\t\t\tmat[0][checkCol] = 1 // speed up future checkings\n break\n }\n }\n specials += special\n }\n return specials \n}\n```
| 7 | 0 |
['Go']
| 1 |
special-positions-in-a-binary-matrix
|
⭐✅|| STORING EACH ROW AND COL SUM || WELL EXPLAINED (HINDI) || BEATS 100% || ✅⭐
|
storing-each-row-and-col-sum-well-explai-nz5m
|
\n Describe your first thoughts on how to solve this problem. \n\n# ALGORITHM\n Describe your approach to solving the problem. \n1)Matrix ke dimensions nikalo:\
|
Sautramani
|
NORMAL
|
2023-12-13T04:18:22.651848+00:00
|
2023-12-13T04:30:02.380696+00:00
| 794 | false |
\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# ALGORITHM\n<!-- Describe your approach to solving the problem. -->\n1)**Matrix ke dimensions nikalo**:\nInput matrix mat ki rows (n) aur columns (m) ka pata lagayein.\n\n2)**Variables ko initialize karein**:\nans naamak ek variable ko 0 se initialize karein. Ye variable special positions ka count store karega.\n\n3)**Row aur column sum vectors ko initialize karein**:\nDo vectors rowsum aur colsum banayein jo har row aur column ke sum ko store karenge.\nrowsum n size ka vector hai jismein shuruwat mein sabhi elements 0 hain.\ncolsum m size ka vector hai jismein shuruwat mein sabhi elements 0 hain.\n\n4)**Row aur column sums nikalein**:\nMatrix ke har element par iterate karein.\nHar element ke liye rowsum aur colsum ko update karein.\n\n5)**Special positions ko check karein**:\nFir se matrix ke har element par iterate karein.\nHar element ke liye check karein ki mat[i][j] 1 hai, rowsum[i] 1 hai, aur colsum[j] 1 hai ya nahi.\nAgar saare conditions satisfy hote hain, to ans ko badhayein.\n\n6)**Result return karein**:\nans mein store kiye gaye special positions ka count return karein.\n\n# Complexity\n- Time complexity:O(n * m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n + m)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```C++ []\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n // Get the number of rows(n) and columns(m) in the matrix\n int n=mat.size();\n int m=mat[0].size();\n int ans=0;\n \n // Vector to store the sum of each row( SIZE OF VECTOR IS n AND ALL ELEMNTS ARE SET 0)\n vector<int>rowsum(n,0);\n // Vector to store the sum of each column of size m and all elements are initially 0\n vector<int>colsum(m,0);\n \n // Calculate the sum of each row and column\n for(int i=0;i<n;i++)\n {\n for(int j=0;j<m;j++)\n {\n rowsum[i]+=mat[i][j];\n colsum[j]+=mat[i][j];\n }\n }\n \n // Check for special positions\n for(int i=0;i<n;i++)\n {\n for(int j=0;j<m;j++)\n {\n // Check if the current position is 1 and the sum of its row and column is 1\n if(mat[i][j]==1 && rowsum[i]==1 && colsum[j]==1)\n {\n // Increment the ans for special positions\n ans++;\n }\n }\n }\n // Return the total count of special positions\n return ans;\n \n }\n};\n```\n```python []\npython 3 []\ndef column(matrix, i):\n return [row[i] for row in matrix]\nclass Solution:\n \n def numSpecial(self, mat: List[List[int]]) -> int:\n c=0\n for i in range(len(mat)):\n if(mat[i].count(1)==1):\n i=mat[i].index(1)\n col=column(mat,i)\n if(col.count(1)==1):\n c+=1\n \n return c \n```\n```java []\nclass Solution {\n public int numSpecial(int[][] mat) {\n // Get the number of rows (n) and columns (m) in the matrix\n int n = mat.length;\n int m = mat[0].length;\n \n // Initialize a counter for special positions\n int ans = 0;\n \n // Array to store the sum of each row (size of the array is n, and all elements are initially set to 0)\n int[] rowSum = new int[n];\n // Array to store the sum of each column (size of the array is m, and all elements are initially set to 0)\n int[] colSum = new int[m];\n \n // Calculate the sum of each row and column\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n rowSum[i] += mat[i][j];\n colSum[j] += mat[i][j];\n }\n }\n \n // Check for special positions\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n // Check if the current position is 1 and the sum of its row and column is 1\n if (mat[i][j] == 1 && rowSum[i] == 1 && colSum[j] == 1) {\n // Increment the counter for special positions\n ans++;\n }\n }\n }\n \n // Return the total count of special positions\n return ans;\n }\n}\n```\n
| 6 | 0 |
['Array', 'Matrix', 'Python', 'C++', 'Java', 'Python3']
| 3 |
special-positions-in-a-binary-matrix
|
EASY DECEMBER ⛄|| BEGINEER FRIENDLY APPROACH 🔥 || C++
|
easy-december-begineer-friendly-approach-wmep
|
Intuition and Appraoch :\nSeems like it all easy december going.. \u26C4\n\nSo, this problem we will do matrix traversal in both row wise and column wise. now
|
DEvilBackInGame
|
NORMAL
|
2023-12-13T03:46:58.366191+00:00
|
2023-12-13T14:04:35.013169+00:00
| 586 | false |
# Intuition and Appraoch :\nSeems like it all easy december going.. \u26C4\n\nSo, this problem we will do matrix traversal in both row wise and column wise. now how we doing lets discuss .\ni will discuss wrt array so that its easy to understand.\n1. First i am assigning` length of array` or can say `number of rows` with `n`. and number of column in each row with `m`.\n2. here taking a `count` variable to store the number of `1` occured in each row first. Then after if there exactly one `1` in a row then we will give the position of that `1` to our `pos` variable. \n3. after getting exactly one`1` in a `row` we will go through `rows` for same `column` whose position index is saved in our `pos `variable.\n4. then there also we will check same thing , if number of one\'s total is `1` then we will increment our `ans` variable. \n5. this how we will traverse through all `rows` and respective `columns`.\n6. return `ans` at last. \n\n# C++ Code :\n```\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n int m =mat[0].size();\n int pos=-1;\n int n =mat.size();\n int ans=0;\n for(int i=0;i<n;i++){\n int count=0;\n//check for number of 1 in each row\n for(int j=0;j<m;j++){\n if(mat[i][j]==1) {\n count++; \n pos=j;\n }\n }\n// if there\'s only one 1 in row ,then we will count total 1 in same column where 1 was found.\n if(count==1){\n count=0;//to count no. of 1 from beginning or you can compare count==2 at last.\n for(int k=0;k<n;k++){\n if(mat[k][pos]==1) count++;\n }\n//if total 1 in a column = 1, ans++\n if(count==1) ans++;\n }\n }\n return ans;\n }\n \n};\n```\n\n# UPVOTE \uD83D\uDE0A\u2B06\n\n
| 6 | 0 |
['Array', 'Matrix', 'C++']
| 1 |
special-positions-in-a-binary-matrix
|
Simple beginner friendly solution involving unordered maps
|
simple-beginner-friendly-solution-involv-puhb
|
Intuition\n Describe your first thoughts on how to solve this problem. \nAs question demands checking if the whole row and column of the current element has a 1
|
maxheap
|
NORMAL
|
2023-12-13T04:08:42.451092+00:00
|
2023-12-13T04:08:42.451141+00:00
| 1,045 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs question demands checking if the whole row and column of the current element has a 1 anywhere , we would obviously need to precompute all the visited elements(tbp 1 here).\n\nElements visited here are tracked via two seperate unordered maps viz. one for rows, and one for columns\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirstly we pre compute and populate the two unordered maps (**vis_rows** and **vis_cols**)\n\nThen we iterate over the matrix elements, whilst checking if the row has more than one 1s. If a row consists of more than one 1, we pass; else, we increment special\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n^2)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\nwhere, $$n$$ is the greater value among (n,m)\n\n{unordered maps contribute towards space complexity}\n\n# Code\n```\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n int rows = mat.size();\n int cols = mat[0].size();\n\n int special = 0;\n\n unordered_map<int,int> vis_rows;\n unordered_map<int,int> vis_cols;\n\n for (int i = 0; i < rows; i++)\n {\n for (int j = 0; j < cols; j++)\n {\n if (mat[i][j]==1)\n {\n vis_rows[i]++;\n vis_cols[j]++;\n }\n }\n }\n\n for (int i = 0; i < rows; i++)\n {\n for (int j = 0; j < cols; j++)\n {\n if (vis_rows.find(i)!=vis_rows.end() && vis_cols.find(j)!=vis_cols.end())\n {\n if (vis_rows[i] == 1 and vis_cols[j]==1)\n {\n if (mat[i][j]==1)\n special++;\n }\n }\n }\n }\n\n return special;\n \n }\n};\n```
| 5 | 0 |
['C++']
| 0 |
special-positions-in-a-binary-matrix
|
C# Solution for Special Positions In A Binary Matrix Problem
|
c-solution-for-special-positions-in-a-bi-vfyy
|
Intuition\n Describe your first thoughts on how to solve this problem. \n1.\tIterate through the matrix and count the number of ones in each row and each column
|
Aman_Raj_Sinha
|
NORMAL
|
2023-12-13T03:04:20.992228+00:00
|
2023-12-13T03:04:20.992263+00:00
| 281 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1.\tIterate through the matrix and count the number of ones in each row and each column.\n2.\tCheck each element of the matrix and verify if it is a special position according to the conditions specified.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.\tInitialize two arrays, rowOnes and colOnes, to keep track of the count of ones in each row and each column, respectively.\n2.\tTraverse the matrix, summing up the number of ones in each row and each column.\n3.\tIterate through the matrix again and check if the current element is 1 and both its row and column have only a single one.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\u2022\tLet the matrix dimensions be m x n.\n\u2022\tCalculating the count of ones in each row and column requires two nested loops, leading to O(m * n) operations.\n\u2022\tChecking for special positions also involves two nested loops, resulting in an additional O(m * n) operations.\n\u2022\tTherefore, the overall time complexity is O(m * n).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\u2022\tTwo arrays, rowOnes and colOnes, of sizes m and n respectively are used to store the count of ones in each row and each column.\n\u2022\tHence, the space complexity is O(m + n) due to the space required for these arrays to store the counts.\n\n# Code\n```\npublic class Solution {\n public int NumSpecial(int[][] mat) {\n int m = mat.Length;\n int n = mat[0].Length;\n int[] rowOnes = new int[m];\n int[] colOnes = new int[n];\n int count = 0;\n\n // Counting the number of ones in each row and column\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n rowOnes[i] += mat[i][j];\n colOnes[j] += mat[i][j];\n }\n }\n\n // Checking for special positions\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (mat[i][j] == 1 && rowOnes[i] == 1 && colOnes[j] == 1) {\n count++;\n }\n }\n }\n\n return count;\n }\n}\n```
| 5 | 0 |
['C#']
| 0 |
special-positions-in-a-binary-matrix
|
[C++] Two Simple Solutions
|
c-two-simple-solutions-by-pankajgupta20-pmu6
|
Solution: 1\nTime Complexity: O(n^3)\nSpace Complexity: O(1)\n\n\tclass Solution {\n\tpublic:\n\t\tint numSpecial(vector>& mat) {\n\t\t\tint nRows = mat.size();
|
pankajgupta20
|
NORMAL
|
2021-05-14T19:16:05.532687+00:00
|
2021-05-14T19:16:05.532735+00:00
| 941 | false |
##### Solution: 1\nTime Complexity: O(n^3)\nSpace Complexity: O(1)\n\n\tclass Solution {\n\tpublic:\n\t\tint numSpecial(vector<vector<int>>& mat) {\n\t\t\tint nRows = mat.size();\n\t\t\tint nCols = mat[0].size();\n\t\t\tint res = 0;\n\t\t\tfor(int i = 0; i < nRows; i++){\n\t\t\t\tfor(int j = 0; j < nCols; j++){\n\t\t\t\t\tif(mat[i][j] == 1){\n\t\t\t\t\t\tint colSum = 0;\n\t\t\t\t\t\tint rowSum = 0;\n\t\t\t\t\t\tfor(int r = 0; r < nRows; r++){\n\t\t\t\t\t\t\tcolSum += mat[r][j];\n\t\t\t\t\t\t}\n\t\t\t\t\t\tfor(int c = 0; c < nCols; c++){\n\t\t\t\t\t\t\trowSum += mat[i][c];\n\t\t\t\t\t\t}\n\t\t\t\t\t\tif(colSum == 1 and rowSum == 1){\n\t\t\t\t\t\t\tres++;\n\t\t\t\t\t\t}\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t}\n\t\t\treturn res;\n\t\t}\n\t};\n##### Solution: 2\nTime Complexity: O(n^2)\nSpace Complexity: O(n)\n\n\tclass Solution {\n\tpublic:\n\t\tint numSpecial(vector<vector<int>>& mat) {\n\t\t\tint nRows = mat.size();\n\t\t\tint nCols = mat[0].size();\n\n\t\t\tvector<int> rowSum(nRows);\n\t\t\tvector<int> colSum(nCols);\n\n\t\t\tfor(int i = 0; i < nRows; i++){\n\t\t\t\tfor(int j = 0; j < nCols; j++){\n\t\t\t\t\trowSum[i] += mat[i][j];\n\t\t\t\t\tcolSum[j] += mat[i][j];\n\t\t\t\t}\n\t\t\t}\n\n\t\t\tint res = 0;\n\t\t\tfor(int i = 0; i < nRows; i++) {\n\t\t\t\tif(rowSum[i] == 1){\n\t\t\t\t\tfor(int j = 0; j < nCols; j++) {\n\t\t\t\t\t\tif(colSum[j] == 1 and mat[i][j] == 1){\n\t\t\t\t\t\t\tres++;\n\t\t\t\t\t\t\tbreak;\n\t\t\t\t\t\t}\n\t\t\t\t\t} \n\t\t\t\t}\n\t\t\t}\n\t\t\treturn res;\n\t\t}\n\t};
| 5 | 0 |
['C', 'C++']
| 0 |
special-positions-in-a-binary-matrix
|
Simple (5 line) efficient (faster than 99.8%) Python solution
|
simple-5-line-efficient-faster-than-998-6rr98
|
\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n count = 0\n cols = list(zip(*mat))\n for row in mat:\n
|
Kartheyan
|
NORMAL
|
2020-10-13T12:17:44.142669+00:00
|
2020-10-13T12:17:44.142700+00:00
| 342 | false |
```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n count = 0\n cols = list(zip(*mat))\n for row in mat:\n if sum(row)==1 and sum(cols[row.index(1)])==1:\n count+=1\n return count\n```
| 5 | 0 |
[]
| 0 |
special-positions-in-a-binary-matrix
|
JavaScript ~[76 ms, 40.2 MB]
|
javascript-76-ms-402-mb-by-dl90-iiue
|
\uD83D\uDE80\njs\nvar numSpecial = function (mat) {\n const rows = mat.length\n const cols = mat[0].length\n const rowArr = new Int8Array(rows)\n const colA
|
dl90
|
NORMAL
|
2020-09-16T06:37:08.997599+00:00
|
2020-09-16T06:37:56.966615+00:00
| 458 | false |
\uD83D\uDE80\n```js\nvar numSpecial = function (mat) {\n const rows = mat.length\n const cols = mat[0].length\n const rowArr = new Int8Array(rows)\n const colArr = new Int8Array(cols)\n const set = new Set()\n\n for (let i = 0; i < rows; i++) {\n for (let j = 0; j < cols; j++) {\n if (mat[i][j]) {\n set.add([i, j])\n rowArr[i]++\n colArr[j]++\n }\n }\n }\n\n let count = 0\n for (const [y, x] of set) {\n if (rowArr[y] === 1 && colArr[x] === 1) count++\n }\n return count\n}\n```
| 5 | 0 |
['JavaScript']
| 0 |
special-positions-in-a-binary-matrix
|
Java | O (M*N) Time | O (M+N) space
|
java-o-mn-time-o-mn-space-by-arizonazerv-zzyk
|
Intuition was to do exactly as the problem asked, count the number of 1\'s in every row and column, store them in a separate array and later whenever we encount
|
arizonazervas
|
NORMAL
|
2020-09-13T04:10:43.427235+00:00
|
2020-09-13T04:10:43.427277+00:00
| 577 | false |
* Intuition was to do exactly as the problem asked, count the number of 1\'s in every row and column, store them in a separate array and later whenever we encounter a 1, look up the value in its column and row (our two arrays) , if both of them are <=1, increment the count.\n\n```\n public int numSpecial(int[][] mat) {\n int nr = mat.length;\n int nc = mat[0].length;\n int[] rowSum = new int[nr];\n int[] colSum = new int[nc];\n int ans = 0;\n for (int i = 0; i < nr; i++) {\n for (int j = 0; j < nc; j++) {\n if (mat[i][j] == 1) {\n rowSum[i]++;\n colSum[j]++;\n }\n }\n }\n\n for (int i = 0; i < nr; i++) {\n for (int j = 0; j < nc; j++) {\n if (mat[i][j] == 1) {\n if (colSum[j] <= 1 && rowSum[i] <= 1)\n ans++;\n }\n }\n }\n return ans;\n }\n```
| 5 | 0 |
[]
| 0 |
special-positions-in-a-binary-matrix
|
✅ One Line Solution
|
one-line-solution-by-mikposp-gp1k
|
(Disclaimer: these are not examples to follow in a real project - they are written for fun and training mostly. PEP 8 is violated intentionally)\n\n# Code #1\nT
|
MikPosp
|
NORMAL
|
2023-12-13T09:49:05.475037+00:00
|
2024-01-13T10:45:35.449724+00:00
| 767 | false |
(Disclaimer: these are not examples to follow in a real project - they are written for fun and training mostly. PEP 8 is violated intentionally)\n\n# Code #1\nTime complexity: $$O(m*n)$$. Space complexity: $$O(1)$$.\n```\nclass Solution:\n def numSpecial(self, M: List[List[int]]) -> int:\n return sum(sum(rr[j] for rr in M)==1 for r in M if sum(r)==1 and (j:=r.index(1))+1)\n```\n\n# Code #2\nTime complexity: $$O(m*n)$$. Space complexity: $$O(m*n)$$.\n```\nclass Solution:\n def numSpecial(self, M: List[List[int]]) -> int:\n return (T:=list(zip(*M))) and sum(sum(T[r.index(1)])==1 for r in M if sum(r)==1)\n```\n\n# Code #3\nTime complexity: $$O(m*n)$$. Space complexity: $$O(m+n)$$.\n```\nclass Solution:\n def numSpecial(self, M: List[List[int]]) -> int:\n return (R:=[sum(r)==1 for r in M]) and (C:=[sum(c)==1 for c in zip(*M)]) and \\\n sum(M[i][j]*R[i]*C[j] for i in range(len(R)) for j in range(len(C)))\n```\n
| 4 | 0 |
['Array', 'Matrix', 'Python', 'Python3']
| 1 |
special-positions-in-a-binary-matrix
|
C++ solutions
|
c-solutions-by-infox_92-wahb
|
\nclass Solution {\npublic:\n\tint numSpecial(vector<vector<int>>& mat) {\n\t\tint nRows = mat.size();\n\t\tint nCols = mat[0].size();\n\t\tint res = 0;\n\t\tfo
|
Infox_92
|
NORMAL
|
2022-11-09T06:41:33.670990+00:00
|
2022-11-09T06:41:33.671033+00:00
| 717 | false |
```\nclass Solution {\npublic:\n\tint numSpecial(vector<vector<int>>& mat) {\n\t\tint nRows = mat.size();\n\t\tint nCols = mat[0].size();\n\t\tint res = 0;\n\t\tfor(int i = 0; i < nRows; i++){\n\t\t\tfor(int j = 0; j < nCols; j++){\n\t\t\t\tif(mat[i][j] == 1){\n\t\t\t\t\tint colSum = 0;\n\t\t\t\t\tint rowSum = 0;\n\t\t\t\t\tfor(int r = 0; r < nRows; r++){\n\t\t\t\t\t\tcolSum += mat[r][j];\n\t\t\t\t\t}\n\t\t\t\t\tfor(int c = 0; c < nCols; c++){\n\t\t\t\t\t\trowSum += mat[i][c];\n\t\t\t\t\t}\n\t\t\t\t\tif(colSum == 1 and rowSum == 1){\n\t\t\t\t\t\tres++;\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t\treturn res;\n\t}\n};\n```
| 4 | 0 |
['C', 'C++']
| 0 |
special-positions-in-a-binary-matrix
|
📌 Python Memory-Efficient Solution
|
python-memory-efficient-solution-by-vand-v79k
|
\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n onesx = []\n onesy = []\n for ri, rv in enumerate(mat):\n
|
vanderbilt
|
NORMAL
|
2022-02-27T04:18:16.261610+00:00
|
2022-03-01T09:34:25.617743+00:00
| 629 | false |
```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n onesx = []\n onesy = []\n for ri, rv in enumerate(mat):\n for ci, cv in enumerate(rv):\n if cv == 1:\n onesx.append(ri)\n onesy.append(ci)\n \n count = 0\n for idx in range(len(onesx)):\n if onesx.count(onesx[idx]) == 1:\n if onesy.count(onesy[idx]) == 1:\n count += 1\n return count\n```
| 4 | 0 |
['Python', 'Python3']
| 1 |
special-positions-in-a-binary-matrix
|
Simple Java Solution O(m*n) (Easy)
|
simple-java-solution-omn-easy-by-shantan-xkvc
|
Up-vote if helpfull\n\nclass Solution {\n public int numSpecial(int[][] mat) {\n int row[]=new int[mat.length];\n int col[]=new int[mat[0].leng
|
ShantanuSinghStrive
|
NORMAL
|
2021-05-25T10:48:04.522140+00:00
|
2021-05-25T10:48:04.522181+00:00
| 533 | false |
**Up-vote if helpfull**\n```\nclass Solution {\n public int numSpecial(int[][] mat) {\n int row[]=new int[mat.length];\n int col[]=new int[mat[0].length];\n int res=0;\n for(int i=0;i<mat.length;i++){\n for(int j=0;j<mat[0].length;j++){\n if(mat[i][j]==1){\n row[i]++;\n col[j]++;\n }\n }\n }\n for(int i=0;i<mat.length;i++){\n for(int j=0;j<mat[0].length;j++){\n if(mat[i][j]==1 && row[i]==1 && col[j]==1){\n res++;\n }\n }\n }\n return res;\n }\n}\n\n```
| 4 | 1 |
['Java']
| 0 |
special-positions-in-a-binary-matrix
|
[Python3] 5-line 2-pass
|
python3-5-line-2-pass-by-ye15-iwag
|
\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n m, n = len(mat), len(mat[0])\n row, col = [0]*m, [0]*n\n for i,
|
ye15
|
NORMAL
|
2020-09-13T04:01:48.682002+00:00
|
2020-09-13T04:01:48.682049+00:00
| 672 | false |
```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n m, n = len(mat), len(mat[0])\n row, col = [0]*m, [0]*n\n for i, j in product(range(m), range(n)): \n if mat[i][j]: row[i], col[j] = 1 + row[i], 1 + col[j]\n return sum(mat[i][j] and row[i] == 1 and col[j] == 1 for i, j in product(range(m), range(n)))\n```
| 4 | 1 |
['Python3']
| 0 |
special-positions-in-a-binary-matrix
|
JavaScript | C++
|
javascript-c-by-nurliaidin-15k1
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Nurliaidin
|
NORMAL
|
2023-12-14T13:53:32.066143+00:00
|
2023-12-14T13:53:32.066182+00:00
| 293 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```javascript []\n/**\n * @param {number[][]} mat\n * @return {number}\n */\nvar numSpecial = function(mat) {\n let row = new Array(mat.length).fill(0);\n let col = new Array(mat[0].length).fill(0);\n\n for(let x=0; x<mat.length; x++) {\n for(let i=0; i<mat[x].length; i++) {\n col[i] += mat[x][i];\n row[x] += mat[x][i];\n }\n }\n let res = 0;\n for(let x=0; x<row.length; x++) {\n if(row[x]==1) {\n for(let i=0; i<col.length; i++) {\n if(col[i]==1 && mat[x][i]==1) res++;\n }\n }\n }\n return res;\n};\n```\n```cpp []\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n vector<int> row(mat.size(), 0);\n vector<int> col(mat[0].size(), 0);\n\n for(int x=0; x<mat.size(); x++) {\n for(int i=0; i<mat[x].size(); i++) {\n row[x] += mat[x][i];\n col[i] += mat[x][i];\n }\n }\n int res = 0;\n for(int x=0; x<row.size(); x++) {\n if(row[x]==1) {\n for(int i=0; i<col.size(); i++) {\n if(col[i]==1 && mat[x][i]==1) res++;\n }\n }\n }\n return res;\n }\n};\n```\n
| 3 | 0 |
['C++', 'JavaScript']
| 2 |
special-positions-in-a-binary-matrix
|
Beats 100% of users with C++ ( BruteForce Approach ) Easy to understand
|
beats-100-of-users-with-c-bruteforce-app-hdo2
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n\n\n\n\n\nif you like the approach please upvote it\n\n\n\n\n\n\nif you like the appr
|
abhirajpratapsingh
|
NORMAL
|
2023-12-13T16:19:55.131442+00:00
|
2023-12-13T16:19:55.131473+00:00
| 16 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n\n\n\n\nif you like the approach please upvote it\n\n\n\n\n\n\nif you like the approach please upvote it\n\n\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> O ( N*M )\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->O ( 1 )\n\n# Code\n```\nclass Solution {\npublic:\n\n int checkOne(vector<vector<int>>& mat , int row , int column)\n {\n int one=0;\n for(int i=0;i<mat[0].size();i++)\n {\n if(mat[row][i]==1)\n one++;\n }\n for(int i=0;i<mat.size();i++)\n {\n if(mat[i][column]==1)\n one++;\n }\n if(one>2)\n return 0;\n return 1;\n }\n int numSpecial(vector<vector<int>>& mat) \n {\n int count=0;\n for(int i=0;i<mat.size();i++)\n {\n for(int j=0;j<mat[0].size();j++)\n {\n if(mat[i][j]==1)\n count=count+checkOne(mat,i,j);\n }\n }\n return count;\n }\n};\n```
| 3 | 0 |
['Array', 'Matrix', 'C++']
| 0 |
special-positions-in-a-binary-matrix
|
Java Approach||beginners friendly
|
java-approachbeginners-friendly-by-hithe-dpxs
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Hitheash
|
NORMAL
|
2023-12-13T14:57:48.835962+00:00
|
2023-12-13T14:57:48.835986+00:00
| 651 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int numSpecial(int[][] mat) {\n int rows = mat.length, cols = mat[0].length;\n int rowSum[] = new int[rows], colSum[] = new int[cols];\n for(int r = 0; r < rows; r++){\n for(int c = 0; c < cols; c++){\n rowSum[r] += mat[r][c];\n }\n }\n\n for(int c = 0; c < cols; c++){\n for(int r = 0; r < rows; r++){\n colSum[c] += mat[r][c];\n }\n }\n int s = 0;\n for(int r = 0; r<rows; r++){\n for(int c = 0; c < cols; c++){\n if(mat[r][c] == 1 && rowSum[r] == 1 && colSum[c] == 1)s++;\n }\n }\n return s;\n }\n}\n```
| 3 | 0 |
['Java']
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.