question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
special-positions-in-a-binary-matrix
|
✅ Fastest Possible Solution ! Beats 100% 🔥 | Easy approach 🐣 | Easy explaination😉.
|
fastest-possible-solution-beats-100-easy-ivf1
|
\n\n# Intuition\n Describe your first thoughts on how to solve this problem. \n All we need to do, is to check for each cell which contains 1, all its sibling c
|
abdelazizSalah
|
NORMAL
|
2023-12-13T07:45:46.287778+00:00
|
2023-12-13T07:45:46.287801+00:00
| 436 | false |
\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n* All we need to do, is to check for each cell which contains 1, all its sibling cells which lay in the same row, and the same column.\n* If any of them contains 1, so we neglect it, otherwise, we should count it with us.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n* The solution relies on two main functions.\n## 1. numSpecial(mat)\n* This is our main function, and it should return the count of the special ones.\n* Its main logic is\n1. create a bool vector with the size of the rows in the given matrix\n - to indicate whethere each row is possible or not.\n - if we found that a certain row contains more than one element, we should just avoid iterating on it in the future to save time.\n2. do the same for the columns. \n3. initialize a **res** counter to store the result inside it.\n4. iterate over all the cells in the given matrix. \n 1. if the cell contains **1**\n 1. check if the current row idx is not marked as violated (contains more than one **1** )\n 2. check if the current col idx is not marked as violated\n 1. call the **check** function on the given row idx and col idx\n 2. if it returned true\n 3. increment the counter by 1 \n5. return the result\n\n## 2. check(mat, i , j , rows, cols )\n### Parameters\n* mat -> the given matrix\n* i -> the current row idx\n* j -> the current col idx\n* rows -> the total number of rows in the matrix\n* cols -> the total number of cols in the matrix\n### Return Type\n* bool -> True if it was a special **1**, False otherwise.\n\n### Main logic\n1. iterate over all rows with fixing the current column.\n 1. if the idx was same as the sent row\n 1. skip this iteration\n 2. if you found that mat[x][j] which is the cell at which you point in this iteration contains 1\n 1. just return false, as our condition is now violated\n2. now do the same logic by iterating over all cols with fixing the current row. \n3. if no violance exist, just return true.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n1. O(m * n * (m + n)*k)\n2. where\n - m -> number of columns\n - n -> number of rows\n - k -> number of ones in the binary matrix, because we apply the check condition only if we have one. \n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n1. O(m + n) \n2. where\n - m -> number of columns\n - n -> number of rows\n\n# Code\n```\n #include <bits/stdc++.h>\n#pragma GCC optimize("O3")\n#pragma GCC optimize("Ofast", "inline", "ffast-math", "unroll-loops", "no-stack-protector")\n#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,avx2,tune=native", "f16c")\nstatic const auto DPSolver = []()\n{ std::ios_base::sync_with_stdio(false); std::cin.tie(nullptr); std::cout.tie(nullptr); return \'c\'; }();\nusing namespace std;\nclass Solution {\npublic:\n\n\nbool check (vector<vector<int>> &mat, int i , int j, int rows, int cols) {\n // loop over the whole row ( other cols)\n for (int x = 0; x < rows; x++)\n if (x == i)\n continue; \n else if (mat[x][j])\n return false; \n // loop over the whole cols\n for (int x = 0; x < cols; x++)\n if (x == j)\n continue; \n else if (mat[i][x])\n return false; \n \n return true; \n}\nint numSpecial(vector<vector<int>> &mat)\n{\n DPSolver; \n int rows = mat.size();\n int cols = mat[0].size();\n vector<bool> rowsFlags(rows); \n vector<bool> colsFlags(cols); \n\n int res = 0; \n for (int i = 0 ; i < rows; i ++){\n for (int j = 0 ; j < cols; j ++){\n if (mat[i][j])\n if(!rowsFlags[i] && !colsFlags[j])\n res += check(mat, i, j, rows, cols); \n }\n }\n return res; \n}\n};\n```
| 3 | 0 |
['Array', 'Math', 'Greedy', 'Matrix', 'C++']
| 0 |
special-positions-in-a-binary-matrix
|
Rust/Python/Go two passes over matrix
|
rustpythongo-two-passes-over-matrix-by-s-kdor
|
Intuition\nWe can fist check how many times have we seen one in each column/row. This can be done by just passing over matrix and incrementing the corresponding
|
salvadordali
|
NORMAL
|
2023-12-13T02:04:57.767255+00:00
|
2023-12-13T02:04:57.767293+00:00
| 199 | false |
# Intuition\nWe can fist check how many times have we seen one in each column/row. This can be done by just passing over matrix and incrementing the corresponding value if `M[y][x] == 1`\n\nThen we do a second pass and if `M[y][x] == 1` and our count is 1 for both rows/columns, then increment the answer\n\n# Complexity\n- Time complexity: $O(n \\cdot m)$\n- Space complexity: $O(n + m)$\n\n# Code\n```Go []\nfunc numSpecial(M [][]int) int {\n nx, ny := len(M[0]), len(M)\n data_x := make([]int, nx)\n data_y := make([]int, ny)\n\n for y := 0; y < ny; y++ {\n for x := 0; x < nx; x++ {\n if M[y][x] == 1 {\n data_x[x]++\n data_y[y]++\n }\n }\n }\n\n res := 0\n for y := 0; y < ny; y++ {\n for x := 0; x < nx; x++ {\n if M[y][x] == 1 && data_x[x] == 1 && data_y[y] == 1 {\n res++\n }\n }\n }\n\n return res\n}\n```\n```python []\nclass Solution:\n def numSpecial(self, M: List[List[int]]) -> int:\n Y, X = len(M), len(M[0])\n list_y = [0] * Y\n list_x = [0] * X\n\n for y in range(Y):\n for x in range(X):\n if M[y][x] == 1:\n list_y[y] += 1\n list_x[x] += 1\n \n res = 0\n for y in range(Y):\n for x in range(X):\n if M[y][x] and list_y[y] == 1 and list_x[x] == 1:\n res += 1\n return res\n```\n```Rust []\nimpl Solution {\n pub fn num_special(M: Vec<Vec<i32>>) -> i32 {\n let (nx, ny) = (M[0].len(), M.len());\n let mut data_x = vec![0; nx];\n let mut data_y = vec![0; ny];\n\n for y in 0 .. ny {\n for x in 0 .. nx {\n if M[y][x] == 1 {\n data_x[x] += 1;\n data_y[y] += 1;\n }\n }\n }\n\n let mut res = 0;\n for y in 0 .. ny {\n for x in 0 .. nx {\n if M[y][x] == 1 && data_x[x] == 1 && data_y[y] == 1 {\n res += 1;\n }\n }\n } \n\n return res;\n }\n}\n```\n
| 3 | 0 |
['Python', 'Go', 'Rust']
| 0 |
special-positions-in-a-binary-matrix
|
[C++] Count 1 in each Row & Column
|
c-count-1-in-each-row-column-by-awesome-xjgyz
|
Intuition\n Describe your first thoughts on how to solve this problem. \n- Count the number of 1 in each row and column\n- Count the number of positions that me
|
pepe-the-frog
|
NORMAL
|
2023-12-13T01:39:36.490706+00:00
|
2023-12-13T01:39:36.490730+00:00
| 597 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- Count the number of `1` in each row and column\n- Count the number of positions that meet the following conditions:\n - `mat[i][j] == 1`\n - `countRow[i] == 1`\n - `countCol[i] == 1`\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- The 1st pass is for counting\n- The 2nd pass is for checking\n\n# Complexity\n- Time complexity: $$O(mn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(m + n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n // time/space: O(mn)/O(m + n)\n int numSpecial(vector<vector<int>>& mat) {\n int m = mat.size(), n = mat[0].size();\n vector<int> countRow(m, 0), countCol(n, 0);\n for (int r = 0; r < m; r++) {\n for (int c = 0; c < n; c++) {\n if (mat[r][c] == 1) {\n countRow[r]++, countCol[c]++;\n }\n }\n }\n\n int result = 0;\n for (int r = 0; r < m; r++) {\n for (int c = 0; c < n; c++) {\n if ((mat[r][c] == 1) && (countRow[r] == 1) && (countCol[c] == 1)) result++;\n }\n }\n return result;\n }\n};\n```
| 3 | 0 |
['Matrix', 'Counting', 'C++']
| 0 |
special-positions-in-a-binary-matrix
|
EASY || BEGINNER
|
easy-beginner-by-abhishekkant135-tdi9
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe algorithm iterates through each position in the matrix and checks if it is a specia
|
Abhishekkant135
|
NORMAL
|
2023-12-13T01:01:02.790664+00:00
|
2023-12-13T01:01:02.790684+00:00
| 201 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe algorithm iterates through each position in the matrix and checks if it is a special position.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Use nested loops to iterate through each position in the matrix.\n2. For each position (i, j) with mat[i][j] == 1, calculate the sum of elements in row i and column j.\n3. If the sum is 2, increment the count as the current position is special.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N * M * (N + M))\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nUPVOTE PLEASE\n# Code\n```\nclass Solution {\n public int numSpecial(int[][] mat) {\n int count=0;\n for(int i=0;i<mat.length;i++){\n for(int j=0;j<mat[0].length;j++){\n int sum=0;\n if(mat[i][j]==1){\n for(int k=0;k<mat.length;k++){\n sum+=mat[k][j];\n }\n for(int k=0;k<mat[0].length;k++){\n sum+=mat[i][k];\n }\n if(sum==2){\n count++;\n }\n\n }\n }\n }\n return count;\n }\n}\n```
| 3 | 0 |
['Java']
| 0 |
special-positions-in-a-binary-matrix
|
[We💕Simple] One Liner! (Beat 100%)
|
wesimple-one-liner-beat-100-by-yooseungk-r6lm
|
Python3\n\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n return sum(\n sum(mat[i][col] for i in range(len(mat))) =
|
YooSeungKim
|
NORMAL
|
2023-12-13T00:29:36.410167+00:00
|
2023-12-13T13:49:10.518926+00:00
| 1,245 | false |
## Python3\n```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n return sum(\n sum(mat[i][col] for i in range(len(mat))) == 1\n for col in [\n row.index(1)\n for row in mat\n if sum(row) == 1\n ]\n )\n\n```\n\n## Kotlin\n``` Kotlin\nclass Solution {\n fun numSpecial(mat: Array<IntArray>): Int =\n mat.mapNotNull { row -> \n row.indexOfFirst { it == 1 }.takeIf { it >= 0 && row.drop(it+1).sum() == 0 }\n }.count { col ->\n mat.sumOf { it[col] } == 1\n }\n}\n```\n\n# Approach\n\n1. **Mapping Rows to Potential Columns**: The function `numSpecial` takes a 2D array `mat` (a matrix) as input. It uses the `mapNotNull` function on this matrix, which processes each row and potentially transforms it to a different value. In this case, the transformation is to identify the column index of the first occurrence of \'1\' in a row.\n\n2. **Identifying Unique \'1\'s in a Row**: Inside `mapNotNull`, `row.indexOfFirst { it == 1 }` finds the index of the first \'1\' in the row. The `takeIf` function is then used to ensure two things:\n - The index is non-negative (i.e., there is at least one \'1\' in the row).\n - All subsequent elements in the row after this \'1\' are zeros (checked by `row.drop(it+1).sum() == 0`).\n3. **Counting Special Elements**: The resulting list from `mapNotNull` contains column indices where there might be a "special" element. The `count` function is then used to count how many of these column indices actually represent a "special" element. This is done by checking for each column index `col` if the sum of all elements in that column (`mat.sumOf { it[col] }`) is equal to 1, which would mean the \'1\' in this column is unique and not shared with other rows.\n\nIn summary, the code strategy is to first identify potential columns for each row where a "special" element could exist. Then, it verifies these potential columns to ensure that they contain only one \'1\' in the entire column. This approach efficiently identifies "special" elements by minimizing the need to repeatedly scan entire rows and columns.\n
| 3 | 0 |
['Python', 'Python3', 'Kotlin']
| 2 |
special-positions-in-a-binary-matrix
|
Java Solution | 91% time | 95% memory
|
java-solution-91-time-95-memory-by-tbekp-d4ej
|
Code\n\nclass Solution {\n public int numSpecial(int[][] mat) {\n int count = 0;\n for (int i = 0; i < mat.length; i++) {\n for (int
|
tbekpro
|
NORMAL
|
2022-11-05T08:37:38.907358+00:00
|
2022-11-05T08:37:38.907383+00:00
| 1,108 | false |
# Code\n```\nclass Solution {\n public int numSpecial(int[][] mat) {\n int count = 0;\n for (int i = 0; i < mat.length; i++) {\n for (int j = 0; j < mat[0].length; j++) {\n if (mat[i][j] == 1 && isSpecialRow(i, mat) && isSpecialCol(j, mat)) {\n count++;\n }\n }\n }\n return count;\n }\n\n private boolean isSpecialRow(int row, int[][] mat) {\n int sum = 0;\n for (int i = 0; i < mat[row].length; i++) {\n sum += mat[row][i];\n if (sum > 1) return false;\n }\n return true;\n }\n\n private boolean isSpecialCol(int col, int[][] mat) {\n int sum = 0;\n for (int i = 0; i < mat.length; i++) {\n sum += mat[i][col];\n if (sum > 1) return false;\n }\n return true;\n }\n}\n```
| 3 | 0 |
['Java']
| 0 |
special-positions-in-a-binary-matrix
|
Java | 100% Faster | Simple Solution
|
java-100-faster-simple-solution-by-sam02-kna1
|
\n// This code is 100% Faster 24 Oct 2022 don\'t know about future\n// If not understanding how to solve ping me with problem no and doubt \n// sahil2001bassan@
|
sam02202001
|
NORMAL
|
2022-10-24T14:18:10.380804+00:00
|
2022-10-24T14:18:10.380839+00:00
| 1,229 | false |
```\n// This code is 100% Faster 24 Oct 2022 don\'t know about future\n// If not understanding how to solve ping me with problem no and doubt \n// [email protected]\n\nclass Solution {\n public int numSpecial(int[][] mat) {\n int n = mat.length;\n int m = mat[0].length;\n int res = 0;\n if(n == 1 && n == 1) return mat[0][0];\n int flag = 0;\n int col = -1;\n for(int i=0; i<n; i++){\n flag = 0;\n for(int j=0; j<m; j++){\n if(mat[i][j] == 1){\n flag += 1;\n col = j;\n } \n }\n if(flag == 1){\n flag = 0;\n for(int row = 0; row<n; row++){\n if(mat[row][col] == 1){\n flag += 1;\n }\n }\n }\n if(flag == 1){\n res += 1; \n }\n }\n return res;\n }\n}\n```
| 3 | 0 |
['Java']
| 0 |
special-positions-in-a-binary-matrix
|
C++ | Easy Code With Explanation
|
c-easy-code-with-explanation-by-ankit460-9a4b
|
Please Upvote :)\n\n\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n int res=0;\n vector<int> row(mat.size(),0);// su
|
ankit4601
|
NORMAL
|
2022-07-24T10:12:06.025174+00:00
|
2022-07-24T10:12:06.025211+00:00
| 468 | false |
Please Upvote :)\n\n```\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n int res=0;\n vector<int> row(mat.size(),0);// sum of row\n vector<int> col(mat[0].size(),0);// sum of col \n \n for(int i=0;i<mat.size();i++)\n {\n int t=0;\n for(int j=0;j<mat[0].size();j++)\n t+=mat[i][j];\n row[i]=t;\n }\n for(int j=0;j<mat[0].size();j++)\n {\n int t=0;\n for(int i=0;i<mat.size();i++)\n t+=mat[i][j];\n col[j]=t;\n }\n \n for(int i=0;i<mat.size();i++)\n {\n for(int j=0;j<mat[0].size();j++)\n {\n // row and col ==1 means mat[i][j]==1 was only the element in the row and col ( special )\n if(mat[i][j]==1 && row[i]==1 && col[j]==1)\n res++;\n }\n }\n return res;\n }\n};\n```
| 3 | 0 |
['C', 'C++']
| 1 |
special-positions-in-a-binary-matrix
|
Java EASY solution
|
java-easy-solution-by-sandip_chanda-k1t2
|
\nclass Solution {\n public int numSpecial(int[][] mat) {\n int[] r = new int[mat.length];\n int[] c = new int[mat[0].length];\n for(int
|
sandip_chanda
|
NORMAL
|
2020-09-26T09:44:37.681902+00:00
|
2020-09-26T09:44:37.681934+00:00
| 488 | false |
```\nclass Solution {\n public int numSpecial(int[][] mat) {\n int[] r = new int[mat.length];\n int[] c = new int[mat[0].length];\n for(int i=0; i<mat.length; i++) {\n for(int j=0; j<mat[0].length; j++) {\n if(mat[i][j] == 1) {\n r[i]++;\n c[j]++;\n }\n }\n }\n int count = 0;\n for(int i=0; i<mat.length; i++) {\n for(int j=0; j<mat[0].length; j++) {\n if(mat[i][j] == 1 && r[i] == 1 && c[j] == 1) {\n count++;\n }\n }\n }\n return count;\n }\n}\n```
| 3 | 0 |
['Java']
| 0 |
special-positions-in-a-binary-matrix
|
[C++] Simple Brute Force Solution Explained | O(mn) Complexity
|
c-simple-brute-force-solution-explained-91su3
|
\nclass Solution\n{\npublic:\n int check(vector<vector<int>> &mat, int row, int col)\n {\n int res = 1;\n /* Checking Column by Traversing e
|
ravireddy07
|
NORMAL
|
2020-09-13T04:02:53.660724+00:00
|
2020-09-13T04:02:53.660766+00:00
| 260 | false |
```\nclass Solution\n{\npublic:\n int check(vector<vector<int>> &mat, int row, int col)\n {\n int res = 1;\n /* Checking Column by Traversing each Row */\n for (int i = 0; i < mat.size(); ++i)\n // If anyone of the row having 1, then it\'s not Special\n if (mat[i][col] != 0)\n if (i != row)\n // If any of the index, matrix having 1, then it\'s not special\n res = 0;\n\n /* Checking Row by Traversing each Column */\n for (int i = 0; i < mat[0].size(); ++i)\n // If anyone of the column having 1, then it\'s not Special\n if (mat[row][i] != 0)\n if (i != col)\n // If any of the index, matrix having 1, then it\'s not special\n res = 0;\n return res;\n }\n\n int numSpecial(vector<vector<int>> &mat)\n {\n int count = 0;\n for (int i = 0; i < mat.size(); ++i)\n for (int j = 0; j < mat[0].size(); ++j)\n if (mat[i][j] == 1)\n // Checking wheither this row & column has only this single 1 or not\n count += check(mat, i, j);\n return count;\n }\n};\n```
| 3 | 1 |
['C']
| 1 |
special-positions-in-a-binary-matrix
|
Easy to Understand Solution || Beginner Friendly Approaches || Beats-->83.13%
|
easy-to-understand-solution-beginner-fri-wryl
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
ADARSH_GAUTAM_576
|
NORMAL
|
2025-03-31T10:36:10.060706+00:00
|
2025-03-31T10:36:10.060706+00:00
| 23 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int numSpecial(int[][] mat) {
int ans=0;
for(int i=0;i<mat.length;i++){
int count=0;
int ptr=-1;
for(int j=0;j<mat[i].length;j++){
if(mat[i][j]==1){
count++;
ptr=j;
}
}
if(count==1){
int acount=0;
for(int k=0;k<mat.length;k++){
if(mat[k][ptr]==1){
acount++;
}
}
if(acount==1){
ans++;
}
}
}
return ans;
}
}
```
| 2 | 0 |
['Array', 'Matrix', 'Java']
| 0 |
special-positions-in-a-binary-matrix
|
Simple Solution 100% ✅
|
simple-solution-100-by-probablylost-f1lr
|
Code\n\nclass Solution {\n func numSpecial(_ mat: [[Int]]) -> Int {\n var rowCounts = [Int](repeating: 0, count: mat.count)\n var colCounts = [
|
ProbablyLost
|
NORMAL
|
2023-12-13T22:23:55.073221+00:00
|
2023-12-14T20:58:36.511930+00:00
| 11 | false |
# Code\n```\nclass Solution {\n func numSpecial(_ mat: [[Int]]) -> Int {\n var rowCounts = [Int](repeating: 0, count: mat.count)\n var colCounts = [Int](repeating: 0, count: mat[0].count)\n var count = 0\n\n for i in 0..<mat.count {\n for j in 0..<mat[i].count {\n if mat[i][j] == 1 {\n rowCounts[i] += 1\n colCounts[j] += 1\n }\n }\n }\n \n for i in 0..<mat.count {\n for j in 0..<mat[i].count {\n if mat[i][j] == 1 && rowCounts[i] == 1 && colCounts[j] == 1 {\n count += 1\n }\n }\n }\n \n return count\n }\n}\n\n```
| 2 | 0 |
['Swift']
| 0 |
special-positions-in-a-binary-matrix
|
Easy Solution || Python
|
easy-solution-python-by-tanya-1109-v7q7
|
Intuition\nFirst iterating through the matrix gives us the position of ones and we calculate if there are any ones in the respective row or column.\nIn the 2nd
|
Tanya-1109
|
NORMAL
|
2023-12-13T17:57:26.816927+00:00
|
2023-12-13T17:57:26.816957+00:00
| 96 | false |
# Intuition\nFirst iterating through the matrix gives us the position of ones and we calculate if there are any ones in the respective row or column.\nIn the 2nd iteration we check if the ones are in special position.\n\n\n\n# Complexity\n- Time complexity:\nO(m*n)\n\n- Space complexity:\nO(m+n)\n\n# Code\n```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n m = len(mat)\n n = len(mat[0])\n row_count = [0] * m\n col_count = [0] * n\n\n special_pos =0 \n for i in range(m):\n for j in range(n):\n if mat[i][j] == 1:\n row_count[i]+=1\n col_count[j]+=1\n for i in range(m):\n for j in range(n):\n if mat[i][j] == 1 and row_count[i] == 1 and col_count[j] == 1:\n special_pos+=1\n return special_pos\n\n \n```\n# **PLEASE DO UPVOTE!!!\uD83E\uDD79**
| 2 | 0 |
['Python3']
| 0 |
special-positions-in-a-binary-matrix
|
Abisheak Marudhu Answer c++
|
abisheak-marudhu-answer-c-by-abisheakmar-i2ih
|
Intuition\nBinary Matrix \n# Approach\nwe have used Btute Force Approch.\n# Complexity\n- Time complexity:\nO(n^3)\n- Space complexity:\nO(n^2)\n\n\n\n# Code c+
|
abisheakmarudhu07
|
NORMAL
|
2023-12-13T16:44:59.502414+00:00
|
2023-12-13T16:55:32.828114+00:00
| 65 | false |
# Intuition\nBinary Matrix \n# Approach\nwe have used Btute Force Approch.\n# Complexity\n- Time complexity:\nO(n^3)\n- Space complexity:\nO(n^2)\n\n\n\n# Code `c++`\n```\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n int c=0;\n for(int i = 0 ; i<mat.size() ; i++)\n {\n for(int j = 0 ; j<mat[0].size() ; j++)\n {\n if(mat[i][j] == 1)\n {\n bool tf = true;\n for(int k = 0 ; k<mat.size() ; k++)\n {\n if(mat[k][j] == 1 && k!=i)\n {\n tf = false;\n break;\n }\n }\n for(int k = 0 ; k<mat[0].size() ; k++)\n {\n if(mat[i][k] == 1 && k!=j)\n {\n tf = false;\n break;\n }\n }\n if(tf)\n {\n c++;\n }\n }\n }\n }\n return c;\n }\n};\n```
| 2 | 0 |
['Array', 'Matrix', 'C++']
| 2 |
special-positions-in-a-binary-matrix
|
C++ | Simple code | Beat 90%
|
c-simple-code-beat-90-by-ankita2905-o16k
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Ankita2905
|
NORMAL
|
2023-12-13T15:54:08.125801+00:00
|
2023-12-13T15:54:08.125823+00:00
| 56 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> check1(vector<int>& vect, int sz){\n vector<int> ans;\n for(int i=0; i<sz; i++){\n if (vect[i]==1) ans.push_back(i);\n }\n return ans;\n }\n int numSpecial(vector<vector<int>>& mat) {\n int m=mat.size(), n=mat[0].size(), ans=0;\n vector<bool> col(n, 0);// check or \n vector<int> col_j(m);\n for(int i=0; i<m; i++){\n auto idx=check1(mat[i], n);\n int j;\n if (idx.size()==1 && col[(j=idx[0])]==0){\n col[j]=1;\n col_j.assign(m, 0);\n for(int k=0; k<m; k++)\n col_j[k]=mat[k][j];\n if (check1(col_j, m).size()==1){\n // cout<<"("<<i<<","<<j<<")";\n ans++;\n } \n }\n else{//cannot be special indices\n for(int j: idx)\n col[j]=1;\n }\n }\n return ans;\n }\n};\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```
| 2 | 0 |
['C++']
| 0 |
special-positions-in-a-binary-matrix
|
Easy C++ Code With Explanation And Comments || C++
|
easy-c-code-with-explanation-and-comment-jqst
|
Intuition\nStep1:Keep track of 1s in each row and in each column in row and col vectors.\n\nStep2:Then again while traversing over matrix, if the current mat[i]
|
abhay0007
|
NORMAL
|
2023-12-13T12:53:02.896674+00:00
|
2023-12-13T12:53:02.896705+00:00
| 1 | false |
# Intuition\n**Step1**:Keep track of 1s in each row and in each column in row and col vectors.\n\n**Step2**:Then again while traversing over matrix, if the current mat[i][j]==1 and current row i.e. row[i]==1 as well as current column i.e.col[j]==1 then count++.\n\n\n# Complexity\n- Time complexity:\nO(n*m)\n\n- Space complexity:\nO(n) if n>=m else O(m)\n\n# Code\n```\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n\n int n=mat.size(),m=mat[0].size(),count=0;\n\n vector<int>row(n,0);\n vector<int>col(m,0);\n\n //Step1: Fill the row and col vector\n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n if(mat[i][j]==1){\n row[i]++;\n col[j]++;\n }\n }\n }\n\n //Step2: Check for all conditions\n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n if(mat[i][j]==1 and row[i]==1 and col[j]==1)\n count++;\n }\n }\n\n return count;\n }\n};\n```
| 2 | 0 |
['Array', 'Matrix', 'C++']
| 0 |
special-positions-in-a-binary-matrix
|
PHP array functions
|
php-array-functions-by-yunniko-f7df
|
\n\n# Code\n\nclass Solution {\n\n /**\n * @param Integer[][] $mat\n * @return Integer\n */\n function numSpecial($mat) {\n $result = 0
|
yunniko
|
NORMAL
|
2023-12-13T10:15:55.514239+00:00
|
2023-12-13T10:15:55.514262+00:00
| 18 | false |
\n\n# Code\n```\nclass Solution {\n\n /**\n * @param Integer[][] $mat\n * @return Integer\n */\n function numSpecial($mat) {\n $result = 0;\n for ($i = 0; $i < count($mat); $i++) {\n if (array_sum($mat[$i]) === 1) {\n $k = array_search(1, $mat[$i]);\n if (array_sum(array_column($mat, $k)) === 1) {\n $result++;\n }\n } \n }\n return $result;\n }\n}\n```
| 2 | 0 |
['PHP']
| 0 |
special-positions-in-a-binary-matrix
|
JAVA solution explained in HINDI
|
java-solution-explained-in-hindi-by-the_-xxy9
|
https://youtu.be/ZIFodfNO6aI\n\nFor explanation, watch the above video and do like share and subscribe the channel\n\n# Code\n\nclass Solution {\n public int
|
The_elite
|
NORMAL
|
2023-12-13T08:37:29.027701+00:00
|
2023-12-13T08:37:29.027724+00:00
| 5 | false |
https://youtu.be/ZIFodfNO6aI\n\nFor explanation, watch the above video and do like share and subscribe the channel\n\n# Code\n```\nclass Solution {\n public int numSpecial(int[][] mat) {\n \n int spcl = 0;\n for(int i = 0; i < mat.length; i++) {\n int idx = isSafeRow(mat, i);\n if(idx >= 0 && isSafeColumn(mat, i, idx)) \n spcl++;\n }\n return spcl;\n }\n\n public int isSafeRow(int mat[][], int i) {\n\n int idx = -1;\n for(int j = 0; j < mat[0].length; j++) {\n if(mat[i][j] == 1) {\n if(idx >= 0) return -1;\n else idx = j;\n }\n }\n return idx;\n }\n\n public boolean isSafeColumn(int mat[][], int i, int idx) {\n for(int j = 0; j < mat.length; j++) {\n if(mat[j][idx] == 1 && j != i) return false;\n }\n return true;\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
special-positions-in-a-binary-matrix
|
Row and Column Sums | Java | C++
|
row-and-column-sums-java-c-by-fly_ing__r-xcrb
|
Intuition\nIf we know how many number of ones in each row and column the special positions can easily be counted.\n\n# Approach\nCount number of ones in each ro
|
Fly_ing__Rhi_no
|
NORMAL
|
2023-12-13T07:41:07.957411+00:00
|
2023-12-13T07:41:07.957440+00:00
| 473 | false |
# Intuition\nIf we know how many number of ones in each row and column the special positions can easily be counted.\n\n# Approach\nCount number of ones in each row and column and then whenever you encounter a value of \'1\' in a cell in input matrix then check the number of ones in row and column of that cell if the number of ones in both row and column is 1 then count it as a special position.\n\n# Complexity\n- Time complexity:\nO(rows * cols), for traversal of the input array\n\n- Space complexity:\nO(rows + col), for row and column sums arrays\n\n# Code\nC++\n```\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n int rows = mat.size(), cols = mat[0].size();\n vector<int> rowSum(rows), colSum(cols);\n for(int r = 0; r < rows; r++){\n for(int c = 0; c < cols; c++){\n rowSum[r] += mat[r][c];\n }\n }\n\n for(int c = 0; c < cols; c++){\n for(int r = 0; r < rows; r++){\n colSum[c] += mat[r][c];\n }\n }\n int spcPosCnt = 0;\n for(int r = 0; r<rows; r++){\n for(int c = 0; c < cols; c++){\n if(mat[r][c] == 1 && rowSum[r] == 1 && colSum[c] == 1)spcPosCnt++;\n }\n }\n return spcPosCnt;\n }\n};\n```\nJava\n```\nclass Solution {\n public int numSpecial(int[][] mat) {\n int rows = mat.length, cols = mat[0].length;\n int rowSum[] = new int[rows], colSum[] = new int[cols];\n for(int r = 0; r < rows; r++){\n for(int c = 0; c < cols; c++){\n rowSum[r] += mat[r][c];\n }\n }\n\n for(int c = 0; c < cols; c++){\n for(int r = 0; r < rows; r++){\n colSum[c] += mat[r][c];\n }\n }\n int spcPosCnt = 0;\n for(int r = 0; r<rows; r++){\n for(int c = 0; c < cols; c++){\n if(mat[r][c] == 1 && rowSum[r] == 1 && colSum[c] == 1)spcPosCnt++;\n }\n }\n return spcPosCnt;\n }\n}\n```
| 2 | 0 |
['C++', 'Java']
| 1 |
special-positions-in-a-binary-matrix
|
Rust 0ms 🔥 2.11Mb ☄️ One Liner Solution 🦀
|
rust-0ms-211mb-one-liner-solution-by-ron-4hgg
|
Complexity\n- Time complexity: O(m * n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(m + n)\n Add your space complexity here, e.g. O(n)
|
rony0000013
|
NORMAL
|
2023-12-13T06:49:44.090255+00:00
|
2023-12-13T06:49:44.090286+00:00
| 54 | false |
# Complexity\n- Time complexity: $$O(m * n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(m + n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code - 0ms\n```\nimpl Solution {\n pub fn num_special(mat: Vec<Vec<i32>>) -> i32 {\n mat.iter().enumerate()\n .fold((0, mat.iter().enumerate()\n .fold((vec![0; mat.len()], vec![0; mat[0].len()]), \n |(mut row, mut col), (i, v)| \n v.iter().enumerate()\n .fold((row, col), \n |(mut row, mut col), (j, &x)| {\n if x==1 {row[i]+=1; col[j]+=1;}\n (row, col)\n }\n )\n )),\n |(mut c, (row, col)), (i, v)| {\n v.iter().enumerate()\n .for_each(|(j, &x)| {\n if x==1 && row[i]==1 && col[j]==1 {c+=1;}\n });\n (c, (row, col))\n }\n ).0\n \n }\n}\n```\n\n# Code - 3ms\n```\nimpl Solution {\n pub fn num_special(mat: Vec<Vec<i32>>) -> i32 {\n mat.iter().enumerate()\n .fold((0, \n mat.iter()\n .map(|v| v.iter().sum())\n .collect::<Vec<i32>>(), \n mat.iter()\n .fold(vec![0; mat[0].len()], \n |x, v| x.iter()\n .zip(v.iter())\n .map(|(&a, &b)| a + b)\n .collect()\n )\n ),\n |(mut c, row, col), (i, v)| {\n v.iter().enumerate()\n .for_each(|(j, &x)| {\n if x==1 && row[i]==1 && col[j]==1 {c+=1;}\n });\n (c, row, col)\n }\n ).0\n \n }\n}\n```
| 2 | 0 |
['Rust']
| 0 |
special-positions-in-a-binary-matrix
|
C++ | C | Solution
|
c-c-solution-by-zhanghx04-jygj
|
Approach\n Describe your approach to solving the problem. \nGet sum of each row and each column, then, find the one-cell, if it\'s row has sum 1 and col has sum
|
zhanghx04
|
NORMAL
|
2023-12-13T03:31:06.073597+00:00
|
2023-12-13T03:31:06.073626+00:00
| 46 | false |
# Approach\n<!-- Describe your approach to solving the problem. -->\nGet sum of each row and each column, then, find the one-cell, if it\'s row has sum 1 and col has sum 1, count it as the special position.\n\n# Complexity\n- Time complexity: $$O(m\\times n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(m + n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n int rows = mat.size();\n int cols = mat[0].size();\n\n vector<int> row_sum(rows);\n vector<int> col_sum(cols);\n\n for (int i = 0; i < rows; ++i) {\n for (int j = 0; j < cols; ++j) {\n row_sum[i] += mat[i][j];\n col_sum[j] += mat[i][j];\n }\n }\n\n int result = 0;\n for (int i = 0; i < rows; ++i) {\n for (int j = 0; j < cols; ++j) {\n result += mat[i][j] == 1 && row_sum[i] == 1 && col_sum[j] == 1;\n }\n }\n\n return result;\n }\n};\n```\n```C []\nint numSpecial(int** mat, int matSize, int* matColSize) {\n int colSize = matColSize[0];\n\n int *row_sum = (int *)calloc(matSize, sizeof(int));\n int *col_sum = (int *)calloc(colSize, sizeof(int));\n\n for (int i = 0; i < matSize; ++i) {\n for (int j = 0; j < colSize; ++j) {\n row_sum[i] += mat[i][j];\n col_sum[j] += mat[i][j];\n }\n }\n\n int result = 0;\n for (int i = 0; i < matSize; ++i) {\n for (int j = 0; j < colSize; ++j) {\n result += mat[i][j] == 1 && row_sum[i] == 1 && col_sum[j] == 1;\n }\n }\n\n free(row_sum);\n free(col_sum);\n\n return result;\n}\n```
| 2 | 0 |
['C', 'C++']
| 0 |
special-positions-in-a-binary-matrix
|
Python3 Solution
|
python3-solution-by-motaharozzaman1996-8xby
|
\n\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n n=len(mat)\n m=len(mat[0])\n ans=0\n transposeMat=list
|
Motaharozzaman1996
|
NORMAL
|
2023-12-13T03:04:14.146497+00:00
|
2023-12-13T03:04:14.146561+00:00
| 620 | false |
\n```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n n=len(mat)\n m=len(mat[0])\n ans=0\n transposeMat=list(zip(*mat))\n for i in range(n):\n for j in range(m):\n if mat[i][j]==1 and sum(mat[i])==1 and sum(transposeMat[j])==1:\n ans+=1\n return ans \n```
| 2 | 0 |
['Python', 'Python3']
| 1 |
special-positions-in-a-binary-matrix
|
Easiest C++ Approach [Beats 70%] | Fastest Solution
|
easiest-c-approach-beats-70-fastest-solu-rrvi
|
Approach\n1. ### Initialization:\n\n - cnt is initialized to 0, which will be used to count the number of special elements.\n2. ### Outer Loop (i):\n\n- The out
|
clickdawg
|
NORMAL
|
2023-12-13T02:53:32.621829+00:00
|
2023-12-13T02:53:32.621850+00:00
| 244 | false |
# Approach\n1. ### Initialization:\n\n - `cnt` is initialized to 0, which will be used to count the number of special elements.\n2. ### Outer Loop (i):\n\n- The outer loop iterates over each row of the matrix (`mat`).\n3. ### Inner Loop (j):\n\n- The inner loop iterates over each column of the matrix for the current row.\n- Check for Special Element `(mat[i][j] == 1)`:\n\n- If the current element is 1, it is considered a potential special element.\n4. ### Row Check (k loop):\n\n- The code checks the entire row of the current element.\n- If there is another 1 in the row (excluding the current element), the flag is set to false.\n5. ### Column Check (l loop):\n\n- The code checks the entire column of the current element.\n- If there is another 1 in the column (excluding the current element), the flag is set to `false`.\n6. ### Special Element Check (flag):\n\n- If the flag is still true after both row and column checks, the current element is considered special.\n- Increment the `cnt` counter.\n7. ### Return Result:\n\n- After both loops are complete, the function returns the total count of special elements (`cnt`).\n\n# Complexity\n- Time complexity:\n$$O(m*n^2)$$ \n\n- Space complexity:\n$$O(1)$$ \n\n# Code\n```\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n int cnt = 0; // Initialize a counter for special elements\n\n // Iterate over each element in the matrix\n for (int i = 0; i < mat.size(); i++) {\n for (int j = 0; j < mat[0].size(); j++) {\n // Check if the current element is 1 (a potential special element)\n if (mat[i][j] == 1) {\n bool flag = true; // Initialize a flag to track if the element is special\n\n // Check the entire row of the current element\n for (int k = 0; k < mat[0].size(); k++) {\n // If there is another 1 in the row (excluding the current element), it\'s not special\n if (mat[i][k] != 0 && k != j)\n flag = false;\n }\n\n // Check the entire column of the current element\n for (int l = 0; l < mat.size(); l++) {\n // If there is another 1 in the column (excluding the current element), it\'s not special\n if (mat[l][j] != 0 && i != l)\n flag = false;\n }\n\n // If the element passed both row and column checks, it\'s a special element\n if (flag)\n cnt++; // Increment the counter\n }\n }\n }\n\n // Return the total count of special elements\n return cnt;\n }\n};\n\n```
| 2 | 0 |
['Array', 'Matrix', 'C++']
| 1 |
special-positions-in-a-binary-matrix
|
Easy Intuition CPP Code.
|
easy-intuition-cpp-code-by-mirtariq-z8hw
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
mirtariq
|
NORMAL
|
2023-12-13T02:24:57.017333+00:00
|
2023-12-13T02:24:57.017352+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n vector<int> row,col;\n for(int i=0;i<mat.size();i++)\n {\n int c=0;\n for(int j=0;j<mat[0].size();j++)\n {\n if(mat[i][j]==1){\n c++;\n }\n }\n row.push_back(c);\n }\n for(int j=0;j<mat[0].size();j++)\n {\n int c=0;\n for(int i=0;i<mat.size();i++)\n {\n if(mat[i][j]==1){\n c++;\n }\n }\n col.push_back(c);\n }\n int ans=0;\n for(int i=0;i<mat.size();i++)\n {\n for(int j=0;j<mat[0].size();j++)\n {\n if(mat[i][j]==1)\n {\n if(row[i]==1&&col[j]==1) ans+=1;\n }\n }\n }\n return ans;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
special-positions-in-a-binary-matrix
|
Very easy python soln
|
very-easy-python-soln-by-jaigurudevcode-c733
|
Very easy Python soln\n\n# Code\n\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n n=len(mat[0])\n m=len(mat)\n c
|
jaiGurudevCode
|
NORMAL
|
2023-12-13T00:24:18.017758+00:00
|
2023-12-13T00:24:18.017775+00:00
| 262 | false |
# Very easy Python soln\n\n# Code\n```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n n=len(mat[0])\n m=len(mat)\n c=0\n trans=[[k[i] for k in mat] for i in range(n)]\n for i in range(m):\n for j in range(n):\n if mat[i][j]==1 and 1 not in mat[i][:j]+mat[i][j+1:] and 1 not in trans[j][:i]+trans[j][i+1:]: c+=1\n return c\n```
| 2 | 0 |
['Python', 'Python3']
| 0 |
special-positions-in-a-binary-matrix
|
🔥TWO SOLUTIONS || Basic Understandable Solution🔥|🔥Clean Code🔥|🔥Daily Challenges🔥
|
two-solutions-basic-understandable-solut-z6d7
|
Complexity\n- Time complexity:\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:\n Add your space complexity here, e.g. O(n) \n\n# Code\nSOLUTI
|
Shree_Govind_Jee
|
NORMAL
|
2023-12-13T00:22:40.920911+00:00
|
2023-12-13T00:34:27.786819+00:00
| 366 | false |
# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n**SOLUTION-1(BRUTEFORCE ONE)**\n```Java []\nclass Solution {\n public int numSpecial(int[][] mat) {\n int cnt=0;\n\n for(int i=0; i<mat.length; i++){\n for(int j=0; j<mat[0].length; j++){\n\n if(mat[i][j]==1){\n int zero1=0, zero2=0;\n \n for(int k=0; k<mat[0].length; k++){\n if(mat[i][k]==0){\n zero1++;\n }\n }\n for(int k=0; k<mat.length; k++){\n if(mat[k][j]==0){\n zero2++;\n }\n }\n\n if(zero1 == mat[0].length-1 && zero2==mat.length-1){\n cnt++;\n }\n }\n }\n }\n return cnt;\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n int cnt=0;\n\n for(int i=0; i<mat.size(); i++){\n for(int j=0; j<mat[0].size(); j++){\n\n if(mat[i][j]==1){\n int zero1=0, zero2=0;\n \n for(int k=0; k<mat[0].size(); k++){\n if(mat[i][k]==0){\n zero1++;\n }\n }\n for(int k=0; k<mat.size(); k++){\n if(mat[k][j]==0){\n zero2++;\n }\n }\n\n if(zero1 == mat[0].size()-1 && zero2==mat.size()-1){\n cnt++;\n }\n }\n }\n }\n return cnt;\n }\n};\n```\n\n---\n\n\n---\n\n\n**SOLUTION-2(OPTIMIZE ONE)**\n```javascript []\nclass Solution {\n public int numSpecial(int[][] mat) {\n //Base Case\n if(mat.length==1 && mat[0].length==1) return mat[0][0];\n\n\n int res=0;\n int flag=0, col=-1;\n for(int i=0; i<mat.length; i++){\n flag=0;\n for(int j=0; j<mat[0].length; j++){\n if(mat[i][j] == 1){\n flag++;\n col=j;\n }\n }\n\n if(flag == 1){\n flag=0;\n for(int rows=0; rows<mat.length; rows++){\n if(mat[rows][col] == 1) flag++;\n }\n }\n if(flag==1) res++;\n }\n return res;\n }\n}\n```\n\n
| 2 | 0 |
['Array', 'Matrix', 'C++', 'Java']
| 0 |
special-positions-in-a-binary-matrix
|
Typescript || Matrix || O(m*n) time || O(m+n) space
|
typescript-matrix-omn-time-omn-space-by-8i2u0
|
Complexity\n- Time complexity:\nO(m*n) \n\n- Space complexity:\nO(m+n) \n\n# Code\n\nfunction numSpecial(grid: number[][]): number {\n const ROW = grid.lengt
|
onifs10
|
NORMAL
|
2023-08-17T20:34:16.494454+00:00
|
2023-08-17T20:34:16.494478+00:00
| 42 | false |
# Complexity\n- Time complexity:\n$$O(m*n)$$ \n\n- Space complexity:\n$$O(m+n)$$ \n\n# Code\n```\nfunction numSpecial(grid: number[][]): number {\n const ROW = grid.length;\n const COL = grid[0].length; \n let rowCounts: number[] = new Array(grid.length).fill(0)\n let colCounts: number[] = new Array(grid[0].length).fill(0)\n\n for(let x = 0; x < ROW;x++){\n for(let y = 0; y < COL; y++){\n if(grid[x][y] == 1){\n rowCounts[x] += 1\n colCounts[y] += 1\n }\n }\n }\n\n let result:number = 0\n for(let x = 0; x < ROW;x++){\n for(let y = 0; y < COL; y++){\n if(grid[x][y] == 1 && rowCounts[x] == 1 && colCounts[y] == 1){\n result++\n }\n }\n }\n\n return result\n};\n```
| 2 | 0 |
['TypeScript']
| 0 |
special-positions-in-a-binary-matrix
|
C++ | Easy Solution With Easy Explaination
|
c-easy-solution-with-easy-explaination-b-mhxm
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
VenisPatel
|
NORMAL
|
2023-07-21T17:54:29.497142+00:00
|
2023-07-21T17:54:29.497166+00:00
| 599 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n bool rowcheck(int row , int column , int m , int n , vector<vector<int>>& mat){\n for(int i=0 ; i<n ; i++){\n if(i!=column && mat[row][i] == 1){\n return false;\n }\n }\n return true;\n }\n bool columncheck(int row , int column , int m , int n , vector<vector<int>>& mat){\n for(int j=0 ; j<m ; j++){\n if(j!=row && mat[j][column] == 1){\n return false;\n }\n }\n return true;\n }\n int numSpecial(vector<vector<int>>& mat) {\n int m = mat.size() ;\n int n = mat[0].size() ;\n int ans = 0 ;\n for(int i=0 ; i<m ; i++){\n for(int j=0 ; j<n ; j++){\n if(mat[i][j] == 1){\n if(rowcheck(i,j,m,n,mat) && columncheck(i,j,m,n,mat)) ans++;\n }\n }\n }\n return ans;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
special-positions-in-a-binary-matrix
|
Easy Solution C++
|
easy-solution-c-by-dhruvp0105-wugf
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
dhruvp0105
|
NORMAL
|
2023-07-21T17:54:28.695234+00:00
|
2023-07-21T17:54:28.695260+00:00
| 358 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n\n bool row_check(int row,int col,int total_row,int total_col,vector<vector<int>> &mat){\n for(int i=0;i<total_col;i++){\n if(i != col && mat[row][i]!=0){\n return false;\n }\n }\n return true;\n }\n\n bool col_check(int row,int col,int total_row,int total_col,vector<vector<int>> &mat){\n for(int i=0;i<total_row;i++){\n if(i != row && mat[i][col]!=0){\n return false;\n }\n }\n return true;\n }\n\n int numSpecial(vector<vector<int>>& mat) {\n\n int m=mat.size();\n int n=mat[0].size();\n int count=0;\n\n for(int i=0;i<m;i++){\n for(int j=0;j<n;j++){\n if(mat[i][j]==1){\n if(row_check(i,j,m,n,mat) && col_check(i,j,m,n,mat)){\n count++;\n }\n }\n }\n }\n return count;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
special-positions-in-a-binary-matrix
|
Python || 95.44% Faster || Easy || O(m*n)
|
python-9544-faster-easy-omn-by-pulkit_up-035t
|
\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n m,n=len(mat),len(mat[0])\n a=[0]*m\n b=[0]*n\n s=set()\n
|
pulkit_uppal
|
NORMAL
|
2023-07-19T04:41:29.798289+00:00
|
2023-07-19T04:41:29.798319+00:00
| 200 | false |
```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n m,n=len(mat),len(mat[0])\n a=[0]*m\n b=[0]*n\n s=set()\n c=0\n for i in range(m):\n for j in range(n):\n if mat[i][j]:\n s.add((i,j))\n b[j]+=1\n a[i]+=1\n \n for i in s:\n x,y=i[0],i[1]\n if a[x]==1 and b[y]==1:\n c+=1\n return c\n```\n**An upvote will be encouraging**
| 2 | 0 |
['Array', 'Python', 'Python3']
| 0 |
special-positions-in-a-binary-matrix
|
Java | 2-pass solution | beats 100%
|
java-2-pass-solution-beats-100-by-steffi-4j9g
|
\n# Code\n\nclass Solution {\n public int numSpecial(int[][] mat) {\n int res = 0;\n int n = mat.length, m = mat[0].length;\n int [] row
|
steffi_keran
|
NORMAL
|
2023-06-25T18:02:42.973751+00:00
|
2023-06-25T18:02:42.973768+00:00
| 125 | false |
\n# Code\n```\nclass Solution {\n public int numSpecial(int[][] mat) {\n int res = 0;\n int n = mat.length, m = mat[0].length;\n int [] rowSum = new int[n], colSum = new int[m];\n\n for(int i = 0; i < n; ++i) {\n for(int j = 0; j < m; ++j) {\n if(mat[i][j]==1) {\n rowSum[i]++; colSum[j]++;\n }\n }\n }\n\n for(int i = 0; i < n; ++i){\n for(int j = 0; j < m; ++j) {\n if(mat[i][j] == 1 && rowSum[i] == 1 && colSum[j] == 1)\n res++;\n }\n }\n\n return res;\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
special-positions-in-a-binary-matrix
|
✅ Beats 96.69% solutions,✅ Easy to understand with Examples Python Code by ✅ BOLT CODING ✅
|
beats-9669-solutions-easy-to-understand-ri4b7
|
Explanation\nFrom the quesiton a number can be said special if there are no other occurence of 1 in same row or column. So first thing we need to do is check is
|
anindya20012001
|
NORMAL
|
2023-01-21T13:35:42.746859+00:00
|
2023-01-21T13:35:42.746902+00:00
| 780 | false |
# Explanation\nFrom the quesiton a number can be said special if there are no other occurence of 1 in same row or column. So first thing we need to do is check is sum(row) == 1 or any other value. Since this is a binary matrix we only need to consider those rows whose sum is exactly 1. Now that\'s our first filter to filter out values row-wise.\nNow its time for column, we use zip(*mat) to get the column wise-matrix. We now check if the index value of column is already present in our row filtered values. If yes we check if sum of that column is == 1. If both conditions satisfy then we increment the counter.\n\n**NOTE:** Many will be confused when using zip(*mat) so here is a small example for easier understanding. \n```\nzip(*variable) # this is used to unzip value\n# Example - 1:\na = [1, 2, 3, 4, 5]\nb = [6, 7, 8, 9, 10]\nc = [11, 12, 13, 14, 15]\nz = zip(a, b, c)\nprint(list(z)) \n# Output : [(1, 6, 11), (2, 7, 12), (3, 8, 13), (4, 9, 14), (5, 10, 15)]\n\n# Unzip Example : \n# Suppose we are given z in this case and we are asked to seperate\n# a, b, c from here\n# We achieve that using unzip operator\n\n# Let\'s take our matrix as z here\nz = [(1, 0, 0), (0, 0, 1), (1, 0, 0)]\n# Our need is to get columns\na, b, c = zip(*z)\n# Output : a ==> [1, 0, 1]\n#. b ==> [0, 0, 0]\n#. c ==> [0, 1, 0]\n\n# Now we are using enumerate function because we need to identify the index \n# of the coloumn.\n```\n\nHope you had a clearer understanding of the solution. If you feel this helpful do upvote and comment your view.\n# Code\n```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n c = 0\n l = []\n for i in range(len(mat)):\n if sum(mat[i]) == 0 or sum(mat[i]) > 1:\n continue\n l.append(mat[i].index(1))\n for idx, col in enumerate(zip(*mat)):\n if idx in l and sum(col) == 1:\n c+=1\n return c\n \n\n```\n# Learning\nTo understand problems in simpler ways, need help with projects, want to learn coding from scratch, work on resume level projects, learn data science ...................\n\nSubscribe to Bolt Coding Channel - https://www.youtube.com/@boltcoding
| 2 | 0 |
['Python3']
| 1 |
special-positions-in-a-binary-matrix
|
C++ solution
|
c-solution-by-_kitish-qrc8
|
\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n int n = mat.size(), m = mat[0].size();\n vector<int> row,col; //no o
|
_kitish
|
NORMAL
|
2022-11-30T20:48:02.068591+00:00
|
2022-11-30T20:48:02.068626+00:00
| 625 | false |
```\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n int n = mat.size(), m = mat[0].size();\n vector<int> row,col; //no of zeros\n int specialPosition = 0;\n for(int i=0; i<n; ++i){\n int zeros = 0;\n for(int j=0; j<m; ++j){\n if(mat[i][j] == 0) zeros++;\n }\n row.push_back(zeros);\n }\n for(int i=0; i<m; ++i){\n int zeros = 0;\n for(int j=0; j<n; ++j){\n if(mat[j][i] == 0) zeros++;\n }\n col.push_back(zeros);\n }\n for(int i=0; i<n; ++i){\n for(int j=0; j<m; ++j){\n if(mat[i][j]){\n if(row[i] == m-1 && col[j] == n-1) specialPosition++;\n }\n }\n }\n return specialPosition;\n }\n};\n```
| 2 | 0 |
['C']
| 0 |
special-positions-in-a-binary-matrix
|
CPP Solution
|
cpp-solution-by-siddharthphalle-bgz1
|
\nint numSpecial(vector<vector<int>>& mat) {\n int m = mat.size(), n = mat[0].size(), sumC = 0, tempC = 0, cnt = 0;\n vector<int>sum(m,0);\n
|
SiddharthPhalle
|
NORMAL
|
2022-07-14T16:20:56.662780+00:00
|
2022-07-14T16:20:56.662821+00:00
| 335 | false |
```\nint numSpecial(vector<vector<int>>& mat) {\n int m = mat.size(), n = mat[0].size(), sumC = 0, tempC = 0, cnt = 0;\n vector<int>sum(m,0);\n for(int i = 0; i < mat.size(); i++)\n sum[i] = accumulate(mat[i].begin(), mat[i].end(), 0);\n for(int i = 0; i < n; i++)\n {\n for(int j = 0; j < m; j++)\n {\n sumC += mat[j][i];\n if(mat[j][i] == 1 && sum[j] == 1)\n ++tempC;\n }\n if(tempC == 1 && sumC ==1)\n cnt++;\n tempC = 0, sumC = 0;\n }\n return cnt;\n }\n```
| 2 | 0 |
['C']
| 0 |
special-positions-in-a-binary-matrix
|
Beginner Friendly Java Solution
|
beginner-friendly-java-solution-by-prish-ru6o
|
\nclass Solution {\n public int numSpecial(int[][] mat) {\n int c=0;\n int m=mat.length;\n int n=mat[0].length;\n for(int i=0;i<m
|
prishita
|
NORMAL
|
2022-06-16T06:59:55.524234+00:00
|
2022-06-16T06:59:55.524273+00:00
| 401 | false |
```\nclass Solution {\n public int numSpecial(int[][] mat) {\n int c=0;\n int m=mat.length;\n int n=mat[0].length;\n for(int i=0;i<m;i++){\n for(int j=0;j<n;j++){\n if(mat[i][j]==1){\n if(checkRow(mat,i,j,m,n) && checkCol(mat,i,j,m,n))\n c++;\n }\n }\n }\n return c;\n }\n public boolean checkRow(int[][] mat,int i,int j,int m,int n){\n for(int x=0;x<n;x++){\n if(x!=j)\n if(mat[i][x]==1) return false;\n }\n return true;\n }\n public boolean checkCol(int[][] mat,int i,int j,int m,int n){\n for(int x=0;x<m;x++){\n if(x!=i)\n if(mat[x][j]==1) return false;\n }\n return true;\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
special-positions-in-a-binary-matrix
|
java easy solution using only for loops
|
java-easy-solution-using-only-for-loops-5wsgz
|
\nclass Solution {\n public int numSpecial(int[][] mat) {\n \n int r = mat.length;\n int c = mat[0].length;\n int row[] = new int
|
aminultension
|
NORMAL
|
2022-06-13T17:01:55.312545+00:00
|
2022-06-13T17:01:55.312588+00:00
| 311 | false |
```\nclass Solution {\n public int numSpecial(int[][] mat) {\n \n int r = mat.length;\n int c = mat[0].length;\n int row[] = new int[r];\n int col[] = new int[c];\n for (int i = 0; i < r; i++) {\n for (int j = 0; j < c; j++) {\n if (mat[i][j] == 1) {\n row[i]++;\n col[j]++;\n }\n }\n }\n int count = 0;\n for (int i = 0; i < r; i++) {\n for (int j = 0; j < c; j++) {\n if (mat[i][j] == 1 && row[i] == 1 && col[j] == 1) {\n count++;\n }\n }\n }\n return count;\n }\n}\n\n```
| 2 | 0 |
['Java']
| 1 |
special-positions-in-a-binary-matrix
|
JavaScript
|
javascript-by-raniketram-h0pt
|
Please upvote, if it helps you!\n\n\nvar numSpecial = function(mat) {\n let count = 0\n \n for (let i = 0; i < mat.length; i++) {\n for (let j =
|
raniketram
|
NORMAL
|
2022-01-18T07:20:44.058073+00:00
|
2022-01-18T07:20:44.058114+00:00
| 367 | false |
## Please upvote, if it helps you!\n\n```\nvar numSpecial = function(mat) {\n let count = 0\n \n for (let i = 0; i < mat.length; i++) {\n for (let j = 0; j < mat[i].length; j++) {\n if (mat[i][j] === 1) {\n if (isValidRow(i) && isValidCol(j)) {\n count++\n }\n }\n }\n }\n \n function isValidRow(index) {\n let count = 0\n let row = mat[index]\n for (let i = 0; i < row.length; i++) {\n if (row[i] === 1) {\n count++\n }\n }\n if (count > 1) {\n return false\n } else {\n return true\n }\n }\n \n function isValidCol(index) {\n let count = 0\n for (let i = 0; i < mat.length; i++) {\n let row = mat[i]\n if (row[index] === 1) {\n count++\n }\n }\n if (count > 1) {\n return false\n } else {\n return true\n }\n }\n \n return count\n};\n```
| 2 | 0 |
['JavaScript']
| 0 |
special-positions-in-a-binary-matrix
|
Python simple solution
|
python-simple-solution-by-beansdata-847v
|
\ndef numSpecial(self, mat: List[List[int]]) -> int:\n\tans = 0\n\tfor i in range(len(mat)):\n\t\tif sum(mat[i]) == 1 and sum([mat[k][mat[i].index(1)] for k in
|
BeansData
|
NORMAL
|
2021-11-02T09:27:47.147431+00:00
|
2021-11-02T09:27:47.147468+00:00
| 94 | false |
```\ndef numSpecial(self, mat: List[List[int]]) -> int:\n\tans = 0\n\tfor i in range(len(mat)):\n\t\tif sum(mat[i]) == 1 and sum([mat[k][mat[i].index(1)] for k in range(len(mat))]) == 1:\n\t\t\t\tans += 1\n\treturn ans\n```
| 2 | 0 |
[]
| 0 |
special-positions-in-a-binary-matrix
|
[Python] Transpose
|
python-transpose-by-dev-josh-qnfo
|
python\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n \n M, N, result = len(mat), len(mat[0]), 0\n \n
|
dev-josh
|
NORMAL
|
2021-09-15T15:06:39.098792+00:00
|
2021-09-15T15:06:39.098828+00:00
| 240 | false |
```python\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n \n M, N, result = len(mat), len(mat[0]), 0\n \n mat_t = list(zip(*mat)) # transpose\n \n for i in range(M):\n for j in range(N):\n if mat[i][j] == 1 and \\\n sum(mat[i]) == 1 and \\\n sum(mat_t[j]) == 1:\n result += 1\n \n return result\n```
| 2 | 0 |
['Python', 'Python3']
| 0 |
special-positions-in-a-binary-matrix
|
Python 3, fast and simple, 152 ms, faster than 97.49%
|
python-3-fast-and-simple-152-ms-faster-t-erc5
|
\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n row_set = {i for i, r in enumerate(mat) if sum(r) == 1}\n return len([
|
MihailP
|
NORMAL
|
2021-07-29T16:44:41.255557+00:00
|
2021-07-29T16:45:08.455700+00:00
| 254 | false |
```\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n row_set = {i for i, r in enumerate(mat) if sum(r) == 1}\n return len(["" for c in zip(*mat) if sum(c) == 1 and c.index(1) in row_set])\n```
| 2 | 0 |
['Python', 'Python3']
| 0 |
special-positions-in-a-binary-matrix
|
C++| 92% faster| EASY TO UNDERSTAND | fast and efficient
|
c-92-faster-easy-to-understand-fast-and-xcgq5
|
Please upvote to motivate me in my quest of documenting all leetcode solutions. HAPPY CODING:)\nAny suggestions and improvements are always welcome\n```\nclass
|
aarindey
|
NORMAL
|
2021-06-15T15:27:17.037026+00:00
|
2021-06-15T15:27:17.037069+00:00
| 188 | false |
***Please upvote to motivate me in my quest of documenting all leetcode solutions. HAPPY CODING:)\nAny suggestions and improvements are always welcome***\n```\nclass Solution {\npublic:\nint numSpecial(vector<vector<int>>& mat) {\n int m=mat.size();\n int n=mat[0].size();\n vector<int> rows(m,0), cols(n,0);\n for (int i = 0; i < m; i++)\n for (int j = 0; j < n; j++) {\n if (mat[i][j]==1)\n rows[i]++, cols[j]++;\n }\n int ans = 0;\n for (int i = 0; i < m; i++)\n for (int j = 0; j < n; j++)\n if (mat[i][j]==1 && rows[i] == 1 && cols[j] == 1)\n ans++;\n return ans;\n}\n};
| 2 | 0 |
['C']
| 1 |
special-positions-in-a-binary-matrix
|
Simple C++ Solution
|
simple-c-solution-by-spiderxm-msts
|
```\nclass Solution {\npublic:\n int numSpecial(vector>& mat) {\n vector rowSum(mat.size(), 0);\n vector columnSum(mat[0].size(), 0);\n
|
spiderxm
|
NORMAL
|
2021-05-06T19:50:45.160203+00:00
|
2021-05-06T19:51:26.063993+00:00
| 74 | false |
```\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n vector<int> rowSum(mat.size(), 0);\n vector<int> columnSum(mat[0].size(), 0);\n for(int i = 0; i < mat[0].size(); i++){\n for(int j = 0; j < mat.size(); j++){\n columnSum[i] += mat[j][i];\n }\n }\n for(int i = 0; i < mat.size(); i++){\n for(int j = 0; j < mat[0].size(); j++){\n rowSum[i] += mat[i][j];\n }\n }\n int count = 0;\n for(int i = 0; i < mat.size(); i++){\n for(int j = 0; j < mat[0].size(); j++){\n if(mat[i][j] == 1){\n if(columnSum[j] == 1 && rowSum[i] == 1){\n count++;\n }\n }\n }\n }\n \n return count;\n }\n};
| 2 | 1 |
[]
| 0 |
special-positions-in-a-binary-matrix
|
Very easy Java solution. Runtime: 1 ms, faster than 99.64%
|
very-easy-java-solution-runtime-1-ms-fas-fem9
|
\nclass Solution \n{\n int r, c;\n int arr[][];\n \n public boolean isSpecial(int row, int col) \n {\n for(int i=0; i<c; i++) //vert
|
ghosharindam195
|
NORMAL
|
2021-04-14T04:16:07.975992+00:00
|
2021-04-14T04:16:07.976025+00:00
| 245 | false |
```\nclass Solution \n{\n int r, c;\n int arr[][];\n \n public boolean isSpecial(int row, int col) \n {\n for(int i=0; i<c; i++) //vertically checking\n {\n if(arr[row][i]==1 && i!=col)\n return false;\n }\n for(int i=0; i<r; i++) //Horizontal checking\n {\n if(arr[i][col]==1 && i!=row)\n return false;\n }\n return true;\n }\n public int numSpecial(int[][] mat) \n {\n r=mat.length;\n c=mat[0].length;\n arr = mat;\n int count=0;\n for(int i=0; i<r; i++)\n {\n for(int j=0; j<c; j++)\n {\n if(mat[i][j]==1 && isSpecial(i, j))\n count++;\n }\n }\n return count;\n }\n}\n//By Arindam Ghosh\n```
| 2 | 0 |
['Java']
| 1 |
special-positions-in-a-binary-matrix
|
Ruby one-liner
|
ruby-one-liner-by-dnnx-eqfw
|
\n# @param {Integer[][]} mat\n# @return {Integer}\ndef num_special(m)\n m.count { |r| r.sum == 1 && (j = r.index(1)) && m.all? { |rr| rr.equal?(r) || rr[j] ==
|
dnnx
|
NORMAL
|
2021-02-14T13:57:30.040562+00:00
|
2021-02-14T13:57:30.040609+00:00
| 68 | false |
```\n# @param {Integer[][]} mat\n# @return {Integer}\ndef num_special(m)\n m.count { |r| r.sum == 1 && (j = r.index(1)) && m.all? { |rr| rr.equal?(r) || rr[j] == 0 } }\nend\n```
| 2 | 0 |
[]
| 1 |
special-positions-in-a-binary-matrix
|
[JAVA] Faster than 99.83%, 1 ms, O(n), best case - 1 pass, worst - 2
|
java-faster-than-9983-1-ms-on-best-case-6lmmh
|
\nclass Solution {\n private static final int NOT_FOUND_IDX = -1;\n \n public int numSpecial(int[][] mat) {\n\t\t// contains coll \'j\' where might be
|
yurokusa
|
NORMAL
|
2021-01-31T22:25:04.865340+00:00
|
2021-01-31T22:47:41.982812+00:00
| 412 | false |
```\nclass Solution {\n private static final int NOT_FOUND_IDX = -1;\n \n public int numSpecial(int[][] mat) {\n\t\t// contains coll \'j\' where might be a lucky number\n var possibleIndexes = new int[mat.length];\n\t\t\n\t\t// no guarantee that it has a full \'j\' sum, but if it is > 2 we already know that we can skip it during counting\n\t\tvar columnSum = new int[mat[0].length];\n\n\t\t// populate indexes and sums\n for (int i = 0; i < mat.length; i++) {\n var colIdx = NOT_FOUND_IDX;\n for (int j = 0; j < columnSum.length; j++) {\n columnSum[j] += mat[i][j];\n if (mat[i][j] == 1) {\n if (colIdx == NOT_FOUND_IDX) {\n colIdx = j;\n } else {\n colIdx = NOT_FOUND_IDX;\n break;\n }\n }\n }\n possibleIndexes[i] = colIdx;\n }\n\n\t\t// count \'1\' values, ignore col \'j\' where we are sure the number is not lucky\n var count = 0;\n for (int p = 0; p < possibleIndexes.length; p++) {\n var j = possibleIndexes[p];\n if (j != NOT_FOUND_IDX && columnSum[j] < 2) {\n var sum = 0;\n for (int i = 0; i < mat.length; i++) {\n sum += mat[i][j];\n if (sum > 1) break;\n }\n if (sum == 1) count++;\n }\n }\n return count;\n }\n}\n```
| 2 | 0 |
['Java']
| 1 |
special-positions-in-a-binary-matrix
|
Easy Solution 32ms c++
|
easy-solution-32ms-c-by-moazmar-67ao
|
\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n int rows=mat.size();\n int cols=mat[0].size();\n int sum=0;\n
|
moazmar
|
NORMAL
|
2020-12-23T21:04:01.456520+00:00
|
2020-12-23T21:04:01.456567+00:00
| 215 | false |
```\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n int rows=mat.size();\n int cols=mat[0].size();\n int sum=0;\n for(int i=0;i<rows;i++){\n int nbe=0;int index;\n for(int j=0;j<cols;j++){\n if(mat[i][j]==1){\n nbe++;\n index=j;\n } \n if(nbe>1)break;\n }\n if(nbe==1){\n for(int k=0;k<rows;k++){\n if(mat[k][index]==1)nbe--;\n }\n if(nbe==0)sum++;\n }\n }\n return sum;\n }\n};\n```
| 2 | 0 |
['C', 'C++']
| 0 |
special-positions-in-a-binary-matrix
|
Java Simple 99.93% Fast Solution
|
java-simple-9993-fast-solution-by-umangl-m2g1
|
This is a very simple and intutive brute force java solution.\nPlease suggest if you\'ve more efficient solution.\n```\npublic int numSpecial(int[][] mat) {\n\t
|
umanglahoti30
|
NORMAL
|
2020-10-12T11:30:34.608701+00:00
|
2020-10-12T11:30:34.608733+00:00
| 274 | false |
This is a very simple and intutive brute force java solution.\nPlease suggest if you\'ve more efficient solution.\n```\npublic int numSpecial(int[][] mat) {\n\tint count = 0;\n\tfor(int i = 0; i < mat.length; i++) {\n\t\tfor(int j = 0; j < mat[0].length; j++) {\n\t\t\tif(mat[i][j] == 1 && special(mat, i, j)) {\n\t\t\t\tcount++;\n\t\t\t}\n\t\t}\n\t}\n\treturn count;\n}\npublic boolean special(int[][] mat, int row, int col){\n\tfor(int i = 0; i < mat.length; i++){\n\t\tif(i == row)\n\t\t\tcontinue;\n\t\tif(mat[i][col] == 1) {\n\t\t\treturn false;\n\t\t}\n\t}\n\tfor(int j = 0; j < mat[0].length; j++) {\n\t\tif(j == col)\n\t\t\tcontinue;\n\t\tif(mat[row][j] == 1) {\n\t\t\treturn false;\n\t\t}\n\t}\n\treturn true;\n}
| 2 | 1 |
['Java']
| 0 |
special-positions-in-a-binary-matrix
|
[C++] Solutions
|
c-solutions-by-zxspring21-luej
|
C++:\n\n(1) Intuition\n\nint numSpecial(vector<vector<int>>& mat) {\n\tconst int row = mat.size(), col = row?mat[0].size():0;\n\tint cnt=0;\n\tfor(int i=0;i<row
|
zxspring21
|
NORMAL
|
2020-10-04T09:03:01.955279+00:00
|
2020-10-04T09:03:17.096468+00:00
| 239 | false |
**C++:**\n\n**(1) Intuition**\n```\nint numSpecial(vector<vector<int>>& mat) {\n\tconst int row = mat.size(), col = row?mat[0].size():0;\n\tint cnt=0;\n\tfor(int i=0;i<row;++i){\n\t\tfor(int j=0;j<col;++j){\n\t\t\tif(mat[i][j]==1){\n\t\t\t\tint sum=0;\n\t\t\t\tfor(int k=0;k<row && sum<=2;++k) sum+=mat[k][j];\n\t\t\t\tfor(int k=0;k<col && sum<=2;++k) sum+=mat[i][k];\n\t\t\t\tif(sum==2) ++cnt;\n\t\t\t}\n\t\t}\n\t}\n\treturn cnt;\n}\n```\n**(2) Two Pass**\n```\nint numSpecial(vector<vector<int>>& mat) {\n\tconst int row = mat.size(), col = row?mat[0].size():0;\n\tvector<int> numbersOfOneInRow(row);\n\tvector<int> numbersOfOneInCol(col);\n\tint cnt=0;\n\tfor(int i=0;i<row;++i)\n\t\tfor(int j=0;j<col;++j)\n\t\t\tif(mat[i][j]) numbersOfOneInRow[i]++, numbersOfOneInCol[j]++;\n\tfor(int i=0;i<row;++i)\n\t\tfor(int j=0;j<col;++j)\n\t\t\tif(mat[i][j] && numbersOfOneInRow[i]==1 && numbersOfOneInCol[j]==1) cnt++;\n\treturn cnt;\n}\n```
| 2 | 0 |
['C']
| 2 |
special-positions-in-a-binary-matrix
|
Python 3 - Runtime faster than 90.88%
|
python-3-runtime-faster-than-9088-by-cc_-61oe
|
\nclass Solution:\n def numSpecial(self, mat: list) -> int:\n # find nums[i][j] == 1\n # find upper lower left right are all 0\n count =
|
CC_CheeseCake
|
NORMAL
|
2020-10-03T15:06:05.527811+00:00
|
2020-10-03T15:06:05.527854+00:00
| 88 | false |
```\nclass Solution:\n def numSpecial(self, mat: list) -> int:\n # find nums[i][j] == 1\n # find upper lower left right are all 0\n count = 0\n lengthRow = len(mat)\n lengthCol = len(mat[0])\n for i in range(lengthRow):\n for j in range(lengthCol):\n if mat[i][j] == 1:\n indexUp = i - 1\n indexDown = i + 1\n indexLeft = j - 1\n indexRigth = j + 1\n foundOne = False\n cont = True\n try:\n if cont:\n while indexUp >= 0:\n if mat[indexUp][j] == 1:\n foundOne = True\n cont = False\n break\n indexUp -= 1\n except:\n pass\n try:\n if cont:\n while indexDown < len(mat):\n if mat[indexDown][j] == 1:\n foundOne = True\n cont = False\n break\n indexDown += 1\n except:\n pass\n try:\n if cont:\n while indexLeft >= 0:\n if mat[i][indexLeft] == 1:\n foundOne = True\n cont = False\n break\n indexLeft -= 1\n except:\n pass\n try:\n if cont:\n while indexRigth < lengthCol:\n if mat[i][indexRigth] == 1:\n foundOne = True\n cont = False\n break\n indexRigth += 1\n except:\n pass\n if not foundOne:\n count += 1\n return count\n\n```
| 2 | 1 |
[]
| 1 |
special-positions-in-a-binary-matrix
|
3 Solutions in C# (100% 100%)
|
3-solutions-in-c-100-100-by-mhorskaya-tn8e
|
\npublic int NumSpecial(int[][] mat) {\n\tvar rows = new List<int>();\n\tfor (var i = 0; i < mat.Length; i++)\n\t\tif (mat[i].Sum() == 1)\n\t\t\trows.Add(i);\n\
|
mhorskaya
|
NORMAL
|
2020-09-14T04:25:40.689818+00:00
|
2020-09-14T05:00:06.924286+00:00
| 147 | false |
```\npublic int NumSpecial(int[][] mat) {\n\tvar rows = new List<int>();\n\tfor (var i = 0; i < mat.Length; i++)\n\t\tif (mat[i].Sum() == 1)\n\t\t\trows.Add(i);\n\n\tvar cols = new List<int>();\n\tfor (var i = 0; i < mat[0].Length; i++)\n\t\tif (mat.Sum(x => x[i]) == 1)\n\t\t\tcols.Add(i);\n\n\treturn rows\n\t\t.SelectMany(r => cols.Select(c => (r, c)))\n\t\t.Count(t => mat[t.r][t.c] == 1);\n}\n```\n```\npublic int NumSpecial(int[][] mat) {\n\tvar rows = Enumerable.Range(0, mat.Length).Where(i => mat[i].Sum() == 1).ToArray();\n\tvar cols = Enumerable.Range(0, mat[0].Length).Where(j => mat.Sum(x => x[j]) == 1).ToArray();\n\treturn rows.SelectMany(r => cols.Select(c => (r, c))).Count(t => mat[t.r][t.c] == 1);\n}\n```\n```\npublic int NumSpecial(int[][] mat) =>\n\tEnumerable.Range(0, mat.Length)\n\t\t.Where(i => mat[i].Sum() == 1)\n\t\t.SelectMany(i => Enumerable.Range(0, mat[0].Length)\n\t\t\t.Where(j => mat.Sum(x => x[j]) == 1)\n\t\t\t.Select(j => (i, j)))\n\t\t.Count(t => mat[t.i][t.j] == 1);\n```
| 2 | 0 |
[]
| 0 |
special-positions-in-a-binary-matrix
|
C++ | HashMap
|
c-hashmap-by-heisenberg-5pa1
|
\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n \n int m=mat.size(), n=mat[0].size(), count=0;\n\t\t\n\t\t//Create t
|
Heisenberg_
|
NORMAL
|
2020-09-13T13:04:07.417286+00:00
|
2020-09-13T13:04:07.417314+00:00
| 128 | false |
```\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n \n int m=mat.size(), n=mat[0].size(), count=0;\n\t\t\n\t\t//Create two HashMap to store the count of 1\'s in the particular Row and Column.\n map<int, int> row, col;\n\t\t\n\t\t//Loop through the Matrix O(N^2)\n for(int i=0; i<m; i++)\n {\n for(int j=0; j<n; j++)\n {\n\t\t\t\t//If 1 if found increment the count of row and col HashMap for that possition.\n if(mat[i][j]==1)\n {\n row[i]++;\n col[j]++;\n }\n }\n }\n \n\t\t//Again loop the Matrix to count.\n for(int i=0; i<m; i++)\n\t\t{\n for(int j=0; j<n; j++)\n\t\t\t{\n\t\t\t\t// If the values at the position and Row count and Column count is 1, Increment the "Count".\n if(mat[i][j]==1 && row[i]==1 && col[j]==1)\n count++;\n\t\t\t}\n\t\t}\n\t\t\n return count;\n }\n};\n```
| 2 | 0 |
['C']
| 0 |
special-positions-in-a-binary-matrix
|
[ IDEA ] with Picture
|
idea-with-picture-by-suneelvarma55-tg9c
|
\n\n To confirm a position as special, it must pass three conditions.\n\t1. cell value must be equal to one\n\t2. No other one should present in column, which m
|
suneelvarma55
|
NORMAL
|
2020-09-13T10:19:44.637616+00:00
|
2020-09-14T05:11:49.209117+00:00
| 81 | false |
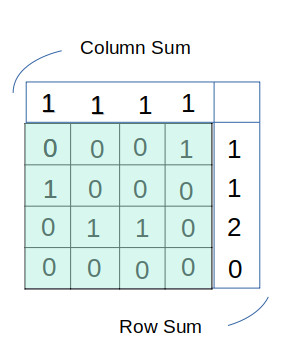\n\n* To confirm a position as special, it must pass three conditions.\n\t1. cell value must be equal to one\n\t2. No other one should present in column, which means\n\t\t\t```sum of vertical cells == 1```\n\t3. No other one should present in row, which means\n\t\t\t```sum of horizontal cells == 1```\n\t\t\t\n* \tCreate arrays for row Sum and column Sum.\n\n\n\n*Upvote, if you understand. Thank you!*
| 2 | 0 |
[]
| 0 |
special-positions-in-a-binary-matrix
|
If i don't want to use extra space. Why this is not working can some one help finding mistake?
|
if-i-dont-want-to-use-extra-space-why-th-s0pj
|
\nclass Solution {\n bool check(int i, int j , int r ,int c, vector<vector<int>>& mat){\n int x = i, y = j;\n while(x>=0) {\n x--;
|
sahilChoudhary16
|
NORMAL
|
2020-09-13T05:06:14.535463+00:00
|
2020-09-13T05:06:14.535494+00:00
| 135 | false |
```\nclass Solution {\n bool check(int i, int j , int r ,int c, vector<vector<int>>& mat){\n int x = i, y = j;\n while(x>=0) {\n x--;\n if (x>= 0 && mat[x][j] == 1) return false;\n }\n x= i;\n while (x < r ){\n x++;\n if (x<r && mat[x][i] == 1) return false;\n }\n \n while(y >=0 ){\n y--;\n if (y>=0 && mat[i][y] == 1 ) return false;\n }\n y = j;\n while(y < c ){\n y++;\n if (y < c && mat[i][y] == 1) return false;\n }\n \n return true;\n \n }\n \n \npublic:\n int numSpecial(vector<vector<int>>& mat) {\n \n int r = mat.size();\n int c = mat[0].size();\n \n int ans = 0;\n for (int i =0 ;i< r ;i++ ){\n for (int j = 0 ;j < c ;j ++ ){\n \n if (mat[i][j] == 1){\n if (check(i,j,r,c,mat)) ans++;\n \n }\n \n }\n }\n return ans;\n }\n};\n```
| 2 | 0 |
[]
| 1 |
special-positions-in-a-binary-matrix
|
Easy Java
|
easy-java-by-satyajit2-zsac
|
\t\tpublic int numSpecial(int[][] mat) {\n\n\n int c = 0;\n for(int i = 0; i < mat.length; i++) {\n for(int j = 0; j < mat[0].length; j
|
satyajit2
|
NORMAL
|
2020-09-13T04:00:42.456183+00:00
|
2020-09-13T04:00:42.456229+00:00
| 383 | false |
\t\tpublic int numSpecial(int[][] mat) {\n\n\n int c = 0;\n for(int i = 0; i < mat.length; i++) {\n for(int j = 0; j < mat[0].length; j++) {\n if(mat[i][j] == 1) {\n if(check(mat, i, j)) {\n c++;\n }\n }\n }\n }\n return c;\n }\n\n public boolean check(int[][] mat, int i, int j) {\n\n int c = 0;\n for(int k = 0; k < mat[0].length; k++) {\n if(mat[i][k] == 0) {\n c++;\n }\n }\n int l = 0;\n\n for(int k = 0; k < mat.length; k++) {\n if(mat[k][j] == 0) {\n l++;\n }\n }\n if(c == mat[0].length - 1 && l == mat.length - 1) {\n return true;\n }\n return false;\n }
| 2 | 0 |
[]
| 0 |
special-positions-in-a-binary-matrix
|
Easy Code | | C++ 👻
|
easy-code-c-by-varuntyagig-i40m
|
Code
|
varuntyagig
|
NORMAL
|
2025-01-16T09:00:55.558571+00:00
|
2025-01-16T09:00:55.558571+00:00
| 43 | false |
# Code
```cpp []
class Solution {
public:
int numSpecial(vector<vector<int>>& mat) {
int specialPositionCount = 0;
int m = mat.size();
int n = mat[0].size();
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (mat[i][j] == 1) {
int countOneRow = 0, countOneCol = 0;
// Traverse Row
// i constant, j vary
for (int k = 0; k < n; k++) {
if (mat[i][k] == 1) {
countOneRow += 1;
}
}
// Traverse Col
// j constant,i vary
for (int k = 0; k < m; k++) {
if (mat[k][j] == 1) {
countOneCol += 1;
}
}
if (countOneCol == 1 && countOneRow == 1) {
specialPositionCount += 1;
}
}
}
}
return specialPositionCount;
}
};
```
| 1 | 0 |
['Matrix', 'Counting', 'C++']
| 0 |
special-positions-in-a-binary-matrix
|
my
|
my-by-sumitraut75147-0qk3
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
sumitraut75147
|
NORMAL
|
2024-09-09T12:47:56.405333+00:00
|
2024-09-09T12:47:56.405364+00:00
| 4 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int numSpecial(int[][] mat) {\n int count=0;\n int rowZero=0;\n int colZero=0;\n for(int i=0;i<mat.length;i++){\n for(int j=0;j<mat[i].length;j++){\n if(mat[i][j]==1){\n for(int k=0;k<mat[i].length;k++){\n if(k!=j){\n if(mat[i][k]==0){\n rowZero=1;\n }else{\n rowZero=0;\n break;\n }\n }\n }\n for(int k=0;k<mat.length;k++){\n if(k!=i){\n if(mat[k][j]==0){\n colZero=1;\n }else{\n colZero=0;\n break;\n }\n }\n }\n if(colZero==1 && rowZero==1){\n count++;\n }\n }\n }\n } \n\n return count;\n\n\n\n }\n}\n```
| 1 | 0 |
['Java']
| 0 |
special-positions-in-a-binary-matrix
|
🔥💯✅✅Best and easyest approch to solve the question beat 99 %
|
best-and-easyest-approch-to-solve-the-qu-1prx
|
Intuition\nThe problem is to find the number of special positions in a binary matrix. A special position is defined as a cell with a value of 1, where all other
|
ishanbagra
|
NORMAL
|
2024-07-14T09:09:47.245465+00:00
|
2024-07-14T09:09:47.245501+00:00
| 2 | false |
Intuition\nThe problem is to find the number of special positions in a binary matrix. A special position is defined as a cell with a value of 1, where all other cells in the same row and column are 0. The approach involves iterating through each cell in the matrix and checking if it is a special position by verifying its row and column.\n\nApproach\nIterate through each cell in the matrix.\nFor each cell with a value of 1, check if all other cells in the same row and column are 0.\nUse two helper functions rows and columns to check the row and column conditions respectively.\nIf both conditions are satisfied, count the cell as a special position.\nReturn the total count of special positions.\nComplexity\nTime complexity: \nO(n\xD7m), where\nn is the number of rows and \nm is the number of columns. This is because for each cell in the matrix, we potentially iterate through all columns and rows.\nSpace complexity: \n\nO(1), since we are only using a fixed amount of extra space.\n\n# Code\n```\n#include <vector>\n\nusing namespace std;\n\nbool rows(vector<vector<int>>& mat, int x, int y) {\n int row = mat.size();\n int col = mat[0].size();\n\n int value = mat[x][y];\n\n for (int i = 0; i < col; i++) {\n if (i != y && mat[x][i]==1) {\n return false;\n }\n }\n return true;\n}\n\nbool columns(vector<vector<int>>& mat, int x, int y) {\n int row = mat.size();\n int col = mat[0].size();\n\n int value = mat[x][y];\n\n for (int i = 0; i < row; i++) {\n if (i != x && mat[i][y]==1) {\n return false;\n }\n }\n return true;\n}\n\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n int row = mat.size();\n int col = mat[0].size();\n\n int count = 0;\n\n for (int i = 0; i < row; i++) {\n for (int j = 0; j < col; j++) {\n if (mat[i][j] == 1) {\n if (rows(mat, i, j) && columns(mat, i, j)) {\n count++;\n }\n }\n }\n }\n\n return count;\n }\n};\n\n```
| 1 | 0 |
['C++']
| 0 |
special-positions-in-a-binary-matrix
|
simple and easy understand solution
|
simple-and-easy-understand-solution-by-s-7bba
|
if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n\n# Code\n\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) \n {\n int n
|
shishirRsiam
|
NORMAL
|
2024-03-19T14:29:36.248548+00:00
|
2024-03-19T14:29:36.248582+00:00
| 238 | false |
# if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n\n# Code\n```\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) \n {\n int n = mat.size(), m = mat[0].size(), ans = 0;\n for(int i=0;i<n;i++)\n {\n for(int j=0;j<m;j++)\n {\n if(mat[i][j]==1)\n {\n int cnt = 0;\n for(int k=0;k<m;k++)\n if(mat[i][k]==1) cnt++;\n for(int k=0;k<n;k++)\n if(mat[k][j]==1) cnt++;\n if(cnt==2) ans++;\n }\n }\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['Array', 'C', 'Matrix', 'Python', 'C++', 'Java', 'Python3', 'Rust', 'JavaScript', 'C#']
| 2 |
special-positions-in-a-binary-matrix
|
C++ || O(n x m) time complexity || hashing approach 🔥🔥🔥|| easy and simple soln.
|
c-on-x-m-time-complexity-hashing-approac-uq2o
|
Intuition\n Describe your first thoughts on how to solve this problem. \nusing hashing technique to count the occurences of 1 in each row and columns.\n\n# Appr
|
ankitsingh07s
|
NORMAL
|
2024-03-13T14:05:36.248177+00:00
|
2024-03-13T14:05:36.248211+00:00
| 0 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nusing hashing technique to count the occurences of 1 in each row and columns.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nwe will use 2 separate arrays for hashing - 1 for rows and 1 for column.\n\nsteps 1- \ntraverse the matrix and whenever a 1 occurs, update its corresponding row and columns in hash arrays\n\nstep 2-\ninitialize a count variable = 0.\n\ntraverse the matrix and again and simultaneously check the hash arrays for value == 1.\n\nNOTE : hash value == 1 in the hash arrays represent that it is the element we are looking for. \n\n# Complexity\n- Time complexity: O(n x m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n + m)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n // approach - use 2 hash arrays to keep count of 1\'s in each row and col.\n\n int n = mat.size(); \n int m = mat[0].size();\n\n vector<int> row(n,0);\n vector<int> col(m,0);\n\n int ans = 0;\n\n for(int i = 0 ; i<n ; i++){\n for(int j = 0 ; j<m ; j++){\n if(mat[i][j] == 1){\n row[i]++;\n col[j]++;\n }\n }\n }\n\n for(int i = 0 ; i<n ; i++){\n for(int j = 0 ; j<m ; j++){\n if(mat[i][j] == 1){\n if(row[i] == 1 && col[j] == 1){\n ans++;\n }\n }\n }\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
special-positions-in-a-binary-matrix
|
JS || Solution by Bharadwaj
|
js-solution-by-bharadwaj-by-manu-bharadw-me3i
|
Intuition\nfunction numSpecial(mat) {\n // Function to calculate the sum of a specific column\n function columnSum(col) {\n return mat.reduce((sum, row) =>
|
Manu-Bharadwaj-BN
|
NORMAL
|
2024-01-11T06:48:32.132723+00:00
|
2024-01-11T06:48:32.132786+00:00
| 16 | false |
# Intuition\nfunction numSpecial(mat) {\n // Function to calculate the sum of a specific column\n function columnSum(col) {\n return mat.reduce((sum, row) => sum + row[col], 0);\n }\n\n // Count of special elements\n let unique = 0;\n\n // Loop through each row\n for (let row of mat) {\n // Check if the row sum is 1\n if (row.reduce((acc, val) => acc + val, 0) === 1) {\n // Find the index of the 1 in the row\n let col = row.indexOf(1);\n // Check if the column sum is also 1\n if (columnSum(col) === 1) {\n // Increment the count of special elements\n unique += 1;\n }\n }\n }\n\n // Return the final count\n return unique;\n}\n\n# Code\n```\nvar numSpecial = function (mat) {\n function columnSum(col) {\n return mat.reduce((sum, row) => sum + row[col], 0);\n }\n let unique = 0;\n for (let row of mat) {\n if (row.reduce((acc, val) => acc + val, 0) === 1) {\n let col = row.indexOf(1);\n unique += columnSum(col) === 1;\n }\n }\n return unique;\n};\n```
| 1 | 0 |
['JavaScript']
| 1 |
special-positions-in-a-binary-matrix
|
Simple easy cpp solution, beats 93% ✅✅
|
simple-easy-cpp-solution-beats-93-by-vai-3e2r
|
Complexity\n- Time complexity: O(m * n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(m + n)\n Add your space complexity here, e.g. O(n)
|
vaibhav2112
|
NORMAL
|
2023-12-14T16:36:21.670205+00:00
|
2023-12-14T16:36:21.670243+00:00
| 5 | false |
# Complexity\n- Time complexity: O(m * n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(m + n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n\n // Logic -> make 2 vectors row and col \n // it will store number of 1 in ith row and jth col\n // iterate matrix again and if mat[i][j] -> check if row[i] = 1 AND col[j] = 1 , ans++\n \n int m = mat.size(), n = mat[0].size(), ans = 0;\n vector<int> row(m,0) , col(n,0);\n\n for(int i = 0 ; i < m ; i++){\n for(int j = 0 ; j < n ; j++){\n if(mat[i][j] == 1){\n row[i]++, col[j]++;\n }\n }\n }\n\n for(int i = 0 ; i < m ; i++){\n for(int j = 0 ; j < n ; j++){\n if(mat[i][j] == 1){\n if(row[i] == 1 && col[j] == 1){\n ans++;\n }\n }\n }\n }\n\n\n return ans;\n\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
special-positions-in-a-binary-matrix
|
✅ C++ Solution 🔥 Fastest Solution , Beats 100%🔥
|
c-solution-fastest-solution-beats-100-by-d00k
|
Intuition\n Describe your first thoughts on how to solve this problem. \nSearch in Only those rows and colums whose matrix[row][column]=="1" to avoid unecessary
|
Rohan80_80
|
NORMAL
|
2023-12-14T06:14:37.359462+00:00
|
2023-12-14T06:14:37.359486+00:00
| 9 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSearch in Only those rows and colums whose matrix[row][column]=="1" to avoid unecessary seaching \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Search matrix [row ][column]== 1 ;\nstart from matrix[0][0] index and search which element\nmatrix[row][column]==1.\n2. If we find the element then call the function which return true and false depending upon the special element is present or not .\n3. In that function Search in matrix[row] [all column elements]==1 ;\nset and temporary counter to count matrix[row][column]==1 ,\nif count greater than 1 return false , to avoid further searching.\n4. In further function Search in matrix[all rows] [column]==1 ;\ncount the element count matrix[row][column]==1 , if count is greater than 2 return false elseif count == 2 return true .\n5. If our function return true then it increase our answer counter element\n6. At last return the answer counter .\n\n# Complexity\n- Time complexity: $$O(M.N.(M+N))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\nprivate: \n bool chk(int i,int j,vector<vector<int>>&mat){\n int temp=0;\n for(int k=0;k< mat[0].size();k++){\n if(mat[i][k]==1) temp++;\n }\n if(temp>1) return false;\n for(int k=0;k<mat.size();k++){\n if(mat[k][j]==1) temp++;\n }\n\n if(temp==2) return 1;\n return 0;\n }\npublic:\n int numSpecial(vector<vector<int>>& mat) {\n int cnt=0;\n for(int i=0;i<mat.size();i++){\n for(int j=0;j<mat[0].size();j++){\n if(mat[i][j]==1){\n if(chk(i,j,mat)){\n cnt++;\n }\n }\n }\n }\n \n return cnt;\n }\n};\n```\n\n\n
| 1 | 0 |
['C++']
| 1 |
special-positions-in-a-binary-matrix
|
🟢 Easy Python & Ruby Solution | 2 Approaches🚀🚀🚀
|
easy-python-ruby-solution-2-approaches-b-jow2
|
Video Explanation\nhttps://youtu.be/nh1M4GGCk1U\n\n# Approach\nPre-calculate Count of 1\n\n# Complexity\n- Time complexity:\nO(m.n)\n\n- Space complexity:\nO(m+
|
mitchell000
|
NORMAL
|
2023-12-13T22:08:40.345381+00:00
|
2023-12-13T22:08:40.345404+00:00
| 12 | false |
# Video Explanation\nhttps://youtu.be/nh1M4GGCk1U\n\n# Approach\nPre-calculate Count of 1\n\n# Complexity\n- Time complexity:\nO(m.n)\n\n- Space complexity:\nO(m+n)\n\n# Code\n```Ruby []\n# @param {Integer[][]} mat\n# @return {Integer}\ndef num_special(mat)\n row, col = mat.length, mat[0].length\n row_count = Array.new(row, 0)\n col_count = Array.new(col, 0)\n\n (0...row).each do |r|\n (0...col).each do |c|\n if mat[r][c] == 1\n row_count[r] += 1\n col_count[c] += 1\n end\n end\n end\n\n result = 0\n (0...row).each do |r|\n (0...col).each do |c|\n result += 1 if mat[r][c] == 1 && row_count[r] == 1 && col_count[c] == 1\n end\n end\n result\nend\n```\n```Python []\nclass Solution:\n def numSpecial(self, mat: List[List[int]]) -> int:\n ROW, COL = len(mat), len(mat[0])\n row_count = [0]*ROW\n col_count = [0]*COL\n for r in range(ROW):\n for c in range(COL):\n if mat[r][c] == 1:\n row_count[r] += 1\n col_count[c] += 1\n \n ans = 0\n for r in range(ROW):\n for c in range(COL):\n if mat[r][c] == 1:\n if row_count[r] == 1 and col_count[c] == 1:\n ans += 1\n return ans\n```
| 1 | 0 |
['Array', 'Matrix', 'Python', 'Python3', 'Ruby']
| 0 |
special-positions-in-a-binary-matrix
|
Swift solution with explanation
|
swift-solution-with-explanation-by-nihad-nzko
|
Approach\nIterate through the matrix keeping track of 1s count in each row and column in variables rowOnesCount and columnOnesCount. Once this done and we have
|
Nihad_s
|
NORMAL
|
2023-12-13T20:18:28.019215+00:00
|
2023-12-13T20:18:28.019244+00:00
| 13 | false |
# Approach\nIterate through the matrix keeping track of 1s count in each row and column in variables $$rowOnesCount$$ and $$columnOnesCount$$. Once this done and we have count of 1s for each row and for each column, we iterate through the matrix again and check if element on current row and column is 1, if it is then we check if current row and column have exactly one count of 1s. If it\'s true then we increment our $$result$$ variable by 1. At the end we just return the $$result$$.\n\n# Complexity\n- Time complexity: $$O(n\\cdot m)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n+m)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n func numSpecial(_ mat: [[Int]]) -> Int {\n var rowOnesCount = Array(repeating: 0, count: mat.count)\n var columnOnesCount = Array(repeating: 0, count: mat[0].count)\n\n for i in 0..<mat.count {\n for j in 0..<mat[0].count {\n if mat[i][j] == 1 {\n rowOnesCount[i] += 1\n columnOnesCount[j] += 1\n }\n }\n }\n\n var result = 0\n for i in 0..<mat.count {\n for j in 0..<mat[0].count {\n if mat[i][j] == 1 && rowOnesCount[i] == 1 && columnOnesCount[j] == 1 {\n result += 1\n }\n }\n }\n\n return result\n }\n}\n```
| 1 | 0 |
['Array', 'Swift', 'Matrix']
| 0 |
mirror-reflection
|
Java solution with an easy-to-understand explanation
|
java-solution-with-an-easy-to-understand-79ls
|
The idea comes from this post: https://leetcode.com/problems/mirror-reflection/discuss/141773, and here I add some explaination.\n\n public int mirrorReflect
|
motorix
|
NORMAL
|
2018-07-07T04:56:27.411436+00:00
|
2018-10-25T06:59:22.820388+00:00
| 18,687 | false |
The idea comes from this post: https://leetcode.com/problems/mirror-reflection/discuss/141773, and here I add some explaination.\n```\n public int mirrorReflection(int p, int q) {\n int m = 1, n = 1;\n while(m * p != n * q){\n n++;\n m = n * q / p;\n }\n if (m % 2 == 0 && n % 2 == 1) return 0;\n if (m % 2 == 1 && n % 2 == 1) return 1;\n if (m % 2 == 1 && n % 2 == 0) return 2;\n return -1;\n }\n```\nFirst, think about the case p = 3 & q = 2.\n\nSo, this problem can be transformed into finding ```m * p = n * q```, where \n```m``` = the number of room extension + 1. \n```n``` = the number of light reflection + 1. \n\n\n1. If the number of light reflection is odd (which means ```n``` is even), it means the corner is on the left-hand side. The possible corner is ```2```.\nOtherwise, the corner is on the right-hand side. The possible corners are ```0``` and ```1```.\n2. Given the corner is on the right-hand side. \nIf the number of room extension is even (which means ```m``` is odd), it means the corner is ```1```. Otherwise, the corner is ```0```.\n\nSo, we can conclude:\n```\nm is even & n is odd => return 0.\nm is odd & n is odd => return 1.\nm is odd & n is even => return 2.\n```\nNote: The case ```m is even & n is even``` is impossible. Because in the equation ``` m * q = n * p```, if ```m``` and ```n``` are even, we can divide both ```m``` and ```n``` by 2. Then, ```m``` or ```n``` must be odd.\n\n--\nBecause we want to find ```m * p = n * q```, where either ```m``` or ```n``` is odd, we can do it this way.\n```\n public int mirrorReflection(int p, int q) {\n int m = q, n = p;\n while(m % 2 == 0 && n % 2 == 0){\n m /= 2;\n n /= 2;\n }\n if (m % 2 == 0 && n % 2 == 1) return 0;\n if (m % 2 == 1 && n % 2 == 1) return 1;\n if (m % 2 == 1 && n % 2 == 0) return 2;\n return -1;\n }\n```
| 455 | 3 |
[]
| 32 |
mirror-reflection
|
[C++/Java/Python] 1-line without using any package or ✖️➗%
|
cjavapython-1-line-without-using-any-pac-0x6c
|
Here is my first solution. When I did it, I just code without any thinking.\n\n def mirrorReflection(self, p, q):\n k = 1\n while (q * k % p):
|
lee215
|
NORMAL
|
2018-06-24T03:04:31.018141+00:00
|
2018-10-25T06:59:14.324750+00:00
| 21,615 | false |
Here is my first solution. When I did it, I just code without any thinking.\n```\n def mirrorReflection(self, p, q):\n k = 1\n while (q * k % p): k += 1\n if q * k / p % 2 and k % 2: return 1\n if q * k / p % 2 == 0 and k % 2: return 0\n if q * k / p % 2 and k % 2 == 0: return 2\n return -1\n```\nWhen I reviewed the problems for my discuss article, I finaly realised only odd or even matter.\n\nDivide `p,q` by `2` until at least one odd.\n\nIf `p = odd, q = even`: return 0\nIf `p = even, q = odd`: return 2\nIf `p = odd, q = odd`: return 1\nI summary it as `return 1 - p % 2 + q % 2`\n\n<img alt="" src="https://s3-lc-upload.s3.amazonaws.com/uploads/2018/06/18/reflection.png" style="width: 218px; height: 217px;" />\n\n**C++:**\n```\n int mirrorReflection(int p, int q) {\n while (p % 2 == 0 && q % 2 == 0) p >>= 1, q >>= 1;\n return 1 - p % 2 + q % 2;\n }\n```\n\n**Java:**\n```\n public int mirrorReflection(int p, int q) {\n while (p % 2 == 0 && q % 2 == 0) {p >>= 1; q >>= 1;}\n return 1 - p % 2 + q % 2;\n }\n```\n**Python:**\n```\n def mirrorReflection(self, p, q):\n while p % 2 == 0 and q % 2 == 0: p, q = p / 2, q / 2\n return 1 - p % 2 + q % 2\n```\n\nBased on this idea, I did this 1-line solutions without any package.\n**C++/Java**\n```\n return (p & -p) > (q & -q) ? 2 : (p & -p) < (q & -q) ? 0:1;\n```\n\n**Python**\n```\n return ((p & -p) >= (q & -q)) + ((p & -p) > (q & -q))\n```\n\n\n**Time Complexity**\nTime for 4 bit manipulations and 2 comparations.
| 191 | 13 |
[]
| 23 |
mirror-reflection
|
Java short solution with a sample drawing
|
java-short-solution-with-a-sample-drawin-s9mg
|
\n\nI draw this graph to help. In this example, p / q = 5 / 2. In this way, we can find some patterns between pq and the result.\n\nI use the extending blocks t
|
wangzi6147
|
NORMAL
|
2018-06-24T03:02:24.886778+00:00
|
2018-10-19T21:06:17.509586+00:00
| 11,704 | false |
\n\nI draw this graph to help. In this example, `p / q = 5 / 2`. In this way, we can find some patterns between pq and the result.\n\nI use the extending blocks to simulate the reflection. As well as the reflection of the corners `0, 1, 2`. Then the laser could go straightly to the top right of the extending blocks until it reaches any of the corners. Then we can use `p/q` to represents the extending blocks `x/y` ratio which is `5/2` in the example above. Then the destination corner could be calculated using this `x/y` ratio.\nThe reason why we used modulo 2 is that if `x/y=10/4` for example, the laser will firstly reach the corner `0` when `x/y=5/2` before `x/y=10/4`. You can draw a similar graph to simulate it.\nIn other words, when the laser first reaches a corner, the `x` and `y` cannot both be even. So we keep using modulo 2 to let `x` and `y` go down. \n\n```\nclass Solution {\n public int mirrorReflection(int p, int q) {\n while (p % 2 == 0 && q % 2 == 0) {\n p /= 2;\n q /= 2;\n }\n if (p % 2 == 0) {\n return 2;\n } else if (q % 2 == 0) {\n return 0;\n } else {\n return 1;\n }\n }\n}\n```
| 153 | 1 |
[]
| 19 |
mirror-reflection
|
Mirror Mirror Flip Flip with Pictures + 10 lines of code [EVERYONE CAN UNDERSTAND! YOU TOO!]
|
mirror-mirror-flip-flip-with-pictures-10-c8ae
|
\n\n\n\n\n\n\n\n\npython\ndef mirrorReflection(p, q):\n\tif q == 0: \n\t\treturn 0\n\n\theight = q\n\twhile height < p or height % p:\n\t\theight += q\n\n\tupFl
|
coolgk
|
NORMAL
|
2020-11-17T18:24:33.139635+00:00
|
2020-11-22T17:34:52.982146+00:00
| 3,079 | false |
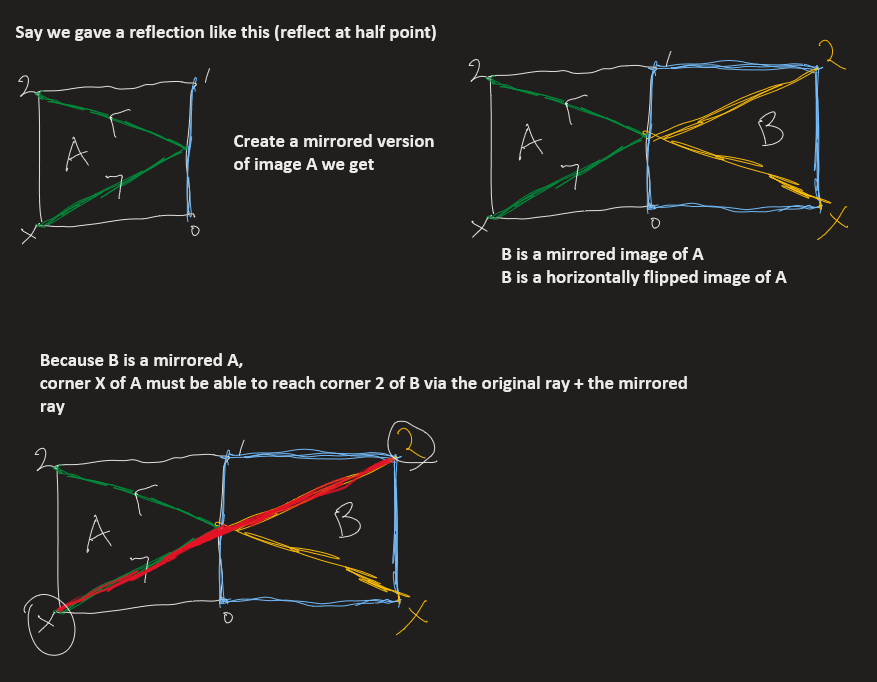\n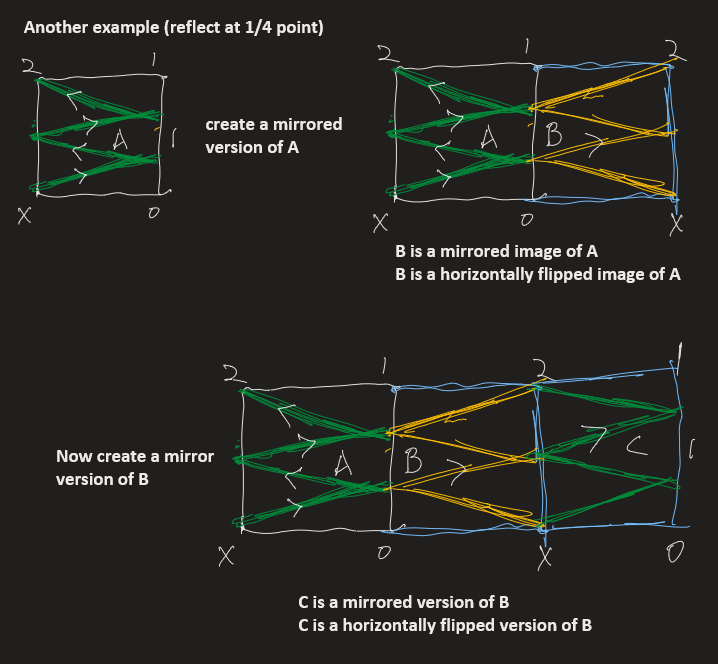\n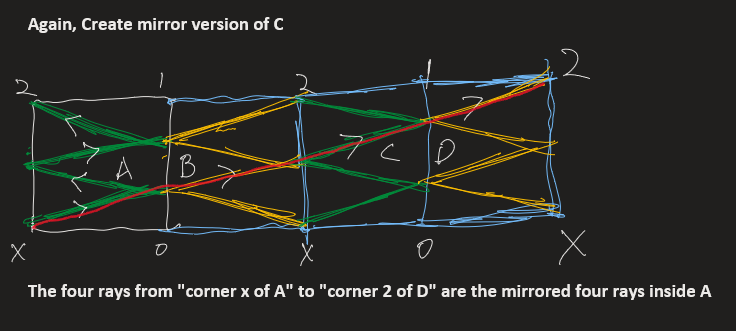\n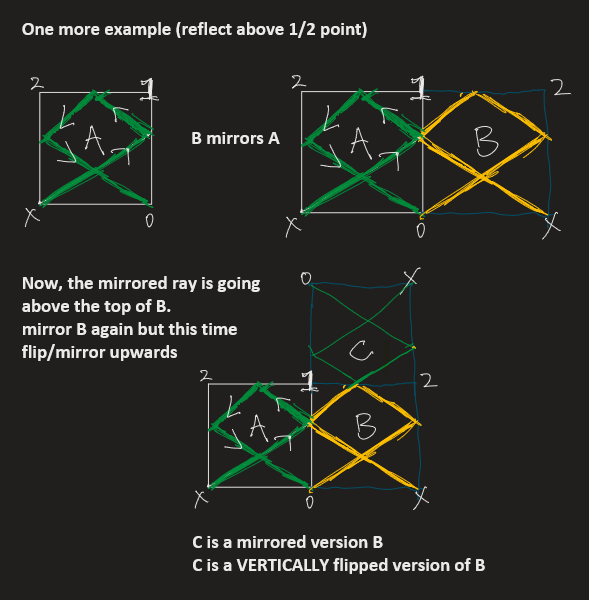\n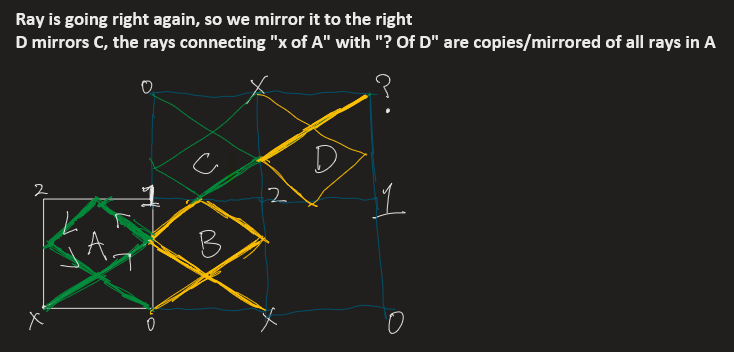\n\n\n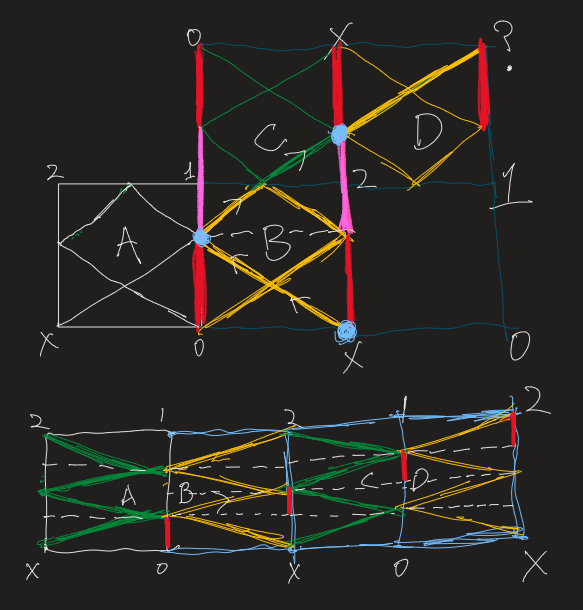\n\n```python\ndef mirrorReflection(p, q):\n\tif q == 0: \n\t\treturn 0\n\n\theight = q\n\twhile height < p or height % p:\n\t\theight += q\n\n\tupFlip = height / p\n\trightFlip = height / q\n\n\ttopCorner = 1 if upFlip % 2 else 0\n\n\treturn topCorner if rightFlip % 2 else 2\n```\n\n```javascript\nfunction mirrorReflection (p, q) { \n if (q === 0) return 0;\n \n let height = q;\n while (height < p || height % p) {\n height += q;\n }\n \n const upFlip = height / p;\n const rightFlip = height / q;\n\n const topCorner = upFlip % 2 ? 1 : 0;\n \n return rightFlip % 2 ? topCorner : 2;\n};\n```
| 128 | 1 |
[]
| 14 |
mirror-reflection
|
✔️ Pseudocode - Explain Why Odd and Even Matter
|
pseudocode-explain-why-odd-and-even-matt-w65f
|
Imagine that after the ray goes over the top edge, it will not reflect back but continue going through another box that stacked on the previous box. \nAnd this
|
Sneeit-Dot-Com
|
NORMAL
|
2022-08-04T06:17:13.874117+00:00
|
2022-08-14T01:41:11.439751+00:00
| 4,432 | false |
Imagine that after the ray goes over the top edge, it will not reflect back but continue going through another box that stacked on the previous box. \n**And this current box is a flipped version of the previous box.**\n\n...\n\n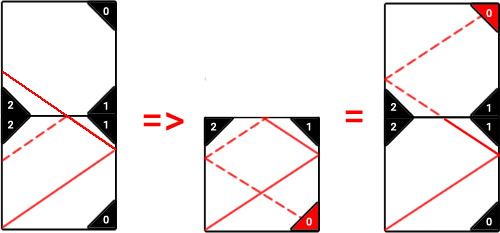\n\n...\n\n\nBecause the ray will hit one of the corners eventually so the total height the ray traveled equals to the total height of stacked boxes. We have this equation:\n```\ns*p = r*q\n// s = number of stacked boxes\n// r = number of reflecting times\n```\n...\n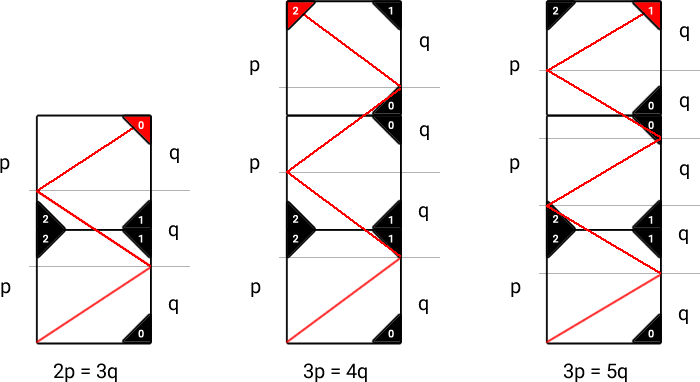\n...\n\nIf `p` and `q` are both even, they are the multiples of 2, so we can divide `p` and `q` by 2 to reduce our equation.\n```\n// For example\ns*p = r*q \n=> s*2*2*x = r*2*2*y\n=> s*x = r*y\n\n// or\ns*p = r*q \n=> s*2*2*x = r*2*2*2*y\n=> s*x = r*2*y\n```\n\nEventually, only `p` or `q` will be even or both are odd.\n\n* If `p` is even then `q` is odd, and because `s*p = r*q` then `r` should be even\n=> **numer of reflecting times is even** means the ray ends at the **top-left corner** which could be only the corner `2`\n\n* Else, the ray ends at the **top-right corner** of a box. \n\t* If `q` is even then `p` is odd, and because `s*p = r*q` then `s` should be even \n\t=> **the number of stacked boxes is even** means the current box is **the flipped version** of the original box so the top-right corner should be only `0`\n\t\n\t* Otherwise, neither `2` or `0` then the ray eventually hits `1`\n\n......\n......\n\n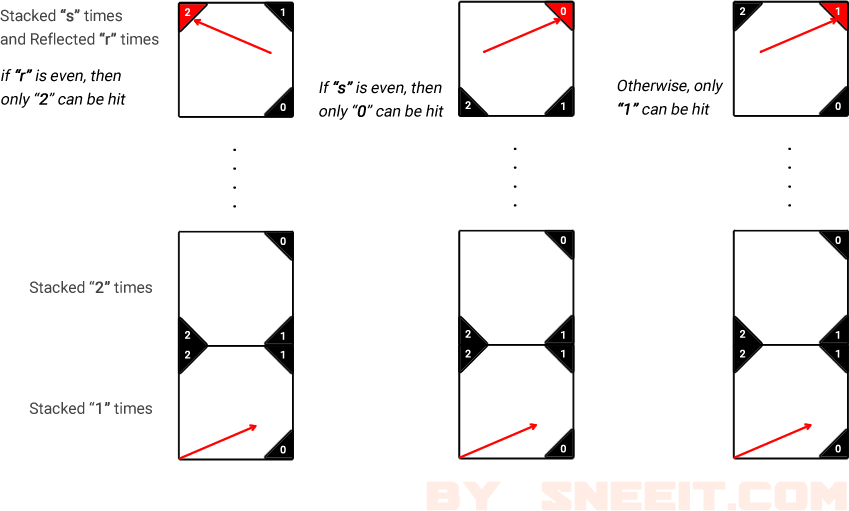\n\n\n```\n// pseudo code\nfunction mirrorReflection(p,q) {\n\t// reduce 2 from the equation\n\twhile (p%2==0 && q%2==0) {\n\t\tp = p / 2\n\t\tq = q / 2\n\t}\n\t\n\t// conclusion\n\tif (p%2 == 0)\n\t\treturn 2\n\t\n\tif (q%2 == 0)\n\t\treturn 0\n\t\n\treturn 1\n}\n```\n\n* Space Complexity is obviously `O(1)`\n* Time Complexity is `O(min(log(p), log(q))` but because q <= p so the worst case is only : `O(log(q))`
| 112 | 1 |
['Math', 'Geometry', 'C', 'Python', 'C++', 'Java', 'JavaScript']
| 9 |
mirror-reflection
|
[C++] Easy to visualize and understand using GCD & LCM
|
c-easy-to-visualize-and-understand-using-8ubf
|
The idea comes from this post: https://leetcode.com/problems/mirror-reflection/discuss/146336, and here I add some explanation.\n\nExplanation\n\n\nObserving th
|
amanahlawat
|
NORMAL
|
2022-08-04T08:04:57.708597+00:00
|
2022-08-04T13:38:43.398687+00:00
| 6,481 | false |
The idea comes from this post: https://leetcode.com/problems/mirror-reflection/discuss/146336, and here I add some explanation.\n\n**Explanation**\n\n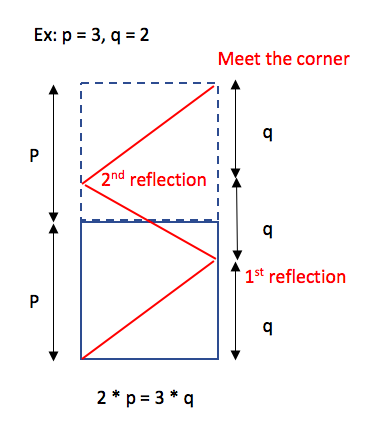\nObserving the above diagram, we can see that we need to find `m`,`n` for the equation `m * p = n * q` which will determine our result as follows -\n\n```\nm is even & n is odd => return 0.\nm is odd & n is odd => return 1.\nm is odd & n is even => return 2.\n```\n\n**Steps**\n\n1. Calculate LCM of `p` and `q` and get the values of `m` and `n`\n2. Apply our understanding for the result\n\n**C++ Code**\n```\nclass Solution {\npublic:\n \n int gcd(int a, int b) {\n while(b) {\n a = a % b;\n swap(a, b);\n }\n return a;\n }\n \n int mirrorReflection(int p, int q) {\n int lcm = (p*q)/gcd(p, q); // calculating lcm using gcd\n int m = lcm/p;\n int n = lcm/q;\n if(m%2==0 && n%2==1) return 0;\n if(m%2==1 && n%2==1) return 1;\n if(m%2==1 && n%2==0) return 2;\n return -1;\n }\n};\n```\n\nPlease upvote if it helped you. Keep on grinding :)
| 103 | 1 |
['Math', 'Geometry', 'C', 'C++']
| 12 |
mirror-reflection
|
Python3 || 2 lines, geometry, w/ explanation || T/S: 98%/ 97%
|
python3-2-lines-geometry-w-explanation-t-j1pz
|
Instead of imagining one room with mirrored walls, imagine an infinite cluster of rooms with glass walls; the light passes through to the next room and on and
|
Spaulding_
|
NORMAL
|
2022-08-04T02:08:20.070288+00:00
|
2024-05-22T19:10:37.927045+00:00
| 4,892 | false |
Instead of imagining one room with mirrored walls, imagine an infinite cluster of rooms with glass walls; the light passes through to the next room and on and on until it evenually hits a corner. \n\n Suppose for example: p = 6, q = 4, which is demonstrated in the figure below.\n\t \n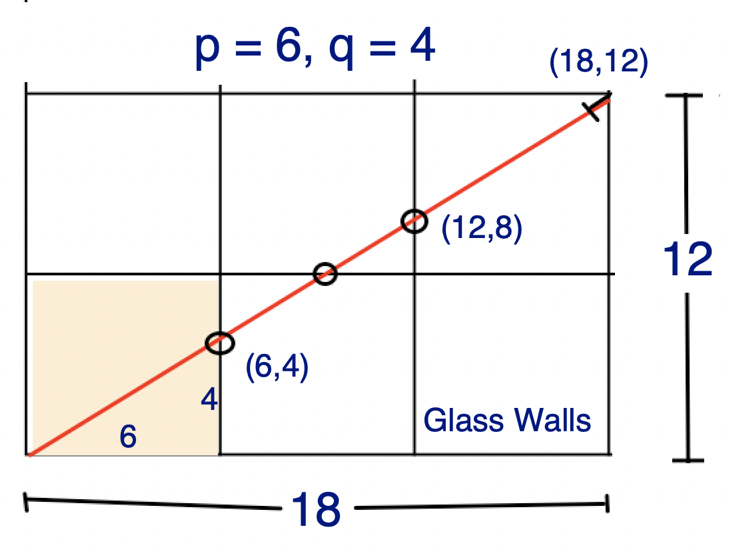\n\nThe least common multiple of 4 and 6 is 12, and 3x4 = 12, so the light will have to pass thru three walls before a multiple of 4 and a multiple of 6 coincide. In the mirrored room, the light would reflect off of three walls before hitting a corner, and three bounces bring us to receptor zero in the bottom right corner\n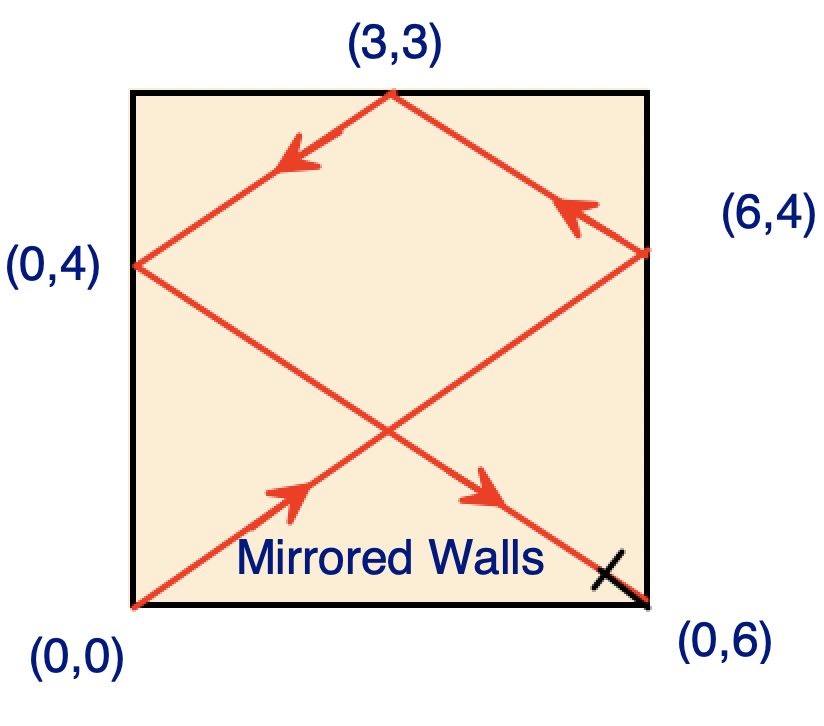\n\nThere\'s still some similar triangles and some other geometry to wrestle with, but the algorithm emerges eventually.\n\nHere\'s my code:\n\n```\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n\n L = lcm(p,q)\n\n return 2 if (L//q)%2 == 0 else (L//p)%2\n```\n[https://leetcode.com/problems/mirror-reflection/submissions/1265163038/](https://leetcode.com/problems/mirror-reflection/submissions/1265163038/)\n\nI could be wrong, but I think that time complexity is *O*(log(min(*P*,*Q*) (due to `lcm`) and space complexity is *O*(1), in which *P*, *Q* ~ `p`,`q`. \n```\n```\nHere\'s another version using the identity lcm(p,q) x gcd(p,q) == p x q:\n```\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n # L*G = p*q <=> L/q = p/G <=> L/p = q/G\n\n G = gcd(p,q)\n p//= G\n q//= G\n \n return 2 if p%2 == 0 else q%2
| 90 | 2 |
['Geometry', 'Python', 'Python3']
| 10 |
mirror-reflection
|
Python [pure geometry illustrated]
|
python-pure-geometry-illustrated-by-gsan-xu96
|
Consider four reflections of the room. Based on the corners these are encoded as A, B, C, D. This is displayed in the figure below (first row). \n\nAs you can s
|
gsan
|
NORMAL
|
2020-11-17T08:55:17.949679+00:00
|
2020-11-17T10:05:59.246489+00:00
| 4,113 | false |
Consider four reflections of the room. Based on the corners these are encoded as `A, B, C, D`. This is displayed in the figure below (first row). \n\nAs you can see we start from a room of type C. An easy way to incorporate reflections is to propagate them thru a stacked set of rooms based on the reflections. We hit a corner at an integer `k` such that `mod(k*q, p) = 0`. In the solution below we first calculate k. Depending on the even/odd values of `k` and `k*q//p` we find the answer.\n\n\n\nIn this case the answer will be 2, as we intersect at `k=2`. I drew a larger diagram for illustrative purposes. (You don\'t need the rest of it for this one.)\n\n```python\nclass Solution:\n def mirrorReflection(self, p, q):\n k = 1\n while k*q%p: k += 1\n if k%2==1 and (k*q//p)%2==0: return 0\n if k%2==1 and (k*q//p)%2==1: return 1\n if k%2==0 and (k*q//p)%2==1: return 2 \n```\n\n**Reduction**\nThe if-conditionals can be compactified as\n```python\nclass Solution:\n def mirrorReflection(self, p, q):\n k = 1\n while k*q%p: k += 1\n return 2 if k%2==0 else (k*q//p)%2\n```
| 88 | 0 |
[]
| 9 |
mirror-reflection
|
🔥Python || Easily Understood✅ || Detailed Explanation || Easy Understand || MATH || Fast || Simple
|
python-easily-understood-detailed-explan-cbdg
|
Appreciate if you could upvote this solution\n\nMath Method:\nFirst, imagining that there are infinity n square rooms and they look like:\n\n\n\nThen, we need t
|
wingskh
|
NORMAL
|
2022-08-04T03:09:30.301696+00:00
|
2022-08-06T05:36:25.342155+00:00
| 1,753 | false |
**Appreciate if you could upvote this solution**\n\n`Math` Method:\nFirst, imagining that there are infinity `n` square rooms and they look like:\n\n\n\nThen, we need to calculate the `height` between the starting point and the first met receptor and let it be `h`.\nSince `h` equals to the first reflection that meet the one of the corners of the room, it fits these two conditions:\n- `h = i * q` \n- `h mod p == 0`\n\nThus, `h` is the **Least Common Multiple** ( LCM ) of `p` and `q`\n\nAfter calculating the h, we can determind \n- whether the laser ray reaches the left receptor`(2)` or right receptors `(0 / 1)`\n- whether the laser ray reaches the bottom receptor`(0)` and top receptors `(1, 2)`\n\n<br/>\n\nCase 1: Right receptors and top receptors\n- Receptor 1\n\nCase 2: Left receptors and top receptors\n- Receptor 2\n\nCase 3: Right receptors and bottom receptors\n- Receptor 3\n\n<br/>\n\n```\nclass Solution:\n def lcm(self, x, y):\n return x * y // self.gcd(x, y)\n\n def gcd(self, x, y):\n while y:\n x, y = y, x % y\n return abs(x)\n\n\n def mirrorReflection(self, p: int, q: int) -> int:\n time_for_reflection = self.lcm(p, q)\n is_right_side = True if time_for_reflection/q % 2 == 1 else False\n is_top_side = True if time_for_reflection/p % 2 == 1 else False\n\n if is_right_side and is_top_side:\n return 1\n elif not is_right_side and is_top_side:\n return 2\n \n return 0\n```\n**Time complexity**: \n- Overall: `O(log(min(p, q)))`\n- Ignore calculation of GCD: `O(1)`\n\n**Space complexity**: \n- Overall: `O(log(min(p, q))`\n- Ignore calculation of GCD: `O(1)`\n<br/>
| 48 | 0 |
['Python']
| 2 |
mirror-reflection
|
The Most Straight Forward Solution.Pure Math.Only 13ms
|
the-most-straight-forward-solutionpure-m-kl1q
|
Just straight forward. Use a while loop to compute every reflection point in bound until the light reaches the corner 0 or 1 or 2. Totally physical imitation.\n
|
sorryble
|
NORMAL
|
2018-06-24T03:15:32.090395+00:00
|
2018-09-11T01:11:03.673638+00:00
| 3,150 | false |
Just straight forward. Use a while loop to compute every reflection point in bound until the light reaches the corner 0 or 1 or 2. Totally physical imitation.\n\n```\nclass Solution {\n \n class Point{\n double x;\n double y;\n \n public Point(double x,double y){\n this.x = x;\n this.y = y;\n }\n }\n \n int p;\n \n Point P_LB; //left - bottom\n Point P_LT;\n Point P_RB;\n Point P_RT; //right - top\n \n public int mirrorReflection(int p, int q) {\n this.p = p;\n P_LB = new Point(0.0,0.0);\n P_LT = new Point(0.0,(double)p);\n P_RB = new Point((double)p,0.0);\n P_RT = new Point((double)p,(double)p);\n \n \n Point start = new Point(0.0,0.0);\n Point end = new Point((double)p,(double)q);\n \n while(!isCorner(end)){\n Point mirror = findMirPoint(start,end);\n Point next = insect(end,mirror);\n \n start = end;\n end = next;\n }\n \n if(isEquals(end,P_LT)){\n return 2;\n }\n \n if(isEquals(end,P_RT)){\n return 1;\n }\n \n if(isEquals(end,P_RB)){\n return 0;\n }\n \n return -1;\n }\n \n private boolean isCorner(Point end){\n if(Math.abs(end.x-0.0)<0.001){\n return Math.abs(end.y-p)<0.001; // corner 2\n }else if(Math.abs(end.x-p)<0.001){\n return Math.abs(end.y-0.0)<0.001 || Math.abs(end.y-p)<0.001; //corner 0 || corner 1\n }else{\n return false;\n }\n \n }\n \n private Point findMirPoint(Point start,Point end){\n if(Math.abs(end.x-0.0)<0.001 || Math.abs(end.x-p)<0.001){ //left or right mirror\n return new Point(start.x,end.y*2-start.y);\n /*\n if(start.y<end.y){\n return new Point(start.x,end.y+(end.y-start.y));\n }else{\n return new Point(start.x,end.y-(start.y-end.y));\n }\n */\n \n }else{ //Math.abs(end.y-0.0)<0.001 || Math.abs(end.y-p)<0.001 //bottom or top mirror\n return new Point(end.x*2-start.x,start.y);\n }\n }\n \n \n private boolean inBound(Point next){\n return next.x>-0.001 && next.x<p+0.001 && next.y>-0.001 && next.y<p+0.001;\n }\n \n private boolean isEquals(Point a,Point b){\n return Math.abs(a.x-b.x)<0.001 && Math.abs(a.y-b.y)<0.001;\n }\n \n private Point insect(Point end,Point next){\n \n Point temp1 = calculateIntersectionPoint(end,next,P_LB,P_LT);\n Point temp2 = calculateIntersectionPoint(end,next,P_LB,P_RB);\n Point temp3 = calculateIntersectionPoint(end,next,P_RT,P_LT);\n Point temp4 = calculateIntersectionPoint(end,next,P_RT,P_RB);\n \n Point[] pArr = new Point[]{temp1,temp2,temp3,temp4};\n \n for(Point temp:pArr){\n if(inBound(temp) && !isEquals(temp,end)) return temp;\n }\n \n return null;\n }\n \n private double calculateVectorProduct(Point P1, Point P2, Point P3, Point P4) { \n return(P2.x-P1.x) * (P4.y-P3.y) - (P2.y-P1.y) * (P4.x-P3.x);\n }\n \n private Point calculateIntersectionPoint(Point A, Point B, Point C, Point D) {\n double t1 = calculateVectorProduct(C, D, A, B);\n double t2 = calculateVectorProduct(A, B, A, C);\n double x = C.x +(D.x-C.x) * t2 / t1;\n double y = C.y +(D.y-C.y) * t2 / t1;\n return new Point(x, y);\n }\n}\n```
| 39 | 2 |
[]
| 13 |
mirror-reflection
|
Mirror Reflection Explanation with Pictures + super short code
|
mirror-reflection-explanation-with-pictu-f1ij
|
\n\n\n\n\n\n\n\n\npython\ndef mirrorReflection(p, q):\n\tif q == 0: \n\t\treturn 0\n\n\theight = q\n\twhile height < p or height % p:\n\t\theight += q\n\n\tupFl
|
coolgk
|
NORMAL
|
2020-11-17T18:21:46.941324+00:00
|
2020-11-22T17:34:27.579805+00:00
| 1,369 | false |
\n\n\n\n\n\n\n\n\n```python\ndef mirrorReflection(p, q):\n\tif q == 0: \n\t\treturn 0\n\n\theight = q\n\twhile height < p or height % p:\n\t\theight += q\n\n\tupFlip = height / p\n\trightFlip = height / q\n\n\ttopCorner = 1 if upFlip % 2 else 0\n\n\treturn topCorner if rightFlip % 2 else 2\n```\n\n```javascript\nfunction mirrorReflection (p, q) { \n if (q === 0) return 0;\n \n let height = q;\n while (height < p || height % p) {\n height += q;\n }\n \n const upFlip = height / p;\n const rightFlip = height / q;\n \n let topCorner = upFlip % 2 ? 1 : 0;\n \n return rightFlip % 2 ? topCorner : 2;\n};\n```
| 38 | 1 |
[]
| 4 |
mirror-reflection
|
[Python] Oneliner solution with diagram, explained
|
python-oneliner-solution-with-diagram-ex-zhla
|
The idea of this problem, instead of reflecting our ray, we will look at it from the point of view of our ray, which is straight line: see the following image f
|
dbabichev
|
NORMAL
|
2020-11-17T08:22:15.543092+00:00
|
2020-11-17T08:22:15.543131+00:00
| 1,683 | false |
The idea of this problem, instead of reflecting our ray, we will look at it from the point of view of our ray, which is straight line: see the following image for better understanding.\n\n\n\n\nHow we can find what we need to return: `0`, `1` or `2`:\n1. If both number of reflections of our room are even, like in our image, we need to return 1.\n2. If horizontal line of reflections is odd and vertical is even, we need to return `0`.\n3. If horizontal line of reflections is even and vertical is odd, we need to return `2`.\n4. Note, that it can not happen that both number are even, than we have one angle before, if we divide these two numbers by 2.\n\nFinally, all this can be written in oneliner as follow:\n\n**Complexity**: time and space complexity is `O(1)` if we assume that we can find `gcd` in `O(1)` time (which is true for int32 numbers). If you want to be more mathematically correct, it is `O(log n)`.\n\n```\nclass Solution:\n def mirrorReflection(self, p, q):\n return (q//gcd(p,q)%2 - p//gcd(p,q)%2 + 1)\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!**
| 33 | 5 |
['Math']
| 2 |
mirror-reflection
|
Easiest solution to understand and write code for (3 liner) | Uncomplicated no brainer
|
easiest-solution-to-understand-and-write-fwhs
|
Intuition 1\nIf you ever see a mirror problem do not start tracing the ray itself, its reflection that goes straight ahead will also reach the same receptor. No
|
numbart
|
NORMAL
|
2022-08-04T08:53:51.187322+00:00
|
2022-08-05T07:22:26.456949+00:00
| 833 | false |
## Intuition 1\nIf you ever see a mirror problem do not start tracing the ray itself, its reflection that goes straight ahead will also reach the same receptor. Now it becomes an old school linear geometry problem instead, where you have straight line starting from (0, 0) and you have to find first integer indices it reaches. If you remember it go ahead and try solving yourself, but if you don\'t remember(like me), lets solve it using some intuition.\n\n<img src="https://assets.leetcode.com/users/images/8860cd36-bfdd-4eee-91b7-9ec95e02a0f0_1659674636.4763405.png" width="400" height="300" border="10"/>\n\nFor every p distance ray goes along x axis, it also goes up by q distance. Since this is square box of side p, we need to find minimum number of "q distances" it needs to travel up before hitting a corner, ie. a multiple of p. This is the lcm of p and q.\n\nNumber of boxes the ray covered to reach receptor in vertical direction(leny) is lcm/p,\nNumber of boxes the ray covered to reach receptor in horizontal direction(lenx) is lcm/q(since for every q distance up it goes p forward),\n___\n## Intuition 2\n\nNow the problem reduces to what is the receptor at (lcm/q , lcm/p)\n\n<img src="https://assets.leetcode.com/users/images/cdd9f65c-c2ab-43cd-9c7f-83ab0a22822c_1659601857.6974719.png" width="600" height="400" border="10"/>\n\nStart writing the receptor number(assume (0, 0) to be 3) in each of the reflected corners for a few corners(image above). You will notice a pattern now. Consider 0 indexing from here on. Notice that odd columns above only have 0, 1 and even ones only have 3, 2. Also notice in the 0, 1 columns 0 is at even position and 1 is at odd positions, same is true for 3, 2 respectively.\n\n___\n## Code\n\nNow for the code no loops no ifs and elses\nHow did I avoid the ifs and elses I created a 2x2 table based on the logic of odd even positions above.\n```\n\t\t\teven y odd y\neven x 3 2\n\nodd x 0 1\n```\n\n\n```cpp\nint mirrorReflection(int p, int q) {\n\tint lcm = p*q/__gcd(p, q), x = lcm/q, y = lcm/p;\n\tint rcp[2][2] = {{3, 2}, {0, 1}};\n\treturn rcp[1&x][1&y];\n}\n```\n\nCould it be easier, leave a like if this made it simple. Here is a small exercise guess why 3 will never be returned as the answer. Check the comments for the answer.
| 21 | 0 |
['C++']
| 4 |
mirror-reflection
|
1 line C++ solution using gcd, only 4ms
|
1-line-c-solution-using-gcd-only-4ms-by-ykf7p
|
The ray hits the left and right wall alternatively. If we ignore the ceiling then the y coordinate of the hit point will be q, 2q, 3q... Now the key point is to
|
mzchen
|
NORMAL
|
2018-06-24T04:36:51.320575+00:00
|
2018-10-19T15:29:13.995263+00:00
| 2,341 | false |
The ray hits the left and right wall alternatively. If we ignore the ceiling then the `y` coordinate of the hit point will be `q`, `2q`, `3q`... Now the key point is to find out the **least common multiplier** (lcm) of `p` and `q` where the ray will be received finally. If the final `y` is an even multiplier of `p` (`lcm / p % 2 == 0`) then the receptor `0` will be hit since the ray is guaranteed to be received. Otherwise we check if a even number of hits (`lcm / q % 2 == 0`) was done before being received by receptor `2`. i.e. if we consider the four corners a 2-row-2-column grid, `lcm / p % 2` is the row number (going bottom-up) while `1 - lcm / q % 2` is the column number (going right-left). Summing them up will get us a [[2,1],[1,0]] grid and this works perfectly as the receptor id. Since `lcm` is `p * q / gcd` we finally get `lcm / p % 2 + 1 - lcm / q % 2 = p * q / gcd / p % 2 + 1 - p * q / gcd / q % 2 = 1 + q / gcd % 2 - p / gcd % 2`.\n```\nclass Solution {\npublic:\n int mirrorReflection(int p, int q) {\n return 1 + q / gcd(p, q) % 2 - p / gcd(p, q) % 2;\n }\n};\n```\nFor C++ 17 or newer `gcd` is built-in. But for C++ 14 (LeetCode default), we have to define `gcd` function ourselves with Euclidean algorithm:\n```\nint gcd(int p, int q) {\n return q ? gcd(q, p % q) : p;\n}\n```\nBelow are explanations:\n
| 21 | 1 |
[]
| 2 |
mirror-reflection
|
Accepted Java Solution
|
accepted-java-solution-by-navid-7kkg
|
public int mirrorReflection(int p, int q) {\n boolean up = true;\n boolean east = true;\n int remain = p;\n while (true) {\n
|
navid
|
NORMAL
|
2018-06-24T03:01:59.168200+00:00
|
2018-06-24T03:01:59.168200+00:00
| 1,248 | false |
public int mirrorReflection(int p, int q) {\n boolean up = true;\n boolean east = true;\n int remain = p;\n while (true) {\n remain -= q;\n if (remain == 0) {\n if (up) {\n if (east)\n return 1;\n else\n return 2;\n }\n else {\n if (east)\n return 0;\n }\n }\n if (remain < 0) {\n remain+=p;\n up=!up;\n }\n east = !east;\n }\n }\n
| 19 | 0 |
[]
| 5 |
mirror-reflection
|
[C++] Geometry mirror game
|
c-geometry-mirror-game-by-codedayday-gtbs
|
\nclass Solution {\npublic:\n int mirrorReflection(int p, int q) {\n int m = 1; // extension count of room\n int n = 1; // reflection count of
|
codedayday
|
NORMAL
|
2020-11-17T15:47:31.605417+00:00
|
2020-11-17T15:50:02.809318+00:00
| 1,069 | false |
```\nclass Solution {\npublic:\n int mirrorReflection(int p, int q) {\n int m = 1; // extension count of room\n int n = 1; // reflection count of laser ray\n while(m * p != n * q){\n n++;\n m = n * q / p;\n }\n if (m % 2 == 0 && n % 2 == 1) return 0;\n if (m % 2 == 1 && n % 2 == 1) return 1;\n if (m % 2 == 1 && n % 2 == 0) return 2;\n return -1;\n }\n};\n// concrete to generic: Example 2: Input: p == 3, q = 2; Output 0\n```\nThe figure is from [1], which really help understand the case which return 0\n\nreference: \n[1] https://leetcode.com/problems/mirror-reflection/discuss/146336/Java-solution-with-an-easy-to-understand-explanation
| 18 | 1 |
[]
| 4 |
mirror-reflection
|
JAVA || Easy Solution with Left and right shift || 100% faster Code
|
java-easy-solution-with-left-and-right-s-bltr
|
\tPLEASE UPVOTE IF YOU LIKE\n\nclass Solution {\n public int mirrorReflection(int p, int q) {\n while(((p|q)&1) == 0){\n p >>= 1;\n
|
shivrastogi
|
NORMAL
|
2022-08-04T01:39:28.788196+00:00
|
2022-08-04T01:48:09.776669+00:00
| 1,827 | false |
\tPLEASE UPVOTE IF YOU LIKE\n```\nclass Solution {\n public int mirrorReflection(int p, int q) {\n while(((p|q)&1) == 0){\n p >>= 1;\n q >>= 1;\n }\n return (q&1) + ((p&1)^1);\n }\n}\n```
| 17 | 2 |
['Java']
| 4 |
mirror-reflection
|
Python clear image explanation ! | loop with direction | O(n) solution ^_^
|
python-clear-image-explanation-loop-with-e618
|
We start at point where height = q, and add q to height each time.\nIfheight + q is smaller than p, it touches left or right border, so we change the left-right
|
luluboy168
|
NORMAL
|
2022-08-04T02:25:47.621227+00:00
|
2022-08-04T08:26:18.967574+00:00
| 849 | false |
We start at point where `height = q`, and add `q` to height each time.\nIf` height + q` is smaller than `p`, it touches left or right border, so we change the left-right direction.\nIf `height + q` is bigger than `p`, it touches left or right border and go through top or bottom, so we change both direction. \n\nFor example: p = 4, q = 3\n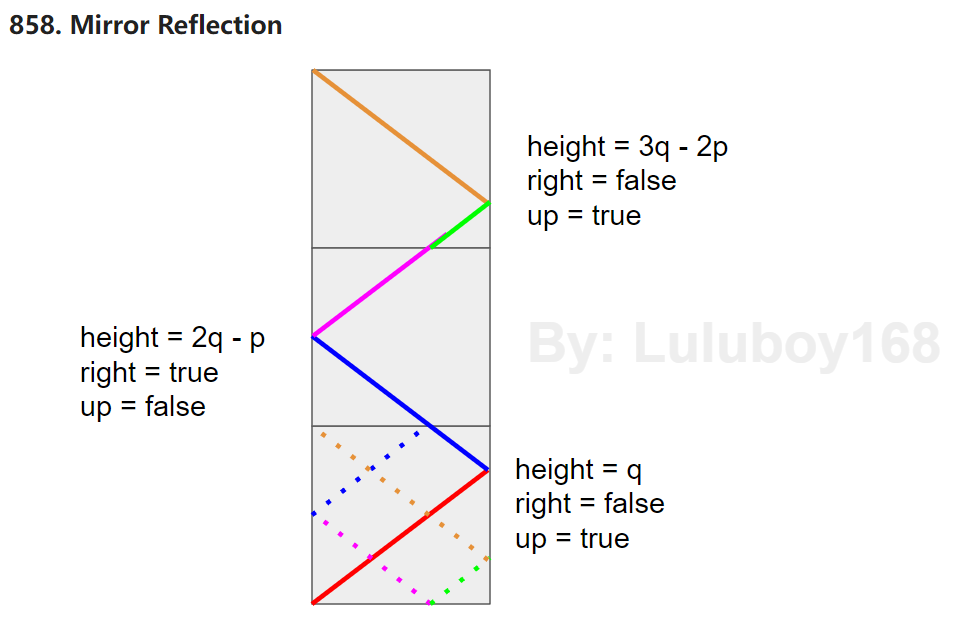\n\n```\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n \n if p == q:\n return 1\n \n height = q\n right, up = False, True\n \n while True:\n if height + q == p:\n if right and up:\n return 1\n elif not right and up:\n return 2\n else:\n return 0\n elif height + q < p: # touch left or right border\n height += q\n right = not right\n else: # touch left or right border and go through top or bottom\n height += q - p\n right = not right\n up = not up\n```\n**Please UPVOTE if you LIKE !!!**
| 15 | 0 |
['Python']
| 2 |
mirror-reflection
|
Math equation solution explained | Short
|
math-equation-solution-explained-short-b-jybb
|
Reflections work nicely enough that we just need to consider the diagram below:\n\nJust fold the diagram into a square to see the trajectory of the ray.\n\nWe c
|
sr_vrd
|
NORMAL
|
2022-08-04T02:00:53.896959+00:00
|
2022-08-04T14:25:14.138628+00:00
| 845 | false |
Reflections work nicely enough that we just need to consider the diagram below:\n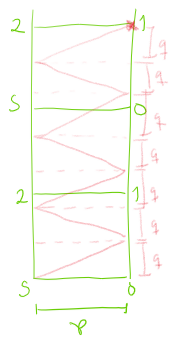\nJust fold the diagram into a square to see the trajectory of the ray.\n\nWe can imagine an infinite tall room, where the ray will continue to reflect over and over again. When the ray hits on a point that has a height that is a multiple of `p`, then we\'ve reached the end. In essence, we need to find the ***smallest positive integer solution*** to the equation `a * q = b * p`<sup>*</sup>. Here `a` would tell us how many times we had the ray bounce and `b` that the "height" of this tall room is `b * p`.\n* To simplify the calculations, we can start by dividing both sides by `gcd(p, q)`, so that `p` and `q` have no factors in common.\n\t* Assuming `p` and `q` are relatively prime, the equation `a * q = b * p` has integer solutions if and only if `q` divides `b`.\n\t* The smallest multiple of `q` is `q` itself, so `b = q`, and `a = p`.\n\nLooking at the diagram we can see that if `a` (the number of times the ray touches a wall) is even, then it is on the left side, and if it is odd, then it is on the right side. We are guaranteed a solution, so if it bounces on the left wall, then it must be on sensor `2`. If it bounces on the right wall, we\'ll have that it hits sensor `0` if `b % 2 == 0` and bounces on sensor `1` otherwise.\n∎\n<sup>* This kind of equation with integer coefficients and integer solutions is called a Diophantine Equation. They are super useful in computational geometry/number theory.</sup> \n\n```\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n # solving equation a * q = b * p\n GCD = gcd(p, q)\n a = p // GCD; b = q // GCD\n \n if a % 2 == 0:\n return 2\n\n return 0 if b % 2 == 0 else 1\n```
| 13 | 0 |
['Math', 'Geometry']
| 2 |
mirror-reflection
|
Simple explanation with java code
|
simple-explanation-with-java-code-by-wil-858v
|
We keep adding q imagining that the right and left edges of the square are infinite, until we reach a height which is divisible by p. Also keep a track of wheth
|
wildrabbit
|
NORMAL
|
2020-11-17T16:48:26.184959+00:00
|
2020-11-18T18:30:41.643607+00:00
| 605 | false |
We keep adding q imagining that the right and left edges of the square are infinite, until we reach a height which is divisible by p. Also keep a track of whether we are on the left, or on the right. \nInitially, we are on the right (since height is already q). \n\n- While `height` is not divisible by `p` (the square\'s side), keep adding `q` to the height, and toggling left.\n- When we have reached a `height` which is multiple of `p`, and we are on the left, it is 2.\n- If we are on the right, and `(height/p)` is an odd number, we are at 1, else we are at 0. \n\t- because the ray actually travels down after reaching height = p, the receptors get reversed in the 2nd, 4th, 6th etc squares for us as we are only going up\n\t- This can be thought of in a simple way where if `q = p`, we will have `height/p = 1`. and if `q = 2 and p = 3`, we will end up with `height = 6`, i.e. `height/p = 2`.\n```\npublic int mirrorReflection(int p, int q) {\n\n\tint height = q;\n\tboolean left = false;\n\n\twhile(height % p != 0) {\n\t\theight += q;\n\t\tleft = !left;\n\t}\n\tif(left)\n\t\treturn 2;\n\telse \n\t\treturn (height/p)%2;\n}\n\t\n\t
| 12 | 0 |
['Java']
| 1 |
mirror-reflection
|
What If the Ray Not Reflected and Expand the Room | Image Explanation
|
what-if-the-ray-not-reflected-and-expand-a0j9
|
What if we assume the Ray Not Reflected and Keeps Going?\n\nConsider that there is a mirrored world behind the mirror, we can expand the room behind the mirror.
|
longluo
|
NORMAL
|
2022-08-04T01:37:38.072904+00:00
|
2022-08-04T10:51:02.619055+00:00
| 1,019 | false |
What if we assume the Ray **Not Reflected and Keeps Going**?\n\nConsider that there is a mirrored world behind the mirror, we can expand the room behind the mirror. The ray has not been reflected and keep going cross the room.\n\nAs the image below shows, we can easily know which receptor will the ray will meet first.\n\n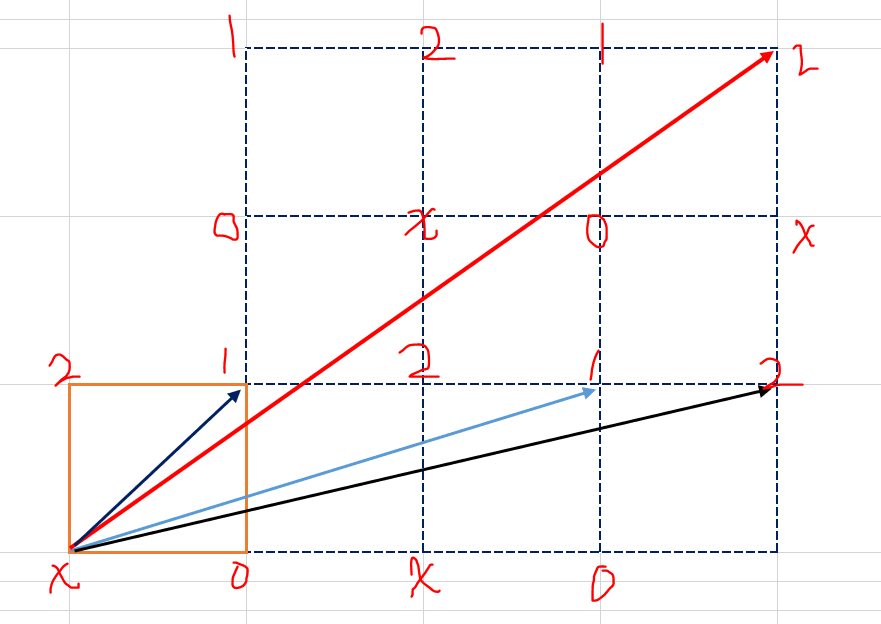\n\n```java\nclass Solution {\n public int mirrorReflection(int p, int q) {\n if (p == q) {\n return 1;\n }\n\n if (q == 0) {\n return 0;\n }\n\n int lcm = p * q / gcd(p, q);\n int x = lcm / p;\n int y = lcm / q;\n\n if (x % 2 == 1 && y % 2 == 1) {\n return 1;\n } else if (x % 2 == 0 && y % 2 == 1) {\n return 0;\n } else {\n return 2;\n }\n }\n\n private int gcd(int a, int b) {\n return b == 0 ? a : gcd(b, a % b);\n }\n}\n```\n\n## Analysis\n\n- **Time Complexity**: `O(log(max(p, q)))`\n- **Space Complexity**: `O(1)`\n\n------------\n\nAll suggestions are welcome. \nIf you have any query or suggestion please comment below.\nPlease upvote\uD83D\uDC4D if you like\uD83D\uDC97 it. Thank you:-)\n\nExplore More [Leetcode Solutions](https://leetcode.com/discuss/general-discussion/1868912/My-Leetcode-Solutions-All-In-One). \uD83D\uDE09\uD83D\uDE03\uD83D\uDC97\n
| 11 | 1 |
['Math', 'Geometry']
| 4 |
mirror-reflection
|
most detailed explanation rather than code, of course including code
|
most-detailed-explanation-rather-than-co-iv5r
|
We should let laser ray keep straight to draw it\'s trajectory, as blowed:\n\n\nWe can get the triangle(x, y) from the triangle(p, q) if the laser ray is straig
|
turnhead
|
NORMAL
|
2019-06-17T03:37:12.173697+00:00
|
2019-06-17T09:25:41.510707+00:00
| 787 | false |
We should let laser ray keep straight to draw it\'s trajectory, as blowed:\n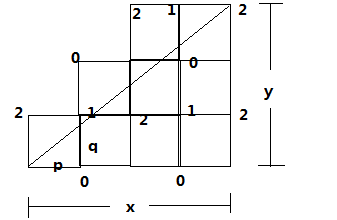\n\nWe can get the triangle(x, y) from the triangle(p, q) if the laser ray is straight\uFF0Cso x/p = y/q. Because the result of x/p is interger, so the result of y/q is interger. In order to find the minimum number that satisfies y, we can start a variable k at one, so y = pk, as pieces of code blowed\n`\n k = 1\n while( p*k % q != 0) k += 1 ;\n` \nSo, we can get k, so we know x and y. Next we can find the answer easily, as the second picture belowed,\n\n1) if we want to make laser ray meet the receptor 0:\n\n\nas showed above, if we want to make laser ray meet the receptor 0, the numbers of reflection must be even numbers, so k is even number\uFF1A\n`\nif( k % 2 ==0 ) return 0;\n`\n\n2) if we want to make laser ray meet the receptor 1 or 2:\n\n\nwe can get : X1/p = 2m + 1 , X2/p = 2m:\n`\nint r = p*k /q;\nif(r % 2 ==0) return 2;\nif(r % 2 ==1) return 1;\n`\nin conclude:\n`\n public int mirrorReflection(int p, int q) {\n \n \n int k = 1;\n while( p*k % q != 0) k += 1 ;\n\t\tif( k % 2 ==0 ) return 0;\n\t\t\n\t\tint r = p*k /q;\n\t\tif(r % 2 ==0) return 2;\n\t\tif(r % 2 ==1) return 1;\n \n return -1;\n }\n` \n\n\n\n\n\n\n
| 11 | 0 |
[]
| 3 |
mirror-reflection
|
C++ Simple Explanation with Diagrams
|
c-simple-explanation-with-diagrams-by-an-z625
|
Approach:\n\n \n ap = bq\n from the above diagram we can see that when b is odd it will hit the right side and when b is even it will hit the left side\n there
|
anis23
|
NORMAL
|
2022-08-04T10:09:14.853303+00:00
|
2022-08-04T10:09:47.564239+00:00
| 447 | false |
**Approach:**\n\n* \n* ```ap = bq```\n* from the above diagram we can see that when b is odd it will hit the right side and when b is even it will hit the left side\n* there can\'t be a case when a=even and b=even because then the laser would have hit the corners twice but we just want to find out first corner that is hit by the laser\n* **Case 1:**\n * a = even\n * b = odd\n * corner = 0\n* **Case 2:**\n * a = odd\n * b = odd\n * corner = 1\n* **Case 3:**\n * a = odd\n * b = even\n * corner = 2\n* we can calculate a and b by lcm(p,q)\n\n**Code:**\n\n```\nclass Solution\n{\npublic:\n int gcd(int a, int b)\n {\n while (b)\n {\n a %= b;\n swap(a, b);\n }\n return a;\n }\n int mirrorReflection(int p, int q)\n {\n int lcm = p * q / gcd(p, q);\n int a = lcm / p;\n int b = lcm / q;\n return (a % 2 == 0) ? 0 : (b % 2 == 0 ? 2 : 1);\n }\n};\n```
| 10 | 0 |
['Math', 'Geometry', 'C', 'C++']
| 2 |
mirror-reflection
|
C++ || Easy to Understand || Logical Approach || GCD
|
c-easy-to-understand-logical-approach-gc-oudw
|
as per the given question we can find a pattern that if the side of square room is even then whatever value of q is there the final receptor will be 2.\n else i
|
Tan_252
|
NORMAL
|
2022-08-04T01:53:11.173214+00:00
|
2022-08-04T01:53:11.173245+00:00
| 1,664 | false |
* as per the given question we can find a pattern that if the **side of square room is even** then whatever value of q is there the final receptor will be 2.\n* else if **p is odd** then there are two probabilities:\n\t* **q is even**: if we draw a room and receptor for this case then we can figure out that the final receptor will be 0.\n\t* **q is odd**: for this case then we can figure out that the final receptor will be 1.\n* if p and q are equal then a line at 45 degrees passes from the initial point and reaches receptor 1.\n* the **most important thing** to consider before we proceed with the above approach is that, p and q can have **mutual factors** at the beginning so if we **divide both the numbers with their gcd** then the above **explained pattern works efficiently** to satisfy the problem statement.\n\n\t\t\tint mirrorReflection(int p, int q) {\n\t\t\t// gcd of p and q using inbuilt function\n\t\t\tint g = __gcd(p,q);\n\t\t\tp/=g;\n\t\t\tq/=g;\n\n\t\t\t// logic as per the above explained pattern\n\t\t\tif(p==q) return 1;\n\n\t\t\tif(p%2==0){\n\t\t\t\treturn 2;\n\t\t\t}else{\n\t\t\t\tif(q%2==0){\n\t\t\t\t\treturn 0;\n\t\t\t\t}else{\n\t\t\t\t\treturn 1;\n\t\t\t\t}\n\t\t\t}\n\t\t\treturn 0;\n\t\t\t}
| 10 | 0 |
['C']
| 4 |
mirror-reflection
|
C# faster than 100% with very simple explanation
|
c-faster-than-100-with-very-simple-expla-tqqt
|
Idea overview\nInstead of calculating all reflections we just need to continously sum input q until we reach value that divides p, i.e. sum % p == 0. To better
|
pawel753
|
NORMAL
|
2020-11-17T20:30:57.336558+00:00
|
2020-11-17T22:19:21.401639+00:00
| 216 | false |
### Idea overview\nInstead of calculating all reflections we just need to continously `sum` input `q` until we reach value that *divides* `p`, i.e. `sum % p == 0`. To better understand let\'s visualise the reflections on on multiple squares instead of one sqare:\n\n\n\n\nAfter we reach the edge condition we need to check are the following: **Have we finished on the *right* or *left* band (side)?**\n1. If we finish on the **left** band it\'s simple because it\'s only corner `2` on the left side. \n2. Otherwise - if we finish on the **right** side - we need to figure out which corner we hit. In order to do this we count the number of additionally created squares (dotted lines on the attached photo)\n\n```\npublic class Solution\n{\n\tpublic int MirrorReflection(int p, int q)\n\t{\n\t\tif (p == q)\n\t\t\treturn 1;\n\t\tif (q == 0)\n\t\t\treturn 0;\n\n\t\tbool rightSide = true;\n\t\tint sum = q;\n\t\tint overflow = 0;\n\t\twhile (sum != 0)\n\t\t{\n\t\t\tsum += q;\n\t\t\tif (sum >= p)\n\t\t\t{\n\t\t\t\tsum %= p;\n\t\t\t\toverflow++;\n\t\t\t}\n\t\t\trightSide = !rightSide;\n\t\t}\n\n\t\tif (!rightSide)\n\t\t\treturn 2;\n\n\t\treturn overflow % 2 == 1 ? 1 : 0;\n\t}\n}\n```\n\nRuntime: 36 ms, faster than 100.00% of C# online submissions for Mirror Reflection.\nMemory Usage: 15.2 MB, less than 66.67% of C# online submissions for Mirror Reflection.
| 10 | 0 |
['C#']
| 0 |
mirror-reflection
|
Simulation. No Convoluted mathematics.
|
simulation-no-convoluted-mathematics-by-cjg8i
|
\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n \n remaining = p\n \n up = True\n \n east
|
bismeet
|
NORMAL
|
2020-11-17T10:22:23.423679+00:00
|
2020-11-17T10:22:23.423709+00:00
| 479 | false |
```\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n \n remaining = p\n \n up = True\n \n east = True\n \n while True:\n \n remaining -= q\n \n if remaining == 0:\n \n if up:\n if east:\n return 1\n else:\n return 2\n elif east:\n return 0\n \n if remaining < 0:\n remaining += p\n up = not up\n \n east = not east\n```
| 8 | 0 |
[]
| 3 |
mirror-reflection
|
✔99.01% FASTER🐍PYTHON🔥EXPLAINED.
|
9901-fasterpythonexplained-by-shubhamdra-bm3i
|
Python Solution\uD83D\uDC0D\nNow picture this, a square with four mirror walls and\nwe\'re given p; the length of each wall \uD83D\uDC49 \uD83D\uDC48and q; dist
|
shubhamdraj
|
NORMAL
|
2022-08-04T15:14:45.172580+00:00
|
2022-08-04T15:15:47.613478+00:00
| 192 | false |
# Python Solution\uD83D\uDC0D\nNow picture this, **a square** with **four mirror walls** and\nwe\'re given **p**; the **length of each wall** \uD83D\uDC49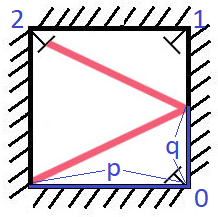 \uD83D\uDC48and **q**; **distance from 0th receptor to where the ray hit**.\n**Examples:** First let\'s see some examples->\n- p = 2, q = 1; the ray first meets 2nd receptor after it gets reflected for 1 time\n- p = 3, q = 1; the ray first meets 1st receptor after it gets reflected for 2 times.\n\nFrom these we can **observe**:\n- if **p is even** and **q is odd**, it\'ll surely **hit 2nd receptor** for the first time\n- if **both p and q is odd**, it\'ll surely **hit 1st receptor** for the first time\n\n**Edge Cases:**\n- p = 4, q = 2; **if both are even**, the ray will **first** definitely meet **2nd receptor**, beacuse the ray gets reflected for q times.\n- p = 2, q = 2; **if both are same**, the ray **first** meets **1st receptor**.\n\n```\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n\t\t# same?\n if p == q: return 1\n\t\t\n # if both are even, we need to keep dividing them by 2, until q becomes 1, \n\t\t# then as we know p even and q is odd, so it first meets 2nd receptor e.g. -> 4, 2\n while p%2 == 0 and q%2 == 0:\n p = p // 2\n q = q // 2\n \n if p%2 == 0 and q%2 == 1: return 2\n elif p%2 == 1 and q%2 == 1: return 1\n elif p%2 == 1 and q%2 == 0: return 0\n```\n## Give it a **Upvote** If You Like My Explanation.\n### Have a Great Day/Night.
| 6 | 0 |
['Math', 'Python']
| 0 |
mirror-reflection
|
C++ || Short & Simple || ✅⭐⭐
|
c-short-simple-by-palashhh-6r0r
|
DO UPVOTE IF IT HELPS !!!!!\n\t\n\tint mirrorReflection(int p, int q) {\n \n while(q % 2 == 0 && p % 2 == 0){\n q /= 2;\n p
|
palashhh
|
NORMAL
|
2022-08-04T12:26:47.794014+00:00
|
2022-08-04T12:26:47.794054+00:00
| 305 | false |
***DO UPVOTE IF IT HELPS !!!!!***\n\t\n\tint mirrorReflection(int p, int q) {\n \n while(q % 2 == 0 && p % 2 == 0){\n q /= 2;\n p /= 2;\n }\n if(q%2==0 && p%2!=0) return 0;\n if(q%2==1 && p%2==0) return 2;\n if(q%2==1 && p%2!=0) return 1;\n\n return -1;\n }
| 6 | 0 |
['Math', 'C']
| 0 |
mirror-reflection
|
C++ using LCM of p and q
|
c-using-lcm-of-p-and-q-by-rupesh_dharme-2563
|
Thought process:\n\n1. It is mentioned that the ray meets a receptor for sure so after a thought we can conclude that the ray will never land on the corner 3 be
|
rupesh_dharme
|
NORMAL
|
2022-08-04T06:01:05.968172+00:00
|
2022-08-04T06:14:13.973436+00:00
| 302 | false |
**Thought process:**\n\n1. It is mentioned that the ray meets a receptor for sure so after a thought we can conclude that the ray will never land on the corner 3 because if it does so, it\'ll follow the same path it followed before and never reach a receptor.\n2. Now we know the movement on axes are independent of each other and definitely as it is a square, the movement along each axis has to be a multiple of ```p```. This hints us that when the ray reaches the receptor the ray should have covered a distance of ```lcm(p, q)``` along vertical axis.\n3. After some more thoughts we can reach the conditions given in the code.\n\n*C++ code:*\n```\nclass Solution {\npublic:\n int mirrorReflection(int p, int q) {\n int lcm = p * q / __gcd(p, q);\n if ((lcm / p) % 2 == 0) return 0;\n if ((lcm / q) % 2 == 0) return 2;\n return 1;\n }\n};\n```\n\nRough work (just in case someone could decode it \uD83D\uDE05):\n\n\n\n\n\nThank you! Do upvote.
| 6 | 0 |
['Math']
| 1 |
mirror-reflection
|
🗓️ Daily LeetCoding Challenge August, Day 4
|
daily-leetcoding-challenge-august-day-4-4bh76
|
This problem is the Daily LeetCoding Challenge for August, Day 4. Feel free to share anything related to this problem here! You can ask questions, discuss what
|
leetcode
|
OFFICIAL
|
2022-08-04T00:00:09.757242+00:00
|
2022-08-04T00:00:09.757310+00:00
| 4,511 | false |
This problem is the Daily LeetCoding Challenge for August, Day 4.
Feel free to share anything related to this problem here!
You can ask questions, discuss what you've learned from this problem, or show off how many days of streak you've made!
---
If you'd like to share a detailed solution to the problem, please create a new post in the discuss section and provide
- **Detailed Explanations**: Describe the algorithm you used to solve this problem. Include any insights you used to solve this problem.
- **Images** that help explain the algorithm.
- **Language and Code** you used to pass the problem.
- **Time and Space complexity analysis**.
---
**📌 Do you want to learn the problem thoroughly?**
Read [**⭐ LeetCode Official Solution⭐**](https://leetcode.com/problems/mirror-reflection/solution) to learn the 3 approaches to the problem with detailed explanations to the algorithms, codes, and complexity analysis.
<details>
<summary> Spoiler Alert! We'll explain these 2 approaches in the official solution</summary>
**Approach 1:** Simulation
**Approach 2:** Mathematical
</details>
If you're new to Daily LeetCoding Challenge, [**check out this post**](https://leetcode.com/discuss/general-discussion/655704/)!
---
<br>
<p align="center">
<a href="https://leetcode.com/subscribe/?ref=ex_dc" target="_blank">
<img src="https://assets.leetcode.com/static_assets/marketing/daily_leetcoding_banner.png" width="560px" />
</a>
</p>
<br>
| 6 | 0 |
[]
| 41 |
mirror-reflection
|
Beautiful easy solution(with explanation)
|
beautiful-easy-solutionwith-explanation-rbhbl
|
Very easy recursive solution. Important observation is that each ray would pass the same distance q on vertical axis on every step. \n\nOnce we realize that, th
|
code_much_more
|
NORMAL
|
2020-11-18T05:25:12.472154+00:00
|
2020-11-18T05:48:42.761571+00:00
| 499 | false |
Very easy recursive solution. Important observation is that each ray would pass the same distance `q` on vertical axis on every step. \n\nOnce we realize that, the solution is straightforward. We go step by step and track the vertical distance that the ray passed. Also keep track in what direction we are going at any given step(variables `up` and `right`). \n\nThere are three base cases for our recursive function:\n1. `distance == p`: We are done, the ray hit one of the corners\n2. `distance > p`: Ray "overshoot". We should change vertical direction. Initial `distance` in opposite direction equals `distance % p`\n3. `distance < p`: Just do another step. Change horizontal direction to the opposite one\n\n```python \nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n \n\t def step(right, up, distance):\n if distance == p:\n return 1 if (up and right) else 2 if up else 0\n elif distance > p:\n return step(not right, not up, distance % p)\n else:\n return step(not right, up, distance+q)\n \n return step(True, True, q)\n ```
| 6 | 0 |
['Recursion', 'Python', 'Python3']
| 0 |
mirror-reflection
|
✅Short || C++ || Java || PYTHON || Explained Solution✔️ || Beginner Friendly ||🔥 🔥 BY MR CODER
|
short-c-java-python-explained-solution-b-fd0s
|
Please UPVOTE if you LIKE!!\nWatch this video \uD83E\uDC83 for the better explanation of the code.\n\nhttps://www.youtube.com/watch?v=gcRdVnBLGbQ&t=145s\n\n\nAl
|
mrcoderrm
|
NORMAL
|
2022-08-15T19:25:32.479991+00:00
|
2022-08-19T20:49:22.594088+00:00
| 118 | false |
**Please UPVOTE if you LIKE!!**\n**Watch this video \uD83E\uDC83 for the better explanation of the code.**\n\nhttps://www.youtube.com/watch?v=gcRdVnBLGbQ&t=145s\n\n\n**Also you can SUBSCRIBE \uD83E\uDC81 \uD83E\uDC81 \uD83E\uDC81 this channel for the daily leetcode challange solution.**\n\nhttps://t.me/dsacoder \u2B05\u2B05 **Telegram link** to discuss leetcode daily questions and other dsa problems\n\n**C++**\n```\n\nclass Solution {\npublic:\n \n int gcd(int a, int b) {\n while(b) {\n a = a % b;\n swap(a, b);\n }\n return a;\n }\n \n int mirrorReflection(int p, int q) {\n int lcm = (p*q)/gcd(p, q); // calculating lcm using gcd\n int m = lcm/p;\n int n = lcm/q;\n if(m%2==0 && n%2==1) return 0;\n if(m%2==1 && n%2==1) return 1;\n if(m%2==1 && n%2==0) return 2;\n return -1;\n }\n};\n```\n**JAVA**\n```\nclass Solution {\n public int mirrorReflection(int p, int q) {\n int incident = q; \n int reflect = p;\n \n while(incident%2 == 0 && reflect%2 == 0){\n incident /= 2;\n reflect /=2;\n }\n \n if(incident%2 == 0 && reflect%2 != 0) return 0;\n if(incident%2 == 1 && reflect%2 == 0) return 2;\n if(incident%2 == 1 && reflect%2 != 0) return 1; \n \n return Integer.MIN_VALUE;\n }\n}\n```\n**PYTHON**\n```\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n\n L = lcm(p,q)\n\n if (L//q)%2 == 0:\n return 2\n\n return (L//p)%2\n```\n**Please do UPVOTE to motivate me to solve more daily challenges like this !!**
| 5 | 0 |
[]
| 0 |
mirror-reflection
|
0 ms Java Easy Code
|
0-ms-java-easy-code-by-janhvi__28-pe90
|
\nclass Solution {\n public int mirrorReflection(int p, int q) {\n int incident = q; \n int reflect = p;\n \n while(incident%2 ==
|
Janhvi__28
|
NORMAL
|
2022-08-09T18:04:52.025668+00:00
|
2022-08-09T18:04:52.025702+00:00
| 131 | false |
```\nclass Solution {\n public int mirrorReflection(int p, int q) {\n int incident = q; \n int reflect = p;\n \n while(incident%2 == 0 && reflect%2 == 0){\n incident /= 2;\n reflect /=2;\n }\n \n if(incident%2 == 0 && reflect%2 != 0) return 0;\n if(incident%2 == 1 && reflect%2 == 0) return 2;\n if(incident%2 == 1 && reflect%2 != 0) return 1; \n \n return Integer.MIN_VALUE;\n }\n}\n```
| 5 | 0 |
[]
| 0 |
mirror-reflection
|
Simple O(log n) Easy to understand Solution
|
simple-olog-n-easy-to-understand-solutio-334k
|
\n#####################################################################################################################\n# Problem: Mirror Reflection\n# Soluti
|
sanjaypm09
|
NORMAL
|
2022-08-04T08:11:43.997288+00:00
|
2022-08-04T08:11:43.997366+00:00
| 297 | false |
```\n#####################################################################################################################\n# Problem: Mirror Reflection\n# Solution : Maths\n# Time Complexity : O(log n) \n# Space Complexity : O(1)\n#####################################################################################################################\n\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n while p % 2 == 0 and q % 2 == 0:\n q /= 2\n p /= 2\n \n if p % 2 == 0:\n return 2\n elif q % 2 == 0:\n return 0\n else:\n return 1\n```
| 5 | 0 |
['Math', 'Python', 'Python3']
| 0 |
mirror-reflection
|
Easy Java Solution | Faster than 100%
|
easy-java-solution-faster-than-100-by-ac-pfr8
|
\nclass Solution {\n public int mirrorReflection(int p, int q) {\n int distance = q;\n int reflection = 0;\n int trip = 0;\n whil
|
acuon
|
NORMAL
|
2022-08-04T07:39:33.044792+00:00
|
2022-08-04T07:41:59.071971+00:00
| 317 | false |
```\nclass Solution {\n public int mirrorReflection(int p, int q) {\n int distance = q;\n int reflection = 0;\n int trip = 0;\n while(distance%p != 0) {\n reflection++;\n distance += q;\n }\n trip = distance/p;\n if(trip%2==1) {\n if(reflection%2==1) return 2;\n return 1;\n }\n return 0;\n }\n}\n```
| 5 | 1 |
['Math', 'Java']
| 0 |
mirror-reflection
|
0 ms, faster than 100.00% of Java online submissions
|
0-ms-faster-than-10000-of-java-online-su-d6n8
|
UPVOTE if u find it useful\n\t\t\t\t\n\t\t\t\t\t \n\t\t\t\t\t class Solution {\n\t\t\t\t\t\t\tpublic int mirrorReflection(int p, int q) {\n\t\t\t\t\t\t\t\n\t\
|
RohiniK98
|
NORMAL
|
2022-08-04T05:12:51.655820+00:00
|
2022-08-04T05:15:49.303442+00:00
| 171 | false |
***UPVOTE if u find it useful***\n\t\t\t\t\n\t\t\t\t\t \n\t\t\t\t\t class Solution {\n\t\t\t\t\t\t\tpublic int mirrorReflection(int p, int q) {\n\t\t\t\t\t\t\t\n\t\t\t\t\t\t\t//both p qnd q even\n\t\t\t\t\t\t\t\twhile ((p%2==0) && (q%2==0)) {\n\t\t\t\t\t\t\t\t\tp/=2;\n\t\t\t\t\t\t\t\t\tq/=2;\n\t\t\t\t\t\t\t\t}\n\t\t\t\t\t\t\t\t\n\t\t\t\t\t\t\t\t//when p is even and q is odd\n\t\t\t\t\t\t\t\tif((p%2)==0 && (q%2)!=0){\n\t\t\t\t\t\t\t\t\treturn 2;\n\t\t\t\t\t\t\t\t} \n\t\t\t\t\t\t\t\t\n\t\t\t\t\t\t\t\t// when both are odd\n\t\t\t\t\t\t\t\tif((p%2)!=0 && (q%2)!=0){\n\t\t\t\t\t\t\t\t\treturn 1;\n\t\t\t\t\t\t\t\t} \n\t\t\t\t\t\t\t\t\n\t\t\t\t\t\t\t\t// when p is odd and q is even\n\t\t\t\t\t\t\t\treturn 0;\n\t\t\t\t\t\t\t}\n\t\t\t\t\t\t}\n\t\t\t\t\t\t\n\t\t\t\t\t\t\n\t\t\t\t\t\t\n# ***THANK YOU***\t\t\t\t\t\t
| 5 | 0 |
['Java']
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.