licenses
sequencelengths 1
3
| version
stringclasses 677
values | tree_hash
stringlengths 40
40
| path
stringclasses 1
value | type
stringclasses 2
values | size
stringlengths 2
8
| text
stringlengths 25
67.1M
| package_name
stringlengths 2
41
| repo
stringlengths 33
86
|
|---|---|---|---|---|---|---|---|---|
[
"Apache-2.0"
] | 0.2.18 | df1e12fb86d1f081833a74249335aa02657be774 | code | 1281 | # Test external function calls / semantic attachments
@testset "external functions" begin
path = joinpath(dirname(pathof(PDDL)), "..", "test", "functions")
# Load domain and define external functions
domain = load_domain(joinpath(path, "domain.pddl"))
throw_range(v, θ) = v^2*sin(2*θ*π/180) / 9.81
domain.funcdefs[:range] = throw_range
throw_height(v, θ, x) = tan(θ*π/180)*x - 9.81*x^2 / (2*v^2 * cos(θ*π/180)^2)
domain.funcdefs[:height] = throw_height
# Load problem
problem = load_problem(joinpath(path, "problem.pddl"))
state = initstate(domain, problem)
# Check that evaluation with external functions works correctly
@test domain[state => pddl"(range 20 45)"] == throw_range(20, 45)
@test domain[state => pddl"(height 20 45 10)"] == throw_height(20, 45, 10)
# Execute plan
state = initstate(domain, problem)
state = execute(domain, state, pddl"(pick ball1)", check=true)
state = execute(domain, state, pddl"(throw ball1 85)", check=true)
state = execute(domain, state, pddl"(pick ball2)", check=true)
state = execute(domain, state, pddl"(throw ball2 75)", check=true)
# Check if goal is satisfied
@test domain[state => pddl"(< (loc ball1) 10)"]
@test domain[state => pddl"(> (loc ball2) 15)"]
@test satisfy(domain, state, problem.goal) == true
end # external functions
| PDDL | https://github.com/JuliaPlanners/PDDL.jl.git |
|
[
"Apache-2.0"
] | 0.2.18 | df1e12fb86d1f081833a74249335aa02657be774 | code | 3882 | @testset "numeric fluents" begin
# Test numeric fluent functionality
path = joinpath(dirname(pathof(PDDL)), "..", "test", "numeric")
domain = load_domain(joinpath(path, "domain.pddl"))
@test domain.name == Symbol("zeno-travel")
@test convert(Term, domain.functions[:distance]) == pddl"(distance ?c1 ?c2)"
@test domain.functions[:fuel].argtypes == (:aircraft,)
problem = load_problem(joinpath(path, "problem.pddl"))
@test problem.metric == pddl"(minimize (+ (* 4 (total-time)) (* 5 (total-fuel-used))))"
Base.show(IOBuffer(), "text/plain", problem)
# Test for static functions
static_fluents = infer_static_fluents(domain)
@test :capacity in static_fluents
@test length(static_fluents) == 5
state = initstate(domain, problem)
implementations = [
"concrete interpreter" => domain,
"ground interpreter" => ground(domain, state),
"abstracted interpreter" => abstracted(domain),
"cached interpreter" => CachedDomain(domain),
"concrete compiler" => first(compiled(domain, state)),
"abstract compiler" => first(compiled(abstracted(domain), state)),
"cached compiler" => CachedDomain(first(compiled(domain, state))),
]
@testset "numeric fluents ($name)" for (name, domain) in implementations
# Execute plan to goal
state = initstate(domain, problem)
# Person 1 boards plane 1
state = execute(domain, state, pddl"(board person1 plane1 city0)", check=true)
@test domain[state => pddl"(onboard plane1)"] ≃ 1
# Plane 1 flies from city 0 to city 2
state = execute(domain, state, pddl"(fly plane1 city0 city2)", check=true)
@test domain[state => pddl"(total-fuel-used)"] ≃ 3100
# Person 1 debarks at city 2
state = execute(domain, state, pddl"(debark person1 plane1 city2)", check=true)
@test domain[state => pddl"(at person1 city2)"] ≃ true
# Plane 1 refuels at city 2
state = execute(domain, state, pddl"(refuel plane1 city2)", check=true)
@test domain[state => pddl"(fuel plane1)"] ≃ 10232
# Person 2 boards plane 1 at city2
state = execute(domain, state, pddl"(board person2 plane1 city2)", check=true)
@test domain[state => pddl"(in person2 plane1)"] ≃ true
# Plane 1 flies from city 2 to city 0
state = execute(domain, state, pddl"(fly plane1 city2 city0)", check=true)
@test domain[state => pddl"(total-fuel-used)"] ≃ 6200
# Person 2 debarks at city 0
state = execute(domain, state, pddl"(debark person2 plane1 city0)", check=true)
@test domain[state => pddl"(at person2 city0)"] ≃ true
# Plane 1 refuels at city 0
state = execute(domain, state, pddl"(refuel plane1 city0)", check=true)
@test domain[state => pddl"(fuel plane1)"] ≃ 10232
# Plane 1 zooms from city 0 to city 1
state = execute(domain, state, pddl"(zoom plane1 city0 city1)", check=true)
@test domain[state => pddl"(total-fuel-used)"] ≃ 16370
# The whole plan took 9 steps
@test domain[state => pddl"(total-time)"] ≃ 9
# Check if goal is satisfied
@test satisfy(domain, state, problem.goal) == true
# Test execution of entire plan
state = initstate(domain, problem)
plan = @pddl(
"(board person1 plane1 city0)",
"(fly plane1 city0 city2)",
"(debark person1 plane1 city2)",
"(refuel plane1 city2)",
"(board person2 plane1 city2)",
"(fly plane1 city2 city0)",
"(debark person2 plane1 city0)",
"(refuel plane1 city0)",
"(zoom plane1 city0 city1)"
)
sim = EndStateSimulator()
state = sim(domain, state, plan)
@test satisfy(domain, state, problem.goal) == true
# Ensure that Base.show does not error
buffer = IOBuffer()
action = first(PDDL.get_actions(domain))
Base.show(buffer, "text/plain", domain)
Base.show(buffer, "text/plain", state)
Base.show(buffer, "text/plain", action)
close(buffer)
end
end # numeric fluents
| PDDL | https://github.com/JuliaPlanners/PDDL.jl.git |
|
[
"Apache-2.0"
] | 0.2.18 | df1e12fb86d1f081833a74249335aa02657be774 | code | 10533 | # Test parsing functionality
@testset "parser" begin
@testset "formula parsing" begin
@test parse_pddl("(ball)") === Const(:ball)
@test parse_pddl("(bouncy-ball)") === Const(Symbol("bouncy-ball"))
@test parse_pddl("(bouncy_ball)") === Const(Symbol("bouncy_ball"))
@test parse_pddl("(1)") === Const(1)
@test parse_pddl("(1.0)") === Const(1.0)
@test parse_pddl("(1.0f)") === Const(1.0f0)
@test parse_pddl("(1f)") === Const(1.0f0)
@test parse_pddl("(?x)") === Var(:X)
@test parse_pddl("(?var-name)") === Var(Symbol("Var-name"))
@test parse_pddl("(?var_name)") === Var(Symbol("Var_name"))
@test parse_pddl("(on a b)") == Compound(:on, [Const(:a), Const(:b)])
@test parse_pddl("(on ?x ?y)") == Compound(:on, [Var(:X), Var(:Y)])
@test parse_pddl("(on-block a b)") == Compound(Symbol("on-block"), [Const(:a), Const(:b)])
@test parse_pddl("(+ cost 1)") == Compound(:+, [Const(:cost), Const(1)])
@test parse_pddl("(= cost 0)") == Compound(:(==), [Const(:cost), Const(0)])
@test parse_pddl("(= cost 0.0)") == Compound(:(==), [Const(:cost), Const(0.0)])
@test parse_pddl("(>= cost 0)") == Compound(:(>=), [Const(:cost), Const(0)])
@test parse_pddl("(!= cost 0)") == Compound(:(!=), [Const(:cost), Const(0)])
@test parse_pddl("(ball)") === @pddl("(ball)") === pddl"(ball)"
@test parse_pddl("(bouncy-ball)") === @pddl("(bouncy-ball)") === pddl"(bouncy-ball)"
@test parse_pddl("(bouncy_ball)") === @pddl("(bouncy_ball)") === pddl"(bouncy_ball)"
@test parse_pddl("(1)") === @pddl("(1)") === pddl"(1)"
@test parse_pddl("(1.0)") === @pddl("(1.0)") === pddl"(1.0)"
@test parse_pddl("(1.0f)") === @pddl("(1.0f)") === pddl"(1.0f)"
@test parse_pddl("(1f)") === @pddl("(1f)") === pddl"(1f)"
@test parse_pddl("(?x)") === @pddl("(?x)") === pddl"(?x)"
@test parse_pddl("(?var-name)") === @pddl("(?var-name)") === pddl"(?var-name)"
@test parse_pddl("(?var_name)") === @pddl("(?var_name)") === pddl"(?var_name)"
@test parse_pddl("(on a b)") == @pddl("(on a b)") == pddl"(on a b)"
@test parse_pddl("(on ?x ?y)") == @pddl("(on ?x ?y)") == pddl"(on ?x ?y)"
@test parse_pddl("(on-block a b)") == @pddl("(on-block a b)") == pddl"(on-block a b)"
@test parse_pddl("(+ cost 1)") == @pddl("(+ cost 1)") == pddl"(+ cost 1)"
@test parse_pddl("(= cost 0)") == @pddl("(= cost 0)") == pddl"(= cost 0)"
@test parse_pddl("(= cost 0.0)") == @pddl("(= cost 0.0)") == pddl"(= cost 0.0)"
@test parse_pddl("(>= cost 0)") == @pddl("(>= cost 0)") == pddl"(>= cost 0)"
@test parse_pddl("(!= cost 0)") == @pddl("(!= cost 0)") == pddl"(!= cost 0)"
@test parse_pddl("(and (on a b) (on b c))") ==
Compound(:and, [pddl"(on a b)", pddl"(on b c)"])
@test parse_pddl("(or (on a b) (on b c))") ==
Compound(:or, [pddl"(on a b)", pddl"(on b c)"])
@test parse_pddl("(not (on a b))") ==
Compound(:not, [pddl"(on a b)"])
@test parse_pddl("(imply (on a b) (on b c))") ==
Compound(:imply, [pddl"(on a b)", pddl"(on b c)"])
@test parse_pddl("(forall (?x) (on ?x b))") ==
Compound(:forall, [pddl"(object ?x)", pddl"(on ?x b)"])
@test parse_pddl("(forall (?x - block) (on ?x b))") ==
Compound(:forall, [pddl"(block ?x)", pddl"(on ?x b)"])
@test parse_pddl("(forall (?x ?y - block) (on ?x ?y))") ==
Compound(:forall, [pddl"(and (block ?x) (block ?y))", pddl"(on ?x ?y)"])
@test parse_pddl("(forall (?x - t1 ?y - t2) (on ?x ?y))") ==
Compound(:forall, [pddl"(and (t1 ?x) (t2 ?y))", pddl"(on ?x ?y)"])
@test parse_pddl("(exists (?x) (on ?x b))") ==
Compound(:exists, [pddl"(object ?x)", pddl"(on ?x b)"])
@test parse_pddl("(exists (?x - block) (on ?x b))") ==
Compound(:exists, [pddl"(block ?x)", pddl"(on ?x b)"])
@test parse_pddl("(exists (?x ?y - block) (on ?x ?y))") ==
Compound(:exists, [pddl"(and (block ?x) (block ?y))", pddl"(on ?x ?y)"])
@test parse_pddl("(exists (?x - t1 ?y - t2) (on ?x ?y))") ==
Compound(:exists, [pddl"(and (t1 ?x) (t2 ?y))", pddl"(on ?x ?y)"])
@test parse_pddl("(when (and (on a b) (on b c)) (on a c))") ==
Compound(:when, [pddl"(and (on a b) (on b c))", pddl"(on a c)"])
@test parse_pddl("(> (+ a b) (* c d))") ==
Compound(:>, [Compound(:+, [Const(:a), Const(:b)]),
Compound(:*, [Const(:c), Const(:d)])])
end
@testset "interpolation" begin
obj1, obj2 = Const(:a), Const(:b)
sym1, sym2 = :a , :b
@test pddl"(on $obj1 $obj2)" == Compound(:on, Term[obj1, obj2])
@test pddl"(on $sym1 $sym2)" == Compound(:on, Term[obj1, obj2])
@test_throws ErrorException parse_pddl("(on \$obj1 \$obj2)")
cval = Const(1)
val = 1
@test pddl"(= cost $cval)" == Compound(:(==), Term[Const(:cost), cval])
@test pddl"(= cost $val)" == Compound(:(==), Term[Const(:cost), cval])
fname = :on
fconst = Const(fname)
@test pddl"($fname $obj1 $obj2)" == Compound(:on, Term[obj1, obj2])
@test_throws MethodError pddl"($fconst $obj1 $obj2)"
var1, var2 = Var(:X), Var(:Y)
ty1, ty2 = :block, :cube
@test pddl"(forall ($var1 $var2 - block) (on $var1 $var2))" ==
pddl"(forall (?x ?y - block) (on ?x ?y))"
@test pddl"(forall ($var1 $var2 - $ty1) (on $var1 $var2))" ==
pddl"(forall (?x ?y - block) (on ?x ?y))"
@test pddl"(forall ($var1 - $ty1 $var2 - $ty2) (on $var1 $var2))" ==
pddl"(forall (?x - block ?y - cube) (on ?x ?y))"
@test pddl"(exists ($var1 $var2 - block) (on $var1 $var2))" ==
pddl"(exists (?x ?y - block) (on ?x ?y))"
@test pddl"(exists ($var1 $var2 - $ty1) (on $var1 $var2))" ==
pddl"(exists (?x ?y - block) (on ?x ?y))"
@test pddl"(exists ($var1 - $ty1 $var2 - $ty2) (on $var1 $var2))" ==
pddl"(exists (?x - block ?y - cube) (on ?x ?y))"
term1, term2 = pddl"(on a b)", pddl"(on b c)"
@test pddl"(and $term1 $term2)" == pddl"(and (on a b) (on b c))"
@test pddl"(or $term1 $term2)" == pddl"(or (on a b) (on b c))"
@test pddl"(not $term1)" == pddl"(not (on a b))"
@test pddl"(imply $term1 $term2)" == pddl"(imply (on a b) (on b c))"
@test pddl"(on ${obj1.name} ${obj2.name})" == Compound(:on, Term[obj1, obj2])
@test pddl"(on ${Const(:a)} ${Const(:b)})" == Compound(:on, Term[obj1, obj2])
@test pddl"""(on ${pddl"a"} ${pddl"b"})""" == Compound(:on, Term[obj1, obj2])
@test pddl"(= cost ${1 + 2})" == Compound(:(==), Term[Const(:cost), Const(3)])
@test pddl"(= cost ${zero(Int)})" == Compound(:(==), Term[Const(:cost), Const(0)])
@test_throws ErrorException parse_pddl("""
(:derived (above \$var1 \$var2)
(or (on \$var1 \$var2)
(exists (?z) (and (on \$var1 ?z) (above ?z \$var2)))))
""")
end
@testset "action parsing" begin
action = pddl"""(:action wait :effect ())"""
@test PDDL.get_name(action) == :wait
@test collect(PDDL.get_argvars(action)) == Var[]
@test collect(PDDL.get_argtypes(action)) == Symbol[]
@test PDDL.get_precond(action) == Const(true)
@test PDDL.get_effect(action) == Const(true)
action = pddl"""
(:action move
:parameters (?a ?b)
:precondition (and (room ?a) (room ?b) (in-room ?a))
:effect (and (not (in-room ?a)) (in-room ?b))
)"""
@test PDDL.get_name(action) == :move
@test collect(PDDL.get_argvars(action)) == [Var(:A), Var(:B)]
@test collect(PDDL.get_argtypes(action)) == [:object, :object]
@test PDDL.get_precond(action) == pddl"(and (room ?a) (room ?b) (in-room ?a))"
@test PDDL.get_effect(action) == pddl"(and (not (in-room ?a)) (in-room ?b))"
action = pddl"""
(:action unstack
:parameters (?x - block ?y - block)
:precondition (and (on ?x ?y) (clear ?x))
:effect (and (holding ?x) (clear ?y) (not (on ?x ?y)) (not (clear ?x)))
)"""
@test PDDL.get_name(action) == :unstack
@test collect(PDDL.get_argvars(action)) == [Var(:X), Var(:Y)]
@test collect(PDDL.get_argtypes(action)) == [:block, :block]
@test PDDL.get_precond(action) ==
pddl"(and (on ?x ?y) (clear ?x))"
@test PDDL.get_effect(action) ==
pddl"(and (holding ?x) (clear ?y) (not (on ?x ?y)) (not (clear ?x)))"
end
@testset "axiom parsing" begin
axiom = pddl"""
(:axiom (above ?x ?y)
(or (on ?x ?y) (exists (?z) (and (on ?x ?z) (above ?z ?y)))))
"""
@test axiom.head == pddl"(above ?x ?y)"
@test axiom.body ==
[pddl"(or (on ?x ?y) (exists (?z) (and (on ?x ?z) (above ?z ?y))))"]
axiom = pddl"""
(:derived (above ?x ?y)
(or (on ?x ?y) (exists (?z) (and (on ?x ?z) (above ?z ?y)))))
"""
@test axiom.head == pddl"(above ?x ?y)"
@test axiom.body ==
[pddl"(or (on ?x ?y) (exists (?z) (and (on ?x ?z) (above ?z ?y))))"]
end
@testset "domain parsing" begin
domain = load_domain(joinpath(@__DIR__, "domain.pddl"))
@test PDDL.get_name(domain) == :shapes
requirements = PDDL.get_requirements(domain)
@test requirements[:adl] == true
@test requirements[:typing] == true
@test requirements[:fluents] == true
@test requirements[Symbol("derived-predicates")] == true
typetree = PDDL.get_typetree(domain)
@test typetree[:object] == [:shape, :color]
@test typetree[:shape] == [:triangle, :rectangle]
@test typetree[:rectangle] == [:square]
@test typetree[:square] == []
@test typetree[:color] == []
constants = PDDL.get_constants(domain)
@test constants == [pddl"(red)", pddl"(green)", pddl"(blue)"]
constypes = PDDL.get_constypes(domain)
@test constypes[pddl"(red)"] == :color
@test constypes[pddl"(green)"] == :color
@test constypes[pddl"(blue)"] == :color
predicates = PDDL.get_predicates(domain)
@test predicates[Symbol("color-of")] ==
PDDL.Signature(Symbol("color-of"), :boolean, [Var(:S), Var(:C)], [:shape, :color])
@test predicates[:colored] ==
PDDL.Signature(:colored, :boolean, [Var(:S)], [:shape])
functions = PDDL.get_functions(domain)
@test functions[:size] ==
PDDL.Signature(:size, :numeric, [Var(:S)], [:shape])
axioms = PDDL.get_axioms(domain)
@test axioms[:colored].head == pddl"(colored ?s)"
@test axioms[:colored].body == [pddl"(exists (?c - color) (color-of ?s ?c))"]
actions = PDDL.get_actions(domain)
@test :recolor in keys(actions)
@test Symbol("grow-all") in keys(actions)
@test Symbol("shrink-all") in keys(actions)
end
@testset "problem parsing" begin
problem = load_problem(joinpath(@__DIR__, "problem.pddl"))
@test PDDL.get_name(problem) == Symbol("shapes-problem")
@test PDDL.get_domain_name(problem) == :shapes
@test PDDL.get_objects(problem) == [pddl"(square1)", pddl"(triangle1)"]
@test PDDL.get_objtypes(problem) ==
Dict{Const,Symbol}(
pddl"(square1)" => :square,
pddl"(triangle1)" => :triangle
)
@test PDDL.get_init_terms(problem) == @pddl(
"(color-of square1 red)",
"(color-of triangle1 red)",
"(= (size square1) 1)",
"(= (size triangle1) 2)"
)
@test PDDL.get_goal(problem) ==
pddl"(and (= (size square1) 3) (= (size triangle1) 1))"
@test PDDL.get_metric(problem) ==
pddl"(minimize (size triangle1))"
end
end # parsing
| PDDL | https://github.com/JuliaPlanners/PDDL.jl.git |
|
[
"Apache-2.0"
] | 0.2.18 | df1e12fb86d1f081833a74249335aa02657be774 | code | 2752 | @testset "set fluents" begin
# Load domain and problem
path = joinpath(dirname(pathof(PDDL)), "..", "test", "sets")
domain = load_domain(joinpath(path, "domain.pddl"))
problem = load_problem(joinpath(path, "problem.pddl"))
Base.show(IOBuffer(), "text/plain", problem)
# Make sure function declarations have the right output type
@test PDDL.get_function(domain, :heard).type == :set
@test PDDL.get_function(domain, :known).type == :set
# State initialization should error if set functions are not registered yet
@test_throws Exception state = initstate(domain, problem)
# Register set theory
PDDL.Sets.@register()
state = initstate(domain, problem)
implementations = [
"concrete interpreter" => domain,
"ground interpreter" => ground(domain, state),
"cached interpreter" => CachedDomain(domain),
"concrete compiler" => first(compiled(domain, state)),
"cached compiler" => CachedDomain(first(compiled(domain, state))),
]
@testset "set fluents ($name)" for (name, domain) in implementations
# Initialize state, test set membership and goal
state = initstate(domain, problem)
@test domain[state => pddl"(member (heard hanau) rumpelstiltskin)"] == 1
@test domain[state => pddl"(member (heard steinau) cinderella)"] == 1
@test domain[state => pddl"(subset (known jacob) story-set)"] == true
@test domain[state => pddl"(subset (known wilhelm) (heard steinau))"] == false
@test satisfy(domain, state, problem.goal) == false
# Jacob tells stories at Steinau, Wilhem at Hanau
state = execute(domain, state, pddl"(entertain jacob steinau)", check=true)
state = execute(domain, state, pddl"(entertain wilhelm hanau)", check=true)
@test domain[state => pddl"(cardinality (heard steinau))"] == 3
@test domain[state => pddl"(cardinality (heard hanau))"] == 3
# Both tell stories at Marburg
state = execute(domain, state, pddl"(entertain jacob marburg)", check=true)
state = execute(domain, state, pddl"(entertain wilhelm marburg)", check=true)
@test domain[state => pddl"(cardinality (heard marburg))"] == 4
# Check that goal is achieved
@test satisfy(domain, state, problem.goal) == true
# Ensure that Base.show does not error
buffer = IOBuffer()
action = first(PDDL.get_actions(domain))
Base.show(buffer, "text/plain", domain)
Base.show(buffer, "text/plain", state)
Base.show(buffer, "text/plain", action)
close(buffer)
end
# Test writing of set-valued fluents
original_state = initstate(domain, problem)
problem_str = write_problem(GenericProblem(original_state))
reparsed_state = initstate(domain, parse_problem(problem_str))
@test reparsed_state == original_state
# Deregister set theory
PDDL.Sets.deregister!()
end # set fluents
| PDDL | https://github.com/JuliaPlanners/PDDL.jl.git |
|
[
"Apache-2.0"
] | 0.2.18 | df1e12fb86d1f081833a74249335aa02657be774 | code | 3275 | # Test basic STRIPS functionality in a gripper domain
@testset "strips" begin
path = joinpath(dirname(pathof(PDDL)), "..", "test", "strips")
domain = load_domain(joinpath(path, "domain.pddl"))
@test domain.name == :gripper
@test convert(Term, domain.predicates[:room]) == pddl"(room ?r)"
problem = load_problem(joinpath(path, "problem.pddl"))
@test problem.name == Symbol("gripper-problem")
@test problem.objects == @pddl("rooma", "roomb", "ball1", "ball2", "left", "right")
Base.show(IOBuffer(), "text/plain", problem)
state = initstate(domain, problem)
implementations = [
"concrete interpreter" => domain,
"ground interpreter" => ground(domain, state),
"abstracted interpreter" => abstracted(domain),
"cached interpreter" => CachedDomain(domain),
"concrete compiler" => first(compiled(domain, state)),
"abstract compiler" => first(compiled(abstracted(domain), state)),
"cached compiler" => CachedDomain(first(compiled(domain, state))),
]
@testset "strips ($name)" for (name, domain) in implementations
# Test forward execution of plans
state = initstate(domain, problem)
state = execute(domain, state, pddl"(pick ball1 rooma left)", check=true)
@test domain[state => pddl"(carry ball1 left)"] ≃ true
state = execute(domain, state, pddl"(move rooma roomb)", check=true)
@test domain[state => pddl"(robbyat roomb)"] ≃ true
state = execute(domain, state, pddl"(drop ball1 roomb left)", check=true)
@test domain[state => pddl"(at ball1 roomb)"] ≃ true
@test satisfy(domain, state, problem.goal) ≃ true
# Test consistency between calls
@test available(domain, state) == available(domain, state)
# Test that available returns a vector of compound terms
if domain isa CachedDomain
@test available(domain, state) isa Vector{Compound}
end
# Test action availability
state = initstate(domain, problem)
@test Set{Term}(available(domain, state)) == Set{Term}(@pddl(
"(pick ball1 rooma right)", "(pick ball1 rooma left)",
"(pick ball2 rooma right)", "(pick ball2 rooma left)",
"(move rooma roomb)", "(move rooma rooma)"
))
# Ensure that Base.show does not error
buffer = IOBuffer()
action = first(PDDL.get_actions(domain))
Base.show(buffer, "text/plain", domain)
Base.show(buffer, "text/plain", state)
Base.show(buffer, "text/plain", action)
close(buffer)
end
# Test backward regression of plans
state = goalstate(domain, problem)
state = regress(domain, state, pddl"(drop ball1 roomb left)")
@test domain[state => pddl"(carry ball1 left)"] == true
state = regress(domain, state, pddl"(move rooma roomb)")
@test domain[state => pddl"(robbyat rooma)"] == true
state = regress(domain, state, pddl"(pick ball1 rooma left)")
@test domain[state => pddl"(at ball1 rooma)"] == true
@test issubset(state, initstate(domain, problem))
# Test action relevance
state = goalstate(domain, problem)
@test Set{Term}(relevant(domain, state)) == Set{Term}(@pddl(
"(drop ball1 roomb left)", "(drop ball1 roomb right)",
"(drop ball1 roomb ball1)", "(drop ball1 roomb ball2)",
"(drop ball1 roomb rooma)", "(drop ball1 roomb roomb)"
))
@test relevant(domain, state) == relevant(CachedDomain(domain), state)
end # strips
| PDDL | https://github.com/JuliaPlanners/PDDL.jl.git |
|
[
"Apache-2.0"
] | 0.2.18 | df1e12fb86d1f081833a74249335aa02657be774 | code | 3306 | # Test typing in a typed gripper domain
@testset "typing" begin
path = joinpath(dirname(pathof(PDDL)), "..", "test", "typing")
domain = load_domain(joinpath(path, "domain.pddl"))
@test domain.name == Symbol("gripper-typed")
@test convert(Term, domain.predicates[:free]) == pddl"(free ?g)"
@test domain.predicates[:carry].argtypes == (:ball, :gripper)
@test :gripper in PDDL.get_types(domain)
problem = load_problem(joinpath(path, "problem.pddl"))
@test problem.name == Symbol("gripper-problem")
@test problem.objects == @pddl("rooma", "roomb", "ball1", "ball2", "left", "right")
@test problem.objtypes[Const(:ball1)] == :ball
Base.show(IOBuffer(), "text/plain", problem)
state = initstate(domain, problem)
implementations = [
"concrete interpreter" => domain,
"ground interpreter" => ground(domain, state),
"abstracted interpreter" => abstracted(domain),
"cached interpreter" => CachedDomain(domain),
"concrete compiler" => first(compiled(domain, state)),
"abstract compiler" => first(compiled(abstracted(domain), state)),
"cached compiler" => CachedDomain(first(compiled(domain, state))),
]
@testset "typing ($name)" for (name, domain) in implementations
# Test forward execution of plans
state = initstate(domain, problem)
state = execute(domain, state, pddl"(pick ball1 rooma left)", check=true)
@test domain[state => pddl"(carry ball1 left)"] ≃ true
state = execute(domain, state, pddl"(move rooma roomb)", check=true)
@test domain[state => pddl"(robbyat roomb)"] ≃ true
state = execute(domain, state, pddl"(drop ball1 roomb left)", check=true)
@test domain[state => pddl"(at ball1 roomb)"] ≃ true
@test satisfy(domain, state, problem.goal) ≃ true
# Test consistency between calls
@test available(domain, state) == available(domain, state)
# Test that available returns a vector of compound terms
if domain isa CachedDomain
@test available(domain, state) isa Vector{Compound}
end
# Test action availability
state = initstate(domain, problem)
@test Set{Term}(available(domain, state)) == Set{Term}(@pddl(
"(pick ball1 rooma right)", "(pick ball1 rooma left)",
"(pick ball2 rooma right)", "(pick ball2 rooma left)",
"(move rooma roomb)", "(move rooma rooma)"
))
# Ensure that Base.show does not error
buffer = IOBuffer()
action = first(PDDL.get_actions(domain))
Base.show(buffer, "text/plain", domain)
Base.show(buffer, "text/plain", state)
Base.show(buffer, "text/plain", action)
close(buffer)
end
# Test backward regression of plans
state = goalstate(domain, problem)
state = regress(domain, state, pddl"(drop ball1 roomb left)")
@test domain[state => pddl"(carry ball1 left)"] == true
state = regress(domain, state, pddl"(move rooma roomb)")
@test domain[state => pddl"(robbyat rooma)"] == true
state = regress(domain, state, pddl"(pick ball1 rooma left)")
@test domain[state => pddl"(at ball1 rooma)"] == true
@test issubset(state, initstate(domain, problem))
# Test action relevance
state = goalstate(domain, problem)
@test Set{Term}(relevant(domain, state)) == Set{Term}(@pddl(
"(drop ball1 roomb left)", "(drop ball1 roomb right)"
))
@test relevant(domain, state) == relevant(CachedDomain(domain), state)
end # typing
| PDDL | https://github.com/JuliaPlanners/PDDL.jl.git |
|
[
"Apache-2.0"
] | 0.2.18 | df1e12fb86d1f081833a74249335aa02657be774 | docs | 5721 | # PDDL.jl
[](https://juliaplanners.github.io/PDDL.jl/stable)
[](https://juliaplanners.github.io/PDDL.jl/dev)



A Julia parser, interpreter, and compiler interface for the Planning Domain Definition Language (PDDL).
Planners not included, but see [`SymbolicPlanners.jl`](https://github.com/JuliaPlanners/SymbolicPlanners.jl).
If you use this software, please cite:
> T. Zhi-Xuan, [“PDDL.jl: An Extensible Interpreter and Compiler Interface for Fast and Flexible AI Planning”](https://dspace.mit.edu/handle/1721.1/143179), MS Thesis, Massachusetts Institute of Technology, 2022.
## Installation
Press `]` at the Julia REPL to enter the package manager, then run:
```
add PDDL
```
For the latest development version, run:
```
add https://github.com/JuliaPlanners/PDDL.jl.git
```
## Features
- Parsing and writing of PDDL domain and problem files
- A high-level symbolic planning API
- Execution of PDDL actions and plans
- Abstract interpretation of PDDL semantics
- Domain grounding and/or compilation for increased performance
- Support for the following PDDL requirements:
- `:strips` - the most restricted functionality
- `:typing` - (hierarchically) typed objects
- `:equality` - comparing equality `=` of objects
- `:quantified-preconditions` - `forall` and `exists`
- `:disjunctive-preconditions` - `or` predicates
- `:conditional-effects` - `when` and `forall` effects
- `:adl` - shorthand for the above 6 requirements
- `:constants` - domain constants
- `:fluents` - numeric fluents
- `:derived-predicates` - a.k.a. domain axioms
`PDDL.jl` does not include any planning algorithms. Rather, it aims to provide an
interface so that planners for PDDL domains can easily be written in Julia, as
in [`SymbolicPlanners.jl`](https://github.com/JuliaPlanners/SymbolicPlanners.jl).
## Example
`PDDL.jl` can be used to parse domains and planning problems written in PDDL.
For example, the following file describes a world of square tiles which are either
white or black, arranged in a grid. To change the color of the tiles one can flip
either a row of tiles or a column of tiles.
```clojure
;; Grid flipping domain with conditional effects and universal quantifiers
(define (domain flip)
(:requirements :adl :typing)
(:types row column)
(:predicates (white ?r - row ?c - column))
(:action flip_row
:parameters (?r - row)
:effect (forall (?c - column)
(and (when (white ?r ?c) (not (white ?r ?c)))
(when (not (white ?r ?c)) (white ?r ?c))))
)
(:action flip_column
:parameters (?c - column)
:effect (forall (?r - row)
(and (when (white ?r ?c) (not (white ?r ?c)))
(when (not (white ?r ?c)) (white ?r ?c))))
)
)
```
A corresponding problem in this domain might be to make all the tiles white,
when the initial state is an alternating pattern of black and white tiles in a 3x3 grid:
```clojure
;; Grid flipping problem
(define (problem flip-problem)
(:domain flip)
(:objects r1 r2 r3 - row c1 c2 c3 - column)
(:init (white r1 c2)
(white r2 c1)
(white r2 c3)
(white r3 c2))
(:goal (forall (?r - row ?c - column) (white ?r ?c)))
)
```
With `PDDL.jl`, we can parse each of these files into Julia constructs:
```julia
domain = load_domain("flip-domain.pddl")
problem = load_problem("flip-problem.pddl")
```
Actions defined by the domain can be executed to solve the problem:
```julia
state = initstate(domain, problem)
state = execute(domain, state, pddl"(flip_column c1)")
state = execute(domain, state, pddl"(flip_column c3)")
state = execute(domain, state, pddl"(flip_row r2)")
```
We can then check that the problem is successfully solved in the final state:
```julia
@assert satisfy(domain, state, problem.goal) == true
```
More examples can be found in the [`test`](test) directory. Documentation can be found [here](https://juliaplanners.github.io/PDDL.jl/stable).
## Interface
PDDL.jl exposes a high-level interface for interacting with planning domains and problems, which can be used to implement planning algorithms and other downstream applications. Full documentation of interface methods can be found [here](https://juliaplanners.github.io/PDDL.jl/stable/ref/interface/#Interface-Functions). A summary is provided below:
- `satisfy` checks whether a logical formula is satisfied (or satisfiable) in a PDDL state.
- `satisfiers` returns all satisfying substitutions to free variables in a logical formula.
- `evaluate` returns the value of a functional or logical expression within the context of a state.
- `initstate` constructs an initial state from a PDDL domain and problem.
- `goalstate` constructs a (partial) goal state from a PDDL domain and problem
- `transition` returns the successor to a state after applying an action or set of actions.
- `execute` applies an action to a state, returning the resulting state.
- `regress` computes the pre-image of an action with respect to a state.
- `available` checks whether an action can be executed in a state.
- If no action is specified, it returns the list of available actions.
- `relevant` checks whether an action can lead to a state.
- If no action is specified, it returns the list of relevant actions.
| PDDL | https://github.com/JuliaPlanners/PDDL.jl.git |
|
[
"Apache-2.0"
] | 0.2.18 | df1e12fb86d1f081833a74249335aa02657be774 | docs | 1422 | # PDDL.jl
A extensible and performant interface for symbolic planning domains specified in the Planning Domain Definition Language (PDDL), with support for PDDL parsing, interpretation, and compilation.
## Features
- Parsing and writing of PDDL domain and problem files
- A high-level symbolic planning API for use by algorithms and applications
- Execution of PDDL actions and plans
- Abstract interpretation of PDDL semantics
- Domain grounding and compilation for increased performance
- Semantic extensibility through modular theories
PDDL.jl does not include any planning algorithms. Rather, it provides an interface so that planners for PDDL domains can easily be written, as in [SymbolicPlanners.jl](https://github.com/JuliaPlanners/SymbolicPlanners.jl).
## Tutorials
Learn how to install and use PDDL.jl by following these tutorials:
```@contents
Pages = [
"tutorials/getting_started.md",
"tutorials/writing_planners.md",
"tutorials/speeding_up.md"
]
Depth = 1
```
## Architecture and Interface
Learn about the architecture of PDDL.jl, its high-level interface for symbolic planning, and the built-in implementations of this interface:
```@contents
Pages = [
"ref/overview.md",
"ref/datatypes.md",
"ref/interface.md",
"ref/parser_writer.md",
"ref/interpreter.md",
"ref/compiler.md",
"ref/absint.md",
"ref/extensions.md",
"ref/utilities.md"
]
Depth = 1
```
| PDDL | https://github.com/JuliaPlanners/PDDL.jl.git |
|
[
"Apache-2.0"
] | 0.2.18 | df1e12fb86d1f081833a74249335aa02657be774 | docs | 1635 | # Abstract Interpretation
PDDL.jl supports [abstract interpretation](https://en.wikipedia.org/wiki/Abstract_interpretation) of PDDL domains. This functionality is exposed by the [`abstracted`](@ref) and [`abstractstate`](@ref) functions:
```@docs
abstracted
abstractstate
```
The behavior of the abstract interpreter can be customized by specifying the Julia type used to represent abstract values for a particular fluent or PDDL type:
```@docs
PDDL.AbstractInterpreter
```
Abstract semantics can also be compiled by calling [`compiled`](@ref) on an abstracted domain and state:
```julia
domain, state = abstracted(domain, state)
domain, state = compiled(domain, state)
```
## Abstract Values and Types
Abstract interpretation requires each concrete value to be mapped to an abstract value of a particular type, which represents an (over-approximation) of the set of the possible values reachable after a series of actions have been executed. By default, Boolean values (i.e. predicates) are mapped to the [`BooleanAbs`](@ref) abstraction, while scalar numbers (corresponding to PDDL types like `integer`, `number` and `numeric`) are mapped to the [`IntervalAbs`](@ref) abstraction. Other types of values may use the [`SetAbs`](@ref) abstraction.
```@docs
PDDL.BooleanAbs
PDDL.IntervalAbs
PDDL.SetAbs
```
When introducing a new global datatype using the PDDL.jl extension interfaces, a default abstraction can be associated with the type by defining a new method for [`PDDL.default_abstype`](@ref):
```@docs
PDDL.default_abstype
```
The [`PDDL.@register`](@ref) macro can also be used to register new default abstractions.
| PDDL | https://github.com/JuliaPlanners/PDDL.jl.git |
|
[
"Apache-2.0"
] | 0.2.18 | df1e12fb86d1f081833a74249335aa02657be774 | docs | 277 | # Compiler
PDDL.jl supports compilation of the semantics of PDDL domains through code-generation for PDDL actions and custom datatypes for PDDL states. See [Speeding Up PDDL.jl](../tutorials/speeding_up.md) for a more detailed explanation.
```@docs
compiled
compilestate
```
| PDDL | https://github.com/JuliaPlanners/PDDL.jl.git |
|
[
"Apache-2.0"
] | 0.2.18 | df1e12fb86d1f081833a74249335aa02657be774 | docs | 9186 | # Concepts and Data Types
Symbolic planning is a general term for approaches to automated planning that describe the environment and its dynamics in terms of high-level symbols. PDDL is one way of representing such symbolic knowledge, but there are many related formalisms which the shared concepts of fluents, states, actions, domains, and problems. Here we provide general definitions of these concepts, and also describe the system of data types in PDDL.jl that mirror these concepts. A graphical overview is shown below.
```@raw html
<div style="text-align:center">
<img src="../../assets/concepts-datatypes.svg" alt="A graphical overview of concepts in symbolic planning and their corresponding datatypes." width="80%"/>
</div>
```
## Fluents and Terms
Fluents define (relational) state variables which may (or may not) change over time. A **fluent** of arity $$n$$ is a predicate (Boolean-valued) or function (non-Boolean) with $$n$$ object arguments, which describes some property or relation over those objects. A **ground fluent** is a fluent defined over particular set of objects (i.e. none of its arguments are free variables). Arguments may optionally be type-restricted.
!!! note "Example"
The fluent `(on ?x ?y)` is named `on`, has arity 2, and describes whether some object denoted by the variable `?x` is stacked on top of `?y`. The ground fluent `(on a b)` denotes that object `a` is stacked on top of object `b` when true.
The `Term` data type is used to represent fluents, but also object constants, variables, logical formulae, effect formulae, and ground actions. Every `Term` has a `name` property, as well as an `args` property, representing the (potentially empty) list of sub-terms it has as arguments. `Term`s are inherited from the [Julog.jl](https://github.com/ztangent/Julog.jl) package for Prolog-style reasoning about first-order logic.
```@docs
Term
```
There are three subtypes of `Term`s:
- `Const` terms, which are used to represent object constants, and have no arguments.
- `Var` terms are used to represent variables in the context of first-order expressions.
- `Compound` terms are terms with arguments. They can be used to represent fluents, action preconditions or effects, logical expressions, or [ground actions](../tutorials/getting_started.md#Instantiating-Actions).
To construct a `Term` using PDDL syntax, the [`@pddl`](@ref) macro or `pddl"..."` [string macro](https://docs.julialang.org/en/v1/manual/metaprogramming/#meta-non-standard-string-literals) can be used:
```julia-repl
julia> pddl"(on a b)" |> dump
Compound
name: Symbol on
args: Array{Term}((2,))
1: Const
name: Symbol a
2: Const
name: Symbol b
```
### Fluent Signatures
In the context of a planning [`Domain`](@ref), (lifted) fluents often have specific type signatures. For example, fluent arguments may be restricted to objects of particular types, and their values may be `:boolean` or `:numeric`. This type information is stored in the [`PDDL.Signature`](@ref) data type:
```@docs
PDDL.Signature
PDDL.arity
```
## States
In symbolic planning, states are symbolic descriptions of the environment and its objects at a particular point in time. Formally, given a finite set of fluents $$\mathcal{F}$$, a **state** $$s$$ is composed of a set of (optionally typed) objects $$\mathcal{O}$$, and valuations of ground fluents $$\mathcal{F}(\mathcal{O})$$ defined over all objects in $$\mathcal{O}$$ of the appropriate types. Each ground fluent thus refers to a state variable. For a ground fluent $$f \in \mathcal{F}(\mathcal{O})$$, we will use the notation $$s[f] = v$$ to denote that $$f$$ has value $$v$$ in state $$s$$.
!!! note "Example"
Given the fluents `(on ?x ?y)` and `(on-table ?x)` that describe a state $s$ with objects `a` and `b`, there are six ground fluents whose values are defined in the state: `(on a a)`, `(on a b)`, `(on b a)`, `(on b b)`, `(on-table a)` and `(on-table b)`. The expression $$s[$$`(on a b)`$$] =$$ `true` means that object `a` is on top of `b` in state $$s$$.
In PDDL.jl, states are represented by the [`State`](@ref) abstract type:
```@docs
State
```
The following accessor methods are defined for a `State`:
```@docs
PDDL.get_objects(::State)
PDDL.get_objtypes(::State)
PDDL.get_objtype(::State, ::Any)
PDDL.get_facts(::State)
PDDL.get_fluent(::State, ::Term)
PDDL.set_fluent!(::State, ::Any, ::Term)
PDDL.get_fluents(::State)
```
## Actions
As described in the [Getting Started](../tutorials/getting_started.md#Instantiating-Actions), symbolic planning formalisms distinguish between **action schemas** (also known as **operators**), which specify the general semantics of an action, and **ground actions**, which represent instantiations of an action schema for specific objects.
An action schema comprises:
- A *name* that identifies the action.
- A list of (optionally typed) *parameters* or *arguments* that an action operates over.
- A *precondition* formula, defined over the parameters, that has to hold true for the action to be executable.
- An *effect* formula, defined over the parameters, specifying how the action modifies the state once it is executed.
!!! note "Example"
An example action schema definition in PDDL is shown below:
```lisp
(:action stack
:parameters (?x ?y - block)
:precondition (and (holding ?x) (clear ?y) (not (= ?x ?y)))
:effect (and (not (holding ?x)) (not (clear ?y)) (clear ?x) (handempty) (on ?x ?y)))
```
This schema defines the semantics of an action named `stack` and has two parameters of type `block`. Its precondition states that block `?x` has to be held, block `?y` has to be clear (no other block is on top of it), and that`?x` is not the same as `?y`. Its effect states that in the next state, `?x` will no longer be held, and that it will be instead be placed on top of block `?y`.
In PDDL.jl, action schemas are represented by the [`Action`](@ref) abstract type:
```@docs
Action
```
The following accessor methods are defined for an `Action`:
```@docs
PDDL.get_argvars(::Action)
PDDL.get_argtypes(::Action)
PDDL.get_precond(::Action)
PDDL.get_effect(::Action)
```
In contrast to action schemas, ground actions are represented with the [`Term`](@ref) data type. This is because the `name` property of a [`Term`](@ref) is sufficient to identify an action schema in the context of a planning domain, and the `args` property can be used to represent action parameters.
There also exists a special no-op action schema, denoted [`PDDL.NoOp()`](@ref) in Julia code. The corresponding ground action can be expressed as [`PDDL.no_op`](@ref) or `pddl"(--)"`.
```@docs
PDDL.NoOp
PDDL.no_op
```
### State Differences
For some use cases, such as [action grounding](utilities.md#Grounding) or [interpreted execution](interpreter.md), it can be helpful to more explicitly represent the effects of an action as a difference between [`State`](@ref)s. PDDL.jl uses the [`PDDL.Diff`](@ref) abstract data type to represent such differences, including [`PDDL.GenericDiff`](@ref)s and [`PDDL.ConditionalDiff`](@ref)s.
```@docs
PDDL.Diff
PDDL.GenericDiff
PDDL.ConditionalDiff
```
Multiple [`PDDL.Diff`](@ref)s can be combined using the [`PDDL.combine!`](@ref) and [`PDDL.combine`](@ref) functions:
```@docs
PDDL.combine!
PDDL.combine
```
## Domains
A **planning domain** is a (first-order) symbolic model of the environment, specifying the predicates and functions that can be used to describe the environment, and the actions that can be taken in the environment, including their preconditions and effects. Some domains may also specify the types of objects that exist, or include domain axioms that specify which predicates can be derived from others.
In PDDL.jl, domains are represented by the [`Domain`](@ref) abstract type:
```@docs
Domain
```
The following accessor methods are defined for a `Domain`:
```@docs
PDDL.get_name(::Domain)
PDDL.get_typetree(::Domain)
PDDL.get_types(::Domain)
PDDL.get_subtypes(::Domain, ::Symbol)
PDDL.get_predicates(::Domain)
PDDL.get_predicate(::Domain, ::Symbol)
PDDL.get_functions(::Domain)
PDDL.get_function(::Domain, ::Symbol)
PDDL.get_fluents(::Domain)
PDDL.get_fluent(::Domain, ::Symbol)
PDDL.get_axioms(::Domain)
PDDL.get_axiom(::Domain, ::Symbol)
PDDL.get_actions(::Domain)
PDDL.get_action(::Domain, ::Symbol)
```
## Problems
A **planning problem** for a particular domain specifies both the
initial state of the environment, and the task specification to be achieved. Typically, the task specification is a goal to be achieved, specified as a logical formula to be satisfied. However, planning problems can also include other specifications, such as a cost metric to minimize, and temporal constraints on the plan or state trajectory.
In PDDL.jl, problems are represented by the [`Problem`](@ref) abstract type:
```@docs
Problem
```
The following accessor methods are defined for a `Problem`:
```@docs
PDDL.get_name(::Problem)
PDDL.get_domain_name(::Problem)
PDDL.get_objects(::Problem)
PDDL.get_objtypes(::Problem)
PDDL.get_init_terms(::Problem)
PDDL.get_goal(::Problem)
PDDL.get_metric(::Problem)
PDDL.get_constraints(::Problem)
```
| PDDL | https://github.com/JuliaPlanners/PDDL.jl.git |
|
[
"Apache-2.0"
] | 0.2.18 | df1e12fb86d1f081833a74249335aa02657be774 | docs | 7581 | # Extension Interfaces
PDDL.jl provides a set of extension interfaces for adding new global predicates, functions, and types. Extensions can be added on a per-predicate or per-function basis, or by registering *theories* that provide a class of related functionality.
## Built-in Types, Predicates and Functions
PDDL.jl stores mappings from (global) names to their implementations by making use of [value-based dispatch](https://github.com/ztangent/ValSplit.jl). These mappings are stored by defining methods for the following functions:
```@docs
PDDL.datatype_def
PDDL.predicate_def
PDDL.function_def
PDDL.modifier_def
```
These mappings can also be accessed in dictionary form with the following utility functions:
```@docs
PDDL.global_datatypes()
PDDL.global_predicates()
PDDL.global_functions()
PDDL.global_modifiers()
```
### Datatypes
By default, PDDL.jl supports fluents with Boolean and numeric values. These correspond to the PDDL datatypes named `boolean`, `integer`, `number` and `numeric`, and are implemented in Julia with the `Bool`, `Int` and `Float64` types:
```julia
PDDL.datatype_def(::Val{:boolean}) = (type=Bool, default=false)
PDDL.datatype_def(::Val{:integer}) = (type=Int, default=0)
PDDL.datatype_def(::Val{:number}) = (type=Float64, default=1.0)
PDDL.datatype_def(::Val{:numeric}) = (type=Float64, default=1.0)
```
When declaring a function in a PDDL domain, it is possible to denote its (output) type as one of the aforementioned types. For example, the `distance` between two cities might be declared to have a `number` type:
```pddl
(distance ?c1 - city ?c2 - city) - number
```
### Predicates and Functions
PDDL.jl also supports built-in predicates and functions for comparisons and arithmetic operations. Since these functions can be used in any PDDL domain, they are called *global* functions. Global predicates and functions are implemented by mapping them to Julia functions:
```julia
# Built-in predicates
PDDL.predicate_def(::Val{:(==)}) = PDDL.equiv
PDDL.predicate_def(::Val{:<=}) = <=
PDDL.predicate_def(::Val{:>=}) = >=
PDDL.predicate_def(::Val{:<}) = <
PDDL.predicate_def(::Val{:>}) = >
# Built-in functions
PDDL.function_def(::Val{:+}) = +
PDDL.function_def(::Val{:-}) = -
PDDL.function_def(::Val{:*}) = *
PDDL.function_def(::Val{:/}) = /
```
### Modifiers
Finally, PDDL.jl supports modifier expressions such as `(increase fluent val)`, which modifies the current value of `fluent` by `val`, setting the new value of `fluent` to the modified `value`. Like global functions, modifiers are implemented by mapping their names to corresponding Julia functions:
```julia
PDDL.modifier_def(::Val{:increase}) = :+
PDDL.modifier_def(::Val{:decrease}) = :-
PDDL.modifier_def(::Val{Symbol("scale-up")}) = :*
PDDL.modifier_def(::Val{Symbol("scale-down")}) = :/
```
## Adding Types, Predicates and Functions
To add a new global datatype, predicate, function, or modifier to PDDL, it is enough to define a new method of [`PDDL.datatype_def`](@ref), [`PDDL.predicate_def`](@ref), [`PDDL.function_def`](@ref), or [`PDDL.modifier_def`](@ref) respectively. Alternatively, one can use the [`@register`](@ref) macro to register new implementations at compile-time:
```@docs
PDDL.@register
```
In scripting contexts, run-time registration and de-registration can be achieved using [`PDDL.register!`](@ref) and [`PDDL.deregister!`](@ref):
```@docs
PDDL.register!
PDDL.deregister!
```
## Defining and Registering Theories
Similar to [Satisfiability Modulo Theories (SMT) solvers](https://en.wikipedia.org/wiki/Satisfiability_modulo_theories), PDDL.jl provides support for [*planning* modulo theories](https://dl.acm.org/doi/10.5555/3038546.3038555). By registering a new theory, developers can extend the semantics of PDDL to handle new mathematical objects such as sets, arrays, and tuples.
A new theory can be implemented by writing a (sub)module annotated with the [`@pddltheory`](@ref) macro:
```@docs
@pddltheory
```
For example, a theory for how to handle sets of PDDL objects can be written as follows (adapting the example by [Gregory et al (2012)](https://dl.acm.org/doi/10.5555/3038546.3038555)):
```julia
@pddltheory module Sets
using PDDL
using PDDL: SetAbs
construct_set(xs::Symbol...) = Set{Symbol}(xs)
empty_set() = Set{Symbol}()
cardinality(s::Set) = length(s)
member(s::Set, x) = in(x, s)
subset(x::Set, y::Set) = issubset(x, y)
union(x::Set, y::Set) = Base.union(x, y)
intersect(x::Set, y::Set) = Base.intersect(x, y)
difference(x::Set, y::Set) = setdiff(x, y)
add_element(s::Set, x) = push!(copy(s), x)
rem_element(s::Set, x) = pop!(copy(s), x)
set_to_term(s::Set) = isempty(s) ? Const(Symbol("(empty-set)")) :
Compound(Symbol("construct-set"), PDDL.val_to_term.(collect(s)))
const DATATYPES = Dict(
"set" => (type=Set{Symbol}, default=Set{Symbol}())
)
const ABSTRACTIONS = Dict(
"set" => SetAbs{Set{Symbol}}
)
const CONVERTERS = Dict(
"set" => set_to_term
)
const PREDICATES = Dict(
"member" => member,
"subset" => subset
)
const FUNCTIONS = Dict(
"construct-set" => construct_set,
"empty-set" => empty_set,
"cardinality" => cardinality,
"union" => union,
"intersect" => intersect,
"difference" => difference,
"add-element" => add_element,
"rem-element" => rem_element
)
end
```
This theory introduces a new PDDL type called `set`, implemented as the Julia datatype `Set{Symbol}`. Sets can be modified with functions such as `union` or `add-element`, and can also serve as arguments to predicates like `subset`. The default abstraction for a set is specified to be a [`SetAbs`](@ref), which means that the abstract interpreter will use a set of sets to represent the abstract value of a set-valued variable.
After defining a new theory, we can *register* it by calling the `@register` macro for that module, and make use of the new functionality in PDDL domains and problems:
```julia
Sets.@register()
domain = pddl"""
(define (domain storytellers)
(:requirements :typing :fluents)
(:types storyteller audience story)
(:functions (known ?t - storyteller) - set
(heard ?a - audience) - set
(story-set) - set
)
(:action entertain
:parameters (?t - storyteller ?a - audience)
:precondition (true)
:effect ((assign (heard ?a) (union (heard ?a) (known ?t))))
)
)
"""
problem = pddl"""
(define (problem storytellers-problem)
(:domain storytellers)
(:objects
jacob wilhelm - storyteller
hanau steinau - audience
snowwhite rumpelstiltskin - story
)
(:init
(= (story-set) (construct-set snowwhite rumpelstiltskin))
(= (known jacob) (construct-set snowwhite))
(= (known wilhelm) (construct-set rumpelstiltskin))
(= (heard hanau) (empty-set))
(= (heard steinau) (empty-set))
)
(:goal (and
; both audiences must hear all stories
(= (heard hanau) (story-set))
(= (heard steinau) (story-set))
))
)
"""
state = initstate(domain, problem)
```
As is the case for registering new predicates and functions, the `@register` macro is preferred whenever packages that depend on PDDL.jl need to be precompiled. However, it is also possible register and deregister theories at runtime with `register!` and `deregister!`:
```julia
Sets.register!()
Sets.deregister!()
```
## Predefined Theories
Alongside the `Sets` example shown above, a theory for handling `Arrays` is predefined as part of PDDL.jl:
```@docs
PDDL.Sets
PDDL.Arrays
```
These theories are not registered by default, and should be registered with the `@register` macro before use.
| PDDL | https://github.com/JuliaPlanners/PDDL.jl.git |
|
[
"Apache-2.0"
] | 0.2.18 | df1e12fb86d1f081833a74249335aa02657be774 | docs | 7475 | # Interface Functions
PDDL.jl defines a set of interface functions that serve as basic operations in a wide variety of symbolic planning algorithms and applications. These functions are intended to be low-level enough such that planning algorithms can be expressed primarily in terms of the operations they represent, but high-level enough so as to abstract away from implementational details. A schematic overview of most of these interface functions is shown below.
```@raw html
<div style="text-align:center">
<img src="../../assets/function-interface.svg" alt="A schematic diagram showing how the PDDL.jl interface functions relate to each other." width="90%"/>
</div>
```
## Evaluating Formulae and Expressions
The key distinguishing feature of symbolic planning is the ability to describe and determine whether certain facts about the world hold true (e.g. is the robot holding a block?), or evaluate numeric properties (e.g. the distance between two cities), with queries expressed in terms of first-order logic. As such, PDDL.jl provides the following functions which satisfy or evaluate first-order expressions in the context of a [`State`](@ref):
### Formula Satisfaction
Given a term representing a well-formed logical formula, or a collection of `terms` (treated as conjunctions of such formulae), the [`satisfy`](@ref) function returns whether they are satisfiable within a domain and state:
```@docs
satisfy
```
When a term has free variables, [`satisfy`](@ref) returns true as long as one satisfying assignment exists. A related function, [`satisfiers`](@ref), returns a list of all satisfying assignments to such variables (a.k.a. substitutions), including the empty list when a variable-free formula is satisfied. If no satisfying assignments exist, `nothing` is returned:
```@docs
satisfiers
```
### Term Evaluation
Given a term representing a ground expression (i.e. one with no free variables), the [`evaluate`](@ref) function returns the value of that expression in the context of a domain and state:
```@docs
evaluate
```
For example, if `term` refers to a fluent, the value of the fluent is returned. Compound numeric expressions (e.g., the sum of two fluents) can also be evaluated.
## State Initialization and Transition
A PDDL domain specifies the transition dynamics of a first order symbolic model of the world, while a PDDL problem specifies the initial state and object set over which these dynamics are grounded. PDDL.jl thus provides functions for constructing an initial state for a domain and problem, and for simulating the transition dynamics:
### State Initialization
Given a domain and problem, the [`initstate`](@ref) function returns the initial state, the type of which is concrete subtype of [`State`](@ref):
```@docs
initstate
```
The type of the returned state may vary depending on the type of the domain or problem provided. For example, providing a compiled domain as an argument leads [`initstate`](@ref) to return a compiled state representation.
### State Transition
Given a domain, state and action, the [`transition`](@ref) function returns a successor state, including the effects of events and processes (as supported by [PDDL+](http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.15.5965&rep=rep1&type=pdf)) and random sampling (in the case of [probabilistic PDDL](http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.94.2335&rep=rep1&type=pdf)). To support future multi-agent extensions of PDDL.jl, [`transition`](@ref) may also accept a set of `actions` to be executed in parallel:
```@docs
transition
transition!
```
## Forward Action Semantics
A widely-used strategy in symbolic planning is forward state space search, guided by a planning heuristic. These algorithms are built upon two basic operations to search forward in state space: querying the actions that are available in any given state, and executing an action to generate a successor state. These operations can be performed using the following functions:
### Action Availability
Given a domain, state, action schema and action arguments, the [`available`](@ref) function returns whether the corresponding action is available in the specified state -- i.e. its precondition is fulfilled. An action may alternatively be provided as a [`Term`](@ref) (e.g. `pddl"(stack a b)"`):
```@docs
available(::Domain, ::State, ::Action, ::Any)
```
When [`available`](@ref) is called without specifying an action, it returns an iterator over all actions available in the specified state, effectively encapsulating the logic for node expansion in a search algorithm:
```@docs
available(::Domain, ::State)
```
### Action Execution
Given a domain, state, action schema and action arguments, the [`execute`](@ref) function returns the result of applying the specified action to the state. An action may also be provided as a [`Term`](@ref):
```@docs
execute
execute!
```
## Inverse Semantics
Regression-based planners (e.g. [the classical STRIPS algorithm](https://en.wikipedia.org/wiki/Stanford_Research_Institute_Problem_Solver)) make use of the fact that is possible to plan by working *backwards* from a goal, repeatedly selecting actions that are relevant to achieving a goal state or specification. This motivates the following interface methods for (i) constructing *abstract* states from goal specifications and (ii) exposing the *inverse* semantics of actions:
### Goal State Construction
In symbolic planning, a logical goal formula ``g`` effectively specifies the set of all concrete goal states where ``g`` holds true. We can represent this set of concrete states as an *abstract* state ``\bar s``. In the special case where the goal ``g`` contains no disjunctions or functions, ``\bar s`` can also be understood as a *partial* state that specifies the values of all predicates in ``g``, and leaves all other predicates unspecified.
To support regression search in this abstract space, PDDL.jl provides the [`goalstate`](@ref) method for constructing an abstract state from the goal specification of a problem:
```@docs
goalstate
```
As with [`initstate`](@ref), the data type of the returned state ``\bar s`` may depend on the type of domain or problem provided.
### Action Relevance
Given a domain, state, action schema and action arguments, the [`relevant`](@ref) function returns whether the action is relevant to achieving the specified state -- i.e., it achieves at least one predicate or numeric constraint in the state, and destroys none through deletion or modification. In the case where the action's effect reduces to a list of predicates to be added and a list to be deleted, this simplifies to checking that at least one added predicate is true in the state, and that none are deleted. An action may also be provided as a [`Term`](@ref):
```@docs
relevant(::Domain, ::State, ::Action, ::Any)
```
When `relevant` is called without specifying an action, it returns an iterator over all actions relevant to the specified state, encapsulating the logic for node expansion in a regression search algorithm:
```@docs
relevant(::Domain, ::State)
```
### Action Regression
Given a domain, state, action schema and action arguments, the [`regress`](@ref) function executes the action in reverse, returning a (potentially abstract) state that represents the pre-image of the action with respect to the input state. An action may also be provided as a [`Term`](@ref):
```@docs
regress
regress!
```
| PDDL | https://github.com/JuliaPlanners/PDDL.jl.git |
|
[
"Apache-2.0"
] | 0.2.18 | df1e12fb86d1f081833a74249335aa02657be774 | docs | 28 | # Interpreter
Coming soon!
| PDDL | https://github.com/JuliaPlanners/PDDL.jl.git |
|
[
"Apache-2.0"
] | 0.2.18 | df1e12fb86d1f081833a74249335aa02657be774 | docs | 4835 | # Architecture Overview
PDDL.jl differs from standard automated planning systems in that it is designed not only for speed and efficiency, but also extensibility and interoperability. This is due to the fact that the design target of PDDL.jl is an *interface*, not just a particular algorithm or application. The diagram below provides an overview of the architecture of PDDL.jl and the ecosystem it enables (**left**), in comparison with the architecture of standard planning systems (**right**).
```@raw html
<div style="text-align:center">
<img src="../../assets/pddl-jl-architecture.svg" alt="A diagram of the architecture and ecosystem of PDDL.jl" width="60%"/>
<img src="../../assets/standard-architecture.svg" alt="A diagram of the architecture of a standard planning system" width="30%"/>
</div>
```
## Standard Planning Architectures
Standard architectures are designed primarily for fast and efficient planning, accepting PDDL domain and problem files as inputs (**right**, *pink*), rapidly translating and compiling them (*orange*) to more efficient representations (*yellow*), running planning algorithms and heuristics (*blue*) over those representations, then producing symbolic plans and metadata as outputs (*green*). This architecture enables performance optimization over the entire pipeline, but limits interaction with external applications to just two channels: (i) receiving domains and problems as inputs; and (ii) providing plans as outputs.
## PDDL.jl Architecture and Ecosystem
In contrast, the core of PDDL.jl is its interface (**left**, *green*): a set of [**abstract data types**](datatypes.md) and [**interface functions**](interface.md) that expose the high-level functionality required to implement planning algorithms and applications. Centering PDDL.jl around its interface means that:
- multiple **implementations** of the interface can coexist (*yellow*), providing either speed, generality or specialized functionality depending on engineering needs
- multiple **applications** (*light blue*) can use the interface to achieve tighter integration between symbolic planning and other AI components
- multiple **extensions** of PDDL are enabled by implementing and extending the interface through additional libraries (*dark blue*). (Note that the extension libraries shown in the diagram are still under development.)
By factoring out these components of traditional planning systems into separate software artifacts, PDDL.jl enables an ecosystem where implementations can evolve independently from applications (e.g. through future compiler improvements), applications can interoperate through a common interface (e.g. [Bayesian agent models](https://arxiv.org/abs/2006.07532) which incorporate planning algorithms), and extensions can be flexibly composed (e.g. multi-agent stochastic domains).
## Built-in Implementations
Given this interface-centered design, PDDL.jl itself does not include any applications or extensions, which are intended to be provided by separate libraries (e.g. [SymbolicPlanners.jl](https://github.com/JuliaPlanners/SymbolicPlanners.jl)). However, PDDL.jl does include several built-in implementations of its interface: a standard interpreter, a compiler, and an abstract interpreter. Each of these implementations plays a different role in the context of a planning application and its development:
- The [**standard interpreter**](interpreter.md) is designed to be easily extended, and also comes with the ease of debugging and inspection usually associated with interpreters. As such, it is ideal for checking correctness when specifying a new PDDL domain, or when implementing a planning algorithm or extension library.
- The [**compiler**](compiler.md) enables efficient planning through just-in-time compilation of specialized state representations and action semantics. While compilation is less easy to extend or debug, it provides orders of magnitude speed-ups over interpretation, allowing PDDL.jl applications to scale to much larger problems.
- The [**abstract interpreter**](absint.md) primary intended use is to compute planning heuristics that rely upon domain relaxation or abstraction. However, abstract interpreters have many other uses which future applications could take advantage of.
## Other Components
In addition to implementations of its interface, PDDL.jl also provides a PDDL [**parser**](parser_writer.md#General-Parsing), [**writer**](parser_writer.md#General-Writing), and a set of [**utilities**](utilities.md) to help analyze and work with PDDL domains. [**Extension interfaces**](extensions.md) also make it easier to support new functionality in PDDL.jl. Collectively, these components allow researchers, developers, and engineers to use symbolic planning in a wide variety of application contexts.
| PDDL | https://github.com/JuliaPlanners/PDDL.jl.git |
|
[
"Apache-2.0"
] | 0.2.18 | df1e12fb86d1f081833a74249335aa02657be774 | docs | 3684 | # Parser and Writer
PDDL.jl supports both parsing and writing of PDDL files and strings. In addition, the parser is designed to be extensible, allowing variants or extensions of PDDL to be easily supported.
## General Parsing
The `PDDL.Parser` submodule contains all functionality related to parsing PDDL strings and loading of PDDL files. To parse a string in PDDL, use the macro [`@pddl`](@ref) or the function [`parse_pddl`](@ref). Both of these return a list of parsed results if multiple strings are provided.
```@docs
@pddl
parse_pddl
```
Below we use [`@pddl`](@ref) to parse a sequence of predicates, and use [`parse_pddl`](@ref) to parse a PDDL axiom (a.k.a. derived predicate):
```julia-repl
julia> @pddl("(on a b)", "(on b c)")
2-element Vector{Compound}:
on(a, b)
on(b, c)
julia> parse_pddl("(:derived (handempty) (forall (?x) (not (holding ?x))))")
handempty <<= forall(object(X), not(holding(X)))
```
In addition, there exists a string macro `pddl"..."`, which is useful for parsing single string literals:
```julia-repl
julia> pddl"(on a b)"
on(a, b)
```
```@docs
@pddl_str
```
## Interpolation
The string macro `pddl"...` (as well as the [`@pddl`](@ref) macro) supports the interpolation of Julia variables using the `$` operator when parsing PDDL formulae. This makes it easier to construct predicates or expressions with a fixed structure but variable contents:
```julia
obj = Const(:a)
sym = :b
pddl"(on $obj $sym)"
# Parses to the same value as pddl"(on a b)"
fname = :on
pddl"($fname a b)"
# Also parses to pddl"(on a b)"
var = pddl"(?x)"
type = :block
pddl"(forall ($var - $type) (on-table $var))"
# Parses to pddl"(forall (?x - block) (on-table ?x))"
```
It is also possible to interpolate entire Julia expressions by surrounding the expression in curly braces (note that the expression itself must not contain any curly braces):
```julia
pddl"(= cost ${1 + 2})" # Parses to pddl"(= cost 3)"
pddl"(= cost ${zero(Int)})" # Parses to pddl"(= cost 0)"
```
Interpolation is **not** supported when parsing larger PDDL constructs, such as actions, domains, and problems.
## Parsing Domains and Problems
To parse domains and problems specified as PDDL strings, use [`parse_domain`](@ref) and [`parse_problem`](@ref).
```@docs
parse_domain
parse_problem
```
To load domains or problems from a file, use [`load_domain`](@ref) and [`load_problem`](@ref).
```@docs
load_domain
load_problem
```
## Extending the Parser
The parser can be extended to handle new PDDL constructs using the following macros:
```@docs
PDDL.Parser.@add_top_level
PDDL.Parser.@add_header_field
PDDL.Parser.@add_body_field
```
## General Writing
The `PDDL.Writer` submodule contains all functionality related to writing PDDL strings and saving of PDDL files. To write a string in PDDL syntax, use the function [`write_pddl`](@ref).
```@docs
write_pddl
```
Below we use [`write_pddl`](@ref) to write out an [`Action`](@ref) from the [Blocksworld domain](https://github.com/JuliaPlanners/PlanningDomains.jl/blob/main/repositories/julia-planners/blocksworld/domain.pddl).
```julia-repl
julia> write_pddl(PDDL.get_action(domain, :stack)) |> print
(:action stack
:parameters (?x ?y - block)
:precondition (and (holding ?x) (clear ?y) (not (= ?x ?y)))
:effect (and (not (holding ?x)) (not (clear ?y)) (clear ?x) (handempty) (on ?x ?y)))
```
## Writing Domains and Problems
To write domains and problem as PDDL strings, use [`write_domain`](@ref) and [`write_problem`](@ref).
```@docs
write_domain
write_problem
```
To save domains or problems as text files to a path, use [`save_domain`](@ref) and [`save_problem`](@ref).
```@docs
save_domain
save_problem
```
| PDDL | https://github.com/JuliaPlanners/PDDL.jl.git |
|
[
"Apache-2.0"
] | 0.2.18 | df1e12fb86d1f081833a74249335aa02657be774 | docs | 3685 | # Utilities
PDDL.jl provides a variety of utilities for working with and manipulating planning domains, including plan simulation, domain grounding, domain caching, and tools for domain and formula analysis.
## Simulation
It is often useful to simulate the results of applying a series of actions to an initial state. PDDL.jl supports this with the [`Simulator`](@ref) data type, and the associated [`PDDL.simulate`](@ref) method.
```@docs
Simulator
PDDL.simulate
```
The following types of [`Simulator`](@ref) are provided, depending on what results are desired:
```@docs
StateRecorder
EndStateSimulator
```
## Grounding
Many planning algorithms and search heuristics benefit from grounding of actions and axioms with respect to the fixed set of objects in the initial state. PDDL.jl provides the [`GroundAction`](@ref) data type to represent grounded actions, as well as the [`groundactions`](@ref) and [`groundaxioms`](@ref) functions to convert lifted [`Action`](@ref)s and axiom `Clause`s into lists of grounded actions:
```@docs
GroundAction
groundactions
groundaxioms
```
PDDL.jl also provides the [`ground`](@ref) function, which can be used to ground specific actions:
```@docs
ground(::Domain, ::State, ::Action, ::Any)
ground(::Domain, ::State, ::GenericAction)
```
The [`ground`](@ref) function can also be used to ground an entire domain with respect to an initial state, returning a [`GroundDomain`](@ref) that can be used in place of the original domain:
```@docs
ground(::Domain, ::State)
GroundDomain
```
## Caching
Some applications of the PDDL.jl interface may result in repeated calls to costly interface functions with the same set of input arguments (e.g. repeatedly determining the set of [`available`](@ref) actions in value iteration). In such cases, it is useful to be able to memoize the outputs of these functions. PDDL.jl supports this via [`CachedDomain`](@ref)s:
```@docs
CachedDomain
CachedDomain(::Domain, ::Any)
```
## Analysis
Static analysis of domains, actions, and formulae is often used in a variety of downstream tasks such as grounding, compilation, and relevance pruning. PDDL.jl provides a suite of analysis tools that can be helpful for these purposes.
### Domain Analysis
Certain analyses are performed on planning domains as whole (e.g. inferring the set of static fluents). The following domain-level analyses are provided by PDDL.jl:
```@docs
infer_static_fluents
infer_affected_fluents
infer_relevant_fluents
infer_axiom_hierarchy
```
An associated set of (un-exported) utility functions are provided:
```@docs
PDDL.is_static
PDDL.is_affected
PDDL.simplify_statics
PDDL.substitute_axioms
```
### Formula Analysis
PDDL.jl also provides a list of utilities for analyzing formula properties (some of which may be specific to the domain they are defined in). Note that these utilities are not exported.
The following utilities determine top-level properties of a [`Term`](@ref).
```@docs
PDDL.is_pred
PDDL.is_derived
PDDL.is_global_pred
PDDL.is_func
PDDL.is_global_func
PDDL.is_attached_func
PDDL.is_external_func
PDDL.is_fluent
PDDL.is_literal
PDDL.is_logical_op
PDDL.is_negation
PDDL.is_quantifier
PDDL.is_type
PDDL.has_subtypes
```
The following utilities determine properties of a [`Term`](@ref) or any of its nested subterms.
```@docs
PDDL.has_name
PDDL.has_pred
PDDL.has_derived
PDDL.has_global_pred
PDDL.has_func
PDDL.has_global_func
PDDL.has_attached_func
PDDL.has_fluent
PDDL.has_logical_op
PDDL.has_negation
PDDL.has_quantifier
PDDL.has_type
```
The [`PDDL.constituents`](@ref) function can be used to decompose a formula into a list of its constituent fluent terms:
```@docs
PDDL.constituents
```
| PDDL | https://github.com/JuliaPlanners/PDDL.jl.git |
|
[
"Apache-2.0"
] | 0.2.18 | df1e12fb86d1f081833a74249335aa02657be774 | docs | 17895 | # Getting Started
```@meta
Description = "A tutorial on getting started with PDDL.jl."
```
Welcome to using PDDL.jl! This tutorial covers how to install PDDL.jl, how to load your first domain and problem, how to manipulate and inspect states and actions, and how to write and execute a plan that achieves a goal.
## Installation
First, download and run Julia, [available here](https://julialang.org/downloads/) (version 1.3 or later required). Optionally, [create your own project](https://pkgdocs.julialang.org/v1/environments/) and activate its environment. Next, press `]` in the Julia REPL to enter the package manager, then install the registered version of PDDL.jl by running:
```
add PDDL
```
To install the latest development version, you may instead run:
```
add https://github.com/JuliaPlanners/PDDL.jl.git
```
PDDL.jl can now be used in the Julia REPL, or at the top of a script:
```julia
using PDDL
```
## Loading Domains and Problems
PDDL stands for the [Planning Domain Definition Language](https://en.wikipedia.org/wiki/Planning_Domain_Definition_Language), a formal language for specifying the semantics of planning domains and problems. PDDL domain and problem definitions are typically saved as text files with the `.pddl` extension.
### Loading Domains
A **PDDL domain** defines the high-level "physics" or transition dynamics of a planning task. A classic example is [Blocksworld](https://en.wikipedia.org/wiki/Blocks_world), a domain where blocks may be stacked on top of each other, or placed on a table:
```lisp
(define (domain blocksworld)
(:requirements :strips :typing :equality)
(:types block)
(:predicates (on ?x ?y - block) (ontable ?x - block) (clear ?x - block)
(handempty) (holding ?x - block))
(:action pick-up
:parameters (?x - block)
:precondition (and (clear ?x) (ontable ?x) (handempty))
:effect (and (not (ontable ?x)) (not (clear ?x))
(not (handempty)) (holding ?x)))
(:action put-down
:parameters (?x - block)
:precondition (holding ?x)
:effect (and (not (holding ?x)) (clear ?x)
(handempty) (ontable ?x)))
(:action stack
:parameters (?x ?y - block)
:precondition (and (holding ?x) (clear ?y) (not (= ?x ?y)))
:effect (and (not (holding ?x)) (not (clear ?y)) (clear ?x)
(handempty) (on ?x ?y)))
(:action unstack
:parameters (?x ?y - block)
:precondition (and (on ?x ?y) (clear ?x) (handempty) (not (= ?x ?y)))
:effect (and (holding ?x) (clear ?y) (not (clear ?x))
(not (handempty)) (not (on ?x ?y))))
)
```
Suppose this domain definition is saved in a file named `blocksworld.pddl` in the current directory. After loading PDDL.jl with `using PDDL`, we can load the Blocksworld domain by calling [`load_domain`](@ref):
```julia
domain = load_domain("blocksworld.pddl")
```
We can then inspect the name of domain, and the list of action names:
```julia-repl
julia> PDDL.get_name(domain)
:blocksworld
julia> PDDL.get_actions(domain) |> keys .|> string
4-element Vector{String}:
"pick-up"
"unstack"
"put-down"
"stack"
```
### Loading Problems
PDDL domains only define the general semantics of the planning task that apply across any set of objects or goals. To fully define a planning task, we also need to load a **PDDL problem**, which defines an initial state, and a goal to be achieved:
```lisp
(define (problem blocksworld-problem)
(:domain blocksworld)
(:objects a b c - block)
(:init (handempty) (ontable a) (ontable b) (ontable c)
(clear a) (clear b) (clear c))
(:goal (and (clear c) (ontable b) (on c a) (on a b)))
)
```
In this problem, there are 3 blocks, `a`, `b`, and `c`, which are all initially placed on the table (`ontable`), with no other blocks placed on them (`clear`). The goal is to stack the blocks such that `c` is on `a` is on `b`.
Suppose the problem definition is saved in `blocksworld-problem.pddl`. We can load it by calling [`load_problem`](@ref):
```julia
problem = load_problem("blocksworld-problem.pddl")
```
We can then inspect the list of objects, and the goal to be reached:
```julia-repl
julia> PDDL.get_objects(problem) |> println
Const[a, b, c]
julia> PDDL.get_goal(problem) |> write_pddl
"(and (clear c) (ontable b) (on c a) (on a b))"
```
### Loading From A Repository
A wide variety of standard PDDL domains and problems can be found online, such as [this repository](https://github.com/potassco/pddl-instances) of instances from the International Planning Competition (IPC). To ease the (down)loading of these domains and problems, the PDDL.jl ecosystem includes [PlanningDomains.jl](https://github.com/JuliaPlanners/PlanningDomains.jl), which contains both a built-in repository of domains and problems, and an interface for accessing domains and problems from other online repositories.
PlanningDomains.jl can be installed from the Pkg REPL as per usual:
```
add PlanningDomains
```
Once installed, we can use PlanningDomains.jl to directly load Blocksworld domains and problems:
```julia
using PlanningDomains
domain = load_domain(:blocksworld)
problem = load_problem(:blocksworld, "problem-2")
```
We can also specify external repositories to download from, such as the previously mentioned repository of [IPC domains and problems](https://github.com/potassco/pddl-instances):
```julia
domain = load_domain(IPCInstancesRepo, "ipc-2000", "blocks-strips-typed")
problem = load_problem(IPCInstancesRepo, "ipc-2000", "blocks-strips-typed", "problem-2")
```
## Constructing and Inspecting States
Now that we've loaded a domain and problem, we can construct the initial state (specified by the problem file) using the [`initstate`](@ref) function:
```julia
state = initstate(domain, problem)
```
### Inspecting Facts and Relations
Conceptually, a **state** consists of a set of objects, and a set of true facts and relations about those objects. We can list the set of facts using [`PDDL.get_facts`](@ref):
```julia-repl
julia> PDDL.get_facts(state)
Set{Term} with 7 elements:
clear(a)
ontable(b)
clear(b)
handempty
ontable(a)
ontable(c)
clear(c)
```
!!! note "PDDL vs. Prolog-style syntax"
Facts are printed in Prolog-style syntax by default: `ontable(a)` in Prolog is the same as `(ontable a)` in PDDL. This is because PDDL.jl uses [Julog.jl](https://github.com/ztangent/Julog.jl) to represent terms and expressions in first-order logic.
In addition to listing facts, we can query the truth value of specific terms using the [`satisfy`](@ref) function:
```julia-repl
julia> satisfy(domain, state, pddl"(ontable a)")
true
julia> satisfy(domain, state, pddl"(on a b)")
false
```
Here, we used the `pddl"..."` string macro to construct a first-order [`Term`](@ref). This allows us to write `pddl"(on a b)"` as syntactic sugar for the expression `Compound(:on, Term[Const(:a), Const(:b)])`. (It is also [possible to *interpolate* values](../ref/parser_writer.md#Interpolation) when using the `pddl"..."` macro.)
Besides querying whether particular terms are true or false, we can also ask PDDL.jl to return all satisfying assignments to a logical formula with free variables using the [`satisfiers`](@ref) function:
```julia-repl
julia> satisfiers(domain, state, pddl"(and (ontable ?x) (clear ?x))")
3-element Vector{Any}:
{X => b}
{X => a}
{X => c}
```
Our query `pddl"(and (ontable ?x) (clear ?x))"` expresses that some object `?x` is on the table, and is clear (i.e. has no other blocks on top of it), where `?x` is PDDL syntax for a variable in a [first-order formula](https://en.wikipedia.org/wiki/First-order_logic#Formulas). Since blocks `a`, `b` and `c` all satisfy the query, [`satisfiers`](@ref) returns a list of corresponding variable substitutions. Note that the PDDL variable `?x` gets rendered in Prolog-style syntax as a capital `X`, by the convention in Prolog that capital letters refer to variables.
### Inspecting Non-Boolean Fluents
PDDL is not limited to domains where object properties and relations must have Boolean values. For example, the [Zeno Travel domain](https://github.com/potassco/pddl-instances/blob/master/ipc-2002/domains/zenotravel-numeric-automatic/domain.pddl) includes numeric properties and relations, such as the distance between two cities, or the amount of fuel in a plane. We can construct and inspect a state in this domain as well:
```julia
zt_domain = load_domain(:zeno_travel)
zt_problem = load_problem(:zeno_travel, "problem-1")
zt_state = initstate(zt_domain, zt_problem)
```
To inspect all properties and relations (Boolean or otherwise) in this state, we can iterate over the list of pairs returned by [`PDDL.get_fluents`](@ref):
```julia-repl
julia> PDDL.get_fluents(zt_state) |> collect
13-element Vector{Pair}:
at(plane1, city0) => true
at(person1, city0) => true
onboard(plane1) => 0
slow-burn(plane1) => 4
⋮
fuel(plane1) => 3956
fast-burn(plane1) => 15
zoom-limit(plane1) => 8
capacity(plane1) => 10232
```
These properties and relations are called [**fluents**](https://en.wikipedia.org/wiki/Fluent_(artificial_intelligence)), a term historically used in AI research to describe facts about the world that may change over time.
Fluents are sometimes also called "state variables", but we avoid that terminology to prevent confusion with variables in the context of first-order terms and formulae. In keeping with the terminology of [first-order logic](https://en.wikipedia.org/wiki/First-order_logic), Boolean fluents such as `(at ?plane ?city)` are also called **predicates**, and non-Boolean fluents such as `(fuel ?plane)` are called **functions** (because they map objects to values).
!!! note "Omitted Predicates"
For conciseness, some implementations of the PDDL.jl interface will omit predicates that are false from the list returned by [`PDDL.get_fluents`](@ref), as is the case above.
In addition to listing fluents, we can evaluate specific fluents using the [`evaluate`](@ref) function. Below, we query the amount of fuel in `plane1`:
```julia-repl
julia> evaluate(zt_domain, zt_state, pddl"(fuel plane1)")
3956
```
We can also evaluate compound expressions of multiple fluents. For example, we might be curious to know the amount of additional fuel that `plane1` can hold. As syntactic sugar for `evaluate(domain, state, term)`, we can also use the syntax `domain[state => term]`:
```julia-repl
julia> evaluate(zt_domain, zt_state, pddl"(- (capacity plane1) (fuel plane1))")
6276
julia> zt_domain[zt_state => pddl"(- (capacity plane1) (fuel plane1))"]
6276
```
For *non-compound* expressions stored directly in the state, we can use [`PDDL.get_fluent`](@ref) to look up the value of a `term` in `state`, or `state[term]` for short:
```julia-repl
julia> state[pddl"(on a b)"] # Blocksworld query
false
julia> zt_state[pddl"(fuel plane1)"] # Zeno Travel query
3956
```
### Inspecting Objects and Object Types
Since PDDL states consist of sets of (optionally typed) objects, PDDL.jl provides the [`PDDL.get_objects`](@ref) function to list all objects in a state, as well as all objects of particular type:
```julia-repl
julia> PDDL.get_objects(state) |> println # Blocksworld objects
Const[c, a, b]
julia> PDDL.get_objects(zt_state, :aircraft) |> println # Zeno Travel aircraft
Const[plane1]
julia> PDDL.get_objects(zt_domain, zt_state, :movable) |> println # Zeno Travel movables
Const[person1, plane1]
```
Note that in the third call to [`PDDL.get_objects`](@ref), we also provided the domain as the first argument. This is because the domain stores information about the type hierarchy, and the `movable` type in the Zeno Travel domain is abstract: There are no objects in the state which have the type `movable`. There only objects of its subtypes, `person` and `aircraft`. We can inspect the type hierarchy of a domain using [`PDDL.get_typetree`](@ref):
```julia-repl
julia> PDDL.get_typetree(zt_domain)
Dict{Symbol, Vector{Symbol}} with 5 entries:
:object => [:movable, :city]
:movable => [:aircraft, :person]
:aircraft => []
:person => []
:city => []
```
Finally, we can inspect the type of a specific object using [`PDDL.get_objtype`](@ref):
```julia-repl
julia> PDDL.get_objtype(zt_state, pddl"(person1)")
:person
```
## Executing Actions and Plans
PDDL domains not only define the predicates and functions which describe a state, but also a set of actions which can modify a state. Having learned how to inspect the contents of a state, we can now modify them using actions.
### Instantiating Actions
In PDDL and symbolic planning more broadly, we distinguish between **action schemas** (also known as **operators**), which specify the general semantics of an action, and **ground actions**, which represent instantiations of actions for specific objects. We can inspect the definition of an action schema in a domain using [`PDDL.get_action`](@ref), such as the definition of `stack` below:
```julia-repl
julia> PDDL.get_action(domain, :stack) |> write_pddl |> print
(:action stack
:parameters (?x ?y - block)
:precondition (and (holding ?x) (clear ?y) (not (= ?x ?y)))
:effect (and (not (holding ?x)) (not (clear ?y)) (clear ?x) (handempty) (on ?x ?y)))
```
The `stack` schema has two **parameters** (or arguments) of type `block`. This means that ground instances of the `stack` schema have to be applied to two `block` objects. The schema also specifies a **precondition** formula, which has to hold true in order for the action to be executable (a.k.a. available) in the current state. Finally, the schema contains an **effect** formula, which specifies facts that will either be added or deleted in the next state. In domains with non-Boolean fluents, effects may also assign or modify the values of fluents.
To refer to a specific application of this action schema to blocks `a` and `b` (i.e., a ground action), we can simply write `pddl"(stack a b)"`, which constructs a `Term` with `stack` as its name, and with `a` and `b` as arguments:
```julia-repl
julia> pddl"(stack a b)" |> dump
Compound
name: Symbol stack
args: Array{Term}((2,))
1: Const
name: Symbol a
2: Const
name: Symbol b
```
If unspecified, whether we are referring to action schemas or ground actions shall be clear from context.
### Listing Available Actions
For our initial state in the Blocksworld domain, we can iterate over the list of available ground actions (i.e. those with satisfied preconditions) using the [`available`](@ref) function:
```julia-repl
julia> available(domain, state) |> collect
3-element Vector{Compound}:
pick-up(a)
pick-up(b)
pick-up(c)
```
Note that [`available`](@ref) returns an iterator over such actions, so we have to `collect` this iterator in order to get a `Vector` result. As before, action `Term`s are printed in Prolog-style syntax.
### Executing Actions
Since we now know which actions are available, we can [`execute`](@ref) one of them to get another state:
```julia-repl
julia> next_state = execute(domain, state, pddl"(pick-up a)");
julia> satisfy(domain, next_state, pddl"(holding a)")
true
```
We see that after executing the `pddl"(pick-up a)"` action, block `a` is now being held. In contrast, if we try to execute a non-available action, PDDL.jl will throw an error:
```julia-repl
julia> next_state = execute(domain, state, pddl"(stack a b)");
ERROR: Precondition (and (holding ?x) (clear ?y) (not (= ?x ?y))) does not hold.
⋮
```
Instead of using [`execute`](@ref), we can also use the [`transition`](@ref) function. For domains written in standard PDDL, these functions have the same behavior, but there are extensions of PDDL which include events and processes that are handled by [`transition`](@ref) only. Note that both [`execute`](@ref) and [`transition`](@ref) do not mutate the original state passed in as an argument. For mutating versions, see [`execute!`](@ref) and [`transition!`](@ref).
### Executing and Simulating Plans
Now that we know how to execute an action, we can execute a series of actions (i.e. a plan) to achieve our goal in the Blocksworld domain. We can do this by repeatedly calling [`transition`](@ref):
```julia
state = initstate(domain, problem)
state = transition(domain, state, pddl"(pick-up a)")
state = transition(domain, state, pddl"(stack a b)")
state = transition(domain, state, pddl"(pick-up c)");
state = transition(domain, state, pddl"(stack c a)");
```
And then check that our goal is indeed satisfied:
```julia-repl
julia> goal = PDDL.get_goal(problem) # Our goal is stack `c` on `a` on `b`
and(clear(c), ontable(b), on(c, a), on(a, b))
julia> satisfy(domain, state, goal)
true
```
Rather than repeatedly call [`transition`](@ref), we can use the [`PDDL.simulate`](@ref) function to directly simulate the end result of a sequence of actions:
```julia
state = initstate(domain, problem)
plan = @pddl("(pick-up a)", "(stack a b)", "(pick-up c)", "(stack c a)")
end_state = PDDL.simulate(EndStateSimulator(), domain, state, plan)
```
As before, the goal is satisfied in the final state:
```julia-repl
julia> satisfy(domain, end_state, goal)
true
```
The first argument to [`PDDL.simulate`](@ref) is a concrete instance of a [`Simulator`](@ref), which controls what information is collected as the simulation progresses. By default, the first argument is a [`StateRecorder`](@ref), which leads [`PDDL.simulate`](@ref) to return the trajectory of all states encountered, including the first:
```julia-repl
julia> traj = PDDL.simulate(domain, state, plan);
julia> eltype(traj)
GenericState
julia> length(traj)
5
```
You've now learned how to load PDDL domains and problems, construct and inspect states, and execute (sequences of) actions -- congratulations! In the [next tutorial](writing_planners.md), you can learn how to write your very own planning algorithms using the functions introduced here.
| PDDL | https://github.com/JuliaPlanners/PDDL.jl.git |
|
[
"Apache-2.0"
] | 0.2.18 | df1e12fb86d1f081833a74249335aa02657be774 | docs | 8899 | # Speeding Up PDDL.jl
```@meta
Description = "How to compile PDDL domains to speed up PDDL.jl."
```
By default, PDDL.jl uses the [built-in PDDL interpreter](../ref/interpreter.md) to execute actions, determine the set of available actions, and perform other basic planning operations. However, because the interpreter is not optimized for speed, planning algorithms that use the interpreter are considerably slower than state-of-the-art planners.
```@raw html
<figure style="text-align:center">
<img src="../../assets/performance-comparison.svg" alt="Blocksworld solution runtimes vs. problem size for PDDL.jl, Pyperplan, and FastDownward, each using A* search with the additive heuristic." width="80%"/>
<figcaption>Blocksworld solution times for PDDL.jl vs. baselines, each using A* search with the additive heuristic.</figcaption>
</figure>
```
Fortunately, PDDL.jl also provides [a PDDL compiler](../ref/compiler.md) that is optimized for speed and low memory consumption. As can be seen in the (log-scale) graph above, using the compiler to solve Blocksworld problems is 10 times faster than the interpreter, within an order of magnitude of the state-of-the-art [FastDownward](https://www.fast-downward.org/) planner, and 20 times faster than [Pyperplan](https://github.com/aibasel/pyperplan), a Python-based planning system. In this tutorial, we show how to use the PDDL compiler to speed up planning algorithms, and explain how these speed-ups are achieved.
## Using the Compiler
To use the PDDL compiler, just call the [`compiled`](@ref) function on a PDDL domain and problem. This returns a compiled domain and initial state:
```julia
using PDDL, PlanningDomains
# Load a generic representation of PDDL domain and problem
domain = load_domain(:blocksworld)
problem = load_problem(:blocksworld, "problem-10")
# Compile the domain and problem to get a compiled domain and state
c_domain, c_state = compiled(domain, problem)
```
Alternatively, [`compiled`](@ref) can be called on a non-compiled domain and (initial) state:
```julia
# Construct initial state from domain and problem
state = initstate(domain, problem)
# Compile the domain and state to get a compiled domain and state
c_domain, c_state = compiled(domain, state)
```
The compiled outputs `c_domain` and `c_state` can then be used with the [PDDL.jl interface](../ref/interpreter.md), or with [an existing planner from SymbolicPlanners.jl](writing_planners.md#Existing-Planners):
```julia
using SymbolicPlanners
# Call A* search on compiled domain and initial state
goal = PDDL.get_goal(problem)
planner = AStarPlanner(HAdd())
sol = planner(c_domain, c_state, goal)
# Execute resulting plan on the compiled initial state
plan = collect(sol)
for act in plan
c_state = transition(c_domain, c_state, act)
end
# Check that the goal is achieved in the final state
@assert satisfy(c_domain, c_state, goal)
```
Factoring out the initial cost of [Julia's just-ahead-of-time compilation](https://discourse.julialang.org/t/so-does-julia-compile-or-interpret/56073/2?u=xuan), planning over the compiled domain and state should lead to runtimes that are 10 times faster or more, compared to the PDDL.jl interpreter.
## State Compilation
One way in which the PDDL.jl compiler reduces runtime is by generating *compiled state representations* that compactly represent the set of facts and fluent values in a state. These representations take advantage of the fixed number of objects in standard PDDL problems, allowing for the generation of finite-object state representations with a known size in advance.
To illustrate the benefits of state compilation, consider the initial state of a Blocksworld problem with 3 blocks, as shown in the [Getting Started](getting_started.md#Loading-Domains-and-Problems) tutorial. The generic state representation used by the PDDL.jl interpreter stores all Boolean fluents in a `Set` data structure, and non-Boolean fluents in a `Dict`. This consumes a fair amount of memory, and suffers from hashing overhead when looking up the value of a fluent:
```
GenericState
types -> Set{Compound} with 3 elements
pddl"(block a)",
pddl"(block b)",
pddl"(block c)"
facts -> Set{Term} with 7 elements
pddl"(handempty)",
pddl"(clear a)",
pddl"(clear b)",
pddl"(clear c)"
pddl"(ontable a)",
pddl"(ontable b)",
pddl"(ontable c)"
values -> Dict{Term,Any} with 0 entries
Size: 1720 bytes
Median Access Time: 394 ns
```
In constrast, the compiled state representation is shown below. Predicate values are stored in memory-efficient bit-arrays, with dimensionality corresponding to the arity of each predicate (1 dimension for `(holding ?x)`, 2 dimensions for `(on ?x ?y)`). Furthermore, each bit array is a field with a fixed name in the compiled data structure. Together, this leads to much lower memory consumption and access times:
```
CompiledBlocksworldState
handempty ->
true
clear -> 3-element BitVector
1 1 1
holding -> 3-element BitVector
0 0 0
ontable -> 3-element BitVector
1 1 1
on -> 3x3 BitMatrix
0 0 0
0 0 0
0 0 0
Size: 336 bytes
Median Access Time: 58.5 ns
```
Generating a compiled state representation requires knowing the number of objects in the problem, their types, and their names. This is why the [`compiled`](@ref) function requires either the problem or initial state as an input.
## Action Compilation
PDDL.jl also supports *compiled action semantics*, generating specialized implementations of the [`execute`](@ref) and [`available`](@ref) interface functions for each action schema in the domain. This makes use of Julia's support for multiple dispatch: By generating concrete subtypes of the [`Action`](@ref) datatype for each action schema, specialized methods can be defined for each subtype.
As an example, consider the compiled implementation of [`execute`](@ref) for the `(stack ?x ?y)` action in the Blocksworld domain. Instead of interpreting the effect formula associated with the action each time it is executed, the compiled version of [`execute`](@ref) directly modifies the appropriate entries of the compiled state representation for the Blocksworld domain (shown below with comments):
```julia
function execute(domain, state, action::CompiledStackAction, args)
state = copy(state)
# Get object indices for arguments
x_idx = objectindex(state, :block, args[1].name)
y_idx = objectindex(state, :block, args[2].name)
# Assign new values to affected fluents
state.handempty = true
state.clear[x_idx] = true
state.clear[y_idx] = false
state.holding[x_idx] = false
state.on[x_idx, y_idx] = true
return state
end
```
All of the above code is compiled from PDDL to Julia, which in turn gets compiled to high performance machine code by Julia's own compiler. By directly modifying the state representation, the compiled implementation can achieve median runtimes up to 60 times faster than the interpreted version of [`execute`](@ref).
## Compiler Limitations
While domain compilation leads to significant performant benefits, the compiler also has several limitations in the current version of PDDL.jl:
- **Top-level only**: Because [`compiled`](@ref) defines new types and methods, it should only be called at the top-level in order to avoid world-age errors.
- **Precompilation not supported**: Since [`compiled`](@ref) evaluates code in the `PDDL` module, it will lead to precompilation errors when used in another module or package. Modules which call [`compiled`](@ref) should hence disable precompilation, or include make calls to [`compiled`](@ref) only in the [`__init__()` function](https://docs.julialang.org/en/v1/manual/modules/#Module-initialization-and-precompilation).
- **Regression not supported**: The compiler does not currently implement the interface functions for reverse action semantics, meaning that it cannot be used for regression search.
- **Compilation overhead**: The cost of compiling generated Julia code on its first run can be significant relative to total runtime for small problems. This means that compilation may not be ideal for one-off use for states with small numbers of objects.
- **No generalization across problems in the same domain**: The compiled code and state representations generated by the compiler currently assume a fixed set of objects. To use the compiler with problems in the same domain, but defined over a different set of of objects the [`compiled`](@ref) function has to be invoked again.
Due to these limitations, it may sometimes be preferable to use the PDDL.jl interpreter instead of the compiler, especially when generality is more important than speed. However, most of these limitations are planned to be removed in future versions of PDDL.jl.
| PDDL | https://github.com/JuliaPlanners/PDDL.jl.git |
|
[
"Apache-2.0"
] | 0.2.18 | df1e12fb86d1f081833a74249335aa02657be774 | docs | 7410 | # Writing Planners
```@meta
Description = "How to write symbolic planners using PDDL.jl."
```
Using the [PDDL.jl interface](..\ref\interface.md), it is straightforward to implement planning algorithms which solve problems in PDDL domains. Since all domain and implementation specific details are encapsulated by the interface, the same algorithm can operate across multiple domains, and even multiple representations of the same domain (e.g. [interpreted](../ref/interpreter.md) vs. [compiled](../ref/compiler.md)).
In this tutorial, we present two simple planners as examples: forward breadth-first search, and backward breadth-first search.
## Forward Search
Our first example is **forward breadth-first search**, shown below. The algorithm accepts a [`Domain`](@ref) and [`Problem`](@ref), then constructs the initial state with the [`initstate`](@ref) function. It also extracts the goal formula using [`PDDL.get_goal`](@ref). The algorithm then searches the state space, iteratively expanding the successors of each state and available action in a [breadth-first order](https://en.wikipedia.org/wiki/Breadth-first_search):
```julia
function forward_bfs(domain::Domain, problem::Problem)
# Initialize state and extract goal
state = initstate(domain, problem)
goal = PDDL.get_goal(problem)
# Initialize search queue
plan = []
queue = [(state, plan)]
while length(queue) > 0
# Pop state and plan
state, plan = popfirst!(queue)
# Check if goal is satisfied
if satisfy(domain, state, goal)
# Return plan if goal is satisfied
return plan
end
# Iterate over available actions and add successors to queue
for action in available(domain, state)
next_state = transition(domain, state, action)
next_plan = [plan; action]
push!(queue, (next_state, next_plan))
end
end
# Return nothing upon failure
return nothing
end
```
As can be seen, search proceeds by popping a state and corresponding plan off the search queue at each iteration, then checking if the state satisfies the goal using [`satisfy`](@ref). If the goal is satisfied, the plan is returned. If not, the state is expanded by iterating over each [`available`](@ref) action, and constructing the successor state for that action using the [`transition`](@ref) function. The successor state and its corresponding plan are added to queue. Search continues until either the queue is exhausted, or the goal is satisfied.
!!! note "Implementation Efficiency"
While easy to understand, the implementation of breadth-first search presented here is memory inefficient because it stores the plan to each state as part of the search queue. Efficient implementations of planners using breadth-first search should be based off [Djikstra's algorithm](https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm) instead.
## Regression Search
PDDL.jl also supports planning via **backward search**, also known as [**regression search**](https://artint.info/2e/html/ArtInt2e.Ch6.S3.html). Backward search operates by treating the goal condition as a *partial* or *abstract* state which only specifies that some predicates must be true. It then searches the space by considering all actions that could possibly achieve the current abstract state (called **relevant** actions), and inverting the semantics of each action (called **regression**). This results in a successor abstract state that represents the pre-image of the action: the set of all states that could have reached the current abstract state through that action.
A breadth-first version of backward search is shown below.
```julia
function backward_bfs(domain::Domain, problem::Problem)
# Construct initial state and goal state
init_state = initstate(domain, problem)
state = goalstate(domain, problem)
# Initialize search queue
plan = []
queue = [(state, plan)]
while length(queue) > 0
# Pop state and plan
state, plan = popfirst!(queue)
# Return plan if initial state implies the current abstract state
if all(evaluate(domain, init_state, fluent) == val
for (fluent, val) in PDDL.get_fluents(state))
return plan
end
# Iterate over relevant actions and add pre-image to queue
for action in relevant(domain, state)
next_state = regress(domain, state, action)
next_plan = [action; plan]
push!(queue, (next_state, next_plan))
end
end
# Return nothing upon failure
return nothing
end
```
This algorithm is very similar to [`forward_bfs`](#forward-search): It first constructs an initial state (using [`initstate`](@ref)) and abstract goal state (using [`goalstate`](@ref)) from the domain and problem. It then searches in a breadth-first order from the abstract goal state, iterating over actions that are [`relevant`](@ref) to achieving the current abstract state, then computing the preimage induced by each action using [`regress`](@ref) and adding the resulting state to the queue. The search terminates when the initial state is found to be in the preimage of some action, i.e., all fluents that are true in the preimage are also true in the initial state.
!!! note "Support for Regression Search"
PDDL.jl currently only provides correct implementations of regression search operations ([`relevant`](@ref) and [`regress`](@ref)) for STRIPS-style domains. This means that regression search is not currently supported for domains with non-Boolean fluents, negative preconditions, disjunctive preconditions, quantified preconditions, or conditional effects.
## Existing Planners
While PDDL.jl makes it relatively easy to implement planning algorithms from scratch, the performance and (re)usability of these algorithms require more careful design. As such, the PDDL.jl ecosystem also includes the [**SymbolicPlanners.jl**](https://github.com/JuliaPlanners/SymbolicPlanners.jl) library, which provides a wide array of planning algorithms and heuristics that have [comparable performance](https://github.com/JuliaPlanners/SymbolicPlanners.jl#performance) to other commonly-used planning systems. Below, we show how to use SymbolicPlanners.jl to solve a Blocksworld problem via [A* search](https://en.wikipedia.org/wiki/A*_search_algorithm) with the [additive heuristic](https://doi.org/10.1016/S0004-3702%2801%2900108-4):
```julia
using PDDL, PlanningDomains, SymbolicPlanners
# Load Blocksworld domain and problem
domain = load_domain(:blocksworld)
problem = load_problem(:blocksworld, "problem-4")
state = initstate(domain, problem)
goal = PDDL.get_goal(problem)
# Construct A* planner with h_add heuristic
planner = AStarPlanner(HAdd())
# Solve the problem using the planner
sol = planner(domain, state, goal)
```
We can check that the resulting solution achieves the goal as desired:
```julia-repl
julia> goal
and(on(d, c), on(c, b), on(b, a), on(a, e))
julia> collect(sol)
10-element Vector{Any}:
unstack(b, a)
put-down(b)
unstack(a, d)
stack(a, e)
pick-up(b)
stack(b, a)
pick-up(c)
stack(c, b)
pick-up(d)
stack(d, c)
julia> satisfy(domain, sol.trajectory[end], goal)
true
```
For more information about the planners and heuristics provided by SymbolicPlanners.jl, consult the [README](https://github.com/JuliaPlanners/SymbolicPlanners.jl).
| PDDL | https://github.com/JuliaPlanners/PDDL.jl.git |
|
[
"MIT"
] | 0.1.0 | 90fbe88ebb4d0f5a1dc07c463eccfa5d13754efa | code | 154 | module SmoothLivePlot
using Observables, WebIO
include("plotFunctions.jl")
export modifyPlotObject!
include("plotMacros.jl")
export @makeLivePlot
end
| SmoothLivePlot | https://github.com/williamjsdavis/SmoothLivePlot.jl.git |
|
[
"MIT"
] | 0.1.0 | 90fbe88ebb4d0f5a1dc07c463eccfa5d13754efa | code | 1011 | # Plotting functions
function smoothLivePlotGeneral(plotFunction, plotArgs)
data_obs = Observable{Any}(plotArgs)
plt_obs = Observable{Any}(plotFunction(plotArgs...))
map!(mapArg -> plotFunction(mapArg...), plt_obs, data_obs)
# Create figure
ui = dom"div"(plt_obs);
display(ui)
sleep(0.4)
return data_obs
end
function modifyPlotObject!(mutablePlotArray; args...)
# Modify plot objects by passing "argX = newValue" pairs
Nargs = length(mutablePlotArray[])
NargsSupplied = length(args)
# Test arguments
if .!all("arg" .== map(x -> string(x)[1:3], args.itr))
error("""Mutable arguments must begin with \"arg\"""")
end
argStringNums = map(x -> parse(Int, string(x)[4:end]), args.itr)
if .!all(argStringNums .<= Nargs)
error("Indices must be less than or equal to length of mutable array")
end
mutablePlotArray[] = map(x -> x in argStringNums ? args.data[findfirst(x .== argStringNums)] : mutablePlotArray[][x], 1:Nargs)
end
| SmoothLivePlot | https://github.com/williamjsdavis/SmoothLivePlot.jl.git |
|
[
"MIT"
] | 0.1.0 | 90fbe88ebb4d0f5a1dc07c463eccfa5d13754efa | code | 382 | # Plotting macros
macro makeLivePlot(plotExpression)
# Turn plotting function into smooth version
plotFunction = plotExpression.args[1]
plotArgs = plotExpression.args[2:end]
arrayArgs = map(x -> :($(esc(x))), plotArgs)
splatArgs = :([$(arrayArgs...)])
outExpression = :(smoothLivePlotGeneral($(esc(plotFunction)), $splatArgs))
return outExpression
end
| SmoothLivePlot | https://github.com/williamjsdavis/SmoothLivePlot.jl.git |
|
[
"MIT"
] | 0.1.0 | 90fbe88ebb4d0f5a1dc07c463eccfa5d13754efa | code | 1067 | # Testing plot examples
using Plots
using SmoothLivePlot
using Test
include("testPlotFunctions.jl")
gr(show = true)
# Test macro
macro no_error(ex)
quote
try
$(esc(ex))
true
catch
false
end
end
end
function main()
@testset "All plots" begin
@testset "Modify Y" begin
@test @no_error testModifyY()
end
@testset "Modify X" begin
@test @no_error testModifyX()
end
@testset "Modify X+Y" begin
@test @no_error testModifyXY()
end
@testset "Modify Z" begin
@test @no_error testModifyZ()
end
@testset "Modify X+Text" begin
@test @no_error testModifyXText()
end
@testset "Modify X+Colour" begin
@test @no_error testModifyXColour()
end
@testset "Add to X+Y" begin
@test @no_error testAddXY()
end
@testset "Add to X+Y+Z" begin
@test @no_error testAddXYZ()
end
end
end
main()
| SmoothLivePlot | https://github.com/williamjsdavis/SmoothLivePlot.jl.git |
|
[
"MIT"
] | 0.1.0 | 90fbe88ebb4d0f5a1dc07c463eccfa5d13754efa | code | 5207 | ## Test plot functions
function testModifyY()
p0, xArray, tArray = getInitialDist()
pMax = maximum(p0)
p = copy(p0)
D = 1E-5
dx = 1/(xArray.len-1);
dt = 0.5*dx*dx/D;
s = D*dt/(dx*dx);
function stepTime(p, s, nx)
p[2:end-1] = s.*p[3:nx]-(2*s-1).*p[2:nx-1]+s.*p[1:nx-2];
end
YplotObject = @makeLivePlot myPlot(xArray, p0)
for tt in tArray
stepTime(p, s, xArray.len)
modifyPlotObject!(YplotObject, arg2 = p)
end
end
function testModifyX()
p0, xArray, tArray = getInitialDist()
pMax = maximum(p0)
XplotObject = @makeLivePlot myPlot(xArray, p0)
for tt in tArray
modifyPlotObject!(XplotObject, arg1 = XplotObject[][1]*0.99)
end
end
function testModifyXY()
p0, xArray, tArray = getInitialDist()
pMax = maximum(p0)
XYplotObject = @makeLivePlot myPlot(xArray, p0)
for tt in tArray
modifyPlotObject!(XYplotObject, arg2 = XYplotObject[][2]*0.99, arg1 = XYplotObject[][1]*1.01)
end
end
function testModifyZ()
x = 1:0.05:20
y = 1:0.05:10
f(x, y, t) = begin
(3x + y^2) * abs(sin(x) + (1-t)*cos(y))
end
X = repeat(reshape(x, 1, :), length(y), 1)
Y = repeat(y, 1, length(x))
Z = map((x, y) -> f(x, y, 0.0), X, Y)
ZplotObject = @makeLivePlot myPlotZ(x, y, Z)
ttt = 0.0:0.1:1.0
for tt in ttt
Z = map((x, y) -> f(x, y, tt), X, Y)
modifyPlotObject!(ZplotObject, arg3 = Z)
end
end
function testModifyXText()
p0, xArray, tArray = getInitialDist()
pMax = maximum(p0)
p = copy(p0)
titleText = "Title, step: "
XtextPlotObject = @makeLivePlot myPlotTitle(xArray, p0, titleText)
for tt in 1:50
modifyPlotObject!(XtextPlotObject, arg3 = string(titleText, tt), arg1 = XtextPlotObject[][1]*0.99)
end
end
function testModifyXColour()
p0, xArray, tArray = getInitialDist()
pMax = maximum(p0)
p = copy(p0)
scatterColour = range(0, 1, length=50)
XColourPlotObject = @makeLivePlot myPlotColour(xArray, p0, scatterColour[1])
for tt in 1:50
modifyPlotObject!(XColourPlotObject, arg3 = scatterColour[tt], arg1 = XColourPlotObject[][1]*0.99)
end
end
function testAddXY()
p0, xArray, tArray = getInitialDist()
pMax = maximum(p0)
p = copy(p0)
addXYPlotObject = @makeLivePlot myPlot(xArray, p0)
for tt in 1:length(xArray)
modifyPlotObject!(addXYPlotObject, arg1 = xArray[1:tt], arg2 = p0[1:tt])
end
end
function testAddXYZ()
attractor = Lorenz()
plt = plot3d(
1,
xlim = (-30, 30),
ylim = (-30, 30),
zlim = (0, 60),
title = "Lorenz Attractor",
label = "",
marker = 2,
)
addXYZPlotObject = @makeLivePlot myPlotXYZ(plt)
for tt in 1:500
step!(attractor)
push!(plt, attractor.x, attractor.y, attractor.z)
modifyPlotObject!(addXYZPlotObject, arg1 = plt)
end
end
function getInitialDist()
tStart = 0.0
tEnd = 2.0
ntSteps = 100
xStart = -5.0
xEnd = 5.0
nxSteps = 20
tArray = range(tStart, tEnd, length = ntSteps)
xArray = range(xStart, xEnd, length = nxSteps)
x0 = 0.0
sig = 2.0
f(x) = exp(-((x - x0)/sig)^2)
p = f.(xArray)
return p, xArray, tArray
end
Base.@kwdef mutable struct Lorenz
dt::Float32 = 0.02
σ::Float32 = 10
ρ::Float32 = 28
β::Float32 = 8/3
x::Float32 = 1
y::Float32 = 1
z::Float32 = 1
end
function step!(l::Lorenz)
dx = l.σ * (l.y - l.x); l.x += l.dt * dx
dy = l.x * (l.ρ - l.z) - l.y; l.y += l.dt * dy
dz = l.x * l.y - l.β * l.z; l.z += l.dt * dz
end
function myPlot(xx, yy)
sleep(0.0001)
plot(
xx, yy,
label = "",
color = :red,
xlim = (-5, 5),
ylim = (0, 1),
title = "Title",
xlabel = "X label",
ylabel = "Y label"
)
scatter!(xx, yy, label = "")
end
function myPlotTitle(xx, yy, titleText)
sleep(0.0001)
plot(
xx, yy,
label = "",
color = :red,
xlim = (-5, 5),
ylim = (0, 1),
title = titleText,
xlabel = "X label",
ylabel = "Y label"
)
scatter!(xx, yy, label = "")
end
function myPlotColour(xx, yy, cc)
sleep(0.0001)
plot(
xx, yy,
label = "",
color = :red,
xlim = (-5, 5),
ylim = (0, 1),
title = "Title text",
xlabel = "X label",
ylabel = "Y label"
)
scatter!(xx, yy, markersize = 20, color = RGBA(cc, 0.5, 0, 0), label = "")
end
function myPlotZ(xx, yy, ZZ)
sleep(0.0001)
p1 = contour(
xx, yy, ZZ,
fill = true, clims=(0,300),
title = "Title text",
xlabel = "X label",
ylabel = "Y label"
);
end
function myPlotXYZ(pltObj)
sleep(0.0001)
xx = getindex(pltObj.series_list[1].plotattributes, :x)
yy = getindex(pltObj.series_list[1].plotattributes, :y)
zz = getindex(pltObj.series_list[1].plotattributes, :z)
plot3d(
xx, yy, zz,
xlim = (-30, 30),
ylim = (-30, 30),
zlim = (0, 60),
title = "Lorenz Attractor",
label = "",
marker = 2,
)
end
| SmoothLivePlot | https://github.com/williamjsdavis/SmoothLivePlot.jl.git |
|
[
"MIT"
] | 0.1.0 | 90fbe88ebb4d0f5a1dc07c463eccfa5d13754efa | docs | 2943 | # SmoothLivePlot.jl
`SmoothLivePlot.jl` is a Julia package for creating live-style plots during calculations.
# Motivation
Updating the Juno plot plane during calculations creates new plots on top of the old ones. This produces a flickering effect e.g.:
- [Can you update a plot in Julia?](https://discourse.julialang.org/t/current-state-of-live-plots-in-atom-juno/30379)
- [Current State of Live Plots in Atom/Juno?](https://discourse.julialang.org/t/current-state-of-live-plots-in-atom-juno/30379)
- [Suppress Plot Window when output to animation](https://discourse.julialang.org/t/suppress-plot-window-when-output-to-animation/30724)
To smoothly update of plots, I generalised a [solution found by user ckneale](https://discourse.julialang.org/t/current-state-of-live-plots-in-atom-juno/30379/7). It uses [Observables.jl](https://github.com/JuliaGizmos/Observables.jl) and [WebIO.jl](https://github.com/JuliaGizmos/WebIO.jl) so that the plot can listen to changes in its elements.
Currently, I have tested the following capabilities:
- Modifying values in X and/or Y array(s) in scatter and plot
- Modifying colours in scatter and plot
- Modifying text elements (e.g. titles, xlabels, etc...)
- Modifying matricies in contour plots
- Adding new elements to X,Y arrays in 2d line and scatter plots
- Adding new elements to X,Y,Z in 3d line and scatter plots
Note: this package is designed to work with the __plot plane in Juno__. If you force it to plot in a gui it will look really weird.
# Using the package
1. Import the module using `using SmoothLivePlot`.
2. Create a live plot with macro `outPlotObject = @makeLivePlot myPlotFunction(argument1, argument2, ...)`.
- Function `myPlotFunction(argument1, argument2, ...)` is a user defined plotting function.
- Output `outPlotObject` is a mutable output array of plot features. Its elements are the input aruments of `myPlotFunction()`.
3. Modify plot elements with function `modifyPlotObject!(outPlotObject, arg2 = newArg2, arg1 = newArg1, ...)`.
- The first argment of `modifyPlotObject!()` must be the mutable output array.
- The following argments are optional and named. The name/value pair must be `arg<x> = newArg1`, where `<x>` in the name is an integer that indicates the position of the argument in the original plotting function `myPlotFunction()`.
- E.g. to modify `argument2` to `newArgument2`, use `modifyPlotObject!(outPlotObject, arg2 = newArgument2)`.
- The modified arguments do not have to be in any specific order, and are updated at the same time.
### Short example
Here's a video showing an output live-plot from some magnetohydrodynamic calculations:

# TODOs
- [ ] Add capability to add additional elements to plots.
- [ ] Benchmark performance.
# Changelog
- Version 0.1.0 - Introduced original version.
| SmoothLivePlot | https://github.com/williamjsdavis/SmoothLivePlot.jl.git |
|
[
"MIT"
] | 0.1.0 | 1c8aa4364d29b8b2e130314849db06203450b756 | code | 13761 | module AtomicLocks
using Base.Threads
@inline function active_wait(i)
ii = 0
for _ in 1:rand(1:min(i,10))
ii+=1
end
end
##########################################################################################################################################################
## AtomicLock
##########################################################################################################################################################
"""
struct AtomicLock
An atomic lock implementation based on atomic boolean flags.
The `AtomicLock` struct provides a simple mechanism for controlling access to a shared resource using atomic operations.
It is similar to `SpinLock`, but introduces a waiting period between acquisition attempts.
# Fields
- `locked::Atomic{Bool}`: A boolean flag indicating whether the lock is currently held. Uses atomic operations to prevent race conditions.
- `wait::Int64`: The wait time (in arbitrary units) between consecutive attempts to acquire the lock. A higher value of `wait` reduces CPU load by spacing out lock acquisition attempts.
# Constructor
AtomicLock(wait=100)
Constructor for `AtomicLock`. Initializes the lock in the unlocked state and sets the `wait` parameter,
which controls the interval between attempts to acquire the lock in the `lock` function.
# Arguments
- `wait`: Optional parameter specifying the delay between acquisition attempts.
Defaults to 100 if not provided. This value allows for some flexibility in
avoiding aggressive spinning in tight loops when attempting to acquire the lock.
# Example
```julia
lock = AtomicLock(200) # Creates a lock with a custom wait time
"""
struct AtomicLock
locked::Atomic{Bool}
wait::Int64
function AtomicLock(wait=100)
new(Atomic{Bool}(false), wait)
end
end
@inline function Base.lock(bl::AtomicLock)
ii = UInt64(0)
while atomic_cas!(bl.locked, false, true)
active_wait(bl.wait)
if mod(ii,100)==0
yield()
end
end
println("lock on thread $(Threads.threadid())")
end
@inline Base.unlock(bl::AtomicLock) = atomic_xchg!(bl.locked,false)
@inline Base.trylock(bl::AtomicLock) = !atomic_cas!(bl.locked, false, true)
@inline Base.islocked(bl::AtomicLock) = bl.locked[]
export AtomicLock
##########################################################################################################################################################
## AtomicFIFOLock
##########################################################################################################################################################
"""
AtomicFIFOLock
An atomic lock that operates on a first-in, first-out (FIFO) basis. This ensures that requests to acquire the lock are handled in the order they are made, providing fairness in lock acquisition.
AtomicFIFOLock(wait=100)
Constructs an `AtomicFIFOLock`, which behaves similarly to a `SpinLock` or `AtomicLock`, but enforces a first-in, first-out (FIFO) order for acquiring the lock. This ensures that the lock is granted in the order in which it was requested, preventing the possibility of starvation that can occur with traditional spinlocks.
# Arguments
- `wait`: Optional parameter that specifies the delay between attempts to acquire the lock. Defaults to 100 if not provided.
# Example
```julia
fifo_lock = AtomicFIFOLock(200) # Creates a FIFO lock with a custom wait time
"""
struct AtomicFIFOLock
head::Atomic{Int64}
tail::Atomic{Int64}
lock::AtomicLock
wait::Int64
function AtomicFIFOLock(wait=100)
new(Atomic{Int64}(0), Atomic{Int64}(0),AtomicLock(),wait)
end
end
@inline function Base.lock(bfl::AtomicFIFOLock)
lock(bfl.lock)
my_tail = atomic_add!(bfl.tail, 1)
unlock(bfl.lock)
i = 1
while (my_tail != bfl.head[])
active_wait(bfl.wait*i)
i += 1
if mod(i,100)==0
yield()
end
end
end
@inline Base.unlock(bfl::AtomicFIFOLock) = atomic_add!(bfl.head,1)
@inline function Base.trylock(bfl::AtomicFIFOLock)
if bfl.tail[] == bfl.head[] && trylock(bfl.lock)
tail = atomic_add!(bfl.tail, 1)
l = true
if (bfl.head[] != tail)
atomic_sub!(bfl.tail, 1)
l = false
end
unlock(bfl.lock)
return l
else
return false
end
end
@inline Base.islocked(bfl::AtomicFIFOLock) = (bfl.head[]<bfl.tail[])
export AtomicFIFOLock
##########################################################################################################################################################
## ReadWriteLock
##########################################################################################################################################################
"""
ReadWriteLock(; kwargs...)
Constructs a `ReadWriteLock`, which allows multiple threads to read in parallel, but only one thread to write at a time.
This lock is designed for managing data that requires very short but frequent access times. It is particularly useful in scenarios where reading operations happen frequently and can occur simultaneously, but writing operations need to be exclusive.
# Keyword Arguments
- `kwargs...`: Currently unused, but allows for future customization of the lock’s behavior.
# Example
```julia
rw_lock = ReadWriteLock() # Creates a new read-write lock
```
ReadWriteLock
A lock that allows one write operation at a time, while multiple read operations can be performed concurrently. This is useful for data management situations with extremely short but frequent access times.
#Fields
head::Threads.Atomic{Int64}: Tracks the current position in the lock queue for managing the order of operations.
tail::Threads.Atomic{Int64}: Tracks the tail of the queue, representing the most recent operation in the queue.
reads_count::Threads.Atomic{Int64}: Keeps track of the number of concurrent read operations. Only one write operation can proceed if no reads are active.
# This lock supports both read and write operations:
readlock(): Acquires a read lock, allowing multiple readers to access the data concurrently.
writelock(): Acquires a write lock, granting exclusive access to the data for writing.
readunlock(): Releases a previously acquired read lock.
writeunlock(): Releases a previously acquired write lock.
"""
struct ReadWriteLock
head::Threads.Atomic{Int64}
tail::Threads.Atomic{Int64}
reads_count::Threads.Atomic{Int64}
ReadWriteLock(;kwargs...) = new(Threads.Atomic{Int64}(0),Threads.Atomic{Int64}(0),Threads.Atomic{Int64}(0))
end
@inline readlock(::Nothing) = nothing
@inline readunlock(::Nothing) = nothing
@inline writelock(::Nothing) = nothing
@inline writeunlock(::Nothing) = nothing
@inline ReadWriteLock(::T) where T = nothing
@inline function readlock(rwl::ReadWriteLock,args...)
this_tail = atomic_add!(rwl.tail,1)
ii = 0
while atomic_add!(rwl.head,0)!=this_tail
active_wait(100)
ii += 1
mod(ii,100)==0 && yield()
end
atomic_add!(rwl.reads_count,1)
atomic_add!(rwl.head,1)
end
@inline function writelock(rwl::ReadWriteLock,args...)
this_tail = atomic_add!(rwl.tail,1)
ii = 0
while atomic_add!(rwl.head,0)!=this_tail || atomic_add!(rwl.reads_count,0)>0
active_wait(100)
ii += 1
mod(ii,100)==0 && yield()
end
end
@inline readunlock(rwl::ReadWriteLock) = atomic_sub!(rwl.reads_count,1)
@inline writeunlock(rwl::ReadWriteLock) = atomic_add!(rwl.head,1)
@inline Base.lock(rwl::ReadWriteLock) = writelock(rwl)
@inline Base.unlock(rwl::ReadWriteLock) = writeunlock(rwl)
export ReadWriteLock
export readlock
export readunlock
export writelock
export writeunlock
##########################################################################################################################################################
## SyncLock
##########################################################################################################################################################
"""An atomic synchronizer. Used to stall tasks until all tasks have reached a particular point in their algorithm."""
struct SyncLock
locks::Threads.Atomic{Int64}
event::Event
SyncLock() = new(Threads.Atomic{Int64}(0),Event())
end
"""Adds `i` counts to the SyncLock. Hence synclock(lock) will stall until synclock(lock) has been called `i` times."""
@inline add_sync!(lock::SyncLock,i) = atomic_add!(lock.locks,i)
@inline Base.lock(lock::SyncLock) = synclock(lock)
""" locks the SyncLock `lock` until all tasks have been completed """
@inline synclock(lock::SyncLock) = begin
a = atomic_sub!(lock.locks,1)
if a<=1
notify(lock.event)
else
wait(lock.event)
end
return a
end
export SyncLock
export synclock
export add_sync!
##########################################################################################################################################################
## ReadWriteLockDebug
##########################################################################################################################################################
const RWLCounter = Threads.Atomic{Int64}(1)
struct RWLTrace
thread::Int64
OP::Int64
all::Int64
point_id::Int64
end
Base.show(io::IO, trace::RWLTrace) = print(io, "(", trace.thread, ",", trace.OP, ",", trace.all,",", trace.point_id, ")")
struct RWLDebugError <: Exception
index::Int64
head::Int64
tail::Int64
reads_count::Int64
trace::Vector{RWLTrace}
end
Base.showerror(io::IO, err::RWLDebugError) = print(io, "$(err.index): $(err.head), $(err.tail), $(err.reads_count), traces: $(err.trace)")
struct ReadWriteLockDebug
head::Threads.Atomic{Int64}
tail::Threads.Atomic{Int64}
reads_count::Threads.Atomic{Int64}
all::Threads.Atomic{Int64}
index::Int64
trace::Vector{RWLTrace}
lock::SpinLock
timelag::Int64
ltrace::Int64
function ReadWriteLockDebug(;traces::Int64=100,timelag::Int64=1000000000,print::Bool=false,location="")
rwl = new(Threads.Atomic{Int64}(0),Threads.Atomic{Int64}(0),Threads.Atomic{Int64}(0),Threads.Atomic{Int64}(0),atomic_add!(AtomicLocks.RWLCounter,1),Vector{RWLTrace}(undef,traces),SpinLock(),timelag,traces)#,cr,cw,ReentrantLock())
if print
println("Initialize ReadWriteLock $(rwl.index) at location: $location")
end
return rwl
end
end
export ReadWriteLockDebug
@inline ReadWriteLockDebug(::T) where T = nothing
@inline function readlock(rwl::ReadWriteLockDebug,id=0)
lock(rwl.lock)
ti = time_ns()
this_tail = atomic_add!(rwl.tail,1)
a = atomic_add!(rwl.all,1)
rwl.trace[mod(a,rwl.ltrace)+1] = RWLTrace(Threads.threadid(),1,a,id)
unlock(rwl.lock)
ii = 0
while atomic_add!(rwl.head,0)<this_tail
active_wait(100)
ii += 1
mod(ii,100)==0 && yield()
if time_ns()-ti>rwl.timelag
#lock(rwl.lock)
a = atomic_add!(rwl.all,1)
rwl.trace[mod(a,rwl.ltrace)+1] = RWLTrace(Threads.threadid(),-1,a,id)
ltrace = length(rwl.trace)
last_index = mod(a,rwl.ltrace)+1
tr = Vector{RWLTrace}(undef,min(ltrace,a+1))
if length(tr)==ltrace
tr[1:(ltrace-last_index)] .= rwl.trace[(last_index+1):ltrace]
tr[(ltrace-last_index+1):ltrace] .= rwl.trace[1:last_index]
else
tr .= rwl.trace[1:(a+1)]
end
#unlock(rwl.lock)
throw(RWLDebugError(rwl.index, atomic_add!(rwl.head, 0), this_tail, atomic_add!(rwl.reads_count, 0), tr))
end
end
println(time_ns()-ti)
atomic_add!(rwl.reads_count,1)
atomic_add!(rwl.head,1)
end
@inline function writelock(rwl::ReadWriteLockDebug,id=0)
lock(rwl.lock)
ti = time_ns()
this_tail = atomic_add!(rwl.tail,1)
#print("$this_tail, $(rwl.head[]), $(rwl.reads_count[])")
a = atomic_add!(rwl.all,1)
rwl.trace[mod(a,rwl.ltrace)+1] = RWLTrace(Threads.threadid(),3,a,id)
unlock(rwl.lock)
ii = 0
while atomic_add!(rwl.head,0)<this_tail || atomic_add!(rwl.reads_count,0)>0
active_wait(100)
ii += 1
mod(ii,100)==0 && yield()
if time_ns()-ti>rwl.timelag
#lock(rwl.lock)
a = atomic_add!(rwl.all,1)
rwl.trace[mod(a,rwl.ltrace)+1] = RWLTrace(Threads.threadid(),-3,a,id)
ltrace = length(rwl.trace)
last_index = mod(a,rwl.ltrace)+1
tr = Vector{RWLTrace}(undef,min(ltrace,a+1))
if length(tr)==ltrace
tr[1:(ltrace-last_index)] .= rwl.trace[(last_index+1):ltrace]
tr[(ltrace-last_index+1):ltrace] .= rwl.trace[1:last_index]
else
tr .= rwl.trace[1:(a+1)]
end
#unlock(rwl.lock)
throw(RWLDebugError(rwl.index, atomic_add!(rwl.head, 0), this_tail, atomic_add!(rwl.reads_count, 0), tr))
end
end
println(time_ns()-ti)
end
@inline function readunlock(rwl::ReadWriteLockDebug,id=0)
lock(rwl.lock)
atomic_sub!(rwl.reads_count,1)
a = atomic_add!(rwl.all,1)
rwl.trace[mod(a,rwl.ltrace)+1] = RWLTrace(Threads.threadid(),2,a,id)
unlock(rwl.lock)
end
@inline function writeunlock(rwl::ReadWriteLockDebug,id=0)
lock(rwl.lock)
atomic_add!(rwl.head,1)
a = atomic_add!(rwl.all,1)
rwl.trace[mod(a,rwl.ltrace)+1] = RWLTrace(Threads.threadid(),4,a,id)
unlock(rwl.lock)
end
@inline Base.lock(rwl::ReadWriteLockDebug,id=0) = writelock(rwl,id)
@inline Base.unlock(rwl::ReadWriteLockDebug,id=0) = writeunlock(rwl,id)
end
| AtomicLocks | https://github.com/martinheida/AtomicLocks.jl.git |
|
[
"MIT"
] | 0.1.0 | 1c8aa4364d29b8b2e130314849db06203450b756 | code | 3546 | using AtomicLocks
using Test
using Base.Threads
@testset "AtomicLocks.jl" begin
function test_thread(_lock)
for i in 1:10
lock(_lock)
print("1 ")
r = rand(1:100)/1000
print("$r -> ")
sleep(r)
print("2 ")
unlock(_lock)
print("3 ")
end
end
function test_lock(lock)
Threads.@threads for i in 1:Threads.nthreads()
test_thread(lock)
end
return true
end
println("Test 1:")
@test test_lock(AtomicLock())
println("Test 1:")
@test test_lock(AtomicFIFOLock())
function sync_thread(slock,lock)
test_thread(lock)
Base.lock(slock)
test_thread(lock)
end
function synctest()
slock = SyncLock()
lock = AtomicFIFOLock()
add_sync!(slock,Threads.nthreads())
Threads.@threads for i in 1:Threads.nthreads()
sync_thread(slock,lock)
end
return true
end
println("Test sync:")
@test synctest()
function reader_task(rwl::ReadWriteLock, thread_id::Int)
println("Thread $thread_id: attempting to acquire read lock.")
readlock(rwl)
println("Thread $thread_id: acquired read lock.")
# Simulate read operation (e.g., with sleep)
sleep(0.1)
println("Thread $thread_id: releasing read lock.")
readunlock(rwl)
end
function writer_task(rwl::ReadWriteLock, thread_id::Int)
println("Thread $thread_id: attempting to acquire write lock.")
writelock(rwl)
println("Thread $thread_id: acquired write lock.")
# Simulate write operation (e.g., with sleep)
sleep(0.1)
println("Thread $thread_id: releasing write lock.")
writeunlock(rwl)
end
function test_read_write_lock()
rwl = ReadWriteLock()
println(typeof(rwl))
# Start threads for read and write operations
nthreads = Threads.nthreads()
println("Using $nthreads threads")
# Create threads that either read or write
@threads for i in 1:nthreads
if mod(i, 2) == 0
reader_task(rwl, i)
else
writer_task(rwl, i)
end
end
return true
end
@test test_read_write_lock()
function test_read(_lock,ii)
for i in 1:10
readlock(_lock)
r = rand(1:55)/1000
sleep(r)
readunlock(_lock)
end
end
function test_write(_lock,ii)
for i in 1:10
writelock(_lock)
r = rand(1:55)/1000
sleep(r)
writeunlock(_lock)
end
end
function test_read_write_lock_debug()
rwl = ReadWriteLockDebug(;traces = 10, timelag=50000000,print=true)
println(typeof(rwl))
# Start threads for read and write operations
nthreads = Threads.nthreads()
println("Using $nthreads threads")
fail = 0
# Create threads that either read or write
@threads for i in 1:nthreads
try
if mod(i, 2) == 0
test_read(rwl, i)
else
test_write(rwl, i)
end
catch e
fail += 1
println(e)
end
end
println("Fails: $fail")
println(rwl.trace[1:rwl.tail[]])
return true
end
@test test_read_write_lock_debug()
end
| AtomicLocks | https://github.com/martinheida/AtomicLocks.jl.git |
|
[
"MIT"
] | 0.1.0 | 1c8aa4364d29b8b2e130314849db06203450b756 | docs | 5150 | # AtomicLocks.jl
`AtomicLocks.jl` is a Julia package that provides a set of thread-safe, atomic-based locks, including traditional read-write locks, FIFO locks, synchronization locks and advanced debug tools for identifying lock contention issues in multithreaded environments. The package is designed for data management scenarios where short but frequent access to data is required and the percentage of data access times is still low compared to the overall computation time.
## Features
- **`AtomicLock`**: A simple atomic lock that provides mutual exclusion with a customizable wait time between attempts to acquire the lock.
- **`AtomicFIFOLock`**: A first-in-first-out (FIFO) atomic lock that ensures fairness by granting the lock to tasks in the order they request it.
- **`ReadWriteLock`**: A read-write lock that allows concurrent reads but exclusive writes.
- **`ReadWriteLockDebug`**: An enhanced version of `ReadWriteLock` with built-in debugging features to detect lock contention and long wait times. In particular, this is made for detecting errors in the usage of ReadWriteLock. Look at `runtests.jl` and play with the time parameters there for getting an insight into the exception management.
- **`SyncLock`**: An atomic synchronizer used to coordinate tasks, making them wait until all have reached a specific synchronization point.
---
## Installation
To install the package, use the Julia package manager:
```julia
] add AtomicLocks
```
## Usage
### 1. AtomicLock
AtomicLock is a simple atomic lock that functions similarly to a SpinLock. The parameter wait controls the time between attempts to acquire the lock.
```julia
using AtomicLocks
# Create an AtomicLock with optional argument 200 that performs approximately 200 simple calculations between two tries to acquire the lock
lock = AtomicLock(200)
# Acquire the lock
lock(lock)
# Release the lock
unlock(lock)
```
### 2. AtomicFIFOLock
AtomicFIFOLock works similarly to AtomicLock but follows a first-in, first-out (FIFO) order for lock acquisition.
```julia
using AtomicLocks
# Create a FIFO lock with optional argument 200 that performs approximately 200 simple calculations between two tries to acquire the lock
fifo_lock = AtomicFIFOLock(200)
# Acquire the lock
lock(fifo_lock)
# Release the lock
unlock(fifo_lock)
```
### 3. ReadWriteLock
ReadWriteLock allows multiple threads to read concurrently, but only one thread can write at any time. Read and write exclude each other. This is particularly useful for managing data with frequent reads and occasional writes, when data access takes only a very small percentage of the code.
The ReadWriteLock will avoid freuent yielding or context switching unless the ressources get stalled in one of the threads. This makes it possible to have many frequent readlocks or writelocks without creating much overhead to the computation.
you can provide the same arguments to ReadWriteLock functions as to ReadWriteLockDebug functions, they will simply be ignored in this context.
```julia
using AtomicLocks
# Create a ReadWriteLock
rw_lock = ReadWriteLock()
# Acquire a read lock
readlock(rw_lock)
# Release a read lock
readunlock(rw_lock)
# Acquire a write lock
writelock(rw_lock)
# Release a write lock
writeunlock(rw_lock)
```
### 4. ReadWriteLockDebug
ReadWriteLockDebug extends ReadWriteLock with debugging features. If a readlock or writelock waits for longer than `timelag` (default: 1 second), an error is raised. It also collects the last few lock operations for debugging purposes.
```julia
using AtomicLocks
# Create a debug read-write lock with traces enabled and 500ms lock-waiting-time before throwing an exception.
rw_lock_debug = ReadWriteLockDebug(traces=200, timelag=500000000, print=true, location="ModuleA")
# Acquire a read lock with trace ID
readlock(rw_lock_debug, 42) # this action will acquire the internal id 42
# Release the read lock
readunlock(rw_lock_debug, 43) # this action will acquire the internal id 42
# If a lock waits for too long, an RWLDebugError will be raised, with trace information:
try
writelock(rw_lock_debug, 100)
catch e::RWLDebugError
println("Lock wait exceeded timelag: ", e)
finally
writeunlock(rw_lock_debug, 101)
end
```
### 5. SyncLock
SyncLock is an atomic synchronizer that ensures tasks wait until all other tasks have reached a specific point in their execution. I developed this lock because I had to implement a synchronized break deep inside my HighVoronoi.jl code and handing all responsibility back to the top would have been counter productive in terms of factorization of code.
```julia
using AtomicLocks
# Create a SyncLock
sync_lock = SyncLock()
function do_stuff(sl)
do_some_stuff()
# Stall until 3 tasks reach this point
synclock(sl) # wait for all threads having completed the first task
do_some_more_stuff()
end
# Warning: The following can only work if there are really at least 3 threads available in Threads.nthreads() and there are three threads available in your OS!!
# Set the lock to wait for 3 tasks
add_sync!(sync_lock, 3)
Threads@threads for i in 1:3
do_stuff(sync_lock)
end
```
| AtomicLocks | https://github.com/martinheida/AtomicLocks.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 1215 | # In Julia register CI, do nothing
if get(ENV, "JULIA_REGISTRYCI_AUTOMERGE", "false") == "true"
exit(0)
end
##
using libcxxwrap_julia_jll
using Scratch
using Pkg.TOML
using UUIDs
##
include("generate_wrapper.jl")
const libpoplar_dir = joinpath(get_scratch!(UUID(TOML.parsefile(joinpath(dirname(@__DIR__), "Project.toml"))["uuid"]), "libpoplar"), "v$(Base.thispatch(VERSION))")
function build_bindings(; path::String=joinpath(libpoplar_dir, "libpoplar_julia.so"), generate_bindings::Bool=true, compile::Bool=true)
if generate_bindings
generate_wrapper()
end
if compile
cxxwrap_include_dir = joinpath(libcxxwrap_julia_jll.artifact_dir, "include")
julia_include_dir = joinpath(dirname(Sys.BINDIR), "include", "julia")
mkpath(dirname(path))
dir = joinpath(@__DIR__, "wrapper")
run(```
$(cxx)
-O0
-std=c++17
-fPIC
-shared
-I$(julia_include_dir)
-I$(cxxwrap_include_dir)
-I$(dir)
-o $(path)
$(joinpath(dir, "template.cpp"))
-lpopops
-lpoplar
```)
end
return nothing
end
build_bindings()
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 24912 | ##
using Clang
using Clang.LibClang
using JSON
##
const allowed_namespaces = ("poplar", "popops")
# TODO: I really shouldn't be using strings everywhere for these
const supported_nodes = ("EnumDecl", "ClassDecl", "StructDecl", "CXXMethod", "FunctionTemplate", "FunctionDecl", "CXXConstructor", "EnumConstantDecl")
const cxx = get(ENV, "CXX", "g++")
abstract type BindgenContext end
mutable struct DefaultBindgenContext <: BindgenContext
searched_headers::Vector{String}
blacklisted_headers::Vector{String}
handled_symbols::Set{String}
seen_symbols::Set{String}
outputDecls::String
outputMembers::String
outputSupertypes::String
end
DefaultBindgenContext() = DefaultBindgenContext([], [], Set([]), Set([]), "", "", "")
function get_system_includes()::Vector{String}
io = IOBuffer()
readchomp(pipeline(`$(cxx) -x c++ -E -Wp,-v - -fsyntax-only`; stdin=IOBuffer(""), stderr=io))
m = match(r"#include <\.\.\.> search starts here:(.*)End of search list\."s, String(take!(io)))[1]
return abspath.(strip.(split(m[2:end - 1], "\n")))
end
# Find the header file in one of the include paths
function resolve_header(header::String, include_paths::Vector{String})::String
for include in include_paths
path = joinpath(include, header)
if isfile(path)
return path
end
end
error("Couldn't find $(header) in $(join(repr.(include_paths), ", "))")
end
# Find header files in the include paths
resolve_headers(headers::Vector{String}, include_paths::Vector{String})::Vector{String} =
resolve_header.(headers, Ref(include_paths))
function get_full_name(cursor, funcargs::Bool=true, buf="")
parent = Clang.getCursorLexicalParent(cursor)
parent_kind = spelling(kind(parent))
cursor_name = name(cursor)
if !funcargs
cursor_name = split(cursor_name, "(")[1]
end
if parent_kind != "TranslationUnit" && parent_kind != "InvalidFile"
buf = get_full_name(parent, funcargs, buf)
end
if buf == ""
return cursor_name
else
return buf * "::" * cursor_name
end
end
function get_namespace(cursor::CLCursor)
tmpcursor = cursor
while spelling(kind(tmpcursor)) != "Namespace" && Clang.getCursorLexicalParent(tmpcursor) != tmpcursor
tmpcursor = Clang.getCursorLexicalParent(tmpcursor)
end
if get_full_name(tmpcursor) == ""
tmpcursor = Clang.clang_getCursorDefinition(cursor)
while spelling(kind(tmpcursor)) != "Namespace" && Clang.getCursorLexicalParent(tmpcursor) != tmpcursor
tmpcursor = Clang.getCursorLexicalParent(tmpcursor)
end
return get_full_name(tmpcursor)
end
return get_full_name(tmpcursor)
end
function get_class_name(cursor::CLCursor)
tmpcursor = cursor
while spelling(kind(tmpcursor)) != "StructDecl" && spelling(kind(tmpcursor)) != "ClassDecl" && Clang.getCursorLexicalParent(tmpcursor) != tmpcursor
tmpcursor = Clang.getCursorLexicalParent(tmpcursor)
end
return get_full_name(tmpcursor)
end
function get_inline_varname(cursor::CLCursor)
vname = get_class_name(cursor)
if !startswith(vname, get_namespace(cursor))
vname = get_namespace(cursor) * vname
end
vname = replace(vname, "poplar::" => "")
vname = uppercasefirst(vname)
replace(vname, "::" => "")
end
function get_julia_name(cursor::CLCursor)
method_name = split(name(cursor), "(")[1]
vname = get_inline_varname(cursor) * titlecase(method_name, strict=false)
vname = replace(vname, "poplar::" => "")
replace(vname, "::" => "")
end
function object_decl_handler(ctx::BindgenContext, classdecl::CLCursor)::Tuple{Union{Nothing, String}, Union{Nothing, String}}
full_name = get_full_name(classdecl)
length(children(classdecl)) == 0 && return nothing, "skip_empty_classdecl"
wrapper_var_name = get_inline_varname(classdecl)
# `VertexPerfEstimate` is a simple struct, we need to map it to a manually
# defined struct on the Julia side.
if wrapper_var_name == "VertexPerfEstimate"
return """mod.map_type<poplar::VertexPerfEstimate>("VertexPerfEstimate");""", nothing
end
# handle simple inheritance
if length(children(classdecl)) > 1 && kind(children(classdecl)[1]) == Clang.CXCursor_CXXBaseSpecifier
if startswith(get_full_name(children(classdecl)[1]), "class ")
base_class = split(get_full_name(children(classdecl)[1]), "class ")[2]
ctx.outputSupertypes *= "template<> struct SuperType<$full_name> { typedef $base_class type; };\n"
return "auto JL$wrapper_var_name = mod.add_type<$full_name>(\"$wrapper_var_name\", jlcxx::julia_base_type<$base_class>());", nothing
end
end
return "auto JL$wrapper_var_name = mod.add_type<$full_name>(\"$wrapper_var_name\");", nothing
end
function optionals(args::Vector)
num = 0
for arg in args
for token in tokenize(arg)
if token.text == "="
num += 1
end
end
end
return num
end
optionals(method::CLCursor) = optionals(get_function_args(method))
function should_wrap(item::AbstractString)
return startswith(item, "ArrayRef") && !contains(item, "poplar") && !contains(item, "std::string") && !contains(item, "program::")
end
function arg_list(method::CLCursor, types=true::Bool, cutoff=Inf, varnames=true::Bool)
Clang.getNumArguments(Clang.getCursorType(method)) == 0 && return ""
cutoff == 0 && return ""
arglist = get_full_name(method)
arglist = split(arglist, "(")[2]
arglist = split(arglist, ")")[1]
# TODO: this is **really** not a good way to do this
argssplit = []
cur = ""
count = 0
for chr in arglist
if chr == '<'
count += 1
end
if chr == '>'
count -= 1
end
if count == 0 && chr == ','
push!(argssplit, cur)
cur = ""
continue
end
cur *= chr
end
if cur != ""
push!(argssplit, cur)
end
total = ""
varname = 'a'
i = 1
for item in argssplit
i > cutoff && break
item = lstrip(item)
item = replace(item, "const poplar::DebugContext &" => "std::string")
item = replace(item, "poplar::DebugContext" => "std::string")
item = replace(item, "poplar::StringRef" => "std::string")
if types
pre = ""
if should_wrap(item)
pre = "jlcxx::"
end
if varnames
total *= "$pre$item $varname, "
else
total *= "$pre$item, "
end
else
if should_wrap(item)
total *= "jlcxxToPoplar($varname), "
else
total *= "$varname, "
end
end
varname += 1
i += 1
end
return total[1:end - 2]
end
function constructor_handler(ctx::BindgenContext, method::CLCursor)::Tuple{Union{Nothing, String}, Union{Nothing, String}}
Clang.clang_getCXXAccessSpecifier(method) != Clang.CX_CXXPublic && return nothing, "insufficient_access"
m_header = spelling(method)
m_name = name(method)
name_small = split(m_name, "(")[1]
m_kind = kind(method)
base_var = get_inline_varname(method)
get_class_name(method) == "" && return nothing, "constructor_missing_class"
# workaround: ostreams really don't like being copied
arglist = arg_list(method)
contains(arglist, "ostream") && return nothing, "ostream_blacklist"
contains(arglist, "istream") && return nothing, "istream_blacklist"
contains(arglist, "&&") && return nothing, "rvalue_unsupported"
contains(m_name, "unique_ptr") && return nothing, "unique_ptr_blacklist"
arglist == "" && return nothing, "default_constructor" # default constructor gets autogenerated
tokenize(method)[end].text == "delete" && return nothing, "deleted_method"
out = "{ using namespace $(get_namespace(method));\n"
args = get_function_args(method)
num_args = length(args)
num_required = num_args - optionals(args)
if num_required == 0
num_required = 1
end
for cutoff in num_required:num_args
out *= "JL$base_var.constructor<$(arg_list(method, true, cutoff, false))>();\n"
end
out *= "}"
return out, nothing
end
function method_handler(ctx::BindgenContext, method::CLCursor)::Tuple{Union{Nothing, String}, Union{Nothing, String}}
Clang.clang_getCXXAccessSpecifier(method) != Clang.CX_CXXPublic && return nothing, "insufficient_access"
m_header = spelling(method)
m_name = name(method)
name_small = split(m_name, "(")[1]
m_kind = kind(method)
base_var = get_inline_varname(method)
julia_name = get_julia_name(method)
func_name = get_full_name(method, false)
get_class_name(method) == "" && return nothing, "constructor_missing_class"
contains(func_name, "::operator") && return nothing, "operator_unsupported"
arglist = arg_list(method)
contains(arglist, "&&") && return nothing, "rvalue_unsupported"
# workaround: ostreams really don't like being copied
contains(arglist, "ostream") && return nothing, "ostream_blacklist"
contains(arglist, "istream") && return nothing, "istream_blacklist"
# Workaround: getImpl (on various poplar types) returns an incomplete class which messes with cxxwrap
(m_name == "getImpl()" || m_name == "getPImpl()") && return nothing, "getimpl_blacklist"
contains(m_name, "connectStreamToCallback") && return nothing, "calls_deleted_function"
contains(m_name, "registerCycleEstimator") && return nothing, "calls_deleted_function"
contains(m_name, "connectHostFunction") && return nothing, "calls_deleted_function"
out = "{ using namespace $(get_namespace(method));\n"
args = get_function_args(method)
num_args = length(args)
num_required = num_args - optionals(args)
if num_required == 0
out = out * """JL$(base_var).method("$(julia_name)", []($(get_class_name(method))& cl) {return cl.$(name_small)();});\n"""
num_required += 1
end
for cutoff in num_required:num_args
# Do not add methods which contains arguments with `TypeTraits::isSimpleType`
if !contains(arg_list(method, true, cutoff), "TypeTraits::isSimpleType")
out = out * """JL$(base_var).method("$(julia_name)", []($(get_class_name(method))& cl, $(arg_list(method, true, cutoff))) {return cl.$(name_small)($(arg_list(method, false, cutoff)));});\n"""
end
end
out = out * "}"
if spelling(kind(method)) == "FunctionTemplate"
if contains(out, "ArrayRef<T>")
# Expand all references to ArrayRef<T> to containers of common types
full = ""
# Not all methods support the same types in `ArrayRef<T>`, so we need to do some
# specialisation.
_types = if julia_name in ("EngineReadTensor", "EngineWriteTensor", "EngineConnectStream", "EngineCopyFromRemoteBuffer")
("unsigned int", "int", "long", "float")
else
("unsigned int", "int", "long", "float", "double")
end
arrayref_types = string.("ArrayRef<", _types, ">")
for type in arrayref_types
full *= replace(out, "ArrayRef<T>" => type)
end
return full, nothing
elseif contains(out, r"GraphConnect\b")
# Manually expand template in poplar::Graph::connect. Ideally this
# would be more automatic.
full = ""
for type in ("unsigned int", "int", "long", "float", "double")
# Note: we have to prevent automatic argument conversion:
# <https://github.com/JuliaInterop/CxxWrap.jl/blob/aec9d9975aec28e9046ad81e7038bbc5319963ea/README.md#automatic-argument-conversion>.
full *= replace(out,
r"\bT\b" => "jlcxx::StrictlyTypedNumber<" * type * ">",
"a, b" => "a, b.value",
)
end
return full, nothing
end
return nothing, "unsupported_template"
end
return out, nothing
end
function func_handler(ctx::BindgenContext, func::CLCursor)::Tuple{Union{Nothing, String}, Union{Nothing, String}}
f_name = name(func)
name_small = split(f_name, "(")[1]
f_kind = kind(func)
julia_name = get_julia_name(func)
func_name = get_full_name(func, false)
# workaround: ostreams really don't like being copied
contains(arg_list(func), "ostream") && return nothing, "ostream_blacklist"
contains(arg_list(func), "istream") && return nothing, "istream_blacklist"
contains(arg_list(func), "&&") && return nothing, "rvalue_unsupported"
contains(func_name, "::operator") && return nothing, "operator_unsupported"
out = "{ using namespace $(get_namespace(func));\n"
return out * "mod.method(\"$julia_name\", []($(arg_list(func))) {return $func_name($(arg_list(func, false)));} ); }", nothing
end
function enum_decl_handler(ctx::BindgenContext, decl::CLCursor)::Tuple{Union{Nothing, String}, Union{Nothing, String}}
!(Clang.clang_getCXXAccessSpecifier(decl) ∈ [Clang.CX_CXXPublic, Clang.CX_CXXInvalidAccessSpecifier]) && return nothing, "insufficient_access"
full_name = get_full_name(decl)
julia_name = get_julia_name(decl)
return "mod.add_bits<$full_name>(\"$julia_name\", jlcxx::julia_type(\"CppEnum\"));", nothing
end
function enum_const_handler(ctx::BindgenContext, decl::CLCursor)::Tuple{Union{Nothing, String}, Union{Nothing, String}}
!(Clang.clang_getCXXAccessSpecifier(decl) ∈ [Clang.CX_CXXPublic, Clang.CX_CXXInvalidAccessSpecifier]) && return nothing, "insufficient_access"
full_name = get_full_name(decl)
julia_name = get_julia_name(decl)
parent_name = get_julia_name(Clang.getCursorLexicalParent(decl))
return "mod.set_const(\"$parent_name$julia_name\", $full_name);", nothing
end
function gen_json(ctx::BindgenContext, decl, id, handled=false, not_handled_reason="")
if not_handled_reason === nothing
not_handled_reason = ""
end
decl_kind = kind(decl)
spelling(decl_kind) ∈ ["EnumDecl", "ClassDecl", "StructDecl", "CXXMethod", "FunctionTemplate", "FunctionDecl", "CXXConstructor", "EnumConstantDecl"] || return
fname = spelling(decl)
tokenstr = ""
for token in tokenize(decl)
tokenstr *= token.text * " "
end
tokenstr = tokenstr[1:end-1]
#if length(tokenstr) > 150
# tokenstr = tokenstr[1:150]
#end
d = Dict("Implemented" => handled, "Text" => tokenstr, "Namespace" => get_namespace(decl), "Token type" => spelling(decl_kind), "Name" => get_full_name(decl), "Filename" => fname, "FailureReason" => not_handled_reason)
open("out.json", "a") do file
write(file, JSON.json(d) * "\n")
end
end
function iterate_children(ctx::BindgenContext, childvec::Vector{CLCursor})
for (i, child) in enumerate(childvec)
valid = true
reason = nothing
child_header = spelling(child)
child_name = name(child)
child_kind = kind(child)
startswith(child_name, "__") && (valid = false; reason = "skip_compiler_definitions") # skip compiler definitions
child_header ∈ ctx.blacklisted_headers && (valid = false; reason = "header_blacklisted")
!any(x -> startswith(get_namespace(child), x), allowed_namespaces) && (valid = false; reason = "not_allowed_namespace")
child_id = get_full_name(child) * "__" * spelling(child_kind)
child_id = replace(child_id, "poplar::StringRef" => "std::string")
# prevents duplicate codegen(+error), TODO: check if still necessary
child_id == "poplar::FieldData::SizeT::size()__CXXMethod" && (valid = false; reason = "filedata_size_blacklist")
# Popops expressions are causing all kinds of problems
contains(child_id, "expr::") && (valid = false; reason = "expr_blacklisted")
contains(child_id, "popops::expr") && (valid = false; reason = "expr_blacklisted")
# TODO: Find and document reason
contains(child_id, "equivalent_device_type") && (valid = false; reason = "equivalent_device_type_blacklist")
# workaround (returning vector of Device causes issues)
contains(child_id, "getDevices") && (valid = false; reason = "getdevices_blacklist")
# Skip everything related to poplar::core (like Target.getTargetOptions)
contains(child_id, "core::") && (valid = false; reason = "core_blacklisted")
contains(child_id, "getTargetOptions") && (valid = false; reason = "core_blacklisted")
# These cause error
# error: static assertion failed: Mirrored types (marked with IsMirroredType) can't be added using add_type, map them directly to a struct instead and use map_type or explicitly disable mirroring for this type, e.g. define template<> struct IsMirroredType<Foo> : std::false_type { };
contains(child_id, "poplar::VertexPerfEstimate::VertexPerfEstimate") && (valid = false; reason = "mirrored_type")
contains(child_id, "poplar::ErrorLocationHash__StructDecl") && (valid = false; reason = "mirrored_type")
# This conversion `ArrayRef<std::string>` to `ArrayRef<poplar::StringRef>` isn't handled correctly
contains(child_id, "poplar::Graph::trace(ArrayRef<std::string>") && (valid = false; reason = "arrayrefstring_blacklisted")
# `DebugContext` constructors which cause ambiguous overload calls
contains(child_id, r"^poplar::DebugContext::DebugContext.*__CXXConstructor$") && (valid = false; reason = "debugcontext_blacklisted")
# This causes the error
# no matching function for call to ‘poplar::program::Sequence::add_many(std::__cxx11::basic_string<char>&)’
contains(child_id, r"poplar::program::Sequence::Sequence.*__CXXConstructor$") && (valid = false; reason = "programsequence_blacklisted")
# Avoid duplicate definition during precompilation of the CxxWrap module
contains(child_id, "poplar::layout::to_string(const poplar::layout::VectorList)__FunctionDecl") && (valid = false; reason = "duplicate_definition")
# Avoid duplicate definition during precompilation of the CxxWrap module.
# Ref: <https://github.com/JuliaIPU/IPUToolkit.jl/issues/12>.
contains(child_id, "poplar::toString") && (valid = false; reason = "duplicate_definition")
# error: invalid use of incomplete type ‘class pva::Report’
contains(child_id, "poplar::Engine::getReport") && (valid = false; reason = "incomplete_type")
# error: invalid application of ‘sizeof’ to incomplete type ‘poplar::core::VertexIntrospector’
contains(child_id, "poplar::VertexIntrospector") && (valid = false; reason = "incomplete_type")
# error: invalid use of incomplete type ‘class poplar::Preallocations’
contains(child_id, "poplar::Preallocations") && (valid = false; reason = "incomplete_type")
# error: no matching function for call to ‘poplar::GlobalExchangeConstraint::GlobalExchangeConstraint()’
contains(child_id, "poplar::Target::getGlobalExchangeConstraints()__CXXMethod") && (valid = false; reason = "getGlobalExchangeConstraints_blacklisted")
# These methods are handled incorrectly by this script and generate lines with
# invalid syntax. They don't seem to be super important, so let's just skip them
# for the time being.
contains(child_id, "poplar::Module::forEachLoadableSegment") && (valid = false; reason = "forEachLoadableSegment_blacklisted")
contains(child_id, "poplar::Module::forEachSegment") && (valid = false; reason = "forEachSegment_blacklisted")
# error: no match for call to ‘(poplar::Engine::copyToRemoteBuffer<unsigned int>::<lambda(unsigned int*)>) (gccs::ArrayRef<const unsigned int>::const_iterator)’
contains(child_id, "poplar::Engine::copyToRemoteBuffer(ArrayRef<T>, std::string, uint64_t, unsigned int)__FunctionTemplate") && (valid = false; reason = "copyToRemoteBuffer_blacklisted")
# IPUAttributes appears only in one method of Device.getAttribute, but it isn't
# documented and it looks troublesome to support in a backward-compatible way, let's
# just skip it.
contains(child_id, "IPUAttributes") && (valid = false; reason = "IPUAttributes_blacklisted")
# Sadly we aren't going to support quarter precision floating-point numbers anytime soon, so let's just skip this.
contains(child_id, "QuarterMetadata") && (valid = false; reason = "QuarterMetadata_blacklisted")
handled = false
if !(child_id ∈ ctx.handled_symbols)
if valid
code, reason = nothing, nothing
res = if spelling(child_kind) == "EnumDecl"
enum_decl_handler(ctx, child)
elseif spelling(child_kind) == "ClassDecl"
object_decl_handler(ctx, child)
elseif spelling(child_kind) == "StructDecl"
object_decl_handler(ctx, child)
end
if res !== nothing
code, reason = res
if code !== nothing
handled = true
ctx.outputDecls *= "// " * child_id * "\n" * code * "\n"
push!(ctx.handled_symbols, child_id)
end
end
res = if spelling(child_kind) == "CXXMethod"
method_handler(ctx, child)
elseif spelling(child_kind) == "FunctionTemplate"
method_handler(ctx, child)
elseif spelling(child_kind) == "FunctionDecl"
func_handler(ctx, child)
elseif spelling(child_kind) == "CXXConstructor"
constructor_handler(ctx, child)
elseif spelling(child_kind) == "EnumConstantDecl"
enum_const_handler(ctx, child)
end
if res !== nothing
code, reason = res
if code !== nothing
handled = true
ctx.outputMembers *= "// " * child_id * "\n" * code * "\n"
push!(ctx.handled_symbols, child_id)
end
end
end
if spelling(child_kind) ∈ supported_nodes
gen_json(ctx, child, child_id, handled, reason)
end
push!(ctx.seen_symbols, child_id)
end
iterate_children(ctx, children(child))
end
end
function gen_bindings(headers::Vector{String}, blacklist::Vector{String})
rm("out.json"; force=true)
touch("out.json")
# Automatically print out the includes of the header files we want to parse
io = IOBuffer()
for header in headers
println(io, "#include <$(header)>")
end
includes = get_system_includes()
ctx = DefaultBindgenContext()
ctx.searched_headers = resolve_headers(headers, includes)
ctx.blacklisted_headers = resolve_headers(blacklist, includes)
# bootstrap a Clang ASTUnit for parsing the headers
flags = CXTranslationUnit_DetailedPreprocessingRecord |
CXTranslationUnit_SkipFunctionBodies
idx = Clang.Index()
tus = []
symbol_names = String[]
# add compiler flags
clang_args = ["-I"*inc for inc in includes]
for h in ctx.searched_headers
tu = Clang.TranslationUnit(idx, h, clang_args, flags)
push!(tus, tu)
end
for trans_unit in tus
root_cursor = Clang.getTranslationUnitCursor(trans_unit)
println(root_cursor)
clang_children = children(root_cursor)
iterate_children(ctx, clang_children)
end
return String(take!(io)), ctx.outputDecls * ctx.outputMembers, ctx.outputSupertypes
end
function generate_wrapper()
gen_headers, gen_inline, gen_inherit = gen_bindings(
[
"poplar/VectorLayout.hpp",
"poplar/DeviceManager.hpp",
"poplar/Engine.hpp",
"poplar/Graph.hpp",
"poplar/CSRFunctions.hpp",
"poplar/IPUModel.hpp",
"popops/ElementWise.hpp",
"popops/codelets.hpp",
],
String[])
#gen_inline = replace(gen_inline, "\n" => "\nprintf(\"Line is %d\\n\", __LINE__);\n")
# Workaround for CxxWrap not liking any types name "Type"
gen_inline = replace(gen_inline, "\"Type\"" => "\"Type_\"")
dir = joinpath(@__DIR__, "wrapper")
write(joinpath(dir, "gen_headers.hpp"), gen_headers)
write(joinpath(dir, "gen_inline.cpp"), gen_inline)
write(joinpath(dir, "gen_inherit.cpp"), gen_inherit)
return nothing
end
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 499 | using Documenter, IPUToolkit, IPUToolkit.Poplar, IPUToolkit.IPUCompiler
makedocs(
modules = [Poplar, IPUCompiler],
sitename = "IPUToolkit.jl",
pages = [
"IPUToolkit" => "index.md",
"Poplar SDK" => "poplar.md",
"Writing codelets" => "compiler.md",
],
format = Documenter.HTML(; edit_link="main"),
)
deploydocs(
repo = "github.com/JuliaIPU/IPUToolkit.jl.git",
target = "build",
deps = nothing,
make = nothing,
devbranch = "main",
)
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 1907 | using IPUToolkit.IPUCompiler, IPUToolkit.Poplar
using Enzyme
IPUCompiler.KEEP_LLVM_FILES[] = true
ENV["POPLAR_RUNTIME_OPTIONS"] = """{"target.hostSyncTimeout":"60"}"""
device = Poplar.get_ipu_device()
target = Poplar.DeviceGetTarget(device)
graph = Poplar.Graph(target)
num_tiles = Int(Poplar.TargetGetNumTiles(target))
initial_points = collect(Float32.(range(-4; stop=4, length=10 * num_tiles)))
minima = similar(initial_points)
∂(f, x) = first(first(autodiff_deferred(Reverse, f, Active(x))))
rosenbrock(x, y=4) = (1 - x) ^ 2 + 100 * (y - x ^ 2) ^ 2
rosenbrock′(x) = ∂(rosenbrock, x)
function adam(∂f, x₀::T) where {T}
x = x₀
# Some constants
α = T(0.001) # learning rate
β₁ = T(0.9)
β₂ = T(0.999)
ϵ = T(1e-8)
# Momenta
m = zero(T)
v = zero(T)
# Stopping criteria
ε = 10 * eps(T)
δ = one(T)
max_t = Int32(1_000_000)
t = one(max_t)
while abs(δ) > ε && t ≤ max_t
g = ∂f(x)
m = β₁ * m + (1 - β₂) * g
v = β₂ * v + (1 - β₂) * g ^ 2
m̂ = m / (1 - β₁ ^ t)
v̂ = v / (1 - β₂ ^ t)
δ = α * m̂ / (√(v̂) + ϵ)
x -= δ
t += one(t)
end
return x
end
@codelet graph function RosenAdam(in::VertexVector{Float32, In}, out::VertexVector{Float32, Out})
for idx in eachindex(out)
out[idx] = adam(rosenbrock′, in[idx])
end
end
initial_points_ipu = Poplar.GraphAddConstant(graph, initial_points)
minima_ipu = similar(graph, minima, "minima");
prog = Poplar.ProgramSequence()
add_vertex(graph, prog, 0:(num_tiles - 1), RosenAdam, initial_points_ipu, minima_ipu)
Poplar.GraphCreateHostRead(graph, "minima-read", minima_ipu)
flags = Poplar.OptionFlags()
Poplar.OptionFlagsSet(flags, "debug.instrument", "true")
engine = Poplar.Engine(graph, prog, flags)
Poplar.EngineLoadAndRun(engine, device)
Poplar.EngineReadTensor(engine, "minima-read", minima)
Poplar.detach_devices()
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 2625 | using IPUToolkit.IPUCompiler
using IPUToolkit.Poplar
using DiffEqGPU
using StaticArrays
using OrdinaryDiffEq
ENV["POPLAR_RUNTIME_OPTIONS"] = """{"target.hostSyncTimeout":"60"}"""
IPUCompiler.PROGRESS_SPINNER[] = false
device = Poplar.get_ipu_device()
target = Poplar.DeviceGetTarget(device)
graph = Poplar.Graph(target)
prog = Poplar.ProgramSequence()
num_tiles = Int(Poplar.TargetGetNumTiles(target))
tiles = 0:(num_tiles - 1)
# Define differential equation
function lorenz(u, p, t)
σ = p[1]
ρ = p[2]
β = p[3]
du1 = σ * (u[2] - u[1])
du2 = u[1] * (ρ - u[3]) - u[2]
du3 = u[1] * u[2] - β * u[3]
return SVector{3}(du1, du2, du3)
end
# Create a range of different input parameters
p = let
σ = repeat(range(0f0; step=0.2f0, length=64); inner=23)
ρ = repeat(range(10f0; step=1f0, length=23); outer=64)
β = repeat([8f0 / 3f0], num_tiles)
zip(σ, ρ, β) |> Iterators.flatten |> collect
end
# Output arrays
n = 10000
u1 = Vector{Float32}(undef, n * num_tiles)
u2 = Vector{Float32}(undef, n * num_tiles)
u3 = Vector{Float32}(undef, n * num_tiles)
# Define kernel
@codelet graph function solve_lorenz(u1::VertexVector{Float32, Out},
u2::VertexVector{Float32, Out},
u3::VertexVector{Float32, Out},
p::VertexVector{Float32, In})
u0 = @SVector [1f0; 0f0; 0f0]
svp = @inbounds SVector{3, Float32}(p)
integ = DiffEqGPU.init(GPUTsit5(), lorenz, false, u0, 0f0, 0.005f0, svp, nothing, CallbackSet(nothing), true, false)
for idx in eachindex(u1, u2)
DiffEqGPU.step!(integ, integ.t + integ.dt, integ.u)
u1[idx] = integ.u[1]
u2[idx] = integ.u[2]
u3[idx] = integ.u[3]
end
return nothing
end
# Input and output tensors on the IPU
p_ipu = Poplar.GraphAddConstant(graph, p)
u1_ipu = similar(graph, u1, "u1")
u2_ipu = similar(graph, u2, "u2")
u3_ipu = similar(graph, u3, "u3")
# Run the codelet defined above on all tiles, with tensors evenly spread across all cores.
add_vertex(graph, prog, tiles, solve_lorenz, u1_ipu, u2_ipu, u3_ipu, p_ipu)
# Prepare tensors read
Poplar.GraphCreateHostRead(graph, "u1-read", u1_ipu)
Poplar.GraphCreateHostRead(graph, "u2-read", u2_ipu)
Poplar.GraphCreateHostRead(graph, "u3-read", u3_ipu)
# Run the program
engine = Poplar.Engine(graph, prog)
Poplar.EngineLoadAndRun(engine, device)
# Read the output tensors back to the CPU
Poplar.EngineReadTensor(engine, "u1-read", u1)
Poplar.EngineReadTensor(engine, "u2-read", u2)
Poplar.EngineReadTensor(engine, "u3-read", u3)
Poplar.detach_devices()
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 2444 | using IPUToolkit.IPUCompiler, IPUToolkit.Poplar
# Define the arrays that will be used during the program. `input` is a host array that will
# be automatically copied to an IPU array, the other `PoplarVector`s are placeholders for
# IPU arrays that will be populated during the execution of the program.
input = Float32[5, 2, 10, 102, -10, 2, 256, 15, 32, 100]
outvec1 = PoplarVector{Float32}(undef, 10)
outvec2 = PoplarVector{Float32}(undef, 10)
outvec3 = PoplarVector{Float32}(undef, 10)
# Get the device.
device = Poplar.get_ipu_device()
# Inside `@ipuprogram` you can do only the following things:
#
# * define functions, which will be used as codelets in the IPU program
# * call these functions, which will automatically build the graph of the calls for you
# * print tensors on the IPU with the "special" function `print_tensor`
# * copy IPU tensors to the host
@ipuprogram device begin
# Define the functions/codelets. All arguments must be `VertexVector`s.
function TimesTwo(inconst::VertexVector{Float32, In}, outvec::VertexVector{Float32, Out})
outvec .= 2 .* inconst
end
function Sort(invec::VertexVector{Float32, In}, outvec::VertexVector{Float32, Out})
outvec .= invec
sort!(outvec)
end
function Sin(invec::VertexVector{Float32, In}, outvec::VertexVector{Float32, Out})
for idx in eachindex(outvec)
@inbounds outvec[idx] = sin(invec[idx])
end
end
# Run the functions. Arguments must be the arrays defined above, either host arrays
# (which will be copied to the IPU automatically) or `PoplarVector`s.
TimesTwo(input, outvec1)
Sort(outvec1, outvec2)
Sin(outvec2, outvec3)
# `print_tensor` is a special function which prints tensors to the host
# using `Poplar.ProgramPrintTensor` under the hood. Syntax is
# print_tensor(<LABEL>, <tensor variable>)
print_tensor("Input", input)
print_tensor("TimesTwo", outvec1)
print_tensor("Sorted", outvec2)
print_tensor("Sin", outvec3)
# Copy IPU tensors to the host. The right-hand side must be one of the tensors defined
# above, the left-hand side is the name of a host array which will be created
# automatically for you, so you will be able to reference them after the `@ipuprogram`.
jl_outvec1 = outvec1
jl_outvec2 = outvec2
jl_outvec3 = outvec3
end
# Detach the device when we're done.
Poplar.detach_devices()
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 3694 | using IPUToolkit.IPUCompiler, IPUToolkit.Poplar
using Enzyme
IPUCompiler.KEEP_LLVM_FILES[] = true
ENV["POPLAR_RUNTIME_OPTIONS"] = """{"target.hostSyncTimeout":"30"}"""
device = Poplar.get_ipu_device()
target = Poplar.DeviceGetTarget(device)
graph = Poplar.Graph(target)
num_tiles = Int(Poplar.TargetGetNumTiles(target))
∂!(f, x, f′) = autodiff_deferred(Reverse, f, Duplicated(x, f′))
neg_log_density(q::AbstractVector{T}) where {T} = (q[1]^2 - q[2])^2 + (q[1]- one(T))^2 / T(100)
# Note: both input and output must have exactly same type (including *all* parameters).
function grad_neg_log_density!(f′::V, x::V) where {T,V<:AbstractVector{T}}
# The derivative is added to duplicated arguments, so we need to zero f′
# before going on.
f′ .= zero(T)
∂!(neg_log_density, x, f′)
return f′
end
function leapfrog!(q::AbstractVector{T}, p::AbstractVector{T}, f′::AbstractVector{T}, dt::T) where {T}
grad_neg_log_density!(f′, q)
p .-= (dt ./ 2) .* f′
q .+= dt .* p
grad_neg_log_density!(f′, q)
p .-= (dt / 2) .* f′
end
function sample_transition!(q_proposed::AbstractVector{T}, p::AbstractVector{T}, f′::AbstractVector{T}, q::AbstractVector{T}, dt::T, n_step) where {T}
randn2!(p)
h_init = sum(abs2, p) / 2 + neg_log_density(q)
q_proposed .= q
for step in UInt32(1):n_step
leapfrog!(q_proposed, p, f′, dt)
end
h_diff = h_init - (sum(abs2, p) / 2 + neg_log_density(q_proposed))
accept_prob = isnan(h_diff) ? zero(T) : exp(min(0, h_diff))
if rand(T) >= accept_prob
q_proposed .= q
end
return accept_prob
end
function sample_chain!(q_chain::AbstractVector{T}, buffer_q::AbstractVector{T}, p::AbstractVector{T}, f′::AbstractVector{T}, orig_q::AbstractVector{T}, n_sample, n_step, dt::T) where {T}
sum_accept_prob = zero(T)
buffer_q .= orig_q
for sample in UInt32(1):n_sample
accept_prob = sample_transition!(buffer_q, p, f′, orig_q, dt, n_step)
for idx in eachindex(buffer_q)
@inbounds q_chain[length(buffer_q) * (sample - 1) + idx] = buffer_q[idx]
end
sum_accept_prob += accept_prob
end
return sum_accept_prob / n_sample
end
n_sample = UInt32(10)
n_step = UInt32(10)
dt = Float32(0.1)
@eval @codelet graph function HamiltonianMonteCarlo(
q_chain::VertexVector{Float32, InOut},
buffer_q::VertexVector{Float32, InOut},
p::VertexVector{Float32, InOut},
gradient::VertexVector{Float32, InOut},
orig_q::VertexVector{Float32, InOut},
)
sample_chain!(q_chain, buffer_q, p, gradient, orig_q, $(n_sample), $(n_step), $(dt))
end
orig_q = randn(Float32, 2 * num_tiles)
orig_q_ipu = Poplar.GraphAddVariable(graph, Poplar.FLOAT(), UInt64[length(orig_q)], "orig_q")
copyto!(graph, orig_q_ipu, orig_q)
buffer_q_ipu = similar(graph, orig_q, "buffer_q")
p_ipu = similar(graph, orig_q, "p")
gradient_ipu = similar(graph, orig_q, "gradient")
q_chain_ipu = Poplar.GraphAddVariable(graph, Poplar.FLOAT(), UInt64[length(orig_q) * n_sample], "q_chain")
q_chain = Matrix{Float32}(undef, length(orig_q), n_sample)
prog = Poplar.ProgramSequence()
add_vertex(graph, prog, 0:(num_tiles - 1), HamiltonianMonteCarlo,
q_chain_ipu, buffer_q_ipu, p_ipu, gradient_ipu, orig_q_ipu)
Poplar.GraphCreateHostRead(graph, "q-chain-read", q_chain_ipu)
flags = Poplar.OptionFlags()
Poplar.OptionFlagsSet(flags, "debug.instrument", "false")
engine = Poplar.Engine(graph, prog, flags)
Poplar.EngineLoadAndRun(engine, device)
Poplar.EngineReadTensor(engine, "q-chain-read", q_chain)
Poplar.detach_devices()
#=
using Plots
sample = 10
scatter(q_chain[1:2:end, sample], q_chain[2:2:end, sample]; xlims=(-3, 3), ylims=(-3, 6))
=#
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 2061 | using IPUToolkit.IPUCompiler
using IPUToolkit.Poplar
device = Poplar.get_ipu_device()
target = Poplar.DeviceGetTarget(device)
graph = Poplar.Graph(target)
tile_clock_frequency = Poplar.TargetGetTileClockFrequency(target)
# Multiply input vector `in` by 2, and store result in vector `out`.
@codelet graph function TimesTwo(in::VertexVector{Float16, In}, out::VertexVector{Float16, Out})
out .= in .* 2
end
# Copy elements of `in` into `out` and sort it in-place. Get cycles counter before and
# after sorting, show the time to sort the vector by divinding the cycles count by the tile
# clock frequency, which has been interpolated inside the kernel with `@eval` (the
# alternative would be to pass it as an extra scalar input argument).
@eval @codelet graph function Sort(in::VertexVector{Float16, In}, out::VertexVector{Float16, Out})
copyto!(out, in)
# We can use the intrinsic `get_scount_l` to get the cycle counter right
# before and after some operations, so that we can benchmark it.
cycles_start = get_scount_l()
sort!(out)
cycles_end = get_scount_l()
# Divide the difference between the two cycle counts by the tile frequency
# clock to get the time.
sort_time = (cycles_end - cycles_start) / $(tile_clock_frequency)
@ipushow sort_time
end
inconst = Poplar.GraphAddConstant(graph, Float16[5, 2, 10, 102, -10, 2, 256, 15, 32, 100])
outvec1 = similar(graph, inconst, "outvec1");
outvec2 = similar(graph, inconst, "outvec2");
prog = Poplar.ProgramSequence()
add_vertex(graph, prog, TimesTwo, inconst, outvec1)
add_vertex(graph, prog, Sort, outvec1, outvec2)
Poplar.ProgramSequenceAdd(prog, Poplar.ProgramPrintTensor("Input", inconst))
Poplar.ProgramSequenceAdd(prog, Poplar.ProgramPrintTensor("Output Times2", outvec1))
Poplar.ProgramSequenceAdd(prog, Poplar.ProgramPrintTensor("Output Sorted", outvec2))
flags = Poplar.OptionFlags()
Poplar.OptionFlagsSet(flags, "debug.instrument", "true")
engine = Poplar.Engine(graph, prog, flags)
Poplar.EngineLoadAndRun(engine, device)
Poplar.detach_devices()
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 3848 | using IPUToolkit.IPUCompiler, IPUToolkit.Poplar
ENV["POPLAR_RUNTIME_OPTIONS"] = """{"target.hostSyncTimeout":"20"}"""
IPUCompiler.KEEP_LLVM_FILES[] = true
device = Poplar.get_ipu_device()
target = Poplar.DeviceGetTarget(device)
graph = Poplar.Graph(target)
function print_usage(unroll, n)
println(stderr, """
Usage:
julia $(@__FILE__) [loop unroll factor] [n]
Default values are
unroll factor: $(unroll)
n: $(n)
Examples:
julia $(@__FILE__) 2
julia $(@__FILE__) 4 729444
""")
end
num_tiles = Int(Poplar.TargetGetNumTiles(target))
n::UInt32, unroll::UInt32 = let
# Default values of n and the loop unrolling factor
n = typemax(UInt32) ÷ num_tiles
unroll = UInt32(1)
# Parse command line arguments, if any
if length(ARGS) ≤ 2
if length(ARGS) ≥ 1
unroll = parse(UInt32, ARGS[1])
end
if length(ARGS) == 2
n = parse(UInt32, ARGS[2])
end
else
print_usage(unroll, n)
exit(1)
end
# Make sure n is an integer multiple of the loop unrolling factor before returning
iszero(rem(n, unroll)) || error("n ($(n)) is not an integer multiple of unroll factor ($(unroll))")
n, unroll
end
num_steps::UInt32 = num_tiles * n
slice::Float32 = 1 / num_steps
tile_clock_frequency = Poplar.TargetGetTileClockFrequency(target)
ids = collect(UInt32.(0:(num_tiles - 1)))
sums = similar(ids, Float32)
cycles = similar(ids)
# Why are we using `@eval`? Because inside a codelet we cannot access non-constant globals,
# so we can either make them constant, or interpolate them via `@eval` and let people play
# with the values without having to restart the session. I think the latter is more
# user-friendly :) And a top-level `@eval` is not _too_ bad.
@eval function pi_kernel(i::T) where {T<:Integer}
sum = 0f0
for j in (i * $(n)):$(unroll):((i + one(T)) * $(n) - one(T))
# Do manual loop unrolling, sometimes this can be better than what the
# compiler can do.
Base.Cartesian.@nexprs $(Int64(unroll)) idx -> begin
x = (j + Float32(idx - 1) - 5f-1) * $(slice)
sum += 4f0 / (1f0 + x ^ 2)
end
end
return sum
end
@codelet graph function Pi(in::VertexVector{UInt32, In},
out::VertexVector{Float32, Out},
cycles::VertexVector{UInt32, Out})
# Each tile deals with one-element vectors only. In `out` we store the result of the
# kernel, in `cycles` we store the cycles count on this tile.
cycles[begin] = @ipuelapsed(out[begin] = pi_kernel(in[begin]))
end
ids_ipu = Poplar.GraphAddConstant(graph, ids)
sums_ipu = similar(graph, sums, "sums");
cycles_ipu = similar(graph, cycles, "cycles");
prog = Poplar.ProgramSequence()
add_vertex(graph, prog, 0:(num_tiles - 1), Pi, ids_ipu, sums_ipu, cycles_ipu)
Poplar.GraphCreateHostRead(graph, "sums-read", sums_ipu)
Poplar.GraphCreateHostRead(graph, "cycles-read", cycles_ipu)
flags = Poplar.OptionFlags()
Poplar.OptionFlagsSet(flags, "debug.instrument", "true")
engine = Poplar.Engine(graph, prog, flags)
Poplar.EngineLoadAndRun(engine, device)
Poplar.EngineReadTensor(engine, "sums-read", sums)
Poplar.EngineReadTensor(engine, "cycles-read", cycles)
Poplar.detach_devices()
pi = sum(sums) * slice
time = round(maximum(cycles) / tile_clock_frequency; sigdigits=4)
print("""
Calculating PI using:
$(num_steps) slices
$(num_tiles) IPU tiles
loop unroll factor $(Int(unroll))
Obtained value of PI: $(pi)
Time taken: $(time) seconds ($(maximum(cycles)) cycles at $(round(tile_clock_frequency / 1e9; sigdigits=3)) GHz)
""")
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 2026 | using IPUToolkit.Poplar
# device = Poplar.get_ipu_model()
device = Poplar.get_ipu_device()
target = Poplar.DeviceGetTarget(device)
graph = Poplar.Graph(target)
h3 = zeros(Float32, 4, 4)
@graph begin
c1 = Poplar.GraphAddConstant(Float32[1.0, 1.5, 2.0, 2.5])
v1 = similar(c1, "v1")
v2 = similar(c1, "v2")
v3 = similar(h3, "v3")
v4 = Poplar.GraphAddVariable(Poplar.INT(), UInt64[10], "v4")
Poplar.GraphSetTileMapping(v1, 0)
Poplar.GraphSetTileMapping(v3, 0)
Poplar.GraphSetTileMapping(v4, 0)
Poplar.GraphSetTileMapping(c1, 0)
end
for i in UInt64(0):UInt64(3)
Poplar.GraphSetTileMapping(graph, v2[i], i)
end
prog = Poplar.ProgramSequence()
Poplar.ProgramSequenceAdd(prog, Poplar.ProgramCopy(c1, v1))
Poplar.ProgramSequenceAdd(prog, Poplar.ProgramPrintTensor("v1-debug", v1))
Poplar.ProgramSequenceAdd(prog, Poplar.ProgramCopy(v1, v2))
Poplar.ProgramSequenceAdd(prog, Poplar.ProgramPrintTensor("v2-debug", v2))
Poplar.GraphCreateHostWrite(graph, "v3-write", v3)
Poplar.GraphCreateHostRead(graph, "v3-read", v3)
v1slice = Poplar.TensorSlice(v1, 0, 3)
v3slice = Poplar.TensorSlice(v3, UInt64[1, 1], UInt64[2, 4])
Poplar.ProgramSequenceAdd(prog, Poplar.ProgramCopy(v1slice, v3slice))
inStream = Poplar.GraphAddHostToDeviceFIFO(graph, "v4-input-stream", Poplar.INT(), 10)
Poplar.ProgramSequenceAdd(prog, Poplar.ProgramCopy(inStream, v4))
Poplar.ProgramSequenceAdd(prog, Poplar.ProgramPrintTensor("v4-0", v4))
Poplar.ProgramSequenceAdd(prog, Poplar.ProgramCopy(inStream, v4))
Poplar.ProgramSequenceAdd(prog, Poplar.ProgramPrintTensor("v4-1", v4))
flags = Poplar.OptionFlags()
Poplar.OptionFlagsSet(flags, "debug.instrument", "true")
engine = Poplar.Engine(graph, prog, flags)
Poplar.EngineLoad(engine, device)
Poplar.EngineWriteTensor(engine, "v3-write", h3)
inData = Int32.(0:29)
Poplar.EngineConnectStream(engine, "v4-input-stream", inData)
Poplar.EngineRun(engine, 0)
Poplar.EngineReadTensor(engine, "v3-read", h3)
print("h3 data: ")
display(h3')
Poplar.detach_devices()
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 1419 | using IPUToolkit.Poplar
# device = Poplar.get_ipu_model()
device = Poplar.get_ipu_device()
target = Poplar.DeviceGetTarget(device)
graph = Poplar.Graph(target)
Poplar.PopopsAddCodelets(graph)
v1 = Poplar.GraphAddVariable(graph, Poplar.FLOAT(), UInt64[2, 2], "v1")
v2 = similar(graph, v1, "v2")
for i in 0:1
for j in 0:1
Poplar.GraphSetTileMapping(graph, v1[i][j], i*2 + j)
Poplar.GraphSetTileMapping(graph, v2[i][j], j*2 + i)
end
end
prog = Poplar.ProgramSequence()
c1 = Poplar.GraphAddConstant(graph, Float32[1.0, 1.5, 2.0, 2.5])
c2 = Poplar.GraphAddConstant(graph, Float32[4.0, 3.0, 2.0, 1.0])
Poplar.GraphSetTileMapping(graph, c1, 0)
Poplar.GraphSetTileMapping(graph, c2, 0)
Poplar.ProgramSequenceAdd(prog, Poplar.ProgramCopy(c1, Poplar.TensorFlatten(v1)))
Poplar.ProgramSequenceAdd(prog, Poplar.ProgramCopy(c2, Poplar.TensorFlatten(v2)))
flags = Poplar.OptionFlags()
v3 = Poplar.PopopsAdd(graph, v1, v2, prog, "Add", flags)
Poplar.ProgramSequenceAdd(prog, Poplar.ProgramPrintTensor("v3", v3))
v4 = Poplar.PopopsAdd(graph, v3, v2, prog, "Add", flags)
Poplar.ProgramSequenceAdd(prog, Poplar.ProgramPrintTensor("v4", v4))
v5 = Poplar.PopopsAdd(graph, v1, Poplar.TensorTranspose(v2), prog, "Add", flags)
Poplar.ProgramSequenceAdd(prog, Poplar.ProgramPrintTensor("v5", v5))
engine = Poplar.Engine(graph, prog, flags)
Poplar.EngineLoadAndRun(engine, device)
Poplar.detach_devices()
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 170 | module IPUToolkit
if get(ENV, "JULIA_REGISTRYCI_AUTOMERGE", "false") != "true"
include("poplar.jl")
include("compiler/compiler.jl")
end
end # module IPUToolkit
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 14201 | module Poplar
using CxxWrap
using Scratch
const libpoplar_dir = joinpath(@get_scratch!("libpoplar"), "v$(Base.thispatch(VERSION))")
get_libpoplar_path() = joinpath(libpoplar_dir, "libpoplar_julia.so")
export @graph
function _graph(g, expr::Expr)
out = copy(expr)
insert!(out.args, 2, g)
return out
end
"""
@graph [graph] expr
This is a convenient macro to automatically inject `graph` as first argument of all function calls in the expression passed as last argument to the macro.
The `graph` argument should be the graph object you want to pass as first argument to the function calls.
If it is a local variable called exactly `graph`, this argument can be omitted and this name will be used automatically.
!!! note
This macro is not very sophisticated and will fail with complex expressions involving, for example, control flows like `if` or `for`.
See the examples below.
## Examples
```julia
julia> @macroexpand @graph begin
c1 = Poplar.GraphAddConstant(Float32[1.0, 1.5, 2.0, 2.5])
v1 = similar(c1, "v1")
copyto!(v1, Float32[4.0, 3.0, 2.0, 1.0])
Poplar.GraphSetTileMapping(c1, 0)
Poplar.GraphSetTileMapping(v1, 0)
end
quote
c1 = Poplar.GraphAddConstant(graph, Float32[1.0, 1.5, 2.0, 2.5])
v1 = similar(graph, c1, "v1")
copyto!(graph, v1, Float32[4.0, 3.0, 2.0, 1.0])
Poplar.GraphSetTileMapping(graph, c1, 0)
Poplar.GraphSetTileMapping(graph, v1, 0)
end
```
"""
macro graph(g, x::Expr)
x.head === :block || error("The last argument to the `@graph` macro must be a begin-end block")
out = Expr(:block)
for expr in x.args
if expr isa LineNumberNode
continue
elseif expr.head === :call
push!(out.args, _graph(g, expr))
elseif expr.head === :(=) && expr.args[2].head === :call
tmp = copy(expr)
tmp.args[2] = _graph(g, expr.args[2])
push!(out.args, tmp)
end
end
return esc(out)
end
macro graph(x::Expr)
esc( :( $(@__MODULE__).@graph graph $(x) ) )
end
# Note: this is really only needed for Poplar SDK ≥ v2.0.0, but at this point we don't know
# the version number yet. It doesn't really hurt defining this struct unconditionally.
struct VertexPerfEstimate
cycles::UInt64
flops::UInt64
VertexPerfEstimate(cycles::Integer=0, flops::Integer=0) =
new(UInt64(cycles), UInt64(flops))
end
@wrapmodule(get_libpoplar_path)
const SDK_VERSION = VersionNumber(match(r"[\d.]+", String(Poplar.getVersionString())).match)
function __init__()
libpoplar = get_libpoplar_path()
if !isfile(libpoplar)
error("""
`$(basename(libpoplar))` expected to exist at path `$(libpoplar)`, but could not be found.
Run `using Pkg; Pkg.build()` to trigger recompilation of `$(basename(libpoplar))`.
""")
end
@initcxx()
end
# More user-friendly methods.
let
# Methods which take 1 pointer as last argument. NOTE: `readTensor` changed API in
# v2.1.0, from taking one pointer to two, like `writeTensor`.
one_ptr = SDK_VERSION < v"2.1.0" ? (:EngineReadTensor,) : ()
# Methods which take 2 pointers as last arguments
two_ptr = SDK_VERSION < v"2.1.0" ? (:EngineWriteTensor, :EngineConnectStream,) : (:EngineWriteTensor, :EngineConnectStream, :EngineReadTensor)
for fun in one_ptr
@eval begin
$(fun)(arg1, arg2, ptr::Ptr{<:Number}) = $(fun)(arg1, arg2, Ptr{Cvoid}(ptr))
$(fun)(arg1, arg2, array::AbstractArray{<:Number}) = $(fun)(arg1, arg2, Ptr{Cvoid}(pointer(array)))
end
end
for fun in two_ptr
@eval begin
$(fun)(arg1, arg2, ptr1::Ptr{<:Number}, ptr2::Ptr{<:Number}) = $(fun)(arg1, arg2, Ptr{Cvoid}(ptr1), Ptr{Cvoid}(ptr2))
$(fun)(arg1, arg2, array::AbstractArray{<:Number}) =
# NOTE: we need to get the pointer to the _end_ of the array, hence `lastindex+1`.
$(fun)(arg1, arg2, Ptr{Cvoid}(pointer(array, firstindex(array))), Ptr{Cvoid}(pointer(array, lastindex(array)+1)))
end
end
end
_get_type(::Type{Bool}) = BOOL()
_get_type(::Type{Cchar}) = CHAR()
_get_type(::Type{Cuchar}) = UNSIGNED_CHAR()
# _get_type(::Type{Cchar}) = SIGNED_CHAR()
_get_type(::Type{Cushort}) = UNSIGNED_SHORT()
_get_type(::Type{Cshort}) = SHORT()
_get_type(::Type{Cuint}) = UNSIGNED_INT()
_get_type(::Type{Cint}) = INT()
_get_type(::Type{Culong}) = UNSIGNED_LONG()
_get_type(::Type{Clong}) = LONG()
# _get_type(::Type{Culonglong}) = UNSIGNED_LONGLONG()
# _get_type(::Type{Clonglong}) = LONGLONG()
_get_type(::Type{Float16}) = HALF()
_get_type(::Type{Cfloat}) = FLOAT()
_get_type(t::Symbol) = _get_type(getfield(@__MODULE__, t))
_get_type(t::TensorAllocated) = Poplar.TensorElementType(t)
_get_type(t::Array) = _get_type(eltype(t))
_size(t::Union{TensorAllocated,Array}) = collect(UInt64.(size(t)))
GraphAddConstant(graph::Graph, tensor::Array{T}) where {T} =
Poplar.GraphAddConstant(graph, _get_type(T), collect(UInt64.(size(tensor))), tensor)
# For `Float16` we need to use the function `graph.addConstantHalf` which takes
# a vector of `uint16_t` in input.
GraphAddConstant(graph::Poplar.Graph, tensor::Array{Float16}) =
GraphAddConstantHalf(graph, Poplar._get_type(Float16), collect(UInt64.(size(tensor))), collect(reinterpret(UInt16, tensor)))
Base.getindex(t::TensorAllocated, r::AbstractUnitRange{<:Integer}) =
TensorSlice(t, first(r), last(r) + step(r))
Base.size(t::TensorAllocated) = Int.((Poplar.TensorShape(t)...,))
Base.length(t::TensorAllocated) = prod(size(t))
Base.eachindex(t::TensorAllocated) = 0:(length(t) - 1)
function Base.eachindex(t1::TensorAllocated, t2::TensorAllocated)
t1_len = length(t1)
t2_len = length(t2)
if t1_len != t2_len
throw(DimensionMismatch("all input tensors to eachindex must have the same lengths, got $(t1) and $(t2)"))
end
return 0:(t1_len - 1)
end
"""
similar(
graph::Poplar.Graph,
tensor::Union{Poplar.TensorAllocated,Array},
[type::DataType],
[debug::String]
) -> Poplar.TensorAllocated
Adds to `graph` a variable tensor with the same shape as `tensor`, which can be either an IPU tensor or a plain CPU host `Array`, using [`Graph::addVariable`](https://docs.graphcore.ai/projects/poplar-api/en/latest/poplar/graph/Graph.html#_CPPv4N6poplar5Graph11addVariableERK4Type8ArrayRefINSt6size_tEERK12DebugContext) under the hood.
If a `type` (this is a Julia type, like `Float32` or `Int32`) argument is not passed, the same element type as `tensor` will be automatically used.
An optional `debug` context can also be passed, as a `String`.
This function returns a pointer to the tensor added to the graph.
"""
Base.similar(graph::Graph, t::Union{TensorAllocated,Array}) =
Poplar.GraphAddVariable(graph, _get_type(t), _size(t))
Base.similar(graph::Graph, t::Union{TensorAllocated,Array}, debug::String) =
Poplar.GraphAddVariable(graph, _get_type(t), _size(t), debug)
Base.similar(graph::Graph, t::Union{TensorAllocated,Array}, type::DataType) =
Poplar.GraphAddVariable(graph, _get_type(type), _size(t))
Base.similar(graph::Graph, t::Union{TensorAllocated,Array}, type::DataType, debug::String) =
Poplar.GraphAddVariable(graph, _get_type(type), _size(t), debug)
"""
copyto!(
graph::Poplar.Graph,
dest::Poplar.TensorAllocated,
src::Array
) -> Poplar.TensorAllocated
In the given `graph` copies the elements of the CPU host array `src` to the IPU tensor `dest`, using [`Graph::setInitialValue`](https://docs.graphcore.ai/projects/poplar-api/en/latest/poplar/graph/Graph.html#_CPPv4I0EN6poplar5Graph15setInitialValueEvRK6Tensor1TPNSt9enable_ifIFN10TypeTraits12isSimpleTypeI1TEEvEE4typeE) under the hood.
The elements of `src` must have a type corresponding to the type of `dest` (e.g. `Float16` for a `half` IPU tensor, or `Float32` for a `float` IPU tensor).
This function returns `dest`.
"""
function Base.copyto!(graph::Poplar.GraphAllocated, dest::Poplar.TensorAllocated, src::Array{T}) where {T}
dest_type = _get_type(dest)
# I think we can't use the `==` operator defined for `Type` in the SDK, so
# we have to compare hashes. Not too bad, but annoying.
if Poplar.TypeHash(dest_type) != Poplar.TypeHash(_get_type(T))
dest_type_string = Poplar.StringRefCloneAsString(Poplar.TypeToString(dest_type))
throw(ArgumentError("The destination tensor has type $(dest_type_string), but the source has type $(T)"))
end
if T == Float16
Poplar.GraphSetInitialValueHalf(graph, dest, collect(reinterpret(UInt16, src)))
else
Poplar.GraphSetInitialValue(graph, dest, src)
end
return dest
end
const ATTACHED_DEVICES = Poplar.DeviceAllocated[]
const ATTACHED_DEVICES_LOCK = ReentrantLock()
# Be sure to quit all julia sessions which hold devices!!!
"""
Poplar.get_ipu_devices(n::Int, hint::Union{AbstractVector{<:Integer},Integer}=0) -> Vector{Poplar.DeviceAllocated}
Try to attach to `n` IPU devices, returns a vector of the pointers to the devices
successfully attached to. You can release them with `Poplar.DeviceDetach` (note that this
function takes a single pointer as input, so you have to use broadcasting
`Poplar.DeviceDetach.(devices)` to release a vector of pointers).
The second optional argument `hint` suggests to which device IDs to try and
attach. It can have different types:
* if of type `Integer`, try to attach to `n` devices, starting from the one
with index `hint`. The default is `hint=0`;
* if of type `AbstractVector`, try to attach to `n` devices from that list of
IDs.
See [`Poplar.get_ipu_device`](@ref) for requesting exactly one IPU device, and [`Poplar.get_ipu_model`](@ref) for requesting an IPU Model.
To release all devices previously attached with `Poplar.get_ipu_devices`, [`Poplar.get_ipu_device`](@ref), or [`Poplar.get_ipu_model`](@ref) use [`Poplar.detach_devices`](@ref).
"""
function get_ipu_devices(n::Int, hint::Union{AbstractVector{<:Integer},Integer}=0)
lock(ATTACHED_DEVICES_LOCK) do
device_manager = Poplar.DeviceManager()
try_ids = if hint isa AbstractVector
hint
else
max_dev_id = Int(Poplar.DeviceManagerGetNumDevices(device_manager))
hint:(max_dev_id - 1)
end
attached_devices = Poplar.DeviceAllocated[]
for id in try_ids
if length(attached_devices) >= n
break
end
device = Poplar.DeviceManagerGetDevice(device_manager, id)
@info "Trying to attach to device $(id)..."
res = Poplar.DeviceAttach(device)
if res
@info "Successfully attached to device $(id)"
push!(attached_devices, device)
end
end
actual_n = length(attached_devices)
if actual_n < n
@warn "Requested $(n) devices, but could attach only to $(actual_n)"
end
if !(actual_n == n == 1)
# Do not print the summary of the attached devices if we requested one and got one.
@info "Attached to devices with IDs $(Int.(Poplar.DeviceGetId.(attached_devices)))"
end
append!(ATTACHED_DEVICES, attached_devices)
attached_devices
end
end
"""
Poplar.get_ipu_device(hint::Union{AbstractVector{<:Integer},Integer}=0) -> Poplar.DeviceAllocated
Similar to [`Poplar.get_ipu_devices`](@ref), but request exactly one IPU device. If it can attach
to a device, return that pointer only (not in a vector, like `get_ipu_devices`), otherwise
return `nothing`.
See [`Poplar.get_ipu_model`](@ref) for requesting an IPU Model.
You can release the device with `Poplar.DeviceDetach(device)`.
To release all devices previously attached with `Poplar.get_ipu_device`, [`Poplar.get_ipu_devices`](@ref), or [`Poplar.get_ipu_model`](@ref) use [`Poplar.detach_devices`](@ref).
The optional argument `hint` suggests to which device IDs to try and
attach. It can have different types:
* if of type `Integer`, try to attach to one device, starting from the one with index `hint`.
The default is `hint=0`;
* if of type `AbstractVector`, try to attach to a device from that list of IDs.
"""
function get_ipu_device(hint::Union{AbstractVector{<:Integer},Integer}=0)
device = get_ipu_devices(1, hint)
if isone(length(device))
return only(device)
end
return nothing
end
"""
Poplar.get_ipu_model(ipu_version::String="ipu2") -> Poplar.DeviceAllocated
Attach to an [IPU Model](https://docs.graphcore.ai/projects/poplar-user-guide/en/latest/poplar_programs.html#programming-with-poplar), and return the attached device.
This uses [`IPUModel::createDevice`](https://docs.graphcore.ai/projects/poplar-api/en/3.4.0/poplar/profiling/IPUModel.html#_CPPv4NK6poplar8IPUModel12createDeviceE11OptionFlagsbj) under the hood.
The optional positional argument `ipu_version::String`, `ipu2` by default, represents the version of the IPU to emulate.
Valid values for `ipu_version` are `ipu1` and `ipu2` (for Mk1 and Mk2 IPU architectures respectively).
See [`Poplar.get_ipu_device`](@ref) and [`Poplar.get_ipu_devices`](@ref) for requesting one or mode hardware IPUs.
You can release the device with `Poplar.DeviceDetach(device)`.
To release all devices previously attached with `Poplar.get_ipu_model`, [`Poplar.get_ipu_device`](@ref) or [`Poplar.get_ipu_devices`](@ref) use [`Poplar.detach_devices`](@ref).
"""
function get_ipu_model(ipu_version::String="ipu2")
lock(ATTACHED_DEVICES_LOCK) do
model = Poplar.IPUModel(ipu_version)
device = Poplar.IPUModelCreateDevice(model)
push!(ATTACHED_DEVICES, device)
device
end
end
"""
Poplar.detach_devices() -> Nothing
Detach all devices previously attached in the current Julia session with [`Poplar.get_ipu_devices`](@ref), [`Poplar.get_ipu_device`](@ref), or [`Poplar.get_ipu_model`](@ref).
"""
function detach_devices()
lock(ATTACHED_DEVICES_LOCK) do
for device in ATTACHED_DEVICES
Poplar.DeviceDetach(device)
end
empty!(ATTACHED_DEVICES)
end
return nothing
end
end # module Poplar
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 15771 | using ProgressMeter
using LLVM
export @codelet
"""
$(@__MODULE__).PROGRESS_SPINNER::$(typeof(PROGRESS_SPINNER))
Option to control whether to display a spinner to show progress during compilation of IPU codelets.
This is forcibly disabled if [`DEBUG_COMPILATION_ERRORS`](@ref) is `true`.
## Example
```julia
$(@__MODULE__).PROGRESS_SPINNER[] = true # enable spinner, default
$(@__MODULE__).PROGRESS_SPINNER[] = false # disable spinner
```
"""
const PROGRESS_SPINNER = Ref(true)
# Build calls like
# VertexVector{T, S}(ccall("extern get_vec_ptr_CodeletName", llvmcall, Ptr{T}, (Int32,), i), ccall("extern get_vec_size_CodeletName", llvmcall, UInt32, (Int32,), i))
# to be passed as argument to the codelet function
function _build_call(arg::Expr, func_ptr::String, func_size::String, i::Int32)
# Some gymnastic to get the type of the argument
type = if arg.args[2].args[1] isa Symbol # arg == :(x::VertexVector{Float32, In})
arg.args[2].args[1]
elseif arg.args[2].args[1] isa Expr # arg == :(x::IPUCompiler.VertexVector{Float32, In}) or :(x::IPUToolkit.IPUCompiler.VertexVector{Float32, In})
arg.args[2].args[1].args[2].value
else
error("Cannot handle argument $(arg)")
end
# TODO: I'd really like to avoid those `getfield`s.
if type === :VertexVector
return :(
$(arg.args[2])( # VertexVector{T,S}
$(Expr(:call, :ccall, func_ptr, :llvmcall, Ptr{getfield(@__MODULE__, arg.args[2].args[2])}, :((Int32,)), i)), # base::Ptr{T}
$(Expr(:call, :ccall, func_size, :llvmcall, UInt32, :((Int32,)), i)) # length::UInt32
)
)
elseif type === :VertexScalar
return :(
$(arg.args[2])( # VertexScalar{T,S}
$(Expr(:call, :ccall, func_ptr, :llvmcall, Ptr{getfield(@__MODULE__, arg.args[2].args[2])}, :((Int32,)), i)), # ptr::Ptr{T}
)
)
else
error("Cannot handle argument of type $(type)")
end
end
function _codelet(graph, usr_kern::Expr)
if usr_kern.head ∉ (:function, :(=)) || usr_kern.args[1].head !== :call
throw(ArgumentError("@codelet takes a named function definition in input"))
end
name = usr_kern.args[1].args[1] # Name of function
args = usr_kern.args[1].args[2:end] # Arguments, with their type annotations: v::VertexVector{T,S}
codelet_fun = gensym(name)
func_ptr = "extern get_vec_ptr_" * String(name)
func_size = "extern get_vec_size_" * String(name)
kernargs = [esc(_build_call(arg, func_ptr, func_size, Int32(i - 1))) for (i, arg) in enumerate(args)]
kern_call = Expr(:call, :($(esc(name))), kernargs...)
return quote
$(esc(usr_kern))
function $(codelet_fun)()
$(kern_call)
return $(esc(nothing))
end
_build_codelet($(esc(graph)), $(codelet_fun), $(esc(name)), $(String(name)))
end
end
"""
@codelet graph <function definition>
Define a codelet and add it to the `graph`.
The `@codelet` macro takes two argument:
* the graph to which to add the codelet with the [`Poplar.GraphAddCodelets`](https://docs.graphcore.ai/projects/poplar-api/en/3.2.0/poplar/graph/Graph.html#_CPPv4N6poplar5Graph11addCodeletsE9StringRef15CodeletFileType9StringRef9StringRef) function;
* the function definition of the codelet that you want to compile for the IPU device.
All the arguments of the function must be either [`VertexVector`](@ref)s, which represent the [`Vector`](https://docs.graphcore.ai/projects/poplar-user-guide/en/3.2.0/vertex_vectors.html) vertex type in the Poplar SDK, or [`VertexScalar`](@ref)s, which represent scalar arguments.
The function passed as second argument to `@codelet` should have a single method.
`@codelet` defines the function passed as argument, generates its LLVM Intermediate Representation (IR) using `GPUCompiler.jl` and then compiles it down to native code using the Poplar compiler `popc`, which must be in [`PATH`](https://en.wikipedia.org/wiki/PATH_(variable)).
By default the LLVM IR of the function is written to a temporary file, but you can choose to keep it in the current directory by customising [`IPUCompiler.KEEP_LLVM_FILES`](@ref).
You can control flags passed to the `popc` compiler like debug and optimisation levels or target types by customising [`IPUCompiler.POPC_FLAGS`](@ref).
During compilation of codelets a spinner is displayed to show the progress, as this step can take a few seconds for each codelet to be generated.
This can be disabled by setting [`IPUCompiler.PROGRESS_SPINNER`](@ref).
All the options mentioned in this section have to be set before the `@codelet` invocation where you want them to have effect.
The codelet is automatically added to the graph but you will have to separately use it in a vertex, by using either the [`add_vertex`](@ref) function, or Poplar's [`Poplar.GraphAddVertex`](https://docs.graphcore.ai/projects/poplar-api/en/3.2.0/poplar/graph/Graph.html#_CPPv4N6poplar5Graph9addVertexE10ComputeSet9StringRef).
## Example
```julia
using IPUToolkit.IPUCompiler, IPUToolkit.Poplar
device = Poplar.get_ipu_device()
target = Poplar.DeviceGetTarget(device)
graph = Poplar.Graph(target)
@codelet graph function test(in::VertexVector{Int32,In}, out::VertexVector{Float32,Out})
for idx in eachindex(out)
out[idx] = sin(in[idx])
end
end
```
This snippet of code defines a codelet called `test`, which takes in input the vector `in`, whose elements are `Int32`s, and modifies the vector `out`, of type `Float32`, by computing the sine of the elements of `in`.
"""
macro codelet(graph, usr_kern::Expr)
return _codelet(graph, usr_kern)
end
# We have experienced some miscompilations of LLVM IR when using optimisation levels `-O1`
# or higher with old `popc`, especially v1.3-2.0. So, we default to `-O0` with older
# versions, and `-O3` for newer versions.
"""
$(@__MODULE__).POPC_FLAGS::$(typeof(POPC_FLAGS))
Options to pass to the `popc` compiler to compile the code.
## Example
```julia
$(@__MODULE__).POPC_FLAGS = `-O3 -g0 -target ipu2`
$(@__MODULE__).POPC_FLAGS = `-O2 -g`
```
"""
const POPC_FLAGS = Ref(Poplar.SDK_VERSION ≥ v"2.2.0" ? `-g -O3` : `-g -O0`)
"""
$(@__MODULE__).KEEP_LLVM_FILES::$(typeof(KEEP_LLVM_FILES))
Option to control whether to keep in the current directory the files with the LLVM Intermediate Representation (IR) generated for the codelets.
## Example
```julia
$(@__MODULE__).KEEP_LLVM_FILES[] = false # Generated LLVM IR files are automatically deleted after compilation, default
$(@__MODULE__).KEEP_LLVM_FILES[] = true # Generated LLVM IR files are kept in the current directory
```
"""
const KEEP_LLVM_FILES = Ref(false)
"""
$(@__MODULE__).TARGET_COLOSSUS::$(typeof(TARGET_COLOSSUS))
Option to control whether to target the Colossus backend when generating the LLVM Intermediate Representation (IR) of the codelets.
If set to `false`, the default, codelets will generate code for the host machine, which may be inefficient, while still being valid.
!!! note
You can target the Colossus backend only if your Julia links to a version of libllvm compiled from [Graphcore's fork of LLVM](https://github.com/graphcore/llvm-project-fork).
!!! warning
This option is experimental, Julia code generation using Graphcore's LLVM has not been tested extensively and is known to cause miscompilations, unexpected errors may happen.
## Example
```julia
$(@__MODULE__).TARGET_COLOSSUS[] = false # Generate LLVM IR for the host, the default
$(@__MODULE__).TARGET_COLOSSUS[] = true # Generate LLVM IR for the Colossus backend
```
"""
const TARGET_COLOSSUS = Ref(false)
"""
$(@__MODULE__).DEBUG_COMPILATION_ERRORS::$(typeof(DEBUG_COMPILATION_ERRORS))
Option to control whether a failure to compile LLVM IR in [`@codelet`](@ref) should drop you into an interactive debug session with [`Cthulhu.jl`](https://github.com/JuliaDebug/Cthulhu.jl).
This forcibly disables the progress spinner enabled by [`PROGRESS_SPINNER`](@ref), as it would not play nicely with the interactive debug session.
!!! note
[`Cthulhu.jl`](https://github.com/JuliaDebug/Cthulhu.jl) must be installed in the environment you are currently using and you have to run `using Cthulhu` before the `@codelet` definition.
`IPUToolkit.jl` does not install `Cthulhu.jl` automatically to limit the number of dependencies.
## Example
```julia
$(@__MODULE__).DEBUG_COMPILATION_ERRORS[] = false # Do not automatically open interactive debug shell when a compilation error arises, the default
$(@__MODULE__).DEBUG_COMPILATION_ERRORS[] = true # Automatically open interactive debug shell when a compilation error arises
```
"""
const DEBUG_COMPILATION_ERRORS = Ref(false)
function _get_target()
if TARGET_COLOSSUS[]
if :Colossus in LLVM.backends()
return Colossus()
end
error("Cannot target the Colossus backend, this is not supported by the version of LLVM that Julia links to.")
end
return NativeCompilerTarget()
end
_print_s(::Type{In}) = "Input"
_print_s(::Type{Out}) = "Output"
_print_s(::Type{InOut}) = "InOut"
_print_t(::Type{Int32}) = "int"
_print_t(::Type{UInt32}) = "unsigned int"
_print_t(::Type{Float16}) = "half"
_print_t(::Type{Float32}) = "float"
_print_arg(io::IO, ::Type{VertexVector{T, S}}, name::String) where {T,S} = println(io, "poplar::", _print_s(S), "<poplar::Vector<", _print_t(T), ">> ", name, ";")
_print_arg(io::IO, ::Type{VertexScalar{T, S}}, name::String) where {T,S} = println(io, "poplar::", _print_s(S), "<", _print_t(T), "> ", name, ";")
# This is an internal function, but it can be used to compile a codelet starting from LLVM
# IR in string form (e.g. if you generated it outside of the current process). NOTE:
# `origKernel` *must* match the name and the signature of the kernel you put in the LLVM IR.
# By default we create the codelet file in temporary directory, so that we don't pollute the
# file system with codelet files everywhere, but you can change that with the `output_path`
# keyword argument.
function ___build_codelet(llvm_ir::String, origKernel::Function, name::String=string(origKernel);
output_path::String=joinpath(mktempdir(), name * ".gp"))
method = methods(origKernel)[end]
args = method.sig.parameters[2:end]
argnames = string.(Base.method_argnames(method)[2:end])
kernel_name = match(Regex("(_Z[\\d_]+$(name)[\\d_]+)"), llvm_ir)[1]
mktempdir() do dir
open(joinpath(dir, "gen_codelet.cpp"), "w") do io
for i in 1:length(args)
_print_arg(io, args[i], argnames[i])
end
end
input_file = joinpath(KEEP_LLVM_FILES[] ? "" : dir, "$(name).ll")
write(input_file, llvm_ir)
# Do not allow references to literal pointers, which are likely to be invalid on the IPU
if contains(llvm_ir, r"inttoptr +\(i64 +\d+")
error("LLVM IR generated for codelet $(name) contains a reference to a literal pointer")
end
# Unless `POPC_FLAGS[]` already sets `-target`, if we have calls to Colossus
# intrinsics we can't target the IPU model on CPU (the `cpu` target), so in that
# case we compile only for `ipu1,ipu2`.
target = if !any(contains("-target"), POPC_FLAGS[].exec) && contains(llvm_ir, "@llvm.colossus.")
`-target ipu1,ipu2`
else
``
end
run(```
popc
$(POPC_FLAGS[])
$(target)
-X -Wno-override-module
-X -Qunused-arguments
-DGET_VEC_PTR_NAME=get_vec_ptr_$(name)
-DGET_VEC_SIZE_NAME=get_vec_size_$(name)
-DCLASS_NAME=$(name)
-DFIRST_NAME=$(argnames[1])
-DKERNEL_NAME=$(kernel_name)
-I$(dir)
$(input_file)
$(joinpath(@__DIR__, "codelet_gen.cpp"))
-o $(output_path)
```)
end
return nothing
end
# Similar to the function above, but it also adds the codelet to the graph.
function ___build_codelet(graph::Poplar.GraphAllocated, llvm_ir::String, origKernel::Function, name::String=string(origKernel);
output_path::String=joinpath(mktempdir(), name * ".gp"))
___build_codelet(llvm_ir, origKernel, name; output_path)
Poplar.GraphAddCodelets(graph, output_path)
return nothing
end
function __build_codelet(graph::Poplar.GraphAllocated, kernel, origKernel::Function, name::String=string(origKernel))
target = _get_target()
source = methodinstance(typeof(kernel), Tuple{})
params = IPUCompilerParams(name)
config = CompilerConfig(target, params)
job = CompilerJob(source, config)
llvm_ir = JuliaContext() do ctx
try
string(GPUCompiler.compile(:llvm, job)[1])
catch err
if err isa InvalidIRError && DEBUG_COMPILATION_ERRORS[]
code_typed(err; interactive = true)
else
rethrow()
end
end
end
# For some reasons the Colossus intrinsics names get dots converted into underscores:
# <https://github.com/JuliaGPU/GPUCompiler.jl/issues/464>. Let's convert them back to
# dots before writing the file to disk.
llvm_ir = replace(llvm_ir,
# Ref for IPU builtins:
# <https://docs.graphcore.ai/projects/poplar-api/en/latest/ipu_intrinsics/ipu_builtins.html>.
"_llvm_colossus_get_scount_l" => "llvm.colossus.get.scount.l",
"_llvm_colossus_get_tile_id" => "llvm.colossus.get.tile.id",
# Random number generation
"_llvm_colossus_urand_f16" => "llvm.colossus.urand.f16",
"_llvm_colossus_urand_f32" => "llvm.colossus.urand.f32",
"_llvm_colossus_urand32" => "llvm.colossus.urand32",
"_llvm_colossus_urand64" => "llvm.colossus.urand64",
"_llvm_colossus_f16v2grand" => "llvm.colossus.f16v2grand",
"_llvm_colossus_f32v2grand" => "llvm.colossus.f32v2grand",
# Float operation
"_llvm_colossus_tanh_f32" => "llvm.colossus.tanh.f32",
# Float comparisons
"_llvm_colossus_f32cmpeq" => "llvm.colossus.f32cmpeq",
"_llvm_colossus_f32cmpge" => "llvm.colossus.f32cmpge",
"_llvm_colossus_f32cmpgt" => "llvm.colossus.f32cmpgt",
"_llvm_colossus_f32cmple" => "llvm.colossus.f32cmple",
"_llvm_colossus_f32cmplt" => "llvm.colossus.f32cmplt",
"_llvm_colossus_f32cmpne" => "llvm.colossus.f32cmpne",
# Float classification (see IEEE 754-2008, § 5.7.2 General operations)
"_llvm_colossus_f32class" => "llvm.colossus.f32class",
)
___build_codelet(graph, llvm_ir, origKernel, name)
end
function _build_codelet(graph::Poplar.GraphAllocated, kernel, origKernel::Function, name::String=string(origKernel))
# Progress spinner is disabled if interactive debugging is enabled.
if PROGRESS_SPINNER[] && !DEBUG_COMPILATION_ERRORS[]
prog = ProgressUnknown("Compiling codelet $(name):"; spinner=true)
task = Threads.@spawn __build_codelet(graph, kernel, origKernel, name)
while !istaskdone(task)
ProgressMeter.next!(prog; spinner="⠋⠙⠹⠸⠼⠴⠦⠧⠇⠏")
sleep(0.1)
end
ProgressMeter.finish!(prog)
fetch(task)
else
__build_codelet(graph, kernel, origKernel, name)
end
end
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 8925 | # based on GPUCompiler example https://github.com/JuliaGPU/GPUCompiler.jl/blob/master/examples/kernel.jl
module IPUCompiler
export @codelet, @ipuprogram, VertexVector, VertexScalar, In, Out, InOut, get_scount_l, get_tile_id, randn2!, add_vertex
include("output.jl")
using GPUCompiler
using ..Poplar
# list of overrides (only for Julia 1.6)
const overrides = Expr[]
# Colossus backend
struct Colossus <: AbstractCompilerTarget
end
GPUCompiler.llvm_triple(::Colossus) = "colossus-graphcore-unknown-elf"
GPUCompiler.runtime_slug(j::CompilerJob{Colossus}) = j.config.params.kernel_name
struct IPUCompilerParams <: AbstractCompilerParams
kernel_name::String
end
# local method table for device functions
@static if isdefined(Base.Experimental, Symbol("@overlay"))
Base.Experimental.@MethodTable(method_table)
else
const method_table = nothing
end
# the method table to use
GPUCompiler.method_table(::CompilerJob{<:Any,IPUCompilerParams}) = method_table
macro device_override(ex)
ex = macroexpand(__module__, ex)
if Meta.isexpr(ex, :call)
ex = eval(ex)
error()
end
return esc(:( Base.Experimental.@overlay($method_table, $ex) ))
end
macro device_function(ex)
ex = macroexpand(__module__, ex)
def = splitdef(ex)
# generate a function that errors
def[:body] = quote
error("This function is not intended for use on the CPU")
end
esc(quote
$(combinedef(def))
@device_override $ex
end)
end
# Functions needed by the runtime
"""
get_scount_l()
Call the [`__builtin_ipu_get_scount_l()`](https://docs.graphcore.ai/projects/poplar-api/en/latest/ipu_intrinsics/ipu_builtins.html#_CPPv426__builtin_ipu_get_scount_lv) builtin:
> Get the value of the control/status register (CSR) `SCOUNT_L`, which is the lower 32 bits of the tile cycle counter value.
"""
function get_scount_l end
"""
get_tile_id()
Call the [`__builtin_ipu_get_tile_id()`](https://docs.graphcore.ai/projects/poplar-api/en/latest/ipu_intrinsics/ipu_builtins.html#_CPPv425__builtin_ipu_get_tile_idv) builtin:
> Get the tile ID of the current tile.
"""
function get_tile_id end
"""
randn2!(v::VertexVector) -> v
Fill the vector `v` with normally-distributed (mean 0, standard deviation 1) random numbers.
The vector *must* have even length.
This function takes advantage of [IPU builtins for random number generation](https://docs.graphcore.ai/projects/poplar-api/en/latest/ipu_intrinsics/ipu_builtins.html#random-number-generation), which return pairs of numbers at a time.
"""
function randn2! end
include("vertices.jl")
include("runtime.jl")
GPUCompiler.runtime_module(::CompilerJob{<:Any,IPUCompilerParams}) = IPURuntime
# `GPUCompiler.isintrinsic` specifies functions which are to be considered intrinsics for
# the current job, and so don't have to be validated by the compilation pipeline. We set
# `getVec$(kernel_name)` to be considered intrinsic, as this is implemented in the
# accompanying C++ codelet, so outside of the LLVM IR generated by GPUCompiler.
GPUCompiler.isintrinsic(@nospecialize(job::CompilerJob{<:Any,IPUCompilerParams}), fn::String) =
contains(fn, Regex("^get_vec_(ptr|size)_" * job.config.params.kernel_name * "\$")) ||
fn ∈ ("printf", "puts", "tanf") || startswith(fn, "_llvm_colossus_")
include("codelet.jl")
include("tensors.jl")
include("program.jl")
include("timing.jl")
function add_vertex(graph::Poplar.GraphAllocated,
compute_set::Poplar.ComputeSetAllocated,
tiles::Union{Integer,AbstractVector{<:Integer}},
codelet::Function,
args::Union{Number,Poplar.TensorAllocated}...)
meths = methods(codelet)
num_tiles = length(tiles)
# Get the names of the arguments of the codelet.
arg_names = string.(Base.method_argnames(meths[begin])[2:end])
# Arguments validation
if length(meths) != 1
throw(ArgumentError("Function $(codelet) does not have exactly one method. Use a different function which has a method only."))
end
if length(arg_names) != length(args)
throw(ArgumentError("Function $(codelet) takes $(length(arg_names)) arguments but you passed $(length(args)) arguments for this vertex."))
end
for (arg_n, arg) in enumerate(args)
if length(arg) < num_tiles
throw(ArgumentError("The argument #$(arg_n) to $(codelet) has $(length(arg)) elements, which is less than the number of tiles ($(num_tiles))"))
end
end
for (idx, tile) in enumerate(tiles)
# Create a vertex on each tile
vertex = Poplar.GraphAddVertex(graph, compute_set, string(codelet))
# Evenly spread the arrays over all tiles.
for (arg_n, arg) in enumerate(args)
arg_slice = if num_tiles > 1 && arg isa Poplar.TensorAllocated
stride = cld(length(arg), num_tiles)
slice = (stride * (idx - 1)):min(length(arg) - 1, (stride * idx - 1))
arg[slice]
else
arg
end
if arg isa Poplar.TensorAllocated
Poplar.GraphSetTileMapping(graph, arg_slice, tile)
end
Poplar.GraphConnect(graph, vertex[arg_names[arg_n]], arg_slice)
end
# Add the vertex on the tile
Poplar.GraphSetTileMapping(graph, vertex, tile)
# TODO: allow setting the perf estimate of the vertex.
if Poplar.SDK_VERSION < v"2.0"
Poplar.GraphSetCycleEstimate(graph, vertex, 1)
else
Poplar.GraphSetPerfEstimate(graph, vertex, 1)
end
end
return nothing
end
function add_vertex(graph::Poplar.GraphAllocated,
program::Poplar.ProgramSequenceAllocated,
tiles::Union{Integer,AbstractVector{<:Integer}},
codelet::Function,
args::Union{Number,Poplar.TensorAllocated}...)
compute_set = Poplar.GraphAddComputeSet(graph, string(codelet))
add_vertex(graph, compute_set, tiles, codelet, args...)
Poplar.ProgramSequenceAdd(program, Poplar.ProgramExecute(compute_set))
return nothing
end
add_vertex(graph::Poplar.GraphAllocated, compute_set::Poplar.ComputeSetAllocated,
codelet::Function, args::Union{Number,Poplar.TensorAllocated}...) =
add_vertex(graph, compute_set, 0, codelet, args...)
add_vertex(graph::Poplar.GraphAllocated, program::Poplar.ProgramSequenceAllocated,
codelet::Function, args::Union{Number,Poplar.TensorAllocated}...) =
add_vertex(graph, program, 0, codelet, args...)
"""
add_vertex(graph::Poplar.GraphAllocated,
compute_set_or_program::Union{Poplar.ComputeSetAllocated, Poplar.ProgramSequenceAllocated},
[tiles::Union{Integer,AbstractVector{<:Integer}},]
codelet::Function,
args::Union{Number,Poplar.TensorAllocated}...) -> Nothing
Add the codelet function `codelet` created with [`@codelet`](@ref) to `graph`, using the tensors `args` as arguments.
The function `codelet` must have exactly one method, no more, no less.
The second argument can be either the program or the compute set to which to add the new vertex/vertices.
If a program is passed, a new compute set will be automatically created.
`add_vertex` also evenly maps all tensors and vertices across all `tiles`, which can be either a single tile ID or an `AbstractVector` of IDs and defaults to single tile 0 if this argument is omitted.
Note that all argument tensors `args` must be longer than or equal to the number of `tiles`.
If you want to have better control over tile mapping, use `Poplar.GraphAddVertex` instead.
"""
add_vertex
# Mapping of the LLVM version used by each version of the Poplar SDK. To find it, use `popc
# --version`.
const POPLAR_SDK_LLVM_MAPPING = Dict(
v"1.3.0" => v"11.0.0",
v"1.4.0" => v"11.0.0",
v"2.0.0" => v"11.0.0",
v"2.1.0" => v"13.0.0",
v"2.2.0" => v"13.0.0",
v"2.3.0" => v"14.0.0",
v"2.4.0" => v"14.0.0",
v"2.5.0" => v"14.0.0",
v"2.6.0" => v"15.0.0",
v"3.0.0" => v"15.0.0",
v"3.1.0" => v"15.0.0",
v"3.2.0" => v"15.0.0",
v"3.3.0" => v"16.0.0",
)
function __init__()
@static if get(POPLAR_SDK_LLVM_MAPPING, Base.thisminor(Poplar.SDK_VERSION), v"0") != Base.thismajor(Base.libllvm_version)
sdk_llvm_version = get(POPLAR_SDK_LLVM_MAPPING, Base.thisminor(Poplar.SDK_VERSION), "UNKNOWN")
if sdk_llvm_version == "UNKNOWN" && !isnothing(Sys.which("popc"))
sdk_llvm_version = match(r"clang version ([\d.]+)", readchomp(`popc --version`))[1]
end
@warn """
You are using Poplar SDK v$(Poplar.SDK_VERSION) which is coupled to LLVM v$(sdk_llvm_version), but your Julia uses LLVM v$(Base.libllvm_version).
IPUCompiler code generation may not work correctly.
"""
end
end
end # module IPUCompiler
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 9758 | # Formatted Output. Adapted from
# <https://github.com/JuliaGPU/CUDA.jl/blob/8ffdf3723ed6224ee7e2c7188ef6ab8d5a498905/src/device/intrinsics/output.jl>.
using LLVM
using LLVM.Interop
using Core: LLVMPtr
export @ipuprintf
"""
$(@__MODULE__).DISABLE_PRINT::$(typeof(DISABLE_PRINT))
Global constant which controls whether printing through the various `@ipuprint*`
macros should be disabled or not. You may want to completely disable printing
for production runs, to avoid the cost of printing on the device, but keep it
enabled during development.
Examples:
```julia
$(@__MODULE__).DISABLE_PRINT[] = false # Do not disable printing, this is the default.
$(@__MODULE__).DISABLE_PRINT[] = true # Disable printing, the `@ipuprint*` macros are no-op.
```
"""
const DISABLE_PRINT = Ref(false)
@generated function promote_c_argument(arg)
# > When a function with a variable-length argument list is called, the variable
# > arguments are passed using C's old ``default argument promotions.'' These say that
# > types char and short int are automatically promoted to int, and type float is
# > automatically promoted to double. Therefore, varargs functions will never receive
# > arguments of type char, short int, or float.
if arg == Cchar || arg == Cshort || arg == Cuchar || arg == Cushort
return :(Cint(arg))
elseif arg == Cfloat
return :(Cdouble(arg))
else
return :(arg)
end
end
"""
@ipuprintf("%Fmt", args...)
Print a formatted string in device context on the host standard output.
Note that this is not a fully C-compliant `printf` implementation.
Also beware that it is an untyped, and unforgiving `printf` implementation. Type widths need
to match, eg. printing a 64-bit Julia integer requires the `%ld` formatting string.
More user-friendly versions of this macro are [`@ipuprint`](@ref), [`@ipuprintln`](@ref).
See also [`@ipushow`](@ref), which is built on top of `@ipuprintf` functionalities.
Printing can be completely disabled by setting [`IPUCompiler.DISABLE_PRINT`](@ref):
```julia
$(@__MODULE__).DISABLE_PRINT[] = true
```
"""
macro ipuprintf(fmt::String, args...)
if DISABLE_PRINT[]
return :()
end
fmt_val = Val(Symbol(fmt))
return :(_ipuprintf($fmt_val, $(map(arg -> :(promote_c_argument($arg)), esc.(args))...)))
end
# Single argument calls can use `puts`, which has a simpler signature.
@generated function _ipuprintf(::Val{fmt}) where {fmt}
@dispose ctx=Context() begin
T_void = LLVM.VoidType()
T_int32 = LLVM.Int32Type()
T_pint8 = LLVM.PointerType(LLVM.Int8Type())
# create functions
llvm_f, llvm_ft = create_function(T_int32, LLVMType[])
mod = LLVM.parent(llvm_f)
# generate IR
@dispose builder=IRBuilder() begin
entry = BasicBlock(llvm_f, "entry")
position!(builder, entry)
str = globalstring_ptr!(builder, String(fmt))
# invoke puts and return
puts_typ = LLVM.FunctionType(T_int32, [T_pint8])
puts = LLVM.Function(mod, "puts", puts_typ)
chars = call!(builder, puts_typ, puts, [str])
ret!(builder, chars)
end
call_function(llvm_f, Int32, Tuple{})
end
end
@generated function _ipuprintf(::Val{fmt}, argspec1, argspec...) where {fmt}
@dispose ctx=Context() begin
arg_exprs = vcat(:( argspec1 ), [:( argspec[$i] ) for i in 1:length(argspec)])
arg_types = [argspec1, argspec...]
T_void = LLVM.VoidType()
T_int32 = LLVM.Int32Type()
T_pint8 = LLVM.PointerType(LLVM.Int8Type())
# create functions
param_types = LLVMType[convert(LLVMType, typ) for typ in arg_types]
llvm_f, llvm_ft = create_function(T_int32, param_types)
mod = LLVM.parent(llvm_f)
# generate IR
@dispose builder=IRBuilder() begin
entry = BasicBlock(llvm_f, "entry")
position!(builder, entry)
str = globalstring_ptr!(builder, String(fmt))
# invoke printf and return
printf_typ = LLVM.FunctionType(T_int32, [T_pint8]; vararg=true)
printf = LLVM.Function(mod, "printf", printf_typ)
chars = call!(builder, printf_typ, printf, [str, parameters(llvm_f)...])
ret!(builder, chars)
end
call_function(llvm_f, Int32, Tuple{arg_types...}, arg_exprs...)
end
end
## print-like functionality
export @ipuprint, @ipuprintln
# simple conversions, defining an expression and the resulting argument type. nothing fancy,
# `@ipuprint` pretty directly maps to `@ipuprintf`; we should just support `write(::IO)`.
const ipuprint_conversions = Dict(
Float32 => (x->:(Float64($x)), Float64),
Float16 => (x->:(Float64($x)), Float64),
Ptr{<:Any} => (x->:(convert(Ptr{Cvoid}, $x)), Ptr{Cvoid}),
LLVMPtr{<:Any} => (x->:(reinterpret(Ptr{Cvoid}, $x)), Ptr{Cvoid}),
Bool => (x->:(Int32($x)), Int32),
)
# format specifiers
const ipuprint_specifiers = Dict(
# integers
Int16 => "%hd",
Int32 => "%d",
Int64 => Sys.iswindows() ? "%lld" : "%ld",
UInt16 => "%hu",
UInt32 => "%u",
UInt64 => Sys.iswindows() ? "%llu" : "%lu",
# floating-point
Float64 => "%f",
# other
Cchar => "%c",
# `Ptr{Cvoid}` should be `%p` but that doesn't seem to be supported. We
# print as an integer until we find a better way.
Ptr{Cvoid} => "%d",
Cstring => "%s",
)
@inline @generated function _ipuprint(parts...)
fmt = ""
args = Expr[]
for i in 1:length(parts)
part = :(parts[$i])
T = parts[i]
# put literals directly in the format string
if T <: Val
fmt *= string(T.parameters[1])
continue
end
# try to convert arguments if they are not supported directly
if !haskey(ipuprint_specifiers, T)
for Tmatch in keys(ipuprint_conversions)
if T <: Tmatch
conv, T = ipuprint_conversions[Tmatch]
part = conv(part)
break
end
end
end
# render the argument
if haskey(ipuprint_specifiers, T)
fmt *= ipuprint_specifiers[T]
push!(args, part)
elseif T <: Tuple
fmt *= "("
for (j, U) in enumerate(T.parameters)
if haskey(ipuprint_specifiers, U)
fmt *= ipuprint_specifiers[U]
push!(args, :($part[$j]))
if j < length(T.parameters)
fmt *= ", "
elseif length(T.parameters) == 1
fmt *= ","
end
else
@error("@ipuprint does not support values of type $U")
end
end
fmt *= ")"
elseif T <: String
@error("@ipuprint does not support non-literal strings")
else
@error("@ipuprint does not support values of type $T")
end
end
quote
$(@__MODULE__).@ipuprintf($fmt, $(args...))
end
end
"""
@ipuprint(xs...)
@ipuprintln(xs...)
Print a textual representation of values `xs` to standard output from the IPU. The
functionality builds on [`@ipuprintf`](@ref), and is intended as a more use friendly alternative of
that API. However, that also means there's only limited support for argument types, handling
16/32/64 signed and unsigned integers, 32 and 64-bit floating point numbers, `Cchar`s and
pointers. For more complex output, use [`@ipuprintf`](@ref) directly.
Limited string interpolation is also possible:
```julia
@ipuprint("Hello, World ", 42, "\\n")
@ipuprint "Hello, World \$(42)\\n"
```
Printing can be completely disabled by setting [`IPUCompiler.DISABLE_PRINT`](@ref):
```julia
$(@__MODULE__).DISABLE_PRINT[] = true
```
"""
macro ipuprint(parts...)
if DISABLE_PRINT[]
return :()
end
args = Union{Val,Expr,Symbol}[]
parts = [parts...]
while true
isempty(parts) && break
part = popfirst!(parts)
# handle string interpolation
if isa(part, Expr) && part.head == :string
parts = vcat(part.args, parts)
continue
end
# expose literals to the generator by using Val types
if isbits(part) # literal numbers, etc
push!(args, Val(part))
elseif isa(part, QuoteNode) # literal symbols
push!(args, Val(part.value))
elseif isa(part, String) # literal strings need to be interned
push!(args, Val(Symbol(part)))
else # actual values that will be passed to printf
push!(args, part)
end
end
quote
_ipuprint($(map(esc, args)...))
end
end
@doc (@doc @ipuprint) ->
macro ipuprintln(parts...)
esc(quote
$(@__MODULE__).@ipuprint($(parts...), "\n")
end)
end
export @ipushow
"""
@ipushow(ex)
IPU analogue of `Base.@show`. It comes with the same type restrictions as [`@ipuprintf`](@ref).
```julia
@ipushow x
```
Printing can be completely disabled by setting [`IPUCompiler.DISABLE_PRINT`](@ref):
```julia
$(@__MODULE__).DISABLE_PRINT[] = true
```
"""
macro ipushow(exs...)
if DISABLE_PRINT[]
return :()
end
blk = Expr(:block)
for ex in exs
push!(blk.args, :(@ipuprintln($(sprint(Base.show_unquoted,ex)*" = "),
begin local value = $(esc(ex)) end)))
end
isempty(exs) || push!(blk.args, :value)
blk
end
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 5019 | function _get_name_args(expr::Expr)
name = expr.args[1].args[1]
args = [(arg.args[1], arg.args[2].args[2], arg.args[2].args[3]) for arg in expr.args[1].args[2:end]]
return name, args
end
function _add_vertex!(initialised_tensors::Dict{Symbol, Symbol}, graph, prog, name_args::Dict, expr::Expr)
name = expr.args[1]
f_args = name_args[name]
compute_set = string(name, "_compute_set")
compute_set_sym = gensym(compute_set)
vertex = gensym(Symbol(name, "_vertex"))
out = quote end
add_vertex = :( $(esc(@__MODULE__().add_vertex))($(esc(graph)), $(esc(prog)), $(esc(name))) )
if length(expr.args) > 1
for (idx, arg) in enumerate(expr.args[2:end])
arg_info = f_args[idx]
vec = gensym(arg_info[1])
if arg ∉ keys(initialised_tensors)
append!(out.args,
(quote
if $(esc(arg)) isa PoplarArray
$(esc(vec)) = $(esc(Poplar.GraphAddVariable))($(esc(graph)), $(esc(Poplar._get_type(arg_info[2]))), collect(UInt64.(size($(esc(arg))))), $(string(arg)))
elseif $(esc(arg)) isa Array
$(esc(vec)) = $(esc(Poplar.GraphAddConstant))($(esc(graph)), $(esc(Poplar._get_type(arg_info[2]))), collect(UInt64.(size($(esc(arg))))), $(esc(arg)))
else
error("`$(string(arg))` is a `$(typeof(esc(arg)))`, it must be either an `Array` or a `PoplarArray`")
end
end).args)
initialised_tensors[arg] = vec
end
push!(add_vertex.args, esc(initialised_tensors[arg]))
end
end
push!(out.args, add_vertex)
return out
end
function _print_tensor(prog::Symbol, initialised_tensors::Dict{Symbol, Symbol}, expr::Expr)
(length(expr.args) == 3 && expr.args[2] isa String && expr.args[3] isa Symbol) || error("""
The `print_tensor` function must have as first argument a `String` and second argument the tensor name:
print_tensor("Description", tensor_name)
""")
return quote
$(esc(Poplar.ProgramSequenceAdd))($(esc(prog)), $(esc(Poplar.ProgramPrintTensor))($(expr.args[2]), $(esc(initialised_tensors[expr.args[3]]))))
end
end
function _read_tensor(engine::Symbol, graph::Symbol, initialised_tensors::Dict{Symbol,Symbol}, expr::Expr)
(length(expr.args) == 2 && expr.args[1] isa Symbol && expr.args[2] isa Symbol) || error("""
Assignment can only be done between two variable names:
jl_var = ipu_tensor
where `jl_var` is a newly created Julia variable on the host, and `ipu_tensor` is the name of a tensor on the IPU.
""")
jl_var = expr.args[1]
ipu_tensor = expr.args[2]
read_name = string(ipu_tensor, "_read")
return (:($(esc(Poplar.GraphCreateHostRead))($(esc(graph)), $(read_name), $(esc(initialised_tensors[ipu_tensor])))),
quote
$(esc(jl_var)) = $(esc(_similar))($(esc(ipu_tensor)))
$(esc(Poplar.EngineReadTensor))($(esc(engine)), $(read_name), $(esc(jl_var)))
end)
end
macro ipuprogram(device, program::Expr)
program.head === :block || error("The second argument to the `@ipuprogram` macro must be a begin-end block")
graph = gensym("graph")
prog = gensym("prog")
engine = gensym("engine")
out = quote
$(esc(graph)) = $(esc(Poplar.Graph))($(esc(Poplar.DeviceGetTarget))($(esc(device))))
$(esc(prog)) = $(esc(Poplar.ProgramSequence))()
end
postamble = quote end
name_args = Dict{Symbol,Any}()
initialised_tensors = Dict{Symbol,Symbol}()
for expr in program.args
expr isa LineNumberNode && continue
if expr.head ∈ (:function, :(=)) && (expr.args[1] isa Expr && expr.args[1].head === :call)
append!(out.args, _codelet(graph, expr).args)
na = _get_name_args(expr)
name_args[na[1]] = na[2]
elseif expr.head === :call
if expr.args[1] === :print_tensor
append!(out.args, _print_tensor(prog, initialised_tensors, expr).args)
else
append!(out.args, _add_vertex!(initialised_tensors, graph, prog, name_args, expr).args)
end
elseif expr.head == :(=)
o, p = _read_tensor(engine, graph, initialised_tensors, expr)
push!(out.args, o)
append!(postamble.args, p.args)
end
end
flags = gensym("flags")
append!(out.args,
(quote
$(esc(flags)) = Poplar.OptionFlags()
$(esc(Poplar.OptionFlagsSet))($(esc(flags)), "debug.instrument", "true")
$(esc(engine)) = $(esc(Poplar.Engine))($(esc(graph)), $(esc(prog)), $(esc(flags)))
$(esc(Poplar.EngineLoadAndRun))($(esc(engine)), $(esc(device)))
end).args)
append!(out.args, postamble.args)
return out
end
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 10390 | module IPURuntime
import ..IPUCompiler: @device_override, @ipuprintf, @ipuprintln, get_scount_l, get_tile_id, randn2!, VertexVector, Out, InOut
using GPUCompiler: reset_runtime
import LinearAlgebra
# reset the runtime cache from global scope, so that any change triggers recompilation
reset_runtime()
# dummy methods
signal_exception() = nothing
# Todo: box/unbox for allowing proper type conversion
# https://github.com/JuliaGPU/CUDAnative.jl/blob/a15d2db96274948d8090457a001e62e14be0d883/src/device/runtime.jl
malloc(sz) = C_NULL
function report_oom(sz)
@ipuprintf("ERROR: Out of memory (trying to allocate %i bytes)\n", sz)
return nothing
end
function report_exception(ex)
@ipuprintf("ERROR: a %s was thrown during kernel execution.", ex)
return nothing
end
function report_exception_name(ex)
@ipuprintf("""
ERROR: a %s was thrown during kernel execution.
Stacktrace:
""", ex)
return nothing
end
function report_exception_frame(idx, func, file, line)
@ipuprintf(" [%i] %s at %s:%i\n", idx, func, file, line)
return nothing
end
# IPU builtins: https://docs.graphcore.ai/projects/poplar-api/en/latest/ipu_intrinsics/ipu_builtins.html
# Note: ideally we'd always call the LLVM intrisics `llvm.colossus....` as is, but that
# works only when targeting a Colossus-aware LLVM, so for the general case we call fake
# external `_llvm_colossus_...` intrinsics and then rename them before writing to file. Not
# great, but it does the job.
get_scount_l() = ccall("extern _llvm_colossus_get_scount_l", llvmcall, Cuint, ())
get_tile_id() = ccall("extern _llvm_colossus_get_tile_id", llvmcall, Cuint, ())
# Random functions, based on IPU intrinsics
@device_override Base.rand(T::Type{Float16}) = ccall("extern _llvm_colossus_urand_f16", llvmcall, Float16, ()) + T(0.5)
@device_override Base.rand(T::Type{Float32}) = ccall("extern _llvm_colossus_urand_f32", llvmcall, Float32, ()) + T(0.5)
@device_override Base.rand(T::Type{UInt32}) = ccall("extern _llvm_colossus_urand32", llvmcall, UInt32, ()) + T(0.5)
@device_override Base.rand(T::Type{UInt64}) = ccall("extern _llvm_colossus_urand64", llvmcall, UInt64, ()) + T(0.5)
# Note: `llvm.colossus.f{16,32}v2grand` return 2-tuples of numbers, but Julia's `Base.randn`
# returns a single number at a time, sadly we have to discard one of the numbers to keep the
# same semantic.
@device_override Base.randn(T::Type{Float16}) = @inbounds ccall("extern _llvm_colossus_f16v2grand", llvmcall, NTuple{2, VecElement{Float16}}, ())[1].value
@device_override Base.randn(T::Type{Float32}) = @inbounds ccall("extern _llvm_colossus_f32v2grand", llvmcall, NTuple{2, VecElement{Float32}}, ())[1].value
function randn2!(v::VertexVector{T}) where {T}
for idx in UInt32(1):UInt32(2):UInt32(length(v))
rnd = if T == Float32
ccall("extern _llvm_colossus_f32v2grand", llvmcall, NTuple{2, VecElement{Float32}}, ())
elseif T == Float16
ccall("extern _llvm_colossus_f16v2grand", llvmcall, NTuple{2, VecElement{Float16}}, ())
end
@inbounds v[idx] = rnd[1].value
@inbounds v[idx+1] = rnd[2].value
end
end
## Math functions.
# There are different reasons why we prefer LLVM intrinsics on the IPU: implementations in
# Julia's Base either require promotion to double (very slow) or require non-existing
# symbols (maybe because they aren't implemented for `double`s on the IPU).
@device_override Base.sin(x::Float32) = ccall("llvm.sin.f32", llvmcall, Float32, (Float32,), x)
@device_override Base.cos(x::Float32) = ccall("llvm.cos.f32", llvmcall, Float32, (Float32,), x)
@device_override Base.sincos(x::Float32) = (sin(x), cos(x))
@device_override Base.tan(x::Float32) = ccall("extern tanf", llvmcall, Float32, (Float32,), x)
@device_override Base.exp(x::Float32) = ccall("llvm.exp.f32", llvmcall, Float32, (Float32,), x)
@device_override Base.exp2(x::Float32) = ccall("llvm.exp2.f32", llvmcall, Float32, (Float32,), x)
@device_override Base.log(x::Float32) = ccall("llvm.log.f32", llvmcall, Float32, (Float32,), x)
@device_override Base.log10(x::Float32) = ccall("llvm.log10.f32", llvmcall, Float32, (Float32,), x)
@device_override Base.log2(x::Float32) = ccall("llvm.log2.f32", llvmcall, Float32, (Float32,), x)
@device_override Base.:^(b::Float32, p::Int32) = ccall("llvm.powi.f32.i32", llvmcall, Float32, (Float32, Int32), b, p)
@device_override Base.:^(b::Float32, p::Float32) = ccall("llvm.pow.f32", llvmcall, Float32, (Float32, Float32), b, p)
@device_override Base.sqrt(x::Float32) = ccall("llvm.sqrt.f32", llvmcall, Float32, (Float32,), x)
# Same, for Float16
@device_override Base.sin(x::Float16) = ccall("llvm.sin.f16", llvmcall, Float16, (Float16,), x)
@device_override Base.cos(x::Float16) = ccall("llvm.cos.f16", llvmcall, Float16, (Float16,), x)
@device_override Base.sincos(x::Float16) = (sin(x), cos(x))
@device_override Base.tan(x::Float16) = Float16(tan(Float32(x)))
@device_override Base.exp(x::Float16) = ccall("llvm.exp.f16", llvmcall, Float16, (Float16,), x)
@device_override Base.exp2(x::Float16) = ccall("llvm.exp2.f16", llvmcall, Float16, (Float16,), x)
@device_override Base.log(x::Float16) = ccall("llvm.log.f16", llvmcall, Float16, (Float16,), x)
@device_override Base.log10(x::Float16) = ccall("llvm.log10.f16", llvmcall, Float16, (Float16,), x)
@device_override Base.log2(x::Float16) = ccall("llvm.log2.f16", llvmcall, Float16, (Float16,), x)
@device_override Base.:^(b::Float16, p::Int16) = ccall("llvm.powi.f16.i16", llvmcall, Float16, (Float16, Int16), b, p)
@device_override Base.:^(b::Float16, p::Float16) = ccall("llvm.pow.f16", llvmcall, Float16, (Float16, Float16), b, p)
@device_override Base.sqrt(x::Float16) = ccall("llvm.sqrt.f16", llvmcall, Float16, (Float16,), x)
# `literal_pow` doesn't support Float16: <https://github.com/JuliaLang/julia/issues/53745>.
@device_override Base.literal_pow(::typeof(^), x::Float16, ::Val{0}) = one(x)
@device_override Base.literal_pow(::typeof(^), x::Float16, ::Val{1}) = x
@device_override Base.literal_pow(::typeof(^), x::Float16, ::Val{2}) = x*x
@device_override Base.literal_pow(::typeof(^), x::Float16, ::Val{3}) = x*x*x
@device_override Base.literal_pow(::typeof(^), x::Float16, ::Val{-1}) = inv(x)
@device_override Base.literal_pow(::typeof(^), x::Float16, ::Val{-2}) = (i=inv(x); i*i)
@device_override Base.min(a::Float32, b::Float32) = ccall("llvm.minnum.f32", llvmcall, Float32, (Float32, Float32), a, b)
@device_override Base.max(a::Float32, b::Float32) = ccall("llvm.maxnum.f32", llvmcall, Float32, (Float32, Float32), a, b)
@device_override Base.tanh(x::Float32) = ccall("extern _llvm_colossus_tanh_f32", llvmcall, Float32, (Float32,), x)
# For some reasons I didn't have the time to investigate the `==` and `!=` methods below cause
# crashes. But also, quick benchmarks didn't show significant performance improvements compared
# to the default behaviour in Julia (also for the other comparison operators), so that they
# don't seem to be too much worth the effort, we keep the code below just for reference.
# @device_override Base.:(==)(a::Float32, b::Float32) = Bool(ccall("extern _llvm_colossus_f32cmpeq", llvmcall, Float32, (Float32, Float32), a, b))
# @device_override Base.:(!=)(a::Float32, b::Float32) = Bool(ccall("extern _llvm_colossus_f32cmpne", llvmcall, Float32, (Float32, Float32), a, b))
## quirks, adapted from
## https://github.com/JuliaGPU/CUDA.jl/blob/5c51766d0a9e7819ea79f314e37ed6a8a5d24369/src/device/quirks.jl
macro print_and_throw(args...)
esc(quote
@ipuprintln "ERROR: " $(args...) "."
throw(nothing)
end)
end
# math.jl
@device_override @noinline Base.Math.throw_complex_domainerror(f::Symbol, x) =
@print_and_throw "This operation requires a complex input to return a complex result"
@device_override @noinline Base.Math.throw_exp_domainerror(x) =
@print_and_throw "Exponentiation yielding a complex result requires a complex argument"
# intfuncs.jl
@device_override @noinline Base.throw_domerr_powbysq(::Any, p) =
@print_and_throw "Cannot raise an integer to a negative power"
@device_override @noinline Base.throw_domerr_powbysq(::Integer, p) =
@print_and_throw "Cannot raise an integer to a negative power"
@device_override @noinline Base.throw_domerr_powbysq(::AbstractMatrix, p) =
@print_and_throw "Cannot raise an integer to a negative power"
@device_override @noinline Base.__throw_gcd_overflow(a, b) =
@print_and_throw "gcd overflow"
# boot.jl
@device_override @noinline Core.throw_inexacterror(f::Symbol, ::Type{T}, val) where {T} =
@print_and_throw "Inexact conversion"
# abstractarray.jl
@device_override @noinline Base.throw_boundserror(A, I) =
@print_and_throw "Out-of-bounds array access"
@device_override @noinline Base.throw_eachindex_mismatch_indices(I, A, B...) =
@print_and_throw "Not all inputs to eachindex have the same axes"
# trig.jl
@device_override @noinline Base.Math.sincos_domain_error(x) =
@print_and_throw "sincos(x) is only defined for finite x, x = " x
@device_override @noinline Base.Math.acos_domain_error(x) =
@print_and_throw "acos(x) not defined for |x| > 1, x = " x
@device_override @noinline Base.Math.asin_domain_error(x) =
@print_and_throw "asin(x) not defined for |x| > 1, x = " x
# range.jl
@eval begin
@device_override function Base.StepRangeLen{T,R,S,L}(ref::R, step::S, len::Integer,
offset::Integer=1) where {T,R,S,L}
if T <: Integer && !isinteger(ref + step)
@print_and_throw("StepRangeLen{<:Integer} cannot have non-integer step")
end
len = convert(L, len)
len >= zero(len) || @print_and_throw("StepRangeLen length cannot be negative")
offset = convert(L, offset)
L1 = oneunit(typeof(len))
L1 <= offset <= max(L1, len) || @print_and_throw("StepRangeLen: offset must be in [1,...]")
$(
Expr(:new, :(StepRangeLen{T,R,S,L}), :ref, :step, :len, :offset)
)
end
end
# LinearAlgebra
@device_override function Base.setindex!(D::LinearAlgebra.Diagonal, v, i::Int, j::Int)
@boundscheck checkbounds(D, i, j)
if i == j
@inbounds D.diag[i] = v
elseif !iszero(v)
@print_and_throw("cannot set off-diagonal entry to a nonzero value")
end
return v
end
end # module IPURuntime
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 852 | # `PoplarArray` is a placeholder type to represent variables to be added to a
# graph. NOTE: these are distincts from `VertexVector`s which represent the
# input/output arguments of codelets (vertices).
export PoplarArray, PoplarVector, PoplarMatrix
struct PoplarArray{T,N} <: AbstractArray{T,N}
size::NTuple{N,Int}
end
const PoplarVector{T} = PoplarArray{T,1}
const PoplarMatrix{T} = PoplarArray{T,2}
PoplarArray{T,N}(::UndefInitializer, size::Vararg{Int,N}) where {T,N} =
PoplarArray{T,N}(size)
Base.size(t::PoplarArray) = t.size
Base.size(t::PoplarArray, d::Int) = size(t)[d]
# Simple methods, don't access the elements
Base.show(io::IO, x::PoplarArray) = Base.show_default(io, x)
Base.show(io::IO, ::MIME"text/plain", x::PoplarArray) = Base.show_default(io, x)
_similar(t::PoplarArray{T,N}) where {T,N} = Array{T,N}(undef, size(t))
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 3947 | # Timing inside a codelet is complicated, because in a codelet you can use
# `__builtin_ipu_get_scount_l` to get the current cycle count, but the clock speed is only
# available from the `target` object (`target.getTileClockFrequency()`). What you can do is
# to get the counters before and after the region you want to benchmark and then divide by
# the clock frequency, interpolated in the codelet code with `@eval`:
#
# device = Poplar.get_ipu_device()
# target = Poplar.DeviceGetTarget(device)
# graph = Poplar.Graph(target)
# tile_clock_frequency = Poplar.TargetGetTileClockFrequency(target)
# @eval IPUCompiler.@codelet graph function Foo(...)
# cycles_start = get_scount_l()
# # Do something here...
# cycles_end = get_scount_l()
# time = (cycles_end - cycles_start) / $(tile_clock_frequency)
# @ipushow time
# end
#
# Here we only provide some macros for easily getting the cycle counts, not the times
# directly. For reference, typical clock counts are either 1.330 GHz on a classic machine
# or 1.850 GHz on a Bow machine.
#
# *NOTE*: cycle counters are `UInt32`, so timing expressions longer than `typemax(UInt32) /
# tile_clock_frequency` (~2 or 3 seconds depending on the model) is unreliable.
export @ipucycles, @ipushowcycles, @ipuelapsed
macro ipucycles(msg, ex)
# `@ipuprintln` is already disabled by `DISABLE_PRINT`, but we want to remove also the
# `get_scount_l` instructions since we aren't going to print anything anyway.
if DISABLE_PRINT[]
return :()
end
return quote
!isnothing($(esc(msg))) && $(@__MODULE__).@ipuprint $(msg) ":"
local cycles_start = get_scount_l()
local value = $(esc(ex))
local cycles_end = get_scount_l()
local Δ = cycles_end - cycles_start
$(@__MODULE__).@ipuprintln Δ " cycles"
value
end
end
macro ipucycles(ex)
return quote
$(@__MODULE__).@ipucycles nothing $(esc(ex))
end
end
"""
@ipucycles ex
@ipucycles "description" ex
Print from inside a codelet the number of cycles spent to compute the expression `ex`.
The corresponding time can be obtained by dividing the number of cycles by the clock frequency of the the tile, which you can get with `Poplar.TargetGetTileClockFrequency(target)` outside of the codelet.
The optional argument `description`, a literal `String`, can be used to print also a label to identify the timed expression.
A label is added automatically by [`@ipushowcycles`](@ref).
See also [`@ipuelapsed`](@ref).
This macro can be made no-op completely by setting
```julia
$(@__MODULE__).DISABLE_PRINT[] = true
```
"""
var"@ipucycles"
"""
@ipushowcycles ex
Print from inside a codelet the expression `ex` and the number of cycles spent to compute it.
This is useful when benchmarking multiple expression, to identify their contributions more easily.
The corresponding time can be obtained by dividing the number of cycles by the clock frequency of the the tile, which you can get with `Poplar.TargetGetTileClockFrequency(target)` outside of the codelet.
See also [`@ipucycles`](@ref), [`@ipuelapsed`](@ref).
This macro can be made no-op completely by setting
```julia
$(@__MODULE__).DISABLE_PRINT[] = true
```
"""
macro ipushowcycles(ex)
return quote
$(@__MODULE__).@ipucycles $(sprint(Base.show_unquoted, ex)) $(esc(ex))
end
end
"""
@ipuelapsed ex
Return number of cycles spent to compute the expression `ex`.
The corresponding time can be obtained by dividing the number of cycles by the clock frequency of the the tile, which you can get with `Poplar.TargetGetTileClockFrequency(target)` outside of the codelet.
See also [`@ipucycles`](@ref), [`@ipushowcycles`](@ref).
"""
macro ipuelapsed(ex)
return quote
local cycles_start = get_scount_l()
$(esc(ex))
local cycles_end = get_scount_l()
cycles_end - cycles_start
end
end
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 4089 | # NOTE: `VertexVector`s are distincts from `PoplarArrays` because they represent
# the variables you can add to a graph.
# Scope of the vectors in codelets. These singletons are used only for dispatch.
struct In end
struct Out end
struct InOut end
"""
VertexVector{T, S} <: AbstractVector{T}
This datatype formally represents vectors to be used in codelets (vertices) in IPU programs.
They are the counterpart of the [vertex vector types](https://docs.graphcore.ai/projects/poplar-user-guide/en/3.2.0/vertex_vectors.html) in the Poplar SDK.
The parameters of `VertexVector{T,S}` are
* `T`: the type of the elements of the vector, e.g. `Int32`, `Float32`, etc.;
* `S`: the scope of the vector in the codelet, `In`, `Out`, or `InOut`.
`VertexVector` is only meant to be used by end-user to define the arguments of codelets with the [`@codelet`](@ref) macro.
You should not try to manually instantiate or access the fields of a `VertexVector`.
For scalar arguments use [`VertexScalar`](@ref).
## Example
```julia
VertexVector{Float32, In} # input-only vector of `Float32` elements
VertexVector{Int32, Out} # output-only vector of `Int32` elements
VertexVector{UInt32, InOut} # input/output vector of `UInt32` elements
```
"""
struct VertexVector{T, S} <: AbstractVector{T}
base::Ptr{T}
length::UInt32
end
VertexVector{T,S}(::UndefInitializer, length::Int) where {T,S} =
VertexVector{T,S}(C_NULL, length)
function Base.setindex!(vec::VertexVector, f, i::Int)
unsafe_store!(vec.base, f, i)
end
function Base.getindex(vec::VertexVector, i::Int)
return unsafe_load(vec.base, i)
end
Base.size(t::VertexVector) = (t.length,)
function Base.size(t::VertexVector, d::Int)
if d <= 0
error("Dimension $(d) out of range")
elseif d == 1
return t.length
else
return 1
end
end
function Base.copyto!(dest::VertexVector, src::VertexVector)
for i in eachindex(dest, src)
dest[i] = src[i]
end
end
# TODO: significantly decreases codesize if set to false but might be actually needed sometimes
@inline function Base.mightalias(A::VertexVector, B::VertexVector)
return false
end
# In Julia v1.9 the default algorithm for sorting arrays requires a scratch area, but we
# can't use it on an IPU because it'd need to allocate an extra array, so let's default to
# the simple fully in-place `QuickSort`.
Base.Sort.defalg(::VertexVector) = QuickSort
# Simple methods, don't access the elements
Base.show(io::IO, x::VertexVector) = Base.show_default(io, x)
Base.show(io::IO, ::MIME"text/plain", x::VertexVector) = Base.show_default(io, x)
"""
VertexScalar{T, S}
This datatype formally represents scalars to be used in codelets (vertices) in IPU programs.
Technically, these are implemented as single-element tensors.
The parameters of `VertexScalar{T,S}` are
* `T`: the type of the scalar, e.g. `Int32`, `Float32`, etc.;
* `S`: the scope of the scalar in the codelet, `In`, `Out`, or `InOut`.
`VertexScalar` is only meant to be used by end-user to define the arguments of codelets with the [`@codelet`](@ref) macro.
You should not try to manually instantiate or access the fields of a `VertexScalar`.
Inside a codelet you can access and set the number by unwrapping it with `[]`.
For vector arguments use [`VertexVector`](@ref).
## Example
Examples of types
```julia
VertexScalar{Float32, In} # input-only `Float32` number
VertexScalar{Int32, Out} # output-only `Int32` number
VertexScalar{UInt32, InOut} # input/output `UInt32` number
```
Inside a codelet, let `x` have type `VertexScalar`, you can access its value if it has scope `In` or `InOut` with
```julia
@ipushow x[]
y = x[] / 3.14
```
If `x` has scope `Out` or `InOut` you can set its value with `x[] = ...`:
```julia
x[] = 3.14
```
"""
struct VertexScalar{T, S}
ptr::Ptr{T}
end
# Scalar arguments are implemented as single-element tensors
Base.getindex(s::VertexScalar{T,<:Union{In,InOut}}) where {T} = unsafe_load(s.ptr)
Base.setindex!(s::VertexScalar{T,<:Union{Out,InOut}}, x::T) where {T} = unsafe_store!(s.ptr, x)
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 687 | using Test
using CxxWrap
# We often want to check that some CxxWrap objects are not NULL.
macro cxxtest(ex)
return quote
local out = $(esc(ex))
Test.@test out.cpp_object != C_NULL
out
end
end
# https://giordano.github.io/blog/2019-05-03-julia-get-pointer-value/
dereference(T::DataType, ptr::Ptr) = unsafe_load(Ptr{T}(ptr))
dereference(T::DataType, ptr::CxxRef) = dereference(T, ptr.cpp_object)
dereference(T::DataType, ptr::Poplar.Type_Allocated) = dereference(T, ptr.cpp_object)
# Do we have access to hardware IPU? If not, we have to skip tests which don't
# work on IPU model.
const USE_HARDWARE_IPU = get(ENV, "GITHUB_ACTIONS", "false") != "true"
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 14157 | module IPUCompilerTest
# Whether bounds are always checked
const check_bounds = Base.JLOptions().check_bounds == 1
using Test
using IPUToolkit.IPUCompiler
using GPUCompiler: GPUCompiler
using IPUToolkit.Poplar
if Poplar.SDK_VERSION ≥ v"2.2.0" || !check_bounds
using Enzyme
using LinearAlgebra
using Statistics
end
if !check_bounds
using StaticArrays
end
# Silence progress spinners.
IPUCompiler.PROGRESS_SPINNER[] = false
include("common.jl")
∂(f, x) = first(first(autodiff_deferred(Reverse, f, Active(x))))
# Define a non-const variable which will lead to a reference to a literal pointer in the IR
# of a codelet below.
non_const_var::Float32 = 0f0
function test_compiler_program(device)
target = @cxxtest Poplar.DeviceGetTarget(device)
graph = @cxxtest Poplar.Graph(target)
# Define a local function to make sure macro hygiene is right
double(x) = x * 2
@codelet graph function TimesTwo(inconst::VertexVector{Float32, In}, outvec::VertexVector{Float32, Out})
outvec .= double.(inconst)
end
@codelet graph function Sort(invec::VertexVector{Float32, In}, outvec::VertexVector{Float32, Out})
copyto!(outvec, invec)
sort!(outvec)
end
@codelet graph function Sin(invec::VertexVector{Float32, In}, outvec::VertexVector{Float32, Out})
for idx in eachindex(outvec)
@inbounds outvec[idx] = sin(invec[idx])
end
end
@codelet graph function Print(pi::VertexScalar{Float32, In})
@ipuprint "Hello, world!"
@ipuprint "Titire tu" " patule" " recubans sub tegmine " "fagi"
@ipuprint "The Answer to the Ultimate Question of Life, the Universe, and Everything is " 42
x = Int32(7)
@ipushow x
@ipushow pi[]
end
# Test some invalid kernels
invalid_error = pkgversion(GPUCompiler) <= v"0.23" ? GPUCompiler.KernelError : GPUCompiler.InvalidIRError
@test_throws invalid_error @codelet graph f_access_out_scalar(x::VertexScalar{Float32, Out}) = @ipushow x[]
@test_throws invalid_error @codelet graph f_set_in_scalar(x::VertexScalar{Float32, In}) = x[] = 3.14f0
# This function would contain a reference to a literal pointer, likely an
# invalid memory address on the IPU.
@test_throws ErrorException @codelet graph literal_pointer(v::VertexVector{Float32,Out}) = v .= non_const_var
input = Float32[5, 2, 10, 102, -10, 2, 256, 15, 32, 100]
inconst = @cxxtest Poplar.GraphAddConstant(graph, input)
outvec1 = @cxxtest similar(graph, inconst, "outvec1");
outvec2 = @cxxtest similar(graph, inconst, "outvec2");
outvec3 = @cxxtest similar(graph, inconst, "outvec3");
prog = @cxxtest Poplar.ProgramSequence()
add_vertex(graph, prog, TimesTwo, inconst, outvec1)
add_vertex(graph, prog, Sort, outvec1, outvec2)
add_vertex(graph, prog, Sin, outvec2, outvec3)
add_vertex(graph, prog, Print, 3.14f0)
# Pass as codelet a function with more than one method
@test_throws ArgumentError add_vertex(graph, prog, +, outvec3)
# Pass wrong number of arguments to the codelet
@test_throws ArgumentError add_vertex(graph, prog, Print, outvec2, outvec3)
# Init some variables which will be used to read back from the IPU
# the results of some basic operations.
output_timestwo = similar(input)
Poplar.GraphCreateHostRead(graph, "timestwo-read", outvec1)
output_sort = similar(input)
Poplar.GraphCreateHostRead(graph, "sort-read", outvec2)
output_sin = similar(input)
Poplar.GraphCreateHostRead(graph, "sin-read", outvec3)
flags = @cxxtest Poplar.OptionFlags()
Poplar.OptionFlagsSet(flags, "debug.instrument", "true")
engine = @cxxtest Poplar.Engine(graph, prog, flags)
# Load and run the program, but capture the stderr, so that we can test that
# it contains what we expect.
pipe = Pipe()
redirect = USE_HARDWARE_IPU ? redirect_stderr : redirect_stdout
redirect(pipe) do
Poplar.EngineLoadAndRun(engine, device)
# Flush streams to make sure everything is printed out, especially
# important when using the IPU model.
Libc.flush_cstdio()
end
output = IOBuffer()
task = @async write(output, pipe)
close(pipe)
wait(task)
lines = split(String(take!(output)), '\n')
@test contains(lines[1], r"Hello, world!$")
@test contains(lines[2], r"Titire tu patule recubans sub tegmine fagi$")
@test contains(lines[3], r"The Answer to the Ultimate Question of Life, the Universe, and Everything is 42$")
@test contains(lines[4], r"x = 7$")
@test contains(lines[5], r"pi\[] = 3.140*$")
@test lines[end] == ""
# Read back some tensors and check the expected values.
Poplar.EngineReadTensor(engine, "timestwo-read", output_timestwo)
@test output_timestwo == 2 .* input
Poplar.EngineReadTensor(engine, "sort-read", output_sort)
@test output_sort == sort(output_timestwo)
Poplar.EngineReadTensor(engine, "sin-read", output_sin)
@test output_sin == sin.(output_sort)
Poplar.detach_devices()
end
function test_ipuprogram(device)
N = 15_000
input = randn(Float32, N)
outvec1 = PoplarVector{Float32}(undef, N)
outvec2 = PoplarVector{Float32}(undef, N)
outvec3 = PoplarVector{Float32}(undef, N)
outvec4 = PoplarVector{Float32}(undef, N)
outvec5 = PoplarVector{Float32}(undef, N)
f(x) = cos(x)
f′(x) = ∂(f, x)
g(x) = tan(x)
g′(x) = ∂(g, x)
@ipuprogram device begin
function TimesTwo(inconst::VertexVector{Float32, In}, outvec::VertexVector{Float32, Out})
outvec .= 2 .* inconst
end
function Scale(invec::VertexVector{Float32, In}, outvec::VertexVector{Float32, Out})
outvec .= invec
# `sum(abs2, v)` is layman norm because we can't statically compile
# `LinearAlgebra.norm!`.
outvec .*= sqrt(length(outvec) / sum(abs2, outvec))
end
function Exp(invec::VertexVector{Float32, In}, outvec::VertexVector{Float32, Out})
for idx in eachindex(outvec)
@inbounds outvec[idx] = exp(invec[idx])
end
end
function DiffCos(invec::VertexVector{Float32, In}, outvec::VertexVector{Float32, Out})
outvec .= f′.(invec)
end
function DiffTan(invec::VertexVector{Float32, In}, outvec::VertexVector{Float32, Out})
for idx in eachindex(outvec)
@inbounds outvec[idx] = g′(invec[idx])
end
end
TimesTwo(input, outvec1)
Scale(outvec1, outvec2)
Exp(outvec2, outvec3)
DiffCos(outvec3, outvec4)
DiffTan(outvec4, outvec5)
jl_outvec1 = outvec1
jl_outvec2 = outvec2
jl_outvec3 = outvec3
jl_outvec4 = outvec4
jl_outvec5 = outvec5
end
Poplar.detach_devices()
@test jl_outvec1 ≈ 2 .* input
@test norm(jl_outvec2) ≈ sqrt(N)
@test jl_outvec3 ≈ exp.(jl_outvec2)
@test jl_outvec4 ≈ @. -sin(jl_outvec3)
@test jl_outvec5 ≈ @. sec(jl_outvec4) ^ 2
end
function test_ipubuiltins(device)
N = 15_000
outvec1 = PoplarVector{Float16}(undef, N)
outvec2 = PoplarVector{Float16}(undef, N)
outvec3 = PoplarVector{Float16}(undef, N)
outvec4 = PoplarVector{Float16}(undef, N)
@ipuprogram device begin
function Random(out::VertexVector{Float16, Out})
for idx in eachindex(out)
out[idx] = rand(Float16)
end
end
function TimesTwoSin(in::VertexVector{Float16,In}, out::VertexVector{Float16, Out})
for idx in eachindex(in, out)
out[idx] = sin(2 * in[idx])
end
end
function Sort16(in::VertexVector{Float16,In}, out::VertexVector{Float16, Out})
copyto!(out, in)
sort!(out; rev=true)
end
function RandomNorm(out::VertexVector{Float16, Out})
for idx in eachindex(out)
out[idx] = randn(Float16)
end
end
Random(outvec1)
TimesTwoSin(outvec1, outvec2)
Sort16(outvec2, outvec3)
RandomNorm(outvec4)
jl_outvec1 = outvec1
jl_outvec2 = outvec2
jl_outvec3 = outvec3
jl_outvec4 = outvec4
end
Poplar.detach_devices()
# There's a non-zero probability that this test may fail, but assuming an
# average relative error of sqrt(N) / N, we multiply by `pi` to be somewhat
# safe (and `pi` is cool).
@test mean(jl_outvec1) ≈ 0.5 rtol=(pi * sqrt(N) / N)
@test jl_outvec2 ≈ sin.(2 .* jl_outvec1)
@test jl_outvec3 ≈ sort(jl_outvec2; rev=true)
@test mean(jl_outvec4) ≈ 0 atol=0.02
@test std(jl_outvec4) ≈ 1 rtol=0.02
end
rosenbrock(x, y=4) = (1 - x) ^ 2 + 100 * (y - x ^ 2) ^ 2
rosenbrock′(x) = ∂(rosenbrock, x)
# See Algorithm 1 at page 2 of https://arxiv.org/abs/1412.6980
function adam(∂f, x₀::T) where {T}
x = x₀
# Some constants
α = T(0.001) # learning rate
β₁ = T(0.9)
β₂ = T(0.999)
ϵ = T(1e-8)
# Momenta
m = zero(T)
v = zero(T)
# Stopping criteria
Δ = 10 * eps(T)
δ = one(T)
max_t = Int32(1_000_000)
t = one(max_t)
while abs(δ) > Δ && t ≤ max_t
g = ∂f(x)
m = β₁ * m + (1 - β₂) * g
v = β₂ * v + (1 - β₂) * g ^ 2
m̂ = m / (1 - β₁ ^ t)
v̂ = v / (1 - β₂ ^ t)
δ = α * m̂ / (√(v̂) + ϵ)
x -= δ
t += one(t)
end
return x
end
function test_adam(device)
input = collect(Float32.(-4:1:4))
output = PoplarVector{Float32}(undef, length(input))
@ipuprogram device begin
function AdamRosenbrock(in::VertexVector{Float32, In}, out::VertexVector{Float32, Out})
for idx in eachindex(out)
out[idx] = adam(rosenbrock′, in[idx])
end
end
AdamRosenbrock(input, output)
jl_output = output
end
Poplar.detach_devices()
@test all(isapprox.(jl_output, [repeat([-2], 4); repeat([2], 5)]; atol=2.6e-3))
end
function test_linalg(device)
N = 16
mat1 = randn(Float32, N)
mat2 = randn(Float32, N)
mul = PoplarVector{Float32}(undef, N)
inverse = PoplarVector{Float32}(undef, N)
@ipuprogram device begin
function LinAlg(in1::VertexVector{Float32, In}, in2::VertexVector{Float32, In}, mul::VertexVector{Float32, Out}, inverse::VertexVector{Float32, Out})
# Arguments can only be vectors, so we need to convert them to
# (static) matrices to do some linear algebra stuff. The conversion
# to `SMatrix` has an internal check about the shape/size of the
# to-be-converted array which would result in dynamic dispatch, we
# need to skip the check with `@inbounds`, but we need to be extra
# sure we're passing consistent data.
m1 = @inbounds SMatrix{4,4,Float32,16}(in1)
m2 = @inbounds SMatrix{4,4,Float32,16}(in2)
m1_m2 = m1 * m2
mul .= (m1_m2)[:]
inverse .= inv(m1_m2)[:]
end
LinAlg(mat1, mat2, mul, inverse)
jl_mul = mul
jl_inv = inverse
end
Poplar.detach_devices()
jl_mul = reshape(jl_mul, 4, 4)
@test reshape(mat1, 4, 4) * reshape(mat2, 4, 4) ≈ jl_mul
@test reshape(jl_inv, 4, 4) ≈ inv(jl_mul)
end
@testset "IPUCompiler" begin
programs = (test_compiler_program, test_adam, test_ipuprogram, test_linalg)
if USE_HARDWARE_IPU
# `test_ipubuiltins` tests IPU builtins which requires compiling for
# hardware IPU, not compatible with an IPU model.
programs = (programs..., test_ipubuiltins)
end
@testset "Test program: $(f)" for f in programs
function skip_test(f)
@warn """
Skipping IPUCompiler test $(f). To run this testset use
import Pkg; Pkg.test("IPUToolkit"; julia_args=`--check-bounds=auto`)
"""
@test_broken false
end
if Poplar.SDK_VERSION ≥ v"2.2.0" || !check_bounds
if f in (test_linalg,) && check_bounds
# * `test_linalg`: converting a `Vector` to `SMatrix` results
# into dynamic dispatch in the error path, this can be skipped
# with `@inbounds`, but `@inbounds` is no-op if we force
# bounds checks so we have no hope to run this nice test when
# using `--check-bounds=yes`.
skip_test(f)
else
device = @cxxtest if USE_HARDWARE_IPU
# Get a device
@test_logs((:info, r"^Trying to attach to device"),
(:info, r"^Successfully attached to device"),
match_mode=:any,
Poplar.get_ipu_device())
else
Poplar.get_ipu_model()
end
# Run a test program
f(device)
end
else
# With --check-bounds=yes GPUCompiler generates a function mentioning an undefined
# symbol `gpu_malloc`. Mark the test as broken until we sort this out. However
# this function is optimised away when compiling with `-O1` or higher, and for
# Poplar.SDK_VERSION ≥ v"2.2.0" we use `-O3`.
skip_test(f)
end
end
@testset "VertexVector" begin
vec = VertexVector{Float32, Out}(undef, 10)
@test vec.base == C_NULL
@test vec.length == 10
@test contains(repr(vec), r"VertexVector{Float32,.*Out}")
end
@testset "Printing to IPU" begin
# Printing is already tested in the program above, here we only check
# that disabling printing makes the `@ipu*` macros no-op.
IPUCompiler.DISABLE_PRINT[] = true
@test @macroexpand(@ipuprintf "Hello, world!") == :()
@test @macroexpand(@ipuprint "Hello, world!") == :()
@test @macroexpand(@ipushow x) == :()
# Restore `DISABLE_PRINT`
IPUCompiler.DISABLE_PRINT[] = false
end
end
end # module IPUCompilerTest
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 5028 | module PoplarTest
using Test
using IPUToolkit.Poplar
include("common.jl")
function test_poplar_program(device)
target = @cxxtest Poplar.DeviceGetTarget(device)
graph = @cxxtest Poplar.Graph(target)
Poplar.PopopsAddCodelets(graph)
v1 = @cxxtest Poplar.GraphAddVariable(graph, Poplar.FLOAT(), UInt64[2, 2], "v1")
@test_throws ArgumentError copyto!(graph, v1, [1, 2, 3, 4])
v2 = @cxxtest similar(graph, v1, "v2")
for i in 0:1
for j in 0:1
@graph begin
Poplar.GraphSetTileMapping(v1[i][j], i*2 + j)
Poplar.GraphSetTileMapping(v2[i][j], j*2 + i)
end
end
end
prog = @cxxtest Poplar.ProgramSequence()
h1 = Float32[1.0, 1.5, 2.0, 2.5]
h2 = Float32[4.0, 3.0, 2.0, 1.0]
# We want to exercise the use of `copyto!` (-> `Graph::setInitialValue`) on
# a tensor allocated with `Graph::addVariable`, but for some reason the test
# below would fail with older SDKs and on an IPU model, so in that case we
# use good ol' `Graph::AddConstant`.
if Poplar.SDK_VERSION < v"2.6" && !USE_HARDWARE_IPU
c1 = @cxxtest Poplar.GraphAddConstant(graph, h1)
else
c1 = @cxxtest Poplar.GraphAddVariable(graph, Poplar.FLOAT(), UInt64[4], "c1")
copyto!(graph, c1, h1)
end
c2 = @cxxtest Poplar.GraphAddConstant(graph, h2)
@graph begin
Poplar.GraphSetTileMapping(c1, 0)
Poplar.GraphSetTileMapping(c2, 0)
end
Poplar.ProgramSequenceAdd(prog, Poplar.ProgramCopy(c1, Poplar.TensorFlatten(v1)))
Poplar.ProgramSequenceAdd(prog, Poplar.ProgramCopy(c2, Poplar.TensorFlatten(v2)))
flags = @cxxtest Poplar.OptionFlags()
v3 = @cxxtest Poplar.PopopsAdd(graph, v1, v2, prog, "Add", flags)
v4 = @cxxtest Poplar.PopopsAdd(graph, v3, v2, prog, "Add", flags)
v5 = @cxxtest Poplar.PopopsAdd(graph, v1, Poplar.TensorTranspose(v2), prog, "Add", flags)
# Init some variables which will be used to read back from the IPU
# (model) the results of some basic operations.
h3 = zeros(Float32, 4)
h4 = zeros(Float32, 4)
h5 = zeros(Float32, 4)
@graph begin
Poplar.GraphCreateHostRead("v3-read", v3)
Poplar.GraphCreateHostRead("v4-read", v4)
Poplar.GraphCreateHostRead("v5-read", v5)
end
engine = @cxxtest Poplar.Engine(graph, prog, flags)
Poplar.EngineLoadAndRun(engine, device)
# Read back some tensors and check the expected values.
Poplar.EngineReadTensor(engine, "v3-read", h3)
@test h3 == h1 + h2
Poplar.EngineReadTensor(engine, "v4-read", h4)
@test h4 == h3 + h2
Poplar.EngineReadTensor(engine, "v5-read", h5)
# TODO: try to write this test in terms of the other tensors.
@test h5 == Float32[5.0, 3.5, 5.0, 3.5]
# Release the device at the end of the program
Poplar.DeviceDetach(device)
end
@testset "Poplar" begin
@cxxtest Poplar.Tensor()
@testset "Device manager" begin
dm = Poplar.DeviceManager()
@test Poplar.DeviceManagerGetNumDevices(dm) > 0
end
# Make sure that dereferencing the types pointers gives a non-totally-useless value.
@testset "Types" begin
@testset "$(type)" for type in (:BOOL, :CHAR, :UNSIGNED_CHAR, :SIGNED_CHAR,
:UNSIGNED_SHORT, :SHORT, :UNSIGNED_INT, :INT,
:UNSIGNED_LONG, :LONG, :UNSIGNED_LONGLONG,
:LONGLONG, :HALF, :FLOAT)
@test dereference(Cint, getfield(Poplar, type)()) != 0
end
end
# Test a simple program using a software-emulated IPU (IPU model)
@testset "IPU Model" begin
device = @cxxtest Poplar.get_ipu_model()
test_poplar_program(device)
end
# Same test, but with a real IPU
USE_HARDWARE_IPU && @testset "Hardware IPU" begin
# Make sure `get_ipu_devices` works when you request 0 devices.
device = @test_logs (:info, r"^Attached to devices with IDs [\w\d]+\[\]") Poplar.get_ipu_devices(0)
@test isempty(device)
# Simple test for `get_ipu_devices` with a range as second argument.
Poplar.DeviceDetach.(@test_logs((:info, r"^Trying to attach to device 0..."),
match_mode=:any,
Poplar.get_ipu_devices(1, 0:0)))
# Couldn't attach to all requested devices
@test_logs((:warn, "Requested 2 devices, but could attach only to 0"),
(:info, r"^Attached to devices with IDs [\w\d]+\[\]"),
Poplar.get_ipu_devices(2, 0:-1))
# Get a device
device = @cxxtest @test_logs((:info, r"^Trying to attach to device"),
(:info, r"^Successfully attached to device"),
match_mode=:any,
Poplar.get_ipu_device())
# Run a test program
test_poplar_program(device)
end
end
end # module PoplarTest
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | code | 44 | include("poplar.jl")
include("compiler.jl")
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | docs | 2162 | # IPUToolkit.jl
[](https://juliaipu.github.io/IPUToolkit.jl/stable)
[](https://juliaipu.github.io/IPUToolkit.jl/dev)
[](https://github.com/JuliaIPU/IPUToolkit.jl/actions/workflows/ci.yml)
This package allows you to interface the [Intelligence Processing Unit (IPU) by Graphcore](https://www.graphcore.ai/products/ipu) using the [Julia programming language](https://julialang.org/).
***Disclaimer**: at the moment this is package is in a proof-of-concept stage, not suitable for production usage.*
## Usage and documentation
The package is called `IPUToolkit` because it provides different tools to interface the IPU from Julia:
* you can use functionalities in the [Poplar SDK](https://www.graphcore.ai/products/poplar);
* you can use Julia's code generation capabilities to automatically compile native code that can be run on the IPU;
* there is a small [embedded Domain-Specific Language](https://en.wikipedia.org/wiki/Domain-specific_language) (eDSL) to automatically generate the code of a program.
These approaches are exploratory of the functionalities, and are often limited in scope and are described in more details in the [documentation](https://juliaipu.github.io/IPUToolkit.jl/).
For examples of usage of this package, see the [`examples/`](https://github.com/JuliaIPU/IPUToolkit.jl/tree/main/examples) directory of the official repository.
## Talks and demos
Here is some material that you may find useful for learning more about Julia on the IPU and trying it out yourself:
* [Pluto notebook](https://giordano.github.io/blog/2023-07-20-julia-ipu/) of presentation given at Graphcore and at JuliaCon in July 2023
* Talk "[Julia meets the Intelligence Processing Unit](https://www.youtube.com/watch?v=-fxB0kmcCVE)" at JuliaCon 2023
* Talk "[Automatic differentiation on the IPU with Enzyme.jl](https://giordano.github.io/talks/2024-03-27-julia-ipu-enzymecon/)" at [EnzymeCon 2024](https://enzyme.mit.edu/conference)
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | docs | 9131 | # Writing codelets in Julia
The `IPUToolkit.IPUCompiler` submodule allows you to write [codelets](https://docs.graphcore.ai/projects/poplar-user-guide/en/3.2.0/vertices_overview.html) for the IPU in Julia.
Codelets are defined with the [`@codelet`](@ref) macro, and then you can use them inside a program, written using the interface to the Poplar SDK described before.
This mechanism uses the [`GPUCompiler.jl`](https://github.com/JuliaGPU/GPUCompiler.jl) package, which is a generic framework for generating LLVM IR code for specialised targets, not limited to GPUs despite the historical name.
Examples of codelets written in Julia are shown in the files [`examples/main.jl`](https://github.com/JuliaIPU/IPUToolkit.jl/blob/main/examples/main.jl), [`examples/pi.jl`](https://github.com/JuliaIPU/IPUToolkit.jl/blob/main/examples/pi.jl), [`examples/adam.jl`](https://github.com/JuliaIPU/IPUToolkit.jl/blob/main/examples/adam.jl), [`examples/diffeq.jl`](https://github.com/JuliaIPU/IPUToolkit.jl/blob/main/examples/diffeq.jl).
The code inside a codelet has the same limitations as all the compilation models based on [`GPUCompiler.jl`](https://github.com/JuliaGPU/GPUCompiler.jl):
* the code has to be statically inferred and compiled, dynamic dispatch is not admitted;
* you cannot use functionalities which require the Julia runtime, most notably the garbage collector;
* you cannot call into any other external binary library at runtime, for example you cannot call into a BLAS library.
After defining a codelet with `@codelet` you can add a vertex calling this codelet to the graph with the function [`add_vertex`](@ref), which also allows controlling the tile mapping in a basic way, or `Poplar.GraphAddVertex`.
```@docs
@codelet
VertexVector
VertexScalar
add_vertex
IPUCompiler.TARGET_COLOSSUS
IPUCompiler.KEEP_LLVM_FILES
IPUCompiler.POPC_FLAGS
IPUCompiler.PROGRESS_SPINNER
```
## IPU builtins
Inside codelets defined with [`@codelet`](@ref) all calls to random functions
* `rand(Float16)`
* `rand(Float32)`
* `rand(UInt32)`
* `rand(UInt64)`
* `randn(Float16)`
* `randn(Float32)`
result to call to corresponding IPU builtins for [random number generation](https://docs.graphcore.ai/projects/poplar-api/en/latest/ipu_intrinsics/ipu_builtins.html#random-number-generation).
The uniformly distributed numbers follow the general semantic of the Julia function `rand` (floating point numbers are uniformely distributed in the $[0, 1)$ range), while the normally distributed numbers have the properties described in the Poplar SDK documentation (numbers are in the range $[-93/16, 93/16]$).
!!! note
The IPU builtins for random numbers return pairs of numbers, but the Julia functions `randn(Float16)` and `randn(Float32)` return only a single number, discarding the second number of the pair.
If you have a vector of even length that you want to fill in-place with normally distributed numbers, you can use the [`randn2!`](@ref) function to do that efficiently, without discarding any number.
Additionally, you can use the [IPU builtins](https://docs.graphcore.ai/projects/poplar-api/en/latest/ipu_intrinsics/ipu_builtins.html) listed below.
```@docs
get_scount_l
get_tile_id
randn2!
```
## Printing
Inside codelets you can print text and value of variables using the macros [`@ipuprintf`](@ref), [`@ipuprint`](@ref), [`@ipuprintln`](@ref), and [`@ipushow`](@ref).
These macros are useful for debugging purposes but printing inside a codelet might incur performance penalty.
To completely disable all printing and make these macros no-op you can set [`IPUCompiler.DISABLE_PRINT`](@ref):
```julia
IPUCompiler.DISABLE_PRINT[] = true
```
```@docs
@ipuprintf
@ipuprint
@ipuprintln
@ipushow
IPUCompiler.DISABLE_PRINT
```
## Benchmarking
To benchmark expressions inside codelets you can use the macros [`@ipucycles`](@ref), [`@ipushowcycles`](@ref), and [`@ipuelapsed`](@ref), which report the number of cycles spent in the wrapped expression.
They are similar to Julia's `@time`, `@showtime`, and `@elapsed` macros, but report the number of cycles, as the clockspeed of tiles cannot be easily obtained _inside_ a codelet.
The corresponding time can be obtained by dividing the number of cycles by the clock frequency of the the tile, which you can get with [`Poplar.TargetGetTileClockFrequency(target)`](https://docs.graphcore.ai/projects/poplar-api/en/latest/poplar/device/Target.html#_CPPv4NK6poplar6Target21getTileClockFrequencyEv) outside of the codelet, and should usually be 1.330 GHz or 1.850 GHz depending on the model of your IPU.
The printing macros `@ipucycles` and `@ipushowcycles` can be made completely no-op by setting [`IPUCompiler.DISABLE_PRINT`](@ref).
!!! warning
Timing of expressions taking longer than `typemax(UInt32) / tile_clock_frequency` (about 2 or 3 seconds depending on your IPU model) is unreliable because the difference between the starting and the ending cycle counts would overflow.
Note also that the `Poplar.TargetGetTileClockFrequency(target)` function [may not return a reliable value](https://github.com/UoB-HPC/ipu-hpc-cookbook/blob/96a37c2f7c745fb4e1ca0bc12fa68fe39df067a7/timing-program-execution/README.md#using-counters-on-the-ipu), but this is an upstream bug (this has been observed at least up to Poplar SDK v3.0).
You may have to use tools like `gc-monitor`, `gc-inventory`, or `gc-info --device-id <N> --tile-clock-speed` to obtain the correct tile clock frequency.
```@docs
@ipucycles
@ipushowcycles
@ipuelapsed
```
## Passing non-constant variables from global scope
If your kernel references a non-constant (`const`) global variable, the generated code will result in a reference to a memory address on the host, and this will fatally fail at runtime because programs running on the IPU don't have access to the host memory.
Constant variables are not affected by this problem because their values are inlined when the function is compiled.
If you can't or don't want to make a variable constant you can interpolate its value with a top-level [`@eval`](https://docs.julialang.org/en/v1/base/base/#Base.@eval) when defining the codelet.
For example:
```julia
using IPUToolkit.IPUCompiler, IPUToolkit.Poplar
device = Poplar.get_ipu_device()
target = Poplar.DeviceGetTarget(device)
graph = Poplar.Graph(target)
tile_clock_frequency = Poplar.TargetGetTileClockFrequency(target)
@eval @codelet graph function test(invec::VertexVector{Float32, In}, outvec::VertexVector{Float32, Out})
# We can use the intrinsic `get_scount_l` to get the cycle counter right
# before and after some operations, so that we can benchmark it.
cycles_start = get_scount_l()
# Do some operations here...
cycles_end = get_scount_l()
# Divide the difference between the two cycle counts by the tile frequency
# clock to get the time.
time = (cycles_end - cycles_start) / $(tile_clock_frequency)
# Show the time spent doing your operations
@ipushow time
end
```
The use of `@eval` allows you not to have to pass an extra argument to your kernel just to use the value of the variable inside the codelet.
## Debugging compilation errors in codelets
Writing codelets for the IPU takes some practice, because you cannot use any arbitrary construct or package as you would normally do when running code on a CPU.
As mentioned above, codelets have to be statically compiled with `GPUCompiler.jl`, with all the limitations of this framework, which can only use a subset of the Julia language.
Therefore, it happens frequently that you run into compilation errors while developing a codelet function, and you have then to resolve the issues, which usually involves removing [dynamic dispatch](https://en.wikipedia.org/wiki/Dynamic_dispatch) calls (which would require the JIT compiler at runtime), resolving [type-instabilities](https://docs.julialang.org/en/v1/manual/performance-tips/#Write-%22type-stable%22-functions), [avoiding memory allocations](https://docs.julialang.org/en/v1/manual/performance-tips/#Measure-performance-with-[@time](@ref)-and-pay-attention-to-memory-allocation), etc...
If you have [`Cthulhu.jl`](https://github.com/JuliaDebug/Cthulhu.jl) installed, you can set [`IPUCompiler.DEBUG_COMPILATION_ERRORS`](@ref) to `true` to automatically open an interactive shell when compiling a codelet results into invalid LLVM IR, to more easily debug the codelet code.
We suggest again taking a look at the code samples in the [`examples/`](https://github.com/JuliaIPU/IPUToolkit.jl/tree/main/examples) directory for learning how to write working IPU codelets in Julia.
```@docs
IPUCompiler.DEBUG_COMPILATION_ERRORS
```
## Domain-Specific Language: `@ipuprogram`
The `IPUCompiler.@ipuprogram` macro provides a very simple and limited DSL to automatically generate most of the boilerplate code needed when writing an IPU program.
You can do *very* little with this DSL, which is mainly a showcase of Julia's meta-programming capabilities.
A fully commented examples of use of the `@ipuprogram` macro is available in the [`examples/dsl.jl`](https://github.com/JuliaIPU/IPUToolkit.jl/blob/main/examples/dsl.jl) file.
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | docs | 4686 | # IPUToolkit.jl
[`IPUToolkit.jl`](https://github.com/JuliaIPU/IPUToolkit.jl) allows you to interface the [Intelligence Processing Unit (IPU) by Graphcore](https://www.graphcore.ai/products/ipu) using the [Julia programming language](https://julialang.org/).
The main motivation for this project is to explore Julia's introspection and metaprogramming capabilities to write high-level code for the IPU using an alternative method to the tools developed by Graphcore, and leverage code-generation through LLVM to generate efficient code for the device: also the IPU compiler is based on this framework, so the LLVM IR constitutes a common language between Julia and the IPU compiler.
!!! warning "Disclaimer"
This effort is not officially endorsed by Graphcore, although we gracefully received help through the public Graphcore support channels.
This package is currently a proof-of-concept, not suitable for production usage.
Its API may be subject to frequent development and breaking changes.
This package was initially created by Emily Dietrich and Luk Burchard, and later expanded by Mosè Giordano.
[Mosè](https://github.com/giordano)'s work on this package was funded by [UCL Centre for Advance Research Computing](https://www.ucl.ac.uk/advanced-research-computing).
## Requirements
This package requires
* Julia v1.6+ (currently tested up to Julia v1.10),
* the Poplar SDK v1.3 or v2.0-v3.2 including the `popc` compiler,
* a C++ compiler supporting C++17 standard for compiling the wrapper around the Poplar SDK (e.g. G++ 9 or following releases).
Other versions of the Poplar SDK are not currently supported.
!!! note "Compatibility between Julia and Poplar SDK"
Both Julia and the Poplar SDK are coupled to a specific version of the LLVM compiler framework, and you will need to match a specific version of the Poplar SDK with a version of Julia using the same major version of LLVM.
For example
* the Poplar SDK version 2.2 uses LLVM 13, which is available in Julia v1.8;
* the Poplar SDK versions 2.3-2.5 use LLVM 14, which is available in Julia v1.9;
* the Poplar SDK versions 2.6-3.2 use LLVM 15, which is available in Julia v1.10;
* the Poplar SDK version 3.3 uses LLVM 16, which is available in Julia v1.11 (NOTE: this combination has ***not*** been tested yet and is likely not to work at the moment).
## Installation
To install the package, run the commands
```julia
using Pkg
Pkg.add("IPUToolkit")
```
You will need to build the wrapper around the Poplar SDK.
This should happen automatically the first time you install the package, in any case you can run it with
```julia
Pkg.build()
```
This step requires a C++ compiler supporting C++17 standard.
You have to set the compiler with the `CXX` environment variable, this can be either its absolute path or simply its name if it is in the [`PATH`](https://en.wikipedia.org/wiki/PATH_(variable)) environment variable.
The compiler must be able to find Poplar header files automatically, depending on your installation of the Poplar SDK you may have to add its `include/` directory to the [`CPATH`](https://gcc.gnu.org/onlinedocs/cpp/Environment-Variables.html) environment variable, but this should be done automatically by the script to activate a Poplar SDK.
!!! note
Compiling the wrapper around the Poplar SDK will take several minutes (up to about 7 minutes, depending on the Poplar version), without printing any progress to screen.
Hold on.
## Usage
The package is called IPUToolkit because it provides different tools to interface the IPU from Julia:
* you can use functionalities in the [Poplar SDK](https://www.graphcore.ai/products/poplar);
* you can use Julia's code generation capabilities to automatically compile native code that can be run on the IPU;
* there is a small [embedded Domain-Specific Language](https://en.wikipedia.org/wiki/Domain-specific_language) (eDSL) to automatically generate the code of a program.
These approaches are exploratory of the functionalities, and are often limited in scope and are described in more details in the following sections.
## Talks and demos
Here is some material that you may find useful for learning more about Julia on the IPU and trying it out yourself:
* [Pluto notebook](https://giordano.github.io/blog/2023-07-20-julia-ipu/) of presentation given at Graphcore and at JuliaCon in July 2023
* Talk "[Julia meets the Intelligence Processing Unit](https://www.youtube.com/watch?v=-fxB0kmcCVE)" at JuliaCon 2023
* Talk "[Automatic differentiation on the IPU with Enzyme.jl](https://giordano.github.io/talks/2024-03-27-julia-ipu-enzymecon/)" at [EnzymeCon 2024](https://enzyme.mit.edu/conference)
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | docs | 4607 | # Interfacing the Poplar SDK
A quick example of use of the Poplar SDK functionalities, available in the `IPUToolkit.Poplar` submodule:
```julia
julia> using IPUToolkit.Poplar
julia> dm = Poplar.DeviceManager();
julia> Int(Poplar.DeviceManagerGetNumDevices(dm))
129
julia> device = Poplar.get_ipu_device();
[ Info: Trying to attach to device 0...
[ Info: Successfully attached to device 0
julia> Int(Poplar.DeviceGetId(device))
0
julia> Poplar.detach_devices()
```
A couple of basic examples of programs running on the IPU written using the interface to the Poplar SDK are available in the files [`examples/tutorial1.jl`](https://github.com/JuliaIPU/IPUToolkit.jl/blob/main/examples/tutorial1.jl) and [`examples/tutorial2.jl`](https://github.com/JuliaIPU/IPUToolkit.jl/blob/main/examples/tutorial2.jl).
We automatically generate the bindings of the Poplar SDK using [`Clang.jl`](https://github.com/JuliaInterop/Clang.jl) and [`CxxWrap.jl`](https://github.com/JuliaInterop/CxxWrap.jl).
There is not automatic documentation at the moment, but functions can be accessed from the `Poplar` submodule.
Also, the `IPUToolkit.Poplar` submodule wraps a subset of the functionalities available in the Poplar SDK, do not expect to be able to use all functionalities.
Remember that Julia does not use class-based object-oriented programming, class instances will usually be first arguments of the methods you want to use.
Function naming convention and signature is usually as follows:
* class name in [CamelCase](https://en.wikipedia.org/wiki/Camel_case), followed by method name also in CamelCase. Note that first letter of method name is always uppercase in this naming convention, even if it is lowercase in the Poplar SDK. For example, the method `getNumDevices` of the `DeviceManager` class can be accessed in the `Poplar` submodule with `Poplar.DeviceManagerGetNumDevices`;
* the first argument of the function is the class instance. For example, to use the Julia function `Poplar.DeviceManagerGetNumDevices`, you need to pass as first argument an instance of `DeviceManager`;
* the following arguments are the same as in the method you want to use in the SDK. For example, the method `getNumDevices` of the `DeviceManager` class doesn't take any argument, so the Julia function `Poplar.DeviceManagerGetNumDevices` will take an instance of `DeviceManager` as *only* argument.
## Convenient methods
In addition to this, for some functions (e.g. `EngineWriteTensor`, `EngineConnectStream`, `EngineReadTensor`) we provide more user-friendly methods where the last argument can be a Julia's `Array`, without having to pass additional arguments for pointers or array size.
Furthermore, the custom functions [`Poplar.get_ipu_device`](@ref) and [`Poplar.get_ipu_devices`](@ref) can be used to access one more IPU devices, as shown in the example above.
Another function for which we provide a convenient method is `Poplar.GraphAddConstant`:
```julia
Poplar.GraphAddConstant(graph, host_array)
```
adds the `host_array` (a plain standard Julia `Array` living on the host) to `graph`, automatically inferring from `host_array` the type and the shape of the tensor in the graph.
This works also with `host_array::Array{Float16}`.
You can slice a tensor with the usual Julia notation `tensor[index1:index2]`, this corresponds to a call to [`Tensor.slice(index1, index2+1)`](https://docs.graphcore.ai/projects/poplar-api/en/latest/poplar/graph/Tensor.html#_CPPv4NK6poplar6Tensor5sliceENSt6size_tENSt6size_tE).
[`similar`](@ref) can be used to add to `graph` a tensor with the same shape and optionally element type as `tensor`, while [`copyto!`](@ref) can be used to copy elements of a CPU host array into an IPU tensor.
## Using `IPUToolkit.jl` without an IPU
While this package requires a physical IPU to use all the available features, you can still experiment with the IPU programming model even if you do not have access to a hardware IPU.
The Poplar SDK provides a feature called IPU Model, which is a software emulation of the behaviour of the IPU hardware.
While the IPU model comes with [some limitations](https://docs.graphcore.ai/projects/poplar-user-guide/en/latest/poplar_programs.html#programming-with-poplar), it can be useful for testing or debugging.
To use the IPU model in `IPUToolkit.jl`, define the device of your IPU program with [`Poplar.get_ipu_model`](@ref):
```julia
device = Poplar.get_ipu_model()
# Then the rest of the program continues as usual
target = Poplar.DeviceGetTarget(device)
graph = Poplar.Graph(target)
# ...
```
```@autodocs
Modules = [IPUToolkit.Poplar]
```
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | docs | 3113 | problem: libpoplar which is needed to interface with ipus (setup data-flow, upload codelets to ipu, ...) only offers a c++ api
projects offering binding to c++ code: Cxx.jl and CxxWrap.jl
Cxx.jl:
* write c++ code inside of julia code
* can directly call into c++ libraries and pass values from julia
+ \+ easy to use
+ \+ doesn't need any additional setup
+ \+ allows more complex c++ snippets
- \- (big one) does not work on current julia
- \- passing values from julia to c++ can be annoying
- \- requires users to write c++ code themselves, no longer pure julia code
CxxWrap.jl:
* bindings are defined from c++ code and compiled to shared library to be loaded by julia
* on julia side everything is pure julia
* \+ no c++ knowledge by endusers required
+ \+ clean interface for programmers
+ \+ comes with integration for various standard c++ data types
- \- every function/constant needs to be manually defined on c++ side
- \- on changes on the c++ side a (potentially huge) library needs to be recompiled
- \- a lot of modern c++ features do not integrate well
Updating cxx.jl would a lot of effort (other people have tried and failed and julia has substantially changed since the last version of cxx.jl released)
CxxWrap approach needs bindings
Manually crafting all bindings would be both a lot of effort (lots of functions)
~~handcrafted boring~~
much more likely to break on updates
- Want to automatically generate c++ side of bindings
- need (libpoplar specific) way to parse c++ headers and generate c++ bindings for them
approach: use Clang.jl (julia libclang) to parse c++ headers (similar: https://github.com/TakekazuKATO/OpenCV.jl/blob/master/generateWrapper.jl)
process:
- Resolve header locations of all the headers which are supposed to get parsed
- parse headers with libclang (clang.jl for julia bindings)
- iterate over the clang abstract syntax tree
- filter out all members which dont belong to poplib namespaces
- generate the cxxwrap c++ code needed to define the binding for relevant member types (class decl, function decl, enum decl, inheritance, ...) (that's the big part)
- compile generated code (templated into handcrafted template.cpp) to shared library (to be loaded by cxxwrap)
- shared library loadable through cxxwrap library
- small additions in handcrafted julia code (nicer ipu management)
problems/hacks:
c++ is big complex language with loads of features which aren't directly supported by cxxwrap which means a lot of functions can't be directly wrapped direcltly with cxxwrap -> generate lambdas instead of passing function directly into cxxwrap
poplar array and string types are different from julia arrays, need to be automatically converted -> convert poplar array types from and to julia arrays automatically
optional parameters aren't directly supported by cxxwrap -> generate multiple function definitions (for all possible combinations of existing/not existing optional parameters)
virtual classes(?) can't be dealocated by cxxwrap properly -> (bad) auto-applied hotfix of cxxwrap to disable calling the dealocator on those types
| IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 1.6.2 | 252cd6243b0780158a2f7e259aefea9e16f965aa | docs | 1909 | skip_empty_classdecl: skips class declarations without a body
insufficient_access: element is private private or protected
constructor_missing_class: skips constructors which don't belong to a "normal" class/struct
ostream_blacklist: skips if arguments contain ostreams as they can't be copied which messes with cxxwrap
istream_blacklist: skips if arguments contain istreams as they can't be copied which messes with cxxwrap
rvalue_unsupported: skips if arguments contain rvalue references as they aren't supported by cxxwrap
unique_ptr_blacklist: skips if arguments contain a unique_pointer as they aren't supported by cxxwrap
default_constructor: skips if the contructor is the default constructor (no arguments) because cxxwrap automatically generates it
deleted_method: skips deleted methods (`func(int i) = delete;`)
operator_unsupported: skips if this method is overloading an operator
getimpl_blacklist: skips functions named "getImpl" or "getPImpl" as those return incomplete classes in poplar libraries which are unsupported in cxxwrap
calls_deleted_function: skips functions which attempt to call deleted functions (currently hardcoded)
unsupported_template: skips functions with templated arguments that aren't of type ArrayRef<T>
skip_compiler_definitions: skips compiler definitions
header_blacklisted: header has been explicitly blacklisted
not_allowed_namespace: namespace of node isn't in the whitelist
fieldata_size_blacklist: workaround to a specific function (poplar::FieldData::SizeT::size) being defined the same way twice(?)
expr_blacklisted: explicitly blacklist poplar expressions due to them using unsupported c++ features
equivalent_device_type_blacklist: explicitly blacklist poplar `equivalent_device_type` as it's using unsupported c++ features
getdevices_blacklist: explicitly blacklists the `getDevices` function as it returns a vector of incomplete classes | IPUToolkit | https://github.com/JuliaIPU/IPUToolkit.jl.git |
|
[
"MIT"
] | 0.15.7 | 3b1dcbf62e469a67f6733ae493401e53d92ff543 | code | 1203 | module StatsPlots
using Reexport
import RecipesBase: recipetype
import Tables
import TableOperations
using RecipesPipeline
@reexport using Plots
import Plots: _cycle
using Plots.PlotMeasures
using StatsBase
using Distributions
using LinearAlgebra: eigen, diagm
using Widgets, Observables
import Observables: AbstractObservable, @map, observe
import Widgets: @nodeps
import DataStructures: OrderedDict
import Clustering: Hclust, nnodes
using Interpolations
using MultivariateStats: MultivariateStats
using AbstractFFTs: fft, ifft
import KernelDensity
using NaNMath
@recipe f(k::KernelDensity.UnivariateKDE) = k.x, k.density
@recipe f(k::KernelDensity.BivariateKDE) = k.x, k.y, permutedims(k.density)
@shorthands cdensity
export @df, dataviewer
include("df.jl")
include("interact.jl")
include("corrplot.jl")
include("cornerplot.jl")
include("distributions.jl")
include("boxplot.jl")
include("dotplot.jl")
include("violin.jl")
include("ecdf.jl")
include("hist.jl")
include("marginalhist.jl")
include("marginalscatter.jl")
include("marginalkde.jl")
include("bar.jl")
include("dendrogram.jl")
include("andrews.jl")
include("ordinations.jl")
include("covellipse.jl")
include("errorline.jl")
end # module
| StatsPlots | https://github.com/JuliaPlots/StatsPlots.jl.git |
|
[
"MIT"
] | 0.15.7 | 3b1dcbf62e469a67f6733ae493401e53d92ff543 | code | 1574 | @userplot AndrewsPlot
"""
andrewsplot(args...; kw...)
Shows each row of an array (or table) as a line. The `x` argument specifies a
grouping variable. This is a way to visualize structure in high-dimensional data.
https://en.wikipedia.org/wiki/Andrews_plot
#Examples
```julia
using RDatasets, StatsPlots
iris = dataset("datasets", "iris")
@df iris andrewsplot(:Species, cols(1:4))
```
"""
andrewsplot
@recipe function f(h::AndrewsPlot)
if length(h.args) == 2 # specify x if not given
x, y = h.args
else
y = h.args[1]
x = ones(size(y, 1))
end
seriestype := :andrews
# series in a user recipe will have different colors
for g in unique(x)
@series begin
label := "$g"
range(-π, stop = π, length = 200), Surface(y[g .== x, :]) #surface needed, or the array will be split into columns
end
end
nothing
end
# the series recipe
@recipe function f(::Type{Val{:andrews}}, x, y, z)
y = y.surf
rows, cols = size(y)
seriestype := :path
# these series are the lines, will keep the same colors
for j = 1:rows
@series begin
primary := false
ys = zeros(length(x))
terms =
[isodd(i) ? cos((i ÷ 2) .* ti) : sin((i ÷ 2) .* ti) for i = 2:cols, ti in x]
for ti in eachindex(x)
ys[ti] = y[j, 1] / sqrt(2) + sum(y[j, i] .* terms[i - 1, ti] for i = 2:cols)
end
x := x
y := ys
()
end
end
x := []
y := []
()
end
| StatsPlots | https://github.com/JuliaPlots/StatsPlots.jl.git |
|
[
"MIT"
] | 0.15.7 | 3b1dcbf62e469a67f6733ae493401e53d92ff543 | code | 2527 | @userplot GroupedBar
recipetype(::Val{:groupedbar}, args...) = GroupedBar(args)
Plots.group_as_matrix(g::GroupedBar) = true
grouped_xy(x::AbstractVector, y::AbstractArray) = x, y
grouped_xy(y::AbstractArray) = 1:size(y, 1), y
@recipe function f(g::GroupedBar; spacing = 0)
x, y = grouped_xy(g.args...)
nr, nc = size(y)
isstack = pop!(plotattributes, :bar_position, :dodge) === :stack
isylog = pop!(plotattributes, :yscale, :identity) ∈ (:log10, :log)
the_ylims = pop!(plotattributes, :ylims, (-Inf, Inf))
# extract xnums and set default bar width.
# might need to set xticks as well
xnums = if eltype(x) <: Number
xdiff = length(x) > 1 ? mean(diff(x)) : 1
bar_width --> 0.8 * xdiff
x
else
bar_width --> 0.8
ux = unique(x)
xnums = (1:length(ux)) .- 0.5
xticks --> (xnums, ux)
xnums
end
@assert length(xnums) == nr
# compute the x centers. for dodge, make a matrix for each column
x = if isstack
x
else
bws = plotattributes[:bar_width] / nc
bar_width := bws * clamp(1 - spacing, 0, 1)
xmat = zeros(nr, nc)
for r = 1:nr
bw = _cycle(bws, r)
farleft = xnums[r] - 0.5 * (bw * nc)
for c = 1:nc
xmat[r, c] = farleft + 0.5bw + (c - 1) * bw
end
end
xmat
end
fill_bottom = if isylog
if isfinite(the_ylims[1])
min(minimum(y) / 100, the_ylims[1])
else
minimum(y) / 100
end
else
0
end
# compute fillrange
y, fr =
isstack ? groupedbar_fillrange(y) :
(y, get(plotattributes, :fillrange, [fill_bottom]))
if isylog
replace!(fr, 0 => fill_bottom)
end
fillrange := fr
seriestype := :bar
x, y
end
function groupedbar_fillrange(y)
nr, nc = size(y)
# bar series fills from y[nr, nc] to fr[nr, nc], y .>= fr
fr = zeros(nr, nc)
y = copy(y)
y[.!isfinite.(y)] .= 0
for r = 1:nr
y_neg = 0
# upper & lower bounds for positive bar
y_pos = sum([e for e in y[r, :] if e > 0])
# division subtract towards 0
for c = 1:nc
el = y[r, c]
if el >= 0
y[r, c] = y_pos
y_pos -= el
fr[r, c] = y_pos
else
fr[r, c] = y_neg
y_neg += el
y[r, c] = y_neg
end
end
end
y, fr
end
| StatsPlots | https://github.com/JuliaPlots/StatsPlots.jl.git |
|
[
"MIT"
] | 0.15.7 | 3b1dcbf62e469a67f6733ae493401e53d92ff543 | code | 7911 |
# ---------------------------------------------------------------------------
# Box Plot
notch_width(q2, q4, N) = 1.58 * (q4 - q2) / sqrt(N)
@recipe function f(
::Type{Val{:boxplot}},
x,
y,
z;
notch = false,
whisker_range = 1.5,
outliers = true,
whisker_width = :half,
sort_labels_by = identity,
xshift = 0.0,
)
# if only y is provided, then x will be UnitRange 1:size(y,2)
if typeof(x) <: AbstractRange
if step(x) == first(x) == 1
x = plotattributes[:series_plotindex]
else
x = [getindex(x, plotattributes[:series_plotindex])]
end
end
xsegs, ysegs = Segments(), Segments()
texts = String[]
glabels = sort(collect(unique(x)))
warning = false
outliers_x, outliers_y = zeros(0), zeros(0)
bw = plotattributes[:bar_width]
isnothing(bw) && (bw = 0.8)
@assert whisker_width === :match || whisker_width == :half || whisker_width >= 0 "whisker_width must be :match, :half, or a positive number"
ww = whisker_width === :match ? bw : whisker_width == :half ? bw / 2 : whisker_width
for (i, glabel) in enumerate(sort(glabels; by = sort_labels_by))
# filter y
values = y[filter(i -> _cycle(x, i) == glabel, 1:length(y))]
# compute quantiles
q1, q2, q3, q4, q5 = quantile(values, range(0, stop = 1, length = 5))
# notch
n = notch_width(q2, q4, length(values))
# warn on inverted notches?
if notch && !warning && ((q2 > (q3 - n)) || (q4 < (q3 + n)))
@warn("Boxplot's notch went outside hinges. Set notch to false.")
warning = true # Show the warning only one time
end
# make the shape
center = Plots.discrete_value!(plotattributes, :x, glabel)[1] + xshift
hw = 0.5_cycle(bw, i) # Box width
HW = 0.5_cycle(ww, i) # Whisker width
l, m, r = center - hw, center, center + hw
lw, rw = center - HW, center + HW
# internal nodes for notches
L, R = center - 0.5 * hw, center + 0.5 * hw
# outliers
if Float64(whisker_range) != 0.0 # if the range is 0.0, the whiskers will extend to the data
limit = whisker_range * (q4 - q2)
inside = Float64[]
for value in values
if (value < (q2 - limit)) || (value > (q4 + limit))
if outliers
push!(outliers_y, value)
push!(outliers_x, center)
end
else
push!(inside, value)
end
end
# change q1 and q5 to show outliers
# using maximum and minimum values inside the limits
q1, q5 = Plots.ignorenan_extrema(inside)
q1, q5 = (min(q1, q2), max(q4, q5)) # whiskers cannot be inside the box
end
# Box
push!(xsegs, m, lw, rw, m, m) # lower T
push!(ysegs, q1, q1, q1, q1, q2) # lower T
push!(
texts,
"Lower fence: $q1",
"Lower fence: $q1",
"Lower fence: $q1",
"Lower fence: $q1",
"Q1: $q2",
"",
)
if notch
push!(xsegs, r, r, R, L, l, l, r, r) # lower box
push!(xsegs, r, r, l, l, L, R, r, r) # upper box
push!(ysegs, q2, q3 - n, q3, q3, q3 - n, q2, q2, q3 - n) # lower box
push!(
texts,
"Q1: $q2",
"Median: $q3 ± $n",
"Median: $q3 ± $n",
"Median: $q3 ± $n",
"Median: $q3 ± $n",
"Q1: $q2",
"Q1: $q2",
"Median: $q3 ± $n",
"",
)
push!(ysegs, q3 + n, q4, q4, q3 + n, q3, q3, q3 + n, q4) # upper box
push!(
texts,
"Median: $q3 ± $n",
"Q3: $q4",
"Q3: $q4",
"Median: $q3 ± $n",
"Median: $q3 ± $n",
"Median: $q3 ± $n",
"Median: $q3 ± $n",
"Q3: $q4",
"",
)
else
push!(xsegs, r, r, l, l, r, r) # lower box
push!(xsegs, r, l, l, r, r, m) # upper box
push!(ysegs, q2, q3, q3, q2, q2, q3) # lower box
push!(
texts,
"Q1: $q2",
"Median: $q3",
"Median: $q3",
"Q1: $q2",
"Q1: $q2",
"Median: $q3",
"",
)
push!(ysegs, q4, q4, q3, q3, q4, q4) # upper box
push!(
texts,
"Q3: $q4",
"Q3: $q4",
"Median: $q3",
"Median: $q3",
"Q3: $q4",
"Q3: $q4",
"",
)
end
push!(xsegs, m, lw, rw, m, m) # upper T
push!(ysegs, q5, q5, q5, q5, q4) # upper T
push!(
texts,
"Upper fence: $q5",
"Upper fence: $q5",
"Upper fence: $q5",
"Upper fence: $q5",
"Q3: $q4",
"",
)
end
if !Plots.isvertical(plotattributes)
# We should draw the plot horizontally!
xsegs, ysegs = ysegs, xsegs
outliers_x, outliers_y = outliers_y, outliers_x
# Now reset the orientation, so that the axes limits are set correctly.
orientation := default(:orientation)
end
@series begin
# To prevent linecolor equal to fillcolor (It makes the median visible)
if plotattributes[:linecolor] == plotattributes[:fillcolor]
plotattributes[:linecolor] = plotattributes[:markerstrokecolor]
end
primary := true
seriestype := :shape
x := xsegs.pts
y := ysegs.pts
()
end
# Outliers
if outliers && !isempty(outliers)
@series begin
primary := false
seriestype := :scatter
if get!(plotattributes, :markershape, :circle) === :none
plotattributes[:markershape] = :circle
end
fillrange := nothing
x := outliers_x
y := outliers_y
()
end
end
# Hover
primary := false
seriestype := :path
marker := false
if Plots.is_attr_supported(Plots.backend(), :hover)
hover := texts
end
linewidth := 0
x := xsegs.pts
y := ysegs.pts
()
end
Plots.@deps boxplot shape scatter
# ------------------------------------------------------------------------------
# Grouped Boxplot
@userplot GroupedBoxplot
recipetype(::Val{:groupedboxplot}, args...) = GroupedBoxplot(args)
@recipe function f(g::GroupedBoxplot; spacing = 0.1)
x, y = grouped_xy(g.args...)
# extract xnums and set default bar width.
# might need to set xticks as well
ux = unique(x)
x = if eltype(x) <: Number
bar_width --> (0.8 * mean(diff(sort(ux))))
float.(x)
else
bar_width --> 0.8
xnums = [findfirst(isequal(xi), ux) for xi in x] .- 0.5
xticks --> (eachindex(ux) .- 0.5, ux)
xnums
end
# shift x values for each group
group = get(plotattributes, :group, nothing)
if group != nothing
gb = RecipesPipeline._extract_group_attributes(group)
labels, idxs = getfield(gb, 1), getfield(gb, 2)
n = length(labels)
bws = plotattributes[:bar_width] / n
bar_width := bws * clamp(1 - spacing, 0, 1)
for i = 1:n
groupinds = idxs[i]
Δx = _cycle(bws, i) * (i - (n + 1) / 2)
x[groupinds] .+= Δx
end
end
seriestype := :boxplot
x, y
end
Plots.@deps groupedboxplot boxplot
| StatsPlots | https://github.com/JuliaPlots/StatsPlots.jl.git |
|
[
"MIT"
] | 0.15.7 | 3b1dcbf62e469a67f6733ae493401e53d92ff543 | code | 3429 | @userplot CornerPlot
recipetype(::Val{:cornerplot}, args...) = CornerPlot(args)
@recipe function f(cp::CornerPlot; compact = false, maxvariables = 30, histpct = 0.1)
mat = cp.args[1]
C = cor(mat)
@assert typeof(mat) <: AbstractMatrix
N = size(mat, 2)
if N > maxvariables
error(
"Requested to plot $N variables in $(N^2) subplots! Likely, the first input needs transposing, otherwise increase maxvariables.",
)
end
# k is the number of rows/columns to hide
k = compact ? 1 : 0
# n is the total number of rows/columns. hists always shown
n = N + 1 - k
labs = pop!(plotattributes, :label, ["x$i" for i = 1:N])
if labs != [""] && length(labs) != N
error("Number of labels not identical to number of datasets")
end
# build a grid layout, where the histogram sizes are a fixed percentage, and we
scatterpcts = ones(n - 1) * (1 - histpct) / (n - 1)
g = grid(
n,
n,
widths = vcat(scatterpcts, histpct),
heights = vcat(histpct, scatterpcts),
)
spidx = 1
indices = zeros(Int, n, n)
for i = 1:n, j = 1:n
isblank = (i == 1 && j == n) || (compact && i > 1 && j < n && j >= i)
g[i, j].attr[:blank] = isblank
if !isblank
indices[i, j] = spidx
spidx += 1
end
end
layout := g
# some defaults
legend := false
foreground_color_border := nothing
margin --> 1mm
titlefont --> font(11)
fillcolor --> Plots.fg_color(plotattributes)
linecolor --> Plots.fg_color(plotattributes)
grid --> true
ticks := nothing
xformatter := x -> ""
yformatter := y -> ""
link := :both
grad = cgrad(get(plotattributes, :markercolor, :RdYlBu))
# figure out good defaults for scatter plot dots:
pltarea = 1 / (2n)
nsamples = size(mat, 1)
markersize --> clamp(pltarea * 800 / sqrt(nsamples), 1, 10)
markeralpha --> clamp(pltarea * 100 / nsamples^0.42, 0.005, 0.4)
# histograms in the right column
for i = 1:N
compact && i == 1 && continue
@series begin
orientation := :h
seriestype := :histogram
subplot := indices[i + 1 - k, n]
grid := false
view(mat, :, i)
end
end
# histograms in the top row
for j = 1:N
compact && j == N && continue
@series begin
seriestype := :histogram
subplot := indices[1, j]
grid := false
view(mat, :, j)
end
end
# scatters
for i = 1:N
vi = view(mat, :, i)
for j = 1:N
# only the lower triangle
if compact && i <= j
continue
end
vj = view(mat, :, j)
@series begin
ticks := :auto
if i == N
xformatter := :auto
xguide := _cycle(labs, j)
end
if j == 1
yformatter := :auto
yguide := _cycle(labs, i)
end
seriestype := :scatter
subplot := indices[i + 1 - k, j]
markercolor := grad[0.5 + 0.5C[i, j]]
smooth --> true
markerstrokewidth --> 0
vj, vi
end
end
# end
end
end
| StatsPlots | https://github.com/JuliaPlots/StatsPlots.jl.git |
|
[
"MIT"
] | 0.15.7 | 3b1dcbf62e469a67f6733ae493401e53d92ff543 | code | 3938 | """
corrplot
This plot type shows the correlation among input variables.
A correlation plot may be produced by a matrix.
A correlation matrix can also be created from the columns of a `DataFrame`
using the [`@df`](@ref) macro like so:
```julia
@df iris corrplot([:SepalLength :SepalWidth :PetalLength :PetalWidth])
```
The marker color in scatter plots reveals the degree of correlation.
Pass the desired colorgradient to `markercolor`.
With the default gradient positive correlations are blue, neutral are yellow
and negative are red. In the 2d-histograms, the color gradient shows the frequency
of points in that bin (as usual, controlled by `seriescolor`).
"""
@userplot CorrPlot
recipetype(::Val{:corrplot}, args...) = CorrPlot(args)
"""
to_corrplot_matrix(mat)
Transforms the input into a correlation plot matrix.
Meant to be overloaded by other types!
"""
to_corrplot_matrix(x) = x
function update_ticks_guides(d::KW, labs, i, j, n)
# d[:title] = (i==1 ? _cycle(labs,j) : "")
# d[:xticks] = (i==n)
d[:xguide] = (i == n ? _cycle(labs, j) : "")
# d[:yticks] = (j==1)
d[:yguide] = (j == 1 ? _cycle(labs, i) : "")
end
@recipe function f(cp::CorrPlot)
mat = to_corrplot_matrix(cp.args[1])
n = size(mat, 2)
C = cor(mat)
labs = pop!(plotattributes, :label, [""])
link := :x # need custom linking for y
layout := (n, n)
legend := false
foreground_color_border := nothing
margin := 1mm
titlefont := font(11)
fillcolor --> Plots.fg_color(plotattributes)
linecolor --> Plots.fg_color(plotattributes)
markeralpha := 0.4
grad = cgrad(get(plotattributes, :markercolor, :RdYlBu))
indices = reshape(1:(n^2), n, n)'
title = get(plotattributes, :title, "")
title_location = get(plotattributes, :title_location, :center)
title := ""
# histograms on the diagonal
for i = 1:n
@series begin
if title != "" && title_location === :left && i == 1
title := title
end
seriestype := :histogram
subplot := indices[i, i]
grid := false
xformatter --> ((i == n) ? :auto : (x -> ""))
yformatter --> ((i == 1) ? :auto : (y -> ""))
update_ticks_guides(plotattributes, labs, i, i, n)
view(mat, :, i)
end
end
# scatters
for i = 1:n
ylink := setdiff(vec(indices[i, :]), indices[i, i])
vi = view(mat, :, i)
for j = 1:n
j == i && continue
vj = view(mat, :, j)
subplot := indices[i, j]
update_ticks_guides(plotattributes, labs, i, j, n)
if i > j
#below diag... scatter
@series begin
seriestype := :scatter
markercolor := grad[0.5 + 0.5C[i, j]]
smooth := true
markerstrokewidth --> 0
xformatter --> ((i == n) ? :auto : (x -> ""))
yformatter --> ((j == 1) ? :auto : (y -> ""))
vj, vi
end
else
#above diag... hist2d
@series begin
seriestype := get(plotattributes, :seriestype, :histogram2d)
if title != "" &&
i == 1 &&
(
(title_location === :center && j == div(n, 2) + 1) ||
(title_location === :right && j == n)
)
if iseven(n)
title_location := :left
end
title := title
end
xformatter --> ((i == n) ? :auto : (x -> ""))
yformatter --> ((j == 1) ? :auto : (y -> ""))
vj, vi
end
end
end
end
end
| StatsPlots | https://github.com/JuliaPlots/StatsPlots.jl.git |
|
[
"MIT"
] | 0.15.7 | 3b1dcbf62e469a67f6733ae493401e53d92ff543 | code | 1333 | """
covellipse(μ, Σ; showaxes=false, n_std=1, n_ellipse_vertices=100)
Plot a confidence ellipse of the 2×2 covariance matrix `Σ`, centered at `μ`.
The ellipse is the contour line of a Gaussian density function with mean `μ`
and variance `Σ` at `n_std` standard deviations.
If `showaxes` is true, the two axes of the ellipse are also plotted.
"""
@userplot CovEllipse
@recipe function f(c::CovEllipse; showaxes = false, n_std = 1, n_ellipse_vertices = 100)
μ, S = _covellipse_args(c.args; n_std = n_std)
θ = range(0, 2π; length = n_ellipse_vertices)
A = S * [cos.(θ)'; sin.(θ)']
@series begin
seriesalpha --> 0.3
Shape(μ[1] .+ A[1, :], μ[2] .+ A[2, :])
end
showaxes && @series begin
label := false
linecolor --> "gray"
([μ[1] + S[1, 1], μ[1], μ[1] + S[1, 2]], [μ[2] + S[2, 1], μ[2], μ[2] + S[2, 2]])
end
end
function _covellipse_args(
(μ, Σ)::Tuple{AbstractVector{<:Real},AbstractMatrix{<:Real}};
n_std::Real,
)
size(μ) == (2,) && size(Σ) == (2, 2) ||
error("covellipse requires mean of length 2 and covariance of size 2×2.")
λ, U = eigen(Σ)
μ, n_std * U * diagm(.√λ)
end
_covellipse_args(args; n_std) = error(
"Wrong inputs for covellipse: $(typeof.(args)). " *
"Expected real-valued vector μ, real-valued matrix Σ.",
)
| StatsPlots | https://github.com/JuliaPlots/StatsPlots.jl.git |
|
[
"MIT"
] | 0.15.7 | 3b1dcbf62e469a67f6733ae493401e53d92ff543 | code | 1640 | function treepositions(hc::Hclust, useheight::Bool, orientation = :vertical)
order = StatsBase.indexmap(hc.order)
nodepos = Dict(-i => (float(order[i]), 0.0) for i in hc.order)
xs = Array{Float64}(undef, 4, size(hc.merges, 1))
ys = Array{Float64}(undef, 4, size(hc.merges, 1))
for i = 1:size(hc.merges, 1)
x1, y1 = nodepos[hc.merges[i, 1]]
x2, y2 = nodepos[hc.merges[i, 2]]
xpos = (x1 + x2) / 2
ypos = useheight ? hc.heights[i] : (max(y1, y2) + 1)
nodepos[i] = (xpos, ypos)
xs[:, i] .= [x1, x1, x2, x2]
ys[:, i] .= [y1, ypos, ypos, y2]
end
if orientation === :horizontal
return ys, xs
else
return xs, ys
end
end
@recipe function f(hc::Hclust; useheight = true, orientation = :vertical)
typeof(useheight) <: Bool || error("'useheight' argument must be true or false")
legend --> false
linecolor --> :black
if orientation === :horizontal
yforeground_color_axis --> :white
ygrid --> false
ylims --> (0.5, length(hc.order) + 0.5)
yticks --> (1:nnodes(hc), string.(1:nnodes(hc))[hc.order])
if useheight
hs = sum(hc.heights)
xlims --> (0, hs + hs * 0.01)
else
xlims --> (0, Inf)
end
xshowaxis --> useheight
else
xforeground_color_axis --> :white
xgrid --> false
xlims --> (0.5, length(hc.order) + 0.5)
xticks --> (1:nnodes(hc), string.(1:nnodes(hc))[hc.order])
ylims --> (0, Inf)
yshowaxis --> useheight
end
treepositions(hc, useheight, orientation)
end
| StatsPlots | https://github.com/JuliaPlots/StatsPlots.jl.git |
|
[
"MIT"
] | 0.15.7 | 3b1dcbf62e469a67f6733ae493401e53d92ff543 | code | 7438 | """
`@df d x`
Convert every symbol in the expression `x` with the respective column in `d` if it exists.
If you want to avoid replacing the symbol, escape it with `^`.
`NA` values are replaced with `NaN` for columns of `Float64` and `""` or `Symbol()`
for strings and symbols respectively.
`x` can be either a plot command or a block of plot commands.
"""
macro df(d, x)
esc(Expr(:call, df_helper(x), d))
end
"""
`@df x`
Curried version of `@df d x`. Outputs an anonymous function `d -> @df d x`.
"""
macro df(x)
esc(df_helper(x))
end
function df_helper(x)
i = gensym()
Expr(:(->), i, df_helper(i, x))
end
function df_helper(d, x)
if isa(x, Expr) && x.head === :block # meaning that there were multiple plot commands
commands = [
df_helper(d, xx) for xx in x.args if
!(isa(xx, Expr) && xx.head === :line || isa(xx, LineNumberNode))
] # apply the helper recursively
return Expr(:block, commands...)
elseif isa(x, Expr) && x.head === :call # each function call is operated on alone
syms = Any[]
vars = Symbol[]
plot_call = parse_table_call!(d, x, syms, vars)
names = gensym()
compute_vars = Expr(
:(=),
Expr(:tuple, Expr(:tuple, vars...), names),
Expr(:call, :($(@__MODULE__).extract_columns_and_names), d, syms...),
)
argnames = _argnames(names, x)
if (length(plot_call.args) >= 2) &&
isa(plot_call.args[2], Expr) &&
(plot_call.args[2].head === :parameters)
label_plot_call = Expr(
:call,
:($(@__MODULE__).add_label),
plot_call.args[2],
argnames,
plot_call.args[1],
plot_call.args[3:end]...,
)
else
label_plot_call =
Expr(:call, :($(@__MODULE__).add_label), argnames, plot_call.args...)
end
return Expr(:block, compute_vars, label_plot_call)
else
error("Second argument ($x) can only be a block or function call")
end
end
parse_table_call!(d, x, syms, vars) = x
function parse_table_call!(d, x::QuoteNode, syms, vars)
new_var = gensym(x.value)
push!(syms, x)
push!(vars, new_var)
return new_var
end
function parse_table_call!(d, x::Expr, syms, vars)
if x.head === :. && length(x.args) == 2
isa(x.args[2], QuoteNode) && return x
elseif x.head === :call
x.args[1] === :^ && length(x.args) == 2 && return x.args[2]
if x.args[1] === :cols
if length(x.args) == 1
push!(x.args, :($(@__MODULE__).column_names($d)))
return parse_table_call!(d, x, syms, vars)
end
range = x.args[2]
new_vars = gensym("range")
push!(syms, range)
push!(vars, new_vars)
return new_vars
end
elseif x.head === :braces # From Query: use curly brackets to simplify writing named tuples
new_ex = Expr(:tuple, x.args...)
for (j, field_in_NT) in enumerate(new_ex.args)
if isa(field_in_NT, Expr) && field_in_NT.head === :(=)
new_ex.args[j] = Expr(:(=), field_in_NT.args...)
elseif field_in_NT isa QuoteNode
new_ex.args[j] = Expr(:(=), field_in_NT.value, field_in_NT)
elseif isa(field_in_NT, Expr)
new_ex.args[j] = Expr(
:(=),
Symbol(filter(t -> t != ':', string(field_in_NT))),
field_in_NT,
)
elseif isa(field_in_NT, Symbol)
new_ex.args[j] = Expr(:(=), field_in_NT, field_in_NT)
end
end
return parse_table_call!(d, new_ex, syms, vars)
end
return Expr(x.head, (parse_table_call!(d, arg, syms, vars) for arg in x.args)...)
end
function column_names(t)
s = Tables.schema(t)
s === nothing ? propertynames(first(Tables.rows(t))) : s.names
end
not_kw(x) = true
not_kw(x::Expr) = !(x.head in [:kw, :parameters])
function insert_kw!(x::Expr, s::Symbol, v)
index = isa(x.args[2], Expr) && x.args[2].head === :parameters ? 3 : 2
x.args = vcat(x.args[1:(index - 1)], Expr(:kw, s, v), x.args[index:end])
end
function _argnames(names, x::Expr)
Expr(:vect, [_arg2string(names, s) for s in x.args[2:end] if not_kw(s)]...)
end
_arg2string(names, x) = stringify(x)
function _arg2string(names, x::Expr)
if x.head === :call && x.args[1] == :cols
return :($(@__MODULE__).compute_name($names, $(x.args[2])))
elseif x.head === :call && x.args[1] == :hcat
return hcat(stringify.(x.args[2:end])...)
elseif x.head === :hcat
return hcat(stringify.(x.args)...)
else
return stringify(x)
end
end
stringify(x) = filter(t -> t != ':', string(x))
compute_name(names, i::Int) = names[i]
compute_name(names, i::Symbol) = i
compute_name(names, i) = reshape([compute_name(names, ii) for ii in i], 1, :)
"""
add_label(argnames, f, args...; kwargs...)
This function ensures that labels are passed to the plotting command, if it accepts them.
If `f` does not accept keyword arguments, and `kwargs` is empty, it will only
forward `args...`.
If the user has provided keyword arguments, but `f` does not accept them,
then it will error.
"""
function add_label(argnames, f, args...; kwargs...)
i = findlast(t -> isa(t, Expr) || isa(t, AbstractArray), argnames)
try
if (i === nothing)
return f(args...; kwargs...)
else
return f(label = stringify.(argnames[i]), args...; kwargs...)
end
catch e
if e isa MethodError ||
(e isa ErrorException && occursin("does not accept keyword arguments", e.msg))
# check if the user has supplied kwargs, then we need to rethrow the error
isempty(kwargs) || rethrow(e)
# transmit only args to `f`
return f(args...)
else
rethrow(e)
end
end
end
get_col(s::Int, col_nt, names) = col_nt[names[s]]
get_col(s::Symbol, col_nt, names) = get(col_nt, s, s)
get_col(syms, col_nt, names) = hcat((get_col(s, col_nt, names) for s in syms)...)
# get the appropriate name when passed an Integer
add_sym!(cols, i::Integer, names) = push!(cols, names[i])
# check for errors in Symbols
add_sym!(cols, s::Symbol, names) = s in names ? push!(cols, s) : cols
# recursively extract column names
function add_sym!(cols, s, names)
for si in s
add_sym!(cols, si, names)
end
cols
end
"""
extract_columns_and_names(df, syms...)
Extracts columns and their names (if the column number is an integer)
into a slightly complex `Tuple`.
The structure goes as `((columndata...), names)`. This is unpacked by the [`@df`](@ref) macro into `gensym`'ed variables, which are passed to the plotting function.
!!! note
If you want to extend the [`@df`](@ref) macro
to work with your custom type, this is the
function you should overload!
"""
function extract_columns_and_names(df, syms...)
Tables.istable(df) || error("Only tables are supported")
names = column_names(df)
# extract selected column names
selected_cols = add_sym!(Symbol[], syms, names)
cols = Tables.columntable(TableOperations.select(df, unique(selected_cols)...))
return Tuple(get_col(s, cols, names) for s in syms), names
end
| StatsPlots | https://github.com/JuliaPlots/StatsPlots.jl.git |
|
[
"MIT"
] | 0.15.7 | 3b1dcbf62e469a67f6733ae493401e53d92ff543 | code | 3279 |
# pick a nice default x range given a distribution
function default_range(dist::Distribution, alpha = 0.0001)
minval = isfinite(minimum(dist)) ? minimum(dist) : quantile(dist, alpha)
maxval = isfinite(maximum(dist)) ? maximum(dist) : quantile(dist, 1 - alpha)
minval, maxval
end
function default_range(m::Distributions.UnivariateMixture, alpha = 0.0001)
mapreduce(_minmax, 1:Distributions.ncomponents(m)) do k
default_range(Distributions.component(m, k), alpha)
end
end
_minmax((xmin, xmax), (ymin, ymax)) = (min(xmin, ymin), max(xmax, ymax))
yz_args(dist) = default_range(dist)
function yz_args(dist::DiscreteUnivariateDistribution)
minval, maxval = extrema(dist)
if isfinite(minval) && isfinite(maxval) # bounded
sup = support(dist)
return sup isa AbstractVector ? (sup,) : ([sup...],)
else # unbounded
return (UnitRange(promote(default_range(dist)...)...),)
end
end
# this "user recipe" adds a default x vector based on the distribution's μ and σ
@recipe function f(dist::Distribution)
if dist isa DiscreteUnivariateDistribution
seriestype --> :sticks
end
(dist, yz_args(dist)...)
end
@recipe function f(m::Distributions.UnivariateMixture; components = true)
if m isa DiscreteUnivariateDistribution
seriestype --> :sticks
end
if components
for k = 1:Distributions.ncomponents(m)
c = Distributions.component(m, k)
@series begin
(c, yz_args(c)...)
end
end
else
(m, yz_args(m)...)
end
end
@recipe function f(distvec::AbstractArray{<:Distribution}, yz...)
for di in distvec
@series begin
seriesargs = isempty(yz) ? yz_args(di) : yz
if di isa DiscreteUnivariateDistribution
seriestype --> :sticks
end
(di, seriesargs...)
end
end
end
# this "type recipe" replaces any instance of a distribution with a function mapping xi to yi
@recipe f(::Type{T}, dist::T; func = pdf) where {T<:Distribution} = xi -> func(dist, xi)
#-----------------------------------------------------------------------------
# qqplots
@recipe function f(h::QQPair; qqline = :identity)
if qqline in (:fit, :quantile, :identity, :R)
xs = [extrema(h.qx)...]
if qqline === :identity
ys = xs
elseif qqline === :fit
itc, slp = hcat(fill!(similar(h.qx), 1), h.qx) \ h.qy
ys = slp .* xs .+ itc
else # if qqline === :quantile || qqline == :R
quantx, quanty = quantile(h.qx, [0.25, 0.75]), quantile(h.qy, [0.25, 0.75])
slp = diff(quanty) ./ diff(quantx)
ys = quanty .+ slp .* (xs .- quantx)
end
@series begin
primary := false
seriestype := :path
xs, ys
end
end
seriestype --> :scatter
legend --> false
h.qx, h.qy
end
loc(D::Type{T}, x) where {T<:Distribution} = fit(D, x), x
loc(D, x) = D, x
@userplot QQPlot
recipetype(::Val{:qqplot}, args...) = QQPlot(args)
@recipe f(h::QQPlot) = qqbuild(loc(h.args[1], h.args[2])...)
@userplot QQNorm
recipetype(::Val{:qqnorm}, args...) = QQNorm(args)
@recipe f(h::QQNorm) = QQPlot((Normal, h.args[1]))
| StatsPlots | https://github.com/JuliaPlots/StatsPlots.jl.git |
|
[
"MIT"
] | 0.15.7 | 3b1dcbf62e469a67f6733ae493401e53d92ff543 | code | 3623 |
# ---------------------------------------------------------------------------
# Dot Plot (strip plot, beeswarm)
@recipe function f(::Type{Val{:dotplot}}, x, y, z; mode = :density, side = :both)
# if only y is provided, then x will be UnitRange 1:size(y, 2)
if typeof(x) <: AbstractRange
if step(x) == first(x) == 1
x = plotattributes[:series_plotindex]
else
x = [getindex(x, plotattributes[:series_plotindex])]
end
end
grouplabels = sort(collect(unique(x)))
barwidth = plotattributes[:bar_width]
barwidth == nothing && (barwidth = 0.8)
getoffsets(halfwidth, y) =
mode === :uniform ? (rand(length(y)) .* 2 .- 1) .* halfwidth :
mode === :density ? violinoffsets(halfwidth, y) : zeros(length(y))
points_x, points_y = zeros(0), zeros(0)
for (i, grouplabel) in enumerate(grouplabels)
# filter y
groupy = y[filter(i -> _cycle(x, i) == grouplabel, 1:length(y))]
center = Plots.discrete_value!(plotattributes, :x, grouplabel)[1]
halfwidth = 0.5_cycle(barwidth, i)
offsets = getoffsets(halfwidth, groupy)
if side === :left
offsets = -abs.(offsets)
elseif side === :right
offsets = abs.(offsets)
end
append!(points_y, groupy)
append!(points_x, center .+ offsets)
end
seriestype := :scatter
x := points_x
y := points_y
()
end
Plots.@deps dotplot scatter
Plots.@shorthands dotplot
function violinoffsets(maxwidth, y)
normalizewidths(maxwidth, widths) = maxwidth * widths / Plots.ignorenan_maximum(widths)
function getlocalwidths(widths, centers, y)
upperbounds =
[violincenters[violincenters .> yval] for yval ∈ y] .|> findmin .|> first
lowercenters = findmax.([violincenters[violincenters .≤ yval] for yval ∈ y])
lowerbounds, lowerindexes = first.(lowercenters), last.(lowercenters)
δs = (y .- lowerbounds) ./ (upperbounds .- lowerbounds)
itp = interpolate(widths, BSpline(Quadratic(Reflect(OnCell()))))
localwidths = itp.(lowerindexes .+ δs)
end
violinwidths, violincenters = violin_coords(y)
violinwidths = normalizewidths(maxwidth, violinwidths)
localwidths = getlocalwidths(violinwidths, violincenters, y)
offsets = (rand(length(y)) .* 2 .- 1) .* localwidths
end
# ------------------------------------------------------------------------------
# Grouped dotplot
@userplot GroupedDotplot
recipetype(::Val{:groupeddotplot}, args...) = GroupedDotplot(args)
@recipe function f(g::GroupedDotplot; spacing = 0.1)
x, y = grouped_xy(g.args...)
# extract xnums and set default bar width.
# might need to set xticks as well
ux = unique(x)
x = if eltype(x) <: Number
bar_width --> (0.8 * mean(diff(sort(ux))))
float.(x)
else
bar_width --> 0.8
xnums = [findfirst(isequal(xi), ux) for xi in x] .- 0.5
xticks --> (eachindex(ux) .- 0.5, ux)
xnums
end
# shift x values for each group
group = get(plotattributes, :group, nothing)
if group != nothing
gb = RecipesPipeline._extract_group_attributes(group)
labels, idxs = getfield(gb, 1), getfield(gb, 2)
n = length(labels)
bws = plotattributes[:bar_width] / n
bar_width := bws * clamp(1 - spacing, 0, 1)
for i = 1:n
groupinds = idxs[i]
Δx = _cycle(bws, i) * (i - (n + 1) / 2)
x[groupinds] .+= Δx
end
end
seriestype := :dotplot
x, y
end
Plots.@deps groupeddotplot dotplot
| StatsPlots | https://github.com/JuliaPlots/StatsPlots.jl.git |
|
[
"MIT"
] | 0.15.7 | 3b1dcbf62e469a67f6733ae493401e53d92ff543 | code | 689 |
# ---------------------------------------------------------------------------
# empirical CDF
@recipe function f(ecdf::StatsBase.ECDF)
seriestype := :steppost
legend --> :topleft
x = [ecdf.sorted_values[1]; ecdf.sorted_values]
if :weights in propertynames(ecdf) && !isempty(ecdf.weights)
# support StatsBase versions >v0.32.0
y = [0; cumsum(ecdf.weights) ./ sum(ecdf.weights)]
else
y = range(0, 1; length = length(x))
end
x, y
end
@userplot ECDFPlot
recipetype(::Val{:ecdfplot}, args...) = ECDFPlot(args)
@recipe function f(p::ECDFPlot)
x = p.args[1]
if !isa(x, StatsBase.ECDF)
x = StatsBase.ecdf(x)
end
x
end
| StatsPlots | https://github.com/JuliaPlots/StatsPlots.jl.git |
|
[
"MIT"
] | 0.15.7 | 3b1dcbf62e469a67f6733ae493401e53d92ff543 | code | 10410 | @userplot ErrorLine
"""
# StatsPlots.errorline(x, y, arg):
Function for parsing inputs to easily make a [`ribbons`] (https://ggplot2.tidyverse.org/reference/geom_ribbon.html),
stick errorbar (https://www.mathworks.com/help/matlab/ref/errorbar.html), or plume
(https://stackoverflow.com/questions/65510619/how-to-prepare-my-data-for-plume-plots) plot while allowing
for easily controlling error type and NaN handling.
# Inputs: default values are indicated with *s
x (vector, unit range) - the values along the x-axis for each y-point
y (matrix [x, repeat, group]) - values along y-axis wrt x. The first dimension must be of equal length to that of x.
The second dimension is treated as the repeated observations and error is computed along this dimension. If the
matrix has a 3rd dimension this is treated as a new group.
error_style (`Symbol` - *:ribbon*, :stick, :plume) - determines whether to use a ribbon style or stick style error
representation.
centertype (symbol - *:mean* or :median) - which approach to use to represent the central value of y at each x-value.
errortype (symbol - *:std*, :sem, :percentile) - which error metric to use to show the distribution of y at each x-value.
percentiles (Vector{Int64} *[25, 75]*) - if using errortype === :percentile then which percentiles to use as bounds.
groupcolor (Symbol, RGB, Vector of Symbol or RGB) - Declares the color for each group. If no value is passed then will use
the default colorscheme. If one value is given then it will use that color for all groups. If multiple colors are
given then it will use a different color for each group.
secondarycolor (`Symbol`, `RGB`, `:matched` - *:Gray60*) - When using stick mode this will allow for the setting of the stick color.
If `:matched` is given then the color of the sticks with match that of the main line.
secondarylinealpha (float *.1*) - alpha value of plume lines.
numsecondarylines (int *100*) - number of plume lines to plot behind central line.
stickwidth (Float64 *.01*) - How much of the x-axis the horizontal aspect of the error stick should take up.
# Example
```julia
x = 1:10
y = fill(NaN, 10, 100, 3)
for i = axes(y,3)
y[:,:,i] = collect(1:2:20) .+ rand(10,100).*5 .* collect(1:2:20) .+ rand()*100
end
y = reshape(1:100, 10, 10);
errorline(1:10, y)
```
"""
errorline
function compute_error(
y::AbstractMatrix,
centertype::Symbol,
errortype::Symbol,
percentiles::AbstractVector,
)
y_central = fill(NaN, size(y, 1))
# NaNMath doesn't accept Ints so convert to AbstractFloat if necessary
if eltype(y) <: Integer
y = float(y)
end
# First compute the center
y_central = if centertype === :mean
mapslices(NaNMath.mean, y, dims = 2)
elseif centertype === :median
mapslices(NaNMath.median, y, dims = 2)
else
error("Invalid center type. Valid symbols include :mean or :median")
end
# Takes 2d matrix [x,y] and computes the desired error type for each row (value of x)
if errortype === :std || errortype === :sem
y_error = mapslices(NaNMath.std, y, dims = 2)
if errortype == :sem
y_error = y_error ./ sqrt(size(y, 2))
end
elseif errortype === :percentile
y_lower = fill(NaN, size(y, 1))
y_upper = fill(NaN, size(y, 1))
if any(isnan.(y)) # NaNMath does not have a percentile function so have to go via StatsBase
for i in axes(y, 1)
yi = y[i, .!isnan.(y[i, :])]
y_lower[i] = percentile(yi, percentiles[1])
y_upper[i] = percentile(yi, percentiles[2])
end
else
y_lower = mapslices(Y -> percentile(Y, percentiles[1]), y, dims = 2)
y_upper = mapslices(Y -> percentile(Y, percentiles[2]), y, dims = 2)
end
y_error = (y_central .- y_lower, y_upper .- y_central) # Difference from center value
else
error("Invalid error type. Valid symbols include :std, :sem, :percentile")
end
return y_central, y_error
end
@recipe function f(
e::ErrorLine;
errorstyle = :ribbon,
centertype = :mean,
errortype = :std,
percentiles = [25, 75],
groupcolor = nothing,
secondarycolor = nothing,
stickwidth = 0.01,
secondarylinealpha = 0.1,
numsecondarylines = 100,
secondarylinewidth = 1,
)
if length(e.args) == 1 # If only one input is given assume it is y-values in the form [x,obs]
y = e.args[1]
x = 1:size(y, 1)
else # Otherwise assume that the first two inputs are x and y
x = e.args[1]
y = e.args[2]
# Check y orientation
ndims(y) > 3 && error("ndims(y) > 3")
if !any(size(y) .== length(x))
error("Size of x and y do not match")
elseif ndims(y) == 2 && size(y, 1) != length(x) && size(y, 2) == length(x) # Check if y needs to be transposed or transmuted
y = transpose(y)
elseif ndims(y) == 3 && size(y, 1) != length(x)
error(
"When passing a 3 dimensional matrix as y, the axes must be [x, repeat, group]",
)
end
end
# Determine if a color palette is being used so it can be passed to secondary lines
if :color_palette ∉ keys(plotattributes)
color_palette = :default
else
color_palette = plotattributes[:color_palette]
end
# Parse different color type
if groupcolor isa Symbol || groupcolor isa RGB{Float64} || groupcolor isa RGBA{Float64}
groupcolor = [groupcolor]
end
# Check groupcolor format
if (groupcolor !== nothing && ndims(y) > 2) && length(groupcolor) == 1
groupcolor = repeat(groupcolor, size(y, 3)) # Use the same color for all groups
elseif (groupcolor !== nothing && ndims(y) > 2) && length(groupcolor) < size(y, 3)
error("$(length(groupcolor)) colors given for a matrix with $(size(y,3)) groups")
elseif groupcolor === nothing
gsi_counter = 0
for i = 1:length(plotattributes[:plot_object].series_list)
if plotattributes[:plot_object].series_list[i].plotattributes[:primary]
gsi_counter += 1
end
end
# Start at next index and allow wrapping of indices
gsi_counter += 1
idx = (gsi_counter:(gsi_counter + size(y, 3))) .% length(palette(color_palette))
idx[findall(x -> x == 0, idx)] .= length(palette(color_palette))
groupcolor = palette(color_palette)[idx]
end
if errorstyle === :plume && numsecondarylines > size(y, 2) # Override numsecondarylines
numsecondarylines = size(y, 2)
end
for g in axes(y, 3) # Iterate through 3rd dimension
# Compute center and distribution for each value of x
y_central, y_error = compute_error(y[:, :, g], centertype, errortype, percentiles)
if errorstyle === :ribbon
seriestype := :path
@series begin
x := x
y := y_central
ribbon := y_error
fillalpha --> 0.1
linecolor := groupcolor[g]
fillcolor := groupcolor[g]
() # Suppress implicit return
end
elseif errorstyle === :stick
x_offset = diff(extrema(x) |> collect)[1] * stickwidth
seriestype := :path
for (i, xi) in enumerate(x)
# Error sticks
@series begin
primary := false
x :=
[xi - x_offset, xi + x_offset, xi, xi, xi + x_offset, xi - x_offset]
if errortype === :percentile
y := [
repeat([y_central[i] - y_error[1][i]], 3)
repeat([y_central[i] + y_error[2][i]], 3)
]
else
y := [
repeat([y_central[i] - y_error[i]], 3)
repeat([y_central[i] + y_error[i]], 3)
]
end
# Set the stick color
if secondarycolor === nothing
linecolor := :gray60
elseif secondarycolor === :matched
linecolor := groupcolor[g]
else
linecolor := secondarycolor
end
linewidth := secondarylinewidth
() # Suppress implicit return
end
end
# Base line
seriestype := :line
@series begin
primary := true
x := x
y := y_central
linecolor := groupcolor[g]
()
end
elseif errorstyle === :plume
num_obs = size(y, 2)
if num_obs > numsecondarylines
sub_sample_idx = sample(1:num_obs, numsecondarylines, replace = false)
y_sub_sample = y[:, sub_sample_idx, g]
else
y_sub_sample = y[:, :, g]
end
seriestype := :path
for i = 1:numsecondarylines
# Background paths
@series begin
primary := false
x := x
y := y_sub_sample[:, i]
# Set the stick color
if secondarycolor === nothing || secondarycolor === :matched
linecolor := groupcolor[g]
else
linecolor := secondarycolor
end
linealpha := secondarylinealpha
linewidth := secondarylinewidth
() # Suppress implicit return
end
end
# Base line
seriestype := :line
@series begin
primary := true
x := x
y := y_central
linecolor := groupcolor[g]
linewidth --> 3 # Make it stand out against the plume better
()
end
else
error("Invalid error style. Valid symbols include :ribbon, :stick, or :plume.")
end
end
end
| StatsPlots | https://github.com/JuliaPlots/StatsPlots.jl.git |
|
[
"MIT"
] | 0.15.7 | 3b1dcbf62e469a67f6733ae493401e53d92ff543 | code | 7346 |
# ---------------------------------------------------------------------------
# density
@recipe function f(
::Type{Val{:density}},
x,
y,
z;
trim = false,
bandwidth = KernelDensity.default_bandwidth(y),
)
newx, newy =
violin_coords(y, trim = trim, wts = plotattributes[:weights], bandwidth = bandwidth)
if Plots.isvertical(plotattributes)
newx, newy = newy, newx
end
x := newx
y := newy
seriestype := :path
()
end
Plots.@deps density path
# ---------------------------------------------------------------------------
# cumulative density
@recipe function f(
::Type{Val{:cdensity}},
x,
y,
z;
trim = false,
npoints = 200,
bandwidth = KernelDensity.default_bandwidth(y),
)
newx, newy =
violin_coords(y, trim = trim, wts = plotattributes[:weights], bandwidth = bandwidth)
if Plots.isvertical(plotattributes)
newx, newy = newy, newx
end
newy = cumsum(float(yi) for yi in newy)
newy ./= newy[end]
x := newx
y := newy
seriestype := :path
()
end
Plots.@deps cdensity path
ea_binnumber(y, bin::AbstractVector) =
error("You cannot specify edge locations for equal area histogram")
ea_binnumber(y, bin::Real) =
(floor(bin) == bin || error("Only integer or symbol values accepted by bins"); Int(bin))
ea_binnumber(y, bin::Int) = bin
ea_binnumber(y, bin::Symbol) = Plots._auto_binning_nbins((y,), 1, mode = bin)
@recipe function f(::Type{Val{:ea_histogram}}, x, y, z)
bin = ea_binnumber(y, plotattributes[:bins])
bins := quantile(y, range(0, stop = 1, length = bin + 1))
normalize := :density
seriestype := :barhist
()
end
Plots.@deps histogram barhist
push!(Plots._histogram_like, :ea_histogram)
@shorthands ea_histogram
@recipe function f(::Type{Val{:testhist}}, x, y, z)
markercolor --> :red
seriestype := :scatter
()
end
@shorthands testhist
# ---------------------------------------------------------------------------
# grouped histogram
@userplot GroupedHist
Plots.group_as_matrix(g::GroupedHist) = true
@recipe function f(p::GroupedHist)
_, v = grouped_xy(p.args...)
group = get(plotattributes, :group, nothing)
bins = get(plotattributes, :bins, :auto)
normed = get(plotattributes, :normalize, false)
weights = get(plotattributes, :weights, nothing)
# compute edges from ungrouped data
h = Plots._make_hist((vec(copy(v)),), bins; normed = normed, weights = weights)
nbins = length(h.weights)
edges = h.edges[1]
bar_width --> mean(map(i -> edges[i + 1] - edges[i], 1:nbins))
x = map(i -> (edges[i] + edges[i + 1]) / 2, 1:nbins)
if group === nothing
y = reshape(h.weights, nbins, 1)
else
gb = RecipesPipeline._extract_group_attributes(group)
labels, idxs = getfield(gb, 1), getfield(gb, 2)
ngroups = length(labels)
ntot = count(x -> !isnan(x), v)
# compute weights (frequencies) by group using those edges
y = fill(NaN, nbins, ngroups)
for i = 1:ngroups
groupinds = idxs[i]
v_i = filter(x -> !isnan(x), v[:, i])
w_i = weights == nothing ? nothing : weights[groupinds]
h_i = Plots._make_hist((v_i,), h.edges; normed = false, weights = w_i)
if normed
y[:, i] .= h_i.weights .* (length(v_i) / ntot / sum(h_i.weights))
else
y[:, i] .= h_i.weights
end
end
end
GroupedBar((x, y))
end
# ---------------------------------------------------------------------------
# Compute binsizes using Wand (1997)'s criterion
# Ported from R code located here https://github.com/cran/KernSmooth/tree/master/R
"Returns optimal histogram edge positions in accordance to Wand (1995)'s criterion'"
Plots.wand_edges(x::AbstractVector, args...) = (binwidth = wand_bins(x, args...);
(minimum(x) - binwidth):binwidth:(maximum(x) + binwidth))
"Returns optimal histogram bin widths in accordance to Wand (1995)'s criterion'"
function wand_bins(x, scalest = :minim, gridsize = 401, range_x = extrema(x), trun = true)
n = length(x)
minx, maxx = range_x
gpoints = range(minx, stop = maxx, length = gridsize)
gcounts = linbin(x, gpoints, trun = trun)
scalest = if scalest === :stdev
sqrt(var(x))
elseif scalest === :iqr
(quantile(x, 3 // 4) - quantile(x, 1 // 4)) / 1.349
elseif scalest === :minim
min((quantile(x, 3 // 4) - quantile(x, 1 // 4)) / 1.349, sqrt(var(x)))
else
error("scalest must be one of :stdev, :iqr or :minim (default)")
end
scalest == 0 && error("scale estimate is zero for input data")
sx = (x .- mean(x)) ./ scalest
sa = (minx - mean(x)) / scalest
sb = (maxx - mean(x)) / scalest
gpoints = range(sa, stop = sb, length = gridsize)
gcounts = linbin(sx, gpoints, trun = trun)
hpi = begin
alpha = ((2 / (11 * n))^(1 / 13)) * sqrt(2)
psi10hat = bkfe(gcounts, 10, alpha, [sa, sb])
alpha = (-105 * sqrt(2 / pi) / (psi10hat * n))^(1 // 11)
psi8hat = bkfe(gcounts, 8, alpha, [sa, sb])
alpha = (15 * sqrt(2 / pi) / (psi8hat * n))^(1 / 9)
psi6hat = bkfe(gcounts, 6, alpha, [sa, sb])
alpha = (-3 * sqrt(2 / pi) / (psi6hat * n))^(1 / 7)
psi4hat = bkfe(gcounts, 4, alpha, [sa, sb])
alpha = (sqrt(2 / pi) / (psi4hat * n))^(1 / 5)
psi2hat = bkfe(gcounts, 2, alpha, [sa, sb])
(6 / (-psi2hat * n))^(1 / 3)
end
scalest * hpi
end
function linbin(X, gpoints; trun = true)
n, M = length(X), length(gpoints)
a, b = gpoints[1], gpoints[M]
gcnts = zeros(M)
delta = (b - a) / (M - 1)
for i = 1:n
lxi = ((X[i] - a) / delta) + 1
li = floor(Int, lxi)
rem = lxi - li
if 1 <= li < M
gcnts[li] += 1 - rem
gcnts[li + 1] += rem
end
if !trun
if lt < 1
gcnts[1] += 1
end
if li >= M
gcnts[M] += 1
end
end
end
gcnts
end
"binned kernel function estimator"
function bkfe(gcounts, drv, bandwidth, range_x)
bandwidth <= 0 && error("'bandwidth' must be strictly positive")
a, b = range_x
h = bandwidth
M = length(gcounts)
gpoints = range(a, stop = b, length = M)
## Set the sample size and bin width
n = sum(gcounts)
delta = (b - a) / (M - 1)
## Obtain kernel weights
tau = 4 + drv
L = min(Int(fld(tau * h, delta)), M)
lvec = 0:L
arg = lvec .* delta / h
kappam = pdf.(Normal(), arg) ./ h^(drv + 1)
hmold0, hmnew = ones(length(arg)), ones(length(arg))
hmold1 = arg
if drv >= 2
for i in (2:drv)
hmnew = arg .* hmold1 .- (i - 1) .* hmold0
hmold0 = hmold1 # Compute mth degree Hermite polynomial
hmold1 = hmnew # by recurrence.
end
end
kappam = hmnew .* kappam
## Now combine weights and counts to obtain estimate
## we need P >= 2L+1L, M: L <= M.
P = nextpow(2, M + L + 1)
kappam = [kappam; zeros(P - 2 * L - 1); reverse(kappam[2:end])]
Gcounts = [gcounts; zeros(P - M)]
kappam = fft(kappam)
Gcounts = fft(Gcounts)
sum(gcounts .* (real(ifft(kappam .* Gcounts)))[1:M]) / (n^2)
end
| StatsPlots | https://github.com/JuliaPlots/StatsPlots.jl.git |
|
[
"MIT"
] | 0.15.7 | 3b1dcbf62e469a67f6733ae493401e53d92ff543 | code | 4107 | plot_function(plt::Function, grouped) = plt
plot_function(plt::Tuple, grouped) = grouped ? plt[2] : plt[1]
combine_cols(dict, ns) = length(ns) > 1 ? hcat((dict[n] for n in ns)...) : dict[ns[1]]
function dataviewer(t; throttle = 0.1, nbins = 30, nbins_range = 1:100)
(t isa AbstractObservable) || (t = Observable{Any}(t))
coltable = map(Tables.columntable, t)
@show names = map(collect ∘ keys, coltable)
dict = @map Dict((key, val) for (key, val) in pairs(&coltable))
x = Widgets.dropdown(names, placeholder = "First axis", multiple = true)
y = Widgets.dropdown(names, placeholder = "Second axis", multiple = true)
y_toggle = Widgets.togglecontent(y, value = false, label = "Second axis")
plot_type = Widgets.dropdown(
OrderedDict(
"line" => Plots.plot,
"scatter" => Plots.scatter,
"bar" => (Plots.bar, StatsPlots.groupedbar),
"boxplot" => (StatsPlots.boxplot, StatsPlots.groupedboxplot),
"corrplot" => StatsPlots.corrplot,
"cornerplot" => StatsPlots.cornerplot,
"density" => StatsPlots.density,
"cdensity" => StatsPlots.cdensity,
"histogram" => StatsPlots.histogram,
"marginalhist" => StatsPlots.marginalhist,
"violin" => (StatsPlots.violin, StatsPlots.groupedviolin),
),
placeholder = "Plot type",
)
# Add bins if the plot allows it
display_nbins =
@map (&plot_type) in [corrplot, cornerplot, histogram, marginalhist] ? "block" :
"none"
nbins = (Widgets.slider(
nbins_range,
extra_obs = ["display" => display_nbins],
value = nbins,
label = "number of bins",
))
nbins.scope.dom = Widgets.div(
nbins.scope.dom,
attributes = Dict("data-bind" => "style: {display: display}"),
)
nbins_throttle = Observables.throttle(throttle, nbins)
by = Widgets.dropdown(names, multiple = true, placeholder = "Group by")
by_toggle = Widgets.togglecontent(by, value = false, label = "Split data")
plt = Widgets.button("plot")
output = @map begin
if (&plt == 0)
plot()
else
args = Any[]
# add first and maybe second argument
push!(args, combine_cols(&dict, x[]))
has_y = y_toggle[] && !isempty(y[])
has_y && push!(args, combine_cols(&dict, y[]))
# compute automatic kwargs
kwargs = Dict()
# grouping kwarg
has_by = by_toggle[] && !isempty(by[])
by_tup = Tuple(getindex(&dict, b) for b in by[])
has_by && (kwargs[:group] = NamedTuple{Tuple(by[])}(by_tup))
# label kwarg
if length(x[]) > 1
kwargs[:label] = x[]
elseif y_toggle[] && length(y[]) > 1
kwargs[:label] = y[]
end
# x and y labels
densityplot1D = plot_type[] in [cdensity, density, histogram]
(length(x[]) == 1 && (densityplot1D || has_y)) && (kwargs[:xlabel] = x[][1])
if has_y && length(y[]) == 1
kwargs[:ylabel] = y[][1]
elseif !has_y && !densityplot1D && length(x[]) == 1
kwargs[:ylabel] = x[][1]
end
plot_func = plot_function(plot_type[], has_by)
plot_func(args...; nbins = &nbins_throttle, kwargs...)
end
end
wdg = Widget{:dataviewer}(
[
"x" => x,
"y" => y,
"y_toggle" => y_toggle,
"by" => by,
"by_toggle" => by_toggle,
"plot_type" => plot_type,
"plot_button" => plt,
"nbins" => nbins,
],
output = output,
)
@layout! wdg Widgets.div(
Widgets.div(:x, :y_toggle, :plot_type, :by_toggle, :plot_button),
Widgets.div(style = Dict("width" => "3em")),
Widgets.div(Widgets.observe(_), :nbins),
style = Dict("display" => "flex", "direction" => "row"),
)
end
| StatsPlots | https://github.com/JuliaPlots/StatsPlots.jl.git |
|
[
"MIT"
] | 0.15.7 | 3b1dcbf62e469a67f6733ae493401e53d92ff543 | code | 1749 | @shorthands marginalhist
@recipe function f(::Type{Val{:marginalhist}}, plt::AbstractPlot; density = false)
x, y = plotattributes[:x], plotattributes[:y]
i = isfinite.(x) .& isfinite.(y)
x, y = x[i], y[i]
bns = get(plotattributes, :bins, :auto)
scale = get(plotattributes, :scale, :identity)
edges1, edges2 = Plots._hist_edges((x, y), bns)
xlims, ylims = map(
x -> Plots.scale_lims(
Plots.ignorenan_extrema(x)...,
Plots.default_widen_factor,
scale,
),
(x, y),
)
# set up the subplots
legend --> false
link := :both
grid --> false
layout --> @layout [
tophist _
hist2d{0.9w,0.9h} righthist
]
# main histogram2d
@series begin
seriestype := :histogram2d
right_margin --> 0mm
top_margin --> 0mm
subplot := 2
bins := (edges1, edges2)
xlims --> xlims
ylims --> ylims
end
# these are common to both marginal histograms
ticks := nothing
xguide := ""
yguide := ""
foreground_color_border := nothing
fillcolor --> Plots.fg_color(plotattributes)
linecolor --> Plots.fg_color(plotattributes)
if density
trim := true
seriestype := :density
else
seriestype := :histogram
end
# upper histogram
@series begin
subplot := 1
bottom_margin --> 0mm
bins := edges1
y := x
xlims --> xlims
end
# right histogram
@series begin
orientation := :h
subplot := 3
left_margin --> 0mm
bins := edges2
y := y
ylims --> ylims
end
end
# # now you can plot like:
# marginalhist(rand(1000), rand(1000))
| StatsPlots | https://github.com/JuliaPlots/StatsPlots.jl.git |
|
[
"MIT"
] | 0.15.7 | 3b1dcbf62e469a67f6733ae493401e53d92ff543 | code | 1534 | @userplot MarginalKDE
@recipe function f(kc::MarginalKDE; levels = 10, clip = ((-3.0, 3.0), (-3.0, 3.0)))
x, y = kc.args
x = vec(x)
y = vec(y)
m_x = median(x)
m_y = median(y)
dx_l = m_x - quantile(x, 0.16)
dx_h = quantile(x, 0.84) - m_x
dy_l = m_y - quantile(y, 0.16)
dy_h = quantile(y, 0.84) - m_y
xmin = m_x + clip[1][1] * dx_l
xmax = m_x + clip[1][2] * dx_h
ymin = m_y + clip[2][1] * dy_l
ymax = m_y + clip[2][2] * dy_h
k = KernelDensity.kde((x, y))
kx = KernelDensity.kde(x)
ky = KernelDensity.kde(y)
ps = pdf.(Ref(k), x, y)
ls = []
for p in range(1.0 / levels, stop = 1 - 1.0 / levels, length = levels - 1)
push!(ls, quantile(ps, p))
end
legend --> false
layout := @layout [
topdensity _
contour{0.9w,0.9h} rightdensity
]
@series begin
seriestype := :contour
levels := ls
fill := false
colorbar := false
subplot := 2
xlims := (xmin, xmax)
ylims := (ymin, ymax)
(collect(k.x), collect(k.y), k.density')
end
ticks := nothing
xguide := ""
yguide := ""
@series begin
seriestype := :density
subplot := 1
xlims := (xmin, xmax)
ylims := (0, 1.1 * maximum(kx.density))
x
end
@series begin
seriestype := :density
subplot := 3
orientation := :h
xlims := (0, 1.1 * maximum(ky.density))
ylims := (ymin, ymax)
y
end
end
| StatsPlots | https://github.com/JuliaPlots/StatsPlots.jl.git |
|
[
"MIT"
] | 0.15.7 | 3b1dcbf62e469a67f6733ae493401e53d92ff543 | code | 1674 | @shorthands marginalscatter
@recipe function f(::Type{Val{:marginalscatter}}, plt::AbstractPlot; density = false)
x, y = plotattributes[:x], plotattributes[:y]
i = isfinite.(x) .& isfinite.(y)
x, y = x[i], y[i]
scale = get(plotattributes, :scale, :identity)
xlims, ylims = map(
x -> Plots.scale_lims(
Plots.ignorenan_extrema(x)...,
Plots.default_widen_factor,
scale,
),
(x, y),
)
# set up the subplots
legend --> false
link := :both
grid --> false
layout --> @layout [
topscatter _
scatter2d{0.9w,0.9h} rightscatter
]
# main scatter2d
@series begin
seriestype := :scatter
right_margin --> 0mm
top_margin --> 0mm
subplot := 2
xlims --> xlims
ylims --> ylims
end
# these are common to both marginal scatter
ticks := nothing
xguide := ""
yguide := ""
fillcolor --> Plots.fg_color(plotattributes)
linecolor --> Plots.fg_color(plotattributes)
if density
trim := true
seriestype := :density
else
seriestype := :scatter
end
# upper scatter
@series begin
subplot := 1
bottom_margin --> 0mm
showaxis := :x
x := x
y := ones(y |> size)
xlims --> xlims
ylims --> (0.95, 1.05)
end
# right scatter
@series begin
orientation := :h
showaxis := :y
subplot := 3
left_margin --> 0mm
# bins := edges2
y := y
x := ones(x |> size)
end
end
# # now you can plot like:
# marginalscatter(rand(1000), rand(1000))
| StatsPlots | https://github.com/JuliaPlots/StatsPlots.jl.git |
|
[
"MIT"
] | 0.15.7 | 3b1dcbf62e469a67f6733ae493401e53d92ff543 | code | 675 | @recipe function f(mds::MultivariateStats.MDS{<:Real}; mds_axes = (1, 2))
length(mds_axes) in [2, 3] || throw(ArgumentError("Can only accept 2 or 3 mds axes"))
xax = mds_axes[1]
yax = mds_axes[2]
tfm = collect(MultivariateStats.predict(mds)')
xlabel --> "MDS$xax"
ylabel --> "MDS$yax"
seriestype := :scatter
aspect_ratio --> 1
if length(mds_axes) == 3
zax = mds_axes[3]
zlabel --> "MDS$zax"
tfm[:, xax], tfm[:, yax], tfm[:, zax]
else
tfm[:, xax], tfm[:, yax]
end
end
#= This needs to wait on a different PCA API in MultivariateStats.jl
@recipe function f(pca::PCA{<:Real}; pca_axes=(1,2))
end
=#
| StatsPlots | https://github.com/JuliaPlots/StatsPlots.jl.git |
|
[
"MIT"
] | 0.15.7 | 3b1dcbf62e469a67f6733ae493401e53d92ff543 | code | 5875 |
# ---------------------------------------------------------------------------
# Violin Plot
const _violin_warned = [false]
function violin_coords(
y;
wts = nothing,
trim::Bool = false,
bandwidth = KernelDensity.default_bandwidth(y),
)
kd =
wts === nothing ? KernelDensity.kde(y, npoints = 200, bandwidth = bandwidth) :
KernelDensity.kde(y, weights = weights(wts), npoints = 200, bandwidth = bandwidth)
if trim
xmin, xmax = Plots.ignorenan_extrema(y)
inside = Bool[xmin <= x <= xmax for x in kd.x]
return (kd.density[inside], kd.x[inside])
end
kd.density, kd.x
end
get_quantiles(quantiles::AbstractVector) = quantiles
get_quantiles(x::Real) = [x]
get_quantiles(b::Bool) = b ? [0.5] : Float64[]
get_quantiles(n::Int) = range(0, 1, length = n + 2)[2:(end - 1)]
@recipe function f(
::Type{Val{:violin}},
x,
y,
z;
trim = true,
side = :both,
show_mean = false,
show_median = false,
quantiles = Float64[],
bandwidth = KernelDensity.default_bandwidth(y),
)
# if only y is provided, then x will be UnitRange 1:size(y,2)
if typeof(x) <: AbstractRange
if step(x) == first(x) == 1
x = plotattributes[:series_plotindex]
else
x = [getindex(x, plotattributes[:series_plotindex])]
end
end
xsegs, ysegs = Segments(), Segments()
qxsegs, qysegs = Segments(), Segments()
mxsegs, mysegs = Segments(), Segments()
glabels = sort(collect(unique(x)))
bw = plotattributes[:bar_width]
bw == nothing && (bw = 0.8)
msc = plotattributes[:markerstrokecolor]
for (i, glabel) in enumerate(glabels)
fy = y[filter(i -> _cycle(x, i) == glabel, 1:length(y))]
widths, centers = violin_coords(
fy,
trim = trim,
wts = plotattributes[:weights],
bandwidth = bandwidth,
)
isempty(widths) && continue
# normalize
hw = 0.5_cycle(bw, i)
widths = hw * widths / Plots.ignorenan_maximum(widths)
# make the violin
xcenter = Plots.discrete_value!(plotattributes, :x, glabel)[1]
xcoords = if (side === :right)
vcat(widths, zeros(length(widths))) .+ xcenter
elseif (side === :left)
vcat(zeros(length(widths)), -reverse(widths)) .+ xcenter
else
vcat(widths, -reverse(widths)) .+ xcenter
end
ycoords = vcat(centers, reverse(centers))
push!(xsegs, xcoords)
push!(ysegs, ycoords)
if show_mean
mea = StatsBase.mean(fy)
mw = maximum(widths)
mx = xcenter .+ [-mw, mw] * 0.75
my = [mea, mea]
if side === :right
mx[1] = xcenter
elseif side === :left
mx[2] = xcenter
end
push!(mxsegs, mx)
push!(mysegs, my)
end
if show_median
med = StatsBase.median(fy)
mw = maximum(widths)
mx = xcenter .+ [-mw, mw] / 2
my = [med, med]
if side === :right
mx[1] = xcenter
elseif side === :left
mx[2] = xcenter
end
push!(qxsegs, mx)
push!(qysegs, my)
end
quantiles = get_quantiles(quantiles)
if !isempty(quantiles)
qy = quantile(fy, quantiles)
maxw = maximum(widths)
for i in eachindex(qy)
qxi = xcenter .+ [-maxw, maxw] * (0.5 - abs(0.5 - quantiles[i]))
qyi = [qy[i], qy[i]]
if side === :right
qxi[1] = xcenter
elseif side === :left
qxi[2] = xcenter
end
push!(qxsegs, qxi)
push!(qysegs, qyi)
end
push!(qxsegs, [xcenter, xcenter])
push!(qysegs, [extrema(qy)...])
end
end
@series begin
seriestype := :shape
x := xsegs.pts
y := ysegs.pts
()
end
if !isempty(mxsegs.pts)
@series begin
primary := false
seriestype := :shape
linestyle := :dot
x := mxsegs.pts
y := mysegs.pts
()
end
end
if !isempty(qxsegs.pts)
@series begin
primary := false
seriestype := :shape
x := qxsegs.pts
y := qysegs.pts
()
end
end
seriestype := :shape
primary := false
x := []
y := []
()
end
Plots.@deps violin shape
# ------------------------------------------------------------------------------
# Grouped Violin
@userplot GroupedViolin
recipetype(::Val{:groupedviolin}, args...) = GroupedViolin(args)
@recipe function f(g::GroupedViolin; spacing = 0.1)
x, y = grouped_xy(g.args...)
# extract xnums and set default bar width.
# might need to set xticks as well
ux = unique(x)
x = if eltype(x) <: Number
bar_width --> (0.8 * mean(diff(sort(ux))))
float.(x)
else
bar_width --> 0.8
xnums = [findfirst(isequal(xi), ux) for xi in x] .- 0.5
xticks --> (eachindex(ux) .- 0.5, ux)
xnums
end
# shift x values for each group
group = get(plotattributes, :group, nothing)
if group != nothing
gb = RecipesPipeline._extract_group_attributes(group)
labels, idxs = getfield(gb, 1), getfield(gb, 2)
n = length(labels)
bws = plotattributes[:bar_width] / n
bar_width := bws * clamp(1 - spacing, 0, 1)
for i = 1:n
groupinds = idxs[i]
Δx = _cycle(bws, i) * (i - (n + 1) / 2)
x[groupinds] .+= Δx
end
end
seriestype := :violin
x, y
end
Plots.@deps groupedviolin violin
| StatsPlots | https://github.com/JuliaPlots/StatsPlots.jl.git |
|
[
"MIT"
] | 0.15.7 | 3b1dcbf62e469a67f6733ae493401e53d92ff543 | code | 6037 | using StatsPlots
using Test
using StableRNGs
using NaNMath
using Clustering
using Distributions
using MultivariateStats
@testset "Grouped histogram" begin
rng = StableRNG(1337)
gpl = groupedhist(
rand(rng, 1000),
yscale = :log10,
ylims = (1e-2, 1e4),
bar_position = :stack,
)
@test NaNMath.minimum(gpl[1][1][:y]) <= 1e-2
@test NaNMath.minimum(gpl[1][1][:y]) > 0
rng = StableRNG(1337)
gpl = groupedhist(
rand(rng, 1000),
yscale = :log10,
ylims = (1e-2, 1e4),
bar_position = :dodge,
)
@test NaNMath.minimum(gpl[1][1][:y]) <= 1e-2
@test NaNMath.minimum(gpl[1][1][:y]) > 0
data = [1, 1, 1, 1, 2, 1]
mask = (collect(1:6) .< 5)
gpl1 = groupedhist(data[mask], group = mask[mask], color = 1)
gpl2 = groupedhist(data[.!mask], group = mask[.!mask], color = 2)
gpl12 = groupedhist(data, group = mask, nbins = 5, bar_position = :stack)
@test NaNMath.maximum(gpl12[1][end][:y]) == NaNMath.maximum(gpl1[1][1][:y])
data = [10 12; 1 1; 0.25 0.25]
gplr = groupedbar(data)
@test NaNMath.maximum(gplr[1][1][:y]) == 10
@test NaNMath.maximum(gplr[1][end][:y]) == 12
gplr = groupedbar(data, bar_position = :stack)
@test NaNMath.maximum(gplr[1][1][:y]) == 22
@test NaNMath.maximum(gplr[1][end][:y]) == 12
end # testset
@testset "dendrogram" begin
# Example from https://en.wikipedia.org/wiki/Complete-linkage_clustering
wiki_example = [
0 17 21 31 23
17 0 30 34 21
21 30 0 28 39
31 34 28 0 43
23 21 39 43 0
]
clustering = hclust(wiki_example, linkage = :complete)
xs, ys = StatsPlots.treepositions(clustering, true, :vertical)
@test xs == [
2.0 1.0 4.0 1.75
2.0 1.0 4.0 1.75
3.0 2.5 5.0 4.5
3.0 2.5 5.0 4.5
]
@test ys == [
0.0 0.0 0.0 23.0
17.0 23.0 28.0 43.0
17.0 23.0 28.0 43.0
0.0 17.0 0.0 28.0
]
end
@testset "Histogram" begin
data = randn(1000)
@test 0.2 < StatsPlots.wand_bins(data) < 0.4
end
@testset "Distributions" begin
@testset "univariate" begin
@testset "discrete" begin
pbern = plot(Bernoulli(0.25))
@test pbern[1][1][:x][1:2] == zeros(2)
@test pbern[1][1][:x][4:5] == ones(2)
@test pbern[1][1][:y][[1, 4]] == zeros(2)
@test pbern[1][1][:y][[2, 5]] == [0.75, 0.25]
pdirac = plot(Dirac(0.25))
@test pdirac[1][1][:x][1:2] == [0.25, 0.25]
@test pdirac[1][1][:y][1:2] == [0, 1]
ppois_unbounded = plot(Poisson(1))
@test ppois_unbounded[1][1][:x] isa AbstractVector
@test ppois_unbounded[1][1][:x][1:2] == zeros(2)
@test ppois_unbounded[1][1][:x][4:5] == ones(2)
@test ppois_unbounded[1][1][:y][[1, 4]] == zeros(2)
@test ppois_unbounded[1][1][:y][[2, 5]] ==
pdf.(Poisson(1), ppois_unbounded[1][1][:x][[1, 4]])
pnonint = plot(Bernoulli(0.75) - 1 // 2)
@test pnonint[1][1][:x][1:2] == [-1 // 2, -1 // 2]
@test pnonint[1][1][:x][4:5] == [1 // 2, 1 // 2]
@test pnonint[1][1][:y][[1, 4]] == zeros(2)
@test pnonint[1][1][:y][[2, 5]] == [0.25, 0.75]
pmix = plot(
MixtureModel([Bernoulli(0.75), Bernoulli(0.5)], [0.5, 0.5]);
components = false,
)
@test pmix[1][1][:x][1:2] == zeros(2)
@test pmix[1][1][:x][4:5] == ones(2)
@test pmix[1][1][:y][[1, 4]] == zeros(2)
@test pmix[1][1][:y][[2, 5]] == [0.375, 0.625]
dzip = MixtureModel([Dirac(0), Poisson(1)], [0.1, 0.9])
pzip = plot(dzip; components = false)
@test pzip[1][1][:x] isa AbstractVector
@test pzip[1][1][:y][2:3:end] == pdf.(dzip, Int.(pzip[1][1][:x][1:3:end]))
end
end
end
@testset "ordinations" begin
@testset "MDS" begin
X = randn(4, 100)
M = fit(MultivariateStats.MDS, X; maxoutdim = 3, distances = false)
Y = MultivariateStats.predict(M)'
mds_plt = plot(M)
@test mds_plt[1][1][:x] == Y[:, 1]
@test mds_plt[1][1][:y] == Y[:, 2]
@test mds_plt[1][:xaxis][:guide] == "MDS1"
@test mds_plt[1][:yaxis][:guide] == "MDS2"
mds_plt2 = plot(M; mds_axes = (3, 1, 2))
@test mds_plt2[1][1][:x] == Y[:, 3]
@test mds_plt2[1][1][:y] == Y[:, 1]
@test mds_plt2[1][1][:z] == Y[:, 2]
@test mds_plt2[1][:xaxis][:guide] == "MDS3"
@test mds_plt2[1][:yaxis][:guide] == "MDS1"
@test mds_plt2[1][:zaxis][:guide] == "MDS2"
end
end
@testset "errorline" begin
rng = StableRNG(1337)
x = 1:10
# Test for floats
y = rand(rng, 10, 100) .* collect(1:2:20)
@test errorline(1:10, y)[1][1][:x] == x # x-input
@test all(
round.(errorline(1:10, y)[1][1][:y], digits = 3) .==
round.(mean(y, dims = 2), digits = 3),
) # mean of y
@test all(
round.(errorline(1:10, y)[1][1][:ribbon], digits = 3) .==
round.(std(y, dims = 2), digits = 3),
) # std of y
# Test for ints
y = reshape(1:100, 10, 10)
@test all(errorline(1:10, y)[1][1][:y] .== mean(y, dims = 2))
@test all(
round.(errorline(1:10, y)[1][1][:ribbon], digits = 3) .==
round.(std(y, dims = 2), digits = 3),
)
# Test colors
y = rand(rng, 10, 100, 3) .* collect(1:2:20)
c = palette(:default)
e = errorline(1:10, y)
@test colordiff(c[1], e[1][1][:linecolor]) == 0.0
@test colordiff(c[2], e[1][2][:linecolor]) == 0.0
@test colordiff(c[3], e[1][3][:linecolor]) == 0.0
end
@testset "marginalhist" begin
rng = StableRNG(1337)
pl = marginalhist(rand(rng, 100), rand(rng, 100))
@test show(devnull, pl) isa Nothing
end
@testset "marginalscatter" begin
rng = StableRNG(1337)
pl = marginalscatter(rand(rng, 100), rand(rng, 100))
@test show(devnull, pl) isa Nothing
end
| StatsPlots | https://github.com/JuliaPlots/StatsPlots.jl.git |
|
[
"MIT"
] | 0.15.7 | 3b1dcbf62e469a67f6733ae493401e53d92ff543 | docs | 1889 |
# StatsPlots.jl NEWS
## 0.10
- Rename package from StatPlots to StatsPlots
## 0.7 current version
### 0.7.3
- fixed out of bound error with `violin` and `boxplot`
- fixed title location in `corrplot`
- better handling of `NaN` and `Inf`
- recipe for `hclust` dendrogram (clustering visualization)
- `dataviewer` recipe for interactive GUIs
### 0.7.2
- fix stack overflow with `@df` and `begin ... end` blocks
- avoid recomputing data unnecessarily in `@df`
### 0.7.1
- remove Loess dependency
- fix hygien macro issue in `@df`
- add curly bracket syntax for automatic naming of groups
- add `cols()` to select all columns
### 0.7.0
- remove DataFrames dependency
- improve tick handling in correlation plots
- add support for discrete distributions
- add automatic legend with `@df`
- allow passing columns of a data table programmatically with `cols`
### 0.6.0
- deprecate the `plot(df, :x, :y)` syntax
- complete the removal of groupederror
- remove shadederror
- suppress axis labels in marginalhist
### 0.5.1
- remove groupederror, as that is now in it's own package
- add `qqnorm` and `qqplot`
- fix 2d density plots
### 0.5.0
- major reconfiguring of the support for tables:
- change the syntax to `@df mydataframe plot(:a, :b)`
- allows using DataFrames automatically in user recipes
- support for all iterable tables, including DataFrame, DataTable, IndexedTable, IterableTable and DataStreams.Source
- better interface to `groupedbar`
- added equal-area histograms
- added the `:wand` binning option for 1-dimensional histograms
### 0.4.2
- improvements to the groupapply function
### 0.4.1
patch release
- reexport Plots
### 0.4.0
- Fix 0.6 deprecations
- support for `_cycle`
### 0.3.0
- added expressions with DataFrame symbols
- added `groupapply` method for population analysis
- updated boxplots to turn off outlier points and improves whiskers
| StatsPlots | https://github.com/JuliaPlots/StatsPlots.jl.git |
|
[
"MIT"
] | 0.15.7 | 3b1dcbf62e469a67f6733ae493401e53d92ff543 | docs | 17974 | # StatsPlots
[](https://travis-ci.org/JuliaPlots/StatsPlots.jl)
[](https://docs.juliaplots.org/latest/generated/statsplots/)
[](https://julialang.zulipchat.com/#narrow/stream/236493-plots)
### Original author: Thomas Breloff (@tbreloff), maintained by the JuliaPlots members
This package is a drop-in replacement for Plots.jl that contains many statistical recipes for concepts and types introduced in the JuliaStats organization.
- Types:
- DataFrames
- Distributions
- Recipes:
- histogram/histogram2d
- groupedhist
- [boxplot](https://en.wikipedia.org/wiki/Box_plot)
- [dotplot](https://en.wikipedia.org/wiki/Dot_plot_(statistics))
- [violin](https://en.wikipedia.org/wiki/Violin_plot)
- marginalhist
- corrplot/cornerplot
- [andrewsplot](https://en.wikipedia.org/wiki/Andrews_plot)
- errorline ([ribbon](https://ggplot2.tidyverse.org/reference/geom_ribbon.html), [stick](https://www.mathworks.com/help/matlab/ref/errorbar.html), [plume](https://www.e-education.psu.edu/files/meteo410/file/Plume.pdf))
- MDS plot
- [qq-plot](https://en.wikipedia.org/wiki/Q%E2%80%93Q_plot)
It is thus slightly less lightweight, but has more functionality.
Initialize:
```julia
#]add StatsPlots # install the package if it isn't installed
using StatsPlots # no need for `using Plots` as that is reexported here
gr(size=(400,300))
```
Table-like data structures, including `DataFrames`, `IndexedTables`, `DataStreams`, etc... (see [here](https://github.com/davidanthoff/IterableTables.jl) for an exhaustive list), are supported thanks to the macro `@df` which allows passing columns as symbols. Those columns can then be manipulated inside the `plot` call, like normal `Arrays`:
```julia
using DataFrames, IndexedTables
df = DataFrame(a = 1:10, b = 10 .* rand(10), c = 10 .* rand(10))
@df df plot(:a, [:b :c], colour = [:red :blue])
@df df scatter(:a, :b, markersize = 4 .* log.(:c .+ 0.1))
t = table(1:10, rand(10), names = [:a, :b]) # IndexedTable
@df t scatter(2 .* :b)
```
Inside a `@df` macro call, the `cols` utility function can be used to refer to a range of columns:
```julia
@df df plot(:a, cols(2:3), colour = [:red :blue])
```
or to refer to a column whose symbol is represented by a variable:
```julia
s = :b
@df df plot(:a, cols(s))
```
`cols()` will refer to all columns of the data table.
In case of ambiguity, symbols not referring to `DataFrame` columns must be escaped by `^()`:
```julia
df[:red] = rand(10)
@df df plot(:a, [:b :c], colour = ^([:red :blue]))
```
The `@df` macro plays nicely with the new syntax of the [Query.jl](https://github.com/davidanthoff/Query.jl) data manipulation package (v0.8 and above), in that a plot command can be added at the end of a query pipeline, without having to explicitly collect the outcome of the query first:
```julia
using Query, StatsPlots
df |>
@filter(_.a > 5) |>
@map({_.b, d = _.c-10}) |>
@df scatter(:b, :d)
```
The `@df` syntax is also compatible with the Plots.jl grouping machinery:
```julia
using RDatasets
school = RDatasets.dataset("mlmRev","Hsb82")
@df school density(:MAch, group = :Sx)
```
To group by more than one column, use a tuple of symbols:
```julia
@df school density(:MAch, group = (:Sx, :Sector), legend = :topleft)
```

To name the legend entries with custom or automatic names (i.e. `Sex = Male, Sector = Public`) use the curly bracket syntax `group = {Sex = :Sx, :Sector}`. Entries with `=` get the custom name you give, whereas entries without `=` take the name of the column.
---
The old syntax, passing the `DataFrame` as the first argument to the `plot` call is no longer supported.
---
## Visualizing a table interactively
A GUI based on the Interact package is available to create plots from a table interactively, using any of the recipes defined below. This small app can be deployed in a Jupyter lab / notebook, Juno plot pane, a Blink window or in the browser, see [here](http://juliagizmos.github.io/Interact.jl/latest/deploying/) for instructions.
```julia
import RDatasets
iris = RDatasets.dataset("datasets", "iris")
using StatsPlots, Interact
using Blink
w = Window()
body!(w, dataviewer(iris))
```

## marginalhist with DataFrames
```julia
using RDatasets
iris = dataset("datasets","iris")
@df iris marginalhist(:PetalLength, :PetalWidth)
```
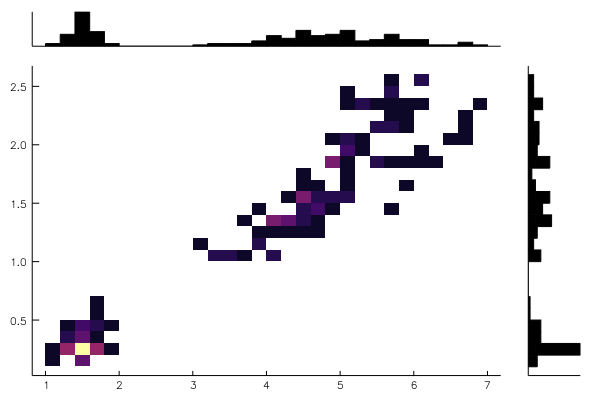
---
## marginalscatter with DataFrames
```julia
using RDatasets
iris = dataset("datasets","iris")
@df iris marginalscatter(:PetalLength, :PetalWidth)
```

---
## marginalkde
```julia
x = randn(1024)
y = randn(1024)
marginalkde(x, x+y)
```
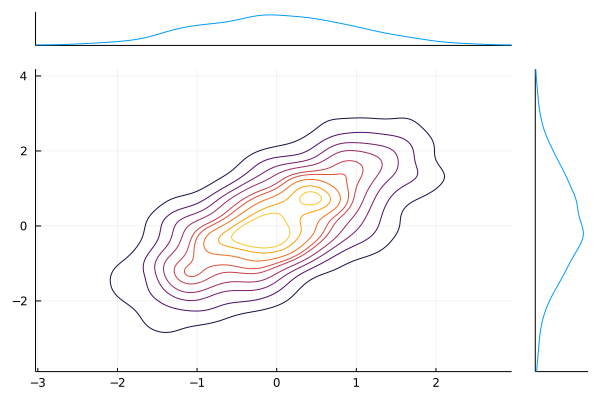
* `levels=N` can be used to set the number of contour levels (default 10); levels are evenly-spaced in the cumulative probability mass.
* `clip=((-xl, xh), (-yl, yh))` (default `((-3, 3), (-3, 3))`) can be used to adjust the bounds of the plot. Clip values are expressed as multiples of the `[0.16-0.5]` and `[0.5,0.84]` percentiles of the underlying 1D distributions (these would be 1-sigma ranges for a Gaussian).
## corrplot and cornerplot
This plot type shows the correlation among input variables. The marker color in scatter plots reveal the degree of correlation. Pass the desired colorgradient to `markercolor`. With the default gradient positive correlations are blue, neutral are yellow and negative are red. In the 2d-histograms the color gradient show the frequency of points in that bin (as usual controlled by `seriescolor`).
```julia
gr(size = (600, 500))
```
then
```julia
@df iris corrplot([:SepalLength :SepalWidth :PetalLength :PetalWidth], grid = false)
```
or also:
```julia
@df iris corrplot(cols(1:4), grid = false)
```

A correlation plot may also be produced from a matrix:
```julia
M = randn(1000,4)
M[:,2] .+= 0.8sqrt.(abs.(M[:,1])) .- 0.5M[:,3] .+ 5
M[:,3] .-= 0.7M[:,1].^2 .+ 2
corrplot(M, label = ["x$i" for i=1:4])
```

```julia
cornerplot(M)
```

```julia
cornerplot(M, compact=true)
```
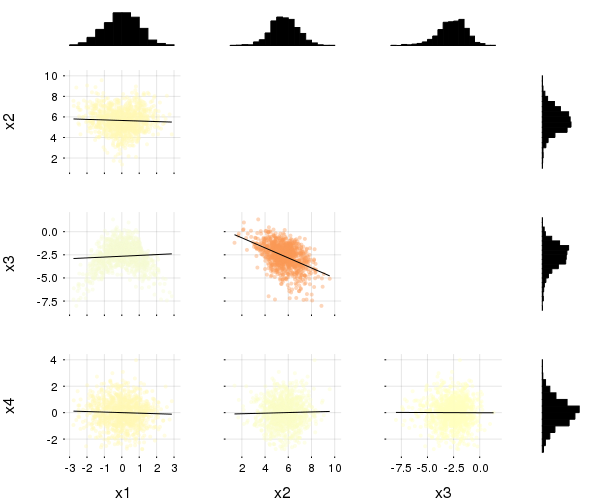
---
## boxplot, dotplot, and violin
```julia
import RDatasets
singers = RDatasets.dataset("lattice", "singer")
@df singers violin(string.(:VoicePart), :Height, linewidth=0)
@df singers boxplot!(string.(:VoicePart), :Height, fillalpha=0.75, linewidth=2)
@df singers dotplot!(string.(:VoicePart), :Height, marker=(:black, stroke(0)))
```

Asymmetric violin or dot plots can be created using the `side` keyword (`:both` - default,`:right` or `:left`), e.g.:
```julia
singers_moscow = deepcopy(singers)
singers_moscow[:Height] = singers_moscow[:Height] .+ 5
@df singers violin(string.(:VoicePart), :Height, side=:right, linewidth=0, label="Scala")
@df singers_moscow violin!(string.(:VoicePart), :Height, side=:left, linewidth=0, label="Moscow")
@df singers dotplot!(string.(:VoicePart), :Height, side=:right, marker=(:black,stroke(0)), label="")
@df singers_moscow dotplot!(string.(:VoicePart), :Height, side=:left, marker=(:black,stroke(0)), label="")
```
Dot plots can spread their dots over the full width of their column `mode = :uniform`, or restricted to the kernel density
(i.e. width of violin plot) with `mode = :density` (default). Horizontal position is random, so dots are repositioned
each time the plot is recreated. `mode = :none` keeps the dots along the center.
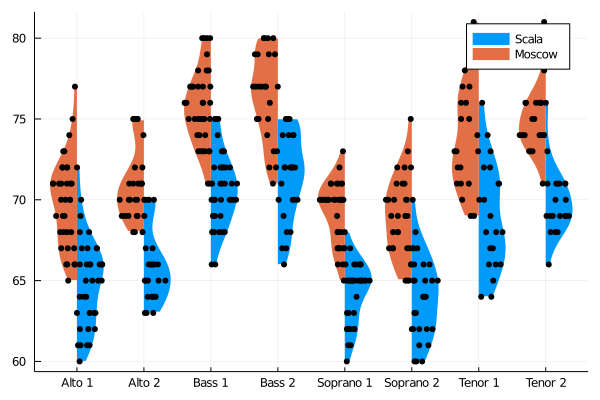
---
## Equal-area histograms
The ea-histogram is an alternative histogram implementation, where every 'box' in
the histogram contains the same number of sample points and all boxes have the same
area. Areas with a higher density of points thus get higher boxes. This type of
histogram shows spikes well, but may oversmooth in the tails. The y axis is not
intuitively interpretable.
```julia
a = [randn(100); randn(100) .+ 3; randn(100) ./ 2 .+ 3]
ea_histogram(a, bins = :scott, fillalpha = 0.4)
```

---
## AndrewsPlot
AndrewsPlots are a way to visualize structure in high-dimensional data by depicting each
row of an array or table as a line that varies with the values in columns.
https://en.wikipedia.org/wiki/Andrews_plot
```julia
using RDatasets
iris = dataset("datasets", "iris")
@df iris andrewsplot(:Species, cols(1:4), legend = :topleft)
```
---
## ErrorLine
The ErrorLine function shows error distributions for lines plots in a variety of styles.
```julia
x = 1:10
y = fill(NaN, 10, 100, 3)
for i = axes(y,3)
y[:,:,i] = collect(1:2:20) .+ rand(10,100).*5 .* collect(1:2:20) .+ rand()*100
end
errorline(1:10, y[:,:,1], errorstyle=:ribbon, label="Ribbon")
errorline!(1:10, y[:,:,2], errorstyle=:stick, label="Stick", secondarycolor=:matched)
errorline!(1:10, y[:,:,3], errorstyle=:plume, label="Plume")
```

---
## Distributions
```julia
using Distributions
plot(Normal(3,5), fill=(0, .5,:orange))
```

```julia
dist = Gamma(2)
scatter(dist, leg=false)
bar!(dist, func=cdf, alpha=0.3)
```

### Quantile-Quantile plots
The `qqplot` function compares the quantiles of two distributions, and accepts either a vector of sample values or a `Distribution`. The `qqnorm` is a shorthand for comparing a distribution to the normal distribution. If the distributions are similar the points will be on a straight line.
```julia
x = rand(Normal(), 100)
y = rand(Cauchy(), 100)
plot(
qqplot(x, y, qqline = :fit), # qqplot of two samples, show a fitted regression line
qqplot(Cauchy, y), # compare with a Cauchy distribution fitted to y; pass an instance (e.g. Normal(0,1)) to compare with a specific distribution
qqnorm(x, qqline = :R) # the :R default line passes through the 1st and 3rd quartiles of the distribution
)
```

## Grouped Bar plots
```julia
groupedbar(rand(10,3), bar_position = :stack, bar_width=0.7)
```

This is the default:
```julia
groupedbar(rand(10,3), bar_position = :dodge, bar_width=0.7)
```

The `group` syntax is also possible in combination with `groupedbar`:
```julia
ctg = repeat(["Category 1", "Category 2"], inner = 5)
nam = repeat("G" .* string.(1:5), outer = 2)
groupedbar(nam, rand(5, 2), group = ctg, xlabel = "Groups", ylabel = "Scores",
title = "Scores by group and category", bar_width = 0.67,
lw = 0, framestyle = :box)
```
## Grouped Histograms
```
using RDatasets
iris = dataset("datasets", "iris")
@df iris groupedhist(:SepalLength, group = :Species, bar_position = :dodge)
```
```
@df iris groupedhist(:SepalLength, group = :Species, bar_position = :stack)
```
## Dendrograms
```julia
using Clustering
D = rand(10, 10)
D += D'
hc = hclust(D, linkage=:single)
plot(hc)
```

The `branchorder=:optimal` option in `hclust()` can be used to minimize
the distance between neighboring leaves:
```julia
using Clustering
using Distances
using StatsPlots
using Random
n = 40
mat = zeros(Int, n, n)
# create banded matrix
for i in 1:n
last = minimum([i+Int(floor(n/5)), n])
for j in i:last
mat[i,j] = 1
end
end
# randomize order
mat = mat[:, randperm(n)]
dm = pairwise(Euclidean(), mat, dims=2)
# normal ordering
hcl1 = hclust(dm, linkage=:average)
plot(
plot(hcl1, xticks=false),
heatmap(mat[:, hcl1.order], colorbar=false, xticks=(1:n, ["$i" for i in hcl1.order])),
layout=grid(2,1, heights=[0.2,0.8])
)
```

Compare to:
```julia
# optimal ordering
hcl2 = hclust(dm, linkage=:average, branchorder=:optimal)
plot(
plot(hcl2, xticks=false),
heatmap(mat[:, hcl2.order], colorbar=false, xticks=(1:n, ["$i" for i in hcl2.order])),
layout=grid(2,1, heights=[0.2,0.8])
)
```

### Dendrogram on the right side
```julia
using Distances
using Clustering
using StatsBase
using StatsPlots
pd=rand(Float64,16,7)
dist_col=pairwise(CorrDist(),pd,dims=2)
hc_col=hclust(dist_col, branchorder=:optimal)
dist_row=pairwise(CorrDist(),pd,dims=1)
hc_row=hclust(dist_row, branchorder=:optimal)
pdz=similar(pd)
for row in hc_row.order
pdz[row,hc_col.order]=zscore(pd[row,hc_col.order])
end
nrows=length(hc_row.order)
rowlabels=(1:16)[hc_row.order]
ncols=length(hc_col.order)
collabels=(1:7)[hc_col.order]
l = grid(2,2,heights=[0.2,0.8,0.2,0.8],widths=[0.8,0.2,0.8,0.2])
plot(
layout = l,
plot(hc_col,xticks=false),
plot(ticks=nothing,border=:none),
plot(
pdz[hc_row.order,hc_col.order],
st=:heatmap,
#yticks=(1:nrows,rowlabels),
yticks=(1:nrows,rowlabels),
xticks=(1:ncols,collabels),
xrotation=90,
colorbar=false
),
plot(hc_row,yticks=false,xrotation=90,orientation=:horizontal,xlim=(0,1))
)
```

## GroupedErrors.jl for population analysis
Population analysis on a table-like data structures can be done using the highly recommended [GroupedErrors](https://github.com/piever/GroupedErrors.jl) package.
This external package, in combination with StatsPlots, greatly simplifies the creation of two types of plots:
### 1. Subject by subject plot (generally a scatter plot)
Some simple summary statistics are computed for each experimental subject (mean is default but any scalar valued function would do) and then plotted against some other summary statistics, potentially splitting by some categorical experimental variable.
### 2. Population plot (generally a ribbon plot in continuous case, or bar plot in discrete case)
Some statistical analysis is computed at the single subject level (for example the density/hazard/cumulative of some variable, or the expected value of a variable given another) and the analysis is summarized across subjects (taking for example mean and s.e.m), potentially splitting by some categorical experimental variable.
For more information please refer to the [README](https://github.com/piever/GroupedErrors.jl/blob/master/README.md).
A GUI based on QML and the GR Plots.jl backend to simplify the use of StatsPlots.jl and GroupedErrors.jl even further can be found [here](https://github.com/piever/PlugAndPlot.jl) (usable but still in alpha stage).
## Ordinations
MDS from [`MultivariateStats.jl`](https://github.com/JuliaStats/MultivariateStats.jl)
can be plotted as scatter plots.
```julia
using MultivariateStats, RDatasets, StatsPlots
iris = dataset("datasets", "iris")
X = convert(Matrix, iris[:, 1:4])
M = fit(MDS, X'; maxoutdim=2)
plot(M, group=iris.Species)
```

PCA will be added once the API in MultivariateStats is changed.
See https://github.com/JuliaStats/MultivariateStats.jl/issues/109 and https://github.com/JuliaStats/MultivariateStats.jl/issues/95.
## Covariance ellipses
A 2×2 covariance matrix `Σ` can be plotted as an ellipse, which is a contour line of a Gaussian density function with variance `Σ`.
```
covellipse([0,2], [2 1; 1 4], n_std=2, aspect_ratio=1, label="cov1")
covellipse!([1,0], [1 -0.5; -0.5 3], showaxes=true, label="cov2")
```

| StatsPlots | https://github.com/JuliaPlots/StatsPlots.jl.git |
|
[
"MIT"
] | 3.13.3 | a4816454042d72e4bae37d13e592591381356a17 | code | 660 | __precompile__()
module ODEInterfaceDiffEq
using Reexport
@reexport using DiffEqBase
using ODEInterface, Compat, DataStructures, FunctionWrappers
using LinearAlgebra
import DiffEqBase: solve
const warnkeywords = (:save_idxs, :d_discontinuities, :unstable_check, :tstops,
:calck, :progress, :dense, :save_start)
function __init__()
global warnlist = Set(warnkeywords)
end
const KW = Dict{Symbol, Any}
include("algorithms.jl")
include("integrator_types.jl")
include("integrator_utils.jl")
include("solve.jl")
export ODEInterfaceAlgorithm, dopri5, dop853, odex, seulex, radau, radau5, rodas,
ddeabm, ddebdf
end # module
| ODEInterfaceDiffEq | https://github.com/SciML/ODEInterfaceDiffEq.jl.git |
|
[
"MIT"
] | 3.13.3 | a4816454042d72e4bae37d13e592591381356a17 | code | 2295 | # ODEInterface.jl Algorithms
abstract type ODEInterfaceAlgorithm <: DiffEqBase.AbstractODEAlgorithm end
abstract type ODEInterfaceImplicitAlgorithm <: ODEInterfaceAlgorithm end
abstract type ODEInterfaceExplicitAlgorithm <: ODEInterfaceAlgorithm end
"""
dopri5: Hairer's classic implementation of the Dormand-Prince 4/5 method.
"""
struct dopri5 <: ODEInterfaceExplicitAlgorithm end
SciMLBase.alg_order(alg::dopri5) = 5
"""
dop853: Explicit Runge-Kutta 8(5,3) by Dormand-Prince.
"""
struct dop853 <: ODEInterfaceExplicitAlgorithm end
SciMLBase.alg_order(alg::dop853) = 8
"""
odex: GBS extrapolation-algorithm based on the midpoint rule.
"""
struct odex <: ODEInterfaceExplicitAlgorithm end
SciMLBase.alg_order(alg::odex) = 12
"""
seulex: Extrapolation-algorithm based on the linear implicit Euler method.
"""
struct seulex{T} <: ODEInterfaceImplicitAlgorithm
jac_lower::T
jac_upper::T
end
SciMLBase.alg_order(alg::seulex) = 12
"""
radau: Implicit Runge-Kutta (Radau IIA) of variable order between 5 and 13.
"""
struct radau{T} <: ODEInterfaceImplicitAlgorithm
jac_lower::T
jac_upper::T
end
SciMLBase.alg_order(alg::radau) = 13
"""
radau5: Implicit Runge-Kutta method (Radau IIA) of order 5.
"""
struct radau5{T} <: ODEInterfaceImplicitAlgorithm
jac_lower::T
jac_upper::T
end
SciMLBase.alg_order(alg::radau5) = 5
"""
rodas: Rosenbrock 4(3) method.
"""
struct rodas{T} <: ODEInterfaceImplicitAlgorithm
jac_lower::T
jac_upper::T
end
SciMLBase.alg_order(alg::rodas) = 4
"""
ddeabm: Adams-Bashforth-Moulton Predictor-Corrector method (order between 1 and 12)
"""
struct ddeabm <: ODEInterfaceExplicitAlgorithm end
SciMLBase.alg_order(alg::ddeabm) = 12
"""
ddebdf: Backward Differentiation Formula (orders between 1 and 5)
"""
struct ddebdf{T} <: ODEInterfaceImplicitAlgorithm
jac_lower::T
jac_upper::T
end
SciMLBase.alg_order(alg::ddebdf) = 5
seulex(; jac_lower = nothing, jac_upper = nothing) = seulex(jac_lower, jac_upper)
radau(; jac_lower = nothing, jac_upper = nothing) = radau(jac_lower, jac_upper)
radau5(; jac_lower = nothing, jac_upper = nothing) = radau5(jac_lower, jac_upper)
rodas(; jac_lower = nothing, jac_upper = nothing) = rodas(jac_lower, jac_upper)
ddebdf(; jac_lower = nothing, jac_upper = nothing) = ddebdf(jac_lower, jac_upper)
| ODEInterfaceDiffEq | https://github.com/SciML/ODEInterfaceDiffEq.jl.git |
|
[
"MIT"
] | 3.13.3 | a4816454042d72e4bae37d13e592591381356a17 | code | 1021 | mutable struct DEOptions{SType, CType}
saveat::SType
save_on::Bool
save_everystep::Bool
callback::CType
end
mutable struct ODEInterfaceIntegrator{F, algType, uType, uPrevType, oType, SType, solType,
P, CallbackCacheType} <:
DiffEqBase.AbstractODEIntegrator{algType, true, uType, Float64}
f::F
u::uType
uprev::uPrevType
t::Float64
tprev::Float64
p::P
opts::oType
u_modified::Bool
tdir::Float64
sizeu::SType
sol::solType
eval_sol_fcn::Any
event_last_time::Int
vector_event_last_time::Int
callback_cache::CallbackCacheType
alg::algType
last_event_error::Float64
end
@inline function (integrator::ODEInterfaceIntegrator)(t, deriv::Type{Val{N}} = Val{0};
idxs = nothing) where {N}
@assert N==0 "ODEInterface does not support dense derivative"
sol = integrator.eval_sol_fcn(t)
return idxs == nothing ? sol : sol[idxs]
end
| ODEInterfaceDiffEq | https://github.com/SciML/ODEInterfaceDiffEq.jl.git |
|
[
"MIT"
] | 3.13.3 | a4816454042d72e4bae37d13e592591381356a17 | code | 4127 | # Carries along the `u` which is an allocation to save when no callbacks
function handle_callbacks!(integrator, eval_sol_fcn)
discrete_callbacks = integrator.opts.callback.discrete_callbacks
continuous_callbacks = integrator.opts.callback.continuous_callbacks
atleast_one_callback = false
continuous_modified = false
discrete_modified = false
saved_in_cb = false
if !(typeof(continuous_callbacks) <: Tuple{})
time, upcrossing, event_occured, event_idx, idx, counter = DiffEqBase.find_first_continuous_callback(integrator,
continuous_callbacks...)
if event_occured
integrator.event_last_time = idx
integrator.vector_event_last_time = event_idx
continuous_modified, saved_in_cb = DiffEqBase.apply_callback!(integrator,
continuous_callbacks[idx],
time, upcrossing,
event_idx)
else
integrator.event_last_time = 0
integrator.vector_event_last_time = 1
end
end
if !(typeof(discrete_callbacks) <: Tuple{})
discrete_modified, saved_in_cb = DiffEqBase.apply_discrete_callback!(integrator,
discrete_callbacks...)
end
if !saved_in_cb
savevalues!(integrator)
end
integrator.u_modified = continuous_modified || discrete_modified
end
function DiffEqBase.savevalues!(integrator::ODEInterfaceIntegrator,
force_save = false)::Tuple{Bool, Bool}
saved, savedexactly = false, false
!integrator.opts.save_on && return saved, savedexactly
uType = eltype(integrator.sol.u)
if integrator.opts.save_everystep || force_save
saved = true
push!(integrator.sol.t, integrator.t)
save_value!(integrator.sol.u, copy(integrator.u), uType, integrator.sizeu)
end
while !isempty(integrator.opts.saveat) &&
integrator.tdir * first(integrator.opts.saveat) < integrator.tdir * integrator.t
saved = true
curt = pop!(integrator.opts.saveat)
tmp = integrator(curt)::Vector{Float64}
push!(integrator.sol.t, curt)
save_value!(integrator.sol.u, tmp, uType, integrator.sizeu)
end
savedexactly = last(integrator.sol.t) == integrator.t
return saved, savedexactly
end
function DiffEqBase.change_t_via_interpolation!(integrator::ODEInterfaceIntegrator, t)
integrator.t = t
tmp = integrator(integrator.t)::Vector{Float64}
if eltype(integrator.sol.u) <: Vector
integrator.u .= tmp
else
integrator.u .= reshape(tmp, integrator.sizeu)
end
nothing
end
DiffEqBase.get_tmp_cache(i::ODEInterfaceIntegrator, args...) = nothing
@inline function Base.getproperty(integrator::ODEInterfaceIntegrator, sym::Symbol)
if sym == :dt
return integrator.t - integrator.tprev
else
return getfield(integrator, sym)
end
end
@inline function DiffEqBase.u_modified!(integrator::ODEInterfaceIntegrator, bool::Bool)
integrator.u_modified = bool
end
function initialize_callbacks!(integrator, initialize_save = true)
t = integrator.t
u = integrator.u
callbacks = integrator.opts.callback
integrator.u_modified = true
u_modified = initialize!(callbacks, u, t, integrator)
# if the user modifies u, we need to fix current values
if u_modified
if initialize_save &&
(any((c) -> c.save_positions[2], callbacks.discrete_callbacks) ||
any((c) -> c.save_positions[2], callbacks.continuous_callbacks))
savevalues!(integrator, true)
end
end
# reset this as it is now handled so the integrators should proceed as normal
integrator.u_modified = false
end
DiffEqBase.set_proposed_dt!(integrator::ODEInterfaceIntegrator, dt) = nothing
| ODEInterfaceDiffEq | https://github.com/SciML/ODEInterfaceDiffEq.jl.git |
|
[
"MIT"
] | 3.13.3 | a4816454042d72e4bae37d13e592591381356a17 | code | 18211 | function DiffEqBase.__solve(prob::DiffEqBase.AbstractODEProblem{uType, tuptType, isinplace},
alg::AlgType,
timeseries = [], ts = [], ks = [];
saveat = Float64[],
verbose = true, save_everystep = isempty(saveat),
save_on = true,
save_start = save_everystep || isempty(saveat) ||
typeof(saveat) <: Number ? true :
prob.tspan[1] in saveat,
timeseries_errors = true, dense_errors = false,
callback = nothing, alias_u0 = false,
kwargs...) where
{uType, tuptType, isinplace, AlgType <: ODEInterfaceAlgorithm}
tType = eltype(tuptType)
isstiff = alg isa ODEInterfaceImplicitAlgorithm
if verbose
warned = !isempty(kwargs) && check_keywords(alg, kwargs, warnlist)
if !(typeof(prob.f) <: DiffEqBase.AbstractParameterizedFunction) && isstiff
if DiffEqBase.has_tgrad(prob.f)
@warn("Explicit t-gradient given to this stiff solver is ignored.")
warned = true
end
end
warned && warn_compat()
end
callbacks_internal = CallbackSet(callback)
max_len_cb = DiffEqBase.max_vector_callback_length(callbacks_internal)
if max_len_cb isa VectorContinuousCallback
callback_cache = DiffEqBase.CallbackCache(max_len_cb.len, uBottomEltype,
uBottomEltype)
else
callback_cache = nothing
end
tspan = prob.tspan
o = KW(kwargs)
u0 = prob.u0
if typeof(u0) <: Number
u = [u0]
else
if alias_u0
u = u0
else
u = deepcopy(u0)
end
end
tdir = sign(tspan[2] - tspan[1])
saveat_internal = saveat_disc_handling(saveat, tdir, tspan, tType)
sizeu = size(u)
o[:RHS_CALLMODE] = ODEInterface.RHS_CALL_INSITU
if save_everystep
_timeseries = Vector{uType}(undef, 0)
ts = Vector{tType}(undef, 0)
else
_timeseries = [copy(u0)]
ts = [tspan[1]]
end
uprev = similar(u)
sol = DiffEqBase.build_solution(prob, alg, ts, _timeseries,
timeseries_errors = timeseries_errors,
calculate_error = false,
stats = DiffEqBase.Stats(0),
retcode = ReturnCode.Default)
opts = DEOptions(saveat_internal, save_on, save_everystep, callbacks_internal)
if !isinplace && typeof(u) <: AbstractArray
f! = (t, u, du) -> (du[:] = vec(prob.f(reshape(u, sizeu), integrator.p, t)); nothing)
elseif !(typeof(u) <: Vector{Float64})
f! = (t, u, du) -> (prob.f(reshape(du, sizeu), reshape(u, sizeu), integrator.p, t);
du = vec(du);
nothing)
else
f! = (t, u, du) -> prob.f(du, u, integrator.p, t)
end
integrator = ODEInterfaceIntegrator(prob.f, u, uprev, tspan[1], tspan[1], prob.p, opts,
false, tdir, sizeu, sol,
(t) -> [t], 0, 1, callback_cache, alg, 0.0)
initialize_callbacks!(integrator)
outputfcn = OutputFunction(integrator)
o[:OUTPUTFCN] = outputfcn
if !(typeof(callbacks_internal.continuous_callbacks) <: Tuple{}) || !isempty(saveat)
if typeof(alg) <: Union{ddeabm, ddebdf}
@warn("saveat and continuous callbacks ignored for ddeabm and ddebdf")
o[:OUTPUTMODE] = ODEInterface.OUTPUTFCN_WODENSE
else
o[:OUTPUTMODE] = ODEInterface.OUTPUTFCN_DENSE
end
else
o[:OUTPUTMODE] = ODEInterface.OUTPUTFCN_WODENSE
end
dict = buildOptions(o,
ODEINTERFACE_OPTION_LIST,
ODEINTERFACE_ALIASES,
ODEINTERFACE_ALIASES_REVERSED)
if prob.f.mass_matrix != I
if typeof(prob.f.mass_matrix) <: Matrix && isstiff
dict[:MASSMATRIX] = prob.f.mass_matrix
elseif !isstiff
error("This solver does not support mass matrices")
else
error("This solver must use full or banded mass matrices.")
end
end
if DiffEqBase.has_jac(prob.f)
dict[:JACOBIMATRIX] = (t, u, J) -> prob.f.jac(J, u, prob.p, t)
end
if isstiff && alg.jac_lower !== nothing
dict[:JACOBIBANDSSTRUCT] = (alg.jac_lower, alg.jac_upper)
end
# Convert to the strings
opts = ODEInterface.OptionsODE([Pair(ODEINTERFACE_STRINGS[k], v) for (k, v) in dict]...)
if typeof(alg) <: dopri5
tend, uend, retcode, stats = ODEInterface.dopri5(f!, tspan[1], tspan[2],
vec(integrator.u), opts)
elseif typeof(alg) <: dop853
tend, uend, retcode, stats = ODEInterface.dop853(f!, tspan[1], tspan[2],
vec(integrator.u), opts)
elseif typeof(alg) <: odex
tend, uend, retcode, stats = ODEInterface.odex(f!, tspan[1], tspan[2],
vec(integrator.u), opts)
elseif typeof(alg) <: seulex
tend, uend, retcode, stats = ODEInterface.seulex(f!, tspan[1], tspan[2],
vec(integrator.u), opts)
elseif typeof(alg) <: radau
tend, uend, retcode, stats = ODEInterface.radau(f!, tspan[1], tspan[2],
vec(integrator.u), opts)
elseif typeof(alg) <: radau5
tend, uend, retcode, stats = ODEInterface.radau5(f!, tspan[1], tspan[2],
vec(integrator.u), opts)
elseif typeof(alg) <: rodas
tend, uend, retcode, stats = ODEInterface.rodas(f!, tspan[1], tspan[2],
vec(integrator.u), opts)
elseif typeof(alg) <: ddeabm
tend, uend, retcode, stats = ODEInterface.ddeabm(f!, tspan[1], tspan[2],
vec(integrator.u), opts)
elseif typeof(alg) <: ddebdf
tend, uend, retcode, stats = ODEInterface.ddebdf(f!, tspan[1], tspan[2],
vec(integrator.u), opts)
end
if !save_everystep
push!(ts, tend)
save_value!(_timeseries, uend, uType, sizeu)
end
if retcode < 0
if retcode == -1
verbose && @warn("Input is not consistent.")
return_retcode = ReturnCode.Failure
elseif retcode == -2
verbose && @warn("Interrupted. Larger maxiters is needed.")
return_retcode = ReturnCode.MaxIters
elseif retcode == -3
verbose && @warn("Step size went too small.")
return_retcode = ReturnCode.DtLessThanMin
elseif retcode == -4
verbose && @warn("Interrupted. Problem is probably stiff.")
return_retcode = ReturnCode.Unstable
end
else
return_retcode = ReturnCode.Success
end
if DiffEqBase.has_analytic(prob.f)
DiffEqBase.calculate_solution_errors!(integrator.sol;
timeseries_errors = timeseries_errors,
dense_errors = dense_errors)
end
destats = sol.stats
destats.nf = stats["no_rhs_calls"]
if haskey(stats, "no_steps_rejected")
destats.nreject = stats["no_steps_rejected"]
destats.naccept = stats["no_steps_accepted"]
end
if haskey(stats, "no_jac_calls")
destats.njacs = stats["no_jac_calls"]
end
if haskey(stats, "no_lu_decomp")
destats.nw = stats["no_lu_decomp"]
end
DiffEqBase.solution_new_retcode(sol, return_retcode)
end
function save_value!(_timeseries, u, ::Type{T}, sizeu) where {T <: Number}
push!(_timeseries, first(u))
end
function save_value!(_timeseries, u, ::Type{T}, sizeu) where {T <: Vector}
push!(_timeseries, u)
end
function save_value!(_timeseries, u, ::Type{T}, sizeu) where {T <: Array}
push!(_timeseries, reshape(u, sizeu))
end
function buildOptions(o, optionlist, aliases, aliases_reversed)
dict1 = Dict{Symbol, Any}([Pair(k, o[k]) for k in (keys(o) ∩ optionlist)])
dict2 = Dict([Pair(aliases_reversed[k], o[k]) for k in (keys(o) ∩ values(aliases))])
merge(dict1, dict2)
end
function saveat_disc_handling(saveat, tdir, tspan, tType)
if typeof(saveat) <: Number
if (tspan[1]:saveat:tspan[end])[end] == tspan[end]
saveat_vec = convert(Vector{tType},
collect(tType, (tspan[1] + saveat):saveat:tspan[end]))
else
saveat_vec = convert(Vector{tType},
collect(tType,
(tspan[1] + saveat):saveat:(tspan[end] - saveat)))
end
else
saveat_vec = vec(collect(tType,
Iterators.filter(x -> tdir * tspan[1] < tdir * x <
tdir * tspan[end], saveat)))
end
if tdir > 0
saveat_internal = BinaryMinHeap(saveat_vec)
else
saveat_internal = BinaryMaxHeap(saveat_vec)
end
saveat_internal
end
const ODEINTERFACE_OPTION_LIST = Set([:RTOL, :ATOL, :OUTPUTFCN, :OUTPUTMODE, :MAXSTEPS,
:STEST, :EPS, :RHO, :SSMINSEL,
:SSMAXSEL, :SSBETA, :MAXSS, :INITIALSS,
:MAXEXCOLUMN, :STEPSIZESEQUENCE,
:MAXSTABCHECKS, :MAXSTABCHECKLINE,
:DENSEOUTPUTWOEE, :INTERPOLDEGRE,
:SSREDUCTION, :SSSELECTPAR1, :SSSELECTPAR2,
:ORDERDECFRAC, :ORDERINCFRAC,
:OPT_RHO, :OPT_RHO2, :RHSAUTONOMOUS, :M1, :M2,
:LAMBDADENSE, :TRANSJTOH,
:STEPSIZESEQUENCE, :JACRECOMPFACTOR, :MASSMATRIX,
:JACOBIMATRIX, :JACOBIBANDSSTRUCT,
:WORKFORRHS, :WORKFORJAC, :WORKFORDEC, :WORKFORSOL,
:MAXNEWTONITER, :NEWTONSTARTZERO, :NEWTONSTOPCRIT,
:DIMFIND1VAR,
:MAXSTAGES, :MINSTAGES, :INITSTAGES,
:STEPSIZESTRATEGY,
:FREEZESSLEFT, :FREEZESSRIGHT, :ORDERDECFACTOR,
:ORDERINCFACTOR, :ORDERDECCSTEPFAC1,
:ORDERDECSTEPFAC2, :RHS_CALLMODE,
])
const ODEINTERFACE_ALIASES = Dict{Symbol, Symbol}(:RTOL => :reltol,
:ATOL => :abstol,
:MAXSTEPS => :maxiters,
:MAXSS => :dtmax,
:INITIALSS => :dt,
#:SSMINSEL=>:qmin,
:SSBETA => :beta2,
:SSMAXSEL => :qmax)
const ODEINTERFACE_ALIASES_REVERSED = Dict{Symbol, Symbol}([(v, k)
for (k, v) in ODEINTERFACE_ALIASES])
const ODEINTERFACE_STRINGS = Dict{Symbol, String}(:LOGIO => "logio",
:LOGLEVEL => "loglevel",
:RHS_CALLMODE => "RightHandSideCallMode",
:RTOL => "RelTol",
:ATOL => "AbsTol",
:MAXSTEPS => "MaxNumberOfSteps",
:EPS => "eps", :OUTPUTFCN => "OutputFcn",
:OUTPUTMODE => "OutputFcnMode",
:STEST => "StiffTestAfterStep",
:RHO => "rho",
:SSMINSEL => "StepSizeMinSelection",
:SSMAXSEL => "StepSizeMaxSelection",
:SSBETA => "StepSizeBeta",
:MAXSS => "MaxStep",
:INITIALSS => "InitialStep",
:MAXEXCOLUMN => "MaxExtrapolationColumn",
:MAXSTABCHECKS => "MaxNumberOfStabilityChecks",
:MAXSTABCHECKLINE => "MaxLineForStabilityCheck",
:INTERPOLDEGREE => "DegreeOfInterpolation",
:ORDERDECFRAC => "OrderDecreaseFraction",
:ORDERINCFRAC => "OrderIncreaseFraction",
:STEPSIZESEQUENCE => "StepSizeSequence",
:SSREDUCTION => "StepSizeReduction",
:SSSELECTPAR1 => "StepSizeSelectionParam1",
:SSSELECTPAR2 => "StepSizeSelectionParam2",
:RHO2 => "rho2",
:DENSEOUTPUTWOEE => "DeactivateErrorEstInDenseOutput",
:TRANSJTOH => "TransfromJACtoHess",
:MAXNEWTONITER => "MaxNewtonIterations",
:NEWTONSTARTZERO => "StartNewtonWithZeros",
:DIMOFIND1VAR => "DimensionOfIndex1Vars",
:DIMOFIND2VAR => "DimensionOfIndex2Vars",
:DIMOFIND3VAR => "DimensionOfIndex3Vars",
:STEPSIZESTRATEGY => "StepSizeStrategy",
:M1 => "M1",
:M2 => "M2",
:JACRECOMPFACTOR => "RecomputeJACFactor",
:NEWTONSTOPCRIT => "NewtonStopCriterion",
:FREEZESSLEFT => "FreezeStepSizeLeftBound",
:FREEZESSRIGHT => "FreezeStepSizeRightBound",
:MASSMATRIX => "MassMatrix",
:JACOBIMATRIX => "JacobiMatrix",
:JACOBIBANDSTRUCT => "JacobiBandStructure",
:MAXSTAGES => "MaximalNumberOfStages",
:MINSTAGES => "MinimalNumberOfStages",
:INITSTAGES => "InitialNumberOfStages",
:ORDERINCFACTOR => "OrderIncreaseFactor",
:ORDERDECFACTOR => "OrderDecreaseFactor",
:ORDERDECSTEPFAC1 => "OrderDecreaseStepFactor1",
:ORDERDECSTEPFAC2 => "OrderDecreaseStepFactor2",
:RHSAUTONOMOUS => "AutonomousRHS",
:LAMBDADENSE => "LambdaForDenseOutput",
:WORKFORRHS => "WorkForRightHandSide",
:WORKFORJAC => "WorkForJacobimatrix",
:WORKFORDEC => "WorkForLuDecomposition",
:WORKFORSOL => "WorkForSubstitution",
:BVPCLASS => "BoundaryValueProblemClass",
:SOLMETHOD => "SolutionMethod",
:IVPOPT => "OptionsForIVPsolver")
struct OutputFunction{T} <: Function
integrator::T
end
function (f::OutputFunction)(reason::ODEInterface.OUTPUTFCN_CALL_REASON,
tprev::Float64, t::Float64, u::Vector{Float64},
eval_sol_fcn, extra_data::Dict)
if reason == ODEInterface.OUTPUTFCN_CALL_STEP
integrator = f.integrator
integrator.uprev .= integrator.u
if eltype(integrator.sol.u) <: Vector
integrator.u .= u
else
integrator.u .= reshape(u, integrator.sizeu)
end
integrator.t = t
integrator.tprev = tprev
integrator.eval_sol_fcn = eval_sol_fcn
handle_callbacks!(integrator, eval_sol_fcn)
if integrator.u_modified
if eltype(integrator.sol.u) <: Vector
u .= integrator.u
else
tmp = reshape(u, integrator.sizeu)
tmp .= integrator.u
end
return ODEInterface.OUTPUTFCN_RET_CONTINUE_XCHANGED
else
return ODEInterface.OUTPUTFCN_RET_CONTINUE
end
# TODO: ODEInterface.OUTPUTFCN_RET_STOP for terminate!
end
ODEInterface.OUTPUTFCN_RET_CONTINUE
end
| ODEInterfaceDiffEq | https://github.com/SciML/ODEInterfaceDiffEq.jl.git |
|
[
"MIT"
] | 3.13.3 | a4816454042d72e4bae37d13e592591381356a17 | code | 1452 | using ODEInterfaceDiffEq, DiffEqBase, Test
import ODEProblemLibrary: prob_ode_linear,
prob_ode_2Dlinear, prob_ode_vanderpol
prob = prob_ode_linear
sol = solve(prob, dopri5(), dt = 1 // 2^(4))
sol = solve(prob, dop853(); dt = 1 // 2^(4))
sol = solve(prob, odex(); dt = 1 // 2^(4))
sol = solve(prob, seulex(); dt = 1 // 2^(4))
sol = solve(prob, radau(); dt = 1 // 2^(4))
sol = solve(prob, radau5(); dt = 1 // 2^(4))
sol = solve(prob, rodas(); dt = 1 // 2^(4))
sol = solve(prob, ddeabm(); dt = 1 // 2^(4))
sol = solve(prob, ddebdf(); dt = 1 // 2^(4))
prob = prob_ode_2Dlinear
sol = solve(prob, dopri5(), dt = 1 // 2^4)
sol = solve(prob, dop853(); dt = 1 // 2^(4))
sol = solve(prob, odex(); dt = 1 // 2^(4))
sol = solve(prob, seulex(); dt = 1 // 2^(4))
sol = solve(prob, radau(); dt = 1 // 2^(4))
sol = solve(prob, radau5(); dt = 1 // 2^(4))
sol = solve(prob, rodas(); dt = 1 // 2^(4))
sol = solve(prob, ddeabm(); dt = 1 // 2^(4))
sol = solve(prob, ddebdf(); dt = 1 // 2^(4))
prob = prob_ode_vanderpol
sol = solve(prob, dopri5(), dt = 1 // 2^4)
sol = solve(prob, dop853(); dt = 1 // 2^(4))
sol = solve(prob, odex(); dt = 1 // 2^(4))
sol = solve(prob, seulex(); dt = 1 // 2^(4))
sol = solve(prob, radau(); dt = 1 // 2^(4))
sol = solve(prob, radau5(); dt = 1 // 2^(4))
sol = solve(prob, rodas(); dt = 1 // 2^(4))
sol = solve(prob, ddeabm(); dt = 1 // 2^(4))
sol = solve(prob, ddebdf(); dt = 1 // 2^(4))
| ODEInterfaceDiffEq | https://github.com/SciML/ODEInterfaceDiffEq.jl.git |
|
[
"MIT"
] | 3.13.3 | a4816454042d72e4bae37d13e592591381356a17 | code | 617 | using ODEInterfaceDiffEq, Test
callback_f = function (du, u, p, t)
du[1] = u[2]
du[2] = -9.81
end
condtion = function (u, t, integrator) # Event when event_f(u,t,k) == 0
u[1]
end
affect! = nothing
affect_neg! = function (integrator)
integrator.u[2] = -integrator.u[2]
end
callback = ContinuousCallback(condtion, affect!, affect_neg!)
u0 = [50.0, 0.0]
tspan = (0.0, 25.0)
prob = ODEProblem(callback_f, u0, tspan)
sol = solve(prob, dopri5(), callback = callback, dtmax = 0.5)
@test sol(4.0)[1] > 0
sol = solve(prob, dopri5(), callback = callback, save_everystep = true)
@test sol(4.0)[1] > -1e-12
| ODEInterfaceDiffEq | https://github.com/SciML/ODEInterfaceDiffEq.jl.git |
|
[
"MIT"
] | 3.13.3 | a4816454042d72e4bae37d13e592591381356a17 | code | 536 | using ODEInterfaceDiffEq, DiffEqBase
using Test
jac_called = false
function Lotka(du, u, p, t)
du[1] = u[1] - u[1] * u[2] # REPL[7], line 3:
du[2] = -3 * u[2] + 1 * u[1] * u[2]
nothing
end
function Lotka_jac(J, u, p, t)
global jac_called
jac_called = true
J[1, 1] = 1.0 - u[2]
J[1, 2] = -u[1]
J[2, 1] = 1 * u[2]
J[2, 2] = -3 + u[1]
nothing
end
prob = ODEProblem(ODEFunction(Lotka, jac = Lotka_jac), ones(2), (0.0, 2.0))
sol = solve(prob, radau5(); dt = 1 // 2^(4))
@test jac_called == true
| ODEInterfaceDiffEq | https://github.com/SciML/ODEInterfaceDiffEq.jl.git |
|
[
"MIT"
] | 3.13.3 | a4816454042d72e4bae37d13e592591381356a17 | code | 617 | using ODEInterfaceDiffEq, DiffEqBase
using Test
import ODEProblemLibrary: prob_ode_mm_linear
prob = prob_ode_mm_linear
@test_throws ErrorException solve(prob, dopri5(), dt = 1 // 2^4)
@test_throws ErrorException solve(prob, dop853(); dt = 1 // 2^(4))
@test_throws ErrorException solve(prob, odex(); dt = 1 // 2^(4))
sol = solve(prob, seulex(); dt = 1 // 2^(4))
sol = solve(prob, radau(); dt = 1 // 2^(4))
sol = solve(prob, radau5(); dt = 1 // 2^(4))
sol = solve(prob, rodas(); dt = 1 // 2^(4))
@test_throws ErrorException solve(prob, ddeabm(); dt = 1 // 2^(4))
sol = solve(prob, ddebdf(); dt = 1 // 2^(4))
| ODEInterfaceDiffEq | https://github.com/SciML/ODEInterfaceDiffEq.jl.git |
|
[
"MIT"
] | 3.13.3 | a4816454042d72e4bae37d13e592591381356a17 | code | 381 | using ODEInterfaceDiffEq, DiffEqBase
using Test
@time @testset "Algorithms" begin include("algorithm_tests.jl") end
@time @testset "Saving" begin include("saving_tests.jl") end
@time @testset "Mass Matrix" begin include("mass_matrix_tests.jl") end
@time @testset "Jacobian Tests" begin include("jac_tests.jl") end
@time @testset "Callback Tests" begin include("callbacks.jl") end
| ODEInterfaceDiffEq | https://github.com/SciML/ODEInterfaceDiffEq.jl.git |
|
[
"MIT"
] | 3.13.3 | a4816454042d72e4bae37d13e592591381356a17 | code | 476 | using ODEInterfaceDiffEq, DiffEqBase
using Test
import ODEProblemLibrary: prob_ode_linear
prob = prob_ode_linear
sol = solve(prob, dopri5(), dt = 1 // 2^(4))
sol = solve(prob, dopri5())
#plot(sol,plot_analytic=true)
sol = solve(prob, dopri5(), save_everystep = false)
@test sol.t == [0.0, 1.0]
sol = solve(prob, dopri5(), saveat = 0.1)
@test sol.t == collect(0:0.1:1)
sol = solve(prob, dopri5(), save_on = false, save_start = false)
@test isempty(sol.t) && isempty(sol.u)
| ODEInterfaceDiffEq | https://github.com/SciML/ODEInterfaceDiffEq.jl.git |
|
[
"MIT"
] | 3.13.3 | a4816454042d72e4bae37d13e592591381356a17 | docs | 2535 | # ODEInterfaceDiffEq
[](https://gitter.im/JuliaDiffEq/Lobby?utm_source=badge&utm_medium=badge&utm_campaign=pr-badge&utm_content=badge)
[](https://github.com/SciML/ODEInterfaceDiffEq.jl/actions?query=workflow%3ACI)
[](https://coveralls.io/github/SciML/ODEInterfaceDiffEq.jl?branch=master)
[](http://codecov.io/github/SciML/ODEInterfaceDiffEq.jl?branch=master)
This package contains bindings for ODEInterface.jl to allow it to be used with the
JuliaDiffEq common interface. For more information on using the solvers from this
package, see the [DifferentialEquations.jl documentation](https://docs.sciml.ai/DiffEqDocs/stable/).
## Installation
A standard installation on MacOSX and Linux should work. On Windows, you need to install mingw32 compilers and add them to the path. [MingW32 can be found here](https://sourceforge.net/projects/mingw-w64/). Then add the path to your environment variables. An example path is:
```
C:\Program Files\mingw-w64\x86_64-6.1.0-posix-seh-rt_v5-rev0\mingw64\bin
```
Note that it is required that you add ODEInterface.jl as well;
```julia
]add ODEInterface
```
Otherwise you may have issues instantiating the solvers.
## Common API Usage
This library adds the common interface to ODEInterface.jl's solvers. [See the DifferentialEquations.jl documentation for details on the interface](https://docs.sciml.ai/DiffEqDocs/stable/). Following the Lorenz example from [the ODE tutorial](https://docs.sciml.ai/DiffEqDocs/stable/tutorials/ode_example/), we can solve this using `dopri5` via the following:
```julia
using ODEInterface, ODEInterfaceDiffEq
function lorenz(du,u,p,t)
du[1] = 10.0(u[2]-u[1])
du[2] = u[1]*(28.0-u[3]) - u[2]
du[3] = u[1]*u[2] - (8/3)*u[3]
end
u0 = [1.0;0.0;0.0]
tspan = (0.0,100.0)
prob = ODEProblem(lorenz,u0,tspan)
sol = solve(prob,dopri5(),abstol=1e-4)
using Plots; plot(sol,vars=(1,2,3))
```
The options available in `solve` are documented [at the common solver options page](https://docs.sciml.ai/DiffEqDocs/stable/basics/common_solver_opts/). The available methods are documented [at the ODE solvers page](https://docs.sciml.ai/DiffEqDocs/stable/solvers/ode_solve/).
| ODEInterfaceDiffEq | https://github.com/SciML/ODEInterfaceDiffEq.jl.git |
|
[
"MIT"
] | 0.8.0 | 2e8ff74c4b7ff2c2bacfcfe24c00aadfd3527f95 | code | 784 | using Pkg
Pkg.activate(@__DIR__)
# As long as it is not registered, this is nice, in general it locally always
# renders docs of the current version checked out in this repo.
Pkg.develop(PackageSpec(; path=(@__DIR__) * "/../"))
using MultiGridBarrier
using Documenter
using PyPlot
DocMeta.setdocmeta!(MultiGridBarrier, :DocTestSetup, :(using MultiGridBarrier); recursive=true)
makedocs(;
modules=[MultiGridBarrier],
authors="Sébastien Loisel",
sitename="MultiGridBarrier.jl",
format=Documenter.HTML(;
canonical="https://sloisel.github.io/MultiGridBarrier.jl",
edit_link="main",
assets=String[],
),
pages=[
"Home" => "index.md",
],
)
deploydocs(;
repo="github.com/sloisel/MultiGridBarrier.jl",
devbranch="main",
)
| MultiGridBarrier | https://github.com/sloisel/MultiGridBarrier.jl.git |
|
[
"MIT"
] | 0.8.0 | 2e8ff74c4b7ff2c2bacfcfe24c00aadfd3527f95 | code | 34015 | export Barrier, AMG, barrier, amgb, amg, newton, illinois, Convex, convex_linear, convex_Euclidian_power, AMGBConvergenceFailure, amgb_core, amg_construct, amg_plot, amg_solve, amg_dim
function blkdiag(M...)
Mat = typeof(M[1])
Mat(blockdiag((sparse.(M))...))
end
struct AMGBConvergenceFailure <: Exception
message
end
Base.showerror(io::IO, e::AMGBConvergenceFailure) = print(io, "AMGBConvergenceFailure:\n", e.message)
"""
Barrier
A type for holding barrier functions. Fields are:
f0::Function
f1::Function
f2::Function
`f0` is the barrier function itself, while `f1` is its gradient and
`f2` is the Hessian.
"""
@kwdef struct Barrier
f0::Function
f1::Function
f2::Function
end
"""
@kwdef struct AMG{T,M,Geometry}
...
end
Objects of this type should probably be assembled by the constructor `amg()`.
A multigrid with `L` level. Denote by `l` between 1 and `L`, a grid level.
Fields are:
* `x::Matrix{T}` the vertices of the fine grid.
* `w::Vector{T}` corresponding quadrature weights.
* `R_fine::Array{M,1}` an array of `L` matrices. The columns of `R_fine[l]` are basis functions for the function space on grid level `l`, interpolated to the fine grid.
* `R_coarse::Array{M,1}` an array of `L` matrices. The columns of `R_coarse[l]` are basis functions for the function space on grid level `l`. Unlike `R_fine[l]`, these basis functions are on grid level `l`, not interpolated to the fine grid.
* `D::Array{M,2}` an array of differential operators. For example, if the barrier parameters are to be `u,ux,s`, with `ux` the derivative of `u`, then `D[l,:] = [I,Dx,I]`, where `Dx` is a numerical differentiation operator on grid level `l`.
* `refine_u::Array{M,1}` an array of `L` grid refinement matrices. If `x[l]` has `n[l]` vertices, then `refine_u[l]` is `n[l+1]` by `n[l]`.
* `coarsen_u::Array{M,1}` an array of `L` grid coarsening matrices. `coarsen_u[l]` is `n[l]` by `n[l+1]`.
* `refine_z::Array{M,1}` an array of `L` grid refining matrices for the "state vector" `z`. For example, if `z` contains the state functions `u` and `s`, then there are `k=2` state functions, and `refine_z[l]` is `k*n[l+1]` by `k*n[l]`.
* `coarsen_z::Array{M,1}` an array of `L` grid coarsening matrices for the "state vector" `z`. `coarsen_z[l]` is `k*n[l]` by `k*n[l+1]`.
These various matrices must satisfy a wide variety of algebraic relations. For this reason, it is recommended to use the constructor `amg()`.
"""
@kwdef struct AMG{T,M,Geometry}
x::Matrix{T}
w::Vector{T}
R_fine::Array{M,1}
R_coarse::Array{M,1}
D::Array{M,2}
refine_u::Array{M,1}
coarsen_u::Array{M,1}
refine_z::Array{M,1}
coarsen_z::Array{M,1}
end
function amg_helper(::Type{Geometry},
x::Matrix{T},
w::Vector{T},
state_variables::Matrix{Symbol},
D::Matrix{Symbol},
subspaces::Dict{Symbol,Vector{M}},
operators::Dict{Symbol,M},
refine::Vector{M},
coarsen::Vector{M}) where {T,M,Geometry}
L = length(refine)
@assert size(w) == (size(x)[1],) && size(refine)==(L,) && size(coarsen)==(L,)
for l=1:L
@assert norm(coarsen[l]*refine[l]-I)<sqrt(eps(T))
end
refine_fine = Array{M,1}(undef,(L,))
refine_fine[L] = refine[L]
coarsen_fine = Array{M,1}(undef,(L,))
coarsen_fine[L] = coarsen[L]
for l=L-1:-1:1
refine_fine[l] = refine_fine[l+1]*refine[l]
coarsen_fine[l] = coarsen[l]*coarsen_fine[l+1]
end
R_coarse = Array{M,1}(undef,(L,))
R_fine = Array{M,1}(undef,(L,))
nu = size(state_variables)[1]
@assert size(state_variables)[2] == 2
for l=1:L
foo = [sparse(subspaces[state_variables[k,2]][l]) for k=1:nu]
R_coarse[l] = M(blockdiag(foo...))
foo = [sparse(refine_fine[l]*subspaces[state_variables[k,2]][l]) for k=1:nu]
R_fine[l] = M(blockdiag(foo...))
end
nD = size(D)[1]
@assert size(D)[2]==2
bar = Dict{Symbol,Int}()
for k=1:nu
bar[state_variables[k,1]] = k
end
D0 = Array{M,2}(undef,(L,nD))
for l=1:L
n = size(coarsen_fine[l],1)
Z = M(spzeros(T,n,n))
for k=1:nD
foo = [Z for j=1:nu]
foo[bar[D[k,1]]] = coarsen_fine[l]*operators[D[k,2]]*refine_fine[l]
D0[l,k] = hcat(foo...)
end
end
refine_z = [blkdiag([refine[l] for k=1:nu]...) for l=1:L]
coarsen_z = [blkdiag([coarsen[l] for k=1:nu]...) for l=1:L]
AMG{T,M,Geometry}(x=x,w=w,R_fine=R_fine,R_coarse=R_coarse,D=D0,
refine_u=refine,coarsen_u=coarsen,refine_z=refine_z,coarsen_z=coarsen_z)
end
"""
function amg(::Type{Geometry};
x::Matrix{T},
w::Vector{T},
state_variables::Matrix{Symbol},
D::Matrix{Symbol},
subspaces::Dict{Symbol,Vector{M}},
operators::Dict{Symbol,M},
refine::Vector{M},
coarsen::Vector{M},
full_space=:full,
id_operator=:id,
feasibility_slack=:feasibility_slack,
generate_feasibility=true) where {T,M,Geometry}
Construct an `AMG` object for use with the `amgb` solver. In many cases, this constructor is not called directly by the user. For 1d and 2d finite elements, use the `fem1d()` or `fem2d()`. For 1d and 2d spectral elements, use `spectral1d()` or `spectral2d()`. You use `amg()` directly if you are implementing your own function spaces.
The `AMG` object shall represent all `L` grid levels of the multigrid hierarchy. Parameters are:
* `x`: the vertices of the fine grid.
* `w`: the quadrature weights for the fine grid.
* `state_variables`: a matrix of symbols. The first column indicates the names of the state vectors or functions, and the second column indicates the names of the corresponding subspaces. A typical example is: `state_variables = [:u :dirichlet; :s :full]`. This would define the solution as being functions named u(x) and s(x). The u function would lie in the space `:dirichlet`, presumably consisting of functions with homogeneous Dirichlet conditions. The s function would lie in the space `:full`, presumably being the full function space, without boundary conditions.
* `D`: a matrix of symbols. The first column indicates the names of various state variables, and the second column indicates the corresponding differentiation operator(s). For example: `D = [:u :id ; :u :dx ; :s :id]`. This would indicate that the barrier should be called as `F(x,y)` with `y = [u,ux,s]`, where `ux` denotes the derivative of `u` with respect to the space variable `x`.
* `subspaces`: a `Dict` mapping each subspace symbol to an array of `L` matrices, e.g. for each `l`, `subspaces[:dirichlet][l]` is a matrix whose columns span the homogeneous Dirichlet subspace of grid level `l`.
* `operators`: a `Dict` mapping each differential operator symbol to a matrix, e.g. `operators[:id]` is an identity matrix, while `operators[:dx]` is a numerical differentiation matrix, on the fine grid level `L`.
* `refine`: an array of length `L` of matrices. For each `l`, `refine[l]` interpolates from grid level `l` to grid level `l+1`. `refine[L]` should be the identity, and `coarsen[l]*refine[l]` should be the identity.
* `coarsen`: an array of length `L` of matrices. For each `l`, `coarsen[l]` interpolates or projects from grid level `l+1` to grid level `l`. `coarsen[L]` should be the identity.
* `generate_feasibility`: if true, `amg()` returns a pair `M` of `AMG` objects. `M[1]` is an `AMG` object to be used for the main optimization problem, while `M[2]` is an `AMG` object for the preliminary feasibility sub problem. In this case, `amg()` also needs to be provided with the following additional information: `feasibility_slack` is the name of a special slack variable that must be unique to the feasibility subproblem (default: `:feasibility_slack`); `full_space` is the name of the "full" vector space (i.e. no boundary conditions, default: `:full`); and `id_operator` is the name of the identity operator (default: `:id`).
"""
function amg(::Type{Geometry};
x::Matrix{T},
w::Vector{T},
state_variables::Matrix{Symbol},
D::Matrix{Symbol},
subspaces::Dict{Symbol,Vector{M}},
operators::Dict{Symbol,M},
refine::Vector{M},
coarsen::Vector{M},
full_space=:full,
id_operator=:id,
feasibility_slack=:feasibility_slack,
generate_feasibility=true) where {T,M,Geometry}
M1 = amg_helper(Geometry,x,w,state_variables,D,subspaces,operators,refine,coarsen)
if !generate_feasibility
return M1
end
s1 = vcat(state_variables,[feasibility_slack full_space])
D1 = vcat(D,[feasibility_slack id_operator])
M2 = amg_helper(Geometry,x,w,s1,D1,subspaces,operators,refine,coarsen)
return M1,M2
end
@doc raw"""
struct Convex
barrier::Function
cobarrier::Function
slack::Function
end
The `Convex` data structure represents a convex domain $Q$ implicitly by way of three functions. The `barrier` function is a barrier for $Q$. `cobarrier` is a barrier for the feasibility subproblem, and `slack` is a function that initializes a valid slack value for the feasibility subproblem. The various `convex_` functions can be used to generate various convex domains.
These function are called as follows: `barrier(x,y)`. `x` is a vertex in a grid, as per the `AMG` object. `y` is some vector. For each fixed `x` variable, `y -> barrier(x,y)` defines a barrier for a convex set in `y`.
"""
struct Convex{T}
barrier::Function
cobarrier::Function
slack::Function
end
"""
function convex_linear(::Type{T}=Float64;idx=Colon(),A::Function=(x)->I,b::Function=(x)->T(0)) where {T}
Generate a `Convex` structure corresponding to the convex domain A(x,k)*y[idx] .+ b(x,k) ≤ 0.
"""
function convex_linear(::Type{T}=Float64;idx=Colon(),A::Function=(x)->I,b::Function=(x)->T(0)) where {T}
F(x,y) = A(x)*y[idx] .+ b(x)
barrier_linear(x,y) = -sum(log.(F(x,y)))
cobarrier_linear(x,yhat) = -sum(log.(F(x,yhat[1:end-1]) .+ yhat[end]))
slack_linear(x,y) = -minimum(F(x,y))
return Convex{T}(barrier_linear,cobarrier_linear,slack_linear)
end
normsquared(z) = dot(z,z)
@doc raw"""
function convex_Euclidian_power(::Type{T}=Float64;idx=Colon(),A::Function=(x)->I,b::Function=(x)->T(0),p::Function=x->T(2)) where {T}
Generate a `Convex` object corresponding to the convex set defined by $z[end] \geq \|z[1:end-1]\|_2^p$ where $z = A(x)*y[idx] .+ b(x)$.
"""
function convex_Euclidian_power(::Type{T}=Float64;idx=Colon(),A::Function=(x)->I,b::Function=(x)->T(0),p::Function=x->T(2)) where {T}
F(x,y) = A(x)*y[idx] .+ b(x)
mu = p->(if (p==2 || p==1) 0 elseif p<2 1 else 2 end)
function barrier_Euclidian_power(x,y)
z = F(x,y)
p0 = p(x) ::T
return -log(z[end]^(2/p0)-normsquared(z[1:end-1]))-mu(p0)*log(z[end])
end
function cobarrier_Euclidian_power(x,yhat)
z = F(x,yhat[1:end-1])
z[end] += yhat[end]
p0 = p(x) ::T
return -log(z[end]^(2/p0)-normsquared(z[1:end-1]))-mu(p0)*log(z[end])
end
function slack_Euclidian_power(x,y)
z = F(x,y)
p0 = p(x) ::T
return -min(z[end]-normsquared(z[1:end-1])^(p0/2),z[end])
end
return Convex{T}(barrier_Euclidian_power,cobarrier_Euclidian_power,slack_Euclidian_power)
end
function convex_piecewise(::Type{T}=Float64;select::Function,Q::Vector{Convex{T}}) where{T}
n = length(Q)
function barrier_piecewise(x,y)
ret = T(0)
sel = select(x)
for k=1:n
if sel[k]
ret += Q[k].barrier(x,y)
end
end
return ret
end
function cobarrier_piecewise(x,y)
ret = T(0)
sel = select(x)
for k=1:n
if sel[k]
ret += Q[k].cobarrier(x,y)
end
end
return ret
end
function slack_piecewise(x,y)
ret = T(0)
sel = select(x)
for k=1:n
if sel[k]
ret = max(ret,Q[k].slack(x,y))
end
end
return ret
end
return Convex{T}(barrier_piecewise,cobarrier_piecewise,slack_piecewise)
end
Base.intersect(U::Convex{T}, V::Convex{T}) where {T} = convex_piecewise(T;select=x->[true,true],Q=[U,V])
@doc raw"""
function barrier(F;
F1=(x,y)->ForwardDiff.gradient(z->F(x,z),y),
F2=(x,y)->ForwardDiff.hessian(z->F(x,z),y))::Barrier
Constructor for barriers.
* `F` is the actual barrier function. It should take parameters `(x,y)`.
* `F1` is the gradient of `F` with respect to `y`.
* `F2` is the Hessian of `F` with respect to `y`.
By default, `F1` and `F2` are automatically generated by the module `ForwardDiff`.
A more specific description of the Barrier object is as follows. The function `Barrier.f0` has parameters:
function Barrier.f0(z,x,w,c,R,D,z0)
Here, `R` is a matrix and `D` is an array of matrices; `x` is a matrix of quadrature nodes with weights `w`, and `c` is a matrix describing the functional we seek to minimize. The value of `Barrier.f0` is given by:
```
p = length(w)
n = length(D)
Rz = z0+R*z
Dz = hcat([D[k]*Rz for k=1:n]...)
y = [F(x[k,:],Dz[k,:]) for k=1:p]
dot(w,y)+sum([dot(w.*c[:,k],Dz[:,k]) for k=1:n])
```
Thus, `Barrier.f0` can be regarded as a quadrature approximation of the integral
```math
\int_{\Omega} \left(\sum_{k=1}^nc_k(x)v_k(x)\right) + F(x,v_1(x),\ldots,v_n(x)) \, dx \text{ where } v_k = D_k(z_0 + Rz).
```
Functions `Barrier.f1` and `Barrier.f2` are the gradient and Hessian, respectively, of `Barrier.f0`, with respect to the `z` parameter. If the underlying matrices are sparse, then sparse arithmetic is used for `Barrier.f2`.
"""
function barrier(F;
F1=(x,y)->ForwardDiff.gradient(z->F(x,z),y),
F2=(x,y)->ForwardDiff.hessian(z->F(x,z),y))::Barrier
function apply_D(z::Vector{T},x,w,R,D,z0) where {T}
@assert all(isfinite.(z))
p = length(w)
n = length(D)
Dz = Array{T,2}(undef,(p,n))
Rz = z0+R*z
for k=1:n
Dz[:,k] = D[k]*Rz
end
return Dz
end
function f0(z::Vector{T},x,w,c,R,D,z0) where {T}
Dz = apply_D(z,x,w,R,D,z0)
p = length(w)
n = length(D)
y = [F(x[k,:],Dz[k,:]) for k=1:p]
dot(w,y)+sum([dot(w.*c[:,k],Dz[:,k]) for k=1:n])
end
function f1(z::Vector{T},x,w,c,R,D,z0) where {T}
Dz = apply_D(z,x,w,R,D,z0)
p = length(w)
n = length(D)
y = Array{T,2}(undef,(p,n))
for k=1:p
y[k,:] = F1(x[k,:],Dz[k,:])
end
y += c
m0 = size(D[1],2)
ret = zeros(T,(m0,))
for k=1:n
ret += D[k]'*(w.*y[:,k])
end
R'*ret
end
function f2(z::Vector{T},x,w,c,R,D,z0) where {T}
Dz = apply_D(z,x,w,R,D,z0)
p = length(w)
n = length(D)
y = Array{T,3}(undef,(p,n,n))
for k=1:p
y[k,:,:] = F2(x[k,:],Dz[k,:])
end
m0 = size(D[1],2)
ret = spzeros(T,m0,m0)
for j=1:n
foo = spdiagm(0=>w.*y[:,j,j])
ret += (D[j])'*foo*D[j]
for k=1:j-1
foo = spdiagm(0=>w.*y[:,j,k])
ret += D[j]'*foo*D[k] + D[k]'*foo*D[j]
end
end
R'*ret*R
end
Barrier(f0=f0,f1=f1,f2=f2)
end
function amgb_phase1(B::Barrier,
M::AMG{T,Mat,Geometry},
x::Matrix{T},
z::Vector{T},
c::Matrix{T};
maxit=10000,
early_stop=z->false) where {T,Mat,Geometry}
L = length(M.R_fine)
cm = Vector{Matrix{T}}(undef,L)
cm[L] = c
zm = Vector{Vector{T}}(undef,L)
zm[L] = z
xm = Vector{Matrix{T}}(undef,L)
xm[L] = x
wm = Vector{Vector{T}}(undef,L)
wm[L] = M.w
passed = falses((L,))
for l=L-1:-1:1
cm[l] = M.coarsen_u[l]*cm[l+1]
xm[l] = M.coarsen_u[l]*xm[l+1]
zm[l] = M.coarsen_z[l]*zm[l+1]
wm[l] = M.refine_u[l]'*wm[l+1]
end
(f0,f1,f2) = (B.f0,B.f1,B.f2)
its = zeros(Int,(L,))
converged = false
for l=1:L
if early_stop(zm[L])
break
end
x = xm[l]
w = wm[l]
R = M.R_coarse[l]
D = M.D[l,:]
z0 = zm[l]
c0 = cm[l]
s0 = zeros(T,(size(R)[2],))
SOL = newton(Mat,
s->f0(s,x,w,c0,R,D,z0),
s->f1(s,x,w,c0,R,D,z0),
s->f2(s,x,w,c0,R,D,z0),
s0,
maxit=maxit)
converged = SOL.converged
if !converged
it = SOL.k
throw(AMGBConvergenceFailure("Damped Newton iteration failed to converge at level $l during phase 1 ($it iterations, maxit=$maxit)."))
end
its[l] = SOL.k
znext = copy(zm)
s = R*SOL.x
znext[l] = zm[l]+s
try
for k=l+1:L
s = M.refine_z[k-1]*s
znext[k] = zm[k]+s
s0 = zeros(T,(size(M.R_coarse[k])[2],))
y0 = f0(s0,xm[k],wm[k],cm[k],M.R_coarse[k],M.D[k,:],znext[k])::T
y1 = f1(s0,xm[k],wm[k],cm[k],M.R_coarse[k],M.D[k,:],znext[k])
@assert isfinite(y0) && all(isfinite.(y1))
end
zm = znext
passed[l] = true
catch
end
end
if !passed[end]
throw(AMGBConvergenceFailure("Phase 1 failed to converge on the finest grid."))
end
(z=zm[L],its=its,passed=passed)
end
function amgb_step(B::Barrier,
M::AMG{T,Mat,Geometry},
x::Matrix{T},
z::Vector{T},
c::Matrix{T};
maxit=Int(ceil(log2(-log2(eps(T)))))+2,
early_stop=z->false) where {T,Mat,Geometry}
L = length(M.R_fine)
(f0,f1,f2) = (B.f0,B.f1,B.f2)
its = zeros(Int,(L,))
converged = false
w = M.w
D = M.D[L,:]
function step(j,J)
R = M.R_fine[J]
s0 = zeros(T,(size(R)[2],))
while true
SOL = newton(Mat,
s->f0(s,x,w,c,R,D,z),
s->f1(s,x,w,c,R,D,z),
s->f2(s,x,w,c,R,D,z),
s0,
maxit=maxit)
its[J] += SOL.k
if SOL.converged
z = z+R*SOL.x
return true
end
jmid = (j+J)÷2
if jmid==j
return false
end
if early_stop(z)
return true
end
if !step(j,jmid)
return false
end
j = jmid
end
end
if step(0,L)
converged = true
end
return (z=z,its=its,converged=converged)
end
"""
function illinois(f,a::T,b::T;fa=f(a),fb=f(b),maxit=10000) where {T}
Find a root of `f` between `a` and `b` using the Illinois algorithm. If `f(a)*f(b)>=0`, returns `b`.
"""
function illinois(f,a::T,b::T;fa=f(a),fb=f(b),maxit=10000) where {T}
@assert isfinite(fa) && isfinite(fb)
if fa==0
return a
end
if fa*fb>=0
return b
end
for k=1:maxit
c = (a*fb-b*fa)/(fb-fa)
fc = f(c)
@assert isfinite(fc)
if c<=min(a,b) || c>=max(a,b) || fc*fa==0 || fc*fb==0
return c
end
if fb*fc<0
a,fa = b,fb
else
fa /= 2
end
b,fb = c,fc
end
throw("Illinois solver failed to converge.")
end
"""
function newton(::Type{Mat},
F0::Function,
F1::Function,
F2::Function,
x::Array{T,1};
maxit=10000,
theta=T(0.1),
beta=T(0.1),
tol=eps(T)) where {T,Mat}
Damped Newton iteration for minimizing a function.
* `F0` the objective function
* `F1` and `F2` are the gradient and Hessian of `F0`, respectively.
* `x` the starting point of the minimization procedure.
The Hessian `F2` return value should be of type `Mat`.
The optional parameters are:
* `maxit`, the iteration aborts with a failure message if convergence is not achieved within `maxit` iterations.
* `tol` is used as a stopping criterion. We stop when the decrement in the objective is sufficiently small.
"""
function newton(::Type{Mat},
F0::Function,
F1::Function,
F2::Function,
x::Array{T,1};
maxit=10000,
theta=T(0.1),
beta=T(0.1),
tol=eps(T)) where {T,Mat}
ss = T[]
ys = T[]
@assert all(isfinite.(x))
y = F0(x) ::T
@assert isfinite(y)
push!(ys,y)
converged = false
k = 0
g = F1(x) ::Array{T,1}
@assert all(isfinite.(g))
ynext,xnext,gnext=y,x,g
while k<maxit && !converged
k+=1
H = F2(x) ::Mat
n = ((H+I*norm(H)*eps(T))\g)::Array{T,1}
@assert all(isfinite.(n))
inc = dot(g,n)
if inc<=0
converged = true
break
end
s = T(1)
while s>T(0)
try
function phi(s)
xn = x-s*n
@assert(isfinite(F0(xn)))
return dot(F1(xn),n)
end
s = illinois(phi,T(0),s,fa=inc)
xnext = x-s*n
ynext,gnext = F0(xnext)::T,F1(xnext)
@assert isfinite(ynext) && all(isfinite.(gnext))
break
catch
end
s = s*beta
end
if ynext>=y && norm(gnext)>=theta*norm(g)
converged = true
end
x,y,g = xnext,ynext,gnext
push!(ss,s)
push!(ys,y)
end
return (x=x,y=y,k=k,converged=converged,ss=ss,ys=ys)
end
"""
function amgb_core(B::Barrier,
M::AMG{T,Mat,Geometry},
x::Matrix{T},
z::Array{T,1},
c::Array{T,2};
tol=(eps(T)),
t=T(0.1),
maxit=10000,
kappa=T(10.0),
early_stop=z->false,
verbose=true) where {T,Mat,Geometry}
The "Algebraic MultiGrid Barrier" method.
* `B` a Barrier object.
* `M` an AMG object.
* `x` a matrix with the same number of rows as `M.x`. This is passed as the `x` parameter of the barrier. Often, `x = M.x`.
* `z` a starting point for the minimization, which should be admissible, i.e. `B.f0(z)<∞`.
* `c` an objective functional to minimize. Concretely, we minimize the integral of `c.*(D*z)`, as computed by the finest quadrature in `M`, subject to `B.f0(z)<∞`. Here, `D` is the differential operator provided in `M`.
Optional parameters:
* `t`: the initial value of `t`
* `tol`: we stop when `1/t<tol`.
* `maxit`: the maximum number of `t` steps.
* `kappa`: the initial size of the t-step. Stepsize adaptation is used in the AMGB algorithm, where the t-step size may be made smaller or large, but it will never exceed the initial size provided here.
* `verbose`: set to `true` to see a progress bar.
* `early_stop`: if `early_stop(z)` is `true` then the minimization is stopped early. This is used when solving the preliminary feasibility problem.
Return value is a named tuple `SOL` with the following fields:
* `SOL.converged` is `true` if convergence was obtained, else it is `false`.
* `SOL.z` the computed solution.
Further `SOL` fields contain various statistics about the solve process.
"""
function amgb_core(B::Barrier,
M::AMG{T,Mat,Geometry},
x::Matrix{T},
z::Array{T,1},
c::Array{T,2};
tol=sqrt(eps(T)),
t=T(0.1),
maxit=10000,
kappa=T(10.0),
early_stop=z->false,
progress=x->nothing,
c0=T(0)) where {T,Mat,Geometry}
t_begin = time()
tinit = t
kappa0 = kappa
L = length(M.R_fine)
its = zeros(Int,(L,maxit))
ts = zeros(T,(maxit,))
kappas = zeros(T,(maxit,))
times = zeros(Float64,(maxit,))
k = 1
times[k] = time()
SOL = amgb_phase1(B,M,x,z,c0 .+ t*c,maxit=maxit,early_stop=early_stop)
passed = SOL.passed
its[:,k] = SOL.its
kappas[k] = kappa
ts[k] = t
z = SOL.z
mi = Int(ceil(log2(-log2(eps(T)))))+2
while t<=1/tol && kappa > 1 && k<maxit && !early_stop(z)
k = k+1
its[:,k] .= 0
times[k] = time()
prog = ((log(t)-log(tinit))/(log(1/tol)-log(tinit)))
progress(prog)
while kappa > 1
t1 = kappa*t
SOL = amgb_step(B,M,x,z,c0 .+ t1*c,maxit=mi,early_stop=early_stop)
its[:,k] += SOL.its
if SOL.converged
if maximum(SOL.its)<=mi*0.5
kappa = min(kappa0,kappa^2)
end
z = SOL.z
t = t1
break
end
kappa = sqrt(kappa)
end
ts[k] = t
kappas[k] = kappa
end
converged = (t>1/tol) || early_stop(z)
if !converged
throw(AMGBConvergenceFailure("Convergence failure in amgb at t=$t, k=$k, kappa=$kappa."))
end
t_end = time()
t_elapsed = t_end-t_begin
return (z=z,c=c,its=its[:,1:k],ts=ts[1:k],kappas=kappas[1:k],M=M,
t_begin=t_begin,t_end=t_end,t_elapsed=t_elapsed,times=times[1:k],passed=passed)
end
"""
function amgb(M::Tuple{AMG{T,Mat,Geometry},AMG{T,Mat,Geometry}},
f::Union{Function,Matrix{T}},
g::Union{Function,Matrix{T}},
Q::Convex;
x::Matrix{T} = M[1].x,
t=T(0.1),
t_feasibility=t,
verbose=true,
return_details=false,
rest...) where {T,Mat,Geometry}
A thin wrapper around `amgb_core()`. Parameters are:
* `M`: obtained from the `amg` constructor, a pair of `AMG` structures. `M[1]` is the main problem while `M[2]` is the feasibility problem.
* `f`: the functional to minimize.
* `g`: the "boundary conditions".
* `Q`: a `Convex` domain for the convex optimization problem.
* `rest...`: any further named arguments are passed on to `amgb_core`.
The initial `z0` guess, and the cost functional `c0`, are computed as follows:
m = size(M[1].x,1)
for k=1:m
z0[k,:] .= g(M[1].x[k,:])
c0[k,:] .= f(M[1].x[k,:])
end
By default, the return value `z` is an `m×n` matrix, where `n` is the number of `state_variables`, see either `fem1d()`, `fem2d()`, `spectral1d()` or `spectral2d()`. If `return_details=true` then the return value is a named tuple with fields `z`, `SOL_feasibility` and `SOL_main`; the latter two fields are named tuples with detailed information regarding the various solves.
"""
function amgb(M::Tuple{AMG{T,Mat,Geometry},AMG{T,Mat,Geometry}},
f::Union{Function,Matrix{T}},
g::Union{Function,Matrix{T}},
Q::Convex;
x::Matrix{T} = M[1].x,
t=T(0.1),
t_feasibility=t,
verbose=true,
return_details=false,
rest...) where {T,Mat,Geometry}
progress = x->nothing
pbar = 0
if verbose
pbar = Progress(1000000; dt=1.0)
progress = x->update!(pbar,Int(floor(1000000*x)))
end
M0 = M[1]
D0 = M0.D[end,1]
xend = M0.x
m = size(xend,1)
ns = Int(size(D0,2)/m)
nD = size(M0.D,2)
w = zeros(T,(m,nD))
c0 = f
if f isa Function
c0 = zeros(T,(m,nD))
for k=1:m
c0[k,:] .= f(x[k,:])
end
end
z0 = g
if g isa Function
z0 = zeros(T,(m,ns))
for k=1:m
z0[k,:] .= g(x[k,:])
end
end
wend = M0.w
z2 = reshape(z0,(:,))
for k=1:nD
w[:,k] = M0.D[end,k]*z2
end
pbarfeas = 0.0
feasible = true
SOL1=nothing
try
for k=1:m
@assert(isfinite(Q.barrier(x[k,:],w[k,:])::T))
end
catch
pbarfeas = 0.1
z1 = hcat(z0,[2*max(Q.slack(x[k,:],w[k,:]),1) for k=1:m])
b = 2*max(1,maximum(z1[:,end]))
c1 = zeros(T,(m,nD+1))
c1[:,end] .= 1
B1 = barrier((x,y)->dot(y,y)+Q.cobarrier(x,y)-log(b^2-y[end]^2))
z1 = reshape(z1,(:,))
early_stop(z) = all(z[end-m+1:end] .< 0)
try
SOL1 = amgb_core(B1,M[2],x,z1,c1,t=t_feasibility,
progress=x->progress(pbarfeas*x),
early_stop=early_stop, rest...)#,c0=hcat(t*c0,zeros(T,(m,1))))
@assert early_stop(SOL1.z)
catch e
if isa(e,AMGBConvergenceFailure)
throw(AMGBConvergenceFailure("Could not solve the feasibility subproblem, probem may be infeasible. Failure was: "+e.message))
end
throw(e)
end
z2 = reshape((reshape(SOL1.z,(m,ns+1)))[:,1:end-1],(:,))
end
B = barrier(Q.barrier)
SOL2 = amgb_core(B,M0,x,z2,c0,t=t,
progress=x->progress((1-pbarfeas)*x+pbarfeas),rest...)
if verbose
progress(1.0)
finish!(pbar)
end
z = reshape(SOL2.z,(m,:))
if return_details
return (z=z,SOL_feasibility=SOL1,SOL_main=SOL2)
end
return z
end
default_f(T) = [(x)->T[0.5,0.0,1.0],(x)->T[0.5,0.0,0.0,1.0]]
default_g(T) = [(x)->T[x[1],2],(x)->T[x[1]^2+x[2]^2,100.0]]
default_D = [[:u :id
:u :dx
:s :id],
[:u :id
:u :dx
:u :dy
:s :id]]
"""
function amg_solve(::Type{T}=Float64;
L::Integer=2, n=nothing,
method=FEM1D,
K = nothing,
state_variables::Matrix{Symbol} = [:u :dirichlet
:s :full],
dim::Integer = amg_dim(method),
D::Matrix{Symbol} = default_D[dim],
M = amg_construct(T,method,L=L,n=n,K=K,state_variables=state_variables,D=D),
p::T = T(1.0),
g::Union{Function,Matrix{T}} = default_g(T)[dim],
f::Union{Function,Matrix{T}} = default_f(T)[dim],
Q::Convex{T} = convex_Euclidian_power(T,idx=2:dim+2,p=x->p),
show=true,
return_details=false, rest...) where {T}
A simplified interface for module MultiGridBarrier to "quickly get started". To solve a p-Laplace problem, do: `amg_solve()`.
Different behaviors can be obtained by supplying various optional keyword arguments, as follows.
* `L=2`: the number of times to subdivide the base mesh.
* The `n` parameter is only used in `spectral` methods, in which case, if `n` is an integer, then `L` is disregarded. `n` is the number of quadrature nodes along each axis.
* `method=FEM1D`: this must be either `FEM1D`, `FEM2D`, `SPECTRAL1D` or `SPECTRAL2D`. This parameter is used twice: once to choose the constructor for the `M` parameter, and again to plot the solution if `show` is `true`. If `show` is `false` and if `M` is constructed "manually", not by its default value, then the `method` parameter is ignored.
* `K`: In most cases, this is `nothing`, but in the `fem2d` case, `K` is the initial mesh.
* `state_variables = [:u :dirichlet ; :s :full]`: the names of the components of the solution vector `z`.
* `dim = size(M[1].x[end],2)`, the dimension of the problem, should be 1 or 2. This is only used in the default values of the `g`, `f`, `Q`, `D` parameters, and is ignored if these parameters do not use default values.
* `D`: the differential operators, see below for defaults.
* `M`: a mesh obtained by one of the constructors `fem1d`, `fem2d`, `spectral1d` or `spectral2d`, corresponding to the `method` parameter.
* `x = M[1].x`: a matrix, same number of rows as `M[1].x`. This matrix will be passed, row by row, to the barrier function, as the x parameter.
* `p = T(1.0)`: the parameter of the p-Laplace operator. This is only relevant if the default value is used for the `Q` parameter, and is ignored otherwise.
* `g`: the "boundary conditions" function. See below for defaults.
* `f`: the "forcing" or "cost functional" to be minimized. See below for defaults.
* `Q`: the convex domain to which the solution should belong. Defaults to `convex_Euclidian_power(T,idx=2:dim+2,p=x->p)`, which corresponds to p-Laplace problems. Change this to solve other variational problems.
* `show=true`: if `true`, plot the solution.
* `return_details=false`: if `false`, return a `Vector{T}` of the solution. If `true`, returned a named tuple with some more details about the solution process.
* `rest...`: any further keyword arguments are passed on to `amgb`.
The default values for the parameters `f`, `g`, `D` are as follows
| `dim` | 1 | 2 |
|:------|:----------------------|:------------------------------|
| `f` | `(x)->T[0.5,0.0,1.0]` | `(x)->T[0.5,0.0,0.0,1.0]` |
| `g` | `(x)->T[x[1],2]` | `(x)->T[x[1]^2+x[2]^2,100.0]` |
| `D` | `[:u :id` | `[:u :id` |
| | ` :u :dx` | ` :u :dx` |
| | ` :s :id]` | ` :u :dy` |
| | | ` :s :id]` |
"""
function amg_solve(::Type{T}=Float64;
L::Integer=2, n=nothing,
method=FEM1D,
K = nothing,
state_variables::Matrix{Symbol} = [:u :dirichlet
:s :full],
dim::Integer = amg_dim(method),
D::Matrix{Symbol} = default_D[dim],
M = amg_construct(T,method,L=L,n=n,K=K,state_variables=state_variables,D=D),
p::T = T(1.0),
g::Union{Function,Matrix{T}} = default_g(T)[dim],
f::Union{Function,Matrix{T}} = default_f(T)[dim],
Q::Convex{T} = convex_Euclidian_power(T,idx=2:dim+2,p=x->p),
show=true,
return_details=false, rest...) where {T}
SOL=amgb(M,f, g, Q,;return_details=return_details,rest...)
if show
z = if return_details SOL.z else SOL end
amg_plot(M[1],z[:,1])
end
SOL
end
function amg_precompile()
fem1d_solve(L=1)
fem2d_solve(L=1)
spectral1d_solve(L=1)
spectral2d_solve(L=1)
end
precompile(amg_precompile,())
| MultiGridBarrier | https://github.com/sloisel/MultiGridBarrier.jl.git |
|
[
"MIT"
] | 0.8.0 | 2e8ff74c4b7ff2c2bacfcfe24c00aadfd3527f95 | code | 4315 | @doc raw"""
module MultiGridBarrier
Module `MultiGridBarrier` solves convex optimization problems in function spaces, for example, solving p-Laplace problems. We recommend to start with the functions `fem1d_solve()`, `fem2d_solve()`, `spectral1d_solve()`, `spectral2d_solve()`. These functions are sufficient to solve p-Laplace problems in 1d or 2d, using finite or spectral elements.
For more general use, the user will need to familiarize themselves with the basic ideas of convex optimization.
* Overview of convex optimization in function spaces by MultiGrid Barrier method.
The general idea is to build a multigrid hierarchy, represented by an `AMG` object, and barrier for a convex set, represented by a `Barrier` object, and then solve a convex optimization problem using the `amgb()` solver.
To generate the multigrid hierarchy represented by the `AMG` object, use either `fem1d()`, `fem2d()`, `spectral1d()` or `spectral2d()` functions. These constructors will assemble suitable `AMG` objects for either FEM or spectral discretizations, in 1d or 2d. One should think of these four constructors as being specialized in constructing some specific function spaces. A user can use the `amg()` constructor directly if custom function spaces are required, but this is more difficult.
We now describe the barrier function.
Assume that ``\Omega \subset \mathbb{R}^d`` is some open set. Consider the example of the p-Laplace problem on ``\Omega``. Let ``f(x)`` be a "forcing" (a function) on ``\Omega``, and ``1 \leq p < \infty``. One wishes to solve the minimization problem
```math
\begin{equation}
\inf_u \int_{\Omega} fu + \|\nabla u\|_2^p \, dx. \tag{1}
\end{equation}
```
Generally speaking, ``u`` will range in some function space, e.g. a space of differentiable functions satisfying homogeneous Dirichlet conditions. Under some conditions, minimizing (1) is equivalent to solving the p-Laplace PDE:
```math
\nabla \cdot (\|\nabla u\|_2^{p-2}\nabla u) = {1 \over p} f.
```
We introduct the "slack function" ``s(x)`` and replace (1) with the following equivalent problem:
```math
\begin{equation}
\inf_{s(x) \geq \|\nabla u(x)\|_2^p} \int_{\Omega} fu + s \, dx. \tag{2}
\end{equation}
```
Define the convex set ``\mathcal{Q} = \{ (u(x),q(x),s(x)) \; : \; s(x) \geq \|q(x)\|_2^p \}``, and
```math
z = \begin{bmatrix} u \\ s \end{bmatrix}, \qquad
c^T = [f,0,1], \qquad
Dz = \begin{bmatrix} u \\ \nabla u \\ s \end{bmatrix}.
```
Then, (2) can be rewritten as
```math
\begin{equation}
\inf_{Dz \in \mathcal{Q}} \int_{\Omega} c^T(x)Dz(x) \, dx. \tag{3}
\end{equation}
```
Recall that a barrier for ``\mathcal{Q}`` is a convex function ``\mathcal{F}`` on ``\mathcal{Q}`` such that ``\mathcal{F} < \infty`` in the interior of ``\mathcal{Q}`` and ``\mathcal{F} = \infty`` on the boundary of ``\mathcal{Q}``. A barrier for the p-Laplace problem is:
```math
\mathcal{F}(u,q,s) = \int_{\Omega} -\log(s^{2 \over p} - \|q\|_2^2) - 2\log s \, dx = \int_{\Omega} F(Dz(x)) \, dx.
```
The central path ``z^*(t)`` minimizes, for each fixed ``t>0``, the quantity
```math
\int_{\Omega} tc^TDz + F(Dz) \, dx.
```
As ``t \to \infty``, ``z^*(t)`` forms a minimizing sequence (or filter) for (3). We think of the function ``c(x)`` as the "functional" that we seek to minimize.
The `Convex{T}` type describes various convex sets (denoted ``Q`` above) by way of functions `barrier()`, `cobarrier()` and `slack()`. `barrier` is indeed a barrier for ``Q``, `cobarrier()` is a barrier for a related feasibility problems, and ``slack()`` is used in solving the feasibility problem. `Convex{T}` objects can be created using the various `convex_...()` constructors, e.g. `convex_Euclidian_power()` for the p-Laplace problem.
Once one has `AMG` and `Convex` objects, and a suitable "functional" `c`, one uses the `amgb()` function to solve the optimization problem by the MultiGrid Barrier method, a variant of the barrier method (or interior point method) that is quasi-optimal for sufficiently regular problems.
"""
module MultiGridBarrier
using SparseArrays
using LinearAlgebra
using PyPlot
using PyCall
using ForwardDiff
using ProgressMeter
using QuadratureRules
include("AlgebraicMultiGridBarrier.jl")
include("fem1d.jl")
include("fem2d.jl")
include("spectral1d.jl")
include("spectral2d.jl")
include("Parabolic.jl")
end
| MultiGridBarrier | https://github.com/sloisel/MultiGridBarrier.jl.git |
|
[
"MIT"
] | 0.8.0 | 2e8ff74c4b7ff2c2bacfcfe24c00aadfd3527f95 | code | 5571 | export parabolic_solve, parabolic_plot
default_D_parabolic = [
[:u :id
:u :dx
:s1 :id
:s2 :id],
[:u :id
:u :dx
:u :dy
:s1 :id
:s2 :id]
]
default_f_parabolic = [
(f1,w1,w2)->[f1,0,w1,w2],
(f1,w1,w2)->[f1,0,0,w1,w2]
]
default_g_parabolic = [
(t,x)->[x[1],0,0],
(t,x)->[x[1]^2+x[2]^2,0,0],
]
@doc raw"""
function parabolic_solve(::Type{T}=Float64;
method = FEM2D,
state_variables = [:u :dirichlet
:s1 :full
:s2 :full],
dim = amg_dim(method),
f1 = x->T(0.5),
f_default = default_f_parabolic[dim],
p = T(1),
h = T(0.2),
f = (t,x)->f_default(h*f1(x)-x[1+dim],T(0.5),h/p),
g = default_g_parabolic[dim],
D = default_D_parabolic[dim],
L = 2,
t0 = T(0),
t1 = T(1),
M = amg_construct(T,method,L=L,D=D,state_variables=state_variables),
Q = (convex_Euclidian_power(;idx=[1,2+dim],p=x->T(2))
∩ convex_Euclidian_power(;idx=vcat(2:1+dim,3+dim),p=x->p)),
verbose = true,
show = true,
interval = 200,
printer=(animation)->display("text/html", animation.to_html5_video(embed_limit=200.0)),
rest...) where {T}
Solves a parabolic (i.e. time-dependent) p-Laplace problem of the form:
```math
u_t - \nabla \cdot (\|\nabla u\|_2^{p-2}\nabla u) = -f_1.
```
We use the implicit Euler scheme ``u_t \approx (u_{k+1}-u_k)/h`` to arrive at:
```math
u_{k+1} - h\nabla \cdot (\|\nabla u_{k+1}\|_2^{p-2}\nabla u_{k+1}) = u_k-hf_1.
```
According to the calculus of variation, we look for a weak solution minimizing
```math
J(u) = \int_{\Omega}{1 \over 2} u^2 + h {1 \over p} \|\nabla u\|_2^p + (hf_1-u_k)u \, dx
```
We introduce the slack functions ``s_1 \geq u^2`` and ``s_2 \geq \|\nabla u\|_2^p`` and minimize instead
```math
\int_{\Omega} {1 \over 2}s_1 + {h \over p} s_2 + (hf_1-u_k)u \, dx.
```
The canonical form is:
```math
z = \begin{bmatrix} u \\ s_1 \\ s_2 \end{bmatrix}
\qquad
f^T = \left[hf_1-u_k,0,0,{1 \over 2},{h \over p}\right]
\qquad
Dz = \begin{bmatrix} u \\ u_x \\ u_y \\ s_1 \\ s_2 \end{bmatrix}
\qquad
g = \begin{bmatrix} g_1 \\ 0 \\ 0 \end{bmatrix}.
```
Here, ``g_1`` encodes boundary conditions for ``u``. Then we minimize:
```math
\int_{\Omega} f^TDz
```
The named arguments `rest...` are passed verbatim to `amg_solve`.
"""
function parabolic_solve(::Type{T}=Float64;
method = FEM2D,
state_variables = [:u :dirichlet
:s1 :full
:s2 :full],
dim = amg_dim(method),
f1 = x->T(0.5),
f_default = default_f_parabolic[dim],
p = T(1),
h = T(0.2),
f = (t,x)->f_default(h*f1(x)-x[1+dim],T(0.5),h/p),
g = default_g_parabolic[dim],
D = default_D_parabolic[dim],
L = 2,
t0 = T(0),
t1 = T(1),
M = amg_construct(T,method,L=L,D=D,state_variables=state_variables),
Q = (convex_Euclidian_power(;idx=[1,2+dim],p=x->T(2))
∩ convex_Euclidian_power(;idx=vcat(2:1+dim,3+dim),p=x->p)),
verbose = true,
show = true,
interval = 200,
printer=(animation)->display("text/html", animation.to_html5_video(embed_limit=200.0)),
rest...) where {T}
ts = t0:h:t1
n = length(ts)
m = size(M[1].x,1)
g0 = g
if g isa Function
foo = g(t0,M[1].x[1,:])
d = length(foo)
g0 = zeros(T,(m,d,n))
for j=1:n
for k=1:m
g0[k,:,j] = g(ts[j],M[1].x[k,:])
end
end
end
d = size(g0,2)
U = g0
pbar = 0
prog = k->nothing
if verbose
pbar = Progress(n; dt=1.0)
prog = k->update!(pbar,k)
end
for k=1:n-1
prog(k-1)
z = amg_solve(;L=L,method=method,M=M,x=hcat(M[1].x,U[:,:,k]),g=U[:,:,k+1],f=x->f(ts[k+1],x),Q=Q,show=false,verbose=false,rest...)
U[:,:,k+1] = z
end
if verbose
finish!(pbar)
end
if show
parabolic_plot(method,M[1],U[:,1,:],interval=interval,printer=printer)
end
return U
end
"""
function parabolic_plot(method,M::AMG{T, Mat,Geometry}, U::Matrix{T};
interval=200, embed_limit=200.0,
printer=(animation)->display("text/html", animation.to_html5_video(embed_limit=embed_limit))) where {T,Mat,Geometry}
Animate the solution of the parabolic problem.
"""
function parabolic_plot(method,M::AMG{T, Mat,Geometry}, U::Matrix{T};
interval=200, embed_limit=200.0,
printer=(animation)->display("text/html", animation.to_html5_video(embed_limit=embed_limit))) where {T,Mat,Geometry}
anim = pyimport("matplotlib.animation")
# anim = matplotlib.animation
m0 = minimum(U)
m1 = maximum(U)
dim = amg_dim(method)
function animate(i)
clf()
ret = amg_plot(M,U[:,i+1])
ax = plt.gca()
if dim==1
ax.set_ylim([m0, m1])
return ret
end
ax.axes.set_zlim3d(bottom=m0, top=m1)
return [ret,]
end
init()=animate(0)
fig = figure()
myanim = anim.FuncAnimation(fig, animate, frames=size(U,2), init_func=init, interval=interval, blit=true)
printer(myanim)
plt.close(fig)
return nothing
end
function parabolic_precompile()
parabolic_solve(method=FEM1D,L=1,h=0.5)
parabolic_solve(method=FEM2D,L=1,h=0.5)
parabolic_solve(method=SPECTRAL1D,L=1,h=0.5)
parabolic_solve(method=SPECTRAL2D,L=2,h=0.5)
end
precompile(parabolic_precompile,())
| MultiGridBarrier | https://github.com/sloisel/MultiGridBarrier.jl.git |
|
[
"MIT"
] | 0.8.0 | 2e8ff74c4b7ff2c2bacfcfe24c00aadfd3527f95 | code | 4644 | export fem1d, FEM1D, fem1d_solve
" abstract type FEM1D end"
abstract type FEM1D end
" amg_dim(::Type{FEM1D}) = 1"
amg_dim(::Type{FEM1D}) = 1
" amg_construct(::Type{T},::Type{FEM1D};rest...) where {T} = fem1d(T;rest...)"
amg_construct(::Type{T},::Type{FEM1D};rest...) where {T} = fem1d(T;rest...)
" fem1d_solve(::Type{T}=Float64;rest...) where {T} = amg_solve(T;method=FEM1D,rest...)"
fem1d_solve(::Type{T}=Float64;rest...) where {T} = amg_solve(T;method=FEM1D,rest...)
"""
function fem1d(::Type{T}=Float64; L::Int=4,
state_variables = [:u :dirichlet
:s :full],
D = [:u :id
:u :dx
:s :id],
generate_feasibility=true) where {T}
Construct an `AMG` object for a 1d piecewise linear finite element grid. The interval is [-1,1]. Parameters are:
* `L`: divide the interval into 2^L subintervals (L for Levels).
* `state_variables`: the "state vector" consists of functions, by default this is `u(x)` and `s(x)`, on the finite element grid.
* `D`: the set of differential operator. The barrier function `F` will eventually be called with the parameters `F(x,Dz)`, where `z` is the state vector. By default, this results in `F(x,u,ux,s)`, where `ux` is the derivative of `u`.
* `generate_feasibility`: if `true`, returns a pair `M` of `AMG` objects. `M[1]` is the `AMG` object for the main problem, and `M[2]` is for the feasibility subproblem.
"""
function fem1d(::Type{T}=Float64; L::Int=4, n=nothing, K=nothing,
state_variables = [:u :dirichlet
:s :full],
D = [:u :id
:u :dx
:s :id],
generate_feasibility=true) where {T}
ls = [2^k for k=1:L]
x = Array{Array{T,2},1}(undef,(L,))
dirichlet = Array{SparseMatrixCSC{T,Int},1}(undef,(L,))
full = Array{SparseMatrixCSC{T,Int},1}(undef,(L,))
uniform = Array{SparseMatrixCSC{T,Int},1}(undef,(L,))
refine = Array{SparseMatrixCSC{T,Int},1}(undef,(L,))
coarsen = Array{SparseMatrixCSC{T,Int},1}(undef,(L,))
for l=1:L
n0 = 2^l
x[l] = reshape(hcat((0:n0-1)./T(n0),(1:n0)./T(n0))',(2*n0,1)) .* 2 .- 1
N = size(x[l])[1]
dirichlet[l] = vcat(spzeros(T,1,n0-1),blockdiag(repeat([sparse(T[1 ; 1 ;;])],outer=(n0-1,))...),spzeros(T,1,n0-1))
full[l] = sparse(T,I,N,N)
uniform[l] = sparse(ones(T,(N,1)))
end
N = size(x[L])[1]
w = repeat([T(2)/N],outer=(N,))
id = sparse(T,I,N,N)
dx = blockdiag(repeat([sparse(T[-2^(L-1) 2^(L-1)
-2^(L-1) 2^(L-1)])],outer=(2^L,))...)
refine[L] = id
coarsen[L] = id
for l=1:L-1
n0 = 2^l
refine[l] = blockdiag(
repeat([sparse(T[1.0 0.0
0.5 0.5
0.5 0.5
0.0 1.0])],outer=(n0,))...)
coarsen[l] = blockdiag(
repeat([sparse(T[1 0 0 0
0 0 0 1])],outer=(n0,))...)
end
subspaces = Dict(:dirichlet => dirichlet, :full => full, :uniform => uniform)
operators = Dict(:id => id, :dx => dx)
return amg(FEM1D,x=x[L],w=w,state_variables=state_variables,
D=D,subspaces=subspaces,operators=operators,refine=refine,coarsen=coarsen,
generate_feasibility=generate_feasibility)
end
"""
function fem1d_interp(x::Vector{T},
y::Vector{T},
t::T) where{T}
Interpolate a 1d piecewise linear function at the given `t` value. If `u(xi)` is the piecewise linear function such that `u(x[k])=y[k]` then this function returns `u(t)`.
"""
function fem1d_interp(x::Vector{T},
y::Vector{T},
t::T) where{T}
b = length(x)
if t<x[1]
return y[1]
elseif t>x[b]
return y[b]
end
a = 1
while b-a>1
c = (a+b)÷2
if x[c]<=t
a=c
else
b=c
end
end
w = (t-x[a])/(x[b]-x[a])
return w*y[b]+(1-w)*y[a]
end
"""
function fem1d_interp(x::Vector{T},
y::Vector{T},
t::Vector{T}) where{T}
Returns `[fem1d_interp(x,y,t[k]) for k=1:length(t)]`.
"""
function fem1d_interp(x::Vector{T},
y::Vector{T},
t::Vector{T}) where{T}
[fem1d_interp(x,y,t[k]) for k=1:length(t)]
end
" amg_plot(M::AMG{T,Mat,FEM1D}, z::Vector{T}) where {T,Mat} = plot(M.x[end],z)"
amg_plot(M::AMG{T,Mat,FEM1D}, z::Vector{T}) where {T,Mat} = plot(M.x,z)
| MultiGridBarrier | https://github.com/sloisel/MultiGridBarrier.jl.git |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.