path
stringlengths 7
265
| concatenated_notebook
stringlengths 46
17M
|
|---|---|
distribuicao-poisson.ipynb
|
###Markdown
UnB AEDI - Analise Estatística de Dados e Informações Professor: João Gabriel de Moraes SouzaAluno: Ivon Miranda Santos*** Distribuição Poisson*** **Importando as bibliotecas** - Sínbolos LaTex https://www.ime.usp.br/~rfarias/simbolos.html
###Code
# biblioteca para escrever fórmulas direto no jupyter notebook
from IPython.display import display, Math, Latex
###Output
_____no_output_____
###Markdown
$$P(k)=\frac{e ^ {-\mu} * \mu ^ k }{k!}$$ - A distribuição de Poisson é largamente empregada quando se deseja contar o numero de eventos de certo tipo que ocorrem em um intervalo de tempo.- Uma das características é que deve haver possibilidade de definir os eventos com sucesso mas não se pode identificar os fracassos- A probabilidade sempre se mantem igual independente da variação do intervalo no tempo, por exemplo: a probabilidade de pessoas que entrarão no shopping na segunda de 12h as 13h, será a mema probabilidade de pessoas que possam entrar na terça feira no mesmo intervalo horário. **Problema 1**- Um restaurante recebe em **média 20 pedidos por hora**. Qual a chance de que, em determinada hora escolhida ao acaso, o restaurante receba 15 pedidos?
###Code
media = 20
media
k = 15
k
import numpy as np
###Output
_____no_output_____
###Markdown
**Solução 1**
###Code
probabilidade = ((np.e ** (-media)) * (media ** k )) / (np.math.factorial(k))
print('Probabilidade : %0.8f ' % probabilidade)
###Output
Probabilidade : 0.05164885
###Markdown
**Solução 2**
###Code
from scipy.stats import poisson
probabilidade = poisson.pmf(k, media)
print('Probabilidae %0.8f ' % probabilidade)
###Output
Probabilidae 0.05164885
###Markdown
**Problema 2**- O número médio de clientes que entram em uma padaria por hora é igual a 20. Obtenha a probabilidade de, na próxima hora, entrarem exatamente 25 clientes.
###Code
media = 20
k = 25
probabilidade = poisson.pmf(k, media)
print('Probabilidade %0.8f ' % probabilidade + ' ou ')
print('Probabilidade %0.4f ' % (probabilidade * 100 ) + ' %')
###Output
Probabilidade 0.04458765 ou
Probabilidade 4.4588 %
|
notebooks/jigsaw-baseline.ipynb
|
###Markdown
Detect TPUs or GPUs:
###Code
# Detect hardware, return appropriate distribution strategy
try:
# TPU detection. No parameters necessary if TPU_NAME environment variable is
# set: this is always the case on Kaggle.
tpu = tf.distribute.cluster_resolver.TPUClusterResolver()
print('Running on TPU ', tpu.master())
except ValueError:
tpu = None
if tpu:
tf.config.experimental_connect_to_cluster(tpu)
tf.tpu.experimental.initialize_tpu_system(tpu)
strategy = tf.distribute.experimental.TPUStrategy(tpu)
else:
# Default distribution strategy in Tensorflow. Works on CPU and single GPU.
strategy = tf.distribute.get_strategy()
print("REPLICAS: ", strategy.num_replicas_in_sync)
###Output
Running on TPU grpc://10.0.0.2:8470
REPLICAS: 8
###Markdown
Set maximum sequence length and path variables.
###Code
SEQUENCE_LENGTH = 128
# Note that private datasets cannot be copied - you'll have to share any pretrained models
# you want to use with other competitors!
GCS_PATH = KaggleDatasets().get_gcs_path('jigsaw-multilingual-toxic-comment-classification')
BERT_GCS_PATH = KaggleDatasets().get_gcs_path('bert-multi')
BERT_GCS_PATH_SAVEDMODEL = BERT_GCS_PATH + "/bert_multi_from_tfhub"
###Output
_____no_output_____
###Markdown
Define the model. We convert m-BERT's output to a final probabilty estimate. We're using an [m-BERT model from TensorFlow Hub](https://tfhub.dev/tensorflow/bert_multi_cased_L-12_H-768_A-12/1).
###Code
def multilingual_bert_model(max_seq_length=SEQUENCE_LENGTH, trainable_bert=True):
"""Build and return a multilingual BERT model and tokenizer."""
input_word_ids = tf.keras.layers.Input(
shape=(max_seq_length,), dtype=tf.int32, name="input_word_ids")
input_mask = tf.keras.layers.Input(
shape=(max_seq_length,), dtype=tf.int32, name="input_mask")
segment_ids = tf.keras.layers.Input(
shape=(max_seq_length,), dtype=tf.int32, name="all_segment_id")
# Load a SavedModel on TPU from GCS. This model is available online at
# https://tfhub.dev/tensorflow/bert_multi_cased_L-12_H-768_A-12/1. You can use your own
# pretrained models, but will need to add them as a Kaggle dataset.
bert_layer = tf.saved_model.load(BERT_GCS_PATH_SAVEDMODEL)
# Cast the loaded model to a TFHub KerasLayer.
bert_layer = hub.KerasLayer(bert_layer, trainable=trainable_bert)
pooled_output, outputs = bert_layer([input_word_ids, input_mask, segment_ids])
print("outputs.shape", outputs.shape)
print("pooled_output.shape", pooled_output.shape)
#outputs = tf.keras.layers.GRU(128) (outputs)
#outputs = tf.keras.layers.Dropout(0.5) (outputs)
#print("outputs.shape after lstms", outputs.shape)
#outputs = tf.keras.layers.Flatten() (outputs)
outputs = tf.keras.layers.GlobalMaxPooling1D() (outputs)
print("outputs.shape after flatten", outputs.shape)
outputs = tf.keras.layers.Dense(32, activation='relu')(outputs)
pooled_output = tf.keras.layers.Dense(32, activation='relu')(pooled_output)
output = tf.keras.layers.Concatenate() ([pooled_output, outputs])
output = tf.keras.layers.Dense(1, activation='sigmoid', name='labels')(output)
return tf.keras.Model(inputs={'input_word_ids': input_word_ids,
'input_mask': input_mask,
'all_segment_id': segment_ids},
outputs=output)
###Output
_____no_output_____
###Markdown
Load the preprocessed dataset. See the demo notebook for sample code for performing this preprocessing.
###Code
def parse_string_list_into_ints(strlist):
s = tf.strings.strip(strlist)
s = tf.strings.substr(
strlist, 1, tf.strings.length(s) - 2) # Remove parentheses around list
s = tf.strings.split(s, ',', maxsplit=SEQUENCE_LENGTH)
s = tf.strings.to_number(s, tf.int32)
s = tf.reshape(s, [SEQUENCE_LENGTH]) # Force shape here needed for XLA compilation (TPU)
return s
def format_sentences(data, label='toxic', remove_language=False):
labels = {'labels': data.pop(label)}
if remove_language:
languages = {'language': data.pop('lang')}
# The remaining three items in the dict parsed from the CSV are lists of integers
for k,v in data.items(): # "input_word_ids", "input_mask", "all_segment_id"
data[k] = parse_string_list_into_ints(v)
return data, labels
def make_sentence_dataset_from_csv(filename, label='toxic', language_to_filter=None):
# This assumes the column order label, input_word_ids, input_mask, segment_ids
SELECTED_COLUMNS = [label, "input_word_ids", "input_mask", "all_segment_id"]
label_default = tf.int32 if label == 'id' else tf.float32
COLUMN_DEFAULTS = [label_default, tf.string, tf.string, tf.string]
if language_to_filter:
insert_pos = 0 if label != 'id' else 1
SELECTED_COLUMNS.insert(insert_pos, 'lang')
COLUMN_DEFAULTS.insert(insert_pos, tf.string)
preprocessed_sentences_dataset = tf.data.experimental.make_csv_dataset(
filename, column_defaults=COLUMN_DEFAULTS, select_columns=SELECTED_COLUMNS,
batch_size=1, num_epochs=1, shuffle=False) # We'll do repeating and shuffling ourselves
# make_csv_dataset required a batch size, but we want to batch later
preprocessed_sentences_dataset = preprocessed_sentences_dataset.unbatch()
if language_to_filter:
preprocessed_sentences_dataset = preprocessed_sentences_dataset.filter(
lambda data: tf.math.equal(data['lang'], tf.constant(language_to_filter)))
#preprocessed_sentences.pop('lang')
preprocessed_sentences_dataset = preprocessed_sentences_dataset.map(
lambda data: format_sentences(data, label=label,
remove_language=language_to_filter))
return preprocessed_sentences_dataset
###Output
_____no_output_____
###Markdown
Set up our data pipelines for training and evaluation.
###Code
def make_dataset_pipeline(dataset, repeat_and_shuffle=True):
"""Set up the pipeline for the given dataset.
Caches, repeats, shuffles, and sets the pipeline up to prefetch batches."""
cached_dataset = dataset.cache()
if repeat_and_shuffle:
cached_dataset = cached_dataset.repeat().shuffle(2048)
cached_dataset = cached_dataset.batch(32 * strategy.num_replicas_in_sync)
cached_dataset = cached_dataset.prefetch(tf.data.experimental.AUTOTUNE)
return cached_dataset
# Load the preprocessed English dataframe.
preprocessed_en_filename = (
GCS_PATH + "/jigsaw-toxic-comment-train-processed-seqlen{}.csv".format(
SEQUENCE_LENGTH))
# Set up the dataset and pipeline.
english_train_dataset = make_dataset_pipeline(
make_sentence_dataset_from_csv(preprocessed_en_filename))
# Process the new datasets by language.
preprocessed_val_filename = (
GCS_PATH + "/validation-processed-seqlen{}.csv".format(SEQUENCE_LENGTH))
nonenglish_val_datasets = {}
for language_name, language_label in [('Spanish', 'es'), ('Italian', 'it'),
('Turkish', 'tr')]:
nonenglish_val_datasets[language_name] = make_sentence_dataset_from_csv(
preprocessed_val_filename, language_to_filter=language_label)
nonenglish_val_datasets[language_name] = make_dataset_pipeline(
nonenglish_val_datasets[language_name])
nonenglish_val_datasets['Combined'] = tf.data.experimental.sample_from_datasets(
(nonenglish_val_datasets['Spanish'], nonenglish_val_datasets['Italian'],
nonenglish_val_datasets['Turkish']))
###Output
_____no_output_____
###Markdown
Compile our model. We'll first evaluate it on our new toxicity dataset in the different languages to see its performance. After that, we'll train it on one of our English datasets, and then again evaluate its performance on the new multilingual toxicity data. As our metric, we'll use the [AUC](https://www.tensorflow.org/api_docs/python/tf/keras/metrics/AUC).
###Code
with strategy.scope():
multilingual_bert = multilingual_bert_model()
# Compile the model. Optimize using stochastic gradient descent.
multilingual_bert.compile(
loss=tf.keras.losses.BinaryCrossentropy(),
optimizer=tf.keras.optimizers.Adam(lr=1e-5),
metrics=[tf.keras.metrics.AUC()])
multilingual_bert.summary()
# Test the model's performance on non-English comments before training.
#for language in nonenglish_val_datasets:
# results = multilingual_bert.evaluate(nonenglish_val_datasets[language],
# steps=100, verbose=0)
# print('{} loss, AUC before training:'.format(language), results)
#results = multilingual_bert.evaluate(english_train_dataset,
# steps=100, verbose=0)
#print('\nEnglish loss, AUC before training:', results)
print()
from keras.callbacks import EarlyStopping
es = EarlyStopping(monitor='val_auc', mode='max', verbose=1, patience=1)
# Train on English Wikipedia comment data.
history = multilingual_bert.fit(
# Set steps such that the number of examples per epoch is fixed.
# This makes training on different accelerators more comparable.
english_train_dataset, steps_per_epoch=4000/strategy.num_replicas_in_sync, #4000
epochs=10, verbose=1, validation_data=nonenglish_val_datasets['Combined'],
validation_steps=100, callbacks=[es]) #100
# Re-evaluate the model's performance on non-English comments after training.
#for language in nonenglish_val_datasets:
# results = multilingual_bert.evaluate(nonenglish_val_datasets[language],
# steps=100, verbose=0)
# print('{} loss, AUC after training:'.format(language), results)
#results = multilingual_bert.evaluate(english_train_dataset,
# steps=100, verbose=0)
#print('\nEnglish loss, AUC after training:', results)
# trian on validation data too
es = EarlyStopping(monitor='auc', mode='max', verbose=1, patience=1)
# Train on English Wikipedia comment data.
history2 = multilingual_bert.fit(
nonenglish_val_datasets['Combined'], steps_per_epoch=4000/strategy.num_replicas_in_sync, #4000
epochs=10, verbose=1, callbacks=[es]) #100
###Output
Train for 500.0 steps, validate for 100 steps
Epoch 1/10
###Markdown
Generate predictionsFinally, we'll use our trained multilingual model to generate predictions for the test data.
###Code
import numpy as np
TEST_DATASET_SIZE = 63812
print('Making dataset...')
preprocessed_test_filename = (
GCS_PATH + "/test-processed-seqlen{}.csv".format(SEQUENCE_LENGTH))
test_dataset = make_sentence_dataset_from_csv(preprocessed_test_filename, label='id')
test_dataset = make_dataset_pipeline(test_dataset, repeat_and_shuffle=False)
print('Computing predictions...')
test_sentences_dataset = test_dataset.map(lambda sentence, idnum: sentence)
probabilities = np.squeeze(multilingual_bert.predict(test_sentences_dataset))
print(probabilities)
print('Generating submission file...')
test_ids_dataset = test_dataset.map(lambda sentence, idnum: idnum).unbatch()
test_ids = next(iter(test_ids_dataset.batch(TEST_DATASET_SIZE)))[
'labels'].numpy().astype('U') # All in one batch
np.savetxt('submission.csv', np.rec.fromarrays([test_ids, probabilities]),
fmt=['%s', '%f'], delimiter=',', header='id,toxic', comments='')
!head submission.csv
###Output
Making dataset...
Computing predictions...
[3.3676624e-06 4.4703484e-07 9.9824965e-01 ... 2.7447939e-05 5.6624413e-07
5.0663948e-07]
Generating submission file...
id,toxic
0,0.000003
1,0.000000
2,0.998250
3,0.000001
4,0.000000
5,0.000000
6,0.000001
7,0.000001
8,0.000003
|
Projects/ABM_DA/experiments/stationsim_gcs_calibration/notebooks/4_simulated_annealing.ipynb
|
###Markdown
Simulated Annealing Simulated annealing algorithm:* Select an initial solution* Select the temperature change counter k=0* Select a temperature cooling schedule* Select an initial temperature* Select a repetition schedule, that defines the number of iterations executed at eachtemperature* For t in \[$t_{max}$, $t_{min}$\]: * For m in \[0, $m_{max}$\] * Generate a solution * Calculate energy diff * If energy diff < 0 then take new state * If energy diff > 0 then take new state with probability exp(-energy diff/t) Imports
###Code
import json
from math import exp
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from random import random, uniform
import seaborn as sns
import sys
import time
%matplotlib inline
sys.path.append('../../../stationsim/')
from stationsim_gcs_model import Model
###Output
_____no_output_____
###Markdown
Constants
###Code
METROPOLIS = 1
TIME_TO_COMPLETION = 5687
MAX_ACTIVE_POPULATION = 85
NEIGHBOURHOOD = 0.5
TEMPERATURE_DROP = 4
###Output
_____no_output_____
###Markdown
Classes
###Code
class State():
def __init__(self, model_params):
self.model_params = model_params
self.model = Model(**self.model_params)
self.population_over_time = [self.model.pop_active]
def get_energy(self):
return abs(self.__get_time_to_completion() - TIME_TO_COMPLETION)
# return abs(self.__get_max_active_population() - MAX_ACTIVE_POPULATION)
def __get_max_active_population(self):
return max(self.population_over_time)
def __get_time_to_completion(self):
return self.model.finish_step_id
def run_model(self):
for _ in range(self.model.step_limit):
self.model.step()
self.population_over_time.append(self.model.pop_active)
###Output
_____no_output_____
###Markdown
Functions
###Code
def get_next_state(current_state):
# Get current parameter values
model_params = current_state.model_params
# Do something to perturb the variable of interest
new_model_params = model_params.copy()
perturbation = uniform(-NEIGHBOURHOOD, NEIGHBOURHOOD)
new_model_params['birth_rate'] += perturbation
# Make new state and run model for new values
state = State(new_model_params)
state.run_model()
return state
def simulated_annealing(initial_state, temp_min=0, temp_max=100):
params = [initial_state.model_params]
state = initial_state
for temp in range(temp_max, temp_min, -TEMPERATURE_DROP):
for i in range(METROPOLIS):
print(f'Run {i} for temperature {temp}')
current_energy = state.get_energy()
next_state = get_next_state(state)
next_energy = next_state.get_energy()
energy_change = next_energy - current_energy
if energy_change < 0:
print('Change state - greed')
state = next_state
elif exp(energy_change / temp) > random():
print('Change state - exploration')
state = next_state
params.append(state.model_params)
return initial_state, state, params
###Output
_____no_output_____
###Markdown
Run
###Code
scaling_factor = 25/14
speed_mean = 1.6026400144010877 / scaling_factor
speed_std = 0.6642343305178546 / scaling_factor
speed_min = 0.31125359137714953 / scaling_factor
print(f'mean: {speed_mean}, std: {speed_std}, min: {speed_min}')
model_params = {'station': 'Grand_Central',
'speed_mean': speed_mean,
'speed_std:': speed_std,
'speed_min': speed_min,
'step_limit': 20000,
'do_print': False,
'pop_total': 274,
'birth_rate': 1.5}
state = State(model_params)
state.run_model()
initial_state, final_state, param_list = simulated_annealing(state)
###Output
Run 0 for temperature 100
|
cnn/mnist-mlp/mnist_mlp_with_validation.ipynb
|
###Markdown
Multi-Layer Perceptron, MNIST---In this notebook, we will train an MLP to classify images from the [MNIST database](http://yann.lecun.com/exdb/mnist/) hand-written digit database.The process will be broken down into the following steps:>1. Load and visualize the data2. Define a neural network3. Train the model4. Evaluate the performance of our trained model on a test dataset!Before we begin, we have to import the necessary libraries for working with data and PyTorch.
###Code
# import libraries
import torch
import numpy as np
###Output
_____no_output_____
###Markdown
--- Load and Visualize the [Data](http://pytorch.org/docs/stable/torchvision/datasets.html)Downloading may take a few moments, and you should see your progress as the data is loading. You may also choose to change the `batch_size` if you want to load more data at a time.This cell will create DataLoaders for each of our datasets.
###Code
from torchvision import datasets
import torchvision.transforms as transforms
from torch.utils.data.sampler import SubsetRandomSampler
# number of subprocesses to use for data loading
num_workers = 0
# how many samples per batch to load
batch_size = 20
# percentage of training set to use as validation
valid_size = 0.2
# convert data to torch.FloatTensor
transform = transforms.ToTensor()
# choose the training and test datasets
train_data = datasets.MNIST(root='data', train=True,
download=True, transform=transform)
test_data = datasets.MNIST(root='data', train=False,
download=True, transform=transform)
# obtain training indices that will be used for validation
num_train = len(train_data)
indices = list(range(num_train))
np.random.shuffle(indices)
split = int(np.floor(valid_size * num_train))
train_idx, valid_idx = indices[split:], indices[:split]
# define samplers for obtaining training and validation batches
train_sampler = SubsetRandomSampler(train_idx)
valid_sampler = SubsetRandomSampler(valid_idx)
# prepare data loaders
train_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size,
sampler=train_sampler, num_workers=num_workers)
valid_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size,
sampler=valid_sampler, num_workers=num_workers)
test_loader = torch.utils.data.DataLoader(test_data, batch_size=batch_size,
num_workers=num_workers)
###Output
_____no_output_____
###Markdown
Visualize a Batch of Training DataThe first step in a classification task is to take a look at the data, make sure it is loaded in correctly, then make any initial observations about patterns in that data.
###Code
import matplotlib.pyplot as plt
%matplotlib inline
# obtain one batch of training images
dataiter = iter(train_loader)
images, labels = dataiter.next()
images = images.numpy()
# plot the images in the batch, along with the corresponding labels
fig = plt.figure(figsize=(25, 4))
for idx in np.arange(20):
ax = fig.add_subplot(2, 20/2, idx+1, xticks=[], yticks=[])
ax.imshow(np.squeeze(images[idx]), cmap='gray')
# print out the correct label for each image
# .item() gets the value contained in a Tensor
ax.set_title(str(labels[idx].item()))
###Output
_____no_output_____
###Markdown
View an Image in More Detail
###Code
img = np.squeeze(images[1])
fig = plt.figure(figsize = (12,12))
ax = fig.add_subplot(111)
ax.imshow(img, cmap='gray')
width, height = img.shape
thresh = img.max()/2.5
for x in range(width):
for y in range(height):
val = round(img[x][y],2) if img[x][y] !=0 else 0
ax.annotate(str(val), xy=(y,x),
horizontalalignment='center',
verticalalignment='center',
color='white' if img[x][y]<thresh else 'black')
###Output
_____no_output_____
###Markdown
--- Define the Network [Architecture](http://pytorch.org/docs/stable/nn.html)The architecture will be responsible for seeing as input a 784-dim Tensor of pixel values for each image, and producing a Tensor of length 10 (our number of classes) that indicates the class scores for an input image. This particular example uses two hidden layers and dropout to avoid overfitting.
###Code
import torch.nn as nn
import torch.nn.functional as F
# define the NN architecture
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
# number of hidden nodes in each layer (512)
hidden_1 = 512
hidden_2 = 512
# linear layer (784 -> hidden_1)
self.fc1 = nn.Linear(28 * 28, hidden_1)
# linear layer (n_hidden -> hidden_2)
self.fc2 = nn.Linear(hidden_1, hidden_2)
# linear layer (n_hidden -> 10)
self.fc3 = nn.Linear(hidden_2, 10)
# dropout layer (p=0.2)
# dropout prevents overfitting of data
self.dropout = nn.Dropout(0.2)
def forward(self, x):
# flatten image input
x = x.view(-1, 28 * 28)
# add hidden layer, with relu activation function
x = F.relu(self.fc1(x))
# add dropout layer
x = self.dropout(x)
# add hidden layer, with relu activation function
x = F.relu(self.fc2(x))
# add dropout layer
x = self.dropout(x)
# add output layer
x = self.fc3(x)
return x
# initialize the NN
model = Net()
print(model)
###Output
Net(
(fc1): Linear(in_features=784, out_features=512, bias=True)
(fc2): Linear(in_features=512, out_features=512, bias=True)
(fc3): Linear(in_features=512, out_features=10, bias=True)
(dropout): Dropout(p=0.2)
)
###Markdown
Specify [Loss Function](http://pytorch.org/docs/stable/nn.htmlloss-functions) and [Optimizer](http://pytorch.org/docs/stable/optim.html)It's recommended that you use cross-entropy loss for classification. If you look at the documentation (linked above), you can see that PyTorch's cross entropy function applies a softmax funtion to the output layer *and* then calculates the log loss.
###Code
# specify loss function (categorical cross-entropy)
criterion = nn.CrossEntropyLoss()
# specify optimizer (stochastic gradient descent) and learning rate = 0.01
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
###Output
_____no_output_____
###Markdown
--- Train the NetworkThe steps for training/learning from a batch of data are described in the comments below:1. Clear the gradients of all optimized variables2. Forward pass: compute predicted outputs by passing inputs to the model3. Calculate the loss4. Backward pass: compute gradient of the loss with respect to model parameters5. Perform a single optimization step (parameter update)6. Update average training lossThe following loop trains for 50 epochs; take a look at how the values for the training loss decrease over time. We want it to decrease while also avoiding overfitting the training data.
###Code
# use gpu if available
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
model.to(device);
# number of epochs to train the model
n_epochs = 50
# initialize tracker for minimum validation loss
valid_loss_min = np.Inf # set initial "min" to infinity
for epoch in range(n_epochs):
# monitor training loss
train_loss = 0.0
valid_loss = 0.0
###################
# train the model #
###################
model.train() # prep model for training
for data, target in train_loader:
# move data and target to device
data, target = data.to(device), target.to(device)
# clear the gradients of all optimized variables
# clear the gradients of all optimized variables
optimizer.zero_grad()
# forward pass: compute predicted outputs by passing inputs to the model
output = model(data)
# calculate the loss
loss = criterion(output, target)
# backward pass: compute gradient of the loss with respect to model parameters
loss.backward()
# perform a single optimization step (parameter update)
optimizer.step()
# update running training loss
train_loss += loss.item()*data.size(0)
######################
# validate the model #
######################
model.eval() # prep model for evaluation
for data, target in valid_loader:
# move data and target to device
data, target = data.to(device), target.to(device)
# clear the gradients of all optimized variables
# forward pass: compute predicted outputs by passing inputs to the model
output = model(data)
# calculate the loss
loss = criterion(output, target)
# update running validation loss
valid_loss += loss.item()*data.size(0)
# print training/validation statistics
# calculate average loss over an epoch
train_loss = train_loss/len(train_loader.dataset)
valid_loss = valid_loss/len(valid_loader.dataset)
print('Epoch: {} \tTraining Loss: {:.6f} \tValidation Loss: {:.6f}'.format(
epoch+1,
train_loss,
valid_loss
))
# save model if validation loss has decreased
if valid_loss <= valid_loss_min:
print('Validation loss decreased ({:.6f} --> {:.6f}). Saving model ...'.format(
valid_loss_min,
valid_loss))
torch.save(model.state_dict(), 'model.pt')
valid_loss_min = valid_loss
###Output
Epoch: 1 Training Loss: 0.767325 Validation Loss: 0.077792
Validation loss decreased (inf --> 0.077792). Saving model ...
Epoch: 2 Training Loss: 0.282707 Validation Loss: 0.059158
Validation loss decreased (0.077792 --> 0.059158). Saving model ...
Epoch: 3 Training Loss: 0.221035 Validation Loss: 0.049745
Validation loss decreased (0.059158 --> 0.049745). Saving model ...
Epoch: 4 Training Loss: 0.182371 Validation Loss: 0.041630
Validation loss decreased (0.049745 --> 0.041630). Saving model ...
Epoch: 5 Training Loss: 0.155042 Validation Loss: 0.037546
Validation loss decreased (0.041630 --> 0.037546). Saving model ...
Epoch: 6 Training Loss: 0.133400 Validation Loss: 0.032389
Validation loss decreased (0.037546 --> 0.032389). Saving model ...
Epoch: 7 Training Loss: 0.118441 Validation Loss: 0.029482
Validation loss decreased (0.032389 --> 0.029482). Saving model ...
Epoch: 8 Training Loss: 0.105242 Validation Loss: 0.027207
Validation loss decreased (0.029482 --> 0.027207). Saving model ...
Epoch: 9 Training Loss: 0.095649 Validation Loss: 0.025199
Validation loss decreased (0.027207 --> 0.025199). Saving model ...
Epoch: 10 Training Loss: 0.086487 Validation Loss: 0.023778
Validation loss decreased (0.025199 --> 0.023778). Saving model ...
Epoch: 11 Training Loss: 0.080151 Validation Loss: 0.022241
Validation loss decreased (0.023778 --> 0.022241). Saving model ...
Epoch: 12 Training Loss: 0.072776 Validation Loss: 0.021167
Validation loss decreased (0.022241 --> 0.021167). Saving model ...
Epoch: 13 Training Loss: 0.066574 Validation Loss: 0.021012
Validation loss decreased (0.021167 --> 0.021012). Saving model ...
Epoch: 14 Training Loss: 0.062729 Validation Loss: 0.019351
Validation loss decreased (0.021012 --> 0.019351). Saving model ...
Epoch: 15 Training Loss: 0.057982 Validation Loss: 0.018499
Validation loss decreased (0.019351 --> 0.018499). Saving model ...
Epoch: 16 Training Loss: 0.053246 Validation Loss: 0.018058
Validation loss decreased (0.018499 --> 0.018058). Saving model ...
Epoch: 17 Training Loss: 0.050015 Validation Loss: 0.017358
Validation loss decreased (0.018058 --> 0.017358). Saving model ...
Epoch: 18 Training Loss: 0.047911 Validation Loss: 0.017159
Validation loss decreased (0.017358 --> 0.017159). Saving model ...
Epoch: 19 Training Loss: 0.044253 Validation Loss: 0.016607
Validation loss decreased (0.017159 --> 0.016607). Saving model ...
Epoch: 20 Training Loss: 0.041105 Validation Loss: 0.016372
Validation loss decreased (0.016607 --> 0.016372). Saving model ...
Epoch: 21 Training Loss: 0.039522 Validation Loss: 0.016244
Validation loss decreased (0.016372 --> 0.016244). Saving model ...
Epoch: 22 Training Loss: 0.037368 Validation Loss: 0.016264
Epoch: 23 Training Loss: 0.035722 Validation Loss: 0.015528
Validation loss decreased (0.016244 --> 0.015528). Saving model ...
Epoch: 24 Training Loss: 0.032814 Validation Loss: 0.015223
Validation loss decreased (0.015528 --> 0.015223). Saving model ...
Epoch: 25 Training Loss: 0.031574 Validation Loss: 0.015718
Epoch: 26 Training Loss: 0.030402 Validation Loss: 0.014802
Validation loss decreased (0.015223 --> 0.014802). Saving model ...
Epoch: 27 Training Loss: 0.028545 Validation Loss: 0.014923
Epoch: 28 Training Loss: 0.026098 Validation Loss: 0.014799
Validation loss decreased (0.014802 --> 0.014799). Saving model ...
Epoch: 29 Training Loss: 0.025808 Validation Loss: 0.014530
Validation loss decreased (0.014799 --> 0.014530). Saving model ...
Epoch: 30 Training Loss: 0.024120 Validation Loss: 0.014249
Validation loss decreased (0.014530 --> 0.014249). Saving model ...
Epoch: 31 Training Loss: 0.023430 Validation Loss: 0.014678
Epoch: 32 Training Loss: 0.022498 Validation Loss: 0.014233
Validation loss decreased (0.014249 --> 0.014233). Saving model ...
Epoch: 33 Training Loss: 0.020586 Validation Loss: 0.014176
Validation loss decreased (0.014233 --> 0.014176). Saving model ...
Epoch: 34 Training Loss: 0.020103 Validation Loss: 0.014318
Epoch: 35 Training Loss: 0.019036 Validation Loss: 0.014375
Epoch: 36 Training Loss: 0.017958 Validation Loss: 0.013878
Validation loss decreased (0.014176 --> 0.013878). Saving model ...
Epoch: 37 Training Loss: 0.017909 Validation Loss: 0.013946
Epoch: 38 Training Loss: 0.016163 Validation Loss: 0.014045
Epoch: 39 Training Loss: 0.016032 Validation Loss: 0.013906
Epoch: 40 Training Loss: 0.015821 Validation Loss: 0.014460
Epoch: 41 Training Loss: 0.014439 Validation Loss: 0.014002
Epoch: 42 Training Loss: 0.014182 Validation Loss: 0.014007
Epoch: 43 Training Loss: 0.013378 Validation Loss: 0.014192
Epoch: 44 Training Loss: 0.013133 Validation Loss: 0.014273
Epoch: 45 Training Loss: 0.013060 Validation Loss: 0.014399
Epoch: 46 Training Loss: 0.012057 Validation Loss: 0.014357
Epoch: 47 Training Loss: 0.011091 Validation Loss: 0.013927
Epoch: 48 Training Loss: 0.011073 Validation Loss: 0.014096
Epoch: 49 Training Loss: 0.010821 Validation Loss: 0.014134
Epoch: 50 Training Loss: 0.010850 Validation Loss: 0.014468
###Markdown
Load the Model with the Lowest Validation Loss
###Code
model.load_state_dict(torch.load('model.pt'))
# check if loaded model is on cuda
next(model.parameters()).is_cuda
###Output
_____no_output_____
###Markdown
--- Test the Trained NetworkFinally, we test our best model on previously unseen **test data** and evaluate it's performance. Testing on unseen data is a good way to check that our model generalizes well. It may also be useful to be granular in this analysis and take a look at how this model performs on each class as well as looking at its overall loss and accuracy.
###Code
# initialize lists to monitor test loss and accuracy
test_loss = 0.0
class_correct = list(0. for i in range(10))
class_total = list(0. for i in range(10))
model.eval() # prep model for evaluation
for data, target in test_loader:
# move data and target to device
data, target = data.to(device), target.to(device)
# forward pass: compute predicted outputs by passing inputs to the model
output = model(data)
# calculate the loss
loss = criterion(output, target)
# update test loss
test_loss += loss.item()*data.size(0)
# convert output probabilities to predicted class
_, pred = torch.max(output, 1)
# compare predictions to true label
correct = np.squeeze(pred.eq(target.data.view_as(pred)))
# calculate test accuracy for each object class
for i in range(batch_size):
label = target.data[i]
class_correct[label] += correct[i].item()
class_total[label] += 1
# calculate and print avg test loss
test_loss = test_loss/len(test_loader.dataset)
print('Test Loss: {:.6f}\n'.format(test_loss))
for i in range(10):
if class_total[i] > 0:
print('Test Accuracy of %5s: %2d%% (%2d/%2d)' % (
str(i), 100 * class_correct[i] / class_total[i],
np.sum(class_correct[i]), np.sum(class_total[i])))
else:
print('Test Accuracy of %5s: N/A (no training examples)' % (classes[i]))
print('\nTest Accuracy (Overall): %2d%% (%2d/%2d)' % (
100. * np.sum(class_correct) / np.sum(class_total),
np.sum(class_correct), np.sum(class_total)))
###Output
Test Loss: 0.059930
Test Accuracy of 0: 98% (970/980)
Test Accuracy of 1: 99% (1126/1135)
Test Accuracy of 2: 97% (1009/1032)
Test Accuracy of 3: 98% (996/1010)
Test Accuracy of 4: 98% (963/982)
Test Accuracy of 5: 98% (875/892)
Test Accuracy of 6: 98% (940/958)
Test Accuracy of 7: 97% (1001/1028)
Test Accuracy of 8: 97% (951/974)
Test Accuracy of 9: 97% (987/1009)
Test Accuracy (Overall): 98% (9818/10000)
###Markdown
Visualize Sample Test ResultsThis cell displays test images and their labels in this format: `predicted (ground-truth)`. The text will be green for accurately classified examples and red for incorrect predictions.
###Code
# obtain one batch of test images
dataiter = iter(test_loader)
images, labels = dataiter.next()
# get sample outputs
output = model(images)
# convert output probabilities to predicted class
_, preds = torch.max(output, 1)
# prep images for display
images = images.numpy()
# plot the images in the batch, along with predicted and true labels
fig = plt.figure(figsize=(25, 4))
for idx in np.arange(20):
ax = fig.add_subplot(2, 20/2, idx+1, xticks=[], yticks=[])
ax.imshow(np.squeeze(images[idx]), cmap='gray')
ax.set_title("{} ({})".format(str(preds[idx].item()), str(labels[idx].item())),
color=("green" if preds[idx]==labels[idx] else "red"))
###Output
_____no_output_____
|
demos/Day 1 - regression .ipynb
|
###Markdown
Feature transformation. The rule should be consistent for training and test data. Z = (x - avg(x)) / std(x) for every feature or column x. Z will have 0 mean and 1 standard deviation
###Code
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train) # Calculates the mean and std for each column
X_train_std = scaler.transform(X_train) # returns the Z-score values for each column
X_test_std = scaler.transform(X_test)
pd.DataFrame(X_train_std)
pd.DataFrame(X_train_std).describe()
from sklearn import linear_model
est = linear_model.LinearRegression()
est.fit(X_train_std, y_train) # find the theta values
est.coef_
est.intercept_
pd.DataFrame({"feature": X.columns, "theta": est.coef_})
from sklearn import pipeline, preprocessing
target = "charges"
X = df.drop(columns=[target])
X = pd.get_dummies(X, drop_first=True)
columns = X.columns
y = df[target]
X_train, X_test, y_train, y_test = model_selection.train_test_split(X.values, y.values
, test_size = 0.3, random_state = 1)
pipe = pipeline.Pipeline([
("scaler", preprocessing.StandardScaler()),
("est", linear_model.LinearRegression())
])
pipe.fit(X_train, y_train)
est = pipe.steps[-1][-1]
est.coef_
y_train_pred = pipe.predict(X_train)
y_test_pred = pipe.predict(X_test)
result = pd.DataFrame({"true": y_test, "predicted": y_test_pred})
result["error"] = result["true"] - result["predicted"]
result
import numpy as np
mse = np.mean(result.error ** 2) # Lower is better
mse
y_test_var = np.var(y_test)
mse/y_test_var
mse / np.mean((y_test - y_train.mean()) ** 2)
r2 = 1 - mse / y_test_var
r2
import pickle
with open("/tmp/insurance.pickle", "wb") as f:
pickle.dump(pipe, f)
with open("/tmp/insurance.pickle", "rb") as f:
pipe = pickle.load(f)
from sklearn import metrics
metrics.mean_squared_error(y_test, pipe.predict(X_test))
target = "charges"
X = df.drop(columns=[target])
X = pd.get_dummies(X, drop_first=True)
columns = X.columns
y = df[target]
X_train, X_test, y_train, y_test = model_selection.train_test_split(X.values, y.values
, test_size = 0.3, random_state = 1)
pipe = pipeline.Pipeline([
("scaler", preprocessing.StandardScaler()),
("est", linear_model.LinearRegression())
])
pipe.fit(X_train, y_train)
y_train_pred = pipe.predict(X_train)
y_test_pred = pipe.predict(X_test)
r2_train = metrics.r2_score(y_train, y_train_pred)
r2_test = metrics.r2_score(y_test, y_test_pred)
mse_train = metrics.mean_squared_error(y_train, y_train_pred)
mse_test = metrics.mean_squared_error(y_test, y_test_pred)
print("r2 Train:", r2_train,
"\nr2 test: ", r2_test,
"\nmse train: ", mse_train,
"\nmse test: ", mse_test
)
target = "charges"
X = df.drop(columns=[target])
X = pd.get_dummies(X, drop_first=True)
columns = X.columns
y = np.log(df[target])
X_train, X_test, y_train, y_test = model_selection.train_test_split(X.values, y.values
, test_size = 0.3, random_state = 1)
pipe = pipeline.Pipeline([
("scaler", preprocessing.StandardScaler()),
("est", linear_model.LinearRegression())
])
pipe.fit(X_train, y_train)
y_train_pred = pipe.predict(X_train)
y_test_pred = pipe.predict(X_test)
r2_train = metrics.r2_score(y_train, y_train_pred)
r2_test = metrics.r2_score(y_test, y_test_pred)
mse_train = metrics.mean_squared_error(np.exp(y_train), np.exp(y_train_pred))
mse_test = metrics.mean_squared_error(np.exp(y_test), np.exp(y_test_pred))
print("r2 Train:", r2_train,
"\nr2 test: ", r2_test,
"\nmse train: ", mse_train,
"\nmse test: ", mse_test
)
69185448/36761456
target = "charges"
#X = df.drop(columns=[target])
X = df.copy()
del X[target]
# bucketizing the continuous vars
def bmi_group(v):
if v > 30:
return "high"
elif v > 22:
return "normal"
else:
return "low"
def age_group(age):
if age > 60:
return "senior"
elif age < 30:
return "young"
else:
return "normal"
def smoker_high_bmi(r):
return (r.smoker == "yes") & (r.bmi > 30)
X["bmi_group"] = X.bmi.apply(bmi_group)
X["age_group"] = X.age.apply(age_group)
X["smoker_high_bmi"] = X.apply(smoker_high_bmi, axis = 1)
X = pd.get_dummies(X, drop_first=True)
columns = X.columns
y = np.log(df[target])
X_train, X_test, y_train, y_test = model_selection.train_test_split(X.values.astype(np.float64)
, y.values
, test_size = 0.3, random_state = 1)
pipe = pipeline.Pipeline([
("scaler", preprocessing.StandardScaler()),
("est", linear_model.LinearRegression())
])
pipe.fit(X_train, y_train)
y_train_pred = pipe.predict(X_train)
y_test_pred = pipe.predict(X_test)
r2_train = metrics.r2_score(y_train, y_train_pred)
r2_test = metrics.r2_score(y_test, y_test_pred)
mse_train = metrics.mean_squared_error(np.exp(y_train), np.exp(y_train_pred))
mse_test = metrics.mean_squared_error(np.exp(y_test), np.exp(y_test_pred))
print("r2 Train:", r2_train,
"\nr2 test: ", r2_test,
"\nmse train: ", mse_train,
"\nmse test: ", mse_test
)
df.head()
target = "charges"
#X = df.drop(columns=[target])
X = df.copy()
del X[target]
# bucketizing the continuous vars
def bmi_group(v):
if v > 30:
return "high"
elif v > 22:
return "normal"
else:
return "low"
def age_group(age):
if age > 60:
return "senior"
elif age < 30:
return "young"
else:
return "normal"
def smoker_high_bmi(r):
return (r.smoker == "yes") & (r.bmi > 30)
X["bmi_group"] = X.bmi.apply(bmi_group)
X["age_group"] = X.age.apply(age_group)
X["smoker_high_bmi"] = X.apply(smoker_high_bmi, axis = 1)
X = pd.get_dummies(X, drop_first=True)
columns = X.columns
y = np.log(df[target])
X_train, X_test, y_train, y_test = model_selection.train_test_split(X.values.astype(np.float64)
, y.values
, test_size = 0.3, random_state = 1)
pipe = pipeline.Pipeline([
("scaler", preprocessing.StandardScaler()),
("est", linear_model.SGDRegressor(max_iter=1000))
])
pipe.fit(X_train, y_train)
y_train_pred = pipe.predict(X_train)
y_test_pred = pipe.predict(X_test)
r2_train = metrics.r2_score(y_train, y_train_pred)
r2_test = metrics.r2_score(y_test, y_test_pred)
mse_train = metrics.mean_squared_error(np.exp(y_train), np.exp(y_train_pred))
mse_test = metrics.mean_squared_error(np.exp(y_test), np.exp(y_test_pred))
print("r2 Train:", r2_train,
"\nr2 test: ", r2_test,
"\nmse train: ", mse_train,
"\nmse test: ", mse_test
)
###Output
r2 Train: 0.7802235733772407
r2 test: 0.8111871236006977
mse train: 69054533.98613885
mse test: 68813337.53454967
###Markdown
Kaggle house price datasethttps://raw.githubusercontent.com/abulbasar/data/master/kaggle-houseprice/data_combined_cleaned.csv
###Code
df = pd.read_csv("/data/kaggle/house-prices/data_combined_cleaned.csv")
df = df[~df.SalesPrice.isnull()]
del df["Id"]
df.info()
target = "SalesPrice"
#X = df.drop(columns=[target])
X = df.copy()
del X[target]
X = pd.get_dummies(X, drop_first=True)
columns = X.columns
y = np.log(df[target])
X_train, X_test, y_train, y_test = model_selection.train_test_split(X.values.astype(np.float64)
, y.values, test_size = 0.3, random_state = 1)
pipe = pipeline.Pipeline([
("scaler", preprocessing.StandardScaler()),
("est", linear_model.LinearRegression())
])
pipe.fit(X_train, y_train)
y_train_pred = pipe.predict(X_train)
y_test_pred = pipe.predict(X_test)
r2_train = metrics.r2_score(y_train, y_train_pred)
r2_test = metrics.r2_score(y_test, y_test_pred)
mse_train = metrics.mean_squared_error(y_train, y_train_pred)
mse_test = metrics.mean_squared_error(y_test, y_test_pred)
print("r2 Train:", r2_train,
"\nr2 test: ", r2_test,
"\nmse train: ", mse_train,
"\nmse test: ", mse_test
)
target = "SalesPrice"
#X = df.drop(columns=[target])
X = df.copy()
del X[target]
X = pd.get_dummies(X, drop_first=True)
columns = X.columns
y = np.log(df[target])
X_train, X_test, y_train, y_test = model_selection.train_test_split(X.values.astype(np.float64)
, y.values, test_size = 0.3, random_state = 1)
weights = []
scores = []
alphas = 10 ** np.linspace(-5, -1, 20)
for alpha in alphas:
pipe = pipeline.Pipeline([
("scaler", preprocessing.StandardScaler()),
("est", linear_model.Lasso(alpha=alpha, max_iter=2000))
])
pipe.fit(X_train, y_train)
y_train_pred = pipe.predict(X_train)
y_test_pred = pipe.predict(X_test)
r2_train = metrics.r2_score(y_train, y_train_pred)
r2_test = metrics.r2_score(y_test, y_test_pred)
mse_train = metrics.mean_squared_error(y_train, y_train_pred)
mse_test = metrics.mean_squared_error(y_test, y_test_pred)
weights.append(pipe.steps[-1][-1].coef_)
"""
print("alpha", alpha,
"\nr2 Train:", r2_train,
"\nr2 test: ", r2_test,
"\nmse train: ", mse_train,
"\nmse test: ", mse_test
)
"""
scores.append(r2_test)
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(alphas, scores)
plt.xlabel("Alpha")
plt.ylabel("R2_test")
plt.xscale("log")
plt.plot(alphas, weights)
plt.legend([])
plt.xscale("log")
plt.xlabel("Alpha")
plt.ylabel("Weights")
plt.title("Effect of regularization param (alpha)\n on magnitude of weights")
est = pipe.steps[-1][-1]
est.coef_
###Output
_____no_output_____
|
.ipynb_checkpoints/arimaPredict-checkpoint.ipynb
|
###Markdown
###Code
!pip install pmdarima
import math
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
from statsmodels.tsa.arima_model import ARIMA
from pmdarima.arima import auto_arima
from sklearn.metrics import mean_squared_error, mean_absolute_error
import warnings
warnings.filterwarnings('ignore')
TSLA = pd.read_csv('Data/FB.csv')
###Output
_____no_output_____
###Markdown
The Dickey-Fuller test is one of the most popular statistical tests. It can be used to determine the presence of unit root in the series and help us understand if the series is stationary.**Null Hypothesis**: The series has a unit root**Alternate Hypothesis**: The series has no unit root.If we fail to reject the Null Hypothesis, then the series is non-stationary.
###Code
def Test_Stationarity(timeseries):
result = adfuller(timeseries['Adj Close'], autolag='AIC')
print("Results of Dickey Fuller Test")
print(f'Test Statistics: {result[0]}')
print(f'p-value: {result[1]}')
print(f'Number of lags used: {result[2]}')
print(f'Number of observations used: {result[3]}')
for key, value in result[4].items():
print(f'critical value ({key}): {value}')
###Output
_____no_output_____
###Markdown
Tesla
###Code
TSLA.head()
TSLA.info()
# Change Dtype of Date column
TSLA["Date"] = pd.to_datetime(TSLA["Date"])
Test_Stationarity(TSLA)
###Output
_____no_output_____
###Markdown
The p-value > 0.05, so we cannot reject the Null hypothesis. Hence, we would need to use the “Integrated (I)” concept, denoted by value ‘d’ in time series, to make the data stationary while building the Auto ARIMA model. Now let's take log of the 'Adj Close' column to reduce the magnitude of the values and reduce the series rising trend.
###Code
TSLA['log Adj Close'] = np.log(TSLA['Adj Close'])
TSLA_log_moving_avg = TSLA['log Adj Close'].rolling(12).mean()
TSLA_log_std = TSLA['log Adj Close'].rolling(12).std()
plt.figure(figsize=(10, 5))
plt.plot(TSLA['Date'], TSLA_log_moving_avg, label="Rolling Mean")
plt.plot(TSLA['Date'], TSLA_log_std, label="Rolling Std")
plt.xlabel('Time')
plt.ylabel('log Adj Close')
plt.legend(loc='best')
plt.title("Rolling Mean and Standard Deviation")
###Output
_____no_output_____
###Markdown
Split the data into training and test set Training Period: 2015-01-02 - 2020-09-30 Testing Period: 2020-10-01 - 2021-02-26
###Code
TSLA_Train_Data = TSLA[TSLA['Date'] < '2021-08-13']
TSLA_Test_Data = TSLA[TSLA['Date'] >= '2021-08-13'].reset_index(drop=True)
plt.figure(figsize=(10, 5))
plt.plot(TSLA_Train_Data['Date'], TSLA_Train_Data['log Adj Close'], label='Train Data')
plt.plot(TSLA_Test_Data['Date'], TSLA_Test_Data['log Adj Close'], label='Test Data')
plt.xlabel('Time')
plt.ylabel('log Adj Close')
plt.legend(loc='best')
###Output
_____no_output_____
###Markdown
Modeling
###Code
TSLA_Auto_ARIMA_Model = auto_arima(TSLA_Train_Data['log Adj Close'], seasonal=False,
error_action='ignore', suppress_warnings=True)
print(TSLA_Auto_ARIMA_Model.summary())
TSLA_ARIMA_Model = ARIMA(TSLA_Train_Data['log Adj Close'], order=(5, 2, 2))
TSLA_ARIMA_Model_Fit = TSLA_ARIMA_Model.fit()
print(TSLA_ARIMA_Model_Fit.summary())
###Output
_____no_output_____
###Markdown
Predicting the closing stock price of Tesla
###Code
TSLA_output = TSLA_ARIMA_Model_Fit.forecast(21, alpha=0.05)
TSLA_predictions = np.exp(TSLA_output[0])
plt.figure(figsize=(10, 5))
plt.plot(TSLA_Train_Data['Date'], TSLA_Train_Data['Adj Close'], label='Training')
plt.plot(TSLA_Test_Data['Date'], TSLA_Test_Data['Adj Close'], label='Testing')
plt.plot(TSLA_Test_Data['Date'], TSLA_predictions, label='Predictions')
plt.xlabel('Time')
plt.ylabel('Closing Price')
plt.legend()
rmse = math.sqrt(mean_squared_error(TSLA_Test_Data['Adj Close'], TSLA_predictions))
mape = np.mean(np.abs(TSLA_predictions - TSLA_Test_Data['Adj Close']) / np.abs(TSLA_Test_Data['Adj Close']))
print(f'RMSE: {rmse}')
print(f'MAPE: {mape}')
###Output
_____no_output_____
|
Data Science Academy/PythonFundamentos/Cap02/Notebooks/DSA-Python-Cap02-01-Numeros.ipynb
|
###Markdown
Data Science Academy - Python Fundamentos - Capítulo 2 Download: http://github.com/dsacademybr
###Code
# Versão da Linguagem Python
from platform import python_version
print('Versão da Linguagem Python Usada Neste Jupyter Notebook:', python_version())
###Output
Versão da Linguagem Python Usada Neste Jupyter Notebook: 3.8.8
###Markdown
Números e Operações Matemáticas Pressione as teclas shift e enter para executar o código em uma célula ou pressione o botão Play no menu superior
###Code
# Soma
4 + 4
# Subtração
4 - 3
# Multiplicação
3 * 3
# Divisão
3 / 2
# Potência
4 ** 2
# Módulo
10 % 3
###Output
_____no_output_____
###Markdown
Função Type
###Code
type(5)
type(5.0)
a = 'Eu sou uma string'
type(a)
###Output
_____no_output_____
###Markdown
Operações com números float
###Code
3.1 + 6.4
4 + 4.0
4 + 4
# Resultado é um número float
4 / 2
# Resultado é um número inteiro
4 // 2
4 / 3.0
4 // 3.0
###Output
_____no_output_____
###Markdown
Conversão
###Code
float(9)
int(6.0)
int(6.5)
###Output
_____no_output_____
###Markdown
Hexadecimal e Binário
###Code
hex(394)
hex(217)
bin(286)
bin(390)
###Output
_____no_output_____
###Markdown
Funções abs, round e pow
###Code
# Retorna o valor absoluto
abs(-8)
# Retorna o valor absoluto
abs(8)
# Retorna o valor com arredondamento
round(3.14151922,2)
# Potência
pow(4,2)
# Potência
pow(5,3)
###Output
_____no_output_____
|
_notebooks/2021-05-05-BivariateNormaldistribution.ipynb
|
###Markdown
Visual Representation of a Bivariate Gaussian> This post depicts various methods of visulalizing the bivariate normal distribution using matplotlib and GeoGebra.- toc: true - badges: true- comments: true- categories: ['bivariate','normal','mean vector','covariance', 'Geogebra']- author : Anand Khandekar- image: images/bivariate.png Dependencies
###Code
#collapse-show
%matplotlib inline
import sys
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from matplotlib import cm # Colormaps
import matplotlib.gridspec as gridspec
from mpl_toolkits.axes_grid1 import make_axes_locatable
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
import seaborn as sns
sns.set_style('darkgrid')
np.random.seed(42)
###Output
_____no_output_____
###Markdown
MultiVariate Normal distributionReal world datasets are seldom univariate. Infact they are often multi variate with large dimensions. Each of these dimensions, also referred to as features, ( columns in a spread sheet) may or maynot be corellated to each other. In particular, we are interested in the multivariate case of this distribution, where each random variable is distributed normally and their joint distribution is also Gaussian. The multivariate Gaussian distribution is defined by a mean vector $\mu$ and a covariance matrix $\Sigma$.The mean vector $\mu$ describes the expected value of the distribution. Each of its components describes the mean of the corresponding dimension. $\Sigma$ models the variance along each dimension and determines how the different random variables are correlated. The covariance matrix is always symmetric and positive semi-definite. The diagonal of $\Sigma$ consists of the variance $\sigma_i^2$ of the $i$-th random variable. And the off-diagonal elements $\sigma_{ij}$ describe the correlation between the $i$-th and the $j$-th random variable. $$X = \begin{bmatrix} X_1 \\ X_2 \\ . \\ .\\ X_n \end{bmatrix} \sim \mathcal{N}(\mathbf{\mu}, \Sigma) $$Wee say that $X$ follows a normal distribution. The covariance $\Sigma$ describs the shape of the distribution. It is defined in terms of the expected value $\mathbb{E}$ :$$ \Sigma = Cov( X_i, X_j) = \mathbb{E}[ ( X_i-\mu_i) (X_i - \mu_j)^T]$$ Let us consider a multi variate normmal random variable $x$ of dimensionality $d$ i.e $d$ numberof features or columns. Then the [joint probability](https://en.wikipedia.org/wiki/Joint_probability_distribution) densit is given by :$$p(\mathbf{x} \mid \mathbf{\mu}, \Sigma) = \frac{1}{\sqrt{(2\pi)^d \lvert\Sigma\rvert}} \exp{ \left( -\frac{1}{2}(\mathbf{x} - \mathbf{\mu})^T \Sigma^{-1} (\mathbf{x} - \mathbf{\mu}) \right)}$$where $ \textbf{x}$ a random sized vector of size $d$, $\textbf{$\mu$}$ is the mean vector, $\Sigma$ is the ( [symmetric](https://en.wikipedia.org/wiki/Symmetric_matrix) , [positive definite](https://en.wikipedia.org/wiki/Positive-definite_matrix) ) covariance matrix ( of size $d\times d$ ), and $\lvert\Sigma\rvert$ its [determinant](https://en.wikipedia.org/wiki/Determinant).We denote the multivariate nornal distribution as : $$\mathcal{N}(\mathbf{\mu}, \Sigma)$$The mean vector $\mathbf{\mu}$, is the expected value of the distribution; and the [covariance](https://en.wikipedia.org/wiki/Covariance) matrix $\Sigma$, which measures how dependent any two random varibales are and how they change with each other. custom defined multivariate normal distribution function.this CODE can be skipped and w can always fall back on Numpy or Scipy who provide in built functions to do the same. But then, who does that ?
###Code
#collapse-show
def multivariate_normal(x, d, mean, covariance):
x_m = x - mean
return (1. / (np.sqrt((2 * np.pi)**d * np.linalg.det(covariance))) *
np.exp(-(np.linalg.solve(covariance, x_m).T.dot(x_m)) / 2))
###Output
_____no_output_____
###Markdown
Bivariate normal distributionLet us consider a r.v with two dimensions $x_1$ and $x_2$ with the covariance between them set to $0$ so that the two are independent : Also, for the sake of siplicity, let us assume a $0$ mean along both the dimensions. $$\mathcal{N}\left(\begin{bmatrix}0 \\0\end{bmatrix}, \begin{bmatrix}1 & 0 \\0 & 1 \end{bmatrix}\right)$$he figure on the right is a bivariate distribution with the covariance between $x_1$ and $x_2$ set to be other than $0$ so that both the variables are correlated. Increasing $x_1$ will increase the probability that $x_2$ will also increase.$$\mathcal{N}\left(\begin{bmatrix}0 \\1\end{bmatrix}, \begin{bmatrix}1 & 0.8 \\0.8 & 1\end{bmatrix}\right)$$ Helper function to generate density surface
###Code
#collapse-show
def generate_surface(mean, covariance, d):
nb_of_x = 100 # grid size
x1s = np.linspace(-5, 5, num=nb_of_x)
x2s = np.linspace(-5, 5, num=nb_of_x)
x1, x2 = np.meshgrid(x1s, x2s) # Generate grid
pdf = np.zeros((nb_of_x, nb_of_x))
# Fill the cost matrix for each combination of weights
for i in range(nb_of_x):
for j in range(nb_of_x):
pdf[i,j] = multivariate_normal(
np.matrix([[x1[i,j]], [x2[i,j]]]),
d, mean, covariance)
return x1, x2, pdf # x1, x2, pdf(x1,x2)
#collapse-show
# subplot
fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, figsize=(18,6))
d = 2 # number of dimensions
# Plot of independent Normals
bivariate_mean = np.matrix([[0.], [0.]]) # Mean
bivariate_covariance = np.matrix([
[1., 0.],
[0., 1.]]) # Covariance
x1, x2, p = generate_surface(
bivariate_mean, bivariate_covariance, d)
# Plot bivariate distribution
con = ax1.contourf(x1, x2, p, 100, cmap=cm.viridis)
ax1.set_xlabel('$x_1$', fontsize=13)
ax1.set_ylabel('$x_2$', fontsize=13)
ax1.axis([-2.5, 2.5, -2.5, 2.5])
ax1.set_aspect('equal')
ax1.set_title('Independent variables', fontsize=12)
# Plot of correlated Normals
bivariate_mean = np.matrix([[0.], [1.]]) # Mean
bivariate_covariance = np.matrix([
[1., 0.8],
[0.8, 1.]]) # Covariance
x1, x2, p = generate_surface(
bivariate_mean, bivariate_covariance, d)
# Plot bivariate distribution
con = ax2.contourf(x1, x2, p, 100, cmap=cm.viridis)
ax2.set_xlabel('$x_1$', fontsize=13)
ax2.set_ylabel('$x_2$', fontsize=13)
ax2.axis([-2.5, 2.5, -1.5, 3.5])
ax2.set_aspect('equal')
ax2.set_title('Correlated variables', fontsize=12)
# Add colorbar and title
fig.subplots_adjust(right=0.8)
cbar_ax = fig.add_axes([0.85, 0.15, 0.02, 0.7])
cbar = fig.colorbar(con, cax=cbar_ax)
cbar.ax.set_ylabel('$p(x_1, x_2)$', fontsize=13)
plt.suptitle("Bivariate normal distributions ", fontsize=13, y=0.95)
plt.show()
###Output
_____no_output_____
###Markdown
Mean vector and Covariance MatricesThe Gaussian on the LHS$$\mathcal{N}\left(\begin{bmatrix}0 \\1\end{bmatrix}, \begin{bmatrix}1 & 0 \\0& 1\end{bmatrix}\right)$$The gaussian on the RHS$$\mathcal{N}\left(\begin{bmatrix}0 \\1\end{bmatrix}, \begin{bmatrix}1 & 0.8 \\0.8 & 1\end{bmatrix}\right)$$ Surface plot in Matplot Lib
###Code
#collapse-show
# Our 2-dimensional distribution will be over variables X and Y
N = 60
X = np.linspace(-3, 3, N)
Y = np.linspace(-3, 4, N)
X, Y = np.meshgrid(X, Y)
# Mean vector and covariance matrix
mu = np.array([0., 1.])
Sigma = np.array([[ 1. , -0.5], [-0.5, 1.5]])
# Pack X and Y into a single 3-dimensional array
pos = np.empty(X.shape + (2,))
pos[:, :, 0] = X
pos[:, :, 1] = Y
def multivariate_gaussian(pos, mu, Sigma):
"""Return the multivariate Gaussian distribution on array pos.
pos is an array constructed by packing the meshed arrays of variables
x_1, x_2, x_3, ..., x_k into its _last_ dimension.
"""
n = mu.shape[0]
Sigma_det = np.linalg.det(Sigma)
Sigma_inv = np.linalg.inv(Sigma)
N = np.sqrt((2*np.pi)**n * Sigma_det)
# This einsum call calculates (x-mu)T.Sigma-1.(x-mu) in a vectorized
# way across all the input variables.
fac = np.einsum('...k,kl,...l->...', pos-mu, Sigma_inv, pos-mu)
return np.exp(-fac / 2) / N
# The distribution on the variables X, Y packed into pos.
Z = multivariate_gaussian(pos, mu, Sigma)
# Create a surface plot and projected filled contour plot under it.
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot_surface(X, Y, Z, rstride=3, cstride=3, linewidth=1, antialiased=True,
cmap=cm.viridis)
cset = ax.contourf(X, Y, Z, zdir='z', offset=-0.15, cmap=cm.viridis)
# Adjust the limits, ticks and view angle
ax.set_zlim(-0.15,0.2)
ax.set_zticks(np.linspace(0,0.2,5))
ax.view_init(27, -21)
plt.show()
###Output
_____no_output_____
|
ptl.ipynb
|
###Markdown
Adversarial Example Generation for Images
###Code
%load_ext autoreload
%autoreload 2
import pdb
import pandas as pd
import numpy as np
from pathlib import Path
from PIL import Image
from collections import OrderedDict
from argparse import Namespace
import matplotlib.pyplot as plt
%matplotlib inline
import torch
import torch.tensor as T
from torch import nn, optim
from torch.nn import functional as F
from torch.utils.data import DataLoader, random_split
from torchvision import transforms, models
from torchvision.datasets import ImageFolder
from torchsummary import summary
import pytorch_lightning as pl
print(f"GPU present: {torch.cuda.is_available()}")
img_size=(150,150)
data_stats = dict(mean=T([0.4302, 0.4575, 0.4539]), std=T([0.2361, 0.2347, 0.2433]))
data_path = Path('./data')
pl.logging.tensorboard
###Output
_____no_output_____
###Markdown
Functions
###Code
def for_disp(img):
img.mul_(data_stats['std'][:, None, None]).add_(data_stats['mean'][:, None, None])
return transforms.ToPILImage()(img)
def get_stats(loader):
mean,std = 0.0,0.0
nb_samples = 0
for imgs, _ in loader:
batch = imgs.size(0)
imgs = imgs.view(batch, imgs.size(1), -1)
mean += imgs.mean(2).sum(0)
std += imgs.std(2).sum(0)
nb_samples += batch
return mean/nb_samples, std/nb_samples
###Output
_____no_output_____
###Markdown
EDA Data
###Code
imgs,labels = [],[]
n_imgs = 5
for folder in (data_path/'train').iterdir():
label = folder.name
for img_f in list(folder.glob('*.jpg'))[:n_imgs]:
with Image.open(img_f) as f:
imgs.append(np.array(f))
labels.append(label)
n_classes = len(np.unique(labels))
fig = plt.figure(figsize=(15, 15))
for i, img in enumerate(imgs):
ax = fig.add_subplot(n_classes, n_imgs, i+1)
ax.imshow(img)
ax.set_title(labels[i], color='r')
ax.set_xticks([])
ax.set_yticks([])
plt.show()
train_tfms = transforms.Compose(
[
transforms.Resize(img_size),
transforms.RandomHorizontalFlip(p=0.5),
transforms.ToTensor(),
transforms.Normalize(**data_stats),
]
)
pred_tfms = transforms.Compose(
[
transforms.Resize(img_size),
transforms.ToTensor(),
transforms.Normalize(**data_stats)
]
)
ds = ImageFolder(data_path/'train', transform=train_tfms)
train_pct = 0.85
n_train = np.int(len(ds) * train_pct)
n_val = len(ds) - n_train
train_ds,val_ds = random_split(ds, [n_train, n_val])
train_ds,val_ds = train_ds.dataset,val_ds.dataset
train_dl = DataLoader(train_ds, batch_size=32, shuffle=True, drop_last=True)
train_itr = iter(train_dl)
val_dl = DataLoader(val_ds, batch_size=32)
val_itr = iter(val_dl)
test_ds = ImageFolder(data_path/'test', transform=pred_tfms)
test_dl = DataLoader(test_ds, batch_size=32)
imgs, labels = next(train_itr)
idx = np.random.randint(len(imgs))
print(train_ds.classes[labels[idx].item()])
img = for_disp(imgs[idx])
img
###Output
_____no_output_____
###Markdown
Training
###Code
class IntelImageClassifier(pl.LightningModule):
def __init__(self, hparams):
super(IntelImageClassifier, self).__init__()
self.hparams = hparams
self.loss_fn = nn.CrossEntropyLoss()
self.img_tfms = self.__define_tfms()
self.train_ds,self.val_ds = self.__split_data()
self.model = self.__build_model()
def __build_model(self):
model = models.vgg16(pretrained=True) # load pretrained model
for param in model.parameters(): param.requires_grad=False # freeze model params
# replace last layer with custom layer
classifier = nn.Sequential(
nn.Linear(in_features=25088, out_features=4096),
nn.ReLU(),
nn.Dropout(p=0.5),
nn.Linear(in_features=4096, out_features=4096),
nn.ReLU(),
nn.Dropout(p=0.5),
nn.Linear(in_features=4096, out_features=6) # 6 classes
)
model.classifier = classifier
return model
def forward(self, x): return self.model(x)
def configure_optimizers(self):
return optim.Adam(self.model.classifier.parameters(), lr=self.hparams.lr)
def __define_tfms(self):
tfms = {}
tfms['train'] = transforms.Compose([
transforms.Resize((150, 150)),
transforms.RandomHorizontalFlip(p=0.5),
transforms.ToTensor(),
transforms.Normalize(**self.hparams.data_stats)
])
tfms['pred'] = transforms.Compose([
transforms.Resize((150, 150)),
transforms.ToTensor(),
transforms.Normalize(**self.hparams.data_stats)
])
return tfms
def training_step(self, batch, batch_idx):
imgs,labels = batch
out = self.forward(imgs)
loss = self.loss_fn(out, labels)
tqdm_dict = {'train_loss': loss}
output = OrderedDict({
'loss': loss,
'progress_bar': tqdm_dict,
})
def __split_data(self):
ds = ImageFolder(self.hparams.data_path/'train', self.img_tfms['train'])
n_train = np.int(len(ds) * self.hparams.train_pct)
n_val = len(ds) - n_train
train_ds,val_ds = random_split(ds, [n_train, n_val])
return train_ds, val_ds
@pl.data_loader
def train_dataloader(self):
return DataLoader(self.train_ds, batch_size=self.hparams.bs, shuffle=True, drop_last=True, num_workers=4)
# @pl.data_loader
# def val_dataloader(self):
# return DataLoader(self.val_ds, batch_size=self.hparams.bs)
hparams = Namespace(
bs=32,
lr=0.001,
train_pct=0.85,
data_path=Path('./data'),
data_stats=dict(mean=T([0.4302, 0.4575, 0.4539]), std=T([0.2361, 0.2347, 0.2433])),
)
model = IntelImageClassifier(hparams)
import logging
logger = logging.getLogger(__name__)
trainer = pl.Trainer(logger=logger,train_percent_check=0.1)
trainer.fit(model)
tfms = {
'train': transforms.Compose([
transforms.Resize((150, 150)),
transforms.RandomHorizontalFlip(p=0.5),
transforms.ToTensor(),
transforms.Normalize(**hparams.data_stats)
]),
'pred': transforms.Compose([
transforms.Resize((150, 150)),
transforms.ToTensor(),
transforms.Normalize(**hparams.data_stats)
]),
}
ds = ImageFolder(data_path/'train', transform=tfms['pred'])
train_pct = 0.85
n_train = np.int(len(ds) * train_pct)
n_val = len(ds) - n_train
train_ds,val_ds = random_split(ds, [n_train, n_val])
train_dl = DataLoader(train_ds, batch_size=32, shuffle=True, drop_last=True)
train_itr = iter(train_dl)
val_dl = DataLoader(val_ds, batch_size=32)
val_itr = iter(val_dl)
test_ds = ImageFolder(data_path/'test', transform=tfms['pred'])
test_dl = DataLoader(test_ds, batch_size=32)
clf = models.vgg16(pretrained=True)
for param in clf.parameters(): param.requires_grad=False
final_clf = nn.Sequential(
nn.Linear(in_features=25088, out_features=4096),
nn.ReLU(),
nn.Dropout(p=0.5),
nn.Linear(in_features=4096, out_features=4096),
nn.ReLU(),
nn.Dropout(p=0.5),
nn.Linear(in_features=4096, out_features=6),
)
clf.classifier = final_clf
loss_fn = nn.CrossEntropyLoss()
opt = optim.Adam(clf.parameters(), lr=0.01)
clf = clf.cuda()
imgs, labels = next(train_itr)
imgs = imgs.cuda()
labels = labels.cuda()
pred = clf(imgs)
loss_fn(pred, labels)
summary(clf, input_size=(3, 150, 150))
summary(clf, input_size=(3,150,150))
###Output
_____no_output_____
|
LAb Data Modeling II/Module6 - Lab4.ipynb
|
###Markdown
DAT210x - Programming with Python for DS Module6- Lab4 This code is intentionally missing! Read the directions on the course lab page!No starter code this time. Instead, take your completed Module6/Module6 - Lab1.ipynb and modify it by adding in a Decision Tree Classifier, setting its max_depth to 9, and random_state=2, but not altering any other setting.Make sure you add in the benchmark and drawPlots call for our new classifier as well.
###Code
import matplotlib as mpl
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import time
C = 1
kernel = 'linear'
iterations = 5000
n_neighbors = 5
max_depth = 9
def drawPlots(model, X_train, X_test, y_train, y_test, wintitle='Figure 1'):
# You can use this to break any higher-dimensional space down,
# And view cross sections of it.
# If this line throws an error, use plt.style.use('ggplot') instead
mpl.style.use('ggplot') # Look Pretty
padding = 3
resolution = 0.5
max_2d_score = 0
y_colors = ['#ff0000', '#00ff00', '#0000ff']
my_cmap = mpl.colors.ListedColormap(['#ffaaaa', '#aaffaa', '#aaaaff'])
colors = [y_colors[i] for i in y_train]
num_columns = len(X_train.columns)
fig = plt.figure()
fig.canvas.set_window_title(wintitle)
fig.set_tight_layout(True)
cnt = 0
for col in range(num_columns):
for row in range(num_columns):
# Easy out
if FAST_DRAW and col > row:
cnt += 1
continue
ax = plt.subplot(num_columns, num_columns, cnt + 1)
plt.xticks(())
plt.yticks(())
# Intersection:
if col == row:
plt.text(0.5, 0.5, X_train.columns[row], verticalalignment='center', horizontalalignment='center', fontsize=12)
cnt += 1
continue
# Only select two features to display, then train the model
X_train_bag = X_train.ix[:, [row,col]]
X_test_bag = X_test.ix[:, [row,col]]
model.fit(X_train_bag, y_train)
# Create a mesh to plot in
x_min, x_max = X_train_bag.ix[:, 0].min() - padding, X_train_bag.ix[:, 0].max() + padding
y_min, y_max = X_train_bag.ix[:, 1].min() - padding, X_train_bag.ix[:, 1].max() + padding
xx, yy = np.meshgrid(np.arange(x_min, x_max, resolution),
np.arange(y_min, y_max, resolution))
# Plot Boundaries
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
# Prepare the contour
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=my_cmap, alpha=0.8)
plt.scatter(X_train_bag.ix[:, 0], X_train_bag.ix[:, 1], c=colors, alpha=0.5)
score = round(model.score(X_test_bag, y_test) * 100, 3)
plt.text(0.5, 0, "Score: {0}".format(score), transform = ax.transAxes, horizontalalignment='center', fontsize=8)
max_2d_score = score if score > max_2d_score else max_2d_score
cnt += 1
print("Max 2D Score: ", max_2d_score)
def benchmark(model, X_train, X_test, y_train, y_test, wintitle='Figure 1'):
print(wintitle + ' Results')
s = time.time()
for i in range(iterations):
# TODO: train the classifier on the training data / labels:
# .. your code here ..
model.fit(X_train, y_train)
print("{0} Iterations Training Time: ".format(iterations), time.time() - s)
s = time.time()
for i in range(iterations):
# TODO: score the classifier on the testing data / labels:
# .. your code here ..
score = model.score(X_test, y_test)
print("{0} Iterations Scoring Time: ".format(iterations), time.time() - s)
print("High-Dimensionality Score: ", round((score*100), 3))
###Output
_____no_output_____
###Markdown
Load up the wheat dataset into dataframe X and verify you did it properly. Indices shouldn't be doubled, nor should you have any headers with weird characters...
###Code
X = pd.read_csv('Datasets/wheat.data')
X = X.drop(labels='id', axis=1)
###Output
_____no_output_____
###Markdown
Go ahead and drop any row with a nan:
###Code
X = X.dropna(axis=0)
X.head()
###Output
_____no_output_____
###Markdown
Copy the labels out of the dataframe into variable `y`, then remove them from `X`.Encode the labels, using the `.map()` trick we showed you in Module 5, such that `canadian:0`, `kama:1`, and `rosa:2`.
###Code
y = X.loc[:, 'wheat_type'].map({'canadian': 0, 'kama': 1, 'rosa': 2})
X = X.drop(labels='wheat_type', axis=1)
###Output
_____no_output_____
###Markdown
Split your data into a `test` and `train` set. Your `test` size should be 30% with `random_state` 7. Please use variable names: `X_train`, `X_test`, `y_train`, and `y_test`:
###Code
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=7)
###Output
_____no_output_____
###Markdown
Create an SVC classifier named `svc` and use a linear kernel. You already have `C` defined at the top of the lab, so just set `C=C`.
###Code
from sklearn.svm import SVC
svc = SVC(C=C, kernel='linear')
###Output
_____no_output_____
###Markdown
Create an KNeighbors classifier named `knn` and set the neighbor count to `5`:
###Code
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=5)
benchmark(knn, X_train, X_test, y_train, y_test, 'KNeighbors')
drawPlots(knn, X_train, X_test, y_train, y_test, 'KNeighbors')
benchmark(svc, X_train, X_test, y_train, y_test, 'SVC')
drawPlots(svc, X_train, X_test, y_train, y_test, 'SVC')
plt.show()
###Output
C:\Users\sasha\Anaconda3\lib\site-packages\matplotlib\figure.py:1742: UserWarning: This figure includes Axes that are not compatible with tight_layout, so its results might be incorrect.
warnings.warn("This figure includes Axes that are not "
###Markdown
Create a Decision Tree classifier named tree Set the neighbor count to 5 and max_depth to 9
###Code
from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier(max_depth=1, random_state=2)
benchmark(knn, X_train, X_test, y_train, y_test, 'KNeighbors')
drawPlots(knn, X_train, X_test, y_train, y_test, 'KNeighbors')
benchmark(svc, X_train, X_test, y_train, y_test, 'SVC')
drawPlots(svc, X_train, X_test, y_train, y_test, 'SVC')
benchmark(tree, X_train, X_test, y_train, y_test, 'Tree')
drawPlots(tree, X_train, X_test, y_train, y_test, 'Tree')
plt.show()
###Output
KNeighbors Results
5000 Iterations Training Time: 2.3180415630340576
5000 Iterations Scoring Time: 5.52967643737793
High-Dimensionality Score: 83.607
Max 2D Score: 90.164
SVC Results
5000 Iterations Training Time: 4.080297470092773
5000 Iterations Scoring Time: 1.7931928634643555
High-Dimensionality Score: 86.885
Max 2D Score: 93.443
Tree Results
5000 Iterations Training Time: 2.1475229263305664
5000 Iterations Scoring Time: 1.4934945106506348
High-Dimensionality Score: 68.852
Max 2D Score: 68.852
|
Semana-12/sklearn2.ipynb
|
###Markdown
Entrenando la regresion logistica con sklearn La libreria sklearn puede implementar la regresion logistica para mas de dos clases, usando OvR.
###Code
# Preprocesado de datos
# =========================================================
from sklearn import datasets
import numpy as np
datos = datasets.load_iris()
X = datos.data[:, [2,3]]
y = datos.target
print(f'Etiquetas en y: {np.unique(y)}')
print(f'Nombres de las categorias: {datos.target_names}.')
# Division de los datos en train y test
# =========================================================
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, stratify = y)
# Escalamiento de variables
# =========================================================
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)
# Creando el modelo de regresion logistica
# =========================================================
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(C = 100.0, random_state=1)
lr.fit(X_train_std, y_train)
# Graficando las regiones
# =========================================================
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
def plot_decision_regions(X, y, classifier, X_test, y_test, resolution=0.02):
# setup marker generator and color map
markers = ('s', 'x', 'o', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
# plot the decision surface
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.3, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0],
y=X[y == cl, 1],
alpha=0.8,
c=colors[idx],
marker=markers[idx],
label=cl,
edgecolor='black')
# highlight test samples
if True:
# plot all samples
#X_test, y_test = X[test_idx, :], y[test_idx]
plt.scatter(X_test[:, 0],
X_test[:, 1],
c='',
edgecolor='black',
alpha=1.0,
linewidth=1,
marker='o',
s=100,
label='test set')
%matplotlib notebook
fig, ax = plt.subplots(figsize = (6, 4))
plot_decision_regions(X_train_std, y_train, lr, X_test_std, y_test)
ax.set_xlabel('petal length [normalizado]')
ax.set_ylabel('petal width [normalizado]')
plt.legend(loc = 'best')
###Output
_____no_output_____
###Markdown
Ahora analizaremos las probabilidades de pertenencia a cada etiqueta de clase. Para ello tomaremos tres filas del conjunto X_test, y evaluaremos con que probabilidad pertenecen a cada clase:
###Code
# Primero observemos a que etiquetas de clase son predichas las muestras de flores:
# Etiquetas en y: [0 1 2]
# Nombres de las categorias: ['setosa' 'versicolor' 'virginica'].
print(X_test[:3, :])
lr.predict(X_test_std[:3, :])
# Luego verifiquemos con que probabilidad pertenecen a dichas clases
lr.predict_proba(X_test_std[:3, :])*100
# Filtrando un poco obtenemos
lr.predict_proba(X_test_std[:3, :]).argmax(axis = 1)
# Sumando las probabilidades por filas comprobamos que suman 1
lr.predict_proba(X_test_std[:3, :]).sum(axis = 1)
# Verifiquemos la precision del modelo
from sklearn.metrics import accuracy_score
y_pred = lr.predict(X_test_std)
np.round(accuracy_score(y_pred, y_test), 2)
###Output
_____no_output_____
###Markdown
EJERCICIO1. Utilice el archivo `usuarios_win_mac_lin.csv` para determinar segun las columnas `duracion,paginas,acciones,valor`, que representan lo siguiente: * Duración de la visita en Segundos * Cantidad de Páginas Vistas durante la Sesión * Cantidad de Acciones del usuario (click, scroll, uso de checkbox, sliders,etc) * Suma del Valor de las acciones (cada acción lleva asociada una valoración de importancia) Si el usuario maneja Windows, Linux o Mac. Ten en cuenta que las etiquetas son las siquientes: * 0 – Windows * 1 – Macintosh * 2 -Linux
###Code
import pandas as pd
df = pd.read_csv('usuarios_win_mac_lin.csv', dtype = str)
df.describe()
def reemplazo(row):
row['duracion'] = row['duracion'].replace('.', '')
return row
df.apply(reemplazo, axis = 1)
df2 = df.astype(int)
df = df.astype(int)
df.columns
X = df.iloc[:, 0:4].values
y = df.iloc[:, -1].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, stratify = y)
sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)
lr = LogisticRegression(C = 10000)
lr.fit(X_train_std, y_train)
lr.coef_
lr.predict_proba(X_test_std)
lr.predict(X_test_std)
accuracy_score(y_train, lr.predict(X_train_std))
accuracy_score(y_test, lr.predict(X_test_std))
import seaborn as sns
sns.pairplot(df, hue = 'clase', height = 1.5)
###Output
_____no_output_____
###Markdown
Abordar el sobreajuste con la regularizacion Algunos de los problemas mas usuales que se suelen encontrar al elaborar modelos de clasificacion y regresion son los conocidos **sobreajuste : overfitting** y **subajuste : underfitting**.El sobreajuste significa simplemente que nuestro modelo se ajusta demasiado bien a los datos de entrenamiento, dando rendimiento muy altos, pero sufre al ajustarse a los datos de test; en el fondo lo que implica es que nuestro modelo es demasiado complejo, y por lo tanto tiene demasiados parametros. Esto generalmente se puede observar cuando el rendimiento en el conjunto de entrenamiento es muy superior que en el conjunto de test.Es importante recordar que el overfitting implica que el modelo tiene alta varianza:**Overfitting $\to$ Alta varianza**El subajuste significa simplemente que nuestro modelo no se ajusta bien a los datos de entrenamiento, y por ende a los de test. Esto significa que nuestro modelo es muy simple y por lo tanto tienen muy pocos parametros. Esto se puede observar cuando el rendimiento es bajo en los datos de entrenamiento.Es importante recordar que el underfitting implica que el modelo tiene alto sesgo:**Underfitting $\to$ Alto sesgo** **Varianza**: Esta mide la consistencia (o variabilidad) de la prediccion del modelo para una instancia de muestra en particular en el caso de tener que entrenar el modelo varias veces, por ejemplo en diferentes subconjuntos de datos de entrenamiento. Podemos decir que _el modelo es sensible a la aleatoriedad en los datos de entrenamiento_ .**Sesgo**: Mide como estarian de lejos las predicciones de los valores correctos si volvieramos a crear el modelo varias veces en distintos conjuntos de datos de entrenamiento; _el sesgo es la medida del error sistematico que no procede de la aleatoriedad_ .Mas sobre este tema en: https://www.analyticslane.com/2019/05/24/los-conceptos-de-sesgo-y-varianza-en-aprendizaje-automaticos/ Como se puede entender, la idea es poder encontrar un equilibrio entre los dos extremos (underfitting y overfitting); la herramienta que se utiliza para hallar ese equilibrio se conoce como **regularizacion** . La que veremos aqui se conoce como **regularizacion L2** , pero mas adelante veremos otras.Dentro de las ventajas de la regularizacion tenemos que:1. La regularizacion es muy util para manejar la colinealidad (alta correlacion entre las caracteristicas).2. Filtrar el ruido de los datos.3. Prevenir el sobreajuste.Lo que hay detras del proceso de regularizacion es la introduccion de un hiperparametro que multiplique a los pesos, y que de esta manera los penalice y los lleve a cero si estos son demasiado grandes, simplificando asi el modelo. Con esta herramienta, se pueden originar modelos mas complejos que luego seran simplificados por la penalizacion introducida. La regularizacion se puede escribir como:$$\frac{\lambda}{2}||\textbf{w}||^2 = \frac{\lambda}{2}\sum_{j=1}^n w_j^2$$**Es importante recordar que si se va a utilizar la regularizacion, es obligatorio la normalizacion de las caracteristicas, pues es importante que estas sean comparables.**La funcion de costo para la regresion logistica, una vez agregada la regularizacion es:$$J(\textbf{w})=\sum_{i=1}^n \big [-y^{(i)}\log(\phi(z^{(i)}))-(1-y^{(i)})\log(1-\phi(z^{(i)})) \big] + \frac{\lambda}{2}||\textbf{w}||^2$$Entiendase que$$||\textbf{w}||^2 = w_0^2+w_1^2+w_2^2+\dots+w_n^2$$Si aumenta el valor del hiperparametro $\lambda$, aumentamos la fuerza de la regularizacion es decir, pondremos una penalidad mas estricta.El parametro $C$ de la regresion logistica es el inverso del parametro $\lambda$, por lo tanto entre mas pequeño sea $C$, mas grande sera la penalizacion.
###Code
datos = datasets.load_iris()
X = datos.data[:, [2, 3]]
y = datos.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, stratify = y)
sc.fit(X_train)
X_train_std = sc.transform(X_train)
datos.target_names
weights, params = [], []
for c in np.arange(-5, 6):
lr = LogisticRegression(C=10.**c, random_state=1)
lr.fit(X_train_std, y_train)
print(lr.coef_)
weights.append(lr.coef_[2])
params.append(10.**c)
weights = np.array(weights)
fig, ax = plt.subplots()
plt.plot(params, weights[:, 0], label='petal length')
plt.plot(params, weights[:, 1], linestyle='--', label='petal width')
plt.ylabel('weight coefficient')
plt.xlabel('C')
plt.legend(loc='best')
plt.xscale('log');
weights
###Output
[[-4.56415218e-04 -4.36331007e-04]
[ 1.01670000e-04 5.34041228e-05]
[ 3.54745218e-04 3.82926884e-04]]
[[-0.0045367 -0.00433589]
[ 0.00101188 0.0005293 ]
[ 0.00352482 0.00380659]]
[[-0.04279415 -0.04079074]
[ 0.00965743 0.00483935]
[ 0.03313671 0.0359514 ]]
[[-0.28170456 -0.26320019]
[ 0.06722777 0.02132152]
[ 0.21447678 0.24187867]]
[[-0.9536221 -0.84903681]
[ 0.21934993 -0.0807552 ]
[ 0.73427217 0.92979202]]
[[-2.30641751 -2.0361802 ]
[ 0.23176496 -0.41264914]
[ 2.07465255 2.44882935]]
[[-4.32419083 -3.81134256]
[-0.41649012 -0.60970102]
[ 4.74068095 4.42104358]]
[[-6.74838687 -5.81332025]
[-1.11905093 -0.64327282]
[ 7.8674378 6.45659307]]
[[-8.78052307 -7.47214464]
[-0.78338287 -0.18068423]
[ 9.56390593 7.65282887]]
[[-10.70320683 -9.0180279 ]
[ 0.07799235 0.53879885]
[ 10.62521448 8.47922906]]
[[-12.67381522 -10.67570423]
[ 1.05196248 1.36151321]
[ 11.62185275 9.31419102]]
###Markdown
EJERCICIO1. Desde el ejercicio anterior, determine cual podria ser el mejor parametro de regularizacion C. Para ello realice varias veces la construccion del modelo, y evalue la precision en cada ejecucion. Los valores C a utilizar son C = [0.1, 1, 10, 100, 1000]
###Code
C = np.arange(1, 50, 1)
for i in C:
lr = LogisticRegression(C = i).fit(X_train_std, y_train)
y_pred = lr.predict(X_test_std)
a = accuracy_score(y_test, y_pred)
print(f'C: {i}, precision: {a}.')
###Output
C: 1, precision: 0.5686274509803921.
C: 2, precision: 0.5882352941176471.
C: 3, precision: 0.6274509803921569.
C: 4, precision: 0.6274509803921569.
C: 5, precision: 0.6274509803921569.
C: 6, precision: 0.6274509803921569.
C: 7, precision: 0.5882352941176471.
C: 8, precision: 0.5882352941176471.
C: 9, precision: 0.6078431372549019.
C: 10, precision: 0.6078431372549019.
C: 11, precision: 0.6078431372549019.
C: 12, precision: 0.5686274509803921.
C: 13, precision: 0.5686274509803921.
C: 14, precision: 0.5686274509803921.
C: 15, precision: 0.5686274509803921.
C: 16, precision: 0.5686274509803921.
C: 17, precision: 0.5686274509803921.
C: 18, precision: 0.5686274509803921.
C: 19, precision: 0.5490196078431373.
C: 20, precision: 0.5490196078431373.
C: 21, precision: 0.5490196078431373.
C: 22, precision: 0.5490196078431373.
C: 23, precision: 0.5490196078431373.
C: 24, precision: 0.5490196078431373.
C: 25, precision: 0.5490196078431373.
C: 26, precision: 0.5490196078431373.
C: 27, precision: 0.5490196078431373.
C: 28, precision: 0.5490196078431373.
C: 29, precision: 0.5490196078431373.
C: 30, precision: 0.5490196078431373.
C: 31, precision: 0.5490196078431373.
C: 32, precision: 0.5490196078431373.
C: 33, precision: 0.5490196078431373.
C: 34, precision: 0.5490196078431373.
C: 35, precision: 0.5490196078431373.
C: 36, precision: 0.5490196078431373.
C: 37, precision: 0.5490196078431373.
C: 38, precision: 0.5490196078431373.
C: 39, precision: 0.5490196078431373.
C: 40, precision: 0.5490196078431373.
C: 41, precision: 0.5490196078431373.
C: 42, precision: 0.5490196078431373.
C: 43, precision: 0.5490196078431373.
C: 44, precision: 0.5490196078431373.
C: 45, precision: 0.5490196078431373.
C: 46, precision: 0.5490196078431373.
C: 47, precision: 0.5490196078431373.
C: 48, precision: 0.5490196078431373.
C: 49, precision: 0.5490196078431373.
|
FinalProject/Code/knn.ipynb
|
###Markdown
Note: EmploymentStatus: 0=Active, 1=TerminatedGender: 0=female, 1=malePerformanceRating: Business Travel: 0=no travel, 1=rarely, 2=frequentlyDepartment: HR=0, R&D=1, Sales=2JobRole: Sales Executive = 0, Sales Representative = 1, Research Scientist = 2, Research Director = 3, Laboratory Technician = 4, Manufacturing Director = 5, Healthcare Representative = 6, Human Resources = 7, Manager = 8
###Code
# Change qualitative data to numeric form
df_skinny['EmploymentStatus'] = df_skinny['EmploymentStatus'].replace(['Yes','No'],[1,0])
df_skinny['Gender']=df_skinny['Gender'].replace(['Female','Male'],[0,1])
df_skinny['BusinessTravel'] = df_skinny['BusinessTravel'].replace(['Travel_Rarely','Travel_Frequently','Non-Travel'],[1,2,0])
df_skinny['Department']=df_skinny['Department'].replace(['Human Resources','Research & Development','Sales'],[0,1,2])
df_skinny['JobRole'] = df_skinny['JobRole'].replace(['Sales Executive','Sales Representative','Research Scientist','Research Director',
'Laboratory Technician','Manufacturing Director','Healthcare Representative','Human Resources','Manager'],[0,1,2,3,4,5,6,7,8])
df_skinny.head()
y = df_skinny["EmploymentStatus"]
target_names = ["Active", "Terminated"]
X = df_skinny.drop("EmploymentStatus",axis=1)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
from sklearn.preprocessing import StandardScaler
X_scaler = StandardScaler().fit(X_train)
X_train_scaled = X_scaler.transform(X_train)
X_test_scaled = X_scaler.transform(X_test)
print(X_test_scaled)
train_scores = []
test_scores = []
for k in range(1, 20, 2):
knn = KNeighborsClassifier(n_neighbors=k)
knn.fit(X_train_scaled, y_train)
train_score = knn.score(X_train_scaled, y_train)
test_score = knn.score(X_test_scaled, y_test)
train_scores.append(train_score)
test_scores.append(test_score)
print(f"k: {k}, Train/Test Score: {train_score:.3f}/{test_score:.3f}")
plt.plot(range(1, 20, 2), train_scores, marker='o')
plt.plot(range(1, 20, 2), test_scores, marker="x")
plt.xlabel("k neighbors")
plt.ylabel("Testing accuracy Score")
plt.show()
knn = KNeighborsClassifier(n_neighbors=9)
knn.fit(X_train_scaled, y_train)
print('k=9 Test Acc: %.3f' % knn.score(X_test_scaled, y_test))
new_X=pd.read_csv("../Resources/newEmployeeData.csv").drop(["EmploymentStatus"], axis=1)
new_predictions = knn.predict(new_X)
print(new_predictions)
###Output
[0 0 0 0 0]
|
notebooks/load_from_mitab_example/load_mitab_data_example.ipynb
|
###Markdown
Example notebook showing how to load and visualize interaction data in mitab format--------------Author: Brin Rosenthal ([email protected])------------
###Code
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import networkx as nx
import mygene
mg = mygene.MyGeneInfo()
# latex rendering of text in graphs
import matplotlib as mpl
mpl.rc('text', usetex = False)
mpl.rc('font', family = 'serif')
% matplotlib inline
import visJS2jupyter.visJS_module
import visJS2jupyter.visualizations
###Output
_____no_output_____
###Markdown
Load the Reactome MI-TAB data- download from http://reactome.org/download/current/interactors/reactome.homo_sapiens.interactions.psi-mitab.txt**NOTE** Make sure you change your path in the cell below to reflect the download location of the Reactome file
###Code
reactome_df = pd.read_csv('../../interactomes/reactome/reactome.homo_sapiens.interactions.psi-mitab.txt',sep='\t')
reactome_df.head()
# create a networkx graph from the pandas dataframe, with all the other columns as edge attributes
attribute_cols = reactome_df.columns.tolist()[2:]
G_reactome = nx.from_pandas_dataframe(reactome_df,source='#ID(s) interactor A',target = 'ID(s) interactor B',
edge_attr = attribute_cols)
len(G_reactome.nodes())
# check that edge attributes have been loaded
list(G_reactome.edges(data=True))[0] # nx 2.0 edgeView object does not support indexing, but a list does!
# only keep nodes which have uniprot ids
uniprot_nodes = []
for n in G_reactome.nodes():
if n.startswith('uniprot'):
uniprot_nodes.append(n)
len(uniprot_nodes)
G_reactome = nx.subgraph(G_reactome,uniprot_nodes)
# take the largest connected component (to speed up visualization)
G_LCC = max(nx.connected_component_subgraphs(G_reactome), key=len)
len(G_LCC.nodes())
#mg_temp = mg.querymany(genes_temp,fields='symbol')
# parse the uniprot ids to HGNC gene symbols
uniprot_temp = [n[n.find(':')+1:] for n in G_LCC.nodes()]
mg_temp = mg.querymany(uniprot_temp,scopes='uniprot',species=9606)
uniprot_list = ['uniprotkb:'+x['query'] for x in mg_temp]
symbol_list = [x['symbol'] if 'symbol' in x.keys() else 'uniprotkb:'+x['query'] for x in mg_temp]
uniprot_to_symbol = dict(zip(uniprot_list,symbol_list))
uniprot_to_symbol = pd.Series(uniprot_to_symbol)
uniprot_to_symbol.head()
# relabel the nodes with their gene names
G_LCC = nx.relabel_nodes(G_LCC,dict(uniprot_to_symbol))
list(G_LCC.nodes())[0:10]
# map from interaction type to integer, and add the integer as an edge attribute
int_types = reactome_df['Interaction type(s)'].unique().tolist()
int_types_2_num = dict(zip(int_types,range(len(int_types))))
num_2_int_types = dict(zip(range(len(int_types)),int_types))
int_num_list = []
for e in G_LCC.edges(data=True):
int_type_temp = e[2]['Interaction type(s)']
int_num_list.append(int_types_2_num[int_type_temp])
# add int_num_list as attribute
int_num_dict = dict(zip(G_LCC.edges(),int_num_list))
nx.set_edge_attributes(G_LCC, name = 'int_type_numeric', values = int_num_dict) # for compatibility with nx 1.11 and 2.0,
# must explicitly define arguments
# set up the edge title for displaying info about interaction type
edge_title = {}
for e in G_LCC.edges():
edge_title[e]=num_2_int_types[int_num_dict[e]]
# add node degree as a node attribute
deg = dict(nx.degree(G_LCC))
nx.set_node_attributes(G_LCC, name = 'degree', values = deg)
# set the layout with networkx spring_layout
pos = nx.spring_layout(G_LCC)
# plot the Reactome largest connected component with edges color-coded by interaction type
nodes = list(G_LCC.nodes())
numnodes = len(nodes)
edges = list(G_LCC.edges())
numedges = len(edges)
edges_with_data = list(G_LCC.edges(data=True))
# draw the graph here
edge_to_color = visJS2jupyter.visJS_module.return_edge_to_color(G_LCC,field_to_map = 'int_type_numeric',cmap=mpl.cm.Set1_r,alpha=.9)
nodes_dict = [{"id":n,"degree":G_LCC.degree(n),"color":'black',
"node_size":deg[n],'border_width':0,
"node_label":n,
"edge_label":'',
"title":n,
"node_shape":'dot',
"x":pos[n][0]*1000,
"y":pos[n][1]*1000} for n in nodes
]
node_map = dict(zip(nodes,range(numnodes))) # map to indices for source/target in edges
edges_dict = [{"source":node_map[edges[i][0]], "target":node_map[edges[i][1]],
"color":edge_to_color[edges[i]],"title":edge_title[edges[i]]} for i in range(numedges)]
visJS2jupyter.visJS_module.visjs_network(nodes_dict,edges_dict,
node_color_border='black',
node_size_field='node_size',
node_size_transform='Math.sqrt',
node_size_multiplier=1,
node_border_width=1,
node_font_size=40,
node_label_field='node_label',
edge_width=2,
edge_smooth_enabled=False,
edge_smooth_type='continuous',
physics_enabled=False,
node_scaling_label_draw_threshold=100,
edge_title_field='title',
graph_title = 'Reactome largest connected component')
###Output
_____no_output_____
|
labs/kubeflow/01_Kubeflow_Pipeline_SDK.ipynb
|
###Markdown
Introduction to the Pipelines SDK The [Kubeflow Pipelines SDK](https://github.com/kubeflow/pipelines/tree/master/sdk) provides a set of Python packages that you can use to specify and run your machine learning (ML) workflows. A pipeline is a description of an ML workflow, including all of the components that make up the steps in the workflow and how the components interact with each other. Kubeflow website has a very detail expaination of kubeflow components, please go to [Introduction to the Pipelines SDK](https://www.kubeflow.org/docs/pipelines/sdk/sdk-overview/) for details Install the Kubeflow Pipelines SDK This guide tells you how to install the [Kubeflow Pipelines SDK](https://github.com/kubeflow/pipelines/tree/master/sdk) which you can use to build machine learning pipelines. You can use the SDK to execute your pipeline, or alternatively you can upload the pipeline to the Kubeflow Pipelines UI for execution.All of the SDK’s classes and methods are described in the auto-generated [SDK reference docs](https://kubeflow-pipelines.readthedocs.io/en/latest/). Run the following command to install the Kubeflow Pipelines SDK
###Code
!pip install kfp --upgrade --user
###Output
_____no_output_____
###Markdown
> Note: Please check official documentation to understand Pipline concetps before your move forward. [Introduction to Pipelines SDK](https://www.kubeflow.org/docs/pipelines/sdk/sdk-overview/) Build simple components and pipelines In this example, we want to calculate sum of three numbers. 1. Let's assume we have a python image to use. It accepts two arguments and return sum of them. 2. The sum of a and b will be used to calculate final result with sum of c and d. In total, we will have three arithmetical operators. Then we use another echo operator to print the result. 1. Create a container image for each componentAssumes that you have already created a program to perform the task required in a particular step of your ML workflow. For example, if the task is to train an ML model, then you must have a program that does the training,Your component can create `outputs` that the downstream components can use as `inputs`. This will be used to build Job Directed Acyclic Graph (DAG) > In this case, we will use a python base image to do the calculation. We skip buiding our own image. 2. Create a Python function to wrap your componentDefine a Python function to describe the interactions with the Docker container image that contains your pipeline component.Here, in order to simplify the process, we use simple way to calculate sum. Ideally, you need to build a new container image for your code change.
###Code
import kfp
from kfp import dsl
def add_two_numbers(a, b):
return dsl.ContainerOp(
name='calculate_sum',
image='python:3.6.8',
command=['python', '-c'],
arguments=['with open("/tmp/results.txt", "a") as file: file.write(str({} + {}))'.format(a, b)],
file_outputs={
'data': '/tmp/results.txt',
}
)
def echo_op(text):
return dsl.ContainerOp(
name='echo',
image='library/bash:4.4.23',
command=['sh', '-c'],
arguments=['echo "Result: {}"'.format(text)]
)
###Output
_____no_output_____
###Markdown
3. Define your pipeline as a Python functionDescribe each pipeline as a Python function.
###Code
@dsl.pipeline(
name='Calcualte sum pipeline',
description='Calculate sum of numbers and prints the result.'
)
def calculate_sum(
a=7,
b=10,
c=4,
d=7
):
"""A four-step pipeline with first two running in parallel."""
sum1 = add_two_numbers(a, b)
sum2 = add_two_numbers(c, d)
sum = add_two_numbers(sum1.output, sum2.output)
echo_task = echo_op(sum.output)
###Output
_____no_output_____
###Markdown
4. Compile the pipelineCompile the pipeline to generate a compressed YAML definition of the pipeline. The Kubeflow Pipelines service converts the static configuration into a set of Kubernetes resources for execution.There are two ways to compile the pipeline. Either use python lib `kfp.compiler.Compiler.compile ` or use binary `dsl-compile` command.
###Code
kfp.compiler.Compiler().compile(calculate_sum, 'calculate-sum-pipeline.zip')
###Output
/home/jovyan/.local/lib/python3.6/site-packages/kfp/components/_data_passing.py:168: UserWarning: Missing type name was inferred as "Integer" based on the value "7".
warnings.warn('Missing type name was inferred as "{}" based on the value "{}".'.format(type_name, str(value)))
/home/jovyan/.local/lib/python3.6/site-packages/kfp/components/_data_passing.py:168: UserWarning: Missing type name was inferred as "Integer" based on the value "10".
warnings.warn('Missing type name was inferred as "{}" based on the value "{}".'.format(type_name, str(value)))
/home/jovyan/.local/lib/python3.6/site-packages/kfp/components/_data_passing.py:168: UserWarning: Missing type name was inferred as "Integer" based on the value "4".
warnings.warn('Missing type name was inferred as "{}" based on the value "{}".'.format(type_name, str(value)))
###Markdown
5. Deploy pipelineThere're two ways to deploy the pipeline. Either upload the generate `.tar.gz` file through the `Kubeflow Pipelines UI`, or use `Kubeflow Pipeline SDK` to deploy it.We will only show sdk usage here.
###Code
client = kfp.Client()
aws_experiment = client.create_experiment(name='aws')
my_run = client.run_pipeline(aws_experiment.id, 'calculate-sum-pipeline',
'calculate-sum-pipeline.zip')
###Output
_____no_output_____
|
Twilio_sms_send.ipynb
|
###Markdown
https://www.twilio.com/docs/sms/tutorials/how-to-send-sms-messages-python
###Code
!pip install twilio
import twilio
import os
import sys
from twilio.rest import Client
# Download the helper library from https://www.twilio.com/docs/python/install
from twilio.rest import Client
# Your Account Sid and Auth Token from twilio.com/console
# DANGER! This is insecure. See http://twil.io/secure
account_sid = 'AC1ae33ab44796f959a4f2d699ae81e8de'
auth_token = '8175fba2b4dad4be1baa241183b00ab0'
client = Client(account_sid, auth_token)
message = client.messages \
.create(
body='This is the ship that made the Kessel Run in fourteen parsecs?',
from_='+12562865877',
to='+918239512468'
)
print(message.sid)
# HACKING HACKJNG HACKING @@@@@@@
account_sid = "AC1ae33ab44796f959a4f2d699ae81e8de"
auth_token = "8175fba2b4dad4be1baa241183b00ab0"
client = Client(account_sid , auth_token)
client.messages.create(
to = "+918482084102", #Enter your mobile number
from_ = "+12562865877" , # Enter your twilio number
body = " this is jsut for testing purpose "
)
###Output
_____no_output_____
|
references/santander-ml-explainability.ipynb
|
###Markdown
Santander ML Explainability CLEAR DATA. MADE MODEL. last update: 20/02/2019You can Fork code and Follow me on:> [ GitHub](https://github.com/mjbahmani/10-steps-to-become-a-data-scientist)> [Kaggle](https://www.kaggle.com/mjbahmani/)------------------------------------------------------------------------------------------------------------- I hope you find this kernel helpful and some UPVOTES would be very much appreciated. ----------- Notebook Content1. [Introduction](1)1. [Load packages](2) 1. [import](21) 1. [Setup](22) 1. [Version](23)1. [Problem Definition](3) 1. [Problem Feature](31) 1. [Aim](32) 1. [Variables](33) 1. [Evaluation](34)1. [Exploratory Data Analysis(EDA)](4) 1. [Data Collection](41) 1. [Visualization](42) 1. [Data Preprocessing](43)1. [Machine Learning Explainability for Santander](5) 1. [Permutation Importance](51) 1. [How to calculate and show importances?](52) 1. [What can be inferred from the above?](53) 1. [Partial Dependence Plots](54)1. [Model Development](6) 1. [lightgbm](61) 1. [RandomForestClassifier](62) 1. [DecisionTreeClassifier](63) 1. [CatBoostClassifier](64) 1. [Funny Combine](65)1. [References](7) 1- IntroductionAt [Santander](https://www.santanderbank.com) their mission is to help people and businesses prosper. they are always looking for ways to help our customers understand their financial health and identify which products and services might help them achieve their monetary goals.In this kernel we are going to create a **Machine Learning Explainability** for **Santander** based this perfect [course](https://www.kaggle.com/learn/machine-learning-explainability) in kaggle.>Note: how to extract **insights** from models? 2- A Data Science Workflow for Santander Of course, the same solution can not be provided for all problems, so the best way is to create a **general framework** and adapt it to new problem.**You can see my workflow in the below image** : **You should feel free to adjust this checklist to your needs** [Go to top](top) 2- Load packages 2-1 Import
###Code
from sklearn.model_selection import train_test_split
from sklearn.model_selection import StratifiedKFold
from sklearn.ensemble import RandomForestClassifier
from sklearn.tree import DecisionTreeClassifier
from catboost import CatBoostClassifier,Pool
from IPython.display import display
import matplotlib.patches as patch
import matplotlib.pyplot as plt
from sklearn.svm import NuSVR
from scipy.stats import norm
from sklearn import svm
import lightgbm as lgb
import xgboost as xgb
import seaborn as sns
import pandas as pd
import numpy as np
import warnings
import time
import glob
import sys
import os
import gc
###Output
_____no_output_____
###Markdown
2-2 Setup
###Code
# for get better result chage fold_n to 5
fold_n=2
folds = StratifiedKFold(n_splits=fold_n, shuffle=True, random_state=10)
%matplotlib inline
%precision 4
warnings.filterwarnings('ignore')
plt.style.use('ggplot')
np.set_printoptions(suppress=True)
pd.set_option("display.precision", 15)
###Output
_____no_output_____
###Markdown
2-3 Version
###Code
print('pandas: {}'.format(pd.__version__))
print('numpy: {}'.format(np.__version__))
print('Python: {}'.format(sys.version))
###Output
pandas: 0.23.4
numpy: 1.16.1
Python: 3.6.6 |Anaconda, Inc.| (default, Oct 9 2018, 12:34:16)
[GCC 7.3.0]
###Markdown
3- Problem DefinitionIn this **challenge**, we should help this **bank** identify which **customers** will make a **specific transaction** in the future, irrespective of the amount of money transacted. The data provided for this competition has the same structure as the real data we have available to solve this **problem**. 3-1 Problem Feature1. train.csv - the training set.1. test.csv - the test set. The test set contains some rows which are not included in scoring.1. sample_submission.csv - a sample submission file in the correct format. 3-2 AimIn this competition, The task is to predict the value of **target** column in the test set. 3-3 VariablesWe are provided with an **anonymized dataset containing numeric feature variables**, the binary **target** column, and a string **ID_code** column.The task is to predict the value of **target column** in the test set. 3-4 evaluation**Submissions** are evaluated on area under the [ROC curve](http://en.wikipedia.org/wiki/Receiver_operating_characteristic) between the predicted probability and the observed target.
###Code
from sklearn.metrics import roc_auc_score, roc_curve
###Output
_____no_output_____
###Markdown
4- Exploratory Data Analysis(EDA) In this section, we'll analysis how to use graphical and numerical techniques to begin uncovering the structure of your data. * Data Collection* Visualization* Data Preprocessing* Data Cleaning 4-1 Data Collection
###Code
print(os.listdir("../input/"))
# import Dataset to play with it
train= pd.read_csv("../input/train.csv")
test = pd.read_csv('../input/test.csv')
sample_submission = pd.read_csv('../input/sample_submission.csv')
sample_submission.head()
train.shape, test.shape, sample_submission.shape
train.head(5)
###Output
_____no_output_____
###Markdown
4-1-1Data set fields
###Code
train.columns
print(len(train.columns))
print(train.info())
###Output
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 200000 entries, 0 to 199999
Columns: 202 entries, ID_code to var_199
dtypes: float64(200), int64(1), object(1)
memory usage: 308.2+ MB
None
###Markdown
4-2-2 numerical values Describe
###Code
train.describe()
###Output
_____no_output_____
###Markdown
4-2 Visualization 4-2-1 hist
###Code
train['target'].value_counts().plot.bar();
f,ax=plt.subplots(1,2,figsize=(20,10))
train[train['target']==0].var_0.plot.hist(ax=ax[0],bins=20,edgecolor='black',color='red')
ax[0].set_title('target= 0')
x1=list(range(0,85,5))
ax[0].set_xticks(x1)
train[train['target']==1].var_0.plot.hist(ax=ax[1],color='green',bins=20,edgecolor='black')
ax[1].set_title('target= 1')
x2=list(range(0,85,5))
ax[1].set_xticks(x2)
plt.show()
###Output
_____no_output_____
###Markdown
4-2-2 Mean Frequency
###Code
train[train.columns[2:]].mean().plot('hist');plt.title('Mean Frequency');
###Output
_____no_output_____
###Markdown
4-2-3 countplot
###Code
f,ax=plt.subplots(1,2,figsize=(18,8))
train['target'].value_counts().plot.pie(explode=[0,0.1],autopct='%1.1f%%',ax=ax[0],shadow=True)
ax[0].set_title('target')
ax[0].set_ylabel('')
sns.countplot('target',data=train,ax=ax[1])
ax[1].set_title('target')
plt.show()
###Output
_____no_output_____
###Markdown
4-2-4 histif you check histogram for all feature, you will find that most of them are so similar
###Code
train["var_0"].hist();
train["var_81"].hist();
train["var_2"].hist();
###Output
_____no_output_____
###Markdown
4-2-6 distplot the target in data set is **imbalance**
###Code
sns.set(rc={'figure.figsize':(9,7)})
sns.distplot(train['target']);
###Output
_____no_output_____
###Markdown
4-2-7 violinplot
###Code
sns.violinplot(data=train,x="target", y="var_0")
sns.violinplot(data=train,x="target", y="var_81")
###Output
_____no_output_____
###Markdown
4-3 Data PreprocessingBefore we start this section let me intrduce you, some other compitation that they were similar to this:1. https://www.kaggle.com/artgor/how-to-not-overfit1. https://www.kaggle.com/c/home-credit-default-risk1. https://www.kaggle.com/c/porto-seguro-safe-driver-prediction 4-3-1 Check missing data for test & train
###Code
def check_missing_data(df):
flag=df.isna().sum().any()
if flag==True:
total = df.isnull().sum()
percent = (df.isnull().sum())/(df.isnull().count()*100)
output = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
data_type = []
# written by MJ Bahmani
for col in df.columns:
dtype = str(df[col].dtype)
data_type.append(dtype)
output['Types'] = data_type
return(np.transpose(output))
else:
return(False)
check_missing_data(train)
check_missing_data(test)
###Output
_____no_output_____
###Markdown
4-3-2 Binary Classification
###Code
train['target'].unique()
###Output
_____no_output_____
###Markdown
4-3-3 Is data set imbalance? A large part of the data is unbalanced, but **how can we solve it?**
###Code
train['target'].value_counts()
def check_balance(df,target):
check=[]
# written by MJ Bahmani for binary target
print('size of data is:',df.shape[0] )
for i in [0,1]:
print('for target {} ='.format(i))
print(df[target].value_counts()[i]/df.shape[0]*100,'%')
###Output
_____no_output_____
###Markdown
1. **Imbalanced dataset** is relevant primarily in the context of supervised machine learning involving two or more classes. 1. **Imbalance** means that the number of data points available for different the classes is different[Image source](http://api.ning.com/files/vvHEZw33BGqEUW8aBYm4epYJWOfSeUBPVQAsgz7aWaNe0pmDBsjgggBxsyq*8VU1FdBshuTDdL2-bp2ALs0E-0kpCV5kVdwu/imbdata.png)
###Code
check_balance(train,'target')
###Output
size of data is: 200000
for target 0 =
89.95100000000001 %
for target 1 =
10.049 %
###Markdown
4-3-4 skewness and kurtosis
###Code
#skewness and kurtosis
print("Skewness: %f" % train['target'].skew())
print("Kurtosis: %f" % train['target'].kurt())
###Output
Skewness: 2.657642
Kurtosis: 5.063112
###Markdown
5- Machine Learning Explainability for SantanderIn this section, I want to try extract insights from models with the help of this excellent [**Course**](https://www.kaggle.com/learn/machine-learning-explainability) in Kaggle.The Goal behind of ML Explainability for Santander is:1. All features are senseless named.(var_1, var2,...) but certainly the importance of each one is different!1. Extract insights from models.1. Find the most inmortant feature in models.1. Affect of each feature on the model's predictions.As you can see from the above, we will refer to three important and practical concepts in this section and try to explain each of them in detail. 5-1 Permutation Importance In this section we will answer following question: 1. What features have the biggest impact on predictions? 1. how to extract insights from models? Prepare our data for our model
###Code
cols=["target","ID_code"]
X = train.drop(cols,axis=1)
y = train["target"]
X_test = test.drop("ID_code",axis=1)
###Output
_____no_output_____
###Markdown
Create a sample model to calculate which feature are more important.
###Code
train_X, val_X, train_y, val_y = train_test_split(X, y, random_state=1)
rfc_model = RandomForestClassifier(random_state=0).fit(train_X, train_y)
###Output
_____no_output_____
###Markdown
5-2 How to calculate and show importances? Here is how to calculate and show importances with the [eli5](https://eli5.readthedocs.io/en/latest/) library:
###Code
import eli5
from eli5.sklearn import PermutationImportance
perm = PermutationImportance(rfc_model, random_state=1).fit(val_X, val_y)
eli5.show_weights(perm, feature_names = val_X.columns.tolist(), top=150)
###Output
_____no_output_____
###Markdown
5-3 What can be inferred from the above?1. As you move down the top of the graph, the importance of the feature decreases.1. The features that are shown in green indicate that they have a positive impact on our prediction1. The features that are shown in white indicate that they have no effect on our prediction1. The features shown in red indicate that they have a negative impact on our prediction1. The most important feature was **Var_110**. 1. 5-4 Partial Dependence PlotsWhile **feature importance** shows what **variables** most affect predictions, **partial dependence** plots show how a feature affects predictions.[6][7]and partial dependence plots are calculated after a model has been fit. [partial-plots](https://www.kaggle.com/dansbecker/partial-plots)
###Code
train_X, val_X, train_y, val_y = train_test_split(X, y, random_state=1)
tree_model = DecisionTreeClassifier(random_state=0, max_depth=5, min_samples_split=5).fit(train_X, train_y)
###Output
_____no_output_____
###Markdown
For the sake of explanation, I use a Decision Tree which you can see below.
###Code
features = [c for c in train.columns if c not in ['ID_code', 'target']]
from sklearn import tree
import graphviz
tree_graph = tree.export_graphviz(tree_model, out_file=None, feature_names=features)
graphviz.Source(tree_graph)
###Output
_____no_output_____
###Markdown
As guidance to read the tree:1. Leaves with children show their splitting criterion on the top1. The pair of values at the bottom show the count of True values and False values for the target respectively, of data points in that node of the tree.>Note: Yes **Var_81** are more effective on our model. 5-5 Partial Dependence PlotIn this section, we see the impact of the main variables discovered in the previous sections by using the [pdpbox](https://pdpbox.readthedocs.io/en/latest/).
###Code
from matplotlib import pyplot as plt
from pdpbox import pdp, get_dataset, info_plots
# Create the data that we will plot
pdp_goals = pdp.pdp_isolate(model=tree_model, dataset=val_X, model_features=features, feature='var_81')
# plot it
pdp.pdp_plot(pdp_goals, 'var_81')
plt.show()
###Output
_____no_output_____
###Markdown
5-6 Chart analysis1. The y axis is interpreted as change in the prediction from what it would be predicted at the baseline or leftmost value.1. A blue shaded area indicates level of confidence
###Code
# Create the data that we will plot
pdp_goals = pdp.pdp_isolate(model=tree_model, dataset=val_X, model_features=features, feature='var_82')
# plot it
pdp.pdp_plot(pdp_goals, 'var_82')
plt.show()
# Create the data that we will plot
pdp_goals = pdp.pdp_isolate(model=tree_model, dataset=val_X, model_features=features, feature='var_139')
# plot it
pdp.pdp_plot(pdp_goals, 'var_139')
plt.show()
# Create the data that we will plot
pdp_goals = pdp.pdp_isolate(model=tree_model, dataset=val_X, model_features=features, feature='var_110')
# plot it
pdp.pdp_plot(pdp_goals, 'var_110')
plt.show()
###Output
_____no_output_____
###Markdown
5-7 SHAP Values**SHAP** (SHapley Additive exPlanations) is a unified approach to explain the output of **any machine learning model**. SHAP connects game theory with local explanations, uniting several previous methods [1-7] and representing the only possible consistent and locally accurate additive feature attribution method based on expectations (see the SHAP NIPS paper for details).[image credits](https://github.com/slundberg/shap)>Note: Shap can answer to this qeustion : **how the model works for an individual prediction?**
###Code
row_to_show = 5
data_for_prediction = val_X.iloc[row_to_show] # use 1 row of data here. Could use multiple rows if desired
data_for_prediction_array = data_for_prediction.values.reshape(1, -1)
rfc_model.predict_proba(data_for_prediction_array);
import shap # package used to calculate Shap values
# Create object that can calculate shap values
explainer = shap.TreeExplainer(rfc_model)
# Calculate Shap values
shap_values = explainer.shap_values(data_for_prediction)
###Output
_____no_output_____
###Markdown
If you look carefully at the code where we created the SHAP values, you'll notice we reference Trees in **shap.TreeExplainer(my_model)**. But the SHAP package has explainers for every type of model.1. shap.DeepExplainer works with Deep Learning models.1. shap.KernelExplainer works with all models, though it is slower than other Explainers and it offers an approximation rather than exact Shap values.
###Code
shap.initjs()
shap.force_plot(explainer.expected_value[1], shap_values[1], data_for_prediction)
# Calculate Shap values
shap_values = explainer.shap_values(val_X)
###Output
_____no_output_____
###Markdown
6- Model DevelopmentSo far, we have used two models, and at this point we add another model and we'll be expanding it soon.in this section you will see following model:1. lightgbm1. RandomForestClassifier1. DecisionTreeClassifier1. CatBoostClassifier 6-1 lightgbm
###Code
# based on following kernel https://www.kaggle.com/dromosys/sctp-working-lgb
params = {'num_leaves': 9,
'min_data_in_leaf': 42,
'objective': 'binary',
'max_depth': 16,
'learning_rate': 0.0123,
'boosting': 'gbdt',
'bagging_freq': 5,
'bagging_fraction': 0.8,
'feature_fraction': 0.8201,
'bagging_seed': 11,
'reg_alpha': 1.728910519108444,
'reg_lambda': 4.9847051755586085,
'random_state': 42,
'metric': 'auc',
'verbosity': -1,
'subsample': 0.81,
'min_gain_to_split': 0.01077313523861969,
'min_child_weight': 19.428902804238373,
'num_threads': 4}
%%time
y_pred_lgb = np.zeros(len(X_test))
for fold_n, (train_index, valid_index) in enumerate(folds.split(X,y)):
print('Fold', fold_n, 'started at', time.ctime())
X_train, X_valid = X.iloc[train_index], X.iloc[valid_index]
y_train, y_valid = y.iloc[train_index], y.iloc[valid_index]
train_data = lgb.Dataset(X_train, label=y_train)
valid_data = lgb.Dataset(X_valid, label=y_valid)
lgb_model = lgb.train(params,train_data,num_boost_round=2000,#change 20 to 2000
valid_sets = [train_data, valid_data],verbose_eval=300,early_stopping_rounds = 200)##change 10 to 200
y_pred_lgb += lgb_model.predict(X_test, num_iteration=lgb_model.best_iteration)/5
###Output
Fold 0 started at Wed Feb 27 03:29:10 2019
Training until validation scores don't improve for 200 rounds.
[300] training's auc: 0.839855 valid_1's auc: 0.81639
[600] training's auc: 0.875365 valid_1's auc: 0.846415
[900] training's auc: 0.894037 valid_1's auc: 0.861257
[1200] training's auc: 0.905897 valid_1's auc: 0.870204
[1500] training's auc: 0.914479 valid_1's auc: 0.876471
[1800] training's auc: 0.920762 valid_1's auc: 0.880908
Did not meet early stopping. Best iteration is:
[2000] training's auc: 0.924285 valid_1's auc: 0.883277
Fold 1 started at Wed Feb 27 03:31:04 2019
Training until validation scores don't improve for 200 rounds.
[300] training's auc: 0.841191 valid_1's auc: 0.816015
[600] training's auc: 0.875354 valid_1's auc: 0.846292
[900] training's auc: 0.892486 valid_1's auc: 0.860744
[1200] training's auc: 0.904462 valid_1's auc: 0.87007
[1500] training's auc: 0.913149 valid_1's auc: 0.876356
[1800] training's auc: 0.919487 valid_1's auc: 0.880811
Did not meet early stopping. Best iteration is:
[2000] training's auc: 0.923097 valid_1's auc: 0.883232
CPU times: user 14min 12s, sys: 7.06 s, total: 14min 19s
Wall time: 3min 44s
###Markdown
6-2 RandomForestClassifier
###Code
y_pred_rfc = rfc_model.predict(X_test)
###Output
_____no_output_____
###Markdown
6-3 DecisionTreeClassifier
###Code
y_pred_tree = tree_model.predict(X_test)
###Output
_____no_output_____
###Markdown
6-4 CatBoostClassifier
###Code
train_pool = Pool(train_X,train_y)
cat_model = CatBoostClassifier(
iterations=3000,# change 25 to 3000 to get best performance
learning_rate=0.03,
objective="Logloss",
eval_metric='AUC',
)
cat_model.fit(train_X,train_y,silent=True)
y_pred_cat = cat_model.predict(X_test)
###Output
_____no_output_____
###Markdown
Now you can change your model and submit the results of other models.
###Code
submission_rfc = pd.DataFrame({
"ID_code": test["ID_code"],
"target": y_pred_rfc
})
submission_rfc.to_csv('submission_rfc.csv', index=False)
submission_tree = pd.DataFrame({
"ID_code": test["ID_code"],
"target": y_pred_tree
})
submission_tree.to_csv('submission_tree.csv', index=False)
submission_cat = pd.DataFrame({
"ID_code": test["ID_code"],
"target": y_pred_cat
})
submission_cat.to_csv('submission_cat.csv', index=False)
submission_lgb = pd.DataFrame({
"ID_code": test["ID_code"],
"target": y_pred_lgb
})
submission_lgb.to_csv('submission_lgb.csv', index=False)
###Output
_____no_output_____
###Markdown
6-5 Funny Combine
###Code
submission_rfc_cat = pd.DataFrame({
"ID_code": test["ID_code"],
"target": (y_pred_rfc +y_pred_cat)/2
})
submission_rfc_cat.to_csv('submission_rfc_cat.csv', index=False)
submission_lgb_cat = pd.DataFrame({
"ID_code": test["ID_code"],
"target": (y_pred_lgb +y_pred_cat)/2
})
submission_lgb_cat.to_csv('submission_lgb_cat.csv', index=False)
submission_rfc_lgb = pd.DataFrame({
"ID_code": test["ID_code"],
"target": (y_pred_rfc +y_pred_lgb)/2
})
submission_rfc_lgb.to_csv('submission_rfc_lgb.csv', index=False)
###Output
_____no_output_____
|
notebooks/011_ASCII_files.ipynb
|
###Markdown
Working with data from ASCII files It's nice, when we can import data from ASCII file with some nice tool like `pandas`, however there are many cases, when you have to parse data line by line by yourself.
###Code
f = open('../data/Bremen_tmin.txt')
###Output
_____no_output_____
###Markdown
`f` is now just a file handler:
###Code
f
###Output
_____no_output_____
###Markdown
Read lines to list
###Code
lines = f.readlines()
f.close()
lines
lines[20]
lines[21]
one_line = lines[21]
one_line
###Output
_____no_output_____
###Markdown
We can separate this line in to several parts (that wil form another list)
###Code
one_line.split()
one_line.split()[0]
one_line.split()[-1]
###Output
_____no_output_____
###Markdown
If we can split one line, we can split many in a loop. Here we use only first 10 data elements:
###Code
for line in lines[21:31]:
print(line)
for line in lines[21:31]:
print(line.split())
###Output
['1890', '1', '1', '-5.50']
['1890', '1', '2', '-7.40']
['1890', '1', '3', '-3.50']
['1890', '1', '4', '-1.90']
['1890', '1', '5', '0.20']
['1890', '1', '6', '6.00']
['1890', '1', '7', '5.80']
['1890', '1', '8', '1.80']
['1890', '1', '9', '0.10']
['1890', '1', '10', '3.00']
###Markdown
Exersice - extract only temperature values from data (create empy list and append to it) We get some values, now, let's write them down.
###Code
odata = [1, 2, 3, 4] # to be replaces by result of the exersise
fout = open('out.txt', 'w') # 'w' means file will be opened for writing
for record in odata:
fout.write(str(record)+'\n')
fout.close()
!head out.txt
# %load out.txt
1
2
3
4
###Output
_____no_output_____
###Markdown
Exersise- extract years, months, days and temperature into four separate variables- create output file that will have records of the type: YYYY:MM:DD temperature - turn this into a function that takes names of the input and output files as arguments.- try to run this function on `../data/Bremen_tmin.txt` file How about other information in this file? How we extract data from less structured data?
###Code
f = open('../data/Bremen_tmin.txt')
lines = f.readlines()
f.close()
lines[1]
lines[1].split()
lines[1].split()[2]
###Output
_____no_output_____
###Markdown
In principle this is where [regular expressions](https://docs.python.org/3/howto/regex.html) can become useful, but we will avoid them, knowing that two last charactes always will be `N,` or `S,`.
###Code
lines[1].split()[2][:-2]
lines[1].split()[3][:-2]
lines[1].split()[4][:-2]
###Output
_____no_output_____
###Markdown
OK, now we know how to parce the line, but how to identify it? If there is some unique word/colelction of charactes in the file, we can always identify it:
###Code
our_line = lines[1]
our_line
our_line.startswith('# coordinates:')
'# coordinates:' in our_line
'# coordinates!' in our_line
f = open('../data/Bremen_tmin.txt')
lines = f.readlines()
f.close()
for line in lines:
if line.startswith('# coordinates:'):
lat = lines[1].split()[2][:-2]
lon = lines[1].split()[3][:-2]
alt = lines[1].split()[4][:-2]
print('Coordinates of the station')
print(f'lon:{lon} lat:{lat} alt:{alt}')
###Output
Coordinates of the station
lon:8.78 lat:53.10 alt:4.0
|
notebooks_Intro.ipynb
|
###Markdown
Introduction to the JupyterLab and Jupyter NotebooksThis is a short introduction to two of the flagship tools created by [the Jupyter Community](https://jupyter.org).> **⚠️Experimental!⚠️**: This is an experimental interface provided by the [JupyterLite project](https://jupyterlite.readthedocs.io/en/latest/). It embeds an entire JupyterLab interface, with many popular packages for scientific computing, in your browser. There may be minor differences in behavior between JupyterLite and the JupyterLab you install locally. You may also encounter some bugs or unexpected behavior. To report any issues, or to get involved with the JupyterLite project, see [the JupyterLite repository](https://github.com/jupyterlite/jupyterlite/issues?q=is%3Aissue+is%3Aopen+sort%3Aupdated-desc). JupyterLab 🧪**JupyterLab** is a next-generation web-based user interface for Project Jupyter. It enables you to work with documents and activities such as Jupyter notebooks, text editors, terminals, and custom components in a flexible, integrated, and extensible manner. It is the interface that you're looking at right now.**For an overview of the JupyterLab interface**, see the **JupyterLab Welcome Tour** on this page, by going to `Help -> Welcome Tour` and following the prompts.> **See Also**: For a more in-depth tour of JupyterLab with a full environment that runs in the cloud, see [the JupyterLab introduction on Binder](https://mybinder.org/v2/gh/jupyterlab/jupyterlab-demo/HEAD?urlpath=lab/tree/demo). Jupyter Notebooks 📓**Jupyter Notebooks** are a community standard for communicating and performing interactive computing. They are a document that blends computations, outputs, explanatory text, mathematics, images, and rich media representations of objects.JupyterLab is one interface used to create and interact with Jupyter Notebooks.**For an overview of Jupyter Notebooks**, see the **JupyterLab Welcome Tour** on this page, by going to `Help -> Notebook Tour` and following the prompts.> **See Also**: For a more in-depth tour of Jupyter Notebooks and the Classic Jupyter Notebook interface, see [the Jupyter Notebook IPython tutorial on Binder](https://mybinder.org/v2/gh/ipython/ipython-in-depth/HEAD?urlpath=tree/binder/Index.ipynb). An example: visualizing data in the notebook ✨Below is an example of a code cell. We'll visualize some simple data using two popular packages in Python. We'll use [NumPy](https://numpy.org/) to create some random data, and [Matplotlib](https://matplotlib.org) to visualize it.Note how the code and the results of running the code are bundled together.
###Code
from matplotlib import pyplot as plt
import numpy as np
# Generate 100 random data points along 3 dimensions
x, y, scale = np.random.randn(3, 100)
fig, ax = plt.subplots()
# Map each onto a scatterplot we'll create with Matplotlib
ax.scatter(x=x, y=y, c=scale, s=np.abs(scale)*500)
ax.set(title="Some random data, created with JupyterLab!")
plt.show()
###Output
_____no_output_____
|
Lecturenotes/10 CRISP-DM and Data Science Libraries.ipynb
|
###Markdown
Module 10: CRISP-DM and Python Libraries for Data ScienceMarch 17, 2021 Last time we discussed the basics of resources on the web, how to access remote resources (files, REST services), how to handle XML files, and how to scrape content form the HTML representation of websites.Today we have a closer look the CRISP-DM reference model for approaching data analysis problems, and at some of the most popular Python libraries for data science applications: Pandas (continued), NumPy and Matplotlib. They all belong to the SciPy collection of libraries for mathematics, science and engineering (https://www.scipy.org/). Always keep in mind that in the lecture we can only discuss a few selected examples, so refer to the respective online documentation for full reference.Next time we will have a look into regular expressions, which can be very useful in practice to find patterns in text – not only useful in Python programs! Approaching Data Analysis Problems: CRISP-DMHow to approach complex data analysis problems? There are of course different ways to do this, one of the most popular is the Cross-Industry Standard Process for Data Mining. CRISP-DM provides a reference model describing how data mining experts typically proceed to address their problems, and thus gives orientation which steps to perform in a data science project. It divides the process into six major phases as shown in the picture below: 1. **Business Understanding**: This initial phase focuses on understanding and determining the general project objectives from a “business” or research perspective. Which (research) questions should the data analysis project answer? It also includes the setup of a project plan.2. **Data Understanding**: This phase is about the familiarization with the available data. This includes to collect, describe, and explore initial data for the project objectives, and also to verify the quality of the data. 3. **Data Preparation**: This phase is about turning the initial data set into the final data set that will be used for the analysis. Depending on the situation, this might include selecting, cleaning, constructing, integrating and formatting data to make them ready for further processing.4. **Modeling**: This phase is about selecting the analysis techniques to be used on the data set, the abstract description of the overall computational process (e.g. with UML Activity Diagrams), its implementation (e.g. with Python) and finally execution on the prepared data set. 5. **Evaluation**: This phase is about critically reviewing the computational model, program and results. Are they correct, and do they achieve the project objectives? If not, the previous phases should be applied again to identify and eliminate the problems. 6. **Deployment**: This last phase is about the deployment of the final data, process, program, results and project report. Furthermore, it should include making plans for monitoring and maintenance of data and software artifacts, and a review of the complete project. Image by Kenneth Jensen, work based on ftp://public.dhe.ibm.com/software/analytics/spss/documentation/modeler/18.0/en/ModelerCRISPDM.pdf (Figure 1), CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=24930610 If you are interested in reading more about CRISP-DM: The "CRISP-DM 1.0 - Step-by-Step Data Mining Guide" (maintained by IBM and freely available online at ftp://ftp.software.ibm.com/software/analytics/spss/support/Modeler/Documentation/14/UserManual/CRISP-DM.pdf) is the official reference for the method. Python Libraries for Data ScienceIn the following we have a look at some of the most important libraries for data science in Python, and discuss some important concepts related to them. Note that we cannot discuss all libraries in detail in this course, and that in the lecture we can only discuss a few selected examples, so refer to the respective online documentation for full reference. PandasThe most important things to know about Pandas we have already covered a while ago: how to use Pandas to read content from CSV files, the data frame and series data structures, indexing operations and basic plotting and statistics methods for data frames and series. Please refer to the Pandas documentation at http://pandas.pydata.org/pandas-docs/stable/ for further details, as we cannot cover the library in depth in this course. In this lecture we only address two other important aspects: handling of missing data and concatenating/joining tables with Pandas. Handling Missing DataFor various reasons it can happen that data are missing in a data frame. They might, for example, already have been missing in the input CSV file due to measurement faults, or have become unavailable because of computations that were not able to return a (good) result.In Pandas the value ```np.nan``` (technically of type ```float```) is the primarily used value for representing missing data. This can look as follows:
###Code
import pandas as pd
df = pd.read_csv("data/table-with-missing-data.csv", sep=",")
print(df)
###Output
name age height
0 Alice 29.0 160.0
1 Bob 45.0 172.0
2 Cindy 63.0 NaN
3 Dennis NaN 197.0
4 Eve 42.0 171.0
5 NaN 75.0 200.0
6 Gina NaN 158.0
7 Harry 35.0 180.0
###Markdown
Note that the value ```None```, should it occur during computations, is usually also interpreted as ```NaN```, and generally the values to be interpreted as missing can be configured in the Python options. This should be done with care, however. By default, Pandas operations simply ignore ```NaN``` values. That is, they simply carry out the computation on the available data in the data frame or series, and/or propagate ```NaN``` values if a meaningful result cannot be derived. For example:
###Code
print(df.describe())
print(df["age"]+1)
###Output
age height
count 6.000000 7.000000
mean 48.166667 176.857143
std 17.486185 16.577380
min 29.000000 158.000000
25% 36.750000 165.500000
50% 43.500000 172.000000
75% 58.500000 188.500000
max 75.000000 200.000000
0 30.0
1 46.0
2 64.0
3 NaN
4 43.0
5 76.0
6 NaN
7 36.0
Name: age, dtype: float64
###Markdown
If such behavior is not wanted, the data frame or series can be manipulated accordingly before applying the operations. One option is to remove rows or columns with missing data completely by using the ```dropna()``` function. The following example shows how to drop all rows where any data are missing, and how to drop all rows where age or height data are missing:
###Code
print(df.dropna())
print(df.dropna(subset=["age", "height"]))
###Output
name age height
0 Alice 29.0 160.0
1 Bob 45.0 172.0
4 Eve 42.0 171.0
7 Harry 35.0 180.0
name age height
0 Alice 29.0 160.0
1 Bob 45.0 172.0
4 Eve 42.0 171.0
5 NaN 75.0 200.0
7 Harry 35.0 180.0
###Markdown
Another possibility is to replace the ```NaN``` values by other/better values:
###Code
print(df.fillna(0))
print(df.fillna(value={"age":0, "height":0}))
print(df.fillna(value={"age":df["age"].mean(), \
"height":df["height"].mean()}))
###Output
name age height
0 Alice 29.0 160.0
1 Bob 45.0 172.0
2 Cindy 63.0 0.0
3 Dennis 0.0 197.0
4 Eve 42.0 171.0
5 0 75.0 200.0
6 Gina 0.0 158.0
7 Harry 35.0 180.0
name age height
0 Alice 29.0 160.0
1 Bob 45.0 172.0
2 Cindy 63.0 0.0
3 Dennis 0.0 197.0
4 Eve 42.0 171.0
5 NaN 75.0 200.0
6 Gina 0.0 158.0
7 Harry 35.0 180.0
name age height
0 Alice 29.000000 160.000000
1 Bob 45.000000 172.000000
2 Cindy 63.000000 176.857143
3 Dennis 48.166667 197.000000
4 Eve 42.000000 171.000000
5 NaN 75.000000 200.000000
6 Gina 48.166667 158.000000
7 Harry 35.000000 180.000000
###Markdown
In some cases also Pandas’ ```interpolate()``` function can be used to come up with values to fill in for missing data. Of course, replacing missing data with values should always be done with great care, as there is a risk of producing distorted or even wrong results when adding data to a data set. Generally, the choice how to handle missing data depends on the specifics of the concrete case, but it is good to know about the different options. Concatenating and Joining TablesWhen working with data frames, often the question arises how to combine two or more of them into one. The following illustrates the most important ways to do that.The easiest case of combining two data frames into one is **concatenation**. It is possible if the two tables have the same columns, but a different set of rows, or if they have the same rows, but different sets of columns. In the former case, they can simply be concatenated vertically, on top of each other, and in the other case horizontally, or next to each other. The following example illustrates how to do that with pandas, simply creating parts of the data frame above that are then concatenated:
###Code
import pandas as pd
df = pd.read_csv("data/table-with-missing-data.csv", sep=",")
three_more_rows = pd.DataFrame(data=\
{"name":["Ines","Joe","Kathy"],"age":[51,18,34],\
"height":[178,185,168]})
print(three_more_rows)
df_concatenated = pd.concat([df, three_more_rows], axis=0)
print(df_concatenated)
###Output
name age height
0 Ines 51 178
1 Joe 18 185
2 Kathy 34 168
name age height
0 Alice 29.0 160.0
1 Bob 45.0 172.0
2 Cindy 63.0 NaN
3 Dennis NaN 197.0
4 Eve 42.0 171.0
5 NaN 75.0 200.0
6 Gina NaN 158.0
7 Harry 35.0 180.0
0 Ines 51.0 178.0
1 Joe 18.0 185.0
2 Kathy 34.0 168.0
###Markdown
Note that the ```concat()``` method does not assign new index values by default. Setting the parameter ```ignore_index=True``` will cause it to re-index, too.Adding a new column to the data frame can be done with the same method, but using the other axis. For example:
###Code
one_more_column = pd.Series([62,70,74,91,65,80,45,95],name="weight")
df_concatenated = pd.concat([df,one_more_column], axis=1)
print(df_concatenated)
###Output
name age height weight
0 Alice 29.0 160.0 62
1 Bob 45.0 172.0 70
2 Cindy 63.0 NaN 74
3 Dennis NaN 197.0 91
4 Eve 42.0 171.0 65
5 NaN 75.0 200.0 80
6 Gina NaN 158.0 45
7 Harry 35.0 180.0 95
###Markdown
Another, and sometimes not-so-easy case is the **joining** of data from different tables that do not come with the same set of rows or columns. In this case, one or more join keys need to be identified that are present in both files and can thus be used to associate the different data items to each other. Sometimes two columns are named the same and do in fact contain the same kind of data. Then it is easy to see that they might be a good key. Here is an example with two simple data frames that both have a key column and can thus easily be joined with merge:
###Code
left = pd.DataFrame({'key': ['key1', 'key2', 'key3', 'key4'],
'A': ['A0', 'A1', 'A2', 'A3'],
'B': ['B0', 'B1', 'B2', 'B3']})
right = pd.DataFrame({'key': ['key1', 'key3', 'key4', 'key2'],
'C': ['C0', 'C1', 'C2', 'C3'],
'D': ['D0', 'D1', 'D2', 'D3']})
join = pd.merge(left, right, on='key')
print(join)
###Output
key A B C D
0 key1 A0 B0 C0 D0
1 key2 A1 B1 C3 D3
2 key3 A2 B2 C1 D1
3 key4 A3 B3 C2 D2
###Markdown
In other cases, it is not so obvious from the name of the column, but if there are two columns with different names that contain the same kind of data, they can also be used as join keys:
###Code
left = pd.DataFrame({'key': ['key1', 'key2', 'key3', 'key4'],
'A': ['A0', 'A1', 'A2', 'A3'],
'B': ['B0', 'B1', 'B2', 'B3']})
right = pd.DataFrame({'ID': ['key5', 'key3', 'key4', 'key2'],
'C': ['C0', 'C1', 'C2', 'C3'],
'D': ['D0', 'D1', 'D2', 'D3']})
join = pd.merge(left, right, left_on="key",right_on="ID")
print(join)
###Output
key A B ID C D
0 key2 A1 B1 key2 C3 D3
1 key3 A2 B2 key3 C1 D1
2 key4 A3 B3 key4 C2 D2
###Markdown
Apparently, only the rows whose keys appear in both data frames are contained in the result. This is the default behavior and corresponds to a so-called inner join. It is also possible to use all data from one or both tables in the joined table, and let the missing values in the rows simply be filled with ```NaN``` values. Those are then called left outer join (if everything from the left table is used, but only the matching keys from the right), right outer join (everything from the right), or outer join (every-thing from both). See the following examples for illustration:
###Code
inner_join = pd.merge(left, right, left_on="key", right_on="ID", how='inner')
print(inner_join)
left_outer_join = pd.merge(left, right, left_on="key", right_on="ID", how='left')
print(left_outer_join)
right_outer_join = pd.merge(left, right, left_on="key",right_on="ID", how='right')
print(right_outer_join)
outer_join = pd.merge(left, right, left_on="key",right_on="ID", how='outer')
print(outer_join)
###Output
key A B ID C D
0 key2 A1 B1 key2 C3 D3
1 key3 A2 B2 key3 C1 D1
2 key4 A3 B3 key4 C2 D2
key A B ID C D
0 key1 A0 B0 NaN NaN NaN
1 key2 A1 B1 key2 C3 D3
2 key3 A2 B2 key3 C1 D1
3 key4 A3 B3 key4 C2 D2
key A B ID C D
0 key2 A1 B1 key2 C3 D3
1 key3 A2 B2 key3 C1 D1
2 key4 A3 B3 key4 C2 D2
3 NaN NaN NaN key5 C0 D0
key A B ID C D
0 key1 A0 B0 NaN NaN NaN
1 key2 A1 B1 key2 C3 D3
2 key3 A2 B2 key3 C1 D1
3 key4 A3 B3 key4 C2 D2
4 NaN NaN NaN key5 C0 D0
###Markdown
For full reference regarding table merging operations with pandas, see https://pandas.pydata.org/pandas-docs/stable/merging.html. NumPyThe NumPy library (http://www.numpy.org/) has been designed to provide specific support for numerical mathematics in Python. In particular, it provides a data structure for n-dimensional arrays/matrices (the ndarray) and operations for working with it. Note that Pandas, itself focusing on functionality for data science applications, has been built on top of NumPy.Here is a small basic NumPy example that shows some of many different ways to create ndarrays:
###Code
import numpy as np
a = np.array([[1,5,6],[6,7,6],[5,4,3]])
b = np.zeros((3,3))
c = np.ones((3,3))
d = np.identity(3)
print(a)
print(b)
print(c)
print(d)
###Output
[[1 5 6]
[6 7 6]
[5 4 3]]
[[0. 0. 0.]
[0. 0. 0.]
[0. 0. 0.]]
[[1. 1. 1.]
[1. 1. 1.]
[1. 1. 1.]]
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
###Markdown
Indexing etc. basically works as with lists, data frames and other collection data structures that we have seen before. Note, however, that ndarrays are homogeneously typed, that is, all contained elements must be of the same type, and that they are usually fixed-size, that is, all rows in a dimension must be of the same length. Also appending new rows or columns to ndarrays is not as easy as with the aforementioned data types, so ideally they are created directly with the size and number of dimensions needed, and values filled in later in the program if needed. The advantage of ndarrays is that numerical operations on large matrices run much faster on them then on the dynamic collection data structures.Python’s standard arithmetic operations can be used on ndarrays, and will be executed elementwise. For example:
###Code
print(a+c)
print(a*a)
print((a-c)<=b)
###Output
[[2. 6. 7.]
[7. 8. 7.]
[6. 5. 4.]]
[[ 1 25 36]
[36 49 36]
[25 16 9]]
[[ True False False]
[False False False]
[False False False]]
###Markdown
For matrix-specific operations, own operators and attributes have been defined, for example for matrix multiplication and transposition:
###Code
print(a@a)
print(a.T)
###Output
[[ 61 64 54]
[ 78 103 96]
[ 44 65 63]]
[[1 6 5]
[5 7 4]
[6 6 3]]
###Markdown
Here is now an example (largely taken from https://www.geeksforgeeks.org/check-given-matrix-is-magic-square-or-not/) that actually does something more useful with ndarrays: A “magic square” is a nxn matrix all of whose row sums, column sums and the sums of the two diagonals are the same. The function ```is_magic(matrix)``` in the program below checks if a ndarray represents a magic square:
###Code
import numpy as np
def is_magic(matrix):
# check if matrix is nxn
dim = matrix.shape
if len(dim)!=2 or dim[0] != dim[1]: return False
N = dim[0]
# calculate the sum of the prime diagonal
s = 0
for i in range(0, N):
s = s + matrix[i][i]
# calculate the sum of the other diagonal
s2 = 0
for i in range(0,N):
s2 = s2 + matrix[i][N-i-1]
if (s != s2): return False
# For sums of Rows
for i in range(0, N):
rowSum = 0;
for j in range(0, N):
rowSum += matrix[i][j]
# check if every row sum is equal to prime diagonal sum
if (rowSum != s):
return False
# For sums of Columns
for i in range(0, N):
colSum = 0
for j in range(0, N):
colSum += matrix[j][i]
# check if every column sum is equal to prime diagonal sum
if (s != colSum):
return False
# if all yes, return true
return True
# test program:
A = np.array([[4,9,2],
[3,5,7],
[8,1,6]])
B = np.array([[3,9,2],
[4,5,7],
[8,1,6]])
print(f"Is A magic? {is_magic(A)}")
print(f"Is B magic? {is_magic(B)}")
###Output
Is A magic? True
Is B magic? False
###Markdown
MatplotlibMatplotlib (https://matplotlib.org/) is Python's 2D plotting library. A number of plotting functions in other libraries, for example the Pandas plotting functions, are actually wrappers around the respective Matplotlib functions. Here is a first simple example with random data:
###Code
import matplotlib.pyplot as plt
x = [1,2,3,4,5,6,7,8,9,10]
y = [34,53,64,10,60,40,73,23,49,10]
plt.plot(x,y)
plt.show()
###Output
_____no_output_____
###Markdown
First the ```matplotlib.pyplot``` module (https://matplotlib.org/api/_as_gen/matplotlib.pyplot.html) is imported and given the shorter name ```plt```. Then two lists x and y of same length are created. X contains a sequence of ascending numbers, and y the same number of random values. The simplest plot is to plot x against y, which is done with the ```plt.plot(x,y)``` statement. ```plt.show()``` then shows the plot.Instead of or in addition to displaying the plots to the user, they can also be saved into raster or vector files for later use with the ```savefig``` function. See the following code for an example that also uses further parameters of the plot function to change the color and add markers to the plotted line:
###Code
plt.plot(x,y, color="r", marker="o")
plt.savefig("img/plot.png")
plt.savefig("img/plot.pdf")
###Output
_____no_output_____
###Markdown
Resulting Files: As another example, consider again the Dutch municipalities data set that we worked with earlier. We can create histograms of population numbers with the following code:
###Code
df = pd.read_csv("data/dutch_municipalities.csv", sep="\t")
plt.hist(df["population"])
plt.show()
plt.hist(df["population"], bins=50)
plt.title("Size of Municipalities")
plt.xlabel("inhabitants")
plt.ylabel("# municipalities")
plt.show()
###Output
_____no_output_____
|
Appendix/Week2/List Operations.ipynb
|
###Markdown
Indexing and Slicing Lists Indexing and slicing work just like in strings. Let's work through some examples:
###Code
my_list = ['one','two','three',4,5]
# Grab element at index 0
my_list[0]
# Grab index 1 and everything past it
my_list[1:]
# Grab everything UP TO index 3
my_list[:3]
###Output
_____no_output_____
###Markdown
We can also use + to concatenate lists, just like we did for strings.
###Code
my_list + ['new item']
###Output
_____no_output_____
###Markdown
Note: This doesn't actually change the original list!
###Code
my_list
###Output
_____no_output_____
###Markdown
You would have to reassign the list to make the change permanent.
###Code
# Reassign
my_list = my_list + ['add new item permanently']
my_list
###Output
_____no_output_____
###Markdown
We can also use the * for a duplication method similar to strings:
###Code
# Make the list double
my_list * 2
# Again doubling not permanent
my_list
###Output
_____no_output_____
|
tests/hmm_example_21a.ipynb
|
###Markdown
HMM EXAMPLES
###Code
# do all the imports
%matplotlib inline
import sys, os,time
import numpy as np
import pandas as pd
from IPython.display import display, HTML, clear_output
import ipywidgets as widgets
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
#homedir = os.path.expanduser('~')
#sys.path.append(os.path.join(homedir,'Nextcloud','github','scikit-speech'))
from pyspch import libhmm
from pyspch import libhmm_plot as hmmplot
from pyspch import utils as spchu
# print all variable statements
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
# graphical and print preferences
cmap_1 = sns.light_palette("caramel",50,input="xkcd")[0:20]
cmap_2 = sns.light_palette("caramel",50,input="xkcd",reverse=True)
cmap = cmap_2
pd.options.display.float_format = '{:,.3f}'.format
mpl.rcParams['figure.figsize'] = [12.0, 6.0]
#mpl.rcParams['ps.papersize'] = 'A4'
mpl.rcParams['xtick.labelsize'] = 14
mpl.rcParams['ytick.labelsize'] = 14
mpl.rcParams['axes.titlepad'] = 15
mpl.rcParams['axes.titlesize'] = 'large'
mpl.rcParams['axes.linewidth'] = 2
mpl.rc('lines', linewidth=3, color='k')
###Output
_____no_output_____
###Markdown
A standard piano keyboard with 88 keys looks like this:The note marked in red is "C4", i.e. the C key in the 4th octave.
###Code
help(hmmplot)
%%HTML
<style type="text/css">
table.dataframe td, table.dataframe th {
border: 2px black solid !important;
column-width: 60px;
color: black !important;
}
###Output
_____no_output_____
###Markdown
Example (1) - Course NotesThe HMM is shown in the drawing below
###Code
# basic initialization creates a model without state transitions
hmm1 = libhmm.DHMM(n_states=3,n_symbols=2,labels=['A','B'],prob_style="lin")
# initialize as a simple left-to-right model
hmm1.init_topology(type="lr",selfprob=0.5)
# or you can with the initialization give transition and emission prob matrices
hmm1 = libhmm.DHMM(n_states=3,n_symbols=2,labels=['A','B'],prob_style="lin")
imat = np.array([1.0, 0.0, 0.])
emat = np.array([[.7,.3],[.1, .9],[.6,.4]])
tmat = np.array([[.6,.4,0.],[0.,.5,.5],[0.,0.,1.]])
hmm1 = libhmm.DHMM(n_states=3,labels=['A','B'],prob_style="lin",
transmat=tmat,initmat=imat,emissionmat=emat)
hmm1.print_model()
#
# set an observation sequence
Xl=['A','B','B','A','B']
X = [hmm1.labels.index(x) for x in Xl]
print("OBSERVATIONS\n")
pd.DataFrame([Xl,X],index=['LABEL','LBL_INDEX'])
###Output
_____no_output_____
###Markdown
Trellis Computations: 1. Forward Pass Probabilities (Viterbi, Forward Algorithm)The **TRELLIS** is a matrix structure of shape (n_states,n_samples) containing in *cell (i,t)* the probability of being in *state S_i*(note: strictly speaking in a discrete density model we have observation *probabilities* and in a continuous density model we work with *observation likelihoods*; when talking about the general case we may use the terms probabilities/likelihoods in a loose way)With *forward pass* we indicate that the Trellis is composed in left-to-right fashion, i.e. a trellis cell contains the probability after having observerd *all observations up to X_t*. When working with an existing HMM we typically only need a forward pass.( A *backward pass* (working from last frame till current) is only needed in the forward-backward training algorithm for HMMs. )It is standard and efficient to fill a Trellis in a left-to-right *time synchronous* way, i.e. all cells (\*,t) are computed as soon as observation X(t) becomes available and for first order Markov models only knowledge of the current observation and the previous column of the trellis is required.Hence the trellis computations are simple recursions (coming in 2 flavors):- Viterbi Probability (computes the probability along the most likely path, it is typically used for decoding/recognition and alignment)$ P(i,t) = \max_j P(j,t-1) * P(j,i) * P(X(t)|i) $- Forward Probability (computes the "true" probability, is mainly used in training HMMs with the Forward-Backward algorithm) $ P(i,t) = \sum_j P(j,t-1) * P(j,i) * P(X(t)|i) $Note:- In both cases the sum- or max-operators need to be applied over all possible states that have a transition leading into *State S_i*- The *state likelihoods* P(X(t)|i) are the likelihood of observing X(t) in State i (also called emmission likelihood)- We further need some initialization probabilities, that tell us the probability of starting in a State with the first observation, so that we can start the recursionThe left-to-right recursive implementation is illustrated below for the basic example using **Viterbi**:- the trellis is the main matrix structure- the annotations above the matrix contain both the label of the observation and the state likelihoods
###Code
for i in range(len(X)):
clear_output(wait=True);
hmmplot.plot_trellis(hmm1,X[0:i+1],plot_frameprobs=True,fmt=".4f")
plt.close()
time.sleep(1)
###Output
_____no_output_____
###Markdown
All the computation in detailsSet Debug True or False for greater levels of detaul
###Code
Debug= True
# initialization routine
def init_trellis(hmm,X):
buf = np.zeros(len(hmm.states))
state_likelihoods = hmm.compute_frameprobs(X)
buf = hmm.initmat * state_likelihoods
return(buf)
# single recursion step
def viterbi_step(hmm,X,buffer):
newbuf = np.zeros(buffer.shape)
state_likelihoods = hmm.compute_frameprobs(X)
print('\nX[t]=',hmm.labels[x],"\nState Likelihoods[.,:]:",state_likelihoods)
for to_state in range(hmm.n_states):
if(Debug):
print("To: %s" % hmm.states[to_state])
for from_state in range(hmm.n_states):
new = hmm.transmat[from_state,to_state] * buffer[from_state]
if(Debug):
print(" -- P(%s,t-1) x P(%s|%s): %.3f x %.3f = %.3f" %
(hmm.states[from_state], hmm.states[to_state],hmm.states[from_state],buffer[from_state],hmm.transmat[from_state,to_state], new) )
if( new > newbuf[to_state] ):
best_tp = new
best_state = from_state
newbuf[to_state] = best_tp * state_likelihoods[to_state]
if(Debug):
print(" --> Best Transition is from state %s: %.3f" %
(hmm.states[best_state], best_tp) )
#print(" --> Observation Probability in state %s for observation %s : %.3f " %
# (hmm.states[best_state], X, state_likelihoods[to_state]))
print(" >>> P(%s,t)= %.3f x %.3f = %.3f " %
(hmm.states[to_state], best_tp, state_likelihoods[to_state], newbuf[to_state]))
return(state_likelihoods,newbuf)
# apply the baseline Viterbi algorithm to our model hmm1 and observation sequence X
buf=init_trellis(hmm1,X[0])
trellis = [buf]
print('INITIALIZATION: X[t]=',hmm1.labels[X[0]],'\n',"Trellis[0,:]:",buf,'\n')
print('RECURSION:')
for x in X[1:]:
likelihoods, newbuf = viterbi_step(hmm1,x,buf)
print('Trellis new buffer [t,:]:',newbuf)
buf = newbuf.copy()
trellis = np.r_[trellis,[buf]]
print("\nFULL TRELLIS")
print(trellis.T)
###Output
_____no_output_____
###Markdown
2. COMPLETION and BACKTRACKING+ a. COMPLETION The probability of the full observation being generated by the underlying HMM is found in final column of the Trellis.We just need to look for the highest scoring cell amongst all states that are admissible ending states.E.g. in a left-to-right model as the one under consideration we implicitly assume that the we need to end in the final state.+ b. BACKPOINTERS and BACKTRACKING Often we are not only interested in the probability that our observation has for the model, but we may also want to know which states have been traversed (e.g. when we do speech recognition and states are phonemes or words). In such situation we need to find the state alignment that underlies the best path. This will only be possible when applying the **Viterbi** algorithm and when maintaining **backpointers of the full trellis**. During the forward path computations we add a backpointers in each cell: i.e. we mark the state from which we entered the current state to give us the max probability. Finally, when we have completed the Trellis, we can do backtracking from the final state following the backpointers all the way to the initial frame.
###Code
frameprobs, trellis, backptrs, alignment = hmm1.viterbi_trellis(X)
for i in range(len(X)):
clear_output(wait=True);
align = False if (i < len(X)-1) else True
hmmplot.plot_trellis(hmm1,X[0:i+1],plot_backptrs=True,plot_frameprobs=True,plot_alignment=align,
plot_norm=True,cmap=cmap_2,vmin=0,vmax=.5)
plt.close()
time.sleep(2)
# plotting it all once more
empty_line = pd.DataFrame([""]*len(Xl),columns=[""]).T
pd.concat([
pd.DataFrame(Xl,columns=[""]).T,
empty_line,
pd.DataFrame(frameprobs.T,index=hmm1.states),
empty_line,
pd.DataFrame(trellis.T,index=hmm1.states),
empty_line,
pd.DataFrame(backptrs.T,index=hmm1.states),
empty_line,
pd.DataFrame([hmm1.states[i] for i in alignment],columns=[""]).T ]
,keys=["OBSERVATIONS",".","LIKELILHOODS","..","TRELLIS","...","BACKPOINTERS","....","ALIGNMENT"] )
# 16 JUNE 2021, PM
# An HMM with single state phonemes (TH,IH,S) that can recognize THIS vs. IS
# - enforced begin silence
# - optional silence at the end
#
# S0 = Silence; S1 = "TH"; S2 = "IH"; S3="S"
# Word 1 = This ( SIL S1 S3 S1 S3 [sil])
# Word 2 = is ( SIL S2 S3 S2 S3 [sil])
#
hmm = libhmm.DHMM(n_states=4,n_symbols=4,prob_style="prob",states= ['SIL','TH','IH ','S'],labels=['A','B','C','D'])
hmm.init_topology(type='lr',selfprob=0.5)
hmm.transmat = np.array([ [0.6, .2, .2, 0.0], [0., .5, .5, .0 ], [ 0., 0.0, .5, .5 ], [0.15, .0, .0, .85] ])
target_emissionprob = np.array([ [0.70, 0.15, 0.1, 0.05 ], [0.2, 0.45, 0.30, 0.05],
[0.2, 0.2 ,.5, .1], [0.1, .15, .15, .60] ])
hmm.emissionmat = spchu.normalize(target_emissionprob,axis=1)
hmm.end_states= [0,3]
#hmm.set_probstyle("log10")
pd.options.display.float_format = '{:,.2f}'.format
hmm.print_model()
# set an observation sequence
Xl=['A','B','C','B','D','A']
X = [hmm.labels.index(x) for x in Xl]
print("OBSERVATION SEQUENCE\n")
print(Xl)
#print(pd.DataFrame([Xl],index=[""]).to_string(index=False))
#
# plotting a partial trellis
print("\nPARTIAL TRELLIS\n")
pd.options.display.float_format = '{:,.4f}'.format
frameprobs, trellis, backptrs, alignment = hmm.viterbi_trellis(X)
empty_line = pd.DataFrame([""]*len(Xl),columns=[""]).T
trellis[3:6,:] = np.nan
df=pd.DataFrame(trellis,index=Xl,columns=hmm.states).T.fillna("")
display(df)
# Solution
fig = hmmplot.plot_trellis(hmm,X,cmap=cmap_caramel,vmin=0,vmax=1,fmt=".2e",
plot_norm=True,
plot_frameprobs=True,plot_backptrs=True,
plot_alignment=True,figsize=(16,6))
#plt.close()
# 17 August 2020
#
# State 0 = Silence; S1 = "P"; S2="M" ; S3 = "AH";
# Word 1 = pa ( SIL S1 S3 [SIL] )
# Word 2 = pap ( SIL S1 S3 S1 [SIL] )
# Word 3 = ma ( SIL S2 S3 [SIL] )
# Word 4 = mam ( SIL S2 S3 S2 [SIL])
# -- papa, mama,
#
hmm = libhmm.DHMM(n_states=4,n_symbols=5,prob_style="prob",states= ['SIL','P ','M ','AH'],labels=['L1','L2','L3','L4','L5'])
hmm.transmat = np.array([ [0.7, .15, .15, 0.0],
[ 0.05, .4, 0.0, 0.6 ],
[ 0.05, 0.0, 0.5, 0.5 ],
[ 0.2, .1, 0.1, 0.7] ])
target_emissionprob = np.array([ [0.65, 0.07, 0.1, 0.1, 0.02 ],
[0.1, 0.6, 0.1, 0.2, 0.1],
[0.1, 0.2 ,.48,.12, 0.1],
[0.05, .05, .05, .40, .45] ])
hmm.emissionmat = spchu.normalize(target_emissionprob,axis=1)
hmm.set_probstyle("log")
hmm.print_model()
hmm.end_states=[0]
X = [ 0, 1, 1, 4, 3, 1, 0 ]
Xl = [hmm.labels[i] for i in X]
print("OBSERVATION SEQUENCE\n")
print(Xl)
#
# plotting a partial trellis
print("\nPARTIAL TRELLIS\n")
pd.options.display.float_format = '{:,.4f}'.format
frameprobs, trellis, backptrs, alignment = hmm.viterbi_trellis(X)
empty_line = pd.DataFrame([""]*len(Xl),columns=[""]).T
trellis[4:8,:] = np.nan
df=pd.DataFrame(trellis,index=Xl,columns=hmm.states).T.fillna("")
display(df)
fig = hmmplot.plot_trellis(hmm,X,cmap=cmap_caramel,vmin=-4,vmax=0,fmt=".2f",
plot_norm=True,
plot_frameprobs=True,plot_backptrs=True,
plot_alignment=True,figsize=(16,6))
plt.close()
display(fig)
###Output
_____no_output_____
|
Kristjan/Naive Bayes with preprocessing and public test.ipynb
|
###Markdown
Last* Prediction accuracy for naive bayes model on train data: 96.494* Prediction accuracy for naive bayes model on validation data: 90.411* F1 score for naive bayes model on train data: 96.879* F1 score for naive bayes model on validation data: 91.954
###Code
ngram_vectorizer = TfidfVectorizer(max_features=40000,
min_df=5,
max_df=0.5,
analyzer='word',
stop_words='english',
ngram_range=(1, 3))
tfidf_train = ngram_vectorizer.fit_transform(df['lemmatized_articles'])
y_train = df['is_adverse_media']
nb_model = MultinomialNB(alpha=best_alpha)
nb_model.fit(tfidf_train, y_train)
public_test = pd.read_csv('../public_test.csv')
!pwd
public_test["article"] = public_test["title"] + " " + public_test["article"]
public_test = public_test.drop(["title"], axis =1)
public_test_lemmatized = public_test[['article', 'label']].copy()
public_test_lemmatized["article"] = public_test_lemmatized["article"].apply(lemmatize)
public_test_lemmatized = public_test_lemmatized.reset_index()
public_test_lemmatized = public_test_lemmatized.drop(['index'], axis=1)
public_test_lemmatized
tfidf_public_test = ngram_vectorizer.transform(public_test_lemmatized.article)
public_test_preds_nb = nb_model.predict(tfidf_public_test)
public_test_accuracy_nb = accuracy_score(public_test.label, public_test_preds_nb)
public_test_f1_score_nb = f1_score(public_test.label, public_test_preds_nb)
print('Prediction accuracy for naive bayes model on public test data:', round(public_test_accuracy_nb*100, 3))
print()
print('F1 score for naive bayes model on public test data:', round(public_test_f1_score_nb*100, 3))
Using Karl's cleaning and lemmatization, title added to article:
Prediction accuracy for naive bayes model on public test data: 90.566
F1 score for naive bayes model on public test data: 92.537
Original cleaned_lemmatized_text.csv for train and lemmatize func is :
Prediction accuracy for naive bayes model on public test data: 91.824
F1 score for naive bayes model on public test data: 93.467
tfidf_public_test = ngram_vectorizer.transform(public_test_lemmatized.article)
public_test_preds_nb = nb_model.predict(tfidf_public_test)
public_test_accuracy_nb = accuracy_score(public_test.label, public_test_preds_nb)
public_test_f1_score_nb = f1_score(public_test.label, public_test_preds_nb)
print('Prediction accuracy for naive bayes model on public test data:', round(public_test_accuracy_nb*100, 3))
print()
print('F1 score for naive bayes model on public test data:', round(public_test_f1_score_nb*100, 3))
###Output
Prediction accuracy for naive bayes model on public test data: 91.824
F1 score for naive bayes model on public test data: 93.333
|
portfolio_planner_hw.ipynb
|
###Markdown
Portfolio PlannerIn this activity, you will use the iedfinance api to grab historical data for a 60/40 portfolio using `SPY` to represent the stock portion and `AGG` to represent the bonds.
###Code
from iexfinance.stocks import get_historical_data
import iexfinance as iex
###Output
_____no_output_____
###Markdown
Data CollectionIn this step, you will need to use the IEX api to fetch closing prices for the `SPY` and `AGG` tickers. Save the results as a pandas DataFrame
###Code
tickers = ["SPY", "AGG"]
end_date = datetime.now()
start_date = end_date + timedelta(-1260)
df = get_historical_data(tickers, start_date, end_date, output_format='pandas')
df.head
df.drop(columns = ['open', 'high', 'low', 'volume'], level=1, inplace=True)
df.head()
###Output
_____no_output_____
###Markdown
Monte Carlo SimulationIn this step, you will run Monte Carlo Simulations for your portfolio to model portfolio performance at different retirement ages. Complete the following steps:1. Calculate the daily returns for the SPY and AGG closing prices.2. Calculate volatility for both the SPY and AGG closing prices.3. Find the last day's closing price for both stocks and save those as variables.4. Run a Monte Carlo Simulation of at least 100 iterations and generate at least 20 years of closing prices HINTS:There are 252 trading days per year, so the number of records to generate for each Monte Carlo run will be 252 days * 20 years
###Code
# Calculate the daily roi for the stocks
daily_returns = df.pct_change()
daily_returns.head()
avg_daily_return_spy = daily_returns.mean()['SPY']['close']
avg_daily_return_agg = daily_returns.mean()['AGG']['close']
print(avg_daily_return_agg)
print(avg_daily_return_spy)
# Calculate volatility
std_daily_return_spy = daily_returns.std()['SPY']['close']
std_daily_return_agg = daily_returns.std()['AGG']['close']
print(std_daily_return_agg)
print(std_daily_return_spy)
# Save the last day's closing price
spy_last_price = df['SPY']['close'][-1]
agg_last_price = df['AGG']['close'][-1]
# Setup the Monte Carlo Parameters
num_simulations = 500
num_trading_days = 252 * 30
monte_carlo = pd.DataFrame()
portfolio_cumulative_returns = pd.DataFrame()
num_simulations = 500
num_trading_days = 252 * 30
spy_last_price = df['SPY']['close'][-1]
agg_last_price = df['AGG']['close'][-1]
monte_carlo = pd.DataFrame()
portfolio_cumulative_returns = pd.DataFrame()
for n in range(num_simulations):
simulated_spy_prices = [spy_last_price]
simulated_agg_prices = [agg_last_price]
for i in range(num_trading_days):
simulated_spy_price = simulated_spy_prices[-1] * (1 + np.random.normal(avg_daily_return_spy, std_daily_return_spy))
simulated_agg_price = simulated_agg_prices[-1] * (1 + np.random.normal(avg_daily_return_agg, std_daily_return_agg))
simulated_spy_prices.append(simulated_spy_price)
simulated_agg_prices.append(simulated_agg_price)
monte_carlo['SPY Prices'] = pd.Series(simulated_spy_prices)
monte_carlo['AGG Prices'] = pd.Series(simulated_agg_prices)
simulated_daily_return = monte_carlo.pct_change()
weights = [0.60, 0.40]
portfolio_daily_return = simulated_daily_return.dot(weights)
portfolio_cumulative_returns[n] = (1+ portfolio_daily_return.fillna(0)).cumprod()
portfolio_cumulative_returns.head()
# Visualize the Simulation
portfolio_cumulative_returns.plot(legend=None)
plt.show()
# Select the last row for the cumulative returns (cumulative returns at 30 years)
ending_cumulative_returns_30 = portfolio_cumulative_returns.iloc[-1, :]
ending_cumulative_returns_30.head()
# Select the last row for the cumulative returns (cumulative returns at 20 years)
ending_cumulative_returns_20 = portfolio_cumulative_returns.iloc[-2521, :]
ending_cumulative_returns_20.head()
# Display the 90% confidence interval for the ending returns
confidence_interval_30 = ending_cumulative_returns_30.quantile(q=[0.05, 0.95])
confidence_interval_20 = ending_cumulative_returns_20.quantile(q=[0.05, 0.95])
print(confidence_interval_30)
print(confidence_interval_20)
# Visualize the distribution of the ending returns
ending_cumulative_returns_30.plot(kind='hist', density=True, bins=20)
ending_cumulative_returns_30.value_counts(bins=10) / len(ending_cumulative_returns_30)
plt.axvline(confidence_interval_30.iloc[0], color='r')
plt.axvline(confidence_interval_30.iloc[1], color='r')
###Output
_____no_output_____
###Markdown
--- Retirement AnalysisIn this section, you will use the monte carlo model to answer the following retirement planning questions:1. What are the expected cumulative returns at 30 years for the 10th, 50th, and 90th percentiles?2. Given an initial investment of `$20,000`, what is the expected portfolio return in dollars at the 10th, 50th, and 90th percentiles?3. Given the current projected annual income from the Plaid analysis, will a 4% withdraw rate from the retirement portfolio meet or exceed that value at the 10th percentile?4. How would a 50% increase in the initial investment amount affect the 4% retirement withdrawal? What are the expected cumulative returns at 30 years for the 10th, 50th, and 90th percentiles?
###Code
initial_investment = 20000
confidence_interval_10 = ending_cumulative_returns_30.quantile(q=[0.95, 0.05])
confidence_interval_50 = ending_cumulative_returns_30.quantile(q=[0.5, 0.5])
investment_pnl_lower_bound_90 = (initial_investment * confidence_interval_30.iloc[0])
investment_pnl_upper_bound_90 = (initial_investment * confidence_interval_30.iloc[1])
investment_pnl_lower_bound_50 = (initial_investment * confidence_interval_50.iloc[0])
investment_pnl_upper_bound_50 = (initial_investment * confidence_interval_50.iloc[1])
investment_pnl_lower_bound_10 = (initial_investment * confidence_interval_10.iloc[0])
investment_pnl_upper_bound_10 = (initial_investment * confidence_interval_10.iloc[1])
ending_cumulative_returns_30.value_counts(bins=10) / len(ending_cumulative_returns_30)
###Output
_____no_output_____
###Markdown
Given an initial investment of `$20,000`, what is the expected portfolio return in dollars at the 10th, 50th, and 90th percentiles?
###Code
print(f"There is a 90% chance that an initial investment of $20,000 in the portfolio"
f" over the next 7560 trading days will end within in the range of"
f" ${investment_pnl_lower_bound_90} and ${investment_pnl_upper_bound_90}")
print()
print()
print(f"There is a 50% chance that an initial investment of $20,000 in the portfolio"
f" over the next 7560 trading days will end within in the range of"
f" ${investment_pnl_lower_bound_50} and ${investment_pnl_upper_bound_50}")
print()
print()
print(f"There is a 10% chance that an initial investment of $20,000 in the portfolio"
f" over the next 7560 trading days will end within in the range of"
f" ${investment_pnl_lower_bound_10} and ${investment_pnl_upper_bound_10}")
###Output
There is a 90% chance that an initial investment of $20,000 in the portfolio over the next 7560 trading days will end within in the range of $66354.83353359034 and $264764.45699693996
There is a 50% chance that an initial investment of $20,000 in the portfolio over the next 7560 trading days will end within in the range of $142715.9358974036 and $142715.9358974036
There is a 10% chance that an initial investment of $20,000 in the portfolio over the next 7560 trading days will end within in the range of $264764.45699693996 and $66354.83353359034
###Markdown
Given the current projected annual income from the Plaid analysis, will a 4% withdraw rate from the retirement portfolio meet or exceed that value at the 10th percentile?Note: This is effectively saying that 90% of the expected returns will be greater than the return at the 10th percentile, so this can help measure the uncertainty about having enough funds at retirement
###Code
withraw = 0.04 * (initial_investment * ending_cumulative_returns_30.sum())
withraw
exceeding value at the 10th percentile
###Output
_____no_output_____
###Markdown
How would a 50% increase in the initial investment amount affect the 4% retirement withdrawal?
###Code
also amount of retirement withdrawl will increased by 50% percent.
###Output
_____no_output_____
###Markdown
Optional ChallengeIn this section, you will calculate and plot the cumulative returns for the median and 90% confidence intervals. This plot shows the expected cumulative returns for any given day between the first day and the last day of investment.
###Code
# YOUR CODE HERE
###Output
_____no_output_____
|
importing interact.ipynb
|
###Markdown
Automated decryption of the Shift CipherImagine you are walking through a forest and you discover a bottle with a sheet of paper in it. On the paper is written the following four passages.
###Code
print '1. TAKDQXMWLDTOTKAAGOHIJFJZRTIOSKFZKZIOSYIOUHKHSBCKRJIWUBMXSZRJUYOJEOYTCHZADSSJUTXRDTCQMCNQFGYNAYDDTZMXWACNHEWPBMIQMVXBJYFCJOHPNUFQSDIBSOQZTEOMRCWIDWQEERKYMZXRBBPXMWBLVRZBWPALLRIBEEIPHJQOYSKAUBMBXGKXQUSITSPQWFHOLKGYFDJUZLPSQNXVVQYMEGCXWQLJVHIVHKRANGLJSDLNDVZFWCTDXABOKBYAJMWYJRKICQMSMGSDHNLHVLNQJQLDWPLOKMXIWUPIHCMWNLBZBFKIPWCNLZDITFGEALEOFRYYPKOBVPVUFTODLFMGIIGVVDHQFAEBCLEDSRMZWXMHUVSJXFTPRSROWRQKDLKKSDWQXOJSTJUOAPAZIZSECFFVNJZYZFOIGKZWHMVMPIBAXKFOYAAXCTCOMDFHQGRHKIDSPRKUQTQ\n\n2. WHKOGHVSPSGHCTHWASGWHKOGHVSKCFGHCTHWASGWHKOGHVSOUSCTKWGRCAWHKOGHVSOUSCTTCCZWGVBSGGWHKOGHVSSDCQVCTPSZWSTWHKOGHVSSDCQVCTWBQFSRIZWHMWHKOGHVSGSOGCBCTZWUVHWHKOGHVSGSOGCBCTROFYBSGGWHKOGHVSGDFWBUCTVCDSWHKOGHVSKWBHSFCTRSGDOWFKSVORSJSFMHVWBUPSTCFSIGKSVORBCHVWBUPSTCFSIGKSKSFSOZZUCWBURWFSQHHCVSOJSBKSKSFSOZZUCWBURWFSQHHVSCHVSFKOMWBGVCFHHVSDSFWCRKOGGCTOFZWYSHVSDFSGSBHDSFWCRHVOHGCASCTWHGBCWGWSGHOIHVCFWHWSGWBGWGHSRCBWHGPSWBUFSQSWJSRTCFUCCRCFTCFSJWZWBHVSGIDSFZOHWJSRSUFSSCTQCADOFWGCBCBZM\n\n3. JCEFOCAQTQOCRPCJDQOJCEFOCAQERGOCRPCJDQOJCEFOCAQFLQRPEJOXRDJCEFOCAQFLQRPPRRVJOAUQOOJCEFOCAQQYRWARPTQVJQPJCEFOCAQQYRWARPJUWGQXKVJCNJCEFOCAQOQFORURPVJLACJCEFOCAQOQFORURPXFGSUQOOJCEFOCAQOYGJULRPARYQJCEFOCAQEJUCQGRPXQOYFJGEQAFXQHQGNCAJULTQPRGQKOEQAFXURCAJULTQPRGQKOEQEQGQFVVLRJULXJGQWCCRAQFHQUEQEQGQFVVLRJULXJGQWCCAQRCAQGEFNJUOARGCCAQYQGJRXEFOORPFGVJSQCAQYGQOQUCYQGJRXCAFCORDQRPJCOURJOJQOCFKCARGJCJQOJUOJOCQXRUJCOTQJULGQWQJHQXPRGLRRXRGPRGQHJVJUCAQOKYQGVFCJHQXQLGQQRPWRDYFGJORURUVN\n\n4. MCDPZAYGXFMBOTDIITRCZUGEAZTXHBXGULNMMBKCGCPALHLYUCOPYTQJWBCIAOKRNPQNJWBNEMVKKJGSDXHFYOOZBAZKDPPDBANLEZJUKJSDAKDFCZLIRAGYNSSKGMWRNHQAEPAONFXVIUGPCKCVRMIGGYBJAHFDHYAETJLYOFQQJPDZYAHHGUJHGCGMKTMAADOJHGTUAPWHEINCTFLBONZVSXCQORRPOFUGUPCKZGKYPDLUFODNFLJTCUYCVEREWDCEERQULFTXEVKKEVVTDPWFOMBRMHUBPYLGCTCUAYVQKKCQNMJDOUGRAWOTRYFOJKYEYZEOGVKFEPASOIOSFGBXIIJTWKTOKLZCMRTVBHGMDKRSEILKYKRDNAQDDKDVJHBPUWAYKSBAAALUTHKSYZDCSMZEVHMKGXBSZBPVGKTERITREBOJIWNKFRRESAPHXBTVEFVAHPXLWXDEGTCLTWBAPUH'
###Output
1. TAKDQXMWLDTOTKAAGOHIJFJZRTIOSKFZKZIOSYIOUHKHSBCKRJIWUBMXSZRJUYOJEOYTCHZADSSJUTXRDTCQMCNQFGYNAYDDTZMXWACNHEWPBMIQMVXBJYFCJOHPNUFQSDIBSOQZTEOMRCWIDWQEERKYMZXRBBPXMWBLVRZBWPALLRIBEEIPHJQOYSKAUBMBXGKXQUSITSPQWFHOLKGYFDJUZLPSQNXVVQYMEGCXWQLJVHIVHKRANGLJSDLNDVZFWCTDXABOKBYAJMWYJRKICQMSMGSDHNLHVLNQJQLDWPLOKMXIWUPIHCMWNLBZBFKIPWCNLZDITFGEALEOFRYYPKOBVPVUFTODLFMGIIGVVDHQFAEBCLEDSRMZWXMHUVSJXFTPRSROWRQKDLKKSDWQXOJSTJUOAPAZIZSECFFVNJZYZFOIGKZWHMVMPIBAXKFOYAAXCTCOMDFHQGRHKIDSPRKUQTQ
2. WHKOGHVSPSGHCTHWASGWHKOGHVSKCFGHCTHWASGWHKOGHVSOUSCTKWGRCAWHKOGHVSOUSCTTCCZWGVBSGGWHKOGHVSSDCQVCTPSZWSTWHKOGHVSSDCQVCTWBQFSRIZWHMWHKOGHVSGSOGCBCTZWUVHWHKOGHVSGSOGCBCTROFYBSGGWHKOGHVSGDFWBUCTVCDSWHKOGHVSKWBHSFCTRSGDOWFKSVORSJSFMHVWBUPSTCFSIGKSVORBCHVWBUPSTCFSIGKSKSFSOZZUCWBURWFSQHHCVSOJSBKSKSFSOZZUCWBURWFSQHHVSCHVSFKOMWBGVCFHHVSDSFWCRKOGGCTOFZWYSHVSDFSGSBHDSFWCRHVOHGCASCTWHGBCWGWSGHOIHVCFWHWSGWBGWGHSRCBWHGPSWBUFSQSWJSRTCFUCCRCFTCFSJWZWBHVSGIDSFZOHWJSRSUFSSCTQCADOFWGCBCBZM
3. JCEFOCAQTQOCRPCJDQOJCEFOCAQERGOCRPCJDQOJCEFOCAQFLQRPEJOXRDJCEFOCAQFLQRPPRRVJOAUQOOJCEFOCAQQYRWARPTQVJQPJCEFOCAQQYRWARPJUWGQXKVJCNJCEFOCAQOQFORURPVJLACJCEFOCAQOQFORURPXFGSUQOOJCEFOCAQOYGJULRPARYQJCEFOCAQEJUCQGRPXQOYFJGEQAFXQHQGNCAJULTQPRGQKOEQAFXURCAJULTQPRGQKOEQEQGQFVVLRJULXJGQWCCRAQFHQUEQEQGQFVVLRJULXJGQWCCAQRCAQGEFNJUOARGCCAQYQGJRXEFOORPFGVJSQCAQYGQOQUCYQGJRXCAFCORDQRPJCOURJOJQOCFKCARGJCJQOJUOJOCQXRUJCOTQJULGQWQJHQXPRGLRRXRGPRGQHJVJUCAQOKYQGVFCJHQXQLGQQRPWRDYFGJORURUVN
4. MCDPZAYGXFMBOTDIITRCZUGEAZTXHBXGULNMMBKCGCPALHLYUCOPYTQJWBCIAOKRNPQNJWBNEMVKKJGSDXHFYOOZBAZKDPPDBANLEZJUKJSDAKDFCZLIRAGYNSSKGMWRNHQAEPAONFXVIUGPCKCVRMIGGYBJAHFDHYAETJLYOFQQJPDZYAHHGUJHGCGMKTMAADOJHGTUAPWHEINCTFLBONZVSXCQORRPOFUGUPCKZGKYPDLUFODNFLJTCUYCVEREWDCEERQULFTXEVKKEVVTDPWFOMBRMHUBPYLGCTCUAYVQKKCQNMJDOUGRAWOTRYFOJKYEYZEOGVKFEPASOIOSFGBXIIJTWKTOKLZCMRTVBHGMDKRSEILKYKRDNAQDDKDVJHBPUWAYKSBAAALUTHKSYZDCSMZEVHMKGXBSZBPVGKTERITREBOJIWNKFRRESAPHXBTVEFVAHPXLWXDEGTCLTWBAPUH
###Markdown
What is the meaning of these passages? Do they have meaning? This can be a very subtle question. The following image is from a 500-year-old document called the Voynich manuscript, and despite the manuscript containing over 200 pages, it is still not known if there is meaning behind the words or if it is an elaborate hoax.  Among our four passages listed above, it turns out that two of them have been encrypted using a cryptosystem and two of them are merely random strings of letters. The goals of this notebook are the following:1. Introduce the shift cipher2. Introduce frequency analysis (both as a method of decryption and as a first approach to the question of whether a piece of text is ciphertext or nonsense)3. Write a function which automatically decrypts messages that were encrypted using the shift cipher We will use some custom functions (i.e., some functions which are not part of the Python programming language, but which instead were written for Math 173). To get access to those functions, we need to load a module defining those functions. Place your cursor in the following cell and hit shift+enter to evaluate it and load the functions.
###Code
import test_interact
test_interact = reload(test_interact)
###Output
_____no_output_____
###Markdown
Perhaps the most basic method of encryption (and perhaps the least secure method of encryption) is the *shift cipher*. The *key* associated to the shift cipher is an integer which specifies how much to shift each letter. The key must be exchanged in secret between the encrypter and the recipient; anyone who knows the key will be able to decrypt the secret message. To get a sense for how the shift cipher works, evaluate the following cell and then use the drop-down menu to try different key values. We use the convention that plaintext is usually written with lower-case letters and ciphertext is usually written with upper-case letters.
###Code
test_interact.shift_encrypt_interact('hello there my name is Chris, what is your name?')
###Output
_____no_output_____
###Markdown
We can make it a little more difficult by removing all spaces and punctuation. Then it's no longer an option to look for words of length one and guess that such a word is "a" or "I". It's also no longer an option to guess that a three-letter word which appears often is likely to be "the". But of course, there is still a very simple naive attack on the shift cipher: if an adversary Eve just tries all 26 possible shift amounts, she will be able to recognize which results in English. (Notice that, even though there are infinitely many integers, a shift of 28 is the same as a shift of 2 and is also the same as a shift of -24, so there are really only 26 possibilities. In the language of modular arithmetic, the only important thing about the key is what is its residue modulo 26.)
###Code
test_interact.shift_encrypt_interact2('Lots of drama')
###Output
_____no_output_____
###Markdown
We would now like to automate the naive attack on the shift cipher; in other words, we would like to input a piece of text encrypted using the shift cipher and we would like computer to return the corresponding plaintext. If there are spaces, we can probably use a dictionary to do this, but what about in general? It turns out there is a strategy which generalizes very well to more elaborate cryptosystems and which has nothing to do with recognizing English words, but instead has to do with recognizing the distribution of English letters. Later in the class we will introduce the Vigenere cipher, which is similar to the shift cipher but much more sophisticated (it was once even thought to be unbreakable). To motivate the attack we will eventually use on the Vigenere cipher, we introduce an attack on the shift cipher based on the idea of *frequency analysis*. Some letters in English occur more often than others. In the orange bar that appears below, the letter frequency which occurs in "average" English is shown. For example, one can tell from the bar chart that E is the most common letter, whereas J, Q, X, Z are much less common. Evaluate the following cell, which will help us to decipher the message written inside the parentheses. In the blue bar chart that appears below, the letter frequency in the ciphertext is shown. By using the dropdown menu, try to find an amount which makes the blue chart match as closely as possible to the shape of the orange chart. Does the resulting text which is displayed look like English?
###Code
test_interact.break_shift_interact("XUBBEJXUHUCODQCUYISXHYIMXQJYIOEKHDQCU")
###Output
_____no_output_____
###Markdown
It turns out we already have all the tools necessary to answer the question from the top of this notebook, about whether the passages are secret messages or are simply random letters? In the following cell, apply the function test_interact.makeplot(Y) to each of the four passages from above. Which one do you think is a shift cipher? Which one do you think is another type of cipher? Which two do you think are random? (Warning: strings have to be inside of quotation marks.)
###Code
test_interact.makeplot('JCEFOCAQTQOCRPCJDQOJCEFOCAQERGOCRPCJDQOJCEFOCAQFLQRPEJOXRDJCEFOCAQFLQRPPRRVJOAUQOOJCEFOCAQQYRWARPTQVJQPJCEFOCAQQYRWARPJUWGQXKVJCNJCEFOCAQOQFORURPVJLACJCEFOCAQOQFORURPXFGSUQOOJCEFOCAQOYGJULRPARYQJCEFOCAQEJUCQGRPXQOYFJGEQAFXQHQGNCAJULTQPRGQKOEQAFXURCAJULTQPRGQKOEQEQGQFVVLRJULXJGQWCCRAQFHQUEQEQGQFVVLRJULXJGQWCCAQRCAQGEFNJUOARGCCAQYQGJRXEFOORPFGVJSQCAQYGQOQUCYQGJRXCAFCORDQRPJCOURJOJQOCFKCARGJCJQOJUOJOCQXRUJCOTQJULGQWQJHQXPRGLRRXRGPRGQHJVJUCAQOKYQGVFCJHQXQLGQQRPWRDYFGJORURUVN')
###Output
_____no_output_____
###Markdown
We've seen how to use frequency analysis (in basic cases) to determine if text is ciphertext or random. Earlier we also saw how to use frequency analysis to determine decrypt text encrypted with the shift cipher. How can we automate that process? In other words, how can we automate the process of "try different shift amounts until the graphs match". The idea is to use the notion of *index of coincidence* from class. We will now implement this strategy. Examples of some of the terms defined in the file are shown in the next two cells.
###Code
test_interact.countletters("XUBBEJXUHUCODQCUYISXHYIMXQJYIOEKHDQCU")
test_interact.englishdictionary
###Output
_____no_output_____
###Markdown
The countletters(X) function lists, for each letter in X, how many times it occurs in X. Using the following template, write a new function which takes as input X and as output returns a dictionary letterprops for which letterprops['A'] is the probability that a randomly chosen letter in X is 'A', and similarly for 'B', etc.
###Code
def makeletterprops(X):
X = test_interact.onlyletters(X).upper()
letterprops = {}
temp = test_interact.countletters(X)
length = sum(test_interact.countletters(X).values())
for ch in test_interact.ascii_uppercase:
if ch in temp:
letterprops[ch] = float(temp[ch])/length
else:
letterprops[ch] = 0
return letterprops
###Output
_____no_output_____
###Markdown
Reality check: Add up all the values in your letterprops dictionary. What answer should you get?
###Code
letterprops = makeletterprops("XUBBEJXUHUCODQCUYISXHYIMXQJYIOEKHDQCU")
sum(letterprops.values())
###Output
_____no_output_____
###Markdown
Using the following template, write a function which takes as input X and as output returns the probability that if you choose a random English letter (according to the probabilities above), call it char1, and you choose a random letter from X, call it char2, that char1 = char2. In other words, write a function that computes the index of coincidence between X and average English.
###Code
def compare_to_english(X):
p = 0;
letterprops = makeletterprops(X)
for ch in test_interact.ascii_uppercase:
p = p + letterprops[ch]*test_interact.englishdictionary[ch]
return p
compare_to_english("XUBBEJXUHUCODQCUYISXHYIMXQJYIOEKHDQCU")
###Output
_____no_output_____
###Markdown
Now try out the function compare_to_english with some text that is actually English. You should get something around .068. You shouldn't expect to get that exactly, but it should be noticeably different from the output you get when you apply the function to ciphertext.
###Code
compare_to_english("hello there, my name is chris, what is your name?")
###Output
_____no_output_____
###Markdown
Exercise: Prove that if the input is random text, with each letter occuring equally likely, then the output of compare_to_english will be 1/26, or more precisely, it will be a decimal approximation of 1/26. (How does 1/26 compare to the result above where we input ciphertext?) Write a function autodecrypt(X) which attempts to decrypt from a shift cipher using the following strategy. For each possible shift amount, shift X by that amount using the function shift_decrypt. For each of these 26 results, run the compare_to_english function. Using the results, guess which is the decrypted text, and return that text.
###Code
def autodecrypt(X):
current_index = 0
current_max = 0
for i in range(0,26):
Y = test_interact.shift_decrypt(X,i)
temp = compare_to_english(Y)
if temp > current_max:
current_max = temp
current_index = i
return test_interact.shift_decrypt(X,current_index)
autodecrypt("PSXWSJHVEQE")
###Output
_____no_output_____
###Markdown
If we run our function on the word jazz, what do we get? What's the longest piece of normal-sounding English that you can find for which autodecrypt does not work? (Notice, you don't have to encrypt the phrase, just type it in directly in plain English.)
###Code
autodecrypt('jazz')
autodecrypt('A jazz xylophone song would be really awful')
###Output
_____no_output_____
|
team_directory/ya/Cook's_Distance.ipynb
|
###Markdown

###Code
# Cook's Distance 기준값보다 큰 아웃라이어 제거 (작은 값 남기기)
cooks_d, pvals = influence.cooks_distance
fox_cr = 4 / (N - K - 1)
#plt.stem(np.arange(len(cooks_d)), cooks_d, marketfmt=",")
idx = np.where(cooks_d > fox_cr)[0]
idx
df2 = df.iloc[idx, :]
df2.head(3550)
sm.graphics.plot_leverage_resid2(result)
plt.show()
###Output
_____no_output_____
|
Exercise 3 - conv nets mnist.ipynb
|
###Markdown
Exercise 3: MNISTLets first look at [this fun video](https://www.youtube.com/watch?v=p_7GWRup-nQ) or [this technical video](https://www.youtube.com/watch?v=FmpDIaiMIeA) to get an understanding of what a convolutional neural network is. Goal in this exerciseWe will create a convolutional neural network that classifies handwritten digits (0-9) from the [MNIST dataset](http://yann.lecun.com/exdb/mnist/). The MNIST dataset has 60,000 training examples and 10,000 test samples. The digits are normalised for size and centred. Q: How many output classes do we have in this problem? Please name the type of problem we are trying to solve.*Answer...*The main difference between the previous exercises is that we are now processing images rather than a vector of numbers. Also, we are going to use the GPU to speed up computation. To use GPU on the Google Colab notebook,Navigate to the "Runtime" tab --> "Change runtime type". In the pop-up window, under "Hardware accelerator" select "GPU". The last step of this exercise contains a task. Import dependenciesStart by importing the dependencies we will need for the project
###Code
import numpy
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import Dropout
from keras.layers import Flatten
from keras.layers.convolutional import Conv2D
from keras.layers.convolutional import MaxPooling2D
from sklearn.model_selection import train_test_split
from keras.utils import np_utils
from keras import backend as K
import matplotlib.pyplot as plt
import numpy as np
from sklearn import metrics
import seaborn as sns
if K.image_dim_ordering() != "tf":
print("Backend image dimension ordering is inappropriate. Change it by typing K.image_dim_ordering('tf')")
def plot_acc_loss(history):
f, (ax1, ax2) = plt.subplots(2,1, figsize=(10,10))
# Summarize history of accuracy
ax1.plot(history.history['loss'])
ax1.plot(history.history['val_loss'])
ax1.set_title('model loss')
ax1.legend(['train', 'validation'], loc='upper left')
# Summarize history of accuracy
ax2.plot(history.history['acc'])
ax2.plot(history.history['val_acc'])
ax2.set_title('model accuracy')
ax2.set_xlabel('epoch')
ax2.legend(['train', 'validation'], loc='upper left')
plt.subplots_adjust(hspace=0.5)
plt.show()
def draw_confusion_matrix(true, pred, labels):
"""
Drawing confusion matrix
"""
cm = metrics.confusion_matrix(true, pred, labels)
ax = plt.subplot()
sns.heatmap(cm, annot=True, ax=ax, fmt="d")
#ax.set_xticklabels(['']+labels)
#ax.set_yticklabels(['']+labels)
ax.set_xlabel("Predicted")
ax.set_ylabel("True")
plt.show()
return cm
###Output
_____no_output_____
###Markdown
Import dataThe MNIST dataset has 60,000 training samples and 10,000 test samples.Keras includes a number of datasets, including MNIST in the `keras.datasets` module. To download the MNIST dataset call `mnist.load_data()`.
###Code
(X_train, y_train), (X_test, y_test) = mnist.load_data()
###Output
Downloading data from https://s3.amazonaws.com/img-datasets/mnist.npz
11493376/11490434 [==============================] - 0s 0us/step
###Markdown
We further split our training data into training and validation data. And we will our validation set size to be 0.2 Set seedSet a seed value so that when we repeatedly run our code we will get the same result. Using the same seed is important when you want to compare algorithms.
###Code
seed = 7
numpy.random.seed(seed)
X_train, X_val, y_train, y_val = train_test_split(X_train, y_train, test_size=0.2, random_state=seed)
###Output
_____no_output_____
###Markdown
A two dimensional convolutional neural network expects data to be arranged in a four dimensional shape: *number of samples* x *width* x *height* x *channels*.For example, assume we have 10 RGB images, with widths and heights of 20 pixels. This would need to be shaped into 10 samples, each RGB channel would be split into three separate images (1 for red, 1 for green and 1 for blue). Each image would then be a 2D array with 20 rows and columns.The MNIST data has the wrong shape for a 2D convolutional neural network (3 dimensions rather than four):
###Code
print(X_train.shape)
###Output
(48000, 28, 28)
###Markdown
The data is missing the dimension for channels, so we need to reshape the data to add it in. The images in the MNIST example are gray scale, so they only have 1 channel.This is done using the numpy `reshape` method.
###Code
X_train = X_train.reshape(X_train.shape[0], 28, 28, 1).astype('float32')
X_test = X_test.reshape(X_test.shape[0], 28, 28, 1).astype('float32')
X_val = X_val.reshape(X_val.shape[0], 28, 28, 1).astype('float32')
X_train.shape
###Output
_____no_output_____
###Markdown
Normalize the pixels to the range 0 - 1 Understanding image data
###Code
X_train = X_train / 255
X_test = X_test / 255
X_val = X_val / 255
# Show the first image in the train dataset and the corresponding output variable
plt.imshow(np.array(X_train[2,:,:,0]), cmap='gray')
print(y_train[2])
# Showing the pixel values
five = X_train[2].reshape(28,28)
for row in range(28):
for col in range(28):
print("%.F " % five[row][col], end="")
print("")
y_train[1:10]
###Output
_____no_output_____
###Markdown
One hot encode the target variables as you did in the Iris classification exercise. The data is already numeric so you do not need to use the LabelEncoder.
###Code
y_train = np_utils.to_categorical(y_train)
y_test = np_utils.to_categorical(y_test)
y_val = np_utils.to_categorical(y_val)
num_classes = y_test.shape[1]
print("Number of classes: {0}".format(num_classes))
###Output
Number of classes: 10
###Markdown
Create the model1. The input layer takes inputs with a dimension 28x28x12. The first hidden layer is a `Conv2D` layer. We have set it to have 30 filters (the number of output filters) and the size of the kernel to 5x5.3. The `MaxPooling2D` has a kernel size of 2x2. This downsamples the output of the previous layer by selecting the maxiumum value in each kernel. An example is illustrated below: 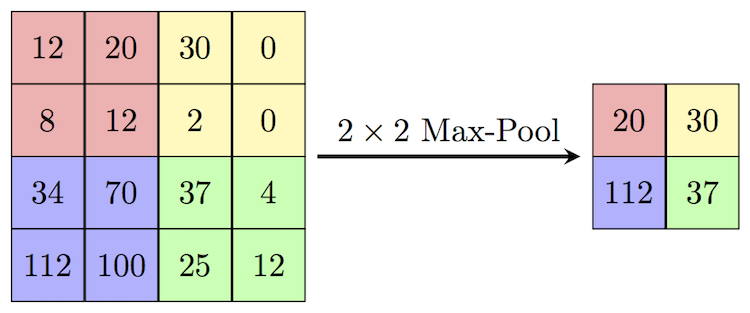4. The `Dropout` layer is used to prevent overfitting. It does this by randomly turning off neurons (50% in this example). 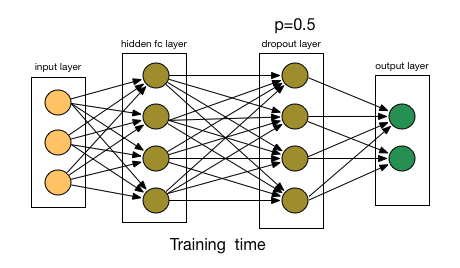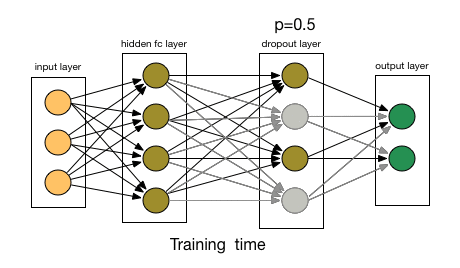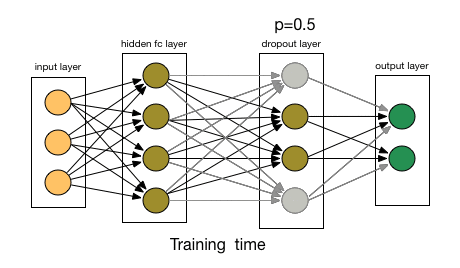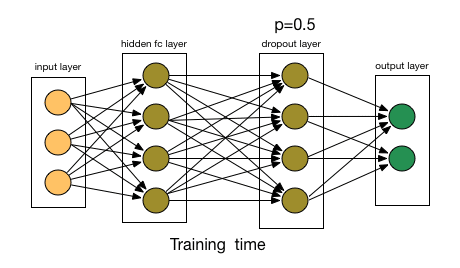5. The `Flatten` layer flattens the Conv2D layers into a normal fully connected layer that can be connected to a Dense layer. 6. A `Dense` fully connected layer is added with 50 neurons.7. The last layer is the output layer, which has 10 neurons (one for each class/digit).
###Code
model = Sequential()
model.add(Conv2D(30, (5, 5), input_shape=(28, 28, 1), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.2))
model.add(Flatten())
model.add(Dense(50, activation='relu'))
model.add(Dense(num_classes, activation='softmax'))
###Output
WARNING: Logging before flag parsing goes to stderr.
W0710 02:31:33.983482 139636698449792 deprecation_wrapper.py:119] From /usr/local/lib/python3.6/dist-packages/keras/backend/tensorflow_backend.py:74: The name tf.get_default_graph is deprecated. Please use tf.compat.v1.get_default_graph instead.
W0710 02:31:34.026873 139636698449792 deprecation_wrapper.py:119] From /usr/local/lib/python3.6/dist-packages/keras/backend/tensorflow_backend.py:517: The name tf.placeholder is deprecated. Please use tf.compat.v1.placeholder instead.
W0710 02:31:34.036042 139636698449792 deprecation_wrapper.py:119] From /usr/local/lib/python3.6/dist-packages/keras/backend/tensorflow_backend.py:4138: The name tf.random_uniform is deprecated. Please use tf.random.uniform instead.
W0710 02:31:34.082878 139636698449792 deprecation_wrapper.py:119] From /usr/local/lib/python3.6/dist-packages/keras/backend/tensorflow_backend.py:3976: The name tf.nn.max_pool is deprecated. Please use tf.nn.max_pool2d instead.
W0710 02:31:34.085995 139636698449792 deprecation_wrapper.py:119] From /usr/local/lib/python3.6/dist-packages/keras/backend/tensorflow_backend.py:133: The name tf.placeholder_with_default is deprecated. Please use tf.compat.v1.placeholder_with_default instead.
W0710 02:31:34.098550 139636698449792 deprecation.py:506] From /usr/local/lib/python3.6/dist-packages/keras/backend/tensorflow_backend.py:3445: calling dropout (from tensorflow.python.ops.nn_ops) with keep_prob is deprecated and will be removed in a future version.
Instructions for updating:
Please use `rate` instead of `keep_prob`. Rate should be set to `rate = 1 - keep_prob`.
###Markdown
Compile the modelThe next step is to compile the model. The loss function (`categorical_crossentropy`) is the same as the Iris multi-class classification exercise.
###Code
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
###Output
W0710 02:31:34.162848 139636698449792 deprecation_wrapper.py:119] From /usr/local/lib/python3.6/dist-packages/keras/optimizers.py:790: The name tf.train.Optimizer is deprecated. Please use tf.compat.v1.train.Optimizer instead.
W0710 02:31:34.196775 139636698449792 deprecation_wrapper.py:119] From /usr/local/lib/python3.6/dist-packages/keras/backend/tensorflow_backend.py:3295: The name tf.log is deprecated. Please use tf.math.log instead.
###Markdown
Fit the modelThe next step is to train the model. It takes a lot more computing resources to train convultional neural networks, so note that far less `epochs` are used, but a much larger `batch_size` is used due to a much larger data set.
###Code
history = model.fit(X_train, y_train, validation_data=(X_val, y_val), epochs=10, batch_size=200)
plot_acc_loss(history)
###Output
_____no_output_____
###Markdown
Evaluate the modelNow that we have trained our model, we can evaluate the performance on the test data.
###Code
scores = model.evaluate(X_test, y_test, verbose=0)
print("Accuracy: {0:.2f}%, Error: {1:.2f}%. ".format(scores[1]*100, 100-scores[1]*100))
y_pred = model.predict_classes(X_test)
y_test = [np.argmax(i) for i in y_test] # Reverse one hot encoded to label encoded
matrix = draw_confusion_matrix(y_test, y_pred, np.unique(y_test)) # (y_true,y_pred)
###Output
_____no_output_____
###Markdown
Visualising errors
###Code
pred_right = y_test == y_pred
wrong = [i for i, pred in enumerate(pred_right) if pred==False]
error_example = wrong[5]
plt.imshow(X_test[error_example,:,:,0], cmap='gray')
print("{0}>{1}".format(y_test[error_example], y_pred[error_example]))
###Output
5>3
###Markdown
Key Points* Convolutional neural network* Image data structure for a 2D convolutional neural network* Some of the layers we can use in our model (e.g., max pooling, dropout)* Materials available on the git repo Network topologiesChanging the structure of a neural network is one of the best methods for improving the accuracy of a neural network. There are two key ways to change your network topology:* Create a deeper network topology* Create a wider network topologyHere are some examples of what this means in the context of the network used in the Iris neural network - exercise 2. BaselineThis was our baseline model for the iris dataset:```pythonmodel = Sequential()model.add(Dense(4, input_dim=4, activation='relu', kernel_initializer='normal'))model.add(Dense(3, activation='sigmoid', kernel_initializer='normal'))``` DeeperIn a deeper network topology you simply increase the number of layers:```pythonmodel = Sequential()model.add(Dense(4, input_dim=4, activation='relu', kernel_initializer='normal'))model.add(Dense(4, activation='relu', kernel_initializer='normal'))model.add(Dense(3, activation='sigmoid', kernel_initializer='normal'))``` WiderIn a wider network topology you increase the number of neurons in the hidden layers:```pythonmodel = Sequential()model.add(Dense(8, input_dim=4, activation='relu', kernel_initializer='normal'))model.add(Dense(3, activation='sigmoid', kernel_initializer='normal'))``` Task 2: create different network topologiesCreate a model with a wider and deeper network topology and see how it performs with regards to the simpler model.Hints:* Think about adding more Conv2D and MaxPooling2D layers, followed by the Flatten layer and Dense layers that decrease in the number of neurons (hundreds -> num_classes)
###Code
###Output
_____no_output_____
|
brfss_clean.ipynb
|
###Markdown
Exploratory Data AnalysisPreparing the BRFSS datasetAllen Downey[MIT License](https://en.wikipedia.org/wiki/MIT_License)
###Code
# If we're running on Colab, install empiricaldist
# https://pypi.org/project/empiricaldist/
import sys
IN_COLAB = 'google.colab' in sys.modules
if IN_COLAB:
!pip install empiricaldist
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from empiricaldist import Pmf, Cdf
###Output
_____no_output_____
###Markdown
Loading and validation
###Code
# Get the data file
import os
if not os.path.exists('LLCP2017ASC.zip'):
!wget https://www.cdc.gov/brfss/annual_data/2017/files/LLCP2017ASC.zip
url16 = 'https://www.cdc.gov/brfss/annual_data/2016/LLCP_VarLayout_16_OneColumn.html'
url17 = 'https://www.cdc.gov/brfss/annual_data/2017/llcp_varlayout_17_onecolumn.html'
tables = pd.read_html(url17)
len(tables)
layout = tables[0]
layout.index = layout['Variable Name']
layout
names = [ 'SEX', 'HTM4', 'WTKG3', 'INCOME2', '_LLCPWT' , '_AGEG5YR', '_VEGESU1']
colspecs = []
for name in names:
start, _, length = layout.loc[name]
colspecs.append((start-1, start+length-1))
colspecs
filename16 = 'LLCP2016ASC.zip'
filename17 = 'LLCP2017ASC.zip'
brfss = pd.read_fwf(filename17,
colspecs=colspecs,
names=names,
compression='zip',
nrows=None)
brfss.head()
brfss.shape
brfss['SEX'].value_counts().sort_index()
brfss['SEX'].replace([9], np.nan, inplace=True)
brfss['INCOME2'].value_counts().sort_index()
brfss['INCOME2'].replace([77, 99], np.nan, inplace=True)
brfss['WTKG3'] /= 100
brfss['WTKG3'].describe()
weight = brfss['WTKG3']
weight.nsmallest(10)
weight.nlargest(10)
height = brfss['HTM4']
height.nsmallest(10)
height.nlargest(10)
brfss['HTM4'].describe()
brfss['_LLCPWT'].describe()
brfss['_AGEG5YR'].describe()
brfss['_AGEG5YR'].value_counts().sort_index()
brfss['_AGEG5YR'].replace([14], np.nan, inplace=True)
brfss['_VEGESU1'] /= 100
Pmf.from_seq(brfss['_VEGESU1']).plot()
bogus = brfss['_VEGESU1'] > 15
brfss.loc[bogus, '_VEGESU1'] = np.nan
brfss['_VEGESU1'].describe()
###Output
_____no_output_____
###Markdown
Add a height group column
###Code
bins = np.arange(0, height.max(), 10)
brfss['_HTMG10'] = pd.cut(brfss['HTM4'], bins=bins, labels=bins[:-1]).astype(float)
brfss._HTMG10.dtype
lower = np.arange(15, 85, 5)
upper = lower + 4
lower[1]= 18
lower = pd.Series(lower, index=range(len(lower)))
lower
upper[-1] = 99
upper = pd.Series(upper, index=range(len(upper)))
upper
midpoint = (lower + upper) / 2
midpoint
age_code = brfss['_AGEG5YR']
brfss['AGE'] = midpoint[age_code].values
brfss['AGE'].describe()
def randint(lower, upper):
for low, high in zip(lower, upper+1):
try:
yield np.random.randint(low, high)
except ValueError:
yield np.nan
###Output
_____no_output_____
###Markdown
Resample
###Code
from utils import resample_rows_weighted
np.random.seed(17)
sample = resample_rows_weighted(brfss, '_LLCPWT')[:100000]
sample.head(10)
!rm brfss.hdf5
sample.to_hdf('brfss.hdf5', 'brfss')
%time brfss = pd.read_hdf('brfss.hdf5', 'brfss')
brfss.shape
brfss.head()
brfss.describe()
###Output
_____no_output_____
|
learntools/python/nbs/ch7-testing.ipynb
|
###Markdown
Welcome to the exercises for day 7 (to go along with the day 7 tutorial notebook on [imports and objects](https://www.kaggle.com/colinmorris/learn-python-challenge-day-7))Run the setup code below before working on the questions (and run it again if you leave this notebook and come back later).
###Code
# This exists to test the learntools implementation of the exercise defined in ex7.py
from learntools.core import binder
binder.bind(globals())
from learntools.python.ex7 import *
###Output
_____no_output_____
###Markdown
Exercises 1.After completing day 5 of the Learn Python Challenge, Jimmy noticed that, according to his `estimate_average_slot_payout` function, the slot machines at the Learn Python Casino are actually rigged *against* the house, and are profitable to play in the long run.Starting with $200 in his pocket, Jimmy has played the slots 500 times, recording his new balance in a list after each spin. He used Python's `matplotlib` library to make a graph of his balance over time:
###Code
# Import the jimmy_slots submodule
from learntools.python import jimmy_slots
# Call the get_graph() function to get Jimmy's graph
graph = jimmy_slots.get_graph()
graph
###Output
_____no_output_____
###Markdown
As you can see, he's hit a bit of bad luck recently. He wants to tweet this along with some choice emojis, but, as it looks right now, his followers will probably find it confusing. He's asked if you can help him make the following changes:1. Add the title "Results of 500 slot machine pulls"2. Make the y-axis start at 0. 3. Add the label "Balance" to the y-axisAfter calling `type(graph)` you see that Jimmy's graph is of type `matplotlib.axes._subplots.AxesSubplot`. Hm, that's a new one. By calling `dir(graph)`, you find three methods that seem like they'll be useful: `.set_title()`, `.set_ylim()`, and `.set_ylabel()`. Use these methods to complete the function `prettify_graph` according to Jimmy's requests. We've already checked off the first request for you (setting a title).(Remember: if you don't know what these methods do, use the `help()` function!)
###Code
def prettify_graph(graph):
"""Modify the given graph according to Jimmy's requests: add a title, make the y-axis
start at 0, label the y-axis. (And, if you're feeling ambitious, format the tick marks
as dollar amounts using the "$" symbol.)
"""
graph.set_title("Results of 500 slot machine pulls")
# Complete steps 2 and 3 here
graph = jimmy_slots.get_graph()
prettify_graph(graph)
graph
###Output
_____no_output_____
###Markdown
**Bonus:** Can you format the numbers on the y-axis so they look like dollar amounts? e.g. $200 instead of just 200.(We're not going to tell you what method(s) to use here. You'll need to go digging yourself with `dir(graph)` and/or `help(graph)`.)
###Code
q1.solution()
def prettify_graph(graph):
"""Modify the given graph according to Jimmy's requests: add a title, make the y-axis
start at 0, label the y-axis. (And, if you're feeling ambitious, format the tick marks
as dollar amounts using the "$" symbol.)
"""
graph.set_title("Results of 500 slot machine pulls")
# Complete steps 2 and 3 here
graph.set_ylim(0)
graph.set_ylabel("Balance")
# An array of the values displayed on the y-axis (150, 175, 200, etc.)
ticks = graph.get_yticks()
# Format those values into strings beginning with dollar sign
new_labels = ['${}'.format(int(amt)) for amt in ticks]
# Set the new labels
graph.set_yticklabels(new_labels)
graph = jimmy_slots.get_graph()
prettify_graph(graph)
graph
###Output
_____no_output_____
###Markdown
2. **Luigi is trying to perform an analysis to determine the best items for winning races on the Mario Kart circuit. He has some data in the form of lists of dictionaries that look like... [ {'name': 'Peach', 'items': ['green shell', 'banana', 'green shell',], 'finish': 3}, {'name': 'Bowser', 'items': ['green shell',], 'finish': 1}, Sometimes the racer's name wasn't recorded {'name': None, 'items': ['mushroom',], 'finish': 2}, {'name': 'Toad', 'items': ['green shell', 'mushroom'], 'finish': 1}, ]`'items'` is a list of all the power-up items the racer picked up in that race, and `'finish'` was their placement in the race (1 for first place, 3 for third, etc.).He wrote the function below to take a list like this and return a dictionary mapping each item to how many times it was picked up by first-place finishers.
###Code
def best_items(racers):
"""Given a list of racer dictionaries, return a dictionary mapping items to the number
of times those items were picked up by racers who finished in first place.
"""
winner_item_counts = {}
for i in range(len(racers)):
# The i'th racer dictionary
racer = racers[i]
# We're only interested in racers who finished in first
if racer['finish'] == 1:
for i in racer['items']:
# Add one to the count for this item (adding it to the dict if necessary)
if i not in winner_item_counts:
winner_item_counts[i] = 0
winner_item_counts[i] += 1
# Data quality issues :/ Print a warning about racers with no name set. We'll take care of it later.
if racer['name'] is None:
print("WARNING: Encountered racer with unknown name on iteration {}/{} (racer = {})".format(
i+1, len(racers), racer['name'])
)
return winner_item_counts
###Output
_____no_output_____
###Markdown
He tried it on a small example list above and it seemed to work correctly:
###Code
# (Don't forget to run the cell above so that the best_items function is defined)
sample = [
{'name': 'Peach', 'items': ['green shell', 'banana', 'green shell',], 'finish': 3},
{'name': 'Bowser', 'items': ['green shell',], 'finish': 1},
{'name': None, 'items': ['mushroom',], 'finish': 2},
{'name': 'Toad', 'items': ['green shell', 'mushroom'], 'finish': 1},
]
best_items(sample)
###Output
WARNING: Encountered racer with unknown name on iteration 3/4 (racer = None)
###Markdown
However, when he tried running it on his full dataset, the program crashed with a `TypeError`.Can you guess why? Try running the code cell below to see the error message Luigi is getting. Once you've identified the bug, fix it in the cell below (so that it runs without any errors).Hint: Luigi's bug is similar to one we encountered in the [day 7 tutorial](https://www.kaggle.com/colinmorris/learn-python-challenge-day-7).
###Code
# Import luigi's full dataset of race data
from learntools.python.luigi_analysis import full_dataset
# Fix me!
def best_items(racers):
winner_item_counts = {}
for i in range(len(racers)):
# The i'th racer dictionary
racer = racers[i]
# We're only interested in racers who finished in first
if racer['finish'] == 1:
for i in racer['items']:
# Add one to the count for this item (adding it to the dict if necessary)
if i not in winner_item_counts:
winner_item_counts[i] = 0
winner_item_counts[i] += 1
# Data quality issues :/ Print a warning about racers with no name set. We'll take care of it later.
if racer['name'] is None:
print("WARNING: Encountered racer with unknown name on iteration {}/{} (racer = {})".format(
i+1, len(racers), racer['name'])
)
return winner_item_counts
# Try analyzing the imported full dataset
try:
best_items(full_dataset)
except TypeError as e:
print("Expected exception:", e)
else:
raise Exception("Should not be reachable!")
q2.hint()
q2.solution()
###Output
_____no_output_____
###Markdown
3.Suppose we wanted to create a new type to represent hands in blackjack. One thing we might want to do with this type is overload the comparison operators like `>` and `<=` so that we could use them to check whether one hand beats another.```python>>> hand1 = BlackjackHand(['K', 'A'])>>> hand2 = BlackjackHand(['7', '10', 'A'])>>> hand1 > hand2True```Well, we're not going to do all that in this question (defining custom classes was a bit too advanced to make the cut for the Learn Python Challenge), but the code we're asking you to write in the function below is very similar to what we'd have to write if we were defining our own BlackjackHand class. (We'd put it in the `__gt__` magic method to define our custom behaviour for `>`.)Fill in the body of `blackjack_hand_greater_than` according to the docstring.
###Code
def blackjack_hand_greater_than(hand_1, hand_2):
"""
Return True if hand_1 beats hand_2, and False otherwise.
In order for hand_1 to beat hand_2 the following must be true:
- The total of hand_1 must not exceed 21
- The total of hand_1 must exceed the total of hand_2 OR hand_2's total must exceed 21
Hands are represented as a list of cards. Each card is represented by a string.
When adding up a hand's total, cards with numbers count for that many points. Face
cards ('J', 'Q', and 'K') are worth 10 points. 'A' can count for 1 or 11.
When determining a hand's total, you should try to count aces in the way that
maximizes the hand's total without going over 21. e.g. the total of ['A', 'A', '9'] is 21,
the total of ['A', 'A', '9', '3'] is 14.
Examples:
>>> blackjack_hand_greater_than(['K'], ['3', '4'])
True
>>> blackjack_hand_greater_than(['K'], ['10'])
False
>>> blackjack_hand_greater_than(['K', 'K', '2'], ['3'])
False
"""
pass
q3.check()
def tot(h):
t = 0
a = 0
for card in h:
if card in 'JKQ':
t += 10
elif card == 'A':
a += 1
else:
t += int(card)
if a and (t + 10 <= 21):
t += 10
return t + a
def blackjack_hand_greater_than(hand_1, hand_2):
t1 = tot(hand_1)
t2 = tot(hand_2)
return t1 <= 21 and (t1 > t2 or t2 > 21)
q3.check()
def tot(h):
t = 0
a = 0
for card in h:
if card in 'JKQ':
t += 10
elif card == 'A':
a += 1
else:
t += int(card)
if a and (t + a + 10 <= 21):
t += 10
return t + a
def blackjack_hand_greater_than(hand_1, hand_2):
t1 = tot(hand_1)
t2 = tot(hand_2)
return t1 <= 21 and (t1 > t2 or t2 > 21)
q3.check()
print(
tot(['2', '8']),
tot(['A']),
tot(['2', '1', 'J', '1', '5', 'K']),
tot(['9', 'A', '2']),
)
q3.hint()
q3.solution()
###Output
_____no_output_____
###Markdown
4.In day 6 of the challenge, you heard a tip-off that the roulette tables at the Learn Python Casino had some quirk where the probability of landing on a particular number was partly dependent on the number the wheel most recently landed on. You wrote a function `conditional_roulette_probs` which returned a dictionary with counts of how often the wheel landed on `x` then `y` for each value of `x` and `y`.After analyzing the output of your function, you've come to the following conclusion: for each wheel in the casino, there is exactly one pair of numbers `a` and `b`, such that, after the wheel lands on `a`, it's significantly more likely to land on `b` than any other number. If the last spin landed on anything other than `a`, then it acts like a normal roulette wheel, with equal probability of landing on any of the 11 numbers (* the casino's wheels are unusually small - they only have the numbers from 0 to 10 inclusive).It's time to exploit this quirk for fun and profit. You'll be writing a roulette-playing agent to beat the house. When called, your agent will have an opportunity to sit down at one of the casino's wheels for 1000 spins. You don't need to bet on every spin. For example, the agent below bets on a random number unless the last spin landed on 4 (in which case it just watches).
###Code
from learntools.python import roulette
import random
def random_and_superstitious(wheel):
"""Interact with the given wheel over 100 spins with the following strategy:
- if the wheel lands on 4, don't bet on the next spin
- otherwise, bet on a random number on the wheel (from 0 to 10)
"""
last_number = 0
while wheel.num_remaining_spins() > 0:
if last_number == 4:
# Unlucky! Don't bet anything.
guess = None
else:
guess = random.randint(0, 10)
last_number = wheel.spin(number_to_bet_on=guess)
roulette.evaluate_roulette_strategy(random_and_superstitious)
###Output
Report:
seconds taken: 6.5
Ran 20,000 simulations with 100 spins each.
Average gain per simulation: $-8.62
Average # bets made: 91.0
Average # bets successful: 8.2 (9.1% success rate)
###Markdown
As you might have guessed, our random/superstitious agent tends to lose more than it wins. Can you write an agent that beats the house? HINT: it might help to go back to the [day 6 exercise notebook]() and review your code for `conditional_roulette_probs` for inspiration.
###Code
from learntools.python import roulette
def my_agent(wheel):
counts = {}
def mostfreq():
if not counts:
return None
maxval = max(counts.values())
maxkeys = [k for k, v in counts.items() if v == maxval]
return maxkeys[0]
while wheel.num_remaining_spins() > 0:
guess = mostfreq()
num = wheel.spin(guess)
counts[num] = counts.get(num, 0) + 1
roulette.evaluate_roulette_strategy(my_agent)
def my_agent(wheel):
pass
roulette.evaluate_roulette_strategy(my_agent)
def my_agent(wheel):
counts = {}
def mostfreq():
if not counts:
return None
maxval = max(counts.values())
maxkeys = [k for k, v in counts.items() if v == maxval]
return maxkeys[0] if len(maxkeys) == 1 else None
while wheel.num_remaining_spins() > 0:
guess = mostfreq()
num = wheel.spin(guess)
counts[num] = counts.get(num, 0) + 1
roulette.evaluate_roulette_strategy(my_agent)
def my_agent(wheel):
counts = {}
def mostfreq():
if not counts:
return None
maxval = max(counts.values())
nonmax = [v for v in counts.values() if v != maxval]
if not nonmax:
return None
maxkeys = [k for k, v in counts.items() if v == maxval]
if len(maxkeys) != 1:
return None
nextmost = max(nonmax)
if maxval - nextmost <= 1:
return None
if maxval / nextmost < 1.5:
return None
return maxkeys[0]
while wheel.num_remaining_spins() > 0:
guess = mostfreq()
num = wheel.spin(guess)
counts[num] = counts.get(num, 0) + 1
roulette.evaluate_roulette_strategy(my_agent)
###Output
Report:
seconds taken: 11.2
Ran 20,000 simulations with 100 spins each.
Average gain per simulation: $1.66
Average # bets made: 13.7
Average # bets successful: 1.5 (11.2% success rate)
|
.ipynb_checkpoints/AppRating-checkpoint.ipynb
|
###Markdown
Importing required libraries
###Code
import pandas as pd
import numpy as np
import seaborn as sns
from sklearn import metrics
from sklearn.model_selection import train_test_split
import random
from scipy import stats
from sklearn import preprocessing
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV
from sklearn.svm import LinearSVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import SGDClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import classification_report
%matplotlib inline
###Output
_____no_output_____
###Markdown
Converting csv file into dataframe
###Code
df=pd.read_csv('Google-Playstore-Full.csv')
###Output
C:\Users\Nikhil\anaconda3\lib\site-packages\IPython\core\interactiveshell.py:3063: DtypeWarning: Columns (2,3,11,12,13) have mixed types.Specify dtype option on import or set low_memory=False.
interactivity=interactivity, compiler=compiler, result=result)
###Markdown
Checking out the data
###Code
df.info()
###Output
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 267052 entries, 0 to 267051
Data columns (total 15 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 App Name 267051 non-null object
1 Category 267051 non-null object
2 Rating 267052 non-null object
3 Reviews 267051 non-null object
4 Installs 267052 non-null object
5 Size 267052 non-null object
6 Price 267052 non-null object
7 Content Rating 267052 non-null object
8 Last Updated 267052 non-null object
9 Minimum Version 267051 non-null object
10 Latest Version 267049 non-null object
11 Unnamed: 11 18 non-null object
12 Unnamed: 12 3 non-null object
13 Unnamed: 13 2 non-null object
14 Unnamed: 14 1 non-null float64
dtypes: float64(1), object(14)
memory usage: 30.6+ MB
###Markdown
Data Cleaning Dropping the null values and unnecessary columns
###Code
df=df.drop(columns=['Unnamed: 11', 'Unnamed: 12','Unnamed: 13','Unnamed: 14', 'Last Updated', 'Minimum Version', 'Latest Version'])
###Output
_____no_output_____
###Markdown
Converting Size column into float from object
###Code
df = df[df.Size.str.contains('\d')]
df.Size[df.Size.str.contains('k')] = "0."+df.Size[df.Size.str.contains('k')].str.replace('.','')
df.Size = df.Size.str.replace('k','')
df.Size = df.Size.str.replace('M','')
df.Size = df.Size.str.replace(',','')
df.Size = df.Size.str.replace('+','')
df.Size = df.Size.astype(float)
df.info()
###Output
<class 'pandas.core.frame.DataFrame'>
Int64Index: 255325 entries, 2 to 267051
Data columns (total 8 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 App Name 255324 non-null object
1 Category 255324 non-null object
2 Rating 255325 non-null object
3 Reviews 255324 non-null object
4 Installs 255325 non-null object
5 Size 255325 non-null float64
6 Price 255325 non-null object
7 Content Rating 255325 non-null object
dtypes: float64(1), object(7)
memory usage: 27.5+ MB
###Markdown
Converting Installs into float from object
###Code
df = df[df.Installs.str.contains('\+')]
df.Installs = df.Installs.str.replace('+','')
df.Installs = df.Installs.str.replace(',','')
df.Installs.astype(int)
df.info()
###Output
<class 'pandas.core.frame.DataFrame'>
Int64Index: 255308 entries, 2 to 267051
Data columns (total 8 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 App Name 255307 non-null object
1 Category 255308 non-null object
2 Rating 255308 non-null object
3 Reviews 255308 non-null object
4 Installs 255308 non-null object
5 Size 255308 non-null float64
6 Price 255308 non-null object
7 Content Rating 255308 non-null object
dtypes: float64(1), object(7)
memory usage: 17.5+ MB
###Markdown
Convert Price into float from object
###Code
df.Price = df.Price.str.contains('1|2|3|4|5|7|8|9').replace(False, 0)
###Output
_____no_output_____
###Markdown
Convert Reviews into float from object
###Code
df = df[df.applymap(np.isreal).Reviews]
df.Reviews = df.Reviews.astype(float)
df.Rating=df.Rating.astype(float)
df.info()
###Output
<class 'pandas.core.frame.DataFrame'>
Int64Index: 191674 entries, 2 to 267051
Data columns (total 8 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 App Name 191674 non-null object
1 Category 191674 non-null object
2 Rating 191674 non-null float64
3 Reviews 191674 non-null float64
4 Installs 191674 non-null object
5 Size 191674 non-null float64
6 Price 191674 non-null float64
7 Content Rating 191674 non-null object
dtypes: float64(4), object(4)
memory usage: 13.2+ MB
###Markdown
Understanding the dataframe
###Code
df=df.reset_index(drop=True)
df.head()
###Output
_____no_output_____
###Markdown
Identifying the categories for apps
###Code
categories = list(df["Category"].unique())
print("There are {0:.0f} categories in our dataset: ".format(len(categories)-1))
print(categories)
df['Rating'].isnull().sum()
###Output
_____no_output_____
###Markdown
Bar Graph of Ratings
###Code
fig,ax = plt.subplots(1,1)
a = df['Rating']
a=a.astype(float)
ax.hist(a, bins = [1,1.5,2,2.5,3,3.5,4,4.5,5])
ax.set_title("Ratings of Apps")
ax.set_xlabel('Rating')
ax.set_ylabel('Number of apps')
plt.show()
###Output
_____no_output_____
###Markdown
As we can see maximum apps get rating froom 4 to 5 which means that there are very few apps with lower rating Splitting The data in Games and Apps to classify better
###Code
df.Category = df.Category.fillna('Unknown')
games = df[df.Category.str.contains('GAME', regex=False)]
other = df[~df.Category.str.contains('GAME', regex=False)]
z_Rating = np.abs(stats.zscore(games.Rating))
games = games[z_Rating < 3]
z_Reviews = np.abs(stats.zscore(games.Reviews))
games = games[z_Reviews < 3]
z_Rating2 = np.abs(stats.zscore(other.Rating))
other = other[z_Rating2 < 3]
z_Reviews2 = np.abs(stats.zscore(other.Reviews))
other = other[z_Reviews2 < 3]
games_mean = np.mean(games.Rating)
games_std = np.std(games.Rating)
other_mean = np.mean(other.Rating)
other_std = np.std(games.Rating)
print("Average Ratings:")
print('Games mean and std: ', games_mean, games_std)
print('Other categories mean and std: ', other_mean, other_std)
###Output
Average Ratings:
Games mean and std: 4.305662207988253 0.39182958482348945
Other categories mean and std: 4.314347154487729 0.39182958482348945
###Markdown
Visualizing the data for Games
###Code
f, ax = plt.subplots(3,2,figsize=(10,15))
games.Category.value_counts().plot(kind='bar', ax=ax[0,0])
ax[0,0].set_title('Frequency of Games per Category')
ax[0,1].scatter(games.Reviews[games.Reviews < 100000], games.Rating[games.Reviews < 100000])
ax[0,1].set_title('Reviews vs Rating')
ax[0,1].set_xlabel('# of Reviews')
ax[0,1].set_ylabel('Rating')
ax[1,0].hist(games.Rating, range=(3,5))
ax[1,0].set_title('Ratings Histogram')
ax[1,0].set_xlabel('Ratings')
d = games.groupby('Category')['Rating'].mean().reset_index()
ax[1,1].scatter(d.Category, d.Rating)
ax[1,1].set_xticklabels(d.Category.unique(),rotation=90)
ax[1,1].set_title('Mean Rating per Category')
ax[2,0].hist(games.Size, range=(0,100),bins=10, label='Size')
ax[2,0].set_title('Size Histogram')
ax[2,0].set_xlabel('Size')
games['Content Rating'].value_counts().plot(kind='bar', ax=ax[2,1])
ax[2,1].set_title('Frequency of Games per Content Rating')
f.tight_layout()
###Output
_____no_output_____
###Markdown
Things we can conclude from above charts:1.Puzzles category in games have more demand with higher ratings too.2.Casino and cards have lesser apps but high rating.3.Size varies a lot in games unlike in apps with majority being in 0-20 MB.4.Unlike what we presumed Teen are not the one being targeted but people with all age group.5.Reviews are generally given for apps with higher rating. Visualizing the data for other Apps
###Code
other = other[other.Category.map(other.Category.value_counts() > 3500)]
f, ax = plt.subplots(3,2,figsize=(10,15))
other.Category.value_counts().plot(kind='bar', ax=ax[0,0])
ax[0,0].set_title('Frequency of Others per Category')
ax[0,1].scatter(other.Reviews[other.Reviews < 100000], other.Rating[other.Reviews < 100000])
ax[0,1].set_title('Reviews vs Rating')
ax[0,1].set_xlabel('# of Reviews')
ax[0,1].set_ylabel('Rating')
ax[1,0].hist(other.Rating, range=(3,5))
ax[1,0].set_title('Ratings Histogram')
ax[1,0].set_xlabel('Ratings')
d = other.groupby('Category')['Rating'].mean().reset_index()
ax[1,1].scatter(d.Category, d.Rating)
ax[1,1].set_xticklabels(d.Category.unique(),rotation=90)
ax[1,1].set_title('Mean Rating per Category')
ax[2,0].hist(other.Size, range=(0,100),bins=10, label='Size')
ax[2,0].set_title('Size Histogram')
ax[2,0].set_xlabel('Size')
other['Content Rating'].value_counts().plot(kind='bar', ax=ax[2,1])
ax[2,1].set_title('Frequency of Others per Content Rating')
f.tight_layout()
###Output
_____no_output_____
###Markdown
From the charts we can conclude following things:1.Apps in category of Education,Tools,Entertainment,Books and Reference are present in heavy numbers their average rating is also better than rest of categories.2.Apps in categories communication,Travel,Finance are in lower numbers with their average rating being low too.3.Apps in category of Finance has low no of apps and lowest average rating which means that people have more demand in Finance and the apps lack in providing the comfort.4.Reviews are generally given for apps with higher rating.5.Apps generally appeal all kind of age group. Considering Apps with Rating above 4
###Code
highRating = df.copy()
highRating = highRating.loc[highRating["Rating"] >= 4.0]
highRateNum = highRating.groupby('Category')['Rating'].nunique()
highRateNum
###Output
_____no_output_____
###Markdown
Apps in Categories of Libraries,House,Events,Dating and Comics have least number of apps rated above 4 Apps with Highest Installs
###Code
popApps = df.copy()
popApps = popApps.drop_duplicates()
popApps = popApps.sort_values(by="Installs",ascending=False)
popApps.reset_index(inplace=True)
popApps.drop(["index"],axis=1,inplace=True)
popApps.loc[:40,['App Name','Installs','Content Rating','Reviews']]
###Output
_____no_output_____
###Markdown
Preprocessing The Data
###Code
df2 = popApps.copy()
label_encoder = preprocessing.LabelEncoder()
df2['Category']= label_encoder.fit_transform(df2['Category'])
df2['Content Rating']= label_encoder.fit_transform(df2['Content Rating'])
df2.Installs=df2.Installs.astype(int)
df2.info()
df2 = df2.drop(["App Name"],axis=1)
df2["Installs"] = (df2["Installs"] > 100000)*1 #Installs Binarized
print("There are {} total rows.".format(df2.shape[0]))
print(df2.head())
###Output
There are 191665 total rows.
Category Rating Reviews Installs Size Price Content Rating
0 41 3.755762 12582.0 1 58.0 0.0 1
1 23 4.440125 9257863.0 1 64.0 0.0 1
2 41 4.390956 1920612.0 1 72.0 0.0 1
3 6 4.185223 11390281.0 1 94.0 0.0 1
4 19 4.330340 10752323.0 1 24.0 0.0 1
###Markdown
Splitting the Data
###Code
X_train,X_test,y_train,y_test = train_test_split(df2[['Category','Rating','Reviews','Size','Price','Content Rating']],df2['Installs'],random_state=30,test_size=0.3)
print(X_train.info())
print(y_train.count())
print(X_test.info())
print(y_test.count())
print("{} Apps are used for Training.".format(X_train.count()))
print("{} Apps are used for Testing.".format(X_test.count()))
###Output
Category 134165
Rating 134165
Reviews 134165
Size 134165
Price 134165
Content Rating 134165
dtype: int64 Apps are used for Training.
Category 57500
Rating 57500
Reviews 57500
Size 57500
Price 57500
Content Rating 57500
dtype: int64 Apps are used for Testing.
###Markdown
Machine Learning Algorithms to see which fits the best Decision Tree Classifier
###Code
popularity_classifier = DecisionTreeClassifier(max_leaf_nodes=30, random_state=0)
popularity_classifier.fit(X_train, y_train)
print('Train Score: ',popularity_classifier.score(X_train, y_train))
print('Test Score: ',popularity_classifier.score(X_test, y_test))
print(classification_report(y_test,popularity_classifier.predict(X_test)))
###Output
Train Score: 0.9595050870197145
Test Score: 0.959391304347826
precision recall f1-score support
0 0.97 0.98 0.98 50481
1 0.87 0.79 0.83 7019
accuracy 0.96 57500
macro avg 0.92 0.88 0.90 57500
weighted avg 0.96 0.96 0.96 57500
###Markdown
Grid Search CV
###Code
classify=GridSearchCV(LogisticRegression(),{'C':[1]})
print(classify.get_params)
classify=classify.fit(X_train,y_train)
print('Train Score: ',classify.score(X_train, y_train))
print('Test Score: ',classify.score(X_test, y_test))
print(classification_report(y_test,classify.predict(X_test)))
###Output
<bound method BaseEstimator.get_params of GridSearchCV(cv=None, error_score=nan,
estimator=LogisticRegression(C=1.0, class_weight=None, dual=False,
fit_intercept=True,
intercept_scaling=1, l1_ratio=None,
max_iter=100, multi_class='auto',
n_jobs=None, penalty='l2',
random_state=None, solver='lbfgs',
tol=0.0001, verbose=0,
warm_start=False),
iid='deprecated', n_jobs=None, param_grid={'C': [1]},
pre_dispatch='2*n_jobs', refit=True, return_train_score=False,
scoring=None, verbose=0)>
###Markdown
SGD Classifier
###Code
classify2=SGDClassifier(alpha=1)
print(classify2.get_params)
classify2=classify2.fit(X_train,y_train)
print('Train Score: ',classify2.score(X_train, y_train))
print('Test Score: ',classify2.score(X_test, y_test))
print(classification_report(y_test,classify2.predict(X_test)))
###Output
<bound method BaseEstimator.get_params of SGDClassifier(alpha=1, average=False, class_weight=None, early_stopping=False,
epsilon=0.1, eta0=0.0, fit_intercept=True, l1_ratio=0.15,
learning_rate='optimal', loss='hinge', max_iter=1000,
n_iter_no_change=5, n_jobs=None, penalty='l2', power_t=0.5,
random_state=None, shuffle=True, tol=0.001,
validation_fraction=0.1, verbose=0, warm_start=False)>
Train Score: 0.9356240450191928
Test Score: 0.9353913043478261
precision recall f1-score support
0 0.93 1.00 0.96 50481
1 0.94 0.50 0.65 7019
accuracy 0.94 57500
macro avg 0.94 0.75 0.81 57500
weighted avg 0.94 0.94 0.93 57500
###Markdown
Grid Search CV
###Code
classify3=GridSearchCV(LinearSVC(C=0.8,dual=False),{'C':[10]})
classify3=classify3.fit(X_train,y_train)
print('Train Score: ',classify3.score(X_train, y_train))
print('Test Score: ',classify3.score(X_test, y_test))
print(classification_report(y_test,classify3.predict(X_test)))
###Output
Train Score: 0.9500018633771848
Test Score: 0.9508
precision recall f1-score support
0 0.95 0.99 0.97 50481
1 0.92 0.66 0.76 7019
accuracy 0.95 57500
macro avg 0.94 0.82 0.87 57500
weighted avg 0.95 0.95 0.95 57500
###Markdown
KNN Classifier
###Code
classify4=KNeighborsClassifier()
classify4.fit(X_train, y_train)
print('Train Score: ',classify4.score(X_train, y_train))
print('Test Score: ',classify4.score(X_test, y_test))
print(classification_report(y_test,classify4.predict(X_test)))
###Output
Train Score: 0.9612790220996534
Test Score: 0.9472347826086956
precision recall f1-score support
0 0.97 0.97 0.97 50481
1 0.80 0.75 0.78 7019
accuracy 0.95 57500
macro avg 0.88 0.86 0.87 57500
weighted avg 0.95 0.95 0.95 57500
###Markdown
Random Forest Classifier
###Code
classify5=RandomForestClassifier(n_estimators=300,max_depth=2.9)
print(classify5.get_params)
classify5=classify5.fit(X_train,y_train)
print('Train Score: ',classify5.score(X_train, y_train))
print('Test Score: ',classify5.score(X_test, y_test))
print(classification_report(y_test,classify5.predict(X_test)))
###Output
<bound method BaseEstimator.get_params of RandomForestClassifier(bootstrap=True, ccp_alpha=0.0, class_weight=None,
criterion='gini', max_depth=2.9, max_features='auto',
max_leaf_nodes=None, max_samples=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=300,
n_jobs=None, oob_score=False, random_state=None,
verbose=0, warm_start=False)>
Train Score: 0.9420787835873737
Test Score: 0.943304347826087
precision recall f1-score support
0 0.94 1.00 0.97 50481
1 0.94 0.57 0.71 7019
accuracy 0.94 57500
macro avg 0.94 0.78 0.84 57500
weighted avg 0.94 0.94 0.94 57500
###Markdown
ADA Boost Classifier
###Code
classify6=AdaBoostClassifier(n_estimators=300,learning_rate=0.02)
print(classify6.get_params)
classify6=classify6.fit(X_train,y_train)
print('Train Score: ',classify6.score(X_train, y_train))
print('Test Score: ',classify6.score(X_test, y_test))
print(classification_report(y_test,classify6.predict(X_test)))
###Output
<bound method BaseEstimator.get_params of AdaBoostClassifier(algorithm='SAMME.R', base_estimator=None, learning_rate=0.02,
n_estimators=300, random_state=None)>
Train Score: 0.9582454440427831
Test Score: 0.9584
precision recall f1-score support
0 0.97 0.98 0.98 50481
1 0.87 0.78 0.82 7019
accuracy 0.96 57500
macro avg 0.92 0.88 0.90 57500
weighted avg 0.96 0.96 0.96 57500
|
.ipynb_checkpoints/SLAM-checkpoint.ipynb
|
###Markdown
Occupancy Grid SLAMSimultaneous Localization And Mapping (SLAM) ist ein klassisches Problem der Robotik. Es gibt Szenarien, in denen Roboter autonom agieren sollen. Dafür ist die Kenntnis der Umgebung und des eigenen Standorts unabdingbar. Eine genaue Karte ist jedoch selten vorhanden, oft ist die Umgebung gar nicht oder nur teilweise bekannt. Ebenso häufig ist die Genauigkeit der Positionsbestimmung unzureichend. Die Lösung ist, dass der Roboter eine eigene Karte erstellt und sich anhand dieser Karte in der Umgebung verortet. Ein großes Forschungsfeld ist beispielsweise seit einigen Jahren der motorisierte Individualverkehr. Mit SLAM werden zwei Aufgaben gelöst:1. Positionsbestimmung in der Umgebung 2. Erstellung einer Karte der UmgebungCharakteristisch ist, dass für die Positionsbestimmung eine Karte und für die Erstellung der Karte eine Position benötigt wird. Da Beides anfangs nicht zur Verfügung steht, wird SLAM oft als Henne-oder-Ei-Problem bezeichnet Das grundsätzliche Vorgehen von SLAM ist, dass der Roboter die Umgebung beobachtet und kartiert. Anschließend bewegt er sich und beobachtet die Umgebung erneut und vergleicht die Beobachtung mit der Karte. Anhand dieses Vergleichs kann die Position bestimmt und die Karte inkrementell aufgebaut werden. Ziel des SLAMs es explizit nicht, sicherheitsrelevante Hinderniserkennung durchzuführen, sondern eine möglichst genaue Positionierung zu erreichen und eine anschaulichen Abbildung der Umgebung zu erstellen. Für die Positionsbestimmung existiert eine Vielzahl von verschiedenen Ortungssensoren und Verfahren. Diese sind jedoch teuer, oft nicht verfügbar und teilweise unzuverlässig. Daher ist das Ziel, diese Sensorik mit SLAM zu ergänzen oder sogar zu ersetzen. Um das SLAM Verfahren verständlich zu erklären wird zunächst auf die Erstellung einer Karte bei bekannten Positionen eingegangen, anschließend wird die Position des Fahrzeugs anhand einer vorhanden Karte und einer Punktwolke des Laserscanners bestimmt und schließlich beide Teile zum SLAM zusammengesetzt. Verwendete DatenIn diesem Notebook werden Daten der [KITTI Vision Benchmark Suite](http://www.cvlibs.net/) verwendet. Im Notebook *Export von KITTI Rohdaten* ist erklärt, wie diese heruntergeladen und exportiert werden. Wenn die dort verwendete Datenstruktur eingehalten wird, ist es möglich andere Daten zu verwenden.Es wird benötigt:1. Eine Textdatei mit der initialen Startposition: x,y,yaw 2. Jede Beobachtung als Punktwolke (x,y,z) im NumPy Binärformat gespeichert3. Die Ground Truth Trajektorie für einen Vergleich als Textdatei: x,y,yawDie Daten, die im ersten Teil für die Erklärung benötigt werden sind im Pfad des Notebooks gespeichert. ParametrierungDie Parametrierung in diesem Notebook ist so gewählt, dass die Ergebnisse anschaulich sind. Für die tatsächliche Parametrierung und weitere Filterung der Punktwolke bitte in die Studienarbeit beziehungsweise in den anderen Code schauen. Teil I: Erstellung der Karte - Mapping With Known Poses Beschreibung der KarteEin Occupancy Grid ist eine belegungsbasierte Karte. Die zweidimensionale Karte wird in eine Zellen aufgeteil. Jede dieser Zellen kann entweder *frei* oder *belegt* sein. Da die Position des Fahrzeugs eine Schätzung ist und die Beobachtungen der Umgebungen ebenfalls Unsicherheiten aufweisen wird der Zustand einer Zelle *m_i* als Wahrscheinlichkeit zwischen 0 und 1 angegeben. Innerhalb dieses Intervalls sind folgende Werte wichtig:Anschaulich werden belegte Zellen schwarz dargestellt, freie weiß und wenn keine Information über den Zustand einer Zelle vorhanden ist, wird sie grau dargestellt. AblaufAusgehend von einer unbekannten Umgebung, bei der zu keiner Zelle Belegungsinformationen werden die Beobachtungen iterativ hinzugefügt:Aus der Punktwolke einer Beobachtung im Fahrzeugkoordinatensystem wird zunächst ein horizontaler Querschnitt ausgeschnitten, der anschließend vom Koordinatensystem des Fahrzeugs anhand der als bekannt vorrausgesetzten Position des Fahrzeugs in das Kartenkoordinatensystem transformiert wird. Für jeden Punkt wird bestimmt, in welcher Zelle der Karte er liegt. Die Wahrscheinlichkeit, dass diese Zelle belegt ist, steigt. Alle Zellen, die sich zwischen dieser belegten Zellen und dem Laserscanner befinden, werden als frei bestimmt. Die Wahrscheinlichkeit, dass diese Zellen belegt sind, sinkt. Analog werden die folgenden Beobachtungen in die Karte integriert. 1. Filterung der PunktwolkeDie folgende Punktwolke enthällt eine gesamte Messung des Velodyne Laserscanners. Die Fahrbahnoberfläche, Hauswände, Personen und ein Fahrradfahrer, eine Straßenbahn und einige Schilder und Autos sind gut sichtbar. Beim Mapping wird nicht die komplette Punktwolke verarbeitet. Es wird lediglich ein horizontaler Querschnitt auf Höhe des Sensors (1.73m +- 0.05m) verwendet.
###Code
%matplotlib notebook
import numpy as np
import matplotlib.pyplot as plt
# load pointcloud
pointcloud = np.load('data/pointcloud_0.npy')
# filter z-Values
zCutMin = -0.05
zCutMax = 0.05
binaryMask = np.logical_and( pointcloud[:,2]>zCutMin, pointcloud[:,2]<zCutMax)
binaryMask = np.column_stack((binaryMask,binaryMask,binaryMask))
pointcloud = pointcloud[binaryMask]
pointcloud = np.reshape(pointcloud,(-1,3))
# project points to xy-plane (delete z-Values)
pointcloud = np.delete(pointcloud,2,1)
# show pointcloud
plt.figure(0)
plt.axis('equal')
plt.scatter(pointcloud[:,0],pointcloud[:,1],c='m',s=10,edgecolors='none')
###Output
_____no_output_____
###Markdown
2. Transformation der Punktwolke in KartenkoordinatensytemDie Punktwolke ist im Koordinatensystem des Laserscanners gespeichert. Um die Beobachtung in die Karte zu integrieren muss sie in das globale Kartenkoordinatensystem transformiert werden. Dazu wird die bekannte Position genutzt:
###Code
# known pose
xPos = 457797.906
yPos = 5428861.825
yaw = -1.222
###Output
_____no_output_____
###Markdown
Die Punktwolke wird zunächst mit dem Gierwinkel des Fahrzeugs rotiert und anschließend verschoben.
###Code
# rotate pointcloud
R = np.matrix([[np.cos(yaw),-np.sin(yaw)], [np.sin(yaw),np.cos(yaw)]])
pointcloud = pointcloud * np.transpose(R)
# translate pointcloud
pointcloud = pointcloud + np.matrix([xPos,yPos])
# show transformed pointcloud
plt.figure(1)
plt.axis('equal')
plt.scatter([pointcloud[:,0]],[pointcloud[:,1]],c='m',s=10,edgecolors='none')
###Output
_____no_output_____
###Markdown
3. Integration der Punktwolke in die KarteJeder der Zellen der Karte ist eine Wahrscheinlichkeit zugeordnet, mit der die Zellen belegt sind. Für die folgende Integration der Punktwolke in die Karte ist es sinnvoll die Wahrscheinlichkeit als logarithmiertes Quotenverhältnis (engl. Log odds) anzugeben:Mit dieser Notation ergeben sich für die oben genannten charakteristischen Wahrscheinlichkeiten folgende Werte:Da die Umgebung am Anfang komplett unbekannt ist, wird die Karte mit 0 initialisiert. Die Zellgröße beträgt beispielsweise 0.1x0.1m.
###Code
# resolution of the grid
resolution = 0.1
# create grid
grid = np.zeros((int(100.0/resolution),int(100.0/resolution)),order='C')
# offset of measurement in grid (x,y)
offset = np.array([xPos+50.0, yPos+50.0])
###Output
_____no_output_____
###Markdown
Wenn eine Messung integriert wird, wird die Wahrscheinlichkeit angepasst. In der Log-Odds Notation kann das sehr effizient über einfache Addition (erhöhen der Wahrscheinlichkeit, dass eine Zelle belegt ist) oder Subtraktion (verringern der Wahrscheinlichkeit) eines konstanten Wertes erfolgen.
###Code
l_occupied = 0.85
l_free = -0.4
###Output
_____no_output_____
###Markdown
Je höher der Wert eine Zelle ist, desto sicherer ist die Information, dass die Zelle belegt ist. Um Messunsicherheiten und Umgebungsveränderungen korrigieren zu können werden die Werte nach oben und unten begrenzt (engl. clamping).
###Code
l_max = 3.5
l_min = -2.0
###Output
_____no_output_____
###Markdown
Nun muss bestimmt werden, welche Zellen anhand der Punktwolke als *frei* und welche als *belegt* bestimmt werden können.Die belegten Zellen zu bestimmen ist einfach: Jeder Punkt der Punktwolke repräsentiert eine Reflektion des Laserstrahls an einem Objekt. Damit ist die Zelle, in die dieser Punkt fällt belegt.Alle Zellen, die zwischen dem Sensor und den belegten Zellen liegen sind frei. Um diese Zellen zu besteimmen wird der ursprünglich für die Darstellung von Geraden in der Computergrafik entwickelte Algorithmus von Bresenham genutzt. Die Bestimmung der Zellen erfolgt effektiv da nahezu nur Additionen genutzt werden.Das verwendete Verfahren ist eine zweidimensionale Variante [dieser](https://gist.github.com/salmonmoose/2760072) Implementierung. Bei Übergabe von Start- und Endpunkt eines Strahls werden alle Zellen zurückgegeben, die nötig sind um diesen Strahl darzustellen.
###Code
import os
import sys
nb_dir = os.path.split(os.getcwd())[0]
if nb_dir not in sys.path:
sys.path.append(nb_dir)
# import bresenham algorithm
from lib import bresenham
###Output
_____no_output_____
###Markdown
Nun kann jeder Punkt der Punktwolke in die Messung integriert werden:
###Code
for ii in range(pointcloud.shape[0]):
# round points to cells
xi = int( (pointcloud[ii,0]-offset[0]) / resolution )
yi = int( (pointcloud[ii,1]-offset[1]) / resolution )
# set beam endpoint-cells as occupied
grid[xi,yi] += l_occupied
# value > threshold? -> clamping
if grid[xi,yi] > l_max:
grid[xi,yi] = l_max
# calculate cells between sensor and endpoint as free with bresenham
startPos = np.array([[int((xPos-offset[0])/resolution),int((yPos-offset[1])/resolution)]])
endPos = np.array([[xi,yi]])
bresenhamPath = bresenham.bresenham2D(startPos, endPos)
# set free cells as free
for jj in range(bresenhamPath.shape[0]):
path_x = int(bresenhamPath[jj,0])
path_y = int(bresenhamPath[jj,1])
grid[path_x, path_y] += l_free
# value < threshold? -> clamping
if grid[path_x, path_y] < l_min:
grid[path_x, path_y] = l_min
plt.figure(3)
plt.imshow(grid[:,:], interpolation ='none', cmap = 'binary')
###Output
_____no_output_____
###Markdown
Weitere Punktwolken werden analog zu der Karte hinzugefügt. Diese Funktion wird für den SLAM Algorithmus in eine Funktion ausgelagert. Eine 3D Implementierung von Mapping With Known Poses gibt es [hier](https://github.com/balzer82/3D-OccupancyGrid-Python).
###Code
%reset
###Output
Once deleted, variables cannot be recovered. Proceed (y/[n])? y
###Markdown
Teil II: Lokalisierung in einer bestehenden Karte mittels Partikelfilter Ablauf Das zweite Teilproblem des SLAM-Prozesses ist die Lokalisierung anhand einer Punktwolke in einer bestehenden Karte. Im SLAM-Prozess wird anhand eines Bewegungsmodells des Fahrzeugs eine erste Schätzung für die Position vorgenommen. Aufgabe der Lokalisierung in einer bestehenden Karte ist es, diese Schätzung anhander der neuen, gefilterten Punktwolke zu verbessern.Die Position des Fahrzeugs wird vollständig mit zwei Koordinaten und einem Winkel beschrieben. **Es wird bestimmt, wie die Punktwolke verschoben und gedreht werden muss, damit sie bestmöglichst zu der Karte passt.** Dafür werden Partikel, die jeweils eine Lösung enthalten zufällig um die erwartete Position verteilt. Für jede dieser Lösungen mit einer Gütefunktion bewertet, wie gut die gefilterte Punktwolke zu der bis hierhin erstellte Karte passt. Das Partikel mit dem höchsten Wert der Gütefunktion stellt die beste Lösung dar.Um die Schätzung zu verbessern können ein oder mehrere der besten Partikel ausgewählt werden und an der Stelle dieser Lösungen neue Partikel verteilt werden. Diesmal wird der Suchradius, und damit das Gebiet, in dem die neuen Partikel erzeugt werden deutlich verkleinert.Dadurch wird die Schätzung genauer. Wie oft diese Schritte durchgeführt werden hängt von der zur Verfügung stehenden Rechenzeit ab. 0. Laden der vorhandenen KarteUm die Funktionsweise des Partikelfilters zu demonstrieren wird eine vorhandene Karte sowie die wie im Mapping gefilterte Punktwolke geladen. Die Punktwolke ist genau die, die als nächstes in die Karte integriert werden soll. Die Information aus dieser Punktwolke ist also noch nicht in die Karte integriert.
###Code
%matplotlib notebook
import numpy as np
import matplotlib.pyplot as plt
# load existing grid and filtered pointcloud
grid = np.loadtxt('data/grid_42.txt')
pointcloud = np.load('data/pointcloud_filtered_43.npy')
# show pointcloud and grid
plt.figure(0)
plt.imshow(grid[:,:], interpolation ='none', cmap = 'binary')
plt.figure(1)
plt.axis('equal')
plt.scatter(pointcloud[:,0],pointcloud[:,1],c='m',s=10,edgecolors='none')
###Output
_____no_output_____
###Markdown
1. Erzeugung Partikel um die geschätzte PositionEs soll die 43. Punktwolke in die Karte integriert werden. Eine erste Schätzung für die Position ist die Lage der 42. Punktwolke:
###Code
firstEstimate_x = 457805.156
firstEstimate_y = 5428851.291
firstEstimate_yaw = -0.697
###Output
_____no_output_____
###Markdown
Außerdem werden wie schon beim mapping die Auflösung sowie Verschiebung der Karte benötigt:
###Code
# resolution of the grid
resolution = 0.1
# offset of measurement in grid (x,y)
offset = np.array([[-50.0, -50.0]])
offsetStartPos = np.array([457797.930, 5428862.694])
###Output
_____no_output_____
###Markdown
Die Lösungen werden als Partikel als spezieller Datentyp in einer Liste gespeichert:
###Code
class Particle(object):
def __init__(self, x, y, yaw, weight):
self.x = x
self.y = y
self.yaw = yaw
self.weight = weight
particles = []
###Output
_____no_output_____
###Markdown
Jetzt muss entschieden werden, wie weit um die letzte Position die neue Position erwartet wird. Entsprechend werden die Standardabweichungen für den Winkel und die Position gesetzt. Außerdem wird die Partikelanzahl festgelegt, dafür muss zwischen Genauigkeit und Rechenzeit abgewogen werden.
###Code
# standard deviation of position and yaw
stddPos = 1.0
stddYaw = 0.02
# number of particels
nrParticle = 500
###Output
_____no_output_____
###Markdown
Die gewünscht Anzahl an Partikeln wird um die zunächste geschätzte Position verteilt:
###Code
for _ in range(0,nrParticle):
x = np.random.normal(firstEstimate_x-offsetStartPos[0],stddPos)
y = np.random.normal(firstEstimate_y-offsetStartPos[1],stddPos)
yaw = np.random.normal(firstEstimate_yaw,stddYaw)
# create particle and append ist to list
p = Particle(x,y,yaw,1)
particles.append(p)
###Output
_____no_output_____
###Markdown
2. Bewertung der LösungenUm die Güte der Lösungen zu bewerten, muss zunächst die Punktwolke anhand der jeweiligen Lösung wie beim Mapping an die entsprechende Position transformiert werden. Für jeden Punkt der Beobachtung wird die dazugehörige Zelle des Grids bestimmt. Die Summe der Log-Odds dieser Zellen beschreibt die Güte der Lösung. Je höher die Summe ist, desto besser ist die gefundene Position.
###Code
def scan2mapDistance(grid,pcl,offset,resolution):
distance = 0;
for i in range(pcl.shape[0]):
# round points to cells
xi = int ( (pcl[i,0]-offset[0,0]) / resolution )
yi = int ( (pcl[i,1]-offset[0,1]) / resolution )
distance += grid[xi,yi]
return distance
###Output
_____no_output_____
###Markdown
Mit der Gütefunktion können alle Lösungen bewertet werden:
###Code
# weight all particles
for p in particles:
# rotate pointcloud
R = np.matrix([[np.cos(p.yaw),-np.sin(p.yaw)], [np.sin(p.yaw),np.cos(p.yaw)]])
pointcloudTransformed = pointcloud * np.transpose(R)
# translate pointcloud
pointcloudTransformed = pointcloudTransformed + np.matrix([p.x,p.y])
# weight particle
p.weight = scan2mapDistance(grid,pointcloudTransformed,offset,resolution)
###Output
_____no_output_____
###Markdown
3. Auswahl der besten PartikelDie Partikel werden in absteigender Reihenfolge nach ihrerem Gewicht sortiert. So können zum Beispiel die besten zehn Partikel ausgewählt werden.
###Code
# sort particles
particles.sort(key = lambda Particle: Particle.weight,reverse=True)
# get ten best particles
bestParticles = particles[:10]
# get best particle
bestParticle = particles[0]
###Output
_____no_output_____
###Markdown
Die Punktwolke anhand der besten Lösung transformiert und passt sehr gut zu der Karte. Zusätzlich sind alle Partikel sowie die besten Partikel dargestellt. Die besten Partikel streuen, sind aber an etwa der gleichen Position.
###Code
# plot grid
plt.figure(2)
plt.imshow(grid[:,:], interpolation ='none', cmap = 'binary')
# get position of all particles
xy = [[p.x,p.y] for p in particles]
x,y = zip(*xy)
# plot all particles
plt.scatter((y-offset[0,1])/resolution,(x-offset[0,0])/resolution,
c='r',s=10,edgecolors='none',label='Partikel')
# plot 10 best particles
plt.scatter((y[0:10]-offset[0,1])/resolution,(x[0:10]-offset[0,0])/resolution,
c='y',s=20,edgecolors='none',label='Beste Partikel')
# plot best estimate pointcloud
R = np.matrix([[np.cos(bestParticle.yaw),-np.sin(bestParticle.yaw)],
[np.sin(bestParticle.yaw),np.cos(bestParticle.yaw)]])
pointcloudTransformed = pointcloud * np.transpose(R)
pointcloudTransformed = pointcloudTransformed + np.matrix([bestParticle.x,bestParticle.y])
plt.scatter([(pointcloudTransformed[:,1]-offset[0,0])/resolution],
[(pointcloudTransformed[:,0]-offset[0,1])/resolution],
c='m',s=10,edgecolors='none',label='Punktwolke')
plt.legend()
###Output
_____no_output_____
###Markdown
4. ResamplingUm die Schätzung weiter zu verbessern werden in der Umgebung der besten Lösungen neue Partikel verteilt. Diesemal ist der Suchradius jedoch deutlich geringer, sodass die Schätzung genauer wird.
###Code
# standard deviation of position and yaw for resampling
stddPosResample = stddPos/5.0
stddYawResample = stddYaw/5.0
# number of particels
nrParticleResample = 50
###Output
_____no_output_____
###Markdown
Verteilung der Partikel um die besten bisherigen Lösungen:
###Code
# delete old particles
particles.clear()
# create 50 particles for each of the best 10 particles
for bp in bestParticles:
for _ in range(0,nrParticleResample):
x = np.random.normal(bp.x,stddPosResample)
y = np.random.normal(bp.y,stddPosResample)
yaw = np.random.normal(bp.yaw,stddYawResample)
# create particle and append ist to list
p = Particle(x,y,yaw,1)
particles.append(p)
###Output
_____no_output_____
###Markdown
Auch diese Lösungen werden bewertet und sortiert:
###Code
# weight all particles
for p in particles:
# rotate pointcloud
R = np.matrix([[np.cos(p.yaw),-np.sin(p.yaw)], [np.sin(p.yaw),np.cos(p.yaw)]])
pointcloudTransformed = pointcloud * np.transpose(R)
# translate pointcloud
pointcloudTransformed = pointcloudTransformed + np.matrix([p.x,p.y])
# weight particle
p.weight = scan2mapDistance(grid,pointcloudTransformed,offset,resolution)
# sort particles
particles.sort(key = lambda Particle: Particle.weight,reverse=True)
###Output
_____no_output_____
###Markdown
5. Auswahl des besten PartikelsDer Schritt zuvor kann beliebig oft wiederholt werden. Am Ende wird die beste Lösung ausgewählt. Es ist gut erkennbar, dass die neuen Partikel durch die geringere Standardabweichung weniger streuen als die ersten.
###Code
# get best particle
bestParticle = particles[0]
# plot grid
plt.figure(3)
plt.imshow(grid[:,:], interpolation ='none', cmap = 'binary')
# get position of all particles
xy = [[p.x,p.y] for p in particles]
x,y = zip(*xy)
# plot all particles
plt.scatter((y-offset[0,1])/resolution,(x-offset[0,0])/resolution,
c='r',s=10,edgecolors='none',label='Partikel')
# plot best particle
plt.scatter((y[0]-offset[0,1])/resolution,(x[0]-offset[0,0])/resolution,
c='y',s=20,edgecolors='none',label='Bestes Partikel')
# plot best estimate pointcloud
R = np.matrix([[np.cos(bestParticle.yaw),-np.sin(bestParticle.yaw)],
[np.sin(bestParticle.yaw),np.cos(bestParticle.yaw)]])
pointcloudTransformed = pointcloud * np.transpose(R)
pointcloudTransformed = pointcloudTransformed + np.matrix([bestParticle.x,bestParticle.y])
plt.scatter([(pointcloudTransformed[:,1]-offset[0,0])/resolution],
[(pointcloudTransformed[:,0]-offset[0,1])/resolution],
c='m',s=10,edgecolors='none',label='Punktwolke')
plt.legend()
%reset
###Output
Once deleted, variables cannot be recovered. Proceed (y/[n])? y
###Markdown
Teil III: Zusammengesetzter SLAM AlgorithmusAls Bindeglied zwischen Mapping with Known Poses und der Lokalisierung in einer bestehenden Karte fehlt die erste Schätzung für die Position, um die bei der Lokalisierung die Partikel verteilt werden.Die ersten beiden Teile sind für eine bessere übersicht in Funktionen ausgelagert worden. Um die Laufzeit zu optimieren werden sie teilweise mit [Numba](https://numba.pydata.org/) zur Laufzeit kompiliert.
###Code
import os
import sys
nb_dir = os.path.split(os.getcwd())[0]
if nb_dir not in sys.path:
sys.path.append(nb_dir)
# import some pointcloud filter functions
from lib import filterPCL
# import mapping algorithm
from lib import mapping
# import particle filter
from lib import posEstimation
###Output
_____no_output_____
###Markdown
BewegungsmodellDie Lokalisierung in einer bestehenden Karte benötigt eine erste Schätzung der Position des Roboters. Eine sehr grobe Näherung wäre die letzte bekannte Position, für eine Verringerung der Laufzeit bei gleichzeitig besserer Lösung muss diese Näherung verbessert werden. Ab der dritten zu integrierenden Beobachtung kenn man die beiden vorherigen Positionen des Roboters. Wenn gleichförmige Bewegung sowohl in der Translation als auch in der Rotation des Roboters angenommen wird, kann über die vorherige Veränderung der Position die erste Schätzung erstellt werden.Diese Schätzung dient als Grundlage für die zuvor erläuterte Lokalisierung in einer bestehenden Karte. Vorteil dieses Bewegungsmodells ist, dass es unabhängig von der Roboterplattform ist und gut mit geringem Aufwand parametrisiert werden kann. AblaufMit dem Bewegungsmodell kann das Mapping With Known Poses und die Lokalisierung in einer bestehenden Karte zum SLAM Prozess zusammengesetzt werden: Zum Startzeitpunkt ist die Umgebung komplett unbekannt, die Startposition wird als bekannt vorausgesetzt beziehungsweise ist beliebig. An dieser Position wird die erste Beobachtung integriert. Dabei steigt für jeden Punkt, der in einer Zelle liegt, die WahrscheinlichkeitDie Karte wird nun genutzt, um die nächste Punktwolke relativ zur Karte zu orientieren. Da noch keine Informationen über die Bewegung des Roboters vorliegen wird in allen Richtungen mit einem verhältnismäßig großen Radius getestet, wo die zweite Punktwolke am besten mit der Karte übereinstimmt. Dafür werden Lösungen zufällig im Suchraum der drei Parameter der Position verteilt und die Lösungen mit der Gütefunktion bewertet. Nach mehreren Iterationen des Partikelfilters wird die beste Lösung ausgewählt und die Beobachtung in die Karte integriert.Da nun zwei Positionen bekannt sind, kann die Differenz und damit die Bewegung des Roboters im letzten Zeitschritt bestimmt werden. Mit dem allgemein gehaltene Bewegungsmodell erfolgt unter Annahme gleichförmiger Bewegung eine erste Schätzung der folgenden Position. Diese Schätzung führt dazu, dass der Suchraum für den Partikelfilter deutlich eingegrenzt wird. Der erneut mehrstufig angewendete Partikelfilter liefert so in kürzerer Zeit eine gute Lokalisierung. Die folgenden Beobachtungen werden auf gleiche Art in der Karte verortet und anschließend in sie integriert. 0. InitialisierungAls Testdaten werden die eingangs beschriebenen Daten der [KITTI Vision Benchmark Suite](http://www.cvlibs.net/) verwendet, die müssen zuvor exportiert und lokal gespeichert werden.
###Code
path = 'E:/KITTI_Daten/2011_09_30_drive_0027_export/'
###Output
_____no_output_____
###Markdown
Laden der Startposition, Angabe der Parameter, der als Vergleich dienenden wahren Trajektorie und Initialisierung des Grids:
###Code
%matplotlib notebook
import numpy as np
import matplotlib.pyplot as plt
import math
import time
"""
Load data
"""
# load start pose
startPose = np.loadtxt(path+'firstPose.txt',delimiter=',')
# load ground truth trajectory
groundTruth = np.asmatrix(np.loadtxt(path+'groundTruth.txt',delimiter=','))
nrOfScans = np.shape(groundTruth)[0]-1
"""
Parameter
"""
# parameter pointlcoud filter
zCutMin = -0.05
zCutMax = 0.05
# parameter mapping from octomap paper
l_occupied = 0.85
l_free = -0.4
l_min = -2.0
l_max = 3.5
# parameter particle Filter
stddPos = 0.1
stddYaw = 0.20
"""
Create empty GRID [m] and initialize it with 0, this Log-Odd
value is maximum uncertainty (P = 0.5)
Use the ground truth trajectory to calculate width and length of the grid
"""
additionalGridSize = 200.0
length = groundTruth[:,0].max()-groundTruth[:,0].min()+additionalGridSize
width = groundTruth[:,1].max()-groundTruth[:,1].min()+additionalGridSize
resolution = 0.25
grid = np.zeros((int(length/resolution),int(width/resolution)),order='C')
"""
Calculate best startposition in grid
"""
offset = np.array([math.fabs(groundTruth[0,0]-groundTruth[:,0].min()+additionalGridSize/2.0),
math.fabs(groundTruth[0,1]-groundTruth[:,1].min()+additionalGridSize/2.0),
0.0])
print('Length: '+str(length))
print('Width: '+str(width))
"""
Other variables
"""
# save estimated pose (x y yaw) in this list
trajectory = []
# save the estimated pose here (mouvement model)
estimatePose = np.matrix([startPose[0],startPose[1],startPose[2]])
###Output
Length: 425.343
Width: 371.525
###Markdown
1. Integration der ersten Punktwolke an initialer PositionDie Position des Fahrzeugs während der Aufnahme der ersten Punktwolke ist bekannt, daher kann die Integration wie beim Mapping With Known Poses erfolgen.
###Code
# load pointcloud
pointcloud = np.load(path+'pointcloudNP_'+str(0)+'.npy')
# filter poinctloud and project it to xy plane
pointcloud = filterPCL.filterZ(pointcloud,zCutMin,zCutMax)
pointcloud = np.delete(pointcloud,2,1)
# transform pointcloud to initial position
R = np.matrix([[np.cos(startPose[2]),-np.sin(startPose[2])],
[np.sin(startPose[2]),np.cos(startPose[2])]])
pointcloud = pointcloud * np.transpose(R)
pointcloud = pointcloud + np.matrix([startPose[0],
startPose[1]])
# add measurement to grid
mapping.addMeasurement(grid,pointcloud[:,0],pointcloud[:,1],
np.matrix([startPose[0],startPose[1],startPose[2]]),
startPose-offset,resolution,
l_occupied,l_free,l_min,l_max)
# add position to trajectory
trajectory.append(startPose)
###Output
_____no_output_____
###Markdown
2. Integration der zweiten PunktwolkeNach nur einer integrierten Punktwolke ist keine Informationen über die Bewegung des Fahrzeugs vorhanden. Daher wird in einem großen Umkreis nach der richtigen Position gesucht. Diese Suche dauert durch die große Partikelanzahl länger, als Teil der Initialisierung ist das vertretbar.
###Code
# load pointcloud
pointcloud = np.load(path+'pointcloudNP_'+str(1)+'.npy')
# filter poinctloud and project it to xy plane
pointcloud = filterPCL.filterZ(pointcloud,zCutMin,zCutMax)
pointcloud = np.delete(pointcloud,2,1)
# estimate position
estimatePose = posEstimation.fitScan2Map(grid,pointcloud,25000,10,2500,
estimatePose,stddPos*10,stddYaw*10,
startPose,offset,resolution)
# transform pointcloud to estimated position
R = np.matrix([[np.cos(estimatePose[0,2]),-np.sin(estimatePose[0,2])],
[np.sin(estimatePose[0,2]),np.cos(estimatePose[0,2])]])
pointcloud = pointcloud * np.transpose(R)
pointcloud = pointcloud + np.matrix([estimatePose[0,0],
estimatePose[0,1]])
# add measurement to grid
mapping.addMeasurement(grid,pointcloud[:,0],pointcloud[:,1],
np.matrix([estimatePose[0,0],estimatePose[0,1],estimatePose[0,2]]),
startPose-offset,resolution,
l_occupied,l_free,l_min,l_max)
# add position to trajectory
trajectory.append(estimatePose)
###Output
_____no_output_____
###Markdown
3. Integration der weiteren PunktwolkenDa nun zwei Positionen bekannt sind, kann das Bewegungsmodell angewendet werden: Es wird gleichförmige Bewegung angenommen, also wird die Differenz der letzten beiden Positionen ausgerechnet und zu der letzten Position addiert. Die erste Schätzung für den Partikelfilter ist so deutlich besser als bei der Integration der zweiten Punktwolke.
###Code
# calculate difference of last to positions
deltaPose = trajectory[-1]-trajectory[-2]
# calculate first estimate for new position
estimatePose = trajectory[-1]+deltaPose
print('Difference of last two postitions:')
print('x='+str(deltaPose[0,0])+'m y='+str(deltaPose[0,1])+'m yaw='+str(deltaPose[0,2])+'rad')
print('First estimate for new position:')
print('x='+str(estimatePose[0,0])+'m y='+str(estimatePose[0,1])+'m yaw='+str(estimatePose[0,2])+'rad')
###Output
Difference of last two postitions:
x=0.056187174865m y=-0.0726430555806m yaw=0.00413078983134rad
First estimate for new position:
x=455637.042374m y=5425990.93371m yaw=-0.548738420337rad
###Markdown
Mit dieser ersten Schätzung können alle weiteren Messungen in die Karte integriert werden:
###Code
t0 = time.time()
for ii in range(2,nrOfScans+1):
# load pointcloud
pointcloud = np.load(path+'pointcloudNP_'+str(ii)+'.npy')
# filter poinctloud and project it to xy plane
pointcloud = filterPCL.filterZ(pointcloud,zCutMin,zCutMax)
pointcloud = np.delete(pointcloud,2,1)
# calculate difference between last to positions
deltaPose = trajectory[-1]-trajectory[-2]
# calculate first estimate for new position
estimatePose = trajectory[-1]+deltaPose
# estimate position with two resamplings
estimatePose = posEstimation.fitScan2Map2(grid,pointcloud,500,1,250,250,
estimatePose,stddPos,stddYaw,
startPose,offset,resolution)
# transform pointcloud to estimated position
R = np.matrix([[np.cos(estimatePose[0,2]),-np.sin(estimatePose[0,2])],
[np.sin(estimatePose[0,2]),np.cos(estimatePose[0,2])]])
pointcloud = pointcloud * np.transpose(R)
pointcloud = pointcloud + np.matrix([estimatePose[0,0],
estimatePose[0,1]])
# add measurement to grid
mapping.addMeasurement(grid,pointcloud[:,0],pointcloud[:,1],
np.matrix([estimatePose[0,0],estimatePose[0,1],estimatePose[0,2]]),
startPose-offset,resolution,
l_occupied,l_free,l_min,l_max)
# add position to trajectory
trajectory.append(estimatePose)
# print update
if ii%10 == 0:
print('Measurement '+str(ii)+' of '+str(nrOfScans)+' processed: '+str(time.time()-t0)+'s')
print('Finished, '+str(ii)+' measurements processed. Timer per measurement: '+str((time.time()-t0)/ii)+'s')
###Output
Measurement 10 of 1105 processed: 2.576207160949707s
Measurement 20 of 1105 processed: 5.194946527481079s
Measurement 30 of 1105 processed: 7.752157211303711s
Measurement 40 of 1105 processed: 10.853665351867676s
Measurement 50 of 1105 processed: 15.920048475265503s
Measurement 60 of 1105 processed: 20.42853832244873s
Measurement 70 of 1105 processed: 23.73824977874756s
Measurement 80 of 1105 processed: 27.152014017105103s
Measurement 90 of 1105 processed: 30.637826204299927s
Measurement 100 of 1105 processed: 33.85546064376831s
Measurement 110 of 1105 processed: 38.11578845977783s
Measurement 120 of 1105 processed: 42.51420497894287s
Measurement 130 of 1105 processed: 45.73684287071228s
Measurement 140 of 1105 processed: 48.72582793235779s
Measurement 150 of 1105 processed: 51.63630676269531s
Measurement 160 of 1105 processed: 55.06708526611328s
Measurement 170 of 1105 processed: 59.237348794937134s
Measurement 180 of 1105 processed: 62.94831371307373s
Measurement 190 of 1105 processed: 67.3497302532196s
Measurement 200 of 1105 processed: 71.37290716171265s
Measurement 210 of 1105 processed: 74.89977979660034s
Measurement 220 of 1105 processed: 78.28552722930908s
Measurement 230 of 1105 processed: 81.9589774608612s
Measurement 240 of 1105 processed: 85.79243588447571s
Measurement 250 of 1105 processed: 89.7520604133606s
Measurement 260 of 1105 processed: 93.3039174079895s
Measurement 270 of 1105 processed: 96.98886108398438s
Measurement 280 of 1105 processed: 100.65279626846313s
Measurement 290 of 1105 processed: 104.43130445480347s
Measurement 300 of 1105 processed: 108.1572756767273s
Measurement 310 of 1105 processed: 111.4014253616333s
Measurement 320 of 1105 processed: 114.31385922431946s
Measurement 330 of 1105 processed: 117.06718516349792s
Measurement 340 of 1105 processed: 119.78148460388184s
Measurement 350 of 1105 processed: 122.79548406600952s
Measurement 360 of 1105 processed: 125.8515293598175s
Measurement 370 of 1105 processed: 128.89555716514587s
Measurement 380 of 1105 processed: 132.1822748184204s
Measurement 390 of 1105 processed: 135.74613976478577s
Measurement 400 of 1105 processed: 139.01230597496033s
Measurement 410 of 1105 processed: 142.1173655986786s
Measurement 420 of 1105 processed: 145.03131365776062s
Measurement 430 of 1105 processed: 147.73263335227966s
Measurement 440 of 1105 processed: 150.69905757904053s
Measurement 450 of 1105 processed: 153.60648727416992s
Measurement 460 of 1105 processed: 156.11314988136292s
Measurement 470 of 1105 processed: 158.59979701042175s
Measurement 480 of 1105 processed: 161.3751380443573s
Measurement 490 of 1105 processed: 164.69333910942078s
Measurement 500 of 1105 processed: 168.31075382232666s
Measurement 510 of 1105 processed: 171.9836871623993s
Measurement 520 of 1105 processed: 175.33240938186646s
Measurement 530 of 1105 processed: 178.29937934875488s
Measurement 540 of 1105 processed: 181.31543135643005s
Measurement 550 of 1105 processed: 184.54157614707947s
Measurement 560 of 1105 processed: 187.7011842727661s
Measurement 570 of 1105 processed: 190.43099784851074s
Measurement 580 of 1105 processed: 193.22736811637878s
Measurement 590 of 1105 processed: 196.56858205795288s
Measurement 600 of 1105 processed: 200.45015668869019s
Measurement 610 of 1105 processed: 203.7753622531891s
Measurement 620 of 1105 processed: 206.81391763687134s
Measurement 630 of 1105 processed: 209.98003244400024s
Measurement 640 of 1105 processed: 213.3917956352234s
Measurement 650 of 1105 processed: 216.4218249320984s
Measurement 660 of 1105 processed: 219.30473566055298s
Measurement 670 of 1105 processed: 222.10460758209229s
Measurement 680 of 1105 processed: 225.08859133720398s
Measurement 690 of 1105 processed: 227.95699310302734s
Measurement 700 of 1105 processed: 230.92746376991272s
Measurement 710 of 1105 processed: 233.65877556800842s
Measurement 720 of 1105 processed: 236.3280975818634s
Measurement 730 of 1105 processed: 238.9278221130371s
Measurement 740 of 1105 processed: 241.55156254768372s
Measurement 750 of 1105 processed: 243.96017456054688s
Measurement 760 of 1105 processed: 246.27774858474731s
Measurement 770 of 1105 processed: 249.0473973751068s
Measurement 780 of 1105 processed: 251.71074223518372s
Measurement 790 of 1105 processed: 254.78028011322021s
Measurement 800 of 1105 processed: 257.8733277320862s
Measurement 810 of 1105 processed: 261.11499404907227s
Measurement 820 of 1105 processed: 264.10747814178467s
Measurement 830 of 1105 processed: 266.90335035324097s
Measurement 840 of 1105 processed: 269.8988358974457s
Measurement 850 of 1105 processed: 272.9493601322174s
Measurement 860 of 1105 processed: 275.95385456085205s
Measurement 870 of 1105 processed: 278.89430356025696s
Measurement 880 of 1105 processed: 281.7872407436371s
Measurement 890 of 1105 processed: 284.61361622810364s
Measurement 900 of 1105 processed: 287.7522089481354s
Measurement 910 of 1105 processed: 290.4294912815094s
Measurement 920 of 1105 processed: 292.90463185310364s
Measurement 930 of 1105 processed: 296.1257724761963s
Measurement 940 of 1105 processed: 300.190966129303s
Measurement 950 of 1105 processed: 303.5737793445587s
Measurement 960 of 1105 processed: 307.1501512527466s
Measurement 970 of 1105 processed: 311.1202883720398s
Measurement 980 of 1105 processed: 314.7707073688507s
Measurement 990 of 1105 processed: 318.4446442127228s
Measurement 1000 of 1105 processed: 321.66282176971436s
Measurement 1010 of 1105 processed: 324.82441687583923s
Measurement 1020 of 1105 processed: 328.12911009788513s
Measurement 1030 of 1105 processed: 331.7370035648346s
Measurement 1040 of 1105 processed: 335.3143997192383s
Measurement 1050 of 1105 processed: 338.8332316875458s
Measurement 1060 of 1105 processed: 341.9012653827667s
Measurement 1070 of 1105 processed: 344.6595950126648s
Measurement 1080 of 1105 processed: 347.2272982597351s
Measurement 1090 of 1105 processed: 349.77899146080017s
Measurement 1100 of 1105 processed: 352.62637996673584s
Finished, 1105 measurements processed. Timer per measurement: 0.32037312391117145s
###Markdown
Der SLAM Prozess ist beendet. Ausgabe des Ergebnisses:
###Code
# show grid
plt.figure(0)
plt.imshow(grid[:,:], interpolation ='none', cmap = 'binary')
# plot trajectory
trajectory = np.vstack(trajectory)
plt.scatter(([trajectory[:,1]]-startPose[1]+offset[1])/resolution,
([trajectory[:,0]]-startPose[0]+offset[0])/resolution,
c='b',s=10,edgecolors='none', label = 'Trajectory SLAM')
# plot ground truth trajectory
plt.scatter(([groundTruth[:,1]]-startPose[1]+offset[1])/resolution,
([groundTruth[:,0]]-startPose[0]+offset[0])/resolution,
c='g',s=10,edgecolors='none', label = 'Trajectory Ground Truth')
# plot last pointcloud
plt.scatter(([pointcloud[:,1]]-startPose[1]+offset[1])/resolution,
([pointcloud[:,0]]-startPose[0]+offset[0])/resolution,
c='m',s=5,edgecolors='none', label = 'Pointcloud')
# plot legend
plt.legend(loc='lower left')
###Output
_____no_output_____
|
35_morphological_analysis/r-evaluate-nblast-clustering.ipynb
|
###Markdown
Read data
###Code
library("h5")
DATASET_DIR = "~/seungmount/research/Jingpeng/14_zfish/01_data/20190415"
f = h5file(file.path(DATASET_DIR,"evaluate3.h5"), mode="r")
neuronIdList = f["/neuronIdList"][]
groundTruthPartition = f["/groundTruthPartition"][]
flyTableDistanceMatrix = - f["flyTable/meanSimilarityMatrix"][]
zfishTableDistanceMatrix = - f["zfishTable/meanSimilarityMatrix"][]
semanticDistanceMatrix = - f["zfishTable/semantic/meanSimilarityMatrix"][]
small2bigDistanceMatrix = - f["zfishTable/small2big/similarityMatrix"][]
semanticSmall2bigDistanceMatrix = - f["zfishTable/semantic/small2big/similarityMatrix"][]
h5close(f)
###Output
_____no_output_____
###Markdown
Clustering
###Code
# Affinity Propagation clustering
# library(apcluster)
# apres <- apcluster(small2bigDistanceMatrix, details=TRUE)
# show(apres)
library("dendextend")
library("dynamicTreeCut")
library(FreeSortR)
distanceMatrix = flyTableDistanceMatrix
evaluate <- function (distanceMatrix){
dist = as.dist(distanceMatrix)
hc = hclust(dist, method="ward.D")
dend <- hc %>% as.dendrogram #%>% set("labels", NULL)
clusters = cutree(hc, k=5)
# clusters <- cutreeDynamic(hc, distM=distanceMatrix, method="tree")
ri = RandIndex(clusters, groundTruthPartition)
ret <- list("randIndex"=ri, "clusters" = clusters, "hc"=hc, "dend"=dend)
return (ret)
}
fly = evaluate(flyTableDistanceMatrix)
zfish = evaluate(zfishTableDistanceMatrix)
semantic = evaluate(semanticDistanceMatrix)
small2big = evaluate(small2bigDistanceMatrix)
semanticSmall2big = evaluate(semanticSmall2bigDistanceMatrix)
cat("metric fly table, zfish table, semantic, small2big, semantic small2big\n")
cat("rand index: ", fly$randIndex$Rand, " ", zfish$randIndex$Rand, " ", semantic$randIndex$Rand,
" ", small2big$randIndex$Rand, " ", semanticSmall2big$randIndex$Rand, "\n")
cat("adjusted rand index: ", fly$randIndex$AdjustedRand, " ", zfish$randIndex$AdjustedRand, " ", semantic$randIndex$AdjustedRand,
" ", small2big$randIndex$AdjustedRand, " ", semanticSmall2big$randIndex$AdjustedRand, "\n")
print_groups <- function(x){
orders = order.hclust(x$hc)
orderedClusters = x$clusters[orders]
orderedNeuronIdList = neuronIdList[orders]
for (groupId in 1:5){
cat("group ", groupId, ": ", orderedNeuronIdList[orderedClusters==groupId], "\n\n")
}
}
# print_groups(fly)
# print_groups(zfish)
print_groups(semantic)
# print_groups(small2big)
library(gplots)
# svg(file=file.path(DATASET_DIR, "figs/evaluate/dend.svg"))
# plot(dend)
# heatmap.2(distanceMatrix)
# dev.off()
# plot(dend)
# heatmap.2(distanceMatrix,
# hclustfun = function(x) hclust(x, method="ward.D"),
# col="heat.colors")
library(d3heatmap)
d3heatmap(distanceMatrix, distfun=as.dist,
hclustfun = function(x) hclust(x, method="ward.D"))
flyTableDistanceMatrix %>% as.dist %>% hclust(method="ward.D") %>% as.dendrogram %>% plot
###Output
_____no_output_____
|
notebooks/General Timeseries with Noise.ipynb
|
###Markdown
Let's simulate a general timeseries, that's been stacked together using the a Central 8/10 strategy:
###Code
# let's create a stacking strategy object
strategy = Central(10)
# let's create a general timeseries
timeseries = Timeseries(model=Transit(a_over_rs=5, period=1.6),
tmin=-5, tmax=5,
cadence=1800.0, subcadence=2.0,
subcadenceuncertainty=0.01,
cosmickw=dict(probability=0.001, height=1))
###Output
_____no_output_____
###Markdown
Now, let's process that timeseries using the stacking strategy.
###Code
# stack the subcadences together into the binned cadence
timeseries.stack(strategy)
# print out the noise associated with these
for k in timeseries.rms.keys():
print('{:>20} noise is {:.3}'.format(k, timeseries.rms[k]))
###Output
unmitigated noise is 0.000468
achieved noise is 0.000363
expected noise is 0.000333
###Markdown
Let's see what this looks like as a static plot.
###Code
timeseries.plot(xlim=[-.5, 0.5])
###Output
_____no_output_____
###Markdown
It'd also be good to show *all* the data points. Let's see what they look like by sliding through the whole light curve as an animation.
###Code
timeseries.movie(filename='generaltransit.mp4')
###Output
100%|██████████| 301/301 [00:13<00:00, 22.74it/s]
|
fig5_annual-cycles.ipynb
|
###Markdown
Figure 5: Annual cyclesconda env: new `phd_v3`, old `work` (in `envs/phd`)
###Code
# To reload external files automatically (ex: utils)
%load_ext autoreload
%autoreload 2
import xarray as xr
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import proplot as plot # New plot library (https://proplot.readthedocs.io/en/latest/)
plot.rc['savefig.dpi'] = 300 # 1200 is too big! #https://proplot.readthedocs.io/en/latest/basics.html#Creating-figures
from scipy import stats
import xesmf as xe # For regridding (https://xesmf.readthedocs.io/en/latest/)
import sys
sys.path.insert(1, '/home/mlalande/notebooks/utils') # to include my util file in previous directory
import utils as u # my personal functions
u.check_python_version()
# u.check_virtual_memory()
###Output
3.8.5 | packaged by conda-forge | (default, Jul 24 2020, 01:25:15)
[GCC 7.5.0]
###Markdown
Set variables
###Code
period = slice('1979','2014')
latlim, lonlim = u.get_domain_HMA()
# Make a extended version for regridding properly on the edges
latlim_ext, lonlim_ext = slice(latlim.start-5, latlim.stop+5), slice(lonlim.start-5, lonlim.stop+5)
# Get zone limits for annual cycle
lonlim_HK, latlim_HK, lonlim_HM, latlim_HM, lonlim_TP, latlim_TP = u.get_zones()
# HMA for full domain and the following for the above zones
zones = ['HMA', 'HK', 'HM', 'TP']
zones_df = pd.DataFrame(
[[lonlim, latlim], [lonlim_HK, latlim_HK], [lonlim_HM, latlim_HM], [lonlim_TP, latlim_TP]],
columns=pd.Index(['lonlim', 'latlim'], name='Limits'),
index=pd.Index(zones, name='Zones')
)
###Output
_____no_output_____
###Markdown
Load observations Topography
###Code
ds = xr.open_dataset('GMTED2010_15n240_1000deg.nc').drop_dims('nbounds').swap_dims(
{'nlat': 'latitude', 'nlon': 'longitude'}).drop({'nlat', 'nlon'}).rename(
{'latitude': 'lat', 'longitude': 'lon'}).sel(lat=latlim_ext, lon=lonlim_ext)
elevation = ds.elevation
elevation_std = ds.elevation_stddev
ds = xr.open_dataset('/data/mlalande/Relief/GMTED2010_15n015_00625deg.nc').drop_dims('nbounds').swap_dims(
{'nlat': 'latitude', 'nlon': 'longitude'}).drop({'nlat', 'nlon'}).rename(
{'latitude': 'lat', 'longitude': 'lon'}).sel(lat=latlim_ext, lon=lonlim_ext)
elevation_HR = ds.elevation
###Output
_____no_output_____
###Markdown
ERA-Interim and ERA5Downloaded from https://cds.climate.copernicus.eu/cdsapp!/dataset/ecv-for-climate-change?tab=doc (there are correction but doesn't seem to affect HMA)For Snow Cover Extent, there is only ERA-Interim on the period 1979-2014 and is computed from snow depth (Appendix A : https://tc.copernicus.org/articles/13/2221/2019/) and https://confluence.ecmwf.int/display/CKB/ERA-Interim%3A+documentationERAInterim:documentation-Computationofnear-surfacehumidityandsnowcover
###Code
path = '/data/mlalande/ERA-ECV/NETCDF'
tas_era5 = xr.open_dataset(path+'/1month_mean_Global_ea_2t_1979-2014_v02.nc').t2m.rename({'latitude': 'lat', 'longitude': 'lon'}).sel(lat=slice(latlim_ext.stop, latlim_ext.start), lon=lonlim_ext) - 273.15
tas_erai = xr.open_dataset(path+'/1month_mean_Global_ei_t2m_1979-2014_v02.nc').t2m.rename({'latitude': 'lat', 'longitude': 'lon'}).sel(lat=slice(latlim_ext.stop, latlim_ext.start), lon=lonlim_ext) - 273.15
pr_era5 = xr.open_dataset(path+'/1month_mean_Global_ea_tp_1979-2014_v02.nc').tp.rename({'latitude': 'lat', 'longitude': 'lon'}).sel(lat=slice(latlim_ext.stop, latlim_ext.start), lon=lonlim_ext) * 10**3
pr_erai = xr.open_dataset(path+'/1month_mean_Global_ei_tp_1979-2014_v02.nc').tp.rename({'latitude': 'lat', 'longitude': 'lon'}).sel(lat=slice(latlim_ext.stop, latlim_ext.start), lon=lonlim_ext) * 10**3
regridder = xe.Regridder(tas_era5, elevation, 'bilinear', periodic=False, reuse_weights=True)
obs_ac_regrid_zones = []
for obs in [tas_era5, tas_erai, pr_era5, pr_erai]:
np.testing.assert_equal((int(period.stop) - int(period.start) + 1)*12, obs.time.size)
obs_ac = u.annual_cycle(obs, calendar=obs.time.encoding['calendar'])
# Compute annual cycle for each zones
temp = [None]*len(zones)
obs_ac_regrid = regridder(obs_ac)
for i, zone in enumerate(zones):
temp[i] = u.spatial_average(
obs_ac_regrid.sel(lat=zones_df.latlim[zone], lon=zones_df.lonlim[zone]).where(elevation > 2500)
)
obs_ac_regrid_zones.append(xr.concat(temp, pd.Index(zones, name="zone")).load())
obs_ac_regrid_zones_tas_era5 = obs_ac_regrid_zones[0]
obs_ac_regrid_zones_tas_erai = obs_ac_regrid_zones[1]
obs_ac_regrid_zones_pr_era5 = obs_ac_regrid_zones[2]
obs_ac_regrid_zones_pr_erai = obs_ac_regrid_zones[3]
###Output
Reuse existing file: bilinear_141x241_35x60.nc
###Markdown
ERA-Interim SCF
###Code
SD = xr.open_mfdataset('/bdd/ERAI/NETCDF/GLOBAL_075/1xmonthly/AN_SF/*/sd.*.asmei.GLOBAL_075.nc').sd.sel(time=period, lat=slice(latlim_ext.stop, latlim_ext.start), lon=lonlim_ext)
RW = 1000
obs = xr.ufuncs.minimum(1, RW*SD/15)*100
# Check if the time steps are ok
np.testing.assert_equal((int(period.stop) - int(period.start) + 1)*12, obs.time.size)
obs_ac = u.annual_cycle(obs, calendar='standard')
regridder = xe.Regridder(obs_ac, elevation, 'bilinear', periodic=False, reuse_weights=True)
# Compute annual cycle for each zones
temp = [None]*len(zones)
obs_ac_regrid = regridder(obs_ac)
for i, zone in enumerate(zones):
temp[i] = u.spatial_average(
obs_ac_regrid.sel(lat=zones_df.latlim[zone], lon=zones_df.lonlim[zone]).where(elevation > 2500)
)
obs_ac_regrid_zones_snc_erai = xr.concat(temp, pd.Index(zones, name="zone")).load()
###Output
Reuse existing file: bilinear_47x80_35x60.nc
###Markdown
ERA5 SCF
###Code
# snow water equivalent (ie parameter SD (141.128))
SD = xr.open_mfdataset('/data/mlalande/ERA5/ERA5_monthly_HMA-ext_SD_1979-2014.nc').sd.rename({'latitude': 'lat', 'longitude': 'lon'}).sel(time=period, lat=slice(latlim_ext.stop, latlim_ext.start), lon=lonlim_ext)
# RSN is density of snow (parameter 33.128)
RSN = xr.open_dataset('/data/mlalande/ERA5/ERA5_monthly_HMA-ext_RSN_1979-2014.nc').rsn.rename({'latitude': 'lat', 'longitude': 'lon'}).sel(time=period, lat=slice(latlim_ext.stop, latlim_ext.start), lon=lonlim_ext)
# RW is density of water equal to 1000
RW = 1000
# https://confluence.ecmwf.int/display/CKB/ERA5%3A+data+documentation#ERA5:datadocumentation-Computationofnear-surfacehumidityandsnowcover
obs = xr.ufuncs.minimum(1, (RW*SD/RSN)/0.1) * 100
# Check if the time steps are ok
np.testing.assert_equal((int(period.stop) - int(period.start) + 1)*12, obs.time.size)
obs_ac = u.annual_cycle(obs, calendar='standard')
regridder = xe.Regridder(obs_ac, elevation, 'bilinear', periodic=False, reuse_weights=True)
# Compute annual cycle for each zones
temp = [None]*len(zones)
obs_ac_regrid = regridder(obs_ac)
for i, zone in enumerate(zones):
temp[i] = u.spatial_average(
obs_ac_regrid.sel(lat=zones_df.latlim[zone], lon=zones_df.lonlim[zone]).where(elevation > 2500)
)
obs_ac_regrid_zones_snc_era5 = xr.concat(temp, pd.Index(zones, name="zone")).load()
###Output
Reuse existing file: bilinear_141x241_35x60.nc
###Markdown
Temperature
###Code
obs = xr.open_dataset('/bdd/cru/cru_ts_4.00/data/tmp/cru_ts4.00.1901.2015.tmp.dat.nc').sel(
time=period, lat=latlim_ext, lon=lonlim_ext).tmp
# Check if the time steps are ok
np.testing.assert_equal((int(period.stop) - int(period.start) + 1)*12, obs.time.size)
obs_ac = u.annual_cycle(obs, calendar=obs.time.encoding['calendar'])
regridder = xe.Regridder(obs, elevation, 'bilinear', periodic=False, reuse_weights=True)
# Compute annual cycle for each zones
temp = [None]*len(zones)
obs_ac_regrid = regridder(obs_ac)
for i, zone in enumerate(zones):
temp[i] = u.spatial_average(
obs_ac_regrid.sel(lat=zones_df.latlim[zone], lon=zones_df.lonlim[zone]).where(elevation > 2500)
)
obs_ac_regrid_zones_tas = xr.concat(temp, pd.Index(zones, name="zone")).load()
###Output
Reuse existing file: bilinear_70x120_35x60.nc
###Markdown
Snow Cover
###Code
ds_rutger = xr.open_dataset('/data/mlalande/RUTGERS/nhsce_v01r01_19661004_20191202.nc').sel(time=period)
with xr.set_options(keep_attrs=True): # Get the snc variable, keep only land data and convert to %
obs = ds_rutger.snow_cover_extent.where(ds_rutger.land == 1)*100
obs.attrs['units'] = '%'
obs = obs.rename({'longitude': 'lon', 'latitude': 'lat'}) # Rename lon and lat for the regrid
# Resamble data per month (from per week)
obs = obs.resample(time='1MS').mean('time', skipna=False, keep_attrs=True)
# Check if the time steps are ok
np.testing.assert_equal((int(period.stop) - int(period.start) + 1)*12, obs.time.size)
obs_ac = u.annual_cycle(obs, calendar='standard')
import scipy
def add_matrix_NaNs(regridder):
X = regridder.weights
M = scipy.sparse.csr_matrix(X)
num_nonzeros = np.diff(M.indptr)
M[num_nonzeros == 0, 0] = np.NaN
regridder.weights = scipy.sparse.coo_matrix(M)
return regridder
regridder = xe.Regridder(obs, elevation, 'bilinear', periodic=False, reuse_weights=True)
regridder = add_matrix_NaNs(regridder)
# Compute annual cycle for each zones
temp = [None]*len(zones)
obs_ac_regrid = regridder(obs_ac)
for i, zone in enumerate(zones):
temp[i] = u.spatial_average(
obs_ac_regrid.sel(lat=zones_df.latlim[zone], lon=zones_df.lonlim[zone]).where(elevation > 2500)
)
obs_ac_regrid_zones_snc = xr.concat(temp, pd.Index(zones, name="zone")).load()
###Output
Reuse existing file: bilinear_88x88_35x60.nc
###Markdown
ESA snow CCIWe keep it at its original resolution because of NaNs values and use higher resolution topography to define the zones.
###Code
path = '/data/mlalande/ESACCI/ESA_CCI_snow_SCFG_v1.0_HKH_gapfilled_monthly'
esa_snc_icefilled = xr.open_dataarray(path+'/ESACCI-L3C_SNOW-SCFG-AVHRR_MERGED-fv1.0_HKH_gapfilled_icefilled_montlhy_1982-2014.nc')
regridder = xe.Regridder(elevation_HR, esa_snc_icefilled, 'bilinear', periodic=False, reuse_weights=True)
elevation_HR_regrid = regridder(elevation_HR)
temp = [None]*len(zones)
esa_snc_ac_icefilled = esa_snc_icefilled.groupby('time.month').mean('time') # otherwise bug with u.annual_cycle (0 on glaciers instead of nan)
for i, zone in enumerate(zones):
temp[i] = u.spatial_average(
esa_snc_ac_icefilled.sel(lat=slice(zones_df.latlim[zone].stop, zones_df.latlim[zone].start), lon=zones_df.lonlim[zone]).where(elevation_HR_regrid > 2500)
)
esa_snc_ac_icefilled_zones = xr.concat(temp, pd.Index(zones, name="zone")).load()
###Output
Reuse existing file: bilinear_560x960_500x920.nc
###Markdown
Precipitation APHRODITE
###Code
obs_longname = 'APHRODITE V1101 (0.5°)'
obs_name = 'APHRODITE'
obs_V1101 = xr.open_mfdataset(
'/data/mlalande/APHRODITE/APHRO_MA_050deg_V1101.*.nc', combine='by_coords'
).precip
obs_V1101_EXR1 = xr.open_mfdataset(
'/data/mlalande/APHRODITE/APHRO_MA_050deg_V1101_EXR1.*.nc', combine='by_coords'
).precip
obs_V1101 = obs_V1101.rename({'longitude': 'lon', 'latitude': 'lat'})
obs = (xr.combine_nested([obs_V1101, obs_V1101_EXR1], concat_dim='time')).sel(time=period)
# Resamble data per month (from per day)
obs = obs.resample(time='1MS').mean('time', skipna=False, keep_attrs=True)
# Check if the time steps are ok
np.testing.assert_equal((int(period.stop) - int(period.start) + 1)*12, obs.time.size)
obs_ac = u.annual_cycle(obs, calendar='standard')
import scipy
def add_matrix_NaNs(regridder):
X = regridder.weights
M = scipy.sparse.csr_matrix(X)
num_nonzeros = np.diff(M.indptr)
M[num_nonzeros == 0, 0] = np.NaN
regridder.weights = scipy.sparse.coo_matrix(M)
return regridder
regridder = xe.Regridder(obs, elevation, 'bilinear', periodic=False, reuse_weights=True)
regridder = add_matrix_NaNs(regridder)
# Compute annual cycle for each zones
temp = [None]*len(zones)
obs_ac_regrid = regridder(obs_ac)
for i, zone in enumerate(zones):
temp[i] = u.spatial_average(
obs_ac_regrid.sel(lat=zones_df.latlim[zone], lon=zones_df.lonlim[zone]).where(elevation > 2500)
)
obs_ac_regrid_zones_pr_aphro = xr.concat(temp, pd.Index(zones, name="zone")).load()
###Output
Reuse existing file: bilinear_140x180_35x60.nc
###Markdown
GPCP
###Code
obs_longname = 'GPCP CDR v2.3 (2.5°)'
obs_name = 'GPCP'
obs = xr.open_mfdataset(
# '/bdd/GPCP/netcdf/surf-rr_gpcp_multi-sat_250d_01mth_*_v2.2-02.nc', combine='by_coords'
# -> missing some month (ex 2014/11)
'/data/mlalande/GPCP/CDR_monthly_v2.3/*/gpcp_v02r03_monthly_d*_c20170616.nc'
).precip.sel(time=period, latitude=latlim_ext, longitude=lonlim_ext)
obs = obs.rename({'longitude': 'lon', 'latitude': 'lat'})
# Check if the time steps are ok
np.testing.assert_equal((int(period.stop) - int(period.start) + 1)*12, obs.time.size)
obs_ac = u.annual_cycle(obs, calendar='standard')
import scipy
def add_matrix_NaNs(regridder):
X = regridder.weights
M = scipy.sparse.csr_matrix(X)
num_nonzeros = np.diff(M.indptr)
M[num_nonzeros == 0, 0] = np.NaN
regridder.weights = scipy.sparse.coo_matrix(M)
return regridder
regridder = xe.Regridder(obs, elevation, 'bilinear', periodic=False, reuse_weights=True)
regridder = add_matrix_NaNs(regridder)
# Compute annual cycle for each zones
temp = [None]*len(zones)
obs_ac_regrid = regridder(obs_ac)
for i, zone in enumerate(zones):
temp[i] = u.spatial_average(
obs_ac_regrid.sel(lat=zones_df.latlim[zone], lon=zones_df.lonlim[zone]).where(elevation > 2500)
)
obs_ac_regrid_zones_pr_gpcp = xr.concat(temp, pd.Index(zones, name="zone")).load()
###Output
Reuse existing file: bilinear_14x24_35x60.nc
###Markdown
Load results
###Code
list_vars = ['tas', 'snc', 'pr']
temp = [None]*len(list_vars)
for i, var in enumerate(list_vars):
temp[i] = xr.open_dataarray(
'results/'+var+'_'+period.start+'-'+period.stop+'multimodel_ensemble_ac.nc'
)
multimodel_ensemble_ac = xr.concat(temp, pd.Index(list_vars, name='var'))
multimodel_ensemble_ac = multimodel_ensemble_ac.sel(model=['BCC-CSM2-MR', 'BCC-ESM1', 'CAS-ESM2-0', 'CESM2', 'CESM2-FV2',
'CESM2-WACCM', 'CESM2-WACCM-FV2', 'CNRM-CM6-1', 'CNRM-CM6-1-HR',
'CNRM-ESM2-1', 'CanESM5', 'GFDL-CM4', 'GISS-E2-1-G',
'GISS-E2-1-H', 'HadGEM3-GC31-LL', 'HadGEM3-GC31-MM', 'IPSL-CM6A-LR',
'MIROC-ES2L', 'MIROC6', 'MPI-ESM1-2-HR', 'MPI-ESM1-2-LR', 'MRI-ESM2-0',
'NorESM2-LM', 'SAM0-UNICON', 'TaiESM1', 'UKESM1-0-LL'])
# multimodel_ensemble_ac
###Output
_____no_output_____
###Markdown
Plot
###Code
f, axs = plot.subplots(ncols=4, nrows=3, aspect=1.3, sharey=0, axwidth=2)
color_model = 'ocean blue'
color_obs = 'black'
color_era = 'pink orange'
n_ax = 0
for i_var, var in enumerate(list_vars):
for i in range(len(zones)):
means = multimodel_ensemble_ac.sel(var=var)[i].mean('model')
# Compute quantiles
shadedata = multimodel_ensemble_ac.sel(var=var)[i].quantile([0.25, 0.75], dim='model') # dark shading
fadedata = multimodel_ensemble_ac.sel(var=var)[i].quantile([0.05, 0.95], dim='model') # light shading
h1 = axs[n_ax].plot(
means,
shadedata=shadedata, fadedata=fadedata,
shadelabel='50% CI', fadelabel='90% CI',
label='Multi-Model Mean', color=color_model,
)
# Add min/max
h2 = axs[n_ax].plot(
multimodel_ensemble_ac.sel(var=var)[i].min('model'),
label='min/max', linestyle='--', color=color_model, linewidth=0.8, alpha=0.8
)
axs[n_ax].plot(
multimodel_ensemble_ac.sel(var=var)[i].max('model'),
linestyle='--', color=color_model, linewidth=0.8, alpha=0.8
)
# Plot observations
if var == 'tas':
h3 = axs[n_ax].plot(obs_ac_regrid_zones_tas[i], label='CRU', color=color_obs, linewidth=2)
h4 = axs[n_ax].plot(obs_ac_regrid_zones_tas_erai[i], label='ERA-Interim', color=color_era, linewidth=1, linestyle='--')
h5 = axs[n_ax].plot(obs_ac_regrid_zones_tas_era5[i], label='ERA5', color=color_era, linewidth=1)
elif var == 'snc':
h3 = axs[n_ax].plot(obs_ac_regrid_zones_snc[i], label='NOAA CDR', color=color_obs, linewidth=2)
h4 = axs[n_ax].plot(esa_snc_ac_icefilled_zones[i], label='ESA CCI (1982-2014)', color=color_obs, linewidth=1, linestyle='--')
h5 = axs[n_ax].plot(obs_ac_regrid_zones_snc_erai[i], label='ERA-Interim', color=color_era, linewidth=1, linestyle='--')
h6 = axs[n_ax].plot(obs_ac_regrid_zones_snc_era5[i], label='ERA5', color=color_era, linewidth=1)
elif var == 'pr':
h3 = axs[n_ax].plot(obs_ac_regrid_zones_pr_aphro[i], label='APHRODITE', color=color_obs, linewidth=2)
h4 = axs[n_ax].plot(obs_ac_regrid_zones_pr_gpcp[i], label='GPCP', color=color_obs, linewidth=1, linestyle='--')
h5 = axs[n_ax].plot(obs_ac_regrid_zones_pr_erai[i], label='ERA-Interim', color=color_era, linewidth=1, linestyle='--')
h6 = axs[n_ax].plot(obs_ac_regrid_zones_pr_era5[i], label='ERA5', color=color_era, linewidth=1)
if i == 0:
axs[n_ax].format(
ylim=(multimodel_ensemble_ac.sel(var=var).min(), multimodel_ensemble_ac.sel(var=var).max()),
xlocator='index', xformatter=['J','F','M','A','M','J','J','A','S','O','N','D'], xtickminor=False,
xlabel=''
)
else:
axs[n_ax].format(
ylim=(multimodel_ensemble_ac.sel(var=var).min(), multimodel_ensemble_ac.sel(var=var).max()),
xlocator='index', xformatter=['J','F','M','A','M','J','J','A','S','O','N','D'], xtickminor=False,
xlabel='',
yticklabels=[]
)
if i_var == 0:
axs[n_ax].format(title=zones[n_ax])
# Add obs legend and ylabel
if i == 0:
if var == 'tas':
h = [h3, h4, h5]
loc = 'lc'
elif var == 'snc':
h = [h3, h4, h5, h6]
loc = 'ur'
elif var == 'pr':
h = [h3, h4, h5, h6]
loc = 'ul'
axs[n_ax].legend(h, loc=loc, frame=False, ncols=1)
labels=['Temperature [°C]', 'Snow Cover Extent [%]', 'Total Precipitation [mm/day]']
axs[n_ax].format(
ylabel = labels[i_var]
)
n_ax += 1
f.legend([h1[0], h1[1], h1[2], h2], loc='b', frame=False, ncols=4, order='F', center=False)
axs.format(
suptitle='Annual cycle from '+period.start+'-'+period.stop+' climatology',
# collabels=zones,
abc=True, abcloc='ur'
)
filename = 'fig5_ac_all_'+period.start+'-'+period.stop+'_v2'
f.save('img/'+filename+'.jpg'); f.save('img/'+filename+'.png'); f.save('img/'+filename+'.pdf')
###Output
_____no_output_____
|
tensorflow_classes/Copy_of_Lab3_What_Are_Convolutions.ipynb
|
###Markdown
What are Convolutions?In the next lab you will explore how to enhance your Computer Vision example using Convolutions. But what are convolutions? In this lab you'll explore what they are and how they work, and then in Lab 4 you'll see how to use them in your neural network. Together with convolutions, you'll use something called 'Pooling', which compresses your image, further emphasising the features. You'll also see how pooling works in this lab. Limitations of the previous DNNIn the last lab you saw how to train an image classifier for fashion items using the Fashion MNIST dataset. This gave you a pretty accuract classifier, but there was an obvious constraint: the images were 28x28, grey scale and the item was centered in the image. For example here are a couple of the images in Fashion MNIST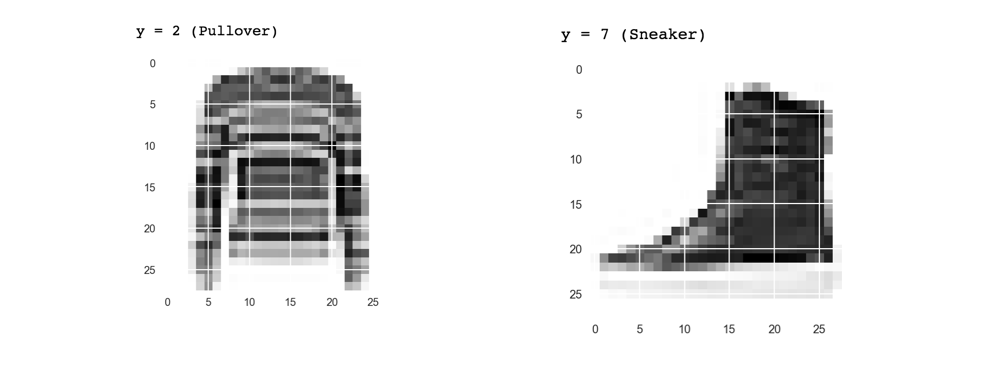The DNN that you created simply learned from the raw pixels what made up a sweater, and what made up a boot in this context. But consider how it might classify this image?While it's clear that there are boots in this image, the classifier would fail for a number of reasons. First, of course, it's not 28x28 greyscale, but more importantly, the classifier was trained on the raw pixels of a left-facing boot, and not the features that make up what a boot is.That's where Convolutions are very powerful. A convolution is a filter that passes over an image, processing it, and extracting features that show a commonolatity in the image. In this lab you'll see how they work, but processing an image to see if you can extract features from it! Generating convolutions is very simple -- you simply scan every pixel in the image and then look at it's neighboring pixels. You multiply out the values of these pixels by the equivalent weights in a filter. So, for example, consider this:In this case a 3x3 Convolution is specified.The current pixel value is 192, but you can calculate the new one by looking at the neighbor values, and multiplying them out by the values specified in the filter, and making the new pixel value the final amount. Let's explore how convolutions work by creating a basic convolution on a 2D Grey Scale image. First we can load the image by taking the 'ascent' image from scipy. It's a nice, built-in picture with lots of angles and lines. Let's start by importing some python libraries.
###Code
import cv2
import numpy as np
from scipy import misc
i = misc.ascent()
###Output
_____no_output_____
###Markdown
Next, we can use the pyplot library to draw the image so we know what it looks like.
###Code
import matplotlib.pyplot as plt
plt.grid(False)
plt.gray()
plt.axis('off')
plt.imshow(i)
plt.show()
###Output
_____no_output_____
###Markdown
We can see that this is an image of a stairwell. There are lots of features in here that we can play with seeing if we can isolate them -- for example there are strong vertical lines.The image is stored as a numpy array, so we can create the transformed image by just copying that array. Let's also get the dimensions of the image so we can loop over it later.
###Code
i_transformed = np.copy(i)
size_x = i_transformed.shape[0]
size_y = i_transformed.shape[1]
###Output
_____no_output_____
###Markdown
Now we can create a filter as a 3x3 array.
###Code
# This filter detects edges nicely
# It creates a convolution that only passes through sharp edges and straight
# lines.
#Experiment with different values for fun effects.
#filter = [ [0, 1, 0], [1, -4, 1], [0, 1, 0]]
# A couple more filters to try for fun!
#filter = [ [-1, -2, -1], [0, 0, 0], [1, 2, 1]]
filter = [ [-1, 0, 1], [-2, 0, 2], [-1, 0, 1]]
# If all the digits in the filter don't add up to 0 or 1, you
# should probably do a weight to get it to do so
# so, for example, if your weights are 1,1,1 1,2,1 1,1,1
# They add up to 10, so you would set a weight of .1 if you want to normalize them
weight = 1
###Output
_____no_output_____
###Markdown
Now let's create a convolution. We will iterate over the image, leaving a 1 pixel margin, and multiply out each of the neighbors of the current pixel by the value defined in the filter. i.e. the current pixel's neighbor above it and to the left will be multiplied by the top left item in the filter etc. etc. We'll then multiply the result by the weight, and then ensure the result is in the range 0-255Finally we'll load the new value into the transformed image.
###Code
for x in range(1,size_x-1):
for y in range(1,size_y-1):
convolution = 0.0
convolution = convolution + (i[x - 1, y-1] * filter[0][0])
convolution = convolution + (i[x, y-1] * filter[0][1])
convolution = convolution + (i[x + 1, y-1] * filter[0][2])
convolution = convolution + (i[x-1, y] * filter[1][0])
convolution = convolution + (i[x, y] * filter[1][1])
convolution = convolution + (i[x+1, y] * filter[1][2])
convolution = convolution + (i[x-1, y+1] * filter[2][0])
convolution = convolution + (i[x, y+1] * filter[2][1])
convolution = convolution + (i[x+1, y+1] * filter[2][2])
convolution = convolution * weight
if(convolution<0):
convolution=0
if(convolution>255):
convolution=255
i_transformed[x, y] = convolution
###Output
_____no_output_____
###Markdown
Now we can plot the image to see the effect of the convolution!
###Code
# Plot the image. Note the size of the axes -- they are 512 by 512
plt.gray()
plt.grid(False)
plt.imshow(i_transformed)
#plt.axis('off')
plt.show()
###Output
_____no_output_____
###Markdown
So, consider the following filter values, and their impact on the image.Using -1,0,1,-2,0,2,-1,0,1 gives us a very strong set of vertical lines:Using -1, -2, -1, 0, 0, 0, 1, 2, 1 gives us horizontal lines:Explore different values for yourself! PoolingAs well as using convolutions, pooling helps us greatly in detecting features. The goal is to reduce the overall amount of information in an image, while maintaining the features that are detected as present. There are a number of different types of pooling, but for this lab we'll use one called MAX pooling. The idea here is to iterate over the image, and look at the pixel and it's immediate neighbors to the right, beneath, and right-beneath. Take the largest (hence the name MAX pooling) of them and load it into the new image. Thus the new image will be 1/4 the size of the old -- with the dimensions on X and Y being halved by this process. You'll see that the features get maintained despite this compression!This code will show a (2, 2) pooling.Run it to see the output, and you'll see that while the image is 1/4 the size of the original, the extracted features are maintained!
###Code
new_x = int(size_x/2)
new_y = int(size_y/2)
newImage = np.zeros((new_x, new_y))
for x in range(0, size_x, 2):
for y in range(0, size_y, 2):
pixels = []
pixels.append(i_transformed[x, y])
pixels.append(i_transformed[x+1, y])
pixels.append(i_transformed[x, y+1])
pixels.append(i_transformed[x+1, y+1])
pixels.sort(reverse=True)
newImage[int(x/2),int(y/2)] = pixels[0]
# Plot the image. Note the size of the axes -- now 256 pixels instead of 512
plt.gray()
plt.grid(False)
plt.imshow(newImage)
#plt.axis('off')
plt.show()
###Output
_____no_output_____
|
secciones/07_operadores_aritmeticos.ipynb
|
###Markdown
Operadores aritméticos> David Quintanar Pérez
###Code
dos = 2
cuatro = 4
dos + cuatro
dos - cuatro
dos * cuatro
cuatro / dos
cuatro % dos
cuatro ** dos
cuatro // dos
###Output
_____no_output_____
###Markdown
Buenas practicas
###Code
1 + 2 * 3 / 4
1 + (2*3 / 4)
###Output
_____no_output_____
|
analyses/seasonality_paper_1/no_temporal_shifts/model_analysis_feature_importance.ipynb
|
###Markdown
Setup
###Code
from specific import *
###Output
_____no_output_____
###Markdown
Retrieve previous results from the 'model' notebook
###Code
X_train, X_test, y_train, y_test = data_split_cache.load()
results, rf = cross_val_cache.load()
###Output
_____no_output_____
###Markdown
ELI5 Permutation Importances (PFI)
###Code
perm_importance_cache = SimpleCache(
"perm_importance", cache_dir=CACHE_DIR, pickler=cloudpickle
)
# Does not seem to work with the dask parallel backend - it gets bypassed
# and every available core on the machine is used up if attempted.
@perm_importance_cache
def get_perm_importance():
rf.n_jobs = 30
with parallel_backend("threading", n_jobs=rf.n_jobs):
return eli5.sklearn.PermutationImportance(rf).fit(X_train, y_train)
# worker = list(client.scheduler_info()['workers'])[0]
# perm_importance = client.run(get_perm_importance, workers=[worker])
perm_importance = get_perm_importance()
perm_df = eli5.explain_weights_df(perm_importance, feature_names=list(X_train.columns))
###Output
_____no_output_____
###Markdown
VIF Calculation
###Code
train_vif_cache = SimpleCache("train_vif", cache_dir=CACHE_DIR)
@train_vif_cache
def get_vifs():
return vif(X_train, verbose=True)
vifs = get_vifs()
vifs = vifs.set_index("Name", drop=True).T
###Output
_____no_output_____
###Markdown
LOCO Calculation - from the LOCO notebook
###Code
loco_cache = SimpleCache("loco_results", cache_dir=CACHE_DIR)
loco_results = loco_cache.load()
baseline_mse = loco_results[""]["mse"]
loco_df = pd.DataFrame(
{
column: [loco_results[column]["mse"] - baseline_mse]
for column in loco_results
if column
}
)
loco_df.columns.name = "Name"
loco_df.index = ["LOCO (MSE)"]
###Output
_____no_output_____
###Markdown
Individual Tree Importances - Gini vs PFI vs SHAPSHAP values are loaded from the shap notebook.
###Code
def plot_importances(df, ax=None):
means = df.mean().sort_values(ascending=False)
df = df.reindex(means.index, axis=1)
if ax is None:
fig, ax = plt.subplots(figsize=(5, 12))
ax = sns.boxplot(data=df, orient="h", ax=ax)
ax.grid(which="both")
###Output
_____no_output_____
###Markdown
Gini
###Code
ind_trees_gini = pd.DataFrame(
[tree.feature_importances_ for tree in rf], columns=X_train.columns,
)
mean_importances = ind_trees_gini.mean().sort_values(ascending=False)
ind_trees_gini = ind_trees_gini.reindex(mean_importances.index, axis=1)
shorten_columns(ind_trees_gini, inplace=True)
def gini_plot(ax, N_col):
sns.boxplot(data=ind_trees_gini.iloc[:, :N_col], ax=ax)
ax.set(
# title="Gini Importances",
ylabel="Gini Importance (MSE)\n"
)
plot_importances(ind_trees_gini)
###Output
_____no_output_____
###Markdown
PFI
###Code
pfi_ind = pd.DataFrame(perm_importance.results_, columns=X_train.columns)
# Re-index according to the same ordering as for the Gini importances!
pfi_ind = pfi_ind.reindex(mean_importances.index, axis=1)
shorten_columns(pfi_ind, inplace=True)
def pfi_plot(ax, N_col):
sns.boxplot(data=pfi_ind.iloc[:, :N_col], ax=ax)
ax.set(
# title="PFI Importances",
ylabel="PFI Importance\n"
)
plot_importances(pfi_ind)
###Output
_____no_output_____
###Markdown
SHAP
###Code
max_index = 995 # Maximum job array index (inclusive).
job_samples = 2000 # Samples per job.
total_samples = (max_index + 1) * job_samples # Sanity check.
# Load the individual data chunks.
shap_chunks = []
for index in tqdm(range(max_index + 1), desc="Loading chunks"):
shap_chunks.append(
SimpleCache(
f"tree_path_dependent_shap_{index}_{job_samples}",
cache_dir=os.path.join(CACHE_DIR, "shap"),
verbose=0,
).load()
)
shap_values = np.vstack(shap_chunks)
mean_abs_shap = np.mean(np.abs(shap_values), axis=0)
mean_shap_importances = (
pd.DataFrame(mean_abs_shap, index=X_train.columns, columns=["SHAP Importance"],)
.sort_values("SHAP Importance", ascending=False)
.T
)
# Re-index according to the same ordering as for the Gini importances!
mean_shap_importances = mean_shap_importances.reindex(mean_importances.index, axis=1)
shorten_columns(mean_shap_importances, inplace=True)
def shap_plot(ax, N_col):
sns.boxplot(data=mean_shap_importances.iloc[:, :N_col], ax=ax)
ax.set(ylabel="SHAP Importance\n")
plot_importances(mean_shap_importances)
###Output
_____no_output_____
###Markdown
LOCO
###Code
loco_df = loco_df.reindex(mean_importances.index, axis=1)
shorten_columns(loco_df, inplace=True)
def loco_plot(ax, N_col):
sns.boxplot(data=loco_df.iloc[:, :N_col], ax=ax)
ax.set(ylabel="LOCO (MSE)\n")
plot_importances(loco_df)
###Output
_____no_output_____
###Markdown
VIF
###Code
# Re-index according to the same ordering as for the Gini importances!
vifs = vifs.reindex(mean_importances.index, axis=1)
shorten_columns(vifs, inplace=True)
def vif_plot(ax, N_col):
sns.boxplot(data=vifs.iloc[:, :N_col], ax=ax)
ax.set(ylabel="VIF\n")
plot_importances(vifs)
###Output
_____no_output_____
###Markdown
ALE 1D
###Code
world_ale_1d_cache = SimpleCache("world_ale_1d", cache_dir=CACHE_DIR)
ptp_values, mc_ptp_values = world_ale_1d_cache.load()
ale_1d_df = pd.DataFrame(ptp_values, index=["ALE 1D (PTP)"])
ale_1d_df.columns.name = "Name"
ale_1d_mc_df = pd.DataFrame(mc_ptp_values, index=["ALE 1D MC (PTP)"])
ale_1d_mc_df.columns.name = "Name"
# Re-index according to the same ordering as for the Gini importances!
ale_1d_df.reindex(mean_importances.index, axis=1)
ale_1d_mc_df.reindex(mean_importances.index, axis=1)
shorten_columns(ale_1d_df, inplace=True)
shorten_columns(ale_1d_mc_df, inplace=True)
def ale_1d_plot(ax, N_col):
sns.boxplot(data=ale_1d_df.iloc[:, :N_col], ax=ax)
ax.set(ylabel="ALE 1D\n")
def ale_1d_mc_plot(ax, N_col):
sns.boxplot(data=ale_1d_mc_df.iloc[:, :N_col], ax=ax)
ax.set(ylabel="ALE 1D MC\n")
fig, axes = plt.subplots(1, 2, figsize=(10, 12))
plot_importances(ale_1d_df, ax=axes[0])
axes[0].set_title("ALE 1D")
plot_importances(ale_1d_mc_df, ax=axes[1])
axes[1].set_title("ALE 1D MC")
for ax in axes:
ax.set_ylabel("")
plt.tight_layout()
###Output
_____no_output_____
###Markdown
ALE 2D - very cursory analysisDoes not take into account which of the 2 variables is the one responsible for the interaction.
###Code
world_ale_2d_cache = SimpleCache("world_ale_2d", cache_dir=CACHE_DIR)
ptp_2d_values = world_ale_2d_cache.load()
interaction_data = defaultdict(float)
for feature in X_train.columns:
for feature_pair, ptp_2d_value in ptp_2d_values.items():
if feature in feature_pair:
interaction_data[feature] += ptp_2d_value
ale_2d_df = pd.DataFrame(interaction_data, index=["ALE 2D (PTP)"])
ale_2d_df.columns.name = "Name"
# Re-index according to the same ordering as for the Gini importances!
ale_2d_df.reindex(mean_importances.index, axis=1)
shorten_columns(ale_2d_df, inplace=True)
def ale_2d_plot(ax, N_col):
sns.boxplot(data=ale_2d_df.iloc[:, :N_col], ax=ax)
ax.set(ylabel="ALE 2D\n")
plot_importances(ale_2d_df)
###Output
_____no_output_____
###Markdown
Combining the plots
###Code
N_col = 20
plot_funcs = (
gini_plot,
pfi_plot,
shap_plot,
loco_plot,
# ale_1d_plot,
# ale_1d_mc_plot,
# ale_2d_plot,
# vif_plot,
)
fig, axes = plt.subplots(
len(plot_funcs), 1, sharex=True, figsize=(7, 1.8 + 2 * len(plot_funcs))
)
for plot_func, ax in zip(plot_funcs, axes):
plot_func(ax, N_col)
# Rotate the last x axis labels (the only visible ones).
axes[-1].set_xticklabels(axes[-1].get_xticklabels(), rotation=45, ha="right")
for _ax in axes:
_ax.grid(which="major", alpha=0.4, linestyle="--")
_ax.tick_params(labelleft=False)
_ax.yaxis.get_major_formatter().set_scientific(False)
for _ax in axes[:-1]:
_ax.set_xlabel("")
# fig.suptitle("Gini, PFI, SHAP, VIF")
plt.tight_layout()
plt.subplots_adjust(top=0.91)
figure_saver.save_figure(
fig,
"_".join(
(
"feature_importances",
*(func.__name__.split("_plot")[0] for func in plot_funcs),
)
),
)
importances = {
"Gini": ind_trees_gini,
"PFI": pfi_ind,
"SHAP": mean_shap_importances,
"LOCO": loco_df,
"ALE 1D": ale_1d_df,
"ALE 1D MC": ale_1d_mc_df,
"ALE 2D": ale_2d_df,
"VIF": vifs,
}
for key, df in importances.items():
importances[key] = df.mean().sort_values(ascending=False)
table_str = np.array([df.index.values for df in importances.values()]).T
def transform(x):
"""Transform x to be in [0, 1]."""
x = np.asanyarray(x)
x = x - np.min(x)
return x / np.max(x)
# 4 groups of variables - vegetation, landcover, human, meteorological
divisions = {
"vegetation": (70, 150), # 4 + 4 x 7: 32.
"landcover": (150, 230), # 4: 4.
"human": (230, 270), # 2: 2.
"meteorology": (270, 430), # 5 + 7: 12.
}
division_members = {
"vegetation": 4,
"landcover": 4,
"human": 2,
"meteorology": 5,
}
division_names = {
"vegetation": ["VOD", "FAPAR", "LAI", "SIF"],
"landcover": ["pftHerb", "ShrubAll", "TreeAll", "AGB Tree",],
"human": ["pftCrop", "popd",],
"meteorology": ["Dry Days", "SWI", "Max Temp", "DTR", "lightning",],
}
var_keys = []
var_H_vals = []
factors = []
for division in divisions:
var_keys.extend(division_names[division])
var_H_vals.extend(
np.linspace(
*divisions[division], division_members["vegetation"], endpoint=False
)
% 360
)
factors.extend(np.linspace(0, 1, division_members["vegetation"]))
shifts = [0, 1, 3, 6, 9, 12, 18, 24]
def combined_get_colors(x):
assert len(x.shape) == 2
out = []
for x_i in x:
out.append([])
for x_ij in x_i:
match_obj = re.search("(.*)\s.{,1}(\d+)\sM", x_ij)
if match_obj:
x_ij_mod = match_obj.group(1)
shift = int(match_obj.group(2))
else:
x_ij_mod = x_ij
shift = 0
index = var_keys.index(x_ij_mod)
H = var_H_vals[index]
S = 1.0 - 0.3 * (shifts.index(shift) / (len(shifts) - 1))
V = 0.85 - 0.55 * (shifts.index(shift) / (len(shifts) - 1))
S -= factors[index] * 0.2
V -= factors[index] * 0.06
out[-1].append(hsluv_to_rgb((H, S * 100, V * 100)))
return out
# Define separate functions for each of the categories on their own.
ind_get_color_funcs = []
for division in divisions:
def get_colors(x, division=division):
assert len(x.shape) == 2
out = []
for x_i in x:
out.append([])
for x_ij in x_i:
match_obj = re.search("(.*)\s.{,1}(\d+)\sM", x_ij)
if match_obj:
x_ij_mod = match_obj.group(1)
shift = int(match_obj.group(2))
else:
x_ij_mod = x_ij
shift = 0
if x_ij_mod not in division_names[division]:
out[-1].append((1, 1, 1))
else:
index = division_names[division].index(x_ij_mod)
desat = 0.85 - 0.7 * (shifts.index(shift) / (len(shifts) - 1))
out[-1].append(
sns.color_palette(
"Set1", n_colors=division_members[division], desat=desat
)[index]
)
return out
ind_get_color_funcs.append(get_colors)
for get_colors, suffix in zip(
(combined_get_colors, *ind_get_color_funcs), ("combined", *divisions),
):
fig = plt.figure(figsize=(12, 6))
spec = fig.add_gridspec(ncols=2, nrows=1, width_ratios=[3, 1])
axes = [fig.add_subplot(s) for s in spec]
def table_importance_plot(x, **kwargs):
axes[1].plot(transform(x), np.linspace(1, 0, len(table_str)), **kwargs)
axes[0].set_axis_off()
table = axes[0].table(
table_str,
loc="left",
rowLabels=range(1, len(table_str) + 1),
bbox=[0, 0, 1, 1],
colLabels=list(importances.keys()),
cellColours=get_colors(table_str),
)
table.auto_set_font_size(False)
table.set_fontsize(8)
color_dict = {
"Gini": "C0",
"PFI": "C1",
"SHAP": "C2",
"LOCO": "C3",
"ALE 1D": "C4",
"ALE 1D MC": "C4",
"ALE 2D": "C4",
"VIF": "C5",
}
ls_dict = {
"Gini": "-",
"PFI": "-",
"SHAP": "-",
"LOCO": "-",
"ALE 1D": "-",
"ALE 1D MC": "--",
"ALE 2D": "-.",
"VIF": "-",
}
for (importance_measure, importance_values), marker in zip(
importances.items(), ["+", "x", "|", "_", "1", "2", "3", "4", "d"],
):
table_importance_plot(
importance_values,
label=importance_measure,
marker=marker,
c=color_dict[importance_measure],
ls=ls_dict[importance_measure],
ms=8,
)
axes[1].yaxis.set_label_position("right")
axes[1].yaxis.tick_right()
cell_height = 1 / (table_str.shape[0] + 1)
axes[1].set_ylim(-cell_height / 2, 1 + (3 / 2) * cell_height)
axes[1].set_yticks(np.linspace(1, 0, table_str.shape[0]))
axes[1].set_yticklabels(range(1, table_str.shape[0] + 1))
axes[1].set_xlim(0, 1)
axes[1].set_xticks([0, 1])
axes[1].set_xticklabels([0, 1])
axes[1].set_xticks(np.linspace(0, 1, 8), minor=True)
axes[1].grid(alpha=0.4, linestyle="--")
axes[1].grid(which="minor", axis="x", alpha=0.4, linestyle="--")
axes[1].legend(loc="best")
plt.tight_layout()
figure_saver.save_figure(
fig, "_".join(("feature_importance_breakdown", suffix)).strip("_")
)
unique_str = np.unique(table_str)
colors = get_colors(unique_str.reshape(1, -1))[0]
def hsluv_conv(hsv):
out = []
for x_i in hsv:
out.append([])
for x_ij in x_i:
out[-1].append(hsluv_to_rgb(x_ij))
return np.array(out)
V, H = np.mgrid[0:1:100j, 0:1:100j]
S = np.ones_like(V) * 1
HSV = np.dstack((H * 360, S * 100, V * 100))
RGB = hsluv_conv(HSV)
plt.figure(figsize=(20, 20))
plt.imshow(RGB, origin="lower", extent=[0, 360, 0, 100], aspect=2)
plt.xlabel("H")
plt.ylabel("V")
for color in colors:
h, s, v = rgb_to_hsluv(color)
for (division, values), marker in zip(divisions.items(), ["+", "x", "_", "|"]):
if (values[0] - 1e-5) < h and h < (values[1] + 1e-5):
break
plt.plot(h, v, marker=marker, linestyle="", c="k")
###Output
_____no_output_____
###Markdown
Choose the 15 most important features using the above metrics
###Code
list(importances)
def transform_series_no_shift(x):
x = x / np.max(np.abs(x))
return x
methods = ["Gini", "PFI", "LOCO", "SHAP"]
combined = transform_series_no_shift(importances[methods[0]])
for method in methods[1:]:
combined += transform_series_no_shift(importances[method])
combined.sort_values(ascending=False, inplace=True)
print(combined[:15].to_latex())
combined[:15]
def transform_series_sum_norm(x):
x = x / np.sum(np.abs(x))
return x
methods = ["Gini", "PFI", "LOCO", "SHAP"]
combined = transform_series_sum_norm(importances[methods[0]])
for method in methods[1:]:
combined += transform_series_sum_norm(importances[method])
combined.sort_values(ascending=False, inplace=True)
print(combined[:15].to_latex())
combined[:15]
###Output
_____no_output_____
|
Python for Finance - Code Files/109 Monte Carlo - Euler Discretization - Part I/CSV/Python 2 CSV/MC - Euler Discretization - Part I - Solution_CSV.ipynb
|
###Markdown
Monte Carlo - Euler Discretization - Part I *Suggested Answers follow (usually there are multiple ways to solve a problem in Python).* Load the data for Microsoft (‘MSFT’) for the period ‘2000-1-1’ until today.
###Code
import numpy as np
import pandas as pd
from pandas_datareader import data as web
from scipy.stats import norm
import matplotlib.pyplot as plt
%matplotlib inline
data = pd.read_csv('D:/Python/MSFT_2000.csv', index_col = 'Date')
###Output
_____no_output_____
###Markdown
Store the annual standard deviation of the log returns in a variable, called “stdev”.
###Code
log_returns = np.log(1 + data.pct_change())
log_returns.tail()
data.plot(figsize=(10, 6));
stdev = log_returns.std() * 250 ** 0.5
stdev
###Output
_____no_output_____
###Markdown
Set the risk free rate, r, equal to 2.5% (0.025).
###Code
r = 0.025
###Output
_____no_output_____
###Markdown
To transform the object into an array, reassign stdev.values to stdev.
###Code
type(stdev)
stdev = stdev.values
stdev
###Output
_____no_output_____
###Markdown
Set the time horizon, T, equal to 1 year, the number of time intervals equal to 250, the iterations equal to 10,000. Create a variable, delta_t, equal to the quotient of T divided by the number of time intervals.
###Code
T = 1.0
t_intervals = 250
delta_t = T / t_intervals
iterations = 10000
###Output
_____no_output_____
###Markdown
Let Z equal a random matrix with dimension (time intervals + 1) by the number of iterations.
###Code
Z = np.random.standard_normal((t_intervals + 1, iterations))
###Output
_____no_output_____
###Markdown
Use the .zeros_like() method to create another variable, S, with the same dimension as Z. S is the matrix to be filled with future stock price data.
###Code
S = np.zeros_like(Z)
###Output
_____no_output_____
###Markdown
Create a variable S0 equal to the last adjusted closing price of Microsoft. Use the “iloc” method.
###Code
S0 = data.iloc[-1]
S[0] = S0
###Output
_____no_output_____
###Markdown
Use the following formula to create a loop within the range (1, t_intervals + 1) that reassigns values to S in time t. $$S_t = S_{t-1} \cdot exp((r - 0.5 \cdot stdev^2) \cdot delta_t + stdev \cdot delta_t^{0.5} \cdot Z_t)$$
###Code
for t in range(1, t_intervals + 1):
S[t] = S[t-1] * np.exp((r - 0.5 * stdev ** 2) * delta_t + stdev * delta_t ** 0.5 * Z[t])
S
S.shape
###Output
_____no_output_____
###Markdown
Plot the first 10 of the 10,000 generated iterations on a graph.
###Code
plt.figure(figsize=(10, 6))
plt.plot(S[:, :10]);
###Output
_____no_output_____
|
Semana3/Tarea3_LagunasDaniel.ipynb
|
###Markdown
Tarea 3: Clases 4 y 5Cada clase que veamos tendrá una tarea asignada, la cual contendrá problemas varios que se pueden resolver con lo visto en clase, de manera que puedas practicar lo que acabas de aprender.En esta ocasión, la tarea tendrá ejercicios relativos a la clases 4 y 5, de la librería NumPy y la librería Matplotlib.Para resolver la tarea, por favor cambiar el nombre del archivo a "Tarea3_ApellidoNombre.ipynb", sin acentos ni letras ñ (ejemplo: en mi caso, el archivo se llamaría "Tarea3_JimenezEsteban.ipynb"). Luego de haber cambiado el nombre, resolver cada uno de los puntos en los espacios provistos.Referencias:- http://www.math.pitt.edu/~sussmanm/3040Summer14/exercisesII.pdf- https://scipy-lectures.org/intro/numpy/exercises.html**Todos los ejercicios se pueden realizar sin usar ciclos `for` ni `while`**___ 1. Cuadrado mágicoUn cuadrado mágico es una matriz cuadrada tal que las sumas de los elementos de cada una de sus filas, las sumas de los elementos de cada una de sus columnas y las sumas de los elementos de cada una de sus diagonales son iguales (hay dos diagonales: una desde el elemento superior izquierdo hasta el elemento inferior derecho, y otra desde el elemento superior derecho hasta el elemento inferior izquierdo).Muestre que la matriz A dada por:
###Code
import numpy as np
A = np.array([[17, 24, 1, 8, 15],
[23, 5, 7, 14, 16],
[ 4, 6, 13, 20, 22],
[10, 12, 19, 21, 3],
[11, 18, 25, 2, 9]])
###Output
_____no_output_____
###Markdown
constituye un cuadrado mágico.Ayuda: las funciones `np.sum()`, `np.diag()` y `np.fliplr()` pueden ser de mucha utilidad
###Code
print(f"La primer diagonal es {np.diag(A)} y suma = {np.diag(A).sum()}")
print(f"La segunda diagonal es {np.diag(np.fliplr(A))} y suma = {np.diag(np.fliplr(A)).sum()}")
i, j = np.shape(A)
for col in range(j):
print(f"La suma de la columna {col + 1}: {A[:, col]} es = {np.sum(A[:, col])}")
for fila in range(i):
print(f"La suma de la fila {fila + 1}: {A[fila, :]} es = {np.sum(A[fila, :])}")
# Función que arroja si es un cuadrado mágico o no.
def cuadrado_magico(M):
sumas = []
sumas.append(np.diag(M).sum())
print(f"La primer diagonal es {np.diag(M)} y suma = {np.diag(M).sum()}")
sumas.append(np.diag(np.fliplr(M)).sum())
print(f"La segunda diagonal es {np.diag(np.fliplr(M))} y suma = {np.diag(np.fliplr(M)).sum()}")
i, j = np.shape(M)
for col in range(j):
print(f"La suma de la columna {col + 1}: {M[:, col]} es = {np.sum(M[:, col])}")
sumas.append(np.sum(M[:, col]))
for fila in range(i):
print(f"La suma de la fila {fila + 1}: {M[fila, :]} es = {np.sum(M[fila, :])}")
sumas.append(np.sum(M[fila, :]))
resultado = True
for i in range(1,len(sumas)):
resultado *= bool(sumas[0]==sumas[i])
return bool(resultado)
cuadrado_magico(A)
###Output
La primer diagonal es [17 5 13 21 9] y suma = 65
La segunda diagonal es [15 14 13 12 11] y suma = 65
La suma de la columna 1: [17 23 4 10 11] es = 65
La suma de la columna 2: [24 5 6 12 18] es = 65
La suma de la columna 3: [ 1 7 13 19 25] es = 65
La suma de la columna 4: [ 8 14 20 21 2] es = 65
La suma de la columna 5: [15 16 22 3 9] es = 65
La suma de la fila 1: [17 24 1 8 15] es = 65
La suma de la fila 2: [23 5 7 14 16] es = 65
La suma de la fila 3: [ 4 6 13 20 22] es = 65
La suma de la fila 4: [10 12 19 21 3] es = 65
La suma de la fila 5: [11 18 25 2 9] es = 65
###Markdown
2. ¿Qué más podemos hacer con NumPy?Este ejercicio es más que nada informativo, para ver qué más pueden hacer con la librería NumPy.Considere el siguiente vector:
###Code
x = np.array([-1., 4., -9.])
###Output
_____no_output_____
###Markdown
1. La función coseno (`np.cos()`) se aplica sobre cada uno de los elementos del vector. Calcular el vector `y = np.cos(np.pi/4*x)`
###Code
y = np.cos(np.pi / 4 * x)
y
###Output
_____no_output_____
###Markdown
2. Puedes sumar vectores y multiplicarlos por escalares. Calcular el vector `z = x + 2*y`
###Code
z = x + (2 * y)
z
###Output
_____no_output_____
###Markdown
3. También puedes calcular la norma de un vector. Investiga como y calcular la norma del vector xAyuda: buscar en las funciones del paquete de algebra lineal de NumPy
###Code
norma_x = np.linalg.norm(x)
norma_x
###Output
_____no_output_____
###Markdown
4. Utilizando la función `np.vstack()` formar una matriz `M` tal que la primera fila corresponda al vector `x`, la segunda al vector `y` y la tercera al vector `z`.
###Code
M = np.vstack((x, y, z))
M
###Output
_____no_output_____
###Markdown
5. Calcule la transpuesta de la matriz `M`, el determinante de la matriz `M`, y la multiplicación matricial de la matriz `M` por el vector `x`.
###Code
M_t = np.transpose(M)
M_t
det_M = np.linalg.det(M)
det_M
Mx = np.dot(M, x)
Mx
###Output
_____no_output_____
###Markdown
3. Graficando funcionesGenerar un gráfico de las funciones $f(x)=e^{-x/10}\sin(\pi x)$ y $g(x)=x e^{-x/3}$ sobre el intervalo $[0, 10]$. Incluya las etiquetas de los ejes y una leyenda con las etiquetas de cada función.
###Code
# Importamos la librería
import matplotlib.pyplot as plt
import numpy as np
# Definimos las funciones
def f(x):
return np.exp(-x / 10) * np.sin(np.pi * x)
def g(x):
return x * np.exp(-x / 3)
# Intervalo
x = np.arange(0, 10.001, 0.001)
# Graficar funciones
plt.figure(figsize=(10, 5))
plt.plot(x, [f(i) for i in x], linestyle = '--', linewidth = 2, label = '$f(x)=e^{-x/10}\sin(\pi x)$')
plt.plot(x, [g(i) for i in x], linestyle = ':', linewidth = 3, label = '$g(x)=x e^{-x/3}$')
plt.xlabel('Eje de las x')
plt.ylabel('Eje de las y')
plt.legend(loc = 'best')
plt.title('Gráfica con 2 funciones')
# Mostrar gráfica
plt.show()
###Output
_____no_output_____
###Markdown
4. Analizando datosLos datos en el archivo `populations.txt` describen las poblaciones de liebres, linces (y zanahorias) en el norte de Canadá durante 20 años.Para poder analizar estos datos con NumPy es necesario importarlos. La siguiente celda importa los datos del archivo `populations.txt`, siempre y cuando el archivo y el notebook de jupyter estén en la misma ubicación:
###Code
data = np.loadtxt('populations.txt')
titulos = ['años', 'liebres', 'linces', 'zanahorias']
data
###Output
_____no_output_____
###Markdown
1. Obtener, usando la indización de NumPy, cuatro arreglos independientes llamados `años`, `liebres`, `linces` y `zanahorias`, correspondientes a los años, a la población de liebres, a la población de linces y a la cantidad de zanahorias, respectivamente.
###Code
años = data[:, 0]
liebres = data[:, 1]
linces = data[:, 2]
zanahorias = data[:, 3]
print(f'Años: {años}\n\nLiebres: {liebres}\n\nLinces: {linces}\n\nZanahorias: {zanahorias}')
###Output
Años: [1900. 1901. 1902. 1903. 1904. 1905. 1906. 1907. 1908. 1909. 1910. 1911.
1912. 1913. 1914. 1915. 1916. 1917. 1918. 1919. 1920.]
Liebres: [30000. 47200. 70200. 77400. 36300. 20600. 18100. 21400. 22000. 25400.
27100. 40300. 57000. 76600. 52300. 19500. 11200. 7600. 14600. 16200.
24700.]
Linces: [ 4000. 6100. 9800. 35200. 59400. 41700. 19000. 13000. 8300. 9100.
7400. 8000. 12300. 19500. 45700. 51100. 29700. 15800. 9700. 10100.
8600.]
Zanahorias: [48300. 48200. 41500. 38200. 40600. 39800. 38600. 42300. 44500. 42100.
46000. 46800. 43800. 40900. 39400. 39000. 36700. 41800. 43300. 41300.
47300.]
###Markdown
2. Calcular e imprimir los valores priomedio y las desviaciones estándar de las poblaciones de cada especie.
###Code
for i in range(1,3):
promedio = round(np.mean(data[:, i]), 4)
des_vest = round(np.std(data[:, i]), 4)
print(f'Para {titulos[i]} el promedio es: {promedio} y su desviación estándar: {des_vest}')
###Output
Para liebres el promedio es: 34080.9524 y su desviación estándar: 20897.9065
Para linces el promedio es: 20166.6667 y su desviación estándar: 16254.5915
###Markdown
3. ¿En qué año tuvo cada especie su población máxima?, y ¿cuál fue la población máxima de cada especie?
###Code
for i in range(1,3):
pob_max = np.max(data[:, i])
year_pob_max = int(data[np.where(data[:, i] == pob_max), 0])
print(f'Para {titulos[i]} la población máxima fue: {pob_max} en el año: {year_pob_max}')
###Output
Para liebres la población máxima fue: 77400.0 en el año: 1903
Para linces la población máxima fue: 59400.0 en el año: 1904
###Markdown
4. Graficar las poblaciones respecto al tiempo. Incluir en la gráfica los puntos de población máxima (resaltarlos con puntos grandes o de color, o con flechas y texto, o de alguna manera que se les ocurra). No olvidar etiquetar los ejes y poner una leyenda para etiquetar los diferentes objetos de la gráfica.
###Code
# Importamos la librería
import matplotlib.pyplot as plt
# Graficar datos
plt.figure(figsize=(12, 5))
for i in range(1,len(data[0])-1):
max_p = np.max(data[:, i])
a_mp = data[np.where(data[:, i] == max_p), 0]
plt.plot(data[:, 0], data[:, i], label = titulos[i])
plt.plot(a_mp, max_p, marker = 'D', markersize = 5, color = 'k')
plt.text(x = a_mp*1.0001, y = max_p*1.015, s = f'máximo {titulos[i]}')
plt.xlabel('Años')
plt.ylabel('Población')
plt.legend(loc = 'best')
plt.title('Poblaciones anuales')
plt.tight_layout()
# Mostrar gráfica
plt.show()
###Output
_____no_output_____
###Markdown
5. Graficar las distribuciones de las diferentes especies utilizando histogramas. Asegúrese de elegir parámetros adecuados de las gráficas.
###Code
# Graficar datos
plt.figure(figsize=(10, 4))
for i in range(1,len(data[0])-1):
plt.subplot(1, 2, i)
plt.hist(x = data[:, i], label = titulos[i])
plt.xlabel('Población')
plt.ylabel('Frecuencia')
plt.legend(loc = 'best')
plt.title(f'Histograma de la población de {titulos[i]}')
plt.tight_layout()
# Mostrar gráfica
plt.show()
###Output
_____no_output_____
###Markdown
6. Calcule el coeficiente de correlación de la población de linces y la población de liebres (ayuda: np.corrcoef). Por otra parte, mediante un gráfico de dispersión de puntos, grafique la población de linces vs. la población de liebres, ¿coincide la forma del gráfico con el coeficiente de correlación obtenido?
###Code
np.corrcoef((data[:,1], data[:,2]))
# Graficar datos
plt.figure(figsize=(5, 4))
max_p = np.max(data[:, i])
a_mp = data[np.where(data[:, i] == max_p), 0]
plt.plot(data[:, 1], data[:, 2], 'o')
plt.xlabel(titulos[1])
plt.ylabel(titulos[2])
plt.title(f'{titulos[1]} y {titulos[2]}')
plt.tight_layout()
# Mostrar gráfica
plt.show()
# Graficar datos
plt.figure(figsize=(5, 4))
max_p = np.max(data[:, i])
a_mp = data[np.where(data[:, i] == max_p), 0]
plt.scatter(data[:, 1], data[:, 2])
plt.xlabel(titulos[1])
plt.ylabel(titulos[2])
plt.title(f'{titulos[1]} y {titulos[2]}')
plt.tight_layout()
# Mostrar gráfica
plt.show()
###Output
_____no_output_____
|
python/numpy_notes.ipynb
|
###Markdown
Remove rows with NaN's from numpy array
###Code
a = np.array([[1, 8], [2,9], [3,10], [4, np.NaN], [5, 12], [6, np.NaN]])
print('Original array:\n', a)
a = a[~np.isnan(a)[:, 1]]
print('With rows containing NaN removed:\n', a)
###Output
Original array:
[[ 1. 8.]
[ 2. 9.]
[ 3. 10.]
[ 4. nan]
[ 5. 12.]
[ 6. nan]]
With rows containing NaN removed:
[[ 1. 8.]
[ 2. 9.]
[ 3. 10.]
[ 5. 12.]]
###Markdown
Find index of nearest value in an arraySee Nov. 20, 2014 answer to [Finding the nearest value and return the index of array in Python](http://stackoverflow.com/questions/8914491/finding-the-nearest-value-and-return-the-index-of-array-in-python)
###Code
def get_index(array, value):
idx = (np.abs(array - value)).argmin()
return idx
a = np.linspace(0., 10., 11)
print(a)
values = [1.2, 5.1, 5.6]
for value in values:
idx = get_index(a, value)
print(value, idx, a[idx])
###Output
[ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.]
1.2 1 1.0
5.1 5 5.0
5.6 6 6.0
###Markdown
Boolean indexing
###Code
a = np.random.randint(0, 100, 10)
a
# Select elements greater than 60
a[a>60]
# Select elements greater than 60 and odd
a[(a>60) & (a%2 == 1)]
a.mean()
a.std()
# Select all of the even numbers greater than the mean
a[a>a.mean()]
# Select all numbers that are within one standard deviation of the mean
a[(a<(a.mean() + a.std())) & (a>(a.mean() - a.std()))]
###Output
_____no_output_____
###Markdown
Clip values in 1D and 2D arrays
###Code
a = np.array([1.0, 0.1, 1.e-3, 0.0, -1.e-3, -0.1, -1.0])
print(a)
a = a.clip(min=0)
print(a)
b = np.array([[0, 1.0], [1, 0.1], [1, 1.e-3], [3, 0.0], [4, -1.e-3], [5, -0.1], [6, -1.0]])
print(b)
print()
b[:,1] = b[:,1].clip(min=0)
print(b)
###Output
[[ 0.e+00 1.e+00]
[ 1.e+00 1.e-01]
[ 1.e+00 1.e-03]
[ 3.e+00 0.e+00]
[ 4.e+00 -1.e-03]
[ 5.e+00 -1.e-01]
[ 6.e+00 -1.e+00]]
[[0.e+00 1.e+00]
[1.e+00 1.e-01]
[1.e+00 1.e-03]
[3.e+00 0.e+00]
[4.e+00 0.e+00]
[5.e+00 0.e+00]
[6.e+00 0.e+00]]
###Markdown
Slice objects[How can I create a slice object for Numpy array?](https://stackoverflow.com/questions/38917173/how-can-i-create-a-slice-object-for-numpy-array) [numpy.s_](https://docs.scipy.org/doc/numpy/reference/generated/numpy.s_.html) Use to give slices meaningful names
###Code
a = np.arange(20).reshape(4, 5)
middle = np.s_[1:3, 1:4]
lowerright = np.s_[2:, 3:]
row2everyother = np.s_[2, 0::2]
lastrow = np.s_[-1, :]
print(a)
print("middle:")
print(a[middle])
print("lowerright:")
print(a[lowerright])
print("row2everyother:")
print(a[row2everyother])
print("lastrow:")
print(a[lastrow])
print(middle)
print(row2everyother)
print(lastrow)
###Output
(slice(1, 3, None), slice(1, 4, None))
(2, slice(0, None, 2))
(-1, slice(None, None, None))
###Markdown
Accessing indices in slice objects
###Code
print(middle)
xslice, yslice = middle[1], middle[0]
print(xslice, yslice)
print(xslice.start, xslice.stop, xslice.step)
print(yslice.start, yslice.stop, yslice.step)
###Output
(slice(1, 3, None), slice(1, 4, None))
slice(1, 4, None) slice(1, 3, None)
1 4 None
1 3 None
###Markdown
Get name of numpy variableSee https://stackoverflow.com/questions/34980833/python-name-of-np-array-variable-as-string
###Code
def namestr(obj, namespace):
return [name for name in namespace if namespace[name] is obj][0]
temp_1D_array = np.linspace(0, 1, 101)
namestr(temp_1D_array, globals())
###Output
_____no_output_____
###Markdown
From articleSee [Top 4 Numpy Functions You Don’t Know About (Probably)](https://towardsdatascience.com/top-4-numpy-functions-you-dont-know-about-probably-28fcd5d7174f) Wherewhere() function will return the index of elements from an array that satisfy a certain condition
###Code
grades = np.array([1, 3, 4, 2, 5, 5])
np.where(grades > 3)
###Output
_____no_output_____
###Markdown
Replace values that do and don't satisfy the given condition
###Code
np.where(grades > 3, 'gt3', 'lt3')
###Output
_____no_output_____
###Markdown
argmin(), argmax(), argsort() allclose()*It will return True if items in two arrays are equal within a tolerance. It will provide you with a great way of checking if two arrays are similar*
###Code
arr1 = np.array([0.15, 0.20, 0.25, 0.17])
arr2 = np.array([0.14, 0.21, 0.27, 0.15])
np.allclose(arr1, arr2, 0.1)
np.allclose(arr1, arr2, 0.2)
###Output
_____no_output_____
|
notebooks/.ipynb_checkpoints/Wind_Stats_with_solutions-checkpoint.ipynb
|
###Markdown
Wind StatisticsCheck out [Wind Statistics Exercises Video Tutorial](https://youtu.be/2x3WsWiNV18) to watch a data scientist go through the exercises Introduction:The data have been modified to contain some missing values, identified by NaN. Using pandas should make this exerciseeasier, in particular for the bonus question.You should be able to perform all of these operations without usinga for loop or other looping construct.1. The data in 'wind.data' has the following format:
###Code
"""
Yr Mo Dy RPT VAL ROS KIL SHA BIR DUB CLA MUL CLO BEL MAL
61 1 1 15.04 14.96 13.17 9.29 NaN 9.87 13.67 10.25 10.83 12.58 18.50 15.04
61 1 2 14.71 NaN 10.83 6.50 12.62 7.67 11.50 10.04 9.79 9.67 17.54 13.83
61 1 3 18.50 16.88 12.33 10.13 11.17 6.17 11.25 NaN 8.50 7.67 12.75 12.71
"""
###Output
_____no_output_____
###Markdown
The first three columns are year, month and day. The remaining 12 columns are average windspeeds in knots at 12 locations in Ireland on that day. More information about the dataset go [here](wind.desc). Step 1. Import the necessary libraries
###Code
import pandas as pd
import datetime
###Output
_____no_output_____
###Markdown
Step 2. Import the dataset from this [address](https://github.com/guipsamora/pandas_exercises/blob/master/06_Stats/Wind_Stats/wind.data) Step 3. Assign it to a variable called data and replace the first 3 columns by a proper datetime index.
###Code
# parse_dates gets 0, 1, 2 columns and parses them as the index
data_url = 'https://raw.githubusercontent.com/guipsamora/pandas_exercises/master/06_Stats/Wind_Stats/wind.data'
data = pd.read_csv(data_url, sep = "\s+")#, parse_dates = [[0,1,2]])
data.head()
data.info()
data.describe().T
###Output
_____no_output_____
###Markdown
Step 4. Year 2061? Do we really have data from this year? Create a function to fix it and apply it.
###Code
data.Yr.unique()
# The problem is that the dates are 2061 and so on...
# function that uses datetime
def fix_century(x):
year = x.year - 100 if x.year > 1989 else x.year
return datetime.date(year, x.month, x.day)
# apply the function fix_century on the column and replace the values to the right ones
data['Yr_Mo_Dy'] = data['Yr_Mo_Dy'].apply(fix_century)
# data.info()
data.head()
###Output
_____no_output_____
###Markdown
Step 5. Set the right dates as the index. Pay attention at the data type, it should be datetime64[ns].
###Code
# transform Yr_Mo_Dy it to date type datetime64
data["Yr_Mo_Dy"] = pd.to_datetime(data["Yr_Mo_Dy"])
data.info()
# set 'Yr_Mo_Dy' as the index
data = data.set_index('Yr_Mo_Dy')
data.head()
# data.info()
###Output
_____no_output_____
###Markdown
Step 6. Compute how many values are missing for each location over the entire record. They should be ignored in all calculations below.
###Code
# "Number of non-missing values for each location: "
data.isnull().sum()
###Output
_____no_output_____
###Markdown
Step 7. Compute how many non-missing values there are in total.
###Code
#number of columns minus the number of missing values for each location
data.shape[0] - data.isnull().sum()
#or
data.notnull().sum()
###Output
_____no_output_____
###Markdown
Step 8. Calculate the mean windspeeds of the windspeeds over all the locations and all the times. A single number for the entire dataset.
###Code
data.sum().sum() / data.notna().sum().sum()
###Output
_____no_output_____
###Markdown
Step 9. Create a DataFrame called loc_stats and calculate the min, max and mean windspeeds and standard deviations of the windspeeds at each location over all the days A different set of numbers for each location.
###Code
data.describe(percentiles=[])
###Output
_____no_output_____
###Markdown
Step 10. Create a DataFrame called day_stats and calculate the min, max and mean windspeed and standard deviations of the windspeeds across all the locations at each day. A different set of numbers for each day.
###Code
# create the dataframe
day_stats = pd.DataFrame()
# this time we determine axis equals to one so it gets each row.
day_stats['min'] = data.min(axis = 1) # min
day_stats['max'] = data.max(axis = 1) # max
day_stats['mean'] = data.mean(axis = 1) # mean
day_stats['std'] = data.std(axis = 1) # standard deviations
day_stats.head()
###Output
_____no_output_____
###Markdown
Step 11. Find the average windspeed in January for each location. Treat January 1961 and January 1962 both as January.
###Code
data.loc[data.index.month == 1].mean()
###Output
_____no_output_____
###Markdown
Step 12. Downsample the record to a yearly frequency for each location.
###Code
data.groupby(data.index.to_period('A')).mean()
###Output
_____no_output_____
###Markdown
Step 13. Downsample the record to a monthly frequency for each location.
###Code
data.groupby(data.index.to_period('M')).mean()
###Output
_____no_output_____
###Markdown
Step 14. Downsample the record to a weekly frequency for each location.
###Code
data.groupby(data.index.to_period('W')).mean()
###Output
_____no_output_____
###Markdown
Step 15. Calculate the min, max and mean windspeeds and standard deviations of the windspeeds across all locations for each week (assume that the first week starts on January 2 1961) for the first 52 weeks.
###Code
# resample data to 'W' week and use the functions
weekly = data.resample('W').agg(['min','max','mean','std'])
# slice it for the first 52 weeks and locations
weekly.loc[weekly.index[1:53], "RPT":"MAL"] .head(10)
###Output
_____no_output_____
|
notebooks/00.0-download-datasets/download-giant-otter.ipynb
|
###Markdown
giant otter vocalizations- ~500 vocalizations from https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0112562
###Code
%load_ext autoreload
%autoreload 2
from avgn.downloading.download import download_tqdm
from avgn.utils.paths import DATA_DIR, ensure_dir
from avgn.utils.general import unzip_file
data_urls = [
('https://journals.plos.org/plosone/article/file?id=10.1371/journal.pone.0112562.s018&type=supplementary', 'adult.zip'),
('https://journals.plos.org/plosone/article/file?id=10.1371/journal.pone.0112562.s019&type=supplementary', 'infant.zip'),
]
output_loc = DATA_DIR /"raw/otter/"
for url, filename in data_urls:
download_tqdm(url, output_location=output_loc/filename)
# unzip
for url, filename in data_urls:
unzip_file(output_loc/filename, output_loc/"zip_contents")
###Output
_____no_output_____
|
eumetsat_tut/.ipynb_checkpoints/class6-checkpoint.ipynb
|
###Markdown
Doing the class 6 exp SRS in python
###Code
import numpy as np
import matplotlib.pyplot as plt
import xarray as xr
import cartopy.crs as ccrs
import cartopy.feature as cfeature
import netCDF4
import pandas as pd
import scipy.interpolate as interp
%matplotlib inline
# Colormap selection
xr.set_options(cmap_divergent='bwr', cmap_sequential='turbo')
mfdataDIR1 = 'data/2009/3B-MO.MS.MRG.3IMERG.*.V06B.HDF5.SUB.nc4'
mfdataDIR2 = 'data/2019/3B-MO.MS.MRG.3IMERG.*.V06B.HDF5.SUB.nc4'
ds1 = xr.open_mfdataset(mfdataDIR1, parallel=True)
ds2 = xr.open_mfdataset(mfdataDIR2, parallel=True)
###Output
_____no_output_____
###Markdown
2009
###Code
ds1
# make preciptation rate to preciptation
def convert_to_precipitaion(ds):
temp = ds * 24
# temp = temp.to_dataset()
return temp
ds1 = convert_to_precipitaion(ds1)
# Transpose the data to get lat first and lon after -
ds1 = ds1.transpose("time", "lat", "lon")
ds1_ind = ds1.sel(lat=slice(5,40), lon=slice(65,100)).dropna("time")
da1 = ds1_ind.precipitation
da1
da1.mean(dim="time").plot()
###Output
_____no_output_____
###Markdown
Attempting to mask the data
###Code
import geopandas as gpd
from rasterio import features
from affine import Affine
def transform_from_latlon(lat, lon):
""" input 1D array of lat / lon and output an Affine transformation
"""
lat = np.asarray(lat)
lon = np.asarray(lon)
trans = Affine.translation(lon[0], lat[0])
scale = Affine.scale(lon[1] - lon[0], lat[1] - lat[0])
return trans * scale
def rasterize(shapes, coords, latitude='lat', longitude='lon',
fill=np.nan, **kwargs):
"""Rasterize a list of (geometry, fill_value) tuples onto the given
xray coordinates. This only works for 1d latitude and longitude
arrays.
usage:
-----
1. read shapefile to geopandas.GeoDataFrame
`states = gpd.read_file(shp_dir+shp_file)`
2. encode the different shapefiles that capture those lat-lons as different
numbers i.e. 0.0, 1.0 ... and otherwise np.nan
`shapes = (zip(states.geometry, range(len(states))))`
3. Assign this to a new coord in your original xarray.DataArray
`ds['states'] = rasterize(shapes, ds.coords, longitude='X', latitude='Y')`
arguments:
---------
: **kwargs (dict): passed to `rasterio.rasterize` function
attrs:
-----
:transform (affine.Affine): how to translate from latlon to ...?
:raster (numpy.ndarray): use rasterio.features.rasterize fill the values
outside the .shp file with np.nan
:spatial_coords (dict): dictionary of {"X":xr.DataArray, "Y":xr.DataArray()}
with "X", "Y" as keys, and xr.DataArray as values
returns:
-------
:(xr.DataArray): DataArray with `values` of nan for points outside shapefile
and coords `Y` = latitude, 'X' = longitude.
"""
transform = transform_from_latlon(coords['lat'], coords['lon'])
out_shape = (len(coords['lat']), len(coords['lon']))
raster = features.rasterize(shapes, out_shape=out_shape,
fill=fill, transform=transform,
dtype=float, **kwargs)
spatial_coords = {latitude: coords['lat'], longitude: coords['lon']}
return xr.DataArray(raster, coords=spatial_coords, dims=('lat', 'lon'))
def add_shape_coord_from_data_array(xr_da, shp_path, coord_name):
""" Create a new coord for the xr_da indicating whether or not it
is inside the shapefile
Creates a new coord - "coord_name" which will have integer values
used to subset xr_da for plotting / analysis/
Usage:
-----
precip_da = add_shape_coord_from_data_array(precip_da, "awash.shp", "awash")
awash_da = precip_da.where(precip_da.awash==0, other=np.nan)
"""
# 1. read in shapefile
shp_gpd = gpd.read_file(shp_path)
# 2. create a list of tuples (shapely.geometry, id)
# this allows for many different polygons within a .shp file (e.g. States of US)
shapes = [(shape, n) for n, shape in enumerate(shp_gpd.geometry)]
# 3. create a new coord in the xr_da which will be set to the id in `shapes`
xr_da[coord_name] = rasterize(shapes, xr_da.coords,
longitude='longitude', latitude='latitude')
return xr_da
shp_dir = './shapefiles/'
da1_ind = add_shape_coord_from_data_array(da1, shp_dir, "awash")
awash_da1 = da1_ind.where(da1_ind.awash==0, other=np.nan)
awash_da1.mean(dim="time").plot()
###Output
/home/aditya/.local/share/virtualenvs/atms_python-xEvIgfwt/lib/python3.9/site-packages/dask/array/numpy_compat.py:39: RuntimeWarning: invalid value encountered in true_divide
x = np.divide(x1, x2, out)
###Markdown
Take the different seasons
###Code
## premonsoon
da1_premon = awash_da1.sel(time=slice("2009-06-01", "2009-09-01"))
da1_premon
fig = plt.figure(figsize=(15, 7))
ax = fig.add_subplot(1, 1, 1, projection=ccrs.PlateCarree())
ax.set_extent([50, 100, 5, 40], crs=ccrs.PlateCarree())
da1_premon.mean(dim="time").plot()
gridliner = ax.gridlines(crs=ccrs.PlateCarree(), draw_labels=True)
gridliner.top_labels = False
gridliner.bottom_labels = True
gridliner.left_labels = True
gridliner.right_labe = False
gridliner.ylines = False # you need False
gridliner.xlines = False # you need False
# ax.set_xlabel("Longitude")
# ax.set_ylabel("Latitude")
ax.set_title("Precipitation plot India (monsoon)", pad=10, fontsize=20)
# ax.add_feature(cfeature.LAND)
# ax.add_feature(cfeature.OCEAN)
ax.add_feature(cfeature.COASTLINE)
# ax.add_feature(cfeature.BORDERS, linestyle=':')
# ax.add_feature(cfeature.STATES.with_scale('10m')) # To add states other than that of USA we have scale 10m
# ax.add_feature(cfeature.LAKES, alpha=0.5)
# ax.add_feature(cfeature.RIVERS)
###Output
/home/aditya/.local/share/virtualenvs/atms_python-xEvIgfwt/lib/python3.9/site-packages/dask/array/numpy_compat.py:39: RuntimeWarning: invalid value encountered in true_divide
x = np.divide(x1, x2, out)
|
linkedList/linkedListIntro.ipynb
|
###Markdown
Title : Linked List Intro1. ListNode 생성2. 1,2,3,4 리스트 노드 연결3. Iterative Print Function4. Recursive Print Function
###Code
class ListNode:
def __init__(self,val):
self.val = val
self.next = None
head_node = ListNode(1)
head_node.next = ListNode(2)
head_node.next.next = ListNode(3)
head_node.next.next.next = ListNode(4)
def printNodes(node:ListNode):
crnt_node = node
while crnt_node is not None:
print(crnt_node.val , end= ' ')
crnt_node = crnt_node.next
printNodes(head_node)
def printNodesRecur(node:ListNode):
print(node.val, end=' ')
if node.next is not None:
printNodesRecur(node.next)
printNodesRecur(head_node)
###Output
_____no_output_____
|
IoU Calculation.ipynb
|
###Markdown
IoU Calculation Code This Python notebook implements the calculation process of IoU score between two segmentation mask images to evaluate the performance of generated segmentation masks. Importing Packages
###Code
import SimpleITK as sitk
import numpy as np
import matplotlib.pyplot as plt
###Output
_____no_output_____
###Markdown
Loading Segmentation Mask Data
###Code
# Loading ground truth segmentation mask
gt_seg_path = 'gt_seg_path'
gt_seg_original = sitk.ReadImage(gt_seg_path)
gt_array = sitk.GetArrayFromImage(gt_seg_original)
print('The size of image is: ', gt_array.shape)
print('The range of intensity is from ', np.min(gt_array), 'to ', np.max(gt_array))
# Loading generated segmentation mask
generated_seg_path = 'generated_seg_path'
generated_seg_original = sitk.ReadImage(generated_seg_path)
generated_array = sitk.GetArrayFromImage(generated_seg_original)
print('The size of image is: ', generated_array.shape)
print('The range of intensity is from ', np.min(generated_array), 'to ', np.max(generated_array))
###Output
_____no_output_____
###Markdown
Calculating IoU score
###Code
TP = np.sum(np.logical_and(generated_array == 1, gt_array == 1)) # True Positive
TN = np.sum(np.logical_and(generated_array == 0, gt_array == 0)) # True Negative
FP = np.sum(np.logical_and(generated_array == 1, gt_array == 0)) # False Positive
FN = np.sum(np.logical_and(generated_array == 0, gt_array == 1)) # False Negative
IoU_score = TP/(FP+FN+TP)
print('IoU Score: ', IoU_score)
###Output
_____no_output_____
|
examples/electric_circuit_problem.ipynb
|
###Markdown
Solving an electric circuit using Particle Swarm Optimization Introduction PSO can be utilized in a wide variety of fields. In this example, the problem consists of analysing a given electric circuit and finding the electric current that flows through it. To accomplish this, the ```pyswarms``` library will be used to solve a non-linear equation by restructuring it as an optimization problem. The circuit is composed by a source, a resistor and a diode, as shown below.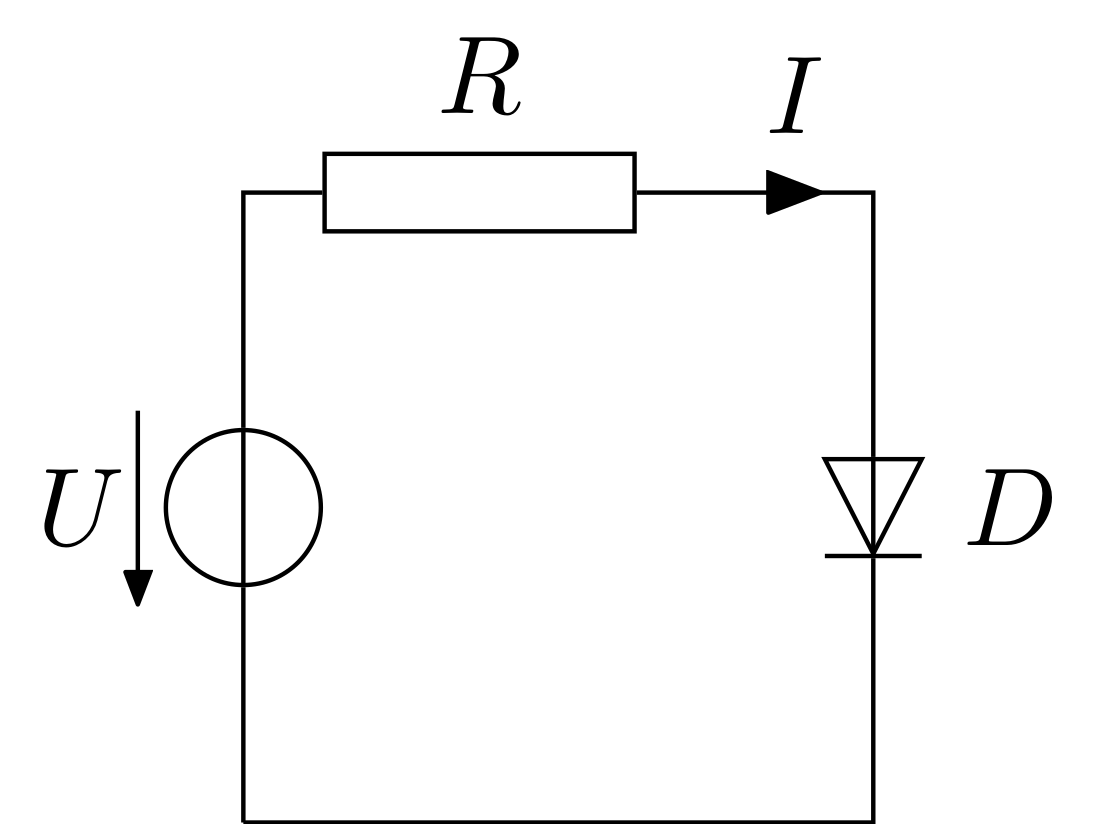 Mathematical FormulationKirchhoff's voltage law states that the directed sum of the voltages around any closed loop is zero. In other words, the sum of the voltages of the passive elements must be equal to the sum of the voltages of the active elements, as expressed by the following equation:$ U = v_D + v_R $, where $U$ represents the voltage of the source and, $v_D$ and $v_R$ represent the voltage of the diode and the resistor, respectively.To determine the current flowing through the circuit, $v_D$ and $v_R$ need to be defined as functions of $I$. A simplified Shockley equation will be used to formulate the current-voltage characteristic function of the diode. This function relates the current that flows through the diode with the voltage across it. Both $I_s$ and $v_T$ are known properties.$I = I_s e^{\frac{v_D}{v_T}}$Where:- $I$ : diode current- $I_s$ : reverse bias saturation current- $v_D$ : diode voltage- $v_T$ : thermal voltageWhich can be formulated over $v_D$:$v_D = v_T \log{\left |\frac{I}{I_s}\right |}$The voltage over the resistor can be written as a function of the resistor's resistance $R$ and the current $I$:$v_R = R I$And by replacing these expressions on the Kirschhoff's voltage law equation, the following equation is obtained:$ U = v_T \log{\left |\frac{I}{I_s}\right |} + R I $ To find the solution of the problem, the previous equation needs to be solved for $I$, which is the same as finding $I$ such that the cost function $c$ equals zero, as shown below. By doing this, solving for $I$ is restructured as a minimization problem. The absolute value is necessary because we don't want to obtain negative currents.$c = \left | U - v_T \log{\left | \frac{I}{I_s} \right |} - RI \right |$ Known parameter valuesThe voltage of the source is $ 10 \space V $ and the resistance of the resistor is $ 100 \space \Omega $. The diode is a silicon diode and it is assumed to be at room temperature.$U = 10 \space V $$R = 100 \space \Omega $$I_s = 9.4 \space pA = 9.4 \times 10^{-12} \space A$ (reverse bias saturation current of silicon diodes at room temperature, $T=300 \space K$)$v_T = 25.85 \space mV = 25.85 \times 10^{-3} \space V $ (thermal voltage at room temperature, $T=300 \space K$) Optimization
###Code
# Import modules
import sys
import numpy as np
import matplotlib.pyplot as plt
# Import PySwarms
import pyswarms as ps
print('Running on Python version: {}'.format(sys.version))
###Output
Running on Python version: 3.7.1 (v3.7.1:260ec2c36a, Oct 20 2018, 14:05:16) [MSC v.1915 32 bit (Intel)]
###Markdown
Defining the cost fuctionThe first argument of the cost function is a ```numpy.ndarray```. Each dimension of this array represents an unknown variable. In this problem, the unknown variable is just $I$, thus the first argument is a unidimensional array. As default, the thermal voltage is assumed to be $25.85 \space mV$.
###Code
def cost_function(I):
#Fixed parameters
U = 10
R = 100
I_s = 9.4e-12
v_t = 25.85e-3
c = abs(U - v_t * np.log(abs(I[:, 0] / I_s)) - R * I[:, 0])
return c
###Output
_____no_output_____
###Markdown
Setting the optimizerTo solve this problem, the global-best optimizer is going to be used.
###Code
%%time
# Set-up hyperparameters
options = {'c1': 0.5, 'c2': 0.3, 'w':0.3}
# Call instance of PSO
optimizer = ps.single.GlobalBestPSO(n_particles=10, dimensions=1, options=options)
# Perform optimization
cost, pos = optimizer.optimize(cost_function, iters=30)
print(pos[0])
print(cost)
###Output
1.1135553828367506e-05
###Markdown
Checking the solutionThe current flowing through the circuit is approximately $ 0.094 \space A$ which yields a cost of almost zero. The graph below illustrates the relationship between the cost $c$ and the current $I$. As shown, the cost reaches its minimum value of zero when $I$ is somewhere close to $0.09$.The use of ```reshape(100, 1)``` is required since ```np.linspace(0.001, 0.1, 100)``` returns an array with shape ```(100,)``` and first argument of the cost function must be a unidimensional array, that is, an array with shape ```(100, 1)```.
###Code
x = np.linspace(0.001, 0.1, 100).reshape(100, 1)
y = cost_function(x)
plt.plot(x, y)
plt.xlabel('Current I [A]')
plt.ylabel('Cost');
###Output
_____no_output_____
###Markdown
Another way of solving non-linear equations is by using non-linear solvers implemented in libraries such as ```scipy```. There are different solvers that one can choose which correspond to different numerical methods. We are going to use ```fsolve```, which is a general non-linear solver that finds the root of a given function. Unlike ```pyswarms```, the function (in this case, the cost function) to be used in ```fsolve``` must have as first argument a single value. Moreover, numerical methods need an initial guess for the solution, which can be made from the graph above.
###Code
# Import non-linear solver
from scipy.optimize import fsolve
c = lambda I: abs(10 - 25.85e-3 * np.log(abs(I / 9.4e-12)) - 100 * I)
initial_guess = 0.09
current_I = fsolve(func=c, x0=initial_guess)
print(current_I[0])
###Output
0.09404768643017938
|
SecureComputing/Project(Secure-File-Sharing)/Server.ipynb
|
###Markdown
Creator Name: Sara Baradaran, Mahdi Heidari, Zahra Khoramian Create Date: Aug 2020 Module Name: Server.py Project Name: Secure File Sharing
###Code
import os
import socket
import hashlib
import base64
import secrets
from Crypto.Util import Counter
from Crypto import Random
import string
import json
import pandas as pd
import pyodbc
import random
from threading import Thread
from uuid import uuid4
from datetime import datetime
from Crypto.Cipher import AES
from cryptography.hazmat.backends import default_backend
from cryptography.hazmat.primitives import hashes,serialization
from cryptography.hazmat.primitives.asymmetric import ec
from cryptography.hazmat.primitives.kdf.hkdf import HKDF
from password_strength import PasswordPolicy, PasswordStats
conn = pyodbc.connect('Driver={SQL Server};'
'Server=DESKTOP-DH5KE9Q\SQLEXPRESS;'
'Database=SecureFileSharing;'
'Trusted_Connection=yes;')
policy = PasswordPolicy.from_names(
length=8, # min length: 8
uppercase=1, # need min. 2 uppercase letters
numbers=1, # need min. 2 digits
special=1, # need min. 2 special characters
nonletters=1, # need min. 2 non-letter characters (digits, specials, anything)
entropybits=30, # need a password that has minimum 30 entropy bits (the power of its alphabet)
)
AouthCode = '0'
def func(connection_sock):
print(str(connection_sock.getsockname()[0]))
key = key_exchange(connection_sock)
if key == None:
print('Connection has been blocked. Failed to set session key')
return 0
while(1):
global AouthCode
data = connection_sock.recv(5000)
if not data:
c_IP , c_port = connection_sock.getpeername()
print('client with ip = {} and port = {} has been disconnected at time {}'
.format(c_IP, c_port, str(datetime.now())))
connection_sock.shutdown()
connection_sock.close()
return 1
data = data.decode('utf-8')
text = decrypt(data, key)
print('received_msg', text)
content = ''
text = text.split("\n")
command = text[0].split()
for i in range(1, len(text) - 1):
content += text[i]
AouthCode = text[len(text) - 1]
print('AouthCode', AouthCode)
print('command', command)
print('content', content)
msg = ''
##############################################################################
if command[0] == "register" and len(command) == 5:
userID = check_username(command[1], conn)
register_status = 0
if userID == None:
pass_str = CheckPasswordStrength(command[1], command[2])
if pass_str == '1':
register_status = user_registeration(command[1], command[2], command[3], command[4], conn)
msg = str(register_status) + " register " + command[1] + " " + str(datetime.now())
else:
msg = "-3 register " + command[1] + " " + str(datetime.now()) + '\n' + pass_str
else:
msg = "-2 register " + command[1] + " " + str(datetime.now())
# register log
add_registre_logs(command[1], command[3], command[4], str(register_status))
cipher_text = encrypt(msg, key)
if cipher_text != None:
connection_sock.send(cipher_text.encode('utf-8'))
##############################################################################
elif command[0] == "login" and len(command) == 3:
ip = str(connection_sock.getsockname()[0])
port = str(connection_sock.getsockname()[1])
ban_min = check_ban(command[1], conn)
if ban_min < 0:
msg = "-4 login " + command[1] + " " + str(datetime.now()) + '\n' + str(-ban_min) + '\n0'
else:
pass_status = check_password(command[1], command[2], conn)
login_status = 0
AuthCode = 0
if pass_status:
login_status, AuthCode = user_login(command[1], ip, port, conn)
if login_status == 1:
msg = "1 login " + command[1] + " " + str(datetime.now()) + '\n\n' + str(AuthCode)
else:
msg = "0 login " + command[1] + " " + str(datetime.now()) + '\n\n0'
else:
msg = "-1 login " + command[1] + " " + str(datetime.now()) + '\n\n0'
#login log
add_login_logs(command[1], command[2], ip, port, AuthCode, str(login_status))
update_ban_state(command[1], login_status, conn)
cipher_text = encrypt(msg, key)
if cipher_text != None:
connection_sock.send(cipher_text.encode('utf-8'))
##############################################################################
elif command[0] == "grant" and len(command) == 4:
ip = str(connection_sock.getsockname()[0])
port = str(connection_sock.getsockname()[1])
fileID = check_file(command[1], conn)
userID = check_AouthCode(ip, port, AouthCode, conn)
owner_status = check_access(userID, fileID, 'o' , conn)
userID_g = check_username(command[2], conn)
file_conf, file_int = get_file_lables(fileID, conn)
grant_status = 0
if userID != None:
if fileID != None:
if owner_status:
insert_access(userID_g, fileID, command[3], conn)
insert_access(userID_g, fileID, command[3], conn)
msg = "1 grant " + command[1] + " " + str(datetime.now())
else:
msg = "0 grant " + command[1] + " " + str(datetime.now())
else:
msg = "-2 grant " + command[1] + " " + str(datetime.now())
else:
msg = "-1 grant " + command[1] + " " + str(datetime.now())
cipher_text = encrypt(msg, key)
if cipher_text != None:
connection_sock.send(cipher_text.encode('utf-8'))
##############################################################################
elif command[0] == "revoce" and len(command) == 4:
ip = str(connection_sock.getsockname()[0])
port = str(connection_sock.getsockname()[1])
fileID = check_file(command[1], conn)
userID = check_AouthCode(ip, port, AouthCode, conn)
owner_status = check_access(userID, fileID, 'o' , conn)
userID_g = check_username(command[2], conn)
file_conf, file_int = get_file_lables(fileID, conn)
grant_status = 0
if userID != None:
if fileID != None:
if owner_status:
revoc_access(userID_g, fileID, command[3], conn)
revoc_access(userID_g, fileID, command[3], conn)
msg = "1 revoce " + command[1] + " " + str(datetime.now())
else:
msg = "0 revoce " + command[1] + " " + str(datetime.now())
else:
msg = "-2 revoce " + command[1] + " " + str(datetime.now())
else:
msg = "-1 revoce " + command[1] + " " + str(datetime.now())
cipher_text = encrypt(msg, key)
if cipher_text != None:
connection_sock.send(cipher_text.encode('utf-8'))
##############################################################################
elif command[0] == "put" and len(command) == 5:
ip = str(connection_sock.getsockname()[0])
port = str(connection_sock.getsockname()[1])
creatorID = check_AouthCode(ip, port, AouthCode, conn)
fileID = check_file(command[1], conn)
put_status = 0
if creatorID != None:
if fileID == None:
put_status = put_file(command[1], content, creatorID, command[2], command[3], command[4], conn)
fileID = check_file(command[1], conn)
msg = str(put_status) + " put " + command[1] + " " + str(datetime.now())
if put_status:
insert_access(creatorID, fileID, 'w', conn)
insert_access(creatorID, fileID, 'r', conn)
else:
msg = "-2 put " + command[1] + " " + str(datetime.now())
else:
msg = "-1 get " + command[1] + " " + str(datetime.now())
#put log
add_put_logs(creatorID, fileID, command[1], command[2], command[3], content, str(put_status))
cipher_text = encrypt(msg, key)
if cipher_text != None:
connection_sock.send(cipher_text.encode('utf-8'))
##############################################################################
elif command[0] == "get" and len(command) == 2:
ip = str(connection_sock.getsockname()[0])
port = str(connection_sock.getsockname()[1])
userID = check_AouthCode(ip, port, AouthCode, conn)
fileID = check_file(command[1], conn)
owner_status = check_access(userID, fileID, 'o' , conn)
file_conf, file_int = get_file_lables(fileID, conn)
if userID != None:
if fileID != None:
if owner_status:
content = get_file(command[1], conn)
msg = "1 get " + command[1] + " " + str(datetime.now()) + "\n" + content
revoc_access(userID, fileID, 'w', conn)
revoc_access(userID, fileID, 'r', conn)
else:
msg = "0 get " + command[1] + " " + str(datetime.now()) + "\n "
else:
msg = "-2 get " + command[1] + " " + str(datetime.now()) + "\n "
else:
msg = "-1 get " + command[1] + " " + str(datetime.now()) + "\n "
#get logs
add_get_logs(userID, fileID, command[1], file_conf, file_int, str(owner_status))
cipher_text = encrypt(msg, key)
if cipher_text != None:
connection_sock.send(cipher_text.encode('utf-8'))
##############################################################################
elif command[0] == "read" and len(command) == 2:
ip = str(connection_sock.getsockname()[0])
port = str(connection_sock.getsockname()[1])
userID = check_AouthCode(ip, port, AouthCode, conn)
fileID = check_file(command[1], conn)
file_conf, file_int = get_file_lables(fileID, conn)
read_status = 0
if userID != None:
if fileID != None:
cond, BIBA_status, BLP_status, ACL = check_access_mode(userID, fileID, 'r' , conn)
if cond:
content = read_file(command[1], conn)
if content == None:
msg = "0 1 1 read " + command[1] + " " + str(datetime.now()) + "\n "
else:
read_status = 1
msg = "1 1 1 read " + command[1] + " " + str(datetime.now()) + "\n" + content
else:
msg = "0 " + str(BLP_status) + " " + str(BIBA_status) + " read " + command[1] + " " + str(datetime.now()) + "\n "
else:
msg = "-2 read " + command[1] + " " + str(datetime.now()) + "\n "
else:
msg = "-1 read " + command[1] + " " + str(datetime.now()) + "\n "
#read logs
add_read_logs(userID, fileID, command[1], file_conf, file_int, str(read_status))
cipher_text = encrypt(msg, key)
if cipher_text != None:
connection_sock.send(cipher_text.encode('utf-8'))
##############################################################################
elif command[0] == "write" and len(command) == 2:
ip = str(connection_sock.getsockname()[0])
port = str(connection_sock.getsockname()[1])
userID = check_AouthCode(ip, port, AouthCode, conn)
fileID = check_file(command[1], conn)
file_conf, file_int = get_file_lables(fileID, conn)
write_status = 0
if userID != None:
if fileID != None:
cond, BIBA_status, BLP_status, ACL = check_access_mode(userID, fileID, 'w' , conn)
if cond:
write_status = write_file(command[1], content, conn)
if write_status == 0:
msg = "0 1 1 write " + command[1] + " " + str(datetime.now())
else:
msg = "1 1 1 write " + command[1] + " " + str(datetime.now())
else:
msg = "0 " + str(BLP_status) + " " + str(BIBA_status) + " write " + command[1] + " " + str(datetime.now())
else:
msg = "-2 write " + command[1] + " " + str(datetime.now())
else:
msg = "-1 write " + command[1] + " " + str(datetime.now())
#write logs
add_write_logs(userID, fileID, command[1], file_conf, file_int, content, str(write_status))
cipher_text = encrypt(msg, key)
if cipher_text != None:
connection_sock.send(cipher_text.encode('utf-8'))
##############################################################################
elif command[0] == "list" and len(command) == 1:
userID = check_AouthCode(ip, port, AouthCode, conn)
ip = str(connection_sock.getsockname()[0])
port = str(connection_sock.getsockname()[1])
if userID == None:
msg = "-1 list " + str(datetime.now())
else:
msg = "1 list " + str(datetime.now()) + "\n "
files = list_files()
msg += files
cipher_text = encrypt(msg, key)
if cipher_text != None:
connection_sock.send(cipher_text.encode('utf-8'))
elif command[0] == "logout" and len(command) == 1:
userID = check_AouthCode(ip, port, AouthCode, conn)
ip = str(connection_sock.getsockname()[0])
port = str(connection_sock.getsockname()[1])
if userID != None:
logout_status = user_logout(userID, ip, port, AouthCode, conn)
else:
msg = "-1 logout " + command[1] + " " + str(datetime.now())
msg = str(logout_status) + " logout " + str(datetime.now())
cipher_text = encrypt(msg, key)
if cipher_text != None:
connection_sock.send(cipher_text.encode('utf-8'))
print(msg)
#Socket handling
#########################################################################################################
def setup_server():
s = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
if s == 0:
print ('error in server socket creation\n')
server_ip = socket.gethostname()
server_port = 8500
s.setsockopt(socket.SOL_SOCKET, socket.SO_REUSEADDR, 1)
s.bind((server_ip, server_port))
s.listen(5)
print("server is listening for any connection ... ")
return s
def server_listening(s):
connection_socket , client_addr = s.accept()
print("client with ip = {} has been connected at time {}".format(client_addr, str(datetime.now())))
return connection_socket
#Cryptography
#########################################################################################################
def key_exchange(client_sock): # first makes a private key, sends and receives public keys, then derives the secret key
try:
backend = default_backend()
client_rcv_pub = client_sock.recv(200) # client_rcv_pub is client received public key in bytes
client_pub = serialization.load_pem_public_key(client_rcv_pub, backend) # client_pub is client public key in curve object
server_pr = ec.generate_private_key(ec.SECP256R1(), backend)
server_pub = server_pr.public_key()
client_sock.send(server_pub.public_bytes(serialization.Encoding.PEM, serialization.PublicFormat.SubjectPublicKeyInfo))
shared_data = server_pr.exchange(ec.ECDH(), client_pub)
secret_key = HKDF(hashes.SHA256(), 32, None, b'Key Exchange', backend).derive(shared_data)
session_key = secret_key[-16:] # to choose the last 128-bit (16-byte) of secret key
print('key exchanged successfully.')
return session_key
except:
print('error in key exchange')
return None
def encrypt(plain_text, key): # returns a json containing ciphertext and nonce for CTR mode
nonce1 = Random.get_random_bytes(8)
countf = Counter.new(64, nonce1)
cipher = AES.new(key, AES.MODE_CTR, counter=countf)
cipher_text_bytes = cipher.encrypt(plain_text.encode('utf-8'))
nonce = base64.b64encode(nonce1).decode('utf-8')
cipher_text = base64.b64encode(cipher_text_bytes).decode('utf-8')
result = json.dumps({'nonce':nonce, 'ciphertext':cipher_text})
return result
def decrypt(data, key):
try:
b64 = json.loads(data)
nonce = base64.b64decode(b64['nonce'].encode('utf-8'))
cipher_text = base64.b64decode(b64['ciphertext'])
countf = Counter.new(64, nonce)
cipher = AES.new(key, AES.MODE_CTR, counter=countf)
plain_text = cipher.decrypt(cipher_text)
return plain_text.decode('utf-8')
except ValueError:
return None
#########################################################################################################
def check_access_mode(userID, fileID, access_type , conn):
MyQuery = '''
select AccessMode
from ValidFiles where FileID = ?
'''
sql_query = pd.read_sql( MyQuery ,conn, params={fileID,} )
acc_mode = int(str(sql_query['AccessMode']).split()[1])
cond = 1
BIBA = check_BIBA(userID, fileID, access_type, conn)
BLP = check_BLP(userID, fileID, access_type, conn)
ACL = check_access(userID, fileID, access_type, conn)
if acc_mode % 2 == 0:
cond = cond & BLP
if acc_mode % 3 == 0:
cond = cond & BIBA
if acc_mode % 5 == 0:
cond = cond & ACL
return cond, BIBA, BLP, ACL
def check_AouthCode(ip, port, AouthCode, conn):
MyQuery = '''
select UserID
from ValidConnections where [AouthCode] = ? and [Ip] = ? and [Port] = ?
'''
sql_query = pd.read_sql( MyQuery ,conn, params=(AouthCode, ip, port,) )
if str(sql_query).split()[0] == 'Empty':
return None
else:
return str(sql_query['UserID']).split()[1]
def list_files():
MyQuery = '''
select FileName, LastModifiedDate
from ValidFiles
'''
sql_query = pd.read_sql( MyQuery ,conn )
return str(sql_query)
def read_file(filename, conn):
MyQuery = '''
select Content
from ValidFiles where FileName = ?
'''
sql_query = pd.read_sql( MyQuery ,conn, params={filename,} )
if str(sql_query).split()[0] == 'Empty':
return None
else:
return str(sql_query['Content'][0])
def write_file(filename, content, conn):
MyQuery = '''
update Files set Content = ?
where [FileName] = ? and [Status] = '1'
'''
cursor = conn.cursor()
cursor.execute( MyQuery, content, filename)
conn.commit()
cursor.close()
new_content = read_file(filename, conn)
if content == new_content:
return 1
return 0
def get_file(filename, conn):
content = read_file(filename, conn)
MyQuery = '''
update Files set [Status] = '0'
where [FileName] = ? and [Status] = '1'
'''
cursor = conn.cursor()
cursor.execute( MyQuery, filename)
conn.commit()
cursor.close()
return content
def check_username(username, conn):
MyQuery = '''
select UserID
from Users where UserName = ?
'''
sql_query = pd.read_sql( MyQuery ,conn, params={username,} )
if str(sql_query).split()[0] == 'Empty':
return None
else:
return str(sql_query['UserID']).split()[1]
#conf_range = ['Top Secret', 'Secret', 'Confidential', 'Unclassified']
#int_range = ['Very Trusted', 'Trusted', 'Slightly Trusted', 'UnTrusted']
int_range = ['1', '2', '3', '4']
conf_range = ['1', '2', '3', '4']
def user_registeration(username, password, conf_label, integrity_label, conn):
if username != "all":
salt = ''.join(secrets.choice(string.ascii_letters) for _ in range(25))
pass_hash = hashlib.sha256((password + salt).encode('utf-8')).hexdigest()
pass_hash = str(pass_hash)
MyQuery = '''
insert into Users ( UserName, PasswordHash, Salt, ConfLable, IntegrityLable) values (?, ?, ?, ?, ? );
'''
if conf_label in conf_range and integrity_label in int_range:
cursor = conn.cursor()
cursor.execute( MyQuery, username, pass_hash,salt, conf_label, integrity_label)
conn.commit()
cursor.close()
if check_username(username, conn) == None:
return 0
return 1
return 0
def CheckPasswordStrength(username, password):
if password.find(username) != -1:
return "password should not include username"
#check condition 1
Condition1 = policy.test(password)
if Condition1:
return ''.join(str(Condition1))
#check condition 2
f = open("PwnedPasswordsTop100k.txt","r")
for x in f:
x = str(x).strip()
if x == password:
return "Password is in top 100,000 pwned passwords"
return '1'
def check_password(username, password, conn):
MyQuery1 = '''
select [Salt]
from Users where UserName = ?
'''
MyQuery2 = '''
select dbo.CheckPassHash(?, ?) as correctness
'''
sql_query = pd.read_sql( MyQuery1 ,conn, params={username,} )
salt = str(sql_query['Salt']).split()[1]
print('salt',salt)
pass_h = str(hashlib.sha256((password + salt).encode('utf-8')).hexdigest())
print('pass_h',pass_h)
print(username)
sql_query2 = pd.read_sql( MyQuery2 ,conn, params=(username, pass_h) )
print(sql_query2)
if str(sql_query2['correctness']).split()[1] == '1':
return 1
else:
return 0
def check_file(filename, conn):
MyQuery = '''
select FileID
from ValidFiles where FileName = ?
'''
sql_query = pd.read_sql( MyQuery ,conn, params={filename,} )
if str(sql_query).split()[0] == 'Empty':
return None
else:
return str(sql_query['FileID']).split()[1]
def put_file(filename, content, creatorID, conf_label, integrity_label, access_mode , conn):
MyQuery = '''
insert into Files ([FileName], [FileCreatorID], [ConfLable], [IntegrityLable], [AccessMode], [Content], [Status])
values (?, ?, ?, ?, ?, ?, ?)
'''
cursor = conn.cursor()
cursor.execute(MyQuery, filename, creatorID, conf_label, integrity_label, access_mode, content, '1')
conn.commit()
cursor.close()
if check_file(filename, conn) == None:
return 0
return 1
def update_ban_state(username, status, conn):
MyQuery1 = '''UPDATE BanUser
SET StartBanTime = CURRENT_TIMESTAMP, BanLvl= ?
where UserID = (select UserID from Users where UserName= ?)
'''
cursor = conn.cursor()
if status:
cursor.execute(MyQuery1, 0, username)
else:
MyQuery2 = '''
select dbo.FindLastFailedLogin(?) as lastfail
'''
sql_query2 = pd.read_sql( MyQuery2 ,conn, params={username,} )
lastfail = str(sql_query2['lastfail']).split()[1]
lastfail = int(lastfail)
if lastfail % 3 == 0:
cursor.execute(MyQuery1, lastfail//3, username)
conn.commit()
cursor.close()
def check_ban(username, conn):
MyQuery2 = '''
select dbo.IsBan(?) as ban_min
'''
sql_query2 = pd.read_sql( MyQuery2 ,conn, params={username,} )
return int(str(sql_query2['ban_min']).split()[1])
#Logs
##############################################################################
def add_registre_logs(username, conf_lable, integrity_lable, status):
MyQuery = '''
INSERT INTO RegisterLogs ( UserName, ConfLable, IntegrityLable, [Status])
VALUES (?, ?, ?, ?);
'''
cursor = conn.cursor()
cursor.execute(MyQuery, username, conf_lable, integrity_lable, status)
conn.commit()
cursor.close()
def add_login_logs(username, password, ip, port, AouthCode, status):
MyQuery = '''
INSERT INTO LoginLogs ( UserName, [password], ConnectionIp, ConnectionPort, AuthenticationCode, [Status])
VALUES (?, ?, ?, ?, ?, ?);
'''
cursor = conn.cursor()
cursor.execute(MyQuery, username, password, ip, port, AouthCode, status)
conn.commit()
cursor.close()
def add_put_logs(creatorID, fileID, filename, file_conf, file_int, content, status):
MyQuery = '''
INSERT INTO PutLogs ( CreatorID, FileID, FileName ,CurFileConfLable, CurFileIntegrityLable, Content, [Status])
VALUES (?, ?, ?, ?, ?, ?, ?);
'''
if fileID == None:
fileID = 0
cursor = conn.cursor()
cursor.execute(MyQuery, creatorID, fileID, filename, file_conf, file_int, content, status)
conn.commit()
cursor.close()
def add_get_logs(userID, fileID, filename, file_conf, file_int, status):
MyQuery = '''
INSERT INTO GetLogs ( UserID, FileID, FileName ,CurFileConfLable, CurFileIntegrityLable, [Status])
VALUES (?, ?, ?, ?, ?, ?);
'''
if fileID == None:
fileID = 0
cursor = conn.cursor()
cursor.execute(MyQuery, userID, fileID, filename, file_conf, file_int, status)
conn.commit()
cursor.close()
def add_read_logs(userID, fileID, filename, file_conf, file_int, status):
MyQuery = '''
INSERT INTO ReadLogs ( UserID, FileID, FileName, CurFileConfLable, CurFileIntegrityLable, [Status])
VALUES (?, ?, ?, ?, ?, ?);
'''
if fileID == None:
fileID = 0
print(userID, fileID, filename, file_conf, file_int, status)
cursor = conn.cursor()
cursor.execute(MyQuery, userID, fileID, filename, file_conf, file_int, status)
conn.commit()
cursor.close()
def add_write_logs(userID, fileID, filename, file_conf, file_int, content, status):
MyQuery = '''
INSERT INTO WriteLogs ( UserID, FileID, FileName, CurFileConfLable, CurFileIntegrityLable, Content, [Status])
VALUES (?, ?, ?, ?, ?, ?, ?);
'''
if fileID == None:
fileID = 0
cursor = conn.cursor()
cursor.execute(MyQuery, userID, fileID, filename, file_conf, file_int, content, status)
conn.commit()
cursor.close()
##############################################################################
#Access Control
##############################################################################
def insert_access(userID, fileID, access_type, conn):
MyQuery = '''
insert into AccessList ([UserID], [FileID], [AccessType])
values (?, ?, ?)
'''
if check_access(userID, fileID, access_type, conn) == 0:
cursor = conn.cursor()
cursor.execute(MyQuery, userID, fileID, access_type)
conn.commit()
cursor.close()
def revoc_access(userID, fileID, access_type, conn):
MyQuery = '''
delete AccessList
where UserID = ? and FileID = ? and AccessType = ?
'''
cursor = conn.cursor()
cursor.execute(MyQuery, userID, fileID, access_type)
conn.commit()
cursor.close()
def check_access(userID, fileID, access_type, conn):
if access_type == 'o':
MyQuery = '''
select *
from Files
where FileID = ? and FileCreatorID = ?
'''
sql_query = pd.read_sql( MyQuery ,conn, params=(fileID, userID,) )
else:
MyQuery = '''
select *
from AccessList
where FileID = ? and UserID = ? and AccessType = ?
'''
sql_query = pd.read_sql( MyQuery ,conn, params=(fileID, userID, access_type,) )
if str(sql_query).split()[0] == 'Empty':
return 0
else:
return 1
def get_file_lables(fileID, conn):
MyQuery = '''
select[IntegrityLable], [ConfLable]
from Files
where FileID = ?
'''
sql_query = pd.read_sql( MyQuery ,conn, params={fileID,} )
if str(sql_query).split()[0] == 'Empty':
file_conf = ''
file_int = ''
else:
file_conf = str(sql_query['ConfLable']).split()[1]
file_int = str(sql_query['IntegrityLable']).split()[1]
return file_conf, file_int
def check_BLP(userID, fileID, access_type, conn):
MyQuery1 = '''
select[ConfLable]
from Users
where UserID = ?
'''
sql_query1 = pd.read_sql( MyQuery1 ,conn, params={userID,} )
MyQuery2 = '''
select[ConfLable]
from Files
where FileID = ?
'''
sql_query2 = pd.read_sql( MyQuery2 ,conn, params={fileID,} )
user_conf = int(str(sql_query1['ConfLable']).split()[1])
file_conf = int(str(sql_query2['ConfLable']).split()[1])
if access_type == 'w':
if(user_conf > file_conf):
return 0
else:
return 1
elif access_type == 'r':
if(user_conf < file_conf):
return 0
else:
return 1
def check_BIBA(userID, fileID, access_type, conn):
MyQuery1 = '''
select[IntegrityLable]
from Users
where UserID = ?
'''
sql_query1 = pd.read_sql( MyQuery1 ,conn, params={userID,} )
MyQuery2 = '''
select[IntegrityLable]
from Files
where FileID = ?
'''
sql_query2 = pd.read_sql( MyQuery2 ,conn, params={fileID,} )
user_int = int(str(sql_query1['IntegrityLable']).split()[1])
file_int = int(str(sql_query2['IntegrityLable']).split()[1])
if access_type == 'w':
if(user_int < file_int):
return 0
else:
return 1
elif access_type == 'r':
if(user_int > file_int):
return 0
else:
return 1
##############################################################################
def user_login(username, Ip, Port, conn):
userID = check_username(username, conn)
MyQuery = '''
insert into Connections ([UserID], [Ip], [Port], [AouthCode], [ConnectionDate], [Status])
values (?, ?, ?, ?, ?, ?)
'''
AouthCode = uuid4()
ConnectionDate = str(datetime.now())[:-3]
cursor = conn.cursor()
cursor.execute( MyQuery, userID, Ip, Port, AouthCode, ConnectionDate, '1')
conn.commit()
cursor.close()
MyQuery2 = '''
select [UserID], [Ip], [Port], [AouthCode], [ConnectionDate], [Status]
from connections
where [UserID] = ? and [Ip] = ? and [Port] = ? and [AouthCode] = ? and [ConnectionDate] = ? and [Status] = '1'
'''
sql_query2 = pd.read_sql( MyQuery2 ,conn, params=(userID, Ip, Port, AouthCode, ConnectionDate,) )
if str(sql_query2).split()[0] == 'Empty':
return 0 , None
return 1, AouthCode
def user_logout(userID, Ip, Port, AouthCode, conn):
MyQuery = '''
update connections set [Status] = '0', ConnectionCloseDate = ?
where [UserID] = ? and [Ip] = ? and [Port] = ? and [AouthCode] = ? and [Status] = '1'
'''
ConnectionCloseDate = str(datetime.now())
cursor = conn.cursor()
cursor.execute( MyQuery, ConnectionCloseDate, userID, Ip, Port, AouthCode)
conn.commit()
cursor.close()
MyQuery2 = '''
select [Status]
from connections
where [UserID] = ? and [Ip] = ? and [Port] = ? and [AouthCode] = ? and [Status] = '0' and ConnectionCloseDate = ?
'''
sql_query2 = pd.read_sql( MyQuery2 ,conn, params=(userID, Ip, Port, AouthCode, ConnectionCloseDate) )
if str(sql_query2).split()[0] == 'Empty':
return 0
return 1
if __name__ == "__main__":
s = setup_server()
while True:
connection_sock = server_listening(s)
try:
Thread(target=func,args=(connection_sock,)).start()
except:
print('Server is busy. Unable to create more threads.')
s.shutdown()
s.close()
###Output
server is listening for any connection ...
client with ip = ('192.168.56.1', 13420) has been connected at time 2021-05-16 09:15:20.098786
192.168.56.1
key exchanged successfully.
|
digit-recognizer/3. CNN.ipynb
|
###Markdown
3. CNN Run name
###Code
import time
project_name = 'DigitRecognizer'
step_name = 'Preprocess'
date_str = time.strftime("%Y%m%d", time.localtime())
time_str = time.strftime("%Y%m%d_%H%M%S", time.localtime())
run_name = '%s_%s_%s' % (project_name, step_name, time_str)
print('run_name: %s' % run_name)
t0 = time.time()
###Output
run_name: DigitRecognizer_Preprocess_20190407_220457
###Markdown
Important Params
###Code
from multiprocessing import cpu_count
batch_size = 8
random_state = 2019
print('cpu_count:\t', cpu_count())
print('batch_size:\t', batch_size)
print('random_state:\t', random_state)
###Output
cpu_count: 4
batch_size: 8
random_state: 2019
###Markdown
Import PKGs
###Code
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
%matplotlib inline
from IPython.display import display
import os
import gc
import math
import shutil
import zipfile
import pickle
import h5py
from PIL import Image
from tqdm import tqdm
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, accuracy_score
from keras.utils.np_utils import to_categorical # convert to one-hot-encoding
from keras.models import Sequential
from keras.layers import Dense, Dropout, Input, Flatten, Conv2D, MaxPooling2D, BatchNormalization
from keras.optimizers import Adam
from keras.preprocessing.image import ImageDataGenerator
from keras.callbacks import LearningRateScheduler, TensorBoard
###Output
Using TensorFlow backend.
###Markdown
Basic folders
###Code
cwd = os.getcwd()
input_folder = os.path.join(cwd, 'input')
log_folder = os.path.join(cwd, 'log')
model_folder = os.path.join(cwd, 'model')
output_folder = os.path.join(cwd, 'output')
print('input_folder: \t\t%s' % input_folder)
print('log_folder: \t\t%s' % log_folder)
print('model_folder: \t\t%s' % model_folder)
print('output_folder: \t\t%s'% output_folder)
train_csv_file = os.path.join(input_folder, 'train.csv')
test_csv_file = os.path.join(input_folder, 'test.csv')
print('\ntrain_csv_file: \t%s' % train_csv_file)
print('test_csv_file: \t\t%s' % test_csv_file)
processed_data_file = os.path.join(input_folder, '%s_%s.p' % (project_name, step_name))
print('processed_data_file: \t%s' % processed_data_file)
###Output
input_folder: D:\Kaggle\digit-recognizer\input
log_folder: D:\Kaggle\digit-recognizer\log
model_folder: D:\Kaggle\digit-recognizer\model
output_folder: D:\Kaggle\digit-recognizer\output
train_csv_file: D:\Kaggle\digit-recognizer\input\train.csv
test_csv_file: D:\Kaggle\digit-recognizer\input\test.csv
processed_data_file: D:\Kaggle\digit-recognizer\input\DigitRecognizer_Preprocess.p
###Markdown
Basic functions
###Code
def show_data_images(rows, fig_column, y_data, *args):
columns = len(args)
figs, axes = plt.subplots(rows, columns, figsize=(rows, fig_column*columns))
print(axes.shape)
for i, ax in enumerate(axes):
y_data_str = ''
if type(y_data) != type(None):
y_data_str = '_' + str(y_data[i])
ax[0].set_title('28x28' + y_data_str)
for j, arg in enumerate(args):
ax[j].imshow(arg[i])
###Output
_____no_output_____
###Markdown
Preview data
###Code
%%time
raw_data = np.loadtxt(train_csv_file, skiprows=1, dtype='int', delimiter=',')
x_data = raw_data[:,1:]
y_data = raw_data[:,0]
x_test = np.loadtxt(test_csv_file, skiprows=1, dtype='int', delimiter=',')
print(x_data.shape)
print(y_data.shape)
print(x_test.shape)
x_data = x_data/255.
x_test = x_test/255.
y_data_cat = to_categorical(y_data)
describe(x_data)
describe(x_test)
describe(y_data)
describe(y_data_cat)
x_data = x_data.reshape(-1, 28, 28, 1)
x_test = x_test.reshape(-1, 28, 28, 1)
describe(x_data)
describe(x_test)
# print(x_data[0])
print(y_data[0: 10])
index = 0
fig, ax = plt.subplots(2, 2, figsize=(12, 6))
ax[0, 0].plot(x_data[index].reshape(784,))
ax[0, 0].set_title('784x1 data')
ax[0, 1].imshow(x_data[index].reshape(28, 28), cmap='gray')
ax[0, 1].set_title('28x28 data => ' + str(y_data[index]))
ax[1, 0].plot(x_test[index].reshape(784,))
ax[1, 0].set_title('784x1 data')
ax[1, 1].imshow(x_test[index].reshape(28, 28), cmap='gray')
ax[1, 1].set_title('28x28 data')
###Output
_____no_output_____
###Markdown
Split train and val
###Code
x_train, x_val, y_train_cat, y_val_cat = train_test_split(x_data, y_data_cat, test_size=0.1, random_state=random_state)
print(x_train.shape)
print(y_train_cat.shape)
print(x_val.shape)
print(y_val_cat.shape)
###Output
_____no_output_____
###Markdown
Build model
###Code
def build_model(input_shape):
model = Sequential()
# Block 1
model.add(Conv2D(filters = 32, kernel_size = (3, 3), activation='relu', padding = 'Same', input_shape = input_shape))
model.add(BatchNormalization())
model.add(Conv2D(filters = 32, kernel_size = (3, 3), activation='relu', padding = 'Same'))
model.add(BatchNormalization())
model.add(MaxPooling2D(strides=(2,2)))
model.add(Dropout(0.25))
# Block 2
model.add(Conv2D(filters = 64, kernel_size = (3, 3), activation='relu', padding = 'Same'))
model.add(BatchNormalization())
model.add(Conv2D(filters = 64, kernel_size = (3, 3), activation='relu', padding = 'Same'))
model.add(BatchNormalization())
model.add(MaxPooling2D(strides=(2,2)))
model.add(Dropout(0.25))
# Output
model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.25))
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.25))
model.add(Dense(10, activation='softmax'))
return model
model = build_model(x_train.shape[1:])
model.compile(loss='categorical_crossentropy', optimizer = Adam(lr=1e-4), metrics=["accuracy"])
train_datagen = ImageDataGenerator(
zoom_range = 0.2,
rotation_range = 20,
height_shift_range = 0.2,
width_shift_range = 0.2
)
val_datagen = ImageDataGenerator()
# annealer = LearningRateScheduler(lambda x: 1e-4 * 0.995 ** x)
def get_lr(x):
if x <= 10:
return 1e-4
elif x <= 20:
return 3e-5
else:
return 1e-5
[print(get_lr(x), end=' ') for x in range(1, 31)]
annealer = LearningRateScheduler(get_lr)
callbacks = [annealer]
%%time
steps_per_epoch = x_train.shape[0] / batch_size
print('steps_per_epoch:\t', steps_per_epoch)
hist = model.fit_generator(
train_datagen.flow(x_train, y_train_cat, batch_size=batch_size, seed=random_state),
steps_per_epoch=steps_per_epoch,
epochs=2, #Increase this when not on Kaggle kernel
verbose=1, #1 for ETA, 0 for silent
callbacks=callbacks,
max_queue_size=batch_size*4,
workers=cpu_count(),
validation_steps=100,
validation_data=val_datagen.flow(x_val, y_val_cat, batch_size=batch_size, seed=random_state)
)
###Output
_____no_output_____
|
notebooks/random_dataset_generation.ipynb
|
###Markdown
Random dataset generationThis example shows generation of two-dimensional dataset follows bivariate Gaussian distribution.[Gsl_randist.bivariate_gaussian](http://mmottl.github.io/gsl-ocaml/api/Gsl_randist.htmlVALbivariate_gaussian)is a binding to [gsl_ran_bivariate_gaussian](https://www.gnu.org/software/gsl/manual/html_node/The-Bivariate-Gaussian-Distribution.html),a function generates a two random numbers following bivariate Gaussian distribution defined as$$\newcommand{d}{\mathrm{d}}p(x,y) \d x \d y =\frac{1}{2 \pi \sigma_x \sigma_y \sqrt{1-\rho^2}}\exp\left( -\frac{x^2 / \sigma_x^2 + y^2 / \sigma_y^2 - 2 \rho x y / (\sigma_x \sigma_y)}{2(1-\rho^2)}\right) \d x \d y$$where $\sigma_x$ and $\sigma_y$ are standard deviations of $x$ and $y$ respectively,and $\rho \in [-1,+1]$ is a correlation coefficient between $x$ and $y$.
###Code
#thread ;;
#require "gsl" ;;
#require "jupyter-archimedes" ;;
let rng = Gsl.Rng.(make MT19937) ;; (* Mersenne Twister *)
(* Generate positive examples *)
let positive_xys =
Array.init 100 (fun _ -> Gsl.Randist.bivariate_gaussian rng ~sigma_x:0.4 ~sigma_y:0.9 ~rho:0.4)
|> Array.map (fun (x, y) -> (x +. 0.5, y -. 0.1))
(* Generate negative examples *)
let negative_xys =
Array.init 100 (fun _ -> Gsl.Randist.bivariate_gaussian rng ~sigma_x:0.6 ~sigma_y:1.2 ~rho:0.3)
|> Array.map (fun (x, y) -> (x -. 0.8, y +. 0.4))
let vp = A.init ["jupyter"] in
A.Axes.box vp ;
A.set_color vp A.Color.red ;
A.Array.xy_pairs vp positive_xys ;
A.set_color vp A.Color.blue ;
A.Array.xy_pairs vp negative_xys ;
A.close vp
let oc = open_out "datasets/bivariate_gaussian_2d.csv" in
let ppf = Format.formatter_of_out_channel oc in
Array.iter
(fun (x, y) -> Format.fprintf ppf "%g,%g,0@." x y)
negative_xys ;
Array.iter
(fun (x, y) -> Format.fprintf ppf "%g,%g,1@." x y)
positive_xys ;
close_out
###Output
_____no_output_____
|
During_experiment/STORM6/20211208-align_10x_positions_seq_DNA_RNA_rnase_treat.ipynb
|
###Markdown
calculate rotation and transposition matrix
###Code
import os
data_folder = r'D:\Pu\20211208-P_brain_CTP11-500_M1_DNA_RNA-seq_hybrid'
before_position_file = os.path.join(data_folder, 'positions_before_align.txt')
after_position_file = os.path.join(data_folder, 'positions_after_align.txt')
import numpy as np
import os, sys
# 1. alignment for manually picked points
def align_manual_points(pos_file_before, pos_file_after,
save=True, save_folder=None, save_filename='', verbose=True):
"""Function to align two manually picked position files,
they should follow exactly the same order and of same length.
Inputs:
pos_file_before: full filename for positions file before translation
pos_file_after: full filename for positions file after translation
save: whether save rotation and translation info, bool (default: True)
save_folder: where to save rotation and translation info, None or string (default: same folder as pos_file_before)
save_filename: filename specified to save rotation and translation points
verbose: say something! bool (default: True)
Outputs:
R: rotation for positions, 2x2 array
T: traslation of positions, array of 2
Here's example for how to translate points
translated_ps_before = np.dot(ps_before, R) + t
"""
# load position_before
if os.path.isfile(pos_file_before):
ps_before = np.loadtxt(pos_file_before, delimiter=',')
# load position_after
if os.path.isfile(pos_file_after):
ps_after = np.loadtxt(pos_file_after, delimiter=',')
# do SVD decomposition to get best fit for rigid-translation
c_before = np.mean(ps_before, axis=0)
c_after = np.mean(ps_after, axis=0)
H = np.dot((ps_before - c_before).T, (ps_after - c_after))
U, _, V = np.linalg.svd(H) # do SVD
# calcluate rotation
R = np.dot(V, U.T).T
if np.linalg.det(R) < 0:
R[:, -1] = -1 * R[:, -1]
# calculate translation
t = - np.dot(c_before, R) + c_after
# here's example for how to translate points
# translated_ps_before = np.dot(ps_before, R) + t
# save
if save:
if save_folder is None:
save_folder = os.path.dirname(pos_file_before)
if not os.path.exists(save_folder):
os.makedirs(save_folder)
if len(save_filename) > 0:
save_filename += '_'
rotation_name = os.path.join(save_folder, save_filename+'rotation')
translation_name = os.path.join(
save_folder, save_filename+'translation')
np.save(rotation_name, R)
np.save(translation_name, t)
return R, t
R, T = align_manual_points(before_position_file, after_position_file, save=False)
R, T
###Output
_____no_output_____
###Markdown
transpose 60x positions
###Code
old_positions = np.loadtxt(os.path.join(data_folder, 'positions_all.txt'), delimiter=',')
new_positions = np.dot(old_positions, R) + T
print(new_positions)
save_filename = os.path.join(data_folder, 'translated_positions_all.txt')
print(save_filename)
np.savetxt(save_filename, new_positions, fmt='%.2f', delimiter=',')
###Output
D:\Pu\20211208-P_brain_CTP11-500_M1_DNA_RNA-seq_hybrid\translated_positions_all.txt
###Markdown
further adjust manually
###Code
manual_shift = np.array([-28.1, -8.7])
adjusted_new_positions = new_positions + manual_shift
adj_save_filename = os.path.join(data_folder, 'adjusted_translated_positions_all.txt')
print(adj_save_filename)
np.savetxt(adj_save_filename, adjusted_new_positions, fmt='%.2f', delimiter=',')
###Output
\\storm6-pc\STORM6-FLASHDrive\Pu\20201127-NOAcr_CTP-08_E14_brain_no_clearing\adjusted_translated_positions_all.txt
|
IMDb+Movie+Assignment.ipynb
|
###Markdown
IMDb Movie Assignment You have the data for the 100 top-rated movies from the past decade along with various pieces of information about the movie, its actors, and the voters who have rated these movies online. In this assignment, you will try to find some interesting insights into these movies and their voters, using Python. Task 1: Reading the data - Subtask 1.1: Read the Movies Data.Read the movies data file provided and store it in a dataframe `movies`.
###Code
# Read the csv file using 'read_csv'. Please write your dataset location here.
movies = pd.read_csv(r'F:\Upgrad Notes\IMDB Assignment\Movie+Assignment+Data.csv')
movies.head()
###Output
_____no_output_____
###Markdown
- Subtask 1.2: Inspect the DataframeInspect the dataframe for dimensions, null-values, and summary of different numeric columns.
###Code
# Check the number of rows and columns in the dataframe
movies.shape
# Check the column-wise info of the dataframe
movies.info()
# Check the summary for the numeric columns
movies.describe()
###Output
_____no_output_____
###Markdown
Task 2: Data AnalysisNow that we have loaded the dataset and inspected it, we see that most of the data is in place. As of now, no data cleaning is required, so let's start with some data manipulation, analysis, and visualisation to get various insights about the data. - Subtask 2.1: Reduce those Digits!These numbers in the `budget` and `gross` are too big, compromising its readability. Let's convert the unit of the `budget` and `gross` columns from `$` to `million $` first.
###Code
# Divide the 'gross' and 'budget' columns by 1000000 to convert '$' to 'million $'
def convert_million(val):
return(val/1000000)
movies.Gross=movies.Gross.apply(convert_million)
movies.budget=movies.budget.apply(convert_million)
movies.head()
###Output
_____no_output_____
###Markdown
- Subtask 2.2: Let's Talk Profit! 1. Create a new column called `profit` which contains the difference of the two columns: `gross` and `budget`. 2. Sort the dataframe using the `profit` column as reference. 3. Extract the top ten profiting movies in descending order and store them in a new dataframe - `top10`. 4. Plot a scatter or a joint plot between the columns `budget` and `profit` and write a few words on what you observed. 5. Extract the movies with a negative profit and store them in a new dataframe - `neg_profit`
###Code
# Create the new column named 'profit' by subtracting the 'budget' column from the 'gross' column
movies['Profit']=movies['Gross']-movies['budget']
movies[['Profit']]
movies.head()
# Sort the dataframe with the 'profit' column as reference using the 'sort_values' function. Make sure to set the argument
#'ascending' to 'False'
movies= movies.sort_values(by='Profit', ascending=False)
movies.head()
# Get the top 10 profitable movies by using position based indexing. Specify the rows till 10 (0-9)
top10= movies.iloc[0:10, :]
top10
#Plot profit vs budget
sns.jointplot(movies.budget, movies.Profit, kind='scatter')
plt.show()
###Output
_____no_output_____
###Markdown
The dataset contains the 100 best performing movies from the year 2010 to 2016. However scatter plot tells a different story. You can notice that there are some movies with negative profit. Although good movies do incur losses, but there appear to be quite a few movie with losses. What can be the reason behind this? Lets have a closer look at this by finding the movies with negative profit.
###Code
#Find the movies with negative profit
neg_profit= movies[movies['Profit']<0]
neg_profit
###Output
_____no_output_____
###Markdown
**`Checkpoint 1:`** Can you spot the movie `Tangled` in the dataset? You may be aware of the movie 'Tangled'. Although its one of the highest grossing movies of all time, it has negative profit as per this result. If you cross check the gross values of this movie (link: https://www.imdb.com/title/tt0398286/), you can see that the gross in the dataset accounts only for the domestic gross and not the worldwide gross. This is true for may other movies also in the list. - Subtask 2.3: The General Audience and the CriticsYou might have noticed the column `MetaCritic` in this dataset. This is a very popular website where an average score is determined through the scores given by the top-rated critics. Second, you also have another column `IMDb_rating` which tells you the IMDb rating of a movie. This rating is determined by taking the average of hundred-thousands of ratings from the general audience. As a part of this subtask, you are required to find out the highest rated movies which have been liked by critics and audiences alike.1. Firstly you will notice that the `MetaCritic` score is on a scale of `100` whereas the `IMDb_rating` is on a scale of 10. First convert the `MetaCritic` column to a scale of 10.2. Now, to find out the movies which have been liked by both critics and audiences alike and also have a high rating overall, you need to - - Create a new column `Avg_rating` which will have the average of the `MetaCritic` and `Rating` columns - Retain only the movies in which the absolute difference(using abs() function) between the `IMDb_rating` and `Metacritic` columns is less than 0.5. Refer to this link to know how abs() funtion works - https://www.geeksforgeeks.org/abs-in-python/ . - Sort these values in a descending order of `Avg_rating` and retain only the movies with a rating equal to higher than `8` and store these movies in a new dataframe `UniversalAcclaim`.
###Code
movies[['MetaCritic']].head()
# Change the scale of MetaCritic
movies['MetaCritic']=movies['MetaCritic']/10
movies[['MetaCritic']].head()
movies[['IMDb_rating']].head()
# Find the average ratings
movies['Avg_rating'] = movies[['MetaCritic', 'IMDb_rating']].mean(axis=1)
x= movies[(abs(movies['IMDb_rating']- movies['MetaCritic'])<0.5)]
x
#Sort in descending order of average rating
x= x.sort_values(by='Avg_rating', ascending=False)
x.head()
# Find the movies with metacritic-rating < 0.5 and also with the average rating of >8
UniversalAcclaim=x[(movies['Avg_rating']>8)]
UniversalAcclaim
###Output
_____no_output_____
###Markdown
**`Checkpoint 2:`** Can you spot a `Star Wars` movie in your final dataset? - Subtask 2.4: Find the Most Popular Trios - IYou're a producer looking to make a blockbuster movie. There will primarily be three lead roles in your movie and you wish to cast the most popular actors for it. Now, since you don't want to take a risk, you will cast a trio which has already acted in together in a movie before. The metric that you've chosen to check the popularity is the Facebook likes of each of these actors.The dataframe has three columns to help you out for the same, viz. `actor_1_facebook_likes`, `actor_2_facebook_likes`, and `actor_3_facebook_likes`. Your objective is to find the trios which has the most number of Facebook likes combined. That is, the sum of `actor_1_facebook_likes`, `actor_2_facebook_likes` and `actor_3_facebook_likes` should be maximum.Find out the top 5 popular trios, and output their names in a list.
###Code
# Write your code here
movies['Total_Likes']=movies[['actor_1_facebook_likes', 'actor_2_facebook_likes', 'actor_3_facebook_likes']].sum(axis=1)
top5_likes = movies.sort_values('Total_Likes', ascending=False).head(5)
top5_likes[['actor_1_name', 'actor_2_name', 'actor_3_name']].values.tolist()
###Output
_____no_output_____
###Markdown
- Subtask 2.5: Find the Most Popular Trios - IIIn the previous subtask you found the popular trio based on the total number of facebook likes. Let's add a small condition to it and make sure that all three actors are popular. The condition is **none of the three actors' Facebook likes should be less than half of the other two**. For example, the following is a valid combo:- actor_1_facebook_likes: 70000- actor_2_facebook_likes: 40000- actor_3_facebook_likes: 50000But the below one is not:- actor_1_facebook_likes: 70000- actor_2_facebook_likes: 40000- actor_3_facebook_likes: 30000since in this case, `actor_3_facebook_likes` is 30000, which is less than half of `actor_1_facebook_likes`.Having this condition ensures that you aren't getting any unpopular actor in your trio (since the total likes calculated in the previous question doesn't tell anything about the individual popularities of each actor in the trio.).You can do a manual inspection of the top 5 popular trios you have found in the previous subtask and check how many of those trios satisfy this condition. Also, which is the most popular trio after applying the condition above? **Write your answers below.**- **`No. of trios that satisfy the above condition:`**- **`Most popular trio after applying the condition:`** **`Optional:`** Even though you are finding this out by a natural inspection of the dataframe, can you also achieve this through some *if-else* statements to incorporate this. You can try this out on your own time after you are done with the assignment.
###Code
# Your answer here (optional)
###Output
_____no_output_____
###Markdown
- Subtask 2.6: Runtime AnalysisThere is a column named `Runtime` in the dataframe which primarily shows the length of the movie. It might be intersting to see how this variable this distributed. Plot a `histogram` or `distplot` of seaborn to find the `Runtime` range most of the movies fall into.
###Code
# Runtime histogram/density plot
sns.distplot(movies.Runtime)
plt.show()
###Output
_____no_output_____
###Markdown
**`Checkpoint 3:`** Most of the movies appear to be sharply 2 hour-long. - Subtask 2.7: R-Rated MoviesAlthough R rated movies are restricted movies for the under 18 age group, still there are vote counts from that age group. Among all the R rated movies that have been voted by the under-18 age group, find the top 10 movies that have the highest number of votes i.e.`CVotesU18` from the `movies` dataframe. Store these in a dataframe named `PopularR`.
###Code
# Write your code here
PopularR= movies[(movies['content_rating']=='R')]
PopularR= PopularR.sort_values('CVotesU18', ascending=False).head(10)
PopularR
###Output
_____no_output_____
###Markdown
**`Checkpoint 4:`** Are these kids watching `Deadpool` a lot? Task 3 : Demographic analysisIf you take a look at the last columns in the dataframe, most of these are related to demographics of the voters (in the last subtask, i.e., 2.8, you made use one of these columns - CVotesU18). We also have three genre columns indicating the genres of a particular movie. We will extensively use these columns for the third and the final stage of our assignment wherein we will analyse the voters across all demographics and also see how these vary across various genres. So without further ado, let's get started with `demographic analysis`. - Subtask 3.1 Combine the Dataframe by GenresThere are 3 columns in the dataframe - `genre_1`, `genre_2`, and `genre_3`. As a part of this subtask, you need to aggregate a few values over these 3 columns. 1. First create a new dataframe `df_by_genre` that contains `genre_1`, `genre_2`, and `genre_3` and all the columns related to **CVotes/Votes** from the `movies` data frame. There are 47 columns to be extracted in total.2. Now, Add a column called `cnt` to the dataframe `df_by_genre` and initialize it to one. You will realise the use of this column by the end of this subtask.3. First group the dataframe `df_by_genre` by `genre_1` and find the sum of all the numeric columns such as `cnt`, columns related to CVotes and Votes columns and store it in a dataframe `df_by_g1`.4. Perform the same operation for `genre_2` and `genre_3` and store it dataframes `df_by_g2` and `df_by_g3` respectively. 5. Now that you have 3 dataframes performed by grouping over `genre_1`, `genre_2`, and `genre_3` separately, it's time to combine them. For this, add the three dataframes and store it in a new dataframe `df_add`, so that the corresponding values of Votes/CVotes get added for each genre.There is a function called `add()` in pandas which lets you do this. You can refer to this link to see how this function works. https://pandas.pydata.org/pandas-docs/version/0.23.4/generated/pandas.DataFrame.add.html6. The column `cnt` on aggregation has basically kept the track of the number of occurences of each genre.Subset the genres that have atleast 10 movies into a new dataframe `genre_top10` based on the `cnt` column value.7. Now, take the mean of all the numeric columns by dividing them with the column value `cnt` and store it back to the same dataframe. We will be using this dataframe for further analysis in this task unless it is explicitly mentioned to use the dataframe `movies`.8. Since the number of votes can't be a fraction, type cast all the CVotes related columns to integers. Also, round off all the Votes related columns upto two digits after the decimal point.
###Code
# Create the dataframe df_by_genre
df_by_genre=movies.drop(columns=['Title', 'title_year', 'budget', 'Gross', 'actor_1_name', 'actor_2_name', 'actor_3_name', 'actor_1_facebook_likes', 'actor_2_facebook_likes', 'actor_3_facebook_likes', 'IMDb_rating', 'MetaCritic', 'Runtime', 'content_rating', 'Country', 'Profit', 'Avg_rating', 'Total_Likes'], axis=1)
df_by_genre.head()
df_by_genre.shape
# Create a column cnt and initialize it to 1
df_by_genre=df_by_genre.assign(cnt=1)
df_by_genre.head()
# Group the movies by individual genres
gp1= df_by_genre.groupby('genre_1')
df_by_g1= gp1.sum()
gp2= df_by_genre.groupby('genre_2')
df_by_g2= gp2.sum()
gp3= df_by_genre.groupby('genre_3')
df_by_g3= gp3.sum()
df_by_g1
df_by_g2
df_by_g3
# Add the grouped data frames and store it in a new data frame
x=df_by_g1.add(df_by_g2, fill_value=0)
df_add= x.add(df_by_g3, fill_value=0)
df_add
#reset column index
df_add= df_add.reset_index()
#rename column name
df_add= df_add.rename(columns={'index': 'genre'})
# Extract genres with atleast 10 occurences
genre_top10=df_add[df_add['cnt']>=10]
genre_top10
# Take the mean for every column by dividing with cnt
genre_top10.loc[:,"CVotes10":"VotesnUS"]= genre_top10.loc[:,"CVotes10":"VotesnUS"].divide(genre_top10["cnt"], axis=0)
genre_top10
# Rounding off the columns of Votes to two decimals
genre_top10.loc[:,"VotesM":"VotesnUS"]= np.round(genre_top10.loc[:,"VotesM":"VotesnUS"], decimals=2)
genre_top10
# Converting CVotes to int type
genre_top10.loc[:,"CVotes10":"CVotesnUS"]= genre_top10.loc[:,"CVotes10":"CVotesnUS"].astype('int32')
genre_top10
###Output
_____no_output_____
###Markdown
If you take a look at the final dataframe that you have gotten, you will see that you now have the complete information about all the demographic (Votes- and CVotes-related) columns across the top 10 genres. We can use this dataset to extract exciting insights about the voters! - Subtask 3.2: Genre Counts!Now let's derive some insights from this data frame. Make a bar chart plotting different genres vs cnt using seaborn.
###Code
# Countplot for genres
plt.figure(figsize=[20, 5])
sns.barplot(data=df_add, x='genre', y='cnt')
plt.show()
###Output
_____no_output_____
###Markdown
**`Checkpoint 5:`** Is the bar for `Drama` the tallest? - Subtask 3.3: Gender and GenreIf you have closely looked at the Votes- and CVotes-related columns, you might have noticed the suffixes `F` and `M` indicating Female and Male. Since we have the vote counts for both males and females, across various age groups, let's now see how the popularity of genres vary between the two genders in the dataframe. 1. Make the first heatmap to see how the average number of votes of males is varying across the genres. Use seaborn heatmap for this analysis. The X-axis should contain the four age-groups for males, i.e., `CVotesU18M`,`CVotes1829M`, `CVotes3044M`, and `CVotes45AM`. The Y-axis will have the genres and the annotation in the heatmap tell the average number of votes for that age-male group. 2. Make the second heatmap to see how the average number of votes of females is varying across the genres. Use seaborn heatmap for this analysis. The X-axis should contain the four age-groups for females, i.e., `CVotesU18F`,`CVotes1829F`, `CVotes3044F`, and `CVotes45AF`. The Y-axis will have the genres and the annotation in the heatmap tell the average number of votes for that age-female group. 3. Make sure that you plot these heatmaps side by side using `subplots` so that you can easily compare the two genders and derive insights.4. Write your any three inferences from this plot. You can make use of the previous bar plot also here for better insights.Refer to this link- https://seaborn.pydata.org/generated/seaborn.heatmap.html. You might have to plot something similar to the fifth chart in this page (You have to plot two such heatmaps side by side).5. Repeat subtasks 1 to 4, but now instead of taking the CVotes-related columns, you need to do the same process for the Votes-related columns. These heatmaps will show you how the two genders have rated movies across various genres.You might need the below link for formatting your heatmap.https://stackoverflow.com/questions/56942670/matplotlib-seaborn-first-and-last-row-cut-in-half-of-heatmap-plot- Note : Use `genre_top10` dataframe for this subtask
###Code
# 1st set of heat maps for CVotes-related columns
x= pd.pivot_table(genre_top10, index='genre', values=['CVotesU18M', 'CVotes1829M', 'CVotes3044M', 'CVotes45AM'])
y= pd.pivot_table(genre_top10, index='genre', values=['CVotesU18F', 'CVotes1829F', 'CVotes3044F', 'CVotes45AF'])
fig, ax =plt.subplots(1,2 ,figsize=(18, 6))
sns.heatmap(x, cmap='Greens', annot=True, ax=ax[0])
sns.heatmap(y, cmap='Greens', annot=True, ax=ax[1])
plt.show()
###Output
_____no_output_____
###Markdown
**`Inferences:`** A few inferences that can be seen from the heatmap above is that males have voted more than females, and Sci-Fi appears to be most popular among the 18-29 age group irrespective of their gender. What more can you infer from the two heatmaps that you have plotted? Write your three inferences/observations below:- Inference 1: Thriller is least voted in male votes category under age 18. - Inference 2: Crime is least voted in female votes category under age18.- Inference 3: Most of the votes are provided by the age group of 18-29 in their respective male, female categories.
###Code
# 2nd set of heat maps for Votes-related columns
x= pd.pivot_table(genre_top10, index='genre', values=['VotesU18M', 'Votes1829M', 'Votes3044M', 'Votes45AM'])
y= pd.pivot_table(genre_top10, index='genre', values=['VotesU18F', 'Votes1829F', 'Votes3044F', 'Votes45AF'])
fig, ax =plt.subplots(1,2 ,figsize=(18,6))
sns.heatmap(x, cmap='Greens', annot=True, ax=ax[0])
sns.heatmap(y, cmap='Greens', annot=True, ax=ax[1])
plt.show()
###Output
_____no_output_____
###Markdown
**`Inferences:`** Sci-Fi appears to be the highest rated genre in the age group of U18 for both males and females. Also, females in this age group have rated it a bit higher than the males in the same age group. What more can you infer from the two heatmaps that you have plotted? Write your three inferences/observations below:- Inference 1: Romance appears to be the lowest rated genre in the age group of 45A for both males and females.- Inference 2: There is almost same vote among all the genre in Male category of 18-29 age group.- Inference 3: Most of the ratings are provided by the age group of U18 in their male, female categories. - Subtask 3.4: US vs non-US Cross AnalysisThe dataset contains both the US and non-US movies. Let's analyse how both the US and the non-US voters have responded to the US and the non-US movies.1. Create a column `IFUS` in the dataframe `movies`. The column `IFUS` should contain the value "USA" if the `Country` of the movie is "USA". For all other countries other than the USA, `IFUS` should contain the value `non-USA`.2. Now make a boxplot that shows how the number of votes from the US people i.e. `CVotesUS` is varying for the US and non-US movies. Make use of the column `IFUS` to make this plot. Similarly, make another subplot that shows how non US voters have voted for the US and non-US movies by plotting `CVotesnUS` for both the US and non-US movies. Write any of your two inferences/observations from these plots.3. Again do a similar analysis but with the ratings. Make a boxplot that shows how the ratings from the US people i.e. `VotesUS` is varying for the US and non-US movies. Similarly, make another subplot that shows how `VotesnUS` is varying for the US and non-US movies. Write any of your two inferences/observations from these plots.Note : Use `movies` dataframe for this subtask. Make use of this documention to format your boxplot - https://seaborn.pydata.org/generated/seaborn.boxplot.html
###Code
# Creating IFUS column
movies['IFUS']= movies['Country'].apply(lambda x: x if x=='USA' else 'non-USA')
# Box plot - 1: CVotesUS(y) vs IFUS(x)
fig, ax =plt.subplots(1,2 ,figsize=(20, 8))
sns.boxplot(movies['IFUS'], movies['CVotesUS'], ax=ax[0])
sns.boxplot(movies['IFUS'], movies['CVotesnUS'], ax=ax[1])
plt.show()
###Output
_____no_output_____
###Markdown
**`Inferences:`** Write your two inferences/observations below:- Inference 1: Median value in CVotesUS for USA movies lies around 5000 whereas for non-USA median lies <5000.- Inference 2: In CVotenUS, median value for for USA and non-USA is almost equal.
###Code
# Box plot - 2: VotesUS(y) vs IFUS(x)
fig, ax =plt.subplots(1,2 ,figsize=(20, 8))
sns.boxplot(movies['IFUS'], movies['VotesUS'], ax=ax[0])
sns.boxplot(movies['IFUS'], movies['VotesnUS'], ax=ax[1])
plt.show()
###Output
_____no_output_____
###Markdown
**`Inferences:`** Write your two inferences/observations below:- Inference 1: Median votes in VotesUS for USA movies lies around 8.0 whereas for non-USA median lies around 7.9.- Inference 2: In VotenUS, median value for for USA is around 7.8 whereas for non-USA it is almost 7.5. - Subtask 3.5: Top 1000 Voters Vs GenresYou might have also observed the column `CVotes1000`. This column represents the top 1000 voters on IMDb and gives the count for the number of these voters who have voted for a particular movie. Let's see how these top 1000 voters have voted across the genres. 1. Sort the dataframe genre_top10 based on the value of `CVotes1000`in a descending order.2. Make a seaborn barplot for `genre` vs `CVotes1000`.3. Write your inferences. You can also try to relate it with the heatmaps you did in the previous subtasks.
###Code
# Sorting by CVotes1000
genre_top10=genre_top10.sort_values('CVotes1000', ascending=False)
genre_top10[['genre','CVotes1000']]
# Bar plot
plt.figure(figsize=[10,5])
sns.barplot(data=genre_top10, x='genre', y='CVotes1000')
plt.show()
###Output
_____no_output_____
|
source/ConstraintProgramming.ipynb
|
###Markdown
Constraint Programming Introduction Constraints naturally arise in a variety of interactions and fields of study such as game theory, social studies, operations research, engineering, and artificial intelligence. A constraint refers to the relationship between the state of objects, such as the constraint that the three angles of a triangle must sum to 180 degrees. Note that this constraint has not precisely stated each angle's value and still allows some flexibility. Said another way, the triangle constraint restricts the values that the three variables (each angle) can take, thus providing information that will be useful in finding values for the three angles.Another example of a constrained problem comes from the recently-aired hit TV series *Buddies*, where a group of five (mostly mutual) friends would like to sit at a table with three chairs in specific arrangements at different times, but have requirements as to who they will and will not sit with.Another example comes from scheduling: at the university level, there is a large number of classes that must be scheduled in various classrooms such that no professor or classroom is double booked. Further, there are some constraints on which classes can be scheduled for the same time, as some students will need to be registered for both.Computers can be employed to solve these types of problems, but in general these tasks are computationally intractable and cannot be solved efficiently in all cases with a single algorithm \cite{Dechter2003}. However, by formalizing these types of problems in a constraint processing framework, we can identify classes of problems that can be solved using efficient algorithms.Below, we discuss generally the three core concepts in constraint programming: **modeling**, **inference**, and **search**. Modeling is an important step that can greatly affect the ability to efficiently solve constrained problems and inference (e.g., constraint propagation) and search are solution methods. Basic constraint propagation and state-space search are building blocks that state of the art solvers incorporate. ModelingA **constraint satisfaction problem** (CSP) is formalized by a *constraint network*, which is the triple $\mathcal{R} = \langle X,D,C\rangle$, where- $X = \{x_i\}_{i=1}^n$ is the set of $n$ variables- $D = \{D_i\}_{i=1}^n$ is the set of variable domains, where the domain of variable $x_k$ is $D_k$- $C = \{C_i\}_{i=1}^m$ is the set of constraints on the values that each $x_i$ can take on. Specifically, - Each constraint $C_i = \langle S_i,R_i\rangle$ specifies allowed variable assignments. - $S_i \subset X$ contains the variables involved in the constraint, called the *scope* of the constraint. - $R_i$ is the constraint's *relation* and represents the simultaneous legal value assignments of variables in the associated scope. - For example, if the scope of the first constraint is $S_1 = \{x_3, x_8\}$, then the relation $R_1$ is a subset of the Cartesian product of those variables' domains: $R_1 \subset D_3 \times D_8$, and an element of the relation $R_1$ could be written as a 2-tuple $(a,b)\in R_1$.Each variable in a CSP can be assigned a value from its domain. A **complete assignment** is one in which every variable is assigned and a **solution** to a CSP is a consistent (or legal w.r.t. the constraints) complete assignment. Note that for a CSP model, *any* consistent complete assignment of the variables (i.e., where all constraints are satisfied) constitutes a valid solution; however, this assignment may not be the "best" solution. Notions of optimality can be captured by introducing an objective function which is used to find a valid solution with the lowest cost. This is referred to as a **constraint *optimization* problem** (COP). We will refer generally to CSPs with the understanding that a CSP can easily become a COP by introducing a heuristic.In this notebook, we will restrict ourselves to CSPs that can be modeled as having **discrete, finite domains**. This helps us to manage the complexity of the constraints so that we can clearly discuss the different aspects of CSPs. Other variations exist such as having discrete but *infinite* domains, where constraints can no longer be enumerated as combinations of values but must be expressed as either linear or nonlinear inequality constraints, such as $T_1 + d_1 \leq T_2$. Therefore, infinite domains require a different constraint language and special algorithms only exist for linear constraints. Additionally, the domain of a CSP may be continuous. With this change, CSPs become mathematical programming problems which are often studied in operations research or optimization theory, for example. Modeling as a GraphIn a general CSP, the *arity* of each constraint (i.e., the number of variables involved) is arbitrary. We can have unary constraints on a single variable, binary constraints between two variables, or $n$-ary constraints between $n$ variables. However, having more than binary constraints adds complexity to the algorithms for solving CSPs. It can be shown that every finite-domain constraint can be reduced to a set of binary constraints by adding enough auxiliary variables \cite{AIMA}. Therefore, since we are only discussing CSPs with finite domains, we will assume that the CSPs we are working with have only unary and binary constraints, meaning that each constraint scope has at most two variables.An important view of a binary constraint network that defines a CSP is as a graph, $\langle\mathcal{V},\mathcal{E}\rangle$. In particular, each vertex corresponds to a variable, $\mathcal{V} = X$, and the edges of the graph $\mathcal{E}$ correspond to various constraints between variables. Since we are only working with binary and unary constraint networks, it is easy to visualize a graph corresponding to a CSP. For constraint networks with more than binary constraints, the constraints must be represented with a hypergraph, where hypernodes are inserted that connect three or more variables together in a constraint.For example, consider a CSP $\mathcal{R}$ with the following definition\begin{align}X &= \{x_1, x_2, x_3\} \\D &= \{D_1, D_2, D_3\},\ \text{where}\; D_1 = \{0,5\},\ D_2 = \{1,2,3\},\ D_3 = \{7\} \\C &= \{C_1, C_2, C_3\},\end{align}where\begin{align}C_1 &= \langle S_1, R_1 \rangle = \langle \{x_1\}, \{5\} \rangle \\C_2 &= \langle S_2, R_2 \rangle = \langle \{x_1, x_2\}, \{(0, 1), (0,3), (5,1)\} \rangle \\C_3 &= \langle S_3, R_3 \rangle = \langle \{x_2, x_3\}, \{(1, 7), (2, 7)\} \rangle.\end{align}The graphical model of this CSP is shown below. SolvingThe goal of formalizing a CSP as a constraint network model is to efficiently solve it using computational algorithms and tools. **Constraint programming** (CP) is a powerful tool to solve combinatorial constraint problems and is the study of computational systems based on constraints. Once the problem has been modeled as a formal CSP, a variety of computable algorithms could be used to find a solution that satisfies all constraints.In general, there are two methods used to solve a CSP: search or inference. In previous 16.410/413 problems, **state-space search** was used to find the best path through some sort of graph or tree structure. Likewise, state-space search could be used to find a valid "path" through the CSP that satisfies each of the local constraints and is therefore a valid global solution. However, this approach would quickly become intractable as the number of variables and the size of each of their domains increase.In light of this, the second solution method becomes more attractive. **Constraint propagation**, a specific type of inference, is used to reduce the number of legal values from a variable's domain by pruning values that would violate the constraints of the given variable. By making a variable locally consistent with its constraints, the domain of adjacent variables may potentially be further reduced as a result of missing values in the pairwise constraint of the two variables. In this way, by making the first variable consistent with its constraints, the constraints of neighboring variables can be re-evaluated, causing a further reduction of domains through the propagation of constraints. These ideas will later be formalized as $k$-consistency.Constraint propagation may be combined with search, using the pros of both methods simultaneously. Alternatively, constraint propagation may be performed as a pre-processing pruning step so that search has a smaller state space to search over. Sometimes, constraint propagation is all that is required and a solution can be found without a search step at all.After giving examples of modeling CSPs, this notebook will explore a variety of solution methods based on constraint propagation and search. --- Problem ModelsGiven a constrained problem, it is desirable to identify an appropriate constraint network model $\mathcal{R} = \langle X,D,C\rangle$ that can be used to find its solution. Modeling for CSPs is an important step that can dramatically affect the difficulty in enumerating the associated constraints or efficiency of finding a solution.Using the general ideas and formalisms from the previous section, we consider two puzzle problems and model them as CSPs in the following sections. N-QueensThe N-Queens problem (depicted below for 4 queens) is a well-know puzzle among computer scientists and will be used as a recurring example throughout this notebook. The problem statement is as follows: given any integer $N$, the goal is to place $N$ queens on an $N\times N$ chessboard satisfying the constraint that no two queens threaten each other. A queen can threaten any other queen that is on the same row, column, or diagonal.
###Code
# Example n-queens
draw_nqueens(nqueens(4))
###Output
_____no_output_____
###Markdown
Now let's try to understand the problem formally. Attempt 1To illustrate the effect of modeling, we first consider a (poor) model for the N-Queens constraint problem, given by the following definitions:\begin{align}X &= \{x_i\}_{i=1}^{N^2} && \text{(Chessboard positions)} \\D &= \{D_i\}_{i=1}^{N^2},\ \text{where}\; D_i = \{0, 1,2,\dots,N\} && \text{(Empty or the $k^\text{th}$ queen)}\end{align}Without considering constraints, the size of the state space (i.e., the number of assignments) is an enormous $(N+1)^{N^2}$. For only $N=4$ queens, this becomes $5^{16} \approx 153$ billion states that could potentially be searched.Expressing the constraints of this problem in terms of the variables and their domains also poses a challenge. Because of the way we have modeled this problem, there are six primary constraints to satisfy:1. Exactly $N$ chess squares shall be filled (i.e., there are only $N$ queens and all of them must be used)1. The $k^\text{th}$ queen, ($1\le k\le N$) shall only be used once.1. No queens share a column1. No queens share a row1. No queens share a positive diagonal (i.e., a diagonal from bottom left to top right)1. No queens share a negative diagonal (i.e., a diagonal from top left to bottom right)To express these constraints mathematically, we first let $Y\triangleq\{1\le i\le N^2|x_i\in X,x_i\ne 0\}$ be the set of chess square numbers that are non-empty and $Z \triangleq \{x\in X|x\ne 0\}$ be the set of queens in those chess squares (unordered). With pointers back to which constraint they satisfy, the expressions are:\begin{align}|Z| = |Y| &= N && (C1) \\z_i-z_j &\ne 0 && (C2) \\|y_i-y_j| &\ne N && (C3) \\\left\lfloor\frac{y_i-1}{N}\right\rfloor &\ne \left\lfloor\frac{y_j-1}{N}\right\rfloor && (C4) \\|y_i-y_j| &\ne (N-1) && (C5) \\|y_i-y_j| &\ne (N+1), && (C6)\end{align}where $z_i, z_j\in Z$ and $y_i,y_j\in Y, \forall i\ne j$, and applying $|\cdot|$ to a set is the set's cardinality (i.e., size) and applied to a scalar is the absolute value. Additionally, we use $\lfloor\cdot\rfloor$ as the floor operator. Notice how we are able to express all the constraints as pairwise (binary).We can count the number of constraints in this model as a function of $N$. In each pairwise constraint (C2)-(C6), there are $N$ choose $2$ pairs. Since we have 5 different types of pairwise constraints, we have that the number of constraints, $\Gamma$, is\begin{equation}\Gamma(N) = 5 {N \choose 2} + 1 = \frac{5N!}{2!(N-2)!} + 1,\end{equation}where the plus one comes from the single constraint for (C1). Thus, $\Gamma(N=4) = 31$.Examining the size of the state space in this model, we see the infeasibility of simply performing a state-space search and then performing a goal test that encodes the problem constraints. This motivates the idea of efficiently using constraints either before or during our solution search, which we will explore in the following sections. Attempt 2Motivated by the desire to do less work in searching and writing constraints, we consider another model of the N-Queens problem. We wish to decrease the size of the state space and number and difficulty of writing the constraints. Good modeling involves cleverly choosing variables and their semantics so that constraints are implicitly encoded, requiring less explicit constraints.We can achieve this by encoding the following assumptions:1. assume one queen per column;1. an assignment determines which row the $i^\text{th}$ queen should be in.With this understanding, we can write the constraint network as\begin{align}X &= \{x_i\}_{i=1}^{N} && \text{(Queen $i$ in the $i^\text{th}$ column)} \\D &= \{D_i\}_{i=1}^{N},\ \text{where}\; D_i = \{1,2,\dots,N\} && \text{(The row in which the $i^\text{th}$ queen should be placed)}.\end{align}Now considering the size of the state space without constraints, we see that this intelligent encoding reduces the size to only $N^N$ assignments.Writing down the constraints is also easier for this model. In fact, we only need to address constraints (C4)-(C6) from above, as (C1)-(C3) are taken care of by intelligently choosing our variables and their domains. The expressions, $\forall x_i,x_j\in X, i\ne j$, are\begin{align}x_i &\ne x_j && \text{(C4)} \\|x_i-x_j| &\ne |i-j|. && \text{(C5, C6)}\end{align}With this reformulation, the number of constraints is\begin{equation}\Gamma(N) = 2 {N \choose 2} = \frac{N!}{(N-2)!}.\end{equation}Thus $\Gamma(N=4) = 12$.We have successfully modeled the N-Queens problem with a reduced state space and with only two pairwise constraints. Both of these properties will allow the solvers discussed next to more efficiently find solutions to this CSP. Map ColoringMap coloring is another classic example of a CSP. Consider the map of Australia shown below (from \cite{AIMA}). The goal is to assign a color to Australia's seven territories such that no neighboring regions share the same color. We are further constrained by only being able to use three colors (e.g., R, G, B). Next to the map is the constraint graph representation of this specific map-coloring problem. The constraint network model $\mathcal{R}=\langle X,D,C \rangle$ for the general map-coloring problem with $N$ regions and $M$ colors is defined as:\begin{align}X &= \{x_i\}_{i=1}^N && \text{(Each region)} \\D &= \{D_i\}_{i=1}^N,\ \text{where}\; D_i = \{c_j\}_{j=1}^M, && \text{(Available colors)}\end{align}and the constraints are encoded as\begin{align}\forall x_i\in X: x_i &\ne n_j,\ \forall n_j\in\mathcal{N}(x_i), && \text{(Each region cannot have the same color as any of its neighbors)}\end{align}where the neighborhood of the region $x_i$ is defined as the set $\mathcal{N}(x_i) = \{x_j\in X| A_{ij}=1,i\ne j, \forall j\}$. The matrix $A\in\mathbb{Z}_{\ge 0}^{N\times N}$ is called the *adjacency matrix* of a graph with $N$ vertices and represents the variables that a given variable is connected to by constraints (i.e., edges). The notation $A_{mn}$ indexes into the matrix by row $m$ and column $n$.We will use the map coloring problem as a COP example later on. First MiniZinc modelWe are now ready to solve our first CPS problem! Let us now introduce [MiniZinc](https://www.minizinc.org/), a **high-level**, **solver-independent** language to express constraint programming problems and solve them. It has a large library of constraints already encoded that we can exploit to encode our problem.A very useful constraint is `alldifferent(array[int] of var int: x)`, which is one of the most studied and used constraint in constraint programming. As the name suggest it takes an array of variables and constrains them to take different values.Let's focus on the N-Queens problem as formulated in attempt 2. The reader can notice that we can write (C1), (C2) and (C3) leveraging the `alldifferent` constraint. As result we get the following model.
###Code
%%minizinc
include "globals.mzn";
int: n = 4;
array[1..n] of var 1..n: queens;
constraint all_different(queens);
constraint all_different([queens[i]+i | i in 1..n]);
constraint all_different([queens[i]-i | i in 1..n]);
solve satisfy;
###Output
_____no_output_____
###Markdown
Here we are asking MiniZinc to solve find any feasible solution (`solve satisfy`) given the constraints.With high-level languages is easy to describe and solve a CSP. The solver at the same time abstract away the complexity of the search process. Let's now focus on how a CSP is actually solved. --- Constraint Propagation MethodsAs previously mentioned, the domain size of a CSP can be dramatically reduced by removing values from variable domains that would violate the relevant constraints. This idea is called **local consistency**. By representing a CSP as a binary constraint graph, making a graph locally consistent amounts to visiting the $i^\text{th}$ node and for each of the values in the domain $D_i$, removing the values of neighboring domains that would cause an illegal assignment.A great example of the power of constraint propagation is seen in Sudoku puzzles. Simple puzzles are designed to be solved by constraint propagation alone. By enforcing local consistency throughout simple formulations of Sudoku common in newspapers, the unique solution is found without the need for search.While there are multiple forms of consistency, we will forgo a discussion of node consistency (single node), path consistency (3 nodes), and generally **$k$-consistency** ($k$ nodes) to focus on arc consistency. Arc ConsistencyThe most well-known notion of local consistency is **arc consistency**, where the key idea is to remove values of variable domains that can never satisfy a specified constraint. The arc $\langle x_i, x_j \rangle$ between two variables $x_i$ and $x_j$ is said to be arc consistent if $\langle x_i, x_j \rangle$ and $\langle x_j, x_i \rangle$ are *directed* arc consistent.The arc $\langle x_i, x_j \rangle$ is **directed arc consistent** (from $x_i$ to $x_j$) if $\forall a_i \in D_i \; \exists a_j \in D_j$ s.t. $\langle a_i, a_j \rangle \in C_{ij}$. The notation $C_{ij}$ represents a constraint between variables $x_i$ and $x_j$ with a relation on their domains $D_i, D_j$. In other words, we write a constraint $\langle \{x_i, x_j\}, R \rangle$ as $C_{ij} = R$, where $R\subset D_i\times D_j$.As an example, consider the following simple constraint network:\begin{align}X &= \{x_1, x_2\} \\D &= \{D_1, D_2\},\ \text{where}\; D_1=\{1,3,5,7\}, D_2=\{2,4,6,8\} \\C &= \{C_{12}\},\end{align}where $C_{12} = \{(1,2),(3,8),(7,4)\}$ lists legal assignment relationships between $x_1$ and $x_2$.To make $\langle x_1, x_2 \rangle$ directed arc consistent, we would remove the values from $D_1$ that could never satisfy the constraint $C_{12}$. The original domains are shown on the left, while the directed arc consistent graph is shown on the right. Note that 6 is not removed from $D_2$ because directed arc consistency only considers consistency in one direction. Similarly, we can make $\langle x_2, x_1 \rangle$ directed arc consistent by removing 6 from $D_2$. This results in an arc consistent graph, shown below. Sound but IncompleteBy making a CSP arc consistent, we are guaranteed that solutions to the CSP will be found in the reduced domain of the arc consistent CSP. However, we are not guaranteed that any arbitrary assignment of variables from the reduced domain will offer a valid CSP solution. In other words, arc consistency is sound (all solutions are arc-consistent solutions) but incomplete (not all arc-consistent solutions are valid solutions). AlgorithmsTo achieve arc consistency in a graph, we can formalize the ideas that we discussed above about removing values from domains that will never participate in a legal constraint. Two widespread algorithms are considered, known `AC-1` and `AC-3`, which are the first and third versions described by Mackworth in \cite{Mackworth1977}.In this section, we give the pseudocode for these algorithms and a discussion of their complexities and trade offs. The `REVISE` AlgorithmFirst, we formalize the procedure of achieving local consistency via the `REVISE` procedure, which is an algorithm that enforces directed arc consistency on a subnetwork. This is the algorithm that we used in the toy example above with $x_1$ and $x_2$.```vhdl1 procedure REVISE(xi,xj)2 for each ai in Di3 if there is no aj in Dj such that (ai,aj) is consistent,4 delete ai from Di5 end if6 end for7 end``` Complexity AnalysisThe complexity of `REVISE` is $O(k^2)$, where $k$ bounds the domain size, i.e., $k=\max_i|D_i|$. The $k^2$ comes from the fact that there is a double `for loop`---the outer loop is on line 2 and the inner loop is on line 3. The `AC-1` AlgorithmA first pass of enforcing arc consistency on an entire constraint network would be to revise each variable domain in a brute-force manner. This is the objective of the following `AC-1` procedure, which takes a CSP definition $\mathcal{R}=\langle X, D, C\rangle$ as input.```vhdl1 procedure AC1(csp)2 loop3 for each cij in C4 REVISE(xi, xj)5 REVISE(xj, xi)6 end for7 until no domain is changed8 end```If after the `AC-1` procedure is run any of the variable domains are empty, then we conclude that the network has no solution. Otherwise, we are guaranteed an arc-consistent network. Complexity AnalysisLet $k$ bound the domain size as before and let $n=|X|$ be the number of variables and $e=|C|$ be the number of constraints. One cycle through all of the constraints (lines 3-6) takes $O(2\,e\,O_\text{REVISE}) = O(ek^2)$. In the worst case, only a single domain is changed in one cycle. In this case, the maximum number of repeats (line 7) will be the total number of values, $nk$. Therefore, the worst-case complexity of the `AC-1` procedure is $O(enk^3)$. The `AC-3` AlgorithmClearly, `AC-1` is straightforward to implement and generates an arc-consistent network, but at great expense. The question we must ask ourselves when using any brute-force method is: Can we do better?A key observation about `AC-1` is that it processes all constraints even if only a single domain was reduced. This is unnecessary because changes in a domain typically only affect a local subgraph around the node in question.The `AC-3` procedure is an improved version that maintains a queue of ordered pairs of variables that participate in a constraint (see lines 2-4). Each arc that is processed is removed from the queue (line 6). If the domain of the arc tail $x_i$ is revised, arcs that have $x_i$ as the head will need to be re-evaluated and are added back to the queue (lines 8-10).```vhdl 1 procedure AC3(csp) 2 for each cij in C do 3 Q ← Q ∪ {, }; 4 end for 5 while Q is not empty 6 select and delete any arc (xi,xj) from Q 7 REVISE(xi,xj) 8 if REVISE(xi,xj) caused a change in Di 9 Q ← Q ∪ { | k ≠ i, k ≠ j, ∀k }10 end if11 end while12 end``` Complexity AnalysisUsing the same notation as before, the time complexity of `AC-3` is computed as follows. Building the initial `Q` is $O(e)$. We know that `REVISE` is $O(k^2)$ (line 7). This algorithm processes constraints at most $2k$ times since each time it is reintroduced into the queue (line 9), the domain of one of its associated variables has just been revised by at least one value, and there are at most $2k$ values. Therefore, the total time complexity of `AC-3` is $O(ek^3)$.Note that the optimal algorithm has complexity $O(ek^2)$ since the worst case of merely verifying the arc consistency of a network requires $ek^2$ operations. There is an `AC-4` algorithm that achieves this performance by not using `REVISE` as a block box, but by exploiting the structures at the constraint level \cite{Dechter2003}. ExampleUsing our efficient CSP model (Attempt 2) from the previous section, consider the following 4-Queens problem, with the chessboard shown to the left and the corresponding constraint graph representation to the right. We have already placed the first queen in the first row, $x_1=1$. We would like to use the `AC-3` algorithm to propagate constraints and eliminate inconsistent values in the domains of variables $x_2$, $x_3$ and $x_4$. Intuitively, we already know which values are inconsistent with our constraints (shown with $\times$ in the chessboard above). Follow the slides below to walk through the `AC-3` algorithm.
###Code
ac3_slides = SlideController('images/4queens_slide%02d.png', 8)
###Output
_____no_output_____
###Markdown
Note how in this example, the efficiencies of `AC-3` were unnecessary. In fact, a single pass of `AC-2` would have achieved the same result. Although this was the case for this specific instance, by adding arcs back to the queue to by examined, `AC-3` is more computationally efficient in general. --- Search MethodsIn the previous 4-Queens example, constraint propagation via `AC-3` was not enough to find a satisfying complete assignment to the CSP. In fact, if `AC-3` had been applied to the empty 4-Queens chessboard, no domains would have been pruned because all variables were already arc consistent. In these cases, we must assign the next variable a value by *guessing and testing*.This trial and error method of guessing a variable and testing if it is consistent is formalized in **search methods** for solving CSPs. As mentioned previously, a simple state-space search would be intractable as the number of variables and their domains increase. However, we will first examine state-space search in more detail and then move to a more clever search algorithm called backtrack search (BT) that checks consistency along the way. Generic Search for CSPsAs we have studied before, a generic search problem can be specified by the following four elements: (1) state space, (2) initial states, (3) operator, and (4) goal test. In a CSP, consider the following definitions of these elements:- state space - partial assignment to variables at the current iteration of the search- initial state - no assignment- operator - add a new assignment to any unassigned variable, e.g., $x_i = a$, where $a\in D_i$. - child extends parent assignments with new- goal test - all variables are assigned - all constraints are satisfied Making Search More Efficient for CSPsThe inefficiency of using the generic state-space search approaches we have previously employed is caused by the size of the state space. Recall that a simple state-space search (using either breadth-first search or depth-first search) has worst case performance of $O(b^d)$, where $b$ is the branching factor and $d$ is the search depth, as illustrated below (from 16.410/413, Lecture 3).In the above formulation of generic state-space search of CSPs, note that the branching factor is calculated as the sum of the maximum domain size $k$ for all variables $n$, i.e., $b = nk$. The search depth of a CSP is exactly $n$, because all variables must be assigned to be considered a solution. Therefore, the performance is exponential in the number of variables, $O([nk]^n)$.This analysis fails to recognize that there are only $k^n$ possible complete assignments of the CSP. That is because the property of **commutativity** is ignored in the above formulation of CSP state-space search. CSPs are commutative because the order in which partial assignments are made do not affect the outcome. Therefore, by restricting the choice of assignment to a single variable at each node in the search tree, the runtime performance becomes only $O(k^n)$.By combining this property with the idea that **extensions to inconsistent partial assignments are always inconsistent**, backtracking search shows how checking consistency after each assignment enables a more efficient CSP search.<!--With a better understanding of how expensive it can become to solve interesting problems with a simple state-space search, we are motivated to find a better searching algorithm. Two factors that contribute to the size of a search space are (1) variable ordering, and (2) consistency level.We have already seen from the `AC-3` example on 4-Queens how enforcing arc-consistency on a network can result in the pruning of variable domains. This clearly reduces the search space of the CSP resulting in better performance from a search algorithm. Therefore, we will focus our discussion on the effects of **variable ordering**.--> Backtracking SearchBacktracking (BT) search is based on depth-first search to choose values for one variable at a time, but it backtracks whenever there are no legal values left to assign. The state space is searched by extending the current partial solution with an assignment to unassigned variables. Starting with the first variable, the algorithm assigns a provisional value to each subsequent variable, checking value consistency along the way. If the algorithm encounters a variable for which no domain value is consistent with the previous assignments, a *dead-end* occurs. At this point, the search *backtracks* and the variable preceding the dead-end assignment is changed and the search continues. The algorithm returns when a solution is found, or when the search is exhausted with no solution. AlgorithmThe following recursive algorithm performs a backtracking search on a given CSP. The recursion base case occurs on line 3, which indicates the halting condition of the algorithm.```vhdl1 procedure backtrack(csp)2 if csp.assignment is complete and feasible then 3 return assignment ; recursion base case4 end if5 var ← csp.get_unassigned_var()6 for next value in csp.var_domain(var)7 original_domain = csp.assign(var, value)8 if csp.assignment is feasible then9 result ← backtrack(csp)10 if result ≠ failure then11 return result12 end if13 csp.restore_domain(original_domain)14 end if15 csp.unassign(var, value)16 return failure17 end``` ExampleWe can apply the backtrack search algorithm to the N-Queens problem. Note that this simple version of the algorithm makes finding a solution tractable for a handful of queens, but there are other improvements that can be made that are discussed in the following section.
###Code
queens, exec_time = nqueens_backtracking(4)
draw_nqueens([queens.assignment])
print("Solution found in %0.4f seconds" % exec_time)
###Output
_____no_output_____
###Markdown
Branch and BoundSuppose we would like to find the *best* solution (in some sense) to the CSP. This amounts to solving the associated constraint optimization problem (COP), where our constraint network is now a 4-tuple, $\langle X, D_X, C, f \rangle$, where $X\in D_X$, $C: D_X \to \{\operatorname{True},\operatorname{False}\}$ and $f: D_x\to\mathbb{R}$ is a cost function. We would like to find the variable assignments $X$ that solve\begin{array}{ll@{}ll}\text{minimize} & f(X) &\\\text{subject to}& C(X) &\end{array}By adding a cost function $f(X)$, we turn a CSP into a COP, and we can use the **branch and bound algorithm** to find the solution with the lowest cost.To find a solution of a COP we could surely explore the whole tree and then pick the leaves with the smallest cost value. However, one may want to integrate the optimization process into the search process allowing to **prune** even if no inconsistency has been detected yet.The main idea behind branch and bound is the following: if the best solution so far has cost $c$, this is a _lower bound_ for all other possible solutions. So, if a partial solution has led to costs of $x$ (cost so far) and the best we can achieve for all other cost components is $y$ with $x + y < c$, then we do not need to continue in this branch.Of course every time we prune a subtree we are implicitly making the search faster compared with full exploration. Therefore with a small overhead in the algorithm, we can improve (in the average case) the runtime. Algorithm```vhdl 1 procedure BranchAndBound(cop) 2 i ← 1; ai ← {} ; initialize variable counter and assignments 3 a_inc ← {}; f_inc ← ∞ ; initialize incumbent assignment and cost 4 Di´ ← Di ; copy domain of first variable 5 while 1 ≤ i ≤ n+1 6 if i = n+1 ; "unfathomed" consistent assignment 7 f_inc ← f(ai) and a_inc ← ai ; updated incumbent 8 i ← i - 2 9 else10 instantiate xi ← SelectValueBB(f_inc) ; Add to assignments ai; update Di11 if xi is null ; if no value was returned,12 i ← i - 1 ; then backtrack13 else14 i ← i + 1 ; else step forward and15 Di´ ← Di ; copy domain of next variable.16 end if17 end if18 end while19 return incumbent X_inc and f_inc ; Assignments exhausted, return incumbent20 end``````vhdl 1 procedure SelectValueBB(f_inc) 2 while Di´ ≠ ∅ 3 select an arbitrary element a ∈ Di´ and remove a from Di´ 4 ai ← ai ∪ {xi = a} 5 if consistent(ai) and b(ai) < f_inc 6 return a; 7 end if 8 end while ; no consistent value 9 return null10 end``` ExampleNow let's revive our discussion on the map coloring problem. Imagine that we work at a company that wishes to print a colored map of the United States, so they need to choose a color for each state. Let's also imagine that the available colors are:
###Code
colors = [
'red',
'green',
'blue',
'#6f2da8', #Grape
'#ffbf00', #Amber
'#01796f', #Pine
'#813f0b', #Clay
'#ff2000', #yellow
'#ff66cc', #pink
'#d21f3c' #raspberry
]
###Output
_____no_output_____
###Markdown
The CEO asks the engineering department (they have one of course) to find a color assignment that satisfies the constraints as specified above in _Map Coloring_ and they arrive at the following solution:
###Code
map_colors, num_colors = us_map_coloring(colors)
draw_us_map(map_colors)
###Output
_____no_output_____
###Markdown
Unfortunately, management is never happy and they complain that {{ num_colors }} colors are really too many. Can we do better? Yes, by adding an objective function $f$ that gives a cost proportional to the number of used colors, we can minimize $f$. This results in the following solution:
###Code
map_colors, opt_num_colors = us_map_coloring(colors, optimize=True)
draw_us_map(map_colors)
###Output
_____no_output_____
###Markdown
Fortunately we saved {{ num_colors - opt_num_colors }} color, well done! --- Extended MethodsThe methods discussed in this section arise from viewing a CSP from different perspectives and from a combination of constraint propagation and search methods. BT Search with Forward Checking (BT-FC)By interleaving inference from constraint propagation and search, we can obtain much more efficient solutions. A well-known way of doing this is by adding an arc consistency step to the backtracking algorithm. The result is called **forward checking**, which allows us to run search on graphs that have not already been pre-processed into arc consistent CSPs. Algorithm**Main Idea**: Maintain n domain copies for resetting, one for each search level i.```vhdl 1 procedure BTwithFC(csp) 2 Di´ ← Di for 1 ≤ i ≤ n ; copy all domains 3 i ← 1; ai = {} ; init variable counter, assignments 4 while 1 ≤ i ≤ n 5 instantiate xi ← SelectValueFC() ; add to assignments, making ai 6 if xi is null ; if no value was returned 7 reset each Dk´ for k>i to 8 its value before xi 9 was last instantiated10 i ← i - 1 ; backtrack11 else12 i ← i + 1 ; step forward13 end if14 end while15 if i = 016 return "inconsistent"17 else18 return ai ; the instantiated values of {xi, ..., xn}19 end``````vhdl 1 procedure SelectValueFC() 2 while Di´ ≠ ∅ 3 select an arbitrary element a ∈ Di´ and remove a from Di´ 4 for all k, i < k ≤ n 5 for all values b ∈ Dk´ 6 if not consistent(a_{i-1}, xi=a, xk=b) 7 remove b from Dk´ 8 end if 9 end for10 if Dk´ = ∅ ; xi=a leads to a dead-end: do not select a11 reset each Dk´, i<k≤n to its value before a was selected12 else13 return a14 end if15 end for16 end while17 return null18 end``` ExampleThe example code below runs a backtracking search with forward checking on the N-Queens problem. For the same value of $N$, note how a solution can be found much faster than without forward checking.
###Code
queens, exec_time = nqueens_backtracking(4, with_forward_checking=True)
draw_nqueens([queens.assignment])
print("Solution found in %0.4f seconds" % exec_time)
###Output
_____no_output_____
###Markdown
BT-FC with Dynamic Variable and Value OrderingTraditional backtracking as it was introduced above uses a fixed ordering over variables and values. However, it is often better to choose ordering dynamically as the search proceeds. The idea is as follows. At each node during the search, choose:- the most constrained variable; picking the variable with the fewest legal variables in its domain will minimize the branching factor,- the least constraining value; choosing a value that rules out the smallest number of values of variables connected to the chosen variable via constraints will leave most options for finding a satisfying assignment.These two ordering heuristics cause the algorithm to choose the variable that fails first and the value that fails last. This helps minimize the search space by pruning larger parts of the tree early on. ExampleThe example code below demonstrates BT-FC with dynamic variable ordering using the most-constrained-variable heurestic. The run time cost of finding a solution to the N-Queens problem is lower than both BT and BT-FC, allowing the problem to be solved for even higher $N$.
###Code
queens, exec_time = nqueens_backtracking(4, with_forward_checking=True, var_ordering='smallest_domain')
draw_nqueens([queens.assignment])
print("Solution found in %0.4f seconds" % exec_time)
###Output
_____no_output_____
###Markdown
Adaptive Consistency: Bucket EliminationAnother method of solving constraint problems entails eliminating constraints through bucket elimination. This method can be understood through the lens of Gaussian elimination, where equations (i.e., constraints) are added and then extra variables are eliminated. More formally, these operations can be thought of from the perspective of relations as **join** and **project** operations.Bucket elimination uses the join and projection operations on the set of constraints in order to transform a constraint graph into a single variable. After solving for that variable, other constraints are solved for by back substitution just as you would in an algebraic system in Gaussian elimination.Using the map coloring problem where an `AllDiff` constraint exists between each neighboring variables, the join and project operators are explained. The constraint graph for the map coloring problem is shown below. The Join OperatorThe map coloring CSP can be trivially solved using the join operation on the constraints, which is defined as the consistent Cartesian product of the constraint relations.Written as tables, the relations of each constraint $C_{12}$, $C_{23}$, and $C_{13}$ are$C_{12}$$C_{23}$$C_{13}$|$V_1$|$V_2$||-----|-----|| R | G || G | R || B | R || B | G ||$V_2$|$V_3$||-----|-----|| R | G ||$V_1$|$V_3$||-----|-----|| R | G || B | G |These constraint relation tables are then joined together as$C_{12}\Join C_{23}$$C_{13}$|$V_1$|$V_2$|$V_3$||-----|-----|-----|| G | R | G || B | R | G ||$V_1$|$V_3$||-----|-----|| R | G || B | G |$C_{12}\Join C_{23}\Join C_{13}$|$V_1$|$V_2$|$V_3$||-----|-----|-----|| B | R | G | The Projection OperatorThe projection operator is akin to the elimination step in Gaussian elimination and is useful for shrinking the size of the constraints. After joining all the constraints in the above example, we can project out all constraints except for one to obtain the value of that variable.For example, the projection of $C_{12}\Join C_{23}\Join C_{13}$ onto $C_1$ is$C_2 = \Pi_2 (C_{12}\Join C_{23}\Join C_{13})$|$V_1$||-----|| B | --- Symmetries M. C. Escher IntroductionA CSP often exhibits some symmetries, which are mappings that preserve satisfiability of the CSP. Symmetries are particularly disadvantageous when we are looking for **all possible solutions** of a CSP, since search can revisit equivalent states over and over again.\begin{definition} \label{def:symmetry}(Symmetry). For any CSP instance $P = \langle X, D, C \rangle$, a solution symmetry of $P$ is a permutation of the set $X\times D$ that preserves the set of solutions to $P$.\end{definition}In other words, a solution symmetry is a bijective mapping defined on the set of possible variable-value pairs of a CSP that maps solutions to solutions. Why is symmetry important? A principal reason for identifying CSP symmetries is to **reduce search efforts** by not exploring assignments that are symmetrically equivalent to assignments considered elsewhere in the search. In other words, if a problem has a lot of symmetric solutions of a small subset of non-symmetric solutions, the search tree is bigger and if we are looking for all those solutions, the search process is forced to visit all the symmetric solutions of the big search tree. Alternatively, if we can prune-out the subtree containing symmetric solutions, the search effort will reduce drastically. Case Study: symmetries in N-Queens problemWe have already seen the N-Queens problem. Let us see all the solutions of a $4 \times 4$ chessboard.
###Code
queens = nqueens(4)
draw_nqueens(queens, all_solutions=True)
###Output
_____no_output_____
###Markdown
There are exactly 2 solutions. It's easy to notice the two are the same solution if we flip (or rotate) the chessboard. Interactive examplesAll the following code snippets are a refinement of the original N-Queens problem where we modify the problem to reduce the number of symmetries. Feel free to explore how the number of solutions to the N-Queens problem changes when we change symmetry breaking strategy and $N$.You can use the following slider to change $N$, than press the button `Update cells...` to quickly update the results of the models.
###Code
n = 5
def update_n(x):
global n
n = x
interact(update_n , x=widgets.IntSlider(value=n, min=1,max=12,step=1, description='Queens:'));
## Update all cells dependent from the slider with the following button
button = widgets.Button(description="Update cells...")
display(button)
button.on_click(autoupdate_cells)
###Output
_____no_output_____
###Markdown
Avoid symmetries Adding Constraints Before SearchIn practice, symmetry in CSPs is usually identified by applying human insight: the programmer sees that some transformation would translate a hypothetical solution into another hypothetical solution. Then, the programmer can try to formalize some constraint that preserves solutions but removes some of the symmetries.For $N$ = {{n}} the N-Queens problem has {{ len(nqueens(n)) }} solutions. One naive way to remove some of the symmetric solutions is to restrict the position for some of the queens, for example, we can say that the first queen should be on the top half of the chess board by imposing an additional constraint like```constraint queens[0] <= n div 2;```This constraint should remove approximately half of the symmetries. Let's try the new model!
###Code
%%minizinc --all-solutions --statistics -m bind
include "globals.mzn";
int: n;
array[0..n-1] of var 0..n-1: queens;
constraint all_different(queens);
constraint all_different([queens[i]+i | i in 0..n-1]);
constraint all_different([queens[i]-i | i in 0..n-1]);
constraint queens[0] <= n div 2;
solve satisfy;
###Output
_____no_output_____
###Markdown
If you play with $N$ you will notice that for $N=4$ all solutions are retained. However, For $N>4$ symmetric solutions will begin to be pruned out.This approach is fine and if done correctly it can greatly reduce the search space. However, this additional constraint can lose solutions if done incorrectly.To address the problem in a better way we need some formal tool. Chessboard symmetriesLooking at the chessboard, we notice that it has eight geometric symmetries---one for each geometric transformation. In particular they are:- identity (no-reflections) $id$ (we always include the identity)- horizontal reflection $r_x$- vertical reflection $r_y$- reflections along the two diagonal axes ($r_{d_1}$ and $r_{d_2}$)- rotations through $90$°, $180$° and $270$° ($r_{90}$, $r_{180}$, $r_{270}$)If we label the sixteen squares of a $4 \times 4$ chessboard with the numbers 1 to 16, we can graphically see how symmetries move cells. Now it's easy to see that a symmetry is a **permutation** that acts on a point: for example, if a queen is at $(2,1)$ (which correspondes to element $2$ in $id$), under the mapping $r_{90}$, it moves to $(4,2)$.One useful form to write a permutation is in _Cauchy form_, for example for $r_{90}$\begin{equation}r_{90} : \left( \begin{array} { c c c c c c c c c } 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16\\ 13 & 9 & 5 & 1 & 14 & 10 & 6 & 2 & 15 & 11 & 7 & 3 & 16 & 12 & 8 & 4\end{array} \right)\end{equation}What this notation says is that an element in position $i$ in the top row, is moved to the corresponding position of the bottom row. For example $1$ → $13$, $2$ → $9$, $3$ → $5$ and so on.This form will help us compactly write constraints to remove unwanted permutations. The Lex-Leader MethodPuget proved that whenever a CSP has symmetry that can be expressed as permutations of the variables, it is possible to find a _reduced form_ with the symmetries eliminated by adding constraints to the original problem \cite{Puget2003}. Puget found such a reduction for three simple constraint problems and showed that this reduced CSP could be solved more efficiently than in its original form.The intuition is rather simple: for each equivalence class of solutions (permutation), we predefine one to be the **canonical solution**. We achieve this by choosing a static variable ordering and imposing the **lexicographic order** for each permutation. This method is called **lex-leader**.For example, let us consider a problem where we have three variables $x_1$, $x_2$, and $x_3$ subject to the `alldifferent` constraint and domain {A,B,C}. This problem has $3!$ solutions, where $3!-1$ are symmetric solutions. Let's say that our canonical solution is `ABC`, and we want to prevent `ACB` from being a solution, the lex-leader method would impose the following additional constraint:$$ x_1\,x_2\,x_3 \preceq_{\text{lex}} x_1\,x_3\,x_2. $$In fact, if $x = (\text{A},\text{C},\text{B})$ the constraint is not satisfied, written as$$ \text{A}\text{C}\text{B}\,\, \npreceq_{\text{lex}} \text{A}\text{B}\text{C}. $$Adding constraints like this for all $3!$ permutations will remove all symmetric solutions, leaving exactly one solution (`ABC`). All other solutions can be recovered by applying each symmetry.In general, if we have a permutation $\pi$ that generates a symmetric solution that we wish to remove, we would impose an additional constraint, usually expressed as$$ x_1 \ldots x_k \preceq_{\text{lex}} x_{\pi (1)} \ldots x_{\pi (k)}, $$where $\pi(i)$ is the index of the variable after the permutation. Unfortunately, for the N-Queens problem formulated as we have seen, this technique does not immediately apply, because some of its symmetries cannot be described as permutations of the `queens` array.The trick to overcoming this limitation is to express the N-Queens problem in terms of Boolean variables for each square of the chessboard that model whether it contains a queen or not (i.e., Attempt 1 from above). Now all the symmetries can be modeled as permutations of this array using Cauchy form.Since the main constraints of the N-Queens problem are much easier to express with the integer `queens` array, we use both models together connecting them using _channeling constraints_.
###Code
%%minizinc --all-solutions --statistics -m bind
include "globals.mzn";
int: n;
array[0..n-1,0..n-1] of var bool: qb;
array[0..n-1] of var 0..n-1: q;
constraint all_different(q);
constraint all_different([q[i]+i | i in 0..n-1]);
constraint all_different([q[i]-i | i in 0..n-1]);
constraint % Channeling constraint
forall (i,j in 0..n-1) ( qb[i,j] <-> (q[i]=j) );
constraint % Lexicographic symmetry breaking constraints
lex_lesseq(array1d(qb), [ qb[j,i] | i in reverse(0..n-1), j in 0..n-1 ]) /\ % r_{90}
lex_lesseq(array1d(qb), [ qb[i,j] | i,j in reverse(0..n-1) ]) /\ % r_{180}
lex_lesseq(array1d(qb), [ qb[j,i] | i in 0..n-1, j in reverse(0..n-1) ]) /\ % r_{270}
lex_lesseq(array1d(qb), [ qb[i,j] | i in reverse(0..n-1), j in 0..n-1 ]) /\ % r_{x}
lex_lesseq(array1d(qb), [ qb[i,j] | i in 0..n-1, j in reverse(0..n-1) ]) /\ % r_{y}
lex_lesseq(array1d(qb), [ qb[j,i] | i,j in 0..n-1 ]) /\ % r_{d_1}
lex_lesseq(array1d(qb), [ qb[j,i] | i,j in reverse(0..n-1) ]); % r_{d_2}
solve satisfy;
###Output
_____no_output_____
|
matplotlib/gallery_jupyter/images_contours_and_fields/layer_images.ipynb
|
###Markdown
Layer ImagesLayer images above one another using alpha blending
###Code
import matplotlib.pyplot as plt
import numpy as np
def func3(x, y):
return (1 - x / 2 + x**5 + y**3) * np.exp(-(x**2 + y**2))
# make these smaller to increase the resolution
dx, dy = 0.05, 0.05
x = np.arange(-3.0, 3.0, dx)
y = np.arange(-3.0, 3.0, dy)
X, Y = np.meshgrid(x, y)
# when layering multiple images, the images need to have the same
# extent. This does not mean they need to have the same shape, but
# they both need to render to the same coordinate system determined by
# xmin, xmax, ymin, ymax. Note if you use different interpolations
# for the images their apparent extent could be different due to
# interpolation edge effects
extent = np.min(x), np.max(x), np.min(y), np.max(y)
fig = plt.figure(frameon=False)
Z1 = np.add.outer(range(8), range(8)) % 2 # chessboard
im1 = plt.imshow(Z1, cmap=plt.cm.gray, interpolation='nearest',
extent=extent)
Z2 = func3(X, Y)
im2 = plt.imshow(Z2, cmap=plt.cm.viridis, alpha=.9, interpolation='bilinear',
extent=extent)
plt.show()
###Output
_____no_output_____
###Markdown
------------References""""""""""The use of the following functions and methods is shownin this example:
###Code
import matplotlib
matplotlib.axes.Axes.imshow
matplotlib.pyplot.imshow
###Output
_____no_output_____
|
Code/.ipynb_checkpoints/FFT analysis-old-checkpoint.ipynb
|
###Markdown
Load data Experiment 2
###Code
Exp2_data_file = 'OptMagData/Exp2/20190406/20190406/AxionWeel000.0500.flt.csv'
Exp2_data = np.loadtxt(Exp2_data_file,delimiter= '\t')
Exp2_time = Exp2_data[:,0]
Exp2_AW_Z = Exp2_data[:,1]
Exp2_AW_X = -Exp2_data[:,2]
Exp2_AV_X = Exp2_data[:,3]
Exp2_AV_Z = Exp2_data[:,4]
plt.figure(figsize = (17,4));plt.plot(Exp2_time,Exp2_AW_X)
## Full useable range
Exp2_Freq = [0.1,0.5, 1, 3, 5]
Exp2_Start_Time = [ 20,150,280,365,440]
Exp2_Stop_Time = [ 140,260,334,427,500]
Exp2_AW_X_FFT = {}
Exp2_AW_Z_FFT = {}
Exp2_AV_X_FFT = {}
Exp2_AV_Z_FFT = {}
Exp2_Freq_FFT = {}
for ii in range(len(Exp2_Freq)):
# loop_nu = Freq[ii]
key = Exp2_Freq[ii]
f_new_sample = sampling_factor*key
if f_new_sample >f_sample:
n_skips = 1
f_new_sample = f_sample
else:
n_skips = int(np.ceil(f_sample/f_new_sample))
# Cut up data
arraybool = (Exp2_time>Exp2_Start_Time[ii] )& (Exp2_time<Exp2_Stop_Time[ii])
Time_Full_Sample = Exp2_time[arraybool]
AW_X_Full = 1e-12*Exp2_AW_X[arraybool]
AW_Z_Full = 1e-12*Exp2_AW_Z[arraybool]
AV_X_Full = 1e-12*Exp2_AV_X[arraybool]
AV_Z_Full = 1e-12*Exp2_AV_Z[arraybool]
# FFT
TimeArrayLength = len(Time_Full_Sample)
Exp2_AW_X_FFT[key] = (np.fft.rfft(AW_X_Full)/TimeArrayLength)
Exp2_AW_Z_FFT[key] = (np.fft.rfft(AW_Z_Full)/TimeArrayLength)
Exp2_AV_X_FFT[key] = (np.fft.rfft(AV_X_Full)/TimeArrayLength)
Exp2_AV_Z_FFT[key] = (np.fft.rfft(AV_Z_Full)/TimeArrayLength)
Exp2_Freq_FFT[key] = f_new_sample/TimeArrayLength*np.arange(1,int(TimeArrayLength/2)+2,1)
# nu = 5
# print(Exp1_Time_cut[nu].shape)
# print(Exp1_Freq_FFT[nu].shape)
# print(Exp1_X_FFT[nu].shape)
# plt.figure(figsize = (12,8))
bigplt_AW = plt.figure()
bigax_AW = bigplt_AW.add_axes([0, 0, 1, 1])
bigplt_AV = plt.figure()
bigax_AV = bigplt_AV.add_axes([0, 0, 1, 1])
for nu in Exp2_Freq:
Bmax_AW = max([max(1e12*abs(Exp2_AW_X_FFT[nu])),max(1e12*abs(Exp2_AW_Z_FFT[nu]))])
Bmax_AV = max([max(1e12*abs(Exp2_AV_X_FFT[nu])),max(1e12*abs(Exp2_AV_Z_FFT[nu]))])
indnu = (np.abs(Exp2_Freq_FFT[nu]-nu)<0.08*nu)
# print(indnu)
ind11nu = (np.abs(Exp2_Freq_FFT[nu]-11*nu)<0.08*nu)
Bmaxatnu_AW = max([1e12*abs(Exp2_AW_X_FFT[nu][indnu]).max(),1e12*abs(Exp2_AW_Z_FFT[nu][indnu]).max()])
Bmaxatnu_AV = max([1e12*abs(Exp2_AV_X_FFT[nu][indnu]).max(),1e12*abs(Exp2_AV_Z_FFT[nu][indnu]).max()])
Bmaxat11nu_AW = max([1e12*abs(Exp2_AW_X_FFT[nu][ind11nu]).max(),1e12*abs(Exp2_AW_Z_FFT[nu][ind11nu]).max()])
Bmaxat11nu_AV = max([1e12*abs(Exp2_AV_X_FFT[nu][ind11nu]).max(),1e12*abs(Exp2_AV_Z_FFT[nu][ind11nu]).max()])
figloop = plt.figure()
plt.loglog(Exp2_Freq_FFT[nu],1e12*abs(Exp2_AW_X_FFT[nu]), label = str(nu)+'Hz X',figure=figloop)
plt.loglog(Exp2_Freq_FFT[nu],1e12*abs(Exp2_AW_Z_FFT[nu]), label = str(nu)+'Hz Z',figure=figloop)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnetic Field (pT)')
plt.grid()
plt.grid(which = 'minor',linestyle = '--')
plt.annotate('$f_\mathrm{rot}$',xy = (nu,Bmaxatnu_AW),xytext=(nu,Bmax_AW),\
arrowprops=dict(color='limegreen',alpha=0.7,width = 3.5,headwidth=8, shrink=0.),\
horizontalalignment='center')
plt.annotate('$11f_\mathrm{rot}$',xy = (11*nu,Bmaxat11nu_AW),xytext=(11*nu,Bmax_AW),\
arrowprops=dict(color='fuchsia',alpha=0.5,width = 3.5,headwidth=8,shrink=0.),\
horizontalalignment='center')
plt.legend(loc='lower left')
if SaveFFTFig:
plt.savefig(SaveDir+'Exp2_AW_'+str(nu)+'Hz_FFT.png',bbox_inches = 'tight',dpi = 1000)
figloop = plt.figure()
plt.loglog(Exp2_Freq_FFT[nu],1e12*abs(Exp2_AV_X_FFT[nu]), label = str(nu)+'Hz X',figure=figloop)
plt.loglog(Exp2_Freq_FFT[nu],1e12*abs(Exp2_AV_Z_FFT[nu]), label = str(nu)+'Hz Z',figure=figloop)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnetic Field (pT)')
plt.grid()
plt.grid(which = 'minor',linestyle = '--')
plt.annotate('$f_\mathrm{rot}$',xy = (nu,Bmaxatnu_AV),xytext=(nu,Bmax_AV),\
arrowprops=dict(color='limegreen',alpha=0.7,width = 3.5,headwidth=8, shrink=0.),\
horizontalalignment='center')
plt.annotate('$11f_\mathrm{rot}$',xy = (11*nu,Bmaxat11nu_AV),xytext=(11*nu,Bmax_AV),\
arrowprops=dict(color='fuchsia',alpha=0.5,width = 3.5,headwidth=8,shrink=0.),\
horizontalalignment='center')
plt.legend(loc='lower left')
if SaveFFTFig:
plt.savefig(SaveDir+'Exp2_AV_'+str(nu)+'Hz_FFT.png',bbox_inches = 'tight',dpi = 1000)
bigax_AW.loglog(Exp2_Freq_FFT[nu],1e12*abs(Exp2_AW_X_FFT[nu]), label = str(nu)+'Hz X',figure=bigplt_AW)
bigax_AW.loglog(Exp2_Freq_FFT[nu],1e12*abs(Exp2_AW_Z_FFT[nu]), label = str(nu)+'Hz Z',figure=bigplt_AW)
bigax_AV.loglog(Exp2_Freq_FFT[nu],1e12*abs(Exp2_AV_X_FFT[nu]), label = str(nu)+'Hz X',figure=bigplt_AV)
bigax_AV.loglog(Exp2_Freq_FFT[nu],1e12*abs(Exp2_AV_Z_FFT[nu]), label = str(nu)+'Hz Z',figure=bigplt_AV)
bigax_AW.set_xlabel('Frequency (Hz)')
bigax_AW.set_ylabel('Magnetic Field (pT)')
bigax_AW.grid()
bigax_AW.grid(which = 'minor',linestyle = '--')
bigax_AW.legend(loc = 'lower left')
if SaveFFTFig:
bigplt_AW.savefig(SaveDir+'Exp2_AW_'+str('all')+'Hz_FFT.png',bbox_inches = 'tight',dpi = 1000)
bigax_AV.set_xlabel('Frequency (Hz)')
bigax_AV.set_ylabel('Magnetic Field (pT)')
bigax_AV.grid()
bigax_AV.grid(which = 'minor',linestyle = '--')
bigax_AV.legend(loc = 'lower left')
if SaveFFTFig:
bigplt_AV.savefig(SaveDir+'Exp2_AV_'+str('all')+'Hz_FFT.png',bbox_inches = 'tight',dpi = 1000)
###Output
C:\Users\Nancy\Anaconda2\lib\site-packages\ipykernel_launcher.py:69: UserWarning: Creating legend with loc="best" can be slow with large amounts of data.
C:\Users\Nancy\Anaconda2\lib\site-packages\ipykernel_launcher.py:77: UserWarning: Creating legend with loc="best" can be slow with large amounts of data.
C:\Users\Nancy\Anaconda2\lib\site-packages\IPython\core\events.py:88: UserWarning: Creating legend with loc="best" can be slow with large amounts of data.
func(*args, **kwargs)
C:\Users\Nancy\Anaconda2\lib\site-packages\IPython\core\pylabtools.py:128: UserWarning: Creating legend with loc="best" can be slow with large amounts of data.
fig.canvas.print_figure(bytes_io, **kw)
|
Fremont_bridge_analysis/Bridge.ipynb
|
###Markdown
Fremont Bridge Bike Traffic Analysis William Gray First, save data location URL so we can access anytime
###Code
%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('seaborn')
from jupyterworkflow.data import get_fremont_data
df = get_fremont_data()
df.resample('W').sum().plot()
ax = df.resample('D').sum().rolling(365).sum().plot()
ax.set_ylim(0, None); # sets y axis to 0 at bottom, and automatic at top
df.groupby(df.index.time).mean().plot()
pivoted = df.pivot_table('Total', index=df.index.time, columns=df.index.date)
pivoted.iloc[:5, :5]
pivoted.plot(legend=False, alpha=0.02);
###Output
_____no_output_____
|
notebooks/26_clustering.ipynb
|
###Markdown
Unsupervised LearningIn contrast to everything we've seen up till now, the data in these problems is **unlabeled**. This means that the metrics that we've used up till now (e.g. accuracy) won't be available to evaluate our models with. Furthermore, the loss functions we've seen also require labels. Unsupervised learning algorithms need to describe the hidden structure in the data. Clustering[Clustering](https://en.wikipedia.org/wiki/Cluster_analysis) is an unsupervised learning problem, where the goal is to split the data into several groups called **clusters**. 
###Code
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
###Output
_____no_output_____
###Markdown
As stated previously, in unsupervised problems the data **isn't** accompanied by labels. We don't even know **how many** groups our data belongs to.To illustrate how unsupervised algorithms cope with the challenge, we'll create an easy example consisting of 100 data points that can easily be split into two categories (of 50 points each). We'll attempt to create an algorithm that can identify the two groups and split the data accordingly.
###Code
# CODE:
# --------------------------------------------
np.random.seed(55) # for reproducibility
p1 = np.random.rand(50,2) * 10 + 1 # 100 random numbers uniformly distributed in [1,11). these are stored in a 50x2 array.
p2 = np.random.rand(50,2) * 10 + 12 # 100 random numbers uniformly distributed in [12,22). these are stored in a 50x2 array.
points = np.concatenate([p1, p2]) # we merge the two into a 100x2 array
# the first column represents the feature x1, while the second represents x2
# subsequently the 30th row represents the two coordinates of the 30th sample
# PLOTTING:
# --------------------------------------------
ax = plt.subplot(111) # create a subplot to get access to the axes object
ax.scatter(points[:,0], points[:,1], c='#7f7f7f') # scatter the points and color them all as gray
# this is done to show that we don't know which
# categories the data can be split into
# Remove ticks from both axes
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
# Remove the spines from the figure
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
# Set labels and title
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.set_title('Data points randomly placed into two groups')
###Output
_____no_output_____
###Markdown
K-Means**[k-means](https://en.wikipedia.org/wiki/K-means_clustering)**, is probably the simplest clustering algorithm. Let's see how it works step by step.The most important hyperparameter is $k$, a number signifying the number of clusters the algorithm would attempt to group the data into. K-means represents clusters through points in space called **centroids**. Initially the centroids are **placed randomly**. Afterwards the distance of each centroid to every data point is computed. These points are **assigned** to the cluster with the closest centroid. Finally, for each cluster, the mean location of all its data points is calculated. Each cluster's centroid is moved to that location (this movement is also referred to as an **update**). The assignment and update stages are repeated until convergence.In the above image:- (a): Data points- (b): Random initialization- (c): Initial assignment- (d): Initial centroid update- (e): Second assignment- (f): Second update The whole training procedure can also be viewed in the image below:In order to better understand the algorithm, we'll attempt to create a simple k-means algorithm on our own. As previously stated, the only hyperparameter we need to define is $k$. The first step is to create $k$ centroids, randomly placed near the data points.
###Code
# CODE:
# --------------------------------------------
np.random.seed(55) # for reproducibility
# Select the value of the hyperparameter k:
k = 2
# STEP 1:
# Randomly place two centroids in the same space as the data points
centroids = np.random.rand(k, 2) * 22
# PLOTTING:
# --------------------------------------------
colors = ['#1f77b4', '#ff7f0e'] # select colors for the two groups
ax = plt.subplot(111)
ax.scatter(points[:, 0], points[:, 1], c='#7f7f7f') # data points in gray
ax.scatter(centroids[:, 0], centroids[:, 1], color=colors, s=80) # centroids in orange and blue
# Aesthetic parameters:
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
###Output
_____no_output_____
###Markdown
In order to continue, we need a way to measure *how close* one point is to another, or in other words a *distance metric*. For this purpose, we will use probably the most common distance metric, [Euclidean distance](https://en.wikipedia.org/wiki/Euclidean_distance).The distance of two points $a$ and $b$ is calculated as follows:$$d \left( a, b \right) = \sqrt{ \left( a_x - b_x \right)^2 + \left( a_y - b_y \right)^2}$$Of course there are many more [distance metrics][1] we can use.[1]: https://en.wikipedia.org/wiki/Metric_(mathematics)
###Code
# CODE:
# --------------------------------------------
def euclidean_distance(point1, point2):
"""
calculates the Euclidean distance between point1 and point2. these points need to be two-dimensional.
"""
return np.sqrt( (point1[0] - point2[0]) ** 2 + (point1[1] - point2[1]) ** 2 )
print('the distance from (5,2) to (2,5) is: ', euclidean_distance((5, 2), (2, 5)))
print('the distance from (3,3) to (3,3) is: ', euclidean_distance((3, 3), (3, 3)))
print('the distance from (1,12) to (12,15) is: ', euclidean_distance((1, 12), (12, 15)))
###Output
the distance from (5,2) to (2,5) is: 4.242640687119285
the distance from (3,3) to (3,3) is: 0.0
the distance from (1,12) to (12,15) is: 11.40175425099138
###Markdown
Tip: Alternatively we could use the built-in function [pdist](https://docs.scipy.org/doc/scipy-0.19.1/reference/generated/scipy.spatial.distance.pdist.html) from scipy.spatial.distance.The second step would be to calculate the distance from each point to every centroid. To do this, we'll use the previously defined function.
###Code
# CODE:
# --------------------------------------------
def calc_distances(centroids, points):
"""
Calculates the Euclidean distance from each centroid to every point.
"""
distances = np.zeros((len(centroids), len(points))) # array with (k x N) dimensions, where we will store the distances
for i in range(len(centroids)):
for j in range(len(points)):
distances[i,j] = euclidean_distance(centroids[i], points[j])
return distances
# The above could also be written as:
# return np.reshape(np.array([euclidean_distance(centroids[i], points[j]) for i in range(len(centroids))
# for j in range(len(points))]), (len(centroids), len(points)))
print('first 10 distances from the first centroid:')
print(calc_distances(centroids, points)[0, :10])
print('...')
###Output
first 10 distances from the first centroid:
[10.66051639 18.34697375 18.03210907 21.35516886 12.70487826 12.63056227
14.22553545 13.44270615 17.74860179 11.96433364]
...
###Markdown
Afterwards, we'll use these distances to assign the data points into clusters (depending on which centroid they are closer to).
###Code
# CODE:
# --------------------------------------------
def assign_cluster(centroids, points):
"""
Calculates the Euclidean distance from each centroid to every point. Assigns the points to clusters.
"""
distances = calc_distances(centroids, points)
return np.argmin(distances, axis=0)
print('Which cluster does each point belong to?')
print(assign_cluster(centroids, points))
###Output
Which cluster does each point belong to?
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 0 1 0 1 1 1 0 0 0 1 0 1 1 1 1 0 1
1 1 1 1 1 1 0 1 1 1 0 0 1 0 1 1 0 1 1 1 1 1 1 1 1 1]
###Markdown
Due to the distance metric we elected, the two groups are geometrically separated through their perpendicular bisector. The lines or planes that separate groups are called [decision boundaries](https://en.wikipedia.org/wiki/Decision_boundary). We'll proceed to draw this line.
###Code
# PLOTTING:
# --------------------------------------------
# First, we'll calculate the perpendicular bisector's function
def generate_perp_bisector(centroids):
midpoint = ((centroids[0, 0] + centroids[1, 0]) / 2, (centroids[0, 1] + centroids[1, 1]) / 2) # the midpoint of the two centroids
slope = (centroids[1, 1] - centroids[0, 1]) / (centroids[1, 0] - centroids[0, 0]) # the angle of the line that connects the two centroids
perpendicular = -1/slope # its perpendicular
return lambda x: perpendicular * (x - midpoint[0]) + midpoint[1] # the function
perp_bisector = generate_perp_bisector(centroids)
# Color mapping
map_colors = {0:'#1f77b4', 1:'#ff7f0e'}
point_colors = [map_colors[i] for i in assign_cluster(centroids, points)]
# Range of values in the x axis
x_range = [points[:, 0].min(), points[:, 0].max()]
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# Scatter the points
ax.scatter(points[:, 0], points[:, 1], c=point_colors, s=50, lw=0, edgecolor='black', label='data points')
ax.scatter(centroids[:, 0], centroids[:, 1], c=colors, s=100, lw=1, edgecolor='black', label='centroids')
# Draw the decision boundary
ax.plot(x_range, [perp_bisector(x) for x in x_range], c='purple', label='decision boundary')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('KMeans: Random Centroid Initialization')
ax.legend(loc='lower right', scatterpoints=3)
###Output
_____no_output_____
###Markdown
The third step involves computing the mean of all points of each class and update the corresponding centroid to that location.
###Code
# CODE:
# --------------------------------------------
def update_centers(centroids, points):
clusters = assign_cluster(centroids, points) # assign points to clusters
new_centroids = np.zeros(centroids.shape) # array where the new positions will be stored
for i in range(len(centroids)):
cluster_points_idx = [j for j in range(len(clusters)) if clusters[j] == i] # finds the positions of the points that belong to cluster i
if cluster_points_idx: # if the centroid has any data points assigned to it, update its position
cluster_points = points[cluster_points_idx] # slice the relevant positions
new_centroids[i, 1] = cluster_points[:,1].sum() / len(cluster_points) # calculate the centroid's new position
new_centroids[i, 0] = cluster_points[:,0].sum() / len(cluster_points)
else: # if the centroid doesn't have any points we keep its old position
new_centroids[i, :] = centroids[i, :]
return new_centroids
# PLOTTING:
# --------------------------------------------
# Compute the new centroid positions and generate the decision boundary and the new assignments
new_centroids = update_centers(centroids, points)
new_boundary = generate_perp_bisector(new_centroids)
new_colors = [map_colors[i] for i in assign_cluster(new_centroids, points)]
# Create figure
fig = plt.figure(figsize=(6, 4))
ax = plt.subplot(111)
# Scatter the points
ax.scatter(points[:, 0], points[:, 1], c=new_colors, s=50, lw=0, edgecolor='black', label='data points')
ax.scatter(centroids[:, 0], centroids[:, 1], c=colors, s=100, lw=1, edgecolor='black', alpha=0.3, label='old centroids')
ax.scatter(new_centroids[:, 0], new_centroids[:, 1], c=colors, s=100, lw=1, edgecolor='black', label='new centroids')
# Draw the decision boundaries
ax.plot(x_range, [perp_bisector(x) for x in x_range], c='black', alpha=0.3, label='old boundary')
ax.plot(x_range, [new_boundary(x) for x in x_range], c='purple', label='new boundary')
# Draw the arrows
for i in range(k):
ax.arrow(centroids[i, 0], centroids[i, 1], new_centroids[i, 0] - centroids[i, 0], new_centroids[i, 1] - centroids[i, 1],
length_includes_head=True, head_width=0.5, color='black')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('KMeans: Boundary changes after first centroid update')
ax.legend(loc='lower right', scatterpoints=3)
###Output
_____no_output_____
###Markdown
The second and third steps are repeated until convergence. An interactive tutorial to try out k-means for different data types and initial conditions is available [here](https://www.naftaliharris.com/blog/visualizing-k-means-clustering/).At this point, we'll attempt to create our own k-means class. For ease we'll try to model it to match the functionality of scikit-learn estimators, as closely as possible. The only hyperparameter, the class will accept, is the number of classes $k$. There will be two methods: `.fit()` which will initialize the centroids and handle the whole training procedure until convergence; and `.predict()` which will compute the distance between one or more points and the centroids and assign them accordingly.
###Code
class KMeans:
def __init__(self, k, term_distance=0.05, max_steps=50, seed=None):
self.k = k
self.seed = seed
self.history = []
# Termination conditions:
self.term_distance = term_distance # minimum allowed centroid update distance before termination
self.max_steps = max_steps # maximum number of epochs
def initialize(self, data):
# Place k centroids in random spots in the space defined by the date
np.random.seed(self.seed)
self.centroids = np.random.rand(self.k,2) * data.max()
self.history = [self.centroids] # holds a history of the centroids' previous locations
def calc_distances(self, points):
# Calculates the distances between the points and centroids
distances = np.zeros((len(self.centroids), len(points)))
for i in range(len(self.centroids)):
for j in range(len(points)):
distances[i,j] = self.euclidean_distance(self.centroids[i], points[j])
return distances
def assign_cluster(self, points):
# Compares the distances between the points ant the centroids and carries out the assignment
distances = self.calc_distances(points)
return np.argmin(distances, axis=0)
def update_centers(self, points):
# Calculates the new positions of the centroids
clusters = self.assign_cluster(points)
new_centroids = np.zeros(self.centroids.shape)
for i in range(len(self.centroids)):
cluster_points_idx = [j for j in range(len(clusters)) if clusters[j] == i]
if cluster_points_idx:
cluster_points = points[cluster_points_idx]
new_centroids[i, 1] = cluster_points[:,1].sum() / len(cluster_points)
new_centroids[i, 0] = cluster_points[:,0].sum() / len(cluster_points)
else:
new_centroids[i, :] = self.centroids[i, :]
return new_centroids
def fit(self, data):
# Undertakes the whole training procedure
# 1) initializes the centroids
# 2, 3) computes the distances and updates the centroids
# Repeats steps (2) and (3) until a termination condition is met
self.initialize(data)
self.previous_positions = [self.centroids]
step = 0
cluster_movement = [self.term_distance + 1] * self.k
while any([x > self.term_distance for x in cluster_movement]) and step < self.max_steps: # checks for both termination conditions
new_centroids = self.update_centers(data)
self.history.append(new_centroids) # store centroids past locations
cluster_movement = [self.euclidean_distance(new_centroids[i,:], self.centroids[i,:]) for i in range(self.k)]
self.centroids = new_centroids
self.previous_positions.append(self.centroids)
step += 1
def predict(self, points):
# Checks if points is an array with multiple points or a tuple with the coordinates of a single point
# and carries out the assignment. This could be done through the built in 'assign_cluster' method,
# but for reasons of clarity we elected to perform it manually.
if isinstance(points, np.ndarray):
if len(points.shape) == 2:
return [np.argmin([self.euclidean_distance(point, centroid) for centroid in self.centroids]) for point in points]
return np.argmin([self.euclidean_distance(points, self.centroids[i]) for i in range(self.k)])
def fit_predict(self, points):
# Runs the training phase and returns the assignment of the training data
self.fit(points)
return self.predict(points)
@staticmethod
def euclidean_distance(point1, point2):
# Computes the Euclidean distance between two points
return np.sqrt( (point1[0] - point2[0]) ** 2 + (point1[1] - point2[1]) ** 2 )
###Output
_____no_output_____
###Markdown
Initially, we'll run a few iterations manually (without the use of `.fit()`) to check if it works correctly.First, let's initialize the $k$ centroids.
###Code
# CODE:
# --------------------------------------------
km = KMeans(2, seed=13)
km.initialize(points)
# PLOTTING:
# --------------------------------------------
# Assign data points and generate decision boundary
point_colors = [map_colors[i] for i in km.predict(points)]
decision_boundary = generate_perp_bisector(km.centroids)
# Create figure
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# Scatter the points and draw the decision boundary
ax.scatter(points[:, 0], points[:, 1], c=point_colors, s=50, lw=0, edgecolor='black', label='data points')
ax.scatter(km.centroids[:, 0], km.centroids[:, 1], c=colors, s=100, lw=1, edgecolor='black', label='centroids')
ax.plot(x_range, [decision_boundary(x) for x in x_range], c='purple', label='new boundary')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('KMeans: Boundary after initialization')
ax.legend(loc='upper left', scatterpoints=3)
###Output
_____no_output_____
###Markdown
Now, we'll run an iteration and update the centroids.
###Code
# CODE:
# --------------------------------------------
old = km.centroids
km.centroids = new = km.update_centers(points)
# PLOTTING:
# --------------------------------------------
# Assign points and generate decision boundary
point_colors = [map_colors[i] for i in km.predict(points)]
new_boundary = generate_perp_bisector(new)
# Create figure
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# Scatter the points and draw the decision boundary
ax.scatter(points[:, 0], points[:, 1], c=point_colors, s=50, lw=0, edgecolor='black', label='data points')
ax.scatter(old[:, 0], old[:, 1], c=colors, s=100, lw=1, edgecolor='black', alpha=0.3, label='old centroids')
ax.scatter(new[:, 0], new[:, 1], c=colors, s=100, lw=1, edgecolor='black', label='new centroids')
ax.plot(x_range, [decision_boundary(x) for x in x_range], c='black', alpha=0.3, label='old boundary')
ax.plot(x_range, [new_boundary(x) for x in x_range], c='purple', label='new boundary')
# Draw arrows
for i in range(km.k):
plt.arrow(old[i, 0], old[i, 1], new[i, 0] - old[i, 0], new[i, 1] - old[i, 1],
length_includes_head=True, head_width=0.5, color='black')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('KMeans: Boundary changes after first centroid update')
ax.legend(loc='upper left', scatterpoints=3)
###Output
_____no_output_____
###Markdown
One more iteration...
###Code
# CODE:
# --------------------------------------------
old = km.centroids
new = km.update_centers(points)
# PLOTTING:
# --------------------------------------------
# Assign points and generate decision boundary
decision_boundary = new_boundary
point_colors = [map_colors[i] for i in km.predict(points)]
new_boundary = generate_perp_bisector(new)
# Create figure
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# Scatter the points and draw the decision boundary
ax.scatter(points[:, 0], points[:, 1], c=point_colors, s=50, lw=0, edgecolor='black', label='data points')
ax.scatter(old[:, 0], old[:, 1], c=colors, s=100, lw=1, edgecolor='black', alpha=0.3, label='old centroids')
ax.scatter(new[:, 0], new[:, 1], c=colors, s=100, lw=1, edgecolor='black', label='new centroids')
ax.plot(x_range, [decision_boundary(x) for x in x_range], c='black', alpha=0.3, label='old boundary')
ax.plot(x_range, [new_boundary(x) for x in x_range], c='purple', label='new boundary')
# Draw arrows
for i in range(km.k):
plt.arrow(old[i, 0], old[i, 1], new[i, 0] - old[i, 0], new[i, 1] - old[i, 1],
length_includes_head=True, head_width=0.5, color='black')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('KMeans: Boundary changes after first centroid update')
ax.legend(loc='upper left', scatterpoints=3)
###Output
_____no_output_____
###Markdown
Now that we confirmed that the class' main functionality works we can try out the `.fit()` method, which handles the training procedure for as many iterations as necessary.
###Code
# CODE:
# --------------------------------------------
km = KMeans(2, seed=44)
km.fit(points)
# PLOTTING:
# --------------------------------------------
# Assign points and generate decision boundary
point_colors = [map_colors[i] for i in km.predict(points)]
decision_boundary = generate_perp_bisector(km.centroids)
# Create figure
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# Scatter the points and draw the decision boundary
ax.scatter(points[:, 0], points[:, 1], c=point_colors, s=50, lw=0, edgecolor='black', label='data points')
ax.scatter(km.centroids[:, 0], km.centroids[:, 1], c=colors, s=100, lw=1, edgecolor='black', label='centroids')
ax.plot(x_range, [new_boundary(x) for x in x_range], c='purple', label='decision boundary')
# We'll use km.history to plot the centroids' previous locations
steps = len(km.history)
for s in range(steps-2): # the last position (where s==steps-1) is already drawn;
# we'll ignore the penultimate position for two reasons:
# 1) it represents the last iteration, where the centroid movement was minimal and
# 2) because the arrows must be 1 less than the points
ax.scatter(km.history[s][:, 0], km.history[s][:, 1], c=colors, s=100, alpha=1.0 / (steps-s))
for i in range(km.k):
ax.arrow(km.history[s][i, 0], km.history[s][i, 1], km.history[s + 1][i, 0] - km.history[s][i, 0],
km.history[s + 1][i, 1] - km.history[s][i, 1], length_includes_head=True, head_width=0.3,
color='black', alpha=1.0 / (steps - s))
# Draw one more time to register the label
ax.scatter(km.history[s][:, 0], km.history[s][:, 1], c=colors, s=100, alpha=1.0 / (steps-s), label='previous positions')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('KMeans: Complete training')
ax.legend(loc='upper left', scatterpoints=3)
###Output
_____no_output_____
###Markdown
Once the system is trained, we can use `.predict()` to figure out which cluster a point belongs to.
###Code
print(' (0,0) belongs to cluster:', km.predict((0, 0)))
print(' (5,5) belongs to cluster:', km.predict((5, 5)))
print('(10,10) belongs to cluster:', km.predict((10, 10)))
print('(15,15) belongs to cluster:', km.predict((15, 15)))
print('(20,20) belongs to cluster:', km.predict((20, 20)))
print('(25,25) belongs to cluster:', km.predict((25, 25)))
###Output
(0,0) belongs to cluster: 0
(5,5) belongs to cluster: 0
(10,10) belongs to cluster: 0
(15,15) belongs to cluster: 1
(20,20) belongs to cluster: 1
(25,25) belongs to cluster: 1
###Markdown
Now that we've covered the basics, let's dive into some more advanced concepts of unsupervised learning. Up till now we haven't given any thought on the selection of $k$. What would happen if we selected a larger value than was necessary?
###Code
# CODE:
# --------------------------------------------
k = 5
km = KMeans(k, seed=13)
km.fit(points)
# PLOTTING:
# --------------------------------------------
# Create figure
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# For ease, from now on, we will allow matplotlib so select the colors on its own
ax.scatter(points[:, 0], points[:, 1], c=km.predict(points), s=50, lw=0, label='data points')
ax.scatter(km.centroids[:, 0], km.centroids[:, 1], c=range(k), s=100, lw=1, edgecolor='black', label='centroids')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('KMeans: k={}'.format(k))
ax.legend(loc='upper left', scatterpoints=3)
###Output
_____no_output_____
###Markdown
Is this a worse solution to the problem than that with $k=2$? Is there a way to confirm this?What if we had a more complex problem where we wouldn't know what $k$ to use?
###Code
# CODE:
# --------------------------------------------
np.random.seed(77)
# We'll create 4 groups of 50 points with centers in the positions (7,7), (7,17), (17,7) και (17,17)
# The points will be highly dispersed so the groups won't be clearly visible
lowb, highb, var = 2, 12, 10
p1 = np.random.rand(50, 2) * var + lowb
p2 = np.random.rand(50, 2) * var + highb
a = np.array([highb] * 50)
b = np.array([lowb] * 50)
c = np.zeros((50, 2))
c[:, 0], c[:, 1] = a, b
p3 = np.random.rand(50, 2) * var + c
c[:, 1], c[:, 0] = a, b
p4 = np.random.rand(50, 2) * var + c
points = np.concatenate([p1, p2, p3, p4])
# PLOTTING:
# --------------------------------------------
# Create figure
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# Scatter new points
ax.scatter(points[:, 0], points[:, 1], c='#7f7f7f')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('Data Points'.format(k))
###Output
_____no_output_____
###Markdown
Select whichever value of $k$ you feel appropriate.
###Code
# CODE:
# --------------------------------------------
k = int(input('Select value for k: '))
km = KMeans(k, seed=77)
km.fit(points)
# PLOTTING:
# --------------------------------------------
# Create figure
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# Scatter new points
ax.scatter(points[:, 0], points[:, 1], c=km.predict(points), lw=0, s=50)
ax.scatter(km.centroids[:, 0], km.centroids[:, 1], c=range(k), lw=1, edgecolor='black', s=100)
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('k-means clustering for k={}'.format(k))
###Output
Select value for k: 5
###Markdown
We'll draw a few more for $k = {2, 3, 4, 5, 6, 7}$.
###Code
# PLOTTING:
# --------------------------------------------
# Create 6 subplots
f, ax = plt.subplots(2, 3, figsize=(10, 5))
seed = 55
# k = 2
km = KMeans(2, seed=seed)
ax[0, 0].scatter(points[:, 0], points[:, 1], c=km.fit_predict(points), lw=0)
ax[0, 0].scatter(km.centroids[:, 0], km.centroids[:, 1], c=range(km.k), lw=1, edgecolor='black', s=80)
ax[0, 0].set_title('k = 2')
ax[0, 0].axis('off')
# k = 3
km = KMeans(3, seed=seed)
ax[0, 1].scatter(points[:, 0], points[:, 1], c=km.fit_predict(points), lw=0)
ax[0, 1].scatter(km.centroids[:, 0], km.centroids[:, 1], c=range(km.k), lw=1, edgecolor='black', s=80)
ax[0, 1].set_title('k = 3')
ax[0, 1].axis('off')
# k = 4
km = KMeans(4, seed=seed)
ax[0, 2].scatter(points[:, 0], points[:, 1], c=km.fit_predict(points), lw=0)
ax[0, 2].scatter(km.centroids[:, 0], km.centroids[:, 1], c=range(km.k), lw=1, edgecolor='black', s=80)
ax[0, 2].set_title('k = 4')
ax[0, 2].axis('off')
# k = 5
km = KMeans(5, seed=seed)
ax[1, 0].scatter(points[:, 0], points[:, 1], c=km.fit_predict(points), lw=0)
ax[1, 0].scatter(km.centroids[:, 0], km.centroids[:, 1], c=range(km.k), lw=1, edgecolor='black', s=80)
ax[1, 0].set_title('k = 5')
ax[1, 0].axis('off')
# k = 6
km = KMeans(6, seed=seed)
ax[1, 1].scatter(points[:, 0], points[:, 1], c=km.fit_predict(points), lw=0)
ax[1, 1].scatter(km.centroids[:, 0], km.centroids[:, 1], c=range(km.k), lw=1, edgecolor='black', s=80)
ax[1, 1].set_title('k = 6')
ax[1, 1].axis('off')
# k = 7
km = KMeans(7, seed=seed)
ax[1, 2].scatter(points[:, 0], points[:, 1], c=km.fit_predict(points), lw=0)
ax[1, 2].scatter(km.centroids[:, 0], km.centroids[:, 1], c=range(km.k), lw=1, edgecolor='black', s=80)
ax[1, 2].set_title('k = 7')
ax[1, 2].axis('off')
###Output
_____no_output_____
###Markdown
So, how should we select the value of $k$ in this task? Is there an objective way to measure whether or not one of the above results is better than the other? Clustering EvaluationIn order to be able to select the value of $k$ that yields the best results, we first need a way to **objectively** evaluate the performance of a clustering algorithm.We can't use any of the metrics we described in previous tutorials (e.g. accuracy, precision, recall), as they compare the algorithm's predictions to the class labels. However, as stated previously, in unsupervised problems there aren't any labels accompanying the data. So how can we measure the performance of a clustering algorithm?One way involves comparing the relationships in the clustered data. The simplest metric we could think of is to compare the variance of the samples of each cluster.For the cluster $C$ this can be calculated through the following formula:$$I_C = \sum_{i \in C}{(x_i - \bar{x}_C)^2}$$where $x_i$ is an example that belongs to cluster $C$ with a centroid $\bar{x}_C$.The smaller the value of $I_C$, the less the variance in cluster $C$, meaning that the cluster is more "compact". Metrics like this are called **inertia**. To calculate the total inertia, we can just sum the inertia of each cluster.$$I = \sum_{C = 1}^k{I_C}$$Many times, this is be divided with the total variance of the data.From now on we will be using the [KMeans](http://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html) estimator from scikit-learn, which provides more features and is better optimized than our simpler implementation.
###Code
# CODE:
# --------------------------------------------
from sklearn.cluster import KMeans
k = 5
km = KMeans(k, random_state=99)
km.fit(points)
# PLOTTING:
# --------------------------------------------
# Create figure
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# Scatter data points and centroids
ax.scatter(points[:, 0], points[:, 1], c=km.predict(points), lw=0, s=50)
ax.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:, 1], c=range(km.n_clusters), lw=1, edgecolor='black', s=100)
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('k-means for k={}\nInertia={:.2f}'.format(k, km.inertia_))
###Output
_____no_output_____
###Markdown
As stated previously, the lower the value of inertia the better. An initial thought would be to try to **minimize** this criterion. Let's run k-means with $k={2, ..., 100}$ to see which value minimizes the inertia.
###Code
# CODE:
# --------------------------------------------
cluster_scores = []
for k in range(2, 101):
km = KMeans(k, random_state=77)
km.fit(points)
cluster_scores.append(km.inertia_)
# PLOTTING:
# --------------------------------------------
# Create figure
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# Plot total inertia for all values of k
ax.plot(range(2, 101), cluster_scores)
# Aesthetic parameters
ax.set_xlabel('k')
ax.set_ylabel('inertia')
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.yaxis.set_ticks_position('left')
ax.xaxis.set_ticks_position('bottom')
ax.set_title('Inertia for different values of k')
###Output
_____no_output_____
###Markdown
From the figure above, we can observe that as $k$ increases, the system's total inertia decreases. This makes sense because more clusters in the system, will result in each of them having only few examples, close to their centroid. This means that the total variance of the system will decrease, as the number of clusters ($k$) increases. Finally, when $k=N$ (where $N$ is the total number of examples) inertia will reach 0.Can inertia help us select the best $k$? Not directly.We can use an **empirical** criterion called the [elbow][1]. To use this, we simply draw the inertia curve and look for where it forms an "elbow".[1]: https://en.wikipedia.org/wiki/Elbow_method_(clustering)
###Code
# PLOTTING:
# --------------------------------------------
# Create figure
fig = plt.figure(figsize=(6, 4))
ax = plt.subplot(111)
# Draw first 6 values of k
plt.plot(range(2,8), cluster_scores[:6])
plt.annotate("elbow", xy=(3, cluster_scores[1]), xytext=(5, 6000),arrowprops=dict(arrowstyle="->"))
plt.annotate("elbow", xy=(4, cluster_scores[2]), xytext=(5, 6000),arrowprops=dict(arrowstyle="->"))
plt.annotate("elbow", xy=(6, cluster_scores[4]), xytext=(5, 6000),arrowprops=dict(arrowstyle="->"))
# Aesthetic parameters
ax.set_xlabel('k')
ax.set_ylabel('inertia')
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.yaxis.set_ticks_position('left')
ax.xaxis.set_ticks_position('bottom')
ax.set_title('Elbow criterion')
###Output
_____no_output_____
###Markdown
In the figure above we could choose $k=3$, $k=4$ or $k=6$. This method however is **highly subjective** and even if we used an objective method of figuring out the "sharpest" elbow (e.g. looking at the curve's second derivative), it still wouldn't produce any objective results, as the criterion is empirical.In order to get an **objective** evaluation on our clustering method's performance we need to dive a bit deeper into [clustering evaluation](https://en.wikipedia.org/wiki/Cluster_analysisEvaluation_and_assessment). There are two main categories here:- Extrinsic evaluation: Involves running the clustering algorithm in a supervised problem, where class labels are available. They are obviously not included during the training phase but are used for evaluation. However, this type of evaluation can't be applied to any truly unsupervised problems.- Intrinsic evaluation: Requires analyzing the structure of the clusters, much like inertia we saw previously. Intrinsic Clustering EvaluationThese metrics analyze the structure of the clusters and try to produce better scores for solutions with more "compact" clusters. Inertia did this by measuring the variance within each cluster. The problem with inertia, was that it rewarded solutions with more clusters. We are now going to examine two metrics that reward solutions with fewer (more sparse) clusters:- [Dunn index](https://en.wikipedia.org/wiki/Dunn_index): This metric consists of two parts: - The nominator is a measure of the **distance between two clusters**. This could be the distance between their centroids, the distance between their closest points, etc. - The denominator is a measure of the **size of the largest cluster**. This could be the largest distance between a centroid and the most remote point assigned to it, the maximum distance between two points of the same cluster, etc.$$DI= \frac{ min \left( \delta \left( C_i, C_j \right) \right)}{ max \, \Delta_p }$$where $C_i, C_j$ are two random centroids, $ \left( C_i, C_j \right)$ is a measure of their distance and $\Delta_p$ in a measure of the size of cluster $p$, where $p \in [0,k]$. The larger Dunn index is, the better the solution. The denominator of this index deals with the size of the clusters. Solutions with smaller (or more "**compact**") clusters produce a smaller denominator, which increases the index's value. The nominator becomes larger the farther apart the clusters are, which rewards **sparse solutions** with fewer clusters. - [Silhouette coefficient][1]: Like Dunn, this metric two can be decomposed into two parts. For cluster $i$: - A measure of cluster **homogeneity** $a(i)$ (e.g. the mean distance of all points assigned to $i$, to its centroid). - A measure of cluster $i$'s **distance to its nearest cluster** $b(i)$ (e.g. the distance of their centroids, the distance of their nearest points etc.)The silhouette coefficient is defined for each cluster separately:$$s \left( i \right) = \frac{b \left( i \right) - a \left( i \right) }{max \left( a \left( i \right) , b \left( i \right) \right)}$$A small value of $a(i)$ means cluster $i$ is more "compact", while a large $b(i)$ means that $i$ is far away from its nearest cluster. It is apparent that larger values of the nominator are better. The denominator scales the index to $[-1, 1]$. The best score we can achieve is $s(i) \approx 1$ for $b(i) >> a(i)$.In order to evaluate our algorithm, we usually average the silhouette coefficients $s(i)$ for all the clusters.We'll now attempt to use the silhouette coefficient to figure out the best $k$ for our previous problem.[1]: https://en.wikipedia.org/wiki/Silhouette_(clustering)
###Code
# CODE:
# --------------------------------------------
from sklearn.metrics import silhouette_score
silhouette_scores = []
for k in range(2, 101):
km = KMeans(k, random_state=77)
km.fit(points)
preds = km.predict(points)
silhouette_scores.append(silhouette_score(points, preds))
# PLOTTING:
# --------------------------------------------
# Find out the value of k which produced the best silhouette score
best_k = np.argmax(silhouette_scores) + 2 # +2 because range() begins from k=2
# Create figure
fig = plt.figure(figsize=(6, 4))
ax = plt.subplot(111)
# Draw figures
ax.plot(range(2, 101), silhouette_scores)
ax.scatter(best_k, silhouette_scores[best_k-2], color='#ff7f0e')
ax.annotate("best k", xy=(best_k, silhouette_scores[best_k-2]), xytext=(50, 0.39), arrowprops=dict(arrowstyle="->"))
# Aesthetic parameters
ax.set_xlabel('k')
ax.set_ylabel('silhouette score')
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.yaxis.set_ticks_position('left')
ax.xaxis.set_ticks_position('bottom')
ax.set_title('Silhouette scores for different values of k')
print('Maximum average silhouette score for k =', best_k)
###Output
Maximum average silhouette score for k = 61
###Markdown
Let's draw the clustering solution for $k=61$.
###Code
# CODE:
# --------------------------------------------
km = KMeans(best_k, random_state=77)
preds = km.fit_predict(points)
# PLOTTING:
# --------------------------------------------
# Create figure
fig = plt.figure(figsize=(6, 4))
ax = plt.subplot(111)
# Draw assigned points
ax.scatter(points[:, 0], points[:, 1], c=preds, lw=0, label='data points')
ax.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:,1], c='#ff7f0e', s=50, lw=1, edgecolor='black', label='centroids')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('k-means for k={}\nSilhouette score={:.2f}'.format(best_k, silhouette_scores[best_k-2]))
plt.legend(loc='upper left', scatterpoints=3)
###Output
_____no_output_____
###Markdown
This result, however, still might not be desirable due to the large number of clusters. In most applications it doesn't help us very much to cluster 200 points into 61 clusters. We could take that into account and add another restriction to our problem: only examine solutions with 20 or less clusters.
###Code
# CODE:
# --------------------------------------------
good_k = np.argmax(silhouette_scores[:10]) + 2
km = KMeans(good_k, random_state=77)
preds = km.fit_predict(points)
# PLOTTING:
# --------------------------------------------
# Create figure
fig = plt.figure(figsize=(6, 4))
ax = plt.subplot(111)
# Draw assigned points
ax.scatter(points[:, 0], points[:, 1], c=preds, lw=0, label='data points')
ax.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:,1], c='#ff7f0e', s=80, lw=1, edgecolor='black', label='centroids')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('k-means for k={}\nSilhouette score={:.2f}'.format(good_k, silhouette_scores[good_k-2]))
ax.legend(loc='upper left', scatterpoints=3)
print('A good value for k is: k =', good_k)
###Output
A good value for k is: k = 6
###Markdown
We can view where this solution's silhouette score ranks compared to the best solution.
###Code
# PLOTTING:
# --------------------------------------------
# Create figure
fig = plt.figure(figsize=(6, 4))
ax = plt.subplot(111)
# Draw figure
ax.plot(range(2, 101), silhouette_scores)
ax.scatter([good_k, best_k], [silhouette_scores[good_k-2], silhouette_scores[best_k-2]], color='#ff7f0e')
ax.annotate("best k", xy=(best_k, silhouette_scores[best_k-2]), xytext=(50, 0.39), arrowprops=dict(arrowstyle="->"))
ax.annotate("good k", xy=(good_k, silhouette_scores[good_k-2]), xytext=(10, 0.43), arrowprops=dict(arrowstyle="->"))
# Aesthetic parameters
ax.set_xlabel('k')
ax.set_ylabel('silhouette score')
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.yaxis.set_ticks_position('left')
ax.xaxis.set_ticks_position('bottom')
ax.set_title('Silhouette scores for different values of k')
###Output
_____no_output_____
###Markdown
Now we normally would want to decide if the drop-off in the silhouette score is acceptable.We could also generate a list of candidate values of $k$ and select the best one manually.
###Code
# PLOTTING:
# --------------------------------------------
# Create figure
fig = plt.figure(figsize=(6, 4))
ax = plt.subplot(111)
# Draw figure
topN = 3
ax.plot(range(2, 22), silhouette_scores[:20])
candidate_k = np.argpartition(silhouette_scores[:20], -topN)[-topN:]
ax.scatter([k+2 for k in candidate_k], [silhouette_scores[k] for k in candidate_k], color='#ff7f0e')
for k in candidate_k:
ax.annotate("candidate k", xy=(k+2, silhouette_scores[k]), xytext=(6, 0.38), arrowprops=dict(arrowstyle="->"))
print('For k = {:<2}, the average silhouette score is: {:.4f}.'.format(k+2, silhouette_scores[k]))
# Aesthetic parameters
ax.set_xlabel('k')
ax.set_ylabel('silhouette score')
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.yaxis.set_ticks_position('left')
ax.xaxis.set_ticks_position('bottom')
ax.set_title('Silhouette scores for different values of k')
###Output
For k = 19, the average silhouette score is: 0.4112.
For k = 9 , the average silhouette score is: 0.4124.
For k = 6 , the average silhouette score is: 0.4126.
###Markdown
It should be noted at this point that cluster evaluation is **highly subjective**. There is no such thing as the "best solution". In the example above one might have preferred the solution that produced the best silhouette score, while another a sparser solution with a worse score.Scikit-learn offers many [metrics](http://scikit-learn.org/stable/modules/classes.htmlclustering-metrics) for cluster evaluation. We need to be careful, however, because some metrics are unfit for use for the selection of $k$.For example [Calinski-Harabaz](http://scikit-learn.org/stable/modules/generated/sklearn.metrics.calinski_harabaz_score.html):$$CH \left( i \right) = \frac{B \left( i \right) / \left( k - 1 \right) }{W \left( i \right) / \left( N - k \right)}$$where $N$ is the number of samples, $k$ is the number of clusters, $i$ is a cluster ($i \in \{1, ..., k \}$), $B \left( i \right)$ is an intra-cluster variance metric (e.g. the mean squared distance between the cluster centroids) and $W \left( i \right)$ is an inter-cluster variance metric (e.g. the mean squared distance between points of the same cluster).
###Code
# CODE:
# --------------------------------------------
from sklearn.metrics import calinski_harabaz_score
ch_scores = []
for k in range(2, 101):
km = KMeans(k, random_state=77)
km.fit(points)
preds = km.predict(points)
ch_scores.append(calinski_harabaz_score(points, preds))
# PLOTTING:
# --------------------------------------------
# Find best score
ch_k = np.argmax(ch_scores) + 2
# Create figure
fig = plt.figure(figsize=(6, 4))
ax = plt.subplot(111)
# Draw figures
ax.plot(range(2, 101), ch_scores)
ax.scatter(ch_k, ch_scores[ch_k-2], color='#ff7f0e')
ax.annotate("best k", xy=(ch_k, ch_scores[ch_k-2]), xytext=(50, 450), arrowprops=dict(arrowstyle="->"))
# Aesthetic parameters
ax.set_xlabel('k')
ax.set_ylabel('Calinski-Harabaz score')
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.yaxis.set_ticks_position('left')
ax.xaxis.set_ticks_position('bottom')
ax.set_title('Calinski-Harabaz scores for different values of k')
print('Maximum Calinski-Harabaz score for k =', ch_k)
###Output
Maximum Calinski-Harabaz score for k = 99
###Markdown
Note: For visualization purposes, in this tutorial, we've used only data with two dimensions. The same principles apply to data of any dimensionality. Bonus material Methods for the selection of **k**:[1](https://datasciencelab.wordpress.com/2013/12/27/finding-the-k-in-k-means-clustering/), [2](http://www.sthda.com/english/articles/29-cluster-validation-essentials/96-determining-the-optimal-number-of-clusters-3-must-know-methods/) InitializationUntil now, we've initialized the algorithm by creating $k$ centroids and placing them randomly, in the same space as the data. The initialization of k-means is very important for optimal convergence. We'll illustrate this through an example.
###Code
# CODE:
# --------------------------------------------
# We'll make 3 groups of 50 points each with centers in the positions (7,7), (17,7) and (17,17)
np.random.seed(77)
lowb, highb, var = 2, 12, 5
p1 = np.random.rand(50, 2) * var + lowb
p2 = np.random.rand(50, 2) * var + highb
a = np.array([highb] * 50)
b = np.array([lowb] * 50)
c = np.zeros((50, 2))
c[:, 0], c[:, 1] = a, b
p3 = np.random.rand(50, 2) * var + c
points = np.concatenate([p1, p2, p3])
# Place 3 centroids in the positions (0,20), (1,19) and (2,18)
centroids = np.array([[0, 20], [1, 19], [2, 18]])
# PLOTTING:
# --------------------------------------------
map_colors = {0: '#1f77b4', 1:'#ff7f0e', 2:'#e377c2'}
color_list = ['#1f77b4', '#ff7f0e', '#e377c2']
# Create figure
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# Draw figures
ax.scatter(points[:, 0], points[:, 1], lw=0, s=50, label='data points')
ax.scatter(centroids[:, 0], centroids[:, 1], c=color_list, s=100, lw=1, edgecolor='black', label='centroids')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('KMeans: Centroid Initialization')
ax.legend(loc='upper right', scatterpoints=3)
###Output
_____no_output_____
###Markdown
There clearly are 3 groups of points and 3 centroids nearby. Normally, we would expect each centroid to claim one group. Let's run the first iteration to see how the centroids move.
###Code
# CODE:
# --------------------------------------------
new_centroids = update_centers(centroids, points)
# PLOTTING:
# --------------------------------------------
colors = [map_colors[i] for i in assign_cluster(new_centroids, points)]
# Create figure
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# Draw figures
ax.scatter(points[:, 0], points[:, 1], c=colors, lw=0, s=50, label='data points')
ax.scatter(new_centroids[:, 0], new_centroids[:, 1], c=color_list, s=100, edgecolors='black', label='new centroids')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('KMeans: First step')
ax.legend(loc='upper right', scatterpoints=3)
ax.arrow(centroids[2, 0], centroids[2, 1], new_centroids[2, 0] - centroids[2, 0], new_centroids[2, 1] - centroids[2, 1],
length_includes_head=True, head_width=0.5, color='black')
###Output
_____no_output_____
###Markdown
The first iteration updated one of the 3 centroids. Let's run one more...
###Code
# CODE:
# --------------------------------------------
centroids = new_centroids
new_centroids = update_centers(centroids, points)
# PLOTTING:
# --------------------------------------------
colors = [map_colors[i] for i in assign_cluster(new_centroids, points)]
# Create figure
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# Draw figures
ax.scatter(points[:, 0], points[:, 1], c=colors, lw=0, s=50, label='data points')
ax.scatter(new_centroids[:, 0], new_centroids[:, 1], c=color_list, s=100, edgecolors='black', label='centroids')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('KMeans: M step')
ax.legend(loc='upper right', scatterpoints=3)
###Output
_____no_output_____
###Markdown
We can run the cell above as many times as we want, the centroids won't move. The reason becomes apparent once we draw the decision boundary.
###Code
# PLOTTING:
# --------------------------------------------
# Generate the decision boudary between the pink and the orange centroids
decision_boundary = generate_perp_bisector(centroids[1:, :])
# Find the range of values along the x axis
x_min = min([points[:, 0].min(), centroids[:, 0].min()])
x_max = max([points[:, 0].max(), centroids[:, 0].max()])
x_range = [x_min, x_max]
# Create figure
fig = plt.figure(figsize=(6, 4))
ax = plt.subplot(111)
# Draw figures
ax.scatter(points[:, 0], points[:, 1], c=colors, lw=0, s=50, label='data points')
ax.scatter(new_centroids[:, 0], new_centroids[:, 1], c=color_list, s=100, edgecolors='black', label='centroids')
ax.plot(x_range, decision_boundary(x_range), c='black', label='decision boundary')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('KMeans: Decision Boundary')
ax.legend(loc='upper right', scatterpoints=3)
###Output
_____no_output_____
|
notebooks/08/1/Applying_a_Function_to_a_Column.ipynb
|
###Markdown
Applying a Function to a Column We have seen many examples of creating new columns of tables by applying functions to existing columns or to other arrays. All of those functions took arrays as their arguments. But frequently we will want to convert the entries in a column by a function that doesn't take an array as its argument. For example, it might take just one number as its argument, as in the function `cut_off_at_100` defined below.
###Code
def cut_off_at_100(x):
"""The smaller of x and 100"""
return min(x, 100)
cut_off_at_100(17)
cut_off_at_100(117)
cut_off_at_100(100)
###Output
_____no_output_____
###Markdown
The function `cut_off_at_100` simply returns its argument if the argument is less than or equal to 100. But if the argument is greater than 100, it returns 100.In our earlier examples using Census data, we saw that the variable `AGE` had a value 100 that meant "100 years old or older". Cutting off ages at 100 in this manner is exactly what `cut_off_at_100` does.To use this function on many ages at once, we will have to be able to *refer* to the function itself, without actually calling it. Analogously, we might show a cake recipe to a chef and ask her to use it to bake 6 cakes. In that scenario, we are not using the recipe to bake any cakes ourselves; our role is merely to refer the chef to the recipe. Similarly, we can ask a table to call `cut_off_at_100` on 6 different numbers in a column. First, we create the table `ages` with a column for people and one for their ages. For example, person `C` is 52 years old.
###Code
ages = Table().with_columns(
'Person', make_array('A', 'B', 'C', 'D', 'E', 'F'),
'Age', make_array(17, 117, 52, 100, 6, 101)
)
ages
###Output
_____no_output_____
###Markdown
`apply` To cut off each of the ages at 100, we will use the a new Table method. The `apply` method calls a function on each element of a column, forming a new array of return values. To indicate which function to call, just name it (without quotation marks or parentheses). The name of the column of input values is a string that must still appear within quotation marks.
###Code
ages.apply(cut_off_at_100, 'Age')
###Output
_____no_output_____
###Markdown
What we have done here is `apply` the function `cut_off_at_100` to each value in the `Age` column of the table `ages`. The output is the array of corresponding return values of the function. For example, 17 stayed 17, 117 became 100, 52 stayed 52, and so on.This array, which has the same length as the original `Age` column of the `ages` table, can be used as the values in a new column called `Cut Off Age` alongside the existing `Person` and `Age` columns.
###Code
ages.with_column(
'Cut Off Age', ages.apply(cut_off_at_100, 'Age')
)
###Output
_____no_output_____
###Markdown
Functions as Values We've seen that Python has many kinds of values. For example, `6` is a number value, `"cake"` is a text value, `Table()` is an empty table, and `ages` is a name for a table value (since we defined it above).In Python, every function, including `cut_off_at_100`, is also a value. It helps to think about recipes again. A recipe for cake is a real thing, distinct from cakes or ingredients, and you can give it a name like "Ani's cake recipe." When we defined `cut_off_at_100` with a `def` statement, we actually did two separate things: we created a function that cuts off numbers at 100, and we gave it the name `cut_off_at_100`.We can refer to any function by writing its name, without the parentheses or arguments necessary to actually call it. We did this when we called `apply` above. When we write a function's name by itself as the last line in a cell, Python produces a text representation of the function, just like it would print out a number or a string value.
###Code
cut_off_at_100
###Output
_____no_output_____
###Markdown
Notice that we did not write `"cut_off_at_100"` with quotes (which is just a piece of text), or `cut_off_at_100()` (which is a function call, and an invalid one at that). We simply wrote `cut_off_at_100` to refer to the function.Just like we can define new names for other values, we can define new names for functions. For example, suppose we want to refer to our function as `cut_off` instead of `cut_off_at_100`. We can just write this:
###Code
cut_off = cut_off_at_100
###Output
_____no_output_____
###Markdown
Now `cut_off` is a name for a function. It's the same function as `cut_off_at_100`, so the printed value is exactly the same.
###Code
cut_off
###Output
_____no_output_____
###Markdown
Let us see another application of `apply`. Example: Prediction Data Science is often used to make predictions about the future. If we are trying to predict an outcome for a particular individual – for example, how she will respond to a treatment, or whether he will buy a product – it is natural to base the prediction on the outcomes of other similar individuals.Charles Darwin's cousin [Sir Francis Galton](https://en.wikipedia.org/wiki/Francis_Galton) was a pioneer in using this idea to make predictions based on numerical data. He studied how physical characteristics are passed down from one generation to the next.The data below are Galton's carefully collected measurements on the heights of parents and their adult children. Each row corresponds to one adult child. The variables are a numerical code for the family, the heights (in inches) of the father and mother, a "midparent height" which is a weighted average [[1]](footnotes) of the height of the two parents, the number of children in the family, as well as the child's birth rank (1 = oldest), gender, and height.
###Code
# Galton's data on heights of parents and their adult children
galton = Table.read_table(path_data + 'galton.csv')
galton
###Output
_____no_output_____
###Markdown
A primary reason for collecting the data was to be able to predict the adult height of a child born to parents similar to those in the dataset. Let us try to do this, using midparent height as the variable on which to base our prediction. Thus midparent height is our *predictor* variable.The table `heights` consists of just the midparent heights and child's heights. The scatter plot of the two variables shows a positive association, as we would expect for these variables.
###Code
heights = galton.select(3, 7).relabeled(0, 'MidParent').relabeled(1, 'Child')
heights
heights.scatter(0)
###Output
_____no_output_____
###Markdown
Now suppose Galton encountered a new couple, similar to those in his dataset, and wondered how tall their child would be. What would be a good way for him to go about predicting the child's height, given that the midparent height was, say, 68 inches?One reasonable approach would be to base the prediction on all the points that correspond to a midparent height of around 68 inches. The prediction equals the average child's height calculated from those points alone.Let's pretend we are Galton and execute this plan. For now we will just make a reasonable definition of what "around 68 inches" means, and work with that. Later in the course we will examine the consequences of such choices.We will take "close" to mean "within half an inch". The figure below shows all the points corresponding to a midparent height between 67.5 inches and 68.5 inches. These are all the points in the strip between the red lines. Each of these points corresponds to one child; our prediction of the height of the new couple's child is the average height of all the children in the strip. That's represented by the gold dot.Ignore the code, and just focus on understanding the mental process of arriving at that gold dot.
###Code
heights.scatter('MidParent')
_ = plots.plot([67.5, 67.5], [50, 85], color='red', lw=2)
_ = plots.plot([68.5, 68.5], [50, 85], color='red', lw=2)
_ = plots.scatter(68, 66.24, color='gold', s=40)
###Output
_____no_output_____
###Markdown
In order to calculate exactly where the gold dot should be, we first need to indentify all the points in the strip. These correspond to the rows where `MidParent` is between 67.5 inches and 68.5 inches.
###Code
close_to_68 = heights.where('MidParent', are.between(67.5, 68.5))
close_to_68
###Output
_____no_output_____
###Markdown
The predicted height of a child who has a midparent height of 68 inches is the average height of the children in these rows. That's 66.24 inches.
###Code
close_to_68.column('Child').mean()
###Output
_____no_output_____
###Markdown
We now have a way to predict the height of a child given any value of the midparent height near those in our dataset. We can define a function `predict_child` that does this. The body of the function consists of the code in the two cells above, apart from choices of names.
###Code
def predict_child(mpht):
"""Predict the height of a child whose parents have a midparent height of mpht.
The prediction is the average height of the children whose midparent height is
in the range mpht plus or minus 0.5.
"""
close_points = heights.where('MidParent', are.between(mpht-0.5, mpht + 0.5))
return close_points.column('Child').mean()
###Output
_____no_output_____
###Markdown
Given a midparent height of 68 inches, the function `predict_child` returns the same prediction (66.24 inches) as we got earlier. The advantage of defining the function is that we can easily change the value of the predictor and get a new prediction.
###Code
predict_child(68)
predict_child(74)
###Output
_____no_output_____
###Markdown
How good are these predictions? We can get a sense of this by comparing the predictions with the data that we already have. To do this, we first apply the function `predict_child` to the column of `Midparent` heights, and collect the results in a new column called `Prediction`.
###Code
# Apply predict_child to all the midparent heights
heights_with_predictions = heights.with_column(
'Prediction', heights.apply(predict_child, 'MidParent')
)
heights_with_predictions
###Output
_____no_output_____
###Markdown
To see where the predictions lie relative to the observed data, we can draw overlaid scatter plots with `MidParent` as the common horizontal axis.
###Code
heights_with_predictions.scatter('MidParent')
###Output
_____no_output_____
|
Homework2/hw2-materials/hw2.ipynb
|
###Markdown
CIS 519 Homework 2: Linear Classifiers- Handed Out: October 5, 2020- Due: October 19, 2020 at 11:59pm.Although the solutions are my own, I consulted with the following peoplewhile working on this homework:Zhijie Qiao Preface- Feel free to talk to other members of the class in doing the homework. I am more concerned that you learn how to solve the problem than that you demonstrate that you solved it entirely on your own. You should, however, **write down your solution yourself**. Please include here the list of people you consulted with in the course of working on the homework:- While we encourage discussion within and outside the class, cheating and copying code is strictly not allowed. Copied code will result in the entire assignment being discarded at the very least.- Please use Piazza if you have questions about the homework. Also, please come to the TAs recitations and to the office hours.- The homework is due at 11:59 PM on the due date. We will be using Gradescope for collecting the homework assignments. You should have been automatically added to Gradescope. If not, please ask a TA for assistance. Post on Piazza and contact the TAs if you are having technical difficulties in submitting the assignment.- Here are some resources you will need for this assignment (https://www.seas.upenn.edu/~cis519/fall2020/assets/HW/HW2/hw2-materials.zip) Overview About Jupyter NotebooksIn this homework assignment, we will use a Jupyter notebook to implement, analyze, and discuss ML classifiers.Knowing and being comfortable with Jupyter notebooks is a must in every data scientist, ML engineer, researcher, etc. They are widely used in industry and are a standard form of communication in ML by intertwining text and code to "tell a story". There are many resources that can introduce you to Jupyter notebooks (they are pretty easy to understand!), and if you still need help any of the TAs are more than willing to help.We will be using a local instance of Jupyter instead of Colab. You are of course free to use Colab, but you will need to understand how to hook your Colab instance with Google Drive to upload the datasets and to save images. About the HomeworkYou will experiment with several different linear classifiers and analyze their performances in both real and synthetic datasets. The goal is to understand the differences andsimilarities between the algorithms and the impact that the dataset characteristics have on thealgorithms' learning behaviors and performances.In total, there are seven different learning algorithms which you will implement.Six are variants of the Perceptron algorithm and the seventh is a support vector machine (SVM).The details of these models is described in Section 1.In order to evaluate the performances of these models, you will use several different datasets.The first two datasets are synthetic datasets that have features and labels that were programaticallygenerated. They were generated using the same script but use different input parameters that produced sparse and dense variants. The second two datasets are for the task of named-entity recognition (NER),identifying the names of people, locations, and organizations within text.One comes from news text and the other from a corpus of emails.For these two datasets, you need to implement the feature extraction yourself.All of the datasets and feature extraction information are described in Section 2.Finally, you will run two sets of experiments, one on the synthetic data and one on the NER data.The first set will analyze how the amount of training data impacts model performance.The second will look at the consequences of having training and testing data that come from different domains.The details of the experiments are described in Section 3. Distribution of PointsThe homework has 4 sections for a total of 100 points + 10 extra credit points:- Section 0: Warmup (5 points)- Section 1: Linear Classifiers (30 points)- Section 2: Datasets (0 points, just text)- Section 3: Experiments (65 points) - Synthetic Experiment: - Parameter Tuning (10 points) - Learning Curves(10 points) - Final Test Accuracies (5 points) - Discussion Questions (5 points) - Noise Experiment (10 points **extra credit**) - NER Experiment: - Feature Extraction (25 points) - Final Test Accuracies (5 points) - $F_1$ Discussion Questions (5 points) Section 0: Warmup Only For ColabIf you want to complete this homework in Colab, you are more than welcome to.You will need a little bit more maneuvering since you will need to uploadthe files of hw2 to your Google Drive and run the following two cells:
###Code
# Uncomment if you want to use Colab for this homework.
# from google.colab import drive
# drive.mount('/content/drive', force_remount=True)
# Uncomment if you want to use Colab for this homework.
# %cd /content/drive/My Drive/Colab Notebooks/YOUR_PATH_TO_HW_FOLDER
###Output
/content/drive/My Drive/Colab Notebooks
###Markdown
Python VersionPython 3.6 or above is required for this homework. Make sure you have it installed.
###Code
# Let's check.
import sys
if sys.version_info[:2] < (3, 6):
raise Exception("You have Python version " + str(sys.version_info))
###Output
_____no_output_____
###Markdown
Imports and Helper Functions (5 points total) Let's import useful modules we will need throughout the homeworkas well as implement helper functions for our experiment. **Read and remember** what each function is doing, as you will probably need some of them down the line.
###Code
# Install necessary libraries for this homework. only need to run once i think
%pip install sklearn
%pip install matplotlib
%pip install numpy
import json
import os
import numpy as np
import matplotlib.pylab as plt
from sklearn.feature_extraction import DictVectorizer
from sklearn.metrics import accuracy_score
DATASETS_PATH = "datasets/"
NER_PATH = os.path.join(DATASETS_PATH, 'ner')
SYNTHETIC_PATH = os.path.join(DATASETS_PATH, 'synthetic')
"""
Helper function that loads a synthetic dataset from the dataset root (e.g. "synthetic/sparse").
You should not need to edit this method.
"""
def load_synthetic_data(dataset_type):
def load_jsonl(file_path):
data = []
with open(file_path, 'r') as f:
for line in f:
data.append(json.loads(line))
return data
def load_txt(file_path):
data = []
with open(file_path, 'r') as f:
for line in f:
data.append(int(line.strip()))
return data
def convert_to_sparse(X):
sparse = []
for x in X:
data = {}
for i, value in enumerate(x):
if value != 0:
data[str(i)] = value
sparse.append(data)
return sparse
path = os.path.join(SYNTHETIC_PATH, dataset_type)
X_train = load_jsonl(os.path.join(path, 'train.X'))
X_dev = load_jsonl(os.path.join(path, 'dev.X'))
X_test = load_jsonl(os.path.join(path, 'test.X'))
num_features = len(X_train[0])
features = [str(i) for i in range(num_features)]
X_train = convert_to_sparse(X_train)
X_dev = convert_to_sparse(X_dev)
X_test = convert_to_sparse(X_test)
y_train = load_txt(os.path.join(path, 'train.y'))
y_dev = load_txt(os.path.join(path, 'dev.y'))
y_test = load_txt(os.path.join(path, 'test.y'))
return X_train, y_train, X_dev, y_dev, X_test, y_test, features
"""
Helper function that loads the NER data from a path (e.g. "ner/conll/train").
You should not need to edit this method.
"""
def load_ner_data(dataset=None, dataset_type=None):
# List of tuples for each sentence
data = []
path = os.path.join(os.path.join(NER_PATH, dataset), dataset_type)
for filename in os.listdir(path):
with open(os.path.join(path, filename), 'r') as file:
sentence = []
for line in file:
if line == '\n':
data.append(sentence)
sentence = []
else:
sentence.append(tuple(line.split()))
return data
"""
A helper function that plots the relationship between number of examples
and accuracies for all the models.
You should not need to edit this method.
"""
def plot_learning_curves(
perceptron_accs,
winnow_accs,
adagrad_accs,
avg_perceptron_accs,
avg_winnow_accs,
avg_adagrad_accs,
svm_accs
):
"""
This function will plot the learning curve for the 7 different models.
Pass the accuracies as lists of length 11 where each item corresponds
to a point on the learning curve.
"""
accuracies = [
('perceptron', perceptron_accs),
('winnow', winnow_accs),
('adagrad', adagrad_accs),
('avg-perceptron', avg_perceptron_accs),
('avg-winnow', avg_winnow_accs),
('avg-adagrad', avg_adagrad_accs),
('svm', svm_accs)
]
x = [500, 1000, 1500, 2000, 2500, 3000, 3500, 4000, 4500, 5000, 10000]
plt.figure()
f, (ax, ax2) = plt.subplots(1, 2, sharey=True, facecolor='w')
for label, acc_list in accuracies:
assert len(acc_list) == 11
ax.plot(x, acc_list, label=label)
ax2.plot(x, acc_list, label=label)
ax.set_xlim(0, 5500)
ax2.set_xlim(9500, 10000)
ax2.set_xticks([10000])
# hide the spines between ax and ax2
ax.spines['right'].set_visible(False)
ax2.spines['left'].set_visible(False)
ax.yaxis.tick_left()
ax.tick_params(labelright='off')
ax2.yaxis.tick_right()
ax2.legend()
plt.show()
###Output
_____no_output_____
###Markdown
F1 Score (5 points)For some part of the homework, you will use the F1 score instead of accuracy to evaluate how well a model does. The F1 score is computed as the harmonic mean of the precision and recall of the classifier. Precision measures the number of correctly identified positive results by the total number of positive results. Recall, on the other hand, measures the number of correctly identified positive results divided by the number of all samples that should have been identified as positive. More formally, we have that$$\begin{align}\text{Precision} &= \frac{TP}{TP + FP} \\\text{Recall} &= \frac{TP}{TP + FN}\end{align}$$where $TP$ is the number of true positives, $FP$ false positives and $FN$ false negatives. Combining these two we define F1 as$$\text{F1} = 2 \cdot \frac{\text{Precision} \cdot \text{Recall}}{\text{Precision} + \text{Recall}}$$You now need to implement the calculation of F1 yourself using the provided function header. It will be unit tested on Gradescope.
###Code
def calculate_f1(y_gold, y_model):
"""
TODO: MODIFY
Computes the F1 of the model predictions using the
gold labels. Each of y_gold and y_model are lists with
labels 1 or -1. The function should return the F1
score as a number between 0 and 1.
"""
import numpy as np
diff = np.zeros(len(y_gold))
for i in range(len(y_gold)):
diff[i] = y_gold[i] - y_model[i]
TP = 0
FP = 0
FN = 0
for i in range(len(diff)):
if diff[i] == 0 and y_gold[i] == 1:
TP += 1
if diff[i] > 0:
FN += 1
if diff[i] < 0:
FP += 1
precision = TP / (TP + FP)
recall = TP / (TP + FN)
F1 = 2 * precision * recall / (precision + recall)
print('TP is',TP)
print('FP is',FP)
print('FN is',FN)
return F1
###Output
_____no_output_____
###Markdown
Looking at the formula for the F1 score, what is the highest and lowest possible value?
###Code
def highest_and_lowest_f1_score():
"""
TODO: MODIFY
Return the highest and lowest possible F1 score
(ie one line solution returning the theoretical max and min)
"""
maxscore = 1
minscore = 0
return maxscore, minscore
###Output
_____no_output_____
###Markdown
Section 1. Linear Classifiers (30 points total) This section details the seven different algorithms that you will use in the experiments. For each of the algorithms, we describe the initialization you should use to start training and the different parameter settings that you should use for the experiment on the synthetic datasets. Each of the update functions for the Perceptron, Winnow, and Perceptron with AdaGrad will be unittested on Gradescope, so please do not edit the function definitions. 1.1 Base Classifier
###Code
class Classifier(object):
"""
DO NOT MODIFY
The Classifier class is the base class for all of the Perceptron-based
algorithms. Your class should override the "process_example" and
"predict_single" functions. Further, the averaged models should
override the "finalize" method, where the final parameter values
should be calculated.
You should not need to edit this class any further.
"""
ITERATIONS = 10
def train(self, X, y):
for iteration in range(self.ITERATIONS):
for x_i, y_i in zip(X, y):
self.process_example(x_i, y_i)
self.finalize()
def process_example(self, x, y):
"""
Makes a prediction using the current parameter values for
the features x and potentially updates the parameters based
on the gradient. Note "x" is a dictionary which maps from the feature
name to the feature value and y is either 1 or -1.
"""
raise NotImplementedError
def finalize(self):
"""Calculates the final parameter values for the averaged models."""
pass
def predict(self, X):
"""
Predicts labels for all of the input examples. You should not need
to override this method.
"""
return [self.predict_single(x) for x in X]
def predict_single(self, x):
"""
Predicts a label, 1 or -1, for the input example. "x" is a dictionary
which maps from the feature name to the feature value.
"""
raise NotImplementedError
###Output
_____no_output_____
###Markdown
1.2 Basic Perceptron (2 points) We do this classifier for you, so enjoy the two free points and pay attention to the techniques and code written. 1.2.1 DescriptionThis is the basic version of the Perceptron Algorithm. In this version, an update will be performed on the example $(\textbf{x}, y)$ if $y(\mathbf{w}^\intercal \mathbf{x} + \theta) \leq 0$. The Perceptron needs to learn both the bias term $\theta$ and the weight vector $\mathbf{w}$ parameters.When the Perceptron makes a mistake on the example $(\textbf{x}, y)$, both $\mathbf{w}$ and $\theta$ need to be updated using the following update equations:$$\begin{align*} \mathbf{w}^\textrm{new} &\gets \mathbf{w} + \eta \cdot y \cdot \mathbf{x} \\ \theta^\textrm{new} &\gets \theta + \eta \cdot y\end{align*}$$where $\eta$ is the learning rate. 1.2.2 HyperparametersWe set $\eta$ to 1, so there are no hyperparameters to tune. Note: If we assume that the order of the examples presented to the algorithm is fixed, we initialize $\mathbf{w} = \mathbf{0}$ and $\theta = 0$, and train both together, then the learning rate $\eta$ does not have any effect. In fact you can show that, if $\mathbf{w}_1$ and $\theta_1$ are the outputs of the Perceptron algorithm with learning rate $\eta_1$, then $\mathbf{w}_1/\eta_1$ and $\theta_1/\eta_1$ will be the result of the Perceptron with learning rate 1 (note that these two hyperplanes give identical predictions). 1.2.3 Initialization$\mathbf{w} = [0, 0, \dots, 0]$ and $\theta = 0$.
###Code
class Perceptron(Classifier):
"""
DO NOT MODIFY THIS CELL
The Perceptron model. Note how we are subclassing `Classifier`.
"""
def __init__(self, features):
"""
Initializes the parameters for the Perceptron model. "features"
is a list of all of the features of the model where each is
represented by a string.
"""
# NOTE: Do not change the names of these 3 data members because
# they are used in the unit tests
self.eta = 1
self.theta = 0
self.w = {feature: 0.0 for feature in features}
def process_example(self, x, y):
y_pred = self.predict_single(x)
if y != y_pred:
for feature, value in x.items():
self.w[feature] += self.eta * y * value
self.theta += self.eta * y
def predict_single(self, x):
score = 0
for feature, value in x.items():
score += self.w[feature] * value
score += self.theta
if score <= 0:
return -1
return 1
###Output
_____no_output_____
###Markdown
For the rest of the Perceptron-based algorithms, you will have to implement the corresponding class like we have done for `Perceptron`.Use the `Perceptron` class as a guide for how to implement the functions. 1.3 Winnow (5 points) 1.3.1 DescriptionThe Winnow algorithm is a variant of the Perceptron algorithm with multiplicative updates. Since the algorithm requires that the target function is monotonic, you will only use it on the synthetic datasets.The Winnow algorithm only learns parameters $\mathbf{w}$.We will fix $\theta = -n$, where $n$ is the number of features.When the Winnow algorithm makes a mistake on the example $(\textbf{x}, y)$, the parameters are updated with the following equation:$$\begin{equation} w^\textrm{new}_i \gets w_i \cdot \alpha^{y \cdot x_i}\end{equation}$$where $w_i$ and $x_i$ are the $i$th components of the corresponding vectors.Here, $\alpha$ is a promotion/demotion hyperparameter. 1.3.2 HyperparametersFor the experiment, choose $\alpha \in \{1.1, 1.01, 1.005, 1.0005, 1.0001\}$. 1.3.3 Initialization$\mathbf{w} = [1, 1, \dots, 1]$ and $\theta = -n$ (constant).
###Code
class Winnow(Classifier):
def __init__(self, alpha, features):
# DO NOT change the names of these 3 data members because
# they are used in the unit tests
self.alpha = alpha
self.w = {feature: 1.0 for feature in features}
self.theta = -len(features)
def process_example(self, x, y):
""" TODO: IMPLEMENT"""
y_pred = self.predict_single(x)
if y != y_pred:
for feature, value in x.items():
self.w[feature] = self.w[feature] * pow(self.alpha,y*value)
def predict_single(self, x):
""" TODO: IMPLEMENT"""
score = 0
for feature, value in x.items():
score += self.w[feature] * value
score += self.theta
if score <= 0:
return -1
return 1
###Output
_____no_output_____
###Markdown
1.4 AdaGrad (10 points) 1.4.1 DescriptionAdaGrad is a variant of the Perceptron algorithm that adapts the learning rate for each parameter based on historical information. The idea is that frequently changing features get smaller learning rates and stable features higher ones.To derive the update equations for this model, we first need to start with the loss function.Instead of using the hinge loss with the elbow at 0 (like the basic Perceptron does), we will instead use the standard hinge loss with the elbow at 1:$$\begin{equation} \mathcal{L}(\mathbf{x}, y, \mathbf{w}, \theta) = \max\left\{0, 1 - y(\mathbf{w}^\intercal \mathbf{x} + \theta)\right\}\end{equation}$$Then, by taking the partial derivative of $\mathcal{L}$ with respect to $\mathbf{w}$ and $\theta$, we can derive the respective graidents (make sure you understand how you could derive these gradients on your own):$$\begin{align} \frac{\partial\mathcal{L}}{\partial\mathbf{w}} &= \begin{cases} \mathbf{0} & \text{if $y(\mathbf{w}^\intercal \mathbf{x} + \theta) > 1$} \\ -y\cdot \mathbf{x} & \textrm{otherwise} \end{cases} \\ \frac{\partial\mathcal{L}}{\partial\theta} &= \begin{cases} 0 & \text{if $y(\mathbf{w}^\intercal \mathbf{x} + \theta) > 1$} \\ -y & \textrm{otherwise} \end{cases}\end{align}$$Then for each parameter, we will keep track of the sum of the parameters' squared gradients.In the following equations, the $k$ superscript refers to the $k$th non-zero gradient (i.e., the $k$th weight vector/misclassified example) and $t$ is the number of mistakes seen thus far.$$\begin{align} G^t_j &= \sum_{k=1}^t \left(\frac{\partial \mathcal{L}}{\partial w^k_j}\right)^2 \\ H^t &= \sum_{k=1}^t \left(\frac{\partial \mathcal{L}}{\partial \theta^k}\right)^2\end{align}$$For example, on the 3rd mistake ($t = 3$), $G^3_j$ is the sum of the squares of the first three non-zero gradients ($\left(\frac{\partial \mathcal{L}}{\partial w^1_j}\right)^2$, $\left(\frac{\partial \mathcal{L}}{\partial w^2_j}\right)^2$, and $\left(\frac{\partial \mathcal{L}}{\partial w^3_j}\right)^2$).Then $\mathbf{G}^3$ is used to calculate the 4th value of the weight vector as follows.On example $(\mathbf{x}, y)$, if $y(\mathbf{w}^\intercal \mathbf{x} + \theta) \leq 1$, then the parameters are updated with the following equations:$$\begin{align} \mathbf{w}^{t+1} &\gets \mathbf{w}^t + \eta \cdot \frac{y \cdot \mathbf{x}}{\sqrt{\mathbf{G}^t}} \\ \theta^{t+1} &\gets \theta^t + \eta \frac{y}{\sqrt{H^t}}\end{align}$$Note that, although we use the hinge loss with the elbow at 1 for training, you still make the prediction based on whether or not $y(\mathbf{w}^\intercal \mathbf{x} + \theta) \leq 0$ during testing. 1.4.2 HyperparametersFor the experiment, choose $\eta \in \{1.5, 0.25, 0.03, 0.005, 0.001\}$ 1.4.3 Initialization$\mathbf{w} = [0, 0, \dots, 0]$ and $\theta = 0$.
###Code
class AdaGrad(Classifier):
def __init__(self, eta, features):
# DO NOT change the names of these 3 data members because
# they are used in the unit tests
self.eta = eta
self.w = {feature: 0.0 for feature in features}
self.theta = 0
self.G = {feature: 1e-5 for feature in features} # 1e-5 prevents divide by 0 problems
self.H = 0
def process_example(self, x, y):
""" TODO: IMPLEMENT"""
import numpy as np
y_pred = self.predict_single(x)
dotpro = 0
if y != y_pred:
# calculate dot product
for feature, value in x.items():
dotpro += self.w[feature] * value
# update w
for feature, value in x.items():
if(y * (dotpro + self.theta) > 1):
dldw = 0
else:
dldw = -y * value
self.G[feature] += dldw ** 2
self.w[feature] += self.eta * y * value / np.sqrt(self.G[feature])
# update theta
if(y * (dotpro + self.theta) > 1):
dldtheta = 0
else:
dldtheta = -y
self.H += dldtheta ** 2
self.theta += self.eta * y / np.sqrt(self.H)
def predict_single(self, x):
""" TODO: IMPLEMENT"""
score = 0
for feature, value in x.items():
score += self.w[feature] * value
score += self.theta
if score <= 0:
return -1
return 1
###Output
_____no_output_____
###Markdown
1.5 Averaged Models (15 points) You will also implement the averaged version of the previous three algorithms.During the course of training, each of the above algorithms will have $K + 1$ different parameter settings for the $K$ different updates it will make during training.The regular implementation of these algorithms uses the parameter values after the $K$th update as the final ones.Instead, the averaged version use the weighted average of the $K + 1$ parameter values as the final parameter values.Let $m_k$ denote the number of correctly classified examples by the $k$th parameter values and $M$ the total number of correctly classified examples.The final parameter values are$$\begin{align} M &= \sum_{k=1}^{K+1} m_k \\ \mathbf{w} &\gets \frac{1}{M} \sum_{k=1}^{K+1} m_k \cdot \mathbf{w}^k \\ \theta &\gets \frac{1}{M} \sum_{k=1}^{K+1} m_k \cdot \theta^k \\\end{align}$$For each of the averaged versions of Perceptron, Winnow, and AdaGrad, use the same hyperparameters and initialization as before. 1.5.1 Implementation NoteImplementing the averaged variants of these algorithms can be tricky. While the final parameter values are based on the sum of $K$ different vectors, there is no need to maintain *all* of these parameters. Instead, you should implement these algorithms by keeping only two vectors, one which maintains the cumulative sum and the current one.Additionally, there are two ways of keeping track of these two vectors.One is more straightforward but prohibitively slow.The second requires some algebra to derive but is significantly faster to run.Try to analyze how the final weight vector is a function of the intermediate updates and their corresponding weights.It should take less than a minute or two for ten iterations for any of the averaged algorithms.**You need to think about how to efficiently implement the averaged algorithms yourself.**Further, the implementation for Winnow is slightly more complicated than the other two, so if you consistently have low accuracy for the averaged Winnow, take a closer look at the derivation.
###Code
class AveragedPerceptron(Classifier):
def __init__(self, features):
self.eta = 1
self.w = {feature: 0.0 for feature in features}
self.theta = 0
"""TODO: You will need to add data members here"""
self.M = 0
self.lastM = 0
self.weightedW = {feature: 0.0 for feature in features}
self.weightedT = 0
self.Mk = []
self.yvec = []
self.xvec = []
def process_example(self, x, y):
""" TODO: IMPLEMENT"""
y_pred = self.predict_single(x)
if y != y_pred:
self.weightedT += (self.M - self.lastM) * self.theta
# append variables for weighted W calculation
self.xvec.append(x)
self.yvec.append(y)
self.Mk.append(self.M - self.lastM)
# update weights
for feature, value in x.items():
self.w[feature] += self.eta * y * value
self.theta += self.eta * y
# reset lastM
self.lastM = self.M
else:
self.M += 1
def predict_single(self, x):
""" TODO: IMPLEMENT"""
score = 0
for feature, value in x.items():
score += self.w[feature] * value
score += self.theta
if score <= 0:
return -1
return 1
def finalize(self):
""" TODO: IMPLEMENT"""
self.M +=1
self.Msum = self.M
self.w = {feature: 0.0 for feature in features}
# sum up rebuild weight vectors from saved x,y,mk values by just summing
# 1/M * (m1+m2+...mk)*y*x and (mi) terms reduces m[i] every iteration
for i in range(len(self.yvec)):
for feature, value in self.xvec[i].items():
self.weightedW[feature] += 1/self.M * self.Msum * \
self.eta * self.yvec[i] * value
# self.w[feature] += 1/self.M * self.Msum * self.eta * self.yvec[i] * value
self.Msum -= self.Mk[i]
self.theta = 1/self.M * self.weightedT
self.w = self.weightedW
# test the averaged perceptron model
X_train, y_train, X_dev, y_dev, X_test, y_test, features = load_synthetic_data('dense')
AvgPerceptron = AveragedPerceptron(features)
iteration = 10
for iter in range(iteration):
for i in range(len(X_train)):
AvgPerceptron.process_example(X_train[i],y_train[i])
AvgPerceptron.finalize()
count = 0
for i in range(len(X_dev)):
x = X_dev[i]
y = AvgPerceptron.predict_single(x)
if y_dev[i] == y:
count += 1
print(count/len(X_dev))
class AveragedWinnow(Classifier):
def __init__(self, alpha, features):
self.alpha = alpha
self.w = {feature: 1.0 for feature in features}
self.theta = -len(features)
"""TODO: You will need to add data members here"""
self.M = 0
self.lastM = 0
self.weightedW = {feature: 1.0 for feature in features}
def process_example(self, x, y):
""" TODO: IMPLEMENT"""
y_pred = self.predict_single(x)
if y != y_pred:
for feature, value in x.items():
self.w[feature] = self.w[feature] * pow(self.alpha,y*value)
for feature in self.weightedW:
self.weightedW[feature] += (self.M - self.lastM) * self.w[feature]
# self.M += 1
self.lastM = self.M
else:
self.M +=1
def predict_single(self, x):
""" TODO: IMPLEMENT"""
score = 0
for feature, value in x.items():
score += self.w[feature] * value
score += self.theta
if score <= 0:
return -1
return 1
def finalize(self):
""" TODO: IMPLEMENT"""
self.M += 1
for feature in self.weightedW:
self.w[feature] = 1/self.M * self.weightedW[feature]
# test the averaged Winnow model
X_train, y_train, X_dev, y_dev, X_test, y_test, features = load_synthetic_data('sparse')
iteration = 10
alpha = 1.1
AvgWinnow = AveragedWinnow(alpha,features)
AvgWinnow.train(X_train,y_train)
# AvgWinnow = Winnow(alpha,features)
# AvgWinnow.train(X_train,y_train)
count = 0
for i in range(len(X_dev)):
x = X_dev[i]
y = AvgWinnow.predict_single(x)
if y_dev[i] == y:
count += 1
print(count/len(X_dev))
class AveragedAdaGrad(Classifier):
def __init__(self, eta, features):
self.eta = eta
self.w = {feature: 0.0 for feature in features}
self.theta = 0
self.G = {feature: 1e-5 for feature in features}
self.H = 0
"""TODO: You will need to add data members here"""
self.M = 0
self.lastM = 0
self.weightedW = {feature: 1.0 for feature in features}
self.weightedT = 0
def process_example(self, x, y):
""" TODO: IMPLEMENT"""
import numpy as np
y_pred = self.predict_single(x)
dotpro = 0
if y != y_pred:
for feature in self.weightedW:
self.weightedW[feature] += (self.M - self.lastM) * self.w[feature]
self.weightedT += (self.M - self.lastM) * self.theta
# append variables for weighted W calculation
self.xvec.append(x)
self.yvec.append(y)
self.Mk.append(self.M - self.lastM)
# calculate dot product
for feature, value in x.items():
dotpro += self.w[feature] * value
# update w
for feature, value in x.items():
if(y * (dotpro + self.theta) > 1):
dldw = 0
else:
dldw = -y * value
self.G[feature] += dldw ** 2
self.w[feature] += self.eta * y * value / np.sqrt(self.G[feature])
# update theta
if(y * (dotpro + self.theta) > 1):
dldtheta = 0
else:
dldtheta = -y
self.H += dldtheta ** 2
self.theta += self.eta * y / np.sqrt(self.H)
self.lastM = self.M
else:
self.M += 1
def predict_single(self, x):
""" TODO: IMPLEMENT"""
score = 0
for feature, value in x.items():
score += self.w[feature] * value
score += self.theta
if score <= 0:
return -1
return 1
def finalize(self):
""" TODO: IMPLEMENT"""
self.M += 1
for feature in self.weightedW:
self.w[feature] = 1/self.M * self.weightedW[feature]
self.theta = 1/self.M * self.weightedT
# test the averaged Adagrad model
X_train, y_train, X_dev, y_dev, X_test, y_test, features = load_synthetic_data('dense')
# 𝜂∈{1.5,0.25,0.03,0.005,0.001}
eta = 1.5
AvgAdaGrad = AveragedAdaGrad(eta,features)
AvgAdaGrad.train(X_train,y_train)
# OrigAdaGrad = AdaGrad(eta,features)
# OrigAdaGrad.train(X_train,y_train)
count = 0
for i in range(len(X_dev)):
x = X_dev[i]
y = AvgAdaGrad.predict_single(x)
if y_dev[i] == y:
count += 1
print(count/len(X_dev))
###Output
0.9445
###Markdown
1.6 Support Vector MachinesAlthough we have not yet covered SVMs in class, you can still train them using the `sklearn` library.We will use a soft margin SVM for non-linearly separable data.You should use the `sklearn` implementation as follows:```from sklearn.svm import LinearSVCclassifier = LinearSVC(loss='hinge')classifier.fit(X, y)````sklearn` requires a different feature representation than what we use for the Perceptron models.The provided Python template code demonstrates how to convert to the require representation.Given training samples $S = \{(\mathbf{x}^1, y^1), (\mathbf{x}^2, y^2), \dots, (\mathbf{x}^m, y^m)\}$, the objective for the SVM is the following:$$\begin{equation} \min_{\mathbf{w}, b, \boldsymbol{\xi}} \frac{1}{2} \vert\vert \mathbf{w}\vert\vert^2_2 + C \sum_{i=1}^m \xi_i\end{equation}$$subject to the following constraints:$$\begin{align} y^i(\mathbf{w}^\intercal \mathbf{x}^i + b) \geq 1 - \xi_i \;\;&\textrm{for } i = 1, 2, \dots, m \\ \xi_i \geq 0 \;\;& \textrm{for } i = 1, 2, \dots, m\end{align}$$
###Code
class SVMClassifier(Classifier):
def __init__(self):
from sklearn.svm import LinearSVC
self.local_classifier = LinearSVC(loss = 'hinge')
self.vectorizer = DictVectorizer()
def trainSVM(self,X_train,y_train):
X_train_dict = self.vectorizer.fit_transform(X_train)
self.local_classifier.fit(X_train_dict,y_train)
def testSVM(self,X_test,y_test):
X_test_dict = self.vectorizer.transform(X_test)
return self.local_classifier.score(X_test_dict,y_test)
"""TODO: Create an SVM classifier"""
X_train, y_train, X_dev, y_dev, X_test, y_test, features = load_synthetic_data('dense')
# This is how you convert from the way we represent features in the
# Perceptron code to how you need to represent features for the SVM.
# You can then train with (X_train_dict, y_train) and test with
# (X_conll_test_dict, y_conll_test) and (X_enron_test_dict, y_enron_test)
vectorizer = DictVectorizer()
X_train_dict = vectorizer.fit_transform(X_train)
X_test_dict = vectorizer.transform(X_test)
from sklearn.svm import LinearSVC
classifier = LinearSVC(loss = 'hinge')
classifier.fit(X_train_dict,y_train)
classifier.score(X_test_dict,y_test)
###Output
_____no_output_____
###Markdown
Section 2. DatasetsIn this section, we describe the synthetic and NER datasets that you will use for your experiments.For the NER datasets, there is also an explanation for the features which you need to extract from the data. 2.1 Synthetic Data 2.1.1 IntroductionThe synthetic datasets have features and labels which are automatically generated from a python script.Each instance will have $n$ binary features and are labeled according to a $l$-of-$m$-of-$n$ Boolean function.Specifically, there is a set of $m$ features such that an example if positive if and only if at least $l$ of these $m$ features are active.The set of $m$ features is the same for the dataset (i.e., it is not a separate set of $m$ features for each individual instance).We provide two versions of the synthetic dataset called sparse and dense.For both datasets, we set $l = 10$ and $m=20$.We set $n = 200$ for the sparse data and $n = 40$ for the dense data.Additionally, we add noise to the data as follows:With probability $0.05$ the label assigned by the function is changed and with probability $0.001$ each feature value is changed.Consequently, the data is not linearly separable.We have provided you with three data splits for both sparse and dense with 10,000 training, 2,000 development, and 2,000 testing examples.Section 3 describes the experiments that you need to run on these datasets. 2.1.2 Feature RepresentationThe features of the synthetic data provided are vectors of 0s and 1s.Storing these large matrices requires lots of memory so we use a sparse representation that stores them as dictionaries instead.For example, the vector $[0,1,0,0,0,1]$ can be stored as `{"x2": 1,"x6": 1}` (using 1-based indexing).We have provided you with the code for parsing and converting the data to this format.You can use these for the all algorithms you develop except the SVM.Since you will be using the implementation of SVM from sklearn, you will need to provide a vector to it. You can use `sklearn.feature_extraction.DictVectorizer` for converting feature-value dictionaries to vectors. 2.2 NER DataIn addition to the synthetic data, we have provided you two datasets for the task of named-entity recognition (NER).The goal is to identify whether strings in text represent names of people, organizations, or locations.An example instance looks like the following:``` [PER Wolff] , currently a journalist in [LOC Argentina] , played with [PER del Bosque] in the final years of the seventies in [ORG Real Madrid] .```In this problem, we will simplify the task to identifying whether a string is named entity or not (that is, you don't have to say which type of entity it is).For each token in the input, we will use the tag $\texttt{I}$ to denote that token is an entity and $\texttt{O}$ otherwise.For example, the full tagging for the above instace is as follows:``` [I Wolff] [O ,] [O currently] [a] [O journalist] [O in] [I Argentina] [O ,] [O played] [O with] [I del] [I Bosque] [O in] [O the] [O final] [O years] [O of] [O the] [O seventies] [O in] [I Real] [I Madrid] .```Given a sentence $S = w_1, w_2, \dots, w_n$, you need to predict the `I`, `O` tag for each word in the sentence.That is, you will produce the sequence $Y = y_1, y_2, \dots, y_n$ where $y_i \in$ {`I`, `O`}. 2.2.1 Datasets: CoNLL and EnronWe have provided two datasets, the CoNLL dataset which is text from news articles, and Enron, a corpus of emails.The files contain one word and one tag per line.For CoNLL, there are training, development, and testing files, whereas Enron only has a test dataset.There are 14,987 training sentences (204,567 words), 336 development sentences (3,779 words), and 303 testing sentences (3,880 words) in CoNLL.For Enron there are 368 sentences (11,852 words).**Please note that the CoNLL dataset is available only for the purposes of this assignment.It is copyrighted, and you are granted access because you are a Penn student, but please delete it when you are done with the homework.** 2.2.2 Feature ExtractionThe NER data is provided as raw text, and you are required to extract features for the classifier.In this assignment, we will only consider binary features based on the context of the word that is supposed to be tagged.Assume that there are $V$ unique words in the dataset and each word has been assigned a unique ID which is a number $\{1, 2, \dots, V\}$.Further, $w_{-k}$ and $w_{+k}$ indicate the $k$th word before and after the target word.The feature templates that you should use to generate features are as follows:| Template | Number of Features ||----------------------|--------------------|| $w_{-3}$ | $V$ || $w_{-2}$ | $V$ || $w_{-1}$ | $V$ || $w_{+1}$ | $V$ || $w_{+2}$ | $V$ || $w_{+3}$ | $V$ || $w_{-1}$ & $w_{-2}$ | $V \times V$ || $w_{+1}$ \& $w_{+2}$ | $V \times V$ || $w_{-1}$ \& $w_{+1}$ | $V \times V$ |Each feature template corresponds to a set of features that you will compute (similar to the features you generated in problem 2 from the first homework assignment).The $w_{-3}$ feature template corresponds to $V$ features where the $i$th feature is 1 if the third word to the left of the target word has ID $i$.The $w_{-1} \& w_{+1}$ feature template corresponds to $V \times V$ features where there is one feature for every unique pair words.For example, feature $(i - 1) \times V + j$ is a binary feature that is 1 if the word 1 to the left of the target has ID $i$ and the first word to the right of the target has ID $j$.In practice, you will not need to keep track of the feature IDs.Instead, each feature will be given a name such as "$w_{-1}=\textrm{the} \& w_{+1}=\textrm{cat}$".In total, all of the above feature templates correspond to a very large number of features.However, for each word, there will be exactly 9 features which are active (non-zero), so the feature vector is quite sparse.You will represent this as a dictionary which maps from the feature name to the value.In the provided Python template, we have implemented a couple of the features for you to demonstrate how to compute them and what the naming scheme should look like.In order to deal with the first two words and the last two words in a sentence, we will add special symbol "SSS" and "EEE" to the vocabulary to represent the words before the first word and the words after the last word.Notice that in the test data you may encounter a word that was not observed in training, and therefore is not in your dictionary.In this case, you cannot generate a feature for it, resulting in less than 7 active features in some of the test examples. Section 3. Experiments (65 points total) You will run two sets of experiments, one using the synthetic data and one using the NER data. 3.1 Synthetic Experiment (30 + 10 extra credit points)This experiment will explore the impact that the amount of training data has on model performance.First, you will do hyperparameter tuning for Winnow and Perceptron with AdaGrad (both standard and averaged versions).Then you will generate learning curves that will plot the size of the training data against the performance.Finally, for each of the models trained on all of the training data, you will find the test score.You should use accuracy to compute the performance of the model.In summary, the experiment consists of three parts1. Parameter Tuning2. Learning Curves3. Final Evaluation 3.1.1 Parameter Tuning (10 points)For both the Winnow and Perceptron with AdaGrad (standard and averaged), there are hyperparameters that you need to choose.(The same is true for SVM, but you should only use the default settings.)Similarly to cross-validation from Homework 1, we will estimate how well each model will do on the true test data using the development dataset (we will not run cross-validation), and choose the hyperparameter settings based on these results.For each hyperparameter value in Section 1, train a model using that value on the training data and compute the accuracy on the development dataset. Each model should be trained for 10 iterations (i.e., 10 passes over the entire dataset).TODO: Fill in the table with the best hyperparameter values and the corresponding validation accuracies.Repeat this for both the sparse and dense data. Winnow Sweep| $\alpha$ | Sparse | Dense ||----------|--------|-------|| 1.1 | 0.8935 | 0.8995 || 1.01 | 0.9270 | 0.9215 || 1.005 | 0.9195 | 0.9080 || 1.0005 | 0.5630 | 0.8615 || 1.0001 | 0.5205 | 0.6140 | Averaged Winnow Sweep| $\alpha$ | Sparse | Dense ||----------|--------|-------|| 1.1 | 0.9390 | 0.9445 || 1.01 | 0.8980 | 0.9335 || 1.005 | 0.8405 | 0.9150 || 1.0005 | 0.5255 | 0.6700 || 1.0001 | 0.5095 | 0.5460 | AdaGrad Sweep| $\eta$ | Sparse | Dense ||----------|--------|-------|| 1.5 | 0.8745 | 0.9325 || 0.25 | 0.8745 | 0.9325 || 0.03 | 0.8745 | 0.9325 || 0.005 | 0.8745 | 0.9325 || 0.001 | 0.8745 | 0.9325 | Averaged AdaGrad Sweep| $\eta$ | Sparse | Dense ||----------|--------|-------|| 1.5 | 0.8935 | 0.9445 || 0.25 | 0.8935 | 0.9445 || 0.03 | 0.8935 | 0.9445 || 0.005 | 0.8935 | 0.9445 || 0.001 | 0.8935 | 0.9445 | 3.1.2 Learning Curves (10 points)Next, you will train all 7 models with different amounts of training data.For Winnow and Perceptron with AdaGrad (standard and averaged), use the best hyperparameters from the parameter tuning experiment.Each of the datasets contains 10,000 training examples.You will train each model 11 times on varying amounts of training data.The first 10 will increase by 500 examples: 500, 1k, 1.5k, 2k, ..., 5k.The 11th model should use all 10k examples.Each Perceptron-based model should be trained for 10 iterations (e.g., 10 passes over the total number of training examples available to that model).The SVM can be run until convergence with the default parameters.For each model, compute the accuracy on the development dataset and plot the results using the provided code.There should be a separate plot for the sparse and dense data.**Note** how we have included an image in markdown. You should do the same for both plots and include them in the output below by running your experiment, saving your plots to the images folder, and linking it to this cell. Sparse Plot  Dense Plot
###Code
# set up the learning curve variables and load the dataset
perceptron_accs = np.zeros(11)
winnow_accs = np.zeros(11)
adagrad_accs = np.zeros(11)
avg_perceptron_accs = np.zeros(11)
avg_winnow_accs = np.zeros(11)
avg_adagrad_accs = np.zeros(11)
svm_accs = np.zeros(11)
X_train, y_train, X_dev, y_dev, X_test, y_test, features = load_synthetic_data('sparse')
# basic perceptron
for i in range(1,12):
X_train_i = X_train[0:(i*500)]
y_train_i = y_train[0:(i*500)]
if i == 11:
X_train_i = X_train
y_train_i = y_train
eta = 1.5
model = Perceptron(features)
model.train(X_train_i,y_train_i)
perceptron_accs[i-1] = compute_accuracy_313(X_dev,y_dev,model)
# averaged perceptron
for i in range(1,12):
X_train_i = X_train[0:(i*500)]
y_train_i = y_train[0:(i*500)]
if i == 11:
X_train_i = X_train
y_train_i = y_train
model = AveragedPerceptron(features)
model.train(X_train_i,y_train_i)
avg_perceptron_accs[i-1] = compute_accuracy_313(X_dev,y_dev,model)
# winnow
for i in range(1,12):
X_train_i = X_train[0:(i*500)]
y_train_i = y_train[0:(i*500)]
if i == 11:
X_train_i = X_train
y_train_i = y_train
alpha = 1.01
model = Winnow(alpha,features)
model.train(X_train_i,y_train_i)
winnow_accs[i-1] = compute_accuracy_313(X_dev,y_dev,model)
# averaged winnow
for i in range(1,12):
X_train_i = X_train[0:(i*500)]
y_train_i = y_train[0:(i*500)]
if i == 11:
X_train_i = X_train
y_train_i = y_train
alpha = 1.1
model = AveragedWinnow(alpha,features)
model.train(X_train_i,y_train_i)
avg_winnow_accs[i-1] = compute_accuracy_313(X_dev,y_dev,model)
# adagrad
for i in range(1,12):
X_train_i = X_train[0:(i*500)]
y_train_i = y_train[0:(i*500)]
if i == 11:
X_train_i = X_train
y_train_i = y_train
eta = 1.5
model = AdaGrad(eta,features)
model.train(X_train_i,y_train_i)
adagrad_accs[i-1] = compute_accuracy_313(X_dev,y_dev,model)
# averaged AdaGrad
for i in range(1,12):
X_train_i = X_train[0:(i*500)]
y_train_i = y_train[0:(i*500)]
if i == 11:
X_train_i = X_train
y_train_i = y_train
eta = 1.5
model = AveragedAdaGrad(eta,features)
model.train(X_train_i,y_train_i)
avg_adagrad_accs[i-1] = compute_accuracy_313(X_dev,y_dev,model)
from sklearn.svm import LinearSVC
for i in range(1,12):
X_train_i = X_train[0:(i*500)]
y_train_i = y_train[0:(i*500)]
if i == 11:
X_train_i = X_train
y_train_i = y_train
vectorizer = DictVectorizer()
X_train_dict = vectorizer.fit_transform(X_train_i)
X_dev_dict = vectorizer.transform(X_dev)
classifier = LinearSVC(loss = 'hinge')
classifier.fit(X_train_dict,y_train_i)
svm_accs[i-1] = classifier.score(X_dev_dict,y_dev)
plot_learning_curves(perceptron_accs,
winnow_accs,
adagrad_accs,
avg_perceptron_accs,
avg_winnow_accs,
avg_adagrad_accs,
svm_accs
)
def compute_accuracy_313(X_dev,y_dev,classifier):
count = 0
for i in range(len(X_dev)):
x = X_dev[i]
y = classifier.predict_single(x)
if y_dev[i] == y:
count += 1
return (count/len(X_dev))
###Output
_____no_output_____
###Markdown
3.1.3 Final Evaluation (5 points)Finally, for each of the 7 models, train the models on all of the training data and compute the test accuracy.For Winnow and Perceptron with AdaGrad, use the best hyperparameter settings you found.Report these accuracies in a table. We will run our models with [500, 1000, 1500, 2000, 2500, 3000, 3500, 4000, 4500, 5000, 10000] examples.
###Code
sample_sizes = [500 * i for i in range(1, 11)] + [10_000]
def run_synthetic_experiment(dataset_type='sparse'):
"""
TODO: IMPLEMENT
Runs the synthetic experiment on either the sparse or dense data
depending on the data path (e.g. "data/sparse" or "data/dense").
We have provided how to train the Perceptron on the training and
test on the testing data (the last part of the experiment). You need
to implement the hyperparameter sweep, the learning curves, and
predicting on the test dataset for the other models.
"""
X_train, y_train, X_dev, y_dev, X_test, y_test, features = load_synthetic_data(dataset_type)
# TODO: YOUR CODE HERE. Determine the best hyperparameters for the relevant models
# report the validation accuracy after training using the best hyper parameters
# i think i did all of these picked the best hyper parameters way above here near the hyper parameter tables
# TOOD: YOUR CODE HERE. Downsample the dataset to the number of desired training
# instances (e.g. 500, 1000), then train all of the models on the
# sampled dataset. Compute the accuracy and add the accuracies to
# the corresponding list. Use plot_learning_curves()
# I did all of these near where the plot is, separated into 7 or 8 cells. please refer to that.
# TODO: Train all 7 models on the training data and make predictions
# for test data
# We will show you how to do it for the basic Perceptron model.
classifier = Perceptron(features)
classifier.train(X_train, y_train)
y_pred = classifier.predict(X_test)
acc = accuracy_score(y_test, y_pred)
print(f"Perceptron's accuracy is {acc}")
# YOUR CODE HERE: Repeat for the other 6 models.
# Averaged Perceptron
classifier = AveragedPerceptron(features)
classifier.train(X_train, y_train)
y_pred = classifier.predict(X_test)
acc = accuracy_score(y_test, y_pred)
print(f"Averaged Perceptron's accuracy is {acc}")
# Winnow
alpha = 1.01
classifier = Winnow(alpha,features)
classifier.train(X_train, y_train)
y_pred = classifier.predict(X_test)
acc = accuracy_score(y_test, y_pred)
print(f"Winnow's accuracy is {acc}")
# Averaged Winnow
alpha = 1.1
classifier = AveragedWinnow(alpha,features)
classifier.train(X_train, y_train)
y_pred = classifier.predict(X_test)
acc = accuracy_score(y_test, y_pred)
print(f"Averged Winnow's accuracy is {acc}")
# Averaged Winnow
eta = 1.5
classifier = AdaGrad(eta,features)
classifier.train(X_train, y_train)
y_pred = classifier.predict(X_test)
acc = accuracy_score(y_test, y_pred)
print(f"AdaGrad's accuracy is {acc}")
# Averaged Winnow
eta = 1.5
classifier = AveragedAdaGrad(eta,features)
classifier.train(X_train, y_train)
y_pred = classifier.predict(X_test)
acc = accuracy_score(y_test, y_pred)
print(f"Averged AdaGrad's accuracy is {acc}")
vectorizer = DictVectorizer()
X_train_dict = vectorizer.fit_transform(X_train)
X_test_dict = vectorizer.transform(X_test)
classifier = LinearSVC(loss = 'hinge')
classifier.fit(X_train_dict,y_train)
acc = classifier.score(X_test_dict,y_test)
print(f"SVM's accuracy is {acc}")
"""
Run the synthetic experiment on the sparse dataset. For reference,
"synthetic/sparse" is the path to where the data is located.
Note: This experiment takes substantial time (around 15 minutes),
so don't worry if it's taking a long time to finish.
"""
run_synthetic_experiment('sparse')
"""
Run the synthetic experiment on the dense dataset. For reference,
"synthetic/dense" is the path to where the data is located.
Note: this experiment should take much less time.
"""
run_synthetic_experiment('dense')
###Output
Perceptron's accuracy is 0.9205
Averaged Perceptron's accuracy is 0.9405
Winnow's accuracy is 0.9255
Averged Winnow's accuracy is 0.9405
AdaGrad's accuracy is 0.9325
Averged AdaGrad's accuracy is 0.9405
SVM's accuracy is 0.9405
###Markdown
Questions (5 points)Answer the following questions:1. Discuss the trends that you see when comparing the standard version of an algorithm to the averaged version (e.g., Winnow versus Averaged Winnow). Is there an observable trend? Typically averaged version of the algorithm has a slightly higher accuracy than the standard version, only 0.01~0.02 improvement but quite consistent. Averaged version also tends to converge a faster than regular version2. We provided you with 10,000 training examples. Were all 10,000 necessary to achieve the best performance for each classifier? If not, how many were necessary? (Rough estimates, no exact numbers required) Not all were necessary. Looking at the learning rate graph, accuracy for both dense and sparse datasets plateau around 6000-7000 training examples for even the worst-performing algorithm. Winnow and averaged winnow converged around 2000 and 4000 examples respectively. For the best-performing algorithm, SVM, it converge to the highest accuracy with only about 1000 training examples. Other algorithm converged between 5000-7000 examples. Further examples did not provide any improvement over accuracy.3. Report your Final Test Accuracies | Model | Sparse | Dense ||---------------------|--------|-------|| Perceptron | 0.7170 | 0.9205 || Winnow | 0.9260 | 0.9255 || AdaGrad | 0.8780 | 0.9325 || Averaged Perceptron | 0.9135 | 0.9405 || Averaged Winnow | 0.9360 | 0.9405 || Averaged AdaGrad | 0.8840 | 0.9405 || SVM | 0.9360 | 0.9405 | 3.1.5 Extra Credit (10 points)Included in the resources for this homework assignment is the code that we used to generate the synthetic data.We used a small amount of noise to create the dataset which you ran the experiments on.For extra credit, vary the amount of noise in either/both of the label and features.Then, plot the models' performances as a function of the amount of noise.Discuss your observations. TODO: Extra Credit observations I ran the experiment with varying random values using the code shown below. Key thing is the 100% random value means that I randomly switched len(y_train) amount of the y_train, but they could've been repeatedly flipped. In the figure below, we can see the perceptron and adagrad approaches 50% which is essentially guess randomly. However, winnow algorithm did not descend to that low of an accuracy because a wrong y_train for winnow means that the added weight goes from w^alpha*y*x to 1/w^alpha*y*x. While for perceptron and adagrad, a wrong y_train means altering the weight vector in the completely opposite direction. Therefore, winnow accuracy decreased but not to a meaningless value while adagrad and perceptron algorithms become obsolete with 100% noise. For some reason SVM did not change. I experiemnted with different ways to make noise but its accuracy end up being a step function not sure why.
###Code
X_train, y_train, X_dev, y_dev, X_test, y_test, features = load_synthetic_data('dense')
noise = np.linspace(0,1,21)
ec_winnowacc = np.zeros(len(noise))
ec_perceptronacc = np.zeros(len(noise))
ec_adagradacc = np.zeros(len(noise))
ec_svmacc = np.zeros(len(noise))
for i in range(len(noise)):
X_train, y_train, X_dev, y_dev, X_test, y_test, features = load_synthetic_data('dense')
classifier = Perceptron(features)
num = int(len(y_train) * noise[i])
for j in range(num):
tempRand = np.random.randint(0,len(y_train))
y_train[tempRand] = -y_train[tempRand]
classifier.train(X_train, y_train)
y_pred = classifier.predict(X_test)
ec_perceptronacc[i] = accuracy_score(y_test, y_pred)
for i in range(len(noise)):
X_train, y_train, X_dev, y_dev, X_test, y_test, features = load_synthetic_data('dense')
classifier = Winnow(1.1,features)
num = int(len(y_train) * noise[i])
for j in range(num):
tempRand = np.random.randint(0,len(y_train))
y_train[tempRand] = -y_train[tempRand]
classifier.train(X_train, y_train)
y_pred = classifier.predict(X_test)
ec_winnowacc[i] = accuracy_score(y_test, y_pred)
for i in range(len(noise)):
X_train, y_train, X_dev, y_dev, X_test, y_test, features = load_synthetic_data('dense')
classifier = AdaGrad(1.5,features)
num = int(len(y_train) * noise[i])
for j in range(num):
tempRand = np.random.randint(0,len(y_train))
y_train[tempRand] = -y_train[tempRand]
classifier.train(X_train, y_train)
y_pred = classifier.predict(X_test)
ec_adagradacc[i] = accuracy_score(y_test, y_pred)
for i in range(len(noise)):
X_train, y_train, X_dev, y_dev, X_test, y_test, features = load_synthetic_data('dense')
num = int(len(y_train) * noise[i])
for j in range(num):
tempRand = np.random.randint(0,len(y_train))
y_train[tempRand] = -y_train[tempRand]
vectorizer = DictVectorizer()
X_train_dict = vectorizer.fit_transform(X_train)
X_test_dict = vectorizer.transform(X_test)
classifier = LinearSVC(loss = 'hinge')
classifier.fit(X_train_dict,y_train)
ec_svmacc[i] = classifier.score(X_test_dict,y_test)
plot_EC_curves(ec_perceptronacc,ec_winnowacc,ec_adagradacc,ec_svmacc)
"""
A helper function that plots the relationship between number of examples
and accuracies for all the models.
You should not need to edit this method.
"""
def plot_EC_curves(
perceptron_accs,
winnow_accs,
adagrad_accs,
svm_accs
):
accuracies = [
('perceptron', perceptron_accs),
('winnow', winnow_accs),
('adagrad', adagrad_accs),
('svm', svm_accs)
]
x = np.linspace(0,1,21)
plt.figure()
# f, (ax, ax2) = plt.subplots(1, 2, sharey=True, facecolor='w')
for label, acc_list in accuracies:
assert len(acc_list) == 21
plt.plot(x, acc_list, label=label)
# ax2.plot(x, acc_list, label=label)
# plt.set_xlim(0,1)
# ax.set_xlim(0, 1)
# ax2.set_xlim(9500, 10000)
# ax2.set_xticks([10000])
# hide the spines between ax and ax2
# plt.spines['right'].set_visible(False)
# ax2.spines['left'].set_visible(False)
# ax.yaxis.tick_left()
# ax.tick_params(labelright='off')
# ax2.yaxis.tick_right()
# ax2.legend()
plt.legend()
plt.title('Extra Credit Noise Plot')
plt.show()
ec_winnowacc
###Output
_____no_output_____
###Markdown
3.2 NER Experiment: Welcome to the Real World (35 points)The experiment with the NER data will analyze how changing the domain of the training and testing data can impact the performance of a model.Instead of accuracy, you will use your $F_1$ score implementation in Section 0 to evaluate how well a model does.Recall measures how many of the actual entities the model successfully tagged as an entity.$$\begin{align} \textrm{Precision} &= \frac{\\textrm{(Actually Entity & Model Predicted Entity)}}{\\textrm{(Model Predicted Entity)}} \\ \textrm{Recall} &= \frac{\\textrm{(Actually Entity & Model Predicted Entity)}}{\\textrm{(Actually Entity)}} \\ \textrm{F}_1 &= 2 \cdot \frac{\textrm{Precision} \times \textrm{Recall}}{\textrm{Precision} + \textrm{Recall}}\end{align}$$For this experiment, you will only use the averaged basic Perceptron and SVM.Hence, no parameter tuning is necessary.Train both models on the CoNLL training data then compute the F$_1$ on the development and testing data of both CoNLL and Enron.Note that the model which is used to predict labels for Enron is trained on CoNLL data, not Enron data.Report the F$_1$ scores in a table. 3.2.1 Extracting NER Features (25 points)Reread Section 2.2.2 to understand how to extract the features required to train the modelsand translate it to the code below.
###Code
def extract_ner_features_train(train):
"""
Extracts feature dictionaries and labels from the data in "train"
Additionally creates a list of all of the features which were created.
We have implemented the w-1 and w+1 features for you to show you how
to create them.
TODO: You should add your additional featurization code here.
(which might require adding and/or changing existing code)
"""
y = []
X = []
features = set()
for sentence in train:
padded = [('SSS', None)] + [('SSS', None)] + [('SSS', None)] + sentence[:]\
+ [('EEE', None)] + [('EEE', None)] + [('EEE', None)]
for i in range(3, len(padded) - 3):
y.append(1 if padded[i][1] == 'I' else -1)
feat1 = 'w-1=' + str(padded[i - 1][0])
feat2 = 'w+1=' + str(padded[i + 1][0])
feat3 = 'w-3=' + str(padded[i - 3][0])
feat4 = 'w-2=' + str(padded[i - 2][0])
feat5 = 'w+2=' + str(padded[i + 2][0])
feat6 = 'w+3=' + str(padded[i + 3][0])
feat7 = 'w-1&w-2=' + str(padded[i - 1][0] + str(padded[i - 2][0]))
feat8 = 'w+1&w+2=' + str(padded[i + 1][0] + str(padded[i + 2][0]))
feat9 = 'w-1&w+1=' + str(padded[i - 1][0] + str(padded[i + 1][0]))
feats = [feat1, feat2, feat3, feat4, feat5, feat6, feat7, feat8, feat9]
features.update(feats)
feats = {feature: 1 for feature in feats}
X.append(feats)
return features, X, y
###Output
_____no_output_____
###Markdown
Now, repeat the process of extracting features from the test data.What is the difference between the code above and below?
###Code
def extract_features_dev_or_test(data, features):
"""
Extracts feature dictionaries and labels from "data". The only
features which should be computed are those in "features". You
should add your additional featurization code here.
TODO: You should add your additional featurization code here.
"""
y = []
X = []
for sentence in data:
padded = [('SSS', None)] + [('SSS', None)] + [('SSS', None)] + sentence[:]\
+ [('EEE', None)] + [('EEE', None)] + [('EEE', None)]
for i in range(3, len(padded) - 3):
y.append(1 if padded[i][1] == 'I' else -1)
feat1 = 'w-1=' + str(padded[i - 1][0])
feat2 = 'w+1=' + str(padded[i + 1][0])
feat3 = 'w-3=' + str(padded[i - 3][0])
feat4 = 'w-2=' + str(padded[i - 2][0])
feat5 = 'w+2=' + str(padded[i + 2][0])
feat6 = 'w+3=' + str(padded[i + 3][0])
feat7 = 'w-1&w-2=' + str(padded[i - 1][0] + str(padded[i - 2][0]))
feat8 = 'w+1&w+2=' + str(padded[i + 1][0] + str(padded[i + 2][0]))
feat9 = 'w-1&w+1=' + str(padded[i - 1][0] + str(padded[i + 1][0]))
feats = [feat1, feat2, feat3, feat4, feat5, feat6, feat7, feat8, feat9]
feats = {feature: 1 for feature in feats if feature in features}
X.append(feats)
return X, y
###Output
_____no_output_____
###Markdown
3.2.2 Running the NER ExperimentAs stated previously, train both models on the CoNLL training data then compute the $F_1$ on the development and testing data of both CoNLL and Enron. Note that the model which is used to predict labels for Enron is trained on CoNLL data, not Enron data.
###Code
def run_ner_experiment(data_path):
"""
Runs the NER experiment using the path to the ner data
(e.g. "ner" from the released resources). We have implemented
the standard Perceptron below. You should do the same for
the averaged version and the SVM.
The SVM requires transforming the features into a different
format. See the end of this function for how to do that.
"""
train = load_ner_data(dataset='conll', dataset_type='train')
conll_test = load_ner_data(dataset='conll', dataset_type='test')
enron_test = load_ner_data(dataset='enron', dataset_type='test')
features, X_train, y_train = extract_ner_features_train(train)
X_conll_test, y_conll_test = extract_features_dev_or_test(conll_test, features)
X_enron_test, y_enron_test = extract_features_dev_or_test(enron_test, features)
# TODO: We show you how to do this for Perceptron.
# You should do this for the Averaged Perceptron and SVM
classifier = Perceptron(features)
classifier.train(X_train, y_train)
y_pred = classifier.predict(X_conll_test)
conll_f1 = calculate_f1(y_conll_test, y_pred)
y_pred = classifier.predict(X_enron_test)
enron_f1 = calculate_f1(y_enron_test, y_pred)
print('Perceptron on NER')
print(' CoNLL', conll_f1)
print(' Enron', enron_f1)
print('Accuracy',accuracy_score(y_enron_test, y_pred))
# Averaged Perceptron
classifier = AveragedPerceptron(features)
classifier.train(X_train, y_train)
y_pred = classifier.predict(X_conll_test)
conll_f1 = calculate_f1(y_conll_test, y_pred)
y_pred = classifier.predict(X_enron_test)
enron_f1 = calculate_f1(y_enron_test, y_pred)
print('Averaged Perceptron on NER')
print(' CoNLL', conll_f1)
print(' Enron', enron_f1)
print('Accuracy',accuracy_score(y_enron_test, y_pred))
# SVM
# This is how you convert from the way we represent features in the
# Perceptron code to how you need to represent features for the SVM.
# You can then train with (X_train_dict, y_train) and test with
# (X_conll_test_dict, y_conll_test) and (X_enron_test_dict, y_enron_test)
vectorizer = DictVectorizer()
X_train_dict = vectorizer.fit_transform(X_train)
X_conll_test_dict = vectorizer.transform(X_conll_test)
X_enron_test_dict = vectorizer.transform(X_enron_test)
classifier = LinearSVC(loss = 'hinge')
classifier.fit(X_train_dict,y_train)
y_pred = classifier.predict(X_conll_test_dict)
conll_f1 = calculate_f1(y_conll_test,y_pred)
y_pred = classifier.predict(X_enron_test_dict)
enron_f1 = calculate_f1(y_enron_test, y_pred)
print('SVM on NER')
print(' CoNLL', conll_f1)
print(' Enron', enron_f1)
print('Accuracy',classifier.score(X_enron_test_dict,y_enron_test))
# Run the NER experiment. "ner" is the path to where the data is located.
run_ner_experiment('ner')
conll_test = load_ner_data(dataset='conll', dataset_type='test')
enron_test = load_ner_data(dataset='enron', dataset_type='test')
X_conll_test, y_conll_test = extract_features_dev_or_test(conll_test, features)
X_enron_test, y_enron_test = extract_features_dev_or_test(enron_test, features)
print(np.shape(y_conll_test))
print(np.shape(y_enron_test))
###Output
(3779,)
(8541,)
|
Ham_Spam.ipynb
|
###Markdown
What is the probability that an email be spam?Resource: [Link](https://github.com/Make-School-Courses/QL-1.1-Quantitative-Reasoning/blob/master/Notebooks/Conditional_Probability/Conditional_probability.ipynb) We know an email is spam, what is the probability that password be a word in it? (What is the frequency of password in a spam email?)* Dictionary of spam where its key would be unique words in spam emails and the value shows the occurance of that word
###Code
spam_data = {
"password": 2,
"review": 1,
"send": 3,
"us": 3,
"your": 3,
"account": 1
}
###Output
_____no_output_____
###Markdown

###Code
p_password_given_spam = float(spam_data['password']) / float(sum(spam_data.values()))
print(p_password_given_spam)
###Output
0.153846153846
###Markdown
Activity: Do the above computation for each word by writing code
###Code
spam = {}
ham = {}
spam_v = float(4)/float(6)
ham_v = float(2)/float(6)
def open_text(text, histogram):
full_text = text.split()
for word in full_text:
if word not in histogram:
histogram[word] = 1
else:
histogram[word] += 1
spam_texts = ['Send us your password', 'review us', 'Send your password', 'Send us your account']
ham_texts = ['Send us your review', 'review your password']
for text in spam_texts:
open_text(text, spam)
for text in ham_texts:
open_text(text, ham)
ls1 = []
ls2 = []
for i in spam:
# obtain the probability of each word by assuming the email is spam
p_word_given_spam = float(spam[i]) / float(sum(spam.values()))
# obtain the probability of each word by assuming the email is ham
p_word_given_ham = 0 if i not in ham else float(ham[i]) / float(sum(ham.values()))
p_word_in_email = float(p_word_given_spam * spam_v) + float(p_word_given_ham * ham_v)
# obtain the probability that for a seen word it belongs to spam email
p_word_is_in_spam = float(p_word_given_spam * spam_v) / float(p_word_in_email)
# obtain the probability that for a seen word it belongs to ham email
p_word_is_in_ham = float(p_word_given_ham * ham_v) / float(p_word_in_email)
print('WORD: {}\nProbability in spam: {}\nProbability in ham: {}\n'. format(i, p_word_is_in_spam, p_word_is_in_ham))
###Output
WORD: account
Probability in spam: 1.0
Probability in ham: 0.0
WORD: review
Probability in spam: 0.35
Probability in ham: 0.65
WORD: us
Probability in spam: 0.763636363636
Probability in ham: 0.236363636364
WORD: Send
Probability in spam: 0.763636363636
Probability in ham: 0.236363636364
WORD: password
Probability in spam: 0.682926829268
Probability in ham: 0.317073170732
WORD: your
Probability in spam: 0.617647058824
Probability in ham: 0.382352941176
|
100days/day 06 - postfix notation.ipynb
|
###Markdown
algorithm
###Code
ops = {
'+': float.__add__,
'-': float.__sub__,
'*': float.__mul__,
'/': float.__truediv__,
'^': float.__pow__,
}
def postfix(expression):
stack = []
for x in expression.split():
if x in ops:
x = ops[x](stack.pop(-2), stack.pop(-1))
else:
x = float(x)
stack.append(x)
return stack.pop()
###Output
_____no_output_____
###Markdown
run
###Code
postfix('1 2 + 4 3 - + 10 5 / *')
postfix('1 2 * 6 2 / + 9 7 - ^')
postfix('1 2 3 4 5 + + + +')
###Output
_____no_output_____
|
docs/examples/data_visualization/grid_layout/custom_layout.ipynb
|
###Markdown
Custom Layout Use the `Layout` class to create a variety of map views for comparison.For more information, run `help(Layout)`.This example uses two different custom layouts. The first with a vertical orientation (2x2) and the second, horizontal (1x4).
###Code
from cartoframes.auth import set_default_credentials
set_default_credentials('cartoframes')
from cartoframes.viz import Map, Layer, Layout
Layout([
Map(Layer('drought_wk_1')),
Map(Layer('drought_wk_2')),
Map(Layer('drought_wk_3')),
Map(Layer('drought_wk_4'))
], 2, 2)
Layout([
Map(Layer('drought_wk_1')),
Map(Layer('drought_wk_2')),
Map(Layer('drought_wk_3')),
Map(Layer('drought_wk_4'))
], 1, 4)
###Output
_____no_output_____
|
parse_and_plot_caffe_log.ipynb
|
###Markdown
Regexps: Text: 02 15:11:28.242069 31983 solver.cpp:341] Iteration 5655, Testing net (0) I1202 15:11:36.076130 374 blocking_queue.cpp:50] Waiting for data I1202 15:11:52.472803 31983 solver.cpp:409] Test net output 0: accuracy = 0.873288 I1202 15:11:52.472913 31983 solver.cpp:409] Test net output 1: loss = 0.605587 (* 1 = 0.605587 loss) Regexp: (?<=Iteration )(.*)(?=, Testing net) Result: 5655 Regexp: (?<=accuracy = )(.*) Result: 0.873288 Regexp: (?<=Test net output 1: loss = )(.*)(?= \()Result: 0.605587 Text:I1202 22:45:56.858299 31983 solver.cpp:237] Iteration 77500, loss = 0.000596309 I1202 22:45:56.858502 31983 solver.cpp:253] Train net output 0: loss = 0.000596309 (* 1 = 0.000596309 loss) Regexp: (?<=Iteration )(.*)(?=, loss) Result: 77500 Regexp: (?<=Train net output 0: loss = )(.*)(?= \() Result: 0.000596309 Text: test_iter: 1456test_interval: 4349base_lr: 5e-05display: 1000max_iter: 4000lr_policy: "fixed"momentum: 0.9weight_decay: 0.004snapshot: 2000 Regexp: (?<=base_lr: )(.*)(?=) Result: 5e-05 imports, and setting for pretty plots.
###Code
import matplotlib as mpl
import seaborn as sns
sns.set(style='ticks', palette='Set2')
sns.despine()
import matplotlib as mpl
mpl.rcParams['xtick.labelsize'] = 20
mpl.rcParams['ytick.labelsize'] = 20
%matplotlib inline
import re
import os
from matplotlib import pyplot as plt
import numpy as np
from scipy.stats import ttest_rel as ttest
import matplotlib
from matplotlib.backends.backend_pgf import FigureCanvasPgf
matplotlib.backend_bases.register_backend('pdf', FigureCanvasPgf)
pgf_with_rc_fonts = {
"font.family": "serif",
}
mpl.rcParams.update(pgf_with_rc_fonts)
test_iteration_regex = re.compile("(?<=Iteration )(.*)(?=, Testing net)")
test_accuracy_regex = re.compile("(?<=accuracy = )(.*)")
test_loss_regex = re.compile("(?<=Test net output #1: loss = )(.*)(?= \()")
train_iteration_regex = re.compile("(?<=Iteration )(.*)(?=, loss)")
train_loss_regex = re.compile("(?<=Train net output #0: loss = )(.*)(?= \()")
learning_rate_regex = re.compile("(?<=base_lr: )(.*)(?=)")
def create_empty_regexp_dict():
regexps_dict = {test_iteration_regex: [], test_accuracy_regex: [], test_loss_regex: [],
train_iteration_regex: [], train_loss_regex: [],
learning_rate_regex: []}
return regexps_dict
def search_regexps_in_file(regexp_dict, file_name):
with open(file_name) as opened_file:
for line in opened_file:
for regexp in regexp_dict:
matches = regexp.search(line)
# Assuming only one match was found
if matches: regexp_dict[regexp].append(float(regexp.search(line).group()))
rgb_dict = create_empty_regexp_dict()
search_regexps_in_file(rgb_dict, '/home/noa/pcl_proj/experiments/cifar10/every_fifth_view/0702/rgb/log.log')
hist_dict = create_empty_regexp_dict()
search_regexps_in_file(hist_dict, '/home/noa/pcl_proj/experiments/cifar10/every_fifth_view/0702/hist/log.log')
rgb_hist_dict = create_empty_regexp_dict()
search_regexps_in_file(rgb_hist_dict, '/home/noa/pcl_proj/experiments/cifar10/every_fifth_view/0702/rgb_hist/log.log')
print rgb_dict[learning_rate_regex][0]
dates_list = ['1601', '1801', '2101', '2701', '0302', '0702', '0902', '1202']
acc = [[],[],[]]
for date_dir in dates_list:
rgb_dict = create_empty_regexp_dict()
search_regexps_in_file(rgb_dict, '/home/noa/pcl_proj/experiments/cifar10/every_fifth_view/'+
date_dir +'/rgb/log.log')
hist_dict = create_empty_regexp_dict()
search_regexps_in_file(hist_dict, '/home/noa/pcl_proj/experiments/cifar10/every_fifth_view/'
+ date_dir+ '/hist/log.log')
rgb_hist_dict = create_empty_regexp_dict()
search_regexps_in_file(rgb_hist_dict, '/home/noa/pcl_proj/experiments/cifar10/every_fifth_view/'
+date_dir+'/rgb_hist/log.log')
acc[0].append(rgb_dict[test_accuracy_regex][-1])
acc[1].append(hist_dict[test_accuracy_regex][-1])
acc[2].append(rgb_hist_dict[test_accuracy_regex][-1])
print np.array(acc[0]).mean()
print np.array(acc[0]).std()
print np.array(acc[1]).mean()
print np.array(acc[1]).std()
print np.array(acc[2]).mean()
print np.array(acc[2]).std()
_, p_1 = ttest(np.array(acc[0]), np.array(acc[1]))
_, p_2 = ttest(np.array(acc[0]), np.array(acc[2]))
_, p_3 = ttest(np.array(acc[2]), np.array(acc[1]))
print 'rgb vs. hist:'
print p_1
print 'rgb vs. rgb_hist'
print p_2
print 'hist vs, rgb_hist'
print p_3
#csfont = {'fontname':'Comic Sans MS'}
#hfont = {'fontname':'Helvetica'}
fig2, axs2 = plt.subplots(1,1, figsize=(40, 20), facecolor='w', edgecolor='k', sharex=True)
spines_to_remove = ['top', 'right']
for spine in spines_to_remove:
axs2.spines[spine].set_visible(False)
axs2.spines['bottom'].set_linewidth(3.5)
axs2.spines['left'].set_linewidth(3.5)
#axs2.set_title('Test set accuracy and loss', fontsize=20)
axs2.xaxis.set_ticks_position('none')
axs2.yaxis.set_ticks_position('none')
axs2.plot(rgb_dict[test_iteration_regex], rgb_dict[test_accuracy_regex], label='RGB', linewidth=8.0)
axs2.plot(hist_dict[test_iteration_regex], hist_dict[test_accuracy_regex], label='FPFH', linewidth=8.0)
axs2.plot(rgb_hist_dict[test_iteration_regex], rgb_hist_dict[test_accuracy_regex], label='RGB+FPFH', linewidth=8.0)
axs2.legend(loc=4, fontsize=60)
axs2.set_ylabel('Test Accuracy', fontsize=70)
plt.yticks(fontsize = 60)
axs2.axes.get_xaxis().set_visible(False)
'''for spine in spines_to_remove:
axs2[1].spines[spine].set_visible(False)
axs2[1].xaxis.set_ticks_position('none')
axs2[1].yaxis.set_ticks_position('none')
axs2[1].plot(rgb_dict[test_iteration_regex], rgb_dict[test_loss_regex], label='rgb')
axs2[1].plot(hist_dict[test_iteration_regex], hist_dict[test_loss_regex], label='histograms')
axs2[1].plot(rgb_hist_dict[test_iteration_regex], rgb_hist_dict[test_loss_regex], label='rgb+histograms')
axs2[1].legend(fontsize=18)
plt.ylabel('Test Accuracy', fontsize=18)
plt.xlabel('Iterations', fontsize=18)'''
#plt.xlim(0,3000)
plt.show()
fig2, axs2 = plt.subplots(1,1, figsize=(40, 15), facecolor='w', edgecolor='k', sharex=True)
for spine in spines_to_remove:
axs2.spines[spine].set_visible(False)
axs2.spines['bottom'].set_linewidth(3.5)
axs2.spines['left'].set_linewidth(3.5)
axs2.xaxis.set_ticks_position('none')
axs2.yaxis.set_ticks_position('none')
axs2.set_yscale('log')
axs2.plot(rgb_dict[train_iteration_regex], (np.array(rgb_dict[train_loss_regex])), label='RGB', linewidth=6.0)
axs2.plot(hist_dict[train_iteration_regex], (np.array(hist_dict[train_loss_regex])), label='FPFH', linewidth=6.0)
axs2.plot(rgb_hist_dict[train_iteration_regex], (np.array(rgb_hist_dict[train_loss_regex])), label='RGB+FPFH', linewidth=6.0)
#axs2.set_title('Training set loss (log-scale)', fontsize=20)
axs2.legend(fontsize=60)
plt.ylabel('Train Loss', fontsize=70)
plt.xlabel('Iterations', fontsize=70)
plt.yticks(fontsize = 60)
plt.xticks(fontsize = 60)
plt.show()
#plt.xlim(47800,48000)
###Output
_____no_output_____
|
notebooks/sentiment_results.ipynb
|
###Markdown
Some sentiment analysis resultsI've only ran some of the models at the sentiment corpora. Performance is not great: 60-70%, SOTA is around 90%
###Code
%cd ~/NetBeansProjects/ExpLosion/
from notebooks.common_imports import *
from gui.output_utils import *
sns.timeseries.algo.bootstrap = my_bootstrap
sns.categorical.bootstrap = my_bootstrap
ids = Experiment.objects.filter(labelled__in=['movie-reviews-tagged', 'aclImdb-tagged'],
clusters__isnull=False).values_list('id', flat=True)
print(ids)
df = dataframe_from_exp_ids(ids, {'id':'id',
'labelled': 'labelled',
'algo': 'clusters__vectors__algorithm',
'unlab': 'clusters__vectors__unlabelled',
'num_cl': 'clusters__num_clusters'}).convert_objects(convert_numeric=True)
performance_table(df)
###Output
[385, 386, 387, 388, 389]
folds has 2500 values
Accuracy has 2500 values
id has 2500 values
unlab has 2500 values
num_cl has 2500 values
algo has 2500 values
labelled has 2500 values
keeping {'unlab', 'num_cl', 'algo', 'labelled'}
|
Task-3.ipynb
|
###Markdown
K- Means Clustering by *Pranjal Bhardwaj* Importing the libraries
###Code
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn import datasets
###Output
/opt/anaconda3/lib/python3.7/site-packages/statsmodels/tools/_testing.py:19: FutureWarning: pandas.util.testing is deprecated. Use the functions in the public API at pandas.testing instead.
import pandas.util.testing as tm
###Markdown
Load the iris dataset
###Code
iris = datasets.load_iris()
iris_df = pd.DataFrame(iris.data, columns = iris.feature_names)
iris_df.head()
iris_df.describe()
###Output
_____no_output_____
###Markdown
Finding the optimum number of clusters for k-means classification > Elbow method> The basic idea behind partitioning methods, such as k-means clustering, is to define clusters such that the total intra-cluster variation or total within-cluster sum of square WSS is minimized. The total WSS measures the compactness of the clustering and we want it to be as small as possible.The Elbow method looks at the total WSS as a function of the number of clusters: One should choose a number of clusters so that adding another cluster doesn’t improve much better the total WSS.The optimal number of clusters can be defined as follow:1. Compute clustering algorithm (e.g., k-means clustering) for different values of k. For instance, by varying k from 1 to 10 clusters.2. For each k, calculate the total within-cluster sum of square (wss).3. Plot the curve of wss according to the number of clusters k.4. The location of a bend (knee) in the plot is generally considered as an indicator of the appropriate number of clusters. Now we will implement 'The elbow method' on the Iris dataset. The elbow method allows us to pick the optimum amount of clusters for classification. although we already know the answer is 3 it is still interesting to run.
###Code
x = iris_df.iloc[:, [0, 1, 2, 3]].values
from sklearn.cluster import KMeans
wcss = []
#this loop will fit the k-means algorithm to our data and
#second we will compute the within cluster sum of squares and #appended to our wcss list.
for i in range(1, 11):
kmeans = KMeans(n_clusters = i, init = 'k-means++',
max_iter = 300, n_init = 10, random_state = 0)
#i above is between 1-10 numbers. init parameter is the random #initialization method
#we select kmeans++ method. max_iter parameter the maximum number of iterations there can be to
#find the final clusters when the K-meands algorithm is running. we #enter the default value of 300
#the next parameter is n_init which is the number of times the #K_means algorithm will be run with
#different initial centroid.
kmeans.fit(x)
#kmeans algorithm fits to the X dataset
wcss.append(kmeans.inertia_)
#kmeans inertia_ attribute is: Sum of squared distances of samples #to their closest cluster center.
# Plotting the results onto a line graph,
# `allowing us to observe 'The elbow'
plt.plot(range(1, 11), wcss)
plt.title('The elbow method')
plt.xlabel('Number of clusters')
plt.ylabel('WCSS') # Within cluster sum of squares
plt.show()
###Output
_____no_output_____
###Markdown
You can clearly see why it is called 'The elbow method' from the above graph, the optimum clusters is where the elbow occurs. This is when the within cluster sum of squares (WCSS) doesn't decrease significantly with every iteration. Now that we have the optimum amount of clusters, we can move on to applying K-means clustering to the Iris dataset. Applying kmeans to the dataset / Creating the kmeans classifier
###Code
kmeans = KMeans(n_clusters = 3, init = 'k-means++',
max_iter = 300, n_init = 10, random_state = 0)
y_kmeans = kmeans.fit_predict(x)
###Output
_____no_output_____
###Markdown
> We are going to use the fit predict method that returns for each observation which cluster it belongs to. The cluster to which client belongs and it will return this cluster numbers into a single vector that is called y K-means Visualising the clusters - On the first two columns
###Code
plt.scatter(x[y_kmeans == 0, 0], x[y_kmeans == 0, 1],
s = 100, c = 'red', label = 'Iris-setosa')
plt.scatter(x[y_kmeans == 1, 0], x[y_kmeans == 1, 1],
s = 100, c = 'green', label = 'Iris-versicolour')
plt.scatter(x[y_kmeans == 2, 0], x[y_kmeans == 2, 1],
s = 100, c = 'blue', label = 'Iris-virginica')
# Plotting the centroids of the clusters
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:,1],
s = 100, c = 'yellow', label = 'Centroids')
plt.legend()
###Output
_____no_output_____
###Markdown
> Average Silhouette Analysis > The average silhouette approach we’ll be described comprehensively in the chapter cluster validation statistics. Briefly, it measures the quality of a clustering. That is, it determines how well each object lies within its cluster. A high average silhouette width indicates a good clustering.> Average silhouette method computes the average silhouette of observations for different values of k. The optimal number of clusters k is the one that maximize the average silhouette over a range of possible values for k (Kaufman and Rousseeuw 1990).The algorithm is similar to the elbow method and can be computed as follow:1. Compute clustering algorithm (e.g., k-means clustering) for different values of k. For instance, by varying k from 1 to 10 clusters.2. For each k, calculate the average silhouette of observations (avg.sil).3. Plot the curve of avg.sil according to the number of clusters k.4. The location of the maximum is considered as the appropriate number of clusters.
###Code
from sklearn.datasets import load_iris
iris = load_iris()
X = iris['data'][:, 1:3]
from __future__ import print_function
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
print(__doc__)
# Generating the sample data from make_blobs
# This particular setting has one distinct cluster and 3 clusters placed close
# together.
X, y = make_blobs(n_samples=500,
n_features=2,
centers=4,
cluster_std=1,
center_box=(-10.0, 10.0),
shuffle=True,
random_state=1) # For reproducibility
range_n_clusters = [2, 3, 4, 5, 6, 7, 8]
for n_clusters in range_n_clusters:
# Create a subplot with 1 row and 2 columns
fig, (ax1, ax2) = plt.subplots(1, 2)
fig.set_size_inches(18, 7)
# The 1st subplot is the silhouette plot
# The silhouette coefficient can range from -1, 1 but in this example all
# lie within [-0.1, 1]
ax1.set_xlim([-0.1, 1])
# The (n_clusters+1)*10 is for inserting blank space between silhouette
# plots of individual clusters, to demarcate them clearly.
ax1.set_ylim([0, len(X) + (n_clusters + 1) * 10])
# Initialize the clusterer with n_clusters value and a random generator
# seed of 10 for reproducibility.
clusterer = KMeans(n_clusters=n_clusters, random_state=10)
cluster_labels = clusterer.fit_predict(X)
# The silhouette_score gives the average value for all the samples.
# This gives a perspective into the density and separation of the formed
# clusters
silhouette_avg = silhouette_score(X, cluster_labels)
print("For n_clusters =", n_clusters,
"The average silhouette_score is :", silhouette_avg)
# Compute the silhouette scores for each sample
sample_silhouette_values = silhouette_samples(X, cluster_labels)
y_lower = 10
for i in range(n_clusters):
# Aggregate the silhouette scores for samples belonging to
# cluster i, and sort them
ith_cluster_silhouette_values = \
sample_silhouette_values[cluster_labels == i]
ith_cluster_silhouette_values.sort()
size_cluster_i = ith_cluster_silhouette_values.shape[0]
y_upper = y_lower + size_cluster_i
color = cm.nipy_spectral(float(i) / n_clusters)
ax1.fill_betweenx(np.arange(y_lower, y_upper),
0, ith_cluster_silhouette_values,
facecolor=color, edgecolor=color, alpha=0.7)
# Label the silhouette plots with their cluster numbers at the middle
ax1.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
# Compute the new y_lower for next plot
y_lower = y_upper + 10 # 10 for the 0 samples
ax1.set_title("The silhouette plot for the various clusters.")
ax1.set_xlabel("The silhouette coefficient values")
ax1.set_ylabel("Cluster label")
# The vertical line for average silhouette score of all the values
ax1.axvline(x=silhouette_avg, color="red", linestyle="--")
ax1.set_yticks([]) # Clear the yaxis labels / ticks
ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])
# 2nd Plot showing the actual clusters formed
colors = cm.nipy_spectral(cluster_labels.astype(float) / n_clusters)
ax2.scatter(X[:, 0], X[:, 1], marker='.', s=30, lw=0, alpha=0.7,
c=colors, edgecolor='k')
# Labeling the clusters
centers = clusterer.cluster_centers_
# Draw white circles at cluster centers
ax2.scatter(centers[:, 0], centers[:, 1], marker='o',
c="white", alpha=1, s=200, edgecolor='k')
for i, c in enumerate(centers):
ax2.scatter(c[0], c[1], marker='$%d$' % i, alpha=1,
s=50, edgecolor='k')
ax2.set_title("The visualization of the clustered data.")
ax2.set_xlabel("Feature space for the 1st feature")
ax2.set_ylabel("Feature space for the 2nd feature")
plt.suptitle(("Silhouette analysis for KMeans clustering on sample data "
"with n_clusters = %d" % n_clusters),
fontsize=14, fontweight='bold')
plt.show()
###Output
Automatically created module for IPython interactive environment
For n_clusters = 2 The average silhouette_score is : 0.7049787496083262
|
Final-Code/Merged-Code-Farah.ipynb
|
###Markdown
Interpolation of VLM Data:
###Code
vlm = vlm_df.drop(columns=['Station', 'VLM_std'])
# Boundary points
# Top point: max latitude
top = vlm.iloc[vlm.idxmax().Latitude]
# Bottom point: min latitude
bottom = vlm.iloc[vlm.idxmin().Latitude]
# Left point: min longitude
left = vlm.iloc[vlm.idxmin().Longitude]
# Right point: max longitude
right = vlm.iloc[vlm.idxmax().Longitude]
# Artificial points for calculating distances
# point = (lon, lat)
# Top counter: lon = top, lat = bottom
top_counter = (top.Longitude, bottom.Latitude)
# Bottom counter: lon = bottom, lat = top
bottom_counter = (bottom.Longitude, top.Latitude)
# Left counter: lon = right, lat = left
left_counter = (right.Longitude, left.Latitude)
# Right counter: lon = left, lat = right
right_counter = (left.Longitude, right.Latitude)
# Arrays for plotting
top_pair = (np.array([top.Longitude, top_counter[0]]), np.array([top.Latitude, top_counter[1]]))
bottom_pair = (np.array([bottom.Longitude, bottom_counter[0]]), np.array([bottom.Latitude, bottom_counter[1]]))
left_pair = (np.array([left.Longitude, left_counter[0]]), np.array([left.Latitude, left_counter[1]]))
right_pair = (np.array([right.Longitude, right_counter[0]]), np.array([right.Latitude, right_counter[1]]))
sns.relplot(x="Longitude", y="Latitude", hue="VLM", data=vlm, palette="mako", height=6, aspect=1.25)
plt.scatter(top_pair[0], top_pair[1], c='r', marker='x', s=200, alpha=0.8)
plt.scatter(bottom_pair[0], bottom_pair[1], c='g', marker='x', s=200, alpha=0.8)
plt.scatter(left_pair[0], left_pair[1], c='b', marker='x', s=200, alpha=0.8)
plt.scatter(right_pair[0], right_pair[1], c='yellow', marker='x', s=200, alpha=0.8)
from math import radians, cos, sin, asin, sqrt
def distance(lon1, lat1, lon2, lat2):
# The math module contains a function named
# radians which converts from degrees to radians.
lon1 = radians(lon1)
lon2 = radians(lon2)
lat1 = radians(lat1)
lat2 = radians(lat2)
# Haversine formula
dlon = lon2 - lon1
dlat = lat2 - lat1
a = sin(dlat / 2)**2 + cos(lat1) * cos(lat2) * sin(dlon / 2)**2
c = 2 * asin(sqrt(a))
# Radius of earth in meters. Use 3956 for miles
r = 6371*1000
# calculate the result
return(c * r)
# Distances of vertical pairs (top & bottom)
ver_top = distance(top.Longitude, top.Latitude, top_counter[0], top_counter[1])
ver_bottom = distance(bottom.Longitude, bottom.Latitude, bottom_counter[0], bottom_counter[1])
# Distances of horizontal pairs (left & right)
hor_left = distance(left.Longitude, left.Latitude, left_counter[0], left_counter[1])
hor_right = distance(right.Longitude, right.Latitude, right_counter[0], right_counter[1])
# There is some slight difference so I'm taking the rounded mean values
dis_ver = np.ceil(np.mean((ver_top, ver_bottom)))
dis_hor = np.ceil(np.mean((hor_left, hor_right)))
# Boundary values
x_min, x_max = vlm.min().Longitude, vlm.max().Longitude
y_min, y_max = vlm.min().Latitude, vlm.max().Latitude
# Divide by distance of 10m seems a bit too detailed. Trying with adding points every 100m instead
nx, ny = (np.int(np.ceil(dis_ver / 100)), np.int(np.ceil(dis_hor / 100)))
x = np.linspace(x_min, x_max, nx)
y = np.linspace(y_min, y_max, ny)
xv, yv = np.meshgrid(x, y)
vlm_points = vlm[['Longitude', 'Latitude']].values
vlm_values = vlm.VLM.values
vlm_grid = griddata(vlm_points, vlm_values, (xv, yv), method='cubic')
sns.relplot(x="Longitude", y="Latitude", hue="VLM", data=vlm, s=50, palette="rocket", height=10)
plt.imshow(vlm_grid, extent=(x_min, x_max, y_min, y_max), origin='lower', alpha=0.6)
plt.show()
elevation_new = copy.deepcopy(elevation)
elevation_new = elevation_new.astype('float')
elevation_new[elevation_new == 32767] = np.nan
plt.imshow(elevation_new)
###Output
_____no_output_____
###Markdown
Idea: flatten the coordinate grid into pairs of coordinates to use as inputs for another interpolation
###Code
vlm_inter_points = np.hstack((xv.reshape(-1, 1), yv.reshape(-1, 1)))
vlm_inter_values = vlm_grid.flatten()
elev_coor = elevation_df[['x', 'y']].values
elev_grid_0 = griddata(vlm_points, vlm_values, elev_coor, method='cubic') # without pre-interpolation
elev_grid_1 = griddata(vlm_inter_points, vlm_inter_values, elev_coor, method='cubic') # with pre-interpolation
plt.scatter(x=elevation_df.x, y=elevation_df.y, c=elev_grid_0)
# Find elevation map boundaries
x_min_elev = dataset.bounds.left
x_max_elev = dataset.bounds.right
y_min_elev = dataset.bounds.bottom
y_max_elev = dataset.bounds.top
# Create elevation meshgrid
nyy, nxx = elevation_new.shape
xx = np.linspace(x_min_elev, x_max_elev, nxx)
yy = np.linspace(y_min_elev, y_max_elev, nyy)
xxv, yyv = np.meshgrid(xx, yy)
xxv.shape, yyv.shape
((1758, 2521), (1758, 2521))
elev_grid = griddata(vlm_inter_points, vlm_inter_values, (xxv, yyv), method='linear')
sns.relplot(x="Longitude", y="Latitude", hue="VLM", data=vlm, s=50, palette="rocket", height=10)
plt.imshow(elev_grid, extent=(x_min_elev, x_max_elev, y_min_elev, y_max_elev), origin="lower", alpha=0.3)
plt.show()
elev_grid_copy = copy.deepcopy(elev_grid)
elev_grid_copy[np.isnan(np.flip(elevation_new, 0))] = np.nan
# Needs to flip elevation array vertically. I don't really understand why.
sns.relplot(x="Longitude", y="Latitude", hue="VLM", data=vlm, s=100, edgecolor="white", palette="rocket", height=10)
plt.imshow(elev_grid_copy, extent=(x_min_elev, x_max_elev, y_min_elev, y_max_elev), origin='lower', alpha=0.8)
plt.show()
###Output
_____no_output_____
###Markdown
**the interpolated VLM values are stored in: elev_grid_copy Calculating AE:
###Code
slr_new = slr_df.loc[(slr_df.Scenario == '0.3 - LOW') | (slr_df.Scenario == '2.5 - HIGH')]
slr_new['SL'] = slr_new.sum(axis=1)
ae_low = copy.deepcopy(elev_grid_copy)
ae_high = copy.deepcopy(elev_grid_copy)
# Division by 100 to fix unit difference
ae_low = np.flip(elevation_new, 0) - slr_new.iloc[0].SL/100 + ae_low
ae_high = np.flip(elevation_new, 0) - slr_new.iloc[1].SL/100 + ae_high
ae_min = min(ae_low[~np.isnan(ae_low)].min(), ae_high[~np.isnan(ae_high)].min())
ae_max = max(ae_low[~np.isnan(ae_low)].max(), ae_high[~np.isnan(ae_high)].max())
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(24, 8))
im1 = ax1.imshow(ae_low, extent=(x_min_elev, x_max_elev, y_min_elev, y_max_elev), origin='lower', alpha=0.8, vmin=ae_min, vmax=ae_max)
im2 = ax2.imshow(ae_high, extent=(x_min_elev, x_max_elev, y_min_elev, y_max_elev), origin='lower', alpha=0.8, vmin=ae_min, vmax=ae_max)
cbar_ax = fig.add_axes([0.9, 0.15, 0.02, 0.7])
fig.colorbar(im2, cax=cbar_ax)
###Output
_____no_output_____
###Markdown
Elevation-Habitat Map: elev_habit_map
###Code
from time import time
from shapely.geometry import Point, Polygon
from shapely.ops import cascaded_union
t00 = time()
# file = gr.from_file('../Week 6/Elevation.tif')
# elevation_df = file.to_geopandas()
habitat_path = r"Data/UAE_habitats_new1.shp"
habitat = gpd.read_file(habitat_path)
elevation_df.to_crs(habitat.crs, inplace=True)
elev_bounds = elevation_df.total_bounds
print("Loading files: %.2fs" % (time() - t00))
# Create boundary points
# Top left - top right - bottom right - bottom left
tl = Point(elev_bounds[0], elev_bounds[3])
tr = Point(elev_bounds[2], elev_bounds[3])
br = Point(elev_bounds[2], elev_bounds[1])
bl = Point(elev_bounds[0], elev_bounds[1])
boundary = Polygon([tl, tr, br, bl])
boundary_df = gpd.GeoSeries(boundary)
# Intersecting original habitat with bounding box
habitat['Intersection'] = habitat.geometry.intersects(boundary)
habitat_cut = habitat[habitat.Intersection == True]
t0 = time()
elev_union_shape = cascaded_union(list(elevation_df.geometry))
print("Merging elevation geometries into one polygon: %.2fs" % (time() - t0))
elev_union = gpd.GeoSeries(elev_union_shape)
elev_union_df = gpd.GeoDataFrame({'geometry': elev_union})
elev_union_df.crs = habitat.crs
elev_union.crs = habitat.crs
elev_union_shape.crs = habitat.crs
t1 = time()
habitat_cut['Intersection_2'] = habitat_cut.geometry.intersects(elev_union_shape)
print("Intersecting reduced habitat map with elevation polygon: %.2fs" % (time() - t1))
habitat_cut_cut = habitat_cut[habitat_cut['Intersection_2'] == True]
t2 = time()
final = gpd.sjoin(elevation_df, habitat_cut_cut, how="left", op="within")
print("Joining elevation df with habitat_cut_cut: %.2fs" % (time() - t2))
def fillna_nearest(series):
fact = series.astype('category').factorize()
series_cat = gpd.GeoSeries(fact[0]).replace(-1, np.nan) # get string as categorical (-1 is NaN)
series_cat_interp = series_cat.interpolate("nearest") # interpolate categorical
cat_to_string = {i:x for i,x in enumerate(fact[1])} # dict connecting category to string
series_str_interp = series_cat_interp.map(cat_to_string) # turn category back to string
return series_str_interp
t3 = time()
final['Fill'] = fillna_nearest(final.Habitats)
print("Interpolating missing values in final df: %.2fs" % (time() - t3))
t4 = time()
f, ax = plt.subplots(1, 1, figsize=(14, 10))
ax = final.plot(column='Fill', ax=ax, legend=True, cmap='magma', edgecolor="face", linewidth=0.)
leg = ax.get_legend()
leg.set_bbox_to_anchor((1.25, 1))
plt.show()
print("Plotting final df: %.2fs" % (time() - t4))
###Output
_____no_output_____
###Markdown
Habitats Grouping:
###Code
elev_habit_map = final.drop(columns=["col", "index_right", "OBJECTID", "Id", "HabitatTyp", "HabitatT_1", "HabitatSub", "HabitatS_1",
"RuleID", "Shape_Leng", "Shape_Area", "Habitats", "Intersection", "Intersection_2"], axis=1)
elev_habit_map.rename(columns={"Fill": "Habitats"}, inplace=True)
# Create New Column for New Habitat Groups:
elev_habit_map['Habitat_Groups'] = ''
elev_habit_map.head(1)
np.unique(elev_habit_map.Habitats)
elev_habit_map.loc[ (elev_habit_map.Habitats == 'Marine Structure')
| (elev_habit_map.Habitats == 'Developed')
| (elev_habit_map.Habitats == 'Dredged Area Wall')
| (elev_habit_map.Habitats == 'Dredged Seabed')
| (elev_habit_map.Habitats == 'Farmland')
, 'Habitat_Groups'] = 'Developed'
elev_habit_map.loc[ (elev_habit_map.Habitats == 'Mountains')
| (elev_habit_map.Habitats == 'Coastal Cliff')
| (elev_habit_map.Habitats == 'Coastal Rocky Plains')
| (elev_habit_map.Habitats == 'Gravel Plains')
| (elev_habit_map.Habitats == 'Rock Armouring / Artificial Reef')
| (elev_habit_map.Habitats == 'Rocky Beaches')
| (elev_habit_map.Habitats == 'Storm Beach Ridges')
, 'Habitat_Groups'] = 'Rocky'
elev_habit_map.loc[ (elev_habit_map.Habitats == 'Mega Dunes')
| (elev_habit_map.Habitats == 'Sand Sheets and Dunes')
| (elev_habit_map.Habitats == 'Sandy Beaches')
| (elev_habit_map.Habitats == 'Coastal Sand Plains')
, 'Habitat_Groups'] = 'Sandy'
elev_habit_map.loc[ (elev_habit_map.Habitats == 'Coastal Salt Flats')
| (elev_habit_map.Habitats == 'Inland Salt Flats')
| (elev_habit_map.Habitats == 'Saltmarsh')
| (elev_habit_map.Habitats == 'Intertidal Habitats')
| (elev_habit_map.Habitats == 'Wetlands')
, 'Habitat_Groups'] = 'Marsh/Salt Flats'
elev_habit_map.loc[ (elev_habit_map.Habitats == 'Coral Reefs')
| (elev_habit_map.Habitats == 'Deep Sub-Tidal Seabed')
| (elev_habit_map.Habitats == 'Hard-Bottom')
| (elev_habit_map.Habitats == 'Seagrass Bed')
| (elev_habit_map.Habitats == 'Lakes or Artificial Lakes')
| (elev_habit_map.Habitats == 'Unconsolidated Bottom')
, 'Habitat_Groups'] = 'Subaqueous'
elev_habit_map.loc[ (elev_habit_map.Habitats == 'Forest Plantations')
| (elev_habit_map.Habitats == 'Mangroves')
, 'Habitat_Groups'] = 'Forest'
# Be carful: it is spelled: 'Coastal Sand Plains' NOT: 'Coastal Sand Planes'
unique_groups = np.unique(elev_habit_map.Habitat_Groups)
print(unique_groups)
print(len(unique_groups))
# elev_habit_map.loc[elev_habit_map.Habitat_Groups == ''] #--> to see which rows still didnt have a group assigned to them
sns.catplot(x="Habitat_Groups", kind="count", palette="mako", data=elev_habit_map, height=5, aspect=1.5)
labels = plt.xticks(rotation=45)
###Output
_____no_output_____
###Markdown
**The Elev-Habit DF now has habitat groups & it is called: 'elev_habit_map' VLM Bins & Habitat Classes: 1. VLM Bins:
###Code
print(len(elev_grid_copy))
print(type(elev_grid_copy))
print(type(elev_grid_copy.flatten()))
# Dropping the NaN values in the array:
nan_array = np.isnan(elev_grid_copy.flatten())
not_nan_array = ~ nan_array
vlm_interpolated_arr = elev_grid_copy.flatten()[not_nan_array]
vlm_interpolated_arr
###Output
_____no_output_____
###Markdown
**The clean, flattened VLM array for interpolated VLM values is called: 'vlm_interpolated_arr'
###Code
# Step 1: Making 3 equal-size bins for VLM data: note: interval differences are irrelevant
vlm_bins = pd.qcut(vlm_interpolated_arr, q=3, precision=1, labels=['Bin #1', 'Bin #2', 'Bin #3'])
# bin definition
bins = vlm_bins.categories
print(bins)
# bin corresponding to each point in data
codes = vlm_bins.codes
print(np.unique(codes))
# Step 2: Making Sure that the Bins are of Almost Equal Size:
size = collections.Counter(codes)
print(size)
d_table = pd.value_counts(codes).to_frame(name='Frequency')
d_table = d_table.reset_index()
d_table = d_table.rename(columns={'index': 'Bin Index'})
fig, ax = plt.subplots()
sns.barplot(x="Bin Index", y="Frequency", data=d_table, label="Size of Each of the 3 Bins", ax=ax)
print(d_table)
# Step 3: Calculating Probability of each Bin:
prob0 = (d_table.loc[0].Frequency)/len(vlm_interpolated_arr)
prob1 = (d_table.loc[1].Frequency)/len(vlm_interpolated_arr)
prob2 = (d_table.loc[2].Frequency)/len(vlm_interpolated_arr)
print(prob0, prob1, prob2)
# Step 4: Joining Everything in a Single Data Frame for aesthetic:
vlm_bins_df = pd.DataFrame()
vlm_bins_df['VLM Values'] = vlm_interpolated_arr
vlm_bins_df['Bins'] = vlm_bins
vlm_bins_df['Intervals'] = pd.qcut(vlm_interpolated_arr, q=3, precision=1)
vlm_bins_df['Probability'] = ''
vlm_bins_df.loc[ (vlm_bins_df.Bins == 'Bin #1'), 'Probability'] = prob0
vlm_bins_df.loc[ (vlm_bins_df.Bins == 'Bin #2'), 'Probability'] = prob1
vlm_bins_df.loc[ (vlm_bins_df.Bins == 'Bin #3'), 'Probability'] = prob2
vlm_bins_df.head()
###Output
_____no_output_____
###Markdown
2. Elevation Classes:
###Code
# Step 1: Create Data Frame:
elevation_classes = pd.DataFrame()
elevation_classes['Elevation_Values'] = elevation_df.value
# Step 2: Get Max and Min Values for Elevation
min_elev = elevation_df.value.min()
max_elev = elevation_df.value.max()
# Step 3: Create Intervals:
interval_0 = pd.cut(x=elevation_df['value'], bins=[1, 5, 10, max_elev])
interval_1 = pd.cut(x=elevation_df['value'], bins=[min_elev, -10, -1, 0], right=False)
interval_2 = pd.cut(x=elevation_df['value'], bins=[0, 1], include_lowest=True)
# Step 4: Add intervals to dataframe:
elevation_classes['Intervals_0'] = interval_0
elevation_classes['Intervals_1'] = interval_1
elevation_classes['Intervals_2'] = interval_2
elevation_classes['Intervals'] = ''
elevation_classes.loc[ ((elevation_classes.Intervals_0.isnull()) & (elevation_classes.Intervals_1.isnull())), 'Intervals'] = interval_2
elevation_classes.loc[ ((elevation_classes.Intervals_0.isnull()) & (elevation_classes.Intervals_2.isnull())), 'Intervals'] = interval_1
elevation_classes.loc[ ((elevation_classes.Intervals_1.isnull()) & (elevation_classes.Intervals_2.isnull())), 'Intervals'] = interval_0
elevation_classes.drop(['Intervals_2', 'Intervals_1', 'Intervals_0'], axis='columns', inplace=True)
# Step 5: Plotting the Size of Each Interval:
size = collections.Counter(elevation_classes.Intervals)
print(size)
d_table_elev = pd.value_counts(elevation_classes.Intervals).to_frame(name='Frequency')
d_table_elev = d_table_elev.reset_index()
d_table_elev = d_table_elev.rename(columns={'index': 'Class Index'})
fig, ax = plt.subplots(figsize=(10, 5))
sns.barplot(x="Class Index", y="Frequency", data=d_table_elev, label="Size of Each Class", ax=ax)
print(d_table_elev)
# Step 6: Calculate Probabilities:
prob0_elev = (d_table_elev.loc[6].Frequency)/len(elevation_classes) # [min_elev, -10)
prob1_elev = (d_table_elev.loc[5].Frequency)/len(elevation_classes) # [-10, -1)
prob2_elev = (d_table_elev.loc[4].Frequency)/len(elevation_classes) # [-1, 0)
prob3_elev = (d_table_elev.loc[2].Frequency)/len(elevation_classes) # [0, 1]
prob4_elev = (d_table_elev.loc[0].Frequency)/len(elevation_classes) # (1, 5]
prob5_elev = (d_table_elev.loc[3].Frequency)/len(elevation_classes) # (5, 10]
prob6_elev = (d_table_elev.loc[1].Frequency)/len(elevation_classes) # (10, max_elev]
print(prob0_elev, prob1_elev, prob2_elev, prob3_elev, prob4_elev, prob5_elev, prob6_elev)
# Step 7: Adding probabilities to d_table_elev for visualization:
d_table_elev['Probability'] = ''
d_table_elev['Probability'].loc[0] = prob4_elev
d_table_elev['Probability'].loc[1] = prob6_elev
d_table_elev['Probability'].loc[2] = prob3_elev
d_table_elev['Probability'].loc[3] = prob5_elev
d_table_elev['Probability'].loc[4] = prob2_elev
d_table_elev['Probability'].loc[5] = prob1_elev
d_table_elev['Probability'].loc[6] = prob0_elev
d_table_elev
###Output
/opt/anaconda3/lib/python3.8/site-packages/pandas/core/indexing.py:1637: SettingWithCopyWarning:
A value is trying to be set on a copy of a slice from a DataFrame
See the caveats in the documentation: https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy
self._setitem_single_block(indexer, value, name)
###Markdown
SLR Scenarios:
###Code
elev_habit_map['Migitation 46-65'] = elev_habit_map.value - 0.27 + elev_habit_map.VLM
elev_habit_map['Intermediate 46-65'] = elev_habit_map.value - 0.3 + elev_habit_map.VLM
elev_habit_map['Intermediate-High 46-65'] = elev_habit_map.value - 0.28 + elev_habit_map.VLM
elev_habit_map['High 46-65'] = elev_habit_map.value - 0.33 + elev_habit_map.VLM
elev_habit_map.head()
###Output
_____no_output_____
###Markdown
AE Bins:
###Code
# Step 1: Create Data Frame for each scenario:
mitigation_df = pd.DataFrame()
mitigation_df['AE_Values'] = elev_habit_map['Migitation 46-65']
inter_df = pd.DataFrame()
inter_df['AE_Values'] = elev_habit_map['Intermediate 46-65']
inter_high_df = pd.DataFrame()
inter_high_df['AE_Values'] = elev_habit_map['Intermediate-High 46-65']
high_df = pd.DataFrame()
high_df['AE_Values'] = elev_habit_map['High 46-65']
# Step 2: Find min and max values for each df:
# Mitigation df:
min_mit = mitigation_df.AE_Values.min()
max_mit = mitigation_df.AE_Values.max()
# Intermediate df:
min_inter = inter_df.AE_Values.min()
max_inter = inter_df.AE_Values.max()
# Intermediate-High df:
min_inter_high = inter_high_df.AE_Values.min()
max_inter_high = inter_high_df.AE_Values.max()
# High df:
min_high = high_df.AE_Values.min()
max_high = high_df.AE_Values.max()
# Step 3: Create Intervals for each df:
# intervals are for all slr data frame:
interval_0_mit = pd.cut(x=mitigation_df['AE_Values'], bins=[1, 5, 10, max_mit])
interval_1_mit = pd.cut(x=mitigation_df['AE_Values'], bins=[min_mit, -12, -1, 0], right=False)
interval_2_mit = pd.cut(x=mitigation_df['AE_Values'], bins=[0, 1], include_lowest=True)
# Step 4: Add intervals to dataframe:
# Intermediate df:
inter_df['Intervals_0'] = interval_0_mit
inter_df['Intervals_1'] = interval_1_mit
inter_df['Intervals_2'] = interval_2_mit
inter_df['Intervals'] = ''
inter_df.loc[ ((inter_df.Intervals_0.isnull()) & (inter_df.Intervals_1.isnull())), 'Intervals'] = interval_2_mit
inter_df.loc[ ((inter_df.Intervals_0.isnull()) & (inter_df.Intervals_2.isnull())), 'Intervals'] = interval_1_mit
inter_df.loc[ ((inter_df.Intervals_1.isnull()) & (inter_df.Intervals_2.isnull())), 'Intervals'] = interval_0_mit
inter_df.drop(['Intervals_2', 'Intervals_1', 'Intervals_0'], axis='columns', inplace=True)
# Mitigation df:
mitigation_df['Intervals_0'] = interval_0_mit
mitigation_df['Intervals_1'] = interval_1_mit
mitigation_df['Intervals_2'] = interval_2_mit
mitigation_df['Intervals'] = ''
mitigation_df.loc[ ((mitigation_df.Intervals_0.isnull()) & (mitigation_df.Intervals_1.isnull())), 'Intervals'] = interval_2_mit
mitigation_df.loc[ ((mitigation_df.Intervals_0.isnull()) & (mitigation_df.Intervals_2.isnull())), 'Intervals'] = interval_1_mit
mitigation_df.loc[ ((mitigation_df.Intervals_1.isnull()) & (mitigation_df.Intervals_2.isnull())), 'Intervals'] = interval_0_mit
mitigation_df.drop(['Intervals_2', 'Intervals_1', 'Intervals_0'], axis='columns', inplace=True)
# Intermediate-High df:
inter_high_df['Intervals_0'] = interval_0_mit
inter_high_df['Intervals_1'] = interval_1_mit
inter_high_df['Intervals_2'] = interval_2_mit
inter_high_df['Intervals'] = ''
inter_high_df.loc[ ((inter_high_df.Intervals_0.isnull()) & (inter_high_df.Intervals_1.isnull())), 'Intervals'] = interval_2_mit
inter_high_df.loc[ ((inter_high_df.Intervals_0.isnull()) & (inter_high_df.Intervals_2.isnull())), 'Intervals'] = interval_1_mit
inter_high_df.loc[ ((inter_high_df.Intervals_1.isnull()) & (inter_high_df.Intervals_2.isnull())), 'Intervals'] = interval_0_mit
inter_high_df.drop(['Intervals_2', 'Intervals_1', 'Intervals_0'], axis='columns', inplace=True)
# High df:
high_df['Intervals_0'] = interval_0_mit
high_df['Intervals_1'] = interval_1_mit
high_df['Intervals_2'] = interval_2_mit
high_df['Intervals'] = ''
high_df.loc[ ((high_df.Intervals_0.isnull()) & (high_df.Intervals_1.isnull())), 'Intervals'] = interval_2_mit
high_df.loc[ ((high_df.Intervals_0.isnull()) & (high_df.Intervals_2.isnull())), 'Intervals'] = interval_1_mit
high_df.loc[ ((high_df.Intervals_1.isnull()) & (high_df.Intervals_2.isnull())), 'Intervals'] = interval_0_mit
high_df.drop(['Intervals_2', 'Intervals_1', 'Intervals_0'], axis='columns', inplace=True)
# Step 5: Plotting the Size of Each Interval:
# Mitigation df:
size = collections.Counter(mitigation_df.Intervals)
print(size)
d_table_mit = pd.value_counts(mitigation_df.Intervals).to_frame(name='Frequency')
d_table_mit = d_table_mit.reset_index()
d_table_mit = d_table_mit.rename(columns={'index': 'Class Index'})
fig, ax = plt.subplots(figsize=(10, 5))
sns.barplot(x="Class Index", y="Frequency", data=d_table_mit, label="Size of Each Class", ax=ax)
print(d_table_mit)
# Intermediate df:
d_table_inter = pd.value_counts(inter_df.Intervals).to_frame(name='Frequency')
d_table_inter = d_table_inter.reset_index()
d_table_inter = d_table_inter.rename(columns={'index': 'Class Index'})
# Intermediate-High df:
d_table_inter_high = pd.value_counts(inter_high_df.Intervals).to_frame(name='Frequency')
d_table_inter_high = d_table_inter_high.reset_index()
d_table_inter_high = d_table_inter_high.rename(columns={'index': 'Class Index'})
# High df:
size = collections.Counter(high_df.Intervals)
print(size)
d_table_high = pd.value_counts(high_df.Intervals).to_frame(name='Frequency')
d_table_high = d_table_high.reset_index()
d_table_high = d_table_high.rename(columns={'index': 'Class Index'})
fig, ax = plt.subplots(figsize=(10, 5))
sns.barplot(x="Class Index", y="Frequency", data=d_table_high, label="Size of Each Class", ax=ax)
print(d_table_high)
mitigation_count = pd.DataFrame(mitigation_df.Intervals.value_counts())
mitigation_count.sort_index(inplace=True)
mitigation_count
sns.barplot(x=mitigation_count.index, y="Intervals", palette="mako", data=mitigation_count)
###Output
_____no_output_____
###Markdown
Calculating Probabilities of Each Scenario:
###Code
# Mitigation:
d_table_mit['Probability'] = (d_table_mit.Frequency)/(d_table_mit.Frequency.sum())
d_table_inter['Probability'] = (d_table_inter.Frequency)/(d_table_inter.Frequency.sum())
d_table_inter_high['Probability'] = (d_table_inter_high.Frequency)/(d_table_inter_high.Frequency.sum())
d_table_high['Probability'] = (d_table_high.Frequency)/(d_table_high.Frequency.sum())
###Output
_____no_output_____
###Markdown
BN Model:
###Code
# Build the networks:
model_mit = pgmpy.models.BayesianModel([('SLR', 'AE'), ('VLM', 'AE'), ('Elevation', 'AE'), ('Elevation', 'Habitat'), ('Habitat', 'CR'), ('AE', 'CR')])
model_inter = pgmpy.models.BayesianModel([('SLR', 'AE'), ('VLM', 'AE'), ('Elevation', 'AE'), ('Elevation', 'Habitat'), ('Habitat', 'CR'), ('AE', 'CR')])
model_inter_high = pgmpy.models.BayesianModel([('SLR', 'AE'), ('VLM', 'AE'), ('Elevation', 'AE'), ('Elevation', 'Habitat'), ('Habitat', 'CR'), ('AE', 'CR')])
model_high = pgmpy.models.BayesianModel([('SLR', 'AE'), ('VLM', 'AE'), ('Elevation', 'AE'), ('Elevation', 'Habitat'), ('Habitat', 'CR'), ('AE', 'CR')])
# CPDs for SLR for models:
cpd_slr_mit = pgmpy.factors.discrete.TabularCPD('SLR', 4, [[1], [0], [0], [0]], state_names={'SLR': ['0.18-0.34', '0.2-0.37', '0.2-0.36', '0.25-0.43']})
cpd_slr_inter = pgmpy.factors.discrete.TabularCPD('SLR', 4, [[0], [1], [0], [0]], state_names={'SLR': ['0.18-0.34', '0.2-0.37', '0.2-0.36', '0.25-0.43']})
cpd_slr_inter_high = pgmpy.factors.discrete.TabularCPD('SLR', 4, [[0], [0], [1], [0]], state_names={'SLR': ['0.18-0.34', '0.2-0.37', '0.2-0.36', '0.25-0.43']})
cpd_slr_high = pgmpy.factors.discrete.TabularCPD('SLR', 4, [[0], [0], [0], [1]], state_names={'SLR': ['0.18-0.34', '0.2-0.37', '0.2-0.36', '0.25-0.43']})
# CPD for VLM:
cpd_vlm = pgmpy.factors.discrete.TabularCPD('VLM', 3, [[prob0], [prob1], [prob2]], state_names={'VLM': ['Bin 1', 'Bin 2', 'Bin 3']})
# CPD for Elevation:
cpd_elevation = pgmpy.factors.discrete.TabularCPD('Elevation', 7, [[prob0_elev], [prob1_elev], [prob2_elev], [prob3_elev], [prob4_elev], [prob5_elev], [prob6_elev]], state_names={'Elevation': ['[min_elev, -10)', '[-10, -1)', '[-1, 0)', '[0, 1]', '(1, 5]', '(5, 10]', '(10, max_elev]']})
# Add CPDs:
model_mit.add_cpds(cpd_slr_mit, cpd_vlm, cpd_elevation)
model_inter.add_cpds(cpd_slr_inter, cpd_vlm, cpd_elevation)
model_inter_high.add_cpds(cpd_slr_inter_high, cpd_vlm, cpd_elevation)
model_high.add_cpds(cpd_slr_high, cpd_vlm, cpd_elevation)
probs_mit = np.array(d_table_mit.Probability).reshape(-1, 1)
probs_inter = np.array(d_table_inter.Probability).reshape(-1, 1)
probs_inter_high = np.array(d_table_inter_high.Probability).reshape(-1, 1)
probs_high = np.array(d_table_high.Probability).reshape(-1, 1)
state_names = ['(1.0, 5.0]', '(10.0, 82.733]', '(5.0, 10.0]', '(-0.001, 1.0]', '[-1.0, 0.0)', '[-12.0, -1.0)', '[-89.269, -12.0)']
cpd_ae_mit = pgmpy.factors.discrete.TabularCPD('AE', 7, probs_mit, state_names={'AE': state_names},
evidence=['SLR', 'VLM', 'Elevation'], evidence_card=[4, 3,7])
cpd_ae_inter = pgmpy.factors.discrete.TabularCPD('AE', 7, probs_inter, state_names={'AE': state_names})
cpd_ae_inter_high = pgmpy.factors.discrete.TabularCPD('AE', 7, probs_inter_high, state_names={'AE': state_names})
cpd_ae_high = pgmpy.factors.discrete.TabularCPD('AE', 7, probs_high, state_names={'AE': state_names})
model_mit.add_cpds(cpd_ae_mit)
model_inter.add_cpds(cpd_ae_inter)
model_inter_high.add_cpds(cpd_ae_inter_high)
model_high.add_cpds(cpd_ae_high)
model_mit.check_model()
###Output
_____no_output_____
###Markdown
Add VLM:
###Code
vlm_interpolated_arr
inter_vlm_df = pd.DataFrame(vlm_interpolated_arr, columns=['VLM'])
elev_habit_map['VLM'] = inter_vlm_df.VLM/1000
elev_habit_map.VLM.value_counts(dropna=False)
###Output
_____no_output_____
|
notebooks/available-questions.ipynb
|
###Markdown
Available questions A note on types- `javaRegex` と `nodeSpec` は `string` のエイリアス。 - Javaの正規表現はPythonとちょっと違うので注意。- `headerConstraint` は、IPv4パケットヘッダーの条件を指定するための特別なタイプ。 Preparing Pybatfishをインポートする。
###Code
from pybatfish.client.commands import *
from pybatfish.question.question import load_questions, list_questions
from pybatfish.question import bfq
###Output
_____no_output_____
###Markdown
クエスチョンテンプレートをBatfishからpybatfishへロードする。
###Code
load_questions()
###Output
Successfully loaded 33 questions from remote
###Markdown
ネットワークスナップショットをアップロードする(スナップショット名の後にいくつかのログが表示される)。bf_init_snapshot()の引数はZipファイルでもいいらしい。
###Code
bf_init_snapshot('networks/example')
###Output
status: TRYINGTOASSIGN
.... no task information
status: ASSIGNED
.... Wed Oct 24 11:14:34 2018 UTC Serializing 'org.batfish.representation.cisco.CiscoConfiguration' instances to disk 6 / 13
status: TERMINATEDNORMALLY
.... Wed Oct 24 11:14:34 2018 UTC Deserializing objects of type 'org.batfish.datamodel.Configuration' from files 15 / 15
Default snapshot is now set to ss_c99bc1c0-c9c2-4308-b799-585d4201bb83
###Markdown
List of questions pybatfish.question.bfq.aaaAuthenticationLogin()AAA認証を必要としないlineを返す。
###Code
aaa_necessity_ans = bfq.aaaAuthenticationLogin().answer()
aaa_necessity_ans.frame().head()
###Output
status: TRYINGTOASSIGN
.... no task information
status: TERMINATEDNORMALLY
.... Wed Oct 24 11:16:39 2018 UTC Begin job
###Markdown
pybatfish.question.bfq.bgpPeerConfiguration()BGPピア設定を返す。
###Code
bgp_peerconf_ans = bfq.bgpPeerConfiguration().answer()
bgp_peerconf_ans.frame().head()
###Output
status: TRYINGTOASSIGN
.... no task information
status: TERMINATEDNORMALLY
.... Wed Oct 24 13:54:57 2018 UTC Begin job
###Markdown
pybatfish.question.bfq.bgpProcessConfiguration()BGPプロセス設定を返す。
###Code
bgp_procconf_ans = bfq.bgpProcessConfiguration().answer()
bgp_procconf_ans.frame().head()
###Output
status: TRYINGTOASSIGN
.... no task information
status: TERMINATEDNORMALLY
.... Wed Oct 24 13:56:21 2018 UTC Begin job
###Markdown
pybatfish.question.bfq.bgpSessionCompatibility()各BGPセッションの情報を返す。
###Code
bgp_sesscomp_ans = bfq.bgpSessionCompatibility().answer()
bgp_sesscomp_ans.frame().head()
###Output
status: TRYINGTOASSIGN
.... no task information
status: TERMINATEDNORMALLY
.... Wed Oct 24 13:59:23 2018 UTC Begin job
###Markdown
pybatfish.question.bfq.bgpSessionStatus()pybatfish.question.bgq.bgpSessionCompatibility()に、ネイバーが確立しているかどうかを示すEstablished_neighborsを加えた情報を返す。
###Code
bgp_sessstat_ans = bfq.bgpSessionStatus().answer()
bgp_sessstat_ans.frame().head()
###Output
status: TRYINGTOASSIGN
.... no task information
status: TERMINATEDNORMALLY
.... Wed Oct 24 14:00:39 2018 UTC Begin job
###Markdown
pybatfish.question.bfq.definedStructures()ネットワーク内で定義されている構造体の一覧を返す。
###Code
def_struct_ans = bfq.definedStructures().answer()
def_struct_ans.frame().head()
###Output
status: TRYINGTOASSIGN
.... no task information
status: TERMINATEDNORMALLY
.... Wed Oct 24 14:05:16 2018 UTC Begin job
###Markdown
pybatfish.question.bfq.edges()様々な種類のエッジを返す。- エッジの種類(edgeTypeとして指定できる。デフォルトはlayer3?) - bgp - eigrp - isis - layer1 - layer2 - layer3 - ospf - rip
###Code
bgp_edges_ans = bfq.edges(edgeType="bgp").answer()
bgp_edges_ans.frame().head()
###Output
status: TRYINGTOASSIGN
.... no task information
status: TERMINATEDNORMALLY
.... Wed Oct 24 14:16:00 2018 UTC Begin job
###Markdown
pybatfish.question.bfq.fileParseStatus()各設定ファイルのパースが成功したかを返す。- pass- fail- partially parsed
###Code
filepstat_ans = bfq.fileParseStatus().answer()
filepstat_ans.frame().head()
###Output
status: TRYINGTOASSIGN
.... no task information
status: TERMINATEDNORMALLY
.... Wed Oct 24 14:16:59 2018 UTC Begin job
###Markdown
pybatfish.question.bfq.filterLineReachability()ACLの中で、評価されないエントリを返す。
###Code
fltreach_ans = bfq.filterLineReachability().answer()
fltreach_ans.frame().head()
###Output
status: TRYINGTOASSIGN
.... no task information
status: ASSIGNED
.... Wed Oct 24 14:19:15 2018 UTC Begin job
status: TERMINATEDNORMALLY
.... Wed Oct 24 14:19:15 2018 UTC Begin job
###Markdown
pybatfish.question.bfq.filterTable()クエスチョンの回答のサブセットを返す。columnsやfilterなどの変数に何か入れて使うっぽいが、よく分からないので後回し。
###Code
filtertable_ans = bfq.filterTable(innerQuestion=bfq.filterLineReachability()).answer()
filtertable_ans.frame().head()
###Output
status: TRYINGTOASSIGN
.... no task information
status: ASSIGNED
.... Wed Oct 24 14:42:50 2018 UTC Begin job
status: TERMINATEDNORMALLY
.... Wed Oct 24 14:42:50 2018 UTC Begin job
###Markdown
pybatfish.question.bfq.interfaceMtu()の条件に合致するインターフェイスを返す。突如answerオブジェクトからframe属性が消える。
###Code
intmtu_ans = bfq.interfaceMtu(mtuBytes=100, comparator='>').answer()
intmtu_ans.frame().head()
###Output
status: TRYINGTOASSIGN
.... no task information
status: TERMINATEDABNORMALLY
.... Wed Oct 24 14:49:15 2018 UTC Begin job
###Markdown
pybatfish.question.bfq.interfaceProperties()各インターフェイスの設定を返す。
###Code
intprop_ans = bfq.interfaceProperties().answer()
intprop_ans.frame().head()
###Output
status: TRYINGTOASSIGN
.... no task information
status: TERMINATEDNORMALLY
.... Wed Oct 24 14:51:14 2018 UTC Begin job
###Markdown
pybatfish.question.bfq.ipOwners()各IPアドレスを保持しているノード、インターフェイスなどの情報を返す。
###Code
ipowners_ans = bfq.ipOwners().answer()
ipowners_ans.frame().head()
###Output
status: TRYINGTOASSIGN
.... no task information
status: TERMINATEDNORMALLY
.... Wed Oct 24 14:56:12 2018 UTC Begin job
###Markdown
pybatfish.question.bfq.ipsecSessionStatus()各IPsec VPNのセッション情報を返す。
###Code
ipsecsesstat_ans = bfq.ipsecSessionStatus().answer()
ipsecsesstat_ans.frame().head()
###Output
status: TRYINGTOASSIGN
.... no task information
status: ASSIGNED
.... Wed Oct 24 14:57:48 2018 UTC Begin job
status: TERMINATEDNORMALLY
.... Wed Oct 24 14:57:48 2018 UTC Begin job
###Markdown
pybatfish.question.bfq.multipathConsistency()マルチパス環境下で、異なる動作をするパスを返す。よく分からない。
###Code
multipathcons_ans = bfq.multipathConsistency().answer()
multipathcons_ans.frame().head()
###Output
status: TRYINGTOASSIGN
.... no task information
status: ASSIGNED
.... Wed Oct 24 15:00:12 2018 UTC Begin job
status: TERMINATEDNORMALLY
.... Wed Oct 24 15:00:12 2018 UTC Begin job
###Markdown
pybatfish.question.bfq.namedStructures()各ノードの名前付き構造体の一覧を返す。構造体って名前がつかないのもあるのか?
###Code
namedstruct_ans = bfq.namedStructures().answer()
namedstruct_ans.frame().head()
###Output
status: TRYINGTOASSIGN
.... no task information
status: ASSIGNED
.... Wed Oct 24 15:02:06 2018 UTC Begin job
status: TERMINATEDNORMALLY
.... Wed Oct 24 15:02:06 2018 UTC Begin job
###Markdown
pybatfish.question.bfq.neighbors()各ネイバーの情報を見られると思ったらframe属性がない。
###Code
neighbors_ans = bfq.neighbors().answer()
neighbors_ans.frame().head()
###Output
status: TRYINGTOASSIGN
.... no task information
status: TERMINATEDNORMALLY
.... Wed Oct 24 15:04:02 2018 UTC Begin job
###Markdown
pybatfish.question.bfq.nodeProperties()各ノードの設定情報が見られる。
###Code
nodeprop_ans = bfq.nodeProperties().answer()
nodeprop_ans.frame().head()
###Output
status: TRYINGTOASSIGN
.... no task information
status: TERMINATEDNORMALLY
.... Wed Oct 24 15:05:49 2018 UTC Begin job
###Markdown
pybatfish.question.bfq.nodes()JSONでノードの設定情報を返してくれるようだが、frame属性がない模様。
###Code
nodes_ans = bfq.nodes().answer()
nodes_ans.frame().head()
###Output
status: ASSIGNED
.... no task information
status: TERMINATEDNORMALLY
.... Wed Oct 24 15:10:19 2018 UTC Begin job
###Markdown
pybatfish.question.bfq.ospfProperties()各ノードのOSPF設定情報を返す。
###Code
ospfprop_ans = bfq.ospfProperties().answer()
ospfprop_ans.frame().head()
###Output
status: TRYINGTOASSIGN
.... no task information
status: TERMINATEDNORMALLY
.... Wed Oct 24 15:12:07 2018 UTC Begin job
###Markdown
pybatfish.question.bfq.parseWarning()スナップショットをパースする時に発生した警告の一覧を返す。
###Code
parsewarn_ans = bfq.parseWarning().answer()
parsewarn_ans.frame().head()
###Output
status: TRYINGTOASSIGN
.... no task information
status: TERMINATEDNORMALLY
.... Wed Oct 24 15:13:18 2018 UTC Begin job
###Markdown
pybatfish.question.bfq.prefixTracer()ネットワーク内でのプレフィックスの伝播を追跡する。frame属性なし。
###Code
preftrace_ans = bfq.prefixTracer().answer()
preftrace_ans.frame().head()
###Output
status: TRYINGTOASSIGN
.... no task information
status: ASSIGNED
.... Wed Oct 24 15:14:36 2018 UTC Loading data plane from disk
status: TERMINATEDABNORMALLY
.... Wed Oct 24 15:14:36 2018 UTC Loading data plane from disk
###Markdown
pybatfish.question.bfq.reachability()headersやpathConstraints、actionsなどで指定した条件に合致したフローを返す。
###Code
reachability_ans = bfq.reachability().answer()
reachability_ans.frame().head()
###Output
status: TRYINGTOASSIGN
.... no task information
status: ASSIGNED
.... Wed Oct 24 15:16:40 2018 UTC Begin job
status: TERMINATEDNORMALLY
.... Wed Oct 24 15:16:40 2018 UTC Begin job
###Markdown
pybatfish.question.bfq.reducedReachability()あるスナップショットでは成功したが、他のスナップショットで成功しなかったフローを返す。スナップショットをまたいで使う?
###Code
redreach_ans = bfq.reducedReachability().answer()
redreach_ans.frame().head()
###Output
_____no_output_____
###Markdown
pybatfish.question.bfq.referencedStructures()
###Code
refstruct_ans = bfq.referencedStructures().answer()
refstruct_ans.frame().head()
###Output
status: TRYINGTOASSIGN
.... no task information
status: TERMINATEDNORMALLY
.... Wed Oct 24 15:24:40 2018 UTC Begin job
###Markdown
pybatfish.question.bfq.routes()各ノードのルート情報を表示する。
###Code
routes_ans = bfq.routes().answer()
routes_ans.frame().head()
###Output
status: TRYINGTOASSIGN
.... no task information
status: TERMINATEDNORMALLY
.... Wed Oct 24 15:26:16 2018 UTC Begin job
|
Breast_Cancer_Dataset_PCA.ipynb
|
###Markdown
Principal Component Analysis with Cancer Data
###Code
#Import all the necessary modules
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from scipy.stats import zscore
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
###Output
_____no_output_____
###Markdown
Q1. Load the Data file ( Breast Cancer CSV) into Python DataFrame and view top 10 rows
###Code
cancer_df = pd.read_csv('breast-cancer-wisconsin-data.csv')
# Id columns is to identify rows hence can be skipped in analysis
# All columns have numerical values
# Class would be the target variable. Should be removed when PCA is done
features_df = cancer_df.drop(['ID'], axis = 1)
features_df.head()
###Output
_____no_output_____
###Markdown
Q2 Print the datatypes of each column and the shape of the dataset. Perform descriptive analysis
###Code
features_df.dtypes
features_df.describe().T
###Output
_____no_output_____
###Markdown
Q3 Check for missing value check, incorrect data, duplicate data and perform imputation with mean, median, mode as necessary.
###Code
# We could see "?" values in column, this should be removed from data set
# Check for missing value in any other column
# No missing values found. So let us try to remove ? from bare nuclei column
# Get count of rows having ?
# 16 values are corrupted. We can either delete them as it forms roughly 2% of data.
# Here we would like to impute it with suitable values
features_df.isnull().sum()
filter1 = features_df['Bare Nuclei'] == '?'
features_df[filter1].shape
features_df.loc[filter1, 'Bare Nuclei'] = np.nan
features_df.isnull().sum()
features_df = features_df.apply(lambda x: x.fillna(x.median()),axis=1)
features_df.isnull().sum()
features_df.shape
features_df.duplicated(keep='first').sum()
features_df.drop_duplicates(keep = 'first', inplace = True)
features_df.shape
features_df['Bare Nuclei'] = features_df['Bare Nuclei'].astype('float64')
###Output
_____no_output_____
###Markdown
Q4. Perform bi variate analysis including correlation, pairplots and state the inferences.
###Code
# Check for correlation of variable
# Cell size shows high significance with cell shape,marginal adhesion, single epithelial cell size,bare nuclei, normal nucleoli
# and bland chromatin
# Target variable shows high correlation with most of these variables
#Let us check for pair plots
# Relationship between variables shows come correlation.
# Distribution of variables shows most of the values are concentrated on lower side, though range remains same for all that is
# Between 1 to 10
corr_matrix = features_df.corr()
corr_matrix
###Output
_____no_output_____
###Markdown
Observations------------------- 1. Clump Thickness is moderatley positively correlated with Cell Size (0.578156)2. Clump Thickness is moderately positively correlated with Cell Shape (0.588956)3. Cell Size is highly positvely correlated with Cell Shape (0.877404)5. Cell Size is moderately positively correlated with Marginal Adhesion(0.640096), Single Epithelial Cell Size(0.689982), Bare Nuclei(0.598223), Normal Nucleoli(0.712986), Bland Chromatin(0.657170)7. Cell Shape is moderately positively correlated with Marginal Adhesion(0.683079), Single Epithelial Cell Size(0.719668), Bare Nuclei(0.715495), Normal Nucleoli(0.735948), Bland Chromatin(0.719446)8. Cell Shape is adequately highly correlated with Class(0.818934)9. Bare Nuclei is adequately correlated with Class (0.820678)10. Normal Nucleoli is moderately highly correlated with Class (0.756618)11. Bland Chromatin is moderately highly correlated with Class (0.715540)
###Code
sns.pairplot(data = features_df, diag_kind = 'kde')
plt.show()
###Output
_____no_output_____
###Markdown
Q5 Remove any unwanted columns or outliers, standardize variables in pre-processing step
###Code
# We could see most of the outliers are now removed.
features_df.boxplot(figsize=(15, 10))
plt.show()
features_df.shape
cols = ['Mitoses', 'Single Epithelial Cell Size']
for col in cols:
Q1 = features_df[col].quantile(0.25)
Q3 = features_df[col].quantile(0.75)
IQR = Q3 - Q1
lower_limit = Q1 - (1.5 * IQR)
upper_limit = Q3 + (1.5 * IQR)
filter2 = features_df[col] > upper_limit
features_df.drop(features_df[filter2].index, inplace = True)
features_df.shape
###Output
_____no_output_____
###Markdown
Q6 Create a covariance matrix for identifying Principal components
###Code
# PCA
# Step 1 - Create covariance matrix
cov_matrix = features_df.cov()
cov_matrix
###Output
_____no_output_____
###Markdown
Q7 Identify eigen values and eigen vector
###Code
# Step 2- Get eigen values and eigen vector
eig_vals, eig_vectors =np.linalg.eig(cov_matrix)
eig_vals
eig_vectors
###Output
_____no_output_____
###Markdown
Q8 Find variance and cumulative variance by each eigen vector
###Code
eig_vectors.var()
total_eigen_vals = sum(eig_vals)
var_explained = [(i/total_eigen_vals * 100) for i in sorted(eig_vals, reverse = True)]
print(var_explained)
print(np.cumsum(var_explained))
###Output
[63.92604980419202, 10.512941043921826, 7.377320792895226, 5.604554209284447, 4.698298814213461, 3.366426653673131, 2.32079139728324, 1.5013775963385572, 0.39658079590952444, 0.2956588922885669]
[ 63.9260498 74.43899085 81.81631164 87.42086585 92.11916466
95.48559132 97.80638272 99.30776031 99.70434111 100. ]
###Markdown
Q9 Use PCA command from sklearn and find Principal Components. Transform data to components formed
###Code
X = features_df.drop('Class', axis = 1)
y = features_df['Class']
pca = PCA()
pca.fit(X)
X_pca = pca.transform(X)
X_pca.shape
###Output
_____no_output_____
###Markdown
Q10 Find correlation between components and features
###Code
pca.components_
pca.explained_variance_
pca.explained_variance_ratio_
corr_df = pd.DataFrame(data = pca.components_, columns = X.columns)
corr_df.head()
sns.heatmap(corr_df)
plt.show()
###Output
_____no_output_____
###Markdown
Popularity Based Recommendation System About Dataset Anonymous Ratings on jokes. 1. Ratings are real values ranging from -10.00 to +10.00 (the value "99" corresponds to "null" = "not rated").2. One row per user3. The first column gives the number of jokes rated by that user. The next 100 columns give the ratings for jokes 01 - 100. Q11 Read the dataset(jokes.csv)
###Code
jokes_df = pd.read_excel('jokes.xlsx')
jokes_df.head()
###Output
_____no_output_____
###Markdown
Q12 Create a new dataframe named `ratings`, with only first 200 rows and all columns from 1(first column is 0) of dataset
###Code
ratings = jokes_df.head(200)
###Output
_____no_output_____
###Markdown
Q13 In the dataset, the null ratings are given as 99.00, so replace all 99.00s with 0Hint: You can use `ratings.replace(, )`
###Code
ratings = ratings_df.replace(99.00, 0)
###Output
_____no_output_____
###Markdown
Q14 Normalize the ratings using StandardScaler and save them in ratings_diff variable
###Code
scaler = StandardScaler()
ratings_diff = scaler.fit_transform(ratings)
ratings_diff
###Output
_____no_output_____
###Markdown
Q15 Find the mean for each column in `ratings_diff` i.e, for each joke
###Code
all_mean = ratings_diff.mean(axis = 0)
all_mean
###Output
_____no_output_____
###Markdown
Q16 Consider all the mean ratings and find the jokes with highest mean value and display the top 10 joke IDs.
###Code
all_mean_df = pd.DataFrame(data = ratings_diff)
all_mean_df
all_mean_df.mean(axis = 0)
new_df = pd.DataFrame(data = all_mean_df)
new_df.iloc[:,0].argsort()[:-10:-1]
###Output
_____no_output_____
|
assets/notebooks/ipynb/Normalization.ipynb
|
###Markdown
Normalization Tutorial
###Code
from IPython.display import HTML, display
def set_css():
display(HTML('''
<style>
pre {
white-space: pre-wrap;
}
</style>
'''))
get_ipython().events.register('pre_run_cell', set_css)
###Output
_____no_output_____
###Markdown
In this part we will be covering Normalization techniques like Stemming and Lemmatization provided by popular NLP/Python Libraries for English and some Non-English languages Morphology - why we normalize
###Code
import spacy
nlp = spacy.load('en') # will download all default pipelines/processors - tokenizer, parser, ner
doc = nlp("I am reading a book")
token = doc[2] # Reading
nlp.vocab.morphology.tag_map[token.tag_]
token.lemma_
doc = nlp("I read a book")
token = doc[1] # Read
nlp.vocab.morphology.tag_map[token.tag_]
token.lemma_
###Output
_____no_output_____
###Markdown
To understand various Morph features eg: 'VerbForm' use https://universaldependencies.org/u/feat/index.html More Examples at : https://spacy.io/usage/linguistic-featuresmorphology NormalizationWord normalization is the task of putting words/tokens in a standard format, choosinga single normal form for words with multiple forms like USA and US or uh-huhand uhhuh. This standardization may be valuable, despite the spelling informationthat is lost in the normalization p**Libraries being used: ntltk, spacy** Eg: * studies - studi (es suffix)* studying - study (ing suffix) 1. Case-FoldingLowercasing ALL your text data - easy but an essential step for normalization
###Code
s1 = "Cat"
s2 = "cat"
s3 = "caT"
print(s1.lower())
print(s2.lower())
print(s3.lower())
# You can Iterate the corpus using the .lower function
sent = "There are fairly good number of registrations for the conference. More people should be registering in the upcoming days"
import nltk
from nltk.tokenize import word_tokenize
# Punkt Sentence Tokenizer - used specially to use a model to identify sentences
nltk.download('punkt')
###Output
_____no_output_____
###Markdown
1. Tokenize sentence
###Code
# Tokenize the sentence
sent = word_tokenize(sent)
print(sent)
###Output
_____no_output_____
###Markdown
2. Remove Punctuations
###Code
# Remove punctuations
def remove_punct(token):
return [word for word in token if word.isalpha()]
sent = remove_punct(sent)
print(sent)
###Output
_____no_output_____
###Markdown
2. Stemming The naive version of morphological analysis is called stemming. Porter Stemmer * One of the oldest stemmer. This stemmer is known for its speed and simplicity.* Limitation: Morphological variants produced are not always real words.
###Code
from nltk.stem import PorterStemmer
ps = PorterStemmer()
# Using the .stem() function for each word in the sentence
ps_stem_sent = [ps.stem(words_sent) for words_sent in sent]
print(ps_stem_sent)
###Output
_____no_output_____
###Markdown
Stemming a word or sentence may result in words that are not actual words.This is due to Over-Stemming and Under-Stemming Snowball Stemmer When compared to the Porter Stemmer, the Snowball Stemmer can map non-English words too. Since it supports other languages the * Snowball Stemmer is a multi-lingual stemmer. * Snowball stemmer is has greater computational speed than Porter Stemmer.
###Code
import nltk
from nltk.stem.snowball import SnowballStemmer
#the stemmer requires a language parameter
snow_stemmer = SnowballStemmer(language='english')
# Using the .stem() function for each word in the sentence
ss_stem_sent = [snow_stemmer.stem(words_sent) for words_sent in sent]
print(ss_stem_sent)
###Output
_____no_output_____
###Markdown
3. Lemmatization1. Wordnet Lemmatizer2. spaCy Lemmatization3. TextBlob Lemmatizer4. Pattern Lemmatizer5. Stanford CoreNLP Lemmatization6. Gensim Lemmatize Wordnet * WordNet is an English dictionary which is a part of Natural Language Tool Kit (NLTK) for Python. This is an extensive library built to make Natural Language Processing (NLP) easy. * WordNet has been used for a number of purposes in information systems, including word-sense disambiguation, information retrieval, automatic text classification, automatic text summarization, machine translation and even automatic crossword puzzle generation.
###Code
import nltk
nltk.download('wordnet')
nltk.download('punkt')
# The perceptron part-of-speech tagger implements part-of-speech tagging using the averaged, structured perceptron algorithm
nltk.download('averaged_perceptron_tagger')
from nltk.stem import WordNetLemmatizer
# Create a lemmatizer object
lemmatizer = WordNetLemmatizer()
# Lemmatize Single Word
# Use lem_object.lemmatize()
print(lemmatizer.lemmatize("bats"))
print(lemmatizer.lemmatize("are"))
print(lemmatizer.lemmatize("feet"))
sentence = "The striped bats are hanging on their feet"
# Tokenize: Split the sentence into words
word_list = nltk.word_tokenize(sentence)
print(word_list)
# Lemmatize list of words and join
print("+==============================+")
lemmatized_output = ' '.join([lemmatizer.lemmatize(w) for w in word_list])
print(lemmatized_output)
###Output
_____no_output_____
###Markdown
Notice how 'hanging' wasnt changed to 'hang', 'are' isnt changed to 'be'. Hence to improve performance we can pass the POS tag alongside with the word
###Code
# Different stemming as a verb and as a noun
print(lemmatizer.lemmatize("stripes", 'v'))
print(lemmatizer.lemmatize("stripes", 'n'))
print(lemmatizer.lemmatize("striped", 'a'))
print(nltk.pos_tag(nltk.word_tokenize(sentence)))
###Output
[('The', 'DT'), ('striped', 'JJ'), ('bats', 'NNS'), ('are', 'VBP'), ('hanging', 'VBG'), ('on', 'IN'), ('their', 'PRP$'), ('feet', 'NNS')]
###Markdown
you can use https://stackoverflow.com/questions/15388831/what-are-all-possible-pos-tags-of-nltk to find out which POS tag corresponds to which part of speech
###Code
# Simple implementation which included POS tag
from nltk.corpus import wordnet
def get_wordnet_pos(word):
tag = nltk.pos_tag([word])[0][1].upper()
tag_dict = {"JJ": wordnet.ADJ,
"NNS": wordnet.NOUN,
"VBP": wordnet.VERB,
"VBG": wordnet.VERB,
}
return tag_dict.get(tag, wordnet.NOUN)
# 3. Lemmatize a Sentence with the appropriate POS tag
sentence = "The striped bats are hanging on their feet"
print([lemmatizer.lemmatize(w, get_wordnet_pos(w)) for w in nltk.word_tokenize(sentence)])
###Output
_____no_output_____
###Markdown
Notice how using POS improved Normalization Spacy
###Code
import spacy
# Initialize spacy 'en' model, keeping only tagger component needed for lemmatization
nlp = spacy.load('en', disable=['parser', 'ner'])
sentence = "The striped bats are hanging on their feet"
# Parse the sentence using the loaded 'en' model object `nlp`
doc = nlp(sentence)
# Extract the lemma for each token using "token.lemma_"
" ".join([token.lemma_ for token in doc])
###Output
_____no_output_____
###Markdown
spacy replaces any pronoun by -PRON- **The spaCy library is one of the most popular NLP libraries along with NLTK. The basic difference between the two libraries is the fact that NLTK contains a wide variety of algorithms to solve one problem whereas spaCy contains only one, but the best algorithm to solve a problem.** Hindi Normalization Non-english languages do not always have their implementations in popular libraries like nltk and spacyFor Indic languages, some available libraries are:* Indic NLP* Stanford NLP* iNLTK  * iNLTK- Hindi, Punjabi, Sanskrit, Gujarati, Kannada, Malyalam, Nepali, Odia, Marathi, Bengali, Tamil, Urdu* Indic NLP Library- Assamese, Sindhi, Sinhala, Sanskrit, Konkani, Kannada, Telugu,* StanfordNLP- Many of the above languages
###Code
!pip install stanfordnlp
import stanfordnlp
stanfordnlp.download('hi')
nlp = stanfordnlp.Pipeline(lang="hi")
###Output
Use device: cpu
---
Loading: tokenize
With settings:
{'model_path': '/root/stanfordnlp_resources/hi_hdtb_models/hi_hdtb_tokenizer.pt', 'lang': 'hi', 'shorthand': 'hi_hdtb', 'mode': 'predict'}
---
Loading: pos
With settings:
{'model_path': '/root/stanfordnlp_resources/hi_hdtb_models/hi_hdtb_tagger.pt', 'pretrain_path': '/root/stanfordnlp_resources/hi_hdtb_models/hi_hdtb.pretrain.pt', 'lang': 'hi', 'shorthand': 'hi_hdtb', 'mode': 'predict'}
---
Loading: lemma
With settings:
{'model_path': '/root/stanfordnlp_resources/hi_hdtb_models/hi_hdtb_lemmatizer.pt', 'lang': 'hi', 'shorthand': 'hi_hdtb', 'mode': 'predict'}
Building an attentional Seq2Seq model...
Using a Bi-LSTM encoder
Using soft attention for LSTM.
Finetune all embeddings.
[Running seq2seq lemmatizer with edit classifier]
---
Loading: depparse
With settings:
{'model_path': '/root/stanfordnlp_resources/hi_hdtb_models/hi_hdtb_parser.pt', 'pretrain_path': '/root/stanfordnlp_resources/hi_hdtb_models/hi_hdtb.pretrain.pt', 'lang': 'hi', 'shorthand': 'hi_hdtb', 'mode': 'predict'}
Done loading processors!
---
###Markdown
Arguments to the function:* lang: str “en” Use recommended models for this language.* models_dir: str ~/stanfordnlp_resources Directory for storing the models.processors str “tokenize,mwt,pos,lemma,depparse” List of processors to use. For a list of all processors supported, see Processors Summary.* treebank: str None Use models for this treebank. If not specified, Pipeline will look up the default treebank for the language requested.* use_gpu: bool True Attempt to use a GPU if possible.
###Code
!pip install torch==1.4.0
# Please install pytorch 1.4.0 version to avoid error in the below command
doc = nlp("मैंने पिछले महीने भारत की यात्रा की थी। मैं अभी भारत यात्रा कर रहा हूँ|")
for word in doc.sentences[0].words:
# Access attributes using word.text or word.lemma
print("{} --> {}".format(word.text,word.lemma))
###Output
मैंने --> मैं
पिछले --> पिछला
महीने --> महीना
भारत --> भारत
की --> का
यात्रा --> यात्रा
की --> कर
थी --> था
। --> ।
###Markdown
Notice:Depending on the Part of speech, the lemmatization for the word has changed* की --> का* की --> कर
###Code
for word in doc.sentences[1].words:
print("{} --> {}".format(word.text,word.lemma))
###Output
मैं --> मैं
अभी --> अभी
भारत --> भारत
यात्रा --> यात्रा
कर --> कर
रहा --> रह
हूँ| --> हूँ
###Markdown
Notice:* मैंने - मैं* मैं - मैं Stemmer- Sanskrithttps://pypi.org/project/sanstem/
###Code
!pip install sanstem
from sanstem import SanskritStemmer
#create a SanskritStemmer object
stemmer = SanskritStemmer()
inflected_noun = 'गजेन'
stemmed_noun = stemmer.noun_stem(inflected_noun)
print(stemmed_noun)
# output : गज्
inflected_verb = 'गच्छामि'
stemmed_verb = stemmer.verb_stem(inflected_verb)
print(stemmed_verb)
# output : गच्छ्
###Output
गच्छ्
|
examples/plot_stack_masks.ipynb
|
###Markdown
Mask and Plot Remote Sensing Data with EarthPy==============================================Learn how to mask out pixels in a raster dataset. This example shows how to apply a cloud mask toLandsat 8 data. Plotting with EarthPy---------------------NoteBelow we walk through a typical workflow using Landsat data with EarthPy.The example below uses Landsat 8 data. In the example below, the landsat_qa layer is thequality assurance data layer that comes with Landsat 8 to identify pixels that may representcloud, shadow and water. The mask values used below are suggested values associated with thelandsat_qa layer that represent pixels with clouds and cloud shadows. Import Packages------------------------------To begin, import the needed packages. You will use a combination of several EarthPymodules including spatial, plot and mask.
###Code
from glob import glob
import os
import matplotlib.pyplot as plt
import rasterio as rio
from rasterio.plot import plotting_extent
import earthpy as et
import earthpy.spatial as es
import earthpy.plot as ep
import earthpy.mask as em
# Get data and set your home working directory
data = et.data.get_data("cold-springs-fire")
###Output
_____no_output_____
###Markdown
Import Example Data------------------------------To get started, make sure your directory is set. Create a stack from all of theLandsat .tif files (one per band) and import the ``landsat_qa`` layer which providesthe locations of cloudy and shadowed pixels in the scene.
###Code
os.chdir(os.path.join(et.io.HOME, "earth-analytics"))
# Stack the landsat bands
# This creates a numpy array with each "layer" representing a single band
landsat_paths_pre = glob(
"data/cold-springs-fire/landsat_collect/LC080340322016070701T1-SC20180214145604/crop/*band*.tif"
)
landsat_paths_pre.sort()
arr_st, meta = es.stack(landsat_paths_pre)
# Import the landsat qa layer
with rio.open(
"data/cold-springs-fire/landsat_collect/LC080340322016070701T1-SC20180214145604/crop/LC08_L1TP_034032_20160707_20170221_01_T1_pixel_qa_crop.tif"
) as landsat_pre_cl:
landsat_qa = landsat_pre_cl.read(1)
landsat_ext = plotting_extent(landsat_pre_cl)
###Output
_____no_output_____
###Markdown
Plot Histogram of Each Band in Your Data----------------------------------------You can view a histogram for each band in your dataset by using the``hist()`` function from the ``earthpy.plot`` module.
###Code
ep.hist(arr_st)
plt.show()
###Output
_____no_output_____
###Markdown
Customize Histogram Plot with Titles and Colors-----------------------------------------------
###Code
ep.hist(
arr_st,
colors=["blue"],
title=[
"Band 1",
"Band 2",
"Band 3",
"Band 4",
"Band 5",
"Band 6",
"Band 7",
],
)
plt.show()
###Output
_____no_output_____
###Markdown
View Single Band Plots-----------------------------------------------Next, have a look at the data, it looks like there is a large cloud that youmay want to mask out.
###Code
ep.plot_bands(arr_st)
plt.show()
###Output
_____no_output_____
###Markdown
Mask the Data-----------------------------------------------You can use the EarthPy ``mask()`` function to handle this cloud.To begin you need to have a layer that defines the pixels thatyou wish to mask. In this case, the ``landsat_qa`` layer will be used.
###Code
ep.plot_bands(
landsat_qa,
title="The Landsat QA Layer Comes with Landsat Data\n It can be used to remove clouds and shadows",
)
plt.show()
###Output
_____no_output_____
###Markdown
Plot The Masked Data~~~~~~~~~~~~~~~~~~~~~Now apply the mask and plot the masked data. The mask applies to every band in your data.The mask values below are values documented in the Landsat 8 documentation that representclouds and cloud shadows.
###Code
# Generate array of all possible cloud / shadow values
cloud_shadow = [328, 392, 840, 904, 1350]
cloud = [352, 368, 416, 432, 480, 864, 880, 928, 944, 992]
high_confidence_cloud = [480, 992]
# Mask the data
all_masked_values = cloud_shadow + cloud + high_confidence_cloud
arr_ma = em.mask_pixels(arr_st, landsat_qa, vals=all_masked_values)
# sphinx_gallery_thumbnail_number = 5
ep.plot_rgb(
arr_ma, rgb=[4, 3, 2], title="Array with Clouds and Shadows Masked"
)
plt.show()
###Output
_____no_output_____
|
src/data/.ipynb_checkpoints/data_load-checkpoint.ipynb
|
###Markdown
Data Load Install Packages, load data
###Code
# Install Kaggle from PIP
! pip install kaggle
# Download the data via API
! kaggle competitions download -c forest-cover-type-prediction
# Import Packages
import kaggle
import numpy as np
import pandas as pd
np.random.seed(0)
# Import Train and Test data from Kaggle
train_kaggle = pd.read_csv('../../data/raw/forest-cover-type-prediction/train.csv')
test_kaggle = pd.read_csv('../../data/raw/forest-cover-type-prediction/test.csv')
# Shuffle the data
# shuffle = np.random.permutation(np.arange(train_kaggle.shape[0]))
train_kaggle = train_kaggle.sample(frac = 1)
# Separate in to train/dev sets
train_pct = .5 # .8 for 80/20 split
split = int(train_kaggle.shape[0] * train_pct)
train_data = train_kaggle.iloc[:split,:-1].set_index('Id')
train_labels = train_kaggle.iloc[:split,].loc[:, ['Id', 'Cover_Type']].set_index('Id')
dev_data = train_kaggle.iloc[split:,:-1].loc[:,].set_index('Id')
dev_labels = train_kaggle.iloc[split:,].loc[:, ['Id', 'Cover_Type']].set_index('Id')
print(train_data.shape)
print(dev_data.shape)
print(train_labels.shape)
print(dev_labels.shape)
# Write data to dataframes
train_data.to_csv('../../data/processed/train_data.csv')
train_labels.to_csv('../../data/processed/train_labels.csv')
dev_data.to_csv('../../data/processed/dev_data.csv')
dev_labels.to_csv('../../data/processed/dev_labels.csv')
###Output
_____no_output_____
|
examples/multi-layer.ipynb
|
###Markdown
CLECC Community Detection
###Code
using MNCD.CommunityDetection.MultiLayer;
var communities = new CLECCCommunityDetection().Apply(network, 1, 2);
display(communities);
VisualizeCommunities(network, communities);
###Output
_____no_output_____
###Markdown
ABACUS
###Code
using MNCD.CommunityDetection.MultiLayer;
using MNCD.CommunityDetection.SingleLayer;
var communities = new ABACUS().Apply(network, n => new Louvain().Apply(n), 2);
display(communities);
VisualizeCommunities(network, communities);
###Output
_____no_output_____
|
dmu1/dmu1_ml_EGS/1.10_PanSTARRS1-3SS.ipynb
|
###Markdown
EGS master catalogue Preparation of Pan-STARRS1 - 3pi Steradian Survey (3SS) dataThis catalogue comes from `dmu0_PanSTARRS1-3SS`.In the catalogue, we keep:- The `uniquePspsSTid` as unique object identifier;- The r-band position which is given for all the sources;- The grizy `FApMag` aperture magnitude (see below);- The grizy `FKronMag` as total magnitude.The Pan-STARRS1-3SS catalogue provides for each band an aperture magnitude defined as “In PS1, an 'optimal' aperture radius is determined based on the local PSF. The wings of the same analytic PSF are then used to extrapolate the flux measured inside this aperture to a 'total' flux.”The observations used for the catalogue where done between 2010 and 2015 ([ref](https://confluence.stsci.edu/display/PANSTARRS/PS1+Image+data+products)).**TODO**: Check if the detection flag can be used to know in which bands an object was detected to construct the coverage maps.**TODO**: Check for stellarity.
###Code
from herschelhelp_internal import git_version
print("This notebook was run with herschelhelp_internal version: \n{}".format(git_version()))
import datetime
print("This notebook was executed on: \n{}".format(datetime.datetime.now()))
%matplotlib inline
#%config InlineBackend.figure_format = 'svg'
import matplotlib.pyplot as plt
plt.rc('figure', figsize=(10, 6))
from collections import OrderedDict
import os
from astropy import units as u
from astropy.coordinates import SkyCoord
from astropy.table import Column, Table
import numpy as np
from herschelhelp_internal.flagging import gaia_flag_column
from herschelhelp_internal.masterlist import nb_astcor_diag_plot, remove_duplicates
from herschelhelp_internal.utils import astrometric_correction, mag_to_flux
OUT_DIR = os.environ.get('TMP_DIR', "./data_tmp")
try:
os.makedirs(OUT_DIR)
except FileExistsError:
pass
RA_COL = "ps1_ra"
DEC_COL = "ps1_dec"
###Output
_____no_output_____
###Markdown
I - Column selection
###Code
imported_columns = OrderedDict({
"objID": "ps1_id",
"raMean": "ps1_ra",
"decMean": "ps1_dec",
"gFApMag": "m_ap_gpc1_g",
"gFApMagErr": "merr_ap_gpc1_g",
"gFKronMag": "m_gpc1_g",
"gFKronMagErr": "merr_gpc1_g",
"rFApMag": "m_ap_gpc1_r",
"rFApMagErr": "merr_ap_gpc1_r",
"rFKronMag": "m_gpc1_r",
"rFKronMagErr": "merr_gpc1_r",
"iFApMag": "m_ap_gpc1_i",
"iFApMagErr": "merr_ap_gpc1_i",
"iFKronMag": "m_gpc1_i",
"iFKronMagErr": "merr_gpc1_i",
"zFApMag": "m_ap_gpc1_z",
"zFApMagErr": "merr_ap_gpc1_z",
"zFKronMag": "m_gpc1_z",
"zFKronMagErr": "merr_gpc1_z",
"yFApMag": "m_ap_gpc1_y",
"yFApMagErr": "merr_ap_gpc1_y",
"yFKronMag": "m_gpc1_y",
"yFKronMagErr": "merr_gpc1_y"
})
catalogue = Table.read("../../dmu0/dmu0_PanSTARRS1-3SS/data/PanSTARRS1-3SS_EGS_v2.fits")[list(imported_columns)]
for column in imported_columns:
catalogue[column].name = imported_columns[column]
epoch = 2012
# Clean table metadata
catalogue.meta = None
# Adding flux and band-flag columns
for col in catalogue.colnames:
if col.startswith('m_'):
errcol = "merr{}".format(col[1:])
# -999 is used for missing values
catalogue[col][catalogue[col] < -900] = np.nan
catalogue[errcol][catalogue[errcol] < -900] = np.nan
flux, error = mag_to_flux(np.array(catalogue[col]), np.array(catalogue[errcol]))
# Fluxes are added in µJy
catalogue.add_column(Column(flux * 1.e6, name="f{}".format(col[1:])))
catalogue.add_column(Column(error * 1.e6, name="f{}".format(errcol[1:])))
# Band-flag column
if "ap" not in col:
catalogue.add_column(Column(np.zeros(len(catalogue), dtype=bool), name="flag{}".format(col[1:])))
# TODO: Set to True the flag columns for fluxes that should not be used for SED fitting.
catalogue[:10].show_in_notebook()
###Output
_____no_output_____
###Markdown
II - Removal of duplicated sources We remove duplicated objects from the input catalogues.
###Code
SORT_COLS = ['merr_ap_gpc1_r', 'merr_ap_gpc1_g', 'merr_ap_gpc1_i', 'merr_ap_gpc1_z', 'merr_ap_gpc1_y']
FLAG_NAME = 'ps1_flag_cleaned'
nb_orig_sources = len(catalogue)
catalogue = remove_duplicates(catalogue, RA_COL, DEC_COL, sort_col=SORT_COLS, flag_name=FLAG_NAME)
nb_sources = len(catalogue)
print("The initial catalogue had {} sources.".format(nb_orig_sources))
print("The cleaned catalogue has {} sources ({} removed).".format(nb_sources, nb_orig_sources - nb_sources))
print("The cleaned catalogue has {} sources flagged as having been cleaned".format(np.sum(catalogue[FLAG_NAME])))
###Output
/opt/anaconda3/envs/herschelhelp_internal/lib/python3.6/site-packages/astropy/table/column.py:1096: MaskedArrayFutureWarning: setting an item on a masked array which has a shared mask will not copy the mask and also change the original mask array in the future.
Check the NumPy 1.11 release notes for more information.
ma.MaskedArray.__setitem__(self, index, value)
###Markdown
III - Astrometry correctionWe match the astrometry to the Gaia one. We limit the Gaia catalogue to sources with a g band flux between the 30th and the 70th percentile. Some quick tests show that this give the lower dispersion in the results.
###Code
gaia = Table.read("../../dmu0/dmu0_GAIA/data/GAIA_EGS.fits")
gaia_coords = SkyCoord(gaia['ra'], gaia['dec'])
catalogue[RA_COL].unit = u.deg
catalogue[DEC_COL].unit = u.deg
nb_astcor_diag_plot(catalogue[RA_COL], catalogue[DEC_COL],
gaia_coords.ra, gaia_coords.dec)
delta_ra, delta_dec = astrometric_correction(
SkyCoord(catalogue[RA_COL], catalogue[DEC_COL]),
gaia_coords
)
print("RA correction: {}".format(delta_ra))
print("Dec correction: {}".format(delta_dec))
catalogue[RA_COL] += delta_ra.to(u.deg)
catalogue[DEC_COL] += delta_dec.to(u.deg)
nb_astcor_diag_plot(catalogue[RA_COL], catalogue[DEC_COL],
gaia_coords.ra, gaia_coords.dec)
###Output
_____no_output_____
###Markdown
IV - Flagging Gaia objects
###Code
catalogue.add_column(
gaia_flag_column(SkyCoord(catalogue[RA_COL], catalogue[DEC_COL]), epoch, gaia)
)
GAIA_FLAG_NAME = "ps1_flag_gaia"
catalogue['flag_gaia'].name = GAIA_FLAG_NAME
print("{} sources flagged.".format(np.sum(catalogue[GAIA_FLAG_NAME] > 0)))
###Output
9109 sources flagged.
###Markdown
V - Saving to disk
###Code
catalogue.write("{}/PS1.fits".format(OUT_DIR), overwrite=True)
###Output
_____no_output_____
|
examples/community/python/example_karateclub.ipynb
|
###Markdown
Zachary's Karate Club Community Detection Using the `NETWORK` Actionset in SAS Viya and Python In this example, we load the Zachary's Karate Club graph into CAS, and show how to detect communities using the network actionset. his example uses Zachary’s Karate Club data (Zachary 1977), which describes social network friendships between 34 members of a karate club at a US university in the 1970s. This is one of the standard publicly available data tables for testing community detection algorithms. It contains 34 nodes and 78 links. The graph is shown below.----------------The basic flow of this notebook is as follows:1. Load the sample graph into a Pandas DataFrame as a set of links that represent the total graph. 2. Connect to our CAS server and load the actionsets we require.3. Upload our sample graph to our CAS server.4. Execute the community detection without fixed nodes using two resolutions (0.5 and 1.0).5. Prepare and display the network plots showing the cliques.----------------__Prepared by:__Damian Herrick (: [dtherrick](www.github.com/dtherrick)) ImportsOur imports are broken out as follows:| Module | Method | Description ||:-----------------|:-----------------:|:----------------------------------------------------------------------------------:|| `os` | all | Allows access to environment variables. || `sys` | all | Used to update our system path so Python can import our custom utility functions. || `swat` | all | SAS Python module that orchestrates communicatoin with a CAS server. || `pandas` | all | Data management module we use for preparation of local data. || `networkx` | all | Used to manage graph data structures when plotting. || `bokeh.io` | `output_notebook` | Utility function that allows rendering of Bokeh plots in Jupyter || `bokeh.io` | `show` | Utility function that displays Bokeh plots || `bokeh.layouts` | `gridplot` | Utility function that arranges Bokeh plots in a multi-plot grid || `bokeh.palettes` | `Spectral8` | Eight-color palette used to differentiate node types. || `bokehvis` | all | Custom module written to simplify plot rendering with Bokeh |
###Code
import os
import sys
import swat
import pandas as pd
import networkx as nx
from bokeh.io import output_notebook, show
from bokeh.layouts import gridplot
from bokeh.palettes import Spectral8
sys.path.append(os.path.join(os.path.dirname(os.getcwd()),r"../../common/python"))
import bokehvis as vis
# tell our notebook we want to output with Bokeh
output_notebook()
###Output
_____no_output_____
###Markdown
Prepare the sample graph. * We pass a set of links, and a set of nodes. Nodes are passed this time because we define fix groups for later calculation on load.
###Code
colNames = ["from", "to"]
links = [
(0, 9), (0, 10), (0, 14), (0, 15), (0, 16), (0, 19), (0, 20), (0, 21), (0, 33),
(0, 23), (0, 24), (0, 27), (0, 28), (0, 29), (0, 30), (0, 31), (0, 32),
(2, 1),
(3, 1), (3, 2),
(4, 1), (4, 2), (4, 3),
(5, 1),
(6, 1),
(7, 1), (7, 5), (7, 6),
(8, 1), (8, 2), (8, 3), (8, 4),
(9, 1), (9, 3),
(10, 3),
(11, 1), (11, 5), (11, 6),
(12, 1),
(13, 1), (13, 4),
(14, 1), (14, 2), (14, 3), (14, 4),
(17, 6), (17, 7),
(18, 1), (18, 2),
(20, 1), (20, 2),
(22, 1), (22, 2),
(26, 24), (26, 25),
(28, 3), (28, 24), (28, 25),
(29, 3),
(30, 24), (30, 27),
(31, 2), (31, 9),
(32, 1), (32, 25), (32, 26), (32, 29),
(33, 3), (33, 9), (33, 15), (33, 16), (33, 19), (33, 21), (33, 23), (33, 24), (33, 30), (33, 31), (33, 32),
]
dfLinkSetIn = pd.DataFrame(links, columns=colNames)
###Output
_____no_output_____
###Markdown
Let's start by looking at the basic network itself.We create a `networkx` graph and pass it to our `bokeh` helper function to create the initial plot.
###Code
G_comm = nx.from_pandas_edgelist(dfLinkSetIn, 'from', 'to')
title = "Zachary's Karate Club"
hover = [('Node', '@index')]
nodeSize = 25
plot = vis.render_plot(graph=G_comm,
title=title,
hover_tooltips=hover,
node_size=nodeSize,
width=1200,
label_font_size="10px",
label_x_offset=-3)
show(plot)
###Output
_____no_output_____
###Markdown
Connect to CAS, load the actionsets we'll need, and upload our graph to the CAS server.
###Code
host = os.environ['CAS_HOST_ORGRD']
port = int(os.environ['CAS_PORT'])
conn = swat.CAS(host, port)
conn.loadactionset("network")
###Output
NOTE: Added action set 'network'.
###Markdown
Upload the local dataframe into CAS
###Code
conn.setsessopt(messageLevel="ERROR")
_ = conn.upload(dfLinkSetIn, casout='LinkSetIn')
conn.setsessopt(messageLevel="DEFAULT")
###Output
_____no_output_____
###Markdown
Step 3: Calculate the communities (without fixed groups) in our graph using the `network` actionset. Since we've loaded our actionset, we can reference it using dot notation from our connection object.We use detection at two resolutions: 0.5 and 1.0Note that the Python code below is equivalent to this block of CASL:```proc network links = mycas.LinkSetIn outNodes = mycas.NodeSetOut; community resolutionList = 1.0 0.5 outLevel = mycas.CommLevelOut outCommunity = mycas.CommOut outOverlap = mycas.CommOverlapOut outCommLinks = mycas.CommLinksOut;run;```
###Code
conn.network.community(links = {'name':'LinkSetIn'},
outnodes = {'name':'nodeSetOut', 'replace':True},
outLevel = {'name':'CommLevelOut', 'replace':True},
outCommunity = {'name':'CommOut', 'replace':True},
outOverlap = {'name':'CommOverlapOut', 'replace':True},
outCommLinks = {'name':'CommLinksOut', 'replace':True},
resolutionList = [0.5, 1]
)
###Output
NOTE: The number of nodes in the input graph is 34.
NOTE: The number of links in the input graph is 78.
NOTE: Processing community detection using 1 threads across 1 machines.
NOTE: At resolution=1, the community algorithm found 4 communities with modularity=0.418803.
NOTE: At resolution=0.5, the community algorithm found 2 communities with modularity=0.371795.
NOTE: Processing community detection used 0.00 (cpu: 0.00) seconds.
###Markdown
Step 4: Get the community results from CAS and prepare data for plotting------In this step we fetch the node results from CAS, then add community assignments and node fill color as node attributes in our `networkx` graph.| Table | Description ||------------|-----------------------------------------------------------|| `NodeSetA` | Results and community labels for resolutions 0.5 and 1.0. || Attribute Label | Description ||-------------------|--------------------------------------|| `community_0` | Community assignment, resolution 1.0 || `community_1` | Community assignment, resolution 0.5 |
###Code
# pull the node set locally so we can plot
comm_nodes_cas = conn.CASTable('NodeSetOut').to_dict(orient='index')
# make our mapping dictionaries that allow us to assign attributes
comm_nodes_0 = {v['node']:v['community_0'] for v in comm_nodes_cas.values()}
comm_nodes_1 = {v['node']:v['community_1'] for v in comm_nodes_cas.values()}
# set the attributes
nx.set_node_attributes(G_comm, comm_nodes_0, 'community_0')
nx.set_node_attributes(G_comm, comm_nodes_1, 'community_1')
# Assign the fill colors for the nodes.
for node in G_comm.nodes:
G_comm.nodes[node]['highlight_0'] = Spectral8[int(G_comm.nodes[node]['community_0'])]
G_comm.nodes[node]['highlight_1'] = Spectral8[int(G_comm.nodes[node]['community_1'])]
###Output
_____no_output_____
###Markdown
Create and display the plots
###Code
title_0 = 'Community Detection Example 1: Resolution 1'
hover_0 = [('Node', '@index'), ('Community', '@community_0')]
title_1 = 'Community Detection Example 2: Resolution 0.5'
hover_1 = [('Node', '@index'), ('Community', '@community_1')]
# render the plots.
# reminder - we set nodeSize earlier in the notebook. Its value is 25.
plot_0 = vis.render_plot(graph=G_comm, title=title_0, hover_tooltips=hover_0, node_size=nodeSize, node_color='highlight_0', width=1200)
plot_1 = vis.render_plot(graph=G_comm, title=title_1, hover_tooltips=hover_1, node_size=nodeSize, node_color='highlight_1', width=1200)
grid = gridplot([plot_0, plot_1], ncols=1)
show(grid)
###Output
_____no_output_____
###Markdown
Clean up everything. Make sure we know what tables we created, drop them, and close our connection.(This is probably overkill, since everything in this session is ephemeral anyway, but good practice nonetheless.
###Code
table_list = conn.tableinfo()["TableInfo"]["Name"].to_list()
for table in table_list:
conn.droptable(name=table, quiet=True)
conn.close()
###Output
_____no_output_____
|
4_archmage/1.1.1. Perceptron and Adaline.ipynb
|
###Markdown
(exceprt from Python Machine Learning Essentials, Supplementary Materials) Sections- [Implementing a perceptron learning algorithm in Python](Implementing-a-perceptron-learning-algorithm-in-Python) - [Training a perceptron model on the Iris dataset](Training-a-perceptron-model-on-the-Iris-dataset)- [Adaptive linear neurons and the convergence of learning](Adaptive-linear-neurons-and-the-convergence-of-learning) - [Implementing an adaptive linear neuron in Python](Implementing-an-adaptive-linear-neuron-in-Python)
###Code
# Display plots in notebook
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
###Output
_____no_output_____
###Markdown
Implementing a perceptron learning algorithm in Python [[back to top](Sections)]
###Code
from ann import Perceptron
Perceptron?
###Output
_____no_output_____
###Markdown
Training a perceptron model on the Iris dataset [[back to top](Sections)] Reading-in the Iris data
###Code
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
data = np.hstack((X, y[:, np.newaxis]))
labels = iris.target_names
features = iris.feature_names
df = pd.DataFrame(data, columns=iris.feature_names+['label'])
df.label = df.label.map({k:v for k,v in enumerate(labels)})
df.tail()
###Output
_____no_output_____
###Markdown
Plotting the Iris data
###Code
# select setosa and versicolor
y = df.iloc[0:100, 4].values
y = np.where(y == 'setosa', -1, 1)
# extract sepal length and petal length
X = df.iloc[0:100, [0, 2]].values
# plot data
plt.scatter(X[:50, 0], X[:50, 1],
color='red', marker='o', label='setosa')
plt.scatter(X[50:100, 0], X[50:100, 1],
color='blue', marker='x', label='versicolor')
plt.xlabel('petal length [cm]')
plt.ylabel('sepal length [cm]')
plt.legend(loc='upper left')
plt.show()
###Output
_____no_output_____
###Markdown
Training the perceptron model
###Code
ppn = Perceptron(eta=0.1, n_iter=10)
ppn.fit(X, y)
plt.plot(range(1, len(ppn.errors_) + 1), ppn.errors_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Number of misclassifications')
plt.tight_layout()
plt.show()
###Output
_____no_output_____
###Markdown
A function for plotting decision regions
###Code
from matplotlib.colors import ListedColormap
def plot_decision_regions(X, y, classifier, resolution=0.02):
# setup marker generator and color map
markers = ('s', 'x', 'o', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
# plot the decision surface
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
# plot class samples
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],
alpha=0.8, c=[cmap(idx)],
marker=markers[idx], label=cl)
plot_decision_regions(X, y, classifier=ppn)
plt.xlabel('sepal length [cm]')
plt.ylabel('petal length [cm]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
###Output
_____no_output_____
###Markdown
Adaptive linear neurons and the convergence of learning [[back to top](Sections)] Implementing an adaptive linear neuron in Python
###Code
from ann import AdalineGD
AdalineGD?
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(8, 4))
ada1 = AdalineGD(n_iter=10, eta=0.01).fit(X, y)
ax[0].plot(range(1, len(ada1.cost_) + 1), np.log10(ada1.cost_), marker='o')
ax[0].set_xlabel('Epochs')
ax[0].set_ylabel('log(Sum-squared-error)')
ax[0].set_title('Adaline - Learning rate 0.01')
ada2 = AdalineGD(n_iter=10, eta=0.0001).fit(X, y)
ax[1].plot(range(1, len(ada2.cost_) + 1), ada2.cost_, marker='o')
ax[1].set_xlabel('Epochs')
ax[1].set_ylabel('Sum-squared-error')
ax[1].set_title('Adaline - Learning rate 0.0001')
plt.tight_layout()
plt.show()
###Output
_____no_output_____
###Markdown
Standardizing features and re-training adaline
###Code
# standardize features
X_std = np.copy(X)
X_std[:,0] = (X[:,0] - X[:,0].mean()) / X[:,0].std()
X_std[:,1] = (X[:,1] - X[:,1].mean()) / X[:,1].std()
ada = AdalineGD(n_iter=15, eta=0.01)
ada.fit(X_std, y)
plot_decision_regions(X_std, y, classifier=ada)
plt.title('Adaline - Gradient Descent')
plt.xlabel('sepal length [standardized]')
plt.ylabel('petal length [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
plt.plot(range(1, len(ada.cost_) + 1), ada.cost_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Sum-squared-error')
plt.tight_layout()
plt.show()
###Output
_____no_output_____
###Markdown
Large scale machine learning and stochastic gradient descent [[back to top](Sections)]
###Code
from ann import AdalineSGD
AdalineSGD?
ada = AdalineSGD(n_iter=15, eta=0.01, random_state=1)
ada.fit(X_std, y)
plot_decision_regions(X_std, y, classifier=ada)
plt.title('Adaline - Stochastic Gradient Descent')
plt.xlabel('sepal length [standardized]')
plt.ylabel('petal length [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
plt.plot(range(1, len(ada.cost_) + 1), ada.cost_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Average Cost')
plt.tight_layout()
plt.show()
ada.partial_fit(X_std[0, :], y[0])
###Output
_____no_output_____
|
GLCIC/demo.ipynb
|
###Markdown
PIL
###Code
pil_img = transforms.functional.to_pil_image(img).resize((n, n), Image.BILINEAR)
plt.imshow(pil_img, cmap='gray')
###Output
_____no_output_____
###Markdown
OpenCV
###Code
cv2_img = cv2.resize(img.numpy(), (n, n), interpolation=cv2.INTER_LINEAR)
plt.imshow(cv2_img, cmap='gray')
###Output
_____no_output_____
###Markdown
TensorFlow
###Code
tensor_img = torch.unsqueeze(img, dim=2)
tensor_img = tf.image.resize(tensor_img, [n, n], antialias=True)
tensor_img = tf.squeeze(tensor_img).numpy()
plt.imshow(tensor_img, cmap='gray')
###Output
_____no_output_____
###Markdown
PyTorch
###Code
torch_img = transforms.functional.to_pil_image(img)
torch_img = torch.unsqueeze(img, dim=2)
transform = transforms.Resize(n)
torch_img = transform(img)
torch_img = torch_img.numpy().reshape(n, n)
plt.imshow(torch_img, cmap='gray')
###Output
_____no_output_____
|
notebooks/drafts/Using Python to Debunk COVID Myths Death Statistic Inflation-checkpoint.ipynb
|
###Markdown
Using Python to Debunk COVID Myths: ‘Death Statistic Inflation’ What is required from Python: - Download most recent death and population data from eurostat - Format data and only select where NUTS3 includes UK - Interpolate weekly population numbers - Age standardise -
###Code
import datetime as dt
import gzip
import io
import numpy as np
import pandas as pd
import requests
import sys
import warnings
%config Completer.use_jedi = False
warnings.filterwarnings('ignore')
pd.set_option('display.max_rows', 500)
pd.set_option('display.max_columns', 500)
###Output
_____no_output_____
###Markdown
1. Population Data 1a. Import, Clean and Munge Raw Data
###Code
r = requests.get('https://ec.europa.eu/eurostat/estat-navtree-portlet-prod/BulkDownloadListing?file=data/demo_r_pjangrp3.tsv.gz')
mlz = gzip.open(io.BytesIO(r.content))
df_pop = pd.read_csv(mlz, sep='\t')
# rename and fix id data column
df_pop = df_pop.rename(columns={"sex,unit,age,geo\\time": "Headings"})
# parse to 4 cols
df_pop["Headings"] = df_pop["Headings"].apply(lambda x: x.split(','))
df_pop[['Sex', 'Unit', 'Age', 'Code']] = pd.DataFrame(df_pop.Headings.tolist(), index= df_pop.index)
df_pop = df_pop.drop(columns=['Headings', 'Unit'])
df_pop = df_pop[(df_pop.Sex == 'T') & (~df_pop.Age.isin(['TOTAL', 'UNK']))]
df_pop = df_pop.drop(columns=['Sex'])
df_pop = pd.melt(df_pop, id_vars=['Age', 'Code'], var_name=['Year'], value_vars=['2014 ', '2015 ', '2016 ', '2017 ', '2018 ', '2019 '], value_name='Pop')
# remove iregs from number col (e.g. p means provisional)
num_iregs = [":", "b", "p", "e", " "]
for ireg in num_iregs:
df_pop.Pop = df_pop.Pop.str.replace(ireg, "")
# cast to numeric
num_cols = ['Pop', 'Year']
for col in num_cols:
df_pop[col] = pd.to_numeric(df_pop[col])
print('We have {:,.0f} observations for annual data by NUTS3 and age group breakdown'.format(len(df_pop)))
df_pop.head()
# give country code to help with chunking
df_pop['Country_Code'] = df_pop.Code.str[:2]
df_pop = pd.merge(left=df_pop, right=df_nuts, on='Code', how='left')
df_pop = df_pop[df_pop.Country == 'United Kingdom']
###Output
_____no_output_____
###Markdown
1b. Create Liner Interp for 2020 and 2021
###Code
# add 2020, 2021 data with NAN for pop to be linearly interpolated forward
df_pop_new = df_pop[['Age', 'Code', 'Country_Code']].drop_duplicates()
df_pop_new['Pop'] = np.nan
df_pop_new['Year'] = 2020
df_pop = pd.concat([df_pop, df_pop_new])
df_pop_new['Year'] = 2021
df_pop = pd.concat([df_pop, df_pop_new])
# just to prove we have a complete data set
df_pop[['Year', 'Code']].groupby('Year').count()
# linear interp 2019 population by group for 2020 and 2021
df_pop = df_pop.sort_values(['Code', 'Age', 'Year'])
df_pop = df_pop.reset_index(drop=True)
df_pop['Pop'] = df_pop['Pop'].ffill()
###Output
_____no_output_____
|
docs/seaman/02.1_seaman_sway_hull_equation.ipynb
|
###Markdown
Sway hull equation
###Code
%load_ext autoreload
%autoreload 2
%matplotlib inline
import sympy as sp
from sympy.plotting import plot as plot
from sympy.plotting import plot3d as plot3d
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
sp.init_printing()
from IPython.core.display import HTML
import seaman.helpers
import seaman_symbol as ss
import sway_hull_equations as equations
import sway_hull_lambda_functions as lambda_functions
from bis_system import BisSystem
###Output
_____no_output_____
###Markdown
Coordinate system Symbols
###Code
from seaman_symbols import *
HTML(ss.create_html_table(symbols=equations.total_sway_hull_equation_SI.free_symbols))
###Output
_____no_output_____
###Markdown
Sway equation
###Code
equations.sway_hull_equation
###Output
_____no_output_____
###Markdown
Force due to drift
###Code
equations.sway_drift_equation
###Output
_____no_output_____
###Markdown
Same equation in SI units
###Code
equations.sway_drift_equation_SI
###Output
_____no_output_____
###Markdown
Force due to yaw rate
###Code
equations.sway_yaw_rate_equation
equations.sway_yaw_rate_equation_SI
###Output
_____no_output_____
###Markdown
Nonlinear forceThe nonlinear force is calculated as the sectional cross flow drag. 
###Code
equations.sway_none_linear_equation
###Output
_____no_output_____
###Markdown
Simple assumption for section draught:
###Code
equations.section_draught_equation
equations.simplified_sway_none_linear_equation
###Output
_____no_output_____
###Markdown
Nonlinear force equation expressed as bis force:
###Code
equations.simplified_sway_none_linear_equation_bis
equations.sway_hull_equation_SI
equations.sway_hull_equation_SI
equations.total_sway_hull_equation_SI
###Output
_____no_output_____
###Markdown
Plotting the total sway hull force equation
###Code
df = pd.DataFrame()
df['v_w'] = np.linspace(-0.3,3,10)
df['u_w'] = 5.0
df['r_w'] = 0.0
df['rho'] = 1025
df['t_a'] = 1.0
df['t_f'] = 1.0
df['L'] = 1.0
df['Y_uv'] = 1.0
df['Y_uuv'] = 1.0
df['Y_ur'] = 1.0
df['Y_uur'] = 1.0
df['C_d'] = 0.5
df['g'] = 9.81
df['disp'] = 23
result = df.copy()
result['fy'] = lambda_functions.Y_h_function(**df)
result.plot(x = 'v_w',y = 'fy');
###Output
_____no_output_____
###Markdown
Plotting with coefficients from a real seaman ship model
###Code
import generate_input
shipdict = seaman.ShipDict.load('../../tests/test_ship.ship')
df = pd.DataFrame()
df['v_w'] = np.linspace(-3,3,20)
df['rho'] = 1025.0
df['g'] = 9.81
df['u_w'] = 5.0
df['r_w'] = 0.0
df_input = generate_input.add_shipdict_inputs(lambda_function=lambda_functions.Y_h_function,
shipdict = shipdict,
df = df)
df_input
result = df_input.copy()
result['fy'] = lambda_functions.Y_h_function(**df_input)
result.plot(x = 'v_w',y = 'fy');
###Output
_____no_output_____
###Markdown
Real seaman++Run real seaman in C++ to verify that the documented model is correct.
###Code
import run_real_seaman
df = pd.DataFrame()
df['v_w'] = np.linspace(-3,3,20)
df['rho'] = 1025.0
df['g'] = 9.81
df['u_w'] = 5.0
df['r_w'] = 0.0
result_comparison = run_real_seaman.compare_with_seaman(lambda_function=lambda_functions.Y_h_function,
shipdict = shipdict,
df = df)
fig,ax = plt.subplots()
result_comparison.plot(x = 'v_w',y = ['fy','fy_seaman'],ax = ax)
ax.set_title('Drift angle variation');
df = pd.DataFrame()
df['r_w'] = np.linspace(-0.1,0.1,20)
df['rho'] = 1025.0
df['g'] = 9.81
df['u_w'] = 5.0
df['v_w'] = 0.0
df_input = generate_input.add_shipdict_inputs(lambda_function=lambda_functions.Y_h_function,
shipdict = shipdict,
df = df)
result_comparison = run_real_seaman.compare_with_seaman(lambda_function=lambda_functions.Y_h_function,
shipdict = shipdict,
df = df,)
fig,ax = plt.subplots()
result_comparison.plot(x = 'r_w',y = ['fy','fy_seaman'],ax = ax)
ax.set_title('Yaw rate variation');
df_input
###Output
_____no_output_____
|
Real_Data/Cusanovich_2018_subset/run_methods/GeneScoring/GeneScoring_cusanovich2018subset.ipynb
|
###Markdown
Installation `conda install bioconductor-genomicranges bioconductor-summarizedexperiment -y` `R` `devtools::install_github("caleblareau/BuenColors")` Import packages
###Code
library(GenomicRanges)
library(SummarizedExperiment)
library(data.table)
library(dplyr)
library(BuenColors)
library(Matrix)
###Output
Loading required package: stats4
Loading required package: BiocGenerics
Loading required package: parallel
Attaching package: ‘BiocGenerics’
The following objects are masked from ‘package:parallel’:
clusterApply, clusterApplyLB, clusterCall, clusterEvalQ,
clusterExport, clusterMap, parApply, parCapply, parLapply,
parLapplyLB, parRapply, parSapply, parSapplyLB
The following objects are masked from ‘package:stats’:
IQR, mad, sd, var, xtabs
The following objects are masked from ‘package:base’:
anyDuplicated, append, as.data.frame, basename, cbind, colMeans,
colnames, colSums, dirname, do.call, duplicated, eval, evalq,
Filter, Find, get, grep, grepl, intersect, is.unsorted, lapply,
lengths, Map, mapply, match, mget, order, paste, pmax, pmax.int,
pmin, pmin.int, Position, rank, rbind, Reduce, rowMeans, rownames,
rowSums, sapply, setdiff, sort, table, tapply, union, unique,
unsplit, which, which.max, which.min
Loading required package: S4Vectors
Attaching package: ‘S4Vectors’
The following object is masked from ‘package:base’:
expand.grid
Loading required package: IRanges
Loading required package: GenomeInfoDb
Loading required package: Biobase
Welcome to Bioconductor
Vignettes contain introductory material; view with
'browseVignettes()'. To cite Bioconductor, see
'citation("Biobase")', and for packages 'citation("pkgname")'.
Loading required package: DelayedArray
Loading required package: matrixStats
Attaching package: ‘matrixStats’
The following objects are masked from ‘package:Biobase’:
anyMissing, rowMedians
Loading required package: BiocParallel
Attaching package: ‘DelayedArray’
The following objects are masked from ‘package:matrixStats’:
colMaxs, colMins, colRanges, rowMaxs, rowMins, rowRanges
The following objects are masked from ‘package:base’:
aperm, apply
Attaching package: ‘data.table’
The following object is masked from ‘package:SummarizedExperiment’:
shift
The following object is masked from ‘package:GenomicRanges’:
shift
The following object is masked from ‘package:IRanges’:
shift
The following objects are masked from ‘package:S4Vectors’:
first, second
Attaching package: ‘dplyr’
The following objects are masked from ‘package:data.table’:
between, first, last
The following object is masked from ‘package:matrixStats’:
count
The following object is masked from ‘package:Biobase’:
combine
The following objects are masked from ‘package:GenomicRanges’:
intersect, setdiff, union
The following object is masked from ‘package:GenomeInfoDb’:
intersect
The following objects are masked from ‘package:IRanges’:
collapse, desc, intersect, setdiff, slice, union
The following objects are masked from ‘package:S4Vectors’:
first, intersect, rename, setdiff, setequal, union
The following objects are masked from ‘package:BiocGenerics’:
combine, intersect, setdiff, union
The following objects are masked from ‘package:stats’:
filter, lag
The following objects are masked from ‘package:base’:
intersect, setdiff, setequal, union
Loading required package: MASS
Attaching package: ‘MASS’
The following object is masked from ‘package:dplyr’:
select
Loading required package: ggplot2
Attaching package: ‘Matrix’
The following object is masked from ‘package:S4Vectors’:
expand
###Markdown
Preprocess `bsub < count_reads_peaks_erisone.sh`
###Code
path = './count_reads_peaks_output/'
files <- list.files(path,pattern = "\\.txt$")
length(files)
#assuming tab separated values with a header
datalist = lapply(files, function(x)fread(paste0(path,x))$V4)
#assuming the same header/columns for all files
datafr = do.call("cbind", datalist)
dim(datafr)
df_regions = read.csv("../../input/combined.sorted.merged.bed",
sep = '\t',header=FALSE,stringsAsFactors=FALSE)
dim(df_regions)
peaknames = paste(df_regions$V1,df_regions$V2,df_regions$V3,sep = "_")
head(peaknames)
head(sapply(strsplit(files,'\\.'),'[', 2))
colnames(datafr) = sapply(strsplit(files,'\\.'),'[', 2)
rownames(datafr) = peaknames
datafr[1:3,1:3]
dim(datafr)
# saveRDS(datafr, file = './datafr.rds')
# datafr = readRDS('./datafr.rds')
filter_peaks <- function (datafr,cutoff = 0.01){
binary_mat = as.matrix((datafr > 0) + 0)
binary_mat = Matrix(binary_mat, sparse = TRUE)
num_cells_ncounted = Matrix::rowSums(binary_mat)
ncounts = binary_mat[num_cells_ncounted >= dim(binary_mat)[2]*cutoff,]
ncounts = ncounts[rowSums(ncounts) > 0,]
options(repr.plot.width=4, repr.plot.height=4)
hist(log10(num_cells_ncounted),main="No. of Cells Each Site is Observed In",breaks=50)
abline(v=log10(min(num_cells_ncounted[num_cells_ncounted >= dim(binary_mat)[2]*cutoff])),lwd=2,col="indianred")
# hist(log10(new_counts),main="Number of Sites Each Cell Uses",breaks=50)
datafr_filtered = datafr[rownames(ncounts),]
return(datafr_filtered)
}
###Output
_____no_output_____
###Markdown
Obtain Feature Matrix
###Code
start_time <- Sys.time()
set.seed(2019)
metadata <- read.table('../../input/metadata.tsv',
header = TRUE,
stringsAsFactors=FALSE,quote="",row.names=1)
datafr_filtered <- filter_peaks(datafr)
dim(datafr_filtered)
# import counts
counts <- data.matrix(datafr_filtered)
dim(counts)
counts[1:3,1:3]
# import gene bodies; restrict to TSS
gdf <- read.table("../../input/mm9/mm9-tss.bed", stringsAsFactors = FALSE)
dim(gdf)
gdf[1:3,1:3]
tss <- data.frame(chr = gdf$V1, gene = gdf$V4, stringsAsFactors = FALSE)
tss$tss <- ifelse(gdf$V5 == "+", gdf$V3, gdf$V2)
tss$start <- ifelse(tss$tss - 50000 > 0, tss$tss - 50000, 0)
tss$stop <- tss$tss + 50000
tss_idx <- makeGRangesFromDataFrame(tss, keep.extra.columns = TRUE)
# import ATAC peaks
# adf <- data.frame(fread('../../input/combined.sorted.merged.bed'))
# colnames(adf) <- c("chr", "start", "end")
adf <- data.frame(do.call(rbind,strsplit(rownames(datafr_filtered),'_')),stringsAsFactors = FALSE)
colnames(adf) <- c("chr", "start", "end")
adf$start <- as.integer(adf$start)
adf$end <- as.integer(adf$end)
dim(adf)
adf$mp <- (adf$start + adf$end)/2
atacgranges <- makeGRangesFromDataFrame(adf, start.field = "mp", end.field = "mp")
# find overlap between ATAC peaks and Ranges linker
ov <- findOverlaps(atacgranges, tss_idx) #(query, subject)
options(repr.plot.width=3, repr.plot.height=3)
# plot a histogram showing peaks per gene
p1 <- qplot(table(subjectHits(ov)), binwidth = 1) + theme(plot.subtitle = element_text(vjust = 1),
plot.caption = element_text(vjust = 1)) +
labs(title = "Histogram of peaks per gene", x = "Peaks / gene", y="Frequency") + pretty_plot()
p1
# calculate distance decay for the weights
dist <- abs(mcols(tss_idx)$tss[subjectHits(ov)] - start(atacgranges)[queryHits(ov)])
exp_dist_model <- exp(-1*dist/5000)
# prepare an outcome matrix
m <- Matrix::sparseMatrix(i = c(queryHits(ov), length(atacgranges)),
j = c(subjectHits(ov), length(tss_idx)),
x = c(exp_dist_model,0))
colnames(m) <- gdf$V4 # gene name
m <- m[,which(Matrix::colSums(m) != 0)]
fm_genescoring <- data.matrix(t(m) %*% counts)
dim(fm_genescoring)
fm_genescoring[1:3,1:3]
end_time <- Sys.time()
end_time - start_time
all(colnames(fm_genescoring) == rownames(metadata))
fm_genescoring = fm_genescoring[,rownames(metadata)]
all(colnames(fm_genescoring) == rownames(metadata))
saveRDS(fm_genescoring, file = '../../output/feature_matrices/FM_GeneScoring_cusanovich2018subset.rds')
sessionInfo()
save.image(file = 'GeneScoring_cusanovich2018subset.RData')
###Output
_____no_output_____
|
DS_Intro_Statistics.ipynb
|
###Markdown
Introduction to Statistics Statistics is the study of how random variables behave in aggregate. It is also the use of that behavior to make inferences and arguments. While much of the math behind statistical calculations is rigorous and precise, its application to real data often involves making imperfect assumptions. In this notebook we'll review some fundamental statistics and pay special attention to the assumptions we make in their application. Hypothesis Testing and Parameter Estimator We often use statistics to describe groups of people or events; for example we compare the current temperature to the *average* temperature for the day or season or we compare a change in stock price to the *volatility* of the stock (in the language of statistics, volatility is called **standard deviation**) or we might wonder what the *average* salary of a data scientist is in a particular country. All of these questions and comparisons are rudimentary forms of statistical inference. Statistical inference often falls into one of two categories: hypothesis testing or parameter estimator.Examples of hypothesis testing are:- Testing if an increase in a stock's price is significant or just random chance- Testing if there is a significant difference in salaries between employees with and without advanced degrees- Testing whether there is a significant correlation between the amount of money a customer spent at a store and which advertisements they'd been shownExamples of parameter estimation are:- Estimating the average annual return of a stock- Estimating the variance of salaries for a particular job across companies- Estimating the correlation coefficient between annual advertising budget and annual revenueWe'll explore the processes of statistical inference by considering the example of salaries with and without advanced degrees.**Exercise:** Decide for each example given in the first sentence whether it is an example of hypothesis testing or parameter estimation. Estimating the Mean Suppose that we know from a prior study that employees with advanced degrees in the USA make on average $70k. To answer the question "do people without advanced degrees earn significantly less than people with advanced degrees?" we must first estimate how much people without advanced degrees earn on average.To do that, we will have to collect some data. Suppose we take a representative, unbiased sample of 1000 employed adults without advanced degrees and learn their salaries. To estimate the mean salary of people without advanced degrees, we simply calculate the mean of this sample:$$ \overline X = \frac{1}{n} \sum_{k=1}^n X_k. $$Let's write some code that will simulate sampling some salaries for employees without advanced degrees.
###Code
import scipy as sp
import numpy as np
import matplotlib.pyplot as plt
from ipywidgets import interact, IntSlider
salaries = sp.stats.lognorm(1, loc=20, scale=25)
def plot_sample(dist):
def plotter(size):
X = dist.rvs(size=size)
ys, bins, _ = plt.hist(X, bins=20, density=True)
plt.ylim([0, ys.max() / (ys * (bins[1] - bins[0])).sum() * 1.25])
plt.axvline(dist.mean(), color='r', label='true mean')
plt.axvline(X.mean(), color='g', label='sample mean')
plt.plot(np.arange(20, 100, .01), salaries.pdf(np.arange(20, 100, .01)), 'k--')
plt.legend()
return plotter
sample_size_slider = IntSlider(min=10, max=200, step=10, value=10, description='sample size')
interact(plot_sample(salaries), size=sample_size_slider)
###Output
_____no_output_____
###Markdown
Standard Error of the Mean Notice that each time we run the code to generate the plot above, we draw a different sample. While the "true" mean remains fixed, the sample mean changes as we draw new samples. In other words, our estimate (the sample mean) of the true mean is noisy and has some error. How noisy is it? How much does it typically differ from the true mean? *What is the **standard deviation** of the sample mean from the true mean*?Let's take many samples and make a histogram of the sample means to visualize the typical difference between the sample mean and the true mean.
###Code
def plot_sampling_dist(dist):
def plotter(sample_size):
means = np.array([dist.rvs(size=sample_size).mean() for _ in range(300)]) - dist.mean()
plt.hist(means, bins=20, density=True, label='sample means')
# plot central limit theorem distribution
Xs = np.linspace(means.min(), means.max(), 1000)
plt.plot(Xs, sp.stats.norm.pdf(Xs, scale=np.sqrt(dist.var()/sample_size)), 'k--',
label='central limit theorem')
plt.legend()
return plotter
sample_size_slider = IntSlider(min=10, max=500, step=10, value=10, description='sample size')
interact(plot_sampling_dist(salaries),
sample_size=sample_size_slider)
###Output
_____no_output_____
###Markdown
As we increase the size of our samples, the distribution of sample means comes to resemble a normal distribution. In fact this occurs regardless of the underlying distribution of individual salaries. This phenomenon is described by the Central Limit Theorem, which states that as the sample size increases, the sample mean will tend to follow a normal distribution with a standard deviation$$ \sigma_{\overline X} = \sqrt{\frac{\sigma^2}{n}}.$$This quantity is called the **standard error**, and it quantifies the standard deviation of the sample mean from the true mean.**Exercise:** In your own words, explain the difference between the standard deviation and the standard error of salaries in our example. Hypothesis Testing and z-scores Now that we can calculate how much we may typically expect the sample mean to differ from the true mean by random chance, we can perform a **hypothesis test**. In hypothesis testing, we assume that the true mean is a known quantity. We then collect a sample and calculate the difference between the sample mean and the assumed true mean. If this difference is large compared to the standard error (i.e. the typical difference we might expect to arise from random chance), then we conclude that the true mean is unlikely to be the value that we had assumed. Let's be more precise with out example.1. Suppose that we know from a prior study that employees with advanced degrees in the USA make on average \$70k. Our **null hypothesis** will be that employees without advanced degrees make the same salary: $H_0: \mu = 70$. We will also choose a threshold of significance for our evidence. In order to decide that our null hypothesis is wrong, we must find evidence that would have less than a certain probability $\alpha$ of occurring due to random chance.
###Code
mu = 70
###Output
_____no_output_____
###Markdown
2. Next we collect a sample of salaries from $n$ employees without advanced degrees and calculate the mean of the sample salaries. Below we'll sample 100 employees.
###Code
sample_salaries = salaries.rvs(size=100)
print('Sample mean: {}'.format(sample_salaries.mean()))
###Output
_____no_output_____
###Markdown
3. Now we compare the difference between the sample mean and the assumed true mean to the standard error. This quantity is called a **z-score**.$$ z = \frac{\overline X - \mu}{\sigma / \sqrt{n}} $$
###Code
z = (sample_salaries.mean() - mu) / np.sqrt(salaries.var() / sample_salaries.size)
print('z-score: {}'.format(z))
###Output
_____no_output_____
###Markdown
4. The z-score can be used with the standard normal distribution (due to the Central Limit Theorem) to calculate the probability that the difference between the sample mean and the null hypothesis is due only to random chance. This probability is called a **p-value**.
###Code
p = sp.stats.norm.cdf(z)
print('p-value: {}'.format(p))
plt.subplot(211)
stderr = np.sqrt(salaries.var() / sample_salaries.size)
Xs = np.linspace(mu - 3*stderr, mu + 3*stderr, 1000)
clt = sp.stats.norm.pdf(Xs, loc=mu, scale=stderr)
plt.plot(Xs, clt, 'k--',
label='central limit theorem')
plt.axvline(sample_salaries.mean(), color='b', label='sample mean')
plt.fill_between(Xs[Xs < mu - 2*stderr], 0, clt[Xs < mu - 2*stderr], color='r', label='critical region')
plt.legend()
plt.subplot(212)
Xs = np.linspace(-3, 3, 1000)
normal = sp.stats.norm.pdf(Xs)
plt.plot(Xs, normal, 'k--', label='standard normal distribution')
plt.axvline(z, color='b', label='z-score')
plt.fill_between(Xs[Xs < -2], 0, normal[Xs < -2], color='r', label='critical region')
plt.legend()
###Output
_____no_output_____
###Markdown
5. If our p-value is less than $\alpha$ then we can reject the null hypothesis; since we found evidence that was very unlikely to arise by random chance, it must be that our initial assumption about the value of the true mean was wrong.This is a very simplified picture of hypothesis testing, but the central idea can be a useful tool outside of the formal hypothesis testing framework. By calculating the difference between an observed quantity and the value we would expect, and then comparing this difference to our expectation for how large the difference might be due to random chance, we can quickly make intuitive judgments about quantities that we have measured or calculated. Confidence Intervals We can also use the Central Limit Theorem to help us perform parameter estimation. Using our sample mean, we estimate the average salary of employees without advanced degrees. However, we also know that this estimate deviates somewhat from the true mean due to the randomness of our sample. Therefore we should put probabilistic bounds on our estimate. We can again use the standard error to help us calculate this probability.
###Code
print("Confidence interval (95%) for average salary: ({:.2f} {:.2f})".format(sample_salaries.mean() - 2 * stderr,
sample_salaries.mean() + 2 * stderr))
Xs = np.linspace(sample_salaries.mean() - 3*stderr,
sample_salaries.mean() + 3*stderr,
1000)
ci = sp.stats.norm.pdf(Xs, loc=sample_salaries.mean(), scale=stderr)
plt.plot(Xs, ci, 'k--',
label='confidence interval pdf')
plt.fill_between(Xs[(Xs > sample_salaries.mean() - 2*stderr) & (Xs < sample_salaries.mean() + 2*stderr)],
0,
clt[(Xs > sample_salaries.mean() - 2*stderr) & (Xs < sample_salaries.mean() + 2*stderr)],
color='r', label='confidence interval')
plt.legend(loc = 'upper right')
###Output
_____no_output_____
###Markdown
Introduction to Statistics Statistics is the study of how random variables behave in aggregate. It is also the use of that behavior to make inferences and arguments. While much of the math behind statistical calculations is rigorous and precise, its application to real data often involves making imperfect assumptions. In this notebook we'll review some fundamental statistics and pay special attention to the assumptions we make in their application. Hypothesis Testing and Parameter Estimator We often use statistics to describe groups of people or events; for example we compare the current temperature to the *average* temperature for the day or season or we compare a change in stock price to the *volatility* of the stock (in the language of statistics, volatility is called **standard deviation**) or we might wonder what the *average* salary of a data scientist is in a particular country. All of these questions and comparisons are rudimentary forms of statistical inference. Statistical inference often falls into one of two categories: hypothesis testing or parameter estimator.Examples of hypothesis testing are:- Testing if an increase in a stock's price is significant or just random chance- Testing if there is a significant difference in salaries between employees with and without advanced degrees- Testing whether there is a significant correlation between the amount of money a customer spent at a store and which advertisements they'd been shownExamples of parameter estimation are:- Estimating the average annual return of a stock- Estimating the variance of salaries for a particular job across companies- Estimating the correlation coefficient between annual advertising budget and annual revenueWe'll explore the processes of statistical inference by considering the example of salaries with and without advanced degrees.**Exercise:** Decide for each example given in the first sentence whether it is an example of hypothesis testing or parameter estimation. Estimating the Mean Suppose that we know from a prior study that employees with advanced degrees in the USA make on average $70k. To answer the question "do people without advanced degrees earn significantly less than people with advanced degrees?" we must first estimate how much people without advanced degrees earn on average.To do that, we will have to collect some data. Suppose we take a representative, unbiased sample of 1000 employed adults without advanced degrees and learn their salaries. To estimate the mean salary of people without advanced degrees, we simply calculate the mean of this sample:$$ \overline X = \frac{1}{n} \sum_{k=1}^n X_k. $$Let's write some code that will simulate sampling some salaries for employees without advanced degrees.
###Code
import scipy as sp
import numpy as np
import matplotlib.pyplot as plt
from ipywidgets import interact, IntSlider
salaries = sp.stats.lognorm(1, loc=20, scale=25)
def plot_sample(dist):
def plotter(size):
X = dist.rvs(size=size)
ys, bins, _ = plt.hist(X, bins=20, density=True)
plt.ylim([0, ys.max() / (ys * (bins[1] - bins[0])).sum() * 1.25])
plt.axvline(dist.mean(), color='r', label='true mean')
plt.axvline(X.mean(), color='g', label='sample mean')
plt.plot(np.arange(20, 100, .01), salaries.pdf(np.arange(20, 100, .01)), 'k--')
plt.legend()
return plotter
sample_size_slider = IntSlider(min=10, max=200, step=10, value=10, description='sample size')
interact(plot_sample(salaries), size=sample_size_slider);
###Output
_____no_output_____
###Markdown
Standard Error of the Mean Notice that each time we run the code to generate the plot above, we draw a different sample. While the "true" mean remains fixed, the sample mean changes as we draw new samples. In other words, our estimate (the sample mean) of the true mean is noisy and has some error. How noisy is it? How much does it typically differ from the true mean? *What is the **standard deviation** of the sample mean from the true mean*?Let's take many samples and make a histogram of the sample means to visualize the typical difference between the sample mean and the true mean.
###Code
def plot_sampling_dist(dist):
def plotter(sample_size):
means = np.array([dist.rvs(size=sample_size).mean() for _ in range(300)]) - dist.mean()
plt.hist(means, bins=20, density=True, label='sample means')
# plot central limit theorem distribution
Xs = np.linspace(means.min(), means.max(), 1000)
plt.plot(Xs, sp.stats.norm.pdf(Xs, scale=np.sqrt(dist.var()/sample_size)), 'k--',
label='central limit theorem')
plt.legend()
return plotter
sample_size_slider = IntSlider(min=10, max=500, step=10, value=10, description='sample size')
interact(plot_sampling_dist(salaries),
sample_size=sample_size_slider);
###Output
_____no_output_____
###Markdown
As we increase the size of our samples, the distribution of sample means comes to resemble a normal distribution. In fact this occurs regardless of the underlying distribution of individual salaries. This phenomenon is described by the Central Limit Theorem, which states that as the sample size increases, the sample mean will tend to follow a normal distribution with a standard deviation$$ \sigma_{\overline X} = \sqrt{\frac{\sigma^2}{n}}.$$This quantity is called the **standard error**, and it quantifies the standard deviation of the sample mean from the true mean.**Exercise:** In your own words, explain the difference between the standard deviation and the standard error of salaries in our example. Hypothesis Testing and z-scores Now that we can calculate how much we may typically expect the sample mean to differ from the true mean by random chance, we can perform a **hypothesis test**. In hypothesis testing, we assume that the true mean is a known quantity. We then collect a sample and calculate the difference between the sample mean and the assumed true mean. If this difference is large compared to the standard error (i.e. the typical difference we might expect to arise from random chance), then we conclude that the true mean is unlikely to be the value that we had assumed. Let's be more precise with out example.1. Suppose that we know from a prior study that employees with advanced degrees in the USA make on average \$70k. Our **null hypothesis** will be that employees without advanced degrees make the same salary: $H_0: \mu = 70$. We will also choose a threshold of significance for our evidence. In order to decide that our null hypothesis is wrong, we must find evidence that would have less than a certain probability $\alpha$ of occurring due to random chance.
###Code
mu = 70
###Output
_____no_output_____
###Markdown
2. Next we collect a sample of salaries from $n$ employees without advanced degrees and calculate the mean of the sample salaries. Below we'll sample 100 employees.
###Code
sample_salaries = salaries.rvs(size=100)
print('Sample mean: {}'.format(sample_salaries.mean()))
###Output
Sample mean: 53.97157385027322
###Markdown
3. Now we compare the difference between the sample mean and the assumed true mean to the standard error. This quantity is called a **z-score**.$$ z = \frac{\overline X - \mu}{\sigma / \sqrt{n}} $$
###Code
z = (sample_salaries.mean() - mu) / np.sqrt(salaries.var() / sample_salaries.size)
print('z-score: {}'.format(z))
###Output
z-score: -2.9665825124241887
###Markdown
4. The z-score can be used with the standard normal distribution (due to the Central Limit Theorem) to calculate the probability that the difference between the sample mean and the null hypothesis is due only to random chance. This probability is called a **p-value**.
###Code
p = sp.stats.norm.cdf(z)
print('p-value: {}'.format(p))
plt.subplot(211)
stderr = np.sqrt(salaries.var() / sample_salaries.size)
Xs = np.linspace(mu - 3*stderr, mu + 3*stderr, 1000)
clt = sp.stats.norm.pdf(Xs, loc=mu, scale=stderr)
plt.plot(Xs, clt, 'k--',
label='central limit theorem')
plt.axvline(sample_salaries.mean(), color='b', label='sample mean')
plt.fill_between(Xs[Xs < mu - 2*stderr], 0, clt[Xs < mu - 2*stderr], color='r', label='critical region')
plt.legend()
plt.subplot(212)
Xs = np.linspace(-3, 3, 1000)
normal = sp.stats.norm.pdf(Xs)
plt.plot(Xs, normal, 'k--', label='standard normal distribution')
plt.axvline(z, color='b', label='z-score')
plt.fill_between(Xs[Xs < -2], 0, normal[Xs < -2], color='r', label='critical region')
plt.legend();
###Output
_____no_output_____
###Markdown
5. If our p-value is less than $\alpha$ then we can reject the null hypothesis; since we found evidence that was very unlikely to arise by random chance, it must be that our initial assumption about the value of the true mean was wrong.This is a very simplified picture of hypothesis testing, but the central idea can be a useful tool outside of the formal hypothesis testing framework. By calculating the difference between an observed quantity and the value we would expect, and then comparing this difference to our expectation for how large the difference might be due to random chance, we can quickly make intuitive judgments about quantities that we have measured or calculated. Confidence Intervals We can also use the Central Limit Theorem to help us perform parameter estimation. Using our sample mean, we estimate the average salary of employees without advanced degrees. However, we also know that this estimate deviates somewhat from the true mean due to the randomness of our sample. Therefore we should put probabilistic bounds on our estimate. We can again use the standard error to help us calculate this probability.
###Code
print("Confidence interval (95%) for average salary: ({:.2f} {:.2f})".format(sample_salaries.mean() - 2 * stderr,
sample_salaries.mean() + 2 * stderr))
Xs = np.linspace(sample_salaries.mean() - 3*stderr,
sample_salaries.mean() + 3*stderr,
1000)
ci = sp.stats.norm.pdf(Xs, loc=sample_salaries.mean(), scale=stderr)
plt.plot(Xs, ci, 'k--',
label='confidence interval pdf')
plt.fill_between(Xs[(Xs > sample_salaries.mean() - 2*stderr) & (Xs < sample_salaries.mean() + 2*stderr)],
0,
clt[(Xs > sample_salaries.mean() - 2*stderr) & (Xs < sample_salaries.mean() + 2*stderr)],
color='r', label='confidence interval')
plt.legend(loc = 'upper right');
###Output
Confidence interval (95%) for average salary: (43.17 64.78)
|
day3/.ipynb_checkpoints/Discrete Convolutions-checkpoint.ipynb
|
###Markdown
Welcome to Convolutional Neural Networks!---ECT* TALENT Summer School 2020*Dr. Michelle P. Kuchera**Davidson College* Research interests: - Machine learning to address challenges in nuclear physics (and high-energy physics) - FRIB experiments - Jefferson Lab experiments - Jefferson Lab Theory Center ----- Convolutional Neural Networks: Convoution OperationsThe convolutional neural network architecture was first described by Kunihiko Fukushima in 1980 (!). *Discrete convolutions* are matrix operations that can, amongst other things, be used to apply *filters* to images. Convolutions (continuous) we first published in 1754 (!!). - In this session, we will be looking at *predefined* filters for images to gain an intuition or understanding as to how the convolutional filters look. - In the next session, we will add them into a neural network architecture to create convolutional neural networks. Given an image `A` and a filter `h` with dimensions of $(2\omega+1) \times (2\omega+1)$, the discrete convolution operation is given by the following mathematics:$$C=x\circledast h$$where$$C[m,n] = \sum_{j=-\omega}^{\omega}\sum_{i=-\omega}^{\omega} h[i+\omega,j+\omega]* A[m+i,n+j]$$Or, graphically: Details * The filter slides across the image and down the image. * *Stride* is how many elements (pixels) you slide the filter by after each operation. This affects the dimensionality of the output of each image. * There are choices to be made at the edges. - for a stride of $1$ and a filter dimension of $3$, as shown here, the outer elements can not be computed as described. - one solution is *padding*, or adding zeros around the outside of the image so that the output can maintain the same shape Now, I will demonstrate the application of discrete convolutions of known filters on an image.First, we `import` our necessary packages:
###Code
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
###Output
_____no_output_____
###Markdown
Now, let's define a function to execute the above operation for any given 2-dimensional image and filter matrices:
###Code
def conv2d(img, filt, stride):
n_rows = len(img)
n_cols = len(img[0])
filt_w = len(filt)
filt_h = len(filt[0])
#store our filtered image
new_img = np.zeros((n_rows//stride+1,n_cols//stride+1))
# print(n_rows,n_cols,filt_w,filt_h) # uncomment for debugging
for i in range(filt_w//2,n_rows-filt_w//2, stride):
for j in range(filt_h//2,n_cols-filt_h//2, stride):
new_img[i//stride,j//stride] = np.sum(img[i-filt_w//2:i+filt_w//2+1,j-filt_h//2:j+filt_h//2+1]*filt)
return new_img
###Output
_____no_output_____
###Markdown
We will first generate a simple synthetic image to which we will apply filters:
###Code
test_img = np.zeros((128,128)) # make an image 128x128 pixels, start by making it entirely black
test_img[30,:] = 255 # add a white row
test_img[:,40] = 255 # add a white column
# add two diagonal lines
for i in range(len(test_img)):
for j in range(len(test_img[i])):
if i == j or i == j+10:
test_img[i,j] = 255
plt.imshow(test_img, cmap="gray")
plt.colorbar()
plt.show()
###Output
_____no_output_____
###Markdown
Let's also investigate the inverse of this image:
###Code
# creating the inverse of test_img
test_img2 = 255 - test_img
plt.imshow(test_img2, cmap="gray")
plt.colorbar()
plt.show()
###Output
_____no_output_____
###Markdown
We will create three filters:
###Code
size = 3 # number of rows and columns for filters
# modify all values
filter1 = np.zeros((size,size))
filter1[:,:] = 0.5
# all values -1 except horizonal stripe in center
filter2 = np.zeros((size,size))
filter2[:,:] = -1
filter2[size//2,:] = 2
# all values -1 except vertical stripe in center
filter3 = np.zeros((size,size))
filter3[:,:] = -1
filter3[:,size//2] = 2
print(filter1,filter2,filter3, sep="\n\n")
###Output
_____no_output_____
###Markdown
And now we call our function `conv2d` with our test images and our first filter:
###Code
filtered_image = conv2d(test_img, filter3,1)
plt.imshow(filtered_image, cmap="gray")
plt.colorbar()
plt.show()
filtered_image2 = conv2d(test_img2, filter3,1)
plt.imshow(filtered_image2, cmap="gray")
plt.colorbar()
plt.show()
###Output
_____no_output_____
###Markdown
In practice, you do not have to code the 2d convolutions (or you can do it in a more vectorized way using the full power of `numpy`).Let's look at the 2d convolutional method from `scipy`. The `mode="same"` argument indicates that our output matrix should match our input matrix.Note that he following import statement was executed at the beginning of this notebook:```pythonfrom scipy import signal```
###Code
spy_image = signal. (test_img, filter3, mode="same")
spy_image2 = signal.convolve2d(test_img2, filter3, mode="same")
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2,sharex=True, sharey=True, figsize = (8,8))
ax1.imshow(spy_image, cmap="gray")
#plt.colorbar()
#plt.show()
ax2.imshow(spy_image2, cmap="gray")
#plt.colorbar()
#fig.add_subplot(f1)
#plt.show()
ax3.imshow(filtered_image, cmap="gray")
ax4.imshow(filtered_image2, cmap="gray")
plt.show()
###Output
_____no_output_____
###Markdown
Filter 1 is a *blurring* filter. It takes an "average" of all of the pixels in the region of the filter, all with the same weight. Let's go back and investigate the other filters. Filter 1 is a *blurring* filter. It takes an "average" of all of the pixels in the region of the filter, all with the same weight. Filter 2 detects horizontal lines. It takes an "average" of all of the pixels in the region of the filter, all with the same weight. Filter 3 detects vertical lines. It takes an "average" of all of the pixels in the region of the filter, all with the same weight.
###Code
residuals = spy_image-filtered_image
plt.imshow(residuals)
plt.title("Residuals")
plt.colorbar()
plt.show()
plt.imshow(residuals[len(filter1):-len(filter1),len(filter1[0]):-len(filter1[0])])
plt.colorbar()
plt.show()
plt.hist(residuals[len(filter1):-len(filter1),len(filter1[0]):-len(filter1[0])].flatten())
plt.show()
print("number of non-zero residuals (removing with of filter all the away around the image):", np.count_nonzero(residuals[len(filter1):-len(filter1),len(filter1[0]):-len(filter1[0])].flatten()))
plt.show()
###Output
_____no_output_____
###Markdown
Let's try with a real photograph.Since we have only defined 2D convolutions for a 2D matrix, we cannot apply our function to color images, which have three channels: (red (R), green (G), blue (B)).Therefore, we make a gray scale image by averaging over the three RGB channels.
###Code
house = plt.imread("house_copy.jpg", format="jpeg")
plt.imshow(house)
plt.show()
bw_house = np.mean(house, axis=2)
plt.imshow(bw_house, cmap="gray")
plt.colorbar()
plt.show()
spy_image = signal.convolve2d(bw_house, filter1, mode="same")
plt.imshow(spy_image, cmap="gray")
plt.colorbar()
plt.show()
spy_image = signal.convolve2d(bw_house, filter2, mode="same")
plt.imshow(spy_image, cmap="gray")
plt.colorbar()
plt.show()
spy_image = signal.convolve2d(bw_house, filter3, mode="same")
plt.imshow(spy_image, cmap="gray")
plt.colorbar()
plt.show()
###Output
_____no_output_____
###Markdown
We can look at the effects of modifying the *stride*
###Code
my_conv = conv2d(bw_house,filter3,5)
plt.imshow(my_conv)
###Output
_____no_output_____
###Markdown
$N$-D convolutionsThe mathmatics of discrete convolutions are the same no matter the dimensionality. Let's first look at 1D convolutions:Given a 1-D data array `a` and a filter `h` with dimensions of $2\omega \times 2\omega$, the discrete convolution operation is given by the following mathematics:$$c[n]=a[n]\circledast h= \sum_{i=-\omega}^{\omega} a[i+n]* h[i+\omega]$$Or, graphically:
###Code
def conv1d(arr, filt, stride):
n = len(arr)
filt_w = len(filt)
#store our filtered image
new_arr = np.zeros(n//stride+1)
# print(n_rows,n_cols,filt_w,filt_h) # uncomment for debugging
for i in range(filt_w//2,n-filt_w//2, stride):
new_arr[i//stride] = np.sum(arr[i-filt_w//2:i+filt_w//2+1]*filt)
return new_arr
from random import random
x = np.linspace(0,1,100)
y = np.sin(15*x)+2*x**2 + np.random.rand(len(x))
plt.plot(y)
###Output
_____no_output_____
###Markdown
Now, we define our filter:
###Code
size = 5
f1 = np.zeros(size)
f1[:] = 0.5
print(f1)
###Output
_____no_output_____
###Markdown
And we convolve our image with our filter aand look at the output:
###Code
new_array = conv1d(y,f1,1)
plt.plot(new_array)
###Output
_____no_output_____
|
src/Chapitre3/figure/2019-01-08_ICP_results_and_figures.ipynb
|
###Markdown
fig, (ax1, ax2) = plt.subplots(1,2, figsize=(8,4))gamma = 1.77coef1 = (gamma - 1)/gammapsindex = 20s = 2.5ax1.plot(x, Te[psindex] + coef1 * (Phi - Phi[psindex] ), "-",alpha=1,linewidth=s, label ="Fluid")ax1.plot(x, Te, "-",alpha=0.8, linewidth=s, label ="PIC values")ax1.set_ylabel("$T_e$ [V]", fontsize=16)ax1.set_xlabel("x [cm]", fontsize=16) ax1.set_title("Sheath model", fontsize=19)ax1.set_xlim((0., 0.4))ax1.set_ylim(bottom = 0) for ax in [ax1]: ax.grid(alpha=0.7) ax.margins(0.01) ax.legend(fontsize=14) psindex = 50phi0 =Phi[psindex]ne0 = ne[psindex]Te0 = Te[psindex]pot_iso = phi0 + np.log(ne/ne0 )*Te0pot_poly = phi0 + ((ne/ne0 )**(gamma-1) -1)*Te0/coef1ax2.plot(x, pot_poly, linewidth=s, label = "Fluid $\gamma = 1.25$")ax2.plot(x, Phi, '-',linewidth=s, alpha=0.8, label = "PIC values")ax2.set_xlabel("x [cm]", fontsize=16)ax2.set_ylabel("$\Phi$ [V]", fontsize=16)ax2.set_xlim((0., 0.4)) ax2.set_ylim(bottom= 0) for ax in [ax2]: ax.grid(alpha=0.7) ax.margins(0.01) ax.legend(fontsize=14) plt.tight_layout() position bottom rightfig.text(1, 0.5, 'Fluid model to update', fontsize=50, color='gray', ha='right', va='bottom', alpha=0.4) plt.savefig("../figures/sheathModelICP.pdf")
###Code
print(data[k]["Pa"])
print(data[k]["Pa"]/(0.1*0.1*7/450))
data[k]["Pn"]
###Output
_____no_output_____
|
Clases/m05_data_science/m05_project01/m05_project01.ipynb
|
###Markdown
MAT281 Aplicaciones de la Matemática en la Ingeniería Proyecto 01: Clasificación de dígitos Instrucciones* Completa tus datos personales (nombre y rol USM) en siguiente celda.* Debes _pushear_ tus cambios a tu repositorio personal del curso.* Como respaldo, debes enviar un archivo .zip con el siguiente formato `mXX_projectYY_apellido_nombre.zip` a [email protected], debe contener todo lo necesario para que se ejecute correctamente cada celda, ya sea datos, imágenes, scripts, etc.* Se evaluará: - Soluciones - Código - Que Binder esté bien configurado. - Al presionar `Kernel -> Restart Kernel and Run All Cells` deben ejecutarse todas las celdas sin error. __Nombre__:__Rol__: Clasificación de dígitosEn este laboratorio realizaremos el trabajo de reconocer un dígito a partir de una imagen. Contenidos* [K Nearest Neighbours](k_nearest_neighbours)* [Exploración de Datos](data_exploration)* [Entrenamiento y Predicción](train_and_prediction)* [Selección de Modelo](model_selection) K Nearest Neighbours El algoritmo **k Nearest Neighbors** es un método no paramétrico: una vez que el parámetro $k$ se ha fijado, no se busca obtener ningún parámetro adicional.Sean los puntos $x^{(i)} = (x^{(i)}_1, ..., x^{(i)}_n)$ de etiqueta $y^{(i)}$ conocida, para $i=1, ..., m$.El problema de clasificación consiste en encontrar la etiqueta de un nuevo punto $x=(x_1, ..., x_m)$ para el cual no conocemos la etiqueta. La etiqueta de un punto se obtiene de la siguiente forma:* Para $k=1$, **1NN** asigna a $x$ la etiqueta de su vecino más cercano. * Para $k$ genérico, **kNN** asigna a $x$ la etiqueta más popular de los k vecinos más cercanos. El modelo subyacente a kNN es el conjunto de entrenamiento completo. A diferencia de otros métodos que efectivamente generalizan y resumen la información (como regresión logística, por ejemplo), cuando se necesita realizar una predicción, el algoritmo kNN mira **todos** los datos y selecciona los k datos más cercanos, para regresar la etiqueta más popular/más común. Los datos no se resumen en parámetros, sino que siempre deben mantenerse en memoria. Es un método por tanto que no escala bien con un gran número de datos. En caso de empate, existen diversas maneras de desempatar:* Elegir la etiqueta del vecino más cercano (problema: no garantiza solución).* Elegir la etiqueta de menor valor (problema: arbitrario).* Elegir la etiqueta que se obtendría con $k+1$ o $k-1$ (problema: no garantiza solución, aumenta tiempo de cálculo). La cercanía o similaridad entre los datos se mide de diversas maneras, pero en general depende del tipo de datos y del contexto.* Para datos reales, puede utilizarse cualquier distancia, siendo la **distancia euclidiana** la más utilizada. También es posible ponderar unas componentes más que otras. Resulta conveniente normalizar para poder utilizar la noción de distancia más naturalmente.* Para **datos categóricos o binarios**, suele utilizarse la distancia de Hamming. A continuación, una implementación de "bare bones" en numpy:
###Code
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
def knn_search(X, k, x):
""" find K nearest neighbours of data among D """
# Distancia euclidiana
d = np.linalg.norm(X - x, axis=1)
# Ordenar por cercania
idx = np.argsort(d)
# Regresar los k mas cercanos
id_closest = idx[:k]
return id_closest, d[id_closest].max()
def knn(X,Y,k,x):
# Obtener los k mas cercanos
k_closest, dmax = knn_search(X, k, x)
# Obtener las etiquetas
Y_closest = Y[k_closest]
# Obtener la mas popular
counts = np.bincount(Y_closest.flatten())
# Regresar la mas popular (cualquiera, si hay empate)
return np.argmax(counts), k_closest, dmax
def plot_knn(X, Y, k, x):
y_pred, neig_idx, dmax = knn(X, Y, k, x)
# plotting the data and the input point
fig = plt.figure(figsize=(8, 8))
plt.plot(x[0, 0], x[0, 1], 'ok', ms=16)
m_ob = Y[:, 0] == 0
plt.plot(X[m_ob, 0], X[m_ob, 1], 'ob', ms=8)
m_sr = Y[:,0] == 1
plt.plot(X[m_sr, 0], X[m_sr, 1], 'sr', ms=8)
# highlighting the neighbours
plt.plot(X[neig_idx, 0], X[neig_idx, 1], 'o', markerfacecolor='None', markersize=24, markeredgewidth=1)
# Plot a circle
x_circle = dmax * np.cos(np.linspace(0, 2*np.pi, 360)) + x[0, 0]
y_circle = dmax * np.sin(np.linspace(0, 2*np.pi, 360)) + x[0, 1]
plt.plot(x_circle, y_circle, 'k', alpha=0.25)
plt.show();
# Print result
if y_pred==0:
print("Prediccion realizada para etiqueta del punto = {} (circulo azul)".format(y_pred))
else:
print("Prediccion realizada para etiqueta del punto = {} (cuadrado rojo)".format(y_pred))
###Output
_____no_output_____
###Markdown
Puedes ejecutar varias veces el código anterior, variando el número de vecinos `k` para ver cómo afecta el algoritmo.
###Code
k = 3 # hyper-parameter
N = 100
X = np.random.rand(N, 2) # random dataset
Y = np.array(np.random.rand(N) < 0.4, dtype=int).reshape(N, 1) # random dataset
x = np.random.rand(1, 2) # query point
# performing the search
plot_knn(X, Y, k, x)
###Output
_____no_output_____
###Markdown
Exploración de los datos A continuación se carga el conjunto de datos a utilizar, a través del sub-módulo `datasets` de `sklearn`.
###Code
import pandas as pd
from sklearn import datasets
digits_dict = datasets.load_digits()
print(digits_dict["DESCR"])
digits_dict.keys()
digits_dict["target"]
###Output
_____no_output_____
###Markdown
A continuación se crea dataframe declarado como `digits` con los datos de `digits_dict` tal que tenga 65 columnas, las 6 primeras a la representación de la imagen en escala de grises (0-blanco, 255-negro) y la última correspondiente al dígito (`target`) con el nombre _target_.
###Code
digits = (
pd.DataFrame(
digits_dict["data"],
)
.rename(columns=lambda x: f"c{x:02d}")
.assign(target=digits_dict["target"])
.astype(int)
)
digits.head()
###Output
_____no_output_____
###Markdown
Ejercicio 1**_(10 puntos)_** **Análisis exploratorio:** Realiza tu análisis exploratorio, no debes olvidar nada! Recuerda, cada análisis debe responder una pregunta.Algunas sugerencias:* ¿Cómo se distribuyen los datos?* ¿Cuánta memoria estoy utilizando?* ¿Qué tipo de datos son?* ¿Cuántos registros por clase hay?* ¿Hay registros que no se correspondan con tu conocimiento previo de los datos?
###Code
## FIX ME PLEASE
###Output
_____no_output_____
###Markdown
Ejercicio 2**_(10 puntos)_** **Visualización:** Para visualizar los datos utilizaremos el método `imshow` de `matplotlib`. Resulta necesario convertir el arreglo desde las dimensiones (1,64) a (8,8) para que la imagen sea cuadrada y pueda distinguirse el dígito. Superpondremos además el label correspondiente al dígito, mediante el método `text`. Esto nos permitirá comparar la imagen generada con la etiqueta asociada a los valores. Realizaremos lo anterior para los primeros 25 datos del archivo.
###Code
digits_dict["images"][0]
###Output
_____no_output_____
###Markdown
Visualiza imágenes de los dígitos utilizando la llave `images` de `digits_dict`. Sugerencia: Utiliza `plt.subplots` y el método `imshow`. Puedes hacer una grilla de varias imágenes al mismo tiempo!
###Code
nx, ny = 5, 5
fig, axs = plt.subplots(nx, ny, figsize=(12, 12))
## FIX ME PLEASE
###Output
_____no_output_____
###Markdown
Entrenamiento y Predicción Se utilizará la implementación de `scikit-learn` llamada `KNeighborsClassifier` (el cual es un _estimator_) que se encuentra en `neighbors`.Utiliza la métrica por defecto.
###Code
from sklearn.neighbors import KNeighborsClassifier
X = digits.drop(columns="target").values
y = digits["target"].values
###Output
_____no_output_____
###Markdown
Ejercicio 3**_(10 puntos)_** Entrenar utilizando todos los datos. Además, recuerda que `k` es un hiper-parámetro, por lo tanto prueba con distintos tipos `k` y obten el `score` desde el modelo.
###Code
k_array = np.arange(1, 101)
## FIX ME PLEASE ##
###Output
_____no_output_____
###Markdown
**Preguntas*** ¿Cuál fue la métrica utilizada?* ¿Por qué entrega estos resultados? En especial para k=1.* ¿Por qué no se normalizó o estandarizó la matriz de diseño? _ RESPONDE AQUÍ _ Ejercicio 4**_(10 puntos)_** Divide los datos en _train_ y _test_ utilizando la función preferida del curso. Para reproducibilidad utiliza `random_state=42`. A continuación, vuelve a ajustar con los datos de _train_ y con los distintos valores de _k_, pero en esta ocasión calcula el _score_ con los datos de _test_.¿Qué modelo escoges?
###Code
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = ## FIX ME PLEASE ##
## FIX ME PLEASE ##
###Output
_____no_output_____
###Markdown
Selección de Modelo Ejercicio 5**_(15 puntos)_** **Curva de Validación**: Replica el ejemplo del siguiente [link](https://scikit-learn.org/stable/auto_examples/model_selection/plot_validation_curve.htmlsphx-glr-auto-examples-model-selection-plot-validation-curve-py) pero con el modelo, parámetros y métrica adecuada.¿Qué podrías decir de la elección de `k`?
###Code
from sklearn.model_selection import validation_curve
param_range = np.arange(1, 101)
## FIX ME PLEASE ##
plt.figure(figsize=(12, 8))
## FIX ME PLEASE ##
plt.show();
###Output
_____no_output_____
###Markdown
**Pregunta*** ¿Qué refleja este gráfico?* ¿Qué conclusiones puedes sacar a partir de él?* ¿Qué patrón se observa en los datos, en relación a los números pares e impares? ¿Porqué sucede esto? _ RESPONDE AQUÍ _ Ejercicio 6**_(15 puntos)_** **Búsqueda de hiper-parámetros con validación cruzada:** Utiliza `sklearn.model_selection.GridSearchCV` para obtener la mejor estimación del parámetro _k_. Prueba con valores de _k_ desde 2 a 100.
###Code
from sklearn.model_selection import GridSearchCV
parameters = ## FIX ME PLEASE ##
digits_gscv = ## FIX ME PLEASE ##
## FIX ME PLEASE ##
# Best params
## FIX ME PLEASE ##
###Output
_____no_output_____
###Markdown
**Pregunta*** ¿Cuál es el mejor valor de _k_?* ¿Es consistente con lo obtenido en el ejercicio anterior? _ RESPONDE AQUÍ _ Ejercicio 7**_(10 puntos)_** __Visualizando datos:__ A continuación se provee código para comparar las etiquetas predichas vs las etiquetas reales del conjunto de _test_. * Define la variable `best_knn` que corresponde al mejor estimador `KNeighborsClassifier` obtenido.* Ajusta el estimador anterior con los datos de entrenamiento.* Crea el arreglo `y_pred` prediciendo con los datos de test._Hint:_ `digits_gscv.best_estimator_` te entrega una instancia `estimator` del mejor estimador encontrado por `GridSearchCV`.
###Code
best_knn =## FIX ME PLEASE ##
## FIX ME PLEASE ##
y_pred = ## FIX ME PLEASE ##
# Mostrar los datos correctos
mask = (y_pred == y_test)
X_aux = X_test[mask]
y_aux_true = y_test[mask]
y_aux_pred = y_pred[mask]
# We'll plot the first 100 examples, randomly choosen
nx, ny = 5, 5
fig, ax = plt.subplots(nx, ny, figsize=(12,12))
for i in range(nx):
for j in range(ny):
index = j + ny * i
data = X_aux[index, :].reshape(8,8)
label_pred = str(int(y_aux_pred[index]))
label_true = str(int(y_aux_true[index]))
ax[i][j].imshow(data, interpolation='nearest', cmap='gray_r')
ax[i][j].text(0, 0, label_pred, horizontalalignment='center', verticalalignment='center', fontsize=10, color='green')
ax[i][j].text(7, 0, label_true, horizontalalignment='center', verticalalignment='center', fontsize=10, color='blue')
ax[i][j].get_xaxis().set_visible(False)
ax[i][j].get_yaxis().set_visible(False)
plt.show()
###Output
_____no_output_____
###Markdown
Modifique el código anteriormente provisto para que muestre los dígitos incorrectamente etiquetados, cambiando apropiadamente la máscara. Cambie también el color de la etiqueta desde verde a rojo, para indicar una mala etiquetación.
###Code
## FIX ME PLEASE ##
###Output
_____no_output_____
###Markdown
**Pregunta*** Solo utilizando la inspección visual, ¿Por qué crees que falla en esos valores? _ RESPONDE AQUÍ _ Ejercicio 8**_(10 puntos)_** **Matriz de confusión:** Grafica la matriz de confusión.**Importante!** Al principio del curso se entregó una versión antigua de `scikit-learn`, por lo cual es importante que actualicen esta librearía a la última versión para hacer uso de `plot_confusion_matrix`. Hacerlo es tan fácil como ejecutar `conda update -n mat281 -c conda-forge scikit-learn` en la terminal de conda.
###Code
from sklearn.metrics import plot_confusion_matrix
fig, ax = plt.subplots(figsize=(12, 12))
## FIX ME PLEASE ##
###Output
_____no_output_____
###Markdown
**Pregunta*** ¿Cuáles son las etiquetas con mejores y peores predicciones?* Con tu conocimiento previo del problema, ¿Por qué crees que esas etiquetas son las que tienen mejores y peores predicciones? _ RESPONDE AQUÍ _ Ejercicio 9**_(10 puntos)_** **Curva de aprendizaje:** Replica el ejemplo del siguiente [link](https://scikit-learn.org/stable/auto_examples/model_selection/plot_learning_curve.htmlsphx-glr-auto-examples-model-selection-plot-learning-curve-py) pero solo utilizando un modelo de KNN con el hiperparámetro _k_ seleccionado anteriormente.
###Code
def plot_learning_curve(estimator, title, X, y, axes=None, ylim=None, cv=None,
n_jobs=None, train_sizes=np.linspace(.1, 1.0, 5)):
"""
Generate 3 plots: the test and training learning curve, the training
samples vs fit times curve, the fit times vs score curve.
Parameters
----------
estimator : object type that implements the "fit" and "predict" methods
An object of that type which is cloned for each validation.
title : string
Title for the chart.
X : array-like, shape (n_samples, n_features)
Training vector, where n_samples is the number of samples and
n_features is the number of features.
y : array-like, shape (n_samples) or (n_samples, n_features), optional
Target relative to X for classification or regression;
None for unsupervised learning.
axes : array of 3 axes, optional (default=None)
Axes to use for plotting the curves.
ylim : tuple, shape (ymin, ymax), optional
Defines minimum and maximum yvalues plotted.
cv : int, cross-validation generator or an iterable, optional
Determines the cross-validation splitting strategy.
Possible inputs for cv are:
- None, to use the default 5-fold cross-validation,
- integer, to specify the number of folds.
- :term:`CV splitter`,
- An iterable yielding (train, test) splits as arrays of indices.
For integer/None inputs, if ``y`` is binary or multiclass,
:class:`StratifiedKFold` used. If the estimator is not a classifier
or if ``y`` is neither binary nor multiclass, :class:`KFold` is used.
Refer :ref:`User Guide <cross_validation>` for the various
cross-validators that can be used here.
n_jobs : int or None, optional (default=None)
Number of jobs to run in parallel.
``None`` means 1 unless in a :obj:`joblib.parallel_backend` context.
``-1`` means using all processors. See :term:`Glossary <n_jobs>`
for more details.
train_sizes : array-like, shape (n_ticks,), dtype float or int
Relative or absolute numbers of training examples that will be used to
generate the learning curve. If the dtype is float, it is regarded as a
fraction of the maximum size of the training set (that is determined
by the selected validation method), i.e. it has to be within (0, 1].
Otherwise it is interpreted as absolute sizes of the training sets.
Note that for classification the number of samples usually have to
be big enough to contain at least one sample from each class.
(default: np.linspace(0.1, 1.0, 5))
"""
if axes is None:
_, axes = plt.subplots(1, 3, figsize=(20, 5))
axes[0].set_title(title)
if ylim is not None:
axes[0].set_ylim(*ylim)
axes[0].set_xlabel("Training examples")
axes[0].set_ylabel("Score")
train_sizes, train_scores, test_scores, fit_times, _ = \
learning_curve(estimator, X, y, cv=cv, n_jobs=n_jobs,
train_sizes=train_sizes,
return_times=True)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
fit_times_mean = np.mean(fit_times, axis=1)
fit_times_std = np.std(fit_times, axis=1)
# Plot learning curve
axes[0].grid()
axes[0].fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="r")
axes[0].fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1,
color="g")
axes[0].plot(train_sizes, train_scores_mean, 'o-', color="r",
label="Training score")
axes[0].plot(train_sizes, test_scores_mean, 'o-', color="g",
label="Cross-validation score")
axes[0].legend(loc="best")
# Plot n_samples vs fit_times
axes[1].grid()
axes[1].plot(train_sizes, fit_times_mean, 'o-')
axes[1].fill_between(train_sizes, fit_times_mean - fit_times_std,
fit_times_mean + fit_times_std, alpha=0.1)
axes[1].set_xlabel("Training examples")
axes[1].set_ylabel("fit_times")
axes[1].set_title("Scalability of the model")
# Plot fit_time vs score
axes[2].grid()
axes[2].plot(fit_times_mean, test_scores_mean, 'o-')
axes[2].fill_between(fit_times_mean, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1)
axes[2].set_xlabel("fit_times")
axes[2].set_ylabel("Score")
axes[2].set_title("Performance of the model")
return plt
from sklearn.model_selection import learning_curve
from sklearn.model_selection import ShuffleSplit
fig, axes = plt.subplots(3, 1, figsize=(10, 15))
## FIX ME PLEASE ##
plt.show()
###Output
_____no_output_____
|
ex09-Advanced Query Techniques of CASE and Subquery.ipynb
|
###Markdown
ex09-Advanced Query Techniques of CASE and SubqueryThe SQLite CASE expression evaluates a list of conditions and returns an expression based on the result of the evaluation. The CASE expression is similar to the IF-THEN-ELSE statement in other programming languages. You can use the CASE statement in any clause or statement that accepts a valid expression. For example, you can use the CASE statement in clauses such as WHERE, ORDER BY, HAVING, IN, SELECT and statements such as SELECT, UPDATE, and DELETE. See more at http://www.sqlitetutorial.net/sqlite-case/. A subquery, simply put, is a query written as a part of a bigger statement. Think of it as a SELECT statement inside another one. The result of the inner SELECT can then be used in the outer query.In this notebook, we put these two query techniques together to calculate seasonal runoff from year-month data in the table of rch.
###Code
%load_ext sql
###Output
_____no_output_____
###Markdown
1. Connet to the given database of demo.db3
###Code
%sql sqlite:///data/demo.db3
###Output
_____no_output_____
###Markdown
If you do not remember the tables in the demo data, you can always use the following command to query.
###Code
%sql SELECT name FROM sqlite_master WHERE type='table'
###Output
* sqlite:///data/demo.db3
Done.
###Markdown
2. Chek the rch tableWe can find that the rch table contains time series data with year and month for each river reach. Therefore, it is natural to calculate some seasonal statistics.
###Code
%sql SELECT * From rch LIMIT 3
###Output
* sqlite:///data/demo.db3
Done.
###Markdown
3. Calculate Seasonal RunoffThere are two key steps: >(1) use the CASE and Subquery to convert months to named seasons;>(2) calculate seasonal mean with aggregate functions on groups.In addition, we also use another filter keyword of ***BETWEEN*** to span months into seasons.
###Code
%%sql sqlite://
SELECT RCH, Quarter, AVG(FLOW_OUTcms) as Runoff
FROM(
SELECT RCH, YR,
CASE
WHEN (MO) BETWEEN 3 AND 5 THEN 'MAM'
WHEN (MO) BETWEEN 6 and 8 THEN 'JJA'
WHEN (MO) BETWEEN 9 and 11 THEN 'SON'
ELSE 'DJF'
END Quarter,
FLOW_OUTcms
from rch)
GROUP BY RCH, Quarter
###Output
Done.
|
matplotlib/gallery_jupyter/event_handling/looking_glass.ipynb
|
###Markdown
Looking GlassExample using mouse events to simulate a looking glass for inspecting data.
###Code
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches
# Fixing random state for reproducibility
np.random.seed(19680801)
x, y = np.random.rand(2, 200)
fig, ax = plt.subplots()
circ = patches.Circle((0.5, 0.5), 0.25, alpha=0.8, fc='yellow')
ax.add_patch(circ)
ax.plot(x, y, alpha=0.2)
line, = ax.plot(x, y, alpha=1.0, clip_path=circ)
ax.set_title("Left click and drag to move looking glass")
class EventHandler:
def __init__(self):
fig.canvas.mpl_connect('button_press_event', self.onpress)
fig.canvas.mpl_connect('button_release_event', self.onrelease)
fig.canvas.mpl_connect('motion_notify_event', self.onmove)
self.x0, self.y0 = circ.center
self.pressevent = None
def onpress(self, event):
if event.inaxes != ax:
return
if not circ.contains(event)[0]:
return
self.pressevent = event
def onrelease(self, event):
self.pressevent = None
self.x0, self.y0 = circ.center
def onmove(self, event):
if self.pressevent is None or event.inaxes != self.pressevent.inaxes:
return
dx = event.xdata - self.pressevent.xdata
dy = event.ydata - self.pressevent.ydata
circ.center = self.x0 + dx, self.y0 + dy
line.set_clip_path(circ)
fig.canvas.draw()
handler = EventHandler()
plt.show()
###Output
_____no_output_____
|
manuscript_analyses/set_cover_analysis/set cover analysis for sgRNA pair design in the gene HSPB1 updated.ipynb
|
###Markdown
Note: this notebook relies on the Jupyter extension [Python Markdown](https://github.com/ipython-contrib/jupyter_contrib_nbextensions/tree/master/src/jupyter_contrib_nbextensions/nbextensions/python-markdown) to properly display the commands below, and in other markdown cells. This notebook describes our process of designing optimal guides for allele-specific excision for the gene *{{gene}}*. *{{gene}}* is a gene located on {{chrom}}. Identify variants to target Identify exhaustive list of targetable variant pairs in the gene with 1000 Genomes data for excision maximum limit = 10kb for the paper.`python ~/projects/AlleleAnalyzer/scripts/ExcisionFinder.py -v /pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/1000genomes_analysis/get_gene_list/gene_list_hg38.tsv {{gene}} /pollard/data/projects/AlleleAnalyzer_data/1kgp_data/hg38_analysis/1kgp_annotated_variants_by_chrom/{{chrom}}_annotated.h5 10000 SpCas9,SaCas9 /pollard/data/genetics/1kg/phase3/hg38/ALL.{{chrom}}_GRCh38.genotypes.20170504.bcf /pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{{gene}}/{{gene_lower}}_var_pairs_ --window=5000 --exhaustive` Generate arcplot input for all populations together and for each superpopulation.`python ~/projects/AlleleAnalyzer/plotting_scripts/gen_arcplot_input.py /pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{{gene}}/{{gene_lower}}_var_pairs_exh.tsv /pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{{gene}}/{{gene_lower}}_arcplot_ALL``parallel " python ~/projects/AlleleAnalyzer/plotting_scripts/gen_arcplot_input.py /pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{{gene}}/{{gene_lower}}_var_pairs_exh.tsv /pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{{gene}}/{{gene_lower}}_arcplot_{} --sample_legend=/pollard/data/projects/AlleleAnalyzer_data/1kgp_data/1kg_allsamples.tsv --pop={} " ::: AFR AMR EAS EUR SAS` Plot arcplots together to demonstrate the different patterns of sharing.`python ~/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/src/superpops_for_arcplot_merged.py ~/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{{gene}}/{{gene_lower}}_arcplot_ ~/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{{gene}}/{{gene_lower}}_``Rscript ~/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/src/arcplot_superpops_for_paper.R ~/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{{gene}}/{{gene_lower}}_all_pops_arcplot_input.tsv ~/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{{gene}}/{{gene_lower}}_filt20_allpops 20 {{start}} {{end}} 5000 {{gene}}` Set Cover Use set cover to identify top 5 variant pairs`python ~/projects/AlleleAnalyzer/scripts/optimize_ppl_covered.py --type=max_probes 5 ~/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{{gene}}/{{gene_lower}}_var_pairs_exh.tsv ~/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{{gene}}/{{gene_lower}}_set_cover_5_pairs`
###Code
set_cover_top_pairs = pd.read_csv(f'/pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{gene}/{gene_lower}_set_cover_5_pairs_pairs_used.txt',
sep='\t')
set_cover_top_pairs
###Output
_____no_output_____
###Markdown
Population coverage for set cover pairs
###Code
def ppl_covered(guides_used_df, cohort_df):
guides_list = guides_used_df['var1'].tolist() + guides_used_df['var2'].tolist()
ppl_covered = cohort_df.query('(var1 in @guides_list) and (var2 in @guides_list)').copy()
return ppl_covered
global pairs_to_ppl
pairs_to_ppl = pd.read_csv(f'/pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{gene}/{gene_lower}_var_pairs_exh.tsv',
sep='\t', low_memory=False)
ptp_sc_5 = ppl_covered(set_cover_top_pairs, pairs_to_ppl)
ptp_sc_5.head()
###Output
_____no_output_____
###Markdown
Top 5 Extract top 5 pairs by population coverage
###Code
top_five_top_pairs = pd.read_csv(f'/pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{gene}/{gene_lower}_arcplot_ALL.tsv',
sep='\t').sort_values(by='percent_pop_covered', ascending=False).head().reset_index(drop=True)
ptp_top_5 = ppl_covered(top_five_top_pairs[['var1','var2']], pairs_to_ppl)
###Output
_____no_output_____
###Markdown
Demonstrate the difference in population coverages between top 5 shared pairs and set cover identified pairs.
###Code
top_five_top_pairs
###Output
_____no_output_____
###Markdown
Make arcplots for set cover and top 5 pairsMake file of set cover pairs for use with arcplot plotting script.
###Code
# set cover
exh = pd.read_csv(f'/pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{gene}/{gene_lower}_var_pairs_exh.tsv',
sep='\t', low_memory=False)
exh_sc = []
for ix, row in set_cover_top_pairs.iterrows():
var1 = row['var1']
var2 = row['var2']
exh_sc.append(pd.DataFrame(exh.query('(var1 == @var1) and (var2 == @var2)')))
exh_sc_df = pd.concat(exh_sc)
exh_sc_df.to_csv(f'/pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{gene}/{gene_lower}_var_pairs_exh_sc.tsv',
sep='\t', index=False)
# top 5
exh = pd.read_csv(f'/pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{gene}/{gene_lower}_var_pairs_exh.tsv',
sep='\t', low_memory=False)
exh_tf = []
for ix, row in top_five_top_pairs.iterrows():
var1 = row['var1']
var2 = row['var2']
exh_tf.append(pd.DataFrame(exh.query('(var1 == @var1) and (var2 == @var2)')))
exh_tf_df = pd.concat(exh_tf)
exh_tf_df.to_csv(f'/pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{gene}/{gene_lower}_var_pairs_exh_tf.tsv',
sep='\t', index=False)
###Output
_____no_output_____
###Markdown
Set coverMake input arcplot-formatted:`python ~/projects/AlleleAnalyzer/plotting_scripts/gen_arcplot_input.py /pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{{gene}}/{{gene_lower}}_var_pairs_exh_sc.tsv /pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{{gene}}/{{gene_lower}}_arcplot_set_cover_ALL`Make arcplot:`Rscript ~/projects/AlleleAnalyzer/plotting_scripts/arcplot_generic.R /pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{{gene}}/{{gene_lower}}_arcplot_set_cover_ALL.tsv /pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{{gene}}/{{gene_lower}}_arcplot_set_cover_ALL 0 {{start}} {{end}} 5000 {{gene}}` Top 5Make input arcplot-formatted:`python ~/projects/AlleleAnalyzer/plotting_scripts/gen_arcplot_input.py /pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{{gene}}/{{gene_lower}}_var_pairs_exh_tf.tsv /pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{{gene}}/{{gene_lower}}_arcplot_top_five_ALL`Make arcplot:`Rscript ~/projects/AlleleAnalyzer/plotting_scripts/arcplot_generic.R /pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{{gene}}/{{gene_lower}}_arcplot_top_five_ALL.tsv /pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{{gene}}/{{gene_lower}}_arcplot_top_five_ALL 0 {{start}} {{end}} 5000 {{gene}}` Compare coverage
###Code
def cov_cat(row):
if row['sample'] in ptp_top_5['ind'].tolist() and row['sample'] in ptp_sc_5['ind'].tolist():
return 'Both'
elif row['sample'] in ptp_top_5['ind'].tolist():
return 'Top 5'
elif row['sample'] in ptp_sc_5['ind'].tolist():
return 'Set Cover'
else:
return 'Neither'
global inds
inds = pd.read_csv('/pollard/data/projects/AlleleAnalyzer_data/1kgp_data/1kg_allsamples.tsv',
sep='\t')
inds_cov = inds.copy()
inds_cov['AlleleAnalyzer'] = inds['sample'].isin(ptp_sc_5['ind'])
inds_cov['Top 5'] = inds['sample'].isin(ptp_top_5['ind'])
inds_cov['Coverage'] = inds_cov.apply(lambda row: cov_cat(row), axis=1)
global superpop_dict
superpop_dict = {
'AMR':'Admixed American',
'AFR':'African',
'SAS':'South Asian',
'EAS':'East Asian',
'EUR':'European'
}
sns.set_palette('Dark2', n_colors=3)
fig, ax = plt.subplots(figsize=(2.8, 1.8))
sns.countplot(y='superpop', hue='AlleleAnalyzer', data=inds_cov.replace(superpop_dict).replace({
True:'Covered',
False:'Not covered'
}).sort_values(by=['superpop','Coverage']))
plt.xlabel('Number of individuals')
plt.ylabel('Super Populations')
plt.xticks(rotation=0)
ax.legend(loc='upper right',prop={'size': 9},
frameon=False,
borderaxespad=0.1)
ax.set_xlim([0,600]) # 600 often works but can be tweaked per gene
plt.title('AlleleAnalyzer')
sns.set_palette('Dark2', n_colors=3)
fig, ax = plt.subplots(figsize=(2.8, 1.8))
sns.countplot(y='superpop', hue='Top 5', data=inds_cov.replace(superpop_dict).replace({
True:'Covered',
False:'Not covered'
}).sort_values(by=['superpop','Coverage']))
plt.xlabel('Number of individuals')
plt.ylabel('Super Populations')
plt.xticks(rotation=0)
ax.legend(loc='upper right',prop={'size': 9},
frameon=False,
borderaxespad=0.1)
ax.set_xlim([0,600]) # 600 often works but can be tweaked per gene
plt.title('Top 5')
###Output
_____no_output_____
###Markdown
Design and score sgRNAs for variants included in Set Cover and Top 5 pairs Set Cover Make BED files for positions for each variant pair
###Code
set_cover_bed = pd.DataFrame()
set_cover_bed['start'] = set_cover_top_pairs['var1'].tolist() + set_cover_top_pairs['var2'].tolist()
set_cover_bed['end'] = set_cover_top_pairs['var1'].tolist() + set_cover_top_pairs['var2'].tolist()
set_cover_bed['region'] = set_cover_bed.index
set_cover_bed['chrom'] = f'{chrom}'
set_cover_bed = set_cover_bed[['chrom','start','end','region']]
set_cover_bed.to_csv(f'/pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{gene}/set_cover_pairs.bed',
sep='\t', index=False, header=False)
###Output
_____no_output_____
###Markdown
Design sgRNAs`python ~/projects/AlleleAnalyzer/scripts/gen_sgRNAs.py -v /pollard/data/genetics/1kg/phase3/hg38/ALL.{{chrom}}_GRCh38.genotypes.20170504.bcf /pollard/data/projects/AlleleAnalyzer_data/1kgp_data/hg38_analysis/1kgp_annotated_variants_by_chrom/{{chrom}}_annotated.h5 /pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{{gene}}/set_cover_pairs.bed /pollard/data/projects/AlleleAnalyzer_data/pam_sites_hg38/ /pollard/data/vertebrate_genomes/human/hg38/hg38/hg38.fa /pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{{gene}}/guides_set_cover_{{gene_lower}} SpCas9,SaCas9 20 --bed --sim -d --crispor=hg38` Top 5 Make BED files for positions for each variant pair
###Code
top_five_bed = pd.DataFrame()
top_five_bed['start'] = top_five_top_pairs['var1'].tolist() + top_five_top_pairs['var2'].tolist()
top_five_bed['end'] = top_five_top_pairs['var1'].tolist() + top_five_top_pairs['var2'].tolist()
top_five_bed['region'] = top_five_bed.index
top_five_bed['chrom'] = f'{chrom}'
top_five_bed = top_five_bed[['chrom','start','end','region']]
top_five_bed.to_csv(f'/pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{gene}/top_five_pairs.bed',
sep='\t', index=False, header=False)
###Output
_____no_output_____
###Markdown
Design sgRNAs`python ~/projects/AlleleAnalyzer/scripts/gen_sgRNAs.py -v /pollard/data/genetics/1kg/phase3/hg38/ALL.{{chrom}}_GRCh38.genotypes.20170504.bcf /pollard/data/projects/AlleleAnalyzer_data/1kgp_data/hg38_analysis/1kgp_annotated_variants_by_chrom/{{chrom}}_annotated.h5 /pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{{gene}}/top_five_pairs.bed /pollard/data/projects/AlleleAnalyzer_data/pam_sites_hg38/ /pollard/data/vertebrate_genomes/human/hg38/hg38/hg38.fa /pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{{gene}}/guides_top_five_{{gene_lower}} SpCas9,SaCas9 20 --bed --sim -d --crispor=hg38` Reanalyze coverage at positions with at least 1 sgRNA with predicted specificity score > threshold Set Cover
###Code
sc_grnas = pd.read_csv(f'/pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{gene}/guides_set_cover_{gene_lower}.tsv',
sep='\t')
def get_pairs(pairs_df, grna_df, min_score=0):
grna_df_spec = grna_df.query('(scores_ref >= @min_score) or (scores_alt >= @min_score)')
positions = grna_df_spec['variant_position'].astype(int).unique().tolist()
pairs_out = pairs_df.query('(var1 in @positions) and (var2 in @positions)').copy()
return(pairs_out)
def plot_coverage(orig_pairs, grnas, min_score_list, xlim, legend_pos='lower right', sc=True):
if sc:
label = 'AlleleAnalyzer'
else:
label = 'Top 5'
inds_cov_df_list = []
for min_score in min_score_list:
pairs_filt = get_pairs(orig_pairs, grnas, min_score = min_score)
ptp = ppl_covered(pairs_filt, pairs_to_ppl)
inds_cov = inds.copy()
inds_cov['Coverage'] = inds['sample'].isin(ptp['ind'])
inds_cov['Minimum Specificity Score'] = min_score
inds_cov_df_list.append(inds_cov)
inds_cov = pd.concat(inds_cov_df_list).query('Coverage').drop_duplicates()
fig, ax = plt.subplots(figsize=(3.8, 5.8))
p = sns.countplot(y='superpop', hue='Minimum Specificity Score',
data=inds_cov.replace(superpop_dict).sort_values(by=['superpop']), palette='magma')
# p = sns.catplot(y='superpop', hue='Minimum Specificity Score', kind='count', row='superpop',
# data=inds_cov.replace(superpop_dict).sort_values(by=['superpop']), palette='magma')
plt.xlabel('Number of individuals')
plt.ylabel('Super Populations')
# plt.xticks(rotation=45)
plt.legend(loc=legend_pos,prop={'size': 9},
frameon=False,
borderaxespad=0.1,
title='Minimum score')
ax.set_xlim([0,xlim])
if sc:
plt.title(f'AlleleAnalyzer coverage at various \nminimum score thresholds, {gene}')
else:
plt.title(f'Top 5 sites at various \nminimum score thresholds, {gene}')
return p
set_cover_top_pairs.head()
sns.swarmplot(x='variant_position', y='scores_ref', data=sc_grnas)
plt.xticks(rotation=90)
p = plot_coverage(set_cover_top_pairs, sc_grnas, list(range(0, 100, 10)), 600, 'lower right')
p.get_figure().savefig(f'/pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{gene}/sc_coverage_all.pdf',
dpi=300, bbox_inches='tight')
def plot_overall(orig_pairs, grnas, max_y):
filters = list(range(0,100,10))
plot_vals = {}
for filt in filters:
pairs_filt = get_pairs(orig_pairs, grnas, min_score = filt)
ptp = ppl_covered(pairs_filt, pairs_to_ppl)
plot_vals[filt] = 100.0* (len(ptp['ind'].unique())/2504.0)
plot_vals_df = pd.DataFrame.from_dict(plot_vals, orient='index')
plot_vals_df['Minimum Score'] = plot_vals_df.index
plot_vals_df.columns = ['% 1KGP Covered','Minimum Score']
fig, ax = plt.subplots(figsize=(3.8, 2.8))
p = sns.barplot(x='Minimum Score', y='% 1KGP Covered',
data=plot_vals_df, palette='magma')
plt.title(f'Overall 1KGP Coverage with Filtering\n by Predicted Specificity Score, {gene}')
plt.xlabel('Minimum Score Threshold')
ax.set_ylim([0,max_y])
return(p)
sc_overall_plot = plot_overall(set_cover_top_pairs, sc_grnas, 60)
sc_overall_plot.get_figure().savefig(f'/pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{gene}/1kgp_cov_overall_set_cover.pdf',
dpi=300, bbox_inches='tight')
###Output
_____no_output_____
###Markdown
Top 5
###Code
tf_grnas = pd.read_csv(f'/pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{gene}/guides_top_five_{gene_lower}.tsv',
sep='\t')
p = plot_coverage(top_five_top_pairs, tf_grnas, list(range(0, 100, 10)), 600, 'lower right', sc=False)
p.get_figure().savefig(f'/pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{gene}/tf_coverage_all.pdf',
dpi=300, bbox_inches='tight')
tf_overall_plot = plot_overall(top_five_top_pairs, tf_grnas, 70)
tf_overall_plot.get_figure().savefig(f'/pollard/home/kathleen/projects/AlleleAnalyzer/manuscript_analyses/set_cover_analysis/{gene}/1kgp_cov_overall_top_five.pdf',
dpi=300, bbox_inches='tight')
###Output
_____no_output_____
|
Test Project.ipynb
|
###Markdown
https://pandas.pydata.org/pandas-docs/stable/user_guide/style.html
###Code
df.head(5)
color = (df.Supplier == 'Matt').map({True: 'background-color: yellow', False: ''})
df.style.apply(lambda s: color)
# df['Amount Agreed'] = df['Amount Agreed'].replace(np.nan, -1)
# df['Buyer'] = df['Buyer'].replace(np.nan, -1)
# df['Effective Date'] = df['Effective Date'].replace(np.nan, -1)
# df['Expires On'] = df['Expires On'].replace(np.nan, -1)
df.loc[:].style.highlight_null(null_color='yellow')
df
color = (df.Supplier == 'Matt').map({True: 'background-color: yellow', False: ''})
df.style.apply(lambda s: color)
df['Amount Agreed'].style.highlight_null('red')
# df['Expires On'] = pd.to_datetime(df['Expires On'])
# df['Effective Date'] = pd.to_datetime(df['Effective Date'])
df
df['Expires On'] = df['Expires On'].dt.strftime('%m/%d/%Y')
start_date = '2000-01-01'
end_date = '2021-12-01'
mask = (df['Expires On'] > start_date) & (df['Expires On'] <= end_date)
expired = df.loc[mask]
expired
df = pd.DataFrame([[2,3,1], [3,2,2], [2,4,4]], columns=list("ABC"))
df.style.apply(lambda x: ["background: red" if v > x.iloc[0] else "" for v in x], axis = 1)
def highlight_max(s, props=''):
return np.where(s == 2, props, '')
df.apply(highlight_max, props='color:white;background-color:darkblue', axis=0)
start_date = '2021-12-01'
end_date = '2030-12-01'
mask = (df['Expires On'] > start_date) & (df['Expires On'] <= end_date)
active_bpas = df.loc[mask]
active_bpas.head()
def highlight_80(y):
if y.Consumed > .8:
return ['background-color: yellow']*14
else:
return ['background-color: white']*14
df.style.apply(highlight_80, axis=1)
def equals(y):
if y.EffectiveDate == 0.997050:
return ['background-color: orange']*14
else:
return ['background-color: white']*14
df.style.apply(equals, axis=1)
# Create some Pandas dataframes from some data.
df1 = pd.DataFrame({'Data': [11, 12, 13, 14]})
df2 = pd.DataFrame({'Data': [21, 22, 23, 24]})
df3 = pd.DataFrame({'Data': [31, 32, 33, 34]})
# Create a Pandas Excel writer using XlsxWriter as the engine.
writer = pd.ExcelWriter('Test2.xlsx', engine='xlsxwriter')
# Write each dataframe to a different worksheet.
df.to_excel(writer, sheet_name='ACTIVE BPAS')
non_emea_bpa.to_excel(writer, sheet_name='NON EMEA BPAS')
expired.to_excel(writer, sheet_name='EXPIRED')
# Close the Pandas Excel writer and output the Excel file.
writer.save()
###Output
_____no_output_____
|
Big-Data-Clusters/CU3/Public/content/diagnose/tsg079-generate-controller-core-dump.ipynb
|
###Markdown
TSG079 - Generate `controller` core dump========================================Steps----- Common functionsDefine helper functions used in this notebook.
###Code
# Define `run` function for transient fault handling, suggestions on error, and scrolling updates on Windows
import sys
import os
import re
import json
import platform
import shlex
import shutil
import datetime
from subprocess import Popen, PIPE
from IPython.display import Markdown
retry_hints = {} # Output in stderr known to be transient, therefore automatically retry
error_hints = {} # Output in stderr where a known SOP/TSG exists which will be HINTed for further help
install_hint = {} # The SOP to help install the executable if it cannot be found
first_run = True
rules = None
debug_logging = False
def run(cmd, return_output=False, no_output=False, retry_count=0):
"""Run shell command, stream stdout, print stderr and optionally return output
NOTES:
1. Commands that need this kind of ' quoting on Windows e.g.:
kubectl get nodes -o jsonpath={.items[?(@.metadata.annotations.pv-candidate=='data-pool')].metadata.name}
Need to actually pass in as '"':
kubectl get nodes -o jsonpath={.items[?(@.metadata.annotations.pv-candidate=='"'data-pool'"')].metadata.name}
The ' quote approach, although correct when pasting into Windows cmd, will hang at the line:
`iter(p.stdout.readline, b'')`
The shlex.split call does the right thing for each platform, just use the '"' pattern for a '
"""
MAX_RETRIES = 5
output = ""
retry = False
global first_run
global rules
if first_run:
first_run = False
rules = load_rules()
# When running `azdata sql query` on Windows, replace any \n in """ strings, with " ", otherwise we see:
#
# ('HY090', '[HY090] [Microsoft][ODBC Driver Manager] Invalid string or buffer length (0) (SQLExecDirectW)')
#
if platform.system() == "Windows" and cmd.startswith("azdata sql query"):
cmd = cmd.replace("\n", " ")
# shlex.split is required on bash and for Windows paths with spaces
#
cmd_actual = shlex.split(cmd)
# Store this (i.e. kubectl, python etc.) to support binary context aware error_hints and retries
#
user_provided_exe_name = cmd_actual[0].lower()
# When running python, use the python in the ADS sandbox ({sys.executable})
#
if cmd.startswith("python "):
cmd_actual[0] = cmd_actual[0].replace("python", sys.executable)
# On Mac, when ADS is not launched from terminal, LC_ALL may not be set, which causes pip installs to fail
# with:
#
# UnicodeDecodeError: 'ascii' codec can't decode byte 0xc5 in position 4969: ordinal not in range(128)
#
# Setting it to a default value of "en_US.UTF-8" enables pip install to complete
#
if platform.system() == "Darwin" and "LC_ALL" not in os.environ:
os.environ["LC_ALL"] = "en_US.UTF-8"
# When running `kubectl`, if AZDATA_OPENSHIFT is set, use `oc`
#
if cmd.startswith("kubectl ") and "AZDATA_OPENSHIFT" in os.environ:
cmd_actual[0] = cmd_actual[0].replace("kubectl", "oc")
# To aid supportabilty, determine which binary file will actually be executed on the machine
#
which_binary = None
# Special case for CURL on Windows. The version of CURL in Windows System32 does not work to
# get JWT tokens, it returns "(56) Failure when receiving data from the peer". If another instance
# of CURL exists on the machine use that one. (Unfortunately the curl.exe in System32 is almost
# always the first curl.exe in the path, and it can't be uninstalled from System32, so here we
# look for the 2nd installation of CURL in the path)
if platform.system() == "Windows" and cmd.startswith("curl "):
path = os.getenv('PATH')
for p in path.split(os.path.pathsep):
p = os.path.join(p, "curl.exe")
if os.path.exists(p) and os.access(p, os.X_OK):
if p.lower().find("system32") == -1:
cmd_actual[0] = p
which_binary = p
break
# Find the path based location (shutil.which) of the executable that will be run (and display it to aid supportability), this
# seems to be required for .msi installs of azdata.cmd/az.cmd. (otherwise Popen returns FileNotFound)
#
# NOTE: Bash needs cmd to be the list of the space separated values hence shlex.split.
#
if which_binary == None:
which_binary = shutil.which(cmd_actual[0])
if which_binary == None:
if user_provided_exe_name in install_hint and install_hint[user_provided_exe_name] is not None:
display(Markdown(f'HINT: Use [{install_hint[user_provided_exe_name][0]}]({install_hint[user_provided_exe_name][1]}) to resolve this issue.'))
raise FileNotFoundError(f"Executable '{cmd_actual[0]}' not found in path (where/which)")
else:
cmd_actual[0] = which_binary
start_time = datetime.datetime.now().replace(microsecond=0)
print(f"START: {cmd} @ {start_time} ({datetime.datetime.utcnow().replace(microsecond=0)} UTC)")
print(f" using: {which_binary} ({platform.system()} {platform.release()} on {platform.machine()})")
print(f" cwd: {os.getcwd()}")
# Command-line tools such as CURL and AZDATA HDFS commands output
# scrolling progress bars, which causes Jupyter to hang forever, to
# workaround this, use no_output=True
#
# Work around a infinite hang when a notebook generates a non-zero return code, break out, and do not wait
#
wait = True
try:
if no_output:
p = Popen(cmd_actual)
else:
p = Popen(cmd_actual, stdout=PIPE, stderr=PIPE, bufsize=1)
with p.stdout:
for line in iter(p.stdout.readline, b''):
line = line.decode()
if return_output:
output = output + line
else:
if cmd.startswith("azdata notebook run"): # Hyperlink the .ipynb file
regex = re.compile(' "(.*)"\: "(.*)"')
match = regex.match(line)
if match:
if match.group(1).find("HTML") != -1:
display(Markdown(f' - "{match.group(1)}": "{match.group(2)}"'))
else:
display(Markdown(f' - "{match.group(1)}": "[{match.group(2)}]({match.group(2)})"'))
wait = False
break # otherwise infinite hang, have not worked out why yet.
else:
print(line, end='')
if rules is not None:
apply_expert_rules(line)
if wait:
p.wait()
except FileNotFoundError as e:
if install_hint is not None:
display(Markdown(f'HINT: Use {install_hint} to resolve this issue.'))
raise FileNotFoundError(f"Executable '{cmd_actual[0]}' not found in path (where/which)") from e
exit_code_workaround = 0 # WORKAROUND: azdata hangs on exception from notebook on p.wait()
if not no_output:
for line in iter(p.stderr.readline, b''):
try:
line_decoded = line.decode()
except UnicodeDecodeError:
# NOTE: Sometimes we get characters back that cannot be decoded(), e.g.
#
# \xa0
#
# For example see this in the response from `az group create`:
#
# ERROR: Get Token request returned http error: 400 and server
# response: {"error":"invalid_grant",# "error_description":"AADSTS700082:
# The refresh token has expired due to inactivity.\xa0The token was
# issued on 2018-10-25T23:35:11.9832872Z
#
# which generates the exception:
#
# UnicodeDecodeError: 'utf-8' codec can't decode byte 0xa0 in position 179: invalid start byte
#
print("WARNING: Unable to decode stderr line, printing raw bytes:")
print(line)
line_decoded = ""
pass
else:
# azdata emits a single empty line to stderr when doing an hdfs cp, don't
# print this empty "ERR:" as it confuses.
#
if line_decoded == "":
continue
print(f"STDERR: {line_decoded}", end='')
if line_decoded.startswith("An exception has occurred") or line_decoded.startswith("ERROR: An error occurred while executing the following cell"):
exit_code_workaround = 1
# inject HINTs to next TSG/SOP based on output in stderr
#
if user_provided_exe_name in error_hints:
for error_hint in error_hints[user_provided_exe_name]:
if line_decoded.find(error_hint[0]) != -1:
display(Markdown(f'HINT: Use [{error_hint[1]}]({error_hint[2]}) to resolve this issue.'))
# apply expert rules (to run follow-on notebooks), based on output
#
if rules is not None:
apply_expert_rules(line_decoded)
# Verify if a transient error, if so automatically retry (recursive)
#
if user_provided_exe_name in retry_hints:
for retry_hint in retry_hints[user_provided_exe_name]:
if line_decoded.find(retry_hint) != -1:
if retry_count < MAX_RETRIES:
print(f"RETRY: {retry_count} (due to: {retry_hint})")
retry_count = retry_count + 1
output = run(cmd, return_output=return_output, retry_count=retry_count)
if return_output:
return output
else:
return
elapsed = datetime.datetime.now().replace(microsecond=0) - start_time
# WORKAROUND: We avoid infinite hang above in the `azdata notebook run` failure case, by inferring success (from stdout output), so
# don't wait here, if success known above
#
if wait:
if p.returncode != 0:
raise SystemExit(f'Shell command:\n\n\t{cmd} ({elapsed}s elapsed)\n\nreturned non-zero exit code: {str(p.returncode)}.\n')
else:
if exit_code_workaround !=0 :
raise SystemExit(f'Shell command:\n\n\t{cmd} ({elapsed}s elapsed)\n\nreturned non-zero exit code: {str(exit_code_workaround)}.\n')
print(f'\nSUCCESS: {elapsed}s elapsed.\n')
if return_output:
return output
def load_json(filename):
"""Load a json file from disk and return the contents"""
with open(filename, encoding="utf8") as json_file:
return json.load(json_file)
def load_rules():
"""Load any 'expert rules' from the metadata of this notebook (.ipynb) that should be applied to the stderr of the running executable"""
try:
# Load this notebook as json to get access to the expert rules in the notebook metadata.
#
j = load_json("tsg079-generate-controller-core-dump.ipynb")
except:
pass # If the user has renamed the book, we can't load ourself. NOTE: Is there a way in Jupyter, to know your own filename?
else:
if "metadata" in j and \
"azdata" in j["metadata"] and \
"expert" in j["metadata"]["azdata"] and \
"rules" in j["metadata"]["azdata"]["expert"]:
rules = j["metadata"]["azdata"]["expert"]["rules"]
rules.sort() # Sort rules, so they run in priority order (the [0] element). Lowest value first.
# print (f"EXPERT: There are {len(rules)} rules to evaluate.")
return rules
def apply_expert_rules(line):
"""Determine if the stderr line passed in, matches the regular expressions for any of the 'expert rules', if so
inject a 'HINT' to the follow-on SOP/TSG to run"""
global rules
for rule in rules:
# rules that have 9 elements are the injected (output) rules (the ones we want). Rules
# with only 8 elements are the source (input) rules, which are not expanded (i.e. TSG029,
# not ../repair/tsg029-nb-name.ipynb)
if len(rule) == 9:
notebook = rule[1]
cell_type = rule[2]
output_type = rule[3] # i.e. stream or error
output_type_name = rule[4] # i.e. ename or name
output_type_value = rule[5] # i.e. SystemExit or stdout
details_name = rule[6] # i.e. evalue or text
expression = rule[7].replace("\\*", "*") # Something escaped *, and put a \ in front of it!
if debug_logging:
print(f"EXPERT: If rule '{expression}' satisfied', run '{notebook}'.")
if re.match(expression, line, re.DOTALL):
if debug_logging:
print("EXPERT: MATCH: name = value: '{0}' = '{1}' matched expression '{2}', therefore HINT '{4}'".format(output_type_name, output_type_value, expression, notebook))
match_found = True
display(Markdown(f'HINT: Use [{notebook}]({notebook}) to resolve this issue.'))
print('Common functions defined successfully.')
# Hints for binary (transient fault) retry, (known) error and install guide
#
retry_hints = {'kubectl': ['A connection attempt failed because the connected party did not properly respond after a period of time, or established connection failed because connected host has failed to respond'], 'azdata': ['Endpoint sql-server-master does not exist', 'Endpoint livy does not exist', 'Failed to get state for cluster', 'Endpoint webhdfs does not exist', 'Adaptive Server is unavailable or does not exist', 'Error: Address already in use']}
error_hints = {'kubectl': [['no such host', 'TSG010 - Get configuration contexts', '../monitor-k8s/tsg010-get-kubernetes-contexts.ipynb'], ['No connection could be made because the target machine actively refused it', 'TSG056 - Kubectl fails with No connection could be made because the target machine actively refused it', '../repair/tsg056-kubectl-no-connection-could-be-made.ipynb']], 'azdata': [['azdata login', 'SOP028 - azdata login', '../common/sop028-azdata-login.ipynb'], ['The token is expired', 'SOP028 - azdata login', '../common/sop028-azdata-login.ipynb'], ['Reason: Unauthorized', 'SOP028 - azdata login', '../common/sop028-azdata-login.ipynb'], ['Max retries exceeded with url: /api/v1/bdc/endpoints', 'SOP028 - azdata login', '../common/sop028-azdata-login.ipynb'], ['Look at the controller logs for more details', 'TSG027 - Observe cluster deployment', '../diagnose/tsg027-observe-bdc-create.ipynb'], ['provided port is already allocated', 'TSG062 - Get tail of all previous container logs for pods in BDC namespace', '../log-files/tsg062-tail-bdc-previous-container-logs.ipynb'], ['Create cluster failed since the existing namespace', 'SOP061 - Delete a big data cluster', '../install/sop061-delete-bdc.ipynb'], ['Failed to complete kube config setup', 'TSG067 - Failed to complete kube config setup', '../repair/tsg067-failed-to-complete-kube-config-setup.ipynb'], ['Error processing command: "ApiError', 'TSG110 - Azdata returns ApiError', '../repair/tsg110-azdata-returns-apierror.ipynb'], ['Error processing command: "ControllerError', 'TSG036 - Controller logs', '../log-analyzers/tsg036-get-controller-logs.ipynb'], ['ERROR: 500', 'TSG046 - Knox gateway logs', '../log-analyzers/tsg046-get-knox-logs.ipynb'], ['Data source name not found and no default driver specified', 'SOP069 - Install ODBC for SQL Server', '../install/sop069-install-odbc-driver-for-sql-server.ipynb'], ["Can't open lib 'ODBC Driver 17 for SQL Server", 'SOP069 - Install ODBC for SQL Server', '../install/sop069-install-odbc-driver-for-sql-server.ipynb'], ['Control plane upgrade failed. Failed to upgrade controller.', 'TSG108 - View the controller upgrade config map', '../diagnose/tsg108-controller-failed-to-upgrade.ipynb']]}
install_hint = {'kubectl': ['SOP036 - Install kubectl command line interface', '../install/sop036-install-kubectl.ipynb'], 'azdata': ['SOP063 - Install azdata CLI (using package manager)', '../install/sop063-packman-install-azdata.ipynb']}
###Output
_____no_output_____
###Markdown
Get the Kubernetes namespace for the big data clusterGet the namespace of the Big Data Cluster use the kubectl command lineinterface .**NOTE:**If there is more than one Big Data Cluster in the target Kubernetescluster, then either:- set \[0\] to the correct value for the big data cluster.- set the environment variable AZDATA\_NAMESPACE, before starting Azure Data Studio.
###Code
# Place Kubernetes namespace name for BDC into 'namespace' variable
if "AZDATA_NAMESPACE" in os.environ:
namespace = os.environ["AZDATA_NAMESPACE"]
else:
try:
namespace = run(f'kubectl get namespace --selector=MSSQL_CLUSTER -o jsonpath={{.items[0].metadata.name}}', return_output=True)
except:
from IPython.display import Markdown
print(f"ERROR: Unable to find a Kubernetes namespace with label 'MSSQL_CLUSTER'. SQL Server Big Data Cluster Kubernetes namespaces contain the label 'MSSQL_CLUSTER'.")
display(Markdown(f'HINT: Use [TSG081 - Get namespaces (Kubernetes)](../monitor-k8s/tsg081-get-kubernetes-namespaces.ipynb) to resolve this issue.'))
display(Markdown(f'HINT: Use [TSG010 - Get configuration contexts](../monitor-k8s/tsg010-get-kubernetes-contexts.ipynb) to resolve this issue.'))
display(Markdown(f'HINT: Use [SOP011 - Set kubernetes configuration context](../common/sop011-set-kubernetes-context.ipynb) to resolve this issue.'))
raise
print(f'The SQL Server Big Data Cluster Kubernetes namespace is: {namespace}')
###Output
_____no_output_____
###Markdown
Get the controller username and passwordGet the controller username and password from the Kubernetes SecretStore and place in the required AZDATA\_USERNAME and AZDATA\_PASSWORDenvironment variables.
###Code
# Place controller secret in AZDATA_USERNAME/AZDATA_PASSWORD environment variables
import os, base64
os.environ["AZDATA_USERNAME"] = run(f'kubectl get secret/controller-login-secret -n {namespace} -o jsonpath={{.data.username}}', return_output=True)
os.environ["AZDATA_USERNAME"] = base64.b64decode(os.environ["AZDATA_USERNAME"]).decode('utf-8')
os.environ["AZDATA_PASSWORD"] = run(f'kubectl get secret/controller-login-secret -n {namespace} -o jsonpath={{.data.password}}', return_output=True)
os.environ["AZDATA_PASSWORD"] = base64.b64decode(os.environ["AZDATA_PASSWORD"]).decode('utf-8')
print(f"Controller username '{os.environ['AZDATA_USERNAME']}' and password stored in environment variables")
###Output
_____no_output_____
###Markdown
Set current directory to temporary directory
###Code
import os
import tempfile
path = tempfile.gettempdir()
os.chdir(path)
print(f"Current directory set to: {path}")
###Output
_____no_output_____
###Markdown
Generate core dump
###Code
run(f'azdata bdc debug dump -n {namespace} -c controller')
print(f'The dump file is in: {os.path.join(path, "output", "dump")}')
print('Notebook execution complete.')
###Output
_____no_output_____
|
DAY 101 ~ 200/DAY141_[BaekJoon] 가장 큰 증가 부분 수열 (Python).ipynb
|
###Markdown
2020년 6월 26일 금요일 BaekJoon - 11055 : 가장 큰 증가 부분 수열 (Python) 문제 : https://www.acmicpc.net/problem/11055 블로그 : https://somjang.tistory.com/entry/BaekJoon-11055%EB%B2%88-%EA%B0%80%EC%9E%A5-%ED%81%B0-%EC%A6%9D%EA%B0%80-%EB%B6%80%EB%B6%84-%EC%88%98%EC%97%B4-Python 첫번째 시도
###Code
inputNum = int(input())
inputNums = input()
inputNums = inputNums.split()
inputNums = [int(num) for num in inputNums]
nc = [0] * (inputNum)
maxNum = 0
for i in range(0, inputNum):
nc[i] = nc[i] + inputNums[i]
for j in range(0, i):
if inputNums[j] < inputNums[i] and nc[i] < nc[j] + inputNums[i]:
nc[i] = nc[j] + inputNums[i]
if maxNum < nc[i]:
maxNum = nc[i]
print(max(nc))
###Output
_____no_output_____
|
intro_neural_networks/StudentAdmissions.ipynb
|
###Markdown
Predicting Student Admissions with Neural NetworksIn this notebook, we predict student admissions to graduate school at UCLA based on three pieces of data:- GRE Scores (Test)- GPA Scores (Grades)- Class rank (1-4)The dataset originally came from here: http://www.ats.ucla.edu/ Loading the dataTo load the data and format it nicely, we will use two very useful packages called Pandas and Numpy. You can read on the documentation here:- https://pandas.pydata.org/pandas-docs/stable/- https://docs.scipy.org/
###Code
# Importing pandas and numpy
import pandas as pd
import numpy as np
import seaborn as sns
sns.set()
# Reading the csv file into a pandas DataFrame
data = pd.read_csv('student_data.csv')
# Printing out the first 10 rows of our data
data.head()
###Output
_____no_output_____
###Markdown
Plotting the dataFirst let's make a plot of our data to see how it looks. In order to have a 2D plot, let's ingore the rank.
###Code
# %matplotlib inline
import matplotlib.pyplot as plt
# Function to help us plot
def plot_points(data):
X = np.array(data[["gre","gpa"]])
y = np.array(data["admit"])
admitted = X[np.argwhere(y==1)]
rejected = X[np.argwhere(y==0)]
plt.scatter([s[0][0] for s in rejected], [s[0][1] for s in rejected], s = 25, color = 'red', edgecolor = 'k')
plt.scatter([s[0][0] for s in admitted], [s[0][1] for s in admitted], s = 25, color = 'cyan', edgecolor = 'k')
plt.xlabel('Test (GRE)')
plt.ylabel('Grades (GPA)')
# Plotting the points
plot_points(data)
plt.show()
###Output
_____no_output_____
###Markdown
Roughly, it looks like the students with high scores in the grades and test passed, while the ones with low scores didn't, but the data is not as nicely separable as we hoped it would. Maybe it would help to take the rank into account? Let's make 4 plots, each one for each rank.
###Code
# Separating the ranks
data_rank1 = data[data["rank"]==1]
data_rank2 = data[data["rank"]==2]
data_rank3 = data[data["rank"]==3]
data_rank4 = data[data["rank"]==4]
print('Rank 1:\n', data_rank1.admit.value_counts())
print('Rank 2:\n', data_rank2.admit.value_counts())
print('Rank 3:\n', data_rank3.admit.value_counts())
print('Rank 4:\n', data_rank4.admit.value_counts())
# Plotting the graphs
plot_points(data_rank1)
plt.title("Rank 1")
plt.show()
plot_points(data_rank2)
plt.title("Rank 2")
plt.show()
plot_points(data_rank3)
plt.title("Rank 3")
plt.show()
plot_points(data_rank4)
plt.title("Rank 4")
plt.show()
###Output
Rank 1:
1 33
0 28
Name: admit, dtype: int64
Rank 2:
0 97
1 54
Name: admit, dtype: int64
Rank 3:
0 93
1 28
Name: admit, dtype: int64
Rank 4:
0 55
1 12
Name: admit, dtype: int64
###Markdown
This looks more promising, as it seems that the lower the rank, the higher the acceptance rate. Let's use the rank as one of our inputs. In order to do this, we should one-hot encode it. TODO: One-hot encoding the rankUse the `get_dummies` function in pandas in order to one-hot encode the data.Hint: To drop a column, it's suggested that you use `one_hot_data`[.drop( )](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.drop.html).
###Code
# TODO: Make dummy variables for rank and concat existing columns
one_hot_data = pd.get_dummies(data, columns=['rank'], drop_first=True)
# Print the first 10 rows of our data
one_hot_data[:10]
###Output
_____no_output_____
###Markdown
TODO: Scaling the dataThe next step is to scale the data. We notice that the range for grades is 1.0-4.0, whereas the range for test scores is roughly 200-800, which is much larger. This means our data is skewed, and that makes it hard for a neural network to handle. Let's fit our two features into a range of 0-1, by dividing the grades by 4.0, and the test score by 800.
###Code
# Making a copy of our data
processed_data = one_hot_data[:]
# TODO: Scale the columns
processed_data['gpa'] = processed_data['gpa'] / 4.0
processed_data['gre'] = processed_data['gre'] / 800
# Printing the first 10 rows of our procesed data
processed_data[:10]
###Output
_____no_output_____
###Markdown
Splitting the data into Training and Testing In order to test our algorithm, we'll split the data into a Training and a Testing set. The size of the testing set will be 10% of the total data.
###Code
sample = np.random.choice(processed_data.index, size=int(len(processed_data)*0.9), replace=False)
train_data, test_data = processed_data.iloc[sample], processed_data.drop(sample)
print("Number of training samples is", len(train_data))
print("Number of testing samples is", len(test_data))
print(train_data[:10])
print(test_data[:10])
###Output
Number of training samples is 360
Number of testing samples is 40
admit gre gpa rank_2 rank_3 rank_4
91 1 0.900 0.227500 0 0 0
28 1 0.975 0.201250 1 0 0
250 0 0.825 0.206875 0 0 1
392 1 0.750 0.211250 0 1 0
177 1 0.775 0.201875 0 1 0
277 1 0.725 0.223750 0 0 0
106 1 0.875 0.222500 0 0 0
158 0 0.825 0.218125 1 0 0
6 1 0.700 0.186250 0 0 0
63 1 0.850 0.240625 0 1 0
admit gre gpa rank_2 rank_3 rank_4
9 0 0.875 0.245000 1 0 0
20 0 0.625 0.198125 0 1 0
31 0 0.950 0.209375 0 1 0
32 0 0.750 0.212500 0 1 0
36 0 0.725 0.203125 0 0 0
58 0 0.500 0.228125 1 0 0
72 0 0.600 0.211875 0 0 1
78 0 0.675 0.195000 0 0 0
83 0 0.475 0.181875 0 0 1
105 1 0.925 0.185625 1 0 0
###Markdown
Splitting the data into features and targets (labels)Now, as a final step before the training, we'll split the data into features (X) and targets (y).
###Code
features = train_data.drop('admit', axis=1)
targets = train_data['admit']
features_test = test_data.drop('admit', axis=1)
targets_test = test_data['admit']
print(features[:10])
print(targets[:10])
###Output
gre gpa rank_2 rank_3 rank_4
91 0.900 0.227500 0 0 0
28 0.975 0.201250 1 0 0
250 0.825 0.206875 0 0 1
392 0.750 0.211250 0 1 0
177 0.775 0.201875 0 1 0
277 0.725 0.223750 0 0 0
106 0.875 0.222500 0 0 0
158 0.825 0.218125 1 0 0
6 0.700 0.186250 0 0 0
63 0.850 0.240625 0 1 0
91 1
28 1
250 0
392 1
177 1
277 1
106 1
158 0
6 1
63 1
Name: admit, dtype: int64
###Markdown
Training the 1-layer Neural NetworkThe following function trains the 1-layer neural network. First, we'll write some helper functions.
###Code
# Activation (sigmoid) function
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_prime(x):
return sigmoid(x) * (1-sigmoid(x))
def error_formula(y, output):
return - y*np.log(output) - (1 - y) * np.log(1-output)
###Output
_____no_output_____
###Markdown
TODO: Backpropagate the errorNow it's your turn to shine. Write the error term. Remember that this is given by the equation $$ (y-\hat{y})x $$ for binary cross entropy loss function and $$ (y-\hat{y})\sigma'(x)x $$ for mean square error.
###Code
# TODO: Write the error term formula
def error_term_formula(x, y, output):
return (y - output) * sigmoid_prime(x) * x
# return (y - output) * x
# Neural Network hyperparameters
epochs = 1000
learnrate = 0.0001
# Training function
def train_nn(features, targets, epochs, learnrate):
# Use to same seed to make debugging easier
np.random.seed(42)
n_records, n_features = features.shape
last_loss = None
# Initialize weights
weights = np.random.normal(scale=1 / n_features**.5, size=n_features)
for e in range(epochs):
del_w = np.zeros(weights.shape)
for x, y in zip(features.values, targets):
# Loop through all records, x is the input, y is the target
# Activation of the output unit
# Notice we multiply the inputs and the weights here
# rather than storing h as a separate variable
output = sigmoid(np.dot(x, weights))
# The error term
error_term = error_term_formula(x, y, output)
# The gradient descent step, the error times the gradient times the inputs
del_w += error_term
# Update the weights here. The learning rate times the
# change in weights
# don't have to divide by n_records since it is compensated by the learning rate
weights += learnrate * del_w #/ n_records
# Printing out the mean square error on the training set
if e % (epochs / 10) == 0:
out = sigmoid(np.dot(features, weights))
loss = np.mean(error_formula(targets, out))
print("Epoch:", e)
if last_loss and last_loss < loss:
print("Train loss: ", loss, " WARNING - Loss Increasing")
else:
print("Train loss: ", loss)
last_loss = loss
print("=========")
print("Finished training!")
return weights
weights = train_nn(features, targets, epochs, learnrate)
###Output
Epoch: 0
Train loss: 0.8199561640044297
=========
Epoch: 100
Train loss: 0.7686526331559296
=========
Epoch: 200
Train loss: 0.730946732954975
=========
Epoch: 300
Train loss: 0.7033446974009928
=========
Epoch: 400
Train loss: 0.6831198631640334
=========
Epoch: 500
Train loss: 0.6682307387719856
=========
Epoch: 600
Train loss: 0.6571865409870233
=========
Epoch: 700
Train loss: 0.6489136758882271
=========
Epoch: 800
Train loss: 0.6426440730921074
=========
Epoch: 900
Train loss: 0.6378292538598115
=========
Finished training!
###Markdown
Calculating the Accuracy on the Test Data
###Code
# Calculate accuracy on test data
test_out = sigmoid(np.dot(features_test, weights))
predictions = test_out > 0.5
accuracy = np.mean(predictions == targets_test)
print("Prediction accuracy: {:.3f}".format(accuracy))
###Output
Prediction accuracy: 0.650
|
3.Modeling/3.3.Clasifation_Random-Forest.ipynb
|
###Markdown
1. Datos
###Code
#Normas
DF_normas = pd.read_csv("normas_binary.csv",
index_col="Número de resolución",
)
#Tribunal
DF_tribunal = pd.read_csv("tribunal_binary.csv",
index_col="Número de resolución")
#Empresas
DF_empresa = pd.read_csv("empresa_binary.csv",
index_col="Número de resolución")
#
CA_WE = np.loadtxt("Criterios_emb.csv", delimiter=",")
#
CA_TFIDF = np.loadtxt("TF-IDF_Vectorization_Criterios.csv",
delimiter=",")
TF_Todas = np.loadtxt("TF-IDF_Vectorization_Todas.csv", delimiter=",")
y = DF_normas.iloc[:, -1].values
normas_numpy = DF_normas.values[:, :-1]
tribunal_numpy = DF_tribunal.values[:, :-1]
empresa_numpy = DF_empresa.values[:, :-1]
###Output
_____no_output_____
###Markdown
2. Clasificación
###Code
def train_test_80_20(X, Y):
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X,
Y,
test_size=0.2,
random_state=10)
return X_train, X_test, Y_train, Y_test
def test_evaluation(model, X_test, y_test):
from sklearn.metrics import classification_report
# evaluación en test del modelo
y_test_pred = model.predict(X_test)
print(classification_report(y_test, y_test_pred))
from sklearn.svm import SVC
from sklearn.model_selection import cross_val_score
from sklearn.neural_network import MLPClassifier
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import KFold
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_classification
# crear un iterador de CV para estandarizar los entrenamientos
# 5-fold cross-validation
kf = KFold(n_splits=5, random_state=0)
###Output
_____no_output_____
###Markdown
**Random Forest - empresa**- bajo rendimiento
###Code
# optimización de hiperparámetros utilizando cross-validation
# MODELO: RF
# VARIABLES DE ENTRADA: empresa
# HYPERPARÁMETROS ÓPTIMOS:
clf = RandomForestClassifier(n_estimators=100,
random_state=0
)
X = np.concatenate([TF_Todas], axis=1)
X_train, X_test, Y_train, Y_test = train_test_80_20(X, y)
scores = cross_val_score(clf, X_train, Y_train,
cv=kf,
scoring="f1"
)
print(f"{scores.mean():.3f} +- {scores.std():.3f}")
%time # pa que aprendas
# enternar el modelo con todos los datos de entrenamiento
clf.fit(X_train, Y_train)
# solo usar cuando ya hayas terminado lo de arriba
test_evaluation(clf, X_test, Y_test)
###Output
precision recall f1-score support
0 0.89 0.55 0.68 31
1 0.63 0.92 0.75 26
accuracy 0.72 57
macro avg 0.76 0.74 0.71 57
weighted avg 0.77 0.72 0.71 57
###Markdown
**Random Forest - normas**
###Code
# optimización de hiperparámetros utilizando cross-validation
# MODELO: RF
# VARIABLES DE ENTRADA: normas
# HYPERPARÁMETROS ÓPTIMOS:
clf = RandomForestClassifier(n_estimators=100, random_state=0)
X = np.concatenate([normas_numpy], axis=1)
X_train, X_test, Y_train, Y_test = train_test_80_20(X, y)
scores = cross_val_score(clf, X_train, Y_train,
cv=kf,
scoring="f1"
)
print(f"{scores.mean():.3f} +- {scores.std():.3f}")
%time
# enternar el modelo con todos los datos de entrenamiento
clf.fit(X_train, Y_train)
# solo usar cuando ya hayas terminado lo de arriba
test_evaluation(clf, X_test, Y_test)
###Output
CPU times: user 2 µs, sys: 1e+03 ns, total: 3 µs
Wall time: 4.05 µs
precision recall f1-score support
0 0.79 0.48 0.60 31
1 0.58 0.85 0.69 26
accuracy 0.65 57
macro avg 0.68 0.67 0.64 57
weighted avg 0.69 0.65 0.64 57
###Markdown
**Random Forest - criterios aplicables (TF-IDF)**
###Code
# optimización de hiperparámetros utilizando cross-validation
# MODELO: RF
# VARIABLES DE ENTRADA: CA (TF-IDF)
# HYPERPARÁMETROS ÓPTIMOS:
clf = RandomForestClassifier(n_estimators=100, random_state=0)
X = np.concatenate([CA_TFIDF], axis=1)
X_train, X_test, Y_train, Y_test = train_test_80_20(X, y)
scores = cross_val_score(clf, X_train, Y_train,
cv=kf,
scoring="f1"
)
print(f"{scores.mean():.3f} +- {scores.std():.3f}")
%time
# enternar el modelo con todos los datos de entrenamiento
clf.fit(X_train, Y_train)
# solo usar cuando ya hayas terminado lo de arriba
test_evaluation(clf, X_test, Y_test)
###Output
CPU times: user 2 µs, sys: 1 µs, total: 3 µs
Wall time: 5.01 µs
precision recall f1-score support
0 0.81 0.55 0.65 31
1 0.61 0.85 0.71 26
accuracy 0.68 57
macro avg 0.71 0.70 0.68 57
weighted avg 0.72 0.68 0.68 57
###Markdown
**Random Forest - normas + criterios aplicables (TF-IDF)**
###Code
# optimización de hiperparámetros utilizando cross-validation
# MODELO: RF
# VARIABLES DE ENTRADA: CA (normas + TF-IDF)
# HYPERPARÁMETROS ÓPTIMOS:
clf = RandomForestClassifier(n_estimators=100, random_state=0)
X = np.concatenate([normas_numpy, CA_TFIDF], axis=1)
X_train, X_test, Y_train, Y_test = train_test_80_20(X, y)
scores = cross_val_score(clf, X_train, Y_train,
cv=kf,
scoring="roc_auc"
)
print(f"{scores.mean():.3f} +- {scores.std():.3f}")
%time
# enternar el modelo con todos los datos de entrenamiento
clf.fit(X_train, Y_train)
# solo usar cuando ya hayas terminado lo de arriba
test_evaluation(clf, X_test, Y_test)
###Output
CPU times: user 2 µs, sys: 1 µs, total: 3 µs
Wall time: 4.05 µs
precision recall f1-score support
0 0.83 0.65 0.73 31
1 0.67 0.85 0.75 26
accuracy 0.74 57
macro avg 0.75 0.75 0.74 57
weighted avg 0.76 0.74 0.74 57
|
notebooks/archive/tutorial_esm4.ipynb
|
###Markdown
IntroductionThis is an introductory tutorial to locate, load, and plot ESM4 biogeochemistry data. Loading dataOutput from the pre-industrial control simulation of ESM4 is located in the file directory: /archive/oar.gfdl.cmip6/ESM4/DECK/ESM4_piControl_D/gfdl.ncrc4-intel16-prod-openmp/pp/ NOTE: it is easiest to navigate the filesystem from the terminal, using the "ls" command.Within this directory are a number of sub-folders in which different variables have been saved. Of relevance for our work are the folders with names starting ocean_ and ocean_cobalt_ (cobalt is the name of the biogeochemistry model used in this simulation). In each of the subfolders, data have been subsampled and time-averaged in different ways. So for example, in the sub-folder ocean_cobalt_omip_tracers_month_z, we find the further sub-folder ts/monthly/5yr/. In this folder are files (separate ones for each biogeochemical tracer) containing monthly averages for each 5 year time period since the beginning of the simulation.Let's load and plot the data from one of these files.
###Code
# Load certain useful packages in python
import xarray as xr
import numpy as np
from matplotlib import pyplot as plt
###Output
_____no_output_____
###Markdown
We will load the oxygen (o2) data from a 5 year window of the simulation - years 711 to 715.
###Code
# Specify the location of the file
rootdir = '/archive/oar.gfdl.cmip6/ESM4/DECK/ESM4_piControl_D/gfdl.ncrc4-intel16-prod-openmp/pp/'
datadir = 'ocean_cobalt_omip_tracers_month_z/ts/monthly/5yr/'
filename = 'ocean_cobalt_omip_tracers_month_z.071101-071512.o2.nc'
# Note the timestamp in the filename: 071101-071512
# which specifies that in this file are data from year 0711 month 01 to year 0715 month 12.
# Load the file using the xarray (xr) command open_dataset
# We load the data to a variable that we call 'oxygen'
oxygen = xr.open_dataset(rootdir+datadir+filename)
# Print to the screen the details of the file
print(oxygen)
###Output
<xarray.Dataset>
Dimensions: (nv: 2, time: 60, xh: 720, yh: 576, z_i: 36, z_l: 35)
Coordinates:
* nv (nv) float64 1.0 2.0
* time (time) object 0711-01-16 12:00:00 ... 0715-12-16 12:00:00
* xh (xh) float64 -299.8 -299.2 -298.8 -298.2 ... 58.75 59.25 59.75
* yh (yh) float64 -77.91 -77.72 -77.54 -77.36 ... 89.47 89.68 89.89
* z_i (z_i) float64 0.0 5.0 15.0 25.0 ... 5.75e+03 6.25e+03 6.75e+03
* z_l (z_l) float64 2.5 10.0 20.0 32.5 ... 5e+03 5.5e+03 6e+03 6.5e+03
Data variables:
average_DT (time) timedelta64[ns] ...
average_T1 (time) object ...
average_T2 (time) object ...
o2 (time, z_l, yh, xh) float32 ...
time_bnds (time, nv) object ...
Attributes:
filename: ocean_cobalt_omip_tracers_month_z.071101-071512.o2.nc
title: ESM4_piControl_D
associated_files: areacello: 07110101.ocean_static.nc
grid_type: regular
grid_tile: N/A
external_variables: volcello areacello
###Markdown
We can see above that the file contains the variable (in this case oxygen - o2), as well as all of the dimensional information - latitude (xh), longitude (yh), depth (z_i and z_l). The two depth coordinates correspond to the layer and interface depths - for our purposes, we will almost always be interested only in the layer depth.We can learn more about a variable (e.g. what it is, and what its units are), by printing it to the screen directly.
###Code
print(oxygen.o2)
###Output
<xarray.DataArray 'o2' (time: 60, z_l: 35, yh: 576, xh: 720)>
[870912000 values with dtype=float32]
Coordinates:
* time (time) object 0711-01-16 12:00:00 ... 0715-12-16 12:00:00
* xh (xh) float64 -299.8 -299.2 -298.8 -298.2 ... 58.75 59.25 59.75
* yh (yh) float64 -77.91 -77.72 -77.54 -77.36 ... 89.47 89.68 89.89
* z_l (z_l) float64 2.5 10.0 20.0 32.5 ... 5e+03 5.5e+03 6e+03 6.5e+03
Attributes:
long_name: Dissolved Oxygen Concentration
units: mol m-3
cell_methods: area:mean z_l:mean yh:mean xh:mean time: mean
cell_measures: volume: volcello area: areacello
time_avg_info: average_T1,average_T2,average_DT
standard_name: mole_concentration_of_dissolved_molecular_oxygen_in_sea_w...
###Markdown
Here we can see that the variable o2 corresponds to the concetration of dissolved oxygen, in moles per cubic metre. *** PlottingNow let's plot some of this data to see what it looks like.We use the package pyplot from matplotlib (plt), with the command pcolormesh. This plots a 2D coloured mesh of whatever variable we specify. We load the generated image to the variable 'im', so that we can point to it later.Within pcolormesh, we use the '.' to pull out the bits that we want from the dataset 'oxygen' In the first instance we take the variable o2: oxygen.o2 Then we select the first time point and the very upper depth level using index selection: oxygen.o2.isel(time=0,z_l=0)
###Code
im = plt.pcolormesh(oxygen.o2.isel(time=0,z_l=0)) # pcolormesh of upper surface at first time step
plt.colorbar(im) # Plot a colorbar
plt.show() # Show the plot
###Output
_____no_output_____
###Markdown
***We can just as easily plot a deeper depth level. Let's look at the 10th level.
###Code
im = plt.pcolormesh(oxygen.o2.isel(time=0,z_l=9)) # remember python indices start from 0
plt.colorbar(im) # Plot a colorbar
plt.show() # Show the plot
###Output
_____no_output_____
###Markdown
Temperature and salinity dataNow we are equipped to load and examine biogeochemical data.Where do we find the coincident physical variables, temperature and salinity? The physical variables are stored in the same root directory, but a different sub-directory: ocean_monthly_z/ts/monthly/5yr/.Let's load the temperature data for the same time period.
###Code
datadir = 'ocean_monthly_z/ts/monthly/5yr/'
filename = 'ocean_monthly_z.071101-071512.thetao.nc'
temperature = xr.open_dataset(rootdir+datadir+filename)
print(temperature.thetao)
###Output
<xarray.DataArray 'thetao' (time: 60, z_l: 35, yh: 576, xh: 720)>
[870912000 values with dtype=float32]
Coordinates:
* time (time) object 0711-01-16 12:00:00 ... 0715-12-16 12:00:00
* xh (xh) float64 -299.8 -299.2 -298.8 -298.2 ... 58.75 59.25 59.75
* yh (yh) float64 -77.91 -77.72 -77.54 -77.36 ... 89.47 89.68 89.89
* z_l (z_l) float64 2.5 10.0 20.0 32.5 ... 5e+03 5.5e+03 6e+03 6.5e+03
Attributes:
long_name: Sea Water Potential Temperature
units: degC
cell_methods: area:mean z_l:mean yh:mean xh:mean time: mean
cell_measures: volume: volcello area: areacello
time_avg_info: average_T1,average_T2,average_DT
standard_name: sea_water_potential_temperature
###Markdown
Let's plot the surface temperature data.
###Code
im = plt.pcolormesh(temperature.thetao.isel(time=0,z_l=0))
plt.colorbar(im) # Plot a colorbar
plt.show() # Show the plot
###Output
_____no_output_____
###Markdown
BinningA lot of what we will be doing is looking at variables such as oxygen in a 'temperature coordinate'. That is to say, 'binning' the oxygen according to the temperature of the water.Let's look at how to do that in xarray.
###Code
# Merge our oxygen and temperature dataarrays
ds = xr.merge([temperature,oxygen])
# Set temperature as a 'coordinate' in the new dataset
ds = ds.set_coords('thetao')
# Use the groupby_bins functionality of xarray to group the o2 measurements into temperature bins
theta_bins = np.arange(-2,30,1) # Specify the range of the bins
o2_in_theta = ds.o2.isel(time=0).groupby_bins('thetao',theta_bins) # Do the grouping
###Output
/nbhome/gam/miniconda/envs/mom6/lib/python3.7/site-packages/numpy/core/numeric.py:538: SerializationWarning: Unable to decode time axis into full numpy.datetime64 objects, continuing using cftime.datetime objects instead, reason: dates out of range
return array(a, dtype, copy=False, order=order)
/nbhome/gam/miniconda/envs/mom6/lib/python3.7/site-packages/numpy/core/numeric.py:538: SerializationWarning: Unable to decode time axis into full numpy.datetime64 objects, continuing using cftime.datetime objects instead, reason: dates out of range
return array(a, dtype, copy=False, order=order)
###Markdown
This series of operations has grouped the o2 datapoints according to their coincident temperature values. (A short example of the functionality of groupby using multi-dimensional coordinates, such as temperature, is provided [here](http://xarray.pydata.org/en/stable/examples/multidimensional-coords.html)) We can now perform new operations on the grouped object (o2_in_theta).For example, we can simply count up the number of data points in each group (like a histogram):
###Code
o2_in_theta.count(xr.ALL_DIMS)
###Output
_____no_output_____
###Markdown
And we can plot that very easily:
###Code
o2_in_theta.count(xr.ALL_DIMS).plot()
###Output
_____no_output_____
###Markdown
Or, we can take the mean value in each group:
###Code
o2_in_theta.mean(xr.ALL_DIMS)
###Output
_____no_output_____
###Markdown
Accounting for volumeDifferent grid cells in the model have different volumes. Thus, when we are doing summations, calculating means, etc., we need to account for this variable volume.So, first load up the gridcell volume data.
###Code
datadir = 'ocean_monthly_z/ts/monthly/5yr/'
filename = 'ocean_monthly_z.071101-071512.volcello.nc'
volume = xr.open_dataset(rootdir+datadir+filename)
print(volume.volcello)
###Output
<xarray.DataArray 'volcello' (time: 60, z_l: 35, yh: 576, xh: 720)>
[870912000 values with dtype=float32]
Coordinates:
* time (time) object 0711-01-16 12:00:00 ... 0715-12-16 12:00:00
* xh (xh) float64 -299.8 -299.2 -298.8 -298.2 ... 58.75 59.25 59.75
* yh (yh) float64 -77.91 -77.72 -77.54 -77.36 ... 89.47 89.68 89.89
* z_l (z_l) float64 2.5 10.0 20.0 32.5 ... 5e+03 5.5e+03 6e+03 6.5e+03
Attributes:
long_name: Ocean grid-cell volume
units: m3
cell_methods: area:sum z_l:sum yh:sum xh:sum time: mean
cell_measures: area: areacello
time_avg_info: average_T1,average_T2,average_DT
standard_name: ocean_volume
###Markdown
As a first example, sum up the volumes of the grid cells within each density class. For this we will need to bin the volume into temperature classes, as we did with oxygen.
###Code
ds = xr.merge([ds,volume])
volcell_in_theta = ds.volcello.isel(time=0).groupby_bins('thetao',theta_bins)
###Output
/nbhome/gam/miniconda/envs/mom6/lib/python3.7/site-packages/numpy/core/numeric.py:538: SerializationWarning: Unable to decode time axis into full numpy.datetime64 objects, continuing using cftime.datetime objects instead, reason: dates out of range
return array(a, dtype, copy=False, order=order)
/nbhome/gam/miniconda/envs/mom6/lib/python3.7/site-packages/numpy/core/numeric.py:538: SerializationWarning: Unable to decode time axis into full numpy.datetime64 objects, continuing using cftime.datetime objects instead, reason: dates out of range
return array(a, dtype, copy=False, order=order)
###Markdown
Summing these binned volumes then provides a true account of the volume of ocean water in each temperature class.
###Code
volcell_in_theta.sum(xr.ALL_DIMS).plot()
###Output
_____no_output_____
###Markdown
I might also want to look at the summed oxygen content. This would involve binning and summing the product of oxygen and grid cell volume.
###Code
o2cont = ds.volcello*ds.o2
o2cont.name='o2cont'
ds = xr.merge([ds,o2cont])
o2cont_in_theta = ds.o2cont.isel(time=0).groupby_bins('thetao',theta_bins)
o2cont_in_theta.sum(xr.ALL_DIMS).plot()
###Output
_____no_output_____
###Markdown
And now the volume-weighted mean oxygen in each temperature class.
###Code
o2mean_in_theta = o2cont_in_theta.sum(xr.ALL_DIMS)/volcell_in_theta.sum(xr.ALL_DIMS)
o2mean_in_theta.plot()
###Output
_____no_output_____
###Markdown
Doing our binning all at onceThe binning process takes some time, since the algorithm has to search through the whole 3D grid. groupby_bins can also operate on DataSets, rather than just DataArrays. As such, it could be more time efficient to do all of the binning at once. Let's have a look at that. Remember, our DataSet ds has all of the variables that we are interested in binning.
###Code
ds_in_theta = ds.isel(time=0).groupby_bins('thetao',theta_bins)
ds_in_theta
###Output
_____no_output_____
|
algorithms/Max-min-fairness.ipynb
|
###Markdown
Max-min fairness https://www.wikiwand.com/en/Max-min_fairness
###Code
from resources.utils import run_tests
def max_min_fairness(demands, capacity):
capacity_remaining = capacity
output = []
for i, demand in enumerate(demands):
share = capacity_remaining / (len(demands) - i)
allocation = min(share, demand)
if i == len(demands) - 1:
allocation = max(share, capacity_remaining)
output.append(allocation)
capacity_remaining -= allocation
return output
tests = [
(dict(demands=[1, 1], capacity=20), [1, 19]),
(dict(demands=[2, 8], capacity=10), [2, 8]),
(dict(demands=[2, 8], capacity=5), [2, 3]),
(dict(demands=[1, 2, 5, 10], capacity=20), [1, 2, 5, 12]),
(dict(demands=[2, 2.6, 4, 5], capacity=10), [2, 2.6, 2.7, 2.7]),
]
run_tests(tests, max_min_fairness)
###Output
✓ All tests successful
|
notebooks/2_seq_modelling/3_task_lm.ipynb
|
###Markdown
3 Task Based Language Model1. Initialisation2. Training3. Fine-tuning4. EvaluationDataset of interest: 1. Long non-coding RNA (lncRNA) vs. messenger RNA (mRNA) - 3.1 Initialisation 3.1.1 Imports
###Code
# Set it to a particular device
import torch
import os
os.environ['CUDA_VISIBLE_DEVICES'] = '1'
%reload_ext autoreload
%autoreload 2
%matplotlib inline
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
import pandas as pd
from pathlib import Path
from functools import partial
from utils import tok_fixed, tok_variable, get_model_LM
import sys; sys.path.append("../tools"); from config import *
from utils import *
###Output
_____no_output_____
###Markdown
3.1.2 mRNA/lncRNA Data initialisation
###Code
data_df = pd.read_csv(HUMAN/'lncRNA.csv', usecols=['Sequence','Name'])
# data for LM fine-tuning
df_ulm = (data_df[data_df['Name'].str.contains('TRAIN.fa')].pipe(partition_data))
df_tr_,df_va_ = df_ulm[df_ulm.set == 'train'], df_ulm[df_ulm.set == 'valid']
# dfs for classification
df_clas = (data_df[data_df['Name'].str.contains('train16K')].pipe(partition_data))
df_clas['Target'] = df_clas['Name'].map(lambda x : x.split('.')[0][:-1])
df_tr,df_va = df_clas[df_clas.set == 'train'], df_clas[df_clas.set == 'valid']
df_te = data_df[data_df['Name'].str.contains('TEST500')]
import matplotlib.pyplot as plt
fig, axes = plt.subplots(nrows=2, figsize = (16,8));
# suptitle = 'Domain Training Data: Distribution by Sample Length'
# _=fig.suptitle(suptitle)
plt.subplots_adjust(hspace=0.4)
_=df_tr_['Sequence'].str.len().sort_values().head(-50).hist(bins=100, log=True, ax=axes[0], alpha=0.5, label='training')
_=df_va_['Sequence'].str.len().sort_values().head(-50).hist(bins=100, log=True, ax=axes[0], alpha=0.5, label='validation')
_=axes[0].set_title('Unsupervised Fine-Tuning'); _=axes[0].set_xlabel('Sample length (base-pairs)'); _=axes[0].legend();
axes[0].grid(False)
# axes[0].set_xscale('log')
_=df_tr['Sequence'].str.len().sort_values().hist(bins=100, ax=axes[1], alpha=0.5, label='training')
_=df_va['Sequence'].str.len().sort_values().hist(bins=100, ax=axes[1], alpha=0.5, label='validation')
_=axes[1].set_title('Classification Fine-Tuning'); _=axes[1].set_xlabel('Sample length (base-pairs)'); _=axes[1].legend()
axes[1].grid(False)
fig.savefig(FIGURES/'ulmfit'/suptitle.lower().replace(' ','_'), dpi=fig.dpi, bbox_inches='tight', pad_inches=0.5)
###Output
_____no_output_____
###Markdown
3.2 LM Fine-Tuning
###Code
%%time
def make_experiments(df_tr, df_va):
"""Construct experiment based on tokenisation parameters explored.
"""
experiments = []
# fixed length
for i,ngram_stride in enumerate(NGRAM_STRIDE):
experiment = {}
experiment['title'] = 'fixed_{}_{}_rows_{}'.format(*ngram_stride,NROWS_TRAIN)
experiment['xdata'], experiment['vocab'] = tok_fixed(df_tr, df_va, *ngram_stride, bs=BS[i])
experiments.append(experiment)
# variable length
for i,max_vocab in enumerate(MAX_VOCAB):
experiment = {}
experiment['title'] = 'variable_{}_rows_{}'.format(max_vocab,NROWS_TRAIN)
experiment['xdata'], experiment['vocab'] = tok_variable(df_tr, df_va, max_vocab, bs=BS[i])
experiments.append(experiment)
return experiments
experiments = make_experiments(df_tr_, df_va_)
TUNE_CONFIG = dict(emb_sz=400,
n_hid=1150,
n_layers=3,
pad_token=0,
qrnn=False,
output_p=0.25,
hidden_p=0.1,
input_p=0.2,
embed_p=0.02,
weight_p=0.15,
tie_weights=True,
out_bias=True)
TUNE_DROP_MULT = 0.25
def tune_model(experiment, epochs=1):
config = TUNE_CONFIG.copy()
drop_mult = TUNE_DROP_MULT
data = experiment['xdata']
learn = get_model_LM(data, drop_mult, config)
learn = learn.to_fp16(dynamic=True); # convert model weights to 16-bit float
model = 'models/' + experiment['title'] + '.pth'
if os.path.exists(HUMAN/model):
print('model found: loading model: {}'.format(experiment['title']))
learn.load(experiment['title'])
learn.data = data
# add callbacks
from fastai.callbacks.csv_logger import CSVLogger
learn.callback_fns.append(partial(CSVLogger,
filename='history_tune_' + experiment['title'],
append=True))
learn.fit(epochs=epochs,wd=1e-4)
learn.save('tune_'+experiment['title'])
learn.save_encoder('tune_'+experiment['title']+'_enc')
# free up cuda
del learn; del data; torch.cuda.empty_cache()
for experiment in experiments[-1:]:
print(experiment['title'])
tune_model(experiment, epochs=4)
###Output
variable_16384_rows_20000
model found: loading model: variable_16384_rows_20000
###Markdown
3.3 Classification
###Code
%%time
def make_experiments(df_tr, df_va):
"""Construct experiment based on tokenisation parameters explored.
"""
experiments = []
# fixed length
for i,ngram_stride in enumerate(NGRAM_STRIDE):
experiment = {}
experiment['title'] = 'fixed_{}_{}_rows_{}'.format(*ngram_stride,NROWS_TRAIN)
experiment['xdata'], experiment['vocab'] = tok_fixed(df_tr, df_va, *ngram_stride,
bs=400, clas=True)
experiments.append(experiment)
# variable length
for i,max_vocab in enumerate(MAX_VOCAB):
experiment = {}
experiment['title'] = 'variable_{}_rows_{}'.format(max_vocab,NROWS_TRAIN)
experiment['xdata'], experiment['vocab'] = tok_variable(df_tr, df_va, max_vocab,
bs=400, clas=True)
experiments.append(experiment)
return experiments
experiments = make_experiments(df_tr, df_va)
CLAS_CONFIG = dict(emb_sz=400,
n_hid=1150,
n_layers=3,
pad_token=0,
qrnn=False,
output_p=0.4,
hidden_p=0.2,
input_p=0.6,
embed_p=0.1,
weight_p=0.5)
CLAS_DROP_MULT = 0.5
def tune_classifier(experiment, epochs=1):
config = CLAS_CONFIG.copy()
drop_mult = CLAS_DROP_MULT
data = experiment['xdata']
learn = get_model_clas(data, CLAS_DROP_MULT, CLAS_CONFIG, max_len=4000*70)
learn.load_encoder(experiment['title']+'_enc')
learn = learn.to_fp16(dynamic=True);
# add callbacks
from fastai.callbacks.csv_logger import CSVLogger
learn.callback_fns.append(partial(CSVLogger,
filename='history_clas' + experiment['title'],
append=True))
learn.freeze()
learn.fit_one_cycle(epochs, 5e-2, moms=(0.8, 0.7))
learn.save('clas_'+experiment['title'])
learn.save_encoder('clas_'+experiment['title']+'_enc')
tune_classifier(experiments[1], epochs=4)
CLAS_CONFIG = dict(emb_sz=400,
n_hid=1150,
n_layers=3,
pad_token=0,
qrnn=False,
output_p=0.4,
hidden_p=0.2,
input_p=0.6,
embed_p=0.1,
weight_p=0.5)
CLAS_DROP_MULT = 0.5
tune_classifier(experiments[1], epochs=4)
###Output
_____no_output_____
###Markdown
3.4 EvaluationWe now evaluate every model trained for classification performance on the `TEST500` dataset.All models have been trained for 10 epochs unsupervised, then fine tuned for an additional 8 epochs on long read ncRNA and mRNA data. We plot confusion matrices for each model, as well as a comparative accuracy plot.
###Code
get_scores(learn)
###Output
_____no_output_____
|
MiniProjects/Calculator.ipynb
|
###Markdown
ProblemAsk user to input the number for simple arthemtic operations
###Code
class SimpleCalculator:
# constructor
def __init__(self):
print('')
# function adds two numbers
def add(self, x, y):
return x + y
# function subtracts two numbers
def subtract(self, x, y):
return x - y
# function multiplies two numbers
def multiply(self, x, y):
return x * y
# function divides two numbers
def divide(self, x, y):
return x / y
# decision function
def calculate(self, num1, num2, userchoice):
if '1' == userchoice:
answer = self.add(num1, num2)
print('\nformula:: num1 + num2 = answer ')
print('{} + {} = {}'.format(num1, num2, answer) )
elif '2' == userchoice:
answer = self.subtract(num1, num2)
print('\nformula:: num1 - num2 = answer ')
print('{} - {} = {}'.format(num1, num2, answer) )
elif '3' == userchoice:
answer = self.multiply(num1, num2)
print('\nformula:: num1 * num2 = answer ')
print('{} * {} = {}'.format(num1, num2, answer) )
elif '4' == userchoice:
answer = self.divide(num1, num2)
print('\nformula:: num1 / num2 = answer ')
print('{} / {} = {}'.format(num1, num2, answer) )
else:
print('Invalid input!')
sc = SimpleCalculator()
while (True):
print('\n\nSelect operation.\n\t {} \n\t {} \n\t {} \n\t {} '. format('1.Add', '2.Subtract', '3.Multiply', '4.Divide' ,'0. EXIT'))
oper = input("Enter choice(0, 1, 2, 3, or 4): ") # Take input from the user
if (oper != "0"):
num1 = float(input("Enter first number: "))
num2 = float(input("Enter second number: "))
sc.calculate(num1, num2, oper)
else:
print('Exited! Happy using Calculator :-)')
break
###Output
Select operation.
1.Add
2.Subtract
3.Multiply
4.Divide
Enter choice(0, 1, 2, 3, or 4): 1
Enter first number: 10
Enter second number: 20
formula:: num1 + num2 = answer
10.0 + 20.0 = 30.0
Select operation.
1.Add
2.Subtract
3.Multiply
4.Divide
Enter choice(0, 1, 2, 3, or 4): 2
Enter first number: 10
Enter second number: 20
formula:: num1 - num2 = answer
10.0 - 20.0 = -10.0
Select operation.
1.Add
2.Subtract
3.Multiply
4.Divide
Enter choice(0, 1, 2, 3, or 4): 3
Enter first number: 10
Enter second number: 20
formula:: num1 * num2 = answer
10.0 * 20.0 = 200.0
Select operation.
1.Add
2.Subtract
3.Multiply
4.Divide
Enter choice(0, 1, 2, 3, or 4): 4
Enter first number: 10
Enter second number: 20
formula:: num1 / num2 = answer
10.0 / 20.0 = 0.5
Select operation.
1.Add
2.Subtract
3.Multiply
4.Divide
Enter choice(0, 1, 2, 3, or 4): 0
Exited! Happy using Calculator :-)
|
examples/grid_2d_examples/supercell_with_arrows.ipynb
|
###Markdown
创建带箭头的supercell
###Code
nodes, edges = [], []
###Output
_____no_output_____
###Markdown
创建 nodes 和 edges top 位相关
###Code
from catplot.grid_components.nodes import Node2D
from catplot.grid_components.edges import Edge2D
top = Node2D([0.0, 0.0], size=800, color="#2A6A9C")
t1 = Node2D([0.0, 1.0])
t2 = Node2D([1.0, 0.0])
nodes.append(top)
e1 = Edge2D(top, t1, width=8)
e2 = Edge2D(top, t2, width=8)
edges.extend([e1, e2])
###Output
_____no_output_____
###Markdown
bridge 相关
###Code
bridge1 = Node2D([0.0, 0.5], style="s", size=600, color="#5A5A5A", alpha=0.6)
bridge2 = Node2D([0.5, 0.0], style="s", size=600, color="#5A5A5A", alpha=0.6)
b1 = bridge1.clone([0.5, 0.5])
b2 = bridge2.clone([0.5, 0.5])
nodes.extend([bridge1, bridge2])
e1 = Edge2D(bridge1, b1)
e2 = Edge2D(bridge1, bridge2)
e3 = Edge2D(bridge2, b2)
e4 = Edge2D(b1, b2)
edges.extend([e1, e2, e3, e4])
###Output
_____no_output_____
###Markdown
hollow 位相关
###Code
h = Node2D([0.5, 0.5], style="h", size=700, color="#5A5A5A", alpha=0.3)
nodes.append(h)
###Output
_____no_output_____
###Markdown
创建箭头
###Code
from catplot.grid_components.edges import Arrow2D
top_bri_1 = Arrow2D(top, bridge1, alpha=0.6, color="#ffffff", zorder=3)
top_bri_2 = Arrow2D(top, bridge2, alpha=0.6, color="#ffffff", zorder=3)
top_hollow = Arrow2D(top, h, alpha=0.6, color="#000000", zorder=3)
arrows = [top_bri_1, top_bri_2, top_hollow]
###Output
_____no_output_____
###Markdown
绘制
###Code
from catplot.grid_components.grid_canvas import Grid2DCanvas
canvas = Grid2DCanvas()
###Output
_____no_output_____
###Markdown
创建supercell
###Code
from catplot.grid_components.supercell import SuperCell2D
supercell = SuperCell2D(nodes, edges, arrows)
canvas.add_supercell(supercell)
canvas.draw()
canvas.figure
###Output
_____no_output_____
###Markdown
扩展supercell
###Code
expanded_supercell = supercell.expand(4, 4)
canvas_big = Grid2DCanvas(figsize=(30, 20), dpi=60)
canvas_big.add_supercell(expanded_supercell)
canvas_big.draw()
canvas_big.figure
###Output
_____no_output_____
|
Consistent Hashing ++.ipynb
|
###Markdown
Improvements to Consistent HashingNormally, [consistent hashing](https://en.wikipedia.org/wiki/Consistent_hashing) is a little expensive, because each node needs the whole set of keys to know which subset it should be working with.But with a little ingenuity in key design, we can enable a pattern that allows each node to only query the work it needs to do! How Consistent Hashing WorksConsistent hashing works by effectively splitting up a ring into multiple parts, and assigning each node a (more or less) equal share.It does this by having each node put the same number of dots on a circle:
###Code
import math
PointNode = namedtuple("PointNode", ["point", "node"])
POINTS_BY_NODE = [
PointNode(0, "a"),
PointNode(math.pi / 2, "b"),
PointNode(math.pi, "c"),
PointNode(math.pi * 3 / 2, "d'")
]
###Output
_____no_output_____
###Markdown
Effectively enabling buckets in between the points. In the example above, we can just find the point that is less than the point we're attempting to bucket:
###Code
import bisect
def get_node_for_point(node_by_point, point):
""" given the node_by_point, return the node that the point belongs to. """
as_point_node = PointNode(point, "_")
index = bisect.bisect_right(node_by_point, as_point_node)
if index == len(node_by_point):
index = -1
return node_by_point[index].node
get_node_for_point(POINTS_BY_NODE, math.pi * 7 / 4)
###Output
_____no_output_____
###Markdown
We can construct our own ring from any arbitrary set of nodes, as long as we have a way to uniquely name on versus the other:
###Code
import bisect
import math
import pprint
from collections import namedtuple
LENGTH = 2 * math.pi
PointNode = namedtuple("PointNode", ["point", "node"])
def _calculate_point_for_node(node, point_num):
""" return back the point for the node, between 0 and 2 * PI """
return hash(node + str(point_num)) % LENGTH
def points_for_node(node, num_points):
return [_calculate_point_for_node(node, i) for i in range(num_points)]
def get_node_by_point(node_names, num_points):
""" return a tuple of (point, node), ordering by point """
point_by_node = [PointNode(p, n) for n in node_names for p in points_for_node(n, num_points)]
point_by_node.sort()
return point_by_node
node_by_point = get_node_by_point(["a", "b", "c", "d"], 4)
get_node_for_point(node_by_point, 2)
###Output
_____no_output_____
###Markdown
Bucketing the Points without all the keysNormaly, consistent hashing requires the one executing the algorithm to be aware of two sets of data: 1. the identifiers of all the nodes in the cluster 2. the set of keys to assign. This is because the standard algorithm runs through the list of all keys, and assigns them:
###Code
def assign_nodes(node_by_point, items):
key_by_bucket = {}
for i in items:
value = hash(i) % LENGTH
node = get_node_for_point(node_by_point, value)
key_by_bucket.setdefault(node, [])
key_by_bucket[node].append(i)
return key_by_bucket
items = list(range(40))
assign_nodes(node_by_point, items)
###Output
_____no_output_____
###Markdown
(note the lack of even distribution here: as a pseudorandom algorithm, you will end up with some minor uneven distribution. We'll talk about that later.)But getting all keys can be inefficient for larger data sets. What happens when we want to consistently hash against a data set of 1 million points?Consistent hashing requires every node to have the full set of keys. But what if each node could just query for the data that's important to it?There is a way to know what those are. Given all the nodes, we can calculate which ranges each node is responsible for:
###Code
def get_ranges_by_node(node_by_point):
""" return a Dict[node, List[Tuple[lower_bound, upper_bound]]] for the raw nodes by point """
range_by_node = {}
previous_point, previous_node = 0, node_by_point[-1].node
for point, node in node_by_point:
point_range = (previous_point, point)
range_by_node.setdefault(node, [])
range_by_node[node].append(point_range)
previous_point, previous_node = point, node
# we close the loop by one last range to the end of the ring
first_node = node_by_point[0].node
range_by_node[first_node].append((previous_point, LENGTH))
return range_by_node
get_ranges_by_node(node_by_point)
###Output
_____no_output_____
###Markdown
Now we have the ranges this node is responsible for. Now we just need a database that knows how to query these ranges.We can accomplish this by storing the range value in the database itself, and index against that:
###Code
import bisect
import random
import string
def _calculate_point(value):
return hash(value) % LENGTH
def _random_string():
return ''.join(random.choices(string.ascii_uppercase + string.digits, k=10))
VALUES = [_random_string() for _ in range(100)]
DATABASE = {_calculate_point(v): v for v in VALUES}
INDEX = sorted(DATABASE.keys())
def query_database(index, database, bounds):
lower, upper = bounds
lower_index = bisect.bisect_right(index, lower)
upper_index = bisect.bisect_left(index, upper)
return [database[index[i]] for i in range(lower_index, upper_index)]
query_database(INDEX, DATABASE, (0.5, 0.6))
###Output
_____no_output_____
###Markdown
At that point, we can pinpoint and query the specific values that are relevant to our node. We can accomplish this with just the information about the nodes themselves:
###Code
def query_values_for_node(node_by_point, index, database, node):
range_by_node = get_ranges_by_node(node_by_point)
values = []
for bounds in range_by_node[node]:
values += query_database(index, database, bounds)
return values
query_values_for_node(node_by_point, INDEX, DATABASE, "a")
###Output
_____no_output_____
|
.ipynb_checkpoints/Fitting a model to data with MCMC-checkpoint.ipynb
|
###Markdown
Fitting a model to data with MCMC
###Code
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import plot_helper as plot_helper
import pandas as pd
import emcee # 2.2.1
import corner
import progressbar
import scipy.optimize as op
###Output
_____no_output_____
###Markdown
This is a very short introduction to using MCMC for fitting a model to data; see references below for much more detailed examples. The ground truth Let us suppose we are interested in some physical process which relates the quantities $x$ and $y$ as\begin{equation}y=y_{max}\frac{x}{x+K},\end{equation}with true parameter values $y_{max}=1$ and $K=2$.
###Code
def model(x,ymax,K):
return ymax*x/(x+K)
ymax=1
K=2
x=np.linspace(0,10,50)
y=model(x,ymax,K)
plot_helper.plot1(x,y,title='Ground truth')
###Output
_____no_output_____
###Markdown
Suppose we make some observations to measure $y_{max}$ and $K$.
###Code
N=9
xobs=(np.random.rand(N))*10
yerrtrue=0.03*np.random.randn(N) # normally distributed errors
yobs=model(xobs,ymax,K)+yerrtrue
yerr=yerrtrue*1 # Our estimated error is not necessarily equal to the true error
plot_helper.plot2(x,y,xobs,yobs,yerr,title='Ground truth+observations')
###Output
_____no_output_____
###Markdown
We would like to estimate the posterior probability distribution for $y_{max}$ and $K$, given these observations. In other words, we want $P(model|data)$, the probability of our model parameters given the data. Bayes' theorem gives an expression for this quantity:\begin{equation}P(model|data)=\frac{P(data|model)P(model)}{P(data)}\end{equation}Let's unpack this equation. The prior $P(model)$ is the prior; it is a description of the uncertainty we palce on the parameters in our model. For instance, let us assume that our parameters are initially normally distributed:\begin{align}y_{max}&=\mathcal{N}(1,0.2) \\K&=\mathcal{N}(2,0.2)\end{align}so that our model becomes \begin{equation}\hat{y}=\mathcal{N}(1,0.2)\frac{x}{x+\mathcal{N}(2,0.2)}.\end{equation}The prior probability of our model given parameters $y_{max}$ and $K$ is\begin{equation}P(model)=\mathcal{N}(y_{max}-1,0.2)\mathcal{N}(\mu-2,0.2).\end{equation}Typically we express these probablities in terms of log-probabilities so that the terms become additive:\begin{equation}\ln P(model)=\ln\mathcal{N}(y_{max}-1,0.2)+\ln\mathcal{N}(\mu-2,0.2).\end{equation}
###Code
def prior(x,mu,sigma):
return 1/np.sqrt(2*np.pi*sigma**2)*np.exp(-(x-mu)**2/(2*sigma**2))
mu1=1
mu2=2
sigma=0.2
xp=np.linspace(0,3,100)
y1=prior(xp,mu1,sigma)
y2=prior(xp,mu2,sigma)
plot_helper.plot3(xp,y1,xp,y2,title='Prior')
###Output
_____no_output_____
###Markdown
The likelihood $P(data|model)$ is known as the likelihood. It's a measure of how likely it is that our model generates the observed data. In order to calculate this term we need a measure of how far our model predictions are from the actual observed data; typically we assume that deviations are due to normally-distributed noise, in which case our likelihood takes the simple form of squared residuals for each of the data points $y_n$ with error $s_n$:\begin{equation}P(data|model)=\prod_n\frac{1}{2\pi s_n^2}\exp\left(-\frac{(y_n-\hat{y}_n)^2}{2s_n^2}\right)\end{equation}The negative log-likelihood is therefore\begin{equation}\ln P(data|model)=-\frac{1}{2}\sum_n \left(\frac{(y_n-\hat{y}_n)^2}{s_n^2}+\ln (2 \pi s_n^2) \right)\end{equation} MCMC What we want to do is determine the posterior probability distribution $\Pi(model|data)$. From this distribution we can determine probabilities as well as the expectation values of any quantity of interest by integrating. In other words, we would like to generate the probability landscape of likely model parameters, given our observations. In order to do this we must sample the landscape by varying the parameters. MCMC allows us to do this, without having to calculate the third term $P(data)$ in the Bayes formula which is nontrivial. The simplest MCMC algorithm is that of Metropolis: The Metropolis algorithm 1) First we start at an initial point for the parameters $y_{max,0}$, $K_0$. We compute the probabilities \begin{equation}P(data|y_{max,0},K_0)P(y_{max,0},K_0).\end{equation}2) Then we move to a new location $y_{max,1}$, $K_1$. This new location is called the proposal, and it's generated by randomly moving to a new point with probability given by a normal distribution centered around the current location, and a fixed variance (the proposal width).3) We calculate the new probabilities \begin{equation}P(data|y_{max,1},K_1)P(y_{max,1},K_1).\end{equation}4) We then calculate the acceptance ratio: \begin{equation}\alpha=\frac{P(data|y_{max,1},K_1)P(y_{max,1},K_1)}{P(data|y_{max,0},K_0)P(y_{max,0},K_0)}.\end{equation}If $\alpha$ is greater than 1, i.e. the probability at the new point is higher, we accept the new point and move there. If $\alpha$ is smaller than 1, then we accept the move with a probability equal to $\alpha$.
###Code
def normalprior(param,mu,sigma):
return np.log( 1.0 / (np.sqrt(2*np.pi)*sigma) ) - 0.5*(param - mu)**2/sigma**2
def like(pos,x,y,yerr):
ymax=pos[0]
K=pos[1]
model=ymax*x/(x+K)
inv_sigma2=1.0/(yerr**2)
return -0.5*(np.sum((y-model)**2*inv_sigma2-np.log(inv_sigma2)))
def prior(pos):
ymax=pos[0]
K=pos[1]
mu1=1
sigma1=0.5
log_Prymax=normalprior(ymax,mu1,sigma1)
mu2=2
sigma2=0.5
log_PrK=normalprior(K,mu2,sigma2)
return log_Prymax+log_PrK
def norm(pos,width):
return pos+width*np.random.randn(2)
def metropolis(pos,MC,steps,width):
for i in range(steps):
proposal=norm(pos,width)
newloglike=like(proposal,xobs,yobs,yerr)+prior(proposal)
oldloglike=like(pos,xobs,yobs,yerr)+prior(pos)
if newloglike>=oldloglike: # If new probability is higher then accept
pos=proposal
else:
a=np.exp(newloglike-oldloglike)
if np.random.rand()<a: # If old probability is higher than only accept with probability a.
pos=proposal
else:
pos=pos
MC[i]=pos
return MC
steps=5000
width=0.1
MC=np.zeros(steps*2).reshape(steps,2)
pos=np.array([1,2])
MC=metropolis(pos,MC,steps,width)
plt.plot(MC[:,0],MC[:,1],'-')
plt.show()
###Output
_____no_output_____
###Markdown
Our Markov chain samples positions in parameter space, spending proportionately more time in regions of high probability mass. While the Metropolis algorithm is intuitive and instructive it is not the most efficient MCMC algorithm, so for the next part we will apply a more efficient ensemble sampler. A more efficient algorithm: Goodman and Weare affine-invariant ensemble samplers
###Code
def lnlike(theta,x,y,yerr):
ymax,K=theta
model=ymax*x/(x+K)
inv_sigma2=1.0/(yerr**2)
return -0.5*(np.sum((y-model)**2*inv_sigma2-np.log(inv_sigma2)))
def lnprior(theta):
ymax,K=theta
if not (0<ymax and 0<K) :
return -np.inf # Hard-cutoff for positive value constraint
mu1=1
sigma1=0.5
log_Prymax=np.log( 1.0 / (np.sqrt(2*np.pi)*sigma1) ) - 0.5*(ymax - mu1)**2/sigma1**2
mu2=2
sigma2=0.5
log_PrK=np.log( 1.0 / (np.sqrt(2*np.pi)*sigma2) ) - 0.5*(K - mu2)**2/sigma2**2
return log_Prymax+log_PrK
def lnprob(theta, x, y, yerr):
lp = lnprior(theta)
if not np.isfinite(lp):
return -np.inf
return lp + lnlike(theta, x, y, yerr)
ndim,nwalkers,threads,iterations,tburn=2,20,8,1000,200
labels=["$y_{max}$","$K$"]
parametertruths=[1,2]
pos=[np.array([
1*(1+0.05*np.random.randn()),
1*(1+0.05*np.random.randn())]) for i in range(nwalkers)]
sampler=emcee.EnsembleSampler(nwalkers,ndim,lnprob,a=2,args=(xobs,yobs,yerr),threads=threads)
### Start MCMC
iterations=iterations
bar=progressbar.ProgressBar(max_value=iterations)
for i, result in enumerate(sampler.sample(pos, iterations=iterations)):
bar.update(i)
### Finish MCMC
samples=sampler.chain[:,:,:].reshape((-1,ndim)) # shape = (nsteps, ndim)
df=pd.DataFrame(samples)
df.to_csv(path_or_buf='samplesout_.csv',sep=',')
df1=pd.read_csv('samplesout_.csv',delimiter=',')
data=np.zeros(df1.shape[0]*(df1.shape[1]-1)).reshape(df1.shape[0],(df1.shape[1]-1))
for i in range(0,int(df1.shape[1]-1)):
data[:,i]=np.array(df1.iloc[:,i+1]) # Put dataframe into array. Dataframe has no. columns = no. parameters.
data2=np.zeros((df1.shape[0]-tburn*nwalkers)*(df1.shape[1]-1)).reshape((df1.shape[0]-(tburn*nwalkers)),(df1.shape[1]-1))
for i in range(0,int(df1.shape[1]-1)):
for j in range(1,nwalkers+1):
data2[(iterations-tburn)*(j-1):(iterations-tburn)*(j),i]=np.array(df1.iloc[iterations*j-iterations+tburn:iterations*j,i+1])
samplesnoburn=data2
#plot_helper.plottraces(samples,labels,parametertruths,nwalkers,iterations,1)
fig=corner.corner(samplesnoburn, labels=labels,truths=parametertruths,quantiles=[0.16, 0.5, 0.84],show_titles=True, title_fmt='.2e', title_kwargs={"fontsize": 10},verbose=False)
fig.savefig("triangle.pdf")
plot_helper.plot4(xp,y1,xp,y2,samplesnoburn,title='Posterior')
plot_helper.plot5(x,y,xobs,yobs,yerr,samplesnoburn,xlabel='x',ylabel='y',legend=False,title=False)
###Output
_____no_output_____
###Markdown
**References*** MacKay 2003 http://www.inference.org.uk/itprnn/book.html - the bible for MCMC and inferential methods in general* Goodman and Weare 2010 https://projecteuclid.org/euclid.camcos/1513731992 - original paper describing affine-invariant ensemble sampling* emcee http://dfm.io/emcee/current/user/line/ - Python implementation of the Goodman and Weare algorithm* Fitting a model to data https://arxiv.org/abs/1008.4686 - excellent tutorial on how to 'properly' fit your data* Hamiltonian Monte Carlo https://arxiv.org/abs/1701.02434 - a more efficient MCMC algorithm, as implemented in Stan (http://mc-stan.org)* Another nice online tutorial http://twiecki.github.io/blog/2015/11/10/mcmc-sampling/ Fit to tellurium ODE model
###Code
import tellurium as te
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import plot_helper as plot_helper
import pandas as pd
import emcee
import corner
import progressbar
###Output
_____no_output_____
###Markdown
Here is a more sophisticated example similar to what you might encounter in the lab. Suppose we have a dynamical system
###Code
def MM_genmodel():
''' Michaelis-Menten enzyme model '''
rr = te.loada('''
J1: E+S->ES ; k1*E*S-k2*ES ;
J2: ES->E+S+P ; k3*ES ;
k1=0;
k2=0;
k3=0;
''')
return(rr)
def simulatemodel(rr,tmax,nsteps,paramdict):
for j in rr.model.getGlobalParameterIds():
rr[j]=paramdict[j] # set parameters
for j in rr.model.getFloatingSpeciesIds():
rr[j]=paramdict[j] # set concentrations
out=rr.simulate(0,tmax,points=nsteps)
return(out,rr)
tmax=20
nsteps=51
keys=['k1','k2','k3','E','S','ES','P']
params=[1,1,1,1,10,0,0]
paramdict=dict(zip(keys,params))
# Generate model
rr=MM_genmodel()
# Simulate model
out,_=simulatemodel(rr,tmax,nsteps,paramdict)
rr.plot()
###Output
_____no_output_____
###Markdown
Let's do a titration experiment and MCMC to extract kinetic parameters for this enzyme.
###Code
np.random.seed(42)
def titration_expt(titration,k1,k2,k3,tmax,nsteps,rr):
Parr=np.zeros((nsteps,len(titration)))
for j in range(len(titration)):
keys=['k1','k2','k3','E','S','ES','P']
params=[k1,k2,k3,1,titration[j],0,0]
paramdict=dict(zip(keys,params))
out,_=simulatemodel(rr,tmax,nsteps,paramdict)
Parr[:,j]=out[:,4]
return Parr
rr=MM_genmodel()
tmax=20
nsteps=51
Parr=titration_expt([0,5,10,15,20],1,10,1,tmax,nsteps,rr)
Parr+=0.2*np.random.randn(Parr.shape[0],Parr.shape[1])*Parr+0.0001*np.random.randn(Parr.shape[0],Parr.shape[1]) # Add noise
plt.plot(Parr,'o') ; plt.show()
# Define MCMC functions
def normalprior(param,mu,sigma):
return np.log( 1.0 / (np.sqrt(2*np.pi)*sigma) ) - 0.5*(param - mu)**2/sigma**2
def lnlike(theta,inputs):
k1,k2,k3=theta
# DATA
y=inputs['y']
yerr=inputs['yerr']
# MODEL INPUTS
tmax=inputs['tmax']
nsteps=inputs['nsteps']
titration=inputs['titration']
rr=inputs['model']
ymodel=titration_expt(titration,k1,k2,k3,tmax,nsteps,rr)
inv_sigma2=1.0/(yerr**2)
return -0.5*(np.sum((y-ymodel)**2*inv_sigma2-np.log(inv_sigma2)))
def lnprior(theta):
k1,k2,k3=theta
if not (0<k1 and 0<k2 and 0<k3) :
return -np.inf # Hard-cutoff for positive value constraint
log_PRs=[normalprior(k1,5,10),
normalprior(k2,10,10),
normalprior(k3,1,0.01)]
return np.sum(log_PRs)
def lnprob(theta,inputs):
lp = lnprior(theta)
if not np.isfinite(lp):
return -np.inf
return lp + lnlike(theta,inputs)
def gelman_rubin(chain):
''' Gelman-Rubin diagnostic for one walker across all parameters. This value should tend to 1. '''
ssq=np.var(chain,axis=1,ddof=1)
W=np.mean(ssq,axis=0)
Tb=np.mean(chain,axis=1)
Tbb=np.mean(Tb,axis=0)
m=chain.shape[0]*1.0
n=chain.shape[1]*1.0
B=n/(m-1)*np.sum((Tbb-Tb)**2,axis=0)
varT=(n-1)/n*W+1/n*B
Rhat=np.sqrt(varT/W)
return Rhat
# Load data
yobs=Parr
yerr=Parr*0.2
# Generate model
rr=MM_genmodel()
inputkeys=['tmax','nsteps','titration','model','y','yerr']
inputvalues=[20,51,[0,5,10,15,20],rr,yobs,yerr]
inputs=dict(zip(inputkeys,inputvalues))
np.random.seed(42)
# MLE
pos=[
5, # k1
10, # k2
1 # k3
]
nll= lambda *args: -lnlike(*args)
result=op.minimize(nll,pos,method='BFGS', args=(inputs))
paramstrue = result["x"]
k1_MLE=paramstrue[0]
k2_MLE=paramstrue[1]
k3_MLE=paramstrue[2]
print(k1_MLE,k2_MLE,k3_MLE)
tmax=20
nsteps=51
titration=[0,5,10,15,20]
ymodel=titration_expt(titration,k1_MLE,k2_MLE,k3_MLE,tmax,nsteps,rr)
plt.plot(yobs,'o')
plt.plot(ymodel,'k-',alpha=1) ; plt.show()
# Run MCMC
ndim,nwalkers,threads,iterations,tburn=3,50,1,3000,1000
labels=["$k_1$","$k_2$","$k_3$"]
parametertruths=[1,10,1]
pos=[np.array([
k1_MLE*(1+0.05*np.random.randn()),
k2_MLE*(1+0.05*np.random.randn()),
k3_MLE*(1+0.05*np.random.randn())]) for i in range(nwalkers)]
sampler=emcee.EnsembleSampler(nwalkers,ndim,lnprob,a=2,args=([inputs]),threads=threads)
### Start MCMC
iterations=iterations
bar=progressbar.ProgressBar(max_value=iterations)
for i, result in enumerate(sampler.sample(pos, iterations=iterations)):
bar.update(i)
### Finish MCMC
samples=sampler.chain[:,:,:].reshape((-1,ndim)) # shape = (nsteps, ndim)
samplesnoburn=sampler.chain[:,tburn:,:].reshape((-1,ndim)) # shape = (nsteps, ndim)
df=pd.DataFrame(samples)
df.to_csv(path_or_buf='samplesout_MM.csv',sep=',')
plot_helper.plottraces(samples,labels,parametertruths,nwalkers,iterations,1)
fig=corner.corner(samplesnoburn, labels=labels,truths=parametertruths,quantiles=[0.16, 0.5, 0.84],show_titles=True, title_fmt='.2e', title_kwargs={"fontsize": 10},verbose=False)
fig.savefig("triangle_MM.pdf")
### Gelman-Rubin diagnostic
# NOT RELIABLE ESTIMATE FOR EMCEE AS WALKERS NOT INDEPENDENT!
plt.close("all")
figure_options={'figsize':(8.27,5.83)} #figure size in inches. A4=11.7x8.3.
font_options={'size':'12','family':'sans-serif','sans-serif':'Arial'}
plt.rc('figure', **figure_options)
plt.rc('font', **font_options)
chain=sampler.chain[:,tburn:,:] # shape = nwalkers, iterations-tburn, ndim
print('Mean acceptance fraction', np.mean(sampler.acceptance_fraction))
print('GR diagnostic for one walker', gelman_rubin(chain)[0]) # Change index to get a different walker
chain_length=chain.shape[1]
step_sampling=np.arange(int(0.2*chain_length),chain_length,50)
rhat=np.array([gelman_rubin(chain[:,:steps,:])[0] for steps in step_sampling])
plt.plot(step_sampling,rhat); ax=plt.gca(); ax.axhline(y=1.1,color='k'); ax.set_title('GR diagnostic');
plt.show()
# Autocorrelation time analysis. 'c' should be as large as possible (default is 5)
tau = np.mean([emcee.autocorr.integrated_time(walker,c=1) for walker in sampler.chain[:,:,:]], axis=0)
print('Tau', tau)
for k1,k2,k3 in samplesnoburn[np.random.randint(len(samplesnoburn), size=10)]:
tmax=20
nsteps=51
titration=[0,5,10,15,20]
ymodel=titration_expt(titration,k1,k2,k3,tmax,nsteps,rr)
plt.plot(ymodel,'k-',alpha=0.1)
plt.plot(yobs,'o'); plt.show()
###Output
_____no_output_____
|
CNN/CNN_implementation_2.ipynb
|
###Markdown
Power Quality Classification using CNN This notebook focusses on developing a Convolutional Neural Network which classifies a particular power signal into its respective power quality condition. The dataset used here contains signals which belong to one of the 6 classes(power quality condition). The sampling rate of this data is 256. This means that each signal is characterized by 256 data points. Here the signals provided are in time domain.
###Code
#importing the required libraries
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import datetime
from scipy.fft import fft,fftfreq
from scipy import signal
from sklearn.preprocessing import StandardScaler
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Dropout, Activation
from tensorflow.keras.optimizers import Adam
#loading the dataset using pandas
x_train = pd.read_csv("../Dataset2/Train/Voltage_L1_train.csv")
y_train = pd.read_csv("../Dataset2/Train/output_train.csv")
x_test = pd.read_csv("../Dataset2/Test/Voltage_L1_test.csv")
y_test = pd.read_csv("../Dataset2/Test/output_test.csv")
print("x_train",x_train.shape)
print("y_train",y_train.shape)
print("x_test",x_test.shape)
print("y_test",y_test.shape)
###Output
x_train (5999, 256)
y_train (5999, 1)
x_test (3599, 256)
y_test (3599, 1)
###Markdown
Data Preprocessing This segment of notebook contains all the preprocessing steps which are performed on the data.
###Code
#dropna() function is used to remove all those rows which contains NA values
x_train.dropna(axis=0,inplace=True)
y_train.dropna(axis=0,inplace=True)
x_test.dropna(axis=0,inplace=True)
y_test.dropna(axis=0,inplace=True)
#shape of the data frames after dropping the rows containing NA values
print("x_train",x_train.shape)
print("y_train",y_train.shape)
print("x_test",x_test.shape)
print("y_test",y_test.shape)
#here we are constructing the array which will finally contain the column names
header =[]
for i in range(1,x_train.shape[1]+1):
header.append("Col"+str(i))
#assigning the column name array to the respectinve dataframes
x_train.columns = header
x_test.columns = header
#assinging the column name for the y_train and y_test
header = ["output"]
y_train.columns = header
y_test.columns = header
x_train.head()
x_test.head()
y_train.head()
y_test.head()
#further splitting the train dataset to train and validation
from sklearn.model_selection import train_test_split
x_train, x_val, y_train, y_val = train_test_split(x_train, y_train, test_size=0.20, random_state=42)
print('x_train',x_train.shape)
print('y_train',y_train.shape)
print('x_val',x_val.shape)
print('y_val',y_val.shape)
print('x_test',x_test.shape)
print('y_test',y_test.shape)
# get_dummies function is used here to perform one hot encoding of the y_* numpy arrays
y_train_hot = pd.get_dummies(y_train['output'])
y_test_hot = pd.get_dummies(y_test['output'])
y_val_hot = pd.get_dummies(y_val['output'])
y_train_hot.head()
y_train_arr = y_train_hot.to_numpy()
y_test_arr = y_test_hot.to_numpy()
y_val_arr = y_val_hot.to_numpy()
print("y_train:",y_train_arr.shape)
print("y_test:",y_test_arr.shape)
print("y_val:",y_val_arr.shape)
no_of_classes = y_train_arr.shape[1]
###Output
y_train: (4799, 6)
y_test: (3599, 6)
y_val: (1200, 6)
###Markdown
Data transformation The data transformation steps employed here are as follows:1) Fourier Transform2) Normalization
###Code
x_train_tr = x_train.to_numpy()
x_test_tr = x_test.to_numpy()
x_val_tr = x_val.to_numpy()
'''for i in range(0,x_train.shape[0]):
x_train_tr[i][:] = np.abs(fft(x_train_tr[i][:]))
for i in range(0,x_test.shape[0]):
x_test_tr[i][:] = np.abs(fft(x_test_tr[i][:]))
for i in range(0,x_val.shape[0]):
x_val_tr[i][:] = np.abs(fft(x_val_tr[i][:]))'''
transform = StandardScaler()
x_train_tr = transform.fit_transform(x_train)
x_test_tr = transform.fit_transform(x_test)
x_val_tr = transform.fit_transform(x_val)
print("Training",x_train_tr.shape)
print(y_train_arr.shape)
print("Validation",x_val_tr.shape)
print(y_val_arr.shape)
print("Test",x_test_tr.shape)
print(y_test_arr.shape)
sampling_rate = x_train_tr.shape[1]
###Output
Training (4799, 256)
(4799, 6)
Validation (1200, 256)
(1200, 6)
Test (3599, 256)
(3599, 6)
###Markdown
Model creation and training
###Code
#Reshaping the Data so that it could be used in 1D CNN
x_train_re = x_train_tr.reshape(x_train_tr.shape[0],x_train_tr.shape[1], 1)
x_test_re = x_test_tr.reshape(x_test_tr.shape[0],x_test_tr.shape[1], 1)
x_val_re = x_val_tr.reshape(x_val_tr.shape[0],x_val_tr.shape[1], 1)
x_train_re.shape
#importing required modules for working with CNN
import tensorflow as tf
from tensorflow.keras.layers import Conv1D
from tensorflow.keras.layers import Convolution1D, ZeroPadding1D, MaxPooling1D, BatchNormalization, Activation, Dropout, Flatten, Dense
from tensorflow.keras.regularizers import l2
#initializing required parameters for the model
batch_size = 64
num_classes = 6
epochs = 20
input_shape=(x_train_tr.shape[1], 1)
model = Sequential()
model.add(Conv1D(128, kernel_size=3,padding = 'same',activation='relu', input_shape=input_shape))
model.add(BatchNormalization())
model.add(MaxPooling1D(pool_size=(2)))
model.add(Conv1D(128,kernel_size=3,padding = 'same', activation='relu'))
model.add(BatchNormalization())
model.add(MaxPooling1D(pool_size=(2)))
model.add(Flatten())
model.add(Dense(16, activation='relu'))
model.add(Dense(num_classes, activation='softmax'))
model.summary()
#compiling the model
log_dir = "logs2/fit/" + datetime.datetime.now().strftime("%Y%m%d-%H%M%S")
tensorboard_callback = tf.keras.callbacks.TensorBoard(log_dir=log_dir, histogram_freq=1)
model.compile(loss=tf.keras.losses.categorical_crossentropy,
optimizer='adam',
metrics=['accuracy'])
#training the model
history = model.fit(x_train_re, y_train_hot, batch_size=batch_size, epochs=epochs, validation_data=(x_val_re, y_val_hot), callbacks=[tensorboard_callback])
%load_ext tensorboard
%tensorboard --logdir logs2/fit
print(model.metrics_names)
###Output
['loss', 'accuracy']
###Markdown
Model evaluation
###Code
print("min val:",min(history.history['val_accuracy']))
print("avg val",np.mean(history.history['val_accuracy']) )
print("max val:",max(history.history['val_accuracy']))
print()
print("min train:",min(history.history['accuracy']))
print("avg train",np.mean(history.history['accuracy']) )
print("max train:",max(history.history['accuracy']))
pred_acc = model.evaluate(x_test_re,y_test_hot)
print("Test accuracy is {}".format(pred_acc))
from sklearn.metrics import confusion_matrix
import seaborn as sn
array = confusion_matrix(y_test_hot.to_numpy().argmax(axis=1), model.predict(x_test_re).argmax(axis=1))
array
to_cm = pd.DataFrame(array, index = [i for i in ["Type-1","Type-2","Type-3","Type-4","Type-5","Type-6"]],
columns = [i for i in ["Type-1","Type-2","Type-3","Type-4","Type-5","Type-6"]])
plt.figure(figsize = (13,9))
sn.heatmap(to_cm, annot=True)
#model.save("CNN_model_data2.h5")
###Output
_____no_output_____
|
Notebooks/How_to_use_Kallisto_on_scRNAseq_data.ipynb
|
###Markdown
ISB-CGC Community NotebooksCheck out more notebooks at our [Community Notebooks Repository](https://github.com/isb-cgc/Community-Notebooks)! Title: How to use Kallisto to quantify genes in 10X scRNA-seqAuthor: David L GibbsCreated: 2019-08-07Purpose: Demonstrate how to use 10X fastq files and produce the gene quantification matrixNotes: In this notebook, we're going to use the 10X genomics fastq files that we generated earlier, to quantify gene expression per cell using Kallisto and Bustools. It is assumed that this notebook is running INSIDE THE CLOUD! By starting up a Jupyter notebook, you are already authenticated, can read and write to cloud storage (buckets) for free, and data transfers are super fast. To start up a notebook, log into your Google Cloud Console, use the main 'hamburger' menu to find the 'AI platform' near the bottom. Select Notebooks and you'll have an interface to start either an R or Python notebook. Resources: Bustools paper:https://www.ncbi.nlm.nih.gov/pubmed/31073610 https://www.kallistobus.tools/getting_started_explained.html https://github.com/BUStools/BUS_notebooks_python/blob/master/dataset-notebooks/10x_hgmm_6k_v2chem_python/10x_hgmm_6k_v2chem.ipynb https://pachterlab.github.io/kallisto/starting
###Code
cd /home/jupyter/
###Output
_____no_output_____
###Markdown
Software install
###Code
!git clone https://github.com/pachterlab/kallisto.git
cd kallisto/
ls -lha
!sudo apt --yes install autoconf cmake
!mkdir build
cd build
!sudo cmake ..
!sudo make
!sudo make install
!kallisto
cd ../..
!git clone https://github.com/BUStools/bustools.git
# we need the devel version due to a bug that stopped compilation ...
!git checkout devel
!git status
cd bustools/
!mkdir build
cd build
!sudo cmake ..
!sudo make
!sudo make install
cd ../..
!bustools
###Output
_____no_output_____
###Markdown
Reference Gathering
###Code
mkdir kallisto_bustools_getting_started/; cd kallisto_bustools_getting_started/
!wget ftp://ftp.ensembl.org/pub/release-96/fasta/homo_sapiens/cdna/Homo_sapiens.GRCh38.cdna.all.fa.gz
!wget ftp://ftp.ensembl.org/pub/release-96/gtf/homo_sapiens/Homo_sapiens.GRCh38.96.gtf.gz
###Output
_____no_output_____
###Markdown
Barcode whitelist
###Code
# Version 3 chemistry
!wget https://github.com/BUStools/getting_started/releases/download/species_mixing/10xv3_whitelist.txt
# Version 2 chemistry
!wget https://github.com/bustools/getting_started/releases/download/getting_started/10xv2_whitelist.txt
###Output
_____no_output_____
###Markdown
Gene map utility
###Code
!wget https://raw.githubusercontent.com/BUStools/BUS_notebooks_python/master/utils/transcript2gene.py
!gunzip Homo_sapiens.GRCh38.96.gtf.gz
!python transcript2gene.py --use_version < Homo_sapiens.GRCh38.96.gtf > transcripts_to_genes.txt
!head transcripts_to_genes.txt
###Output
_____no_output_____
###Markdown
Data
###Code
mkdir data
!gsutil -m cp gs://your-bucket/bamtofastq_S1_* data
mkdir output
cd /home/jupyter
ls -lha data
###Output
_____no_output_____
###Markdown
Indexing
###Code
!kallisto index -i Homo_sapiens.GRCh38.cdna.all.idx -k 31 Homo_sapiens.GRCh38.cdna.all.fa.gz
###Output
_____no_output_____
###Markdown
Kallisto
###Code
!kallisto bus -i Homo_sapiens.GRCh38.cdna.all.idx -o output -x 10xv3 -t 8 \
data/bamtofastq_S1_L005_R1_001.fastq.gz data/bamtofastq_S1_L005_R2_001.fastq.gz \
data/bamtofastq_S1_L005_R1_002.fastq.gz data/bamtofastq_S1_L005_R2_002.fastq.gz \
data/bamtofastq_S1_L005_R1_003.fastq.gz data/bamtofastq_S1_L005_R2_003.fastq.gz \
data/bamtofastq_S1_L005_R1_004.fastq.gz data/bamtofastq_S1_L005_R2_004.fastq.gz \
data/bamtofastq_S1_L005_R1_005.fastq.gz data/bamtofastq_S1_L005_R2_005.fastq.gz \
data/bamtofastq_S1_L005_R1_006.fastq.gz data/bamtofastq_S1_L005_R2_006.fastq.gz \
data/bamtofastq_S1_L005_R1_007.fastq.gz data/bamtofastq_S1_L005_R2_007.fastq.gz
###Output
_____no_output_____
###Markdown
Bustools
###Code
cd /home/jupyter/output/
!mkdir genecount;
!mkdir tmp;
!mkdir eqcount
!bustools correct -w ../10xv3_whitelist.txt -o output.correct.bus output.bus
!bustools sort -t 8 -o output.correct.sort.bus output.correct.bus
!bustools text -o output.correct.sort.txt output.correct.sort.bus
!bustools count -o eqcount/output -g ../transcripts_to_genes.txt -e matrix.ec -t transcripts.txt output.correct.sort.bus
!bustools count -o genecount/output -g ../transcripts_to_genes.txt -e matrix.ec -t transcripts.txt --genecounts output.correct.sort.bus
!gzip output.bus
!gzip output.correct.bus
###Output
_____no_output_____
###Markdown
Copyting out results
###Code
cd /home/jupyter
!gsutil -m cp -r output gs://my-output-bucket/my-results
###Output
_____no_output_____
|
Foundations_of_Private_Computation/Federated_Learning/duet_basics/exercise/Exercise_Duet_Basics_Data_Scientist.ipynb
|
###Markdown
Part 1: Join the Duet Server the Data Owner connected to
###Code
duet = sy.join_duet(loopback=True)
###Output
_____no_output_____
###Markdown
Checkpoint 0 : Now STOP and run the Data Owner notebook until Checkpoint 1. Part 2: Search for Available Data
###Code
# The data scientist can check the list of searchable data in Data Owner's duet store
duet.store.pandas
# Data Scientist finds that there are Heights and Weights of a group of people. There are some analysis he/she can do with them together.
heights_ptr = duet.store[0]
weights_ptr = duet.store[1]
# heights_ptr is a reference to the height dataset remotely available on data owner's server
print(heights_ptr)
# weights_ptr is a reference to the weight dataset remotely available on data owner's server
print(weights_ptr)
###Output
_____no_output_____
###Markdown
Calculate BMI (Body Mass Index) and weight statusUsing the heights and weights pointers of the people of Group A, calculate their BMI and get a pointer to their individual BMI. From the BMI pointers, you can check if a person is normal-weight, overweight or obese, without knowing their actual heights and weights and even BMI values. BMI from 19 to 24 - Normal BMI from 25 to 29 - Overweight BMI from 30 to 39 - Obese BMI = [weight (kg) / (height (cm)^2)] x 10,000 Hint: run duet.torch and find the required operators One amazing thing about pointers is that from a pointer to a list of items, we can get the pointers to each item in the list. As example, here we have weights_ptr pointing to the weight-list, but from that we can also get the pointer to each weight and perform computation on each of them without even the knowing the value! Below code will show you how to access the pointers to each weight and height from the list pointer.
###Code
for i in range(6):
print("Pointer to Weight of person", i + 1, weights_ptr[i])
print("Pointer to Height of person", i + 1, heights_ptr[i])
def BMI_calculator(w_ptr, h_ptr):
bmi_ptr = 0
##TODO
"Write your code here for calculating bmi_ptr"
###
return bmi_ptr
def weight_status(w_ptr, h_ptr):
status = None
bmi_ptr = BMI_calculator(w_ptr, h_ptr)
##TODO
"""Write your code here.
Possible values for status:
Normal,
Overweight,
Obese,
Out of range
"""""
###
return status
for i in range(0, 6):
bmi_ptr = BMI_calculator(weights_ptr[i], heights_ptr[i])
statuses = []
for i in range(0, 6):
status = weight_status(weights_ptr[i], heights_ptr[i])
print("Weight of Person", i + 1, "is", status)
statuses.append(status)
assert statuses == ["Normal", "Overweight", "Obese", "Normal", "Overweight", "Normal"]
###Output
_____no_output_____
|
examples/PLSR/.ipynb_checkpoints/PLSR_on_NIR_and_octane_data-checkpoint.ipynb
|
###Markdown
Partial Least Squares Regression (PLSR) on Near Infrared Spectroscopy (NIR) data and octane data This notebook illustrates how to use the **hoggorm** package to carry out partial least squares regression (PLSR) on multivariate data. Furthermore, we will learn how to visualise the results of the PLSR using the **hoggormPlot** package. --- Import packages and prepare data First import **hoggorm** for analysis of the data and **hoggormPlot** for plotting of the analysis results. We'll also import **pandas** such that we can read the data into a data frame. **numpy** is needed for checking dimensions of the data.
###Code
import hoggorm as ho
import hoggormplot as hop
import pandas as pd
import numpy as np
###Output
_____no_output_____
###Markdown
Next, load the data that we are going to analyse using **hoggorm**. After the data has been loaded into the pandas data frame, we'll display it in the notebook.
###Code
# Load fluorescence data
X_df = pd.read_csv('gasoline_NIR.txt', header=None, sep='\s+')
X_df
# Load response data, that is octane measurements
y_df = pd.read_csv('gasoline_octane.txt', header=None, sep='\s+')
y_df
###Output
_____no_output_____
###Markdown
The ``nipalsPLS1`` class in hoggorm accepts only **numpy** arrays with numerical values and not pandas data frames. Therefore, the pandas data frames holding the imported data need to be "taken apart" into three parts: * two numpy array holding the numeric values* two Python list holding variable (column) names* two Python list holding object (row) names. The numpy arrays with values will be used as input for the ``nipalsPLS2`` class for analysis. The Python lists holding the variable and row names will be used later in the plotting function from the **hoggormPlot** package when visualising the results of the analysis. Below is the code needed to access both data, variable names and object names.
###Code
# Get the values from the data frame
X = X_df.values
y = y_df.values
# Get the variable or columns names
X_varNames = list(X_df.columns)
y_varNames = list(y_df.columns)
# Get the object or row names
X_objNames = list(X_df.index)
y_objNames = list(y_df.index)
###Output
_____no_output_____
###Markdown
--- Apply PLSR to our data Now, let's run PLSR on the data using the ``nipalsPLS1`` class, since we have a univariate response. The documentation provides a [description of the input parameters](https://hoggorm.readthedocs.io/en/latest/plsr.html). Using input paramter ``arrX`` and ``vecy`` we define which numpy array we would like to analyse. ``vecy`` is what typically is considered to be the response vector, while the measurements are typically defined as ``arrX``. By setting input parameter ``Xstand=False`` we make sure that the variables are only mean centered, not scaled to unit variance, if this is what you want. This is the default setting and actually doesn't need to expressed explicitly. Setting paramter ``cvType=["loo"]`` we make sure that we compute the PLS2 model using full cross validation. ``"loo"`` means "Leave One Out". By setting paramter ``numpComp=10`` we ask for four components to be computed.
###Code
model = ho.nipalsPLS1(arrX=X, Xstand=False,
vecy=y,
cvType=["loo"],
numComp=10)
###Output
loo
###Markdown
That's it, the PLS2 model has been computed. Now we would like to inspect the results by visualising them. We can do this using plotting functions of the separate [**hoggormPlot** package](https://hoggormplot.readthedocs.io/en/latest/). If we wish to plot the results for component 1 and component 2, we can do this by setting the input argument ``comp=[1, 2]``. The input argument ``plots=[1, 6]`` lets the user define which plots are to be plotted. If this list for example contains value ``1``, the function will generate the scores plot for the model. If the list contains value ``6`` the explained variance plot for y will be plotted. The hoggormPlot documentation provides a [description of input paramters](https://hoggormplot.readthedocs.io/en/latest/mainPlot.html).
###Code
hop.plot(model, comp=[1, 2],
plots=[1, 6],
objNames=X_objNames,
XvarNames=X_varNames,
YvarNames=y_varNames)
###Output
_____no_output_____
###Markdown
Plots can also be called separately.
###Code
# Plot cumulative explained variance (both calibrated and validated) using a specific function for that.
hop.explainedVariance(model)
# Plot cumulative validated explained variance in X.
hop.explainedVariance(model, which=['X'])
hop.scores(model)
# Plot X loadings in line plot
hop.loadings(model, weights=True, line=True)
# Plot regression coefficients
hop.coefficients(model, comp=[3])
###Output
_____no_output_____
###Markdown
--- Accessing numerical results Now that we have visualised the PLSR results, we may also want to access the numerical results. Below are some examples. For a complete list of accessible results, please see this part of the documentation.
###Code
# Get X scores and store in numpy array
X_scores = model.X_scores()
# Get scores and store in pandas dataframe with row and column names
X_scores_df = pd.DataFrame(model.X_scores())
X_scores_df.index = X_objNames
X_scores_df.columns = ['Comp {0}'.format(x+1) for x in range(model.X_scores().shape[1])]
X_scores_df
help(ho.nipalsPLS1.X_scores)
# Dimension of the X_scores
np.shape(model.X_scores())
###Output
_____no_output_____
###Markdown
We see that the numpy array holds the scores for all countries and OECD (35 in total) for four components as required when computing the PCA model.
###Code
# Get X loadings and store in numpy array
X_loadings = model.X_loadings()
# Get X loadings and store in pandas dataframe with row and column names
X_loadings_df = pd.DataFrame(model.X_loadings())
X_loadings_df.index = X_varNames
X_loadings_df.columns = ['Comp {0}'.format(x+1) for x in range(model.X_loadings().shape[1])]
X_loadings_df
help(ho.nipalsPLS1.X_loadings)
np.shape(model.X_loadings())
###Output
_____no_output_____
###Markdown
Here we see that the array holds the loadings for the 10 variables in the data across four components.
###Code
# Get Y loadings and store in numpy array
Y_loadings = model.Y_loadings()
# Get Y loadings and store in pandas dataframe with row and column names
Y_loadings_df = pd.DataFrame(model.Y_loadings())
Y_loadings_df.index = y_varNames
Y_loadings_df.columns = ['Comp {0}'.format(x+1) for x in range(model.Y_loadings().shape[1])]
Y_loadings_df
# Get X correlation loadings and store in numpy array
X_corrloadings = model.X_corrLoadings()
# Get X correlation loadings and store in pandas dataframe with row and column names
X_corrloadings_df = pd.DataFrame(model.X_corrLoadings())
X_corrloadings_df.index = X_varNames
X_corrloadings_df.columns = ['Comp {0}'.format(x+1) for x in range(model.X_corrLoadings().shape[1])]
X_corrloadings_df
help(ho.nipalsPLS1.X_corrLoadings)
# Get Y loadings and store in numpy array
Y_corrloadings = model.X_corrLoadings()
# Get Y loadings and store in pandas dataframe with row and column names
Y_corrloadings_df = pd.DataFrame(model.Y_corrLoadings())
Y_corrloadings_df.index = y_varNames
Y_corrloadings_df.columns = ['Comp {0}'.format(x+1) for x in range(model.Y_corrLoadings().shape[1])]
Y_corrloadings_df
help(ho.nipalsPLS1.Y_corrLoadings)
# Get calibrated explained variance of each component in X
X_calExplVar = model.X_calExplVar()
# Get calibrated explained variance in X and store in pandas dataframe with row and column names
X_calExplVar_df = pd.DataFrame(model.X_calExplVar())
X_calExplVar_df.columns = ['calibrated explained variance in X']
X_calExplVar_df.index = ['Comp {0}'.format(x+1) for x in range(model.X_loadings().shape[1])]
X_calExplVar_df
help(ho.nipalsPLS1.X_calExplVar)
# Get calibrated explained variance of each component in Y
Y_calExplVar = model.Y_calExplVar()
# Get calibrated explained variance in Y and store in pandas dataframe with row and column names
Y_calExplVar_df = pd.DataFrame(model.Y_calExplVar())
Y_calExplVar_df.columns = ['calibrated explained variance in Y']
Y_calExplVar_df.index = ['Comp {0}'.format(x+1) for x in range(model.Y_loadings().shape[1])]
Y_calExplVar_df
help(ho.nipalsPLS1.Y_calExplVar)
# Get cumulative calibrated explained variance in X
X_cumCalExplVar = model.X_cumCalExplVar()
# Get cumulative calibrated explained variance in X and store in pandas dataframe with row and column names
X_cumCalExplVar_df = pd.DataFrame(model.X_cumCalExplVar())
X_cumCalExplVar_df.columns = ['cumulative calibrated explained variance in X']
X_cumCalExplVar_df.index = ['Comp {0}'.format(x) for x in range(model.X_loadings().shape[1] + 1)]
X_cumCalExplVar_df
help(ho.nipalsPLS1.X_cumCalExplVar)
# Get cumulative calibrated explained variance in Y
Y_cumCalExplVar = model.Y_cumCalExplVar()
# Get cumulative calibrated explained variance in Y and store in pandas dataframe with row and column names
Y_cumCalExplVar_df = pd.DataFrame(model.Y_cumCalExplVar())
Y_cumCalExplVar_df.columns = ['cumulative calibrated explained variance in Y']
Y_cumCalExplVar_df.index = ['Comp {0}'.format(x) for x in range(model.Y_loadings().shape[1] + 1)]
Y_cumCalExplVar_df
help(ho.nipalsPLS1.Y_cumCalExplVar)
# Get cumulative calibrated explained variance for each variable in X
X_cumCalExplVar_ind = model.X_cumCalExplVar_indVar()
# Get cumulative calibrated explained variance for each variable in X and store in pandas dataframe with row and column names
X_cumCalExplVar_ind_df = pd.DataFrame(model.X_cumCalExplVar_indVar())
X_cumCalExplVar_ind_df.columns = X_varNames
X_cumCalExplVar_ind_df.index = ['Comp {0}'.format(x) for x in range(model.X_loadings().shape[1] + 1)]
X_cumCalExplVar_ind_df
help(ho.nipalsPLS1.X_cumCalExplVar_indVar)
# Get calibrated predicted Y for a given number of components
# Predicted Y from calibration using 1 component
Y_from_1_component = model.Y_predCal()[1]
# Predicted Y from calibration using 1 component stored in pandas data frame with row and columns names
Y_from_1_component_df = pd.DataFrame(model.Y_predCal()[1])
Y_from_1_component_df.index = y_objNames
Y_from_1_component_df.columns = y_varNames
Y_from_1_component_df
# Get calibrated predicted Y for a given number of components
# Predicted Y from calibration using 4 component
Y_from_4_component = model.Y_predCal()[4]
# Predicted Y from calibration using 1 component stored in pandas data frame with row and columns names
Y_from_4_component_df = pd.DataFrame(model.Y_predCal()[4])
Y_from_4_component_df.index = y_objNames
Y_from_4_component_df.columns = y_varNames
Y_from_4_component_df
help(ho.nipalsPLS1.X_predCal)
# Get validated explained variance of each component X
X_valExplVar = model.X_valExplVar()
# Get calibrated explained variance in X and store in pandas dataframe with row and column names
X_valExplVar_df = pd.DataFrame(model.X_valExplVar())
X_valExplVar_df.columns = ['validated explained variance in X']
X_valExplVar_df.index = ['Comp {0}'.format(x+1) for x in range(model.X_loadings().shape[1])]
X_valExplVar_df
help(ho.nipalsPLS1.X_valExplVar)
# Get validated explained variance of each component Y
Y_valExplVar = model.Y_valExplVar()
# Get calibrated explained variance in X and store in pandas dataframe with row and column names
Y_valExplVar_df = pd.DataFrame(model.Y_valExplVar())
Y_valExplVar_df.columns = ['validated explained variance in Y']
Y_valExplVar_df.index = ['Comp {0}'.format(x+1) for x in range(model.Y_loadings().shape[1])]
Y_valExplVar_df
help(ho.nipalsPLS1.Y_valExplVar)
# Get cumulative validated explained variance in X
X_cumValExplVar = model.X_cumValExplVar()
# Get cumulative validated explained variance in X and store in pandas dataframe with row and column names
X_cumValExplVar_df = pd.DataFrame(model.X_cumValExplVar())
X_cumValExplVar_df.columns = ['cumulative validated explained variance in X']
X_cumValExplVar_df.index = ['Comp {0}'.format(x) for x in range(model.X_loadings().shape[1] + 1)]
X_cumValExplVar_df
help(ho.nipalsPLS1.X_cumValExplVar)
# Get cumulative validated explained variance in Y
Y_cumValExplVar = model.Y_cumValExplVar()
# Get cumulative validated explained variance in Y and store in pandas dataframe with row and column names
Y_cumValExplVar_df = pd.DataFrame(model.Y_cumValExplVar())
Y_cumValExplVar_df.columns = ['cumulative validated explained variance in Y']
Y_cumValExplVar_df.index = ['Comp {0}'.format(x) for x in range(model.Y_loadings().shape[1] + 1)]
Y_cumValExplVar_df
help(ho.nipalsPLS1.Y_cumValExplVar)
help(ho.nipalsPLS1.X_cumValExplVar_indVar)
# Get validated predicted Y for a given number of components
# Predicted Y from validation using 1 component
Y_from_1_component_val = model.Y_predVal()[1]
# Predicted Y from calibration using 1 component stored in pandas data frame with row and columns names
Y_from_1_component_val_df = pd.DataFrame(model.Y_predVal()[1])
Y_from_1_component_val_df.index = y_objNames
Y_from_1_component_val_df.columns = y_varNames
Y_from_1_component_val_df
# Get validated predicted Y for a given number of components
# Predicted Y from validation using 3 components
Y_from_3_component_val = model.Y_predVal()[3]
# Predicted Y from calibration using 3 components stored in pandas data frame with row and columns names
Y_from_3_component_val_df = pd.DataFrame(model.Y_predVal()[3])
Y_from_3_component_val_df.index = y_objNames
Y_from_3_component_val_df.columns = y_varNames
Y_from_3_component_val_df
help(ho.nipalsPLS1.Y_predVal)
# Get predicted scores for new measurements (objects) of X
# First pretend that we acquired new X data by using part of the existing data and overlaying some noise
import numpy.random as npr
new_X = X[0:4, :] + npr.rand(4, np.shape(X)[1])
np.shape(X)
# Now insert the new data into the existing model and compute scores for two components (numComp=2)
pred_X_scores = model.X_scores_predict(new_X, numComp=2)
# Same as above, but results stored in a pandas dataframe with row names and column names
pred_X_scores_df = pd.DataFrame(model.X_scores_predict(new_X, numComp=2))
pred_X_scores_df.columns = ['Comp {0}'.format(x+1) for x in range(2)]
pred_X_scores_df.index = ['new object {0}'.format(x+1) for x in range(np.shape(new_X)[0])]
pred_X_scores_df
help(ho.nipalsPLS1.X_scores_predict)
# Predict Y from new X data
pred_Y = model.Y_predict(new_X, numComp=2)
# Predict Y from nex X data and store results in a pandas dataframe with row names and column names
pred_Y_df = pd.DataFrame(model.Y_predict(new_X, numComp=2))
pred_Y_df.columns = y_varNames
pred_Y_df.index = ['new object {0}'.format(x+1) for x in range(np.shape(new_X)[0])]
pred_Y_df
###Output
_____no_output_____
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.