question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
network-delay-time
|
Dijkstra's algorithm solution explanation (with Python 3)
|
dijkstras-algorithm-solution-explanation-0ld1
|
Since the graph of network delay times is a weighted, connected graph (if the graph isn\'t connected, we can return -1) with non-negative weights, we can find t
|
enmingliu
|
NORMAL
|
2020-05-17T04:19:08.330246+00:00
|
2020-05-17T04:19:08.330282+00:00
| 13,183
| false
|
Since the graph of network delay times is a weighted, connected graph (if the graph isn\'t connected, we can return -1) with non-negative weights, we can find the shortest path from root node K into any other node using Dijkstra\'s algorithm. If we want to find how long it will take for all nodes to receive the signal, we need to find the maximum of the shortest paths from node K to any other node. \n\nWe can do this by running dijkstra\'s algorithm starting with node K, and shortest path length to node K, 0. We can keep track of the lengths of the shortest paths from K to every other node in a set S, and if the length of S is equal to N, we know that the graph is connected (if not, return -1). We can then return the maximum of the shortest path lengths in S to get how long it will take for all nodes to receive the signal.\n\n```\ndef networkDelayTime(self, times: List[List[int]], N: int, K: int) -> int:\n graph = collections.defaultdict(list)\n for (u, v, w) in times:\n graph[u].append((v, w))\n \n priority_queue = [(0, K)]\n shortest_path = {}\n while priority_queue:\n w, v = heapq.heappop(priority_queue)\n if v not in shortest_path:\n shortest_path[v] = w\n for v_i, w_i in graph[v]:\n heapq.heappush(priority_queue, (w + w_i, v_i))\n \n if len(shortest_path) == N:\n return max(shortest_path.values())\n else:\n return -1\n```\n
| 33
| 0
|
['Queue', 'Heap (Priority Queue)', 'Ordered Set', 'Python', 'Python3']
| 7
|
network-delay-time
|
Clean JavaScript Bellman-Ford solution
|
clean-javascript-bellman-ford-solution-b-0s9d
|
Introduction to Bellman-Ford https://www.youtube.com/watch?v=obWXjtg0L64\n\n\nconst networkDelayTime = (times, N, K) => {\n const time = Array(N + 1).fill(Infi
|
hongbo-miao
|
NORMAL
|
2019-10-28T06:44:12.569384+00:00
|
2020-09-02T15:48:27.248283+00:00
| 2,746
| false
|
Introduction to Bellman-Ford https://www.youtube.com/watch?v=obWXjtg0L64\n\n```\nconst networkDelayTime = (times, N, K) => {\n const time = Array(N + 1).fill(Infinity);\n time[K] = 0;\n for (let i = 0; i < N; i++) {\n for (const [u, v, t] of times) {\n if (time[u] === Infinity) continue;\n if (time[v] > time[u] + t) {\n time[v] = time[u] + t;\n }\n }\n }\n\n let res = 0;\n for (let i = 1; i <= N; i++) {\n res = Math.max(res, time[i]);\n }\n return res === Infinity ? -1 : res;\n};\n```\n
| 29
| 0
|
['JavaScript']
| 3
|
network-delay-time
|
c++ dijkstra with priority queue
|
c-dijkstra-with-priority-queue-by-kelvin-qgft
|
\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int N, int K) {\n // build graph \n vector<vector<pair<int, int>
|
kelvinshcn
|
NORMAL
|
2019-07-21T18:16:11.913404+00:00
|
2019-07-21T18:16:11.913436+00:00
| 2,359
| false
|
```\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int N, int K) {\n // build graph \n vector<vector<pair<int, int> > > graph(N+1);\n for (auto edge : times) {\n int fr_node = edge[0];\n int to_node = edge[1];\n int cost = edge[2];\n graph[fr_node].push_back(make_pair(cost, to_node)); \n }\n vector<int> dist(N+1, INT_MAX);\n priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>>> pq;\n dist[K] = 0;\n pq.push(make_pair(0, K)); \n while (!pq.empty()) {\n pair<int,int> x = pq.top();\n pq.pop();\n for (auto neighbor : graph[x.second]) {\n int ar = dist[x.second] + neighbor.first;\n if (ar < dist[neighbor.second]) {\n dist[neighbor.second] = ar;\n pq.push(make_pair(ar, neighbor.second));\n }\n } \n } \n int max_time = INT_MIN;\n for (int i = 1; i < dist.size(); ++i) {\n if (max_time < dist[i]) {\n max_time = dist[i];\n }\n }\n \n return max_time == INT_MAX? -1 : max_time;\n }\n};\n```
| 24
| 0
|
['C', 'Heap (Priority Queue)']
| 2
|
network-delay-time
|
Shortest Path Faster Algorithm (SPFA) - Java 26ms beats 86.85%
|
shortest-path-faster-algorithm-spfa-java-e50b
|
SPFA is an improvement on top of Bellman-Ford, and prabably easier to understand than Dijkstra. It is popular with students who take part in NOIP and ACM-ICPC.
|
xiong6
|
NORMAL
|
2019-03-04T00:59:59.481689+00:00
|
2019-03-04T00:59:59.481733+00:00
| 2,467
| false
|
SPFA is an improvement on top of Bellman-Ford, and prabably easier to understand than Dijkstra. It is popular with students who take part in NOIP and ACM-ICPC. The key points are\n1. We use a FIFO queue to store vertices that are about to be relaxed.\n2. Vertices should be reinserted into the queue whenever its distance is updated.\n\nAs claimed in wikipedia https://en.wikipedia.org/wiki/Shortest_Path_Faster_Algorithm the worst case comlexity is the same as Bellman-Ford, but the average running time is O(|E|) .\n```\n public int networkDelayTime(int[][] times, int N, int K) {\n // construct the graph\n Map<Integer, Map<Integer, Integer>> costs = new HashMap<>();\n for (int[] e: times) {\n costs.putIfAbsent(e[0], new HashMap<Integer, Integer>());\n costs.get(e[0]).put(e[1], e[2]);\n }\n \n int[] distances = new int[N+1];\n Arrays.fill(distances, Integer.MAX_VALUE);\n distances[K] = 0;\n \n Queue<Integer> que = new LinkedList<>();\n boolean[] inQue = new boolean[N+1]; // indicate whether the element is inside the queue or not\n que.offer(K);\n while (!que.isEmpty()) {\n int node = que.poll();\n inQue[node] = false;\n if (!costs.containsKey(node)) continue;\n for (int next: costs.get(node).keySet()) {\n int d = costs.get(node).get(next);\n if (distances[next] > distances[node] + d) {\n distances[next] = distances[node] + d;\n if (!inQue[next]) {\n que.offer(next);\n inQue[next] = true;\n }\n }\n }\n }\n \n int result = 0;\n for (int i = 1; i <= N; i++) {\n result = Math.max(result, distances[i]); \n }\n \n return result == Integer.MAX_VALUE ? -1 : result;\n }\n```
| 22
| 0
|
[]
| 2
|
network-delay-time
|
[Java] | 🔥 100% | Dijkstra | Bellman Ford | SPFA | Floyd-Warshall
|
java-100-dijkstra-bellman-ford-spfa-floy-wwj8
|
Dijkstra\n- TC: O(E + Elog(E))\n- SC: O(V+E)\n- 8 ms\n## Two different ways\njava []\nclass Solution {\n record Node(int i, int t) {}\n public int network
|
byegates
|
NORMAL
|
2023-01-16T07:22:17.948276+00:00
|
2023-03-05T07:04:17.304909+00:00
| 4,259
| false
|
# Dijkstra\n- TC: O(E + Elog(E))\n- SC: O(V+E)\n- [8 ms](https://leetcode.com/problems/network-delay-time/submissions/879004707/)\n## Two different ways\n```java []\nclass Solution {\n record Node(int i, int t) {}\n public int networkDelayTime(int[][] times, int n, int k) {\n // create graph\n List<Node>[] g = new List[n];\n for (int i = 0; i < n; i++) g[i] = new ArrayList<>();\n for (var t : times) g[t[0]-1].add(new Node(t[1]-1, t[2]));\n\n int[] time = new int[n];\n Queue<Integer> q = new PriorityQueue<>((u, v) -> time[u]-time[v]);\n Arrays.fill(time, Integer.MAX_VALUE);\n time[--k] = 0;\n q.offer(k);\n\n while (!q.isEmpty()) {\n var cur = q.poll();\n for (var next : g[cur]) {\n int t2 = time[cur] + next.t;\n if (t2 >= time[next.i]) continue;\n time[next.i] = t2;\n q.offer(next.i);\n }\n }\n\n int res = time[0];\n for (var t : time) if (t == Integer.MAX_VALUE) return -1; else if (t > res) res = t;\n return res;\n }\n}\n```\n```java []\nclass Solution {\n record Node (int i, int t) {}\n public int networkDelayTime(int[][] times, int n, int k) {\n // create graph\n List<Node>[] g = new List[n];\n for (int i = 0; i < n; i++) g[i] = new ArrayList<>();\n for (var t : times) g[t[0]-1].add(new Node(t[1]-1, t[2]));\n\n Queue<Node> q = new PriorityQueue<>((a, b) -> a.t - b.t);\n q.offer(new Node(--k, 0));\n int[] time = new int[n];\n Arrays.fill(time, Integer.MAX_VALUE);\n time[k] = 0;\n\n while (!q.isEmpty()) {\n var cur = q.poll();\n for (var next : g[cur.i]) {\n int t2 = cur.t + next.t;\n if (t2 >= time[next.i]) continue;\n time[next.i] = t2;\n q.offer(new Node(next.i, t2));\n }\n }\n\n int res = time[0];\n for (var t : time) if (t == Integer.MAX_VALUE) return -1; else if (t > res) res = t;\n return res;\n }\n}\n```\n\n# Bellman Ford\n- TC: O(V*E) ==> n^3 (best O(E) => O(n^2))\n- SC: O(N)\n- [2ms with early termination 100%](https://leetcode.com/problems/network-delay-time/submissions/879012500/)\n- [13 ms without early termination](https://leetcode.com/problems/network-delay-time/submissions/879011956/)\n# Code\n```java\nclass Solution {\n private final static int MAX = 1_000_000_000;\n public int networkDelayTime(int[][] times, int n, int k) {\n int[] time = new int[n+1];\n Arrays.fill(time, MAX);\n time[k] = time[0] = 0; // time[0] is garbage\n\n for (int i = 1; i < n; i++) { // for n nodes, we iterate max n-1 times\n boolean canRelax = false;\n for (var e : times) if (time[e[0]] + e[2] < time[e[1]]) {\n time[e[1]] = time[e[0]] + e[2];\n canRelax = true;\n }\n if (!canRelax) break;\n }\n\n int res = time[1];\n for (var t : time) if (t == MAX) return -1; else if (t > res) res = t;\n return res;\n }\n}\n```\n# SPFA\n- TC: Worst:\xA0O(V*E) same as\xA0Bellman-Ford. Avg:\xA0O(E)\n- SC: O(V)\n- [6ms](https://leetcode.com/problems/network-delay-time/submissions/879056523/)\n- [wiki SFPA](https://en.wikipedia.org/wiki/Shortest_Path_Faster_Algorithm)\n# Code\n```java\nclass Solution {\n record Node (int i, int t) {} \n public int networkDelayTime(int[][] times, int n, int k) {\n // create graph\n List<Node>[] g = new List[n];\n for (int i = 0; i < n; i++) g[i] = new ArrayList<>();\n for (var t : times) g[t[0]-1].add(new Node(t[1]-1, t[2]));\n\n int[] time = new int[n];\n Arrays.fill(time, Integer.MAX_VALUE);\n time[--k] = 0;\n boolean[] inQ = new boolean[n];\n Queue<Integer> q = new ArrayDeque<>();\n q.offer(k);\n\n while (!q.isEmpty()) {\n int cur = q.poll();\n inQ[cur] = false;\n for (var next : g[cur]) {\n if (time[cur] + next.t < time[next.i]) {\n time[next.i] = time[cur] + next.t;\n if (!inQ[next.i]) {\n q.offer(next.i);\n inQ[next.i] = true;\n }\n }\n }\n }\n\n int res = time[0];\n for (var t : time) if (t == Integer.MAX_VALUE) return -1; else if (t > res) res = t;\n return res;\n }\n}\n```\n# Floyd-Warshall\n- TC: O(V^3)\n- SC: O(V^2)\n- [10ms](https://leetcode.com/problems/network-delay-time/submissions/879057269/)\n\n# Code\n```java\nclass Solution {\n private final static int MAX = 1_000_000_000; // for convenience\n public int networkDelayTime(int[][] times, int n, int k) {\n int[][] time = new int[n][n]; // we dont use 0\n for (var t : time) Arrays.fill(t, MAX);\n for (int i = 0; i < n; i++) time[i][i] = 0;\n for (var t : times) time[t[0]-1][t[1]-1] = t[2]; // fill in the init matrix\n\n // m as middle, intermediate\n for (int m = 0; m < n; m++) for (int i = 0; i < n; i++) for (int j = 0; j < n; j++)\n if (time[i][m] + time[m][j] < time[i][j]) time[i][j] = time[i][m] + time[m][j];\n\n int res = time[--k][0];\n for (var t : time[k]) if (t == MAX) return -1; else if (t > res) res = t;\n return res;\n }\n}\n```
| 20
| 1
|
['Dynamic Programming', 'Java']
| 3
|
network-delay-time
|
DFS / BFS / Dijkstra / Bellman Ford / Floyd Warshall easy to understand [Python]
|
dfs-bfs-dijkstra-bellman-ford-floyd-wars-54ca
|
```\nclass Solution:\n \n def BellmanFord(self, times, N, K):\n \n # Bellman Ford\n cost = {i:float(\'inf\') for i in range(1, N+1)}\
|
prabhjyot28
|
NORMAL
|
2020-06-24T16:07:49.908541+00:00
|
2020-06-24T16:24:18.531546+00:00
| 2,118
| false
|
```\nclass Solution:\n \n def BellmanFord(self, times, N, K):\n \n # Bellman Ford\n cost = {i:float(\'inf\') for i in range(1, N+1)}\n cost[K] = 0\n for i in range(N-1):\n update = False\n for u, v, c in times:\n if cost[u]+c<cost[v]:\n update = True\n cost[v] = cost[u]+c\n if not update:\n break\n \n ans = max(cost.values())\n return ans if ans!=float(\'inf\') else -1\n \n \n \n \n def Dijkstra(self, times, N, K):\n g = collections.defaultdict(list) # [(node, cost)]\n for u, v, c in times:\n g[u].append((v, c))\n \n cost = {i:float(\'inf\') for i in range(1, N+1)}\n cost[K] = 0\n from queue import PriorityQueue\n pq = PriorityQueue()\n pq.put((0, K))\n \n while not pq.empty():\n curr_cost, curr_node = pq.get()\n \n for nei, c in g[curr_node]:\n if curr_cost+c<cost[nei]:\n cost[nei] = curr_cost+c\n pq.put((cost[nei], nei))\n \n ans = max(cost.values())\n return ans if ans!=float(\'inf\') else -1\n \n \n \n \n \n def DFS(self, times, n, k):\n cost = {i:float(\'inf\') for i in range(1, N+1)}\n g = collections.defaultdict(list)\n for u, v, c in times:\n g[u].append((v, c))\n \n def DFS(curr, curr_cost):\n if curr_cost<cost[curr]:\n cost[curr] = curr_cost\n for nei, c in g[curr]:\n DFS(nei, curr_cost+c)\n \n DFS(K, 0)\n ans = max(cost.values())\n return ans if ans!=float(\'inf\') else -1\n \n \n \n \n \n \n \n \n def BFS(self, times, N, K):\n g = collections.defaultdict(list)\n for u, v, c in times:\n g[u].append((v, c))\n \n cost = {i:float(\'inf\') for i in range(1, N+1)}\n cost[K] = 0\n curr = collections.deque()\n curr.append((K, 0))\n \n while curr:\n curr_node, curr_cost = curr.popleft()\n for nei, c in g[curr_node]:\n if curr_cost+c < cost[nei]:\n cost[nei] = curr_cost+c\n curr.append((nei, curr_cost+c))\n \n ans = max(cost.values())\n return ans if ans!=float(\'inf\') else -1\n\n def FloydWarshall(self, times, N, K):\n # APSP\n cost = {}\n for i in range(1, N+1):\n for j in range(1, N+1):\n if i==j:\n cost[(i, j)] = 0\n else:\n cost[(i, j)] = float(\'inf\')\n \n for u,v,c in times:\n cost[(u, v)] = c\n \n for k in range(1, N+1):\n for i in range(1, N+1):\n for j in range(1, N+1):\n cost[(i, j)] = min(cost[(i, j)], cost[(i, k)]+cost[(k, j)])\n \n \n ans = float(\'-inf\')\n for i in range(1, N+1):\n ans = max(ans, cost[(K, i)])\n\n return ans if ans!=float(\'inf\') else -1\n\n \n
| 19
| 0
|
['Depth-First Search', 'Breadth-First Search', 'Python3']
| 2
|
network-delay-time
|
JAVA Djikstra's Solution
|
java-djikstras-solution-by-wssx12138-n61i
|
Someone would use Queue instead of PriorityQueue.\n\n public int networkDelayTime(int[][] times, int N, int K) {\n if (times == null || times.length =
|
wssx12138
|
NORMAL
|
2017-12-13T02:53:07.755000+00:00
|
2018-10-21T15:27:18.475589+00:00
| 3,919
| false
|
Someone would use Queue instead of PriorityQueue.\n```\n public int networkDelayTime(int[][] times, int N, int K) {\n if (times == null || times.length == 0 || times[0].length == 0) {\n return -1;\n }\n int[][] grid = new int[N + 1][N + 1];\n for (int[] arr : grid) {\n Arrays.fill(arr, Integer.MAX_VALUE);\n }\n for (int[] curEdge : times) {\n grid[curEdge[0]][curEdge[1]] = curEdge[2];\n }\n\n int[] res = new int[N + 1];\n Arrays.fill(res, Integer.MAX_VALUE);\n PriorityQueue<Integer> minHeap = new PriorityQueue<Integer>(N, new Comparator<Integer>() {\n @Override\n public int compare(Integer c1, Integer c2) {\n return res[c1] - res[c2];\n }\n });\n minHeap.offer(K);\n res[K] = 0;\n while (!minHeap.isEmpty()) {\n Integer start = minHeap.poll();\n for (int i = 1; i <= N; i++) {\n int curWeight = grid[start][i];\n if (curWeight != Integer.MAX_VALUE && res[i] > res[start] + curWeight) {\n res[i] = res[start] + curWeight;\n minHeap.offer(i);\n }\n }\n }\n int count = 0;\n for (int i = 1; i <= N; i++) {\n if (res[i] == Integer.MAX_VALUE) {\n return -1;\n }\n count = Math.max(count, res[i]);\n }\n return count;\n }\n```
| 19
| 4
|
[]
| 4
|
network-delay-time
|
Java || best question to understand Dijkastras
|
java-best-question-to-understand-dijkast-o6ca
|
\nclass Solution {\n public int networkDelayTime(int[][] times, int n, int K) {\n int[][] graph = new int[n][n];\n for(int i = 0; i < n ; i++)
|
achyutav
|
NORMAL
|
2022-05-14T01:17:44.392245+00:00
|
2022-05-18T09:52:48.096798+00:00
| 3,736
| false
|
```\nclass Solution {\n public int networkDelayTime(int[][] times, int n, int K) {\n int[][] graph = new int[n][n];\n for(int i = 0; i < n ; i++) Arrays.fill(graph[i], Integer.MAX_VALUE);\n for( int[] rows : times) graph[rows[0] - 1][rows[1] - 1] = rows[2]; \n \n int[] distance = new int[n];\n Arrays.fill(distance, Integer.MAX_VALUE);\n distance[K - 1] = 0;\n \n boolean[] visited = new boolean[n];\n for(int i = 0; i < n ; i++){\n int v = minIndex(distance, visited);\n if(v == -1)continue;\n visited[v] = true;\n for(int j = 0; j < n; j++){\n if(graph[v][j] != Integer.MAX_VALUE){\n int newDist = graph[v][j] + distance[v];\n if(newDist < distance[j]) distance[j] = newDist;\n }\n }\n }\n int result = 0;\n for(int dist : distance){\n if(dist == Integer.MAX_VALUE) return -1;\n result = Math.max(result, dist);\n }\n return result;\n }\n\t\n private int minIndex(int[] distance, boolean[] visited){\n int min = Integer.MAX_VALUE, minIndex = -1;\n for(int i = 0; i < distance.length; i++){\n if(!visited[i] && distance[i] < min){\n min = distance[i];\n minIndex = i;\n }\n }\n return minIndex;\n }\n}\n```
| 16
| 0
|
['Java']
| 3
|
network-delay-time
|
Straightforward Python Dijkstra's
|
straightforward-python-dijkstras-by-yang-p2fw
|
Nothing fancy, just apply Dijkstra's algorithm to the input. The only pitfall is that you have to check that all nodes are reachable from source node, else retu
|
yangshun
|
NORMAL
|
2017-12-10T06:37:18.770000+00:00
|
2022-03-18T01:01:22.136449+00:00
| 5,046
| false
|
Nothing fancy, just apply Dijkstra's algorithm to the input. The only pitfall is that you have to check that all nodes are reachable from source node, else return -1.\n\n*- Yangshun*\n\n```\nclass Solution(object):\n def networkDelayTime(self, times, N, K):\n from collections import defaultdict\n nodes = defaultdict(dict)\n Q = set(range(N))\n for u, v, w in times:\n nodes[u - 1][v - 1] = w\n dist = [float('inf')] * N\n dist[K - 1] = 0\n while len(Q):\n u = None\n for node in Q:\n if u == None or dist[node] < dist[u]:\n u = node\n Q.remove(u)\n for v in nodes[u]:\n alt = dist[u] + nodes[u][v]\n if alt < dist[v]:\n dist[v] = alt\n d = max(dist)\n return -1 if d == float('inf') else d\n```
| 16
| 3
|
[]
| 3
|
network-delay-time
|
Simple Java Solution using BFS (similar to dijkstra's shortest path algorithm) with explanation
|
simple-java-solution-using-bfs-similar-t-dffd
|
The idea is to find the time to reach every other node from given node K\nThen, to check if all nodes can be reached and if it can be reached then return the ti
|
ashish53v
|
NORMAL
|
2017-12-10T04:02:52.038000+00:00
|
2018-09-26T05:34:41.934968+00:00
| 6,912
| false
|
The idea is to find the time to reach every other node from given node K\nThen, to check if all nodes can be reached and if it can be reached then return the time taken to reach the farthest node (node which take longest to get the signal).\nAs the signal traverses concurrently to all nodes, we have to find the maximum time it takes to reach a node among all nodes from given node K.\nIf any single node takes Integer.MAX_Value, then return -1, as not all nodes can be reached\n\nadd the index of all the nodes which can be reached from a node to a list and store this list in a hashmap\n\nthen its similar to dijkstra's shortest path algorithm except that I am not using Priority Queue to get the minimum distance node. See comments.\n```\nclass Solution {\n public int networkDelayTime(int[][] times, int N, int K) {\n int r = times.length, max = Integer.MAX_VALUE;\n \n Map<Integer,List<Integer>> map = new HashMap<>();\n for(int i=0;i<r;i++){\n int[] nums = times[i];\n int u = nums[0];\n int v = nums[1];\n List<Integer> list = map.getOrDefault(u,new ArrayList<>());\n \n list.add(i);\n \n map.put(u,list);\n }\n if(map.get(K) == null){\n return -1;// no immediate neighbor of node K, so return -1\n }\n int[] dist = new int[N+1];//dist[i] is the time taken to reach node i from node k\n Arrays.fill(dist,max);\n \n dist[K] = 0;\n Queue<Integer> queue = new LinkedList<>();\n \n queue.add(K);\n \n while(!queue.isEmpty()){\n int u = queue.poll();\n int t = dist[u];\n List<Integer> list = map.get(u);// get the indices of all the neighbors of node u\n if(list == null)\n continue;\n \n for(int n:list){\n int v = times[n][1];\n int time = times[n][2];// time taken to reach from u to v\n if(dist[v] > t + time){// if time taken to reach v from k is greater than time taken to reach from k to u + time taken to reach from u to v, then update dist[v]\n dist[v] = t + time;\n queue.add(v);// as we have found shorter distance to node v, explore all neighbors of v\n } \n }\n }\n \n int res = -1;\n \n for(int i=1;i<=N;i++){\n int d = dist[i];\n if(d == max){// if d is max, it means node i can not be reached from K, so return -1\n return -1;\n }\n res = d > res ? d : res;\n }\n \n return res;\n }\n}\n```\n\nNote: I have updated the solution description and solution. Yes, my solution is not exactly dijkstra, but it was inspired by it and I thought it was very similar except that it is not very similar.
| 16
| 4
|
[]
| 9
|
network-delay-time
|
Simple Dijkstra's Solution in Java along with great intuition using Priority Queue
|
simple-dijkstras-solution-in-java-along-oai2g
|
Intuition\nUsing the simple generic Dijkstras algorithm with little tweak to solve the problem.\nData Structures to be used here is:\n1. Array: to store distanc
|
sarja830
|
NORMAL
|
2022-11-09T14:44:53.191414+00:00
|
2024-05-02T12:08:41.347082+00:00
| 1,728
| false
|
# Intuition\nUsing the simple generic Dijkstras algorithm with little tweak to solve the problem.\nData Structures to be used here is:\n1. **Array**: to store distance from source\n*In the code*: d - to store distance of each vertex from source node.\nInitially make it infinity for all the vertex except source.\nFor source set it to 0 since from source we can reach the source in 0.\n\n2. **HashMap**: to store the graph in the form of adjacency list(adjacent vertex connected from a vertex) for fast traversal\n*In the code*: map - convert the given times[i] to this form for fast traversal\nKey - vertex\nValue - List of integer array which contains the adjacent vertex and their distances to that particular vertex in the format source,target and the weight (times[i] = (ui, vi, wi)).\n\n3. **Priority Queue** to get the shortest distance vertex from source in O(1) time\nIt contains an integer array which contains the vertex and the distance from source of that vertex.\nPriority is determined based on distance from the source.\nSyntax in java: PriorityQueue<int[]> pq = new PriorityQueue<>((a,b)->a[1]-b[1]);\n\n4. **Set**: To keep track of the processed nodes\nIntially empty.\nfill it one by one by the nodes that are getting processed.\n\n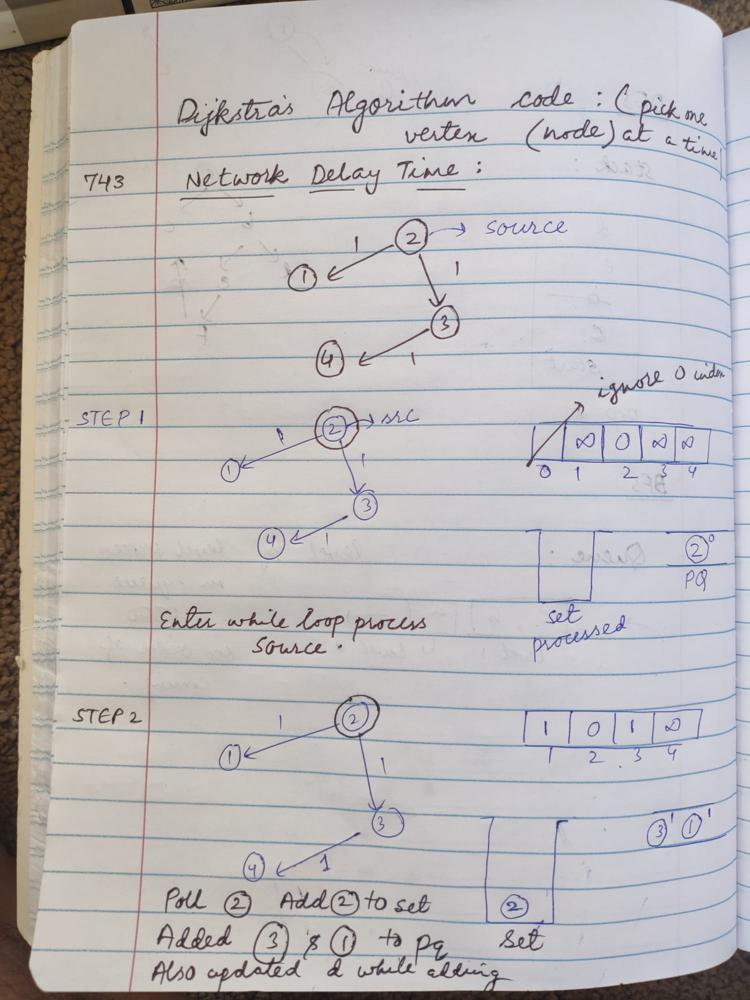\n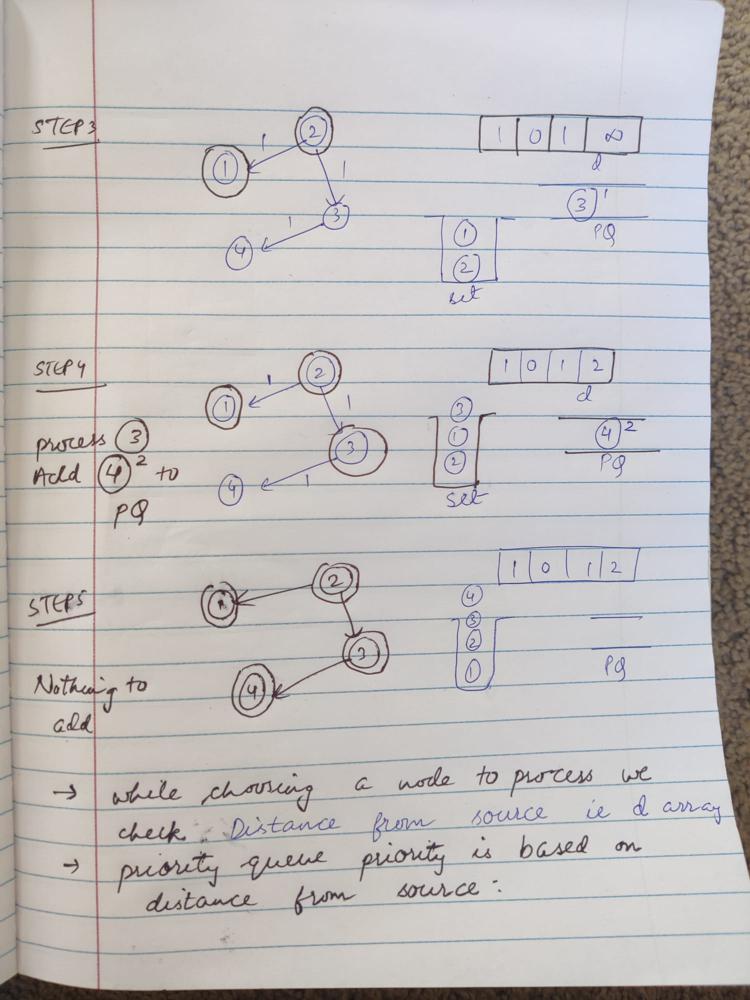\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Pick a vertex everytime starting from the source.\n2. update the distance of its adjacent vertices from source which is updating the d array which stores the distance of the source.\n3. As soon as you relax the adjacent edges add it to the priority queue which will pick the vertex with minimum distance from source for the next iteration \nA vertex is processed when its adjacent vertices are relaxed.\n\nRepeat:\n - Pick a node everytime based on shortest distance from source\n - relax adjacent vertices\nuntil all vertices are processed.\n\nRealxing the Vertices:\n Picked a vertex u;\n Relaxing vertex v which is adjacent to vertex u using the logic:\n if(d[v]>d[u]+distance)\n d[v]=d[u]+distance;\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(V+E(Log(V)))\n V vertices in the graph each need to be traversed. Logn is the insertion time for each vertices in the heap (priority queue) here n is V;\nif a vertex is added twice in priority queue the maximum number of time it can be added is the number of edges. hence ElogV.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int networkDelayTime(int[][] times, int n, int source) {\n\n HashMap<Integer,List<int[]>> map = new HashMap();\n\n for(int[] time:times)\n {\n if(!map.containsKey(time[0]))\n {\n List<int[]> l = new LinkedList();\n l.add(time);\n map.put(time[0],l);\n }\n else\n {\n List<int[]> lk =map.get(time[0]);\n lk.add(time);\n map.put(time[0],lk);\n }\n }\n\n\n // intialize the distance array and fill it as infinity\n int[] d = new int[n+1];\n Arrays.fill(d,10000);\n d[source]=0;\n\n// priority based on distance in pq int[]{node , distance_from_source}\n// priority based on distance\n PriorityQueue<int[]> pq = new PriorityQueue<>((a,b)->a[1]-b[1]);\n pq.add(new int[]{source,d[source]});\n\n HashSet<Integer> processed = new HashSet();\n\n\n while(pq.size()!=0)\n {\n int[] current =pq.poll();\n int u =current[0];\n// int distance = current[1];\n\n if(processed.contains(u)) continue;\n\n processed.add(u);\n\n// update all the distance of adjacent nodes from the selected node\n// relaxing step\n if(map.containsKey(u))\n for(int[] nodes:map.get(u))\n {\n int v =nodes[1];\n int distance=nodes[2];\n if(d[v]>d[u]+distance)\n d[v]=d[u]+distance;\n pq.add(new int[]{v,d[v]});\n }\n }\n\n<!-- return the maximum time taken -->\n int max=0;\n for(int i=1;i<d.length;i++)\n {\n if(i==source) continue;\n else\n max=Math.max(max,d[i]);\n }\n\n<!-- if we are unable to reach a node return -1 -->\n if(processed.size()!=n) return -1;\n else return max;\n }\n}\n```
| 15
| 0
|
['Greedy', 'Graph', 'Heap (Priority Queue)', 'Java']
| 0
|
network-delay-time
|
Easy C++ Solution | Dijkstras Algo | Explained
|
easy-c-solution-dijkstras-algo-explained-rzqu
|
\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n vector <vector<pair<int, int>>> neighs(n+1); //
|
ahanavish
|
NORMAL
|
2022-02-08T17:52:03.766911+00:00
|
2022-05-15T08:02:57.031163+00:00
| 1,376
| false
|
```\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n vector <vector<pair<int, int>>> neighs(n+1); //to store the neighbors and weights corresponding to each vertices\n for(auto t: times) //pushing vertex, neighbor, weight in the proper format\n neighs[t[0]].push_back({t[1], t[2]});\n \n vector <int> res(n+1, INT_MAX); //to store the time taken by signal to reach each vertices\n priority_queue <pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq; //min heap\n pq.push({0, k}); //starting with the starting vertex\n res[k]=0; //since no time is required for starting vertex to reach itself\n \n while(!pq.empty()){\n int vertex=pq.top().second; \n pq.pop();\n \n for(auto neigh:neighs[vertex]){ //considering each neighbors\n //if time taken to reach end point(neigh.first) is more than time taken to reach \n //starting point(i.e vertex) initially+time taken(i.e neigh.second) to reach from\n //starting to end with another path\n if(res[vertex]+neigh.second<res[neigh.first]){ \n //updating time for shorter path\n res[neigh.first]=res[vertex]+neigh.second;\n //pushing for the further journey from end point(i.e neigh.first)\n pq.push({res[neigh.first], neigh.first});\n }\n }\n }\n \n int ans=*max_element(res.begin()+1, res.end()); //to get max time taken\n //if it is impossible for all nodes to receive signal, i.e we still have INT_MAX in res \n //array, so return -1. Else return ans\n return ans==INT_MAX?-1:ans; \n }\n};\n```
| 13
| 1
|
['Graph', 'C', 'Heap (Priority Queue)', 'C++']
| 3
|
network-delay-time
|
Java Simple Bellman-Ford Algorithm Solution - 2 Approaches with Explanation
|
java-simple-bellman-ford-algorithm-solut-e38l
|
1) This approach shows that we can use the times array given to us as number of edges and perform Bellman-Ford Algorithm to be able to also detect any negative
|
algosolver
|
NORMAL
|
2020-04-13T02:28:05.773969+00:00
|
2020-04-13T02:28:05.774019+00:00
| 1,374
| false
|
1) This approach shows that we can use the times array given to us as number of edges and perform Bellman-Ford Algorithm to be able to also detect any negative cycles.\n```\nclass Solution {\n public int networkDelayTime(int[][] times, int N, int K) {\n //create distance array and set them to MAX_VALUE except the starting node K to 0.\n int[] dist = new int[N+1];\n for(int i=1; i<dist.length; i++) {\n dist[i] = Integer.MAX_VALUE;\n }\n dist[K] = 0;\n \n //try to relax all the edges\n for(int i=1; i<N; i++) {\n for(int[] edge: times) {\n int source = edge[0];\n int dest = edge[1];\n int weight = edge[2];\n if(dist[source]!=Integer.MAX_VALUE && dist[source] + weight < dist[dest]) {\n dist[dest] = dist[source] + weight;\n }\n }\n }\n \n int max = Integer.MIN_VALUE;\n // check to see if any of the distances are MAX_VALUE, this will\n // show that the node was never relaxed so return -1\n for(int i=0; i<dist.length; i++) {\n if(dist[i]==Integer.MAX_VALUE){\n return -1;\n }\n max = Math.max(max, dist[i]);\n }\n \n return max;\n }\n}\n```\n2. In this approach I created an Edge class to transform the times array into a graph of edges and then perform Bellman-Ford algorithm.\n```\nclass Solution {\n public int networkDelayTime(int[][] times, int N, int K) {\n List<Edge> edges = new ArrayList<>();\n \n for(int i=0; i<times.length; i++) {\n edges.add(new Edge(times[i][0], times[i][1], times[i][2]));\n }\n \n int[] dist = new int[N+1];\n for(int i=1; i<dist.length; i++) {\n dist[i] = Integer.MAX_VALUE;\n }\n dist[K] = 0;\n \n for(int i=1; i<N; i++) {\n for(Edge currEdge: edges) {\n int source = currEdge.v;\n int dest = currEdge.u;\n int weight = currEdge.weight;\n if(dist[source]!=Integer.MAX_VALUE && dist[source] + weight < dist[dest]) {\n dist[dest] = dist[source] + weight;\n }\n }\n }\n \n int max = Integer.MIN_VALUE;\n // check to see if any of the distance are MAX_VALUE, this will\n // show that the node was never relaxed so return -1\n for(int i=0; i<dist.length; i++) {\n if(dist[i]==Integer.MAX_VALUE){\n return -1;\n }\n max = Math.max(max, dist[i]);\n }\n \n return max;\n }\n \n class Edge {\n int v;\n int u;\n int weight;\n \n Edge(int v, int u, int weight) {\n this.v = v;\n this.u = u;\n this.weight = weight;\n }\n \n public String toString() {\n return " " + this.v + ", " + this.u + ", " + this.weight;\n }\n }\n}\n```
| 13
| 0
|
['Java']
| 1
|
network-delay-time
|
c++ dijkstra concise
|
c-dijkstra-concise-by-laiden-7yc9
|
\nclass Solution {\npublic:\n vector<int> dijkstra(vector<vector<pair<int,int>>>& g, int src){\n int n = g.size();\n vector<int> ret(n, -1);\n
|
laiden
|
NORMAL
|
2018-04-25T19:20:30.052890+00:00
|
2018-10-20T16:55:06.404394+00:00
| 2,047
| false
|
```\nclass Solution {\npublic:\n vector<int> dijkstra(vector<vector<pair<int,int>>>& g, int src){\n int n = g.size();\n vector<int> ret(n, -1);\n \n priority_queue<pair<int,int>, vector<pair<int,int>>, greater<void>> q;\n q.push({0,src});\n\n while(!q.empty()){\n auto x = q.top(); q.pop();\n int c = x.first, v = x.second;\n \n if(ret[v] != -1) continue;\n ret[v] = c;\n for(auto p : g[v]) q.push({p.second + c, p.first});\n }\n\n return ret;\n }\n \n int networkDelayTime(vector<vector<int>>& a, int n, int k) {\n vector<vector<pair<int,int>>> g(n);\n \n for(int i=0; i<a.size(); i++){\n int u = a[i][0] - 1, v = a[i][1] - 1, c = a[i][2];\n g[u].push_back({v,c});\n }\n \n auto ret = dijkstra(g, k-1);\n int hi = 0;\n for(int i=0; i<n; i++){\n if(ret[i] == -1) return -1;\n hi = max(hi, ret[i]);\n }\n return hi;\n }\n};\n```
| 13
| 0
|
[]
| 3
|
network-delay-time
|
Dijkstra's Algorithm, but it's shortest time instead of shortest distance.
|
dijkstras-algorithm-but-its-shortest-tim-72wx
|
IntuitionBasically using Dijsktra's algorithm but instead of distance and weight, its just using time.ApproachUse exact ditto-copy paste of dijsktra algorithm..
|
akhi_101
|
NORMAL
|
2025-02-18T14:32:57.623383+00:00
|
2025-02-18T14:32:57.623383+00:00
| 1,743
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Basically using Dijsktra's algorithm but instead of distance and weight, its just using time.
# Approach
<!-- Describe your approach to solving the problem. -->
Use exact ditto-copy paste of dijsktra algorithm... But,
the distance we usually calculate, consider it to be now time to be calculated.
Make sure to convert it from 1-based index to 0-based index, by simply subtracting the nodes with -1. it is given in the code when i add the adjaceny list.
Add the first node to the PriorityQueue, that is the k node, as per the question.
then extract it from the queue, store it in the variable, so that you can take it's adjacent nodes (as shown in the for loop from the adjaceny list)
now take the nodes from teh adjaceny list, of the adjacent node
that is adj.get(node) -> the node's adjacent-node.
then basically just check that if the time you you have now, and the time it already took for the first node, is smaller than the current one... here is where the dijsktra algo is taken place.
In Dijkstra, we check for shortest distance, similarly, we see the shortest time taken.
so update it to the visitedtime array, and add the new nodes (that is the adjacent-node of the current node which you took from the queue.)
then it will be repeated
the rest just check if any of the elment is infinite, retun -1 else add the total time
and thats it, you solved it!
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(N + E) becuase its graph quesiton lol
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(N) visited time extra space.
# Code
```java []
import java.util.*;
class Tuple {
int first, second;
public Tuple(int first, int second) {
this.first = first;
this.second = second;
}
}
class Solution {
public int networkDelayTime(int[][] times, int n, int k) {
List<List<Tuple>> adj = new ArrayList<>();
for (int i = 0; i < n; i++) {
adj.add(new ArrayList<>());
}
// Convert 1-based indexing to 0-based indexing
for (int[] time : times) {
adj.get(time[0] - 1).add(new Tuple(time[1] - 1, time[2]));
}
// Priority queue for Dijkstra’s algorithm
PriorityQueue<Tuple> q = new PriorityQueue<>(Comparator.comparingInt(a -> a.second));
// Distance array, initialized with infinity (MAX_VALUE)
int[] visitedtime = new int[n];
Arrays.fill(visitedtime, Integer.MAX_VALUE);
visitedtime[k - 1] = 0; // Convert source node `k` to 0-based
q.add(new Tuple(k - 1, 0));
while (!q.isEmpty()) {
Tuple it = q.poll();
int node = it.first;
int t = it.second;
for (Tuple iter : adj.get(node)) {
int adjnode = iter.first;
int edgetime = iter.second;
if (t + edgetime < visitedtime[adjnode]) {
visitedtime[adjnode] = t + edgetime;
q.add(new Tuple(adjnode, visitedtime[adjnode]));
}
}
}
// Find the maximum time taken to reach any node
int maxTime = 0;
for (int time : visitedtime) {
if (time == Integer.MAX_VALUE) {
return -1; // Some nodes are unreachable
}
maxTime = Math.max(maxTime, time);
}
return maxTime;
}
}
```
| 12
| 0
|
['Breadth-First Search', 'Graph', 'Heap (Priority Queue)', 'Shortest Path', 'Java']
| 6
|
network-delay-time
|
Javascript Using Dijikstra Algorithm and Priority Queue (faster than 88.14% of js submissions)
|
javascript-using-dijikstra-algorithm-and-tj9g
|
Based on Dijikstra Algorithm (using Priority Queue). Finding distance from source node K\n\n\nclass QElement { \n constructor(element, priority) \n { \n
|
sanketnitk
|
NORMAL
|
2020-09-25T13:41:25.040145+00:00
|
2020-09-25T13:44:45.192783+00:00
| 1,735
| false
|
Based on Dijikstra Algorithm (using Priority Queue). Finding distance from source node K\n\n```\nclass QElement { \n constructor(element, priority) \n { \n this.element = element; \n this.priority = priority; \n } \n}\n\nclass PriorityQueue {\n constructor() {\n this.items = [];\n }\n enqueue(element, priority) {\n var qElement = new QElement(element, priority); \n var contain = false; \n for (var i = 0; i < this.items.length; i++) {\n if (this.items[i].priority > qElement.priority) {\n this.items.splice(i, 0, qElement);\n contain = true;\n break;\n }\n }\n if (!contain) {\n this.items.push(qElement);\n }\n }\n dequeue() {\n if (this.isEmpty()) \n return "Underflow"; \n return this.items.shift(); \n }\n isEmpty() {\n return this.items.length == 0;\n }\n}\n \n\nclass Graph {\n constructor(N) {\n this.num_vertices = N;\n this.AdjList = new Map();\n }\n addVertex(v) {\n this.AdjList.set(v, []);\n }\n addEdge(x, y, wt) {\n this.AdjList.get(x).push({node: y, wt: wt}); \n }\n};\n\n\nvar networkDelayTime = function(times, N, K) {\n let graph = new Graph(N);\n let distance = {};\n let pq = new PriorityQueue();\n for (var i = 1; i <= N; i++) {\n graph.addVertex(i);\n distance[i] = Infinity;\n }\n times.forEach(function(time){\n graph.addEdge(time[0], time[1], time[2]);\n });\n distance[K] = 0;\n pq.enqueue(K, 0);\n while (!pq.isEmpty()) {\n let minNode = pq.dequeue();\n let currNode = minNode.element;\n let weight = minNode.priority;\n let adjVertexes = graph.AdjList.get(currNode);\n adjVertexes.forEach(function(neigh){\n let temp = distance[currNode] + neigh.wt;\n if (temp < distance[neigh.node]) {\n distance[neigh.node] = temp;\n pq.enqueue(neigh.node, distance[neigh.node]);\n }\n }) \n }\n let time = 0;\n Object.keys(distance).forEach(function(node) {\n if (distance[node] > time) {\n time = distance[node];\n } \n });\n return time == Infinity ? -1 : time;\n};\n```
| 12
| 0
|
['Graph', 'Heap (Priority Queue)', 'JavaScript']
| 3
|
network-delay-time
|
Java DFS
|
java-dfs-by-fllght-xkxl
|
java\nprivate final Map<Integer, List<Node>> connected = new HashMap<>();\n\n public int networkDelayTime(int[][] times, int n, int k) {\n for (int[]
|
FLlGHT
|
NORMAL
|
2022-05-14T07:22:07.956850+00:00
|
2022-05-14T07:22:07.956891+00:00
| 1,735
| false
|
```java\nprivate final Map<Integer, List<Node>> connected = new HashMap<>();\n\n public int networkDelayTime(int[][] times, int n, int k) {\n for (int[] time : times) {\n connected.putIfAbsent(time[0], new ArrayList<>());\n connected.get(time[0]).add(new Node(time[2], time[1]));\n }\n connected.forEach((source, nodes) -> nodes.sort(Comparator.comparing(Node::travelTime)));\n int[] receivedTime = new int[n + 1]; Arrays.fill(receivedTime, 1, receivedTime.length, Integer.MAX_VALUE);\n dfs(receivedTime, 0, k);\n \n int max = Arrays.stream(receivedTime).max().orElseThrow(RuntimeException::new);\n return max == Integer.MAX_VALUE ? -1 : max;\n }\n\n private void dfs(int[] receivedTime, int currentTime, int currentNode) {\n if (receivedTime[currentNode] <= currentTime) return;\n receivedTime[currentNode] = currentTime;\n if (connected.containsKey(currentNode))\n connected.get(currentNode).forEach(node -> dfs(receivedTime, currentTime + node.travelTime(), node.destination()));\n }\n\n public record Node(int travelTime, int destination) {}\n```
| 11
| 0
|
['Depth-First Search', 'Java']
| 1
|
network-delay-time
|
Very very Simple | C++ | BFS
|
very-very-simple-c-bfs-by-megamind-zt6a
|
Initialize the queue with the node currNode as k and store the corresponding time required in signal vector as 0. The signal from node currNode will travel to e
|
megamind_
|
NORMAL
|
2022-05-14T02:12:35.471420+00:00
|
2022-05-14T02:12:35.471481+00:00
| 2,775
| false
|
Initialize the queue with the node currNode as k and store the corresponding time required in signal vector as 0. The signal from node currNode will travel to every adjacent node. Iterate over every adjacent node neighborNode. We will add each adjacent node to the queue only if the signal from currNode via the current edge takes less time than the fastest signal to reach the adjacent node so far. Time taken by the fastest signal for currNode is denoted by signal[currNode]\n```\n vector<vector<pair<int,int>>> vec(n+1);\n \n for(int i=0;i<times.size();i++){\n \n int j = times[i][0];\n vec[j].push_back({times[i][1],times[i][2]}); \n }\n \n vector<int> signal(n+1,INT_MAX);\n\n queue<int> q;\n q.push(k);\n \n \n signal[k] = 0;\n \n while (!q.empty()) {\n int currNode = q.front(); \n q.pop();\n \n \n for (pair<int,int> p : vec[currNode]) {\n \n \n int time = p.second;\n int neighbor = p.first;\n \n int arrival = signal[currNode] + time;\n if (signal[neighbor] > arrival) {\n signal[neighbor] = arrival;\n q.push(neighbor);\n }\n \n }\n }\n \n int maxi = 0;\n for(int i =1;i<=n;i++){\n \n if(signal[i]==INT_MAX)return -1;\n \n maxi = max(maxi,signal[i]);\n \n }\n \n return maxi;\n\n }\n \n```\n**Time complexity: O(N\u22C5E)\nSpace complexity: O(N\u22C5E)**
| 11
| 0
|
['Breadth-First Search']
| 4
|
network-delay-time
|
[C++] Djikstra's Algorithm || Bellman Ford || Concise and very easy to understand
|
c-djikstras-algorithm-bellman-ford-conci-p79t
|
Approach : Dijkstra\'s Shortest Path Algorithm (Using Priority queue)\n\nFirst, from the given input vector, we have to make the adjacency list for the required
|
devrajsingh
|
NORMAL
|
2022-05-14T05:22:52.041591+00:00
|
2022-05-14T05:22:52.041621+00:00
| 1,786
| false
|
***Approach : Dijkstra\'s Shortest Path Algorithm (Using Priority queue)***\n\nFirst, from the given input vector, we have to make the adjacency list for the required directed weighted graph for Dijkstra\'s Algorithm\n\nTo calculate the minimum distance to all other nodes from given "k" node. For minimum distance , we make a minimum heap using C++ STL priority queue.\n\n If our maximum distance is INT_MAX, that means we have not visited some nodes (hence distance vector was initialized with INT_MAX in starting). So we will return -1.\nElse we will return maximum distance.\n\n***Dijkstra (Time Complexity)- V + ElogV***\n\n```\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n vector<int>dis(n+1,INT_MAX);\n priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>>pq;\n \n vector<vector<int>>adj[n+1];\n \n for(int j=0;j<times.size();j++) // Graph creation\n {\n int u=times[j][0];\n int v=times[j][1];\n int w=times[j][2];\n adj[u].push_back({v,w});\n }\n \n dis[k]=0; // Time from K to K is 0\n pq.push({0,k});\n \n while(!pq.empty())\n {\n int u=pq.top().second;\n pq.pop();\n \n for(auto vec:adj[u]) // vec is vector containing v and w\n {\n int v=vec[0];\n int w=vec[1];\n \n if(dis[u]+w<dis[v])\n {\n pq.push({dis[u]+w,v});\n dis[v]=w+dis[u];\n }\n }\n }\n\t \n int ans=0;\n for(int i=1;i<=n;i++)\n {\n if(dis[i]==INT_MAX) return -1;\n ans=max(ans,dis[i]);\n }\n return ans;\n }\n};\n```\nWe can further optimize this last loop, by keeping the count of nodes which are processed and also we can store answer in another variable in while loop too.\n```\n int ans=0;\n for(int i=1;i<=n;i++)\n {\n if(dis[i]==INT_MAX) return -1;\n ans=max(ans,dis[i]);\n }\n return ans;\n```\n\n----------------------------------------------------------------------------------------\n----------------------------------------------------------------------------------------\n----------------------------------------------------------------------------------------\n----------------------------------------------------------------------------------------\n\n\n***2nd Approach Using [ Bellman Ford ]***\n\n***Bellman Ford(Time Complexity) - VE***\n\n```\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n \n \n vector<int>dis(n+1,INT_MAX);\n dis[k]=0;\n for(int i=1;i<n;i++)\n {\n for(int j=0;j<times.size();j++)\n {\n int u=times[j][0];\n int v=times[j][1];\n int w=times[j][2];\n \n if(dis[u]!=INT_MAX && dis[u]+w<dis[v])\n {\n dis[v]=w+dis[u];\n }\n }\n }\n\t\t \n int ans=0;\n for(int i=1;i<=n;i++)\n {\n if(dis[i]==INT_MAX) return -1; // If any node is not reachable from k\n ans=max(ans,dis[i]);\n }\n return ans;\n \n }\n};\n```\n
| 9
| 0
|
['Graph', 'C', 'C++']
| 0
|
network-delay-time
|
python 10 line Optimized Djikstra solution & 8 line Bellman Ford
|
python-10-line-optimized-djikstra-soluti-c0mp
|
Solution 1: Djikstra O(NlogN + len(times)) \npython\nclass Solution:\n def networkDelayTime(self, times: List[List[int]], N: int, K: int) -> int:\n gr
|
jason003
|
NORMAL
|
2019-03-09T14:00:04.002165+00:00
|
2019-06-11T11:43:45.500495+00:00
| 571
| false
|
Solution 1: Djikstra O(NlogN + len(times)) \n```python\nclass Solution:\n def networkDelayTime(self, times: List[List[int]], N: int, K: int) -> int:\n graph, seen, heap = collections.defaultdict(dict), set(), [(0, K)]\n for u, v, w in times:\n graph[u][v] = w\n while heap:\n w, u = heapq.heappop(heap)\n if u in seen: continue\n seen, res = seen | {u}, w\n for v in graph[u]:\n if v not in seen: heapq.heappush(heap, (w + graph[u][v], v))\n return res if len(seen) == N else -1\n```\n\nSolution 2: Bellman Ford O(Nlen(times))\n```python\nclass Solution:\n def networkDelayTime(self, times: List[List[int]], N: int, K: int) -> int:\n dp = [0] + [float(\'inf\')] * N\n dp[K] = 0\n for _ in range(N):\n for u, v, w in times:\n if dp[u] != float(\'inf\') and dp[u] + w < dp[v]:\n dp[v] = dp[u] + w\n res = max(dp or [0])\n return -1 if res == float(\'inf\') else res\n```
| 9
| 0
|
[]
| 1
|
network-delay-time
|
Simple Solution with Diagrams in Video - JavaScript, C++, Java, Python
|
simple-solution-with-diagrams-in-video-j-0w6m
|
Video\nPlease upvote here so others save time too!\n\nLike the video on YouTube if you found it useful\n\nClick here to subscribe on YouTube:\nhttps://www.youtu
|
danieloi
|
NORMAL
|
2024-12-04T16:36:05.759520+00:00
|
2024-12-04T16:36:05.759550+00:00
| 1,759
| false
|
# Video\nPlease upvote here so others save time too!\n\nLike the video on YouTube if you found it useful\n\nClick here to subscribe on YouTube:\nhttps://www.youtube.com/@mayowadan?sub_confirmation=1\n\nThanks!\n\nhttps://youtu.be/mJT48XM9g9g?si=l_zKDD8aCgzvo5vi\n\n```Javascript []\n/**\n * @param {number[][]} times\n * @param {number} n\n * @param {number} k\n * @return {number}\n */\nvar networkDelayTime = function (times, n, k) {\n const adjacency = new Map();\n for (const time of times) {\n const src = time[0];\n const dst = time[1];\n const t = time[2];\n if (!adjacency.has(src)) {\n adjacency.set(src, []);\n }\n adjacency.get(src).push([dst, t]);\n }\n\n const pq = [];\n pq.push({ node: k, time: 0 });\n const visited = new Set();\n let delays = 0;\n\n while (pq.length > 0) {\n pq.sort((a, b) => a.time - b.time);\n const { time, node } = pq.shift();\n\n if (visited.has(node)) {\n continue;\n }\n\n visited.add(node);\n delays = Math.max(delays, time);\n const neighbors = adjacency.get(node) || []; // Handle case when there are no neighbors\n\n for (const neighbor of neighbors) {\n const neighborNode = neighbor[0];\n const neighborTime = neighbor[1];\n if (!visited.has(neighborNode)) {\n const newTime = time + neighborTime;\n pq.push({ node: neighborNode, time: newTime });\n }\n }\n }\n\n if (visited.size === n) {\n return delays;\n }\n\n return -1;\n};\n```\n```Python []\nclass Solution:\n def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:\n # Create adjacency list\n adjacency = {i: [] for i in range(1, n + 1)}\n for src, dst, time in times:\n adjacency[src].append((dst, time))\n\n # Priority queue for Dijkstra\'s algorithm (min-heap based on time)\n pq = [(0, k)] # (time, node)\n visited = set()\n delays = 0\n\n while pq:\n time, node = heapq.heappop(pq)\n\n # Skip if the node has been visited\n if node in visited:\n continue\n\n visited.add(node)\n delays = max(delays, time)\n\n for neighbor, neighbor_time in adjacency.get(node, []):\n if neighbor not in visited:\n heapq.heappush(pq, (time + neighbor_time, neighbor))\n\n # Check if all nodes have been visited\n return delays if len(visited) == n else -1\n\n```\n```Java []\nclass Solution {\n public int networkDelayTime(int[][] times, int n, int k) {\n // Create adjacency list\n Map<Integer, List<int[]>> adjacency = new HashMap<>();\n for (int[] time : times) {\n int src = time[0];\n int dst = time[1];\n int t = time[2];\n adjacency.computeIfAbsent(src, key -> new ArrayList<>()).add(new int[] { dst, t });\n }\n\n // Priority queue for Dijkstra\'s algorithm (min-heap based on time)\n PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[1]));\n pq.add(new int[] { k, 0 });\n Set<Integer> visited = new HashSet<>();\n int delays = 0;\n\n while (!pq.isEmpty()) {\n int[] current = pq.poll();\n int time = current[1];\n int node = current[0];\n\n // Skip if the node has been visited\n if (!visited.add(node)) {\n continue;\n }\n\n delays = Math.max(delays, time);\n List<int[]> neighbors = adjacency.getOrDefault(node, new ArrayList<>());\n\n for (int[] neighbor : neighbors) {\n int neighborNode = neighbor[0];\n int neighborTime = neighbor[1];\n if (!visited.contains(neighborNode)) {\n pq.add(new int[] { neighborNode, time + neighborTime });\n }\n }\n }\n\n // Check if all nodes have been visited\n return visited.size() == n ? delays : -1;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n // Create adjacency list\n unordered_map<int, vector<pair<int, int>>> adjacency;\n for (const auto& time : times) {\n int src = time[0];\n int dst = time[1];\n int t = time[2];\n adjacency[src].emplace_back(dst, t);\n }\n\n // Priority queue for Dijkstra\'s algorithm (min-heap based on time)\n priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;\n pq.emplace(0, k);\n set<int> visited;\n int delays = 0;\n\n while (!pq.empty()) {\n auto [time, node] = pq.top();\n pq.pop();\n\n // Skip if the node has been visited\n if (visited.count(node)) {\n continue;\n }\n\n visited.insert(node);\n delays = max(delays, time);\n for (const auto& neighbor : adjacency[node]) {\n int neighborNode = neighbor.first;\n int neighborTime = neighbor.second;\n if (!visited.count(neighborNode)) {\n pq.emplace(time + neighborTime, neighborNode);\n }\n }\n }\n\n // Check if all nodes have been visited\n return visited.size() == n ? delays : -1;\n }\n};\n\n```
| 8
| 0
|
['Python', 'C++', 'Java', 'Python3', 'JavaScript']
| 0
|
network-delay-time
|
Easy classic DIJKSTRA C++ | easy to understand :)
|
easy-classic-dijkstra-c-easy-to-understa-s4p5
|
Intuition\nshortest path / distance nikalna ho jaha bhi sidha dijkstra lagado..\nwe get the distance from node k to every node sabse kam length ka.\nphir check
|
sach_code
|
NORMAL
|
2023-07-31T18:51:19.490410+00:00
|
2023-08-01T20:33:29.026826+00:00
| 538
| false
|
# Intuition\nshortest path / distance nikalna ho jaha bhi sidha dijkstra lagado..\nwe get the distance from node k to every node sabse kam length ka.\nphir check karlo dist m konsa sabse dur hai..\nutna hi time lagega max spread hone m..\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n\nsimilar to the classic ques in tree\ninfection problem on geegsforgeeks\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: Elog V due to priority queue use\n\nhere we cant use normal queue becuase weights are different matlab distance alag hai sab jagah ki to hame khudse min chhaiye har iteration me\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: space of adjacency list and distance vector\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n\n // adjacency list banado mast, use classic pair method\n vector<pair<int,int>> adj[n+1]; \n // <!-- min heap banadia ek jo min distance dega bar bar priority queue m -->\n priority_queue<pair<int,int> , vector<pair<int,int>> , greater <pair<int,int>>> pq;\n\n // <!-- directed hai to ek sided list define kardi -->\n\n for( auto it : times){\n adj[it[0]].push_back({it[1] , it[2]});\n }\n\n // <!-- sabki distance ko k node se initially infinite mark krdia -->\n vector<int> dist(n+1, 1e9);\n\n // <!-- node k ki node k se distance to 0 hi hogi -->\n dist[k] =0;\n pq.push({0,k});\n\n // <!-- iteration traversal BFS starts -->\n\n while(!pq.empty()){\n auto it = pq.top();\n pq.pop();\n int dis = it.first;\n int node = it.second;\n\n // <!-- ab har node ko pura check karna hai ek edge at a time -->\n\n for( auto it : adj[node]){\n int adjnode = it.first;\n int wt = it.second;\n\n // <!-- agar distance kam ayi kisi tarah to us node ki dist update kardo kam wali -->\n\n if(dist[adjnode] > dis +wt){\n dist[adjnode] = wt+dis;\n pq.push({dis+wt, adjnode});\n }\n }\n }\n\n // <!-- max distance node k se is the weight taken to spread in whole graph -->\n int ans = 0; \n for ( int i=1;i<dist.size(); i++){\n ans = max(ans, dist[i]);\n }\n\n // <!-- agar visit hi nahi hua to -1 return karo -->\n \n if( ans == 1e9) return -1;\n return ans;\n\n\n\n\n \n }\n};\n```
| 8
| 0
|
['Breadth-First Search', 'Heap (Priority Queue)', 'C++']
| 1
|
network-delay-time
|
3 APPROACHES || DIFFERENCE BETWEEN DIJKSTRA | BELMAN FORD | FLOYDD WARSHELL || C++
|
3-approaches-difference-between-dijkstra-e0qd
|
DIJKSTRA ALGORITHM\n\n HELPS TO FIND SSSP ( SINGLE SOURCE SHORTEST PATH ) TO EVERY OTHER NODES\n CAN BE IMPLEMENTED BY BOTH PRIORITY QUEUES AND SETS\n\nAD
|
dikshant_sh
|
NORMAL
|
2023-03-30T10:03:14.767829+00:00
|
2023-03-30T10:15:19.532409+00:00
| 803
| false
|
**DIJKSTRA ALGORITHM**\n\n* HELPS TO FIND SSSP ( **SINGLE SOURCE SHORTEST PATH** ) TO EVERY OTHER NODES\n* CAN BE IMPLEMENTED BY BOTH PRIORITY QUEUES AND SETS\n\n*ADVANTAGES*\n1. T.C - O( ElogV )\n\n*DISADVANTAGES*\n1. IT WON\'T WORKS FOR THE NEGATIVE EDGES\n2. UNABLE TO IDENTIFY NEGATIVE CYCLES\n```\nclass Solution\n{\npublic:\n int networkDelayTime(vector<vector<int>> ×, int n, int k)\n {\n vector<pair<int, int>> adj[n + 1];\n vector<int> dis(n + 1, 1e4);\n dis[k] = 0;\n priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;\n for (auto it : times)\n adj[it[0]].push_back({it[1], it[2]});\n pq.push({0, k});\n int ans = 0;\n while (!pq.empty())\n {\n auto it = pq.top();\n pq.pop();\n int distance = it.first;\n int node = it.second;\n for (auto i : adj[node])\n {\n if (distance + i.second < dis[i.first])\n {\n dis[i.first] = distance + i.second;\n pq.push({distance + i.second, i.first});\n }\n }\n }\n for (int i = 1; i <= n; i++)\n {\n if (dis[i] == 1e4)\n return -1;\n ans = max(ans, dis[i]);\n }\n return ans;\n }\n};\n```\n\n\n**BELMAN FORD ALGORITHM**\n\n* SIMLIAR TO DIJKSTRA\n* HELPS TO FIND SSSP( **SINGLE SOURCE SHORTEST PATH** ) TO EVERY OTHER NODES\n\n*INTUITION*\n* JUST RELAX ALL THE EDGES N-1 TIMES SIMPLE !\n* REALAXATION IS IF THE NEW DISTANCE IS SMALLER THAN PREVIOUS ONE JUST UPDATE IT OR ( *if( dist[u] + weight < dist[v] ) THAN JUST UPDATE --> dist[v] = dist[u] + weight* !\n\n*ADVANTAGES*\n1. WORKS FOR NEGATIVE EDGES\n2. ALSO HELPS US TO IDENTIFY NEGATIVE CYCLE !\n3. SIMILIAR TO DIJKSTRA\n \n **HOW TO IDENTIFY -VE CYLCES ???** ----> IF IT IS STILL RELAXING IN THE Nth ITERATION THAN DEFINITELY IT WILL CONSIST A NEGATIVE CYCLE\n \n *DISADVANTAGES*\n1. T.C - O ( V*E )\n\n```\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n// BELMAN FORD ALGORITHM\n vector<int>dist(n+1,1e8);\n dist[k]=0;\n for(int i=0;i<n;i++)\n {\n for(auto &it:times)\n {\n int u=it[0];\n int v=it[1];\n int wt=it[2];\n if(dist[u]!=1e8 && dist[u]+wt<dist[v])\n {\n dist[v]=dist[u]+wt;\n }\n }\n }\n // for the -ve cycle if there is a -ve cycle the distance matrix will definitely reduce\n for(auto &it:times)\n {\n int u=it[0];\n int v=it[1];\n int wt=it[2];\n if(dist[u]!=1e8 && dist[u]+wt<dist[v])\n {\n return -1;\n }\n }\n // if no -ve cycles\n int ans=INT_MIN;\n for(int i=1;i<=n;i++)\n {\n if(dist[i]==1e4) return -1;\n ans=max(ans,dist[i]);\n }\n return ans==1e8?-1:ans;\n }\n};\n```\n\n\n**FLOYD WARSHELL ALGORITHM**\n\n* HELPS TO FIND THE MSSP (**MULTI SOURCE SHORTEST PATH**)\n* USES ADJAENCY MATRIX NOT ADJEANCY LIST LIKE DIJKSTRA AND BELMAN FORD\n* IT\'S A NORMAL BRUTE FORCE\n\n*ADVANTAGES*\n1. HELPS TO FIND MSSP WHERE AS DUJKSTRA AND BELMAN FORD DON\'T GIVES U THIS LUXURY !\n2. DETECTS -VE CYCLE\n3. WORKS -VE EDGES TOO !\n\nDISADVANTAGES\n1. T.C- O( N^3 )\n\n```\nclass Solution\n{\npublic:\n int networkDelayTime(vector<vector<int>> ×, int n, int k)\n {\n // FLOYDD WARSHELL ALGORITHM\n vector<vector<int>> adjaencyMatrix(n + 1, vector<int>(n + 1, 1e9));\n for (auto it : times)\n {\n int src = it[0];\n int dst = it[1];\n int wt = it[2];\n adjaencyMatrix[src][dst] = wt;\n }\n // created adjaency matrix finally !\n for (int i = 0; i < n + 1; i++)\n {\n for (int j = 0; j < n + 1; j++)\n {\n if (j == 0)\n adjaencyMatrix[i][j] = 0;\n if (i == j)\n adjaencyMatrix[i][j] = 0;\n }\n }\n for (int via = 0; via < n + 1; via++)\n {\n for (int i = 0; i < n + 1; i++)\n {\n for (int j = 0; j < n + 1; j++)\n {\n adjaencyMatrix[i][j] = min(adjaencyMatrix[i][j], adjaencyMatrix[i][via] + adjaencyMatrix[via][j]);\n }\n }\n }\n\n int ans = -1;\n for (auto it : adjaencyMatrix[k])\n {\n if (it == 1e9)\n return -1;\n if (it != 0)\n ans = max(it, ans);\n }\n return ans;\n }\n};\n```\n\n**UPVOTE IF THIS WAS HELPFUL !**\n\n\n
| 8
| 0
|
['Graph', 'C']
| 2
|
network-delay-time
|
Java Dijkstra With Clean and Commented Solution 100%
|
java-dijkstra-with-clean-and-commented-s-cx0e
|
\nclass Solution {\n \n public int total = 0; // to return the max value\n \n public class Edge // As graph is arrayList of edges so firstly creati
|
sandeepbk01
|
NORMAL
|
2022-05-14T02:40:50.553925+00:00
|
2023-06-06T17:45:50.320661+00:00
| 1,088
| false
|
```\nclass Solution {\n \n public int total = 0; // to return the max value\n \n public class Edge // As graph is arrayList of edges so firstly creating an edge class\n {\n int src; // source\n int nbr; // its destination or source\'s neighbour\n int wt; // corresponding edge weight\n \n Edge(int src , int nbr , int wt) // constructor to initialise the new Edge object\n {\n this.src = src;\n this.nbr = nbr;\n this.wt = wt;\n }\n }\n \n public int networkDelayTime(int[][] times, int n, int k) {\n \n List<Edge>[] graph = new ArrayList[n+1]; // Adjacency List for representation of graph {n+1} because edge starts from **1 to N**\n \n Set<Integer> set = new HashSet(); // if all nodes are visited then return result else return -1 as mentioned\n \n for(int i=1;i<=n;i++)\n {\n graph[i] = new ArrayList(); // Creating the Adjacency list like for Node 1 ----> [] , Node 2 -----> []\n }\n \n \n \n for(int i=0;i<times.length;i++)\n {\n // Graph creation\n int v1 = times[i][0];\n int v2 = times[i][1];\n int wt = times[i][2];\n graph[v1].add(new Edge(v1, v2, wt)); // as it is directed graph obviously only one edge to be connected\n \n }\n \n\t\t// At this point our graph is ready and ready to execute this problem\n\t\t\n\t\t// As the source is K is the question and from K we need to visit all the nodes\n\t\t\n PriorityQueue<Pair> pq = new PriorityQueue<>(); // Min PriorityQueue for Dijkstras\n \n boolean[] vis = new boolean[n+1]; // {n+1} because 1toN nodes not 0 to N-1\n \n pq.add(new Pair(k,0)); //initialising the priorityQueue \n \n while(pq.size() > 0)\n {\n Pair rem = pq.remove();\n \n if(vis[rem.v]) // If the node is already visited then just continue\n {\n continue;\n }\n \n vis[rem.v] = true; //else mark it as true\n set.add(rem.v); // this is for final result comparing\n total = Math.max(total , rem.wsf); // max until now\n \n for(Edge e : graph[rem.v]) // visiting the neighbours using the current node \n {\n if(vis[e.nbr] == false)\n {\n pq.add(new Pair(e.nbr , rem.wsf+e.wt)); // prev wt + curr wt\n \n }\n }\n \n }\n \n if(set.size() == n)\n {\n return total;\n }\n return -1;\n \n \n }\n \n public class Pair implements Comparable<Pair> // As pq is of type Pair we need to mention how it is been compared with hence we go on with comparable class\n {\n int v;\n int wsf;\n Pair(int v , int wsf)\n {\n this.v = v;\n this.wsf = wsf;\n }\n \n public int compareTo(Pair o) // Inbuilt method when used comparable interface and has to be compulsorily defined\n {\n return this.wsf - o.wsf;\n }\n }\n}\n\n//Please upvote if you found this informative\n```
| 8
| 0
|
['Heap (Priority Queue)', 'Java']
| 2
|
network-delay-time
|
Python 3 | Different 4 Methods | No Explanation
|
python-3-different-4-methods-no-explanat-llts
|
Approach \#1. Dijkstra\npython\nclass Solution:\n def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:\n dp = [sys.maxsize] * n\
|
idontknoooo
|
NORMAL
|
2021-12-06T06:30:38.975330+00:00
|
2021-12-06T07:07:41.616163+00:00
| 1,153
| false
|
### Approach \\#1. Dijkstra\n```python\nclass Solution:\n def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:\n dp = [sys.maxsize] * n\n dp[k-1] = 0\n graph = collections.defaultdict(list)\n for s, e, w in times:\n graph[s].append((e, w))\n visited = set() \n heap = [(0, k)] \n while heap:\n cur, node = heapq.heappop(heap)\n dp[node-1] = cur\n if node not in visited:\n visited.add(node)\n n -= 1\n for nei, w in graph[node]:\n if dp[nei-1] > cur + w:\n dp[nei-1] = cur + w\n if nei not in visited:\n heapq.heappush(heap, (cur + w, nei))\n if not n: return cur\n return -1\n```\n### Approach \\#2. Floyd-Warshall \n```python\nclass Solution:\n def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:\n dp = [[sys.maxsize] * n for _ in range(n)] \n graph = collections.defaultdict(list)\n for s, e, w in times:\n graph[s].append((e, w))\n dp[s-1][e-1] = w\n \n for i in range(n):\n dp[i][i] = 0\n \n for kk in range(n):\n for i in range(n):\n for j in range(n):\n if dp[i][kk] != sys.maxsize and dp[kk][j] != sys.maxsize:\n dp[i][j] = min(dp[i][j], dp[i][kk] + dp[kk][j])\n ans = 0 \n for j in range(n):\n ans = max(ans, dp[k-1][j])\n return ans if ans != sys.maxsize else -1\n```\n### Approach \\#3. Bellman-Ford\n```python\nclass Solution:\n def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:\n dp = [sys.maxsize] * n\n dp[k-1] = 0\n \n for _ in range(n-1):\n for s, e, w in times:\n if dp[e-1] > dp[s-1] + w:\n dp[e-1] = dp[s-1] + w\n \n ans = 0 \n for i in range(n):\n if i != k-1:\n ans = max(ans, dp[i])\n return ans if ans != sys.maxsize else -1\n```\n### Approach \\#4. SPFA (deque implementation)\n```python\nclass Solution:\n def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:\n dp = [sys.maxsize] * n\n dp[k-1] = 0\n graph = collections.defaultdict(list)\n for s, e, w in times:\n graph[s].append((e, w))\n \n dq = collections.deque([k])\n visited = set([k])\n while dq:\n node = dq.popleft()\n cost = dp[node-1]\n visited.remove(node)\n for nei, w in graph[node]:\n if dp[nei-1] > cost + w:\n dp[nei-1] = cost + w\n if nei not in visited:\n visited.add(nei)\n dq.append(nei)\n \n ans = 0 \n for i in range(n):\n if i != k-1:\n ans = max(ans, dp[i])\n return ans if ans != sys.maxsize else -1\n```
| 8
| 1
|
['Python', 'Python3']
| 0
|
network-delay-time
|
Understanding Djikstra Algorithm for Beginners - Java Solution 9ms ✨
|
understanding-djikstra-algorithm-for-beg-okxd
|
Approach\n- Find shortest path (minimum time) to reach all the nodes from node \'k\'\n- Find the max of all the minimum time\n- keep track of number of visited
|
anurag0608
|
NORMAL
|
2021-06-14T10:57:19.323000+00:00
|
2023-11-22T11:34:38.922462+00:00
| 1,036
| false
|
# Approach\n- Find shortest path (minimum time) to reach all the nodes from node \'k\'\n- Find the max of all the minimum time\n- keep track of number of visited nodes\n- if you ae able to reach all the nodes from \'k\' then minimum time to reach all the nodes is the maxmimum of all the reaching times.\n\nIf time taken to reach node `N1` and `N2` is `3` and` 4 `seconds respectively\nSo when will the sender recognize that both received the signal successfully?\n(ignoring round trip) **The answer is 4s**\nBy keeping this in mind lets move forward...\n### So how to do this ?\nBasically we\'ve to find shortest path (least delay path) from the starting node \'k\'\nAs we know DFS is not good for finding shortest path (dfs simply jumps to the first adjacent node and goes depth wise)\nWe\'ll do BFS here.. for good results.\n* First we\'ll have a queue \n* We\'ll also maintain a distance array containing final cost to reach each vertex from source vertex i.e for vertex \'v\' shortest distance from source to \'v\' will be `distance[v]` \n* We\'ll put the starting vertex.. since cost to reach starting vertex is zero.. mark the distance[start] = 0 \n* As we proceed the exploration on vertex start.. we\'ll visit all of its adjacent neighbors and add it to the queue\n**But** wait a minute before we add **we\'ll update the distance to reach those neighbors in there corresponding indices in distance array**.\nThis is called **relaxation**.\n\n### How we will do this ?\nI\'ll take an example...\nImagine this -\n```text\n dis[u] = 0;\n dis[v] = INT_MAX; //initially we don\'t know the shortest path to reach there \n dis[w] = INT_MAX; // this is called over-estimating the distance\n\n u--------v----------w\n 0 (1) Max (2) MAX\n\n cost(u,v) = 1\n cost(v,w) = 2\n\n Start vertex 0\n neighbor is vertex \'v\'\n What is the min cost to reach v ?\n do this..\n (distance to reach u + cost to reach v) If less than current distance to reach v i.e old distance[v]\n then we update the distance of v\n\n Since (o+1) < MAX\n dis[v] = 1\n\n Similarly to reach w from v\n (dis[v] + cost(v, w)) < dist[w] or MAX\n dis[w] = 1+2 = 3\n\n distance array [0 1 3]\n u v w\n\t\t\t\t\t\t\n This tells us that\n If we start from u then..\n Minimum cost to reach v is 1 and w is 3\n\n We continue doing this.. and every time we select a vertex with minimum distance value. (unlike normal BFS there we directly remove the node from top of the queue)\n\n This modified verision of BFS is also known as Dijkstra\'s Algorithm :)\n```\n# Complexity\n- Time:\n $$O(Vlog(E))$$, here V = vertices, E = number of edges\n- Space:\n $$O(V+E)$$\n```\nclass Solution {\n public int networkDelayTime(int[][] times, int n, int k) {\n // construct adj list\n List[] adj = new List[n+1]; // given 1-indexed nodes\n //O(times.length)\n for(int[] time:times){\n int u = time[0];\n int v = time[1];\n int t = time[2];\n if(adj[u]==null){\n adj[u] = new ArrayList<int[]>();\n }\n adj[u].add(new int[]{v,t}); // u->(v,t)\n }\n // we have to find shortest reaching time to all the other nodes from k\n // and find max of all the reaching time\n PriorityQueue<int[]> pq = new PriorityQueue<>((a,b)->Integer.compare(a[1],b[1]));\n boolean[] vis = new boolean[n+1]; \n \n int[] reachTime = new int[n+1]; // store the optimal reach time to reach nodes\n Arrays.fill(reachTime, Integer.MAX_VALUE); // infinity\n\n int count = 0; // keep track of all the visited nodes\n int max = 0; // max of all the shortest reaching time\n \n pq.add(new int[]{k,0});// cost to start node is zero\n reachTime[k] = 0;\n\n // use dijkstra algorithm\n while(!pq.isEmpty()){\n int[] node = pq.poll();\n int u = node[0];\n int reachTime_u = node[1];\n if(vis[u]){\n continue;\n }\n vis[u] = true;\n count++; // count visited nodes\n max = Math.max(max, reachTime_u); // update max\n if(adj[u]!=null){\n Iterator<int[]> it = adj[u].iterator();\n while(it.hasNext()){\n int[] neighbor = it.next();\n int v = neighbor[0];\n int cost_uv = neighbor[1];\n // relaxation\n if(!vis[v] && (reachTime_u+cost_uv)<reachTime[v]){\n // if current estimation for reaching node \'v\' < previously estimated value\n reachTime[v] = reachTime_u+cost_uv;\n // dont mark as visited, there could be another path for reaching v \n // with lesses reach time\n pq.add(new int[]{v, reachTime[v]});\n }\n }\n }\n }\n return count==n?max:-1;\n }\n}\n```\n\n
| 8
| 0
|
['Greedy', 'Breadth-First Search', 'Graph', 'Heap (Priority Queue)', 'Shortest Path', 'Java']
| 2
|
network-delay-time
|
Java Simple Djikstra
|
java-simple-djikstra-by-hobiter-1v37
|
1, based on Djikstra\n2, check shortes dist from origin for each node. Once found the shortest, put it in vs to avoid duplicate. before put in set, compare to r
|
hobiter
|
NORMAL
|
2020-07-03T00:52:31.040961+00:00
|
2020-07-03T00:52:31.040989+00:00
| 717
| false
|
1, based on Djikstra\n2, check shortes dist from origin for each node. Once found the shortest, put it in vs to avoid duplicate. before put in set, compare to res, and record the longest node to reach\n3, nit: check if all nodes could be reachable.\n\n```\n public int networkDelayTime(int[][] times, int N, int K) {\n Map<Integer, Map<Integer, Integer>> g = new HashMap<>();\n for (int[] time : times) {\n g.computeIfAbsent(time[0], k -> new HashMap<>());\n g.get(time[0]).put(time[1], time[2]);\n }\n PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[1] - b[1]);\n Set<Integer> vs = new HashSet<>();\n pq.offer(new int[]{K, 0});\n int res = 0;\n while (!pq.isEmpty()) {\n int[] curr = pq.poll(); \n if (vs.contains(curr[0])) continue;\n vs.add(curr[0]);\n res = Math.max(res, curr[1]); // this must be after vs check, say[[1,2,1],[2,1,3]] 2, 2\n for (int neig : g.getOrDefault(curr[0], new HashMap<Integer,Integer>()).keySet()) {\n if (vs.contains(neig)) continue;\n pq.offer(new int[]{neig, g.get(curr[0]).get(neig) + curr[1]});\n }\n }\n return vs.size() == N ? res : -1; // check if all nods visited; say [[1,2,1]], 2, 2\n }\n```
| 8
| 1
|
[]
| 1
|
network-delay-time
|
BFS | 99 % beats | Java
|
bfs-99-beats-java-by-eshwaraprasad-fe02
|
\n\n\n# Approach\n Describe your approach to solving the problem. \nApproach is very simple, Instead of using any Priorityqueue or any normal queue, we can simp
|
eshwaraprasad
|
NORMAL
|
2024-08-30T06:43:46.308085+00:00
|
2024-08-30T06:43:46.308117+00:00
| 631
| false
|
> \n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nApproach is very simple, Instead of using any Priorityqueue or any normal queue, we can simply traverse through given edges and each time we can perform operation like virus spreading. That is, right from source vertex, at each iteration, it\'s neighbours `time` gets updates to the min possible time.\n\nAt the end when all the nodes are visited, we can return the Max value from them.\n\n\n# Code\n```java []\nclass Solution {\n public int networkDelayTime(int[][] times, int n, int k) {\n int result[] = new int[n + 1];\n int int_max = Integer.MAX_VALUE;\n Arrays.fill(result, int_max);\n result[k] = 0;\n\n for(int i = 0; i < n - 1; i++) {\n boolean found = false;\n\n for(int time[] : times) {\n int src = time[0];\n int dest = time[1];\n int t = time[2];\n\n if(result[src] == int_max) continue;\n if(result[src] + t < result[dest]) {\n found = true;\n result[dest] = result[src] + t;\n }\n }\n if(found == false) break;\n }\n int answer = -1;\n for(int i = 1; i < n + 1; i++) {\n if(result[i] == int_max) return -1;\n answer = Math.max(answer, result[i]);\n }\n return answer;\n }\n}\n```
| 7
| 0
|
['Java']
| 0
|
network-delay-time
|
Javascript | Priority Queue
|
javascript-priority-queue-by-shekhar90-w4pu
|
\nvar networkDelayTime = function (times, n, k) {\n const edges = [];\n for (let [u, v, w] of times) {\n if (!edges[u]) edges[u] = [];\n edg
|
shekhar90
|
NORMAL
|
2022-05-22T15:27:36.061296+00:00
|
2022-05-22T15:27:36.061341+00:00
| 705
| false
|
```\nvar networkDelayTime = function (times, n, k) {\n const edges = [];\n for (let [u, v, w] of times) {\n if (!edges[u]) edges[u] = [];\n edges[u].push([v, w]);\n }\n\n function bfs() {\n const pQueue = new MinPriorityQueue({ compare: (a, b) => a[1] > b[1] });\n const visit = new Set();\n pQueue.enqueue([k, 0]);\n let maxPathTill = 0;\n\n while (!pQueue.isEmpty()) {\n const [node, w] = pQueue.dequeue();\n if (visit.has(node)) continue;\n visit.add(node);\n maxPathTill = Math.max(maxPathTill, w);\n if (edges[node]) {\n const adjNodes = edges[node];\n for (let [adjNode, adjW] of adjNodes) {\n if (!visit.has(adjNode)) pQueue.enqueue([adjNode, w + adjW])\n }\n }\n }\n return visit.size === n ? maxPathTill : -1;\n }\n\n return bfs()\n}\n```
| 7
| 0
|
['Queue', 'Heap (Priority Queue)', 'JavaScript']
| 0
|
network-delay-time
|
C++ | Dijkstra's Shortest Path Algorithm Explained | 99.61% Faster
|
c-dijkstras-shortest-path-algorithm-expl-o503
|
Firstly, from the given input vector, we have to make the adjacency list for the required directed weighted graph. \n\nA corner condition: If node k has no outg
|
cyber-venom003
|
NORMAL
|
2021-09-24T06:35:03.478649+00:00
|
2021-09-24T06:35:03.478696+00:00
| 1,307
| false
|
Firstly, from the given input vector, we have to make the adjacency list for the required **directed weighted graph**. \n\nA corner condition: If node k has no outgoing connections, then it is impossible for signal to reach to all nodes, we return -1 in this case.\n\n### Approach : Dijkstra\'s Shortest Path Algorithm (99.61% faster)\n\nHere, our priority is to reach to all nodes anyhow. So, we calculate the minimum distance to all other nodes from given "k" node. For getting minimum distance every time, we make a minimum heap using C++ STL priority queue. \n\nOnce we have visited all feasible nodes from given "k" node, we have the minimum distances of the nodes which we have visited from "k". So now, our answer would be the maximum distance in these all distances. \n\nIf our maximum distance is INT_MAX, that means we have not visited some nodes (hence distance vector was initialized with INT_MAX in starting). So we will return -1.\nElse we will return maximum distance.\n\nMy Submission:\n```\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n vector<pair<int , int>> adj[n + 1]; // Graph Container (Adjacency List)\n \n for(int i = 0 ; i < times.size() ; ++i){\n adj[times[i][0]].push_back(make_pair(times[i][1] , times[i][2])); //Constructing the graph.\n }\n \n vector<bool> visited(n + 1 , false); // Visited Array\n vector<int> distances(n + 1 , INT_MAX); // Minimum Distance of each node from k, initialized by INT_MAX.\n if(adj[k].size() == 0){ // If there is no outgoing edge from k, return -1.\n return -1;\n } else { // Standard Dijkstra Algorithm Implementation\n priority_queue<pair<int , int> , vector<pair<int , int>> , greater<pair<int , int>>> dijkstra_queue;\n distances[k] = 0;\n int count = 0;\n dijkstra_queue.push(make_pair(0 , k));\n while(count < n && !dijkstra_queue.empty()){\n int distance = dijkstra_queue.top().first;\n int node = dijkstra_queue.top().second;\n dijkstra_queue.pop();\n if(visited[node]){\n continue;\n }\n visited[node] = true;\n distances[node] = distance;\n count++;\n for(auto it : adj[node]){\n int next_node = it.first;\n int next_distance = it.second;\n if(!visited[next_node]){\n dijkstra_queue.push(make_pair(distance + next_distance , next_node));\n }\n }\n }\n }\n int answer = 0;\n for(int i = 1 ; i < distances.size() ; ++i){ \n answer = max(answer , distances[i]); // Distance of farthest node would be our answer.\n }\n if(answer == INT_MAX){ // Means we have missed some node.\n return -1;\n }\n return answer; \n }\n};\n```\n**PLEASE UPVOTE IT IF YOU LIKED IT, IT REALLY MOTIVATES :)**
| 7
| 0
|
['C', 'C++']
| 1
|
network-delay-time
|
Bellman Ford and Dijkstra / short and Easy to understand
|
bellman-ford-and-dijkstra-short-and-easy-kuvg
|
** Bellmann ford\n\n \nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int N, int K) {\n int n = times.size();\n\t\t\tif (
|
rmn_8743
|
NORMAL
|
2021-09-16T05:00:29.827079+00:00
|
2021-09-16T05:07:26.388411+00:00
| 460
| false
|
** Bellmann ford**\n```\n \nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int N, int K) {\n int n = times.size();\n\t\t\tif (!n) return 0;\n\t\t\t\n\t\t\tvector<int>dist(N+1, INT_MAX);\n\t\t\tint res = 0;\n\t\t\t\n\t\t\tdist[K] = 0;\n\t\t\tfor (int i = 0; i < N; i++) {\n\t\t\t\tfor (int j = 0; j < n; j++) {\n\t\t\t\t\tint u = times[j][0];\n\t\t\t\t\tint v = times[j][1];\n\t\t\t\t\tint w = times[j][2];\n\t\t\t\t\tif (dist[u] != INT_MAX && dist[u] + w < dist[v])\n\t\t\t\t\t\tdist[v] = w + dist[u];\n\t\t\t\t}\n\t\t\t}\n\t\t\t\n\t\t\tfor (int i = 1; i <= N; i++)\n\t\t\t\tres = max(res, dist[i]);\n\n\t\t\treturn res == INT_MAX ? -1 : res;\n\t\t}\n};\n```\n** Dijkstra**\n```\nclass Solution {\n\tpublic:\n\t\tint networkDelayTime(vector<vector<int>>& times, int N, int K) {\n\t\t\t\n\t\t\tpriority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>>pq;\n\t\t\tvector<int>dist(N+1, INT_MAX);\n\t\t\t\n\t\t\tpq.push({0, K});\n\t\t\tdist[K] = 0;\n\t\t\t\n\t\t\tunordered_map<int, vector<pair<int, int>>>adj;\n\t\t\tfor (auto i:times)\n\t\t\t\tadj[i[0]].push_back({i[1],i[2]});\n\t\t\t\n\t\t\twhile (!pq.empty()) {\n\t\t\t\tauto p = pq.top();\n\t\t\t\tpq.pop();\n\t\t\t\t\n\t\t\t\tint u = p.second;\n\t\t\t\tfor (auto i:adj[u]) {\n\t\t\t\t\tint v = i.first;\n\t\t\t\t\tint w = i.second;\n\t\t\t\t\t\n\t\t\t\t\tif (dist[v] > dist[u] + w) {\n\t\t\t\t\t\tdist[v] = dist[u] + w;\n\t\t\t\t\t\tpq.push({dist[v], v});\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t}\n\t\t\t\n\t\t\tint res = 0;\n\t\t\tfor (int i = 1; i <= N; i++)\n\t\t\t\tres = max(res, dist[i]);\n\t\t\t\n\t\t\treturn res == INT_MAX ? -1 : res;\n\t\t}\n\t};\n\t```
| 7
| 0
|
['C']
| 1
|
network-delay-time
|
Dijkstra | Bellman Ford | Floyd Warshall
|
dijkstra-bellman-ford-floyd-warshall-by-i7kku
|
Time Complexity\nDijkstra - V + ElogE\nBellman Ford - VE\nFloyd Warshall - V^3\n\nDijkstra\n\n\nclass Solution {\n public int networkDelayTime(int[][] times,
|
i18n
|
NORMAL
|
2021-01-23T06:35:45.970619+00:00
|
2021-01-23T06:35:45.970659+00:00
| 253
| false
|
**Time Complexity**\nDijkstra - V + ElogE\nBellman Ford - VE\nFloyd Warshall - V^3\n\n**Dijkstra**\n\n```\nclass Solution {\n public int networkDelayTime(int[][] times, int N, int K) {\n List<int[]>[] adj = new ArrayList[N];\n for (int i = 0; i < N; i++) {\n adj[i] = new ArrayList<>();\n }\n\n for (int[] t : times) {\n adj[t[0] - 1].add(new int[]{t[1] - 1, t[2]});\n }\n\n int[] dist = new int[N];\n Arrays.fill(dist, -1);\n\n dist[K - 1] = 0;\n Queue<int[]> minHeap = new PriorityQueue<>((a, b) -> Integer.compare(a[1], b[1]));\n minHeap.offer(new int[]{K - 1, 0});\n\n while (minHeap.size() > 0) {\n int curr = minHeap.peek()[0];\n minHeap.poll();\n for (int[] pair : adj[curr]) {\n int next = pair[0];\n int weight = pair[1];\n int d = dist[curr] + weight;\n if (dist[next] == -1 || dist[next] > d) {\n dist[next] = d;\n minHeap.offer(new int[]{next, dist[next]});\n }\n }\n }\n\n int maxwait = 0;\n for (int i = 0; i < N; i++) {\n if(dist[i] == -1) \n return -1;\n maxwait = Math.max(maxwait, dist[i]);\n }\n return maxwait;\n }\n}\n```\n\n************\n\n**Bellman Ford**\n\n```\nclass Solution {\n public int networkDelayTime(int[][] times, int N, int K) {\n int[] dist = new int[N + 1];\n Arrays.fill(dist, Integer.MAX_VALUE);\n \n dist[K] = 0;\n for(int i = 1; i < N; i++) {\n for(int[] e : times) {\n int u = e[0], v = e[1], w = e[2];\n if(dist[u] != Integer.MAX_VALUE && dist[v] > dist[u] + w)\n dist[v] = dist[u] + w;\n }\n }\n \n int maxwait = 0;\n for (int i = 1; i <= N; i++)\n maxwait = Math.max(maxwait, dist[i]);\n return maxwait == Integer.MAX_VALUE ? -1 : maxwait;\n }\n}\n```\n\n\n**Bellman Short Code**\n\n```\nclass Solution {\n public int networkDelayTime(int[][] times, int N, int K) {\n int[] dist = new int[N];\n Arrays.fill(dist, Integer.MAX_VALUE);\n dist[K - 1] = 0;\n for(int i = 1; i < N; i++)\n for(int[] e : times)\n if(dist[e[0] - 1] != Integer.MAX_VALUE && dist[e[1] - 1] > dist[e[0] - 1] + e[2])\n dist[e[1] - 1] = dist[e[0] - 1] + e[2];\n \n int maxwait = Arrays.stream(dist).max().getAsInt();\n return maxwait == Integer.MAX_VALUE ? -1 : maxwait;\n }\n}\n```\n\n************\n\n**Floyd Warshall **\n\n```\nclass Solution {\n public int networkDelayTime(int[][] times, int N, int K) {\n int MAX = 1000000;\n int[][] dist = new int[N][N];\n for(int i = 0; i < N; i++)\n Arrays.fill(dist[i], MAX);\n for(int i = 0; i < N; i++)\n dist[i][i] = 0;\n for(int[] e : times)\n dist[e[0] - 1][e[1] - 1] = e[2];\n \n for(int k = 0; k < N; k++)\n for(int i = 0; i < N; i++)\n for(int j = 0; j < N; j++) \n dist[i][j] = Math.min(dist[i][j], dist[i][k] + dist[k][j]);\n \n int maxwait = 0;\n for(int i = 0; i < N; i++)\n maxwait = Math.max(maxwait, dist[K - 1][i]);\n return maxwait == MAX ? -1 : maxwait;\n }\n}\n```
| 7
| 0
|
[]
| 0
|
network-delay-time
|
Go Dijkstra with Heap
|
go-dijkstra-with-heap-by-waydi1-15tt
|
\nimport "container/heap"\n\ntype Distance struct {\n W int\n V int\n}\n\ntype DistanceHeap []Distance\n\nfunc (h DistanceHeap) Len() int { return len(h)
|
waydi1
|
NORMAL
|
2021-01-04T09:01:43.837529+00:00
|
2021-01-04T09:01:43.837558+00:00
| 535
| false
|
```\nimport "container/heap"\n\ntype Distance struct {\n W int\n V int\n}\n\ntype DistanceHeap []Distance\n\nfunc (h DistanceHeap) Len() int { return len(h) }\nfunc (h DistanceHeap) Less(i, j int) bool { return h[i].W < h[j].W }\nfunc (h DistanceHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }\n\nfunc (h *DistanceHeap) Push(x interface{}) {\n *h = append(*h, x.(Distance))\n}\n\nfunc (h *DistanceHeap) Pop() interface{} {\n value := (*h)[len(*h)-1]\n *h = (*h)[:len(*h)-1]\n return value\n}\n\nfunc networkDelayTime(times [][]int, N int, K int) int {\n graph := map[int][]Distance{}\n \n for _, time := range times {\n u, v, w := time[0], time[1], time[2]\n graph[u] = append(graph[u], Distance{w, v})\n }\n \n q := &DistanceHeap{\n Distance{0, K},\n }\n \n arrivalTime := map[int]int{}\n \n for q.Len() > 0 {\n d := heap.Pop(q).(Distance)\n \n if _, ok := arrivalTime[d.V]; ok {\n continue\n }\n \n arrivalTime[d.V] = d.W\n \n for _, next := range graph[d.V] {\n next.W += d.W\n heap.Push(q, next)\n }\n }\n \n if len(arrivalTime) < N {\n return -1\n }\n \n maxTime := 0\n for _, v := range arrivalTime {\n if v > maxTime {\n maxTime = v\n }\n }\n \n return maxTime\n}\n```
| 7
| 0
|
['Go']
| 0
|
network-delay-time
|
Java | Dijkstra's algorithm & Fibonacci Heap explained
|
java-dijkstras-algorithm-fibonacci-heap-gwkeb
|
This question is a classic example for using Dijkstra\'s single-source shortest path finiding algorithm. But why is that?\n\nIntuition\nThe problem statement ma
|
levimor
|
NORMAL
|
2020-10-29T12:20:47.007345+00:00
|
2020-10-29T12:20:47.007378+00:00
| 1,548
| false
|
This question is a classic example for using Dijkstra\'s single-source shortest path finiding algorithm. But why is that?\n\n**Intuition**\nThe problem statement makes it clear that this is a graph problem, all we need to do is to decied which algorithm to use in order to solve it.\nSince we are dealling with weighted edges, *BFS* will not work here (unless all weights were equal, which really mean no weights at all).\n*DFS* won\'t cut it too (even if we wouldn\'t have any weights), since it doesn\'t find the shortest path.\nYou can use *Bellman-Ford* for this question, however it won\'t be optimal and it doesn\'t necessary given that all weights are positive integers (which is a classic hint for using Dijkstra).\nAnother option is *Floyd-Warshall*, but it isn\'t necessary either given that we have a single source.\n\nAfter we decided to use Dijkstra, we just need to add the functionality of tracking the longest path in the graph - which is the answer.\n\n**Fibonacci Heap**\nIf you pay close attention you would notice that in the worst case our heap will have O(E) nodes in it. Since we never poll out outdated paths from our heap and only offering new ones. That means we pay O(logE) for each heap.offer() call. A standard Priority Queue doesn\'t have the functionality of decreasing a key value. This is where Fibonacci heaps comes into play. Fibonacci Heaps have a decreasePriority in O(logN) where N is the heap size. With that we can secure the promise of O(ElogV) for Dijksta\'s algorithm.\nI haven\'t used Fibonacci Heap in my solution because the standard Java collections API does not contain an implementation of it, and implementing it during a real interview will be an overkill for this type of question. However I would definitely mention it. \n\n**Algorithm**\n```\nclass Solution {\n public int networkDelayTime(int[][] times, int N, int K) {\n Map<Integer, List<int[]>> adjacencyMap = new HashMap<>();\n for (int[] edge : times) {\n adjacencyMap.putIfAbsent(edge[0], new ArrayList<>());\n adjacencyMap.get(edge[0]).add(new int[]{edge[1], edge[2]});\n }\n \n Queue<int[]> heap = new PriorityQueue<>(\n (e1, e2) -> Integer.compare(e1[1], e2[1]));\n heap.offer(new int[]{K, 0});\n Map<Integer, Integer> distanceByNode = new HashMap<>();\n \n int elapsedTime = 0;\n while (!heap.isEmpty()) {\n int[] current = heap.poll();\n int node = current[0], distance = current[1];\n if (distanceByNode.containsKey(node)) continue;\n elapsedTime = Math.max(elapsedTime, distance);\n distanceByNode.put(node, distance);\n if (!adjacencyMap.containsKey(node)) continue;\n for (int[] edge : adjacencyMap.get(node)) {\n int neighbour = edge[0], weight = edge[1];\n if (distanceByNode.containsKey(neighbour)) continue;\n heap.offer(new int[]{neighbour, distance+weight});\n }\n }\n return distanceByNode.size() != N ? -1 : elapsedTime;\n }\n}\n```
| 7
| 1
|
['Heap (Priority Queue)', 'Java']
| 0
|
network-delay-time
|
Java BFS Solution
|
java-bfs-solution-by-jianhuilin1124-ll1z
|
\nclass Solution {\n public int networkDelayTime(int[][] times, int N, int K) {\n Map<Integer, Map<Integer, Integer>> map = new HashMap<>();\n
|
jianhuilin1124
|
NORMAL
|
2020-09-07T22:14:29.692762+00:00
|
2020-09-07T22:14:29.692871+00:00
| 803
| false
|
```\nclass Solution {\n public int networkDelayTime(int[][] times, int N, int K) {\n Map<Integer, Map<Integer, Integer>> map = new HashMap<>();\n for (int[] t : times) {\n int from = t[0];\n int to = t[1];\n int weight = t[2];\n map.putIfAbsent(from, new HashMap<>());\n map.get(from).put(to, weight);\n }\n int[] res = new int[N + 1];\n Arrays.fill(res, Integer.MAX_VALUE);\n res[K] = 0;\n Queue<int[]> queue = new ArrayDeque<>();\n queue.offer(new int[]{K, 0});\n while (!queue.isEmpty()) {\n int[] cur = queue.poll();\n int node = cur[0];\n int weight = cur[1];\n for (int next : map.getOrDefault(node, new HashMap<>()).keySet()) {\n int w = map.get(node).get(next);\n if (w + weight < res[next]) {\n res[next] = w + weight;\n queue.offer(new int[]{next, w + weight});\n }\n }\n }\n int max = 0;\n for (int i = 1; i <= N; ++i) {\n if (res[i] == Integer.MAX_VALUE) {\n return -1;\n }\n max = Math.max(max, res[i]);\n }\n return max;\n }\n}\n```
| 7
| 0
|
['Java']
| 1
|
network-delay-time
|
Swift solution with comments, very concise
|
swift-solution-with-comments-very-concis-mr3o
|
It uses a standard BFS and doesn\'t appear to need a priority queue. Please enlighten me if in any case a priority queue will help reduce the time. \nI love Swi
|
wds8807
|
NORMAL
|
2019-04-23T01:18:53.687571+00:00
|
2019-04-23T01:18:53.687601+00:00
| 380
| false
|
It uses a standard BFS and doesn\'t appear to need a priority queue. Please enlighten me if in any case a priority queue will help reduce the time. \nI love Swift language dealing with hashmaps in such a concise manner.\n```\nclass Solution {\n\tfunc networkDelayTime(_ times: [[Int]], _ N: Int, _ K: Int) -> Int {\n\t\t\n\t\tvar graph: [Int: [Int: Int]] = [:]\n\t\t\n\t\t/* Build graph: [source: [destination: weight]] */\n\t\tfor t in times {\n\t\t\tgraph[t[0], default: [:]][t[1]] = t[2]\n\t\t}\n\t\t\n\t\t/* Distance map: [node: distance from K to here] */\n\t\tvar distMap: [Int: Int] = [:]\n\t\tdistMap[K] = 0\n\t\tvar q: [(node: Int, dist: Int)] = []\n\t\t\n\t\tq.append((node: K, dist: 0))\n\t\t\n\t\twhile !q.isEmpty {\n\t\t\tlet curr = q.removeLast()\n\t\t\t\n\t\t\t/* Get all neighbors of current node from graph */\n\t\t\tguard let nexts = graph[curr.node] else { continue }\n\t\t\t\n\t\t\tfor (dest, weight) in nexts {\n\t\t\t\tif let distToNext = distMap[dest], curr.dist + weight >= distToNext {\n\t\t\t\t\t/* If there already exists a shorter distance to this neighbor,\n\t\t\t\t\t we do not update distance to this neighbor */\n\t\t\t\t\tcontinue\n\t\t\t\t}\n\t\t\t\t/* Update the distance to this neighbor\n\t\t\t\t/ Add this neighbor in the queue */\n\t\t\t\tdistMap[dest] = curr.dist + weight\n\t\t\t\tq.append((node: dest, dist: curr.dist + weight))\n\t\t\t}\n\t\t}\n\t\treturn distMap.count == N ? distMap.values.max() ?? -1 : -1\n\t}\n}\n\n```
| 7
| 0
|
[]
| 2
|
network-delay-time
|
Solution using Bellman-Ford shortest path algorithm
|
solution-using-bellman-ford-shortest-pat-iip1
|
My solution using Bellman-Ford algorithm to find the shortest paths. The max of the shortest path is the time it takes to reach all the nodes.\n\n\nclass Soluti
|
arvindrs
|
NORMAL
|
2019-01-17T02:12:40.869865+00:00
|
2019-01-17T02:12:40.869905+00:00
| 15,444
| false
|
My solution using Bellman-Ford algorithm to find the shortest paths. The max of the shortest path is the time it takes to reach all the nodes.\n\n```\nclass Solution {\n // TC = O(T * N), SC = O(N), T-> length of times\n // Using Bellman-Ford to find shortest paths from node K\n public int networkDelayTime(int[][] times, int N, int K) {\n int[] dist = new int[N];\n for (int i = 0; i < dist.length; i++)\n dist[i] = (int)1e9;\n dist[K - 1] = 0;\n for (int i = 0; i < N; i++) {\n for (int[] time: times) {\n if (dist[time[0] - 1] + time[2] < dist[time[1] - 1]) {\n dist[time[1] - 1] = dist[time[0] - 1] + time[2]; \n }\n } \n }\n if (Arrays.stream(dist).anyMatch(i -> i == (int)1e9)) return -1;\n return Arrays.stream(dist).max().orElse(-1);\n }\n}\n```
| 7
| 1
|
[]
| 5
|
network-delay-time
|
✅C++ || Bellman Ford || Easy Explanation || 🗓️ Daily LeetCoding Challenge May, Day 14
|
c-bellman-ford-easy-explanation-daily-le-tkff
|
Please Upvote If It Helps\n\n\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) \n {\n // just created a
|
mayanksamadhiya12345
|
NORMAL
|
2022-05-14T17:20:06.765467+00:00
|
2022-05-14T17:23:02.748595+00:00
| 405
| false
|
**Please Upvote If It Helps**\n\n```\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) \n {\n // just created a dis vector that will contain the distance for reaching nodes\n // and make dik[k] initially 0 because we will start dearching from k \n vector<int>dis(n+1,INT_MAX);\n dis[k]=0;\n \n // we are using here bellman ford algorithm\n // we will update our dis vector upto (n-1) times according to bellman\'s ford algo\n for(int i=1;i<n;i++)\n {\n // just checking for all the nodes that are available in our graph\n for(int j=0;j<times.size();j++)\n {\n // extracting the information form the current value\n int u=times[j][0]; // source\n int v=times[j][1]; // destination\n int w=times[j][2]; // weight\n \n // current source is not finite value then we can not pick that path \n \n // so just check current source is finite or not\n // and we are having better path for reaching V from U by using W\n if(dis[u]!=INT_MAX && dis[u]+w<dis[v])\n {\n // if we are having better path available then just update our dis\n dis[v]=w+dis[u];\n }\n }\n }\n\t\t \n // take out the best value to reach n from k\n int ans=0;\n for(int i=1;i<=n;i++)\n {\n // If any node is not reachable from k\n if(dis[i]==INT_MAX) \n return -1; \n \n // else take best\n ans=max(ans,dis[i]);\n }\n return ans;\n \n }\n};\n```
| 6
| 0
|
[]
| 0
|
network-delay-time
|
✅ [python] | Simple BFS approach
|
python-simple-bfs-approach-by-addejans-0rry
|
The Algorithm:\n Create an adjacency list from source to target nodes along with the weight of their edges\n Create a dictionary to keep track of the current sh
|
addejans
|
NORMAL
|
2022-05-14T03:34:49.553554+00:00
|
2022-05-14T03:34:49.553608+00:00
| 832
| false
|
**The Algorithm:**\n* Create an adjacency list from source to target nodes along with the weight of their edges\n* Create a dictionary to keep track of the current shortest time to traverse to each node in the graph (starting with infinity)\n* In a breadth first search (BFS) fashion, traverse neighbors starting at `k` until no new shortest times to a node are found\n* The maximum time to any given node after no new updates is the time it must take to traverse the whole network since each node in the network must be visited at least once\n* If the maximum is infinity, then it means that node was never updated and thus unreachable from starting node `k`\n\n---\n\n**The Code:**\n```\ndef networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:\n \n\t# establish graph and data structures\n\ttotal_time_to_reach_node = {i: float(\'inf\') for i in range(1, n+1)}\n\tgraph = defaultdict(list)\n\tfor src, target, time in times:\n\t\tif src in graph: \n\t\t\tgraph[src].append((target, time))\n\t\telse:\n\t\t\tgraph[src] = [(target, time)]\n\n\tqueue = [(k, 0)]\n\n\t# bfs until no new updates are made\n\twhile queue:\n\t\tsrc, total_time = queue.pop(0)\n\t\tif total_time < total_time_to_reach_node[src]:\n\t\t\ttotal_time_to_reach_node[src] = total_time\n\t\t\tfor target, time in graph[src]:\n\t\t\t\tqueue.append((target, total_time + time)) \n\n\t# if possible, return the total time to traverse network\n\ttime_to_traverse_network = max(total_time_to_reach_node.values())\n\tif time_to_traverse_network < float(\'inf\'):\n\t\treturn time_to_traverse_network\n\telse:\n\t\treturn -1\n```
| 6
| 0
|
['Breadth-First Search', 'Python']
| 0
|
network-delay-time
|
WITH EXPLAINATION POSSIBLE 2 SOLUTIONS IN c++
|
with-explaination-possible-2-solutions-i-846k
|
1.bellman Ford solution\n\n // Solution1: Bellman Ford or dfs\n // TC: O(nE), E = no. of edges\n // SC: O(n)\n int bellmanFord(vector<vector<int>>& ti
|
kkg2002
|
NORMAL
|
2022-05-14T00:32:14.959001+00:00
|
2022-05-14T00:35:10.293121+00:00
| 623
| false
|
1.bellman Ford solution\n```\n // Solution1: Bellman Ford or dfs\n // TC: O(nE), E = no. of edges\n // SC: O(n)\n int bellmanFord(vector<vector<int>>& times, int n, int k) {\n // delay[i] = time to reach kth node\n vector<int> delay(n+1, INT_MAX);\n // we start from node kth node as source, all other nodes are destinations\n delay[k] = 0;\n \n for(int i = 0; i < n; i++) {\n for(auto edge: times) {\n // delay[dst] > delay[src] + wt\n delay[edge[1]] = min(delay[edge[1]], \n delay[edge[0]] == INT_MAX ? INT_MAX : delay[edge[0]] + edge[2]);\n }\n }\n // 0th element is dummy, so skip . Find the max delay time, this will decide the overall delay\n int max_delay = *max_element(delay.begin() + 1, delay.end());\n \n return max_delay == INT_MAX ? -1 : max_delay;\n }\n\t int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n return bellmanFord(times, n, k);\n }\n```\nOPTIMISE SOLUTION\n\n2.djikstra solution\n```\nint djikstra(vector<vector<int>>& times, int n, int k) {\n // create graph, 0th node is dummy\n // node: <dst, time>\n vector<vector<pair<int, int> > > g(n+1);\n \n for(auto edge: times) \n g[edge[0]].emplace_back(make_pair(edge[1], edge[2]));\n \n // delay[i] = min time to reach kth node\n vector<int> delay(n+1, INT_MAX);\n \n auto comp = [&](const array<int, 2>& a, const array<int, 2>& b) { return a[1] >= b[1]; }; \n // <node, time>\n priority_queue<array<int, 2>, vector<array<int, 2>>, decltype(comp)> min_heap(comp);\n min_heap.push({k, 0});\n // starting dist will be 0\n delay[k] = 0;\n \n while(!min_heap.empty()) {\n auto [curr, curr_time] = min_heap.top();\n min_heap.pop();\n \n if(delay[curr] > curr_time)\n continue;\n \n for(auto [dst, t]: g[curr]) {\n if(delay[dst] > delay[curr] + t) {\n delay[dst] = delay[curr] + t;\n min_heap.push({dst, delay[curr] + t});\n }\n }\n }\n \n int max_delay = *max_element(delay.begin() + 1, delay.end());\n return max_delay == INT_MAX ? -1 : max_delay;\n }\n \n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n return djikstra(times, n, k);\n }\n};\n// TC: O(ElogE) + O(V+E)\n```
| 6
| 0
|
['Depth-First Search', 'C']
| 0
|
network-delay-time
|
JavaScript Solution - Dijkstra's algorithm
|
javascript-solution-dijkstras-algorithm-7bshl
|
Runtime: 100 ms, faster than 92.92% of JavaScript online submissions for Network Delay Time.\nMemory Usage: 47.1 MB, less than 53.54% of JavaScript online submi
|
godscode
|
NORMAL
|
2021-12-21T13:07:50.043815+00:00
|
2021-12-21T13:07:50.043856+00:00
| 1,133
| false
|
Runtime: 100 ms, faster than 92.92% of JavaScript online submissions for Network Delay Time.\nMemory Usage: 47.1 MB, less than 53.54% of JavaScript online submissions for Network Delay Time.\n\n```\nvar networkDelayTime = function(times, n, k) {\n let graph = {};\n let costs = {};\n let parents = {};\n let processed = {};\n let processedCounter = 0;\n \n for (let time of times) {\n if (!graph[time[0]]) {\n graph[time[0]] = {};\n } \n graph[time[0]][time[1]] = time[2];\n \n }\n \n for (let i = 1; i <= n; i++) {\n costs[i] = Infinity;\n processed[i] = false;\n }\n costs[k] = 0;\n \n node = k;\n \n while (node !== -1) {\n let cost = costs[node];\n let neighbours = graph[node];\n for (let neighbor in neighbours) {\n let newCostOfNeighbor = cost + neighbours[neighbor];\n if (newCostOfNeighbor < costs[neighbor]) {\n costs[neighbor] = newCostOfNeighbor;\n parents[neighbor] = node;\n }\n }\n processed[node] = true;\n processedCounter++;\n node = findLowestCostNode(costs)\n } \n \n function findLowestCostNode(costs) {\n lowestCost = Infinity;\n lowestCostNode = -1;\n for (let node in costs) {\n cost = costs[node];\n if (cost < lowestCost && !processed[node]) {\n lowestCost = cost;\n lowestCostNode = node;\n }\n }\n return lowestCostNode;\n }\n \n if (processedCounter !== n) return -1;\n\n let set = new Set();\n for (let node in costs) {\n\t set.add(costs[node]);\n }\n let max = Math.max(...set);\n \n return max;\n};\n```
| 6
| 0
|
['JavaScript']
| 1
|
network-delay-time
|
Need help with a test case, what am I missing? [[1,2,1],[2,1,3]] 2 2
|
need-help-with-a-test-case-what-am-i-mis-5r5u
|
Greetings,\n\nI want to understand this specific test case. The expected return value is 3, but from where I sit, I think it should be 4.\n\n\n[[1,2,1],[2,1,3]]
|
TGPSKI
|
NORMAL
|
2021-04-06T22:38:36.311099+00:00
|
2021-04-06T22:40:11.150732+00:00
| 131
| false
|
Greetings,\n\nI want to understand this specific test case. The expected return value is 3, but from where I sit, I think it should be 4.\n\n```\n[[1,2,1],[2,1,3]]\n2\n2\n```\n\nThis adj list describes a network of two nodes, 1 and 2. \n\n1 -> 2 at a delay of 1, and 2 -> 1 at a delay of 3. The signal input node is 2, and the signal output node is 2. \n\nHow long does it take a signal input at node 2 to reach node 2? The answer must be 0 or 4. From 2, you can travel to 1 at a cost of 3, but the signal is now at node 1 and has to return to node 2 with an additional delay of 1. Or, you could take the case that when a signal is input to node 2, node 2 has the signal and no additional travel is required, so the answer is 0.\n\nWhat am I doing wrong here? How can one come up with a return value of 3?\n
| 6
| 0
|
[]
| 2
|
network-delay-time
|
JavaScript Clean, Easy Bellman-Ford 97% | 91%
|
javascript-clean-easy-bellman-ford-97-91-36io
|
\n\n\n\nfunction networkDelayTime(times, N, K) {\n //Initialize array to track times to each node from start node.\n const time = Array(N).fill(Infinity);\n
|
casmith1987
|
NORMAL
|
2021-03-11T16:24:24.696440+00:00
|
2021-09-24T22:32:06.231757+00:00
| 427
| false
|
\n\n\n```\nfunction networkDelayTime(times, N, K) {\n //Initialize array to track times to each node from start node.\n const time = Array(N).fill(Infinity);\n //Initialize Start node to be 0 since signal begins here.\n //The -1 here and below is so node value === index value\n //in time array\n time[K-1] = 0;\n let changed = true;\n //Iterate through signal times lowering time-to-node each iteration\n //until no changes are made to time array. Best possible\n //times to node at index from start node will then be stored \n //in time array.\n while (changed) {\n changed = false;\n for (let [node1, node2, timeToNode] of times) {\n\t node1--, node2--;\n\t //If time to first node === Infinity, we haven\'t figured out\n\t //How to reach this node yet. Continue until we have.\n if (time[node1] === Infinity) continue;\n if (time[node2] > time[node1] + timeToNode) {\n time[node2] = time[node1] + timeToNode;\n changed = true;\n }\n }\n }\n \n //Return maximum time in time array since this is how long\n //it will take for signal to reach last node.\n let res = Math.max(...time)\n //If max time is infinity, at least one node cannot be reached, return -1.\n //Else return max value from time array.\n return res === Infinity ? -1 : res;\n};\n```
| 6
| 0
|
['JavaScript']
| 0
|
network-delay-time
|
C++ // DIJKSTRA // PRIORITY_QUEUE nothing more than that
|
c-dijkstra-priority_queue-nothing-more-t-f9rb
|
\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int N, int K) {\n // nodes from 1 to N\n\t vector<vector<pair<int,int>>>
|
seonwoo960000
|
NORMAL
|
2021-01-04T04:28:53.223956+00:00
|
2021-01-04T04:28:53.223980+00:00
| 494
| false
|
```\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int N, int K) {\n // nodes from 1 to N\n\t vector<vector<pair<int,int>>> graph(N+1);\n\t // table is to store time it takes from node K \n vector<int> table(N+1, INT_MAX);\n // starts from K\n\t table[K] = 0;\n \n\t // making graph\n for (auto vec : times) {\n int u = vec[0], v = vec[1], w = vec[2];\n graph[u].push_back(make_pair(v, w));\n }\n \n\t // maybe this question is checking us if we know the usage of priority queue\n\t // the priority queue will sort(in not increasing order) based on time from K node \n priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>>> pq;\n pq.push(make_pair(0, K));\n \n while (!pq.empty()) {\n int cur_dis = pq.top().first;\n int cur_node = pq.top().second;\n pq.pop();\n \n for (int i=0; i<graph[cur_node].size(); i++) {\n int next_node = graph[cur_node][i].first;\n int next_weight = graph[cur_node][i].second;\n \n\t\t // add node to priority queue whenever the time recorded is larger than currently computed time\n if (table[next_node] > table[cur_node] + next_weight) {\n table[next_node] = table[cur_node] + next_weight;\n pq.push(make_pair(table[next_node], next_node));\n }\n }\n }\n \n int result = 0;\n\t // checking if there is unvisited node and the maximum result for our question\n for (int i=1; i<=N; i++) {\n if (table[i] == INT_MAX) return -1;\n if (table[i] > result) result = table[i]; \n }\n \n return result;\n }\n};\n```
| 6
| 0
|
['C', 'Heap (Priority Queue)', 'C++']
| 1
|
network-delay-time
|
Djikstra : CLRS Implementation : O((E+V) Log V)
|
djikstra-clrs-implementation-oev-log-v-b-u6zz
|
I came across several implementaiton of the Djikstra\'s while browsing through LeetCode disccuss. Most of the people have implemented Djikstra which is very sim
|
codiberal
|
NORMAL
|
2020-06-14T11:45:58.277264+00:00
|
2020-06-14T11:45:58.277305+00:00
| 579
| false
|
I came across several implementaiton of the Djikstra\'s while browsing through LeetCode disccuss. Most of the people have implemented Djikstra which is very similar to BFS but is different from the version mentioned in CLRS. Also, that implementation involves enqueuing element more than once in priority queue, though the later occurence of same element are tackled using maintaining a visited array.\n```\nclass Solution {\n public int networkDelayTime(int[][] times, int N, int K) {\n List<int[]>[] graph = new List[N+1];\n for(int i=1;i<=N;i++)\n graph[i]=new ArrayList<>();\n for(int[] time : times)\n graph[time[0]].add(new int[]{time[1],time[2]});\n return djikstra(graph,N,K);\n }\n public int djikstra(List<int[]>[] graph, int n, int k){\n int[] dist = new int[n+1];\n Arrays.fill(dist,Integer.MAX_VALUE);\n dist[k]=0;\n TreeSet<Integer> q = new TreeSet<>((a,b) -> dist[a]!=dist[b]?dist[a]-dist[b]:a-b);//Sotring indices instead of distance, also when distances are same we compare based on index, it allows more than one vertex to have same distance.\n for(int i=1;i<=n;i++)\n q.add(i);\n int res=0;\n while(!q.isEmpty()){\n int u = q.pollFirst();\n res=Math.max(res,dist[u]);\n for(int[] vertex : graph[u]){\n int v = vertex[0];\n int w = vertex[1];\n if(dist[v]>dist[u]+w){\n q.remove(v);//removing and reinserting to ensure elements in treeset remain sorted\n dist[v]=dist[u]+w;\n q.add(v);\n }\n }\n\n }\n return res==Integer.MAX_VALUE?-1:res;\n }\n}\n\n```\n\nComplexity Anaylysis : \nV : number of vertices, E : number of edges\n1. Leave aside the for loop inside while for the moment, remaining statement takes O(log V) for q.pollFirst() + Constant time, thsi poll operation happens at most V time => Time Complexity = O(v log v)\n2. Aggregate Analysis of inner for loop(inside while) : Here we are basically going through adjacency list of all vertices, that mean it will get executed E times, also each iteration will take O(log V) time.\n=>Time Complexity = O(E Log V)\n3. Overall Time Complexity : O((E+V) Log V))
| 6
| 0
|
[]
| 2
|
network-delay-time
|
C++ | Dijkstra's Algorithm
|
c-dijkstras-algorithm-by-rohitmahajan281-02su
|
\nclass Solution {\n\tpublic:\n\t\t int networkDelayTime(vector<vector<int>>& times, int N, int K) {\t\n\t\t // smallest element will be on top (as we require
|
rohitmahajan2810
|
NORMAL
|
2020-06-11T20:23:15.142411+00:00
|
2020-06-13T15:58:25.307635+00:00
| 422
| false
|
```\nclass Solution {\n\tpublic:\n\t\t int networkDelayTime(vector<vector<int>>& times, int N, int K) {\t\n\t\t // smallest element will be on top (as we require to choose next smallest distace node to select)\n\t\t // Node (u,v,w) : u=>v with weight as w\n\t\t // pq(min_distace of vertex v, v)\n\t\t priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>>pq;\n\t\t // as node range from (1,N)\n\t\t // initialize all distance as infinity excluding starting vertex \n\t\t vector<int>dist(N+1, INT_MAX);\n\t\t // as we are starting from vertex K so its distance is considered as 0\n\t\t pq.push(make_pair(0, K));\n\t\t dist[K] = 0;\n\n\t\t // Creating adjacency list from given times \n\t\t unordered_map<int, vector<pair<int, int>>>adj;\n\t\t for (int i = 0; i < times.size(); i++)\n\t\t\t adj[times[i][0]].push_back(make_pair(times[i][1], times[i][2]));\n\t\t // times = [[2,1,1],[2,3,1],[3,4,1]]\n\t\t // adj = 2=>{(1,1), (3,1)}, 3=>{(4,1)}\n\n\t\t // Till we visited all the vertex in the graph\n\t\t while (!pq.empty()) {\n\t\t\t pair<int, int>p = pq.top();\n\t\t\t pq.pop();\n\t\t\t int u = p.second;\n\t\t\t // Main Dijistra\'s Algorithm starts here updating distance of each vertex to minimum\n\t\t\t for (auto it = adj[u].begin(); it != adj[u].end(); it++) {\n\t\t\t\tint v = it->first;\n\t\t\t\tint w = it->second;\n\t\t\t\tif (dist[v] > dist[u] + w) {\n\t\t\t\t\t\tdist[v] = dist[u] + w;\n\t\t\t\t\t\tpq.push(make_pair(dist[v], v));\n\t\t\t\t}\n\t\t\t }\n\t\t\t}\n\n\t\t // Maximum value of dist will be the max value of time taken to visit all vertex in graph\n\t\t int t = 0;\n\t\t for (int i = 1; i <= N; i++)\n\t\t\t t = max(t, dist[i]);\n\n\t\t // if not possible return -1 else return t \n\t\t return t == INT_MAX ? -1 : t;\n\t\t}\n\t};\n```
| 6
| 0
|
[]
| 0
|
network-delay-time
|
Readable Dijkstra's - Java - Pure template based
|
readable-dijkstras-java-pure-template-ba-877o
|
What is Dijkstra\'s Algorithm (we call it D.A here) and why do we care here ?\n\n1. D.A is an algorithm to find hte shortest distance from 1 ROOT NODE to ALL OT
|
bordoisila
|
NORMAL
|
2020-04-24T15:17:46.919062+00:00
|
2020-04-24T18:54:08.111205+00:00
| 694
| false
|
**What is Dijkstra\'s Algorithm (we call it D.A here) and why do we care here ?**\n\n1. D.A is an algorithm to find hte shortest distance from 1 ROOT NODE to ALL OTHER ROOT NODES in a GRAPH. \n2. Think about finding the shortest distance from San Jose to San Francisco, Los Angeles and Fremont in a Graph of 4 Cities [San Jose, San Francisco, Los Angeles, Fremont] \n3. If we have the starting City given and the distance between some cities in a Connected Manner ( path from any city A to any city B exists in some manner ) we should be able to calculate the Shortest Distance. \n4. We can ALSO COLLECT THE CITIES in the shortest paths but we dont care currently\n\n**How is it related to this question?**\n\n1. We have a source network node ( San Jose )\n2. We have many destination nodes ( Other cities )\n3. We are calculating the shortest time to propagate info from source to ALL other nodes ( Shortest distance from San Jose to others and then MAX of the Shortest Distances or times taken gives the EVENTUAL TIME TAKEN to propagate the messages from ROOT NODE to the LAST NODE )\n\n**What do we do then ?**\n\n1. Have a set of visited nodes which is initially empty\n```visited = {}```\n2. Have a Graph built from the provided times array as : \n```\nu = times[i][0] //Source\nv = times[i][1] // Destination\nw = times[i][2] // Edge Weight - Distance - time -> Anything you wanna call it\n\nGraph = [{u, [v, w]}, {u2, [v2, w2]}...)\n```\n3. Maintain a distance array that contains the distances of ALL nodes from the root K. This means distance[K] = 0\n```\nArrays.fill(distance, Integer.MAX_VALUE) // Initially infinite distance\ndistance[K] = 0; // Root to Root is 0\ndistance[0] = 0; //There is no node called 0 and we just set it to 0 to prevent calculations. \n//If you are starting you nodes with 0 itself, make sure you calculate all nodes n as distance[n - 1]. \n//We will start from 1. So, ignore distance[0];\n```\n4. Create min heap to prioritize based on least distance from ROOT\n```\nComparator.comparing(node -> node[1]) where it will be the distace\n```\n5. Now, offer to the heap the ROOT with distance to itself as 0\n```\nheap.offer(new int[]{K, 0});\n```\n6. Now, for every item in the heap, repeat the following : \n```\ncurrent_source = heap.poll();\ndistance_from_root_to_current_source = current_source[1]; // Based on values offered to heap\nif(not_visited_current_source) {\n\t//for all neighbors of current source \n\t//if neighbor not visited as well\n\t//distance[neighbor] = Math.min(distance[neighbor], distance_from_root_to_current_source + weight of edge from u to current neighbor\n\theap.offer(new int[]{current_neighbor, distance[neighbor] });\n}\n```\n7. Now, return the MAX value from distance array as it is the max time taken to send signal to the LAST NODE from the ROOT only if all nodes have been visited. Else return - 1\n\n**CODE BELOW**\n```\nclass Solution {\n public int networkDelayTime(int[][] times, int N, int K) {\n if(N == 0 || K < 1 || K > N || times == null || times.length == 0) return 0;\n \n int[] distance = new int[N + 1];\n int[] visited = new int[N + 1];\n PriorityQueue<int[]> heap = new PriorityQueue<>(Comparator.comparing(a -> a[1]));\n Map<Integer, List<int[]>> graph = new HashMap<>();\n \n Arrays.fill(distance, Integer.MAX_VALUE);\n distance[K] = 0;\n distance[0] = 0;\n \n for(int i = 0; i < times.length; i++) {\n List<int[]> neighbors = graph.getOrDefault(times[i][0], new LinkedList<>());\n neighbors.add(new int[]{times[i][1], times[i][2]});\n graph.put(times[i][0], neighbors);\n }\n \n heap.offer(new int[]{K, 0});\n \n while(!heap.isEmpty()) {\n int u = heap.peek()[0];\n int distUFromRoot = heap.poll()[1];\n if(visited[u] == 1) continue;\n visited[u] = 1;\n \n if(graph.containsKey(u)) {\n for(int[] neighbor : graph.get(u)) {\n int v = neighbor[0];\n int w = neighbor[1];\n if(visited[v] == 0) {\n int newDistanceVFromRoot = Math.min(distance[v], w + distUFromRoot);\n distance[v] = newDistanceVFromRoot;\n heap.offer(new int[]{v, newDistanceVFromRoot});\n }\n }\n }\n }\n \n for(int i = 1; i <= N; i++) {\n if(visited[i] == 0) return -1;\n }\n \n return Arrays.stream(distance).max().getAsInt();\n }\n}
| 6
| 0
|
[]
| 1
|
network-delay-time
|
[Java] DijkstraSP using IndexMinPQ with time complexity O(ElogV)
|
java-dijkstrasp-using-indexminpq-with-ti-fjws
|
If you use a built-in PriorityQueue to implements dijkstra shortest path algorithm, the time complexity will be O(ElogE), since you may add several edges with d
|
zmy3324
|
NORMAL
|
2020-04-08T12:28:58.216281+00:00
|
2020-04-08T12:28:58.216330+00:00
| 497
| false
|
If you use a built-in PriorityQueue to implements dijkstra shortest path algorithm, the time complexity will be O(ElogE), since you may add several edges with different distances. By using the indexMinPQ, you could avoid the duplicates and get a O(ElogV). The runtime also improves from [31ms](https://leetcode.com/problems/network-delay-time/discuss/210698/Java-Djikstrabfs-Concise-and-very-easy-to-understandp://)(test from the most voted dijkstra solution) to 8ms.\n\n```\nclass Solution {\n public int networkDelayTime(int[][] times, int n, int k) {\n List<Pair<Integer, Integer>>[] g = new List[n];\n for (int i = 0; i < n; i++) g[i] = new ArrayList<>();\n for (int[] edge : times) {\n g[edge[0] - 1].add(new Pair(edge[1] - 1, edge[2]));\n }\n IndexMinPQ<Integer> pq = new IndexMinPQ(n);\n pq.insert(k - 1, 0);\n int[] distTo = new int[n];\n Arrays.fill(distTo, Integer.MAX_VALUE);\n distTo[k - 1] = 0;\n while (!pq.isEmpty()) {\n int idx = pq.delMin();\n int dist = distTo[idx];\n for (Pair<Integer, Integer> next : g[idx]) {\n int nidx = next.getKey();\n int ndist = next.getValue() + dist;\n if (ndist< distTo[nidx]) {\n distTo[nidx] = ndist;\n if (!pq.contains(nidx)) pq.insert(nidx, ndist);\n else pq.decreaseKey(nidx, ndist);\n }\n }\n }\n int ans = 0;\n for (int dist : distTo) ans = Math.max(ans, dist);\n return ans == Integer.MAX_VALUE ? -1 : ans;\n }\n}\n\nclass IndexMinPQ<Key extends Comparable<Key>> {\n private int maxN; // maximum number of elements on PQ\n private int n; // number of elements on PQ\n private int[] pq; // binary heap using 1-based indexing\n private int[] qp; // inverse of pq - qp[pq[i]] = pq[qp[i]] = i\n private Key[] keys; // keys[i] = priority of i\n\n public IndexMinPQ(int maxN) {\n if (maxN < 0) throw new IllegalArgumentException();\n this.maxN = maxN;\n n = 0;\n keys = (Key[]) new Comparable[maxN + 1];\n pq = new int[maxN + 1];\n qp = new int[maxN + 1]; \n for (int i = 0; i <= maxN; i++)\n qp[i] = -1;\n }\n \n public boolean isEmpty() {\n return n == 0;\n }\n\n public boolean contains(int i) {\n return qp[i] != -1;\n }\n\n public int size() {\n return n;\n }\n\n public void insert(int i, Key key) {\n n++;\n qp[i] = n;\n pq[n] = i;\n keys[i] = key;\n swim(n);\n } \n \n public int minIndex() {\n return pq[1];\n }\n\n public Key minKey() {\n return keys[pq[1]];\n }\n\n public int delMin() {\n int min = pq[1];\n exch(1, n--);\n sink(1);\n assert min == pq[n+1];\n qp[min] = -1; // delete\n keys[min] = null; // to help with garbage collection\n pq[n+1] = -1; // not needed\n return min;\n }\n \n public void decreaseKey(int i, Key key) {\n keys[i] = key;\n swim(qp[i]);\n }\n \n private boolean greater(int i, int j) {\n return keys[pq[i]].compareTo(keys[pq[j]]) > 0;\n }\n\n private void exch(int i, int j) {\n int swap = pq[i];\n pq[i] = pq[j];\n pq[j] = swap;\n qp[pq[i]] = i;\n qp[pq[j]] = j;\n }\n\n private void swim(int k) {\n while (k > 1 && greater(k/2, k)) {\n exch(k, k/2);\n k = k/2;\n }\n }\n\n private void sink(int k) {\n while (2*k <= n) {\n int j = 2*k;\n if (j < n && greater(j, j+1)) j++;\n if (!greater(k, j)) break;\n exch(k, j);\n k = j;\n }\n }\n}\n```
| 6
| 0
|
[]
| 1
|
network-delay-time
|
Python - Dijkstra
|
python-dijkstra-by-cool_shark-6g3h
|
py\n\nclass Solution:\n def networkDelayTime(self, times: List[List[int]], N: int, K: int) -> int:\n \n\t\t# build graph\n g = collections.defa
|
cool_shark
|
NORMAL
|
2020-02-13T15:18:14.416485+00:00
|
2020-02-13T15:31:12.275228+00:00
| 698
| false
|
```py\n\nclass Solution:\n def networkDelayTime(self, times: List[List[int]], N: int, K: int) -> int:\n \n\t\t# build graph\n g = collections.defaultdict(list)\n for u, v, cost in times:\n g[u].append((cost,v))\n \n min_heap = [(0, K)] # cost, u\n visited = set()\n distance = {i:float(\'inf\') for i in range(1, N+1)}\n distance[K] = 0\n while min_heap:\n cost, u = heapq.heappop(min_heap)\n if u in visited:\n continue\n visited.add(u)\n if len(visited) == N: # Found!\n return cost\n \n for cost2, v in g[u]:\n if cost + cost2 < distance[v] and v not in visited:\n distance[v] = cost + cost2\n heapq.heappush(min_heap, (cost + cost2, v))\n return -1\n \n```
| 6
| 0
|
[]
| 2
|
network-delay-time
|
[Python] Dijkstra || Bellman-Ford || Floyd-Warshall
|
python-dijkstra-bellman-ford-floyd-warsh-73ei
|
Dijkstra\nTime: O(ElogV)\nSpace: O(V+E)\n\n- Single Source Shortest Path\n- Finds the shortest path from one node to all other nodes. \n- A greedy algorithm th
|
teampark
|
NORMAL
|
2020-02-10T23:25:38.227426+00:00
|
2020-02-10T23:29:17.810948+00:00
| 540
| false
|
**Dijkstra**\nTime: ```O(ElogV)```\nSpace: ```O(V+E)```\n\n- Single Source Shortest Path\n- Finds the shortest path from one node to all other nodes. \n- A greedy algorithm that works by always exploring the shortest available path first. \n```\nclass Solution(object):\n\n def networkDelayTime(self, times, N, K):\n adj_list = self.get_adj_list(times, N)\n heap = [(0, K)]\n distance_from_k = {}\n \n while heap:\n curr_dist, curr_node = heapq.heappop(heap)\n distance_from_k[curr_node] = curr_dist\n if len(distance_from_k) == N:\n break\n for neighbor, weight in adj_list[curr_node]:\n if neighbor not in distance_from_k:\n heapq.heappush(heap, (curr_dist + weight, neighbor))\n \n return max(distance_from_k.values()) if len(distance_from_k) == N else -1\n \n def get_adj_list(self, times, N):\n temp = {i:[] for i in range(1,N+1)}\n for node1, node2, weight in times:\n temp[node1].append((node2, weight))\n return temp \n```\n\n**Bellman Ford**\nTime: ```O(VE)```\nSpace: ```O(V)```\n\n- Single Source Shortest Path \n- A Dynamic Programming algorithm that can handle negative edge weights\n```\n def networkDelayTime(self, times, N, K):\n\t\tdistance = {i:float(\'inf\') for i in range(1, N+1)}\n\t\tdistance[K] = 0 \n\t\t\n\t\tfor _ in range(N-1):\n\t\t\tfor node1, node2, weight in times:\n\t\t\t\tif distance[node1] + weight < distance[node2]:\n\t\t\t\t\tdistance[node2] = distance[node1] + weight\n\t\treturn max(distance.values()) if max(distance.values()) != float(\'inf\') else -1 \n```\n\n**Floyd-Warshall**\nTime: ```O(n^3)```\nSpace: ```O(n^2)```\n\n- All Pairs Shortest Path\n- Finds the shortest path between all pairs of nodes\n```\n def networkDelayTime(self, times, N, K):\n\t\t# Initial Matrix Setup\n matrix = [[float(\'inf\') for _ in range(N)] for _ in range(N)]\n \n for node1, node2, weight in times:\n matrix[node1-1][node2-1] = weight\n \n for i in range(len(matrix)):\n matrix[i][i] = 0 \n \n\t\t# Actual Iteration and Finding of Shortest Path\n for k in range(N):\n for node1 in range(N):\n for node2 in range(N):\n matrix[node1][node2] = min(matrix[node1][node2], matrix[node1][k] + matrix[k][node2])\n \n\t\treturn max(matrix[K-1]) if max(matrix[K-1]) != float(\'inf\') else -1\n```
| 6
| 0
|
[]
| 0
|
network-delay-time
|
Simple Python BFS solution
|
simple-python-bfs-solution-by-otoc-2yvc
|
\n def networkDelayTime(self, times: List[List[int]], N: int, K: int) -> int:\n graph = [dict() for _ in range(N + 1)]\n for u, v, w in times:\
|
otoc
|
NORMAL
|
2019-09-25T17:52:09.284494+00:00
|
2019-09-25T17:52:09.284542+00:00
| 572
| false
|
```\n def networkDelayTime(self, times: List[List[int]], N: int, K: int) -> int:\n graph = [dict() for _ in range(N + 1)]\n for u, v, w in times:\n graph[u][v] = w\n finished = [float(\'inf\') for _ in range(N + 1)]\n # BFS visit\n curr_level = {K}\n finished[0], finished[K] = 0, 0\n while curr_level:\n next_level = set()\n for u in curr_level:\n for v in graph[u]:\n if finished[v] > finished[u] + graph[u][v]:\n finished[v] = finished[u] + graph[u][v]\n next_level.add(v)\n curr_level = next_level\n t = max(finished)\n return t if t != float(\'inf\') else -1\n```
| 6
| 0
|
[]
| 0
|
network-delay-time
|
Dijkstra’s Algorithm || Priority Queue || BFS || Explanation || Complexities
|
dijkstras-algorithm-priority-queue-bfs-e-wmen
|
IntuitionWe need to determine the shortest time required for a signal to reach all nodes in a network. This problem is similar to finding the shortest path in a
|
Anurag_Basuri
|
NORMAL
|
2025-02-01T08:14:14.603242+00:00
|
2025-02-01T08:14:14.603242+00:00
| 1,363
| false
|
## **Intuition**
We need to determine the shortest time required for a signal to reach all nodes in a network. This problem is similar to finding the **shortest path** in a weighted graph, where each edge represents the travel time.
The best approach to solve this problem is **Dijkstra’s Algorithm**, which efficiently finds the shortest path from a single source to all other nodes.
---
## **Approach**
1. **Graph Representation:**
- Convert the list of `times` into an **adjacency list**, where each node stores its neighbors and the corresponding travel time.
- Since node numbers start from `1` to `n`, we use **1-based indexing**.
2. **Dijkstra’s Algorithm with Min-Heap (Priority Queue):**
- Use a **min-heap (priority queue)** to always process the node with the **smallest known delay** first.
- Start from node `k`, initializing its delay to `0`.
- Maintain a `network[]` array to store the **shortest time** to reach each node, initialized to `∞` (a large value).
3. **Process Nodes Efficiently:**
- Extract the node with the **smallest current delay** from the heap.
- Update its neighbors if a **shorter** travel time is found.
- Push the updated node into the heap for further processing.
4. **Find the Maximum Time:**
- Once all reachable nodes are processed, the **maximum value** in `network[]` gives the total delay time.
- If any node remains `∞`, return `-1` as it's **not reachable**.
---
## **Algorithm Name**
This problem is solved using **Dijkstra’s Algorithm** with a **Min-Heap (Priority Queue)** for efficiency.
---
## **Complexity Analysis**
### **Time Complexity:**
- **Graph Construction:** \(O(E)\), where \(E\) is the number of edges.
- **Dijkstra’s Algorithm:**
- Each node is processed once: \(O(N)\).
- Each edge is relaxed once: \(O(E)\).
- The priority queue operations take \(O(log N)\).
- **Overall Complexity:** O((N + E) log N), where \(N\) is the number of nodes and \(E\) is the number of edges.
### **Space Complexity:**
- **Adjacency list storage:** \(O(N + E)\).
- **Priority queue storage:** \(O(N)\).
- **Distance array:** \(O(N)\).
- **Overall Complexity:** \(O(N + E)\).
---
## **Edge Cases Considered**
✅ **Disconnected Nodes:** If any node is unreachable, return `-1`.
✅ **Single Node Case:** If `n == 1`, return `0`.
✅ **All Nodes Connected:** The algorithm efficiently finds the shortest delay time.
✅ **Multiple Paths:** The algorithm correctly updates nodes only when a shorter path is found.
This ensures the solution is **robust and efficient** for all cases. 🚀
# Code
```cpp []
class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
// Create adjacency list representation of the graph
vector<vector<pair<int, int>>> adj(n + 1); // Using 1-based indexing
for (const auto& time : times)
adj[time[0]].push_back({time[1], time[2]});
// Min-heap (priority queue) to always process the shortest known path first
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
pq.push({0, k}); // {current time, current node}
// Distance array to store the shortest time to each node
vector<int> network(n + 1, INT_MAX);
network[k] = 0;
while (!pq.empty()) {
auto [cur_time, cur] = pq.top();
pq.pop();
// Explore all adjacent nodes
for (const auto& [new_cur, weight] : adj[cur]) {
int new_time = cur_time + weight;
if (new_time < network[new_cur]) {
network[new_cur] = new_time;
pq.push({new_time, new_cur});
}
}
}
// Find the maximum delay time among all reachable nodes
int min_time = 0;
for (int i = 1; i <= n; i++) {
if (network[i] == INT_MAX) return -1; // If any node is unreachable
min_time = max(min_time, network[i]);
}
return min_time;
}
};
```
```java []
class Solution {
public int networkDelayTime(int[][] times, int n, int k) {
// Create adjacency list representation of the graph
ArrayList<ArrayList<int[]>> adj = new ArrayList<>();
for (int i = 0; i <= n; i++) // Using 1-based indexing
adj.add(new ArrayList<>());
// Fill adjacency list with edges
for (int[] time : times)
adj.get(time[0]).add(new int[]{time[1], time[2]});
// Min-heap (priority queue) to always process the shortest known path first
PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] - b[0]);
pq.add(new int[]{0, k}); // {current time, current node}
// Distance array to store the shortest time to each node
int[] network = new int[n + 1];
Arrays.fill(network, Integer.MAX_VALUE);
network[k] = 0;
while (!pq.isEmpty()) {
int[] top = pq.poll();
int cur_time = top[0], cur = top[1];
// Explore all adjacent nodes
for (int[] time : adj.get(cur)) {
int new_cur = time[0];
int new_time = cur_time + time[1];
if (new_time < network[new_cur]) {
network[new_cur] = new_time;
pq.add(new int[]{new_time, new_cur});
}
}
}
// Find the maximum delay time among all reachable nodes
int min_time = 0;
for (int i = 1; i <= n; i++) {
if (network[i] == Integer.MAX_VALUE) return -1; // If any node is unreachable
min_time = Math.max(min_time, network[i]);
}
return min_time;
}
}
```
``` python []
class Solution:
def networkDelayTime(self, times: list[list[int]], n: int, k: int) -> int:
# Create adjacency list representation of the graph
adj = {i: [] for i in range(1, n + 1)} # Using 1-based indexing
for u, v, w in times:
adj[u].append((v, w))
# Min-heap (priority queue) to always process the shortest known path first
pq = [(0, k)] # (current time, current node)
network = {i: float('inf') for i in range(1, n + 1)}
network[k] = 0
while pq:
cur_time, cur = heapq.heappop(pq)
# Explore all adjacent nodes
for new_cur, weight in adj[cur]:
new_time = cur_time + weight
if new_time < network[new_cur]:
network[new_cur] = new_time
heapq.heappush(pq, (new_time, new_cur))
# Find the maximum delay time among all reachable nodes
max_time = max(network.values())
return max_time if max_time != float('inf') else -1
```
| 5
| 0
|
['Breadth-First Search', 'Graph', 'Heap (Priority Queue)', 'Shortest Path', 'C++', 'Java', 'Python3']
| 0
|
network-delay-time
|
90.1 (Approach 1: Dijkstra's algorithm) | O(E * log V)✅ | Python & C++(Step by step explanation)✅
|
901-approach-1-dijkstras-algorithm-oe-lo-1qg6
|
Intuition\nThe problem can be approached using Dijkstra\'s algorithm, which is a popular algorithm for finding the shortest paths between nodes in a graph. Here
|
monster0Freason
|
NORMAL
|
2024-02-18T11:01:31.309441+00:00
|
2024-02-18T11:01:31.309476+00:00
| 671
| false
|
# Intuition\nThe problem can be approached using Dijkstra\'s algorithm, which is a popular algorithm for finding the shortest paths between nodes in a graph. Here, each node represents a point in the network, and the edges represent the time it takes for a signal to travel between two points.\n\n# Approach\n1. **Build the Graph**:\n - In this step, we convert the given list of times into a graph representation. Each node in the network is represented as a key in the `edges` dictionary, and its value is a list of tuples containing the target node and the time it takes to travel from the source node to the target node.\n - This step is crucial because it helps us efficiently traverse the network and compute the minimum time for all nodes to receive the signal. By organizing the data into a graph structure, we can easily access the neighboring nodes of any given node.\n\n2. **Apply Dijkstra\'s Algorithm**:\n - Dijkstra\'s algorithm is a popular method for finding the shortest path from a source node to all other nodes in a weighted graph. Since our problem involves finding the minimum time for all nodes to receive the signal from a given source node, Dijkstra\'s algorithm is a suitable choice.\n - We utilize a min-heap to efficiently select the node with the minimum time to propagate the signal. This ensures that we explore the paths with the shortest cumulative time first, leading to an optimal solution.\n\n3. **Process Nodes**:\n - In each iteration of the algorithm, we pop the node with the minimum time from the min-heap. This node represents the next node to be processed.\n - We check if the node has already been visited. If it has, we skip processing it further to avoid revisiting nodes unnecessarily.\n - If the node has not been visited, we mark it as visited and update the current time to the time taken to reach this node. This ensures that we keep track of the cumulative time as we traverse the network.\n\n4. **Update Neighbors**:\n - For each neighbor of the current node, we calculate the total time taken to reach that neighbor by adding the time taken to travel from the current node to the neighbor to the current time.\n - We then push this updated time and the neighbor node into the min-heap if the neighbor node has not been visited yet. This allows us to explore all possible paths from the current node efficiently.\n\n5. **Check Completeness**:\n - After processing all nodes, we check if all nodes have been visited. If all nodes have been visited, it means that the signal has successfully reached all nodes in the network.\n - In this case, we return the current time as the minimum time taken for all nodes to receive the signal.\n - If not all nodes have been visited, it indicates that some nodes could not receive the signal within the given network structure. In such a scenario, we return -1 to signify that it is impossible for all nodes to receive the signal.\n\n# Example\n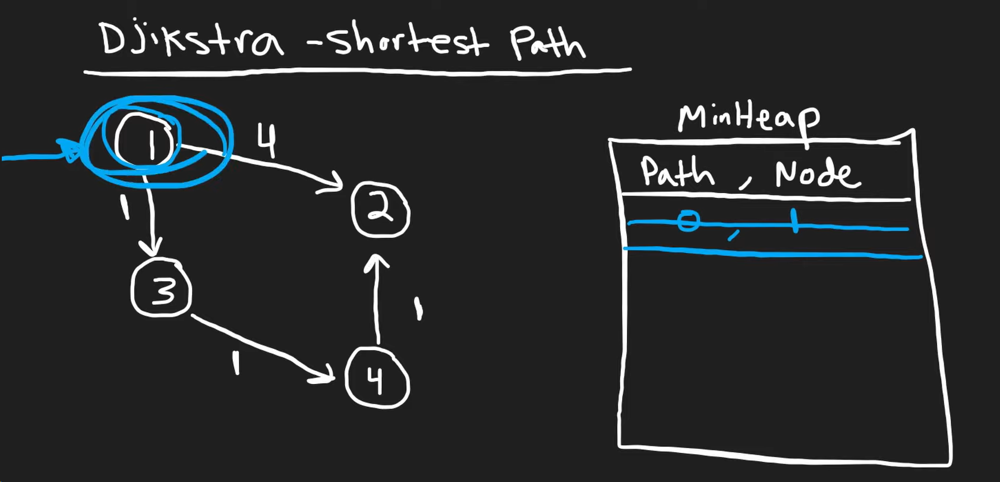\n\n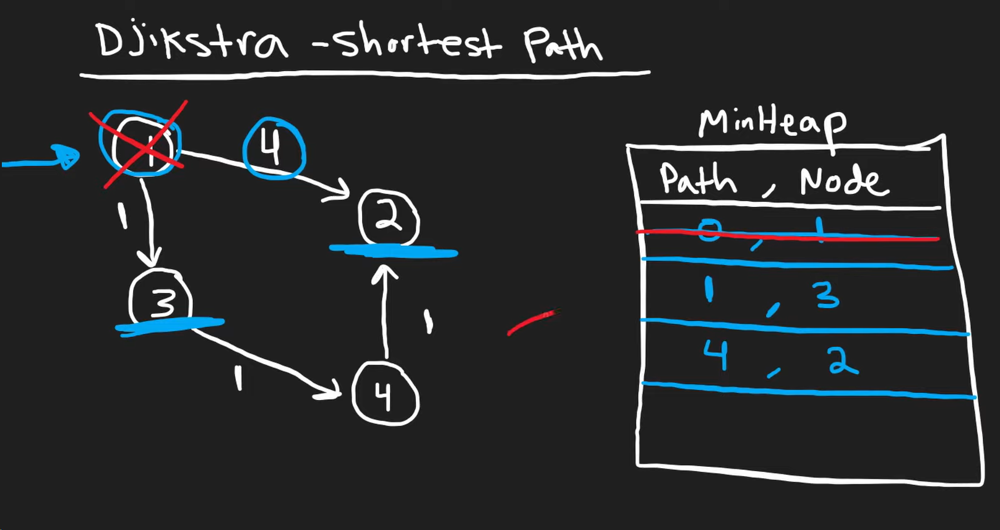\n\n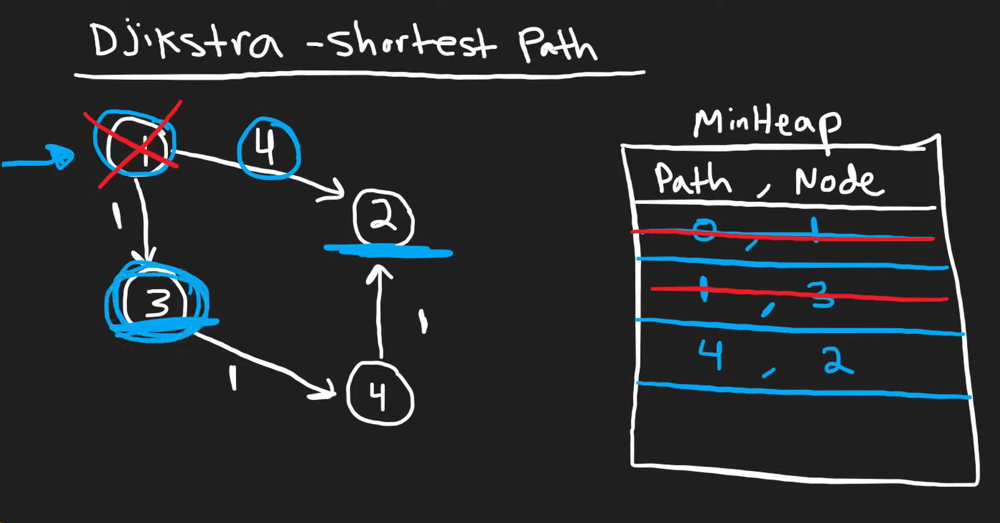\n\n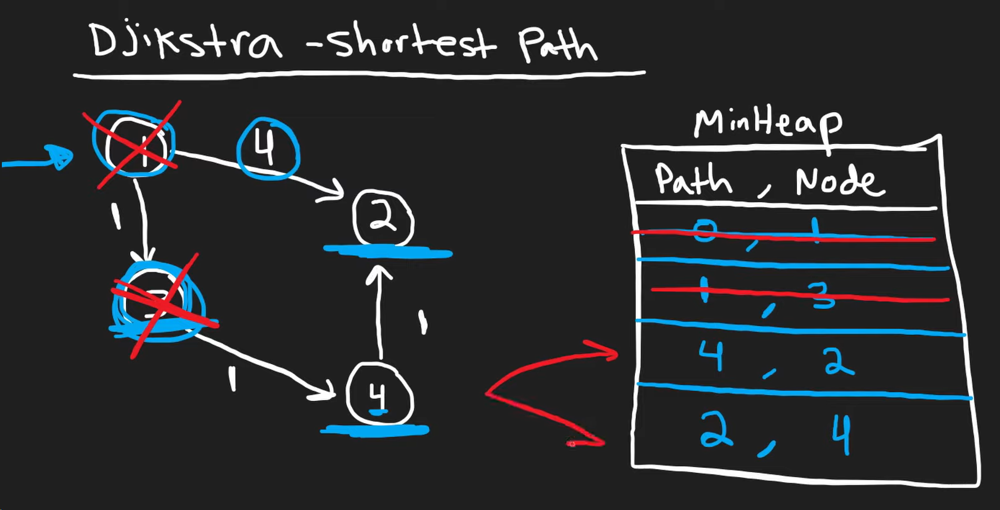\n\n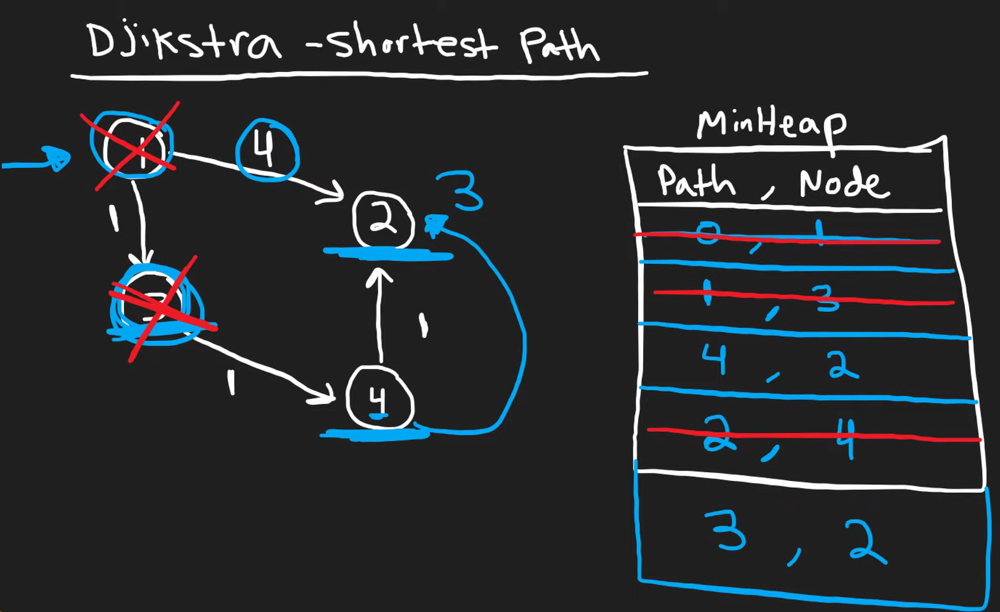\n\n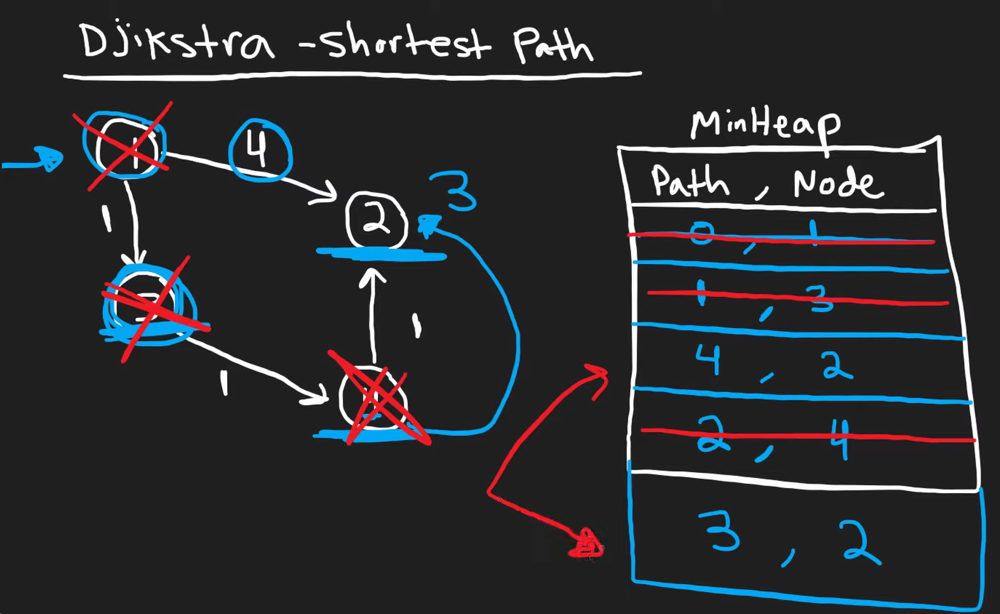\n\n# Complexity\n- Time complexity: \\(O(E * log V)\\), where \\(E\\) is the number of edges and \\(V\\) is the number of vertices (nodes) in the graph. Dijkstra\'s algorithm has a time complexity of \\(O(E \\log V)\\) when implemented using a min-heap.\n- Space complexity: \\(O(V + E)\\) for storing the graph and the min-heap.\n\n## Python Implementation:\n```python\nclass Solution:\n def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:\n # Create a defaultdict to store the adjacency list representation of the graph\n edges = collections.defaultdict(list)\n \n # Populate the adjacency list with the given edges and weights\n for u, v, w in times:\n edges[u].append((v, w))\n\n # Initialize a minHeap with (0, k), where k is the starting node and 0 is the distance to k\n minHeap = [(0, k)]\n \n # Initialize a set to keep track of visited nodes\n visit = set()\n \n # Initialize the time variable to track the maximum time taken to reach all nodes\n t = 0\n \n # While there are elements in the minHeap\n while minHeap:\n # Pop the node with the minimum distance from the minHeap\n w1, n1 = heapq.heappop(minHeap)\n \n # If the node has been visited, continue to the next iteration\n if n1 in visit:\n continue\n \n # Mark the current node as visited\n visit.add(n1)\n \n # Update the time to the current distance\n t = w1\n\n # Iterate over the neighbors of the current node\n for n2, w2 in edges[n1]:\n # If the neighbor has not been visited yet\n if n2 not in visit:\n # Add the neighbor to the minHeap with updated distance\n heapq.heappush(minHeap, (w1 + w2, n2))\n \n # If all nodes have been visited, return the maximum time taken\n return t if len(visit) == n else -1\n```\n\n## C++ Implementation:\n```c++\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n // Create an adjacency list to represent the graph\n vector<pair<int, int>> adj[n + 1];\n \n // Populate the adjacency list with the given edges and weights\n for (int i = 0; i < times.size(); i++) {\n int source = times[i][0];\n int dest = times[i][1];\n int time = times[i][2];\n adj[source].push_back({time, dest});\n }\n \n // Initialize a vector to store the time taken to receive signals at each node\n vector<int> signalReceiveTime(n + 1, INT_MAX);\n \n // Initialize a priority queue to keep track of nodes with the minimum time\n priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;\n \n // Push the starting node k with time 0 into the priority queue\n pq.push({0, k});\n \n // Update the signalReceiveTime of the starting node to 0\n signalReceiveTime[k] = 0;\n \n // While the priority queue is not empty\n while (!pq.empty()) {\n // Extract the node with the minimum time from the priority queue\n int currNodeTime = pq.top().first;\n int currNode = pq.top().second;\n pq.pop();\n \n // If the current time to reach the node is greater than the recorded time, skip\n if (currNodeTime > signalReceiveTime[currNode]) {\n continue;\n }\n \n // Iterate over the neighbors of the current node\n for (int i = 0; i < adj[currNode].size(); i++) {\n pair<int, int> edge = adj[currNode][i];\n int time = edge.first;\n int neighborNode = edge.second;\n \n // If the time to reach the neighbor node through the current node is less than the recorded time\n if (signalReceiveTime[neighborNode] > currNodeTime + time) {\n // Update the time and push the neighbor node into the priority queue\n signalReceiveTime[neighborNode] = currNodeTime + time;\n pq.push({signalReceiveTime[neighborNode], neighborNode});\n }\n }\n }\n \n // Find the maximum time taken to reach all nodes\n int result = INT_MIN;\n for (int i = 1; i <= n; i++) {\n result = max(result, signalReceiveTime[i]);\n }\n \n // If any node cannot receive a signal, return -1\n if (result == INT_MAX) {\n return -1;\n }\n return result;\n }\n};\n```\n\n\n# Please upvote the solution if you understood it.\n\n
| 5
| 0
|
['Graph', 'Heap (Priority Queue)', 'C++', 'Python3']
| 2
|
network-delay-time
|
C++ || Dijkstra✅ + Bellman Ford✅ + (Some idea on Floyd-Warshall)✅ || Easy💡 and Fast🔥
|
c-dijkstra-bellman-ford-some-idea-on-flo-joyg
|
Here question asks to return minimum time it takes for all the n nodes to receive the signal. Which means it wants to say that find the shortest time to reach a
|
UjjwalAgrawal
|
NORMAL
|
2023-06-02T11:05:46.683087+00:00
|
2023-06-02T11:05:46.683123+00:00
| 1,220
| false
|
Here question asks to return minimum time it takes for all the n nodes to receive the signal. Which means it wants to say that find the shortest time to reach all the nodes and then return maximum time out of it.\n\nBasically there is some node which will take more time then other nodes. So have to minimize that time.\n\nMinimum time to reach all nodes = max({src to 1, src to 2, ..... , src to N})\n\n---\n\n# Dijkstra Algo\n- Time complexity: $$O(ElogV)$$\n- Space complexity: $$O(E+V)$$\n\n```\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n vector<vector<pair<int, int>>> adj(n); // Adj List\n for(auto e: times){\n // Storing vertices by subtracting 1 as nodes given as 1 to N.\n int u = e[0]-1, v = e[1]-1, wt = e[2]; \n adj[u].push_back({v, wt});\n }\n\n vector<int> dist(n, 1e9); //Distance array\n\n // Min Heap to arrange distance from low to high \n // {Distance, Node}\n priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;\n\n dist[k-1] = 0; // Distance of src to src will be 0\n pq.push({0, k-1}); // Push the current state of source node\n\n while(!pq.empty()){\n auto [nDist, node] = pq.top(); // Getting top node\n pq.pop();\n \n // If dist of node has been updated to lower value then skip further calculation. \n if(nDist > dist[node]) continue;\n\n // Traversing all adjacent nodes\n for(auto [adjNode, edgeWt] : adj[node]){\n\n //Usual bellman equation checking and pushing node\'s state\n if(dist[adjNode] > nDist + edgeWt){\n dist[adjNode] = nDist + edgeWt;\n pq.push({dist[adjNode], adjNode});\n }\n }\n }\n\n // Getting maximum answer\n int ans = 0;\n for(int i = 0; i<n; i++){\n // If any node\'s distance is still 1e9 (infinite) return -1\n if(dist[i] == 1e9) return -1;\n ans = max(ans, dist[i]);\n }\n\n return ans;\n }\n};\n```\n---\n\n\n# Bellman Ford Algo\n- Time complexity: $$O(EV)$$\n- Space complexity: $$O(V)$$\n```\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n vector<int> dist(n+1, 1e9); //Distance array\n dist[k] = 0; // Distance of src to src is 0\n\n // Relaxing all edges N-1 times\n for(int i = 0; i<n-1; i++){\n // Traversing all edges\n for(auto e : times){\n int u = e[0], v = e[1], wt = e[2];\n\n // Relaxing only if distance of u is not infinite\n if(dist[u] != 1e9)\n dist[v] = min(dist[v], dist[u] + wt);\n }\n }\n\n // Getting maximum answer\n int ans = 0;\n for(int i = 1; i<=n; i++){\n if(dist[i] == 1e9) return -1;\n ans = max(ans, dist[i]);\n }\n\n return ans;\n }\n};\n```\n\n---\n\n# Floyd Warshall Algo\n- Time complexity: $$O(V^3)$$\n- Space complexity: $$O(V^2)$$\n\n\nThis algo is Multi-Source shortest path algorithm and is the costliest shortest path algorithm.\nIt works well when we have find the shortest of each pair of nodes or graph has negative weights cycle. But here we have to find distance from single source only and here don\'t have any negative weight cycles.\nIf you want to try that algo it can applied to this question easily without any changes to algo.\n\n---\n\n```\nThank you\nIf you learn/found something new, please Upvote \uD83D\uDC4D\n```\n---\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n
| 5
| 0
|
['Breadth-First Search', 'Heap (Priority Queue)', 'Shortest Path', 'C++']
| 0
|
network-delay-time
|
Dijkstra's Algorithms
|
dijkstras-algorithms-by-ganjinaveen-wmnk
|
Dijkstra\'s Algorithm\n\nclass Solution:\n def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:\n edges=defaultdict(list)\n
|
GANJINAVEEN
|
NORMAL
|
2023-04-30T13:05:17.958975+00:00
|
2023-04-30T13:05:17.959010+00:00
| 1,536
| false
|
# Dijkstra\'s Algorithm\n```\nclass Solution:\n def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:\n edges=defaultdict(list)\n for u, v, w in times:\n #graph[u-1].append((v-1, w))\n edges[u].append((v,w))\n minheap=[(0,k)]\n visit=set()\n t=0\n while minheap:\n w1,n1=heapq.heappop(minheap)\n if n1 in visit:\n continue\n visit.add(n1)\n t=max(t,w1)\n for n2,w2 in edges[n1]:\n if n2 not in visit:\n heapq.heappush(minheap,((w1+w2),n2))\n return t if len(visit)==n else -1\n```\n# please upvote me it would encourage me alot\n
| 5
| 0
|
['Python3']
| 1
|
network-delay-time
|
Java | using MinHeap
|
java-using-minheap-by-venkat089-qrtk
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Venkat089
|
NORMAL
|
2023-02-16T05:37:16.860536+00:00
|
2023-02-16T05:37:16.860582+00:00
| 817
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int networkDelayTime(int[][] times, int n, int k) {\n Map<Integer,List<int[]>> map=new HashMap<>();\n for(int i[]:times)\n {\n if(!map.containsKey(i[0]))map.put(i[0],new ArrayList<>());\n map.get(i[0]).add(new int[]{i[1],i[2]});\n }\n \n Set<Integer> visited=new HashSet<>();\n Queue<int[]> minheap=new PriorityQueue<>((a,b)->a[1]-b[1]);\n\n minheap.add(new int[]{k,0});\n int ans=0;\n while(!minheap.isEmpty())\n {\n int val[]=minheap.poll();\n int src=val[0],w=val[1];\n if(visited.contains(src))continue;\n visited.add(src);\n ans=w;\n if(!map.containsKey(src))continue;\n for(int i[]:map.get(src))\n {\n minheap.add(new int[]{i[0],i[1]+w});\n }\n }\n return visited.size()==n?ans:-1;\n\n }\n}\n```
| 5
| 0
|
['Java']
| 0
|
network-delay-time
|
✅C++ || CLEAN && Easy to Understand CODE || Dijkstra's Algo
|
c-clean-easy-to-understand-code-dijkstra-hrg4
|
\n\nLogic - > No Logic! Strightforward question, just Apply Dijkstra\'s or Bellman Ford and you are good to go!\n\nT-> O(E log V) && S->O(V)\n\n\n\tclass Soluti
|
abhinav_0107
|
NORMAL
|
2022-12-30T15:00:24.976446+00:00
|
2022-12-30T15:01:46.401321+00:00
| 601
| false
|
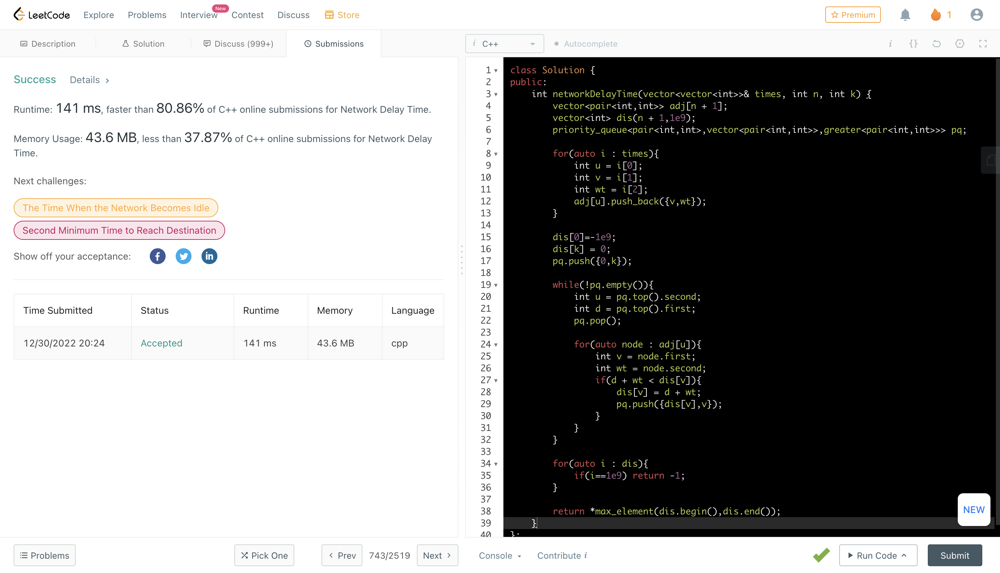\n\n***Logic - > No Logic! Strightforward question, just Apply Dijkstra\'s or Bellman Ford and you are good to go!***\n\n**T-> O(E log V) && S->O(V)**\n\n\n\tclass Solution {\n\t\tpublic:\n\t\t\tint networkDelayTime(vector<vector<int>>& times, int n, int k) {\n\t\t\t\tvector<pair<int,int>> adj[n + 1];\n\t\t\t\tvector<int> dis(n + 1,1e9);\n\t\t\t\tpriority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> pq;\n\n\t\t\t\tfor(auto i : times){\n\t\t\t\t\tint u = i[0];\n\t\t\t\t\tint v = i[1];\n\t\t\t\t\tint wt = i[2];\n\t\t\t\t\tadj[u].push_back({v,wt});\n\t\t\t\t}\n\n\t\t\t\tdis[0]=-1e9;\n\t\t\t\tdis[k] = 0;\n\t\t\t\tpq.push({0,k});\n\n\t\t\t\twhile(!pq.empty()){\n\t\t\t\t\tint u = pq.top().second;\n\t\t\t\t\tint d = pq.top().first;\n\t\t\t\t\tpq.pop();\n\n\t\t\t\t\tfor(auto node : adj[u]){\n\t\t\t\t\t\tint v = node.first;\n\t\t\t\t\t\tint wt = node.second;\n\t\t\t\t\t\tif(d + wt < dis[v]){\n\t\t\t\t\t\t\tdis[v] = d + wt;\n\t\t\t\t\t\t\tpq.push({dis[v],v});\n\t\t\t\t\t\t}\n\t\t\t\t\t}\n\t\t\t\t}\n\n\t\t\t\tfor(auto i : dis){\n\t\t\t\t\tif(i==1e9) return -1;\n\t\t\t\t}\n\n\t\t\t\treturn *max_element(dis.begin(),dis.end());\n\t\t\t}\n\t\t};
| 5
| 0
|
['C', 'Heap (Priority Queue)', 'C++']
| 1
|
network-delay-time
|
✅ [Python] propagation through all paths using Dijkstra's Algorithm (with detailed comments)
|
python-propagation-through-all-paths-usi-70v4
|
\u2705 IF YOU LIKE THIS SOLUTION, PLEASE UPVOTE.\n*\nThis solution employs Dijkstra\'s algorithm to propagate signal through the network. \n\n*Comment. To get m
|
stanislav-iablokov
|
NORMAL
|
2022-11-03T18:14:00.422947+00:00
|
2022-11-03T18:17:11.982517+00:00
| 455
| false
|
**\u2705 IF YOU LIKE THIS SOLUTION, PLEASE UPVOTE.**\n****\nThis solution employs Dijkstra\'s algorithm to propagate signal through the network. \n\n**Comment**. To get minimal signal arrival time for each node, we propagate through all paths using double-ended queue. On each iteration, we send signal from a source node to all its destination nodes (according to the network\'s graph) and update time. We also note that there is no point to propagate further if the signal has already reached some node via another path with better time.\n\n```\nclass Solution:\n def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:\n \n # [1] convert edge data to a hashmap\n graph = defaultdict(list)\n for u, v, w in times: graph[u].append((v, w))\n \n # [2] signal minimal time to reach each node\n MAX_TIME = 6000*100+1\n signal = [MAX_TIME] * (n+1)\n signal[k] = 0\n \n # [3] propagate signal through all possible\n # paths iteratively using deque\n dq = deque([k])\n while dq:\n node_from = dq.popleft()\n time_from = signal[node_from]\n for node_to, time_to in graph[node_from]:\n # [4] there is no point to propagate further if the signal has\n # already reached this node via another path with better time\n time = time_from + time_to\n if time < signal[node_to]:\n signal[node_to] = time\n dq.append(node_to)\n\n # [5] check time for all nodes\n if all(map(lambda t: t < MAX_TIME, signal[1:n+1])):\n return max(signal[1:n+1])\n else: \n return -1\n```
| 5
| 0
|
[]
| 3
|
network-delay-time
|
📍 C++ Solution with Pattern for future Questions
|
c-solution-with-pattern-for-future-quest-doyq
|
\uD83D\uDD25 Please Upvote It is FREE from your side\n\nWhere this Approach can be used [Pattern]\n- Whenever we want to find max or min cost path from a source
|
AlphaDecodeX
|
NORMAL
|
2022-09-06T06:09:08.553575+00:00
|
2022-09-06T06:09:29.659420+00:00
| 446
| false
|
\uD83D\uDD25 Please **Upvote** It is **FREE** from your side\n\n**Where this Approach can be used** [Pattern]\n- Whenever we want to find max or min cost path from a source to destination. \n- It will also work if the nodes are disconnected means more than one graph present which are not connected with each other\n- We can use this algorithm in both directed and undirected graph.\n\n**Approach:-** We can use **Dijkastra here alongwith prioirty_queue** which ensures that a node will always visit its neighbours with minimum distance possible. Maintain a distance vector which is time in this case. **One mistake that I was doing** is in the if condition ```time[node] + x.second < time[x.first] && !visited[x.first]``` I was not putting visited and was using <= inequality. It will make us looping infinitely incase graph has a cycle and equal cost of reaching the nodes.\n\nDry run a case you\'ll understand.\n\n```\n#define pii pair<int, int>\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n vector<vector<pair<int, int>>> adj(n+1); // (node, time)\n for(int i = 0; i<times.size(); i++){\n adj[times[i][0]].push_back({times[i][1], times[i][2]});\n }\n vector<int> visited(n+1,0);\n vector<int> time(n+1,INT_MAX);\n time[k] = 0;\n priority_queue<pii, vector<pii>,greater<pii>> nodes;\n nodes.push({0,k});\n while(!nodes.empty()){\n int node = nodes.top().second;\n nodes.pop();\n visited[node] = 1;\n for(auto &x: adj[node]){\n if(time[node] + x.second < time[x.first] && !visited[x.first]){\n time[x.first] = min(time[node]+x.second, time[x.first]);\n nodes.push({time[x.first], x.first});\n }\n }\n }\n for(int i = 1; i<=n; i++){\n if(visited[i]==0){\n return -1;\n }\n }\n int timeToReach = time[1];\n for(int i = 1; i<=n; i++){\n // cout<<time[i]<<\' \';\n timeToReach = max(timeToReach, time[i]);\n }\n return timeToReach;\n }\n};\n```
| 5
| 0
|
['C', 'C++']
| 0
|
network-delay-time
|
✅C++ | ✅Use Bellman Ford Algorithm
|
c-use-bellman-ford-algorithm-by-yash2arm-amzq
|
\nclass Solution {\npublic:\n \n // I\'m going to use Bellman Ford Algorithm\n int networkDelayTime(vector<vector<int>>& times, int n, int k) \n {\n
|
Yash2arma
|
NORMAL
|
2022-05-14T19:12:23.117230+00:00
|
2022-05-14T19:12:23.117272+00:00
| 395
| false
|
```\nclass Solution {\npublic:\n \n // I\'m going to use Bellman Ford Algorithm\n int networkDelayTime(vector<vector<int>>& times, int n, int k) \n {\n // just created a dis vector that will store the distance for reaching the node\n // and assign dis[k]=0 because we will start searching from k \n vector<int>dis(n+1,INT_MAX);\n dis[k]=0;\n \n \n // we will update our dis vector upto (n-1) times according to bellman\'s ford algo\n for(int i=1;i<n;i++)\n {\n // just checking for all the nodes that are available in our graph\n for(int j=0;j<times.size();j++)\n {\n // extracting source, destination, weight\n int u=times[j][0]; // source\n int v=times[j][1]; // destination\n int w=times[j][2]; // weight\n \n // if current source is not finite value then we can not pick that path \n // so just check current source is finite or not\n // and if we have better path for reaching V from U by using W then we update dis[v]\n if(dis[u]!=INT_MAX && dis[u]+w<dis[v])\n {\n // if we are having better path available then just update our dis\n dis[v]=w+dis[u];\n }\n }\n }\n\t\t \n // take out the best value to reach n from k\n int ans=0;\n for(int i=1;i<=n;i++)\n {\n // If any node is not reachable from k return -1\n if(dis[i]==INT_MAX) \n return -1; \n \n // else take best path\n ans=max(ans,dis[i]);\n }\n return ans;\n \n }\n};\n```
| 5
| 0
|
['Graph', 'C', 'C++']
| 0
|
network-delay-time
|
Simple Java, Dijkstra, heap, COMMENTS,
|
simple-java-dijkstra-heap-comments-by-fo-o4ff
|
I could not find many solutions with comments so I decieded to write one up. I hope this helps someone. I am using Dijkstra\'s Algorithm.\n\n\nclass Solution {\
|
fourgates
|
NORMAL
|
2022-01-16T04:54:26.151827+00:00
|
2022-01-16T04:54:26.151856+00:00
| 437
| false
|
I could not find many solutions with comments so I decieded to write one up. I hope this helps someone. I am using Dijkstra\'s Algorithm.\n\n```\nclass Solution {\n public int networkDelayTime(int[][] times, int n, int k) {\n // init\n Map<Integer, List<int[]>> graph = new HashMap<>();\n \n // create graph\n // i usually use List<List<Integer>> graph..., but this graph is not zero based :(\n for (int[] time : times) {\n if(graph.get(time[0]) == null){\n graph.put(time[0], new ArrayList<>());\n }\n graph.get(time[0]).add(new int[]{time[1], time[2]});\n }\n \n // min heap to process cheapest edges first\n PriorityQueue<int[]> queue = new PriorityQueue<>((a,b)->a[1] - b[1]);\n \n // start with edge k!\n // k = starting edge\n // 0 = the initial weight\n queue.offer(new int[]{k, 0});\n \n // a map to keep track of distance for each node\n Map<Integer, Integer> dist = new HashMap<>();\n \n // lets get started!\n while(!queue.isEmpty()){\n int[] curr = queue.poll();\n \n int node = curr[0];\n int weight = curr[1];\n \n // since we are using a min heap we only need to iterate over each node once\n if(dist.containsKey(node)){\n continue;\n }\n dist.put(node, weight);\n \n // queue up the neighbors\n if(graph.containsKey(node)){\n for(int[] edge : graph.get(node)){\n // add the weight between this edge and the current node we are visiting\n // the weight to get from the src to this egde is n-1 + n\n queue.offer(new int[]{edge[0], edge[1] + weight});\n }\n }\n \n }\n // we are missing a node :(\n if(dist.size() != n){\n return -1;\n }\n \n // essentially, the max delay time is going to be the longest path\n int result = Integer.MIN_VALUE;\n \n // iterate over each node and find the max distance (total weight) \n for(int node : dist.keySet()){\n result = Math.max(result, dist.get(node));\n }\n return result;\n }\n}\n```
| 5
| 0
|
['Heap (Priority Queue)', 'Java']
| 0
|
network-delay-time
|
[Java] Dijkstra's Algo with Heap
|
java-dijkstras-algo-with-heap-by-jocelyn-7mub
|
Runtime: 17ms (beat 62%)\nMemory Usage: 42MB(beat 83.23%)\n\n\nclass Solution {\n public int networkDelayTime(int[][] times, int n, int k) {\n Map<Int
|
jocelyn23
|
NORMAL
|
2021-07-29T03:49:35.262719+00:00
|
2021-07-29T03:49:55.016555+00:00
| 480
| false
|
Runtime: 17ms (beat 62%)\nMemory Usage: 42MB(beat 83.23%)\n\n```\nclass Solution {\n public int networkDelayTime(int[][] times, int n, int k) {\n Map<Integer, List<Cell>> graph = new HashMap<>();\n for (int[] edge: times) {\n graph.computeIfAbsent(edge[0], v->new ArrayList<>()).add(new Cell(edge[1],edge[2]));\n }\n \n Map<Integer, Integer> costs = new HashMap<>();\n PriorityQueue<Cell> heap = new PriorityQueue<>();\n heap.add(new Cell(k, 0));\n \n while(!heap.isEmpty()) {\n Cell curr = heap.poll();\n if(costs.containsKey(curr.node)) continue;\n costs.put(curr.node, curr.time);\n \n if (graph.containsKey(curr.node)) {\n for(Cell neig: graph.get(curr.node)) {\n if (!costs.containsKey(neig.node)) {\n heap.add(new Cell(neig.node, neig.time+curr.time));\n }\n }\n }\n }\n int ans = -1;\n if (costs.size() != n) return ans;\n for (int cost: costs.values()) {\n ans = Math.max(ans, cost);\n }\n return ans; \n }\n}\n\nclass Cell implements Comparable<Cell> {\n int node, time;\n Cell(int node, int time) {\n this.node = node;\n this.time = time;\n } \n public int compareTo(Cell c2) {\n return time-c2.time;\n }\n}\n```
| 5
| 0
|
['Java']
| 2
|
network-delay-time
|
C# Belman-Ford implementation
|
c-belman-ford-implementation-by-and85-5mgn
|
\npublic class Solution\n{\n\tpublic int NetworkDelayTime(int[][] times, int n, int k)\n\t{\n\t\t// implementation of Belman-Ford Algorithm\n\t\t// https://www.
|
and85
|
NORMAL
|
2021-01-30T17:22:53.334634+00:00
|
2021-01-30T17:25:19.831676+00:00
| 427
| false
|
```\npublic class Solution\n{\n\tpublic int NetworkDelayTime(int[][] times, int n, int k)\n\t{\n\t\t// implementation of Belman-Ford Algorithm\n\t\t// https://www.youtube.com/watch?v=FtN3BYH2Zes \n\t\t// run relaxation of each vertex exactly n - 1 times\n\t\t// source vertex should have 0 cost to visit, all other vertexes should start from infinity cost\n\t\tvar costs = new Dictionary<int, double>();\n\t\tfor (int i = 1; i <= n; i++)\n\t\t\tcosts[i] = double.PositiveInfinity;\n\t\tcosts[k] = 0;\n\n\t\tint u, v, w;\n\n\t\tfor (int i = 0; i < n - 1; i++)\n\t\t{\n\t\t\tbool isRelaxed = false;\n\t\t\tfor (int t = 0; t < times.Length; t++)\n\t\t\t{\n\t\t\t\tu = times[t][0];\n\t\t\t\tv = times[t][1];\n\t\t\t\tw = times[t][2];\n\n\t\t\t\tdouble candidateCost = costs[u] + w;\n\t\t\t\tif (costs[v] > candidateCost)\n\t\t\t\t{\n\t\t\t\t\tcosts[v] = candidateCost;\n\t\t\t\t\tisRelaxed = true;\n\t\t\t\t}\n\t\t\t}\n\n\t\t\tif (!isRelaxed) \n\t\t\t\tbreak;\n\t\t}\n\n\t\tdouble maxCost = costs.Values.Max();\n\t\treturn (maxCost < double.PositiveInfinity) ? (int)maxCost : -1;\n\t}\n}\n```
| 5
| 0
|
[]
| 1
|
network-delay-time
|
Comparison between standard Dijlstra and BFS solution, kind for beginners.
|
comparison-between-standard-dijlstra-and-9pz4
|
The goal is to compute the shorhest path from one single node to all nodes in directed weighted graph.\nWe can do this in both Dijlstra\'s Algorithm and BFS. \n
|
green077
|
NORMAL
|
2019-10-17T05:46:44.742620+00:00
|
2019-10-17T05:46:44.742670+00:00
| 1,108
| false
|
The goal is to compute the shorhest path from one single node to all nodes in directed weighted graph.\nWe can do this in both Dijlstra\'s Algorithm and BFS. \nMy solution is not the quickest, but it\'s easy to understand and standard. \nFor Dijlstra: \n1. put node number and temporary distance into priority queue. \n2. distance array is used to store the final result\n3. Visited array needs to be used to mark the visited nodes\n\nFor BFS: \n1. put node number into queue\n2. distance array is used to store the temporary result, updated during BFS search\n3. No need to track visited nodes\n\nSolution one: Dijlstra\'s Algorithm (26ms, faster than 74.68%)\n```\nclass intComparator implements Comparator<int[]>{\n @Override\n public int compare(int[] o1, int[] o2){\n return o1[1] - o2[1];\n }\n}\nclass Solution {\n public int networkDelayTime(int[][] times, int N, int K) {\n \n //build graph\n Map<Integer, List<List<Integer>>> map = new HashMap<>();\n for (int[] time : times) {\n if (!map.containsKey(time[0])) {\n map.put(time[0], new ArrayList<>());\n }\n List<Integer> temp = new ArrayList<>();\n temp.add(time[1]);\n temp.add(time[2]);\n map.get(time[0]).add(temp);\n }\n \n //visited array + distance array + priority queue\n boolean[] visited = new boolean[N];\n int[] dists = new int[N];\n Arrays.fill(dists, -1);\n PriorityQueue<int[]> pq = new PriorityQueue<>(new intComparator());\n //<current node number, temporary distance>\n pq.offer(new int[] {K, 0});\n \n while (!pq.isEmpty()) {\n int[] cur = pq.poll();\n //when one node is polled out from queue\n //the temporary distance is the final result\n if (visited[cur[0] - 1]) continue;\n dists[cur[0] - 1] = cur[1];\n visited[cur[0] - 1] = true;\n if (map.containsKey(cur[0])) {\n List<List<Integer>> nodes = map.get(cur[0]);\n for (List<Integer> node : nodes) {\n if (visited[node.get(0) - 1]) continue;\n pq.offer(new int[] {node.get(0), dists[cur[0] - 1] + node.get(1)});\n }\n }\n }\n int maxPath = 0;\n for (int i = 0; i < dists.length; i ++) {\n if (dists[i] == -1) {\n return -1;\n } \n maxPath = Math.max(maxPath, dists[i]);\n }\n return maxPath;\n }\n}\n```\nSolution two: BFS (27ms, faster than 73.78%)\n```\nclass Solution {\n public int networkDelayTime(int[][] times, int N, int K) {\n // build graph\n Map<Integer, List<List<Integer>>> map = new HashMap<>();\n for (int[] time : times) {\n if (!map.containsKey(time[0])) {\n map.put(time[0], new ArrayList<>());\n }\n List<Integer> temp = new ArrayList<>();\n temp.add(time[1]);\n temp.add(time[2]);\n map.get(time[0]).add(temp);\n }\n \n //dists array to keep temporary results, needs to be updated during bfs\n int[] dists = new int[N];\n Arrays.fill(dists, Integer.MAX_VALUE);\n Queue<Integer> q = new LinkedList<>();\n q.offer(K);\n dists[K - 1] = 0;\n while (!q.isEmpty()) {\n int cur = q.poll();\n int dist = dists[cur - 1];\n if (map.containsKey(cur)) {\n List<List<Integer>> nodes = map.get(cur);\n for (List<Integer> node : nodes) {\n //update dists\n if (dists[node.get(0) - 1] <= dist + node.get(1)) continue;\n dists[node.get(0) - 1] = dist + node.get(1);\n q.offer(node.get(0));\n }\n }\n }\n int maxPath = 0;\n for (int i = 0; i < dists.length; i ++) {\n if (dists[i] == Integer.MAX_VALUE) {\n return -1;\n } \n maxPath = Math.max(maxPath, dists[i]);\n }\n return maxPath;\n }\n}\n```
| 5
| 0
|
['Breadth-First Search', 'Java']
| 3
|
network-delay-time
|
经典Dijkstra + 优先队列优化Dijkstra + 经典Bellman-Ford
|
jing-dian-dijkstra-you-xian-dui-lie-you-e6dyp
|
solution 1 \u7ECF\u5178Dijkstra\njava\n public int networkDelayTime(int[][] times, int N, int K) {\n int maxValue=6005;\n int[][] graph = new i
|
greatgeek
|
NORMAL
|
2019-08-24T09:22:49.621691+00:00
|
2019-08-24T09:22:49.621739+00:00
| 597
| false
|
**solution 1 \u7ECF\u5178Dijkstra**\n```java\n public int networkDelayTime(int[][] times, int N, int K) {\n int maxValue=6005;\n int[][] graph = new int[N+1][N+1];\n for(int i=0;i<graph.length;i++){\n for(int j=0;j<graph[i].length;j++){\n graph[i][j]=maxValue;\n }\n }\n int[] distance=new int[N+1];\n for(int i=1;i<distance.length;i++){\n distance[i]=maxValue;\n }\n \n for(int i=0;i<times.length;i++){\n int src=times[i][0];\n int des=times[i][1];\n int time=times[i][2];\n graph[src][des]=time;\n }\n \n \n for(int i=1;i<graph[K].length;i++){\n distance[i]=graph[K][i];\n }\n distance[K]=0;\n boolean[] visited=new boolean[N+1];\n visited[K]=true;\n \n for(int i=1;i<=N;i++){\n int minValue=Integer.MAX_VALUE;\n int node=-1;\n for(int j=1;j<distance.length;j++){\n if(visited[j]==true) continue;\n if(distance[j]<minValue){\n minValue=distance[j];\n node=j;\n }\n }\n if(node==-1) break;\n else visited[node]=true;\n for(int k=1;k<graph[node].length;k++){\n if(visited[k]==true) continue;\n if(distance[k]>distance[node]+graph[node][k]){\n distance[k]=distance[node]+graph[node][k];\n }\n }\n \n }\n \n int res=0;\n for(int i=1;i<distance.length;i++){\n res=Math.max(res,distance[i]);\n }\n return res==maxValue ? -1 : res;\n }\n```\n\n**solution 2 \u4F18\u5148\u961F\u5217\u4F18\u5316Dijkstra**\n```java\nclass Node{\n int node;\n int distance;\n public Node(int node,int distance){\n this.node=node;\n this.distance=distance;\n }\n }\n \n class NodeComparator implements Comparator<Node>{\n @Override\n public int compare(Node o1,Node o2){\n return o1.distance-o2.distance;\n }\n }\n \n public int networkDelayTime(int[][] times, int N, int K) {\n int maxValue=6005;\n int[][] graph = new int[N+1][N+1];\n for(int i=0;i<graph.length;i++){\n for(int j=0;j<graph[i].length;j++){\n graph[i][j]=maxValue;\n }\n }\n int[] distance=new int[N+1];\n for(int i=1;i<distance.length;i++){\n distance[i]=maxValue;\n }\n \n for(int i=0;i<times.length;i++){\n int src=times[i][0];\n int des=times[i][1];\n int time=times[i][2];\n graph[src][des]=time;\n }\n \n distance[K]=0;\n boolean[] visited=new boolean[N+1];\n\n Queue<Node> priorityQueue = new PriorityQueue<Node>(new NodeComparator());\n priorityQueue.offer(new Node(K,0));\n while(!priorityQueue.isEmpty()){\n Node curNode = priorityQueue.poll();\n visited[curNode.node]=true;\n for(int i=1;i<graph[curNode.node].length;i++){\n if(visited[i]==true) continue;\n else{\n if(distance[i] > distance[curNode.node]+graph[curNode.node][i]){\n distance[i]=distance[curNode.node]+graph[curNode.node][i];\n priorityQueue.offer(new Node(i,distance[i]));\n }\n }\n }\n }\n \n int res=0;\n for(int i=1;i<distance.length;i++){\n res=Math.max(res,distance[i]);\n }\n return res==maxValue ? -1 : res;\n }\n```\n\n**\u7ECF\u5178Bellman-Ford**\n```java\npublic int networkDelayTime(int[][] times, int N, int K) {\n int maxValue = 6005;\n int[] distance = new int[N+1];\n for(int i=1;i<distance.length;i++){\n distance[i]=maxValue;\n }\n distance[K]=0;\n for(int j=1;j<N;j++){\n for(int i=0;i<times.length;i++){\n int u=times[i][0],v=times[i][1],w=times[i][2];\n i f(distance[v] > distance[u]+w ){\n distance[v]=distance[u]+w;\n }\n }\n }\n\n \n int res=0;\n for(int i=1;i<distance.length;i++){\n res=Math.max(res,distance[i]);\n }\n return res==maxValue ? -1 : res;\n }\n```
| 5
| 0
|
['Java']
| 0
|
network-delay-time
|
[3 Ways to Solve Java]Floyd Warshall && Dijkstra && Bellman Ford
|
3-ways-to-solve-javafloyd-warshall-dijks-o3dy
|
It\'s kind of brute force. Floyd Warshall:\n\nclass Solution {\n public int networkDelayTime(int[][] times, int N, int K) {\n int[][] M = new int[N +
|
flusteredying
|
NORMAL
|
2018-03-30T00:09:24.110658+00:00
|
2018-03-30T00:09:24.110658+00:00
| 643
| false
|
It\'s kind of brute force. Floyd Warshall:\n```\nclass Solution {\n public int networkDelayTime(int[][] times, int N, int K) {\n int[][] M = new int[N + 1][N + 1];\n for(int[] row : M){\n Arrays.fill(row, 10000);\n }\n for(int[] t : times){\n int v1 = t[0];\n int v2 = t[1];\n int cost = t[2];\n M[v1][v2] = cost;\n }\n for(int m = 1; m <= N; m ++){\n \tfor(int i = 1; i <= N; i ++){\n \t\tfor(int j = 1; j <= N; j ++){\n \t\t\tif(M[i][m] + M[m][j] < M[i][j]){\n \t\t\t\tM[i][j] = M[i][m] + M[m][j];\n \t\t\t}\n \t\t}\n \t}\n }\n int max = Integer.MIN_VALUE;\n for(int i = 1; i <= N; i ++){\n if(i == K){\n continue;\n }\n if(M[K][i] == 10000){\n return -1;\n }\n max = Math.max(max, M[K][i]);\n }\n return max == 10000 ? -1 : max;\n }\n}\n```\n\nDijkstra:\n```\nclass Solution {\n public int networkDelayTime(int[][] times, int N, int K) {\n PriorityQueue<int[]> heap = new PriorityQueue<>((a, b) -> (a[2] - b[2]));\n int[][] graph = new int[N + 1][N + 1];\n for(int[] row : graph){\n Arrays.fill(row, -1);\n }\n for(int[] t : times){\n graph[t[0]][t[1]] = t[2];\n }\n for(int i = 1; i <= N; i ++){\n if(graph[K][i] != -1){\n heap.offer(new int[]{K, i, graph[K][i]});\n }\n }\n int[] minCost = new int[N + 1];\n Arrays.fill(minCost, -1);\n while(!heap.isEmpty()){\n int[] cur = heap.poll();\n int u = cur[0];\n int v = cur[1];\n int cost = cur[2];\n if(minCost[v] == -1){\n minCost[v] = cost;\n }\n for(int i = 1; i <= N; i ++){\n if(graph[v][i] != -1 && minCost[i] == -1){\n heap.offer(new int[]{K, i, cost + graph[v][i]});\n }\n }\n }\n int max = Integer.MIN_VALUE;\n for(int i = 1; i <= N; i ++){\n if(i == K){\n continue;\n }\n if(minCost[i] == -1){\n return -1;\n }\n max = Math.max(minCost[i], max);\n }\n return max == Integer.MIN_VALUE ? -1 : max;\n }\n}\n```\nHowever, Dijkstra takes around 150ms. Floyd takes around 80ms, faster than Dijkstra. \nFloyd time complexity should be O(V^3), while Dijkstra should be O(E*logE).(Correct me if im wrong)\nIdk what happend behind the scene, could anyone tell me why? \nE can be upto V^2, even in worst case, E*logE = V^2 * logV^2 = 2V^2logV.\nV^3 is still greater 2V^2logV.\n\nBellman Ford:\n```\nclass Solution {\n public int networkDelayTime(int[][] times, int N, int K) {\n int[] dis = new int[N + 1];\n Arrays.fill(dis, Integer.MAX_VALUE);\n dis[K] = 0;\n for(int i = 1; i <= N; i ++){\n if(i == K){\n continue;\n }\n for(int[] edge : times){\n int u = edge[0];\n int v = edge[1];\n int cost = edge[2];\n if(dis[u] != Integer.MAX_VALUE && dis[u] + cost < dis[v]){\n dis[v] = dis[u] + cost;\n }\n }\n }\n int max = Integer.MIN_VALUE;\n for(int i = 1; i <= N; i ++){\n if(i == K){\n continue;\n }\n max = Math.max(max, dis[i]);\n }\n return max == Integer.MAX_VALUE ? -1 : max;\n }\n}\n```\nBellmanFord is faster, around 50 ms.
| 5
| 0
|
[]
| 3
|
network-delay-time
|
Simple Python solution using Djikstra's
|
simple-python-solution-using-djikstras-b-lkqx
|
BFS is used to iterate through the nodes, where next node is determined using priority queue ordered by its distance from starting node K.\n\n def networkDel
|
incog
|
NORMAL
|
2017-12-10T04:04:12.617000+00:00
|
2017-12-10T04:04:12.617000+00:00
| 1,295
| false
|
BFS is used to iterate through the nodes, where next node is determined using priority queue ordered by its distance from starting node K.\n```\n def networkDelayTime(self, times, N, K):\n pq = []\n adj = [[] for _ in range(N+1)]\n for time in times:\n adj[time[0]].append((time[1], time[2]))\n\n fin, res = set(), 0\n heapq.heappush(pq, (0, K))\n\n while len(pq) and len(fin) != N:\n cur = heapq.heappop(pq)\n fin.add(cur[1])\n res = cur[0]\n for child, t in adj[cur[1]]:\n if child in fin: continue\n heapq.heappush(pq, (t+cur[0], child))\n\n return res if len(fin) == N else -1\n```
| 5
| 2
|
[]
| 2
|
network-delay-time
|
✅BEST | GRAPH | JAVA | Explained🔥🔥🔥
|
best-graph-java-explained-by-adnannshaik-1quu
|
Intuition
The problem requires us to determine the time it takes for a signal to reach all nodes in a directed weighted graph. Since this is a shortest path pro
|
AdnanNShaikh
|
NORMAL
|
2025-02-17T02:04:57.891759+00:00
|
2025-02-17T02:04:57.891759+00:00
| 331
| false
|
**Intuition**
The problem requires us to determine the time it takes for a signal to reach all nodes in a directed weighted graph. Since this is a shortest path problem where we need to find the minimum time from a source node to all other nodes, Dijkstra's algorithm is a natural fit because it efficiently finds the shortest path in a graph with positive weights.
**Approach**
**Graph Representation:**
We represent the graph using an adjacency list stored in a HashMap<Integer, List<int[]>>.
Each node maps to a list of integer arrays [neighbor, travel_time], where neighbor is the destination node and travel_time is the time taken to reach it.
Dijkstra's Algorithm (Priority Queue / Min-Heap):
We use a Priority Queue (Min-Heap) to always expand the node with the smallest known time first.
Start with the given node k with time 0 (i.e., pq.offer(new int[]{k, 0})).
Maintain a distance map (dist) to store the shortest time to reach each node.
Process nodes in the priority queue:
Extract the node with the smallest recorded time.
If it has already been processed, skip it.
Otherwise, update its shortest known time and push its neighbors to the queue.
Repeat until all nodes are visited or the queue is empty.
Final Result Calculation:
If we have visited all n nodes, return the maximum time among all shortest paths (Collections.max(dist.values())).
If some nodes are unreachable, return -1.
**Complexity Analysis**
**Time Complexity:**
Constructing the adjacency list takes O(E) time, where E is the number of edges.
The priority queue operations (insertion/removal) take O(log V) time, where V is the number of nodes.
Since each node is processed once and each edge is relaxed once, the total time complexity is O((V + E) log V).
**Space Complexity:**
O(V + E) for storing the graph adjacency list.
O(V) for the priority queue (since at most all nodes can be in the queue at once).
O(V) for the dist map.
Overall, the space complexity is O(V + E).
# Code
```java []
class Solution {
public int networkDelayTime(int[][] times, int n, int k) {
// Create adjacency list for graph representation
Map<Integer, List<int[]>> graph = new HashMap<>();
for (int i = 1; i <= n; i++) graph.put(i, new ArrayList<>());
for (int[] time : times) {
graph.get(time[0]).add(new int[]{time[1], time[2]});
}
// Priority Queue (Min-Heap) for Dijkstra's Algorithm
PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[1]));
pq.offer(new int[]{k, 0}); // Start with the source node
Map<Integer, Integer> dist = new HashMap<>();
while (!pq.isEmpty()) {
int[] curr = pq.poll(); // Get the node with the smallest time
int node = curr[0], time = curr[1];
if (dist.containsKey(node)) continue; // Skip if already visited
dist.put(node, time);
for (int[] neighbor : graph.get(node)) {
int nextNode = neighbor[0], nextTime = neighbor[1];
if (!dist.containsKey(nextNode)) {
pq.offer(new int[]{nextNode, time + nextTime});
}
}
}
if (dist.size() != n) return -1; // If not all nodes are reached, return -1
return Collections.max(dist.values()); // Return the maximum time taken
}
}
```
| 4
| 0
|
['Java']
| 0
|
network-delay-time
|
DFS C++ SOLUTION
|
dfs-c-solution-by-jeffrin2005-c876
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Jeffrin2005
|
NORMAL
|
2024-07-04T03:49:50.172902+00:00
|
2024-07-04T03:49:50.172922+00:00
| 288
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nclass Solution {\npublic:\n void dfs(int node, vector<vector<pair<int, int>>>& graph, vector<int>& dist, int elapsed) {\n if (elapsed >= dist[node]) return; // If the current time is not better, skip\n dist[node] = elapsed;\n for (auto& edge : graph[node]) {\n int neighbor = edge.first;\n int time = edge.second;\n dfs(neighbor, graph, dist, elapsed + time);\n }\n }\n\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n vector<vector<pair<int, int>>> graph(n + 1);\n for (auto& x : times) {\n graph[x[0]].push_back({x[1], x[2]});\n }\n vector<int> dist(n + 1, INT_MAX);\n dfs(k, graph, dist, 0); \n\n int maxDelay = 0;\n for (int i = 1; i <= n; i++) {\n if (dist[i] == INT_MAX) return -1; \n maxDelay = max(maxDelay, dist[i]);\n }\n return maxDelay;\n }\n};\n```
| 4
| 0
|
['C++']
| 0
|
network-delay-time
|
Dijkstra's BFS C++ SOLUTION
|
dijkstras-bfs-c-solution-by-jeffrin2005-mmen
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Jeffrin2005
|
NORMAL
|
2024-07-04T03:46:54.561749+00:00
|
2024-07-04T03:46:54.561781+00:00
| 758
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n vector<vector<pair<int,int>>> graph(n + 1);\n for(auto& x : times){\n graph[x[0]].push_back({x[1], x[2]}); \n }\n vector<int> dist(n + 1, INT_MAX);\n priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>>> pq;\n dist[k] = 0;\n pq.push({0, k});\n while(!pq.empty()){\n int u = pq.top().second;\n int d = pq.top().first;\n pq.pop();\n if(d > dist[u]) continue;\n for(auto& newnode : graph[u]){\n int v = newnode.first;\n int weight = newnode.second;\n if(dist[u] + weight < dist[v]){\n dist[v] = dist[u] + weight;\n pq.push({dist[v], v});\n }\n }\n }\n int ans = -1;\n for(int i = 1; i <= n; i++){\n if(dist[i] == INT_MAX) return -1;\n ans = max(ans, dist[i]);\n }\n return ans; \n }\n};\n```
| 4
| 0
|
['C++']
| 0
|
network-delay-time
|
Dijkstra's Algorithm || Simple C++ Solution ||
|
dijkstras-algorithm-simple-c-solution-by-fkrz
|
Code\n\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n vector<vector<pair<int,int>>> adj(n+1,vector<pa
|
abhijeet5000kumar
|
NORMAL
|
2023-12-19T22:53:55.243370+00:00
|
2023-12-19T22:53:55.243386+00:00
| 1,228
| false
|
# Code\n```\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n vector<vector<pair<int,int>>> adj(n+1,vector<pair<int,int>>{} );\n for(auto x:times){\n adj[x[0]].push_back({x[1],x[2]});\n }\n\n vector<int> dist(n+1,1e9);\n dist[k]=0;\n priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>>> pq;\n pq.push({0,k});\n\n while(!pq.empty()){\n int node=pq.top().second;\n int dis=pq.top().first;\n pq.pop();\n\n for(auto x:adj[node]){\n int adjNode=x.first;\n int adjDist=x.second;\n if(dis+adjDist < dist[adjNode]){\n dist[adjNode]=dis+adjDist;\n pq.push({adjDist+dis,adjNode});\n }\n }\n }\n int ans=-1;\n for(int i=1;i<=n;i++){\n ans=max(ans,dist[i]);\n }\n if(ans==1e9){return -1;}\n return ans;\n }\n};\n```
| 4
| 0
|
['Depth-First Search', 'Breadth-First Search', 'Graph', 'Heap (Priority Queue)', 'Shortest Path', 'C++']
| 0
|
network-delay-time
|
Best O(ElogV) Solution
|
best-oelogv-solution-by-kumar21ayush03-riod
|
Approach\nDijkstra\'s Algorithm\n\n# Complexity\n- Time complexity:\nO(ElogV)\n\n- Space complexity:\nO(V + E)\n\n# Code\n\nclass Solution {\npublic:\n int n
|
kumar21ayush03
|
NORMAL
|
2023-03-18T13:54:58.048732+00:00
|
2023-03-18T13:54:58.048778+00:00
| 246
| false
|
# Approach\nDijkstra\'s Algorithm\n\n# Complexity\n- Time complexity:\n$$O(ElogV)$$\n\n- Space complexity:\n$$O(V + E)$$\n\n# Code\n```\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n vector <pair<int, int>> adj[n+1];\n for (auto it: times) \n adj[it[0]].push_back({it[1], it[2]});\n priority_queue <pair<int, int>, vector<pair<int, int>>, greater<pair<int,int>>> pq;\n pq.push({0, k});\n vector <int> time(n+1, 1e9);\n time[k] = 0;\n while (!pq.empty()) {\n int t = pq.top().first;\n int node = pq.top().second;\n pq.pop();\n for (auto it: adj[node]) {\n int adjNode = it.first;\n int wt = it.second;\n if (t + wt < time[adjNode]) {\n time[adjNode] = t + wt;\n pq.push({t + wt, adjNode});\n }\n }\n }\n int minTime = INT_MIN;\n for (int i = 1; i <= n; i++) {\n if (time[i] == 1e9)\n return -1;\n minTime = max (time[i], minTime); \n }\n return minTime;\n }\n};\n```
| 4
| 0
|
['C++']
| 0
|
network-delay-time
|
Java || Dijkstra || PriorityQueue (Heap) || Fast
|
java-dijkstra-priorityqueue-heap-fast-by-kjwv
|
An leetcode a day, doctors are always on the way.\n\n\n\nclass Solution {\n public int networkDelayTime(int[][] times, int n, int k) {\n \n //R
|
yining_xu
|
NORMAL
|
2022-08-30T23:56:06.418600+00:00
|
2022-08-30T23:56:06.418637+00:00
| 357
| false
|
An leetcode a day, doctors are always on the way.\n\n```\n\nclass Solution {\n public int networkDelayTime(int[][] times, int n, int k) {\n \n //Represente the graph using adjacency list\n List<int[]>[] graph = new List[n + 1];\n for(int i = 0; i <= n; i++){\n graph[i] = new ArrayList<int[]>();\n }\n for(int[] time : times){\n int from = time[0];\n int to = time[1];\n int value = time[2];\n graph[from].add(new int[]{to, value});\n }\n \n //the distance array\n int[] dist = new int[n + 1];\n\t\t\n\t\t//a big enough number which the distance will never reach out\n Arrays.fill(dist, 50000);\n dist[k] = 0;\n \n //non-decending order\n PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] != b[0] ? a[0] - b[0] : a[1] - b[1]);\n pq.offer(new int[]{0, k});\n while(!pq.isEmpty()){\n int[] curr = pq.poll();\n int time = curr[0];\n int currNode = curr[1];\n if(dist[currNode] < time){\n continue;\n }\n for(int[] edge : graph[currNode]){\n int toNode = edge[0];\n int distance = edge[1] + dist[currNode];\n if(distance < dist[toNode]){\n dist[toNode] = distance;\n pq.offer(new int[]{distance, toNode});\n }\n }\n }\n int ans = 0;\n\t\t\n\t\t//remember it should be 1\n for(int i = 1; i < n + 1; i++){\n ans = Math.max(ans, dist[i]);\n }\n return ans == 50000 ? -1 : ans;\n }\n}\n\n```
| 4
| 0
|
['Java']
| 0
|
network-delay-time
|
Using Dijkstra Algorithm, [C++]
|
using-dijkstra-algorithm-c-by-akashsahuj-41is
|
Implementation\n\nUsing Dijkstra Algorithm\nTime Complexity = O(N + ElogN)\nSpace Complexity = (O(N+E) + O(N) + O(N)) => O(N+E)\nWhere N is the nunber of vertic
|
akashsahuji
|
NORMAL
|
2022-06-02T18:17:38.817723+00:00
|
2022-06-02T18:17:38.817768+00:00
| 273
| false
|
Implementation\n\n**Using Dijkstra Algorithm\nTime Complexity = O(N + ElogN)\nSpace Complexity = (O(N+E) + O(N) + O(N)) => O(N+E)\nWhere N is the nunber of vertices in the graph and E is the number of edges**\n\n```\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n \n vector<pair<int, int>> graph[n+1];\n \n for(auto time : times){\n graph[time[0]].push_back({time[1], time[2]});\n }\n \n vector<int> distance(n+1, INT_MAX); \n distance[k] = 0;\n\t\t\n\t\t// to create min heap we need to take pass these 3 parameters\n // data type, vector type, comparison\n priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;\n \n pq.push({0, k});\n \n while(!pq.empty()){\n int dis = pq.top().first;\n int node = pq.top().second;\n pq.pop();\n \n for(auto adjacentNode : graph[node]){\n int destinationNode = adjacentNode.first;\n int weight = adjacentNode.second;\n \n if(dis + weight < distance[destinationNode]){\n distance[destinationNode] = dis + weight;\n pq.push({dis + weight, destinationNode});\n }\n }\n }\n \n int res = INT_MIN;\n for(int i = 1; i < distance.size(); i++){\n res = max(res, distance[i]);\n }\n \n return (res == INT_MAX) ? -1 : res;\n }\n};\n```\nIf you find any issue in understanding the solution then comment below, will try to help you.\nIf you found my solution useful.\nSo **please do upvote and encourage me** to document all leetcode problems\uD83D\uDE03\nHappy Coding :)
| 4
| 0
|
['Graph', 'C', 'Heap (Priority Queue)', 'Shortest Path']
| 0
|
network-delay-time
|
Python Solution - Dijkstra's Shortest Path Algorithm using minHeap
|
python-solution-dijkstras-shortest-path-9qb1z
|
\n# Implement Dijkstra\'s Shortest Path Algorithm\n\nclass Solution:\n def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:\n #
|
SamirPaulb
|
NORMAL
|
2022-05-23T05:35:20.166134+00:00
|
2022-05-23T05:44:37.106873+00:00
| 789
| false
|
```\n# Implement Dijkstra\'s Shortest Path Algorithm\n\nclass Solution:\n def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:\n # create Adjacency List \n adjList = {i:[] for i in range(1, n+1)}\n for u, v, w in times:\n adjList[u].append((v, w))\n \n minHeap = [(0, k)] # taking min-heap so that pop() will give node with lowest distance\n t = 0 # total time require\n visited = set() # to keep a track of visited nodes\n \n while minHeap:\n w1, n1 = heapq.heappop(minHeap) # w1 = time to reach from source k(weight); n1 = value of node\n if n1 in visited: continue\n visited.add(n1)\n t = max(t, w1) # as w1 is the total time to reach to n1 from k\n for n2, w2 in adjList[n1]:\n if n2 not in visited:\n heapq.heappush(minHeap, (w1 + w2, n2)) # added current time(w1) + time between n1 and n2\n \n # if we can visit all nodes then only return total time t\n return t if len(visited) == n else -1 \n\n# number of edges, e = len(times)\n# n = total no. of nodes\n\n# Time: O(e * log(n)) \n# Space: O(n)\n```
| 4
| 0
|
['Heap (Priority Queue)', 'Python', 'Python3']
| 2
|
network-delay-time
|
All Three Approaches | Easy Solution | Commented Explanation |
|
all-three-approaches-easy-solution-comme-g1h1
|
Upvote if you like it and finds helpful !\n\nApproach 1 : DFS\n\n Time complexity: O((N - 1)! + ElogE\n Space complexity: O(N + E)O(N+E)\n\n\n\nclass Solution
|
nitin_05
|
NORMAL
|
2022-05-14T09:21:08.130690+00:00
|
2022-05-14T09:35:54.818406+00:00
| 431
| false
|
***Upvote if you like it and finds helpful !***\n\n**Approach 1 : DFS**\n\n ***Time complexity: O((N - 1)! + ElogE***\n ***Space complexity: O(N + E)O(N+E)***\n\n\n```\nclass Solution {\npublic:\n static bool sortbysec ( const pair<int,int>&a , const pair<int,int>&b )\n {\n return a.second < b.second ;\n }\n \n void dfsutil(int src , vector<vector<pair<int,int>>>& adj, vector<bool>& visited ,vector <int>& receiving_time , int t )\n {\n receiving_time[src] = t; \n visited[src] = true;\n for(int i = 0 ; i < adj[src].size(); i++)\n {\n int neigbhour = adj[src][i].first;\n int time = adj[src][i].second;\n \n if(!visited[neigbhour])\n {\n dfsutil(neigbhour , adj ,visited , receiving_time , t+time);\n }\n else if( visited[neigbhour] && receiving_time[neigbhour] > t+time)\n {\n dfsutil(neigbhour , adj, visited , receiving_time , t+time);\n }\n }\n }\n \n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n vector<vector<pair<int,int>>> adj(n+1); \n vector<bool>visited(n+1,false); visited[0] = true;\n vector<int>timestramp(n+1,INT_MAX); timestramp[0] = 0;\n \n for(auto &time : times ) // creating adj list by adding edges from source to destination node.\n {\n adj[time[0]].push_back({time[1],time[2]});\n }\n \n for(int i =0 ; i< n+1 ; i++) // Sort pair according to timestramp in ascending order.\n {\n sort(adj[i].begin(), adj[i].end() , sortbysec); \n }\n \n dfsutil(k , adj ,visited ,timestramp , 0); \n \n for(int i = 1 ; i < visited.size(); i++)\n if(!visited[i]) return -1;\n \n return *max_element(timestramp.begin(), timestramp.end());\n }\n};\n```\n\n##### Approach 2 : Bellman Ford Solution \n\n**Time complexity: O(NE)\nSpace complexity: O(N)**\n\n```\nint bellmanFord(vector<vector<int>>& times, int n, int k) {\n // delay[i] = time to reach kth node\n vector<int> delay(n+1, INT_MAX);\n // we start from node kth node as source, all other nodes are destinations\n delay[k] = 0;\n \n for(int i = 0; i < n; i++) {\n for(auto edge: times) {\n // delay[dst] > delay[src] + wt\n delay[edge[1]] = min(delay[edge[1]], \n delay[edge[0]] == INT_MAX ? INT_MAX : delay[edge[0]] + edge[2]);\n }\n }\n // 0th element is dummy, so skip . Find the max delay time, this will decide the overall delay\n int max_delay = *max_element(delay.begin() + 1, delay.end());\n \n return max_delay == INT_MAX ? -1 : max_delay;\n }\n\t int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n return bellmanFord(times, n, k);\n }\n```\n\n\n##### Optimised Solution\n##### Approach 3 : Djikstra Using DFS Solution \n\n##### Time complexity: O(V+E)\n##### Space complexity: O(N)\n\n```\nclass Solution {\npublic:\nint networkDelayTime(vector<vector>& times, int n, int k) {\n\n vector<vector<pair<int, int>>> graph(n + 1);\n for(auto &i : times)\n graph[i[0]].push_back({i[1], i[2]});\n \n vector<int> d(n + 1, INT_MAX);\n vector<bool> visited(n + 1, false);\n d[k] = 0;\n dfs(graph, k, d, 0, visited);\n \n for(int i = 1; i <= n; i++)\n if(!visited[i])\n return -1;\n \n int ans = 0;\n for(int i = 1; i <= n; i++)\n ans = max(ans, d[i]);\n \n return ans;\n}\n\nvoid dfs(vector<vector<pair<int, int>>> &graph, int i, vector<int> &d, int tmp, vector<bool> &visited)\n{\n visited[i] = true;\n for(auto &j : graph[i])\n if(tmp + j.second < d[j.first])\n d[j.first] = tmp + j.second, dfs(graph, j.first, d, d[j.first], visited);\n}\n};\n```\n\n###### Comment down if You have any doubt !
| 4
| 0
|
['Depth-First Search', 'C']
| 1
|
network-delay-time
|
C++ Dijkstra
|
c-dijkstra-by-midnightsimon-1zu9
|
Solved live on stream. Link in profile\n\n\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n using pii
|
midnightsimon
|
NORMAL
|
2022-05-14T01:28:48.804232+00:00
|
2022-05-14T01:28:48.804256+00:00
| 556
| false
|
Solved live on stream. Link in profile\n\n```\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n using pii = pair<int,int>;\n vector<vector<pii>> adjList(n);\n priority_queue<pii, vector<pii>, greater<pii>> pq;\n for(auto& time : times) {\n int src = time[0]-1;\n int dst = time[1]-1;\n int wt = time[2];\n adjList[src].push_back({wt, dst});\n }\n vector<int> dists(n, INT_MAX);\n dists[k-1] = 0;\n pq.push({0, k-1});\n \n while(!pq.empty()) {\n auto [wt, src] = pq.top();\n pq.pop();\n if(dists[src] < wt) continue;\n auto& children = adjList[src];\n for(auto& [childWt, dst] : children) {\n int newWt = wt + childWt;\n if(newWt < dists[dst]) {\n dists[dst] = newWt;\n pq.push({newWt, dst});\n }\n }\n }\n int ans = 0;\n for(int x : dists) {\n if(x == INT_MAX) return -1;\n ans = max(ans, x);\n }\n \n return ans;\n }\n};\n```
| 4
| 0
|
[]
| 0
|
network-delay-time
|
C++ | Code Explained With Proper Comment | Dijkstra Algorithm
|
c-code-explained-with-proper-comment-dij-z8uv
|
\n// 1. DijkstraAlgorithm => TC O(nlogn) | SC O(n)\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n pri
|
itsmdasifraza
|
NORMAL
|
2022-02-10T17:10:57.591698+00:00
|
2022-02-10T17:10:57.591747+00:00
| 254
| false
|
```\n// 1. DijkstraAlgorithm => TC O(nlogn) | SC O(n)\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>>pq; // min heap\n pq.push({0, k});\n vector<vector<pair<int, int>>> adj(n + 1); // declare adjacency matrix for easy node access\n for(auto it : times){ // initialize adjacency matrix\n adj[it[0]].push_back({it[1], it[2]});\n }\n vector<int> wt(n + 1, INT_MAX); // saving weight of each node to infinity\n wt[k] = 0; // weight of source is zero\n while(!pq.empty()){ // dijkstra algo to find min distance of each node from source\n int prevDis = pq.top().first;\n int node = pq.top().second;\n pq.pop();\n for(auto it: adj[node]){\n int adjNode = it.first;\n int adjDis = it.second;\n if(wt[adjNode] > prevDis + adjDis){\n wt[adjNode] = prevDis + adjDis;\n pq.push({prevDis + adjDis, adjNode});\n }\n }\n }\n int maxi = -1;\n for(int i = 1; i <= n; i++){\n if(wt[i] == INT_MAX) return -1; // if node consist INT_MAX, means all nodes not visited\n maxi = max(wt[i], maxi);\n }\n return maxi;\n }\n};\n\n// please upvote\n// if you find this helpful \n```
| 4
| 0
|
['C++']
| 0
|
network-delay-time
|
Python DFS vs BFS vs Djikstra's(Flavor or BFS)
|
python-dfs-vs-bfs-vs-djikstrasflavor-or-8y3kz
|
\nfrom collections import defaultdict\nimport heapq\nfrom collections import deque\nclass Solution:\n def networkDelayTime(self, times: List[List[int]], n: i
|
ashm4478
|
NORMAL
|
2021-11-08T03:32:45.378929+00:00
|
2021-11-08T03:32:45.378962+00:00
| 558
| false
|
```\nfrom collections import defaultdict\nimport heapq\nfrom collections import deque\nclass Solution:\n def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:\n\t\n # Common code for all\n\t\t\n graph = defaultdict(list)\n for u, v , w in times:\n graph[u].append((w,v))\n \n dist = {node: float(\'inf\') for node in range(1,n+1)}\n\n# DFS\n def dfs(node, elapsed):\n if elapsed >= dist[node]: return # Recursion hence base case,\n # If elapsed time > the optimal distance in dist[node]\n #We break\n # If its equal\n # we still break\n dist[node] = elapsed\n for time, nei in sorted(graph[node]):\n # Why Sorted? --> Does TLE otherwise, \n # It is a greedy Strategy, It is not neccessarily required in DFS\n \n # To speed things up, at each visited node we\'ll consider signals exiting the node that are faster first, by sorting the edges.\n dfs(nei, elapsed + time)\n\n dfs(k, 0)\n ans = max(dist.values())\n #print(dist)\n return ans if ans < float(\'inf\') else -1\n\n\n\n# QUEUE\n \n pq = deque() # Queue\n pq.appendleft((0,k))\n dist = [float(\'inf\') for _ in range(1, n+2)]\n dist[k]=0\n \n while pq:\n elapsed_time, node = pq.popleft()\n for time, nei in graph[node]:\n if elapsed_time + time < dist[nei]:\n dist[nei] = elapsed_time + time\n pq.appendleft((elapsed_time + time,nei))\n ans = max(dist[1:])\n print(dist)\n return ans if ans < float(\'inf\') else -1\n \n# Dijkstra\'s Algorithm \n \n pq = [(0,k)]\n dist = {} # visit all nodes with weight so hashmap works...\n \n while pq:\n elapsed_time, node = heapq.heappop(pq) # always select shortest weight from graph\n if node not in dist:\n dist[node] = elapsed_time\n for nei, time in graph[node]:\n if nei not in dist:\n heapq.heappush(pq,(time + elapsed_time,nei))\n \n return max(dist.values()) if len(dist) == n else -1\n```\n\nThis resource gives you an understanding of how Djikstra\'s is actually just a flavor of BFS\nhttps://devtut.github.io/algorithm/dijkstras-algorithm.html#dijkstra-s-shortest-path-algorithm\n\nIt is a no-brainer for all newbies and advanced leetcoders to use\nBFS as the strategy for shortest path. \n**Shortest path ---> BFS** Be it single source, from specific vertex / overall top-bottom in tree-like\n\nWhy BFS over Djikstra\'s \n* We are considering non-negative/ postive weighted graphs*\n1. BFS used on **unweighted** graph --> Treats each edge of same weight\n\t\ta. We can still use BFS and store the cost/ elapsed time in a tuple.\n\t\tb. Visit 1 hop away nodes. \n\t\tc. Next hop away nodes.\n2. Djikstra\'s used on Weighted graph (positve weighted only)\n3. We can use DFS which is teh slowest of the three and offer slight optimization by picking fast exiting nodes by sorting the distances.\n\nThese above axioms are just best practices for getting best Complexity!!\nNo body can tell you, that you can\'t implement anything a certain way..\nIf you want to get better though, start chewing more than you can swallow and then get comfortable taking bigger bites\n\n\nVanilla BFS, apart from being utterly vanilla, causes double updates --> More computation\n*Reasoning here *--> https://devtut.github.io/algorithm/dijkstras-algorithm.html#dijkstra-s-shortest-path-algorithm\n\nDjikstras uses Greedy strategy to pick and "Update" the optimal distance in each step.\nand uses\'s priority queue to pick the smallest weight from current_node.\nTo relax/update and push to the queue...\n\nThis greedy strategy somehow reduces the # updates make the algo faster...\n\n\nGraph Algorithms are quite philosophical if you think about them..\nDFS: You start from 0, see each choice to completion --> You will get to your goal, eventually.\nBFS: You start from 0, see each choice just 1 hop away ----->>>\n\t\t\t\t\t\t---------> If it fits your constraints/ you go to the next level or you abandon that path. Who knows the right *HOP*, will help you reach your dest quickly, as if by magic! \nNaaw Son, it Aint Magic, Its Logic. :P\nDjikstra\'s : Lets Optimized the Magic from BFS shall we ? You start same as BFS, just selectively chose your hops... Increasing probability for that magically hop, all the while reducing effort and knowing fully that, even as we try to be greedy and careful with our energy and updates some situations will be no better the vanilla BFS. \nMagic Arrives on its own time. \nIn some problems all distances have to be traversed. All Vertices to be visited. \nThere is no easy Pruning and result.\nWe have to see all things through..just like the distances to all the vertices from source, where you are at currently. How smartly you do it is upto you ^_^\n\nIgnore my post guys, Just ranting\n\t\t\t\n\t\t\t\n
| 4
| 0
|
['Depth-First Search', 'Breadth-First Search', 'Recursion', 'Python']
| 0
|
network-delay-time
|
C++ || Dijkstra's Algorithm || priority_queue || Time:-O(NlogN) || space:-O(N) + O(N)
|
c-dijkstras-algorithm-priority_queue-tim-sqv3
|
Time :- O((N+E)*logN) =O(NlogN)\nSpace:-O(N) {for dist arrays } + O(N) {for priority_queue}\n\nclass Solution {\npublic:\n int networkDelayTime(vector<vector
|
Pitbull_45
|
NORMAL
|
2021-11-03T22:27:14.985086+00:00
|
2021-11-03T22:27:14.985126+00:00
| 155
| false
|
*Time* :- O((N+E)*logN) =O(NlogN)\nSpace:-O(N) {for dist arrays } + O(N) {for priority_queue}\n```\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n int m=times.size();\n vector<pair<int,int>>graph[n+1];\n for(int i=0;i<m;i++)\n {\n graph[times[i][0]].push_back({times[i][1],times[i][2]});\n }\n // Dijkstra algorithm begins from here...\n priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>>pq; \n vector<int> disto(n+1,INT_MAX); // (dis,from)\n disto[k]=0;\n pq.push({0,k});\n \n while(!pq.empty())\n {\n int dist=pq.top().first; // dis\n int prev=pq.top().second; // node\n pq.pop();\n \n vector<pair<int,int>>::iterator it;\n for(auto it:graph[prev])\n {\n int next=it.first; // next adjcent node \n int nextdist=it.second; // distance b/w the nodes\n \n if(disto[next] > disto[prev]+nextdist)\n {\n disto[next]=disto[prev]+nextdist; // next dist = prev dist + weight of edge \n pq.push({disto[next],next}); // (dist,node)\n }\n }\n }\n int res=0;\n for(int i=1;i<disto.size();i++)\n {\n res=max(res,disto[i]);\n }\n if(res==INT_MAX)\n {\n return -1;\n }\n else\n {\n return res;\n }\n }\n};\n```
| 4
| 0
|
[]
| 0
|
network-delay-time
|
c++ solution | BFS
|
c-solution-bfs-by-xor09-qd5p
|
\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n int size=times.size();\n int max_time=0, des,
|
xor09
|
NORMAL
|
2021-03-05T15:24:11.928231+00:00
|
2021-03-05T15:24:35.425558+00:00
| 343
| false
|
```\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n int size=times.size();\n int max_time=0, des, time; \n vector<pair<int,int>>graph[n+1];\n vector<int> t(n+1,INT_MAX);\n \n for(int i=0;i<size;i++){\n graph[times[i][0]].push_back({times[i][1],times[i][2]});\n }\n\n queue<pair<int,int>> q;\n q.push({k,0});\n \n while(!q.empty()){\n pair<int,int>p = q.front(); \n q.pop();\n des=p.first;\n time=p.second;\n t[des]=min(t[des],time);\n for(auto x : graph[des]){\n if(x.second+time < t[x.first]) q.push({x.first,(x.second+time)});\n } \n }\n \n for(int i=1;i<n+1;i++){\n if(t[i]==INT_MAX) return -1;\n max_time=max(max_time,t[i]);\n }\n return max_time;\n }\n};\n```\nPlease **UPVOTE**
| 4
| 2
|
['Breadth-First Search', 'C']
| 0
|
network-delay-time
|
Two algorithms JS Solution
|
two-algorithms-js-solution-by-hbjorbj-5v05
|
\nvar networkDelayTime = function(times, N, K) {\n // Converting data into adjacency list\n let adjList = new Array(N).fill(0).map(() => []);\n for (le
|
hbjorbj
|
NORMAL
|
2020-10-28T08:41:08.597780+00:00
|
2020-10-29T06:43:22.249881+00:00
| 444
| false
|
```\nvar networkDelayTime = function(times, N, K) {\n // Converting data into adjacency list\n let adjList = new Array(N).fill(0).map(() => []);\n for (let edge of times) {\n adjList[edge[0]-1].push([edge[1]-1,edge[2]]);\n }\n \n let travelTime = new Array(N).fill(Infinity);\n travelTime[K-1] = 0;\n let heap = new PriorityQueue((a,b) => travelTime[a-1] < travelTime[b-1]);\n heap.push(K-1);\n \n while (!heap.isEmpty()) {\n let curV = heap.pop();\n for (let pair of adjList[curV]) {\n let nextV = pair[0], weight = pair[1];\n let tempTime = travelTime[curV] + weight;\n if (travelTime[nextV] > tempTime) {\n travelTime[nextV] = tempTime;\n heap.push(nextV);\n // costs to vertices connected to this nextV might change\n // if cost to this nextV changed\n // but if cost to this nextV didn\'t change, there is no need to push\n // this vertex to heap again\n }\n }\n }\n \n // travelTime[v] represents the lowest-cost path from K to v vertex \n // Find the highest cost to reach a vertex because at this cost\n // K must have visited all other vertices already\n let totalTime = Math.max(...travelTime);\n return totalTime === Infinity ? -1 : totalTime;\n};\n\n// Dijkstra\'s algorithm\n// Time Complexity: O(N + ELog(E)) where E can be N^2 in the worst case\n// Space Complexity: O(N + E)\n\n// Priority Queue implementation\nclass PriorityQueue {\n constructor(comparator = (a, b) => a > b) {\n this._heap = [];\n this._comparator = comparator;\n }\n\n size() {\n return this._heap.length;\n }\n\n peek() {\n return this._heap[0];\n }\n\n isEmpty() {\n return this._heap.length === 0;\n }\n\n _parent(idx) {\n return Math.floor((idx - 1) / 2);\n }\n\n _leftChild(idx) {\n return idx * 2 + 1;\n }\n\n _rightChild(idx) {\n return idx * 2 + 2;\n }\n\n _swap(i, j) {\n [this._heap[i], this._heap[j]] = [this._heap[j], this._heap[i]];\n }\n\n _compare(i, j) {\n return this._comparator(this._heap[i], this._heap[j]);\n }\n\n push(value) {\n this._heap.push(value);\n this._siftUp();\n\n return this.size();\n }\n\n _siftUp() {\n let nodeIdx = this.size() - 1;\n\n while (0 < nodeIdx && this._compare(nodeIdx, this._parent(nodeIdx))) {\n this._swap(nodeIdx, this._parent(nodeIdx));\n nodeIdx = this._parent(nodeIdx);\n }\n }\n\n pop() {\n if (this.size() > 1) {\n this._swap(0, this.size() - 1);\n }\n\n const poppedValue = this._heap.pop();\n this._siftDown();\n return poppedValue;\n }\n\n _siftDown() {\n let nodeIdx = 0;\n\n while (\n (this._leftChild(nodeIdx) < this.size() &&\n this._compare(this._leftChild(nodeIdx), nodeIdx)) ||\n (this._rightChild(nodeIdx) < this.size() &&\n this._compare(this._rightChild(nodeIdx), nodeIdx))\n ) {\n const greaterChildIdx =\n this._rightChild(nodeIdx) < this.size() &&\n this._compare(this._rightChild(nodeIdx), this._leftChild(nodeIdx))\n ? this._rightChild(nodeIdx)\n : this._leftChild(nodeIdx);\n\n this._swap(greaterChildIdx, nodeIdx);\n nodeIdx = greaterChildIdx;\n }\n }\n}\n```\n\n```\nvar networkDelayTime = function(times, N, K) {\n let distances = new Array(N).fill(Infinity);\n distances[K-1] = 0;\n \n for (let i = 0; i < N-1; i++) {\n let cost = 0;\n for (let edge of times) {\n let source = edge[0], target = edge[1], weight = edge[2];\n let newDistance = distances[source-1] + weight;\n if (newDistance < distances[target-1]) {\n distances[target-1] = newDistance;\n cost++;\n }\n }\n if (cost === 0) break; // already found all shortest distances to every vertex\n }\n let res = Math.max(...distances);\n return res === Infinity ? -1 : res;\n}\n// Bellman-Ford\'s algorithm\n// Time Complexity: O(N*E) where E can be N^2 in the worst case\n// Space Complexity: O(N)\n```
| 4
| 0
|
['JavaScript']
| 0
|
network-delay-time
|
C++ Dijkstra Algorithm and BFS
|
c-dijkstra-algorithm-and-bfs-by-dj55427-ifjo
|
Solution 1: Dijkstra Algorithm\n\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int N, int K) {\n \n vector<vect
|
dj55427
|
NORMAL
|
2020-10-05T05:18:26.418571+00:00
|
2020-10-05T07:25:48.306789+00:00
| 532
| false
|
Solution 1: Dijkstra Algorithm\n```\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int N, int K) {\n \n vector<vector<pair<int,int>>> G(N);\n for(auto itr: times)\n G[itr[0]-1].push_back({itr[1]-1,itr[2]});\n \n vector<int> timetaken(N,INT_MAX);\n return Dijkstra(K-1,G,N,timetaken);\n }\n int Dijkstra(int s, vector<vector<pair<int,int>>> &G, int N, vector<int> &timetaken)\n {\n priority_queue< pair<int,int> , vector<pair<int,int>> , greater<pair<int,int>> > pq;\n pq.push({0,s});\n timetaken[s]=0;\n while(!pq.empty())\n {\n int time=pq.top().first;\n int source=pq.top().second;\n pq.pop();\n for(auto itr: G[source])\n {\n if(timetaken[itr.first]>(time+itr.second))\n {\n pq.push({time+itr.second,itr.first});\n timetaken[itr.first]=time+itr.second;\n }\n }\n }\n \n int max_val=0;\n for(int i=0; i<N; ++i)\n {\n if(timetaken[i]==INT_MAX)\n return -1;\n max_val=max(max_val,timetaken[i]);\n }\n return max_val;\n }\n};\n```\nSolution 2: BFS\n```\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int N, int K) {\n \n vector<vector<pair<int,int>>> G(N);\n for(auto itr: times)\n G[itr[0]-1].push_back({itr[1]-1,itr[2]});\n \n vector<int> timetaken(N,INT_MAX);\n return BFS(K-1,G,N,timetaken);\n }\n int BFS(int s, vector<vector<pair<int,int>>> &G, int N, vector<int> &timetaken)\n {\n queue<pair<int,int>> pq;\n pq.push({0,s});\n timetaken[s]=0;\n while(!pq.empty())\n {\n int time=pq.front().first;\n int source=pq.front().second;\n pq.pop();\n for(auto itr: G[source])\n {\n if(timetaken[itr.first]>(time+itr.second))\n {\n pq.push({time+itr.second,itr.first});\n timetaken[itr.first]=time+itr.second;\n }\n }\n }\n \n int max_val=0;\n for(int i=0; i<N; ++i)\n {\n if(timetaken[i]==INT_MAX)\n return -1;\n max_val=max(max_val,timetaken[i]);\n }\n return max_val;\n }\n};\n```
| 4
| 0
|
['C', 'Heap (Priority Queue)']
| 0
|
network-delay-time
|
Java Solution - Dijkstra Algorithm (Inbuilt min-heap trick)
|
java-solution-dijkstra-algorithm-inbuilt-laow
|
Since the inbuilt implementation of priorty queue in java does not support updating the keys once they are inserted, we could insert duplicate nodes in the queu
|
itsmastersam
|
NORMAL
|
2020-04-25T15:54:31.951961+00:00
|
2020-04-25T15:58:20.432657+00:00
| 228
| false
|
Since the inbuilt implementation of priorty queue in java does not support updating the keys once they are inserted, we could insert duplicate nodes in the queue. Once we have visited a node, we can discard all of its duplicates whenever they appear.\n\n```\nclass Solution {\n int ans = 0;\n \n public int networkDelayTime(int[][] times, int N, int K) {\n ArrayList<int[]> adj[] = new ArrayList[N]; // (node, weight)\n for(int i = 0; i < N; i++){\n adj[i] = new ArrayList<>();\n }\n \n for(int t[]: times){\n adj[t[0] - 1].add(new int[]{t[1] - 1, t[2]});\n }\n \n boolean visited[] = new boolean[N];\n dijkstra(K-1, adj, visited);\n \n for(boolean v: visited){\n if(!v){\n return -1;\n }\n }\n \n return ans;\n }\n \n public void dijkstra(int source, ArrayList<int[]> adj[], boolean visited[]){\n PriorityQueue<int[]> pq = new PriorityQueue<>(new Comparator<>(){\n public int compare(int a[], int b[]){\n return a[1] - b[1];\n } \n });\n \n pq.add(new int[]{source, 0});\n while(!pq.isEmpty()){ \n int node[] = pq.poll();\n\n // skip duplicate nodes\n if(visited[node[0]]){\n continue;\n }\n \n visited[node[0]] = true; \n ans = node[1];\n \n for(int neighbor[]: adj[node[0]]){\n pq.add(new int[]{neighbor[0], neighbor[1] + node[1]});\n }\n }\n }\n}\n```
| 4
| 0
|
[]
| 1
|
network-delay-time
|
C++ concise solution
|
c-concise-solution-by-jasperjoe-7d51
|
\tclass Solution {\n\tpublic:\n\t\tint networkDelayTime(vector>& times, int N, int K) {\n\t\t\tint MAX=100101;\n\t\t\tvector dp(N+1,MAX);\n\t\t\tdp[0]=0;\n\t\t\
|
jasperjoe
|
NORMAL
|
2020-01-02T10:43:34.075032+00:00
|
2020-01-02T10:43:34.075065+00:00
| 619
| false
|
\tclass Solution {\n\tpublic:\n\t\tint networkDelayTime(vector<vector<int>>& times, int N, int K) {\n\t\t\tint MAX=100*101;\n\t\t\tvector<int> dp(N+1,MAX);\n\t\t\tdp[0]=0;\n\t\t\tdp[K]=0;\n\t\t\tfor(int i=0;i<N;i++){\n\t\t\t\tfor(auto v:times){\n\t\t\t\t\tint a=v[0];\n\t\t\t\t\tint b=v[1];\n\t\t\t\t\tdp[b]=min(dp[b],dp[a]+v[2]);\n\t\t\t\t}\n\t\t\t}\n\t\t\tint res=*max_element(dp.begin(),dp.end());\n\t\t\treturn res==MAX ? -1:res;\n\n\t\t}\n\t};
| 4
| 1
|
['C', 'C++']
| 0
|
successful-pairs-of-spells-and-potions
|
✔️✔️Easy Solutions in Java ✔️✔️, Python ✔️, and C++ ✔️🧐Look at once 💻 with Exaplanation
|
easy-solutions-in-java-python-and-c-look-gzvy
|
Intuition\n Describe your first thoughts on how to solve this problem. \nFor each spell, we need to find the number of potions that can form a successful pair w
|
Vikas-Pathak-123
|
NORMAL
|
2023-04-02T00:58:19.785541+00:00
|
2023-04-02T01:16:07.236021+00:00
| 35,211
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFor each spell, we need to find the number of potions that can form a successful pair with it. A pair is successful if the product of their strengths is at least the given success value. To find the number of successful pairs for each spell, we can iterate through the potions array and check if the product of the spell strength and the potion strength is greater than or equal to the success value. If it is, we can increment a counter for that spell. We can then return the counters as an array.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. We start by initializing the output array `pairs` with all zeros, and sorting the `potions` array in ascending order.\n \n2. For each `spell` in `spells`, we perform a binary search on the `potions` array to find the number of `potions` that form a successful pair with the current `spell`. We maintain two pointers `left` and `right` that initially point to the first and last indices\nof the `potions` array, respectively.\n\n3. We repeat the binary search until the `left` and `right` pointers meet or cross each other. In each iteration, we compute the product of the current `spell` and the middle `potion` using long integer multiplication to avoid integer overflow. If the product is greater than or equal to the `success` threshold, we move the `right` pointer to the left of the middle index. Otherwise, we move the `left` pointer to the right of the middle index.\n\n4. Once the binary search is complete, we set the corresponding element of `pairs` to the number of `potions` that come after the `left` pointer in the sorted `potions` array, which are guaranteed to form a successful pair with the current `spell`.\n\n5. Finally, we return the `pairs` array as the result.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this solution is $$O(n log m)$$, where n is the length of `spells` and m is the length of `potions`, due to the binary search. The space complexity is O(1).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is $$O(1)$$, since we only use a constant amount of extra memory to store the `pairs` array and the binary search pointers.\n\n\n\n\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution.\uD83D\uDE0A Keep Learning\nPlease give my solution an upvote! \uD83D\uDC4D\nIt\'s a simple way to show your appreciation and\nkeep me motivated. Thank you! \uD83D\uDE0A\n```\n\n# Code\n``` Java []\nclass Solution {\n public int[] successfulPairs(int[] spells, int[] potions, long success) {\n int n = spells.length;\n int m = potions.length;\n int[] pairs = new int[n];\n Arrays.sort(potions);\n for (int i = 0; i < n; i++) {\n int spell = spells[i];\n int left = 0;\n int right = m - 1;\n while (left <= right) {\n int mid = left + (right - left) / 2;\n long product = (long) spell * potions[mid];\n if (product >= success) {\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n }\n pairs[i] = m - left;\n }\n return pairs;\n }\n}\n\n```\n``` Python []\nclass Solution(object):\n def successfulPairs(self, spells, potions, success):\n n = len(spells)\n m = len(potions)\n pairs = [0] * n\n potions.sort()\n for i in range(n):\n spell = spells[i]\n left = 0\n right = m - 1\n while left <= right:\n mid = left + (right - left) // 2\n product = spell * potions[mid]\n if product >= success:\n right = mid - 1\n else:\n left = mid + 1\n pairs[i] = m - left\n return pairs\n\n```\n``` C++ []\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n int n = spells.size();\n int m = potions.size();\n vector<int> pairs(n, 0);\n sort(potions.begin(), potions.end());\n for (int i = 0; i < n; i++) {\n int spell = spells[i];\n int left = 0;\n int right = m - 1;\n while (left <= right) {\n int mid = left + (right - left) / 2;\n long long product = (long long)spell * (long long)potions[mid];\n if (product >= success) {\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n }\n pairs[i] = m - left;\n }\n return pairs;\n }\n};\n\n```\n# Please Comment\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution comment below if you like it.\uD83D\uDE0A\n```
| 342
| 1
|
['Array', 'Binary Search', 'Python', 'C++', 'Java']
| 23
|
successful-pairs-of-spells-and-potions
|
[JavaC++/Python] Straignt Forward with Explantion
|
javacpython-straignt-forward-with-explan-ciws
|
Explanation\nFor each spell,\nit needs ceil integer of need = success * 1.0 / spell.\n\nBinary search the index of first potion >= need in the sorted potions.\n
|
lee215
|
NORMAL
|
2022-06-11T16:02:03.039386+00:00
|
2022-06-11T16:17:53.490459+00:00
| 18,207
| false
|
# **Explanation**\nFor each `spell`,\nit needs ceil integer of `need = success * 1.0 / spell`.\n\nBinary search the `index` of first `potion >= need` in the sorted `potions`.\nThe number of potions that are successful are `potions.length - index`\n\nAccumulate the result `res` and finally return it.\n<br>\n\n# **Complexity**\nTime `O(mlogm + nlogm)`\nSpace `O(n)`\n<br>\n\n**Java**\n```java\n\tpublic int[] successfulPairs(int[] spells, int[] potions, long success) {\n\t\tArrays.sort(potions);\n\t\tTreeMap<Long, Integer> map = new TreeMap<>();\n map.put(Long.MAX_VALUE, potions.length);\n\t\tfor (int i = potions.length - 1; i >= 0; i--) {\n\t\t\tmap.put((long) potions[i], i);\n\t\t}\n\t\tfor (int i = 0; i < spells.length; i++) {\n long need = (success + spells[i] - 1) / spells[i];\n\t\t\tspells[i] = potions.length - map.ceilingEntry(need).getValue();\n\t\t}\n\t\treturn spells;\n\t}\n```\n**C++**\n```cpp\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n sort(potions.begin(), potions.end());\n vector<int> res;\n for (int a: spells) {\n long need = (success + a - 1) / a;\n auto it = lower_bound(potions.begin(), potions.end(), need);\n res.push_back(potions.end() - it);\n }\n return res;\n }\n```\n\n**Python**\n```py\n def successfulPairs(self, spells, potions, success):\n potions.sort()\n return [len(potions) - bisect_left(potions, (success + a - 1) // a) for a in spells]\n```\n<br>\n\n# Solution II: Two Sum\nSort `spells`\nSort `potions`\nNow it\'s basic two sum question, though it\'s two mulplication.\n\nTime `O(nlogn + mlogm)`\nSpace `O(n)`\n\n**Java**\n```java\n public int[] successfulPairs(int[] spells, int[] potions, long success) {\n int[] spells0 = spells.clone();\n Arrays.sort(potions);\n Arrays.sort(spells);\n HashMap<Integer, Integer> count = new HashMap<>();\n int n = spells.length, m = potions.length, j = m - 1, res[] = new int[n];\n for (int i = 0; i < n; ++i) {\n while (j >= 0 && 1L * spells[i] * potions[j] >= success)\n j--;\n count.put(spells[i], m - j - 1);\n }\n for (int i = 0; i < n; ++i) {\n res[i] = count.get(spells0[i]);\n }\n return res;\n }\n```
| 109
| 3
|
['C', 'Python', 'Java']
| 18
|
successful-pairs-of-spells-and-potions
|
C++ | Clean | Easy ✅
|
c-clean-easy-by-ritik_pcl-p6sf
|
\u2764 Please Upvote if you find helpful \u2764\n\nExplanation (Step by Step)\n\nStep 1. \nThe function starts by initializing the vector v with zeros and then
|
ritik_pcl
|
NORMAL
|
2022-06-11T16:06:28.477177+00:00
|
2023-04-02T07:50:18.083439+00:00
| 8,829
| false
|
\u2764 Please Upvote if you find helpful \u2764\n\n**Explanation (Step by Step)**\n\n**Step 1.** \nThe function starts by initializing the vector `v` with `zeros` and then `sorting` the vector `p` in `non-decreasing` order.\n\n**Step 2.** \nFor each element `s[i]` in vector `s`, a `binary search` is performed on vector `p` to find the index of the `largest` element whose product with `s[i]` is `less than eqaul` to `suc`. The binary search is performed by maintaining two indices `l` and `h` representing the lower and upper bounds of the search range, respectively. The search continues until `l` is `less than equal` to `h`.\n\n**Step 3** \nInside the loop, the middle index `mid` is computed as the average of `l` and `h`. If the product of `s[i]` and `p[mid]` is greater than or equal to suc, the upper bound `h` is adjusted to search the `left half` of the array, otherwise the lower bound `l` is adjusted to search the `right half` of the array.\n\n**Step 4**\nAfter the binary search, the number of successful pairs for the element `s[i]` is calculated by `subtracting` the `index of the last element` found in the search from the `size of p`. This is because all elements in `p` starting from this index `satisfy` the condition for a successful pair.\n\n**Step 5**\nFinally, the vector `v` is returned, containing the number of `successful pairs` for each element in `s`. \n\n**FAQ** : `Why binary search is used ?` \n=> By using binary search, the code avoids the need to compare the current element in s with all elements in p, which would have a time complexity of $$O(n\xB2)$$. Instead, the binary search algorithm efficiently reduces the search space by dividing it in half at each step, resulting in a much faster search time $$O(nlog(n))$$.\n\n```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& s, vector<int>& p, long long suc) {\n \n vector<int> v(s.size(),0);\n sort(p.begin(),p.end());\n \n for(int i=0;i<s.size();i++)\n {\n int h=p.size()-1;\n int l=0;\n int mid;\n while(l<=h)\n {\n mid = l + (h-l)/2;\n \n if((long long int)s[i]*(long long int)p[mid] >= suc)\n h = mid-1;\n \n else\n l = mid+1;\n }\n \n v[i] = p.size()-1-h;\n }\n \n return v;\n }\n};\n```\n\n \u2227,,,\u2227\n( \u0333\u2022 \xB7 \u2022 \u0333)\n/ \u3065\u2661\n
| 75
| 3
|
['Binary Search', 'C', 'C++']
| 4
|
successful-pairs-of-spells-and-potions
|
Image Explanation🏆- [Binary Search with & without Inbuild Libraries] - C++/Java/Python
|
image-explanation-binary-search-with-wit-4asr
|
Video Solution (Aryan Mittal) - Link in LeetCode Profile\nSuccessful Pairs of Spells and Potions by Aryan Mittal\n\n\n# Approach & Intution\n\n\n\n\n\n\n\n\n\n\
|
aryan_0077
|
NORMAL
|
2023-04-02T01:05:37.488111+00:00
|
2023-04-02T02:27:09.694000+00:00
| 14,068
| false
|
# Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Successful Pairs of Spells and Potions` by `Aryan Mittal`\n\n\n# Approach & Intution\n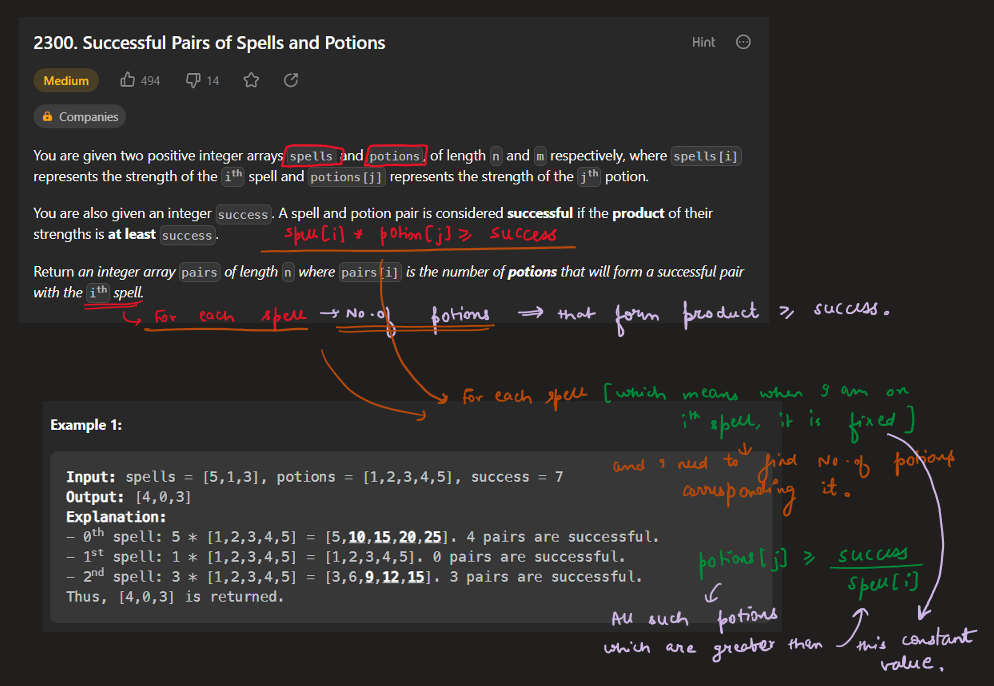\n\n\n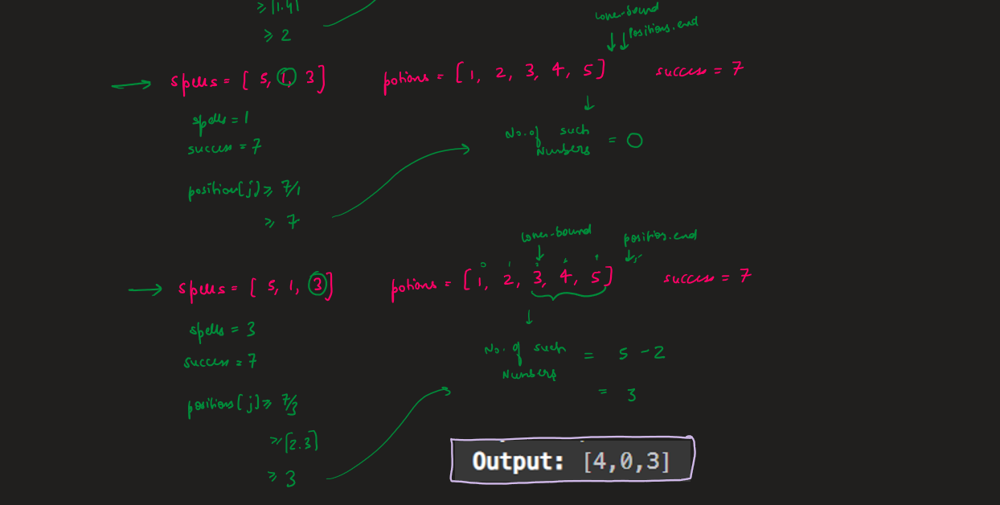\n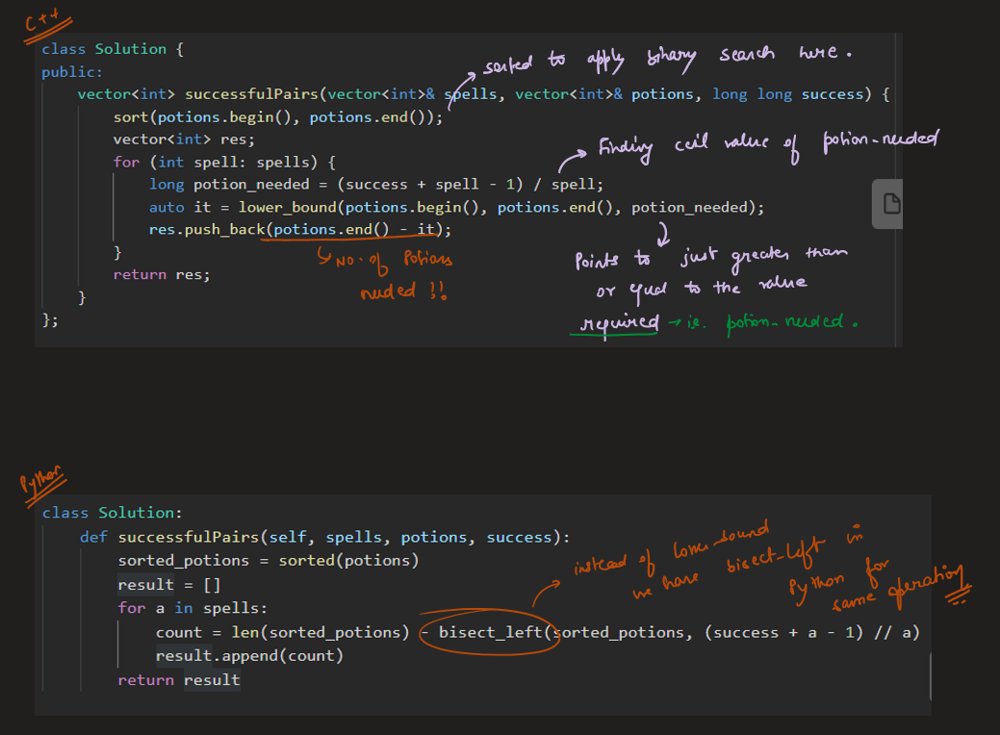\n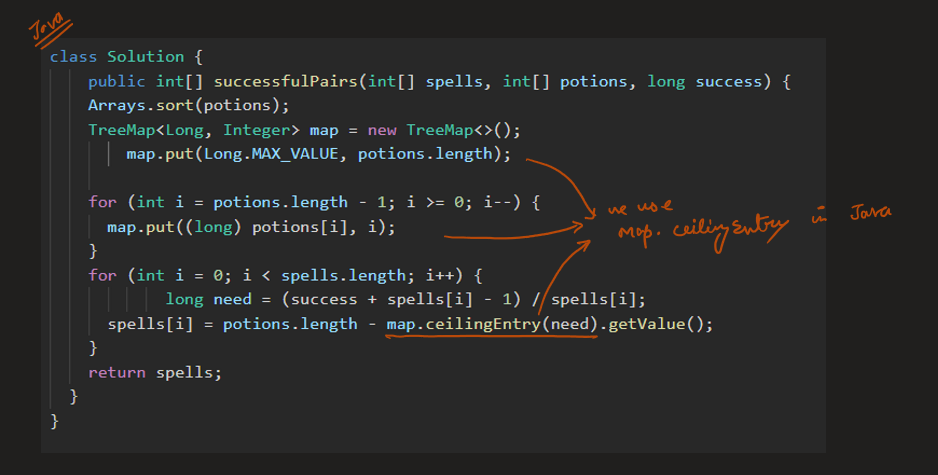\n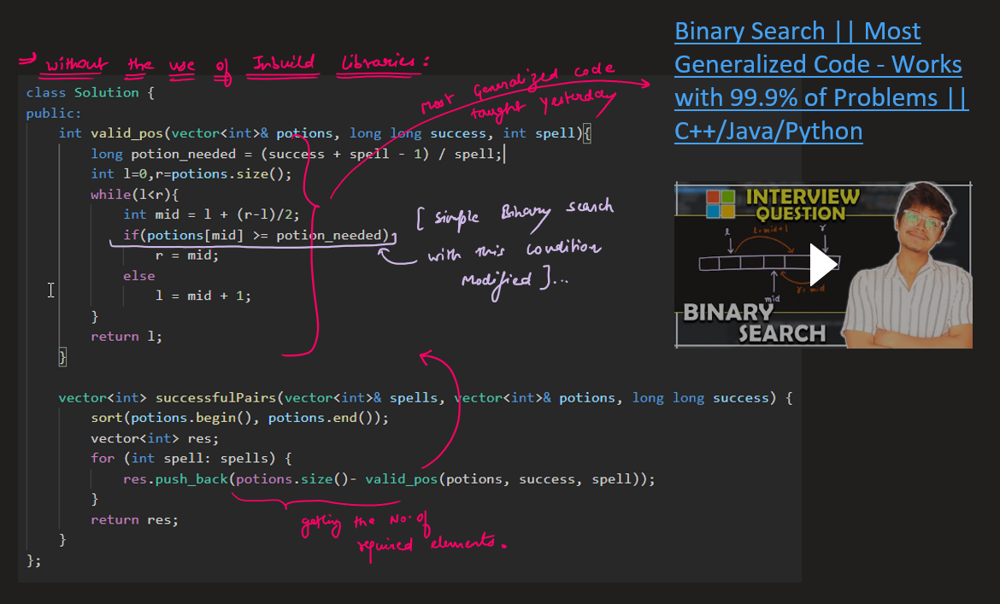\n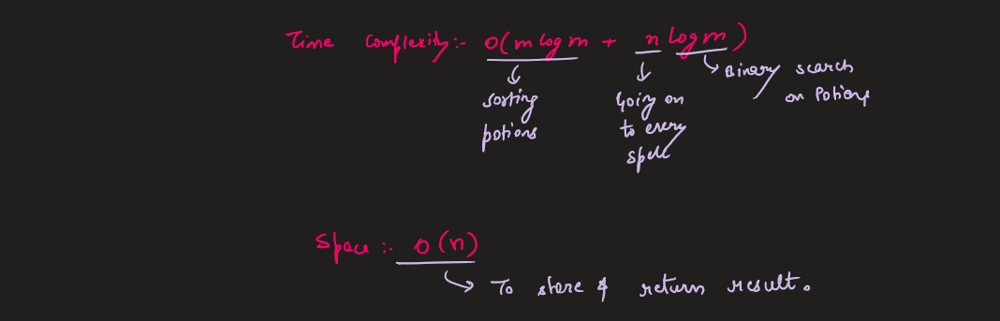\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n sort(potions.begin(), potions.end());\n vector<int> res;\n for (int spell: spells) {\n long potion_needed = (success + spell - 1) / spell;\n auto it = lower_bound(potions.begin(), potions.end(), potion_needed);\n res.push_back(potions.end() - it);\n }\n return res;\n }\n};\n```\n```Java []\nclass Solution {\n public int[] successfulPairs(int[] spells, int[] potions, long success) {\n\t\tArrays.sort(potions);\n\t\tTreeMap<Long, Integer> map = new TreeMap<>();\n map.put(Long.MAX_VALUE, potions.length);\n \n\t\tfor (int i = potions.length - 1; i >= 0; i--) {\n\t\t\tmap.put((long) potions[i], i);\n\t\t}\n\t\tfor (int i = 0; i < spells.length; i++) {\n long need = (success + spells[i] - 1) / spells[i];\n\t\t\tspells[i] = potions.length - map.ceilingEntry(need).getValue();\n\t\t}\n\t\treturn spells;\n\t}\n}\n```\n```Python []\nclass Solution:\n def successfulPairs(self, spells, potions, success):\n sorted_potions = sorted(potions)\n result = []\n for a in spells:\n count = len(sorted_potions) - bisect_left(sorted_potions, (success + a - 1) // a)\n result.append(count)\n return result\n```\n\n\n# Code Without Inbuild Libraries\nExact same [Generalized Binary Search code](https://leetcode.com/problems/binary-search/solutions/3363888/image-explanation-most-generalized-binary-search-cjavapython/) discussed for C++/Java/Python.\n```C++ []\nclass Solution {\npublic:\n int valid_pos(vector<int>& potions, long long success, int spell){\n long potion_needed = (success + spell - 1) / spell;\n\n int l=0,r=potions.size();\n while(l<r){\n int mid = l + (r-l)/2;\n if(potions[mid] >= potion_needed)\n r = mid;\n else\n l = mid + 1;\n }\n return l;\n }\n\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n sort(potions.begin(), potions.end());\n vector<int> res;\n for (int spell: spells) {\n res.push_back(potions.size()- valid_pos(potions, success, spell));\n }\n return res;\n }\n};\n```\n```Java []\nclass Solution {\n public int valid_pos(int[] potions, long success, int spell) {\n long potion_needed = (success + spell - 1) / spell;\n int l = 0, r = potions.length;\n while (l < r) {\n int mid = l + (r - l) / 2;\n if (potions[mid] >= potion_needed)\n r = mid;\n else\n l = mid + 1;\n }\n return l;\n }\n\n public int[] successfulPairs(int[] spells, int[] potions, long success) {\n Arrays.sort(potions);\n int[] res = new int[spells.length];\n for (int i = 0; i < spells.length; i++) {\n res[i] = potions.length - valid_pos(potions, success, spells[i]);\n }\n return res;\n }\n}\n```\n```Python []\nclass Solution:\n def valid_pos(self, potions: List[int], success: int, spell: int) -> int:\n potion_needed = (success + spell - 1) // spell\n l, r = 0, len(potions)\n while l < r:\n mid = l + (r - l) // 2\n if potions[mid] >= potion_needed:\n r = mid\n else:\n l = mid + 1\n return l\n\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n potions.sort()\n res = []\n for spell in spells:\n res.append(len(potions) - self.valid_pos(potions, success, spell))\n return res\n```
| 52
| 2
|
['Binary Search', 'C++', 'Java', 'Python3']
| 5
|
successful-pairs-of-spells-and-potions
|
Why and How Binary Search || Intuition Explained
|
why-and-how-binary-search-intuition-expl-5dds
|
\n\n\n\nclass Solution {\npublic:\n int getPairCount(vector<int>& potions, int& spell, long long& target)\n {\n int n = potions.size(), bestIdx = n
|
mohakharjani
|
NORMAL
|
2023-04-02T01:11:29.188166+00:00
|
2023-04-02T01:19:07.303627+00:00
| 6,981
| false
|
\n\n\n```\nclass Solution {\npublic:\n int getPairCount(vector<int>& potions, int& spell, long long& target)\n {\n int n = potions.size(), bestIdx = n;\n int low = 0, high = n - 1;\n //=============================================================\n while(low <= high)\n {\n int mid = low + (high - low) / 2;\n long long product = (long long)spell * potions[mid];\n \n if (product >= target)\n {\n bestIdx = mid;\n high = mid - 1;\n }\n else low = mid + 1;\n }\n //================================================================\n return (n - bestIdx);\n }\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success)\n {\n int n = spells.size();\n vector<int>ans(n);\n sort(potions.begin(), potions.end());\n for (int i = 0; i < n; i++) \n ans[i] = getPairCount(potions, spells[i], success);\n \n return ans;\n }\n};\n```\n\n
| 50
| 4
|
['C', 'Binary Tree', 'C++']
| 6
|
successful-pairs-of-spells-and-potions
|
✅ Java | Easy Solution with Detailed Explaination and Similar problems 📝 | Binary Search
|
java-easy-solution-with-detailed-explain-wj1w
|
Intuition\nQuestion reduces to finding no of potions for each spell which have \nproduct greater than success where product is (each spell * potions[i])\n\nNow
|
nikeMafia
|
NORMAL
|
2023-04-02T03:37:43.811014+00:00
|
2023-04-02T07:30:19.087866+00:00
| 3,318
| false
|
# Intuition\nQuestion reduces to finding no of potions for each spell which have \n***product greater than success*** where product is (each spell * potions[i])\n\nNow decision is whether to keep the potions array sorted or not.\n\n- ***NON-SORTED*** Another is to traverse entire array of potions and count no of products(spell * potions[i]) greater than success. But this will take more time as for each spell we will need to traverse entire potions array.\n\n- ***SORTED*** Immediate thought to reduce time complexity of above case is to keep potions array sorted, then question reduces to finding the first occurrence of the product( each spell * potions[i]) which is greater than success, so we go with ***Binary search***\n\n---\n\n\n# Approach\n1) Sort potions array.\n2) For every spell we will find min Index where the product( spell * potion[i]) is greater than success\n3) Once we find such an index via binary search anser for that spell is \npotions.length - minIndex\n4) It is ***important*** how we choose left and right pointers of binary search\n5) I intialised with left = 0, *right = potion.length and not potion.length-1*, since we can have a case where we donot find any minIndex in that case the minIndex will be potion.length and hence result[i] of such spell[i] = potion.length -minIndex = 0\n\n**Similar question[ LC 35 Search and Insert](https://leetcode.com/problems/search-insert-position/) to make you understand point 5 better and how to choose boundaries wisely depending on the question type.**\n\n***Generic binary search [understanding](https://leetcode.com/problems/binary-search/solutions/3364223/java-easy-solution-explained-why-leftright-left2-instead-of-leftright2/)***\n\n\n---\n- Time Complexity\nO(nlogm): where m is the length of potions array and n of spells array\n\n***NOTE***: Reason why 1l is done in ***long product = (1l * spell) * potions[mid];*** because (spell * potions[i]) both being integer will overflow and will result in wrong product value. \nI wasted a lot of time in this.\n\n---\n\nHope it is easy to understand.\nLet me know if there is something unclear and i can fix it.\n\nOtherwise, please upvote if you like the solution, it would be encouraging\n\n\n\n\n# Code\n```\nclass Solution {\n public int[] successfulPairs(int[] spells, int[] potions, long success) {\n int [] result = new int[spells.length];\n int potionsLength = potions.length;\n Arrays.sort(potions);\n\n for(int i=0; i<spells.length; i++){\n int minIndex = binarySearch(potions, success, spells[i]);\n result[i] = potionsLength - minIndex;\n }\n return result;\n }\n\n private int binarySearch(int [] potions, long success, int spell){\n int left= 0;\n int right= potions.length;\n \n while(left<right){\n int mid = left + (right-left)/2;\n long product = (1l * spell) * potions[mid];\n if(product<success){\n left=mid+1;\n }else{\n right=mid;\n }\n }\n\n return left;\n }\n}\n\n```
| 32
| 0
|
['Binary Search', 'Java']
| 1
|
successful-pairs-of-spells-and-potions
|
Prefix/Postfix sum C++ | 99% Faster in time
|
prefixpostfix-sum-c-99-faster-in-time-by-yrpi
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem asks us to find out the number of potion values that has product with a spe
|
HenryNguyen101
|
NORMAL
|
2023-04-02T03:42:14.109940+00:00
|
2023-04-02T03:42:14.109966+00:00
| 5,239
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem asks us to find out the number of potion values that has product with a specific spell value which is greater than (or equal to) a threshold.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSince we have to find the amount of values that is greater than a value, the easiest way is to sort the whole array, then do binary search to find out the position that has the smallest element that satisfy the problem. However, since this approach takes `O(nlogn)` times, which might not be the best idea (in my opinion), for the input with size of 10^5, so I got another idea.\n\nMy idea was, couting occurences of all numbers, then add from the end, using postfix sum, so that, `postfix[n]` is the number of numbers that has value greater than or equal to value `n` in `potions`. Then, that would take `O(1)`, instead of `O(log n)` for each time do searching for each spell, and `O(n)` for counting, instead of `O(nlogn)` do sorting.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n int postfix[100001] = {0};\n for(auto potion: potions) postfix[potion]++;\n for(int i=99999; i>=0; --i) postfix[i] += postfix[i+1];\n\n //No need extra space at all for storing final result\n for(int i=0; i<spells.size(); ++i){\n long long val = success / (long long) spells[i];\n if(success % (long long) spells[i] != 0) val++;\n\n spells[i] = val <= 1e5 ? postfix[val] : 0;\n }\n return spells;\n }\n};\n```
| 28
| 0
|
['C++']
| 2
|
successful-pairs-of-spells-and-potions
|
Binary Search
|
binary-search-by-kamisamaaaa-ppn5
|
\nIf ith potion is successful then all the potions after will be successful.\n So find the first potion which is successful using Binary Search.\n\nclass Sol
|
kamisamaaaa
|
NORMAL
|
2022-06-11T16:01:56.128551+00:00
|
2022-06-11T16:15:28.284463+00:00
| 3,311
| false
|
\n***If ith potion is successful then all the potions after will be successful.\n So find the first potion which is successful using Binary Search.***\n```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n \n vector<int> res;\n int n(size(potions));\n sort(begin(potions), end(potions));\n \n for (auto& spell : spells) {\n int start(0), end(n);\n while (start < end) {\n int mid = start + (end-start)/2;\n ((long long)spell*potions[mid] >= success) ? end = mid : start = mid+1;\n }\n res.push_back(n-start);\n }\n return res;\n }\n};\n```
| 26
| 1
|
['C', 'Binary Tree']
| 4
|
successful-pairs-of-spells-and-potions
|
✅✅Python🔥Simple Solution🔥Easy to Understand🔥
|
pythonsimple-solutioneasy-to-understand-1uxta
|
Please UPVOTE \uD83D\uDC4D\n\n!! BIG ANNOUNCEMENT !!\nI am currently Giving away my premium content well-structured assignments and study materials to clear int
|
cohesk
|
NORMAL
|
2023-04-02T13:53:21.909086+00:00
|
2023-04-02T13:53:21.909128+00:00
| 3,138
| false
|
# Please UPVOTE \uD83D\uDC4D\n\n**!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers this week. I planned to give for next 10,000 Subscribers as well. So **DON\'T FORGET** to Subscribe\n\n**Search \uD83D\uDC49`Tech Wired leetcode` on YouTube to Subscribe**\n# OR \n**Click the Link in my Leetcode Profile to Subscribe**\n\n# Video Solution\n**Search \uD83D\uDC49 `Successful Pairs of Spells and Potions by Tech Wired` on YouTube**\n\n\n\n\nHappy Learning, Cheers Guys \uD83D\uDE0A\n\n# Approach:\n\nThe approach for solving the problem is fairly straightforward. We start by sorting the potions list in non-decreasing order. Next, we loop through each spell strength a in the spells list. For each spell, we calculate the minimum strength required for a successful pair by using the formula (success + a - 1) // a. This formula ensures that the result is rounded up to the nearest integer. Once we have the minimum strength required, we use the bisect_left function to find the index of the first potion in the sorted potions list that has strength greater than or equal to the minimum strength required for a successful pair. Finally, we subtract this index from the length of potions to get the number of potions that can form a successful pair for the given spell strength. We repeat this process for each spell strength and store the counts in the result list. Finally, we return the result list.\n\n# Intuition:\n\nThe problem requires us to find the number of successful pairs of spells and potions. The key to finding a successful pair is to ensure that the strength of the potion is greater than or equal to the minimum strength required for a successful pair for the given spell strength. This minimum strength is calculated by using the formula (success + a - 1) // a, which ensures that the result is rounded up to the nearest integer. Sorting the potions list in non-decreasing order makes it easier to find the right potion for each spell. We use the bisect_left function to find the index of the first potion in the sorted potions list that has strength greater than or equal to the minimum strength required for a successful pair. The difference between the length of potions and this index gives the number of potions that can form a successful pair for the given spell strength. We repeat this process for each spell strength, and the counts are stored in the result list.\n\n```\nclass Solution:\n def successfulPairs(self, spells, potions, success):\n sorted_potions = sorted(potions)\n result = []\n for a in spells:\n count = len(sorted_potions) - bisect_left(sorted_potions, (success + a - 1) // a)\n result.append(count)\n return result\n\n\n```\n\n\n# Please UPVOTE \uD83D\uDC4D
| 22
| 1
|
['Array', 'Binary Search', 'Python', 'Python3']
| 1
|
successful-pairs-of-spells-and-potions
|
[Java/Python 3] Sort and Binary search w/ brief explanation and analysis.
|
javapython-3-sort-and-binary-search-w-br-qitd
|
Q & A\n\nQ1: Why and how do we need to compute the factor?\nA1: \n1) We need a factor from potions to multiply with current spells[i] in order to get a product
|
rock
|
NORMAL
|
2022-06-11T16:02:52.895284+00:00
|
2022-06-13T16:53:15.037791+00:00
| 3,240
| false
|
**Q & A**\n\nQ1: Why and how do we need to compute the factor?\nA1: \n1) We need a factor from `potions` to multiply with current `spells[i]` in order to get a product at least `success`. Therefore, computing before hand will obtain a key (the factor) for binary search.\n2) `(success + s) // s = success / s + 1`, which is not ceiling of `success / s`; In contrast, `success / s <= (success + s - 1) // s < success / s + 1`, and therefore `(success + s - 1) // s` is the ceiling. \n\nQ2: Why in Python 3 code do we need to compute the ceiling `(success + s - 1) // s`, not `success / s`?\nA2: For this problem we can use either. ~~~However, if `potions` is a float array then the ceiling way is a must. `success / s` is a float, which has a limited precision. In extreme case it may cause error; Use the ceiling, an int, will guarantee the correctness of the code.~~~\n\n~~~e.g., `success = 10, s = 3`, `potions[i] = 3.3333333333...33` (there are `k + 1` 3\'s) is in `potions`.~~~\n\n~~~If we use float `factor = success / s = 10 / 3 = 3.3333333333...3` (there are `k` 3\'s), then we will miss the correct `potions[i]` in binary search;~~~\n~~~In contrast, `(success + s - 1) // s = (10 + 3 - 1) // 3 = 4` will guarantee to obtain correct result.~~~\n\n**End of Q & A**\n\n----\n\n1. Sort `potions` for binary search;\n2. Traverse `spells`, for each element `s`, compute the ceiling of the quotient of `success / s`, `(success + s - 1) / s`;\n3. Binary search the corresponding ceiling of each quotient in 2. to find out how many pairs with a product at least `success`.\n\n```java\n public int[] successfulPairs(int[] spells, int[] potions, long success) {\n Arrays.sort(potions);\n int[] pairs = new int[spells.length];\n for (int i = 0; i < spells.length; ++i) {\n if ((success + spells[i] - 1) / spells[i] > 100_000) { // boundary check to avoid int overflow.\n int s = spells[i], factor = (int)((success + s - 1) / s);\n pairs[i] = potions.length - binarySearch(potions, factor);\n } \n }\n return pairs;\n }\n private int binarySearch(int[] potions, int key) {\n int lo = 0, hi = potions.length; \n while (lo < hi) {\n int mid = lo + (hi - lo) / 2;\n if (potions[mid] < key) {\n lo = mid + 1;\n }else {\n hi = mid;\n } \n }\n return lo;\n }\n```\nWe can modify signature of `binarySearch(int[], int)` to `binarySearch(int[], long)` to avoid int overflow problem.\n```java\n public int[] successfulPairs(int[] spells, int[] potions, long success) {\n Arrays.sort(potions);\n int[] pairs = new int[spells.length];\n for (int i = 0; i < spells.length; ++i) {\n long factor = (success + spells[i] - 1) / spells[i];\n pairs[i] = potions.length - binarySearch(potions, factor);\n }\n return pairs;\n }\n private int binarySearch(int[] potions, long key) {\n int lo = 0, hi = potions.length; \n while (lo < hi) {\n int mid = lo + (hi - lo) / 2;\n if (potions[mid] < key) {\n lo = mid + 1;\n }else {\n hi = mid;\n } \n }\n return lo;\n }\n```\n\n```python\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n potions.sort()\n pairs = []\n for s in spells:\n factor = (success + s - 1) // s\n pairs.append(len(potions) - bisect.bisect_left(potions, factor))\n return pairs\n```\n\nFor Python 3 code, we can use `success / s` as key for binary search:\n\n```python\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n potions.sort()\n return [len(potions) - bisect.bisect_left(potions, success / s) for s in spells]\n```\n\n**Analysis:**\n\nTime: `O((m + n)logm)`, space: `O(n + m)` - including sorting space, where `n = spells.length, m = potions.length`.
| 19
| 0
|
['Binary Search', 'Sorting', 'Java', 'Python3']
| 7
|
successful-pairs-of-spells-and-potions
|
Binary Search vs. Two Pointers
|
binary-search-vs-two-pointers-by-votruba-jev0
|
In the first approach, we sort potions, and use binary search to find the position of the weakest potion that produces a success. All potions to the right would
|
votrubac
|
NORMAL
|
2022-06-11T16:46:39.681160+00:00
|
2022-06-11T17:44:28.458594+00:00
| 2,738
| false
|
In the first approach, we sort `potions`, and use binary search to find the position of the weakest potion that produces a success. All potions to the right would work also.\n\nIn the second approach, we sort both `potions` and `spells` (we actually sort indexes `idx` to preserve the order of spells). Then, we use two pointers to track the weakest `potions[j]` that works for `spells[i]`. Since we process spells from weakest to the strongest, pointer `j` is moved in one direction - from strongest to weakest.\n\n#### Binary Search\n**C++**\n```cpp\nvector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n sort(begin(potions), end(potions));\n for (int i = 0; i < spells.size(); ++i) {\n long long comp = (success + spells[i] - 1) / spells[i];\n spells[i] = potions.size() - (lower_bound(begin(potions), end(potions), comp) - begin(potions));\n }\n return spells;\n}\n```\n#### Two Pointers\n**C++**\n```cpp\nvector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n vector<int> idx(spells.size());\n iota(begin(idx), end(idx), 0);\n sort(begin(potions), end(potions), greater<int>());\n sort(begin(idx), end(idx), [&](int i, int j){ return spells[i] < spells[j]; });\n for (int i = 0, j = 0; i < idx.size(); ++i) {\n while (j < potions.size() && (long long)potions[j] * spells[idx[i]] >= success)\n ++j;\n spells[idx[i]] = j;\n }\n return spells;\n}\n```
| 17
| 0
|
['C']
| 4
|
successful-pairs-of-spells-and-potions
|
✅ Java | Sorting + Binary Search Approach
|
java-sorting-binary-search-approach-by-p-t2fl
|
\n// Approach 2: Sorting + Binary Search (Lower Bound)\n\n// Time complexity: O((m + n) log m)\n// Space complexity: O(log m)\n\npublic int[] successfulPairs(i
|
prashantkachare
|
NORMAL
|
2023-04-02T05:48:08.556994+00:00
|
2023-04-02T06:14:53.023709+00:00
| 1,533
| false
|
```\n// Approach 2: Sorting + Binary Search (Lower Bound)\n\n// Time complexity: O((m + n) log m)\n// Space complexity: O(log m)\n\npublic int[] successfulPairs(int[] spells, int[] potions, long success) {\n\tint n = spells.length;\n\tint m = potions.length;\n\tint[] pairs = new int[n];\n\n\tArrays.sort(potions); // m log m\n\n\tfor (int i = 0; i < n; i++) { // n log m\n\t\tint left = 0, right = m;\n\n\t\twhile (left < right) {\n\t\t\tint mid = left + (right - left) / 2;\n\n\t\t\tif ((long) spells[i] * (long) potions[mid] >= success)\n\t\t\t\tright = mid;\n\t\t\telse\n\t\t\t\tleft = mid + 1;\n\t\t}\n\n\t\tpairs[i] = m - left;\n\t}\n\n\treturn pairs;\n}\n```\n\n**Please upvote if you find this solution useful. Happy Coding!**
| 15
| 0
|
['Sorting', 'Binary Tree', 'Java']
| 1
|
successful-pairs-of-spells-and-potions
|
Linear Solution c++
|
linear-solution-c-by-user5376zt-2v7z
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n1. Find maximum Spell power.\n2. Create an array counts of length max spe
|
user5376Zt
|
NORMAL
|
2023-04-02T05:42:05.845796+00:00
|
2023-04-02T05:42:05.845843+00:00
| 947
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Find maximum Spell power.\n2. Create an array `counts` of length `max spell power` filled with zeros.\n3. For each potion calculate minimum required spell. If required spell <= maximum spell power, increment counts of required Spell.\n4. Update `counts` , so `counts[i] = sum(counts[0]...counts[i])`. So `counts` now contains total number of "good" potions.\n5. Fill the results, so `results[i] = counts[spells[i]]`. To save some space, we can use spells as results.\n\n# Complexity\n- Time complexity: O(n + m + k)\n spells.size() = n\n potions.size() = m\n max spells power = k\n\n It can be optimized a little bit. `k` could be `max spells power` - `min spells power`\n\n- Space complexity: O(k)\n We only use additional space for `counts` array. If we consider `results` as additional space, then O(k+n).\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n int maxSpell = 0;\n for(int i=0; i<spells.size(); ++i){ //O(n)\n maxSpell = max(maxSpell, spells[i]);\n }\n vector<int> counts(maxSpell+1, 0);\n\n for(int i=0; i<potions.size(); ++i){ //O(m)\n auto index = (success+potions[i]-1)/potions[i]; //minimum required spell power\n if(index<counts.size()) counts[index]++;\n }\n\n for(int i=1; i<counts.size(); ++i){ //O(k)\n counts[i] +=counts[i-1];\n }\n\n vector<int> result(spells.size(), 0);\n for(int i=0; i<spells.size(); ++i){ //O(n)\n result[i] = counts[spells[i]];\n }\n return result;\n }\n};\n```
| 13
| 0
|
['C++']
| 4
|
successful-pairs-of-spells-and-potions
|
🔥 C++ Beginner Friendly Explanation - Brute Force to Optimized Intuition 🤔
|
c-beginner-friendly-explanation-brute-fo-ulk4
|
Brute Force [Time Limit Exceeded]\n\n## Intuition\nInitially, it sounds like we can just multiply each spell for each potion, but this is not fast enough.\n\n##
|
hotpotmaster
|
NORMAL
|
2023-04-02T02:50:04.157798+00:00
|
2023-04-02T02:52:51.670892+00:00
| 2,480
| false
|
# Brute Force [Time Limit Exceeded]\n\n## Intuition\nInitially, it sounds like we can just multiply each `spell` for each `potion`, but this is not fast enough.\n\n## Algorithm Design\n- Loop for each `spell`\n - Loop for each `potion`\n - Increase count if the product is $$>=$$ `success`\n\n## Code\n```cpp\nclass Solution {\npublic:\n // T:O(n*m), S:O(1)\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n vector<int> numPairs(spells.size(), 0);\n\n // Loop through all spells\n for(int i = 0; i < spells.size(); i++) { // O(n)\n int spell = spells[i];\n int count = 0;\n\n // Loop through all potions for each spell\n for(int potion: potions) { // O(m)\n\n // Increment count if it exceeds success\n long long pair = (long long)potion * (long long)spell;\n if(pair >= success) count++;\n }\n numPairs[i] = count;\n }\n\n return numPairs;\n }\n};\n```\n\n## Complexity\nLet\'s define `m` as the length of `spells` and `n` as the length of `potions`.\n\n- Time Complexity: $$O(n*m)$$\n- Space Complexity: $$O(1)$$\n - The resulting array is not considered as space.\n\n# Binary Search [Accepted]\n\n## Intuition\nTo reduce search time, we can almost always use binary search. However, the prequisite is sorting. Here, we only need to sort `potions` and find the minimum potion needed to be $$>=$$ `success`.\n\n## Algorithm Design\n- Sort potions\n- Loop for each `spell`\n - Find index of the minimum potion needed\n - Calculate the distance since every greater idx is $$>=$$ `success`\n\n## Code\n```cpp\nclass Solution {\npublic:\n // T:O(m log m + n log m), S:O(log m)\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n vector<int> numPairs(spells.size(), 0);\n\n // Sort potions\n sort(potions.begin(), potions.end()); // O(m log m)\n\n // Loop through all spells\n for(int i = 0; i < spells.size(); i++) { // O(n)\n // Find the minimum potion needed for success\n long long potionNeeded = ceil(static_cast<double>(success) / spells[i]);\n\n // Find the smallest idx position\n auto it = lower_bound(potions.begin(), potions.end(), potionNeeded); // O(log m)\n int idx = it - potions.begin();\n\n // Calculate count based on the index\n int numPair = potions.size() - (it - potions.begin());\n numPairs[i] = max(0, numPair);\n }\n\n return numPairs;\n }\n};\n```\n\n## Complexity\nLet\'s define `m` as the length of `spells` and `n` as the length of `potions`.\n\n- Time Complexity: $$O((m + n)log m)$$\n- Space Complexity: $$O(log m)$$\n - Sorting in C++ takes $$O(log m)$$ space.\n - The resulting array is not considered as space.\n \n# Two Pointers [Accepted]\n\n## Intuition\nSince a larger number will always be able to form products $$>=$$ `success` compared to a smaller number, we can use a greedy two pointer approach. \n\n#### For example:\nspells: [1,2,3]\npotions: [1,2]\nsuccess: 4\n\nIf we take the leftmost `spell` (1) and multiply with rightmost `potion` (2), we get a product of 2. This means any potion of a smaller index will not be possible. If we are able to form a product $$>=$$ `success`, that means any greater `spell` number can form it too.\n\n## Algorithm Design\n- Remember the index of `spells` since we will be sorting\n- Sort `potions` and `spells`\n- Initialize two pointers:\n - Leftmost of `spells`\n - Rightmost of `potions`\n- While we can form product $$>=$$ `success`, we should decrement `potion` pointer. \n\n## Code\n```cpp\nclass Solution {\npublic:\n // T:O(n log n + m log m), S:O(n + log m)\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n unordered_map<int, pair<int, int>> pairsMap; // {spells[i], {idx, numPair}}\n\n // Copy spells into numPairs\n vector<int> numPairs(spells); // O(n)\n \n // Add each number into the map\n for(int i = 0; i < spells.size(); i++) { // O(n)\n pairsMap[spells[i]] = {i, -1};\n }\n\n // Sort both spells and potion\n sort(spells.begin(), spells.end()); // O(n log n)\n sort(potions.begin(), potions.end()); // O(m log m)\n\n // Two pointer approach\n // Spell pointer starts from the left\n // Potion pointer starts from the right\n int potionPtr = potions.size() - 1;\n for(int i = 0; i < spells.size(); i++) { // O(m)\n int spell = spells[i];\n while(potionPtr >= 0 && (long long) spell * potions[potionPtr] >= success) {\n potionPtr--;\n }\n pairsMap[spell] = {pairsMap[spell].first, potions.size() - 1 - potionPtr};\n }\n\n // Put data into vector\n int idx = 0;\n for(int spell: numPairs) { // O(n)\n numPairs[idx++] = pairsMap[spell].second;\n }\n\n return numPairs;\n }\n};\n```\n\n## Complexity\nLet\'s define `m` as the length of `spells` and `n` as the length of `potions`.\n\n- Time Complexity: $$O(n log n + m log m)$$\n- Space Complexity: $$O(n + log m)$$\n - Sorting in C++ takes $$O(log n)$$ space.\n - The resulting array is not considered as space.
| 13
| 0
|
['Two Pointers', 'Binary Search', 'Sorting', 'C++']
| 2
|
successful-pairs-of-spells-and-potions
|
Day 92 || Binary Search || Easiest Beginner Friendly Sol
|
day-92-binary-search-easiest-beginner-fr-xhid
|
NOTE - PLEASE READ INTUITION AND APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.\n \nNOTE 2 -
|
singhabhinash
|
NORMAL
|
2023-04-02T00:51:35.880659+00:00
|
2023-04-02T01:19:24.160785+00:00
| 4,697
| false
|
**NOTE - PLEASE READ INTUITION AND APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n \n**NOTE 2 - I WILL HIGHLY RECOMMEND YOU GUYS BEFORE SOLVING THIS PROBLEM PLEASE SOLVE BINARY SEARCH PROBLEM.**\n\n**704. Binary Search Problem -** https://leetcode.com/problems/binary-search/\n**704. Binary Search Solution -** https://leetcode.com/problems/binary-search/solutions/3364016/day-91-binary-search-o-logn-time-easiest-beginner-friendly-sol/\n\n# Intuition of this Problem :\n*The problem is asking to find the number of successful pairings between the spells and potions arrays such that the product of their strengths is at least a given integer "success".*\n\n***To solve this problem, we can iterate through each spell and for each spell, we can find the index of the first potion whose strength is at least "success". This can be done using binary search since the potions array is sorted. Once we have the index, the number of successful pairings can be calculated by subtracting the index from the total number of potions. We can repeat this process for each spell and store the number of successful pairings in an array.***\n\n*Finally, we return the array containing the number of successful pairings for each spell.*\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach for this Problem :\n1. Define a function binarySearch which takes the input integer spell, a vector of integers potions, and a long integer success and returns an integer value.\n2. Initialize the integer startIndex to 0, lastIndex to potions.size() - 1, and ansIndex to -1.\n3. Run a while loop until startIndex is less than or equal to lastIndex.\n4. Within the loop, calculate the midIndex using (startIndex + (lastIndex - startIndex) / 2) to avoid integer overflow.\n5. If the product of spell and the midIndex element of potions is greater than or equal to success, then set ansIndex to midIndex and update lastIndex to midIndex - 1.\n6. Else, update startIndex to midIndex + 1.\n7. Return ansIndex.\n8. Initialize an integer m to the size of the potions vector and create an empty vector ans.\n9. Sort the potions vector in ascending order using sort.\n10. Iterate through each element spell in the spells vector.\n11. Initialize an integer countPair to 0.\n12. Call the binarySearch function with spell, potions, and success as arguments and store the result in the index variable.\n13. If index is equal to -1, then add 0 to countPair, else add m - index to countPair.\n14. Append countPair to ans.\n15. Return ans.\n<!-- Describe your approach to solving the problem. -->\n\n# Code :\n```C++ []\n//1st Approach\n\nclass Solution {\npublic:\n int binarySearch(int spell, vector<int>& potions, long long success) {\n int startIndex = 0; \n int lastIndex = potions.size() - 1;\n int ansIndex = -1;\n while(startIndex <= lastIndex){\n //helps to prevent from out of bound\n int midIndex = (startIndex + (lastIndex - startIndex) / 2);\n if ((long long) spell * potions[midIndex] >= success){\n ansIndex = midIndex;\n lastIndex = midIndex - 1;\n }\n else{\n startIndex = midIndex + 1;\n }\n }\n return ansIndex; \n }\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n sort(potions.begin(), potions.end());\n int m = potions.size();\n vector<int> ans;\n for (int spell : spells) {\n int countPair = 0;\n int index = binarySearch(spell, potions, success);\n if (index == -1) \n countPair += 0;\n else\n countPair += (m - index);\n ans.push_back(countPair);\n }\n return ans;\n }\n};\n```\n```C++ []\n//2nd Approach\n\nclass Solution {\npublic:\n int binarySearch(int spell, vector<int>& potions, long long success) {\n int startIndex = 0; \n int lastIndex = potions.size() - 1;\n while(startIndex <= lastIndex){\n //helps to prevent from out of bound\n int midIndex = (startIndex + (lastIndex - startIndex) / 2);\n if ((long long) spell * potions[midIndex] >= success){\n lastIndex = midIndex - 1;\n }\n else{\n startIndex = midIndex + 1;\n }\n }\n return lastIndex + 1; \n }\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n sort(potions.begin(), potions.end());\n int m = potions.size();\n vector<int> ans;\n for (int spell : spells) {\n int index = binarySearch(spell, potions, success);\n ans.push_back(m - index);\n }\n return ans;\n }\n};\n```\n```Java []\nclass Solution {\n public int binarySearch(int spell, int[] potions, long success) {\n int startIndex = 0; \n int lastIndex = potions.length - 1;\n int ansIndex = -1;\n while(startIndex <= lastIndex){\n int midIndex = (startIndex + (lastIndex - startIndex) / 2);\n if ((long) spell * potions[midIndex] >= success){\n ansIndex = midIndex;\n lastIndex = midIndex - 1;\n }\n else{\n startIndex = midIndex + 1;\n }\n }\n return ansIndex; \n }\n public int[] successfulPairs(int[] spells, int[] potions, long success) {\n Arrays.sort(potions);\n int m = potions.length;\n int[] ans = new int[spells.length];\n for (int i = 0; i < spells.length; i++) {\n int countPair = 0;\n int index = binarySearch(spells[i], potions, success);\n if (index == -1) \n countPair += 0;\n else\n countPair += (m - index);\n ans[i] = countPair;\n }\n return ans;\n }\n}\n\n```\n```Python []\nclass Solution:\n def binarySearch(self, spell: int, potions: List[int], success: int) -> int:\n startIndex = 0\n lastIndex = len(potions) - 1\n ansIndex = -1\n while startIndex <= lastIndex:\n midIndex = (startIndex + (lastIndex - startIndex) // 2)\n if spell * potions[midIndex] >= success:\n ansIndex = midIndex\n lastIndex = midIndex - 1\n else:\n startIndex = midIndex + 1\n return ansIndex\n \n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n potions.sort()\n m = len(potions)\n ans = []\n for spell in spells:\n countPair = 0\n index = self.binarySearch(spell, potions, success)\n if index == -1:\n countPair += 0\n else:\n countPair += (m - index)\n ans.append(countPair)\n return ans\n\n```\n\n# Time Complexity and Space Complexity:\n- **Time Complexity :** **O((n + m) log m)**, where n is the length of the spells vector and m is the length of the potions vector.\n\n*The sort function takes O(m log m) time where \'m\' is the size of the potions vector.\nFor each spell, the binarySearch function is called which takes O(log m) time.\nTherefore, the time complexity of the entire solution is O(n log m + m log m), where \'n\' is the size of the spells vector.*\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- **Space Complexity :** **O(m + n)**, since we need to store the result in the ans vector.\n\n*The space complexity of the solution is O(m) to store the sorted potions vector, and O(n) to store the output vector of size \'n\'.\nTherefore, the total space complexity of the solution is O(m + n).*\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->
| 13
| 1
|
['Array', 'Binary Search', 'C++', 'Java', 'Python3']
| 1
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.