question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
symmetric-tree
|
👏🏻 Python | DFS - 公瑾™
|
python-dfs-gong-jin-tm-by-yuzhoujr-vwar
|
101. Symmetric Tree\n\n\u8FD9\u9053\u9898\u5177\u4F53\u7684Recursion Rule\u4E0D\u662F\u4F20\u9012Root\u672C\u8EAB\uFF0C\u800C\u662F\u5BF9\u4E24\u4E2A\u5B50\u5B
|
yuzhoujr
|
NORMAL
|
2018-10-19T21:18:33.051304+00:00
|
2018-10-19T21:18:33.051368+00:00
| 915
| false
|
### 101. Symmetric Tree\n\n\u8FD9\u9053\u9898\u5177\u4F53\u7684Recursion Rule\u4E0D\u662F\u4F20\u9012Root\u672C\u8EAB\uFF0C\u800C\u662F\u5BF9\u4E24\u4E2A\u5B50\u5B69\u5B50\u7684\u6BD4\u8F83\uFF0C\u6240\u4EE5Helper\u7684\u53C2\u6570\u5B9A\u4E49\u4E3A`root.left` \u548C `root.right`. \u7136\u540E\u6839\u636E\u9898\u76EE\u7684\u7279\u6027\uFF0C\u5728\u6BCF\u4E00\u5C42\u5F80\u4E0B\u4F20\u9012\u4E4B\u524D\u8981\u505A\u6BD4\u8F83\uFF0C\u6240\u4EE5\u662F`preorder`\u7684\u5199\u6CD5\uFF0C\u5148\u5199\u6BD4\u8F83\u7684\u51E0\u79CD\u683C\u5F0F\uFF0C\u7136\u540E\u5728\u505A\u9012\u5F52\u3002\u9012\u5F52\u5411\u4E0A\u8FD4\u56DE\u7684\u53C2\u6570\u662F\u4E00\u4E2ABoolean\u3002\n\n\u65F6\u95F4\u590D\u6742\u5EA6 : O(N)\n\u7A7A\u95F4\u590D\u6742\u5EA6 : O(N) or O(Height)\n\n```python\nclass Solution(object):\n def isSymmetric(self, root):\n if not root: return True\n return self.dfs_helper(root.left, root.right)\n \n \n def dfs_helper(self, n1, n2):\n if not n1 and not n2: return True\n if not n1 or not n2: return False\n if n1.val != n2.val: return False\n left = self.dfs_helper(n1.left, n2.right)\n right = self.dfs_helper(n1.right, n2.left)\n return left and right\n```
| 9
| 1
|
[]
| 1
|
symmetric-tree
|
My 16ms C++ solution
|
my-16ms-c-solution-by-skillness-8pyc
|
\n bool DFS(TreeNode *left,TreeNode *right)\n {\n if(left == NULL || right == NULL)\n return left == right;\n return (left->val =
|
skillness
|
NORMAL
|
2014-12-02T13:34:43+00:00
|
2014-12-02T13:34:43+00:00
| 1,135
| false
|
\n bool DFS(TreeNode *left,TreeNode *right)\n {\n if(left == NULL || right == NULL)\n return left == right;\n return (left->val == right->val)&DFS(left->right,right->left)&DFS(left->left,right->right);\n }\n bool isSymmetric(TreeNode *root) {\n if(root == NULL)\n return true;\n return DFS(root->left,root->right);\n }
| 9
| 0
|
[]
| 1
|
symmetric-tree
|
Two Simple Accepted Java solutions. Recursion and Iteration.
|
two-simple-accepted-java-solutions-recur-b3bu
|
The idea is simple. Traverse both on left an right branches of the root symmetricaly and check if the values are equal.\n\n\nRecursion.\n\n public boolean is
|
pavel-shlyk
|
NORMAL
|
2015-01-18T17:24:56+00:00
|
2015-01-18T17:24:56+00:00
| 1,288
| false
|
The idea is simple. Traverse both on left an right branches of the root symmetricaly and check if the values are equal.\n\n\nRecursion.\n\n public boolean isSymmetric(TreeNode root) {\n return root == null ? true : symmetric(root.left, root.right);\n }\n\t\n\tpublic boolean symmetric(TreeNode left, TreeNode right) {\n if (left == null && right == null) {\n \treturn true;\n } else if (left != null && right != null && left.val == right.val) {\n \treturn symmetric(left.left, right.right) && symmetric(left.right, right.left);\n } else {\n \treturn false;\n }\n }\n\n\n\nIteration.\n\n public boolean isSymmetric(TreeNode root) {\n if (root == null || (root.left == null && root.right == null)) return true;\n Stack<TreeNode> L = new Stack<TreeNode>();\n Stack<TreeNode> R = new Stack<TreeNode>();\n L.push(root.left);\n R.push(root.right);\n \n while(!L.isEmpty() && !R.isEmpty()) {\n \tTreeNode left = L.pop();\n \tTreeNode right = R.pop();\n \tif (left == null && right == null) continue;\n \tif (left != null && right != null && left.val == right.val) {\n \t\tL.push(left.left);\n \t\tR.push(right.right);\n \t\tL.push(left.right);\n \t\tR.push(right.left);\n \t\tcontinue;\n \t}\n \treturn false;\n }\n return true;\n }
| 9
| 0
|
[]
| 2
|
symmetric-tree
|
[Recusive solution for symmetric tree]: is it an optimal solution to use inorderTraversal?
|
recusive-solution-for-symmetric-tree-is-c2z7l
|
The approach I have is:\n1. get two vectors which saves both left and right sides of the root in inorderTraversal format.\n2. compare the vectors to see if they
|
wshaoxuan
|
NORMAL
|
2013-11-12T23:41:48+00:00
|
2013-11-12T23:41:48+00:00
| 9,297
| false
|
The approach I have is:\n1. get two vectors which saves both left and right sides of the root in inorderTraversal format.\n2. compare the vectors to see if they are symmetric.\nIt needs extra O(2n) space, not sure if this is an accepted solution. Or is there any better to solve this problem recursively.\n\n /*recusive*/\n class inorderTraversal {\n public:\n vector<int> solution(TreeNode *root) {\n // IMPORTANT: Please reset any member data you declared, as\n // the same Solution instance will be reused for each test case.\n vector <int> results;\n \t\tvector <int> rightResults;\n \t\tif(!root) return results;\n \t\tresults=solution(root->left);\n results.insert(results.end(),root->val);\n \t\trightResults=solution(root->right);\n \t\tif(!rightResults.empty())\n \t\t\tresults.insert(results.end(),rightResults.begin(), rightResults.end());\n }\n };\n \n class Solution {\n public:\n bool isSymmetric(TreeNode *root) {\n // IMPORTANT: Please reset any member data you declared, as\n // the same Solution instance will be reused for each test case.\n if(!root) return true;\n \t\tinorderTraversal instance;\n \t\tvector <int> leftResults=instance.solution(root->left);\n \t\tvector <int> rightResults=instance.solution(root->right);\n \t\tif(leftResults.size()!=rightResults.size())\n \t\t\treturn false;\n \t\tint size=leftResults.size();\n \t\tif(!size) return true;\n \n \t\tfor(int i=0; i< size; i++)\n \t\t{\n \t\t\tif(leftResults[i]!=rightResults[size-1-i])\n \t\t\t\treturn false;\n \t\t}\n \t\treturn true;\n }\n };
| 9
| 2
|
[]
| 5
|
symmetric-tree
|
7 lines c++ solution
|
7-lines-c-solution-by-wuhaibing-yzfj
|
/\nThe key is to traverse the left subtree with order root -> left -> right, \nand the right subtree with order root -> right-> left\n/\n\n\n bool isSymmetri
|
wuhaibing
|
NORMAL
|
2015-07-13T03:38:10+00:00
|
2015-07-13T03:38:10+00:00
| 1,314
| false
|
/*\nThe key is to traverse the left subtree with order root -> left -> right, \nand the right subtree with order root -> right-> left\n*/\n\n\n bool isSymmetric(TreeNode* root) {\n if (!root) return true;\n return isSymmetric_helper(root->left, root->right);\n }\n bool isSymmetric_helper(TreeNode* root1, TreeNode* root2) {\n if (root1==NULL && root2==NULL) return true;\n if (root1==NULL || root2==NULL) return false;\n if (root1->val != root2->val) return false;\n return isSymmetric_helper(root1->left, root2->right) && isSymmetric_helper(root1->right, root2->left);\n }
| 9
| 0
|
[]
| 1
|
symmetric-tree
|
✅BEATS 100% | DFS | JAVA | EXPLAINED🔥🔥🔥
|
beats-100-dfs-java-explained-by-adnannsh-lk5d
|
Approach:\n\nEmploys a recursive approach to compare the left and right subtrees of the root node.\nThe isSameTree function compares two nodes for equality and
|
AdnanNShaikh
|
NORMAL
|
2024-08-31T17:56:09.254533+00:00
|
2024-08-31T17:56:09.254584+00:00
| 1,510
| false
|
**Approach:**\n\nEmploys a recursive approach to compare the left and right subtrees of the root node.\nThe isSameTree function compares two nodes for equality and recursively compares their corresponding subtrees.\nThe isSymmetric function calls isSameTree with the root node as both arguments, effectively comparing the left and right subtrees of the entire tree.\n\n**Time Complexity: O(n)**\n\nThe code visits each node of the tree once, resulting in linear time complexity with respect to the number of nodes (n).\n\n**Space Complexity: O(h)**\n\nThe space complexity is determined by the maximum depth of the tree (h). In the worst case (a skewed tree), the recursion stack can reach a depth of h, leading to O(h) space usage.\n\n# Code\n```java []\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n public boolean isSymmetric(TreeNode root) {\n boolean ans= isSameTree(root.left, root.right);\n return ans;\n }\n//(Imp) here we want a mirror so for that , Ro Ro will be same and for Tree 1 when we are moving left at the same time for tree2 we will moce right\n //when for tree1 moving right at same time mmove tree2 to right which will give you a mirror \n public boolean isSameTree(TreeNode p, TreeNode q) {\n if(p == null || q == null){\n return p == q;\n }\n\n return (p.val == q.val) && isSameTree(p.left , q.right) && isSameTree(p.right, q.left); \n // it means the curr vals , the ones coming from left and coming from right all 3 should be true then return true , if either on is false it will reuturn false\n }\n \n}\n```
| 8
| 0
|
['Java']
| 0
|
symmetric-tree
|
Nice and clear 🟩🟩🟩 beats 89.91%
|
nice-and-clear-beats-8991-by-teklumt-7oe7
|
\n\n# Approach\n Describe your approach to solving the problem. \nNice and clear \uD83D\uDFE9\uD83D\uDFE9\uD83D\uDFE9 beats 89.91% \n\n# Complexity\n- Time comp
|
teklumt
|
NORMAL
|
2024-01-14T20:47:18.211885+00:00
|
2024-01-14T20:47:18.211943+00:00
| 2,580
| false
|
\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nNice and clear \uD83D\uDFE9\uD83D\uDFE9\uD83D\uDFE9 beats 89.91% \n\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(H)\n- where \'H\' is the height of the tree\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isSymmetric(self, root: Optional[TreeNode]) -> bool:\n \n def dfs(left,right):\n if not left and not right:\n return True\n if not left or not right: \n return False\n \n return left.val==right.val and dfs(left.left,right.right) and dfs(left.right,right.left)\n return dfs(root.left,root.right)\n```
| 8
| 0
|
['Python', 'Python3']
| 3
|
symmetric-tree
|
c++ solution
|
c-solution-by-loverdrama699-4s3f
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
loverdrama699
|
NORMAL
|
2023-03-13T11:31:27.762117+00:00
|
2023-03-13T11:31:27.762144+00:00
| 1,239
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n bool isSymmetric(TreeNode* root) {\n return isMirror(root, root);\n }\n\n bool isMirror(TreeNode* t1, TreeNode* t2) {\n if (t1 == nullptr && t2 == nullptr) {\n return true;\n }\n if (t1 == nullptr || t2 == nullptr) {\n return false;\n }\n return t1->val == t2->val && isMirror(t1->right, t2->left) && isMirror(t1->left, t2->right);\n }\n};\n```
| 8
| 0
|
['C++']
| 2
|
symmetric-tree
|
C# Iterative DFS
|
c-iterative-dfs-by-ilya-a-f-5kuf
|
\npublic class Solution\n{\n public bool IsSymmetric(TreeNode root)\n {\n if (root == null)\n {\n return true;\n }\n\n
|
ilya-a-f
|
NORMAL
|
2023-03-13T10:38:18.947843+00:00
|
2023-03-13T11:12:35.377034+00:00
| 1,712
| false
|
```\npublic class Solution\n{\n public bool IsSymmetric(TreeNode root)\n {\n if (root == null)\n {\n return true;\n }\n\n var stack = new Stack<(TreeNode, TreeNode)>();\n stack.Push((root.left, root.right));\n\n while (stack.Any())\n {\n switch (stack.Pop())\n {\n case (null, null):\n continue;\n\n case (null, _) or (_, null):\n return false;\n\n case (TreeNode l, TreeNode r) when l.val != r.val:\n return false;\n\n case (TreeNode l, TreeNode r) when l.val == r.val:\n stack.Push((l.left, r.right));\n stack.Push((l.right, r.left));\n break;\n }\n }\n\n return true;\n }\n}\n```
| 8
| 0
|
['C#']
| 1
|
symmetric-tree
|
Easy C++ Solution|| DFS || Beats 100% ✔✔ || Explanation ✔✔
|
easy-c-solution-dfs-beats-100-explanatio-gh8c
|
Approach\n Describe your approach to solving the problem. \n1. Do preorder traversal in the left subtree (node-left-right) and preorder traversal in reverse man
|
mamatva004
|
NORMAL
|
2023-02-17T06:17:10.214001+00:00
|
2023-03-13T04:42:33.321697+00:00
| 1,622
| false
|
# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Do preorder traversal in the left subtree (node-left-right) and preorder traversal in reverse manner (node-right-left) in the right subtree. \n2. At any point, if we find any dissimilarity then the tree is not symmetric, otherwise it is symmetric.\n\n# Complexity\n- Time complexity:\n O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity:\n O(h)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass Solution {\npublic:\n bool check(TreeNode *root1, TreeNode *root2){\n if(root1==NULL && root2==NULL) return true;\n if(!(root1 && root2)) return false;\n\n if(root1->val!=root2->val) return false;\n bool l=check(root1->left,root2->right);\n bool r=check(root1->right,root2->left);\n return l&&r;\n }\n bool isSymmetric(TreeNode* root) {\n return check(root->left,root->right);\n\n }\n};\n```
| 8
| 0
|
['C++']
| 0
|
symmetric-tree
|
Tree || 100% Beat || 0ms runtime || Easy-to-understand
|
tree-100-beat-0ms-runtime-easy-to-unders-i9qd
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
mridulxtiwari
|
NORMAL
|
2023-01-16T14:32:26.810695+00:00
|
2023-01-16T14:32:26.810728+00:00
| 1,306
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n bool tra(TreeNode* root1,TreeNode* root2){\n if(root1==0&&root2==0){\n return true;\n }\n if(root1==0||root2==0||root1->val!=root2->val){\n return false;\n }\n return tra(root1->left,root2->right)&&tra(root1->right,root2->left);\n }\n bool isSymmetric(TreeNode* root) {\n return tra(root->left,root->right);\n }\n};\n```
| 8
| 0
|
['C++']
| 0
|
symmetric-tree
|
Recursive and iterative JS versions
|
recursive-and-iterative-js-versions-by-r-4yp1
|
Recursive:\n\nvar isSymmetric = function(root) {\n/**\n * Compares two TreeNode\'s\n * @param {TreeNode} root1\n * @param {TreeNode} root2\n * @return {boolean}
|
rinat_a
|
NORMAL
|
2021-09-06T19:06:27.031358+00:00
|
2021-09-07T07:45:58.279405+00:00
| 765
| false
|
Recursive:\n```\nvar isSymmetric = function(root) {\n/**\n * Compares two TreeNode\'s\n * @param {TreeNode} root1\n * @param {TreeNode} root2\n * @return {boolean}\n */\n function isEqual(root1, root2) {\n if (!root1 && !root2) return true;\n if (!root1 || !root2) return false;\n return root1.val === root2.val\n && isEqual(root1.left, root2.right)\n && isEqual(root1.right, root2.left);\n }\n if (!root) return true;\n return isEqual(root.left, root.right)\n};\n```\n\nIterative: \n```\nvar isSymmetric = function(root) {\n if (!root) return true;\n \n const stack = [root.left, root.right];\n while (stack.length) {\n const currLeft = stack.shift();\n const currRight = stack.shift();\n if (!currLeft && !currRight) continue;\n if ((!currLeft || !currRight) || currLeft.val !== currRight.val) return false;\n stack.push(currLeft.left, currRight.right, currLeft.right, currRight.left);\n }\n return true;\n};\n```
| 8
| 0
|
['JavaScript']
| 2
|
symmetric-tree
|
0 ms, faster than 100.00% of Java online submissions
|
0-ms-faster-than-10000-of-java-online-su-9gq1
|
Runtime: 0 ms, faster than 100.00% of Java online submissions for Symmetric Tree.\nMemory Usage: 37.4 MB, less than 74.15% of Java online submissions for Symmet
|
aroraharsh010
|
NORMAL
|
2020-05-20T20:09:00.026813+00:00
|
2020-05-21T08:29:33.095790+00:00
| 483
| false
|
Runtime: 0 ms, faster than 100.00% of Java online submissions for Symmetric Tree.\nMemory Usage: 37.4 MB, less than 74.15% of Java online submissions for Symmetric Tree.\n```\nclass Solution {\n public boolean isSymmetric(TreeNode root) {\n return root==null || traverse(root.left,root.right);\n }\n private boolean traverse(TreeNode one,TreeNode two){\n if(one==null && two==null)return true;\n if(one==null || two==null)return false;\n if(one.val!=two.val)return false;\n boolean resl=traverse(one.left,two.right);\n if(!resl)return false;\n boolean resr=traverse(one.right,two.left);\n if(!resr)return false;\n return true;\n }\n}\n```
| 8
| 1
|
['Recursion', 'Java']
| 0
|
symmetric-tree
|
Share 3 methods to solve this problem (Java)
|
share-3-methods-to-solve-this-problem-ja-nuap
|
First.\nWe can define a binary tree by mid-order and post-order or pre-order and mid-order, the mirror tree is same to the origin tree. So we can check these tw
|
tovenja
|
NORMAL
|
2015-03-22T09:48:14+00:00
|
2015-03-22T09:48:14+00:00
| 876
| false
|
First.\nWe can define a binary tree by mid-order and post-order or pre-order and mid-order, the mirror tree is same to the origin tree. So we can check these two trees' mid-order and post-order are all same?\n\n public boolean isSymmetric(TreeNode root) {\n if (root==null)\n return true;\n return getMidOrderSeq(root).equals(getReMidOrderSeq(root))&&getPostOrderSeq(root).equals(getRePostOrderSeq(root));\n }\n \n public String getMidOrderSeq(TreeNode node) {\n if (node == null) {\n return "";\n }\n return getMidOrderSeq(node.left) + node.val + getMidOrderSeq(node.right);\n }\n public String getReMidOrderSeq(TreeNode node) {\n if (node == null) {\n return "";\n }\n return getReMidOrderSeq(node.right) + node.val + getReMidOrderSeq(node.left);\n }\n public String getPostOrderSeq(TreeNode node) {\n if (node == null) {\n return "";\n }\n return getPostOrderSeq(node.left) +getPostOrderSeq(node.right)+ node.val ;\n }\n public String getRePostOrderSeq(TreeNode node) {\n if (node == null) {\n return "";\n }\n return getRePostOrderSeq(node.right) +getRePostOrderSeq(node.left)+ node.val ;\n }\n\n\nSecond. Normal recursion.\n\n public boolean isSymmetric(TreeNode root) {\n if (root == null)\n return true;\n return isSymmetric(root, root);\n \n }\n \n public boolean isSymmetric(TreeNode left, TreeNode right) {\n if (left == null || right == null) {\n return left == right;\n }\n return left.val == right.val && isSymmetric(left.left, right.right) && isSymmetric(left.right, right.left);\n }\n\nThird. Iteration.\n\n public boolean isSymmetricIter(TreeNode root) {\n if (root == null || (root.left == null && root.right == null))\n return true;\n Stack<TreeNode> leftStack = new Stack<>();\n Stack<TreeNode> rightStack = new Stack<>();\n leftStack.push(root.left);\n rightStack.push(root.right);\n while (!leftStack.isEmpty() && !rightStack.isEmpty()) {\n TreeNode left = leftStack.pop();\n TreeNode right = rightStack.pop();\n if (left == null && right == null) {\n continue;\n }\n if (left == null || right == null)\n return false;\n if (left.val != right.val)\n return false;\n leftStack.push(left.left);\n rightStack.push(right.right);\n leftStack.push(left.right);\n rightStack.push(right.left);\n }\n return true;\n }
| 8
| 0
|
['Java']
| 1
|
moving-stones-until-consecutive-ii
|
[Java/C++/Python] Sliding Window
|
javacpython-sliding-window-by-lee215-7anh
|
Lower Bound\nAs I mentioned in my video last week,\nin case of n stones, \nwe need to find a consecutive n positions and move the stones in.\n\nThis idea led th
|
lee215
|
NORMAL
|
2019-05-05T04:11:08.235416+00:00
|
2020-03-12T15:17:15.969095+00:00
| 16,742
| false
|
## Lower Bound\nAs I mentioned in my video last week,\nin case of `n` stones, \nwe need to find a consecutive `n` positions and move the stones in.\n\nThis idea led the solution with sliding windows.\n\nSlide a window of size `N`, and find how many stones are already in this window.\nWe want moves other stones into this window.\nFor each missing stone, we need at least one move.\n\nGenerally, the number of missing stones and the moves we need are the same.\nOnly one corner case in this problem, we need to move the endpoint to no endpoint.\n\n\nFor case `1,2,4,5,10`,\n1 move needed from `10` to `3`.\n\nFor case `1,2,3,4,10`,\n2 move needed from `1` to `6`, then from `10` to `5`.\n<br>\n\n## Upper Bound\nWe try to move all stones to leftmost or rightmost.\nFor example of to rightmost.\nWe move the `A[0]` to `A[1] + 1`.\nThen each time, we pick the stone of left endpoint, move it to the next empty position.\nDuring this process, the position of leftmost stones increment 1 by 1 each time.\nUntil the leftmost is at `A[n - 1] - n + 1`.\n<br>\n\n## Complexity\nTime of quick sorting `O(NlogN)`\nTime of sliding window `O(N)`\nSpace `O(1)`\n<br>\n\n**Java:**\n```\n public int[] numMovesStonesII(int[] A) {\n Arrays.sort(A);\n int i = 0, n = A.length, low = n;\n int high = Math.max(A[n - 1] - n + 2 - A[1], A[n - 2] - A[0] - n + 2);\n for (int j = 0; j < n; ++j) {\n while (A[j] - A[i] >= n) ++i;\n if (j - i + 1 == n - 1 && A[j] - A[i] == n - 2)\n low = Math.min(low, 2);\n else\n low = Math.min(low, n - (j - i + 1));\n }\n return new int[] {low, high};\n }\n```\n\n**C++:**\n```\n vector<int> numMovesStonesII(vector<int>& A) {\n sort(A.begin(), A.end());\n int i = 0, n = A.size(), low = n;\n int high = max(A[n - 1] - n + 2 - A[1], A[n - 2] - A[0] - n + 2);\n for (int j = 0; j < n; ++j) {\n while (A[j] - A[i] >= n) ++i;\n if (j - i + 1 == n - 1 && A[j] - A[i] == n - 2)\n low = min(low, 2);\n else\n low = min(low, n - (j - i + 1));\n }\n return {low, high};\n }\n```\n\n**Python:**\n```\n def numMovesStonesII(self, A):\n A.sort()\n i, n, low = 0, len(A), len(A)\n high = max(A[-1] - n + 2 - A[1], A[-2] - A[0] - n + 2)\n for j in range(n):\n while A[j] - A[i] >= n: i += 1\n if j - i + 1 == n - 1 and A[j] - A[i] == n - 2:\n low = min(low, 2)\n else:\n low = min(low, n - (j - i + 1))\n return [low, high]\n```\n
| 179
| 8
|
[]
| 38
|
moving-stones-until-consecutive-ii
|
c++ with picture
|
c-with-picture-by-xiongqiangcs-9m14
|
the max move\n\nintuition we need the max move A[n-1]-A[0]-n+1\n\nuse the case 1 2 99 100\n\n\n\n\nbut the endpoint stone exist an hole, if you move the endpoi
|
xiongqiangcs
|
NORMAL
|
2019-05-09T10:29:20.602394+00:00
|
2019-05-10T08:07:57.823176+00:00
| 6,086
| false
|
## the max move\n\n**intuition we need the max move** `A[n-1]-A[0]-n+1`\n\nuse the case `1 2 99 100`\n\n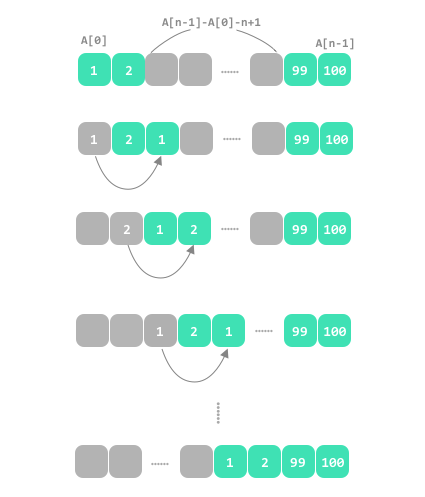\n\n\n**but the endpoint stone exist an hole**, if you move the endpoint stone firstly, the hole will disappear\n\nuse the case `1 100 102 105 200`\n\n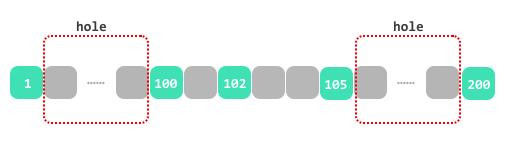\n\n\n* move the leftmost endpoint stone firstly, the left hole disappear, and the move is `A[n-1]-A[1]-n+2`\n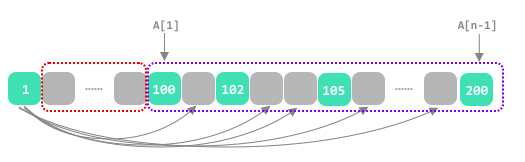\n\n* samely\uFF0Cmove the rightmost endpoint stone firstly, the right hole disappear, and the max move is `A[n-2]-A[0]-n+2`\n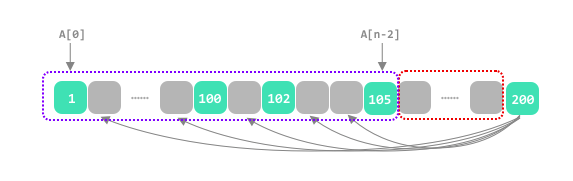\n\n* last, the max move is `min(A[n-1]-A[1]-n+2, A[n-2]-A[0]-n+2)`\n\n### the min move\n\n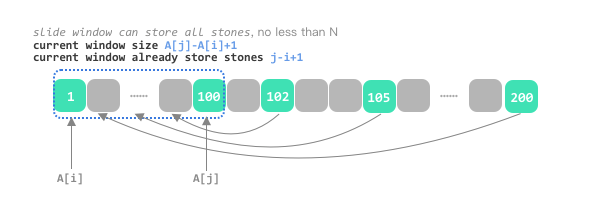\n\n\n```\nvector<int> numMovesStonesII(vector<int>& A) {\n\tsort(A.begin(), A.end());\n\tint n = A.size(), low = n;\n\tfor (int i = 0, j = 0; j < n; ++ j) {\n\t\twhile (A[j]-A[i]+1 > n) ++ i;\n\t\tint already_store = (j-i+1);\n\t\tif (already_store == n - 1 && A[j] - A[i] + 1 == n-1) {\n\t\t\tlow = min(low, 2);\n\t\t} else {\n\t\t\tlow = min(low, n - already_store);\n\t\t}\n\t}\n\treturn {low, max(A[n-1]-A[1]-n+2, A[n-2]-A[0]-n+2)};\n}\n```
| 125
| 1
|
[]
| 14
|
moving-stones-until-consecutive-ii
|
C++ O(nlogn) with detailed explanation
|
c-onlogn-with-detailed-explanation-by-hk-ibjh
|
Sort it first.\n1. How to get the minimum steps?\n\tWe can transfer this question into a problem like:\n\tFind the longest subsequence of a sorted array with ma
|
hkreporter
|
NORMAL
|
2019-05-05T04:32:47.306303+00:00
|
2019-05-06T19:57:07.859762+00:00
| 3,964
| false
|
Sort it first.\n1. How to get the minimum steps?\n\tWe can transfer this question into a problem like:\n\tFind the longest subsequence of a sorted array with max difference==n-1;\n\tFor example, [1, 4, 5, 6, 10], the longest subsequence is 4,5,6, we just need to move 1 and 10 close to 4, 5, 6, so we just need n - len: 5-3 = 2 steps.\n\tNotice that 3,4,5,6,10 is a special case, 2 steps too, so if there are n-1 consecutive numbers, add 1 to minimum steps.\n\t\n2. How to find maximum steps?\nSuppose 1, 10, 20, 30, 100;\nif we move100, then;\n1,10,20,29,30\n1,10,20,28,29\n....\n1,2,3,4,5\nif we move 1, then:\n\t\t\t10,11,20,30,100\n\t\t\t11,12,20,30,100\n\t\t\t....\n\t\t\t96,97,98,99,100\n\t\t\t\n\tGOT IT?\n\tWe just need to compute the largest interval not including 1 endpoint.\n\tfor example, in the previous example, \n\tlargest_interval = max(100-10, 30-1);\n\tso slots_betweet_largest_interval = 100-10-1=89\n\tthen we know there are n-3 stones between the largest interval, so the remaining slots are the maximized steps we can move.\n\tthat is 89-(n-3)=89-(5-3)=87\n```\n\tclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& A) {\n int n = A.size();\n int maxcon = 1, start, end, j = 0;\n int si=0, ei=0;\n sort(A.begin(), A.end());\n for(int i = 0; i < n; i++) {\n start = A[i];\n end = start+n;\n while(j<n&&A[j]<end) {\n j++;\n }\n if(j-i>maxcon||(j-i==maxcon&&A[j-1]-A[i]>ei-si)){\n si=A[i];\n ei=A[j-1];\n maxcon=j-i;\n }\n }\n \n int minimum = n-maxcon;\n if(maxcon==n-1&&ei-si==maxcon-1) minimum++;\n if(maxcon==n) minimum=0;\n int largest_interval = max(A[n-1]-A[1], A[n-2]-A[0])-1;\n int maximum = largest_interval-(n-3);\n return {minimum, maximum};\n }\n}\n```;
| 39
| 2
|
[]
| 11
|
moving-stones-until-consecutive-ii
|
C++ solution | Sliding window for minimum moves
|
c-solution-sliding-window-for-minimum-mo-pmmf
|
First, sort the given stones array.\n1. To find minimum moves, we approach the problem by checking each window which has a size not greater than stones.size().
|
shivamxarora
|
NORMAL
|
2020-03-29T20:33:47.651301+00:00
|
2020-06-12T07:04:04.003635+00:00
| 2,466
| false
|
First, **sort** the given stones array.\n1. To find **minimum** moves, we approach the problem by checking each window which has a size not greater than **stones.size()**. The intitution is that in a window which has size less than or equal to the number of stones, we can always get the unoccupied spaces and accordingly put the other stones inside and outside that window to make them consecutive. We just have to get that window in which we can do so in least number of moves.\n2. To find **maximum** moves, we just have to make the stones jump only to their **nearest** unoccupied space in a move and keep doing this until all the stones are consecutive.\n```\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n int n = stones.size();\n vector<int> result;\n \n\t\t// sorting the stones array\n sort(stones.begin(), stones.end());\n \n\t\t// window size, stones count in a window\n int i = 0, j = 0, wsize, scount, minMoves = INT_MAX;\n \n while (j < n) {\n wsize = stones[j] - stones[i] + 1;\n scount = j - i + 1;\n \n\t\t\t// if window size becomes greater than number of stones\n if (wsize > n) {\n i++;\n continue;\n }\n \n\t\t\t/* To handle some corner cases\n\t\t\t Example - _ _ 3 4 5 6 _ _ 10\n\t\t\t Here, putting, stone at 10th position, next to stone at 6th position is an invalid move.\n\t\t\t*/\n if (wsize == n - 1 && scount == n - 1)\n minMoves = min(minMoves, 2);\n \n else minMoves = min(minMoves, n - scount);\n \n j++;\n }\n \n result.push_back(minMoves);\n \n int maxMoves;\n\t\t\n\t\t// consecutive stones at the beginning or consecutive stones at the end or both\n if (stones[1] == stones[0] + 1 || stones[n - 1] == stones[n - 2] + 1)\n maxMoves = stones[n - 1] - stones[0] + 1 - n;\n \n\t\t// non-consecutive stones at both the beginning and the end\n else \n maxMoves = max(((stones[n - 1] - stones[1]) - (n - 1) + 1), ((stones[n - 2] - stones[0]) - (n - 1) + 1));\n \n result.push_back(maxMoves);\n \n return result;\n }\n};
| 16
| 0
|
['C', 'Sliding Window']
| 2
|
moving-stones-until-consecutive-ii
|
Python solution w/ comments
|
python-solution-w-comments-by-haoyangfan-so40
|
py\nclass Solution:\n def numMovesStonesII(self, stones: List[int]) -> List[int]:\n A = sorted(stones)\n n = len(stones)\n \n # e
|
haoyangfan
|
NORMAL
|
2019-07-28T18:49:21.115767+00:00
|
2019-07-28T18:49:21.115803+00:00
| 1,460
| false
|
```py\nclass Solution:\n def numMovesStonesII(self, stones: List[int]) -> List[int]:\n A = sorted(stones)\n n = len(stones)\n \n # either keep moving the stone at right endpoint to the left interval between A[0] ... A[n - 2]\n # basically each empty spot can consume 1 move, so total moves = total # of empty spots inside A[0] .. A[n - 2]\n # A[n - 2] - A[0] + 1 - 2 - (n - 3)\n # ------------------- - ---------\n # interval length A[0], A[n-2] stones already inside\n #\n # similar idea for keeping moving the stone at left endpoint to the right interval between A[1] ... A[n - 1]\n # total # of empty spots = A[n - 1] - stone[1] + 1 - 2 - (n - 3)\n # we take the maximum of these two moves\n max_moves = max(A[-1] - A[1] + 1 - 2 - (n - 3), A[-2] - A[0] + 1 - 2 - (n - 3))\n \n # for min moves, use a sliding window\n # idea: https://leetcode.com/problems/moving-stones-until-consecutive-ii/discuss/286886/No-code-just-chinese-explanation\n # https://leetcode.com/problems/moving-stones-until-consecutive-ii/discuss/289357/c++-with-picture\n l, min_moves = 0, n\n \n for r in range(n):\n # in case current window can hold more than n stones, shrink the window\n while A[r] - A[l] + 1 > n:\n l += 1\n \n # a special case: A[l] ... A[r] currently is consecutive and there is only one stone (endpoint) outside\n # in this case we oneed 2 move\n if A[r] - A[l] == r - l and r - l + 1 == n - 1:\n min_moves = min(min_moves, 2)\n else:\n # refer: leetcode.com/problems/moving-stones-until-consecutive-ii/discuss/286886/No-code-just-chinese-explanation/275066\n min_moves = min(min_moves, n - (r - l + 1))\n \n return [min_moves, max_moves]\n \n```\nHappy Coding~
| 15
| 0
|
[]
| 3
|
moving-stones-until-consecutive-ii
|
This should by no means be a Medium question
|
this-should-by-no-means-be-a-medium-ques-6f1t
|
\tclass Solution {\n\tpublic:\n\t\tvector numMovesStonesII(vector& stones) {\n\t\t\tsort(stones.begin(),stones.end());\n\t\t\tint n=stones.size();\n\t\t\tint MA
|
jasperjoe
|
NORMAL
|
2019-12-28T13:23:33.719636+00:00
|
2019-12-28T13:23:33.719669+00:00
| 2,021
| false
|
\tclass Solution {\n\tpublic:\n\t\tvector<int> numMovesStonesII(vector<int>& stones) {\n\t\t\tsort(stones.begin(),stones.end());\n\t\t\tint n=stones.size();\n\t\t\tint MAX=0;\n\t\t\tint MIN=INT_MAX;\n\t\t\tint a=stones.back()-stones[1]+1-(n-1);\n\t\t\tint b=stones[n-2]-stones[0]+1-(n-1);\n\t\t\tint j=0;\n\t\t\tMAX=max(a,b);\n\t\t\tfor(int i=0;i<n;i++){\n\t\t\t\twhile(j<n && stones[j]-stones[i]+1<n){\n\t\t\t\t\tj++;\n\t\t\t\t}\n\t\t\t\tif(j>=n){\n\t\t\t\t\tbreak;\n\t\t\t\t}\n\t\t\t\tint gap;\n\t\t\t\tif(stones[j]-stones[i]+1==n){\n\t\t\t\t\tgap=n-(j-i+1);\n\t\t\t\t}\n\t\t\t\telse if(j-1-i+1==n-1){\n\t\t\t\t\tgap=2;\n\t\t\t\t}\n\t\t\t\telse{\n\t\t\t\t\tgap=n-(j-1-i+1);\n\t\t\t\t}\n\t\t\t\tMIN=min(MIN,gap);\n\t\t\t}\n\t\t\treturn {MIN,MAX};\n\t\t}\n\t};
| 10
| 1
|
['C', 'Sliding Window', 'C++']
| 1
|
moving-stones-until-consecutive-ii
|
C++ Code With Easy Explanation
|
c-code-with-easy-explanation-by-chronovi-lxag
|
```\nclass Solution {\npublic:\n vector numMovesStonesII(vector& A) {\n int n = A.size(); //number of stones\n \n sort(A.begin(), A.end()
|
chronoviser
|
NORMAL
|
2020-06-10T15:19:18.288356+00:00
|
2020-06-10T15:19:18.288386+00:00
| 1,339
| false
|
```\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& A) {\n int n = A.size(); //number of stones\n \n sort(A.begin(), A.end());\n \n //To find max_moves:\n //move either starting endstone, or end endstone : this consumes one Move\n //after this we calculate the number of free spaces now available, and we will now go through all these \n //spaces one by one. \n //Number of spaces available after moving first stone : A[n-1] - A[1] + 1,\n //Number of spaces available after moving last stone : A[n-2] - A[0] + 1\n // + 1, for the initial move we made \n int max_moves = max(A[n-1] - A[1] -n + 1, A[n-2] - A[0] - n + 1) + 1;\n \n //To find min_moves we\'ll use Sliding Window approach:\n //We will consider a sliding a window of size <=n, which has maximum number of stones init.\n //minimum_moves will be then equal to n - number of stones already in max_sliding window\n //Corner case : sliding window size : n-1 and number of stones : n-1,\n //then minimum number of moves will be atleast 2,consider cases : {1,2,3,4,10} --> 2 , {1,2,3,4,6} --> 1\n //\n //window_size = A[end] - A[start] + 1, stone_count = start - end + 1\n int start = 0, end = 0, min_moves = n; \n while(end < n) {\n int window_size = A[end] - A[start] + 1;\n int stone_count = end - start + 1;\n \n if(window_size > n) {\n start++;\n continue;\n }\n \n if(window_size == n-1 and stone_count == n-1) {\n min_moves = min(min_moves, 2);\n }\n else\n min_moves = min(min_moves, n - stone_count);\n \n end++;\n }\n return {min_moves, max_moves};\n }\n};
| 9
| 1
|
[]
| 2
|
moving-stones-until-consecutive-ii
|
Short C++ O(nlogn) solution, 7 lines
|
short-c-onlogn-solution-7-lines-by-mzche-y6vp
|
\nvector<int> numMovesStonesII(vector<int>& s) {\n sort(s.begin(), s.end());\n int n = s.size(), gaps = s[n - 1] - s[0] + 1 - n, low = INT_MAX;\n if (s
|
mzchen
|
NORMAL
|
2019-05-05T06:14:06.919899+00:00
|
2019-05-05T06:14:06.919947+00:00
| 1,233
| false
|
```\nvector<int> numMovesStonesII(vector<int>& s) {\n sort(s.begin(), s.end());\n int n = s.size(), gaps = s[n - 1] - s[0] + 1 - n, low = INT_MAX;\n if (s[1] - s[0] == gaps + 1 || s[n - 1] - s[n - 2] == gaps + 1)\n low = min(2, gaps);\n else for (int i = 0; i < n; i++) // window slides here\n low = min<int>(low, n - (upper_bound(s.begin() + i, s.end(), s[i] + n - 1) - s.begin() - i));\n return {low, max(s[n - 1] - s[1], s[n - 2] - s[0]) - n + 2};\n}\n```
| 9
| 3
|
[]
| 0
|
moving-stones-until-consecutive-ii
|
Python 3 || 8 lines, sliding window w/ bin search || T/S: 66% / 57%
|
python-3-8-lines-sliding-window-w-bin-se-8rcd
|
Pretty much what everyone else has, but for what it\'s worth, it does use a bin search to locate the windows.\n\nclass Solution:\n def numMovesStonesII(self,
|
Spaulding_
|
NORMAL
|
2022-11-16T16:38:17.688096+00:00
|
2024-05-31T21:47:47.678289+00:00
| 877
| false
|
Pretty much what everyone else has, but for what it\'s worth, it does use a bin search to locate the windows.\n```\nclass Solution:\n def numMovesStonesII(self, stones: List[int]) -> List[int]:\n \n stones.sort()\n n, lo = len(stones), inf\n\n for right in range(n):\n\n left= bisect_right(stones,stones[right]-n)\n\n if right-left == stones[right]-stones[left] == n-2: lo = min(lo, 2)\n \n else: lo = min(lo, n - (right-left+1))\n\n hi = max(stones[n-1]-stones[1], stones[n-2]-stones[0]) - n + 2 \n\n return [lo, hi]\n\n```\n[https://leetcode.com/problems/moving-stones-until-consecutive-ii/submissions/1273657024/](https://leetcode.com/problems/moving-stones-until-consecutive-ii/submissions/1273657024/)\n\nI could be wrong, but I think that time complexity is *O*(*N* log *N*) and space complexity is *O*(1), in which *N* ~ `len(stones)`.\n
| 8
| 0
|
['Python']
| 0
|
moving-stones-until-consecutive-ii
|
Is it really Medium?
|
is-it-really-medium-by-ayush33-e9hy
|
Is it only me who feels this should be very hard or I am just a noob with coding?
|
ayush33
|
NORMAL
|
2022-02-27T13:13:05.786939+00:00
|
2022-02-27T13:13:05.786979+00:00
| 659
| false
|
Is it only me who feels this should be very hard or I am just a noob with coding?
| 7
| 0
|
[]
| 1
|
moving-stones-until-consecutive-ii
|
[Python] Sliding window with detailed expalanation
|
python-sliding-window-with-detailed-expa-aeoc
|
python\nclass Solution:\n def numMovesStonesII(self, stones: list[int]) -> list[int]:\n """\n 1. For the higher bound, it is determined by eith
|
eroneko
|
NORMAL
|
2021-09-27T04:41:41.067924+00:00
|
2021-09-27T04:41:41.067968+00:00
| 1,156
| false
|
```python\nclass Solution:\n def numMovesStonesII(self, stones: list[int]) -> list[int]:\n """\n 1. For the higher bound, it is determined by either moving the leftmost\n to the right side, or by moving the rightmost to the left side:\n 1.1 If moving leftmost to the right side, the available moving\n positions are A[n - 1] - A[1] + 1 - (n - 1) = \n A[n - 1] - A[1] - n + 2\n 1.2 If moving rightmost to the left side, the available moving\n positions are A[n - 2] - A[0] + 1 - (n - 1) = \n A[n - 2] - A[0] - n + 2.\n 2. For the lower bound, we could use sliding window to find a window\n that contains the most consecutive stones (A[i] - A[i - 1] = 1):\n 2.1 Generally the moves we need are the same as the number of\n missing stones in the current window.\n 2.3 When the window is already consecutive and contains all the\n n - 1 stones, we need at least 2 steps to move the last stone\n into the current window. For example, 1,2,3,4,10:\n 2.3.1 We need to move 1 to 6 first as we are not allowed to\n move 10 to 5 as it will still be an endpoint stone.\n 2.3.2 Then we need to move 10 to 5 and now the window becomes\n 2,3,4,5,6.\n """\n A, N = sorted(stones), len(stones)\n maxMoves = max(A[N - 1] - A[1] - N + 2, A[N - 2] - A[0] - N + 2)\n minMoves = N\n\n # Calculate minimum moves through sliding window.\n start = 0\n for end in range(N):\n while A[end] - A[start] + 1 > N:\n start += 1\n\n if end - start + 1 == N - 1 and A[end] - A[start] + 1 == N - 1:\n # Case: N - 1 stones with N - 1 positions.\n minMoves = min(minMoves, 2)\n else:\n minMoves = min(minMoves, N - (end - start + 1))\n\n return [minMoves, maxMoves]\n```
| 6
| 0
|
['Sliding Window', 'Python3']
| 2
|
moving-stones-until-consecutive-ii
|
Python sliding window approach O(N)
|
python-sliding-window-approach-on-by-abh-lofx
|
For minimum number of moves, the final arrangement will be of the form [a, a+1, a+2, ... a+L-1] for L stones for some \'a\'. \nThe possible values of \'a\' are
|
abhi2iitk
|
NORMAL
|
2020-02-23T18:51:08.162011+00:00
|
2020-02-23T18:53:47.245875+00:00
| 767
| false
|
For minimum number of moves, the final arrangement will be of the form [a, a+1, a+2, ... a+L-1] for L stones for some \'a\'. \nThe possible values of \'a\' are all the stone positions in the given input array.\nFor each possible \'a\' check how many positions (from a to a+L-1) already have stones. We need to fill in the missing remaining positions. Thus if there are K missing positions we need K moves to fill them. Compute K for each value of \'a\' and take their minimum.\n\nFor maximum it is just the sum of the gaps between each stone. But if we take the 1st stone then we cannot count the gaps betwwen 1st and 2nd stone. Similarly if we take the last stone then we cannot count the gaps between last and 2nd last stone. Thus we need to take the maximum of these two cases.\n\n```\nclass Solution(object):\n def get_min_moves(self, stones):\n min_cnts = float("Inf")\n \n start, end = 0, 1\n cnts = 1\n while end < len(stones):\n if stones[end] < stones[start]+len(stones):\n cnts += 1\n end += 1\n else:\n rem = len(stones)-cnts\n if (rem == 1 and stones[end-1] == stones[start]+len(stones)-1) or rem != 1:\n min_cnts = min(min_cnts, rem)\n \n start += 1\n cnts -= 1\n \n rem = len(stones)-cnts\n \n if (rem == 1 and stones[end-1] == stones[start]+len(stones)-1) or rem != 1:\n min_cnts = min(min_cnts, rem)\n \n return min_cnts\n \n \n def get_max_moves(self, stones):\n return max(sum([stones[i]-stones[i-1]-1 for i in range(2, len(stones))]), \n sum([stones[i+1]-stones[i]-1 for i in range(len(stones)-3, -1, -1)]))\n \n \n def numMovesStonesII(self, stones):\n stones = sorted(stones)\n \n a = self.get_min_moves(stones)\n b = self.get_max_moves(stones)\n \n return [a, b]
| 5
| 4
|
[]
| 2
|
moving-stones-until-consecutive-ii
|
Java || Easy
|
java-easy-by-pankaj1417-3bv2
|
\n\t\tclass Solution {\n\t\t\tpublic int[] numMovesStonesII(int[] stones) {\n\t\t\t\tint n = stones.length;\n\t\t\t\t int[] ans = new int[2];\n\t\t\t\t int i =
|
Pankaj1417
|
NORMAL
|
2021-06-01T13:39:33.114103+00:00
|
2021-06-01T13:40:27.949200+00:00
| 865
| false
|
\n\t\tclass Solution {\n\t\t\tpublic int[] numMovesStonesII(int[] stones) {\n\t\t\t\tint n = stones.length;\n\t\t\t\t int[] ans = new int[2];\n\t\t\t\t int i = 0, j = 0, wsize, scount, minMoves = Integer.MAX_VALUE;\n\t\t\t\tArrays.sort(stones);\n\t\t\t\t while (j < n) {\n\t\t\t\t\twsize = stones[j] - stones[i] + 1;\n\t\t\t\t\tscount = j - i + 1;\n\n\t\t\t\t\tif (wsize > n) {\n\t\t\t\t\t\ti++;\n\t\t\t\t\t\tcontinue;\n\t\t\t\t\t}\n\n\t\t\t\t\tif (wsize == n - 1 && scount == n - 1)\n\t\t\t\t\t\tminMoves = Math.min(minMoves, 2);\n\n\t\t\t\t\telse minMoves = Math.min(minMoves, n - scount);\n\n\t\t\t\t\tj++;\n\t\t\t\t}\n\t\t\t\tans[0] = minMoves;\n\t\t\t\tint maxMoves = 0;\n\t\t\t\t if (stones[1] == stones[0] + 1 || stones[n - 1] == stones[n - 2] + 1)\n\t\t\t\t\tmaxMoves = stones[n - 1] - stones[0] + 1 - n;\n\t\t\t\telse \n\t\t\t\t\tmaxMoves = Math.max(((stones[n - 1] - stones[1]) - (n - 1) + 1), ((stones[n - 2] - stones[0]) - (n - 1) + 1));\n\n\t\t\t\tans[1] = maxMoves;\n\t\t\t\treturn ans;\n\t\t\t}\n\t\t}
| 4
| 1
|
['Sliding Window', 'Java']
| 0
|
moving-stones-until-consecutive-ii
|
Use Interval to Get Max Moves
|
use-interval-to-get-max-moves-by-nullpoi-4cnl
|
I failed to figure out the min moves... The following is an intuitive solution for max moves.\n1. Sort and get the intervals.\n2. Check the first and last inter
|
nullpointer01
|
NORMAL
|
2019-05-05T10:20:53.429414+00:00
|
2019-05-05T10:26:33.524443+00:00
| 592
| false
|
I failed to figure out the min moves... The following is an intuitive solution for max moves.\n1. Sort and get the intervals.\n2. Check the first and last interval, if either is `0`, we are able to reduce every non-zero interval to zero at every smallest move (`1`). Thus, the number of moves is the sum of intervals.\n3. If both first and last intervals are not `0`, we need to drop the smaller one with 1 move, put the stone into the larger one and stick to the outer edge. Then the problem becomes Step 2 above. Node the larger one is reduced by 1, but is done with 1 move, so we can simplify it as: drop smaller one, then sum up the remaining intervals.\n\n```java\nclass Solution {\n public int[] numMovesStonesII(int[] stones) {\n Arrays.sort(stones);\n \n List<Integer> intervals = new ArrayList<Integer>();\n for (int i = 1; i <stones.length; i++) {\n int interval = stones[i] - stones[i-1] - 1;\n intervals.add(interval);\n }\n int maxMove = getMaxMove(new ArrayList<Integer>(intervals));\n ...\n }\n\n private int getMaxMove(List<Integer> intervals) {\n if (intervals.get(0) != 0 && intervals.get(intervals.size() - 1) != 0) {\n if (intervals.get(0) > intervals.get(intervals.size() - 1)) {\n intervals.remove(intervals.size() - 1);\n } else {\n intervals.remove(0);\n }\n }\n int count = 0;\n for (int interval : intervals) {\n count += interval;\n }\n return count;\n }\n}\n```
| 3
| 0
|
[]
| 0
|
moving-stones-until-consecutive-ii
|
Moving Stones Until Consecutive II
|
moving-stones-until-consecutive-ii-by-an-x2oy
|
Code
|
Ansh1707
|
NORMAL
|
2025-03-28T16:21:10.137501+00:00
|
2025-03-28T16:21:10.137501+00:00
| 29
| false
|
# Code
```python []
class Solution(object):
def numMovesStonesII(self, stones):
"""
:type stones: List[int]
:rtype: List[int]
"""
stones.sort()
n = len(stones)
maxMoves = max(stones[-1] - stones[1] - (n - 2), stones[-2] - stones[0] - (n - 2))
minMoves = n
left = 0
for right in range(n):
while stones[right] - stones[left] + 1 > n:
left += 1
current_window_size = right - left + 1
if current_window_size == n - 1 and stones[right] - stones[left] + 1 == n - 1:
minMoves = min(minMoves, 2)
else:
minMoves = min(minMoves, n - current_window_size)
return [minMoves, maxMoves]
```
| 2
| 0
|
['Array', 'Math', 'Sorting', 'Python']
| 0
|
moving-stones-until-consecutive-ii
|
Solution in Java
|
solution-in-java-by-shree_govind_jee-em0f
|
Intuition\nLower Bound\nAs I mentioned in my video last week,\nin case of n stones,\nwe need to find a consecutive n positions and move the stones in.\n\nThis i
|
Shree_Govind_Jee
|
NORMAL
|
2023-12-06T08:46:30.359179+00:00
|
2023-12-06T08:46:30.359207+00:00
| 374
| false
|
# Intuition\n**Lower Bound**\nAs I mentioned in my video last week,\nin case of n stones,\nwe need to find a consecutive n positions and move the stones in.\n\nThis idea led the solution with sliding windows.\n\nSlide a window of size N, and find how many stones are already in this window.\nWe want moves other stones into this window.\nFor each missing stone, we need at least one move.\n\nGenerally, the number of missing stones and the moves we need are the same.\nOnly one corner case in this problem, we need to move the endpoint to no endpoint.\n\nFor case `1,2,4,5,10,`\n1 move needed from `10` to `3`.\n\nFor case `1,2,3,4,10,`\n2 move needed from `1` to `6,` then from `10` to `5`.\n\n\n**Upper Bound**\nWe try to move all stones to leftmost or rightmost.\nFor example of to rightmost.\nWe move the `A[0]` to `A[1] + 1`.\nThen each time, we pick the stone of left endpoint, move it to the next empty position.\nDuring this process, the position of leftmost stones increment 1 by 1 each time.\nUntil the leftmost is at `A[n - 1] - n + 1`.\n\n# Complexity\n- Time complexity:$$O(N * log(N))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] numMovesStonesII(int[] stones) {\n Arrays.sort(stones);\n\n int i=0, n=stones.length;\n int high = Math.max(stones[n-1] - n+2 -stones[1], stones[n-2]-stones[0]- n+2);\n\n int low=n;\n for(int j=0; j<n; j++){\n while(stones[j]-stones[i] >= n) i++;\n\n if(j-i+1 == n-1 && stones[j]-stones[i]==n-2) low = Math.min(low, 2);\n else low = Math.min(low, n-(j-i+1));\n }\n return new int[]{low, high};\n }\n}\n```
| 2
| 0
|
['Array', 'Math', 'Two Pointers', 'Sorting', 'Java']
| 0
|
moving-stones-until-consecutive-ii
|
100 T and S | Commented and Explained With Examples
|
100-t-and-s-commented-and-explained-with-0xme
|
Intuition\n Describe your first thoughts on how to solve this problem. \nAt the base of this problem is a linear scan. This is because we are trying to achieve
|
laichbr
|
NORMAL
|
2023-07-29T13:03:47.946264+00:00
|
2023-07-29T13:03:47.946284+00:00
| 117
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAt the base of this problem is a linear scan. This is because we are trying to achieve the pairing of minimum number of moves and maximum number of moves. As such, we are trying to sort the move value space and scan over it linearly. This can be achieved with a few key insights from the problem that keep it at a medium level. \n\nFirst, we have a list size lower bound of 3. This is actually dreadfully important for one of our key edge cases that make this easily solvable so don\'t discard such things when they come up! \n\nSecond, we have that all the stone values are unique. \n\nThird, we have that all the stone values are positive integers from 1 to 10^9. This is important both as an insight into the fact that we are working with only positive values, and that we are working with a very large value space compared to a much relatively smaller value ordination (there are 10^9 values for the stones, but only 10^4 positions at most for them) \n\nWe are also provided with a helpful hint \n>For the minimum, how many cows are already in place? For the maximum, we have to lose either the gap A[1] - A[0] or A[N-1] - A[N-2] (where N = A.length), but every other space can be occupied ? \n\nWe turn first to the idea of the maximum, where we have a gap we will need to lose of either between the first and second position or ultimate and penultimate position. \n\nIf we consider a list of 3 items, our minimum, what is our minimum values to get our minimal return? Not to spoil anything, but it is 1, 2, 3 \n\nThis is key to the problem, since there are no spaces provided between the values, so our return should be [0, 0] \n\nBy realizing the impact of this the approach follows below. Try to work out for a few values and sizes to get the feel for it and you\'ll likely find an understanding either intuitively or by action. I recommend working with small list sizes and trying to generate [0, 1], [0, 2], [1, 2], and [2, 2] with only 3 or so items. It\'ll be difficult, but worth it for the understanding pay off. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe original ordering of the stones is not valid compared to their ordinal positioning, and since we know we have a size limit much less than a value limit, we start by sorting. \n\nThen, we want to know how much space we have to work witin, so get the size of your listing (how many stones do you have regardless of how much they are worth?) \n\nThen, we need to calculate the two largest costs, move penultimate and move ultimate (final in the code) \n\nMove penultimate is the cost of swapping the stones at the second to last spot and the first spot, minus the cost of the number of stones you have (Since you moved over the whole thing!) plus 2 to deal with the fact that they are unique\n\nMove ultimate is the cost of swapping the stones at the last spot and second spot, minus the cost of the number of stones you have plus 2 to deal with the fact that they are unique\n\nIf either of these is 0, the other must be locked in as most moves, as most moves will be the max of these two options (try to convince yourself of why that is the case! This relates to the idea of the list sizings, and is really clearly seen with a list of size 3)\n\nIf either is 0, \n- min legal moves is min of 2 and most moves \n- return min legal moves and most moves \n\nOtherwise we now must consider how many max legal moves are there really? \n\nSet max legal moves to 0 \nSet starting index to 0 \nenumerate index and stone in stones \n- while stones at starting index lte stone - stone length \n - increment starting index \n- our max legal moves here is the max of itself (so it preserves good discoveries) and index - starting index + 1 (+1 for the fact we use 0 indexing) \n- but, it cannot get too big! Remember, we already found the actual max, so don\'t let anything in here fool you! Set max legal moves as such to min(max(max_legal_moves, index - starting_index + 1), max_moves) \n- this keeps our newly found max legal less than our actual max moves \n\nWhen done enumerating return length - max legal moves, max moves \n\n# Complexity\n- Time complexity : O(S log S + S)\n - O(S log S) to sort the stones \n - O(S) to loop over (while loop is incindental, as it can only run as many times as the length of stones as well in total, so it does not add to this) \n\n- Space complexity : O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nNo additional space utilized \n\n# Code\n```\nclass Solution:\n \'\'\'\n Test cases walk through \n Given 7, 4, 9 prove 1, 2 6, 5, 4, 3, 10, prove 2, 3 \n\n Sort stones -> 4, 7, 9 3, 4, 5, 6, 10 \n Stone length -> 3 5\n Move penultimate = 7 - 4 - 3 + 2 = 2 6-3-5+2 = 0 \n Move final = 9 - 7 - 3 + 2 = 1 10-4-5+2 = 3 \n Neither is 0, so we cannot return for sure Move penultimate is 0, so move final is assured \n This means we can return [min(2, 3), 3] -> [2, 3]\n\n Max legal moves is 0 For completeness, max legal moves is 0, max moves is 3 \n starting index is 0 starting index is 0 \n\n Enumeration Enumeration\n index is 0, stone is 4 index is 0, stone is 3 \n stones[0] lte 4 - 3 ? No, skip while loop stones[0] lte 3 - 5 ? No, skip while \n max legal moves is min of (max of self and 0 - 0 + 1, most moves) max legal moves is min of (max of self and 0 - 0 + 1), max moves -> max legal moves is 1 \n -> max legal moves is 1 \n\n index is 1, stone is 7 index is 1, stone is 4 \n stones[0] <= 7 - 3 ? Yes, enter while stones[0] lte 4 - 5 ? No, skip while \n starting index is now 1 max legal moves is min of (max of self and 1 - 0 + 1), max moves -> max legal moves is 2\n stones[1] <= 7 - 3 ? No, skip while \n max legal moves -> min(max of self and 1 - 1 + 1), max_moves \n -> max legal moves is 1 index is 2, stone is 5 \n stones[0] lte 5 - 5 ? No skip while \n index is 2, stone is 9 max legal moves is min of (max of self and 2 - 0 + 1), max_moves -> max legal moves is 3 \n stones[1] <= 9 - 3 ? No, skip while \n max legal moves is min(max of self and 2-1 + 1), max_moves\n -> max legal moves is 2 index is 3, stone is 6 \n End enumeration stones[0] lte 6 - 5 ? No skip while \n max legal moves is min (max of self and 3 - 0 + 1), max_moves -> max legal moves is 3 \n Return [3 - 2, 2] -> [1, 2] checks out \n index is 4, stones is 10 \n stones[0] lte 10 - 5 ? Yes, enter while \n starting index is 1 \n stones[1] lte 10 - 5 ? Yes, enter while \n starting index is 2 \n stones[2] lte 10 - 5 ? Yes, enter while \n starting index is 3 \n max legal moves is min (max of self and 4 - 3 + 1), max moves -> max legal moves is 3 \n End enumeration\n\n Return [5 - 3, 3] -> [2, 3]\n \'\'\'\n def numMovesStonesII(self, stones: List[int]) -> List[int] :\n # order does not need to be maintained, so sorting is optimal \n stones.sort()\n # want to work within stone physical space since 10^9 >> 10^4 (stone weight vs length)\n stone_length = len(stones)\n # what is the cost of moving the second to last stone and the 0th stone? \n move_penultimate = stones[-2] - stones[0] - stone_length + 2 \n # what is the cost of moving the last stone and the 1st stone? \n move_final = stones[-1] - stones[1] - stone_length + 2 \n # in both of these, the cost is the positional exchange in stones along the stone length + 2 for the two stones moving \n # our most moves possible are the max of these two \n most_moves = max(move_penultimate, move_final)\n # since the stones are unique, if either is 0, the one that we have must be max legal moves \n # if move penultimate is 0, that means that the second largest stone less the least stone less the length + 2 is 0 \n # this means that the largest stone, which must be at least one larger than the largest, less the second to least stone which is at least one larger than the least stone less the length + 2 is move final \n # our minimal length is 3 \n # let a, b, c be stones in order \n # b - a - 3 + 2 = 0 -> b = a + 1 move penultimate \n # c - b - 3 + 2 = 0 -> b = c - 1 move final \n # c - 1 = a + 1 -> c = a + 2 \n # all stones must be at least 1 to 10^9 and are unique \n # so at minimum a is 1, b is 2 and c is 3 \n # in this case, move final is also 0 so we get 0, 0 \n # if a = 4, b = 5, c = 7 \n # 5 - 4 - 3 + 2 = 0 move penultimate is 0 \n # 7 - 5 - 3 + 2 -> 1 move ultimate is 1 \n # min legal moves is min of 2 and 1 -> min legal moves is 1 -> 1, 1 is returned \n # from this it can be seen that the movement of c relative to b impacts the return here when one is 0, and that if either is 0 it does not preclude the other. However it does entail a relation to 2 as most that min could become \n # this is because if most moves is greater than 2, we could always do the move alternate that was 0 in two steps. This is what locks in to place the ability to use 2 here as the min argument. \n if move_penultimate == 0 or move_final == 0 : \n min_legal_moves = min(2, most_moves)\n return [min_legal_moves, most_moves]\n # how many legal moves are there in sorted order? \n max_legal_moves = 0 \n # starting from 0th index \n starting_index = 0\n # enumerate each stone and index \n for index, stone in enumerate(stones) :\n # while the stone at starting index is lte this stone minus stone length (cost of a move) \n while stones[starting_index] <= stone - stone_length : \n # increment \n starting_index += 1\n # max legal moves is then set to maxima of self and indexed difference with 1 for 0 based indexing \n max_legal_moves = min(max(max_legal_moves, index - starting_index + 1), most_moves) \n # return length - max legal moves when in sorted order (your minimal move state) and most moves in sorted order \n return [stone_length - max_legal_moves, most_moves]\n```
| 2
| 0
|
['Python3']
| 0
|
moving-stones-until-consecutive-ii
|
[ C++ ] [ Sliding Window ]
|
c-sliding-window-by-sosuke23-9bsr
|
Code\n\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n sort(stones.begin(), stones.end());\n\n int N = stone
|
Sosuke23
|
NORMAL
|
2023-04-25T14:45:07.410143+00:00
|
2023-04-25T14:45:07.410187+00:00
| 935
| false
|
# Code\n```\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n sort(stones.begin(), stones.end());\n\n int N = stones.size(), low = N;\n for (int i = 0, j = 0; j < N; ++j) {\n while (stones[j] - stones[i] + 1 > N) {\n ++i;\n }\n if (N - (j - i + 1) == 1 && N - (stones[j] - stones[i] + 1) == 1) {\n low = min(low, 2);\n } else {\n low = min(low, N - (j - i + 1));\n }\n }\n\n int high = 1 + max((stones[N - 1] - stones[1] + 1) - N, // Move to right most\n (stones[N - 2] - stones[0] + 1) - N); // Move to left most\n return {low, high};\n }\n};\n```
| 2
| 0
|
['C++']
| 0
|
moving-stones-until-consecutive-ii
|
[Java] simple+clean sliding window
|
java-simpleclean-sliding-window-by-66bro-ufti
|
\nclass Solution {\n public int[] numMovesStonesII(int[] A) {\n Arrays.sort(A);\n int N=A.length;\n if(A[N-1]-A[0]+1==A.length)return ne
|
66brother
|
NORMAL
|
2020-10-07T22:55:36.371305+00:00
|
2020-10-07T22:55:36.371336+00:00
| 670
| false
|
```\nclass Solution {\n public int[] numMovesStonesII(int[] A) {\n Arrays.sort(A);\n int N=A.length;\n if(A[N-1]-A[0]+1==A.length)return new int[]{0,0};\n \n int max=1+Math.max(A[N-1]-A[1]+1-N,A[N-2]-A[0]+1-N); \n int min=Integer.MAX_VALUE;\n \n \n Queue<Integer>q=new LinkedList<>();\n q.add(A[0]);\n for(int i=1;i<A.length;i++){\n if(A[i]-q.peek()+1>=N){\n if(A[i]-q.peek()+1==N){\n min=Math.min(min,N-q.size()-1);\n }else{\n if(A[i]-q.peek()==N)min=1;\n else{\n int M=Math.max(2,N-q.size());\n min=Math.min(min,M);\n }\n }\n \n q.poll();\n }\n q.add(A[i]);\n }\n \n return new int[]{min,max};\n }\n \n}\n```
| 2
| 1
|
[]
| 1
|
moving-stones-until-consecutive-ii
|
Not shortest but easiest to understand solution
|
not-shortest-but-easiest-to-understand-s-jsvs
|
\nclass Solution { \n public int[] numMovesStonesII(int[] stones) {\n int max;\n Arrays.sort(stones);\n int len = stones.length;\n int
|
privatetrain
|
NORMAL
|
2019-06-17T06:29:26.033407+00:00
|
2019-06-17T06:29:26.033446+00:00
| 681
| false
|
```\nclass Solution { \n public int[] numMovesStonesII(int[] stones) {\n int max;\n Arrays.sort(stones);\n int len = stones.length;\n int gaps = stones[len - 1] - stones[0] + 1 - len;\n if (stones[0] + 1 == stones[1] || stones[len - 1] == stones[len - 2] + 1) {\n max = gaps;\n } else {\n int minE = Math.min(stones[1] - stones[0] - 1, stones[len - 1] - stones[len - 2] - 1);\n max = gaps - minE;\n }\n \n int cnt = 0;\n int b = 0;\n int sc = 0;\n int min = Integer.MAX_VALUE;\n while (true) {\n int lst = stones[b] + len - 1;\n if (lst > stones[len - 1]) {\n break;\n }\n while (true) {\n if (sc < len && stones[sc] <= lst) {\n cnt++;\n sc++;\n } else {\n break;\n }\n }\n gaps = len - cnt;\n if (!(b == 0 && gaps == 1 && sc == len - 1)) {\n min = Math.min(min, gaps);\n }\n \n b++;\n cnt--;\n }\n \n int fst = stones[len - 1] - (len - 1);\n sc = len - 1;\n cnt = 0;\n while (sc >= 0 && stones[sc] >= fst) {\n cnt++;\n sc--;\n }\n \n gaps = len - cnt;\n if (!(gaps == 1 && sc == 0)) {\n min = Math.min(min, len - cnt);\n }\n int[] res = new int[2];\n res[0] = min;\n res[1] = max;\n return res;\n }\n}\n\n```
| 2
| 0
|
[]
| 1
|
moving-stones-until-consecutive-ii
|
Easy to understand JavaScript solution
|
easy-to-understand-javascript-solution-b-teq7
|
\nvar numMovesStonesII = function(stones) {\n stones.sort((a, b) => a - b);\n const { length: size } = stones;\n const max = Math.max(stones[size - 1]
|
tzuyi0817
|
NORMAL
|
2023-02-18T07:29:55.636042+00:00
|
2023-02-18T07:29:55.636092+00:00
| 73
| false
|
```\nvar numMovesStonesII = function(stones) {\n stones.sort((a, b) => a - b);\n const { length: size } = stones;\n const max = Math.max(stones[size - 1] - stones[1] - size + 2, stones[size - 2] - stones[0] - size + 2);\n let start = 0;\n let min = size;\n\n for (let end = 1; end < size; end++) {\n while (stones[end] - stones[start] + 1 > size) start += 1;\n const already = end - start + 1;\n\n if (already === size - 1 && stones[end] - stones[start] + 1 === size - 1) {\n min = Math.min(min, 2);\n } else {\n min = Math.min(min, size - already);\n }\n }\n return [min, max];\n};\n```
| 1
| 0
|
['JavaScript']
| 0
|
moving-stones-until-consecutive-ii
|
c++ | easy | fast
|
c-easy-fast-by-venomhighs7-jeac
|
\n\n# Code\n\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& A) {\n sort(A.begin(), A.end());\n int i = 0, n = A.size
|
venomhighs7
|
NORMAL
|
2022-11-17T04:52:18.328214+00:00
|
2022-11-17T04:52:18.328256+00:00
| 853
| false
|
\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& A) {\n sort(A.begin(), A.end());\n int i = 0, n = A.size(), low = n;\n int high = max(A[n - 1] - n + 2 - A[1], A[n - 2] - A[0] - n + 2);\n for (int j = 0; j < n; ++j) {\n while (A[j] - A[i] >= n) ++i;\n if (j - i + 1 == n - 1 && A[j] - A[i] == n - 2)\n low = min(low, 2);\n else\n low = min(low, n - (j - i + 1));\n }\n return {low, high};\n }\n};\n```
| 1
| 0
|
['C++']
| 0
|
moving-stones-until-consecutive-ii
|
c++ | easy | fast
|
c-easy-fast-by-venomhighs7-plzo
|
\n\n# Code\n\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& A) {\n sort(A.begin(), A.end());\n int i = 0, n = A.size
|
venomhighs7
|
NORMAL
|
2022-11-17T04:51:41.997741+00:00
|
2022-11-17T04:51:41.997773+00:00
| 340
| false
|
\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& A) {\n sort(A.begin(), A.end());\n int i = 0, n = A.size(), low = n;\n int high = max(A[n - 1] - n + 2 - A[1], A[n - 2] - A[0] - n + 2);\n for (int j = 0; j < n; ++j) {\n while (A[j] - A[i] >= n) ++i;\n if (j - i + 1 == n - 1 && A[j] - A[i] == n - 2)\n low = min(low, 2);\n else\n low = min(low, n - (j - i + 1));\n }\n return {low, high};\n }\n};\n```
| 1
| 0
|
['C++']
| 0
|
moving-stones-until-consecutive-ii
|
💯EASIEST || C++ || SLIDING WINDOW
|
easiest-c-sliding-window-by-maheshwari__-chrg
|
\n\nDo upvote if you like it!\n\n\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n sort(begin(stones), end(stones));
|
maheshwari__apoorv
|
NORMAL
|
2022-09-11T13:14:33.349973+00:00
|
2022-09-11T13:14:33.350017+00:00
| 503
| false
|
\n\n**Do upvote if you like it!**\n\n```\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n sort(begin(stones), end(stones)); \n int n = size(stones), ii = 0, low = INT_MAX; \n int high = max(stones[n-2] - stones[0], stones[n-1] - stones[1]) - (n - 2); \n \n for (int i = 0; i < n; ++i) {\n while (stones[i] - stones[ii] >= n) ++ii; \n if (i - ii + 1 == n - 1 && stones[i] - stones[ii] == n - 2) \n low = min(low, 2); \n else low = min(low, n - (i - ii + 1)); \n }\n return {low, high}; \n }\n};\n```\n\n\n
| 1
| 0
|
['C++']
| 0
|
moving-stones-until-consecutive-ii
|
easy sliding window using binary search
|
easy-sliding-window-using-binary-search-7q157
|
\nFor the max step just skip the first gap or last gap. detail https://leetcode.com/problems/moving-stones-until-consecutive-ii/discuss/289357/c%2B%2B-with-pict
|
th160887
|
NORMAL
|
2021-08-09T06:41:41.237409+00:00
|
2021-08-09T06:41:41.237455+00:00
| 322
| false
|
\nFor the max step just skip the first gap or last gap. detail https://leetcode.com/problems/moving-stones-until-consecutive-ii/discuss/289357/c%2B%2B-with-picture\nFor the min step, just do a sliding window and try to move everyone inside the window. result is, window with minimum movement. (one edge case)\n\n\n````\nclass Solution {\n public:\n vector<int> numMovesStonesII(vector<int>& stones) {\n int n = stones.size();\n int minMove = numeric_limits<int>::max();\n sort(stones.begin(), stones.end());\n int gap = stones[n - 1] - stones[0] - n + 1;\n\n // if there is gap in only one side then minimum move is min(2, gap size)\n if (stones[n - 1] - stones[n - 2] - 1 == gap || stones[1] - stones[0] - 1 == gap) {\n // 3,4,5,6,_,_,_,_,_,_13 --> 4,5,6,_,3,_,_,_,_,13 --> 4,5,6,13,3\n minMove = min(2, gap);\n } else {\n // we do a simple sliding window with helo of binary search\n for (int i = 0; i < n; i++) {\n int inside = upper_bound(stones.begin() + i, stones.end(), stones[i] + n - 1) - stones.begin() - i;\n minMove = min(minMove, n - inside);\n }\n }\n return {minMove, max(stones[n - 2] - stones[0] - n + 2, stones[n - 1] - stones[1] - n + 2)};\n }\n};\n````
| 1
| 0
|
[]
| 0
|
moving-stones-until-consecutive-ii
|
(C++) 1040. Moving Stones Until Consecutive II
|
c-1040-moving-stones-until-consecutive-i-7b1e
|
\n\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n sort(begin(stones), end(stones)); \n int n = size(stones)
|
qeetcode
|
NORMAL
|
2021-06-24T17:03:34.574866+00:00
|
2021-06-24T17:03:34.574909+00:00
| 559
| false
|
\n```\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n sort(begin(stones), end(stones)); \n int n = size(stones), ii = 0, low = INT_MAX, high = max(stones[n-2] - stones[0], stones[n-1] - stones[1]) - (n - 2); \n \n for (int i = 0; i < n; ++i) {\n while (stones[i] - stones[ii] >= n) ++ii; \n if (i - ii + 1 == n - 1 && stones[i] - stones[ii] == n - 2) low = min(low, 2); \n else low = min(low, n - (i - ii + 1)); \n }\n return {low, high}; \n }\n};\n```
| 1
| 0
|
['C']
| 1
|
moving-stones-until-consecutive-ii
|
C++ short solution
|
c-short-solution-by-guccigang-iuns
|
Run-time is O(NlogN), space is O(1). \n\n\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n std::sort(stones.begin(),
|
guccigang
|
NORMAL
|
2021-02-03T22:30:42.656556+00:00
|
2021-02-03T22:30:42.656591+00:00
| 519
| false
|
Run-time is `O(NlogN)`, space is `O(1)`. \n\n```\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n std::sort(stones.begin(), stones.end());\n int size{(int)stones.size()}, maxSum{0};\n for(int i{1}; i < size; ++i) maxSum += stones[i]-stones[i-1]-1;\n maxSum -= std::min(stones[1]-stones[0]-1, stones[size-1]-stones[size-2]-1);\n int len{0};\n for(int i{0}, j{0}; j < size; ++j) {\n while(stones[j]-stones[i] >= size) ++i;\n bool add{stones[j]-stones[i] != size-1 && (i == 0 || j == size-1 && i < 2)};\n len = std::max(len, j-i+1-add);\n }\n \n return {size-len, maxSum};\n }\n};\n```
| 1
| 0
|
[]
| 0
|
moving-stones-until-consecutive-ii
|
Golang solution with explanation, not good enough
|
golang-solution-with-explanation-not-goo-t1kd
|
go\nfunc numMovesStonesII(stones []int) []int {\n\tsort.Ints(stones)\n\t// calc all gaps\n\tgap := make([]int, 0)\n\tfor i := 1; i < len(stones); i++ {\n\t\tdif
|
tjucoder
|
NORMAL
|
2020-07-26T06:52:53.124361+00:00
|
2020-07-26T07:02:57.406237+00:00
| 169
| false
|
```go\nfunc numMovesStonesII(stones []int) []int {\n\tsort.Ints(stones)\n\t// calc all gaps\n\tgap := make([]int, 0)\n\tfor i := 1; i < len(stones); i++ {\n\t\tdiff := stones[i] - stones[i-1]\n\t\tif diff > 1 {\n\t\t\tgap = append(gap, diff-1)\n\t\t}\n\t}\n\t// calc max here\n\t// each move, we will lost one gap\n\t// we may lose more than one gap at the first move\n\tmax := 0\n\tfor _, v := range gap {\n\t\tmax += v\n\t}\n\tgapBoundL := stones[1] - stones[0] - 1\n\tgapBoundR := stones[len(stones)-1] - stones[len(stones)-2] - 1\n\tif gapBoundL < gapBoundR {\n\t\tmax -= gapBoundL\n\t} else {\n\t\tmax -= gapBoundR\n\t}\n\t// calc min here\n // we need move stones until they are all continuously\n\tcount := 1\n\tfor l, r := 0, 1; r < len(stones); {\n\t\tif stones[r] - stones[l] < len(stones) {\n\t\t\tif current := r - l + 1; current > count {\n\t\t\t\tcount = current\n\t\t\t}\n\t\t\tr++\n\t\t} else {\n\t\t\tl++\n\t\t}\n\t}\n\tmin := len(stones) - count\n if min == 1 && len(gap) == 1 && gap[0] != 1 {\n // [6,5,4,3,10], cap = [3]\n // we need 2-moves\n // [4,5,6,8,10]\n // [4,5,6,7,8]\n \n // [6,5,4,3,8], cap = [1]\n // one move is enough\n \n // [6,5,10,3,7], cap = [1,2]\n // one move is enough\n min++\n }\n\treturn []int{min, max}\n}\n```
| 1
| 0
|
['Go']
| 0
|
moving-stones-until-consecutive-ii
|
C# beat 100%
|
c-beat-100-by-wwjuan-ecn5
|
\npublic class Solution {\n public int[] NumMovesStonesII(int[] stones) {\n Array.Sort(stones);\n \n int i = 0, n = stones.Length, low =
|
wwjuan
|
NORMAL
|
2020-03-03T19:50:10.364386+00:00
|
2020-03-03T19:50:10.364431+00:00
| 182
| false
|
```\npublic class Solution {\n public int[] NumMovesStonesII(int[] stones) {\n Array.Sort(stones);\n \n int i = 0, n = stones.Length, low = n;\n int high = Math.Max(stones[n-1] - n + 2 - stones[1], stones[n-2] - stones[0] - n + 2);\n \n for(int j = 0; j<n; j++){\n while(stones[j] - stones[i] >= n)\n i++;\n if(j - i + 1 == n - 1 && stones[j] - stones[i] == n-2)\n low = Math.Min(low, 2);\n else\n low = Math.Min(low, n-(j-i+1));\n }\n \n return new int[] {low, high};\n }\n}\n\n```
| 1
| 0
|
[]
| 0
|
moving-stones-until-consecutive-ii
|
Go Solution with Detailed Explanation
|
go-solution-with-detailed-explanation-by-v2wj
|
For more golang solution, please check: https://github.com/yinfirefire/LeetCode-GoSol\ngo\nfunc numMovesStonesII(stones []int) []int {\n\tsort.Ints(stones)\n\t/
|
shuoyan
|
NORMAL
|
2019-12-18T02:26:08.763628+00:00
|
2019-12-18T02:26:08.763684+00:00
| 374
| false
|
For more golang solution, please check: https://github.com/yinfirefire/LeetCode-GoSol\n```go\nfunc numMovesStonesII(stones []int) []int {\n\tsort.Ints(stones)\n\t// Upper bound:\n\t// 1, move the first stone A[0] to A[n-1]-n+1\n\t// the total number between new left bound and A[1] is the steps to take\n\t// A[n-1]-n+1-A[1]+1\n\t// 2, or move the last stone A[n-1] to A[0]+n-1\n\t// the total number between new right bound and A[n-2] is the steps to take\n\t// A[n-2]-(A[0]+n-1)+1\n\t//\n\t// Lower bound:\n\t// Sliding window size of len(stones), find vacancy in the current window, and the number of vacancy is the number\n\t// of steps\n\t// Edge Case: A[j]-A[i]==n-2 && j-i+1==n-1\n\t// e.g. 1,2,3,4,10: we need to move 1 to 6, then 10 to 5\n\tn := len(stones)\n\ti := 0\n\tmin := float64(n)\n\tmax := 0\n\tif stones[n-1]-n+1-stones[1]+1 < stones[n-2]-stones[0]-n+2 {\n\t\tmax = stones[n-2]-stones[0]-n+2\n\t}else{\n\t\tmax = stones[n-1]-stones[1]-n+2\n\t}\n\tfor j:=0; j<n; j++{\n\t\tfor stones[j]-stones[i]>=n{\n\t\t\ti++\n\t\t}\n\t\tif stones[j]-stones[i]==n-2&&j-i==n-2{\n\t\t\tmin = math.Min(min, float64(2))\n\t\t}else{\n\t\t\tmin = math.Min(min, float64(n-(j-i+1)))\n\t\t}\n\t}\n\treturn []int{int(min), max}\n}\n```
| 1
| 0
|
[]
| 0
|
moving-stones-until-consecutive-ii
|
C++ slide window
|
c-slide-window-by-sanzenin_aria-3tbi
|
```\nclass Solution {\npublic:\n vector numMovesStonesII(vector& stones) {\n sort(stones.begin(), stones.end());\n return { minMove(stones), maxMove
|
sanzenin_aria
|
NORMAL
|
2019-06-16T17:19:36.454563+00:00
|
2019-06-16T17:19:36.454617+00:00
| 496
| false
|
```\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n sort(stones.begin(), stones.end());\n return { minMove(stones), maxMove(stones) };\n }\n\n int maxMove(vector<int>& v) {\n const int n = v.size();\n int left = v[1] - v[0] - 1;\n int right = v[n - 1] - v[n - 2] - 1;\n int total_interval = v[n - 1] - v[0] - n + 1;\n return total_interval - min(left, right);\n }\n\n int minMove(vector<int>& v) {\n int l = 0, r = 1, minMove = v.size();\n while (r < v.size()) {\n int interval = v[r] - v[l] - (r - l);\n int numStoneOutsideLR = v.size() - (r - l + 1);\n if (numStoneOutsideLR >= interval) {\n if (numStoneOutsideLR == 1 && interval == 0)\n minMove = min(minMove, 2); //shit corner case\n else\n minMove = min(minMove, numStoneOutsideLR);\n r++;\n }\n else {\n l++;\n }\n }\n return minMove;\n }\n};
| 1
| 0
|
[]
| 1
|
moving-stones-until-consecutive-ii
|
C++ super easy and short 9-line solution, beats 100% time and 100% space!
|
c-super-easy-and-short-9-line-solution-b-dnbm
|
```\n\tvector numMovesStonesII(vector& stones) {\n int mx=INT_MAX, ct=0, size=stones.size(), pre=0;\n sort(stones.begin(), stones.end());\n
|
michaelz
|
NORMAL
|
2019-05-08T05:55:43.666380+00:00
|
2019-05-08T05:55:43.666447+00:00
| 720
| false
|
```\n\tvector<int> numMovesStonesII(vector<int>& stones) {\n int mx=INT_MAX, ct=0, size=stones.size(), pre=0;\n sort(stones.begin(), stones.end());\n for(int i=0;i<stones.size();i++) {\n while(stones[i]-stones[pre]>size-1) pre++;\n ct=max(ct, i-pre+1);\n }\n mx=max(stones[size-2]-stones[0]-size+2, stones.back()-stones[1]-size+2);\n if(stones.back()-stones[0]>size&&(stones[size-2]-stones[0]==size-2||stones[size-1]-stones[1]==size-2)) ct--;\n return {size-ct, mx};\n }
| 1
| 1
|
[]
| 3
|
moving-stones-until-consecutive-ii
|
Python3: 84 ms
|
python3-84-ms-by-kzhang14-1qtr
|
\nclass Solution:\n def numMovesStonesII(self, stones: List[int]) -> List[int]:\n stones.sort()\n ma=max(stones[-1]-stones[1]-len(stones)+2,sto
|
kzhang14
|
NORMAL
|
2019-05-05T18:13:30.008262+00:00
|
2019-05-05T18:16:23.228979+00:00
| 348
| false
|
```\nclass Solution:\n def numMovesStonesII(self, stones: List[int]) -> List[int]:\n stones.sort()\n ma=max(stones[-1]-stones[1]-len(stones)+2,stones[-2]-stones[0]-len(stones)+2)\n mi=0\n l=len(stones)\n for i in range(l-1):\n if stones[i]<=stones[-1]-l+1:\n k=bisect.bisect(stones,stones[i]+l-1)\n if i==0:\n if stones[0]+l-1 in stones:\n mi=max(mi,k)\n else:\n mi=max(mi,min(l-2,k))\n else:\n mi=max(mi,k-i)\n return [l-mi,ma]\n```
| 1
| 1
|
[]
| 0
|
moving-stones-until-consecutive-ii
|
Crude and undecorated solution
|
crude-and-undecorated-solution-by-quadpi-wga7
|
This is a direct dump of my thinking process ...\n To make many moves as possible, we form a "blob" of numbers and have the "blob" crawl to the other end. With
|
quadpixels
|
NORMAL
|
2019-05-05T04:43:14.613971+00:00
|
2019-05-05T04:45:08.952760+00:00
| 466
| false
|
This is a direct dump of my thinking process ...\n* To make many moves as possible, we form a "blob" of numbers and have the "blob" crawl to the other end. With this approach the answer will be related to the total width of the gaps;\n * However, if both endpoints are "lonely" (meaning they have no neighbors), then we must sacrifice either endpoints\n ```\n\t Initial: 1 _ _ _ _ _ 100 ... 10000 _ _ _ _ _ _ _ _ _ _ _ 10100\n\t Move 1 to the middle: 100 ... 10000 _ _ _ _ _ _ _ _ _ _ _ 10100\n\t Move 100 to 10001: 101 ... 10001_ _ _ _ _ _ _ _ _ _ _ 10100\n\t Move 101 to 10002: 102 ... 10002 _ _ _ _ _ _ _ _ _ _ 10100\n\t Move 102 to 10003: 103 ... 10003_ _ _ _ _ _ _ _ _ _ 10100\n\t ^^^^^^^^^^^^^\n\t This "blob" just keeps moving to the right at unit length at a time \n\t\t\t\t\t and eating up whatever gets in the way\n\t However to form the "blob" either gap next to a "lonely" endpoint must be dropped\n\t```\n\t\n* To make as few moves as possible, we move a sliding window over the initial configuration of the stones. However, there will be an extra processing for the "lonely" endpoints: We must make one extra move so that we could move the lone endpoint, just like in the second example:\n ```\n\tInitial: 3 4 5 6 _ _ _ 10\n\tMove 3 to 8: 4 5 6 _ 8 _ 10 <-- 10 is lonely 10 cannot be moved to 7 (it will still be endpoint if directly moved to 7)\n\tMove 10 to 7: 4 5 6 7 8\n\t```\n\tWe must do this exactly once whenever there is a "lonely" endpoint. (We do not need to do this twice when both endpoints are lonely)\n\n\n```\nclass Solution {\npublic:\n\tint GetGapCount(vector<int>& stones, int* total_gap_length, int* first_gap_len, int* last_gap_len) {\n\t\tif (stones.size() < 2) return 0;\n\t\tint ret = 0, tl = 0;\n\t\tint prev = stones[0];\n\t\tfor (int i=1; i<stones.size(); i++) {\n\t\t\tint x = stones[i];\n\t\t\tif (x != prev + 1) {\n\t\t\t\tret ++;\n\t\t\t\tint gap_len = (x - prev - 1);\n\t\t\t\ttl += gap_len;\n\t\t\t\tif (i == 1) *first_gap_len = gap_len;\n\t\t\t\tif (i == (stones.size()-1)) *last_gap_len = gap_len;\n\t\t\t}\n\t\t\tprev = x;\n\t\t}\n\t\t*total_gap_length = tl;\n\t\treturn ret;\n\t}\n\tvector<int> numMovesStonesII(vector<int>& stones) {\n\t\tconst int N = int(stones.size());\n\t\tsort(stones.begin(), stones.end());\n\n\t\tvector<int> ret = { 0, 0 };\n\t\tint total_gap_length = 0;\n\t\tint first_gap_len = 0;\n\t\tint last_gap_len = 0;\n\t\tint num_gaps = GetGapCount(stones, &total_gap_length, &first_gap_len, &last_gap_len);\n\t\t//printf("num_gaps=%d\\n", num_gaps);\n\n\t\tif (num_gaps == 0) { }\n\t\telse {\n\t\t\tint min_skips = 2147483647;\n\t\t\tint idx0 = 0, idx1 = 0;\n\t\t\twhile (idx1 < N) {\n\t\t\t\tint num_in_window = idx1 - idx0 + 1;\n\t\t\t\tint gap_len = N - num_in_window;\n\t\t\t\tint num_skips = gap_len;\n\t\t\t\tif (num_skips < min_skips) { min_skips = num_skips; }\n\n\t\t\t\tidx1 ++;\n\t\t\t\tif (idx1 < N) {\n\t\t\t\t\twhile (stones[idx1] - stones[idx0] > (N-1)) idx0 ++;\n\t\t\t\t}\n\t\t\t}\n\n\t\t\tret[0] = min_skips;\n\t\t\tret[1] = total_gap_length;\n\n\t\t\tif (num_gaps >= 2) {\n\t\t\t\tif (stones[1] > stones[0]+1 && stones[N-2] < stones[N-1]-1) {\n\t\t\t\t\tret[1] -= min(first_gap_len, last_gap_len);\n\t\t\t\t}\n\t\t\t} else if (num_gaps == 1) {\n\t\t\t\t//printf("first_gap_len = %d\\n", first_gap_len);\n\t\t\t\tif ((stones[1] > stones[0]+1 && first_gap_len > 1) || \n\t\t\t\t (stones[N-2] < stones[N-1]-1 && last_gap_len > 1)) {\n\t\t\t\t\tret[0] += 1;\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t\treturn ret;\n\t}\n};\n\n\n```
| 1
| 1
|
[]
| 1
|
moving-stones-until-consecutive-ii
|
Python3 solution O(NlogN) with explaination
|
python3-solution-onlogn-with-explainatio-bdju
|
\nclass Solution:\n def numMovesStonesII(self, stones: List[int]) -> List[int]:\n stones.sort()\n minM = float(\'inf\')\n for i in range
|
davyjing
|
NORMAL
|
2019-05-05T04:06:27.787236+00:00
|
2019-05-05T04:48:37.094377+00:00
| 550
| false
|
```\nclass Solution:\n def numMovesStonesII(self, stones: List[int]) -> List[int]:\n stones.sort()\n minM = float(\'inf\')\n for i in range(1,len(stones)-1):\n loc = bisect.bisect_left(stones, stones[i]+len(stones)-1, lo=0, hi=len(stones)-1)\n if stones[loc] == stones[i]+len(stones)-1:\n minM = min(minM,len(stones)-(loc-i)-1)\n else:\n minM = min(minM,len(stones)-loc+i)\n if stones[-1]-stones[0]+1 == len(stones):\n minM = 0\n maxM = max(stones[-2]-stones[0]-len(stones)+2,stones[-1]-stones[1]-len(stones)+2)\n return [minM,maxM]\n```\nFor max moves, after first move, we can move the end one as "outside" as possible, thus this is easy to compute.\nFor mim moves, we examine how the final state is like, (consective from ith position), we just need to check how many vacancies there are in this range.
| 1
| 1
|
[]
| 0
|
moving-stones-until-consecutive-ii
|
scala sliding window
|
scala-sliding-window-by-vititov-50a6
| null |
vititov
|
NORMAL
|
2025-02-26T21:17:03.163454+00:00
|
2025-02-26T21:17:03.163454+00:00
| 4
| false
|
```scala []
object Solution {
def numMovesStonesII(stones: Array[Int]): Array[Int] = {
lazy val sorted = stones.sorted
lazy val delta = (stones.length - List(0,1).map{i => sorted(sorted.length-2+i)-sorted(i)-1}
.min - 2) max 0
lazy val mn = sorted.indices.foldLeft(0){case (lo,hi) =>
if(sorted(hi)-sorted(lo) > stones.length) lo+1 else lo
} + delta
lazy val mx = sorted.last-sorted.head+1-sorted.length-
List(1,sorted.length-1).map{i =>sorted(i)-sorted(i-1)-1}.min
if(sorted.last-sorted.head+1==sorted.length) Array(0,0) else Array(mn,mx)
}
}
```
| 0
| 0
|
['Two Pointers', 'Sliding Window', 'Scala']
| 0
|
moving-stones-until-consecutive-ii
|
Sort and Binary Search O(nlgn)
|
sort-and-binary-search-onlgn-by-lilongxu-a1mh
|
IntuitionSort and analyze.Approach
Sort the stones.
To obtain the max moves, we choose the endpoint that has a smaller gap with its (sole) neighbour stone, in o
|
lilongxue
|
NORMAL
|
2025-02-16T02:20:59.271364+00:00
|
2025-02-16T02:20:59.271364+00:00
| 6
| false
|
# Intuition
Sort and analyze.
# Approach
1. Sort the stones.
2. To obtain the max moves, we choose the endpoint that has a smaller gap with its (sole) neighbour stone, in order to diminish the least space. The max moves = total gaps - min(leftmost gap, rightmost gap).
3. To obtain the min moves, we need to binary search.
4. For each stones, we should try to make it as the leftmost stone when the movements are completed. In this way, the rightmost stone is its position + len - 1. If the rightmost stone is beyond the initial rightmost one, it's impossible, and we will skip it.
5. We use binary search to find how many existing stones will be covered in this way, and here outcome = len - covered.
6. We should also try to make it the rightmost stone when done. It's similar.
7. There is an exception: when the initial leftmost or rightmost stone can't be moved, we must skip it. We need to determine this case: when its gap with its neighbour is 0, and there is at most 1 consecutive gap segment, it's that case.
8. The result is the min of the outcomes.
# Complexity
- Time complexity:
O(nlgn)
- Space complexity:
O(1)
# Code
```javascript []
/**
* @param {number[]} stones
* @return {number[]}
*/
var numMovesStonesII = function(stones) {
stones.sort((a, b) => a - b)
const minVal = stones[0], maxVal = stones.at(-1)
const len = stones.length
const gapCount = 1 + maxVal - minVal - len
let emptyCount = 0, hasEnoughEmpty = false
for (let i = 1; i < len; i++) {
if (stones[i] > stones[i - 1] + 1) {
emptyCount++
if (emptyCount > 1) {
hasEnoughEmpty = true
break
}
}
}
const gapL = stones[1] - minVal - 1
const gapR = maxVal - stones.at(-2) - 1
const maxResult = gapCount - Math.min(gapL, gapR)
let minResult = maxResult
const leftStart = gapL === 0 && !hasEnoughEmpty ? 1 : 0
const rightStart = gapR === 0 && !hasEnoughEmpty ? len - 2 : len - 1
if (rightStart === len - 1) {
for (let i = leftStart; i < len; i++) {
const from = stones[i], to = from + len - 1
if (to > maxVal) break
let low = i, high = len - 1
// find latest low where
// stones[low] <= to
while (low < high) {
const mid = Math.ceil((low + high) / 2)
if (stones[mid] <= to) low = mid
else high = mid - 1
}
const covered = 1 + low - i
const outcome = len - covered
minResult = Math.min(minResult, outcome)
}
}
if (leftStart === 0) {
for (let i = rightStart; i > -1; i--) {
const from = stones[i], to = from - len + 1
if (to < minVal) break
let low = 0, high = i
// find earliest high where
// stones[high] >= to
while (low < high) {
const mid = Math.floor((low + high) / 2)
if (stones[mid] >= to) high = mid
else low = mid + 1
}
const covered = 1 + i - high
const outcome = len - covered
minResult = Math.min(minResult, outcome)
}
}
return [minResult, maxResult]
};
```
| 0
| 0
|
['JavaScript']
| 0
|
moving-stones-until-consecutive-ii
|
I have no idea how I solved this
|
i-have-no-idea-how-i-solved-this-by-bori-s4g5
|
Code\npython3 []\nclass Solution:\n def numMovesStonesII(self, a: List[int]) -> List[int]:\n n = len(a)\n a.sort()\n \n maxi = 1
|
boriswilliams
|
NORMAL
|
2024-09-26T19:29:31.215477+00:00
|
2024-09-26T19:30:55.489873+00:00
| 53
| false
|
# Code\n```python3 []\nclass Solution:\n def numMovesStonesII(self, a: List[int]) -> List[int]:\n n = len(a)\n a.sort()\n \n maxi = 1 - min(a[1] - a[0], a[-1] - a[-2])\n for i in range(1, n):\n maxi += a[i] - a[i-1] - 1\n \n mini = sys.maxsize\n j = 0\n for i in range(n):\n while j < n and a[j] - a[i] <= n - 1:\n j += 1\n x = n - j + i\n if x == 1 and a[j-1] - a[i] == j - i - 1:\n x += 1\n mini = min(mini, x)\n\n return [mini, maxi]\n```
| 0
| 0
|
['Python3']
| 0
|
moving-stones-until-consecutive-ii
|
[Accepted] Swift
|
accepted-swift-by-vasilisiniak-waps
|
\nclass Solution {\n func numMovesStonesII(_ stones: [Int]) -> [Int] {\n\n guard stones.count > 2 else { return [0, 0] }\n \n var st = s
|
vasilisiniak
|
NORMAL
|
2024-06-28T16:12:10.743612+00:00
|
2024-06-28T16:12:10.743667+00:00
| 9
| false
|
```\nclass Solution {\n func numMovesStonesII(_ stones: [Int]) -> [Int] {\n\n guard stones.count > 2 else { return [0, 0] }\n \n var st = stones.sorted()\n\n let ma = st[st.count - 1] - st[0] - min(st[1] - st[0], st[st.count - 1] - st[st.count - 2]) + 2 - st.count\n \n let mi: Int = {\n var mi = Int.max\n var l = 0\n var r = 0\n\n while r + 1 < st.count, st[r + 1] - st[l] < stones.count { r += 1 }\n\n while r < st.count {\n while st[r] - st[l] >= stones.count { l += 1 }\n\n let innerfree = st[r] - st[l] - r + l\n let outerfree = st.count - st[r] + st[l] - 1\n\n if outerfree == 1, innerfree == 0 { mi = min(mi, 2) }\n else { mi = min(mi, innerfree + outerfree) }\n \n r += 1\n }\n\n return mi\n }()\n\n return [mi, ma]\n }\n}\n\n\n\n/*\n\nxx.........................x\n\nx..x.xxxx.xx....x\nx.xxxx.xx...xx\n\n*/\n```
| 0
| 0
|
['Swift']
| 0
|
moving-stones-until-consecutive-ii
|
C++ Code
|
c-code-by-lucifer_2214-ya54
|
class Solution {\npublic:\n vector numMovesStonesII(vector& stones) {\n sort(stones.begin(), stones.end());\n\n int N = stones.size(), low = N;
|
lucifer_2214
|
NORMAL
|
2024-06-25T04:06:43.006297+00:00
|
2024-06-25T04:06:43.006328+00:00
| 24
| false
|
class Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n sort(stones.begin(), stones.end());\n\n int N = stones.size(), low = N;\n for (int i = 0, j = 0; j < N; ++j) {\n while (stones[j] - stones[i] + 1 > N) {\n ++i;\n }\n if (N - (j - i + 1) == 1 && N - (stones[j] - stones[i] + 1) == 1) {\n low = min(low, 2);\n } else {\n low = min(low, N - (j - i + 1));\n }\n }\n\n int high = 1 + max((stones[N - 1] - stones[1] + 1) - N, // Move to right most\n (stones[N - 2] - stones[0] + 1) - N); // Move to left most\n return {low, high};\n }\n};
| 0
| 0
|
['C++']
| 0
|
moving-stones-until-consecutive-ii
|
Java Code
|
java-code-by-kpuniya-d81m
|
class Solution {\n public int[] numMovesStonesII(int[] stones) {\n Arrays.sort(stones);\n\n int i=0, n=stones.length;\n int high = Math.
|
Kpuniya
|
NORMAL
|
2024-06-25T04:02:00.098952+00:00
|
2024-06-25T04:02:00.098995+00:00
| 5
| false
|
class Solution {\n public int[] numMovesStonesII(int[] stones) {\n Arrays.sort(stones);\n\n int i=0, n=stones.length;\n int high = Math.max(stones[n-1] - n+2 -stones[1], stones[n-2]-stones[0]- n+2);\n\n int low=n;\n for(int j=0; j<n; j++){\n while(stones[j]-stones[i] >= n) i++;\n\n if(j-i+1 == n-1 && stones[j]-stones[i]==n-2) low = Math.min(low, 2);\n else low = Math.min(low, n-(j-i+1));\n }\n return new int[]{low, high};\n }\n}
| 0
| 0
|
[]
| 0
|
moving-stones-until-consecutive-ii
|
Sliding Window with edge case
|
sliding-window-with-edge-case-by-3aarong-sz5r
|
\n\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n vector<int> res;\n sort(stones.begin(),stones.end());\n
|
3aarongan
|
NORMAL
|
2024-06-14T18:39:14.778877+00:00
|
2024-06-14T18:39:14.778907+00:00
| 20
| false
|
\n```\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n vector<int> res;\n sort(stones.begin(),stones.end());\n int n = stones.size();\n int l = 0, r = 0;\n int result = 0;\n while(l < n){\n while(r < n && stones[r]-stones[l] < n){\n r++;\n }\n if(r-l == n-1 && stones[r-1]-stones[l] == n-2){\n result = max(r-l-1,result);\n }\n else\n result = max(r-l,result);\n r--;\n l++;\n }\n res.push_back(n-result);\n res.push_back(max(stones[n-2]-stones[0],stones[n-1]-stones[1])-n+2);\n return res;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
moving-stones-until-consecutive-ii
|
USACO 2019 February Contest, Silver Problem 1. Sleepy Cow Herding
|
usaco-2019-february-contest-silver-probl-ieza
|
This is USACO 2019 February Contest, Silver, Problem 1. Sleepy Cow Herding\n\nIt\'s medium, if you\'re in the contest :)\n\nHow to solve it? https://www.youtube
|
vokasik
|
NORMAL
|
2024-06-07T03:03:53.389208+00:00
|
2024-06-07T03:03:53.389234+00:00
| 94
| false
|
This is [USACO 2019 February Contest, Silver, Problem 1. Sleepy Cow Herding](]https://usaco.org/index.php?page=viewproblem2&cpid=918)\n\nIt\'s medium, if you\'re in the contest :)\n\nHow to solve it? https://www.youtube.com/watch?v=BvgV7f3pwcI\n\n```\nclass Solution:\n def numMovesStonesII(self, stones: List[int]) -> List[int]:\n N = len(stones)\n stones.sort()\n min_res = 0\n if stones[N - 2] - stones[0] == N - 2 and stones[N - 1] - stones[N - 2] > 2:\n min_res = 2\n elif stones[N - 1] - stones[1] == N - 2 and stones[1] - stones[0] > 2:\n min_res = 2\n else:\n l = r = max_range = 0\n while l < N:\n while r < N - 1 and stones[r + 1] - stones[l] <= N - 1:\n r += 1\n max_range = max(max_range, r - l + 1)\n l += 1\n min_res = N - max_range\n max_res = max(stones[N - 2] - stones[0], stones[N - 1] - stones[1]) - (N - 2)\n return (min_res, max_res)\n```
| 0
| 0
|
['Python', 'Python3']
| 1
|
moving-stones-until-consecutive-ii
|
1040. Moving Stones Until Consecutive II.cpp
|
1040-moving-stones-until-consecutive-iic-1yfl
|
Code\n\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n sort(stones.begin(), stones.end());\n int n = stones.
|
202021ganesh
|
NORMAL
|
2024-04-28T09:43:00.204857+00:00
|
2024-04-28T09:43:00.204891+00:00
| 32
| false
|
**Code**\n```\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n sort(stones.begin(), stones.end());\n int n = stones.size(), i = 0, low = n;\n int high = max(stones[n-1] - n + 2 - stones[1], stones[n-2] - stones[0] - n + 2);\n for (int j = 0; j < n; ++j) {\n while (stones[j] - stones[i] >= n) ++i;\n if (j - i + 1 == n - 1 && stones[j] - stones[i] == n - 2)\n low = min(low, 2);\n else\n low = min(low, n - (j - i + 1));\n }\n return {low, high};\n }\n};\n```
| 0
| 0
|
['C']
| 0
|
moving-stones-until-consecutive-ii
|
Solution Moving Stones Until Consecutive
|
solution-moving-stones-until-consecutive-40d2
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Suyono-Sukorame
|
NORMAL
|
2024-03-15T06:55:08.657176+00:00
|
2024-03-15T06:55:08.657201+00:00
| 4
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n\n /**\n * @param Integer[] $stones\n * @return Integer[]\n */\n function numMovesStonesII($stones) {\n sort($stones);\n $n = count($stones);\n $total = $stones[$n - 1] - $stones[0] + 1 - $n;\n \n $maxMoves = max($stones[$n - 1] - $stones[1] - $n + 2, $stones[$n - 2] - $stones[0] - $n + 2);\n \n $left = 0;\n $minMoves = $n;\n \n for ($right = 0; $right < $n; $right++) {\n while ($stones[$right] - $stones[$left] >= $n) {\n $left++;\n }\n \n if ($right - $left + 1 === $n - 1 && $stones[$right] - $stones[$left] === $n - 2) {\n $minMoves = min($minMoves, 2);\n } else {\n $minMoves = min($minMoves, $n - ($right - $left + 1));\n }\n }\n \n return [$minMoves, $maxMoves];\n }\n}\n\n```
| 0
| 0
|
['PHP']
| 0
|
moving-stones-until-consecutive-ii
|
DAY75 || ABHINAV
|
day75-abhinav-by-abhijha1-1ai7
|
Intuition\n Describe your first thoughts on how to solve this problem. \n1. Sort the stones to make it easier to analyze the positions. Find the minimum number
|
abhijha1
|
NORMAL
|
2024-02-08T18:26:19.853088+00:00
|
2024-02-08T19:51:36.658825+00:00
| 35
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1. Sort the stones to make it easier to analyze the positions. Find the minimum number of moves required to make the stones consecutive by iterating through the sorted list of stones.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Sort the stones to make it easier to analyze their positions.\n2. Determine the minimum number of moves required to make the stones consecutive by iterating through the sorted list of stones.\n3. Calculate the maximum number of moves required by considering the possibilities at both ends of the sorted list of stones.\n4. Return the minimum and maximum number of moves as a pair.\n\n# Complexity\n- Time complexity: O(NlogN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n sort(stones.begin(), stones.end());\n\n int N = stones.size(), low = N;\n for (int i = 0, j = 0; j < N; ++j) {\n while (stones[j] - stones[i] + 1 > N) {\n ++i;\n }\n if (N - (j - i + 1) == 1 && N - (stones[j] - stones[i] + 1) == 1) {\n low = min(low, 2);\n } \n else {\n low = min(low, N - (j - i + 1));\n }\n }\n\n int high = 1 + max((stones[N - 1] - stones[1] + 1) - N, (stones[N - 2] - stones[0] + 1) - N);\n return {low, high};\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
moving-stones-until-consecutive-ii
|
Moving Stones Until Consecutive II || JAVASCRIPT || Solution by Bharadwaj
|
moving-stones-until-consecutive-ii-javas-hryn
|
Approach\nSliding Window\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(1)\n\n# Code\n\nvar numMovesStonesII = function(stones) {\n st
|
Manu-Bharadwaj-BN
|
NORMAL
|
2023-12-18T11:29:17.454734+00:00
|
2023-12-18T11:29:17.454765+00:00
| 27
| false
|
# Approach\nSliding Window\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nvar numMovesStonesII = function(stones) {\n stones.sort((a, b) => a - b);\n let { length: size } = stones;\n let max = Math.max(stones[size - 1] - stones[1] - size + 2, stones[size - 2] - stones[0] - size + 2);\n let start = 0;\n let min = size;\n\n for(let end = 1; end < size; end++){\n while(stones[end] - stones[start] + 1 > size) start += 1;\n let already = end - start + 1;\n\n if(already === size - 1 && stones[end] - stones[start] + 1 === size - 1){\n min = Math.min(min, 2);\n } else {\n min = Math.min(min, size - already);\n }\n } \n return [min, max];\n};\n```
| 0
| 0
|
['JavaScript']
| 0
|
moving-stones-until-consecutive-ii
|
aaa
|
aaa-by-user3043sb-ckyv
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
user3043SB
|
NORMAL
|
2023-12-17T10:06:38.355520+00:00
|
2023-12-17T10:06:38.355542+00:00
| 105
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport java.util.*;\n\nclass Solution {\n\n // 1,2,_,_,5\n // 2,1,_,5 -> 1,2,5\n // 2,_,1,5 -> 2,5,1\n\n\n // 1,2,x,x,x,6\n // 2,1,x,x,6\n // 1,2,x,6\n // 2,1,6\n\n // 1,2,x,x,x,6\n // 2,x,x,1,6\n // 2,6,x,1\n // 6,2,1\n\n // a,x,b,x,x,x,c\n // a,c,b spaces removed = right + 1\n // b,a,x,x,c spaces removed = left + 1\n\n // MAX: left/right + 1 always\n // 3,4,5,6,x,x,x,10\n\n // MIN:\n // 3,4,5,6,x ,x ,x ,10\n // 4,5,6,x ,3 ,x ,10\n // 4,5,6,10,3\n\n // a,b,c,x,x,x,x,d gap = 4 max = 4 min = 2\n // b,c,x,a,x,x,d min = 2; merge island of 1 to main island\n // b,c,d,a\n\n // a,b,x,x,x,x,c,d min = 2; merge island of 2 to main island\n // b,x,x,a,x,c,d\n // a,b,c,d\n\n // gaps 1,2\n\n // max = 4\n // 2 2 3\n // C AAAAAA BBBBBBBBBBBBBB DDD\n // AAAAAAC BBBBBBBBBBBBBB DDD\n // AAAAAAC BBBBBBBBBBBBBB D DD\n // AAAAAAC BBBBBBBBBBBBBBDD D\n // AAAAAACDBBBBBBBBBBBBBBDD\n\n // C AAAAAA BBBBBBBBBBBBBB DDD max = 7\n // CD AAAAAA BBBBBBBBBBBBBB DD\n // CDDAAAAAA BBBBBBBBBBBBBB D\n // DDAAAAAAC BBBBBBBBBBBBBB D\n // DAAAAAAC BBBBBBBBBBBBBBD D\n // AAAAAAC BBBBBBBBBBBBBBDD D\n // AAAAAC BBBBBBBBBBBBBBDDAD\n // AAAAACDBBBBBBBBBBBBBBDDA\n\n // MAX STRATEGY depends on OUTER ISLAND SIZE:\n // 1) outer island > 1 => cost = size of gap; we remove outer gap 1 by 1\n // moreover we can keep rotating the outer island; total cost = sum of all gaps\n // 2) outer island == 1 => cost = 1 and we remove (left/right gap) + 1 spaces\n // HOWEVER need to only do step 2) ONCE; then we can do step 1!!!!!!!\n\n // MIN STRATEGY:\n // 1) try all possible windows of size N; and check how many spaces need to be filled\n\n public int[] numMovesStonesII(int[] A) {\n int min = A.length, max = 0, n = A.length;\n Arrays.sort(A);\n int leftMostSpace = A[1] - A[0] - 1;\n int rightMostSpace = A[n - 1] - A[n - 2] - 1; // no need to even loop for the spaces; because the vals are on the X-axis\n int numsInRange = (A[n - 1] - A[0] + 1); // nums in range INCLUSIVE\n int spaces = numsInRange - n; // nums in range INCLUSIVE - numbers in range = gaps\n max = spaces;\n if (leftMostSpace > 0 && rightMostSpace > 0)\n max -= Math.min(leftMostSpace, rightMostSpace); // 1 more removed space but cost + 1 too; cancels out\n\n // 4,7,9\n for (int l = 0, r = 1; l < n; l++) {\n while (r < n - 1 && (A[r] - A[l] + 1) < n) r++;\n int numsInWindowRange = A[r] - A[l] + 1;\n int stonesInWindow = r - l + 1;\n int positionsToFill = n - stonesInWindow; // moves needed\n if (numsInWindowRange > n) { // window too big, need to shrink it with 1 step; a,b,x,x,x,x,x,c,d\n positionsToFill++;\n stonesInWindow--; // rightmost stone is outside the first N spaces of window\n }\n // nums in window == N => spaces are in MIDDLE\n // nums in window != N => spaces in front or at the back; handle single missing elem !!!\n if (numsInWindowRange != n && stonesInWindow == n - 1) positionsToFill ++; // edge case a,b,x,x,c\n min = Math.min(min, positionsToFill);\n }\n // 4,7,9\n // 4,x,x,7,x,9\n\n // 2,5,6,7,8\n // 2,x,x,5,6,7,8\n\n return new int[]{min, max};\n }\n\n}\n```
| 0
| 0
|
['Java']
| 0
|
moving-stones-until-consecutive-ii
|
Solution
|
solution-by-deleted_user-1icu
|
C++ []\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& A) {\n sort(A.begin(), A.end());\n int i = 0, n = A.size(), low =
|
deleted_user
|
NORMAL
|
2023-05-25T08:49:10.107167+00:00
|
2023-05-25T09:17:37.544366+00:00
| 293
| false
|
```C++ []\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& A) {\n sort(A.begin(), A.end());\n int i = 0, n = A.size(), low = n;\n int high = max(A[n - 1] - n + 2 - A[1], A[n - 2] - A[0] - n + 2);\n for (int j = 0; j < n; ++j) {\n while (A[j] - A[i] >= n) ++i;\n if (j - i + 1 == n - 1 && A[j] - A[i] == n - 2)\n low = min(low, 2);\n else\n low = min(low, n - (j - i + 1));\n }\n return {low, high};\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def numMovesStonesII(self, s: List[int]) -> List[int]:\n s.sort()\n n = len(s)\n d1 = s[-2] - s[0] - n + 2\n d2 = s[-1] - s[1] - n + 2\n max_move = max(d1, d2)\n if d1 == 0 or d2 == 0:\n return [min(2, max_move), max_move]\n max_cnt = left = 0\n for right, x in enumerate(s):\n while s[left] <= x - n:\n left += 1\n max_cnt = max(max_cnt, right - left + 1)\n return [n - max_cnt, max_move]\n```\n\n```Java []\n\tclass Solution {\n\t\tpublic int[] numMovesStonesII(int[] stones) {\n\t\t\tint n = stones.length;\n\t\t\t int[] ans = new int[2];\n\t\t\t int i = 0, j = 0, wsize, scount, minMoves = Integer.MAX_VALUE;\n\t\t\tArrays.sort(stones);\n\t\t\t while (j < n) {\n\t\t\t\twsize = stones[j] - stones[i] + 1;\n\t\t\t\tscount = j - i + 1;\n\n\t\t\t\tif (wsize > n) {\n\t\t\t\t\ti++;\n\t\t\t\t\tcontinue;\n\t\t\t\t}\n\t\t\t\tif (wsize == n - 1 && scount == n - 1)\n\t\t\t\t\tminMoves = Math.min(minMoves, 2);\n\n\t\t\t\telse minMoves = Math.min(minMoves, n - scount);\n\n\t\t\t\tj++;\n\t\t\t}\n\t\t\tans[0] = minMoves;\n\t\t\tint maxMoves = 0;\n\t\t\t if (stones[1] == stones[0] + 1 || stones[n - 1] == stones[n - 2] + 1)\n\t\t\t\tmaxMoves = stones[n - 1] - stones[0] + 1 - n;\n\t\t\telse \n\t\t\t\tmaxMoves = Math.max(((stones[n - 1] - stones[1]) - (n - 1) + 1), ((stones[n - 2] - stones[0]) - (n - 1) + 1));\n\t\t\tans[1] = maxMoves;\n\t\t\treturn ans;\n\t\t}\n\t}\n```
| 0
| 0
|
['C++', 'Java', 'Python3']
| 0
|
moving-stones-until-consecutive-ii
|
Swift solution with comments, using sliding window
|
swift-solution-with-comments-using-slidi-7kjs
|
Complexity\n- Time complexity: O(n*log(n)), where n is stones count\n- Space complexity: O(n)\n\n# Code\n\nclass Solution {\n func numMovesStonesII(_ stones:
|
VladimirTheLeet
|
NORMAL
|
2023-04-12T20:27:02.321607+00:00
|
2023-04-12T20:30:44.014595+00:00
| 33
| false
|
# Complexity\n- Time complexity: O(n*log(n)), where n is stones count\n- Space complexity: O(n)\n\n# Code\n```\nclass Solution {\n func numMovesStonesII(_ stones: [Int]) -> [Int]\n {\n let stonesCount = stones.count\n let stones = stones.sorted() // that gives O(n*log(n)) complexity\n\n // distances from the edge stones to their nearest neighbors\n let edgeDist = [stones[1] - stones[0], stones[stonesCount-1] - stones[stonesCount-2]]\n let minEdgeDist = edgeDist.min()!, maxEdgeDist = edgeDist.max()!\n\n // for max number of turns we first move the edge stone to the nearest position\n // on the other side of its neighbor, losing minEdgeDist-1 empty spaces\n // after that we will always have a group of stones on that edge,\n // we\'ll move the last of them, losing one space per turn till the end\n let maxMovesNumber = stones[stonesCount-1] - stones[0] - stonesCount - minEdgeDist + 2\n\n\n // we use the sliding window with the width of stonesCount,\n // finding max possible number of stones fit in this window.\n // for min number of turns we just jump the remaining \n // outside stones into this range one by one\n\n // index for element that is left border of the sliding window\n var leftIndex = 0\n // index for element after right border of the sliding window\n guard var rightIndex = stones.firstIndex(where: { $0 >= stones[0] + stonesCount })\n else { return [0, 0] }\n \n var count = 0, maxCount = 0\n while rightIndex <= stonesCount\n {\n count = rightIndex - leftIndex\n maxCount = max(count, maxCount)\n // left border always advance to the next stone\n leftIndex += 1\n // if we have the rightmost stone inside the window, there is \n // no point moving further, as the count can only go down\n if rightIndex == stonesCount { break }\n\n // move right border by finding the next stone\n // that is outside advanced window range.\n // could use binary search to speed up the searching a bit,\n // but the complexity here is just O(n), as we only traverse\n // the array once, so didn\'t bother\n while rightIndex < stonesCount\n {\n if stones[rightIndex] >= stones[leftIndex] + stonesCount { break }\n rightIndex += 1\n }\n }\n var minMovesNumber = stonesCount - maxCount\n // one special case with all stones but one already grouped together\n if maxCount == stonesCount - 1, minEdgeDist == 1, maxEdgeDist > 2 {\n minMovesNumber += 1\n }\n\n return [minMovesNumber, maxMovesNumber]\n }\n}\n```
| 0
| 0
|
['Swift', 'Sliding Window']
| 0
|
moving-stones-until-consecutive-ii
|
C
|
c-by-tinachien-azy7
|
\n/**\n * Note: The returned array must be malloced, assume caller calls free().\n */\nint cmp(const void* a, const void* b){\n return *(int*)a - *(int*)b ;\
|
TinaChien
|
NORMAL
|
2023-03-19T12:08:12.747740+00:00
|
2023-03-19T12:08:12.747772+00:00
| 34
| false
|
```\n/**\n * Note: The returned array must be malloced, assume caller calls free().\n */\nint cmp(const void* a, const void* b){\n return *(int*)a - *(int*)b ;\n}\nint* numMovesStonesII(int* stones, int stonesSize, int* returnSize){\n int n = stonesSize ;\n *returnSize = 2 ;\n qsort(stones, n, sizeof(int), cmp) ;\n int* ans = malloc(2 * sizeof(int)) ;\n int upper , lower = n ;\n upper = fmax(stones[n-1] - stones[1] + 1 - n + 1, stones[n-2] - stones[0] + 1 - n + 1) ;\n int left = 0 ;\n for(int right = 0; right < n; right++){\n while(stones[right] - stones[left] + 1 > n)\n left++ ;\n \n if( stones[right] - stones[left] + 1 == n-1 && right - left + 1 == n-1 )\n lower = fmin(lower, 2) ;\n else\n lower = fmin(lower, n - (right - left + 1)) ;\n }\n ans[0] = lower ;\n ans[1] = upper ;\n return ans ;\n}\n```
| 0
| 0
|
[]
| 0
|
moving-stones-until-consecutive-ii
|
C++||Sliding Window|| Easy to Understand
|
csliding-window-easy-to-understand-by-re-enp3
|
\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) \n {\n sort(stones.begin(),stones.end());\n int n=stones.siz
|
return_7
|
NORMAL
|
2023-02-13T08:39:09.583980+00:00
|
2023-02-13T08:39:09.584013+00:00
| 95
| false
|
```\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) \n {\n sort(stones.begin(),stones.end());\n int n=stones.size();\n int low=n;\n for(int i=0,j=0;j<n;j++)\n {\n while(stones[j]-stones[i]+1>n)\n i++;\n int already_store=j-i+1;\n if(already_store==n-1&&(stones[j]-stones[i]+1==n-1))\n {\n low=min(low,2);\n }\n else\n {\n low=min(low,n-already_store);\n }\n }\n return {low,max(stones[n-1]-stones[1]-n+1,stones[n-2]-stones[0]-n+1)+1};\n \n }\n};\n```\nIf you like the solution plz upvote.
| 0
| 0
|
['C', 'Sorting']
| 0
|
moving-stones-until-consecutive-ii
|
Fast C++ solution
|
fast-c-solution-by-obose-qlk0
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem is to find the minimum number of moves required to move all the stones to c
|
Obose
|
NORMAL
|
2023-01-20T18:28:54.094064+00:00
|
2023-01-20T18:28:54.094110+00:00
| 123
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is to find the minimum number of moves required to move all the stones to consecutive positions. We need to find the minimum number of moves required to move the stones to their final positions and the maximum number of moves required to move the stones to their final positions.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach is to first sort the stones, then use two pointers to find the minimum and maximum number of moves required to move the stones to their final positions. The first pointer i is used to keep track of the leftmost stone that can be included in the sliding window, and the second pointer j is used to iterate through the stones. The size of the sliding window is represented by the variable n. The variable low is used to keep track of the minimum number of moves required to move the stones to their final positions, and the variable high is used to keep track of the maximum number of moves required to move the stones to their final positions.\n# Complexity\n- Time complexity: $$O(n log n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n sort(stones.begin(), stones.end());\n int n = stones.size(), i = 0, low = n;\n int high = max(stones[n-1] - n + 2 - stones[1], stones[n-2] - stones[0] - n + 2);\n for (int j = 0; j < n; ++j) {\n while (stones[j] - stones[i] >= n) ++i;\n if (j - i + 1 == n - 1 && stones[j] - stones[i] == n - 2)\n low = min(low, 2);\n else\n low = min(low, n - (j - i + 1));\n }\n return {low, high};\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
moving-stones-until-consecutive-ii
|
Clean Python | 8 Lines | High Speed | O(n) time, O(1) space | Beats 96.9% | With Explanation
|
clean-python-8-lines-high-speed-on-time-x7sy3
|
Intuition & Approach\n\n## Lower Bound\nAs I mentioned in my video last week,\nin case of n stones,\nwe need to find a consecutive n positions and move the ston
|
avs-abhishek123
|
NORMAL
|
2023-01-19T06:15:20.822605+00:00
|
2023-01-19T06:15:20.822650+00:00
| 170
| false
|
# Intuition & Approach\n\n## Lower Bound\nAs I mentioned in my video last week,\nin case of `n` stones,\nwe need to find a consecutive `n` positions and move the stones in.\n\nThis idea led the solution with sliding windows.\n\nSlide a window of size `N`, and find how many stones are already in this window.\nWe want moves other stones into this window.\nFor each missing stone, we need at least one move.\n\nGenerally, the number of missing stones and the moves we need are the same.\nOnly one corner case in this problem, we need to move the endpoint to no endpoint.\n\nFor case `1,2,4,5,10`\n1 move needed from `10` to `3`.\n\nFor case `1,2,3,4,10`\n2 move needed from `1` to `6`, then from `10` to `5`.\n\n\n## Upper Bound\nWe try to move all stones to leftmost or rightmost.\nFor example of to rightmost.\nWe move the `A[0]` to `A[1] + 1`.\nThen each time, we pick the stone of left endpoint, move it to the next empty position.\nDuring this process, the position of leftmost stones increment 1 by 1 each time.\nUntil the leftmost is at `A[n - 1] - n + 1`.\n\n# Complexity\n#### Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- Time of quick sorting `O(NlogN)`\n- Time of sliding window `O(N)`\n#### Space complexity: `O(1)`\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numMovesStonesII(self, A):\n A.sort()\n i, n, low = 0, len(A), len(A)\n high = max(A[-1] - n + 2 - A[1], A[-2] - A[0] - n + 2)\n for j in range(n):\n while A[j] - A[i] >= n: i += 1\n if j - i + 1 == n - 1 and A[j] - A[i] == n - 2: low = min(low, 2)\n else: low = min(low, n - (j - i + 1))\n return [low, high]\n```
| 0
| 2
|
['Python3']
| 0
|
moving-stones-until-consecutive-ii
|
Just a runnable solution
|
just-a-runnable-solution-by-ssrlive-awgh
|
Code\n\nimpl Solution {\n pub fn num_moves_stones_ii(stones: Vec<i32>) -> Vec<i32> {\n let mut stones = stones;\n stones.sort();\n let n
|
ssrlive
|
NORMAL
|
2023-01-11T07:53:49.945791+00:00
|
2023-01-11T07:53:49.945834+00:00
| 66
| false
|
# Code\n```\nimpl Solution {\n pub fn num_moves_stones_ii(stones: Vec<i32>) -> Vec<i32> {\n let mut stones = stones;\n stones.sort();\n let n = stones.len();\n let mut i = 0;\n let mut low = n as i32;\n let high = std::cmp::max(stones[n - 1] - n as i32 + 2 - stones[1], stones[n - 2] - stones[0] - n as i32 + 2);\n for j in 0..n {\n while stones[j] - stones[i] >= n as i32 {\n i += 1;\n }\n if j - i + 1 == n - 1 && stones[j] - stones[i] == n as i32 - 2 {\n low = std::cmp::min(low, 2);\n } else {\n low = std::cmp::min(low, n as i32 - (j - i + 1) as i32);\n }\n }\n vec![low, high]\n }\n}\n```
| 0
| 0
|
['Rust']
| 0
|
moving-stones-until-consecutive-ii
|
Python solution: try to explain more extensively
|
python-solution-try-to-explain-more-exte-hxxh
|
First thing first, this problem is ridiculous to be used for interviews. The given example 2 is actually an edge case....\n\n\nclass Solution:\n # This probl
|
huikinglam02
|
NORMAL
|
2022-08-21T07:31:31.408332+00:00
|
2022-08-21T07:31:31.408375+00:00
| 68
| false
|
First thing first, this problem is ridiculous to be used for interviews. The given example 2 is actually an edge case....\n\n```\nclass Solution:\n # This problem is separated into two parts: the max and the min\n # They use totally different strategies\n # Max is a little easier: it involves moving all the stones step by step from left to right or right to left\n # For example: [1,100,102,105,200]\n # It depends on whether we first move 1 to 101, then 102 to 103, 101 to 104... etc.\n # Or the other way round, 200 to 104, 105 to 103, 104 to 101, etc.\n # The max move is max(stones[-1]-stones[1]-1-(n-3), stones[-2]-stones[0]-1-(n-3)) \n # Getting the min move is more tricky. Because the final result will be a window of size n, the best strategy is it started with a stone position and in the n-size subwindow after it, it contains the most stones possible\n # For example as in the case [1,100,102,105,200], min move will be\n # move 1 to 101, move 200 to 104, move 105 to 103\n # The appropriate technique is to use sliding window. we first set start and try to extend end, and for each end, we ensure stones[end] - stones[start] + 1 <= n\n # Then for each valid sliding window, we calculate the number of free slots in the window: n - (end - start + 1)\n # There is a special case: stones = [3,4,5,6,10]\n # We see that what start = 0, end = 3, the only free slot in the window is at the ends. The proper move is move 3 to position 8 and 10 to position 7. 2 moves\n \n def numMovesStonesII(self, stones: List[int]) -> List[int]:\n stones.sort()\n n = len(stones)\n maxmoves = max(stones[-1]-stones[1], stones[-2]-stones[0]) - n + 2\n start, minmoves = 0, maxmoves\n for end in range(n):\n while stones[end] - stones[start] >= n:\n start += 1\n if end-start+1 == n-1 and stones[end]-stones[start]+1== n-1:\n minmoves = min(minmoves, 2)\n else:\n minmoves = min(minmoves, n - (end-start+1))\n #print(start, end, minmoves)\n return [minmoves, maxmoves]\n```
| 0
| 0
|
[]
| 0
|
moving-stones-until-consecutive-ii
|
C++| Sliding Window for min + Greedy for max | O(n)
|
c-sliding-window-for-min-greedy-for-max-86xsz
|
\nclass Solution {\npublic:\n int cal_min(vector<int>& nums){\n unordered_map<int,int> mp; \n int left = 0, m = INT_MAX;\n for(int i = 0
|
kumarabhi98
|
NORMAL
|
2022-07-02T08:24:05.218782+00:00
|
2022-07-02T08:24:05.218848+00:00
| 209
| false
|
```\nclass Solution {\npublic:\n int cal_min(vector<int>& nums){\n unordered_map<int,int> mp; \n int left = 0, m = INT_MAX;\n for(int i = 0; i<nums.size();++i) mp[nums[i]] = i;\n for(int i = 0; i<nums.size();++i){\n int e = nums[i]+nums.size()-1;\n if(e>nums[nums.size()-1]) continue;\n int n = nums.size()-(upper_bound(nums.begin(),nums.end(),e)-nums.begin());\n if(left || mp.find(e)!=mp.end() || n>1) m = min(left+n,m);\n left++;\n }\n return m;\n }\n int cal_max(vector<int>& nums){\n int sum = 0,n = nums.size();\n for(int i = 1; i<nums.size();++i) sum+=(nums[i]-nums[i-1]-1);\n int a = nums[1]-nums[0]-1, b = nums[n-1]-nums[n-2]-1;\n return sum - min(a,b);\n }\n vector<int> numMovesStonesII(vector<int>& nums) {\n sort(nums.begin(),nums.end());\n return {cal_min(nums),cal_max(nums)};\n }\n};\n```
| 0
| 0
|
['C', 'Sliding Window']
| 0
|
moving-stones-until-consecutive-ii
|
What is max move and what is min?
|
what-is-max-move-and-what-is-min-by-rand-uauq
|
The question huanted me for a while is that what does it mean by max and min move?\nTake max first - how to make sure we move as many times as possible?\nThe an
|
randysheriff
|
NORMAL
|
2022-01-20T21:17:33.332852+00:00
|
2022-01-20T21:29:51.585592+00:00
| 239
| false
|
The question huanted me for a while is that what does it mean by max and min move?\nTake max first - how to make sure we move as many times as possible?\nThe answer is to visit as many gaps as we can. Assume we have [7,4,9], after sort, it is [4,7,9], the number of visitable gaps between each pair of positions are 2 and 1, or specifically, position 5,6 and 8. So the max move means that we try to visit the gaps as many as possible. \nOne way is to move rightbound, we could move leftmost stone to 8 to have [7,8,9], then we are done with the count of move equals 1. \nThen we could try move leftbound - move 9 to 6 to have [4,6,7] and move 7 to 5 to have [4,5,6], so we have moved twice and the max_move = max(1,2) = 2.\nAnother example - [1,3,7,10], the gaps are 2,4,5,6,8,9, if we move rightbound, we could visit 4,5,6,8,9, while leftbound we could visit 2,4,5,6, so max_move = max(5,4) = 5.\nOk ... then what does it mean by min move? \nThe answer is try to keep as many stones as where they are, and move in every other outside stone.\nTo achieve this, we could setup a window of size >= N (N is the number of all stones), then we slide the windows from left to right, during which for each occurrance of such an window we count how many stones need to move in, the min of all those counts is the min_move.\n\n```\nvector<int> numMovesStonesII(vector<int>& stones) {\n sort(stones.begin(), stones.end());\n int min_move = (int)1e9;\n int max_move = 0;\n int gap_sum = 0;\n int size = stones.size();\n for (int i = 1; i < size; ++i) {\n gap_sum += stones[i] - stones[i-1] - 1; // sum of all gaps\n }\n\t\t// max_move = max(rightbound moves, leftbound moves)\n max_move = max(gap_sum - stones[1] + stones[0] + 1, gap_sum - stones[size-1] + stones[size-2] + 1);\n int st = 0;\n int ed = 1; //[st, ed] is the sliding window\n while (ed < size) {\n int space = stones[ed] - stones[st] + 1;\n if (space < size) ed += 1; // window too small, need to expand\n else if (space == size) { // window size is N, borders are all in right place, only need to move in all outside stones.\n min_move = min(min_move, st + size - ed - 1);\n st += 1;\n } else { // window size bigger than N, need to move one of the border inside the window in the end.\n int not_included = st + size - ed - 1;\n\t\t\t\t// mind the case that there is no outside stone, moving is impossible, so skip.\n if (not_included > 0) min_move = min(min_move, st + size - ed);\n st += 1;\n }\n }\n \n return {min_move, max_move};\n }\n```
| 0
| 0
|
[]
| 0
|
moving-stones-until-consecutive-ii
|
[Python3] sliding window
|
python3-sliding-window-by-ye15-imfl
|
\n\nclass Solution:\n def numMovesStonesII(self, stones: List[int]) -> List[int]:\n stones.sort()\n high = max(stones[-1] - stones[1], stones[-
|
ye15
|
NORMAL
|
2021-06-24T16:56:55.349729+00:00
|
2021-06-24T17:02:30.915382+00:00
| 312
| false
|
\n```\nclass Solution:\n def numMovesStonesII(self, stones: List[int]) -> List[int]:\n stones.sort()\n high = max(stones[-1] - stones[1], stones[-2] - stones[0]) - (len(stones) - 2)\n \n ii, low = 0, inf\n for i in range(len(stones)): \n while stones[i] - stones[ii] >= len(stones): ii += 1\n if i - ii + 1 == stones[i] - stones[ii] + 1 == len(stones) - 1: low = min(low, 2)\n else: low = min(low, len(stones) - (i - ii + 1))\n return [low, high]\n```
| 0
| 0
|
['Python3']
| 0
|
moving-stones-until-consecutive-ii
|
Go | 100% speed + mem
|
go-100-speed-mem-by-ducthanh98-4zj6
|
\nfunc numMovesStonesII(stones []int) []int {\n\tsort.Ints(stones)\n\treturn []int{minStep(stones),maxStep(stones)}\n}\n\nfunc minStep(stones []int) int {\n\tle
|
ducthanh98
|
NORMAL
|
2021-06-20T14:29:50.690333+00:00
|
2021-06-20T14:29:50.690364+00:00
| 130
| false
|
```\nfunc numMovesStonesII(stones []int) []int {\n\tsort.Ints(stones)\n\treturn []int{minStep(stones),maxStep(stones)}\n}\n\nfunc minStep(stones []int) int {\n\tleft,right := 0,1\n\tminStep := math.MaxInt32\n\tgaps := 0\n\texistStones := 1\n\tlength := len(stones)\n\tfor right < length {\n\n\t\tif stones[right] <= stones[left] + length - 1 {\n\t\t\tright++\n\t\t\texistStones++\n\t\t} else {\n\n\t\t\tgaps = length - existStones\n\t\t\tif gaps == 1 && stones[right-1] == stones[left]+length-1 || gaps != 1 {\n\t\t\t\tminStep = min(gaps,minStep)\n\t\t\t}\n\t\t\tleft++\n\t\t\texistStones--\n\n\t\t}\n\n\t}\n\tgaps = length - existStones\n\tif gaps == 1 && stones[right-1] == stones[left]+length-1 || gaps != 1 {\n\t\tminStep = min(gaps,minStep)\n\t}\n\treturn minStep\n\n}\n\nfunc maxStep(stones []int) int {\n\ttotal := stones[len(stones) - 1] - stones[0] + 1\n\tspace := total - len(stones)\n\treturn max(space -( stones[1] - stones[0] - 1),space - ( stones[len(stones) - 1] - stones[len(stones) - 2] - 1))\n}\n\nfunc min(a, b int) int {\n\tif a < b {\n\t\treturn a\n\t}\n\treturn b\n}\n\nfunc max(a, b int) int {\n\tif a > b {\n\t\treturn a\n\t}\n\treturn b\n}\n```
| 0
| 0
|
[]
| 0
|
moving-stones-until-consecutive-ii
|
cpp14 solution
|
cpp14-solution-by-divkr98-81dw
|
max idea : https://leetcode.com/problems/moving-stones-until-consecutive-ii/discuss/286920/Use-Interval-to-Get-Max-Moves\n\nmin idea : https://leetcode.com/prob
|
divkr98
|
NORMAL
|
2020-10-23T08:47:19.243655+00:00
|
2020-10-23T08:48:43.514109+00:00
| 278
| false
|
max idea : https://leetcode.com/problems/moving-stones-until-consecutive-ii/discuss/286920/Use-Interval-to-Get-Max-Moves\n\nmin idea : https://leetcode.com/problems/moving-stones-until-consecutive-ii/discuss/555907/C%2B%2B-solution-or-Sliding-window-for-minimum-moves\n\n\n```\nclass Solution {\npublic:\n\n int calculatemax(vector<int> &stones)\n {\n vector<int> intervals;\n for(int i = 1 ; i < stones.size() ; ++i){\n intervals.push_back(stones[i] - stones[i-1] - 1);\n }\n int maxx = 0;\n if(intervals[0] != 0 and intervals[intervals.size()-1] != 0){\n if(intervals[0] > intervals[intervals.size() -1]){\n intervals.pop_back();\n }\n else{\n intervals.erase(intervals.begin());\n }\n }\n maxx = accumulate(intervals.begin() , intervals.end() , 0);\n return maxx;\n }\n\n int calculatemin(vector<int> &stones)\n {\n int i = 0 , j = 0;\n int minn = INT_MAX;\n int n = stones.size() ; \n while(1){\n if(j >= n or i >= n) break; \n int windowsize = stones[j] - stones[i] + 1;\n int totalstones = j - i + 1;\n if(windowsize > n){\n ++i;\n continue;\n }\n if(windowsize == n-1 and totalstones == n-1){\n minn = min(minn , 2);\n }\n else{\n minn = min(minn , n - totalstones);\n }\n ++j;\n }\n return minn;\n }\n\n vector<int> numMovesStonesII(vector<int>& stones) {\n sort(stones.begin() , stones.end());\n int maxx = calculatemax(stones);\n int minn = calculatemin(stones);\n vector<int> res = {minn , maxx} ;\n return res;\n }\n};\n\n```
| 0
| 0
|
[]
| 0
|
moving-stones-until-consecutive-ii
|
Rust translated, 0ms 100%
|
rust-translated-0ms-100-by-qiuzhanghua-hvwa
|
rust\nimpl Solution {\n pub fn num_moves_stones_ii(mut a: Vec<i32>) -> Vec<i32> {\n a.sort();\n let mut i = 0;\n let n = a.len();\n
|
qiuzhanghua
|
NORMAL
|
2020-09-18T00:38:22.561633+00:00
|
2020-09-18T00:38:22.561666+00:00
| 164
| false
|
```rust\nimpl Solution {\n pub fn num_moves_stones_ii(mut a: Vec<i32>) -> Vec<i32> {\n a.sort();\n let mut i = 0;\n let n = a.len();\n let mut lo = n as i32;\n let hi = std::cmp::max(\n a[n - 1] - n as i32 + 2 - a[1],\n a[n - 2] - a[0] - n as i32 + 2,\n );\n for j in 0..n {\n while a[j] - a[i] >= n as i32 {\n i += 1;\n }\n if j - i + 1 == n - 1 && a[j] - a[i] == n as i32 - 2 {\n lo = std::cmp::min(lo, 2);\n } else {\n lo = std::cmp::min(lo, n as i32 - (j - i + 1) as i32);\n }\n }\n vec![lo, hi]\n }\n}\n\n#[cfg(test)]\nmod tests {\n use super::*;\n\n #[test]\n fn test_num_moves_stones_ii() {\n assert_eq!(Solution::num_moves_stones_ii(vec![7, 4, 9]), vec![1, 2]);\n }\n\n #[test]\n fn test_num_moves_stones_ii_02() {\n assert_eq!(\n Solution::num_moves_stones_ii(vec![6, 5, 4, 3, 10]),\n vec![2, 3]\n );\n }\n\n #[test]\n fn test_num_moves_stones_ii_03() {\n assert_eq!(\n Solution::num_moves_stones_ii(vec![100, 101, 104, 102, 103]),\n vec![0, 0]\n );\n }\n}\n```
| 0
| 0
|
[]
| 0
|
moving-stones-until-consecutive-ii
|
JavaScript Sliding Window
|
javascript-sliding-window-by-zckpp1992-z5c8
|
Maximum\nThe idea of getting the maximum is to use up all the empty slots available.\nAnd since left most item cannot be left most item again and same to right
|
zckpp1992
|
NORMAL
|
2020-08-23T21:28:19.070066+00:00
|
2020-08-23T21:28:19.070104+00:00
| 298
| false
|
**Maximum**\nThe idea of getting the maximum is to use up all the empty slots available.\nAnd since left most item cannot be left most item again and same to right most item, we have to move left most item to the right of A[1], and right most item to the left of A[n-2].\nThus all the empty slots available is either A[n-1] - A[1] - 1 - (n-3) (start with moving left most item), or A[n-2] - A[0] - 1 - (n-3) (start with moving right most item), n-3 is the number of items that already there.\n\n**Minimum**\nThe idea of getting the minimum is to use as many items that we do not need to move as possible.\nWe have the sliding window [i,j], where window length(A[j]-A[i]) is smaller than the length of n, which means items within the window are deff within the consecutive list, so that they do not need to move.\nNow we just need to count the items outside the sliding window which need to be moved, which is n - (j - i + 1).\nThough we need to consider when the items within the window are already consecutive and we have one item left, it takes 2 moves to make all of them consecutive.\ne.g.\n2,3,4,8\n\n```\n/**\n * @param {number[]} stones\n * @return {number[]}\n */\nvar numMovesStonesII = function(stones) {\n let min = +Infinity;\n let n = stones.length;\n stones.sort((a,b) => a-b);\n let max = Math.max(\n stones[n-2]-stones[0]-1-(n-3), \n stones[n-1]-stones[1]-1-(n-3));\n let i = 0;\n for (let j = 0; j < n; j++) {\n while (stones[j] - stones[i] >= n) i++;\n if (j - i + 1 == n - 1 && stones[j] - stones[i] == n - 2)\n min = Math.min(min, 2);\n else\n min = Math.min(min, n - (j - i + 1));\n }\n return [min,max];\n};\n```
| 0
| 0
|
[]
| 0
|
moving-stones-until-consecutive-ii
|
[C++] lots of subtle corner cases, learned from forum
|
c-lots-of-subtle-corner-cases-learned-fr-kywm
|
\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n const int n = stones.size();\n std::sort(stones.begin(), st
|
huangdachuan
|
NORMAL
|
2020-06-18T05:56:51.381140+00:00
|
2020-06-18T05:56:51.381190+00:00
| 317
| false
|
```\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n const int n = stones.size();\n std::sort(stones.begin(), stones.end());\n\n int j = 0;\n for (; j < n && stones[j] - stones[0] + 1 <= n; ++j) {}\n int maxOccupied = j;\n for (int i = 0; j < n; ++j) {\n while (stones[j] - stones[i] + 1 > n) { ++i; }\n maxOccupied = std::max(maxOccupied, j - i + 1);\n }\n int minimumMoves = n - maxOccupied;\n if (stones[n - 2] - stones[0] + 1 == n - 1 && stones[n - 1] > stones[n - 2] + 2) {\n minimumMoves = 2;\n }\n if (stones[n - 1] - stones[1] + 1 == n - 1 && stones[1] > stones[0] + 2) {\n minimumMoves = 2;\n }\n\n const int spaces = stones.back() - stones.front() + 1 - n;\n const int maximumMoves = std::max(spaces - (stones[1] - stones[0] - 1),\n spaces - (stones.back() - stones[n - 2] - 1));\n return {minimumMoves, maximumMoves};\n }\n};\n```
| 0
| 0
|
[]
| 0
|
moving-stones-until-consecutive-ii
|
Miss test case @LeetCodeOffical(Actually not)
|
miss-test-case-leetcodeofficalactually-n-xyto
|
If input is [1,5], we cannot make any movements, because all stones are endpoint stones. So the result should be [0,0]. \nHowever, for now, the reuslt from OJ i
|
hanzhoutang
|
NORMAL
|
2020-03-25T04:19:37.842553+00:00
|
2020-03-25T15:54:49.595235+00:00
| 184
| false
|
If input is [1,5], we cannot make any movements, because all stones are endpoint stones. So the result should be [0,0]. \nHowever, for now, the reuslt from OJ is [2,0]. \nI believe it\'s a bug, we need to add this testcase. \n@LeetCodeOffical
| 0
| 0
|
[]
| 1
|
moving-stones-until-consecutive-ii
|
c++ solution
|
c-solution-by-hanzhoutang-ngjy
|
In my opinion, I think the problem is really not as easy as you think. \n\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n
|
hanzhoutang
|
NORMAL
|
2020-03-25T04:05:10.997508+00:00
|
2020-03-25T04:21:16.104671+00:00
| 370
| false
|
In my opinion, I think the problem is really not as easy as you think. \n```\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n if(stones.empty()||stones.size()==1){\n return {0,0};\n }\n if(stones.size() == 2){\n return {0,0};\n }\n sort(stones.begin(),stones.end());\n deque<int> window; \n window.push_back(stones[0]);\n int n = stones.size();\n int count = 0;\n int _min = INT_MAX; \n int total = 0;\n for(int i = 1;i<n;i++){\n total += stones[i] - stones[i-1]-1;\n int r = window[0] + n - 1; \n if(stones[i]<=r){\n count += stones[i] - window.back() - 1; \n window.push_back(stones[i]);\n } else {\n if(window.back() == r) {\n _min = min(_min,count);\n }\n else if(window.size() + 1 != n) {\n _min = min(_min,count + r - window.back());\n }\n int front = window.front();\n window.pop_front();\n if(window.size()){\n total -= stones[i] - stones[i-1] -1;\n count -= window.front() - front - 1; \n i--;\n } else {\n count = 0; \n window.push_back(stones[i]);\n }\n \n }\n }\n int l = window.back() - n + 1; \n if(window.front() == l){\n _min = min(_min,count);\n } else if(window.size() + 1 != n){\n _min = min(_min,count + window.front() - l);\n }\n int x = min(stones[1] - stones[0] - 1, stones[stones.size()-1] - stones[stones.size()-2] - 1);\n int _max = total - x;\n return {_min,_max};\n }\n};\nconst int _ = [](){\n ios_base::sync_with_stdio(false);\n cin.tie(NULL);\n cout.tie(NULL);\n return 0;\n}();\n```
| 0
| 0
|
[]
| 0
|
moving-stones-until-consecutive-ii
|
[python] 100%
|
python-100-by-fukuzawa_yumi-l6kf
|
\n def numMovesStonesII(self, stones):\n stones.sort()\n n,i=len(stones),0\n for j in range(n):\n if stones[j]-stones[i]>=n:
|
fukuzawa_yumi
|
NORMAL
|
2020-01-21T05:28:51.240380+00:00
|
2020-01-21T05:28:51.240414+00:00
| 387
| false
|
```\n def numMovesStonesII(self, stones):\n stones.sort()\n n,i=len(stones),0\n for j in range(n):\n if stones[j]-stones[i]>=n: i+=1\n return [2 if i==1 and stones[-1]-stones[0]!=n and (stones[-2]-stones[0]==n-2 or stones[-1]-stones[1]==n-2) else i,stones[-1]-stones[0]-n-min(stones[1]-stones[0],stones[-1]-stones[-2])+2]\n```
| 0
| 1
|
[]
| 1
|
moving-stones-until-consecutive-ii
|
Go solution
|
go-solution-by-sabakunoarashi-llt8
|
go\nimport "sort"\n\nfunc max(a, b int) int {\n if a > b {\n return a\n } else {\n return b\n }\n}\n\nfunc min(a, b int) int {\n if a
|
sabakunoarashi
|
NORMAL
|
2019-12-19T15:22:56.964442+00:00
|
2019-12-19T15:22:56.964489+00:00
| 118
| false
|
```go\nimport "sort"\n\nfunc max(a, b int) int {\n if a > b {\n return a\n } else {\n return b\n }\n}\n\nfunc min(a, b int) int {\n if a > b {\n return b\n } else {\n return a\n }\n}\n\nfunc numMovesStonesII(stones []int) []int {\n sort.Ints(stones)\n i, n := 0, len(stones)\n max_step := max(stones[n-1] - stones[1] - n + 2, stones[n-2] - stones[0] - n + 2)\n \n min_step := len(stones)\n for j := 0; j < n; j++ {\n for stones[j] - stones[i] >= n {\n i++\n }\n if j - i + 1 == n - 1 && stones[j] - stones[i] == n - 2 {\n min_step = min(min_step, 2)\n } else {\n min_step = min(min_step, n - (j - i + 1))\n }\n }\n \n return []int{min_step, max_step}\n}\n```
| 0
| 0
|
[]
| 0
|
moving-stones-until-consecutive-ii
|
C++ solution 10~20ms
|
c-solution-1020ms-by-danyanglee-98fk
|
\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& A) {\n int mx = 0, sz = A.size(), i = A[0], l = 0, r = 0;\n vector<int>
|
danyanglee
|
NORMAL
|
2019-11-03T08:48:31.095882+00:00
|
2019-11-03T08:56:25.020513+00:00
| 318
| false
|
```\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& A) {\n int mx = 0, sz = A.size(), i = A[0], l = 0, r = 0;\n vector<int> res;\n ios::sync_with_stdio(false);\n \n sort(A.begin(), A.end());\n \n while(r < sz && A[r] <= A[0]+sz-1) r++;\n i = A[0]+sz - 1;//right point of window\n \n //The count of points outside of the window must be larger than the count of right and left unocuppied point of the window\n if(l + sz - r == 0 || l + sz - r > ((i+1-sz!=A[l])+(i!=A[r-1])))\n mx = max(mx, r - l); \n \n while(r < sz && i <= A[sz - 1]){\n //move window\n i = min(A[l+1] + sz - 1, A[r]);\n if(i >= A[r]){\n r++;\n }\n if(i+1-sz > A[l])\n l++;\n \n //update max\n if(l + sz - r == 0 || l + sz - r > ((i-sz+1!=A[l])+(i!=A[r-1])))\n mx = max(mx, r - l);\n }\n res.push_back(sz - mx);\n res.push_back(A[sz - 1] - A[0] - sz + 1 - min(A[sz - 1] - A[sz - 2] - 1, A[1] - A[0] - 1));\n return res;\n }\n};\n```
| 0
| 0
|
[]
| 0
|
moving-stones-until-consecutive-ii
|
C++ sliding window solution
|
c-sliding-window-solution-by-eminem18753-q5lz
|
\nclass Solution \n{\n public:\n vector<int> numMovesStonesII(vector<int>& a) \n {\n int n=a.size();\n sort(a.begin(),a.end());\n
|
eminem18753
|
NORMAL
|
2019-10-08T02:56:48.881374+00:00
|
2019-10-08T02:56:48.881412+00:00
| 474
| false
|
```\nclass Solution \n{\n public:\n vector<int> numMovesStonesII(vector<int>& a) \n {\n int n=a.size();\n sort(a.begin(),a.end());\n int M=max(a[n-2]-a[0]-n+2,a[n-1]-a[1]-n+2);\n int m=2147483647;\n \n int p1=0;\n int p2=0;\n while(true)\n {\n int last=a[p1]+n-1;\n if(p1+1>=n&&p2+1>=n)\n {\n break;\n }\n else if(p2+1>=n)\n {\n if(a[p2]<=last)\n {\n int s=p2-p1+1;\n \n if(a[p2]==last-1&&s==n-1)\n {\n m=min(m,n-s+1);\n }\n else\n {\n m=min(m,n-s);\n }\n }\n p1++;\n }\n else if(a[p2]<=last)\n {\n int s=p2-p1+1;\n if(a[p2]==last-1&&s==n-1)\n {\n m=min(m,n-s+1);\n }\n else\n {\n m=min(m,n-s);\n }\n p2++;\n }\n else\n {\n p1++;\n }\n }\n \n return {m,M};\n }\n};\n```
| 0
| 0
|
[]
| 0
|
moving-stones-until-consecutive-ii
|
C++ O(NlogN) solution
|
c-onlogn-solution-by-jokerkeny-9z14
|
\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n sort(stones.begin(),stones.end());\n int n = stones.size();
|
jokerkeny
|
NORMAL
|
2019-05-05T04:10:14.097606+00:00
|
2019-05-05T04:21:47.846037+00:00
| 646
| false
|
```\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n sort(stones.begin(),stones.end());\n int n = stones.size();\n int minmove = n;\n \n auto i = stones.begin();\n auto j = upper_bound(stones.begin(), stones.end(), stones[0]+n-1);\n minmove = min (minmove, n - (int)(j - i));\n j = stones.end();\n i = lower_bound(stones.begin(), stones.end(), stones[n-1]-n+1);\n minmove = min (minmove, n - (int)(j - i));\n if (minmove == 1) {\n if(stones.back()-stones.front() > n && (stones[n-1]- stones[1] == n -2 || stones[n-2]-stones[0] == n-2)) minmove++;\n }\n \n //both side have outlier\n for (int s = 1, t = 1; t < n; t++) {\n if (stones[t] - stones[s] + 1 > n) {\n minmove = min (minmove, n - (t - s) );\n while (stones[t] - stones[s] + 1 > n)\n s++;\n }\n }\n int maxmove=stones[n-1] - stones[0] + 1 - n;\n if(stones[1]-stones[0]>1 && stones[n-1]-stones[n-2]>1) {\n maxmove -= min(stones[1]-stones[0] - 1, stones[n-1]-stones[n-2] -1);\n }\n return vector{minmove,maxmove};\n }\n};\n```\n
| 0
| 0
|
['C']
| 1
|
moving-stones-until-consecutive-ii
|
C++ O(N log(N))
|
c-on-logn-by-murkyautomata-q6ez
|
\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n int N= stones.size(), max_in_N=0, min_steps, max_steps, first_gap;
|
murkyautomata
|
NORMAL
|
2019-05-05T04:06:59.083496+00:00
|
2019-05-05T04:07:33.463681+00:00
| 351
| false
|
```\nclass Solution {\npublic:\n vector<int> numMovesStonesII(vector<int>& stones) {\n int N= stones.size(), max_in_N=0, min_steps, max_steps, first_gap;\n \n if(N<3) return {0,0};\n \n sort(stones.begin(), stones.end());\n \n for(int i=0, j=0; i<N; ++i){\n while( j < N && stones[i] + N > stones[j]) ++j;\n max_in_N= max(max_in_N, j-i);\n }\n \n min_steps= N - max_in_N ;\n \n if(max_in_N==N-1 && N>3 && max(stones[1]-stones[0], stones[N-1]-stones[N-2]) > 2) min_steps= 2;\n \n \n first_gap= min(stones[1]-stones[0], stones[N-1]-stones[N-2]);\n max_steps= (stones[N-1] - stones[0] + 1) - N - (first_gap - 1);\n \n return {min_steps, max_steps};\n }\n};\n```
| 0
| 0
|
[]
| 0
|
network-delay-time
|
Java, Djikstra/bfs, Concise and very easy to understand
|
java-djikstrabfs-concise-and-very-easy-t-1qt4
|
I think bfs and djikstra are very similar problems. It\'s just that djikstra cost is different compared with bfs, so use priorityQueue instead a Queue for a sta
|
alizhiyu46
|
NORMAL
|
2018-12-28T21:39:46.215798+00:00
|
2019-06-16T22:41:05.329730+00:00
| 55,694
| false
|
I think bfs and djikstra are very similar problems. It\'s just that djikstra cost is different compared with bfs, so use priorityQueue instead a Queue for a standard bfs search.\n```\nclass Solution {\n public int networkDelayTime(int[][] times, int N, int K) {\n Map<Integer, Map<Integer,Integer>> map = new HashMap<>();\n for(int[] time : times){\n map.putIfAbsent(time[0], new HashMap<>());\n map.get(time[0]).put(time[1], time[2]);\n }\n \n //distance, node into pq\n Queue<int[]> pq = new PriorityQueue<>((a,b) -> (a[0] - b[0]));\n \n pq.add(new int[]{0, K});\n \n boolean[] visited = new boolean[N+1];\n int res = 0;\n \n while(!pq.isEmpty()){\n int[] cur = pq.remove();\n int curNode = cur[1];\n int curDist = cur[0];\n if(visited[curNode]) continue;\n visited[curNode] = true;\n res = curDist;\n N--;\n if(map.containsKey(curNode)){\n for(int next : map.get(curNode).keySet()){\n pq.add(new int[]{curDist + map.get(curNode).get(next), next});\n }\n }\n }\n return N == 0 ? res : -1;\n \n }\n}\n```
| 292
| 9
|
[]
| 36
|
network-delay-time
|
[C++] Bellman Ford
|
c-bellman-ford-by-alexander-7buu
|
C++\n\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int N, int K) {\n vector<int> dist(N + 1, INT_MAX);\n dist[
|
alexander
|
NORMAL
|
2017-12-10T04:01:53.214000+00:00
|
2018-10-21T03:47:07.559308+00:00
| 33,922
| false
|
**C++**\n```\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int N, int K) {\n vector<int> dist(N + 1, INT_MAX);\n dist[K] = 0;\n for (int i = 0; i < N; i++) {\n for (vector<int> e : times) {\n int u = e[0], v = e[1], w = e[2];\n if (dist[u] != INT_MAX && dist[v] > dist[u] + w) {\n dist[v] = dist[u] + w;\n }\n }\n }\n\n int maxwait = 0;\n for (int i = 1; i <= N; i++)\n maxwait = max(maxwait, dist[i]);\n return maxwait == INT_MAX ? -1 : maxwait;\n }\n};\n```
| 233
| 10
|
[]
| 37
|
network-delay-time
|
Python concise queue & heap solutions
|
python-concise-queue-heap-solutions-by-c-dtvk
|
Heap\n\nclass Solution:\n def networkDelayTime(self, times, N, K):\n q, t, adj = [(0, K)], {}, collections.defaultdict(list)\n for u, v, w in t
|
cenkay
|
NORMAL
|
2018-10-30T14:07:26.087090+00:00
|
2018-10-30T14:07:26.087153+00:00
| 20,656
| false
|
* Heap\n```\nclass Solution:\n def networkDelayTime(self, times, N, K):\n q, t, adj = [(0, K)], {}, collections.defaultdict(list)\n for u, v, w in times:\n adj[u].append((v, w))\n while q:\n time, node = heapq.heappop(q)\n if node not in t:\n t[node] = time\n for v, w in adj[node]:\n heapq.heappush(q, (time + w, v))\n return max(t.values()) if len(t) == N else -1\n```\n* Queue\n```\nclass Solution:\n def networkDelayTime(self, times, N, K):\n t, graph, q = [0] + [float("inf")] * N, collections.defaultdict(list), collections.deque([(0, K)])\n for u, v, w in times:\n graph[u].append((v, w))\n while q:\n time, node = q.popleft()\n if time < t[node]:\n t[node] = time\n for v, w in graph[node]:\n q.append((time + w, v))\n mx = max(t)\n return mx if mx < float("inf") else -1\n```
| 158
| 2
|
['Queue', 'Heap (Priority Queue)', 'Python']
| 20
|
network-delay-time
|
[c++] Easy to understand Dijkstra's algorithm
|
c-easy-to-understand-dijkstras-algorithm-dg76
|
\ntypedef pair<int, int> pii;\n\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n vector<vector<pii> > g
|
flyingmouse
|
NORMAL
|
2018-09-25T19:48:14.623051+00:00
|
2022-04-20T09:51:28.593678+00:00
| 39,305
| false
|
```\ntypedef pair<int, int> pii;\n\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n vector<vector<pii> > g(n + 1);\n for (const auto& t : times) {\n g[t[0]].emplace_back(t[1], t[2]);\n }\n const int inf = 1e9;\n vector<int> dist(n + 1, inf);\n\t\tvector<bool> vis(n + 1, false);\n dist[k] = 0;\n priority_queue<pii, vector<pii>, greater<pii> > pq;\n pq.emplace(0, k);\n int u, v, w;\n while (!pq.empty()) {\n u = pq.top().second; pq.pop();\n\t\t\tif (vis[u]) continue;\n\t\t\tvis[u] = true;\n for (auto& to : g[u]) {\n v = to.first, w = to.second;\n if (dist[v] > dist[u] + w) {\n dist[v] = dist[u] + w;\n pq.emplace(dist[v], v);\n }\n }\n }\n int ans = *max_element(dist.begin() + 1, dist.end());\n return ans == inf ? -1 : ans;\n }\n};\n```
| 144
| 7
|
[]
| 23
|
network-delay-time
|
Java solutions using Dijkstra, Floyd–Warshall and Bellman-Ford algorithm
|
java-solutions-using-dijkstra-floyd-wars-qrni
|
Floyd\u2013Warshall algorithm\nTime complexity: O(N^3), Space complexity: O(N^2)\n\npublic int networkDelayTime_FW(int[][] times, int N, int K) {\n double[][
|
lakemorning
|
NORMAL
|
2018-10-21T03:12:24.978940+00:00
|
2018-10-24T13:19:29.959742+00:00
| 16,528
| false
|
1. Floyd\u2013Warshall algorithm\nTime complexity: O(N^3), Space complexity: O(N^2)\n```\npublic int networkDelayTime_FW(int[][] times, int N, int K) {\n double[][] disTo = new double[N][N];\n for (int i = 0; i < N; i++) {\n Arrays.fill(disTo[i], Double.POSITIVE_INFINITY);\n }\n for (int i = 0; i < N; i++) {\n disTo[i][i] = 0;\n }\n for (int[] edge: times) {\n disTo[edge[0] - 1][edge[1] - 1] = edge[2];\n }\n for (int k = 0; k < N; k++) {\n for (int i = 0; i < N; i++) {\n for (int j = 0; j < N; j++) {\n if (disTo[i][j] > disTo[i][k] + disTo[k][j])\n disTo[i][j] = disTo[i][k] + disTo[k][j];\n }\n }\n }\n double max = Double.MIN_VALUE;\n for (int i = 0; i < N; i++) {\n if (disTo[K - 1][i] == Double.POSITIVE_INFINITY) return -1;\n max = Math.max(max, disTo[K - 1][i]);\n }\n return (int) max;\n}\n```\n\n2. Bellman-Ford algorithm\nTime complexity: O(N*E), Space complexity: O(N)\n```\npublic int networkDelayTime_BF(int[][] times, int N, int K) {\n double[] disTo = new double[N];\n Arrays.fill(disTo, Double.POSITIVE_INFINITY);\n disTo[K - 1] = 0;\n for (int i = 1; i < N; i++) {\n for (int[] edge : times) {\n int u = edge[0] - 1, v = edge[1] - 1, w = edge[2];\n disTo[v] = Math.min(disTo[v], disTo[u] + w);\n }\n }\n double res = Double.MIN_VALUE;\n for (double i: disTo) {\n res = Math.max(i, res);\n }\n return res == Double.POSITIVE_INFINITY ? -1 : (int) res;\n}\n```\n\n3. Dijkstra\'s algorithm\nTime complexity: O(Nlog(N) + E), Space complexity: O(N + E)\n```\npublic int networkDelayTime_Dijkstra(int[][] times, int N, int K) {\n Map<Integer, List<int[]>> graph = new HashMap<>();\n for (int[] edge: times) {\n graph.putIfAbsent(edge[0], new ArrayList<>());\n graph.get(edge[0]).add(new int[]{edge[1], edge[2]});\n }\n PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> (a[0] - b[0]));\n boolean[] visited = new boolean[N + 1];\n int[] minDis = new int[N + 1];\n Arrays.fill(minDis, Integer.MAX_VALUE);\n minDis[K] = 0;\n pq.offer(new int[]{0, K});\n int max = 0;\n while (!pq.isEmpty()) {\n int[] curr = pq.poll();\n int currNode = curr[1];\n if (visited[currNode]) continue;\n visited[currNode] = true;\n int currDis = curr[0];\n max = currDis;\n N--;\n if (!graph.containsKey(currNode)) continue;\n for (int[] next : graph.get(currNode)) {\n if (!visited[next[0]] && currDis + next[1] < minDis[next[0]])\n pq.offer(new int[]{currDis + next[1], next[0]});\n }\n }\n return N == 0 ? max : -1;\n}\n```\n
| 133
| 1
|
[]
| 19
|
network-delay-time
|
Python Bellman-Ford, SPFA, Dijkstra, Floyd, clean and easy to understand
|
python-bellman-ford-spfa-dijkstra-floyd-3hnmg
|
Since the input is edges, it naturally occured to me to use Bellman-Ford. Of course we can process the edges and use SPFA (Shortest Path Faster Algorithm) and D
|
sfdye
|
NORMAL
|
2019-04-29T12:53:42.168292+00:00
|
2019-04-29T12:53:42.168338+00:00
| 10,395
| false
|
Since the input is edges, it naturally occured to me to use Bellman-Ford. Of course we can process the edges and use [SPFA](https://en.wikipedia.org/wiki/Shortest_Path_Faster_Algorithm) (Shortest Path Faster Algorithm) and Dijkstra.\n\n**Bellman-Ford**\nTime: `O(VE)`\nSpace: `O(N)`\n\n```python\nclass Solution:\n def networkDelayTime(self, times: List[List[int]], N: int, K: int) -> int:\n dist = [float("inf") for _ in range(N)]\n dist[K-1] = 0\n for _ in range(N-1):\n for u, v, w in times:\n if dist[u-1] + w < dist[v-1]:\n dist[v-1] = dist[u-1] + w\n return max(dist) if max(dist) < float("inf") else -1\n```\n\n**SPFA**\nTime: average `O(E)`, worst `O(VE)`\nSpace: `O(V+E)`\n\n```python\nclass Solution:\n def networkDelayTime(self, times: List[List[int]], N: int, K: int) -> int:\n dist = [float("inf") for _ in range(N)]\n K -= 1\n dist[K] = 0\n weight = collections.defaultdict(dict)\n for u, v, w in times:\n weight[u-1][v-1] = w\n queue = collections.deque([K])\n while queue:\n u = queue.popleft()\n for v in weight[u]:\n if dist[u] + weight[u][v] < dist[v]:\n dist[v] = dist[u] + weight[u][v]\n queue.append(v)\n return max(dist) if max(dist) < float("inf") else -1\n```\n\n**Dijkstra**\nTime: `O(E+VlogV)`\nSpace: `O(V+E)`\n\n```python\nclass Solution:\n def networkDelayTime(self, times: List[List[int]], N: int, K: int) -> int:\n weight = collections.defaultdict(dict)\n for u, v, w in times:\n weight[u][v] = w\n heap = [(0, K)]\n dist = {}\n while heap:\n time, u = heapq.heappop(heap)\n if u not in dist:\n dist[u] = time\n for v in weight[u]:\n heapq.heappush(heap, (dist[u] + weight[u][v], v))\n return max(dist.values()) if len(dist) == N else -1\n```\n\n**Floyd-Warshall**\nTime: `O(V^3)`\nSpace: `O(V^2)`\n\n```python\nclass Solution:\n def networkDelayTime(self, times: List[List[int]], N: int, K: int) -> int:\n dist = [[float("inf") for _ in range(N)] for _ in range(N)]\n for u, v, w in times:\n dist[u-1][v-1] = w\n for i in range(N):\n dist[i][i] = 0\n for k in range(N):\n for i in range(N):\n for j in range(N):\n dist[i][j] = min(dist[i][j], dist[i][k]+dist[k][j])\n return max(dist[K-1]) if max(dist[K-1]) < float("inf") else -1\n```
| 121
| 0
|
[]
| 12
|
network-delay-time
|
[Python] - DFS, BFS, Dijkstra, Bellman Ford, SPFA, Floyd Warshall
|
python-dfs-bfs-dijkstra-bellman-ford-spf-jw6b
|
\nimport heapq\nfrom collections import deque\nfrom collections import defaultdict\n\n# """\n# Uses simple DFS - Accepted\nclass Solution(object):\n def net
|
parthobiswas007
|
NORMAL
|
2020-01-05T09:00:23.670647+00:00
|
2021-11-28T17:34:39.476394+00:00
| 10,204
| false
|
```\nimport heapq\nfrom collections import deque\nfrom collections import defaultdict\n\n# """\n# Uses simple DFS - Accepted\nclass Solution(object):\n def networkDelayTime(self, times, N, K):\n graph = defaultdict(list)\n for u, v, w in times:\n graph[u].append((v, w))\n distance = {node: float("inf") for node in range(1, N + 1)}\n self.DFS(graph, distance, K, 0)\n totalTime = max(distance.values())\n return totalTime if totalTime < float("inf") else -1\n\n def DFS(self, graph, distance, node, elapsedTimeSoFar):\n if elapsedTimeSoFar >= distance[node]: # signal aalreaady reached to this node. so no need to explore for this node\n return\n distance[node] = elapsedTimeSoFar\n for neighbour, time in sorted(graph[node]):\n self.DFS(graph, distance, neighbour, elapsedTimeSoFar + time)\n# """\n\n\n# """\n# Uses simple BFS - Accepted\nclass Solution:\n def networkDelayTime(self, times, N, K):\n elapsedTime, graph, queue = [0] + [float("inf")] * N, defaultdict(list), deque([(0, K)])\n for u, v, w in times:\n graph[u].append((v, w))\n while queue:\n time, node = queue.popleft()\n if time < elapsedTime[node]:\n elapsedTime[node] = time\n for v, w in graph[node]:\n queue.append((time + w, v))\n mx = max(elapsedTime)\n return mx if mx < float("inf") else -1\n# """\n\n\n\n# """\n# Dijkstra algorithm - Accepted\nclass Solution:\n def networkDelayTime(self, times, N, K):\n elapsedTime, graph, heap = [0] + [float("inf")] * N, defaultdict(list), [(0, K)] # it\'s a min-heap\n for u, v, w in times:\n graph[u].append((v, w))\n while heap:\n time, node = heapq.heappop()\n if time < elapsedTime[node]:\n elapsedTime[node] = time\n for v, w in graph[node]:\n heapq.heappush(heap, (time + w, v))\n mx = max(elapsedTime)\n return mx if mx < float("inf") else -1\n# """\n\n\n\n# """\n# Original Bellman\u2013Ford algorithm - Accepted\nclass Solution:\n def networkDelayTime(self, times, N, K):\n distance = [float("inf") for _ in range(N)]\n distance[K-1] = 0\n for _ in range(N-1):\n for u, v, w in times:\n if distance[u-1] + w < distance[v-1]:\n distance[v-1] = distance[u-1] + w\n return max(distance) if max(distance) < float("inf") else -1\n# """\n\n\n\n# """\n# Shortest Path Faster Algorithm (SPFA): An improvement of the Bellman\u2013Ford algorithm - Accepted\nclass Solution:\n def networkDelayTime(self, times, N, K):\n elapsedTime, graph, queue = [0] + [float("inf")] * N, defaultdict(list), deque([(0, K)])\n elapsedTime[K] = 0\n for u, v, w in times:\n graph[u].append((v, w))\n while queue:\n time, node = queue.popleft()\n for neighbour in graph[node]:\n v, w = neighbour\n if time + w < elapsedTime[v]:\n elapsedTime[v] = time + w\n queue.append((time + w, v))\n mx = max(elapsedTime)\n return mx if mx < float("inf") else -1\n# """\n\n\n\n\n\n# """\n# Floyd Warshall - Accepted\nclass Solution:\n def networkDelayTime(self, times, N, K):\n elapsedTimeMatrix = [[float("inf") for _ in range(N)] for _ in range(N)]\n for u, v, w in times:\n elapsedTimeMatrix[u - 1][v - 1] = w\n for i in range(N): # Assigning 0 to the diagonal cells\n elapsedTimeMatrix[i][i] = 0\n for k in range(N):\n for i in range(N):\n for j in range(N):\n elapsedTimeMatrix[i][j] = min(elapsedTimeMatrix[i][j], elapsedTimeMatrix[i][k] + elapsedTimeMatrix[k][j])\n mx = max(elapsedTimeMatrix[K - 1])\n return mx if mx < float("inf") else -1\n# """\n\n```
| 87
| 2
|
['Depth-First Search', 'Breadth-First Search', 'Python']
| 9
|
network-delay-time
|
Python Simple Dijkstra Beats ~90%
|
python-simple-dijkstra-beats-90-by-const-p64k
|
Time - O(N + ELogN) -Standard Time complexity of Dijkstra\'s algorithm\n\nSpace - O(N + E) - for adjacency list and maintaining Heap.\n\n\nclass Solution:\n
|
constantine786
|
NORMAL
|
2022-05-14T03:13:19.541575+00:00
|
2022-05-14T03:29:46.795649+00:00
| 8,776
| false
|
**Time - O(N + ELogN)** -Standard Time complexity of [Dijkstra\'s algorithm](https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm#Running_time)\n\n**Space - O(N + E)** - for adjacency list and maintaining Heap.\n\n```\nclass Solution:\n def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int: \n adj_list = defaultdict(list)\n \n for x,y,w in times:\n adj_list[x].append((w, y))\n \n visited=set()\n heap = [(0, k)]\n while heap:\n travel_time, node = heapq.heappop(heap)\n visited.add(node)\n \n if len(visited)==n:\n return travel_time\n \n for time, adjacent_node in adj_list[node]:\n if adjacent_node not in visited:\n heapq.heappush(heap, (travel_time+time, adjacent_node))\n \n return -1\n```\n\n--- \n\n***Please upvote if you find it useful***
| 66
| 0
|
['Python', 'Python3']
| 4
|
network-delay-time
|
[C++] Djikstra's Algorithm (Very Easy To Understand) (Beats 85%)
|
c-djikstras-algorithm-very-easy-to-under-yj08
|
\n // Using Priority queue (Min-heap)\n int networkDelayTime(vector<vector<int>>& times, int N, int K) {\n vector<pair<int,int>> g[N+1];\n f
|
not_a_cp_coder
|
NORMAL
|
2020-07-17T21:23:22.026165+00:00
|
2020-07-17T21:23:22.026206+00:00
| 10,908
| false
|
```\n // Using Priority queue (Min-heap)\n int networkDelayTime(vector<vector<int>>& times, int N, int K) {\n vector<pair<int,int>> g[N+1];\n for(int i=0;i<times.size();i++)\n g[times[i][0]].push_back(make_pair(times[i][1],times[i][2]));\n vector<int> dist(N+1, 1e9);\n dist[K] = 0;\n priority_queue<pair<int,int>, vector<pair<int,int>> , greater<pair<int,int>>> q;\n q.push(make_pair(0,K));\n pair<int,int> temp;\n bool visit[N+1];\n memset(visit, false, sizeof(visit));\n while(!q.empty()){\n temp = q.top();\n q.pop();\n int u = temp.second;\n visit[u] = true;\n for(int i=0;i<g[u].size();i++){\n int v = g[u][i].first;\n int weight = g[u][i].second;\n if(visit[v]==false && dist[v] > dist[u] + weight){\n dist[v] = dist[u] + weight;\n q.push(make_pair(dist[v], v));\n }\n }\n }\n int ans = 0;\n for(int i=1;i<dist.size();i++){\n ans = max(ans, dist[i]);\n }\n if(ans==1e9) return -1;\n return ans;\n }\n```\nFeel free to ask any doubts in the **comment** section.\nIf you like this solution, do **UPVOTE**.\nHappy Coding :)
| 56
| 2
|
['C', 'Heap (Priority Queue)', 'C++']
| 6
|
network-delay-time
|
Dijkstra's Algorithm - Template - List of Problems
|
dijkstras-algorithm-template-list-of-pro-8xbv
|
Dijlstra\'s Algorithm\n\n743. Network Delay Time\n\n\n/*\nStep 1: Create a Map of start and end nodes with weight\n 1 -> {2,1},{3,2}\n 2 -> {4,4},
|
letsdoitthistime
|
NORMAL
|
2022-07-21T01:33:17.762402+00:00
|
2024-02-12T03:37:51.604706+00:00
| 8,309
| false
|
Dijlstra\'s Algorithm\n\n**743. Network Delay Time**\n\n```\n/*\nStep 1: Create a Map of start and end nodes with weight\n 1 -> {2,1},{3,2}\n 2 -> {4,4},{5,5}\n 3 -> {5,3}\n 4 ->\n 5 ->\n\nStep 2: create a result array where we will keep track the minimum distance to rech end of the node from start node\n\nStep 3: Create a Queue and add starting position with it\'s weight and add it\'s reachable distance with increament of own\'t weight plus a weight require to reach at the end node from start node.\n We keep adding and removing pairs from queue and updating result array as well.\n\nStep 4: find the maximum value from result array:\n\n*/\n\nclass Solution {\n public int networkDelayTime(int[][] times, int n, int k) {\n \n //Step 1\n Map<Integer, Map<Integer, Integer>> map = new HashMap<>();\n \n for(int[] time : times) {\n int start = time[0];\n int end = time[1];\n int weight = time[2];\n \n map.putIfAbsent(start, new HashMap<>());\n map.get(start).put(end, weight);\n }\n \n // Step 2\n int[] dis = new int[n+1];\n Arrays.fill(dis, Integer.MAX_VALUE);\n dis[k] = 0;\n \n Queue<int[]> queue = new LinkedList<>();\n queue.add(new int[]{k,0});\n \n //Step 3:\n while(!queue.isEmpty()) {\n int[] cur = queue.poll();\n int curNode = cur[0];\n int curWeight = cur[1];\n \n for(int next : map.getOrDefault(curNode, new HashMap<>()).keySet()) {\n int nextweight = map.get(curNode).get(next);\n \n if(curWeight + nextweight < dis[next]) {\n dis[next] = curWeight + nextweight;\n queue.add(new int[]{next, curWeight + nextweight});\n }\n }\n }\n \n //Step 4:\n int res = 0;\n for(int i=1; i<=n; i++) {\n if(dis[i] > res) {\n res = Math.max(res, dis[i]);\n } \n }\n \n return res == Integer.MAX_VALUE ? -1 : res;\n }\n}\n\n```\n\n**1514. Path with Maximum Probability**\n\n```\nclass Solution {\n public double maxProbability(int n, int[][] edges, double[] succProb, int start, int end) {\n Map<Integer, Map<Integer, Double>> map = new HashMap<>();\n \n for(int i=0; i<edges.length; i++){\n map.putIfAbsent(edges[i][0], new HashMap<>());\n map.putIfAbsent(edges[i][1], new HashMap<>());\n map.get(edges[i][0]).put(edges[i][1], succProb[i]);\n map.get(edges[i][1]).put(edges[i][0], succProb[i]);\n }\n \n Set<Integer> visited = new HashSet<>();\n \n PriorityQueue<double[]> queue = new PriorityQueue<double[]>((a, b) -> new Double(b[1]).compareTo(new Double(a[1])));\n queue.add(new double[]{start, 1.0});\n \n while(!queue.isEmpty()) {\n double[] cur = queue.poll();\n \n int curNode = (int)cur[0];\n double curWeight = cur[1];\n \n if(curNode == end) {\n return curWeight;\n }\n \n if(!visited.contains(curNode)) {\n visited.add(curNode);\n \n for(Map.Entry<Integer, Double> next: map.getOrDefault(curNode, new HashMap<>()).entrySet()) {\n int nKey = next.getKey();\n double nextWeight = next.getValue();\n \n queue.add(new double[]{nKey, curWeight * nextWeight});\n }\n }\n }\n return 0;\n }\n}\n```\n\n**787. Cheapest Flights Within K Stops**\n\n```\n/*\nIt\'s same as Dijkstra algorithm to calculate distance btween two nodes when we have weights. I use BFS approach. \n\nFor Example: 4\n (1) |\n | (4)\n 0--------1 In this Example if my src is 0 and destination is 3 and K = 2\n | | then the total cost of ticket is 4: (0->2->3)\n (2) | | (5)\n | |\n 2--------3\n (2)\n\nStep 1: Create an adjacency list from given Matrix\n 0-> [(4,1) -> (1,4) -> (2,2)]\n 1-> [(3,5)]\n 2-> [(3,2)]\n 3-> [(1,5)]\n 4-> []\n\nStep 2: Sort Every int[] arr ({nextDestination, totalCostToReachThatDestination, K-1}) based on cost.\n So Low cost will be at the starting of the PQ. It\'s min PQ\n\n\nStep 3: Get Node int[] from PQ and get it\'s sub next destination places and put back to the Queue to sort based on cost.Once u get destination return cost. \n*/\n\nclass Solution {\n public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {\n Map<Integer, List<int[]>> map = new HashMap<>();\n \n //Step 1:\n for(int[] flight : flights) {\n map.putIfAbsent(flight[0], new ArrayList<>());\n map.get(flight[0]).add(new int[]{flight[1], flight[2]});\n }\n \n Map<Integer, Integer> visited = new HashMap<>(); // This is extra step to avoid TLE\n \n // Step 2:\n PriorityQueue<int[]> queue = new PriorityQueue<>((a,b) -> (a[1]-b[1]));\n queue.add(new int[]{src, 0, k});\n \n \n // Step 3:\n while(!queue.isEmpty()) {\n int[] cur = queue.poll();\n \n int curNode = cur[0];\n int curPrice = cur[1];\n int remainingStop = cur[2];\n \n if(curNode == dst) {\n return curPrice;\n }\n \n visited.put(curNode, remainingStop); // To avoid TLE\n \n if(remainingStop >= 0 ) {\n for(int[] temp : map.getOrDefault(curNode, new ArrayList<>())) { \n if(!visited.containsKey(temp[0]) || remainingStop > visited.get(temp[0])) // This condition is to avoid TLE otherwise we add in PQ\n {\n queue.add(new int[]{temp[0], temp[1]+curPrice, remainingStop-1});\n }\n }\n }\n }\n return -1;\n }\n}\n```\n\n**1584. Min Cost to Connect All Points**\n\n```\n// This problem is to create MST from so we use Prim\'s Algorithm. Prims Algo is almost similar to Dijkstra\'s Algo\n\nclass Solution {\n public int minCostConnectPoints(int[][] points) {\n PriorityQueue<int[]> queue = new PriorityQueue<>((a,b) -> a[2] - b[2]);\n queue.add(new int[]{0,0,0});\n \n Set<Integer> visited = new HashSet();\n \n int cost = 0;\n int len = points.length;\n \n while(!queue.isEmpty() && visited.size()<len) {\n int[] pq = queue.poll();\n int curNode = pq[0];\n int endNode = pq[1];\n int curCost = pq[2];\n \n if(visited.contains(endNode)) {\n continue;\n }\n cost = cost + curCost;\n \n visited.add(endNode);\n \n for(int i=0; i<len; i++) {\n if(!visited.contains(i)) {\n queue.add(new int[]{endNode, i, distance(points, endNode, i)});\n }\n }\n }\n \n return cost;\n \n }\n \n private int distance(int[][] points, int i, int j) {\n return Math.abs(points[i][0]-points[j][0]) + Math.abs(points[i][1] - points[j][1]);\n }\n}\n```\n\n**778. Swim in Rising Water**\n\n```\nclass Solution {\n public int swimInWater(int[][] grid) {\n int result = 0;\n int m = grid.length;\n int n = grid[0].length;\n\n PriorityQueue<int[]> minHeap = new PriorityQueue<>((a,b) -> a[0] - b[0]);\n minHeap.add(new int[]{grid[0][0],0,0});\n\n boolean[][] visited = new boolean[m][n];\n visited[0][0] = true;\n\n int[][] dirs = {{0,-1}, {0,1}, {1,0}, {-1,0}};\n\n while(!minHeap.isEmpty()) {\n int[] temp = minHeap.poll();\n\n int curHeight = temp[0];\n int curRow = temp[1];\n int curCol = temp[2];\n\n if(curRow == m-1 && curCol == n-1) {\n return curHeight;\n }\n\n for(int[] dir : dirs) {\n int x = curRow + dir[0];\n int y = curCol + dir[1];\n\n if(x>=0 && x<m && y>=0 && y<n && visited[x][y] == false) {\n visited[x][y] = true;\n minHeap.add(new int[]{Math.max(curHeight, grid[x][y]), x, y});\n }\n }\n }\n\n return -1;\n }\n}\n\n```\n\n**1976. Number of Ways to Arrive at Destination**\n\n```\n/* \nThis Problem is same as Dijkstra\'s algortim. It\'s \njust modulo(10^9 + 7) in the given input is making it slightly complex. stick to the same logic for the Dijsktra\'s algo \nand you will easily come up with the solution in the interview. \n*/\n\nclass Solution {\n public int countPaths(int n, int[][] roads) {\n Map<Integer, Map<Integer, Long>> map = new HashMap<>();\n\n for(int i=0; i<roads.length; i++) {\n map.putIfAbsent(roads[i][0], new HashMap<>());\n map.putIfAbsent(roads[i][1], new HashMap<>());\n \n map.get(roads[i][0]).put(roads[i][1], (long)roads[i][2]);\n map.get(roads[i][1]).put(roads[i][0], (long)roads[i][2]);\n }\n\n int[] ways = new int[n];\n long[] distance = new long[n];\n Arrays.fill(distance, Long.MAX_VALUE/2);\n Arrays.fill(ways, 0);\n\n ways[0] = 1;\n distance[0] = 0;\n\n int mod = (int)(1e9+7);\n\n PriorityQueue<int[]> minHeap = new PriorityQueue<>((a,b) -> a[0] - b[0]);\n minHeap.add(new int[]{0,0,0});\n\n while(!minHeap.isEmpty()) {\n int[] temp = minHeap.poll();\n\n long curDist = temp[0];\n int curNode = temp[1];\n int endNode = temp[2];\n\n for(int next : map.getOrDefault(curNode, new HashMap<>()).keySet()) {\n long nextDist = map.get(curNode).get(next);\n\n if(curDist + nextDist < distance[next]) {\n distance[next] = curDist + nextDist;\n minHeap.add(new int[]{(int)(curDist + nextDist), next, endNode});\n ways[next] = ways[curNode];\n\n } else if(curDist + nextDist == distance[next]) {\n ways[next] = (ways[next] + ways[curNode]) % mod; \n }\n }\n }\n\n return ways[n-1] % mod;\n }\n}\n\n```\n\n**1334. Find the City With the Smallest Number of Neighbors at a Threshold Distance**\n\n```\nclass Solution {\n public int findTheCity(int n, int[][] edges, int distanceThreshold) {\n int result = -1;\n int minRechable = Integer.MAX_VALUE;\n\n Map<Integer, Map<Integer, Integer>> map = new HashMap<>();\n\n for(int i=0; i<edges.length; i++) {\n map.putIfAbsent(edges[i][0], new HashMap<>());\n map.putIfAbsent(edges[i][1], new HashMap<>());\n\n map.get(edges[i][0]).put(edges[i][1], edges[i][2]);\n map.get(edges[i][1]).put(edges[i][0], edges[i][2]);\n }\n\n PriorityQueue<int[]> minHeap = new PriorityQueue<>((a,b) -> a[0] - b[0]);\n\n for(int i=0; i<n; i++) {\n int[] distance = new int[n];\n minHeap.add(new int[]{0,i});\n\n Arrays.fill(distance, Integer.MAX_VALUE/2);\n distance[i] = 0;\n \n while(!minHeap.isEmpty()) {\n int[] temp = minHeap.poll();\n \n int curDist = temp[0];\n int curNode = temp[1];\n\n for(int next : map.getOrDefault(curNode, new HashMap<>()).keySet()) {\n int nextDist = map.get(curNode).get(next);\n\n if(curDist + nextDist < distance[next]) {\n distance[next] = curDist + nextDist;\n minHeap.add(new int[]{curDist + nextDist, next});\n } \n }\n }\n int rechable = 0;\n\n for(int k=0; k<distance.length; k++) {\n if(distance[k] <= distanceThreshold) {\n distance[k] = distanceThreshold;\n rechable++;\n }\n }\n\n if(minRechable >= rechable) {\n minRechable = rechable;\n result = i;\n }\n }\n\n return result;\n }\n}\n```
| 55
| 0
|
['Java']
| 7
|
network-delay-time
|
[C++] 3 Solutions ( BFS, Dijkstra, Bellman-Ford )
|
c-3-solutions-bfs-dijkstra-bellman-ford-uzo63
|
BFS \nTC = 108ms\n\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n vector<pair<int,int>> adj[n+1];\n
|
sheldonbang
|
NORMAL
|
2021-05-19T15:44:22.077697+00:00
|
2021-08-19T03:35:21.553539+00:00
| 4,969
| false
|
**BFS** \n*TC = 108ms*\n```\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n vector<pair<int,int>> adj[n+1];\n for(int i=0;i<times.size();i++)\n adj[times[i][0]].push_back({times[i][1],times[i][2]});\n vector<int> dist(n+1,INT_MAX);\n queue<int> q;\n q.push(k);\n dist[k]=0;\n while(!q.empty())\n {\n int t=q.front();\n q.pop();\n for(pair<int,int> it:adj[t])\n {\n if(dist[it.first]>dist[t]+it.second)\n {\n dist[it.first]=dist[t]+it.second;\n q.push(it.first);\n }\n }\n }\n int res=0;\n for(int i=1;i<=n;i++)\n {\n if(dist[i]==INT_MAX)\n return -1;\n res=max(res,dist[i]);\n }\n return res;\n }\n};\n```\n\n**Dijkstra Algorithm**\n*TC = 112ms*\n```\nclass Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n vector<pair<int,int>> adj[n+1];\n for(int i=0;i<times.size();i++)\n adj[times[i][0]].push_back({times[i][1],times[i][2]});\n vector<int> dist(n+1,INT_MAX);\n priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> pq;\n pq.push({0,k});\n dist[k]=0;\n while(!pq.empty())\n {\n pair<int,int> t=pq.top();\n pq.pop();\n for(pair<int,int> it:adj[t.second])\n {\n if(dist[it.first]>t.first+it.second)\n {\n dist[it.first]=t.first+it.second;\n pq.push({dist[it.first],it.first});\n }\n }\n }\n int res=0;\n for(int i=1;i<=n;i++)\n {\n if(dist[i]==INT_MAX)\n return -1;\n res=max(res,dist[i]);\n }\n\t\treturn res;\n\t}\n};\n ```\n \n **Bellman-Ford Algorithm**\n *TC = 208ms*\n ```\n class Solution {\npublic:\n int networkDelayTime(vector<vector<int>>& times, int n, int k) {\n vector<int> dist(n+1,INT_MAX);\n dist[k]=0;\n \n for(int i=0;i<n-1;i++)\n {\n bool flag=false;\n for(auto node:times)\n {\n int src=node[0];\n int des=node[1];\n int time=node[2];\n if(dist[src]!=INT_MAX&&dist[des]>dist[src]+time)\n {\n dist[des]=dist[src]+time;\n flag=true;\n }\n }\n if(flag==false)\n break;\n }\n int res=0;\n for(int i=1;i<=n;i++)\n {\n if(dist[i]==INT_MAX)\n return -1;\n res=max(res,dist[i]);\n }\n return res;\n }\n};\n```\n\n*Do upvote if you find it useful!!!*\n
| 41
| 0
|
['Breadth-First Search', 'C', 'C++']
| 3
|
network-delay-time
|
Efficient O(E log V) Python Dijkstra min heap with explanation
|
efficient-oe-log-v-python-dijkstra-min-h-h2ih
|
Good video to visualize what\'s happening in Dijkstra with minimal fuss https://www.youtube.com/watch?v=pVfj6mxhdMw\n\nPython implementation details:\n\n1. Cons
|
mereck
|
NORMAL
|
2019-07-07T16:26:31.358865+00:00
|
2019-07-07T16:46:05.129240+00:00
| 19,294
| false
|
Good video to visualize what\'s happening in Dijkstra with minimal fuss https://www.youtube.com/watch?v=pVfj6mxhdMw\n\nPython implementation details:\n\n1. Construct adjacency list representation of a directional graph using a defaultdict of dicts\n2. Track visited vertices in a set\n3. Track known distances from K to all other vertices in a dict. Initialize this with a 0 to K.\n4. Use a `min_dist` heapq to maintain minheap of (distance, vertex) tuples. Initialize with (0,K). \n\nMain algorithm:\n1. While the `min_dist` is not empty, pop vertices in the order of minimal `cur_dist` , skip visited\n2. Visit the current vertex and check if any of its unvisited neighbors\' known `distances` can be improved. This is the case if `this_dist` is less than `distances[neighbor]`. \n3. Update the known distances and add new shorter distances onto the `min_dist` min heap if above is true.\n3. If we have not visited all of the nodes in the graph, we need to return -1 per problem statement\n4. Our answer is the largest known distance to any node from K\n\nThere is no efficient find method in a min heap. Whenever a new shorter distance to a vertex becomes known, we push onto the `min_dist` heap. This will result in duplicate vertices being on the min queue. Use `visited` set to skip duplicates in constant time. \n\nThis approach is not very space efficient for dense graphs because we will have O(|E|) items on the `min_dist` queue. However, this will allow for log |E| = 2 log |V| lookups of the next minimum distance edge to process.\n\nTime complexity: O(|E| log |E| ) = O(|E| 2 log |V|) = O(|E| log |V|)\n\n\n```\n def networkDelayTime(self, times: List[List[int]], N: int, K: int) -> int:\n \n graph = collections.defaultdict(dict)\n \n for frm, to, cost in times:\n graph[frm][to] = cost\n \n distances = { i: float("inf") for i in range(1, N+1)}\n distances[K] = 0\n min_dist = [(0,K)]\n visited = set()\n\n while min_dist:\n \n cur_dist, cur = heapq.heappop(min_dist)\n if cur in visited: continue\n visited.add(cur) \n \n for neighbor in graph[cur]:\n if neighbor in visited: continue\n this_dist = cur_dist + graph[cur][neighbor]\n if this_dist < distances[neighbor]:\n distances[neighbor] = this_dist\n heapq.heappush(min_dist, (this_dist, neighbor))\n \n if len(visited) != len(distances): return -1\n return distances[max(distances,key=distances.get)]\n```
| 37
| 0
|
[]
| 5
|
network-delay-time
|
Simple JAVA Djikstra's (PriorityQueue optimized) Solution with explanation
|
simple-java-djikstras-priorityqueue-opti-wxhp
|
It is a direct graph. \n1. Use Map> to store the source node, target node and the distance between them.\n2. Offer the node K to a PriorityQueue.\n3. Then keep
|
samuel_ji
|
NORMAL
|
2017-12-16T00:04:42.431000+00:00
|
2018-10-24T04:33:31.185932+00:00
| 18,076
| false
|
It is a direct graph. \n1. Use Map<Integer, Map<Integer, Integer>> to store the source node, target node and the distance between them.\n2. Offer the node K to a PriorityQueue.\n3. Then keep getting the closest nodes to the current node and calculate the distance from the source (K) to this node (absolute distance). Use a Map to store the shortest absolute distance of each node.\n4. Return the node with the largest absolute distance.\n\n```\npublic int networkDelayTime(int[][] times, int N, int K) {\n if(times == null || times.length == 0){\n return -1;\n }\n // store the source node as key. The value is another map of the neighbor nodes and distance.\n Map<Integer, Map<Integer, Integer>> path = new HashMap<>();\n for(int[] time : times){\n Map<Integer, Integer> sourceMap = path.get(time[0]);\n if(sourceMap == null){\n sourceMap = new HashMap<>();\n path.put(time[0], sourceMap);\n }\n Integer dis = sourceMap.get(time[1]);\n if(dis == null || dis > time[2]){\n sourceMap.put(time[1], time[2]);\n }\n \n }\n\n //Use PriorityQueue to get the node with shortest absolute distance \n //and calculate the absolute distance of its neighbor nodes.\n Map<Integer, Integer> distanceMap = new HashMap<>();\n distanceMap.put(K, 0);\n PriorityQueue<int[]> pq = new PriorityQueue<>((i1, i2) -> {return i1[1] - i2[1];});\n pq.offer(new int[]{K, 0});\n int max = -1;\n while(!pq.isEmpty()){\n int[] cur = pq.poll();\n int node = cur[0];\n int distance = cur[1];\n\n // Ignore processed nodes\n if(distanceMap.containsKey(node) && distanceMap.get(node) < distance){\n continue;\n }\n \n Map<Integer, Integer> sourceMap = path.get(node);\n if(sourceMap == null){\n continue;\n }\n for(Map.Entry<Integer, Integer> entry : sourceMap.entrySet()){\n int absoluteDistence = distance + entry.getValue();\n int targetNode = entry.getKey();\n if(distanceMap.containsKey(targetNode) && distanceMap.get(targetNode) <= absoluteDistence){\n continue;\n }\n distanceMap.put(targetNode, absoluteDistence);\n pq.offer(new int[]{targetNode, absoluteDistence});\n }\n }\n // get the largest absolute distance.\n for(int val : distanceMap.values()){\n if(val > max){\n max = val;\n }\n }\n return distanceMap.size() == N ? max : -1;\n}\n```
| 36
| 4
|
[]
| 16
|
network-delay-time
|
Not sure why this is a medium
|
not-sure-why-this-is-a-medium-by-elmubar-tzsh
|
This seems like a problem that should be labeled hard. Dijkstra\'s isn\'t a super commonly known algorithm.
|
elmubark
|
NORMAL
|
2018-09-14T16:29:33.980764+00:00
|
2018-09-14T16:29:33.980810+00:00
| 6,069
| false
|
This seems like a problem that should be labeled hard. Dijkstra\'s isn\'t a super commonly known algorithm.
| 34
| 12
|
[]
| 15
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.