problem
stringlengths 18
4.46k
| answer
stringlengths 1
942
| pass_at_n
float64 0.08
0.92
|
|---|---|---|
In a trapezoid with bases 3 and 4, find the length of the segment parallel to the bases that divides the area of the trapezoid in the ratio $5:2$, counting from the shorter base. | \sqrt{14} | 0.75 |
Compute the number of sequences of integers \((a_{1}, \ldots, a_{200})\) such that the following conditions hold:
- \(0 \leq a_{1}<a_{2}<\cdots<a_{200} \leq 202\).
- There exists a positive integer \(N\) with the following property: for every index \(i \in \{1, \ldots, 200\}\) there exists an index \(j \in \{1, \ldots, 200\}\) such that \(a_{i}+a_{j}-N\) is divisible by 203. | 20503 | 0.625 |
The area of a quadrilateral is \( S \). Find the area of a parallelogram whose sides are equal and parallel to the diagonals of the quadrilateral. | 2S | 0.75 |
Buses. At the stop near Absent-Minded Scientist's house, buses of two routes stop: No. 152 and No. 251. Both go to the metro station. The interval between buses No. 152 is exactly 5 minutes, and the interval between buses No. 251 is exactly 7 minutes. The intervals are strictly observed, but these two routes are not coordinated with each other and their schedules do not depend on each other. At a completely random moment, the Absent-Minded Scientist arrives at the stop and boards the first bus that arrives to get to the metro. What is the probability that the Scientist will board bus No. 251? | \frac{5}{14} | 0.125 |
Among the numbers greater than 2013, find the smallest even number \( N \) for which the fraction \(\frac{15N-7}{22N-5}\) is reducible. | 2144 | 0.75 |
Given the sets:
$$
\begin{array}{l}
U=\{1,2, \cdots, 8\}, \\
A=\{1,2, \cdots, 5\}, \\
B=\{4,5, \cdots, 8\} .
\end{array}
$$
Find the number of subsets of $U$ that are not subsets of $A$ and also not subsets of $B$. | 196 | 0.625 |
A circle with its center on the line \( y = b \) intersects the parabola \( y = \frac{3}{4} x^{2} \) at least at three points; one of these points is the origin, and two of the remaining points lie on the line \( y = \frac{3}{4} x + b \). Find all values of \( b \) for which the described configuration is possible. | \frac{25}{12} | 0.5 |
Find the area of the figure defined on the coordinate plane by the inequality \( 2(2-x) \geq \left| y - x^2 \right| + \left| y + x^2 \right| \). | 15 | 0.125 |
The binomial expansion of $\left(\sqrt{x}+\frac{1}{2 \sqrt[4]{x}}\right)^{n}$ is arranged in descending powers of $x$. If the coefficients of the first three terms form an arithmetic sequence, then there are ___ terms in the expansion in which the exponent of $x$ is an integer. | 3 | 0.75 |
Gosha entered a natural number into the calculator. Then, he performed the following operation three times: first, he extracted the square root, and then took the integer part of the resulting number. As a result, he obtained the number 1. What is the largest number that Gosha could have initially entered?
Note: The integer part of a number is the largest integer that does not exceed the given number. | 255 | 0.875 |
Given that \(\cos \alpha + \cos \beta + \cos \gamma = \sqrt{\frac{1}{5}}\) and \(\sin \alpha + \sin \beta + \sin \gamma = \sqrt{\frac{4}{5}}\), find \(\cos (\alpha - \beta) + \cos (\beta - \gamma) + \cos (\gamma - \alpha)\). | -1 | 0.625 |
Given \( f(x)=\frac{a^{x}}{a^{x}+\sqrt{a}} \) (where \( a \) is a positive constant), find the value of \( f\left(\frac{1}{1001}\right)+f\left(\frac{2}{1001}\right)+\cdots+ f\left(\frac{1000}{1001}\right) \). | 500 | 0.375 |
Given the point \( P(x, y) \) satisfies
\[ y = \frac{2x + 2018}{x - 1} \quad (x > y, \; x, y \in \mathbf{Z}_+) , \]
find the number of such points \( P(x, y) \). | 6 | 0.625 |
Let's accept without proof that for every natural number $n$, there exists a polynomial $P_{n}$ such that the identity $\sin(nx) = P_{n}(\cos x) \cdot \sin x$ holds. Show that $P_{n}(1)=n$. | P_n(1) = n | 0.375 |
Calculate the limit of the function:
$$\lim _{x \rightarrow 1} \frac{\sqrt{x^{2}-x+1}-1}{\operatorname{tg} \pi x}$$ | \frac{1}{2\pi} | 0.875 |
Inside the square $ABCD$, a point $M$ is taken such that $\angle MAB = 60^{\circ}$ and $\angle MCD = 15^{\circ}$. Find $\angle MBC$. | 30^\circ | 0.625 |
Natural numbers from 1 to 1982 are arranged in some order. A computer examines pairs of adjacent numbers from left to right (the first and second, the second and third, etc. up to the last pair) and swaps the numbers in the examined pair if the larger number is on the left. Then it examines all pairs, moving from the last pair to the first, swapping numbers in the pairs by the same rule. After this examination, the operator received information that the number in the hundredth position did not move both times. Find this number. | 100 | 0.375 |
On the sides of triangle \(ABC\), points were marked: 10 on side \(AB\), 11 on side \(BC\), and 12 on side \(AC\). None of the vertices of the triangle were marked. How many triangles with vertices at the marked points exist? | 4951 | 0.875 |
Given \( a, b, c \) are all greater than 1, satisfying
$$
\left\{\begin{array}{l}
\lg a+\log_{b} c=3, \\
\lg b+\log_{a} c=4 .
\end{array}\right.
$$
Find the maximum value of \( \lg a \cdot \lg c \). | \frac{16}{3} | 0.875 |
Evaluate: \( 3.416 \cos \frac{\pi}{33} \cdot \cos \frac{2 \pi}{33} \cdot \cos \frac{4 \pi}{33} \cdot \cos \frac{8 \pi}{33} \cdot \cos \frac{16 \pi}{33} \) and verify that it equals \( \frac{1}{32} \). | \frac{1}{32} | 0.75 |
Find \(\log _{n}\left(\frac{1}{2}\right) \log _{n-1}\left(\frac{1}{3}\right) \cdots \log _{2}\left(\frac{1}{n}\right)\) in terms of \(n\). | (-1)^{n-1} | 0.875 |
In triangle \( ABC \), the angle bisectors \( BP \) and \( CT \) intersect at point \( O \). It is known that points \( A, P, O \), and \( T \) lie on the same circle. Find angle \( A \). | 60^\circ | 0.875 |
Find the volume of a regular triangular prism if the side of its base is \(a\) and the lateral surface area is equal to the sum of the areas of the bases. | \frac{a^3}{8} | 0.375 |
A motorcyclist departed from point $A$ with an initial speed of 90 km/h, uniformly increasing the speed (i.e., the speed increases by the same amount over equal time intervals). After three hours, the motorcyclist arrived at point $B$, passing through $C$ along the way. Then, the motorcyclist turned around and, still uniformly increasing speed, set off back. Two hours later, he passed by point $C$ again at a speed of 110 km/h and continued on to $A$. Find the distance between points $A$ and $C$. | 76 \ \text{km} | 0.375 |
Calculate the degree of ionization using the formula:
$$
\alpha=\sqrt{ } K_{\mathrm{HCN}} \mathrm{C}
$$
Given values:
$$
\alpha_{\text {ion }}=\sqrt{ }\left(7,2 \cdot 10^{-10}\right) / 0,1=\sqrt{ } 7,2 \cdot 10^{-9}=8,5 \cdot 10^{-5}, \text{ or } 8,5 \cdot 10^{-5} \cdot 10^{2}=0,0085\%
$$
Alternatively, if the concentration of ions is known, you can calculate $\alpha$ as:
$$
\mathrm{C} \cdot \alpha=[\mathrm{H}^{+}]=[\mathrm{CN}^{-}], [\mathrm{H}^{+}]=[\mathrm{CN}^{-}]=8,5 \cdot 10^{-6} \text{ mol/L}
$$
Then:
$$
\alpha_{\text{ion }}=8,5 \cdot 10^{-6}, 0,1=8,5 \cdot 10^{-5} \text{ or } 8,5 \cdot 10^{-5} \cdot 10^{2}=0,0085\%
$$ | 0.0085\% | 0.375 |
Three students proposed different methods to tackle the problem: "For the inequality $x^{2}+25+\left|x^{3}-5 x^{2}\right| \geqslant a x$ to hold for all $x$ in the interval $[1,12]$, find the range of the real number $a$."
Each student suggested a different approach:
- Student A: "We only need the minimum value on the left-hand side of the inequality to be no smaller than the maximum value on the right-hand side."
- Student B: "Transform the inequality into a function involving variable $x$ on the left side and a constant on the right side, then find the extremum of the function."
- Student C: "Consider both sides of the inequality as functions of $x$ and plot their graphs."
Based on their proposed methods, determine the correct conclusion for the range of $a$. | (-\infty, 10] | 0.375 |
Find the sum $\sin x+\sin y+\sin z$, given that $\sin x=\operatorname{tg} y$, $\sin y=\operatorname{tg} z$, and $\sin z=\operatorname{tg} x$. | 0 | 0.375 |
Find all possible pairs of prime numbers \((p, q)\) such that the equation
\[ x^{4} + p x^{3} - q = 0 \]
has an integer root. | (2, 3) | 0.75 |
8. On an island of knights, who always tell the truth, and liars, who always lie, a school was opened. All $2N$ students of different heights lined up in pairs (forming two columns). The first two people said: "I am taller than two: my partner and the person behind me." The last two said: "I am also taller than two: my partner and the person in front of me." Finally, all the others said: "And I am taller than three: my partner, the person in front of me, and the person behind me."
a) What is the maximum number of knights in the school?
b) Can only liars study in the school? | \text{No} | 0.125 |
Calculate the limit of the numerical sequence:
\[
\lim_{{n \to \infty}} \frac{2n - \sin n}{\sqrt{n} - \sqrt[3]{n^3 - 7}}
\] | -2 | 0.875 |
Using the diagram below, a seven-digit integer can be created as follows: trace a path that uses each line segment exactly once and use the labels on the line segments as digits. For example, the path that goes from \( C \) to \( A \) to \( B \) to \( C \) to \( E \) to \( B \) to \( D \) and finally to \( E \) gives the positive integer 3264715. What is the largest possible positive integer that can be created in this way?
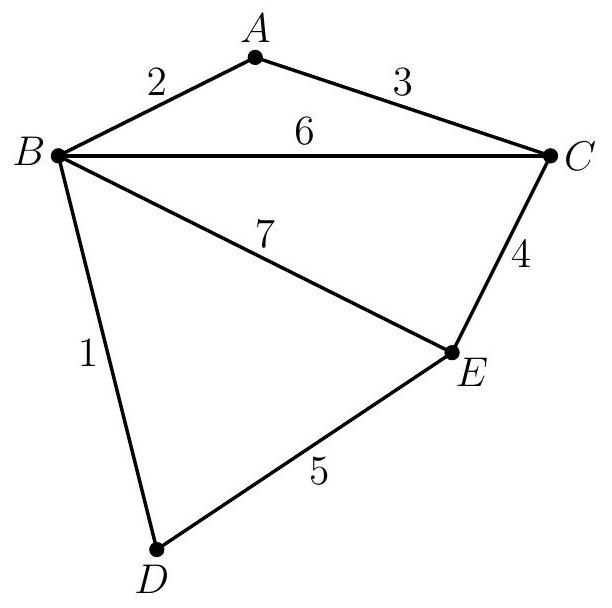 | 7645123 | 0.125 |
Calculate the area of the figures bounded by the lines given in polar coordinates.
$$
r=\sin 3 \phi
$$ | \frac{\pi}{4} | 0.625 |
Given the real numbers \( a \geq b \geq c \geq d \) with \( a + b + c + d = 9 \) and \( a^2 + b^2 + c^2 + d^2 = 21 \), find the minimum possible value of \( \text{ab} - \text{cd} \). | 2 | 0.375 |
If \( a \) and \( b \) are positive integers that can each be written as a sum of two squares, then \( ab \) is also a sum of two squares. Find the smallest positive integer \( c \) such that \( c = ab \), where \( a = x^3 + y^3 \) and \( b = x^3 + y^3 \) each have solutions in integers \( (x, y) \), but \( c = x^3 + y^3 \) does not. | 4 | 0.125 |
Let $n$ be a given natural number. Find all continuous functions $f(x)$ such that
$$
(0) f(x) + (1) f\left(x^{2}\right) + (2) f\left(x^{2^{2}}\right) + \cdots + (n-1) f\left(x^{2^{n-1}}\right) + (n) f\left(x^{2^{n}}\right) = 0.
$$ | f(x) = 0 | 0.875 |
Find all composite positive integers \( n \) such that all the divisors of \( n \) can be written in the form \( a^{r} + 1 \), where \( a \) and \( r \) are integers with \( a \geq 0 \) and \( r \geq 2 \). | 10 | 0.75 |
A group of cows and horses are randomly divided into two equal rows. Each animal in one row is directly opposite an animal in the other row. If 75 of the animals are horses and the number of cows opposite cows is 10 more than the number of horses opposite horses, determine the total number of animals in the group. | 170 | 0.75 |
On an island, there are only 50 knights, who always tell the truth, and 15 civilians, who can either tell the truth or lie. A forgetful professor, who came to the island to give a lecture, forgot what color hat he is wearing. What is the minimum number of local inhabitants that the professor needs to ask about the color of his hat in order to be certain about its color? | 31 | 0.875 |
In 1900, a reader asked the following question in 1930: He knew a person who died at an age that was $\frac{1}{29}$ of the year of his birth. How old was this person in 1900? | 44 | 0.25 |
Find the number of ordered integer pairs \((a, b)\) such that the equation \(x^{2} + a x + b = 167 y\) has integer solutions \((x, y)\), where \(1 \leq a, b \leq 2004\). | 2020032 | 0.75 |
Let \( n \) be a given positive integer. Determine the minimum of the polynomial \( f(x) = x^{2n} + 2x^{2n-1} + 3x^{2n-2} + \cdots + (2n+1-k)x^k + \cdots + 2n x + (2n+1) \) defined for real numbers. | n+1 | 0.875 |
For what smallest natural number \( a \) are there exactly 50 perfect squares in the numerical interval \( (a, 3a) \)? | 4486 | 0.125 |
An urn contains nine balls, numbered from 1 to 9. José and Maria each simultaneously draw one ball from the urn. They form a two-digit number with the number on José's ball as the tens digit and the number on Maria's ball as the units digit. What is the probability that this number is even? | \frac{4}{9} | 0.75 |
The sets \( A \) and \( B \) are bounded subsets of the real line. The set \( A \) is the union of \( n \) disjoint and open intervals, and the set \( B \) is the union of \( m \) disjoint and open intervals. What is the maximum number of disjoint intervals that the set \( A \cap B \) can consist of? | n + m - 1 | 0.5 |
In a tournament with 10 teams, each team faces each other exactly once. Additionally, there are no ties, and each team has a 50% chance of winning any match. What is the probability that, after counting the scores of the $\frac{10 \cdot 9}{2} = 45$ games, no two players have the same number of wins? | \frac{10!}{2^{45}} | 0.875 |
For an integer \( n \geq 0 \), let \( f(n) \) be the smallest possible value of \( |x+y| \), where \( x \) and \( y \) are integers such that \( 3x - 2y = n \). Evaluate \( f(0) + f(1) + f(2) + \cdots + f(2013) \). | 2416 | 0.75 |
A rectangular strip of length 16 was cut into two strips of lengths 9 and 7. These two strips were placed on a table as shown in the picture.
It is known that the area of the part of the table covered only by the left strip is 27, and the area of the part of the table covered only by the right strip is 18. Find the area of the part of the table covered by both strips. | 13.5 | 0.875 |
$ABCD$ is a square of side length 1. $P$ is a point on $AC$, and the circumcircle of $\triangle BPC$ intersects $CD$ at $Q$. If the area of $\triangle CPQ$ is $\frac{6}{25}$, find $CQ$. | \frac{3}{5} | 0.75 |
A cylinder of base radius 1 is cut into two equal parts along a plane passing through the center of the cylinder and tangent to the two base circles. Suppose that each piece's surface area is \( m \) times its volume. Find the greatest lower bound for all possible values of \( m \) as the height of the cylinder varies. | 3 | 0.125 |
One tea bag can brew either two or three cups of tea. Mila and Tanya equally divided a box of tea bags. Mila brewed 57 cups of tea, and Tanya brewed 83 cups. How many tea bags could have been in the box? | 56 | 0.875 |
The result of the expression \( 210 \times 6 - 52 \times 5 \) is \(\qquad\) | 1000 | 0.875 |
Let the random variables $\xi$ and $\eta$ denote the lifetimes of the blue and red light bulbs, respectively. The lifetime of the flashlight is equal to the minimum of these two values. Clearly, $\min (\xi, \eta) \leq \xi$. Let's move to the expected values: $\operatorname{E} \min (\xi, \eta) \leq \mathrm{E} \xi=2$. Therefore, the expected lifetime of the flashlight is no more than 2 years. | 2 | 0.875 |
Consider the sequence \(a_1, a_2, a_3, \cdots, a_n, \cdots \) which satisfies \(a_1 = a_2 = 1\), \(a_3 = 2\), and for any natural number \(n\), \(a_n \cdot a_{n+1} \cdot a_{n+2} \neq 1\). Additionally, it holds that \( a_n \cdot a_{n+1} \cdot a_{n+2} \cdot a_{n+3} = a_n + a_{n+1} + a_{n+2} + a_{n+3} \). What is the value of \(a_1 + a_2 + \cdots + a_{100}\)? | 200 | 0.25 |
Find the smallest natural number \( N \) that is divisible by \( p \), ends with \( p \), and has a digit sum equal to \( p \), given that \( p \) is a prime number and \( 2p+1 \) is a cube of a natural number. | 11713 | 0.75 |
Katya wrote a four-digit number on the board which was divisible by each of its digits without remainder (the number did not contain any zeros). Then she erased the first and last digits, leaving the number 89 on the board. What could have been the original number on the board? (Find all variants and show that there are no others.) | 4896 | 0.875 |
There are 4 bookstores that subscribed to a total of 400 "Mathematical and Physical World" magazines. Each bookstore subscribed to at least 98 and at most 101 magazines. How many different ways can they subscribe to these magazines? | 31 | 0.75 |
Find the largest four-digit number that is divisible by 7 and consists of four different digits. | 9870 | 0.375 |
Divide the set \( M = \{1, 2, \ldots, 12\} \) of the first 12 positive integers into four subsets each containing three elements, such that in each subset, one number is the sum of the other two. Find the number of different ways to do this. | 8 | 0.25 |
Divide 23 cards, each labeled with numbers 1 to 23, into three piles. It is known that the average numbers of the three piles are 13, 4, and 17, respectively. What is the minimum number of cards in the pile with an average number of 13? | 6 | 0.375 |
The clock shows $00:00$, with both the hour and minute hands coinciding. Considering this coincidence as number 0, determine after what time interval (in minutes) they will coincide for the 21st time. If the answer is not an integer, round the result to the nearest hundredth. | 1374.55 | 0.625 |
A firecracker was thrown vertically upward with a speed of \(20 \text{ m/s}\). One second after the flight began, it exploded into two fragments of equal mass. The first fragment flew horizontally immediately after the explosion with a speed of 48 m/s. Find the magnitude of the speed of the second fragment (in m/s) immediately after the explosion. The acceleration due to gravity is \(10 \text{ m/s}^2\). | 52 | 0.875 |
Find all functions \( f: \mathbf{R} \rightarrow \mathbf{R} \) such that for any real numbers \( x \) and \( y \), the following holds:
\[ f(f(x) + y) = 2x + f(f(y) - x). \] | f(x) = x + c | 0.75 |
A regular triangular prism \(ABC-A_1B_1C_1\) has a base edge length of \(a\) and a lateral edge length of \(\sqrt{2}a\). Find the angle between \(AC_1\) and the lateral face \(ABB_1A_1\). | 30^\circ | 0.875 |
In a fixed $3 \times 3$ grid, 4 identical chess pieces are to be placed into the cells. No more than one piece can be placed in any single cell. If each row and each column must contain at least one piece, how many different ways can this be done? | 45 | 0.25 |
There are three batches of parts, each containing 30 parts. The number of standard parts in the first, second, and third batches is 20, 15, and 10, respectively. A part is randomly selected from a randomly chosen batch and it turns out to be standard. Then, a second part is randomly selected from the same batch, and it also turns out to be standard. Find the probability that the parts were drawn from the third batch. | \frac{9}{68} | 0.625 |
Which number is greater: \(100^{100}\) or \(50^{50} \cdot 150^{50}\)? | 100^{100} | 0.5 |
Given that the positive integer \( m \) satisfies that \( m^{4} + 16m + 8 \) can be expressed as the product of two or more consecutive integers, determine the maximum value of \( m \). | 2 | 0.75 |
To enter Ali Baba's cave, it is necessary to reset 28 counters, each of which is set to a natural number from 1 to 2017. In one move, treasure seekers are allowed to decrease the values of some counters by the same number, which can be changed from move to move. Indicate the minimum number of moves in which the treasure seekers will definitely reset the counters (regardless of the initial values) and enter the cave. | 11 | 0.75 |
On the sides \( AB, BC \), and \( AC \) of triangle \( ABC \), points \( C_1, A_1 \) and \( B_1 \) are taken respectively, such that \( AC_1 : C_1B = BA_1 : A_1C = CB_1 : B_1A = 2 : 1 \).
Find the area of the triangle whose vertices are the pairwise intersections of segments \( AA_1, BB_1 \), and \( CC_1 \), given that the area of triangle \( ABC \) is 1. | \frac{1}{7} | 0.875 |
In the figure, \(ABCD\) is a square with a side length of \(1 \text{ cm}\). \(E\) is the midpoint of the diagonal \(BD\), and \(F\) is the midpoint of the segment \(BE\). What is the area of the triangle \(\triangle BCF\)? | 0.125 \text{ cm}^2 | 0.375 |
Find the minimum value of the expression $\cos (x+y)$, given that $\cos x + $\cos y = \frac{1}{3}$. | -\frac{17}{18} | 0.875 |
A real number \(x\) is chosen uniformly at random from the interval \([0, 1000]\). Find the probability that
\[
\left\lfloor\frac{\left\lfloor\frac{x}{2.5}\right\rfloor}{2.5}\right\rfloor = \left\lfloor\frac{x}{6.25}\right\rfloor.
\] | \frac{9}{10} | 0.125 |
There are ten cards each of the digits "3", "4", and "5". Choose any 8 cards such that their sum is 27. At most, how many of these cards can be "3"? | 6 | 0.5 |
In the dream market, a Sphinx offered a traveler seven illusions, two naps, and one nightmare for four dreams. To another traveler, the same Sphinx offered four illusions, four naps, and two nightmares for seven dreams. The Sphinx measures equally for all travelers.
How many illusions did one dream cost?
| 10 | 0.625 |
Is it possible to place 12 ships of size $1 \times 4$ in a $10 \times 10$ square (for a game like "battleship") such that the ships do not touch each other (even at the corners)? | \text{No} | 0.5 |
Find the mass of a plate \(D\) with surface density \(\mu = \frac{x}{y^5}\), bounded by the curves
\[
\frac{x^2}{16} + y^2 = 1, \quad \frac{x^2}{16} + y^2 = 3, \quad y = \frac{x}{4}, \quad x = 0 \quad \left(y \geq \frac{x}{4}, x \geq 0\right)
\] | 4 | 0.25 |
Let \( A \) be the sum of the digits of the number \( 16^{16} \), and \( B \) be the sum of the digits of the number \( A \). Find the sum of the digits of the number \( B \) without calculating \( 16^{16} \). | 7 | 0.625 |
Given the sequence $\left\{A_{n}\right\}$ defined by
$$
A_{1}=1, \quad A_{2}=3, \quad A_{n}=4 A_{n-1}-A_{n-2},
$$
find the value of $\sum_{n=1}^{+\infty} \operatorname{arccot} 2 A_{n}^{2}$. | \frac{\pi}{6} | 0.5 |
Let \( S \) be a subset of \(\{1,2,3, \ldots, 199,200\}\). We say that \( S \) is pretty if, for every pair of elements \( a \) and \( b \) in \( S \), the number \( a - b \) is not a prime number. What is the maximum number of elements in a pretty subset of \(\{1,2,3, \ldots, 199,200\}\)? | 50 | 0.375 |
We successively write all the numbers from 1 to one million. Then, we replace each number by the sum of its digits. We repeat this process until only single-digit numbers remain. Which digit appears the most frequently? | 1 | 0.875 |
Kolya drew 10 line segments and marked all their intersection points in red. After counting the red points, he noticed the following property: on each segment, there are exactly three red points.
a) Provide an example of the arrangement of 10 line segments with this property.
b) What can be the maximum number of red points for 10 segments with this property? | 15 | 0.875 |
Let \( a, b, c, x, y, \) and \( z \) be complex numbers such that
\[ a = \frac{b+c}{x-2}, \quad b = \frac{c+a}{y-2}, \quad c = \frac{a+b}{z-2}. \]
If \( x y + y z + z x = 67 \) and \( x + y + z = 2010 \), find the value of \( x y z \). | -5892 | 0.75 |
Let the function \( y = f(x) \) satisfy: for all \( x \in \mathbb{R} \), \( y = f(x) \geqslant 0 \), and \( f(x+1) = \sqrt{9 - f(x)^2} \). When \( x \in [0,1) \),
$$
f(x) = \begin{cases}
2^x, & 0 \leqslant x < \frac{1}{2}, \\
\log_{10} (x + 31), & \frac{1}{2} \leqslant x < 1
\end{cases}
$$
Find \( f(\sqrt{1000}) \). | \frac{3\sqrt{3}}{2} | 0.875 |
We define a sequence \( u_n \) as follows: \( u_1 \) and \( u_2 \) are integers between 1 and 10000 (inclusive), and \( u_{k+1} \) is the smallest absolute value of the pairwise differences of the previous terms. Show that \( u_{21} = 0 \). | u_{21} = 0 | 0.875 |
As shown in the figure, \(BC = 3 BE\) and \(AC = 4 CD\). The area of triangle \(ABC\) is how many times the area of triangle \(ADE\)? | 2 | 0.25 |
It is said that whoever pulls out the sword from the stone can rule England. King Arthur wanted to obtain the sword from the stone, so he sought advice from the prophet Merlin. To test King Arthur's sincerity, Merlin gave him a problem composed entirely of prime numbers:
\[ 5 \times A + 7 \times B = 7 \times 7 \]
Merlin said: "If you can tell me how much greater \( A \) is than \( B \), I will help you." After thinking about it, King Arthur gave Merlin the correct answer. This correct answer is ____. | 5 | 0.875 |
Two natural numbers \( a \) and \( b \), their least common multiple is 60. Then, the number of possible values for the difference between these two natural numbers is _____. | 23 | 0.375 |
As shown in Figure 1, in the regular triangular prism \(ABC-A_1B_1C_1\), \(D\) and \(E\) are points on the lateral edges \(BB_1\) and \(CC_1\), respectively. Given that \(EC = BC = 2BD\), find the measure of the dihedral angle between the section \(ADE\) and the base \(ABC\). | 45^\circ | 0.5 |
Find the number of 7-digit integers formed by some or all of the five digits, namely, 0, 1, 2, 3, and 4, such that these integers contain none of the three blocks 22, 33, and 44. | 29776 | 0.375 |
Let \( a, b, c \) be positive real numbers such that \( a + b + c = 2013 \). Find the maximum value of \( \sqrt{3a + 12} + \sqrt{3b + 12} + \sqrt{3c + 12} \). | 135 | 0.75 |
In a convex quadrilateral \(ABCD\), side \(AB\) is equal to diagonal \(BD\), \(\angle A=65^\circ\), \(\angle B=80^\circ\), and \(\angle C=75^\circ\). What is \(\angle CAD\) (in degrees)? | 15^\circ | 0.25 |
A natural number \( A \) has exactly 100 different divisors (including 1 and \( A \) ). Find the product of these divisors. | A^{50} | 0.625 |
Given that the real numbers \( x, y \) and \( z \) satisfy the condition \( x + y + z = 3 \), find the maximum value of \( f(x, y, z) = \sqrt{2x + 13} + \sqrt[3]{3y + 5} + \sqrt[4]{8z + 12} \). | 8 | 0.625 |
Determine the smallest integer $n$ such that there exist $n$ real numbers $x_{1}, \ldots, x_{n}$ all belonging to the interval $(-1, 1)$ and for which
$$
x_{1}+\cdots+x_{n}=0 \quad \text{and} \quad x_{1}^{2}+\cdots+x_{n}^{2}=2020
$$ | 2022 | 0.75 |
If \(\frac{1}{x}+\frac{1}{2x}+\frac{1}{3x}=\frac{1}{12}\), what is the value of \(x\)? | 22 | 0.875 |
A natural number is written on the board. If its last digit (in the units place) is erased, the remaining non-zero number is divisible by 20. If the first digit is erased, the remaining number is divisible by 21. What is the smallest number that could be on the board if its second digit is not 0? | 1609 | 0.875 |
At the olympiad, gymnasium students, lyceum students, and regular school students gathered. Some of them stood in a circle. Gymnasium students always lie to regular school students, lyceum students lie to gymnasium students, and regular school students lie to lyceum students. In all other cases, the students tell the truth. Each person told their neighbor to the right, "I am a gymnasium student." How many regular school students were in this circle? | 0 | 0.875 |
Count the number of permutations \( a_{1} a_{2} \ldots a_{7} \) of 1234567 with the longest decreasing subsequence of length at most two (i.e. there does not exist \( i < j < k \) such that \( a_{i} > a_{j} > a_{k} \)). | 429 | 0.75 |
Find the greatest number among \(5^{100}\), \(6^{91}\), \(7^{90}\), \(8^{85}\). | 8^{85} | 0.625 |
Find all values of \( n \) for which the sum
\[
1! + 2! + 3! + \cdots + n!
\]
is a perfect square, where \( n! = 1 \cdot 2 \cdot 3 \cdots n \). | 1 \text{ and } 3 | 0.75 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.