question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
alternating-groups-ii
|
1-pass | O( n + k - 2 ) & O(1)
|
1-pass-o2n-o1-c-easy-2-methods-by-iitian-wu29
|
IntuitionTo find number of aternating member groups in Binary circular array.Method-1Instead of making a new array of size 2*N, use circular indexing to track.
|
iitian_010u
|
NORMAL
|
2025-03-09T00:35:01.094175+00:00
|
2025-03-09T00:45:06.506374+00:00
| 1,289 | false |
# Intuition
To find number of aternating member groups in Binary circular array.
# Method-1
Instead of making a new array of size 2*N, use circular indexing to track. **( i%n wali )**
- Use current_count to track alternating members.
- If not equal → current_count++
- Else → Reset to 1 (adjacents are equal).
- If current_count >= k, add to result.
# Complexity
- Time complexity: O( n + k - 2 )
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int n = colors.size(), current_count =1, result = 0;
/*
1. loop upto n + k - 2(because it is circular array)
2. check condition is if not equal current_count ++,
else adjust. are equal, so reset the current_count.
3. if the current_count value reach to k. means if found a group.
*/
for(int i=0;i<n+k-2;++i){
if(colors[i%n]!=colors[(i+1)%n]){
current_count++;
}else{
current_count =1;
}
result += (current_count>=k);
}
return result;
}
};
```
```javascript []
class Solution {
numberOfAlternatingGroups(colors, k) {
let n = colors.length, current_count = 1, result = 0;
// Loop up to n + k - 2 (circular array)
for (let i = 0; i < n + k - 2; ++i) {
if (colors[i % n] !== colors[(i + 1) % n]) {
current_count++;
} else {
current_count = 1;
}
result += (current_count >= k) ? 1 : 0;
}
return result;
}
}
```
```python []
class Solution:
def numberOfAlternatingGroups(self, colors: list[int], k: int) -> int:
n, current_count, result = len(colors), 1, 0
# Loop up to n + k - 2 (circular array)
for i in range(n + k - 2):
if colors[i % n] != colors[(i + 1) % n]:
current_count += 1
else:
current_count = 1
result += (current_count >= k)
return result
```
```Java []
class Solution {
public int numberOfAlternatingGroups(int[] colors, int k) {
int n = colors.length, current_count = 1, result = 0;
// Loop up to n + k - 2 (circular array)
for (int i = 0; i < n + k - 2; ++i) {
if (colors[i % n] != colors[(i + 1) % n]) {
current_count++;
} else {
current_count = 1;
}
result += (current_count >= k) ? 1 : 0;
}
return result;
}
}
```
# Method 2
Approach is exactly the same, but instead of using circular indexing, create a new array by copying colors twice. Now, use normal indexing and apply a sliding window technique.
| 7 | 0 |
['Array', 'Sliding Window', 'Python', 'C++', 'Java', 'Python3', 'JavaScript']
| 1 |
alternating-groups-ii
|
Sliding Window || simple and easy Python solution 😍❤️🔥
|
sliding-window-simple-and-easy-python-so-7d4m
|
if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n\n# Code\n\nclass Solution(object):\n def numberOfAlternatingGroups(self, nums, k):\n n = len(nu
|
shishirRsiam
|
NORMAL
|
2024-07-07T02:10:19.125286+00:00
|
2024-07-07T02:13:23.405484+00:00
| 439 | false |
# if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n\n# Code\n```\nclass Solution(object):\n def numberOfAlternatingGroups(self, nums, k):\n n = len(nums)\n i, j, cnt, ans = 0, 0, 0, 0\n nums += nums\n\n while j < (n+k)-1:\n if nums[j] == nums[j+1]: i = j\n j += 1\n if j-i >= k: ans += 1\n\n return ans\n```
| 7 | 0 |
['Array', 'Greedy', 'Sliding Window', 'Simulation', 'Python', 'Python3']
| 4 |
alternating-groups-ii
|
Alternating Groups II || Best Ever Solution || Cpp Solution
|
alternating-groups-ii-best-ever-solution-7f9f
|
Intuitionour condition is to find how many subarray of size k with alternating colors contiguously present. so we need to circularly approach to find whether to
|
user3161EP
|
NORMAL
|
2025-03-09T16:47:09.573031+00:00
|
2025-03-09T16:47:09.573031+00:00
| 104 | false |
# Intuition
our condition is to find how many subarray of size k with alternating colors contiguously present. so we need to circularly approach to find whether to check they are alternative, so when we hit the index that cannot be reached, we use modulo technique, that is if color's size is 6 and index we cannot reach is also 6 means, we perform modulo operation so 6%6=0, 7%6=1, and so on so that we can approach circularly.
# Approach
I initially used a approach where it runs in a Time Complexity of O(N*K) this condition leads to TLE, but that is the very solution, where i add each element for size k to a temporary array and check whether it is alternative. if yes, we increment that count and return it.
Optimised Solution Approach:
Here we check each element and its neighbour element next to it if not same we increment its count, if at somepoint that count reaches a size of k we add it to our result and check if the next following index to follows alternative approach we add it to the result count. that is if from and to ind(0->4),k=5 all are alternative we increment the count and next to our suprise, (1->5),k=5 all are also alternative we found another subarray that is circular that is contiguously next to it. thus, we add it to our result count and return the number of alternating groups.
# Complexity
- Time complexity:
O(N+K)
- Space complexity:
O(1)
***PLEASE DO UPVOTE ME, IF YOU FOUND THIS SOLUTION VERY HELPFUL.THANK YOU.*😊**
# Code
```cpp []
// class Solution { // Time Limit Exceeded
// public:
// bool isAlternative(vector<int>&nums)
// {
// for(int i=1;i<nums.size();i++)
// {
// if(nums[i]==nums[i-1]) return false;
// }
// return true;
// }
// int numberOfAlternatingGroups(vector<int>& colors, int k) {
// int count=0;
// for(int i=0;i<colors.size();i++)
// {
// bool isTrue=true;
// vector<int>temp;
// int start=1;
// int ind=i;
// while(start<=k)
// {
// temp.push_back(colors[ind%colors.size()]);
// start++;
// ind++;
// }
// if(isAlternative(temp)) count++;
// }
// return count==0?0:count;
// }
// };
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int cnt=1;
int res=0;
for(int i=0;i<colors.size()+k-2;i++)
{
if(colors[i%colors.size()]!=colors[(i+1)%colors.size()]) cnt++;
else cnt=1;
if(cnt>=k)
{
res+=1;
}
}
return res;
}
};
```
| 6 | 0 |
['Array', 'Sliding Window', 'C++']
| 0 |
alternating-groups-ii
|
Sliding Window - JAVA
|
sliding-window-java-by-ayeshakhan7-si10
|
Code
|
ayeshakhan7
|
NORMAL
|
2025-03-09T08:28:35.689836+00:00
|
2025-03-09T08:28:35.689836+00:00
| 1,021 | false |
# Code
```java []
class Solution {
public int numberOfAlternatingGroups(int[] colors, int k) {
int res=0;
int left=0;
int n = colors.length;
// N+K
for(int right=1;right < (n + k -1); right++){ // exp..
// skip entire subarray
if(colors[right%n] == colors[(right-1)%n]){
left = right;
}
if(right - left + 1 == k){
res++;
left++; // move to next subarray or shrinking phase
}
}
return res;
}
}
```
| 6 | 0 |
['Java']
| 0 |
alternating-groups-ii
|
EASY WINDOW || In Depth Explanation || JAVA
|
easy-window-in-depth-explanation-java-by-487r
|
Understanding the Code\n\nProblem:\n Given a circular array of colors (red or blue), find the number of alternating groups of size k.\n An alternating group is
|
Abhishekkant135
|
NORMAL
|
2024-07-18T12:25:07.323638+00:00
|
2024-07-18T12:25:07.323676+00:00
| 286 | false |
## Understanding the Code\n\n**Problem:**\n* Given a circular array of colors (red or blue), find the number of alternating groups of size `k`.\n* An alternating group is a sequence of `k` tiles where the colors alternate (except for the first and last tiles).\n\n**Solution Approach:**\n\n* The code uses a sliding window approach to count the number of alternating groups.\n* It maintains a window of size `k` and checks if the current window is an alternating group.\n* To handle the circular nature of the array, the code effectively extends the array by appending `k - 1` elements from the beginning to the end.\n\n**Code Breakdown:**\n\n1. **Initialization:**\n * `ans`: Stores the count of alternating groups.\n * `i` and `j`: Pointers for the sliding window, initially set to 0.\n * `prev`: Stores the previous color encountered.\n\n2. **Sliding Window and Checking:**\n * The `while` loop iterates until `j` reaches `colors.length + k - 1`.\n * `end`: Represents the current index in the circular array, calculated using modulo (`%`).\n * If the current color (`colors[end]`) is the same as the previous color (`prev`), it means the current window cannot be an alternating group, so `i` is updated to `j` to start a new potential group.\n * If the window size reaches `k`, it means a complete group of size `k` is formed. If it\'s an alternating group, `ans` is incremented, and `i` is moved to the next position to start checking the next group.\n * The `prev` variable is updated with the current color.\n\n3. **Return the Count:**\n * Finally, the function returns the total count of alternating groups (`ans`).\n\n**Key Points:**\n\n* The use of `prev` efficiently tracks the previous color to determine if the current window is alternating.\n* The sliding window approach effectively handles the circular nature of the problem.\n* The code ensures that only complete windows of size `k` are considered for alternating groups.\n\n**Example:**\n\nConsider the array `colors = [0, 1, 0, 1, 1, 0, 0, 1]`, and `k = 3`.\n\n- The first window is `[0, 1, 0]`, which is an alternating group, so `ans` is incremented.\n- The next window is `[1, 0, 1]`, also an alternating group, so `ans` is incremented again.\n- The third window is `[0, 1, 1]`, not an alternating group.\n- The process continues until the end of the extended array.\n\nThe final value of `ans` will be the number of alternating groups in the circular array.\n\nThis code provides an efficient and clear solution for finding alternating groups in a circular array.\n\n\n# Code\n```\nclass Solution {\n public int numberOfAlternatingGroups(int[] colors, int k) {\n int ans=0;\n int i=0;\n int j=0;\n int prev=-1;\n while(i<colors.length && j<colors.length+k){\n int end=j%colors.length;\n if(colors[end]==prev){\n i=j;\n }\n if(j-i+1==k){\n ans++;\n i++;\n }\n j++;\n prev=colors[end];\n \n }\n return ans;\n }\n}\n```
| 6 | 0 |
['Sliding Window', 'Java']
| 0 |
alternating-groups-ii
|
✅ One Line Solution
|
one-line-solution-by-mikposp-zqwp
|
(Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)Code #1Time complexity: O(n). Space complexity: O(1)
|
MikPosp
|
NORMAL
|
2025-03-09T09:00:24.477784+00:00
|
2025-03-09T09:00:24.477784+00:00
| 538 | false |
(Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)
# Code #1
Time complexity: $$O(n)$$. Space complexity: $$O(1)$$.
```python3
class Solution:
def numberOfAlternatingGroups(self, a: List[int], k: int) -> int:
return sum(max(0,sum(g)-k+2) for _,g in groupby(starmap(ne,pairwise(a+a[:k-1]))))
```
[Ref](https://leetcode.com/problems/alternating-groups-ii/solutions/5443075/python-3-one-line-fast-and-short)
# Code #2
Time complexity: $$O(n)$$. Space complexity: $$O(1)$$.
```python3
class Solution:
def numberOfAlternatingGroups(self, a: List[int], k: int) -> int:
return sum(q>=k-1 for q in accumulate(starmap(ne,pairwise(a+a[:k-1])),lambda q,v:q*v+v))
```
# Code #3 - Two Lines
Time complexity: $$O(n)$$. Space complexity: $$O(1)$$.
```python3
class Solution:
def numberOfAlternatingGroups(self, a: List[int], k: int) -> int:
b = chain([0],(i for (i,v),(j,u) in pairwise(enumerate(a+a[:k])) if v==u),[len(a)+k-1])
return sum(max(0,j-i-k+1) for i,j in pairwise(b))
```
(Disclaimer 2: code above is just a product of fantasy packed into one line, it is not declared to be 'true' oneliners - please, remind about drawbacks only if you know how to make it better)
| 5 | 0 |
['Array', 'Python', 'Python3']
| 1 |
alternating-groups-ii
|
Super easy approach ever || using sliding window || without modifying array(vector) || beats 97%
|
super-easy-approach-ever-using-sliding-w-ikmd
|
Code
|
Aditya_4444
|
NORMAL
|
2025-03-09T05:34:35.100724+00:00
|
2025-03-09T05:34:35.100724+00:00
| 663 | false |
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int n=colors.size();
if (k>n)
return 0;
int c=0;
int res=0;
for (int i=1; i<n+k; i++) {
if (colors[(i-1)%n] != colors[i%n]) {
c++;
} else {
c=1;
}
if (c>=k) {
res++;
}
}
return res;
}
};
```
| 5 | 0 |
['Array', 'Sliding Window', 'C++']
| 0 |
alternating-groups-ii
|
Python | Simple Counter | O(n + k), O(1) | Beats 90%
|
simple-simple-counter-on-k-o1-beats-90-b-itjz
|
CodeComplexity
Time complexity: O(n+k). Iterates over circular list, list is n and circle adds k - 1 more elements, so n + k - 1 total. Each check is constant
|
2pillows
|
NORMAL
|
2025-03-09T01:53:49.274418+00:00
|
2025-03-09T02:05:04.587600+00:00
| 349 | false |
# Code
```python3 []
class Solution:
def numberOfAlternatingGroups(self, colors: List[int], k: int) -> int:
groups = alt_count = 0 # num alt groups and tracker for consecutive alt colors
for a, b in pairwise(chain(colors, colors[:k])): # use chain to extend colors for circular check
alt_count = alt_count + 1 if a != b else 1 # either add to or reset counter
groups += 1 if alt_count >= k else 0 # add to group if count length is at least k
return groups
```
# Complexity
- Time complexity: $$O(n + k)$$. Iterates over circular list, list is n and circle adds k - 1 more elements, so n + k - 1 total. Each check is constant time, overall is (n + k).
- Space complexity: $$O(1)$$. Only uses constant space variables, pairwise() and chain() are both iterators and don't create a new list.
# Performance
| 5 | 0 |
['Python3']
| 1 |
alternating-groups-ii
|
[Python3] Two Pointers + Sliding Window - Simple Solution
|
python3-two-pointers-sliding-window-simp-pyfp
|
Intuition\n- We need to keep a sliding window range smaller or equal to k, which is alternating group.\n- We can use queue to do that. However, using only 2 poi
|
dolong2110
|
NORMAL
|
2024-07-16T18:10:19.735903+00:00
|
2024-07-16T18:10:19.735933+00:00
| 121 | false |
# Intuition\n- We need to keep a sliding window range smaller or equal to `k`, which is alternating group.\n- We can use **queue** to do that. However, using only **2 pointers** to maintain both ends of the window is more efficient.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfAlternatingGroups(self, colors: List[int], k: int) -> int:\n colors += colors[: k - 1]\n i, j, res = 0, 1, 0\n while j < len(colors):\n if colors[j] == colors[j - 1]: i = j\n if j - i + 1 == k: \n res += 1\n i += 1\n j += 1\n return res\n```
| 5 | 0 |
['Array', 'Two Pointers', 'Sliding Window', 'Python3']
| 0 |
alternating-groups-ii
|
Sliding Window || simple and easy C++ solution 😍❤️🔥
|
sliding-window-simple-and-easy-c-solutio-it0r
|
if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n\n# Code\n\nclass Solution {\npublic:\n int numberOfAlternatingGroups(vector<int>& nums, int k) \n {
|
shishirRsiam
|
NORMAL
|
2024-07-07T02:04:31.296584+00:00
|
2024-07-07T02:13:53.441832+00:00
| 304 | false |
# if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfAlternatingGroups(vector<int>& nums, int k) \n {\n int cnt = 0, ans = 0;\n int i = 0, j = 0, n = nums.size();\n for(int i=0;i<k;i++)\n nums.push_back(nums[i]);\n\n while(j<(n+k)-1)\n {\n if(nums[j++] == nums[j]) i = j-1;\n if(j-i >= k) ans++;\n }\n return ans;\n }\n};\n```
| 5 | 0 |
['Array', 'Greedy', 'Sliding Window', 'Simulation', 'C++']
| 4 |
alternating-groups-ii
|
Simple C++ O(n) solution
|
simple-c-on-solution-by-spyy-a7vy
|
Array represents circle so first and last are connected. So I pushed the same array at the end to make it simple.\nThink greedily from each index we need to fin
|
spyy_
|
NORMAL
|
2024-07-06T16:03:43.832424+00:00
|
2024-07-06T16:03:43.832466+00:00
| 307 | false |
Array represents circle so first and last are connected. So I pushed the same array at the end to make it simple.\nThink greedily from each index we need to find length = k which satisfies the given condition.\nbounds of traversal -> assume last index n-1 is the starting point so we need to check elements till n - 1 + k.\nWe check if the element\'s previous is equal to the element, if it is equal we make length = 1 (as it makes our condition false) our new group should not have the previous element!!!!.\n\n```\nclass Solution {\npublic:\n int numberOfAlternatingGroups(vector<int>& colors, int k) {\n vector<int> edit = colors;\n for(auto it : colors) edit.push_back(it);\n int ans = 0;\n int length = 1;\n int n = colors.size();\n for(int i = 1;i < n + k - 1 ; i++){ \n if(edit[i]==edit[i-1]){\n length = 1;\n }\n else length++;\n if(length >= k) ans++;\n }\n return ans;\n }\n};\n```
| 5 | 1 |
['C++']
| 2 |
alternating-groups-ii
|
🔥Beats 100% 🎯| ✨Easy Approach | C++ | Java
|
beats-100-easy-approach-c-java-by-panvis-7t9e
|
IntuitionThe problem is ti find the alternating groups of length k. We need to extend the array by k to simulate a cyclic sequence, ensuring we check all possib
|
panvishdowripilli
|
NORMAL
|
2025-03-09T15:34:38.358721+00:00
|
2025-03-09T15:34:38.358721+00:00
| 326 | false |
# Intuition
The problem is ti find the alternating groups of length `k`. We need to extend the array by `k` to simulate a cyclic sequence, ensuring we check all possible groups.
****
# Approach
1. **Extended Iteration:**
- We need to iterate the `colors` array form `0` to `n + k -1` to check all the possible windows in the array.
- Now compare `i` and `i + 1` positions in the `colors` array.
2. **Sliding Window Technique:**
- Maintain two variable `i` and `j`, where `i` is the left of the `colors` array and `j` is the right of the `colors` array.
- If two consecutive elements are the same, the reset `i = j`, breaking the alternating sequence.
- Whenever the window size reaches at least `k`, increment the `count`.
****
# Complexity
- **Time complexity:**
- **O(N + K)** -> For iterating over the `colors` array from `0` to `n + k - 1`.
- **Space complexity:**
- **O(1)** -> No extra space is used
****
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int n = colors.size(), count = 0, i = 0;
for(int j = 0; j < n + k -1; j++){
if(colors[j % n] == colors[(j + 1) % n]){
i = j;
}
if(j - i + 1 >= k){
count++;
}
}
return count;
}
};
```
```java []
class Solution {
public int numberOfAlternatingGroups(int[] colors, int k) {
int n = colors.length, count = 0, i = 0;
for(int j = 0; j < n + k -1; j++){
if(colors[j % n] == colors[(j + 1) % n]){
i = j;
}
if(j - i + 1 >= k){
count++;
}
}
return count;
}
}
```
| 4 | 0 |
['Array', 'Sliding Window', 'C++', 'Java']
| 0 |
alternating-groups-ii
|
CPP || 100% beats || 2 solution || Sliding Window || very easy to understand
|
cpp-100-beats-2-solution-sliding-window-b0pzj
|
Complexity
Time complexity: O(N*k)
Space complexity: O(1)
Code (Sliding Window) --> TLE (Brute Force)Complexity (OPTIMIZED SOLUTION)
Time complexity: O(N)
Spa
|
apoorvjain7222
|
NORMAL
|
2025-03-09T12:27:00.360374+00:00
|
2025-03-09T12:27:00.360374+00:00
| 87 | false |
# Complexity
- Time complexity: O(N*k)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
<br/>

# Code (Sliding Window) --> TLE (Brute Force)
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int n = colors.size();
int count =0;
for(int i=0;i<n;i++){
bool flag = true;
for(int j=i;j<i+k-1;j++){
if(colors[j%n] == colors[(j+1)%n]){
flag = false;
break;
}
}
if(flag){
count++;
}
}
return count;
}
};
```
# Complexity (OPTIMIZED SOLUTION)
- Time complexity: O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
<br/>

# Code (Sliding Window)
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int n = colors.size();
int count =0;
int left=0;
for(int i=1;i<n+k-1;i++){
if(colors[i%n] == colors[(i-1)%n]){
left = i;
continue;
}
if(i-left+1 == k){
count++;
left++;
}
}
return count;
}
};
```
| 4 | 0 |
['Array', 'Sliding Window', 'C++']
| 0 |
alternating-groups-ii
|
beats 94% simple and easy solution ever
|
beats-94-simple-and-easy-solution-ever-b-gnmg
|
Complexity
Time complexity:O(n+k)
Space complexity:O(1)
Code
|
s_malay
|
NORMAL
|
2025-03-09T05:18:40.290020+00:00
|
2025-03-09T05:18:40.290020+00:00
| 359 | false |
# Complexity
- Time complexity:O(n+k)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
colors.insert(colors.end(), colors.begin(), colors.begin() + k);
int n = colors.size();
if (k > n)
return 0;
int cnt = 0;
int ans = 0;
for (int i = 1; i < n; i++) {
if (colors[i - 1] != colors[i]) {
cnt++;
} else {
cnt = 1;
}
if (cnt >= k) {
ans++;
}
}
return ans;
}
};
```
| 4 | 0 |
['Array', 'Sliding Window', 'C++']
| 1 |
alternating-groups-ii
|
1-PASS || Easy to understand
|
1-pass-easy-to-understand-by-jayanthmaru-xbd5
|
Intuitionsliding windowApproachComplexity
Time complexity:O(n+k)
Space complexity: O(1)
Code
|
jayanthmarupaka29
|
NORMAL
|
2025-03-09T01:07:28.851132+00:00
|
2025-03-09T01:07:28.851132+00:00
| 420 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
sliding window
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:O(n+k)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int window=1;
int n=colors.size(),cnt=0;
for(int i=0;i<n+k-2;i++){
if(colors[i%n]!=colors[(i+1)%n]){
window++;
if(window>=k){
cnt++;
}
}else{
window=1;
}
}
return cnt;
}
};
```
| 4 | 0 |
['Array', 'Sliding Window', 'C++']
| 2 |
alternating-groups-ii
|
Circular Alternating Groups 🔄: Beginner-Friendly with Visualization
|
circular-alternating-groups-beginner-fri-22c2
|
Possible - 18/07/2024\n---\n# Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem involves identifying alternating groups in a
|
sambhav22435
|
NORMAL
|
2024-07-18T08:24:16.211865+00:00
|
2024-07-18T08:24:16.211897+00:00
| 183 | false |
> Possible - 18/07/2024\n---\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem involves identifying alternating groups in a circular array of colors. \n\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Handling Circularity**: Repeat the first `k-1` elements at the end of the vector to handle circularity.\n2. **Marking Alternating Groups**: Iterate through the colors vector to identify positions where alternating groups start.\n3. **Counting Alternating Groups**: Count the number of valid alternating groups of size `k-2` or more based on the marked positions.\n\n---\n\n# Complexity\n- Time complexity:\n <!-- Add your time complexity here, e.g. $$O(n)$$ -->\n **O(n)** where **n** is the size of the original colors vector.\n- Space complexity:\n <!-- Add your space complexity here, e.g. $$O(n)$$ -->\n **O(n)** due to the extra space used for the `alternatingMarks` vector.\n\n---\n# Step-by-Step Visualization\n**Initial Input:**\n\n```\ncolors = [0, 1, 0, 1, 0]\nk = 3\n```\n\n**Handling Circularity:**\n\nWe repeat the first **k-1** elements at the end of the vector:\n\n```\ncolors = [0, 1, 0, 1, 0, 0, 1]\n```\n\n**Marking Alternating Groups:**\n\nWe create a vector ***alternatingMarks*** to mark positions of alternating groups.\n\n**Colors Vector and Alternating Groups:**\n\n| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |\n|---------------|---|---|---|---|---|---|---|\n| Colors | 0 | 1 | 0 | 1 | 0 | 0 | 1 |\n| Alternating | 0 | 1 | 1 | 1 | 0 | 0 | 0 |\n\n**Explanation:**\n- **colors[1]** (1) and **colors[2]**(0) form an alternating group with **colors[0]** (0).\n- **colors[2]** (0) and **colors[3]** (1) form an alternating group with **colors[1]** (1).\n- **colors[3]** (1) and **colors[4]** (0) form an alternating group with **colors[2]**(0).\n\nTherefore, ***alternatingMarks*** becomes:\n\n```\nalternatingMarks = [0, 1, 1, 1, 0, 0, 0]\n```\n\n**Counting Alternating Groups:**\n\nWe initialize **result** and **currentGroupCount** to 0, then iterate through *alternatingMarks* to count valid alternating groups.\n\n**Iterating through Alternating Marks:**\n\n| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |\n|---------------|---|---|---|---|---|---|---|\n| Alternating | 0 | 1 | 1 | 1 | 0 | 0 | 0 |\n| Group Count | - | 1 | 2 | 3 | 0 | 0 | 0 |\n| Result | 0 | 1 | 2 | 3 | 3 | 3 | 3 |\n\n**Explanation:**\n- **alternatingMarks[1]** = 1: increase **currentGroupCount** to 1, increment **result** to 1 (as **currentGroupCount >= k-2**), reset **currentGroupCount** to 0.\n- **alternatingMarks[2]** = 1: increase **currentGroupCount** to 1, increment **result** to 2 (as **currentGroupCount >= k-2**), reset **currentGroupCount** to 0.\n- **alternatingMarks[3]** = 1: increase **currentGroupCount** to 1, increment **result** to 3 (as **currentGroupCount >= k-2**), reset **currentGroupCount** to 0.\n- **alternatingMarks[4]** = 0: reset **currentGroupCount** to 0.\n- **alternatingMarks[5]** = 0: no change.\n- **alternatingMarks[6]** = 0: no change.\nTherefore, the total number of alternating groups is **3**.\n\n\n---\n# Code\n``` cpp []\n#include <vector>\nusing namespace std;\n\nclass Solution {\npublic:\n int numberOfAlternatingGroups(vector<int>& colors, int k) {\n // Repeat the first k-1 elements of the vector at the end to handle circularity\n for(int i = 0; i < k - 1; i++) {\n colors.push_back(colors[i]);\n }\n \n // Vector to mark positions of alternating groups\n vector<int> alternatingMarks;\n alternatingMarks.push_back(0); // Start with a non-alternating mark\n \n // Iterate through the colors vector to find alternating groups\n for(int i = 1; i < colors.size() - 1; i++) {\n if(colors[i] != colors[i + 1] && colors[i + 1] == colors[i - 1]) {\n // Found an alternating group\n alternatingMarks.push_back(1);\n } else {\n // No alternating group\n alternatingMarks.push_back(0);\n }\n }\n alternatingMarks.push_back(0); // End with a non-alternating mark\n \n int result = 0; // Count of alternating groups\n int currentGroupCount = 0; // Counter for current alternating group\n \n // Count the number of valid alternating groups of size k-2 or more\n for(int i = 0; i < alternatingMarks.size(); i++) {\n if(alternatingMarks[i] == 1) {\n currentGroupCount++;\n if(currentGroupCount >= (k - 2)) {\n result++;\n currentGroupCount--;\n }\n } else {\n currentGroupCount = 0; // Reset counter if no alternating group\n }\n }\n\n return result;\n }\n};\n```\n---\n\n
| 4 | 0 |
['Array', 'C', 'Sliding Window', 'C++']
| 2 |
alternating-groups-ii
|
✅ Java Easy solution | O(n) runtime
|
java-easy-solution-on-runtime-by-tanmoy_-soeh
|
IntuitionThe problem requires finding the number of alternating groups of length at least k in a circular array. An alternating group means consecutive elements
|
TANMOY_123
|
NORMAL
|
2025-03-09T14:05:24.038370+00:00
|
2025-03-09T14:05:24.038370+00:00
| 98 | false |
# Intuition
The problem requires finding the number of alternating groups of length at least `k` in a circular array. An alternating group means consecutive elements must have different values. Since the array is circular, we extend our checks beyond its length by considering indices in a modular fashion.
# Approach
1. **Initialization:**
- We define `count` to store the number of valid alternating groups.
- Use `left` as the starting index of a potential group.
- Define `limit = n + k - 1` to account for the circular nature of the array.
2. **Sliding Window Expansion:**
- For each `left`, set `right = left + 1` and expand `right` while elements are alternating (`colors[right-1] != colors[right]`), wrapping around using modulo indexing.
- Stop expanding when we encounter a repeated color or exceed the `limit`.
3. **Validating Alternating Groups:**
- If the length `(right - left) >= k`, we count all possible subarrays of length at least `k` within this segment.
- The number of valid groups in this segment is `(right - left) - k + 1`.
4. **Move `left` to `right` and repeat.**
# Complexity
- Time complexity: $$O(n)$$
- The `left` pointer iterates through `n` elements, and `right` moves forward without backtracking, leading to a **linear O(n) time complexity**.
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(1)$$
- There was no extra space we have used that is dependent on the `colors` array 's size.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int numberOfAlternatingGroups(int[] colors, int k)
{
int n=colors.length;
int count=0;
int left = 0;
int limit = n+k-1;
while(left<n)
{
int right= left+1;
while(right<limit && (colors[(right-1)%n]!=colors[right%n]))
{
right++;
}
if((right-left)>=k)
{
count += (right-left) - k +1;
}
left=right;
}
return count;
}
}
```

| 3 | 0 |
['Array', 'Sliding Window', 'Java']
| 0 |
alternating-groups-ii
|
2ms✅|| 98% beats🔥|| Beginner Friendly💯|| just single loop👍|| just create one array❤️
|
2ms-98-beats-beginner-friendly-just-sing-yhnr
|
IntuitionApproachsliding windowComplexity
Time complexity:
Space complexity:
Code
|
Sorna_Prabhakaran
|
NORMAL
|
2025-03-09T10:35:57.035524+00:00
|
2025-03-09T10:37:57.198213+00:00
| 166 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
sliding window
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution
{
public int numberOfAlternatingGroups(int[] c, int k)
{
int start = 0, cnt = 0;
boolean isEven = k % 2 == 0;
int[] nums = Arrays.copyOf(c, (c.length + (k-1)));
System.arraycopy(c, 0, nums, c.length, k-1);
for(int end = 1; end < nums.length; end++)
{
if((end - start) < k-1)
{
if(nums[end] == nums[end-1]) start = end;
}
else
{
if(isEven)
{
if(nums[start++] != nums[end]) cnt++;
else start = end;
}
else
{
if(nums[start++] == nums[end]) cnt++;
else start = end;
}
}
}
return cnt;
}
}
```
| 3 | 0 |
['Java']
| 1 |
alternating-groups-ii
|
✅ Easy to Understand | Fixed Sliding Window | Detailed Video Explanation🔥
|
easy-to-understand-fixed-sliding-window-d2sbz
|
IntuitionThe problem requires finding contiguous subarrays of length k that alternate in color, considering the circular nature of the array. Since the last and
|
sahilpcs
|
NORMAL
|
2025-03-09T09:07:56.383975+00:00
|
2025-03-09T09:07:56.383975+00:00
| 185 | false |
# Intuition
The problem requires finding contiguous subarrays of length `k` that alternate in color, considering the circular nature of the array. Since the last and first elements are adjacent, a direct approach would be complex. Instead, extending the array simplifies handling circular behavior.
# Approach
1. **Extend the Array:** Copy the `colors` array into a new array and append its first `(k - 1)` elements to handle circular adjacency.
2. **Use a Sliding Window:** Maintain a window `[i, j]` to check for valid alternating groups.
3. **Expand the Window:** Increase `j` while ensuring adjacent elements are alternating.
4. **Reset on Failure:** If two consecutive elements match, reset `i` and `j`.
5. **Count Valid Groups:** If the window reaches size `k` and maintains alternation, count it as a valid group and slide the window forward.
# Complexity
- **Time complexity:**
- The algorithm processes each element once in the sliding window approach, leading to an overall complexity of $$O(n)$$.
- **Space complexity:**
- The extended array requires extra space of size `k - 1`, making the space complexity $$O(n)$$.
# Code
```java []
class Solution {
public int numberOfAlternatingGroups(int[] colors, int k) {
// Extend the colors array to handle the circular nature
int[] extended = new int[colors.length + k - 1];
// Copy the original colors array into the extended array
for (int i = 0; i < colors.length; i++) {
extended[i] = colors[i];
}
// Append the first (k - 1) elements to the end to simulate circular behavior
for (int i = 0; i < k - 1; i++) {
extended[colors.length + i] = colors[i];
}
int n = extended.length; // New extended array size
int i = 0, j = 0; // Two pointers for the sliding window
int ans = 0; // Counter for the alternating groups
while (j < n - 1) {
// If two consecutive tiles have the same color, reset the window
if (extended[j] == extended[j + 1]) {
j = j + 1;
i = j;
continue;
}
j++; // Expand the window
// If window size is smaller than k, continue expanding
if (j - i + 1 < k) continue;
// Valid alternating group found, increment the count
ans++;
i++; // Slide the window forward
}
return ans; // Return total count of alternating groups
}
}
```
https://youtu.be/51E6hoWVigo
| 3 | 0 |
['Array', 'Sliding Window', 'Java']
| 1 |
alternating-groups-ii
|
[C++] One pass
|
c-one-pass-by-bora_marian-ch0f
|
To solve that colors are put in a circle add k elements to the end.
Iterate from 1 to n + k - 1 and remember when you see last time non alternating elements (c
|
bora_marian
|
NORMAL
|
2025-03-09T07:20:19.380938+00:00
|
2025-03-09T07:20:19.380938+00:00
| 96 | false |
- To solve that colors are put in a circle add k elements to the end.
- Iterate from `1` to `n + k - 1` and remember when you see last time non alternating elements (`colors[i]` and colors`[i-1]`).
- If the distance between i and the last non_alternating position is >= k, than we can increase the result.
---
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int n = colors.size();
for (int i = 0; i < k; i++) {
colors.push_back(colors[i]);
}
int non_alternating = -1, res = 0;
for (int i = 1; i < n + k - 1; i++) {
if (colors[i] == colors[i-1]) {
non_alternating = i-1;
continue;
}
if (i - non_alternating >= k) {
res++;
}
}
return res;
}
};
```
| 3 | 0 |
['C++']
| 0 |
alternating-groups-ii
|
TS PMO icl🗣️‼️. But simple ahh Sliding window solution ngl fr vroski.
|
ts-pmo-icl-but-simple-ahh-sliding-window-v02s
|
Code
|
Ishaan_P
|
NORMAL
|
2025-03-09T02:17:17.695987+00:00
|
2025-03-09T02:17:33.118546+00:00
| 231 | false |
# Code
```java []
class Solution {
public int numberOfAlternatingGroups(int[] colors, int k) {
//keep track of most recent index where disruption happened while doing sliding window
//as long as disruption is outside of the bounds of the sliding window, add 1 to the count
int L = 0;
int R = k-1;
int count = 0;
int mostRecentDisruptionIdx = -1;
for(int i = 1; i <= R; i++){
if(colors[i] == colors[i-1])
mostRecentDisruptionIdx = i-1;
}
while(R < colors.length + k-1){
if(mostRecentDisruptionIdx < L)
count++;
R++;
L++;
if(R < colors.length + k -1)
if(colors[R%colors.length] == colors[(R-1)%colors.length])
mostRecentDisruptionIdx = R-1;
}
return count;
}
}
```
| 3 | 0 |
['Java']
| 0 |
alternating-groups-ii
|
SLIDING WINDOW || Neat code with comments || JAVA || easy to understand code
|
sliding-window-neat-code-with-comments-j-6v1t
|
IntuitionA straightforward approach would be checking every possible subarray of length k, but this would be inefficient. Instead, we can use a sliding window t
|
QuantamBee
|
NORMAL
|
2025-03-09T02:00:09.170408+00:00
|
2025-03-09T02:00:09.170408+00:00
| 107 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
A straightforward approach would be checking every possible subarray of length $$k$$, but this would be inefficient. Instead, we can use a sliding window technique to efficiently track alternating groups in $$ O(n)$$ time complexity.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Use a sliding window
- Expand the window by moving `end`.
- Use modulo indexing` (% n) `to handle circular traversal.
- Reset window if consecutive colors are same
- check for valid alternating sequences of size k
# Complexity
- Time complexity: $$O(n)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int numberOfAlternatingGroups(int[] colors, int k) {
int totalGroups = 0;
int start = 0;
int end = 0;
int lastColor = -1;
int n = colors.length;
while (start < n && end < n + k) {
int currentIndex = end % n; // Handle circular indexing
// Reset window if consecutive colors are the same
if (colors[currentIndex] == lastColor) {
start = end;
}
// Check if we have a valid alternating sequence of size k
if (end - start + 1 == k) {
totalGroups++;
start++; // Move start to check the next window
}
end++;
lastColor = colors[currentIndex]; // Update last seen color
}
return totalGroups;
}
}
```
| 3 | 0 |
['Array', 'Two Pointers', 'Sliding Window', 'Java']
| 0 |
alternating-groups-ii
|
38 ms JS/C++. Beats 100.00% time, 100.00% mem
|
four-approaches-beats-10000-time-10000-m-r6qk
|
ApproachSliding windows, only you need to circle the array. To do this, you can either duplicate k-1 elements to the end, or use the index mod k to access the e
|
nodeforce
|
NORMAL
|
2025-03-09T01:46:38.861325+00:00
|
2025-03-09T02:57:13.603454+00:00
| 342 | false |
# Approach
Sliding windows, only you need to circle the array. To do this, you can either duplicate `k-1` elements to the end, or use the index mod `k` to access the elements. You can also use two pointers or a index and the width of the window. Copying works faster and the module does not require additional space.
Copy beats 100.00% runtime with a significant margin:
Mod beats 100% memory, and still 100% time, but worse than copy runtime:
Branchless
# Complexity
- Time complexity: $$O(n + k)$$.
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: Copy $$O(k)$$, Mod $$O(1)$$.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code JS
```javascript [Copy + 2P]
const numberOfAlternatingGroups = (a, k) => {
const n = a.length;
for (let i = 0; i < k - 1; ++i) a.push(a[i]);
let g = 0;
for (let l = 0, r = 1; l < n; ++r) {
if (a[r - 1] === a[r]) l = r;
if (r - l < k - 1) continue;
++g;
++l;
}
return g;
};
```
```javascript [Copy + W]
const numberOfAlternatingGroups = (a, k) => {
for (let i = 0; i < k - 1; ++i) a.push(a[i]);
let g = 0;
for (let i = 1, w = 1; i < a.length; ++i) {
if (a[i - 1] !== a[i]) {
if (++w >= k) ++g;
} else w = 1;
}
return g;
};
```
```javascript [Mod + 2P]
const numberOfAlternatingGroups = (a, k) => {
const n = a.length;
let g = 0;
for (let l = 0, r = 1; l < n; ++r) {
if (a[(r - 1) % n] === a[r % n]) l = r;
if (r - l < k - 1) continue;
++g;
++l;
}
return g;
};
```
```javascript [Mod + W]
const numberOfAlternatingGroups = (a, k) => {
const n = a.length;
let g = 0;
for (let i = 1, w = 1; i < n + k - 1; ++i) {
if (a[(i - 1) % n] !== a[i % n]) {
if (++w >= k) ++g;
} else w = 1;
}
return g;
};
```
```javascript [Branchless]
const numberOfAlternatingGroups = (a, k) => {
for (let i = 0; i < k - 1; ++i) a.push(a[i]);
let g = 0;
const { length } = a;
for (let i = 1, w = 1, p = a[0]; i < length; ++i) {
w *= p !== a[i];
g += ++w >= k;
p = a[i];
}
return g;
};
```
# Code C++
```cpp [Copy]
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& a, int k) {
for (int i = 0; i < k - 1; ++i) a.push_back(a[i]);
int g = 0;
for (int i = 1, w = 1, p = a[0]; i < a.size(); ++i) {
w *= p != a[i];
g += ++w >= k;
p = a[i];
}
return g;
}
};
```
```cpp [Mod]
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& a, int k) {
const int n = a.size();
int g = 0;
for (int i = 1, w = 1, p = a[0]; i < n + k - 1; ++i) {
const int c = a[i % n];
w *= p != c;
g += ++w >= k;
p = c;
}
return g;
}
};
```
| 3 | 0 |
['Array', 'C', 'Sliding Window', 'C++', 'TypeScript', 'JavaScript']
| 0 |
alternating-groups-ii
|
Very easy sol || cpp || beginner friendly
|
very-easy-sol-cpp-beginner-friendly-by-a-nyft
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
skipper_108
|
NORMAL
|
2024-08-12T06:06:01.142328+00:00
|
2024-08-12T06:06:01.142361+00:00
| 43 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- o(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nstatic auto speedup = []() {\n ios_base::sync_with_stdio(false);\n cout.tie(NULL);\n cin.tie(NULL);\n return\xA0NULL;\n}();\nclass Solution {\npublic:\n int numberOfAlternatingGroups(vector<int>& colors, int k) {\n int count = 1,ans = 0;\n int n = colors.size();\n int prev = colors[0];\n\n for(int i = 1; i < n + k-1 ;i++){\n \n\n if(prev == colors[i%n]){\n count = 1;\n }\n else{\n count++;\n if(count >= k){\n ans++;\n }\n }\n prev = colors[i%n];\n }\n return ans;\n }\n};\n```
| 3 | 0 |
['C++']
| 0 |
alternating-groups-ii
|
Very Short (String | RegExp) Approach
|
very-short-string-regexp-recursion-appro-vy1x
|
it's a challenge for you to explain how it works
|
charnavoki
|
NORMAL
|
2024-07-07T10:09:48.435151+00:00
|
2025-03-09T01:34:14.552880+00:00
| 51 | false |
```
const numberOfAlternatingGroups = (colors, k, s = colors.join(''), str = s + s.slice(0, k - 1)) =>
(str.match(/(?:10)+1?|(?:01)+0?/g) || []).reduce((s, c) => s + Math.max(0, c.length - k + 1), 0);
```
it's a challenge for you to explain how it works
| 3 | 0 |
['JavaScript']
| 0 |
alternating-groups-ii
|
Sliding Window Easy
|
sliding-window-easy-by-maneesh5164-p5mi
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
maneesh5164
|
NORMAL
|
2024-07-06T18:33:47.966702+00:00
|
2024-07-06T18:33:47.966724+00:00
| 171 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfAlternatingGroups(vector<int>& col, int k) {\n\n for(int i=0;i<k-1;i++){\n col.push_back(col[i]);\n }\n\n int n=col.size();\n\n int left=0;\n int right=1;\n int count=0;\n\n while(right<n){\n \n if(col[right]!=col[right-1]){\n if(right-left+1==k){\n count++;\n left++;\n }\n right++;\n }else{\n left=right;\n right++;\n }\n }\n\n return count;\n \n }\n};\n```
| 3 | 0 |
['Two Pointers', 'Sliding Window', 'Counting', 'C++']
| 1 |
alternating-groups-ii
|
🔥WITH EXPLANATION!!ROLLING HASH TECHNIQUE🔥 Very EASY to UNDERSTAND and BEGINNER FRIENDLY CODE
|
with-explanationrolling-hash-technique-v-0qpy
|
\n\n# Approach\nHash Function:\n\nThe get_hash function computes a hash value for a given vector a. The hash is computed using a polynomial rolling hash techniq
|
Saksham_Gulati
|
NORMAL
|
2024-07-06T17:46:02.131532+00:00
|
2024-07-06T17:51:35.862260+00:00
| 56 | false |
\n\n# Approach\nHash Function:\n\nThe `get_hash` function computes a hash value for a given vector a. The hash is computed using a polynomial rolling hash technique where each element of the array is transformed and summed with a multiplying factor, modulo 1e9+7.\nThis hash function is used to quickly compare subarrays.\nAlternating Patterns:\n\nThe function `numberOfAlternatingGroups` aims to find subarrays of length k in colors that alternate between two patterns: 010101... and 101010....\nIt first constructs these two patterns and computes their hash values (h1 and h2).\nHandling Circular Case:\n\nThe input vector colors is extended by appending the first k elements again. This handles the circular nature of the problem, ensuring that subarrays wrapping around the end of the array are considered.\nInitial Subarray Hash:\n\nThe hash of the first subarray of length k is computed and compared with h1 and h2.\nSliding Window:\n\nThe main part of the algorithm uses a sliding window approach to move through the vector colors.\nFor each new subarray starting at index l and ending at index r, the hash is updated by removing the contribution of the element that is sliding out of the window and adding the contribution of the new element sliding into the window.\nThis allows for efficient computation of the hash for each subarray in constant time after the initial hash computation.\nComparison:\n\nFor each subarray hash computed, it is compared against `h1` and `h2`. If it matches either, the count `c` is incremented.\n# Complexity\n- Time complexity:\n $$O(n)$$\n\n- Space complexity:\n $$O(n)$$ \n\n# Code\n```\nclass Solution {\npublic:\n const int mod=1e9+7;\n \n long long get_hash(vector<int>& a) {\n long long h=0;\n long long p=1;\n int n=a.size();\n for(int i=n-1;i>=0;i--) {\n h=(h+(a[i]+1)*p*1ll)%mod;\n p=(p*31*1ll)%mod;\n }\n return h;\n }\n\n int numberOfAlternatingGroups(vector<int>& colors, int k) {\n int n=colors.size();\n long long p=1;\n vector<int> a;\n \n // Create alternating pattern 010101... or 101010...\n for(int i=0; i<k; i++) {\n a.push_back(p);\n p^=1;\n }\n\n // Get hash of alternating pattern 010101...\n long long h1=get_hash(a);\n \n // Flip pattern to 101010...\n for(int i=0; i<k; i++) {\n a[i]^=1;\n }\n\n // Get hash of alternating pattern 101010...\n long long h2=get_hash(a);\n\n // Initialize hash of first window in the vector\n a.clear();\n for(int i=0; i<k; i++) a.push_back(colors[i]);\n \n // Extend the vector to handle circular case\n for(int i=0; i<k; i++) colors.push_back(colors[i]);\n\n long long ht=get_hash(a);\n long long c=0;\n\n // Compare initial hash with alternating patterns\n if(ht==h1 || ht==h2) c++;\n \n p=1;\n for(int i=0; i<k-1; i++) p=(long long)(p*31*1ll)%mod;\n\n // Slide the window\n for(int l=1, r=k; l<n; l++, r++) {\n long long del=((colors[l-1]+1)*p)%mod;\n long long add=colors[r]+1;\n ht=((ht-del+mod)*31*1ll+add)%mod;\n if(h1==ht || ht==h2) c++;\n }\n\n return c;\n }\n};\n```\n\n\n\n\n
| 3 | 0 |
['C++']
| 0 |
alternating-groups-ii
|
Two Pointers / Sliding Window Approach (Detailed Explanation Probably)
|
two-pointers-sliding-window-approach-det-f2ez
|
Intuition\nObservations:\n- Suppose you know colors[i...j] is alternating group of length k. We can find that colors[i...j+1] to be alternating iff colors[j+1]!
|
jonteo2001
|
NORMAL
|
2024-07-06T16:37:50.731092+00:00
|
2024-07-06T16:37:50.731118+00:00
| 179 | false |
# Intuition\nObservations:\n- Suppose you know `colors[i...j]` is alternating group of length `k`. We can find that `colors[i...j+1]` to be alternating iff `colors[j+1]!=colors[j]`\n - If it is alternating, you can shift the window to `colors[i+1...j+1]` because we are only interested in length `k` groups.\n - If `colors[i...j+1]` is **NOT** alternating, any subarray with `colors[j,j+1]` will not be alternating. So you can skip to index `j+1` and check the subarray `colors[j+1...j+1+k]`.\n\n- Suppose `colors[i...j]` is a subarray of length `k` but is **NOT** alternating. We can just do a simple check to see if the colors on the left and right alternate.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- First concatenate `colors[0...k-1]` to the end of colors to mimic the circle. We take the first `k-1` elements because the last group we consider is the subarray `colors[n-1,0...,k-1]`\n- Maintain a variable `start` that maintains the start index of the subarray we are considering. Let `start = 0`\n- Maintain a variable `is_alt` that is `true` when the **previous** subarray is alternating (ie. `colors[start-1...end-1]`is alternating) and false otherwise.\n\n(See Pseudocode)\n```\ncount = 0\nstart = 0\nis_alt = False\nWHILE start < number of original elements:\n end = start + k - 1 # subarray of start...end of k elements\n IF start-1...end-1 is alternating:\n IF colors[end] != colors[end-1]:\n count += 1\n ELSE:\n is_alt = False\n start = end # don\'t need to consider others\n ELSE:\n Check if colors[start...end] is alternating\n IF alternating:\n is_alt = True\n start += 1 # check colors[start+1...end+1] next iter\n ELSE:\n start = first index where it stops alternating\n``` \n\n# Complexity\n- Time complexity: $O(N)$ , where N is the number of elements.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(k)$, where N is the number of elements\nIn order to simplify my implementation, I copied the first `k-1` elements to the end. Technically you can optimize this further by removing that and adding more logic. \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python\nclass Solution:\n def numberOfAlternatingGroups(self, colors: List[int], k: int) -> int:\n n = len(colors)\n for i in range(k-1): # copy k-1 elements to end to simulate the cycle\n colors.append(colors[i])\n num = 0\n is_alt = False\n start = 0\n k -= 1 # this is because I considered [start, end] inclusive\n # print(colors)\n while start < n:\n end = start + k\n # print("end = ",end)\n if not is_alt:\n s = colors[start]\n invalid_idx = 0\n for i in range(start+1, end+1): # check alternating\n if colors[i] == 1 - s:\n s = 1 - s\n else:\n invalid_idx = i\n break\n else:\n is_alt = True\n num += 1\n start += 1\n continue\n start = invalid_idx\n else:\n if colors[end] == 1 - colors[end-1]:\n num += 1\n # print("start = ", start)\n start += 1\n else:\n is_alt = False\n start = end\n return num\n```
| 3 | 0 |
['Two Pointers', 'Sliding Window', 'Python3']
| 0 |
alternating-groups-ii
|
One Pass Solution Without Using DP 🔥✅🚀 | Intuitive Solution
|
one-pass-solution-without-using-dp-intui-oegm
|
Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n\n# Code\n\nclass Solution(object):\n def numberOfAlternatingGroups(self,
|
Gargeya
|
NORMAL
|
2024-07-06T16:31:01.971172+00:00
|
2024-07-06T16:31:01.971194+00:00
| 36 | false |
# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass Solution(object):\n def numberOfAlternatingGroups(self, colors, k):\n nums=colors[:]\n n=len(nums)\n r=0\n c=0\n s=set()\n for i in range(len(nums)+k-1):\n if nums[i%n]!=nums[(i+1)%n]:\n r+=1\n if r>=k-1:\n if i%n not in s:\n c+=1\n s.add(i%n)\n else:\n r=0\n return c\n """\n :type colors: List[int]\n :type k: int\n :rtype: int\n """\n \n```\n
| 3 | 0 |
['Python', 'Python3']
| 1 |
alternating-groups-ii
|
🚨 Linear scan and check || 5 Lines Faster 100%
|
linear-scan-and-check-5-lines-faster-100-5p0g
|
Intuition\n- Linear scan\n- Traverse upto n + k to calculate elements across circle\n- If any element does not equal previous element, shrink the window by upda
|
t86
|
NORMAL
|
2024-07-06T16:04:34.384821+00:00
|
2024-07-06T16:17:41.036993+00:00
| 247 | false |
**Intuition**\n- Linear scan\n- Traverse upto `n + k` to calculate elements across circle\n- If any element does not equal previous element, shrink the window by updating `l`, or maintain a window of `k` len\n- if a window of `k` len is valid it means all elements inside this is alternating thereby increment result\n\n**Code**\n```c++\nint numberOfAlternatingGroups(vector<int>& colors, int k) {\n int n = colors.size(), res = 0;\n for (auto i = 1, l = 0; i < n + k; i++) \n if (colors[i % n] == colors[ (i - 1 ) % n]) l = i - 1;\n else {\n l = max(l, i - k);\n if (i - l == k) res++;\n }\n return res;\n}\n```\n\n**Complexity**\n`Time`: O(n)\n`Space`: O(1)\n\n**For more solutions and concepts, check out this \uD83D\uDCD6 [BLOG](https://github.com/MuhtasimTanmoy/notebook) and \uD83C\uDFC6 [GITHUB REPOSITORY](https://github.com/MuhtasimTanmoy/playground) with over 2000+ solutions.**
| 3 | 0 |
['C']
| 1 |
alternating-groups-ii
|
c++ 2 solution kmp algorithm and alternative index solution
|
c-2-solution-kmp-algorithm-and-alternati-ot9h
|
1 Alternative index\n\nclass Solution {\npublic:\n int numberOfAlternatingGroups(vector<int>& nums, int k) {\n int missMatch=0;\n int ans=0;\n
|
dilipsuthar17
|
NORMAL
|
2024-07-06T16:01:28.903498+00:00
|
2024-07-06T16:26:15.194532+00:00
| 400 | false |
**1 Alternative index**\n```\nclass Solution {\npublic:\n int numberOfAlternatingGroups(vector<int>& nums, int k) {\n int missMatch=0;\n int ans=0;\n int n=nums.size();\n for(int i=0;i<n+k-1;i++){\n if(nums[i%n]!=nums[(i+1)%n]) missMatch++;\n else missMatch=1;\n if(missMatch>=k) ans++;\n }\n return ans;\n }\n};\n```\n** kmp algorithm to find pattern**\n```\nclass Solution {\npublic:\n vector<int>kmp(string s,string p){\n s=p+"###"+s;\n int n=s.size();\n vector<int>result(n,0);\n int i=1;\n int len=0;\n while(i<n){\n if(s[i]==s[len]){\n result[i]=++len;\n i++;\n }\n else{\n if(len){\n len=result[len-1];\n }\n else{\n i++;\n }\n }\n }\n return result;\n }\n int numberOfAlternatingGroups(vector<int>& nums, int k) {\n for(int i=0;i<k-1;i++){\n nums.push_back(nums[i]);\n }\n string s="";\n for(int i=0;i<nums.size();i++){\n if(nums[i]==0) s.push_back(\'0\');\n if(nums[i]==1) s.push_back(\'1\');\n }\n string p1="";\n string p2="";\n for(int i=0;i<k;i++){\n if(i%2==0){\n p1.push_back(\'0\');\n p2.push_back(\'1\');\n }\n else{\n p1.push_back(\'1\');\n p2.push_back(\'0\');\n }\n }\n int count=0;\n vector<int>result1=kmp(s,p1);\n vector<int>result2=kmp(s,p2);\n \n for(int i=0;i<result2.size();i++){\n if(result1[i]==k||result2[i]==k){\n count++;\n }\n }\n return count;\n }\n};\n```
| 3 | 0 |
['C', 'C++']
| 1 |
alternating-groups-ii
|
Simple and Easy Solution here. using Sliding window concept
|
simple-and-easy-solution-here-using-slid-o1bt
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
HYDRO2070
|
NORMAL
|
2025-03-09T19:30:43.925930+00:00
|
2025-03-09T19:30:43.925930+00:00
| 29 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& temp, int &k) {
for(int i = 0;i < k-1;i++) temp.push_back(temp[i]);
int n = temp.size();
int ans = 0;
int i = 0;
bool pass = false;
while(i < n){
if(pass){
if(temp[i] == temp[i-1]){
pass = false;
}
else{
ans++;
i++;
}
}
else{
if(i > n-k) break;
int j = i;
int last = -1;
while(j < i+k && temp[j] != last){
last = temp[j];
j++;
}
if(j == i+k){
ans++;
pass = true;
}
i = j;
}
}
return ans;
}
};
```
| 2 | 0 |
['Array', 'Sliding Window', 'C++']
| 0 |
alternating-groups-ii
|
simple sliding window solution
|
simple-sliding-window-solution-by-singh_-epge
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Singh_abhiishek
|
NORMAL
|
2025-03-09T18:52:58.256619+00:00
|
2025-03-09T18:52:58.256619+00:00
| 27 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int numberOfAlternatingGroups(int[] colors, int k) {
int n = colors.length;
int ans = 0, l = 0, r = 0;
while(l < n && r < n+k){
if(r-l+1 == k){
l++;
ans++;
}
if(colors[r%n] == colors[(r+1)%n]) l = r+1;
r++;
}
return ans;
}
}
```
| 2 | 0 |
['Sliding Window', 'Java']
| 0 |
alternating-groups-ii
|
💪O(N) || EXTEND, SLIDE, AND CONQUER || SLIDING WINDOW
|
on-extend-slide-and-conquer-sliding-wind-yfke
|
IntuitionSince colors represents a circular array, the first and last elements are adjacent. A naive approach would involve manually handling wraparounds, which
|
Kartik_7
|
NORMAL
|
2025-03-09T17:56:43.651779+00:00
|
2025-03-09T17:56:43.651779+00:00
| 12 | false |
# Intuition
Since colors represents a circular array, the first and last elements are adjacent. A naive approach would involve manually handling wraparounds, which complicates the logic. Instead, we extend colors by appending it to itself. This allows us to treat the problem as a simple sliding window without special handling for circular cases. We only need to ensure left < mid to avoid counting beyond the original array.
# Approach
1. Extend colors by appending it to itself to simplify the circular handling.
1. Use a sliding window approach with left and right pointers.
1. Maintain Notalt, which tracks consecutive same-colored tiles in the window.
1. Expand right, updating Notalt when encountering consecutive same colors.
1. Shrink from left when the window exceeds k, adjusting Notalt.
1. If Notalt == 0, count the alternating group.
# Complexity
- Time complexity: O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
bool isalternate(int left, int right, vector<int>&temp){
for(int i=left; i<right; i++){
if(temp[i]==temp[i+1]) return false;
}
return true;
}
int numberOfAlternatingGroups(vector<int>& colors, int k) {
vector<int>temp=colors;
for(int i=0; i<colors.size(); i++){
temp.push_back(colors[i]);
}
int n=temp.size(); int cnt=0; int alt = 0;
int left=0; int right=0; int mid=n/2;
while(left<mid &&right<n){
if(right > left && temp[right] == temp[right - 1]) alt++;
if(right-left+1>k){
if(temp[left] == temp[left + 1]) alt--;
left++;
}
if(left<mid && right-left+1==k && alt==0){
cnt++;
}
right++;
}
return cnt;
}
};
```
| 2 | 0 |
['Sliding Window', 'C++']
| 0 |
alternating-groups-ii
|
✅ ☕️JAVA || Sliding Window || O(n) Solution || 2 ms Beats 98%
|
java-sliding-window-on-solution-2-ms-bea-hpba
|
IntuitionAs other developer, my first intution was double for loop and slidingWindow. However, the system won't allow this due to time limit exceeded exception.
|
wilsonthiesman17
|
NORMAL
|
2025-03-09T16:38:52.976089+00:00
|
2025-03-09T16:38:52.976089+00:00
| 42 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
As other developer, my first intution was double for loop and $$slidingWindow$$. However, the system won't allow this due to time limit exceeded exception.
This new approach uses the idea of counting **how many times a color (element) is changing** inside the `colors` array and assess their validity.
# Approach
<!-- Describe your approach to solving the problem. -->
As given in the problem statement where the group needs to alternate, this approach considers something as valid when `arr[i] != arr[i - 1]`.
Everytime a **valid** scenario happens, we increment our counter `count`.
In contrast, when an **invalid** scenario happens, we **assess** our alternate-groupings condition and reset the `count` to `0`.
The assessment in `assess(int count, int k, int length)` function is simple.
1. If the `count` is below `k`, the alternating elements are smaller than `k`, thus it can't be considered as a valid $$alternatingGroup$$ in this sub-group.
2. If the `count` has the same value as `k`, then there can only be one valid $$alternatingGroup$$ in this sub-group.
3. If the `count` is as big as the number of elements inside of `colors`, then if we think using $$sliding Window$$ approach, there can be `colors.length` valid $$alternatingGroup$$ in this sub-group.
4. Other than that, the number of valid $$alternatingGroup$$ in this sub-group can follow the rule of **"how many slidingWindow can be performed inside an array of size m"** : $$m - slidingWindow.size + 1$$
One special condition is added:
When the **first** and **last** elements are valid, we need to concatenate the `count` of the two sub-groups.
Due to this extra checking condition, we need to make sure of two things:
- Skip the first `assess(int count, int k, int length)` function call to avoid double counting and saving the value into a variable (`firstSum`) **only if** the sub-group includes the first element of the array (`connected = true`).
- Perform `assess(int count, int k, int length)` into the first valid $$alternatingGroup$$ sub-group when the **first** and **last** elements are **invalid**.
# Complexity
- Time complexity: $$O(n)$$
We run a loop for `colors.length` iterations, disregarding the factor of `k` into the number of iteration that needs to be performed.
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(1)$$
Fixed number of variables are used and does not create any array nor collections.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
private int assess(int count, int k, int length) {
if (count + 1 < k) {
return 0;
} else if (count + 1 == k) {
return 1;
} else if (count == length) {
return length;
}
return (count + 1 - k + 1);
}
public int numberOfAlternatingGroups(int[] colors, int k) {
int result = 0;
int count = 0;
boolean connected = false;
int firstSum = 0;
for (int i = 1; i <= colors.length; ++i) {
if (colors[i % colors.length] != colors[i - 1]) {
count++;
if (i == 1) {
connected = true;
}
if (i == colors.length && connected) {
count += firstSum;
firstSum = 0;
}
}else {
if (connected && firstSum == 0) {
firstSum = count;
if (i != colors.length) {
count = 0;
}
continue;
}
result += this.assess(count, k, colors.length);
count = 0;
}
}
if (firstSum != 0) {
count = firstSum;
}
result += this.assess(count, k, colors.length);
return result;
}
}
```
---

**p.s This is my first ever post... please leave any construction feedbacks if any :)**
| 2 | 0 |
['Java']
| 0 |
alternating-groups-ii
|
Optimized Solution || Explanation || Complexities
|
optimized-solution-explanation-complexit-p792
|
IntuitionThe problem asks to count the number of alternating groups of size k in a circular array.
An alternating group is a sequence where consecutive elements
|
Anurag_Basuri
|
NORMAL
|
2025-03-09T16:26:07.809345+00:00
|
2025-03-09T16:26:07.809345+00:00
| 43 | false |
# Intuition
The problem asks to count the number of **alternating groups** of size `k` in a **circular array**.
An **alternating group** is a sequence where consecutive elements are different, following a pattern like `A → B → A → B`.
Since the array is **circular**, special handling is required to manage the wrap-around condition.
---
# Approach
1. **Initialization:**
- Create `count` to track the number of valid alternating groups.
- Initialize `curLen = 1` to track the current alternating sequence length.
- Use `prevColor = colors[0]` as the starting reference color.
2. **Iterate Through the Array:**
- Loop from index `1` to `n + k - 1`.
- Use `idx = i % n` to calculate the circular index.
3. **Check Conditions:**
- **If `colors[idx] == prevColor`:**
➤ The pattern breaks.
➤ Reset `curLen = 1`.
➤ Update `prevColor` to the current color.
- **If `colors[idx] != prevColor`:**
➤ The alternating pattern continues.
➤ Increment `curLen`.
➤ If `curLen >= k`, increment `count`.
4. **Return the Result:**
- Return `count` as the final answer.
---
# Complexity Analysis
- **Time Complexity:** $$O(n+k)$$ — Each element is processed once with constant-time checks.
- **Space Complexity:** $$O(1)$$ — Only a few variables are used; no extra data structures are required.
---
# Edge Cases
✅ **Single element array:** Handles the smallest possible input.
✅ **All identical elements:** Correctly returns `0` when no alternating groups exist.
✅ **Perfect alternating pattern:** Efficiently identifies maximum alternating sequences.
✅ **Circular boundary conditions:** Properly manages groups that wrap around the array’s endpoints.
# Code
``` cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int n = colors.size();
int count = 0;
int curLen = 1;
int prevColor = colors[0];
// Loop through the array with circular traversal logic
for (int i = 1; i < n + k - 1; i++) {
int idx = i % n; // Circular index calculation
// If the current color matches the previous one
if (colors[idx] == prevColor) {
curLen = 1; // Reset the alternating sequence length
prevColor = colors[idx]; // Update the previous color
continue;
}
// Extend the alternating sequence
curLen++;
// If alternating sequence reaches at least k, count it
if (curLen >= k) {
count++;
}
// Update previous color for the next iteration
prevColor = colors[idx];
}
return count;
}
};
```
```java []
class Solution {
public int numberOfAlternatingGroups(int[] colors, int k) {
int n = colors.length;
int count = 0;
int curLen = 1;
int prevColor = colors[0];
// Loop through the array with circular traversal logic
for (int i = 1; i < n + k - 1; i++) {
int idx = i % n; // Circular index calculation
// If the current color matches the previous one
if (colors[idx] == prevColor) {
curLen = 1; // Reset the alternating sequence length
prevColor = colors[idx]; // Update the previous color
continue;
}
// Extend the alternating sequence
curLen++;
// If alternating sequence reaches at least k, count it
if (curLen >= k) {
count++;
}
// Update previous color for the next iteration
prevColor = colors[idx];
}
return count;
}
}
```
``` python []
class Solution:
def numberOfAlternatingGroups(self, colors: list[int], k: int) -> int:
n = len(colors)
count = 0
curLen = 1
prevColor = colors[0]
# Loop through the array with circular traversal logic
for i in range(1, n + k - 1):
idx = i % n # Circular index calculation
# If the current color matches the previous one
if colors[idx] == prevColor:
curLen = 1 # Reset the alternating sequence length
prevColor = colors[idx] # Update the previous color
continue
# Extend the alternating sequence
curLen += 1
# If alternating sequence reaches at least k, count it
if curLen >= k:
count += 1
# Update previous color for the next iteration
prevColor = colors[idx]
return count
```
| 2 | 0 |
['Array', 'Sliding Window', 'Python3']
| 0 |
alternating-groups-ii
|
CRAZY FAST & EASY TO UNDERSTAND 🚀 TWO POINTERS 🎯 SLIDING WINDOW 🔄 O(N) ⏳ Beats 💯% 🔥
|
crazy-fast-easy-to-understand-two-pointe-iw7s
|
Intuition 🧠💡We need to count the number of groups of size k where the colors alternate without repeating. Since the array is circular, we can simulate it by usi
|
Adiverse_7
|
NORMAL
|
2025-03-09T12:34:56.724879+00:00
|
2025-03-09T12:34:56.724879+00:00
| 52 | false |
# Intuition 🧠💡
We need to count the number of groups of size `k` where the colors **alternate** without repeating. Since the array is circular, we can simulate it by using the modulo operator while iterating.
# Approach 🚀🔄
- Use a **sliding window** technique to track alternating groups.
- Keep two pointers:
- `l` (left) tracks the start of the valid group.
- `r` (right) expands the window.
- If two consecutive colors are the same, **reset** the window.
- If the window size exceeds `k`, **move `l` forward**.
- When the window reaches size `k`, **increment the count**.
# Complexity ⏳📊
- Time complexity: $$O(n)$$ ✅
- Space complexity: $$O(1)$$ ✅
# Code 💻🔥
```cpp []
class Solution
{
public:
int numberOfAlternatingGroups(vector<int> &colors, int k)
{
//brother below is the wrong approach because we consume more space
// colors.insert(colors.end(), colors.begin(), colors.end());
int n = colors.size();
int l = 0, r = 1;
int count = 0;
while (r < (n + (k - 1)))
{
if (colors[r % n] == colors[(r - 1) % n])
{
l = r;
}
if (r - l + 1 > k)
l++;
if (r - l + 1 == k)
count++;
r++;
}
return count;
}
};
```
| 2 | 0 |
['Array', 'Sliding Window', 'C++']
| 0 |
alternating-groups-ii
|
C++✅✅| One pass | Simplest approach🚀🚀
|
c-one-pass-simplest-approach-by-aayu_t-qkit
|
Code
|
aayu_t
|
NORMAL
|
2025-03-09T12:04:07.473398+00:00
|
2025-03-09T12:04:07.473398+00:00
| 117 | false |
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int ans = 0, cnt = 1, n = colors.size();
for(int i = 1; i < (n + k - 1); i++) {
if(colors[i % n] != colors[(i - 1) % n]) {
cnt++;
}
else cnt = 1;
if(cnt >= k) ans++;
}
return ans;
}
};
```
| 2 | 0 |
['Array', 'C++']
| 0 |
alternating-groups-ii
|
✅✅ Sliding Window || Beginner Friendly || Easy Solution
|
sliding-window-beginner-friendly-easy-so-tnho
|
Intuition
We need to count alternating groups of length at least k, considering a circular array behavior.
Instead of handling circular behavior separately, we
|
Karan_Aggarwal
|
NORMAL
|
2025-03-09T10:14:48.516334+00:00
|
2025-03-09T10:14:48.516334+00:00
| 15 | false |
# Intuition
- We need to count alternating groups of length at least `k`, considering a circular array behavior.
- Instead of handling circular behavior separately, we extend the array by appending the first `k-1` elements to the end.
- This ensures we can check valid groups that might wrap around the end.
# Approach
1. Extend `colors` by appending the first `k-1` elements to handle circular cases.
2. Use two pointers (`i` and `j`) to track an alternating sequence.
3. If consecutive elements are the same, reset `i = j`.
4. If the alternating sequence reaches `k`, increment `ans` and move `i` forward.
5. Continue iterating until we process all `N = n + (k-1)` elements.
# Time Complexity
- The loop runs **O(n + k)**, which simplifies to **O(n)**.
- Appending `k-1` elements takes **O(k)** but remains within **O(n)**.
# Space Complexity
- Since we modify the input array, extra space used is **O(1)**.
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int n=colors.size();
int ans=0;
int N=n+(k-1);
for(int i=0;i<k-1;i++) colors.push_back(colors[i]);
int i=0,j=1;
while(j<N){
if(colors[j]==colors[j-1]){
i=j;
j++;
continue;
}
if(j-i+1==k){
i++;
ans++;
}
j++;
}
return ans;
}
};
```
# Have a Good Day 😊 UpVote?
| 2 | 0 |
['Array', 'Sliding Window', 'C++']
| 0 |
alternating-groups-ii
|
✅✅ Sliding Window || Easy Solution
|
sliding-window-easy-solution-by-karan_ag-nblh
|
Intuition
We need to count the number of valid alternating groups of length at least k.
An alternating group is a contiguous subarray where adjacent elements ar
|
Karan_Aggarwal
|
NORMAL
|
2025-03-09T09:40:11.556871+00:00
|
2025-03-09T09:40:11.556871+00:00
| 14 | false |
# Intuition
- We need to count the number of valid alternating groups of length at least `k`.
- An alternating group is a contiguous subarray where adjacent elements are different.
- We traverse the array while tracking the length of the current alternating sequence.
- If the sequence length reaches `k`, we increment our answer.
# Approach
1. Initialize `length = 1` and `last = colors[0]` to track the current alternating group.
2. Traverse the array:
- If `colors[i] == last`, reset `length = 1`.
- Otherwise, increase `length` and check if it reaches `k`.
- Update `last = colors[i]` after each iteration.
3. Handle edge cases separately if necessary.
4. Return the total count of valid alternating groups.
# Time Complexity
- We iterate through the array once, making the time complexity **O(n)**.
# Space Complexity
- We use only a few integer variables, so the space complexity is **O(1)**.
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int n=colors.size();
int ans=0;
int length=1;
int last=colors[0];
for(int i=1;i<n;i++){
if(colors[i]==last){
length=1;
last=colors[i];
continue;
}
length++;
if(length>=k) ans++;
last=colors[i];
}
for(int i=0;i<k-1;i++){
if(colors[i]==last){
length=1;
last=colors[i];
break;
}
length++;
if(length>=k) ans++;
last=colors[i];
}
return ans;
}
};
```
# Have a Good Day 😊 UpVote?
| 2 | 0 |
['Array', 'Sliding Window', 'C++']
| 0 |
alternating-groups-ii
|
simple py solution
|
simple-py-solution-by-noam971-1fjs
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
noam971
|
NORMAL
|
2025-03-09T09:28:43.092864+00:00
|
2025-03-09T09:28:43.092864+00:00
| 29 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def numberOfAlternatingGroups(self, colors: List[int], k: int) -> int:
n = len(colors)
res, l = 0, 0
for r in range(1, n + k - 1):
if colors[r % n] == colors[(r - 1) % n]:
l = r
if k <= r - l + 1:
res += 1
return res
```
| 2 | 0 |
['Python3']
| 0 |
alternating-groups-ii
|
Sliding Window/ Deque/ Easy to Understand for Java Users
|
sliding-window-deque-easy-to-understand-4s5q9
|
IntuitionThe problem involves finding the number of alternating groups of size k in a circular array colours[]. An alternating group is defined as a sequence of
|
Shashwata_32
|
NORMAL
|
2025-03-09T08:06:33.446870+00:00
|
2025-03-09T08:06:33.446870+00:00
| 105 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem involves finding the number of alternating groups of size k in a circular array colours[]. An alternating group is defined as a sequence of elements where no two consecutive elements are the same. The array is circular, meaning that after the last element, the sequence wraps around to the first element. So we need to take an hypothetical array of size n+k-1.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Deque Usage: We use a deque (double-ended queue) to keep track of the current sequence of elements. The deque allows us to efficiently add elements to the front and remove elements from the back.
2. Iterating Through the Array: We iterate through the array, considering each element and its position in the circular array (using i % n to handle the circular nature).
3. Checking for Alternating Sequence:
If the deque is empty or the current element is different from the first element in the deque, we add it to the front of the deque.
4. If the current element is the same as the first element in the deque, we reset the deque by clearing it and then adding the current element.
5. Counting Valid Groups:
Whenever the size of the deque reaches k, it means we have found a valid alternating group of size k. We increment the count and then remove the last element from the deque to make room for the next element.
6. Final Count: After iterating through the array, the count will hold the total number of valid alternating groups of size k.
# Complexity
Time complexity:
=
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Outer Loop:
1. The loop runs for i = 0 to i = n + k - 2, which means it iterates n + k - 1 times.
2. Here, n is the length of the array col, and k is the size of the alternating group.
- Deque Operations:
1. q.getFirst(): This operation is O(1) because accessing the first element of a deque is constant time.
2. q.addFirst(): Adding an element to the front of the deque is O(1).
3. q.clear(): Clearing the deque is O(m), where m is the number of elements in the deque. In the worst case, m can be up to k.
4. q.removeLast(): Removing the last element of the deque is O(1).
- Condition Checks:
All condition checks (e.g., q.isEmpty(), q.getFirst() != col[i % n]) are O(1).
- Worst-Case Scenario:
The worst case occurs when the deque is frequently cleared. For example, if the array has many consecutive duplicates, the q.clear() operation will be called often.
Each q.clear() operation takes O(k) time, and in the worst case, it can happen O(n) times.
Therefore, the total time complexity is:
O((n+k−1)⋅k)=O(nk+k^2)
Since k is typically much smaller than n, we can simplify this to O(nk).
Space complexity:
=
1. Deque Usage:
The deque q stores at most k elements at any point in time. Therefore the space used by the deque is O(k).
2. Other Variables:
The variables i, count, rob, and n use constant space, i.e., O(1).
3. Total Space Complexity:
The dominant space usage comes from the deque, so the total space complexity is O(k).
Summary:
=
1. Time Complexity: O(nk)
The loop runs n + k - 1 times, and in the worst case, each iteration involves operations that depend on k.
2. Space Complexity: O(k)
The deque stores at most k elements, and no additional significant space is used.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int numberOfAlternatingGroups(int[] col, int k) {
int i,count=0,rob=-1,n=col.length;
Deque<Integer> q=new ArrayDeque<>();
for(i=0;i<n+k-1;i++)
{
if(q.isEmpty()||q.getFirst()!=col[i%n])
q.addFirst(col[i%n]);
else if(q.getFirst()==col[i%n])
{
q.clear();
q.addFirst(col[i%n]);
}
if(q.size()==k)
{
count++;
q.removeLast();
}
}
return count;
}
}
```
| 2 | 0 |
['Java']
| 1 |
alternating-groups-ii
|
EASY , intuitive and Time and Space optimizing solution, GOOD for competitive coding
|
easy-intuitive-and-time-and-space-optimi-g9ex
|
IntuitionKey Insight
The problem requires checking k-length groups in a circular array where each group has alternating colors. Each valid group must have exact
|
SUJALAHAR
|
NORMAL
|
2025-03-09T07:45:15.616450+00:00
|
2025-03-09T07:56:23.009688+00:00
| 78 | false |
# Intuition
Key Insight
The problem requires checking k-length groups in a circular array where each group has alternating colors. Each valid group must have exactly k-1 color switches between adjacent tiles.
# Approach
Solution Steps(only three steps)
1.Handle Circular Nature
Extend the original array by appending the first k-1 elements (to simulate circular wrapping without complex modulo operations).
2.Track Color Switches
Create a prefix array where each entry counts the total switches (0→1 or 1→0) from the start up to that position.
3.Check Valid Groups
For every possible window of k tiles, check if the number of switches in that window equals k-1 (indicating perfect alternation).
Example Walkthrough
Input: colors =, k = 3
Extended Array: `` (add first 2 elements to handle circular wrap)
Prefix Array (Switches Counted):
Indices: 0 1 2 3 4 5 6
Values: 0 1 2 3 4 4 5
Valid Groups (3 switches with 2 transitions each):
Positions 0-2: ``
Positions 1-3: ``
Positions 2-4: ``
Result: 3 valid groups ✅
Code Explanation
Step 1: Extend the Array
# Code
```cpp []
vector<int>v = colors;
for(int i=1; i<k; i++){
v.push_back(v[i-1]);
}
```
Appends the first k-1 elements of colors to itself.
Simplifies checking groups that wrap around the array's end.
Step 2: Build Prefix Array
# Code
```cpp []
vector<int>cprefix(v.size());
cprefix[0] = 0;
for(int i=1; i<v.size(); i++){
cprefix[i] = (v[i]!=v[i-1]) + cprefix[i-1];
}
```
cprefix[i] stores the total switches between v and v[i].
Example: For v =, cprefix becomes `` (two switches at positions 0→1 and 1→2).
Step 3: Count Valid Groups
# Code
```cpp []
int cnt = 0;
for(int i=k-1; i<v.size(); i++){
if((cprefix[i]-cprefix[i-(k-1)]) == k-1) cnt++;
}
```
For each window ending at index i, check if the difference in switches equals k-1.
Mathematically, this ensures exactly k-1 transitions in the current window of k elements.
Why This Works
Circular Handling: The extended array allows seamless checks for groups crossing the original array's end.
Switch Counting: The prefix array efficiently tracks transitions, enabling O(1) window checks.
Time Complexity: O(n + k) (linear time), making it highly efficient for large inputs.
This approach cleverly combines preprocessing and prefix sums to solve the problem optimally! 🚀
# Complexity
- Time complexity: Time Complexity: O(n + k) (linear time), making it highly efficient for large inputs.
- Space complexity: The prefix array efficiently tracks transitions, enabling O(1) window checks.
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
vector<int>v = colors;
for(int i=1;i<k;i++){
v.push_back(v[i-1]);
}
vector<int>cprefix(v.size());
cprefix[0] = 0;
for(int i=1;i<v.size();i++){
cprefix[i] = (v[i]!=v[i-1]) + cprefix[i-1];
}
int cnt = 0;
for(int i=k-1;i<v.size();i++){
if((cprefix[i]-cprefix[i-(k-1)]) == k-1) cnt++;
}
return cnt;
}
};
```
| 2 | 0 |
['Array', 'Two Pointers', 'Sliding Window', 'Prefix Sum', 'C++']
| 0 |
alternating-groups-ii
|
✅💥BEATS 100%✅💥 || 🔥Easy CODE🔥 || ✅💥EASY EXPLAINATION✅💥 || JAVA || C++ || PYTHON
|
beats-100-easy-code-easy-explaination-ja-30bl
|
IntuitionThe problem requires counting subarrays of consecutive elements in a given array, colors, where the subarrays meet specific conditions. Specifically, w
|
chaitanyameshram_07
|
NORMAL
|
2025-03-09T07:43:14.901179+00:00
|
2025-03-09T07:43:14.901179+00:00
| 132 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem requires counting subarrays of consecutive elements in a given array, colors, where the subarrays meet specific conditions. Specifically, we track consecutive subarrays of length k or greater and handle transitions between colors. The idea is to efficiently count these subarrays by keeping track of consecutive runs and handling special cases when the sequence of colors transitions or loops.
1. Consecutive Elements: If consecutive elements are the same, we increment the length of the run. When the colors change, the current run ends, and we compare it to the threshold k.
2. First Color Transition: After encountering the first color change, we track the minimum of the previous consecutive run and the threshold k.
3. Final Handling: If the last element is the same as the first one, the loop of colors might affect the result, and adjustments are made accordingly.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Initialize variables to track the current run (cnt), the minimum length for the first transition (firstcnt), and the final result (ans).
2. Iterate over the colors array to count runs and handle transitions.
3. Adjust the final result for edge cases, such as when the first and last elements are the same and the length of the array matches the condition.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(n)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(1)
# Code
```java []
class Solution {
public int numberOfAlternatingGroups(int[] colors, int k) {
// int cnt = 1;
// int res = 0;
// int firstcnt = 0;
// for (int i = 1; i < colors.length; i++) {
// if (colors[i] != colors[i-1]) cnt++;
// else {
// if (firstcnt == 0) firstcnt = Math.min(k-1, cnt);
// cnt = 1;
// }
// if (cnt >= k) res++;
// }
// if (colors[colors.length-1] == colors[0]) cnt = -1000;
// if (cnt == colors.length) return cnt;
// return res + Math.max(0, firstcnt + Math.min(cnt, k-1) - k + 1);
int cnt =1;
int firstcnt=0;
int ans =0;
for(int i =1;i<colors.length;i++){
if(colors[i]!=colors[i-1])cnt++;
else{
if(firstcnt==0){
firstcnt =Math.min(k-1,cnt);
}
cnt =1;
}
if(cnt>=k) ans++;
}
if(colors[colors.length-1] ==colors[0]) cnt =-1000;
if(cnt==colors.length)return cnt;
return ans+ Math.max(0,firstcnt+Math.min(cnt,k-1)-k+1);
}
}
```
``` python []
class Solution:
def countSubarrays(self, colors, k):
cnt = 1
firstcnt = 0
ans = 0
for i in range(1, len(colors)):
if colors[i] != colors[i - 1]:
cnt += 1
else:
if firstcnt == 0:
firstcnt = min(k - 1, cnt)
cnt = 1
if cnt >= k:
ans += 1
if colors[-1] == colors[0]:
cnt = -1000
if cnt == len(colors):
return cnt
return ans + max(0, firstcnt + min(cnt, k - 1) - k + 1)
```
``` c++ []
class Solution {
public:
int countSubarrays(vector<int>& colors, int k) {
int cnt = 1;
int firstcnt = 0;
int ans = 0;
for (int i = 1; i < colors.size(); i++) {
if (colors[i] != colors[i - 1]) {
cnt++;
} else {
if (firstcnt == 0) {
firstcnt = min(k - 1, cnt);
}
cnt = 1;
}
if (cnt >= k) {
ans++;
}
}
if (colors[colors.size() - 1] == colors[0]) {
cnt = -1000;
}
if (cnt == colors.size()) {
return cnt;
}
return ans + max(0, firstcnt + min(cnt, k - 1) - k + 1);
}
};
```
| 2 | 0 |
['Array', 'Math', 'Dynamic Programming', 'Bit Manipulation', 'Sliding Window', 'Enumeration', 'C++', 'Java', 'Python3']
| 0 |
alternating-groups-ii
|
🚀 Count Alternating Groups in Python — Super Simple & Efficient!
|
count-alternating-groups-in-python-super-d1jy
|
🧠 Intuition
💡 First Thought: The goal is to count alternating groups of colors of length k.
🔄 Since the array is cyclic, we extend it to handle wraparounds easi
|
kaushik0325kumar
|
NORMAL
|
2025-03-09T07:09:00.338200+00:00
|
2025-03-09T07:09:00.338200+00:00
| 7 | false |
🧠 Intuition
💡 First Thought: The goal is to count alternating groups of colors of length k.
🔄 Since the array is cyclic, we extend it to handle wraparounds easily.
🛠️ Approach
1️⃣ Extend the colors list by adding the first k-1 elements to the end to handle cyclic groups.
2️⃣ Iterate through the list, grouping alternating colors.
3️⃣ Store these groups in b, ensuring each segment alternates.
4️⃣ Check if the last element needs to be handled separately.
5️⃣ Count the groups that match k, and if longer, break them down accordingly.
⏳ Complexity
Time Complexity: 🚀 O(n) – We iterate through the list a few times.
Space Complexity: 💾 O(n) – Extra space used for storing alternating groups.
# Code
```python3 []
class Solution:
def numberOfAlternatingGroups(self, colors: List[int], k: int) -> int:
colors.extend(colors[:k-1])
b=[]
count=0
a=[]
for i in range(0,len(colors)-1):
if colors[i]!=colors[i+1]:
a.append(colors[i])
else:
a.append(colors[i])
b.append(a)
a=[]
b.append(a)
if( len(b) > 0 and len(b[-1]) > 0 and colors[-1] == b[-1][-1]):
b.append(colors[-1])
else:
b[-1].append(colors[-1])
for i in b:
if(len(i)==k):
count+=1
elif(len(i)>k):
count+=(1+len(i)-k)
return count
```
| 2 | 0 |
['Python3']
| 0 |
alternating-groups-ii
|
Simple and easy Iterative Solution | O(n) | JAVA | C++ | PYTHON
|
simple-and-easy-iterative-solution-on-ja-lqew
|
IntuitionIf we have an alternating group of length n, the number of alternating groups of length k we can create is:Explanation:
An alternating group of length
|
deepanshu2202
|
NORMAL
|
2025-03-09T06:12:51.902292+00:00
|
2025-03-09T06:12:51.902292+00:00
| 19 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
If we have an **alternating group** of length `n`, the number of alternating groups of length `k` we can create is:
(n - k + 1)
### Explanation:
- An alternating group of length **n** consists of **n** consecutive elements.
- To form an alternating group of length **k**, we take **k** consecutive elements at a time.
- The first group starts at index **0** (covering indices `0` to `k-1`), the second group starts at index **1** (`1` to `k`), and so on.
- The last possible group starts at index **n - k** (`n-k` to `n-1`).
- Thus, the total number of groups is **(n - k + 1)**.
### Example
Number of alternating groups = (n - k + 1)
let colors = [1, 0, 1, 0, 1], k = 3
groups => (1, 0, 1), (0, 1, 0), (1, 0, 1) = 3
(5 - 3 + 1) = 3
# Approach
<!-- Describe your approach to solving the problem. -->
- We'll use two variables, `currCount` and `totalCount`, to keep track of the length of the current alternating group and the total number of alternating groups.
- If adjacent elements are different, we can simply increment `currCount` by `1`. Otherwise, we'll add `(currCount - k + 1)` to `totalCount` if `currCount >= k`.
- If the first and last elements are the same, we can simply return `totalCount` because there won't be a cyclic group. However, if they are different, we'll continue to increment `currCount`, iterating from the `0th` index to the `(k - 1)th` index because we have already counted from the `0th` index to the `kth` index in the first iteration. Finally, we can simply return `totalCount`.
# Complexity
- Time complexity: O(n + k)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int numberOfAlternatingGroups(int[] colors, int k) {
int currCount = 1, totalCount = 0;
int i = 0;
while (i < colors.length - 1) {
if (colors[i] == colors[i + 1]) {
totalCount += (currCount >= k) ? (currCount - k + 1) : 0;
currCount = 1;
} else {
currCount++;
}
i++;
}
if (colors[0] != colors[colors.length - 1]) {
currCount++;
for (i = 0; i < (k - 2) && colors[i] != colors[i + 1]; i++)
currCount++;
}
totalCount += (currCount >= k) ? (currCount - k + 1) : 0;
return totalCount;
}
}
```
```C++ []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int currCount = 1, totalCount = 0;
int i = 0;
while (i < colors.size() - 1) {
if (colors[i] == colors[i + 1]) {
totalCount += (currCount >= k) ? (currCount - k + 1) : 0;
currCount = 1;
} else {
currCount++;
}
i++;
}
if (colors[0] != colors[colors.size() - 1]) {
currCount++;
for (i = 0; i < (k - 2) && colors[i] != colors[i + 1]; i++)
currCount++;
}
totalCount += (currCount >= k) ? (currCount - k + 1) : 0;
return totalCount;
}
};
```
```Python []
class Solution:
def numberOfAlternatingGroups(self, colors: list[int], k: int) -> int:
curr_count, total_count = 1, 0
i = 0
while i < len(colors) - 1:
if colors[i] == colors[i + 1]:
total_count += (curr_count - k + 1) if curr_count >= k else 0
curr_count = 1
else:
curr_count += 1
i += 1
if colors[0] != colors[-1]:
curr_count += 1
for i in range(min(k - 2, len(colors) - 1)):
if colors[i] == colors[i + 1]:
break
curr_count += 1
total_count += (curr_count - k + 1) if curr_count >= k else 0
return total_count
```
| 2 | 0 |
['Python', 'C++', 'Java']
| 0 |
alternating-groups-ii
|
Easy code | Must try | In Java
|
easy-code-must-try-in-java-by-notaditya0-zru7
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
NotAditya09
|
NORMAL
|
2025-03-09T06:07:27.860775+00:00
|
2025-03-09T06:07:27.860775+00:00
| 203 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int numberOfAlternatingGroups(int[] colors, int k) {
final int n = colors.length;
int ans = 0;
int alternating = 1;
for (int i = 0; i < n + k - 2; ++i) {
alternating = colors[i % n] == colors[(i - 1 + n) % n] ? 1 : alternating + 1;
if (alternating >= k)
++ans;
}
return ans;
}
}
```
| 2 | 0 |
['Java']
| 0 |
alternating-groups-ii
|
Simplest Java Solution🚀|| Well Explained🔥|| Beginner Friendly✅
|
simplest-java-solution-well-explained-be-fzsg
|
IntuitionThe problem requires finding contiguous subarrays of length k in a circular array that follow an alternating pattern (0,1,0,1, etc.). Since the array i
|
ghumeabhi04
|
NORMAL
|
2025-03-09T05:50:55.598978+00:00
|
2025-03-09T05:50:55.598978+00:00
| 126 | false |
# Intuition
The problem requires finding contiguous subarrays of length k in a circular array that follow an alternating pattern (0,1,0,1, etc.). Since the array is circular, we must also check sequences that wrap around from the end to the beginning.
# Approach
1. Extend the Array for Circularity:
- Since the array is circular, we append the first k−1 elements to the end to handle wrap-around cases seamlessly.
2. Sliding Window Approach:
- Maintain a sliding window of size k while iterating through the extended array.
- Use two pointers:
- i (start of window)
- j (end of window, moving forward).
- If a non-alternating pattern is found, reset the window (i = j).
- If the window reaches size k, count it as a valid alternating group and move i forward to slide the window.
3. Return the Count:
- Count the valid alternating groups found.
# Complexity
- Time complexity: O(n)
- Space complexity: O(n)
# Code
```java []
class Solution {
public int numberOfAlternatingGroups(int[] colors, int k) {
ArrayList<Integer> list = new ArrayList<>();
for(int i: colors) list.add(i);
for(int i=0; i<k-1; i++) list.add(colors[i]);
// System.out.println(list);
int l = list.size();
int cnt = 0;
int i=0;
int j=1;
while(j<l) {
if(list.get(j) == list.get(j-1)) {
i = j;
}
if(j-i+1 == k) {
i++;
cnt++;
}
j++;
}
return cnt;
}
}
```
| 2 | 0 |
['Array', 'Sliding Window', 'Java']
| 0 |
alternating-groups-ii
|
Count Alternating Groups in a Circular Array
|
count-alternating-groups-in-a-circular-a-tjqr
|
IntuitionThe problem involves identifying groups of size k in a circular array where colors alternate. To achieve this efficiently:
Identify indices where adjac
|
jeetkarena3
|
NORMAL
|
2025-03-09T05:48:29.998688+00:00
|
2025-03-09T05:48:29.998688+00:00
| 38 | false |
## Intuition
The problem involves identifying groups of size `k` in a circular array where colors alternate. To achieve this efficiently:
1. Identify indices where adjacent elements fail to alternate (failure points).
2. Calculate the number of valid `k`-sized groups that exist between these failure points.
---
## Approach
1. **Identify Failure Points:**
Loop through the array and record indices where adjacent colors are the same (`colors[i] == colors[i + 1]`). Additionally, check the circular edge (last and first elements).
2. **Handle Full Alternation Case:**
If no failure points exist, the entire array is alternating, and the result is the total number of possible groups (`n`).
3. **Extend for Circular Wrap-Around:**
Append the first failure index plus the array size (`fails[0] + n`) to handle groups spanning the end and start of the array.
4. **Compute Valid Groups:**
Use sliding windows of consecutive failure points to calculate the gap between them. For each gap:
- The number of valid `k`-sized groups is given by `gap = pair[1] - pair[0] - k + 1` (only positive gaps contribute to the count).
---
## Complexity
- **Time complexity:**
$$O(n)$$ for identifying failure points and computing valid groups (single pass through the array and failure points).
- **Space complexity:**
$$O(n)$$ for storing failure points.
---
## Code
```rust []
impl Solution {
pub fn number_of_alternating_groups(colors: Vec<i32>, k: i32) -> i32 {
let n = colors.len();
let k = k as i32;
let n_i32 = n as i32;
// Step 1: Collect indices where adjacent colors fail to alternate
let mut fails: Vec<i32> = (0..n - 1)
.filter(|&i| colors[i] == colors[i + 1])
.map(|i| i as i32)
.collect();
// Step 2: Check the wrap-around case (last and first elements)
if colors[n - 1] == colors[0] {
fails.push((n - 1) as i32);
}
// Step 3: Handle full alternation (no failures)
if fails.is_empty() {
return n_i32;
}
// Step 4: Extend failure points for circular wrap-around
fails.push(fails[0] + n_i32);
// Step 5: Calculate valid groups using sliding windows of failure points
fails
.windows(2)
.map(|pair| {
let gap = pair[1] - pair[0] - k + 1;
if gap > 0 {
gap
} else {
0
}
})
.sum()
}
}
```
| 2 | 0 |
['Array', 'Sliding Window', 'Rust']
| 0 |
alternating-groups-ii
|
Easy explanation of javaScript solution
|
easy-explanation-of-javascript-solution-objwu
|
IntuitionThe problem requires finding contiguous subarrays of length k in a circular array where elements alternate in color. Since the array is circular, the l
|
Samandardev02
|
NORMAL
|
2025-03-09T05:46:27.616088+00:00
|
2025-03-09T05:46:27.616088+00:00
| 74 | false |
# Intuition
The problem requires finding contiguous subarrays of length `k` in a circular array where elements alternate in color. Since the array is circular, the last and first elements are considered adjacent. The naive approach would be to iterate over every possible subarray and check if it alternates, but this would be inefficient for large inputs.
# Approach
We use a **sliding window approach** to optimize the solution. Instead of checking every possible subarray separately, we maintain a **valid alternating count** while iterating through the array. If the current tile alternates with the previous one, we increase the count; otherwise, we reset it. If the alternating count reaches at least `k`, we increase the result counter. The circular nature is handled using modulo indexing (`i % n`).
# Complexity
- Time complexity:
- $$O(n)$$ — We traverse the array only once, making this an optimal approach.
- Space complexity:
- $$O(1)$$ — We only use a few extra variables, independent of `n`.
# Code
```javascript
/**
* @param {number[]} colors
* @param {number} k
* @return {number}
*/
var numberOfAlternatingGroups = function(colors, k) {
let count = 0, valid = 1;
const n = colors.length;
for (let i = 1; i < n + k - 1; i++) {
let currIndex = i % n;
let prevIndex = (i - 1) % n;
if (colors[currIndex] !== colors[prevIndex]) {
valid++;
} else {
valid = 1;
}
if (valid >= k) count++;
}
return count;
};
| 2 | 0 |
['JavaScript']
| 1 |
alternating-groups-ii
|
3 Different Approaches💯 || C++ & Java || 1 pass || 30ms Beats 100%😎
|
3-different-approaches-c-java-1-pass-30m-9ead
|
IntuitionApproach - 1 (Brute Force)Complexity
Time complexity: O(n*k)
Space complexity: O(1)
CodeApproach - 2 (Sliding Window using Khandani Template)Complexit
|
Uchariya
|
NORMAL
|
2025-03-09T04:12:54.529685+00:00
|
2025-03-09T04:12:54.529685+00:00
| 39 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach - 1 (Brute Force)
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(n*k)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int n = colors.size();
for (int i = 0; i < k - 1; i++) {
colors.push_back(colors[i]);
}
int result = 0;
for (int i = 0; i < n; i++) {
bool isAlternating = true;
for (int j = i; j < i + k - 1; j++) {
if (colors[j] == colors[j + 1]) {
isAlternating = false;
break;
}
}
if (isAlternating) {
result++;
}
}
return result;
}
};
```
```java []
class Solution {
public int numberOfAlternatingGroups(int[] colors, int k) {
int n = colors.length;
int[] extended = new int[n + k - 1];
System.arraycopy(colors, 0, extended, 0, n);
for (int i = 0; i < k - 1; i++) {
extended[n + i] = colors[i];
}
int result = 0;
for (int i = 0; i < n; i++) {
boolean isAlternating = true;
for (int j = i; j < i + k - 1; j++) {
if (extended[j] == extended[j + 1]) {
isAlternating = false;
break;
}
}
if (isAlternating) {
result++;
}
}
return result;
}
}
```
# Approach - 2 (Sliding Window using Khandani Template)
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(n*k)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int n = colors.size();
int N = n + (k-1);
for(int i = 0; i < k-1; i++) {
colors.push_back(colors[i]); //to handle wrap around (circular array)
}
int result = 0;
int i = 0;
int j = 1; //because we have to check index j-1 for checking alterate
while(j < N) {
if(colors[j] == colors[j-1]) {
i = j;
j++;
continue;
}
if(j - i + 1 == k) {
result++;
i++;
}
j++;
}
return result;
}
};
```
```java []
class Solution {
public int numberOfAlternatingGroups(int[] colors, int k) {
int n = colors.length;
int N = n + (k - 1);
int[] extended = new int[N];
System.arraycopy(colors, 0, extended, 0, n);
for (int i = 0; i < k - 1; i++) {
extended[n + i] = colors[i]; // to handle wrap-around (circular array)
}
int result = 0;
int i = 0, j = 1; // because we have to check index j-1 for checking alternate
while (j < N) {
if (extended[j] == extended[j - 1]) {
i = j;
j++;
continue;
}
if (j - i + 1 == k) {
result++;
i++;
}
j++;
}
return result;
}
}
```
# Approach - 3 (Using simple counting in 2 Pass)
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(n*k)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int n = colors.size();
int result = 0;
int length = 1; //i = 0 index wala element
int last = colors[0];
//1st Pass
for(int i = 1; i < n; i++) {
if(colors[i] == last) {
length = 1;
last = colors[i];
continue;
}
length++;
if(length >= k) {
result++;
}
last = colors[i];
}
//T.C : O(n)
//2nd Pass
for(int i = 0; i < k-1; i++) { //checking starting (k-1) elements
if(colors[i] == last) {
length = 1;
last = colors[i];
break;
}
length++;
if(length >= k) {
result++;
}
last = colors[i];
}
return result;
}
};
```
```java []
class Solution {
public int numberOfAlternatingGroups(int[] colors, int k) {
int n = colors.length;
int result = 0;
int length = 1; // i = 0 index wala element
int last = colors[0];
// 1st Pass
for (int i = 1; i < n; i++) {
if (colors[i] == last) {
length = 1;
last = colors[i];
continue;
}
length++;
if (length >= k) {
result++;
}
last = colors[i];
}
// T.C : O(n)
// 2nd Pass
for (int i = 0; i < k - 1; i++) { // checking starting (k-1) elements
if (colors[i] == last) {
length = 1;
last = colors[i];
break;
}
length++;
if (length >= k) {
result++;
}
last = colors[i];
}
return result;
}
}
```
# upvote a solution
| 2 | 0 |
['C++']
| 0 |
alternating-groups-ii
|
🔥 Two Pointer Magic 🚀 | O(N) Sliding Window + Trick to Handle Cycle| Super Easy Explanation!
|
super-easy-beginner-friendly-solution-by-hdfx
|
Number of Alternating GroupsProblem StatementGiven an array c consisting of integers and an integer k, determine the number of alternating groups of length k.
A
|
Harshit___at___work
|
NORMAL
|
2025-03-09T04:11:50.858776+00:00
|
2025-03-09T04:16:36.535927+00:00
| 33 | false |
# Number of Alternating Groups
## Problem Statement
Given an array `c` consisting of integers and an integer `k`, determine the number of alternating groups of length `k`.
An alternating group is defined as a contiguous subarray of length `k` in which adjacent elements are different.
## Intuition
The goal is to identify subarrays of length `k` that satisfy the alternating property.
Since the array is cyclic, we can extend the array by appending the first `k-1` elements to its end.
By using a two-pointer approach, we can efficiently track valid alternating groups.
## Approach
1. **Extend the array:**
- Append the first `k-1` elements of `c` to its end to handle the cyclic property.
2. **Two-pointer traversal:**
- Use two pointers `i` and `j` to traverse the array while checking for valid alternating groups.
- If `c[j]` is different from `c[j-1]`, we continue extending the window.
- If we find a valid alternating group of length `k`, increment the count and shift `i`.
- If a repetition is encountered, reset the start pointer `i` to `j`.
3. **Return the count of valid alternating groups.**
## Complexity Analysis
- **Time Complexity:**
- Since we traverse the array once using a two-pointer approach, the complexity is **O(n)**.
- **Space Complexity:**
- We only modify the existing array by appending `k-1` elements, so the extra space used is **O(k)**.
## Code Implementation
```cpp
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& c, int k)
{
int i = 0;
int j = 1;
int ans = 0;
// Extend the array to handle cyclic cases
for(int i = 0; i < k - 1; i++)
c.push_back(c[i]);
int n = c.size();
while (j < n) {
if (c[j] != c[j - 1] && (j - i + 1) != k) {
j++;
}
else if (c[j] == c[j - 1]) {
i = j;
j++;
}
else {
ans++;
i++;
j++;
}
}
return ans;
}
};
| 2 | 0 |
['Two Pointers', 'Sliding Window', 'C++']
| 0 |
alternating-groups-ii
|
[Rust] One-liner!
|
rust-one-liner-by-discreaminant2809-u65o
|
Complexity
Time complexity:
O(n+k)
Space complexity:
O(1)
Code
|
discreaminant2809
|
NORMAL
|
2025-03-09T04:07:46.419148+00:00
|
2025-03-09T04:07:46.419148+00:00
| 39 | false |
# Complexity
- Time complexity:
$$O(n + k)$$
- Space complexity:
$$O(1)$$
# Code
```rust []
impl Solution {
pub fn number_of_alternating_groups(colors: Vec<i32>, k: i32) -> i32 {
colors[1..]
.iter()
.chain(&colors[0..k as usize - 1])
.copied()
.fold((colors[0], 1, 0), |(prev, count, ans), color| {
if color != prev {
(color, count + 1, ans + (count + 1 >= k) as i32)
} else {
(color, 1, ans)
}
})
.2
}
}
```
| 2 | 0 |
['Sliding Window', 'Iterator', 'Rust']
| 1 |
alternating-groups-ii
|
Simple O(n) solution
|
simple-on-solution-by-stddaa-xbpk
|
Complexity
Time complexity: O(n)
Space complexity: O(1)
Code
|
stddaa
|
NORMAL
|
2025-03-09T03:10:05.635034+00:00
|
2025-03-09T03:10:05.635034+00:00
| 132 | false |
# Complexity
- Time complexity: $$O(n)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```golang []
func numberOfAlternatingGroups(colors []int, groupSize int) int {
left := 0 // Left pointer to track the start of the current window
right := 0 // Right pointer to expand the window
result := 0 // Count of valid alternating groups
n := len(colors) // Length of the colors array
// Iterate through the array to find valid alternating groups
for left < n {
// Move the right pointer forward
right++
// Check if the current tile and the previous tile have the same color
if colors[right % n] == colors[(right - 1) % n] {
// If they are the same, the alternating sequence breaks
// Move the left pointer to the current position to start a new window
left = right
} else if right - left + 1 == groupSize {
// If the window size equals the required group size, it's a valid group
result++ // Increment the result count
left++ // Move the left pointer to slide the window forward
}
}
return result
}
```
| 2 | 0 |
['Go']
| 0 |
alternating-groups-ii
|
python3
|
python3-by-jamesandersonswe_001-6xba
|
Code
|
jamesandersonswe_001
|
NORMAL
|
2025-03-09T03:09:59.782636+00:00
|
2025-03-09T03:09:59.782636+00:00
| 626 | false |
# Code
```python3 []
class Solution:
def numberOfAlternatingGroups(self, colors: List[int], k: int) -> int:
colors.extend(colors[:(k-1)])
count = 0
left = 0
for right in range(len(colors)):
if right > 0 and colors[right] == colors[right - 1]:
left = right
if right - left + 1 >= k:
count += 1
return count
```
| 2 | 1 |
['Python3']
| 1 |
alternating-groups-ii
|
🌈 Count Alternating Subsequences in a Circular Array
|
count-alternating-subsequences-in-a-circ-g40f
|
Approach
Extend the array
Concatenate the first k-1 elements to the end of the original string to simulate the circular behavior.
Iterate through the extende
|
lehieu99666
|
NORMAL
|
2025-03-09T02:49:24.297635+00:00
|
2025-03-09T02:49:24.297635+00:00
| 80 | false |
# Approach
<!-- Describe your approach to solving the problem. -->
1. Extend the array
- Concatenate the first `k-1` elements to the end of the original string to simulate the circular behavior.
2. Iterate through the extended sequence
- Maintain a variable `curr_length` to track the length of the current alternating segment.
- If the current character differs from the previous one, increment `curr_length`.
- Otherwise, reset `curr_length` to 1 (since alternating condition breaks).
- If `curr_length` reaches at least `k`, increment the total count.
3. Return the total count of valid alternating subsequences.
# Complexity
- Time complexity: $$O(n + k)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(n)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def numberOfAlternatingGroups(self, colors: List[int], k: int) -> int:
# Extend colors to handle circular cases
extended = colors + colors[:k-1]
total = 0
curr_length = 1 # Current alternating segment length
for i in range(1, len(extended)):
if extended[i] != extended[i-1]:
curr_length += 1
else:
curr_length = 1 # Reset if not alternating
if curr_length >= k:
total += 1
return total
```
| 2 | 0 |
['Sliding Window', 'Python3']
| 0 |
alternating-groups-ii
|
Beginner friendly Sliding Window Python Solution
|
beginner-friendly-sliding-window-python-mxt4m
|
ApproachSliding Window
We use a sliding window technique to track valid windows of size k. Since the array is circular, we extend the original array by appendin
|
khoisday
|
NORMAL
|
2025-03-09T02:17:18.962912+00:00
|
2025-03-09T02:17:18.962912+00:00
| 43 | false |
# Approach
**Sliding Window**
- We use a sliding window technique to track valid windows of size k. Since the array is circular, we extend the original array by appending the first k-1 elements to the end.
- The key insight is to reset our left pointer whenever we encounter two adjacent elements with the same color. This invalidates that sequence as a potential alternating group.
# Complexity
- Time complexity: O(n + k)
- Space complexity: O(n + k) for the extended array
# Code
```python3 []
class Solution:
def numberOfAlternatingGroups(self, colors: List[int], k: int) -> int:
# Extend the colors list to handle circular nature
colors = colors + colors[:(k-1)]
res = 0
l = 0
for r in range(1, len(colors)):
# Set left equal to right when finding two same adjacent elements
if r > 0 and colors[r] == colors[r - 1]:
l = r
# If we have a valid window size, count it
if r - l + 1 >= k:
res += 1
return res
```
# Code no extra space needed
```python3 []
class Solution:
def numberOfAlternatingGroups(self, colors: List[int], k: int) -> int:
class Solution:
def numberOfAlternatingGroups(self, colors: List[int], k: int) -> int:
n = len(colors)
res = 0
l = 0
# Loop through the array and consider the circular property
# We need to go up to n+k-1 to handle all possible windows
for r in range(n + k - 1):
# If we find two consecutive same colors, reset our left pointer
# We use modulo to handle circular nature of the array
if r > 0 and colors[r % n] == colors[(r - 1) % n]:
l = r
# If our current window is at least size k, it's a valid alternating group
if r - l + 1 >= k:
res += 1
return res
```
| 2 | 0 |
['Python3']
| 0 |
alternating-groups-ii
|
sliding window without using external space simple solution
|
sliding-window-without-using-external-sp-sydb
|
ApproachWe use sliding window mechanism to solve this problem. First we initialize i, j and res to 0. Then start the sliding window with the condition that i sh
|
samarthpai9870
|
NORMAL
|
2025-03-09T00:47:47.408623+00:00
|
2025-03-09T00:47:47.408623+00:00
| 108 | false |
# Approach
We use sliding window mechanism to solve this problem. First we initialize `i`, `j` and `res` to 0. Then start the sliding window with the condition that i should iterate only till n. Inside he while loop we check if the window size is less than k and is expandable, then we expand the window and proceed else we set `i` = `j` that means there is a repeating element in the window hence it cannot be grouped. If the window size is equal to n(else statement) we check if the group is valid, if yes then we increment both i and j so that the window size remains k otherwise we set `i` = `j` and proceed.
# Complexity
- Time complexity:
$$O(2n)$$
- Space complexity:
$$O(1)$$
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& arr, int k) {
int n = arr.size(), i = 0,j = 0, res = 0;
while(i < n){
if(j - i + 1 < k){
if(j - i == 0 or arr[j%n]!=arr[(j-1)%n]){
j++;
}
else{
i = j;
}
}
else{
if(arr[j%n]!=arr[(j-1)%n]){
i++;
j++;
res++;
}
else{
i = j;
}
}
}
return res;
}
};
```
| 2 | 0 |
['Sliding Window', 'C++']
| 0 |
alternating-groups-ii
|
💡 The Most Easiest and Simple Sliding Window Approach 🚀
|
the-most-easiest-and-simple-sliding-wind-qrmi
|
Upvote if this is helpful :) happy coding\n\n# Approach\n1. Extend the array by appending the first \( k-1 \) elements to account for circularity.\n2. Use a sli
|
hopmic
|
NORMAL
|
2024-11-23T22:59:49.642295+00:00
|
2024-11-23T22:59:49.642345+00:00
| 26 | false |
# ***Upvote if this is helpful :) happy coding***\n\n# Approach\n1. Extend the array by appending the first \\( k-1 \\) elements to account for circularity.\n2. Use a sliding window to evaluate each group of size \\( k \\).\n3. Validate if the group alternates by ensuring adjacent elements differ.\n4. If adjacent elements are equal or simmilar set the left pointer to the right pointer to keep a valid window\n5. Count valid alternating groups.\n\n\n# Complexity\n- Time complexity: \n $$O(n)$$ (for validating each sliding window of size \\( k \\)).\n\n- Space complexity: \n $$O(n)$$ (due to extending the array by \\( k-1 \\) where 3 <= k <= colors.length).\n\n\n# Code\n```python3 []\nclass Solution:\n def numberOfAlternatingGroups(self, colors: List[int], k: int) -> int:\n count = 0\n\n colors.extend(colors[:k-1]) # if k = 3 we add the first 2 numbers to account for circularity\n print(colors)\n\n L = 0\n for R in range(1, len(colors)):\n \n if colors[R] == colors[R-1]:\n L = R\n if R - L + 1 == k:\n count += 1\n L += 1\n\n return count\n```\n\n# ***Upvote if this was helpful :) happy coding***\n
| 2 | 0 |
['Array', 'Sliding Window', 'Python', 'C++', 'Java', 'Python3', 'JavaScript']
| 0 |
alternating-groups-ii
|
Simple C++ solution
|
simple-c-solution-by-dhawalsingh564-0e4z
|
Complexity\n- Time complexity: O(n+k)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n+k)\n Add your space complexity here, e.g. O(n) \n\n
|
dhawalsingh564
|
NORMAL
|
2024-07-09T06:00:10.576234+00:00
|
2024-07-09T06:00:10.576320+00:00
| 67 | false |
# Complexity\n- Time complexity: O(n+k)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n+k)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n**1. Duplicate Initial Segment:** Extend the list by appending its first k-1 elements to the end. This ensures that any potential wrapping alternating groups are captured in a linear scan.\n\n**2. Count Alternations:** As you iterate through the extended list, keep a count of consecutive alternating elements. When the count reaches k, it indicates a valid alternating group, so increase the answer counter.\n\n**3. Reset Count:** If a consecutive element is not alternating, reset the count and start anew.\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfAlternatingGroups(vector<int>& colors, int k) {\n int ans=0;\n for(int i=0;i<k-1;i++){\n colors.push_back(colors[i]);\n }\n int n = colors.size();\n int count=1;\n for(int i=1;i<n;i++){\n if(colors[i]!=colors[i-1]){\n count++;\n if(count>=k){\n ans++;\n }\n }\n else{\n count=1;\n }\n }\n return ans;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
alternating-groups-ii
|
Easy Java Solution
|
easy-java-solution-by-ravikumar50-v325
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
ravikumar50
|
NORMAL
|
2024-07-07T09:54:13.602479+00:00
|
2024-07-07T09:54:13.602512+00:00
| 74 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int numberOfAlternatingGroups(int[] colors, int k) {\n int n = colors.length;\n int arr[] = new int[n+k-1];\n for(int i=0; i<n; i++){\n arr[i] = colors[i];\n }\n int idx = n;\n for(int i=0; i<k-1; i++) arr[idx++] = colors[i];\n\n int w = 1;\n int ans = 0;\n for(int i=1; i<n+k-1; i++){\n if(arr[i]!=arr[i-1]) w++;\n else w = 1;\n\n if(w>=k) ans++;\n }\n return ans;\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
alternating-groups-ii
|
Java solution easy to understand
|
java-solution-easy-to-understand-by-keet-mjpg
|
Prerequisites: Sliding Window\n Describe your first thoughts on how to solve this problem. \n\n\n# Approach\n Describe your approach to solving the problem. \nI
|
keetarpjai
|
NORMAL
|
2024-07-06T18:34:56.595233+00:00
|
2024-07-06T18:34:56.595269+00:00
| 141 | false |
# Prerequisites: Sliding Window\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nInstead of checking modulo as we have a circular array I created another array of size n+k-1. It will definitely increase space but that we can bear if you want to you can easily avoid using extra space by using modulo operator\n\nWe took n+k-1 because at max we can go to last index n-1 and then if we take k-1 elements we can have an answer.\n\nStep1: update last k-1 elements with the 1st k-1 elements as it is a circular.\n\nStep2: I ran a loop till n+k-1 and check **if it similar to previous index** if yes keep on increase vc which indicates the length of the subarray which is having all element alternative.\nIf length (vc) increases k I start increasing count like a sliding window. because if it is continuously satisfying the above condition so it will increase the overall count.\nAs we need groups of size k and if for ex. overall vc goes to suppose k+5 then it will eventually give us 6 distinct groups.\n\nIf it is not similar to previous we will update vc to 0\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N) \n\n\n# Code\n```\nclass Solution {\n public int numberOfAlternatingGroups(int[] colors, int k) {\n int n= colors.length;\n\n int a[]=new int[n+k-1];\n for(int i=0;i<n;i++) {\n a[i]=colors[i];\n }\n for(int i=n;i<n+k-1;i++) {\n a[i]=colors[i-n];\n }\n int flag=0,i=1,cnt=0,vc=0;\n while(i<n+k-1) {\n if(a[i]!=a[i-1]) {\n vc++;\n if(vc>=k-1) cnt++;\n \n } else {\n vc=0;\n }\n i++;\n }\n return cnt;\n }\n}\n```
| 2 | 0 |
['Java']
| 2 |
alternating-groups-ii
|
Java || Simple 3 Step Process🔥🔥using DP|| Beats 100% ☑☑||Line by Line Code Explaination🥳
|
java-simple-3-step-processusing-dp-beats-fllo
|
\n\n# Intuition\n- An "alternating group" of length k means every k contiguous elements should alternate in color, and since the array is circular, the end of t
|
SKSingh0703
|
NORMAL
|
2024-07-06T16:48:20.272939+00:00
|
2024-07-06T16:48:20.272968+00:00
| 131 | false |
\n\n# Intuition\n- An "alternating group" of length k means **every k contiguous elements should alternate in color**, and since the array is circular, the end of the array wraps around to the start.\n- To handle the circular nature of the array easily, duplicate the array by appending the first k-1 elements to the end. This allows you to consider groups that span across the end and start of the array without complex modulo operations.\n\n# Approach\n1. **Circular Array Handling:** The code duplicates the colors array by appending it to itself (colorList). This removes thhe need of using modulo operations.\n2. **Dynamic Programming (DP) Approach:**\n i) Use a DP array to keep track of the length of the current alternating sequence ending at each position.\n\n ii) **If the current element (colors[i]) is different from the previous element (colors[i-1]), increment the length of the current alternating sequence (dp[i] = dp[i-1] + 1)**.\n\n iii) **If the current element is the same as the previous one, reset the alternating sequence length (dp[i] = 1).**\n\n3. **Counting Valid Groups:**\n\n- If the length of the alternating sequence (dp[i]) becomes k, it signifies a valid alternating group of length k. Increase count by 1.\n# Complexity\n\n- **Time complexity :** O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- **Space complexity :** O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n\n# Code\n```\nclass Solution {\n\n\n public int numberOfAlternatingGroups(int[] colors, int k) {\n int ans = 0 , dp = 0;\n List<Integer> colorList = new ArrayList<>();\n //Initialization\n for (int color : colors) {\n colorList.add(color);\n }\n for (int color : colors) {\n colorList.add(color);\n }\n for (int i = 0;i - k + 1 < colors.length;i ++) {\n if (i == 0) {\n dp = 1;\n } else {\n //If alternate increase size\n if (colorList.get(i) != colorList.get(i - 1)) {\n dp ++;\n }\n //Else reset the size\n else {\n dp = 1;\n }\n }\n //Condition check for length=k\n if (i >= k - 1) {\n if (dp >= k) {\n ans ++;\n }\n }\n }\n return ans;\n }\n\n}\n```
| 2 | 0 |
['Dynamic Programming', 'Java']
| 0 |
alternating-groups-ii
|
I solved it with soooo much difficulty!!!
|
i-solved-it-with-soooo-much-difficulty-b-2ykd
|
Problem Description\n\nThere is a circle of red and blue tiles. You are given an array of integers colors and an integer k. The color of tile i is represented b
|
KhadimHussainDev
|
NORMAL
|
2024-07-06T16:14:04.745388+00:00
|
2024-07-06T16:17:33.111764+00:00
| 161 | false |
# Problem Description\n\nThere is a circle of red and blue tiles. You are given an array of integers `colors` and an integer `k`. The color of tile `i` is represented by `colors[i]`:\n\n- `colors[i] == 0` means that tile `i` is red.\n- `colors[i] == 1` means that tile `i` is blue.\n\nAn alternating group is every `k` contiguous tiles in the circle with alternating colors (each tile in the group except the first and last one has a different color from its left and right tiles).\n\nReturn the number of alternating groups.\n\nNote that since `colors` represents a circle, the first and the last tiles are considered to be next to each other.\n\n# Approach\n\nThe approach involves extending the `colors` array to handle the circular nature and then checking for alternating groups in a sliding window manner.\n\n1. **Extend the Array**: Extend the `colors` array by appending the first `k-1` elements to the end. This handles the circular nature of the problem by allowing contiguous checks that wrap around.\n\n2. **Initialize Variables**: Initialize `count` to 0 to keep track of the number of alternating groups, and `is_group` to `False` to indicate if the current window is an alternating group.\n\n3. **Initial Check**: Perform an initial check for the first `k` elements to see if they form an alternating group. If they do, set `is_group` to `True` and increment `count`.\n\n4. **Sliding Window**: Use a sliding window approach to move through the array:\n\n - If the current window is an alternating group, continue to the next window.\n - If not, check the next window of `k` elements to see if it forms an alternating group.\n\n5. **Final Count**: After processing all windows, return the `count` of alternating groups.\n\n# Code\n\n```python\nclass Solution:\n def numberOfAlternatingGroups(self, colors: List[int], k: int) -> int:\n n = len(colors)\n count = 0\n arr = colors + colors[:k - 1]\n is_group = False\n check = True\n for i in range (1 , k):\n if arr[i] == arr[i - 1]:\n check = False\n break\n if check:\n is_group = True\n count += 1\n while i < n:\n if is_group:\n if arr[i] == arr[i + 1]:\n is_group = False\n i += 1\n else:\n count += 1\n i += 1\n else:\n check = True\n for j in range (i + 1 ,i + k ):\n if arr[j] == arr[j - 1]:\n check = False\n is_group = False\n i = j\n break\n if check:\n is_group = True\n count += 1\n i += k - 1 \n for j in range(i + 1 , len(arr)):\n if is_group:\n if arr[j] == arr [ j - 1]:\n break\n count += 1\n else:\n break\n \n \n return count\n\n```\n\n# Complexity Analysis\n\n- **Time Complexity**:\n\n - The time complexity of this solution is O(n), where n is the length of the `colors` array. This is because each element is processed at most twice: once in the initial pass and once in the sliding window check.\n\n- **Space Complexity**:\n - The space complexity is O(n + k) due to the extended array `arr` which is created by appending the first `k-1` elements to the original array.\n\n# Summary\n\nThis approach efficiently counts the number of alternating groups in a circular array by leveraging an extended array to handle the circular nature and using a sliding window method to check for alternating groups. The complexity analysis ensures the solution is scalable with respect to the length of the input array and the group size.\n\n\n---\n> #### ***If You Found it helpful, please upvote it. Thanks***\n
| 2 | 0 |
['Python3']
| 1 |
alternating-groups-ii
|
Python Unwrap + Sliding window
|
python-unwrap-sliding-window-by-dyxuki-hjij
|
\n\nclass Solution:\n def numberOfAlternatingGroups(self, colors: List[int], k: int) -> int:\n for i in range(k):\n colors.append(colors[i]
|
dyxuki
|
NORMAL
|
2024-07-06T16:07:10.850752+00:00
|
2024-07-06T16:07:10.850785+00:00
| 57 | false |
\n```\nclass Solution:\n def numberOfAlternatingGroups(self, colors: List[int], k: int) -> int:\n for i in range(k):\n colors.append(colors[i])\n ans = 0\n l = 0\n for r in range(1, len(colors)-1):\n if colors[r] == colors[r-1]:\n l = r\n \n if r-l+1 >= k:\n ans += 1\n return ans \n\n```
| 2 | 0 |
['Sliding Window', 'Python3']
| 0 |
alternating-groups-ii
|
✅Easy and simple Solution ✅Sliding Window
|
easy-and-simple-solution-sliding-window-4ze5s
|
Guy\'s if you find this solution helpful \uD83D\uDE0A, PLEASE do UPVOTE. By doing that it motivate\'s me to create more better post like this \u270D\uFE0F\nFoll
|
ayushluthra62
|
NORMAL
|
2024-07-06T16:04:05.428519+00:00
|
2024-07-07T03:50:05.566766+00:00
| 316 | false |
***Guy\'s if you find this solution helpful \uD83D\uDE0A, PLEASE do UPVOTE. By doing that it motivate\'s me to create more better post like this \u270D\uFE0F***<br>\n**Follow me on LinkeDin [[click Here](https://www.linkedin.com/in/ayushluthra62/)]**\n\n# Complexity\n- Time complexity:\nO(N *k)\n\n- Space complexity:\nO(1)\n\n# Code\n```\n\n\nclass Solution {\npublic:\n int numberOfAlternatingGroups(std::vector<int>& colors, int k) {\n int n = colors.size();\n if (k > n) return 0;\n\n int count = 0;\n\n \n bool check = true;\n for (int i = 0; i < k - 1; ++i) {\n if (colors[i] == colors[i + 1]) {\n check = false;\n break;\n }\n }\n\n if (check) {\n ++count;\n }\n\n \n for (int i = 1; i < n; ++i) {\n \n int last = i - 1;\n int first = (i + k - 1) % n;\n if (check) {\n if (colors[last] == colors[(last + 1) % n] || colors[first] == colors[(first - 1 + n) % n]) {\n check = false;\n }\n } else {\n check = true;\n for (int j = i; j < i + k - 1; ++j) {\n if (colors[j % n] == colors[(j + 1) % n]) {\n check = false;\n break;\n }\n }\n }\n\n if (check) {\n ++count;\n }\n }\n\n return count;\n }\n};\n\n```\n***Guy\'s if you find this solution helpful \uD83D\uDE0A, PLEASE do UPVOTE. By doing that it motivate\'s me to create more better post like this \u270D\uFE0F***<br>\n**Follow me on LinkeDin [[click Here](https://www.linkedin.com/in/ayushluthra62/)]**
| 2 | 0 |
['Sliding Window', 'C++']
| 4 |
alternating-groups-ii
|
O(n) runtime alternating
|
on-runtime-alternating-by-tin_le-zclp
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
tin_le
|
NORMAL
|
2024-07-06T16:03:54.067708+00:00
|
2024-07-06T19:53:48.433660+00:00
| 222 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfAlternatingGroups(vector<int>& colors, int k) {\n int res = 0, n = colors.size(), count = 1, last = -1;\n for(int i = 1; i < 2 * n && last != i % n; i++)\n {\n count = colors[i % n] != colors[(i - 1) % n] ? count + 1 : 1;\n if(count >= k) \n {\n if(last == -1) last =i; \n res++;\n }\n }\n return res;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
alternating-groups-ii
|
KMP || SET to reduce overlapping cases
|
kmp-set-to-reduce-overlapping-cases-by-t-lewu
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
hmaan
|
NORMAL
|
2024-07-06T16:02:41.736322+00:00
|
2024-07-06T16:02:41.736353+00:00
| 16 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int kmp(string& temp, string& b) {\n int n = b.size();\n vector<int> lps(n, 0);\n int i = 1, len = 0;\n while (i < n) {\n if (b[i] == b[len]) {\n len++;\n lps[i] = len;\n i++;\n } else {\n if (len != 0) {\n len = lps[len - 1];\n } else {\n lps[i] = 0;\n i++;\n }\n }\n }\n int m = temp.size();\n int p = 0, j = 0, count = 0;\n unordered_set<int> visited;\n while (p < m) {\n if (temp[p] == b[j]) {\n p++;\n j++;\n } else if (p < m && temp[p] != b[j]) {\n if (j != 0) {\n j = lps[j - 1];\n } else {\n p++;\n }\n }\n if (j == n) {\n int startPos = (p - n) % (m / 2); \n if (visited.find(startPos) != visited.end()) {\n return count;\n }\n visited.insert(startPos);\n count++;\n j = lps[j-1]; \n }\n }\n return count;\n }\n\n int numberOfAlternatingGroups(vector<int>& colors, int k) {\n int n = colors.size();\n if (k > n) return 0;\n\n string a = "", b = "";\n for (int i = 0; i < k; i++) {\n if (i % 2 == 0) {\n a += \'0\';\n b += \'1\';\n } else {\n a += \'1\';\n b += \'0\';\n }\n }\n\n string temp = "";\n for (int i = 0; i < n; i++) {\n temp += to_string(colors[i]);\n }\n temp += temp; \n\n int ans = kmp(temp, a) ;\n cout<<ans<<endl;\n ans+= kmp(temp, b);\n return ans;\n }\n};\n\n```
| 2 | 0 |
['C++']
| 0 |
alternating-groups-ii
|
🧠 Detecting Perfectly Alternating Color Groups – The Circular Trick No One Tells You!
|
detecting-perfectly-alternating-color-gr-m0io
|
IntuitionWe want to count how many circular subsequences of length k exist in the array colors where every adjacent pair alternates (e.g. R-G-R-G).The naive way
|
loginov-kirill
|
NORMAL
|
2025-03-30T06:53:26.273469+00:00
|
2025-04-01T19:23:34.932443+00:00
| 1,101 | false |
### Intuition
We want to count how many **circular subsequences** of length `k` exist in the array `colors` where every adjacent pair alternates (e.g. R-G-R-G).
The naive way would be to manually check every group — but there's a smarter way:
convert the alternating condition into a binary array, and use prefix sums to make group checks lightning fast.
---
### Approach
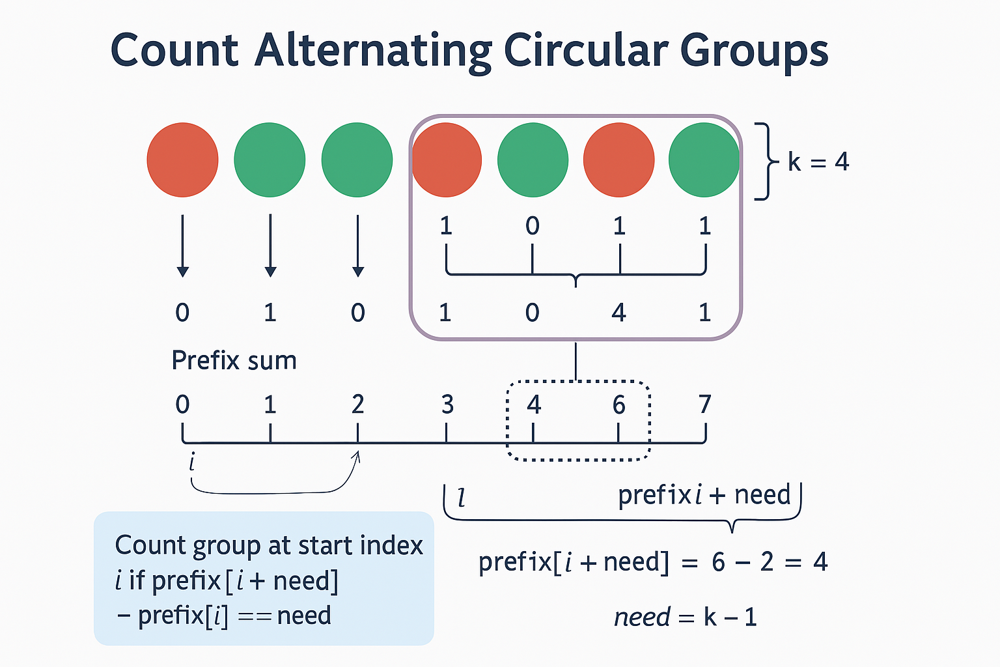
1. Create a binary array `alt` where `alt[i] = 1` if `colors[i] != colors[i+1]` (wrapping around the circle), otherwise 0.
2. Duplicate the array (simulate circular behavior).
3. Build a prefix sum array to quickly count how many alternating transitions exist in any window.
4. For each window of size `k`, check if it contains exactly `k-1` alternating transitions.
If yes — we found a valid alternating group!
---
### Complexity
**Time Complexity:**
( O(n) ) to build the binary `alt` array
( O(n) ) for prefix sums and window checks
**Overall:** ( O(n) )
**Space Complexity:**
( O(n) ) to store prefix sums and alt array
---
### Code
```python []
class Solution(object):
def numberOfAlternatingGroups(self, colors, k):
n = len(colors)
alt = [1 if colors[i] != colors[(i + 1) % n] else 0 for i in range(n)]
a = alt + alt
cum = [0] * (len(a) + 1)
for i in range(len(a)):
cum[i + 1] = cum[i] + a[i]
cnt = 0
need = k - 1
for i in range(n):
if cum[i + need] - cum[i] == need:
cnt += 1
return cnt
```
```javascript []
var numberOfAlternatingGroups = function(colors, k) {
const n = colors.length;
const alt = Array.from({ length: n }, (_, i) =>
colors[i] !== colors[(i + 1) % n] ? 1 : 0
);
const extended = [...alt, ...alt];
const prefix = new Array(extended.length + 1).fill(0);
for (let i = 0; i < extended.length; i++) {
prefix[i + 1] = prefix[i] + extended[i];
}
const need = k - 1;
let count = 0;
for (let i = 0; i < n; i++) {
if (prefix[i + need] - prefix[i] === need) {
count++;
}
}
return count;
};
```
<img src="https://assets.leetcode.com/users/images/b91de711-43d7-4838-aabe-07852c019a4d_1743313174.0180438.webp" width="270"/>
| 1 | 0 |
['Array', 'Math', 'Sliding Window', 'Python', 'JavaScript']
| 1 |
alternating-groups-ii
|
C# solution (sliding window)
|
c-solution-sliding-window-by-newbiecoder-3pqx
|
IntuitionKeep a sliding window of size k. Check if all colors form a valid alternating group.Complexity
Time complexity:O(n)
Space complexity:O(1)
Code
|
newbiecoder1
|
NORMAL
|
2025-03-29T07:02:39.677250+00:00
|
2025-03-29T07:03:49.968702+00:00
| 7 | false |
# Intuition
Keep a sliding window of size k. Check if all colors form a valid alternating group.
# Complexity
- Time complexity:O(n)
- Space complexity:O(1)
# Code
```csharp []
public class Solution {
public int NumberOfAlternatingGroups(int[] colors, int k) {
int result = 0;
int left = 0, right = 1, n = colors.Length;
while(right <= n + k - 2)
{
if(colors[right % n] == colors[(right - 1) % n])
{
left = right;
}
right++;
if(right - left == k)
{
result++;
left++;
}
}
return result;
}
}
```
| 1 | 0 |
['C#']
| 0 |
alternating-groups-ii
|
Simple O(N) Solution !!!
|
simple-on-solution-by-dipak__patil-wm2l
|
Complexity
Time complexity:
O(n)
Space complexity:
O(1)
Code
|
dipak__patil
|
NORMAL
|
2025-03-13T16:55:31.021029+00:00
|
2025-03-13T16:55:31.021029+00:00
| 6 | false |
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(1)
# Code
```golang []
func numberOfAlternatingGroups(colors []int, k int) int {
res := 0
validTiles := 1
prevTile := colors[0]
for i := 1; i < len(colors)+k-1; i++ {
if colors[i%len(colors)] == prevTile {
validTiles = 1
continue
}
validTiles++
if validTiles >= k {
res++
}
prevTile = colors[i%len(colors)]
}
return res
}
```
| 1 | 0 |
['Array', 'Sliding Window', 'Go']
| 0 |
alternating-groups-ii
|
Simple easy sol.
|
simple-easy-sol-by-hanumana_ram-irr0
|
Complexity
Time complexity: O(n)
Space complexity: O(1)
Code
|
Hanumana_ram
|
NORMAL
|
2025-03-11T13:55:26.192034+00:00
|
2025-03-11T13:55:26.192034+00:00
| 7 | false |
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int ans = 0;
int n = colors.size();
int pre = -1;
int l =0;
int cp = 0;
for(int i=0;i<n+k;i++){
int j = i %n;
if(cp>=n)break;
if(pre==-1){
pre = colors[j];
cp=j;
l++;
}
else{
if(colors[j]==pre){
int a = l-k+1;
l=1;
pre = colors[j];
cp=i;
if(a>0)ans+=a;
}
else{
l++;
pre = colors[j];
}
}
}
if(cp<n){
ans+=(n-cp);
}
return ans;
}
};
```
| 1 | 0 |
['C++']
| 0 |
alternating-groups-ii
|
Sliding Window (Approach 2) | Maths | Easy Explanation | Optimal O(n)
|
sliding-window-approach-2-maths-easy-exp-908t
|
IntuitionThe intuition is to apply a sliding window.
When two adjacent elements are equal, we restart our window (ie, move left pointer to where the current poi
|
ashhar_24
|
NORMAL
|
2025-03-10T22:48:25.366028+00:00
|
2025-03-10T22:48:38.078300+00:00
| 6 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The intuition is to apply a sliding window.
When two adjacent elements are equal, we restart our window (ie, move left pointer to where the current pointer is, as the subarray between these two pointers can never contribute to alternating subarray).
And when the size of the window becomes equal to k, ie the distance between left pointer (`i`) and the current pointer (`j`) becomes equal to `k (j - i + 1 == k)`, we move our left pointer to explore next probable alternating subarray by updating the `cnt` value by 1.
# Approach
<!-- Describe your approach to solving the problem. -->
Use Two - Pointers (i and j), `i` will be the left pointer while j will be the current pointer.
When `colors[j] == colors[j-1]`, the subarray between i and j will never contribute to the required alternating subarray, hence we `shrink` the window and bring `i to j`.
Else, when they aren't equal we check if the distance between both the pointers is k or not, if it is, we increase the value of `cnt` and increment the `left pointer` by `1` to explore the next possible alternating subarray.
**NOTE**: Since here we have to consider circular array as well, and at max while standing at index `n-1`, we will need `k-1` more elements from the front of the array, we simply use `modulo (%)`, operator to handle this.
Instead of `j`, we use `j%n` and for `(j-1)`, we use `(j-1+n)%n`
The current moves total `(n+k-1)` indices, for j>n, we use modulo to bring it back to the starting indices.
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int n = colors.size();
int i = 0, j = 1; // left and right pointer
int cnt = 0; // keeps the cnt of required subarrays
while(j<(n+k-1)){
if(colors[j%n]==colors[(j-1+n)%n]) i = (j%n);
else{
if(j-i+1==k){
cnt++; i++;
}
}
j++;
}
return cnt;
}
};
```
| 1 | 0 |
['Array', 'Sliding Window', 'C++']
| 0 |
alternating-groups-ii
|
gg
|
gg-by-somesh9421-vw9g
|
Code
|
somesh9421
|
NORMAL
|
2025-03-10T19:04:33.246542+00:00
|
2025-03-10T19:04:33.246542+00:00
| 6 | false |
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int length=1,ans=0;
int n=colors.size();
for( int i=1;i<=n-1+k-1;i++ ){
if( colors[i%n] != colors[(i-1+n)%n] ){
length++;
}else{
length=1;
}
if(length>=k){
ans++;
}
}
return ans;
}
};
```
| 1 | 0 |
['C++']
| 0 |
alternating-groups-ii
|
✅ 🌟 JAVA SOLUTION ||🔥 BEATS 100% PROOF🔥|| 💡 CONCISE CODE ✅ || 🧑💻 BEGINNER FRIENDLY
|
java-solution-beats-100-proof-concise-co-2osn
|
Complexity
Time complexity:O(n+k)
Space complexity:O(1)
Code
|
Shyam_jee_
|
NORMAL
|
2025-03-10T18:25:46.779391+00:00
|
2025-03-10T18:25:46.779391+00:00
| 11 | false |
# Complexity
- Time complexity:$$O(n+k)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:$$O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int numberOfAlternatingGroups(int[] colors, int k) {
int n=colors.length;
int left=0;
int res=0;
for(int right=1;right<colors.length+k-1;right++)
{
// skip entire subArray
if(colors[(right)%n]==colors[(right-1)%n]) left=right;
if(right-left+1==k)
{
res++;
left++; // move to next subArray Or shrinking phase
}
}
return res;
}
}
```
| 1 | 0 |
['Array', 'Sliding Window', 'Java']
| 0 |
alternating-groups-ii
|
Sliding Window (Approach 1) | Maths | Easy Explanation | Optimal O(n)
|
sliding-window-maths-easy-explanation-op-3hep
|
IntuitionHere, if we observe carefully, if we have two same numbers adjacent to each other, then that subarray can never be counted in our alternating group.
Al
|
ashhar_24
|
NORMAL
|
2025-03-10T10:26:44.481985+00:00
|
2025-03-10T22:39:30.670107+00:00
| 7 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Here, if we observe carefully, if we have two same numbers adjacent to each other, then that subarray can never be counted in our alternating group.
Also since the subarray can be cyclic as well, we use some modulo properties:
- (a - b) % m => (a - b + m) % m (to handle cases when a - b < 0)
- And to move in cyclic fashion, we do %n (n: size of array)
Using above two things, we approach this question.


# Approach
<!-- Describe your approach to solving the problem. -->
Here, we imagine having a `window` which contains alternating numbers. When we come across a number which is equal to it's previous number, we reset the `size` of the window to 1 (ie, shrink our window).
If it is not equal to it's previous element, we increase the size of the window by 1.
And if the size of window is `>= k`, we increase the `cnt` value by 1.
Also, since the array can be cyclic and if we stand at the last index, we need to move `k-1` indices more in order to have `k` elements. Hence the max value of our pointer is `(n+k-1)` starting from index `1`.
# Complexity
- Time complexity: O(n+k) ~ O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int n = colors.size();
int cnt = 0;
int j = 1, len = 1; // j-> pointer | len-> window size
while(j < (n+k-1)){
if(colors[j%n] == colors[(j-1)%n]) len = 1;
else len++;
if(len>=k) cnt++;
j++;
}
return cnt;
}
};
```
| 1 | 0 |
['Array', 'Math', 'Sliding Window', 'C++']
| 0 |
alternating-groups-ii
|
✅ Sliding Window + Modulus Trick 🚀🔥| C++ | Easy Logical Approach ✅
|
count-alternating-color-groups-in-circul-vh7z
|
IntuitionThe problem requires finding the number of alternating groups of length at least k in a circular array. Since the array is circular, we need to handle
|
akshayanithan
|
NORMAL
|
2025-03-09T23:27:00.789712+00:00
|
2025-03-09T23:28:36.905630+00:00
| 6 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem requires finding the number of alternating groups of length at least k in a circular array. Since the array is circular, we need to handle the wrap-around case, ensuring elements at the end connect to the beginning. The goal is to count how many contiguous subarrays have alternating colors of length at least k.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Initialize variables:
- maxLen keeps track of the current length of alternating elements.
- ans stores the count of valid alternating groups.
n is the size of the array.
2. Traverse the array:
- Iterate from 1 to n + k - 1 to handle the circular array. The additional k-1 iterations ensure any valid alternating group that wraps around the array is counted.
- Compare the current element colors[i % n] with the previous element colors[(i + n - 1) % n].
- If they are different, increase maxLen (as it forms an alternating group).
- If they are same, reset maxLen to 1.
3. Count valid groups:
- After updating maxLen, if its value becomes >= k, increment ans (since we found a valid alternating group).
4. Return the result:
- After traversing the array, ans will contain the count of alternating groups of size k or greater.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
The loop runs from $$1$$ to $$n+k-1$$, so the time complexity is $$O(n+k)$$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
We are using only constant extra space, hence $$O(1)$$
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int maxLen = 1, ans = 0, n = colors.size();
for (int i = 1; i < n + k - 1; i++) {
if (colors[i % n] != colors[(i + n - 1) % n]) {
maxLen++;
} else {
maxLen = 1;
}
if (maxLen >= k)
ans++;
}
return ans;
}
};
```
| 1 | 0 |
['Array', 'Sliding Window', 'C++']
| 0 |
alternating-groups-ii
|
I'm a disappointment. Anyways... Scans for alternating regions through circular array. O(n) O(1)
|
im-a-disappointment-anyways-scans-for-al-hs8m
|
Intuitionlet n = size of found alternating region (non-circular)
let k = size of alternating region (as described by problem)
the number of groups then is n-k+1
|
sohamvam
|
NORMAL
|
2025-03-09T22:51:56.028541+00:00
|
2025-03-09T22:51:56.028541+00:00
| 8 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
let n = size of found alternating region (non-circular)
let k = size of alternating region (as described by problem)
the number of groups then is n-k+1
we want to find all the alternating regions in the circular array.
Note if the alternating region is circular (ie the whole array alternates perfectly). n-k+1 does not hold and the number of k regions is the size of the circular array itself.
We should be wise about what point we start looking for an alternating region in the circle. Suppose there are 2 alternating regions, but one of them is alternating past the 0 index (such as index -2(size-2) to 5). If we start looking for alternating regions starting at index 0, we will count 3 alternating regions. The alternating region that crossed index 0 got cut in half! That region in 2 cells short and our answer become inaccurate. To solve this we must choose an index that can't be cutting into an alternating region (ie two cells with the same color).
***I realize as of writing this I could have optimized my algorithm as at this point, because whether or not the array is fully alternating should be identifiable at this point.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Find the start index by scanning from i=1, compare i and i-1 for being same colors. If yes then i is the start index
b) If we get through the whole array, then default to index 0. Note that if index 0 and size-1 don't match the whole array is alternating, so we can early return groups as the size of the input array
2. Consider the start cell to be the initial alternating region of size 1.
a) If the next cell is not the same color as the last color then increment the region size by 1. Continue to next cell
b) Else use the n-k+1 formula and add result to groups if result was positive. Reset region size to 1 and next cell is the region
3. At the end of the loop we may need to add the region to groups (In the case an alternating region ends at the cell before the starting cell)
Note the last line was to accomodate for the case the whole array is a circular alternating region (which again could have been deduced earlier).
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```c []
#define MAX(a,b) (a>=b ? a:b)
int numberOfAlternatingGroups(int* colors, int size, int k) {
//We are interested in all the regions along the circle that actually alternate
//If there is a alternating region of size n there are n-k+1 alternating groups of size k
//If an alternating region is smaller than k then n-k+1 < 0 and we can consider it as 0
int groups = 0;
//Note we should find a spot with two same colors so as to not cut an alternating region in half
//Step 1 find a optimal start point (if not present then default to 0)
int start=0;
for (int i=1; i<size; ++i) {
if (colors[i] == colors[i-1]) {
start = i;
break;
}
}
//Step 2 scan for alternating region
int reg_size = 1; //initial region is first tile at 0
int last_color = colors[start];
for (int i=start+1; i<size+start; ++i) {
if (last_color != colors[i%size]) {
++reg_size;
}
else {
groups += MAX(reg_size-k+1, 0);
reg_size = 1;
}
last_color = colors[i%size];
}
//If the whole thing is an alternating series, the last cell won't make it add to groups
groups += MAX(reg_size-k+1, 0);
reg_size = 1;
//Also if the entire thing is alternating there are size number of groups of k for as long as k <= size
if (last_color != colors[start] && k <= size)
groups = size;
return groups;
}
```
| 1 | 0 |
['Array', 'C', 'Sliding Window']
| 0 |
alternating-groups-ii
|
Reuse LC 3206 | Sliding Window Template
|
reuse-lc-3206-sliding-window-template-by-04y4
|
Idea:
This problem is a generic case for LC 3206. Alternating Groups I
Use the Sliding Window Template discussed here
T/S: O(n + k)/O(1), where n = size(nums)
|
prashant404
|
NORMAL
|
2025-03-09T21:39:40.351902+00:00
|
2025-03-09T22:32:36.908623+00:00
| 19 | false |
**Idea:**
* This problem is a generic case for [LC 3206. Alternating Groups I](https://leetcode.com/problems/alternating-groups-i/solutions/6518629/sliding-window-template-explained-by-pra-48z5/)
* Use the Sliding Window Template discussed [here](https://leetcode.com/discuss/post/1773891/sliding-window-technique-and-question-ba-9tt4/)
>T/S: O(n + k)/O(1), where n = size(nums)
```java []
public int numberOfAlternatingGroups(int[] colors, int k) {
var left = 0;
var count = 0;
var n = colors.length;
var end = n + k - 1;
for (var right = 1; right < end; right++)
if (colors[(right - 1) % n] == colors[right % n]) {
left = right;
} else if (right - left + 1 == k) {
count++;
left++;
}
return count;
}
```
***Please upvote if this helps***
| 1 | 0 |
['Java']
| 0 |
alternating-groups-ii
|
Easy Java Solution || Beats 98% of Java Users .
|
easy-java-solution-beats-98-of-java-user-oah6
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
zzzz9
|
NORMAL
|
2025-03-09T21:17:30.040886+00:00
|
2025-03-09T21:17:30.040886+00:00
| 10 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int numberOfAlternatingGroups(int[] colors, int k) {
int n = colors.length ;
int rs = 0 ;
int curr = 1 ;
for( int i=1 ; i<n ; ++i ){
if( colors[i] != colors[i-1] ){
curr++;
}else {
curr =1 ;
}
if( curr >= k ){
rs++ ;
}
}
if( colors[n-1] != colors[0] ){
curr++ ;
if( curr >= k ) rs++ ;
for( int i=1 ; i<k-1 ; ++i ){
if( colors[i-1] != colors[i] ){
curr++;
}else {
break ;
}
if( curr >= k ){
rs++ ;
}
}
}
return rs ;
}
}
```
| 1 | 0 |
['Array', 'Sliding Window', 'Java']
| 0 |
alternating-groups-ii
|
Easy | Solved 🚀
|
easy-solved-by-nirmal100754-e4ma
|
IntuitionWe need to count alternating groups of size at least k in a circular array colors.
An alternating group means adjacent elements have different values.A
|
nirmal100754
|
NORMAL
|
2025-03-09T20:44:49.320048+00:00
|
2025-03-09T20:44:49.320048+00:00
| 12 | false |
# Intuition
We need to count **alternating groups** of size at least `k` in a **circular** array `colors`.
An alternating group means **adjacent elements have different values**.
---
# Approach
1. **Use a counter (`c`)** to track the length of the current alternating group.
2. **Iterate through `colors` twice** (`size * 2` iterations) to handle circular behavior.
- If the current element is **equal to the previous one**, reset `c = 1` (new group starts).
- Otherwise, increment `c`.
- If we have completed **one full cycle** and `c >= k`, increment the result `res`.
3. **Return `res`** as the total count of valid alternating groups.
---
# Complexity
- **Time Complexity**:
$$O(N)$$ since we iterate twice over `colors`.
- **Space Complexity**:
$$O(1)$$ since only a few integer variables are used.
---
# Upvote 🚀
If this helped, **upvote** and keep coding! 🔥
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int c=0,res=0,size=colors.size();
for(int a=1;a<size*2;a++)
{
if(colors[a%size]==colors[(a-1)%size])
c=1;
else
c++;
if(a>=size && c>=k)
res++;
}
return res;
}
};
```
| 1 | 0 |
['Array', 'Sliding Window', 'C++']
| 0 |
alternating-groups-ii
|
Sliding Window | Intuition Explained | Made Easy
|
sliding-window-intuition-explained-made-kgxzz
|
Intuition
The problem requires us to find the number of alternating groups of length 𝑘 in a circular array of red and blue tiles.
Since the array is circular, t
|
tharun55
|
NORMAL
|
2025-03-09T20:44:27.750444+00:00
|
2025-03-09T20:59:07.513652+00:00
| 14 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
1. The problem requires us to find the number of alternating groups of length 𝑘 in a circular array of red and blue tiles.
2. Since the array is circular, the first and last elements are adjacent. This makes it tricky to iterate linearly because we need to ensure continuity even when reaching the end of the array. Here where % operator helps!
3. To efficiently find valid alternating groups, we need a way to check each group of 𝑘 elements while ensuring that adjacent elements alternate between red (0) and blue (1).
---
# Approach
<!-- Describe your approach to solving the problem. -->
We use a sliding window approach to check all possible contiguous subarrays of length 𝑘. Steps involved:
1. Use Two Pointers (i and j):
i represents the start of a window.
j expands the window until it reaches length 𝑘.
2. Check Alternating Property:
Every tile inside the window (except the first and last one) should be different from its neighbors.
If we find a mismatch, move i forward to restart checking.
3. Handle Circular Property:
Since the array is circular, we use the modulus operator (%) to wrap around indices.
4. Counting Valid Groups:
If a valid alternating group of size 𝑘 is found, increase the count and move i forward.
# Complexity
- Time complexity: O(n+k)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
i pointer moves at most 𝑛 times.
j pointer moves at most 𝑛+k times.
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int n = colors.size();
int ans = 0;
int i = 0, j = 1;
// For each window till it reaches end
// Either (i < n) or (j < n+k-1)
while (i < n) {
// Ensure current window is alternating
if (colors[j % n] != colors[(j - 1) % n]) {
if (j - i + 1 == k) { // Found valid group
ans++;
i++; // Move i to check next possibility
}
} else {
i = j; // Reset window if alternation breaks
}
j++; // Expand window
}
return ans;
}
};
```
| 1 | 0 |
['Two Pointers', 'Sliding Window', 'C++']
| 0 |
alternating-groups-ii
|
One Pass Sliding Window with Hash Set
|
one-pass-sliding-window-with-hash-set-by-7ovh
|
IntuitionWe can simply just store all color violations in a hash set and update this hash set when expanding and shrinking the window.ApproachOnce we encounter
|
TomGoh
|
NORMAL
|
2025-03-09T20:36:22.881438+00:00
|
2025-03-09T20:36:22.881438+00:00
| 9 | false |
# Intuition
We can simply just store all color violations in a hash set and update this hash set when expanding and shrinking the window.
# Approach
Once we encounter a color violation when expanding the window, i.e., a same color for two adjacent array elements, we insert the index into the hash set, and when we shrinking the window and find the left bound of the window is in the violation set, remove it from the set.
If the violation set for the current window is empty, we increase the answer by one, and if it is not empty, we do nothing.
# Complexity
- Time complexity:
O(n+k)
- Space complexity:
O(k)
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int n = colors.size();
if(k>n){
return 0;
}
int right=1;
unordered_set<int> violations;
while(right<k){
if(colors[right]==colors[right-1]){
violations.insert(right-1);
}
right++;
}
int ans = violations.size() == 0 ? 1 : 0;
for(int left=0; left<n-1; left++){
if(violations.find(left)!=violations.end()){
violations.erase(left);
}
if(colors[(right+n)%n]==colors[(right+n-1)%n]){
violations.insert(right-1);
}
right++;
ans += violations.empty() ? 1 : 0;
}
return ans;
}
};
```
| 1 | 0 |
['Sliding Window', 'C++']
| 0 |
alternating-groups-ii
|
Sliding Window || C++ || Beats 77% || Easiest Approach
|
sliding-window-c-beats-77-easiest-approa-l6aq
|
IntuitionApproachComplexity
Time complexity: O(N)
Space complexity: O(1)
Code
|
DevilishAxis09
|
NORMAL
|
2025-03-09T20:03:50.039853+00:00
|
2025-03-09T20:03:50.039853+00:00
| 10 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
int n = colors.size();
int left = 0;
int cnt = 0;
for(int right = 1; right < (n + k-1); right++)
{
if(colors[(right) % n] == colors[(right - 1) % n]) // skip entire subarray if not alt colors
{
left = right;
}
else if(right - left + 1 == k) // move to nxt subarray
{
cnt++;
left++;
}
}
return cnt;
}
};
```
| 1 | 0 |
['C++']
| 0 |
alternating-groups-ii
|
c++ || Easy To Understand || Beats 90% || Sliding Window ||
|
c-easy-two-understand-beats-90-sliding-w-ecvy
|
ApproachStep 1:Extending the ArraySince we are considering contiguous subarrays, we must also account for cyclic subarrays where elements wrap around from the e
|
rohith1002
|
NORMAL
|
2025-03-09T19:26:59.578311+00:00
|
2025-03-09T19:28:11.720631+00:00
| 16 | false |
Approach
Step 1:Extending the Array
Since we are considering contiguous subarrays, we must also account for cyclic subarrays where elements wrap around from the end to the beginning. To achieve this, we append the first k-1 elements to the end of the array.
for(int i = 0; i < k - 1; i++)
a.push_back(a[i]);
Step 2: Sliding Window Technique
We use two pointers:
s (start) tracks the beginning of the subarray.
e (end) tracks valid subarrays where elements alternate.
We traverse the array while ensuring that adjacent elements are different. If a valid subarray of size k is found, we increment the count and move the start index forward.
Step 3: Counting Valid Subarrays
For each position, we check whether adjacent elements are different. If so, we continue the subarray. If the subarray reaches size k, we count it and shift the window forward.
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& a, int k) {
int ans = 0;
int n = a.size();
// Extend array to handle cyclic subarrays
for(int i = 0; i < k - 1; i++)
a.push_back(a[i]);
int e = 0;
int s = 1;
while (s < n + k - 1) {
if (a[s - 1] != a[s]) { // Check alternating property
if (s - e + 1 == k) { // Check subarray length
ans++;
e++; // Move start forward
}
} else {
e = s; // Reset start if two consecutive elements are same
}
s++;
}
return ans;
}
};
```
| 1 | 0 |
['Two Pointers', 'Sliding Window', 'C++']
| 0 |
alternating-groups-ii
|
Alternating Groups II
|
alternating-groups-ii-by-sachin-kr10-76cn
|
IntuitionFirst approch is doing without sliding Window just using arrayApproachComplexity
Time complexity: O(n*k)
Space complexity: O(n)
Code
|
sachin-kr10
|
NORMAL
|
2025-03-09T19:26:46.151777+00:00
|
2025-03-09T19:26:46.151777+00:00
| 6 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
First approch is doing without sliding Window just using array
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(n*k)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(n)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int numberOfAlternatingGroups(vector<int>& colors, int k) {
for(int i=0;i<k;i++){
colors.push_back(colors[i]);
}
int count=0;
int c=1;
int n=colors.size();
bool flag=true;
for(int i=0;i<n-k;i++){
if(flag){
for(int j=i;j<i+(k-1);j++){
if(colors[j]!=colors[j+1]){
c++;
}
}
}
if(!flag){
if(colors[i+(k-1)]!=colors[i+(k-2)]){
count++;
}
else{
i=i+(k-2);
flag=true;
}
}
if(c==k){
count++;
flag=false;
}
c=1;
}
return count;
}
};
```
| 1 | 0 |
['C++']
| 0 |
alternating-groups-ii
|
Sliding Window & Circular Array Traversal Approach
|
sliding-window-circular-array-traversal-tot6z
|
**🔼 Please Upvote
🔼 Please Upvote
🔼 Please Upvote
🔼 Please Upvote💡If this helped, don’t forget to upvote! 🚀🔥**IntuitionWe need to count the number of contiguous
|
alperensumeroglu
|
NORMAL
|
2025-03-09T19:18:29.407283+00:00
|
2025-03-09T19:18:29.407283+00:00
| 23 | false |
**🔼 Please Upvote
🔼 Please Upvote
🔼 Please Upvote
🔼 Please Upvote
💡If this helped, don’t forget to upvote! 🚀🔥**
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
We need to count the number of contiguous alternating subarrays of length at least k.
An alternating group means that adjacent elements are different.
# Approach
<!-- Describe your approach to solving the problem. -->
Maintain a counter `w` to track the length of the current alternating sequence.
Iterate through the colors array in a circular manner.
If the current color is different from the previous one, increment `w`.
Otherwise, reset `w` to 1.
If `w` reaches `k` or more, increment the result counter `ans`.
# Complexity
- Time Complexity: O(n) since we iterate through the array once.
- Space Complexity: O(1) as we use only a few extra variables.
**🔼 Please Upvote
🔼 Please Upvote
🔼 Please Upvote
🔼 Please Upvote
💡If this helped, don’t forget to upvote! 🚀🔥**
# Code
```python3 []
class Solution:
def numberOfAlternatingGroups(self, colors, k):
w = 1 # Tracks the length of the current alternating sequence
ans = 0 # Counts valid alternating groups
n = len(colors)
for i in range(1, n + k - 2 + 1): # Loop through circular array
if colors[i % n] != colors[(i - 1 + n) % n]: # Check if alternating
w += 1 # Increase alternating sequence length
else:
w = 1 # Reset if pattern breaks
if w >= k:
ans += 1 # Count valid alternating groups
return ans # Return total count of valid alternating groups
```
| 1 | 0 |
['Hash Table', 'Linked List', 'Dynamic Programming', 'Stack', 'Greedy', 'Bit Manipulation', 'Sliding Window', 'Suffix Array', 'Bitmask', 'Python3']
| 0 |
maximum-frequency-after-subarray-operation
|
Kadane Algorithm | 100% BEATS | Counting | Well Expained
|
kadane-algorithm-100-beats-counting-well-n3m2
|
IntuitionThe goal is to maximize the frequency of the value k after adding a chosen integer x to a subarray. The optimal approach involves converting as many el
|
shubham6762
|
NORMAL
|
2025-01-26T04:24:56.877392+00:00
|
2025-01-26T04:24:56.877392+00:00
| 6,560 | false |
### Intuition
The goal is to maximize the frequency of the value `k` after adding a chosen integer `x` to a subarray. The optimal approach involves converting as many elements as possible to `k` by selecting a subarray and an appropriate `x`.
### Approach
1. **Original Count**: First, count the existing occurrences of `k` in the array.
2. **Transformation for Each Value**: For each possible value `m` (1 to 50, except `k`), create a transformed array where:
- `m` elements contribute `+1` (gain if converted to `k`),
- `k` elements contribute `-1` (loss if converted away from `k`),
- Others contribute `0`.
3. **Kadane's Algorithm**: Use Kadane's algorithm on this transformed array to find the maximum subarray sum, which represents the best possible gain for converting `m` to `k`.
4. **Maximize Frequency**: The maximum frequency of `k` is the sum of the original count and the best gain from all possible `m`.
### Complexity
- **Time Complexity**: O(n)
- **Space Complexity**: O(1)
### Code
```cpp []
class Solution {
public:
int maxFrequency(vector<int>& nums, int k) {
int orig = count(nums.begin(), nums.end(), k), mx = 0;
for (int m = 1; m <= 50; ++m) {
if (m == k) continue;
int cur = 0, mxCur = 0;
for (int n : nums) {
cur += n == m ? 1 : n == k ? -1 : 0;
cur = max(cur, 0);
mxCur = max(mxCur, cur);
}
mx = max(mx, mxCur);
}
return orig + mx;
}
};
```
``` Java []
public class Solution {
public int maxFrequency(int[] nums, int k) {
int orig = 0;
for (int num : nums) {
if (num == k) orig++;
}
int maxGain = 0;
for (int m = 1; m <= 50; m++) {
if (m == k) continue;
int current = 0, maxCurrent = 0;
for (int num : nums) {
current += (num == m) ? 1 : (num == k) ? -1 : 0;
current = Math.max(current, 0);
maxCurrent = Math.max(maxCurrent, current);
}
maxGain = Math.max(maxGain, maxCurrent);
}
return orig + maxGain;
}
}
```
``` Python []
class Solution(object):
def maxFrequency(self, nums, k):
orig = nums.count(k)
max_gain = 0
for m in range(1, 51):
if m == k:
continue
current = max_current = 0
for num in nums:
if num == m:
current += 1
elif num == k:
current -= 1
current = max(current, 0)
max_current = max(max_current, current)
max_gain = max(max_gain, max_current)
return orig + max_gain
```
### Explanation
- **Original Count**: Count how many times `k` appears initially.
- **Transformation**: For each `m`, transform the array to track potential gains/losses when converting `m` to `k`.
- **Kadane's Algorithm**: Find the subarray with the maximum net gain (converted `m` elements minus existing `k` elements in the subarray).
- **Result Calculation**: Add the best possible gain from any `m` to the original count of `k` to get the maximum frequency after the operation.
| 81 | 0 |
['Array', 'Counting', 'Prefix Sum', 'C++']
| 11 |
maximum-frequency-after-subarray-operation
|
[Java/C++/Python] One Pass, O(n)
|
javacpython-kadane-by-lee215-xzfq
|
Solution 1: KadaneNot sure if it's appropriate to name it as Kadane.Pick a subarray, count the biggest frequency of any value.
For the rest part of this subarra
|
lee215
|
NORMAL
|
2025-01-26T04:12:48.882829+00:00
|
2025-01-30T07:36:31.762267+00:00
| 3,838 | false |
# **Solution 1: Kadane**
Not sure if it's appropriate to name it as Kadane.
Pick a subarray, count the biggest frequency of any value.
For the rest part of this subarray, count the frequency of `k`.
This equals to:
Pick a subarray, find out the biggest gap between
the most frequent element and `k`.
The values range is small,
we can check the every element with kadane alogorithm.
Time `O(50n)`
Space `O(50)`
<br>
```py [Python3]
def maxFrequency(self, A: List[int], k: int) -> int:
count = Counter(A)
def kadane(b):
res = cur = 0
for a in A:
if a == k:
cur -= 1
if a == b:
cur += 1
if cur < 0:
cur = 0
res = max(res, cur)
return res
res = max(kadane(b) for b in count)
return count[k] + res
```
```Java [Java]
public int maxFrequency(int[] A, int k) {
Map<Integer, Integer> count = new HashMap<>();
for (int a : A) {
count.put(a, count.getOrDefault(a, 0) + 1);
}
int res = 0;
for (int b : count.keySet()) {
res = Math.max(res, kadane(A, k, b));
}
return count.getOrDefault(k, 0) + res;
}
private int kadane(int[] A, int k, int b) {
int res = 0, cur = 0;
for (int a : A) {
if (a == k) {
cur--;
}
if (a == b) {
cur++;
}
if (cur < 0) {
cur = 0;
}
res = Math.max(res, cur);
}
return res;
}
```
```C++ [C++]
int maxFrequency(vector<int>& A, int k) {
unordered_map<int, int> count;
for (int a : A) {
count[a]++;
}
auto kadane = [&](int b) {
int res = 0, cur = 0;
for (int a : A) {
if (a == k) {
cur--;
}
if (a == b) {
cur++;
}
if (cur < 0) {
cur = 0;
}
res = max(res, cur);
}
return res;
};
int res = 0;
for (const auto& [b, _] : count) {
res = max(res, kadane(b));
}
return count[k] + res;
}
```
# Solution 2
Same `res` mean the maximum increase from `count[k]`
But we can merge the usage of `cur` in solution 1 to `count`.
`count[a]` means the current number of `k,k,k,a,a,a...` sequence,
`k` first then `a`.
Time `O(n)`
Space `O(50)`
```py [Python3]
def maxFrequency(self, A: List[int], k: int) -> int:
cnt = Counter()
res = 0
for a in A:
cnt[a] = max(cnt[a], cnt[k]) + 1;
res = max(res, cnt[a] - cnt[k])
return cnt[k] + res
```
```Java [Java]
public int maxFrequency(int[] A, int k) {
int count[] = new int[51], res = 0;
for (int a : A) {
count[a] = Math.max(count[a], count[k]) + 1;
res = Math.max(res, count[a] - count[k]);
}
return count[k] + res;
}
```
```C++ [C++]
int maxFrequency(vector<int>& A, int k) {
unordered_map<int, int> count;
int res = 0;
for (int a : A) {
count[a] = max(count[a], count[k]) + 1;
res = max(res, count[a] - count[k]);
}
return count[k] + res;
}
```
| 52 | 0 |
['Array', 'Hash Table', 'Dynamic Programming', 'Python', 'C++', 'Java']
| 13 |
maximum-frequency-after-subarray-operation
|
One Pass
|
try-all-numbers-by-votrubac-gd52
|
Update: this optimized solution is doing pretty much the same as the longer (original) solution below.CodeThe key observation is that numbers are limited to 50.
|
votrubac
|
NORMAL
|
2025-01-26T04:01:59.534952+00:00
|
2025-01-26T04:51:47.126243+00:00
| 2,793 | false |
**Update:** this optimized solution is doing pretty much the same as the longer (original) solution below.
**Code**
```cpp []
int maxFrequency(vector<int>& nums, int k) {
int cnt[51] = {}, res = 0, cnt_k = 0;
for (int n : nums) {
cnt[n] = max(cnt[n], cnt_k) + 1;
res += n == k;
cnt_k += n == k;
res = max(res, cnt[n]);
}
return res;
}
```
The key observation is that numbers are limited to `50`.
We can just compute the result for each number `n` and return the best one.
The approach below finds the prefix and suffix where it is best to keep `k` unchanged. And, we change `n` into `k` in between.
We go left-to-right and count `k` and `n`.
When `cnt_k >= cnt_n`, we extend the prefix. So, the best result so far is `prefix + cnt_n`. We do the same right-to-left to find the best suffix.
**Complexity Analysis**
- Time: O(nm), where `m` is maximum number.
- O(n) for this problem since `m` is limited to 50.
- Memory: O(n)
**Code**
```cpp []
int cnt[100001];
class Solution {
public:
int maxFrequency(vector<int>& nums, int k) {
int res = 0, max_n = *max_element(begin(nums), end(nums));
for (int n = 1; n <= max_n; ++n) {
fill_n(begin(cnt),0, nums.size() + 1);
for (int i = 0, pref = 0, cnt_k = 0, cnt_n = 0; i < nums.size(); ++i) {
cnt_k += nums[i] == k;
cnt_n += nums[i] == n;
if (cnt_k >= cnt_n) {
pref += cnt_k;
cnt_k = cnt_n = 0;
}
cnt[i + 1] = pref + cnt_n;
}
for (int i = nums.size() - 1, suf = 0, cnt_n = 0, cnt_k = 0; i >= 0; --i) {
cnt_k += nums[i] == k;
cnt_n += nums[i] == n;
if (cnt_k >= cnt_n) {
suf += cnt_k;
cnt_k = cnt_n = 0;
}
res = max(res, cnt[i] + suf + cnt_n);
}
}
return res;
}
};
```
| 21 | 1 |
['C++']
| 6 |
maximum-frequency-after-subarray-operation
|
Simple Kadane Algorithm Solution
|
simple-kadane-algorithm-solution-by-pran-yf7y
|
IntuitionTo maximize the frequency of k, we need to strategically use the operation to convert other values into k while maximizing the size of the subarray.App
|
pranavjarande
|
NORMAL
|
2025-01-26T04:05:57.283000+00:00
|
2025-01-26T04:05:57.283000+00:00
| 1,518 | false |
### Intuition
To maximize the frequency of `k`, we need to strategically use the operation to convert other values into `k` while maximizing the size of the subarray.
### Approach
1. **Count Initial Frequency of `k`:**
- First, count how many elements in `nums` are equal to `k` and store this count in `cnt`.
2. **Kadane's Algorithm for Maximum Subarray Transformation:**
- Use **Kadane's Algorithm** to calculate the maximum frequency of `k` that can be achieved by converting subarrays with another target value.
- For each value `i` (from 1 to 50):
- Treat `i` as the target value to convert into `k`.
- Calculate the maximum contribution of elements being converted from `i` to `k` using a sliding window (Kadane's approach).
- Skip processing if `i == k` since no transformation is needed for `k`.
3. **Update the Maximum Frequency:**
- Combine the result of the current transformation with the initial frequency (`cnt`) of `k` to get the potential maximum frequency.
### Complexity
- **Time Complexity:**
- The outer loop runs for 50 iterations (fixed range).
- For each target value, we loop through the array once (`O(n)`).
- Hence, the overall complexity is **O(50 * n) ≈ O(n)**.
- **Space Complexity:**
- We use only a few variables for counting and calculations.
- Hence, the space complexity is **O(1)**.
# Code
```cpp []
class Solution {
public:
int maxFrequency(vector<int>& nums, int k)
{
int cnt=0;
for(int x:nums)if(x==k)cnt++;
int ans=cnt;
for(int i=1;i<=50;i++)
{
if(i==k)continue;
int maxi=0;
int s=0;
for(int x:nums)
{
if(x==i)s++;
else if(x==k)s--;
if(s<0)s=0;
maxi=max(maxi,s);
}
//cout<<i<<" "<<maxi<<endl;
ans=max(ans,cnt+maxi);
}
//cout<<endl;
return ans;
}
};
```
| 12 | 0 |
['Greedy', 'C++']
| 1 |
maximum-frequency-after-subarray-operation
|
Intuition of Kadane (Max Subarray) Algorithm | Clean Code
|
intuition-of-kadanemax-subarray-algorith-c039
|
Approach
Traverse the array, count the initial occurrence times of k kFreq, and record all non-k elements with unordered_set.
For each non-k element nonKNum,
|
Attention2000
|
NORMAL
|
2025-01-26T04:14:58.674070+00:00
|
2025-01-26T08:05:01.695138+00:00
| 1,212 | false |
# Approach
<!-- Describe your approach to solving the problem. -->
1. Traverse the array, count the initial occurrence times of k `kFreq`, and record all non-k elements with `unordered_set`.
2. For each non-k element `nonKNum`, use [Kadane algorithm](https://en.wikipedia.org/wiki/Maximum_subarray_problem) to calculate its corresponding maximum gain subarray. The contribution rules of the gain subarray are: +1 when `nonKNum` appears, -1 when `k` appears, and other elements don't matter.
3. Maintain the current maximum gain value `maxGain`, and get the maximum gain after traversing all non-k elements.
4. The final result is: `kFreq + maxGain`.
# Complexity
- Time complexity: $$O(mn)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(m)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
Where $$m$$ is the number of different non-k elements in `nums` and $$n$$ is the length of `nums`.
# Code
```cpp []
class Solution {
public:
int maxFrequency(vector<int>& nums, int k) {
int kFreq = 0;
unordered_set<int> nonKNums;
for (int num : nums) {
if (num == k) {
kFreq++;
} else {
nonKNums.insert(num);
}
}
int maxGain = 0;
for (int nonKNum : nonKNums) {
int curMax = 0;
int maxSubarray = 0;
for (int num : nums) {
if (num == nonKNum) {
curMax += 1;
} else if (num == k) {
curMax -= 1;
}
maxSubarray = max(maxSubarray, curMax);
if (curMax < 0) {
curMax = 0;
}
}
maxGain = max(maxGain, maxSubarray);
}
return kFreq + maxGain;
}
};
```
| 10 | 0 |
['Greedy', 'C++']
| 1 |
maximum-frequency-after-subarray-operation
|
100%Beat || Using HashMap || Counting Freq
|
100beat-using-hashmap-counting-freq-by-a-wqww
|
IntuitionApproachInitial Frequency Calculation: First, the frequency of k in the original array is calculatedSubarray Transformation: The next part of the solut
|
AlgoAce2004
|
NORMAL
|
2025-01-26T04:14:46.797424+00:00
|
2025-01-26T04:16:21.851561+00:00
| 860 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
Initial Frequency Calculation: First, the frequency of k in the original array is calculated
Subarray Transformation: The next part of the solution is to simulate the effect of selecting a subarray and adding a number x to all elements in that subarray. The goal is to find subarrays that, after adding a specific number x, increase the frequency of k. To do this, the code iterates over all possible numbers v in the array (except k), and checks how adding x can result in a transformation that creates more ks.
Maximizing the Frequency of k: The variable curr_sum tracks the ongoing "balance" between occurrences of v and k.
If we encounter a v, we increase curr_sum because it's becoming more like k (after adding the appropriate x).
If we encounter k, we decrease curr_sum because we are subtracting the influence of k in the current subarray.
If at any point curr_sum becomes negative, it is reset to zero, as continuing with a negative sum wouldn't help maximize the result. The maximum value of curr_sum (temp_max) represents the largest potential increase in the frequency of k for that specific value v.
This loop runs for all values of v (from 1 to 50), ensuring that every possible subarray transformation is considered.
Final Result: After iterating through all values of v, the maximum possible increase in the frequency of k is stored in max. The final frequency of k after the transformation is the sum of the initial frequency (k_freq) and the maximum increase (max):
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public static int solve(int[] nums, int k) {
int k_freq = 0;
HashMap<Integer, Integer> map = new HashMap<>();
for (int i : nums) {
map.put(i, map.getOrDefault(i, 0) + 1);
}
if (map.containsKey(k)) {
k_freq += map.get(k);
}
int max = 0;
for (int v = 1; v <= 50; v++) {
if (v == k) continue;
int curr_sum = 0;
int temp_max = 0;
for (int num : nums) {
if (num == v) {
curr_sum += 1;
} else if (num == k) {
curr_sum -= 1;
}
if (curr_sum < 0) {
curr_sum = 0;
}
if (curr_sum > temp_max) {
temp_max = curr_sum;
}
}
if (temp_max > max) {
max = temp_max;
}
}
int maxfreq = k_freq + max;
return maxfreq;
}
public int maxFrequency(int[] nums, int k) {
return solve(nums, k);
}
}
```
| 5 | 0 |
['Java']
| 2 |
maximum-frequency-after-subarray-operation
|
Easy solution using kadane algorithm. Better than other solutions available
|
easy-solution-using-kadane-algorithm-bet-4t31
|
IntuitionIf u see the testcases (they are <=50). So what if we try making all numbers in the array from 1 to 50 equal to k.
and then see what is our best soluti
|
madhavgarg2213
|
NORMAL
|
2025-01-26T06:49:27.451464+00:00
|
2025-01-26T06:49:27.451464+00:00
| 504 | false |
# Intuition
If u see the testcases (they are <=50). So what if we try making all numbers in the array from 1 to 50 equal to k.
and then see what is our best solution.
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
So to check the longest subarray of integer i, we use kadane. we will create a copy array where that element is 1 and k = -1 and rest all 0. so if k comes in between of the longest subarray it automatically subtracts the 1 k occcurance from the total k occurances.
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: 50 * O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: 50* O(n)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int kadane(vector<int>& v){
int sum = 0;
int m = 0;
for(int i : v){
sum+=i;
m = max(m, sum);
sum = max(sum, 0);
}
return m;
}
int maxFrequency(vector<int>& nums, int k) {
int maxSum = 0;
int n = nums.size();
for(int i = 1; i<=50; i++){
if(i==k){
continue;
}
vector<int> copy = nums;
for(int& j: copy){
if(j==k){
j = -1;
}else if(j==i){
j = 1;
}else{
j = 0;
}
}
maxSum = max(maxSum, kadane(copy));
}
int cnt=0;
for(int a: nums){
if(a==k){
cnt++;
}
}
if(maxSum == n || cnt == n){
return n;
}
return maxSum + cnt;
}
};
```
| 4 | 0 |
['C++']
| 0 |
maximum-frequency-after-subarray-operation
|
Simplest Python solution O(50*n). Try all numbers only
|
simplest-python-solution-o50n-try-all-nu-ul6m
|
Code
|
112115046
|
NORMAL
|
2025-01-26T04:07:22.397912+00:00
|
2025-01-26T04:07:22.397912+00:00
| 677 | false |
# Code
```python3 []
class Solution:
def maxFrequency(self, nums: List[int], k: int) -> int:
mxx = 0
kc = nums.count(k)
for i in range(1,51):
if i == k: continue
mx = 0
c = 0
for num in nums:
if num == i: c += 1
elif num == k: c -= 1
mx = max(mx, c)
c = max(0, c)
mxx = max(mxx, mx)
return kc + mxx
```
| 4 | 1 |
['Python3']
| 2 |
maximum-frequency-after-subarray-operation
|
SLIDING WINDOW WITH FREQUENCY COUNT - BEATS 100%
|
sliding-window-with-frequency-count-beat-3mu2
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
rryn
|
NORMAL
|
2025-01-26T04:06:16.333987+00:00
|
2025-01-26T04:06:16.333987+00:00
| 1,074 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int maxFrequency(vector<int>& a, int k) {
int n = a.size(), ans = 0;
vector<vector<int>> g(n, vector<int> (51, 0));
for(int i=0; i<n; i++){
for(int j=1; j<=50; j++){
if(i > 0) g[i][j] = g[i-1][j];
if(j == a[i]) g[i][j]++;
}
}
for(int i=1; i<=50; i++){
vector<vector<int>> t(n, vector<int>(2, 0));
int mini = -1;
for(int j=0; j<n; j++){
if(j > 0){
t[j][0] = t[j-1][0] + (a[j] == i);
t[j][1] = t[j-1][1] + (a[j] == k);
}
else {
t[j][0] = (a[j] == i);
t[j][1] = (a[j] == k);
}
int cur = t[j][0] - t[j][1];
int minVal = mini >= 0 ? t[mini][0] - t[mini][1] : 0;
int rem = g[n-1][i] - g[j][i] + ( j < n-1 and a[n-1] == k ? 1 : 0);
ans = max(ans, rem + (cur - minVal) + (mini >= 0 ? t[mini][1] : 0));
if(cur < minVal) mini = j;
}
}
return ans;
}
};
```
| 4 | 1 |
['C++']
| 1 |
maximum-frequency-after-subarray-operation
|
DP with explanation
|
dp-with-explanation-by-aianhuipanhui-011s
|
IntuitionWhen you have no idea how to solve medium problem, try DP.Approach
First count maximal number of k we can get considering only nums[:i] (i included).
|
aianhuipanhui
|
NORMAL
|
2025-01-26T04:15:56.385145+00:00
|
2025-01-26T04:15:56.385145+00:00
| 676 | false |
# Intuition
When you have no idea how to solve medium problem, try DP.
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
- First count maximal number of k we can get considering only nums[:i] (i included).
- Suppose last position of nums[i] is at index j (this can be recorded with dict), we either take res[j] + 1 or start a new chapter by counting number of k between index 0 and i-1 and adding an additional 1.
- If nums[i] = k, update k_cnt to record number of k between index 0 and i.
- Add number of k between i+1 and n-1 to res[i].
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: $O(n)$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $O(n)$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def maxFrequency(self, nums: List[int], k: int) -> int:
n = len(nums)
last_pos = {}
res = [0 for i in range(n)]
k_cnt = [0 for i in range(n+1)]
for i, ele in enumerate(nums):
k_cnt[i+1] = k_cnt[i] + int(ele == k)
res[i] = 1 + k_cnt[i]
if ele in last_pos:
res[i] = max(res[i], res[last_pos[ele]] + 1)
last_pos[ele] = i
for i in range(n):
res[i] += (k_cnt[-1] - k_cnt[i+1])
return max(res)
```
| 3 | 0 |
['Python3']
| 0 |
maximum-frequency-after-subarray-operation
|
easy to understand
|
easy-to-understand-by-enigmaler-ewfc
|
Time complexity:
O(n)
Code
|
enigmaler
|
NORMAL
|
2025-02-07T00:42:23.669717+00:00
|
2025-02-17T07:23:05.822922+00:00
| 53 | false |
- Time complexity:
O(n)
# Code
```java []
class Solution {
public int maxFrequency(int[] nums, int k) {
int[][] frq = new int[50][];// inner array: 0 -> counter(increment),
//1 -> count of K, 2 -> frq Of value - CntK(index[1]), reset array if 2 index value goes negative;
int cntK = 0, max = 1;
for(int i = 0; i < nums.length; i++){
if(nums[i] == k){cntK++;continue;}
int[] curr = frq[nums[i] - 1];
if(curr == null || curr[0] == -100 || (curr != null && (curr[0] - (cntK - curr[1]) <= 0))) {
frq[nums[i] - 1] = new int[]{1, cntK, 1};//frq, cntK, difference
}else{
curr[0]++;curr[2] = curr[0] - (cntK - curr[1]);
if( curr[2] > max ){
max = curr[2];
}
if(curr[2] <= 0){curr[0] = -100;}//-100 -> reset(if count of k is more)
}
}
return (max + cntK > nums.length) ? nums.length : max + cntK;
}
}
```
| 2 | 0 |
['Java']
| 0 |
maximum-frequency-after-subarray-operation
|
Contest 434 || Queu-3
|
contest-434-queu-3-by-sajaltiwari007-0ifx
|
Approach & Intuition:
Count occurrences of k
The first loop counts how many times k appears in nums (countk).
If all elements in nums are k, return countk imm
|
sajaltiwari007
|
NORMAL
|
2025-01-30T16:08:40.338475+00:00
|
2025-01-30T16:08:40.338475+00:00
| 38 | false |
## **Approach & Intuition:**
1. **Count occurrences of `k`**
- The first loop counts how many times `k` appears in `nums` (`countk`).
- If all elements in `nums` are `k`, return `countk` immediately.
2. **Create a 2D frequency array (`arr`)**
- The `arr` array is structured to keep track of how often each number appears in different segments split by occurrences of `k`.
- `arr[ind][nums[i]-1]++` is used to store frequency counts.
3. **Find the most frequent number (excluding `k`)**
- While populating `arr`, it also keeps track of the most frequently occurring number (`ele`) and its count (`maxi`).
4. **Calculate the maximum frequency of any number**
- A nested loop iterates over possible numbers (1 to 50) and determines the maximum frequency by summing values across different segments.
- The condition `if(j+1>count) count = j+1;` ensures that the frequency count is at least `j+1`.
- The final answer is determined using `Math.max()`.
---
## **Complexity Analysis:**
- **First loop:** `O(N)` → Counts occurrences of `k`.
- **Second loop:** `O(N)` → Fills the `arr` matrix.
- **Nested loops:** `O(50 * countk)`
- Outer loop runs 50 times (for numbers from 1 to 50).
- Inner loop runs `countk + 1` times (number of segments).
Thus, the overall complexity is approximately **O(N + 50 * countk)**.
### **Optimizations:**
1. **Avoid unnecessary storage (`arr` matrix)**
- Instead of a `countk+1 × 50` matrix, a **HashMap** could track segment frequencies dynamically, reducing space.
2. **More efficient frequency computation**
- Using a **sliding window or prefix sum approach** could make frequency counting more efficient.
# Code
```java []
class Solution {
public int maxFrequency(int[] nums, int k) {
int countk =0;
for(int i:nums){
if(i==k) countk++;
}
if(countk==nums.length) return countk;
int[][] arr = new int[countk+1][50];
int ind =0;
int maxi =0;
int ele = -1;
for(int i=0;i<nums.length;i++){
if(nums[i]==k){
ind++;
continue;
}
else{
arr[ind][nums[i]-1]++;
if(arr[ind][nums[i]-1]>maxi){
maxi = arr[ind][nums[i]-1];
ele = nums[i];
}
}
}
int maxFreq = 0;
int answer =0;
for(int i=1;i<=50;i++){
int count =0;
int temp =0;
for(int j=0;j<arr.length;j++){
count+=arr[j][i-1];
if(j+1>count) count =j+1;
answer = Math.max(answer,count+countk-j);
}
answer = Math.max(answer,count);
}
return answer;
}
}
```
| 2 | 0 |
['Java']
| 0 |
maximum-frequency-after-subarray-operation
|
✅Easy to understand✅ Beats 100%
|
easy-to-understand-beats-100-by-mithun00-l5wz
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Mithun005
|
NORMAL
|
2025-01-27T05:19:57.139847+00:00
|
2025-01-27T05:19:57.139847+00:00
| 119 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def maxFrequency(self, nums: List[int], k: int) -> int:
m=0
c=nums.count(k)
for i in range(1,51):
if(i!=k):
n=0
v=0
for j in nums:
if(j==k):
v-=1
elif(j==i):
v+=1
v=max(v,0)
n=max(n,v)
m=max(m,n)
return m+c
```
| 2 | 1 |
['Python3']
| 1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.