question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
minimum-bit-flips-to-convert-number
|
xor bitset->1 line||beats 100%
|
xor-bitset-1-linebeats-100-by-anwendeng-ynjf
|
Intuition\n Describe your first thoughts on how to solve this problem. \nEasy question.\n1-line solution is provided.\n# Approach\n Describe your approach to so
|
anwendeng
|
NORMAL
|
2024-09-11T01:02:33.893466+00:00
|
2024-09-11T11:45:23.436705+00:00
| 2,811 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nEasy question.\n1-line solution is provided.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nxx=x^y;\nzz=x&y&xx;//in fact zz=0\n\nxb.count()+zb.count() is the answer\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code||0ms beats 100%\n```cpp []\nclass Solution {\npublic:\n int minBitFlips(int x, int y) {\n int xx=x^y;\n int zz=x&y&xx;\n bitset<32> xb(xx), zb(zz);\n return xb.count()+zb.count();\n }\n};\n```\n# C++ revised 1-liner\n```\nclass Solution {\npublic:\n int minBitFlips(int x, int y) {\n return bitset<32>(x^y).count();\n }\n};\n```
| 24 | 1 |
['Bit Manipulation', 'C++']
| 8 |
minimum-bit-flips-to-convert-number
|
Java - XOR and counting bits - beats 100%
|
java-xor-and-counting-bits-beats-100-by-cuup8
|
We need to count the number of corresponding bits of start and goal that are different.\nxor-ing start and goal will result in a new number with binary represen
|
abanoubcs
|
NORMAL
|
2022-04-02T16:17:07.965214+00:00
|
2022-04-02T22:43:00.069103+00:00
| 3,141 | false |
We need to count the number of corresponding bits of start and goal that are different.\nxor-ing start and goal will result in a new number with binary representation of 0 where the corresponding bits of start and goal are equal and 1 where the corresponding bits are different.\n\nFor example: 10 and 7 \n10 = 1010\n 7 = 0111\n \n10 xor 7 = 1101 (3 ones)\n\nNext we need to count the number of 1s (different bits)\nThe quickest way to count the number of 1s in a number is by eliminating the right most 1 each time and count the number of eliminations, this is done by and-ing the number with (number-1)\nSubtracting a 1 from a number flips all right most bits until the first right most 1 and by and-ing with the number itself we eliminating the all bits until the first tight most 1 (inclusive)\nex. \nnumber =1101\nnumber -1 = 1100\nnumber and (number -1) = 1100 (we eliminated the right most 1)\n\n```\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int xor =start ^ goal;\n int count=0;\n while(xor>0){\n count++;\n xor=xor & (xor-1);\n }\n return count;\n \n }\n}\n```
| 24 | 0 |
['Java']
| 8 |
minimum-bit-flips-to-convert-number
|
Simple Two lines code using XOR
|
simple-two-lines-code-using-xor-by-user0-rxy0
|
Intuition\n# XOR Operation (^):\n\nThe XOR operation returns a bit that is 1 where the bits of start and goal differ, and 0 where they are the same.\nBy calcula
|
user0197ub
|
NORMAL
|
2024-09-11T01:11:51.171047+00:00
|
2024-09-11T01:11:51.171066+00:00
| 5,602 | false |
# Intuition\n# XOR Operation (^):\n\nThe XOR operation returns a bit that is 1 where the bits of start and goal differ, and 0 where they are the same.\nBy calculating xor_value = start ^ goal, you create a number where each 1 represents a bit that differs between start and goal.\n# Counting the Number of Differing Bits:\n\nThe number of differing bits (or the number of 1s in xor_value) is exactly the number of bit flips required to convert start to goal.\nbin(xor_value) converts the number to its binary representation, and .count(\'1\') counts the number of 1s.\n\n# Complexity\n- Time complexity:\nO(1)\n\n- Space complexity:\n O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def minBitFlips(self, start: int, goal: int) -> int:\n xor_value = start ^ goal\n return bin(xor_value).count(\'1\')\n \n```\n\n# Code\n```c++ []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int xor_value = start ^ goal;\n int res = 0;\n while (xor_value > 0) {\n res += xor_value & 1; \n xor_value >>= 1; \n }\n \n return res;\n }\n};\n```\n\n\n
| 21 | 2 |
['Bit Manipulation', 'C++', 'Python3']
| 9 |
minimum-bit-flips-to-convert-number
|
C++/Java/JavaScript || Easy Solution || Beats 100% || Bit Manipulation
|
cjavajavascript-easy-solution-beats-100-rlgau
|
Intuition\n - Question -> Here given Two numbers. If both no. are represented in Binary then how many minimum bits are required to change in one no. so it conve
|
shivang21007
|
NORMAL
|
2023-05-11T19:57:43.918196+00:00
|
2023-05-11T19:57:43.918241+00:00
| 2,059 | false |
# Intuition\n - Question -> Here given Two numbers. If both no. are represented in Binary then how many minimum bits are required to change in one no. so it convert into second no. \n\n*example* -> \n```\n 10 = 1 0 (1) 0\n 7 = 0 1 (1) 1\n```\nhere, 3 bits are different in both no.s and need to be change in one of them to covert into another.\n\n# Approach \nHere, we have to identify the different bits so , XOR operator can help us -->\n``` \n A | B | A XOR B\n 0 | 0 | 0\n 10 = 1 0 1 0 0 | 1 | 1 \n 7 = 0 1 1 1 1 | 0 | 1 \n____________________________ 1 | 1 | 0\nxor(10,7) = 1 1 0 1\n```\nNow , We have to just count the Set Bits(1) in result of xor.\n no.of Set bits = 3. So, There is minimum 3 flips required.\n# Complexity\n- Time complexity:\n\n Best case - O(1)\n Worst Case - O(n)\n\n- Space complexity:\n \n Constant Space - O(1)\n\n# Code\n\n- C++ Code ->\n```\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n \n int a = (start ^ goal); // this will do xor of given numbers\n //now count set bits\n int count = 0; \n while(a){\n if(a&1){\n count++;\n }\n a = a>>1; // this is right shift operator\n }\n return count;\n }\n};\n```\n- Java Code ->\n```\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int a = (start ^ goal);\n int count = 0;\n \n while(a != 0) {\n if((a & 1) == 1) {\n count++;\n }\n \n a = a >> 1;\n }\n \n return count;\n }\n}\n\n```\n- JavaScript code ->\n```\nvar minBitFlips = function(start, goal) {\n let a = start ^ goal;\n let count = 0;\n \n while (a !== 0) {\n if (a & 1) {\n count++;\n }\n \n a = a >> 1;\n }\n \n return count;\n};\n```
| 18 | 0 |
['Bit Manipulation', 'C++', 'Java', 'JavaScript']
| 3 |
minimum-bit-flips-to-convert-number
|
O(1) | 0 - ms beats 100 % | Java | Python | Go | C++ | Rust | JavaScript
|
o1-0-ms-beats-100-java-python-go-c-rust-jlb2c
|
\n### Code 1\n\n\n\njava []\npublic class Solution {\n public int minBitFlips(int start, int goal) {\n return Integer.bitCount(start ^ goal);\n }\n
|
kartikdevsharma_
|
NORMAL
|
2024-09-11T04:33:07.520883+00:00
|
2024-09-11T14:26:09.368333+00:00
| 2,493 | false |
\n### Code 1\n\n\n\n```java []\npublic class Solution {\n public int minBitFlips(int start, int goal) {\n return Integer.bitCount(start ^ goal);\n }\n}\n\n```\n\n\n```cpp []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n return __builtin_popcount(start ^ goal);\n }\n};\n\n```\n\n\n\n\n\n```python []\nclass Solution:\n def minBitFlips(self, start: int, goal: int) -> int:\n return bin(start ^ goal).count(\'1\')\n\n```\n\n\n\n\n```go []\nfunc minBitFlips(start int, goal int) int {\n return bits.OnesCount(uint(start ^ goal))\n}\n\n```\n\n\n\n\n```rust []\nimpl Solution {\n pub fn min_bit_flips(start: i32, goal: i32) -> i32 {\n (start ^ goal).count_ones() as i32\n }\n}\n\n```\n\n\n\n\n```javascript []\nvar minBitFlips = function(start, goal) {\n return (start ^ goal).toString(2).split(\'1\').length - 1;\n};\n\n```\n\n### Code 2\n\n```Java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int flipCount = 0;\n int mask = 1;\n \n for (int i = 0; i < 32; i++) { \n boolean startBit = (start & mask) != 0;\n boolean goalBit = (goal & mask) != 0;\n \n if (startBit != goalBit) {\n flipCount++;\n }\n \n mask <<= 1;\n }\n \n return flipCount;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int flipCount = 0;\n unsigned int mask = 1;\n \n for (int i = 0; i < 32; i++) {\n bool startBit = (start & mask) != 0;\n bool goalBit = (goal & mask) != 0;\n \n if (startBit != goalBit) {\n flipCount++;\n }\n \n mask <<= 1;\n }\n \n return flipCount;\n }\n};\n```\n```Python []\nclass Solution:\n def minBitFlips(self, start: int, goal: int) -> int:\n flip_count = 0\n mask = 1\n \n for _ in range(32): # Assuming 32-bit integers\n start_bit = bool(start & mask)\n goal_bit = bool(goal & mask)\n \n if start_bit != goal_bit:\n flip_count += 1\n \n mask <<= 1\n \n return flip_count\n```\n```Go []\nfunc minBitFlips(start int, goal int) int {\n flipCount := 0\n mask := 1\n\n for i := 0; i < 32; i++ {\n startBit := (start & mask) != 0\n goalBit := (goal & mask) != 0\n\n if startBit != goalBit {\n flipCount++\n }\n\n mask <<= 1\n }\n\n return flipCount\n}\n```\n```Rust []\nimpl Solution {\n pub fn min_bit_flips(start: i32, goal: i32) -> i32 {\n let mut flip_count = 0;\n let mut mask: u32 = 1;\n \n for _ in 0..32 {\n let start_bit = (start & (mask as i32)) != 0;\n let goal_bit = (goal & (mask as i32)) != 0;\n \n if start_bit != goal_bit {\n flip_count += 1;\n }\n \n mask <<= 1;\n }\n \n flip_count\n }\n}\n```\n```JavaScript []\n/**\n * @param {number} start\n * @param {number} goal\n * @return {number}\n */\nvar minBitFlips = function(start, goal) {\n let flipCount = 0;\n let mask = 1;\n \n for (let i = 0; i < 32; i++) {\n const startBit = (start & mask) !== 0;\n const goalBit = (goal & mask) !== 0;\n \n if (startBit !== goalBit) {\n flipCount++;\n }\n \n mask <<= 1;\n }\n \n return flipCount;\n};\n```
| 14 | 0 |
['Bit Manipulation', 'C++', 'Java', 'Go', 'Python3', 'Rust', 'JavaScript']
| 5 |
minimum-bit-flips-to-convert-number
|
c++ | Easy O(N) solution | Basic Maths
|
c-easy-on-solution-basic-maths-by-yash2a-qd3s
|
Please upvote if you find this solution helpful\nCode:\n\nclass Solution {\npublic:\n //we just check whether binary bit is equal or not \n //if it is we
|
Yash2arma
|
NORMAL
|
2022-04-05T08:37:52.408073+00:00
|
2022-04-05T08:40:26.193274+00:00
| 1,540 | false |
**Please upvote if you find this solution helpful**\n**Code:**\n```\nclass Solution {\npublic:\n //we just check whether binary bit is equal or not \n //if it is we do nothing otherwise we flips the bit and increase the count\n int minBitFlips(int start, int goal) \n { \n int flips=0;\n\t\t\n\t\t//iterate until both numbers get 0\n while(start || goal)\n {\n\t\t\t//check whether bits are equal or not, if not we flip the bit\n if(start%2 != goal%2)\n flips++;\n \n start /= 2;\n goal /= 2;\n }\n return flips;\n \n }\n};\n```
| 12 | 0 |
['Math', 'C', 'C++']
| 3 |
minimum-bit-flips-to-convert-number
|
__builtin_popcount(start ^ goal)
|
builtin_popcountstart-goal-by-votrubac-1w89
|
C++\ncpp\nint minBitFlips(int start, int goal) {\n return __builtin_popcount(start ^ goal);\n}\n
|
votrubac
|
NORMAL
|
2022-04-03T19:19:24.871537+00:00
|
2022-04-03T19:19:24.871572+00:00
| 904 | false |
**C++**\n```cpp\nint minBitFlips(int start, int goal) {\n return __builtin_popcount(start ^ goal);\n}\n```
| 12 | 0 |
['C']
| 5 |
minimum-bit-flips-to-convert-number
|
✔ python | easy | interview thinking
|
python-easy-interview-thinking-by-peb-dx0h
|
The given question requires us to count the total number of flips we need to do inorder to make start -> goal.\nEx: \n7 - 0111\n10 - 1010\nHere, we only flip t
|
peb
|
NORMAL
|
2022-07-09T21:34:30.613365+00:00
|
2022-12-04T15:22:16.507182+00:00
| 1,923 | false |
The given question requires us to count the total number of flips we need to do inorder to make `start -> goal`.\nEx: \n7 - 0111\n10 - 1010\nHere, we only flip the bits which are different in both **start** and **goal**, i.e. `01` or `10`. And, what helps us to find if the bits are different? **XOR**. \nNow, we count these bits (i.e. different bits). And how do we calculate the number of `1\'s` in a number? `n & (n-1)` technique.\n\nSo, the number of flips required is **3**.\n\nTherefore, the solution is divided into two parts - identify the distinct bits in both numbers and then, count these bits.\n\nSolution:\n```python\nclass Solution(object):\n def minBitFlips(self, start, goal):\n res = start ^ goal\n cnt = 0\n while res:\n res &= res - 1\n cnt += 1\n return cnt\n```\n\n
| 9 | 0 |
['Bit Manipulation', 'Python', 'Python3']
| 3 |
minimum-bit-flips-to-convert-number
|
Java solution with explaination
|
java-solution-with-explaination-by-shubh-xjzd
|
Intuition\nWe want to check how many bits need to flipped in the input number to get the output number. So we would need to check the bits which are different i
|
shubhampawar16298
|
NORMAL
|
2023-01-07T17:56:26.053480+00:00
|
2023-01-07T17:56:26.053529+00:00
| 1,828 | false |
# Intuition\nWe want to check how many bits need to flipped in the input number to get the output number. So we would need to check the bits which are different in both numbers (No point in counting bits which are same in both) and count them.\n\n# Approach\nE.g. \n10 = 1010\n7 = 0111\nso different bits are, from rightmost bit, 1st, 3rd and 4th. \nWe know XOR operation between two numbers will give us these different bits.\n\n 1010\n ^ 0111\n ____________ \n 1101\nAs we see here, in the output number only bits are set which are different in both numbers. (1 ^ 1) = 0 and (1 ^ 0) = 1\n\nNow, we just have to count these set bits and for that we will use Kernighan\u2019s algorithm to find the number of set bits in a number. The idea behind the algorithm is that when we subtract one from an integer, all the bits following the rightmost set of bits are inverted, turning 1 to 0 and 0 to 1. The rightmost set bit also gets inverted with the bits right to it.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int minBitFlips(int start, int goal) {\n if(start == goal) return 0;\n int xor = start ^ goal;\n int counter=0;\n while(xor > 0) {\n xor = xor & (xor-1);\n counter++;\n }\n return counter;\n }\n}\n```
| 8 | 0 |
['Java']
| 1 |
minimum-bit-flips-to-convert-number
|
Simple Java Code ☠️
|
simple-java-code-by-abhinandannaik1717-em31
|
Code\njava []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n String str1 = Integer.toBinaryString(start);\n String str2 =
|
abhinandannaik1717
|
NORMAL
|
2024-09-11T07:03:08.513339+00:00
|
2024-09-11T07:03:08.513373+00:00
| 584 | false |
# Code\n```java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n String str1 = Integer.toBinaryString(start);\n String str2 = Integer.toBinaryString(goal);\n int n1 = str1.length();\n int n2 = str2.length();\n int count = 0,i=n1-1,j=n2-1;\n while(i>=0 && j>=0){\n if(str1.charAt(i) != str2.charAt(j)){\n count++;\n }\n i--;\n j--;\n }\n while(i>=0){\n if(str1.charAt(i)==\'1\'){\n count++;\n }\n i--;\n }\n while(j>=0){\n if(str2.charAt(j)==\'1\'){\n count++;\n }\n j--;\n } \n return count; \n }\n}\n```\n\n### Explanation\n\n#### Step 1: Convert the Integers to Binary Strings\n```java\nString str1 = Integer.toBinaryString(start);\nString str2 = Integer.toBinaryString(goal);\n```\n- **`Integer.toBinaryString(start)`**: This method converts the integer `start` into its binary representation as a string.\n - For example, if `start = 5`, the result would be `"101"`.\n- **`Integer.toBinaryString(goal)`**: Similarly, this converts the integer `goal` into its binary representation.\n - For example, if `goal = 1`, the result would be `"1"`.\n\n#### Step 2: Get the Length of Both Binary Strings\n```java\nint n1 = str1.length();\nint n2 = str2.length();\n```\n- `n1` holds the length of the binary string of `start`.\n- `n2` holds the length of the binary string of `goal`.\n \nThis is needed to determine the size of both binary strings for comparison.\n\n#### Step 3: Initialize Variables for Comparison\n```java\nint count = 0, i = n1 - 1, j = n2 - 1;\n```\n- **`count`**: This variable tracks the number of bit flips.\n- **`i` and `j`**: These indices represent the positions of the bits in the binary strings of `start` and `goal`, respectively. They are initialized to point to the last character of each string (`n1-1` and `n2-1`), so we can compare the binary strings from right to left (least significant bit first).\n\n#### Step 4: Compare Both Binary Strings\n```java\nwhile(i >= 0 && j >= 0){\n if(str1.charAt(i) != str2.charAt(j)){\n count++;\n }\n i--;\n j--;\n}\n```\nThis loop iterates over both binary strings from right to left (starting with the least significant bits) and compares each bit:\n- **`if(str1.charAt(i) != str2.charAt(j))`**: If the bits at the same position in `start` and `goal` are different, a flip is required, so we increment `count`.\n- The loop continues until either string is fully traversed (i.e., `i < 0` or `j < 0`).\n\n#### Step 5: Handle Remaining Bits in `start`\n```java\nwhile(i >= 0){\n if(str1.charAt(i) == \'1\'){\n count++;\n }\n i--;\n}\n```\nOnce the common part of both strings has been compared, we check if there are any remaining bits in the `start` binary string:\n- **`if(str1.charAt(i) == \'1\')`**: If there are remaining bits in `start` and the current bit is `1`, it means we need to flip this bit to `0` to match the shorter `goal` binary string (which effectively has leading `0`s).\n- **`count++`**: If a bit is `1`, a flip is counted.\n\n#### Step 6: Handle Remaining Bits in `goal`\n```java\nwhile(j >= 0){\n if(str2.charAt(j) == \'1\'){\n count++;\n }\n j--;\n}\n```\nSimilarly, if the `goal` string has remaining bits that haven\'t been compared:\n- **`if(str2.charAt(j) == \'1\')`**: If the current bit is `1`, we need to flip it to `0` (since the `start` string has effectively `0`s in these positions).\n- **`count++`**: A flip is counted for each `1` in the remaining part of the `goal`.\n\n#### Step 7: Return the Total Count of Flips\n```java\nreturn count;\n```\nFinally, the total number of bit flips needed is returned.\n\n### Example Walkthrough\n\nLet\u2019s walk through an example where:\n- **start = 5** (binary: `"101"`)\n- **goal = 1** (binary: `"1"`)\n\n1. **Convert to binary**:\n - `start = "101"`\n - `goal = "1"`\n\n2. **Comparison**:\n - Start comparing from the rightmost bits:\n - First comparison: `start[2] = 1` and `goal[0] = 1` (no flip needed).\n - We run out of bits in `goal`, so we move to the next step.\n \n3. **Remaining bits in `start`**:\n - We have two more bits left in `start`: `"10"`.\n - For `start[1] = 0`, no flip is needed.\n - For `start[0] = 1`, we need a flip (flip to `0`).\n\n4. **Result**:\n - The total number of flips required is 1.\n\n### Time Complexity\n- **O(max(n1, n2))**: The algorithm compares the two binary strings from right to left, so the time complexity is proportional to the length of the longer binary string between `start` and `goal`.\n\n### Space Complexity\n- **O(n1 + n2)**: We store the binary representations of `start` and `goal` as strings. Therefore, the space complexity depends on the size of these binary strings.\n\n
| 7 | 0 |
['String', 'Java']
| 0 |
minimum-bit-flips-to-convert-number
|
💢☠💫Easiest👾Faster✅💯 Lesser🧠 🎯 C++✅Python3🐍✅Java✅C✅Python🐍✅C#✅💥🔥💫Explained☠💥🔥 Beats 100
|
easiestfaster-lesser-cpython3javacpython-mmf1
|
Intuition\n\n Describe your first thoughts on how to solve this problem. \njavascript []\n/**\n * @param {number} start\n * @param {number} goal\n * @return {nu
|
Edwards310
|
NORMAL
|
2024-09-11T05:29:06.114252+00:00
|
2024-09-11T05:29:06.114289+00:00
| 160 | false |
# Intuition\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n```javascript []\n/**\n * @param {number} start\n * @param {number} goal\n * @return {number}\n */\nvar minBitFlips = function (start, goal) {\n let cnt = 0, xor = start ^ goal\n while (xor !== 0) {\n cnt++\n xor = xor & (xor - 1)\n }\n return cnt\n};\n```\n```C++ []\nclass Solution {\npublic:\n int minBitFlips(int s, int g) {\n return __builtin_popcount(s ^ g);\n }\n};\n```\n```Python3 []\nclass Solution:\n def minBitFlips(self, start: int, goal: int) -> int:\n return bin(start ^ goal).count(\'1\')\n```\n```Java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int num = start ^ goal, cnt = 0;\n while (num != 0) {\n cnt++;\n num = num & (num - 1);\n }\n return cnt;\n }\n}\n```\n```C []\n#include<stdio.h>\n#include<stdlib.h>\n#define Rep(i, n) for (int i = 0; i < n; ++i)\n#define Rep1(i, n) for (int i = 1; i <=n ;i++)\n\nint minBitFlips(int start, int goal) {\n int webinar = start ^ goal;\n int cnt = 0;\n Rep(i, 31) {\n int mask = (1 << i);\n if (mask & webinar)\n cnt++;\n }\n return cnt;\n}\n```\n```Python []\nclass Solution(object):\n def minBitFlips(self, s, g):\n """\n :type start: int\n :type goal: int\n :rtype: int\n """\n web = s ^ g\n cnt = 0\n while web:\n cnt += 1\n web = web & (web - 1)\n \n return cnt\n```\n```C# []\npublic class Solution {\n public int MinBitFlips(int start, int goal) {\n var xor = start ^ goal;\n int count = 0;\n while (xor != 0){\n xor = xor & (xor - 1);\n count++;\n }\n return count;\n }\n}\n```\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(logn)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n# Code\n```cpp []\nclass Solution {\npublic:\n int minBitFlips(int s, int g) {\n return __builtin_popcount(s ^ g);\n }\n};\n```\n
| 7 | 0 |
['Bit Manipulation', 'C', 'Python', 'C++', 'Java', 'Python3', 'JavaScript']
| 0 |
minimum-bit-flips-to-convert-number
|
not bit manipulation just plain string conversion
|
not-bit-manipulation-just-plain-string-c-hz20
|
Intuition\n Describe your first thoughts on how to solve this problem. \nwe convert the bigger number to string and convert the smaller number to string and we
|
srinivas_bodduru
|
NORMAL
|
2024-09-11T02:19:04.147008+00:00
|
2024-09-11T02:19:04.147035+00:00
| 1,330 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nwe convert the bigger number to string and convert the smaller number to string and we compare the two strings and increment the counter where ever we find differences \n# Approach\n<!-- Describe your approach to solving the problem. -->\nnormal to strig () method \npadStart will add leading zeroes to our string \nsimply compare and increase count as needed \nreturn count \n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```javascript []\nvar minBitFlips = function (start, goal) {\n let count = 0\n let s1\n let s2\n if (start > goal) {\n s1 = start.toString(2)\n s2 = goal.toString(2).padStart(s1.length, 0)\n }\n else {\n s1 = goal.toString(2)\n s2 = start.toString(2).padStart(s1.length, 0)\n }\n for (let i = 0; i < s1.length; i++) {\n if (s1[i] !== s2[i]) count++\n }\n return count\n};\n```\n```python []\ndef min_bit_flips(start: int, goal: int) -> int:\n # XOR the numbers to find differing bits\n xor = start ^ goal\n \n # Count the number of 1s in the binary representation of xor\n count = bin(xor).count(\'1\')\n \n return count\n\n# Example usage\nstart = 29 # Example start\ngoal = 15 # Example goal\nprint(min_bit_flips(start, goal)) # Output the number of bit flips\n\n```\n```java []\npublic class BitFlips {\n public static int minBitFlips(int start, int goal) {\n // Convert start and goal to binary strings\n String s1 = Integer.toBinaryString(start);\n String s2 = Integer.toBinaryString(goal);\n \n // Pad the shorter binary string with leading zeros\n int maxLength = Math.max(s1.length(), s2.length());\n s1 = String.format("%" + maxLength + "s", s1).replace(\' \', \'0\');\n s2 = String.format("%" + maxLength + "s", s2).replace(\' \', \'0\');\n \n // Count the number of differing bits\n int count = 0;\n for (int i = 0; i < s1.length(); i++) {\n if (s1.charAt(i) != s2.charAt(i)) {\n count++;\n }\n }\n return count;\n }\n\n public static void main(String[] args) {\n int start = 29; // Example start\n int goal = 15; // Example goal\n System.out.println(minBitFlips(start, goal)); // Output the number of bit flips\n }\n}\n\n```\n```c []\n#include <stdio.h>\n\nint minBitFlips(int start, int goal) {\n int count = 0;\n int xor = start ^ goal; // XOR to find differing bits\n \n // Count the number of set bits in xor\n while (xor > 0) {\n count += xor & 1;\n xor >>= 1;\n }\n \n return count;\n}\n\nint main() {\n int start = 29; // Example start\n int goal = 15; // Example goal\n printf("%d\\n", minBitFlips(start, goal)); // Output the number of bit flips\n return 0;\n}\n\n```
| 7 | 1 |
['Bit Manipulation', 'C', 'Python', 'C++', 'TypeScript', 'Python3', 'JavaScript']
| 4 |
minimum-bit-flips-to-convert-number
|
🔥Beats 100%🔥✅Without Inbuilt Function Super Easy (C++/Java/Python) Bit Manipulation Solution✅
|
beats-100without-inbuilt-function-super-gxso5
|
Intuition\nThe intuition is to iteratively checks each bit of the two numbers using a loop, which continues until the larger of start and goal becomes zero (ind
|
suyogshete04
|
NORMAL
|
2024-03-22T03:37:51.196328+00:00
|
2024-03-22T03:41:09.421277+00:00
| 1,108 | false |
# Intuition\nThe intuition is to iteratively checks each bit of the two numbers using a loop, which continues until the larger of `start` and `goal` becomes zero (indicating all bits have been checked). Within each iteration, it applies a bitwise AND with 1 to both numbers to extract their least significant bits, compares them, and increments a counter if they differ, indicating a flip is needed. Then, it right shifts both numbers to compare the next set of bits.\n\n\n\n\n# Approach\n\n1. **Initialization**: The solution begins by identifying the maximum of `start` and `goal`. This is used to determine the number of iterations needed, as the loop continues until `maxi` is reduced to zero. A variable `res` is initialized to count the number of bit flips required.\n\n2. **Looping through Bits**: The solution uses a `while` loop that continues as long as `maxi` is not zero. This ensures that all the bits in the larger of the two numbers (`start` or `goal`) are examined.\n\n3. **Bitwise Comparison and Shift**:\n - At each iteration, the least significant bit (LSB) of both `start` and `goal` is compared using the bitwise AND (`&`) operation with `1`. The expression `(start & 1)` extracts the LSB of `start`, and similarly `(goal & 1)` for `goal`. If these two LSBs are not equal, it signifies that a bit flip is needed at this position, and the `res` counter is incremented.\n - After the comparison, both `start` and `goal` are right-shifted (`>>`) by 1. This discards the LSB just examined and moves the next bit into the LSB position for comparison in the next iteration. Similarly, `maxi` is also right-shifted by 1 to eventually terminate the loop.\n\n4. **Result**: Once all bits in the larger number have been examined, the loop ends, and the function returns `res`, the total number of bit flips required.\n\n## Complexity Analysis:\n- **Time Complexity**: O(log(max(start, goal))).\n - The loop iterates over each bit of the maximum of `start` and `goal`. Since the number of bits in a binary representation of a number `n` is `O(log n)`, the time complexity is determined by the maximum of `start` and `goal`.\n- **Space Complexity**: O(1).\n - The solution uses a fixed amount of extra space, regardless of the input size. Variables `maxi`, `res`, `start`, and `goal` are the only additional storage used, and their size does not scale with the size of the input.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int maxi = max(start, goal);\n int res = 0;\n while (maxi) {\n if ((start & 1) != (goal & 1))\n res++;\n\n start = start >> 1;\n goal = goal >> 1;\n maxi = maxi >> 1;\n }\n\n return res;\n }\n};\n```\n```Java []\npublic class Solution {\n public int minBitFlips(int start, int goal) {\n int res = 0;\n // The \'maxi\' variable is not needed since we\'re iterating until both start and goal are 0.\n while (start != 0 || goal != 0) {\n // Check if the least significant bits of start and goal are different\n if ((start & 1) != (goal & 1))\n res++;\n\n // Right shift start and goal to check the next bit in the next iteration\n start = start >> 1;\n goal = goal >> 1;\n }\n\n return res;\n }\n}\n\n```\n```Python []\nclass Solution:\n def minBitFlips(self, start: int, goal: int) -> int:\n maxi = max(start, goal)\n res = 0\n while maxi:\n if (start & 1) != (goal & 1):\n res += 1\n\n start = start >> 1\n goal = goal >> 1\n maxi = maxi >> 1\n\n return res\n\n```\n## Please Upvote If It Helped You \u2764\uFE0F
| 7 | 0 |
['Bit Manipulation', 'C++', 'Java', 'Python3']
| 1 |
minimum-bit-flips-to-convert-number
|
Python Solution | One liner
|
python-solution-one-liner-by-tejpratap1-ju4n
|
Just xor so we get 1 at places where bits are different and then count those bits.\n\nclass Solution:\n def minBitFlips(self, start: int, goal: int) -> int:\
|
TejPratap1
|
NORMAL
|
2022-04-02T16:20:21.723192+00:00
|
2022-04-02T16:20:21.723223+00:00
| 911 | false |
**Just xor so we get 1 at places where bits are different and then count those bits.**\n```\nclass Solution:\n def minBitFlips(self, start: int, goal: int) -> int:\n return (bin(start^goal).count("1"))\n```
| 7 | 0 |
['Bit Manipulation', 'Python']
| 3 |
minimum-bit-flips-to-convert-number
|
👍One liner solution✅As fast as wind💨! Shortest🔥Fastest🔥Easiest🔥Full explanation🌟
|
one-liner-solutionas-fast-as-wind-shorte-n1bm
|
\n### Explanation of the Problem\n\nThe problem asks us to determine the minimum number of "bit flips" required to convert one number, start, into another numbe
|
aijcoder
|
NORMAL
|
2024-09-11T09:08:59.201923+00:00
|
2024-09-11T09:11:20.980378+00:00
| 1,090 | false |
\n### Explanation of the Problem\n\nThe problem asks us to determine the minimum number of "bit flips" required to convert one number, `start`, into another number, `goal`. A "bit flip" means changing a bit in a binary number from 0 to 1, or from 1 to 0.\n\n#### Binary Representation of Numbers\nEach integer can be represented as a sequence of bits (binary digits), which are either 0 or 1. For example, the number 10 is represented as `1010` in binary, and the number 7 is represented as `0111`. To convert one number to another, you would need to change some bits in one number\'s binary representation so that it becomes equal to the other number\'s binary form.\n\n### Key Idea\n\nTo determine how many bit flips are needed, the main task is to:\n1. Compare the binary representation of `start` and `goal`.\n2. Count how many bits differ between the two numbers. A differing bit is where a flip is necessary.\n\nThis can be easily achieved using a bitwise XOR (exclusive OR) operation. XOR between two bits returns:\n- 1 if the bits are different (one is 0, the other is 1),\n- 0 if the bits are the same (both are 0 or both are 1).\n\nThus, by performing a bitwise XOR on `start` and `goal`, we get a new number where each bit represents whether the corresponding bits in `start` and `goal` differ. The number of `1`s in the result tells us how many bit flips are required.\n\n### Steps to Solve\n\n1. **Bitwise XOR**: Perform a bitwise XOR on `start` and `goal`. This operation compares the binary representations of the two numbers.\n2. **Count the 1s**: Count the number of `1`s in the result of the XOR operation. Each `1` represents a difference between `start` and `goal` that requires a bit flip.\n\n### Detailed Example Walkthrough\n\n#### Example 1: \n**Input**: \n`start = 10`, `goal = 7`\n\n**Binary Representation**: \n- `start (10)` in binary is `1010`\n- `goal (7)` in binary is `0111`\n\n**XOR Operation**: \n- `1010 (10)`\n- `0111 (7)`\n- XOR result: `1101`\n\nThe XOR result `1101` means that the 1st, 2nd, and 4th bits (from the right) differ between `start` and `goal`. So, we need to flip those bits.\n\n**Flips**:\n- Flip the 1st bit: `1010` \u2192 `1011`\n- Flip the 3rd bit: `1011` \u2192 `1111`\n- Flip the 4th bit: `1111` \u2192 `0111`\n\nThus, it takes **3 flips** to convert `start` (10) to `goal` (7).\n\n**Output**: `3`\n\n#### Example 2:\n**Input**: \n`start = 3`, `goal = 4`\n\n**Binary Representation**: \n- `start (3)` in binary is `011`\n- `goal (4)` in binary is `100`\n\n**XOR Operation**: \n- `011 (3)`\n- `100 (4)`\n- XOR result: `111`\n\nThe XOR result `111` means that all three bits differ between `start` and `goal`. So, we need to flip all three bits.\n\n**Flips**:\n- Flip the 1st bit: `011` \u2192 `010`\n- Flip the 2nd bit: `010` \u2192 `000`\n- Flip the 3rd bit: `000` \u2192 `100`\n\nThus, it takes **3 flips** to convert `start` (3) to `goal` (4).\n\n**Output**: `3`\n\n### Constraints:\n- The numbers `start` and `goal` are non-negative integers.\n- Both numbers can be represented in binary within the range of typical integer sizes (e.g., 32-bit integers).\n\n### General Approach:\n1. Compute `start XOR goal`.\n2. Count the number of `1`s in the binary representation of the XOR result.\n3. Return the count, which is the number of bit flips required.\n\nThis approach runs efficiently in O(1) time due to the constant size of integers and O(1) space for the same reason.\n1. C++:\n\n```cpp\n// Built-in approach\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n return __builtin_popcount(start ^ goal);\n }\n};\n\n// Manual approach\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int xorResult = start ^ goal;\n int count = 0;\n while (xorResult) {\n count += xorResult & 1;\n xorResult >>= 1;\n }\n return count;\n }\n};\n```\n\n2. Python:\n\n```python\n# Built-in approach\nclass Solution:\n def minBitFlips(self, start: int, goal: int) -> int:\n return bin(start ^ goal).count(\'1\')\n\n# Manual approach\nclass Solution:\n def minBitFlips(self, start: int, goal: int) -> int:\n xor_result = start ^ goal\n count = 0\n while xor_result:\n count += xor_result & 1\n xor_result >>= 1\n return count\n```\n\n3. Java:\n\n```java\n// Built-in approach\nclass Solution {\n public int minBitFlips(int start, int goal) {\n return Integer.bitCount(start ^ goal);\n }\n}\n\n// Manual approach\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int xorResult = start ^ goal;\n int count = 0;\n while (xorResult != 0) {\n count += xorResult & 1;\n xorResult >>>= 1;\n }\n return count;\n }\n}\n```\n\n4. JavaScript:\n\n```javascript\n// Built-in approach (Note: JS doesn\'t have a built-in popcount function)\n/**\n * @param {number} start\n * @param {number} goal\n * @return {number}\n */\nvar minBitFlips = function(start, goal) {\n return (start ^ goal).toString(2).split(\'1\').length - 1;\n};\n\n// Manual approach\n/**\n * @param {number} start\n * @param {number} goal\n * @return {number}\n */\nvar minBitFlips = function(start, goal) {\n let xorResult = start ^ goal;\n let count = 0;\n while (xorResult) {\n count += xorResult & 1;\n xorResult >>>= 1;\n }\n return count;\n};\n```\n\nEach language solution includes both the built-in approach (where available) and a manual bit-counting approach. The manual approach is more universal and works across all languages, while the built-in approach may be more efficient in languages that support it.\n\nThe basic idea in all solutions is to:\n1. XOR the start and goal numbers to get the differing bits.\n2. Count the number of set bits (1s) in the XOR result.\n\nThis count represents the minimum number of bit flips required to convert the start number to the goal number.
| 6 | 0 |
['Bit Manipulation', 'C++', 'Java', 'Python3', 'JavaScript']
| 2 |
minimum-bit-flips-to-convert-number
|
Flip Different Bits Only | Java | C++ | [Video Solution]
|
flip-different-bits-only-java-c-video-so-a9lr
|
Intuition, approach, and complexity discussed in video solution in detail.\nhttps://youtu.be/lqSsY0EXnb0\n# Code\njava []\nclass Solution {\n public int minB
|
Lazy_Potato_
|
NORMAL
|
2024-09-11T04:36:46.484551+00:00
|
2024-09-11T04:36:46.484572+00:00
| 1,195 | false |
# Intuition, approach, and complexity discussed in video solution in detail.\nhttps://youtu.be/lqSsY0EXnb0\n# Code\n``` java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int diffNum = (start ^ goal);\n return setBitCnt(diffNum);\n }\n private int setBitCnt(int num){\n int bitCnt=0;\n while(num > 0){\n bitCnt++;\n num &= (num - 1);\n }\n return bitCnt;\n }\n}\n```\n```cpp []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int diffNum = (start ^ goal);\n return setBitCnt(diffNum);\n }\nprivate:\n int setBitCnt(int num){\n int bitCnt=0;\n while(num > 0){\n bitCnt++;\n num &= (num - 1);\n }\n return bitCnt; \n }\n};\n```
| 6 | 0 |
['Bit Manipulation', 'C++', 'Java']
| 4 |
minimum-bit-flips-to-convert-number
|
simple and easy Javascript solution 😍❤️🔥
|
simple-and-easy-javascript-solution-by-s-19gw
|
\n\n# Complexity\n- Time complexity: O(1)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n
|
shishirRsiam
|
NORMAL
|
2024-09-11T00:36:01.324947+00:00
|
2024-09-11T00:36:01.324980+00:00
| 348 | false |
\n\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```javascript []\nvar minBitFlips = function(start, goal) \n{\n // Perform bitwise XOR between \'start\' and \'goal\'.\n // The XOR operation results in a number where each bit is 1 if the corresponding bits of \'start\' and \'goal\' are different, otherwise it\'s 0.\n let xor = start ^ goal;\n\n // Initialize a variable \'ans\' to count the number of bit flips required.\n let ans = 0;\n\n // Loop while there are still bits set to 1 in \'xor\'.\n // The loop will terminate when \'xor\' becomes 0, meaning all bits have been checked.\n while (xor) \n {\n // Use bitwise AND with 1 to check if the least significant bit (rightmost) of \'xor\' is 1.\n // If it\'s 1, it means there\'s a difference between the corresponding bits of \'start\' and \'goal\', so increment \'ans\'.\n ans += xor & 1;\n\n // Right shift \'xor\' by 1 bit to move to the next bit in the XOR result.\n // This effectively divides \'xor\' by 2, discarding the least significant bit.\n xor >>= 1;\n }\n\n // Return the total number of bit flips needed.\n return ans;\n};\n```\n\n# if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n###### Let\'s Connect on LinkedIn: www.linkedin.com/in/shishirrsiam\n###### Let\'s Connect on Facebook: www.fb.com/shishirrsiam
| 6 | 0 |
['Bit Manipulation', 'JavaScript']
| 8 |
minimum-bit-flips-to-convert-number
|
one line solution
|
one-line-solution-by-shishirrsiam-i4el
|
\n# Complexity\n- Time complexity: O(1)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n
|
shishirRsiam
|
NORMAL
|
2024-09-11T00:26:09.678792+00:00
|
2024-09-11T00:26:09.678811+00:00
| 1,359 | false |
\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nclass Solution(object):\n def minBitFlips(self, start, goal):\n return bin(start ^ goal).count(\'1\') \n```\n\n\n# if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n###### Let\'s Connect on LinkedIn: www.linkedin.com/in/shishirrsiam\n###### Let\'s Connect on Facebook: www.fb.com/shishirrsiam
| 6 | 0 |
['Bit Manipulation', 'Python', 'Python3']
| 10 |
minimum-bit-flips-to-convert-number
|
C 0ms simple solution by using & and ^
|
c-0ms-simple-solution-by-using-and-by-ro-4rb6
|
Intuition\nI thought that if I find the number of differing bits between \'start\' and \'goal\' and assign them to a variable, then I can count them.\n\n# Appro
|
camogluserkan
|
NORMAL
|
2023-11-02T10:07:31.352033+00:00
|
2023-11-02T10:07:31.352062+00:00
| 293 | false |
# Intuition\nI thought that if I find the number of differing bits between \'start\' and \'goal\' and assign them to a variable, then I can count them.\n\n# Approach\nFirstly, I determined how many differing bits exist between \'start\' and \'goal\'.\nThe XOR operation returns 1 if the bits of \'goal\' and \'start\' are different.\nI stored this value in a variable named \'DifferentBits\'.\nAfterward, I counted the differing bits using the \'&\' operation. If the rightmost bit of \'DifferentBits\' is 1, it signifies that the bits were different, and the XOR operation returns 1 to the \'DifferentBits\' value.\nIf so, I incremented \'count\' by 1.\nIn the end, I returned \'count\'.\n\n# Complexity\n- Time complexity:\nO(1)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nint minBitFlips(int start, int goal){\n int DifferentBits = start ^ goal,count=0; // DifferentBits hold how many bits are different\n while (DifferentBits != 0) {\n if (DifferentBits & 1) // if DifferentBits = 1, these bits are different. So, count++\n count++;\n DifferentBits >>= 1;\n }\n return count;\n}\n```
| 6 | 0 |
['C']
| 1 |
minimum-bit-flips-to-convert-number
|
✅[cpp || Beats 100% || O(1) TC || O(1) SC || Thorough Explanation]✅
|
cpp-beats-100-o1-tc-o1-sc-thorough-expla-yf2q
|
Intuition\n1 ^ 1 = 0\n0 ^ 0 = 0\n1 ^ 0 = 1\n0 ^ 1 = 1\n\nIf we xor a and b we can find the bits that are distinct in a and b\n\nA ---> 1 1 1 0 0 1\nB ---> 1 0 1
|
mayanksinghchouhan
|
NORMAL
|
2023-10-19T04:27:32.620912+00:00
|
2023-10-21T01:24:40.585074+00:00
| 841 | false |
# Intuition\n1 ^ 1 = 0\n0 ^ 0 = 0\n1 ^ 0 = 1\n0 ^ 1 = 1\n\nIf we xor a and b we can find the bits that are distinct in a and b\n\nA ---> 1 1 1 0 0 1\nB ---> 1 0 1 0 1 0\nA^B->0 1 0 0 1 1 \n\n# Approach\n- All you need to do is count the number of set bits in A ^ B and you will have your answer.\n- You can do this using the kernighans algorithm as in the code below.\n\n# Complexity\n- Time complexity: O(1)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int sxorg = start ^ goal;\n int count = 0;\n while(sxorg != 0) {\n int rsb = sxorg & -sxorg;\n sxorg -= rsb;\n count++;\n }\n return count;\n }\n};\n```\n# \u270C\uFE0FUpvote if it helps\n
| 6 | 0 |
['Bit Manipulation', 'C++']
| 3 |
minimum-bit-flips-to-convert-number
|
Rust solution
|
rust-solution-by-bigmih-u3if
|
\nimpl Solution {\n pub fn min_bit_flips(start: i32, goal: i32) -> i32 {\n (start ^ goal).count_ones() as _\n }\n}\n
|
BigMih
|
NORMAL
|
2022-04-03T08:46:11.616165+00:00
|
2022-04-03T08:46:11.616193+00:00
| 189 | false |
```\nimpl Solution {\n pub fn min_bit_flips(start: i32, goal: i32) -> i32 {\n (start ^ goal).count_ones() as _\n }\n}\n```
| 6 | 0 |
['Rust']
| 1 |
minimum-bit-flips-to-convert-number
|
✅ C++ | Easy | 2 different ways
|
c-easy-2-different-ways-by-chandanagrawa-cwe2
|
We have to count all positions where the i\'th bit of number A and B is different , so just iterate from bit 32 to 0 and check.\n\n\nclass Solution\n{\n publ
|
chandanagrawal23
|
NORMAL
|
2022-04-02T16:11:12.953189+00:00
|
2022-04-02T16:41:10.490701+00:00
| 1,277 | false |
We have to count all positions where the i\'th bit of number **A** and **B** is different , so just iterate from bit 32 to 0 and check.\n\n```\nclass Solution\n{\n public:\n int minBitFlips(int start, int goal)\n {\n int cnt = 0;\n for (int i = 32; i >= 0; i--)\n {\n\t\t\t\tint current = (1LL << i) & start;\n int required = (1LL << i) & goal;\n if (required != current)\n cnt++;\n }\n return cnt;\n }\n};\n```\n\nAfter submitting , I realised that we can get different bit when we will do **XOR** of **A** and **B** \nlike A = 101111\nlike B = 110001\nA^B = 011110 , so just count how many ones in A^B , to count 1\'s in a number we have a fucntion called **__builtin_popcount(N)** where N = A^B\n```\nclass Solution {\npublic:\n int minBitFlips(int A, int B) {\n return __builtin_popcount(A^B);\n }\n};\n\n```
| 6 | 0 |
['C']
| 6 |
minimum-bit-flips-to-convert-number
|
⚡ Easy approach, O(N) time | No Bit Manipulation
|
easy-approach-on-time-no-bit-manipulatio-vx3h
|
\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int ans = 0;\n while(start && goal) { \n if(start%2 != goal%2
|
abanoub7asaad
|
NORMAL
|
2022-04-02T16:01:10.003140+00:00
|
2022-04-03T21:34:39.872690+00:00
| 655 | false |
```\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int ans = 0;\n while(start && goal) { \n if(start%2 != goal%2)\n ans++;\n start /= 2;\n goal /= 2;\n } \n while(start) { \n if(start%2)\n ans++;\n start /= 2;\n } \n while(goal) { \n if(goal%2)\n ans++; \n goal /= 2;\n } \n return ans;\n }\n};\n```
| 6 | 0 |
['C']
| 3 |
minimum-bit-flips-to-convert-number
|
Easy Soln✅✅||Bit Manipulation Mastery 🔥🔥||Beats 100% ✅✅
|
easy-solnbit-manipulation-mastery-beats-6z7cb
|
Here the problem is to convert the bit value start to bit value of goal.\n\nEx. \nstart = 4 -> 0100\ngoal = 10 -> 1010\n\nwe just have to check the difference
|
21eca01
|
NORMAL
|
2024-09-11T09:22:04.066969+00:00
|
2024-09-11T09:22:04.067006+00:00
| 222 | false |
Here the problem is to convert the bit value start to bit value of goal.\n\nEx. \nstart = 4 -> 0100\ngoal = 10 -> 1010\n\nwe just have to check the differences between these two number\'s bits.\nWe can just check each bit similarity using XOR(^) method and shift every digit with the help of right shift\n \n**Walkthrough the solution**\n\nAfter each step both the start and goal are right shifted so that new unit value can be obtained.\n\n\n-> count=0:\n1. 0100 unit bit=0 \n 1010 unit bit=0 ```No diff``` count=0:\n\n2. 010 unit bit=0 \n 101 unit bit=1 ``Diff Bit`` count=1:\n\n3. 01 unit bit=1\n 10 unit bit=0 ``Diff Bit`` count=2:\n\n4. 0 unit bit=0 \n 1 unit bit=1 ``Diff Bit`` count=3:\n\nHence count =3\n\n\n\n**Unit Digit Calculation**\nThe unit bit of each number is found out using &(and) operator which will give us the last unit digit \nif `` (x&1) =0 `` then the unit digit =0:\nelse `(x&1) =1 ` then the unit digit =1:\n\n**The Diff Between the two digits**\nThe Answer to whether the the two digits are same or not can be found out using the the ``XOR(^)`` operator which can state whether the two digits are same or different.\n* (0^1) =1\n* (1^0) =1\n* (1^1) =0\n* (0^0) =0\n\nWhen the two digits are same the ans ans is 0 , when the two digits are different the ans is 1. Thus this can be achieved.\n\nThus out differences in count can be achieved.\n\n# Code\n```java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int count=0;\n while(start!=0||goal!=0){\n count+=((start&1)^(goal&1));\n start=start>>1;\n goal=goal>>1;\n }\n return count;\n }\n}\n```\n\n``` python3 []\nclass Solution:\n def minBitFlips(self, start: int, goal: int) -> int:\n count = 0\n while start != 0 or goal != 0:\n count += (start & 1) ^ (goal & 1)\n start = start >> 1\n goal = goal >> 1\n return count\n\n```\n``` C++ []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int count = 0;\n while (start != 0 || goal != 0) {\n count += (start & 1) ^ (goal & 1);\n start = start >> 1;\n goal = goal >> 1;\n }\n return count;\n }\n};\n```\n``` JavaScript []\n/**\n * @param {number} start\n * @param {number} goal\n * @return {number}\n */\nvar minBitFlips = function(start, goal) {\n let count = 0;\n while (start !== 0 || goal !== 0) {\n count += (start & 1) ^ (goal & 1);\n start = start >> 1;\n goal = goal >> 1;\n }\n return count;\n};\n```
| 5 | 0 |
['Bit Manipulation', 'C++', 'Java', 'Python3']
| 1 |
minimum-bit-flips-to-convert-number
|
1 Line Solution | 100 % Beats | Java
|
1-line-solution-100-beats-java-by-eshwar-d319
|
Code\njava []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n return Integer.bitCount(start ^ goal);\n }\n}\n
|
eshwaraprasad
|
NORMAL
|
2024-09-11T05:52:17.220076+00:00
|
2024-09-11T05:52:17.220115+00:00
| 196 | false |
# Code\n```java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n return Integer.bitCount(start ^ goal);\n }\n}\n```
| 5 | 0 |
['Java']
| 1 |
minimum-bit-flips-to-convert-number
|
Java | Brute Force | 6 lines | Clean code
|
java-brute-force-6-lines-clean-code-by-j-ru8d
|
Complexity\n- Time complexity: O(max.bits)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \
|
judgementdey
|
NORMAL
|
2024-09-11T00:06:26.027471+00:00
|
2024-09-11T00:06:26.027502+00:00
| 561 | false |
# Complexity\n- Time complexity: $$O(max.bits)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n var res = 0;\n\n while (start > 0 || goal > 0) {\n res += (start & 1) == (goal & 1) ? 0 : 1;\n\n start >>= 1;\n goal >>= 1;\n }\n return res;\n }\n}\n```\nIf you like my solution, please upvote it!
| 5 | 0 |
['Bit Manipulation', 'Java']
| 1 |
minimum-bit-flips-to-convert-number
|
Very Intuitive approach
|
very-intuitive-approach-by-dixon_n-dsqx
|
take a xor why? \n\nsee what you take a xor the 1 will remaing zero meaning we dont want to filp that bit, and if its zero it will remain as zero so we dont wan
|
Dixon_N
|
NORMAL
|
2024-09-04T10:42:49.482454+00:00
|
2024-09-04T10:42:49.482486+00:00
| 423 | false |
take a xor why? \n\nsee what you take a xor the 1 will remaing zero meaning we dont want to filp that bit, and if its zero it will remain as zero so we dont want to flip it \nso wha are the reamingin one\'s ? we need to count the ones\' in the bits after doing xor ithats is the problem is reduced simple\n\n\n# Code\n```java []\n//Approach -2\n\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int ans=start ^ goal;\n int count=0;\n while(ans!=0){\n count++;\n ans = (ans&(ans-1));\n }\n return count;\n }\n}\n```\n```java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int ans=start ^ goal;\n int count=0;\n for(int i=0;i<32;i++){\n if ((ans & (1 << i)) != 0) {\n count++;\n }\n }\n return count;\n }\n}\n```
| 5 | 0 |
['Bit Manipulation', 'Java']
| 5 |
minimum-bit-flips-to-convert-number
|
Curious Logic Python3
|
curious-logic-python3-by-ganjinaveen-1ec4
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
GANJINAVEEN
|
NORMAL
|
2023-02-26T11:21:08.016021+00:00
|
2023-02-26T11:21:08.016065+00:00
| 900 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minBitFlips(self, start: int, goal: int) -> int:\n s=bin(start)[2:].zfill(50)\n g=bin(goal)[2:].zfill(50)\n count=0\n for i in range(50):\n if s[i]!=g[i]:\n count+=1\n return count\n```
| 5 | 0 |
['Python3']
| 2 |
minimum-bit-flips-to-convert-number
|
👋 CPP EZ Amazon + Google😬 Interview O(set bits)
|
cpp-ez-amazon-google-interview-oset-bits-dpza
|
UPVOTE PLZ \u2763\n# Approach-1 Always takes O(N)\nclass Solution { //O(N) soln.\npublic:\n int minBitFlips(int start, int goal) {\n
|
AdityaBhate
|
NORMAL
|
2022-07-18T07:48:18.918473+00:00
|
2022-11-16T05:55:52.630071+00:00
| 1,206 | false |
# ***UPVOTE PLZ \u2763***\n# **Approach-1** Always takes O(N)\nclass Solution { //O(N) soln.\npublic:\n int minBitFlips(int start, int goal) {\n int c=0, i=0;\n while(start != goal){\n int mask=1<<i;\n if((start & mask) == (goal & mask))\n i++;\n else{\n start=start ^ mask;\n c++;\n i++;\n } \n }\n return c;\n }\n};\n\n# **Approach-2** Faster :)\nclass Solution { // O(No. of set bits in start^goal)\npublic:\n int minBitFlips(int start, int goal) {\n int res = start ^ goal;\n int c=0;\n while(res!=0){\n res = res & (res-1);\n c++;\n }\n return c;\n }\n};
| 5 | 2 |
['Bit Manipulation', 'C', 'C++', 'Java', 'Python3']
| 2 |
minimum-bit-flips-to-convert-number
|
Python Solution | Hamming Distance Based | One Liner
|
python-solution-hamming-distance-based-o-ljxd
|
Hamming Distance\nHamming Distance between two integers is the number of bits that are different at the same position in both numbers. \n\nAlgorithm\n- XOR the
|
Gautam_ProMax
|
NORMAL
|
2022-04-26T15:17:42.700131+00:00
|
2022-04-26T15:17:42.700165+00:00
| 428 | false |
## Hamming Distance\nHamming Distance between two integers is the number of bits that are different at the same position in both numbers. \n\nAlgorithm\n- XOR the numbers\n- Count set bits (1)\n\n```\nclass Solution:\n def minBitFlips(self, start: int, goal: int) -> int:\n return bin(start ^ goal).count("1")\n```
| 5 | 0 |
['Bit Manipulation', 'Python', 'Python3']
| 0 |
minimum-bit-flips-to-convert-number
|
C++ 0ms solution without bit manipulation
|
c-0ms-solution-without-bit-manipulation-oijvf
|
\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int count=0;\n while(start && goal){\n if(start%2!=goal%2) co
|
zdy012
|
NORMAL
|
2022-04-02T17:06:07.442494+00:00
|
2022-04-02T17:06:07.442539+00:00
| 750 | false |
```\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int count=0;\n while(start && goal){\n if(start%2!=goal%2) count++;\n start/=2;\n goal/=2;\n }\n while(start){\n if(start%2)count++;\n start/=2;\n }\n while(goal){\n if(goal%2)count++;\n goal/=2;\n }\n return count;\n }\n};\n```
| 5 | 0 |
['C++']
| 2 |
minimum-bit-flips-to-convert-number
|
C++ | Easy | And Operation
|
c-easy-and-operation-by-kamisamaaaa-6lcn
|
\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n \n int res(0);\n for (int i=32; ~i; i--) {\n if ((star
|
kamisamaaaa
|
NORMAL
|
2022-04-02T16:54:11.783841+00:00
|
2022-04-02T16:54:21.143616+00:00
| 327 | false |
```\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n \n int res(0);\n for (int i=32; ~i; i--) {\n if ((start & 1) != (goal & 1)) res++;\n start >>= 1; goal >>= 1;\n }\n return res;\n } \n};\n```
| 5 | 1 |
['C']
| 0 |
minimum-bit-flips-to-convert-number
|
Easy Solution✅✅||using XOR 🔥🔥||Beats 100% ✅✅
|
easy-solutionusing-xor-beats-100-by-mr_a-9bhx
|
Intuition\n\nThe goal of the problem is to find the minimum number of bit flips required to convert start to goal. A bit flip means changing a bit from 0 to 1 o
|
mr_ajagiya
|
NORMAL
|
2024-09-11T19:39:38.090936+00:00
|
2024-09-11T19:39:38.090957+00:00
| 127 | false |
# Intuition\n\nThe goal of the problem is to find the minimum number of bit flips required to convert `start` to `goal`. A bit flip means changing a bit from 0 to 1 or from 1 to 0.\n\n1. **XOR Operation (`^`)**:\n - The XOR of two numbers, `start ^ goal`, gives a number where each bit is `1` if the corresponding bits in `start` and `goal` are different, and `0` if they are the same.\n - So, the XOR result highlights all the bits where a flip is needed to convert `start` into `goal`.\n\n2. **Counting Set Bits (`__builtin_popcount(k)`)**:\n - The number of `1`s in the XOR result tells us exactly how many bits need to be flipped. This is efficiently counted using the `__builtin_popcount()` function, which counts the number of set bits (1s) in the XOR result.\n\n3. **Helper Function `count(int n)`**:\n - The function `count(int n)` determines how many bits are needed to represent the larger of `start` or `goal`. This function runs by repeatedly dividing `n` by 2, which mimics counting the number of bits in the binary representation of `n`.\n\n4. **Logic Flow**:\n - The algorithm calculates the number of bit flips by:\n - Finding the XOR between `start` and `goal`.\n - Counting how many bits differ using `__builtin_popcount()`.\n - The final result is directly the count of differing bits (i.e., the number of bits to flip).\n\n\n# Approach\n\n1. **Step 1**: Calculate the larger of `start` and `goal` using `max(start, goal)`. This is stored in `n`.\n \n2. **Step 2**: Use the `count(n)` function to calculate the number of bits required to represent `n`. This is needed to determine how many bits we are comparing between `start` and `goal`.\n\n3. **Step 3**: Compute `k = start ^ goal`, which gives a number where the bits are `1` wherever `start` and `goal` differ.\n\n4. **Step 4**: Use `__builtin_popcount(k)` to count the number of `1`s in `k`, which is the number of differing bits (i.e., bits to flip).\n\n5. **Step 5**: Calculate the number of `0`s that do not need to be flipped as `nOf0 = mx - b`. This step is based on how many bits we have in total versus how many need to be flipped.\n\n6. **Step 6**: The result is `mx - nOf0`, which simplifies to the number of differing bits (i.e., `b`). Thus, the return value is simply the number of bits to flip.\n\n### Simplified Explanation:\n1. Compute XOR between `start` and `goal`, which marks where bits differ.\n2. Count the number of `1`s in the XOR result (using `__builtin_popcount()`), which represents the number of bits that need to be flipped.\n3. Return the count as the minimum number of flips required.\n\n\n# Complexity\n- Time complexity:\nO(log n)\n\n- Space complexity:\nO(1)\n\n# Code\n```cpp []\nclass Solution {\n private: int count(int n){\n int c=0;\n while(n>0){\n c++;\n n=n/2;\n }\n return c;\n}\npublic:\n int minBitFlips(int start, int goal) {\n int n = max(start,goal);\n int mx = count(n);\n int k = start ^ goal;\n int b = __builtin_popcount(k);\n int nOf0 = mx-b;\n return mx-nOf0;\n }\n};\n```\n\nt
| 4 | 0 |
['Bit Manipulation', 'C++']
| 0 |
minimum-bit-flips-to-convert-number
|
Simple and Easy CPP Code!💯✅☮️
|
simple-and-easy-cpp-code-by-siddharth_si-d0md
|
\n# Code\ncpp []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n bitset<32> bs(start);\n bitset<32> bg(goal);\n in
|
siddharth_sid_k
|
NORMAL
|
2024-09-11T16:45:21.292129+00:00
|
2024-09-11T16:45:21.292164+00:00
| 137 | false |
\n# Code\n```cpp []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n bitset<32> bs(start);\n bitset<32> bg(goal);\n int c=0;\n for(int i=bs.size();i>=0;i--)\n {\n if(bs[i]!=bg[i])\n {\n c++;\n }\n }\n return c; \n }\n};\n```\n### Intuition:\nThe problem asks for the minimum number of bit flips required to transform `start` into `goal`. A bit flip changes a `0` to `1` or a `1` to `0`. To solve this, we need to compare the binary representations of `start` and `goal` and count how many bits are different between them.\n\n### Approach:\n1. **Binary Representation:** First, we convert `start` and `goal` into 32-bit binary representations using `bitset<32>`. The bitset will help us represent the numbers in binary format.\n \n2. **Bit Comparison:** We iterate through each bit of the binary representation from the most significant bit (MSB) to the least significant bit (LSB). For each position, we check if the corresponding bits in `start` and `goal` are different.\n \n3. **Counting Bit Flips:** If the bits differ at any position, it means we need a flip, so we increment the counter `c`.\n\n4. **Return the Result:** After comparing all the bits, we return the count `c`, which represents the minimum number of bit flips required to transform `start` into `goal`.\n\n### Code:\n\n```cpp\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n bitset<32> bs(start);\n bitset<32> bg(goal);\n int c = 0;\n for (int i = bs.size(); i >= 0; i--) {\n if (bs[i] != bg[i]) {\n c++;\n }\n }\n return c;\n }\n};\n```\n\n### Complexity Analysis:\n\n- **Time Complexity:** `O(32)` \n We are comparing 32 bits (since we use `bitset<32>`) and for each bit, we perform a constant-time comparison, so the total time complexity is `O(32)` which simplifies to `O(1)`.\n\n- **Space Complexity:** `O(1)` \n We are using only a fixed amount of space for the `bitset` objects and the counter `c`. Thus, the space complexity is constant.\n
| 4 | 0 |
['C++']
| 0 |
minimum-bit-flips-to-convert-number
|
✅BEATS 100.00% ⌚2 Approaches ✔using Bit Manipulation and Second one Simplest BRUTE FORCE⛔
|
beats-10000-2-approaches-using-bit-manip-ahju
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nApproach 1:\nWe use XOR to check where the two numbers (start and goal) a
|
ArcuLus
|
NORMAL
|
2024-09-11T07:12:35.436835+00:00
|
2024-09-11T07:12:35.436866+00:00
| 13 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nApproach 1:\nWe use XOR to check where the two numbers (start and goal) are different. XOR gives us a new number where every 1 means a difference between the bits, and every 0 means they\u2019re the same. Then, we just count how many 1s are in that XOR result\u2014each 1 means we need to flip a bit to match the numbers. Simple as that: compare, count, done!\n\nApproach 2:\nSo, we\u2019re converting both numbers (start and goal) into their binary forms (basically, how computers see them as 0s and 1s). But sometimes, one number has more bits than the other, so we add extra 0s at the front to make them the same length. Then, we just compare the two numbers bit by bit, counting how many times they\u2019re different. Each difference means you\u2019d need to flip that bit to make the two numbers match. In the end, the total flips is your answer!\n\nthen just straight-up comparing 0s and 1s!\n\n# Complexity\n- Time complexity:\nboth approaches have O(n)(n is no of bits in the larger one)time complexity, but XOR is a bit more efficient in practice since it avoids string operations.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\n// class Solution {\n// public int minBitFlips(int start, int goal) {\n // int x = start ^ goal;\n // int count = 0;\n // while (x > 0) {\n // count += x & 1;\n // x >>= 1;\n // }\n // return count;\n// }\n// }\nclass Solution {\n public int minBitFlips(int start, int goal) {\n String st = Integer.toBinaryString(start);\n String go = Integer.toBinaryString(goal);\n \n int l = st.length();\n int m = go.length();\n \n if (l < m) {\n st = "0".repeat(m - l) + st;\n } else if (m < l) {\n go = "0".repeat(l - m) + go;\n }\n \n int flips = 0;\n \n for (int i = 0; i < st.length(); i++) {\n if (st.charAt(i) != go.charAt(i)) {\n flips++;\n }\n }\n \n return flips;\n }\n}\n\n```
| 4 | 0 |
['Bit Manipulation', 'Java']
| 1 |
minimum-bit-flips-to-convert-number
|
EASY SOLUTION
|
easy-solution-by-viratkohli-ts6v
|
USE XOR THEN COUNT EVERY SET BIT\n# Complexity\n- Time complexity:O(log n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(1)\n Add your spa
|
viratkohli_
|
NORMAL
|
2024-09-11T03:57:59.521740+00:00
|
2024-09-11T03:57:59.521772+00:00
| 264 | false |
- USE XOR THEN COUNT EVERY SET BIT\n# Complexity\n- Time complexity:O(log n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int count = 0;\n int num = start^goal;\n\n while(num){\n int x = num%2;\n if(x && 1) count++;\n num /= 2;\n }\n return count;\n }\n};\n```
| 4 | 0 |
['Bit Manipulation', 'C++']
| 2 |
minimum-bit-flips-to-convert-number
|
simple and easy C++ solution 😍❤️🔥
|
simple-and-easy-c-solution-by-shishirrsi-3aqg
|
\n# Complexity\n- Time complexity: O(1)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n
|
shishirRsiam
|
NORMAL
|
2024-09-11T00:21:07.862880+00:00
|
2024-09-11T00:21:07.862900+00:00
| 964 | false |
\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) \n {\n // Convert the \'start\' and \'goal\' integers into 32-bit binary representation using bitset\n bitset<32> startBit(start), goalBit(goal);\n\n // Initialize a variable \'ans\' to store the number of bit flips needed\n int ans = 0;\n\n // Loop through each bit from 0 to 31 (since we are dealing with 32-bit integers)\n for(int i = 0; i < 32; i++) \n // If the bit at position \'i\' in startBit is different from the bit in goalBit, increment \'ans\'\n if(startBit[i] != goalBit[i]) ans += 1;\n\n // Return the total number of bit flips needed\n return ans;\n }\n};\n```\n\n# if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n###### Let\'s Connect on LinkedIn: www.linkedin.com/in/shishirrsiam\n###### Let\'s Connect on Facebook: www.fb.com/shishirrsiam
| 4 | 1 |
['Bit Manipulation', 'C++']
| 9 |
minimum-bit-flips-to-convert-number
|
BEATS 100% || O(1) || EASY BEGINERS
|
beats-100-o1-easy-beginers-by-abhishekka-lvk1
|
The provided code defines a function minBitFlips(start, goal) that calculates the minimum number of bit flips required to convert one integer (start) to another
|
Abhishekkant135
|
NORMAL
|
2024-06-24T15:23:39.192808+00:00
|
2024-06-24T15:23:39.192837+00:00
| 912 | false |
The provided code defines a function `minBitFlips(start, goal)` that calculates the minimum number of bit flips required to convert one integer (`start`) to another (`goal`). Here\'s a detailed explanation:\n\n**Concept:**\n\nThe code leverages the XOR (^) operator and bit manipulation to efficiently determine the number of bits that differ between `start` and `goal`.\n\n**Steps:**\n\n1. **XOR Operation:**\n - `int ans = start ^ goal;`: This line calculates the XOR between `start` and `goal`. The XOR operation returns 1 for bits that are different between the two operands and 0 for bits that are the same. By storing this result in `ans`, we essentially have a bitmask where 1s indicate positions where the bits differ.\n\n2. **Counting Set Bits:**\n - `int count = 0;`: Initializes a variable `count` to store the number of bit flips needed.\n - `for (int i = 0; i < 32; i++) { ... }`: This loop iterates 32 times, considering all 32 bits of a 32-bit integer (assuming integer size).\n - `if ((ans & (1 << i)) != 0) { ... }`: This condition checks if the `i`th bit in `ans` is set to 1. Here\'s how it works:\n - `(1 << i)`: This expression creates a bitmask with a single 1 at the `i`th position (left shift 1 by `i` positions).\n - `&`: The bitwise AND operation between `ans` and this bitmask checks if the `i`th bit in `ans` is 1.\n - `!= 0`: If the result of the AND operation is not zero (meaning the `i`th bit in `ans` is 1), it signifies a difference between `start` and `goal` at that position.\n - `count++`: If the condition is true, it means a bit flip is needed, so `count` is incremented.\n\n3. **Returning the Result:**\n - `return count;`: After iterating through all bits, the `count` variable holds the minimum number of bit flips required to convert `start` to `goal`.\n\n**Explanation:**\n\n- The XOR operation effectively identifies the bits that differ between `start` and `goal`.\n- The loop iterates through each bit position and checks if the corresponding bit in the XOR result (`ans`) is 1. If it\'s 1, it means a bit flip is needed in the original `start` to match the `goal`.\n- By counting the number of such occurrences, the code determines the minimum number of bit flips required.\n\n**Efficiency:**\n\nThis approach is efficient because it leverages bitwise operations, which are typically faster than traditional loop-based comparisons for identifying and counting differing bits.\n\n**Example:**\n\nConsider `start = 10 (binary: 1010)` and `goal = 17 (binary: 10001)`.\n\n- `ans = start ^ goal = 7 (binary: 0111)`.\n- The loop iterates and finds three 1s in `ans` (positions 0, 1, and 3).\n- `count` is incremented three times.\n- The function returns `count = 3`, indicating three bit flips are needed (from 0 to 1 in positions 0, 1, and 3 of `start` to match `goal`).\n\n# Code\n```\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int ans=start ^ goal;\n int count=0;\n for(int i=0;i<32;i++){\n if ((ans & (1 << i)) != 0) {\n count++;\n }\n }\n return count;\n }\n}\n```
| 4 | 0 |
['Bit Manipulation', 'Java']
| 1 |
minimum-bit-flips-to-convert-number
|
Java Simplest! Code (Beats 100%)
|
java-simplest-code-beats-100-by-ravinder-xzx7
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n- Compare least significant bits of both start and goal and keep right sh
|
Ravinder_1834
|
NORMAL
|
2023-10-22T18:14:26.146111+00:00
|
2023-10-22T18:14:26.146134+00:00
| 915 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- Compare least significant bits of both start and goal and keep right shifting by 1 until it is greater than 0. \n- Simultaneously count the no. of steps(which increases when the bits are not equal).\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int steps=0;\n \n while(start>0 || goal>0){\n if((start&(1))!=(goal&(1))){\n steps++;\n }\n start=start>>1;\n goal=goal>>1;\n }\n return steps;\n }\n}\n```
| 4 | 0 |
['Java']
| 1 |
minimum-bit-flips-to-convert-number
|
✅Beats 100% || Easiest Code using inbuilt function
|
beats-100-easiest-code-using-inbuilt-fun-fxsu
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
vishu_0123
|
NORMAL
|
2023-05-15T08:30:03.101596+00:00
|
2023-05-15T08:30:03.101636+00:00
| 1,056 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int ans=0;\n string s= bitset<32> (start).to_string();\n string str= bitset<32> (goal).to_string();\n for(int i=0;i<32;i++){\n if(s[i]!=str[i]) ans++;\n }\n return ans;\n }\n};\nDo UPVOTE\n```
| 4 | 0 |
['C++']
| 2 |
minimum-bit-flips-to-convert-number
|
💡 C++ | Simple Logic | With Full Explanation ✏️
|
c-simple-logic-with-full-explanation-by-m2gez
|
Intuition\nThe goal is to find how many bit flips (changing a bit from 0 to 1 or vice versa) are required to convert one number (start) to another number (goal)
|
Tusharr2004
|
NORMAL
|
2024-09-11T17:54:31.588632+00:00
|
2024-09-11T17:54:31.588665+00:00
| 12 | false |
# Intuition\nThe goal is to find how many bit flips (changing a bit from `0` to `1` or vice versa) are required to convert one number (`start`) to another number (`goal`).\n\nThe idea is based on the following key points:\n\n1. **Binary Representation:**\n\n- Every integer can be represented as a sequence of bits (binary digits). For instance, the number `5` is `101` in binary, and `1` is `001`. By comparing the bits of two numbers, we can determine how different they are.\n2. **Bit Comparison:**\n\n- The key observation here is that the number of positions where the bits differ between `start` and `goal` will tell us how many flips are needed to convert one number into the other.\n3. **Handling Different Binary Lengths:**\n\n- When converting numbers to binary, their bit-lengths (number of binary digits) might be different. For instance, the binary representation of `1` is `001`, while the binary representation of `5` is `101`. We need to compare all bits, so the shorter binary number should be padded with leading zeros to ensure both numbers have the same length.\n4. **Step-by-Step Process:**\n\n- Convert `start` and `goal` into their binary representations.\nIf the binary representations have different lengths, pad the shorter one with zeros to match the lengths.\nCompare the bits at each position. If the bits at a position are different, increment the flip count.\nThe final count gives the number of bit flips needed.\n\nThis approach simplifies the problem of converting one number to another by directly comparing their bit patterns, which is both intuitive and efficient for binary manipulation.\n\n# Approach\nTo solve the problem of finding the minimum number of bit flips required to convert `start` to `goal`, we can break down the approach into the following steps:\n\n1. **Binary Conversion:**\n\n- Convert the decimal numbers `start` and `goal` into their binary representations. This can be done by continuously dividing the number by 2 and storing the remainder (0 or 1) in a string, which gives the binary form of the number.\n2. **Padding to Equal Length:**\n\n- Once we have the binary strings for both `start` and `goal`, they may not be of the same length. For instance, `5` is `101` in binary and `1` is `001`. To ensure we can compare the two numbers bit by bit, we pad the shorter binary string with leading zeros until both strings are of equal length.\n3. **Bitwise Comparison:**\n\n- After ensuring both binary strings have the same length, we iterate through both strings bit by bit. For every position where the bits differ (i.e., one is `1` and the other is `0`), it means a bit flip is required to make the bits equal.\n4. **Counting the Bit Flips:**\n\n- Every time the bits differ at a particular position, we increment a counter that tracks how many bit flips are needed.\n5. **Return the Result:**\n\n- Finally, the counter will hold the total number of bit flips required to convert `start` into `goal`, which is returned as the result.\n\n# Example Walkthrough:\n\n**Input:**\n\n`start = 5` \u2192 Binary: `101`\n`goal = 1` \u2192 Binary: `001`\n**Step-by-step:**\n\nConvert start to binary: `5 \u2192 101`\nConvert goal to binary: `1 \u2192 001`\nBoth strings are already of the same length (101 and 001), so no padding is needed.\nCompare bit by bit:\n`1 != 0` (bit flip needed)\n`0 == 0` (no flip needed)\n`1 != 1` (no flip needed)\nTotal number of bit flips = `1`\n\n# Complexity\n- Time complexity:\n```O(Log(Max(Start,Goal)))```\n\n- Space complexity:\n``` O(logn)```\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int ans = 0; // To store the number of bit flips needed\n string x = "", y = ""; // Strings to store binary representations of \'start\' and \'goal\'\n\n // Convert \'start\' to binary and store in \'x\'\n while (start != 0) {\n x += to_string(start % 2); // Get the least significant bit (0 or 1)\n start /= 2; // Divide \'start\' by 2 to process the next bit\n }\n\n // Convert \'goal\' to binary and store in \'y\'\n while (goal != 0) {\n y += to_string(goal % 2); // Get the least significant bit (0 or 1)\n goal /= 2; // Divide \'goal\' by 2 to process the next bit\n }\n\n // If the lengths of the binary strings are not equal, pad the shorter one with \'0\'s\n if (x.size() != y.size()) {\n if (x.size() < y.size()) {\n // If \'x\' is shorter, add \'0\'s to its end to match the size of \'y\'\n while (x.size() != y.size()) {\n x += "0";\n }\n } else {\n // If \'y\' is shorter, add \'0\'s to its end to match the size of \'x\'\n while (y.size() != x.size()) {\n y += "0";\n }\n }\n }\n\n // Compare the bits of \'x\' and \'y\' to count the number of positions where they differ\n for (int i = 0; i < x.size(); i++) {\n if (x[i] != y[i]) {\n ans++; // Increment the count if the bits differ at the current position\n }\n }\n\n return ans; // Return the total number of bit flips required\n }\n};\n```\n\n\n\n\n# Ask any doubt !!!\nReach out to me \uD83D\uDE0A\uD83D\uDC47\n\uD83D\uDD17 https://tushar-bhardwaj.vercel.app/
| 3 | 0 |
['C++']
| 0 |
minimum-bit-flips-to-convert-number
|
✅ One Line Solution
|
one-line-solution-by-mikposp-0fhs
|
(Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)\n\n# Code #1\nTime complexity: O(digits). Space com
|
MikPosp
|
NORMAL
|
2024-09-11T09:04:55.753107+00:00
|
2024-09-11T09:04:55.753127+00:00
| 355 | false |
(Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)\n\n# Code #1\nTime complexity: $$O(digits)$$. Space complexity: $$O(1)$$.\n```python3\nclass Solution:\n def minBitFlips(self, v: int, u: int) -> int:\n return (v^u).bit_count()\n```\n\n# Code #2\nTime complexity: $$O(digits)$$. Space complexity: $$O(digits)$$.\n```python3\nclass Solution:\n def minBitFlips(self, v: int, u: int) -> int:\n return bin(v^u).count(\'1\')\n```\n\n# Code #3\nTime complexity: $$O(digits)$$. Space complexity: $$O(digits)$$.\n```python3\nclass Solution:\n def minBitFlips(self, v: int, u: int) -> int:\n return sum(map(int,f\'{v^u:b}\'))\n```\n\n# Code #4\nTime complexity: $$O(digits)$$. Space complexity: $$O(digits)$$.\n```python3\nclass Solution:\n def minBitFlips(self, v: int, u: int) -> int:\n return (f:=lambda q:q and q%2+f(q>>1))(v^u)\n```\n\n# Code #5\nTime complexity: $$O(digits)$$. Space complexity: $$O(digits)$$.\n```python3\nclass Solution:\n def minBitFlips(self, v: int, u: int) -> int:\n return (f:=lambda v,u:(v or u) and (v%2!=u%2)+f(v//2,u//2))(v,u)\n```\n\n# Code #6\nTime complexity: $$O(digits)$$. Space complexity: $$O(digits)$$.\n```python3\nclass Solution:\n def minBitFlips(self, v: int, u: int) -> int:\n return sum(starmap(ne,zip_longest(bin(v)[:1:-1],bin(u)[:1:-1],fillvalue=\'0\')))\n```\n\n(Disclaimer 2: code above is just a product of fantasy packed into one line, it is not claimed to be \'true\' oneliners - please, remind about drawbacks only if you know how to make it better)
| 3 | 0 |
['String', 'Bit Manipulation', 'Recursion', 'Python', 'Python3']
| 0 |
minimum-bit-flips-to-convert-number
|
Simple and Easy C++ code ||☠️💯✅
|
simple-and-easy-c-code-by-shodhan_ak-g43i
|
Code\ncpp []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n bitset<32> binary1(start);\n bitset<32> binary2(goal);\n
|
Shodhan_ak
|
NORMAL
|
2024-09-11T07:13:03.449448+00:00
|
2024-09-11T07:13:03.449473+00:00
| 94 | false |
# Code\n```cpp []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n bitset<32> binary1(start);\n bitset<32> binary2(goal);\n int count = 0;\n for (int i = 0; i < binary1.size(); i++) {\n if (binary1[i] != binary2[i]) { \n count++;\n }\n }\n return count;\n }\n};\n\n```\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem asks us to find the minimum number of bit flips required to convert one integer `start` into another integer `goal`. A bit flip is simply changing a bit from `0 to 1` or from `1 to 0`.\n\n **To solve this, consider:**\n\nEach integer can be represented in binary form, where each bit is either 0 or 1.\nThe task can be viewed as finding the number of positions where the binary representations of start and goal differ.\n\nFor every bit position that is different between start and goal, we will need one flip.\nThus, the goal is to compare the binary representations of the two numbers and count how many bits differ.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n**Convert to Binary:**\nWe first convert both start and goal into their binary representations. This can be done using a bitset of fixed size (in this case, 32 bits to handle standard integers in C++).\n\n**Bit Comparison:**\nOnce we have the binary representations of start and goal, we need to compare the bits at each position. For every bit that is different between start and goal, we increment a count.\n\n**Iterate through Each Bit:**\nWe loop through all the bits (32 in total for a 32-bit integer) and compare corresponding bits in start and goal. If the bits are different at a given position, we increase the count.\n\n**Return the Count:**\nAfter iterating through all the bits, the final value of count will be the minimum number of flips required to convert start to goal.\n\n# Code walkthrough\n`bitset<32> binary1(start);:` This line converts start into a 32-bit binary representation.\n`bitset<32> binary2(goal);:` Similarly, this converts goal into a 32-bit binary representation.\n`for (int i = 0; i < binary1.size(); i++):` A loop that iterates through each bit position (from 0 to 31).\n`if (binary1[i] != binary2[i]) { count++; }: `For each position, we compare the bits in binary1 and binary2. If they differ, increment the count by 1.\n`return count;:` Finally, return the total number of differing bits, which is the required number of bit flips.\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n
| 3 | 0 |
['C++']
| 0 |
minimum-bit-flips-to-convert-number
|
Easy to understand || beats 100%
|
easy-to-understand-beats-100-by-yash9325-3kgt
|
\n\n# Approach\n Describe your approach to solving the problem. \nThe goal is to calculate the minimum number of bit flips required to convert one integer (star
|
yash9325
|
NORMAL
|
2024-09-11T05:31:39.076545+00:00
|
2024-09-11T05:31:39.076581+00:00
| 4 | false |
\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe goal is to calculate the minimum number of bit flips required to convert one integer (`start`) to another integer (`goal`). The basic idea is to compare the binary representation of both integers and identify the positions where the bits differ. Here\'s a step-by-step breakdown of the approach:\n\n### 1. **Understand XOR Operation**:\n - The XOR operation (`^`) compares the bits of two numbers:\n - If the bits are the same at a particular position (both 0 or both 1), XOR returns 0 for that position.\n - If the bits differ (one is 0 and the other is 1), XOR returns 1 for that position.\n - So, by performing `start ^ goal`, the result will have `1`s in positions where the bits of `start` and `goal` differ. These positions represent where bit flips are needed.\n\n\n### 2. **Count the Number of 1\'s in the XOR Result**:\n - The number of `1`s in the XOR result represents how many bits need to be flipped to convert `start` to `goal`.\n - We can count the `1`s by:\n - Using the bitwise AND operation (`& 1`) to check the least significant bit.\n - Right-shifting the XOR result by 1 position in each iteration to check the next bit.\n\n### 3. **Steps in the Algorithm**:\n 1. Perform XOR between `start` and `goal` to get the positions of differing bits.\n 2. Initialize a counter (`flipCount`) to keep track of how many bits need to be flipped.\n 3. Use a loop to iterate through each bit of the XOR result:\n - Check if the least significant bit is `1` (indicating a differing bit).\n - Right-shift the XOR result to move to the next bit.\n 4. Return the `flipCount` after processing all bits.\n\n# Complexity\n- Time complexity:O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int xorResult = start ^ goal;\n // Count the number of 1s in the XOR result, which represents differing bits\n int flipCount = 0;\n \n // Count the number of set bits (1s)\n while (xorResult != 0) {\n flipCount += xorResult & 1; // Check if the last bit is 1\n xorResult >>= 1; // Shift right by 1 to check the next bit\n }\n \n return flipCount;\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int xorResult = start ^ goal;\n int flipCount = 0;\n \n // Count the number of set bits (1s) in xorResult\n while (xorResult != 0) {\n flipCount += xorResult & 1; // Check if the least significant bit is 1\n xorResult >>= 1; // Shift right by 1 to move to the next bit\n }\n \n return flipCount;\n }\n};\n\n```
| 3 | 0 |
['C++', 'Java']
| 0 |
minimum-bit-flips-to-convert-number
|
0ms Solution in Java👀
|
0ms-solution-in-java-by-starboy609-z5jk
|
Intuition\n Describe your first thoughts on how to solve this problem. \n1.XOR Operation: By using start ^ goal, you get a number that shows which bits are diff
|
starboy609
|
NORMAL
|
2024-09-11T05:14:40.461634+00:00
|
2024-09-11T05:14:40.461670+00:00
| 3 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1.XOR Operation: By using start ^ goal, you get a number that shows which bits are different between start and goal.\n\n2.Count Differences: Count how many 1s are in the result of this XOR operation. Each 1 represents a bit that is different and needs to be flipped.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.Calculate Differences:\nCompute x = start ^ goal. This highlights the bits where start and goal differ.\nCount the 1s:\n\n2.Initialize a counter to zero.\nCheck each bit of x. If the bit is 1, add 1 to the counter.\nMove to the next bit by shifting x right.\n\n3.Return the Count: This count is the number of bit flips needed.\n\n# Complexity\n- Time complexity: O(k), where k is the number of bits in the numbers\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1), because only a few extra variables are used\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int x = start ^ goal; // Step 1\n\n int c = 0;\n\n while(x > 0) // Step 2\n {\n c += (x & 1);\n x >>= 1;\n }\n\n return c; // Step 3\n }\n}\n```
| 3 | 0 |
['Java']
| 0 |
minimum-bit-flips-to-convert-number
|
Kotlin simple solution || Detailed explanation
|
kotlin-simple-solution-detailed-explanat-7ahr
|
Intuition\n Describe your first thoughts on how to solve this problem. \nIn order to count the number of bit flips required to convert start to goal. We need to
|
sushanth_grandhi
|
NORMAL
|
2024-09-11T02:49:55.853012+00:00
|
2024-09-11T21:40:17.064038+00:00
| 43 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIn order to count the number of bit flips required to convert start to goal. We need to find the bit positions which differ in both the numbers.\n\nSo, we can go bit by bit to check if it varies or same.\n\nIf the bits in both the numbers vary, we need to flip it and hence needed to be counted.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nWe can use "X-or" bitwise operator. Since xor of 2 numbers result in a number which has set bits (1) in positions that vary in both the numbers.\n\nOnce we found the xor result, we can use right shift operator to traverse bit by bit and count the set bits.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n1. Finding xor is linear - in terms of number of bits.\n2. Finding bit count is linear - in terms of number of bits.\n3. Given that numbers are in range of [0, 10^9].\n4. A number 2^x can be represented in \'x+1\' bits => 4 - 3 bits, 8 - 4 bits, 16 - 5 bits, ...etc\n5. 1000 = 10^3 ~ 1024 = 2^10 => 10^9 ~ 2^30 => At max 31 bits.\n6. Hence, it takes O(31) ~ constant time.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n1. No extra space is required ~ O(1).\n\n# Code\n```kotlin []\nclass Solution {\n fun minBitFlips(start: Int, goal: Int): Int {\n // 1 xor 1 = 0; 0 xor 1 = 1\n // Hence, xor of 2 numbers will result in number with 1 in bits that differ\n\n var xorVal = start xor goal\n var bitFlips = 0\n\n // Starting with LSB, \n // check if there is 1 at each bit and count accordingly\n while (xorVal > 0) {\n // bitFlips += if (xorVal and 1 == 1) 1 else 0\n\n bitFlips += (xorVal and 1)\n // or if (xorVal and 1 == 1) bitFlips++\n\n xorVal = xorVal shr 1\n }\n\n return bitFlips\n }\n}\n```\n\n```python3 []\nclass Solution:\n def minBitFlips(self, start: int, goal: int) -> int:\n\n // 1 ^ 1 = 0; 0 ^ 1 = 1\n // Hence, xor of 2 numbers will result in number with 1 in bits that differ\n\n xorVal = start ^ goal\n bitFlips = 0\n\n // Starting with LSB, \n // check if there is 1 at each bit and count accordingly\n while xorVal:\n bitFlips += 1 if (xorVal & 1) else 0\n xorVal >>= 1\n \n return bitFlips\n \n```\n\nPlease upvote if you like my solution :)\nLeave a comment for any suggestions
| 3 | 0 |
['Bit Manipulation', 'Bitmask', 'Python3', 'Kotlin']
| 1 |
minimum-bit-flips-to-convert-number
|
Golang solution with explanation
|
golang-solution-with-explanation-by-alek-w6pp
|
Intuition\nTo solve the problem of finding the minimum number of bit flips required to convert one integer (start) to another integer (goal), we need to identif
|
alekseiapa
|
NORMAL
|
2024-09-11T01:53:17.234681+00:00
|
2024-09-11T01:53:17.234710+00:00
| 93 | false |
# Intuition\nTo solve the problem of finding the minimum number of bit flips required to convert one integer (`start`) to another integer (`goal`), we need to identify the bits that differ between the two numbers. Each differing bit represents a necessary bit flip. The most efficient way to find these differing bits is by using the XOR bitwise operation (`^`). The XOR operation produces a binary number with `1`s at every position where the corresponding bits of `start` and `goal` differ. The task then reduces to counting the number of `1`s in the result of this XOR operation, which gives the minimum number of bit flips required.\n\n# Approach\n1. **Use XOR to Find Differing Bits**:\n - Perform an XOR operation on `start` and `goal`. The result will have `1`s at positions where the bits of `start` and `goal` differ.\n \n2. **Count the Number of 1s in the XOR Result**:\n - To find the number of differing bits, we count the number of `1`s in the result of the XOR operation. This can be done by continuously shifting the bits to the right and checking the least significant bit.\n \n3. **Return the Count**:\n - The count of `1`s represents the minimum number of bit flips required to convert `start` to `goal`.\n\n# Complexity\n- **Time complexity**: \n The time complexity is **O(log N)**, where `N` is the maximum of `start` and `goal`. This is because we are iterating through the bits of the XOR result, which takes logarithmic time relative to the size of the number.\n\n- **Space complexity**: \n The space complexity is **O(1)**, as the solution only uses a constant amount of extra space to store the count and intermediate values.\n\n# Code\n```golang []\nfunc countOnes(n int) int {\n count := 0\n for n > 0 {\n count += n & 1 // Increment count if the last bit is 1\n n >>= 1 // Right shift n by 1 to check the next bit\n }\n return count\n}\n\n// Function to calculate the minimum number of bit flips to convert start to goal\nfunc minBitFlips(start int, goal int) int {\n xorResult := start ^ goal // XOR to find differing bits\n return countOnes(xorResult) // Count the number of 1s in the XOR result\n}\n```
| 3 | 0 |
['Go']
| 0 |
minimum-bit-flips-to-convert-number
|
C++ || Easy Video Solution || Faster than 100%
|
c-easy-video-solution-faster-than-100-by-jboc
|
The video solution for the below code is\nhttps://youtu.be/kDSXbCOT6tg\n\n# Code\ncpp []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\
|
__SAI__NIVAS__
|
NORMAL
|
2024-09-11T01:47:45.962795+00:00
|
2024-09-11T01:47:45.962824+00:00
| 173 | false |
The video solution for the below code is\nhttps://youtu.be/kDSXbCOT6tg\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n ios_base::sync_with_stdio(false);\n cin.tie(NULL);\n cout.tie(NULL);\n // Note:\n // Bit flip is nothing but considering a bit in the number and flipping it i.e. either 1 is converted to 0 or 0 is converted to 1.\n // We need to find the minimum number of flips to convert the start to goal number.\n // Example - 1\n // start 10\n // goal 7\n // start 1010 32 16 8 4 2 1\n // goal 0111\n // 10\n // 2)10( Rem 0\n // 2)5( Rem 1\n // 2)2( Rem 0\n // 1\n int ans = 0;\n while(start or goal){\n ans += ((start % 2) != (goal % 2));\n start /= 2;\n goal /= 2;\n }\n return ans;\n }\n};\n```
| 3 | 0 |
['C++']
| 1 |
minimum-bit-flips-to-convert-number
|
Cpp || Bit Manipulation
|
cpp-bit-manipulation-by-imsej_al-q0p1
|
Intuition\n Describe your first thoughts on how to solve this problem. \n1. Each bit flip operation changes a 0 bit to a 1 bit or a 1 bit to a 0 bit.\n2. The XO
|
imsej_al
|
NORMAL
|
2024-06-07T11:02:57.440588+00:00
|
2024-06-07T11:02:57.440621+00:00
| 506 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1. Each bit flip operation changes a 0 bit to a 1 bit or a 1 bit to a 0 bit.\n2. The XOR (exclusive OR) operation between two bits will be 1 if the bits are different and 0 if they are the same. Thus, start ^ goal will produce a number where each 1 bit represents a position where start and goal have different bits.\n\n# Approach\n1. Compute XOR: Compute start ^ goal. This result will have 1 bits in positions where start and goal differ.\n2. Count the Number of 1 Bits: Count the number of 1 bits in the result of the XOR operation. This count gives the minimum number of bit flips required to convert start to goal.\n\n# Complexity\n#### Time Complexity:\nThe loop runs for 31 iterations (assuming a 32-bit integer, but using 31 since it generally suffices to consider up to the most significant bit in typical constraints). Thus, the time complexity is O(1) because it is a constant-time operation regardless of the specific values of start and goal.\n#### Space Complexity:\nThe space complexity is O(1) because only a fixed amount of extra space is used for variables ans and cnt, and no additional space that scales with input size is required.\n\n# Code\n```\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int ans = start ^ goal;\n int cnt = 0;\n for(int i = 0;i<31;i++){\n if(ans & (1 << i))\n cnt++;\n }\n return cnt;\n }\n};\n```
| 3 | 0 |
['Bit Manipulation', 'C++']
| 1 |
minimum-bit-flips-to-convert-number
|
Most easy solution with all bit manipulation concepts covered
|
most-easy-solution-with-all-bit-manipula-9cia
|
Intuition\nBit Manipultaion\n\n\n\n\n# Approach\n- In this solution, I have taken the XOR of start and goal because, with the XOR operation, if both bits are th
|
Pulkit28
|
NORMAL
|
2024-05-19T02:58:19.489160+00:00
|
2024-05-19T20:17:30.886109+00:00
| 173 | false |
# Intuition\nBit Manipultaion\n\n\n\n\n# Approach\n- In this solution, I have taken the XOR of start and goal because, with the XOR operation, if both bits are the same (both 0 or both 1), the result is 0. If the bits are different (one is 0 and the other is 1), the result is 1. This allows us to identify the positions where the bits differ.\n\n- Next, to count the number of differing bits (which correspond to the number of 1s in the result of the XOR operation), we convert the result to its binary form and count the number of 1s. Instead of using the modulo operation to check each bit, we can use the right shift (>>) operator to improve efficiency. The updated dtb function using the right shift operator looks like this:\n\n```\nint dtb(int n) {\n int cnt = 0;\n while (n > 0) {\n if (n & 1) { // Check if the least significant bit is 1\n cnt++;\n }\n n >>= 1; // Right shift the number by 1 bit\n }\n cout << cnt << endl;\n return cnt;\n}\n```\n# Tip\n- Be careful Bitmanipulation questions are little tricky and needs knowledge of ^, <<, >>, |, & and many more.\n\n1) Bitwise AND (&)\n\nCompares each bit of two numbers and returns a new number whose bits are set to 1 only if both corresponding bits of the operands are 1.\nExample:\n```\nint a = 5; // Binary: 0101\nint b = 3; // Binary: 0011\nint c = a & b; // Binary: 0001 (c is 1)\n```\n\n2) Bitwise OR (|)\n\nCompares each bit of two numbers and returns a new number whose bits are set to 1 if at least one of the corresponding bits of the operands is 1.\nExample:\n\n```\nint a = 5; // Binary: 0101\nint b = 3; // Binary: 0011\nint c = a | b; // Binary: 0111 (c is 7)\n```\n\n3) Bitwise XOR (^)\n\nCompares each bit of two numbers and returns a new number whose bits are set to 1 if exactly one of the corresponding bits of the operands is 1 (but not both).\nExample:\n\n```\nint a = 5; // Binary: 0101\nint b = 3; // Binary: 0011\nint c = a ^ b; // Binary: 0110 (c is 6)\n\n```\n4)Bitwise NOT (~)\n\nInverts all the bits of a number, changing 0s to 1s and 1s to 0s.\nExample:\n\n```\nint a = 5; // Binary: 0101\nint c = ~a; // Binary: 1010 (c is -6 in two\'s complement representation)\n```\n\n5)Left Shift (<<)\n\nShifts the bits of a number to the left by a specified number of positions, inserting 0s from the right.\nExample:\n\n```\nint a = 5; // Binary: 0101\nint c = a << 1; // Binary: 1010 (c is 10)\n```\n\n6)Right Shift (>>)\n\nShifts the bits of a number to the right by a specified number of positions. For positive numbers, 0s are inserted from the left; for negative numbers, 1s are typically inserted from the left.\nExample:\n```\nint a = 5; // Binary: 0101\nint c = a >> 1; // Binary: 0010 (c is 2)\n```\n\n7) Bit Masking\n\nUsing bitwise operators to manipulate specific bits within a number.\nExample: To set the 3rd bit of a to 1:\n\n```\nint a = 5; // Binary: 0101\nint mask = 1 << 2; // Binary: 0100\na = a | mask; // a becomes 1101 (a is 13)\nBit Counting\n```\n\n8) Counting the number of 1s (set bits) in a binary representation.\nExample: Using the built-in function __builtin_popcount in GCC:\n\n```\nint count = __builtin_popcount(a);\n```\n9) Checking if a Number is a Power of Two\n\nA number is a power of two if it has exactly one set bit.\nExample:\n```\nbool isPowerOfTwo(int n) {\n return n > 0 && (n & (n - 1)) == 0;\n}\n```\n\n10) Using XOR to swap two numbers.\nSwapping Numbers Without a Temporary Variable\nExample:\n\n```\nint a = 5;\nint b = 3;\na = a ^ b;\nb = a ^ b;\na = a ^ b;\n```\n\n11) Clearing a Bit\n\nSetting a specific bit to 0.\nExample: To clear the 2nd bit of a:\n\n```\nint a = 5; // Binary: 0101\nint mask = ~(1 << 1); // Binary: 1111 1101\na = a & mask; // a becomes 0101 (a is 5)\n```\n\n12) Setting a Bit\n\nSetting a specific bit to 1.\nExample: To set the 1st bit of a:\n\n```\nint a = 5; // Binary: 0101\nint mask = 1 << 1; // Binary: 0010\na = a | mask; // a becomes 0111 (a is 7)\n```\n\n\n13) Flipping a specific bit.\nExample: To toggle the 2nd bit of a:\n\n```\nint a = 5; // Binary: 0101\nint mask = 1 << 1; // Binary: 0010\na = a ^ mask; // a becomes 0111 (a is 7)\n\n```\n- These concepts are enough to solve any Bit Problem.\n\n# Complexity\n- Time complexity:\nO(logn)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n int dtb(int n){\n int cnt=0;\n while(n>0){\n int rem = n%2;\n if(rem == 1){\n cnt++;\n }\n n = n/2;\n }\n cout<<cnt<<endl;\n return cnt;\n }\n int minBitFlips(int start, int goal) {\n int decimal = start^goal;\n int a = dtb(decimal);\n return a;\n }\n};\n```
| 3 | 0 |
['C++']
| 1 |
minimum-bit-flips-to-convert-number
|
One line solution 🔥🔥 | Beats 100% | Java, Python, C++
|
one-line-solution-beats-100-java-python-8rij7
|
\n\n# \uD83D\uDCD2Complexity\n- \u23F0Time complexity:O(1)\n Add your time complexity here, e.g. O(n) \n\n- \uD83E\uDDFASpace complexity:O(1)\n Add your space c
|
saikrishnanaidu
|
NORMAL
|
2024-05-06T05:37:28.907900+00:00
|
2024-05-06T05:37:28.907936+00:00
| 457 | false |
\n\n# \uD83D\uDCD2Complexity\n- \u23F0Time complexity:O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- \uD83E\uDDFASpace complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n return Integer.bitCount(start^goal);\n }\n}\n```\n```python []\nclass Solution:\n def minBitFlips(self, start: int, goal: int) -> int:\n return bin(start ^ goal).count(\'1\')\n\n```\n```C++ []\n#include <bitset>\n\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n return std::bitset<32>(start ^ goal).count();\n }\n};\n\'\n```\n\n
| 3 | 0 |
['Python', 'C++', 'Java', 'Python3']
| 2 |
minimum-bit-flips-to-convert-number
|
✅💯Solution With Actual CONCEPT!! || UNDERSTAND THE INTUITION || NO USE OF PREDEFINED FUNCTIONS ||
|
solution-with-actual-concept-understand-x0f0c
|
Intuition\n Describe your first thoughts on how to solve this problem. \nBefore starting to asses this problem lets understand the concept of Bit Shifting.\n\nB
|
piyuzh
|
NORMAL
|
2024-04-29T04:40:03.611859+00:00
|
2024-04-29T16:55:55.683988+00:00
| 204 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBefore starting to asses this problem lets understand the concept of Bit Shifting.\n\nBit shifting involves ***```moving the bits of a binary number to the left or right by a specified number of positions.```***\n\nLeft shift (<<) multiplies the number by 2 raised to the power of the shift amount. For example, 5 << 1 shifts the bits of 5 one position to the left, resulting in 10 (binary 1010 becomes 10100).\n\nOr in simpler words Left Shift removes bits from the MSB side of the binary representation\n\nRight shift (>>) divides the number by 2 raised to the power of the shift amount, discarding the remainder. For example, 10 >> 1 shifts the bits of 10 one position to the right, resulting in 5 (binary 1010 becomes 101).\n\nYou guessed it!! Right shift removes bits from the LSB side of the binary representation\n# Approach\n<!-- Describe your approach to solving the problem. -->\nNow the question pretty much says what to do, the main trick here was to find a way to get to the number of set bits.\n\nFirstly one thing that we can notice from examples is that the number of bit flips were always equal to the number of bits of the resultant value\'s binary representation that was pretty obv to look for, and dont worry if you didnt youll get an eye for it soon\n\nNow how do we get the number of required set bits? We XOR the value that we are starting from and the value we need to reach to.\n\nHere\'s why we use XOR:\n\nWhen we XOR two bits-\n- If the two bits are different (one is 0 and the other is 1), the result is 1.\n- If the two bits are the same (both 0 or both 1), the result is 0.\n\n- By XORing start and goal, we obtain a result where each set bit (1) indicates a position where the corresponding bits in start and goal are different.\n\n- Any bit that needs to be flipped from 0 to 1 or from 1 to 0 in start to match goal will have a set bit in the XOR result.\n\n---\n\nNow the thing that no one is talking about\nThe bitCounut() function\nUsing the predefined function is a good way to quickly wrap up the solutionn but its important to understand how the function works\n\nfirstly we use bitwise AND and get the LSB \nHow does that work?\nAssume a number n=`101101`\ndoing bitwise AND with 1 on only the LSB we get\n\n`101101 & 000001= 1 `\n\nnow if thats 1 (refer truth table of AND if confused), which means its a set bit then we just increase our count by one\nand then remove the LSB from the number n by rightshifting one position ( >> 1 )\n\nn becomes: `010110` (we remove the last bit by right shifting the number by 1 and to maintain the number of total bits we add a 0 at the start)\n\nnow lets do it one last time to understand what\'ll happen if the LSB is 0\n\n`010110 & 000001= 0`\n\nwhich means the count is not going to increase\n\nand we right shift again to get to the next value\n\nwe do this until n becomes 0 and now we return the value of count.\n___\n# **CODE**\n```java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n return bitCount(start^goal);\n }\n public int bitCount(int num){\n int count=0;\n while(num!=0){\n count+=num&1; //count the number of set bits\n num>>=1; //right shift one bit to change the LSB\n }\n return count;\n }\n}\n\n// 011^100=111\n```\n
| 3 | 0 |
['Math', 'Bit Manipulation', 'Brainteaser', 'Bitmask', 'Java']
| 2 |
minimum-bit-flips-to-convert-number
|
2220. 🔥 Java | Bit Manipulation | 100% Efficient 🔥
|
2220-java-bit-manipulation-100-efficient-6ohi
|
Complexity\n- Time complexity: O(N)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n# Co
|
thecompetitivedev
|
NORMAL
|
2023-07-26T21:32:16.031584+00:00
|
2023-07-26T21:33:18.931967+00:00
| 376 | false |
# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int count=0;\n for(int i=0;i<32;i++)\n {\n int mask=(1<<i);\n if(((start & mask)==0 && (goal & mask)!=0) || ((start & mask)!=0 && (goal & mask)==0))\n count++;\n\n }\n return count;\n }\n}\n```
| 3 | 0 |
['Bit Manipulation', 'Java']
| 3 |
minimum-bit-flips-to-convert-number
|
✅ One of the most easiest solutions 💯
|
one-of-the-most-easiest-solutions-by-riy-4er5
|
Intuition\nWe need to just count to total number of different bits of start and end.\n\n# Approach\nFind XOR of start and end and then count 1. Because after XO
|
Riyad-Hossain
|
NORMAL
|
2023-07-06T03:00:59.695207+00:00
|
2023-07-06T03:00:59.695226+00:00
| 360 | false |
# Intuition\nWe need to just count to total number of different bits of `start` and `end`.\n\n# Approach\nFind `XOR` of `start` and `end` and then count 1. Because after `XOR` any two value, we get 1 only when where the bit is different.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int count = 0;\n\n long long diffBits = start ^ goal;\n while(diffBits != 0){\n if(diffBits & 1) count++;\n diffBits >>= 1;\n }\n\n return count;\n }\n};\n```\n\n**Please upvote if you really like the approach. \uD83D\uDC4D\uD83C\uDFFB**\n\nCheckout my GitHub repo: [GitHub](https://github.com/RiyaadHossain/LeetCode-Problem)
| 3 | 0 |
['Bit Manipulation', 'C++']
| 1 |
minimum-bit-flips-to-convert-number
|
JAVA && BIT MANIPULATION && BEATS 100% (Kernighan's Algorithm approach)
|
java-bit-manipulation-beats-100-kernigha-dw7m
|
Intuition\n Describe your first thoughts on how to solve this problem. \nUsing XOR operator the bits that are different will become 1 and same bits will become
|
Pratham_Upadhyay
|
NORMAL
|
2023-06-08T13:46:59.726075+00:00
|
2023-06-08T13:46:59.726144+00:00
| 702 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUsing XOR operator the bits that are different will become 1 and same bits will become 0 . After that we just need to count the number of 1\'s using the Kernighan\'s Algorithm.\n\n# Approach\n\nFirst we store the XOR operator result in n and then we initialize a counter with 0 . Now we loop until the n!=0 and inside the loop we are initializing rsbm (right most set bit mask ) for the n. And after that we subtract the rightmost set bit from n using n -= rsbm. This clears the rightmost set bit from n. The counter variable is incremented by 1. At last we return counter .\n\n# Complexity\n- Time complexity:\n O(Log(n))\n\n- Space complexity:\n O(1)\n\n# Code\n```\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int n = start^goal;\n int counter = 0;\n \n while(n!=0){\n int rsbm = n & -n;\n n -= rsbm;\n counter++;\n }\n\n return counter;\n\n }\n}\n```
| 3 | 0 |
['Bit Manipulation', 'Java']
| 1 |
minimum-bit-flips-to-convert-number
|
0ms Solution || Bit Manipulation
|
0ms-solution-bit-manipulation-by-vpavank-aq9k
|
Intuition\nJust try to make the $start$ equals to $goal$ using $Bit Manipulations$.\n\n# Approach\nIf the $goal$ bit is set, check if the $start$ bit is set, if
|
vpavankalyan
|
NORMAL
|
2023-06-07T07:54:59.152628+00:00
|
2023-06-07T07:54:59.152665+00:00
| 1,712 | false |
# Intuition\nJust try to make the $start$ equals to $goal$ using $Bit Manipulations$.\n\n# Approach\nIf the $goal$ bit is **set**, check if the $start$ bit is **set**, if not increase the count, as we will use one $flip$ operation.\n\nIf the $goal$ bit is **unset**, check if the $start$ bit is **unset**, if not increase the count, as we will use one $flip$ operation \n\n# Complexity\n- Time complexity: $$O(log(max(start, goal)))$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int cnt = 0;\n while(goal || start)\n {\n bool goalBit = (goal&1);\n bool startBit = (start&1);\n if(goalBit)\n {\n if(startBit)\n {\n // Do Nothing\n }\n else\n {\n cnt++;\n }\n }\n else\n {\n if(startBit)\n {\n cnt++;\n }\n else\n {\n // Do Nothing\n }\n }\n start >>= 1;\n goal >>= 1;\n }\n return cnt;\n }\n};\n```\n# Follow up Question:\nhttps://leetcode.com/problems/minimum-flips-to-make-a-or-b-equal-to-c/\n**My Solution:** https://leetcode.com/problems/minimum-flips-to-make-a-or-b-equal-to-c/solutions/3607616/0ms-solution-bit-manipulation/
| 3 | 0 |
['Bit Manipulation', 'C++']
| 1 |
minimum-bit-flips-to-convert-number
|
Kernighan's algorithm || Easy to understand || With Explaination
|
kernighans-algorithm-easy-to-understand-41h6n
|
\n\n\n class Solution {\n public:\n int minBitFlips(int start, int goal) {\n int cnt=0;\n \n // # Here we get he number if set bit
|
harsh_patell21
|
NORMAL
|
2023-05-01T03:34:35.465514+00:00
|
2023-05-01T03:34:35.465559+00:00
| 234 | false |
\n\n\n class Solution {\n public:\n int minBitFlips(int start, int goal) {\n int cnt=0;\n \n // # Here we get he number if set bits which are required for getting our goal number\n int set=start^goal;\n \n // # kernighan\'s algo for finding no of set bits\n while(set!=0){\n \n // # a mask in which only right most bit is set\n int rsb=(set&(-set));\n set=set-rsb;\n cnt++;\n }\n return cnt;\n }\n };
| 3 | 0 |
['C']
| 1 |
minimum-bit-flips-to-convert-number
|
Easy And Understandable Solution
|
easy-and-understandable-solution-by-kada-gtxb
|
Intuition\n Describe your first thoughts on how to solve this problem. \nFirstly On Reading The Problem, We have to find How Many Bits \nAre Different in start
|
kadavakallulokesh
|
NORMAL
|
2023-02-23T18:52:49.408652+00:00
|
2023-02-23T18:52:49.408693+00:00
| 561 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirstly On Reading The Problem, We have to find How Many Bits \nAre Different in **start** And **goal**.\n\nfor finding How many different bits,we use X-OR Gate .(0^1=1 and 1^0=1)\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n**_step1_** : find x-or of start and goal\n**_step2_** : now find no.of set bits (i.e., no.of 1s) in xOredResult.\n (this is becuase \'1\' in xOredResult denotes the bits are different,so we have to flip them) \n**_step3_** : the no.of set bits gives the no.of bits to flip actually\n\n(Read $$Brian-Kerninghan algorithm$$ to count no.of set bits in a particular number) \n\n# Complexity\n- Time complexity: $$O(logn)$$ where \'n\' is the number whose set bits need to be calculated\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n**Please upvote my solution if you really liked it**\n\n# Code\n```\nclass Solution {\n private int count = 0;\n public int minBitFlips(int start, int goal) {\n\n // Find X-OR of start and goal to know no.of different bits\n int xOredResult = (start^goal);\n\n // now Count no.of SetBits in xOredResult\n // using Brian-Kerninghan Algorithm\n return brianKerninghanAlgo(xOredResult);\n }\n public int brianKerninghanAlgo(int num)\n {\n while(num != 0)\n {\n num&=(num-1);\n count++;\n }\n return count;\n }\n}\n```
| 3 | 0 |
['Bit Manipulation', 'Java']
| 3 |
minimum-bit-flips-to-convert-number
|
C# Simple Solution With Explanation
|
c-simple-solution-with-explanation-by-gr-qumu
|
Please upvote if my solution was helpful ;)\n# Explanation\nExample: start = 10, goal = 7, in binary representation are 1010 and 0111 respectively\n\n\n\n\n1101
|
gregsklyanny
|
NORMAL
|
2022-12-10T08:04:20.437857+00:00
|
2022-12-12T15:29:34.918885+00:00
| 211 | false |
**Please upvote if my solution was helpful ;)**\n# Explanation\nExample: start = 10, goal = 7, in binary representation are 1010 and 0111 respectively\n\n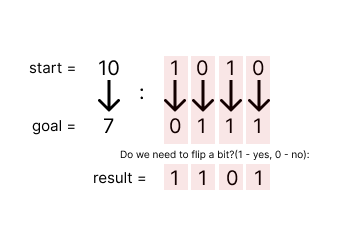\n\n\n1101 is a result of XOR operation - result = start^goal. Answer is a count of "1" bits in result.\n\n# Algorithm\n1) Initialize "result" as a start^goal (xor operation)\n2) Count "1" bits in result and return it\n\n# Code\n```\npublic class Solution \n{\n public int MinBitFlips(int start, int goal)\n {\n int result = start^goal;\n int output = 0;\n while(result > 0)\n {\n if((result & 1) == 1) output++;\n result = result>>1;\n }\n return output;\n }\n}\n```\n# Code 2(memory optimization)\n\nIn the code below we are using method parameters start and goal as a local variables \n\n```\npublic class Solution \n{\n public int MinBitFlips(int start, int goal)\n {\n start = start^goal;\n goal = 0;\n while(start > 0)\n {\n if((start & 1) == 1) goal++;\n start = start>>1;\n }\n return goal;\n }\n}\n```
| 3 | 0 |
['Bit Manipulation', 'C#']
| 0 |
minimum-bit-flips-to-convert-number
|
JAVA easy solution using Kernighan's Algorithm
|
java-easy-solution-using-kernighans-algo-wafg
|
First we find xor of the two input numbers and count the number of set bits in the result using kernighan\'s algorithm\n\nhere result=start^goal\n\nkernighan\'s
|
21Arka2002
|
NORMAL
|
2022-09-04T03:31:27.034028+00:00
|
2022-09-04T03:31:27.034055+00:00
| 370 | false |
First we find xor of the two input numbers and count the number of set bits in the result using kernighan\'s algorithm\n\nhere result=start^goal\n\nkernighan\'s algorithm-\n\nIn a loop till the result > 0\nStep 1 increase the count by 1\nStep 2 result=result xor (result - 1)\n\n\n```\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int n=start^goal,c=0;\n while(n>0)\n {\n n&=(n-1);\n c+=1;\n }\n return c;\n }\n}\n```
| 3 | 0 |
['Bit Manipulation', 'Java']
| 1 |
minimum-bit-flips-to-convert-number
|
🏌️ One Liner - Python
|
one-liner-python-by-robbiebusinessacc-gaxn
|
\n\nreturn(start^goal).bit_count()\n\nPlease upvote if you want to see more one liners and simple solutions
|
robbiebusinessacc
|
NORMAL
|
2022-08-04T17:39:35.948463+00:00
|
2022-08-04T17:39:35.948502+00:00
| 310 | false |
\n```\nreturn(start^goal).bit_count()\n```\n**Please upvote if you want to see more one liners and simple solutions**
| 3 | 0 |
['Python']
| 2 |
minimum-bit-flips-to-convert-number
|
C++ solution well explained, faster than 100%
|
c-solution-well-explained-faster-than-10-cvmw
|
\nclass Solution {\npublic:\n // Function to count the set bits\n int countSetBits(int n)\n {\n int count = 0;\n while(n > 0){\n
|
Striver27
|
NORMAL
|
2022-06-15T06:11:27.168147+00:00
|
2022-06-15T06:11:27.168184+00:00
| 175 | false |
```\nclass Solution {\npublic:\n // Function to count the set bits\n int countSetBits(int n)\n {\n int count = 0;\n while(n > 0){\n n &= (n-1);\n count++;\n }\n return count;\n }\n \n int minBitFlips(int start, int goal) {\n \n return countSetBits(start ^ goal); // start ^ goal : gives the differenciating bits\n \n }\n};\n```\n\n**Liked it ? Do upvote it, it do motivates !**
| 3 | 0 |
['Bit Manipulation', 'C']
| 1 |
minimum-bit-flips-to-convert-number
|
C++ Simple Xor Operation 100% Faster
|
c-simple-xor-operation-100-faster-by-kis-m2y2
|
```\n//let start = 1101\n//goal = 1000\n// Xor = 0101\n//NUmber of set bits in Xor\nclass Solution {\npublic:\n int minBitFlips(int start, int goal
|
kissingtheworld
|
NORMAL
|
2022-04-11T08:17:57.589277+00:00
|
2022-04-11T08:17:57.589317+00:00
| 192 | false |
```\n//let start = 1101\n//goal = 1000\n// Xor = 0101\n//NUmber of set bits in Xor\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) \n {\n int xorr = start xor goal;\n unsigned int ans=0;\n //Count number of bits to be flipped\n while(xorr)\n {\n ans++;\n xorr = xorr&(xorr-1);// Brian Kernighan\'s Algorithm to count set bit;\n }\n return ans;\n }\n};\n//Please Do Upvote \n//If you find Anything Incorrect or have doubt drop it down;
| 3 | 0 |
['Counting']
| 0 |
minimum-bit-flips-to-convert-number
|
Kotlin Solution: XOR then count set bit
|
kotlin-solution-xor-then-count-set-bit-b-vif0
|
\nclass Solution {\n fun minBitFlips(start: Int, goal: Int): Int {\n var result = start xor goal\n var answer = 0\n while (result > 0) {\
|
ogbe
|
NORMAL
|
2022-04-05T00:51:24.480890+00:00
|
2022-04-05T00:51:41.479517+00:00
| 56 | false |
```\nclass Solution {\n fun minBitFlips(start: Int, goal: Int): Int {\n var result = start xor goal\n var answer = 0\n while (result > 0) {\n if (result % 2 == 1) {\n answer++\n }\n result /= 2\n }\n return answer\n }\n}\n```
| 3 | 0 |
['Kotlin']
| 1 |
minimum-bit-flips-to-convert-number
|
Bits Manipulation + XOR(^)
|
bits-manipulation-xor-by-aditya_jain_258-7nkw
|
\nclass Solution {\n\tpublic static int minBitFlips(int a1, int a2) {\n\t\tint n = (a1 ^ a2);\n\t\tint res = 0;\n\t\twhile (n != 0) {\n\t\t\tres++;\n\t\t\tn &=
|
Aditya_jain_2584550188
|
NORMAL
|
2022-04-03T06:21:18.397805+00:00
|
2022-04-03T06:21:18.397876+00:00
| 225 | false |
```\nclass Solution {\n\tpublic static int minBitFlips(int a1, int a2) {\n\t\tint n = (a1 ^ a2);\n\t\tint res = 0;\n\t\twhile (n != 0) {\n\t\t\tres++;\n\t\t\tn &= (n - 1);\n\t\t}\n\t\treturn res;\n\t}\n}\n```
| 3 | 0 |
['Bit Manipulation', 'Java']
| 1 |
minimum-bit-flips-to-convert-number
|
C++ XOR + __builtinpop_count
|
c-xor-__builtinpop_count-by-lzl124631x-bosw
|
See my latest update in repo LeetCode\n## Solution 1.\n\nXOR sets the bits that are different between start and goal, and unsets bits that are the same.\n\n__bu
|
lzl124631x
|
NORMAL
|
2022-04-02T16:44:28.062210+00:00
|
2022-04-02T16:44:28.062240+00:00
| 267 | false |
See my latest update in repo [LeetCode](https://github.com/lzl124631x/LeetCode)\n## Solution 1.\n\nXOR sets the bits that are different between `start` and `goal`, and unsets bits that are the same.\n\n`__builtin_popcount(mask)` counts the `1`s in `mask`.\n\nExample:\n\nExpression | Value\n---|--\nstart| `0011010`\ngoal| `0101100`\nstart^goal| `0110110`\n__builtin_popcount(start^goal) | 4\n\n\n```cpp\n// OJ: https://leetcode.com/problems/minimum-bit-flips-to-convert-number/\n// Author: github.com/lzl124631x\n// Time: O(1)\n// Space: O(1)\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n return __builtin_popcount(start ^ goal);\n }\n};\n```
| 3 | 0 |
[]
| 1 |
minimum-bit-flips-to-convert-number
|
✅ || BITWISE || Easiest || LOGIC || Complexity Analysis || C++
|
bitwise-easiest-logic-complexity-analysi-4z42
|
Solution\n\n\n#### LOGIC\n This is simpliy asking about Hamming distance\n Take XOR, because it will set bit to 1 only when both bits are different\n Then simpl
|
siddp6
|
NORMAL
|
2022-04-02T16:05:55.058269+00:00
|
2022-04-02T16:35:19.485186+00:00
| 342 | false |
## **Solution**\n\n\n#### **LOGIC**\n* This is simpliy asking about [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance)\n* Take [XOR](https://en.wikipedia.org/wiki/Exclusive_or), because it will set bit to 1 only when both bits are different\n* Then simply count the bits\n\n\n#### **Code** \n```cpp\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int a = start ^ goal;\n int sol = 0;\n \n while (a > 0) {\n sol += a & 1;\n a >>= 1;\n }\n \n return sol;\n }\n};\n```\n\n## **Complexity**\n\n##### __Apporach : 1__ \n##### Time Complexity: **O(floor(log10(n) + 1))**, where is ```n``` is ```max(start, goal)```.\n\n##### Space Complexity: **O(1)**\n\n\n<br>\n\n __Check out all [my](https://leetcode.com/siddp6/) recent solutions [here](https://github.com/sidd6p/LeetCode)__\n\n \n __Feel Free to Ask Doubts\nAnd Please Share Some Suggestions\nHAPPY CODING :)__\n\n\n
| 3 | 0 |
['Bit Manipulation', 'C']
| 3 |
minimum-bit-flips-to-convert-number
|
✅ 🌟 JAVA SOLUTION ||🔥 BEATS 100% PROOF🔥|| 💡 CONCISE CODE ✅ || 🧑💻 BEGINNER FRIENDLY
|
java-solution-beats-100-proof-concise-co-2z7h
|
Complexity
Time complexity:O(No.OfSetBit(startgoal))
Space complexity:O(1)
Code
|
Shyam_jee_
|
NORMAL
|
2025-03-09T18:17:38.801367+00:00
|
2025-03-09T18:17:38.801367+00:00
| 64 | false |
# Complexity
- Time complexity:$$O(No.OfSetBit(start^goal))$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:$$O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int minBitFlips(int start, int goal) {
int num=start^goal;
int cnt=0;
while(num>0)
{
cnt++;
num=num&(num-1);
}
return cnt;
}
}
```
| 2 | 0 |
['Bit Manipulation', 'Java']
| 0 |
minimum-bit-flips-to-convert-number
|
✅Effortless and Efficient Solution by Dhandapani✅|| 🔥🔥Beats 100% in Java🚀🚀
|
effortless-and-efficient-solution-by-dha-qbjw
|
🧠IntuitionTo find the minimum number of bit flips required to convert one integer to another, we can use a simple XOR operation. The XOR of two numbers will hav
|
Dhandapanimaruthasalam
|
NORMAL
|
2025-01-27T08:05:14.456744+00:00
|
2025-01-27T08:05:14.456744+00:00
| 82 | false |
# 🧠Intuition
To find the minimum number of bit flips required to convert one integer to another, we can use a simple XOR operation. The XOR of two numbers will have set bits (1s) in positions where the corresponding bits of the two numbers are different. Therefore, counting the number of set bits in the XOR result gives us the number of bit flips needed.
# 🔍Approach
1. Perform an XOR operation between the `start` and `goal` integers.
2. Count the number of set bits (1s) in the result of the XOR operation.
3. Each set bit represents a bit position where the `start` and `goal` differ, hence requires a flip.
# ⏳Complexity
- Time complexity: $$O(\log_{2}(n))$$, where `n` is the maximum value between `start` and `goal`. This complexity arises because we may need to examine each bit of the integers.
- Space complexity: $$O(1)$$, since we are only using a few variables for calculations and the memory usage doesn't scale with the input size.
# 📜Code(Java)
```java []
class Solution {
public int minBitFlips(int start, int goal) {
int ans = 0;
int xor = start ^ goal;
while(xor != 0) {
ans += xor & 1;
xor >>= 1;
}
return ans;
}
}
```
##### I hope this helps! Feel free to reach out if you need more assistance. Happy coding! 🚀✨
| 2 | 0 |
['Java']
| 0 |
minimum-bit-flips-to-convert-number
|
Easy solution || Beats 100%
|
easy-solution-beats-100-by-hriii11-ypdm
|
Intuition\n- XOR (^) gives us 0 if same digits and 1 if different \n- we can XOR the two no to know how many have to be switched\n- different positons will have
|
Hriii11
|
NORMAL
|
2024-11-07T04:24:23.941679+00:00
|
2024-11-07T04:24:23.941717+00:00
| 8 | false |
# Intuition\n- XOR (^) gives us 0 if same digits and 1 if different \n- we can XOR the two no to know how many have to be switched\n- different positons will have 1 so we will just count the no of 1s and return them\n\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int count = 0;\n int toggle= start^goal; // same zero different one\n // now count 1s to know how many were different aka will need flipping\n while(toggle){\n count += toggle & 1;\n toggle>>=1;\n }\n return count;\n }\n};\n```
| 2 | 0 |
['C++']
| 1 |
minimum-bit-flips-to-convert-number
|
❤️🔥 [EASY] APPROACH & EXPLANATION
|
easy-approach-explanation-by-ramitgangwa-j9yg
|
Intuition\nTo solve this problem, I thought about the nature of binary representation and how XOR can help us determine the differences between two integers. Wh
|
ramitgangwar
|
NORMAL
|
2024-10-05T10:31:25.537893+00:00
|
2024-10-05T10:31:25.537932+00:00
| 53 | false |
# Intuition\nTo solve this problem, I thought about the nature of binary representation and how XOR can help us determine the differences between two integers. When two bits are the same, the result of XOR is 0; when they differ, the result is 1. Therefore, by performing an XOR operation between the `start` and `goal`, I can identify the bits that need to be flipped.\n\n# Approach\n1. Calculate the XOR of the `start` and `goal` integers. This will give us a new integer where each bit represents whether the corresponding bits of the two integers are different.\n2. Count the number of 1s in the XOR result. Each 1 indicates a position where the bits differ, meaning a flip is required.\n3. Return the count of 1s, which represents the minimum number of bit flips needed.\n\n# Example\n* **Input**: \n```\nstart = 10, goal = 7\n```\n* **Output**: \n```\n3\n```\n* **Explanation**:\n - The binary representation of 10 is `1010`, and that of 7 is `0111`.\n - Perform XOR: 1010 \u2295 0111 = 1101\n - The XOR result is `1101`, indicating the differing bits.\n - The positions where the bits differ (1s in the XOR result) are:\n - 1st bit (from the right): 0 vs 1\n - 2nd bit: 1 vs 1 (same)\n - 3rd bit: 0 vs 1\n - 4th bit: 1 vs 0\n\n So, we need to flip the 1st, 3rd, and 4th bits, totaling 3 flips.\n\n\n# Complexity\n- Time complexity: $$O(k)$$, where $$k$$ is the number of bits in the integer representation (constant time for 32 bits in practice).\n \n- Space complexity: $$O(1)$$, since we are using a fixed amount of space regardless of the input size.\n\n# Code\n```java\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int xor = start ^ goal;\n\n int count = 0;\n while(xor > 0){\n count += xor & 1;\n xor = xor >> 1;\n }\n\n return count;\n }\n}\n```
| 2 | 0 |
['Bit Manipulation', 'Java']
| 0 |
minimum-bit-flips-to-convert-number
|
Flipping the Minimum Bits for Transformation!
|
flipping-the-minimum-bits-for-transforma-q52p
|
Intuition\n Describe your first thoughts on how to solve this problem. \n- To find the number of bit flips required to convert start to goal, we can compare the
|
ROHAN_SHETTY
|
NORMAL
|
2024-09-12T08:58:58.069666+00:00
|
2024-09-12T08:58:58.069706+00:00
| 6 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- To find the number of bit flips required to convert start to goal, we can compare the binary representation of the two numbers. The bit positions where the two numbers differ correspond to the bits that need to be flipped.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- XOR the start and goal numbers. The result will have 1s in the positions where the bits of start and goal differ, and 0s where they are the same.\n```\nint xorr = start ^ goal;\n\n```\n- Checking the Least Significant Bit: The expression (xorr & 1) checks the Least Significant Bit (LSB) of the xorr result: The bitwise AND operation (&) between xorr and 1 isolates the LSB.\nIf xorr & 1 equals 1, it means the LSB of xorr is 1, indicating a difference between the corresponding bits of start and goal. In this case, you increment the flip counter because that bit needs to be flipped.\n```\nflip += (xorr & 1);\n\n```\n- Shifting Right: After checking the LSB, you right shift xorr by one bit. This operation discards the current LSB and moves the next bit into the LSB position. This allows you to examine the next bit in the next iteration of the loop.\n```\nxorr >>= 1;\n\n```\n\n# Complexity\n- Time complexity:$$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int xorr = start ^ goal;\n int flip = 0;\n while(xorr > 0)\n {\n flip += (xorr & 1);\n xorr >>= 1;\n }\n return flip;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
minimum-bit-flips-to-convert-number
|
Beats 97.89%✅🔥| Python, C++💻| SUPER EASY, CLEAR Explanation📕
|
beats-9789-python-c-super-easy-clear-exp-nzpg
|
Beats 97.89%\u2705\uD83D\uDD25| Python, C++\uD83D\uDCBB| SUPER EASY, CLEAR Explanation\uD83D\uDCD5\n\n## 1. Proof (Python3)\n\n\n## 2. Algorithms\n* XOR\n\n## 3
|
kcp_1410
|
NORMAL
|
2024-09-12T02:07:41.532724+00:00
|
2024-09-12T02:07:41.532755+00:00
| 15 | false |
# Beats 97.89%\u2705\uD83D\uDD25| Python, C++\uD83D\uDCBB| SUPER EASY, CLEAR Explanation\uD83D\uDCD5\n\n## 1. Proof (Python3)\n\n\n## 2. Algorithms\n* XOR\n\n## 3. Code (with inline explanation)\n```python3 []\nclass Solution:\n def minBitFlips(self, start: int, goal: int) -> int:\n # XOR `start` and `goal` to get all `1`s in the columns where start[i] != goal[i]\n xor = bin(start ^ goal)\n # Count the `1`s (aka the differences that need to be flipped)\n return xor.count(\'1\')\n```\n\n## 4. Complexity\n\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\n### Upvote if you find this solution helpful, thank you \uD83E\uDD0D
| 2 | 0 |
['Bit Manipulation', 'Python', 'Python3']
| 0 |
minimum-bit-flips-to-convert-number
|
1 line fast c++ 100%
|
1-line-fast-c-100-by-amanraox-s4od
|
Approach\nPerform a bitwise XOR between start and goal. The result will have 1 in positions where the bits are different between the two numbers.\nCount the num
|
amanraox
|
NORMAL
|
2024-09-11T18:17:23.097728+00:00
|
2024-09-11T18:17:23.097782+00:00
| 4 | false |
# Approach\nPerform a bitwise XOR between start and goal. The result will have 1 in positions where the bits are different between the two numbers.\nCount the number of 1s in the XOR result using builtin popcount and return it.\n\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n return __builtin_popcount(start^goal);\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
minimum-bit-flips-to-convert-number
|
Beats 100%😎😎 || Easy To Understand || Explained Solution
|
beats-100-easy-to-understand-explained-s-e0qe
|
\n### Intuition\nThe problem asks us to find the minimum number of bit flips needed to convert one integer (start) into another (goal). The most intuitive appro
|
Yash_RajSingh
|
NORMAL
|
2024-09-11T17:42:02.378090+00:00
|
2024-09-11T17:42:02.378131+00:00
| 13 | false |
\n### Intuition\nThe problem asks us to find the minimum number of bit flips needed to convert one integer (`start`) into another (`goal`). The most intuitive approach is to compare the binary representations of both numbers bit by bit and count the differences. A difference between corresponding bits indicates a necessary flip.\n\n### Approach\n1. **Binary Conversion**: First, convert both `start` and `goal` into their binary forms.\n2. **Equalize Lengths**: To easily compare the binary forms, ensure both vectors are of equal length by padding the shorter one with leading zeros.\n3. **Count Flips**: Traverse both binary vectors, and for each differing bit, increment the flip count.\n4. **Return Result**: The count represents the minimum number of flips needed.\n\n### Complexity\n- **Time Complexity**: \n - The time complexity is $$O(\\log \\max(\\text{start}, \\text{goal}))$$ due to converting numbers to binary and comparing bit-by-bit.\n \n- **Space Complexity**: \n - The space complexity is $$O(\\log \\max(\\text{start}, \\text{goal}))$$ because of the storage of binary vectors.\n\n\n\n\n\n### Code\n```cpp\nclass Solution {\npublic:\n // Function to convert a number to its binary representation\n vector<int> solve(int temp) {\n vector<int> bin;\n while (temp != 0) {\n bin.push_back(temp % 2); // Get the remainder when divided by 2 (binary digit)\n temp = temp / 2; // Divide by 2 for the next bit\n }\n reverse(bin.begin(), bin.end()); // Reverse to get the correct order\n return bin;\n }\n\n // Function to find the minimum bit flips needed to convert start to goal\n int minBitFlips(int start, int goal) {\n vector<int> s = solve(start); // Binary representation of start\n vector<int> g = solve(goal); // Binary representation of goal\n\n int m = s.size(); // Size of start\'s binary representation\n int n = g.size(); // Size of goal\'s binary representation\n\n // Equalize the length of both binary vectors by padding with zeros\n if (m > n) {\n int extraBit = m - n;\n for (int i = 0; i < extraBit; i++) {\n g.push_back(0); // Add zeros to goal\n }\n reverse(g.begin(), g.end());\n reverse(g.begin() + extraBit, g.end());\n } else {\n int extraBit = n - m;\n for (int i = 0; i < extraBit; i++) {\n s.push_back(0); // Add zeros to start\n }\n reverse(s.begin(), s.end());\n reverse(s.begin() + extraBit, s.end());\n }\n\n // Count the number of differing bits\n int count = 0;\n for (int i = 0; i < s.size(); i++) {\n if (s[i] ^ g[i]) { // XOR to check if bits are different\n count++;\n }\n }\n\n return count; // Return the number of flips needed\n }\n};\n```\n\n---\n\n
| 2 | 0 |
['Bit Manipulation', 'C++']
| 1 |
minimum-bit-flips-to-convert-number
|
✅🔥BEATS 100.00% || ALL LANGUAGES || BEGINNER FRIENDLY 🔥✅
|
beats-10000-all-languages-beginner-frien-cwxt
|
Intuition\n Describe your first thoughts on how to solve this problem. \n- To convert one number into another, we need to focus on the positions where the two n
|
surajdivekarsd27
|
NORMAL
|
2024-09-11T15:26:48.096692+00:00
|
2024-09-11T15:26:48.096716+00:00
| 15 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- To convert one number into another, we need to focus on the positions where the two numbers have different bits. Each bit represents either a 0 or a 1, and if the bits at the same position in both numbers are different, we need to "flip" that bit to make the numbers match.\n\n- Imagine two numbers as sequences of binary digits (0s and 1s). By comparing them digit by digit, whenever we find a mismatch, it means a flip is required to make the numbers identical. We count how many times this happens.\n\n- To do this efficiently, instead of checking every bit manually, we use a clever way to identify and count only the differing bits, then "turn off" those bits one by one until none remain. This allows us to quickly determine the exact number of bit flips needed.\n\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Calculate xor = start ^ goal to identify which bits differ.\n2. Count the number of 1s in the result (since each 1 represents a differing bit).\n2. To count the number of 1s, repeatedly perform the operation xor = xor & (xor - 1) until xor becomes 0. This operation clears the least significant set bit, which allows us to count the number of set bits in xor.\n\n# Complexity\n- Time complexity: O(k) => where k is the number of set bits in xor. In the worst case, it could be O(32) since the number of bits in an integer is limited to 32.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1) => as no extra space other than a few variables is used.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n```java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int xor = start ^ goal;\n int count = 0;\n while(xor>0){\n xor = xor & (xor-1);\n count++;\n }\n return count;\n }\n}\n```\n```c++ []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int xorVal = start ^ goal;\n int count = 0;\n while (xorVal > 0) {\n xorVal = xorVal & (xorVal - 1);\n count++;\n }\n return count;\n }\n};\n\n```\n```python []\nclass Solution:\n def minBitFlips(self, start: int, goal: int) -> int:\n xor = start ^ goal\n count = 0\n while xor > 0:\n xor = xor & (xor - 1)\n count += 1\n return count\n\n```\n```javascipt []\nvar minBitFlips = function(start, goal) {\n let xor = start ^ goal;\n let count = 0;\n while (xor > 0) {\n xor = xor & (xor - 1);\n count++;\n }\n return count;\n};\n\n\n```\n
| 2 | 0 |
['Bit Manipulation', 'C++', 'Java', 'Python3', 'JavaScript']
| 0 |
minimum-bit-flips-to-convert-number
|
simplest || common sense || 4 languages
|
simplest-common-sense-4-languages-by-pra-yu7z
|
Intuition\n Describe your first thoughts on how to solve this problem. \nTo find the minimum number of bits needed to make two numbers equal, we can compare the
|
prajwal_nimbalkar
|
NORMAL
|
2024-09-11T13:37:51.445076+00:00
|
2024-09-11T13:37:51.445100+00:00
| 73 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo find the minimum number of bits needed to make two numbers equal, we can compare their corresponding bits. For example, if the goal is 111011 and the start is 001011, we can see that the last four bits are already identical. Therefore, we only need to modify the bits that differ between the two numbers.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirst, perform a bitwise XOR operation between the start and target numbers. The resulting value will have 1s in positions where the corresponding bits differ between the two numbers\n\nNext, count the number of 1s in the XOR result. This count represents the number of positions where the bits differ, which is equivalent to the number of required bit flips.\n\nTo count the 1s, use a loop to repeatedly check the least significant bit of the XOR result using a bitwise AND with 1. After checking the least significant bit, right-shift the XOR result by 1 to process the next bit. Continue this process until all bits have been examined.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int cnt=0;\n int temp=start ^ goal;\n while(temp){\n cnt=cnt+(temp & 1);\n temp=temp>>1;\n }\n\n return cnt;\n }\n};\n\n```\n```python []\nclass Solution:\n def minBitFlips(self, start, goal):\n """\n Calculates the minimum number of bit flips required to convert\n the integer `start` into the integer `goal`.\n\n Args:\n start: The starting integer.\n goal: The target integer.\n\n Returns:\n The minimum number of bit flips needed.\n """\n\n xor_result = start ^ goal\n count = 0\n\n while xor_result != 0:\n count += xor_result & 1\n xor_result >>= 1\n\n return count\n\n```\n```java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int xorResult = start ^ goal;\n int count = 0;\n\n while (xorResult != 0) {\n count += xorResult & 1;\n xorResult >>= 1;\n }\n\n return count;\n }\n}\n```\n```C []\nint minBitFlips(int start, int goal) {\n int cnt=0;\n int temp=start ^ goal;\n while(temp){\n cnt=cnt+(temp & 1);\n temp=temp>>1;\n }\n\n return cnt;\n}\n```
| 2 | 0 |
['Math', 'Bit Manipulation', 'C', 'Python', 'C++', 'Java']
| 0 |
minimum-bit-flips-to-convert-number
|
🔥Beats 100%🔥 || ✅2 SOLUTION✅ || WITH BITCOUNT METHOD & WITHOUT✅
|
beats-100-2-solution-with-bitcount-metho-wp2l
|
\n# Code\njava []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n return Integer.bitCount(start^goal);\n }\n}\n\n\n# Code\n```j
|
717822f143
|
NORMAL
|
2024-09-11T09:12:49.555746+00:00
|
2024-09-11T09:12:49.555766+00:00
| 37 | false |
\n# Code\n```java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n return Integer.bitCount(start^goal);\n }\n}\n\n```\n# Code\n```java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int a=start^goal,c=0;\n while(a>0){\n if(a%2==1){\n c++;\n }\n a>>=1;\n }\n return c;\n }\n}\n\n
| 2 | 0 |
['Java']
| 0 |
minimum-bit-flips-to-convert-number
|
Solution By Dare2Solve | Detailed Explanation | Clean Code
|
solution-by-dare2solve-detailed-explanat-b5jo
|
Explanation []\nauthorslog.com/blog/TtRI8mE2NY\n\n# Code\n\ncpp []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int num = sta
|
Dare2Solve
|
NORMAL
|
2024-09-11T08:31:43.879821+00:00
|
2024-09-11T17:24:24.767541+00:00
| 21 | false |
```Explanation []\nauthorslog.com/blog/TtRI8mE2NY\n```\n# Code\n\n```cpp []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int num = start ^ goal; // XOR to find differing bits\n return countSetBits(num);\n }\n\nprivate:\n int countSetBits(int num) {\n int count = 0;\n while (num != 0) {\n num = num & (num - 1); // Clear the least significant set bit\n count++;\n }\n return count;\n }\n};\n```\n\n```python []\nclass Solution:\n def minBitFlips(self, start: int, goal: int) -> int:\n num = start ^ goal # XOR to find differing bits\n return self.countSetBits(num)\n\n def countSetBits(self, num: int) -> int:\n count = 0\n while num != 0:\n num = num & (num - 1) # Clear the least significant set bit\n count += 1\n return count\n```\n\n```java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int num = start ^ goal; // XOR to find differing bits\n return countSetBits(num);\n }\n\n private int countSetBits(int num) {\n int count = 0;\n while (num != 0) {\n num = num & (num - 1); // Clear the least significant set bit\n count++;\n }\n return count;\n }\n}\n```\n\n```javascript []\nvar minBitFlips = function (start, goal) {\n let num = start ^ (goal);\n return countSetBits(num);\n}\nvar countSetBits = (num) => {\n\n let count = 0;\n while (num != 0) {\n num = num & num - 1;\n count++;\n }\n return count;\n}\n```
| 2 | 0 |
['Bit Manipulation', 'Python', 'C++', 'Java', 'Python3', 'JavaScript']
| 0 |
minimum-bit-flips-to-convert-number
|
"Efficient Bitwise Approach to Minimum Bit Flips Calculation"
|
efficient-bitwise-approach-to-minimum-bi-nt2f
|
Intuition\nTo solve the problem of finding the minimum number of bit flips required to convert one integer (start) to another integer (goal), the key observatio
|
muthupalani
|
NORMAL
|
2024-09-11T08:12:49.664892+00:00
|
2024-09-11T08:12:49.664930+00:00
| 14 | false |
**Intuition**\nTo solve the problem of finding the minimum number of bit flips required to convert one integer (start) to another integer (goal), the key observation is that a bit flip is needed whenever the corresponding bits in start and goal differ. By examining the binary representation of both integers, you can determine which bits need to be flipped to achieve the conversion.\n\n**Approach**\nBitwise Comparison: Use bitwise operations to compare the bits of start and goal. Specifically, check if the least significant bit (rightmost bit) of start is different from that of goal.\nCount Flips: If the bits are different, increment the count of flips required.\n\nShift Right: Move to the next bit by shifting start and goal right by one position (dividing by 2).\n\nRepeat: Continue this process until both start and goal are reduced to 0. At this point, all necessary bit flips have been counted.\n\nThe approach leverages the fact that bitwise operations are efficient, and shifting right effectively reduces the size of the integers, so the solution operates in constant time with respect to the number of bits.\n\n**Complexity**\nTime complexity: \nO(log(max(start,goal)))\n\nThis is because the number of bits to process is proportional to the logarithm of the larger of the two numbers.\n\nSpace complexity: \nO(1)\nThe algorithm uses a constant amount of extra space regardless of the input size.\n\n# Code\n```java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int count=0;\n while(start>0 || goal>0){\n if(((start&1) ^ (goal&1))==1){\n count+=1;\n }\n start=start>>1;\n goal=goal>>1;\n }return count;\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
minimum-bit-flips-to-convert-number
|
Easy solution to code and understand fast
|
easy-solution-to-code-and-understand-fas-jsab
|
Intuition\n Describe your first thoughts on how to solve this problem. \nusing some logical operator\n\n# Approach\n Describe your approach to solving the probl
|
KARTHICK2605
|
NORMAL
|
2024-09-11T07:51:20.029066+00:00
|
2024-09-11T07:51:20.029090+00:00
| 64 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nusing some logical operator\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nuse xor and make count buy reducing the bit by and\n# Complexity\n- Time complexity:0ms\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:40mb\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int count=0;\n int bit=start^goal;\n while(bit!=0){\n bit&=(bit-1);\n count++;\n }return count;\n }\n}\n```
| 2 | 0 |
['Bit Manipulation', 'Java']
| 1 |
minimum-bit-flips-to-convert-number
|
Minimum Bit Flips to Convert Start to Goal
|
minimum-bit-flips-to-convert-start-to-go-e4d5
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem involves determining the number of bit flips required to convert one intege
|
Suryanshrajs
|
NORMAL
|
2024-09-11T07:38:33.484329+00:00
|
2024-09-11T07:38:33.484353+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem involves determining the number of bit flips required to convert one integer into another. To find this, we can leverage XOR. The XOR operation between two numbers will give a result where the bits are 1 wherever the two numbers differ. The problem then reduces to counting the number of 1s in the result.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Perform an XOR between start and goal. This will give a number (val) that has 1s in positions where the bits of start and goal are different.\n2. To count how many bits differ (i.e., how many flips are needed), we use the function countSetBits which counts the number of 1s in the binary representation of a number. This is done using the operation x = x & (x - 1) which removes the lowest set bit from x until x becomes 0.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity for counting the set bits is proportional to the number of set bits in val, which in the worst case can be the number of bits in an integer (typically O(log N) where N is the value of the number in binary representation).\nTherefore, the overall time complexity is: O(logn)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is constant because we only use a few variables.\nTherefore, the overall space complexity is: O(1)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int countSetBits(int x) {\n int setBits = 0;\n while (x != 0) {\n x = x & (x - 1);\n setBits++;\n }\n\n return setBits;\n }\n int minBitFlips(int start, int goal) {\n \n int val = start ^ goal;\n cout << val;\n\nreturn countSetBits(val);\n\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
minimum-bit-flips-to-convert-number
|
Using right shift operator
|
using-right-shift-operator-by-piratehunt-olyo
|
Code\ncpp []\nclass Solution {\npublic:\n int minBitFlips(int A, int B) {\n int C=A^B;\n int ans=0;\n while(C)\n { \n
|
piratehunter
|
NORMAL
|
2024-09-11T06:46:16.743807+00:00
|
2024-09-11T06:46:16.743836+00:00
| 57 | false |
# Code\n```cpp []\nclass Solution {\npublic:\n int minBitFlips(int A, int B) {\n int C=A^B;\n int ans=0;\n while(C)\n { \n if(C&1)\n ans++;\n C = C >> 1;\n }\n return ans;\n }\n};\n```
| 2 | 0 |
['Bit Manipulation', 'C++']
| 2 |
minimum-bit-flips-to-convert-number
|
Simple Easy "%" Approach - Beats 95% - Time O(n) Space O(1)
|
simple-easy-approach-beats-95-time-on-sp-i4zv
|
Intuition\nWe can use the % operator to extract the bits of a number from right to left (from the least significant bit to the most significant oane). \n\nExamp
|
bogdanctdev
|
NORMAL
|
2024-09-11T06:25:03.793893+00:00
|
2024-09-11T06:25:03.793939+00:00
| 141 | false |
# Intuition\nWe can use the `%` operator to extract the bits of a number from right to left (from the least significant bit to the most significant oane). \n\nExample:\n- `10` in binary is `1010`. Using `% 2` iteratively on `10` gives the bits `0101` (starting from the least significant bit);\n- `7` in binary is `111` (or `0111` to match the bit count with `10`). Using `% 2` four times on `7` gives `1110`.\n\n**Note**: To iterate through all bits of a number, divide the number by `2` repeatedly until it becomes `0`.\n\n# Approach\nIn order to find the minimum number of bit flips required to convert the binary representation of `start` into `goal`, we can compare the least significant bits of `start` and `goal` and increments the flip count if they differ.\nWe divide by 2 both `start` and `goal` until both are 0.\n\n# Complexity\n- Time complexity:\n**O(n)** where n is the number of bits of the biggest number between "$$start$$" and "$$goal$$";\n\n- Space complexity:\n**O(1)**, no extra data structures were used;\n\n# Results\n\n\n# Code\n```csharp []\npublic class Solution {\n public int MinBitFlips(int start, int goal) {\n int flips = 0;\n\n while (!(start == 0) || !(goal == 0))\n {\n if ((start %2) != (goal % 2))\n flips++;\n\n start /= 2;\n goal /= 2; \n }\n\n return flips;\n }\n}\n```
| 2 | 0 |
['Bit Manipulation', 'C#']
| 0 |
minimum-bit-flips-to-convert-number
|
XOR operation (Playing with bits) explained about XOR operation!! with Dry run 💯✅
|
xor-operation-playing-with-bits-explaine-gbd4
|
Understanding XOR operation\n- If both the bits are same results in 0, otherwise 1.\n\n\n# Approach\n Describe your approach to solving the problem. \n - Perfor
|
PavanKumarMeesala
|
NORMAL
|
2024-09-11T06:20:19.612226+00:00
|
2024-09-11T06:20:19.612258+00:00
| 5 | false |
# Understanding XOR operation\n- If both the bits are same results in 0, otherwise 1.\n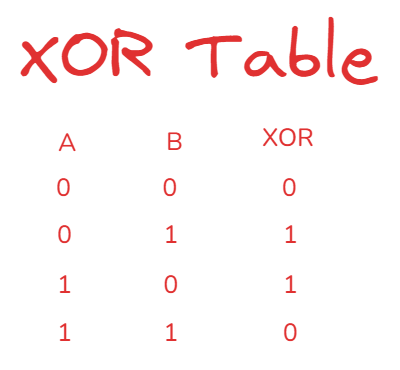\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n - Perform the XOR operation between `start and goal`.\n - Count the set bits in the XOR result.\n - Return the count.\n\n\n\n# Dry run\n### Example:\n- `start = 10` (binary: `1010`)\n- `goal = 7` (binary: `0111`)\n\nThe steps are as follows:\n\n### Initial Setup:\n- `start = 10 (1010)`\n- `goal = 7 (0111)`\n- `counter = 0`\n\n### Step 1: XOR Operation\nPerform `start ^ goal`:\n\n- `1010 ^ 0111 = 1101` (This will be our `XOR` result)\n\nThe XOR operation results in `1101` because XOR returns `1` for different bits and `0` for the same bits. Now, we need to count the number of `1`s in this XOR result, as each `1` indicates a bit flip is required.\n\n### Step 2: Counting Set Bits (Flips)\nWe initialize `counter = 0` and process the XOR result:\n\n- `XOR = 1101` (decimal 13)\n\n1. Check if the least significant bit (LSB) is `1`: \n - `1101 & 1 = 1`, so increment `counter`: \n - `counter = 1`\n - Right shift `XOR`: \n - `XOR >>= 1` \u2192 `XOR = 110 (decimal 6)`\n \n2. Check the new LSB: \n - `110 & 1 = 0`, no increment. \n - Right shift `XOR`: \n - `XOR >>= 1` \u2192 `XOR = 11 (decimal 3)`\n\n3. Check the new LSB: \n - `11 & 1 = 1`, increment `counter`: \n - `counter = 2`\n - Right shift `XOR`: \n - `XOR >>= 1` \u2192 `XOR = 1 (decimal 1)`\n\n4. Check the new LSB: \n - `1 & 1 = 1`, increment `counter`: \n - `counter = 3`\n - Right shift `XOR`: \n - `XOR >>= 1` \u2192 `XOR = 0` (stop)\n\n### Step 3: Final Counter\n- The XOR result has `3` set bits, so `counter = 3`.\n\n### Conclusion:\nThe function returns `3`, which means 3 bit flips are needed to transform `start = 10` to `goal = 7`.\n# Complexity\n- Time complexity: XOR Operation will take O(`1`) and While counting the set bits in XOR will take O(`log N`), hence O(`log N`) is our time complexity.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(`1`) not using any extra space.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int counter = 0;\n\n int XOR = start ^ goal;\n\n while(XOR > 0)\n {\n counter += (XOR & 1);\n XOR >>= 1;\n }\n\n return counter;\n }\n}\n```\n\n\n
| 2 | 0 |
['Math', 'Bit Manipulation', 'Java']
| 0 |
minimum-bit-flips-to-convert-number
|
One Line code with Explanation
|
one-line-code-with-explanation-by-psriji-a8q8
|
Explanation \n Describe your first thoughts on how to solve this problem. \n For start = 10 and goal = 7:\n 10 in binary is 1010\n 7 in binary is 0111\
|
psrijith
|
NORMAL
|
2024-09-11T06:05:04.398742+00:00
|
2024-09-11T06:05:04.398774+00:00
| 29 | false |
# Explanation \n<!-- Describe your first thoughts on how to solve this problem. -->\n For start = 10 and goal = 7:\n 10 in binary is 1010\n 7 in binary is 0111\n 10 ^ 7 gives 1101\n The binary 1101 contains three 1s, \n so the number of bit flips required is 3.\n\n# Code\n```python3 []\nclass Solution:\n def minBitFlips(self, s: int, g: int) -> int:\n return (bin(s^g)).count(\'1\')\n```
| 2 | 0 |
['Python3']
| 0 |
minimum-bit-flips-to-convert-number
|
Minimum Bit Flips to Convert Integer - Efficient Bitwise Solution
|
minimum-bit-flips-to-convert-integer-eff-gkm1
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem asks us to determine how many bit flips are needed to convert one integer (
|
namratha2604
|
NORMAL
|
2024-09-11T05:51:16.314040+00:00
|
2024-09-11T05:51:16.314073+00:00
| 15 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem asks us to determine how many bit flips are needed to convert one integer (start) into another (goal). My intuition is that this problem can be solved by comparing the binary representations of both numbers and counting the positions where the bits differ.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nConvert both integers start and goal into 32-bit binary representations.\nCompare the two bitsets bit by bit, counting how many positions differ.\nThe total number of differing bits will be the minimum number of bit flips required.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nTime complexity:\n1. The time complexity is \uD835\uDC42(1)\n2. \uD835\uDC42(1) because we are always comparing 32 bits, regardless of the input values.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n1. The space complexity is \uD835\uDC42(1)\n\n2. \uD835\uDC42(1) as we are only using a fixed amount of extra space (two bitsets of size 32 and a counter).\n\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n bitset<32> b1(start);\n bitset<32> b2(goal);\n int c = 0;\n for(int i=31;i>=0;i--){\n if(b1[i]!=b2[i]) c++;\n }\n return c;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
minimum-bit-flips-to-convert-number
|
Straight forward C++ solution | Beats 100%🚀
|
straight-forward-c-solution-beats-100-by-ojko
|
\n# Approach\nLet\'s consider start to be 10 and end to be 7\nbinary representation of these two \n1 0 1 0\n0 1 1 1\nwe have to check number of bits not matchin
|
ChinmayaRao
|
NORMAL
|
2024-09-11T05:30:45.380805+00:00
|
2024-09-11T05:30:45.380843+00:00
| 31 | false |
\n# Approach\nLet\'s consider start to be 10 and end to be 7\nbinary representation of these two \n1 0 1 0\n0 1 1 1\nwe have to check number of bits not matching.\n(XOR approach) if bits are different result is 1. Else result is 0.\nwe have to compare the leftmost bits.\nif the bits are different then we have to flip it.\nso xor can say if the bits are different.\n\nNote:\nDon\'t directly xor start and end. Because we have to compare only leftmost bits. \nSo start&1 ^ end&1.\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int res = 0;\n while(start > 0 || goal > 0)\n {\n res += ((start&1 )^ (goal&1));\n start >>= 1;\n goal >>= 1;\n \n }\n return res;\n }\n};\n```
| 2 | 0 |
['Bit Manipulation', 'C++']
| 0 |
minimum-bit-flips-to-convert-number
|
Best way of approach in java using XOR operation ~cksolutions.. (O(1))
|
best-way-of-approach-in-java-using-xor-o-r1a8
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nOne of yhe best approa
|
kandiah_01
|
NORMAL
|
2024-09-11T05:00:05.000479+00:00
|
2024-09-11T05:00:05.000507+00:00
| 76 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nOne of yhe best approach is to use *XOR OPERATION* \n#Remember XOR operation#\nRule-1: 1 ^ 0 = 1 or 0 ^ 1 = 1\nRule-2: 0 ^ 0 = 0 or 1 ^ 1 = 0\n\nFirst step is to do xor for the *start* and *goal* \nThen, you count the number of bits are \'1\' ,\nHer is your answer.\n\n**PLEASE UPVOTE**\n# Complexity\n- Time complexity:O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n String ad=String.valueOf(start^goal);\n int a=(start^goal);\n int c=0;\n String ans=Integer.toBinaryString(a);\n System.out.println(ans);\n for(int i=0;i<ans.length();i++){\n if(ans.charAt(i)!=\'0\') c+=1;\n }\n return c;\n }\n}\n```
| 2 | 0 |
['Bit Manipulation', 'Java']
| 1 |
minimum-bit-flips-to-convert-number
|
🔥✅💯1 Line Most Easy Solution With Detailed Explanation💯✅🔥
|
1-line-most-easy-solution-with-detailed-tgwv7
|
Intuition\nThe problem is asking for the minimum number of bit flips required to convert one number (start) into another number (goal). A bit flip means changin
|
Ajay_Kartheek
|
NORMAL
|
2024-09-11T04:22:22.839062+00:00
|
2024-09-11T04:22:22.839097+00:00
| 23 | false |
# Intuition\nThe problem is asking for the minimum number of bit flips required to convert one number (start) into another number (goal). A bit flip means changing a 0 to 1 or a 1 to 0.\n\nTo solve this, we can use the XOR operation. XOR (^ operator in Python) will give a 1 wherever the bits of start and goal differ, and a 0 where they are the same.\n\n# Approach\n1. XOR Operation:\n\n - Perform the XOR operation between start and goal. This will result in a number where each bit is 1 if the corresponding bits in start and goal are different, and 0 if they are the same.\n2. Counting Bit Differences:\n \n - To find the number of differing bits, convert the result of the XOR operation to its binary representation and count the number of 1s. Each 1 in the result corresponds to a bit that differs between start and goal, which is exactly where a bit flip is needed.\n \n3. Return the Result:\n\n - The number of bit flips required will be the count of 1s in the binary representation of the XOR result.\n\n# Complexity\n- Time complexity:\n O(b)\n\n- Space complexity:\nO(1)\n\n# Code\n```python3 []\nclass Solution:\n def minBitFlips(self, start: int, goal: int) -> int:\n return bin(start^goal).count("1")\n```\n```Java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n // XOR start and goal to find differing bits, then count the number of 1\'s\n return Integer.bitCount(start ^ goal);\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n // XOR start and goal, then use __builtin_popcount to count the number of 1\'s\n return __builtin_popcount(start ^ goal);\n }\n};\n\n```
| 2 | 0 |
['Bit Manipulation', 'C++', 'Java', 'Python3']
| 0 |
minimum-bit-flips-to-convert-number
|
Beginner-to-Advanced Solution with explanation CPP
|
beginner-to-advanced-solution-with-expla-nzth
|
Intuition\nThe problem asks for the minimum number of bit flips required to convert one integer (start) to another (goal). To solve this, we can leverage the bi
|
jaydeep-pro
|
NORMAL
|
2024-09-11T04:11:33.072548+00:00
|
2024-09-11T04:11:33.072578+00:00
| 21 | false |
# Intuition\nThe problem asks for the minimum number of bit flips required to convert one integer (start) to another (goal). To solve this, we can leverage the binary representations of both numbers. By comparing the binary digits of start and goal, we can determine how many positions differ, and each difference corresponds to a required bit flip.\n\n# Approach\nConvert both integers to binary strings: We\'ll first create a helper function that converts an integer to its binary string representation.\nEqualize the lengths of the binary strings: Since the lengths of the binary representations of start and goal may differ, we pad the shorter string with leading zeroes so that both strings have the same length.\nCount differing bits: Compare the two binary strings bit by bit. For each position where the bits differ, we increment a counter, as each difference requires a bit flip.\nReturn the count of differing bits: This count will represent the minimum number of bit flips needed.\n\n# Complexity\n# Time complexity:\nThe time complexity of converting a number to a binary string is proportional to the number of bits in the number, which is O(log n) where n is the value of the number. Comparing the two binary strings takes O(m), where m is the length of the binary strings (which is log(max(start, goal))).\nTherefore, the overall time complexity is O(log(max(start, goal))).\n\n# Space complexity:\nThe space complexity is also O(log(max(start, goal))) due to the space used to store the binary string representations of the numbers.\n# Code\n```cpp []\nclass Solution {\npublic:\n string numberToBitsString(int n) {\n string ans = "";\n while (n > 0) {\n if (n % 2 == 0) {\n ans += "0";\n } else {\n ans += "1";\n }\n n = n / 2;\n }\n\n if (ans == "")\n ans = "0";\n\n reverse(ans.begin(), ans.end());\n\n return ans;\n }\n int minBitFlips(int start, int goal) {\n string startBits = numberToBitsString(start);\n string goalBits = numberToBitsString(goal);\n\n // Make the lengths of the two strings equal by padding with leading\n // zeroes\n int maxLength = max(startBits.length(), goalBits.length());\n while (startBits.length() < maxLength)\n startBits = "0" + startBits;\n while (goalBits.length() < maxLength)\n goalBits = "0" + goalBits;\n\n // Count the number of differing bits\n int flips = 0;\n for (int i = 0; i < maxLength; i++) {\n if (startBits[i] != goalBits[i]) {\n flips++;\n }\n }\n\n return flips;\n // this returns minimum bit flips\n }\n};\n```\n\n\n\n\n\n\n\n\n# Advanced Approach\n\n\n\n\n# Intuition\nThe minimum number of bit flips required to convert start to goal can be determined by analyzing which bits differ between the two numbers. The XOR (^) operation directly reveals the differing bits. If a bit is different between start and goal, the result of XOR will have a 1 at that position. Counting the number of 1s in the result gives the number of bit flips required.\n\n# Approach\nXOR operation:\nPerform the XOR operation on start and goal. The result of this operation will have 1s in positions where start and goal differ, and 0s where the bits are the same.\nCount set bits:\nAfter XOR, we count the number of 1s in the result (i.e., the number of differing bits). This can be done by checking the least significant bit of the result and shifting right bit by bit.\nReturn the count of differing bits: The total number of 1s in the XOR result is the number of flips required to convert start to goal.\n\n# Complexity\n- Time complexity:\nThe time complexity of this approach is O(1), as we\'re working with a fixed number of bits (typically 32 or 64 bits depending on the system). The number of operations is proportional to the number of bits in the integer representation of start and goal.\n\n- Space complexity:\nThe space complexity is O(1), as no additional space beyond a few variables is used.\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) { \n \n int xorFlips = start ^ goal;\n int flips =0;\n \n while(xorFlips){\n flips += xorFlips & 1;\n\n xorFlips = xorFlips >> 1;\n }\n return flips;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
minimum-bit-flips-to-convert-number
|
Easy ✅, VERY Easy❎ || Beats 100%🚀
|
easy-very-easy-beats-100-by-ayushiivarsh-1s3s
|
\n# Code\njava []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n //checking how many bits has been flipped\n int xor = sta
|
AyushiiVarshney
|
NORMAL
|
2024-09-11T04:08:15.164387+00:00
|
2024-09-11T04:08:15.164417+00:00
| 29 | false |
\n# Code\n```java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n //checking how many bits has been flipped\n int xor = start ^ goal;\n \n // to count the no. of changed bits\n int count = 0;\n \n while (xor != 0) {\n // Increment count for each 1-bit\n count += xor & 1;\n // Right shift to check the next bit\n xor >>= 1;\n }\n return count;\n }\n}\n```
| 2 | 0 |
['Bit Manipulation', 'Java']
| 1 |
minimum-bit-flips-to-convert-number
|
💡🔥💥 Easy Python Solution Without Bit Manipulation 💥🔥💡
|
easy-python-solution-without-bit-manipul-i5fj
|
Approach\n Describe your approach to solving the problem. \n1. Convert to Binary Representation:\n\nConvert both start and goal to their binary representations
|
eknath_mali_002
|
NORMAL
|
2024-09-11T03:58:43.463397+00:00
|
2024-09-11T03:58:43.463427+00:00
| 28 | false |
# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Convert to Binary Representation:**\n\nConvert both start and goal to their binary representations using the bin() function.\nRemove the `\'0b\'` prefix that Python includes in the output of bin() by slicing the string [2:].\n2. **Pad the Shorter Binary String:**\n\nTo compare the binary representations bit-by-bit, make sure both binary strings have the same length.\nIf start is shorter than goal, prepend leading zeros to start until both are of equal length, and vice versa.\n3. **Count the Number of Different Bits:**\n\nUse a loop to compare each bit in the binary representations of start and goal.\nIf a bit `differs`, `increment a counter (ans)`to keep track of the required number of flips.\n4. **Return the Total Count:**\n\nThe counter ans will represent the minimum number of bit flips required to convert start to goal.\n# Complexity\n- Time complexity:$$O(log n)$$\n - where `n` is the larger of the two numbers, start or goal.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(log n)$$\n - where `n` is the larger of the two numbers, start or goal.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def minBitFlips(self, start: int, goal: int) -> int:\n start_bin, goal_bin = bin(start)[2:], bin(goal)[2:]\n if len(start_bin) < len(goal_bin):\n start_bin = "0"* (len(goal_bin) - len(start_bin)) + start_bin\n if len(goal_bin) < len(start_bin):\n goal_bin = "0"* (len(start_bin) - len(goal_bin)) + goal_bin\n ans = 0\n print(f"start {start_bin} end {goal_bin}")\n for s, g in zip(start_bin, goal_bin):\n if s != g:\n ans += 1\n return ans\n\n# With Bit Manipulation .. Optimized version\n # def minBitFlips(self, start: int, goal: int) -> int:\n # # XOR of same no is 0 else 1\n # xor = start ^ goal\n # ans = 0\n # while xor:\n # ans += xor&1 # taking last bit if 1 then +1 else +0\n # xor >>= 1\n # return ans\n```
| 2 | 0 |
['Bit Manipulation', 'Python3']
| 0 |
minimum-bit-flips-to-convert-number
|
𝑂(log 𝑛) | 0ms Beats 100.00% | Easy Solution
|
olog-n-0ms-beats-10000-easy-solution-by-a5a98
|
\n\n---\n# Intuition\nTo convert the binary representation of start to goal, we need to count the number of bit positions where the two numbers differ. This is
|
user4612MW
|
NORMAL
|
2024-09-11T03:08:15.322095+00:00
|
2024-09-11T03:16:19.179325+00:00
| 17 | false |
#\n\n---\n# Intuition\nTo convert the binary representation of start to goal, we need to count the number of bit positions where the two numbers differ. This is equivalent to counting the number of 1\'s in the XOR of start and goal, as XOR highlights the differing bits (1 for different, 0 for the same).\n\n# Approach\nThe solution involves XORing start and goal, and then counting the number of 1\'s in the result. This can be done efficiently by checking each bit using the & operator and shifting the XOR result to the right until all bits are processed.\n\n# Complexity\n- **Time complexity** $$\uD835\uDC42(log \uD835\uDC5B)$$ where n is the maximum value of start or goal. We process each bit of the XOR result.\n- **Space complexity** $$\uD835\uDC42(1)$$, since we only use a few variables.\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minBitFlips(int start, int goal) {\n int count{0};\n for (int x = start ^ goal; x; x >>= 1) count += x & 1;\n return count;\n }\n};\n\n```\n```java []\nclass Solution {\n public int minBitFlips(int start, int goal) {\n int count = 0;\n for (int x = start ^ goal; x != 0; x >>= 1) {\n count += x & 1;\n }\n return count;\n }\n}\n```\n```python []\nclass Solution:\n def minBitFlips(self, start: int, goal: int) -> int:\n count = 0\n x = start ^ goal\n while x:\n count += x & 1\n x >>= 1\n return count\n```\n\n---\n- \n\n---
| 2 | 0 |
['C++', 'Java', 'Python3']
| 0 |
apply-operations-to-make-all-array-elements-equal-to-zero
|
[Java/C++/Python] Greedy + Sliding Window
|
javacpython-greedy-sliding-window-by-lee-jshg
|
Intuition\nFor the first A[i] > 0,\nwe need to select the array A[i],A[i+1]..A[i+k-1]\nand decrease all these elements by A[i].\n\n\n# Explanation\nThe subarray
|
lee215
|
NORMAL
|
2023-07-09T04:12:16.758961+00:00
|
2023-07-09T04:12:16.758979+00:00
| 13,788 | false |
# **Intuition**\nFor the first `A[i] > 0`,\nwe need to select the array `A[i],A[i+1]..A[i+k-1]`\nand decrease all these elements by `A[i]`.\n<br>\n\n# **Explanation**\nThe subarray deleted starting at `A[i]`,\nwill affect the `A[i+1], A[i+2], ...A[i+k-1]`.\n\nSo we can use `cur` to record the sum of previous `k - 1` elements,\nwhere `cur = A[i - 1] + A[i - 2] + A[i - k + 1]`.\n\nSo there is a sense of sliding window here,\nwith window size of `k`.\n\nNow to solve this problem,\nwe iterate `A[i]`,\nand compare `A[i]` with `cur`.\n\n\nIf `cur > A[i]`,\nit means A[i] will be over-decreased to negative,\nreturn `false`.\nFor example,\n`A = [2,1]` and `k = 2` will return `false`.\n\nIf `cur <= A[i]`,\n`A[i]` will be decresed `cur` times,\nso `A[i] -= cur`,\nthen still need to decrese `A[i]` times,\nso `cur += A[i]`.\n\nWe continue doing this for all `A[i]`,\nand finally we check if `cur == 0`.\nFor example,\n`A = [0,0,1]` and `k = 2` will return `false`.\n<br>\n\n# **Complexity**\nTime `O(n)`\nSpace `O(1)`, needs `O(k)` if not change the input `A`\n<br>\n\n**Java**\n```java\n public boolean checkArray(int[] A, int k) {\n int cur = 0, n = A.length;\n for (int i = 0; i < n; ++i) {\n if (cur > A[i])\n return false;\n A[i] -= cur;\n cur += A[i];\n if (i >= k - 1)\n cur -= A[i - k + 1];\n }\n return cur == 0;\n }\n```\n\n**C++**\n```cpp\n bool checkArray(vector<int>& A, int k) {\n int cur = 0, n = A.size();\n for (int i = 0; i < n; ++i) {\n if (cur > A[i])\n return false;\n A[i] -= cur;\n cur += A[i];\n if (i >= k - 1)\n cur -= A[i - k + 1];\n }\n return cur == 0;\n }\n```\n\n**Python**\n```py\n def checkArray(self, A: List[int], k: int) -> bool:\n cur = 0\n for i, a in enumerate(A):\n if cur > a:\n return False\n A[i], cur = a - cur, a\n if i >= k - 1:\n cur -= A[i - k + 1]\n return cur == 0\n```\n<br>\n\n\n# More Similar Sliding Window Problems\nHere are some similar sliding window problems.\nAlso find more explanations and discussion.\nGood luck and have fun.\n\n- 2730. [Find the Longest Semi-Repetitive Substring](https://leetcode.com/problems/find-the-longest-semi-repetitive-substring/discuss/3629621/JavaC%2B%2BPython-Sliding-Window)\n- 2555. [Maximize Win From Two Segments](https://leetcode.com/problems/maximize-win-from-two-segments/discuss/3141449/JavaC%2B%2BPython-DP-%2B-Sliding-Segment-O(n))\n- 2537. [Count the Number of Good Subarrays](https://leetcode.com/problems/count-the-number-of-good-subarrays/discuss/3052559/C%2B%2BPython-Sliding-Window)\n- 2401. [Longest Nice Subarray](https://leetcode.com/problems/longest-nice-subarray/discuss/2527496/Python-Sliding-Window)\n- 2398. [Maximum Number of Robots Within Budget](https://leetcode.com/problems/maximum-number-of-robots-within-budget/discuss/2524838/Python-Sliding-Window-O(n))\n- 1838. [Frequency of the Most Frequent Element](https://leetcode.com/problems/frequency-of-the-most-frequent-element/discuss/1175090/JavaC%2B%2BPython-Sliding-Window)\n- 1493. [Longest Subarray of 1\'s After Deleting One Element](https://leetcode.com/problems/longest-subarray-of-1s-after-deleting-one-element/discuss/708112/JavaC%2B%2BPython-Sliding-Window-at-most-one-0)\n- 1425. [Constrained Subsequence Sum](https://leetcode.com/problems/constrained-subsequence-sum/discuss/597751/JavaC++Python-O(N)-Decreasing-Deque)\n- 1358. [Number of Substrings Containing All Three Characters](https://leetcode.com/problems/number-of-substrings-containing-all-three-characters/discuss/516977/JavaC++Python-Easy-and-Concise)\n- 1248. [Count Number of Nice Subarrays](https://leetcode.com/problems/count-number-of-nice-subarrays/discuss/419378/JavaC%2B%2BPython-Sliding-Window-atMost(K)-atMost(K-1))\n- 1234. [Replace the Substring for Balanced String](https://leetcode.com/problems/replace-the-substring-for-balanced-string/discuss/408978/javacpython-sliding-window/)\n- 1004. [Max Consecutive Ones III](https://leetcode.com/problems/max-consecutive-ones-iii/discuss/247564/JavaC%2B%2BPython-Sliding-Window)\n- 930. [Binary Subarrays With Sum](https://leetcode.com/problems/binary-subarrays-with-sum/discuss/186683/)\n- 992. [Subarrays with K Different Integers](https://leetcode.com/problems/subarrays-with-k-different-integers/discuss/523136/JavaC%2B%2BPython-Sliding-Window)\n- 904. [Fruit Into Baskets](https://leetcode.com/problems/fruit-into-baskets/discuss/170740/Sliding-Window-for-K-Elements)\n- 862. [Shortest Subarray with Sum at Least K](https://leetcode.com/problems/shortest-subarray-with-sum-at-least-k/discuss/143726/C%2B%2BJavaPython-O(N)-Using-Deque)\n- 209. [Minimum Size Subarray Sum](https://leetcode.com/problems/minimum-size-subarray-sum/discuss/433123/JavaC++Python-Sliding-Window)\n<br>\n
| 131 | 1 |
['C', 'Python', 'Java']
| 20 |
apply-operations-to-make-all-array-elements-equal-to-zero
|
+1/-1 trick | c++, python, javascript and extra segment tree/BIT solution
|
1-1-trick-c-python-javascript-and-extra-w7tv2
|
Approach\nLet\'s look for the first non-zero value from left to right, let\'s call the index $i$, since it is the first one if we use a window starting at a low
|
BetoSCL
|
NORMAL
|
2023-07-09T04:03:40.232586+00:00
|
2023-07-12T04:00:36.695988+00:00
| 5,662 | false |
# Approach\nLet\'s look for the first non-zero value from left to right, let\'s call the index $i$, since it is the first one if we use a window starting at a lower index than $i$ we will affect some zero values and transform them into negative which is not valid, and a window starting greater than $i$ cannot help either since they left $nums[i] \\neq 0$ so the only option is to apply exactly $nums[i]$ operations with a window starting at $i$, however when we apply these operations we will also affect the indices in the range $[i,(i+k)-1]$ so we need to update efficiently. \n\nAfter the updates we move to the next non-zero element and repeat the algorithm, checking for negative values. \n\nHow to do this efficiently? For advanced users perhaps a segment tree may come to mind, but we can apply the +1,-1 trick. \n\nThe trick is to take an array of prefix sums, in which we can apply updates in ranges, let\'s see an example to understand it well. \n\n$prefix = [0,0,0,0,0,0,0,0,0,0]$\n\n\nfirst we start with an array of prefixes for each index in zeros,for a range update for example $l = 1,r = 4$ we will update the prefix array with $prefix[l]++$ and $prefix[r+1]--$ in our example the array would look like this.\n$prefix = [0,1,0,0,0,0,-1,0]$ \n\nBut how is this useful?, once we do all the updates (it is necessary to have all the updates before the queries) if we get the prefix sums for each index we can know for each one how much it increased/decreased taking into account all the updates that affected that index, leaving the example as follows. \n$prefix\\_sum = [0,1,1,1,1,1,0,0]$ \n\nWe can see that the prefix sums perfectly describe the update $l = 1,r = 4$.\n\nNow for our problem we can apply as we go along, note that we iterate from left to right and apply some update starting exactly at $i$ and affect only later elements so all possible updates affecting the index $i$ already happened so as we go along doing the checks we can know how much the previous updates modified the current element.\n\n# Complexity\n- Time complexity:\n$O(n)$\n\n```c++ []\nclass Solution {\npublic:\n bool checkArray(vector<int>& nums, int k) {\n int n = nums.size();\n \n vector<long long> pref(n+1,0);\n long long ac = 0;\n \n for(int i = 0;i<n;i++){\n ac-=pref[i];\n nums[i]-=ac;\n \n if(nums[i]<0) return false;\n if(i+k<=n){ \n ac+=nums[i];\n pref[i+k]+=nums[i];\n nums[i] = 0;\n }\n else if(nums[i]>0)return false;\n }\n return true;\n }\n};\n```\n\n```javascript []\n/**\n * @param {number[]} nums\n * @param {number} k\n * @return {boolean}\n */\nvar checkArray = function(nums, k) {\n let n = nums.length\n let pref = Array(n+1).fill(0)\n let ac = 0\n for(let [i, val] of nums.entries()){\n ac-=pref[i]\n val-=ac\n console.log(val,i)\n\n if(val<0)return false\n if(i+k<=n){\n ac+=val\n pref[i+k]+=val\n val = 0\n }\n else if(val>0)return false\n }\n\n return true\n};\n```\n```python []\nclass Solution:\n def checkArray(self, nums: List[int], k: int) -> bool:\n n = len(nums)\n pref = [0]*(n+1)\n ac = 0\n for i in range(0,n):\n ac-=pref[i]\n nums[i]-=ac\n\n if nums[i]<0:\n return False\n if i+k<=n:\n ac+=nums[i]\n pref[i+k]+=nums[i]\n nums[i] = 0\n elif nums[i]>0:\n return False\n\n return True\n \n```\nExtra solution using segment tree for the updates in range\n$O(nlog(n))$\n# Code\n```c++\n class Solution {\npublic:\n vector<long long> st,lazy;\n int n;\n void propagate(int v,int l,int r){\n if(lazy[v]==0)return ;\n st[v] += ((r-l)+1)*lazy[v];\n\n if(l!=r){\n lazy[v<<1]+=lazy[v];\n lazy[v<<1|1]+=lazy[v];\n }\n lazy[v] = 0;\n }\n\n void update(int l,int r,int val,int v ,int sl,int sr){\n propagate(v,sl,sr);\n if(sl>r || sr<l)return ;\n if(sl>=l && sr<=r){\n lazy[v]+=val;\n propagate(v,sl,sr);\n return ;\n }\n int m = (sl+sr)>>1;\n update(l,r,val,v<<1,sl,m);\n update(l,r,val,v<<1|1,m+1,sr);\n }\n\n long long query(int l,int r,int v,int sl,int sr ){\n propagate(v,sl,sr);\n if(sl>r || sr<l)return 0;\n if(sl>=l && sr<=r)return st[v];\n\n int m = (sl+sr)>>1;\n return query(l,r,v<<1,sl,m)+query(l,r,v<<1|1,m+1,sr);\n }\n\n void update(int l,int r,int val){\n update(l,r,val,1,0,n-1);\n }\n\n long long query(int l,int r){\n return query(l,r,1,0,n-1);\n }\n\n bool checkArray(vector<int>& nums, int k) {\n n=nums.size();\n st.resize(4*n);\n lazy.resize(4*n);\n \n for(int i = 0;i<n;i++)update(i,i,nums[i]);\n\n for(int i=0;i<n;i++){\n int x = query(i,i);\n if(x>0 && i+k<=n)\n update(i,(i+k)-1,-x); \n if(query(i,i)!=0) return false;\n }\n return true;\n }\n};\n```\n# Fenwick tree / BIT solution\nAnd finally a solution with fenwick tree also called Binary Index Tree, this solution is interesting because the BIT is much easier to code, but the most important thing is that it also uses the trik +1/-1 \uD83E\uDD2F. \n\nDepending on where you learn the BIT structure you may not know that the fenwick tree can also deal with updates in ranges and not with a complex lazy propagation like the segment tree, in fact if you understand the structure well you can see the BIT as a prefix sum on steroids, basically it is a clever way to build ranges based on the binary representation of some index in such a way that those ranges help you to get the prefix sum up to an index, evidently with the ability to update when desired.\n\nSo since the BIT updates a particular values based on a particular index, at first the update in range is not possible ***(since the combination of the ranges needed for all the indexes in the range cannot be achieved in logarithmic time, so it will degenerate into an O(n) update in the worst case using the basic update)***, but since with that structure you can also get the prefix sums you can apply the trick and be able to update a range but sacrificing the query in range just make $update(l,val)$ and $update(r+1,-val)$.\n\nWhy if you want to have updates in ranges you can not get the query in range? ***(actually it is possible but I never learned it as it doesn\'t seem very useful, in that case I better use a segment tree)*** this is because the information in the indexes by itself no longer represents the prefix sums but represents a kind of accumulated change for each prefix. in a common BIT to get the query in range you have something like $query(r)-query(l-1)$ ,you subtract the prefix that you don\'t need, but when you use the update in range the information is not what we think, now we have some information from the end of the ranges that we need to subtract so you need the full prefix information to get the correct value, therefore if you subtract some prefix you will have incomplete information (like we do in the query in range) and the result will be wrong.\n\nAlthough I will not explain in depth the BIT or the segment tree, I hope it will be useful or that you will learn something new, maybe in another problem I will write more in depth about these structures \uD83D\uDE09.\n\n```c++\nclass Solution {\npublic:\n \n vector<int> bit;\n void add(int idx,int val){\n for(++idx;idx<bit.size();idx+= idx&-idx)bit[idx]+=val;\n }\n\n void add(int l,int r,int val){\n add(l,val);\n add(r+1,-val);\n }\n\n int sum(int idx){\n int res = 0;\n for(++idx;idx>0;idx-=idx&-idx)res+=bit[idx];\n return res;\n }\n\n bool checkArray(vector<int>& nums, int k) {\n int n=nums.size();\n bit.resize(n+1);\n \n for(int i = 0;i<n;i++)add(i,i,nums[i]);\n\n for(int i=0;i<n;i++){\n int x = sum(i);\n if(x>0 && i+k<=n)\n add(i,(i+k)-1,-x); \n if(sum(i)!=0) return false;\n }\n return true;\n }\n};\n```\n
| 29 | 2 |
['Binary Indexed Tree', 'Segment Tree', 'C++', 'Python3', 'JavaScript']
| 9 |
apply-operations-to-make-all-array-elements-equal-to-zero
|
| [JAVA] | Simple Solution | Sliding Window |
|
java-simple-solution-sliding-window-by-k-1g7u
|
Intuition | [JAVA] | Simple Solution | Sliding Window\n Describe your first thoughts on how to solve this problem. \n\n# Approach : Sliding Window\n Describe y
|
kartikeylapy
|
NORMAL
|
2023-07-09T07:30:59.781653+00:00
|
2023-07-09T07:30:59.781683+00:00
| 954 | false |
# Intuition | [JAVA] | Simple Solution | Sliding Window\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach : Sliding Window\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n*k)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public boolean checkArray(int[] nums, int k) {\n int n = nums.length; //size of array\n int c = 0;\n for (int i = 0; i <= n-k; i++) { //iterating through array\n if(nums[i] == 0) continue; //no operation performed\n if(nums[i] < 0) return false; //negative value\n if(nums[i] > 0) c = nums[i]; //save the value for operation\n for(int j = i;j <i+k;j++) nums[j]-= c; //perfoming the operation\n }\n for (int i = n-k; i < n; i++) { //checking for values\n if (nums[i] != 0) {\n return false; //elements not zero after perfoming max operations\n }\n }\n return true;\n }\n}\n```
| 18 | 1 |
['Java']
| 1 |
apply-operations-to-make-all-array-elements-equal-to-zero
|
✅ [C++] | Simple Solution | Range Prefix Sum
|
c-simple-solution-range-prefix-sum-by-00-o9xm
|
Approach : Range Prefix Sum\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n# Code\n\nclass Solution {\npublic:\n bool checkArray(vec
|
007_abhishek
|
NORMAL
|
2023-07-09T04:03:04.979715+00:00
|
2023-07-09T16:07:24.356618+00:00
| 4,498 | false |
# Approach : Range Prefix Sum\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n# Code\n```\nclass Solution {\npublic:\n bool checkArray(vector<int>& nums, int k) {\n int n=nums.size();\n if(n==1) return true;\n \n vector<int> temp(n,0);\n int i=0;\n temp[i]=nums[i];\n if(k<n) temp[k]=-nums[i];\n\n // i will be 1 even if first condition is false\n for(i=1;i<n-k+1;i++) { \n temp[i]+=temp[i-1];\n \n if(temp[i]>nums[i]) return false;\n\n int x = nums[i]-temp[i];\n temp[i]+=x;\n if(i+k<n) temp[i+k]-=x;\n else { i++; break; } // Last Window\n }\n // Checking if Last Window element is equals to our temp array element or not\n while(i<n) {\n temp[i]+=temp[i-1];\n if(temp[i]!=nums[i]) return false;\n i++;\n }\n return true;\n }\n};\n```
| 17 | 1 |
['Prefix Sum', 'C++']
| 2 |
apply-operations-to-make-all-array-elements-equal-to-zero
|
C++ || Sliding window technique || Beginner Friendly
|
c-sliding-window-technique-beginner-frie-xtyw
|
Intuition\n Describe your first thoughts on how to solve this problem. \n When I am at the start position of current window, my goal will be to make this first
|
ChelsiGarg
|
NORMAL
|
2023-07-10T08:53:57.862444+00:00
|
2023-07-10T08:53:57.862469+00:00
| 1,377 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n When I am at the start position of current window, my goal will be to make this first element zero so that i can go for next window (window size will be of length k). Now, let first element of this current window is ***sub*** then I will subtract \'sub\' from each element of this current window & will move to next window.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Move ahead in the array till we don\'t encounter any non-zero number.\n2. Let *i* is the index of first non-zero element. So, my window will start from *i* to *(i+k)* positions. My goal is to make nums[i]=0. For this, I will subtract nums[i] from each element in the window.\n3. If in the current window, any element < nums[i] then I can not apply operation on k elements simultaneously & hence return false otherwise subtract nums[i].\n4. Now, do i++ & move ahead.\n5. If you are able to successfully complete the traversal, return true\n6. In the starting, I have reversed the array. Without reversing also, the solution will run fine but will give TLE when initial elements are much much smaller than upcoming elements. This is because we are subtracting, say 1 from 1e5.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n bool checkArray(vector<int>& nums, int k) {\n int n=nums.size();\n int i=0;\n if(nums[0]<nums[n-1])\n reverse(nums.begin(),nums.end());\n \n while(i<n){\n while(i<n){\n if(nums[i]==0)\n i++;\n else\n break;\n }\n \n if(i==n)\n return true;\n \n int sub=nums[i];\n for(int count=0; count<k; count++){\n if((i+count)>=n || nums[i+count]<sub)\n return false;\n nums[i+count]-=sub;\n }\n i++;\n }\n return true;\n }\n};\n\n---\n\n**Please upvote if you find the solution to be helpful**\n
| 13 | 0 |
['C++']
| 3 |
apply-operations-to-make-all-array-elements-equal-to-zero
|
Line by Line explained Short Simple C++ solution
|
line-by-line-explained-short-simple-c-so-qh2k
|
Intuition\nWindow size is k .\nWe don\'t care how many times we have to apply operations.\n \nWe just care about whether it is possible to convert all elements
|
Bijay293
|
NORMAL
|
2023-07-10T06:29:24.755074+00:00
|
2023-07-12T13:29:38.193435+00:00
| 1,286 | false |
# Intuition\nWindow size is k .\nWe don\'t care how many times we have to apply operations.\n \nWe just care about whether it is possible to convert all elements to 0 or not.\n\nSo for example :\n2 2 3 1 1 taking k = 3 and window starting at index 0 we can get \n0 0 1 1 1 by applying some number of operations (we dont care about number of operations)\n\ncontinue applying operations we get all 0s.\n\n**So we can Conclude**\nEvery element at index i is influenced by elements at \n**i - 1 , i - 2 , i - 3 , ... , i - (k-1)**.\n\n\n# Approach\nKeep a prefixSum variable that has contribution from **i - 1 , i - 2 , i - 3 , ... , i - (k-1)** elements .\n\nEvery element will contribute **nums[ i ] - (current prefixSum value)** for the next k - 1 elements . \n\nThus keeping contrubution of every element in mind we will calculate the next prefixSum\n\n# Complexity\n- Time complexity:\n $$O(n)$$ \n\n- Space complexity:\n$$O(n)$$ just for storing the contribution of each elements\nYou can optimize it by using the nums array instead.\n\n# Cleaner Code\n```\nclass Solution {\npublic:\n bool checkArray(vector<int>& nums, int k) {\n int prefixsumk = 0;\n int n = nums.size();\n vector<int> contribution(n,0);\n for(int i=0;i<n; i++){\n if(prefixsumk > nums[i])\n return false;\n contribution[i] = nums[i] - prefixsumk;\n prefixsumk = prefixsumk + contribution[i];\n if(i>=k-1)\n prefixsumk-= contribution[i-k+1];\n }\n return prefixsumk == 0;\n }\n};\n```\n\n\n# Code with comments explaining line by line\n```\nclass Solution {\npublic:\n bool checkArray(vector<int>& nums, int k) {\n\n// stores contribution of previous k-1 elements\n int prefixsumk = 0;\n\n int n = nums.size();\n// stores contribution for every element \n vector<int> contribution(n,0);\n\n// for first element contribution is 0 since there are no element b4 it\n for(int i=0;i<n; i++){\n// if we have prefixsum greater than current element that means after subtracting\n// (performing operations) we will get negative number rather than 0 .\n if(prefixsumk > nums[i])\n return false;\n// the current element will contribute value = what is left \n// after performing operations on previous windows of size k.\n contribution[i] = nums[i] - prefixsumk;\n\n// calculate prefix sum for next element \n// for that we need to add contribution of current element \n prefixsumk = prefixsumk + contribution[i];\n\n// and subtract contribution of i-(k-1) th element before it if it exists\n if(i>=k-1)\n prefixsumk-= contribution[i-k+1];\n }\n// At the end of all operations there are no elements left so last contribution\n// should be 0 otherwise we will be left with some numbers at end that were not converted to 0 .\n return prefixsumk == 0;\n }\n};\n```
| 10 | 0 |
['Sliding Window', 'C++']
| 2 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.