question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
minimize-the-maximum-adjacent-element-difference
|
[Java/C++/Python] No Binary Search, O(1) Space
|
javacpython-no-binary-search-o1-space-by-ykbd
|
Complexity\nTime O(n)\nSpace O(1)\n\n# Intuition 1\nAssume r is the maximum absolute difference between adjacent elements.\nr is short for radius.\nx can cover
|
lee215
|
NORMAL
|
2024-11-17T15:30:49.526769+00:00
|
2024-11-18T14:52:24.658074+00:00
| 1,067
| false
|
# **Complexity**\nTime `O(n)`\nSpace `O(1)`\n\n# **Intuition 1**\nAssume `r` is the maximum absolute difference between adjacent elements.\n`r` is short for radius.\n`x` can cover the range of `[x - r, x + r]`\n`y` can cover the range of `[y - r, y + r]`\n\nNotice that these two range could overlap.\n\n# **Intuition 2**\nAssume `a > 0` and `b > 0`\nFor subarray `[a, b]`,\nwe can do nothing to improve.\n\nFor subarray `[a,x,b]`,\nlet\'s say `[a, b]` limits a single `x`.\n\nFor subarray `[a,x,x,b]`,\nlet\'s say `[a, b]` limits multiple `x`.\n\nFor prefix `[x, x, a]` starting with `-1`,\nall `x` in prefix will take the same value,\nlet\'s say `[a, a]` limits single `x`.\n\nFor suffix `[a, x, x]` ending with `-1`,\nall `x` in suffix will take the same value,\nlet\'s say `[a, a]` limits single `x`.\n\n\n# **Explanation**\nOne pass iterate the `A`,\nfind the max diff of adjacent positive `max_adj`,\nfind the max number `mina` adjacent to `-1`,\nfind the min number `maxb` adjacent to `-1`.\n\nThe core idea of this solution is that,\nfind the minimum radius `r`\nso that all limits `[a,b]` can be covered by either `[x - r, x + r]` or `[y - r, y + r]`.\n\nOne more biggest observation,\nassume `x < y`,\n`mina` must be covered by `x`\nand `maxb` must be covered by `y`.\nTo minimize `r`,\n`x - r == mina` and `y + r == maxb`.\n\nThus the progress can be easy greed:\nSecond pass the `A`,\nfor each limit `[a, b]`,\nfind if `[a, b]` is closer to left bound `mina` or right bound `maxb`,\n`res` is the diameter that we can minimize.\n\nIn addition to the limit for multiple `x`,\nit can be same result for single `x`,\nor will take a radius `r >= (maxa - mina) / 3`.\n(There\'s a difficult thinking process but an easy conclusion)\n<br>\n\n\n\n```Java [Java]\n public int minDifference(int[] A) {\n int n = A.length, max_adj = 0, mina = Integer.MAX_VALUE, maxb = 0;\n for (int i = 0; i < n - 1; ++i) {\n int a = A[i], b = A[i + 1];\n if (a > 0 && b > 0) {\n max_adj = Math.max(max_adj, Math.abs(a - b));\n } else if (a > 0 || b > 0) {\n mina = Math.min(mina, Math.max(a, b));\n maxb = Math.max(maxb, Math.max(a, b));\n }\n }\n\n int res = 0, min_2r = (maxb - mina + 2) / 3 * 2;\n for (int i = 0; i < n; ++i) {\n if ((i > 0 && A[i - 1] == -1) || A[i] > 0) continue;\n int j = i;\n while (j < n && A[j] == -1) {\n j++;\n }\n int a = Integer.MAX_VALUE, b = 0;\n if (i > 0) {\n a = Math.min(a, A[i - 1]);\n b = Math.max(b, A[i - 1]);\n }\n if (j < n) {\n a = Math.min(a, A[j]);\n b = Math.max(b, A[j]);\n }\n if (j - i == 1) {\n res = Math.max(res, Math.min(maxb - a, b - mina));\n } else {\n res = Math.max(res, Math.min(maxb - a, Math.min(b - mina, min_2r)));\n }\n }\n return Math.max(max_adj, (res + 1) / 2);\n }\n```\n\n```C++ [C++]\n int minDifference(vector<int>& A) {\n int n = A.size(), max_adj = 0, mina = INT_MAX, maxb = 0;\n for (int i = 0; i < n - 1; ++i) {\n int a = A[i], b = A[i + 1];\n if (a > 0 && b > 0) {\n max_adj = max(max_adj, abs(a - b));\n } else if (a > 0 || b > 0) {\n mina = min(mina, max(a, b));\n maxb = max(maxb, max(a, b));\n }\n }\n\n int res = 0, min_2r = (maxb - mina + 2) / 3 * 2;\n for (int i = 0; i < n; ++i) {\n if ((i > 0 && A[i - 1] == -1) || A[i] > 0) continue;\n int j = i;\n while (j < n && A[j] == -1) {\n j++;\n }\n int a = INT_MAX, b = 0;\n if (i > 0) {\n a = min(a, A[i - 1]);\n b = max(b, A[i - 1]);\n }\n if (j < n) {\n a = min(a, A[j]);\n b = max(b, A[j]);\n }\n if (j - i == 1) {\n res = max(res, min(maxb - a, b - mina));\n } else {\n res = max(res, min({maxb - a, b - mina, min_2r}));\n }\n }\n return max(max_adj, (res + 1) / 2);\n }\n```\n\n```py [Python3]\n def minDifference(self, A: List[int]) -> int:\n n = len(A)\n max_adj, mina, maxb = 0, inf, 0\n for a,b in pairwise(A):\n if a > 0 and b > 0:\n max_adj = max(max_adj, abs(a - b))\n elif a > 0 or b > 0:\n mina = min(mina, max(a, b))\n maxb = max(maxb, max(a, b))\n res = 0\n min_2r = (maxb - mina + 2) // 3 * 2 # min 2r if [a,x,y,b] is better\n for i in range(n):\n if (i > 0 and A[i - 1] == -1) or A[i] > 0: continue\n j = i\n while j < n and A[j] == -1:\n j += 1\n a, b = inf, 0\n if i > 0:\n a = min(a, A[i - 1])\n b = max(b, A[i - 1])\n if j < n:\n a = min(a, A[j])\n b = max(b, A[j])\n res = max(res, min(maxb - a, b - mina, min_2r if j - i > 1 else inf))\n return max(max_adj, (res + 1) // 2)\n```\n
| 22
| 1
|
['C', 'Python', 'Java']
| 3
|
minimize-the-maximum-adjacent-element-difference
|
C++ | easiest solution with detailed explanation and comment on code
|
c-easiest-solution-with-detailed-explana-31ms
|
\n### 1. Intuition\n\n- You are given an array nums that contains integers and -1 values representing missing elements.\n- You are allowed to replace the -1 ele
|
blue106
|
NORMAL
|
2024-11-17T04:16:42.841801+00:00
|
2024-11-17T04:16:42.841829+00:00
| 1,627
| false
|
\n### **1. Intuition**\n\n- You are given an array `nums` that contains integers and `-1` values representing missing elements.\n- You are allowed to replace the `-1` elements with two positive integers (`minValue` and `maxValue`), which are chosen once for the entire array.\n- The task is to replace the `-1` values in such a way that the maximum absolute difference between any two adjacent elements in the array is minimized.\n\n---\n\n### **2. Functions definitions**\n\n#### **`isValidDifference()` Function**\n\nThis function checks whether it\'s possible to replace all `-1` values in the array `nums` such that the maximum absolute difference between any two adjacent elements does not exceed a given `maxDiff`.\n\n- **Inputs**:\n - `nums`: The original array, including `-1` values.\n - `maxDiff`: The maximum allowed difference between adjacent elements.\n\n- **Process**:\n 1. **Create bounds**: For each non-missing element in the array, compute two possible values: \n - The lower bound (`minValue`) is `nums[i] - maxDiff`.\n - The upper bound (`maxValue`) is `nums[i] + maxDiff`.\n These bounds are stored in two arrays: `lowerBounds` and `upperBounds`.\n \n 2. **Calculate range**: The range of values that can be used to replace the `-1` values is constrained by the values in `lowerBounds` and `upperBounds`. We calculate:\n - `minValue = min(lowerBounds) + 2 * maxDiff` (the smallest possible value considering the allowed difference).\n - `maxValue = max(upperBounds) - 2 * maxDiff` (the largest possible value considering the allowed difference).\n\n 3. **Test replacements**: For each `-1` value in `nums`, attempt to replace it with either `minValue` or `maxValue`. The replacement must ensure that the new value does not cause the difference with adjacent values to exceed `maxDiff`.\n - If it\'s possible to replace all `-1` values while satisfying the constraint, return `true`.\n - If not, return `false`.\n\n#### **`minDifference()` Function**\n\nThis is the main function that solves the problem. It uses **binary search** to find the smallest possible `maxDiff` that works.\n\n- **Inputs**:\n - `nums`: The array with integers and `-1` values.\n\n- **Process**:\n 1. **Count missing values**: First, count the number of `-1` values in `nums` and store the count in `missingCount`.\n\n 2. **Handle edge cases**:\n - If there are no missing values (`missingCount == 0`), calculate the maximum absolute difference between adjacent elements in the array. This is the answer.\n - If the entire array consists of `-1` values, return `0` because all elements can be set to the same value (e.g., both `minValue` and `maxValue` are the same).\n \n 3. **Binary search**:\n - Initialize the binary search bounds: `low = 0` and `high = 1000000005` (an arbitrarily large value to cover possible differences).\n - While `low` is not equal to `high`, compute the middle value `mid` as the average of `low` and `high`.\n - Call the `isValidDifference()` function to check if a difference of `mid` is possible.\n - If it is possible, update the upper bound `high = mid` to search for a smaller difference.\n - If it\u2019s not possible, update the lower bound `low = mid + 1` to search for a larger difference.\n \n 4. **Return the result**: Once the binary search ends, `low` will be the smallest possible maximum difference that works.\n\n---\n\n### **3. Edge Cases Noticed**\n\n- **No missing values**: If there are no `-1` values in `nums`, simply calculate the maximum difference between adjacent elements.\n \n- **All elements are missing**: If all elements are `-1`, we can set them all to the same value (e.g., both `minValue` and `maxValue` are the same), making the maximum difference `0`.\n\n- **Sparse or dense missing values**: The code handles cases where missing values are spread out or are adjacent to non-missing values.\n\n---\n\n### **4. Example Walkthrough**\n\nLet\u2019s go through an example:\n\n#### **Example 1:**\n\n```cpp\nvector<int> nums = [1, 2, -1, 10, 8];\n```\n\nWe are looking for the smallest possible `maxDiff` after replacing the `-1` value.\n\n- **Initial Array**: `[1, 2, -1, 10, 8]`\n \n- **Binary Search**:\n - We start with `low = 0` and `high = 1000000005`.\n - In each iteration, we check if a given `maxDiff` works by calling `isValidDifference()`. This involves calculating possible replacements for `-1` and checking if the maximum difference between adjacent elements remains within the allowed `maxDiff`.\n \n- **Result**: The smallest possible `maxDiff` that works is `4`.\n\n#### **Example 2:**\n\n```cpp\nvector<int> nums = [-1, -1, -1];\n```\n\n- **Initial Array**: `[-1, -1, -1]`\n \n- **Handling Edge Case**: Since all elements are `-1`, we can replace them all with the same value (e.g., both `minValue` and `maxValue` can be `4`), resulting in a `maxDiff` of `0`.\n\n- **Result**: The minimum possible `maxDiff` is `0`.\n\n---\n\n### **5. Time and Space Complexity**\n\n- **Time Complexity**:\n - The binary search runs in `O(log(maxDiff))`, where `maxDiff` is a large constant.\n - For each binary search iteration, the `isValidDifference()` function checks each element of the array, which takes `O(n)` time.\n - Overall time complexity: `O(n * log(maxDiff))`, where `n` is the size of the array.\n\n- **Space Complexity**:\n - The space complexity is `O(n)` due to the additional storage used for `lowerBounds`, `upperBounds`, and the array copy passed to `isValidDifference()`.\n\n---\n\n### Conclusion\n\nThis code leverages **binary search** and **greedy filling** techniques to minimize the maximum difference between adjacent elements in the array after replacing missing values (`-1`). The binary search narrows down the smallest feasible `maxDiff`, while the greedy approach ensures that replacements of `-1` values maintain this difference. The solution is efficient with a time complexity of `O(n * log(maxDiff))`.\n\n# Code\n```cpp []\nclass Solution {\npublic:\n // Helper function to check if a given maxDiff is feasible\n bool isValidDifference(vector<int> nums, int maxDiff) {\n vector<int> lowerBounds, upperBounds;\n\n // Traverse through the nums array\n for (int i = 0; i < nums.size(); i++) {\n // When an element is not -1 and is adjacent to a -1, compute possible values\n if (nums[i] != -1 && (i && nums[i-1] == -1 || (i != nums.size()-1) && nums[i+1] == -1)) {\n lowerBounds.push_back(nums[i] - maxDiff); // Minimum possible value for the element\n upperBounds.push_back(nums[i] + maxDiff); // Maximum possible value for the element\n }\n }\n\n // Calculate the minimum and maximum values considering the allowed difference\n int minValue = *min_element(lowerBounds.begin(), lowerBounds.end()) + 2 * maxDiff; // The lower bound value\n int maxValue = *max_element(upperBounds.begin(), upperBounds.end()) - 2 * maxDiff; // The upper bound value\n\n // Now, for each -1 in the array, try to fill it with either `minValue` or `maxValue`\n for (int i = 0; i < nums.size(); i++) {\n if (nums[i] == -1) { // If it\'s a missing value\n // Try replacing with `minValue` first\n if (\n (i == 0 || abs(nums[i-1] - minValue) <= maxDiff) && // Check left neighbor\n (i == (nums.size() - 1) || nums[i+1] == -1 || abs(nums[i+1] - minValue) <= maxDiff)) // Check right neighbor\n {\n nums[i] = minValue; // Replace with `minValue`\n } else {\n nums[i] = maxValue; // Otherwise, replace with `maxValue`\n }\n }\n }\n\n // After replacing all -1 values, check if the difference between adjacent elements is within `maxDiff`\n for (int i = 0; i < nums.size()-1; i++) {\n if (abs(nums[i] - nums[i+1]) > maxDiff) { // If any difference exceeds `maxDiff`, return false\n return false;\n }\n }\n\n // If no differences exceeded the allowed maxDiff, return true\n return true;\n }\n\n // Main function to find the minimum possible difference between adjacent elements\n int minDifference(vector<int>& nums) { \n int missingCount = 0;\n\n // Count how many missing values (-1) are in the array\n for (int x: nums) if (x == -1) missingCount++;\n\n // If no missing values, calculate the maximum difference between adjacent elements\n if (missingCount == 0) {\n int maxDiff = 0;\n for (int i = 0; i < nums.size()-1; i++) {\n maxDiff = max(maxDiff, abs(nums[i] - nums[i+1])); // Find the largest difference\n }\n return maxDiff;\n } \n // If all elements are missing, the minimum difference is 0 since we can set them to the same value\n else if (missingCount == nums.size()) return 0;\n\n // Perform binary search to find the minimum possible `maxDiff`\n int low = 0;\n int high = 1000000005; // A large enough number to represent the upper bound\n\n // Binary search for the minimum `maxDiff`\n while (low != high) {\n int mid = (low + high) / 2; // Find the midpoint of the current range\n\n // Test if the current maxDiff is feasible\n if (isValidDifference(nums, mid)) {\n high = mid; // If feasible, try a smaller `maxDiff`\n } else {\n low = mid + 1; // If not feasible, try a larger `maxDiff`\n }\n }\n\n // Return the smallest `maxDiff` that worked\n return low;\n }\n};\n\n```\n\n\n
| 20
| 6
|
['Array', 'Two Pointers', 'Binary Search', 'Greedy', 'C++']
| 7
|
minimize-the-maximum-adjacent-element-difference
|
[Python] Binary Search + Interval Stabbing
|
python-binary-search-interval-stabbing-b-28ke
|
Binary search for the answer.\n\nLet\'s say we are trying to decide whether bound is an answer. Every wildcard ? next to a positive value a induces an interval
|
awice
|
NORMAL
|
2024-11-17T04:23:41.385222+00:00
|
2024-11-17T04:23:41.385246+00:00
| 947
| false
|
Binary search for the answer.\n\nLet\'s say we are trying to decide whether `bound` is an answer. Every wildcard `?` next to a positive value `a` induces an interval `[a-bound, a+bound]`. Wildcards like `a?b` induce the interval `[a-bound,a+bound] INTERSECT [b-bound,b+bound]`.\n\nAt the end, we have some intervals and we want to know whether all of them can be stabbed by two points. The choice for these points will be greedy from the left and right as these extreme intervals must have a point on them chosen.\n\nIf we have chosen points `lo, hi`, then additionally they must have `abs(lo - hi) <= bound`, or the choice is valid without having to switch between `lo` and `hi`.\n\n# Code\n```python3 []\nclass Solution:\n def minDifference(self, A: List[int]) -> int:\n groups = [list(grp) for k, grp in groupby(A, key=lambda x: x>0)]\n singles = [] # a? or a??\n doubles = [] # a?b or a??b\n base = 0 # the max diff of two positive elements\n\n for i, grp in enumerate(groups):\n if grp[0] != -1:\n for j in range(len(grp) - 1):\n base = max(base, abs(grp[j] - grp[j+1]))\n continue\n\n neis = []\n if i - 1 >= 0:\n neis.append(groups[i-1][-1])\n if i + 1 < len(groups):\n neis.append(groups[i+1][0])\n neis.sort()\n\n if len(neis) == 1:\n singles.append([*neis, len(grp) > 1])\n if len(neis) == 2:\n doubles.append([*neis, len(grp) > 1])\n\n if not singles and not doubles:\n return base\n\n def possible(bound):\n intervals = []\n for a, len2 in singles:\n intervals.append([a-bound, a+bound])\n for a, b, len2 in doubles:\n if len2:\n intervals.append([a-bound, a+bound])\n intervals.append([b-bound, b+bound])\n else:\n lo = b - bound\n hi = a + bound\n if lo > hi: return 0\n intervals.append([lo, hi])\n\n # we have a bunch of intervals, and we want to know if we can stab twice\n # to hit all intervals\n lo = min(e for s,e in intervals)\n hi = max(s for s,e in intervals)\n \n if lo + bound < hi:\n if not all(\n any(abs(a-p) <= bound and abs(b-p) <= bound for p in [lo, hi]) \n for a,b,l in doubles\n ):\n return 0\n\n return all(s <= lo <= e or s <= hi <= e for s,e in intervals)\n \n return bisect_left(range(10**9), 1, base, max(A), key=possible)\n```
| 12
| 0
|
['Python3']
| 1
|
minimize-the-maximum-adjacent-element-difference
|
C++ - Binary Search - O(NlogM)
|
c-binary-search-onlogm-by-facug91-nab5
|
Intuition\nThe main idea is to have a function to check if the problem can be solved with a difference smaller or equals to a given value.\nWith that in mind, w
|
facug91
|
NORMAL
|
2024-11-17T05:22:18.763869+00:00
|
2024-11-17T06:17:17.390595+00:00
| 680
| false
|
# Intuition\nThe main idea is to have a function to check if the problem can be solved with a difference smaller or equals to a given value.\nWith that in mind, we can use a binary search over the possible range of answers, to check which difference is the smallest.\n\n# Approach\nFirst I try to solve some special cases, like N == 2, and an array of -1. This cases are trivial and don\'t need an explanation. \nThen I create a more compact version of `nums`, canculating the minimum value that has an adjacent -1. I also use -2 for the case when there are multiple consecutive -1 values, because it\'s the same to have 2 or 10000, it has the same possible solutions: (x,...,x), (y,...,y), (x,...y), (y,...x). I also calculate the current maximum diffence, in order to avoid further checks about this in the `check` function. \nAfter that, there\'s the binary search, which uses the function `check` to see if the a diffence of mid (smaller or equals to mid) can be used to solve the problem. \nI think the most important part to explain about `check`, is how to calculate the (x,y) values (which I called `p1` and `p2`). This can be done using the smallest value that has an adjacent -1 and the greatest value that has an adjacent -1. If we use a `p1` greater than the minimum value + diff, the difference will surely be greater than diff, nd using a smaller value won\'t help at all, because we want to solve it with a difference smaller or equals than `diff`. The same logic applies for `p2` and the maximum value. \n\nI don\'t usually write tutorials, so this may be a bit messy. I appreciate any suggestions for improvement.\n\n\n# Complexity\n- Time complexity:\nBeing N the number of elements in `nums` and M the maximum range (which is ~1e9), this solutions is O(NlogM).\n\n- Space complexity:\nI used a secondary array to simplify the check function (at least for me it does), so it is O(N), but I think it can be done in O(1).\n\n# Code\n```cpp []\nstatic const int fastIO = [] {\n\tstd::ios_base::sync_with_stdio(false), std::cin.tie(nullptr), std::cout.tie(nullptr);\n\treturn 0;\n}();\n\nclass Solution {\nprivate:\n\tbool check(vector<int>& nums, int mn, int mx, int diff) {\n\t\tint p1 = mn + diff, p2 = mx - diff, n = (int)nums.size();\n\t\tif (nums[0] == -1 && abs(nums[1] - p1) > diff && abs(nums[1] - p2) > diff) return false;\n\t\tif (nums[n - 1] == -1 && abs(nums[n - 2] - p1) > diff && abs(nums[n - 2] - p2) > diff) return false;\n\t\tfor (int i = 1; i + 1 < nums.size(); i++)\n\t\t\tif (nums[i] < 0) {\n\t\t\t\tif (abs(nums[i - 1] - p1) <= diff && abs(nums[i + 1] - p1) <= diff) continue;\n\t\t\t\tif (abs(nums[i - 1] - p2) <= diff && abs(nums[i + 1] - p2) <= diff) continue;\n\t\t\t\tif (nums[i] == -2) {\n\t\t\t\t\tif (abs(p2 - p1) <= diff) {\n\t\t\t\t\t\tif (abs(nums[i - 1] - p1) <= diff && abs(nums[i + 1] - p2) <= diff) continue;\n\t\t\t\t\t\tif (abs(nums[i - 1] - p2) <= diff && abs(nums[i + 1] - p1) <= diff) continue;\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t\treturn false;\n\t\t\t}\n\t\treturn true;\n\t}\n\npublic:\n\tint minDifference(vector<int>& nums) {\n\t\tconst int n = (int)nums.size();\n\n\t\tif (n == 2) {\n\t\t\tif (nums[0] != -1 && nums[1] != -1) return abs(nums[0] - nums[1]);\n\t\t\treturn 0;\n\t\t}\n\n\t\tbool allMinus1 = true;\n\t\tfor (int num: nums)\n\t\t\tif (num != -1) {\n\t\t\t\tallMinus1 = false;\n\t\t\t\tbreak;\n\t\t\t}\n\t\tif (allMinus1) return 0;\n\n\t\tint mn = 1e9, mx = 0, currMx = 0, cnt = 0;\n\t\tvector<int> nums2;\n\t\tfor (int i = 0; i < n; i++) {\n\t\t\tif (nums[i] != -1) {\n\t\t\t\tif (i > 0 && nums[i - 1] != -1) currMx = max(currMx, abs(nums[i] - nums[i - 1]));\n\t\t\t\tif (cnt == 1) nums2.push_back(-1);\n\t\t\t\tif (cnt > 1) nums2.push_back(-2);\n\t\t\t\tcnt = 0;\n\t\t\t\tif (i == 0 || i + 1 == n || nums[i - 1] == -1 || nums[i + 1] == -1)\n\t\t\t\t\tnums2.push_back(nums[i]);\n\t\t\t\tif (i > 0 && nums[i - 1] == -1 || i + 1 < n && nums[i + 1] == -1) {\n\t\t\t\t\tmn = min(mn, nums[i]);\n\t\t\t\t\tmx = max(mx, nums[i]);\n\t\t\t\t}\n\t\t\t} else {\n\t\t\t\tcnt++;\n\t\t\t}\n\t\t}\n\t\tif (cnt > 1) nums2.push_back(-1);\n\t\tif (nums2[0] == -2) nums[0] = -1;\n\n\t\tint lo = currMx, hi = mx - mn + 1;\n\t\twhile (lo < hi) {\n\t\t\tint mid = (lo + hi) / 2;\n\t\t\tif (check(nums2, mn, mx, mid)) hi = mid;\n\t\t\telse lo = mid + 1;\n\t\t}\n\t\treturn lo;\n\t}\n};\n```
| 6
| 0
|
['Binary Search', 'C++']
| 1
|
minimize-the-maximum-adjacent-element-difference
|
Binary Search (29th place solution)
|
binary-search-29th-place-solution-by-ton-wd4i
|
Intuition\nBinary search, greedy\n\n\n# Approach\nBinary search on the possible result.\n\nThen the question is reduced to - given a specific maximum distance t
|
tonghuikang
|
NORMAL
|
2024-11-17T04:03:49.606950+00:00
|
2024-11-17T18:01:30.980213+00:00
| 782
| false
|
# Intuition\nBinary search, greedy\n\n\n# Approach\nBinary search on the possible result.\n\nThen the question is reduced to - given a specific maximum distance `target_diff`, can you find a pair of (x,y) that satisifies the constraint?\n\nThe input can be reduced to three types of element pairs (a,b)\n- There are no missing numbers between the element pair (we do not need to consider this after we reject the solution if the specified maximum distance is smaller than the difference between this element pair)\n- There is one missing numbers between the element pair (if the array starts or ends with the missing elements, consider the leftmost and rightmost non-missing element to pair with itself)\n- There are at least two missing numbers between the element pair (in this case you can just consider that there are only two missing numbers)\n\nWithout loss of generality, assume a <= b.\n\nYou have to choose an (x,y) such that it is possible fit into all element pairs within the specified maximum distance.\n\nChoose `x = min(a) + target_diff` to guarantee that we can at least satisfy the element pair with `min(a)`.\nChoose `y = max(b) - target_diff` to guarantee that we can at least satisfy the element pair with `max(b)`.\n\nThen just try to fix all possible combinations of (x,y) into each pair.\n- Note that for element pairs with two missing numbers, it is possible to put `(x,x)` or `(y,y)`.\n- If you are putting both x and y into element pairs with two missing numbers, make sure x and y differ at most by `target_diff`.\n\nIf you can do it, the specified maximum distance is achievable (and also any larger maximum distances). Then continue with the binary search.\n\n\n# Complexity\n- Time complexity:\nO(n log k)\n\n- Space complexity:\nO(n)\n\n# Code\n```python3 []\nfrom typing import List\n\n\ndef binary_search(\n func_, # condition function\n first=True, # else last\n target=True, # else False\n left=0,\n right=2**31 - 1,\n) -> int:\n # https://leetcode.com/discuss/general-discussion/786126/\n # ASSUMES THAT THERE IS A TRANSITION\n # MAY HAVE ISSUES AT THE EXTREMES\n\n def func(val):\n # if first True or last False, assume search space is in form\n # [False, ..., False, True, ..., True]\n\n # if first False or last True, assume search space is in form\n # [True, ..., True, False, ..., False]\n # for this case, func will now be negated\n if first ^ target:\n return not func_(val)\n return func_(val)\n\n while left < right:\n mid = (left + right) // 2\n if func(mid):\n right = mid\n else:\n left = mid + 1\n if first: # find first True\n return left\n else: # find last False\n return left - 1\n\n\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n # left, right, count (1 or 2)\n n = len(nums)\n \n if nums.count(-1) == 0:\n return max(abs(a-b) for a,b in zip(nums, nums[1:]))\n if nums.count(-1) == n:\n return 0\n \n arr = []\n \n if nums[-1] == -1:\n while nums[-1] == -1:\n nums.pop()\n arr.append((nums[-1], nums[-1], 1))\n \n nums.reverse()\n if nums[-1] == -1:\n while nums[-1] == -1:\n nums.pop()\n arr.append((nums[-1], nums[-1], 1))\n \n maxdiff = 0\n \n prev_val = nums[0]\n prev_idx = 0\n for i,x in enumerate(nums[1:], start=1):\n if x != -1:\n if i - prev_idx == 1:\n maxdiff = max(maxdiff, abs(x - prev_val))\n elif i - prev_idx == 2:\n left = min(prev_val, x)\n right = max(prev_val, x)\n arr.append((left, right, 1))\n else:\n left = min(prev_val, x)\n right = max(prev_val, x)\n arr.append((left, right, 2))\n prev_val = x\n prev_idx = i\n \n def func(target_diff):\n if target_diff < maxdiff:\n return False\n \n xval = 10**10 + 10\n yval = -10**10 - 10\n for a,b,c in arr:\n xval = min(xval, a + target_diff) # can be smaller and ok\n yval = max(yval, b - target_diff) # can be larger and ok\n \n for a,b,c in arr:\n if c == 1:\n if abs(a - xval) <= target_diff and abs(b - xval) <= target_diff:\n continue\n if abs(a - yval) <= target_diff and abs(b - yval) <= target_diff:\n continue\n return False\n if c == 2:\n if abs(a - xval) <= target_diff and abs(b - yval) <= target_diff and abs(yval - xval) <= target_diff:\n continue\n if abs(a - yval) <= target_diff and abs(b - xval) <= target_diff and abs(yval - xval) <= target_diff:\n continue\n if abs(a - xval) <= target_diff and abs(b - xval) <= target_diff:\n continue\n if abs(a - yval) <= target_diff and abs(b - yval) <= target_diff:\n continue\n return False\n return True\n \n return binary_search(func, first=True, target=True, left=0, right=10**10 + 10)\n \n \n \n \n \n```
| 5
| 0
|
['Python3']
| 0
|
minimize-the-maximum-adjacent-element-difference
|
[Python] 🔥 Binary Search | Very Detailed Explanation | Visual Diagrams|
|
python-binary-search-very-detailed-expla-7env
|
Intuition\n\n Describe your first thoughts on how to solve this problem. \n\nThanks for the inspiration of @Alex Wi\'s solution. \n\nConsidering it as a convex
|
Yosemiti
|
NORMAL
|
2024-11-18T03:45:04.877971+00:00
|
2024-11-18T07:03:50.506286+00:00
| 74
| false
|
# Intuition\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nThanks for the inspiration of [@Alex Wi](https://leetcode.com/problems/minimize-the-maximum-adjacent-element-difference/solutions/6053410/python-binary-search-interval-stabbing/)\'s solution. \n\nConsidering it as a convex optimization problem `bound = f(x, y)` is a dead end. `bound` is not differentiable. Trick 1 here is to convert the problem of `(x,y)` to a problem of `bound`. \n\nNow consider a function `isValid(bound)`and if return boolean value for if `bound` is valid. Then `isValid()` is monotone non-decreasing.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nWe calculate gaps between existing elements as`existing_gap` and binary search `min_bound` in `[0, max(nums)]` and find the minimal valid `bound`. The final result will be `max(existing_gap, min_bound)`\n\n## Q1 How do we determine if `bound` is valid?\nWe know that the adjacent elements will bound our unfilled elements (-1s). For one-sided bound `[a, -1]`, x or y should be in interval`[a-bound, a+bound]`. For double sided bound `[a, -1, b]`, x or y should be in interval `[a-bound, a+bound]`$$\\cap$$ `[b-bound, b+bound]`.\n\nConsider the intervals like this:\n```\n---- #interval 0 \n ------- #interval 1 \n ----- #interval 2 \n ---- #interval 3 \n ----------- #interval 4 \n```\nit should be penetrate by (at most) two parameter x and y like:\n```\n---x #interval 0 \n --x---- #interval 1 \n x---- #interval 2 \n ---y #interval 3 \n y---------- #interval 4\n```\nThen how do we know if these x, y exists?\n\n### 1.1 Greedy approach\n\nIf the intervals we have can be penentrated by at most 2 points, then\n`x = min(right_points)`\n`y = max(left_points)`\nmust satisfy the condition, which are chosen by greedy approach.\n#### 1.1.1 Case 1: There exists one point that can penetrate all intervals. \nThis is a easier case. For example\n```\n------------x #interval 0 \n -----------x- #interval 1 \n ---------x--- #interval 2 \n -------x----- #interval 3 \n -----x------- #interval 4\n```\nThe most greedy option is the **minimal right endpoint** (`x` above) . Greedy here means "if this point cannot satisfy, then no points can satisfy." (maximal left endpoint is another greedy solution)\n\n#### 1.1.2 Case 2: There need at least 2 points to penetrate all intervals.\n\nSuppose `x < y`\n\n\nIf these two don\'t satisfy, then no other two poins statisfy. For example:\n```\n---x #interval 0 \n --x---- #interval 1 \n x---- #interval 2 \n ---- #interval 3\n ---y #interval 4 \n y---------- #interval 5\n```\n\n\n**Conclusion**: for any given `bound` and `intervals`, by checking if `x_0` or `y_0` can penetrate each interval, we can determine if this `bound` is valid for both case 1 and case 2.\n\n<details>\n<summary>Detailed Proof</summary>\n\n\n**Claim 1**: The most greedy `x` is the **minimal right endpoint** of the all interval.\n\nIf `x_0` is not valid, then no `x` such that `x > x_0` can do it. Because `x > x_0` it will not penentrate the left most one (interval 0 in the example above.). And y will also not if y > x. \n\nIf there exists `x` such that `x < x_0`, it can not penentrate more intervals than what `x_0` can.\n\nProof by contradiction: suppose there exists an interval `[s, e]` that `x_1 = x_0 -1` can penentrate but `x_0` cannot. Then `e < x_0`, there exist another right endpoint. Thus `x_0` is not the **minimal right endpoint**, contradiction.\n\n**Claim 2**: The the most greedy y is the **max left endpoint** of the right most interval. \n\nThe proof is similar to claim 1.\n</details>\n\n## 2 How do we collect intervals?\nThis part is trickier than it seems. The intervals are created by double-sided and single-sided conditions.\n\n### 2.1 Single sided\n**Important**: There are two kinds of single-sided case. If we just fill the naive way like we discussed in the chapter 0, it will be problematic.Now consider these case:\n- case 1: [-1, 14, 30, 46, -1]\n- case 2: [14, -1, -1, 46]\n- case 3: [14, -1, -1, 14, 46, -1, -1, 46]\n\n(Reminder: we are now finding the `min_bound` for unfilled elements. Not filled ones)\n\nRecall we build intervals from `-1`\'s neighbors. \n\nIn case1, suppose we check `bound=0`. Intervals are `[[14, 14], [46, 46]]`, then we we can fill `x=14` and `y=46` to make it [14, 14, 30, 46, 46] and return `True`. \n\nIn case2, suppose we check `bound=0`. Intervals are `[[14, 14], [46, 46]]`. By greedy approach, we should `x=14` and `y=46` and the difference will be `max(14-14, 46-14, 46-46)` and return `False`.\n\nIn case3, suppose we check `bound=0`. Intervals are `[[14, 14], [14, 14], [46, 46], [46, 46]]`. By greedy approach, we should `x=14` and `y=46` and the difference will be `0` and return` True`.\n\n#### 2.1.1 Why same intervals but different result?\n\nBecause we filled [14, x, y, 46] and only considered if x and y bounded by existing elements. But here x is bounded by y also. Then when should we check if a position is bounded by another position?\n\nThe problem is actually these positions have **non-adjacent neighbors**. They are not adjacent, but unfilled value between them are bounded by them.\n\nIn case 1, there is no non-adjacent neighbors.\nIn case 2, 14 has non-adjacent neighbors 46.\nIn case 3, 14 has non-adjacent neighbors 14 and 46 has non-adjacent neighbors 46.\n\n<!-- **Can we just check `y > x+ bound`?**\n\nIf we input `bound=0`, our function should return `True` for the minimal unfilled difference is actually `0`. -->\n\n#### 2.1.2 Sollution \n\nFor any one-sided case, we check if it has non-adjacent neighbor by check its previous filled digit and next filled digit.\n\n\nWe record the true neighbor and non-adjacent neighbor as `[a, b]`, we need to check if these two conditions both hold:\n- `y > x + bound` (condition 2-1)\n- Not `x` or `y` in both `[a-bound,a+bound]` and `[b-bound,b+bound]` (condition 2-2)\n\nThis is because if (2-1) holds, we can only fill all `-1` position in beteen with either `x` or `y`. If no `x` or `y` can fit this, then we return `False`.\n\n### 2.2 Double sided\nEasier than signle-sided. For case like `[a, -1, b]`, we can do `lo = min(a, b)` and `hi = max(a, b)`. \n\nIf `lo + bound < hi - bound`, the interval is an empty set. No point can penetrate this interval and we should return `False`. Other wise, check if `x` or `y` can penntrate this interval.\n\n\n# Complexity\n- Time complexity: $$O(Nlog(M))$$, where $$M$$ is `max(nums)`, $$N$$ is the length of `nums`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n n = len(nums)\n # For detect non-adjacent neighbors.\n next_filled = [-100] * n\n prev_filled = [-100] * n\n p = -100\n for i in range(n):\n prev_filled[i] = p\n if nums[i] != -1:\n p = i\n p = -100\n for i in range(n-1, -1, -1):\n next_filled[i] = p\n if nums[i] != -1:\n p = i\n\n double_sided = []\n single_sided = []\n # extra_check is used for saving non-adjacent neighbor\n extra_check = []\n\n for i in range(n):\n if nums[i] == -1:\n p, q = prev_filled[i], next_filled[i]\n # Double sided condition\n if prev_filled[i] == i-1 and next_filled[i] == i+1:\n double_sided.append([nums[p], nums[q]])\n\n # Single-sided condition\n elif prev_filled[i] == i-1:\n single_sided.append([nums[p]])\n # Non-adjacent neighbors\n if 0 <= q < n:\n extra_check.append([nums[p], nums[q]])\n\n # Single-sided condition\n elif next_filled[i] == i+1:\n single_sided.append([nums[q]])\n # Non-adjacent neighbors\n if 0 <= p >= 0:\n extra_check.append([nums[p], nums[q]])\n\n # Skip zero-sided condition.\n\n # Max difference between filled elements\n existed_gap = 0\n for i in range(n-1):\n if nums[i] != -1 and nums[i+1] != -1:\n existed_gap = max(existed_gap, abs(nums[i]-nums[i+1]))\n\n # If there is no conditions created. min_bound will be 0.\n if not double_sided and not single_sided:\n return existed_gap\n\n def isValid(bound):\n # Create intervals by both coditions and input `bound`\n intervals = []\n for eq in double_sided:\n lo, hi = min(eq), max(eq)\n # Empty set (Chapter 2.2)\n if lo + bound < hi - bound:\n return False\n intervals.append([hi-bound, lo+bound])\n for eq in single_sided:\n intervals.append([eq[0]-bound, eq[0]+bound])\n \n # Two greedy point for checking (Chapter 1.1)\n x = min(r for l, r in intervals)\n y = max(l for l, r in intervals)\n \n # Check Non-adjacent neighbors (Chapter 2.1.2)\n if abs(y-x) > bound and not all(any(abs(a-param) <= bound and abs(b-param) <= bound for param in (x, y)) for a, b in extra_check):\n return False\n\n # Each intervals should be penetrate by x or y\n return all(l<= x <=r or l <= y <= r for l, r in intervals)\n\n # Left side Binary Search\n l = 0\n r = max(nums)+1\n while l < r:\n m = (l+r) // 2\n if not isValid(m):\n l = m + 1\n else:\n r = m\n return max(existed_gap, l)\n```
| 1
| 0
|
['Python3']
| 0
|
minimize-the-maximum-adjacent-element-difference
|
Python 3 | Detailed Explanation with Extensive Comments on My Thinking Process
|
python-3-detailed-explanation-with-exten-kbrx
|
Observations\n\n## Which algorithm to use?\n\nIt\'s hard to direcly choose x and y to minimize the maximum absolute difference, but it\'s not as hard to check i
|
ianlo0511
|
NORMAL
|
2024-11-17T17:07:12.789193+00:00
|
2024-11-17T17:07:12.789228+00:00
| 89
| false
|
# Observations\n\n## Which algorithm to use?\n\nIt\'s hard to direcly choose `x` and `y` to minimize the maximum absolute difference, but it\'s not as hard to check if we can find a pair of `(x, y)` to achieve the maximum absolute difference as some arbitrary number `d` \u2014 binary search can be a good fit.\n\n## How to check?\n\nNote that if we know the minimum and maximum positive integers that are adjacent to some -1 (denoted as `min_val` and `max_val`), it\'s clear that we should always choose `x` as `min_val + d` and `y` as `max_val - d` (assuming `x <= y`), since they are the two furthest numbers we can go away from `min_val` and `max_val`, respectively.\n\nThis observation also tells us that if `2 * d <= min_val + max_val`, we can skip the check, since if we choose `x` as `min_val + d`, no integer between `[min_val, max_val]` can lead to a maximum absolute difference larger than `d`.\n\nTo check, we can simply confirm if we can fill in each -1 segment with either `x` or `y` individually (note that each segment is independent from each other). It leads to an exponential solution at the first glance (as we have to enumerate through all permutations), but can be optimized with the following observation.\n\n## Compression\n\nWe can compress the array with two observations below:\n\n1. An integer that is not adjacent to any -1 doesn\'t matter to the check (it does potentially give us a lower bound of the maximum absolute difference, though).\n2. Any -1 that is adjacent to -1 on both sides doesn\'t matter to the check \u2014 we\'ll just always choose `x` or `y`, and the absolute difference it incurs would eitehr be `0` or `x - y`. If it\'s `x - y`, it means that the two -1 adjacent to it has different values, and removing the -1 in between doesn\'t have any impact on the analysis.\n\nThe second observation is important to eliminate the exponential factor in the check, as the number of permutations becomes at most 4 for each segment after the compression.\n\n# Approach\nEquipped with all the observations, a high-level overview of the approach can be described as (1) compress the array, then (2) do binary search on the maximum distance `d` to find the answer.\n\nSee comments in the code for detailed explanation.\n\n# Complexity\n- Time complexity: $O(N\\log M)$, where $N$ is the legnth of the array, and `M` is the difference between the maximum and minimum integers in the array.\n\n- Space complexity: $O(N)$\n\n# Code\n```python3 []\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n n = len(nums)\n min_val, max_val = 10 ** 9 + 1, 0\n first, last = None, None\n arr = []\n lower = 0\n\n # step 1: "squeeze" the array to remove unneeded numbers\n for idx, num in enumerate(nums):\n if num == -1:\n # squeeze -1 segments to have length at most 2\n if len(arr) >= 2 and arr[-2] == -1 and arr[-1] == -1:\n continue\n arr.append(num)\n else:\n if first is None:\n first = num\n last = num\n if (\n (idx > 0 and nums[idx - 1] == -1) or\n (idx < n - 1 and nums[idx + 1] == -1)\n ):\n # only consider positive integers actually adjacent to -1\n arr.append(num)\n min_val = min(min_val, num)\n max_val = max(max_val, num)\n\n # the lower bound of the max abs diff is the diff between existing nums\n lower = max(\n lower,\n (\n -1 if idx <= 0 or nums[idx - 1] == -1\n else abs(nums[idx] - nums[idx - 1])\n ),\n (\n -1 if idx >= n - 1 or nums[idx + 1] == -1\n else abs(nums[idx] - nums[idx + 1])\n )\n )\n\n # if the length of the squeezed array is 0, it means\n # (1) there is no -1, or\n # (2) there is no positive integer\n # in either case, the answer should be the lower bound\n # note that the lower bound is initialized to 0, which covers (1)\n if len(arr) == 0:\n return lower\n\n # not required, but will eliminate some annoying boundary check\n # it doesn\'t affect the final answer, as\n # (1) if the first number in the array is -1, it means that the very\n # first positive integer we see is definitely adjacent to some -1\n # (2) if the last number in the array is -1, it means that the very\n # last positive integer we see is also adjacent to some -1\n arr = (\n ([] if arr[0] != -1 else [first]) +\n arr +\n ([] if arr[-1] != -1 else [last])\n )\n\n # check if we can acheive the max abs diff as d\n # min_val and max_val are the min / max integers adjacent to some -1\n def check(arr, min_val, max_val, d):\n # if max_val - min_val <= 2 * d, choosing x as min_val + d would naturally\n # satisfy the condition\n if max_val - min_val <= 2 * d:\n return True\n\n # otherwise, we check if we can acheive the condition by setting x and y\n # as min_val + d and max_val - d, respectively\n i, n = 0, len(arr)\n x, y = min_val + d, max_val - d\n while i < n:\n if arr[i] == -1:\n # two (or more) consecutive -1, enumerate through all combinations\n if arr[i + 1] == -1:\n flag = False\n for v1, v2 in [(x, x), (x, y), (y, x), (y, y)]:\n if (\n abs(arr[i - 1] - v1) <= d and\n abs(arr[i + 2] - v2) <= d and\n abs(v1 - v2) <= d\n ):\n flag = True\n break\n i += 2\n # single -1\n else:\n flag = False\n for v in [x, y]:\n if abs(arr[i - 1] - v) <= d and abs(arr[i + 1] - v) <= d:\n flag = True\n break\n i += 1\n\n if not flag:\n return False\n else:\n i += 1\n\n return True\n\n # a naive upper bound of the answer is max_val - min_val\n left, right = lower, max_val - min_val\n # early stop if the max abs diff between existing integers is already larger\n # than the naive upper bound\n if left >= right:\n return left\n\n # binary search\n while left < right:\n mid = (left + right) // 2\n if check(arr, min_val, max_val, mid):\n right = mid\n else:\n left = mid + 1\n\n return right\n\n```
| 1
| 0
|
['Python3']
| 0
|
minimize-the-maximum-adjacent-element-difference
|
Binary Search on diff. || maintain range L - R and if R-L>=1... detailed explanation. MUST CHECK!!
|
binary-search-on-diff-maintain-range-l-r-yf2k
|
Hard problem made easy.
Observation + Binary Search = AC
Reconstruct array bcz repeatation of adjacent element does'nt affect solution and consecutive 2 and m
|
Priyanshu_pandey15
|
NORMAL
|
2024-11-17T07:39:20.172115+00:00
|
2024-12-25T20:01:46.554037+00:00
| 188
| false
|

---
- Hard problem made easy.
- Observation + Binary Search = AC
- Reconstruct array bcz repeatation of adjacent element does'nt affect solution and consecutive 2 and more -1 can be treated as 2, -1's.
- Since we know, our abs. diff should not exceed "x", so every possible -1 and its adjacent req = [(x - arr[i]) ... (x + arr[i])]
- And compute this range for every -1 with keep on truncating the range and at last if range L to R satisfies R-L >=1 then true.
- If R-L == 0, then replace every -1 with R(or L) & then check if array satisfies the abs diff condition of "x" or not, if yes then true else false.
- If L > R then we have only two posiibilities for -1 replacement as either 'L' or 'R', check if array satisfies the abs diff condition of "x" or not by replacing -1 with either of L or R, if yes then true else false.
---
`UPVOTE IF YOU UNDERSTAND OR COMMENT FOR DOUBT.`
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(n.logn)$$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(n)$$
# Code
```java []
class Solution {
static int[] reConstruct(int[] nums) {
int n = nums.length, i = 0, x = 0, freq = 0;
int[] temp = new int[n];
while (i < n) {
int current = nums[i];
freq = 0;
while (i < n && current == nums[i]) {
freq++;
i++;
}
if (current == -1 && freq >= 2) {
temp[x++] = current;
}
temp[x++] = current;
}
int[] res = new int[x];
for (int j = 0; j < x; j++) {
res[j] = temp[j];
}
return res;
}
static int maxStartDiff(int[] arr) {
int n = arr.length, max = 0;
for (int i = 0; i < n - 1; i++) {
if (arr[i] != -1 && arr[i + 1] != -1) {
max = Math.max(max, Math.abs(arr[i] - arr[i + 1]));
}
}
return max;
}
static public int minDifference(int[] nums) {
nums = reConstruct(nums);
int ans = -1;
int start = maxStartDiff(nums), end = 1000000000, mid = 0;
while (start <= end) {
mid = start + (end - start) / 2;
boolean can = canBe(nums, mid);
if (can) {
ans = mid;
end = mid - 1;
} else
start = mid + 1;
}
return ans;
}
static boolean canBe(int[] arr, int mid) {
int to = Integer.MAX_VALUE, from = -1, n = arr.length;
for (int i = 0; i < arr.length; i++) {
if (arr[i] == -1) {
if (i > 0) {
if (arr[i - 1] != -1) {
int left = -1;
left = arr[i - 1] - mid;
int right = mid + arr[i - 1];
from = Math.max(from, left);
to = Math.min(to, right);
}
}
if (i < n - 1) {
if (arr[i + 1] != -1) {
int left = arr[i + 1] - mid;
int right = mid + arr[i + 1];
from = Math.max(from, left);
to = Math.min(to, right);
}
}
}
}
if (from < to)
return true;
if (from == to) {
int[] temp = Arrays.copyOf(arr, n);
int maxDiff = -1;
for (int i = 0; i < n; i++) {
if (arr[i] == -1)
temp[i] = from;
}
for (int i = 0; i < n - 1; i++) {
maxDiff = Math.max(maxDiff, Math.abs(temp[i] - temp[i + 1]));
}
if (maxDiff > mid)
return false;
return true;
}
int[] temp = Arrays.copyOf(arr, n);
for (int i = 0; i < n; i++) {
if (temp[i] == -1) {
if (i == 0) {
if (temp[i + 1] != -1) {
if (Math.abs(temp[i + 1] - from) <= mid) {
temp[i] = from;
} else if (Math.abs(temp[i + 1] - to) <= mid) {
temp[i] = to;
}else
return false;
}
} else if (i == n - 1) {
if (temp[i - 1] != -1) {
if (Math.abs(temp[i - 1] - from) <= mid) {
temp[i] = from;
} else if (Math.abs(temp[i - 1] - to) <= mid) {
temp[i] = to;
}else
return false;
}
} else {
if (temp[i - 1] == -1) {
if (Math.abs(temp[i + 1] - from) <= mid) {
temp[i] = from;
} else if (Math.abs(temp[i + 1] - to) <= mid) {
temp[i] = to;
} else
return false;
} else {
if (temp[i + 1] == -1) {
if (Math.abs(temp[i - 1] - from) <= mid) {
temp[i] = from;
} else if (Math.abs(temp[i - 1] - to) <= mid) {
temp[i] = to;
} else
return false;
} else {
if (Math.abs(temp[i - 1] - from) <= mid && Math.abs(temp[i + 1] - from) <= mid)
temp[i] = from;
else if (Math.abs(temp[i - 1] - to) <= mid && Math.abs(temp[i + 1] - to) <= mid)
temp[i] = to;
else
return false;
}
}
}
}
}
return true;
}
}
```
| 1
| 0
|
['Binary Search', 'Java']
| 1
|
minimize-the-maximum-adjacent-element-difference
|
BEATS 100% || Java Solution || Optimum Solution
|
beats-100-java-solution-optimum-solution-iliy
|
Intuition\n- The problem requires determining the minimal difference that ensures an array remains sorted after replacing -1 values in the array. The approach i
|
yallavamsipavan1234
|
NORMAL
|
2024-11-17T04:14:51.245919+00:00
|
2024-11-17T04:14:51.245951+00:00
| 285
| false
|
# Intuition\n- The problem requires determining the minimal difference that ensures an array remains sorted after replacing -1 values in the array. The approach involves analyzing intervals where -1s appear and ensuring the replacements maintain the sorted property of the array.\n\n# Approach\n- **Identify Segments :**\n\n - Traverse the array and identify segments where -1 values appear.\n\n - Track the boundaries of each segment and their lengths.\n\n- **Binary Search for Minimal Difference :**\n\n - Use binary search to find the minimum possible value that ensures the array remains sorted.\n\n - For each middle value during the binary search, use a helper function to check if the array can be sorted.\n\n- **Checking Validity :**\n\n - The helper function applies the minimal difference constraint and checks if the array remains sorted.\n\n - It calculates potential values for boundaries and ensures they fit within the constraints.\n\n# Complexity\n- Time complexity: `O(n * log(max_element))`\n\n- Space complexity: `O(n)`\n\n# Code\n```java []\nclass Solution {\n public int minDifference(int[] nums) {\n ArrayList<int[]> arr = new ArrayList<>();\n int n = nums.length;\n int last = -1;\n int min = 0;\n for(int i=0;i<n;i++) {\n if(nums[i] != -1) {\n if(i>0 && nums[i-1] != -1) min = Math.max(min,Math.abs(nums[i]-nums[i-1]));\n last = i;\n continue;\n }\n int p = i;\n while(p<n && nums[p] == -1) p++;\n int cnt = p-i;\n if(p==n) {\n arr.add(new int[]{last,-1,cnt});\n break;\n } else {\n arr.add(new int[]{last,p,cnt});\n }\n i = p-1;\n }\n if(arr.size() == 0) return min;\n int l=min,r=(int)1e9;\n while(l<r) {\n int mid = l+(r-l)/2;\n boolean flag = check(arr,mid,nums);\n if(flag) {\n r = mid;\n } else {\n l = mid+1;\n }\n }\n return l;\n }\n boolean check(ArrayList<int[]> arr,int l,int[] nums) {\n int min = Integer.MAX_VALUE;\n int max = 0;\n for(int[] seg:arr) {\n if(seg[0] != -1) {\n min = Math.min(nums[seg[0]]+l,min);\n max = Math.max(nums[seg[0]]-l,max);\n }\n if(seg[1] != -1) {\n min = Math.min(nums[seg[1]]+l,min);\n max = Math.max(nums[seg[1]]-l,max); \n }\n }\n if(min>=max) return true;\n for(int[] seg:arr) {\n if(seg[0] == -1 || seg[1] == -1) continue;\n int m1 = Math.max(nums[seg[0]],nums[seg[1]]);\n int m2 = Math.min(nums[seg[0]],nums[seg[1]]);\n if((Math.abs(m1-min)<=l && Math.abs(m2-min)<=l) || (Math.abs(m1-max)<=l && Math.abs(m2-max)<=l)) continue;\n if(Math.abs(max-m1)<=l && Math.abs(min-m2)<=l && Math.abs(min-max)<=l && seg[2]>1) continue;\n return false;\n }\n return true;\n }\n}\n```
| 1
| 1
|
['Java']
| 1
|
minimize-the-maximum-adjacent-element-difference
|
DP + Greedy [EXPLAINED]
|
dp-greedy-explained-by-r9n-wxo2
|
IntuitionFind the minimum difference between adjacent elements in an array, where some elements are missing and represented by -1. We can replace these -1 value
|
r9n
|
NORMAL
|
2025-02-12T06:09:31.251597+00:00
|
2025-02-12T06:09:31.251597+00:00
| 9
| false
|
# Intuition
Find the minimum difference between adjacent elements in an array, where some elements are missing and represented by -1. We can replace these -1 values to minimize the difference between adjacent elements. The challenge is to fill in the missing elements optimally.
# Approach
First, count how many -1 values there are and if there are none, just find the largest difference between adjacent numbers directly. If all values are -1, the answer is 0 since we can assign the same value to all positions. If not all values are -1, calculate the minimum and maximum values around the missing elements and use DP to try filling them in. A binary search approach helps to find the smallest maximum difference by testing various possible values.
# Complexity
- Time complexity:
O(n * log(max_diff)), where n is the length of the array and max_diff is the range of possible differences, making it efficient for large inputs.
- Space complexity:
O(n), due to the dp table used for dynamic programming to store intermediate results.
# Code
```rust []
use std::cmp::{min, max};
impl Solution {
fn find(nums: &Vec<i32>) -> i32 {
let n = nums.len();
let mut ans = 0;
for i in 1..n {
ans = max(ans, (nums[i] - nums[i - 1]).abs());
}
ans
}
fn find_min(arr: &Vec<i32>, p: usize, x: i32, y: i32, i: usize, dp: &mut Vec<Vec<i32>>) {
let n = arr.len();
dp[n][0] = 0;
dp[n][1] = 0;
for ind in (1..n).rev() {
for pre in 0..=1 {
let mut ans = i32::MAX;
if arr[ind] == -1 {
let mut prev = arr[ind - 1];
if prev == -1 && pre == 0 {
prev = x;
} else if pre == 1 {
prev = y;
}
ans = min(ans, max((x - prev).abs(), dp[ind + 1][0]));
ans = min(ans, max((y - prev).abs(), dp[ind + 1][1]));
} else {
let mut prev = arr[ind - 1];
if prev == -1 && pre == 0 {
prev = x;
} else if pre == 1 {
prev = y;
}
ans = min(ans, max((arr[ind] - prev).abs(), dp[ind + 1][0]));
}
dp[ind][pre] = ans;
}
}
}
pub fn min_difference(nums: Vec<i32>) -> i32 {
let n = nums.len();
let mut one = 0;
for &it in &nums {
if it == -1 {
one += 1;
}
}
if one == n {
return 0;
}
if one == 0 {
return Solution::find(&nums);
}
let mut max_bound = i32::MIN;
let mut min_bound = i32::MAX;
for i in 0..n {
if nums[i] != -1 {
if i > 0 && nums[i - 1] == -1 {
min_bound = min(min_bound, nums[i]);
max_bound = max(max_bound, nums[i]);
}
if i != n - 1 && nums[i + 1] == -1 {
max_bound = max(max_bound, nums[i]);
min_bound = min(min_bound, nums[i]);
}
}
}
let mut dp = vec![vec![-1; 2]; n + 1];
// Make solve mutable by adding `mut` here
let mut solve = |max_diff: i32| -> bool {
let x = min_bound + max_diff;
let y = max_bound - max_diff;
for i in 0..=n {
dp[i][0] = -1;
dp[i][1] = -1;
}
let mut ans = i32::MAX;
Solution::find_min(&nums, 0, x, y, 1, &mut dp);
if nums[0] == -1 {
ans = min(ans, min(dp[1][0], dp[1][1]));
} else {
ans = min(ans, dp[1][0]);
}
ans <= max_diff
};
let mut low = 0;
let mut high = 1_000_000_000;
let mut ans = -1;
while low <= high {
let mid = low + (high - low) / 2;
if solve(mid) {
ans = mid;
high = mid - 1;
} else {
low = mid + 1;
}
}
ans
}
}
```
| 0
| 0
|
['Array', 'Binary Search', 'Dynamic Programming', 'Greedy', 'Rust']
| 0
|
minimize-the-maximum-adjacent-element-difference
|
Explanation with video - Java
|
explanation-with-video-java-by-gvp-w6g6
|
Intuition\nStarting with a basic use case like [2, -1, 16] for example, where the answer to the above simple case is 7 which is quite easy to see because (16 -
|
gvp
|
NORMAL
|
2024-12-05T22:28:27.210141+00:00
|
2024-12-06T07:43:26.095363+00:00
| 49
| false
|
# Intuition\nStarting with a basic use case like [2, -1, 16] for example, where the answer to the above simple case is `7` which is quite easy to see because `(16 - 2) / 2 = 7` therefore `d` is 7 and `x = 9`.\n\nLets expand to a bit more complicated use case like `[2, -1, 16, 12, -1, 4, 5, -1, 16, 19, -1, 18, 19, -1, 32]` Could we still use x in place of -1 and satisfy the condition `<= d` for all adjacent elements? We see it does not work for this case and we can see why thats because as the range of numbers increase (in the above case 32 for example) we have to also increase our range `d`. \n\nBut, whats the optimal value for d, increase by how much?\n\nI have putup a youtube video explaining my thought process and approach. Please give it a watch if you would like.\n\n[Youtube Video](https://www.youtube.com/watch?v=2fCtjA_eitU)\n\n\n# Approach\n- if array contains all -1; simply return 0\n- calculate currMax\n- calculate min and max from array\n- find d by doing a binarySearch\n- calculate x = min + d; y = max - d;\n- check if this x and y meets the criteria that difference between adjacent elements does not exceed d. i.e |a - b| <= d\n - If |a - b| > d binary search the upper bound [d, high]\n - if |a - b| <= d save this as an potential ans and binary search the lower bound [low, d - 1]\n- Finally return max(currMax, ans)\n\n# Complexity\n- Time complexity:\n`O(n log k)`\nwhere n is the number of elements in the array\nk is the max array element\n\n- Space complexity:\nO(n)\n\n# Code\n```java []\nimport java.util.ArrayList;\nimport java.util.Arrays;\nimport java.util.List;\n\nclass Solution {\n record Interval(int s, int e, boolean hasMoreThanOne){\n static boolean check(int a, int mid, int b, int range){\n return Math.abs(mid - a) <= range && Math.abs(mid - b) <= range;\n }\n static boolean check(int a, int mid1, int mid2, int b, int range){\n return Math.abs(mid1 - a) <= range && Math.abs(mid1 - mid2) <= range && Math.abs(mid2 - b) <= range;\n }\n }\n\n public int minDifference(int[] nums) {\n boolean noPositiveNum = Arrays.stream(nums).filter(i -> i != -1).findAny().isEmpty();\n if(noPositiveNum){\n return 0;\n }\n int currentMax = getCurrentMax(nums);\n List<Interval> intervals = buildIntervals(nums);\n int minStart = Integer.MAX_VALUE, maxEnd = Integer.MIN_VALUE;\n for (Interval interval : intervals) {\n minStart = Math.min(minStart, Math.min(interval.e, interval.s));\n maxEnd = Math.max(maxEnd, Math.max(interval.e, interval.s));\n }\n int l = 0, h = maxEnd, m;\n int ans = -1;\n while(l <= h){\n m = l + (h - l) / 2;\n boolean result = calculateFromIntervals(intervals, minStart + m, maxEnd - m, m);\n if(result){\n ans = m;\n h = m - 1;\n } else {\n l = m + 1;\n }\n }\n return Math.max(ans, currentMax);\n }\n\n private int getCurrentMax(int[] nums){\n int currMax = Integer.MIN_VALUE;\n int previous = nums[0];\n for(int i = 1; i < nums.length; i ++){\n if(nums[i] != -1){\n if(previous != -1){\n currMax = Math.max(currMax, Math.abs(previous - nums[i]));\n }\n previous = nums[i];\n } else {\n previous = -1;\n }\n }\n return currMax;\n }\n\n private List<Interval> buildIntervals(int[] nums) {\n int previous = -1;\n int minusOneCount = 0;\n List<Interval> intervals = new ArrayList<>();\n for (int num : nums) {\n if (num == -1) {\n minusOneCount ++;\n } else {\n if (minusOneCount > 0) {\n intervals.add(new Interval(previous != -1 ? previous : num, num, minusOneCount > 1));\n minusOneCount = 0;\n }\n previous = num;\n }\n }\n if(nums[nums.length - 1] == -1){\n intervals.add(new Interval(previous, previous, minusOneCount > 1));\n }\n return intervals;\n }\n\n boolean calculateFromIntervals(List<Interval> intervals, int minStart, int maxEnd, int maxDiff){\n for (Interval interval : intervals) {\n if (interval.hasMoreThanOne) {\n boolean res1 = Interval.check(interval.s, minStart, minStart, interval.e, maxDiff);\n boolean res2 = Interval.check(interval.s, minStart, maxEnd, interval.e, maxDiff);\n boolean res3 = Interval.check(interval.s, maxEnd, minStart, interval.e, maxDiff);\n boolean res4 = Interval.check(interval.s, maxEnd, maxEnd, interval.e, maxDiff);\n if (!res1 && !res2 && !res3 && !res4) {\n return false;\n }\n } else {\n boolean res1 = Interval.check(interval.s, minStart, interval.e, maxDiff);\n boolean res2 = Interval.check(interval.s, maxEnd, interval.e, maxDiff);\n if (!res1 && !res2) {\n return false;\n }\n }\n }\n return true;\n }\n}\n```
| 0
| 0
|
['Java']
| 0
|
minimize-the-maximum-adjacent-element-difference
|
C# Solution
|
c-solution-by-advalas-kvnt
|
Intuition\n Describe your first thoughts on how to solve this problem. \nI wasnt able to complete this during the contest a few weeks ago but it was bugging me
|
advalas
|
NORMAL
|
2024-12-04T15:40:20.390406+00:00
|
2024-12-04T15:41:12.743428+00:00
| 5
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI wasnt able to complete this during the contest a few weeks ago but it was bugging me that i didnt finish it. I decided to come back to it and see if i could finish it in C# since nobody else has done that.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe algorithm processes the input array in two main passes:\nFirst pass: Calculates initial values\nSecond pass: Handles sequences of -1 values\n## First Pass\nIn the first loop, the function iterates through adjacent pairs of elements in the array and does the following:\nIf both elements are positive, it updates maxAdj with the maximum absolute difference between adjacent positive elements.\nIf at least one element is positive, it updates minA (minimum of positive elements) and maxB (maximum of positive elements).\n## Second Pass\nThe second loop is more complex and handles sequences of -1 values in the array:\nIt identifies sequences of -1 values.\nFor each sequence, it considers the values immediately before and after the sequence (if they exist).\nIt calculates a local result based on these surrounding values and the length of the -1 sequence.\nThe global result res is updated with the maximum of these local results.\n\n## Key Variables\n\n- maxAdj: Maximum difference between adjacent positive elements\n- minA: Minimum value among positive elements\n- maxB: Maximum value among positive elements\n- res: Accumulates the maximum result from the second pass\n- min2R: A threshold value used in calculations\n\n## Final Result\n\nThe function returns the maximum of two values:\nmaxAdj: The maximum difference between adjacent positive elements\n(res + 1) / 2: Half of the maximum result from the second pass, rounded up\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```csharp []\npublic class Solution {\n public int MinDifference(int[] A) {\n int n = A.Length, maxAdj = 0, minA = int.MaxValue, maxB = 0;\n for (int i = 0; i < n - 1; ++i) {\n int a = A[i], b = A[i + 1];\n if (a > 0 && b > 0) {\n maxAdj = Math.Max(maxAdj, Math.Abs(a - b));\n }\n else if (a > 0 || b > 0) {\n minA = Math.Min(minA, Math.Max(a, b));\n maxB = Math.Max(maxB, Math.Max(a, b));\n }\n }\n\n int res = 0, min2R = (maxB - minA + 2) / 3 * 2;\n for (int i = 0; i < n; ++i) {\n if ((i > 0 && A[i - 1] == -1) || A[i] > 0) continue;\n\n int j = i;\n\n while (j < n && A[j] == -1) {\n j++;\n }\n\n int a = int.MaxValue, b = 0;\n\n if (i > 0) {\n a = Math.Min(a, A[i - 1]);\n b = Math.Max(b, A[i - 1]);\n }\n\n if (j < n) {\n a = Math.Min(a, A[j]);\n b = Math.Max(b, A[j]);\n }\n\n if (j - i == 1) {\n res = Math.Max(res, Math.Min(maxB - a, b - minA));\n }\n\n else {\n res = Math.Max(res, Math.Min(maxB - a, Math.Min(b - minA, min2R)));\n }\n }\n return Math.Max(maxAdj, (res + 1) / 2);\n }\n}\n```
| 0
| 0
|
['C#']
| 0
|
minimize-the-maximum-adjacent-element-difference
|
C# Solution
|
c-solution-by-advalas-8egn
|
Intuition\n Describe your first thoughts on how to solve this problem. \nI wasnt able to complete this during the contest a few weeks ago but it was bugging me
|
advalas
|
NORMAL
|
2024-12-04T15:40:04.363158+00:00
|
2024-12-04T15:40:04.363182+00:00
| 3
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI wasnt able to complete this during the contest a few weeks ago but it was bugging me that i didnt finish it. I decided to come back to it and see if i could finish it in C# since nobody else has done that.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe algorithm processes the input array in two main passes:\nFirst pass: Calculates initial values\nSecond pass: Handles sequences of -1 values\n## First Pass\nIn the first loop, the function iterates through adjacent pairs of elements in the array and does the following:\nIf both elements are positive, it updates maxAdj with the maximum absolute difference between adjacent positive elements.\nIf at least one element is positive, it updates minA (minimum of positive elements) and maxB (maximum of positive elements).\n## Second Pass\nThe second loop is more complex and handles sequences of -1 values in the array:\nIt identifies sequences of -1 values.\nFor each sequence, it considers the values immediately before and after the sequence (if they exist).\nIt calculates a local result based on these surrounding values and the length of the -1 sequence.\nThe global result res is updated with the maximum of these local results.\n\n## Key Variables\n\n- maxAdj: Maximum difference between adjacent positive elements\n- minA: Minimum value among positive elements\n- maxB: Maximum value among positive elements\n- res: Accumulates the maximum result from the second pass\n- min2R: A threshold value used in calculations\n\n## Final Result\n\nThe function returns the maximum of two values:\nmaxAdj: The maximum difference between adjacent positive elements\n(res + 1) / 2: Half of the maximum result from the second pass, rounded up\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```csharp []\npublic class Solution {\n public int MinDifference(int[] A) {\n int n = A.Length, maxAdj = 0, minA = int.MaxValue, maxB = 0;\n for (int i = 0; i < n - 1; ++i) {\n int a = A[i], b = A[i + 1];\n if (a > 0 && b > 0) {\n maxAdj = Math.Max(maxAdj, Math.Abs(a - b));\n }\n else if (a > 0 || b > 0) {\n minA = Math.Min(minA, Math.Max(a, b));\n maxB = Math.Max(maxB, Math.Max(a, b));\n }\n }\n\n int res = 0, min2R = (maxB - minA + 2) / 3 * 2;\n for (int i = 0; i < n; ++i) {\n if ((i > 0 && A[i - 1] == -1) || A[i] > 0) continue;\n\n int j = i;\n\n while (j < n && A[j] == -1) {\n j++;\n }\n\n int a = int.MaxValue, b = 0;\n\n if (i > 0) {\n a = Math.Min(a, A[i - 1]);\n b = Math.Max(b, A[i - 1]);\n }\n\n if (j < n) {\n a = Math.Min(a, A[j]);\n b = Math.Max(b, A[j]);\n }\n\n if (j - i == 1) {\n res = Math.Max(res, Math.Min(maxB - a, b - minA));\n }\n\n else {\n res = Math.Max(res, Math.Min(maxB - a, Math.Min(b - minA, min2R)));\n }\n }\n return Math.Max(maxAdj, (res + 1) / 2);\n }\n}\n```
| 0
| 0
|
['C#']
| 0
|
minimize-the-maximum-adjacent-element-difference
|
Simple Code to Avoid Corner Cases O(N)
|
simple-code-to-avoid-corner-cases-on-by-ntian
|
Intuition\n Describe your first thoughts on how to solve this problem. \n For data size(10^5) provided and the problem aims to find minimaml difference, the fir
|
HaixinShi
|
NORMAL
|
2024-11-26T07:17:36.017874+00:00
|
2024-11-26T07:17:36.017906+00:00
| 27
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n For data size(10^5) provided and the problem aims to find minimaml difference, the first thought came to my mind is binary search. We can simply set min_diff = 0 and max_diff = 10^9 and do binary search. The question became how to check if a candidate difference is valid.\n\nPreviously, I tried to deal it with interval intersection. At the beginning, we have two candidate intervals [1, 10**9] since we can select x and y independently. For each number n adjacent to -1, we aim to have non-empty intersection between [n - diff, n + diff] and at least candidate intervals. After iterating all numbers adjacent to -1, we want to see there are valid candidate non-empty intervals left.\n\nThe above contains a lot of trivial corner cases. Inspired by [Val\'s solution](https://leetcode.com/problems/minimize-the-maximum-adjacent-element-difference/solutions/6054022/binary-search/), we can conservatively select x, y instead of intervals. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n## Preprocessing\nWe will iterate number list and convert [n1, -1, ..., -1, n2] to **tuple (n1, n2, cnt)** where **cnt** is the number of -1s and **cnt > 0**. These sequences contains the gaps that we want to fill.\n\nAmong all **numbers adjcent to -1s**, we want to find the maxmimum and minimum as **max_n** and **min_n**. \n\n\n## Binary Search\n### (x, y) Selection by Candidate d\nFor each candidate difference **d** of binary search, we have **x = min_n + d** and **y = max_n - d** and we want to check if the number list can be filled with x and y. The reason can be explained as follows:\n\n\nFor all (1), (2), (3) cases, we can ensure all numbers will have at most d as difference with x or y.\n\n### Check with given (x, y) and d\nFor a given candidate difference d, when iterating preprocessed sequence, we have two scenarios:\n- For only one -1 between n1 and n2 **(cnt == 1)**, we can only select (x, x) or (y, y).\n- For more than one -1 between n1 and n2 **(cnt > 1)**, we can select (x, x), (y, y), (x, y), (y, x).\n\nAs long as one option can be valid, we can go to check next pairs of numbers.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n# Code\n```python3 []\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n # find the number pairs that have -1s in the gap\n seqs = []\n \n # previous positive number\n prev = None \n \n # count the number of -1s in the gap\n cnt = 0 \n \n # find the max and min of all numbers adjacent to -1\n min_n, max_n = float(\'inf\'), -float(\'inf\') \n \n # find the max gap that we could not improve, where no -1s is in the gap\n max_gap = 0\n \n for i in range(len(nums)):\n if nums[i] == -1:\n cnt += 1\n else:\n if cnt > 0:\n min_n = min(min_n, nums[i])\n max_n = max(max_n, nums[i])\n if prev is None:\n seqs.append((nums[i], nums[i], cnt))\n else:\n seqs.append((prev, nums[i], cnt))\n min_n = min(min_n, prev)\n max_n = max(max_n, prev)\n elif prev is not None:\n # for consecutive positive numbers without -1s in the gap\n max_gap = max(max_gap, abs(nums[i] - prev))\n cnt = 0\n prev = nums[i]\n \n # dealing with trailing -1s\n if cnt > 0 and prev is not None:\n seqs.append((prev, prev, cnt))\n min_n = min(min_n, prev)\n max_n = max(max_n, prev)\n \n # we don\'t have -1 in gaps\n if (min_n, max_n) == (float(\'inf\'), -float(\'inf\')):\n return max_gap\n\n # the following function \n def check(x, y, d):\n for n1, n2, cnt in seqs:\n valid = False\n if cnt > 1:# we can put two numbers in the gap\n ops = [(x, x), (y, y), (x, y), (y, x)]\n else:# we can only put one number in the gap\n ops = [(x, x), (y, y)]\n for g1, g2 in ops:\n if abs(g1 - g2) <= d and abs(n1 - g1) <= d and abs(n2 - g2) <= d:\n valid = True\n if not valid:\n return False\n return True\n\n # start binary search, min_d is the difference we could not change, \n # max_d is aiming to conservatively cover [min_n, -1, -1, max_n] extreme cases\n min_d = max_gap\n max_d = int(math.ceil((max_n - min_n) / 2))\n if min_d >= max_d:\n return min_d\n ans = None\n while min_d <= max_d:\n d = min_d + (max_d - min_d) // 2\n # (min_n + d) and (max_n - d) is most conservative choices\n if check(min_n + d, max_n - d, d):\n ans = d\n max_d = d - 1\n else:\n min_d = d + 1\n return ans\n \n```
| 0
| 0
|
['Binary Search', 'Python3']
| 0
|
minimize-the-maximum-adjacent-element-difference
|
C++ || Binary Search || Dp
|
c-binary-search-dp-by-ks404536-dee4
|
Complexity\n- Time complexity:\n Add your time complexity here, e.g. O(n) \nO(log(1e9) * (n * 2))\n\n- Space complexity:\n Add your space complexity here, e.g.
|
ks404536
|
NORMAL
|
2024-11-24T18:20:41.559721+00:00
|
2024-11-24T18:20:41.559755+00:00
| 63
| false
|
# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(log(1e9) * (n * 2))\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n * 2)\n\n# Code\n```cpp []\nclass Solution {\n int find(vector<int> &nums){\n int n = nums.size();\n int ans = 0;\n for(int i=1;i<n;i++){\n ans = max(ans,abs(nums[i] - nums[i-1]) );\n }\n return ans;\n }\n\n // int findMin(vector<int> &arr, int pre, int x, int y, int ind, vector<vector<int>> &dp){\n // int n = arr.size();\n // if(ind == n) return 0;\n\n // if(dp[ind][pre] != -1) return dp[ind][pre];\n\n // int ans = 1e9;\n\n // if(arr[ind] == -1) {\n\n // int prev = arr[ind-1];\n // if(prev == -1 && pre == 0) {\n // prev = x;\n // }\n // else if(pre == 1) {\n // prev = y;\n // }\n\n // ans = min(ans, max({abs(x - prev), findMin(arr, 0, x, y, ind+1, dp)}));\n // ans = min(ans, max({abs(y - prev), findMin(arr, 1, x, y, ind+1, dp)}));\n // }\n // else {\n // int prev = arr[ind-1];\n // if(prev == -1 && pre == 0) {\n // prev = x;\n // }\n // else if(pre == 1) {\n // prev = y;\n // }\n\n // ans = min(ans, max({abs(arr[ind] - prev), findMin(arr, 0, x, y, ind+1, dp)}));\n // }\n\n // return dp[ind][pre] = ans;\n // }\n\n void findMin(vector<int> &arr, int p, int x, int y, int i, vector<vector<int>> &dp){\n int n = arr.size();\n // if(ind == n) return 0;\n dp[n][0] = 0;\n dp[n][1] = 0;\n\n for(int ind=n-1;ind>=1;ind--){\n for(int pre=0;pre<=1;pre++){\n int ans = 1e9;\n if(arr[ind] == -1) {\n\n int prev = arr[ind-1];\n if(prev == -1 && pre == 0) {\n prev = x;\n }\n else if(pre == 1) {\n prev = y;\n }\n\n ans = min(ans, max({abs(x - prev), dp[ind+1][0]}));\n ans = min(ans, max({abs(y - prev), dp[ind+1][1]}));\n }\n else {\n int prev = arr[ind-1];\n if(prev == -1 && pre == 0) {\n prev = x;\n }\n else if(pre == 1) {\n prev = y;\n }\n\n ans = min(ans, max({abs(arr[ind] - prev), dp[ind+1][0]}));\n }\n dp[ind][pre] = ans;\n }\n }\n }\n\npublic:\n int minDifference(vector<int>& nums) {\n int n = nums.size();\n\n int one = 0;\n for(auto it : nums){\n if(it == -1) one++;\n }\n\n if(one == n) return 0;\n\n if(one == 0){\n return find(nums);\n }\n\n int maxBound = -1e9;\n int minBound = 1e9;\n for(int i=0;i<n;i++){\n if(nums[i] != -1) {\n if(i > 0 && nums[i-1] == -1) {\n minBound = min(minBound, nums[i]);\n maxBound = max(maxBound, nums[i]);\n }\n if(i != n-1 && nums[i + 1] == -1) {\n maxBound = max(maxBound, nums[i]);\n minBound = min(minBound, nums[i]);\n }\n }\n }\n\n vector<vector<int>> dp(n+1, vector<int> (2, -1));\n\n\n auto solve = [&] (int maxDiff) -> bool {\n // return true;\n int x = minBound + maxDiff;\n int y = maxBound - maxDiff;\n\n for(int i=0;i<=n;i++) {\n dp[i][0] = -1;\n dp[i][1] = -1;\n }\n\n int ans = 1e9;\n findMin(nums, 0, x, y, 1, dp);\n if(nums[0] == -1){\n ans = min({ans,dp[1][0], dp[1][1] });\n }\n else ans = min(ans, dp[1][0]);\n\n return ans <= maxDiff;\n };\n\n int low = 0;\n int high = 1e9;\n int ans = -1;\n\n while(low <= high) {\n int mid = low + (high - low)/2;\n\n if(solve(mid)){\n ans = mid;\n high = mid-1;\n }\n else low = mid+1;\n }\n\n return ans;\n }\n};\n```
| 0
| 0
|
['Binary Search', 'Dynamic Programming', 'C++']
| 0
|
minimize-the-maximum-adjacent-element-difference
|
binary search, interval, and special treatment of adjacent -1's
|
binary-search-interval-and-special-treat-pl3n
|
Intuition\nWhen first looking at this problem of filling in missing values (-1s) while minimizing the maximum difference between adjacent numbers, the key insig
|
phi9t
|
NORMAL
|
2024-11-24T03:12:11.562460+00:00
|
2024-11-24T03:12:11.562496+00:00
| 17
| false
|
# Intuition\nWhen first looking at this problem of filling in missing values (-1s) while minimizing the maximum difference between adjacent numbers, the key insight is that we\'re looking for a minimum maximum difference. Whenever we see a "minimize the maximum" or "maximize the minimum" pattern, binary search often proves to be a useful approach.\n\nThe first thought might be to try every possible value for each -1 position, but this would be inefficient. Instead, we can ask a simpler question: "Given a maximum allowed difference D, can we fill in the numbers to satisfy this constraint?" This transforms our optimization problem into a decision problem that we can solve efficiently.\n\n# Approach\nThe solution uses several key techniques:\n\n1. **Preprocessing**\n - First, we clean up the input by only keeping -1s that have at least one non-missing neighbor\n - This removes irrelevant -1s that won\'t affect our final answer\n\n2. **Binary Search Framework**\n - We use binary search on the answer (the maximum difference)\n - For each potential maximum difference D, we check if it\'s possible to fill all -1s while keeping adjacent differences \u2264 D\n - Our search space is from the current maximum difference to the maximum value in the array\n\n3. **Interval-based Validation**\n For each maximum difference D we try:\n ```python\n def get_interval(i, diff):\n # For position i, find valid range of values that keep\n # differences with neighbors \u2264 diff\n # Returns (min_valid, max_valid)\n ```\n\n4. **Greedy Validation**\n ```python\n def validate_diff_range(diff):\n # Get valid intervals for each missing position\n # Sort intervals and check if they can be satisfied greedily\n # Handle special case of consecutive missing values\n ```\n\n5. **Special Cases**\n - Handle consecutive missing values separately\n - Consider boundary conditions (start/end of array)\n - Empty cases (no values to fill)\n\nThe key insight in the validation step is that if we can find valid intervals for each missing position, we can greedily assign values starting from the leftmost interval. If we encounter a gap between intervals that can\'t be bridged with our current maximum difference, we\'ve found an impossible case.\n\n# Complexity\n- Time complexity: $$O(n \\log M)$$ where:\n - n is the length of the array\n - M is the maximum value in the array\n - We do binary search on the range [0, max_value], and each validation takes O(n)\n\n- Space complexity: $$O(n)$$ where:\n - We store indices to fill and intervals\n - The validation process uses additional O(n) space for storing intervals\n - All other operations use constant extra space\n\nThe binary search approach gives us a significant improvement over trying all possible values (which would be exponential). The interval-based validation allows us to efficiently check if a particular maximum difference is achievable without having to try all possible combinations of values.\n\nThe most elegant part of this solution is how it transforms a complex optimization problem into a series of simpler decision problems through binary search, and then uses interval intersection and greedy techniques to efficiently solve each decision problem.\n\nThis approach is not only efficient but also robust, handling various edge cases like consecutive missing values and boundary conditions. The greedy validation step is particularly clever, as it proves that if we can\'t satisfy the constraints greedily, no other assignment of values would work either.\n# Code\n```python3 []\nclass Solution:\n def minDifference(self, original_nums: List[int]) -> int:\n nums = []\n for i, val in enumerate(original_nums):\n if val != -1:\n nums.append(val)\n continue\n if any(True for j in [i - 1, i + 1] if (0 <= j < len(original_nums) and original_nums[j] != -1)):\n nums.append(-1)\n\n inds_to_fill = []\n max_diff = 0\n for i, val in enumerate(nums):\n if val == -1:\n inds_to_fill.append(i)\n continue\n for j in [i - 1, i + 1]:\n if not (0 <= j < len(nums)):\n continue\n if nums[j] == -1:\n continue\n max_diff = max(abs(nums[j] - val), max_diff)\n\n if not inds_to_fill:\n return max_diff\n\n inds_to_validate = []\n for i in inds_to_fill:\n if i - 1 < 0 or i + 2 >= len(nums):\n continue\n if nums[i + 1] != -1:\n continue\n inds_to_validate.append(i)\n\n def get_interval(i, diff):\n curr_intervals = []\n for j in [i - 1, i + 1]:\n if not (0 <= j < len(nums)):\n continue\n val = nums[j]\n if val == -1:\n continue \n curr_intervals.append((val - diff, val + diff))\n assert curr_intervals\n if len(curr_intervals) == 1:\n lhs, rhs = curr_intervals[0]\n else:\n lhs = max(curr_intervals[0][0], curr_intervals[1][0])\n rhs = min(curr_intervals[0][1], curr_intervals[1][1])\n return lhs, rhs\n\n def validate_diff_range(diff):\n intervals = []\n for i in inds_to_fill:\n lhs, rhs = get_interval(i, diff)\n if lhs > rhs:\n return False \n intervals.append((lhs, rhs))\n\n assert intervals\n intervals.sort()\n\n if len(intervals) == 1:\n return True\n\n min_last = intervals[0][-1]\n min_chosen = intervals[0][-1]\n max_chosen = intervals[-1][0]\n num_breaks = 0\n for curr_init, curr_last in intervals:\n if curr_init > min_last:\n min_chosen = min_last\n num_breaks += 1\n if num_breaks > 1:\n return False\n min_last = curr_last\n else:\n min_last = min(curr_last, min_last)\n if num_breaks == 0:\n return True\n\n for i in inds_to_validate:\n can_fit = False\n for lhs, rhs in [\n (min_chosen, min_chosen),\n (max_chosen, max_chosen),\n (max_chosen, min_chosen),\n (min_chosen, max_chosen),\n ]:\n if abs(lhs - rhs) > diff:\n continue\n if abs(nums[i - 1] - lhs) > diff or abs(nums[i + 2] - rhs) > diff:\n continue \n can_fit = True\n break\n if not can_fit:\n return False\n\n return True\n\n\n lower = max_diff\n upper = max(nums) + 1\n while lower < upper:\n diff = lower + (upper - lower) // 2\n if validate_diff_range(diff):\n upper = diff\n else:\n lower = diff + 1\n \n return upper\n\n\n\n\n```
| 0
| 0
|
['Python3']
| 0
|
minimize-the-maximum-adjacent-element-difference
|
C++ | binary search + check constraints case by case
|
c-binary-search-check-constraints-case-b-obe3
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThis approach is based on the hints.\n\nFirstly, some definitions:\n let\'s call the po
|
baihuaxie
|
NORMAL
|
2024-11-20T10:09:54.208525+00:00
|
2024-11-20T10:26:35.457579+00:00
| 52
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis approach is based on the hints.\n\nFirstly, some definitions:\n* let\'s call the positions with -1 as the value the wildcards and I will denote them using ? instead of -1 for better clarity\n* let\'s use $$d_{total}$$ to denote the maximal adjacent difference of the entire array, after some assignment scheme of (x,y), which we don\'t know yet, but we can make some useful observations\n* let\'s call a position in the array that neighbors a wildcard a critical position. for instance, in a case {1, 3, ?, 4}, both elements 3 and 4 are critical positions. we denote these elements by $$a_i$$ and we gather them into a subarray $$a=\\{a_1,a_2,...\\}$$\nnote that it is possible that $$a$$ is empty\nwe denote the maximal adjacent differences of these critical positions with their neighboring wildcards, after some assignments of $$(x,y)$$, simply as $$d$$\n* if we then calculate the adjacent differences on the remaining elements in the array (not critical positions or wildcards), we would obtain some value, let\'s denote it as $$d_l$$, this value will be constant regardless of any assignments of $$(x,y)$$, therefore it forms a lower-bound on the final $$d_{total}$$. in other words, $$d_{total}=\\max(d_l,d)$$\n* in addition, it is useful to find the max and min of $$a$$, and we call them $$\\max(a)$$ and $$\\min(a)$$, respectively\n* I\'ll always assume $$0< x\\le y$$ without loss of generality\n\nNow let\'s make some useful observations. note that henceforth we don\'t need to consider the non-critical positions anymore, so all of the $$d$$\'s in the rest of the notes refer to the maximal adjacent differences produced by the wildcard replacements:\n1. we should always pick $$(x,y)\\in[\\min(a),\\max(a)]$$\nthe choice of $$(x,y)$$ only affects the adjacent differences with the critical positions. suppose we had picked an $$x<\\min(a)$$ and used it to replace some of the wildcards in the original array, and obtained a $$d$$ value. we could always pick another $$x\'=x+1$$ and use $$x\'$$ in the same replacements, since $$x\'$$ is still smaller than all other critical elements in the array, this will only reduce the final $$d$$. we can do this until $$x=\\min(a)$$, therefore there is no reason to pick a value less than $$\\min(a)$$. a similar observation can be made on $$\\max(a)$$.\n2. the optimal $$d\\le\\max(a)-\\min(a)$$\nin other words the upper-bound of the optimal value of $$d$$ is bounded by the difference between the max and min elements in the subarray of critical positions $$a$$.\nwe can prove this by simple contradiction: suppose the maximal adjacent distance $$d>\\max(a)-\\min(a)$$, then there exists two adjacent elements $$a$$ and $$b$$ in the array (wildcards replaced) such that $$a-b=d$$, but $$a-b\\le\\max(a)-\\min(b)<d$$, so there is a direct contradiction. note that I have used observation #1 here implicitly.\n3. the possible values of the maximal adjacent difference of the entire array, given wildcards assigned to either $$x$$ or $$y$$, denoted by $$d_{total}$$, is limited to the range $$[d_l,\\max(a)-\\min(a)]$$\nif instead $$d_l>\\max(a)-\\min(a)$$, then $$d_{total}=d_l$$ and we cannot find any $$(x,y)$$ to reduce it further\n4. it is very easy to get a larger $$d$$ by assigning $$(x,y)$$ deliberately, e.g. pick very large or very small numbers can always produce large $$d$$\n5. the optimal $$d$$ is the smallest possible value, and as we tried to reduce $$d$$, the process is limited by whether or not there exists such a pair of $$(x,y)$$ and a corresponding replacement scheme such that a given $$d$$ is achieved\nwe can see this in a simple example, suppose the array is just $$\\{a,?,b\\}$$, and without loss of generality we assume $$a\\le b$$. suppose we want to pick an $$x$$ to replace the wildcard such that the resulting maximal adjacent difference is $$d$$\nby definition we have:\n$$a-d\\le x\\le a+d$$ and\n$$b-d\\le x\\le b+d$$\nfor them to simultaneously hold we have: $$a+d\\ge b-d$$\nor a lower-bound on $$d$$ is $$d\\ge\\frac{b-a}{2}$$\nif we tried to reduce $$d$$ to even smaller value, it is not possible to find such an $$x$$ that makes it so.\n\nNow let\'s summarize the observations so far:\nthe optimal $$d$$ is limited in a range $$[d_l,\\max(a)-\\min(a)]$$\nwe want to find the lowest possible value of $$d$$ within this range and satisfying the constraints that there exists $$(x,y)$$ replacements to make this $$d$$ possible.\na natural way to do this is to binary search $$d$$ on the range, and write a sub-routine that works in at most $$\\mathcal{O}(N)$$ to check if the the constraints are met, so the total complexity is kept at at most $$\\mathcal{O}(N\\log N)$$ and we will be fine from TLE.\nNow let\'s consider the subroutine. the problem is this: given the subsrray $$a$$ of critical positions and a desired result $$d$$, we need to pick $$(x,y)$$ and assign to wildcard positions such that all resulting adjacent differences are no greater than $$d$$.\nspecifically, we need to meet two constraints:\n1. for all critical positions $$a_i$$ we must have either $$|a_i-x|\\le d$$ or $$|a_i-y|\\le d$$\n2. for consecutive wildcards, it might be necessary to check that $$|x-y|\\le d$$\nthe second constraint is not necessarily required by all test cases, because in some cases we can use only one value to replace all wildcards in a row, but in other cases we must use both values. I\'ll go through this in details later.\n\nwe make the following observation on the optimal choices of $$x$$ and $$y$$, here without loss of generality I have assumed $$x\\le y$$:\nit is optimal to pick $$x=\\min(a)+d$$ and $$y=\\max(a)-d$$\nthe reasoning is illustrated in the following sketch:\n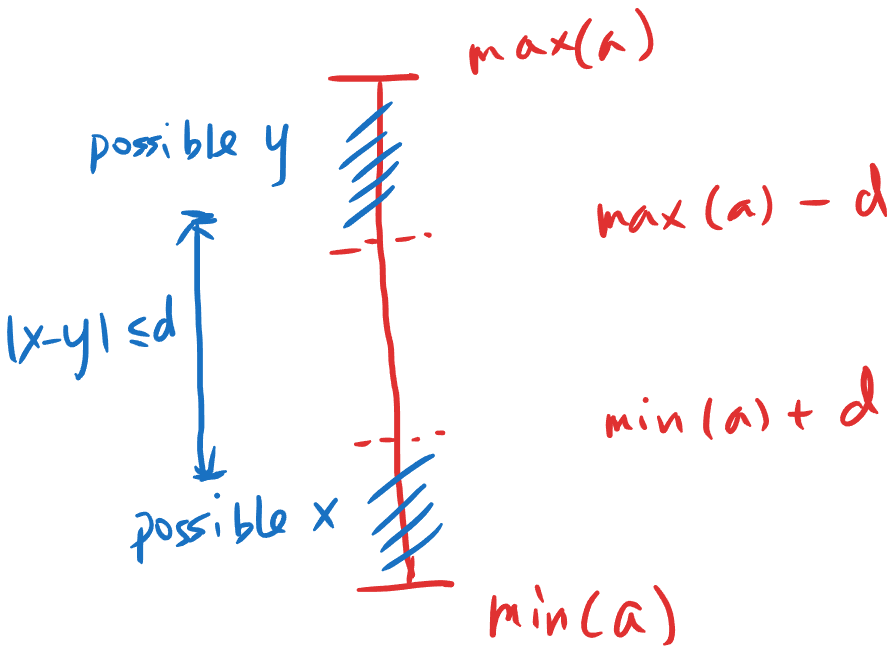\nwe start from the element whose value is $$\\min(a)$$, we know it is neighboring a wildcard since it is by definition in the subarray of critical positions, therefore we must have $$|x-\\min(a)|\\le d$$, or that $$\\min(a)-d\\le x\\le \\min(a)+d$$. similarly we can say for $$y$$ we must have $$\\max(a)-d\\le y\\le\\max(a)+d$$. now considering that it\'s possible that we need to satisfy the constraint that $$|x-y|\\le d$$, it is therfore desirable to choose $$x$$ as large as possible and $$y$$ as small as possible. the choice of $$x=\\min(a)+d$$ and $$y=\\max(a)-d$$ would make it more likely that a smaller $$d$$ is attainable. this is not exactly a strict proof of optimality, but it seems to work fine enough in the test cases.\n\nWith the above observations and analysis, we can present the following approach using binary search.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nAs per the discusions above, the key for the solution is to find a linear time subroutine that checks if the chosen $$(x,y)$$ pair can satisfy the constraints of $$d$$ at all positions neighboring a wildcard (this includes consecutive wildcards).\nConcretely, we need to consider the folowing cases:\n1. $$\\{a,?,b\\}$$\na single wildcard surrounded by two regular numbers.\nwe can put either $$x$$ or $$y$$ here\nif we pick $$x$$ then we must have $$|a-x|\\le d$$ && $$|b-x|\\le d$$\nsimilarly if we pick $$y$$ we have similar constraints.\none of these two sets of constraints must be true\n2. $$\\{?,a\\}$$ or $$\\{a,?\\}$$\na single wildcard as the first or the last of the array\nwe can append $$a$$ to the start or the end of the array in preprocessing, so it reduces to case #1 without impact on the result\n3. $$\\{a, ?, ?\\}$$\ntwo consecutive wildcards following a regular number\nwe consider only the adjacent difference between $$a$$ and the first widlcard, we\'ll defer the constraint on the two wildcards later. pick either $$x$$ or $$y$$ to satisfy the constraint.\nit is necessary that we keep track of which value we\'ve picked, or rather, which value can be picked. I use a 2-bit bitmask to represent this information, so if mask=00 means neither $$x$$ nor $$y$$ satisfy the constraint, we return false directly; mask=01 and mask=10 means only $$x$$ or $$y$$ satisfy the constraint, respectively; and mask=11 means both values are ok, we will choose based on later constraints.\n4. $$\\{?,?,b\\}$$\ntwo consecutive wildcards ending with a regular number\nfirst we consider the constraints on $$b$$ in the usual way. we put our choices of $$(x,y)$$ similarly in a 2-bit mask, call it mask_b.\nthen we have to consider the constraints on the two wildcards, and this can be determined by the values of mask_a and mask_b.\nif mask_a is a default value 0, it means neither $$x$$ nor $$y$$ had been assinged, we are free to pick which one, and obviously we pick the same value as constrained by $$b$$ so as to make the difference zero.\nif mask_a == 11, it means both $$x$$ and $$y$$ are fine, the result is the same, we pick the one to make difference zero.\nif mask_a == 10 or 01, only one of the values $$(x,y)$$ had been assigned to previous wildcards. now there is definitily going to be two adjacent wildcards such that one is constrained by $$b$$ and the other is constrained by a previous assignment. so we take an XOR on mask_a ^ mask_b, if we find that we these two assignments differ, i.e., one picks $$x$$, the other picks $$y$$, we must additionally check the constraint that $$|x-y|\\le d$$.\n\nI\'ll give an example here. suppose nums=[2,-1,4,-1,-1,6]. the optimal $$d$$ is 1, and we have $$x=3$$ and $$y=5$$. we assign $$x$$ to the first wildcard. now for the second wildcard to the right of element 4, it is possible to assign either 3 or 5. so we set mask_a=11 and defer our decision later. for the last wildcard we must assign 5, so mask_b=10. since we determined that we could have picked either 3 or 5 at the previous wildcard, by checking that mask_a ^ mask_b != 11, we can now pick 5 to fill the second wildcard, therefore it is not necessary that $$|x-y|\\le d$$ in this example. had we enforced this constraint we could not have found the lowest possible $$d$$.\n\nBelow is the code in C++ (>=85% submissions) that implements the sketched approach.\n\n\n# Complexity\n- Time complexity: $$\\mathcal{O}(N\\log M)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$N$$ is number of elements in array, $$M$$ is the determined by the values of the array and could be up to 10^9.\n\n- Space complexity: $$\\mathcal{O}(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n bool checkConstraints(vector<int>& nums, int d, int x, int y) {\n\n int n = nums.size();\n\n // two 2-bit bitmasks\n // prev[0] = 1 if using x to replace the wildcard satisfies the constraint\n // prev[1] = 1 if using y to replace the wildcard satisfies the constraint\n // same for post\n int prev = 0, post = 0;\n\n for (int i = 1; i < n-1; ++i) {\n // skip regular positions because we only focus on wildcards to check constraints\n if (nums[i] != -1) continue;\n\n // case: {a, ?, b}\n if (nums[i-1] != -1 && nums[i+1] != -1) {\n if (!((abs(nums[i-1]-x) <= d && abs(nums[i+1]-x) <= d)\n || (abs(nums[i-1]-y) <= d && abs(nums[i+1]-y) <= d)))\n return false;\n }\n \n // case: {a, ?, ?}\n // set prev bits\n if (nums[i-1] != -1 && nums[i+1] == -1) {\n if (abs(nums[i-1]-x) <= d )\n prev = prev | 1;\n if (abs(nums[i-1]-y) <= d)\n prev = prev | (1 << 1);\n if (prev == 0) {\n return false;\n }\n }\n\n // case: {?, ?, a}\n // set post bits\n if (nums[i-1] == -1 && nums[i+1] != -1) {\n if (abs(nums[i+1]-x) <= d)\n post = post | 1;\n if (abs(nums[i+1]-y) <= d)\n post = post | (1 << 1);\n if (post == 0)\n return false;\n\n // if prev==01 && post==10, or prev=10 && post==01\n // this means I have used both x and y as replacements in the consecutive wildcard sequence\n // in this case I must check if |x-y| satisifies the constraint\n // in all other cases, I could use just either x or y (but not both) in the sequence\n // so I don\'t need to check this global constraint\n if ((prev ^ post) == 3) {\n if (abs(x-y) > d)\n return false;\n }\n\n // reset bitmasks after the current consecutive wildcard sequence is finished\n prev = 0;\n post = 0;\n }\n }\n\n return true;\n }\n\n int minDifference(vector<int>& nums) {\n\n // first we check if either the first or the last element is a wildcard\n // that is also neighboring a regular number\n // we reduce these edge cases to a regular case by appending the neighboring regular number\n // so e.g. {?, a} becomes {a, ?, a}, and {a, ?} becomes {a, ?, a}\n // this won\'t have any effect on the result\n // but it simplies the edges cases so that we don\'t have to take special care in subroutines\n // note that nums size might be changed so be careful here\n if (nums[0] == -1 && nums[1] != -1)\n nums.insert(nums.begin(), nums[1]);\n if (nums[nums.size()-1] == -1 && nums[nums.size()-2] != -1)\n nums.push_back(nums[nums.size()-2]);\n int n = nums.size();\n\n // preprocess the array to identify the subarray of elements neighboring a wildcard\n // we need to find the min and max of this subarray to form the initial bound on\n // the maximal adjacent different, d\n int min_a = INT_MAX, max_a = -1;\n int low_d = 0;\n for (int i = 0; i < n-1; ++i) {\n if (nums[i] != -1 && nums[i+1] == -1) {\n min_a = min(min_a, nums[i]);\n max_a = max(max_a, nums[i]);\n }\n if (nums[i] == -1 && nums[i+1] != -1) {\n min_a = min(min_a, nums[i+1]);\n max_a = max(max_a, nums[i+1]);\n }\n \n // if we find two adjacent regular numbers, calculate their difference\n // the max of these regular differences is the lower-bound on d regardless of replacements\n if (nums[i] != -1 && nums[i+1] != -1) {\n low_d = max(low_d, abs(nums[i+1]-nums[i]));\n }\n\n // consecutive widlcards do not require preprocessing\n }\n\n // edge case #1: when there are no critical positions\n // in these cases min_a and max_a are not updated from initial values\n // 1) all elements are regular numbers \n // 2) all elements are wildcards\n // in both cases we return low_d i.e. the lower-bound on d found on all regular numbers\n // in the latter case low_d = initial value 0\n if (min_a == INT_MAX && max_a == -1) \n return low_d;\n \n // edge case #2: min_a == max_a\n // 1) exactly one critical position\n // 2) all critical positions have identical elements\n // in both cases, the critical position\'s adjacent difference can be made zero by picking\n // the right (x,y), so the global d comes down to just low_d\n if (min_a == max_a)\n return low_d;\n \n // the bound on d is [low_d, max_a - min_a]\n // we do a binary search on this range to find the lowest possible d\n // the constraint is checked by making sure there exists an assignment of (x,y) to obtain this d\n int low = max(low_d, 1);\n int high = max_a - min_a;\n int d = max(low_d, high);\n while (low <= high ){\n int mid = low + (high - low) / 2;\n // cout << mid << " | ";\n\n // for a given d, the optimal choice of (x, y) is that\n // x = min_a + d, y = max_a -d\n // if constraints are satisfied, we can reduce d by going to the lower half\n // this process guarantees we find the smallest possible d that satisfies the constraint\n if (checkConstraints(nums, mid, min_a+mid, max_a-mid)) {\n d = mid;\n high = mid-1;\n }\n else {\n low = mid+1;\n }\n }\n\n return d;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
minimize-the-maximum-adjacent-element-difference
|
[Binary Search] Left & Right Neighbours - Easy C++ Solution
|
binary-search-left-right-neighbours-easy-0mwg
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
pran-2110
|
NORMAL
|
2024-11-20T00:00:22.272300+00:00
|
2024-11-20T00:00:22.272347+00:00
| 38
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(N\\log{M})$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n int n=nums.size();\n vector <int> le(n,0),ri(n,0);\n int m=INT_MAX,M=-INT_MAX;\n int flag=1;\n int no1=1;\n int st=-1,en=-1;\n for(int i=0;i<n;i++){\n if(nums[i]!=-1 && ((i>0 && nums[i-1]==-1)||(i<(n-1) && nums[i+1]==-1))){\n m=min(m,nums[i]);\n M=max(M,nums[i]);\n }\n if(nums[i]==-1) no1=0;\n else{\n flag=0;\n if(st==-1) st=nums[i];\n en=nums[i];\n }\n }\n le[0]=st;\n ri[n-1]=en;\n for(int i=1;i<(n-1);i++){\n int j=n-1-i;\n if(nums[i-1]!=-1) {\n le[i]=nums[i-1];\n }\n else{\n le[i]=le[i-1];\n }\n if(nums[j+1]!=-1) {\n ri[j]=nums[j+1];\n }\n else{\n ri[j]=ri[j+1];\n }\n }\n if(nums[n-2]!=-1) le[n-1]=nums[n-2];\n else le[n-1]=le[n-2];\n if(nums[1]!=-1) ri[0]=nums[1];\n else ri[0]=ri[1];\n if(flag) return 0;\n if(no1) m=0,M=0;\n int l=0, r=1e9;\n int ans=r;\n while(l<=r){\n int mid=(l+r)/2;\n int x = m+mid;\n int y = M-mid;\n vector <int> cop(n,0);\n flag=1;\n for(int i=0;i<n;i++){\n if(nums[i]==-1){\n int a = max(abs(le[i]-x),abs(ri[i]-x));\n int b = max(abs(le[i]-y),abs(ri[i]-y));\n cop[i] = (a < b) ? x : y;\n\n }\n else{\n cop[i]=nums[i];\n }\n }\n for(int i=1;i<(n-1);i++){\n if(nums[i]==-1){\n int a = max(abs(cop[i - 1] - x), abs(cop[i + 1] - x));\n int b = max(abs(cop[i - 1] - y), abs(cop[i + 1] - y));\n cop[i] = (a > b) ? y : x;\n }\n }\n for(int i=1;i<n;i++){\n if(abs(cop[i]-cop[i-1])> mid) flag=0;\n }\n if(flag){\n ans=mid;\n r=mid-1;\n }\n else{\n l=mid+1;\n }\n }\n return ans;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
minimize-the-maximum-adjacent-element-difference
|
Two pass, O(n) time
|
two-pass-on-time-by-solid_kalium-r8g4
|
Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Intuition\n- When choosing x and y, we only care about the numbers adjacent to them\n- x an
|
solid_kalium
|
NORMAL
|
2024-11-19T01:47:54.564168+00:00
|
2024-11-19T01:53:36.474209+00:00
| 61
| false
|
# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\n# Intuition\n- When choosing `x` and `y`, we only care about the numbers adjacent to them\n- `x` and `y` will each have a set of adjacent numbers\n - One set will include the smallest adjacent number: `minAdj`\n - The other will include the largest adjacent number: `maxAdj`\n - Since each set is "anchored" at one side and we only care about the variable that is furthest from its "anchor," we can assume both of them are equally far away from their anchor. We\'ll call this `minDist`.\n - We now have only one "actual" variable from which we can calculate our original variables. `x = minAdj + minDist` `y = maxAdj - minDist`\n - *Note that we don\'t actually care about `x` or `y`, so they won\'t appear in the code. And we don\'t care about the actual sets of values, so we don\'t calculate those either. Since we already know one extreme of each set, we can just calculate the relevant metric, the difference between the min and max elements, each time we "assign" an element to a set.*\n- Each sequence of -1\'s can be treated as either one variable or both variables back to back if there at least two -1\'s in a row.\n- Because we are dealing with integers and maximum distances, whenever we split a range into 2 or 3 ranges, we need to round up.\n\n# Approach\nFor each pair of adjacent known numbers, we need to find the minimum distance (`minDist`) that can work for it. Then we need to are forced to choose the maximum of those values. That is, the distance the meets the minimum required by each pair.\n- If two known numbers are adjacent, `minDist` is just the distance between them\n- If a single unknown number is between two known numbers, the variable we will use is the one whose "half" of the overall range covers more of the interval between the two known numbers. Let\'s say I have values for `minAdj`, `loNum`, `hiNum`, and `maxAdj`. Then I\'m trying to decide whether `loNum` and `hiNum` are in the set with `minAdj` or the one with `maxAdj`. To do this, I pick the set that minimizes the distance between it\'s lowest and highest elements. Meaning, I pick the smaller of `hiNum - minAdj` or `maxAdj - loNum`. We can now calculate the necessary `minDist` by dividing that number in half (and rounding up).\n- If two or more unknown numbers are between two known numbers, we have a choice. They can all be the same variable as described in the previous point. Or they can include both variables. In this case, we would be dividing the range between minAdj and maxAdj into three parts. If `x` and `y` are distinct, `minDist` can\'t go any higher.\n - You might wonder, can we stop early then? No. Consider `[10,-1,-1,30,-1,12]`. We can bridge the first gap with `minDist = 7` by dividing the range in thirds. But later we find that we are forced to include a low number in the high set, causing `minDist` to be even larger.\n - We could stop early if we find that the `minAdj` and `maxAdj` numbers are adjacent to the same single unknown value, but I personally didn\'t think it was worth checking for this condition.\n\n# Alternate Thoughts\n\n- I did consider applying my basic rules to calculate `minDiff` for each of the three scenarios (0, 1, 2+ unknowns in a row). Then choosing `x` and `y` using that and `minAdj` and `maxAdj` and calculating the observed `minDiff`. And finally doing a binary search between the two. But it just felt like there was likely enough information to calculate the answer without the search.\n- I also thought the constraints made it an LP problem, but that seemed like overkill and I haven\'t used it recently enough for it to be quick. Plus, leetcode rarely, if ever, assumes you\'ll import a Linear Programming library.\n- Clustering algorithms as a general concept came to mind, but I never got around to looking for a way to use one.\n- I think the key realizations for me were:\n - That values on either side of an unknown are forced into a common set, a la union-find.\n - We can assign one variable to the top half and one to the bottom half of the range `[minAdj, maxAdj]`.\n - If one variable is forced to be far from it\'s bound, we may as well move the other one too because there is no penalty. This allows us to have only one variable.\n\n# Code\n```python3 []\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n n = len(nums)\n\n ### First pass to get minAdj and maxAdj\n\n # Quickly get to first known number\n iFirstNonVar = 0\n while iFirstNonVar < n and nums[iFirstNonVar] == -1:\n iFirstNonVar += 1\n\n # If there are no known numbers\n if iFirstNonVar == n:\n return 0\n\n # Find minAdj and maxAdj\n minAdj = inf\n maxAdj = -inf\n prev = nums[iFirstNonVar] \n unknowns = iFirstNonVar\n for i in range(iFirstNonVar, n):\n num = nums[i]\n\n if num == -1:\n unknowns += 1\n continue\n\n if unknowns >= 1:\n minAdj = min(minAdj, num, prev)\n maxAdj = max(maxAdj, num, prev)\n unknowns = 0\n\n prev = num\n\n if unknowns >= 1:\n minAdj = min(minAdj, prev)\n maxAdj = max(maxAdj, prev)\n\n\n ### Second pass to calculate minDiff\n # One variable will be in each half of [minAdj, maxAdj]\n\n minDiff = 0\n\n prev = nums[iFirstNonVar]\n unknowns = iFirstNonVar\n for i in range(iFirstNonVar, n):\n num = nums[i]\n\n if num == -1:\n unknowns += 1\n continue\n\n if unknowns == 0:\n # No unknowns\n minDiff = max(minDiff, abs(num - prev))\n elif unknowns >= 1:\n # If there is effectively one unknown,\n # find the relevant distance based on which variable would be used\n numLo, numHi = sorted((num, prev))\n pairDiff = min(numHi - minAdj, maxAdj - numLo)\n\n if unknowns == 1:\n # Exactly 1 unknown\n minDiff = max(minDiff, (pairDiff + 1) // 2)\n else:\n # Two cases:\n # 1) Both are the same variable: treat as 1 unknown.\n # 2) Different variables: they need to be evenly spaced between ends of the range\n case1 = (pairDiff + 1) // 2\n case2 = (maxAdj - minAdj + 2) // 3\n minDiff = max(minDiff, min(case1, case2))\n\n unknowns = 0\n\n prev = num\n\n return minDiff\n\n```
| 0
| 0
|
['Greedy', 'Union Find', 'Python3']
| 0
|
minimize-the-maximum-adjacent-element-difference
|
Binary Search | All Test Cases Passes
|
binary-search-all-test-cases-passes-by-f-4jzs
|
Approach\nSame as @votrubac except the extra checkpoint where nums start with -1\n\n# Complexity\n- Time complexity:\nO(nlog(m)) ---- m is of size 10^9 and n is
|
mfarqua00
|
NORMAL
|
2024-11-18T16:48:04.731416+00:00
|
2024-11-18T17:29:14.216411+00:00
| 59
| false
|
# Approach\nSame as [@votrubac](https://leetcode.com/problems/minimize-the-maximum-adjacent-element-difference/solutions/6054022/binary-search/) except the extra checkpoint where nums start with -1\n\n# Complexity\n- Time complexity:\nO(nlog(m)) ---- m is of size 10^9 and n is 10^5\n\n- Space complexity:\nO(1)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n bool checkDiffComp(vector<int>& nums, int x, int y, int gap){\n int count = 0, prev = 0;\n for(int i = 0; i < nums.size(); i++){\n if(nums[i] != -1){\n if(count && prev){\n int diff = min(max(abs(prev-x), abs(nums[i]-x)), max(abs(prev-y), abs(nums[i]-y)));\n if(diff > gap && (count == 1 || abs(y-x) > gap))\n return false;\n }\n else if(count){\n int diff = min(abs(nums[i]-x), abs(nums[i]-y));\n if(diff > gap)\n return false;\n }\n\n count = 0;\n prev = nums[i];\n }\n else{\n count++;\n }\n }\n return true;\n }\n int minDifference(vector<int>& nums) {\n int max_gap = 0, min_mis = INT_MAX, max_mis = 0;\n\n for(int i = 1; i < nums.size(); i++){\n int curr_max = max(nums[i], nums[i-1]);\n if(min(nums[i], nums[i-1]) == -1 && curr_max != -1){\n min_mis = min(min_mis, curr_max);\n max_mis = max(max_mis, curr_max);\n }\n else{\n max_gap = max(max_gap, abs(nums[i] - nums[i-1]));\n }\n }\n\n int l = max_gap, h = (max_mis - min_mis + 1)/2;\n while(l < h){\n int m = (l+h)/2;\n\n if(checkDiffComp(nums, min_mis+m, max_mis-m, m))\n h = m;\n else\n l = m+1;\n }\n return l;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
minimize-the-maximum-adjacent-element-difference
|
My Solution
|
my-solution-by-hope_ma-j82r
|
\n/**\n * Time Complexity: O(n)\n * Space Complexity: O(1)\n * where `n` is the length of the vector `nums`\n */\nclass Solution {\n public:\n int minDifferenc
|
hope_ma
|
NORMAL
|
2024-11-18T10:33:24.555708+00:00
|
2024-11-18T12:40:44.725240+00:00
| 8
| false
|
```\n/**\n * Time Complexity: O(n)\n * Space Complexity: O(1)\n * where `n` is the length of the vector `nums`\n */\nclass Solution {\n public:\n int minDifference(const vector<int> &nums) {\n constexpr int missing = -1;\n const int n = static_cast<int>(nums.size());\n int min_left = numeric_limits<int>::max();\n int max_right = numeric_limits<int>::min();\n for (int i = 0; i < n; ++i) {\n if (nums[i] != missing && ((i > 0 && nums[i - 1] == missing) || (i + 1 < n && nums[i + 1] == missing))) {\n min_left = min(min_left, nums[i]);\n max_right = max(max_right, nums[i]);\n }\n }\n \n int ret = 0;\n for (int i_left = -1, i_right = 0; i_right < n + 1; ++i_right) {\n if (i_right < n && nums[i_right] == missing) {\n continue;\n }\n \n if (i_left == -1 || i_right == n) {\n if (i_right < n && i_right > 0) {\n // at this time, `i_left` == `-1` holds\n ret = max(ret, min((nums[i_right] - min_left + 1) >> 1, (max_right - nums[i_right] + 1) >> 1));\n } else if (i_left > -1 && i_left < n - 1) {\n // at this time, `i_right` == `n` holds\n ret = max(ret, min((nums[i_left] - min_left + 1) >> 1, (max_right - nums[i_left] + 1) >> 1));\n }\n } else {\n if (i_left + 1 == i_right) {\n ret = max(ret, abs(nums[i_left] - nums[i_right]));\n } else {\n const int left = min(nums[i_left], nums[i_right]);\n const int right = max(nums[i_left], nums[i_right]);\n ret = max(\n ret,\n min({\n (right - min_left + 1) >> 1,\n (max_right - left + 1) >> 1,\n i_right - i_left > 2 ? (max_right - min_left + 2) / 3 : numeric_limits<int>::max()\n })\n );\n }\n }\n i_left = i_right;\n }\n return ret;\n }\n};\n```
| 0
| 0
|
[]
| 0
|
minimize-the-maximum-adjacent-element-difference
|
Finding x and y via interval intersections and binary search on answer
|
finding-x-and-y-via-interval-intersectio-zwel
|
Approach\n\n## Key Idea\n1. It is obvious that if we can obtain the answer as mid, then we can obtain a larger answer by choosing x and y accordingly. \n Thu
|
NastyWaterEspresso
|
NORMAL
|
2024-11-18T09:27:57.475774+00:00
|
2024-11-18T13:29:56.455920+00:00
| 55
| false
|
# Approach\n\n## Key Idea\n1. It is obvious that if we can obtain the answer as `mid`, then we can obtain a larger answer by choosing `x` and `y` accordingly. \n Thus, we can apply **binary search** on the answer.\n\n---\n\n## Obtaining `x` and `y` via Interval Intersections\n1. For every `nums[i]` with at least one neighbor with value `-1`, store the interval `[nums[i] - mid, nums[i] + mid]`.\n2. Sort the intervals.\n3. Keep finding common segments of the intervals, allowing at most **two different common segments**.\n4. Note:\n - `x` can lie in the first common segment, and `y` can lie in the second common segment, and vice versa.\n5. If there are **two common segments intersecting**, then replace all the `-1`s in the array with a value that lies in the intersection of the two common segments.\n6. If there is only **one common segment**, then replace all the `-1`s in the array with any one value in that common range.\n7. Suppose the common segments are `[l1, r1]`, `[l2, r2]` and, WLOG (Without Loss of Generality), let `l1 <= l2`. \n - Then it is better to take `x = r1` and `y = l2`, or vice versa.\n\n---\n\n## Dynamic Programming Step\n1. Use **dynamic programming** to solve the following:\n - Given the array `arr`, `x`, `y`, and `mid`, check if we can replace `-1`s by `x` or `y` such that the **maximum adjacent absolute difference** of the array is less than or equal to `mid`.\n\n---\n\n## Steps Summary\n1. Apply **binary search** on the answer.\n2. For each value of `mid`, determine `x` and `y` using interval intersections.\n3. Use dynamic programming to verify whether replacing `-1`s with `x` or `y` satisfies the condition.\n\n\n\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n // Determine the initial low bound\n int negs_cnt = 0;\n int low = 0, high = 1e9;\n for (int i = 1; i < nums.size(); ++i) {\n if (nums[i] != -1 && nums[i - 1] != -1) {\n low = max(low, abs(nums[i] - nums[i - 1]));\n }\n }\n for (int num : nums) {\n if (num == -1)\n negs_cnt++;\n }\n\n if (negs_cnt == 0)\n return low;\n\n // Perform binary search for the minimum possible maximum difference\n int result = INT_MAX;\n\n while (low <= high) {\n int mid = low + (high - low) / 2;\n\n if (isPossible(nums, mid, negs_cnt)) {\n result = mid; // Update result\n high = mid - 1; // Try for a smaller max difference\n } else {\n low = mid + 1; // Try for a larger max difference\n }\n }\n if (result == INT_MAX)\n return low;\n\n return result;\n }\n\nprivate:\n bool isPossible(vector<int>& nums, int mid, const int& cnt) {\n // Form the intervals\n vector<pair<int, int>> intervals;\n for (int i = 0, n = nums.size(); i < n; i++) {\n if (nums[i] != -1 && ((i > 0 && nums[i - 1] == -1) ||\n (i < n - 1 && nums[i + 1] == -1))) {\n intervals.push_back({nums[i] - mid, nums[i] + mid});\n }\n }\n\n // Sort intervals based on their starting points\n sort(intervals.begin(), intervals.end());\n\n // To store the common intervals\n vector<pair<int, int>> common_intervals;\n\n for (auto& interval : intervals) {\n bool merged = false;\n // Try to merge with existing common intervals\n for (auto& common : common_intervals) {\n if (interval.first <= common.second) { // There\'s an overlap\n common.first = max(common.first, interval.first);\n common.second = min(common.second, interval.second);\n merged = true;\n break;\n }\n }\n\n // If it can\'t be merged into any existing common interval\n if (!merged) {\n if (common_intervals.size() < cnt) {\n // Create a new common interval if we can\n common_intervals.push_back(interval);\n } else {\n // If more than `cnt` disjoint intervals are needed, not\n // possible\n return false;\n }\n }\n }\n if (common_intervals.size() == 0)\n return true;\n if (common_intervals.size() == 1)\n return true;\n else {\n sort(common_intervals.begin(), common_intervals.end());\n int x = common_intervals[0].second;\n int y = common_intervals[1].first;\n if (x >= y)\n return true;\n // printf("mid: %d, x: %d, y: %d, possible: %d\\n", mid, x, y,\n // canReplaceAndSatisfy(nums, x, y, mid));\n return canReplaceAndSatisfy(nums, x, y, mid);\n }\n }\n // Function to check if replacing satisfies conditions\n bool canReplaceAndSatisfy(vector<int>& arr, int x, int y, int mid) {\n int n = arr.size();\n vector<vector<int>> dp(n, vector<int>(2, 0));\n dp[0][0] = 1;\n dp[0][1] = 1;\n\n for (int i = 1; i < n; i++) {\n if (arr[i] != -1) {\n if (arr[i - 1] == -1) {\n if (abs(x - arr[i]) <= mid) {\n dp[i][0] = dp[i - 1][0];\n }\n if (abs(y - arr[i]) <= mid) {\n dp[i][1] = dp[i - 1][1];\n }\n if (dp[i][0] == 0 && dp[i][1] == 0)\n return false;\n } else {\n dp[i][0] = 1;\n dp[i][1] = 1;\n }\n } else {\n if (arr[i - 1] == -1) {\n dp[i][0] = dp[i - 1][0];\n dp[i][1] = dp[i - 1][1];\n if (abs(x - y) <= mid) {\n dp[i][0] = dp[i][0] || dp[i - 1][1];\n dp[i][1] = dp[i][1] || dp[i - 1][0];\n if (dp[i][0] == 0 && dp[i][1] == 0)\n return false;\n }\n\n } else {\n if (abs(x - arr[i - 1]) <= mid) {\n dp[i][0] = 1;\n }\n if (abs(y - arr[i - 1]) <= mid) {\n dp[i][1] = 1;\n }\n if (dp[i][0] == 0 && dp[i][1] == 0)\n return false;\n }\n }\n }\n return true;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
minimize-the-maximum-adjacent-element-difference
|
Binary Search
|
binary-search-by-tensortrove-h352
|
Intuition\nThe problem revolves around minimizing the maximum difference between adjacent elements in an array where missing elements (denoted as -1) can be rep
|
20241219.tensortrove
|
NORMAL
|
2024-11-18T07:20:37.427010+00:00
|
2024-11-18T07:25:54.208436+00:00
| 48
| false
|
# Intuition\nThe problem revolves around minimizing the maximum difference between adjacent elements in an array where missing elements (denoted as -1) can be replaced by one of two chosen integers, x or y. To achieve the optimal solution:\n\n1. Observe that replacing -1 with two values allows us to control the adjacent differences.\n2. If we have many -1s, we can consider them as blocks, surrounded by known numbers, which simplifies the problem.\n3. Binary search over the possible maximum differences helps efficiently find the minimum possible maximum difference.\n\n# Approach\n1. **Identify Blocks of -1s:**\n\nTraverse the array, and replace consecutive -1s with markers like -1 or -2 to denote isolated or consecutive blocks.\nCollect the minimum and maximum values of the known elements adjacent to -1s for further calculations.\n2. **Binary Search to Minimize Maximum Difference:**\n\nDefine a search space (low to high) for the possible maximum difference. Initially, low is the largest existing adjacent difference, and high is the range between the minimum and maximum values of known elements.\nFor a mid-value (diff), validate whether replacing -1s with two values (x and y) allows all adjacent differences to stay within diff.\n3. **Validation of a Difference (diff):**\n\nReplace -1 with two possible values such that all adjacent differences are less than or equal to diff.\nCheck each segment of the modified array to ensure feasibility.\n4. **Optimize Using Binary Search:**\n\nIf a difference diff is valid, try smaller values to minimize it further.\nOtherwise, increase the value of diff.\n5. **Return the Result:**\n\nThe smallest valid difference obtained from binary search is the result.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n - The binary search runs in O(log(range)), where the range is the difference between high and low.\n - For each binary search iteration, validation takes O(n) as we traverse the array.\n - Overall time complexity is O(n\u22C5log(range)).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n - The solution uses an auxiliary array (nums2) to simplify handling of -1s and requires O(n) space.\n - Overall space complexity is O(n).\n\n# Code\n```python3 []\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n n = len(nums)\n\n if n == 2:\n if nums[0] != -1 and nums[1] != -1:\n return abs(nums[0] - nums[1])\n return 0\n\n if all(num == -1 for num in nums):\n return 0\n\n mn = int(1e9)\n mx = 0\n currMx = 0\n cnt = 0\n nums2 = []\n \n for i in range(n):\n if nums[i] != -1:\n if i > 0 and nums[i - 1] != -1:\n currMx = max(currMx, abs(nums[i] - nums[i - 1]))\n if cnt == 1:\n nums2.append(-1)\n if cnt > 1:\n nums2.append(-2)\n cnt = 0\n if i == 0 or i + 1 == n or nums[i - 1] == -1 or nums[i + 1] == -1:\n nums2.append(nums[i])\n if (i > 0 and nums[i - 1] == -1) or (i + 1 < n and nums[i + 1] == -1):\n mn = min(mn, nums[i])\n mx = max(mx, nums[i])\n else:\n cnt += 1\n \n if cnt > 1:\n nums2.append(-1)\n if nums2[0] == -2:\n nums2[0] = -1\n\n low = currMx\n high = mx - mn + 1\n\n while low < high:\n mid = (low + high) // 2\n p1 = mn + mid\n p2 = mx - mid\n valid = True\n\n if nums2[0] == -1 and abs(nums2[1] - p1) > mid and abs(nums2[1] - p2) > mid:\n valid = False\n if nums2[-1] == -1 and abs(nums2[-2] - p1) > mid and abs(nums2[-2] - p2) > mid:\n valid = False\n\n for i in range(1, len(nums2) - 1):\n if nums2[i] < 0:\n if abs(nums2[i - 1] - p1) <= mid and abs(nums2[i + 1] - p1) <= mid:\n continue\n if abs(nums2[i - 1] - p2) <= mid and abs(nums2[i + 1] - p2) <= mid:\n continue\n if nums2[i] == -2:\n if abs(p2 - p1) <= mid:\n if abs(nums2[i - 1] - p1) <= mid and abs(nums2[i + 1] - p2) <= mid:\n continue\n if abs(nums2[i - 1] - p2) <= mid and abs(nums2[i + 1] - p1) <= mid:\n continue\n valid = False\n break\n \n if valid:\n high = mid\n else:\n low = mid + 1\n \n return low\n\n```
| 0
| 0
|
['Python3']
| 0
|
minimize-the-maximum-adjacent-element-difference
|
Rust Solution
|
rust-solution-by-abhineetraj1-f3bm
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem asks us to find the minimum difference between adjacent values in an array
|
abhineetraj1
|
NORMAL
|
2024-11-18T04:29:52.586027+00:00
|
2024-11-18T04:29:52.586062+00:00
| 12
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem asks us to find the minimum difference between adjacent values in an array while possibly replacing `-1` entries with values from adjacent elements. The key idea is to minimize the maximum difference between adjacent values, possibly taking advantage of the `-1` values as flexible placeholders.\n\n- First, we need to find the largest difference between adjacent positive values, `max_adj`.\n- Then, we need to find the smallest and largest values around the `-1` entries (treated as gaps). We want to replace `-1` values in such a way that the differences between adjacent numbers are minimized.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n 1. **Initial Pass**:\n - Traverse the array to identify the largest absolute difference between consecutive positive integers (`max_adj`).\n - Track the smallest (`mina`) and largest (`maxb`) positive numbers that are adjacent to a `-1`. This helps us understand how to fill in gaps caused by `-1`s.\n \n2. **Second Pass (Gap Handling)**:\n - Traverse the array again to handle sequences of `-1` values. For each such sequence:\n - Identify the values before and after the gap (if they exist).\n - Attempt to minimize the maximum difference that would result from replacing the `-1` values with those before and after the gap.\n \n3. **Final Result**:\n - The final result will be the larger of `max_adj` (the largest difference found in the first pass) or half of the calculated result from handling the gaps.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```rust []\nimpl Solution {\n pub fn min_difference(nums: Vec<i32>) -> i32 {\n let n = nums.len();\n let mut max_adj = 0;\n let mut mina = i32::MAX;\n let mut maxb = i32::MIN;\n\n // First pass: find max_adj, mina, maxb\n for i in 0..(n - 1) {\n let a = nums[i];\n let b = nums[i + 1];\n if a > 0 && b > 0 {\n max_adj = max_adj.max((a - b).abs());\n } else if a > 0 || b > 0 {\n mina = mina.min(a.max(b));\n maxb = maxb.max(a.max(b));\n }\n }\n\n let mut res = 0;\n\n // Second pass: check gaps between -1\'s and find the maximum result\n let mut i = 0;\n while i < n {\n if (i > 0 && nums[i - 1] == -1) || nums[i] > 0 {\n i += 1;\n continue;\n }\n\n let mut j = i;\n while j < n && nums[j] == -1 {\n j += 1;\n }\n\n let mut a = i32::MAX;\n let mut b = i32::MIN;\n\n if i > 0 {\n a = a.min(nums[i - 1]);\n b = b.max(nums[i - 1]);\n }\n if j < n {\n a = a.min(nums[j]);\n b = b.max(nums[j]);\n }\n\n if a <= b {\n if j - i == 1 {\n res = res.max((maxb - a).min(b - mina));\n } else {\n res = res.max((maxb - a).min(b - mina).min((maxb - mina + 2) / 3 * 2));\n }\n }\n\n i = j;\n }\n\n max_adj.max((res + 1) / 2)\n }\n}\n\n```
| 0
| 0
|
['Rust']
| 0
|
minimize-the-maximum-adjacent-element-difference
|
Binary Search Solution to Minimize Maximum Adjacent Difference in an Array [c++ with explaination]
|
binary-search-solution-to-minimize-maxim-fz5f
|
Intuition\n Describe your first thoughts on how to solve this problem. \nWe aim to find the minimum possible maximum difference between adjacent elements in the
|
sumanth977
|
NORMAL
|
2024-11-17T16:57:32.177376+00:00
|
2024-11-17T16:57:32.177476+00:00
| 48
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe aim to find the minimum possible maximum difference between adjacent elements in the array. This involves two key steps:\n1.\tBinary Search: Use binary search on the maximum difference (maxDiff) to minimize it.\n2.\tValidation: For each candidate maxDiff, check if it\u2019s possible to replace -1 values with a pair (x, y) such that all adjacent differences are within the limit.\n\n# Steps\n<!-- Describe your approach to solving the problem. -->\n1.\tBinary Search Setup:\n\t\u2022\tDefine a range [low, high] for possible maxDiff.\n\t\u2022\tStart with low = 0 and high = 1e9 (the maximum possible value in the constraints).\n2.\tValidation with isPossible:\n\t\u2022\tFor a given maxDiff, find the minimum and maximum values from existing non--1 neighbors.\n\t\u2022\tReplace -1 values using x = minNum + maxDiff and y = maxNum - maxDiff if they satisfy the constraints.\n\t\u2022\tValidate the array to ensure all adjacent differences are within maxDiff.\n3.\tEdge Cases:\n\t\u2022\tIf all elements are -1, the array can have a constant value, so the result is 0.\n\t\u2022\tIf there are no -1 values, return the maximum absolute difference directly.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n \u2022\tBinary search runs in O(log(maxNum)).\n\t\u2022\tFor each candidate maxDiff, isPossible scans the array, taking O(n).\n\t\u2022\tOverall complexity: $$O(n * log(maxNum))$$.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe solution uses a few variables and copies the array during validation, leading to $$O(n)$$ space usage.\n\n# Code\n```cpp []\nclass Solution {\nprivate:\n int n;\n\n // Helper function to check if the array can satisfy the given maxDiff\n bool isPossible(vector<int> nums, int maxDiff) {\n int max_num = INT_MIN;\n int min_num = INT_MAX;\n\n // Identify min and max from neighbors of `-1`\n for (int i = 0; i < n; i++) {\n if (nums[i] != -1 && \n ((i > 0 && nums[i - 1] == -1) || (i < n - 1 && nums[i + 1] == -1))) {\n max_num = max(nums[i], max_num); // Update maximum neighbor value\n min_num = min(nums[i], min_num); // Update minimum neighbor value\n }\n }\n\n // If no valid neighbors are found, return false\n if (min_num == INT_MAX || max_num == INT_MIN) \n return false;\n\n // Candidate values for replacing `-1`\n int x = min_num + maxDiff;\n int y = max_num - maxDiff;\n\n // Replace `-1` values\n for (int i = 0; i < n; i++) {\n if (nums[i] == -1) {\n // Check if replacing with `x` satisfies maxDiff\n if ((i == 0 || abs(nums[i - 1] - x) <= maxDiff) && \n (i == n - 1 || nums[i + 1] == -1 || abs(nums[i + 1] - x) <= maxDiff)) {\n nums[i] = x;\n } else {\n // Otherwise replace with `y`\n nums[i] = y;\n }\n }\n }\n\n // Validate the array for maxDiff constraint\n for (int i = 1; i < n; i++) {\n if (abs(nums[i] - nums[i - 1]) > maxDiff)\n return false; // Constraint violated\n }\n return true;\n }\n\npublic:\n int minDifference(vector<int>& nums) {\n n = nums.size();\n\n // Count missing values\n int missingCount = count(nums.begin(), nums.end(), -1);\n\n // Edge case: All elements are `-1`\n if (missingCount == n)\n return 0;\n\n // Edge case: No missing elements\n if (missingCount == 0) {\n int absDiff = INT_MIN;\n for (int i = 1; i < n; i++) {\n absDiff = max(absDiff, abs(nums[i] - nums[i - 1]));\n }\n return absDiff; // Return the maximum difference\n }\n\n // Binary search for the minimum possible maxDiff\n int low = 0, high = 1e9, ans = high;\n\n while (low <= high) {\n int mid = low + (high - low) / 2; // Midpoint for binary search\n if (isPossible(nums, mid)) {\n ans = mid; // If valid, update answer\n high = mid - 1; // Search for smaller maxDiff\n } else {\n low = mid + 1; // Search for larger maxDiff\n }\n }\n\n return ans; // Return the minimized maxDiff\n }\n};\n```
| 0
| 0
|
['Binary Search', 'C++']
| 0
|
minimize-the-maximum-adjacent-element-difference
|
Explained + well documented code
|
explained-well-documented-code-by-ivangn-zi51
|
Ideas\n1. Reduce sequences of missing numbers: length >= 3 to only 2\n2. Use a "meet in middle" strategy to get upper bound\n3. Binary searching for the minimum
|
ivangnilomedov
|
NORMAL
|
2024-11-17T16:56:51.679557+00:00
|
2024-11-17T16:56:51.679597+00:00
| 41
| false
|
# Ideas\n1. Reduce sequences of missing numbers: length >= 3 to only 2\n2. Use a "meet in middle" strategy to get upper bound\n3. Binary searching for the minimum possible difference\n\n# Approach\n1. **Preprocessing**\n - Collapse 3+ consecutive -1s to just 2 since with only two values (x,y), longer sequences can always be optimally filled\n - Track min/max values adjacent to missing numbers as they constrain our x,y choices\n\n2. **Binary Search Bounds**\n - Lower bound: max difference between existing adjacent numbers (can\'t do better)\n - Upper bound: (max_miss_adj - min_miss_adj + 1) / 2 (from "meet in middle" strategy)\n\n3. **Optimal x,y Selection** \n For target difference d:\n - x = min_miss_adj + d // higher x will not satisfy existing element for min_miss_adj\n - y = max_miss_adj - d // lower y will not satisfy existing element for max_miss_adj\n\n4. **Validation Strategy**\n For each missing single -1 or double -1,-1:\n - Try single value (all x or all y)\n - For double -1,-1 also try combinations (x,y) or (y,x)\n - Ensure all adjacent differences \u2264 d\n\n# Complexity\n- Time complexity: $$O(N \\log M)$$ where N is array length and M is the range of numbers\n- Space complexity: $$O(1)$$ (array is modified in place)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n // We can collapse 3 or more consecutive -1s to just 2\n int sz = 0;\n for (int i = 0, last_pos = -1; i < nums.size(); ++i) {\n if (nums[i] > -1)\n last_pos = i;\n if (i - last_pos < 3)\n nums[sz++] = nums[i];\n }\n nums.resize(sz);\n\n const int N = nums.size();\n int max_adj_diff = 0;\n // Track min/max values adjacent to missing numbers\n int min_miss_adj = numeric_limits<int>::max() / 3;\n int max_miss_adj = 0;\n for (int i = 0; i < N; ++i) {\n if (i > 0 && nums[i] > -1 && nums[i - 1] > -1)\n max_adj_diff = max(max_adj_diff, abs(nums[i] - nums[i - 1]));\n if (nums[i] > -1 && (i > 0 && nums[i - 1] == -1 || i + 1 < N && nums[i + 1] == -1)) {\n min_miss_adj = min(min_miss_adj, nums[i]);\n max_miss_adj = max(max_miss_adj, nums[i]);\n }\n }\n\n // Bisect:\n int beg = max_adj_diff; // can\'t do better than existing differences\n int end = (max_miss_adj - min_miss_adj + 1) / 2; // is derived from "meet in middle" strategy, apparently\n // this answer works, but can be not the lowest\n while (beg < end) {\n int mid = beg + (end - beg) / 2;\n // Proof: (assume x < y)\n // x = min_miss_adj + d\n // we will not be able to achieve answer=mid if lower(x, y) > min_miss_adj + d\n // since the case of min_miss_adj element will not be covered\n // y = max_miss_adj - mid\n // similar reason why upper(x, y) can not be > max_miss_adj - mid\n if (are_x_y_valid(nums, mid, min_miss_adj + mid, max_miss_adj - mid))\n end = mid;\n else\n beg = mid + 1;\n }\n return beg;\n }\n\nprivate:\n // For each missing number or sequence of two missing numbers:\n // - Try placing single x or single y\n // - For sequences of 2, also try x,y or y,x combination\n // All adjacent differences must be <= d\n bool are_x_y_valid(const vector<int>& nums, int d, int x, int y) {\n // Check if we can fill missing positions, for case of sequential [ .. -1, -1 .. ]\n // check only the first -1\n for (int i = 0; i < nums.size(); ++i) if (nums[i] == -1 && (i == 0 || nums[i - 1] != -1)) {\n bool left_ok_for_x = i == 0 || abs(nums[i - 1] - x) <= d;\n bool left_ok_for_y = i == 0 || abs(nums[i - 1] - y) <= d;\n\n // single -1 => j same as i\n // sequential -1,-1 => j - rightmost of -1\n int j = i == nums.size() - 1 ? i : // at end of array\n nums[i + 1] != -1 ? i : // next is defined\n i + 1; // rightmost of -1\n bool right_ok_for_x = j == nums.size() - 1 || abs(nums[j + 1] - x) <= d;\n bool right_ok_for_y = j == nums.size() - 1 || abs(nums[j + 1] - y) <= d;\n\n // if can use single value x|y\n bool one_of_xy_pass = (left_ok_for_x && right_ok_for_x) ||\n (left_ok_for_y && right_ok_for_y);\n // either (x then y) or (y then x), also validate |x-y| <= d\n bool combine_xy_pass = abs(x - y) <= d &&\n (left_ok_for_x && right_ok_for_y ||\n left_ok_for_y && right_ok_for_x);\n\n if (i == j && !one_of_xy_pass) return false; // None of x, y fits for single -1\n if (i < j && !( one_of_xy_pass || combine_xy_pass ))\n // Neither single nor combination can fill\n return false;\n }\n return true;\n }\n};\n\n```
| 0
| 0
|
['C++']
| 0
|
minimize-the-maximum-adjacent-element-difference
|
Python3 binary search 42 lines
|
python3-binary-search-42-lines-by-nguyen-hkhd
|
Intuition\n Describe your first thoughts on how to solve this problem. \nFind the maximum, minimum of elements in nums that next to -1\nFor the maximum absolute
|
nguyenquocthao00
|
NORMAL
|
2024-11-17T14:08:26.106017+00:00
|
2024-11-17T14:08:26.106055+00:00
| 38
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFind the maximum, minimum of elements in nums that next to -1\nFor the maximum absolute distance dif, we can always choose the optimal x,y that: x=lo+dif, y=hi-dif, and check whether the chosen x,y can satisfy the requirement.\n\nIf we have (-1, a) or (a, -1), treat it as (a, -1, a) and replace -1 by either x or y.\nIf we have (a, -1, -1, b), we can replace by (a, x, x, b), (a, x, y, b), (a, y, y, b), (a, y, x, b). If there are more than 3 -1, treat as 2.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n n=len(nums)\n avai = [i for i,v in enumerate(nums) if v>0]\n if len(avai)<=1: return 0\n neighbors = set()\n data=[]\n if avai[0]!=0: neighbors.add(nums[avai[0]])\n if avai[-1]!=n-1: neighbors.add(nums[avai[-1]])\n maxdif=0\n for i in range(len(avai)-1):\n ii,jj = avai[i], avai[i+1]\n x,y = nums[ii], nums[jj]\n if x>y: x,y=y,x\n if ii+1==jj:\n maxdif =max(maxdif, y-x)\n else:\n neighbors.add(x)\n neighbors.add(y)\n data.append((x,y,min(jj-ii-1,2)))\n if len(data)==0: return maxdif\n nb = sorted(neighbors)\n if maxdif > nb[-1]-nb[0]: return maxdif\n def feasible(dif):\n if dif<maxdif: return False\n x,y = nb[0]+dif, nb[-1]-dif\n if x>y: x,y=y,x\n for d in data:\n if max(abs(d[0]-x),abs(d[1]-x))<=dif or max(abs(d[0]-y), abs(d[1]-y))<=dif: continue\n if d[2]>=2 and max(abs(d[0]-x), abs(d[1]-y), abs(y-x))<=dif: continue\n return False\n return True\n l,r,res = 0, nb[-1]-nb[0], 0\n while l<=r:\n mid=(l+r)//2\n if feasible(mid): res,r=mid,mid-1\n else: l=mid+1\n return res\n \n \n\n \n \n \n```
| 0
| 0
|
['Python3']
| 0
|
minimize-the-maximum-adjacent-element-difference
|
Hardest problem I ever solved. (though with minor look at hints) ;)
|
hardest-problem-i-ever-solved-though-wit-jdni
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
user7634ri
|
NORMAL
|
2024-11-17T11:41:14.941679+00:00
|
2024-11-17T11:41:14.941709+00:00
| 162
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n\n vector<int> preprocess(vector<int>& nums) {\n vector<int> reduced = {};\n int n = nums.size();\n\n for(int i = 0; i < n; i ++) {\n if(nums[i] != -1) {\n reduced.push_back(nums[i]);\n continue;\n }\n\n if(i - 1 >= 0 && nums[i - 1] != -1) {\n reduced.push_back(nums[i]);\n continue;\n }\n\n if(i + 1 <= n - 1 && nums[i + 1] != -1) {\n reduced.push_back(nums[i]);\n }\n }\n return reduced;\n }\n\n bool is_intersecting(vector<int> s1, vector<int> s2) {\n return max(s1[0], s2[0]) <= min(s1[1], s2[1]);\n }\n\n vector<int> segment_intersection(vector<int> s1, vector<int> s2) {\n return {max(s1[0], s2[0]), min(s1[1], s2[1])};\n }\n\n bool are_2_points_covering_all_segments(vector<vector<int>> segments) {\n // minimum points needed to cover all the segments.\n vector<vector<int>> pointwise;\n \n for(int i = 0; i < segments.size(); i ++) {\n pointwise.push_back({segments[i][0], -1, i}); // -1 denotes start;\n pointwise.push_back({segments[i][1], 1, i});\n }\n sort(pointwise.begin(), pointwise.end());\n\n unordered_map<int, int> mp;\n\n queue<int> starts;\n\n int points = 0;\n\n for(auto it: pointwise) {\n if(mp[it[2]] == 1) {\n continue;\n }\n\n if(it[1] > 0) {\n \n points ++;\n while(!starts.empty()) {\n auto u = starts.front();\n mp[u] = 1;\n starts.pop();\n }\n } else {\n starts.push(it[2]);\n }\n }\n return points <= 1;\n }\n\n bool is_mid_possible(int mid, vector<int> v) {\n int n = v.size();\n \n \n int d = INT_MAX;\n for(int i = 0; i < n; i ++) {\n if(v[i] != -1 && i > 0 && v[i - 1] == -1) {\n d = min(d, v[i]);\n } else if(v[i] != -1 && i + 1 < n && v[i + 1] == -1) {\n d = min(d, v[i]);\n }\n }\n if(d == INT_MAX) return true;\n d += mid;\n for(int i = 0; i < n; i ++) {\n if(v[i] != -1 && i > 0 && v[i - 1] == -1) {\n\n if(abs(v[i] - d) > mid) continue;\n \n if(i >= 2 && v[i - 2] != -1 && abs(v[i - 2] - d) > mid) continue;\n\n v[i - 1] = d;\n\n }\n }\n\n\n for(int i = 0; i < n; i ++) {\n if(v[i] != -1 && i + 1 < n && v[i + 1] == -1) {\n if(abs(v[i] - d) > mid) continue;\n if(i + 2 < n && v[i + 2] != -1 && abs(v[i + 2] - d) > mid) continue;\n v[i + 1] = d;\n }\n }\n\n // if post this there are 2 consecutive -1s then bro both of them have to converge to same value and intersection logic shall be useful.\n if(mid <= 15) {\n cout << "mid " << mid << endl;\n\n for(auto it: v) {\n cout << it << " ";\n }\n cout << endl;\n }\n\n vector<vector<int>> found_segments = {};\n\n\n for(int i = 0; i < n; i ++) {\n if(v[i] == - 1 && i + 1 < n && v[i + 1] == -1) {\n // this means v[i - 1] , v[i + 2] are positive.\n vector<int> s1 = {v[i - 1] - mid, v[i - 1] + mid};\n vector<int> s2 = {v[i + 2] - mid, v[i + 2] + mid};\n if(is_intersecting(s1, s2)) {\n found_segments.push_back(segment_intersection(s1, s2));\n } else {\n return false;\n }\n i ++;\n } else if(v[i] == -1 && i + 1 < n && v[i + 1] != -1) {\n vector<int> s1 = {v[i + 1] - mid, v[i + 1] + mid};\n vector<int> s2 = {v[i + 1] - mid, v[i + 1] + mid};\n if(i > 0 && v[i - 1] != -1) {\n s1 = {v[i - 1] - mid, v[i - 1] + mid};\n }\n if(is_intersecting(s1, s2)) {\n found_segments.push_back(segment_intersection(s1, s2));\n } else {\n return false;\n }\n } else if(v[i] == -1 && i > 0 && v[i - 1] != -1) {\n vector<int> s1 = {v[i - 1] - mid, v[i - 1] + mid};\n vector<int> s2 = {v[i - 1] - mid, v[i - 1] + mid};\n if(is_intersecting(s1, s2)) {\n found_segments.push_back(segment_intersection(s1, s2));\n } else {\n return false;\n }\n }\n }\n return are_2_points_covering_all_segments(found_segments);\n }\n\n int minDifference(vector<int>& nums) {\n vector<int> v = preprocess(nums);\n if(v.size() == 0) {\n return 0;\n }\n\n int start = 0, end = 1e9, ans = - 1;\n for(int i = 1; i < nums.size(); i ++) {\n if(nums[i] != - 1 && nums[i - 1] != -1)\n start = max(start, abs(nums[i] - nums[i - 1]));\n }\n\n while(start <= end) {\n int mid = (start + end) / 2;\n if(is_mid_possible(mid, v)) {\n ans = mid;\n end = mid - 1;\n } else {\n start = mid + 1;\n }\n }\n\n return ans;\n // cout << are_2_points_covering_all_segments({{1, 2}, {3, 4}, {1, 4}}) << endl;\n }\n};\n```
| 0
| 0
|
['C++']
| 1
|
minimize-the-maximum-adjacent-element-difference
|
[C++] Binary Search + Classified discussion
|
c-binary-search-classified-discussion-by-xr7y
|
CODE:\n\n\nclass Solution {\npublic:\n int minDifference(vector<int>& a) { int n = a.size();\n // Prework 0\uFF1A The maximum diffe
|
projectcoder
|
NORMAL
|
2024-11-17T10:00:48.930560+00:00
|
2024-11-17T10:18:50.202844+00:00
| 31
| false
|
**CODE:**\n\n```\nclass Solution {\npublic:\n int minDifference(vector<int>& a) { int n = a.size();\n // Prework 0\uFF1A The maximum difference between consecutive numbers.\n int low = 0, cnt = 0;\n for (int l = 0, r = 0; l < n; l = r) {\n for (l = r; l < n && a[l]==-1; l++) cnt++;\n for (r = l+1; r < n && a[r]!=-1; r++) low = max(low, abs(a[r]-a[r-1]));\n }\n\n \n // Prework 1\uFF1A Obtain all the numbers.\n int s[n+10];\n int m = 0;\n\n for (int i = 0; i < n; i++) if (a[i] != -1) {\n if ((i-1>=0 && a[i-1]==-1) || (i+1<n && a[i+1]==-1)) s[++m] = a[i];\n }\n sort(s+1, s+m+1);\n m = unique(s+1, s+m+1) - s - 1;\n\n unordered_map<int,int> pos;\n for (int i = 1; i <= m; i++) pos[s[i]] = i;\n\n\n // Prework 2\uFF1A Find the farthest right position each element can connect to.\n int f[n+10]; memset(f, 0, sizeof(f)); // "u,-1,v"\n int g[n+10]; memset(g, 0, sizeof(g)); // "u,-1,...,-1,v"\n for (int l = 0, r = 0; l < n; l = r) {\n for (l = r; l < n && a[l]!=-1; l++);\n for (r = l; r < n && a[r]==-1; r++);\n if (l-1 >= 0 && r < n) {\n int u = min(pos[a[l-1]], pos[a[r]]), v = max(pos[a[l-1]], pos[a[r]]);\n if (r-l == 1) f[u] = max(f[u], v);\n if (r-l > 1) g[u] = max(g[u], v);\n }\n }\n\n \n if (m == 0) return low;\n if (cnt == 0) return low;\n if (cnt == 1) return max(low, (s[m]-s[1]+1)/2);\n\n\n auto check = [&](int limit) -> bool {\n // Decision 1\uFF1A X == Y\n if (s[m]-s[1] <= 2*limit) return true;\n\n // Decision 2: abs(X-Y) <= limit\n for (int i = 1, e = 0; i+1 <= m; i++) {\n if (s[i] < s[m]-2*limit) e = max(e, f[i]);\n if (e <= i && (s[i]-s[1]) <= 2*limit && (s[m]-s[i+1]) <= 2*limit && (s[m]-limit)-(s[1]+limit) <= limit) return true;\n }\n\n // Decision 3\uFF1A abs(X-Y) > limit\n for (int i = 1, e = 0; i+1 <= m; i++) {\n if (s[i] < s[m]-2*limit) e = max(e, max(f[i], g[i])); // Forced connection: two elements connected by a consecutive segment of -1.\n if (e <= i && (s[i]-s[1]) <= 2*limit && (s[m]-s[i+1]) <= 2*limit) return true;\n }\n\n return false;\n };\n\n int l = low, r = 1e9;\n while (l <= r) {\n int mid = (l+r)>>1;\n if (!check(mid)) l = mid+1;\n else r = mid-1; \n }\n return l;\n }\n};\n```\n
| 0
| 0
|
[]
| 0
|
minimize-the-maximum-adjacent-element-difference
|
Binary Search + DP Solution || Interval Merging || Beats 50%
|
binary-search-dp-solution-interval-mergi-tmhp
|
Complexity\n- Time complexity:O(n * log(max(nums)))\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(n)\n Add your space complexity here, e.g
|
dubeyad2003
|
NORMAL
|
2024-11-17T07:18:08.485055+00:00
|
2024-11-17T07:18:08.485105+00:00
| 59
| false
|
# Complexity\n- Time complexity:$$O(n * log(max(nums)))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nint dp[100005][3];\nint val[3];\nclass Solution {\npublic:\n bool possible(int diff, vector<int>& arr, vector<int>& nums){\n int n = arr.size(), m = nums.size();\n for(int i=0; i<=m; i++)\n dp[i][0] = dp[i][1] = dp[i][2] = 0;\n int cnt = 1, mx = arr[0] + diff, x = -1, y = -1;\n for(int i=1; i<n; i++){\n if(mx < (arr[i] - diff)){\n x = mx;\n mx = (arr[i] + diff);\n cnt++;\n }else{\n mx = min(mx, (arr[i] + diff));\n }\n }\n if(cnt > 2) return false;\n if(cnt == 2) y = arr[n-1] - diff;\n else x = y = arr[n-1] - diff;\n n = m;\n dp[n][0] = dp[n][1] = dp[n][2] = 1;\n for(int i=n-1; i>=0; i--){\n for(int prev=0; prev<=2; prev++){\n int el = i ? nums[i-1] : -1;\n val[0] = x, val[1] = y, val[2] = el;\n int ans = 0;\n if(nums[i] == -1){\n if(i){\n ans |= (abs(val[prev] - x) <= diff) & dp[i+1][0];\n ans |= (abs(val[prev] - y) <= diff) & dp[i+1][1];\n }else{\n ans |= dp[i+1][0];\n ans |= dp[i+1][1];\n }\n }else{\n if(i){\n ans |= (abs(val[prev] - nums[i]) <= diff) & dp[i+1][2];\n }else{\n ans |= dp[i+1][2];\n }\n }\n dp[i][prev] = ans;\n }\n }\n return dp[0][2];\n }\n int minDifference(vector<int>& nums) {\n ios_base::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);\n int n = nums.size();\n int lo = 0, hi = 1e9, cnt = 0;\n vector<int> arr;\n for(int i=0; i<n; i++){\n if(nums[i] == -1) cnt++;\n if(i > 0 && nums[i] != -1 && nums[i-1] != -1)\n lo = max(lo, abs(nums[i] - nums[i-1]));\n if(nums[i] == -1){\n if(i > 0 && nums[i-1] != -1) arr.push_back(nums[i-1]);\n if(i+1 < n && nums[i+1] != -1) arr.push_back(nums[i+1]);\n }\n }\n if(cnt >= (n-1)) return 0;\n if(!cnt) return lo;\n sort(arr.begin(), arr.end());\n int ans = hi;\n while(lo <= hi){\n int mid = lo + (hi - lo) / 2;\n if(possible(mid, arr, nums)){\n ans = mid;\n hi = mid - 1;\n }else{\n lo = mid + 1;\n }\n }\n return ans;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
minimize-the-maximum-adjacent-element-difference
|
[c++] Binary Search
|
c-binary-search-by-lyronly-g1eh
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n1 Fix one smaller ele
|
lyronly
|
NORMAL
|
2024-11-17T05:14:49.949509+00:00
|
2024-11-17T05:14:49.949544+00:00
| 73
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n1 Fix one smaller element x, \n2 For bigger element y ,given min gap m, try to figure out range of y to determine if y exists.\n\nPreprocess all pair of \n1 : a, -1, b\n2 : a, -1, -1, b\na <= b\n\nFor case 2\nif x > a, then it is a, x, y, b\notherwise it is a, y, y, b\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\ntypedef long long ll;\nclass Solution {\npublic:\n int n;\n int md = 0;\n vector<pair<int, int>> dp1;\n vector<pair<int, int>> dp2;\n int a = INT_MAX;\n int minv = INT_MAX;\n int maxv = INT_MIN;\n\n pair<int, int> rang(int l, int r, int m)\n {\n return {r - m, l + m}; \n }\n bool test(int m)\n {\n int x = a + m;\n\n int y1 = minv;\n int y2 = maxv;\n for (auto&[l, r] : dp1)\n {\n if (abs(x - l) <= m && abs(x - r) <= m) continue;\n auto r1 = rang(l, r, m);\n if (r1.second < r1.first) return false;\n y1 = max(y1, r1.first);\n y2 = min(y2, r1.second);\n if (y1 > y2) return false;\n }\n\n for (auto&[l, r] : dp2)\n {\n if (abs(x - l) <= m && abs(x - r) <= m) continue;\n // first x\n if (x > l) \n {\n if ((x - l) > m) return false;\n pair<int, int> r1 = {max(x , r - m), min(x + m, r + m)};\n if (r1.second < r1.first) return false;\n y1 = max(y1, r1.first);\n y2 = min(y2, r1.second);\n if (y1 > y2) return false;\n } \n else \n {\n // both y\n auto r1 = rang(l, r, m);\n if (r1.second < r1.first) return false;\n y1 = max(y1, r1.first);\n y2 = min(y2, r1.second);\n if (y1 > y2) return false;\n }\n }\n if (y1 > y2) return false;\n return true;\n }\n void push(vector<pair<int, int>>& cur, int x, int y)\n {\n cur.push_back({min(x, y), max(x, y)});\n }\n int minDifference(vector<int>& nums) {\n n = nums.size();\n int pre = -1;\n int last = -1;\n minv = INT_MAX;\n maxv = INT_MIN;\n for (int i = 0; i < n; i++)\n {\n if (nums[i] > 0)\n {\n if (pre == -1) pre = nums[i];\n last = nums[i];\n\n if (i - 1 >= 0 && nums[i - 1] > 0)\n {\n md = max(md, abs(nums[i] - nums[i - 1]));\n }\n\n minv = min(minv, nums[i]);\n maxv = max(maxv, nums[i]);\n }\n }\n if (last == -1) return 0;\n\n int i = 0;\n while (i < n)\n {\n if (nums[i] != -1) {\n pre = nums[i];\n i++;\n continue;\n }\n int cnt = 0;\n while (i < n && nums[i] == -1)\n {\n cnt++;\n i++;\n }\n int e = (i >= n) ? last : nums[i];\n if (cnt == 1)\n {\n a = min(pre, a);\n a = min(e, a);\n push(dp1, pre, e);\n // dp1.push_back({pre, e});\n }\n else \n {\n a = min(pre, a);\n a = min(e, a);\n push(dp2, pre, e);\n // dp2.push_back({pre, e});\n }\n\n }\n if (dp1.empty() && dp2.empty()) return md;\n\n ll l = md;\n ll r = maxv - minv;\n ll ans = r;\n //cout << minv << "," << maxv << "," << a << endl;\n while (l <= r)\n {\n ll m = (l + r)/2;\n bool res = test(m);\n //cout << m << "," << res << endl;\n if (res)\n {\n ans = m;\n r = m - 1;\n }\n else \n {\n l = m + 1;\n }\n }\n\n return ans;\n\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
minimize-the-maximum-adjacent-element-difference
|
python3
|
python3-by-harshitasree-jeyg
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
harshitasree
|
NORMAL
|
2024-11-17T04:14:39.872538+00:00
|
2024-11-17T04:14:39.872563+00:00
| 111
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nfrom typing import List\n\n\ndef binary_search(\n func_, # condition function\n first=True, # else last\n target=True, # else False\n left=0,\n right=2**31 - 1,\n) -> int:\n # https://leetcode.com/discuss/general-discussion/786126/\n # ASSUMES THAT THERE IS A TRANSITION\n # MAY HAVE ISSUES AT THE EXTREMES\n\n def func(val):\n # if first True or last False, assume search space is in form\n # [False, ..., False, True, ..., True]\n\n # if first False or last True, assume search space is in form\n # [True, ..., True, False, ..., False]\n # for this case, func will now be negated\n if first ^ target:\n return not func_(val)\n return func_(val)\n\n while left < right:\n mid = (left + right) // 2\n if func(mid):\n right = mid\n else:\n left = mid + 1\n if first: # find first True\n return left\n else: # find last False\n return left - 1\n\n\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n # left, right, count (1 or 2)\n n = len(nums)\n \n if nums.count(-1) == 0:\n return max(abs(a-b) for a,b in zip(nums, nums[1:]))\n if nums.count(-1) == n:\n return 0\n \n arr = []\n \n if nums[-1] == -1:\n while nums[-1] == -1:\n nums.pop()\n arr.append((nums[-1], nums[-1], 1))\n \n nums.reverse()\n if nums[-1] == -1:\n while nums[-1] == -1:\n nums.pop()\n arr.append((nums[-1], nums[-1], 1))\n \n maxdiff = 0\n \n prev_val = nums[0]\n prev_idx = 0\n for i,x in enumerate(nums[1:], start=1):\n if x != -1:\n if i - prev_idx == 1:\n maxdiff = max(maxdiff, abs(x - prev_val))\n elif i - prev_idx == 2:\n left = min(prev_val, x)\n right = max(prev_val, x)\n arr.append((left, right, 1))\n else:\n left = min(prev_val, x)\n right = max(prev_val, x)\n arr.append((left, right, 2))\n prev_val = x\n prev_idx = i\n \n def func(target_diff):\n if target_diff < maxdiff:\n return False\n \n xval = 10**10 + 10\n yval = -10**10 - 10\n for a,b,c in arr:\n xval = min(xval, a + target_diff) # can be smaller and ok\n yval = max(yval, b - target_diff) # can be larger and ok\n \n for a,b,c in arr:\n if c == 1:\n if abs(a - xval) <= target_diff and abs(b - xval) <= target_diff:\n continue\n if abs(a - yval) <= target_diff and abs(b - yval) <= target_diff:\n continue\n return False\n if c == 2:\n if abs(a - xval) <= target_diff and abs(b - yval) <= target_diff and abs(yval - xval) <= target_diff:\n continue\n if abs(a - yval) <= target_diff and abs(b - xval) <= target_diff and abs(yval - xval) <= target_diff:\n continue\n if abs(a - xval) <= target_diff and abs(b - xval) <= target_diff:\n continue\n if abs(a - yval) <= target_diff and abs(b - yval) <= target_diff:\n continue\n return False\n return True\n \n return binary_search(func, first=True, target=True, left=0, right=10**10 + 10)\n \n \n \n \n \n```
| 0
| 0
|
['Python3']
| 1
|
stone-game-iv
|
Easy Explanation, you will definitely gonna understand
|
easy-explanation-you-will-definitely-gon-9g2i
|
\n\n\n\nWell to be honest this is really not a hard problem. But, anyways our JOB is to solve it. Let\'s do it\n\n\n\n\n\nFirst understand this problem with an
|
hi-malik
|
NORMAL
|
2022-01-22T05:00:08.739044+00:00
|
2022-01-22T08:41:42.098321+00:00
| 5,419
| false
|
<hr>\n<hr>\n\n```\nWell to be honest this is really not a hard problem. But, anyways our JOB is to solve it. Let\'s do it\n```\n\n<hr>\n<hr>\n\n`First understand this problem with an example`. Take **n = 7** where n denotes no. of **stone**\n\n\n\nAs, **Alice always start game first** to remove stone. So, how many choices can he make to remove **7** stones is:\n> **1 ^ 1 = 1**\n> **2 ^ 2 = 4**\n\n`So, he can only make 2 choices`\n\n\n\n* `So, from 7 stones Alice 1st remove 1 stone & then Alice remove 4 stones` \n* * When **Alice remove 1 stone** the remaining stone **left is 6**. \n* * But If **Alice remove 4 stones** then remaining stones **left are 3.**\n* `Now it\'s Bob turn. Bob as well can make only 2 moves i.e. 1 OR 4 which is less than 6`\n* * When **Bob remove 1 stone** from branch **6** the remaining stone **left is 5**. But If **Bob remove 4 stones** from branch **6** then remaining stones **left are 2**.\n* * But in **Branch 3 Bob can only remove 1 stone**, so remaining **left is 2.**\n* `Now it\'s Alice turn.` \n* * From **branch 5 if Alice decide to remove 1 stone** remaining stone **left is 4**. But, if **alice** decide to **remove 4 stone** remaining stone **left is 1.**\n* * From **branch 2 if Alice decide to remove 1 stone** remaining stone **left is 1.** \n* * From **another branch 2 if Alice decide to remove 1 stone** remaining stone **left is 1**\n* `Now the Bob turn and every branch is ending with perfect square`. So, **Bob can remove from any branch because there is no branch from Alice can win.**\n\nSo, as you see there are **no. of repeated sub problems**, like 2, 4 so we will use the `Dynamic Programming` to solve this problem.\n\nI hope you understand, and let\'s code it\n\n**Top down Approach code Explained**\n\n```\n{\n Boolean[] dp = new Boolean[100001]; // craeted dp on n which size is 10^5\n\n public boolean winnerSquareGame(int n) {\n if (n == 0) return false;\n if (dp[n] != null) return dp[n];\n boolean winner = false;\n for (int i = 1; i * i <= n; i++) { // looping for the perfect square which has to be less then n\n if (!winnerSquareGame(n - i * i)) { // if the previous branch has false, we will check the winner of this game. \n\t\t\t\t// n - perfect square which can be possible in all branches.\n // if any of the branch gives us true.\n winner = true; // update our winner variable to true.\n break; // break that branch, because alice can win in that\n\n }\n }\n return dp[n] = winner;\n }\n```\n\n**Java - Top down Approach**\n```\nclass Solution {\n Boolean[] dp = new Boolean[100001];\n\n public boolean winnerSquareGame(int n) {\n if (n == 0) return false;\n if (dp[n] != null) return dp[n];\n boolean winner = false;\n for (int i = 1; i * i <= n; i++) {\n if (!winnerSquareGame(n - i * i)) {\n winner = true;\n break;\n\n }\n }\n return dp[n] = winner;\n }\n}\n```\nANALYSIS :- \n* **Time Complexity :-** BigO(N^1.5)\n\n* **Space Complexity :-** BigO(N)\n\n<hr>\n<hr>\n\n**Another Approach** We taking the same example where no of stone, **n =** **7**\n\n\n\n\n```\nFor finding out wether alice win or not, we had written some test cases, \nbecause for all the game theory question try to write down some of the starting values and \nthen try to calculate some further values using the backward values because the answer will be pre-defined \nif they are playing optimally.\n```\n\n* `For only 1` **Alice will win**, so answer is **true**\n* `For 2` **Alice will lose**, so answer is **false**. \n* `If there are **3 stones**` and you can only take out **1** because **1 is not greater then 3**, answer is **true**\n* * **Why** because **Alice** take out one **->** **Bob** take out one **->** **Alice** take out one\n* `Now **4**` is a **perfect square** **Alice** can take out the whole no in the **1st chance**. Since **Alice** take out the whole number, no chance left for **Bob**, so **Alice will win** & answer is **true**\n* `For **5** there are 2 chances, wether take out 1 OR 4.`\n* * If **Alice** take **1**, then **Bob left with 4 stones** & in **previous** condition we had **true**. So **Bob** will take out whole **4 stone**, & answer beome **false** \n* * If **Alice** take **4**, then **Bob left with 1 stones** & in **that** condition we had **true**. So **Bob** will win as well & answer beome **false**\n* `For **6** there are 2 chances, wether take out 1 OR 4.`\n* * If **Alice** take **1**, then **Bob left with 5 stones** & in **previous** condition we had **false**. So **Bob** will definitely lose in that condition & our **Alice** will win. So, answer beome **true** \n* * If **Alice** take **4**, then **Bob left with 2 stones** & in **that** condition we had **false**. So **Bob** will definitely lose in that condition & our **Alice** will win. So, answer beome **true** \n* `For **7** there are 2 chances, wether take out 1 OR 4.`\n* * If **Alice** take **1**, then **Bob left with 6 stones** & in **previous** condition we had **true**. So **Bob** will definitely win in that condition & our **Alice** will lose. So, answer beome **false** \n* * If **Alice** take **4**, then **Bob left with 3 stones** & in **that** condition we had **true**. So **Bob** will definitely win in that condition & our **Alice** will lose. So, answer beome **false**\n\n**Let\'s code it up**\n\n**Java - Bottom Up Approach**\n```\nclass Solution {\n public boolean winnerSquareGame(int n) {\n boolean dp[] = new boolean[n + 1];\n for(int i = 1; i <= n; i++){\n for(int j = 1; j * j <= i; j++){\n if(!dp[i - j * j]){\n dp[i] = true;\n break;\n }\n }\n }\n return dp[n];\n }\n}\n```\n**C++ Bottom Up Approach**\n```\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<bool> dp(n + 1);\n for(int i = 1; i <= n; i++){\n for(int j = 1; j * j <= i; j++){\n if(!dp[i - j * j]){\n dp[i] = true;\n break;\n }\n }\n }\n return dp[n];\n }\n};\n```\nANALYSIS :- \n* **Time Complexity :-** BigO(N^1.5)\n\n* **Space Complexity :-** BigO(N)
| 270
| 106
|
['C', 'Java']
| 14
|
stone-game-iv
|
[Java/C++/Python] DP
|
javacpython-dp-by-lee215-fbfj
|
Explanation\ndp[i] means the result for n = i.\n\nif there is any k that dp[i - k * k] == false,\nit means we can make the other lose the game,\nso we can win t
|
lee215
|
NORMAL
|
2020-07-11T16:05:26.901392+00:00
|
2020-07-11T16:13:46.031484+00:00
| 13,760
| false
|
# **Explanation**\n`dp[i]` means the result for `n = i`.\n\nif there is any `k` that `dp[i - k * k] == false`,\nit means we can make the other lose the game,\nso we can win the game an `dp[i] = true`.\n<br>\n\n# **Complexity**\nTime `O(n^1.5)`\nSpace `O(N)`\n<br>\n\n**Java**\n```java\n public boolean winnerSquareGame(int n) {\n boolean[] dp = new boolean[n + 1];\n for (int i = 1; i <= n; ++i) {\n for (int k = 1; k * k <= i; ++k) {\n if (!dp[i - k * k]) {\n dp[i] = true;\n break;\n }\n }\n }\n return dp[n];\n }\n```\n**C++**\n```cpp\n bool winnerSquareGame(int n) {\n vector<bool> dp(n + 1, false);\n for (int i = 1; i <= n; ++i) {\n for (int k = 1; k * k <= i; ++k) {\n if (!dp[i - k * k]) {\n dp[i] = true;\n break;\n }\n }\n }\n return dp[n];\n }\n```\n**Python:**\n```py\n def winnerSquareGame(self, n):\n dp = [False] * (n + 1)\n for i in xrange(1, n + 1):\n dp[i] = not all(dp[i - k * k] for k in xrange(1, int(i**0.5) + 1))\n return dp[-1]\n```\n
| 182
| 6
|
[]
| 24
|
stone-game-iv
|
Java | Heavily Commented | Subproblems Visualised
|
java-heavily-commented-subproblems-visua-rm4l
|
Let\'s enumerate all possible moves for n = 7: \n\n\n\nAs you can see, for Alice, there is no subtree that can make him win.\n\nNow let\'s consider for n = 8. C
|
khaufnak
|
NORMAL
|
2020-07-11T16:00:46.185843+00:00
|
2020-07-12T05:23:14.805436+00:00
| 3,403
| false
|
Let\'s enumerate all possible moves for ```n = 7```: \n\n\n\nAs you can see, for Alice, there is no subtree that can make him win.\n\nNow let\'s consider for ```n = 8```. Can Alice choose a subtree that can make him win?\n\n\n\nYes. Alive will go (-1) first move which can make him win.\n\n>Observation: Each of the players asks this question to themselves to play optimally: Can I make a move that will push the other person to a subtree which will eventually make me win.\n\nNote: You can see repeating subproblems, therefore, dynamic programming.\n\n```\nclass Solution {\n Boolean[] dp = new Boolean[100000 + 1];\n public boolean winnerSquareGame(int n) {\n if (dp[n] != null) {\n return dp[n];\n }\n Boolean answer = false;\n for (int move = 1; n - move * move >= 0; ++move) {\n if (n - move * move == 0) {\n // current player won\n answer = true;\n break;\n } else {\n // Hand over turn to other player.\n // If there is any subtree, where the other person loses. We use that subtree.\n // 1. OR means we choose any winning subtree.\n // 2. ! in !solve(n - move*move, dp) means we hand over turn to other player after reducing n by move*move\n answer |= !winnerSquareGame(n - move * move);\n }\n }\n return dp[n] = answer;\n }\n}\n```\n\nComplexity: ```O(sqrt(n) * n)```
| 100
| 2
|
[]
| 10
|
stone-game-iv
|
[Python] DP solution, using game theory, explained
|
python-dp-solution-using-game-theory-exp-x1f3
|
In this problems we have game with two persons, and we need to understand who is winning, if they play with optimal strategies. In this game at each moment of t
|
dbabichev
|
NORMAL
|
2020-10-25T07:32:12.805115+00:00
|
2020-10-25T07:32:12.805148+00:00
| 2,446
| false
|
In this problems we have game with two persons, and we need to understand who is winning, if they play with optimal strategies. In this game at each moment of time we have several (say `k`) stones, and we say that it is **position** in our game. At each step, each player can go from one position to another. Let us use classical definitions:\n\n1. The empty game (the game where there are no moves to be made) is a losing position.\n2. A position is a winning position if at least one of the positions that can be obtained from this position by a single move is a losing position.\n3. A position is a losing position if every position that can be obtained from this position by a single move is a winning position.\n\nWhy people use definitions like this? Imagine that we are in winning position, then there exists at least one move to losing position (**property 2**), so you make it and you force your opponent to be in loosing position. You opponent have no choice to return to winning position, because every position reached from losing position is winning (**property 3**). So, by following this strategy we can say, that for loosing positions Alice will loose and she will win for all other positions.\n\nSo, what we need to check now for position **state**: all positions, we can reach from it and if at least one of them is `False`, our position is winning and we can immedietly return `True`. If all of them are `True`, our position is loosing, and we return `False`. Also we return `False`, if it is our terminal position.\n\n**Complexity**: For each of `n` positions we check at most `sqrt(n)` different moves, so overall time complexity is `O(n sqrt(n))`. Space complexity is `O(n)`, we keep array of length `n`.\n\n```\nclass Solution:\n def winnerSquareGame(self, n):\n \n @lru_cache(None)\n def dfs(state):\n if state == 0: return False\n for i in range(1, int(math.sqrt(state))+1):\n if not dfs(state - i*i): return True\n return False\n \n return dfs(n)\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!**
| 49
| 3
|
['Dynamic Programming']
| 4
|
stone-game-iv
|
📌[ Java ] A very detailed explanation | From Brute Force to Optimised
|
java-a-very-detailed-explanation-from-br-vi5y
|
*\nPlease upvote if the explanation helps, as it keeps up the motivation to provide such posts.\n\n\u2714\uFE0F Given statements:\nAlice starts the game\nEach t
|
Kaustubh_22
|
NORMAL
|
2022-01-22T03:14:35.932050+00:00
|
2022-01-22T19:10:09.332022+00:00
| 1,439
| false
|
****\nPlease upvote if the explanation helps, as it keeps up the motivation to provide such posts.\n****\n\u2714\uFE0F **Given statements**:\nAlice starts the game\nEach time, a player takes `any non-zero square number` of stones in the pile.\n\n**\u2714\uFE0F Obervations:**\nWe don\'t know how much stones does Alice/Bob picks up but we can assume they both play optimally and we need to check if Alice wins the game by doing so.\nIf we are given `n` number of stones, there are `x` number of `square-numbers` in between and to guarantee a win, Alice needs to pick such a number so that Bob is left with a non-square `n-x` stones.\n\n`For eg:`\nIf `n=9`, \nChoices Alice has : \n1. `x=1 ` Bob is left with `n-x` stones -> `8`\n2. `x=4` Bob is left with -> `5`\n3. `x=9` bob is left with -> `0` ( should pick )\n\nWe need to check if there is any situation by which Alice wins a game, or a situation where Bob can not make a move.\n\n# \u2714\uFE0FRecursive Approach : \nWe need to pick every `square number (x = [1,sqrt(n)] )` and reduce the search space for Bob.\n\n****\n\n\n****\n```\nclass Solution {\n public boolean winnerSquareGame(int n) {\n return winnerUtil(n);\n }\n private boolean winnerUtil(int n) {\n // base case\n if(n<=0)\n return false;\n \n // main logic\n for(int i=1;i*i<=n;i++) {\n // The move Alice makes = i*i\n int opponent = n-i*i;\n if( ! winnerUtil(opponent) )\n return true;\n }\n return false;\n }\n}\n```\n\n**Observation** : We are checking if for `n`, if there is some `i` for which `n-i*i` is false. `[ This will help us in implementing to Bottom-Up DP ] `\n\n# \u2714\uFE0FTop-Down DP : \nMemoizing a recursive code is easy.\n\n```\nclass Solution {\n public boolean winnerSquareGame(int n) {\n HashMap<Integer, Boolean> map = new HashMap<>();\n return winnerUtil(n, map);\n }\n private boolean winnerUtil(int n, HashMap<Integer, Boolean> map) {\n // base case\n if(n<=0)\n return false;\n \n if(map.containsKey(n))\n return map.get(n);\n \n // main logic\n for(int i=1;i*i<=n;i++) {\n // The move Alice makes = i*i\n int opponent = n-i*i;\n if(!winnerUtil(opponent, map))\n {\n map.put(n, true);\n return true;\n }\n }\n map.put(n, false);\n return false;\n }\n}\n```\n\n# \u2714\uFE0FBottom-Up Dp : \ndp[i] stores the result for `n = i.`\n\nif there is any `x` that `dp[i - x * x] == false`,\nit means we can make the other lose the game, \nso we can win the game if `dp[i] = true`.\n\nFor `i`, we are checking if `i-j*j` is false, where `j = [1, i]`\n\n```\nclass Solution {\n public boolean winnerSquareGame(int n) {\n boolean[]dp = new boolean[n+1];\n // dp[0] = false;\n for(int i=1;i<n+1;i++) {\n for(int j=1;j*j<=i;j++) {\n if(!dp[i-j*j]) {\n dp[i] = true;\n break;\n }\n }\n }\n return dp[n];\n }\n}\n```\n\n\u2714\uFE0F Complexity Analysis:\n* TC : `O(n * \u221An )`\n* SC : `O(n)`
| 36
| 14
|
['Dynamic Programming', 'Recursion', 'Java']
| 3
|
stone-game-iv
|
C++ DP solution | Explained
|
c-dp-solution-explained-by-asthacs-11td
|
Both the players play optimally. dp[i] = true represents that for i th number, Alice can win. False means Alice loses.\nLets assume Alice loses for n=j.\nThus,
|
asthacs
|
NORMAL
|
2020-07-11T16:08:32.084833+00:00
|
2020-07-11T17:37:23.657748+00:00
| 2,849
| false
|
Both the players play optimally. dp[i] = true represents that for i th number, Alice can win. False means Alice loses.\nLets assume Alice loses for n=j.\nThus, if at any point i Alice can remove a square number such that the remaining number is equal to j, and j is false, then Alice can win at the point i.\n\n*Time complexity: O(n sqrt(n) )\nSpace complexity: O(n)*\n\n```\nbool winnerSquareGame(int n) {\n if(n==0)\n return false;\n\t\t\t\n vector<bool> dp(n+1, false); \n for(int i=1; i<=n; i++)\n {\n for(int j=1; j*j<=i; j++)\n {\n if(dp[i-(j*j)]==false)\n {\n dp[i] = true;\n break;\n }\n }\n }\n \n return dp[n];\n }\n\t
| 31
| 4
|
['Dynamic Programming', 'C']
| 4
|
stone-game-iv
|
💎 C++ || ❌ DFS 🆚 ✔ DP || Easy Understanding
|
c-dfs-vs-dp-easy-understanding-by-intell-qru4
|
\uD83D\uDC68\u200D\uD83D\uDCBB Friend\'s if you find this solution helpful \uD83D\uDE0A, PLEASE do UPVOTE. By doing that motivates me to create a better post li
|
intellisense
|
NORMAL
|
2022-01-22T03:22:13.721556+00:00
|
2022-01-22T13:53:21.181364+00:00
| 1,532
| false
|
\uD83D\uDC68\u200D\uD83D\uDCBB Friend\'s if you find this solution helpful \uD83D\uDE0A, PLEASE do UPVOTE. By doing that motivates me to create a better post like this \u270D\uFE0F\n____________________________________________________________________________________________________________\n____________________________________________________________________________________________________________\n\n### DRY RUN for Both DFS and DP.\n\n\n\n#### \u2714\uFE0F **Question Conclusion**\n* Lets assume it as a number game. two player are playing Alice and Bob. Alice has given the first chance.\n* Here Both the player want to win the game and to win they have to make the number 0 for other player.\n* Bound by the rules they can only choose single move they can subtract a square which is smaller or equal to the number so the number given to other player is equal to 0.\n* Here both the player want to win the game so they will find every permutation if there is any possiblity to win the game.\n#### \u2714\uFE0F **Solution - I (Naive Approach will give time limit exceed)**\n##### **Intuition :-**\n* Lets go for the naive one first.\n* Lets check for every possible combination and find weather that we can make the number zero for the other player to lose the game.\n* If we could not make the number 0 we have to decrement the number such that bob will not able to make the number 0. But keep in mind the rules of the game Cheating is not allowed \uD83D\uDE05.\n* Here we have used a recursive function helper with the base conditon as if who every player will give 0 to the other player will win the game as return 1.\n##### **Code :-**\n```\nclass Solution\n{\npublic:\n bool winnerSquareGame(int n)\n {\n if (n <= 0)\n {\n return false;\n }\n for (int j = 1; j * j < n + 1; j++)\n {\n if (!winnerSquareGame(n - j * j))\n {\n return true;\n }\n }\n return false;\n }\n};\n```\n**Time Complexity** : `O(still figuring out)`, we are using DFS for every condition. suggestion are welcomed.\n**Space Complexity** : `O(1)`, no extra space is being used.\n#### \u2714\uFE0F **Solution - II (Best Approach)**\n##### **Intuition :-**\n* Here we are going to check the same as earlier but now we will store the answer in a DP vector so that we can directly check weather the result have been checked for that number as its value will always be same for a number that is earlier check.\n* DP vector of size 100001 is created as max size is given in question.\n* Thus in the end we will return value at index n of the DP.\n##### **Code :-**\n```\nclass Solution\n{\npublic:\n bool winnerSquareGame(int n)\n {\n vector<bool> dp(n + 1);\n for (int i = 1; i < n + 1; i++)\n {\n for (int j = 1; j * j < i + 1; j++)\n {\n if (!dp[i - j * j])\n {\n dp[i] = true;\n break;\n }\n }\n }\n return dp[n];\n }\n};\n```\n**Time Complexity** : `O(n^1.5)`, there are n loop outer and inside it n^0.5 loop will be checked.\n**Space Complexity** : `O(n)`, Here we are using space of 10^5 element as given max limit in ques.\n_____________________________________________________________________________________________________________\n_____________________________________________________________________________________________________________\n\n\uD83D\uDCBBIf there are any suggestions/questions in my post, comment below \uD83D\uDC47
| 30
| 23
|
['Dynamic Programming', 'C']
| 11
|
stone-game-iv
|
✔️ [Python3] JUST 4-LINES, (ノ゚0゚)ノ~ OMG!!!, Explained
|
python3-just-4-lines-no0no-omg-explained-99jg
|
UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.\n\nIn the beginning, it may seem that we would need to do a hug
|
artod
|
NORMAL
|
2022-01-22T02:31:06.992887+00:00
|
2022-01-22T18:11:01.571328+00:00
| 1,649
| false
|
**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nIn the beginning, it may seem that we would need to do a huge amount of scans, recursive calls and take lots of space doing backtracking since the input `n` is in the range `1..10e5`. But the thing is that a player can remove only **squared number** of stones from the pile. That is, if we got `100000` as an input, the number of possible moves is in the more modest range `1..floor(sqrt(100000))` = `1 .. 316`. So it\'s perfectly doable to recursively verify all possible moves of Alice and Bob using memoization.\n\nWe iterate over the range `floor(sqrt(n)) .. 1`, square the index, and recursively call the function asking the question: Can the next player win if he/she starts with the pile of stones `n - i^2`?. If yes that means the current player loses, and we need to check the remaining options.\n\nWhy do we scan in the reversed range? Try to answer this question yourself as an exercise in the comments (\u0E07\u30C4)\u0E27\n\nTime: **O(N*sqrt(N))** - scan\nSpace: **O(N)** - memo and recursive stack\n\nRuntime: 404 ms, faster than **82.63%** of Python3 online submissions for Stone Game IV.\nMemory Usage: 22.7 MB, less than **40.72%** of Python3 online submissions for Stone Game IV.\n\n```\n @cache\n def winnerSquareGame(self, n: int) -> bool:\n if not n: return False\n\t\t\n for i in reversed(range(1, floor(sqrt(n)) + 1)):\n if not self.winnerSquareGame(n - i**2): return True\n\n return False\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**
| 28
| 17
|
['Dynamic Programming', 'Python3']
| 5
|
stone-game-iv
|
Beginners Solution with image
|
beginners-solution-with-image-by-java_pr-9k62
|
\nclass Solution {\n public boolean winnerSquareGame(int n) {\n HashSet<Integer> losingState = new HashSet<>();\n HashSet<Integer> winingState
|
Java_Programmer_Ketan
|
NORMAL
|
2022-01-22T04:48:46.388078+00:00
|
2022-01-22T06:18:04.667122+00:00
| 709
| false
|
```\nclass Solution {\n public boolean winnerSquareGame(int n) {\n HashSet<Integer> losingState = new HashSet<>();\n HashSet<Integer> winingState = new HashSet<>();\n losingState.add(0);\n for(int cur=1;cur<=n;cur++){\n for(int i=1;i*i<=cur;i++){\n if(losingState.contains(cur-i*i)){\n winingState.add(cur);\n break;\n }\n }\n if(!winingState.contains(cur)) losingState.add(cur);\n }\n return winingState.contains(n);\n }\n}\n```\n**Method 2**\nfalse in the array means losing state\n```\nclass Solution {\n public boolean winnerSquareGame(int n) {\n boolean[] dp = new boolean[n+1];\n for(int cur=1;cur<=n;cur++){\n for(int i=1;i*i<=cur;i++){\n if(!dp[cur-i*i]){\n dp[cur]=true;\n break;\n }\n }\n }\n return dp[n];\n }\n}\n```\n\n
| 24
| 10
|
[]
| 1
|
stone-game-iv
|
C++ || Easy to Understand || Explanation
|
c-easy-to-understand-explanation-by-__ph-xmcv
|
See, in this types of game problem, you have to be one of the player & play optimally for this player. Lets say, I become Alice & want to defeat bob. Playing op
|
__phoenixer__
|
NORMAL
|
2022-01-22T07:17:06.745005+00:00
|
2022-01-22T07:19:11.701107+00:00
| 1,440
| false
|
See, in this types of game problem, you have to be one of the player & play optimally for this player. Lets say, I become Alice & want to defeat bob. Playing optimally means:\n**at any turn I will look after every possiblity & see that at which possibility I can win. If no such possibility found, then it means that now I will loose for sure**.\n\nHere I will discuss 2 approaches. One is Brute force recursion, & other is memoization.\nBut I recommend you to see **Brute Force approach first** (because **I had explained it in details**).\n\n**APPROACH 1 : BRUTE FORCE RECURSION** (TLE)\n```\n bool winnerSquareGame(int n) {\n\t\t// Remember, Alice will play first turn (Alice will start the game)\n\t // Base Case\n if(n==0){ // Alice can not pick any coins, so he genuinely lost\n return false;\n }\n\t\t\n\t\t//Possibility 1\n if(n==1){ // as 1 is a perfect square, so alice picks it up & wins\n return true;\n }\n \n // Possibility 2: check if n is a perfect Square number or not\n long double x= sqrt(n);\n\n\t if((int)x * (int)x == n){ // then it is a perfect square number, alice picks it up & wins\n\t\t return true; // Alice picks it up\n\t }\n \n\t\t// We have checked for 1, and perfect_square. Now check every other remaining possibility\n\t\t// That is, every perfectSquare number that alice can pick which are in range [1, n].\n\t\t\n for(int i=1; i*i<=n; i++){\n bool prevAns= winnerSquareGame(n-(i*i)); // who will win if piles contains n-(i*i) stones\n if(prevAns==false){ // If Alice losses the game when piles contains n-(i*i) stones. Then Alice will dafinately win if piles contains "n" stones. (by picking remaining i*i stones)\n return true;\n }\n }\n // Loop ends, that means at none of the above possiblities Alice wins.\n return false; // so, Alice loose the game\n }\n```\n\n**Approach 2 : MEMOIZATION** (Passed)\n\n```\n bool winnerSquareGameHelper(int n, char* arr) {\n if(n==0){ // Alice can not pick any coins, so he genuinely lost\n arr[0]=\'F\';\n return false;\n }\n if(n==1){\n arr[1]=\'T\';\n return true;\n }\n \n if(arr[n]!=\'N\'){\n if(arr[n]==\'T\'){\n return true;\n }\n return false;\n }\n \n // check if n is a perfect number or not\n long double x= sqrt(n);\n\n\t if((int)x * (int)x == n){ // then it is a perfect square number\n arr[n]=\'T\';\n\t\t return true; // Alice picks it up\n\t }\n \n for(int i=1; i*i<=n; i++){\n bool prevAns= winnerSquareGameHelper(n-(i*i), arr);\n if(prevAns==false){\n arr[n]=\'T\';\n return true;\n }\n }\n arr[n]=\'F\';\n return false;\n }\n \n bool winnerSquareGame(int n){\n \n char* arr= new char[n+1];\n for(int i=0; i<=n; i++){\n arr[i]=\'N\'; // initialize with some some random char\n }\n \n return winnerSquareGameHelper(n, arr);\n }\n```\n\nThanking you !\nIf you have any doubt then don\'t hesitate to ask in comments.
| 21
| 4
|
['Dynamic Programming', 'Recursion', 'Memoization', 'C']
| 3
|
stone-game-iv
|
C++ dp code in just 4 lines with explanation
|
c-dp-code-in-just-4-lines-with-explanati-k36j
|
Logic for Code\n\nAlice have to pick the square numbers only e.g. 1,4,9,16..............\nLet\'s say that Alice pick number k*k then remaining number of stones
|
rahulrajdav699
|
NORMAL
|
2022-01-22T12:16:51.477788+00:00
|
2022-01-23T07:00:43.357528+00:00
| 896
| false
|
**Logic for Code**\n\nAlice have to pick the square numbers only e.g. 1,4,9,16..............\nLet\'s say that Alice pick number **k*k** then remaining number of stones in piles will be **n-k*k**\nNow its Bob\'s turn and he has **n-k*k** stones in pile.\nIf there is a force win for **n-k*k** stones in piles then Bob will definitely win.\nSo, Alice can only win if there exists a number **k** such that Bob(with **n-k*k** stones) will not have force win.\n\n\n\nSo we will make a dp table.\n\ndp[i] means the result for n = i.\n\nif there is any k that dp[i - k * k] == false,\nit means we can make the other lose the game,\nso we can win the game an dp[i] = true.\n\n**Complexity**\n\nTime O(n * sqrt(n))\nSpace O(N)\n\n```\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<bool> dp(n+1,0);\n for(int i=1;i<=n;i++)\n for(int j=1;j*j<=i;j++)\n if(!dp[i-j*j]) { dp[i]=true; break;}\n return dp[n];\n }\n};
| 15
| 3
|
['Dynamic Programming']
| 1
|
stone-game-iv
|
Java Simple Top Down DP
|
java-simple-top-down-dp-by-hobiter-ps35
|
DFS, caching result with a hashmap, aka, top-down DP;\n\nclass Solution {\n Map<Integer, Boolean> map = new HashMap<>();\n public boolean winnerSquareGame
|
hobiter
|
NORMAL
|
2020-07-11T23:14:22.111406+00:00
|
2020-07-11T23:14:22.111452+00:00
| 634
| false
|
DFS, caching result with a hashmap, aka, top-down DP;\n```\nclass Solution {\n Map<Integer, Boolean> map = new HashMap<>();\n public boolean winnerSquareGame(int n) {\n if (n == 0) return false;\n if (map.containsKey(n)) return map.get(n);\n boolean res = false;\n for (int i = 1; i * i <= n; i++) {\n if (!winnerSquareGame(n - i * i)) {\n res = true;\n break;\n }\n }\n map.put(n, res);\n return res;\n }\n}\n```
| 12
| 2
|
[]
| 0
|
stone-game-iv
|
🎨 The ART of Dynamic Programming
|
the-art-of-dynamic-programming-by-clayto-q5dn
|
Synopsis:\n\n\uD83C\uDFA8 The ART of Dynamic Programming:\n\n1. All possible jth squared amount of stones which can be taken are considered for each ith amount
|
claytonjwong
|
NORMAL
|
2020-07-15T16:33:12.668093+00:00
|
2023-05-25T01:52:54.938330+00:00
| 608
| false
|
**Synopsis:**\n\n[\uD83C\uDFA8 The ART of Dynamic Programming:](https://leetcode.com/discuss/general-discussion/712010/the-art-of-dynamic-programming-an-intuitive-approach-from-apprentice-to-master/)\n\n1. **A**ll possible `j`<sup>th</sup> squared amount of stones which can be taken are considered for each `i`<sup>th</sup> amount of stones\n2. **R**emember each subproblem\'s optimal solution via a DP memo\n3. **T**urn the top-down solution upside-down to create the bottom-up solution\n\n---\n\n**Note:** Prerequisites to properly understanding this solution are a handful of [game theory](https://en.wikipedia.org/wiki/Game_theory) concepts:\n* [Zero-sum game](https://en.wikipedia.org/wiki/Zero-sum_game)\n* [Minimax (in Zero-sum games)](https://en.wikipedia.org/wiki/Minimax#In_zero-sum_games)\n* [Nash Equilibrium](https://en.wikipedia.org/wiki/Nash_equilibrium)\n\n---\n\n**Kotlin:**\n\n*Top-Down (TLE)*\n```\nclass Solution {\n fun winnerSquareGame(N: Int): Boolean {\n fun go(i: Int): Boolean {\n if (i == 0)\n return false // \uD83D\uDED1 base case: no stones left\n var take = 0\n for (j in Math.sqrt(i.toDouble()).toInt() downTo 1) { // \u2B50\uFE0F take each (j * j) amount of stones\n if (!go(i - j * j))\n return true // \uD83C\uDFAF if next player lost, then current player wins\n }\n return false\n }\n return go(N)\n }\n}\n```\n\n*Top-Down Memo (AC)*\n```\nclass Solution {\n fun winnerSquareGame(N: Int): Boolean {\n var m = mutableMapOf<Int, Boolean>();\n fun go(i: Int): Boolean {\n if (m.contains(i))\n return m[i]!! // \uD83E\uDD14 memo\n if (i == 0) {\n m[i] = false // \uD83D\uDED1 base case: no stones left\n return m[i]!!\n }\n for (j in Math.sqrt(i.toDouble()).toInt() downTo 1) { // \u2B50\uFE0F take each (j * j) amount of stones\n if (!go(i - j * j)) {\n m[i] = true\n return m[i]!! // \uD83C\uDFAF if next player lost, then current player wins\n }\n }\n m[i] = false\n return m[i]!!\n }\n return go(N)\n }\n}\n```\n\n*Bottom-Up (AC)*\n```\nclass Solution {\n fun winnerSquareGame(N: Int): Boolean {\n var dp = Array<Boolean>(N + 1) { false } // \uD83E\uDD14 memo + \uD83D\uDED1 base case dp[0]: no stones left\n for (i in 1..N) {\n for (j in Math.sqrt(i.toDouble()).toInt() downTo 1) { // \u2B50\uFE0F take each (j * j) amount of stones\n if (!dp[i - j * j])\n dp[i] = true // \uD83C\uDFAF if next player lost, then current player wins\n }\n }\n return dp[N]\n }\n}\n```\n\n**Javascript Solutions:**\n\n*Top-Down (TLE)*\n```\nlet winnerSquareGame = N => {\n let go = i => {\n if (!i)\n return false; // \uD83D\uDED1 base case: no stones left\n for (let j = Math.floor(Math.sqrt(i)); 1 <= j; --j) // \u2B50\uFE0F take each (j * j) amount of stones\n if (!go(i - (j * j)))\n return true; // \uD83C\uDFAF if next player lost, then current player wins\n return false;\n };\n return go(N);\n};\n```\n\n*Top-Down Memo (AC)*\n```\nlet winnerSquareGame = N => {\n let m = Array(N).fill(null);\n let go = i => {\n if (m[i] != null)\n return m[i]; // \uD83E\uDD14 memo\n if (!i)\n return m[i] = false; // \uD83D\uDED1 base case: no stones left\n for (let j = Math.floor(Math.sqrt(i)); 1 <= j; --j) // \u2B50\uFE0F take each (j * j) amount of stones, \uD83D\uDC8E avoid TLE by taking largest (j * j) first\n if (!go(i - (j * j)))\n return m[i] = true; // \uD83C\uDFAF if next player lost, then current player wins\n return m[i] = false;\n };\n return go(N);\n};\n```\n\n*Bottom-Up (AC)*\n```\nlet winnerSquareGame = N => {\n let dp = Array(N + 1).fill(false); // \uD83E\uDD14 memo\n dp[0] = false; // \uD83D\uDED1 base case: no stones left\n for (let i = 1; i <= N; ++i)\n for (let j = Math.floor(Math.sqrt(i)); 1 <= j; --j) // \u2B50\uFE0F take each (j * j) amount of stones\n if (!dp[i - (j * j)])\n dp[i] = true; // \uD83C\uDFAF if next player lost, then current player wins\n return dp[N];\n};\n```\n\n---\n\n**Python3 Solutions:**\n\n*Top-Down (TLE)*\n```\nclass Solution:\n def go(self, i: int) -> bool:\n if not i:\n return False # \uD83D\uDED1 base case: no stones left\n for j in range(math.floor(math.sqrt(i)), 0, -1): # \u2B50\uFE0F take each (j * j) stones\n if not self.go(i - (j * j)):\n return True # \uD83C\uDFAF if next player lost, then current player wins\n return False\n def winnerSquareGame(self, N: int) -> bool:\n return self.go(N)\n```\n\n*Top-Down Memo (AC)*\n```\nclass Solution:\n def go(self, i: int, m = {}) -> bool:\n if i in m:\n return m[i] # \uD83E\uDD14 memo\n if not i:\n m[i] = False\n return False # \uD83D\uDED1 base case: no stones left\n for j in range(math.floor(math.sqrt(i)), 0, -1): # \u2B50\uFE0F take each (j * j) stones, \uD83D\uDC8E avoid TLE by taking largest (j * j) first\n if not self.go(i - (j * j)):\n m[i] = True\n return True # \uD83C\uDFAF if next player lost, then current player wins\n m[i] = False\n return False\n def winnerSquareGame(self, N: int) -> bool:\n return self.go(N)\n```\n\n*Bottom-Up (AC)*\n```\nclass Solution:\n def winnerSquareGame(self, N: int) -> bool:\n dp = [False] * (N + 1)\n dp[0] = False # \uD83D\uDED1 base case: no stones left\n for i in range(0, N + 1):\n for j in range(math.floor(math.sqrt(i)), 0, -1): # \u2B50\uFE0F take each (j * j) stones\n if not dp[i - (j * j)]:\n dp[i] = True # \uD83C\uDFAF if next player lost, then current player wins\n return dp[N]\n```\n\n---\n\n**C++ Solutions:**\n\n*Top-Down (TLE)*\n```\nclass Solution {\n bool go(int i) {\n if (!i)\n return false; // \uD83D\uDED1 base case: no stones left\n for (int j = sqrt(i); 1 <= j; --j) // \u2B50\uFE0F take each (j * j) stones\n if (!go(i - (j * j)))\n return true; // \uD83C\uDFAF if next player lost, then current player wins\n return false;\n }\npublic:\n bool winnerSquareGame(int N) {\n return go(N);\n }\n};\n```\n\n*Top-Down Memo (AC)*\n```\nclass Solution {\n using Map = unordered_map<int, int>;\n bool go(int i, Map&& m = {}) {\n if (m.find(i) != m.end())\n return m[i]; // \uD83E\uDD14 memo\n if (!i)\n return m[i] = false; // \uD83D\uDED1 base case: no stones left\n for (int j = sqrt(i); 1 <= j; --j) // \u2B50\uFE0F take each (j * j) stones, \uD83D\uDC8E avoid TLE by taking largest (j * j) first\n if (!go(i - (j * j), move(m)))\n return m[i] = true; // \uD83C\uDFAF if next player lost, then current player wins\n return m[i] = false;\n }\npublic:\n bool winnerSquareGame(int N) {\n return go(N);\n }\n};\n```\n\n*Bottom-Up (AC)*\n```\nclass Solution {\npublic:\n bool winnerSquareGame(int N) {\n bitset<100001> dp; // \uD83E\uDD14 memo\n dp[0] = 0; // \uD83D\uDED1 base case: no stones left\n for (auto i{ 1 }; i <= N; ++i)\n for (int j = sqrt(i); 1 <= j; --j) // \u2B50\uFE0F take each (j * j) stones\n if (!dp[i - (j * j)])\n dp[i] = 1; // \uD83C\uDFAF if next player lost, then current player wins\n return dp[N];\n }\n};\n```
| 11
| 0
|
[]
| 1
|
stone-game-iv
|
Python Recursion + Memo = DP
|
python-recursion-memo-dp-by-wsy19970125-65bw
|
Recursion + Memo:\n\tclass Solution:\n\t\t@lru_cache(None)\n\t\tdef winnerSquareGame(self, n: int) -> bool:\n\t\t\tif n == 0:\n\t\t\t\treturn False\n\t\t\ti = i
|
wsy19970125
|
NORMAL
|
2020-07-11T16:20:01.866237+00:00
|
2020-07-11T23:52:36.554624+00:00
| 1,028
| false
|
### Recursion + Memo:\n\tclass Solution:\n\t\t@lru_cache(None)\n\t\tdef winnerSquareGame(self, n: int) -> bool:\n\t\t\tif n == 0:\n\t\t\t\treturn False\n\t\t\ti = int(math.sqrt(n))\n\t\t\twhile i >= 1:\n\t\t\t\tif not self.winnerSquareGame(n - i * i):\n\t\t\t\t\treturn True\n\t\t\t\ti -= 1\n\t\t\treturn False\n### DP:\n\tclass Solution:\n\t\tdef winnerSquareGame(self, n: int) -> bool:\n\n\t\t\tdp = [None] * (n + 1)\n\t\t\tdp[0] = False\n\t\t\tsteps = sorted([ele ** 2 for ele in range(1, int(math.sqrt(n)) + 1)], reverse=True)\n\n\t\t\tfor i in range(n):\n\t\t\t\tfor step in steps:\n\t\t\t\t\tif i + step <= n:\n\t\t\t\t\t\tif dp[i + step]:\n\t\t\t\t\t\t\tcontinue\n\t\t\t\t\t\telse:\n\t\t\t\t\t\t\tdp[i + step] = (False if dp[i] else True)\n\t\t\t\tif dp[-1]:\n\t\t\t\t\treturn True\n\t\t\treturn False
| 11
| 0
|
[]
| 3
|
stone-game-iv
|
JAVA | Stone Game IV | 100% Fast | Explained
|
java-stone-game-iv-100-fast-explained-by-0yfq
|
\n\n\nclass Solution {\n public boolean winnerSquareGame(int n) {\n //if dp[i]==false, it means Alice will loose anyway, dp[i]==true, Alice will win non
|
sanket_64
|
NORMAL
|
2020-10-25T08:16:15.366263+00:00
|
2020-10-25T08:16:15.366297+00:00
| 264
| false
|
\n\n```\nclass Solution {\n public boolean winnerSquareGame(int n) {\n //if dp[i]==false, it means Alice will loose anyway, dp[i]==true, Alice will win nonetheless\n boolean dp[] = new boolean[n+1];\n \n //for all numbers, \n for(int i=0;i<=n;i++){\n \n // if already true, nothing to do\n if(dp[i])\n continue;\n \n //as dp[i] is false, any square numbers from here onwards should return true,\n //so if dp[17] is false, dp[17+4], dp[17+9] and so on are true, as ALice can remove 4 and 9 from stones and return dp[17] to Bob and hence bob will fail\n for(int k=1;i+k*k<=n;k++)\n dp[i+k*k]=true;\n }\n \n return dp[n];\n}\n}\n```
| 9
| 4
|
[]
| 3
|
stone-game-iv
|
[Python3] DP
|
python3-dp-by-patrickoweijane-ep0y
|
Below is the code, please let me know if you have any questions!\n\nclass Solution:\n def winnerSquareGame(self, n: int) -> bool:\n dp = [False] * (n
|
PatrickOweijane
|
NORMAL
|
2022-01-22T00:56:31.257366+00:00
|
2022-01-22T17:04:39.432984+00:00
| 778
| false
|
Below is the code, please let me know if you have any questions!\n```\nclass Solution:\n def winnerSquareGame(self, n: int) -> bool:\n dp = [False] * (n + 1)\n squares = []\n curSquare = 1\n for i in range(1, n + 1):\n if i == curSquare * curSquare:\n squares.append(i)\n curSquare += 1\n dp[i] = True\n else:\n for square in squares:\n if not dp[i - square]:\n dp[i] = True\n break\n return dp[n]\n```\n\nEdit: For a clear explanation of the algorithm, check the comment of @Cavalier_Poet below!
| 8
| 0
|
['Dynamic Programming', 'Python', 'Python3']
| 3
|
stone-game-iv
|
Standard DP question Explained BEST - ALL you need to know
|
standard-dp-question-explained-best-all-meiu1
|
We are asked to find the solution for an input of n. So,we find solution for all numbers from [0,n] and we do this because the previous answers help us in findi
|
akhil_ak
|
NORMAL
|
2020-07-11T18:21:59.710620+00:00
|
2020-07-12T09:16:58.011578+00:00
| 758
| false
|
We are asked to find the solution for an input of n. So,we find solution for all numbers from [0,n] and we do this because the previous answers help us in finding the solution for a potentially larger number. We have n states of dp,each state represents the solution of that specific state. states = [0,n]. let dp[i] be the state representation.\n\nAnd we have to find the optimal answer.Even if in one possibility alice wins,its a True.\n```\nFor each state i:\n\tj = find all the perfect squares less than i.\n\tfor each j:\n\t\tAssume that the perfectsquare j is taken by alice.\n\t\tThen the game continues as` dp[i-j*j]` for bob as start player.\n\t\tSince we calculated all answers for such states with alice as start player,its the same even if bob becomes the start player because both play optimally.\n\t\tIf bob could wins ,alice loses i.e ` dp[i-j*j]` = True\n\t\telse if bob loses alice wins i.e ` dp[i-j*j]` = False\n\t\tSo,we choose the case where alice wins with alice as start player(In essence we find if atleast one j returns True for dp[i]). or dp[i] |= ! dp[i-j*j]\n```\t\n\t\t\n`Time:O(n^1.5) | Space:O(n) `\nApproach`:DynamicProgramming` Bottom-up\n\n\tclass Solution:\n\t\t\tdef winnerSquareGame(self, n: int) -> bool:\n\t\t\t\tdp = [False]*(n+1)\n\t\t\t\tfor i in range(1,n+1):\n\t\t\t\t\tj = 1\n\t\t\t\t\twhile j*j <= i:\n\t\t\t\t\t\tdp[i] |= not dp[i-j*j]\n\t\t\t\t\t\tj+=1\n\t\t\t\treturn dp[n]\n\nplease leave an upvote if you find it helpful :)\n
| 8
| 0
|
['Python', 'Python3']
| 1
|
stone-game-iv
|
✅ [Python] ULTIMATE ONE-LINER
|
python-ultimate-one-liner-by-stanislav-i-yhow
|
\u2705 IF YOU LIKE THIS SOLUTION, PLEASE UPVOTE.\n*\nThis solution employs recursion to explore all possible games. Time complexity is O(N\sqrtN). Space complex
|
stanislav-iablokov
|
NORMAL
|
2022-11-11T17:06:04.544367+00:00
|
2022-11-14T09:37:59.333183+00:00
| 307
| false
|
**\u2705 IF YOU LIKE THIS SOLUTION, PLEASE UPVOTE.**\n****\nThis solution employs recursion to explore all possible games. Time complexity is **O(N\\*sqrtN)**. Space complexity is **O(N)**.\n\n**Comment.** (don\'t have time for that now, but If you want explanation, please leave a comment)\n\n**Python.**\n```\nclass Solution:\n @lru_cache(None)\n def winnerSquareGame(self, n: int) -> bool:\n return any(not self.winnerSquareGame(n-m**2) for m in reversed(range(1, int(n**0.5)+1))) or False\n```
| 6
| 0
|
[]
| 0
|
stone-game-iv
|
Easy || recursion || memoization || easy explaination
|
easy-recursion-memoization-easy-explaina-1px8
|
We want a sequence of choices for alice such that bob always loose no mater what choices he make.\nSo for all the choices bob make we\'ll check if in all cases
|
Sandy_14
|
NORMAL
|
2022-09-22T09:00:18.672551+00:00
|
2022-09-22T09:00:18.672597+00:00
| 411
| false
|
We want a sequence of choices for alice such that bob always loose no mater what choices he make.\nSo for all the choices bob make we\'ll check if in all cases alice wins (that\'s why the AND operation in bob\'s choices).\nSimilarly, for alice choice we\'\'ll check any choice that lead to his win.\nSee code for more explaination.\n\n```\nclass Solution {\npublic:\n int t[100001][2]; //memoization\n bool solve(int n,int c)\n {\n if(n==0)\n {\n if(c==1) return true;\n else return false;\n }\n if(t[n][c]!=-1) return t[n][c];\n if(c==0) //if it\'s alice turn\n {\n bool ans=false;\n for(int x=1;x*x<=n;x++)\n {\n ans=ans || solve(n-(x*x),1-c);\n }\n return t[n][c]=ans;\n }\n else //if it\'s bob turn\n {\n bool ans=true;\n for(int x=1;x*x<=n;x++)\n {\n ans=ans && solve(n-(x*x),1-c);\n }\n return t[n][c]=ans;\n }\n }\n bool winnerSquareGame(int n) {\n memset(t,-1,sizeof(t));\n return solve(n,0);\n }\n};\n```
| 6
| 0
|
['Dynamic Programming', 'Recursion', 'C']
| 0
|
stone-game-iv
|
💚[C++] Fast & Easy Solution Explained | O(N(sqrt (N)) | Philosophy
|
c-fast-easy-solution-explained-onsqrt-n-tic2k
|
Welcome to abivilion\'s solution. Kindly upvote for more documentation\n\n## Philosophy\n\n\n1. I don\'t know what can Alice take or Bob take for himself/herse
|
abivilion
|
NORMAL
|
2022-01-22T01:52:54.039412+00:00
|
2022-01-22T02:42:53.513840+00:00
| 432
| false
|
**Welcome to abivilion\'s solution. Kindly upvote for more documentation**\n\n## ***Philosophy***\n\n```\n1. I don\'t know what can Alice take or Bob take for himself/herself , But I do know they are playing optimally.\n\n2. And playing optimally means first perferences should be PERFECT SQUARE. Other choices are totally depends on the situation.\n\n3. So,After understanding this I confirm that the for both guys I need to find PERFECT SQUARES <=n;\n\n4. The word CHOICE comes with recursion So, I need recursion...\n\nBut How? Lets find out.\n\n5. Situation- If any of guys make any choices optimally then I have to work upon those choices for ANOTHER person.\nSo, It means I need to traverse every choices and search for PERFECT SQUARE if possible. Then tailor the choice after selecting a number <=N. Then, same logic should be applied to different choices.\n\n6. SO, I can use FOR\n WORKING ON EACH CHOICES -> RECURSION\n WHAT WORK TO PERFORM ON EACH CHOICE -> Traverse till the choice and look out for perfect square.\n\n 7. Thier may form redundant calls . I can use dp[] to store ans.\n\n```\n\n\n\n\n\n\n***SOLUTION***\n\n```\nclass Solution {\npublic:\n \n int dp[100001];\n \n int opr(int n)\n {\n if(n<=0) return 0;\n if(dp[n]!=-1) return dp[n]; \n for(int i=1;i*i<=n;i++)\n {\n // if 2nd player return false then first will win; \n if(opr(n-i*i)==0) return dp[n]=1;\n }\n \n return dp[n]=false;\n \n }\n bool winnerSquareGame(int n) {\n cout<<sizeof(dp);\n memset(dp,-1,sizeof(dp));\n \n return opr(n);\n }\n};\n```
| 6
| 3
|
['Dynamic Programming', 'Memoization', 'C']
| 2
|
stone-game-iv
|
Python simple and very short DP solution
|
python-simple-and-very-short-dp-solution-4n8w
|
\nclass Solution:\n def winnerSquareGame(self, n: int) -> bool:\n dp = [0]*(n+1)\n for i in range(1, n+1):\n j = 1\n whil
|
yehudisk
|
NORMAL
|
2020-10-25T08:07:16.893465+00:00
|
2020-10-25T08:07:16.893507+00:00
| 417
| false
|
```\nclass Solution:\n def winnerSquareGame(self, n: int) -> bool:\n dp = [0]*(n+1)\n for i in range(1, n+1):\n j = 1\n while j*j <= i and not dp[i]:\n dp[i] = dp[i-j*j]^1\n j+=1\n return dp[n]\n```\n**Like it? please upvote...**
| 6
| 0
|
['Python3']
| 1
|
stone-game-iv
|
💥Runtime beats 92.86%, Memory beats 100.00% [EXPLAINED]
|
runtime-beats-9286-memory-beats-10000-ex-o6fz
|
Intuition\nThe intuition behind this problem is that each player can only remove a certain number of stones defined by perfect squares, and the goal is to deter
|
r9n
|
NORMAL
|
2024-09-26T18:30:59.875510+00:00
|
2024-09-26T18:30:59.875549+00:00
| 28
| false
|
# Intuition\nThe intuition behind this problem is that each player can only remove a certain number of stones defined by perfect squares, and the goal is to determine if the first player (Alice) can always win if both play optimally.\n\n# Approach\nThe approach involves using dynamic programming to build a solution where we create an array that tracks whether the current player can win with a given number of stones; we fill this array by checking all possible square removals to see if they leave the opponent in a losing position.\n\n# Complexity\n- Time complexity:\nO(n\u221An) because we iterate through all stone counts up to n and for each, we check perfect squares up to \u221An.\n\n- Space complexity:\nO(n) due to the storage needed for the dynamic programming array.\n\n# Code\n```csharp []\npublic class Solution {\n public bool WinnerSquareGame(int n) {\n bool[] dp = new bool[n + 1];\n \n for (int i = 1; i <= n; i++) {\n for (int j = 1; j * j <= i; j++) {\n if (!dp[i - j * j]) {\n dp[i] = true;\n break;\n }\n }\n }\n \n return dp[n];\n }\n}\n\n```
| 5
| 0
|
['C#']
| 0
|
stone-game-iv
|
[Python3] Game Theory + DP - Simple Solution
|
python3-game-theory-dp-simple-solution-b-lrks
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
dolong2110
|
NORMAL
|
2024-09-10T09:28:32.749730+00:00
|
2024-09-10T09:28:32.749760+00:00
| 105
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def winnerSquareGame(self, n: int) -> bool:\n @cache\n def dp(player: int, stones: int) -> int:\n sqrt = int(math.sqrt(stones))\n for i in range(sqrt, 0, -1):\n if i ** 2 == stones or not dp(player ^ 1, stones - i ** 2): return True\n return False\n return dp(0, n)\n```
| 5
| 0
|
['Math', 'Dynamic Programming', 'Game Theory', 'Python3']
| 0
|
stone-game-iv
|
[Template Solution] DP = DFS + memoization
|
template-solution-dp-dfs-memoization-by-svvg6
|
\n/*\nDP = DFS + memoization\nAssume NN is the length of arr.\nTime complexity: O}(N*sqrt(N)) since we spend O(sqrt(N)) at most for each dfs call, and there a
|
codedayday
|
NORMAL
|
2020-10-25T19:17:46.435643+00:00
|
2022-01-23T00:27:07.875379+00:00
| 362
| false
|
```\n/*\nDP = DFS + memoization\nAssume NN is the length of arr.\nTime complexity: O}(N*sqrt(N)) since we spend O(sqrt(N)) at most for each dfs call, and there are O(N) dfs calls in total.\nSpace complexity: O(N) since we need spaces of O(N) to store the result of dfs.\n*/\nclass Solution {// DP = DFS + memoization\npublic://Time/Space: O(N); O(N)\n bool winnerSquareGame(int n) {\n if(n == 0) return false;\n if(n == 1) return true;\n if(_map.count(n)) return _map[n];\n //for(int i = 1; i<=sqrt(n); ++i) //i*i:1, 4, ..., n. this suboptimal: dfs(n) -> dfs(n-1)\n\t\t//for(int i = sqrt(n); i >=0; --i) //This will cause dfs(n) -> dfs(n) deap infinite loop\n\t\tfor(int i = sqrt(n); i >=1; --i) //i*i:n, ..., 4, 1. this is better. dfs(n) -> dfs(SMALL_NUMBER)\t\t\n if(!winnerSquareGame(n-i*i)) return _map[n]=true; \n return _map[n]=false;\n }\n \nprivate:\n unordered_map<int,bool> _map; \n};\n```\nNote[1]: It\'s 10x faster if you do the recursion from sqrt(n) to 1:\n\n If we use 1 to sqrt(n), then the recursive call will go as: winnerSquareGame(n), then winnerSquareGame(n-1), which in turn calls winnerSquareGame(n-2) etc; meaning we will always get the worst case.\n\nIf reversed, winnerSquareGame(n) may call winnerSquareGame(<small_number>), which, if returns False, means that winnerSquareGame(n) will return True immediately (without checking n-1)\n\nReference:\n[1] https://leetcode.com/problems/stone-game-iv/solution/
| 4
| 0
|
['C']
| 1
|
stone-game-iv
|
Easy python DP solution with explanation
|
easy-python-dp-solution-with-explanation-gjov
|
Approach\n\nAt every state user has the option to choose one of the square numbers less than or equal to the current number. The player should choose a number t
|
surakshith
|
NORMAL
|
2020-10-25T07:57:08.454418+00:00
|
2020-10-25T07:58:50.647104+00:00
| 215
| false
|
**Approach**\n\nAt every state user has the option to choose one of the square numbers less than or equal to the current number. The player should choose a number that guarantees the next player to lose. This is a choice based problem and the player has square numbers as choices\n\nExample:\nif n = 1 -> Player1 will chose 1 and wins\nif n == 2 -> Player1 has only option of chosing 1 and he loses because player2 will get n = 1 and he\'ll choose 1\nif n == 3 -> Player1 has only option of chosing 1 and he will win because player2 will get n = 2 and he\'ll always lose\n\nif n == 10 -> Player1 has 3 options [1, 4, 9] to choose. \n1. \tIf P1 chooses 1 then P2 will get 9 and he\'ll chose 9 to win\n2. \tif P1 chooses 4 then P2 will get 6 and he\'ll choose 4 to win\n3. \tIf P1 chooses 9 then P2 will get 1 and he\'ll choose 1 to win\n\nSo n == 10 is an impossible state to win. \n\nAs you can observe there are subproblems for every n . These subproblems can be stored in a map to be reused gain (DP!!!!!!)\n\n```\nclass Solution(object):\n def winnerSquareGame(self, n):\n\n\n """\n\t\tPrecompute all possible sqaure numbers\n """\n def get_squares():\n squares = []\n for i in range(1, int(n ** (0.5)) + 1):\n squares.append(i * i)\n return squares\n \n \n squares = get_squares()\n squares_set = set(squares) # have a set to check if the number is a square so that we can return immediately\n self.cache = {}\n def solve(n):\n if n in squares_set: # No need to check other numbers. Return immediately\n return True\n if n in self.cache:\n return self.cache[n]\n\t\t\t\n\t\t\t """\n\t\t\tCheck for all squares less than n\n\t\t\t"""\n for i in squares:\n if i > n:\n break\n\n ans = solve(n - i)\n if not ans: # if the next player loses then we have found the number\n self.cache[n] = not ans\n return not ans\n self.cache[n] = False\n return False # We have exhausested all posibilities so return False\n \n return solve(n)\n```
| 4
| 0
|
['Dynamic Programming', 'Python', 'Python3']
| 0
|
stone-game-iv
|
C++ | DP
|
c-dp-by-di_b-b75i
|
```\nbool winnerSquareGame(int n) {\n if(sqrt(n) - floor(sqrt(n)) == 0)\n return true;\n vector dp(n+1,false);\n for(int i = 1;
|
di_b
|
NORMAL
|
2020-07-11T16:08:52.119583+00:00
|
2020-07-11T16:08:52.119660+00:00
| 400
| false
|
```\nbool winnerSquareGame(int n) {\n if(sqrt(n) - floor(sqrt(n)) == 0)\n return true;\n vector<bool> dp(n+1,false);\n for(int i = 1; i <= n; ++i)\n {\n for(int j = 1; j*j <= i; ++j)\n {\n int x = j*j;\n if(!dp[i-x])\n {\n dp[i] = true;\n break;\n }\n }\n }\n return dp[n];\n }
| 4
| 0
|
[]
| 0
|
stone-game-iv
|
DP || Almost 95% Beats || Easy to Understand ||
|
dp-almost-95-beats-easy-to-understand-by-uag6
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
kdhakal
|
NORMAL
|
2025-03-27T02:10:36.370891+00:00
|
2025-03-27T02:10:36.370891+00:00
| 29
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public boolean winnerSquareGame(int n) {
boolean[] winner = new boolean[n + 1];
for(int i = 1; i <= n; i++) {
for(int k = 1; k * k <= i; k++) {
if(!winner[i - k * k]) {
winner[i] = true;
break;
}
}
}
return winner[n];
}
}
```
| 3
| 0
|
['Java']
| 0
|
stone-game-iv
|
Simple C++ best intutition | Dynamic programming
|
simple-c-best-intutition-dynamic-program-1xbr
|
Here we simply define our dp state as whether the person performing currently can win or not . Base case is that a person loses is he has 0 left . Then for ever
|
rachit_17
|
NORMAL
|
2023-05-27T06:43:02.811255+00:00
|
2023-05-27T06:43:45.785876+00:00
| 450
| false
|
Here we simply define our dp state as whether the person performing currently can win or not . Base case is that a person loses is he has 0 left . Then for every i , I subtract squares less than i and see whether I can make the other person reach a state where he loses . So if dp[i-(j*j)]==false , the current person can win . So , for given n we see if alice can take bob to a state where he loses .\n\n``` bool winnerSquareGame(int n) {\n vector<bool>dp(n+1,true);\n // dp[n] represents whether the person having the current chance with n number left can win or not\n dp[0]=false; //base case is when you reach zero current person can no longer make move so he loses\n for(int i=1;i<=n;i++){\n bool ans=false;\n for(int j=1;j*j<=i;j++){\n if(dp[i-(j*j)]==false){ans=true;break;} \n // here for all squares upto i , we check whether the next person can be moved to a state in which he loses, that is dp[state]==false, if exist current person wins the game\n }\n dp[i]=ans;\n }\n return a[n];\n }\n\t
| 3
| 0
|
['Dynamic Programming']
| 0
|
stone-game-iv
|
[C++] Easy solution, dynamic programming-bottom up
|
c-easy-solution-dynamic-programming-bott-62zz
|
\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n if(sqrt(n) == floor(sqrt(n))) return true;\n \n vector<bool> firstPlayerWin(n
|
harshuljain
|
NORMAL
|
2022-01-22T10:53:43.342415+00:00
|
2022-01-22T10:53:43.342504+00:00
| 368
| false
|
```\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n if(sqrt(n) == floor(sqrt(n))) return true;\n \n vector<bool> firstPlayerWin(n+1);\n firstPlayerWin[1] = true;\n \n for(int i = 2; i <= n; i++) {\n if(sqrt(i) == floor(sqrt(i))) {\n firstPlayerWin[i] = true;\n continue;\n }\n \n // check if first player can force the other player into a losing state\n int j = 1;\n while(i - j*j > 0) {\n if(!firstPlayerWin[i-j*j]) {\n firstPlayerWin[i] = true;\n break;\n }\n j++;\n }\n }\n return firstPlayerWin[n];\n }\n};\n```\n
| 3
| 0
|
['Dynamic Programming', 'C', 'C++']
| 1
|
stone-game-iv
|
C++ || Explained with examples || O(kN) time,
|
c-explained-with-examples-okn-time-by-ke-fcok
|
Intution\nNotice the pattern, I am taking A as Alice here and B as Bob\nn = 1 , A wins\nn = 2 , B wins\nn = 3 , A wins\nn = 4 , A wins\nn = 5 , B wins\nn = 6,
|
kevinujunior
|
NORMAL
|
2022-01-22T07:44:28.738707+00:00
|
2022-01-23T09:08:34.771950+00:00
| 134
| false
|
**Intution**\nNotice the pattern, I am taking A as Alice here and B as Bob\nn = 1 , A wins\nn = 2 , B wins\nn = 3 , A wins\nn = 4 , A wins\nn = 5 , B wins\nn = 6, A wins\nn = 7, B wins\n\nnow let us understand what\'s happening let us start with example n=5\nso as Alice is starting first he has two choices either he can remove 1 stone (4 left for Bob) or remove 4 stones (1 left for Bob).\nCase 1: Alice remove 1 stone, Bob has 4 stones with him now so Bob can just make a move and win, \nSo in case 1 Alice can not win.\nCase 2: Alice remove 4 stones, Bob has 1 stone and he can remove it and win, \nSo Alice loses here as well.\n\nSo there\'s no possible way for Alice to win.\n\nConsider second example n=6\nAlice can remove 1 stone or 4 stone \nif Alice remove 1 stone then Bob cannot win (How do we know this)??? \nNotice the outcomes I have written above if n=5 the current player(which is Bob now) will lose.\nand in second case when Alice remove 4 stones, Bob left with 3 stones, and Bob will win now,\n(look at n=3 and Bob is current player now).\n\nAs players are playing optimally Alice will choose to remove 1(not 4) stone and win, same goes for Bob when his chance comes.\n\nHope you\'ve got the idea now.\nWe can maintain a **dp** array to keep track of the outcomes we know so far.\nAnd a **squares** vector to maintain squares we know so far \n\n***Algorithm:***\n\n* If n is a perfect square then Alice make one move and wins, i,e if(n = perfect square) ->Alice wins\n* If it is not a perfect square, we find if he can win by making any square move. i.e if(n != perfect square)-> find from all possible moves if he can win or not.\n\nTime complexity : O(nk) (We can have 315 perfect squares when n= 100000)\nSpace complexity : O(n+k)\n\n\nPS: My code might not be very efficient, but i hope you guys got the feel.\n\n```\n bool winnerSquareGame(int n) {\n //vector to keep track of squares we have got so far\n vector<int> squares;\n bool dp[n+2];\n dp[1] = true;\n squares.push_back(1);\n \n \n for(int i=2;i<=n;i++){\n \n //if it is a perfect square then current player wins\n if(sqrt(i)==int(sqrt(i))){\n dp[i] = true;\n squares.push_back(i);\n }\n \n else\n {\n int flag = 0;\n \n //otherwise make square moves and check if Alice can win or not\n for(int j=0;j<squares.size();j++){\n \n //for current player if second player loses then current player wins\n if(dp[i-squares[j]]==false){\n dp[i] = true;\n flag = 1;\n break;\n }\n }\n \n //if no move can be made by current player or if second player wins then current player loses\n if(flag==0)\n dp[i]= false;\n \n }\n }\n return dp[n];\n }\n```\n\n\n
| 3
| 0
|
['Dynamic Programming']
| 1
|
stone-game-iv
|
Simple DP solution with Explanation (C++)
|
simple-dp-solution-with-explanation-c-by-4i28
|
Alice makes a move removing square number of stones and remaining stones are passed to Bob and Bob does the same. So, when there are odd number of moves made,
|
umsisamess
|
NORMAL
|
2022-01-22T06:57:06.234651+00:00
|
2022-01-22T06:57:06.234683+00:00
| 95
| false
|
Alice makes a move removing square number of stones and remaining stones are passed to Bob and Bob does the same. So, when there are **odd number of moves** made, **Alice wins** and when there are **even number of moves** made, **Bob wins**, as Alice is the one starting the game. \n\nTherefore, here we use **dynamic programming** concept. We run a **loop from 1 to n** and inside that we run **loop of square numbers from 1 to i**. The formula for i number of stones can be written as :-\n\n**dp[i] = 1 + dp[i-j*j]**\n\nNow, if we have any **possibility of dp[i] being odd**, we break the loop, otherwise we continue the loop. \n\nFor the final answer, if dp[n] is odd, Alice wins, else, Bob wins.\n\n```\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<int> dp(n+1,0);\n dp[0] = 0;\n dp[1] = 1;\n for(int i=2;i<n+1;i++){\n for(int j=1;j*j<=i;j++){\n dp[i] = 1+dp[i-j*j];\n if(dp[i]%2==1) break;\n }\n }\n return dp[n]%2==1?true:false;\n }\n};\n```
| 3
| 0
|
['Dynamic Programming']
| 0
|
stone-game-iv
|
Diagram | Easy DP solution
|
diagram-easy-dp-solution-by-abhay_kumar_-fu52
|
The basic idea is very simple: if the count of stone is a square number, Alice can easily win by removing all the stones at once, leaving nothing for Bob to rem
|
abhay_kumar_singh
|
NORMAL
|
2022-01-22T00:41:07.010371+00:00
|
2022-01-22T01:59:06.878360+00:00
| 151
| false
|
The basic idea is very simple: if the count of stone is a square number, Alice can easily win by removing all the stones at once, leaving nothing for Bob to remove. Otherwise, by jumping square numbers backwards, we look for a previous solution (at least one) where Alice would actually lose and mark the current solution to be true if we could find such previously losing solution, because it is Bob who would be put in that tough spot to lose once Alice has made her move.\n\nFor example in the following diagram, we are calculating ```dp[8]```. We look 1, 4, 9 steps back for previous solutions to see if Alice had lost. We find that in ```dp[7]``` she had lost the match, so she will force Bob to lose by taking just 1 stone out.\n\n\n```\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<bool> dp(n + 1);\n int sq_n = 1;\n for(int i = 1; i <= n ; ++i){\n if(i == sq_n * sq_n){\n dp[i] = true;\n ++sq_n;\n }\n else{\n bool effect = false;\n for(int j = 1; i-j*j >= 1 ; ++j){\n effect |= !dp[i-j*j];\n if(effect)\n break;\n }\n dp[i] = effect;\n }\n }\n return dp[n];\n }\n};\n```\nTime Complexity: **O(N * sqrt(N))**\nSpace Complexity: **O(N)**\n\nPS: Please write down in comments if something was unclear.
| 3
| 2
|
['Dynamic Programming', 'C', 'C++']
| 1
|
stone-game-iv
|
not a best solution like others but better understanding using my solution
|
not-a-best-solution-like-others-but-bett-cg4c
|
\n\n\nt=0 alice \nt=1 bob \nboth try to win and plays optimally but one thing bob will win when he gets one 0 means false and alice will win when he get one 1
|
asppanda
|
NORMAL
|
2021-11-10T07:53:23.499714+00:00
|
2021-11-10T07:53:23.499750+00:00
| 102
| false
|
\n\n\nt=0 alice \nt=1 bob \nboth try to win and plays optimally but one thing bob will win when he gets one 0 means false and alice will win when he get one 1 means true so i hv done for getting one zero u can use and operator and for getting 1 1 you have to do or operator\n\n\n```\nclass Solution\n{\n public static int val(int n,int dp[][],int t)\n {\n if(n==0)\n {\n if(t==0)\n {\n return 0;\n }\n return 1;\n }\n if(dp[n][t]!=-1)\n {\n return dp[n][t];\n }\n int tp=(int)(Math.sqrt(n));\n int k=1;\n if(t==1)\n {\n for(int i=1;i<=tp;i++)\n {\n k&=val(n-(int)Math.pow(i,2),dp,0); \n }\nreturn dp[n][t]=k;\n }\n else\n {\n int k1=0;\n for(int i=1;i<=tp;i++)\n {\n k1|=val(n-(int)Math.pow(i,2),dp,1); \n }\n return dp[n][t]=k1;\n }\n \n }\n public boolean winnerSquareGame(int n) \n {\n int dp[][]=new int[n+1][2];\n for(int i=0;i<=n;i++)\n {\n Arrays.fill(dp[i],-1);\n }\n int flag=val(n,dp,0);\n if(flag==1)\n {\n return true;\n }\n else\n {\n return false;\n }\n }\n}\n```\n\n# ******pls upvote if u like the solution and feel free to ask doubt in comment section\n
| 3
| 0
|
['Dynamic Programming', 'Java']
| 0
|
stone-game-iv
|
C++ Simple Top Down DP solution
|
c-simple-top-down-dp-solution-by-deepans-y850
|
class Solution {\npublic:\n\n int dp[100002] ;\n bool fun(int n ){\n \n if(n<0){\n return false ;\n }\n \n i
|
deepanshugupta134
|
NORMAL
|
2021-05-04T06:58:11.556009+00:00
|
2021-05-04T06:58:11.556055+00:00
| 338
| false
|
class Solution {\npublic:\n\n int dp[100002] ;\n bool fun(int n ){\n \n if(n<0){\n return false ;\n }\n \n if(dp[n] != -1){\n return dp[n]==1?true:false ;\n }\n\n bool ans = false ;\n for(int i=1 ; i*i<=n ; i++){\n ans = ans || !fun(n- (i*i));\n }\n ans?dp[n]=1:dp[n]=0 ;\n return ans ;\n }\n \n bool winnerSquareGame(int n) {\n memset(dp , -1 , sizeof(dp));\n bool ans = fun(n) ;\n return ans ;\n }\n};
| 3
| 1
|
['Dynamic Programming', 'Recursion', 'Memoization', 'C']
| 1
|
stone-game-iv
|
C++
|
c-by-ashuruntimeterror-9jiy
|
```\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector dp(n + 1);\n \n for(int i = 1; i <= n; ++i) {\n for(
|
ashuruntimeterror
|
NORMAL
|
2020-10-27T05:44:15.678986+00:00
|
2020-10-27T05:44:15.679039+00:00
| 130
| false
|
```\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<int> dp(n + 1);\n \n for(int i = 1; i <= n; ++i) {\n for(int j = 1; j * j <= i; ++j) dp[i] |= !dp[i - j * j];\n }\n \n return dp[n];\n}\n};
| 3
| 0
|
[]
| 0
|
stone-game-iv
|
[C++] DP Bottom-Up Solution Explained, ~95% Time, 75% Space
|
c-dp-bottom-up-solution-explained-95-tim-b3vy
|
The intuition: the result for number n can be computed as solving subtracting from it all the squares which are < n and checking for the most convenient path, b
|
ajna
|
NORMAL
|
2020-10-26T09:56:10.832022+00:00
|
2020-10-26T09:56:10.832055+00:00
| 377
| false
|
The intuition: the result for number `n` can be computed as solving subtracting from it all the squares which are `< n` and checking for the most convenient path, boiling it down to a few base cases.\n\nIn fewer words, it is a bit like solving the classical problem of finding the nth Fibonacci number, in terms of general pattern.\n\nThinking that if Alice wins we have a value of `1` (`true`) and if Bob wins we will have a value of `0` (`false`), we can start thinking in those terms:\n\n```cpp\n// value of n\n0 // I know it is not a valid input, but just to build up the general case\n// value of the result\n0 // Alice cannot do any meaningful move\n\n// value of n\n0 1\n// value of the result\n0 1 // Alice can only pick 1, Bob can just lost\n\n// value of n\n0 1 2\n// value of the result\n0 1 0 // Alice can only pick 1, after Bob can only do the same, then she loses\n\n// value of n\n0 1 2 3 \n// value of the result\n0 1 0 1 // Alice picks 1, Bob picks 1, Alice picks 1, Bob loses\n\n// value of n\n0 1 2 3 4\n// value of the result\n0 1 0 1 1 // Alice picks 4 (remember she needs to do her most convenient move), Bob loses\n\n// value of n\n0 1 2 3 4 5\n// value of the result\n0 1 0 1 1 0 // if Alice picks 4, then Bob picks 1 or the other way around - in any case Alice loses\n\n// And so on\n```\n\nIf that does not scream "dynamic programming" to your frontal cortex, I don\'t know what else might!\n\nSo, let\'s get down to business then and for starters let\'s try something funny, as in defining our `dp` array outside our `Solution` class, statically, and same for an initialiser of the first 2 elements; I am not 100% sure of how things work with testing on LC, but I tried to do so, in order to save on computation (moving from the assumption that the results for each cell of dp will always be the same) and it seems like I got some slight advantage in that sense - but not too sure about it.\n\nSimilarly, we will also statically initialise its first 2 values using a static lambda (hacky, I know).\n\nTime to put effort in our main function, then, starting with support variables: we will only compute `maxSquareRoot`, setting it to a minimum of `2` in order not to have the code die on us, and `squares` to be filled with all the squares up to `n`, starting from `4` (so, for example, for `n == 50` we would have `squares == {4, 9, 16, 25, 36, 49}`). I thought about declaring it statically too, but it such a minor computation that I doubt it would have made any difference for the currently given 72 tests or so, particularly considering a good chunk of them are on numbers much smaller than the top limit.\n\nNow, time for the main loop, going with `i` from `2` (remember we already initialised for indexes `0` and `1` above) up to `n`.\n\nFor each value `i`, we initially set it to have the opposite of the previous value, because if Alice takes `1` from `i`, then the winning/losing situation will be reverted and the other way around.\n\nWe then proceed looping through all the values in `squares` with `sq` to find if there are more convenient moves, updating the value of `dp[i]` as a logical OR between its current value and what you would get with `dp[i - sq]`.\n\nHere is the tricky bit: we will stop with this inner loop of course as soon as we arrive to values of `sq` which are bigger than `i`; but there is another stopping condition to be considered: since both players are supposed to make the best move, but Alice moves first, we will stop as soon as we find a `true` value (also considering that it would not make sense anyway to continue ORing with a `true` value).\n\nAnd if you think this second `break`ing condition is trivial, consider that adding it allowed me to push the time down from about 120ms to just 20ms!\n\nOnce we are all set and done, we can just return `dp[n]` :)\n\nThe code:\n\n```cpp\nstatic bool dp[100001];\n\nstatic auto setup = [](){\n dp[0] = false;\n dp[1] = true;\n return NULL;\n}();\n\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n // checking if we already computed this value\n if (int(dp[n]) == 1) return true;\n // support variables\n int maxSquareRoot = max(2, (int)pow(n, 0.5)), squares[maxSquareRoot - 1];\n // populating squares\n for (int i = 2; i <= maxSquareRoot; i++) squares[i - 2] = i * i;\n // dping up to n\n for (int i = 2; i <= n; i++) {\n // initialising dp[i] to a boolean\n dp[i] = !dp[i - 1];\n // checking all the possible back moves\n for (int sq: squares) {\n if (dp[i] || sq > i) break;\n dp[i] |= !dp[i - sq];\n }\n }\n return dp[n];\n }\n};\n```
| 3
| 0
|
['Dynamic Programming', 'Memoization', 'C', 'C++']
| 0
|
stone-game-iv
|
C++ 4 lines using bitset, no nested for loops
|
c-4-lines-using-bitset-no-nested-for-loo-t4ir
|
The idea is the same as using a bool array, but you can update the entire data by simply << and |, instead of going through a for loop.\n\ncpp\nbool winnerSquar
|
alvin-777
|
NORMAL
|
2020-10-26T04:43:46.599680+00:00
|
2020-10-26T04:59:21.152032+00:00
| 222
| false
|
The idea is the same as using a bool array, but you can update the entire data by simply `<<` and `|`, instead of going through a for loop.\n\n```cpp\nbool winnerSquareGame(int n) {\n\tbitset<100001> dp(0), mask(0);\n\tfor (int i = 1; i*i <= n; ++i) mask.set(i*i); // Marks all square numbers\n\tfor (int i = 0; i < n && !dp.test(n); ++i) if (!dp.test(i)) dp |= mask << i; // If the number i leads to a loss, then i + any square number will lead to a win\n\t // And once we find a way to win, we are done.\n\treturn dp.test(n);\n}\n```\n
| 3
| 0
|
['Dynamic Programming', 'C']
| 1
|
stone-game-iv
|
Stone Game IV | java | c++| kotlin| dp
|
stone-game-iv-java-c-kotlin-dp-by-cygnus-xyo5
|
Let\'s say we have a boolean array dp with size n+1. each number dp[i] in the aray means if a player(either A or B) can win when there are i stones. \n\nSo for
|
cygnus
|
NORMAL
|
2020-10-25T09:09:10.072216+00:00
|
2020-10-25T09:20:02.123864+00:00
| 234
| false
|
Let\'s say we have a boolean array dp with size n+1. each number dp[i] in the aray means if a player(either A or B) can win when there are i stones. \n\nSo for dp[i], we need to check the value of dp[i - j * j ] for every possible j. If this number is false, this means the other play B will lose with i -j * j stones and player A will win for dp[i]. If none of them is false, it means player B can always win and player A will lose. dp[0] will be false (if there are 0 stones, player A will lose)\n\nThis is a standard dp solution with Time complexity of **O(N^1.5)** and space complexity of **O(N)** \n\njava\n```\nclass Solution {\n public boolean winnerSquareGame(int n) {\n boolean [] dp = new boolean[n+1];\n for (int i = 1; i <= n; i++)\n {\n for (int j = 1; j*j <= i; j++)\n {\n if (!dp[i-j*j])\n {\n dp[i] = true;\n break;\n }\n }\n }\n return dp[n];\n }\n}\n```\n\nc++\n```\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<bool> dp(n+1, false);\n for (int i = 1; i <= n; i++)\n {\n for (int j = 1; j*j <= i; j++)\n {\n if (!dp[i-j*j])\n {\n dp[i] = true;\n break;\n }\n }\n }\n return dp[n];\n }\n};\n```\n\nkotlin\n```\nclass Solution {\n fun winnerSquareGame(n: Int): Boolean {\n var dp = BooleanArray(n+1){false}\n for (i in 1..n) {\n var j = 1;\n while (j * j <= i) {\n if (!dp[i-j*j]) {\n dp[i] = true\n break\n }\n j++\n }\n }\n return dp[n]\n }\n}\n```
| 3
| 1
|
['Dynamic Programming', 'C', 'Java', 'Kotlin']
| 1
|
stone-game-iv
|
C++ super-simple and short DP solution
|
c-super-simple-and-short-dp-solution-by-d84yf
|
\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<bool> dp(n+1, false);\n for (int i=1; i<=n; i++) {\n \n
|
yehudisk
|
NORMAL
|
2020-10-25T08:10:47.644149+00:00
|
2020-10-25T08:10:47.644191+00:00
| 230
| false
|
```\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<bool> dp(n+1, false);\n for (int i=1; i<=n; i++) {\n \n int j = 1;\n while ((j*j <= i) && (!dp[i])) \n dp[i] = !dp[i-j*j++];\n }\n \n return dp[n];\n }\n};\n```\n**Like it? please upvote...**
| 3
| 0
|
['C']
| 0
|
stone-game-iv
|
Easy C++ solution
|
easy-c-solution-by-nc-26cg
|
Should be rated medium imo\n\n\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<bool> dp(n+1, false);\n \n for (int
|
nc_
|
NORMAL
|
2020-07-21T06:56:47.237117+00:00
|
2020-07-21T06:56:47.237164+00:00
| 207
| false
|
Should be rated medium imo\n\n```\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<bool> dp(n+1, false);\n \n for (int i = 1; i <= n; ++i) {\n for (int j = 1; j * j <= i; ++j) {\n if (!dp[i - j * j]) {\n dp[i] = true;\n break;\n }\n }\n }\n \n return dp[n];\n }\n};\n```
| 3
| 0
|
[]
| 0
|
stone-game-iv
|
Simple DP solution. top-down.
|
simple-dp-solution-top-down-by-chejianch-mdop
|
\nclass Solution {\npublic:\n int dp[100010][2];\n bool winnerSquareGame(int n) {\n memset(dp, -1, sizeof(dp));\n return dfs(n, true);\n
|
chejianchao
|
NORMAL
|
2020-07-11T21:44:51.618239+00:00
|
2020-07-11T21:48:06.930364+00:00
| 134
| false
|
```\nclass Solution {\npublic:\n int dp[100010][2];\n bool winnerSquareGame(int n) {\n memset(dp, -1, sizeof(dp));\n return dfs(n, true);\n }\n \n bool dfs(int n, bool isAlice) {\n if(n == 0) return isAlice ? false : true;\n if(dp[n][isAlice] >= 0) return dp[n][isAlice];\n bool res = false;\n for(int i = sqrt(n); i >= 1; --i) {\n res = dfs(n - i * i, !isAlice);\n if(res == isAlice)\n break;\n }\n return dp[n][isAlice] = res;\n }\n};\n```
| 3
| 0
|
[]
| 1
|
stone-game-iv
|
[Python3] bottom-up dp
|
python3-bottom-up-dp-by-ye15-4smd
|
Algo\nDefine ans as indicator of Alice winning the game given k stones. Then, \nans[0] = False (boundary condition)\nans[k] = True if ans[k-i*i] == False for i
|
ye15
|
NORMAL
|
2020-07-11T16:26:19.596064+00:00
|
2022-01-22T01:43:02.357738+00:00
| 274
| false
|
Algo\nDefine `ans` as indicator of Alice winning the game given `k` stones. Then, \n`ans[0] = False` (boundary condition)\n`ans[k] = True` if `ans[k-i*i] == False` for `i in range(1, int(sqrt(k))+1)`. \n\n`O(N^(3/2))` time & `O(N)` space \n```\nclass Solution:\n def winnerSquareGame(self, n: int) -> bool:\n dp = [False] * (n+1)\n for x in range(1, n+1): \n for k in range(1, int(sqrt(x))+1):\n if not dp[x-k*k]: \n dp[x] = True\n break \n return dp[-1]\n```\n\nTop-down implementation is given below. However, note that it suffers from "maximum recursion depth exceeded" issue as some test case is too large to handle recursively. \n```\nclass Solution:\n def winnerSquareGame(self, n: int) -> bool:\n \n @cache\n def fn(x): \n if x == 0: return False \n for k in range(1, int(sqrt(x))+1):\n if not fn(x-k*k): return True \n return False \n \n return fn(n)\n```
| 3
| 0
|
['Python3']
| 0
|
stone-game-iv
|
[Java] Recursive concise solution
|
java-recursive-concise-solution-by-hydro-24n0
|
java\nclass Solution {\n Boolean[] memo;\n public boolean winnerSquareGame(int n) {\n memo = new Boolean[n + 1];\n\t\tmemo[0] = false; // 0 mean pl
|
hydro_0
|
NORMAL
|
2020-07-11T16:04:48.233043+00:00
|
2020-07-12T14:52:45.675418+00:00
| 344
| false
|
```java\nclass Solution {\n Boolean[] memo;\n public boolean winnerSquareGame(int n) {\n memo = new Boolean[n + 1];\n\t\tmemo[0] = false; // 0 mean player lost\n return f(n); \n }\n \n boolean f(int n) {\n if (memo[n] != null) return memo[n];\n for (int i = (int) Math.sqrt(n); i > 0; i--) {\n if (!f(n - (i * i))) { // if there is a way when another player definitely lose - current player wins\n return memo[n] = true; \n }\n }\n return memo[n] = false; // there is no way for this player to win\n }\n}\n```
| 3
| 0
|
['Java']
| 1
|
stone-game-iv
|
[Javascript] DP Problem
|
javascript-dp-problem-by-alanchanghsnu-qbpq
|
\n// DP problem\nvar winnerSquareGame = function(n) {\n\n// //////////////////////////////////\n// 1. Define an array that Alice will win or los
|
alanchanghsnu
|
NORMAL
|
2020-07-11T16:01:12.870576+00:00
|
2020-07-11T16:01:12.870623+00:00
| 247
| false
|
```\n// DP problem\nvar winnerSquareGame = function(n) {\n\n// //////////////////////////////////\n// 1. Define an array that Alice will win or loss (T/F)\n// //////////////////////////////////\n\n const res = new Array(n+1).fill(false);\n let k = 1;\n \n for (let i = 1; i <= n; i++) {\n\n// //////////////////////////////////\n// 2. if it is square number, obviously, Alice win\n// //////////////////////////////////\n \n if (k*k === i) {\n res[i] = true;\n k++;\n continue;\n }\n\n// //////////////////////////////////\n// 3. after Alice removes j*j (1 <= j < k) stones, find whether res[i-j*j] is T/F (= Bob win/loss)\n// if j exists that res[i-j*j] = false, it means that Bob will lose the game with the remaining i-j*j stones => Alice wins\n// otherwise, Alice lose \n// //////////////////////////////////\n\n let AliceWin = false;\n for (let j = 1; j < k && j*j <= i; j++) {\n if (!res[i-j*j]) {\n AliceWin = true;\n break;\n }\n }\n res[i] = AliceWin;\n }\n \n return res[n];\n};\n```
| 3
| 0
|
['JavaScript']
| 0
|
stone-game-iv
|
[Python3] Basic Nims game theory
|
python3-basic-nims-game-theory-by-ironic-07ku
|
\n#!/usr/bin/python3.8\n\n# https://en.wikipedia.org/wiki/Nim\n\nimport math\nimport functools\nclass Solution:\n @functools.lru_cache(maxsize=None)\n def
|
ironic_arrow
|
NORMAL
|
2020-07-11T16:01:04.593547+00:00
|
2020-07-11T16:01:04.593588+00:00
| 241
| false
|
```\n#!/usr/bin/python3.8\n\n# https://en.wikipedia.org/wiki/Nim\n\nimport math\nimport functools\nclass Solution:\n @functools.lru_cache(maxsize=None)\n def winnerSquareGame(self, n: int) -> bool:\n if n<=0:\n return False\n i = int(math.sqrt(n))+1\n while i:\n if i*i<=n and not self.winnerSquareGame(n-i*i):\n return True\n i-=1\n return False\n```
| 3
| 1
|
[]
| 1
|
stone-game-iv
|
C++ | | DP Memoization Approach | | Explained Steps
|
c-dp-memoization-approach-explained-step-2kqb
|
Intuition\n- The problem requires determining if Alice will win a game given an initial number of stones n where players take turns removing a perfect square nu
|
Satyamjha_369
|
NORMAL
|
2024-08-20T06:13:27.969680+00:00
|
2024-08-20T06:13:27.969714+00:00
| 234
| false
|
# Intuition\n- The problem requires determining if Alice will win a game given an initial number of stones n where players take turns removing a perfect square number of stones. \n- The game continues until a player cannot make a valid move, causing them to lose. \n- To solve this problem, we need to evaluate all possible moves to see if Alice, starting first, can guarantee a win assuming both players play optimally.\n\n# Approach\nThe approach involves using dynamic programming (DP) with recursion and memoization to efficiently determine the outcome of the game. Here\u2019s a detailed explanation of the approach:\n\n**Base Case:**\nWhen there are no stones left (n == 0), the current player loses since they cannot make a move `return (n % 2);`\nThis can also have been simply limited to `return false`\n**Recursive Case:**\n\n- For a given number of stones n, the algorithm explores all possible moves where a player can remove a perfect square number of stones.\n- For each possible move, it recursively checks if removing that number of stones would leave the opponent in a losing position.\n- If there exists any move that forces the opponent into a losing state, the current player can win and thus dp[n] is set to true.\n- Otherwise, if all moves lead to states where the opponent can win, then dp[n] is set to false.\n\n## Memoization:\nThe dp vector is used to store results of previously computed states to avoid redundant calculations and improve efficiency. The dp array is initialized with -1 to denote that a state has not been computed yet.\n\n**Recursive Function:**\nThe function `solve(n, cnt, dp)` recursively explores all possible perfect square moves.\n\n# Complexity\n## Time Complexity:\n\n## Space Complexity:\n\n\n# Code\n```cpp []\nclass Solution {\npublic:\n bool solve(int n, int cnt, vector<int>& dp){\n if(n == 0){\n return (n % 2);\n }\n\n if(dp[n] != -1)\n return dp[n];\n \n for (int i = 1; i*i <= n; i++) {\n if(i*i > n)\n break;\n if (!solve(n - i*i, cnt + 1, dp)) {\n dp[n] = 1; \n return true;\n }\n }\n return dp[n] = 0;\n }\n\n bool winnerSquareGame(int n) {\n vector<int> dp(n+1, -1); \n return solve(n, 0, dp);\n }\n};\n```
| 2
| 0
|
['Dynamic Programming', 'Game Theory', 'C++']
| 1
|
stone-game-iv
|
Pictorial Representation || Simple Game Theory || easy to understand
|
pictorial-representation-simple-game-the-34cj
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem is about determining if the first player (Alice) will win the game if both
|
tinku_tries
|
NORMAL
|
2024-05-31T08:27:11.218262+00:00
|
2024-05-31T08:27:11.218294+00:00
| 293
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is about determining if the first player (Alice) will win the game if both players play optimally. The game involves taking turns removing a square number of stones, and the player who cannot make a move loses. This can be approached using dynamic programming to track winning and losing states.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Dynamic Programming Table:** Use a 1D DP table `dp` where `dp[i]` indicates whether the state with `i` stones is a winning (1) or losing (0) state.\n2. **Base Case:** If there are no stones left (`n == 0`), it is a losing state (`dp[0] = 0`).\n3. **Recursive Case:** For each state `n`, check all possible square numbers `i*i` that can be removed. If removing `i*i` stones leads to a losing state for the opponent (`f(n - i*i) == 0`), then the current state is a winning state (`dp[n] = 1`). If no such move leads to a losing state for the opponent, then the current state is a losing state (`dp[n] = 0`).\n4. **Memoization:** Store the results in the DP table to avoid redundant calculations.\n5. **Final Result:** Start with `n` stones and determine if it is a winning or losing state.\n\n# Complexity\n- **Time complexity:** \\(O(n \\sqrt{n})\\) because for each `n`, we check all possible square numbers up to \\(\\sqrt{n}\\).\n- **Space complexity:** \\(O(n)\\) for storing the DP table.\n\n# Pictorial Representation\nIf you can go to a `loss state` from `initial state `, then its a `win state`.\n`Blue` coloured is `Win State` and `Grey` colored is `Loss` state. \n\n\n# Code\n```cpp\nclass Solution {\npublic:\n vector<int> dp; // -1 --> not touched yet, 0 --> loss state, 1 --> win state\n\n // Recursive function to determine if the current state is a winning state\n int f(int n) {\n if (n < 0) return 0;\n // If DP already evaluated the state, then return the state\n if (dp[n] != -1) return dp[n];\n // Finding if it\'s a win or loss state\n for (int i = 1; i * i <= n; i++) {\n if (f(n - i * i) == 0) {\n return dp[n] = 1; \n }\n }\n // Didn\'t find any winning state, return that it\'s a loss state\n return dp[n] = 0;\n }\n\n bool winnerSquareGame(int n) {\n // Initializing DP\n dp.clear();\n dp.resize(n + 1, -1);\n // 0th state is a loss one\n dp[0] = 0;\n return f(n);\n }\n};\n```
| 2
| 0
|
['Math', 'Dynamic Programming', 'Game Theory', 'C++']
| 0
|
stone-game-iv
|
Java | Recursive | Tabulation | Dynamic Programming solution
|
java-recursive-tabulation-dynamic-progra-fte7
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
PrachiSaid
|
NORMAL
|
2024-01-31T11:12:34.218153+00:00
|
2024-01-31T11:15:20.523993+00:00
| 120
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(N^2)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nclass Solution {\n public boolean winnerSquareGame(int n) {\n // return recursive(n);\n return tabulation(n);\n }\n\n private boolean recursive(int n) {\n // if we have n = 0 then we cannot further find its square number hence return false\n if(n == 0) return false;\n\n // we know that any number multiplied by 1 is always a square number\n if(n == 1) return true;\n\n // we check from 1 until we find a number which multiplication gives us the answer we are looking for\n for(int i = 1; i * i <= n; i++) {\n int square = i * i;\n if(square <= n) {\n // check if the next player is winning or loosing\n if(recursive(n - square) == false) {\n // if the next player is loosing by taking the current number then we win\n return true;\n }\n }\n }\n\n // return false if by applying all the combinations the next player wins\n return false;\n }\n\n private boolean tabulation(int ind) {\n boolean[] dp = new boolean[ind + 1];\n\n for(int n = 1; n <= ind; n++) {\n for(int i = 1; i * i <= n; i++) {\n if(dp[n - (i * i)] == false) {\n dp[n] = true;\n break;\n }\n }\n }\n\n // System.out.println(Arrays.toString(dp));\n\n return dp[ind];\n }\n}\n```
| 2
| 0
|
['Java']
| 0
|
stone-game-iv
|
Python short and clean 1-liners. Multiple solutions. Functional programming.
|
python-short-and-clean-1-liners-multiple-urun
|
Approach 1: Top-Down DP\n\n# Complexity\n- Time complexity: O(n \cdot \sqrt{n})\n\n- Space complexity: O(n)\n\n# Code\nMultiline Recursive:\npython\nclass Solut
|
darshan-as
|
NORMAL
|
2023-07-28T08:00:28.814512+00:00
|
2023-07-28T08:01:34.588675+00:00
| 385
| false
|
# Approach 1: Top-Down DP\n\n# Complexity\n- Time complexity: $$O(n \\cdot \\sqrt{n})$$\n\n- Space complexity: $$O(n)$$\n\n# Code\nMultiline Recursive:\n```python\nclass Solution:\n def winnerSquareGame(self, n: int) -> bool:\n squares = lambda x: (i * i for i in range(isqrt(x), 0, -1))\n \n @cache\n def can_win(n: int) -> bool:\n return n and not all(can_win(n - s) for s in squares(n))\n \n return can_win(n)\n\n\n```\n\nFunctional. Can be restructured into a 1-liner:\n```python\nclass Solution:\n def winnerSquareGame(self, n: int) -> bool:\n squares = lambda x: (i * i for i in range(isqrt(x), 0, -1))\n can_win = cache(lambda n: n and not all(can_win(n - s) for s in squares(n)))\n return can_win(n)\n\n\n```\n\n---\n\n# Approach 2: Bottom-Up DP\n\n# Complexity\n- Time complexity: $$O(n \\cdot \\sqrt{n})$$\n\n- Space complexity: $$O(n)$$\n\n# Code\nMultiline Iterative:\n```python\nclass Solution:\n def winnerSquareGame(self, n: int) -> bool:\n squares = lambda x: (i * i for i in range(isqrt(x), 0, -1))\n\n dp = [False] * (n + 1)\n for i in range(1, n + 1):\n dp[i] = not all(dp[i - s] for s in squares(i))\n return dp[-1]\n\n\n```\n\nFunctional. Can be restructured into a 1-liner:\n# Code\n```python\nclass Solution:\n def winnerSquareGame(self, n: int) -> bool:\n squares = lambda x: (i * i for i in range(isqrt(x), 0, -1))\n next_wins = lambda dp, i: setitem(dp, i, not all(dp[i - s] for s in squares(i))) or dp\n return reduce(next_wins, range(n + 1), [False] * (n + 1))[-1]\n\n\n```
| 2
| 0
|
['Math', 'Dynamic Programming', 'Game Theory', 'Python', 'Python3']
| 0
|
stone-game-iv
|
Simple Game theory
|
simple-game-theory-by-techtinkerer-mbgg
|
\n\n# Complexity\n- Time complexity:O(root(n))\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(n)\n Add your space complexity here, e.g. O(n
|
TechTinkerer
|
NORMAL
|
2023-07-10T11:27:43.395955+00:00
|
2023-07-10T11:46:32.776701+00:00
| 46
| false
|
\n\n# Complexity\n- Time complexity:O(root(n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int dp[100001];\n Solution(){\n memset(dp,-1,sizeof(dp));\n }\n bool winnerSquareGame(int n) {\n if(n==0)\n return false;\n if(n==1)\n return true;\n if(dp[n]!=-1)\n return dp[n];\n bool ans=0;\n for(int i=1;i*i<=n;i++){\n ans|=!winnerSquareGame(n-i*i);\n if(ans==true)\n break;\n }\n \n return dp[n]= ans;\n }\n};\n```
| 2
| 0
|
['Dynamic Programming', 'Game Theory', 'C++']
| 0
|
stone-game-iv
|
Simple C++ Solution
|
simple-c-solution-by-lotus18-mk4l
|
Code\n\nclass Solution \n{\npublic:\n int dp[100011];\n bool f(int n) \n {\n if(n==0) return 0;\n int i=1;\n if(dp[n]!=-1) return
|
lotus18
|
NORMAL
|
2023-02-03T11:00:50.559986+00:00
|
2023-02-03T11:00:50.560032+00:00
| 346
| false
|
# Code\n```\nclass Solution \n{\npublic:\n int dp[100011];\n bool f(int n) \n {\n if(n==0) return 0;\n int i=1;\n if(dp[n]!=-1) return dp[n];\n while(i*i<=n)\n {\n if(!f(n-i*i)) return dp[n]=1;\n i++;\n }\n return dp[n]=0;\n }\n bool winnerSquareGame(int n) \n {\n memset(dp,-1,sizeof(dp));\n return f(n);\n }\n};\n```
| 2
| 0
|
['C++']
| 0
|
stone-game-iv
|
c++ | easy | short
|
c-easy-short-by-venomhighs7-4yly
|
\n# Code\n\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<bool> dp(n + 1, false);\n for (int i = 1; i <= n; ++i) {\n
|
venomhighs7
|
NORMAL
|
2022-10-11T04:02:23.030481+00:00
|
2022-10-11T04:02:23.030513+00:00
| 1,376
| false
|
\n# Code\n```\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<bool> dp(n + 1, false);\n for (int i = 1; i <= n; ++i) {\n for (int k = 1; k * k <= i; ++k) {\n if (!dp[i - k * k]) {\n dp[i] = true;\n break;\n }\n }\n }\n return dp[n];\n }\n};\n```
| 2
| 0
|
['C++']
| 1
|
stone-game-iv
|
[C++]✅ || Easiest Solution || DP / Game Theory
|
c-easiest-solution-dp-game-theory-by-ros-srua
|
class Solution {\npublic:\n\n vector dp;\n\t\n bool fun(int n){\n \n if(n <= 0) // Base Case\n return 0;\n\t\t\t\n
|
rosario1975
|
NORMAL
|
2022-07-26T19:37:07.804893+00:00
|
2022-07-26T19:37:07.804925+00:00
| 289
| false
|
class Solution {\npublic:\n\n vector<int> dp;\n\t\n bool fun(int n){\n \n if(n <= 0) // Base Case\n return 0;\n\t\t\t\n if(dp[n] != -1)\n return dp[n]; // If already solved, return\n \n \n bool ans = 0;\n for(int i = 1; i*i <= n; i++){\n \n int rem = n - (i*i); // remaining stones for bob\n \n // Alice wins, when bob looses\n ans = ans || !fun(rem); \n \n }\n \n return dp[n] = ans; // memoize\n }\n bool winnerSquareGame(int n) {\n \n dp = vector<int>(n+1,-1);\n \n return fun(n);\n }\n};
| 2
| 0
|
['Dynamic Programming', 'C', 'Game Theory', 'C++']
| 0
|
stone-game-iv
|
Recursion + Memoization || C++
|
recursion-memoization-c-by-user0382o-upjc
|
\nclass Solution {\npublic:\n int dp[100001];\n bool util(int n){\n if(n == 1) return true;\n if(n == 2) return false;\n if(dp[n] !=
|
user0382o
|
NORMAL
|
2022-06-19T14:26:27.077006+00:00
|
2022-06-19T14:26:27.077046+00:00
| 197
| false
|
```\nclass Solution {\npublic:\n int dp[100001];\n bool util(int n){\n if(n == 1) return true;\n if(n == 2) return false;\n if(dp[n] != -1) return dp[n];\n bool temp = false;\n for(int i = 1; i*i <= n; i++){ //checking for each and every square number\n temp = !(util(n-(i*i))); //taking ~ because if bob got loosing state then only alice can win\n if(temp) break; //as alice got any of the winning state return true\n }\n \n return dp[n] = temp;\n }\n \n bool winnerSquareGame(int n) { \n memset(dp, -1, sizeof(dp));\n return util(n);\n }\n};\n```
| 2
| 0
|
['Dynamic Programming', 'Recursion', 'Memoization']
| 0
|
stone-game-iv
|
Java || easy explanation|| understandable
|
java-easy-explanation-understandable-by-4rbum
|
\nclass Solution {\n Boolean[] dp = new Boolean[100001];// taking constraints under consideration\n public boolean winnerSquareGame(int n) {\n \n
|
abhay270901
|
NORMAL
|
2022-01-23T07:15:21.805449+00:00
|
2022-01-23T07:15:21.805478+00:00
| 81
| false
|
```\nclass Solution {\n Boolean[] dp = new Boolean[100001];// taking constraints under consideration\n public boolean winnerSquareGame(int n) {\n \n if(dp[n]!=null)// not empty\n {\n return dp[n];//return \n }\n Boolean win=false;// default win is false..\n for(int i=1;n>=i*i;i++)// looping for squares\n {\n if(n-i*i==0)// after removing square number from pile if diff is 0 \n {\n win=true;// the alice player wins..\n break;\n }\n else// if the diff isn\'t zero\n {\n win=win||!winnerSquareGame(n-i*i);// assigning win used ! for negate bob winning situation recursive call\n }\n }\n return dp[n]=win;// update to dp and return\n }\n}\n```
| 2
| 0
|
[]
| 1
|
stone-game-iv
|
Dp, Game Theory
|
dp-game-theory-by-dev2104rumal-6xva
|
\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<int> dp(n+1);\n dp[0] = 0; // loosing state\n for(int i=1;i<=n;i++
|
dev2104rumal
|
NORMAL
|
2022-01-23T06:13:12.269952+00:00
|
2022-01-23T06:13:12.269997+00:00
| 113
| false
|
```\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<int> dp(n+1);\n dp[0] = 0; // loosing state\n for(int i=1;i<=n;i++){\n for(int j=1;j*j<=i;j++){\n if(dp[i-(j*j)] == 0) {dp[i] = 1; break;} // using one step I can make him stand at loosing state\n }\n }\n return dp[n];\n }\n};\n```
| 2
| 0
|
[]
| 0
|
stone-game-iv
|
Recursion->memoization || beginner friendly code
|
recursion-memoization-beginner-friendly-hytxv
|
\n//Recursive solution\nclass Solution {\npublic: \n bool winnerSquareGame(int n) \n {\n if(n<=0) return false;\n for(int i=1; i*i<=n; i++)
|
bhagyajeet
|
NORMAL
|
2022-01-22T15:15:38.448485+00:00
|
2022-01-22T15:15:38.448514+00:00
| 289
| false
|
```\n//Recursive solution\nclass Solution {\npublic: \n bool winnerSquareGame(int n) \n {\n if(n<=0) return false;\n for(int i=1; i*i<=n; i++)\n if(!solve(n-i*i, dp)) return true;\n return false;\n } \n}; \n\n//memoization solution- same code as recursion solution, used dp vector for storing value and avoiding multiple recursion.\nclass Solution {\npublic: \n bool solve(int n, vector<int>&dp) \n {\n if(n<=0) return false;\n if(dp[n]!=-1) return dp[n];\n for(int i=1; i*i<=n; i++)\n if(!solve(n-i*i, dp)) return dp[n]=true;\n return dp[n]=false;\n } \n bool winnerSquareGame(int n) \n {\n vector<int>dp(100001, -1);\n return solve(n, dp);\n }\n};\n\n//If the solution helps you, please upvote.\n```
| 2
| 0
|
['Dynamic Programming', 'Recursion', 'Memoization', 'C', 'C++']
| 0
|
stone-game-iv
|
Simple proof | Easy to understand | C++
|
simple-proof-easy-to-understand-c-by-gun-on46
|
Proof\nKey Points\n- Alice plays first\n- Alice wins if there are odd number of moves\n- Bob wins if there are even number of moves \n\nWhen the game is played
|
gunzaan
|
NORMAL
|
2022-01-22T13:27:07.205956+00:00
|
2022-01-22T13:27:07.205984+00:00
| 90
| false
|
## Proof\n**Key Points**\n- Alice plays first\n- Alice wins if there are odd number of moves\n- Bob wins if there are even number of moves \n\nWhen the game is played Alice plays the first move and thats in her control. Other moves may depend on Bobs move. So if there is any first move for which we can force even number of moves then the total moves become odd and Alice wins. So when we check for certaiin first move we get n1 = (n - square number) we have to again check if there is another square number for which we can force an odd number of moves and so on until we reach zero.\n\n## Approach\nHere we take the bottom up approach. We assume that, if we have zero move we cannot win. This will be our base condition. First we check for smaller numbers that if we can choose the first square number and for the remaining stone we always lose. And then we build the solution for larger numbers.\n\n## Code\n```cpp\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n vector<bool> dp(n+1);\n dp[0] = false;\n int x;\n for(int cur = 1; cur<=n; ++cur){ \n for(int i=1; i*i<=cur; ++i){\n dp[cur] = dp[cur] | (!dp[cur-i*i]);\n }\n }\n return dp[n];\n }\n};\n```\n\n**Please give an upvote if it was helpful**
| 2
| 0
|
['Dynamic Programming', 'C']
| 0
|
stone-game-iv
|
c++ DP explained with comments
|
c-dp-explained-with-comments-by-antonkru-pt6j
|
\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n\t\t// Create vector n + 1 because on top of 1..n for the game we will hold the 0 for the loss
|
antonkrug
|
NORMAL
|
2022-01-22T12:53:31.188392+00:00
|
2022-01-22T22:49:05.029356+00:00
| 99
| false
|
```\nclass Solution {\npublic:\n bool winnerSquareGame(int n) {\n\t\t// Create vector n + 1 because on top of 1..n for the game we will hold the 0 for the loss state\n vector<bool> dp(n + 1, false); // Populate whole vector with \'false\' (including the dp[0])\n\n // For each number (upto the N we were requested to calculate)\n for (int i=1; i<=n; i++) {\n \n // Check if the previous move was loss\n if (!dp[i-1]) {\n // If previous move was loss, then Alice can subtract 1 to get to winning state by forcing Bob\n // into the previous loss move\n dp[i] = true;\n \n } else {\n // If the previous move was not loss, try to find as Alice any (starting from biggest)\n // squareNumber to subtract and reach a lossing state\n \n // We do not need the set current dp[i]=false as the whole vector is intialized as false\n\t\t\t\t// Start with sqrt(i) because (int)sqrt(i)*(int)sqrt(i) is the biggest sqaure number we\n\t\t\t\t// can subtract from position i\n for (int j=sqrt(i); j>1; j--) {\n int squareNumber = j*j;\n if (!dp[i- squareNumber]) {\n // Found loss state, no need to process further\n dp[i] = true;\n break;\n }\n }\n \n } \n }\n return dp[n];\n }\n};\n```
| 2
| 0
|
['Dynamic Programming', 'C']
| 0
|
stone-game-iv
|
JAVA DP Solution
|
java-dp-solution-by-piyushja1n-621p
|
\nclass Solution {\n \n public boolean winnerSquareGame(int n) {\n \n boolean dp[] = new boolean[n + 1];\n \n for(int i = 0; i
|
piyushja1n
|
NORMAL
|
2022-01-22T05:39:46.479990+00:00
|
2022-01-22T05:39:46.480029+00:00
| 198
| false
|
```\nclass Solution {\n \n public boolean winnerSquareGame(int n) {\n \n boolean dp[] = new boolean[n + 1];\n \n for(int i = 0; i <= n; i++){\n \n if(dp[i]) continue;\n \n for(int j = 1; i + j * j <= n; j++)\n dp[i + j * j] = true;\n }\n \n // System.out.println(Arrays.toString(dp));\n return dp[n];\n }\n}\n```
| 2
| 0
|
['Dynamic Programming', 'Java']
| 0
|
stone-game-iv
|
✅ [Solution] Swift: Stone Game IV (+ test cases)
|
solution-swift-stone-game-iv-test-cases-wmhrg
|
swift\nclass Solution {\n func winnerSquareGame(_ n: Int) -> Bool {\n var dp = [Bool](repeating: false, count: n + 1)\n \n for i in 1...
|
AsahiOcean
|
NORMAL
|
2022-01-22T04:30:35.267730+00:00
|
2022-01-22T04:30:35.267771+00:00
| 1,174
| false
|
```swift\nclass Solution {\n func winnerSquareGame(_ n: Int) -> Bool {\n var dp = [Bool](repeating: false, count: n + 1)\n \n for i in 1...n {\n var val = 1\n while val * val <= i {\n if !dp[i - val * val] {\n dp[i] = true\n break\n }\n val += 1\n }\n }\n \n return dp[n]\n }\n}\n```\n\n---\n\n<p>\n<details>\n<summary>\n<img src="https://git.io/JDblm" height="24">\n<b>TEST CASES</b>\n</summary>\n\n<p><pre>\n<b>Result:</b> Executed 3 tests, with 0 failures (0 unexpected) in 0.014 (0.016) seconds\n</pre></p>\n\n```swift\nimport XCTest\n\nclass Tests: XCTestCase {\n \n private let solution = Solution()\n \n // Alice can remove 1 stone winning the game because Bob doesn\'t have any moves.\n func test0() {\n let value = solution.winnerSquareGame(1)\n XCTAssertEqual(value, true)\n }\n \n // Alice can only remove 1 stone, after that Bob removes the last one winning the game (2 -> 1 -> 0).\n func test1() {\n let value = solution.winnerSquareGame(2)\n XCTAssertEqual(value, false)\n }\n \n // n is already a perfect square, Alice can win with one move, removing 4 stones (4 -> 0).\n func test2() {\n let value = solution.winnerSquareGame(4)\n XCTAssertEqual(value, true)\n }\n}\n\nTests.defaultTestSuite.run()\n```\n\n</details>\n</p>
| 2
| 0
|
['Dynamic Programming', 'Swift']
| 0
|
stone-game-iv
|
Simple C solution with DP
|
simple-c-solution-with-dp-by-linhbk93-uelt
|
\nbool winnerSquareGame(int n){\n int dp[100001] = {0};\n for(int i = 0; i <= n; i++)\n {\n if(dp[i]) continue;\n for(int j = 1; i + j *
|
linhbk93
|
NORMAL
|
2022-01-22T01:42:06.151485+00:00
|
2022-01-22T01:42:06.151526+00:00
| 147
| false
|
```\nbool winnerSquareGame(int n){\n int dp[100001] = {0};\n for(int i = 0; i <= n; i++)\n {\n if(dp[i]) continue;\n for(int j = 1; i + j * j <= n; j++)\n dp[i + j * j] = 1;\n }\n return dp[n];\n}\n```
| 2
| 0
|
['Dynamic Programming', 'C']
| 0
|
stone-game-iv
|
Java Simple and easy DP Memoization solution, clean code with comments
|
java-simple-and-easy-dp-memoization-solu-gvj7
|
PLEASE UPVOTE IF YOU LIKE THIS SOLUTION\n\n\n\nclass Solution {\n HashMap<Integer, Boolean> cache;\n public boolean winnerSquareGame(int n) {\n cac
|
satyaDcoder
|
NORMAL
|
2021-06-17T16:06:10.927555+00:00
|
2021-06-17T16:06:10.927604+00:00
| 168
| false
|
**PLEASE UPVOTE IF YOU LIKE THIS SOLUTION**\n\n\n```\nclass Solution {\n HashMap<Integer, Boolean> cache;\n public boolean winnerSquareGame(int n) {\n cache = new HashMap();\n return canAliceWin(n);\n }\n \n private boolean canAliceWin(int n){\n if(n <= 0) return false;\n \n //reterive from cache \n if(cache.containsKey(n)) return cache.get(n);\n \n //find anytime Bob will lose the game\n boolean isBobLose = false;\n \n //just iterate 1 to the square root(n)\n for(int i = 1; i* i <= n; i++){\n if(!canAliceWin(n - (i * i))){\n isBobLose = true;\n break;\n }\n }\n \n //save in the cache\n cache.put(n, isBobLose);\n \n return isBobLose;\n }\n }\n```
| 2
| 0
|
['Dynamic Programming', 'Memoization', 'Java']
| 0
|
stone-game-iv
|
10% :: Python (Sprague-Grundy Function)
|
10-python-sprague-grundy-function-by-tuh-exhm
|
\n# A Modified Nim Game\n# Use Sprague Grundy Functions for the same\n\nclass Solution:\n def getMex(self, arr):\n counter = 0\n arr.sort()\n
|
tuhinnn_py
|
NORMAL
|
2021-05-06T12:10:50.639358+00:00
|
2021-05-06T12:10:50.639398+00:00
| 203
| false
|
```\n# A Modified Nim Game\n# Use Sprague Grundy Functions for the same\n\nclass Solution:\n def getMex(self, arr):\n counter = 0\n arr.sort()\n for num in arr:\n if num != counter:\n return counter\n counter += 1\n return arr[-1] + 1\n # Alternatively\n # return min(set([num for num in range(max(arr) + 2)]) - set(arr))\n \n def winnerSquareGame(self, n: int) -> bool:\n dp = [0 for i in range(n + 1)]\n dp[0] = 0\n for i in range(1, n + 1):\n start = math.floor(math.sqrt(i))\n arr = []\n while start > 0:\n arr.append(dp[i - start * start])\n start -= 1\n dp[i] = self.getMex(arr)\n\n return dp[-1]\n```
| 2
| 0
|
[]
| 0
|
stone-game-iv
|
C# solution dp+back tracking approach
|
c-solution-dpback-tracking-approach-by-v-eg0p
|
\n var dp = new bool[n+1];\n var ps = new List<int>(){1};\n dp[1] = true;\n for (int i = 2; i <= n; i++)\n {\n if
|
victorsdk
|
NORMAL
|
2020-10-25T21:32:51.446878+00:00
|
2020-10-25T21:34:16.314227+00:00
| 92
| false
|
```\n var dp = new bool[n+1];\n var ps = new List<int>(){1};\n dp[1] = true;\n for (int i = 2; i <= n; i++)\n {\n if (Math.Sqrt(i) % 1 == 0)\n {\n ps.Add(i);\n dp[i] = true;\n }\n else\n {\n foreach (int s in ps)\n {\n if (!dp[i-s])\n {\n dp[i] = true;\n break;\n } \n } \n }\n } \n return dp[n];\n```
| 2
| 0
|
['Dynamic Programming', 'Backtracking']
| 0
|
stone-game-iv
|
Animated Explanation | Both Recursive + Iterative Solutions | C++ Implementations
|
animated-explanation-both-recursive-iter-u9sb
|
Animated explanation:\nhttps://www.youtube.com/watch?v=akGqO-cFodE\n\nIterative implementation:\n\nbool winnerSquareGame(int n) {\n vector<bool> dp(n + 1); //
|
procedurecall
|
NORMAL
|
2020-10-25T11:37:32.929607+00:00
|
2020-10-25T11:37:32.929649+00:00
| 132
| false
|
Animated explanation:\nhttps://www.youtube.com/watch?v=akGqO-cFodE\n\nIterative implementation:\n```\nbool winnerSquareGame(int n) {\n vector<bool> dp(n + 1); // same as our memo before, but now a vector\n // dp[0] is already false by default\n // iterate through the remaining values bottom-up\n // note that compared to our previous implementation, i takes on the value of\n // our "current" n\n for (int i = 1; i <= n; ++i) {\n // for every possible move:\n for (int sq = 1; sq * sq <= i; ++sq) {\n if (!dp[i - sq * sq]) {\n // found a winning move!\n dp[i] = true;\n break;\n }\n }\n }\n return dp[n];\n}\n```\n\nRecursive implementation:\n```\n// top-down dynamic programming approach: add a memo to the brute force\nbool CanWin(int n, unordered_map<int, bool> &memo) { // pass memo by reference\n if (memo.count(n) > 0)\n return memo[n];\n // base case: if nothing left, immediate loss (no possible move)\n if (n == 0) {\n memo[n] = false;\n return false;\n }\n // otherwise, iterate through the next moves\n // for every possible square number (the square number is sq*sq)\n for (int sq = 1; sq * sq <= n; ++sq) {\n // do we win by taking sq*sq from n\n // we win when the other player loses\n if (!CanWin(n - sq * sq, memo)) {\n memo[n] = true;\n return true;\n }\n }\n // if we never found a winning move, they\'re all losing moves\n memo[n] = false;\n return false;\n}\nbool winnerSquareGame(int n) {\n unordered_map<int, bool> memo;\n return CanWin(n, memo);\n}
| 2
| 1
|
[]
| 0
|
stone-game-iv
|
Stone Game IV (python DP)
|
stone-game-iv-python-dp-by-qianzechang-vpd6
|
\nclass Solution:\n def winnerSquareGame(self, n: int) -> bool:\n square=[i**2 for i in range(1,int(n**0.5)+1)]\n dp=[False]*(n+1)\n for
|
qianzechang
|
NORMAL
|
2020-10-25T07:31:23.170215+00:00
|
2020-10-25T07:31:23.170260+00:00
| 127
| false
|
```\nclass Solution:\n def winnerSquareGame(self, n: int) -> bool:\n square=[i**2 for i in range(1,int(n**0.5)+1)]\n dp=[False]*(n+1)\n for i in range(1,n+1):\n for s in square:\n if s>i:\n break\n if dp[i-s]==False:\n dp[i]=True\n break\n return dp[-1]\n```
| 2
| 1
|
[]
| 0
|
stone-game-iv
|
Java DP O(N)time. faster than 100%.
|
java-dp-ontime-faster-than-100-by-103sty-oj52
|
Runtime: 2 ms, faster than 100.00%, Memory Usage: 36.6 MB, less than 100.00% of Java online submissions\n\n\n//O(N)time\n//O(N)space\npublic boolean winnerSquar
|
103style
|
NORMAL
|
2020-07-17T05:42:31.240641+00:00
|
2020-07-17T05:42:31.240677+00:00
| 239
| false
|
**Runtime: 2 ms, faster than 100.00%, Memory Usage: 36.6 MB, less than 100.00% of Java online submissions**\n\n```\n//O(N)time\n//O(N)space\npublic boolean winnerSquareGame(int n) {\n boolean[] dp = new boolean[n + 1];\n for(int i = 0; i <= n; i++){\n if(dp[i]){\n continue;\n }\n for(int j = 1; i + j * j <= n; j++){\n dp[i + j * j] = true;\n }\n }\n return dp[n];\n}\n```
| 2
| 1
|
[]
| 1
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.