2021 Problems
Browse filesThis view is limited to 50 files because it contains too many changes.
See raw diff
- .gitattributes +15 -0
- 2021/finals/and.cpp +147 -0
- 2021/finals/and.in +0 -0
- 2021/finals/and.md +44 -0
- 2021/finals/and.out +0 -0
- 2021/finals/and_sol.md +19 -0
- 2021/finals/antisocial.cpp +456 -0
- 2021/finals/antisocial.in +3 -0
- 2021/finals/antisocial.md +41 -0
- 2021/finals/antisocial.out +1007 -0
- 2021/finals/antisocial_sol.md +20 -0
- 2021/finals/hire_flyers.cpp +354 -0
- 2021/finals/hire_flyers.in +3 -0
- 2021/finals/hire_flyers.md +50 -0
- 2021/finals/hire_flyers.out +118 -0
- 2021/finals/hire_flyers_sol.md +15 -0
- 2021/finals/ssssss.cpp +113 -0
- 2021/finals/ssssss.in +3 -0
- 2021/finals/ssssss.md +62 -0
- 2021/finals/ssssss.out +105 -0
- 2021/finals/ssssss_sol.md +19 -0
- 2021/finals/table_flipping.cpp +430 -0
- 2021/finals/table_flipping.in +3 -0
- 2021/finals/table_flipping.md +48 -0
- 2021/finals/table_flipping.out +100 -0
- 2021/finals/table_flipping_sol.md +67 -0
- 2021/finals/vacation.cpp +115 -0
- 2021/finals/vacation.in +3 -0
- 2021/finals/vacation.md +40 -0
- 2021/finals/vacation.out +101 -0
- 2021/finals/vacation_sol.md +16 -0
- 2021/quals/160428912890161.jpg +3 -0
- 2021/quals/271244381102893.jpg +3 -0
- 2021/quals/328916612261658.jpg +3 -0
- 2021/quals/375673720664225.jpg +3 -0
- 2021/quals/541711107152146.jpg +3 -0
- 2021/quals/consistency_ch1.cpp +35 -0
- 2021/quals/consistency_ch1.in +54 -0
- 2021/quals/consistency_ch1.md +33 -0
- 2021/quals/consistency_ch1.out +53 -0
- 2021/quals/consistency_ch1_sol.md +5 -0
- 2021/quals/consistency_ch2.cpp +48 -0
- 2021/quals/consistency_ch2.in +7292 -0
- 2021/quals/consistency_ch2.md +44 -0
- 2021/quals/consistency_ch2.out +51 -0
- 2021/quals/consistency_ch2_sol.md +7 -0
- 2021/quals/gold_mine_ch1.cpp +56 -0
- 2021/quals/gold_mine_ch1.in +956 -0
- 2021/quals/gold_mine_ch1.md +57 -0
- 2021/quals/gold_mine_ch1.out +56 -0
.gitattributes
CHANGED
|
@@ -83,3 +83,18 @@ saved_model/**/* filter=lfs diff=lfs merge=lfs -text
|
|
| 83 |
2020/quals/running_on_fumes_ch1.in filter=lfs diff=lfs merge=lfs -text
|
| 84 |
2020/quals/running_on_fumes_ch2.in filter=lfs diff=lfs merge=lfs -text
|
| 85 |
2020/quals/timber.in filter=lfs diff=lfs merge=lfs -text
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 83 |
2020/quals/running_on_fumes_ch1.in filter=lfs diff=lfs merge=lfs -text
|
| 84 |
2020/quals/running_on_fumes_ch2.in filter=lfs diff=lfs merge=lfs -text
|
| 85 |
2020/quals/timber.in filter=lfs diff=lfs merge=lfs -text
|
| 86 |
+
2021/finals/antisocial.in filter=lfs diff=lfs merge=lfs -text
|
| 87 |
+
2021/finals/hire_flyers.in filter=lfs diff=lfs merge=lfs -text
|
| 88 |
+
2021/finals/ssssss.in filter=lfs diff=lfs merge=lfs -text
|
| 89 |
+
2021/finals/table_flipping.in filter=lfs diff=lfs merge=lfs -text
|
| 90 |
+
2021/finals/vacation.in filter=lfs diff=lfs merge=lfs -text
|
| 91 |
+
2021/round1/blockchain.in filter=lfs diff=lfs merge=lfs -text
|
| 92 |
+
2021/round2/chainblock.in filter=lfs diff=lfs merge=lfs -text
|
| 93 |
+
2021/round2/runway.in filter=lfs diff=lfs merge=lfs -text
|
| 94 |
+
2021/round2/valet_parking_ch2.in filter=lfs diff=lfs merge=lfs -text
|
| 95 |
+
2021/round3/auth-ore-ization.in filter=lfs diff=lfs merge=lfs -text
|
| 96 |
+
2021/round3/expl-ore-ation_ch1.in filter=lfs diff=lfs merge=lfs -text
|
| 97 |
+
2021/round3/expl-ore-ation_ch2.in filter=lfs diff=lfs merge=lfs -text
|
| 98 |
+
2021/round3/expl-ore-ation_ch3.in filter=lfs diff=lfs merge=lfs -text
|
| 99 |
+
2021/round3/perf-ore-mance.in filter=lfs diff=lfs merge=lfs -text
|
| 100 |
+
2021/round3/rep-ore-ting.in filter=lfs diff=lfs merge=lfs -text
|
2021/finals/and.cpp
ADDED
|
@@ -0,0 +1,147 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
#include <algorithm>
|
| 2 |
+
#include <iostream>
|
| 3 |
+
#include <vector>
|
| 4 |
+
using namespace std;
|
| 5 |
+
|
| 6 |
+
const int LIM = 4000005;
|
| 7 |
+
|
| 8 |
+
struct UnionFind {
|
| 9 |
+
int N;
|
| 10 |
+
vector<int> root, diff_to_root, rank, sz, diffsum;
|
| 11 |
+
|
| 12 |
+
UnionFind(int _N):
|
| 13 |
+
N(_N), root(_N), diff_to_root(_N), rank(_N), sz(_N, 1), diffsum(_N) {
|
| 14 |
+
for (int i = 0; i < N; i++) {
|
| 15 |
+
root[i] = i;
|
| 16 |
+
}
|
| 17 |
+
}
|
| 18 |
+
|
| 19 |
+
int find(int i) {
|
| 20 |
+
int r = root[i];
|
| 21 |
+
if (r != i) {
|
| 22 |
+
root[i] = find(r);
|
| 23 |
+
diff_to_root[i] ^= diff_to_root[r];
|
| 24 |
+
}
|
| 25 |
+
return root[i];
|
| 26 |
+
}
|
| 27 |
+
|
| 28 |
+
bool merge(int i, int j, int d) {
|
| 29 |
+
int ri = find(i), rj = find(j);
|
| 30 |
+
d ^= diff_to_root[i] ^ diff_to_root[j];
|
| 31 |
+
if (ri == rj) {
|
| 32 |
+
return !d;
|
| 33 |
+
}
|
| 34 |
+
if (rank[ri] > rank[rj]) {
|
| 35 |
+
swap(ri, rj);
|
| 36 |
+
}
|
| 37 |
+
root[ri] = rj;
|
| 38 |
+
diff_to_root[ri] = d;
|
| 39 |
+
sz[rj] += sz[ri];
|
| 40 |
+
diffsum[rj] += d ? sz[ri] - diffsum[ri] : diffsum[ri];
|
| 41 |
+
if (rank[ri] == rank[rj]) {
|
| 42 |
+
rank[rj]++;
|
| 43 |
+
}
|
| 44 |
+
return true;
|
| 45 |
+
}
|
| 46 |
+
};
|
| 47 |
+
|
| 48 |
+
int N, K;
|
| 49 |
+
|
| 50 |
+
void solve() {
|
| 51 |
+
vector<int> both(LIM), ans(LIM);
|
| 52 |
+
vector<vector<vector<int>>> ind(LIM, vector<vector<int>>(2));
|
| 53 |
+
int maxL = 0;
|
| 54 |
+
// Input.
|
| 55 |
+
cin >> N >> K;
|
| 56 |
+
for (int i = 0; i < N; i++) {
|
| 57 |
+
string s[2];
|
| 58 |
+
cin >> s[0] >> s[1];
|
| 59 |
+
int len = max(s[0].size(), s[1].size());
|
| 60 |
+
maxL = max(maxL, len);
|
| 61 |
+
for (int b = 0; b < len; b++) {
|
| 62 |
+
int ch[2];
|
| 63 |
+
for (int j : {0, 1}) {
|
| 64 |
+
int slen = s[j].size();
|
| 65 |
+
ch[j] = b < slen ? s[j][slen - b - 1] - '0' : 0;
|
| 66 |
+
}
|
| 67 |
+
if (ch[0] && ch[1]) {
|
| 68 |
+
both[b]++;
|
| 69 |
+
} else {
|
| 70 |
+
for (int j : {0, 1}) {
|
| 71 |
+
if (ch[j]) {
|
| 72 |
+
ind[b][j].push_back(i);
|
| 73 |
+
}
|
| 74 |
+
}
|
| 75 |
+
}
|
| 76 |
+
}
|
| 77 |
+
}
|
| 78 |
+
// Consider each bit, starting from the most significant.
|
| 79 |
+
UnionFind U(N);
|
| 80 |
+
for (int b = maxL - 1; b >= 0; b--) {
|
| 81 |
+
ans[b] = 0;
|
| 82 |
+
// Bit included twice?
|
| 83 |
+
if (both[b] == N) {
|
| 84 |
+
ans[b] = 2;
|
| 85 |
+
continue;
|
| 86 |
+
}
|
| 87 |
+
// Bit not included at all?
|
| 88 |
+
if (both[b] + ind[b][0].size() + ind[b][1].size() < N) {
|
| 89 |
+
continue;
|
| 90 |
+
}
|
| 91 |
+
// Include bit once if possible.
|
| 92 |
+
int k = 0;
|
| 93 |
+
bool imp = false;
|
| 94 |
+
UnionFind U2 = U;
|
| 95 |
+
for (int i = 0; !imp && i < 2; i++) {
|
| 96 |
+
for (int j = 0; !imp && j < (int)ind[b][i].size() - 1; j++) {
|
| 97 |
+
if (!U2.merge(ind[b][i][j], ind[b][i][j + 1], 0)) {
|
| 98 |
+
imp = true;
|
| 99 |
+
}
|
| 100 |
+
}
|
| 101 |
+
}
|
| 102 |
+
if (imp) {
|
| 103 |
+
continue;
|
| 104 |
+
}
|
| 105 |
+
if (ind[b][0].size() > 0 && ind[b][1].size() > 0) {
|
| 106 |
+
if (!U2.merge(ind[b][0][0], ind[b][1][0], 1)) {
|
| 107 |
+
continue;
|
| 108 |
+
}
|
| 109 |
+
}
|
| 110 |
+
for (int i = 0; i < N; i++) {
|
| 111 |
+
if (U2.find(i) == i) {
|
| 112 |
+
k += min(U2.diffsum[i], U2.sz[i] - U2.diffsum[i]);
|
| 113 |
+
}
|
| 114 |
+
}
|
| 115 |
+
if (k > K) {
|
| 116 |
+
continue;
|
| 117 |
+
}
|
| 118 |
+
U = U2;
|
| 119 |
+
ans[b] = 1;
|
| 120 |
+
}
|
| 121 |
+
// Add up answer in binary.
|
| 122 |
+
for (int i = 0; i < maxL; i++) {
|
| 123 |
+
if (i == maxL - 1 && ans[i] >= 2) {
|
| 124 |
+
ans[maxL++] = 0;
|
| 125 |
+
}
|
| 126 |
+
ans[i + 1] += ans[i] / 2;
|
| 127 |
+
ans[i] %= 2;
|
| 128 |
+
}
|
| 129 |
+
// Output.
|
| 130 |
+
while (maxL > 1 && !ans[maxL - 1]) {
|
| 131 |
+
maxL--;
|
| 132 |
+
}
|
| 133 |
+
for (int i = maxL - 1; i >= 0; i--) {
|
| 134 |
+
cout << ans[i];
|
| 135 |
+
}
|
| 136 |
+
cout << endl;
|
| 137 |
+
}
|
| 138 |
+
|
| 139 |
+
int main() {
|
| 140 |
+
int T;
|
| 141 |
+
cin >> T;
|
| 142 |
+
for (int t = 1; t <= T; t++) {
|
| 143 |
+
cout << "Case #" << t << ": ";
|
| 144 |
+
solve();
|
| 145 |
+
}
|
| 146 |
+
return 0;
|
| 147 |
+
}
|
2021/finals/and.in
ADDED
|
The diff for this file is too large to render.
See raw diff
|
|
|
2021/finals/and.md
ADDED
|
@@ -0,0 +1,44 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Andy has no time for ores, he's just here for the `AND`s.
|
| 2 |
+
|
| 3 |
+
Andy has \(N\) pairs of integers, with each integer given in binary as a bitstring. The \(i\)th pair consists of bitstrings \(A_i\) and \(B_i\). No bitstring has leading zeros (except for the bitstring `"0"` itself).
|
| 4 |
+
|
| 5 |
+
Andy may choose at most \(K\) of these pairs for swapping. For each chosen pair \(i\), he'll swap its bitstrings \(A_i\) and \(B_i\).
|
| 6 |
+
|
| 7 |
+
After all of these swaps, he'll compute \(X\) as the bitwise `AND` of the \(N\) bitstrings \(A_{1..N}\), and \(Y\) as the bitwise `AND` of the \(N\) bitstrings \(B_{1..N}\), and finally add \(X\) and \(Y\) together. What's the maximum sum of \(X + Y\) that Andy can achieve?
|
| 8 |
+
|
| 9 |
+
Note that:
|
| 10 |
+
|
| 11 |
+
- The integer value of a bitstring \(S\) is equal to \(S_1 * 2^{|S|-1} + S_2 * 2^{|S|-2} + ... + S_{|S|} * 2^0\).
|
| 12 |
+
- The bitwise `AND` of a set of bitstrings \(S\) is a bitstring \(V\) such that, if leading zeros were appended to bitstrings in \(S\) until they all had the same length, then \(V\) also has that same length, with \(V_i\) equal to `1` if and only if all bitstrings in \(S\) have a `1` at index \(i\).
|
| 13 |
+
|
| 14 |
+
|
| 15 |
+
# Constraints
|
| 16 |
+
|
| 17 |
+
\(1 \le T \le 90\)
|
| 18 |
+
\(1 \le N \le 2{,}000{,}000\)
|
| 19 |
+
\(0 \le K \le N\)
|
| 20 |
+
\(0 \le A_{i,j}, B_{i,j} \le 1\)
|
| 21 |
+
|
| 22 |
+
The total length of all bitstrings \(A_{1..N}\) and \(B_{1..N}\) is at most \(4{,}000{,}000\).
|
| 23 |
+
The total length of all bitstrings across all test cases is at most \(10{,}000{,}000\).
|
| 24 |
+
|
| 25 |
+
|
| 26 |
+
# Input
|
| 27 |
+
|
| 28 |
+
Input begins with an integer \(T\), the number of test cases. For each test case, there is first a line containing \(2\) space-separated integers, \(N\) and \(K\). Then, \(N\) lines follow, the \(i\)th of which contains \(2\) space-separated bitstrings, \(A_i\) and \(B_i\).
|
| 29 |
+
|
| 30 |
+
|
| 31 |
+
# Output
|
| 32 |
+
|
| 33 |
+
For the \(i\)th test case, print a line containing *"Case #i: "* followed by a single bitstring, the maximum achievable sum of bitstring `AND`s, with no leading zeros (unless the bitstring is ``"0"``).
|
| 34 |
+
|
| 35 |
+
|
| 36 |
+
# Sample Explanation
|
| 37 |
+
|
| 38 |
+
In the first case, \(X = 1011011_2 \,(91_{10})\), \(Y = 101101_2 \,(45_{10})\), and \(X + Y = 10001000_2 \,(136_{10})\).
|
| 39 |
+
|
| 40 |
+
In the second case, no swaps are allowed, so we must have \(X = 1011011_2\) `AND` \(0_2 = 0_2\) and \(Y = 0_2 \) `AND` \(101101_2 = 0_2\).
|
| 41 |
+
|
| 42 |
+
In the third case, one option is to swap \(A_1\) and \(B_1\). This yields \(X = 0_2\) `AND` \(0_2 = 0_2\) and \(Y = 1011011_2\) `AND` \(101101_2 = 1001_2\).
|
| 43 |
+
|
| 44 |
+
In the fourth case, one option is to swap \(A_1\) and \(B_1\) as well as \(A_3\) and \(B_3\), resulting in \(X = 111_2 \,(7_{10})\), \(Y = 1_2 \,(1_{10})\), and \(X + Y = 1000_2 \,(8_{10})\).
|
2021/finals/and.out
ADDED
|
The diff for this file is too large to render.
See raw diff
|
|
|
2021/finals/and_sol.md
ADDED
|
@@ -0,0 +1,19 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Let \(L\) be the length of the longest bitstring. Each bit index \(i\) (counting from the right, starting at \(0\)) between \(0\) and \(L-1\) (inclusive) will contribute either \(0\), \(2^i\), or \(2*2^i\) to the answer, depending on whether it's set in all bitstrings \(A_{1..N}\) and/or in all bitstrings \(B_{1..N}\). Once we determine which of these each bit index will contribute in the optimal solution, we'll be able to compute the resulting summed bitstring in \(O(L)\) time.
|
| 2 |
+
|
| 3 |
+
Considering bit indices \(i\) in order from most to least significant (from \(L-1\) down to \(0\)), each will fall into one of three categories:
|
| 4 |
+
|
| 5 |
+
1. If \(i\) is set in all \(2N\) bitstrings \(A_{1..N}\) and \(B_{1..N}\), then it must always contribute \(2*2^i\) to the answer.
|
| 6 |
+
|
| 7 |
+
2. If, for at least one pair \(j\), \(i\) is set in neither \(A_j\) nor \(B_j\), then it must always contribute \(0\) to the answer.
|
| 8 |
+
|
| 9 |
+
3. Otherwise, it may either contribute \(0\) or \(2^i\) to the answer. We should greedily cause it to contribute \(2^i\) if possible (without compromising previously-considered bit indices), as doing so would be strictly better than doing so for all later bit indices combined (as \(2^i \gt \sum_{j=0}^{i-1}{2^j}\)).
|
| 10 |
+
|
| 11 |
+
Let \(O_j\) be the "orientation" of pair \(j\) (whether or not it's being swapped), \(X\) be the set of pairs \(j\) for which \(i\) is set in \(A_j\) but not \(B_j\), and \(Y\) be the set of pairs \(j\) for which \(i\) set in \(B_j\) but not \(A_j\).
|
| 12 |
+
|
| 13 |
+
Bit index \(i\) will then contribute to the answer if and only if all pairs in \(X\) have equal \(O\) values, all pairs in \(Y\) have equal \(O\) values, and the \(X\) pairs' \(O\) values are the opposite of the \(Y\) pairs' \(O\) values. This can be expressed as a set of at most \(|X|+|Y|+1\) pairwise relationships, each stating whether a certain pair of pairs must have equal or opposite \(O\) values.
|
| 14 |
+
|
| 15 |
+
We'll maintain information about these relationships using a [disjoint set union](https://en.wikipedia.org/wiki/Disjoint-set_data_structure) data structure (over the \(N\) pairs), augmented such that the root of each set stores its total number of pairs and the number of pairs which must have opposite \(O\) values to the root, and such that each pair stores whether or not it must have the opposite \(O\) value to the root of its set.
|
| 16 |
+
|
| 17 |
+
So, when considering each bit index \(i\), we'll make a copy of the DSU and attempt to add all of the newly-required relationships to it in \(O(N*α(N))\) time. If that proves possible without introducing conflicts, we'll take another \(O(N)\) time to compute the minimum total number of swaps required (by greedily choosing between the two possible arrangements of orientations for each set). If that comes out to at most \(K\), then we'll add \(2^i\) to the answer and keep the new state of the DSU, while we'll otherwise roll back to the DSU's prior state.
|
| 18 |
+
|
| 19 |
+
Each time a bit index falls into the third category described above, there must have been at least \(N\) set bits in the input (at that index). Therefore, if \(S\) is the sum of all \(2N\) bitstring lengths, then only \(O(S/N)\) bit indices can fall into that category. This means that the time complexity of this algorithm is \(O(S/N * N * α(N)) = O(S α(N))\) (effectively \(O(S)\)).
|
2021/finals/antisocial.cpp
ADDED
|
@@ -0,0 +1,456 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
#include <algorithm>
|
| 2 |
+
#include <cassert>
|
| 3 |
+
#include <cmath>
|
| 4 |
+
#include <functional>
|
| 5 |
+
#include <iostream>
|
| 6 |
+
#include <queue>
|
| 7 |
+
#include <utility>
|
| 8 |
+
#include <vector>
|
| 9 |
+
using namespace std;
|
| 10 |
+
|
| 11 |
+
const int LIM = 6000006;
|
| 12 |
+
const long double EPS = 1e-9;
|
| 13 |
+
|
| 14 |
+
using LD = long double;
|
| 15 |
+
using pii = pair<int, int>;
|
| 16 |
+
|
| 17 |
+
// From https://github.com/zigui-ps/VoronoiDiagram
|
| 18 |
+
struct point {
|
| 19 |
+
LD x, y;
|
| 20 |
+
|
| 21 |
+
point(): x(0), y(0) {}
|
| 22 |
+
point(LD _x, LD _y): x(_x), y(_y) {}
|
| 23 |
+
|
| 24 |
+
LD operator/(point p) const { return x * p.y - y * p.x; }
|
| 25 |
+
point operator+(point p) const { return point(x + p.x, y + p.y); }
|
| 26 |
+
point operator-(point p) const { return point(x - p.x, y - p.y); }
|
| 27 |
+
friend point operator*(LD b, point a) { return point(b * a.x, b * a.y); }
|
| 28 |
+
|
| 29 |
+
LD size() const { return hypot(x, y); }
|
| 30 |
+
LD sz2() const { return x * x + y * y; }
|
| 31 |
+
point r90() const { return point(-y, x); }
|
| 32 |
+
LD dot(point p) { return x * p.x + y * p.y; }
|
| 33 |
+
};
|
| 34 |
+
|
| 35 |
+
int dcmp(LD x) {
|
| 36 |
+
return x < -EPS ? -1 : x > EPS ? 1 : 0;
|
| 37 |
+
}
|
| 38 |
+
|
| 39 |
+
point line_intersect(point a, point b, point u, point v) {
|
| 40 |
+
return u + (((a - u) / b) / (v / b)) * v;
|
| 41 |
+
}
|
| 42 |
+
|
| 43 |
+
point get_circumcenter(point p0, point p1, point p2) {
|
| 44 |
+
return line_intersect(
|
| 45 |
+
0.5 * (p0 + p1), (p0 - p1).r90(), 0.5 * (p1 + p2), (p1 - p2).r90()
|
| 46 |
+
);
|
| 47 |
+
}
|
| 48 |
+
|
| 49 |
+
point project_point_segment(point a, point b, point c) {
|
| 50 |
+
LD r = (b - a).dot(b - a);
|
| 51 |
+
if (fabs(r) < EPS) {
|
| 52 |
+
return a;
|
| 53 |
+
}
|
| 54 |
+
r = (c - a).dot(b - a) / r;
|
| 55 |
+
if (r < 0) {
|
| 56 |
+
return a;
|
| 57 |
+
}
|
| 58 |
+
if (r > 1) {
|
| 59 |
+
return b;
|
| 60 |
+
}
|
| 61 |
+
return a + r * (b - a);
|
| 62 |
+
}
|
| 63 |
+
|
| 64 |
+
bool point_in_polygon_incl(const vector<point> &p, point q) {
|
| 65 |
+
bool c = 0;
|
| 66 |
+
for (int i = 0; i < p.size(); i++) {
|
| 67 |
+
int j = (i + 1) % p.size();
|
| 68 |
+
if ((project_point_segment(p[i], p[j], q) - q).sz2() < EPS) {
|
| 69 |
+
return true;
|
| 70 |
+
}
|
| 71 |
+
if (
|
| 72 |
+
(p[i].y <= q.y && q.y < p[j].y || p[j].y <= q.y && q.y < p[i].y) &&
|
| 73 |
+
q.x < p[i].x + (p[j].x - p[i].x) * (q.y - p[i].y) / (p[j].y - p[i].y)
|
| 74 |
+
) {
|
| 75 |
+
c = !c;
|
| 76 |
+
}
|
| 77 |
+
}
|
| 78 |
+
return c;
|
| 79 |
+
}
|
| 80 |
+
|
| 81 |
+
// https://www.youtube.com/watch?v=h_vvP4ah6Ck
|
| 82 |
+
LD parabola_intersect(point left, point right, LD sweepline) {
|
| 83 |
+
auto f2 = [](point left, point right, LD sweepline) {
|
| 84 |
+
int sign = left.x < right.x ? 1 : -1;
|
| 85 |
+
point m = 0.5 * (left + right);
|
| 86 |
+
point v = line_intersect(
|
| 87 |
+
m, (right - left).r90(), point(0, sweepline), point(1, 0)
|
| 88 |
+
);
|
| 89 |
+
point w = line_intersect(m, (left - v).r90(), v, left - v);
|
| 90 |
+
LD l1 = (v - w).size();
|
| 91 |
+
LD l2 = sqrt(pow(sweepline - m.y, 2) - (m - w).sz2());
|
| 92 |
+
LD l3 = (left - v).size();
|
| 93 |
+
return v.x + (m.x - v.x) * l3 / (l1 + sign * l2);
|
| 94 |
+
};
|
| 95 |
+
if (fabs(left.y - right.y) < fabs(left.x - right.x) * EPS) {
|
| 96 |
+
return f2(left, right, sweepline);
|
| 97 |
+
}
|
| 98 |
+
int sign = left.y < right.y ? -1 : 1;
|
| 99 |
+
point v = line_intersect(
|
| 100 |
+
left, right - left, point(0, sweepline), point(1, 0)
|
| 101 |
+
);
|
| 102 |
+
LD d1 = (0.5 * (left + right) - v).sz2(), d2 = (0.5 * (left - right)).sz2();
|
| 103 |
+
return v.x + sign * sqrt(max(0.0L, d1 - d2));
|
| 104 |
+
}
|
| 105 |
+
|
| 106 |
+
struct Beachline {
|
| 107 |
+
struct node {
|
| 108 |
+
point pt;
|
| 109 |
+
int idx;
|
| 110 |
+
int end;
|
| 111 |
+
node *link[2], *par, *prv, *nxt;
|
| 112 |
+
|
| 113 |
+
node() {}
|
| 114 |
+
node(point _pt, int idx):
|
| 115 |
+
pt(_pt), idx(idx), end(0), link{0, 0}, par(0), prv(0), nxt(0) {}
|
| 116 |
+
} *root;
|
| 117 |
+
|
| 118 |
+
LD sweepline;
|
| 119 |
+
|
| 120 |
+
Beachline() : sweepline(-1e20), root(NULL) { }
|
| 121 |
+
|
| 122 |
+
inline int dir(node* x) {
|
| 123 |
+
return x->par->link[0] != x;
|
| 124 |
+
}
|
| 125 |
+
|
| 126 |
+
// p n p n
|
| 127 |
+
// / \ / \ / \ / \
|
| 128 |
+
// n d => a p or a n => p d
|
| 129 |
+
// / \ / \ / \ / \
|
| 130 |
+
// a b b d c d a c
|
| 131 |
+
void rotate(node* n) {
|
| 132 |
+
node* p = n->par;
|
| 133 |
+
int d = dir(n);
|
| 134 |
+
p->link[d] = n->link[!d];
|
| 135 |
+
if (n->link[!d]) {
|
| 136 |
+
n->link[!d]->par = p;
|
| 137 |
+
}
|
| 138 |
+
n->par = p->par;
|
| 139 |
+
if (p->par) {
|
| 140 |
+
p->par->link[dir(p)] = n;
|
| 141 |
+
}
|
| 142 |
+
n->link[!d] = p;
|
| 143 |
+
p->par = n;
|
| 144 |
+
}
|
| 145 |
+
|
| 146 |
+
void splay(node* x, node* f = NULL) {
|
| 147 |
+
while (x->par != f) {
|
| 148 |
+
if (x->par->par == f) {
|
| 149 |
+
// no-op
|
| 150 |
+
} else if (dir(x) == dir(x->par)) {
|
| 151 |
+
rotate(x->par);
|
| 152 |
+
} else {
|
| 153 |
+
rotate(x);
|
| 154 |
+
}
|
| 155 |
+
rotate(x);
|
| 156 |
+
}
|
| 157 |
+
if (f == NULL) {
|
| 158 |
+
root = x;
|
| 159 |
+
}
|
| 160 |
+
}
|
| 161 |
+
|
| 162 |
+
void insert(node* n, node* p, int d) {
|
| 163 |
+
splay(p);
|
| 164 |
+
node *c = p->link[d];
|
| 165 |
+
n->link[d] = c;
|
| 166 |
+
if (c) {
|
| 167 |
+
c->par = n;
|
| 168 |
+
}
|
| 169 |
+
p->link[d] = n;
|
| 170 |
+
n->par = p;
|
| 171 |
+
node *prv = !d ? p->prv : p, *nxt = !d ? p : p->nxt;
|
| 172 |
+
n->prv = prv;
|
| 173 |
+
if (prv) {
|
| 174 |
+
prv->nxt = n;
|
| 175 |
+
}
|
| 176 |
+
n->nxt = nxt;
|
| 177 |
+
if (nxt) {
|
| 178 |
+
nxt->prv = n;
|
| 179 |
+
}
|
| 180 |
+
}
|
| 181 |
+
|
| 182 |
+
void erase(node* n) {
|
| 183 |
+
node *prv = n->prv, *nxt = n->nxt;
|
| 184 |
+
if (!prv && !nxt) {
|
| 185 |
+
if (n == root) {
|
| 186 |
+
root = NULL;
|
| 187 |
+
}
|
| 188 |
+
return;
|
| 189 |
+
}
|
| 190 |
+
n->prv = NULL;
|
| 191 |
+
if (prv) {
|
| 192 |
+
prv->nxt = nxt;
|
| 193 |
+
}
|
| 194 |
+
n->nxt = NULL;
|
| 195 |
+
if (nxt) {
|
| 196 |
+
nxt->prv = prv;
|
| 197 |
+
}
|
| 198 |
+
splay(n);
|
| 199 |
+
if (!nxt) {
|
| 200 |
+
root->par = NULL;
|
| 201 |
+
n->link[0] = NULL;
|
| 202 |
+
root = prv;
|
| 203 |
+
} else {
|
| 204 |
+
splay(nxt, n);
|
| 205 |
+
node* c = n->link[0];
|
| 206 |
+
nxt->link[0] = c;
|
| 207 |
+
c->par = nxt;
|
| 208 |
+
n->link[0] = NULL;
|
| 209 |
+
n->link[1] = NULL;
|
| 210 |
+
nxt->par = NULL;
|
| 211 |
+
root = nxt;
|
| 212 |
+
}
|
| 213 |
+
}
|
| 214 |
+
|
| 215 |
+
bool get_event(node *cur, LD &next_sweep) {
|
| 216 |
+
if (!cur->prv || !cur->nxt) {
|
| 217 |
+
return false;
|
| 218 |
+
}
|
| 219 |
+
point u = (cur->pt - cur->prv->pt).r90();
|
| 220 |
+
point v = (cur->nxt->pt - cur->pt).r90();
|
| 221 |
+
if (dcmp(u / v) != 1) {
|
| 222 |
+
return false;
|
| 223 |
+
}
|
| 224 |
+
point p = get_circumcenter(cur->pt, cur->prv->pt, cur->nxt->pt);
|
| 225 |
+
next_sweep = p.y + (p - cur->pt).size();
|
| 226 |
+
return true;
|
| 227 |
+
}
|
| 228 |
+
|
| 229 |
+
node* find_beachline(LD x) {
|
| 230 |
+
node* cur = root;
|
| 231 |
+
while (cur) {
|
| 232 |
+
LD left = cur->prv
|
| 233 |
+
? parabola_intersect(cur->prv->pt, cur->pt, sweepline)
|
| 234 |
+
: -1e30;
|
| 235 |
+
LD right = cur->nxt
|
| 236 |
+
? parabola_intersect(cur->pt, cur->nxt->pt, sweepline)
|
| 237 |
+
: 1e30;
|
| 238 |
+
if (left <= x && x <= right) {
|
| 239 |
+
splay(cur);
|
| 240 |
+
return cur;
|
| 241 |
+
}
|
| 242 |
+
cur = cur->link[x > right];
|
| 243 |
+
}
|
| 244 |
+
return NULL;
|
| 245 |
+
}
|
| 246 |
+
};
|
| 247 |
+
|
| 248 |
+
using BeachNode = Beachline::node;
|
| 249 |
+
|
| 250 |
+
static BeachNode arr[LIM];
|
| 251 |
+
static int sz;
|
| 252 |
+
static BeachNode* new_node(point point, int idx) {
|
| 253 |
+
arr[sz] = BeachNode(point, idx);
|
| 254 |
+
return arr + (sz++);
|
| 255 |
+
}
|
| 256 |
+
|
| 257 |
+
struct event {
|
| 258 |
+
int type, idx, prv, nxt;
|
| 259 |
+
BeachNode *cur;
|
| 260 |
+
LD sweep;
|
| 261 |
+
|
| 262 |
+
event(LD sweep, int idx) : type(0), sweep(sweep), idx(idx) {}
|
| 263 |
+
event(LD sweep, BeachNode* cur) :
|
| 264 |
+
type(1), sweep(sweep), prv(cur->prv->idx), cur(cur), nxt(cur->nxt->idx) {}
|
| 265 |
+
|
| 266 |
+
bool operator>(const event& l) const { return sweep > l.sweep; }
|
| 267 |
+
};
|
| 268 |
+
|
| 269 |
+
void voronoi_diagram(
|
| 270 |
+
vector<point> &input,
|
| 271 |
+
vector<point> &vertex,
|
| 272 |
+
vector<pii> &edge,
|
| 273 |
+
vector<pii> &area
|
| 274 |
+
) {
|
| 275 |
+
Beachline beachline = Beachline();
|
| 276 |
+
priority_queue<event, vector<event>, greater<event>> events;
|
| 277 |
+
|
| 278 |
+
auto add_edge = [&](int u, int v, int a, int b, BeachNode* c1, BeachNode* c2) {
|
| 279 |
+
if (c1) {
|
| 280 |
+
c1->end = edge.size() * 2;
|
| 281 |
+
}
|
| 282 |
+
if (c2) {
|
| 283 |
+
c2->end = edge.size() * 2 + 1;
|
| 284 |
+
}
|
| 285 |
+
edge.emplace_back(u, v);
|
| 286 |
+
area.emplace_back(a, b);
|
| 287 |
+
};
|
| 288 |
+
auto write_edge = [&](int idx, int v) {
|
| 289 |
+
if (idx % 2 == 0) {
|
| 290 |
+
edge[idx / 2].first = v;
|
| 291 |
+
} else {
|
| 292 |
+
edge[idx / 2].second = v;
|
| 293 |
+
}
|
| 294 |
+
};
|
| 295 |
+
auto add_event = [&](BeachNode* cur) {
|
| 296 |
+
LD nxt;
|
| 297 |
+
if (beachline.get_event(cur, nxt)) {
|
| 298 |
+
events.emplace(nxt, cur);
|
| 299 |
+
}
|
| 300 |
+
};
|
| 301 |
+
|
| 302 |
+
int n = input.size(), cnt = 0;
|
| 303 |
+
/*arr = new BeachNode[n * 4]; */sz = 0;
|
| 304 |
+
sort(input.begin(), input.end(), [](const point &l, const point &r) {
|
| 305 |
+
return l.y != r.y ? l.y < r.y : l.x < r.x;
|
| 306 |
+
});
|
| 307 |
+
|
| 308 |
+
BeachNode *tmp = beachline.root = new_node(input[0], 0), *t2;
|
| 309 |
+
for (int i = 1; i < n; i++) {
|
| 310 |
+
if (dcmp(input[i].y - input[0].y) == 0) {
|
| 311 |
+
add_edge(-1, -1, i - 1, i, 0, tmp);
|
| 312 |
+
beachline.insert(t2 = new_node(input[i], i), tmp, 1);
|
| 313 |
+
tmp = t2;
|
| 314 |
+
} else {
|
| 315 |
+
events.emplace(input[i].y, i);
|
| 316 |
+
}
|
| 317 |
+
}
|
| 318 |
+
|
| 319 |
+
while (events.size()) {
|
| 320 |
+
event q = events.top();
|
| 321 |
+
events.pop();
|
| 322 |
+
BeachNode *prv, *cur, *nxt, *site;
|
| 323 |
+
int v = vertex.size(), idx = q.idx;
|
| 324 |
+
beachline.sweepline = q.sweep;
|
| 325 |
+
if (q.type == 0) {
|
| 326 |
+
point pt = input[idx];
|
| 327 |
+
cur = beachline.find_beachline(pt.x);
|
| 328 |
+
beachline.insert(site = new_node(pt, idx), cur, 0);
|
| 329 |
+
beachline.insert(prv = new_node(cur->pt, cur->idx), site, 0);
|
| 330 |
+
add_edge(-1, -1, cur->idx, idx, site, prv);
|
| 331 |
+
add_event(prv);
|
| 332 |
+
add_event(cur);
|
| 333 |
+
} else {
|
| 334 |
+
cur = q.cur;
|
| 335 |
+
prv = cur->prv;
|
| 336 |
+
nxt = cur->nxt;
|
| 337 |
+
if (!prv || !nxt || prv->idx != q.prv || nxt->idx != q.nxt) {
|
| 338 |
+
continue;
|
| 339 |
+
}
|
| 340 |
+
vertex.push_back(get_circumcenter(prv->pt, nxt->pt, cur->pt));
|
| 341 |
+
write_edge(prv->end, v);
|
| 342 |
+
write_edge(cur->end, v);
|
| 343 |
+
add_edge(v, -1, prv->idx, nxt->idx, 0, prv);
|
| 344 |
+
beachline.erase(cur);
|
| 345 |
+
add_event(prv);
|
| 346 |
+
add_event(nxt);
|
| 347 |
+
}
|
| 348 |
+
}
|
| 349 |
+
// delete arr;
|
| 350 |
+
}
|
| 351 |
+
|
| 352 |
+
int XR, YR;
|
| 353 |
+
int N, M;
|
| 354 |
+
vector<pair<int, LD>> adj[LIM];
|
| 355 |
+
point KP[2];
|
| 356 |
+
int KN[2];
|
| 357 |
+
LD ans;
|
| 358 |
+
|
| 359 |
+
void process_voronoi_diagrams(vector<point> P) {
|
| 360 |
+
int i, j, k;
|
| 361 |
+
vector<point> vertex;
|
| 362 |
+
vector<pii> edge, area;
|
| 363 |
+
voronoi_diagram(P, vertex, edge, area);
|
| 364 |
+
M = vertex.size();
|
| 365 |
+
for (int i = 0; i < area.size(); i++) {
|
| 366 |
+
int e1 = edge[i].first, e2 = edge[i].second;
|
| 367 |
+
if (e1 < 0 || e2 < 0) {
|
| 368 |
+
continue; // Infinite edge.
|
| 369 |
+
}
|
| 370 |
+
point v1 = vertex[e1], v2 = vertex[e2];
|
| 371 |
+
if (
|
| 372 |
+
min(v1.x, v2.x) < -EPS || max(v1.x, v2.x) > XR + EPS ||
|
| 373 |
+
min(v1.y, v2.y) < -EPS || max(v1.y, v2.y) > YR + EPS
|
| 374 |
+
) {
|
| 375 |
+
continue; // Edge outside rectangle.
|
| 376 |
+
}
|
| 377 |
+
// Add edge to graph with appropriate weight.
|
| 378 |
+
int pi1 = area[i].first, pi2 = area[i].second;
|
| 379 |
+
point p1 = P[pi1], p2 = P[pi2];
|
| 380 |
+
LD d = (p1 - project_point_segment(v1, v2, p1)).size();
|
| 381 |
+
adj[e1].emplace_back(e2, d);
|
| 382 |
+
adj[e2].emplace_back(e1, d);
|
| 383 |
+
// Consider any key points in triangles adjacent to this edge.
|
| 384 |
+
point mid = 0.5 * (p1 + p2);
|
| 385 |
+
for (int j : {0, 1}) {
|
| 386 |
+
for (int k : {0, 1}) {
|
| 387 |
+
point kp = KP[j], p = k ? p2 : p1;
|
| 388 |
+
ans = min(ans, (kp - p).size()); // Must be this close to a point.
|
| 389 |
+
if (point_in_polygon_incl({p, v1, mid}, kp)) {
|
| 390 |
+
KN[j] = e1;
|
| 391 |
+
}
|
| 392 |
+
if (point_in_polygon_incl({p, mid, v2}, kp)) {
|
| 393 |
+
KN[j] = e2;
|
| 394 |
+
}
|
| 395 |
+
}
|
| 396 |
+
}
|
| 397 |
+
}
|
| 398 |
+
}
|
| 399 |
+
|
| 400 |
+
LD solve() {
|
| 401 |
+
vector<point> P;
|
| 402 |
+
for (int i = 0; i < LIM; i++) {
|
| 403 |
+
adj[i].clear();
|
| 404 |
+
}
|
| 405 |
+
// Input.
|
| 406 |
+
cin >> XR >> YR;
|
| 407 |
+
cin >> KP[0].x >> KP[0].y >> KP[1].x >> KP[1].y;
|
| 408 |
+
cin >> N;
|
| 409 |
+
for (int i = 0; i < N; i++) {
|
| 410 |
+
int a, b;
|
| 411 |
+
cin >> a >> b;
|
| 412 |
+
P.emplace_back(a, b);
|
| 413 |
+
// Additionally mirror each point across each side of the rectangle.
|
| 414 |
+
P.emplace_back(-a, b);
|
| 415 |
+
P.emplace_back(a, -b);
|
| 416 |
+
P.emplace_back(2 * XR - a, b);
|
| 417 |
+
P.emplace_back(a, 2 * YR - b);
|
| 418 |
+
}
|
| 419 |
+
// Compute Voronoi diagram and corresponding graph.
|
| 420 |
+
ans = 1e18;
|
| 421 |
+
KN[0] = KN[1] = -1;
|
| 422 |
+
process_voronoi_diagrams(P);
|
| 423 |
+
assert(KN[0] >= 0 && KN[1] >= 0);
|
| 424 |
+
// MST.
|
| 425 |
+
vector<bool> visit(M);
|
| 426 |
+
priority_queue<pair<LD, int>> Q;
|
| 427 |
+
Q.emplace(ans, KN[0]);
|
| 428 |
+
while (!Q.empty()) {
|
| 429 |
+
ans = min(ans, Q.top().first);
|
| 430 |
+
int i = Q.top().second;
|
| 431 |
+
Q.pop();
|
| 432 |
+
if (i == KN[1]) {
|
| 433 |
+
break;
|
| 434 |
+
}
|
| 435 |
+
if (visit[i]) {
|
| 436 |
+
continue;
|
| 437 |
+
}
|
| 438 |
+
visit[i] = true;
|
| 439 |
+
for (auto c : adj[i]) {
|
| 440 |
+
if (!visit[c.first]) {
|
| 441 |
+
Q.emplace(c.second, c.first);
|
| 442 |
+
}
|
| 443 |
+
}
|
| 444 |
+
}
|
| 445 |
+
return ans;
|
| 446 |
+
}
|
| 447 |
+
|
| 448 |
+
int main() {
|
| 449 |
+
cout.precision(10);
|
| 450 |
+
int T;
|
| 451 |
+
cin >> T;
|
| 452 |
+
for (int t = 1; t <= T; t++) {
|
| 453 |
+
cout << "Case #" << t << ": " << fixed << solve() << endl;
|
| 454 |
+
}
|
| 455 |
+
return 0;
|
| 456 |
+
}
|
2021/finals/antisocial.in
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:3775e7403b65e0a26f30ac7a55f82b9ff51e744f4436e97ba01226840e6619f0
|
| 3 |
+
size 29523370
|
2021/finals/antisocial.md
ADDED
|
@@ -0,0 +1,41 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Cole is a programmer in the coal division of Metal (previously Facebulk), working across \(T\) office buildings with very pleasant coworkers and unlimited free ice cream. However, as a self-proclaimed antisocial code monkey, he still prefers to "mine" his own business when possible.
|
| 2 |
+
|
| 3 |
+
A given office building can be represented by an axis-aligned rectangle with opposite corners \((0, 0)\) and \((X_R, Y_R)\) on a 2D plane. Inside, there are \(N\) friendly coworkers, the \(i\)th of whom is permanently seated at position \((X_i, Y_i)\), distinct from all other coworkers.
|
| 4 |
+
|
| 5 |
+
Cole is currently at position \((X_A, Y_A)\), and would like to reach the unlimited free ice cream at a different position \((X_B, Y_B)\). Neither position is located at a coworker's seat.
|
| 6 |
+
|
| 7 |
+
Please help Cole determine the closest distance he'll need to get to another coworker in order to travel from \((X_A, Y_A)\) to \((X_B, Y_B)\) without leaving the building. Your answer will be accepted if it is within either \(10^{-6}\) or \(0.000001\%\) of the right answer.
|
| 8 |
+
|
| 9 |
+
# Constraints
|
| 10 |
+
|
| 11 |
+
\(1 \le T \le 800\)
|
| 12 |
+
\(1 \le N \le 800{,}000\)
|
| 13 |
+
\(2 \le X_R, Y_R \le 1{,}000{,}000{,}000\)
|
| 14 |
+
\(0 < X_i, X_A, X_B < X_R\)
|
| 15 |
+
\(0 < Y_i, Y_A, Y_B < Y_R\)
|
| 16 |
+
|
| 17 |
+
The sum of \(N\) across all buildings is at most \(3{,}000{,}000\).
|
| 18 |
+
|
| 19 |
+
# Input
|
| 20 |
+
|
| 21 |
+
Input begins with a single integer \(T\), the number of office buildings. For each building, there is first a line containing \(2\) space-separated integers, \(X_R\) and \(Y_R\). Then, there is a line containing \(4\) space-separated integers, \(X_A\), \(Y_A\), \(X_B\), and \(Y_B\). Then, there a line containing a single integer \(N\). Then, \(N\) lines follow, the \(i\)th of which consists of \(2\) space-separated integers, \(X_i\) and \(Y_i\).
|
| 22 |
+
|
| 23 |
+
# Output
|
| 24 |
+
|
| 25 |
+
For the \(i\)th building, print a line containing *"Case #i: "* followed by a single real number, the closest that Cole will need to get to another coworker in order to reach the free ice cream.
|
| 26 |
+
|
| 27 |
+
# Sample Explanation
|
| 28 |
+
|
| 29 |
+
In the first building, walking directly from \((3, 1)\) to \((17, 1)\) would take Cole within just 2 units of the coworker at \((10, 3)\). Instead, one optimal route might involve walking upward first, then across, and then back down, as illustrated below:
|
| 30 |
+
|
| 31 |
+
{{PHOTO_ID:441536274154579|WIDTH:450}}
|
| 32 |
+
|
| 33 |
+
The closest such a route gets to the coworker is \(7\) units (for example at coordinates \((10, 10)\).
|
| 34 |
+
|
| 35 |
+
In the second building, Cole's route must begin and end at a distance of \(\sqrt{4^2 + 2^2} \approx 4.47\) units from the coworker at \((10, 3)\). It's possible for Cole to get around them without getting any closer than that, for example with the following route:
|
| 36 |
+
|
| 37 |
+
{{PHOTO_ID:4816243665107323|WIDTH:450}}
|
| 38 |
+
|
| 39 |
+
In the third building, one optimal route for Cole might look as follows:
|
| 40 |
+
|
| 41 |
+
{{PHOTO_ID:440615224330860|WIDTH:280}}
|
2021/finals/antisocial.out
ADDED
|
@@ -0,0 +1,1007 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Case #1: 7.00000000
|
| 2 |
+
Case #2: 4.47213595
|
| 3 |
+
Case #3: 1.50000000
|
| 4 |
+
Case #4: 1.00000000
|
| 5 |
+
Case #5: 0.70710678
|
| 6 |
+
Case #6: 20.67002661
|
| 7 |
+
Case #7: 80.21533519
|
| 8 |
+
Case #8: 1414210.02683937
|
| 9 |
+
Case #9: 4.92442890
|
| 10 |
+
Case #10: 4.00000000
|
| 11 |
+
Case #11: 2.23606798
|
| 12 |
+
Case #12: 2.23606798
|
| 13 |
+
Case #13: 3.00000000
|
| 14 |
+
Case #14: 3.00000000
|
| 15 |
+
Case #15: 3.00000000
|
| 16 |
+
Case #16: 1.00000000
|
| 17 |
+
Case #17: 3.60555128
|
| 18 |
+
Case #18: 3.00000000
|
| 19 |
+
Case #19: 2.00000000
|
| 20 |
+
Case #20: 2.23606798
|
| 21 |
+
Case #21: 2.50000000
|
| 22 |
+
Case #22: 4.12310563
|
| 23 |
+
Case #23: 2.00000000
|
| 24 |
+
Case #24: 1.00000000
|
| 25 |
+
Case #25: 6.40312424
|
| 26 |
+
Case #26: 1.41421356
|
| 27 |
+
Case #27: 28.44292531
|
| 28 |
+
Case #28: 156.78010078
|
| 29 |
+
Case #29: 24.08318916
|
| 30 |
+
Case #30: 64.12487817
|
| 31 |
+
Case #31: 17.26267650
|
| 32 |
+
Case #32: 72.71863585
|
| 33 |
+
Case #33: 30.00000000
|
| 34 |
+
Case #34: 5.83095189
|
| 35 |
+
Case #35: 5.65685425
|
| 36 |
+
Case #36: 33.01514804
|
| 37 |
+
Case #37: 2.00000000
|
| 38 |
+
Case #38: 1.00000000
|
| 39 |
+
Case #39: 3.60555128
|
| 40 |
+
Case #40: 1.41421356
|
| 41 |
+
Case #41: 1.00000000
|
| 42 |
+
Case #42: 3.16227766
|
| 43 |
+
Case #43: 1.41421356
|
| 44 |
+
Case #44: 2.23606798
|
| 45 |
+
Case #45: 1.00000000
|
| 46 |
+
Case #46: 1.00000000
|
| 47 |
+
Case #47: 9543.00000000
|
| 48 |
+
Case #48: 128840.13542371
|
| 49 |
+
Case #49: 208298.03709589
|
| 50 |
+
Case #50: 104872.11421536
|
| 51 |
+
Case #51: 107938.38446540
|
| 52 |
+
Case #52: 1.00000000
|
| 53 |
+
Case #53: 1.00000000
|
| 54 |
+
Case #54: 1.00000000
|
| 55 |
+
Case #55: 1.00000000
|
| 56 |
+
Case #56: 1.41421356
|
| 57 |
+
Case #57: 1.00000000
|
| 58 |
+
Case #58: 1.41421356
|
| 59 |
+
Case #59: 1.00000000
|
| 60 |
+
Case #60: 1.00000000
|
| 61 |
+
Case #61: 1.00000000
|
| 62 |
+
Case #62: 1.00000000
|
| 63 |
+
Case #63: 1.00000000
|
| 64 |
+
Case #64: 1.00000000
|
| 65 |
+
Case #65: 1.00000000
|
| 66 |
+
Case #66: 1.00000000
|
| 67 |
+
Case #67: 1.00000000
|
| 68 |
+
Case #68: 1.00000000
|
| 69 |
+
Case #69: 1.00000000
|
| 70 |
+
Case #70: 1.00000000
|
| 71 |
+
Case #71: 1.00000000
|
| 72 |
+
Case #72: 35976.61908796
|
| 73 |
+
Case #73: 42938.23665744
|
| 74 |
+
Case #74: 58489.66686518
|
| 75 |
+
Case #75: 116585.96945173
|
| 76 |
+
Case #76: 6369.86860147
|
| 77 |
+
Case #77: 123579.24923708
|
| 78 |
+
Case #78: 55709.89155437
|
| 79 |
+
Case #79: 21791.00000000
|
| 80 |
+
Case #80: 120268.51226319
|
| 81 |
+
Case #81: 445241.52874255
|
| 82 |
+
Case #82: 1.00000000
|
| 83 |
+
Case #83: 1.00000000
|
| 84 |
+
Case #84: 1.00000000
|
| 85 |
+
Case #85: 1.00000000
|
| 86 |
+
Case #86: 1.00000000
|
| 87 |
+
Case #87: 3.00000000
|
| 88 |
+
Case #88: 1.00000000
|
| 89 |
+
Case #89: 1.00000000
|
| 90 |
+
Case #90: 1.00000000
|
| 91 |
+
Case #91: 1.00000000
|
| 92 |
+
Case #92: 1.00000000
|
| 93 |
+
Case #93: 2.23606798
|
| 94 |
+
Case #94: 1.00000000
|
| 95 |
+
Case #95: 1.00000000
|
| 96 |
+
Case #96: 1.00000000
|
| 97 |
+
Case #97: 1.00000000
|
| 98 |
+
Case #98: 1.00000000
|
| 99 |
+
Case #99: 1.00000000
|
| 100 |
+
Case #100: 1.00000000
|
| 101 |
+
Case #101: 1.00000000
|
| 102 |
+
Case #102: 1.00000000
|
| 103 |
+
Case #103: 0.70710678
|
| 104 |
+
Case #104: 3.16227766
|
| 105 |
+
Case #105: 1.00000000
|
| 106 |
+
Case #106: 1.00000000
|
| 107 |
+
Case #107: 1.00000000
|
| 108 |
+
Case #108: 1.00000000
|
| 109 |
+
Case #109: 1.00000000
|
| 110 |
+
Case #110: 1.00000000
|
| 111 |
+
Case #111: 1.41421356
|
| 112 |
+
Case #112: 78704.90217420
|
| 113 |
+
Case #113: 44624.42169933
|
| 114 |
+
Case #114: 15757.11880389
|
| 115 |
+
Case #115: 27250.00000000
|
| 116 |
+
Case #116: 17927.39251118
|
| 117 |
+
Case #117: 13889.43231381
|
| 118 |
+
Case #118: 35204.23625077
|
| 119 |
+
Case #119: 131886.18824578
|
| 120 |
+
Case #120: 29047.53876407
|
| 121 |
+
Case #121: 8179.31745319
|
| 122 |
+
Case #122: 18736.13321900
|
| 123 |
+
Case #123: 109403.20688627
|
| 124 |
+
Case #124: 15882.17834555
|
| 125 |
+
Case #125: 25585.01033809
|
| 126 |
+
Case #126: 44822.85592195
|
| 127 |
+
Case #127: 28679.92440715
|
| 128 |
+
Case #128: 17528.28508440
|
| 129 |
+
Case #129: 39216.44272496
|
| 130 |
+
Case #130: 23306.10780461
|
| 131 |
+
Case #131: 15247.12671293
|
| 132 |
+
Case #132: 2.82842712
|
| 133 |
+
Case #133: 1.00000000
|
| 134 |
+
Case #134: 5.38516481
|
| 135 |
+
Case #135: 4.00000000
|
| 136 |
+
Case #136: 3.16227766
|
| 137 |
+
Case #137: 1.00000000
|
| 138 |
+
Case #138: 2.23606798
|
| 139 |
+
Case #139: 1.00000000
|
| 140 |
+
Case #140: 2.23606798
|
| 141 |
+
Case #141: 1.00000000
|
| 142 |
+
Case #142: 1.00000000
|
| 143 |
+
Case #143: 2.82842712
|
| 144 |
+
Case #144: 2.00000000
|
| 145 |
+
Case #145: 4.92442890
|
| 146 |
+
Case #146: 1.41421356
|
| 147 |
+
Case #147: 3.16227766
|
| 148 |
+
Case #148: 1.00000000
|
| 149 |
+
Case #149: 2.23606798
|
| 150 |
+
Case #150: 2.00000000
|
| 151 |
+
Case #151: 2.91547595
|
| 152 |
+
Case #152: 849.21257645
|
| 153 |
+
Case #153: 612.24341564
|
| 154 |
+
Case #154: 864.87976043
|
| 155 |
+
Case #155: 363.88047488
|
| 156 |
+
Case #156: 209.30360723
|
| 157 |
+
Case #157: 434.00115207
|
| 158 |
+
Case #158: 227.90568225
|
| 159 |
+
Case #159: 303.64617567
|
| 160 |
+
Case #160: 255.00000000
|
| 161 |
+
Case #161: 564.00000000
|
| 162 |
+
Case #162: 12.04159458
|
| 163 |
+
Case #163: 5.00000000
|
| 164 |
+
Case #164: 4.00000000
|
| 165 |
+
Case #165: 10.04987562
|
| 166 |
+
Case #166: 7.81024968
|
| 167 |
+
Case #167: 3.16227766
|
| 168 |
+
Case #168: 1.41421356
|
| 169 |
+
Case #169: 22.20360331
|
| 170 |
+
Case #170: 1.00000000
|
| 171 |
+
Case #171: 4.24264069
|
| 172 |
+
Case #172: 6.32455532
|
| 173 |
+
Case #173: 1.41421356
|
| 174 |
+
Case #174: 1.00000000
|
| 175 |
+
Case #175: 1.00000000
|
| 176 |
+
Case #176: 1.00000000
|
| 177 |
+
Case #177: 1.00000000
|
| 178 |
+
Case #178: 13.03840481
|
| 179 |
+
Case #179: 10.00000000
|
| 180 |
+
Case #180: 4.47213595
|
| 181 |
+
Case #181: 2.00000000
|
| 182 |
+
Case #182: 172138.00000290
|
| 183 |
+
Case #183: 61871.00029093
|
| 184 |
+
Case #184: 193561.86906000
|
| 185 |
+
Case #185: 2603.00691509
|
| 186 |
+
Case #186: 115472.29394534
|
| 187 |
+
Case #187: 6695.00067214
|
| 188 |
+
Case #188: 45248.57161281
|
| 189 |
+
Case #189: 1538.00130039
|
| 190 |
+
Case #190: 267166.22841220
|
| 191 |
+
Case #191: 72714.38709086
|
| 192 |
+
Case #192: 161.91355718
|
| 193 |
+
Case #193: 139.03237033
|
| 194 |
+
Case #194: 132.83448347
|
| 195 |
+
Case #195: 182.00274723
|
| 196 |
+
Case #196: 588.16409275
|
| 197 |
+
Case #197: 61.13100686
|
| 198 |
+
Case #198: 294.17001887
|
| 199 |
+
Case #199: 386.42981251
|
| 200 |
+
Case #200: 677.83257520
|
| 201 |
+
Case #201: 143.31521203
|
| 202 |
+
Case #202: 216.17816726
|
| 203 |
+
Case #203: 137.38267722
|
| 204 |
+
Case #204: 39.05124838
|
| 205 |
+
Case #205: 158.34456101
|
| 206 |
+
Case #206: 460.00978250
|
| 207 |
+
Case #207: 452.63368191
|
| 208 |
+
Case #208: 4.47213595
|
| 209 |
+
Case #209: 2.23606798
|
| 210 |
+
Case #210: 2.23606798
|
| 211 |
+
Case #211: 5.09901951
|
| 212 |
+
Case #212: 2.23606798
|
| 213 |
+
Case #213: 2.00000000
|
| 214 |
+
Case #214: 1.00000000
|
| 215 |
+
Case #215: 5.09901951
|
| 216 |
+
Case #216: 1.41421356
|
| 217 |
+
Case #217: 1.41421356
|
| 218 |
+
Case #218: 8.60232527
|
| 219 |
+
Case #219: 2.82842712
|
| 220 |
+
Case #220: 1.00000000
|
| 221 |
+
Case #221: 10.00000000
|
| 222 |
+
Case #222: 4.47213595
|
| 223 |
+
Case #223: 1.00000000
|
| 224 |
+
Case #224: 3.60555128
|
| 225 |
+
Case #225: 1.41421356
|
| 226 |
+
Case #226: 3.00000000
|
| 227 |
+
Case #227: 4.00000000
|
| 228 |
+
Case #228: 2.23606798
|
| 229 |
+
Case #229: 2.00000000
|
| 230 |
+
Case #230: 6.70820393
|
| 231 |
+
Case #231: 2.00000000
|
| 232 |
+
Case #232: 1.00000000
|
| 233 |
+
Case #233: 1.00000000
|
| 234 |
+
Case #234: 3.60555128
|
| 235 |
+
Case #235: 6.70820393
|
| 236 |
+
Case #236: 7.28010989
|
| 237 |
+
Case #237: 1.41421356
|
| 238 |
+
Case #238: 1.00000000
|
| 239 |
+
Case #239: 5.00000000
|
| 240 |
+
Case #240: 2.00000000
|
| 241 |
+
Case #241: 1.41421356
|
| 242 |
+
Case #242: 5.00000000
|
| 243 |
+
Case #243: 2.00000000
|
| 244 |
+
Case #244: 2.23606798
|
| 245 |
+
Case #245: 2.23606798
|
| 246 |
+
Case #246: 5.83095189
|
| 247 |
+
Case #247: 1.41421356
|
| 248 |
+
Case #248: 2.23606798
|
| 249 |
+
Case #249: 2.82842712
|
| 250 |
+
Case #250: 3.00000000
|
| 251 |
+
Case #251: 1.00000000
|
| 252 |
+
Case #252: 3.16227766
|
| 253 |
+
Case #253: 1.00000000
|
| 254 |
+
Case #254: 1.00000000
|
| 255 |
+
Case #255: 3.16227766
|
| 256 |
+
Case #256: 1.00000000
|
| 257 |
+
Case #257: 1.41421356
|
| 258 |
+
Case #258: 3.60555128
|
| 259 |
+
Case #259: 2.82842712
|
| 260 |
+
Case #260: 1.41421356
|
| 261 |
+
Case #261: 2.23606798
|
| 262 |
+
Case #262: 7.28010989
|
| 263 |
+
Case #263: 3.00000000
|
| 264 |
+
Case #264: 1.00000000
|
| 265 |
+
Case #265: 2.23606798
|
| 266 |
+
Case #266: 1.00000000
|
| 267 |
+
Case #267: 3.16227766
|
| 268 |
+
Case #268: 4.12310563
|
| 269 |
+
Case #269: 2.00000000
|
| 270 |
+
Case #270: 1.41421356
|
| 271 |
+
Case #271: 2.00000000
|
| 272 |
+
Case #272: 2.00000000
|
| 273 |
+
Case #273: 6.40312424
|
| 274 |
+
Case #274: 3.16227766
|
| 275 |
+
Case #275: 8.06225775
|
| 276 |
+
Case #276: 8.24621125
|
| 277 |
+
Case #277: 2.23606798
|
| 278 |
+
Case #278: 2.82842712
|
| 279 |
+
Case #279: 3.80788655
|
| 280 |
+
Case #280: 1.00000000
|
| 281 |
+
Case #281: 9.21954446
|
| 282 |
+
Case #282: 2.23606798
|
| 283 |
+
Case #283: 3.16227766
|
| 284 |
+
Case #284: 2.82842712
|
| 285 |
+
Case #285: 3.60555128
|
| 286 |
+
Case #286: 5.09901951
|
| 287 |
+
Case #287: 3.60555128
|
| 288 |
+
Case #288: 9.05538514
|
| 289 |
+
Case #289: 2.23606798
|
| 290 |
+
Case #290: 3.16227766
|
| 291 |
+
Case #291: 5.83095189
|
| 292 |
+
Case #292: 1.00000000
|
| 293 |
+
Case #293: 8.00000000
|
| 294 |
+
Case #294: 4.00000000
|
| 295 |
+
Case #295: 2.00000000
|
| 296 |
+
Case #296: 1.41421356
|
| 297 |
+
Case #297: 2.00000000
|
| 298 |
+
Case #298: 5.09901951
|
| 299 |
+
Case #299: 1.00000000
|
| 300 |
+
Case #300: 1.00000000
|
| 301 |
+
Case #301: 7.00000000
|
| 302 |
+
Case #302: 1.00000000
|
| 303 |
+
Case #303: 2.23606798
|
| 304 |
+
Case #304: 8.06225775
|
| 305 |
+
Case #305: 2.00000000
|
| 306 |
+
Case #306: 2.00000000
|
| 307 |
+
Case #307: 4.12310563
|
| 308 |
+
Case #308: 1.41421356
|
| 309 |
+
Case #309: 1.41421356
|
| 310 |
+
Case #310: 2.82842712
|
| 311 |
+
Case #311: 1.41421356
|
| 312 |
+
Case #312: 1.41421356
|
| 313 |
+
Case #313: 2.23606798
|
| 314 |
+
Case #314: 2.23606798
|
| 315 |
+
Case #315: 2.23606798
|
| 316 |
+
Case #316: 1.41421356
|
| 317 |
+
Case #317: 5.40832691
|
| 318 |
+
Case #318: 2.23606798
|
| 319 |
+
Case #319: 6.08276253
|
| 320 |
+
Case #320: 5.38516481
|
| 321 |
+
Case #321: 1.00000000
|
| 322 |
+
Case #322: 2.23606798
|
| 323 |
+
Case #323: 1.00000000
|
| 324 |
+
Case #324: 4.12310563
|
| 325 |
+
Case #325: 3.60555128
|
| 326 |
+
Case #326: 2.00000000
|
| 327 |
+
Case #327: 5.00000000
|
| 328 |
+
Case #328: 4.00000000
|
| 329 |
+
Case #329: 6.00000000
|
| 330 |
+
Case #330: 3.60555128
|
| 331 |
+
Case #331: 4.47213595
|
| 332 |
+
Case #332: 1.00000000
|
| 333 |
+
Case #333: 1.00000000
|
| 334 |
+
Case #334: 1.41421356
|
| 335 |
+
Case #335: 3.16227766
|
| 336 |
+
Case #336: 12.16552506
|
| 337 |
+
Case #337: 4.00000000
|
| 338 |
+
Case #338: 2.23606798
|
| 339 |
+
Case #339: 2.23606798
|
| 340 |
+
Case #340: 3.16227766
|
| 341 |
+
Case #341: 9.43398113
|
| 342 |
+
Case #342: 2.82842712
|
| 343 |
+
Case #343: 1.41421356
|
| 344 |
+
Case #344: 5.65685425
|
| 345 |
+
Case #345: 4.12310563
|
| 346 |
+
Case #346: 3.00000000
|
| 347 |
+
Case #347: 6.08276253
|
| 348 |
+
Case #348: 6.70820393
|
| 349 |
+
Case #349: 3.00000000
|
| 350 |
+
Case #350: 5.38516481
|
| 351 |
+
Case #351: 4.12310563
|
| 352 |
+
Case #352: 6.08276253
|
| 353 |
+
Case #353: 6.70820393
|
| 354 |
+
Case #354: 2.82842712
|
| 355 |
+
Case #355: 1.00000000
|
| 356 |
+
Case #356: 2.82842712
|
| 357 |
+
Case #357: 2.82842712
|
| 358 |
+
Case #358: 1.41421356
|
| 359 |
+
Case #359: 2.82842712
|
| 360 |
+
Case #360: 1.00000000
|
| 361 |
+
Case #361: 3.16227766
|
| 362 |
+
Case #362: 5.09901951
|
| 363 |
+
Case #363: 1.41421356
|
| 364 |
+
Case #364: 1.00000000
|
| 365 |
+
Case #365: 4.00000000
|
| 366 |
+
Case #366: 8.06225775
|
| 367 |
+
Case #367: 1.41421356
|
| 368 |
+
Case #368: 2.23606798
|
| 369 |
+
Case #369: 2.00000000
|
| 370 |
+
Case #370: 7.00000000
|
| 371 |
+
Case #371: 2.23606798
|
| 372 |
+
Case #372: 1.41421356
|
| 373 |
+
Case #373: 2.00000000
|
| 374 |
+
Case #374: 2.82842712
|
| 375 |
+
Case #375: 2.82842712
|
| 376 |
+
Case #376: 5.65685425
|
| 377 |
+
Case #377: 3.16227766
|
| 378 |
+
Case #378: 8.06225775
|
| 379 |
+
Case #379: 4.24264069
|
| 380 |
+
Case #380: 1.00000000
|
| 381 |
+
Case #381: 3.60555128
|
| 382 |
+
Case #382: 2.23606798
|
| 383 |
+
Case #383: 1.41421356
|
| 384 |
+
Case #384: 1.00000000
|
| 385 |
+
Case #385: 4.12310563
|
| 386 |
+
Case #386: 2.23606798
|
| 387 |
+
Case #387: 3.60555128
|
| 388 |
+
Case #388: 3.00000000
|
| 389 |
+
Case #389: 2.23606798
|
| 390 |
+
Case #390: 3.60555128
|
| 391 |
+
Case #391: 3.16227766
|
| 392 |
+
Case #392: 1.41421356
|
| 393 |
+
Case #393: 4.12310563
|
| 394 |
+
Case #394: 3.00000000
|
| 395 |
+
Case #395: 3.00000000
|
| 396 |
+
Case #396: 1.41421356
|
| 397 |
+
Case #397: 5.00000000
|
| 398 |
+
Case #398: 1.00000000
|
| 399 |
+
Case #399: 1.41421356
|
| 400 |
+
Case #400: 2.23606798
|
| 401 |
+
Case #401: 4.47213595
|
| 402 |
+
Case #402: 2.00000000
|
| 403 |
+
Case #403: 3.16227766
|
| 404 |
+
Case #404: 1.41421356
|
| 405 |
+
Case #405: 3.60555128
|
| 406 |
+
Case #406: 2.23606798
|
| 407 |
+
Case #407: 2.23606798
|
| 408 |
+
Case #408: 3.16227766
|
| 409 |
+
Case #409: 3.60555128
|
| 410 |
+
Case #410: 1.41421356
|
| 411 |
+
Case #411: 2.82842712
|
| 412 |
+
Case #412: 2.23606798
|
| 413 |
+
Case #413: 5.00000000
|
| 414 |
+
Case #414: 2.00000000
|
| 415 |
+
Case #415: 2.00000000
|
| 416 |
+
Case #416: 5.00000000
|
| 417 |
+
Case #417: 3.60555128
|
| 418 |
+
Case #418: 6.70820393
|
| 419 |
+
Case #419: 2.82842712
|
| 420 |
+
Case #420: 5.00000000
|
| 421 |
+
Case #421: 5.38516481
|
| 422 |
+
Case #422: 2.00000000
|
| 423 |
+
Case #423: 5.83095189
|
| 424 |
+
Case #424: 3.00000000
|
| 425 |
+
Case #425: 4.00000000
|
| 426 |
+
Case #426: 3.16227766
|
| 427 |
+
Case #427: 3.16227766
|
| 428 |
+
Case #428: 1.00000000
|
| 429 |
+
Case #429: 7.21110255
|
| 430 |
+
Case #430: 3.60555128
|
| 431 |
+
Case #431: 1.00000000
|
| 432 |
+
Case #432: 2.23606798
|
| 433 |
+
Case #433: 1.41421356
|
| 434 |
+
Case #434: 8.06225775
|
| 435 |
+
Case #435: 6.32455532
|
| 436 |
+
Case #436: 1.00000000
|
| 437 |
+
Case #437: 4.12310563
|
| 438 |
+
Case #438: 1.41421356
|
| 439 |
+
Case #439: 6.40312424
|
| 440 |
+
Case #440: 3.16227766
|
| 441 |
+
Case #441: 3.60555128
|
| 442 |
+
Case #442: 2.23606798
|
| 443 |
+
Case #443: 3.16227766
|
| 444 |
+
Case #444: 3.00000000
|
| 445 |
+
Case #445: 3.60555128
|
| 446 |
+
Case #446: 1.41421356
|
| 447 |
+
Case #447: 13.41640786
|
| 448 |
+
Case #448: 3.00000000
|
| 449 |
+
Case #449: 3.16227766
|
| 450 |
+
Case #450: 5.09901951
|
| 451 |
+
Case #451: 2.23606798
|
| 452 |
+
Case #452: 1.41421356
|
| 453 |
+
Case #453: 2.23606798
|
| 454 |
+
Case #454: 5.09901951
|
| 455 |
+
Case #455: 4.00000000
|
| 456 |
+
Case #456: 1.41421356
|
| 457 |
+
Case #457: 2.00000000
|
| 458 |
+
Case #458: 3.80788655
|
| 459 |
+
Case #459: 1.00000000
|
| 460 |
+
Case #460: 3.16227766
|
| 461 |
+
Case #461: 6.40312424
|
| 462 |
+
Case #462: 2.23606798
|
| 463 |
+
Case #463: 2.00000000
|
| 464 |
+
Case #464: 6.08276253
|
| 465 |
+
Case #465: 1.00000000
|
| 466 |
+
Case #466: 1.41421356
|
| 467 |
+
Case #467: 2.23606798
|
| 468 |
+
Case #468: 3.60555128
|
| 469 |
+
Case #469: 2.00000000
|
| 470 |
+
Case #470: 4.00000000
|
| 471 |
+
Case #471: 3.00000000
|
| 472 |
+
Case #472: 2.23606798
|
| 473 |
+
Case #473: 2.23606798
|
| 474 |
+
Case #474: 10.00000000
|
| 475 |
+
Case #475: 3.16227766
|
| 476 |
+
Case #476: 1.00000000
|
| 477 |
+
Case #477: 1.00000000
|
| 478 |
+
Case #478: 5.09901951
|
| 479 |
+
Case #479: 3.16227766
|
| 480 |
+
Case #480: 3.00000000
|
| 481 |
+
Case #481: 3.16227766
|
| 482 |
+
Case #482: 10.77032961
|
| 483 |
+
Case #483: 2.00000000
|
| 484 |
+
Case #484: 3.00000000
|
| 485 |
+
Case #485: 7.28010989
|
| 486 |
+
Case #486: 2.23606798
|
| 487 |
+
Case #487: 5.00000000
|
| 488 |
+
Case #488: 1.00000000
|
| 489 |
+
Case #489: 1.41421356
|
| 490 |
+
Case #490: 1.00000000
|
| 491 |
+
Case #491: 1.00000000
|
| 492 |
+
Case #492: 5.00000000
|
| 493 |
+
Case #493: 1.41421356
|
| 494 |
+
Case #494: 4.47213595
|
| 495 |
+
Case #495: 2.23606798
|
| 496 |
+
Case #496: 4.12310563
|
| 497 |
+
Case #497: 1.41421356
|
| 498 |
+
Case #498: 3.60555128
|
| 499 |
+
Case #499: 1.41421356
|
| 500 |
+
Case #500: 3.00000000
|
| 501 |
+
Case #501: 3.60555128
|
| 502 |
+
Case #502: 1.00000000
|
| 503 |
+
Case #503: 5.00000000
|
| 504 |
+
Case #504: 2.23606798
|
| 505 |
+
Case #505: 1.41421356
|
| 506 |
+
Case #506: 1.00000000
|
| 507 |
+
Case #507: 2.00000000
|
| 508 |
+
Case #508: 2.82842712
|
| 509 |
+
Case #509: 4.47213595
|
| 510 |
+
Case #510: 3.60555128
|
| 511 |
+
Case #511: 4.12310563
|
| 512 |
+
Case #512: 6.70820393
|
| 513 |
+
Case #513: 1.41421356
|
| 514 |
+
Case #514: 1.00000000
|
| 515 |
+
Case #515: 5.09901951
|
| 516 |
+
Case #516: 5.83095189
|
| 517 |
+
Case #517: 3.00000000
|
| 518 |
+
Case #518: 2.00000000
|
| 519 |
+
Case #519: 1.41421356
|
| 520 |
+
Case #520: 4.24264069
|
| 521 |
+
Case #521: 1.00000000
|
| 522 |
+
Case #522: 5.09901951
|
| 523 |
+
Case #523: 1.00000000
|
| 524 |
+
Case #524: 1.00000000
|
| 525 |
+
Case #525: 5.83095189
|
| 526 |
+
Case #526: 11.66190379
|
| 527 |
+
Case #527: 1.00000000
|
| 528 |
+
Case #528: 5.09901951
|
| 529 |
+
Case #529: 1.00000000
|
| 530 |
+
Case #530: 2.23606798
|
| 531 |
+
Case #531: 5.83095189
|
| 532 |
+
Case #532: 4.47213595
|
| 533 |
+
Case #533: 2.82842712
|
| 534 |
+
Case #534: 1.00000000
|
| 535 |
+
Case #535: 8.06225775
|
| 536 |
+
Case #536: 2.00000000
|
| 537 |
+
Case #537: 2.23606798
|
| 538 |
+
Case #538: 1.41421356
|
| 539 |
+
Case #539: 6.32455532
|
| 540 |
+
Case #540: 5.38516481
|
| 541 |
+
Case #541: 6.32455532
|
| 542 |
+
Case #542: 3.16227766
|
| 543 |
+
Case #543: 8.06225775
|
| 544 |
+
Case #544: 5.00000000
|
| 545 |
+
Case #545: 2.23606798
|
| 546 |
+
Case #546: 1.41421356
|
| 547 |
+
Case #547: 3.60555128
|
| 548 |
+
Case #548: 2.82842712
|
| 549 |
+
Case #549: 1.00000000
|
| 550 |
+
Case #550: 2.00000000
|
| 551 |
+
Case #551: 6.00000000
|
| 552 |
+
Case #552: 1.00000000
|
| 553 |
+
Case #553: 2.00000000
|
| 554 |
+
Case #554: 2.00000000
|
| 555 |
+
Case #555: 2.23606798
|
| 556 |
+
Case #556: 3.16227766
|
| 557 |
+
Case #557: 1.41421356
|
| 558 |
+
Case #558: 1.00000000
|
| 559 |
+
Case #559: 1.00000000
|
| 560 |
+
Case #560: 3.16227766
|
| 561 |
+
Case #561: 1.00000000
|
| 562 |
+
Case #562: 1.00000000
|
| 563 |
+
Case #563: 2.23606798
|
| 564 |
+
Case #564: 1.00000000
|
| 565 |
+
Case #565: 13.03840481
|
| 566 |
+
Case #566: 1.00000000
|
| 567 |
+
Case #567: 7.28010989
|
| 568 |
+
Case #568: 1.41421356
|
| 569 |
+
Case #569: 12.04159458
|
| 570 |
+
Case #570: 2.00000000
|
| 571 |
+
Case #571: 2.00000000
|
| 572 |
+
Case #572: 1.41421356
|
| 573 |
+
Case #573: 3.16227766
|
| 574 |
+
Case #574: 1.00000000
|
| 575 |
+
Case #575: 3.16227766
|
| 576 |
+
Case #576: 4.12310563
|
| 577 |
+
Case #577: 1.00000000
|
| 578 |
+
Case #578: 2.00000000
|
| 579 |
+
Case #579: 10.44030651
|
| 580 |
+
Case #580: 1.00000000
|
| 581 |
+
Case #581: 2.00000000
|
| 582 |
+
Case #582: 1.41421356
|
| 583 |
+
Case #583: 4.00000000
|
| 584 |
+
Case #584: 1.41421356
|
| 585 |
+
Case #585: 2.23606798
|
| 586 |
+
Case #586: 1.41421356
|
| 587 |
+
Case #587: 5.00000000
|
| 588 |
+
Case #588: 4.12310563
|
| 589 |
+
Case #589: 2.00000000
|
| 590 |
+
Case #590: 4.12310563
|
| 591 |
+
Case #591: 2.00000000
|
| 592 |
+
Case #592: 1.00000000
|
| 593 |
+
Case #593: 7.28010989
|
| 594 |
+
Case #594: 3.00000000
|
| 595 |
+
Case #595: 2.23606798
|
| 596 |
+
Case #596: 10.29563014
|
| 597 |
+
Case #597: 7.21110255
|
| 598 |
+
Case #598: 1.41421356
|
| 599 |
+
Case #599: 1.00000000
|
| 600 |
+
Case #600: 4.47213595
|
| 601 |
+
Case #601: 5.00000000
|
| 602 |
+
Case #602: 2.23606798
|
| 603 |
+
Case #603: 2.00000000
|
| 604 |
+
Case #604: 9.43398113
|
| 605 |
+
Case #605: 5.83095189
|
| 606 |
+
Case #606: 3.60555128
|
| 607 |
+
Case #607: 2.23606798
|
| 608 |
+
Case #608: 2.23606798
|
| 609 |
+
Case #609: 1.00000000
|
| 610 |
+
Case #610: 5.09901951
|
| 611 |
+
Case #611: 1.00000000
|
| 612 |
+
Case #612: 1.41421356
|
| 613 |
+
Case #613: 1.00000000
|
| 614 |
+
Case #614: 2.00000000
|
| 615 |
+
Case #615: 1.00000000
|
| 616 |
+
Case #616: 5.09901951
|
| 617 |
+
Case #617: 2.82842712
|
| 618 |
+
Case #618: 1.41421356
|
| 619 |
+
Case #619: 9.21954446
|
| 620 |
+
Case #620: 2.82842712
|
| 621 |
+
Case #621: 2.00000000
|
| 622 |
+
Case #622: 4.24264069
|
| 623 |
+
Case #623: 2.00000000
|
| 624 |
+
Case #624: 2.23606798
|
| 625 |
+
Case #625: 1.00000000
|
| 626 |
+
Case #626: 2.23606798
|
| 627 |
+
Case #627: 1.41421356
|
| 628 |
+
Case #628: 3.00000000
|
| 629 |
+
Case #629: 4.12310563
|
| 630 |
+
Case #630: 3.16227766
|
| 631 |
+
Case #631: 4.24264069
|
| 632 |
+
Case #632: 6.70820393
|
| 633 |
+
Case #633: 2.00000000
|
| 634 |
+
Case #634: 7.07106781
|
| 635 |
+
Case #635: 1.00000000
|
| 636 |
+
Case #636: 2.23606798
|
| 637 |
+
Case #637: 2.00000000
|
| 638 |
+
Case #638: 1.00000000
|
| 639 |
+
Case #639: 5.09901951
|
| 640 |
+
Case #640: 1.00000000
|
| 641 |
+
Case #641: 1.00000000
|
| 642 |
+
Case #642: 2.00000000
|
| 643 |
+
Case #643: 3.16227766
|
| 644 |
+
Case #644: 4.47213595
|
| 645 |
+
Case #645: 6.08276253
|
| 646 |
+
Case #646: 2.00000000
|
| 647 |
+
Case #647: 10.44030651
|
| 648 |
+
Case #648: 3.16227766
|
| 649 |
+
Case #649: 2.23606798
|
| 650 |
+
Case #650: 6.08276253
|
| 651 |
+
Case #651: 2.00000000
|
| 652 |
+
Case #652: 15.55634919
|
| 653 |
+
Case #653: 3.60555128
|
| 654 |
+
Case #654: 5.09901951
|
| 655 |
+
Case #655: 3.16227766
|
| 656 |
+
Case #656: 3.60555128
|
| 657 |
+
Case #657: 1.41421356
|
| 658 |
+
Case #658: 1.41421356
|
| 659 |
+
Case #659: 2.00000000
|
| 660 |
+
Case #660: 1.00000000
|
| 661 |
+
Case #661: 4.24264069
|
| 662 |
+
Case #662: 8.06225775
|
| 663 |
+
Case #663: 2.23606798
|
| 664 |
+
Case #664: 1.00000000
|
| 665 |
+
Case #665: 5.00000000
|
| 666 |
+
Case #666: 1.00000000
|
| 667 |
+
Case #667: 4.47213595
|
| 668 |
+
Case #668: 5.00000000
|
| 669 |
+
Case #669: 4.12310563
|
| 670 |
+
Case #670: 6.00000000
|
| 671 |
+
Case #671: 3.00000000
|
| 672 |
+
Case #672: 1.41421356
|
| 673 |
+
Case #673: 3.00000000
|
| 674 |
+
Case #674: 2.00000000
|
| 675 |
+
Case #675: 1.00000000
|
| 676 |
+
Case #676: 3.90512484
|
| 677 |
+
Case #677: 5.09901951
|
| 678 |
+
Case #678: 6.08276253
|
| 679 |
+
Case #679: 5.00000000
|
| 680 |
+
Case #680: 3.60555128
|
| 681 |
+
Case #681: 1.00000000
|
| 682 |
+
Case #682: 3.16227766
|
| 683 |
+
Case #683: 3.00000000
|
| 684 |
+
Case #684: 4.12310563
|
| 685 |
+
Case #685: 2.23606798
|
| 686 |
+
Case #686: 4.00000000
|
| 687 |
+
Case #687: 2.00000000
|
| 688 |
+
Case #688: 2.82842712
|
| 689 |
+
Case #689: 2.23606798
|
| 690 |
+
Case #690: 2.00000000
|
| 691 |
+
Case #691: 1.00000000
|
| 692 |
+
Case #692: 12.04159458
|
| 693 |
+
Case #693: 1.41421356
|
| 694 |
+
Case #694: 6.70820393
|
| 695 |
+
Case #695: 2.23606798
|
| 696 |
+
Case #696: 3.00000000
|
| 697 |
+
Case #697: 3.60555128
|
| 698 |
+
Case #698: 3.16227766
|
| 699 |
+
Case #699: 2.00000000
|
| 700 |
+
Case #700: 1.00000000
|
| 701 |
+
Case #701: 2.82842712
|
| 702 |
+
Case #702: 5.09901951
|
| 703 |
+
Case #703: 8.06225775
|
| 704 |
+
Case #704: 6.70820393
|
| 705 |
+
Case #705: 1.00000000
|
| 706 |
+
Case #706: 4.00000000
|
| 707 |
+
Case #707: 4.00000000
|
| 708 |
+
Case #708: 1.00000000
|
| 709 |
+
Case #709: 6.08276253
|
| 710 |
+
Case #710: 1.41421356
|
| 711 |
+
Case #711: 4.00000000
|
| 712 |
+
Case #712: 4.00000000
|
| 713 |
+
Case #713: 5.00000000
|
| 714 |
+
Case #714: 1.41421356
|
| 715 |
+
Case #715: 2.23606798
|
| 716 |
+
Case #716: 3.00000000
|
| 717 |
+
Case #717: 2.82842712
|
| 718 |
+
Case #718: 2.82842712
|
| 719 |
+
Case #719: 1.00000000
|
| 720 |
+
Case #720: 1.41421356
|
| 721 |
+
Case #721: 5.09901951
|
| 722 |
+
Case #722: 6.32455532
|
| 723 |
+
Case #723: 1.41421356
|
| 724 |
+
Case #724: 2.82842712
|
| 725 |
+
Case #725: 1.00000000
|
| 726 |
+
Case #726: 2.23606798
|
| 727 |
+
Case #727: 4.00000000
|
| 728 |
+
Case #728: 1.00000000
|
| 729 |
+
Case #729: 11.00000000
|
| 730 |
+
Case #730: 2.00000000
|
| 731 |
+
Case #731: 3.60555128
|
| 732 |
+
Case #732: 6.32455532
|
| 733 |
+
Case #733: 5.00000000
|
| 734 |
+
Case #734: 1.41421356
|
| 735 |
+
Case #735: 4.12310563
|
| 736 |
+
Case #736: 1.00000000
|
| 737 |
+
Case #737: 6.08276253
|
| 738 |
+
Case #738: 2.82842712
|
| 739 |
+
Case #739: 1.00000000
|
| 740 |
+
Case #740: 3.00000000
|
| 741 |
+
Case #741: 3.16227766
|
| 742 |
+
Case #742: 1.00000000
|
| 743 |
+
Case #743: 2.82842712
|
| 744 |
+
Case #744: 2.23606798
|
| 745 |
+
Case #745: 3.00000000
|
| 746 |
+
Case #746: 4.12310563
|
| 747 |
+
Case #747: 1.00000000
|
| 748 |
+
Case #748: 1.00000000
|
| 749 |
+
Case #749: 3.16227766
|
| 750 |
+
Case #750: 5.65685425
|
| 751 |
+
Case #751: 5.65685425
|
| 752 |
+
Case #752: 1.41421356
|
| 753 |
+
Case #753: 3.60555128
|
| 754 |
+
Case #754: 2.00000000
|
| 755 |
+
Case #755: 3.16227766
|
| 756 |
+
Case #756: 1.00000000
|
| 757 |
+
Case #757: 2.00000000
|
| 758 |
+
Case #758: 4.00000000
|
| 759 |
+
Case #759: 5.65685425
|
| 760 |
+
Case #760: 1.41421356
|
| 761 |
+
Case #761: 5.00000000
|
| 762 |
+
Case #762: 1.41421356
|
| 763 |
+
Case #763: 4.47213595
|
| 764 |
+
Case #764: 4.47213595
|
| 765 |
+
Case #765: 7.81024968
|
| 766 |
+
Case #766: 2.00000000
|
| 767 |
+
Case #767: 2.23606798
|
| 768 |
+
Case #768: 1.00000000
|
| 769 |
+
Case #769: 1.00000000
|
| 770 |
+
Case #770: 4.47213595
|
| 771 |
+
Case #771: 1.00000000
|
| 772 |
+
Case #772: 7.28010989
|
| 773 |
+
Case #773: 2.23606798
|
| 774 |
+
Case #774: 2.23606798
|
| 775 |
+
Case #775: 4.47213595
|
| 776 |
+
Case #776: 1.41421356
|
| 777 |
+
Case #777: 2.23606798
|
| 778 |
+
Case #778: 1.00000000
|
| 779 |
+
Case #779: 1.00000000
|
| 780 |
+
Case #780: 3.16227766
|
| 781 |
+
Case #781: 1.41421356
|
| 782 |
+
Case #782: 1.41421356
|
| 783 |
+
Case #783: 1.00000000
|
| 784 |
+
Case #784: 3.60555128
|
| 785 |
+
Case #785: 1.00000000
|
| 786 |
+
Case #786: 10.29563014
|
| 787 |
+
Case #787: 2.23606798
|
| 788 |
+
Case #788: 2.23606798
|
| 789 |
+
Case #789: 4.12310563
|
| 790 |
+
Case #790: 5.65685425
|
| 791 |
+
Case #791: 2.00000000
|
| 792 |
+
Case #792: 3.60555128
|
| 793 |
+
Case #793: 8.06225775
|
| 794 |
+
Case #794: 1.41421356
|
| 795 |
+
Case #795: 2.82842712
|
| 796 |
+
Case #796: 1.00000000
|
| 797 |
+
Case #797: 2.00000000
|
| 798 |
+
Case #798: 4.47213595
|
| 799 |
+
Case #799: 7.21110255
|
| 800 |
+
Case #800: 12.36931688
|
| 801 |
+
Case #801: 2.00000000
|
| 802 |
+
Case #802: 1.41421356
|
| 803 |
+
Case #803: 2.23606798
|
| 804 |
+
Case #804: 3.16227766
|
| 805 |
+
Case #805: 5.00000000
|
| 806 |
+
Case #806: 2.23606798
|
| 807 |
+
Case #807: 3.60555128
|
| 808 |
+
Case #808: 4.00000000
|
| 809 |
+
Case #809: 3.16227766
|
| 810 |
+
Case #810: 5.09901951
|
| 811 |
+
Case #811: 6.70820393
|
| 812 |
+
Case #812: 4.47213595
|
| 813 |
+
Case #813: 3.16227766
|
| 814 |
+
Case #814: 4.12310563
|
| 815 |
+
Case #815: 1.00000000
|
| 816 |
+
Case #816: 3.00000000
|
| 817 |
+
Case #817: 3.16227766
|
| 818 |
+
Case #818: 2.00000000
|
| 819 |
+
Case #819: 4.12310563
|
| 820 |
+
Case #820: 1.00000000
|
| 821 |
+
Case #821: 4.47213595
|
| 822 |
+
Case #822: 1.41421356
|
| 823 |
+
Case #823: 3.00000000
|
| 824 |
+
Case #824: 1.00000000
|
| 825 |
+
Case #825: 2.23606798
|
| 826 |
+
Case #826: 3.00000000
|
| 827 |
+
Case #827: 1.41421356
|
| 828 |
+
Case #828: 7.28010989
|
| 829 |
+
Case #829: 1.41421356
|
| 830 |
+
Case #830: 8.60232527
|
| 831 |
+
Case #831: 2.82842712
|
| 832 |
+
Case #832: 4.24264069
|
| 833 |
+
Case #833: 4.12310563
|
| 834 |
+
Case #834: 1.41421356
|
| 835 |
+
Case #835: 1.00000000
|
| 836 |
+
Case #836: 4.12310563
|
| 837 |
+
Case #837: 1.41421356
|
| 838 |
+
Case #838: 2.00000000
|
| 839 |
+
Case #839: 3.16227766
|
| 840 |
+
Case #840: 1.41421356
|
| 841 |
+
Case #841: 1.00000000
|
| 842 |
+
Case #842: 6.08276253
|
| 843 |
+
Case #843: 1.00000000
|
| 844 |
+
Case #844: 3.60555128
|
| 845 |
+
Case #845: 6.32455532
|
| 846 |
+
Case #846: 3.16227766
|
| 847 |
+
Case #847: 2.23606798
|
| 848 |
+
Case #848: 9.43398113
|
| 849 |
+
Case #849: 3.16227766
|
| 850 |
+
Case #850: 1.00000000
|
| 851 |
+
Case #851: 5.38516481
|
| 852 |
+
Case #852: 7.61577311
|
| 853 |
+
Case #853: 4.47213595
|
| 854 |
+
Case #854: 3.60555128
|
| 855 |
+
Case #855: 1.00000000
|
| 856 |
+
Case #856: 2.82842712
|
| 857 |
+
Case #857: 6.08276253
|
| 858 |
+
Case #858: 4.00000000
|
| 859 |
+
Case #859: 3.60555128
|
| 860 |
+
Case #860: 9.84885780
|
| 861 |
+
Case #861: 1.00000000
|
| 862 |
+
Case #862: 2.23606798
|
| 863 |
+
Case #863: 1.00000000
|
| 864 |
+
Case #864: 2.23606798
|
| 865 |
+
Case #865: 4.12310563
|
| 866 |
+
Case #866: 5.00000000
|
| 867 |
+
Case #867: 1.41421356
|
| 868 |
+
Case #868: 1.00000000
|
| 869 |
+
Case #869: 5.00000000
|
| 870 |
+
Case #870: 5.38516481
|
| 871 |
+
Case #871: 4.00000000
|
| 872 |
+
Case #872: 4.47213595
|
| 873 |
+
Case #873: 5.38516481
|
| 874 |
+
Case #874: 1.00000000
|
| 875 |
+
Case #875: 6.00000000
|
| 876 |
+
Case #876: 2.00000000
|
| 877 |
+
Case #877: 2.23606798
|
| 878 |
+
Case #878: 2.82842712
|
| 879 |
+
Case #879: 5.38516481
|
| 880 |
+
Case #880: 4.12310563
|
| 881 |
+
Case #881: 4.00000000
|
| 882 |
+
Case #882: 2.82842712
|
| 883 |
+
Case #883: 3.00000000
|
| 884 |
+
Case #884: 1.41421356
|
| 885 |
+
Case #885: 7.07106781
|
| 886 |
+
Case #886: 5.38516481
|
| 887 |
+
Case #887: 3.00000000
|
| 888 |
+
Case #888: 3.00000000
|
| 889 |
+
Case #889: 1.41421356
|
| 890 |
+
Case #890: 1.00000000
|
| 891 |
+
Case #891: 2.82842712
|
| 892 |
+
Case #892: 3.53553391
|
| 893 |
+
Case #893: 1.41421356
|
| 894 |
+
Case #894: 1.00000000
|
| 895 |
+
Case #895: 3.00000000
|
| 896 |
+
Case #896: 3.60555128
|
| 897 |
+
Case #897: 4.47213595
|
| 898 |
+
Case #898: 1.00000000
|
| 899 |
+
Case #899: 2.23606798
|
| 900 |
+
Case #900: 1.00000000
|
| 901 |
+
Case #901: 3.60555128
|
| 902 |
+
Case #902: 1.41421356
|
| 903 |
+
Case #903: 1.41421356
|
| 904 |
+
Case #904: 6.08276253
|
| 905 |
+
Case #905: 5.83095189
|
| 906 |
+
Case #906: 2.23606798
|
| 907 |
+
Case #907: 1.00000000
|
| 908 |
+
Case #908: 2.00000000
|
| 909 |
+
Case #909: 1.00000000
|
| 910 |
+
Case #910: 8.24621125
|
| 911 |
+
Case #911: 5.00000000
|
| 912 |
+
Case #912: 3.16227766
|
| 913 |
+
Case #913: 2.00000000
|
| 914 |
+
Case #914: 2.23606798
|
| 915 |
+
Case #915: 4.12310563
|
| 916 |
+
Case #916: 2.00000000
|
| 917 |
+
Case #917: 2.23606798
|
| 918 |
+
Case #918: 1.00000000
|
| 919 |
+
Case #919: 2.23606798
|
| 920 |
+
Case #920: 4.12310563
|
| 921 |
+
Case #921: 1.41421356
|
| 922 |
+
Case #922: 1.41421356
|
| 923 |
+
Case #923: 2.23606798
|
| 924 |
+
Case #924: 2.23606798
|
| 925 |
+
Case #925: 1.41421356
|
| 926 |
+
Case #926: 8.54400375
|
| 927 |
+
Case #927: 2.23606798
|
| 928 |
+
Case #928: 3.60555128
|
| 929 |
+
Case #929: 1.41421356
|
| 930 |
+
Case #930: 4.24264069
|
| 931 |
+
Case #931: 3.00000000
|
| 932 |
+
Case #932: 2.82842712
|
| 933 |
+
Case #933: 5.38516481
|
| 934 |
+
Case #934: 2.23606798
|
| 935 |
+
Case #935: 2.23606798
|
| 936 |
+
Case #936: 3.00000000
|
| 937 |
+
Case #937: 1.41421356
|
| 938 |
+
Case #938: 2.00000000
|
| 939 |
+
Case #939: 2.23606798
|
| 940 |
+
Case #940: 2.00000000
|
| 941 |
+
Case #941: 6.00000000
|
| 942 |
+
Case #942: 2.23606798
|
| 943 |
+
Case #943: 1.00000000
|
| 944 |
+
Case #944: 1.00000000
|
| 945 |
+
Case #945: 2.00000000
|
| 946 |
+
Case #946: 3.60555128
|
| 947 |
+
Case #947: 1.00000000
|
| 948 |
+
Case #948: 3.60555128
|
| 949 |
+
Case #949: 4.24264069
|
| 950 |
+
Case #950: 3.60555128
|
| 951 |
+
Case #951: 1.00000000
|
| 952 |
+
Case #952: 5.00000000
|
| 953 |
+
Case #953: 1.00000000
|
| 954 |
+
Case #954: 3.60555128
|
| 955 |
+
Case #955: 2.00000000
|
| 956 |
+
Case #956: 3.16227766
|
| 957 |
+
Case #957: 1.00000000
|
| 958 |
+
Case #958: 1.00000000
|
| 959 |
+
Case #959: 2.00000000
|
| 960 |
+
Case #960: 1.00000000
|
| 961 |
+
Case #961: 1.00000000
|
| 962 |
+
Case #962: 2.23606798
|
| 963 |
+
Case #963: 5.09901951
|
| 964 |
+
Case #964: 1.00000000
|
| 965 |
+
Case #965: 7.28010989
|
| 966 |
+
Case #966: 1.00000000
|
| 967 |
+
Case #967: 2.23606798
|
| 968 |
+
Case #968: 1.00000000
|
| 969 |
+
Case #969: 1.00000000
|
| 970 |
+
Case #970: 3.16227766
|
| 971 |
+
Case #971: 2.00000000
|
| 972 |
+
Case #972: 4.24264069
|
| 973 |
+
Case #973: 2.82842712
|
| 974 |
+
Case #974: 2.23606798
|
| 975 |
+
Case #975: 12.64911064
|
| 976 |
+
Case #976: 1.00000000
|
| 977 |
+
Case #977: 1.00000000
|
| 978 |
+
Case #978: 5.65685425
|
| 979 |
+
Case #979: 1.00000000
|
| 980 |
+
Case #980: 10.44030651
|
| 981 |
+
Case #981: 1.41421356
|
| 982 |
+
Case #982: 6.08276253
|
| 983 |
+
Case #983: 2.23606798
|
| 984 |
+
Case #984: 3.04138127
|
| 985 |
+
Case #985: 1.00000000
|
| 986 |
+
Case #986: 3.60555128
|
| 987 |
+
Case #987: 1.41421356
|
| 988 |
+
Case #988: 2.00000000
|
| 989 |
+
Case #989: 4.24264069
|
| 990 |
+
Case #990: 2.00000000
|
| 991 |
+
Case #991: 3.60555128
|
| 992 |
+
Case #992: 2.23606798
|
| 993 |
+
Case #993: 3.00000000
|
| 994 |
+
Case #994: 3.00000000
|
| 995 |
+
Case #995: 3.16227766
|
| 996 |
+
Case #996: 1.00000000
|
| 997 |
+
Case #997: 4.47213595
|
| 998 |
+
Case #998: 3.00000000
|
| 999 |
+
Case #999: 2.82842712
|
| 1000 |
+
Case #1000: 9.84885780
|
| 1001 |
+
Case #1001: 5.38516481
|
| 1002 |
+
Case #1002: 1.00000000
|
| 1003 |
+
Case #1003: 3.16227766
|
| 1004 |
+
Case #1004: 1.00000000
|
| 1005 |
+
Case #1005: 1.00000000
|
| 1006 |
+
Case #1006: 3.60555128
|
| 1007 |
+
Case #1007: 3.16227766
|
2021/finals/antisocial_sol.md
ADDED
|
@@ -0,0 +1,20 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
We can imagine "danger circles" around all coworkers increase at a constant size until there is no path to the finish. This idea is very similar to the construction of a Voronoi diagram, which can be done in \(O(N \log(N))\) time using Fortune's algorithm. If we remove the restriction that you are not allowed to leave the building's borders, the optimal path maximizing the distance to the nearest person will be a sequence of edges on the Voronoi diagram, as well as a segment from the start position to a Voronoi node and a segment from the end position to a Voronoi node. For the first and last segment, we simply want to walk to a Voronoi node that isn't *closer* to our nearest neighbor than we are, of the Voronoi nodes tangential to this neighbor's corresponding node in the Delaunay triangulation. Valid start and end Voronoi nodes can be found by iterating through all neighboring Voronoi nodes to the nearest person, and simply taking the one which is most in the direction away from the nearest coworker. Then, we can handle the path of Voronoi edges by sorting the edges and using a disjoint set (similarly to Kruskal's minimum spanning tree algorithm, though in this case as a maximum spanning tree), stopping once the start and end Voronoi nodes are unioned.
|
| 2 |
+
|
| 3 |
+
Note that there are also 2 cases in which the path might not remain on the Voronoi diagram's edges:
|
| 4 |
+
|
| 5 |
+
1. At the start (and similarly at the end), the path must move from the the starting point \(a = (X_A, Y_A)\) to some graph node. If it's in the Voronoi cell of some closest point \(x\), then it should move to some node on the boundary of that cell without getting closer to \(x\) (any such node will do). A valid choice of node is the one which is closest angle-wise (relative to \(x\)) to \(a\).
|
| 6 |
+
|
| 7 |
+
2. The path can also travel along the borders of the building's rectangle — there should effectively be a graph node at each rectangle corner and at each intersection of an (infinite) Voronoi edge with the rectangle's border, with these nodes connected around the border by edges (weighted like the other edges). A good way of constructing this situation is to begin by mirroring all \(N\) points across the rectangle's \(4\) sides, and then computing the Voronoi diagram for all \(5N\) resulting points. Provided that we then include Voronoi edges lying inside or on the border of the rectangle (excluding ones lying outside it), the set of edges will then be exactly what we need.
|
| 8 |
+
This is because the introduction of the mirrored points doesn't affect the portion of the Voronoi diagram strictly inside the rectangle (as no mirrored point can be the closest point to a point inside the rectangle; the corresponding original point must be closer), while at each point along the rectangle's boundary, whatever original point was closest to it, the corresponding mirrored point must now be equidistant (resulting in a Voronoi node/edge at the border).
|
| 9 |
+
For a visualization of this concept with a 3-point example, check out [this tool](http://alexbeutel.com/webgl/voronoi.html) with the following input data: `{"sites":[220,240,270,250,290,220,180,240,220,160,380,240,220,360,270,150,270,350,130,250,330,250,290,180,290,380,110,220,310,220],"queries":[]}`.
|
| 10 |
+
|
| 11 |
+
The time complexity of the above algorithm is \(O(N \log(N))\).
|
| 12 |
+
|
| 13 |
+
It's worth noting that it's also possible to solve this problem for many (e.g. \(10^5\)) queries of start/end points, though that extension was not included in the contest as its implementation would be rather long.
|
| 14 |
+
|
| 15 |
+
Computation of which Voronoi cell and graph node each starting/ending point corresponds to must now be done more efficiently, in less than \(O(N)\) time per such point. It's possible to augment Fortune's algorithm to determine which Voronoi cell each such point lies within. Alternatively, you can do a line sweep from left to right, finding for each query point which Voronoi edge is above it (form which you can determine which Voronoi cell it is in). For each cell, if the angles of its surrounding Voronoi vertices (relative to the cell's central point) are precomputed and sorted, it's possible to binary search over them for each starting/ending point to find its enclosing triangle. These changes take a total of \(O((N+K) \log(N))\) time.
|
| 16 |
+
|
| 17 |
+
To solve the second part of the problem, one approach involves still generating a maximum spanning tree using Kruskal's algorithm. The answer for a query is then based on the minimum edge weight on the path connecting its starting/ending points' corresponding nodes in this tree. This can be computed for each query using binary lifting (or other methods). Thus, the time complexity of this portion also comes out to \(O((N+K) \log(N))\) time.
|
| 18 |
+
|
| 19 |
+
Another approach for the second part of the problem is to use a parallel binary search. For each query, we can store its minimum and maximum possible answer, and iterate through all edges until these ranges are sufficiently small. At each iteration, the range for each query's possible answer will be halved. An iteration consists of maintaining a disjoint set of all components, processing queries and edges in decreasing order of weight. When we get to a query, we simply check if its two nodes are in the same component, and adjust either the high or low value of that queries binary search accordingly (this will change its mid for where it is sorted in the next iteration). At a Voronoi edge, we simply union the two components.
|
| 20 |
+
|
2021/finals/hire_flyers.cpp
ADDED
|
@@ -0,0 +1,354 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
#include <algorithm>
|
| 2 |
+
#include <iostream>
|
| 3 |
+
#include <map>
|
| 4 |
+
#include <set>
|
| 5 |
+
#include <tuple>
|
| 6 |
+
#include <utility>
|
| 7 |
+
#include <vector>
|
| 8 |
+
using namespace std;
|
| 9 |
+
|
| 10 |
+
const int MOD = 1000000007;
|
| 11 |
+
|
| 12 |
+
int N;
|
| 13 |
+
|
| 14 |
+
struct Seg { // Directions: U / R / D / L
|
| 15 |
+
int i = -1, r, c, p, d, t = 0;
|
| 16 |
+
|
| 17 |
+
long long get_time_val() {
|
| 18 |
+
return N * ((long long)t - r - c) + i;
|
| 19 |
+
}
|
| 20 |
+
|
| 21 |
+
bool operator<(const Seg& b) const {
|
| 22 |
+
return make_pair(r, c) < make_pair(b.r, b.c);
|
| 23 |
+
}
|
| 24 |
+
};
|
| 25 |
+
|
| 26 |
+
struct BIT {
|
| 27 |
+
int N;
|
| 28 |
+
vector<int> V;
|
| 29 |
+
|
| 30 |
+
BIT() {}
|
| 31 |
+
|
| 32 |
+
BIT(int _N): N(_N) {
|
| 33 |
+
init(_N);
|
| 34 |
+
}
|
| 35 |
+
|
| 36 |
+
void init(int _N) {
|
| 37 |
+
N = _N;
|
| 38 |
+
V.resize(N + 1);
|
| 39 |
+
}
|
| 40 |
+
|
| 41 |
+
void clear() {
|
| 42 |
+
fill(V.begin(), V.end(), 0);
|
| 43 |
+
}
|
| 44 |
+
|
| 45 |
+
void update(int i, int v) {
|
| 46 |
+
for (i++; i <= N; i += (i & -i)) {
|
| 47 |
+
V[i] += v;
|
| 48 |
+
}
|
| 49 |
+
}
|
| 50 |
+
|
| 51 |
+
int query(int i) {
|
| 52 |
+
int v = 0;
|
| 53 |
+
i = min(i, N - 1);
|
| 54 |
+
for (i++; i > 0; i -= (i & -i)) {
|
| 55 |
+
v += V[i];
|
| 56 |
+
}
|
| 57 |
+
return v;
|
| 58 |
+
}
|
| 59 |
+
};
|
| 60 |
+
|
| 61 |
+
struct SegTree {
|
| 62 |
+
int N, sz;
|
| 63 |
+
vector<vector<long long>> keys;
|
| 64 |
+
vector<BIT> B;
|
| 65 |
+
|
| 66 |
+
SegTree() {}
|
| 67 |
+
|
| 68 |
+
SegTree(int _N) {
|
| 69 |
+
init(_N);
|
| 70 |
+
}
|
| 71 |
+
|
| 72 |
+
void init(int _N) {
|
| 73 |
+
N = _N;
|
| 74 |
+
for (sz = 1; sz < N; sz <<= 1)
|
| 75 |
+
;
|
| 76 |
+
keys.resize(sz << 1);
|
| 77 |
+
B.resize(sz << 1);
|
| 78 |
+
}
|
| 79 |
+
|
| 80 |
+
void init_keys() {
|
| 81 |
+
for (int i = sz; i < sz + N; i++) {
|
| 82 |
+
auto &K = keys[i];
|
| 83 |
+
sort(K.begin(), K.end());
|
| 84 |
+
B[i].init(K.size());
|
| 85 |
+
}
|
| 86 |
+
for (int i = sz - 1; i >= 1; i--) {
|
| 87 |
+
auto &K = keys[i];
|
| 88 |
+
auto &c1 = keys[i << 1], &c2 = keys[(i << 1) + 1];
|
| 89 |
+
int a = 0, b = 0;
|
| 90 |
+
while (a < c1.size() || b < c2.size()) {
|
| 91 |
+
if (b == c2.size() || (a < c1.size() && c1[a] < c2[b])) {
|
| 92 |
+
K.push_back(c1[a++]);
|
| 93 |
+
} else {
|
| 94 |
+
K.push_back(c2[b++]);
|
| 95 |
+
}
|
| 96 |
+
}
|
| 97 |
+
B[i].init(K.size());
|
| 98 |
+
}
|
| 99 |
+
}
|
| 100 |
+
|
| 101 |
+
int query_larger(int a, int b, long long v, int i = 1, int r1 = 0, int r2 = -1) {
|
| 102 |
+
if (r2 < 0) {
|
| 103 |
+
a = max(a, 0);
|
| 104 |
+
b = min(b, sz - 1);
|
| 105 |
+
if (a > b) {
|
| 106 |
+
return 0;
|
| 107 |
+
}
|
| 108 |
+
r2 = sz - 1;
|
| 109 |
+
}
|
| 110 |
+
if (a <= r1 && r2 <= b) {
|
| 111 |
+
auto &K = keys[i];
|
| 112 |
+
v = lower_bound(K.begin(), K.end(), v) - K.begin();
|
| 113 |
+
return B[i].query(K.size() - 1) - B[i].query(v - 1);
|
| 114 |
+
}
|
| 115 |
+
int m = (r1 + r2) >> 1, c = i << 1;
|
| 116 |
+
int res = 0;
|
| 117 |
+
if (a <= m) {
|
| 118 |
+
res += query_larger(a, b, v, c, r1, m);
|
| 119 |
+
}
|
| 120 |
+
if (b > m) {
|
| 121 |
+
res += query_larger(a, b, v, c + 1, m + 1, r2);
|
| 122 |
+
}
|
| 123 |
+
return res;
|
| 124 |
+
}
|
| 125 |
+
|
| 126 |
+
void update_one(int i, long long v, int d) {
|
| 127 |
+
i += sz;
|
| 128 |
+
while (i >= 1) {
|
| 129 |
+
auto &K = keys[i];
|
| 130 |
+
B[i].update(lower_bound(K.begin(), K.end(), v) - K.begin(), d);
|
| 131 |
+
i >>= 1;
|
| 132 |
+
}
|
| 133 |
+
}
|
| 134 |
+
};
|
| 135 |
+
|
| 136 |
+
vector<Seg> SS;
|
| 137 |
+
|
| 138 |
+
Seg trim_seg(Seg s, int a, int b, bool hor) {
|
| 139 |
+
if (s.d == 1 || s.d == 2) { // Forward segment.
|
| 140 |
+
int& sv1 = hor ? s.c : s.r; // First value.
|
| 141 |
+
int sv2 = sv1 + s.p - 1; // Last value.
|
| 142 |
+
int t1 = max(0, a - sv1); // Truncation at start.
|
| 143 |
+
int t2 = max(0, sv2 - b); // Truncation at end.
|
| 144 |
+
sv1 += t1, s.t += t1;
|
| 145 |
+
s.p -= t1 + t2;
|
| 146 |
+
} else { // Backward segment.
|
| 147 |
+
int& sv2 = hor ? s.c : s.r; // Last value.
|
| 148 |
+
int sv1 = sv2 - (s.p - 1); // First value.
|
| 149 |
+
int t1 = max(0, a - sv1); // Truncation at start.
|
| 150 |
+
int t2 = max(0, sv2 - b); // Truncation at end.
|
| 151 |
+
sv2 -= t2, s.t += t2;
|
| 152 |
+
s.p -= t1 + t2;
|
| 153 |
+
}
|
| 154 |
+
return s;
|
| 155 |
+
}
|
| 156 |
+
|
| 157 |
+
vector<Seg> merge_opp_segs(Seg s1, Seg s2, bool hor) {
|
| 158 |
+
int nc = (hor ? s2.c - s1.c : s2.r - s1.r) + 1;
|
| 159 |
+
int t1 = s1.t; // Time for s1 to reach start.
|
| 160 |
+
int t2 = s2.t + nc - 1 - (s2.i < s1.i ? 1 : 0); // Time for s2 to reach start.
|
| 161 |
+
int m = (hor ? s1.c : s1.r) + (t2 - t1 + 2) / 2 -
|
| 162 |
+
1; // Last value painted over by s2.
|
| 163 |
+
vector<Seg> S;
|
| 164 |
+
S.push_back(trim_seg(s2, -1e9 - 1, m, hor));
|
| 165 |
+
S.push_back(trim_seg(s1, m + 1, 2e9 + 1, hor));
|
| 166 |
+
return S;
|
| 167 |
+
}
|
| 168 |
+
|
| 169 |
+
void process_linear_segs(vector<Seg> V, bool hor) {
|
| 170 |
+
// Collect and sort forward / backward segments.
|
| 171 |
+
int d1, d2;
|
| 172 |
+
if (hor) {
|
| 173 |
+
d1 = 1;
|
| 174 |
+
d2 = 3;
|
| 175 |
+
} else {
|
| 176 |
+
d1 = 2;
|
| 177 |
+
d2 = 0;
|
| 178 |
+
}
|
| 179 |
+
vector<tuple<int, int, Seg>> P1, P2;
|
| 180 |
+
for (auto s : V) {
|
| 181 |
+
if (s.d == d1) {
|
| 182 |
+
P1.emplace_back(s.r + s.c, -s.i, s);
|
| 183 |
+
} else {
|
| 184 |
+
P2.emplace_back(-(s.r + s.c), -s.i, s);
|
| 185 |
+
}
|
| 186 |
+
}
|
| 187 |
+
sort(P1.begin(), P1.end());
|
| 188 |
+
sort(P2.begin(), P2.end());
|
| 189 |
+
// Reduce forward / backward segments independently.
|
| 190 |
+
vector<Seg> S1, S2;
|
| 191 |
+
int last = -1e9 - 1;
|
| 192 |
+
for (auto p : P1) {
|
| 193 |
+
Seg s = trim_seg(get<2>(p), last + 1, 2e9 + 1, hor); // Trim to after last.
|
| 194 |
+
if (s.p > 0) { // Include if not obsolete.
|
| 195 |
+
S1.push_back(s);
|
| 196 |
+
}
|
| 197 |
+
last = max(last, (hor ? s.c : s.r) + (s.p - 1));
|
| 198 |
+
}
|
| 199 |
+
last = 2e9 + 1;
|
| 200 |
+
for (auto p : P2) {
|
| 201 |
+
Seg s = trim_seg(get<2>(p), -1e9 - 1, last - 1, hor); // Trim to before last.
|
| 202 |
+
if (s.p > 0) { // Include if not obsolete.
|
| 203 |
+
S2.push_back(s);
|
| 204 |
+
}
|
| 205 |
+
last = min(last, (hor ? s.c : s.r) - (s.p - 1));
|
| 206 |
+
}
|
| 207 |
+
// Merge forward / backward segments.
|
| 208 |
+
vector<tuple<int, int, int>> E;
|
| 209 |
+
for (int i = 0; i < S1.size(); i++) {
|
| 210 |
+
Seg s = S1[i];
|
| 211 |
+
int sv = hor ? s.c : s.r;
|
| 212 |
+
E.emplace_back(sv, 1, i);
|
| 213 |
+
E.emplace_back(sv + s.p, 0, i);
|
| 214 |
+
}
|
| 215 |
+
for (int i = 0; i < S2.size(); i++) {
|
| 216 |
+
Seg s = S2[i];
|
| 217 |
+
int sv = hor ? s.c : s.r;
|
| 218 |
+
E.emplace_back(sv - (s.p - 1), 3, i);
|
| 219 |
+
E.emplace_back(sv + 1, 2, i);
|
| 220 |
+
}
|
| 221 |
+
sort(E.begin(), E.end());
|
| 222 |
+
vector<int> inds{-1, -1};
|
| 223 |
+
for (int i = 0; i < E.size(); i++) {
|
| 224 |
+
int v = get<0>(E[i]), e = get<1>(E[i]);
|
| 225 |
+
// Update set of ongoing segments.
|
| 226 |
+
int j = e / 2;
|
| 227 |
+
if (e % 2) {
|
| 228 |
+
inds[j] = get<2>(E[i]);
|
| 229 |
+
} else {
|
| 230 |
+
inds[j] = -1;
|
| 231 |
+
}
|
| 232 |
+
// Process ongoing segments?
|
| 233 |
+
if (i + 1 < E.size() && v < get<0>(E[i + 1])) {
|
| 234 |
+
vector<Seg> S;
|
| 235 |
+
if (inds[0] >= 0 && inds[1] >= 0) {
|
| 236 |
+
S = merge_opp_segs(S1[inds[0]], S2[inds[1]], hor);
|
| 237 |
+
} else if (inds[0] >= 0) {
|
| 238 |
+
S.push_back(S1[inds[0]]);
|
| 239 |
+
} else if (inds[1] >= 0) {
|
| 240 |
+
S.push_back(S2[inds[1]]);
|
| 241 |
+
}
|
| 242 |
+
for (auto s : S) {
|
| 243 |
+
Seg s2 = trim_seg(s, v, get<0>(E[i + 1]) - 1, hor);
|
| 244 |
+
if (s2.p > 0) {
|
| 245 |
+
SS.push_back(s2);
|
| 246 |
+
}
|
| 247 |
+
}
|
| 248 |
+
}
|
| 249 |
+
}
|
| 250 |
+
}
|
| 251 |
+
|
| 252 |
+
int solve() {
|
| 253 |
+
SS.clear();
|
| 254 |
+
map<int, vector<Seg>> rowS, colS;
|
| 255 |
+
// Input.
|
| 256 |
+
cin >> N;
|
| 257 |
+
for (int i = 0; i < N; i++) {
|
| 258 |
+
Seg s;
|
| 259 |
+
s.i = i + 1;
|
| 260 |
+
char d;
|
| 261 |
+
cin >> s.r >> s.c >> s.p >> d;
|
| 262 |
+
s.d = d == 'N' ? 0 : d == 'E' ? 1 : d == 'S' ? 2 : 3;
|
| 263 |
+
if (s.d % 2) {
|
| 264 |
+
rowS[s.r].push_back(s);
|
| 265 |
+
} else {
|
| 266 |
+
colS[s.c].push_back(s);
|
| 267 |
+
}
|
| 268 |
+
}
|
| 269 |
+
// Reduce each relevant row / column to disjoint segments
|
| 270 |
+
for (auto p : rowS) {
|
| 271 |
+
process_linear_segs(p.second, true);
|
| 272 |
+
}
|
| 273 |
+
for (auto p : colS) {
|
| 274 |
+
process_linear_segs(p.second, false);
|
| 275 |
+
}
|
| 276 |
+
// Compute base answer.
|
| 277 |
+
int ans = 0;
|
| 278 |
+
for (auto s : SS) {
|
| 279 |
+
ans = (ans + (long long)s.i * s.p) % MOD;
|
| 280 |
+
}
|
| 281 |
+
// Consider 4 different rotations of the grid.
|
| 282 |
+
for (int r = 0; r < 4; r++) {
|
| 283 |
+
// Rotate everything 90 degrees clockwise.
|
| 284 |
+
for (int i = 0; i < SS.size(); i++) {
|
| 285 |
+
Seg &s = SS[i];
|
| 286 |
+
int r = s.r, c = s.c, d = s.d;
|
| 287 |
+
s.r = c;
|
| 288 |
+
s.c = -r;
|
| 289 |
+
s.d = (d + 1) % 4;
|
| 290 |
+
}
|
| 291 |
+
// Consider 2 different vertical flips of the grid.
|
| 292 |
+
for (int _ : {0, 1}) {
|
| 293 |
+
// Flip everything vertically.
|
| 294 |
+
for (int i = 0; i < SS.size(); i++) {
|
| 295 |
+
Seg &s = SS[i];
|
| 296 |
+
s.r = -s.r;
|
| 297 |
+
if (s.d % 2 == 0) {
|
| 298 |
+
s.d = 2 - s.d;
|
| 299 |
+
}
|
| 300 |
+
}
|
| 301 |
+
// Assemble list of line sweep events and distinct D segment columns.
|
| 302 |
+
vector<tuple<int, int, Seg>> E;
|
| 303 |
+
vector<int> cc;
|
| 304 |
+
for (auto s : SS) {
|
| 305 |
+
if (s.d == 1) { // R
|
| 306 |
+
E.emplace_back(s.r, 1, s);
|
| 307 |
+
} else if (s.d == 2) { // D
|
| 308 |
+
E.emplace_back(s.r, 0, s);
|
| 309 |
+
E.emplace_back(s.r + s.p - 1, 2, s);
|
| 310 |
+
cc.push_back(s.c);
|
| 311 |
+
}
|
| 312 |
+
}
|
| 313 |
+
sort(E.begin(), E.end());
|
| 314 |
+
sort(cc.begin(), cc.end());
|
| 315 |
+
cc.resize(unique(cc.begin(), cc.end()) - cc.begin());
|
| 316 |
+
// Initialize 2D segment tree.
|
| 317 |
+
SegTree ST(cc.size());
|
| 318 |
+
for (auto s : SS) {
|
| 319 |
+
if (s.d == 2) { // D
|
| 320 |
+
ST.keys[ST.sz + (lower_bound(cc.begin(), cc.end(), s.c) - cc.begin())]
|
| 321 |
+
.push_back(s.get_time_val());
|
| 322 |
+
}
|
| 323 |
+
}
|
| 324 |
+
ST.init_keys();
|
| 325 |
+
// Line sweep to subtract R segments covered by D ones.
|
| 326 |
+
for (auto p : E) {
|
| 327 |
+
int e = get<1>(p);
|
| 328 |
+
Seg s = get<2>(p);
|
| 329 |
+
if (e == 1) {
|
| 330 |
+
int a = lower_bound(cc.begin(), cc.end(), s.c) - cc.begin();
|
| 331 |
+
int b = lower_bound(cc.begin(), cc.end(), s.c + s.p) - cc.begin() - 1;
|
| 332 |
+
long long v = s.get_time_val();
|
| 333 |
+
ans = (ans + MOD - (long long)s.i * ST.query_larger(a, b, v) % MOD) % MOD;
|
| 334 |
+
} else {
|
| 335 |
+
ST.update_one(
|
| 336 |
+
lower_bound(cc.begin(), cc.end(), s.c) - cc.begin(),
|
| 337 |
+
s.get_time_val(),
|
| 338 |
+
e == 0 ? 1 : -1
|
| 339 |
+
);
|
| 340 |
+
}
|
| 341 |
+
}
|
| 342 |
+
}
|
| 343 |
+
}
|
| 344 |
+
return ans;
|
| 345 |
+
}
|
| 346 |
+
|
| 347 |
+
int main() {
|
| 348 |
+
int T;
|
| 349 |
+
cin >> T;
|
| 350 |
+
for (int t = 1; t <= T; t++) {
|
| 351 |
+
cout << "Case #" << t << ": " << solve() << endl;
|
| 352 |
+
}
|
| 353 |
+
return 0;
|
| 354 |
+
}
|
2021/finals/hire_flyers.in
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:ec067e73d4e7660125c8b0e7f05c676243bd6de76bb7fe2d619a564f925d1b41
|
| 3 |
+
size 35952813
|
2021/finals/hire_flyers.md
ADDED
|
@@ -0,0 +1,50 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
The market is hot for geological talent! Hiring agents are competing to display their job flyers on street intersections across \(T\) towns.
|
| 2 |
+
|
| 3 |
+
A town's streets can be represented as an infinite 2D grid with rows numbered by increasing integers from North to South and columns numbered by increasing integers from West to East.
|
| 4 |
+
|
| 5 |
+
There are \(N\) hiring agents, numbered from \(1\) to \(N\). Agent \(i\) starts at the intersection of row \(R_i\) and column \(C_i\), holding \(P_i\) flyers, and facing the cardinal direction \(D_i\) (`"N"` for North, `"S"` for South, `"E"` for East, or `"W"` for West). Each *turn* taken by an agent consists of the following:
|
| 6 |
+
|
| 7 |
+
1. Post one of their own flyers at their current intersection, shredding any competing flyer that may have previously been there.
|
| 8 |
+
2. If the agent has more flyers, move to the adjacent intersection in direction \(D_i\).
|
| 9 |
+
|
| 10 |
+
The agents will take turns posting one flyer at a time. Agent \(1\) will take a turn, followed by agent \(2\), and so on until agent \(N\) takes a turn, at which point agent \(1\) will go again (if necessary). Note that there may be multiple agents occupying the same intersection at any point in time.
|
| 11 |
+
|
| 12 |
+
Let \(F_i\) be the number of flyers placed by agent \(i\) which remain will unshredded at the end. Your job is to compute the sum of \(i * F_i\) over all agents \(i\). As this sum may be very large, you should only compute it modulo \(1{,}000{,}000{,}007\).
|
| 13 |
+
|
| 14 |
+
|
| 15 |
+
# Constraints
|
| 16 |
+
|
| 17 |
+
\(1 \le T \le 75\)
|
| 18 |
+
\(1 \le N \le 800{,}000\)
|
| 19 |
+
\(0 \le R_i, C_i \le 1{,}000{,}000{,}000\)
|
| 20 |
+
\(1 \le P_i \le 1{,}000{,}000{,}000\)
|
| 21 |
+
\(D_i \in \{\)`"N"`, `"S"`, `"E"`, `"W"`\(\}\)
|
| 22 |
+
|
| 23 |
+
The sum of \(N\) across all towns is at most \(2{,}000{,}000\).
|
| 24 |
+
|
| 25 |
+
|
| 26 |
+
# Input
|
| 27 |
+
|
| 28 |
+
Input begins with an integer \(T\), the number of towns. For each town, there is first a line containing a single integer \(N\). Then, \(N\) lines follow, the \(i\)th of which consists of \(3\) space-separated integers \(R_i\), \(C_i\), and \(P_i\), followed by a space-separated character, \(D_i\).
|
| 29 |
+
|
| 30 |
+
|
| 31 |
+
# Output
|
| 32 |
+
|
| 33 |
+
For the \(i\)th town, print a line containing *"Case #i: "* followed by a single integer, the sum of \(i * F_i\) over all agents \(i\), modulo \(1{,}000{,}000{,}007\).
|
| 34 |
+
|
| 35 |
+
|
| 36 |
+
# Sample Explanation
|
| 37 |
+
|
| 38 |
+
In the first town, the relevant portion of the grid will end up with the following flyers (with `"."` representing an intersection with no flyer), yielding an answer of \((1 * 3 + 2 * 2 + 3 * 1 + 4 * 1) \;\mathrm{mod}\; 1{,}000{,}000{,}007 = 14\):
|
| 39 |
+
|
| 40 |
+
{{PHOTO_ID:1597395337265553|WIDTH:180}}
|
| 41 |
+
|
| 42 |
+
In the second town, the relevant portion of the grid will end up with the following flyers, yielding an answer of \((1 * 2 + 2 * 2 + 3 * 2 + 4 * 2) \;\mathrm{mod}\; 1{,}000{,}000{,}007 = 20\):
|
| 43 |
+
|
| 44 |
+
{{PHOTO_ID:4543454065770744|WIDTH:234}}
|
| 45 |
+
|
| 46 |
+
In the third town, each of agent \(2\)'s turns will involve shredding the last flyer placed by agent \(1\) and replacing it with her own. This will result in \(1{,}000{,}000{,}000\) intersections containing agent \(2\)'s flyers, for an answer of \((2 * 1{,}000{,}000{,}000) \;\mathrm{mod}\; 1{,}000{,}000{,}007 = 999999993\).
|
| 47 |
+
|
| 48 |
+
In the fourth town, the relevant portion of the grid will end up with the following flyers:
|
| 49 |
+
|
| 50 |
+
{{PHOTO_ID:451563133198975|WIDTH:360}}
|
2021/finals/hire_flyers.out
ADDED
|
@@ -0,0 +1,118 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Case #1: 14
|
| 2 |
+
Case #2: 20
|
| 3 |
+
Case #3: 999999993
|
| 4 |
+
Case #4: 40
|
| 5 |
+
Case #5: 431
|
| 6 |
+
Case #6: 99999993
|
| 7 |
+
Case #7: 999999994
|
| 8 |
+
Case #8: 99999994
|
| 9 |
+
Case #9: 1000000002
|
| 10 |
+
Case #10: 1000000000
|
| 11 |
+
Case #11: 999999993
|
| 12 |
+
Case #12: 999999993
|
| 13 |
+
Case #13: 999999993
|
| 14 |
+
Case #14: 999999897
|
| 15 |
+
Case #15: 999999871
|
| 16 |
+
Case #16: 423
|
| 17 |
+
Case #17: 199999229
|
| 18 |
+
Case #18: 217073425
|
| 19 |
+
Case #19: 33397706
|
| 20 |
+
Case #20: 485540721
|
| 21 |
+
Case #21: 357736831
|
| 22 |
+
Case #22: 9508
|
| 23 |
+
Case #23: 23
|
| 24 |
+
Case #24: 18
|
| 25 |
+
Case #25: 6628
|
| 26 |
+
Case #26: 17604
|
| 27 |
+
Case #27: 616191825
|
| 28 |
+
Case #28: 856214908
|
| 29 |
+
Case #29: 616087243
|
| 30 |
+
Case #30: 471216968
|
| 31 |
+
Case #31: 38733402
|
| 32 |
+
Case #32: 936491239
|
| 33 |
+
Case #33: 730649978
|
| 34 |
+
Case #34: 306373993
|
| 35 |
+
Case #35: 65225585
|
| 36 |
+
Case #36: 285757320
|
| 37 |
+
Case #37: 930974524
|
| 38 |
+
Case #38: 372468607
|
| 39 |
+
Case #39: 928733717
|
| 40 |
+
Case #40: 275995039
|
| 41 |
+
Case #41: 836627363
|
| 42 |
+
Case #42: 65664903
|
| 43 |
+
Case #43: 983496873
|
| 44 |
+
Case #44: 519454660
|
| 45 |
+
Case #45: 90348890
|
| 46 |
+
Case #46: 684422234
|
| 47 |
+
Case #47: 513902139
|
| 48 |
+
Case #48: 669592753
|
| 49 |
+
Case #49: 357034246
|
| 50 |
+
Case #50: 43918841
|
| 51 |
+
Case #51: 521394249
|
| 52 |
+
Case #52: 564353372
|
| 53 |
+
Case #53: 855226307
|
| 54 |
+
Case #54: 239432065
|
| 55 |
+
Case #55: 625583995
|
| 56 |
+
Case #56: 513611137
|
| 57 |
+
Case #57: 275942363
|
| 58 |
+
Case #58: 587689801
|
| 59 |
+
Case #59: 731508246
|
| 60 |
+
Case #60: 231112528
|
| 61 |
+
Case #61: 854323953
|
| 62 |
+
Case #62: 174113343
|
| 63 |
+
Case #63: 183976986
|
| 64 |
+
Case #64: 521066588
|
| 65 |
+
Case #65: 22830859
|
| 66 |
+
Case #66: 326336345
|
| 67 |
+
Case #67: 272982133
|
| 68 |
+
Case #68: 598100830
|
| 69 |
+
Case #69: 150190138
|
| 70 |
+
Case #70: 391017847
|
| 71 |
+
Case #71: 486836356
|
| 72 |
+
Case #72: 820516557
|
| 73 |
+
Case #73: 908604859
|
| 74 |
+
Case #74: 640323950
|
| 75 |
+
Case #75: 616284508
|
| 76 |
+
Case #76: 31141531
|
| 77 |
+
Case #77: 226022048
|
| 78 |
+
Case #78: 320220618
|
| 79 |
+
Case #79: 599198956
|
| 80 |
+
Case #80: 306153532
|
| 81 |
+
Case #81: 725058056
|
| 82 |
+
Case #82: 569982633
|
| 83 |
+
Case #83: 199539090
|
| 84 |
+
Case #84: 908976066
|
| 85 |
+
Case #85: 306805906
|
| 86 |
+
Case #86: 190096232
|
| 87 |
+
Case #87: 350305906
|
| 88 |
+
Case #88: 692998074
|
| 89 |
+
Case #89: 675835976
|
| 90 |
+
Case #90: 342816784
|
| 91 |
+
Case #91: 816435451
|
| 92 |
+
Case #92: 685089027
|
| 93 |
+
Case #93: 74992281
|
| 94 |
+
Case #94: 935277973
|
| 95 |
+
Case #95: 512924016
|
| 96 |
+
Case #96: 231908365
|
| 97 |
+
Case #97: 42789399
|
| 98 |
+
Case #98: 329880680
|
| 99 |
+
Case #99: 645685346
|
| 100 |
+
Case #100: 937296473
|
| 101 |
+
Case #101: 342175151
|
| 102 |
+
Case #102: 606419669
|
| 103 |
+
Case #103: 725071734
|
| 104 |
+
Case #104: 267317223
|
| 105 |
+
Case #105: 679712553
|
| 106 |
+
Case #106: 198107887
|
| 107 |
+
Case #107: 703671316
|
| 108 |
+
Case #108: 365207939
|
| 109 |
+
Case #109: 635956066
|
| 110 |
+
Case #110: 917227680
|
| 111 |
+
Case #111: 77831067
|
| 112 |
+
Case #112: 934581893
|
| 113 |
+
Case #113: 820657774
|
| 114 |
+
Case #114: 59748552
|
| 115 |
+
Case #115: 494746701
|
| 116 |
+
Case #116: 962057137
|
| 117 |
+
Case #117: 687849975
|
| 118 |
+
Case #118: 199374792
|
2021/finals/hire_flyers_sol.md
ADDED
|
@@ -0,0 +1,15 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Each contiguous portion of a hiring agent's path can be represented as a 2D segment with \(6\) properties (agent's index, segment's initial row, segment's initial column, turns taken by the agent before reaching the segment's initial row/column, direction, and segment length). Each agent's full path corresponds to one such segment (with \(0\) turns taken before reaching it), but we may want to split/trim/remove some of these segments, based on which portions of them "cover" portions of others (visit cells later, thus replacing their flyers).
|
| 2 |
+
|
| 3 |
+
For each relevant row containing \(a_1\) `'E'` agents and \(a_2\) `'W'` agents (with \(a_1 + a_2 \gt 0\)), our first goal will be to transform all of its `'E'` agents' segments into a disjoint set of segments. For these, if segment \(s_1\) begins in an earlier column than segment \(s_2\) (or also in the same column if \(s_1\)'s agent index is greater than \(s_2\)'s), then \(s_1\) will cover \(s_2\) up to the end of \(s_1\), meaning that \(s_2\) should be trimmed to begin past that column (or removed entirely if it would become empty). Based on this idea, the `'E'` agents can be handled in \(O(a_1 \log(a_1))\) time, involving sorting them by their initial columns. We can repeat much the same process to transform all of the `'W'` agents' segments into a disjoint set of segments.
|
| 4 |
+
|
| 5 |
+
Our next step will be to combine the `'E'` and `'W'` segments together into a single disjoint set of segments. This can be done in \(O((a_1 + a_2)\log(a_1 + a_2))\) time using a line sweep across the segments' endpoints. For each interval between such endpoints, if it has at most ongoing segment (either `'E'` or a `'W'`), we'll simply keep that segment (trimmed down to that interval). On the other hand, if the interval has both a `'E'` and a `'W'` segment ongoing, we can compute how they interact within that interval, with the `'E'` segment potentially covering some right portion of the `'W'` segment and vice versa (resulting in at most disjoint \(2\) segments for the interval). Note that we'll end up with \(O(a_1 + a_2)\) segments overall.
|
| 6 |
+
|
| 7 |
+
Finally, all of the above should be repeated for each relevant column, transforming all of the `'S'` and `'N'` agents' segments into a disjoint set of segments. Based on the \(O(N)\) transformed segments, we can then trivially compute a base answer, ignoring interactions of horizontal segments with vertical ones.
|
| 8 |
+
|
| 9 |
+
What remains is subtracting from the answer based on each cell at which a horizontal segment intersects with a vertical one, with one segment covering the other there. We'll consider each possible pair of directions (`'E'` covered by `'S'`, `'N'` covered by `'W'`, etc.) independently. Through a combination of \(90 \degree\) rotations and axis-aligned flips of the entire grid and its segments, all \(8\) direction pairs can be transformed into just considering `'E'` covered by `'S'`.
|
| 10 |
+
|
| 11 |
+
We'll perform a line sweep downward through the `'E'` segments' rows and the `'S'` segments top/bottom rows, while maintaining some info about the ongoing `'S'` segments. It's possible to compute a constant "time value" for each `'E'`/`'S'` segment such that, whenever \(2\) segments intersect, the one with the larger time value will cover the other. In particular, a way to compute this time value (properly accounting for row/column offsets and breaking ties based on agent indices) is \(N*(\)(turns previously taken by agent) \(-\) (initial row) \(-\) (initial column)\() + \) (agent index).
|
| 12 |
+
|
| 13 |
+
We can therefore maintain a 2D segment tree (over the \(O(N)\) coordinate-compressed relevant columns), with each node of the tree storing the set of time values of ongoing `'S'` segments in its interval of columns (most conveniently in an order statistics tree, though a coordinate-compressed Fenwick tree can also work). Whenever a `'S'` segment starts or ends, we'll update the segment tree accordingly, and whenever an `'E'` segment is encountered, we can compute the number of its cells which are covered by querying for the number of time values greater than its own time value present in its interval of columns.
|
| 14 |
+
|
| 15 |
+
The total time complexity of this solution is \(O(N \log^2(N))\), due to updating and querying the 2D segment tree \(O(N)\) times.
|
2021/finals/ssssss.cpp
ADDED
|
@@ -0,0 +1,113 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
#include <algorithm>
|
| 2 |
+
#include <iostream>
|
| 3 |
+
#include <set>
|
| 4 |
+
#include <tuple>
|
| 5 |
+
#include <utility>
|
| 6 |
+
#include <vector>
|
| 7 |
+
using namespace std;
|
| 8 |
+
|
| 9 |
+
const int LIM = 800008;
|
| 10 |
+
|
| 11 |
+
int N;
|
| 12 |
+
int A[LIM], B[LIM];
|
| 13 |
+
|
| 14 |
+
void solve() {
|
| 15 |
+
vector<tuple<int, bool, int>> E;
|
| 16 |
+
set<pair<int, int>> S;
|
| 17 |
+
// Input, while finding tallest grounded ladder.
|
| 18 |
+
int ng = 0, mg = -1;
|
| 19 |
+
cin >> N;
|
| 20 |
+
for (int i = 0; i < N; i++) {
|
| 21 |
+
cin >> A[i] >> B[i];
|
| 22 |
+
if (!A[i]) {
|
| 23 |
+
ng++;
|
| 24 |
+
if (mg < 0 || B[i] > B[mg]) {
|
| 25 |
+
mg = i;
|
| 26 |
+
}
|
| 27 |
+
} else {
|
| 28 |
+
E.emplace_back(A[i], 0, i);
|
| 29 |
+
E.emplace_back(B[i], 1, i);
|
| 30 |
+
}
|
| 31 |
+
}
|
| 32 |
+
// None grounded?
|
| 33 |
+
if (ng == 0) {
|
| 34 |
+
cout << "0 0" << endl;
|
| 35 |
+
return;
|
| 36 |
+
}
|
| 37 |
+
// Sort endpoints (including tallest grounded ladder).
|
| 38 |
+
E.emplace_back(B[mg], 1, mg);
|
| 39 |
+
sort(E.begin(), E.end());
|
| 40 |
+
|
| 41 |
+
// Line sweep.
|
| 42 |
+
int ans1 = ng, ans2 = 0;
|
| 43 |
+
int a = mg, b = mg;
|
| 44 |
+
S.clear();
|
| 45 |
+
for (auto e : E) {
|
| 46 |
+
int i = get<2>(e);
|
| 47 |
+
if (!get<1>(e)) {
|
| 48 |
+
// Bottom of ladder i.
|
| 49 |
+
S.emplace(B[i], i);
|
| 50 |
+
continue;
|
| 51 |
+
}
|
| 52 |
+
// Top of ladder i.
|
| 53 |
+
if (B[a] > B[b]) {
|
| 54 |
+
swap(a, b);
|
| 55 |
+
}
|
| 56 |
+
auto it = S.find(make_pair(B[i], i));
|
| 57 |
+
if (it != S.end()) {
|
| 58 |
+
// Ladder i not used yet, so jump from ladder a to it.
|
| 59 |
+
S.erase(it);
|
| 60 |
+
ans1++;
|
| 61 |
+
ans2++;
|
| 62 |
+
a = i;
|
| 63 |
+
} else if (i == b) {
|
| 64 |
+
// Consider ladder i to be ladder a rather than b.
|
| 65 |
+
swap(a, b);
|
| 66 |
+
} else if (i != a) {
|
| 67 |
+
// Ladder i is irrelevant.
|
| 68 |
+
continue;
|
| 69 |
+
}
|
| 70 |
+
// Top of ladder a, so need to jump off of it.
|
| 71 |
+
if (!S.empty()) {
|
| 72 |
+
// There are other unused ladders, so jump from ladder a to the one with
|
| 73 |
+
// lowest top.
|
| 74 |
+
bool isB = a == b;
|
| 75 |
+
a = S.begin()->second;
|
| 76 |
+
S.erase(make_pair(B[a], a));
|
| 77 |
+
ans1++;
|
| 78 |
+
ans2++;
|
| 79 |
+
if (isB) {
|
| 80 |
+
// This is also ladder b, so repeat for it.
|
| 81 |
+
if (!S.empty()) {
|
| 82 |
+
// Jump from ladder b to another unused ladder.
|
| 83 |
+
b = S.begin()->second;
|
| 84 |
+
S.erase(make_pair(B[b], b));
|
| 85 |
+
ans1++;
|
| 86 |
+
ans2++;
|
| 87 |
+
} else {
|
| 88 |
+
// Jump from ladder b to the new ladder a.
|
| 89 |
+
ans2++;
|
| 90 |
+
b = a;
|
| 91 |
+
}
|
| 92 |
+
}
|
| 93 |
+
} else if (a != b) {
|
| 94 |
+
// Jump from ladder a to ladder b.
|
| 95 |
+
ans2++;
|
| 96 |
+
a = b;
|
| 97 |
+
} else {
|
| 98 |
+
// Nowhere else to go, so stop.
|
| 99 |
+
break;
|
| 100 |
+
}
|
| 101 |
+
}
|
| 102 |
+
cout << ans1 << " " << ans2 << endl;
|
| 103 |
+
}
|
| 104 |
+
|
| 105 |
+
int main() {
|
| 106 |
+
int T;
|
| 107 |
+
cin >> T;
|
| 108 |
+
for (int t = 1; t <= T; t++) {
|
| 109 |
+
cout << "Case #" << t << ": ";
|
| 110 |
+
solve();
|
| 111 |
+
}
|
| 112 |
+
return 0;
|
| 113 |
+
}
|
2021/finals/ssssss.in
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:fe48271e0b6976f5bd39e98bcd684756097fcab280e70694910643f0411d0e9b
|
| 3 |
+
size 72370704
|
2021/finals/ssssss.md
ADDED
|
@@ -0,0 +1,62 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
The mining company Facebulk Inc. has just rebranded to Metal Platforms Inc. In order to move fast with stable infrastructure, Metal has contracted the serpentine safety inspector, Solid Snake, to inspect \(T\) walls across its mine shafts.
|
| 2 |
+
|
| 3 |
+
A given wall has \(N\) vertical ladders (numbered from \(1\) to \(N\)) for Solid Snake to inspect. The wall can be represented as a 2D plane, with \(y=0\) being the lowest part of the wall, where it touches the ground. The \(i\)th ladder is positioned at x-coordinate \(i\), with its bottom at y-coordinate \(A_i\) and its top at y-coordinate \(B_i\).
|
| 4 |
+
|
| 5 |
+
Solid Snake is initially on the ground at coordinates \((0, 0)\) and hopes to inspect as many ladders as possible, ensuring they meet Solid Snake's Strict Serpentine Safety Specifications (SSSSSS), before finally returning to any position on the ground.
|
| 6 |
+
|
| 7 |
+
For example, the fourth sample case is depicted below:
|
| 8 |
+
|
| 9 |
+
{{PHOTO_ID:426120359137830|WIDTH:300}}
|
| 10 |
+
|
| 11 |
+
Solid Snake can perform the following actions:
|
| 12 |
+
|
| 13 |
+
1. If he's on the ground, he can freely move left and right, and can climb onto any ladder \(i\) which touches the ground at his current x-coordinate (i.e. \(A_i = 0\))
|
| 14 |
+
2. If he's on a ladder \(i\), he can:
|
| 15 |
+
1. **Inspect** it (if he hasn't already inspected that ladder)
|
| 16 |
+
2. Freely move up and down on that ladder — in other words, decrease his y-coordinate as low as \(A_i\) or increase it as high as \(B_i\) (while keeping his x-coordinate equal to \(i\))
|
| 17 |
+
3. Freely move onto the ground if the ladder touches the ground (i.e. \(A_i = 0\))
|
| 18 |
+
4. **Jump** horizontally to any other ladder \(j\) such that \(A_j \le y \le B_j\), where \(y\) is his current y-coordinate (note that he can jump directly to *any* such ladder, potentially passing by and ignoring other ladders along the way)
|
| 19 |
+
|
| 20 |
+
Please help Solid Snake determine the maximum number of ladders that he can inspect. Furthermore, determine the minimum number of jumps required for him to inspect that many ladders and then end up back on the ground at the end. Note that Solid Snake is allowed to intermediately return to the ground before he's done with all of his ladder inspections.
|
| 21 |
+
|
| 22 |
+
|
| 23 |
+
# Constraints
|
| 24 |
+
|
| 25 |
+
\(1 \le T \le 80\)
|
| 26 |
+
\(1 \le N \le 800{,}000\)
|
| 27 |
+
\(0 \le A_i < B_i \le 1{,}000{,}000{,}000\)
|
| 28 |
+
|
| 29 |
+
The sum of \(N\) across all walls is at most \(4{,}000{,}000\).
|
| 30 |
+
|
| 31 |
+
|
| 32 |
+
# Input
|
| 33 |
+
|
| 34 |
+
Input begins with an integer \(T\), the number of mine shaft walls to be inspected. For each wall, there is first a line containing a single integer \(N\). Then, \(N\) lines follow, the \(i\)th of which consists of \(2\) space-separated integers, \(A_i\) and \(B_i\).
|
| 35 |
+
|
| 36 |
+
|
| 37 |
+
# Output
|
| 38 |
+
|
| 39 |
+
For the \(i\)th wall, print a line containing *"Case #i: "* followed by \(2\) space-separated integers, the maximum number of ladders which Solid Snake can inspect and the minimum number of jumps required for him to do so.
|
| 40 |
+
|
| 41 |
+
|
| 42 |
+
# Sample Explanation
|
| 43 |
+
|
| 44 |
+
On the first wall, Solid Snake can move along the ground to each ladder, climb onto it, inspect it, and return to the ground, all without performing any jumps.
|
| 45 |
+
|
| 46 |
+
{{PHOTO_ID:525571725505702|WIDTH:240}}
|
| 47 |
+
|
| 48 |
+
On the second wall, Solid Snake cannot climb onto or inspect any ladders.
|
| 49 |
+
|
| 50 |
+
{{PHOTO_ID:247278897354943|WIDTH:240}}
|
| 51 |
+
|
| 52 |
+
On the third wall, one possible solution is for Solid Snake to:
|
| 53 |
+
- climb onto (and inspect) the third ladder at coordinates \((3, 0)\),
|
| 54 |
+
- move up to \((3, 10)\),
|
| 55 |
+
- jump to (and inspect) the second ladder at \((2, 10)\),
|
| 56 |
+
- move up to \((2, 15)\),
|
| 57 |
+
- jump to (and inspect) the first ladder at \((1, 15)\), and
|
| 58 |
+
- retrace his path by jumping to the second ladder, jumping to the third ladder, and finally returning to the ground.
|
| 59 |
+
|
| 60 |
+
Along the way, he will have inspected all \(3\) ladders while performing \(4\) jumps.
|
| 61 |
+
|
| 62 |
+
{{PHOTO_ID:436214534714219|WIDTH:240}}
|
2021/finals/ssssss.out
ADDED
|
@@ -0,0 +1,105 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Case #1: 3 0
|
| 2 |
+
Case #2: 0 0
|
| 3 |
+
Case #3: 3 4
|
| 4 |
+
Case #4: 3 3
|
| 5 |
+
Case #5: 10 12
|
| 6 |
+
Case #6: 1 0
|
| 7 |
+
Case #7: 5 8
|
| 8 |
+
Case #8: 5 5
|
| 9 |
+
Case #9: 6 8
|
| 10 |
+
Case #10: 6 5
|
| 11 |
+
Case #11: 6 7
|
| 12 |
+
Case #12: 7 8
|
| 13 |
+
Case #13: 11 12
|
| 14 |
+
Case #14: 72 74
|
| 15 |
+
Case #15: 197 196
|
| 16 |
+
Case #16: 500 740
|
| 17 |
+
Case #17: 501 501
|
| 18 |
+
Case #18: 800000 970282
|
| 19 |
+
Case #19: 84752 84831
|
| 20 |
+
Case #20: 800000 1599998
|
| 21 |
+
Case #21: 800000 800001
|
| 22 |
+
Case #22: 0 0
|
| 23 |
+
Case #23: 1 0
|
| 24 |
+
Case #24: 0 0
|
| 25 |
+
Case #25: 1 0
|
| 26 |
+
Case #26: 10 0
|
| 27 |
+
Case #27: 10 0
|
| 28 |
+
Case #28: 1 0
|
| 29 |
+
Case #29: 10 14
|
| 30 |
+
Case #30: 1 0
|
| 31 |
+
Case #31: 10000 14601
|
| 32 |
+
Case #32: 200000 293133
|
| 33 |
+
Case #33: 1 0
|
| 34 |
+
Case #34: 0 0
|
| 35 |
+
Case #35: 0 0
|
| 36 |
+
Case #36: 0 0
|
| 37 |
+
Case #37: 0 0
|
| 38 |
+
Case #38: 10 0
|
| 39 |
+
Case #39: 10 9
|
| 40 |
+
Case #40: 0 0
|
| 41 |
+
Case #41: 0 0
|
| 42 |
+
Case #42: 0 0
|
| 43 |
+
Case #43: 100 0
|
| 44 |
+
Case #44: 100 86
|
| 45 |
+
Case #45: 100 99
|
| 46 |
+
Case #46: 100 100
|
| 47 |
+
Case #47: 0 0
|
| 48 |
+
Case #48: 1000 0
|
| 49 |
+
Case #49: 1000 822
|
| 50 |
+
Case #50: 1000 976
|
| 51 |
+
Case #51: 0 0
|
| 52 |
+
Case #52: 0 0
|
| 53 |
+
Case #53: 10000 0
|
| 54 |
+
Case #54: 10000 8232
|
| 55 |
+
Case #55: 10000 9789
|
| 56 |
+
Case #56: 10000 9978
|
| 57 |
+
Case #57: 0 0
|
| 58 |
+
Case #58: 10 0
|
| 59 |
+
Case #59: 10 0
|
| 60 |
+
Case #60: 10 0
|
| 61 |
+
Case #61: 15 8
|
| 62 |
+
Case #62: 10 0
|
| 63 |
+
Case #63: 1000 1045
|
| 64 |
+
Case #64: 10 0
|
| 65 |
+
Case #65: 1000 1790
|
| 66 |
+
Case #66: 675 666
|
| 67 |
+
Case #67: 10 0
|
| 68 |
+
Case #68: 1000 991
|
| 69 |
+
Case #69: 10 0
|
| 70 |
+
Case #70: 31 0
|
| 71 |
+
Case #71: 31 0
|
| 72 |
+
Case #72: 31 0
|
| 73 |
+
Case #73: 36 8
|
| 74 |
+
Case #74: 31 0
|
| 75 |
+
Case #75: 1000 988
|
| 76 |
+
Case #76: 31 0
|
| 77 |
+
Case #77: 1000 1778
|
| 78 |
+
Case #78: 999 973
|
| 79 |
+
Case #79: 31 0
|
| 80 |
+
Case #80: 1000 970
|
| 81 |
+
Case #81: 31 0
|
| 82 |
+
Case #82: 10 0
|
| 83 |
+
Case #83: 11 2
|
| 84 |
+
Case #84: 10 0
|
| 85 |
+
Case #85: 18710 20988
|
| 86 |
+
Case #86: 10 0
|
| 87 |
+
Case #87: 19999 20033
|
| 88 |
+
Case #88: 28 21
|
| 89 |
+
Case #89: 20000 36516
|
| 90 |
+
Case #90: 20000 19991
|
| 91 |
+
Case #91: 10 0
|
| 92 |
+
Case #92: 20000 19991
|
| 93 |
+
Case #93: 10 0
|
| 94 |
+
Case #94: 141 0
|
| 95 |
+
Case #95: 142 2
|
| 96 |
+
Case #96: 141 0
|
| 97 |
+
Case #97: 15972 17798
|
| 98 |
+
Case #98: 142 2
|
| 99 |
+
Case #99: 20000 19940
|
| 100 |
+
Case #100: 163 26
|
| 101 |
+
Case #101: 20000 36504
|
| 102 |
+
Case #102: 20000 19860
|
| 103 |
+
Case #103: 141 0
|
| 104 |
+
Case #104: 20000 19860
|
| 105 |
+
Case #105: 141 0
|
2021/finals/ssssss_sol.md
ADDED
|
@@ -0,0 +1,19 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
If there are no ladders touching the ground, the answer is \(0\). Otherwise, those can all be inspected for free, and only the one with the largest \(B\) value is relevant.
|
| 2 |
+
|
| 3 |
+
We can perform a line sweep upwards over the ladders' endpoints (including the top of the tallest grounded ladder) while greedily constructing \(2\) "paths" of ladders simultaneously (one for the way up from the ground, and another for the way back down).
|
| 4 |
+
|
| 5 |
+
We'll maintain the ongoing ladders \(a\) and \(b\) for the \(2\) paths (not necessarily distinct, and both initially equal to the grounded ladder), the set \(U\) of ongoing ladders not yet used in either path (ordered by their \(B\) values, and initially empty), and the number of ladders inspected \(I\) and number of jumps used \(J\). We'll maintain an invariant that \(B_b\) is always greater than or equal to the \(B\) values of all other ongoing ladders not in \(U\) (including \(a\)). For convenience, we'll also assume that \(b\)'s top comes after \(a\)'s top in the line sweep (in case \(a \ne b\) and \(B_a = B_b\)).
|
| 6 |
+
|
| 7 |
+
When we encounter the bottom of a ladder, we'll simply add it to \(U\).
|
| 8 |
+
|
| 9 |
+
When we encounter the top of ladder \(i\), if \(i\) is in \(U\), then this is our last chance to visit it. So, we'll jump from ladder a to ladder \(i\) (leaving ladder \(b\) alone), removing \(i\) from \(U\), setting a to equal \(i\), and incrementing \(I\) and \(J\).
|
| 10 |
+
|
| 11 |
+
Either way, ladder \(i\)'s top being reached is then only relevant if \(i = a\) (and potentially also \(i = b\)), as we must jump to different ladder(s) to continue the path(s). One of the following situations will apply:
|
| 12 |
+
|
| 13 |
+
1. If \(U\) is empty and \(i = a = b\), we should terminate the line sweep, as both paths have converged and there are no higher ladders to jump to.
|
| 14 |
+
|
| 15 |
+
2. If \(U\) is empty but \(a \ne b\) (with \(i = a\)), we'll jump from ladder \(a\) to ladder \(b\) (necessary to attempt to continue \(a\)'s path or at least converge with \(b\)'s path), setting \(a\) to equal \(b\) and incrementing \(J\).
|
| 16 |
+
|
| 17 |
+
3. Otherwise, if \(U\) is non-empty, we'll jump from ladder \(a\) to the ladder \(j\) in \(U\) with the smallest \(B\) value, removing \(j\) from \(U\), setting \(a\) to equal \(j\), and incrementing \(I\) and \(J\). If \(i = b\), then we'll repeat this process to similarly jump from ladder \(b\) to the ladder in \(U\) with the next-smallest \(B\) value (though if \(U\) has become empty, then we'll instead need to jump from ladder \(b\) to the new ladder \(a\)). We may need to then swap \(a\) and \(b\) to maintain the aforementioned invariant regarding ladder \(b\).
|
| 18 |
+
|
| 19 |
+
The time complexity of this algorithm is \(O(N \log(N))\).
|
2021/finals/table_flipping.cpp
ADDED
|
@@ -0,0 +1,430 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
#include <algorithm>
|
| 2 |
+
#include <cstring>
|
| 3 |
+
#include <iostream>
|
| 4 |
+
#include <tuple>
|
| 5 |
+
#include <utility>
|
| 6 |
+
#include <vector>
|
| 7 |
+
using namespace std;
|
| 8 |
+
|
| 9 |
+
const int LIM = 300003;
|
| 10 |
+
using pii = pair<int, int>;
|
| 11 |
+
#define x first
|
| 12 |
+
#define y second
|
| 13 |
+
|
| 14 |
+
struct Compressor {
|
| 15 |
+
int N;
|
| 16 |
+
vector<pii> V;
|
| 17 |
+
|
| 18 |
+
Compressor() {}
|
| 19 |
+
Compressor(vector<pii> _V) {
|
| 20 |
+
V = _V;
|
| 21 |
+
comp();
|
| 22 |
+
}
|
| 23 |
+
|
| 24 |
+
void insert(pii v) {
|
| 25 |
+
V.push_back(v);
|
| 26 |
+
}
|
| 27 |
+
|
| 28 |
+
void comp() {
|
| 29 |
+
sort(V.begin(), V.end());
|
| 30 |
+
N = unique(V.begin(), V.end()) - V.begin();
|
| 31 |
+
V.resize(N);
|
| 32 |
+
}
|
| 33 |
+
|
| 34 |
+
int get(pii v) {
|
| 35 |
+
return lower_bound(V.begin(), V.end(), v) - V.begin();
|
| 36 |
+
}
|
| 37 |
+
};
|
| 38 |
+
|
| 39 |
+
const int TLIM = 2100000;
|
| 40 |
+
const int ZERO_VAL = 0;
|
| 41 |
+
const int ZERO_LAZY = 0;
|
| 42 |
+
|
| 43 |
+
struct MaxRangeSegTree {
|
| 44 |
+
static void update_value(int &a, int v, int r1, int r2) { a += v; }
|
| 45 |
+
static void update_lazy(int &a, int v, int r1, int r2) { a += v; }
|
| 46 |
+
static int join_values(int v1, int v2) { return max(v1, v2); }
|
| 47 |
+
|
| 48 |
+
int N, sz;
|
| 49 |
+
int tree[TLIM];
|
| 50 |
+
int lazy[TLIM];
|
| 51 |
+
|
| 52 |
+
MaxRangeSegTree() {}
|
| 53 |
+
MaxRangeSegTree(int _N) { init(_N); }
|
| 54 |
+
|
| 55 |
+
void init(int _N) {
|
| 56 |
+
N = _N;
|
| 57 |
+
for (sz = 1; sz < N; sz <<= 1)
|
| 58 |
+
;
|
| 59 |
+
clear();
|
| 60 |
+
}
|
| 61 |
+
|
| 62 |
+
void clear() {
|
| 63 |
+
for (int i = 0; i < (sz << 1); i++) {
|
| 64 |
+
tree[i] = ZERO_VAL;
|
| 65 |
+
lazy[i] = ZERO_LAZY;
|
| 66 |
+
}
|
| 67 |
+
}
|
| 68 |
+
|
| 69 |
+
void propagate(int i, int r1, int r2) {
|
| 70 |
+
int v = lazy[i];
|
| 71 |
+
lazy[i] = ZERO_LAZY;
|
| 72 |
+
update_value(tree[i], v, r1, r2);
|
| 73 |
+
if (i < sz) {
|
| 74 |
+
int m = (r1 + r2) >> 1, c1 = i << 1, c2 = c1 + 1;
|
| 75 |
+
update_lazy(lazy[c1], v, r1, m);
|
| 76 |
+
update_lazy(lazy[c2], v, m + 1, r2);
|
| 77 |
+
}
|
| 78 |
+
}
|
| 79 |
+
|
| 80 |
+
void comp(int i) {
|
| 81 |
+
int c1 = i << 1, c2 = c1 + 1;
|
| 82 |
+
tree[i] = join_values(tree[c1], tree[c2]);
|
| 83 |
+
}
|
| 84 |
+
|
| 85 |
+
int query(int a, int b, int i = 1, int r1 = 0, int r2 = -1) {
|
| 86 |
+
if (r2 < 0) {
|
| 87 |
+
a = max(a, 0);
|
| 88 |
+
b = min(b, sz - 1);
|
| 89 |
+
if (a > b) {
|
| 90 |
+
return ZERO_VAL;
|
| 91 |
+
}
|
| 92 |
+
r2 = sz - 1;
|
| 93 |
+
}
|
| 94 |
+
propagate(i, r1, r2);
|
| 95 |
+
if (a <= r1 && r2 <= b) {
|
| 96 |
+
return tree[i];
|
| 97 |
+
}
|
| 98 |
+
int m = (r1 + r2) >> 1, c = i << 1;
|
| 99 |
+
int res = ZERO_VAL;
|
| 100 |
+
if (a <= m) {
|
| 101 |
+
res = join_values(res, query(a, b, c, r1, m));
|
| 102 |
+
}
|
| 103 |
+
if (b > m) {
|
| 104 |
+
res = join_values(res, query(a, b, c + 1, m + 1, r2));
|
| 105 |
+
}
|
| 106 |
+
return res;
|
| 107 |
+
}
|
| 108 |
+
|
| 109 |
+
void update(int a, int b, int v, int i = 1, int r1 = 0, int r2 = -1) {
|
| 110 |
+
if (r2 < 0) {
|
| 111 |
+
a = max(a, 0);
|
| 112 |
+
b = min(b, sz - 1);
|
| 113 |
+
if (a > b) {
|
| 114 |
+
return;
|
| 115 |
+
}
|
| 116 |
+
r2 = sz - 1;
|
| 117 |
+
}
|
| 118 |
+
if (r2 < 0) {
|
| 119 |
+
r2 = sz - 1;
|
| 120 |
+
}
|
| 121 |
+
propagate(i, r1, r2);
|
| 122 |
+
if (a <= r1 && r2 <= b) {
|
| 123 |
+
update_lazy(lazy[i], v, r1, r2);
|
| 124 |
+
propagate(i, r1, r2);
|
| 125 |
+
return;
|
| 126 |
+
}
|
| 127 |
+
int m = (r1 + r2) >> 1, c = i << 1;
|
| 128 |
+
if (a <= m) {
|
| 129 |
+
update(a, b, v, c, r1, m);
|
| 130 |
+
}
|
| 131 |
+
if (b > m) {
|
| 132 |
+
update(a, b, v, c + 1, m + 1, r2);
|
| 133 |
+
}
|
| 134 |
+
propagate(c, r1, m);
|
| 135 |
+
propagate(c + 1, m + 1, r2);
|
| 136 |
+
comp(i);
|
| 137 |
+
}
|
| 138 |
+
};
|
| 139 |
+
|
| 140 |
+
const pii NONE{-1, -1};
|
| 141 |
+
|
| 142 |
+
struct MaxElemSegTree {
|
| 143 |
+
pii join_values(pii v1, pii v2) { return max(v1, v2); }
|
| 144 |
+
|
| 145 |
+
int N, sz;
|
| 146 |
+
vector<pii> tree;
|
| 147 |
+
|
| 148 |
+
MaxElemSegTree() {}
|
| 149 |
+
MaxElemSegTree(int _N) { init(_N); }
|
| 150 |
+
|
| 151 |
+
void init(int _N) {
|
| 152 |
+
N = _N;
|
| 153 |
+
for (sz = 1; sz < N; sz <<= 1)
|
| 154 |
+
;
|
| 155 |
+
clear();
|
| 156 |
+
}
|
| 157 |
+
|
| 158 |
+
void clear() {
|
| 159 |
+
tree.clear();
|
| 160 |
+
tree.resize(sz << 1, NONE);
|
| 161 |
+
}
|
| 162 |
+
|
| 163 |
+
void comp(int i) {
|
| 164 |
+
int c1 = i << 1, c2 = c1 + 1;
|
| 165 |
+
tree[i] = join_values(tree[c1], tree[c2]);
|
| 166 |
+
}
|
| 167 |
+
|
| 168 |
+
pii query(int a, int b, int i = 1, int r1 = 0, int r2 = -1) {
|
| 169 |
+
if (r2 < 0) {
|
| 170 |
+
a = max(a, 0);
|
| 171 |
+
b = min(b, sz - 1);
|
| 172 |
+
if (a > b) {
|
| 173 |
+
return NONE;
|
| 174 |
+
}
|
| 175 |
+
r2 = sz - 1;
|
| 176 |
+
}
|
| 177 |
+
if (a <= r1 && r2 <= b) {
|
| 178 |
+
return tree[i];
|
| 179 |
+
}
|
| 180 |
+
int m = (r1 + r2) >> 1, c = i << 1;
|
| 181 |
+
pii res = NONE;
|
| 182 |
+
if (a <= m) {
|
| 183 |
+
res = join_values(res, query(a, b, c, r1, m));
|
| 184 |
+
}
|
| 185 |
+
if (b > m) {
|
| 186 |
+
res = join_values(res, query(a, b, c + 1, m + 1, r2));
|
| 187 |
+
}
|
| 188 |
+
return res;
|
| 189 |
+
}
|
| 190 |
+
|
| 191 |
+
void update_one(int i, pii p) {
|
| 192 |
+
i += sz;
|
| 193 |
+
tree[i] = p;
|
| 194 |
+
while (i > 1) {
|
| 195 |
+
i >>= 1;
|
| 196 |
+
comp(i);
|
| 197 |
+
}
|
| 198 |
+
}
|
| 199 |
+
};
|
| 200 |
+
|
| 201 |
+
struct NestedSegTree {
|
| 202 |
+
int N, sz;
|
| 203 |
+
bool has_init_keys;
|
| 204 |
+
vector<int> keys[TLIM];
|
| 205 |
+
MaxElemSegTree T[TLIM];
|
| 206 |
+
|
| 207 |
+
NestedSegTree() {}
|
| 208 |
+
NestedSegTree(int _N) { init(_N); }
|
| 209 |
+
|
| 210 |
+
void init(int _N) {
|
| 211 |
+
N = _N;
|
| 212 |
+
for (sz = 1; sz < N; sz <<= 1)
|
| 213 |
+
;
|
| 214 |
+
has_init_keys = false;
|
| 215 |
+
}
|
| 216 |
+
|
| 217 |
+
void init_keys() {
|
| 218 |
+
for (int i = sz; i < sz + N; i++) {
|
| 219 |
+
auto &k = keys[i];
|
| 220 |
+
sort(k.begin(), k.end());
|
| 221 |
+
k.resize(unique(k.begin(), k.end()) - k.begin());
|
| 222 |
+
T[i].init(k.size());
|
| 223 |
+
}
|
| 224 |
+
for (int i = sz - 1; i >= 1; i--) {
|
| 225 |
+
auto &k = keys[i], &c1 = keys[i << 1], &c2 = keys[(i << 1) + 1];
|
| 226 |
+
int a = 0, b = 0;
|
| 227 |
+
while (a < c1.size() || b < c2.size()) {
|
| 228 |
+
if (a < c1.size() && b < c2.size() && c1[a] == c2[b]) {
|
| 229 |
+
k.push_back(c1[a++]);
|
| 230 |
+
b++;
|
| 231 |
+
} else if (b == c2.size() || (a < c1.size() && c1[a] < c2[b])) {
|
| 232 |
+
k.push_back(c1[a++]);
|
| 233 |
+
} else {
|
| 234 |
+
k.push_back(c2[b++]);
|
| 235 |
+
}
|
| 236 |
+
}
|
| 237 |
+
T[i].init(k.size());
|
| 238 |
+
}
|
| 239 |
+
has_init_keys = true;
|
| 240 |
+
}
|
| 241 |
+
|
| 242 |
+
pii query_max_up_to_k(int a, int b, int k, int i = 1, int r1 = 0, int r2 = -1) {
|
| 243 |
+
if (r2 < 0) {
|
| 244 |
+
a = max(a, 0);
|
| 245 |
+
b = min(b, sz - 1);
|
| 246 |
+
if (a > b) {
|
| 247 |
+
return NONE;
|
| 248 |
+
}
|
| 249 |
+
r2 = sz - 1;
|
| 250 |
+
}
|
| 251 |
+
if (a <= r1 && r2 <= b) {
|
| 252 |
+
k = lower_bound(keys[i].begin(), keys[i].end(), k + 1) - keys[i].begin() - 1;
|
| 253 |
+
return T[i].query(0, k);
|
| 254 |
+
}
|
| 255 |
+
int m = (r1 + r2) >> 1, c = i << 1;
|
| 256 |
+
pii res = NONE;
|
| 257 |
+
if (a <= m) {
|
| 258 |
+
res = max(res, query_max_up_to_k(a, b, k, c, r1, m));
|
| 259 |
+
}
|
| 260 |
+
if (b > m) {
|
| 261 |
+
res = max(res, query_max_up_to_k(a, b, k, c + 1, m + 1, r2));
|
| 262 |
+
}
|
| 263 |
+
return res;
|
| 264 |
+
}
|
| 265 |
+
|
| 266 |
+
void update_one(int i, int k, pii p) {
|
| 267 |
+
i += sz;
|
| 268 |
+
if (!has_init_keys) {
|
| 269 |
+
keys[i].push_back(k);
|
| 270 |
+
return;
|
| 271 |
+
}
|
| 272 |
+
while (i >= 1) {
|
| 273 |
+
T[i].update_one(
|
| 274 |
+
lower_bound(keys[i].begin(), keys[i].end(), k) - keys[i].begin(), p
|
| 275 |
+
);
|
| 276 |
+
i >>= 1;
|
| 277 |
+
}
|
| 278 |
+
}
|
| 279 |
+
};
|
| 280 |
+
|
| 281 |
+
int N;
|
| 282 |
+
pair<pii, pii> A[LIM], B[LIM];
|
| 283 |
+
int Axx[LIM], Axy[LIM];
|
| 284 |
+
int lowerX[3 * LIM], lowerY[3 * LIM];
|
| 285 |
+
bool visit[LIM];
|
| 286 |
+
NestedSegTree STX, STY;
|
| 287 |
+
|
| 288 |
+
void update_A_rect(int i, bool ins) {
|
| 289 |
+
STX.update_one(A[i].x.x, Axy[i], ins ? make_pair(A[i].y.y, i) : NONE);
|
| 290 |
+
STX.update_one(A[i].y.x, Axy[i], ins ? make_pair(A[i].y.y, i) : NONE);
|
| 291 |
+
STY.update_one(A[i].x.y, Axx[i], ins ? make_pair(A[i].y.x, i) : NONE);
|
| 292 |
+
STY.update_one(A[i].y.y, Axx[i], ins ? make_pair(A[i].y.x, i) : NONE);
|
| 293 |
+
}
|
| 294 |
+
|
| 295 |
+
int get_A_rect_for_B_rect(int i) {
|
| 296 |
+
pii p = STX.query_max_up_to_k(B[i].x.x, B[i].y.x, B[i].y.y);
|
| 297 |
+
if (p.x >= B[i].x.y) {
|
| 298 |
+
return p.y;
|
| 299 |
+
}
|
| 300 |
+
p = STY.query_max_up_to_k(B[i].x.y, B[i].y.y, B[i].y.x);
|
| 301 |
+
if (p.x >= B[i].x.x) {
|
| 302 |
+
return p.y;
|
| 303 |
+
}
|
| 304 |
+
return -1;
|
| 305 |
+
}
|
| 306 |
+
|
| 307 |
+
bool rec(int i) {
|
| 308 |
+
visit[i] = true;
|
| 309 |
+
for (;;) {
|
| 310 |
+
int j = get_A_rect_for_B_rect(i);
|
| 311 |
+
if (j < 0) {
|
| 312 |
+
break;
|
| 313 |
+
}
|
| 314 |
+
if (visit[j]) {
|
| 315 |
+
return true;
|
| 316 |
+
}
|
| 317 |
+
if (rec(j)) {
|
| 318 |
+
return true;
|
| 319 |
+
}
|
| 320 |
+
}
|
| 321 |
+
update_A_rect(i, 0);
|
| 322 |
+
return false;
|
| 323 |
+
}
|
| 324 |
+
|
| 325 |
+
bool solve() {
|
| 326 |
+
Compressor cx, cy;
|
| 327 |
+
// Input, and compute flipped rectangles.
|
| 328 |
+
cin >> N;
|
| 329 |
+
for (int i = 0; i < N; i++) {
|
| 330 |
+
char c;
|
| 331 |
+
cin >> A[i].x.x >> A[i].x.y >> A[i].y.x >> A[i].y.y >> c;
|
| 332 |
+
B[i] = A[i];
|
| 333 |
+
switch (c) {
|
| 334 |
+
case 'U': B[i].x.y += A[i].y.y; break;
|
| 335 |
+
case 'D': B[i].x.y -= A[i].y.y; break;
|
| 336 |
+
case 'L': B[i].x.x -= A[i].y.x; break;
|
| 337 |
+
case 'R': B[i].x.x += A[i].y.x; break;
|
| 338 |
+
}
|
| 339 |
+
A[i].y.x += A[i].x.x;
|
| 340 |
+
A[i].y.y += A[i].x.y;
|
| 341 |
+
B[i].y.x += B[i].x.x;
|
| 342 |
+
B[i].y.y += B[i].x.y;
|
| 343 |
+
cx.insert({A[i].x.x, i});
|
| 344 |
+
cx.insert({A[i].y.x, i}),
|
| 345 |
+
cx.insert({B[i].x.x, i});
|
| 346 |
+
cx.insert({B[i].y.x, i});
|
| 347 |
+
cy.insert({A[i].x.y, i});
|
| 348 |
+
cy.insert({A[i].y.y, i});
|
| 349 |
+
cy.insert({B[i].x.y, i});
|
| 350 |
+
cy.insert({B[i].y.y, i});
|
| 351 |
+
}
|
| 352 |
+
// Compress coordinates.
|
| 353 |
+
cx.comp(), cy.comp();
|
| 354 |
+
auto V = cx.V;
|
| 355 |
+
for (int i = 0; i < V.size(); i++) {
|
| 356 |
+
lowerX[i] = (i == 0 || V[i - 1].x != V[i].x) ? i : lowerX[i - 1];
|
| 357 |
+
}
|
| 358 |
+
V = cy.V;
|
| 359 |
+
for (int i = 0; i < V.size(); i++) {
|
| 360 |
+
lowerY[i] = (i == 0 || V[i - 1].x != V[i].x) ? i : lowerY[i - 1];
|
| 361 |
+
}
|
| 362 |
+
for (int i = 0; i < N; i++) {
|
| 363 |
+
A[i].x.x = cx.get({A[i].x.x, i});
|
| 364 |
+
A[i].x.y = cy.get({A[i].x.y, i}),
|
| 365 |
+
A[i].y.x = cx.get({A[i].y.x, i});
|
| 366 |
+
A[i].y.y = cy.get({A[i].y.y, i});
|
| 367 |
+
B[i].x.x = cx.get({B[i].x.x, i});
|
| 368 |
+
B[i].x.y = cy.get({B[i].x.y, i}),
|
| 369 |
+
B[i].y.x = cx.get({B[i].y.x, i});
|
| 370 |
+
B[i].y.y = cy.get({B[i].y.y, i});
|
| 371 |
+
// Remember exact (unique) lower coordinates.
|
| 372 |
+
Axx[i] = A[i].x.x, Axy[i] = A[i].x.y;
|
| 373 |
+
// Round coordinates up to value boundaries (with exclusive upper
|
| 374 |
+
// coordinates).
|
| 375 |
+
A[i].x.x = lowerX[A[i].x.x];
|
| 376 |
+
B[i].x.x = lowerX[B[i].x.x];
|
| 377 |
+
A[i].x.y = lowerY[A[i].x.y];
|
| 378 |
+
B[i].x.y = lowerY[B[i].x.y];
|
| 379 |
+
A[i].y.x = lowerX[A[i].y.x] - 1;
|
| 380 |
+
B[i].y.x = lowerX[B[i].y.x] - 1;
|
| 381 |
+
A[i].y.y = lowerY[A[i].y.y] - 1;
|
| 382 |
+
B[i].y.y = lowerY[B[i].y.y] - 1;
|
| 383 |
+
}
|
| 384 |
+
// Check for any overlap between final tables via line sweep.
|
| 385 |
+
vector<tuple<int, int, int, int>> E;
|
| 386 |
+
for (int i = 0; i < N; i++) {
|
| 387 |
+
E.emplace_back(B[i].x.y, 1, B[i].x.x, B[i].y.x);
|
| 388 |
+
E.emplace_back(B[i].y.y + 1, -1, B[i].x.x, B[i].y.x);
|
| 389 |
+
}
|
| 390 |
+
sort(E.begin(), E.end());
|
| 391 |
+
MaxRangeSegTree ST(cx.V.size());
|
| 392 |
+
for (auto e : E) {
|
| 393 |
+
ST.update(get<2>(e), get<3>(e), get<1>(e));
|
| 394 |
+
if (ST.query(0, cx.V.size() - 1) > 1) {
|
| 395 |
+
return false;
|
| 396 |
+
}
|
| 397 |
+
}
|
| 398 |
+
// Initialize segment trees of initial tables, over x and y coordinates.
|
| 399 |
+
STX = NestedSegTree(cx.V.size());
|
| 400 |
+
STY = NestedSegTree(cy.V.size());
|
| 401 |
+
for (int j : {0, 1}) {
|
| 402 |
+
if (j) { // Initialize keys second time around.
|
| 403 |
+
STX.init_keys();
|
| 404 |
+
STY.init_keys();
|
| 405 |
+
}
|
| 406 |
+
for (int i = 0; i < N; i++) {
|
| 407 |
+
// Set up keys first time around, then perform actual updates.
|
| 408 |
+
update_A_rect(i, 1);
|
| 409 |
+
}
|
| 410 |
+
}
|
| 411 |
+
// Search for cycles via DFS.
|
| 412 |
+
memset(visit, 0, sizeof visit);
|
| 413 |
+
for (int i = 0; i < N; i++) {
|
| 414 |
+
if (!visit[i]) {
|
| 415 |
+
if (rec(i)) {
|
| 416 |
+
return false; // Cycle found.
|
| 417 |
+
}
|
| 418 |
+
}
|
| 419 |
+
}
|
| 420 |
+
return true;
|
| 421 |
+
}
|
| 422 |
+
|
| 423 |
+
int main() {
|
| 424 |
+
int T;
|
| 425 |
+
cin >> T;
|
| 426 |
+
for (int t = 1; t <= T; t++) {
|
| 427 |
+
cout << "Case #" << t << ": " << (solve() ? "YES" : "NO") << endl;
|
| 428 |
+
}
|
| 429 |
+
return 0;
|
| 430 |
+
}
|
2021/finals/table_flipping.in
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:6165ba7ac7b576b2c2eeef3bc6342a5d831a6282bfe0c64934a2f20cfd83bba4
|
| 3 |
+
size 47880833
|
2021/finals/table_flipping.md
ADDED
|
@@ -0,0 +1,48 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Tabitha is tired of tricky Hacker Cup problems, and is hosting a table flipping after-party for the finalists to let out some steam. Her party will be held with finalists distributed across \(T\) rooms.
|
| 2 |
+
|
| 3 |
+
A given room has \(N\) tables (numbered from \(1\) to \(N\)), with one finalist at each table. Each table \(i\) is represented as an axis-aligned rectangle of positive area on a 2D plane, with bottom-left vertex at \((X_i, Y_i)\), a width of \(W_i\), and a height of \(H_i\). No two tables overlap (intersect with positive area).
|
| 4 |
+
|
| 5 |
+
Finalists will take turns flipping their tables in one of the \(4\) cardinal directions by reflecting the rectangle across an edge. Table \(i\) must be flipped in direction \(D_i\) (`"U"` if the table is to be flipped over its upper edge, `"D"` for its lower edge, `"L"` for its left edge, or `"R"` for its right edge). Finalists must flip their tables one-by-one, i.e., no two tables may be flipped at the exact same time.
|
| 6 |
+
|
| 7 |
+
Every finalist knows which direction each table must be flipped, and do not wish to interfere with each other. Tabitha would like to know if there exists some permutation in which the tables can be flipped, such that at no time do any two tables overlap (intersect with positive area).
|
| 8 |
+
|
| 9 |
+
# Constraints
|
| 10 |
+
|
| 11 |
+
\(1 \le T \le 70\)
|
| 12 |
+
\(1 \le N \le 300{,}000\)
|
| 13 |
+
\(0 \le X_i, Y_i \le 500{,}000{,}000\)
|
| 14 |
+
\(1 \le W_i, H_i \le 500{,}000{,}000\)
|
| 15 |
+
\(D_i \in \{\)`"U"`, `"D"`, `"L"`, `"R"`\(\}\)
|
| 16 |
+
|
| 17 |
+
The sum of \(N\) across all test cases is at most \(3{,}000{,}000\).
|
| 18 |
+
|
| 19 |
+
# Input
|
| 20 |
+
|
| 21 |
+
Input begins with a single integer \(T\), the number of rooms. For each room, there is first a line containing a single integer \(N\). Then, \(N\) lines follow, the \(i\)th of which contains \(4\) space-separated integers, \(X_i\), \(Y_i\), \(W_i\), and \(H_i\), followed by a space-separated character \(D_i\).
|
| 22 |
+
|
| 23 |
+
# Output
|
| 24 |
+
|
| 25 |
+
For the \(i\)th room, print a line containing *"Case #i: "* followed by `"YES"` if there exists a permutation of tables as described above, or `"NO"` otherwise.
|
| 26 |
+
|
| 27 |
+
# Sample Explanation
|
| 28 |
+
|
| 29 |
+
In the first room, the two tables (along with their flipping directions) are arranged as follows:
|
| 30 |
+
|
| 31 |
+
{{PHOTO_ID:616805819746914|WIDTH:420}}
|
| 32 |
+
|
| 33 |
+
Flipping the left table first would result in it overlapping with the right table. On the other hand, if the right table is flipped first, then the left table can be validly flipped as well, leaving the tables looking as follows:
|
| 34 |
+
|
| 35 |
+
{{PHOTO_ID:382533823663612|WIDTH:420}}
|
| 36 |
+
|
| 37 |
+
In the second room, the left table is to be flipped to the right instead. No matter which order the tables are flipped in, they will overlap with one another at some point.
|
| 38 |
+
|
| 39 |
+
The third room is arranged as follows:
|
| 40 |
+
|
| 41 |
+
{{PHOTO_ID:462323098803710|WIDTH:420}}
|
| 42 |
+
|
| 43 |
+
No matter which order the tables are flipped in, they will touch but not overlap with one another.
|
| 44 |
+
|
| 45 |
+
The fourth room is arranged as follows, and has no valid table-flipping order:
|
| 46 |
+
|
| 47 |
+
{{PHOTO_ID:1268827100291056|WIDTH:320}}
|
| 48 |
+
|
2021/finals/table_flipping.out
ADDED
|
@@ -0,0 +1,100 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Case #1: YES
|
| 2 |
+
Case #2: NO
|
| 3 |
+
Case #3: YES
|
| 4 |
+
Case #4: NO
|
| 5 |
+
Case #5: YES
|
| 6 |
+
Case #6: NO
|
| 7 |
+
Case #7: YES
|
| 8 |
+
Case #8: NO
|
| 9 |
+
Case #9: NO
|
| 10 |
+
Case #10: NO
|
| 11 |
+
Case #11: YES
|
| 12 |
+
Case #12: NO
|
| 13 |
+
Case #13: NO
|
| 14 |
+
Case #14: NO
|
| 15 |
+
Case #15: NO
|
| 16 |
+
Case #16: YES
|
| 17 |
+
Case #17: NO
|
| 18 |
+
Case #18: NO
|
| 19 |
+
Case #19: YES
|
| 20 |
+
Case #20: NO
|
| 21 |
+
Case #21: NO
|
| 22 |
+
Case #22: NO
|
| 23 |
+
Case #23: NO
|
| 24 |
+
Case #24: NO
|
| 25 |
+
Case #25: NO
|
| 26 |
+
Case #26: NO
|
| 27 |
+
Case #27: NO
|
| 28 |
+
Case #28: YES
|
| 29 |
+
Case #29: YES
|
| 30 |
+
Case #30: YES
|
| 31 |
+
Case #31: YES
|
| 32 |
+
Case #32: NO
|
| 33 |
+
Case #33: NO
|
| 34 |
+
Case #34: NO
|
| 35 |
+
Case #35: NO
|
| 36 |
+
Case #36: NO
|
| 37 |
+
Case #37: YES
|
| 38 |
+
Case #38: NO
|
| 39 |
+
Case #39: NO
|
| 40 |
+
Case #40: YES
|
| 41 |
+
Case #41: YES
|
| 42 |
+
Case #42: YES
|
| 43 |
+
Case #43: YES
|
| 44 |
+
Case #44: YES
|
| 45 |
+
Case #45: YES
|
| 46 |
+
Case #46: YES
|
| 47 |
+
Case #47: YES
|
| 48 |
+
Case #48: YES
|
| 49 |
+
Case #49: YES
|
| 50 |
+
Case #50: YES
|
| 51 |
+
Case #51: YES
|
| 52 |
+
Case #52: YES
|
| 53 |
+
Case #53: YES
|
| 54 |
+
Case #54: YES
|
| 55 |
+
Case #55: YES
|
| 56 |
+
Case #56: YES
|
| 57 |
+
Case #57: YES
|
| 58 |
+
Case #58: YES
|
| 59 |
+
Case #59: NO
|
| 60 |
+
Case #60: NO
|
| 61 |
+
Case #61: NO
|
| 62 |
+
Case #62: NO
|
| 63 |
+
Case #63: NO
|
| 64 |
+
Case #64: NO
|
| 65 |
+
Case #65: YES
|
| 66 |
+
Case #66: YES
|
| 67 |
+
Case #67: YES
|
| 68 |
+
Case #68: NO
|
| 69 |
+
Case #69: NO
|
| 70 |
+
Case #70: NO
|
| 71 |
+
Case #71: NO
|
| 72 |
+
Case #72: NO
|
| 73 |
+
Case #73: NO
|
| 74 |
+
Case #74: NO
|
| 75 |
+
Case #75: NO
|
| 76 |
+
Case #76: NO
|
| 77 |
+
Case #77: NO
|
| 78 |
+
Case #78: YES
|
| 79 |
+
Case #79: YES
|
| 80 |
+
Case #80: NO
|
| 81 |
+
Case #81: NO
|
| 82 |
+
Case #82: NO
|
| 83 |
+
Case #83: NO
|
| 84 |
+
Case #84: NO
|
| 85 |
+
Case #85: NO
|
| 86 |
+
Case #86: NO
|
| 87 |
+
Case #87: NO
|
| 88 |
+
Case #88: NO
|
| 89 |
+
Case #89: NO
|
| 90 |
+
Case #90: NO
|
| 91 |
+
Case #91: NO
|
| 92 |
+
Case #92: NO
|
| 93 |
+
Case #93: NO
|
| 94 |
+
Case #94: NO
|
| 95 |
+
Case #95: NO
|
| 96 |
+
Case #96: NO
|
| 97 |
+
Case #97: NO
|
| 98 |
+
Case #98: NO
|
| 99 |
+
Case #99: NO
|
| 100 |
+
Case #100: NO
|
2021/finals/table_flipping_sol.md
ADDED
|
@@ -0,0 +1,67 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
For each table, we know which direction it is going to be flipped over, so we can create two rectangle objects for each table. The rectangle of the starting position will be denoted as \(S\), and the rectangle for the ending position will be denoted as \(E\). We can coordinate compress all the values across these rectangles to make the problem slightly easier.
|
| 2 |
+
|
| 3 |
+
First, we can check if any of the tables overlap in their ending states. A standard line sweep can be done over all of the \(E\) rectangles in one dimension, with a segment tree of ongoing rectangles maintained over the other dimension. If any overlap is found, the answer for the test case is `"NO"`.
|
| 4 |
+
|
| 5 |
+
The tables must start in a valid position, and now we know that they also end in a valid position. We must now check if there is an ordering where they stay valid at each step. Let’s create a graph \(G\) with \(N\) nodes, one for each table. Let there be a directed edge from table \(A\) to table \(B\) if flipping over table \(A\) would cause it to intersect with a non-flipped over table \(B\) (\(E\) rectangle from \(A\) intersects with \(S\) rectangle from \(B\)). This means that rectangle \(B\) must be flipped over before rectangle \(A\). If this graph is acyclic then an ordering exists such that the tables never overlap at any step. The ordering would be the reverse of the topological sort based on how edges are defined above. This leads to a simple \(O(N^2)\) solution. Construct the graph above naively by checking every pair of rectangles and adding the edge if it exists, then run a cycle check or topological sorting on the graph. There are \(N\) vertices and \(N^2\) edges so any cycle check or topo sort algorithm will take \(O(V+E) = O(N^2)\).
|
| 6 |
+
|
| 7 |
+
Due to the properties of the graph, it is actually possible to perform a cycle check on this graph on the order of number of vertices, and not edges. Consider the following interactive problem:
|
| 8 |
+
|
| 9 |
+
There is a graph \(G\) with \(V\) vertices and \(E\) edges. There are no self-loops or multi-edges. You are not given the graph, only the number of vertices \(V\) (labeled \(1\) to \(V\)). You may perform \(2\) queries on this graph:
|
| 10 |
+
|
| 11 |
+
Query 1) Remove vertex with label \(X\) from the graph. This will remove all incoming and outgoing edges from this node.
|
| 12 |
+
|
| 13 |
+
Query 2) Ask for any outgoing edge from vertex \(X\). If vertex \(X\) contains any outgoing edges, this will return the vertex of any of them at random. If vertex \(X\) is already removed or contains no outgoing edges, this will return \(-1\).
|
| 14 |
+
|
| 15 |
+
Your task is to determine whether the original graph (before removing any vertices) contains a cycle in no more than \(4*V\) queries.
|
| 16 |
+
|
| 17 |
+
This can be solved via the following algorithm:
|
| 18 |
+
```
|
| 19 |
+
void dfs(int n) {
|
| 20 |
+
seen[n] = true;
|
| 21 |
+
while (!hasCycle) {
|
| 22 |
+
int to = query2(n);
|
| 23 |
+
if (to == -1) break;
|
| 24 |
+
else if (seen[to]) hasCycle = true;
|
| 25 |
+
else dfs(to);
|
| 26 |
+
}
|
| 27 |
+
query1(n);
|
| 28 |
+
}
|
| 29 |
+
|
| 30 |
+
boolean hasCycle = false;
|
| 31 |
+
boolean[] seen = new boolean[N];
|
| 32 |
+
for (int i = 0; i < N; i++) if (!seen[i]) dfs(i);
|
| 33 |
+
```
|
| 34 |
+
|
| 35 |
+
Query 1 is performed on each node at most once amounting to \(N\) queries. For query 2, if a returned node has previously been visited then a cycle is found and the process ends. Otherwise we visit that node, so query 2 is performed at most once for each time a node is entered, and then potentially once more on each node when no more edges are found. The total amount of queries is at most \(N + N + N + 1\).
|
| 36 |
+
|
| 37 |
+
Since this DFS only follows edges of the original graph, it is easy to see that if no cycle exists in the original graph, no false positive will be found. If a cycle exists, this solution will find it. Consider the initial path of nodes the DFS visits right before calling query 1 on any node:
|
| 38 |
+
|
| 39 |
+
\(A \to B \to C \to D \to E\)
|
| 40 |
+
|
| 41 |
+
We know each of these nodes are distinct because if there were any duplicates, a cycle would be found. We also know that node \(E\) has no outgoing edges in the original graph since no node has been destroyed yet and query 1 is about to be called (if \(E\) had an outgoing edge to \(A-D\), then this cycle would get found and the process would end). Since node \(E\) has no outgoing edges, we can guarantee that it is not part of any cycle in the graph. Node \(E\) then gets safely removed and now the stack looks like
|
| 42 |
+
|
| 43 |
+
\(A \to B \to C \to D\)
|
| 44 |
+
|
| 45 |
+
Now we will take any outgoing edge from \(D\) (if any exist) until we reach another point where a node has no more outgoing edges:
|
| 46 |
+
|
| 47 |
+
\(A \to B \to C \to D \to F \to G\)
|
| 48 |
+
|
| 49 |
+
If we do not reach a point where a node has no more outgoing edges, that means a cycle will get reached and be found.
|
| 50 |
+
|
| 51 |
+
If none of the nodes reachable from \(A\) (including \(A\) itself) are part of a cycle, then this function will eventually remove all of these nodes from the graph and finish without finding a cycle. Then search then starts from another node (if available).
|
| 52 |
+
|
| 53 |
+
Let’s consider the case where one of the reachable nodes is part of a cycle. Let’s consider the stack right after the first node that is part of a cycle is reached:
|
| 54 |
+
|
| 55 |
+
\(A \to B \to C \to D\)
|
| 56 |
+
|
| 57 |
+
Here \(D\) is the first node on the stack that is part of a cycle. It has been shown that nodes are only removed when they are not part of any cycle, and if we call DFS on node \(X\) then eventually all nodes reachable from \(X\) including \(X\) itself will be removed if they are not part of a cycle. This means that we will certainly find and reach any outgoing edges from \(D\) to nodes that also belong to a cycle containing \(D\). This logic continues until we eventually reach a node with an outgoing edge to \(D\) itself. Once we process this edge, we find the cycle and the process ends.
|
| 58 |
+
|
| 59 |
+
Now that we’ve shown we can do cycle section on a graph with these two queries, the original problem needs to be translated to this new problem. We can create a data structure to store/remove rectangles and query for some rectangle if there is another rectangle that intersects with it, and return one of them.
|
| 60 |
+
|
| 61 |
+
Create a segment tree across the \(X\) values of the rectangles. Each node stores an implicit segment tree across \(Y\) values. When adding a rectangle, for its left \(X\) and right \(X\) boundaries, for all \(\log(N)\) nodes including that \(X\), set the index of the lower \(Y\) to be the value of the upper \(Y\). To support insertion and deletion of multiple rectangles with the same lower \(Y\) without disrupting each other, one approach is to give each rectangle a unique lower \(Y\) "key" rather than compressing them all to exactly the same one.
|
| 62 |
+
|
| 63 |
+
Add all the \(S\) rectangles to this data structure. Now to check if a node has any outgoing edges, query from left X to right X for the corresponding \(E\) rectangle of that node. For each \(\log(N)\) nodes in this range, query the max from \([0, \) upper \(Y]\) and check if that value is \(\ge\) lower \(Y\). If this is true, then there is some intersecting rectangle and we can return the index of it by storing extra data.
|
| 64 |
+
|
| 65 |
+
There is one case this will not find: If the intersecting \(S\) rectangle starts at a smaller \(X\) and ends at a larger \(X\) than the \(E\) rectangle we are checking, the \(\log(N)\) nodes in the segment tree will not find this rectangle. If we rotate the problem and also check by having a segment tree across \(Y\) values and implicit segment tree across \(X\), then it will be instead found in the other structure. Since \(E\) rectangles are formed by reflecting across its corresponding \(S\) rectangle, then if there were any case such that an \(E\) rectangle is completely contained inside an \(S\) rectangle (without touching its borders) then there would be an intersection between the two \(S\) rectangles and this would be found during the sweep line.
|
| 66 |
+
|
| 67 |
+
Each insertion into and deletion from this data structure takes \(O(\log^2(N))\) time, and querying for an intersecting rectangle also takes \(O(\log^2(N))\) time. Since these queries are called \(O(N)\) times in the algorithm described above, the overall runtime of this solution is \(O(N \log^2(N))\).
|
2021/finals/vacation.cpp
ADDED
|
@@ -0,0 +1,115 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
#include <algorithm>
|
| 2 |
+
#include <cassert>
|
| 3 |
+
#include <cstring>
|
| 4 |
+
#include <iostream>
|
| 5 |
+
#include <vector>
|
| 6 |
+
#include <utility>
|
| 7 |
+
using namespace std;
|
| 8 |
+
|
| 9 |
+
const int LIM = 1000001;
|
| 10 |
+
|
| 11 |
+
int N;
|
| 12 |
+
long long K;
|
| 13 |
+
int C[LIM];
|
| 14 |
+
vector<int> ch[LIM];
|
| 15 |
+
|
| 16 |
+
// <sum, negative # of paths>
|
| 17 |
+
pair<long long, int> DP[LIM][3]; // [node][# of incoming paths]
|
| 18 |
+
pair<long long, int> DP2[3][2], nxt[3][2]; // [# of ongoing paths][counted node?]
|
| 19 |
+
|
| 20 |
+
void rec(int i, int p, long long P) {
|
| 21 |
+
for (auto c : ch[i]) {
|
| 22 |
+
rec(c, i, P);
|
| 23 |
+
}
|
| 24 |
+
memset(DP2, 0, sizeof DP2);
|
| 25 |
+
DP2[1][1] = make_pair(C[i], 0);
|
| 26 |
+
memcpy(nxt, DP2, sizeof nxt);
|
| 27 |
+
for (auto c : ch[i]) {
|
| 28 |
+
for (int j = 2; j >= 0; j--) {
|
| 29 |
+
for (int b = 1; b >= 0; b--) {
|
| 30 |
+
auto d = DP2[j][b];
|
| 31 |
+
for (int j2 = 0; j2 <= 2; j2++) {
|
| 32 |
+
auto d2 = DP[c][j2];
|
| 33 |
+
for (int u = 0; u <= j2; u++) {
|
| 34 |
+
int r = j2 - u;
|
| 35 |
+
if (r > j) {
|
| 36 |
+
continue;
|
| 37 |
+
}
|
| 38 |
+
int j3 = j + u - r;
|
| 39 |
+
if (j3 < 0 || j3 > 2) {
|
| 40 |
+
continue;
|
| 41 |
+
}
|
| 42 |
+
int b2 = b | (j2 ? 1 : 0);
|
| 43 |
+
long long dv = d.first + d2.first + (!b && b2 ? C[i] : 0) - r * P;
|
| 44 |
+
int dk = d.second + d2.second - r;
|
| 45 |
+
nxt[j3][b2] = max(nxt[j3][b2], make_pair(dv, dk));
|
| 46 |
+
}
|
| 47 |
+
}
|
| 48 |
+
}
|
| 49 |
+
}
|
| 50 |
+
memcpy(DP2, nxt, sizeof nxt);
|
| 51 |
+
}
|
| 52 |
+
for (int j = 0; j <= 2; j++) {
|
| 53 |
+
for (int j2 = 0; j2 <= j; j2++) {
|
| 54 |
+
int e = j - j2;
|
| 55 |
+
for (int b : {0, 1}) {
|
| 56 |
+
auto d = DP2[j][b];
|
| 57 |
+
DP[i][j2] = max(DP[i][j2], make_pair(d.first - e * P, d.second - e));
|
| 58 |
+
}
|
| 59 |
+
}
|
| 60 |
+
}
|
| 61 |
+
}
|
| 62 |
+
|
| 63 |
+
pair<long long, int> solve(long long P) {
|
| 64 |
+
memset(DP, 0, sizeof DP);
|
| 65 |
+
rec(0, -1, P);
|
| 66 |
+
auto d = DP[0][0];
|
| 67 |
+
return make_pair(d.first + -d.second * P, -d.second - 1);
|
| 68 |
+
}
|
| 69 |
+
|
| 70 |
+
int solve() {
|
| 71 |
+
for (int i = 0; i < LIM; i++) {
|
| 72 |
+
ch[i].clear();
|
| 73 |
+
}
|
| 74 |
+
// Input.
|
| 75 |
+
cin >> N >> K;
|
| 76 |
+
for (int i = 0; i < N; i++) {
|
| 77 |
+
cin >> C[i];
|
| 78 |
+
}
|
| 79 |
+
for (int i = 1, j; i <= N - 1; i++) {
|
| 80 |
+
cin >> j;
|
| 81 |
+
ch[j - 1].push_back(i);
|
| 82 |
+
}
|
| 83 |
+
// Binary search for appropriate path penalty.
|
| 84 |
+
long long r1 = -1, r2 = (long long)N * 1e9 + 1;
|
| 85 |
+
while (r2 > r1) {
|
| 86 |
+
long long m = (r1 + r2 + 1) >> 1;
|
| 87 |
+
auto ans = solve(m);
|
| 88 |
+
if (ans.first < K) {
|
| 89 |
+
r2 = m - 1;
|
| 90 |
+
} else {
|
| 91 |
+
r1 = m;
|
| 92 |
+
}
|
| 93 |
+
}
|
| 94 |
+
// Compute final answer.
|
| 95 |
+
int ans = -1;
|
| 96 |
+
if (r1 >= 0) {
|
| 97 |
+
pair<long long, int> ans1 = solve(r1), ans2 = solve(r1 + 1);
|
| 98 |
+
assert(ans2.first < K && K <= ans1.first && ans2.second < ans1.second);
|
| 99 |
+
long long diffV = ans1.first - ans2.first;
|
| 100 |
+
int diffK = ans1.second - ans2.second;
|
| 101 |
+
long long need = K - ans2.first;
|
| 102 |
+
ans = ans2.second + (need * diffK + diffV - 1) / diffV;
|
| 103 |
+
assert(ans2.second < ans && ans <= ans1.second);
|
| 104 |
+
}
|
| 105 |
+
return ans;
|
| 106 |
+
}
|
| 107 |
+
|
| 108 |
+
int main() {
|
| 109 |
+
int T;
|
| 110 |
+
cin >> T;
|
| 111 |
+
for (int t = 1; t <= T; t++) {
|
| 112 |
+
cout << "Case #" << t << ": " << solve() << endl;
|
| 113 |
+
}
|
| 114 |
+
return 0;
|
| 115 |
+
}
|
2021/finals/vacation.in
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:81ebf295afac73c8c95cf13046266c11072057ac4d463f6af778aa03f9d4bd2c
|
| 3 |
+
size 61315378
|
2021/finals/vacation.md
ADDED
|
@@ -0,0 +1,40 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Melody is planning her Christmas vacation in the Metalverse, an ore-rich VR experience consisting of \(T\) virtual worlds.
|
| 2 |
+
|
| 3 |
+
A given world has \(N\) cities (numbered from \(1\) to \(N\)) with \(N - 1\) roads running between them. The \(i\)th road allows Melody to drive between cities \(P_i\) and \(i+1\) in either direction (with \(1 \le P_i \le i\)). City \(i\) also contains \(C_i\) ore-naments which Melody can collect as souvenirs while she's there.
|
| 4 |
+
|
| 5 |
+
Melody's vacation consists of starting in any city of her choice, and then repeatedly performing either of the following actions:
|
| 6 |
+
|
| 7 |
+
1. Drive along a road to another city, unless her previous action was to drive *from* that city
|
| 8 |
+
2. Teleport to any other city
|
| 9 |
+
|
| 10 |
+
Melody may visit a city multiple times, but may only collect its ore-naments once. She may stop her vacation at any point.
|
| 11 |
+
|
| 12 |
+
Please help Melody evaluate, for each world, the minimum number of times she must teleport to collect at least K ore-naments, if it's possible at all.
|
| 13 |
+
|
| 14 |
+
# Constraints
|
| 15 |
+
|
| 16 |
+
\(1 \le T \le 95\)
|
| 17 |
+
\(2 \le N \le 10^6\)
|
| 18 |
+
\(1 \le K \le 10^{12}\)
|
| 19 |
+
\(0 \le C_i \le 10^9\)
|
| 20 |
+
\(1 \le P_i \le i\)
|
| 21 |
+
|
| 22 |
+
The sum of \(N\) across all worlds is at most \(5{,}000{,}000\).
|
| 23 |
+
|
| 24 |
+
# Input
|
| 25 |
+
|
| 26 |
+
Input begins with an integer \(T\), the number of virtual worlds to be evaluated. For each world, there is first a line containing \(2\) space-separated integers, \(N\) and \(K\). Then, there is a line containing \(N\) space-separated integers, \(C_{1..N}\). Then, there is a line containing \(N-1\) space-separated integers, \(P_{1..(N-1)}\).
|
| 27 |
+
|
| 28 |
+
# Output
|
| 29 |
+
|
| 30 |
+
For the \(i\)th world, print a line containing *"Case #i: "* followed a single integer, the minimum number of times Melody must teleport to collect at least \(K\) ore-naments, or \(-1\) if it's impossible to do so.
|
| 31 |
+
|
| 32 |
+
# Sample Explanation
|
| 33 |
+
|
| 34 |
+
In the first three worlds, the cities are arranged as follows:
|
| 35 |
+
|
| 36 |
+
{{PHOTO_ID:2893643357566792|WIDTH:300}}
|
| 37 |
+
|
| 38 |
+
In the first world, one option is to start in city \(4\), drive to city \(2\), and finally drive to city \(3\). This will yield \(40 + 20 + 30 = 90\) ore-naments.
|
| 39 |
+
|
| 40 |
+
In the second world, one option is to start in city \(2\), drive to city \(1\), teleport to city \(3\), drive to city \(2\), and finally drive to city \(4\). This will yield \(20 + 10 + 30 + 0 + 40 = 100\) ore-naments.
|
2021/finals/vacation.out
ADDED
|
@@ -0,0 +1,101 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Case #1: 0
|
| 2 |
+
Case #2: 1
|
| 3 |
+
Case #3: -1
|
| 4 |
+
Case #4: 1
|
| 5 |
+
Case #5: 1
|
| 6 |
+
Case #6: 2
|
| 7 |
+
Case #7: 0
|
| 8 |
+
Case #8: 0
|
| 9 |
+
Case #9: 1
|
| 10 |
+
Case #10: 2
|
| 11 |
+
Case #11: 2
|
| 12 |
+
Case #12: 2
|
| 13 |
+
Case #13: 3
|
| 14 |
+
Case #14: 4
|
| 15 |
+
Case #15: -1
|
| 16 |
+
Case #16: 15
|
| 17 |
+
Case #17: 75
|
| 18 |
+
Case #18: 73180
|
| 19 |
+
Case #19: 0
|
| 20 |
+
Case #20: 499
|
| 21 |
+
Case #21: 499999
|
| 22 |
+
Case #22: -1
|
| 23 |
+
Case #23: -1
|
| 24 |
+
Case #24: -1
|
| 25 |
+
Case #25: 0
|
| 26 |
+
Case #26: 0
|
| 27 |
+
Case #27: 0
|
| 28 |
+
Case #28: 0
|
| 29 |
+
Case #29: 0
|
| 30 |
+
Case #30: 0
|
| 31 |
+
Case #31: 0
|
| 32 |
+
Case #32: 0
|
| 33 |
+
Case #33: 0
|
| 34 |
+
Case #34: 0
|
| 35 |
+
Case #35: 0
|
| 36 |
+
Case #36: 0
|
| 37 |
+
Case #37: -1
|
| 38 |
+
Case #38: -1
|
| 39 |
+
Case #39: -1
|
| 40 |
+
Case #40: 51
|
| 41 |
+
Case #41: 12
|
| 42 |
+
Case #42: 0
|
| 43 |
+
Case #43: 0
|
| 44 |
+
Case #44: 0
|
| 45 |
+
Case #45: 0
|
| 46 |
+
Case #46: 0
|
| 47 |
+
Case #47: 0
|
| 48 |
+
Case #48: 0
|
| 49 |
+
Case #49: 0
|
| 50 |
+
Case #50: -1
|
| 51 |
+
Case #51: -1
|
| 52 |
+
Case #52: -1
|
| 53 |
+
Case #53: -1
|
| 54 |
+
Case #54: 51
|
| 55 |
+
Case #55: 12
|
| 56 |
+
Case #56: 0
|
| 57 |
+
Case #57: 0
|
| 58 |
+
Case #58: 0
|
| 59 |
+
Case #59: 0
|
| 60 |
+
Case #60: 0
|
| 61 |
+
Case #61: 0
|
| 62 |
+
Case #62: 0
|
| 63 |
+
Case #63: 51
|
| 64 |
+
Case #64: 11
|
| 65 |
+
Case #65: 0
|
| 66 |
+
Case #66: 0
|
| 67 |
+
Case #67: 0
|
| 68 |
+
Case #68: 0
|
| 69 |
+
Case #69: 439
|
| 70 |
+
Case #70: 60
|
| 71 |
+
Case #71: 0
|
| 72 |
+
Case #72: 27
|
| 73 |
+
Case #73: 4
|
| 74 |
+
Case #74: 0
|
| 75 |
+
Case #75: 0
|
| 76 |
+
Case #76: 0
|
| 77 |
+
Case #77: 0
|
| 78 |
+
Case #78: 5541
|
| 79 |
+
Case #79: 1661
|
| 80 |
+
Case #80: 510
|
| 81 |
+
Case #81: 26
|
| 82 |
+
Case #82: 4
|
| 83 |
+
Case #83: 0
|
| 84 |
+
Case #84: 0
|
| 85 |
+
Case #85: 0
|
| 86 |
+
Case #86: 0
|
| 87 |
+
Case #87: 0
|
| 88 |
+
Case #88: 0
|
| 89 |
+
Case #89: 0
|
| 90 |
+
Case #90: 5571
|
| 91 |
+
Case #91: 1627
|
| 92 |
+
Case #92: 518
|
| 93 |
+
Case #93: 26
|
| 94 |
+
Case #94: 4
|
| 95 |
+
Case #95: 0
|
| 96 |
+
Case #96: 0
|
| 97 |
+
Case #97: 0
|
| 98 |
+
Case #98: 0
|
| 99 |
+
Case #99: 448
|
| 100 |
+
Case #100: 70
|
| 101 |
+
Case #101: 0
|
2021/finals/vacation_sol.md
ADDED
|
@@ -0,0 +1,16 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Note that the network of cities and roads form a tree (which we consider to be rooted at node \(1\)), and that a vacation using \(t\) teleports is equivalent to a set of \(t+1\) simple paths on the tree, with ore-naments collected from all nodes present in at least one path.
|
| 2 |
+
|
| 3 |
+
We'll begin by considering a different variation of this problem, in which each path used incurs some constant penalty of \(P\) ore-naments (such that, if \(o\) ore-naments are collected using \(p\) paths, the final ore-nament count \(x\) will be \(o - p * P\)). In this variation, let's maximize \(x\), breaking ties by minimizing \(p\).
|
| 4 |
+
|
| 5 |
+
This variation is solvable using DP, letting \(DP_{i,j}\) be the optimal pair of \((x, p)\) for node \(i\)'s subtree, such that \(j\) paths are ongoing between node \(i\) and its parent (with those \(j\) paths not included in \(x\) and \(p\)). The overall answer will then be \(DP_{1,0}\). We can observe that values of \(j\) up to \(2\) are relevant (as there must be an optimal set of paths such that no tree edge is part of \(3\) or more paths). This means there are only \(O(N)\) states, which are all possible to evaluate in linear time. A key aspect of the implementation is only counting each path and its penalty once, for example only at its topmost node (when it doesn't continue from node \(i\) up to its parent, due to either ending there or feeding into two of \(i\)'s children).
|
| 6 |
+
|
| 7 |
+
To now solve the original problem, we can employ a technique which goes by various names, including "parameter search" or the "Aliens optimization" — its workings and requirements are described in greater detail [here](http://www.serbanology.com/article/The%20Trick%20From%20Aliens).
|
| 8 |
+
|
| 9 |
+
In short, we'll binary search for the largest per-path penalty \(P\) (between \(0\) and \(\sum_{i=1}^N C_i)\)) which results in an ore-nament count of \(o\) (excluding subtraction from path penalties) of at least \(K\). Note that \(o = x + p * P\). We can do so because:
|
| 10 |
+
|
| 11 |
+
- As \(P\) increases, the path count \(p\) and corresponding ore-nament count \(o\) decrease or stays equal
|
| 12 |
+
- If we define a function \(F(p)\) as the maximum ore-nament count \(o\) for a given path count \(p\), \(F(p)\) is concave (the more paths are used, the more diminished are their returns)
|
| 13 |
+
|
| 14 |
+
Let \(o_1\) and \(p_1\) be the optimal ore-nament and path counts for the penalty \(P\) produced by the binary search, and \(o_2\) and \(p_2\) be the corresponding counts for penalty \(P+1\). Note that \(o_2 \lt K \le o_1\) and \(p_2 \lt p_1\). The minimum number of paths required to collect \(K\) ore-naments is then somewhere in the interval \((p_2, p_1]\). In particular, we can linearly interpolate between \((o_1, p_1)\) and \((o_2, p_2)\) to compute our final answer as \(p_2 + \lceil(K - o_2)(p_1 - p_2) / (o_1 - o_2)\rceil + 1\).
|
| 15 |
+
|
| 16 |
+
The time complexity of this solution is \(O(N * \log(\sum_{i=1}^N C_i))\).
|
2021/quals/160428912890161.jpg
ADDED

|
Git LFS Details
|
2021/quals/271244381102893.jpg
ADDED

|
Git LFS Details
|
2021/quals/328916612261658.jpg
ADDED
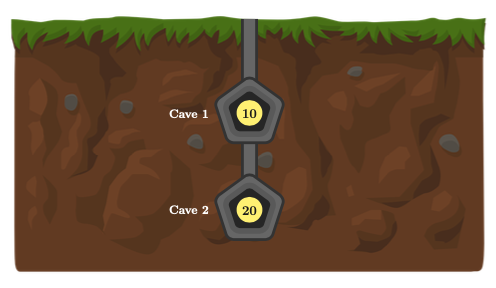
|
Git LFS Details
|
2021/quals/375673720664225.jpg
ADDED
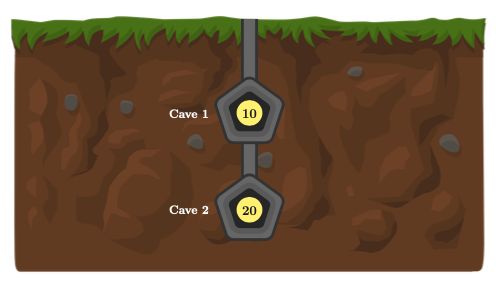
|
Git LFS Details
|
2021/quals/541711107152146.jpg
ADDED

|
Git LFS Details
|
2021/quals/consistency_ch1.cpp
ADDED
|
@@ -0,0 +1,35 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
#include <algorithm>
|
| 2 |
+
#include <iostream>
|
| 3 |
+
using namespace std;
|
| 4 |
+
|
| 5 |
+
const int INF = 1e6;
|
| 6 |
+
|
| 7 |
+
bool is_vowel(char c) {
|
| 8 |
+
return c == 'A' || c == 'E' || c == 'I' || c == 'O' || c == 'U';
|
| 9 |
+
}
|
| 10 |
+
|
| 11 |
+
string S;
|
| 12 |
+
|
| 13 |
+
int solve() {
|
| 14 |
+
cin >> S;
|
| 15 |
+
int ans = INF;
|
| 16 |
+
for (char c1 = 'A'; c1 <= 'Z'; c1++) {
|
| 17 |
+
int curr = 0;
|
| 18 |
+
for (char c2 : S) {
|
| 19 |
+
if (c1 != c2) {
|
| 20 |
+
curr += is_vowel(c1) == is_vowel(c2) ? 2 : 1;
|
| 21 |
+
}
|
| 22 |
+
}
|
| 23 |
+
ans = min(ans, curr);
|
| 24 |
+
}
|
| 25 |
+
return ans;
|
| 26 |
+
}
|
| 27 |
+
|
| 28 |
+
int main() {
|
| 29 |
+
int T;
|
| 30 |
+
cin >> T;
|
| 31 |
+
for (int t = 1; t <= T; t++) {
|
| 32 |
+
cout << "Case #" << t << ": " << solve() << endl;
|
| 33 |
+
}
|
| 34 |
+
return 0;
|
| 35 |
+
}
|
2021/quals/consistency_ch1.in
ADDED
|
@@ -0,0 +1,54 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
53
|
| 2 |
+
ABC
|
| 3 |
+
F
|
| 4 |
+
BANANA
|
| 5 |
+
FBHC
|
| 6 |
+
FOXEN
|
| 7 |
+
CONSISTENCY
|
| 8 |
+
HAAACKEEERCUUUP
|
| 9 |
+
OOEUEUIUUOOAUEIOIEEUIAIUAUOOAUUIIEUUOAAIOAEAUEIAOAOOAOOAAIEOAEOEIOIAAEAAIOEEOIIIEEIOIUEIEEEAAEEEEOAA
|
| 10 |
+
QPQWJXRJJXBTKKGBKVXNSCQBHZTSFZRYCDZFYQJQWHWHYJVDRXSGWRLJNTHBXYBRBTVXBBPPCXRBFVXVNDQQTHHBKXZDPQZGSHWF
|
| 11 |
+
EDHHDGFGCFHBHCAFGHHCBDHHECAEGGAGAGDGEGGFDGBCDFDCBHFGBDBCGHEACCGFAGEFBFGECFGFCGGBEDGDBFCEHEDHEHHFGCEB
|
| 12 |
+
AAAAAAAAAAEEEEEEEEEEIIIIIIIIIIOOOOOOOOOOUUUUUUUUUUBBBBBBBBBBBCCCCDDDDFFFFGGGGHHHHJJJJKKKKLLLLMMMMNNN
|
| 13 |
+
AAAAAEEEEEIIIIIOOOOOOUUUUUXYZ
|
| 14 |
+
IOIWOWIOIWOWIOIWOWIOIWOWIOIWOWIOIWOWIOIWOWIOIWOWIOIWOWIOIWOWIOIWOWIOIWOWIOIWOWIOIWOWIOIWOWIOIWOWIOI
|
| 15 |
+
OEOUAEOUAUAEIEIIIAIOOUAUIAEEUUIAIAIOUIIAUUIIUAUUEAOAOAEEUEUOUAOAIOUUEEIEAUOAIOEEOUIOAUOEOIAEO
|
| 16 |
+
EJZITADGAAAKTEIQVEWLLIIZXWLKSEAIUUUIERFKEUOXONORJRXGKGLIUIUBNXINNJHHAEAACBEQWXZ
|
| 17 |
+
OIOUAUOAIEUOEUIUIIUAAAAUOEIEUAIEEOIAOEUEAOOEAIIEEAEIUIOAUIIOEEUEAOEOOAAIAUAO
|
| 18 |
+
OWAMBXIRMUNOIXEUJILQLAPGLHQSFXUNAJLIERKUQEGCIYNHHEEYFHOFIAMH
|
| 19 |
+
ZVOIAGIMOLAHOAIAJEIUBHLNDDFIHGZHCIUWRMGIHIUOPICDOURTUVAOO
|
| 20 |
+
IOAOIAAOAEOIEIEAIIEAOUEIEIOOIEIEOIEIOEOUUOEUEOAOEIOOUUUIIOAEIAIEIOIEUOIUUEIEAEIAAIEOE
|
| 21 |
+
HLVTMEAUMYEDMFIMUMEEBEUKEAITNWOIIOSGTIAUPBUINUQGYOAAAETCJGOEMWQEAOPUTTDAAQEESKISO
|
| 22 |
+
AIIOEAAAUEUUOEOOUAIIIIOEEIEAAAAUAIAEUUOUEUOAUAOIUAOUAAIUIIIE
|
| 23 |
+
EMLEKLIXUPNUEAUEAXUCKHPUEJBUIAKJTKCYIGITCIAUPIQAZUO
|
| 24 |
+
RGQQRTUSHOIUEJBEYZSHIIRDASATUUPUBKTHHUZNTPNLOILOOQYU
|
| 25 |
+
SYMPHXFDDRQRPMZTJBVFYWMPLGBRBPRYMTTBDBNTMTJFYJ
|
| 26 |
+
AOEEUOAOOUEUUUUEEOAOIOOAAEIEAIEUOIAOOAIOUAAUIUEUIOIUUEEOOAEOIEUIUOOOIEIUEIAEEIIEIEEEEAUIOEIIUE
|
| 27 |
+
UVZVEOMIJOOAWGLCIEIAUBSQPRM
|
| 28 |
+
UUKWEQAESOAANZPGYMYEDHQEQZWUPZRZIHIIYEUEICKALGANOHKMIEXMXCUAXXYLODOZKEOUGDFKCNI
|
| 29 |
+
OOKMHREFNKYAYIIGKZTIQBUUAEOIOUAKXFIYTGLBZAEEGIEBZEUVUW
|
| 30 |
+
OAAOOEUIEOIEAOIOEOAOEIUAEOAAAEAUEOUIAEEOAUOEIEOAOOAAUAUAOAIUAIIAOAAOAOUOEAEAIUUUUIOAOO
|
| 31 |
+
AYOOZMUIADIDNXXHTMDEFFDDJIMPJANSTOAUHSAIGAFXJHTAABWUZBURBOVJEDZICDOBEAXIJADNLMSKHAOAFEJPHWIAHC
|
| 32 |
+
KDIYULAIEGHARWVOIKBAUTEINPMEBAPRETFOUL
|
| 33 |
+
OBHMEAIJAJEROOFEHOHEYEVGHHOOUTIPAETOEAQOJVICAUNLWNUL
|
| 34 |
+
GLZIAUAIULAYREOPAALTETAGFHAAURKILIEAAZAOOLJNBZKKICUIZOQUOEUKKIDUBUTQOUVRAUWNYIQAPASQA
|
| 35 |
+
PTCJRYMLRWZVMZZPBKPNSDMFTCFKLCZXLPQLNQCLDXQVQZMYHBXPLQMXMHJQFKLHNXTKCRZMRKBWDTBBPYFTMLBQZMVVRBTXBCM
|
| 36 |
+
OKMEOEQIUSFATUOTONBRYEEUUUDGEITUGRARKUIUGOJIAOEGUKJOPIAYZBGKOEFOFHOXIJTCEOOEMSSOFCEXIUYOF
|
| 37 |
+
ALECOEAGWFOIEERMFTABOYKUCIXJRZMV
|
| 38 |
+
OEOQUIAFDWEXDKOSAFVUMBBYVEUUWDETZUGNHWJEIWAIHITNAMFLYPIGJOLAOCPFOTOEHVEARVPXCSTITMHA
|
| 39 |
+
OXEOURJOEUEJUUTUEIEQORXSBGLUIIARAVUBPUICEIJAIILEQDBIIQONE
|
| 40 |
+
UFOVKZEOUTPUJSWEITEUAIYDRIBGUIUIOEII
|
| 41 |
+
XHWYBOALEKWBXNTCUJUZUMPMXULCJQUELATALEPLSAGAWOVOULNCOFYIUZGORZGAHIVAQTFJLUEHAREICHTTJCBNIEEXXPIIA
|
| 42 |
+
IPQALOOEQAWOTODUOFNIAZGQPUTHFFSAEZWOOGYEVQSHRIKCALEUSDAVBUFKIACUSIAKSBLU
|
| 43 |
+
LNJYCVQZUUIKAFAIJSVMZPT
|
| 44 |
+
IEOFAAANDPZTKXEOBULZIEL
|
| 45 |
+
GJNZWNDWKKNPLRRBSSDNHXFZ
|
| 46 |
+
KTNIUDNSSOOFAMLGAXJGKXOEBHGEOGQQELSAAEZAGKEFEYYRLETFAEBOAHASLIZUUEAGCP
|
| 47 |
+
GMJAIDRIBTPAOJATREMCOOVXODUIHEUBSAGF
|
| 48 |
+
MYNTULUYAUBJWTUHTUUOWEOUUIQPGPKFPEAUUAOOARIVSDIQEIMCUIQUQDAUAIIENPILCBGIOCVNUR
|
| 49 |
+
OOOYSRHWNQELBPPMEPOMAZUEZWZAUBAOHNEEYXACMAKUUHUEAULHHBILUHWIONXKNFEAIAZOEUXIZOKJBUONPQAXPEOIRCX
|
| 50 |
+
LEAEJOUUJOHCANBFJVIEEAZAEBUEWFXDECKUN
|
| 51 |
+
AOWESABWHAIARBELWCPEMRJSIE
|
| 52 |
+
AHKELEGPWUNIMUEIUAFOEMAJVFNAEGDOIPASOCLZGPBEAZECGJUUOKHFZSIICWUGRGEAAIZANQIEFVNANAITXIOVDVAEOE
|
| 53 |
+
EASAYUEOXQXEAKAFIUOEAALAUIIUUGPA
|
| 54 |
+
FBBNOBTGQYATFOVKWIHAHOXQRNOAAIEUUUIKGFQMGEWYYINOIIEQNQHOQKOOLIXIAKOFEURNOZUKAGAVQAYNQ
|
2021/quals/consistency_ch1.md
ADDED
|
@@ -0,0 +1,33 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
**Note: This problem shares similarities with [Chapter 2](https://www.facebook.com/codingcompetitions/hacker-cup/2021/qualification-round/problems/A2). The solution to either chapter may help with solving the other, so please consider reading both first.**
|
| 2 |
+
|
| 3 |
+
Connie received a string \(S\) for her birthday, consisting entirely of uppercase letters (each between `"A"` and `"Z"`, inclusive).
|
| 4 |
+
|
| 5 |
+
However, Connie really only likes nice, *consistent* strings. She considers a string to be consistent if and only if all of its letters are the same.
|
| 6 |
+
|
| 7 |
+
Each second, Connie may choose one letter in \(S\) and replace it with a different letter. **If her chosen letter is a vowel, then she may replace it with any consonant of her choice. On the other hand, if her chosen letter is a consonant, then she may replace it with any vowel of her choice.** The \(5\) letters `"A"`, `"E"`, `"I"`, `"O"`, and `"U"` are considered vowels, while the remaining \(21\) letters of the alphabet are considered consonants. If a letter appears multiple times in \(S\), she may only replace a single occurrence per second.
|
| 8 |
+
|
| 9 |
+
Help her determine the minimum number of seconds required to change \(S\) into any consistent string. Note that \(S\) might already be consistent, in which case \(0\) seconds would be required.
|
| 10 |
+
|
| 11 |
+
# Constraints
|
| 12 |
+
|
| 13 |
+
\(1 \le T \le 45\)
|
| 14 |
+
\(1 \le |S| \le 100\)
|
| 15 |
+
`"A"` \(\le S_i \le\) `"Z"`
|
| 16 |
+
|
| 17 |
+
The sum of \(|S|\) across all test cases is at most \(4{,}500\).
|
| 18 |
+
|
| 19 |
+
# Input
|
| 20 |
+
|
| 21 |
+
Input begins with an integer \(T\), the number of birthdays Connie has had. For each birthday, there is a single line containing the string \(S\).
|
| 22 |
+
|
| 23 |
+
# Output
|
| 24 |
+
|
| 25 |
+
For the \(i\)th string, print a line containing *"Case #i: "* followed by the minimum number of seconds required to change \(S\) into any consistent string.
|
| 26 |
+
|
| 27 |
+
# Sample Explanation
|
| 28 |
+
|
| 29 |
+
In the first case, Connie could replace the second and third letters (`"B"` and `"C"`) each with `"A"`, yielding the string `"AAA"` in \(2\) seconds.
|
| 30 |
+
|
| 31 |
+
In the second case, `"F"` is already consistent.
|
| 32 |
+
|
| 33 |
+
In the third case, Connie could replace the first, third, and fifth letters (`"B"`, `"N"`, and `"N"`) each with `"A"`, yielding the string `"AAAAAA"` in \(3\) seconds.
|
2021/quals/consistency_ch1.out
ADDED
|
@@ -0,0 +1,53 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Case #1: 2
|
| 2 |
+
Case #2: 0
|
| 3 |
+
Case #3: 3
|
| 4 |
+
Case #4: 4
|
| 5 |
+
Case #5: 5
|
| 6 |
+
Case #6: 12
|
| 7 |
+
Case #7: 17
|
| 8 |
+
Case #8: 100
|
| 9 |
+
Case #9: 100
|
| 10 |
+
Case #10: 94
|
| 11 |
+
Case #11: 128
|
| 12 |
+
Case #12: 30
|
| 13 |
+
Case #13: 67
|
| 14 |
+
Case #14: 93
|
| 15 |
+
Case #15: 95
|
| 16 |
+
Case #16: 76
|
| 17 |
+
Case #17: 70
|
| 18 |
+
Case #18: 66
|
| 19 |
+
Case #19: 85
|
| 20 |
+
Case #20: 99
|
| 21 |
+
Case #21: 60
|
| 22 |
+
Case #22: 60
|
| 23 |
+
Case #23: 57
|
| 24 |
+
Case #24: 46
|
| 25 |
+
Case #25: 94
|
| 26 |
+
Case #26: 33
|
| 27 |
+
Case #27: 94
|
| 28 |
+
Case #28: 67
|
| 29 |
+
Case #29: 86
|
| 30 |
+
Case #30: 102
|
| 31 |
+
Case #31: 47
|
| 32 |
+
Case #32: 62
|
| 33 |
+
Case #33: 98
|
| 34 |
+
Case #34: 99
|
| 35 |
+
Case #35: 106
|
| 36 |
+
Case #36: 37
|
| 37 |
+
Case #37: 102
|
| 38 |
+
Case #38: 72
|
| 39 |
+
Case #39: 43
|
| 40 |
+
Case #40: 114
|
| 41 |
+
Case #41: 86
|
| 42 |
+
Case #42: 25
|
| 43 |
+
Case #43: 28
|
| 44 |
+
Case #44: 24
|
| 45 |
+
Case #45: 80
|
| 46 |
+
Case #46: 43
|
| 47 |
+
Case #47: 88
|
| 48 |
+
Case #48: 117
|
| 49 |
+
Case #49: 41
|
| 50 |
+
Case #50: 29
|
| 51 |
+
Case #51: 114
|
| 52 |
+
Case #52: 38
|
| 53 |
+
Case #53: 100
|
2021/quals/consistency_ch1_sol.md
ADDED
|
@@ -0,0 +1,5 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
There are only \(26\) possible consistent strings which \(S\) might be changed into, with all characters in \(S\) ending up equal to some character \(x\) (`"A"` \(\le x \le\) `"Z"`). We'll consider each possible value of \(x\) and compute the total number of seconds required to change all characters in \(S\) into \(x\), with the minimum of those \(26\) possible totals being our final answer.
|
| 2 |
+
|
| 3 |
+
For each character \(x\), we'll need to consider each character \(c\) in \(S\) and compute the number of seconds required to change \(c\) into \(x\). If \(c = x\), then \(0\) seconds are required. If \(c\) is a vowel while \(x\) is a consonant (or vice versa), then \(1\) second is required. Otherwise (that is, \(c\) and \(x\) differ but are either both vowels or both consonants), \(2\) seconds are required.
|
| 4 |
+
|
| 5 |
+
[See David Harmeyer's solution video here](https://youtu.be/p5yPTHNUTlc).
|
2021/quals/consistency_ch2.cpp
ADDED
|
@@ -0,0 +1,48 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
#include <algorithm>
|
| 2 |
+
#include <iostream>
|
| 3 |
+
using namespace std;
|
| 4 |
+
|
| 5 |
+
const int INF = 1e6;
|
| 6 |
+
|
| 7 |
+
string S;
|
| 8 |
+
int K;
|
| 9 |
+
int dist[26][26];
|
| 10 |
+
|
| 11 |
+
int solve() {
|
| 12 |
+
for (int i = 0; i < 26; i++) {
|
| 13 |
+
for (int j = 0; j < 26; j++) {
|
| 14 |
+
dist[i][j] = (i == j) ? 0 : INF;
|
| 15 |
+
}
|
| 16 |
+
}
|
| 17 |
+
cin >> S >> K;
|
| 18 |
+
for (int i = 0; i < K; i++) {
|
| 19 |
+
char a, b;
|
| 20 |
+
cin >> a >> b;
|
| 21 |
+
dist[a - 'A'][b - 'A'] = 1;
|
| 22 |
+
}
|
| 23 |
+
for (int k = 0; k < 26; k++) {
|
| 24 |
+
for (int i = 0; i < 26; i++) {
|
| 25 |
+
for (int j = 0; j < 26; j++) {
|
| 26 |
+
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
|
| 27 |
+
}
|
| 28 |
+
}
|
| 29 |
+
}
|
| 30 |
+
int ans = INF;
|
| 31 |
+
for (int i = 0; i < 26; i++) {
|
| 32 |
+
int curr = 0;
|
| 33 |
+
for (char c : S) {
|
| 34 |
+
curr += dist[c - 'A'][i];
|
| 35 |
+
}
|
| 36 |
+
ans = min(ans, curr);
|
| 37 |
+
}
|
| 38 |
+
return ans == INF ? -1 : ans;
|
| 39 |
+
}
|
| 40 |
+
|
| 41 |
+
int main() {
|
| 42 |
+
int T;
|
| 43 |
+
cin >> T;
|
| 44 |
+
for (int t = 1; t <= T; t++) {
|
| 45 |
+
cout << "Case #" << t << ": " << solve() << endl;
|
| 46 |
+
}
|
| 47 |
+
return 0;
|
| 48 |
+
}
|
2021/quals/consistency_ch2.in
ADDED
|
@@ -0,0 +1,7292 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
51
|
| 2 |
+
ABC
|
| 3 |
+
2
|
| 4 |
+
BA
|
| 5 |
+
CA
|
| 6 |
+
ABC
|
| 7 |
+
2
|
| 8 |
+
AB
|
| 9 |
+
AC
|
| 10 |
+
F
|
| 11 |
+
0
|
| 12 |
+
BANANA
|
| 13 |
+
4
|
| 14 |
+
AB
|
| 15 |
+
AN
|
| 16 |
+
BA
|
| 17 |
+
NA
|
| 18 |
+
FBHC
|
| 19 |
+
4
|
| 20 |
+
FB
|
| 21 |
+
BF
|
| 22 |
+
HC
|
| 23 |
+
CH
|
| 24 |
+
FOXEN
|
| 25 |
+
8
|
| 26 |
+
NI
|
| 27 |
+
OE
|
| 28 |
+
NX
|
| 29 |
+
EW
|
| 30 |
+
OI
|
| 31 |
+
FE
|
| 32 |
+
FN
|
| 33 |
+
XW
|
| 34 |
+
CONSISTENCY
|
| 35 |
+
26
|
| 36 |
+
AB
|
| 37 |
+
BC
|
| 38 |
+
CD
|
| 39 |
+
DE
|
| 40 |
+
EF
|
| 41 |
+
FG
|
| 42 |
+
GH
|
| 43 |
+
HI
|
| 44 |
+
IJ
|
| 45 |
+
JK
|
| 46 |
+
KL
|
| 47 |
+
LM
|
| 48 |
+
MN
|
| 49 |
+
NO
|
| 50 |
+
OP
|
| 51 |
+
PQ
|
| 52 |
+
QR
|
| 53 |
+
RS
|
| 54 |
+
ST
|
| 55 |
+
TU
|
| 56 |
+
UV
|
| 57 |
+
VW
|
| 58 |
+
WX
|
| 59 |
+
XY
|
| 60 |
+
YZ
|
| 61 |
+
ZA
|
| 62 |
+
ABC
|
| 63 |
+
9
|
| 64 |
+
AB
|
| 65 |
+
BX
|
| 66 |
+
BZ
|
| 67 |
+
CY
|
| 68 |
+
IJ
|
| 69 |
+
JK
|
| 70 |
+
KC
|
| 71 |
+
XI
|
| 72 |
+
YZ
|
| 73 |
+
KJJQTQEURABTEDFLTDPQTQLULKXAVSMDHZBQWUNNRUSZQLXNXT
|
| 74 |
+
50
|
| 75 |
+
PF
|
| 76 |
+
VM
|
| 77 |
+
MW
|
| 78 |
+
FG
|
| 79 |
+
QP
|
| 80 |
+
WD
|
| 81 |
+
XV
|
| 82 |
+
QF
|
| 83 |
+
YG
|
| 84 |
+
MG
|
| 85 |
+
DJ
|
| 86 |
+
VB
|
| 87 |
+
ZY
|
| 88 |
+
VN
|
| 89 |
+
UK
|
| 90 |
+
SL
|
| 91 |
+
NI
|
| 92 |
+
LG
|
| 93 |
+
GQ
|
| 94 |
+
PU
|
| 95 |
+
KX
|
| 96 |
+
XD
|
| 97 |
+
UR
|
| 98 |
+
NY
|
| 99 |
+
JL
|
| 100 |
+
XK
|
| 101 |
+
XF
|
| 102 |
+
OV
|
| 103 |
+
DV
|
| 104 |
+
KJ
|
| 105 |
+
HF
|
| 106 |
+
AM
|
| 107 |
+
CG
|
| 108 |
+
GF
|
| 109 |
+
XM
|
| 110 |
+
RY
|
| 111 |
+
DY
|
| 112 |
+
MR
|
| 113 |
+
FR
|
| 114 |
+
MS
|
| 115 |
+
RN
|
| 116 |
+
UD
|
| 117 |
+
JT
|
| 118 |
+
XP
|
| 119 |
+
YF
|
| 120 |
+
BP
|
| 121 |
+
RQ
|
| 122 |
+
TV
|
| 123 |
+
EA
|
| 124 |
+
BM
|
| 125 |
+
CTIRHZXUMSTXXFUGBFFCKODOCDVJXDNJPWSILUQPKLWOEXLKRSDUYLTENZIZXMAVSHVTJXTRIHZOFKDBPWTZLEIOXKCIQCIDHEKL
|
| 126 |
+
300
|
| 127 |
+
HJ
|
| 128 |
+
YF
|
| 129 |
+
WS
|
| 130 |
+
KQ
|
| 131 |
+
SV
|
| 132 |
+
EV
|
| 133 |
+
YV
|
| 134 |
+
MC
|
| 135 |
+
CF
|
| 136 |
+
IV
|
| 137 |
+
YS
|
| 138 |
+
LK
|
| 139 |
+
LF
|
| 140 |
+
RC
|
| 141 |
+
SC
|
| 142 |
+
WY
|
| 143 |
+
JO
|
| 144 |
+
SM
|
| 145 |
+
US
|
| 146 |
+
CE
|
| 147 |
+
QY
|
| 148 |
+
SE
|
| 149 |
+
UY
|
| 150 |
+
GQ
|
| 151 |
+
RQ
|
| 152 |
+
SF
|
| 153 |
+
RH
|
| 154 |
+
LP
|
| 155 |
+
QH
|
| 156 |
+
CU
|
| 157 |
+
TR
|
| 158 |
+
CH
|
| 159 |
+
DV
|
| 160 |
+
OS
|
| 161 |
+
TV
|
| 162 |
+
BI
|
| 163 |
+
WB
|
| 164 |
+
DM
|
| 165 |
+
RB
|
| 166 |
+
MO
|
| 167 |
+
DE
|
| 168 |
+
OT
|
| 169 |
+
UT
|
| 170 |
+
DY
|
| 171 |
+
VC
|
| 172 |
+
MN
|
| 173 |
+
WF
|
| 174 |
+
WV
|
| 175 |
+
XR
|
| 176 |
+
HI
|
| 177 |
+
NE
|
| 178 |
+
VB
|
| 179 |
+
GV
|
| 180 |
+
PW
|
| 181 |
+
FG
|
| 182 |
+
NY
|
| 183 |
+
KR
|
| 184 |
+
UH
|
| 185 |
+
KJ
|
| 186 |
+
FR
|
| 187 |
+
MG
|
| 188 |
+
ME
|
| 189 |
+
VL
|
| 190 |
+
IO
|
| 191 |
+
EJ
|
| 192 |
+
BK
|
| 193 |
+
NI
|
| 194 |
+
WR
|
| 195 |
+
GP
|
| 196 |
+
WM
|
| 197 |
+
MS
|
| 198 |
+
NP
|
| 199 |
+
BE
|
| 200 |
+
BT
|
| 201 |
+
CP
|
| 202 |
+
HF
|
| 203 |
+
XQ
|
| 204 |
+
EI
|
| 205 |
+
NR
|
| 206 |
+
FY
|
| 207 |
+
WD
|
| 208 |
+
YD
|
| 209 |
+
KB
|
| 210 |
+
KN
|
| 211 |
+
XJ
|
| 212 |
+
FJ
|
| 213 |
+
QS
|
| 214 |
+
LJ
|
| 215 |
+
JV
|
| 216 |
+
OW
|
| 217 |
+
TY
|
| 218 |
+
UE
|
| 219 |
+
MJ
|
| 220 |
+
GL
|
| 221 |
+
NB
|
| 222 |
+
WL
|
| 223 |
+
HK
|
| 224 |
+
OG
|
| 225 |
+
CJ
|
| 226 |
+
KL
|
| 227 |
+
AB
|
| 228 |
+
KT
|
| 229 |
+
XH
|
| 230 |
+
EX
|
| 231 |
+
DH
|
| 232 |
+
HE
|
| 233 |
+
KO
|
| 234 |
+
KU
|
| 235 |
+
EU
|
| 236 |
+
PB
|
| 237 |
+
MA
|
| 238 |
+
PD
|
| 239 |
+
XU
|
| 240 |
+
AT
|
| 241 |
+
XK
|
| 242 |
+
FH
|
| 243 |
+
ST
|
| 244 |
+
TG
|
| 245 |
+
XA
|
| 246 |
+
YR
|
| 247 |
+
WC
|
| 248 |
+
CO
|
| 249 |
+
OQ
|
| 250 |
+
QC
|
| 251 |
+
JU
|
| 252 |
+
AE
|
| 253 |
+
HR
|
| 254 |
+
VS
|
| 255 |
+
BX
|
| 256 |
+
EK
|
| 257 |
+
OU
|
| 258 |
+
VW
|
| 259 |
+
SD
|
| 260 |
+
DR
|
| 261 |
+
UG
|
| 262 |
+
MB
|
| 263 |
+
LE
|
| 264 |
+
TK
|
| 265 |
+
KE
|
| 266 |
+
PY
|
| 267 |
+
LU
|
| 268 |
+
YK
|
| 269 |
+
HP
|
| 270 |
+
XG
|
| 271 |
+
LX
|
| 272 |
+
AR
|
| 273 |
+
CV
|
| 274 |
+
GI
|
| 275 |
+
OI
|
| 276 |
+
PK
|
| 277 |
+
GN
|
| 278 |
+
EO
|
| 279 |
+
BS
|
| 280 |
+
FU
|
| 281 |
+
XO
|
| 282 |
+
OL
|
| 283 |
+
AW
|
| 284 |
+
OH
|
| 285 |
+
RO
|
| 286 |
+
QB
|
| 287 |
+
GO
|
| 288 |
+
YQ
|
| 289 |
+
VJ
|
| 290 |
+
WE
|
| 291 |
+
IX
|
| 292 |
+
TS
|
| 293 |
+
DI
|
| 294 |
+
FQ
|
| 295 |
+
UA
|
| 296 |
+
RT
|
| 297 |
+
IF
|
| 298 |
+
QE
|
| 299 |
+
OE
|
| 300 |
+
JM
|
| 301 |
+
SW
|
| 302 |
+
CS
|
| 303 |
+
XM
|
| 304 |
+
BU
|
| 305 |
+
AU
|
| 306 |
+
SB
|
| 307 |
+
MR
|
| 308 |
+
FC
|
| 309 |
+
TO
|
| 310 |
+
SP
|
| 311 |
+
YJ
|
| 312 |
+
QM
|
| 313 |
+
MK
|
| 314 |
+
CI
|
| 315 |
+
HT
|
| 316 |
+
IJ
|
| 317 |
+
RY
|
| 318 |
+
XP
|
| 319 |
+
HM
|
| 320 |
+
BC
|
| 321 |
+
RP
|
| 322 |
+
DA
|
| 323 |
+
BA
|
| 324 |
+
YE
|
| 325 |
+
WN
|
| 326 |
+
GD
|
| 327 |
+
SO
|
| 328 |
+
PM
|
| 329 |
+
NL
|
| 330 |
+
HS
|
| 331 |
+
PE
|
| 332 |
+
LD
|
| 333 |
+
XE
|
| 334 |
+
QN
|
| 335 |
+
MT
|
| 336 |
+
BL
|
| 337 |
+
PV
|
| 338 |
+
KX
|
| 339 |
+
CK
|
| 340 |
+
JS
|
| 341 |
+
QR
|
| 342 |
+
CM
|
| 343 |
+
PH
|
| 344 |
+
FE
|
| 345 |
+
HU
|
| 346 |
+
UP
|
| 347 |
+
SN
|
| 348 |
+
QI
|
| 349 |
+
RF
|
| 350 |
+
ED
|
| 351 |
+
TP
|
| 352 |
+
AO
|
| 353 |
+
UW
|
| 354 |
+
XL
|
| 355 |
+
DS
|
| 356 |
+
BV
|
| 357 |
+
MX
|
| 358 |
+
JH
|
| 359 |
+
DG
|
| 360 |
+
EY
|
| 361 |
+
FL
|
| 362 |
+
HL
|
| 363 |
+
EF
|
| 364 |
+
WQ
|
| 365 |
+
XI
|
| 366 |
+
UB
|
| 367 |
+
EP
|
| 368 |
+
CY
|
| 369 |
+
SX
|
| 370 |
+
BP
|
| 371 |
+
WX
|
| 372 |
+
QD
|
| 373 |
+
FO
|
| 374 |
+
LR
|
| 375 |
+
HY
|
| 376 |
+
LA
|
| 377 |
+
VR
|
| 378 |
+
FX
|
| 379 |
+
AQ
|
| 380 |
+
BY
|
| 381 |
+
LM
|
| 382 |
+
TE
|
| 383 |
+
FW
|
| 384 |
+
OD
|
| 385 |
+
SY
|
| 386 |
+
CA
|
| 387 |
+
RE
|
| 388 |
+
KF
|
| 389 |
+
VX
|
| 390 |
+
OP
|
| 391 |
+
NV
|
| 392 |
+
WU
|
| 393 |
+
EQ
|
| 394 |
+
HC
|
| 395 |
+
WG
|
| 396 |
+
KC
|
| 397 |
+
KG
|
| 398 |
+
WH
|
| 399 |
+
SQ
|
| 400 |
+
GK
|
| 401 |
+
VQ
|
| 402 |
+
FV
|
| 403 |
+
BJ
|
| 404 |
+
JN
|
| 405 |
+
EN
|
| 406 |
+
KA
|
| 407 |
+
VD
|
| 408 |
+
TA
|
| 409 |
+
EL
|
| 410 |
+
LN
|
| 411 |
+
PG
|
| 412 |
+
OV
|
| 413 |
+
UO
|
| 414 |
+
XV
|
| 415 |
+
OJ
|
| 416 |
+
WA
|
| 417 |
+
KP
|
| 418 |
+
DN
|
| 419 |
+
QP
|
| 420 |
+
QK
|
| 421 |
+
YT
|
| 422 |
+
GE
|
| 423 |
+
DT
|
| 424 |
+
YN
|
| 425 |
+
KW
|
| 426 |
+
JE
|
| 427 |
+
UETNRSJASUXUTTLLGAJVQXKWSJBLTPCFMFIIPTUEYYNUVUETUKKIQMWCHJADPRAUPKWNSUCJHVBSBXMHUGNUHYNVHAIMAOIGZCUO
|
| 428 |
+
300
|
| 429 |
+
GM
|
| 430 |
+
LX
|
| 431 |
+
CE
|
| 432 |
+
FN
|
| 433 |
+
CM
|
| 434 |
+
EQ
|
| 435 |
+
HU
|
| 436 |
+
XZ
|
| 437 |
+
KS
|
| 438 |
+
RV
|
| 439 |
+
CX
|
| 440 |
+
CJ
|
| 441 |
+
CZ
|
| 442 |
+
CL
|
| 443 |
+
CG
|
| 444 |
+
BE
|
| 445 |
+
OS
|
| 446 |
+
FI
|
| 447 |
+
FS
|
| 448 |
+
IT
|
| 449 |
+
FU
|
| 450 |
+
LQ
|
| 451 |
+
GV
|
| 452 |
+
AV
|
| 453 |
+
MP
|
| 454 |
+
CD
|
| 455 |
+
KV
|
| 456 |
+
HS
|
| 457 |
+
BM
|
| 458 |
+
IY
|
| 459 |
+
AB
|
| 460 |
+
NV
|
| 461 |
+
AD
|
| 462 |
+
KY
|
| 463 |
+
VX
|
| 464 |
+
AR
|
| 465 |
+
GQ
|
| 466 |
+
HI
|
| 467 |
+
LS
|
| 468 |
+
GJ
|
| 469 |
+
FY
|
| 470 |
+
OQ
|
| 471 |
+
DO
|
| 472 |
+
JS
|
| 473 |
+
MX
|
| 474 |
+
MV
|
| 475 |
+
JU
|
| 476 |
+
AZ
|
| 477 |
+
AS
|
| 478 |
+
PR
|
| 479 |
+
DT
|
| 480 |
+
JM
|
| 481 |
+
EI
|
| 482 |
+
CH
|
| 483 |
+
IM
|
| 484 |
+
QU
|
| 485 |
+
GZ
|
| 486 |
+
RZ
|
| 487 |
+
GR
|
| 488 |
+
SY
|
| 489 |
+
LZ
|
| 490 |
+
JN
|
| 491 |
+
DU
|
| 492 |
+
UX
|
| 493 |
+
AU
|
| 494 |
+
DN
|
| 495 |
+
EH
|
| 496 |
+
BC
|
| 497 |
+
RU
|
| 498 |
+
CT
|
| 499 |
+
FJ
|
| 500 |
+
QY
|
| 501 |
+
IK
|
| 502 |
+
DJ
|
| 503 |
+
QS
|
| 504 |
+
KW
|
| 505 |
+
NW
|
| 506 |
+
RW
|
| 507 |
+
KT
|
| 508 |
+
JT
|
| 509 |
+
GS
|
| 510 |
+
GO
|
| 511 |
+
AO
|
| 512 |
+
NT
|
| 513 |
+
WX
|
| 514 |
+
HX
|
| 515 |
+
QR
|
| 516 |
+
SU
|
| 517 |
+
HY
|
| 518 |
+
MU
|
| 519 |
+
KX
|
| 520 |
+
NP
|
| 521 |
+
JZ
|
| 522 |
+
DZ
|
| 523 |
+
LP
|
| 524 |
+
NY
|
| 525 |
+
VY
|
| 526 |
+
ER
|
| 527 |
+
PQ
|
| 528 |
+
PS
|
| 529 |
+
TW
|
| 530 |
+
EX
|
| 531 |
+
NS
|
| 532 |
+
FO
|
| 533 |
+
JK
|
| 534 |
+
KQ
|
| 535 |
+
FH
|
| 536 |
+
DW
|
| 537 |
+
HK
|
| 538 |
+
HJ
|
| 539 |
+
MS
|
| 540 |
+
XY
|
| 541 |
+
GI
|
| 542 |
+
TZ
|
| 543 |
+
TX
|
| 544 |
+
BV
|
| 545 |
+
LW
|
| 546 |
+
IW
|
| 547 |
+
JO
|
| 548 |
+
ST
|
| 549 |
+
IS
|
| 550 |
+
GU
|
| 551 |
+
GH
|
| 552 |
+
EP
|
| 553 |
+
AJ
|
| 554 |
+
MN
|
| 555 |
+
EV
|
| 556 |
+
BL
|
| 557 |
+
TY
|
| 558 |
+
CP
|
| 559 |
+
UY
|
| 560 |
+
OZ
|
| 561 |
+
EM
|
| 562 |
+
JR
|
| 563 |
+
BO
|
| 564 |
+
ET
|
| 565 |
+
EG
|
| 566 |
+
MY
|
| 567 |
+
AM
|
| 568 |
+
DQ
|
| 569 |
+
BF
|
| 570 |
+
FG
|
| 571 |
+
LY
|
| 572 |
+
AQ
|
| 573 |
+
FX
|
| 574 |
+
CY
|
| 575 |
+
OP
|
| 576 |
+
GW
|
| 577 |
+
JQ
|
| 578 |
+
CI
|
| 579 |
+
CF
|
| 580 |
+
QT
|
| 581 |
+
AG
|
| 582 |
+
KN
|
| 583 |
+
GP
|
| 584 |
+
IV
|
| 585 |
+
SZ
|
| 586 |
+
HM
|
| 587 |
+
AX
|
| 588 |
+
FR
|
| 589 |
+
FM
|
| 590 |
+
HL
|
| 591 |
+
DH
|
| 592 |
+
CN
|
| 593 |
+
HN
|
| 594 |
+
RY
|
| 595 |
+
WY
|
| 596 |
+
OY
|
| 597 |
+
OX
|
| 598 |
+
IN
|
| 599 |
+
EU
|
| 600 |
+
RX
|
| 601 |
+
BW
|
| 602 |
+
NQ
|
| 603 |
+
CQ
|
| 604 |
+
DX
|
| 605 |
+
MW
|
| 606 |
+
UV
|
| 607 |
+
PU
|
| 608 |
+
QV
|
| 609 |
+
AC
|
| 610 |
+
AF
|
| 611 |
+
IU
|
| 612 |
+
EO
|
| 613 |
+
HW
|
| 614 |
+
DY
|
| 615 |
+
MO
|
| 616 |
+
WZ
|
| 617 |
+
CK
|
| 618 |
+
HR
|
| 619 |
+
EK
|
| 620 |
+
IX
|
| 621 |
+
KU
|
| 622 |
+
LR
|
| 623 |
+
DI
|
| 624 |
+
BY
|
| 625 |
+
CR
|
| 626 |
+
KR
|
| 627 |
+
BZ
|
| 628 |
+
BK
|
| 629 |
+
YZ
|
| 630 |
+
BR
|
| 631 |
+
EY
|
| 632 |
+
DF
|
| 633 |
+
EN
|
| 634 |
+
AW
|
| 635 |
+
SV
|
| 636 |
+
EF
|
| 637 |
+
FT
|
| 638 |
+
HZ
|
| 639 |
+
DK
|
| 640 |
+
CU
|
| 641 |
+
PZ
|
| 642 |
+
HO
|
| 643 |
+
IP
|
| 644 |
+
BS
|
| 645 |
+
AN
|
| 646 |
+
ES
|
| 647 |
+
EZ
|
| 648 |
+
HP
|
| 649 |
+
CS
|
| 650 |
+
IR
|
| 651 |
+
VZ
|
| 652 |
+
VW
|
| 653 |
+
AH
|
| 654 |
+
GY
|
| 655 |
+
LN
|
| 656 |
+
FW
|
| 657 |
+
AI
|
| 658 |
+
RT
|
| 659 |
+
FK
|
| 660 |
+
HV
|
| 661 |
+
CO
|
| 662 |
+
MQ
|
| 663 |
+
LM
|
| 664 |
+
NX
|
| 665 |
+
UZ
|
| 666 |
+
JV
|
| 667 |
+
EL
|
| 668 |
+
MZ
|
| 669 |
+
FP
|
| 670 |
+
EW
|
| 671 |
+
KZ
|
| 672 |
+
HQ
|
| 673 |
+
DR
|
| 674 |
+
NU
|
| 675 |
+
BN
|
| 676 |
+
BD
|
| 677 |
+
JY
|
| 678 |
+
IZ
|
| 679 |
+
JX
|
| 680 |
+
SW
|
| 681 |
+
KL
|
| 682 |
+
PT
|
| 683 |
+
BP
|
| 684 |
+
GN
|
| 685 |
+
GL
|
| 686 |
+
TV
|
| 687 |
+
PW
|
| 688 |
+
GX
|
| 689 |
+
BX
|
| 690 |
+
AE
|
| 691 |
+
QX
|
| 692 |
+
IQ
|
| 693 |
+
KO
|
| 694 |
+
IJ
|
| 695 |
+
NZ
|
| 696 |
+
NO
|
| 697 |
+
OT
|
| 698 |
+
DG
|
| 699 |
+
LT
|
| 700 |
+
LU
|
| 701 |
+
OW
|
| 702 |
+
CW
|
| 703 |
+
FQ
|
| 704 |
+
JW
|
| 705 |
+
GK
|
| 706 |
+
DL
|
| 707 |
+
JP
|
| 708 |
+
AP
|
| 709 |
+
NR
|
| 710 |
+
MT
|
| 711 |
+
DE
|
| 712 |
+
OR
|
| 713 |
+
SX
|
| 714 |
+
MR
|
| 715 |
+
RS
|
| 716 |
+
DS
|
| 717 |
+
OU
|
| 718 |
+
EJ
|
| 719 |
+
PX
|
| 720 |
+
UW
|
| 721 |
+
BT
|
| 722 |
+
IO
|
| 723 |
+
FV
|
| 724 |
+
TU
|
| 725 |
+
PY
|
| 726 |
+
BG
|
| 727 |
+
CV
|
| 728 |
+
LO
|
| 729 |
+
UXATTHDNUSYAKHRQFPXSYGLNNHSBIELBBTRLWYLMQGFTOOBSQPQOGQGMNZVHDUEEAJNBFXWHJVOZEBEJTZADPGCDINUJTVUISZJQ
|
| 730 |
+
300
|
| 731 |
+
DL
|
| 732 |
+
DY
|
| 733 |
+
AK
|
| 734 |
+
GI
|
| 735 |
+
CU
|
| 736 |
+
NR
|
| 737 |
+
BZ
|
| 738 |
+
IO
|
| 739 |
+
BL
|
| 740 |
+
DJ
|
| 741 |
+
GU
|
| 742 |
+
PS
|
| 743 |
+
LZ
|
| 744 |
+
OP
|
| 745 |
+
MX
|
| 746 |
+
JN
|
| 747 |
+
EV
|
| 748 |
+
DS
|
| 749 |
+
FM
|
| 750 |
+
FT
|
| 751 |
+
DP
|
| 752 |
+
IQ
|
| 753 |
+
PY
|
| 754 |
+
JL
|
| 755 |
+
CK
|
| 756 |
+
DN
|
| 757 |
+
BY
|
| 758 |
+
KO
|
| 759 |
+
EO
|
| 760 |
+
QZ
|
| 761 |
+
KT
|
| 762 |
+
MR
|
| 763 |
+
KS
|
| 764 |
+
TW
|
| 765 |
+
ET
|
| 766 |
+
JS
|
| 767 |
+
BM
|
| 768 |
+
AY
|
| 769 |
+
JP
|
| 770 |
+
LO
|
| 771 |
+
CZ
|
| 772 |
+
KL
|
| 773 |
+
AU
|
| 774 |
+
DU
|
| 775 |
+
NU
|
| 776 |
+
DW
|
| 777 |
+
BF
|
| 778 |
+
OV
|
| 779 |
+
KP
|
| 780 |
+
CI
|
| 781 |
+
AJ
|
| 782 |
+
JQ
|
| 783 |
+
SX
|
| 784 |
+
DK
|
| 785 |
+
UW
|
| 786 |
+
LM
|
| 787 |
+
IK
|
| 788 |
+
IZ
|
| 789 |
+
GJ
|
| 790 |
+
YZ
|
| 791 |
+
EQ
|
| 792 |
+
HK
|
| 793 |
+
KR
|
| 794 |
+
QR
|
| 795 |
+
EN
|
| 796 |
+
TZ
|
| 797 |
+
PQ
|
| 798 |
+
MV
|
| 799 |
+
HZ
|
| 800 |
+
RS
|
| 801 |
+
NT
|
| 802 |
+
FQ
|
| 803 |
+
FJ
|
| 804 |
+
DM
|
| 805 |
+
CQ
|
| 806 |
+
PT
|
| 807 |
+
BC
|
| 808 |
+
DT
|
| 809 |
+
HP
|
| 810 |
+
VZ
|
| 811 |
+
FL
|
| 812 |
+
AG
|
| 813 |
+
AR
|
| 814 |
+
CP
|
| 815 |
+
TV
|
| 816 |
+
NX
|
| 817 |
+
LR
|
| 818 |
+
FK
|
| 819 |
+
JU
|
| 820 |
+
AH
|
| 821 |
+
EI
|
| 822 |
+
GN
|
| 823 |
+
AS
|
| 824 |
+
GK
|
| 825 |
+
VY
|
| 826 |
+
FP
|
| 827 |
+
GP
|
| 828 |
+
MQ
|
| 829 |
+
SY
|
| 830 |
+
QX
|
| 831 |
+
KX
|
| 832 |
+
EZ
|
| 833 |
+
DZ
|
| 834 |
+
OR
|
| 835 |
+
AT
|
| 836 |
+
FH
|
| 837 |
+
AD
|
| 838 |
+
GR
|
| 839 |
+
JY
|
| 840 |
+
HQ
|
| 841 |
+
BE
|
| 842 |
+
FO
|
| 843 |
+
HW
|
| 844 |
+
EW
|
| 845 |
+
OY
|
| 846 |
+
LY
|
| 847 |
+
SW
|
| 848 |
+
EY
|
| 849 |
+
HS
|
| 850 |
+
MY
|
| 851 |
+
GS
|
| 852 |
+
IN
|
| 853 |
+
FS
|
| 854 |
+
CY
|
| 855 |
+
RY
|
| 856 |
+
OU
|
| 857 |
+
GW
|
| 858 |
+
TU
|
| 859 |
+
AQ
|
| 860 |
+
BO
|
| 861 |
+
ST
|
| 862 |
+
BR
|
| 863 |
+
CL
|
| 864 |
+
CT
|
| 865 |
+
IR
|
| 866 |
+
EH
|
| 867 |
+
HL
|
| 868 |
+
SV
|
| 869 |
+
AI
|
| 870 |
+
SZ
|
| 871 |
+
ES
|
| 872 |
+
HU
|
| 873 |
+
MW
|
| 874 |
+
EJ
|
| 875 |
+
AX
|
| 876 |
+
GQ
|
| 877 |
+
RW
|
| 878 |
+
PW
|
| 879 |
+
WZ
|
| 880 |
+
VX
|
| 881 |
+
DQ
|
| 882 |
+
FX
|
| 883 |
+
NY
|
| 884 |
+
AW
|
| 885 |
+
KM
|
| 886 |
+
OT
|
| 887 |
+
FY
|
| 888 |
+
GO
|
| 889 |
+
SU
|
| 890 |
+
CG
|
| 891 |
+
JT
|
| 892 |
+
IW
|
| 893 |
+
AE
|
| 894 |
+
RZ
|
| 895 |
+
HN
|
| 896 |
+
NV
|
| 897 |
+
FU
|
| 898 |
+
DI
|
| 899 |
+
BW
|
| 900 |
+
MP
|
| 901 |
+
HJ
|
| 902 |
+
BK
|
| 903 |
+
RX
|
| 904 |
+
WX
|
| 905 |
+
OS
|
| 906 |
+
PX
|
| 907 |
+
LS
|
| 908 |
+
BG
|
| 909 |
+
LT
|
| 910 |
+
RV
|
| 911 |
+
EK
|
| 912 |
+
CW
|
| 913 |
+
TX
|
| 914 |
+
JR
|
| 915 |
+
GX
|
| 916 |
+
GY
|
| 917 |
+
KU
|
| 918 |
+
GL
|
| 919 |
+
CX
|
| 920 |
+
CM
|
| 921 |
+
LN
|
| 922 |
+
MT
|
| 923 |
+
CR
|
| 924 |
+
HM
|
| 925 |
+
CH
|
| 926 |
+
UV
|
| 927 |
+
MS
|
| 928 |
+
BH
|
| 929 |
+
HO
|
| 930 |
+
RT
|
| 931 |
+
DE
|
| 932 |
+
DV
|
| 933 |
+
AB
|
| 934 |
+
WY
|
| 935 |
+
NP
|
| 936 |
+
KY
|
| 937 |
+
HT
|
| 938 |
+
BU
|
| 939 |
+
RU
|
| 940 |
+
QS
|
| 941 |
+
GT
|
| 942 |
+
LP
|
| 943 |
+
BI
|
| 944 |
+
JV
|
| 945 |
+
AO
|
| 946 |
+
XZ
|
| 947 |
+
AP
|
| 948 |
+
IJ
|
| 949 |
+
AZ
|
| 950 |
+
IM
|
| 951 |
+
IT
|
| 952 |
+
BT
|
| 953 |
+
JW
|
| 954 |
+
EF
|
| 955 |
+
MZ
|
| 956 |
+
BQ
|
| 957 |
+
DR
|
| 958 |
+
LX
|
| 959 |
+
CS
|
| 960 |
+
NQ
|
| 961 |
+
HX
|
| 962 |
+
PV
|
| 963 |
+
HV
|
| 964 |
+
GZ
|
| 965 |
+
BN
|
| 966 |
+
EM
|
| 967 |
+
PU
|
| 968 |
+
DG
|
| 969 |
+
HR
|
| 970 |
+
CV
|
| 971 |
+
NO
|
| 972 |
+
IV
|
| 973 |
+
JO
|
| 974 |
+
MO
|
| 975 |
+
MU
|
| 976 |
+
CO
|
| 977 |
+
MN
|
| 978 |
+
DO
|
| 979 |
+
FZ
|
| 980 |
+
PZ
|
| 981 |
+
JX
|
| 982 |
+
FN
|
| 983 |
+
GH
|
| 984 |
+
EL
|
| 985 |
+
KN
|
| 986 |
+
JZ
|
| 987 |
+
JM
|
| 988 |
+
EP
|
| 989 |
+
AN
|
| 990 |
+
CE
|
| 991 |
+
OX
|
| 992 |
+
QT
|
| 993 |
+
EU
|
| 994 |
+
LQ
|
| 995 |
+
CF
|
| 996 |
+
IU
|
| 997 |
+
CD
|
| 998 |
+
LV
|
| 999 |
+
NS
|
| 1000 |
+
NW
|
| 1001 |
+
XY
|
| 1002 |
+
KZ
|
| 1003 |
+
PR
|
| 1004 |
+
IY
|
| 1005 |
+
IS
|
| 1006 |
+
LU
|
| 1007 |
+
BP
|
| 1008 |
+
HY
|
| 1009 |
+
KQ
|
| 1010 |
+
IL
|
| 1011 |
+
FW
|
| 1012 |
+
AL
|
| 1013 |
+
UX
|
| 1014 |
+
DH
|
| 1015 |
+
QW
|
| 1016 |
+
BV
|
| 1017 |
+
LW
|
| 1018 |
+
BX
|
| 1019 |
+
IX
|
| 1020 |
+
CN
|
| 1021 |
+
EG
|
| 1022 |
+
DX
|
| 1023 |
+
GV
|
| 1024 |
+
VW
|
| 1025 |
+
AM
|
| 1026 |
+
FI
|
| 1027 |
+
FV
|
| 1028 |
+
IP
|
| 1029 |
+
OQ
|
| 1030 |
+
GM
|
| 1031 |
+
KWHOFYWRATTBFMFQKHRAYNZTSQYFEXNYZCSMCBOMALUVXAIBAXFFWSRPTBGIXJIEXKBFKLSAGHZJVFIHGETPUSVLIBXXDOYWRWPG
|
| 1032 |
+
300
|
| 1033 |
+
WQ
|
| 1034 |
+
MK
|
| 1035 |
+
QD
|
| 1036 |
+
HR
|
| 1037 |
+
OK
|
| 1038 |
+
XI
|
| 1039 |
+
GC
|
| 1040 |
+
BC
|
| 1041 |
+
XT
|
| 1042 |
+
YN
|
| 1043 |
+
IB
|
| 1044 |
+
TW
|
| 1045 |
+
FQ
|
| 1046 |
+
HD
|
| 1047 |
+
MY
|
| 1048 |
+
XM
|
| 1049 |
+
EG
|
| 1050 |
+
QM
|
| 1051 |
+
US
|
| 1052 |
+
HJ
|
| 1053 |
+
PK
|
| 1054 |
+
FD
|
| 1055 |
+
MU
|
| 1056 |
+
YC
|
| 1057 |
+
WH
|
| 1058 |
+
LO
|
| 1059 |
+
TG
|
| 1060 |
+
TC
|
| 1061 |
+
AO
|
| 1062 |
+
AR
|
| 1063 |
+
WU
|
| 1064 |
+
CE
|
| 1065 |
+
AH
|
| 1066 |
+
CB
|
| 1067 |
+
AC
|
| 1068 |
+
XG
|
| 1069 |
+
NT
|
| 1070 |
+
AB
|
| 1071 |
+
GM
|
| 1072 |
+
NF
|
| 1073 |
+
SY
|
| 1074 |
+
BH
|
| 1075 |
+
XD
|
| 1076 |
+
XH
|
| 1077 |
+
FU
|
| 1078 |
+
VT
|
| 1079 |
+
VW
|
| 1080 |
+
WB
|
| 1081 |
+
AI
|
| 1082 |
+
GT
|
| 1083 |
+
ER
|
| 1084 |
+
EC
|
| 1085 |
+
GQ
|
| 1086 |
+
MJ
|
| 1087 |
+
HC
|
| 1088 |
+
KM
|
| 1089 |
+
QU
|
| 1090 |
+
HN
|
| 1091 |
+
QS
|
| 1092 |
+
WS
|
| 1093 |
+
QP
|
| 1094 |
+
YH
|
| 1095 |
+
TH
|
| 1096 |
+
NU
|
| 1097 |
+
UQ
|
| 1098 |
+
WL
|
| 1099 |
+
CP
|
| 1100 |
+
WG
|
| 1101 |
+
RB
|
| 1102 |
+
BF
|
| 1103 |
+
CX
|
| 1104 |
+
JG
|
| 1105 |
+
IY
|
| 1106 |
+
SH
|
| 1107 |
+
DX
|
| 1108 |
+
NI
|
| 1109 |
+
CR
|
| 1110 |
+
DY
|
| 1111 |
+
EO
|
| 1112 |
+
NB
|
| 1113 |
+
QE
|
| 1114 |
+
CI
|
| 1115 |
+
JR
|
| 1116 |
+
MP
|
| 1117 |
+
GL
|
| 1118 |
+
BW
|
| 1119 |
+
JT
|
| 1120 |
+
GP
|
| 1121 |
+
SK
|
| 1122 |
+
GK
|
| 1123 |
+
EN
|
| 1124 |
+
JY
|
| 1125 |
+
FI
|
| 1126 |
+
IJ
|
| 1127 |
+
OT
|
| 1128 |
+
HM
|
| 1129 |
+
FP
|
| 1130 |
+
FE
|
| 1131 |
+
FW
|
| 1132 |
+
NQ
|
| 1133 |
+
CQ
|
| 1134 |
+
QL
|
| 1135 |
+
AW
|
| 1136 |
+
VC
|
| 1137 |
+
UR
|
| 1138 |
+
KW
|
| 1139 |
+
IC
|
| 1140 |
+
GS
|
| 1141 |
+
TN
|
| 1142 |
+
PV
|
| 1143 |
+
LE
|
| 1144 |
+
PJ
|
| 1145 |
+
TK
|
| 1146 |
+
UV
|
| 1147 |
+
OS
|
| 1148 |
+
IH
|
| 1149 |
+
EY
|
| 1150 |
+
AP
|
| 1151 |
+
QV
|
| 1152 |
+
OL
|
| 1153 |
+
SQ
|
| 1154 |
+
QC
|
| 1155 |
+
QW
|
| 1156 |
+
OB
|
| 1157 |
+
OX
|
| 1158 |
+
DG
|
| 1159 |
+
LM
|
| 1160 |
+
WI
|
| 1161 |
+
VD
|
| 1162 |
+
JQ
|
| 1163 |
+
YX
|
| 1164 |
+
SA
|
| 1165 |
+
OH
|
| 1166 |
+
IM
|
| 1167 |
+
TD
|
| 1168 |
+
XF
|
| 1169 |
+
NJ
|
| 1170 |
+
JP
|
| 1171 |
+
QJ
|
| 1172 |
+
AY
|
| 1173 |
+
XQ
|
| 1174 |
+
RP
|
| 1175 |
+
MA
|
| 1176 |
+
WV
|
| 1177 |
+
PM
|
| 1178 |
+
JN
|
| 1179 |
+
DV
|
| 1180 |
+
LX
|
| 1181 |
+
LR
|
| 1182 |
+
KV
|
| 1183 |
+
UH
|
| 1184 |
+
XN
|
| 1185 |
+
YP
|
| 1186 |
+
WC
|
| 1187 |
+
YG
|
| 1188 |
+
SG
|
| 1189 |
+
BD
|
| 1190 |
+
VM
|
| 1191 |
+
VY
|
| 1192 |
+
EQ
|
| 1193 |
+
KE
|
| 1194 |
+
WY
|
| 1195 |
+
BU
|
| 1196 |
+
VI
|
| 1197 |
+
YO
|
| 1198 |
+
RO
|
| 1199 |
+
HO
|
| 1200 |
+
MV
|
| 1201 |
+
SL
|
| 1202 |
+
UW
|
| 1203 |
+
OM
|
| 1204 |
+
YM
|
| 1205 |
+
OR
|
| 1206 |
+
YQ
|
| 1207 |
+
DJ
|
| 1208 |
+
VF
|
| 1209 |
+
JU
|
| 1210 |
+
VU
|
| 1211 |
+
RC
|
| 1212 |
+
KH
|
| 1213 |
+
DH
|
| 1214 |
+
KS
|
| 1215 |
+
YF
|
| 1216 |
+
RQ
|
| 1217 |
+
OC
|
| 1218 |
+
NY
|
| 1219 |
+
JL
|
| 1220 |
+
YB
|
| 1221 |
+
KU
|
| 1222 |
+
RK
|
| 1223 |
+
TM
|
| 1224 |
+
PD
|
| 1225 |
+
VH
|
| 1226 |
+
GF
|
| 1227 |
+
PU
|
| 1228 |
+
HP
|
| 1229 |
+
MD
|
| 1230 |
+
LD
|
| 1231 |
+
JC
|
| 1232 |
+
JX
|
| 1233 |
+
DA
|
| 1234 |
+
JK
|
| 1235 |
+
BK
|
| 1236 |
+
GV
|
| 1237 |
+
CO
|
| 1238 |
+
XO
|
| 1239 |
+
TU
|
| 1240 |
+
WA
|
| 1241 |
+
EJ
|
| 1242 |
+
VN
|
| 1243 |
+
SB
|
| 1244 |
+
NC
|
| 1245 |
+
FL
|
| 1246 |
+
DP
|
| 1247 |
+
GE
|
| 1248 |
+
ED
|
| 1249 |
+
HQ
|
| 1250 |
+
XW
|
| 1251 |
+
PN
|
| 1252 |
+
TX
|
| 1253 |
+
CD
|
| 1254 |
+
BL
|
| 1255 |
+
VK
|
| 1256 |
+
MQ
|
| 1257 |
+
CU
|
| 1258 |
+
EA
|
| 1259 |
+
NL
|
| 1260 |
+
BY
|
| 1261 |
+
PE
|
| 1262 |
+
TL
|
| 1263 |
+
UO
|
| 1264 |
+
NX
|
| 1265 |
+
NM
|
| 1266 |
+
VX
|
| 1267 |
+
YU
|
| 1268 |
+
MC
|
| 1269 |
+
LW
|
| 1270 |
+
FM
|
| 1271 |
+
OU
|
| 1272 |
+
HB
|
| 1273 |
+
YT
|
| 1274 |
+
QB
|
| 1275 |
+
NE
|
| 1276 |
+
JO
|
| 1277 |
+
CM
|
| 1278 |
+
AE
|
| 1279 |
+
SC
|
| 1280 |
+
UK
|
| 1281 |
+
TP
|
| 1282 |
+
CJ
|
| 1283 |
+
DI
|
| 1284 |
+
MG
|
| 1285 |
+
HL
|
| 1286 |
+
KP
|
| 1287 |
+
GH
|
| 1288 |
+
QA
|
| 1289 |
+
CG
|
| 1290 |
+
XR
|
| 1291 |
+
GD
|
| 1292 |
+
JB
|
| 1293 |
+
CW
|
| 1294 |
+
TO
|
| 1295 |
+
YA
|
| 1296 |
+
KJ
|
| 1297 |
+
WJ
|
| 1298 |
+
PS
|
| 1299 |
+
ET
|
| 1300 |
+
KR
|
| 1301 |
+
OV
|
| 1302 |
+
JS
|
| 1303 |
+
RE
|
| 1304 |
+
BQ
|
| 1305 |
+
KY
|
| 1306 |
+
FA
|
| 1307 |
+
GW
|
| 1308 |
+
UT
|
| 1309 |
+
IA
|
| 1310 |
+
DU
|
| 1311 |
+
AF
|
| 1312 |
+
QN
|
| 1313 |
+
IT
|
| 1314 |
+
ON
|
| 1315 |
+
FG
|
| 1316 |
+
AL
|
| 1317 |
+
PW
|
| 1318 |
+
SE
|
| 1319 |
+
EX
|
| 1320 |
+
JI
|
| 1321 |
+
MX
|
| 1322 |
+
SF
|
| 1323 |
+
VA
|
| 1324 |
+
PQ
|
| 1325 |
+
NG
|
| 1326 |
+
KX
|
| 1327 |
+
XL
|
| 1328 |
+
LJ
|
| 1329 |
+
UM
|
| 1330 |
+
FX
|
| 1331 |
+
YV
|
| 1332 |
+
VE
|
| 1333 |
+
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAZ
|
| 1334 |
+
25
|
| 1335 |
+
AB
|
| 1336 |
+
BC
|
| 1337 |
+
CD
|
| 1338 |
+
DE
|
| 1339 |
+
EF
|
| 1340 |
+
FG
|
| 1341 |
+
GH
|
| 1342 |
+
HI
|
| 1343 |
+
IJ
|
| 1344 |
+
JK
|
| 1345 |
+
KL
|
| 1346 |
+
LM
|
| 1347 |
+
MN
|
| 1348 |
+
NO
|
| 1349 |
+
OP
|
| 1350 |
+
PQ
|
| 1351 |
+
QR
|
| 1352 |
+
RS
|
| 1353 |
+
ST
|
| 1354 |
+
TU
|
| 1355 |
+
UV
|
| 1356 |
+
VW
|
| 1357 |
+
WX
|
| 1358 |
+
XY
|
| 1359 |
+
YZ
|
| 1360 |
+
QRDFWDOMXARXHNHTCYAEDCQKSPKJIKVADIATJRYFQFMAXOVO
|
| 1361 |
+
230
|
| 1362 |
+
KZ
|
| 1363 |
+
LQ
|
| 1364 |
+
JQ
|
| 1365 |
+
HT
|
| 1366 |
+
RS
|
| 1367 |
+
IV
|
| 1368 |
+
LT
|
| 1369 |
+
GH
|
| 1370 |
+
CK
|
| 1371 |
+
PT
|
| 1372 |
+
IP
|
| 1373 |
+
CO
|
| 1374 |
+
BO
|
| 1375 |
+
GZ
|
| 1376 |
+
JV
|
| 1377 |
+
SW
|
| 1378 |
+
LS
|
| 1379 |
+
GQ
|
| 1380 |
+
EH
|
| 1381 |
+
QY
|
| 1382 |
+
FS
|
| 1383 |
+
NQ
|
| 1384 |
+
FP
|
| 1385 |
+
CR
|
| 1386 |
+
HO
|
| 1387 |
+
DR
|
| 1388 |
+
AN
|
| 1389 |
+
IQ
|
| 1390 |
+
FU
|
| 1391 |
+
GL
|
| 1392 |
+
DN
|
| 1393 |
+
RZ
|
| 1394 |
+
KT
|
| 1395 |
+
EO
|
| 1396 |
+
NO
|
| 1397 |
+
AE
|
| 1398 |
+
RT
|
| 1399 |
+
CM
|
| 1400 |
+
CU
|
| 1401 |
+
FK
|
| 1402 |
+
KV
|
| 1403 |
+
JN
|
| 1404 |
+
OR
|
| 1405 |
+
CG
|
| 1406 |
+
DL
|
| 1407 |
+
ES
|
| 1408 |
+
GU
|
| 1409 |
+
CH
|
| 1410 |
+
PS
|
| 1411 |
+
KU
|
| 1412 |
+
DU
|
| 1413 |
+
IW
|
| 1414 |
+
NZ
|
| 1415 |
+
SU
|
| 1416 |
+
KW
|
| 1417 |
+
BF
|
| 1418 |
+
DS
|
| 1419 |
+
IX
|
| 1420 |
+
EJ
|
| 1421 |
+
XZ
|
| 1422 |
+
CQ
|
| 1423 |
+
CS
|
| 1424 |
+
SY
|
| 1425 |
+
TW
|
| 1426 |
+
JL
|
| 1427 |
+
BK
|
| 1428 |
+
BL
|
| 1429 |
+
IM
|
| 1430 |
+
HL
|
| 1431 |
+
JT
|
| 1432 |
+
EG
|
| 1433 |
+
MU
|
| 1434 |
+
AF
|
| 1435 |
+
MZ
|
| 1436 |
+
CP
|
| 1437 |
+
NX
|
| 1438 |
+
JK
|
| 1439 |
+
TV
|
| 1440 |
+
RY
|
| 1441 |
+
JS
|
| 1442 |
+
ER
|
| 1443 |
+
GO
|
| 1444 |
+
LW
|
| 1445 |
+
KL
|
| 1446 |
+
HX
|
| 1447 |
+
BC
|
| 1448 |
+
FV
|
| 1449 |
+
KN
|
| 1450 |
+
VW
|
| 1451 |
+
AG
|
| 1452 |
+
CI
|
| 1453 |
+
KS
|
| 1454 |
+
CL
|
| 1455 |
+
FR
|
| 1456 |
+
DI
|
| 1457 |
+
PQ
|
| 1458 |
+
DG
|
| 1459 |
+
LO
|
| 1460 |
+
QR
|
| 1461 |
+
AB
|
| 1462 |
+
BJ
|
| 1463 |
+
FT
|
| 1464 |
+
NS
|
| 1465 |
+
DY
|
| 1466 |
+
DH
|
| 1467 |
+
UX
|
| 1468 |
+
KR
|
| 1469 |
+
AS
|
| 1470 |
+
HM
|
| 1471 |
+
DE
|
| 1472 |
+
IO
|
| 1473 |
+
RW
|
| 1474 |
+
FM
|
| 1475 |
+
GS
|
| 1476 |
+
AZ
|
| 1477 |
+
PY
|
| 1478 |
+
DZ
|
| 1479 |
+
UY
|
| 1480 |
+
OV
|
| 1481 |
+
IR
|
| 1482 |
+
YZ
|
| 1483 |
+
OY
|
| 1484 |
+
MN
|
| 1485 |
+
EF
|
| 1486 |
+
MQ
|
| 1487 |
+
HV
|
| 1488 |
+
CJ
|
| 1489 |
+
NV
|
| 1490 |
+
HZ
|
| 1491 |
+
GT
|
| 1492 |
+
LZ
|
| 1493 |
+
GW
|
| 1494 |
+
IT
|
| 1495 |
+
BV
|
| 1496 |
+
LY
|
| 1497 |
+
OW
|
| 1498 |
+
GP
|
| 1499 |
+
BR
|
| 1500 |
+
AT
|
| 1501 |
+
FW
|
| 1502 |
+
HN
|
| 1503 |
+
AH
|
| 1504 |
+
BT
|
| 1505 |
+
KQ
|
| 1506 |
+
BY
|
| 1507 |
+
FI
|
| 1508 |
+
QX
|
| 1509 |
+
IZ
|
| 1510 |
+
FJ
|
| 1511 |
+
IN
|
| 1512 |
+
AI
|
| 1513 |
+
UZ
|
| 1514 |
+
HS
|
| 1515 |
+
CZ
|
| 1516 |
+
MW
|
| 1517 |
+
ST
|
| 1518 |
+
EN
|
| 1519 |
+
LP
|
| 1520 |
+
LU
|
| 1521 |
+
OU
|
| 1522 |
+
TZ
|
| 1523 |
+
GK
|
| 1524 |
+
RX
|
| 1525 |
+
BP
|
| 1526 |
+
HK
|
| 1527 |
+
DX
|
| 1528 |
+
OX
|
| 1529 |
+
EY
|
| 1530 |
+
GR
|
| 1531 |
+
CX
|
| 1532 |
+
EK
|
| 1533 |
+
IY
|
| 1534 |
+
DQ
|
| 1535 |
+
FG
|
| 1536 |
+
QV
|
| 1537 |
+
AD
|
| 1538 |
+
MR
|
| 1539 |
+
QZ
|
| 1540 |
+
NR
|
| 1541 |
+
GI
|
| 1542 |
+
TX
|
| 1543 |
+
GV
|
| 1544 |
+
AQ
|
| 1545 |
+
RV
|
| 1546 |
+
AW
|
| 1547 |
+
BX
|
| 1548 |
+
AJ
|
| 1549 |
+
SV
|
| 1550 |
+
CD
|
| 1551 |
+
AK
|
| 1552 |
+
GJ
|
| 1553 |
+
NW
|
| 1554 |
+
JZ
|
| 1555 |
+
QU
|
| 1556 |
+
VX
|
| 1557 |
+
BU
|
| 1558 |
+
BM
|
| 1559 |
+
GX
|
| 1560 |
+
HP
|
| 1561 |
+
MP
|
| 1562 |
+
LV
|
| 1563 |
+
EL
|
| 1564 |
+
FO
|
| 1565 |
+
DV
|
| 1566 |
+
HJ
|
| 1567 |
+
BG
|
| 1568 |
+
KX
|
| 1569 |
+
EZ
|
| 1570 |
+
AY
|
| 1571 |
+
BW
|
| 1572 |
+
AR
|
| 1573 |
+
AC
|
| 1574 |
+
JU
|
| 1575 |
+
OP
|
| 1576 |
+
FH
|
| 1577 |
+
EM
|
| 1578 |
+
ET
|
| 1579 |
+
XY
|
| 1580 |
+
UW
|
| 1581 |
+
HY
|
| 1582 |
+
DF
|
| 1583 |
+
JO
|
| 1584 |
+
OQ
|
| 1585 |
+
AU
|
| 1586 |
+
JY
|
| 1587 |
+
MO
|
| 1588 |
+
SX
|
| 1589 |
+
HQ
|
| 1590 |
+
AM
|
| 1591 |
+
BZ
|
| 1592 |
+
BDKCZAWSSOBNYFYKMILGTPZFTGVUQXDSMZRTJIRLKTQRTBR
|
| 1593 |
+
244
|
| 1594 |
+
DP
|
| 1595 |
+
KS
|
| 1596 |
+
SW
|
| 1597 |
+
IW
|
| 1598 |
+
EU
|
| 1599 |
+
OW
|
| 1600 |
+
DN
|
| 1601 |
+
IJ
|
| 1602 |
+
CF
|
| 1603 |
+
FY
|
| 1604 |
+
IM
|
| 1605 |
+
BK
|
| 1606 |
+
IX
|
| 1607 |
+
EP
|
| 1608 |
+
WY
|
| 1609 |
+
RV
|
| 1610 |
+
VX
|
| 1611 |
+
CO
|
| 1612 |
+
AM
|
| 1613 |
+
CN
|
| 1614 |
+
CM
|
| 1615 |
+
FV
|
| 1616 |
+
LM
|
| 1617 |
+
XY
|
| 1618 |
+
QR
|
| 1619 |
+
DE
|
| 1620 |
+
UY
|
| 1621 |
+
OP
|
| 1622 |
+
EQ
|
| 1623 |
+
AV
|
| 1624 |
+
CX
|
| 1625 |
+
FZ
|
| 1626 |
+
AD
|
| 1627 |
+
GQ
|
| 1628 |
+
EO
|
| 1629 |
+
MW
|
| 1630 |
+
BN
|
| 1631 |
+
EZ
|
| 1632 |
+
GX
|
| 1633 |
+
AS
|
| 1634 |
+
BW
|
| 1635 |
+
AK
|
| 1636 |
+
RT
|
| 1637 |
+
GY
|
| 1638 |
+
IN
|
| 1639 |
+
FQ
|
| 1640 |
+
EI
|
| 1641 |
+
BG
|
| 1642 |
+
GO
|
| 1643 |
+
PR
|
| 1644 |
+
UX
|
| 1645 |
+
HU
|
| 1646 |
+
NU
|
| 1647 |
+
BF
|
| 1648 |
+
CZ
|
| 1649 |
+
CJ
|
| 1650 |
+
LZ
|
| 1651 |
+
EV
|
| 1652 |
+
KX
|
| 1653 |
+
VZ
|
| 1654 |
+
OQ
|
| 1655 |
+
HZ
|
| 1656 |
+
DM
|
| 1657 |
+
PZ
|
| 1658 |
+
TZ
|
| 1659 |
+
HM
|
| 1660 |
+
OV
|
| 1661 |
+
NR
|
| 1662 |
+
QX
|
| 1663 |
+
KO
|
| 1664 |
+
CW
|
| 1665 |
+
AW
|
| 1666 |
+
NV
|
| 1667 |
+
HO
|
| 1668 |
+
VY
|
| 1669 |
+
IO
|
| 1670 |
+
GP
|
| 1671 |
+
CL
|
| 1672 |
+
RX
|
| 1673 |
+
AZ
|
| 1674 |
+
PX
|
| 1675 |
+
LP
|
| 1676 |
+
DK
|
| 1677 |
+
LO
|
| 1678 |
+
BM
|
| 1679 |
+
MU
|
| 1680 |
+
BC
|
| 1681 |
+
JU
|
| 1682 |
+
IQ
|
| 1683 |
+
BO
|
| 1684 |
+
NY
|
| 1685 |
+
EM
|
| 1686 |
+
HJ
|
| 1687 |
+
CS
|
| 1688 |
+
AU
|
| 1689 |
+
PS
|
| 1690 |
+
DG
|
| 1691 |
+
AY
|
| 1692 |
+
KU
|
| 1693 |
+
DI
|
| 1694 |
+
OY
|
| 1695 |
+
HP
|
| 1696 |
+
JM
|
| 1697 |
+
JK
|
| 1698 |
+
GW
|
| 1699 |
+
FN
|
| 1700 |
+
RU
|
| 1701 |
+
IU
|
| 1702 |
+
RZ
|
| 1703 |
+
JS
|
| 1704 |
+
ER
|
| 1705 |
+
CK
|
| 1706 |
+
MQ
|
| 1707 |
+
LX
|
| 1708 |
+
QZ
|
| 1709 |
+
EX
|
| 1710 |
+
DY
|
| 1711 |
+
UZ
|
| 1712 |
+
GT
|
| 1713 |
+
QY
|
| 1714 |
+
AE
|
| 1715 |
+
AX
|
| 1716 |
+
FJ
|
| 1717 |
+
AP
|
| 1718 |
+
SY
|
| 1719 |
+
MR
|
| 1720 |
+
MY
|
| 1721 |
+
BX
|
| 1722 |
+
TU
|
| 1723 |
+
KT
|
| 1724 |
+
CY
|
| 1725 |
+
AI
|
| 1726 |
+
CP
|
| 1727 |
+
KN
|
| 1728 |
+
HI
|
| 1729 |
+
AJ
|
| 1730 |
+
KY
|
| 1731 |
+
BD
|
| 1732 |
+
PU
|
| 1733 |
+
KV
|
| 1734 |
+
JR
|
| 1735 |
+
GU
|
| 1736 |
+
PQ
|
| 1737 |
+
DS
|
| 1738 |
+
NW
|
| 1739 |
+
AC
|
| 1740 |
+
IV
|
| 1741 |
+
WZ
|
| 1742 |
+
NZ
|
| 1743 |
+
QV
|
| 1744 |
+
EF
|
| 1745 |
+
NX
|
| 1746 |
+
DQ
|
| 1747 |
+
HK
|
| 1748 |
+
FT
|
| 1749 |
+
FG
|
| 1750 |
+
DX
|
| 1751 |
+
AQ
|
| 1752 |
+
FW
|
| 1753 |
+
AF
|
| 1754 |
+
SV
|
| 1755 |
+
GI
|
| 1756 |
+
CG
|
| 1757 |
+
EJ
|
| 1758 |
+
DU
|
| 1759 |
+
JW
|
| 1760 |
+
WX
|
| 1761 |
+
EL
|
| 1762 |
+
IP
|
| 1763 |
+
DV
|
| 1764 |
+
LN
|
| 1765 |
+
FL
|
| 1766 |
+
BP
|
| 1767 |
+
BV
|
| 1768 |
+
CV
|
| 1769 |
+
MX
|
| 1770 |
+
FU
|
| 1771 |
+
BI
|
| 1772 |
+
GJ
|
| 1773 |
+
FK
|
| 1774 |
+
FI
|
| 1775 |
+
QW
|
| 1776 |
+
PT
|
| 1777 |
+
CH
|
| 1778 |
+
BU
|
| 1779 |
+
YZ
|
| 1780 |
+
FO
|
| 1781 |
+
EN
|
| 1782 |
+
BE
|
| 1783 |
+
SX
|
| 1784 |
+
TV
|
| 1785 |
+
AB
|
| 1786 |
+
DJ
|
| 1787 |
+
IY
|
| 1788 |
+
KR
|
| 1789 |
+
CU
|
| 1790 |
+
HQ
|
| 1791 |
+
SU
|
| 1792 |
+
LV
|
| 1793 |
+
DL
|
| 1794 |
+
JL
|
| 1795 |
+
HX
|
| 1796 |
+
JO
|
| 1797 |
+
EG
|
| 1798 |
+
IR
|
| 1799 |
+
MN
|
| 1800 |
+
IK
|
| 1801 |
+
AN
|
| 1802 |
+
LY
|
| 1803 |
+
OU
|
| 1804 |
+
HN
|
| 1805 |
+
AH
|
| 1806 |
+
MV
|
| 1807 |
+
LR
|
| 1808 |
+
BL
|
| 1809 |
+
TX
|
| 1810 |
+
EW
|
| 1811 |
+
CI
|
| 1812 |
+
MP
|
| 1813 |
+
CD
|
| 1814 |
+
EH
|
| 1815 |
+
LQ
|
| 1816 |
+
GN
|
| 1817 |
+
NS
|
| 1818 |
+
AG
|
| 1819 |
+
HS
|
| 1820 |
+
KZ
|
| 1821 |
+
PV
|
| 1822 |
+
IZ
|
| 1823 |
+
JY
|
| 1824 |
+
DH
|
| 1825 |
+
BH
|
| 1826 |
+
GH
|
| 1827 |
+
KP
|
| 1828 |
+
JN
|
| 1829 |
+
AO
|
| 1830 |
+
KQ
|
| 1831 |
+
KL
|
| 1832 |
+
MT
|
| 1833 |
+
UV
|
| 1834 |
+
DF
|
| 1835 |
+
HV
|
| 1836 |
+
BR
|
| 1837 |
+
CT
|
| 1838 |
+
ECYHYKWGQTYLYBDXPMGFOLLYJFQUURMRUHWKEPSQ
|
| 1839 |
+
124
|
| 1840 |
+
RV
|
| 1841 |
+
ZH
|
| 1842 |
+
HW
|
| 1843 |
+
GS
|
| 1844 |
+
BQ
|
| 1845 |
+
HS
|
| 1846 |
+
ZW
|
| 1847 |
+
CJ
|
| 1848 |
+
BA
|
| 1849 |
+
AG
|
| 1850 |
+
VH
|
| 1851 |
+
DI
|
| 1852 |
+
MH
|
| 1853 |
+
UR
|
| 1854 |
+
KD
|
| 1855 |
+
OH
|
| 1856 |
+
JI
|
| 1857 |
+
VR
|
| 1858 |
+
MX
|
| 1859 |
+
UE
|
| 1860 |
+
HG
|
| 1861 |
+
QC
|
| 1862 |
+
DX
|
| 1863 |
+
SK
|
| 1864 |
+
WD
|
| 1865 |
+
KT
|
| 1866 |
+
VO
|
| 1867 |
+
LV
|
| 1868 |
+
BM
|
| 1869 |
+
XF
|
| 1870 |
+
DE
|
| 1871 |
+
AD
|
| 1872 |
+
CP
|
| 1873 |
+
OB
|
| 1874 |
+
DC
|
| 1875 |
+
GB
|
| 1876 |
+
IV
|
| 1877 |
+
EC
|
| 1878 |
+
KX
|
| 1879 |
+
AZ
|
| 1880 |
+
UX
|
| 1881 |
+
PC
|
| 1882 |
+
DP
|
| 1883 |
+
PE
|
| 1884 |
+
GR
|
| 1885 |
+
YC
|
| 1886 |
+
RS
|
| 1887 |
+
AW
|
| 1888 |
+
IF
|
| 1889 |
+
SV
|
| 1890 |
+
BK
|
| 1891 |
+
DW
|
| 1892 |
+
JG
|
| 1893 |
+
ZN
|
| 1894 |
+
LK
|
| 1895 |
+
OX
|
| 1896 |
+
SZ
|
| 1897 |
+
WH
|
| 1898 |
+
ND
|
| 1899 |
+
UB
|
| 1900 |
+
OR
|
| 1901 |
+
SQ
|
| 1902 |
+
TH
|
| 1903 |
+
UK
|
| 1904 |
+
DH
|
| 1905 |
+
NT
|
| 1906 |
+
UA
|
| 1907 |
+
BY
|
| 1908 |
+
ED
|
| 1909 |
+
OS
|
| 1910 |
+
NY
|
| 1911 |
+
LO
|
| 1912 |
+
JD
|
| 1913 |
+
CS
|
| 1914 |
+
JF
|
| 1915 |
+
GW
|
| 1916 |
+
LY
|
| 1917 |
+
NL
|
| 1918 |
+
RE
|
| 1919 |
+
WM
|
| 1920 |
+
RM
|
| 1921 |
+
PT
|
| 1922 |
+
LG
|
| 1923 |
+
DF
|
| 1924 |
+
CV
|
| 1925 |
+
QL
|
| 1926 |
+
OP
|
| 1927 |
+
GC
|
| 1928 |
+
QH
|
| 1929 |
+
HE
|
| 1930 |
+
US
|
| 1931 |
+
VU
|
| 1932 |
+
JH
|
| 1933 |
+
EQ
|
| 1934 |
+
JQ
|
| 1935 |
+
VN
|
| 1936 |
+
JS
|
| 1937 |
+
JT
|
| 1938 |
+
RP
|
| 1939 |
+
XY
|
| 1940 |
+
RW
|
| 1941 |
+
NH
|
| 1942 |
+
QE
|
| 1943 |
+
KJ
|
| 1944 |
+
ES
|
| 1945 |
+
HK
|
| 1946 |
+
RI
|
| 1947 |
+
UY
|
| 1948 |
+
CW
|
| 1949 |
+
FR
|
| 1950 |
+
XR
|
| 1951 |
+
FK
|
| 1952 |
+
WX
|
| 1953 |
+
HY
|
| 1954 |
+
RH
|
| 1955 |
+
IU
|
| 1956 |
+
EH
|
| 1957 |
+
HO
|
| 1958 |
+
QW
|
| 1959 |
+
AC
|
| 1960 |
+
QZ
|
| 1961 |
+
NM
|
| 1962 |
+
MF
|
| 1963 |
+
YK
|
| 1964 |
+
ZGYDGANSWZKXKIUEQXKKFLWUBAJUYHDMEETESIPGEGCEKIUSFEXKHSZVNMTBWGJOPMHIRB
|
| 1965 |
+
198
|
| 1966 |
+
DJ
|
| 1967 |
+
ET
|
| 1968 |
+
IQ
|
| 1969 |
+
AO
|
| 1970 |
+
OQ
|
| 1971 |
+
FR
|
| 1972 |
+
MV
|
| 1973 |
+
NX
|
| 1974 |
+
KR
|
| 1975 |
+
QS
|
| 1976 |
+
JL
|
| 1977 |
+
IN
|
| 1978 |
+
BJ
|
| 1979 |
+
IZ
|
| 1980 |
+
JQ
|
| 1981 |
+
CI
|
| 1982 |
+
MN
|
| 1983 |
+
DY
|
| 1984 |
+
KZ
|
| 1985 |
+
BN
|
| 1986 |
+
ES
|
| 1987 |
+
DK
|
| 1988 |
+
EQ
|
| 1989 |
+
DH
|
| 1990 |
+
ST
|
| 1991 |
+
MP
|
| 1992 |
+
OT
|
| 1993 |
+
YZ
|
| 1994 |
+
LT
|
| 1995 |
+
MZ
|
| 1996 |
+
BI
|
| 1997 |
+
HQ
|
| 1998 |
+
HS
|
| 1999 |
+
SZ
|
| 2000 |
+
EI
|
| 2001 |
+
RY
|
| 2002 |
+
JR
|
| 2003 |
+
RV
|
| 2004 |
+
IX
|
| 2005 |
+
HJ
|
| 2006 |
+
HR
|
| 2007 |
+
IJ
|
| 2008 |
+
TW
|
| 2009 |
+
JP
|
| 2010 |
+
AX
|
| 2011 |
+
IT
|
| 2012 |
+
AD
|
| 2013 |
+
DU
|
| 2014 |
+
QX
|
| 2015 |
+
FO
|
| 2016 |
+
QV
|
| 2017 |
+
CW
|
| 2018 |
+
EK
|
| 2019 |
+
DT
|
| 2020 |
+
BH
|
| 2021 |
+
EW
|
| 2022 |
+
EN
|
| 2023 |
+
KU
|
| 2024 |
+
BK
|
| 2025 |
+
DL
|
| 2026 |
+
AH
|
| 2027 |
+
KM
|
| 2028 |
+
WZ
|
| 2029 |
+
AV
|
| 2030 |
+
FN
|
| 2031 |
+
IL
|
| 2032 |
+
TV
|
| 2033 |
+
HZ
|
| 2034 |
+
JW
|
| 2035 |
+
NR
|
| 2036 |
+
DG
|
| 2037 |
+
JN
|
| 2038 |
+
PR
|
| 2039 |
+
LO
|
| 2040 |
+
GW
|
| 2041 |
+
LP
|
| 2042 |
+
CL
|
| 2043 |
+
TZ
|
| 2044 |
+
DE
|
| 2045 |
+
LN
|
| 2046 |
+
SX
|
| 2047 |
+
FS
|
| 2048 |
+
CF
|
| 2049 |
+
DI
|
| 2050 |
+
BP
|
| 2051 |
+
DP
|
| 2052 |
+
UZ
|
| 2053 |
+
IM
|
| 2054 |
+
KV
|
| 2055 |
+
GR
|
| 2056 |
+
GT
|
| 2057 |
+
QT
|
| 2058 |
+
HP
|
| 2059 |
+
FV
|
| 2060 |
+
FM
|
| 2061 |
+
CN
|
| 2062 |
+
KO
|
| 2063 |
+
VZ
|
| 2064 |
+
GH
|
| 2065 |
+
DR
|
| 2066 |
+
GX
|
| 2067 |
+
MY
|
| 2068 |
+
EH
|
| 2069 |
+
DW
|
| 2070 |
+
HN
|
| 2071 |
+
TY
|
| 2072 |
+
GV
|
| 2073 |
+
EF
|
| 2074 |
+
BE
|
| 2075 |
+
MU
|
| 2076 |
+
OY
|
| 2077 |
+
GO
|
| 2078 |
+
HW
|
| 2079 |
+
KX
|
| 2080 |
+
DZ
|
| 2081 |
+
HU
|
| 2082 |
+
AW
|
| 2083 |
+
EU
|
| 2084 |
+
KY
|
| 2085 |
+
VW
|
| 2086 |
+
CQ
|
| 2087 |
+
HI
|
| 2088 |
+
AE
|
| 2089 |
+
DO
|
| 2090 |
+
JU
|
| 2091 |
+
FU
|
| 2092 |
+
PU
|
| 2093 |
+
HK
|
| 2094 |
+
FY
|
| 2095 |
+
KN
|
| 2096 |
+
AN
|
| 2097 |
+
JV
|
| 2098 |
+
GP
|
| 2099 |
+
AT
|
| 2100 |
+
DV
|
| 2101 |
+
BU
|
| 2102 |
+
AF
|
| 2103 |
+
OV
|
| 2104 |
+
CY
|
| 2105 |
+
TU
|
| 2106 |
+
FG
|
| 2107 |
+
HO
|
| 2108 |
+
DS
|
| 2109 |
+
CV
|
| 2110 |
+
EV
|
| 2111 |
+
JZ
|
| 2112 |
+
IK
|
| 2113 |
+
VX
|
| 2114 |
+
RT
|
| 2115 |
+
CE
|
| 2116 |
+
HM
|
| 2117 |
+
EX
|
| 2118 |
+
OR
|
| 2119 |
+
UW
|
| 2120 |
+
QZ
|
| 2121 |
+
AR
|
| 2122 |
+
BL
|
| 2123 |
+
LZ
|
| 2124 |
+
AG
|
| 2125 |
+
LS
|
| 2126 |
+
BT
|
| 2127 |
+
HL
|
| 2128 |
+
CR
|
| 2129 |
+
CD
|
| 2130 |
+
DQ
|
| 2131 |
+
BM
|
| 2132 |
+
GN
|
| 2133 |
+
PQ
|
| 2134 |
+
KW
|
| 2135 |
+
MO
|
| 2136 |
+
IO
|
| 2137 |
+
FL
|
| 2138 |
+
UY
|
| 2139 |
+
QW
|
| 2140 |
+
PX
|
| 2141 |
+
TX
|
| 2142 |
+
IS
|
| 2143 |
+
JT
|
| 2144 |
+
GS
|
| 2145 |
+
FI
|
| 2146 |
+
ER
|
| 2147 |
+
NZ
|
| 2148 |
+
GU
|
| 2149 |
+
GI
|
| 2150 |
+
QR
|
| 2151 |
+
BY
|
| 2152 |
+
BX
|
| 2153 |
+
RZ
|
| 2154 |
+
DN
|
| 2155 |
+
IU
|
| 2156 |
+
MR
|
| 2157 |
+
LV
|
| 2158 |
+
AZ
|
| 2159 |
+
AJ
|
| 2160 |
+
UV
|
| 2161 |
+
GZ
|
| 2162 |
+
PY
|
| 2163 |
+
CH
|
| 2164 |
+
OIHWQMOCQNHZRROYFBACXTJBTVRGECUKVMDWAQGOIYRBJBYVAIQLHFVDLQCOAOOBAACSMIHQTH
|
| 2165 |
+
95
|
| 2166 |
+
YZ
|
| 2167 |
+
QI
|
| 2168 |
+
MT
|
| 2169 |
+
MD
|
| 2170 |
+
BR
|
| 2171 |
+
HG
|
| 2172 |
+
KR
|
| 2173 |
+
KW
|
| 2174 |
+
QC
|
| 2175 |
+
KP
|
| 2176 |
+
DP
|
| 2177 |
+
CY
|
| 2178 |
+
RA
|
| 2179 |
+
LQ
|
| 2180 |
+
EG
|
| 2181 |
+
AM
|
| 2182 |
+
NE
|
| 2183 |
+
XR
|
| 2184 |
+
QM
|
| 2185 |
+
FB
|
| 2186 |
+
BZ
|
| 2187 |
+
PA
|
| 2188 |
+
GD
|
| 2189 |
+
CF
|
| 2190 |
+
MC
|
| 2191 |
+
JO
|
| 2192 |
+
BC
|
| 2193 |
+
AW
|
| 2194 |
+
ER
|
| 2195 |
+
FA
|
| 2196 |
+
PE
|
| 2197 |
+
UV
|
| 2198 |
+
CD
|
| 2199 |
+
MK
|
| 2200 |
+
GA
|
| 2201 |
+
AK
|
| 2202 |
+
ZL
|
| 2203 |
+
HR
|
| 2204 |
+
UA
|
| 2205 |
+
BN
|
| 2206 |
+
LO
|
| 2207 |
+
PR
|
| 2208 |
+
VM
|
| 2209 |
+
WX
|
| 2210 |
+
UP
|
| 2211 |
+
CO
|
| 2212 |
+
KX
|
| 2213 |
+
RN
|
| 2214 |
+
MU
|
| 2215 |
+
IE
|
| 2216 |
+
KH
|
| 2217 |
+
RX
|
| 2218 |
+
WH
|
| 2219 |
+
PX
|
| 2220 |
+
ZD
|
| 2221 |
+
MB
|
| 2222 |
+
XI
|
| 2223 |
+
BE
|
| 2224 |
+
IL
|
| 2225 |
+
TI
|
| 2226 |
+
SP
|
| 2227 |
+
KV
|
| 2228 |
+
DU
|
| 2229 |
+
EL
|
| 2230 |
+
ES
|
| 2231 |
+
NV
|
| 2232 |
+
BA
|
| 2233 |
+
JQ
|
| 2234 |
+
AL
|
| 2235 |
+
RH
|
| 2236 |
+
PY
|
| 2237 |
+
XK
|
| 2238 |
+
KJ
|
| 2239 |
+
ZJ
|
| 2240 |
+
XG
|
| 2241 |
+
BH
|
| 2242 |
+
OU
|
| 2243 |
+
YP
|
| 2244 |
+
WE
|
| 2245 |
+
XH
|
| 2246 |
+
VY
|
| 2247 |
+
JM
|
| 2248 |
+
WR
|
| 2249 |
+
ON
|
| 2250 |
+
KN
|
| 2251 |
+
LD
|
| 2252 |
+
IX
|
| 2253 |
+
RT
|
| 2254 |
+
WC
|
| 2255 |
+
RF
|
| 2256 |
+
CE
|
| 2257 |
+
ZW
|
| 2258 |
+
OY
|
| 2259 |
+
OD
|
| 2260 |
+
SF
|
| 2261 |
+
RJAKSGJOHUOGVHBVCRBJTUVBDZGEIFSUEWQHJWKLBJJW
|
| 2262 |
+
107
|
| 2263 |
+
FN
|
| 2264 |
+
CO
|
| 2265 |
+
BJ
|
| 2266 |
+
FQ
|
| 2267 |
+
DG
|
| 2268 |
+
QX
|
| 2269 |
+
OS
|
| 2270 |
+
DE
|
| 2271 |
+
BU
|
| 2272 |
+
SZ
|
| 2273 |
+
JP
|
| 2274 |
+
PZ
|
| 2275 |
+
LS
|
| 2276 |
+
DU
|
| 2277 |
+
FP
|
| 2278 |
+
DK
|
| 2279 |
+
VW
|
| 2280 |
+
JT
|
| 2281 |
+
FW
|
| 2282 |
+
BL
|
| 2283 |
+
AM
|
| 2284 |
+
BQ
|
| 2285 |
+
AU
|
| 2286 |
+
EX
|
| 2287 |
+
PQ
|
| 2288 |
+
IJ
|
| 2289 |
+
FY
|
| 2290 |
+
AN
|
| 2291 |
+
MS
|
| 2292 |
+
NT
|
| 2293 |
+
OY
|
| 2294 |
+
GY
|
| 2295 |
+
IT
|
| 2296 |
+
AE
|
| 2297 |
+
CM
|
| 2298 |
+
DW
|
| 2299 |
+
JR
|
| 2300 |
+
MO
|
| 2301 |
+
BG
|
| 2302 |
+
KU
|
| 2303 |
+
KY
|
| 2304 |
+
OQ
|
| 2305 |
+
DP
|
| 2306 |
+
RX
|
| 2307 |
+
QU
|
| 2308 |
+
RT
|
| 2309 |
+
HX
|
| 2310 |
+
HY
|
| 2311 |
+
BD
|
| 2312 |
+
FL
|
| 2313 |
+
MP
|
| 2314 |
+
IX
|
| 2315 |
+
BW
|
| 2316 |
+
GP
|
| 2317 |
+
FZ
|
| 2318 |
+
CJ
|
| 2319 |
+
CZ
|
| 2320 |
+
VX
|
| 2321 |
+
EG
|
| 2322 |
+
MX
|
| 2323 |
+
ST
|
| 2324 |
+
GS
|
| 2325 |
+
AW
|
| 2326 |
+
OV
|
| 2327 |
+
CF
|
| 2328 |
+
UY
|
| 2329 |
+
MU
|
| 2330 |
+
TX
|
| 2331 |
+
OU
|
| 2332 |
+
LM
|
| 2333 |
+
LZ
|
| 2334 |
+
BE
|
| 2335 |
+
PU
|
| 2336 |
+
FO
|
| 2337 |
+
HV
|
| 2338 |
+
EV
|
| 2339 |
+
MR
|
| 2340 |
+
CD
|
| 2341 |
+
DY
|
| 2342 |
+
AV
|
| 2343 |
+
KS
|
| 2344 |
+
KV
|
| 2345 |
+
RZ
|
| 2346 |
+
GZ
|
| 2347 |
+
AG
|
| 2348 |
+
JO
|
| 2349 |
+
AF
|
| 2350 |
+
CN
|
| 2351 |
+
GR
|
| 2352 |
+
DJ
|
| 2353 |
+
JM
|
| 2354 |
+
JL
|
| 2355 |
+
QW
|
| 2356 |
+
CY
|
| 2357 |
+
VZ
|
| 2358 |
+
RS
|
| 2359 |
+
OT
|
| 2360 |
+
AJ
|
| 2361 |
+
RY
|
| 2362 |
+
AT
|
| 2363 |
+
JS
|
| 2364 |
+
BP
|
| 2365 |
+
TZ
|
| 2366 |
+
FJ
|
| 2367 |
+
KP
|
| 2368 |
+
UX
|
| 2369 |
+
GL
|
| 2370 |
+
OUAUVIGHMLNYZDPWXUNBRKHFUEORZOGLGTVHBXILSSIEXQCGDEXYUTRZUOQIMYYIQFGS
|
| 2371 |
+
270
|
| 2372 |
+
AK
|
| 2373 |
+
HO
|
| 2374 |
+
BJ
|
| 2375 |
+
UD
|
| 2376 |
+
MI
|
| 2377 |
+
MQ
|
| 2378 |
+
AT
|
| 2379 |
+
NL
|
| 2380 |
+
UE
|
| 2381 |
+
OP
|
| 2382 |
+
TM
|
| 2383 |
+
VB
|
| 2384 |
+
XY
|
| 2385 |
+
NJ
|
| 2386 |
+
BQ
|
| 2387 |
+
GO
|
| 2388 |
+
PH
|
| 2389 |
+
AB
|
| 2390 |
+
ML
|
| 2391 |
+
SE
|
| 2392 |
+
GF
|
| 2393 |
+
TG
|
| 2394 |
+
HF
|
| 2395 |
+
SX
|
| 2396 |
+
QJ
|
| 2397 |
+
NU
|
| 2398 |
+
KD
|
| 2399 |
+
WU
|
| 2400 |
+
YO
|
| 2401 |
+
QI
|
| 2402 |
+
NE
|
| 2403 |
+
KU
|
| 2404 |
+
FN
|
| 2405 |
+
SW
|
| 2406 |
+
XS
|
| 2407 |
+
BE
|
| 2408 |
+
CH
|
| 2409 |
+
JM
|
| 2410 |
+
VN
|
| 2411 |
+
KP
|
| 2412 |
+
DF
|
| 2413 |
+
LC
|
| 2414 |
+
UP
|
| 2415 |
+
YP
|
| 2416 |
+
PN
|
| 2417 |
+
SD
|
| 2418 |
+
LU
|
| 2419 |
+
UO
|
| 2420 |
+
WG
|
| 2421 |
+
AQ
|
| 2422 |
+
SO
|
| 2423 |
+
PW
|
| 2424 |
+
XR
|
| 2425 |
+
HV
|
| 2426 |
+
MK
|
| 2427 |
+
VI
|
| 2428 |
+
DM
|
| 2429 |
+
TK
|
| 2430 |
+
CG
|
| 2431 |
+
RX
|
| 2432 |
+
CO
|
| 2433 |
+
BA
|
| 2434 |
+
YD
|
| 2435 |
+
VP
|
| 2436 |
+
RS
|
| 2437 |
+
DN
|
| 2438 |
+
LY
|
| 2439 |
+
UX
|
| 2440 |
+
AY
|
| 2441 |
+
JF
|
| 2442 |
+
FK
|
| 2443 |
+
QD
|
| 2444 |
+
FC
|
| 2445 |
+
WT
|
| 2446 |
+
KT
|
| 2447 |
+
NG
|
| 2448 |
+
AF
|
| 2449 |
+
DK
|
| 2450 |
+
CF
|
| 2451 |
+
EM
|
| 2452 |
+
MR
|
| 2453 |
+
KE
|
| 2454 |
+
XE
|
| 2455 |
+
WM
|
| 2456 |
+
FQ
|
| 2457 |
+
VK
|
| 2458 |
+
EW
|
| 2459 |
+
WS
|
| 2460 |
+
YK
|
| 2461 |
+
YG
|
| 2462 |
+
DY
|
| 2463 |
+
NR
|
| 2464 |
+
YN
|
| 2465 |
+
MD
|
| 2466 |
+
PU
|
| 2467 |
+
TH
|
| 2468 |
+
UH
|
| 2469 |
+
EI
|
| 2470 |
+
YV
|
| 2471 |
+
HI
|
| 2472 |
+
SF
|
| 2473 |
+
JU
|
| 2474 |
+
JI
|
| 2475 |
+
FW
|
| 2476 |
+
DU
|
| 2477 |
+
IB
|
| 2478 |
+
QY
|
| 2479 |
+
AO
|
| 2480 |
+
GR
|
| 2481 |
+
OU
|
| 2482 |
+
YU
|
| 2483 |
+
PG
|
| 2484 |
+
GT
|
| 2485 |
+
KL
|
| 2486 |
+
ME
|
| 2487 |
+
XH
|
| 2488 |
+
BV
|
| 2489 |
+
AX
|
| 2490 |
+
UM
|
| 2491 |
+
IE
|
| 2492 |
+
UL
|
| 2493 |
+
BM
|
| 2494 |
+
SZ
|
| 2495 |
+
JE
|
| 2496 |
+
IV
|
| 2497 |
+
TI
|
| 2498 |
+
YQ
|
| 2499 |
+
VZ
|
| 2500 |
+
HS
|
| 2501 |
+
QP
|
| 2502 |
+
EC
|
| 2503 |
+
DB
|
| 2504 |
+
FA
|
| 2505 |
+
HL
|
| 2506 |
+
KR
|
| 2507 |
+
LX
|
| 2508 |
+
PI
|
| 2509 |
+
MN
|
| 2510 |
+
UK
|
| 2511 |
+
CM
|
| 2512 |
+
LP
|
| 2513 |
+
IC
|
| 2514 |
+
FO
|
| 2515 |
+
AM
|
| 2516 |
+
BC
|
| 2517 |
+
UZ
|
| 2518 |
+
ES
|
| 2519 |
+
OS
|
| 2520 |
+
WO
|
| 2521 |
+
SK
|
| 2522 |
+
EG
|
| 2523 |
+
QF
|
| 2524 |
+
JG
|
| 2525 |
+
CR
|
| 2526 |
+
IX
|
| 2527 |
+
KX
|
| 2528 |
+
RL
|
| 2529 |
+
ZK
|
| 2530 |
+
CY
|
| 2531 |
+
VY
|
| 2532 |
+
AG
|
| 2533 |
+
HC
|
| 2534 |
+
GK
|
| 2535 |
+
YT
|
| 2536 |
+
PR
|
| 2537 |
+
XT
|
| 2538 |
+
RV
|
| 2539 |
+
NK
|
| 2540 |
+
HZ
|
| 2541 |
+
BW
|
| 2542 |
+
GU
|
| 2543 |
+
LN
|
| 2544 |
+
DR
|
| 2545 |
+
BK
|
| 2546 |
+
KH
|
| 2547 |
+
BS
|
| 2548 |
+
CK
|
| 2549 |
+
ST
|
| 2550 |
+
ID
|
| 2551 |
+
RJ
|
| 2552 |
+
EQ
|
| 2553 |
+
MB
|
| 2554 |
+
MV
|
| 2555 |
+
XD
|
| 2556 |
+
HR
|
| 2557 |
+
BG
|
| 2558 |
+
ND
|
| 2559 |
+
PQ
|
| 2560 |
+
LG
|
| 2561 |
+
BD
|
| 2562 |
+
IY
|
| 2563 |
+
XA
|
| 2564 |
+
UG
|
| 2565 |
+
RH
|
| 2566 |
+
RC
|
| 2567 |
+
YI
|
| 2568 |
+
UB
|
| 2569 |
+
RT
|
| 2570 |
+
UJ
|
| 2571 |
+
ZO
|
| 2572 |
+
UI
|
| 2573 |
+
QH
|
| 2574 |
+
GZ
|
| 2575 |
+
NB
|
| 2576 |
+
JS
|
| 2577 |
+
DS
|
| 2578 |
+
QX
|
| 2579 |
+
SP
|
| 2580 |
+
OG
|
| 2581 |
+
HB
|
| 2582 |
+
ZJ
|
| 2583 |
+
WP
|
| 2584 |
+
WA
|
| 2585 |
+
LI
|
| 2586 |
+
EO
|
| 2587 |
+
NX
|
| 2588 |
+
SI
|
| 2589 |
+
WD
|
| 2590 |
+
SM
|
| 2591 |
+
DH
|
| 2592 |
+
SJ
|
| 2593 |
+
HM
|
| 2594 |
+
PY
|
| 2595 |
+
PF
|
| 2596 |
+
KM
|
| 2597 |
+
IM
|
| 2598 |
+
TW
|
| 2599 |
+
DT
|
| 2600 |
+
YF
|
| 2601 |
+
SN
|
| 2602 |
+
KC
|
| 2603 |
+
ED
|
| 2604 |
+
HX
|
| 2605 |
+
OL
|
| 2606 |
+
DI
|
| 2607 |
+
ZX
|
| 2608 |
+
ZV
|
| 2609 |
+
GP
|
| 2610 |
+
ZT
|
| 2611 |
+
JK
|
| 2612 |
+
VQ
|
| 2613 |
+
CX
|
| 2614 |
+
AP
|
| 2615 |
+
AD
|
| 2616 |
+
EP
|
| 2617 |
+
GS
|
| 2618 |
+
LW
|
| 2619 |
+
MY
|
| 2620 |
+
EU
|
| 2621 |
+
IK
|
| 2622 |
+
MC
|
| 2623 |
+
QE
|
| 2624 |
+
PM
|
| 2625 |
+
IO
|
| 2626 |
+
BX
|
| 2627 |
+
NS
|
| 2628 |
+
VS
|
| 2629 |
+
AC
|
| 2630 |
+
GJ
|
| 2631 |
+
XQ
|
| 2632 |
+
LZ
|
| 2633 |
+
PA
|
| 2634 |
+
PK
|
| 2635 |
+
AL
|
| 2636 |
+
OF
|
| 2637 |
+
SH
|
| 2638 |
+
GY
|
| 2639 |
+
RF
|
| 2640 |
+
GE
|
| 2641 |
+
TP
|
| 2642 |
+
GHZPCGJFWNVJEYFSUGKJFQLTFWDQSJQHDETBALMGABUFRNIPMHQAEADZNYAGTZLBP
|
| 2643 |
+
35
|
| 2644 |
+
OS
|
| 2645 |
+
GS
|
| 2646 |
+
IV
|
| 2647 |
+
JN
|
| 2648 |
+
BZ
|
| 2649 |
+
FM
|
| 2650 |
+
JV
|
| 2651 |
+
PX
|
| 2652 |
+
LT
|
| 2653 |
+
NQ
|
| 2654 |
+
DV
|
| 2655 |
+
AS
|
| 2656 |
+
IT
|
| 2657 |
+
JM
|
| 2658 |
+
QW
|
| 2659 |
+
AL
|
| 2660 |
+
JR
|
| 2661 |
+
HO
|
| 2662 |
+
MZ
|
| 2663 |
+
RX
|
| 2664 |
+
DT
|
| 2665 |
+
OU
|
| 2666 |
+
EX
|
| 2667 |
+
BT
|
| 2668 |
+
TV
|
| 2669 |
+
HZ
|
| 2670 |
+
UV
|
| 2671 |
+
EQ
|
| 2672 |
+
MY
|
| 2673 |
+
QV
|
| 2674 |
+
KW
|
| 2675 |
+
GM
|
| 2676 |
+
IJ
|
| 2677 |
+
HT
|
| 2678 |
+
BG
|
| 2679 |
+
EDHTCBCSRZOMGPQERBHHAW
|
| 2680 |
+
180
|
| 2681 |
+
WU
|
| 2682 |
+
BG
|
| 2683 |
+
IQ
|
| 2684 |
+
AU
|
| 2685 |
+
GD
|
| 2686 |
+
TM
|
| 2687 |
+
VS
|
| 2688 |
+
CR
|
| 2689 |
+
IE
|
| 2690 |
+
VL
|
| 2691 |
+
NU
|
| 2692 |
+
UA
|
| 2693 |
+
IW
|
| 2694 |
+
DQ
|
| 2695 |
+
CT
|
| 2696 |
+
WD
|
| 2697 |
+
HJ
|
| 2698 |
+
KP
|
| 2699 |
+
QZ
|
| 2700 |
+
TC
|
| 2701 |
+
FN
|
| 2702 |
+
XE
|
| 2703 |
+
XB
|
| 2704 |
+
RT
|
| 2705 |
+
ZI
|
| 2706 |
+
GW
|
| 2707 |
+
QB
|
| 2708 |
+
DT
|
| 2709 |
+
AZ
|
| 2710 |
+
QN
|
| 2711 |
+
IJ
|
| 2712 |
+
DG
|
| 2713 |
+
PR
|
| 2714 |
+
EY
|
| 2715 |
+
NM
|
| 2716 |
+
UV
|
| 2717 |
+
MH
|
| 2718 |
+
AX
|
| 2719 |
+
GS
|
| 2720 |
+
QP
|
| 2721 |
+
FU
|
| 2722 |
+
AD
|
| 2723 |
+
JC
|
| 2724 |
+
GQ
|
| 2725 |
+
HD
|
| 2726 |
+
OJ
|
| 2727 |
+
KE
|
| 2728 |
+
BY
|
| 2729 |
+
TV
|
| 2730 |
+
KF
|
| 2731 |
+
RV
|
| 2732 |
+
MR
|
| 2733 |
+
JV
|
| 2734 |
+
GK
|
| 2735 |
+
RN
|
| 2736 |
+
GH
|
| 2737 |
+
PQ
|
| 2738 |
+
SL
|
| 2739 |
+
CN
|
| 2740 |
+
BI
|
| 2741 |
+
PS
|
| 2742 |
+
UH
|
| 2743 |
+
UJ
|
| 2744 |
+
GM
|
| 2745 |
+
VK
|
| 2746 |
+
AM
|
| 2747 |
+
OH
|
| 2748 |
+
LG
|
| 2749 |
+
HG
|
| 2750 |
+
YE
|
| 2751 |
+
QY
|
| 2752 |
+
MG
|
| 2753 |
+
MT
|
| 2754 |
+
ZM
|
| 2755 |
+
IB
|
| 2756 |
+
CL
|
| 2757 |
+
RE
|
| 2758 |
+
NW
|
| 2759 |
+
NR
|
| 2760 |
+
KA
|
| 2761 |
+
OD
|
| 2762 |
+
QA
|
| 2763 |
+
DY
|
| 2764 |
+
SQ
|
| 2765 |
+
SY
|
| 2766 |
+
CW
|
| 2767 |
+
SB
|
| 2768 |
+
KZ
|
| 2769 |
+
VW
|
| 2770 |
+
QW
|
| 2771 |
+
VX
|
| 2772 |
+
AH
|
| 2773 |
+
SI
|
| 2774 |
+
ZX
|
| 2775 |
+
IU
|
| 2776 |
+
CS
|
| 2777 |
+
WI
|
| 2778 |
+
BJ
|
| 2779 |
+
OL
|
| 2780 |
+
XT
|
| 2781 |
+
VO
|
| 2782 |
+
QF
|
| 2783 |
+
CX
|
| 2784 |
+
AE
|
| 2785 |
+
GT
|
| 2786 |
+
GZ
|
| 2787 |
+
NE
|
| 2788 |
+
YS
|
| 2789 |
+
UR
|
| 2790 |
+
XP
|
| 2791 |
+
SV
|
| 2792 |
+
RH
|
| 2793 |
+
WR
|
| 2794 |
+
HC
|
| 2795 |
+
MB
|
| 2796 |
+
BQ
|
| 2797 |
+
UK
|
| 2798 |
+
SZ
|
| 2799 |
+
MU
|
| 2800 |
+
NZ
|
| 2801 |
+
ZQ
|
| 2802 |
+
KS
|
| 2803 |
+
JO
|
| 2804 |
+
JR
|
| 2805 |
+
AT
|
| 2806 |
+
NV
|
| 2807 |
+
IF
|
| 2808 |
+
FO
|
| 2809 |
+
EX
|
| 2810 |
+
FD
|
| 2811 |
+
WS
|
| 2812 |
+
ND
|
| 2813 |
+
AV
|
| 2814 |
+
IR
|
| 2815 |
+
UI
|
| 2816 |
+
IO
|
| 2817 |
+
EF
|
| 2818 |
+
OR
|
| 2819 |
+
MF
|
| 2820 |
+
EJ
|
| 2821 |
+
DA
|
| 2822 |
+
KC
|
| 2823 |
+
VH
|
| 2824 |
+
UO
|
| 2825 |
+
MC
|
| 2826 |
+
TQ
|
| 2827 |
+
BM
|
| 2828 |
+
VC
|
| 2829 |
+
DS
|
| 2830 |
+
UL
|
| 2831 |
+
TG
|
| 2832 |
+
KL
|
| 2833 |
+
XG
|
| 2834 |
+
HB
|
| 2835 |
+
IG
|
| 2836 |
+
BH
|
| 2837 |
+
EG
|
| 2838 |
+
SR
|
| 2839 |
+
DM
|
| 2840 |
+
IA
|
| 2841 |
+
WY
|
| 2842 |
+
LP
|
| 2843 |
+
EO
|
| 2844 |
+
BD
|
| 2845 |
+
MN
|
| 2846 |
+
JZ
|
| 2847 |
+
CK
|
| 2848 |
+
JE
|
| 2849 |
+
WN
|
| 2850 |
+
DW
|
| 2851 |
+
YX
|
| 2852 |
+
CJ
|
| 2853 |
+
ZP
|
| 2854 |
+
JF
|
| 2855 |
+
SK
|
| 2856 |
+
OY
|
| 2857 |
+
QH
|
| 2858 |
+
PV
|
| 2859 |
+
CV
|
| 2860 |
+
TS
|
| 2861 |
+
FOQSTAHIPOJEBFJMSXHEPZOJOYFOKBYVCWSBMWQQCBNCISQ
|
| 2862 |
+
70
|
| 2863 |
+
KN
|
| 2864 |
+
MN
|
| 2865 |
+
NU
|
| 2866 |
+
GN
|
| 2867 |
+
BU
|
| 2868 |
+
AW
|
| 2869 |
+
CK
|
| 2870 |
+
RU
|
| 2871 |
+
XY
|
| 2872 |
+
MS
|
| 2873 |
+
NP
|
| 2874 |
+
ER
|
| 2875 |
+
KQ
|
| 2876 |
+
MX
|
| 2877 |
+
AB
|
| 2878 |
+
GL
|
| 2879 |
+
LM
|
| 2880 |
+
IJ
|
| 2881 |
+
CY
|
| 2882 |
+
PY
|
| 2883 |
+
WZ
|
| 2884 |
+
OT
|
| 2885 |
+
DU
|
| 2886 |
+
NT
|
| 2887 |
+
TW
|
| 2888 |
+
NQ
|
| 2889 |
+
DK
|
| 2890 |
+
BR
|
| 2891 |
+
CT
|
| 2892 |
+
KM
|
| 2893 |
+
DI
|
| 2894 |
+
FQ
|
| 2895 |
+
CW
|
| 2896 |
+
SW
|
| 2897 |
+
EM
|
| 2898 |
+
JY
|
| 2899 |
+
OY
|
| 2900 |
+
FH
|
| 2901 |
+
AP
|
| 2902 |
+
JR
|
| 2903 |
+
GO
|
| 2904 |
+
LU
|
| 2905 |
+
GP
|
| 2906 |
+
UV
|
| 2907 |
+
OR
|
| 2908 |
+
BG
|
| 2909 |
+
FR
|
| 2910 |
+
GI
|
| 2911 |
+
MW
|
| 2912 |
+
CS
|
| 2913 |
+
LY
|
| 2914 |
+
FT
|
| 2915 |
+
CM
|
| 2916 |
+
DE
|
| 2917 |
+
UZ
|
| 2918 |
+
CN
|
| 2919 |
+
BV
|
| 2920 |
+
JK
|
| 2921 |
+
EF
|
| 2922 |
+
AV
|
| 2923 |
+
RZ
|
| 2924 |
+
LV
|
| 2925 |
+
RY
|
| 2926 |
+
KY
|
| 2927 |
+
BP
|
| 2928 |
+
CF
|
| 2929 |
+
OQ
|
| 2930 |
+
KT
|
| 2931 |
+
OU
|
| 2932 |
+
AG
|
| 2933 |
+
ONOQLUUAMOSDUYAGNDFKDJEMSKLMMBFSFRHGSRHUPJWHTNAZPSKMXZTLNZZEYRYPIEHYUTSESWTDJXCXFLSHTGOW
|
| 2934 |
+
184
|
| 2935 |
+
LB
|
| 2936 |
+
TE
|
| 2937 |
+
WQ
|
| 2938 |
+
KM
|
| 2939 |
+
QP
|
| 2940 |
+
GX
|
| 2941 |
+
VN
|
| 2942 |
+
JF
|
| 2943 |
+
BA
|
| 2944 |
+
KD
|
| 2945 |
+
IZ
|
| 2946 |
+
JZ
|
| 2947 |
+
YH
|
| 2948 |
+
DN
|
| 2949 |
+
EF
|
| 2950 |
+
TZ
|
| 2951 |
+
ZW
|
| 2952 |
+
OC
|
| 2953 |
+
AM
|
| 2954 |
+
ON
|
| 2955 |
+
GK
|
| 2956 |
+
XP
|
| 2957 |
+
OD
|
| 2958 |
+
FS
|
| 2959 |
+
HJ
|
| 2960 |
+
NW
|
| 2961 |
+
WP
|
| 2962 |
+
SF
|
| 2963 |
+
IJ
|
| 2964 |
+
UE
|
| 2965 |
+
YK
|
| 2966 |
+
NR
|
| 2967 |
+
DA
|
| 2968 |
+
DP
|
| 2969 |
+
JO
|
| 2970 |
+
UK
|
| 2971 |
+
MX
|
| 2972 |
+
ET
|
| 2973 |
+
AI
|
| 2974 |
+
NQ
|
| 2975 |
+
NO
|
| 2976 |
+
EP
|
| 2977 |
+
KS
|
| 2978 |
+
XE
|
| 2979 |
+
PK
|
| 2980 |
+
BK
|
| 2981 |
+
QV
|
| 2982 |
+
BQ
|
| 2983 |
+
NB
|
| 2984 |
+
AQ
|
| 2985 |
+
DS
|
| 2986 |
+
IK
|
| 2987 |
+
RH
|
| 2988 |
+
RT
|
| 2989 |
+
SR
|
| 2990 |
+
GJ
|
| 2991 |
+
BC
|
| 2992 |
+
KY
|
| 2993 |
+
AN
|
| 2994 |
+
VB
|
| 2995 |
+
YT
|
| 2996 |
+
HT
|
| 2997 |
+
KR
|
| 2998 |
+
WS
|
| 2999 |
+
YP
|
| 3000 |
+
QH
|
| 3001 |
+
TW
|
| 3002 |
+
FY
|
| 3003 |
+
ZD
|
| 3004 |
+
OK
|
| 3005 |
+
WY
|
| 3006 |
+
IA
|
| 3007 |
+
JV
|
| 3008 |
+
VM
|
| 3009 |
+
MD
|
| 3010 |
+
YR
|
| 3011 |
+
UQ
|
| 3012 |
+
AS
|
| 3013 |
+
YI
|
| 3014 |
+
HA
|
| 3015 |
+
FK
|
| 3016 |
+
VR
|
| 3017 |
+
AU
|
| 3018 |
+
GF
|
| 3019 |
+
XT
|
| 3020 |
+
EO
|
| 3021 |
+
ZO
|
| 3022 |
+
NS
|
| 3023 |
+
AZ
|
| 3024 |
+
SM
|
| 3025 |
+
LN
|
| 3026 |
+
OF
|
| 3027 |
+
FR
|
| 3028 |
+
PL
|
| 3029 |
+
SZ
|
| 3030 |
+
SG
|
| 3031 |
+
DM
|
| 3032 |
+
DO
|
| 3033 |
+
JB
|
| 3034 |
+
JT
|
| 3035 |
+
QY
|
| 3036 |
+
TL
|
| 3037 |
+
SQ
|
| 3038 |
+
RE
|
| 3039 |
+
DK
|
| 3040 |
+
EH
|
| 3041 |
+
LE
|
| 3042 |
+
OT
|
| 3043 |
+
UP
|
| 3044 |
+
LH
|
| 3045 |
+
BX
|
| 3046 |
+
AV
|
| 3047 |
+
EN
|
| 3048 |
+
CQ
|
| 3049 |
+
FP
|
| 3050 |
+
HQ
|
| 3051 |
+
CA
|
| 3052 |
+
ZJ
|
| 3053 |
+
KP
|
| 3054 |
+
HO
|
| 3055 |
+
SO
|
| 3056 |
+
CY
|
| 3057 |
+
KU
|
| 3058 |
+
PW
|
| 3059 |
+
SU
|
| 3060 |
+
MY
|
| 3061 |
+
QN
|
| 3062 |
+
RN
|
| 3063 |
+
NC
|
| 3064 |
+
RW
|
| 3065 |
+
DY
|
| 3066 |
+
XJ
|
| 3067 |
+
LU
|
| 3068 |
+
KB
|
| 3069 |
+
AF
|
| 3070 |
+
TO
|
| 3071 |
+
UT
|
| 3072 |
+
HB
|
| 3073 |
+
WL
|
| 3074 |
+
ID
|
| 3075 |
+
DI
|
| 3076 |
+
TS
|
| 3077 |
+
KO
|
| 3078 |
+
DE
|
| 3079 |
+
DU
|
| 3080 |
+
QS
|
| 3081 |
+
QW
|
| 3082 |
+
CZ
|
| 3083 |
+
TN
|
| 3084 |
+
MJ
|
| 3085 |
+
FE
|
| 3086 |
+
SN
|
| 3087 |
+
RU
|
| 3088 |
+
BH
|
| 3089 |
+
BM
|
| 3090 |
+
MR
|
| 3091 |
+
MO
|
| 3092 |
+
TC
|
| 3093 |
+
FX
|
| 3094 |
+
UB
|
| 3095 |
+
VF
|
| 3096 |
+
CI
|
| 3097 |
+
DV
|
| 3098 |
+
BO
|
| 3099 |
+
AJ
|
| 3100 |
+
OR
|
| 3101 |
+
SP
|
| 3102 |
+
JG
|
| 3103 |
+
WC
|
| 3104 |
+
NX
|
| 3105 |
+
EB
|
| 3106 |
+
HF
|
| 3107 |
+
WU
|
| 3108 |
+
BD
|
| 3109 |
+
TA
|
| 3110 |
+
OM
|
| 3111 |
+
HD
|
| 3112 |
+
JC
|
| 3113 |
+
MH
|
| 3114 |
+
ND
|
| 3115 |
+
VQ
|
| 3116 |
+
JN
|
| 3117 |
+
HS
|
| 3118 |
+
UF
|
| 3119 |
+
KXAVSMDHZBQWUNNRUSZQLXNXTKJJQTQEURABTEDFLTDPQTQLULVLQBQZMMQNSCQG
|
| 3120 |
+
69
|
| 3121 |
+
TU
|
| 3122 |
+
WD
|
| 3123 |
+
XV
|
| 3124 |
+
QF
|
| 3125 |
+
PN
|
| 3126 |
+
YG
|
| 3127 |
+
MG
|
| 3128 |
+
DJ
|
| 3129 |
+
VB
|
| 3130 |
+
ZY
|
| 3131 |
+
VN
|
| 3132 |
+
UX
|
| 3133 |
+
OP
|
| 3134 |
+
UK
|
| 3135 |
+
SL
|
| 3136 |
+
VF
|
| 3137 |
+
BY
|
| 3138 |
+
JU
|
| 3139 |
+
BD
|
| 3140 |
+
NI
|
| 3141 |
+
LG
|
| 3142 |
+
QH
|
| 3143 |
+
DA
|
| 3144 |
+
GQ
|
| 3145 |
+
PU
|
| 3146 |
+
KX
|
| 3147 |
+
XD
|
| 3148 |
+
UR
|
| 3149 |
+
NY
|
| 3150 |
+
JL
|
| 3151 |
+
DR
|
| 3152 |
+
UZ
|
| 3153 |
+
XK
|
| 3154 |
+
IE
|
| 3155 |
+
IF
|
| 3156 |
+
XF
|
| 3157 |
+
OV
|
| 3158 |
+
DV
|
| 3159 |
+
KJ
|
| 3160 |
+
HF
|
| 3161 |
+
AM
|
| 3162 |
+
CG
|
| 3163 |
+
GF
|
| 3164 |
+
XM
|
| 3165 |
+
RY
|
| 3166 |
+
DY
|
| 3167 |
+
MR
|
| 3168 |
+
FR
|
| 3169 |
+
MS
|
| 3170 |
+
RN
|
| 3171 |
+
UD
|
| 3172 |
+
JT
|
| 3173 |
+
XP
|
| 3174 |
+
YF
|
| 3175 |
+
BP
|
| 3176 |
+
RQ
|
| 3177 |
+
VD
|
| 3178 |
+
TV
|
| 3179 |
+
EA
|
| 3180 |
+
BM
|
| 3181 |
+
YV
|
| 3182 |
+
VP
|
| 3183 |
+
PF
|
| 3184 |
+
VM
|
| 3185 |
+
YC
|
| 3186 |
+
TN
|
| 3187 |
+
MW
|
| 3188 |
+
FG
|
| 3189 |
+
QP
|
| 3190 |
+
IVYPGYOYQEZVMNVZTBJOJSAWJHQBMOFLQVWUTKBWUIERBXZVVDOTQSVRQLXULSYJPRJQ
|
| 3191 |
+
111
|
| 3192 |
+
RH
|
| 3193 |
+
KC
|
| 3194 |
+
PS
|
| 3195 |
+
QF
|
| 3196 |
+
SF
|
| 3197 |
+
JR
|
| 3198 |
+
LK
|
| 3199 |
+
IR
|
| 3200 |
+
TL
|
| 3201 |
+
HZ
|
| 3202 |
+
PR
|
| 3203 |
+
PO
|
| 3204 |
+
ZY
|
| 3205 |
+
IT
|
| 3206 |
+
WH
|
| 3207 |
+
BN
|
| 3208 |
+
MG
|
| 3209 |
+
DM
|
| 3210 |
+
RN
|
| 3211 |
+
EM
|
| 3212 |
+
RI
|
| 3213 |
+
DV
|
| 3214 |
+
FO
|
| 3215 |
+
OD
|
| 3216 |
+
FZ
|
| 3217 |
+
AP
|
| 3218 |
+
UQ
|
| 3219 |
+
JZ
|
| 3220 |
+
QC
|
| 3221 |
+
WA
|
| 3222 |
+
YT
|
| 3223 |
+
FC
|
| 3224 |
+
GD
|
| 3225 |
+
UA
|
| 3226 |
+
ZR
|
| 3227 |
+
ZC
|
| 3228 |
+
AF
|
| 3229 |
+
OK
|
| 3230 |
+
NA
|
| 3231 |
+
UH
|
| 3232 |
+
HP
|
| 3233 |
+
EL
|
| 3234 |
+
HL
|
| 3235 |
+
GX
|
| 3236 |
+
ZI
|
| 3237 |
+
LO
|
| 3238 |
+
AU
|
| 3239 |
+
UE
|
| 3240 |
+
RG
|
| 3241 |
+
DP
|
| 3242 |
+
XT
|
| 3243 |
+
MB
|
| 3244 |
+
ZP
|
| 3245 |
+
IJ
|
| 3246 |
+
FV
|
| 3247 |
+
FT
|
| 3248 |
+
FA
|
| 3249 |
+
BS
|
| 3250 |
+
ML
|
| 3251 |
+
ZW
|
| 3252 |
+
OB
|
| 3253 |
+
DQ
|
| 3254 |
+
FK
|
| 3255 |
+
GJ
|
| 3256 |
+
ZA
|
| 3257 |
+
BL
|
| 3258 |
+
LW
|
| 3259 |
+
BF
|
| 3260 |
+
US
|
| 3261 |
+
TI
|
| 3262 |
+
YP
|
| 3263 |
+
TA
|
| 3264 |
+
GP
|
| 3265 |
+
BP
|
| 3266 |
+
EC
|
| 3267 |
+
LH
|
| 3268 |
+
YL
|
| 3269 |
+
LG
|
| 3270 |
+
HX
|
| 3271 |
+
UJ
|
| 3272 |
+
KM
|
| 3273 |
+
IG
|
| 3274 |
+
SM
|
| 3275 |
+
CU
|
| 3276 |
+
AK
|
| 3277 |
+
LM
|
| 3278 |
+
VM
|
| 3279 |
+
QD
|
| 3280 |
+
HR
|
| 3281 |
+
UY
|
| 3282 |
+
OI
|
| 3283 |
+
KX
|
| 3284 |
+
GB
|
| 3285 |
+
VH
|
| 3286 |
+
FN
|
| 3287 |
+
KI
|
| 3288 |
+
CQ
|
| 3289 |
+
KE
|
| 3290 |
+
UD
|
| 3291 |
+
UT
|
| 3292 |
+
VR
|
| 3293 |
+
KF
|
| 3294 |
+
XJ
|
| 3295 |
+
YU
|
| 3296 |
+
GY
|
| 3297 |
+
ZH
|
| 3298 |
+
RZ
|
| 3299 |
+
EZ
|
| 3300 |
+
TJ
|
| 3301 |
+
HM
|
| 3302 |
+
FR
|
| 3303 |
+
MNTQELQJFKDLDKNZTCINIPWRESPQZNWUNESWGJZ
|
| 3304 |
+
207
|
| 3305 |
+
FL
|
| 3306 |
+
UW
|
| 3307 |
+
BJ
|
| 3308 |
+
EX
|
| 3309 |
+
AH
|
| 3310 |
+
PQ
|
| 3311 |
+
EV
|
| 3312 |
+
VZ
|
| 3313 |
+
FG
|
| 3314 |
+
IT
|
| 3315 |
+
RS
|
| 3316 |
+
GQ
|
| 3317 |
+
GW
|
| 3318 |
+
ER
|
| 3319 |
+
NZ
|
| 3320 |
+
BK
|
| 3321 |
+
IR
|
| 3322 |
+
HP
|
| 3323 |
+
OQ
|
| 3324 |
+
MO
|
| 3325 |
+
NX
|
| 3326 |
+
AK
|
| 3327 |
+
AX
|
| 3328 |
+
AV
|
| 3329 |
+
DS
|
| 3330 |
+
FS
|
| 3331 |
+
JV
|
| 3332 |
+
GV
|
| 3333 |
+
HT
|
| 3334 |
+
QR
|
| 3335 |
+
GP
|
| 3336 |
+
KZ
|
| 3337 |
+
AD
|
| 3338 |
+
IJ
|
| 3339 |
+
KY
|
| 3340 |
+
QT
|
| 3341 |
+
XY
|
| 3342 |
+
EN
|
| 3343 |
+
FN
|
| 3344 |
+
DY
|
| 3345 |
+
JQ
|
| 3346 |
+
LZ
|
| 3347 |
+
RX
|
| 3348 |
+
CP
|
| 3349 |
+
CK
|
| 3350 |
+
DN
|
| 3351 |
+
OZ
|
| 3352 |
+
MR
|
| 3353 |
+
HV
|
| 3354 |
+
BD
|
| 3355 |
+
CZ
|
| 3356 |
+
OV
|
| 3357 |
+
CO
|
| 3358 |
+
GX
|
| 3359 |
+
JW
|
| 3360 |
+
EP
|
| 3361 |
+
RT
|
| 3362 |
+
OT
|
| 3363 |
+
IV
|
| 3364 |
+
KM
|
| 3365 |
+
DI
|
| 3366 |
+
FW
|
| 3367 |
+
SV
|
| 3368 |
+
TX
|
| 3369 |
+
WZ
|
| 3370 |
+
TZ
|
| 3371 |
+
PV
|
| 3372 |
+
DO
|
| 3373 |
+
DG
|
| 3374 |
+
HY
|
| 3375 |
+
UZ
|
| 3376 |
+
EQ
|
| 3377 |
+
EH
|
| 3378 |
+
BP
|
| 3379 |
+
HI
|
| 3380 |
+
GS
|
| 3381 |
+
GM
|
| 3382 |
+
DZ
|
| 3383 |
+
KN
|
| 3384 |
+
LU
|
| 3385 |
+
TV
|
| 3386 |
+
CW
|
| 3387 |
+
RW
|
| 3388 |
+
AJ
|
| 3389 |
+
FM
|
| 3390 |
+
KS
|
| 3391 |
+
CT
|
| 3392 |
+
SX
|
| 3393 |
+
SZ
|
| 3394 |
+
BI
|
| 3395 |
+
CR
|
| 3396 |
+
DK
|
| 3397 |
+
PX
|
| 3398 |
+
JK
|
| 3399 |
+
AF
|
| 3400 |
+
GT
|
| 3401 |
+
SU
|
| 3402 |
+
JO
|
| 3403 |
+
CQ
|
| 3404 |
+
KR
|
| 3405 |
+
QZ
|
| 3406 |
+
DH
|
| 3407 |
+
BT
|
| 3408 |
+
WX
|
| 3409 |
+
EW
|
| 3410 |
+
LS
|
| 3411 |
+
AT
|
| 3412 |
+
HQ
|
| 3413 |
+
NS
|
| 3414 |
+
NU
|
| 3415 |
+
JM
|
| 3416 |
+
AR
|
| 3417 |
+
GH
|
| 3418 |
+
QV
|
| 3419 |
+
CJ
|
| 3420 |
+
HK
|
| 3421 |
+
DV
|
| 3422 |
+
BL
|
| 3423 |
+
IO
|
| 3424 |
+
OY
|
| 3425 |
+
MQ
|
| 3426 |
+
LX
|
| 3427 |
+
PT
|
| 3428 |
+
BG
|
| 3429 |
+
AW
|
| 3430 |
+
EI
|
| 3431 |
+
LN
|
| 3432 |
+
EG
|
| 3433 |
+
IP
|
| 3434 |
+
MU
|
| 3435 |
+
KT
|
| 3436 |
+
JY
|
| 3437 |
+
QY
|
| 3438 |
+
RY
|
| 3439 |
+
MN
|
| 3440 |
+
AI
|
| 3441 |
+
EM
|
| 3442 |
+
EO
|
| 3443 |
+
LM
|
| 3444 |
+
UV
|
| 3445 |
+
DQ
|
| 3446 |
+
EY
|
| 3447 |
+
BU
|
| 3448 |
+
JZ
|
| 3449 |
+
CX
|
| 3450 |
+
JR
|
| 3451 |
+
FH
|
| 3452 |
+
HN
|
| 3453 |
+
HL
|
| 3454 |
+
CY
|
| 3455 |
+
DU
|
| 3456 |
+
CD
|
| 3457 |
+
MP
|
| 3458 |
+
AC
|
| 3459 |
+
RV
|
| 3460 |
+
BH
|
| 3461 |
+
EZ
|
| 3462 |
+
DT
|
| 3463 |
+
NV
|
| 3464 |
+
AN
|
| 3465 |
+
QW
|
| 3466 |
+
HR
|
| 3467 |
+
NO
|
| 3468 |
+
YZ
|
| 3469 |
+
OU
|
| 3470 |
+
CU
|
| 3471 |
+
JX
|
| 3472 |
+
BF
|
| 3473 |
+
FT
|
| 3474 |
+
IY
|
| 3475 |
+
AM
|
| 3476 |
+
BM
|
| 3477 |
+
LT
|
| 3478 |
+
HM
|
| 3479 |
+
FP
|
| 3480 |
+
AQ
|
| 3481 |
+
DP
|
| 3482 |
+
WY
|
| 3483 |
+
AL
|
| 3484 |
+
BN
|
| 3485 |
+
SY
|
| 3486 |
+
OR
|
| 3487 |
+
CI
|
| 3488 |
+
BV
|
| 3489 |
+
GN
|
| 3490 |
+
OW
|
| 3491 |
+
UY
|
| 3492 |
+
GI
|
| 3493 |
+
LP
|
| 3494 |
+
JP
|
| 3495 |
+
LW
|
| 3496 |
+
LR
|
| 3497 |
+
MX
|
| 3498 |
+
AG
|
| 3499 |
+
HU
|
| 3500 |
+
JS
|
| 3501 |
+
PZ
|
| 3502 |
+
PR
|
| 3503 |
+
DL
|
| 3504 |
+
CH
|
| 3505 |
+
ST
|
| 3506 |
+
LQ
|
| 3507 |
+
CS
|
| 3508 |
+
HX
|
| 3509 |
+
LO
|
| 3510 |
+
QX
|
| 3511 |
+
FZ
|
| 3512 |
+
WARHBSPIFYYINCLNJIFUHKDCYYZCWYUZYNCJ
|
| 3513 |
+
162
|
| 3514 |
+
KR
|
| 3515 |
+
VL
|
| 3516 |
+
AF
|
| 3517 |
+
XW
|
| 3518 |
+
TW
|
| 3519 |
+
US
|
| 3520 |
+
OX
|
| 3521 |
+
SY
|
| 3522 |
+
WE
|
| 3523 |
+
KC
|
| 3524 |
+
TI
|
| 3525 |
+
ES
|
| 3526 |
+
FS
|
| 3527 |
+
ME
|
| 3528 |
+
NG
|
| 3529 |
+
RK
|
| 3530 |
+
ZW
|
| 3531 |
+
JM
|
| 3532 |
+
LX
|
| 3533 |
+
PT
|
| 3534 |
+
VF
|
| 3535 |
+
NA
|
| 3536 |
+
UM
|
| 3537 |
+
GN
|
| 3538 |
+
WA
|
| 3539 |
+
DP
|
| 3540 |
+
HJ
|
| 3541 |
+
HG
|
| 3542 |
+
XC
|
| 3543 |
+
GV
|
| 3544 |
+
RD
|
| 3545 |
+
BI
|
| 3546 |
+
PS
|
| 3547 |
+
HX
|
| 3548 |
+
XZ
|
| 3549 |
+
HK
|
| 3550 |
+
DQ
|
| 3551 |
+
MI
|
| 3552 |
+
AT
|
| 3553 |
+
QB
|
| 3554 |
+
HW
|
| 3555 |
+
SG
|
| 3556 |
+
SO
|
| 3557 |
+
NV
|
| 3558 |
+
AY
|
| 3559 |
+
PM
|
| 3560 |
+
LO
|
| 3561 |
+
JC
|
| 3562 |
+
HZ
|
| 3563 |
+
TC
|
| 3564 |
+
SL
|
| 3565 |
+
PB
|
| 3566 |
+
BH
|
| 3567 |
+
ID
|
| 3568 |
+
OI
|
| 3569 |
+
HE
|
| 3570 |
+
JO
|
| 3571 |
+
UW
|
| 3572 |
+
YJ
|
| 3573 |
+
DZ
|
| 3574 |
+
JF
|
| 3575 |
+
HT
|
| 3576 |
+
MJ
|
| 3577 |
+
XI
|
| 3578 |
+
ZU
|
| 3579 |
+
XA
|
| 3580 |
+
YX
|
| 3581 |
+
OD
|
| 3582 |
+
RL
|
| 3583 |
+
EQ
|
| 3584 |
+
MU
|
| 3585 |
+
PF
|
| 3586 |
+
IY
|
| 3587 |
+
VI
|
| 3588 |
+
QD
|
| 3589 |
+
EL
|
| 3590 |
+
XJ
|
| 3591 |
+
QM
|
| 3592 |
+
CD
|
| 3593 |
+
NP
|
| 3594 |
+
QR
|
| 3595 |
+
YE
|
| 3596 |
+
KU
|
| 3597 |
+
ON
|
| 3598 |
+
AJ
|
| 3599 |
+
WO
|
| 3600 |
+
UR
|
| 3601 |
+
ZX
|
| 3602 |
+
PK
|
| 3603 |
+
QO
|
| 3604 |
+
UN
|
| 3605 |
+
SA
|
| 3606 |
+
ZS
|
| 3607 |
+
VE
|
| 3608 |
+
QS
|
| 3609 |
+
CW
|
| 3610 |
+
WH
|
| 3611 |
+
KB
|
| 3612 |
+
IG
|
| 3613 |
+
LY
|
| 3614 |
+
KL
|
| 3615 |
+
PY
|
| 3616 |
+
RG
|
| 3617 |
+
GR
|
| 3618 |
+
XF
|
| 3619 |
+
QY
|
| 3620 |
+
MK
|
| 3621 |
+
TF
|
| 3622 |
+
DR
|
| 3623 |
+
OA
|
| 3624 |
+
JW
|
| 3625 |
+
DU
|
| 3626 |
+
IW
|
| 3627 |
+
MD
|
| 3628 |
+
NX
|
| 3629 |
+
BJ
|
| 3630 |
+
RW
|
| 3631 |
+
XH
|
| 3632 |
+
IQ
|
| 3633 |
+
JU
|
| 3634 |
+
WU
|
| 3635 |
+
WZ
|
| 3636 |
+
XK
|
| 3637 |
+
UP
|
| 3638 |
+
PH
|
| 3639 |
+
ZC
|
| 3640 |
+
DH
|
| 3641 |
+
YZ
|
| 3642 |
+
LC
|
| 3643 |
+
UV
|
| 3644 |
+
WM
|
| 3645 |
+
FJ
|
| 3646 |
+
UE
|
| 3647 |
+
XN
|
| 3648 |
+
KG
|
| 3649 |
+
XV
|
| 3650 |
+
YO
|
| 3651 |
+
ND
|
| 3652 |
+
OG
|
| 3653 |
+
XO
|
| 3654 |
+
DO
|
| 3655 |
+
YP
|
| 3656 |
+
FE
|
| 3657 |
+
BX
|
| 3658 |
+
WS
|
| 3659 |
+
CJ
|
| 3660 |
+
DC
|
| 3661 |
+
FO
|
| 3662 |
+
LG
|
| 3663 |
+
KI
|
| 3664 |
+
BO
|
| 3665 |
+
CV
|
| 3666 |
+
EF
|
| 3667 |
+
MG
|
| 3668 |
+
OC
|
| 3669 |
+
BN
|
| 3670 |
+
PI
|
| 3671 |
+
XP
|
| 3672 |
+
WT
|
| 3673 |
+
UX
|
| 3674 |
+
KM
|
| 3675 |
+
RO
|
| 3676 |
+
MITBPNHKDFBKQBJDWSMEWJGCPZXVYTEUBPEROWBBOCBJKXWGLEPDNLZJZPKKZUIVAHGLAZZRTYJPFJSNFGRKP
|
| 3677 |
+
211
|
| 3678 |
+
QX
|
| 3679 |
+
KR
|
| 3680 |
+
HP
|
| 3681 |
+
ZQ
|
| 3682 |
+
AJ
|
| 3683 |
+
AB
|
| 3684 |
+
GA
|
| 3685 |
+
TU
|
| 3686 |
+
RD
|
| 3687 |
+
HZ
|
| 3688 |
+
WR
|
| 3689 |
+
IR
|
| 3690 |
+
UY
|
| 3691 |
+
WP
|
| 3692 |
+
PH
|
| 3693 |
+
YW
|
| 3694 |
+
ML
|
| 3695 |
+
OQ
|
| 3696 |
+
TR
|
| 3697 |
+
AL
|
| 3698 |
+
TA
|
| 3699 |
+
DT
|
| 3700 |
+
QT
|
| 3701 |
+
WS
|
| 3702 |
+
WC
|
| 3703 |
+
VO
|
| 3704 |
+
YH
|
| 3705 |
+
UV
|
| 3706 |
+
DL
|
| 3707 |
+
SF
|
| 3708 |
+
XU
|
| 3709 |
+
TD
|
| 3710 |
+
TE
|
| 3711 |
+
LY
|
| 3712 |
+
EF
|
| 3713 |
+
LO
|
| 3714 |
+
WG
|
| 3715 |
+
IJ
|
| 3716 |
+
OL
|
| 3717 |
+
LM
|
| 3718 |
+
YZ
|
| 3719 |
+
JX
|
| 3720 |
+
VI
|
| 3721 |
+
GJ
|
| 3722 |
+
WM
|
| 3723 |
+
YD
|
| 3724 |
+
LR
|
| 3725 |
+
MV
|
| 3726 |
+
IT
|
| 3727 |
+
SP
|
| 3728 |
+
NQ
|
| 3729 |
+
HR
|
| 3730 |
+
RA
|
| 3731 |
+
YE
|
| 3732 |
+
PE
|
| 3733 |
+
RY
|
| 3734 |
+
SZ
|
| 3735 |
+
JD
|
| 3736 |
+
YQ
|
| 3737 |
+
BD
|
| 3738 |
+
UT
|
| 3739 |
+
NU
|
| 3740 |
+
CP
|
| 3741 |
+
FU
|
| 3742 |
+
WA
|
| 3743 |
+
RE
|
| 3744 |
+
UB
|
| 3745 |
+
IZ
|
| 3746 |
+
SL
|
| 3747 |
+
YJ
|
| 3748 |
+
LF
|
| 3749 |
+
EC
|
| 3750 |
+
DK
|
| 3751 |
+
JB
|
| 3752 |
+
LG
|
| 3753 |
+
NI
|
| 3754 |
+
DU
|
| 3755 |
+
MI
|
| 3756 |
+
UX
|
| 3757 |
+
LA
|
| 3758 |
+
AC
|
| 3759 |
+
YC
|
| 3760 |
+
ZH
|
| 3761 |
+
CG
|
| 3762 |
+
BY
|
| 3763 |
+
ZC
|
| 3764 |
+
KL
|
| 3765 |
+
YF
|
| 3766 |
+
ND
|
| 3767 |
+
NV
|
| 3768 |
+
ED
|
| 3769 |
+
MG
|
| 3770 |
+
PZ
|
| 3771 |
+
KS
|
| 3772 |
+
CH
|
| 3773 |
+
ZA
|
| 3774 |
+
TN
|
| 3775 |
+
EW
|
| 3776 |
+
SN
|
| 3777 |
+
BA
|
| 3778 |
+
UJ
|
| 3779 |
+
VA
|
| 3780 |
+
UI
|
| 3781 |
+
EA
|
| 3782 |
+
BN
|
| 3783 |
+
PL
|
| 3784 |
+
UA
|
| 3785 |
+
KT
|
| 3786 |
+
FC
|
| 3787 |
+
IA
|
| 3788 |
+
DI
|
| 3789 |
+
BS
|
| 3790 |
+
UZ
|
| 3791 |
+
RI
|
| 3792 |
+
GY
|
| 3793 |
+
QU
|
| 3794 |
+
RZ
|
| 3795 |
+
QC
|
| 3796 |
+
HA
|
| 3797 |
+
NY
|
| 3798 |
+
BM
|
| 3799 |
+
MP
|
| 3800 |
+
NB
|
| 3801 |
+
SE
|
| 3802 |
+
HM
|
| 3803 |
+
JM
|
| 3804 |
+
VU
|
| 3805 |
+
XE
|
| 3806 |
+
GF
|
| 3807 |
+
ER
|
| 3808 |
+
PJ
|
| 3809 |
+
RB
|
| 3810 |
+
MW
|
| 3811 |
+
YG
|
| 3812 |
+
EO
|
| 3813 |
+
OJ
|
| 3814 |
+
HN
|
| 3815 |
+
IV
|
| 3816 |
+
JZ
|
| 3817 |
+
IX
|
| 3818 |
+
LK
|
| 3819 |
+
VQ
|
| 3820 |
+
QR
|
| 3821 |
+
DG
|
| 3822 |
+
EX
|
| 3823 |
+
UW
|
| 3824 |
+
JE
|
| 3825 |
+
QJ
|
| 3826 |
+
SU
|
| 3827 |
+
BK
|
| 3828 |
+
WD
|
| 3829 |
+
LD
|
| 3830 |
+
GW
|
| 3831 |
+
ZX
|
| 3832 |
+
XZ
|
| 3833 |
+
KU
|
| 3834 |
+
LS
|
| 3835 |
+
HD
|
| 3836 |
+
XD
|
| 3837 |
+
KA
|
| 3838 |
+
EK
|
| 3839 |
+
FT
|
| 3840 |
+
TS
|
| 3841 |
+
QA
|
| 3842 |
+
YO
|
| 3843 |
+
QW
|
| 3844 |
+
KF
|
| 3845 |
+
OW
|
| 3846 |
+
GZ
|
| 3847 |
+
RN
|
| 3848 |
+
IC
|
| 3849 |
+
GN
|
| 3850 |
+
OV
|
| 3851 |
+
ZV
|
| 3852 |
+
XL
|
| 3853 |
+
YI
|
| 3854 |
+
TC
|
| 3855 |
+
TF
|
| 3856 |
+
VY
|
| 3857 |
+
VJ
|
| 3858 |
+
YX
|
| 3859 |
+
JI
|
| 3860 |
+
AF
|
| 3861 |
+
EQ
|
| 3862 |
+
HK
|
| 3863 |
+
DX
|
| 3864 |
+
BQ
|
| 3865 |
+
GC
|
| 3866 |
+
PV
|
| 3867 |
+
AK
|
| 3868 |
+
WY
|
| 3869 |
+
ZB
|
| 3870 |
+
LP
|
| 3871 |
+
FK
|
| 3872 |
+
UL
|
| 3873 |
+
MX
|
| 3874 |
+
BZ
|
| 3875 |
+
QP
|
| 3876 |
+
PA
|
| 3877 |
+
JA
|
| 3878 |
+
AY
|
| 3879 |
+
AP
|
| 3880 |
+
KZ
|
| 3881 |
+
RG
|
| 3882 |
+
FQ
|
| 3883 |
+
RJ
|
| 3884 |
+
YR
|
| 3885 |
+
UO
|
| 3886 |
+
LU
|
| 3887 |
+
ZI
|
| 3888 |
+
XQ
|
| 3889 |
+
YJQESDHZLXMOTUEPTUORYIIYQFJMAJTFPNQYSLBFKCBQTEFXLAMSWUZYBUUGXNPYSDBZLOJUUKSQHTSUESHFJFKVGPWVSIYJBN
|
| 3890 |
+
135
|
| 3891 |
+
HI
|
| 3892 |
+
HX
|
| 3893 |
+
AW
|
| 3894 |
+
XZ
|
| 3895 |
+
GM
|
| 3896 |
+
BU
|
| 3897 |
+
JR
|
| 3898 |
+
KR
|
| 3899 |
+
FZ
|
| 3900 |
+
SY
|
| 3901 |
+
RY
|
| 3902 |
+
ER
|
| 3903 |
+
KW
|
| 3904 |
+
EQ
|
| 3905 |
+
GV
|
| 3906 |
+
SZ
|
| 3907 |
+
AG
|
| 3908 |
+
CX
|
| 3909 |
+
OX
|
| 3910 |
+
LQ
|
| 3911 |
+
MV
|
| 3912 |
+
GX
|
| 3913 |
+
LZ
|
| 3914 |
+
CK
|
| 3915 |
+
BW
|
| 3916 |
+
BC
|
| 3917 |
+
AX
|
| 3918 |
+
NP
|
| 3919 |
+
FV
|
| 3920 |
+
OW
|
| 3921 |
+
IS
|
| 3922 |
+
OV
|
| 3923 |
+
GN
|
| 3924 |
+
DR
|
| 3925 |
+
FY
|
| 3926 |
+
IO
|
| 3927 |
+
LY
|
| 3928 |
+
IT
|
| 3929 |
+
HN
|
| 3930 |
+
KO
|
| 3931 |
+
AV
|
| 3932 |
+
LW
|
| 3933 |
+
MX
|
| 3934 |
+
EI
|
| 3935 |
+
ST
|
| 3936 |
+
BJ
|
| 3937 |
+
AL
|
| 3938 |
+
LT
|
| 3939 |
+
QX
|
| 3940 |
+
HP
|
| 3941 |
+
FX
|
| 3942 |
+
TZ
|
| 3943 |
+
AB
|
| 3944 |
+
JK
|
| 3945 |
+
EL
|
| 3946 |
+
KQ
|
| 3947 |
+
QS
|
| 3948 |
+
GY
|
| 3949 |
+
FI
|
| 3950 |
+
SW
|
| 3951 |
+
DX
|
| 3952 |
+
CF
|
| 3953 |
+
RW
|
| 3954 |
+
OY
|
| 3955 |
+
QY
|
| 3956 |
+
GU
|
| 3957 |
+
DN
|
| 3958 |
+
IV
|
| 3959 |
+
DI
|
| 3960 |
+
KZ
|
| 3961 |
+
CS
|
| 3962 |
+
HL
|
| 3963 |
+
FR
|
| 3964 |
+
IZ
|
| 3965 |
+
PX
|
| 3966 |
+
GR
|
| 3967 |
+
OZ
|
| 3968 |
+
LS
|
| 3969 |
+
DL
|
| 3970 |
+
RT
|
| 3971 |
+
KP
|
| 3972 |
+
QZ
|
| 3973 |
+
GO
|
| 3974 |
+
DP
|
| 3975 |
+
LO
|
| 3976 |
+
MT
|
| 3977 |
+
BO
|
| 3978 |
+
SV
|
| 3979 |
+
FH
|
| 3980 |
+
IN
|
| 3981 |
+
IU
|
| 3982 |
+
HQ
|
| 3983 |
+
DF
|
| 3984 |
+
FS
|
| 3985 |
+
FU
|
| 3986 |
+
BQ
|
| 3987 |
+
PY
|
| 3988 |
+
BI
|
| 3989 |
+
OT
|
| 3990 |
+
PS
|
| 3991 |
+
GL
|
| 3992 |
+
HV
|
| 3993 |
+
MW
|
| 3994 |
+
DQ
|
| 3995 |
+
UW
|
| 3996 |
+
ET
|
| 3997 |
+
HT
|
| 3998 |
+
BZ
|
| 3999 |
+
OR
|
| 4000 |
+
NY
|
| 4001 |
+
MQ
|
| 4002 |
+
EH
|
| 4003 |
+
EY
|
| 4004 |
+
IR
|
| 4005 |
+
HY
|
| 4006 |
+
PV
|
| 4007 |
+
OU
|
| 4008 |
+
CW
|
| 4009 |
+
JP
|
| 4010 |
+
JW
|
| 4011 |
+
BX
|
| 4012 |
+
FM
|
| 4013 |
+
JL
|
| 4014 |
+
CD
|
| 4015 |
+
EF
|
| 4016 |
+
LU
|
| 4017 |
+
CR
|
| 4018 |
+
GZ
|
| 4019 |
+
KY
|
| 4020 |
+
NO
|
| 4021 |
+
AH
|
| 4022 |
+
PQ
|
| 4023 |
+
AC
|
| 4024 |
+
BT
|
| 4025 |
+
KM
|
| 4026 |
+
LSKUGECWHUTLKILFVIWFFQLUSMJMYHTQFOWEOTRMTRCCLZLTRKUCEBERD
|
| 4027 |
+
168
|
| 4028 |
+
OD
|
| 4029 |
+
MV
|
| 4030 |
+
ZF
|
| 4031 |
+
JP
|
| 4032 |
+
HX
|
| 4033 |
+
VW
|
| 4034 |
+
VK
|
| 4035 |
+
SC
|
| 4036 |
+
CF
|
| 4037 |
+
SV
|
| 4038 |
+
OR
|
| 4039 |
+
BV
|
| 4040 |
+
MX
|
| 4041 |
+
AI
|
| 4042 |
+
DC
|
| 4043 |
+
FU
|
| 4044 |
+
YV
|
| 4045 |
+
HZ
|
| 4046 |
+
MT
|
| 4047 |
+
AB
|
| 4048 |
+
RH
|
| 4049 |
+
PN
|
| 4050 |
+
SJ
|
| 4051 |
+
NP
|
| 4052 |
+
QN
|
| 4053 |
+
XA
|
| 4054 |
+
PM
|
| 4055 |
+
NR
|
| 4056 |
+
IF
|
| 4057 |
+
OG
|
| 4058 |
+
EO
|
| 4059 |
+
MB
|
| 4060 |
+
DV
|
| 4061 |
+
WC
|
| 4062 |
+
TE
|
| 4063 |
+
OT
|
| 4064 |
+
FR
|
| 4065 |
+
AS
|
| 4066 |
+
VS
|
| 4067 |
+
DF
|
| 4068 |
+
PJ
|
| 4069 |
+
GM
|
| 4070 |
+
ZO
|
| 4071 |
+
WF
|
| 4072 |
+
RY
|
| 4073 |
+
HO
|
| 4074 |
+
MK
|
| 4075 |
+
BE
|
| 4076 |
+
GY
|
| 4077 |
+
EW
|
| 4078 |
+
MD
|
| 4079 |
+
QH
|
| 4080 |
+
ND
|
| 4081 |
+
HS
|
| 4082 |
+
RF
|
| 4083 |
+
KX
|
| 4084 |
+
GE
|
| 4085 |
+
IZ
|
| 4086 |
+
ZL
|
| 4087 |
+
DR
|
| 4088 |
+
ZV
|
| 4089 |
+
PZ
|
| 4090 |
+
UD
|
| 4091 |
+
JK
|
| 4092 |
+
GU
|
| 4093 |
+
JS
|
| 4094 |
+
RO
|
| 4095 |
+
KE
|
| 4096 |
+
BR
|
| 4097 |
+
WR
|
| 4098 |
+
OM
|
| 4099 |
+
TD
|
| 4100 |
+
TR
|
| 4101 |
+
OU
|
| 4102 |
+
LF
|
| 4103 |
+
IL
|
| 4104 |
+
TU
|
| 4105 |
+
LD
|
| 4106 |
+
KU
|
| 4107 |
+
JI
|
| 4108 |
+
WK
|
| 4109 |
+
YF
|
| 4110 |
+
TA
|
| 4111 |
+
BM
|
| 4112 |
+
DK
|
| 4113 |
+
DW
|
| 4114 |
+
GN
|
| 4115 |
+
WD
|
| 4116 |
+
IQ
|
| 4117 |
+
CH
|
| 4118 |
+
WO
|
| 4119 |
+
ZK
|
| 4120 |
+
VP
|
| 4121 |
+
GR
|
| 4122 |
+
NO
|
| 4123 |
+
FI
|
| 4124 |
+
YU
|
| 4125 |
+
BQ
|
| 4126 |
+
ET
|
| 4127 |
+
JW
|
| 4128 |
+
CQ
|
| 4129 |
+
PW
|
| 4130 |
+
SO
|
| 4131 |
+
VO
|
| 4132 |
+
JD
|
| 4133 |
+
JB
|
| 4134 |
+
MU
|
| 4135 |
+
AC
|
| 4136 |
+
FH
|
| 4137 |
+
HU
|
| 4138 |
+
QZ
|
| 4139 |
+
XZ
|
| 4140 |
+
PB
|
| 4141 |
+
OX
|
| 4142 |
+
UQ
|
| 4143 |
+
FC
|
| 4144 |
+
WZ
|
| 4145 |
+
XG
|
| 4146 |
+
RE
|
| 4147 |
+
UA
|
| 4148 |
+
OP
|
| 4149 |
+
MQ
|
| 4150 |
+
CU
|
| 4151 |
+
VD
|
| 4152 |
+
PO
|
| 4153 |
+
YD
|
| 4154 |
+
BF
|
| 4155 |
+
MZ
|
| 4156 |
+
MJ
|
| 4157 |
+
XQ
|
| 4158 |
+
DA
|
| 4159 |
+
IO
|
| 4160 |
+
RD
|
| 4161 |
+
XK
|
| 4162 |
+
DJ
|
| 4163 |
+
UW
|
| 4164 |
+
ZA
|
| 4165 |
+
QF
|
| 4166 |
+
LJ
|
| 4167 |
+
GV
|
| 4168 |
+
CL
|
| 4169 |
+
DU
|
| 4170 |
+
PR
|
| 4171 |
+
GT
|
| 4172 |
+
TV
|
| 4173 |
+
LZ
|
| 4174 |
+
ID
|
| 4175 |
+
ER
|
| 4176 |
+
FE
|
| 4177 |
+
TM
|
| 4178 |
+
DG
|
| 4179 |
+
XB
|
| 4180 |
+
HI
|
| 4181 |
+
OL
|
| 4182 |
+
ZI
|
| 4183 |
+
WS
|
| 4184 |
+
GK
|
| 4185 |
+
IG
|
| 4186 |
+
PL
|
| 4187 |
+
GP
|
| 4188 |
+
JE
|
| 4189 |
+
AW
|
| 4190 |
+
XY
|
| 4191 |
+
JL
|
| 4192 |
+
UN
|
| 4193 |
+
OI
|
| 4194 |
+
HD
|
| 4195 |
+
QR
|
| 4196 |
+
WVBZCPYIQMATGVVRPFVJQQXRYPJIIATPRKIICLWKHZEJMHEYRWUPAXP
|
| 4197 |
+
163
|
| 4198 |
+
XQ
|
| 4199 |
+
KR
|
| 4200 |
+
IW
|
| 4201 |
+
JI
|
| 4202 |
+
FE
|
| 4203 |
+
AP
|
| 4204 |
+
GF
|
| 4205 |
+
VK
|
| 4206 |
+
LN
|
| 4207 |
+
WB
|
| 4208 |
+
FJ
|
| 4209 |
+
TC
|
| 4210 |
+
MQ
|
| 4211 |
+
OJ
|
| 4212 |
+
OU
|
| 4213 |
+
XC
|
| 4214 |
+
EL
|
| 4215 |
+
WM
|
| 4216 |
+
HZ
|
| 4217 |
+
HQ
|
| 4218 |
+
SI
|
| 4219 |
+
BC
|
| 4220 |
+
DP
|
| 4221 |
+
CL
|
| 4222 |
+
ID
|
| 4223 |
+
BJ
|
| 4224 |
+
OV
|
| 4225 |
+
DL
|
| 4226 |
+
PQ
|
| 4227 |
+
GM
|
| 4228 |
+
GY
|
| 4229 |
+
AG
|
| 4230 |
+
BA
|
| 4231 |
+
ML
|
| 4232 |
+
NP
|
| 4233 |
+
LM
|
| 4234 |
+
TF
|
| 4235 |
+
MK
|
| 4236 |
+
WF
|
| 4237 |
+
UF
|
| 4238 |
+
QW
|
| 4239 |
+
QG
|
| 4240 |
+
CT
|
| 4241 |
+
AH
|
| 4242 |
+
IA
|
| 4243 |
+
XP
|
| 4244 |
+
OK
|
| 4245 |
+
PI
|
| 4246 |
+
RS
|
| 4247 |
+
LA
|
| 4248 |
+
DB
|
| 4249 |
+
JA
|
| 4250 |
+
TB
|
| 4251 |
+
CV
|
| 4252 |
+
DU
|
| 4253 |
+
TU
|
| 4254 |
+
BE
|
| 4255 |
+
FX
|
| 4256 |
+
BK
|
| 4257 |
+
SW
|
| 4258 |
+
ZI
|
| 4259 |
+
BI
|
| 4260 |
+
EX
|
| 4261 |
+
SD
|
| 4262 |
+
ED
|
| 4263 |
+
ZT
|
| 4264 |
+
SF
|
| 4265 |
+
NB
|
| 4266 |
+
EW
|
| 4267 |
+
WO
|
| 4268 |
+
QP
|
| 4269 |
+
RM
|
| 4270 |
+
GU
|
| 4271 |
+
RB
|
| 4272 |
+
AZ
|
| 4273 |
+
SC
|
| 4274 |
+
TE
|
| 4275 |
+
BF
|
| 4276 |
+
HR
|
| 4277 |
+
UR
|
| 4278 |
+
HL
|
| 4279 |
+
PR
|
| 4280 |
+
QZ
|
| 4281 |
+
CH
|
| 4282 |
+
ZQ
|
| 4283 |
+
GK
|
| 4284 |
+
LH
|
| 4285 |
+
VU
|
| 4286 |
+
JV
|
| 4287 |
+
CU
|
| 4288 |
+
TV
|
| 4289 |
+
HS
|
| 4290 |
+
RY
|
| 4291 |
+
FU
|
| 4292 |
+
AK
|
| 4293 |
+
XH
|
| 4294 |
+
NJ
|
| 4295 |
+
US
|
| 4296 |
+
TD
|
| 4297 |
+
WA
|
| 4298 |
+
IF
|
| 4299 |
+
LC
|
| 4300 |
+
RP
|
| 4301 |
+
VO
|
| 4302 |
+
OQ
|
| 4303 |
+
PD
|
| 4304 |
+
CS
|
| 4305 |
+
HD
|
| 4306 |
+
LJ
|
| 4307 |
+
QJ
|
| 4308 |
+
HE
|
| 4309 |
+
IM
|
| 4310 |
+
XY
|
| 4311 |
+
LR
|
| 4312 |
+
DG
|
| 4313 |
+
AM
|
| 4314 |
+
SB
|
| 4315 |
+
DX
|
| 4316 |
+
AQ
|
| 4317 |
+
PK
|
| 4318 |
+
UE
|
| 4319 |
+
OD
|
| 4320 |
+
KB
|
| 4321 |
+
ZD
|
| 4322 |
+
YA
|
| 4323 |
+
HM
|
| 4324 |
+
AT
|
| 4325 |
+
SQ
|
| 4326 |
+
YD
|
| 4327 |
+
KE
|
| 4328 |
+
SH
|
| 4329 |
+
QA
|
| 4330 |
+
ZS
|
| 4331 |
+
NC
|
| 4332 |
+
JG
|
| 4333 |
+
ME
|
| 4334 |
+
IU
|
| 4335 |
+
TN
|
| 4336 |
+
RG
|
| 4337 |
+
HY
|
| 4338 |
+
PV
|
| 4339 |
+
PF
|
| 4340 |
+
HC
|
| 4341 |
+
FC
|
| 4342 |
+
ZX
|
| 4343 |
+
DO
|
| 4344 |
+
SZ
|
| 4345 |
+
HU
|
| 4346 |
+
NM
|
| 4347 |
+
YX
|
| 4348 |
+
WZ
|
| 4349 |
+
WK
|
| 4350 |
+
XI
|
| 4351 |
+
NR
|
| 4352 |
+
JH
|
| 4353 |
+
UH
|
| 4354 |
+
UX
|
| 4355 |
+
GR
|
| 4356 |
+
XM
|
| 4357 |
+
QY
|
| 4358 |
+
EY
|
| 4359 |
+
CF
|
| 4360 |
+
JP
|
| 4361 |
+
CDHHMSCCCAUQDSUCBDLVVURXLBUNOWNOQIBUIURZRTBSPWMPXYYVTNOVWDQUXAIQTVOMZSIESNQHWMGALDQXKRBPZCCPUGU
|
| 4362 |
+
267
|
| 4363 |
+
KX
|
| 4364 |
+
OP
|
| 4365 |
+
GU
|
| 4366 |
+
DO
|
| 4367 |
+
EU
|
| 4368 |
+
VZ
|
| 4369 |
+
HK
|
| 4370 |
+
GM
|
| 4371 |
+
NO
|
| 4372 |
+
DX
|
| 4373 |
+
DI
|
| 4374 |
+
TY
|
| 4375 |
+
CQ
|
| 4376 |
+
BW
|
| 4377 |
+
MT
|
| 4378 |
+
SV
|
| 4379 |
+
DG
|
| 4380 |
+
NS
|
| 4381 |
+
BU
|
| 4382 |
+
EW
|
| 4383 |
+
DJ
|
| 4384 |
+
NY
|
| 4385 |
+
DW
|
| 4386 |
+
CK
|
| 4387 |
+
LM
|
| 4388 |
+
KT
|
| 4389 |
+
BD
|
| 4390 |
+
CO
|
| 4391 |
+
HZ
|
| 4392 |
+
LV
|
| 4393 |
+
GV
|
| 4394 |
+
PY
|
| 4395 |
+
DS
|
| 4396 |
+
LP
|
| 4397 |
+
AX
|
| 4398 |
+
QY
|
| 4399 |
+
FJ
|
| 4400 |
+
XZ
|
| 4401 |
+
KY
|
| 4402 |
+
XY
|
| 4403 |
+
KL
|
| 4404 |
+
AU
|
| 4405 |
+
WZ
|
| 4406 |
+
FP
|
| 4407 |
+
BF
|
| 4408 |
+
FO
|
| 4409 |
+
WX
|
| 4410 |
+
MS
|
| 4411 |
+
BG
|
| 4412 |
+
HJ
|
| 4413 |
+
RW
|
| 4414 |
+
AK
|
| 4415 |
+
SX
|
| 4416 |
+
BY
|
| 4417 |
+
AS
|
| 4418 |
+
FQ
|
| 4419 |
+
LQ
|
| 4420 |
+
IW
|
| 4421 |
+
YZ
|
| 4422 |
+
DR
|
| 4423 |
+
QT
|
| 4424 |
+
OZ
|
| 4425 |
+
QS
|
| 4426 |
+
FW
|
| 4427 |
+
HT
|
| 4428 |
+
CX
|
| 4429 |
+
CH
|
| 4430 |
+
DE
|
| 4431 |
+
DQ
|
| 4432 |
+
CW
|
| 4433 |
+
MW
|
| 4434 |
+
SU
|
| 4435 |
+
BV
|
| 4436 |
+
EQ
|
| 4437 |
+
FG
|
| 4438 |
+
IJ
|
| 4439 |
+
JQ
|
| 4440 |
+
LS
|
| 4441 |
+
BO
|
| 4442 |
+
AG
|
| 4443 |
+
BJ
|
| 4444 |
+
AY
|
| 4445 |
+
OS
|
| 4446 |
+
JP
|
| 4447 |
+
CE
|
| 4448 |
+
AP
|
| 4449 |
+
NQ
|
| 4450 |
+
NU
|
| 4451 |
+
AW
|
| 4452 |
+
PV
|
| 4453 |
+
DK
|
| 4454 |
+
IU
|
| 4455 |
+
EF
|
| 4456 |
+
OQ
|
| 4457 |
+
HP
|
| 4458 |
+
FI
|
| 4459 |
+
OW
|
| 4460 |
+
NV
|
| 4461 |
+
IX
|
| 4462 |
+
KV
|
| 4463 |
+
EO
|
| 4464 |
+
PX
|
| 4465 |
+
RT
|
| 4466 |
+
UZ
|
| 4467 |
+
CV
|
| 4468 |
+
GS
|
| 4469 |
+
UX
|
| 4470 |
+
FR
|
| 4471 |
+
IL
|
| 4472 |
+
JN
|
| 4473 |
+
EX
|
| 4474 |
+
RX
|
| 4475 |
+
MN
|
| 4476 |
+
AL
|
| 4477 |
+
VW
|
| 4478 |
+
HW
|
| 4479 |
+
DV
|
| 4480 |
+
CG
|
| 4481 |
+
FV
|
| 4482 |
+
LR
|
| 4483 |
+
TX
|
| 4484 |
+
FM
|
| 4485 |
+
DZ
|
| 4486 |
+
NZ
|
| 4487 |
+
LZ
|
| 4488 |
+
ST
|
| 4489 |
+
CI
|
| 4490 |
+
BS
|
| 4491 |
+
ES
|
| 4492 |
+
JX
|
| 4493 |
+
AV
|
| 4494 |
+
AE
|
| 4495 |
+
KZ
|
| 4496 |
+
CN
|
| 4497 |
+
HX
|
| 4498 |
+
KN
|
| 4499 |
+
OR
|
| 4500 |
+
IS
|
| 4501 |
+
DY
|
| 4502 |
+
AR
|
| 4503 |
+
MY
|
| 4504 |
+
NX
|
| 4505 |
+
BQ
|
| 4506 |
+
HL
|
| 4507 |
+
JL
|
| 4508 |
+
AT
|
| 4509 |
+
QW
|
| 4510 |
+
OT
|
| 4511 |
+
BL
|
| 4512 |
+
BN
|
| 4513 |
+
EP
|
| 4514 |
+
TW
|
| 4515 |
+
FY
|
| 4516 |
+
FT
|
| 4517 |
+
DT
|
| 4518 |
+
AO
|
| 4519 |
+
FZ
|
| 4520 |
+
RV
|
| 4521 |
+
HR
|
| 4522 |
+
BC
|
| 4523 |
+
CJ
|
| 4524 |
+
AI
|
| 4525 |
+
LX
|
| 4526 |
+
GP
|
| 4527 |
+
QX
|
| 4528 |
+
CF
|
| 4529 |
+
QR
|
| 4530 |
+
AQ
|
| 4531 |
+
VY
|
| 4532 |
+
CZ
|
| 4533 |
+
GN
|
| 4534 |
+
MR
|
| 4535 |
+
LW
|
| 4536 |
+
DF
|
| 4537 |
+
DL
|
| 4538 |
+
GO
|
| 4539 |
+
EJ
|
| 4540 |
+
IN
|
| 4541 |
+
GQ
|
| 4542 |
+
PW
|
| 4543 |
+
OX
|
| 4544 |
+
AZ
|
| 4545 |
+
OY
|
| 4546 |
+
JY
|
| 4547 |
+
DM
|
| 4548 |
+
AD
|
| 4549 |
+
FH
|
| 4550 |
+
WY
|
| 4551 |
+
CP
|
| 4552 |
+
AJ
|
| 4553 |
+
PT
|
| 4554 |
+
MQ
|
| 4555 |
+
JS
|
| 4556 |
+
IM
|
| 4557 |
+
IV
|
| 4558 |
+
JK
|
| 4559 |
+
MX
|
| 4560 |
+
FN
|
| 4561 |
+
KQ
|
| 4562 |
+
SW
|
| 4563 |
+
KO
|
| 4564 |
+
NT
|
| 4565 |
+
TU
|
| 4566 |
+
IO
|
| 4567 |
+
RU
|
| 4568 |
+
JR
|
| 4569 |
+
SZ
|
| 4570 |
+
CM
|
| 4571 |
+
EV
|
| 4572 |
+
BX
|
| 4573 |
+
AB
|
| 4574 |
+
JO
|
| 4575 |
+
EG
|
| 4576 |
+
GL
|
| 4577 |
+
NW
|
| 4578 |
+
BM
|
| 4579 |
+
EY
|
| 4580 |
+
LU
|
| 4581 |
+
AF
|
| 4582 |
+
RZ
|
| 4583 |
+
BI
|
| 4584 |
+
HI
|
| 4585 |
+
PU
|
| 4586 |
+
MZ
|
| 4587 |
+
JZ
|
| 4588 |
+
MP
|
| 4589 |
+
GK
|
| 4590 |
+
FS
|
| 4591 |
+
AN
|
| 4592 |
+
MV
|
| 4593 |
+
CY
|
| 4594 |
+
CT
|
| 4595 |
+
CL
|
| 4596 |
+
FX
|
| 4597 |
+
EM
|
| 4598 |
+
HV
|
| 4599 |
+
JM
|
| 4600 |
+
JW
|
| 4601 |
+
CU
|
| 4602 |
+
OV
|
| 4603 |
+
DN
|
| 4604 |
+
KR
|
| 4605 |
+
BT
|
| 4606 |
+
PS
|
| 4607 |
+
HQ
|
| 4608 |
+
JV
|
| 4609 |
+
BH
|
| 4610 |
+
QZ
|
| 4611 |
+
UV
|
| 4612 |
+
KU
|
| 4613 |
+
CR
|
| 4614 |
+
PR
|
| 4615 |
+
LT
|
| 4616 |
+
EH
|
| 4617 |
+
LO
|
| 4618 |
+
HU
|
| 4619 |
+
DU
|
| 4620 |
+
AC
|
| 4621 |
+
IZ
|
| 4622 |
+
BZ
|
| 4623 |
+
RS
|
| 4624 |
+
RY
|
| 4625 |
+
HN
|
| 4626 |
+
TZ
|
| 4627 |
+
MU
|
| 4628 |
+
ER
|
| 4629 |
+
IY
|
| 4630 |
+
HLIIMZYUODTKROGRZGIBECKBWVEZ
|
| 4631 |
+
51
|
| 4632 |
+
US
|
| 4633 |
+
OP
|
| 4634 |
+
KW
|
| 4635 |
+
UC
|
| 4636 |
+
QP
|
| 4637 |
+
PR
|
| 4638 |
+
DW
|
| 4639 |
+
IY
|
| 4640 |
+
BV
|
| 4641 |
+
QK
|
| 4642 |
+
BZ
|
| 4643 |
+
MH
|
| 4644 |
+
KA
|
| 4645 |
+
JE
|
| 4646 |
+
TJ
|
| 4647 |
+
ZL
|
| 4648 |
+
PN
|
| 4649 |
+
DK
|
| 4650 |
+
EF
|
| 4651 |
+
DE
|
| 4652 |
+
IH
|
| 4653 |
+
HV
|
| 4654 |
+
BL
|
| 4655 |
+
ZX
|
| 4656 |
+
TX
|
| 4657 |
+
UX
|
| 4658 |
+
GW
|
| 4659 |
+
JB
|
| 4660 |
+
OQ
|
| 4661 |
+
RX
|
| 4662 |
+
TY
|
| 4663 |
+
IX
|
| 4664 |
+
XY
|
| 4665 |
+
BU
|
| 4666 |
+
KB
|
| 4667 |
+
LG
|
| 4668 |
+
EV
|
| 4669 |
+
MB
|
| 4670 |
+
YC
|
| 4671 |
+
BD
|
| 4672 |
+
AO
|
| 4673 |
+
XI
|
| 4674 |
+
DB
|
| 4675 |
+
GX
|
| 4676 |
+
EJ
|
| 4677 |
+
SK
|
| 4678 |
+
FR
|
| 4679 |
+
MF
|
| 4680 |
+
OV
|
| 4681 |
+
NL
|
| 4682 |
+
QA
|
| 4683 |
+
GXIENJCPYBWMGJJPTUZZDWIOAMHHWWNSYRCPJNYBVXBBARCILOFNPHH
|
| 4684 |
+
94
|
| 4685 |
+
ZS
|
| 4686 |
+
NZ
|
| 4687 |
+
OZ
|
| 4688 |
+
MW
|
| 4689 |
+
SJ
|
| 4690 |
+
CY
|
| 4691 |
+
OX
|
| 4692 |
+
KB
|
| 4693 |
+
YQ
|
| 4694 |
+
DY
|
| 4695 |
+
EN
|
| 4696 |
+
CU
|
| 4697 |
+
FO
|
| 4698 |
+
KO
|
| 4699 |
+
OI
|
| 4700 |
+
LP
|
| 4701 |
+
NP
|
| 4702 |
+
VO
|
| 4703 |
+
MN
|
| 4704 |
+
GW
|
| 4705 |
+
PZ
|
| 4706 |
+
IV
|
| 4707 |
+
LD
|
| 4708 |
+
UF
|
| 4709 |
+
AO
|
| 4710 |
+
WV
|
| 4711 |
+
JT
|
| 4712 |
+
FZ
|
| 4713 |
+
VA
|
| 4714 |
+
YW
|
| 4715 |
+
WS
|
| 4716 |
+
IA
|
| 4717 |
+
JR
|
| 4718 |
+
OC
|
| 4719 |
+
NK
|
| 4720 |
+
QE
|
| 4721 |
+
XH
|
| 4722 |
+
CF
|
| 4723 |
+
PD
|
| 4724 |
+
PE
|
| 4725 |
+
UK
|
| 4726 |
+
TY
|
| 4727 |
+
AK
|
| 4728 |
+
PF
|
| 4729 |
+
VD
|
| 4730 |
+
DH
|
| 4731 |
+
FV
|
| 4732 |
+
KY
|
| 4733 |
+
JW
|
| 4734 |
+
RC
|
| 4735 |
+
QF
|
| 4736 |
+
AI
|
| 4737 |
+
IN
|
| 4738 |
+
KA
|
| 4739 |
+
CP
|
| 4740 |
+
LA
|
| 4741 |
+
QV
|
| 4742 |
+
UE
|
| 4743 |
+
FD
|
| 4744 |
+
PN
|
| 4745 |
+
LO
|
| 4746 |
+
XI
|
| 4747 |
+
JH
|
| 4748 |
+
XL
|
| 4749 |
+
CL
|
| 4750 |
+
QT
|
| 4751 |
+
AZ
|
| 4752 |
+
SI
|
| 4753 |
+
DA
|
| 4754 |
+
PH
|
| 4755 |
+
SL
|
| 4756 |
+
SF
|
| 4757 |
+
IJ
|
| 4758 |
+
NY
|
| 4759 |
+
IT
|
| 4760 |
+
QW
|
| 4761 |
+
ZN
|
| 4762 |
+
NO
|
| 4763 |
+
DM
|
| 4764 |
+
DF
|
| 4765 |
+
ID
|
| 4766 |
+
NU
|
| 4767 |
+
XB
|
| 4768 |
+
GL
|
| 4769 |
+
OJ
|
| 4770 |
+
SK
|
| 4771 |
+
IP
|
| 4772 |
+
RS
|
| 4773 |
+
RQ
|
| 4774 |
+
CE
|
| 4775 |
+
SB
|
| 4776 |
+
QK
|
| 4777 |
+
XW
|
| 4778 |
+
XM
|
| 4779 |
+
GHHSMPAYWLAHVTCTOMTDXIPXIVTPBOQKDLLCBMPONYELWQRQAVBANRPJSKBAFRGYQOJIAL
|
| 4780 |
+
229
|
| 4781 |
+
TX
|
| 4782 |
+
DW
|
| 4783 |
+
EG
|
| 4784 |
+
CT
|
| 4785 |
+
VW
|
| 4786 |
+
EW
|
| 4787 |
+
CY
|
| 4788 |
+
NO
|
| 4789 |
+
FV
|
| 4790 |
+
OV
|
| 4791 |
+
BS
|
| 4792 |
+
HU
|
| 4793 |
+
CZ
|
| 4794 |
+
JW
|
| 4795 |
+
LQ
|
| 4796 |
+
OY
|
| 4797 |
+
CN
|
| 4798 |
+
BD
|
| 4799 |
+
AU
|
| 4800 |
+
GI
|
| 4801 |
+
LO
|
| 4802 |
+
MU
|
| 4803 |
+
TY
|
| 4804 |
+
HO
|
| 4805 |
+
HV
|
| 4806 |
+
HR
|
| 4807 |
+
PV
|
| 4808 |
+
JT
|
| 4809 |
+
BQ
|
| 4810 |
+
DR
|
| 4811 |
+
AV
|
| 4812 |
+
EO
|
| 4813 |
+
LV
|
| 4814 |
+
RT
|
| 4815 |
+
MO
|
| 4816 |
+
QW
|
| 4817 |
+
DV
|
| 4818 |
+
GM
|
| 4819 |
+
KW
|
| 4820 |
+
LT
|
| 4821 |
+
NW
|
| 4822 |
+
FJ
|
| 4823 |
+
IZ
|
| 4824 |
+
KV
|
| 4825 |
+
HQ
|
| 4826 |
+
UV
|
| 4827 |
+
RX
|
| 4828 |
+
AG
|
| 4829 |
+
JO
|
| 4830 |
+
AW
|
| 4831 |
+
TZ
|
| 4832 |
+
AF
|
| 4833 |
+
EL
|
| 4834 |
+
CK
|
| 4835 |
+
CO
|
| 4836 |
+
RS
|
| 4837 |
+
IV
|
| 4838 |
+
IN
|
| 4839 |
+
JN
|
| 4840 |
+
FG
|
| 4841 |
+
IL
|
| 4842 |
+
DS
|
| 4843 |
+
GU
|
| 4844 |
+
QS
|
| 4845 |
+
OS
|
| 4846 |
+
KO
|
| 4847 |
+
DF
|
| 4848 |
+
HS
|
| 4849 |
+
GS
|
| 4850 |
+
UZ
|
| 4851 |
+
DL
|
| 4852 |
+
GO
|
| 4853 |
+
RW
|
| 4854 |
+
MY
|
| 4855 |
+
IP
|
| 4856 |
+
CL
|
| 4857 |
+
CP
|
| 4858 |
+
CV
|
| 4859 |
+
LY
|
| 4860 |
+
AR
|
| 4861 |
+
FH
|
| 4862 |
+
GH
|
| 4863 |
+
IK
|
| 4864 |
+
HJ
|
| 4865 |
+
EZ
|
| 4866 |
+
PZ
|
| 4867 |
+
DO
|
| 4868 |
+
HI
|
| 4869 |
+
BE
|
| 4870 |
+
JL
|
| 4871 |
+
AJ
|
| 4872 |
+
AX
|
| 4873 |
+
AM
|
| 4874 |
+
UX
|
| 4875 |
+
MR
|
| 4876 |
+
BW
|
| 4877 |
+
QY
|
| 4878 |
+
OP
|
| 4879 |
+
CX
|
| 4880 |
+
ER
|
| 4881 |
+
CG
|
| 4882 |
+
BR
|
| 4883 |
+
BU
|
| 4884 |
+
CR
|
| 4885 |
+
KP
|
| 4886 |
+
GK
|
| 4887 |
+
IU
|
| 4888 |
+
KL
|
| 4889 |
+
MX
|
| 4890 |
+
CQ
|
| 4891 |
+
XZ
|
| 4892 |
+
EY
|
| 4893 |
+
CI
|
| 4894 |
+
HX
|
| 4895 |
+
AK
|
| 4896 |
+
UY
|
| 4897 |
+
LZ
|
| 4898 |
+
AH
|
| 4899 |
+
NZ
|
| 4900 |
+
DU
|
| 4901 |
+
EK
|
| 4902 |
+
BM
|
| 4903 |
+
XY
|
| 4904 |
+
TV
|
| 4905 |
+
GP
|
| 4906 |
+
NU
|
| 4907 |
+
GL
|
| 4908 |
+
BJ
|
| 4909 |
+
SV
|
| 4910 |
+
HY
|
| 4911 |
+
IJ
|
| 4912 |
+
BN
|
| 4913 |
+
OT
|
| 4914 |
+
KR
|
| 4915 |
+
FR
|
| 4916 |
+
BG
|
| 4917 |
+
GT
|
| 4918 |
+
AS
|
| 4919 |
+
HM
|
| 4920 |
+
ST
|
| 4921 |
+
EJ
|
| 4922 |
+
PU
|
| 4923 |
+
RV
|
| 4924 |
+
MV
|
| 4925 |
+
EU
|
| 4926 |
+
TW
|
| 4927 |
+
AB
|
| 4928 |
+
LX
|
| 4929 |
+
JZ
|
| 4930 |
+
SX
|
| 4931 |
+
MT
|
| 4932 |
+
GQ
|
| 4933 |
+
AN
|
| 4934 |
+
DG
|
| 4935 |
+
EV
|
| 4936 |
+
IW
|
| 4937 |
+
AT
|
| 4938 |
+
JR
|
| 4939 |
+
GY
|
| 4940 |
+
LW
|
| 4941 |
+
LS
|
| 4942 |
+
IX
|
| 4943 |
+
OW
|
| 4944 |
+
SZ
|
| 4945 |
+
HT
|
| 4946 |
+
DY
|
| 4947 |
+
FX
|
| 4948 |
+
EM
|
| 4949 |
+
PW
|
| 4950 |
+
DI
|
| 4951 |
+
BP
|
| 4952 |
+
KQ
|
| 4953 |
+
QZ
|
| 4954 |
+
RY
|
| 4955 |
+
WZ
|
| 4956 |
+
QT
|
| 4957 |
+
NT
|
| 4958 |
+
OQ
|
| 4959 |
+
DM
|
| 4960 |
+
YZ
|
| 4961 |
+
EF
|
| 4962 |
+
IR
|
| 4963 |
+
BI
|
| 4964 |
+
DH
|
| 4965 |
+
IT
|
| 4966 |
+
LN
|
| 4967 |
+
KZ
|
| 4968 |
+
BY
|
| 4969 |
+
CM
|
| 4970 |
+
FT
|
| 4971 |
+
IQ
|
| 4972 |
+
UW
|
| 4973 |
+
EN
|
| 4974 |
+
BF
|
| 4975 |
+
SU
|
| 4976 |
+
CH
|
| 4977 |
+
PS
|
| 4978 |
+
GJ
|
| 4979 |
+
BC
|
| 4980 |
+
BO
|
| 4981 |
+
AE
|
| 4982 |
+
RZ
|
| 4983 |
+
PX
|
| 4984 |
+
DJ
|
| 4985 |
+
DX
|
| 4986 |
+
CD
|
| 4987 |
+
CW
|
| 4988 |
+
LP
|
| 4989 |
+
LU
|
| 4990 |
+
CJ
|
| 4991 |
+
FM
|
| 4992 |
+
JY
|
| 4993 |
+
FI
|
| 4994 |
+
FL
|
| 4995 |
+
AP
|
| 4996 |
+
NR
|
| 4997 |
+
FN
|
| 4998 |
+
EQ
|
| 4999 |
+
SY
|
| 5000 |
+
LR
|
| 5001 |
+
GN
|
| 5002 |
+
JX
|
| 5003 |
+
HP
|
| 5004 |
+
AO
|
| 5005 |
+
BK
|
| 5006 |
+
QV
|
| 5007 |
+
PQ
|
| 5008 |
+
FP
|
| 5009 |
+
DP
|
| 5010 |
+
AWWFIZHMUNEZAJRAGNKLWKSOCTMATGFHYDEACOHKYRQTEEIHLEBH
|
| 5011 |
+
222
|
| 5012 |
+
GQ
|
| 5013 |
+
HL
|
| 5014 |
+
ZU
|
| 5015 |
+
IX
|
| 5016 |
+
DK
|
| 5017 |
+
UK
|
| 5018 |
+
JY
|
| 5019 |
+
WV
|
| 5020 |
+
CB
|
| 5021 |
+
PJ
|
| 5022 |
+
UM
|
| 5023 |
+
XE
|
| 5024 |
+
SW
|
| 5025 |
+
TN
|
| 5026 |
+
LW
|
| 5027 |
+
JP
|
| 5028 |
+
SD
|
| 5029 |
+
MU
|
| 5030 |
+
ZF
|
| 5031 |
+
UJ
|
| 5032 |
+
KG
|
| 5033 |
+
HO
|
| 5034 |
+
ZP
|
| 5035 |
+
NZ
|
| 5036 |
+
KS
|
| 5037 |
+
OX
|
| 5038 |
+
XT
|
| 5039 |
+
ZD
|
| 5040 |
+
PC
|
| 5041 |
+
JI
|
| 5042 |
+
EQ
|
| 5043 |
+
AO
|
| 5044 |
+
XR
|
| 5045 |
+
WE
|
| 5046 |
+
WP
|
| 5047 |
+
MT
|
| 5048 |
+
IN
|
| 5049 |
+
QK
|
| 5050 |
+
FA
|
| 5051 |
+
HI
|
| 5052 |
+
IU
|
| 5053 |
+
KY
|
| 5054 |
+
KI
|
| 5055 |
+
TS
|
| 5056 |
+
MO
|
| 5057 |
+
ZH
|
| 5058 |
+
AY
|
| 5059 |
+
DZ
|
| 5060 |
+
BI
|
| 5061 |
+
FN
|
| 5062 |
+
BF
|
| 5063 |
+
PM
|
| 5064 |
+
JZ
|
| 5065 |
+
AR
|
| 5066 |
+
UI
|
| 5067 |
+
UQ
|
| 5068 |
+
OS
|
| 5069 |
+
XP
|
| 5070 |
+
RV
|
| 5071 |
+
CS
|
| 5072 |
+
MV
|
| 5073 |
+
PX
|
| 5074 |
+
VC
|
| 5075 |
+
JC
|
| 5076 |
+
FY
|
| 5077 |
+
KO
|
| 5078 |
+
SF
|
| 5079 |
+
GL
|
| 5080 |
+
BE
|
| 5081 |
+
CZ
|
| 5082 |
+
QZ
|
| 5083 |
+
QV
|
| 5084 |
+
CV
|
| 5085 |
+
YN
|
| 5086 |
+
XH
|
| 5087 |
+
EY
|
| 5088 |
+
UN
|
| 5089 |
+
TC
|
| 5090 |
+
GC
|
| 5091 |
+
SX
|
| 5092 |
+
RJ
|
| 5093 |
+
IR
|
| 5094 |
+
PH
|
| 5095 |
+
NC
|
| 5096 |
+
MA
|
| 5097 |
+
PE
|
| 5098 |
+
NF
|
| 5099 |
+
IV
|
| 5100 |
+
US
|
| 5101 |
+
SH
|
| 5102 |
+
VS
|
| 5103 |
+
KE
|
| 5104 |
+
YF
|
| 5105 |
+
EI
|
| 5106 |
+
QM
|
| 5107 |
+
UZ
|
| 5108 |
+
HK
|
| 5109 |
+
NL
|
| 5110 |
+
GA
|
| 5111 |
+
FD
|
| 5112 |
+
HY
|
| 5113 |
+
RU
|
| 5114 |
+
EK
|
| 5115 |
+
OF
|
| 5116 |
+
ZO
|
| 5117 |
+
IO
|
| 5118 |
+
EP
|
| 5119 |
+
BQ
|
| 5120 |
+
SY
|
| 5121 |
+
XW
|
| 5122 |
+
FI
|
| 5123 |
+
GZ
|
| 5124 |
+
KJ
|
| 5125 |
+
OI
|
| 5126 |
+
UD
|
| 5127 |
+
DU
|
| 5128 |
+
MH
|
| 5129 |
+
IY
|
| 5130 |
+
GE
|
| 5131 |
+
WO
|
| 5132 |
+
VH
|
| 5133 |
+
JR
|
| 5134 |
+
DG
|
| 5135 |
+
GD
|
| 5136 |
+
KC
|
| 5137 |
+
TK
|
| 5138 |
+
ZW
|
| 5139 |
+
RE
|
| 5140 |
+
WY
|
| 5141 |
+
XJ
|
| 5142 |
+
GF
|
| 5143 |
+
IP
|
| 5144 |
+
LA
|
| 5145 |
+
NY
|
| 5146 |
+
BX
|
| 5147 |
+
ZJ
|
| 5148 |
+
ZA
|
| 5149 |
+
NG
|
| 5150 |
+
OC
|
| 5151 |
+
VR
|
| 5152 |
+
OL
|
| 5153 |
+
XL
|
| 5154 |
+
ET
|
| 5155 |
+
AQ
|
| 5156 |
+
GS
|
| 5157 |
+
XS
|
| 5158 |
+
WA
|
| 5159 |
+
OY
|
| 5160 |
+
FB
|
| 5161 |
+
FZ
|
| 5162 |
+
CL
|
| 5163 |
+
SB
|
| 5164 |
+
VA
|
| 5165 |
+
IW
|
| 5166 |
+
HM
|
| 5167 |
+
PO
|
| 5168 |
+
QO
|
| 5169 |
+
ZB
|
| 5170 |
+
FV
|
| 5171 |
+
LN
|
| 5172 |
+
VP
|
| 5173 |
+
ID
|
| 5174 |
+
VU
|
| 5175 |
+
IE
|
| 5176 |
+
ZR
|
| 5177 |
+
LP
|
| 5178 |
+
KW
|
| 5179 |
+
TY
|
| 5180 |
+
TD
|
| 5181 |
+
NR
|
| 5182 |
+
XC
|
| 5183 |
+
KZ
|
| 5184 |
+
TV
|
| 5185 |
+
BM
|
| 5186 |
+
QE
|
| 5187 |
+
MX
|
| 5188 |
+
MC
|
| 5189 |
+
TH
|
| 5190 |
+
EB
|
| 5191 |
+
CF
|
| 5192 |
+
YZ
|
| 5193 |
+
BY
|
| 5194 |
+
SV
|
| 5195 |
+
SE
|
| 5196 |
+
NT
|
| 5197 |
+
OP
|
| 5198 |
+
OD
|
| 5199 |
+
VG
|
| 5200 |
+
YU
|
| 5201 |
+
VT
|
| 5202 |
+
MB
|
| 5203 |
+
JD
|
| 5204 |
+
JG
|
| 5205 |
+
BT
|
| 5206 |
+
YS
|
| 5207 |
+
GO
|
| 5208 |
+
DC
|
| 5209 |
+
XV
|
| 5210 |
+
RH
|
| 5211 |
+
OJ
|
| 5212 |
+
EF
|
| 5213 |
+
DI
|
| 5214 |
+
QA
|
| 5215 |
+
DE
|
| 5216 |
+
JX
|
| 5217 |
+
JE
|
| 5218 |
+
QS
|
| 5219 |
+
AF
|
| 5220 |
+
FK
|
| 5221 |
+
PY
|
| 5222 |
+
RW
|
| 5223 |
+
NQ
|
| 5224 |
+
XI
|
| 5225 |
+
DA
|
| 5226 |
+
AL
|
| 5227 |
+
OZ
|
| 5228 |
+
JU
|
| 5229 |
+
DS
|
| 5230 |
+
HR
|
| 5231 |
+
QG
|
| 5232 |
+
BL
|
| 5233 |
+
DY
|
| 5234 |
+
RCVJXGWPXOOCEFZLVNSHQ
|
| 5235 |
+
276
|
| 5236 |
+
VL
|
| 5237 |
+
YJ
|
| 5238 |
+
HI
|
| 5239 |
+
GJ
|
| 5240 |
+
IA
|
| 5241 |
+
XI
|
| 5242 |
+
WT
|
| 5243 |
+
CJ
|
| 5244 |
+
CR
|
| 5245 |
+
GX
|
| 5246 |
+
MI
|
| 5247 |
+
YM
|
| 5248 |
+
OX
|
| 5249 |
+
YZ
|
| 5250 |
+
XP
|
| 5251 |
+
YV
|
| 5252 |
+
EC
|
| 5253 |
+
ZY
|
| 5254 |
+
HD
|
| 5255 |
+
XB
|
| 5256 |
+
UD
|
| 5257 |
+
KQ
|
| 5258 |
+
UM
|
| 5259 |
+
CW
|
| 5260 |
+
FX
|
| 5261 |
+
FV
|
| 5262 |
+
RK
|
| 5263 |
+
QT
|
| 5264 |
+
PM
|
| 5265 |
+
QO
|
| 5266 |
+
MD
|
| 5267 |
+
VT
|
| 5268 |
+
JN
|
| 5269 |
+
GP
|
| 5270 |
+
QW
|
| 5271 |
+
FC
|
| 5272 |
+
DQ
|
| 5273 |
+
VM
|
| 5274 |
+
CM
|
| 5275 |
+
GT
|
| 5276 |
+
PY
|
| 5277 |
+
PC
|
| 5278 |
+
VX
|
| 5279 |
+
FZ
|
| 5280 |
+
EU
|
| 5281 |
+
AH
|
| 5282 |
+
WM
|
| 5283 |
+
UT
|
| 5284 |
+
KJ
|
| 5285 |
+
AD
|
| 5286 |
+
TR
|
| 5287 |
+
RC
|
| 5288 |
+
LS
|
| 5289 |
+
CV
|
| 5290 |
+
OD
|
| 5291 |
+
VB
|
| 5292 |
+
LA
|
| 5293 |
+
ZH
|
| 5294 |
+
ZE
|
| 5295 |
+
YA
|
| 5296 |
+
IX
|
| 5297 |
+
TS
|
| 5298 |
+
AS
|
| 5299 |
+
FS
|
| 5300 |
+
ZV
|
| 5301 |
+
QS
|
| 5302 |
+
NK
|
| 5303 |
+
AG
|
| 5304 |
+
VU
|
| 5305 |
+
JF
|
| 5306 |
+
OF
|
| 5307 |
+
HB
|
| 5308 |
+
SO
|
| 5309 |
+
EN
|
| 5310 |
+
UQ
|
| 5311 |
+
RY
|
| 5312 |
+
QX
|
| 5313 |
+
OV
|
| 5314 |
+
XK
|
| 5315 |
+
TM
|
| 5316 |
+
ZA
|
| 5317 |
+
NH
|
| 5318 |
+
FM
|
| 5319 |
+
ZQ
|
| 5320 |
+
ZO
|
| 5321 |
+
KZ
|
| 5322 |
+
UA
|
| 5323 |
+
DH
|
| 5324 |
+
VN
|
| 5325 |
+
XQ
|
| 5326 |
+
BH
|
| 5327 |
+
RS
|
| 5328 |
+
YQ
|
| 5329 |
+
GQ
|
| 5330 |
+
MO
|
| 5331 |
+
OA
|
| 5332 |
+
HU
|
| 5333 |
+
EV
|
| 5334 |
+
ZI
|
| 5335 |
+
JQ
|
| 5336 |
+
PX
|
| 5337 |
+
JE
|
| 5338 |
+
SA
|
| 5339 |
+
IT
|
| 5340 |
+
DS
|
| 5341 |
+
FK
|
| 5342 |
+
LT
|
| 5343 |
+
JX
|
| 5344 |
+
YI
|
| 5345 |
+
OU
|
| 5346 |
+
IN
|
| 5347 |
+
FU
|
| 5348 |
+
DM
|
| 5349 |
+
FH
|
| 5350 |
+
HC
|
| 5351 |
+
CF
|
| 5352 |
+
TD
|
| 5353 |
+
CB
|
| 5354 |
+
MF
|
| 5355 |
+
TW
|
| 5356 |
+
TK
|
| 5357 |
+
AJ
|
| 5358 |
+
VQ
|
| 5359 |
+
WL
|
| 5360 |
+
AQ
|
| 5361 |
+
YE
|
| 5362 |
+
JO
|
| 5363 |
+
YK
|
| 5364 |
+
ZT
|
| 5365 |
+
NL
|
| 5366 |
+
YG
|
| 5367 |
+
WQ
|
| 5368 |
+
XR
|
| 5369 |
+
OK
|
| 5370 |
+
ZX
|
| 5371 |
+
YX
|
| 5372 |
+
KW
|
| 5373 |
+
KE
|
| 5374 |
+
SE
|
| 5375 |
+
CI
|
| 5376 |
+
UC
|
| 5377 |
+
FO
|
| 5378 |
+
CT
|
| 5379 |
+
IY
|
| 5380 |
+
HZ
|
| 5381 |
+
FB
|
| 5382 |
+
UZ
|
| 5383 |
+
DB
|
| 5384 |
+
WZ
|
| 5385 |
+
AY
|
| 5386 |
+
PD
|
| 5387 |
+
MX
|
| 5388 |
+
QV
|
| 5389 |
+
JZ
|
| 5390 |
+
FR
|
| 5391 |
+
NI
|
| 5392 |
+
XV
|
| 5393 |
+
NB
|
| 5394 |
+
SN
|
| 5395 |
+
VA
|
| 5396 |
+
GU
|
| 5397 |
+
QH
|
| 5398 |
+
UG
|
| 5399 |
+
JA
|
| 5400 |
+
GI
|
| 5401 |
+
HR
|
| 5402 |
+
PS
|
| 5403 |
+
DG
|
| 5404 |
+
YL
|
| 5405 |
+
SF
|
| 5406 |
+
TA
|
| 5407 |
+
DF
|
| 5408 |
+
FN
|
| 5409 |
+
PJ
|
| 5410 |
+
YO
|
| 5411 |
+
KB
|
| 5412 |
+
UJ
|
| 5413 |
+
WH
|
| 5414 |
+
BC
|
| 5415 |
+
FY
|
| 5416 |
+
FP
|
| 5417 |
+
CQ
|
| 5418 |
+
YC
|
| 5419 |
+
KN
|
| 5420 |
+
RJ
|
| 5421 |
+
PN
|
| 5422 |
+
KC
|
| 5423 |
+
LE
|
| 5424 |
+
PO
|
| 5425 |
+
BQ
|
| 5426 |
+
AK
|
| 5427 |
+
SL
|
| 5428 |
+
BI
|
| 5429 |
+
XM
|
| 5430 |
+
QP
|
| 5431 |
+
UV
|
| 5432 |
+
NY
|
| 5433 |
+
OE
|
| 5434 |
+
ML
|
| 5435 |
+
MQ
|
| 5436 |
+
ZP
|
| 5437 |
+
TF
|
| 5438 |
+
FL
|
| 5439 |
+
CY
|
| 5440 |
+
XJ
|
| 5441 |
+
FI
|
| 5442 |
+
XO
|
| 5443 |
+
TH
|
| 5444 |
+
ND
|
| 5445 |
+
PL
|
| 5446 |
+
CN
|
| 5447 |
+
JC
|
| 5448 |
+
GW
|
| 5449 |
+
OM
|
| 5450 |
+
RO
|
| 5451 |
+
XF
|
| 5452 |
+
DN
|
| 5453 |
+
ON
|
| 5454 |
+
FG
|
| 5455 |
+
BV
|
| 5456 |
+
UP
|
| 5457 |
+
DK
|
| 5458 |
+
PQ
|
| 5459 |
+
WA
|
| 5460 |
+
AP
|
| 5461 |
+
FQ
|
| 5462 |
+
JG
|
| 5463 |
+
ZM
|
| 5464 |
+
ZK
|
| 5465 |
+
HX
|
| 5466 |
+
TL
|
| 5467 |
+
DE
|
| 5468 |
+
EF
|
| 5469 |
+
LO
|
| 5470 |
+
RD
|
| 5471 |
+
DV
|
| 5472 |
+
KA
|
| 5473 |
+
EQ
|
| 5474 |
+
HG
|
| 5475 |
+
LJ
|
| 5476 |
+
IJ
|
| 5477 |
+
SG
|
| 5478 |
+
FE
|
| 5479 |
+
ZL
|
| 5480 |
+
AZ
|
| 5481 |
+
PT
|
| 5482 |
+
BW
|
| 5483 |
+
VW
|
| 5484 |
+
KM
|
| 5485 |
+
LH
|
| 5486 |
+
SX
|
| 5487 |
+
OR
|
| 5488 |
+
EK
|
| 5489 |
+
SZ
|
| 5490 |
+
BS
|
| 5491 |
+
XT
|
| 5492 |
+
HM
|
| 5493 |
+
BJ
|
| 5494 |
+
BN
|
| 5495 |
+
CS
|
| 5496 |
+
PK
|
| 5497 |
+
QN
|
| 5498 |
+
XN
|
| 5499 |
+
RH
|
| 5500 |
+
IQ
|
| 5501 |
+
IB
|
| 5502 |
+
WO
|
| 5503 |
+
JT
|
| 5504 |
+
OW
|
| 5505 |
+
BF
|
| 5506 |
+
WB
|
| 5507 |
+
NE
|
| 5508 |
+
WG
|
| 5509 |
+
EP
|
| 5510 |
+
WF
|
| 5511 |
+
BG
|
| 5512 |
+
NKIBMKPUTAZPXRGNNKOAOQUVFLDFZISACTXIGBLAOMHRNEKGHOUCOD
|
| 5513 |
+
39
|
| 5514 |
+
OH
|
| 5515 |
+
KD
|
| 5516 |
+
FX
|
| 5517 |
+
AL
|
| 5518 |
+
ND
|
| 5519 |
+
NP
|
| 5520 |
+
QV
|
| 5521 |
+
VS
|
| 5522 |
+
BU
|
| 5523 |
+
PM
|
| 5524 |
+
BQ
|
| 5525 |
+
PR
|
| 5526 |
+
FL
|
| 5527 |
+
LE
|
| 5528 |
+
KU
|
| 5529 |
+
KM
|
| 5530 |
+
WJ
|
| 5531 |
+
ER
|
| 5532 |
+
JQ
|
| 5533 |
+
YX
|
| 5534 |
+
OT
|
| 5535 |
+
IF
|
| 5536 |
+
YW
|
| 5537 |
+
VY
|
| 5538 |
+
BO
|
| 5539 |
+
HW
|
| 5540 |
+
WQ
|
| 5541 |
+
YM
|
| 5542 |
+
DB
|
| 5543 |
+
LU
|
| 5544 |
+
AT
|
| 5545 |
+
RM
|
| 5546 |
+
IR
|
| 5547 |
+
GJ
|
| 5548 |
+
TD
|
| 5549 |
+
HQ
|
| 5550 |
+
QR
|
| 5551 |
+
DC
|
| 5552 |
+
UN
|
| 5553 |
+
MOKWSMAHEGIXZJIEWICZAFMORDIKHTKNIOFRGAA
|
| 5554 |
+
50
|
| 5555 |
+
SZ
|
| 5556 |
+
TV
|
| 5557 |
+
HL
|
| 5558 |
+
EO
|
| 5559 |
+
WJ
|
| 5560 |
+
AF
|
| 5561 |
+
VL
|
| 5562 |
+
VQ
|
| 5563 |
+
HE
|
| 5564 |
+
JV
|
| 5565 |
+
ME
|
| 5566 |
+
XL
|
| 5567 |
+
CV
|
| 5568 |
+
JG
|
| 5569 |
+
FC
|
| 5570 |
+
CM
|
| 5571 |
+
KC
|
| 5572 |
+
EL
|
| 5573 |
+
EK
|
| 5574 |
+
SG
|
| 5575 |
+
LG
|
| 5576 |
+
EU
|
| 5577 |
+
NT
|
| 5578 |
+
KD
|
| 5579 |
+
ON
|
| 5580 |
+
EQ
|
| 5581 |
+
OD
|
| 5582 |
+
ZQ
|
| 5583 |
+
PD
|
| 5584 |
+
WT
|
| 5585 |
+
SL
|
| 5586 |
+
WH
|
| 5587 |
+
NW
|
| 5588 |
+
FN
|
| 5589 |
+
VZ
|
| 5590 |
+
DQ
|
| 5591 |
+
UL
|
| 5592 |
+
UK
|
| 5593 |
+
IV
|
| 5594 |
+
VT
|
| 5595 |
+
UP
|
| 5596 |
+
LY
|
| 5597 |
+
KP
|
| 5598 |
+
MR
|
| 5599 |
+
FY
|
| 5600 |
+
NP
|
| 5601 |
+
DC
|
| 5602 |
+
JX
|
| 5603 |
+
KB
|
| 5604 |
+
GW
|
| 5605 |
+
BACEVZIGKSKCUZCUSFMWDWMVIVQHGOMTMF
|
| 5606 |
+
114
|
| 5607 |
+
GO
|
| 5608 |
+
AC
|
| 5609 |
+
NS
|
| 5610 |
+
QW
|
| 5611 |
+
DK
|
| 5612 |
+
DE
|
| 5613 |
+
HN
|
| 5614 |
+
LQ
|
| 5615 |
+
OU
|
| 5616 |
+
IV
|
| 5617 |
+
CU
|
| 5618 |
+
XZ
|
| 5619 |
+
GI
|
| 5620 |
+
OQ
|
| 5621 |
+
CZ
|
| 5622 |
+
AQ
|
| 5623 |
+
MO
|
| 5624 |
+
BJ
|
| 5625 |
+
IY
|
| 5626 |
+
IT
|
| 5627 |
+
KQ
|
| 5628 |
+
EZ
|
| 5629 |
+
AE
|
| 5630 |
+
OR
|
| 5631 |
+
IL
|
| 5632 |
+
TV
|
| 5633 |
+
LS
|
| 5634 |
+
ER
|
| 5635 |
+
EK
|
| 5636 |
+
DV
|
| 5637 |
+
FR
|
| 5638 |
+
DM
|
| 5639 |
+
IW
|
| 5640 |
+
RV
|
| 5641 |
+
LY
|
| 5642 |
+
GQ
|
| 5643 |
+
JQ
|
| 5644 |
+
UW
|
| 5645 |
+
CG
|
| 5646 |
+
ES
|
| 5647 |
+
PV
|
| 5648 |
+
JZ
|
| 5649 |
+
JK
|
| 5650 |
+
AI
|
| 5651 |
+
JU
|
| 5652 |
+
BF
|
| 5653 |
+
AX
|
| 5654 |
+
HO
|
| 5655 |
+
RX
|
| 5656 |
+
GU
|
| 5657 |
+
CL
|
| 5658 |
+
LV
|
| 5659 |
+
MP
|
| 5660 |
+
KX
|
| 5661 |
+
BN
|
| 5662 |
+
MX
|
| 5663 |
+
KU
|
| 5664 |
+
FL
|
| 5665 |
+
TX
|
| 5666 |
+
IR
|
| 5667 |
+
LW
|
| 5668 |
+
AG
|
| 5669 |
+
RT
|
| 5670 |
+
HZ
|
| 5671 |
+
EV
|
| 5672 |
+
GW
|
| 5673 |
+
CK
|
| 5674 |
+
EL
|
| 5675 |
+
NV
|
| 5676 |
+
VY
|
| 5677 |
+
DR
|
| 5678 |
+
CP
|
| 5679 |
+
MN
|
| 5680 |
+
FO
|
| 5681 |
+
BX
|
| 5682 |
+
TZ
|
| 5683 |
+
DW
|
| 5684 |
+
TU
|
| 5685 |
+
KY
|
| 5686 |
+
FM
|
| 5687 |
+
WX
|
| 5688 |
+
KO
|
| 5689 |
+
EI
|
| 5690 |
+
GR
|
| 5691 |
+
FT
|
| 5692 |
+
QV
|
| 5693 |
+
BL
|
| 5694 |
+
GN
|
| 5695 |
+
CQ
|
| 5696 |
+
AD
|
| 5697 |
+
EP
|
| 5698 |
+
EG
|
| 5699 |
+
HX
|
| 5700 |
+
DS
|
| 5701 |
+
DN
|
| 5702 |
+
KR
|
| 5703 |
+
HV
|
| 5704 |
+
MY
|
| 5705 |
+
JL
|
| 5706 |
+
JY
|
| 5707 |
+
TW
|
| 5708 |
+
MS
|
| 5709 |
+
ET
|
| 5710 |
+
LO
|
| 5711 |
+
FW
|
| 5712 |
+
WZ
|
| 5713 |
+
CO
|
| 5714 |
+
PZ
|
| 5715 |
+
HT
|
| 5716 |
+
UV
|
| 5717 |
+
XY
|
| 5718 |
+
MZ
|
| 5719 |
+
NU
|
| 5720 |
+
RU
|
| 5721 |
+
BVSTPGPUDKCKTIYHTXJKI
|
| 5722 |
+
71
|
| 5723 |
+
IP
|
| 5724 |
+
EF
|
| 5725 |
+
XZ
|
| 5726 |
+
HL
|
| 5727 |
+
JT
|
| 5728 |
+
PX
|
| 5729 |
+
UX
|
| 5730 |
+
LU
|
| 5731 |
+
QZ
|
| 5732 |
+
KR
|
| 5733 |
+
EO
|
| 5734 |
+
QS
|
| 5735 |
+
SU
|
| 5736 |
+
QW
|
| 5737 |
+
ES
|
| 5738 |
+
JO
|
| 5739 |
+
NV
|
| 5740 |
+
BS
|
| 5741 |
+
HP
|
| 5742 |
+
UV
|
| 5743 |
+
GX
|
| 5744 |
+
HY
|
| 5745 |
+
BT
|
| 5746 |
+
UW
|
| 5747 |
+
GQ
|
| 5748 |
+
KT
|
| 5749 |
+
MX
|
| 5750 |
+
GI
|
| 5751 |
+
TY
|
| 5752 |
+
AT
|
| 5753 |
+
BG
|
| 5754 |
+
GP
|
| 5755 |
+
GN
|
| 5756 |
+
FL
|
| 5757 |
+
SX
|
| 5758 |
+
FU
|
| 5759 |
+
DI
|
| 5760 |
+
AS
|
| 5761 |
+
CV
|
| 5762 |
+
CM
|
| 5763 |
+
ST
|
| 5764 |
+
PR
|
| 5765 |
+
GJ
|
| 5766 |
+
LW
|
| 5767 |
+
BI
|
| 5768 |
+
BX
|
| 5769 |
+
DE
|
| 5770 |
+
HU
|
| 5771 |
+
TZ
|
| 5772 |
+
DP
|
| 5773 |
+
CO
|
| 5774 |
+
OX
|
| 5775 |
+
CQ
|
| 5776 |
+
CL
|
| 5777 |
+
RX
|
| 5778 |
+
JW
|
| 5779 |
+
AV
|
| 5780 |
+
RY
|
| 5781 |
+
IO
|
| 5782 |
+
EJ
|
| 5783 |
+
GR
|
| 5784 |
+
EU
|
| 5785 |
+
YZ
|
| 5786 |
+
DK
|
| 5787 |
+
MU
|
| 5788 |
+
RW
|
| 5789 |
+
EV
|
| 5790 |
+
MO
|
| 5791 |
+
AH
|
| 5792 |
+
MQ
|
| 5793 |
+
JZ
|
| 5794 |
+
LHAGGCKQQIXKCRFYUWTCQUEKCVUHS
|
| 5795 |
+
192
|
| 5796 |
+
DT
|
| 5797 |
+
HX
|
| 5798 |
+
TY
|
| 5799 |
+
AZ
|
| 5800 |
+
DO
|
| 5801 |
+
PY
|
| 5802 |
+
JS
|
| 5803 |
+
HV
|
| 5804 |
+
FK
|
| 5805 |
+
HJ
|
| 5806 |
+
OU
|
| 5807 |
+
HO
|
| 5808 |
+
GW
|
| 5809 |
+
EJ
|
| 5810 |
+
FT
|
| 5811 |
+
CG
|
| 5812 |
+
JY
|
| 5813 |
+
MU
|
| 5814 |
+
DR
|
| 5815 |
+
KS
|
| 5816 |
+
GR
|
| 5817 |
+
HU
|
| 5818 |
+
BN
|
| 5819 |
+
FU
|
| 5820 |
+
CL
|
| 5821 |
+
LS
|
| 5822 |
+
BU
|
| 5823 |
+
HM
|
| 5824 |
+
NR
|
| 5825 |
+
LW
|
| 5826 |
+
EX
|
| 5827 |
+
AN
|
| 5828 |
+
LY
|
| 5829 |
+
LP
|
| 5830 |
+
SV
|
| 5831 |
+
CF
|
| 5832 |
+
AR
|
| 5833 |
+
PS
|
| 5834 |
+
RV
|
| 5835 |
+
QV
|
| 5836 |
+
DG
|
| 5837 |
+
GS
|
| 5838 |
+
JU
|
| 5839 |
+
TZ
|
| 5840 |
+
JO
|
| 5841 |
+
DK
|
| 5842 |
+
DF
|
| 5843 |
+
FR
|
| 5844 |
+
CR
|
| 5845 |
+
LZ
|
| 5846 |
+
EP
|
| 5847 |
+
PR
|
| 5848 |
+
IR
|
| 5849 |
+
MO
|
| 5850 |
+
KW
|
| 5851 |
+
SX
|
| 5852 |
+
NU
|
| 5853 |
+
IM
|
| 5854 |
+
AP
|
| 5855 |
+
AG
|
| 5856 |
+
IX
|
| 5857 |
+
LV
|
| 5858 |
+
RT
|
| 5859 |
+
HS
|
| 5860 |
+
JN
|
| 5861 |
+
IT
|
| 5862 |
+
ET
|
| 5863 |
+
AC
|
| 5864 |
+
AX
|
| 5865 |
+
SW
|
| 5866 |
+
OP
|
| 5867 |
+
GX
|
| 5868 |
+
FL
|
| 5869 |
+
TU
|
| 5870 |
+
QU
|
| 5871 |
+
PQ
|
| 5872 |
+
CI
|
| 5873 |
+
GO
|
| 5874 |
+
FZ
|
| 5875 |
+
QT
|
| 5876 |
+
QX
|
| 5877 |
+
JW
|
| 5878 |
+
EM
|
| 5879 |
+
MN
|
| 5880 |
+
WZ
|
| 5881 |
+
QZ
|
| 5882 |
+
DJ
|
| 5883 |
+
BS
|
| 5884 |
+
ST
|
| 5885 |
+
CD
|
| 5886 |
+
RU
|
| 5887 |
+
JL
|
| 5888 |
+
BI
|
| 5889 |
+
DS
|
| 5890 |
+
GH
|
| 5891 |
+
VY
|
| 5892 |
+
BR
|
| 5893 |
+
RS
|
| 5894 |
+
HZ
|
| 5895 |
+
KP
|
| 5896 |
+
KZ
|
| 5897 |
+
KQ
|
| 5898 |
+
MV
|
| 5899 |
+
KR
|
| 5900 |
+
GP
|
| 5901 |
+
AQ
|
| 5902 |
+
GT
|
| 5903 |
+
HW
|
| 5904 |
+
GZ
|
| 5905 |
+
UZ
|
| 5906 |
+
IS
|
| 5907 |
+
OV
|
| 5908 |
+
BT
|
| 5909 |
+
MZ
|
| 5910 |
+
DM
|
| 5911 |
+
VZ
|
| 5912 |
+
JZ
|
| 5913 |
+
CP
|
| 5914 |
+
FY
|
| 5915 |
+
IP
|
| 5916 |
+
QW
|
| 5917 |
+
BD
|
| 5918 |
+
FW
|
| 5919 |
+
LR
|
| 5920 |
+
OY
|
| 5921 |
+
LO
|
| 5922 |
+
CW
|
| 5923 |
+
BM
|
| 5924 |
+
NY
|
| 5925 |
+
WY
|
| 5926 |
+
NQ
|
| 5927 |
+
DQ
|
| 5928 |
+
OW
|
| 5929 |
+
MQ
|
| 5930 |
+
GN
|
| 5931 |
+
RY
|
| 5932 |
+
FJ
|
| 5933 |
+
PV
|
| 5934 |
+
HI
|
| 5935 |
+
FH
|
| 5936 |
+
AM
|
| 5937 |
+
FG
|
| 5938 |
+
NP
|
| 5939 |
+
KU
|
| 5940 |
+
JP
|
| 5941 |
+
JT
|
| 5942 |
+
LM
|
| 5943 |
+
HP
|
| 5944 |
+
LN
|
| 5945 |
+
DY
|
| 5946 |
+
MX
|
| 5947 |
+
AS
|
| 5948 |
+
FM
|
| 5949 |
+
HR
|
| 5950 |
+
FQ
|
| 5951 |
+
PT
|
| 5952 |
+
UW
|
| 5953 |
+
AJ
|
| 5954 |
+
IU
|
| 5955 |
+
OT
|
| 5956 |
+
FN
|
| 5957 |
+
AD
|
| 5958 |
+
DZ
|
| 5959 |
+
IL
|
| 5960 |
+
XZ
|
| 5961 |
+
FO
|
| 5962 |
+
EY
|
| 5963 |
+
GU
|
| 5964 |
+
GY
|
| 5965 |
+
MW
|
| 5966 |
+
MT
|
| 5967 |
+
CY
|
| 5968 |
+
CK
|
| 5969 |
+
VW
|
| 5970 |
+
LU
|
| 5971 |
+
EI
|
| 5972 |
+
CH
|
| 5973 |
+
NO
|
| 5974 |
+
LQ
|
| 5975 |
+
GL
|
| 5976 |
+
AY
|
| 5977 |
+
DH
|
| 5978 |
+
EZ
|
| 5979 |
+
LX
|
| 5980 |
+
CX
|
| 5981 |
+
TX
|
| 5982 |
+
AL
|
| 5983 |
+
SY
|
| 5984 |
+
IW
|
| 5985 |
+
CE
|
| 5986 |
+
PU
|
| 5987 |
+
HL
|
| 5988 |
+
GGAIHCJQVGNWNYVTKUANBYKVVWKHPHRUPYORRPUFXNPNFJITASYISXCTBXBHLHHPCPEWLMLUDEUAUIF
|
| 5989 |
+
234
|
| 5990 |
+
LI
|
| 5991 |
+
XO
|
| 5992 |
+
PI
|
| 5993 |
+
AX
|
| 5994 |
+
EU
|
| 5995 |
+
SP
|
| 5996 |
+
BI
|
| 5997 |
+
WV
|
| 5998 |
+
PV
|
| 5999 |
+
WS
|
| 6000 |
+
AH
|
| 6001 |
+
KU
|
| 6002 |
+
NK
|
| 6003 |
+
JM
|
| 6004 |
+
UV
|
| 6005 |
+
YQ
|
| 6006 |
+
LT
|
| 6007 |
+
WD
|
| 6008 |
+
NV
|
| 6009 |
+
BD
|
| 6010 |
+
MZ
|
| 6011 |
+
OR
|
| 6012 |
+
MJ
|
| 6013 |
+
XE
|
| 6014 |
+
ZV
|
| 6015 |
+
PM
|
| 6016 |
+
PD
|
| 6017 |
+
IE
|
| 6018 |
+
XI
|
| 6019 |
+
UE
|
| 6020 |
+
GE
|
| 6021 |
+
BJ
|
| 6022 |
+
UG
|
| 6023 |
+
ST
|
| 6024 |
+
BS
|
| 6025 |
+
VL
|
| 6026 |
+
PF
|
| 6027 |
+
CG
|
| 6028 |
+
BQ
|
| 6029 |
+
GV
|
| 6030 |
+
EI
|
| 6031 |
+
WK
|
| 6032 |
+
SQ
|
| 6033 |
+
LH
|
| 6034 |
+
KH
|
| 6035 |
+
TO
|
| 6036 |
+
JE
|
| 6037 |
+
TN
|
| 6038 |
+
YA
|
| 6039 |
+
UN
|
| 6040 |
+
VK
|
| 6041 |
+
UK
|
| 6042 |
+
VP
|
| 6043 |
+
TQ
|
| 6044 |
+
GO
|
| 6045 |
+
HL
|
| 6046 |
+
SE
|
| 6047 |
+
VI
|
| 6048 |
+
BG
|
| 6049 |
+
LB
|
| 6050 |
+
KA
|
| 6051 |
+
YK
|
| 6052 |
+
UR
|
| 6053 |
+
JW
|
| 6054 |
+
DQ
|
| 6055 |
+
FU
|
| 6056 |
+
PU
|
| 6057 |
+
GQ
|
| 6058 |
+
SH
|
| 6059 |
+
NS
|
| 6060 |
+
RP
|
| 6061 |
+
LY
|
| 6062 |
+
VX
|
| 6063 |
+
OC
|
| 6064 |
+
UI
|
| 6065 |
+
UH
|
| 6066 |
+
RI
|
| 6067 |
+
NB
|
| 6068 |
+
UL
|
| 6069 |
+
DI
|
| 6070 |
+
VT
|
| 6071 |
+
TK
|
| 6072 |
+
IK
|
| 6073 |
+
TS
|
| 6074 |
+
XW
|
| 6075 |
+
IN
|
| 6076 |
+
WF
|
| 6077 |
+
QL
|
| 6078 |
+
PR
|
| 6079 |
+
MI
|
| 6080 |
+
RW
|
| 6081 |
+
LG
|
| 6082 |
+
HE
|
| 6083 |
+
TD
|
| 6084 |
+
UX
|
| 6085 |
+
RC
|
| 6086 |
+
WU
|
| 6087 |
+
BT
|
| 6088 |
+
YL
|
| 6089 |
+
AY
|
| 6090 |
+
MU
|
| 6091 |
+
XR
|
| 6092 |
+
MH
|
| 6093 |
+
PG
|
| 6094 |
+
CD
|
| 6095 |
+
XL
|
| 6096 |
+
SA
|
| 6097 |
+
RU
|
| 6098 |
+
BL
|
| 6099 |
+
PX
|
| 6100 |
+
OS
|
| 6101 |
+
MA
|
| 6102 |
+
XB
|
| 6103 |
+
XH
|
| 6104 |
+
AN
|
| 6105 |
+
KB
|
| 6106 |
+
AO
|
| 6107 |
+
JF
|
| 6108 |
+
OL
|
| 6109 |
+
HJ
|
| 6110 |
+
NA
|
| 6111 |
+
KN
|
| 6112 |
+
ZO
|
| 6113 |
+
VB
|
| 6114 |
+
KZ
|
| 6115 |
+
OT
|
| 6116 |
+
GL
|
| 6117 |
+
AS
|
| 6118 |
+
YR
|
| 6119 |
+
QP
|
| 6120 |
+
MO
|
| 6121 |
+
NE
|
| 6122 |
+
IP
|
| 6123 |
+
FI
|
| 6124 |
+
RO
|
| 6125 |
+
HB
|
| 6126 |
+
XC
|
| 6127 |
+
YT
|
| 6128 |
+
GS
|
| 6129 |
+
PL
|
| 6130 |
+
WC
|
| 6131 |
+
ZD
|
| 6132 |
+
EN
|
| 6133 |
+
DV
|
| 6134 |
+
FK
|
| 6135 |
+
FE
|
| 6136 |
+
BN
|
| 6137 |
+
IJ
|
| 6138 |
+
IY
|
| 6139 |
+
FO
|
| 6140 |
+
EA
|
| 6141 |
+
ZN
|
| 6142 |
+
WZ
|
| 6143 |
+
KQ
|
| 6144 |
+
AD
|
| 6145 |
+
ZM
|
| 6146 |
+
ZI
|
| 6147 |
+
FS
|
| 6148 |
+
YI
|
| 6149 |
+
DY
|
| 6150 |
+
AC
|
| 6151 |
+
YH
|
| 6152 |
+
HT
|
| 6153 |
+
YM
|
| 6154 |
+
HI
|
| 6155 |
+
OB
|
| 6156 |
+
SX
|
| 6157 |
+
XF
|
| 6158 |
+
RF
|
| 6159 |
+
HO
|
| 6160 |
+
LM
|
| 6161 |
+
XG
|
| 6162 |
+
TC
|
| 6163 |
+
ON
|
| 6164 |
+
PO
|
| 6165 |
+
CX
|
| 6166 |
+
IT
|
| 6167 |
+
PJ
|
| 6168 |
+
AU
|
| 6169 |
+
RG
|
| 6170 |
+
HD
|
| 6171 |
+
QS
|
| 6172 |
+
MK
|
| 6173 |
+
FJ
|
| 6174 |
+
MD
|
| 6175 |
+
WH
|
| 6176 |
+
RT
|
| 6177 |
+
GK
|
| 6178 |
+
BM
|
| 6179 |
+
KW
|
| 6180 |
+
ER
|
| 6181 |
+
FN
|
| 6182 |
+
QU
|
| 6183 |
+
MY
|
| 6184 |
+
JK
|
| 6185 |
+
AQ
|
| 6186 |
+
DJ
|
| 6187 |
+
CU
|
| 6188 |
+
KT
|
| 6189 |
+
NC
|
| 6190 |
+
SD
|
| 6191 |
+
RN
|
| 6192 |
+
YD
|
| 6193 |
+
OZ
|
| 6194 |
+
QE
|
| 6195 |
+
DZ
|
| 6196 |
+
QT
|
| 6197 |
+
RQ
|
| 6198 |
+
ZX
|
| 6199 |
+
QV
|
| 6200 |
+
LP
|
| 6201 |
+
BV
|
| 6202 |
+
CY
|
| 6203 |
+
SK
|
| 6204 |
+
YX
|
| 6205 |
+
SR
|
| 6206 |
+
GM
|
| 6207 |
+
WR
|
| 6208 |
+
WO
|
| 6209 |
+
HW
|
| 6210 |
+
QO
|
| 6211 |
+
NW
|
| 6212 |
+
JP
|
| 6213 |
+
JB
|
| 6214 |
+
FL
|
| 6215 |
+
PC
|
| 6216 |
+
IW
|
| 6217 |
+
EG
|
| 6218 |
+
UO
|
| 6219 |
+
LS
|
| 6220 |
+
IS
|
| 6221 |
+
PY
|
| 6222 |
+
EF
|
| 6223 |
+
MN
|
| 6224 |
+
FMYLOQNETTJSVVJBCSHYKTPWRZYQBTIPPZMLYSCVTTAHIKEHVXPWDOM
|
| 6225 |
+
128
|
| 6226 |
+
IR
|
| 6227 |
+
WK
|
| 6228 |
+
AW
|
| 6229 |
+
CL
|
| 6230 |
+
GH
|
| 6231 |
+
FJ
|
| 6232 |
+
UN
|
| 6233 |
+
WQ
|
| 6234 |
+
BD
|
| 6235 |
+
RW
|
| 6236 |
+
TP
|
| 6237 |
+
WN
|
| 6238 |
+
ZK
|
| 6239 |
+
AX
|
| 6240 |
+
CJ
|
| 6241 |
+
XL
|
| 6242 |
+
VM
|
| 6243 |
+
CS
|
| 6244 |
+
PR
|
| 6245 |
+
UR
|
| 6246 |
+
JF
|
| 6247 |
+
TF
|
| 6248 |
+
KC
|
| 6249 |
+
RH
|
| 6250 |
+
ZD
|
| 6251 |
+
ZO
|
| 6252 |
+
YS
|
| 6253 |
+
JD
|
| 6254 |
+
PW
|
| 6255 |
+
PK
|
| 6256 |
+
OR
|
| 6257 |
+
JN
|
| 6258 |
+
ER
|
| 6259 |
+
OB
|
| 6260 |
+
NR
|
| 6261 |
+
BX
|
| 6262 |
+
SZ
|
| 6263 |
+
TV
|
| 6264 |
+
MK
|
| 6265 |
+
RG
|
| 6266 |
+
LE
|
| 6267 |
+
JL
|
| 6268 |
+
VQ
|
| 6269 |
+
ME
|
| 6270 |
+
KB
|
| 6271 |
+
ZS
|
| 6272 |
+
KJ
|
| 6273 |
+
HJ
|
| 6274 |
+
NQ
|
| 6275 |
+
YF
|
| 6276 |
+
WJ
|
| 6277 |
+
VZ
|
| 6278 |
+
EN
|
| 6279 |
+
RP
|
| 6280 |
+
VF
|
| 6281 |
+
NE
|
| 6282 |
+
SP
|
| 6283 |
+
NX
|
| 6284 |
+
KH
|
| 6285 |
+
LJ
|
| 6286 |
+
HL
|
| 6287 |
+
XS
|
| 6288 |
+
UI
|
| 6289 |
+
EP
|
| 6290 |
+
ZR
|
| 6291 |
+
AS
|
| 6292 |
+
OP
|
| 6293 |
+
IC
|
| 6294 |
+
AF
|
| 6295 |
+
LN
|
| 6296 |
+
TE
|
| 6297 |
+
NU
|
| 6298 |
+
KX
|
| 6299 |
+
PD
|
| 6300 |
+
IO
|
| 6301 |
+
FY
|
| 6302 |
+
MN
|
| 6303 |
+
RJ
|
| 6304 |
+
PH
|
| 6305 |
+
YX
|
| 6306 |
+
KR
|
| 6307 |
+
ED
|
| 6308 |
+
QM
|
| 6309 |
+
DI
|
| 6310 |
+
QL
|
| 6311 |
+
QG
|
| 6312 |
+
VW
|
| 6313 |
+
BH
|
| 6314 |
+
VL
|
| 6315 |
+
AQ
|
| 6316 |
+
CB
|
| 6317 |
+
FG
|
| 6318 |
+
RD
|
| 6319 |
+
GV
|
| 6320 |
+
OS
|
| 6321 |
+
GB
|
| 6322 |
+
PU
|
| 6323 |
+
ZV
|
| 6324 |
+
EF
|
| 6325 |
+
MW
|
| 6326 |
+
YL
|
| 6327 |
+
TM
|
| 6328 |
+
PJ
|
| 6329 |
+
RZ
|
| 6330 |
+
CR
|
| 6331 |
+
XK
|
| 6332 |
+
IV
|
| 6333 |
+
YJ
|
| 6334 |
+
ES
|
| 6335 |
+
XV
|
| 6336 |
+
DS
|
| 6337 |
+
HF
|
| 6338 |
+
DN
|
| 6339 |
+
LI
|
| 6340 |
+
IU
|
| 6341 |
+
UY
|
| 6342 |
+
XH
|
| 6343 |
+
YU
|
| 6344 |
+
EL
|
| 6345 |
+
KM
|
| 6346 |
+
FZ
|
| 6347 |
+
XP
|
| 6348 |
+
OV
|
| 6349 |
+
FK
|
| 6350 |
+
FT
|
| 6351 |
+
UZ
|
| 6352 |
+
AT
|
| 6353 |
+
ZH
|
| 6354 |
+
IAZDJPGDBWOWNPTMFMSOOFWYHBAWQ
|
| 6355 |
+
182
|
| 6356 |
+
OM
|
| 6357 |
+
NK
|
| 6358 |
+
PD
|
| 6359 |
+
MR
|
| 6360 |
+
WI
|
| 6361 |
+
YM
|
| 6362 |
+
YH
|
| 6363 |
+
GQ
|
| 6364 |
+
JB
|
| 6365 |
+
PS
|
| 6366 |
+
ED
|
| 6367 |
+
AW
|
| 6368 |
+
YD
|
| 6369 |
+
DN
|
| 6370 |
+
WJ
|
| 6371 |
+
HR
|
| 6372 |
+
NF
|
| 6373 |
+
LC
|
| 6374 |
+
MZ
|
| 6375 |
+
WG
|
| 6376 |
+
XL
|
| 6377 |
+
LJ
|
| 6378 |
+
YS
|
| 6379 |
+
YZ
|
| 6380 |
+
IW
|
| 6381 |
+
ZM
|
| 6382 |
+
QB
|
| 6383 |
+
JH
|
| 6384 |
+
NR
|
| 6385 |
+
WY
|
| 6386 |
+
UO
|
| 6387 |
+
NA
|
| 6388 |
+
PW
|
| 6389 |
+
TK
|
| 6390 |
+
XK
|
| 6391 |
+
FW
|
| 6392 |
+
AP
|
| 6393 |
+
PU
|
| 6394 |
+
VS
|
| 6395 |
+
MS
|
| 6396 |
+
TF
|
| 6397 |
+
QZ
|
| 6398 |
+
JC
|
| 6399 |
+
BE
|
| 6400 |
+
FK
|
| 6401 |
+
EG
|
| 6402 |
+
LX
|
| 6403 |
+
RM
|
| 6404 |
+
RB
|
| 6405 |
+
JT
|
| 6406 |
+
PO
|
| 6407 |
+
OW
|
| 6408 |
+
EO
|
| 6409 |
+
OE
|
| 6410 |
+
XC
|
| 6411 |
+
NB
|
| 6412 |
+
LO
|
| 6413 |
+
KB
|
| 6414 |
+
NO
|
| 6415 |
+
CO
|
| 6416 |
+
UT
|
| 6417 |
+
MA
|
| 6418 |
+
BA
|
| 6419 |
+
KH
|
| 6420 |
+
PZ
|
| 6421 |
+
BW
|
| 6422 |
+
PN
|
| 6423 |
+
SP
|
| 6424 |
+
QL
|
| 6425 |
+
OY
|
| 6426 |
+
LM
|
| 6427 |
+
BJ
|
| 6428 |
+
VE
|
| 6429 |
+
QO
|
| 6430 |
+
FS
|
| 6431 |
+
FL
|
| 6432 |
+
OU
|
| 6433 |
+
YX
|
| 6434 |
+
DG
|
| 6435 |
+
OT
|
| 6436 |
+
VU
|
| 6437 |
+
UB
|
| 6438 |
+
DB
|
| 6439 |
+
RV
|
| 6440 |
+
PV
|
| 6441 |
+
EQ
|
| 6442 |
+
ZF
|
| 6443 |
+
JI
|
| 6444 |
+
DM
|
| 6445 |
+
XD
|
| 6446 |
+
HA
|
| 6447 |
+
AR
|
| 6448 |
+
BT
|
| 6449 |
+
MD
|
| 6450 |
+
EI
|
| 6451 |
+
AE
|
| 6452 |
+
SZ
|
| 6453 |
+
DU
|
| 6454 |
+
KL
|
| 6455 |
+
KR
|
| 6456 |
+
YQ
|
| 6457 |
+
LT
|
| 6458 |
+
HF
|
| 6459 |
+
EF
|
| 6460 |
+
XR
|
| 6461 |
+
TZ
|
| 6462 |
+
JG
|
| 6463 |
+
GI
|
| 6464 |
+
UL
|
| 6465 |
+
XI
|
| 6466 |
+
VM
|
| 6467 |
+
XZ
|
| 6468 |
+
TR
|
| 6469 |
+
WU
|
| 6470 |
+
MU
|
| 6471 |
+
KD
|
| 6472 |
+
XU
|
| 6473 |
+
IQ
|
| 6474 |
+
VP
|
| 6475 |
+
UN
|
| 6476 |
+
HL
|
| 6477 |
+
XG
|
| 6478 |
+
CQ
|
| 6479 |
+
HN
|
| 6480 |
+
CZ
|
| 6481 |
+
IX
|
| 6482 |
+
KE
|
| 6483 |
+
MP
|
| 6484 |
+
RA
|
| 6485 |
+
QF
|
| 6486 |
+
NT
|
| 6487 |
+
AV
|
| 6488 |
+
GR
|
| 6489 |
+
GM
|
| 6490 |
+
QW
|
| 6491 |
+
TY
|
| 6492 |
+
TE
|
| 6493 |
+
OQ
|
| 6494 |
+
QJ
|
| 6495 |
+
WC
|
| 6496 |
+
IS
|
| 6497 |
+
FO
|
| 6498 |
+
YB
|
| 6499 |
+
DA
|
| 6500 |
+
BI
|
| 6501 |
+
SM
|
| 6502 |
+
EA
|
| 6503 |
+
BG
|
| 6504 |
+
IN
|
| 6505 |
+
NQ
|
| 6506 |
+
PE
|
| 6507 |
+
JN
|
| 6508 |
+
HC
|
| 6509 |
+
ZS
|
| 6510 |
+
VI
|
| 6511 |
+
IH
|
| 6512 |
+
GO
|
| 6513 |
+
AN
|
| 6514 |
+
AX
|
| 6515 |
+
HP
|
| 6516 |
+
IA
|
| 6517 |
+
LG
|
| 6518 |
+
GK
|
| 6519 |
+
GZ
|
| 6520 |
+
IL
|
| 6521 |
+
ZR
|
| 6522 |
+
CJ
|
| 6523 |
+
HT
|
| 6524 |
+
LV
|
| 6525 |
+
VF
|
| 6526 |
+
KX
|
| 6527 |
+
RS
|
| 6528 |
+
NY
|
| 6529 |
+
QA
|
| 6530 |
+
ZH
|
| 6531 |
+
KN
|
| 6532 |
+
WV
|
| 6533 |
+
XW
|
| 6534 |
+
SI
|
| 6535 |
+
DE
|
| 6536 |
+
PB
|
| 6537 |
+
YA
|
| 6538 |
+
LPEHATOJCOZCHJWENYRQXBQLWLMCDAWLEAXKKYRYRUQQVUJKCMVFFOX
|
| 6539 |
+
280
|
| 6540 |
+
KW
|
| 6541 |
+
JR
|
| 6542 |
+
GX
|
| 6543 |
+
WZ
|
| 6544 |
+
CS
|
| 6545 |
+
IW
|
| 6546 |
+
QX
|
| 6547 |
+
TU
|
| 6548 |
+
GH
|
| 6549 |
+
JL
|
| 6550 |
+
AL
|
| 6551 |
+
FQ
|
| 6552 |
+
SY
|
| 6553 |
+
GQ
|
| 6554 |
+
FW
|
| 6555 |
+
IM
|
| 6556 |
+
FX
|
| 6557 |
+
EK
|
| 6558 |
+
HY
|
| 6559 |
+
PZ
|
| 6560 |
+
AE
|
| 6561 |
+
UY
|
| 6562 |
+
GN
|
| 6563 |
+
SZ
|
| 6564 |
+
KM
|
| 6565 |
+
BR
|
| 6566 |
+
HJ
|
| 6567 |
+
LQ
|
| 6568 |
+
XZ
|
| 6569 |
+
ER
|
| 6570 |
+
AC
|
| 6571 |
+
ST
|
| 6572 |
+
ES
|
| 6573 |
+
HO
|
| 6574 |
+
NU
|
| 6575 |
+
EU
|
| 6576 |
+
FP
|
| 6577 |
+
XY
|
| 6578 |
+
KS
|
| 6579 |
+
CP
|
| 6580 |
+
TZ
|
| 6581 |
+
RW
|
| 6582 |
+
HU
|
| 6583 |
+
BN
|
| 6584 |
+
AN
|
| 6585 |
+
PQ
|
| 6586 |
+
KT
|
| 6587 |
+
EN
|
| 6588 |
+
OU
|
| 6589 |
+
LM
|
| 6590 |
+
IN
|
| 6591 |
+
AT
|
| 6592 |
+
EH
|
| 6593 |
+
IU
|
| 6594 |
+
FV
|
| 6595 |
+
ET
|
| 6596 |
+
MO
|
| 6597 |
+
BP
|
| 6598 |
+
EX
|
| 6599 |
+
KP
|
| 6600 |
+
BL
|
| 6601 |
+
DP
|
| 6602 |
+
DT
|
| 6603 |
+
GO
|
| 6604 |
+
RZ
|
| 6605 |
+
BE
|
| 6606 |
+
CT
|
| 6607 |
+
BV
|
| 6608 |
+
JQ
|
| 6609 |
+
UW
|
| 6610 |
+
IL
|
| 6611 |
+
LZ
|
| 6612 |
+
HT
|
| 6613 |
+
JZ
|
| 6614 |
+
NP
|
| 6615 |
+
HN
|
| 6616 |
+
JX
|
| 6617 |
+
BM
|
| 6618 |
+
JM
|
| 6619 |
+
BU
|
| 6620 |
+
KV
|
| 6621 |
+
SX
|
| 6622 |
+
RS
|
| 6623 |
+
CH
|
| 6624 |
+
MQ
|
| 6625 |
+
CI
|
| 6626 |
+
MX
|
| 6627 |
+
DV
|
| 6628 |
+
QR
|
| 6629 |
+
AV
|
| 6630 |
+
DK
|
| 6631 |
+
MS
|
| 6632 |
+
KR
|
| 6633 |
+
HR
|
| 6634 |
+
FL
|
| 6635 |
+
AB
|
| 6636 |
+
IO
|
| 6637 |
+
OX
|
| 6638 |
+
EO
|
| 6639 |
+
PT
|
| 6640 |
+
CN
|
| 6641 |
+
NT
|
| 6642 |
+
DE
|
| 6643 |
+
OV
|
| 6644 |
+
TX
|
| 6645 |
+
CJ
|
| 6646 |
+
AW
|
| 6647 |
+
BY
|
| 6648 |
+
DW
|
| 6649 |
+
QU
|
| 6650 |
+
HX
|
| 6651 |
+
AQ
|
| 6652 |
+
YZ
|
| 6653 |
+
AD
|
| 6654 |
+
IK
|
| 6655 |
+
AG
|
| 6656 |
+
IJ
|
| 6657 |
+
SU
|
| 6658 |
+
BW
|
| 6659 |
+
CV
|
| 6660 |
+
CY
|
| 6661 |
+
IV
|
| 6662 |
+
CE
|
| 6663 |
+
DH
|
| 6664 |
+
HV
|
| 6665 |
+
NS
|
| 6666 |
+
RU
|
| 6667 |
+
LS
|
| 6668 |
+
HS
|
| 6669 |
+
MP
|
| 6670 |
+
AS
|
| 6671 |
+
KZ
|
| 6672 |
+
DO
|
| 6673 |
+
LY
|
| 6674 |
+
EL
|
| 6675 |
+
KN
|
| 6676 |
+
KU
|
| 6677 |
+
NW
|
| 6678 |
+
HK
|
| 6679 |
+
DF
|
| 6680 |
+
CO
|
| 6681 |
+
CU
|
| 6682 |
+
GS
|
| 6683 |
+
OQ
|
| 6684 |
+
GJ
|
| 6685 |
+
GW
|
| 6686 |
+
LV
|
| 6687 |
+
TY
|
| 6688 |
+
VY
|
| 6689 |
+
FI
|
| 6690 |
+
GT
|
| 6691 |
+
GR
|
| 6692 |
+
JV
|
| 6693 |
+
MU
|
| 6694 |
+
AY
|
| 6695 |
+
AF
|
| 6696 |
+
CL
|
| 6697 |
+
CZ
|
| 6698 |
+
DM
|
| 6699 |
+
PW
|
| 6700 |
+
RX
|
| 6701 |
+
EQ
|
| 6702 |
+
AP
|
| 6703 |
+
SW
|
| 6704 |
+
NX
|
| 6705 |
+
EM
|
| 6706 |
+
PX
|
| 6707 |
+
BQ
|
| 6708 |
+
BC
|
| 6709 |
+
AM
|
| 6710 |
+
LN
|
| 6711 |
+
VZ
|
| 6712 |
+
JT
|
| 6713 |
+
AK
|
| 6714 |
+
IT
|
| 6715 |
+
AI
|
| 6716 |
+
LX
|
| 6717 |
+
JO
|
| 6718 |
+
BO
|
| 6719 |
+
FY
|
| 6720 |
+
DI
|
| 6721 |
+
OW
|
| 6722 |
+
DX
|
| 6723 |
+
TV
|
| 6724 |
+
VX
|
| 6725 |
+
FU
|
| 6726 |
+
BX
|
| 6727 |
+
NR
|
| 6728 |
+
HW
|
| 6729 |
+
VW
|
| 6730 |
+
LO
|
| 6731 |
+
PR
|
| 6732 |
+
CF
|
| 6733 |
+
DJ
|
| 6734 |
+
BF
|
| 6735 |
+
RV
|
| 6736 |
+
FO
|
| 6737 |
+
OP
|
| 6738 |
+
HQ
|
| 6739 |
+
LT
|
| 6740 |
+
KO
|
| 6741 |
+
FG
|
| 6742 |
+
MW
|
| 6743 |
+
JN
|
| 6744 |
+
IY
|
| 6745 |
+
CQ
|
| 6746 |
+
PY
|
| 6747 |
+
EF
|
| 6748 |
+
QT
|
| 6749 |
+
PV
|
| 6750 |
+
FR
|
| 6751 |
+
IP
|
| 6752 |
+
BZ
|
| 6753 |
+
RT
|
| 6754 |
+
IX
|
| 6755 |
+
MV
|
| 6756 |
+
DR
|
| 6757 |
+
JK
|
| 6758 |
+
JY
|
| 6759 |
+
EP
|
| 6760 |
+
EV
|
| 6761 |
+
UX
|
| 6762 |
+
UV
|
| 6763 |
+
DU
|
| 6764 |
+
BJ
|
| 6765 |
+
GM
|
| 6766 |
+
KQ
|
| 6767 |
+
FH
|
| 6768 |
+
WY
|
| 6769 |
+
MT
|
| 6770 |
+
JW
|
| 6771 |
+
IQ
|
| 6772 |
+
QZ
|
| 6773 |
+
BI
|
| 6774 |
+
AU
|
| 6775 |
+
GL
|
| 6776 |
+
CG
|
| 6777 |
+
FM
|
| 6778 |
+
BD
|
| 6779 |
+
LU
|
| 6780 |
+
DN
|
| 6781 |
+
DY
|
| 6782 |
+
EI
|
| 6783 |
+
LR
|
| 6784 |
+
OS
|
| 6785 |
+
AX
|
| 6786 |
+
DQ
|
| 6787 |
+
GZ
|
| 6788 |
+
QV
|
| 6789 |
+
NO
|
| 6790 |
+
MN
|
| 6791 |
+
EY
|
| 6792 |
+
HI
|
| 6793 |
+
BH
|
| 6794 |
+
AH
|
| 6795 |
+
FT
|
| 6796 |
+
MY
|
| 6797 |
+
NY
|
| 6798 |
+
JU
|
| 6799 |
+
FZ
|
| 6800 |
+
GK
|
| 6801 |
+
IR
|
| 6802 |
+
HZ
|
| 6803 |
+
AR
|
| 6804 |
+
DS
|
| 6805 |
+
CX
|
| 6806 |
+
UZ
|
| 6807 |
+
GP
|
| 6808 |
+
WX
|
| 6809 |
+
KY
|
| 6810 |
+
BG
|
| 6811 |
+
GI
|
| 6812 |
+
TW
|
| 6813 |
+
KL
|
| 6814 |
+
AZ
|
| 6815 |
+
FK
|
| 6816 |
+
BS
|
| 6817 |
+
OZ
|
| 6818 |
+
GY
|
| 6819 |
+
CK
|
| 6820 |
+
SZSASTHPDPSNSAMCCKXHMKF
|
| 6821 |
+
231
|
| 6822 |
+
SX
|
| 6823 |
+
GJ
|
| 6824 |
+
DL
|
| 6825 |
+
YG
|
| 6826 |
+
WO
|
| 6827 |
+
GZ
|
| 6828 |
+
UQ
|
| 6829 |
+
MF
|
| 6830 |
+
MQ
|
| 6831 |
+
SO
|
| 6832 |
+
DV
|
| 6833 |
+
YX
|
| 6834 |
+
WI
|
| 6835 |
+
HI
|
| 6836 |
+
JZ
|
| 6837 |
+
ZJ
|
| 6838 |
+
XD
|
| 6839 |
+
GK
|
| 6840 |
+
TR
|
| 6841 |
+
LC
|
| 6842 |
+
HX
|
| 6843 |
+
ER
|
| 6844 |
+
LK
|
| 6845 |
+
SR
|
| 6846 |
+
DQ
|
| 6847 |
+
ZM
|
| 6848 |
+
BV
|
| 6849 |
+
VZ
|
| 6850 |
+
US
|
| 6851 |
+
QV
|
| 6852 |
+
KB
|
| 6853 |
+
LD
|
| 6854 |
+
FI
|
| 6855 |
+
TS
|
| 6856 |
+
JR
|
| 6857 |
+
UX
|
| 6858 |
+
WN
|
| 6859 |
+
EF
|
| 6860 |
+
OD
|
| 6861 |
+
RH
|
| 6862 |
+
LB
|
| 6863 |
+
KR
|
| 6864 |
+
BA
|
| 6865 |
+
SB
|
| 6866 |
+
UT
|
| 6867 |
+
QZ
|
| 6868 |
+
XG
|
| 6869 |
+
HK
|
| 6870 |
+
AF
|
| 6871 |
+
GE
|
| 6872 |
+
UL
|
| 6873 |
+
VY
|
| 6874 |
+
IO
|
| 6875 |
+
UG
|
| 6876 |
+
GL
|
| 6877 |
+
JU
|
| 6878 |
+
NM
|
| 6879 |
+
OI
|
| 6880 |
+
LG
|
| 6881 |
+
QP
|
| 6882 |
+
CD
|
| 6883 |
+
IB
|
| 6884 |
+
FQ
|
| 6885 |
+
NH
|
| 6886 |
+
BG
|
| 6887 |
+
OK
|
| 6888 |
+
NV
|
| 6889 |
+
YV
|
| 6890 |
+
BM
|
| 6891 |
+
HO
|
| 6892 |
+
WK
|
| 6893 |
+
PC
|
| 6894 |
+
ST
|
| 6895 |
+
BR
|
| 6896 |
+
BI
|
| 6897 |
+
VR
|
| 6898 |
+
KG
|
| 6899 |
+
NO
|
| 6900 |
+
NX
|
| 6901 |
+
ES
|
| 6902 |
+
MY
|
| 6903 |
+
ZH
|
| 6904 |
+
HS
|
| 6905 |
+
EW
|
| 6906 |
+
YR
|
| 6907 |
+
IL
|
| 6908 |
+
CB
|
| 6909 |
+
WJ
|
| 6910 |
+
FL
|
| 6911 |
+
NF
|
| 6912 |
+
EP
|
| 6913 |
+
PA
|
| 6914 |
+
ZL
|
| 6915 |
+
HP
|
| 6916 |
+
PH
|
| 6917 |
+
TD
|
| 6918 |
+
VS
|
| 6919 |
+
VB
|
| 6920 |
+
CX
|
| 6921 |
+
RP
|
| 6922 |
+
BF
|
| 6923 |
+
PF
|
| 6924 |
+
ZS
|
| 6925 |
+
XB
|
| 6926 |
+
FC
|
| 6927 |
+
YI
|
| 6928 |
+
GC
|
| 6929 |
+
FT
|
| 6930 |
+
RZ
|
| 6931 |
+
GT
|
| 6932 |
+
KN
|
| 6933 |
+
VQ
|
| 6934 |
+
XO
|
| 6935 |
+
GH
|
| 6936 |
+
NA
|
| 6937 |
+
WH
|
| 6938 |
+
MO
|
| 6939 |
+
HG
|
| 6940 |
+
QH
|
| 6941 |
+
QW
|
| 6942 |
+
XU
|
| 6943 |
+
BH
|
| 6944 |
+
XR
|
| 6945 |
+
PZ
|
| 6946 |
+
WL
|
| 6947 |
+
LN
|
| 6948 |
+
VC
|
| 6949 |
+
RX
|
| 6950 |
+
OR
|
| 6951 |
+
EB
|
| 6952 |
+
KU
|
| 6953 |
+
ET
|
| 6954 |
+
UD
|
| 6955 |
+
TL
|
| 6956 |
+
JK
|
| 6957 |
+
TO
|
| 6958 |
+
CR
|
| 6959 |
+
DT
|
| 6960 |
+
JC
|
| 6961 |
+
OP
|
| 6962 |
+
CQ
|
| 6963 |
+
OS
|
| 6964 |
+
WM
|
| 6965 |
+
ZX
|
| 6966 |
+
PE
|
| 6967 |
+
DY
|
| 6968 |
+
VE
|
| 6969 |
+
LQ
|
| 6970 |
+
OX
|
| 6971 |
+
JX
|
| 6972 |
+
TX
|
| 6973 |
+
HJ
|
| 6974 |
+
JT
|
| 6975 |
+
GA
|
| 6976 |
+
KT
|
| 6977 |
+
NI
|
| 6978 |
+
MD
|
| 6979 |
+
FA
|
| 6980 |
+
WG
|
| 6981 |
+
VO
|
| 6982 |
+
QC
|
| 6983 |
+
FS
|
| 6984 |
+
YZ
|
| 6985 |
+
PM
|
| 6986 |
+
VP
|
| 6987 |
+
RT
|
| 6988 |
+
LZ
|
| 6989 |
+
OW
|
| 6990 |
+
QS
|
| 6991 |
+
EJ
|
| 6992 |
+
BN
|
| 6993 |
+
SU
|
| 6994 |
+
NP
|
| 6995 |
+
MT
|
| 6996 |
+
WZ
|
| 6997 |
+
FE
|
| 6998 |
+
QY
|
| 6999 |
+
ZW
|
| 7000 |
+
MZ
|
| 7001 |
+
AU
|
| 7002 |
+
OY
|
| 7003 |
+
SQ
|
| 7004 |
+
CA
|
| 7005 |
+
IJ
|
| 7006 |
+
MP
|
| 7007 |
+
AK
|
| 7008 |
+
JO
|
| 7009 |
+
QM
|
| 7010 |
+
JF
|
| 7011 |
+
LE
|
| 7012 |
+
CF
|
| 7013 |
+
IF
|
| 7014 |
+
OF
|
| 7015 |
+
AL
|
| 7016 |
+
VT
|
| 7017 |
+
GS
|
| 7018 |
+
BY
|
| 7019 |
+
YO
|
| 7020 |
+
TK
|
| 7021 |
+
QG
|
| 7022 |
+
KA
|
| 7023 |
+
EQ
|
| 7024 |
+
RJ
|
| 7025 |
+
EM
|
| 7026 |
+
AN
|
| 7027 |
+
UP
|
| 7028 |
+
RO
|
| 7029 |
+
ZQ
|
| 7030 |
+
VD
|
| 7031 |
+
PO
|
| 7032 |
+
DH
|
| 7033 |
+
DR
|
| 7034 |
+
XC
|
| 7035 |
+
PR
|
| 7036 |
+
XQ
|
| 7037 |
+
CW
|
| 7038 |
+
PV
|
| 7039 |
+
HW
|
| 7040 |
+
NU
|
| 7041 |
+
ZO
|
| 7042 |
+
YT
|
| 7043 |
+
NZ
|
| 7044 |
+
HL
|
| 7045 |
+
JN
|
| 7046 |
+
MR
|
| 7047 |
+
RG
|
| 7048 |
+
ED
|
| 7049 |
+
YP
|
| 7050 |
+
RU
|
| 7051 |
+
XM
|
| 7052 |
+
VH
|
| 7053 |
+
PDJNSTZVPMSVOILLVNFYHBKOQDBTFZQMERMBGZOZIJBCI
|
| 7054 |
+
177
|
| 7055 |
+
NT
|
| 7056 |
+
YC
|
| 7057 |
+
XO
|
| 7058 |
+
UT
|
| 7059 |
+
YH
|
| 7060 |
+
OT
|
| 7061 |
+
ON
|
| 7062 |
+
RE
|
| 7063 |
+
WF
|
| 7064 |
+
JT
|
| 7065 |
+
OF
|
| 7066 |
+
VS
|
| 7067 |
+
QM
|
| 7068 |
+
RA
|
| 7069 |
+
EI
|
| 7070 |
+
EH
|
| 7071 |
+
AD
|
| 7072 |
+
NX
|
| 7073 |
+
LZ
|
| 7074 |
+
GX
|
| 7075 |
+
QY
|
| 7076 |
+
IW
|
| 7077 |
+
OX
|
| 7078 |
+
JR
|
| 7079 |
+
JL
|
| 7080 |
+
RQ
|
| 7081 |
+
BK
|
| 7082 |
+
SG
|
| 7083 |
+
DQ
|
| 7084 |
+
HC
|
| 7085 |
+
AO
|
| 7086 |
+
QS
|
| 7087 |
+
QA
|
| 7088 |
+
HO
|
| 7089 |
+
MW
|
| 7090 |
+
VK
|
| 7091 |
+
JN
|
| 7092 |
+
HL
|
| 7093 |
+
JD
|
| 7094 |
+
HA
|
| 7095 |
+
JE
|
| 7096 |
+
AE
|
| 7097 |
+
AH
|
| 7098 |
+
FR
|
| 7099 |
+
VJ
|
| 7100 |
+
CA
|
| 7101 |
+
AN
|
| 7102 |
+
IQ
|
| 7103 |
+
ZE
|
| 7104 |
+
GP
|
| 7105 |
+
MO
|
| 7106 |
+
PM
|
| 7107 |
+
OP
|
| 7108 |
+
IF
|
| 7109 |
+
GO
|
| 7110 |
+
GI
|
| 7111 |
+
OE
|
| 7112 |
+
FM
|
| 7113 |
+
YW
|
| 7114 |
+
DV
|
| 7115 |
+
UJ
|
| 7116 |
+
PW
|
| 7117 |
+
RU
|
| 7118 |
+
JC
|
| 7119 |
+
KI
|
| 7120 |
+
SH
|
| 7121 |
+
DY
|
| 7122 |
+
OZ
|
| 7123 |
+
SK
|
| 7124 |
+
VB
|
| 7125 |
+
WN
|
| 7126 |
+
KD
|
| 7127 |
+
UE
|
| 7128 |
+
XN
|
| 7129 |
+
EW
|
| 7130 |
+
BN
|
| 7131 |
+
LK
|
| 7132 |
+
WU
|
| 7133 |
+
VL
|
| 7134 |
+
PU
|
| 7135 |
+
KN
|
| 7136 |
+
FL
|
| 7137 |
+
XH
|
| 7138 |
+
XG
|
| 7139 |
+
ZS
|
| 7140 |
+
MY
|
| 7141 |
+
CG
|
| 7142 |
+
GK
|
| 7143 |
+
IS
|
| 7144 |
+
FD
|
| 7145 |
+
WM
|
| 7146 |
+
SP
|
| 7147 |
+
VX
|
| 7148 |
+
HS
|
| 7149 |
+
US
|
| 7150 |
+
TL
|
| 7151 |
+
GA
|
| 7152 |
+
JX
|
| 7153 |
+
EL
|
| 7154 |
+
MZ
|
| 7155 |
+
PV
|
| 7156 |
+
ZR
|
| 7157 |
+
KX
|
| 7158 |
+
XK
|
| 7159 |
+
XT
|
| 7160 |
+
HI
|
| 7161 |
+
DT
|
| 7162 |
+
IO
|
| 7163 |
+
PG
|
| 7164 |
+
HV
|
| 7165 |
+
NY
|
| 7166 |
+
UP
|
| 7167 |
+
DL
|
| 7168 |
+
RS
|
| 7169 |
+
EU
|
| 7170 |
+
YX
|
| 7171 |
+
MB
|
| 7172 |
+
VM
|
| 7173 |
+
ZT
|
| 7174 |
+
HM
|
| 7175 |
+
LQ
|
| 7176 |
+
BJ
|
| 7177 |
+
TJ
|
| 7178 |
+
FA
|
| 7179 |
+
RK
|
| 7180 |
+
ZY
|
| 7181 |
+
KM
|
| 7182 |
+
EG
|
| 7183 |
+
SV
|
| 7184 |
+
XF
|
| 7185 |
+
VR
|
| 7186 |
+
GW
|
| 7187 |
+
ZA
|
| 7188 |
+
RY
|
| 7189 |
+
KH
|
| 7190 |
+
DF
|
| 7191 |
+
UF
|
| 7192 |
+
UW
|
| 7193 |
+
PF
|
| 7194 |
+
KW
|
| 7195 |
+
BZ
|
| 7196 |
+
OB
|
| 7197 |
+
FS
|
| 7198 |
+
DK
|
| 7199 |
+
ZB
|
| 7200 |
+
NO
|
| 7201 |
+
FH
|
| 7202 |
+
YM
|
| 7203 |
+
SO
|
| 7204 |
+
TK
|
| 7205 |
+
DS
|
| 7206 |
+
MC
|
| 7207 |
+
FO
|
| 7208 |
+
PL
|
| 7209 |
+
YL
|
| 7210 |
+
WI
|
| 7211 |
+
FE
|
| 7212 |
+
PO
|
| 7213 |
+
YS
|
| 7214 |
+
FX
|
| 7215 |
+
DR
|
| 7216 |
+
RT
|
| 7217 |
+
QE
|
| 7218 |
+
WH
|
| 7219 |
+
WT
|
| 7220 |
+
RW
|
| 7221 |
+
JS
|
| 7222 |
+
MA
|
| 7223 |
+
AR
|
| 7224 |
+
IZ
|
| 7225 |
+
DZ
|
| 7226 |
+
VT
|
| 7227 |
+
YQ
|
| 7228 |
+
UH
|
| 7229 |
+
PI
|
| 7230 |
+
IP
|
| 7231 |
+
DM
|
| 7232 |
+
JYGPXSWTIJHUAKYHSUMBECDZWJOPOVNKHF
|
| 7233 |
+
59
|
| 7234 |
+
UR
|
| 7235 |
+
OE
|
| 7236 |
+
LC
|
| 7237 |
+
UY
|
| 7238 |
+
UD
|
| 7239 |
+
UO
|
| 7240 |
+
KU
|
| 7241 |
+
YO
|
| 7242 |
+
LJ
|
| 7243 |
+
KX
|
| 7244 |
+
OK
|
| 7245 |
+
FW
|
| 7246 |
+
YV
|
| 7247 |
+
LV
|
| 7248 |
+
WV
|
| 7249 |
+
UA
|
| 7250 |
+
XA
|
| 7251 |
+
CX
|
| 7252 |
+
BL
|
| 7253 |
+
SN
|
| 7254 |
+
FT
|
| 7255 |
+
TG
|
| 7256 |
+
GA
|
| 7257 |
+
VE
|
| 7258 |
+
ZN
|
| 7259 |
+
AT
|
| 7260 |
+
PI
|
| 7261 |
+
GE
|
| 7262 |
+
ND
|
| 7263 |
+
BV
|
| 7264 |
+
HC
|
| 7265 |
+
AP
|
| 7266 |
+
RS
|
| 7267 |
+
XT
|
| 7268 |
+
PH
|
| 7269 |
+
AE
|
| 7270 |
+
WD
|
| 7271 |
+
PZ
|
| 7272 |
+
VM
|
| 7273 |
+
HL
|
| 7274 |
+
CH
|
| 7275 |
+
SW
|
| 7276 |
+
FA
|
| 7277 |
+
WZ
|
| 7278 |
+
PN
|
| 7279 |
+
QD
|
| 7280 |
+
FR
|
| 7281 |
+
LT
|
| 7282 |
+
ZQ
|
| 7283 |
+
EJ
|
| 7284 |
+
BF
|
| 7285 |
+
CN
|
| 7286 |
+
JB
|
| 7287 |
+
WA
|
| 7288 |
+
UC
|
| 7289 |
+
GC
|
| 7290 |
+
ET
|
| 7291 |
+
AJ
|
| 7292 |
+
HM
|
2021/quals/consistency_ch2.md
ADDED
|
@@ -0,0 +1,44 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
**Note: This problem shares similarities with [Chapter 1](https://www.facebook.com/codingcompetitions/hacker-cup/2021/qualification-round/problems/A1). The solution to either chapter may help with solving the other, so please consider reading both first.**
|
| 2 |
+
|
| 3 |
+
Connie received a string \(S\) for her birthday, consisting entirely of uppercase letters (each between `"A"` and `"Z"`, inclusive).
|
| 4 |
+
|
| 5 |
+
However, Connie really only likes nice, *consistent* strings. She considers a string to be consistent if and only if all of its letters are the same.
|
| 6 |
+
|
| 7 |
+
Each second, Connie may choose one letter in \(S\) and replace it with a different letter. **There are \(K\) different types of replacements she may make, with the \(i\)th one involving choosing letter \(A_i\) anywhere in \(S\) and replacing it with letter \(B_i\).** No type of replacement (ordered pair of \(A_i\) and \(B_i\)) is given twice. There is no limit on how many times she may end up using each type of replacement. If a letter appears multiple times in \(S\), she may only replace a single occurrence per second.
|
| 8 |
+
|
| 9 |
+
Help her determine the minimum number of seconds required to change \(S\) into any consistent string, if possible. If it's impossible to ever do so, output \(-1\) instead. Note that \(S\) might already be consistent, in which case \(0\) seconds would be required.
|
| 10 |
+
|
| 11 |
+
# Constraints
|
| 12 |
+
|
| 13 |
+
\(1 \le T \le 40\)
|
| 14 |
+
\(1 \le |S| \le 100\)
|
| 15 |
+
\(0 \le K \le 300 \)
|
| 16 |
+
`"A"` \(\le S_i, A_i, B_i \le\) `"Z"`
|
| 17 |
+
\(A_i \ne B_i\)
|
| 18 |
+
|
| 19 |
+
The sum of \(|S|\) across all test cases is at most \(4{,}000\).
|
| 20 |
+
|
| 21 |
+
|
| 22 |
+
|
| 23 |
+
|
| 24 |
+
# Input
|
| 25 |
+
|
| 26 |
+
Input begins with an integer \(T\), the number of birthdays Connie has had. For each birthday, there is one line containing the string \(S\), then another line containing the integer \(K\), then \(K\) more lines, the \(i\)th of which contains the two characters \(A_i\) and \(B_i\).
|
| 27 |
+
|
| 28 |
+
|
| 29 |
+
# Output
|
| 30 |
+
|
| 31 |
+
For the \(i\)th string, print a line containing *"Case #i: "* followed by the minimum number of seconds required to change \(S\) into any consistent string, or \(-1\) if it's impossible to do so.
|
| 32 |
+
|
| 33 |
+
|
| 34 |
+
# Sample Explanation
|
| 35 |
+
|
| 36 |
+
In the first case, Connie could replace the second and third letters (`"B"` and `"C"`) each with `"A"`, yielding the string `"AAA"` in \(2\) seconds.
|
| 37 |
+
|
| 38 |
+
In the second case, Connie cannot apply either available type of replacement to `"ABC"`, meaning that she cannot change it into a consistent string.
|
| 39 |
+
|
| 40 |
+
In the third case, `"F"` is already consistent.
|
| 41 |
+
|
| 42 |
+
In the fourth case, Connie could replace the first, third, and fifth letters (`"B"`, `"N"`, and `"N"`) each with `"A"`, yielding the string `"AAAAAA"` in \(3\) seconds.
|
| 43 |
+
|
| 44 |
+
In the sixth case, Connie could change "`FOXEN"` into the string `"WWWWW"` in \(8\) seconds. Note that she may apply a sequence of multiple replacements to any of the letters in \(S\).
|
2021/quals/consistency_ch2.out
ADDED
|
@@ -0,0 +1,51 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Case #1: 2
|
| 2 |
+
Case #2: -1
|
| 3 |
+
Case #3: 0
|
| 4 |
+
Case #4: 3
|
| 5 |
+
Case #5: -1
|
| 6 |
+
Case #6: 8
|
| 7 |
+
Case #7: 100
|
| 8 |
+
Case #8: 5
|
| 9 |
+
Case #9: 108
|
| 10 |
+
Case #10: -1
|
| 11 |
+
Case #11: 103
|
| 12 |
+
Case #12: 111
|
| 13 |
+
Case #13: -1
|
| 14 |
+
Case #14: 2475
|
| 15 |
+
Case #15: -1
|
| 16 |
+
Case #16: 59
|
| 17 |
+
Case #17: 61
|
| 18 |
+
Case #18: -1
|
| 19 |
+
Case #19: 138
|
| 20 |
+
Case #20: -1
|
| 21 |
+
Case #21: 91
|
| 22 |
+
Case #22: -1
|
| 23 |
+
Case #23: 29
|
| 24 |
+
Case #24: -1
|
| 25 |
+
Case #25: 122
|
| 26 |
+
Case #26: 120
|
| 27 |
+
Case #27: 112
|
| 28 |
+
Case #28: 41
|
| 29 |
+
Case #29: 53
|
| 30 |
+
Case #30: 104
|
| 31 |
+
Case #31: -1
|
| 32 |
+
Case #32: 78
|
| 33 |
+
Case #33: 88
|
| 34 |
+
Case #34: 99
|
| 35 |
+
Case #35: -1
|
| 36 |
+
Case #36: -1
|
| 37 |
+
Case #37: 98
|
| 38 |
+
Case #38: 64
|
| 39 |
+
Case #39: 26
|
| 40 |
+
Case #40: -1
|
| 41 |
+
Case #41: -1
|
| 42 |
+
Case #42: -1
|
| 43 |
+
Case #43: -1
|
| 44 |
+
Case #44: -1
|
| 45 |
+
Case #45: 105
|
| 46 |
+
Case #46: 86
|
| 47 |
+
Case #47: 37
|
| 48 |
+
Case #48: 61
|
| 49 |
+
Case #49: 30
|
| 50 |
+
Case #50: 66
|
| 51 |
+
Case #51: -1
|
2021/quals/consistency_ch2_sol.md
ADDED
|
@@ -0,0 +1,7 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
As in Chapter 1, we'll consider each possible character \(x\) (`"A"` \(\le x \le\) `"Z"`) such that all characters in \(S\) are to be changed into \(x\). The only difference is in computing the minimum number of seconds it takes to change some character \(c\) into another character \(x\) (if it's possible at all).
|
| 2 |
+
|
| 3 |
+
If we imagine an unweighted graph with \(26\) nodes (one for each letter from `"A"` to `"Z"`), such that there's a directed edge from node \(A_i\) to node \(B_i\) for each type of replacement \(i\), then the minimum number of seconds required to change \(c\) into \(x\) is equal to the shortest length of any path from node \(c\) to node \(x\) (if any such path exists).
|
| 4 |
+
|
| 5 |
+
We can precompute a \(26*26\) table of these shortest distances between all pairs of nodes by using the [Floyd–Warshall algorithm](https://en.wikipedia.org/wiki/Floyd%E2%80%93Warshall_algorithm) or by performing a [BFS (breadth-first search)](https://en.wikipedia.org/wiki/Breadth-first_search) from each possible starting node, taking care to mark unreachable pairs of nodes as effectively having an infinite distance and being unusable in the final answer. For each character \(x\) and for each character \(c\) in \(S\), we can then look up the shortest distance from node \(c\) to node \(x\) in the table.
|
| 6 |
+
|
| 7 |
+
[See David Harmeyer's solution video here](https://youtu.be/p5yPTHNUTlc).
|
2021/quals/gold_mine_ch1.cpp
ADDED
|
@@ -0,0 +1,56 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
#include <algorithm>
|
| 2 |
+
#include <iostream>
|
| 3 |
+
#include <vector>
|
| 4 |
+
using namespace std;
|
| 5 |
+
|
| 6 |
+
const int LIM = 52;
|
| 7 |
+
|
| 8 |
+
int N, C[LIM];
|
| 9 |
+
vector<int> adj[LIM];
|
| 10 |
+
|
| 11 |
+
// Maximum path sum from i down to any leaf.
|
| 12 |
+
int rec(int i, int parent) {
|
| 13 |
+
int m = 0;
|
| 14 |
+
for (int j : adj[i]) {
|
| 15 |
+
if (j != parent) {
|
| 16 |
+
m = max(m, rec(j, i));
|
| 17 |
+
}
|
| 18 |
+
}
|
| 19 |
+
return C[i] + m;
|
| 20 |
+
}
|
| 21 |
+
|
| 22 |
+
int solve() {
|
| 23 |
+
cin >> N;
|
| 24 |
+
for (int i = 0; i < N; i++) {
|
| 25 |
+
cin >> C[i];
|
| 26 |
+
adj[i].clear();
|
| 27 |
+
}
|
| 28 |
+
for (int i = 0; i < N - 1; i++) {
|
| 29 |
+
int a, b;
|
| 30 |
+
cin >> a >> b;
|
| 31 |
+
a--, b--;
|
| 32 |
+
adj[a].push_back(b);
|
| 33 |
+
adj[b].push_back(a);
|
| 34 |
+
}
|
| 35 |
+
// Find up to 2 best children of root.
|
| 36 |
+
int m1 = 0, m2 = 0;
|
| 37 |
+
for (auto c : adj[0]) {
|
| 38 |
+
int v = rec(c, 0);
|
| 39 |
+
if (v > m1) {
|
| 40 |
+
m2 = m1;
|
| 41 |
+
m1 = v;
|
| 42 |
+
} else {
|
| 43 |
+
m2 = max(m2, v);
|
| 44 |
+
}
|
| 45 |
+
}
|
| 46 |
+
return C[0] + m1 + m2;
|
| 47 |
+
}
|
| 48 |
+
|
| 49 |
+
int main() {
|
| 50 |
+
int T;
|
| 51 |
+
cin >> T;
|
| 52 |
+
for (int t = 1; t <= T; t++) {
|
| 53 |
+
cout << "Case #" << t << ": " << solve() << endl;
|
| 54 |
+
}
|
| 55 |
+
return 0;
|
| 56 |
+
}
|
2021/quals/gold_mine_ch1.in
ADDED
|
@@ -0,0 +1,956 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
56
|
| 2 |
+
2
|
| 3 |
+
10 20
|
| 4 |
+
1 2
|
| 5 |
+
4
|
| 6 |
+
1 1 1 1
|
| 7 |
+
2 1
|
| 8 |
+
4 2
|
| 9 |
+
1 3
|
| 10 |
+
4
|
| 11 |
+
1 1 1 1
|
| 12 |
+
2 1
|
| 13 |
+
4 1
|
| 14 |
+
1 3
|
| 15 |
+
6
|
| 16 |
+
5 4 1 3 2 4
|
| 17 |
+
5 1
|
| 18 |
+
5 4
|
| 19 |
+
5 3
|
| 20 |
+
5 2
|
| 21 |
+
6 3
|
| 22 |
+
9
|
| 23 |
+
2 14 7 6 11 3 6 1 8
|
| 24 |
+
4 5
|
| 25 |
+
6 7
|
| 26 |
+
8 9
|
| 27 |
+
1 3
|
| 28 |
+
6 8
|
| 29 |
+
2 4
|
| 30 |
+
4 1
|
| 31 |
+
1 8
|
| 32 |
+
1
|
| 33 |
+
0
|
| 34 |
+
1
|
| 35 |
+
20000000
|
| 36 |
+
50
|
| 37 |
+
10781795 9557808 1853831 8423199 13742134 9391909 16578911 1493660 4495014 12643630 8281227 14100842 1245098 18524652 2988334 14561137 16666695 9299012 15862790 17721246 9922966 1225383 17847177 6262771 19901037 14907244 6631578 6927800 19177901 7008600 13196264 2973903 11068968 12618816 15130596 6490405 2343468 14699973 6213468 13011780 16035761 18356031 18155449 12593158 1363995 12257973 1752529 16612197 17458347 15297287
|
| 38 |
+
1 33
|
| 39 |
+
7 33
|
| 40 |
+
29 7
|
| 41 |
+
15 29
|
| 42 |
+
44 15
|
| 43 |
+
44 12
|
| 44 |
+
45 12
|
| 45 |
+
45 42
|
| 46 |
+
42 37
|
| 47 |
+
37 20
|
| 48 |
+
20 40
|
| 49 |
+
26 40
|
| 50 |
+
26 19
|
| 51 |
+
19 24
|
| 52 |
+
24 13
|
| 53 |
+
13 6
|
| 54 |
+
38 6
|
| 55 |
+
38 49
|
| 56 |
+
18 49
|
| 57 |
+
18 36
|
| 58 |
+
36 50
|
| 59 |
+
27 50
|
| 60 |
+
8 27
|
| 61 |
+
3 8
|
| 62 |
+
3 5
|
| 63 |
+
16 5
|
| 64 |
+
31 16
|
| 65 |
+
2 31
|
| 66 |
+
48 2
|
| 67 |
+
48 25
|
| 68 |
+
25 22
|
| 69 |
+
22 43
|
| 70 |
+
4 43
|
| 71 |
+
3 14
|
| 72 |
+
14 10
|
| 73 |
+
10 23
|
| 74 |
+
23 47
|
| 75 |
+
47 21
|
| 76 |
+
21 34
|
| 77 |
+
30 34
|
| 78 |
+
32 30
|
| 79 |
+
46 32
|
| 80 |
+
41 46
|
| 81 |
+
41 39
|
| 82 |
+
39 17
|
| 83 |
+
35 17
|
| 84 |
+
11 35
|
| 85 |
+
9 11
|
| 86 |
+
28 9
|
| 87 |
+
49
|
| 88 |
+
17302004 10273548 5740500 17973923 13685251 15645774 622007 1492681 4327318 3323822 14848368 13996716 15111113 7731583 5968618 4352086 11385157 4010472 15722800 13378328 14902259 15121331 2892404 8049510 13094347 14804404 4593452 2330703 19144650 14047444 4521047 7793047 15549186 16288441 2108382 2618482 396235 15495700 10244373 11687135 4683031 15349894 17699168 10705055 8220388 12126767 17928434 11570898 3110858
|
| 89 |
+
40 1
|
| 90 |
+
22 40
|
| 91 |
+
22 5
|
| 92 |
+
18 5
|
| 93 |
+
18 21
|
| 94 |
+
21 12
|
| 95 |
+
12 14
|
| 96 |
+
14 32
|
| 97 |
+
34 32
|
| 98 |
+
20 1
|
| 99 |
+
15 20
|
| 100 |
+
15 31
|
| 101 |
+
13 31
|
| 102 |
+
13 24
|
| 103 |
+
30 24
|
| 104 |
+
45 30
|
| 105 |
+
45 3
|
| 106 |
+
7 3
|
| 107 |
+
41 7
|
| 108 |
+
9 1
|
| 109 |
+
4 9
|
| 110 |
+
4 23
|
| 111 |
+
23 49
|
| 112 |
+
19 49
|
| 113 |
+
19 44
|
| 114 |
+
16 44
|
| 115 |
+
27 16
|
| 116 |
+
28 27
|
| 117 |
+
28 37
|
| 118 |
+
1 17
|
| 119 |
+
17 2
|
| 120 |
+
6 2
|
| 121 |
+
6 38
|
| 122 |
+
47 38
|
| 123 |
+
25 47
|
| 124 |
+
11 25
|
| 125 |
+
11 46
|
| 126 |
+
46 48
|
| 127 |
+
42 48
|
| 128 |
+
1 39
|
| 129 |
+
39 35
|
| 130 |
+
43 35
|
| 131 |
+
29 43
|
| 132 |
+
29 8
|
| 133 |
+
8 36
|
| 134 |
+
10 36
|
| 135 |
+
10 33
|
| 136 |
+
33 26
|
| 137 |
+
48
|
| 138 |
+
19468394 11245085 96422 2258067 19303323 8694050 17794081 8162102 18142289 5914229 15522922 10467206 1482294 14252202 5651542 1702350 11149417 15283645 11245775 14478157 9029416 15182710 7217297 4789867 15226391 19566312 8644990 17618951 8105007 16907283 17782431 3762411 10795846 18161833 4452792 3566945 18590774 12366830 17579655 7050719 9915565 13715896 10665880 2962653 5977489 9893270 5673672 5937608
|
| 139 |
+
40 1
|
| 140 |
+
1 43
|
| 141 |
+
13 40
|
| 142 |
+
40 31
|
| 143 |
+
43 2
|
| 144 |
+
43 5
|
| 145 |
+
35 13
|
| 146 |
+
15 13
|
| 147 |
+
31 26
|
| 148 |
+
20 31
|
| 149 |
+
2 7
|
| 150 |
+
2 29
|
| 151 |
+
5 33
|
| 152 |
+
17 5
|
| 153 |
+
9 35
|
| 154 |
+
35 4
|
| 155 |
+
15 22
|
| 156 |
+
16 15
|
| 157 |
+
26 37
|
| 158 |
+
38 26
|
| 159 |
+
19 20
|
| 160 |
+
23 20
|
| 161 |
+
3 7
|
| 162 |
+
18 7
|
| 163 |
+
29 47
|
| 164 |
+
29 24
|
| 165 |
+
33 12
|
| 166 |
+
39 33
|
| 167 |
+
17 6
|
| 168 |
+
17 27
|
| 169 |
+
10 9
|
| 170 |
+
9 48
|
| 171 |
+
25 4
|
| 172 |
+
4 11
|
| 173 |
+
42 22
|
| 174 |
+
28 22
|
| 175 |
+
16 32
|
| 176 |
+
30 16
|
| 177 |
+
37 44
|
| 178 |
+
14 37
|
| 179 |
+
21 38
|
| 180 |
+
46 38
|
| 181 |
+
34 19
|
| 182 |
+
19 8
|
| 183 |
+
23 45
|
| 184 |
+
23 36
|
| 185 |
+
41 3
|
| 186 |
+
19
|
| 187 |
+
53 908 148 709 390 629 17 695 434 219 503 759 839 251 436 723 566 625 584
|
| 188 |
+
6 1
|
| 189 |
+
1 3
|
| 190 |
+
3 4
|
| 191 |
+
6 15
|
| 192 |
+
4 18
|
| 193 |
+
4 5
|
| 194 |
+
5 14
|
| 195 |
+
14 8
|
| 196 |
+
2 8
|
| 197 |
+
10 2
|
| 198 |
+
8 9
|
| 199 |
+
16 2
|
| 200 |
+
13 16
|
| 201 |
+
16 7
|
| 202 |
+
9 17
|
| 203 |
+
11 7
|
| 204 |
+
12 13
|
| 205 |
+
19 12
|
| 206 |
+
50
|
| 207 |
+
18912310 18898464 9703986 18912689 2009993 4434239 9954547 19121924 2609372 18973224 14435844 13483385 3626463 2358310 660000 5989543 4964520 11365947 11345297 17094483 7809461 10905240 5814466 9676595 3331964 2183977 10303843 4902860 3732401 4909127 16038707 15024764 16354836 11631505 11285869 7612564 6859251 9943765 18178513 6007965 19332675 5418023 11461709 11572412 14616407 8894484 4313416 8458288 7368507 10417137
|
| 208 |
+
1 8
|
| 209 |
+
23 8
|
| 210 |
+
35 23
|
| 211 |
+
35 16
|
| 212 |
+
34 16
|
| 213 |
+
29 34
|
| 214 |
+
29 48
|
| 215 |
+
48 15
|
| 216 |
+
15 4
|
| 217 |
+
4 43
|
| 218 |
+
43 11
|
| 219 |
+
11 39
|
| 220 |
+
39 32
|
| 221 |
+
50 32
|
| 222 |
+
50 26
|
| 223 |
+
26 17
|
| 224 |
+
17 25
|
| 225 |
+
25 38
|
| 226 |
+
33 38
|
| 227 |
+
33 20
|
| 228 |
+
20 44
|
| 229 |
+
5 44
|
| 230 |
+
12 5
|
| 231 |
+
12 46
|
| 232 |
+
46 18
|
| 233 |
+
18 37
|
| 234 |
+
40 37
|
| 235 |
+
14 40
|
| 236 |
+
14 45
|
| 237 |
+
45 47
|
| 238 |
+
47 27
|
| 239 |
+
10 27
|
| 240 |
+
30 10
|
| 241 |
+
30 9
|
| 242 |
+
31 9
|
| 243 |
+
31 19
|
| 244 |
+
42 19
|
| 245 |
+
7 42
|
| 246 |
+
49 7
|
| 247 |
+
49 36
|
| 248 |
+
36 22
|
| 249 |
+
3 22
|
| 250 |
+
41 3
|
| 251 |
+
6 41
|
| 252 |
+
2 6
|
| 253 |
+
2 24
|
| 254 |
+
21 24
|
| 255 |
+
13 21
|
| 256 |
+
13 28
|
| 257 |
+
50
|
| 258 |
+
18722046 12710434 16020009 4888908 14836429 6218620 11504022 6626860 9294133 8048471 3189363 4648600 4622144 2470903 1984131 8809675 7697925 18471764 11138701 11257526 14865598 19460650 7447560 5368676 2059911 19869997 8209250 13119358 10952374 1918042 12594669 8057835 9985489 6766697 6026342 13136271 4568624 12938079 1685284 12127285 18825520 14743872 19963610 9009543 4560145 12243425 14921993 3056186 18857581 11345370
|
| 259 |
+
46 1
|
| 260 |
+
46 38
|
| 261 |
+
45 38
|
| 262 |
+
27 45
|
| 263 |
+
47 27
|
| 264 |
+
47 40
|
| 265 |
+
40 23
|
| 266 |
+
50 23
|
| 267 |
+
50 26
|
| 268 |
+
3 26
|
| 269 |
+
3 10
|
| 270 |
+
49 10
|
| 271 |
+
13 49
|
| 272 |
+
13 33
|
| 273 |
+
33 8
|
| 274 |
+
41 8
|
| 275 |
+
41 25
|
| 276 |
+
17 25
|
| 277 |
+
17 24
|
| 278 |
+
28 24
|
| 279 |
+
36 28
|
| 280 |
+
36 14
|
| 281 |
+
20 14
|
| 282 |
+
20 43
|
| 283 |
+
21 43
|
| 284 |
+
6 1
|
| 285 |
+
35 6
|
| 286 |
+
35 42
|
| 287 |
+
42 11
|
| 288 |
+
11 18
|
| 289 |
+
2 18
|
| 290 |
+
19 2
|
| 291 |
+
19 9
|
| 292 |
+
32 9
|
| 293 |
+
30 32
|
| 294 |
+
30 44
|
| 295 |
+
44 4
|
| 296 |
+
4 5
|
| 297 |
+
5 31
|
| 298 |
+
22 31
|
| 299 |
+
22 15
|
| 300 |
+
15 34
|
| 301 |
+
48 34
|
| 302 |
+
48 12
|
| 303 |
+
39 12
|
| 304 |
+
16 39
|
| 305 |
+
37 16
|
| 306 |
+
37 7
|
| 307 |
+
29 7
|
| 308 |
+
50
|
| 309 |
+
13859433 18628942 7347267 4813943 16978714 15303963 6580609 7087898 1282597 17231025 12811294 9673049 3538611 18865997 15180831 13520772 8715179 14281497 2489079 16929588 10106875 6867369 2611428 11334811 9897608 11174561 5757160 7529719 11068080 4630901 10974819 17483809 14382456 7754057 8912970 4341058 1061719 7392247 13464838 14706852 539294 1847086 15492075 19938470 8518530 10316215 12941651 13247946 6510792 19914451
|
| 310 |
+
1 37
|
| 311 |
+
18 37
|
| 312 |
+
14 18
|
| 313 |
+
14 23
|
| 314 |
+
34 23
|
| 315 |
+
34 35
|
| 316 |
+
48 35
|
| 317 |
+
43 48
|
| 318 |
+
43 7
|
| 319 |
+
39 7
|
| 320 |
+
12 39
|
| 321 |
+
49 12
|
| 322 |
+
49 13
|
| 323 |
+
11 13
|
| 324 |
+
11 16
|
| 325 |
+
16 27
|
| 326 |
+
22 27
|
| 327 |
+
17 22
|
| 328 |
+
25 17
|
| 329 |
+
40 25
|
| 330 |
+
50 40
|
| 331 |
+
50 24
|
| 332 |
+
24 3
|
| 333 |
+
3 4
|
| 334 |
+
8 4
|
| 335 |
+
8 41
|
| 336 |
+
33 41
|
| 337 |
+
33 6
|
| 338 |
+
6 31
|
| 339 |
+
10 31
|
| 340 |
+
15 10
|
| 341 |
+
2 15
|
| 342 |
+
5 2
|
| 343 |
+
30 4
|
| 344 |
+
30 29
|
| 345 |
+
29 28
|
| 346 |
+
38 28
|
| 347 |
+
38 19
|
| 348 |
+
45 19
|
| 349 |
+
44 45
|
| 350 |
+
26 44
|
| 351 |
+
20 26
|
| 352 |
+
20 42
|
| 353 |
+
47 42
|
| 354 |
+
46 47
|
| 355 |
+
21 46
|
| 356 |
+
36 21
|
| 357 |
+
36 32
|
| 358 |
+
9 32
|
| 359 |
+
50
|
| 360 |
+
1059625 7399861 4160424 8188362 17502519 13530183 3225904 2167562 7695292 6667986 1369655 272121 18991240 4580900 6451404 17036126 9630706 1191067 14628869 18615863 11287266 4569815 3646051 617070 10649864 5791744 2384211 2057530 4568367 3469488 6736337 2670613 13142188 15840383 16961319 11253589 5117424 6674474 348116 1690218 13320765 11690591 254343 17334707 9879670 18598952 15285578 12291069 9084174 12436465
|
| 361 |
+
1 47
|
| 362 |
+
47 24
|
| 363 |
+
15 24
|
| 364 |
+
48 15
|
| 365 |
+
27 48
|
| 366 |
+
27 16
|
| 367 |
+
16 22
|
| 368 |
+
22 4
|
| 369 |
+
4 43
|
| 370 |
+
43 45
|
| 371 |
+
45 44
|
| 372 |
+
20 44
|
| 373 |
+
20 21
|
| 374 |
+
21 10
|
| 375 |
+
10 19
|
| 376 |
+
19 8
|
| 377 |
+
1 11
|
| 378 |
+
33 11
|
| 379 |
+
33 36
|
| 380 |
+
5 36
|
| 381 |
+
5 23
|
| 382 |
+
23 40
|
| 383 |
+
18 40
|
| 384 |
+
29 18
|
| 385 |
+
38 29
|
| 386 |
+
12 38
|
| 387 |
+
12 17
|
| 388 |
+
2 17
|
| 389 |
+
37 2
|
| 390 |
+
37 13
|
| 391 |
+
13 46
|
| 392 |
+
31 46
|
| 393 |
+
31 9
|
| 394 |
+
50 1
|
| 395 |
+
7 50
|
| 396 |
+
7 35
|
| 397 |
+
32 35
|
| 398 |
+
32 41
|
| 399 |
+
39 41
|
| 400 |
+
6 39
|
| 401 |
+
6 28
|
| 402 |
+
14 28
|
| 403 |
+
14 30
|
| 404 |
+
26 30
|
| 405 |
+
26 34
|
| 406 |
+
42 34
|
| 407 |
+
3 42
|
| 408 |
+
25 3
|
| 409 |
+
25 49
|
| 410 |
+
50
|
| 411 |
+
15348007 15930520 7862316 8776851 7767735 2058353 13822633 8327546 15305367 1051015 13144842 11788841 1356503 16948905 7467273 14305319 14345609 18738710 5040710 10238368 18185530 18735728 11323225 17420201 9164812 6084560 3900278 1684386 15231345 8205555 19500476 14225333 10566022 10026385 19187482 2185594 10017545 2812622 1856478 19705789 8295929 4546762 9436380 258647 11279049 8832083 18064695 14269496 15520576 6156730
|
| 412 |
+
6 1
|
| 413 |
+
25 6
|
| 414 |
+
43 25
|
| 415 |
+
19 43
|
| 416 |
+
19 5
|
| 417 |
+
5 49
|
| 418 |
+
12 49
|
| 419 |
+
15 12
|
| 420 |
+
26 15
|
| 421 |
+
47 1
|
| 422 |
+
8 47
|
| 423 |
+
14 8
|
| 424 |
+
14 41
|
| 425 |
+
40 41
|
| 426 |
+
7 40
|
| 427 |
+
7 23
|
| 428 |
+
23 37
|
| 429 |
+
37 17
|
| 430 |
+
17 27
|
| 431 |
+
45 1
|
| 432 |
+
45 30
|
| 433 |
+
28 30
|
| 434 |
+
28 50
|
| 435 |
+
50 42
|
| 436 |
+
39 42
|
| 437 |
+
33 39
|
| 438 |
+
18 33
|
| 439 |
+
4 18
|
| 440 |
+
4 46
|
| 441 |
+
1 36
|
| 442 |
+
36 29
|
| 443 |
+
29 34
|
| 444 |
+
34 22
|
| 445 |
+
21 22
|
| 446 |
+
20 21
|
| 447 |
+
20 2
|
| 448 |
+
35 2
|
| 449 |
+
35 3
|
| 450 |
+
48 3
|
| 451 |
+
1 10
|
| 452 |
+
10 11
|
| 453 |
+
31 11
|
| 454 |
+
31 13
|
| 455 |
+
13 9
|
| 456 |
+
24 9
|
| 457 |
+
44 24
|
| 458 |
+
44 16
|
| 459 |
+
16 32
|
| 460 |
+
32 38
|
| 461 |
+
50
|
| 462 |
+
11886753 14396775 13790329 16324347 18497188 11945684 7004094 13185557 11553720 8824602 5705261 4810797 16291852 11701920 17863995 12390470 14961622 16542723 16380400 5753246 15447735 19992783 2236447 18811132 14750269 18578906 12849328 19840925 725634 15855933 11960601 2553781 3274993 15990512 11631083 5908132 10679849 2074625 11425928 14075574 5485305 475761 14396659 10192279 18475915 2545579 15898304 4097874 2395806 14762401
|
| 463 |
+
1 6
|
| 464 |
+
1 46
|
| 465 |
+
6 2
|
| 466 |
+
29 6
|
| 467 |
+
46 47
|
| 468 |
+
23 46
|
| 469 |
+
2 3
|
| 470 |
+
27 2
|
| 471 |
+
10 29
|
| 472 |
+
29 30
|
| 473 |
+
47 32
|
| 474 |
+
47 18
|
| 475 |
+
39 23
|
| 476 |
+
23 37
|
| 477 |
+
3 17
|
| 478 |
+
3 11
|
| 479 |
+
27 26
|
| 480 |
+
4 27
|
| 481 |
+
33 10
|
| 482 |
+
28 10
|
| 483 |
+
30 36
|
| 484 |
+
30 7
|
| 485 |
+
32 16
|
| 486 |
+
34 32
|
| 487 |
+
18 50
|
| 488 |
+
18 44
|
| 489 |
+
5 39
|
| 490 |
+
39 41
|
| 491 |
+
37 35
|
| 492 |
+
24 37
|
| 493 |
+
17 9
|
| 494 |
+
48 17
|
| 495 |
+
11 40
|
| 496 |
+
11 25
|
| 497 |
+
26 8
|
| 498 |
+
26 12
|
| 499 |
+
4 13
|
| 500 |
+
4 43
|
| 501 |
+
14 33
|
| 502 |
+
33 49
|
| 503 |
+
28 15
|
| 504 |
+
19 28
|
| 505 |
+
36 21
|
| 506 |
+
36 38
|
| 507 |
+
7 42
|
| 508 |
+
31 7
|
| 509 |
+
20 16
|
| 510 |
+
22 16
|
| 511 |
+
45 34
|
| 512 |
+
50
|
| 513 |
+
8080772 15272279 16956387 9264291 13249675 16538490 747726 5595331 15422402 9728532 4109565 2617489 1581766 10252507 8366478 19972632 8915273 3209563 153782 6596774 14507637 16038678 13127217 10536120 4122362 11944133 5982819 18209556 4304310 16038589 2615568 3414774 10539776 9153389 17082805 13191010 8510609 5599236 18926721 1607576 12365328 20271 19898611 17742502 15914297 16537088 1432337 12400663 8207273 12180714
|
| 514 |
+
1 47
|
| 515 |
+
43 1
|
| 516 |
+
3 1
|
| 517 |
+
1 17
|
| 518 |
+
1 26
|
| 519 |
+
5 1
|
| 520 |
+
1 36
|
| 521 |
+
37 1
|
| 522 |
+
21 1
|
| 523 |
+
1 33
|
| 524 |
+
1 16
|
| 525 |
+
35 1
|
| 526 |
+
29 1
|
| 527 |
+
1 30
|
| 528 |
+
1 39
|
| 529 |
+
1 28
|
| 530 |
+
46 1
|
| 531 |
+
27 1
|
| 532 |
+
18 1
|
| 533 |
+
7 1
|
| 534 |
+
50 1
|
| 535 |
+
1 2
|
| 536 |
+
20 1
|
| 537 |
+
49 1
|
| 538 |
+
1 11
|
| 539 |
+
1 22
|
| 540 |
+
4 1
|
| 541 |
+
1 8
|
| 542 |
+
1 14
|
| 543 |
+
1 41
|
| 544 |
+
1 40
|
| 545 |
+
1 44
|
| 546 |
+
1 19
|
| 547 |
+
32 1
|
| 548 |
+
1 15
|
| 549 |
+
45 1
|
| 550 |
+
31 1
|
| 551 |
+
1 38
|
| 552 |
+
1 23
|
| 553 |
+
25 1
|
| 554 |
+
1 12
|
| 555 |
+
42 1
|
| 556 |
+
13 1
|
| 557 |
+
48 1
|
| 558 |
+
1 24
|
| 559 |
+
1 34
|
| 560 |
+
9 1
|
| 561 |
+
10 1
|
| 562 |
+
6 1
|
| 563 |
+
50
|
| 564 |
+
3207047 8503498 17230684 400553 10550055 4615982 3755920 10392641 5838806 702516 12415512 16704449 16696162 900946 3850500 18625414 641526 8254892 16079374 14993250 13703938 15492942 7302736 16172137 9770551 13933574 1461014 13568857 13554094 3541980 4689102 1642403 4852264 19211312 5094684 19954714 8374384 8326254 13540362 379959 1728989 8379247 10896477 8095751 6752500 16562287 16880642 2105777 12860970 10614439
|
| 565 |
+
35 1
|
| 566 |
+
1 16
|
| 567 |
+
18 16
|
| 568 |
+
7 18
|
| 569 |
+
25 18
|
| 570 |
+
25 3
|
| 571 |
+
3 26
|
| 572 |
+
26 30
|
| 573 |
+
6 30
|
| 574 |
+
42 6
|
| 575 |
+
44 42
|
| 576 |
+
13 42
|
| 577 |
+
17 44
|
| 578 |
+
13 36
|
| 579 |
+
12 36
|
| 580 |
+
22 12
|
| 581 |
+
20 12
|
| 582 |
+
4 22
|
| 583 |
+
4 34
|
| 584 |
+
34 10
|
| 585 |
+
29 34
|
| 586 |
+
21 10
|
| 587 |
+
15 21
|
| 588 |
+
15 8
|
| 589 |
+
46 8
|
| 590 |
+
8 19
|
| 591 |
+
40 46
|
| 592 |
+
5 19
|
| 593 |
+
40 31
|
| 594 |
+
23 31
|
| 595 |
+
14 23
|
| 596 |
+
33 23
|
| 597 |
+
24 33
|
| 598 |
+
43 24
|
| 599 |
+
48 24
|
| 600 |
+
45 48
|
| 601 |
+
45 49
|
| 602 |
+
49 39
|
| 603 |
+
49 50
|
| 604 |
+
27 39
|
| 605 |
+
2 27
|
| 606 |
+
2 38
|
| 607 |
+
2 32
|
| 608 |
+
38 28
|
| 609 |
+
28 47
|
| 610 |
+
47 9
|
| 611 |
+
41 9
|
| 612 |
+
9 11
|
| 613 |
+
37 41
|
| 614 |
+
11
|
| 615 |
+
506 696 439 932 126 77 596 953 635 750 476
|
| 616 |
+
6 1
|
| 617 |
+
3 1
|
| 618 |
+
6 8
|
| 619 |
+
11 6
|
| 620 |
+
2 8
|
| 621 |
+
8 5
|
| 622 |
+
11 4
|
| 623 |
+
9 2
|
| 624 |
+
7 9
|
| 625 |
+
10 9
|
| 626 |
+
14
|
| 627 |
+
529 916 700 489 652 598 253 40 981 950 658 271 372 25
|
| 628 |
+
1 13
|
| 629 |
+
13 12
|
| 630 |
+
1 5
|
| 631 |
+
12 11
|
| 632 |
+
13 3
|
| 633 |
+
4 13
|
| 634 |
+
3 8
|
| 635 |
+
9 12
|
| 636 |
+
11 7
|
| 637 |
+
14 3
|
| 638 |
+
11 10
|
| 639 |
+
6 8
|
| 640 |
+
2 11
|
| 641 |
+
9
|
| 642 |
+
640 190 883 390 249 293 50 28 181
|
| 643 |
+
2 1
|
| 644 |
+
5 2
|
| 645 |
+
3 5
|
| 646 |
+
4 3
|
| 647 |
+
8 4
|
| 648 |
+
7 8
|
| 649 |
+
7 6
|
| 650 |
+
9 6
|
| 651 |
+
10
|
| 652 |
+
972 146 694 61 605 692 109 104 374 199
|
| 653 |
+
1 5
|
| 654 |
+
10 5
|
| 655 |
+
10 2
|
| 656 |
+
2 3
|
| 657 |
+
3 7
|
| 658 |
+
7 9
|
| 659 |
+
8 9
|
| 660 |
+
8 6
|
| 661 |
+
4 6
|
| 662 |
+
10
|
| 663 |
+
780 301 621 12 911 224 109 144 232 811
|
| 664 |
+
2 1
|
| 665 |
+
1 10
|
| 666 |
+
10 8
|
| 667 |
+
9 10
|
| 668 |
+
9 4
|
| 669 |
+
4 6
|
| 670 |
+
5 8
|
| 671 |
+
4 3
|
| 672 |
+
7 6
|
| 673 |
+
11
|
| 674 |
+
362 497 398 159 99 522 67 94 112 176 166
|
| 675 |
+
2 1
|
| 676 |
+
1 3
|
| 677 |
+
3 10
|
| 678 |
+
3 6
|
| 679 |
+
9 1
|
| 680 |
+
2 5
|
| 681 |
+
5 8
|
| 682 |
+
7 8
|
| 683 |
+
11 2
|
| 684 |
+
2 4
|
| 685 |
+
12
|
| 686 |
+
71 393 381 505 160 957 793 905 720 443 912 55
|
| 687 |
+
8 1
|
| 688 |
+
1 6
|
| 689 |
+
4 8
|
| 690 |
+
10 6
|
| 691 |
+
7 6
|
| 692 |
+
7 5
|
| 693 |
+
10 11
|
| 694 |
+
5 3
|
| 695 |
+
3 12
|
| 696 |
+
3 2
|
| 697 |
+
2 9
|
| 698 |
+
7
|
| 699 |
+
271 700 622 314 774 954 374
|
| 700 |
+
5 1
|
| 701 |
+
7 1
|
| 702 |
+
7 4
|
| 703 |
+
1 2
|
| 704 |
+
6 5
|
| 705 |
+
2 3
|
| 706 |
+
8
|
| 707 |
+
635 846 256 438 511 374 480 182
|
| 708 |
+
1 8
|
| 709 |
+
4 1
|
| 710 |
+
8 5
|
| 711 |
+
5 7
|
| 712 |
+
2 5
|
| 713 |
+
7 3
|
| 714 |
+
6 7
|
| 715 |
+
4
|
| 716 |
+
717 848 767 290
|
| 717 |
+
3 1
|
| 718 |
+
2 1
|
| 719 |
+
1 4
|
| 720 |
+
14
|
| 721 |
+
717 926 430 917 235 131 547 205 69 433 526 629 2 411
|
| 722 |
+
1 4
|
| 723 |
+
1 9
|
| 724 |
+
9 6
|
| 725 |
+
6 14
|
| 726 |
+
9 8
|
| 727 |
+
11 14
|
| 728 |
+
8 5
|
| 729 |
+
5 2
|
| 730 |
+
4 13
|
| 731 |
+
10 5
|
| 732 |
+
14 7
|
| 733 |
+
12 14
|
| 734 |
+
10 3
|
| 735 |
+
7
|
| 736 |
+
240 680 69 238 365 424 727
|
| 737 |
+
4 1
|
| 738 |
+
7 1
|
| 739 |
+
3 4
|
| 740 |
+
1 2
|
| 741 |
+
3 5
|
| 742 |
+
6 7
|
| 743 |
+
4
|
| 744 |
+
724 352 867 399
|
| 745 |
+
1 2
|
| 746 |
+
4 1
|
| 747 |
+
3 2
|
| 748 |
+
15
|
| 749 |
+
920 874 869 256 565 750 247 622 2 852 151 208 67 662 65
|
| 750 |
+
1 8
|
| 751 |
+
1 4
|
| 752 |
+
7 1
|
| 753 |
+
12 8
|
| 754 |
+
11 12
|
| 755 |
+
15 12
|
| 756 |
+
14 4
|
| 757 |
+
2 14
|
| 758 |
+
5 7
|
| 759 |
+
6 8
|
| 760 |
+
13 14
|
| 761 |
+
14 9
|
| 762 |
+
10 12
|
| 763 |
+
3 7
|
| 764 |
+
5
|
| 765 |
+
732 218 246 356 475
|
| 766 |
+
4 1
|
| 767 |
+
4 2
|
| 768 |
+
2 5
|
| 769 |
+
5 3
|
| 770 |
+
10
|
| 771 |
+
518 303 729 430 405 209 136 632 882 161
|
| 772 |
+
1 2
|
| 773 |
+
3 1
|
| 774 |
+
9 2
|
| 775 |
+
6 2
|
| 776 |
+
5 9
|
| 777 |
+
9 7
|
| 778 |
+
10 7
|
| 779 |
+
4 5
|
| 780 |
+
8 10
|
| 781 |
+
6
|
| 782 |
+
6 130 306 143 365 524
|
| 783 |
+
1 2
|
| 784 |
+
3 1
|
| 785 |
+
2 5
|
| 786 |
+
2 4
|
| 787 |
+
6 4
|
| 788 |
+
10
|
| 789 |
+
957 679 994 834 959 868 379 444 709 451
|
| 790 |
+
5 1
|
| 791 |
+
6 1
|
| 792 |
+
9 5
|
| 793 |
+
9 2
|
| 794 |
+
5 3
|
| 795 |
+
1 7
|
| 796 |
+
10 1
|
| 797 |
+
4 2
|
| 798 |
+
6 8
|
| 799 |
+
9
|
| 800 |
+
873 911 850 505 731 92 0 917 185
|
| 801 |
+
7 1
|
| 802 |
+
5 1
|
| 803 |
+
7 3
|
| 804 |
+
3 4
|
| 805 |
+
5 2
|
| 806 |
+
8 4
|
| 807 |
+
2 9
|
| 808 |
+
9 6
|
| 809 |
+
11
|
| 810 |
+
836 849 330 879 721 15 953 26 168 552 209
|
| 811 |
+
6 1
|
| 812 |
+
1 5
|
| 813 |
+
8 5
|
| 814 |
+
2 5
|
| 815 |
+
7 2
|
| 816 |
+
2 9
|
| 817 |
+
8 10
|
| 818 |
+
11 8
|
| 819 |
+
3 1
|
| 820 |
+
10 4
|
| 821 |
+
7
|
| 822 |
+
798 64 888 566 249 246 94
|
| 823 |
+
1 7
|
| 824 |
+
1 6
|
| 825 |
+
6 3
|
| 826 |
+
3 2
|
| 827 |
+
6 5
|
| 828 |
+
5 4
|
| 829 |
+
8
|
| 830 |
+
25 673 12 948 616 712 691 775
|
| 831 |
+
1 6
|
| 832 |
+
1 3
|
| 833 |
+
7 3
|
| 834 |
+
6 2
|
| 835 |
+
5 2
|
| 836 |
+
8 2
|
| 837 |
+
4 2
|
| 838 |
+
9
|
| 839 |
+
396 829 598 685 793 397 944 25 190
|
| 840 |
+
1 8
|
| 841 |
+
4 1
|
| 842 |
+
5 8
|
| 843 |
+
6 4
|
| 844 |
+
7 8
|
| 845 |
+
2 1
|
| 846 |
+
7 9
|
| 847 |
+
6 3
|
| 848 |
+
7
|
| 849 |
+
444 584 100 717 804 491 731
|
| 850 |
+
1 7
|
| 851 |
+
1 6
|
| 852 |
+
6 3
|
| 853 |
+
5 6
|
| 854 |
+
3 2
|
| 855 |
+
3 4
|
| 856 |
+
10
|
| 857 |
+
28 560 811 351 755 636 869 300 186 642
|
| 858 |
+
5 1
|
| 859 |
+
1 9
|
| 860 |
+
10 9
|
| 861 |
+
5 7
|
| 862 |
+
3 10
|
| 863 |
+
2 7
|
| 864 |
+
4 7
|
| 865 |
+
8 2
|
| 866 |
+
6 7
|
| 867 |
+
14
|
| 868 |
+
100 595 973 106 110 265 834 208 840 54 817 305 832 522
|
| 869 |
+
6 1
|
| 870 |
+
13 1
|
| 871 |
+
8 13
|
| 872 |
+
5 1
|
| 873 |
+
14 5
|
| 874 |
+
4 13
|
| 875 |
+
7 8
|
| 876 |
+
12 6
|
| 877 |
+
11 13
|
| 878 |
+
10 7
|
| 879 |
+
9 5
|
| 880 |
+
7 3
|
| 881 |
+
2 10
|
| 882 |
+
3
|
| 883 |
+
761 421 546
|
| 884 |
+
2 1
|
| 885 |
+
3 2
|
| 886 |
+
3
|
| 887 |
+
847 236 563
|
| 888 |
+
1 2
|
| 889 |
+
3 1
|
| 890 |
+
7
|
| 891 |
+
535 70 182 504 689 485 731
|
| 892 |
+
1 7
|
| 893 |
+
1 5
|
| 894 |
+
7 2
|
| 895 |
+
6 5
|
| 896 |
+
5 4
|
| 897 |
+
7 3
|
| 898 |
+
5
|
| 899 |
+
593 392 426 79 532
|
| 900 |
+
3 1
|
| 901 |
+
4 3
|
| 902 |
+
5 4
|
| 903 |
+
5 2
|
| 904 |
+
6
|
| 905 |
+
120 272 703 997 592 407
|
| 906 |
+
4 1
|
| 907 |
+
1 5
|
| 908 |
+
6 5
|
| 909 |
+
6 2
|
| 910 |
+
3 2
|
| 911 |
+
4
|
| 912 |
+
729 897 271 687
|
| 913 |
+
1 4
|
| 914 |
+
1 2
|
| 915 |
+
3 1
|
| 916 |
+
3
|
| 917 |
+
742 235 854
|
| 918 |
+
1 2
|
| 919 |
+
3 1
|
| 920 |
+
9
|
| 921 |
+
576 860 132 449 971 236 91 763 481
|
| 922 |
+
7 1
|
| 923 |
+
4 1
|
| 924 |
+
8 4
|
| 925 |
+
1 9
|
| 926 |
+
5 9
|
| 927 |
+
3 9
|
| 928 |
+
7 2
|
| 929 |
+
2 6
|
| 930 |
+
12
|
| 931 |
+
500 151 201 711 664 719 708 380 597 329 668 789
|
| 932 |
+
1 11
|
| 933 |
+
4 11
|
| 934 |
+
3 4
|
| 935 |
+
2 3
|
| 936 |
+
2 5
|
| 937 |
+
12 5
|
| 938 |
+
12 6
|
| 939 |
+
8 6
|
| 940 |
+
9 8
|
| 941 |
+
10 9
|
| 942 |
+
7 10
|
| 943 |
+
5
|
| 944 |
+
148 720 790 669 396
|
| 945 |
+
3 1
|
| 946 |
+
4 1
|
| 947 |
+
4 5
|
| 948 |
+
3 2
|
| 949 |
+
7
|
| 950 |
+
394 979 854 329 446 51 349
|
| 951 |
+
7 1
|
| 952 |
+
4 1
|
| 953 |
+
7 2
|
| 954 |
+
4 5
|
| 955 |
+
6 7
|
| 956 |
+
5 3
|
2021/quals/gold_mine_ch1.md
ADDED
|
@@ -0,0 +1,57 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
**Note: This problem shares similarities with [Chapter 2](https://www.facebook.com/codingcompetitions/hacker-cup/2021/qualification-round/problems/C2). The solution to either chapter may help with solving the other, so please consider reading both first.**
|
| 2 |
+
|
| 3 |
+
Just like [logging](https://www.youtube.com/watch?v=7AheBqBk0iQ), mining is a key industry in Canada's primary sector. Prospectors use geological tools to find ore deposits, then [drill, and blast](https://www.youtube.com/watch?v=zPbY--IXGg8&t=463s) to excavate a system of underground tunnels for access to the ores.
|
| 4 |
+
|
| 5 |
+
Minerva is a contract miner who spends her days extracting gold ore from underground mines across Ontario. One particular gold mine she's contracting for consists of \(N\) underground caves, numbered from \(1\) to \(N\), with cave \(1\) having an exit to the surface. There are also \(N - 1\) tunnels running among the caves, the \(i\)th of which allows one to travel in either direction between caves \(A_i\) and \(B_i\). Each cave is reachable from cave \(1\) by a sequence of these tunnels.
|
| 6 |
+
|
| 7 |
+
Cave \(i\) is known to contain \(C_i\) ounces of gold ore. With her trusty dump truck, Minerva plans to drive underground starting in cave \(1\), collect as much gold ore as possible, and exit back to the surface through cave \(1\).
|
| 8 |
+
|
| 9 |
+
There's just one issue: the tunnels are highly unstable, and will cave in after Minerva drives through them. Therefore, she is only able to traverse each tunnel at most once. Fortunately, the caves themselves are reinforced with pillars and will never collapse — she may visit each cave any number of times (though she can only collect its gold ore at most once).
|
| 10 |
+
|
| 11 |
+
This safety measure may limit mobility. Thankfully, Minerva's truck is also equipped to be a drill rig. As she travels through the system of caves, she may at any point use it to travel from her current cave to *any* other cave by drilling a new tunnel. **In this chapter, the rig only has the energy to drill at most one such tunnel.** Unfortunately, this new tunnel will be just as unstable as the existing ones — Minerva will only dare travel through it once.
|
| 12 |
+
|
| 13 |
+
Please help Minerva determine the maximum weight of gold ore that can be collected if she begins in cave \(1\), spends any amount of time exploring the mine (traveling through tunnels, drilling at most one new tunnel, and collecting ore from any visited caves), and end up once again in cave \(1\).
|
| 14 |
+
|
| 15 |
+
|
| 16 |
+
# Constraints
|
| 17 |
+
|
| 18 |
+
\(1 \le T \le 35\)
|
| 19 |
+
\(1 \le N \le 50\)
|
| 20 |
+
\(0 \le C_i \le 20{,}000{,}000\)
|
| 21 |
+
\(1 \le A_i, B_i \le N\)
|
| 22 |
+
|
| 23 |
+
The sum of \(N\) across all mines is at most \(1{,}000\).
|
| 24 |
+
|
| 25 |
+
|
| 26 |
+
# Input
|
| 27 |
+
|
| 28 |
+
Input begins with an integer \(T\), the number of mines that Minerva is contracted to work. For each mine, there is first a line containing the single integer \(N\). Then, there is a second line containing \(N\) space-separated integers, \(C_{1..N}\). Then, \(N - 1\) lines follow, the \(i\)th of which contains the space-separated integers \(A_i\) and \(B_i\).
|
| 29 |
+
|
| 30 |
+
|
| 31 |
+
# Output
|
| 32 |
+
|
| 33 |
+
For the \(i\)th mine, output a line containing *"Case #i: "* followed by a single integer, the maximum weight of gold ore (in ounces) that Minerva can collect before leaving the mine.
|
| 34 |
+
|
| 35 |
+
|
| 36 |
+
|
| 37 |
+
# Sample Explanation
|
| 38 |
+
|
| 39 |
+
The first mine looks as follows:
|
| 40 |
+
|
| 41 |
+
{{PHOTO_ID:328916612261658}}
|
| 42 |
+
|
| 43 |
+
It's possible to visit both caves (collecting \(30\) ounces of ore) and then return to cave \(1\), for example by taking the tunnel from cave \(1\) to cave \(2\) and then drilling a tunnel back to cave \(1\).
|
| 44 |
+
|
| 45 |
+
|
| 46 |
+
The second mine looks as follows:
|
| 47 |
+
|
| 48 |
+
{{PHOTO_ID:271244381102893}}
|
| 49 |
+
|
| 50 |
+
It's possible to end up with the ore from all \(4\) caves, for example by taking the tunnel to cave \(3\), drilling to cave \(4\), and then taking tunnels to cave \(2\) followed by cave \(1\).
|
| 51 |
+
|
| 52 |
+
|
| 53 |
+
The third mine looks as follows:
|
| 54 |
+
|
| 55 |
+
{{PHOTO_ID:160428912890161}}
|
| 56 |
+
|
| 57 |
+
It's possible to end up with \(3\) ounces of ore, but Minerva cannot collect all \(4\) ounces while still returning to cave \(1\) and only drilling one tunnel.
|
2021/quals/gold_mine_ch1.out
ADDED
|
@@ -0,0 +1,56 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Case #1: 30
|
| 2 |
+
Case #2: 4
|
| 3 |
+
Case #3: 3
|
| 4 |
+
Case #4: 12
|
| 5 |
+
Case #5: 32
|
| 6 |
+
Case #6: 0
|
| 7 |
+
Case #7: 20000000
|
| 8 |
+
Case #8: 430281141
|
| 9 |
+
Case #9: 260237126
|
| 10 |
+
Case #10: 155055536
|
| 11 |
+
Case #11: 7124
|
| 12 |
+
Case #12: 493215271
|
| 13 |
+
Case #13: 501845900
|
| 14 |
+
Case #14: 399532193
|
| 15 |
+
Case #15: 284199587
|
| 16 |
+
Case #16: 271952925
|
| 17 |
+
Case #17: 139158830
|
| 18 |
+
Case #18: 47952015
|
| 19 |
+
Case #19: 361976459
|
| 20 |
+
Case #20: 4056
|
| 21 |
+
Case #21: 3432
|
| 22 |
+
Case #22: 2904
|
| 23 |
+
Case #23: 3956
|
| 24 |
+
Case #24: 2947
|
| 25 |
+
Case #25: 2039
|
| 26 |
+
Case #26: 4885
|
| 27 |
+
Case #27: 3321
|
| 28 |
+
Case #28: 2620
|
| 29 |
+
Case #29: 2332
|
| 30 |
+
Case #30: 3071
|
| 31 |
+
Case #31: 2071
|
| 32 |
+
Case #32: 2342
|
| 33 |
+
Case #33: 4394
|
| 34 |
+
Case #34: 2027
|
| 35 |
+
Case #35: 3361
|
| 36 |
+
Case #36: 1109
|
| 37 |
+
Case #37: 5450
|
| 38 |
+
Case #38: 5064
|
| 39 |
+
Case #39: 3689
|
| 40 |
+
Case #40: 2090
|
| 41 |
+
Case #41: 3061
|
| 42 |
+
Case #42: 3235
|
| 43 |
+
Case #43: 2483
|
| 44 |
+
Case #44: 4151
|
| 45 |
+
Case #45: 3897
|
| 46 |
+
Case #46: 1728
|
| 47 |
+
Case #47: 1646
|
| 48 |
+
Case #48: 2641
|
| 49 |
+
Case #49: 2022
|
| 50 |
+
Case #50: 3091
|
| 51 |
+
Case #51: 2313
|
| 52 |
+
Case #52: 1831
|
| 53 |
+
Case #53: 3240
|
| 54 |
+
Case #54: 6417
|
| 55 |
+
Case #55: 2723
|
| 56 |
+
Case #56: 3351
|