2020 Problems
Browse filesThis view is limited to 50 files because it contains too many changes.
See raw diff
- .gitattributes +5 -0
- 2020/finals/1094784447639382.jpg +3 -0
- 2020/finals/1173260263089522.jpg +3 -0
- 2020/finals/127321889008596.jpg +3 -0
- 2020/finals/139722534273576.jpg +3 -0
- 2020/finals/1583104035206937.jpg +3 -0
- 2020/finals/186542789854750.jpg +3 -0
- 2020/finals/2008456099296384.jpg +3 -0
- 2020/finals/2722961511304050.jpg +3 -0
- 2020/finals/2854957798069201.jpg +3 -0
- 2020/finals/299743861289784.jpg +3 -0
- 2020/finals/3047534892140325.jpg +3 -0
- 2020/finals/311416436611683.jpg +3 -0
- 2020/finals/3533638723394837.jpg +3 -0
- 2020/finals/386528679257402.jpg +3 -0
- 2020/finals/408936830244710.jpg +3 -0
- 2020/finals/424906348725741.jpg +3 -0
- 2020/finals/477696676534167.jpg +3 -0
- 2020/finals/493376864970463.jpg +3 -0
- 2020/finals/747829032476688.jpg +3 -0
- 2020/finals/825086724953069.jpg +3 -0
- 2020/finals/862340924576901.jpg +3 -0
- 2020/finals/863939674419710.jpg +3 -0
- 2020/finals/cake_cutting_committee.cpp +353 -0
- 2020/finals/cake_cutting_committee.in +0 -0
- 2020/finals/cake_cutting_committee.md +67 -0
- 2020/finals/cake_cutting_committee.out +112 -0
- 2020/finals/cake_cutting_committee_sol.md +18 -0
- 2020/finals/cryptoconference.cpp +158 -0
- 2020/finals/cryptoconference.in +3 -0
- 2020/finals/cryptoconference.md +41 -0
- 2020/finals/cryptoconference.out +110 -0
- 2020/finals/cryptoconference_sol.md +9 -0
- 2020/finals/pond_precipitation.cpp +178 -0
- 2020/finals/pond_precipitation.in +129 -0
- 2020/finals/pond_precipitation.md +76 -0
- 2020/finals/pond_precipitation.out +64 -0
- 2020/finals/pond_precipitation_sol.md +5 -0
- 2020/finals/somebody_elses_problem.cpp +152 -0
- 2020/finals/somebody_elses_problem.in +3 -0
- 2020/finals/somebody_elses_problem.md +44 -0
- 2020/finals/somebody_elses_problem.out +109 -0
- 2020/finals/somebody_elses_problem_sol.md +18 -0
- 2020/finals/spider_spring.cpp +310 -0
- 2020/finals/spider_spring.in +1189 -0
- 2020/finals/spider_spring.md +104 -0
- 2020/finals/spider_spring.out +108 -0
- 2020/finals/spider_spring_sol.md +11 -0
- 2020/finals/tree_training.cpp +201 -0
- 2020/finals/tree_training.in +0 -0
.gitattributes
CHANGED
|
@@ -78,3 +78,8 @@ saved_model/**/* filter=lfs diff=lfs merge=lfs -text
|
|
| 78 |
2019/finals/little_boat_on_the_sea.in filter=lfs diff=lfs merge=lfs -text
|
| 79 |
2019/finals/temporal_revision.in filter=lfs diff=lfs merge=lfs -text
|
| 80 |
2019/round3/chain_of_command.in filter=lfs diff=lfs merge=lfs -text
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 78 |
2019/finals/little_boat_on_the_sea.in filter=lfs diff=lfs merge=lfs -text
|
| 79 |
2019/finals/temporal_revision.in filter=lfs diff=lfs merge=lfs -text
|
| 80 |
2019/round3/chain_of_command.in filter=lfs diff=lfs merge=lfs -text
|
| 81 |
+
2020/finals/cryptoconference.in filter=lfs diff=lfs merge=lfs -text
|
| 82 |
+
2020/finals/somebody_elses_problem.in filter=lfs diff=lfs merge=lfs -text
|
| 83 |
+
2020/quals/running_on_fumes_ch1.in filter=lfs diff=lfs merge=lfs -text
|
| 84 |
+
2020/quals/running_on_fumes_ch2.in filter=lfs diff=lfs merge=lfs -text
|
| 85 |
+
2020/quals/timber.in filter=lfs diff=lfs merge=lfs -text
|
2020/finals/1094784447639382.jpg
ADDED

|
Git LFS Details
|
2020/finals/1173260263089522.jpg
ADDED

|
Git LFS Details
|
2020/finals/127321889008596.jpg
ADDED

|
Git LFS Details
|
2020/finals/139722534273576.jpg
ADDED
|
Git LFS Details
|
2020/finals/1583104035206937.jpg
ADDED
|
Git LFS Details
|
2020/finals/186542789854750.jpg
ADDED
|
Git LFS Details
|
2020/finals/2008456099296384.jpg
ADDED

|
Git LFS Details
|
2020/finals/2722961511304050.jpg
ADDED
|
Git LFS Details
|
2020/finals/2854957798069201.jpg
ADDED

|
Git LFS Details
|
2020/finals/299743861289784.jpg
ADDED

|
Git LFS Details
|
2020/finals/3047534892140325.jpg
ADDED
|
Git LFS Details
|
2020/finals/311416436611683.jpg
ADDED

|
Git LFS Details
|
2020/finals/3533638723394837.jpg
ADDED

|
Git LFS Details
|
2020/finals/386528679257402.jpg
ADDED
|
Git LFS Details
|
2020/finals/408936830244710.jpg
ADDED
|
Git LFS Details
|
2020/finals/424906348725741.jpg
ADDED
|
Git LFS Details
|
2020/finals/477696676534167.jpg
ADDED

|
Git LFS Details
|
2020/finals/493376864970463.jpg
ADDED
|
Git LFS Details
|
2020/finals/747829032476688.jpg
ADDED

|
Git LFS Details
|
2020/finals/825086724953069.jpg
ADDED

|
Git LFS Details
|
2020/finals/862340924576901.jpg
ADDED

|
Git LFS Details
|
2020/finals/863939674419710.jpg
ADDED
|
Git LFS Details
|
2020/finals/cake_cutting_committee.cpp
ADDED
|
@@ -0,0 +1,353 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
// Cake-Cutting Committee
|
| 2 |
+
// Solution by Jacob Plachta
|
| 3 |
+
|
| 4 |
+
#include <algorithm>
|
| 5 |
+
#include <functional>
|
| 6 |
+
#include <numeric>
|
| 7 |
+
#include <iostream>
|
| 8 |
+
#include <iomanip>
|
| 9 |
+
#include <cstdio>
|
| 10 |
+
#include <cmath>
|
| 11 |
+
#include <complex>
|
| 12 |
+
#include <cstdlib>
|
| 13 |
+
#include <ctime>
|
| 14 |
+
#include <cstring>
|
| 15 |
+
#include <cassert>
|
| 16 |
+
#include <string>
|
| 17 |
+
#include <vector>
|
| 18 |
+
#include <list>
|
| 19 |
+
#include <map>
|
| 20 |
+
#include <set>
|
| 21 |
+
#include <unordered_map>
|
| 22 |
+
#include <unordered_set>
|
| 23 |
+
#include <deque>
|
| 24 |
+
#include <queue>
|
| 25 |
+
#include <stack>
|
| 26 |
+
#include <bitset>
|
| 27 |
+
#include <sstream>
|
| 28 |
+
using namespace std;
|
| 29 |
+
|
| 30 |
+
#define LL long long
|
| 31 |
+
#define LD long double
|
| 32 |
+
#define PR pair<int,int>
|
| 33 |
+
|
| 34 |
+
#define Fox(i,n) for (i=0; i<n; i++)
|
| 35 |
+
#define Fox1(i,n) for (i=1; i<=n; i++)
|
| 36 |
+
#define FoxI(i,a,b) for (i=a; i<=b; i++)
|
| 37 |
+
#define FoxR(i,n) for (i=(n)-1; i>=0; i--)
|
| 38 |
+
#define FoxR1(i,n) for (i=n; i>0; i--)
|
| 39 |
+
#define FoxRI(i,a,b) for (i=b; i>=a; i--)
|
| 40 |
+
#define Foxen(i,s) for (auto i:s)
|
| 41 |
+
#define Min(a,b) a=min(a,b)
|
| 42 |
+
#define Max(a,b) a=max(a,b)
|
| 43 |
+
#define Sz(s) int((s).size())
|
| 44 |
+
#define All(s) (s).begin(),(s).end()
|
| 45 |
+
#define Fill(s,v) memset(s,v,sizeof(s))
|
| 46 |
+
#define pb push_back
|
| 47 |
+
#define mp make_pair
|
| 48 |
+
#define x first
|
| 49 |
+
#define y second
|
| 50 |
+
|
| 51 |
+
template<typename T> T Abs(T x) { return(x < 0 ? -x : x); }
|
| 52 |
+
template<typename T> T Sqr(T x) { return(x * x); }
|
| 53 |
+
string plural(string s) { return(Sz(s) && s[Sz(s) - 1] == 'x' ? s + "en" : s + "s"); }
|
| 54 |
+
|
| 55 |
+
const int INF = (int)1e9;
|
| 56 |
+
const LD EPS = 1e-12;
|
| 57 |
+
const LD PI = acos(-1.0);
|
| 58 |
+
|
| 59 |
+
#define GETCHAR getchar_unlocked
|
| 60 |
+
|
| 61 |
+
bool Read(int& x) {
|
| 62 |
+
char c, r = 0, n = 0;
|
| 63 |
+
x = 0;
|
| 64 |
+
for (;;) {
|
| 65 |
+
c = GETCHAR();
|
| 66 |
+
if ((c < 0) && (!r))
|
| 67 |
+
return(0);
|
| 68 |
+
if ((c == '-') && (!r))
|
| 69 |
+
n = 1;
|
| 70 |
+
else if ((c >= '0') && (c <= '9'))
|
| 71 |
+
x = x * 10 + c - '0', r = 1;
|
| 72 |
+
else if (r)
|
| 73 |
+
break;
|
| 74 |
+
}
|
| 75 |
+
if (n)
|
| 76 |
+
x = -x;
|
| 77 |
+
return(1);
|
| 78 |
+
}
|
| 79 |
+
|
| 80 |
+
#define LIM 800
|
| 81 |
+
|
| 82 |
+
#define TVAL int
|
| 83 |
+
#define TLAZY int
|
| 84 |
+
#define TLIM 4100
|
| 85 |
+
|
| 86 |
+
TVAL ZERO_VAL = 0;
|
| 87 |
+
TLAZY ZERO_LAZY = 0;
|
| 88 |
+
|
| 89 |
+
struct SegTree
|
| 90 |
+
{
|
| 91 |
+
void UpdateValForUpdateOrLazy(TVAL& a, TLAZY v)
|
| 92 |
+
{
|
| 93 |
+
a += v;
|
| 94 |
+
}
|
| 95 |
+
|
| 96 |
+
void UpdateLazyForUpdateOrLazy(TLAZY& a, TLAZY v)
|
| 97 |
+
{
|
| 98 |
+
a += v;
|
| 99 |
+
}
|
| 100 |
+
|
| 101 |
+
TVAL CombVals(TVAL v1, TVAL v2)
|
| 102 |
+
{
|
| 103 |
+
return(max(v1, v2));
|
| 104 |
+
}
|
| 105 |
+
|
| 106 |
+
int N, sz;
|
| 107 |
+
TVAL tree[TLIM];
|
| 108 |
+
TLAZY lazy[TLIM];
|
| 109 |
+
|
| 110 |
+
SegTree() {}
|
| 111 |
+
|
| 112 |
+
SegTree(int _N)
|
| 113 |
+
{
|
| 114 |
+
Init(_N);
|
| 115 |
+
}
|
| 116 |
+
|
| 117 |
+
void Init(int _N)
|
| 118 |
+
{
|
| 119 |
+
N = _N;
|
| 120 |
+
for (sz = 1; sz < N; sz <<= 1);
|
| 121 |
+
Clear();
|
| 122 |
+
}
|
| 123 |
+
|
| 124 |
+
void Clear()
|
| 125 |
+
{
|
| 126 |
+
int i;
|
| 127 |
+
Fox(i, sz << 1)
|
| 128 |
+
tree[i] = ZERO_VAL;
|
| 129 |
+
Fox(i, sz << 1)
|
| 130 |
+
lazy[i] = ZERO_LAZY;
|
| 131 |
+
}
|
| 132 |
+
|
| 133 |
+
void Prop(int i)
|
| 134 |
+
{
|
| 135 |
+
TLAZY v = lazy[i];
|
| 136 |
+
lazy[i] = ZERO_LAZY;
|
| 137 |
+
UpdateValForUpdateOrLazy(tree[i], v);
|
| 138 |
+
if (i < sz)
|
| 139 |
+
{
|
| 140 |
+
int c1 = i << 1, c2 = c1 + 1;
|
| 141 |
+
UpdateLazyForUpdateOrLazy(lazy[c1], v);
|
| 142 |
+
UpdateLazyForUpdateOrLazy(lazy[c2], v);
|
| 143 |
+
}
|
| 144 |
+
}
|
| 145 |
+
|
| 146 |
+
void Comp(int i)
|
| 147 |
+
{
|
| 148 |
+
int c1 = i << 1, c2 = c1 + 1;
|
| 149 |
+
tree[i] = CombVals(tree[c1], tree[c2]);
|
| 150 |
+
}
|
| 151 |
+
|
| 152 |
+
TVAL Query(
|
| 153 |
+
int a, int b,
|
| 154 |
+
int i = 1, int r1 = 0, int r2 = -1
|
| 155 |
+
) {
|
| 156 |
+
if (r2 < 0)
|
| 157 |
+
{
|
| 158 |
+
Max(a, 0);
|
| 159 |
+
Min(b, sz - 1);
|
| 160 |
+
if (a > b)
|
| 161 |
+
return ZERO_VAL;
|
| 162 |
+
r2 = sz - 1;
|
| 163 |
+
}
|
| 164 |
+
Prop(i);
|
| 165 |
+
if (a <= r1 && r2 <= b)
|
| 166 |
+
return(tree[i]);
|
| 167 |
+
int m = (r1 + r2) >> 1, c = i << 1;
|
| 168 |
+
TVAL ret = ZERO_VAL;
|
| 169 |
+
if (a <= m)
|
| 170 |
+
ret = CombVals(ret, Query(a, b, c, r1, m));
|
| 171 |
+
if (b > m)
|
| 172 |
+
ret = CombVals(ret, Query(a, b, c + 1, m + 1, r2));
|
| 173 |
+
return(ret);
|
| 174 |
+
}
|
| 175 |
+
|
| 176 |
+
void Update(
|
| 177 |
+
int a, int b,
|
| 178 |
+
TLAZY v,
|
| 179 |
+
int i = 1, int r1 = 0, int r2 = -1
|
| 180 |
+
) {
|
| 181 |
+
if (r2 < 0)
|
| 182 |
+
{
|
| 183 |
+
Max(a, 0);
|
| 184 |
+
Min(b, sz - 1);
|
| 185 |
+
if (a > b)
|
| 186 |
+
return;
|
| 187 |
+
r2 = sz - 1;
|
| 188 |
+
}
|
| 189 |
+
Prop(i);
|
| 190 |
+
if (a <= r1 && r2 <= b)
|
| 191 |
+
{
|
| 192 |
+
UpdateLazyForUpdateOrLazy(lazy[i], v);
|
| 193 |
+
Prop(i);
|
| 194 |
+
return;
|
| 195 |
+
}
|
| 196 |
+
int m = (r1 + r2) >> 1, c = i << 1;
|
| 197 |
+
if (a <= m)
|
| 198 |
+
Update(a, b, v, c, r1, m);
|
| 199 |
+
if (b > m)
|
| 200 |
+
Update(a, b, v, c + 1, m + 1, r2);
|
| 201 |
+
Prop(c), Prop(c + 1), Comp(i);
|
| 202 |
+
}
|
| 203 |
+
};
|
| 204 |
+
|
| 205 |
+
struct Event
|
| 206 |
+
{
|
| 207 |
+
int x, y1, y2, c;
|
| 208 |
+
bool s;
|
| 209 |
+
};
|
| 210 |
+
|
| 211 |
+
const bool operator<(const Event& a, const Event& b)
|
| 212 |
+
{
|
| 213 |
+
return(mp(a.x, !a.s) < mp(b.x, !b.s));
|
| 214 |
+
}
|
| 215 |
+
|
| 216 |
+
int S, N;
|
| 217 |
+
int C[LIM], P[LIM][4];
|
| 218 |
+
|
| 219 |
+
bool IsBetween(int a, int b, int p, bool ex)
|
| 220 |
+
{
|
| 221 |
+
if (b < a)
|
| 222 |
+
b += INF;
|
| 223 |
+
if (p < a)
|
| 224 |
+
p += INF;
|
| 225 |
+
return ex ? a < p && p < b : a <= p && p <= b;
|
| 226 |
+
}
|
| 227 |
+
|
| 228 |
+
int GetPosAfter(int a, int p)
|
| 229 |
+
{
|
| 230 |
+
if (p < a)
|
| 231 |
+
p += INF;
|
| 232 |
+
return(p - a);
|
| 233 |
+
}
|
| 234 |
+
|
| 235 |
+
int SolveForLine(vector<int> h)
|
| 236 |
+
{
|
| 237 |
+
int i, j, s;
|
| 238 |
+
// compare all pieces against dividing line, and assemble line sweep events
|
| 239 |
+
int base = 0;
|
| 240 |
+
vector<int> CY;
|
| 241 |
+
vector<Event> E;
|
| 242 |
+
Fox(i, N)
|
| 243 |
+
{
|
| 244 |
+
// full intersection?
|
| 245 |
+
if (
|
| 246 |
+
(IsBetween(P[i][0], P[i][2], h[0], 0) || IsBetween(P[i][3], P[i][1], h[0], 0)) &&
|
| 247 |
+
(IsBetween(P[i][0], P[i][2], h[1], 0) || IsBetween(P[i][3], P[i][1], h[1], 0))
|
| 248 |
+
)
|
| 249 |
+
{
|
| 250 |
+
base += C[i];
|
| 251 |
+
continue;
|
| 252 |
+
}
|
| 253 |
+
// look for orientation of line segments such that at least one spans crosses from the 1st to the 2nd half
|
| 254 |
+
Fox(s, 2)
|
| 255 |
+
{
|
| 256 |
+
int p[4];
|
| 257 |
+
memcpy(p, P[i], sizeof(p));
|
| 258 |
+
if (s)
|
| 259 |
+
reverse(p, p + 4);
|
| 260 |
+
// check which points are on their required halves
|
| 261 |
+
bool bx[2], by[2];
|
| 262 |
+
Fox(j, 2)
|
| 263 |
+
{
|
| 264 |
+
bx[j] = IsBetween(h[0], h[1], p[j * 2], 0);
|
| 265 |
+
by[j] = IsBetween(h[1], h[0], p[j * 2 + 1], 0);
|
| 266 |
+
}
|
| 267 |
+
// neither line segment is entirely valid?
|
| 268 |
+
if ((!bx[0] || !by[0]) && (!bx[1] || !by[1]))
|
| 269 |
+
continue;
|
| 270 |
+
assert(bx[0] + by[0] + bx[1] + by[1] >= 3); // other one must be at least half-valid
|
| 271 |
+
// map points to positions on their halves
|
| 272 |
+
int x[2], y[2];
|
| 273 |
+
Fox(j, 2)
|
| 274 |
+
{
|
| 275 |
+
x[j] = bx[j] ? GetPosAfter(h[0], p[j * 2]) : 2 * INF * (j ? 1 : -1);
|
| 276 |
+
y[j] = by[j] ? -GetPosAfter(h[1], p[j * 2 + 1]) : 2 * INF * (j ? 1 : -1);
|
| 277 |
+
}
|
| 278 |
+
assert(x[0] < x[1] && y[0] < y[1]);
|
| 279 |
+
E.pb({ x[0], y[0], y[1], C[i], 1 });
|
| 280 |
+
E.pb({ x[1], y[0], y[1], C[i], 0 });
|
| 281 |
+
CY.pb(y[0]), CY.pb(y[1]);
|
| 282 |
+
break;
|
| 283 |
+
}
|
| 284 |
+
}
|
| 285 |
+
// compress Y-coordinates
|
| 286 |
+
sort(All(CY));
|
| 287 |
+
int K = unique(All(CY)) - CY.begin();
|
| 288 |
+
CY.resize(K);
|
| 289 |
+
// line sweep
|
| 290 |
+
SegTree ST(K);
|
| 291 |
+
sort(All(E));
|
| 292 |
+
Foxen(e, E)
|
| 293 |
+
{
|
| 294 |
+
e.y1 = lower_bound(All(CY), e.y1) - CY.begin();
|
| 295 |
+
e.y2 = lower_bound(All(CY), e.y2) - CY.begin();
|
| 296 |
+
// left edge of a rectangle?
|
| 297 |
+
if (e.s)
|
| 298 |
+
{
|
| 299 |
+
ST.Update(e.y1, K - 1, e.c);
|
| 300 |
+
continue;
|
| 301 |
+
}
|
| 302 |
+
// right edge of a rectangle
|
| 303 |
+
ST.Update(e.y2, e.y2, ST.Query(e.y2, K - 1) - ST.Query(e.y2, e.y2));
|
| 304 |
+
ST.Update(e.y2 + 1, K - 1, -e.c);
|
| 305 |
+
}
|
| 306 |
+
return(base + ST.Query(0, K - 1));
|
| 307 |
+
}
|
| 308 |
+
|
| 309 |
+
int ProcessCase()
|
| 310 |
+
{
|
| 311 |
+
int i, j;
|
| 312 |
+
// input
|
| 313 |
+
Read(S), Read(N);
|
| 314 |
+
Fox(i, N)
|
| 315 |
+
{
|
| 316 |
+
Read(C[i]);
|
| 317 |
+
Fox(j, 4)
|
| 318 |
+
{
|
| 319 |
+
int x, y;
|
| 320 |
+
Read(x), Read(y);
|
| 321 |
+
if (!x)
|
| 322 |
+
P[i][j] = y;
|
| 323 |
+
else if (y == S)
|
| 324 |
+
P[i][j] = S + x;
|
| 325 |
+
else if (x == S)
|
| 326 |
+
P[i][j] = 3 * S - y;
|
| 327 |
+
else
|
| 328 |
+
P[i][j] = 4 * S - x;
|
| 329 |
+
}
|
| 330 |
+
// normalize lines
|
| 331 |
+
if (IsBetween(P[i][1], P[i][0], P[i][2], 1))
|
| 332 |
+
swap(P[i][0], P[i][1]);
|
| 333 |
+
if (IsBetween(P[i][2], P[i][3], P[i][0], 1))
|
| 334 |
+
swap(P[i][2], P[i][3]);
|
| 335 |
+
}
|
| 336 |
+
// consider all possible dividing lines
|
| 337 |
+
int ans = 0;
|
| 338 |
+
Fox(i, N)
|
| 339 |
+
{
|
| 340 |
+
Fox(j, 2)
|
| 341 |
+
Max(ans, SolveForLine({ P[i][j * 2], P[i][j * 2 + 1] }));
|
| 342 |
+
}
|
| 343 |
+
return(ans);
|
| 344 |
+
}
|
| 345 |
+
|
| 346 |
+
int main()
|
| 347 |
+
{
|
| 348 |
+
int T, t;
|
| 349 |
+
Read(T);
|
| 350 |
+
Fox1(t, T)
|
| 351 |
+
printf("Case #%d: %d\n", t, ProcessCase());
|
| 352 |
+
return(0);
|
| 353 |
+
}
|
2020/finals/cake_cutting_committee.in
ADDED
|
The diff for this file is too large to render.
See raw diff
|
|
|
2020/finals/cake_cutting_committee.md
ADDED
|
@@ -0,0 +1,67 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Melody is preparing a cake for a very special occasion. She's starting off with a square cake, though she'd like it cut down into a more unique shape. When viewed from above, it can be represented as a square on a 2D plane, with opposite corners at coordinates \((0, 0)\) and \((S, S)\).
|
| 2 |
+
|
| 3 |
+
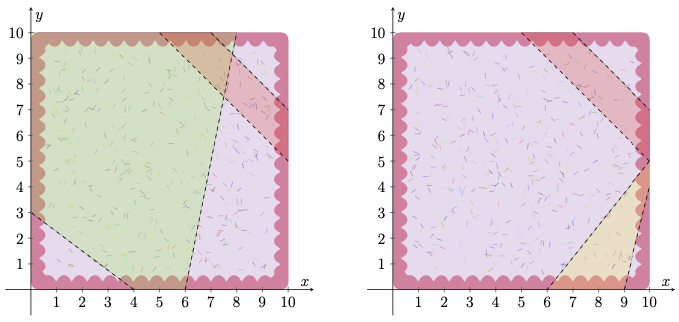
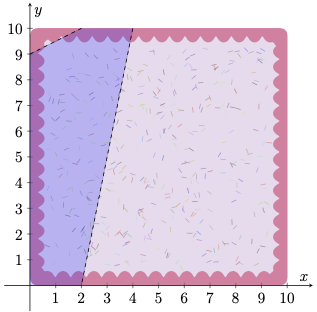
Out of countless contenders, Melody has interviewed \(N\) certified cake-cutting consultants, asking how the cake should be cut down. The \(i\)th consultant, who has a competence value of \(C_i\), has proposed that two cuts should be performed: the first being a line segment between coordinates \((X_{i,1}, Y_{i,1})\) and \((X_{i,2}, Y_{i,2})\), and the second between \((X_{i,3}, Y_{i,3})\) and \((X_{i,4}, Y_{i,4})\). Each of these four points is exactly on a side of the cake (but not on a corner), the two points describing each line segment are not on the same side of the cake, and the two line segments do not share any points in common (in other words, they don't intersect nor have any equal endpoints). Therefore, the two cuts would split the cake into three non-empty polygonal sections. Of those, the middle section (the one between the two cuts) would become their **proposed cake shape**, with the other two sections discarded.
|
| 4 |
+
|
| 5 |
+
For example, the following diagram illustrates a cake with \(S = 10\) and a consultant's pair of proposed cuts (from \((4, 10)\) to \((2, 0)\) and from \((0, 9)\) to \((2, 10)\)), with their resulting proposed cake shape highlighted in blue:
|
| 6 |
+
|
| 7 |
+
{{PHOTO_ID:186542789854750}}
|
| 8 |
+
|
| 9 |
+
Melody wants to hire one or more of the consultants to form a committee, whose members will then deliberate on the final shape of the cake. That is, she calls for a completely competent consulting committee capable of coming to a consensus on a commendable cake-cutting configuration. Clearly.
|
| 10 |
+
|
| 11 |
+
She wants the sum of the hired consultants' competence values to be as large as possible, no matter how many of them she has to hire. However, she won't allow a pair of consultants to both be part of the committee if their cake-cutting proposals *fundamentally differ*, which is the case if their proposed cake shapes do not share any points in common (in other words, if those two polygons are entirely disjoint, including at their edges and vertices).
|
| 12 |
+
|
| 13 |
+
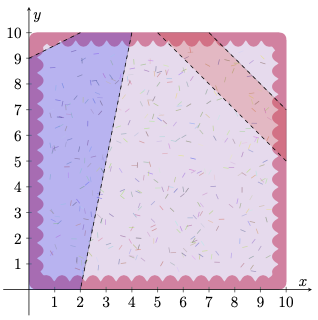
For example, the following diagram additionally includes another consultant's pair of proposed cuts (from (7, 10) to (10, 7) and from (10, 5) to (5, 10)), with their proposed cake shape highlighted in red. Since these two proposed cake shapes do not overlap at all, the two proposals fundamentally differ, meaning that if one of these consultants is hired, the other cannot also be hired:
|
| 14 |
+
|
| 15 |
+
{{PHOTO_ID:3047534892140325}}
|
| 16 |
+
|
| 17 |
+
On the other hand, each of the following cakes features a pair of proposals which do not fundamentally differ, due to the proposed cake shapes sharing at least one point in common (meaning that, for each cake, the two consultants could be hired together):
|
| 18 |
+
|
| 19 |
+
{{PHOTO_ID:139722534273576}}
|
| 20 |
+
|
| 21 |
+
Help Melody determine the maximum combined competence of consultants who can form the committee, such that no two of them have fundamentally differing cake-cutting proposals.
|
| 22 |
+
|
| 23 |
+
# Constraints
|
| 24 |
+
|
| 25 |
+
\(1 \le T \le 80\)
|
| 26 |
+
\(1 \le N \le 800\)
|
| 27 |
+
\(2 \le S \le 100,000,000\)
|
| 28 |
+
\(1 \le C_i \le 500,000\)
|
| 29 |
+
\(0 \le X_{i,j}, Y_{i,j} \le S\)
|
| 30 |
+
|
| 31 |
+
The sum of \(N\) across all special occasions is at most 20,000.
|
| 32 |
+
|
| 33 |
+
# Input
|
| 34 |
+
|
| 35 |
+
Input begins with an integer \(T\), the number of special occasions. For each occasion, there are \(N + 1\) lines. The first line contains 2 space-separated integers, \(S\) and \(N\). \(N\) lines follow, the \(i\)th of which contains the 9 space-separated integers \(C_i\), \(X_{i,1}\), \(Y_{i,1}\), \(X_{i,2}\), \(Y_{i,2}\), \(X_{i,3}\), \(Y_{i,3}\), and \(X_{i,4}\), \(Y_{i,4}\).
|
| 36 |
+
|
| 37 |
+
|
| 38 |
+
# Output
|
| 39 |
+
|
| 40 |
+
For the \(i\)th special occasion, print a line containing *"Case #i: "*, followed by a single integer, the maximum combined competence of cake-cutting consultants who can form the committee.
|
| 41 |
+
|
| 42 |
+
|
| 43 |
+
# Explanation of Sample
|
| 44 |
+
|
| 45 |
+
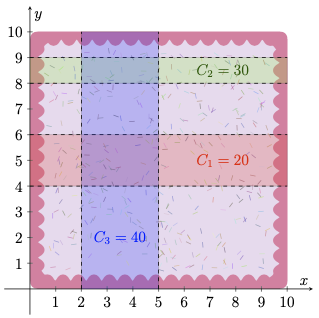
The first cake (along with the consultants' proposed cake shapes) looks as follows:
|
| 46 |
+
|
| 47 |
+
{{PHOTO_ID:2722961511304050}}
|
| 48 |
+
|
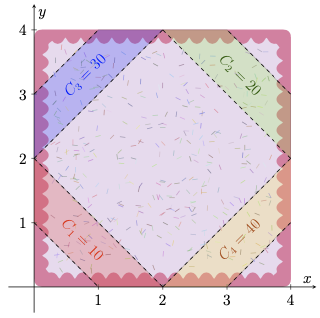
| 49 |
+
The 1st and 2nd consultants can't both be hired together, but either can be hired alongside the 3rd consultant. So, the best Melody can do is to hire the 2nd and 3rd consultants for a combined competence of \(30 + 40 = 70\).
|
| 50 |
+
|
| 51 |
+
The second cake looks as follows:
|
| 52 |
+
|
| 53 |
+
{{PHOTO_ID:408936830244710}}
|
| 54 |
+
|
| 55 |
+
Melody can hire all three consultants.
|
| 56 |
+
|
| 57 |
+
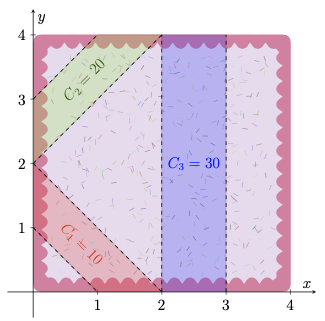
The third cake looks as follows:
|
| 58 |
+
|
| 59 |
+
{{PHOTO_ID:386528679257402}}
|
| 60 |
+
|
| 61 |
+
The fourth cake looks as follows:
|
| 62 |
+
|
| 63 |
+
{{PHOTO_ID:863939674419710}}
|
| 64 |
+
|
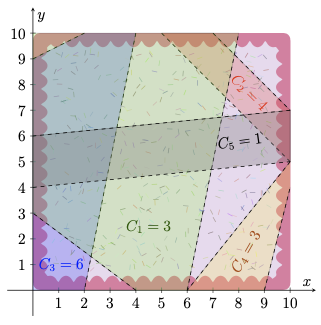
| 65 |
+
The fifth cake looks as follows:
|
| 66 |
+
|
| 67 |
+
{{PHOTO_ID:424906348725741}}
|
2020/finals/cake_cutting_committee.out
ADDED
|
@@ -0,0 +1,112 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Case #1: 70
|
| 2 |
+
Case #2: 60
|
| 3 |
+
Case #3: 60
|
| 4 |
+
Case #4: 14
|
| 5 |
+
Case #5: 11
|
| 6 |
+
Case #6: 15
|
| 7 |
+
Case #7: 26
|
| 8 |
+
Case #8: 62
|
| 9 |
+
Case #9: 59
|
| 10 |
+
Case #10: 33
|
| 11 |
+
Case #11: 10
|
| 12 |
+
Case #12: 4
|
| 13 |
+
Case #13: 8160
|
| 14 |
+
Case #14: 7207
|
| 15 |
+
Case #15: 7
|
| 16 |
+
Case #16: 59
|
| 17 |
+
Case #17: 41008
|
| 18 |
+
Case #18: 52938
|
| 19 |
+
Case #19: 17272
|
| 20 |
+
Case #20: 250000000
|
| 21 |
+
Case #21: 81000
|
| 22 |
+
Case #22: 81000
|
| 23 |
+
Case #23: 195153474
|
| 24 |
+
Case #24: 157757408
|
| 25 |
+
Case #25: 148427301
|
| 26 |
+
Case #26: 33268941
|
| 27 |
+
Case #27: 31942779
|
| 28 |
+
Case #28: 29651063
|
| 29 |
+
Case #29: 31340125
|
| 30 |
+
Case #30: 29857414
|
| 31 |
+
Case #31: 29451361
|
| 32 |
+
Case #32: 29524220
|
| 33 |
+
Case #33: 27477273
|
| 34 |
+
Case #34: 30685666
|
| 35 |
+
Case #35: 30626812
|
| 36 |
+
Case #36: 27372492
|
| 37 |
+
Case #37: 29689094
|
| 38 |
+
Case #38: 5215
|
| 39 |
+
Case #39: 55269
|
| 40 |
+
Case #40: 3394
|
| 41 |
+
Case #41: 1870
|
| 42 |
+
Case #42: 3902
|
| 43 |
+
Case #43: 1656
|
| 44 |
+
Case #44: 22432
|
| 45 |
+
Case #45: 61590
|
| 46 |
+
Case #46: 2693
|
| 47 |
+
Case #47: 11236
|
| 48 |
+
Case #48: 4765
|
| 49 |
+
Case #49: 11836
|
| 50 |
+
Case #50: 25810
|
| 51 |
+
Case #51: 17702
|
| 52 |
+
Case #52: 69830
|
| 53 |
+
Case #53: 13183
|
| 54 |
+
Case #54: 39633
|
| 55 |
+
Case #55: 16641
|
| 56 |
+
Case #56: 20295
|
| 57 |
+
Case #57: 8134
|
| 58 |
+
Case #58: 371
|
| 59 |
+
Case #59: 4361
|
| 60 |
+
Case #60: 15012
|
| 61 |
+
Case #61: 667
|
| 62 |
+
Case #62: 7749
|
| 63 |
+
Case #63: 7587
|
| 64 |
+
Case #64: 66822
|
| 65 |
+
Case #65: 13309
|
| 66 |
+
Case #66: 8544
|
| 67 |
+
Case #67: 62661
|
| 68 |
+
Case #68: 22366
|
| 69 |
+
Case #69: 1235
|
| 70 |
+
Case #70: 12477
|
| 71 |
+
Case #71: 12164
|
| 72 |
+
Case #72: 7031
|
| 73 |
+
Case #73: 21198
|
| 74 |
+
Case #74: 15176
|
| 75 |
+
Case #75: 6046
|
| 76 |
+
Case #76: 1149
|
| 77 |
+
Case #77: 35941
|
| 78 |
+
Case #78: 810
|
| 79 |
+
Case #79: 23259
|
| 80 |
+
Case #80: 1335
|
| 81 |
+
Case #81: 2950
|
| 82 |
+
Case #82: 7170
|
| 83 |
+
Case #83: 41925
|
| 84 |
+
Case #84: 8782
|
| 85 |
+
Case #85: 1107
|
| 86 |
+
Case #86: 15565
|
| 87 |
+
Case #87: 17094
|
| 88 |
+
Case #88: 1250
|
| 89 |
+
Case #89: 27818
|
| 90 |
+
Case #90: 10246
|
| 91 |
+
Case #91: 5690
|
| 92 |
+
Case #92: 17200
|
| 93 |
+
Case #93: 6868
|
| 94 |
+
Case #94: 7621
|
| 95 |
+
Case #95: 24280
|
| 96 |
+
Case #96: 15790
|
| 97 |
+
Case #97: 806
|
| 98 |
+
Case #98: 24283
|
| 99 |
+
Case #99: 21818
|
| 100 |
+
Case #100: 636
|
| 101 |
+
Case #101: 39706
|
| 102 |
+
Case #102: 9505
|
| 103 |
+
Case #103: 16829
|
| 104 |
+
Case #104: 59786
|
| 105 |
+
Case #105: 5017
|
| 106 |
+
Case #106: 23559
|
| 107 |
+
Case #107: 48806
|
| 108 |
+
Case #108: 7429
|
| 109 |
+
Case #109: 35980
|
| 110 |
+
Case #110: 62511
|
| 111 |
+
Case #111: 2200
|
| 112 |
+
Case #112: 45468
|
2020/finals/cake_cutting_committee_sol.md
ADDED
|
@@ -0,0 +1,18 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
We can number the possible positions of line segment endpoints from \(1\) to \(4(N-1)\) in clockwise order around the edge of the square, and then simply map all of the given line segment endpoints to these indices, noting that only their relative order is relevant for determining which proposed cake shapes overlap with one another.
|
| 2 |
+
|
| 3 |
+
It's possible to show that, for any valid set of proposed cake shapes, there must exist at least one *key line segment* amongst them such that every polygon in the set overlaps with that line segment. We'll therefore consider all \(2N\) possible key line segments.
|
| 4 |
+
|
| 5 |
+
For a given key line segment, each polygon either doesn't overlap with it at all (and so should be ignored), overlaps with all of it (and so may always be used), or overlaps with only part of it. For polygons falling into this final category, we're interested in the maximum combined value of any set of them such that each pair of them overlaps.
|
| 6 |
+
|
| 7 |
+
The key line segment splits the full set of possible endpoint indices into two sections, which we'll call the X and Y sections. We can map each polygon's endpoints to new indices along these two sections, both numbered starting from the same ("first") endpoint of the key line segment (meaning that one section's sequence of indices is equivalent to increasing original indices, while the other section's is equivalent to decreasing original indices). If a polygon has 3 endpoints in one section and 1 endpoint in the other (as opposed to 2 in each), then we'll shift one of them over to one of the key line segment's endpoints without changing which other polygons it overlaps with.
|
| 8 |
+
|
| 9 |
+
The result is that, for each line segment of each polygon, one endpoint will have been mapped to a new index in the X section, with the other mapped to a new index in the Y section. This allows us to represent each polygon by a pair of intervals \([x_1, x_2]\) and \([y_1, y_2]\) (consisting of its two X section indices and its two Y section indices, respectively). With this representation, we can then observe that a pair of polygons don't overlap if and only one of the polygons' X and Y intervals are both strictly to the right (or strictly to the left) of the other polygon's respective X and Y intervals.
|
| 10 |
+
|
| 11 |
+
If we now visualize each such polygon as a rectangle on a 2D plane, with coordinates based on its X and Y intervals (in particular, with lower-left corner \((x_1, y_1)\) and upper-right corner \((x_1, y_1)\)), we're interested in the maximum combined value of any set of them such that no rectangle is strictly both above and to the right of any other rectangle. This may be accomplished in \(O(N log(N))\) time with a line sweep over the x-coordinates. We'll let \(M_y\) be the maximum combined value of a valid set of rectangles encountered so far, such that the lowest of their top-right corners encountered so far has y-coordinate `y`, and maintain this with the help of a segment tree:
|
| 12 |
+
|
| 13 |
+
- When we encounter the left edge of a rectangle with bottom edge `y_1`, we should increase each of \(M_{y_1..\infty}\) by that rectangle's value (as this rectangle may be added to any such set).
|
| 14 |
+
- When we encounter the right edge of a rectangle with top edge `y_2`, we should first set \(M_{y_2}\) to \(\max(M_{(y_2+1)..\infty})\) (as including this rectangle in any such set would decrease its lowest top-right corner to \(y_2\)). We should then decrease each of \(M_{(y_2+1)..\infty}\) by that rectangle's value (as this rectangle may no longer be added to any such set).
|
| 15 |
+
|
| 16 |
+
Repeating the above process for all \(2N\) possible key line segments yields a solution with a time complexity of \(O(N^2 log(N))\) (though a less efficient, \(O(N^3)\) implementation would also suffice).
|
| 17 |
+
|
| 18 |
+
For further reading, if we consider mapping the line segment endpoint indices to positions around the circumference of a circle instead (essentially treating the original square as a circle), each proposed cake shape is known as a *circle trapezoid*. The intersection graph of these polygons (a graph in which there's an edge between two pieces if and only if they overlap) is then known as a [*circle trapezoid graph*](https://en.wikipedia.org/wiki/Trapezoid_graph#Circle_trapezoid_graphs). The problem of computing the maximum clique weight in such a graph (equivalent to what's asked for in Cake-Cutting Committee), and other related problems, are explored further in [this paper](https://www.sciencedirect.com/science/article/pii/S0166218X96000133?via%3Dihub).
|
2020/finals/cryptoconference.cpp
ADDED
|
@@ -0,0 +1,158 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
// Cryptoconference
|
| 2 |
+
// Solution by Jacob Plachta
|
| 3 |
+
|
| 4 |
+
#include <algorithm>
|
| 5 |
+
#include <functional>
|
| 6 |
+
#include <numeric>
|
| 7 |
+
#include <iostream>
|
| 8 |
+
#include <iomanip>
|
| 9 |
+
#include <cstdio>
|
| 10 |
+
#include <cmath>
|
| 11 |
+
#include <complex>
|
| 12 |
+
#include <cstdlib>
|
| 13 |
+
#include <ctime>
|
| 14 |
+
#include <cstring>
|
| 15 |
+
#include <cassert>
|
| 16 |
+
#include <string>
|
| 17 |
+
#include <vector>
|
| 18 |
+
#include <list>
|
| 19 |
+
#include <map>
|
| 20 |
+
#include <set>
|
| 21 |
+
#include <unordered_map>
|
| 22 |
+
#include <unordered_set>
|
| 23 |
+
#include <deque>
|
| 24 |
+
#include <queue>
|
| 25 |
+
#include <stack>
|
| 26 |
+
#include <bitset>
|
| 27 |
+
#include <sstream>
|
| 28 |
+
using namespace std;
|
| 29 |
+
|
| 30 |
+
#define LL long long
|
| 31 |
+
#define LD long double
|
| 32 |
+
#define PR pair<int,int>
|
| 33 |
+
|
| 34 |
+
#define Fox(i,n) for (i=0; i<n; i++)
|
| 35 |
+
#define Fox1(i,n) for (i=1; i<=n; i++)
|
| 36 |
+
#define FoxI(i,a,b) for (i=a; i<=b; i++)
|
| 37 |
+
#define FoxR(i,n) for (i=(n)-1; i>=0; i--)
|
| 38 |
+
#define FoxR1(i,n) for (i=n; i>0; i--)
|
| 39 |
+
#define FoxRI(i,a,b) for (i=b; i>=a; i--)
|
| 40 |
+
#define Foxen(i,s) for (i=s.begin(); i!=s.end(); i++)
|
| 41 |
+
#define Min(a,b) a=min(a,b)
|
| 42 |
+
#define Max(a,b) a=max(a,b)
|
| 43 |
+
#define Sz(s) int((s).size())
|
| 44 |
+
#define All(s) (s).begin(),(s).end()
|
| 45 |
+
#define Fill(s,v) memset(s,v,sizeof(s))
|
| 46 |
+
#define pb push_back
|
| 47 |
+
#define mp make_pair
|
| 48 |
+
#define x first
|
| 49 |
+
#define y second
|
| 50 |
+
|
| 51 |
+
template<typename T> T Abs(T x) { return(x < 0 ? -x : x); }
|
| 52 |
+
template<typename T> T Sqr(T x) { return(x * x); }
|
| 53 |
+
string plural(string s) { return(Sz(s) && s[Sz(s) - 1] == 'x' ? s + "en" : s + "s"); }
|
| 54 |
+
|
| 55 |
+
const int INF = (int)1e9;
|
| 56 |
+
const LD EPS = 1e-12;
|
| 57 |
+
const LD PI = acos(-1.0);
|
| 58 |
+
|
| 59 |
+
#define GETCHAR getchar_unlocked
|
| 60 |
+
|
| 61 |
+
bool Read(int& x) {
|
| 62 |
+
char c, r = 0, n = 0;
|
| 63 |
+
x = 0;
|
| 64 |
+
for (;;) {
|
| 65 |
+
c = GETCHAR();
|
| 66 |
+
if ((c < 0) && (!r))
|
| 67 |
+
return(0);
|
| 68 |
+
if ((c == '-') && (!r))
|
| 69 |
+
n = 1;
|
| 70 |
+
else if ((c >= '0') && (c <= '9'))
|
| 71 |
+
x = x * 10 + c - '0', r = 1;
|
| 72 |
+
else if (r)
|
| 73 |
+
break;
|
| 74 |
+
}
|
| 75 |
+
if (n)
|
| 76 |
+
x = -x;
|
| 77 |
+
return(1);
|
| 78 |
+
}
|
| 79 |
+
|
| 80 |
+
#define MOD 1000000007
|
| 81 |
+
|
| 82 |
+
int N, K;
|
| 83 |
+
LL cur, ans;
|
| 84 |
+
set<PR> S;
|
| 85 |
+
|
| 86 |
+
// returns the # of valid intervals with start positions in:
|
| 87 |
+
// (this interval's start, next interval's start]
|
| 88 |
+
LL Count(set<PR>::iterator I)
|
| 89 |
+
{
|
| 90 |
+
// get key points from this interval and the next one
|
| 91 |
+
int a = I->x + 1;
|
| 92 |
+
I++;
|
| 93 |
+
int b = I->x;
|
| 94 |
+
int c = I->y - 1;
|
| 95 |
+
// count intervals which start in [a, b] and end no later than c
|
| 96 |
+
int v1 = c - b;
|
| 97 |
+
int v2 = c - a;
|
| 98 |
+
return (LL)(v1 + v2) * (v2 - v1 + 1) / 2;
|
| 99 |
+
}
|
| 100 |
+
|
| 101 |
+
// inserts interval [a, b] into the set, while updating the total # of valid intervals
|
| 102 |
+
void Insert(int a, int b)
|
| 103 |
+
{
|
| 104 |
+
set<PR>::iterator I, J;
|
| 105 |
+
I = S.lower_bound(mp(a, -1));
|
| 106 |
+
// is the new interval obsolete (covers existing interval)?
|
| 107 |
+
if (a <= I->x && I->y <= b)
|
| 108 |
+
return;
|
| 109 |
+
// erase any existing obsolete intervals (covering the new one)
|
| 110 |
+
if (I->x > a)
|
| 111 |
+
I--;
|
| 112 |
+
for (;;)
|
| 113 |
+
{
|
| 114 |
+
if (I->y < b)
|
| 115 |
+
break;
|
| 116 |
+
J = I, I--;
|
| 117 |
+
cur -= Count(J) + Count(I);
|
| 118 |
+
S.erase(J);
|
| 119 |
+
cur += Count(I);
|
| 120 |
+
}
|
| 121 |
+
// insert the new interval
|
| 122 |
+
cur -= Count(I);
|
| 123 |
+
S.insert(mp(a, b));
|
| 124 |
+
cur += Count(I);
|
| 125 |
+
I++;
|
| 126 |
+
cur += Count(I);
|
| 127 |
+
}
|
| 128 |
+
|
| 129 |
+
LL ProcessCase()
|
| 130 |
+
{
|
| 131 |
+
int i;
|
| 132 |
+
// input
|
| 133 |
+
Read(N), Read(K);
|
| 134 |
+
// init
|
| 135 |
+
S.clear();
|
| 136 |
+
S.insert(mp(-1, -1));
|
| 137 |
+
S.insert(mp(K, K + 1));
|
| 138 |
+
ans = 1;
|
| 139 |
+
cur = Count(S.begin());
|
| 140 |
+
// process intervals
|
| 141 |
+
Fox(i, N)
|
| 142 |
+
{
|
| 143 |
+
int s, d;
|
| 144 |
+
Read(s), Read(d);
|
| 145 |
+
Insert(s, s + d);
|
| 146 |
+
ans = ans * (cur % MOD) % MOD;
|
| 147 |
+
}
|
| 148 |
+
return(ans);
|
| 149 |
+
}
|
| 150 |
+
|
| 151 |
+
int main()
|
| 152 |
+
{
|
| 153 |
+
int T, t;
|
| 154 |
+
Read(T);
|
| 155 |
+
Fox1(t, T)
|
| 156 |
+
printf("Case #%d: %lld\n", t, ProcessCase());
|
| 157 |
+
return(0);
|
| 158 |
+
}
|
2020/finals/cryptoconference.in
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:a50294e575c083ccf35a9f1298d80e950fb199d926cc2203e9d7f80970603d6e
|
| 3 |
+
size 14176322
|
2020/finals/cryptoconference.md
ADDED
|
@@ -0,0 +1,41 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Crys just invented a new cryptocurrency and is planning to present it at \(T\) blockchain conferences around the world. The conference schedules are already on their way to being finalized, but Crys is considering how she might get her own talks in at the last minute.
|
| 2 |
+
|
| 3 |
+
A certain conference is \(K\) hours long, with talks to start and end on the hour. Each talk will span a non-empty inclusive time interval of hours \([x, y]\), such that \(x\) and \(y\) are integers and \(0 \le x \lt y \le K\). \(N\) talks are gradually being added to the schedule, one after another, with the \(i\)th added talk scheduled to span the time interval \([S_i, S_i + D_i]\). The \(N\) talks are not necessarily added in order of starting or ending time. Their time intervals may arbitrarily overlap with one another, and are not necessarily distinct.
|
| 4 |
+
|
| 5 |
+
Each time a talk is added to the schedule, Crys will then consider submitting a request for her own talk to also be included. This involves proposing a time interval for her talk, which must similarly be an integral interval \([x, y]\) such that \(0 \le x \lt y \le K\). Crys suspects that her request would be rejected if the inclusion of her talk might prevent an attendee from hearing another talk due to her proposed time interval entirely subsuming an already-scheduled one. As such, after the first \(i\) talks have been added to the schedule, she will *not* propose a time interval \([x, y]\) if there exists any existing talk \(j\) \((1 \le j \le i)\) such that \(x \le S_j\) and \(S_j + D_j \le y\).
|
| 6 |
+
|
| 7 |
+
Letting \(C_i\) be the number of different time intervals which Crys could validly propose for her talk after the first \(i\) talks have been added to the schedule, please determine the value of \((C_1 * C_2 * ... * C_N)\) modulo 1,000,000,007.
|
| 8 |
+
|
| 9 |
+
# Constraints
|
| 10 |
+
|
| 11 |
+
\(1 \le T \le 95\)
|
| 12 |
+
\(1 \le N \le 300,000\)
|
| 13 |
+
\(1 \le K \le 1,000,000,000\)
|
| 14 |
+
\(0 \le S_i < K\)
|
| 15 |
+
\(1 \le D_i \le K\)
|
| 16 |
+
\(1 \le S_i + D_i \le K\)
|
| 17 |
+
|
| 18 |
+
The sum of \(N\) across all conferences is at most 1,500,000.
|
| 19 |
+
|
| 20 |
+
# Input
|
| 21 |
+
|
| 22 |
+
Input begins with an integer \(T\), the number of conferences. For each conference there are \(N + 1\) lines. The first line contains the space-separated integers \(N\) and \(K\). \(N\) lines follow, the \(i\)th of which contains the space-separated integers \(S_i\) and \(D_i\).
|
| 23 |
+
|
| 24 |
+
|
| 25 |
+
# Output
|
| 26 |
+
|
| 27 |
+
For the \(i\)th conference, print a line containing *"Case #i: "*, followed by a single integer, the product of \(C_{1..N}\) modulo 1,000,000,007.
|
| 28 |
+
|
| 29 |
+
|
| 30 |
+
|
| 31 |
+
|
| 32 |
+
|
| 33 |
+
# Explanation of Sample
|
| 34 |
+
|
| 35 |
+
In the first conference, once a talk spanning time interval \([1, 2]\) exists, Crys can only propose time intervals \([0, 1]\) and \([2, 3]\) for her talk without subsuming \([1, 2]\). Therefore, \(C = [2]\).
|
| 36 |
+
|
| 37 |
+
In the second conference, after the first talk (spanning time interval \([1, 3]\)) has been added to the schedule, Crys can propose any of the time intervals \([0, 1]\), \([0, 2]\), \([1, 2]\), or \([2, 3]\). After the introduction of the second talk (spanning time interval \([0, 2]\)), she can only propose \([0, 1]\), \([1, 2]\), or \([2, 3]\). Therefore, \(C = [4, 3]\), and the final answer is (4 * 3) modulo 1,000,000,007 = 12.
|
| 38 |
+
|
| 39 |
+
In the third conference, \(C = [8, 4]\).
|
| 40 |
+
|
| 41 |
+
In the fourth conference, \(C = [4126, 3631, 3239, 2687, 2687]\).
|
2020/finals/cryptoconference.out
ADDED
|
@@ -0,0 +1,110 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Case #1: 2
|
| 2 |
+
Case #2: 12
|
| 3 |
+
Case #3: 32
|
| 4 |
+
Case #4: 352996146
|
| 5 |
+
Case #5: 751550872
|
| 6 |
+
Case #6: 20
|
| 7 |
+
Case #7: 83444858
|
| 8 |
+
Case #8: 572887886
|
| 9 |
+
Case #9: 598916604
|
| 10 |
+
Case #10: 470820377
|
| 11 |
+
Case #11: 174927279
|
| 12 |
+
Case #12: 896919730
|
| 13 |
+
Case #13: 541761571
|
| 14 |
+
Case #14: 515822691
|
| 15 |
+
Case #15: 228409848
|
| 16 |
+
Case #16: 659858375
|
| 17 |
+
Case #17: 190419874
|
| 18 |
+
Case #18: 948002069
|
| 19 |
+
Case #19: 495164089
|
| 20 |
+
Case #20: 989289949
|
| 21 |
+
Case #21: 313062055
|
| 22 |
+
Case #22: 317384968
|
| 23 |
+
Case #23: 381355941
|
| 24 |
+
Case #24: 861250172
|
| 25 |
+
Case #25: 21268787
|
| 26 |
+
Case #26: 426473611
|
| 27 |
+
Case #27: 174566443
|
| 28 |
+
Case #28: 270050563
|
| 29 |
+
Case #29: 247721801
|
| 30 |
+
Case #30: 128678835
|
| 31 |
+
Case #31: 141554145
|
| 32 |
+
Case #32: 589771144
|
| 33 |
+
Case #33: 703459805
|
| 34 |
+
Case #34: 770102403
|
| 35 |
+
Case #35: 32994412
|
| 36 |
+
Case #36: 98689617
|
| 37 |
+
Case #37: 146465775
|
| 38 |
+
Case #38: 429027202
|
| 39 |
+
Case #39: 249562463
|
| 40 |
+
Case #40: 939240223
|
| 41 |
+
Case #41: 366445856
|
| 42 |
+
Case #42: 629076290
|
| 43 |
+
Case #43: 856574351
|
| 44 |
+
Case #44: 816923530
|
| 45 |
+
Case #45: 988573584
|
| 46 |
+
Case #46: 227744671
|
| 47 |
+
Case #47: 136671501
|
| 48 |
+
Case #48: 552031554
|
| 49 |
+
Case #49: 637297699
|
| 50 |
+
Case #50: 0
|
| 51 |
+
Case #51: 407393317
|
| 52 |
+
Case #52: 648160821
|
| 53 |
+
Case #53: 453730949
|
| 54 |
+
Case #54: 626850629
|
| 55 |
+
Case #55: 77514078
|
| 56 |
+
Case #56: 776033559
|
| 57 |
+
Case #57: 981403229
|
| 58 |
+
Case #58: 164846153
|
| 59 |
+
Case #59: 486727330
|
| 60 |
+
Case #60: 181718458
|
| 61 |
+
Case #61: 794033109
|
| 62 |
+
Case #62: 741574342
|
| 63 |
+
Case #63: 145879918
|
| 64 |
+
Case #64: 171838401
|
| 65 |
+
Case #65: 417158876
|
| 66 |
+
Case #66: 725642265
|
| 67 |
+
Case #67: 472767853
|
| 68 |
+
Case #68: 740493091
|
| 69 |
+
Case #69: 89444180
|
| 70 |
+
Case #70: 608421866
|
| 71 |
+
Case #71: 393203295
|
| 72 |
+
Case #72: 879337785
|
| 73 |
+
Case #73: 915216546
|
| 74 |
+
Case #74: 290037518
|
| 75 |
+
Case #75: 248932214
|
| 76 |
+
Case #76: 953715588
|
| 77 |
+
Case #77: 167356836
|
| 78 |
+
Case #78: 317540564
|
| 79 |
+
Case #79: 991575711
|
| 80 |
+
Case #80: 879687486
|
| 81 |
+
Case #81: 322773218
|
| 82 |
+
Case #82: 589228118
|
| 83 |
+
Case #83: 466166842
|
| 84 |
+
Case #84: 748094367
|
| 85 |
+
Case #85: 248333831
|
| 86 |
+
Case #86: 515789417
|
| 87 |
+
Case #87: 951341566
|
| 88 |
+
Case #88: 948722510
|
| 89 |
+
Case #89: 517082433
|
| 90 |
+
Case #90: 535310061
|
| 91 |
+
Case #91: 102636817
|
| 92 |
+
Case #92: 805901472
|
| 93 |
+
Case #93: 546788335
|
| 94 |
+
Case #94: 684359382
|
| 95 |
+
Case #95: 454605467
|
| 96 |
+
Case #96: 310565738
|
| 97 |
+
Case #97: 700636353
|
| 98 |
+
Case #98: 266780658
|
| 99 |
+
Case #99: 383812708
|
| 100 |
+
Case #100: 664630757
|
| 101 |
+
Case #101: 289228410
|
| 102 |
+
Case #102: 957511402
|
| 103 |
+
Case #103: 584046200
|
| 104 |
+
Case #104: 58349857
|
| 105 |
+
Case #105: 730036244
|
| 106 |
+
Case #106: 945387917
|
| 107 |
+
Case #107: 744001995
|
| 108 |
+
Case #108: 854694249
|
| 109 |
+
Case #109: 644309315
|
| 110 |
+
Case #110: 801361727
|
2020/finals/cryptoconference_sol.md
ADDED
|
@@ -0,0 +1,9 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
We'll maintain a set \(R\) of all "relevant" talk time intervals. An interval \([x, y]\) is considered irrelevant if ignoring it does not change the set of time intervals which may be proposed, which is the case if and only if there exists another interval which is inclusively contained within it (an interval \([x', y']\) such that \(x \le x'\) and \(y' \le y\)).
|
| 2 |
+
|
| 3 |
+
We'll maintain \(R\) ordered by intervals' start times, in strictly increasing order. Note that this also means that the intervals' end times must be strictly increasing (otherwise, they cannot all be relevant). For convenience, we'll also begin by including dummy intervals \([-1, -1]\) and \([K, K+1]\) in \(R\), whose significance is explained below. From there, updating the set for each new interval may be done relatively straightforwardly in amortized \(O(log(N))\) time, with the new interval either already being irrelevant, or being relevant and causing 0 or more existing intervals to become irrelevant.
|
| 4 |
+
|
| 5 |
+
What remains is maintaining the corresponding answer for \(R\) — that is, the number of time intervals which may be proposed without subsuming any interval in \(R\). For this purpose, let \(F([x_1, y_1], [x_2, y_2])\) be the number of different intervals \([x_p, y_p]\) which may be proposed such that \(x_1 < x_p \le x_2\), given that \([x_1, y_1]\) and \([x_2, y_2]\) form a pair of consecutive relevant intervals in \(R\). Note that \(F([x_1, y_1], [x_2, y_2])\) does not depend on any intervals in \(R\) besides those two, and may be easily computed in \(O(1)\) time using the fact that the only constraints are \(x_1 < x_p \le x_2\) and \(x_p < y_p < y_2\).
|
| 6 |
+
|
| 7 |
+
We can observe that the sum of \(F([x_1, y_1], [x_2, y_2])\) over all pairs of consecutive relevant intervals (of which there are \(|R| - 1\)) is equal to the total answer — for example, this is the case when \(R\) consists only of the initial pair of dummy intervals \([-1, -1]\) and \([K, K+1]\), with additional intervals simply partitioning the set of possible start times. We can then maintain this sum with no additional time complexity as we go. For example, when inserting an interval \(X\) between two existing intervals \(A\) and \(B\), we should increase the sum by \(F(A, X) + F(X, B) - F(A, B)\), with deletions handled similarly.
|
| 8 |
+
|
| 9 |
+
This gives us an algorithm with a time complexity of \(O(N log(N))\).
|
2020/finals/pond_precipitation.cpp
ADDED
|
@@ -0,0 +1,178 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
// Pond Precipitation
|
| 2 |
+
// Solution by Jacob Plachta
|
| 3 |
+
|
| 4 |
+
#include <algorithm>
|
| 5 |
+
#include <functional>
|
| 6 |
+
#include <numeric>
|
| 7 |
+
#include <iostream>
|
| 8 |
+
#include <iomanip>
|
| 9 |
+
#include <cstdio>
|
| 10 |
+
#include <cmath>
|
| 11 |
+
#include <complex>
|
| 12 |
+
#include <cstdlib>
|
| 13 |
+
#include <ctime>
|
| 14 |
+
#include <cstring>
|
| 15 |
+
#include <cassert>
|
| 16 |
+
#include <string>
|
| 17 |
+
#include <vector>
|
| 18 |
+
#include <list>
|
| 19 |
+
#include <map>
|
| 20 |
+
#include <unordered_map>
|
| 21 |
+
#include <set>
|
| 22 |
+
#include <deque>
|
| 23 |
+
#include <queue>
|
| 24 |
+
#include <stack>
|
| 25 |
+
#include <bitset>
|
| 26 |
+
#include <sstream>
|
| 27 |
+
using namespace std;
|
| 28 |
+
|
| 29 |
+
#define LL long long
|
| 30 |
+
#define LD long double
|
| 31 |
+
#define PR pair<int,int>
|
| 32 |
+
|
| 33 |
+
#define Fox(i,n) for (i=0; i<n; i++)
|
| 34 |
+
#define Fox1(i,n) for (i=1; i<=n; i++)
|
| 35 |
+
#define FoxI(i,a,b) for (i=a; i<=b; i++)
|
| 36 |
+
#define FoxR(i,n) for (i=(n)-1; i>=0; i--)
|
| 37 |
+
#define FoxR1(i,n) for (i=n; i>0; i--)
|
| 38 |
+
#define FoxRI(i,a,b) for (i=b; i>=a; i--)
|
| 39 |
+
#define Foxen(i,s) for (i=s.begin(); i!=s.end(); i++)
|
| 40 |
+
#define Min(a,b) a=min(a,b)
|
| 41 |
+
#define Max(a,b) a=max(a,b)
|
| 42 |
+
#define Sz(s) int((s).size())
|
| 43 |
+
#define All(s) (s).begin(),(s).end()
|
| 44 |
+
#define Fill(s,v) memset(s,v,sizeof(s))
|
| 45 |
+
#define pb push_back
|
| 46 |
+
#define mp make_pair
|
| 47 |
+
#define x first
|
| 48 |
+
#define y second
|
| 49 |
+
|
| 50 |
+
template<typename T> T Abs(T x) { return(x < 0 ? -x : x); }
|
| 51 |
+
template<typename T> T Sqr(T x) { return(x * x); }
|
| 52 |
+
string plural(string s) { return(Sz(s) && s[Sz(s) - 1] == 'x' ? s + "en" : s + "s"); }
|
| 53 |
+
|
| 54 |
+
const int INF = (int)1e9;
|
| 55 |
+
const LD EPS = 1e-12;
|
| 56 |
+
const LD PI = acos(-1.0);
|
| 57 |
+
|
| 58 |
+
#define GETCHAR getchar_unlocked
|
| 59 |
+
|
| 60 |
+
bool Read(int& x)
|
| 61 |
+
{
|
| 62 |
+
char c, r = 0, n = 0;
|
| 63 |
+
x = 0;
|
| 64 |
+
for (;;)
|
| 65 |
+
{
|
| 66 |
+
c = GETCHAR();
|
| 67 |
+
if ((c < 0) && (!r))
|
| 68 |
+
return(0);
|
| 69 |
+
if ((c == '-') && (!r))
|
| 70 |
+
n = 1;
|
| 71 |
+
else
|
| 72 |
+
if ((c >= '0') && (c <= '9'))
|
| 73 |
+
x = x * 10 + c - '0', r = 1;
|
| 74 |
+
else
|
| 75 |
+
if (r)
|
| 76 |
+
break;
|
| 77 |
+
}
|
| 78 |
+
if (n)
|
| 79 |
+
x = -x;
|
| 80 |
+
return(1);
|
| 81 |
+
}
|
| 82 |
+
|
| 83 |
+
#define LIM 32
|
| 84 |
+
#define LIM2 500
|
| 85 |
+
#define MOD 1000000007
|
| 86 |
+
|
| 87 |
+
int N;
|
| 88 |
+
int D[LIM], C[LIM];
|
| 89 |
+
int ch[LIM2][LIM2];
|
| 90 |
+
int dyn[LIM][LIM2];
|
| 91 |
+
|
| 92 |
+
int Exp(int a, int b)
|
| 93 |
+
{
|
| 94 |
+
LL p = a, v = 1;
|
| 95 |
+
while (b)
|
| 96 |
+
{
|
| 97 |
+
if (b & 1)
|
| 98 |
+
v = v * p % MOD;
|
| 99 |
+
p = p * p % MOD;
|
| 100 |
+
b >>= 1;
|
| 101 |
+
}
|
| 102 |
+
return(v);
|
| 103 |
+
}
|
| 104 |
+
|
| 105 |
+
void Add(int& a, int b)
|
| 106 |
+
{
|
| 107 |
+
a = (a + b) % MOD;
|
| 108 |
+
}
|
| 109 |
+
|
| 110 |
+
int Prod(int a, int b)
|
| 111 |
+
{
|
| 112 |
+
return((LL)a * b % MOD);
|
| 113 |
+
}
|
| 114 |
+
|
| 115 |
+
int Div(int a, int b)
|
| 116 |
+
{
|
| 117 |
+
return Prod(a, Exp(b, MOD - 2));
|
| 118 |
+
}
|
| 119 |
+
|
| 120 |
+
int ProcessCase()
|
| 121 |
+
{
|
| 122 |
+
int i, j, k;
|
| 123 |
+
// input
|
| 124 |
+
Read(N);
|
| 125 |
+
Fox(i, N)
|
| 126 |
+
Read(D[i]);
|
| 127 |
+
// compute max prefix capacities
|
| 128 |
+
int p = 0, s = 0;
|
| 129 |
+
Fox(i, N + 1)
|
| 130 |
+
{
|
| 131 |
+
if (i == N || D[i] < D[p])
|
| 132 |
+
{
|
| 133 |
+
FoxI(j, p, i - 1)
|
| 134 |
+
s += D[j] - D[p];
|
| 135 |
+
FoxI(j, p + (p ? 1 : 0), i)
|
| 136 |
+
C[j] = s;
|
| 137 |
+
p = i;
|
| 138 |
+
}
|
| 139 |
+
}
|
| 140 |
+
// DP
|
| 141 |
+
Fill(dyn, 0);
|
| 142 |
+
dyn[0][0] = 1;
|
| 143 |
+
Fox(i, N)
|
| 144 |
+
{
|
| 145 |
+
Fox(j, (i ? C[i - 1] : 0) + 1)
|
| 146 |
+
{
|
| 147 |
+
Fox(k, C[i] - j + 1)
|
| 148 |
+
Add(dyn[i + 1][j + k], Prod(dyn[i][j], ch[j + k][k]));
|
| 149 |
+
}
|
| 150 |
+
}
|
| 151 |
+
// compute answer
|
| 152 |
+
int ans = 0;
|
| 153 |
+
Fox(i, s + 1)
|
| 154 |
+
Add(ans, Div(dyn[N][i], Exp(N, i)));
|
| 155 |
+
return(ans);
|
| 156 |
+
}
|
| 157 |
+
|
| 158 |
+
int main()
|
| 159 |
+
{
|
| 160 |
+
int T, t;
|
| 161 |
+
int i, j;
|
| 162 |
+
// precompute choose table
|
| 163 |
+
ch[0][0] = 1;
|
| 164 |
+
Fox1(i, LIM2 - 1)
|
| 165 |
+
{
|
| 166 |
+
Fox(j, i + 1)
|
| 167 |
+
{
|
| 168 |
+
ch[i][j] = ch[i - 1][j];
|
| 169 |
+
if (j)
|
| 170 |
+
Add(ch[i][j], ch[i - 1][j - 1]);
|
| 171 |
+
}
|
| 172 |
+
}
|
| 173 |
+
// testcase loop
|
| 174 |
+
Read(T);
|
| 175 |
+
Fox1(t, T)
|
| 176 |
+
printf("Case #%d: %d\n", t, ProcessCase());
|
| 177 |
+
return(0);
|
| 178 |
+
}
|
2020/finals/pond_precipitation.in
ADDED
|
@@ -0,0 +1,129 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
64
|
| 2 |
+
2
|
| 3 |
+
2 1
|
| 4 |
+
2
|
| 5 |
+
1 2
|
| 6 |
+
1
|
| 7 |
+
30
|
| 8 |
+
3
|
| 9 |
+
3 1 2
|
| 10 |
+
3
|
| 11 |
+
1 3 2
|
| 12 |
+
5
|
| 13 |
+
3 5 4 1 2
|
| 14 |
+
8
|
| 15 |
+
3 7 5 8 2 6 1 4
|
| 16 |
+
15
|
| 17 |
+
11 29 12 10 13 28 15 6 5 25 17 8 9 3 24
|
| 18 |
+
2
|
| 19 |
+
30 1
|
| 20 |
+
2
|
| 21 |
+
1 30
|
| 22 |
+
16
|
| 23 |
+
10 28 18 17 20 19 21 29 5 14 11 8 7 25 3 27
|
| 24 |
+
19
|
| 25 |
+
22 27 26 14 24 17 10 9 30 12 19 28 1 13 25 23 8 20 18
|
| 26 |
+
20
|
| 27 |
+
30 15 29 14 28 13 27 12 26 11 25 10 24 9 23 8 22 7 21 6
|
| 28 |
+
30
|
| 29 |
+
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
|
| 30 |
+
30
|
| 31 |
+
3 30 22 20 14 17 27 19 24 1 23 25 5 12 11 15 29 13 2 8 21 16 26 28 18 4 6 7 9 10
|
| 32 |
+
30
|
| 33 |
+
30 23 9 4 14 10 20 29 26 19 3 22 16 13 24 11 2 15 18 8 7 17 5 28 27 12 6 1 21 25
|
| 34 |
+
29
|
| 35 |
+
23 24 25 30 14 26 22 12 27 19 18 7 8 28 13 9 15 29 10 4 20 17 6 11 3 21 5 1 2
|
| 36 |
+
29
|
| 37 |
+
21 26 6 14 19 27 9 8 23 3 20 4 25 12 17 16 10 22 13 30 24 11 18 15 7 5 1 29 2
|
| 38 |
+
28
|
| 39 |
+
21 28 18 26 10 30 13 19 6 17 24 23 11 3 2 29 4 27 22 14 9 8 1 12 7 20 15 16
|
| 40 |
+
28
|
| 41 |
+
4 12 28 9 15 5 1 17 26 20 27 22 13 29 3 2 21 25 14 6 24 23 10 18 30 16 8 11
|
| 42 |
+
27
|
| 43 |
+
30 24 25 27 20 29 26 15 11 28 23 13 16 10 14 19 3 6 17 8 22 18 2 12 5 1 4
|
| 44 |
+
27
|
| 45 |
+
27 22 21 1 5 7 26 23 13 18 14 28 25 19 29 6 11 3 17 30 24 10 12 16 4 15 8
|
| 46 |
+
26
|
| 47 |
+
22 11 2 16 1 25 15 9 29 12 4 21 8 26 24 18 6 30 13 19 5 23 17 20 7 3
|
| 48 |
+
26
|
| 49 |
+
2 25 29 20 21 27 28 8 23 10 18 17 26 22 24 13 7 12 3 5 14 4 1 15 6 9
|
| 50 |
+
6
|
| 51 |
+
18 25 26 8 10 20
|
| 52 |
+
13
|
| 53 |
+
16 26 25 2 30 27 19 24 22 9 6 4 14
|
| 54 |
+
14
|
| 55 |
+
1 7 20 26 17 11 30 14 15 27 28 5 24 12
|
| 56 |
+
4
|
| 57 |
+
30 7 26 2
|
| 58 |
+
11
|
| 59 |
+
30 24 29 9 18 17 25 13 8 11 4
|
| 60 |
+
16
|
| 61 |
+
10 28 18 17 20 19 21 29 5 14 11 8 7 25 3 27
|
| 62 |
+
5
|
| 63 |
+
30 21 18 9 8
|
| 64 |
+
13
|
| 65 |
+
19 13 24 7 8 21 16 20 3 15 2 30 11
|
| 66 |
+
2
|
| 67 |
+
1 25
|
| 68 |
+
8
|
| 69 |
+
13 12 23 22 25 20 30 15
|
| 70 |
+
13
|
| 71 |
+
20 8 13 3 17 9 30 22 28 2 21 5 12
|
| 72 |
+
19
|
| 73 |
+
22 27 26 14 24 17 10 9 30 12 19 28 1 13 25 23 8 20 18
|
| 74 |
+
9
|
| 75 |
+
30 27 28 13 5 6 2 19 15
|
| 76 |
+
4
|
| 77 |
+
12 25 23 11
|
| 78 |
+
11
|
| 79 |
+
24 6 29 16 14 22 11 1 7 15 2
|
| 80 |
+
20
|
| 81 |
+
11 29 12 10 13 28 15 2 3 25 21 17 8 9 5 24 27 16 23 26
|
| 82 |
+
17
|
| 83 |
+
11 7 6 9 20 14 21 30 23 19 24 8 27 25 2 15 12
|
| 84 |
+
3
|
| 85 |
+
24 20 2
|
| 86 |
+
18
|
| 87 |
+
30 16 25 8 6 23 14 27 29 3 12 18 22 19 9 15 13 11
|
| 88 |
+
6
|
| 89 |
+
17 15 14 12 3 11
|
| 90 |
+
12
|
| 91 |
+
4 22 23 15 13 1 19 8 12 27 14 21
|
| 92 |
+
7
|
| 93 |
+
1 16 25 13 23 7 6
|
| 94 |
+
1
|
| 95 |
+
3
|
| 96 |
+
19
|
| 97 |
+
7 27 24 30 23 29 8 28 25 19 13 21 12 18 1 11 16 10 4
|
| 98 |
+
7
|
| 99 |
+
10 29 30 9 8 5 11
|
| 100 |
+
6
|
| 101 |
+
29 27 25 17 7 2
|
| 102 |
+
6
|
| 103 |
+
29 25 12 10 15 9
|
| 104 |
+
7
|
| 105 |
+
26 21 24 19 20 14 13
|
| 106 |
+
17
|
| 107 |
+
7 25 27 17 21 28 29 24 10 2 4 19 5 8 26 3 11
|
| 108 |
+
16
|
| 109 |
+
18 28 14 7 26 21 17 10 16 13 12 4 8 2 6 1
|
| 110 |
+
16
|
| 111 |
+
23 15 30 16 4 29 1 9 14 2 12 11 22 24 21 17
|
| 112 |
+
6
|
| 113 |
+
30 18 24 17 8 5
|
| 114 |
+
5
|
| 115 |
+
27 30 17 15 5
|
| 116 |
+
15
|
| 117 |
+
29 26 20 28 10 17 19 9 15 5 6 4 8 11 3
|
| 118 |
+
7
|
| 119 |
+
26 27 24 10 17 2 4
|
| 120 |
+
13
|
| 121 |
+
26 22 30 18 28 14 9 20 3 10 5 2 4
|
| 122 |
+
8
|
| 123 |
+
15 20 24 26 14 5 1 2
|
| 124 |
+
1
|
| 125 |
+
26
|
| 126 |
+
4
|
| 127 |
+
17 5 22 7
|
| 128 |
+
6
|
| 129 |
+
28 24 17 5 1 3
|
2020/finals/pond_precipitation.md
ADDED
|
@@ -0,0 +1,76 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Cherry the turtle lives in a long, narrow pond. When cross-sectionally viewed from the side, the floor of the pond can be divided into \(N\) columns, each flat and 1 metre wide. The \(i\)th column from the left is at a depth of \(D_i\) metres below ground level, and all \(N\) column depths are distinct. The pond is surrounded by dirt (at ground level), just to the left of column 1 and the right of column \(N\). Cherry loves to sit on the floor in the leftmost column and bask as much as possible — but only when it's dry. Fortunately for her, the pond is initially devoid of water.
|
| 2 |
+
|
| 3 |
+
For example, if \(D = [3, 5, 4, 1, 2]\), the pond would look as follows (with Cherry's position indicated in green):
|
| 4 |
+
|
| 5 |
+
{{PHOTO_ID:311416436611683}}
|
| 6 |
+
|
| 7 |
+
Unusually enormous drops of rainwater are about to begin falling into the pond, one by one, each onto a random column (drawn uniformly at random from the set of \(N\) columns). Each drop contains 1 cross-sectional square metre of water, and obeys the following process:
|
| 8 |
+
|
| 9 |
+
1. It falls until it hits a flat *surface*. This surface consists of the highest (least deep) point in its column (which might be either the floor of the pond itself or an existing layer of water atop it), as well as all contiguous equally-deep points to the left and right of it.
|
| 10 |
+
2. If that surface is immediately surrounded by any deeper columns to its left and/or right, then the drop's water flows down onto one of them. If there's only one such adjacent deeper column, then the drop flows onto that one. If the columns to the left and right are both deeper than the surface (note that this can only occur if the surface consists of a single column), then the drop's water all flows to the *left* one. Either way, once the drop flows into a different column, the process repeats back from Step 1.
|
| 11 |
+
3. Otherwise, the drop's 1 cross-sectional square metre of water spreads itself out evenly across the entire surface it landed on (which will never cause that surface to "overflow" by becoming strictly higher than the columns to its left or right).
|
| 12 |
+
|
| 13 |
+
Cherry will be forced to stop basking as soon as a non-zero amount of water comes to rest atop column 1. She doesn't mind if raindrops fall directly on column 1 but then immediately flow away from it.
|
| 14 |
+
|
| 15 |
+
For example, if a raindrop were to fall in column 4 of the above pond, it would flow to the left (onto column 3), and then flow left again to settle in column 2:
|
| 16 |
+
|
| 17 |
+
{{PHOTO_ID:3533638723394837}}
|
| 18 |
+
|
| 19 |
+
If a raindrop then fell in column 1, it would flow to the right and spread itself out over the surface spanning columns 2 and 3:
|
| 20 |
+
|
| 21 |
+
{{PHOTO_ID:299743861289784}}
|
| 22 |
+
|
| 23 |
+
If a raindrop then fell in column 5, it would remain there:
|
| 24 |
+
|
| 25 |
+
{{PHOTO_ID:1094784447639382}}
|
| 26 |
+
|
| 27 |
+
Another raindrop falling in column 5 (or *any* column) would then yield the following state:
|
| 28 |
+
|
| 29 |
+
{{PHOTO_ID:747829032476688}}
|
| 30 |
+
|
| 31 |
+
And one more raindrop falling in any column would yield the following state (forcing Cherry to stop basking due to column 1 becoming submerged in water):
|
| 32 |
+
|
| 33 |
+
{{PHOTO_ID:477696676534167}}
|
| 34 |
+
|
| 35 |
+
Determine the expected number of drops which will fall before Cherry is forced to stop basking. This will always occur after a finite number of drops have fallen, and before any water overflows the pond.
|
| 36 |
+
|
| 37 |
+
Let this expected number of drops be represented as a quotient of integers \(p/q\) in lowest terms. Output the value of this quotient modulo 1,000,000,007 — in other words, output the unique integer \(x\) such that \(0 \le x \lt 1,000,000,007\) and \(p \equiv x*q\text{ }(\text{modulo }1,000,000,007)\).
|
| 38 |
+
|
| 39 |
+
|
| 40 |
+
# Constraints
|
| 41 |
+
|
| 42 |
+
\(1 \le T \le 50\)
|
| 43 |
+
\(1 \le N \le 30\)
|
| 44 |
+
\(1 \le D_i \le 30\)
|
| 45 |
+
\(D_{1..N}\) are distinct
|
| 46 |
+
|
| 47 |
+
The sum of \(N\) across all ponds is at most 1000.
|
| 48 |
+
|
| 49 |
+
|
| 50 |
+
# Input
|
| 51 |
+
|
| 52 |
+
Input begins with an integer \(T\), the number of ponds. For each pond, there are 2 lines. The first line contains a single integer \(N\). The second line contains the \(N\) space-separated integers \(D_{1..N}\).
|
| 53 |
+
|
| 54 |
+
|
| 55 |
+
# Output
|
| 56 |
+
|
| 57 |
+
For the \(i\)th pond, print a line containing *"Case #i: "*, followed by a single integer, the expected number of drops which will fall before the leftmost column becomes covered in water, expressed as a quotient of integers modulo 1,000,000,007.
|
| 58 |
+
|
| 59 |
+
|
| 60 |
+
# Explanation of Sample
|
| 61 |
+
|
| 62 |
+
The first pond initially looks as follows:
|
| 63 |
+
|
| 64 |
+
{{PHOTO_ID:1173260263089522}}
|
| 65 |
+
|
| 66 |
+
If the first raindrop falls in column 1, it will settle there, and if it falls in column 2 instead, it will flow into column 1. Either way, Cherry's position will be submerged and she'll be forced to stop basking.
|
| 67 |
+
|
| 68 |
+
The second pond initially looks as follows:
|
| 69 |
+
|
| 70 |
+
{{PHOTO_ID:127321889008596}}
|
| 71 |
+
|
| 72 |
+
The first raindrop will always settle in column 2, leaving Cherry uninterrupted. However, the second raindrop will then always land on the surface spanning both columns, filling both up to a depth of 0.5 metres below ground level and thus forcing Cherry to stop basking.
|
| 73 |
+
|
| 74 |
+
The third pond only has a single column, and Cherry will need to stop basking as soon as the first raindrop falls in it.
|
| 75 |
+
|
| 76 |
+
The fourth pond may end up in various states depending on which columns the raindrops fall in. If the first drop falls in either column 1 or 2, then it will immediately settle in column 1, while if it falls in column 3, it will remain there and it will take a second drop to force Cherry to stop basking. The answer is therefore \(\frac{2}{3} 1 + \frac{1}{3} 2 = \frac{4}{3}\). \(4 \equiv 333,333,337 * 3\text{ }(\text{modulo }1,000,000,007)\), meaning that \(333,333,337\) should be outputted.
|
2020/finals/pond_precipitation.out
ADDED
|
@@ -0,0 +1,64 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Case #1: 1
|
| 2 |
+
Case #2: 2
|
| 3 |
+
Case #3: 1
|
| 4 |
+
Case #4: 333333337
|
| 5 |
+
Case #5: 4
|
| 6 |
+
Case #6: 772800010
|
| 7 |
+
Case #7: 600238862
|
| 8 |
+
Case #8: 777291572
|
| 9 |
+
Case #9: 1
|
| 10 |
+
Case #10: 30
|
| 11 |
+
Case #11: 937030791
|
| 12 |
+
Case #12: 413793850
|
| 13 |
+
Case #13: 839435693
|
| 14 |
+
Case #14: 436
|
| 15 |
+
Case #15: 443547255
|
| 16 |
+
Case #16: 396227790
|
| 17 |
+
Case #17: 466103174
|
| 18 |
+
Case #18: 817567450
|
| 19 |
+
Case #19: 617077188
|
| 20 |
+
Case #20: 328627652
|
| 21 |
+
Case #21: 923842801
|
| 22 |
+
Case #22: 461892853
|
| 23 |
+
Case #23: 120289842
|
| 24 |
+
Case #24: 898611294
|
| 25 |
+
Case #25: 639276210
|
| 26 |
+
Case #26: 153140977
|
| 27 |
+
Case #27: 224
|
| 28 |
+
Case #28: 64313891
|
| 29 |
+
Case #29: 492753435
|
| 30 |
+
Case #30: 937030791
|
| 31 |
+
Case #31: 1
|
| 32 |
+
Case #32: 147204623
|
| 33 |
+
Case #33: 25
|
| 34 |
+
Case #34: 748059186
|
| 35 |
+
Case #35: 716331815
|
| 36 |
+
Case #36: 413793850
|
| 37 |
+
Case #37: 351458863
|
| 38 |
+
Case #38: 25
|
| 39 |
+
Case #39: 510316599
|
| 40 |
+
Case #40: 840006893
|
| 41 |
+
Case #41: 943180527
|
| 42 |
+
Case #42: 1
|
| 43 |
+
Case #43: 249621861
|
| 44 |
+
Case #44: 746767720
|
| 45 |
+
Case #45: 981645522
|
| 46 |
+
Case #46: 85
|
| 47 |
+
Case #47: 1
|
| 48 |
+
Case #48: 509775157
|
| 49 |
+
Case #49: 3252335
|
| 50 |
+
Case #50: 1
|
| 51 |
+
Case #51: 646090541
|
| 52 |
+
Case #52: 822157443
|
| 53 |
+
Case #53: 357912021
|
| 54 |
+
Case #54: 532071843
|
| 55 |
+
Case #55: 723030647
|
| 56 |
+
Case #56: 799725660
|
| 57 |
+
Case #57: 4
|
| 58 |
+
Case #58: 124032548
|
| 59 |
+
Case #59: 677744521
|
| 60 |
+
Case #60: 752783508
|
| 61 |
+
Case #61: 893366069
|
| 62 |
+
Case #62: 1
|
| 63 |
+
Case #63: 64313891
|
| 64 |
+
Case #64: 194444447
|
2020/finals/pond_precipitation_sol.md
ADDED
|
@@ -0,0 +1,5 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Let \(C_i\) be the maximum number of raindrops which can fall in the first \(i\) columns without causing any water to settle atop column 1. We can compute \(C_{1..N}\) in \(O(N)\) time by iterating over the columns from left to right, looking for each new highest (least deep) column, and considering filling the columns before it (back to the previous highest column) with water up to the depth of that previous highest column.
|
| 2 |
+
|
| 3 |
+
Then, let \(\textit{DP}_{i,d}\) be the number of different ways for \(d\) raindrops to fall in the first \(i\) columns without causing any water to settle atop column 1. \(\textit{DP}_{0,0}\) = 1, with the remaining values computable using dynamic programming as follows. We can consider all triples \((i, d, d')\) in increasing order of \(i\) such that \(d\) drops have fallen in the first \(i\) columns (such that \(d \le C_i\)) and \(d'\) drops will fall in column \(i + 1\) (such that \(d + d' \le C_{i+1}\)). This allows us to increase \(\textit{DP}_{i+1,d+d'}\) by \(\textit{DP}_{i,d} * {d+d' \choose d'}\), given that the new \(d'\) drops may be mixed in anywhere amongst the total \(d+d'\) drops. Overall, this process takes \(O(N * \sum(D_{1..N})^2)\) time.
|
| 4 |
+
|
| 5 |
+
Finally, let \(S_d\) be the probability that, once \(d\) drops have fallen, no water has yet settled atop column 1. Note that \(S_d = \textit{DP}_{N,d} / N^i\). The answer may then be computed as \(\sum(S_{0..C_N})\).
|
2020/finals/somebody_elses_problem.cpp
ADDED
|
@@ -0,0 +1,152 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
// Somebody Else's Problem
|
| 2 |
+
// Solution by Jacob Plachta
|
| 3 |
+
|
| 4 |
+
#include <algorithm>
|
| 5 |
+
#include <functional>
|
| 6 |
+
#include <numeric>
|
| 7 |
+
#include <iostream>
|
| 8 |
+
#include <iomanip>
|
| 9 |
+
#include <cstdio>
|
| 10 |
+
#include <cmath>
|
| 11 |
+
#include <complex>
|
| 12 |
+
#include <cstdlib>
|
| 13 |
+
#include <ctime>
|
| 14 |
+
#include <cstring>
|
| 15 |
+
#include <cassert>
|
| 16 |
+
#include <string>
|
| 17 |
+
#include <vector>
|
| 18 |
+
#include <list>
|
| 19 |
+
#include <map>
|
| 20 |
+
#include <set>
|
| 21 |
+
#include <unordered_map>
|
| 22 |
+
#include <unordered_set>
|
| 23 |
+
#include <deque>
|
| 24 |
+
#include <queue>
|
| 25 |
+
#include <stack>
|
| 26 |
+
#include <bitset>
|
| 27 |
+
#include <sstream>
|
| 28 |
+
using namespace std;
|
| 29 |
+
|
| 30 |
+
#define LL long long
|
| 31 |
+
#define LD long double
|
| 32 |
+
#define PR pair<int,int>
|
| 33 |
+
|
| 34 |
+
#define Fox(i,n) for (i=0; i<n; i++)
|
| 35 |
+
#define Fox1(i,n) for (i=1; i<=n; i++)
|
| 36 |
+
#define FoxI(i,a,b) for (i=a; i<=b; i++)
|
| 37 |
+
#define FoxR(i,n) for (i=(n)-1; i>=0; i--)
|
| 38 |
+
#define FoxR1(i,n) for (i=n; i>0; i--)
|
| 39 |
+
#define FoxRI(i,a,b) for (i=b; i>=a; i--)
|
| 40 |
+
#define Foxen(i,s) for (auto i:s)
|
| 41 |
+
#define Min(a,b) a=min(a,b)
|
| 42 |
+
#define Max(a,b) a=max(a,b)
|
| 43 |
+
#define Sz(s) int((s).size())
|
| 44 |
+
#define All(s) (s).begin(),(s).end()
|
| 45 |
+
#define Fill(s,v) memset(s,v,sizeof(s))
|
| 46 |
+
#define pb push_back
|
| 47 |
+
#define mp make_pair
|
| 48 |
+
#define x first
|
| 49 |
+
#define y second
|
| 50 |
+
|
| 51 |
+
template<typename T> T Abs(T x) { return(x < 0 ? -x : x); }
|
| 52 |
+
template<typename T> T Sqr(T x) { return(x * x); }
|
| 53 |
+
string plural(string s) { return(Sz(s) && s[Sz(s) - 1] == 'x' ? s + "en" : s + "s"); }
|
| 54 |
+
|
| 55 |
+
const int INF = (int)1e9;
|
| 56 |
+
const LD EPS = 1e-12;
|
| 57 |
+
const LD PI = acos(-1.0);
|
| 58 |
+
|
| 59 |
+
#define GETCHAR getchar_unlocked
|
| 60 |
+
|
| 61 |
+
bool Read(int& x) {
|
| 62 |
+
char c, r = 0, n = 0;
|
| 63 |
+
x = 0;
|
| 64 |
+
for (;;) {
|
| 65 |
+
c = GETCHAR();
|
| 66 |
+
if ((c < 0) && (!r))
|
| 67 |
+
return(0);
|
| 68 |
+
if ((c == '-') && (!r))
|
| 69 |
+
n = 1;
|
| 70 |
+
else if ((c >= '0') && (c <= '9'))
|
| 71 |
+
x = x * 10 + c - '0', r = 1;
|
| 72 |
+
else if (r)
|
| 73 |
+
break;
|
| 74 |
+
}
|
| 75 |
+
if (n)
|
| 76 |
+
x = -x;
|
| 77 |
+
return(1);
|
| 78 |
+
}
|
| 79 |
+
|
| 80 |
+
#define MOD 1000000007
|
| 81 |
+
#define LIM 1000001
|
| 82 |
+
|
| 83 |
+
int N, ans;
|
| 84 |
+
vector<int> ch[LIM];
|
| 85 |
+
int dyn1[LIM]; // max. len. of downward i -> leaf
|
| 86 |
+
int dyn2[LIM]; // max. len. of downward root -> leaf outside i's subtree
|
| 87 |
+
int dyn3[LIM]; // max. disjoint len. of downward root -> leaf plus other path ongoing from i's parent
|
| 88 |
+
|
| 89 |
+
void rec1(int i)
|
| 90 |
+
{
|
| 91 |
+
// recurse, and compute dyn1[i]
|
| 92 |
+
dyn1[i] = 0;
|
| 93 |
+
Foxen(c, ch[i])
|
| 94 |
+
{
|
| 95 |
+
rec1(c);
|
| 96 |
+
Max(dyn1[i], dyn1[c] + 1);
|
| 97 |
+
}
|
| 98 |
+
}
|
| 99 |
+
|
| 100 |
+
void rec2(int i, int d)
|
| 101 |
+
{
|
| 102 |
+
// compute answer for i
|
| 103 |
+
ans = ans * (LL)max(dyn1[i] + dyn2[i] + (!i ? 0 : 1), dyn3[i]) % MOD;
|
| 104 |
+
// compute max 2 (dyn1[c] + 1, c) pairs
|
| 105 |
+
PR m1, m2;
|
| 106 |
+
m1 = m2 = mp(0, -1);
|
| 107 |
+
Foxen(c, ch[i])
|
| 108 |
+
{
|
| 109 |
+
PR p = mp(dyn1[c] + 1, c);
|
| 110 |
+
if (p > m1)
|
| 111 |
+
m2 = m1, m1 = p;
|
| 112 |
+
else if (p > m2)
|
| 113 |
+
m2 = p;
|
| 114 |
+
}
|
| 115 |
+
// compute dyn2[c] and dyn3[c], and recurse
|
| 116 |
+
Foxen(c, ch[i])
|
| 117 |
+
{
|
| 118 |
+
int m = (m1.y == c ? m2 : m1).x;
|
| 119 |
+
dyn2[c] = max(d + m, dyn2[i]);
|
| 120 |
+
dyn3[c] = max(dyn3[i] + 1, dyn2[i] + m + 1 + (!i ? 0 : 1));
|
| 121 |
+
rec2(c, d + 1);
|
| 122 |
+
}
|
| 123 |
+
}
|
| 124 |
+
|
| 125 |
+
int ProcessCase()
|
| 126 |
+
{
|
| 127 |
+
int i, j;
|
| 128 |
+
// input
|
| 129 |
+
Read(N);
|
| 130 |
+
Fox1(i, N - 1)
|
| 131 |
+
{
|
| 132 |
+
Read(j), j--;
|
| 133 |
+
ch[j].pb(i);
|
| 134 |
+
}
|
| 135 |
+
// DP
|
| 136 |
+
ans = 1;
|
| 137 |
+
rec1(0);
|
| 138 |
+
rec2(0, 0);
|
| 139 |
+
// reset
|
| 140 |
+
Fox(i, N)
|
| 141 |
+
ch[i].clear();
|
| 142 |
+
return(ans);
|
| 143 |
+
}
|
| 144 |
+
|
| 145 |
+
int main()
|
| 146 |
+
{
|
| 147 |
+
int T, t;
|
| 148 |
+
Read(T);
|
| 149 |
+
Fox1(t, T)
|
| 150 |
+
printf("Case #%d: %d\n", t, ProcessCase());
|
| 151 |
+
return(0);
|
| 152 |
+
}
|
2020/finals/somebody_elses_problem.in
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:42fb026894d3a2c67d12bff5c8c7605976525e17fb94ed2dfc18ae0b5a91a494
|
| 3 |
+
size 29992845
|
2020/finals/somebody_elses_problem.md
ADDED
|
@@ -0,0 +1,44 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
H Combinator (HC) is a business incubator that provides seed funding to startups. It operates on the core value that "nothing is somebody else's problem" (since businesses slow down when tasks get perpetually passed from person to person). HC currently supports \(T\) companies. As a managing director hoping to weed out some bad investments, you would like to assess how well the structure of each company holds up to this important principle.
|
| 2 |
+
|
| 3 |
+
Suppose a company has \(N\) employees, numbered \(1\) to \(N\) in decreasing order of seniority. Employee \(1\) is the CEO, while each other employee \(i\) \((i \ge 2)\) has a manager, employee \(M_i\) \((M_i \lt i)\).
|
| 4 |
+
|
| 5 |
+
When employee \(i\) is assigned a task to complete, they may instead reassign it to one of the following employees:
|
| 6 |
+
|
| 7 |
+
1. One of their direct reports (any employee \(j\) such that \(M_j = i\)), if any exist
|
| 8 |
+
2. Their manager (employee \(M_i\)), if \(i \ge 2\)
|
| 9 |
+
3. The CEO (employee \(1\)), if \(i \ge 2\)
|
| 10 |
+
|
| 11 |
+
That employee may then reassign the task to yet another employee, and so on. However, an employee may never be reassigned a task that has ever been previously assigned to them, as the lack of responsibility would become too apparent. For example, an employee and manager cannot repeatedly pass a task back and forth.
|
| 12 |
+
|
| 13 |
+
Let \(R_i\) be the maximum number of times that a task could be reassigned from one employee to another if it were initially assigned to employee \(i\). For each company, you would like to calculate the product \((R_1 * R_2 * ... * R_N)\), modulo 1,000,000,007.
|
| 14 |
+
|
| 15 |
+
# Constraints
|
| 16 |
+
|
| 17 |
+
\(1 \le T \le 100\)
|
| 18 |
+
\(2 \le N \le 1,000,000\)
|
| 19 |
+
\(1 \le M_i \lt i\)
|
| 20 |
+
|
| 21 |
+
The sum of \(N\) across all companies is at most 6,000,000.
|
| 22 |
+
|
| 23 |
+
|
| 24 |
+
# Input
|
| 25 |
+
|
| 26 |
+
Input begins with an integer \(T\), the number of companies. For each company there are 2 lines. The first line contains the single integer \(N\). The second line contains \(N - 1\) space-separated integers, \(M_{2..N}\).
|
| 27 |
+
|
| 28 |
+
|
| 29 |
+
# Output
|
| 30 |
+
|
| 31 |
+
For the \(i\)th company, print a line containing *"Case #i: "*, followed by a single integer, the product of \(R_{1..N}\) modulo 1,000,000,007.
|
| 32 |
+
|
| 33 |
+
|
| 34 |
+
# Explanation of Sample
|
| 35 |
+
|
| 36 |
+
For the first company, if the CEO is initially assigned a task, all they can do is reassign it to one of their reports, who cannot then assign it back. On the other hand, if another employee is initially assigned a task, they can reassign it to the CEO, who can then assign it to the other remaining employee. Therefore, \(R = [1, 2, 2]\), and the final answer is (1 * 2 * 2) modulo 1,000,000,007 = 4.
|
| 37 |
+
|
| 38 |
+
For the second company, no matter which employee is initially assigned a task, it can then be reassigned twice. For example, employee 2 can assign their task to their report (employee 3), who can then assign it to the CEO. Therefore, \(R = [2, 2, 2]\).
|
| 39 |
+
|
| 40 |
+
For the third company, \(R = [2, 2, 3, 3]\).
|
| 41 |
+
|
| 42 |
+
For the fourth company, \(R = [3, 6, 6, 6, 7, 7, 7, 7, 8, 8]\).
|
| 43 |
+
|
| 44 |
+
For the fifth company, \(R = [4, 6, 6, 7, 8, 6, 7, 7, 8, 7, 7, 8, 8, 9, 9]\).
|
2020/finals/somebody_elses_problem.out
ADDED
|
@@ -0,0 +1,109 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Case #1: 4
|
| 2 |
+
Case #2: 8
|
| 3 |
+
Case #3: 36
|
| 4 |
+
Case #4: 99574272
|
| 5 |
+
Case #5: 801542729
|
| 6 |
+
Case #6: 512
|
| 7 |
+
Case #7: 110638080
|
| 8 |
+
Case #8: 100755024
|
| 9 |
+
Case #9: 609548256
|
| 10 |
+
Case #10: 449377614
|
| 11 |
+
Case #11: 697200545
|
| 12 |
+
Case #12: 40681884
|
| 13 |
+
Case #13: 801335875
|
| 14 |
+
Case #14: 912420599
|
| 15 |
+
Case #15: 828211555
|
| 16 |
+
Case #16: 222945837
|
| 17 |
+
Case #17: 794621467
|
| 18 |
+
Case #18: 539189349
|
| 19 |
+
Case #19: 153951545
|
| 20 |
+
Case #20: 403356442
|
| 21 |
+
Case #21: 158834216
|
| 22 |
+
Case #22: 757493143
|
| 23 |
+
Case #23: 124049818
|
| 24 |
+
Case #24: 157599195
|
| 25 |
+
Case #25: 210009530
|
| 26 |
+
Case #26: 934651967
|
| 27 |
+
Case #27: 846283835
|
| 28 |
+
Case #28: 135977128
|
| 29 |
+
Case #29: 96550718
|
| 30 |
+
Case #30: 460241648
|
| 31 |
+
Case #31: 168595112
|
| 32 |
+
Case #32: 212089364
|
| 33 |
+
Case #33: 533764564
|
| 34 |
+
Case #34: 887365886
|
| 35 |
+
Case #35: 959297767
|
| 36 |
+
Case #36: 518707324
|
| 37 |
+
Case #37: 926754190
|
| 38 |
+
Case #38: 800571094
|
| 39 |
+
Case #39: 352762395
|
| 40 |
+
Case #40: 446732699
|
| 41 |
+
Case #41: 137078595
|
| 42 |
+
Case #42: 82460488
|
| 43 |
+
Case #43: 63988313
|
| 44 |
+
Case #44: 368079615
|
| 45 |
+
Case #45: 874039636
|
| 46 |
+
Case #46: 259792328
|
| 47 |
+
Case #47: 680495316
|
| 48 |
+
Case #48: 310927912
|
| 49 |
+
Case #49: 159825100
|
| 50 |
+
Case #50: 757078864
|
| 51 |
+
Case #51: 11192700
|
| 52 |
+
Case #52: 815983871
|
| 53 |
+
Case #53: 221642594
|
| 54 |
+
Case #54: 881701383
|
| 55 |
+
Case #55: 233697937
|
| 56 |
+
Case #56: 842482923
|
| 57 |
+
Case #57: 765406592
|
| 58 |
+
Case #58: 989866696
|
| 59 |
+
Case #59: 898464379
|
| 60 |
+
Case #60: 345934457
|
| 61 |
+
Case #61: 451190753
|
| 62 |
+
Case #62: 322496398
|
| 63 |
+
Case #63: 475160557
|
| 64 |
+
Case #64: 996799426
|
| 65 |
+
Case #65: 211994997
|
| 66 |
+
Case #66: 690657310
|
| 67 |
+
Case #67: 971619993
|
| 68 |
+
Case #68: 440397393
|
| 69 |
+
Case #69: 481512798
|
| 70 |
+
Case #70: 186452849
|
| 71 |
+
Case #71: 708281413
|
| 72 |
+
Case #72: 357202043
|
| 73 |
+
Case #73: 777137428
|
| 74 |
+
Case #74: 841177015
|
| 75 |
+
Case #75: 825117615
|
| 76 |
+
Case #76: 853698291
|
| 77 |
+
Case #77: 594949860
|
| 78 |
+
Case #78: 404255967
|
| 79 |
+
Case #79: 458058760
|
| 80 |
+
Case #80: 589833391
|
| 81 |
+
Case #81: 311188915
|
| 82 |
+
Case #82: 858709805
|
| 83 |
+
Case #83: 457598660
|
| 84 |
+
Case #84: 291250389
|
| 85 |
+
Case #85: 89919554
|
| 86 |
+
Case #86: 964724850
|
| 87 |
+
Case #87: 87366696
|
| 88 |
+
Case #88: 253283539
|
| 89 |
+
Case #89: 417747428
|
| 90 |
+
Case #90: 10644788
|
| 91 |
+
Case #91: 95418217
|
| 92 |
+
Case #92: 560671530
|
| 93 |
+
Case #93: 326047040
|
| 94 |
+
Case #94: 463949173
|
| 95 |
+
Case #95: 905018983
|
| 96 |
+
Case #96: 201781788
|
| 97 |
+
Case #97: 955583192
|
| 98 |
+
Case #98: 319780485
|
| 99 |
+
Case #99: 514572911
|
| 100 |
+
Case #100: 92757427
|
| 101 |
+
Case #101: 829713327
|
| 102 |
+
Case #102: 367443664
|
| 103 |
+
Case #103: 932977208
|
| 104 |
+
Case #104: 247500328
|
| 105 |
+
Case #105: 387055634
|
| 106 |
+
Case #106: 191909169
|
| 107 |
+
Case #107: 421840147
|
| 108 |
+
Case #108: 730451318
|
| 109 |
+
Case #109: 493473473
|
2020/finals/somebody_elses_problem_sol.md
ADDED
|
@@ -0,0 +1,18 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
The employees can be considered nodes of a tree rooted at node 1 (the CEO), with each node \(i\)'s set of children \(C_i\) consisting of all nodes \(j\) such that \(M_j = i\). We'll additionally let \(D_i\) be the depth of node \(i\), and \(S_i\) be its set of siblings.
|
| 2 |
+
|
| 3 |
+
We can observe that \(R_i\) corresponds to either of the following:
|
| 4 |
+
|
| 5 |
+
- The maximum length of any single simple path starting at node \(i\) (potentially going upwards to some ancestor and then back downwards)
|
| 6 |
+
- 1 plus the maximum combined length of any node-disjoint pair of simple paths, the first one starting at node \(i\) (potentially going upwards to some ancestor and then back downwards) and the second starting at the root (and only going downwards)
|
| 7 |
+
|
| 8 |
+
We'll approach computing these lengths and sums with dynamic programming.
|
| 9 |
+
|
| 10 |
+
First, let \(\textit{DP1}_i\) be the maximum length of any path starting at node \(i\) and contained within \(i\)'s subtree. \(\textit{DP1}_{1..N}\) may be computed in standard fashion based on the recurrence \(\textit{DP1}_i = \max(c \in C_i | \textit{DP1}_c + 1)\).
|
| 11 |
+
|
| 12 |
+
Next, let \(\textit{DP2}_i\) be the maximum length of any path starting at the root and never entering node \(i\)'s subtree. If \(i\) is the root, then \(\textit{DP2}_i = 0\). Otherwise, \(\textit{DP2}_i = \max(D_{M_i} + \max(s \in S_i | \textit{DP1}_s + 1), \textit{DP2}_{M_i})\).
|
| 13 |
+
|
| 14 |
+
Now, let \(\textit{DP3}_i\) be 1 plus the maximum combined length of any node-disjoint pair of simple paths, the first one starting at node \(i\) but not including any of \(i\)'s children, and the second starting at the root. If \(i\) is the root, then \(\textit{DP3}_i = 0\). Otherwise, \(\textit{DP3}_i = \max(\textit{DP3}_{M_i} + 1, \textit{DP2}_{M_i} + \max(s \in S_i | \textit{DP1}_s + 1) + 2)\).
|
| 15 |
+
|
| 16 |
+
Finally, if \(i\) is the root, then \(R_i = \textit{DP1}_i\). Otherwise, \(R_i = \max(\textit{DP1}_i + \textit{DP2}_i + 1, \textit{DP3}_i)\).
|
| 17 |
+
|
| 18 |
+
We can compute all of the above values in \(O(N)\) time through two recursive (or iterative) passes over the tree.
|
2020/finals/spider_spring.cpp
ADDED
|
@@ -0,0 +1,310 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
// Spider Spring
|
| 2 |
+
// Solution by Jacob Plachta
|
| 3 |
+
|
| 4 |
+
#include <algorithm>
|
| 5 |
+
#include <functional>
|
| 6 |
+
#include <numeric>
|
| 7 |
+
#include <iostream>
|
| 8 |
+
#include <iomanip>
|
| 9 |
+
#include <cstdio>
|
| 10 |
+
#include <cmath>
|
| 11 |
+
#include <complex>
|
| 12 |
+
#include <cstdlib>
|
| 13 |
+
#include <ctime>
|
| 14 |
+
#include <cstring>
|
| 15 |
+
#include <cassert>
|
| 16 |
+
#include <string>
|
| 17 |
+
#include <vector>
|
| 18 |
+
#include <list>
|
| 19 |
+
#include <map>
|
| 20 |
+
#include <set>
|
| 21 |
+
#include <unordered_map>
|
| 22 |
+
#include <unordered_set>
|
| 23 |
+
#include <deque>
|
| 24 |
+
#include <queue>
|
| 25 |
+
#include <stack>
|
| 26 |
+
#include <bitset>
|
| 27 |
+
#include <sstream>
|
| 28 |
+
using namespace std;
|
| 29 |
+
|
| 30 |
+
#define LL long long
|
| 31 |
+
#define LD long double
|
| 32 |
+
#define PR pair<int,int>
|
| 33 |
+
|
| 34 |
+
#define Fox(i,n) for (i=0; i<n; i++)
|
| 35 |
+
#define Fox1(i,n) for (i=1; i<=n; i++)
|
| 36 |
+
#define FoxI(i,a,b) for (i=a; i<=b; i++)
|
| 37 |
+
#define FoxR(i,n) for (i=(n)-1; i>=0; i--)
|
| 38 |
+
#define FoxR1(i,n) for (i=n; i>0; i--)
|
| 39 |
+
#define FoxRI(i,a,b) for (i=b; i>=a; i--)
|
| 40 |
+
#define Foxen(i,s) for (i=s.begin(); i!=s.end(); i++)
|
| 41 |
+
#define Min(a,b) a=min(a,b)
|
| 42 |
+
#define Max(a,b) a=max(a,b)
|
| 43 |
+
#define Sz(s) int((s).size())
|
| 44 |
+
#define All(s) (s).begin(),(s).end()
|
| 45 |
+
#define Fill(s,v) memset(s,v,sizeof(s))
|
| 46 |
+
#define pb push_back
|
| 47 |
+
#define mp make_pair
|
| 48 |
+
#define x first
|
| 49 |
+
#define y second
|
| 50 |
+
|
| 51 |
+
template<typename T> T Abs(T x) { return(x < 0 ? -x : x); }
|
| 52 |
+
template<typename T> T Sqr(T x) { return(x * x); }
|
| 53 |
+
string plural(string s) { return(Sz(s) && s[Sz(s) - 1] == 'x' ? s + "en" : s + "s"); }
|
| 54 |
+
|
| 55 |
+
const int INF = (int)1e9;
|
| 56 |
+
const LD EPS = 1e-12;
|
| 57 |
+
const LD PI = acos(-1.0);
|
| 58 |
+
|
| 59 |
+
#define GETCHAR getchar_unlocked
|
| 60 |
+
|
| 61 |
+
bool Read(int& x) {
|
| 62 |
+
char c, r = 0, n = 0;
|
| 63 |
+
x = 0;
|
| 64 |
+
for (;;) {
|
| 65 |
+
c = GETCHAR();
|
| 66 |
+
if ((c < 0) && (!r))
|
| 67 |
+
return(0);
|
| 68 |
+
if ((c == '-') && (!r))
|
| 69 |
+
n = 1;
|
| 70 |
+
else if ((c >= '0') && (c <= '9'))
|
| 71 |
+
x = x * 10 + c - '0', r = 1;
|
| 72 |
+
else if (r)
|
| 73 |
+
break;
|
| 74 |
+
}
|
| 75 |
+
if (n)
|
| 76 |
+
x = -x;
|
| 77 |
+
return(1);
|
| 78 |
+
}
|
| 79 |
+
|
| 80 |
+
void ReadSeq(int* V, int N, int K)
|
| 81 |
+
{
|
| 82 |
+
int i, A, B, C, D;
|
| 83 |
+
Fox(i, K)
|
| 84 |
+
Read(V[i]);
|
| 85 |
+
Read(A), Read(B), Read(C), Read(D);
|
| 86 |
+
FoxI(i, K, N - 1)
|
| 87 |
+
V[i] = ((LL)A * V[i - 2] + (LL)B * V[i - 1] + C) % D + 1;
|
| 88 |
+
}
|
| 89 |
+
|
| 90 |
+
#define MOD 1000000007
|
| 91 |
+
#define LIM 1000001
|
| 92 |
+
|
| 93 |
+
#define TVAL LL
|
| 94 |
+
#define TLAZY pair<LL,LL> // (set, increase)
|
| 95 |
+
#define TLIM 2100000
|
| 96 |
+
|
| 97 |
+
TVAL ZERO_VAL = 0;
|
| 98 |
+
TLAZY ZERO_LAZY = mp(0, 0);
|
| 99 |
+
|
| 100 |
+
struct SegTree
|
| 101 |
+
{
|
| 102 |
+
void UpdateValForUpdateOrLazy(TVAL& a, TLAZY v)
|
| 103 |
+
{
|
| 104 |
+
if (v.x)
|
| 105 |
+
a = v.x;
|
| 106 |
+
if (v.y)
|
| 107 |
+
a += v.y;
|
| 108 |
+
}
|
| 109 |
+
|
| 110 |
+
void UpdateLazyForUpdateOrLazy(TLAZY& a, TLAZY v)
|
| 111 |
+
{
|
| 112 |
+
if (v.x)
|
| 113 |
+
a.x = v.x;
|
| 114 |
+
if (v.y)
|
| 115 |
+
a.y += v.y;
|
| 116 |
+
}
|
| 117 |
+
|
| 118 |
+
TVAL CombVals(TVAL v1, TVAL v2)
|
| 119 |
+
{
|
| 120 |
+
return(v1 + v2);
|
| 121 |
+
}
|
| 122 |
+
|
| 123 |
+
int N, sz;
|
| 124 |
+
TVAL tree[TLIM];
|
| 125 |
+
TLAZY lazy[TLIM];
|
| 126 |
+
|
| 127 |
+
SegTree() {}
|
| 128 |
+
|
| 129 |
+
SegTree(int _N)
|
| 130 |
+
{
|
| 131 |
+
Init(_N);
|
| 132 |
+
}
|
| 133 |
+
|
| 134 |
+
void Init(int _N)
|
| 135 |
+
{
|
| 136 |
+
N = _N;
|
| 137 |
+
for (sz = 1; sz < N; sz <<= 1);
|
| 138 |
+
Clear();
|
| 139 |
+
}
|
| 140 |
+
|
| 141 |
+
void Clear()
|
| 142 |
+
{
|
| 143 |
+
int i;
|
| 144 |
+
Fox(i, sz << 1)
|
| 145 |
+
tree[i] = ZERO_VAL;
|
| 146 |
+
Fox(i, sz << 1)
|
| 147 |
+
lazy[i] = ZERO_LAZY;
|
| 148 |
+
}
|
| 149 |
+
|
| 150 |
+
void Prop(int i)
|
| 151 |
+
{
|
| 152 |
+
TLAZY v = lazy[i];
|
| 153 |
+
lazy[i] = ZERO_LAZY;
|
| 154 |
+
UpdateValForUpdateOrLazy(tree[i], v);
|
| 155 |
+
if (i < sz)
|
| 156 |
+
{
|
| 157 |
+
int c1 = i << 1, c2 = c1 + 1;
|
| 158 |
+
UpdateLazyForUpdateOrLazy(lazy[c1], v);
|
| 159 |
+
UpdateLazyForUpdateOrLazy(lazy[c2], v);
|
| 160 |
+
}
|
| 161 |
+
}
|
| 162 |
+
|
| 163 |
+
void Comp(int i)
|
| 164 |
+
{
|
| 165 |
+
int c1 = i << 1, c2 = c1 + 1;
|
| 166 |
+
tree[i] = CombVals(tree[c1], tree[c2]);
|
| 167 |
+
}
|
| 168 |
+
|
| 169 |
+
TVAL Query(
|
| 170 |
+
int a, int b,
|
| 171 |
+
int i = 1, int r1 = 0, int r2 = -1
|
| 172 |
+
) {
|
| 173 |
+
if (r2 < 0)
|
| 174 |
+
r2 = sz - 1;
|
| 175 |
+
Prop(i);
|
| 176 |
+
if (a <= r1 && r2 <= b)
|
| 177 |
+
return(tree[i]);
|
| 178 |
+
int m = (r1 + r2) >> 1, c = i << 1;
|
| 179 |
+
TVAL ret = ZERO_VAL;
|
| 180 |
+
if (a <= m)
|
| 181 |
+
ret = CombVals(ret, Query(a, b, c, r1, m));
|
| 182 |
+
if (b > m)
|
| 183 |
+
ret = CombVals(ret, Query(a, b, c + 1, m + 1, r2));
|
| 184 |
+
return(ret);
|
| 185 |
+
}
|
| 186 |
+
|
| 187 |
+
void Update(
|
| 188 |
+
int a, int b,
|
| 189 |
+
TLAZY v,
|
| 190 |
+
int i = 1, int r1 = 0, int r2 = -1
|
| 191 |
+
) {
|
| 192 |
+
if (r2 < 0)
|
| 193 |
+
r2 = sz - 1;
|
| 194 |
+
Prop(i);
|
| 195 |
+
if (a <= r1 && r2 <= b)
|
| 196 |
+
{
|
| 197 |
+
UpdateLazyForUpdateOrLazy(lazy[i], v);
|
| 198 |
+
Prop(i);
|
| 199 |
+
return;
|
| 200 |
+
}
|
| 201 |
+
int m = (r1 + r2) >> 1, c = i << 1;
|
| 202 |
+
if (a <= m)
|
| 203 |
+
Update(a, b, v, c, r1, m);
|
| 204 |
+
if (b > m)
|
| 205 |
+
Update(a, b, v, c + 1, m + 1, r2);
|
| 206 |
+
Prop(c), Prop(c + 1), Comp(i);
|
| 207 |
+
}
|
| 208 |
+
|
| 209 |
+
void UpdateOne(int i, TLAZY v) {
|
| 210 |
+
i += sz;
|
| 211 |
+
UpdateValForUpdateOrLazy(tree[i], v);
|
| 212 |
+
while (i > 1)
|
| 213 |
+
{
|
| 214 |
+
i >>= 1;
|
| 215 |
+
Comp(i);
|
| 216 |
+
}
|
| 217 |
+
}
|
| 218 |
+
};
|
| 219 |
+
|
| 220 |
+
int N, M, K;
|
| 221 |
+
int H[LIM], X[LIM], Y[LIM], Z[LIM], W[LIM];
|
| 222 |
+
set<int> LS;
|
| 223 |
+
|
| 224 |
+
// 0: height of column i
|
| 225 |
+
// 1: sum of A endpoint weights with endpoint value i
|
| 226 |
+
// 2: sum of A endpoint weighted values with endpoint value i
|
| 227 |
+
// 3: sum of B endpoint weights with endpoint value i
|
| 228 |
+
// 4: sum of B endpoint weighted values with endpoint value i
|
| 229 |
+
SegTree ST[5];
|
| 230 |
+
|
| 231 |
+
void UpdateHeights(int a, int b, int h)
|
| 232 |
+
{
|
| 233 |
+
ST[0].Update(a, b, mp(h, 0));
|
| 234 |
+
}
|
| 235 |
+
|
| 236 |
+
void UpdateLineSegment(int i, int d) // d = 1 (add) / -1 (remove)
|
| 237 |
+
{
|
| 238 |
+
if (i < 0 || i + 1 >= N)
|
| 239 |
+
return;
|
| 240 |
+
int a = ST[0].Query(i, i), b = ST[0].Query(i + 1, i + 1);
|
| 241 |
+
if (a > b)
|
| 242 |
+
swap(a, b);
|
| 243 |
+
LL w = (LL)(i + 1) * (N - i - 1);
|
| 244 |
+
ST[1].UpdateOne(a, mp(0, w % MOD * d));
|
| 245 |
+
ST[2].UpdateOne(a, mp(0, a * w % MOD * d));
|
| 246 |
+
ST[3].UpdateOne(b, mp(0, w % MOD * d));
|
| 247 |
+
ST[4].UpdateOne(b, mp(0, b * w % MOD * d));
|
| 248 |
+
if (d > 0)
|
| 249 |
+
LS.insert(i);
|
| 250 |
+
else
|
| 251 |
+
LS.erase(i);
|
| 252 |
+
}
|
| 253 |
+
|
| 254 |
+
int ProcessCase()
|
| 255 |
+
{
|
| 256 |
+
int i;
|
| 257 |
+
// input
|
| 258 |
+
Read(N), Read(M), Read(K);
|
| 259 |
+
ReadSeq(H, N, K);
|
| 260 |
+
ReadSeq(X, M, K);
|
| 261 |
+
ReadSeq(Y, M, K);
|
| 262 |
+
ReadSeq(Z, M, K);
|
| 263 |
+
ReadSeq(W, M, K);
|
| 264 |
+
// init segment trees, line segment set, and horizontal sum
|
| 265 |
+
Fox(i, 5)
|
| 266 |
+
ST[i].Init(!i ? N : LIM);
|
| 267 |
+
LS.clear();
|
| 268 |
+
LL horiz = 0;
|
| 269 |
+
Fox(i, N)
|
| 270 |
+
{
|
| 271 |
+
UpdateHeights(i, i, H[i]);
|
| 272 |
+
UpdateLineSegment(i - 1, 1);
|
| 273 |
+
horiz = (horiz + (LL)i * (N - i)) % MOD;
|
| 274 |
+
}
|
| 275 |
+
// process events
|
| 276 |
+
int ans = 1;
|
| 277 |
+
Fox(i, M)
|
| 278 |
+
{
|
| 279 |
+
// update
|
| 280 |
+
int x = X[i] - 1;
|
| 281 |
+
int y = min(x + Y[i], N) - 1;
|
| 282 |
+
int z = Z[i];
|
| 283 |
+
auto I = LS.lower_bound(x - 1);
|
| 284 |
+
while (I != LS.end() && *I <= y)
|
| 285 |
+
{
|
| 286 |
+
int k = *I;
|
| 287 |
+
I++;
|
| 288 |
+
UpdateLineSegment(k, -1);
|
| 289 |
+
}
|
| 290 |
+
UpdateHeights(x, y, z);
|
| 291 |
+
UpdateLineSegment(x - 1, 1);
|
| 292 |
+
UpdateLineSegment(y, 1);
|
| 293 |
+
// query
|
| 294 |
+
int w = W[i];
|
| 295 |
+
LL d1 = ST[4].Query(w + 1, LIM - 1) - ST[2].Query(w + 1, LIM - 1);
|
| 296 |
+
LL d2 = ST[3].Query(w + 1, LIM - 1) - ST[1].Query(w + 1, LIM - 1);
|
| 297 |
+
LL vert = ((d1 - d2 % MOD * w) % MOD + MOD) % MOD;
|
| 298 |
+
ans = (LL)ans * (horiz + vert) * 2 % MOD;
|
| 299 |
+
}
|
| 300 |
+
return(ans);
|
| 301 |
+
}
|
| 302 |
+
|
| 303 |
+
int main()
|
| 304 |
+
{
|
| 305 |
+
int T, t;
|
| 306 |
+
Read(T);
|
| 307 |
+
Fox1(t, T)
|
| 308 |
+
printf("Case #%d: %d\n", t, ProcessCase());
|
| 309 |
+
return(0);
|
| 310 |
+
}
|
2020/finals/spider_spring.in
ADDED
|
@@ -0,0 +1,1189 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
108
|
| 2 |
+
2 2 2
|
| 3 |
+
2 3
|
| 4 |
+
0 0 0 100
|
| 5 |
+
2 1
|
| 6 |
+
0 0 0 2
|
| 7 |
+
1 1
|
| 8 |
+
0 0 0 2
|
| 9 |
+
4 1
|
| 10 |
+
0 0 0 100
|
| 11 |
+
1 3
|
| 12 |
+
0 0 0 100
|
| 13 |
+
3 3 3
|
| 14 |
+
1 2 4
|
| 15 |
+
0 0 0 100
|
| 16 |
+
2 3 1
|
| 17 |
+
0 0 0 3
|
| 18 |
+
1 1 2
|
| 19 |
+
0 0 0 3
|
| 20 |
+
2 4 6
|
| 21 |
+
0 0 0 100
|
| 22 |
+
1 5 5
|
| 23 |
+
0 0 0 100
|
| 24 |
+
6 6 6
|
| 25 |
+
13 4 7 11 2 5
|
| 26 |
+
0 0 0 100
|
| 27 |
+
1 3 6 1 1 4
|
| 28 |
+
0 0 0 6
|
| 29 |
+
1 2 1 1 3 2
|
| 30 |
+
0 0 0 6
|
| 31 |
+
13 9 5 4 10 12
|
| 32 |
+
0 0 0 100
|
| 33 |
+
8 2 9 3 6 11
|
| 34 |
+
0 0 0 100
|
| 35 |
+
10 12 2
|
| 36 |
+
37 11
|
| 37 |
+
1 2 3 45
|
| 38 |
+
2 7
|
| 39 |
+
2 3 4 9
|
| 40 |
+
2 1
|
| 41 |
+
3 4 5 4
|
| 42 |
+
24 38
|
| 43 |
+
4 5 6 78
|
| 44 |
+
16 9
|
| 45 |
+
5 6 7 87
|
| 46 |
+
100 200 3
|
| 47 |
+
470 104 185
|
| 48 |
+
213 20 226 692
|
| 49 |
+
76 35 8
|
| 50 |
+
499 768 377 92
|
| 51 |
+
23 9 12
|
| 52 |
+
880 205 286 31
|
| 53 |
+
165 249 43
|
| 54 |
+
883 477 453 674
|
| 55 |
+
385 68 409
|
| 56 |
+
853 105 54 410
|
| 57 |
+
903 930 2
|
| 58 |
+
1633 1521
|
| 59 |
+
701 815 358 1878
|
| 60 |
+
753 662
|
| 61 |
+
656 986 148 901
|
| 62 |
+
1 1
|
| 63 |
+
401 8 25 5
|
| 64 |
+
165 131
|
| 65 |
+
282 747 129 1191
|
| 66 |
+
116 123
|
| 67 |
+
618 891 846 1164
|
| 68 |
+
1000000 1000000 2
|
| 69 |
+
1000000 1000000
|
| 70 |
+
0 0 999999 1000000
|
| 71 |
+
1000000 1000000
|
| 72 |
+
0 0 999999 1000000
|
| 73 |
+
1000000 1000000
|
| 74 |
+
0 0 999999 1000000
|
| 75 |
+
1000000 1000000
|
| 76 |
+
0 0 999999 1000000
|
| 77 |
+
1000000 1000000
|
| 78 |
+
0 0 999999 1000000
|
| 79 |
+
1000000 1000000 2
|
| 80 |
+
1000000 1
|
| 81 |
+
1 0 999999 1000000
|
| 82 |
+
1 1
|
| 83 |
+
0 0 0 1
|
| 84 |
+
1 1
|
| 85 |
+
0 0 0 1
|
| 86 |
+
1000000 1000000
|
| 87 |
+
0 0 999999 1000000
|
| 88 |
+
1 2
|
| 89 |
+
0 1 0 1000000
|
| 90 |
+
1000000 1000000 2
|
| 91 |
+
178 556
|
| 92 |
+
584 595 823 1000000
|
| 93 |
+
1 4
|
| 94 |
+
433 783 232 1000000
|
| 95 |
+
2 2
|
| 96 |
+
0 0 1 3
|
| 97 |
+
177 100
|
| 98 |
+
680 28 717 1000000
|
| 99 |
+
528 410
|
| 100 |
+
60 815 683 1000000
|
| 101 |
+
1000000 1000000 2
|
| 102 |
+
19 24
|
| 103 |
+
350 303 365 1000000
|
| 104 |
+
51 52
|
| 105 |
+
216 967 821 1000000
|
| 106 |
+
2 3
|
| 107 |
+
106 327 154 20
|
| 108 |
+
82 163
|
| 109 |
+
744 449 414 1000000
|
| 110 |
+
464 306
|
| 111 |
+
362 471 820 1000000
|
| 112 |
+
1000000 1000000 2
|
| 113 |
+
324 111
|
| 114 |
+
101 937 252 1000000
|
| 115 |
+
33 171
|
| 116 |
+
175 798 441 12345
|
| 117 |
+
987654 987654
|
| 118 |
+
0 0 987654 1000000
|
| 119 |
+
44 811
|
| 120 |
+
459 777 237 1000000
|
| 121 |
+
257 35
|
| 122 |
+
704 951 629 1000000
|
| 123 |
+
1000000 1000000 2
|
| 124 |
+
430 157
|
| 125 |
+
514 758 528 1000000
|
| 126 |
+
548 141
|
| 127 |
+
945 926 558 1000000
|
| 128 |
+
47 42
|
| 129 |
+
268 531 962 1000000
|
| 130 |
+
3 162
|
| 131 |
+
86 400 6 1000000
|
| 132 |
+
1 2
|
| 133 |
+
154 756 683 1000000
|
| 134 |
+
100000 100000 2
|
| 135 |
+
125 149
|
| 136 |
+
311 576 518 100000
|
| 137 |
+
6 32
|
| 138 |
+
563 173 458 100000
|
| 139 |
+
4 4
|
| 140 |
+
544 210 328 100000
|
| 141 |
+
14 286
|
| 142 |
+
340 267 60 100000
|
| 143 |
+
369 57
|
| 144 |
+
509 315 521 100000
|
| 145 |
+
100000 100000 2
|
| 146 |
+
44 88
|
| 147 |
+
242 300 281 100000
|
| 148 |
+
25 30
|
| 149 |
+
634 853 304 100000
|
| 150 |
+
2 1
|
| 151 |
+
208 685 950 100000
|
| 152 |
+
327 11
|
| 153 |
+
289 357 883 100000
|
| 154 |
+
135 93
|
| 155 |
+
891 910 259 100000
|
| 156 |
+
903 930 2
|
| 157 |
+
633 521
|
| 158 |
+
701 815 358 878
|
| 159 |
+
753 662
|
| 160 |
+
656 986 148 901
|
| 161 |
+
1 1
|
| 162 |
+
401 8 25 2
|
| 163 |
+
65 31
|
| 164 |
+
282 747 129 191
|
| 165 |
+
16 23
|
| 166 |
+
618 891 846 164
|
| 167 |
+
560 696 2
|
| 168 |
+
169 198
|
| 169 |
+
198 539 496 255
|
| 170 |
+
140 17
|
| 171 |
+
282 82 691 446
|
| 172 |
+
24 14
|
| 173 |
+
831 13 414 42
|
| 174 |
+
376 39
|
| 175 |
+
882 608 720 885
|
| 176 |
+
227 52
|
| 177 |
+
261 461 789 381
|
| 178 |
+
972 540 2
|
| 179 |
+
331 334
|
| 180 |
+
648 253 91 489
|
| 181 |
+
530 322
|
| 182 |
+
732 335 927 893
|
| 183 |
+
6 7
|
| 184 |
+
301 667 399 18
|
| 185 |
+
48 178
|
| 186 |
+
430 392 172 301
|
| 187 |
+
284 653
|
| 188 |
+
32 807 789 962
|
| 189 |
+
855 600 2
|
| 190 |
+
145 135
|
| 191 |
+
920 730 668 224
|
| 192 |
+
247 646
|
| 193 |
+
898 870 550 833
|
| 194 |
+
67 10
|
| 195 |
+
744 620 881 82
|
| 196 |
+
392 316
|
| 197 |
+
553 191 883 424
|
| 198 |
+
79 223
|
| 199 |
+
71 463 361 248
|
| 200 |
+
301 113 2
|
| 201 |
+
52 155
|
| 202 |
+
208 684 646 784
|
| 203 |
+
33 215
|
| 204 |
+
736 691 995 259
|
| 205 |
+
9 23
|
| 206 |
+
76 461 136 25
|
| 207 |
+
293 85
|
| 208 |
+
823 97 279 420
|
| 209 |
+
695 133
|
| 210 |
+
239 888 885 698
|
| 211 |
+
530 859 2
|
| 212 |
+
70 763
|
| 213 |
+
70 537 870 950
|
| 214 |
+
18 262
|
| 215 |
+
866 322 130 508
|
| 216 |
+
3 18
|
| 217 |
+
93 713 359 21
|
| 218 |
+
21 77
|
| 219 |
+
85 331 644 197
|
| 220 |
+
309 496
|
| 221 |
+
866 213 902 580
|
| 222 |
+
634 721 2
|
| 223 |
+
60 231
|
| 224 |
+
468 492 479 357
|
| 225 |
+
178 412
|
| 226 |
+
811 454 239 522
|
| 227 |
+
21 45
|
| 228 |
+
414 524 132 49
|
| 229 |
+
325 45
|
| 230 |
+
207 720 216 638
|
| 231 |
+
570 43
|
| 232 |
+
534 876 111 875
|
| 233 |
+
561 329 2
|
| 234 |
+
614 541
|
| 235 |
+
832 480 598 697
|
| 236 |
+
261 76
|
| 237 |
+
873 340 462 436
|
| 238 |
+
31 20
|
| 239 |
+
243 979 906 32
|
| 240 |
+
292 107
|
| 241 |
+
447 597 189 468
|
| 242 |
+
59 146
|
| 243 |
+
582 280 677 290
|
| 244 |
+
330 749 2
|
| 245 |
+
142 499
|
| 246 |
+
701 963 70 583
|
| 247 |
+
186 108
|
| 248 |
+
622 896 827 249
|
| 249 |
+
13 11
|
| 250 |
+
290 282 580 13
|
| 251 |
+
371 522
|
| 252 |
+
619 692 591 594
|
| 253 |
+
144 302
|
| 254 |
+
942 108 659 661
|
| 255 |
+
251 322 2
|
| 256 |
+
30 135
|
| 257 |
+
399 56 251 226
|
| 258 |
+
190 52
|
| 259 |
+
456 382 867 239
|
| 260 |
+
7 2
|
| 261 |
+
149 100 640 13
|
| 262 |
+
360 48
|
| 263 |
+
959 859 940 492
|
| 264 |
+
48 237
|
| 265 |
+
282 686 565 240
|
| 266 |
+
958 436 2
|
| 267 |
+
533 818
|
| 268 |
+
59 810 553 950
|
| 269 |
+
540 762
|
| 270 |
+
177 425 49 954
|
| 271 |
+
27 4
|
| 272 |
+
552 414 728 27
|
| 273 |
+
209 180
|
| 274 |
+
622 438 998 496
|
| 275 |
+
32 16
|
| 276 |
+
6 969 88 72
|
| 277 |
+
513 902 2
|
| 278 |
+
301 435
|
| 279 |
+
779 823 750 519
|
| 280 |
+
175 356
|
| 281 |
+
750 231 89 418
|
| 282 |
+
31 28
|
| 283 |
+
265 947 489 32
|
| 284 |
+
39 7
|
| 285 |
+
316 983 505 48
|
| 286 |
+
30 369
|
| 287 |
+
103 713 87 480
|
| 288 |
+
206 517 2
|
| 289 |
+
151 118
|
| 290 |
+
85 178 267 834
|
| 291 |
+
22 69
|
| 292 |
+
859 466 727 186
|
| 293 |
+
7 7
|
| 294 |
+
418 864 848 8
|
| 295 |
+
328 411
|
| 296 |
+
358 164 939 696
|
| 297 |
+
287 427
|
| 298 |
+
127 386 335 604
|
| 299 |
+
594 981 2
|
| 300 |
+
1 2
|
| 301 |
+
163 999 302 18
|
| 302 |
+
334 239
|
| 303 |
+
508 223 271 581
|
| 304 |
+
5 5
|
| 305 |
+
327 457 791 5
|
| 306 |
+
433 13
|
| 307 |
+
471 904 69 461
|
| 308 |
+
617 534
|
| 309 |
+
756 256 43 737
|
| 310 |
+
833 242 2
|
| 311 |
+
209 103
|
| 312 |
+
939 521 682 243
|
| 313 |
+
97 67
|
| 314 |
+
373 545 125 730
|
| 315 |
+
78 43
|
| 316 |
+
341 224 763 82
|
| 317 |
+
661 289
|
| 318 |
+
475 751 558 938
|
| 319 |
+
540 43
|
| 320 |
+
641 407 96 834
|
| 321 |
+
479 552 2
|
| 322 |
+
773 95
|
| 323 |
+
561 14 84 873
|
| 324 |
+
138 298
|
| 325 |
+
434 550 678 363
|
| 326 |
+
5 11
|
| 327 |
+
96 820 744 15
|
| 328 |
+
5 16
|
| 329 |
+
479 790 808 20
|
| 330 |
+
316 544
|
| 331 |
+
890 507 177 827
|
| 332 |
+
408 650 2
|
| 333 |
+
7 797
|
| 334 |
+
495 737 239 825
|
| 335 |
+
90 89
|
| 336 |
+
766 944 708 370
|
| 337 |
+
16 16
|
| 338 |
+
580 975 345 28
|
| 339 |
+
445 239
|
| 340 |
+
142 720 688 462
|
| 341 |
+
140 210
|
| 342 |
+
571 928 250 224
|
| 343 |
+
791 957 2
|
| 344 |
+
615 452
|
| 345 |
+
42 934 832 710
|
| 346 |
+
781 48
|
| 347 |
+
319 308 733 782
|
| 348 |
+
7 4
|
| 349 |
+
364 533 596 34
|
| 350 |
+
334 346
|
| 351 |
+
261 705 922 421
|
| 352 |
+
90 92
|
| 353 |
+
529 138 584 158
|
| 354 |
+
546 301 2
|
| 355 |
+
393 679
|
| 356 |
+
919 681 106 789
|
| 357 |
+
425 523
|
| 358 |
+
792 958 404 533
|
| 359 |
+
1 1
|
| 360 |
+
589 283 628 1
|
| 361 |
+
59 239
|
| 362 |
+
903 702 401 373
|
| 363 |
+
123 247
|
| 364 |
+
942 685 70 608
|
| 365 |
+
76 542 2
|
| 366 |
+
211 172
|
| 367 |
+
144 246 457 352
|
| 368 |
+
27 42
|
| 369 |
+
500 977 733 75
|
| 370 |
+
3 2
|
| 371 |
+
523 893 924 8
|
| 372 |
+
21 15
|
| 373 |
+
329 889 114 57
|
| 374 |
+
33 178
|
| 375 |
+
960 453 552 778
|
| 376 |
+
360 84 2
|
| 377 |
+
2 29
|
| 378 |
+
707 417 370 29
|
| 379 |
+
40 196
|
| 380 |
+
696 131 893 327
|
| 381 |
+
1 12
|
| 382 |
+
465 830 658 27
|
| 383 |
+
539 401
|
| 384 |
+
518 768 936 566
|
| 385 |
+
357 18
|
| 386 |
+
242 566 931 464
|
| 387 |
+
820 98 2
|
| 388 |
+
3 295
|
| 389 |
+
587 398 408 407
|
| 390 |
+
525 548
|
| 391 |
+
225 646 190 797
|
| 392 |
+
7 6
|
| 393 |
+
340 738 936 18
|
| 394 |
+
303 31
|
| 395 |
+
314 951 152 343
|
| 396 |
+
32 24
|
| 397 |
+
592 101 794 55
|
| 398 |
+
930 117 2
|
| 399 |
+
143 444
|
| 400 |
+
445 505 199 931
|
| 401 |
+
34 859
|
| 402 |
+
225 935 398 926
|
| 403 |
+
62 13
|
| 404 |
+
815 727 139 74
|
| 405 |
+
382 610
|
| 406 |
+
938 136 78 976
|
| 407 |
+
91 162
|
| 408 |
+
374 20 826 578
|
| 409 |
+
263 745 2
|
| 410 |
+
153 59
|
| 411 |
+
315 654 700 172
|
| 412 |
+
5 186
|
| 413 |
+
581 314 479 218
|
| 414 |
+
14 7
|
| 415 |
+
816 774 927 26
|
| 416 |
+
65 27
|
| 417 |
+
817 265 822 70
|
| 418 |
+
18 77
|
| 419 |
+
368 696 166 85
|
| 420 |
+
279 738 2
|
| 421 |
+
159 142
|
| 422 |
+
898 425 339 318
|
| 423 |
+
43 150
|
| 424 |
+
769 530 503 259
|
| 425 |
+
8 3
|
| 426 |
+
672 517 872 18
|
| 427 |
+
83 551
|
| 428 |
+
732 669 499 685
|
| 429 |
+
257 456
|
| 430 |
+
947 301 419 789
|
| 431 |
+
598 555 2
|
| 432 |
+
30 7
|
| 433 |
+
575 679 622 37
|
| 434 |
+
536 186
|
| 435 |
+
41 588 65 537
|
| 436 |
+
43 2
|
| 437 |
+
966 616 818 59
|
| 438 |
+
248 256
|
| 439 |
+
926 345 362 320
|
| 440 |
+
7 212
|
| 441 |
+
450 360 668 365
|
| 442 |
+
264 577 2
|
| 443 |
+
15 2
|
| 444 |
+
717 154 500 21
|
| 445 |
+
102 111
|
| 446 |
+
656 620 658 219
|
| 447 |
+
8 2
|
| 448 |
+
892 626 865 8
|
| 449 |
+
743 525
|
| 450 |
+
179 112 70 876
|
| 451 |
+
429 679
|
| 452 |
+
880 3 973 825
|
| 453 |
+
897 144 2
|
| 454 |
+
540 332
|
| 455 |
+
840 455 830 627
|
| 456 |
+
562 400
|
| 457 |
+
212 814 564 861
|
| 458 |
+
6 8
|
| 459 |
+
967 216 433 48
|
| 460 |
+
53 397
|
| 461 |
+
720 766 244 636
|
| 462 |
+
135 196
|
| 463 |
+
803 924 987 262
|
| 464 |
+
429 612 2
|
| 465 |
+
17 55
|
| 466 |
+
996 594 794 123
|
| 467 |
+
226 321
|
| 468 |
+
720 686 277 385
|
| 469 |
+
1 1
|
| 470 |
+
890 830 894 1
|
| 471 |
+
899 590
|
| 472 |
+
168 359 680 933
|
| 473 |
+
331 402
|
| 474 |
+
446 717 585 638
|
| 475 |
+
839 233 2
|
| 476 |
+
521 845
|
| 477 |
+
61 640 876 975
|
| 478 |
+
551 296
|
| 479 |
+
911 703 495 798
|
| 480 |
+
34 29
|
| 481 |
+
763 214 43 49
|
| 482 |
+
159 144
|
| 483 |
+
728 711 733 707
|
| 484 |
+
687 417
|
| 485 |
+
766 235 436 919
|
| 486 |
+
365 586 2
|
| 487 |
+
84 74
|
| 488 |
+
448 91 430 285
|
| 489 |
+
4 97
|
| 490 |
+
110 366 424 305
|
| 491 |
+
2 9
|
| 492 |
+
867 175 438 15
|
| 493 |
+
415 156
|
| 494 |
+
819 867 368 520
|
| 495 |
+
517 426
|
| 496 |
+
533 851 639 597
|
| 497 |
+
465 60 2
|
| 498 |
+
330 409
|
| 499 |
+
767 64 479 424
|
| 500 |
+
343 275
|
| 501 |
+
386 527 467 353
|
| 502 |
+
1 1
|
| 503 |
+
921 595 49 1
|
| 504 |
+
324 322
|
| 505 |
+
605 22 541 475
|
| 506 |
+
480 415
|
| 507 |
+
753 135 614 850
|
| 508 |
+
801 771 2
|
| 509 |
+
63 291
|
| 510 |
+
144 684 80 412
|
| 511 |
+
555 472
|
| 512 |
+
749 518 924 684
|
| 513 |
+
55 38
|
| 514 |
+
775 334 474 65
|
| 515 |
+
5 233
|
| 516 |
+
907 805 320 742
|
| 517 |
+
8 10
|
| 518 |
+
213 117 454 404
|
| 519 |
+
783 771 2
|
| 520 |
+
598 530
|
| 521 |
+
846 857 583 798
|
| 522 |
+
553 176
|
| 523 |
+
508 278 568 603
|
| 524 |
+
7 25
|
| 525 |
+
290 565 235 33
|
| 526 |
+
3 94
|
| 527 |
+
656 619 860 237
|
| 528 |
+
529 436
|
| 529 |
+
236 48 762 662
|
| 530 |
+
432 863 2
|
| 531 |
+
704 427
|
| 532 |
+
213 389 808 976
|
| 533 |
+
275 77
|
| 534 |
+
851 125 737 385
|
| 535 |
+
4 9
|
| 536 |
+
957 52 233 15
|
| 537 |
+
595 365
|
| 538 |
+
905 284 117 861
|
| 539 |
+
647 91
|
| 540 |
+
292 115 735 765
|
| 541 |
+
992 300 2
|
| 542 |
+
525 297
|
| 543 |
+
649 530 454 720
|
| 544 |
+
834 212
|
| 545 |
+
934 685 909 883
|
| 546 |
+
28 12
|
| 547 |
+
805 982 864 51
|
| 548 |
+
24 511
|
| 549 |
+
505 668 249 578
|
| 550 |
+
187 182
|
| 551 |
+
153 428 304 235
|
| 552 |
+
427 382 2
|
| 553 |
+
190 227
|
| 554 |
+
759 686 149 442
|
| 555 |
+
159 204
|
| 556 |
+
313 771 135 420
|
| 557 |
+
7 29
|
| 558 |
+
294 207 468 30
|
| 559 |
+
323 129
|
| 560 |
+
44 983 618 527
|
| 561 |
+
385 130
|
| 562 |
+
837 293 873 478
|
| 563 |
+
509 937 2
|
| 564 |
+
73 76
|
| 565 |
+
121 923 553 257
|
| 566 |
+
370 177
|
| 567 |
+
415 250 899 453
|
| 568 |
+
3 7
|
| 569 |
+
435 812 337 11
|
| 570 |
+
252 311
|
| 571 |
+
623 186 732 401
|
| 572 |
+
180 470
|
| 573 |
+
238 772 839 514
|
| 574 |
+
842 577 2
|
| 575 |
+
273 625
|
| 576 |
+
269 271 271 657
|
| 577 |
+
748 140
|
| 578 |
+
414 784 901 768
|
| 579 |
+
29 5
|
| 580 |
+
721 553 330 37
|
| 581 |
+
583 440
|
| 582 |
+
69 152 381 723
|
| 583 |
+
368 364
|
| 584 |
+
414 820 333 689
|
| 585 |
+
477 441 2
|
| 586 |
+
89 1
|
| 587 |
+
78 356 819 110
|
| 588 |
+
90 387
|
| 589 |
+
433 743 609 408
|
| 590 |
+
16 3
|
| 591 |
+
516 625 885 28
|
| 592 |
+
75 65
|
| 593 |
+
939 438 215 281
|
| 594 |
+
566 739
|
| 595 |
+
555 353 992 913
|
| 596 |
+
356 406 2
|
| 597 |
+
531 300
|
| 598 |
+
232 72 584 972
|
| 599 |
+
288 202
|
| 600 |
+
971 588 35 346
|
| 601 |
+
9 25
|
| 602 |
+
199 601 573 30
|
| 603 |
+
26 46
|
| 604 |
+
124 574 366 169
|
| 605 |
+
387 451
|
| 606 |
+
384 662 131 637
|
| 607 |
+
913 20 2
|
| 608 |
+
21 81
|
| 609 |
+
695 806 658 88
|
| 610 |
+
628 413
|
| 611 |
+
737 3 576 755
|
| 612 |
+
2 21
|
| 613 |
+
351 988 165 61
|
| 614 |
+
256 57
|
| 615 |
+
837 302 864 324
|
| 616 |
+
55 653
|
| 617 |
+
881 641 578 882
|
| 618 |
+
698 679 2
|
| 619 |
+
47 673
|
| 620 |
+
551 473 606 997
|
| 621 |
+
184 28
|
| 622 |
+
216 911 779 691
|
| 623 |
+
2 4
|
| 624 |
+
704 423 546 14
|
| 625 |
+
347 196
|
| 626 |
+
792 634 838 689
|
| 627 |
+
74 59
|
| 628 |
+
915 525 986 842
|
| 629 |
+
393 922 2
|
| 630 |
+
240 570
|
| 631 |
+
965 583 455 776
|
| 632 |
+
330 323
|
| 633 |
+
698 365 640 364
|
| 634 |
+
8 16
|
| 635 |
+
245 373 833 20
|
| 636 |
+
152 449
|
| 637 |
+
532 500 183 745
|
| 638 |
+
62 14
|
| 639 |
+
832 222 151 243
|
| 640 |
+
315 43 2
|
| 641 |
+
86 16
|
| 642 |
+
395 803 569 187
|
| 643 |
+
92 258
|
| 644 |
+
828 665 547 273
|
| 645 |
+
6 8
|
| 646 |
+
667 827 876 12
|
| 647 |
+
429 194
|
| 648 |
+
346 346 589 843
|
| 649 |
+
170 319
|
| 650 |
+
206 272 331 385
|
| 651 |
+
669 404 2
|
| 652 |
+
258 490
|
| 653 |
+
527 689 745 524
|
| 654 |
+
212 388
|
| 655 |
+
130 943 920 546
|
| 656 |
+
8 13
|
| 657 |
+
574 788 848 29
|
| 658 |
+
43 119
|
| 659 |
+
64 487 333 496
|
| 660 |
+
243 140
|
| 661 |
+
183 95 468 526
|
| 662 |
+
273 706 2
|
| 663 |
+
414 353
|
| 664 |
+
436 437 355 942
|
| 665 |
+
244 23
|
| 666 |
+
640 387 315 251
|
| 667 |
+
15 13
|
| 668 |
+
553 925 689 18
|
| 669 |
+
4 11
|
| 670 |
+
370 471 315 119
|
| 671 |
+
166 161
|
| 672 |
+
569 223 990 208
|
| 673 |
+
531 32 2
|
| 674 |
+
506 504
|
| 675 |
+
486 554 489 654
|
| 676 |
+
384 77
|
| 677 |
+
170 520 889 507
|
| 678 |
+
7 41
|
| 679 |
+
825 153 339 49
|
| 680 |
+
123 129
|
| 681 |
+
683 207 26 378
|
| 682 |
+
240 222
|
| 683 |
+
879 356 276 426
|
| 684 |
+
745 956 2
|
| 685 |
+
141 202
|
| 686 |
+
874 518 913 207
|
| 687 |
+
385 554
|
| 688 |
+
787 532 492 617
|
| 689 |
+
31 24
|
| 690 |
+
474 781 354 42
|
| 691 |
+
269 339
|
| 692 |
+
239 554 367 389
|
| 693 |
+
44 73
|
| 694 |
+
590 458 10 280
|
| 695 |
+
958 776 2
|
| 696 |
+
176 226
|
| 697 |
+
362 980 71 565
|
| 698 |
+
83 658
|
| 699 |
+
113 657 2 790
|
| 700 |
+
5 18
|
| 701 |
+
15 701 673 49
|
| 702 |
+
75 308
|
| 703 |
+
715 108 614 541
|
| 704 |
+
269 339
|
| 705 |
+
416 733 949 423
|
| 706 |
+
798 353 2
|
| 707 |
+
296 63
|
| 708 |
+
499 720 142 388
|
| 709 |
+
261 325
|
| 710 |
+
590 147 182 693
|
| 711 |
+
9 7
|
| 712 |
+
421 916 646 11
|
| 713 |
+
628 103
|
| 714 |
+
50 562 658 982
|
| 715 |
+
605 446
|
| 716 |
+
323 289 464 610
|
| 717 |
+
796 595 2
|
| 718 |
+
49 46
|
| 719 |
+
842 758 506 57
|
| 720 |
+
101 616
|
| 721 |
+
224 112 764 703
|
| 722 |
+
10 3
|
| 723 |
+
847 990 147 12
|
| 724 |
+
172 574
|
| 725 |
+
537 366 920 667
|
| 726 |
+
439 108
|
| 727 |
+
729 34 95 661
|
| 728 |
+
350 73 2
|
| 729 |
+
466 42
|
| 730 |
+
546 898 16 895
|
| 731 |
+
214 24
|
| 732 |
+
585 290 713 280
|
| 733 |
+
1 1
|
| 734 |
+
931 720 958 11
|
| 735 |
+
344 379
|
| 736 |
+
387 158 827 552
|
| 737 |
+
335 182
|
| 738 |
+
928 388 807 397
|
| 739 |
+
382 1000 2
|
| 740 |
+
68 52
|
| 741 |
+
911 968 211 82
|
| 742 |
+
266 319
|
| 743 |
+
398 831 183 353
|
| 744 |
+
4 6
|
| 745 |
+
898 78 585 25
|
| 746 |
+
539 288
|
| 747 |
+
804 190 800 698
|
| 748 |
+
18 30
|
| 749 |
+
107 564 732 36
|
| 750 |
+
73 276 2
|
| 751 |
+
118 139
|
| 752 |
+
573 84 696 174
|
| 753 |
+
56 37
|
| 754 |
+
228 872 892 58
|
| 755 |
+
2 2
|
| 756 |
+
83 435 585 7
|
| 757 |
+
785 430
|
| 758 |
+
481 464 27 981
|
| 759 |
+
367 105
|
| 760 |
+
399 788 560 464
|
| 761 |
+
52 65 2
|
| 762 |
+
765 384
|
| 763 |
+
369 187 978 776
|
| 764 |
+
22 24
|
| 765 |
+
501 428 954 47
|
| 766 |
+
5 2
|
| 767 |
+
656 300 499 6
|
| 768 |
+
494 546
|
| 769 |
+
5 402 392 548
|
| 770 |
+
75 278
|
| 771 |
+
606 745 297 309
|
| 772 |
+
241 627 2
|
| 773 |
+
12 586
|
| 774 |
+
549 559 189 779
|
| 775 |
+
137 4
|
| 776 |
+
46 958 7 194
|
| 777 |
+
18 19
|
| 778 |
+
526 740 817 21
|
| 779 |
+
186 92
|
| 780 |
+
340 447 970 236
|
| 781 |
+
771 140
|
| 782 |
+
717 71 787 885
|
| 783 |
+
341 917 2
|
| 784 |
+
562 425
|
| 785 |
+
783 957 382 739
|
| 786 |
+
218 190
|
| 787 |
+
498 57 390 299
|
| 788 |
+
1 1
|
| 789 |
+
233 320 920 1
|
| 790 |
+
49 233
|
| 791 |
+
219 332 549 248
|
| 792 |
+
480 359
|
| 793 |
+
969 659 769 718
|
| 794 |
+
500 77 2
|
| 795 |
+
800 453
|
| 796 |
+
506 665 520 821
|
| 797 |
+
412 21
|
| 798 |
+
871 378 204 478
|
| 799 |
+
20 40
|
| 800 |
+
172 963 747 44
|
| 801 |
+
163 109
|
| 802 |
+
846 564 775 277
|
| 803 |
+
411 509
|
| 804 |
+
709 367 247 699
|
| 805 |
+
913 517 2
|
| 806 |
+
438 495
|
| 807 |
+
242 879 176 652
|
| 808 |
+
374 102
|
| 809 |
+
216 69 835 708
|
| 810 |
+
30 58
|
| 811 |
+
524 794 32 71
|
| 812 |
+
397 26
|
| 813 |
+
88 571 386 886
|
| 814 |
+
232 481
|
| 815 |
+
333 192 794 809
|
| 816 |
+
434 729 2
|
| 817 |
+
353 664
|
| 818 |
+
739 708 624 916
|
| 819 |
+
14 49
|
| 820 |
+
520 853 9 376
|
| 821 |
+
1 3
|
| 822 |
+
340 496 434 3
|
| 823 |
+
283 657
|
| 824 |
+
349 85 955 800
|
| 825 |
+
215 830
|
| 826 |
+
21 251 109 899
|
| 827 |
+
290 327 2
|
| 828 |
+
221 488
|
| 829 |
+
425 90 815 561
|
| 830 |
+
97 159
|
| 831 |
+
109 760 64 267
|
| 832 |
+
4 2
|
| 833 |
+
801 242 69 7
|
| 834 |
+
209 220
|
| 835 |
+
97 574 13 286
|
| 836 |
+
131 302
|
| 837 |
+
729 106 277 333
|
| 838 |
+
628 337 2
|
| 839 |
+
23 130
|
| 840 |
+
161 406 455 224
|
| 841 |
+
389 430
|
| 842 |
+
793 896 886 605
|
| 843 |
+
7 11
|
| 844 |
+
871 715 940 13
|
| 845 |
+
309 149
|
| 846 |
+
833 43 29 317
|
| 847 |
+
14 101
|
| 848 |
+
206 619 221 323
|
| 849 |
+
950 324 2
|
| 850 |
+
382 386
|
| 851 |
+
237 285 492 788
|
| 852 |
+
539 532
|
| 853 |
+
842 746 526 809
|
| 854 |
+
62 60
|
| 855 |
+
641 128 580 92
|
| 856 |
+
5 7
|
| 857 |
+
137 119 15 9
|
| 858 |
+
402 563
|
| 859 |
+
446 248 393 842
|
| 860 |
+
642 580 2
|
| 861 |
+
253 437
|
| 862 |
+
451 745 475 753
|
| 863 |
+
288 48
|
| 864 |
+
34 290 884 620
|
| 865 |
+
18 40
|
| 866 |
+
148 37 74 65
|
| 867 |
+
52 25
|
| 868 |
+
564 791 334 77
|
| 869 |
+
4 93
|
| 870 |
+
823 63 646 284
|
| 871 |
+
533 381 2
|
| 872 |
+
93 295
|
| 873 |
+
942 79 375 684
|
| 874 |
+
83 23
|
| 875 |
+
422 291 917 430
|
| 876 |
+
10 15
|
| 877 |
+
692 613 456 23
|
| 878 |
+
155 464
|
| 879 |
+
142 558 663 557
|
| 880 |
+
126 444
|
| 881 |
+
764 906 703 768
|
| 882 |
+
956 610 2
|
| 883 |
+
175 203
|
| 884 |
+
642 420 108 632
|
| 885 |
+
199 335
|
| 886 |
+
658 874 715 779
|
| 887 |
+
27 26
|
| 888 |
+
37 956 739 53
|
| 889 |
+
103 240
|
| 890 |
+
251 232 222 614
|
| 891 |
+
262 326
|
| 892 |
+
697 623 521 527
|
| 893 |
+
473 209 2
|
| 894 |
+
38 26
|
| 895 |
+
435 450 519 65
|
| 896 |
+
167 341
|
| 897 |
+
714 563 948 358
|
| 898 |
+
20 7
|
| 899 |
+
890 511 311 32
|
| 900 |
+
241 98
|
| 901 |
+
585 209 622 316
|
| 902 |
+
415 83
|
| 903 |
+
194 145 527 543
|
| 904 |
+
769 340 2
|
| 905 |
+
240 205
|
| 906 |
+
149 511 59 939
|
| 907 |
+
447 428
|
| 908 |
+
834 906 987 702
|
| 909 |
+
10 1
|
| 910 |
+
783 226 664 20
|
| 911 |
+
368 469
|
| 912 |
+
177 445 637 850
|
| 913 |
+
328 22
|
| 914 |
+
492 283 357 619
|
| 915 |
+
16 568 2
|
| 916 |
+
380 542
|
| 917 |
+
445 325 581 683
|
| 918 |
+
13 10
|
| 919 |
+
101 971 396 15
|
| 920 |
+
1 2
|
| 921 |
+
234 168 442 2
|
| 922 |
+
9 152
|
| 923 |
+
945 89 932 172
|
| 924 |
+
348 248
|
| 925 |
+
689 627 696 447
|
| 926 |
+
769 864 2
|
| 927 |
+
345 114
|
| 928 |
+
182 290 472 452
|
| 929 |
+
355 601
|
| 930 |
+
481 609 643 710
|
| 931 |
+
53 19
|
| 932 |
+
133 829 577 76
|
| 933 |
+
378 66
|
| 934 |
+
348 336 433 519
|
| 935 |
+
574 271
|
| 936 |
+
847 252 667 608
|
| 937 |
+
330 330 2
|
| 938 |
+
245 597
|
| 939 |
+
684 89 256 650
|
| 940 |
+
30 46
|
| 941 |
+
417 409 636 312
|
| 942 |
+
5 2
|
| 943 |
+
236 943 280 6
|
| 944 |
+
117 146
|
| 945 |
+
615 775 832 223
|
| 946 |
+
7 12
|
| 947 |
+
353 186 107 16
|
| 948 |
+
462 280 2
|
| 949 |
+
824 24
|
| 950 |
+
243 589 242 946
|
| 951 |
+
368 74
|
| 952 |
+
480 415 75 375
|
| 953 |
+
5 8
|
| 954 |
+
589 223 293 8
|
| 955 |
+
647 594
|
| 956 |
+
981 952 541 983
|
| 957 |
+
284 257
|
| 958 |
+
427 632 555 365
|
| 959 |
+
816 159 2
|
| 960 |
+
519 623
|
| 961 |
+
519 756 873 679
|
| 962 |
+
435 609
|
| 963 |
+
891 719 333 632
|
| 964 |
+
6 6
|
| 965 |
+
874 500 522 28
|
| 966 |
+
49 210
|
| 967 |
+
954 657 739 388
|
| 968 |
+
20 36
|
| 969 |
+
473 708 831 251
|
| 970 |
+
998 170 2
|
| 971 |
+
455 327
|
| 972 |
+
12 321 890 469
|
| 973 |
+
236 78
|
| 974 |
+
255 637 797 818
|
| 975 |
+
34 1
|
| 976 |
+
167 191 237 39
|
| 977 |
+
608 27
|
| 978 |
+
187 494 159 649
|
| 979 |
+
249 180
|
| 980 |
+
935 825 164 533
|
| 981 |
+
514 863 2
|
| 982 |
+
212 139
|
| 983 |
+
951 359 544 272
|
| 984 |
+
393 233
|
| 985 |
+
742 52 391 425
|
| 986 |
+
1 3
|
| 987 |
+
210 583 168 47
|
| 988 |
+
59 33
|
| 989 |
+
371 633 77 179
|
| 990 |
+
707 806
|
| 991 |
+
522 643 958 903
|
| 992 |
+
497 712 2
|
| 993 |
+
58 80
|
| 994 |
+
786 316 104 173
|
| 995 |
+
141 341
|
| 996 |
+
397 937 967 468
|
| 997 |
+
12 6
|
| 998 |
+
485 909 296 36
|
| 999 |
+
426 270
|
| 1000 |
+
687 160 576 493
|
| 1001 |
+
28 177
|
| 1002 |
+
932 726 631 685
|
| 1003 |
+
351 490 2
|
| 1004 |
+
588 656
|
| 1005 |
+
867 187 989 903
|
| 1006 |
+
149 14
|
| 1007 |
+
408 504 113 343
|
| 1008 |
+
11 2
|
| 1009 |
+
116 72 65 21
|
| 1010 |
+
91 36
|
| 1011 |
+
146 590 781 140
|
| 1012 |
+
80 42
|
| 1013 |
+
547 6 173 267
|
| 1014 |
+
296 633 2
|
| 1015 |
+
48 8
|
| 1016 |
+
421 784 83 58
|
| 1017 |
+
34 89
|
| 1018 |
+
315 421 241 278
|
| 1019 |
+
7 13
|
| 1020 |
+
573 626 111 26
|
| 1021 |
+
361 257
|
| 1022 |
+
265 39 8 364
|
| 1023 |
+
14 44
|
| 1024 |
+
674 303 876 46
|
| 1025 |
+
136 801 2
|
| 1026 |
+
99 483
|
| 1027 |
+
436 695 919 618
|
| 1028 |
+
22 41
|
| 1029 |
+
666 715 388 127
|
| 1030 |
+
1 2
|
| 1031 |
+
482 583 478 2
|
| 1032 |
+
458 234
|
| 1033 |
+
39 160 420 496
|
| 1034 |
+
438 484
|
| 1035 |
+
349 709 431 537
|
| 1036 |
+
387 85 2
|
| 1037 |
+
82 221
|
| 1038 |
+
596 268 556 924
|
| 1039 |
+
97 246
|
| 1040 |
+
608 39 236 344
|
| 1041 |
+
30 16
|
| 1042 |
+
607 604 162 36
|
| 1043 |
+
284 611
|
| 1044 |
+
656 372 886 676
|
| 1045 |
+
31 47
|
| 1046 |
+
160 324 970 297
|
| 1047 |
+
165 354 2
|
| 1048 |
+
597 760
|
| 1049 |
+
538 219 926 859
|
| 1050 |
+
110 91
|
| 1051 |
+
283 621 671 150
|
| 1052 |
+
5 11
|
| 1053 |
+
49 404 158 13
|
| 1054 |
+
42 17
|
| 1055 |
+
345 31 409 61
|
| 1056 |
+
41 16
|
| 1057 |
+
160 448 354 120
|
| 1058 |
+
249 540 2
|
| 1059 |
+
918 839
|
| 1060 |
+
400 927 410 996
|
| 1061 |
+
186 176
|
| 1062 |
+
669 393 88 213
|
| 1063 |
+
1 1
|
| 1064 |
+
788 628 528 1
|
| 1065 |
+
402 528
|
| 1066 |
+
181 22 523 543
|
| 1067 |
+
175 141
|
| 1068 |
+
799 997 402 644
|
| 1069 |
+
445 287 2
|
| 1070 |
+
361 156
|
| 1071 |
+
628 174 747 369
|
| 1072 |
+
237 314
|
| 1073 |
+
12 879 291 424
|
| 1074 |
+
22 20
|
| 1075 |
+
452 512 387 40
|
| 1076 |
+
57 384
|
| 1077 |
+
864 339 957 421
|
| 1078 |
+
501 8
|
| 1079 |
+
827 151 78 520
|
| 1080 |
+
763 374 2
|
| 1081 |
+
321 421
|
| 1082 |
+
601 323 70 456
|
| 1083 |
+
527 148
|
| 1084 |
+
642 74 93 748
|
| 1085 |
+
20 15
|
| 1086 |
+
244 11 914 23
|
| 1087 |
+
350 191
|
| 1088 |
+
807 860 574 939
|
| 1089 |
+
620 156
|
| 1090 |
+
279 634 675 809
|
| 1091 |
+
425 39 2
|
| 1092 |
+
752 385
|
| 1093 |
+
811 187 622 948
|
| 1094 |
+
292 222
|
| 1095 |
+
12 143 608 386
|
| 1096 |
+
9 5
|
| 1097 |
+
633 146 514 23
|
| 1098 |
+
211 215
|
| 1099 |
+
894 693 864 310
|
| 1100 |
+
709 396
|
| 1101 |
+
135 691 837 778
|
| 1102 |
+
865 348 2
|
| 1103 |
+
278 484
|
| 1104 |
+
166 576 304 730
|
| 1105 |
+
533 474
|
| 1106 |
+
903 642 498 670
|
| 1107 |
+
3 2
|
| 1108 |
+
495 32 416 4
|
| 1109 |
+
9 10
|
| 1110 |
+
607 416 472 10
|
| 1111 |
+
83 112
|
| 1112 |
+
647 116 990 327
|
| 1113 |
+
800 954 2
|
| 1114 |
+
144 117
|
| 1115 |
+
710 703 439 245
|
| 1116 |
+
389 75
|
| 1117 |
+
133 615 901 646
|
| 1118 |
+
3 10
|
| 1119 |
+
537 481 182 16
|
| 1120 |
+
544 483
|
| 1121 |
+
369 91 585 618
|
| 1122 |
+
489 423
|
| 1123 |
+
403 858 268 524
|
| 1124 |
+
930 12 2
|
| 1125 |
+
304 30
|
| 1126 |
+
304 916 887 305
|
| 1127 |
+
638 32
|
| 1128 |
+
26 625 967 930
|
| 1129 |
+
40 52
|
| 1130 |
+
68 475 73 54
|
| 1131 |
+
67 31
|
| 1132 |
+
645 729 529 171
|
| 1133 |
+
392 703
|
| 1134 |
+
120 969 483 710
|
| 1135 |
+
715 72 2
|
| 1136 |
+
441 540
|
| 1137 |
+
423 115 917 570
|
| 1138 |
+
467 94
|
| 1139 |
+
100 549 243 565
|
| 1140 |
+
1 1
|
| 1141 |
+
227 199 797 1
|
| 1142 |
+
33 123
|
| 1143 |
+
977 775 857 1000
|
| 1144 |
+
2 6
|
| 1145 |
+
280 958 590 8
|
| 1146 |
+
663 16 2
|
| 1147 |
+
169 477
|
| 1148 |
+
510 376 476 540
|
| 1149 |
+
339 503
|
| 1150 |
+
614 248 494 604
|
| 1151 |
+
39 15
|
| 1152 |
+
843 132 278 48
|
| 1153 |
+
520 459
|
| 1154 |
+
313 584 80 718
|
| 1155 |
+
285 173
|
| 1156 |
+
41 67 913 870
|
| 1157 |
+
338 665 2
|
| 1158 |
+
173 140
|
| 1159 |
+
267 792 521 276
|
| 1160 |
+
304 187
|
| 1161 |
+
868 923 970 337
|
| 1162 |
+
12 2
|
| 1163 |
+
992 923 463 16
|
| 1164 |
+
73 195
|
| 1165 |
+
775 24 288 296
|
| 1166 |
+
224 406
|
| 1167 |
+
686 197 913 564
|
| 1168 |
+
656 687 2
|
| 1169 |
+
18 20
|
| 1170 |
+
490 573 447 150
|
| 1171 |
+
420 57
|
| 1172 |
+
25 789 37 648
|
| 1173 |
+
14 21
|
| 1174 |
+
606 571 686 22
|
| 1175 |
+
72 180
|
| 1176 |
+
282 131 414 219
|
| 1177 |
+
158 618
|
| 1178 |
+
51 585 489 751
|
| 1179 |
+
589 797 2
|
| 1180 |
+
470 11
|
| 1181 |
+
213 20 226 692
|
| 1182 |
+
376 35
|
| 1183 |
+
499 768 377 478
|
| 1184 |
+
23 9
|
| 1185 |
+
880 205 286 41
|
| 1186 |
+
165 249
|
| 1187 |
+
883 477 453 674
|
| 1188 |
+
385 68
|
| 1189 |
+
853 105 54 410
|
2020/finals/spider_spring.md
ADDED
|
@@ -0,0 +1,104 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
A family of water spiders lives at a spring located on an earthquake hotspot. The spring features \(N\) columns of rocks in a row, numbered \(1\) to \(N\) from left to right. Each rocky column \(i\) has a width of 1 cm and a height of \(H_i\) cm.
|
| 2 |
+
|
| 3 |
+
The spring always has some global water level. The rocky columns can each be below the water, at water level, or protrude above its surface. A spider in a given column must float on the surface of the water (if the rock is below water level) or stand atop the rock (if it's at or above water level). This means that, when the water level is W cm, the **effective elevation** at column \(i\) is \(max(H_i, W)\) cm.
|
| 4 |
+
|
| 5 |
+
For example, the following diagram illustrates a spring with \(H = [2, 1, 3, 1]\) and \(W = 2\), with the effective elevations outlined in black:
|
| 6 |
+
|
| 7 |
+
{{PHOTO_ID:1583104035206937}}
|
| 8 |
+
|
| 9 |
+
Water spiders sometimes want to travel from one column \(a\) to another column \(b\). This involves starting horizontally in the middle of column \(a\), at its effective elevation, and walking along the outline of the effective elevations until ending up horizontally in the middle of column \(b\). This may include walking left/right across the tops of rocks or the surface of the water, as well as up/down along the sides of the protruding rocks. Note that a spider's route will never take it left of column \(1\), right of column \(N\), below the surface of the water, nor into mid-air.
|
| 10 |
+
|
| 11 |
+
For example, the path which a water spider would follow from column 1 to column 4 (having a length of 5 cm) is indicated in red below:
|
| 12 |
+
|
| 13 |
+
{{PHOTO_ID:862340924576901}}
|
| 14 |
+
|
| 15 |
+
Unfortunately for the spring's inhabitants, frequent earthquakes occur, altering the heights of the rocky columns and the water. The spiders would like to survey the accessibility of the spring after each earthquake.
|
| 16 |
+
|
| 17 |
+
Specifically, \(M\) earthquakes are about to occur, one after another. As part of the \(i\)th earthquake, the height of each rocky column \(c\) such that \(X_i \le c \le min(X_i + Y_i - 1, N)\) will become equal to \(Z_i\) cm, and the global water level will become \(W_i\) cm. After each earthquake \(i\), the spiders are interested in the current sum of travel distances (in cm) over all \(N*(N - 1)\) ordered pairs of starting and ending columns — we'll call this quantity \(S_i\).
|
| 18 |
+
|
| 19 |
+
Please determine the value of \((S_1 * S_2 * ... * S_M)\) modulo 1,000,000,007.
|
| 20 |
+
|
| 21 |
+
In order to reduce the size of the input, the above values will not all be provided explicitly. Instead, you'll be given the first \(K\) values \(H_{1..K}\), \(X_{1..K}\), \(Y_{1..K}\), \(Z_{1..K}\), and \(W_{1..K}\), as well as the five quadruples of constants \((A_H, B_H, C_H, D_H)\), \((A_X, B_X, C_X, D_X)\), \((A_Y, B_Y, C_Y, D_Y)\), \((A_Z, B_Z, C_Z, D_Z)\), and \((A_W, B_W, C_W, D_W)\), and must then compute \(H_{(K+1)..N}\), \(X_{(K+1)..M}\), \(Y_{(K+1)..M}\), \(Z_{(K+1)..M}\), and \(W_{(K+1)..M}\) as follows:
|
| 22 |
+
|
| 23 |
+
\(H_i = ((A_H * H_{i-2} + B_H * H_{i-1} + C_H) \text{ modulo } D_H) + 1\) for \(i > K\)
|
| 24 |
+
\(X_i = ((A_X * X_{i-2} + B_X * X_{i-1} + C_X) \text{ modulo } D_X) + 1\) for \(i > K\)
|
| 25 |
+
\(Y_i = ((A_Y * Y_{i-2} + B_Y * Y_{i-1} + C_Y) \text{ modulo } D_Y) + 1\) for \(i > K\)
|
| 26 |
+
\(Z_i = ((A_Z * Z_{i-2} + B_Z * Z_{i-1} + C_Z) \text{ modulo } D_Z) + 1\) for \(i > K\)
|
| 27 |
+
\(W_i = ((A_W * W_{i-2} + B_W * W_{i-1} + C_W) \text{ modulo } D_W) + 1\) for \(i > K\)
|
| 28 |
+
|
| 29 |
+
|
| 30 |
+
# Constraints
|
| 31 |
+
|
| 32 |
+
\(1 \le T \le 90\)
|
| 33 |
+
\(2 \le N \le 1,000,000\)
|
| 34 |
+
\(2 \le M \le 1,000,000\)
|
| 35 |
+
\(2 \le K \le min(N, M)\)
|
| 36 |
+
\(0 \le A_H, B_H, C_H, A_X, B_X, C_X, A_Y, B_Y, C_Y, A_Z, B_Z, C_Z, A_W, B_W, C_W \le 1,000,000\)
|
| 37 |
+
\(1 \le D_H, D_Z, D_W \le 1,000,000\)
|
| 38 |
+
\(1 \le D_X, D_Y \le N\)
|
| 39 |
+
\(1 \le H_i \le D_H\)
|
| 40 |
+
\(1 \le X_i \le D_X\)
|
| 41 |
+
\(1 \le Y_i \le D_Y\)
|
| 42 |
+
\(1 \le Z_i \le D_Z\)
|
| 43 |
+
\(1 \le W_i \le D_W\)
|
| 44 |
+
|
| 45 |
+
The sum of \(N + M\) across all springs is at most 15,000,000.
|
| 46 |
+
|
| 47 |
+
|
| 48 |
+
# Input:
|
| 49 |
+
|
| 50 |
+
Input begins with an integer \(T\), the number of springs. For each spring there are 11 lines:
|
| 51 |
+
|
| 52 |
+
The first line contains the 3 space-separated integers \(N\), \(M\), and \(K\).
|
| 53 |
+
|
| 54 |
+
The second line contains the \(K\) space-separated integers \(H_{1..K}\).
|
| 55 |
+
|
| 56 |
+
The third line contains the 4 space-separated integers \(A_H\), \(B_H\), \(C_H\), and \(D_H\).
|
| 57 |
+
|
| 58 |
+
The fourth line contains the \(K\) space-separated integers \(X_{1..K}\).
|
| 59 |
+
|
| 60 |
+
The fifth line contains the 4 space-separated integers \(A_X\), \(B_X\), \(C_X\), and \(D_X\).
|
| 61 |
+
|
| 62 |
+
The sixth line contains the \(K\) space-separated integers \(Y_{1..K}\).
|
| 63 |
+
|
| 64 |
+
The seventh line contains the 4 space-separated integers \(A_Y\), \(B_Y\), \(C_Y\), and \(D_Y\).
|
| 65 |
+
|
| 66 |
+
The eighth line contains the \(K\) space-separated integers \(Z_{1..K}\).
|
| 67 |
+
|
| 68 |
+
The ninth line contains the 4 space-separated integers \(A_Z\), \(B_Z\), \(C_Z\), and \(D_Z\).
|
| 69 |
+
|
| 70 |
+
The tenth line contains the \(K\) space-separated integers \(W_{1..K}\).
|
| 71 |
+
|
| 72 |
+
The eleventh line contains the 4 space-separated integers \(A_W\), \(B_W\), \(C_W\), and \(D_W\).
|
| 73 |
+
|
| 74 |
+
|
| 75 |
+
# Output
|
| 76 |
+
|
| 77 |
+
For the \(i\)th spring, print a line containing *"Case #i: "*, followed by a single integer, the product of \(S_{1..M}\) modulo 1,000,000,007.
|
| 78 |
+
|
| 79 |
+
|
| 80 |
+
# Explanation of Sample
|
| 81 |
+
|
| 82 |
+
For the first spring, after the first earthquake, the spring looks as follows (with the 3 cm-long path which a water spider would follow from column 1 to column 2, or vice versa, indicated in red):
|
| 83 |
+
|
| 84 |
+
{{PHOTO_ID:825086724953069}}
|
| 85 |
+
|
| 86 |
+
After the second earthquake, the spring looks as follows (with the path now only being 2 cm long in either direction):
|
| 87 |
+
|
| 88 |
+
{{PHOTO_ID:2854957798069201}}
|
| 89 |
+
|
| 90 |
+
Therefore, \(S = [6, 4]\), and the final answer is (6 * 4) modulo 1,000,000,007 = 24.
|
| 91 |
+
|
| 92 |
+
For the second spring, \(S = [20, 8, 12]\), with the spring left in the following state after the final earthquake:
|
| 93 |
+
|
| 94 |
+
{{PHOTO_ID:2008456099296384}}
|
| 95 |
+
|
| 96 |
+
For the third spring, \(S = [222, 382, 110, 266, 136, 98]\).
|
| 97 |
+
|
| 98 |
+
For the fourth spring:
|
| 99 |
+
- \(H = [37, 11, 18, 6, 34, 33, 14, 20, 13, 5]\)
|
| 100 |
+
- \(X = [2, 7, 3, 1, 5, 4, 9, 4, 8, 1, 6, 7]\)
|
| 101 |
+
- \(Y = [2, 1, 4, 1, 2, 1, 4, 1, 2, 1, 4, 1]\)
|
| 102 |
+
- \(Z = [24, 38, 59, 64, 17, 36, 21, 22, 45, 8, 71, 4]\)
|
| 103 |
+
- \(W = [16, 9, 55, 35, 58, 9, 4, 77, 55, 27, 10, 29]\)
|
| 104 |
+
- \(S = [2926, 3736, 650, 2754, 518, 6108, 5844, 330, 788, 3844, 7096, 9186]\)
|
2020/finals/spider_spring.out
ADDED
|
@@ -0,0 +1,108 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Case #1: 24
|
| 2 |
+
Case #2: 1920
|
| 3 |
+
Case #3: 633021623
|
| 4 |
+
Case #4: 26104609
|
| 5 |
+
Case #5: 222201367
|
| 6 |
+
Case #6: 294984794
|
| 7 |
+
Case #7: 126230317
|
| 8 |
+
Case #8: 701835095
|
| 9 |
+
Case #9: 476355486
|
| 10 |
+
Case #10: 569072565
|
| 11 |
+
Case #11: 770890219
|
| 12 |
+
Case #12: 331545300
|
| 13 |
+
Case #13: 586465964
|
| 14 |
+
Case #14: 527373588
|
| 15 |
+
Case #15: 660459755
|
| 16 |
+
Case #16: 300060524
|
| 17 |
+
Case #17: 334130994
|
| 18 |
+
Case #18: 388975932
|
| 19 |
+
Case #19: 463042989
|
| 20 |
+
Case #20: 304920201
|
| 21 |
+
Case #21: 113772377
|
| 22 |
+
Case #22: 930176068
|
| 23 |
+
Case #23: 769102540
|
| 24 |
+
Case #24: 408615819
|
| 25 |
+
Case #25: 38456416
|
| 26 |
+
Case #26: 151183167
|
| 27 |
+
Case #27: 495825208
|
| 28 |
+
Case #28: 379977285
|
| 29 |
+
Case #29: 464573744
|
| 30 |
+
Case #30: 54753620
|
| 31 |
+
Case #31: 245195659
|
| 32 |
+
Case #32: 641620440
|
| 33 |
+
Case #33: 598545150
|
| 34 |
+
Case #34: 537132549
|
| 35 |
+
Case #35: 923113036
|
| 36 |
+
Case #36: 526657807
|
| 37 |
+
Case #37: 842401388
|
| 38 |
+
Case #38: 419985955
|
| 39 |
+
Case #39: 964642955
|
| 40 |
+
Case #40: 740556252
|
| 41 |
+
Case #41: 841709531
|
| 42 |
+
Case #42: 878347921
|
| 43 |
+
Case #43: 312086860
|
| 44 |
+
Case #44: 955911834
|
| 45 |
+
Case #45: 276614878
|
| 46 |
+
Case #46: 487022859
|
| 47 |
+
Case #47: 795786176
|
| 48 |
+
Case #48: 343190954
|
| 49 |
+
Case #49: 74385760
|
| 50 |
+
Case #50: 321245598
|
| 51 |
+
Case #51: 965080929
|
| 52 |
+
Case #52: 823067303
|
| 53 |
+
Case #53: 135908834
|
| 54 |
+
Case #54: 585300036
|
| 55 |
+
Case #55: 926495473
|
| 56 |
+
Case #56: 931152045
|
| 57 |
+
Case #57: 894178522
|
| 58 |
+
Case #58: 787600444
|
| 59 |
+
Case #59: 293173412
|
| 60 |
+
Case #60: 68209924
|
| 61 |
+
Case #61: 209830385
|
| 62 |
+
Case #62: 912463885
|
| 63 |
+
Case #63: 575215794
|
| 64 |
+
Case #64: 685242113
|
| 65 |
+
Case #65: 444403624
|
| 66 |
+
Case #66: 962706125
|
| 67 |
+
Case #67: 248763200
|
| 68 |
+
Case #68: 792547224
|
| 69 |
+
Case #69: 91173824
|
| 70 |
+
Case #70: 826460523
|
| 71 |
+
Case #71: 236496818
|
| 72 |
+
Case #72: 562509057
|
| 73 |
+
Case #73: 910930512
|
| 74 |
+
Case #74: 534456170
|
| 75 |
+
Case #75: 3476227
|
| 76 |
+
Case #76: 336398749
|
| 77 |
+
Case #77: 196148390
|
| 78 |
+
Case #78: 715823122
|
| 79 |
+
Case #79: 83714804
|
| 80 |
+
Case #80: 641318271
|
| 81 |
+
Case #81: 725243218
|
| 82 |
+
Case #82: 573492387
|
| 83 |
+
Case #83: 510219501
|
| 84 |
+
Case #84: 199176480
|
| 85 |
+
Case #85: 612804801
|
| 86 |
+
Case #86: 425635646
|
| 87 |
+
Case #87: 969437741
|
| 88 |
+
Case #88: 378662112
|
| 89 |
+
Case #89: 507530203
|
| 90 |
+
Case #90: 513904049
|
| 91 |
+
Case #91: 848838110
|
| 92 |
+
Case #92: 322953305
|
| 93 |
+
Case #93: 517889920
|
| 94 |
+
Case #94: 334400162
|
| 95 |
+
Case #95: 466456064
|
| 96 |
+
Case #96: 798068428
|
| 97 |
+
Case #97: 300601975
|
| 98 |
+
Case #98: 64947010
|
| 99 |
+
Case #99: 468758813
|
| 100 |
+
Case #100: 34487030
|
| 101 |
+
Case #101: 259390400
|
| 102 |
+
Case #102: 457033816
|
| 103 |
+
Case #103: 683157728
|
| 104 |
+
Case #104: 793162616
|
| 105 |
+
Case #105: 992419153
|
| 106 |
+
Case #106: 429921572
|
| 107 |
+
Case #107: 165351954
|
| 108 |
+
Case #108: 782762430
|
2020/finals/spider_spring_sol.md
ADDED
|
@@ -0,0 +1,11 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Let a line segment \((a, b)\) refer to a consecutive pair of columns with distinct heights \(a\) and \(b\), such that \(a < b\). If the column indices are \(i\) and \(i+1\), then we'll refer to \(i\) as the line segment's *position*.
|
| 2 |
+
|
| 3 |
+
We'll define the *weight* \(w\) of a line segment to be the number of spider paths which would cross it. If its index is \(i\), then \(w = i*(N-i)\). We'll say that each line segment has two separate *endpoints* with values \(a\) and \(b\), each with weight \(w\), and with weighted values \(w*a\) and \(w*b\).
|
| 4 |
+
|
| 5 |
+
When evaluating an \(S\) value for a water level \(W\), we'll define a *relevant line segment endpoint* as one with a value greater than \(W\). We'll start by computing the sum of relevant \(b\) endpoints' weighted values, and subtract the sum of relevant \(a\) endpoints' weighted values. There may be line segments for which we only added the \(b\) endpoint but didn't subtract the \(a\) endpoint (due to it being having a value no greater than \(W\)). To account for this, we'll take the sum of relevant \(b\) endpoints' weights, subtract the sum of relevant \(a\) endpoints' weights, multiply that difference by \(W\), and finally subtract that product to arrive at our final answer.
|
| 6 |
+
|
| 7 |
+
In order to compute the above values efficiently, we can maintain 4 Fenwick (binary indexed) trees, containing the \(a\) / \(b\) endpoints' weights / weighted values (in each case indexed by the endpoints' values). Assuming these have been maintained, we can compute each \(S\) value in \(O(log(N))\) time.
|
| 8 |
+
|
| 9 |
+
At first glance, it appears we'll need to perform up to \(O(NM)\) updates to these trees, given that up to \(N\) line segments may be affected by each of the \(M\) earthquakes. However, we can observe that setting the heights of an interval of columns \([L, R]\) causes all line segments at positions in \([L, R-1]\) to disappear, causes at most 2 new line segments (at positions \(L-1\) and \(R\)) to appear, and doesn't update any other line segments. Therefore, across all of the earthquakes, only \(O(N + M)\) line segments need to be updated, and we just need to not waste time iterating over positions not featuring line segments.
|
| 10 |
+
|
| 11 |
+
This can be done either by maintaining a set of intervals of equal-height columns (such that there's a line segment between each consecutive pair of intervals), or by maintaining a segment tree of column heights combined with a set of line segment positions. Either way, these data structures may be updated in amortized \(O(log(N))\) time per earthquake and allow us to only update the Fenwick trees described above for \(O(N + M)\) line segments overall. The total complexity is therefore \(O((N + M) log(N))\).
|
2020/finals/tree_training.cpp
ADDED
|
@@ -0,0 +1,201 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
// Tree Training
|
| 2 |
+
// Solution by Jacob Plachta
|
| 3 |
+
|
| 4 |
+
#include <algorithm>
|
| 5 |
+
#include <functional>
|
| 6 |
+
#include <numeric>
|
| 7 |
+
#include <iostream>
|
| 8 |
+
#include <iomanip>
|
| 9 |
+
#include <cstdio>
|
| 10 |
+
#include <cmath>
|
| 11 |
+
#include <complex>
|
| 12 |
+
#include <cstdlib>
|
| 13 |
+
#include <ctime>
|
| 14 |
+
#include <cstring>
|
| 15 |
+
#include <cassert>
|
| 16 |
+
#include <string>
|
| 17 |
+
#include <vector>
|
| 18 |
+
#include <list>
|
| 19 |
+
#include <map>
|
| 20 |
+
#include <set>
|
| 21 |
+
#include <unordered_map>
|
| 22 |
+
#include <unordered_set>
|
| 23 |
+
#include <deque>
|
| 24 |
+
#include <queue>
|
| 25 |
+
#include <stack>
|
| 26 |
+
#include <bitset>
|
| 27 |
+
#include <sstream>
|
| 28 |
+
using namespace std;
|
| 29 |
+
|
| 30 |
+
#define LL long long
|
| 31 |
+
#define LD long double
|
| 32 |
+
#define PR pair<int,int>
|
| 33 |
+
|
| 34 |
+
#define Fox(i,n) for (i=0; i<n; i++)
|
| 35 |
+
#define Fox1(i,n) for (i=1; i<=n; i++)
|
| 36 |
+
#define FoxI(i,a,b) for (i=a; i<=b; i++)
|
| 37 |
+
#define FoxR(i,n) for (i=(n)-1; i>=0; i--)
|
| 38 |
+
#define FoxR1(i,n) for (i=n; i>0; i--)
|
| 39 |
+
#define FoxRI(i,a,b) for (i=b; i>=a; i--)
|
| 40 |
+
#define Foxen(i,s) for (i=s.begin(); i!=s.end(); i++)
|
| 41 |
+
#define Min(a,b) a=min(a,b)
|
| 42 |
+
#define Max(a,b) a=max(a,b)
|
| 43 |
+
#define Sz(s) int((s).size())
|
| 44 |
+
#define All(s) (s).begin(),(s).end()
|
| 45 |
+
#define Fill(s,v) memset(s,v,sizeof(s))
|
| 46 |
+
#define pb push_back
|
| 47 |
+
#define mp make_pair
|
| 48 |
+
#define x first
|
| 49 |
+
#define y second
|
| 50 |
+
|
| 51 |
+
template<typename T> T Abs(T x) { return(x < 0 ? -x : x); }
|
| 52 |
+
template<typename T> T Sqr(T x) { return(x * x); }
|
| 53 |
+
string plural(string s) { return(Sz(s) && s[Sz(s) - 1] == 'x' ? s + "en" : s + "s"); }
|
| 54 |
+
|
| 55 |
+
const int INF = (int)1e9;
|
| 56 |
+
const LD EPS = 1e-12;
|
| 57 |
+
const LD PI = acos(-1.0);
|
| 58 |
+
|
| 59 |
+
#define GETCHAR getchar_unlocked
|
| 60 |
+
|
| 61 |
+
bool Read(int& x) {
|
| 62 |
+
char c, r = 0, n = 0;
|
| 63 |
+
x = 0;
|
| 64 |
+
for (;;) {
|
| 65 |
+
c = GETCHAR();
|
| 66 |
+
if ((c < 0) && (!r))
|
| 67 |
+
return(0);
|
| 68 |
+
if ((c == '-') && (!r))
|
| 69 |
+
n = 1;
|
| 70 |
+
else if ((c >= '0') && (c <= '9'))
|
| 71 |
+
x = x * 10 + c - '0', r = 1;
|
| 72 |
+
else if (r)
|
| 73 |
+
break;
|
| 74 |
+
}
|
| 75 |
+
if (n)
|
| 76 |
+
x = -x;
|
| 77 |
+
return(1);
|
| 78 |
+
}
|
| 79 |
+
|
| 80 |
+
#define MOD 1000000007
|
| 81 |
+
#define LIM 1000005
|
| 82 |
+
#define LOG 20
|
| 83 |
+
|
| 84 |
+
int N, M;
|
| 85 |
+
char S[LIM];
|
| 86 |
+
int Z[LIM];
|
| 87 |
+
int DS[LIM];
|
| 88 |
+
|
| 89 |
+
int TreeCnt(int h) // # of nodes in binary tree with height h
|
| 90 |
+
{
|
| 91 |
+
return((1 << (h + 1)) - 1);
|
| 92 |
+
}
|
| 93 |
+
|
| 94 |
+
// E(z, s, h) = max. *s which can fit alongside z 0s (with s *s before the 1st 0) in a tree of height at most h (only relevant for z > 0)
|
| 95 |
+
int E(int z, int s, int h)
|
| 96 |
+
{
|
| 97 |
+
if (h >= LOG)
|
| 98 |
+
return(N);
|
| 99 |
+
int left = min(s, h + 1 - z); // *s at root and along leftmost branch
|
| 100 |
+
int cnt = TreeCnt(h); // full tree
|
| 101 |
+
cnt -= TreeCnt(h - left); // subtract subtree of 1st 0
|
| 102 |
+
if (cnt >= s)
|
| 103 |
+
cnt += TreeCnt(h - left - 1); // add back right subtree of 1st 0
|
| 104 |
+
return(cnt);
|
| 105 |
+
}
|
| 106 |
+
|
| 107 |
+
// F(p, z, s) = min. tree height for p *s, z 0s, and s *s before 1st 0 (s ignored if z = 0)
|
| 108 |
+
int F(int p, int z, int s)
|
| 109 |
+
{
|
| 110 |
+
int r1 = z ? (s > 0 ? z : z - 1) : 0;
|
| 111 |
+
int r2 = max(r1, min(LOG, p + z - 1));
|
| 112 |
+
while (r1 < r2)
|
| 113 |
+
{
|
| 114 |
+
int m = (r1 + r2) >> 1;
|
| 115 |
+
if ((z ? E(z, s, m) : TreeCnt(m)) >= p)
|
| 116 |
+
r2 = m;
|
| 117 |
+
else
|
| 118 |
+
r1 = m + 1;
|
| 119 |
+
}
|
| 120 |
+
return(r1);
|
| 121 |
+
}
|
| 122 |
+
|
| 123 |
+
int ProcessCase()
|
| 124 |
+
{
|
| 125 |
+
int i, j, z;
|
| 126 |
+
// input
|
| 127 |
+
scanf("%s", &S);
|
| 128 |
+
N = strlen(S);
|
| 129 |
+
// find 0s
|
| 130 |
+
M = 0;
|
| 131 |
+
Z[M++] = -1;
|
| 132 |
+
Fox(i, N)
|
| 133 |
+
if (S[i] == '0')
|
| 134 |
+
Z[M++] = i;
|
| 135 |
+
Z[M++] = N;
|
| 136 |
+
// A) z = 0
|
| 137 |
+
int ans = 0;
|
| 138 |
+
int v = 0, s = 0;
|
| 139 |
+
Fill(DS, 0);
|
| 140 |
+
Fox1(i, M - 1)
|
| 141 |
+
{
|
| 142 |
+
int x = Z[i] - Z[i - 1] - 1; // sequence of x *s before ith 0
|
| 143 |
+
v += x;
|
| 144 |
+
DS[2]--, DS[x + 2]++;
|
| 145 |
+
}
|
| 146 |
+
Fox1(i, N)
|
| 147 |
+
{
|
| 148 |
+
s += DS[i];
|
| 149 |
+
v += s;
|
| 150 |
+
ans = (ans + (LL)v * F(i, 0, 0)) % MOD;
|
| 151 |
+
}
|
| 152 |
+
// B) 1 <= z <= LOG
|
| 153 |
+
Fox1(z, LOG) // z 0s
|
| 154 |
+
{
|
| 155 |
+
Fox1(i, M - z - 1) // ith 0 as the leftmost 0
|
| 156 |
+
{
|
| 157 |
+
int j = i + z - 1;
|
| 158 |
+
int c1 = Z[i] - Z[i - 1] - 1; // c1 *s to the left
|
| 159 |
+
int c2 = Z[j + 1] - Z[j] - 1; // c2 *s to the right
|
| 160 |
+
int m = Z[j] - Z[i] + 1 - z; // m *s in between
|
| 161 |
+
Fox(s, c1 + 1) // use s *s to the left
|
| 162 |
+
{
|
| 163 |
+
int p = s + m, mp = s + m + c2;
|
| 164 |
+
int h = F(p, z, s);
|
| 165 |
+
while (p <= mp)
|
| 166 |
+
{
|
| 167 |
+
int p2 = min(mp, E(z, s, h));
|
| 168 |
+
ans = (ans + (LL)(p2 - p + 1) * h) % MOD;
|
| 169 |
+
p = p2 + 1, h++;
|
| 170 |
+
}
|
| 171 |
+
}
|
| 172 |
+
}
|
| 173 |
+
}
|
| 174 |
+
// C) z > LOG
|
| 175 |
+
Fox1(i, M - 2) // count contribution of the ith 0
|
| 176 |
+
{
|
| 177 |
+
// add # of intervals containing it
|
| 178 |
+
ans = (ans + (LL)(Z[i] + 1) * (N - Z[i])) % MOD;
|
| 179 |
+
// subtract # of intervals containing it, with <= LOG 0s
|
| 180 |
+
FoxI(j, max(1, i - LOG + 1), i) // jth 0 as the leftmost 0
|
| 181 |
+
{
|
| 182 |
+
int k = min(M - 1, j + LOG); // first disallowed 0
|
| 183 |
+
int c = (LL)(Z[j] - Z[j - 1]) * (Z[k] - Z[i]) % MOD;
|
| 184 |
+
ans = (ans + MOD - c) % MOD;
|
| 185 |
+
}
|
| 186 |
+
// subtract # of intervals starting with it, with > LOG 0s
|
| 187 |
+
int j = i + LOG;
|
| 188 |
+
if (j < M)
|
| 189 |
+
ans = (ans + MOD - (N - Z[j])) % MOD;
|
| 190 |
+
}
|
| 191 |
+
return(ans);
|
| 192 |
+
}
|
| 193 |
+
|
| 194 |
+
int main()
|
| 195 |
+
{
|
| 196 |
+
int T, t;
|
| 197 |
+
Read(T);
|
| 198 |
+
Fox1(t, T)
|
| 199 |
+
printf("Case #%d: %d\n", t, ProcessCase());
|
| 200 |
+
return(0);
|
| 201 |
+
}
|
2020/finals/tree_training.in
ADDED
|
The diff for this file is too large to render.
See raw diff
|
|
|