text
stringlengths 100
500k
| subset
stringclasses 4
values |
|---|---|
Only show open access (3)
Over 3 years (6)
Statistics and Probability (1)
operational semantics
Theory and Practice of Logic Programming (5)
Mathematical Structures in Computer Science (3)
RAIRO - Theoretical Informatics and Applications (1)
Cambridge University Press (1)
14 - Tabular: Probabilistic Inference from the Spreadsheet
By Andrew D. Gordon, Claudio Russo, Marcin Szymczak, Johannes Borgström, Nicolas Rolland, Thore Graepel, Daniel Tarlow
Edited by Gilles Barthe, Joost-Pieter Katoen, RWTH Aachen University, Germany, Alexandra Silva, University College London
Book: Foundations of Probabilistic Programming
Print publication: 03 December 2020, pp 489-532
View extract
Tabular is a domain-specific language for expressing probabilistic models of relational data. Tabular has several features that set it apart from other probabilistic programming languages including: (1) programs and data are stored as spreadsheet tables; (2) programs consist of probabilistic annotations on the relational schema of the data; and (3) inference returns estimations of missing values and latent columns, as well as parameters. Our primary implementation is for Microsoft Excel and relies on Infer.NET for inference. Still, the language can be called independently of Excel and can target alternative inference engines.
Petri nets based on Lawvere theories
Jade Master
Journal: Mathematical Structures in Computer Science / Volume 30 / Issue 7 / August 2020
Published online by Cambridge University Press: 09 November 2020, pp. 833-864
We give a definition of Q-net, a generalization of Petri nets based on a Lawvere theory Q, for which many existing variants of Petri nets are a special case. This definition is functorial with respect to change in Lawvere theory, and we exploit this to explore the relationships between different kinds of Q-nets. To justify our definition of Q-net, we construct a family of adjunctions for each Lawvere theory explicating the way in which Q-nets present free models of Q in Cat. This gives a functorial description of the operational semantics for an arbitrary category of Q-nets. We show how this can be used to construct the semantics for Petri nets, pre-nets, integer nets, and elementary net systems.
Flexible coinductive logic programming
FRANCESCO DAGNINO, DAVIDE ANCONA, ELENA ZUCCA
Journal: Theory and Practice of Logic Programming / Volume 20 / Issue 6 / November 2020
Published online by Cambridge University Press: 22 September 2020, pp. 818-833
Add to cart £26.00 Added to cart An error has occurred,
Recursive definitions of predicates are usually interpreted either inductively or coinductively. Recently, a more powerful approach has been proposed, called flexible coinduction, to express a variety of intermediate interpretations, necessary in some cases to get the correct meaning. We provide a detailed formal account of an extension of logic programming supporting flexible coinduction. Syntactically, programs are enriched by coclauses, clauses with a special meaning used to tune the interpretation of predicates. As usual, the declarative semantics can be expressed as a fixed point which, however, is not necessarily the least, nor the greatest one, but is determined by the coclauses. Correspondingly, the operational semantics is a combination of standard SLD resolution and coSLD resolution. We prove that the operational semantics is sound and complete with respect to declarative semantics restricted to finite comodels.
Open Petri nets
John C. Baez, Jade Master
Journal: Mathematical Structures in Computer Science / Volume 30 / Issue 3 / March 2020
Published online by Cambridge University Press: 07 April 2020, pp. 314-341
The reachability semantics for Petri nets can be studied using open Petri nets. For us, an "open" Petri net is one with certain places designated as inputs and outputs via a cospan of sets. We can compose open Petri nets by gluing the outputs of one to the inputs of another. Open Petri nets can be treated as morphisms of a category Open(Petri), which becomes symmetric monoidal under disjoint union. However, since the composite of open Petri nets is defined only up to isomorphism, it is better to treat them as morphisms of a symmetric monoidal double category ${\mathbb O}$ pen(Petri). We describe two forms of semantics for open Petri nets using symmetric monoidal double functors out of ${\mathbb O}$ pen(Petri). The first, an operational semantics, gives for each open Petri net a category whose morphisms are the processes that this net can carry out. This is done in a compositional way, so that these categories can be computed on smaller subnets and then glued together. The second, a reachability semantics, simply says which markings of the outputs can be reached from a given marking of the inputs.
A deterministic rewrite system for the probabilistic λ-calculus
Thomas Leventis
Journal: Mathematical Structures in Computer Science / Volume 29 / Issue 10 / November 2019
Published online by Cambridge University Press: 06 June 2019, pp. 1479-1512
In this paper we present an operational semantics for the 'call-by-name' probabilistic λ-calculus, whose main feature is to use only deterministic relations and to have no constraint on the reduction strategy. The calculus enjoys similar properties to the usual λ-calculus. In particular we prove it to be confluent, and we prove a standardisation theorem.
Probabilistic operational semantics for the lambda calculus
Ugo Dal Lago, Margherita Zorzi
Journal: RAIRO - Theoretical Informatics and Applications / Volume 46 / Issue 3 / July 2012
Published online by Cambridge University Press: 22 June 2012, pp. 413-450
Probabilistic operational semantics for a nondeterministic extension of pure λ-calculus is studied. In this semantics, a term evaluates to a (finite or infinite) distribution of values. Small-step and big-step semantics, inductively and coinductively defined, are given. Moreover, small-step and big-step semantics are shown to produce identical outcomes, both in call-by-value and in call-by-name. Plotkin's CPS translation is extended to accommodate the choice operator and shown correct with respect to the operational semantics. Finally, the expressive power of the obtained system is studied: the calculus is shown to be sound and complete with respect to computable probability distributions.
A simple correctness proof for magic transformation
WŁODZIMIERZ DRABENT
Published online by Cambridge University Press: 04 March 2011, pp. 929-936
The paper presents a simple and concise proof of correctness of the magic transformation. We believe that it may provide a useful example of formal reasoning about logic programs. The correctness property concerns the declarative semantics. The proof, however, refers to the operational semantics (LD-resolution) of the source programs. Its conciseness is due to applying a suitable proof method.
A complete and terminating execution model for Constraint Handling Rules
HARIOLF BETZ, FRANK RAISER, THOM FRÜHWIRTH
Journal: Theory and Practice of Logic Programming / Volume 10 / Issue 4-6 / July 2010
We observe that the various formulations of the operational semantics of Constraint Handling Rules proposed over the years fall into a spectrum ranging from the analytical to the pragmatic. While existing analytical formulations facilitate program analysis and formal proofs of program properties, they cannot be implemented as is. We propose a novel operational semantics ω!, which has a strong analytical foundation, while featuring a terminating execution model. We prove its soundness and completeness with respect to existing analytical formulations and we provide an implementation in the form of a source-to-source transformation to CHR with rule priorities.
Graphs and colorings for answer set programming
KATHRIN KONCZAK, THOMAS LINKE, TORSTEN SCHAUB
Journal: Theory and Practice of Logic Programming / Volume 6 / Issue 1-2 / January 2006
Published online by Cambridge University Press: 27 January 2006, pp. 61-106
We investigate the usage of rule dependency graphs and their colorings for characterizing and computing answer sets of logic programs. This approach provides us with insights into the interplay between rules when inducing answer sets. We start with different characterizations of answer sets in terms of totally colored dependency graphs that differ in graph-theoretical aspects. We then develop a series of operational characterizations of answer sets in terms of operators on partial colorings. In analogy to the notion of a derivation in proof theory, our operational characterizations are expressed as (non-deterministically formed) sequences of colorings, turning an uncolored graph into a totally colored one. In this way, we obtain an operational framework in which different combinations of operators result in different formal properties. Among others, we identify the basic strategy employed by the noMoRe system and justify its algorithmic approach. Furthermore, we distinguish operations corresponding to Fitting's operator as well as to well-founded semantics.
The witness properties and the semantics of the Prolog cut
JAMES H. ANDREWS
Journal: Theory and Practice of Logic Programming / Volume 3 / Issue 1 / January 2003
Published online by Cambridge University Press: 18 December 2002, pp. 1-59
The semantics of the Prolog 'cut' construct is explored in the context of some desirable properties of logic programming systems, referred to as the witness properties. The witness properties concern the operational consistency of responses to queries. A generalization of Prolog with negation as failure and cut is described, and shown not to have the witness properties. A restriction of the system is then described, which preserves the choice and first-solution behaviour of cut but allows the system to have the witness properties. The notion of cut in the restricted system is more restricted than the Prolog hard cut, but retains the useful first-solution behaviour of hard cut, not retained by other proposed cuts such as the 'soft cut'. It is argued that the restricted system achieves a good compromise between the power and utility of the Prolog cut and the need for internal consistency in logic programming systems. The restricted system is given an abstract semantics, which depends on the witness properties; this semantics suggests that the restricted system has a deeper connection to logic than simply permitting some computations which are logical. Parts of this paper appeared previously in a different form in the Proceedings of the 1995 International Logic Programming Symposium (Andrews, 1995). | CommonCrawl |
Are there Soliton Solutions for Maxwell's Equations?
Some non-linear differential equations (such as Korteweg–de Vries and Kadomtsev–Petviashvili equations) have "solitary waves" solutions (solitons).
Does the set of partial differential equations known as "Maxwell's equations" theoretically admit such kind of solutions?
In that case, should these solutions appear in the form of "stationary shells" of electromagnetic field? By "stationary", I mean do the solutions maintain their shape?
Thanks for your comments!
partial-differential-equations mathematical-physics nonlinear-system electromagnetism soliton-theory
$\begingroup$ What means "solitary wave solution" for you? Something like compact support and "not changing form"? $\endgroup$
– Severin Schraven
$\begingroup$ @SeverinSchraven Yes! Something like this. I would say, the equivalent of the solitons in the (shallow) water. $\endgroup$
$\begingroup$ @andrea.prunotto: Could you please clarify what you mean by "stationary shells"? $\endgroup$
– Adrian Keister
$\begingroup$ @SeverinSchraven With this term I mean "a bubble" of electromagnetic field, sorry if I cannot be more precise, the 3D equivalent of the 1-D soliton in the water (i.e. a wave that does not involve crests and troughs, but is made only of a crest, or a trough). $\endgroup$
$\begingroup$ @AdrianKeister Sorry, the previous comment was for you! $\endgroup$
The answer is yes to both questions. If you cast Maxwell's Equations in cylindrical coordinates for a fiber optic cable, and you take birefringence into account, you get the coupled nonlinear Schrödinger equations. You can then solve those by means of the Inverse Scattering Transform, which takes the original system of nonlinear pde's (nonlinear because of the coordinate system), transforms them into a coupled system of linear ode's (the Manakov system) which are straight-forward to solve, and then, by means of the Gel'fand-Levitan-Marchenko integral equation, you arrive at the soliton solutions of the original pde's. For references, see C. Menyuk, Application of multiple-length-scale methods to the study of optical fiber transmission, Journal of Engineering Mathematics 36: 113-136, 1999, Kluwer Academic Publishers, Netherlands, and my own dissertation, which includes other references of interest. In particular, Shaw's book Mathematical Principles of Optical Fiber Communication has most of these derivations in it.
The resulting soliton solutions behave mostly like waves, but they also interact in a particle-like fashion; for example, in a collision, they can alter each others' phase - a decidedly non-wave-like behavior. Solitons do not stay in one place; in the case above, they would travel down the fiber cable (indeed, solitons are the reason fiber is the backbone of the Internet!), and self-correct their shape as they go. And, as Maxwell's equations are all about electromagnetic fields, the solutions are, indeed, stationary (in your sense) "shells" of electromagnetic fields.
Adrian KeisterAdrian Keister
$\begingroup$ Thanks for the detailed and illuminating answer, Adrian! A further question for you: Do you know if there are macroscopic conditions in which such phenomenon occurs? I mean, a case in which such solitons can have dimensions of meters, rather than the dimensions of the diameter of a fiber cable? $\endgroup$
$\begingroup$ @andrea.prunotto: Thank you for your kind words. An interesting question, that. I don't know the answer; my hunch/intuition would be no, but I don't have much of anything to back that up. $\endgroup$
$\begingroup$ @andrea.prunotto I googled: High power, pulsed soliton generation at radio and microwave frequencies. $\endgroup$
– Keith McClary
$\begingroup$ Also en.wikipedia.org/wiki/Ball_lightning#Soliton_hypothesis. $\endgroup$
$\begingroup$ @Adrian,Keith Thanks for your comments! $\endgroup$
Adrian has given an interesting answer already, but I think it is worth pointing out two key points which were necessary for his soliton situation. Firstly, it was necessary to impose some specific form of initial-boundary data (to constrain the waves to inside the fibre optic cable), and secondly it was necessary to impose physical assumptions on the medium which actually changed the underlying PDE.
If one considers the source-free Maxwells equations in a vacuum, then you know that the electric and magnetic fields $E$ and $B$ satisfy the standard wave equations $\Box E=0$, $\Box B =0$. If you work on the domain $(x,t)\in \mathbb{R}^3 \times [0,\infty)$ of "open space", and if you pose a Cauchy problem for the equations, which means if you specify some initial data (which must of course satisfy divergence free conditions) along the initial surface $t=0$, then it follows from Kirchoff's formula for the solution that the fields $E$ and $B$ have to decay in time. Specifically, one has $\|D^\alpha E(\cdot,t), D^\alpha B(\cdot,t)\|_{L^\infty(\mathbb{R}^3)} \to 0$ as $t\to \infty$ where $D^\alpha$ represents any chosen choice of composition of partial derivatives.
Thus solutions to Maxwell's equations on an unbounded domain must always "scatter at infinity", and you can't hope to find soliton type solutions.
Aerinmund FagelsonAerinmund Fagelson
$\begingroup$ Thanks for your answer! Very interesting, and neat. I wonder if our atmosphere (where these ball-lightnings occur) can be considered a "bound domain", and how. $\endgroup$
$\begingroup$ Interesting thought! I must admit I don't know much about the physics of lightening, but I think the lightening storm would be a much more complicated electrodynamics problem. My answer is really only supposed to apply to electromagnetic waves travelling in a vacuum (such as those induced by the lightening storm which carry the image to your eye, for instance). $\endgroup$
– Aerinmund Fagelson
$\begingroup$ Also you raise a good point that in reality there is no such thing as an unbounded domain, but for initial disturbances that are sufficiently localized with respect to the scale of the problem (i.e. the size of the of the lightening cloud compared with the distance to an astronaut on the moon) the model should be quite good and one would expect the waves to decay as they travel through space (i.e. the lightening storm may appear bright to you, but will look very dim from the perspective of the astronaut). $\endgroup$
$\begingroup$ Was just looking at some of the videos of this "ball lightning". I do see your point that it is not clear the soliton behaviour there is driven at all by boundedness constraints on the domain. The lightning ball just sits their localized in the middle of a huge cloud! Probably some very complicated nonlinear phenomena going on! Afraid I'm out of my depth :p $\endgroup$
$\begingroup$ I share the same feeling! That's way I was trying to address the problem in a theoretical way. But I have studied non-linear equations only for the water (tidal waves, etc.). By the way, there is the theory due to Kapitza, et al (1955), but it does not explain why these monsters (the ball lightnings) are extremely charged! $\endgroup$
A Learning Roadmap to the "foundations" of Nonlinear Analysis (and certain specific topics)
Can we model finite propagation speeds through parabolic PDEs?
Solve non-linear differential equation with boundary conditions
reference for soliton solutions
Conservation of mass in hyperbolic PDE [reference request]
Derivation of 2D Korteweg-de-Vries equation
What constitutes a gauge theory? Help me understand electromagnetism as the prototype of all gauge theories
Help understanding the derivation of Maxwell's equations from Euler-Lagrange equations
Maxwell's equations as general partial differential equations
Why are soliton solutions interesting mathematically or physically? | CommonCrawl |
When the Angles of a Triangle Don't Add up to 180 Degrees
Article by Toni Beardon
Published May 2002,February 2011.
Do the angles of a triangle add up to 180 degrees or $\pi$ radians? The answer is 'sometimes yes, sometimes no'. Is this an important question? Yes, because it leads to an understanding that there are different geometries based on different axioms or 'rules of the game of geometry'. Is it a meaningful question? Well no, at least not until we have agreed on the meaning of the words 'angle' and 'triangle', not until we know the rules of the game. In this article we briefly discuss the underlying axioms and give a simple proof that the sum of the angles of a triangle on the surface of a unit sphere is not equal to $\pi$ but to $\pi$ plus the area of the triangle. We shall use the fact that the area of the surface of a unit sphere is $4\pi$.
2. The Big Theorem
Before we can say what a triangle is we need to agree on what we mean by points and lines. We are working on spherical geometry (literally geometry on the surface of a sphere). In this geometry the space is the surface of the sphere; the points are points on that surface, and the line of shortest distance between two points is the great circle containing the two points. A great circle (like the Equator) cuts the sphere into two equal hemispheres. This geometry has obvious applications to distances between places and air-routes on the Earth.
Rotating sphere showing great circle
The angle between two great circles at a point P is the Euclidean angle between the directions of the circles (or strictly between the tangents to the circles at P). This presents no difficulty in navigation on the Earth because at any given point we think of the angle between two directions as if the Earth were flat at that point.
A lune is a part of the surface of the sphere bounded by two great circles which meet at antipodal points. We first consider the area of a lune and then introduce another great circle that splits the lune into triangles.
Rotating sphere showing 4 lunes
Lemma.
The area of a lune on a circle of unit radius is twice its angle, that is if the angle of the lune is A then its area is 2A. Two great circles intersecting at antipodal points P and P' divide the sphere into 4 lunes. The area of the surface of a unit sphere is $4\pi$.
The areas of the lunes are proportional to their angles at P so the area of a lune with angle A is
${\frac{A}{2\pi}\times {4\pi}= {2A}}$
Exercise 1.
What are the areas of the other 3 lunes? Do your 4 areas add up to $4\pi$?
Check your answers here .
The sides of a triangle ABC are segments of three great circles which actually cut the surface of the sphere into eight spherical triangles. Between the two great circles through the point A there are four angles. We label the angle inside triangle ABC as angle A, and similarly the other angles of triangle ABC as angle B and angle C.
Rotating sphere showing 8 triangles
Rotating the sphere can you name the eight triangles and say whether any of them have the same area? Check your answers here .
Theorem.
Consider a spherical triangle ABC on the unit sphere with angles A, B and C. Then the area of triangle ABC is
A + B + C - $\pi$.
The diagram shows a view looking down on the hemisphere which has the line through AC as its boundary. The regions marked Area 1 and Area 3 are lunes with angles A and C respectively. Consider the lunes through B and B'. Triangle ABC is congruent to triangle A'B'C' so the bow-tie shaped shaded area, marked Area 2, which is the sum of the areas of the triangles ABC and A'BC', is equal to the area of the lune with angle B, that is equal to 2B.
So in the diagram we see the areas of three lunes and, using the lemma, these are:
Area 1 = 2A
Area 2 = 2B
Area 3 = 2C
In adding up these three areas we include the area of the triangle ABC three times. Hence
Area 1 + Area 2 + Area 3 = Area of hemisphere +2(Area of triangle ABC)
2A + 2B + 2C
2 $\pi$ + 2(Area of triangle ABC)
Area of triangle ABC
A + B + C - $\pi$ .
3. Non-Euclidean Geometry
Sometimes revolutionary discoveries are nothing more than actually seeing what has been under our noses all the time. This was the case over the discovery of Non-Euclidean Geometry in the nineteenth century. For some 2000 years after Euclid wrote his 'Elements' in 325 BC people tried to prove the parallel postulate as a theorem in the geometry from the other axioms but always failed and that is a long story. Meanwhile mathematicians were using spherical geometry all the time, a geometry which obeys the other axioms of Euclidean Geometry and contains many of the same theorems, but in which the parallel postulate does not hold. All along they had an example of a Non-Euclidean Geometry under their noses.
Think of a line L and a point P not on L. The big question is: "How many lines can be drawn through P parallel to L?" In Euclidean Geometry the answer is ``exactly one" and this is one version of the parallel postulate. If the sum of the angles of every triangle in the geometry is $\pi$ radians then the parallel postulate holds and vice versa, the two properties are equivalent.
In spherical geometry, the basic axioms which we assume (the rules of the game) are different from Euclidean Geometry - this is a Non-Euclidean Geometry. We have seen that in spherical geometry the angles of triangles do not always add up to $\pi$ radians so we would not expect the parallel postulate to hold. In spherical geometry, the straight lines (lines of shortest distance or geodesics) are great circles and every line in the geometry cuts every other line in two points. The answer to the big question about parallels is``If we have a line L and a point P not on L then there are no lines through P parallel to the line L."
The Greek mathematicians (for example Ptolemy c 150) computed the measurements of right angled spherical triangles and worked with formulae of spherical trigonometry and Arab mathematicians (for example Jabir ibn Aflah c 1125 and Nasir ed-din c 1250) extended the work even further. The formula discussed in this article was discovered by Harriot in 1603 and published by Girard in 1629. Further ideas of the subject were developed by Saccerhi (1667 - 1733).
All this went largely un-noticed by the 19th century discoverers of hyperbolic geometry, which is another Non-Euclidean Geometry where the parallel postulate does not hold. In spherical geometry (also called elliptic geometry) the angles of triangles add up to more than $\pi$ radians and in hyperbolic geometry the angles of triangles add up to less than $\pi$ radians.
For further reading see the article by Alan Beardon 'How many Geometries Are There?' and the article by Keith Carne 'Strange Geometries' . There are some practical activities that you can try for yourself to explore these geometries further to be found at http://nrich.maths.org/MOTIVATE/conf8/index.html | CommonCrawl |
Scalable techniques and algorithms for computational genomics (part 2)
Predicting metabolic pathway membership with deep neural networks by integrating sequential and ontology information
Imam Cartealy1 &
Li Liao ORCID: orcid.org/0000-0002-1197-18791
Inference of protein's membership in metabolic pathways has become an important task in functional annotation of protein. The membership information can provide valuable context to the basic functional annotation and also aid reconstruction of incomplete pathways. Previous works have shown success of inference by using various similarity measures of gene ontology.
In this work, we set out to explore integrating ontology and sequential information to further improve the accuracy. Specifically, we developed a neural network model with an architecture tailored to facilitate the integration of features from different sources. Furthermore, we built models that are able to perform predictions from pathway-centric or protein-centric perspectives. We tested the classifiers using 5-fold cross validation for all metabolic pathways reported in KEGG database.
The testing results demonstrate that by integrating ontology and sequential information with a tailored architecture our deep neural network method outperforms the existing methods significantly in the pathway-centric mode, and in the protein-centric mode, our method either outperforms or performs comparably with a suite of existing GO term based semantic similarity methods.
Metabolic pathways are series of biochemical reactions occurring within the cell which involve catalytic reactions of protein enzymes converting substrate compounds into product compounds. Because each reaction in the pathway requires a protein enzyme as catalysis in order to happen, from an enzyme centric perspective, a metabolic pathway can be represented as a list of these proteins. Identification of organism's metabolism usually involves laborious experimental techniques mainly in characterization of protein enzymes in metabolic pathways. It requires advanced technologies, expensive equipments, and highly skilled manpower to perform the experiments. To shorten the steps required in the characterization process, computational methods are often deployed for modeling the pathway and inferring specific tasks. The prediction step might provide a higher level of network organization that facilitate human comprehension of the system and aid in identifying the missing information such as missing proteins or reactions in the network. One example of such prediction tasks is pathway membership inference, which is to determine whether a protein is a member in the enzyme list of a given pathway. This is an important annotation task that can not only provide context to the basic function annotation of proteins but also more importantly aid reconstruction of incomplete metabolic pathways, which can subsequently help better understand metabolism and physiology of cells and provide complementary perspective to study evolutionary [1].
However, traditional sequence similarity-based homology approaches to characterizing proteins for their enzymatic properties run into difficulties when sequence identity is lower than 60% [2]. Facing this challenge, various efforts have been made to go beyond individual proteins and their homologs to leverage the large amount of annotations for proteins in their functional context, such as from curated reference dataset or features extracted from proteins. The example of curated reference dataset is Gene Ontology (GO), which provide a hierarchy of controlled terms defining protein functions with varied levels of specificity for different cellular functions/processes [3, 4]. The semantic similarity between two proteins can be used to replace the sequence-based similarity method.
Various similarity measures have been developed to quantify the semantic similarity of GO terms and applied it in quantitative comparison of functional similarity of gene products, although most of these methods are not developed for metabolic pathway membership inference [5–10]. Essentially, those measures mainly involve two steps of calculation : 1) calculation of GO term similarity, and 2) calculation of protein similarity, based on GO term similarity. In the first step, the semantic similarity between two GO terms is calculated to incorporate the GO hierarchy, via information contains in the GO tree such as node, edge or combination of the two. In the second step, protein similarities are aggregated from their terms' similarities. To infer the protein's membership in the pathway, the similarity between the proteins are then used [7, 11]. More recently, in [5], a hybrid approach to take into account of both information content of individual GO terms and the whole GO hierarchy with a simple Cosine similarity is shown to be advantageous in both prediction accuracy and running time as compared with other semantic similarity-based methods.
In general, however, the prediction task of proteins' annotation, including the prediction of protein's metabolic pathway annotation, may come from two perspectives. One perspective is the pathway centric perspective and the other is protein centric perspective. In the pathway centric perspective, the relevant question is: given a pathway, predict the proteins participate in the pathway, thus this perspective leads to prediction problem of association of pathway and its enzymatic reaction. On the other hand, the protein centric problem asks a different question: given a protein and its annotation, predict enzymatic reaction that they catalyzed. This question can be translated into prediction of set of metabolic pathways of which a given protein is likely to be a member. While the protein centric perspective is more natural in protein annotation, it turns out more computationally challenging as it is multi-class classification problem, as compared to the binary classification problem for pathway centric membership prediction.
In this work, we set out to develop new computational approach based on neural networks for predicting pathway membership from both directions: the protein centric and pathway centric problems. In doing so, we also explore integrating both ontology and sequential information to further improve the accuracy. Specifically, we develop a neural network model with an architecture tailored to facilitate the integration of features from different sources.
Table 1 shows the performance of our method for pathway membership prediction, in comparison to using a suite of different ontology-based gene similarity methods mentioned in the Methods. Because GO has three separate hierarchies: BP, CC, and MF, we thus evaluated the prediction performance for using each hierarchy. In addition, we also evaluated the performance of different featured used in this experiment separately.
Table 1 The ROC score of different methods in pathway membership prediction for all ontologies. NN is neural network model, NN 1/0 is neural network model that use binary representation of GO terms as features. The number of layers in neural network are three and the
We developed a method to include the graph structure information of gene ontology and the information contain in ontology terms as feature representation of proteins. The inclusion of both graph structure and information content in our method can significantly improve performance of pathway prediction membership. When a simple approach of binary vector 1 or 0 to represent the presence of GO term for a given protein, the performances of prediction are lower than our method for all ontologies, for example when BP ontology is used the performances are.941 and.953 respectively (statistically significant, p <0.05)
In comparison across three ontologies, the best results are obtained when BP ontology terms are used as features to predict the membership of metabolic pathway for all methods. It is clear that the neural network model outperformed other methods. For example, when BP terms are used, the ROC score for neural network,,cosine, SVM, RF, and KNN are.953,.931,.920,.935, and.830 respectively. When cosine method is used as a baseliner method, our method's performance is statistically significant higher (p <0.05), while other machine learning methods such as KNN and SVM are lower. However, it is interesting to note that the performance of methods that are designed specifically to use the ontology-based semantic similarity such as SimGIC, and Resnik, are mostly the worst performance in all ontologies, even below the baseline cosine method. The reason behind this may be explained by the fact that most of ontology-based semantic similarity methods are based on calculating the similarity distance between the proteins only, without the learning process such as SVM classifier.
The good performances of prediction methods when using GO terms ontology are expected since the GO terms are curated data. The BP terms are especially information rich of protein function dataset. Other ontology terms, i.e. MF and CC, are not as rich as the BP in terms of function information, thus the performance of methods in predicting protein membership of pathway when using these ontologies are below the BP ontology. This pattern is consistent with our intuition that metabolic pathways are better characterized as biological processes (BP). Realizing this, we tested the performances of neural network method and base classifier when using non function based curated data, such as k-mer which transform the sequence information into frequency of k-mer amino acids, as input features to the models. Compared to the performances when GO terms are used as features, the sequence-based features are less effective in pathway membership prediction task (Table 2). The top model performance when using this feature are.786 for neural networks model.
Table 2 ROC score of different methods when k-mer is used as input features
We also tested the effect of multi modal features as input to our neural network model. We tested two different possibilities of combining the multi modal features in our NN model, by concatenating the features at early stage and at later stage. Addition of information to the method can improve the prediction performance of NN model (Table 3), although in other models it can lower the prediction performance. For example, compare to single modal of GO term in NN architecture, the use of multi-modal data can increase the performance from.952 to.957 (p=0.17), from.849 to.880 (p <0.05), and from.895 to.907 (p <0.05) when BP, CC, and MF ontologies are used. However, in cosine method, the use of multi-modal data of GO terms and k-mer frequency can deteriorate the prediction performance. We believe this attributed to the learning power of the neural network, in which individual neurons can adjust their weights adapting to different type of features, whereas the cosine method treats all features equally.
Table 3 The ROC score of methods for multi-modal data. NN is neural network model, NN 1/0 is neural network model that use binary representation of GO terms as features. (concat) is approach where GO terms and k-mer is concatenated as single vector to represent each protein, (multi-input) approach where GO terms and k-mer are used as two input to the model. The number of layers in neural network are three and the dimension of neurons in each layer are 128,64, and 1
When we considered the metabolic membership prediction task as a pathway centric problem, we needed to build many models, one for each pathway. Thus, for a given protein to be classified, we need to run it for every model and obtained the predicted output. The protein centric prediction task, on the other hand, will predict multiple classes at once thus can be built from one model. Table 4 shows the performance of neural network method in comparison to other methods by using either single modal or multi modal features.
Table 4 The performance comparison of models in protein centric task. The table reports the true positive (TP), false negative (FN), false positive (FP), number of proteins that have at least 1 prediction label (NP), the precision, recall, F measure, and Matthews correlation coefficient (MCC) for different features used in the models. The features used are k-mer, GO terms (BP, CC, and MF), and when both k-mer and GO terms are combined. The number of layers in neural network are three where the dimension of the first two layers are 128 and 64, and the last layer dimension is equal to the number of metabolic pathways
Similar to pathway-centric prediction task, the performances of the protein-centric methods are best when BP ontology is used as feature. The F measure of NN for example, are.572,.386, and.462 when BP, CC and MF ontology are used respectively. When NN model being compared to other classifiers, it outperforms most of the classifiers, especially when using the MF and CC dataset, while when using BP dataset, it is second under SVM classifier. However, it is important to note that of all classifiers, neural network produced the highest number of proteins that have at least one predicted label in all ontologies and highest number of true positive, which suggest that the neural network being more sensitive (thus higher recall) in detecting the metabolic pathway to the proteins, while other classifiers are more being specific (hence higher precision). Consequently, NN produces highest number of false positive and lowest number of false negative of all methods, while SVM produces lower false positive and higher false negative than NN. Overall, however, as measured by the F1 score that takes into account both recall and precision, NN either outperforms other methods (CC, CC+k-mer, MP, MP+k-mer)or performs comparably with other methods (BP, BP+k-mer). It is worth noting that, the protein-centric membership prediction is a multi-class classification whereas the pathway-centric membership prediction is a binary classification, which means that the former one is much more challenging, as reflected in the prediction performance. Therefore, while performance for protein-centric membership prediction may seem low, it should be assessed in the context of multi-class (320 classes to be exact) classification with a 1/320 = 0.3% accuracy from a random classifier.
In this work, we developed a neural network-based method for pathway membership inference using both gene ontology (GO) similarity and sequential features between a query protein and proteins that are known to the members of a given pathway. By replacing binary vector of the GO term annotation for a gene with the information content of individual GO terms and incorporating GO hierarchy with ancestor nodes that are directly present in gene annotation, we can create information rich vector representation for a gene. We built multilayer forward feeding neural networks that are able to integrate the GO term features and sequential features. We demonstrated that our NN based method outperformed other classifiers including SVM and random forest and the methods that are specifically designed to use the GO term features alone. Moreover, the NN based method is also able to answer question from both the pathway centric and protein centric perspectives, which makes the method more versatile in scaled up application for protein annotation.
We used the gene ontology and gene annotation from GeneOntology (GO, http://geneontology.org), version 2019-07-01. The GO's ontology consists of three ontologies, i.e. biological process (BP), cellular components (CC) and molecular functions (MF). This version of GO contains 31043 BP, 11973 MF, and 4397 CC terms. The annotation provides association between proteins and their corresponding GO terms either manually reviewed by curator or automatically generated by prediction tools. Out all of available evidence codes, only IEA (Inferred from Electronic Annotation) has not assigned manually by a curator. Therefore, it is necessary to exclude the IEA evidence code to prevent cyclic prediction: predict the protein annotations by using predicted data. In this experiment, we exclude annotations encoded by IEA.
We downloaded human KEGG pathway data set from Kyoto Encyclopedia of Genes and Genomes database [12], http://rest.kegg.jp. The database consists of 320 human pathways. We excluded pathways that consists less than 10 proteins to ensure adequate training and testing in the cross-validation scheme and mapped the NCBI gene id to its corresponding Uniprot identifier. As a result, we obtained 308 pathways and the number of proteins in the pathways range from 10 to 521 proteins with most of the pathways having proteins less than 100 proteins (Fig. 1).
Distribution of pathways and the number of their proteins used in this experiment
Data representation
We used multimodal data as input to our model, including the GO terms and k-mer information from protein sequences. While a simplistic approach to represent GO terms is a binary vector with 1 or 0 representing the presence or absence of GO terms in annotation of given gene, our method adopts a scheme from [5], which considers both of the structure of the GO graph and the information content of the GO terms in building the vector of the gene and their corresponding annotations (Fig. 2).
Generation of vector representation from GO dataset. In this example, the protein is annotated with t3 and t4. To generate protein's feature vector, the normalized IC of t3 and t4 is used in the first stage. On second stage, the semantic value (SV) of all term ancestors of t3 and t4 are calculated. Since t3 and t4 share common ancestor, t1 and t2, the semantic value for t1 and t2 are average semantic value (\(\overline {SV} \)). See Material and Methods for detail description
Specifically, before we build the gene vector, we first calculated the semantic value (SV) for each GO term in the annotation of a given protein. We used a normalized information content of term ti by dividing the information content of term ti with the maximum IC in whole set of GO terms T as follows:
$$ IC_{n}(t_{i}) = \frac{IC(t_{i})}{ \max\limits_{t_{j} \in T} IC(t_{j})} $$
Then we expanded the annotation of a given protein by including all of the ancestor terms: for each annotation term ti in a given protein, we assigned the weighted semantic value for all ancestor terms of term ti, defined as follows:
$$ SV(t_{{pi}}) = w^{d_{p}}IC_{n}(t_{{pi}}), $$
wherew is the weight, in this case we use a fix constant of 0.5, tpi is all ancestor terms of term ti and dpi is the path length of term ti to its ancestor tpi. The path length is defined as the difference of the maximum depth between the two terms in the GO tree.
When there are multiple GO terms in the annotation of a given protein, it is possible that these GO terms may have ancestor terms in common. Therefore, during expansion of the annotation vector for a given protein, a common ancestor term will have multiple semantic values, each for annotation term in the original annotation, as the common ancestor term may receive a semantic value from all of its descendants. Hence, we calculated the average of these values (\(\overline {SV(t_{p})} \)) as the new semantic values for a common ancestor term tp. Note that, in GO hierarchy, there are other relationships such as "NOT" and "contribute to", between two GO terms; in this study, however, we only include "is_a" relationship for calculating the semantic value, following the same practice as in other method such as [7], which we compare with.
After this procedure, a gene is represented as a vector of n-dimension, where n = |T|, each dimension corresponding to one GO term in the gene ontology hierarchy, with a semantic value being either a) the normalized information content if the GO term is present in the gene annotation, or b) a value assigned as above for a GO term whose descendant(s) is present, or c) a value of zero if a GO term is not of either of the two former cases.
In addition to gene annotation data as input to our model, we also used sequence-based features, such k-mer. The k-mer feature represents the sequence information as the frequency of k-mer, in this case we used k=2.
Neural network architecture
Artificial neural network is inspired by biological process [13]. It consists of layers of neurons that are fully connected between layers, but no connection between neurons in the same layer. Each neuron performs linear transformation operation of weighted information summation coming from all neurons in previous layer adjusted by some biases followed by nonlinear activation function f, as define by following equation:
$$ x = f \left(\sum{w_{i} x_{i}} +b \right) $$
While there are many activation options available for neural network. The two most used activation functions are ReLU and Sigmoid. The ReLu set the lower bound output of neuron to 0 the output of neuron to be minimum of 0, while sigmoid squashing the output of neuron and bounded to be between 0 and 1. In this experiment, we used the ReLU activation in the hidden layer, while Sigmoid is used in the output layer. The formal definition of ReLU (4) and Sigmoid (5) are:
$$ y = max (0,x) $$
$$ y = \frac{1}{1+ e^{(-x)}} $$
We implemented a multi-layer feed forward deep neural network in our model. We stacked three fully connected layers where the first layer is the input layer, the second layer is hidden layer, and the last layer is output layer. The input of the network is the n-dimensional vector of protein's features (Fig. 4). We used multi-modal features, i.e. GO terms and k-mer, and we either used a single modal or multi-modal features. For a single modal feature, we adopt architecture in Fig. 3. For multi-modal features, we combined the features' vectors at early stage or at later stage. At early stage, we concatenate multiple vectors into one vector as input to the model, thus the architecture similar to single input vector (Fig. 3). On the other hand, the concatenation at later stage happens inside the model where multi input model accept multiple input of vectors, then the model combine it in hidden layer while processing the inputs (NN multi input, Fig. 4). Note that convolution neural networks were attempted and did not get good performance, which we believe may be attributed to lack of convoluted patterns/features in protein sequences, unlike 2d images. Depending upon the classification task, the dimension of output layer is either 1 or n, where n is the number of classes to be predicted (n=308). In binary classification, the dimension of output layer is 1, while in multi-label classification the dimension of output layer is n. For binary classification task, we built one model for each class, while for multi-label classification task, we built one model. We performed optimization by comparing different number of neurons in each layer (data not shown).
Neural network architecture for single vector input
Neural network architecture for multi input vector
We implemented the Keras library to build our model. We chose to minimize the binary cross entropy function loss using the Adam optimizer with learning rate 0.001 for binary classification task. For multi label classification task, we chose to minimize the F1 function loss. To prevent overfitting in our model, we implemented the dropout (0.5) regularization. Note that unless explicitly mentioned otherwise, the default values of the hyperparameters are used in this study, and it is conceivable that better performance than reported in Tables 1, 2, and 3 can be achieved should these hyperparameters be optimally tuned.
In our experiment, we trained individual model separately for each pathway in the binary classification task. We performed 5-fold cross validation for each pathway. For each pathway, positive dataset consists of proteins that belong to the pathway while negative dataset is generated by selecting equal number of random proteins that do not belong to the pathway or interacting with proteins in the pathway. We followed this procedure since proteins in the pathway tend to interact each other, and by using this approach we ensured that there are no proteins in the negative dataset that are interacting with proteins in the positive dataset. We used BioGrid dataset to determine the interacting protein. We also excluded proteins that have no GO terms information in the pathways.
For multi-label classification task, we followed different approach. Since in both multi class or multi label classification task a positive sample can be a negative sample for other classes, we did not generate negative dataset. We simply consider negative dataset of a given pathways are proteins in other pathways. We also did not perform 5-fold cross validation, instead we randomly held 5 proteins from each pathway as testing dataset and the rest as training dataset.
Baseline classifiers
We used several GO based semantic similarity measures and baseline classifier as comparison to our method. We used the most commonly used semantic similarity measures, Resnik [10] and simGIC [9]. These measures mainly use the information content (IC) of each node to quantify the GO terms in the GO graph. The IC is described as:
$$ IC(t) = -log[p(t)] $$
where p(t) is term frequency of t in a given annotation corpus, such as Gene Ontology Annotation (GOA). These measures use same principal in calculating similarity between two proteins, which is based on the similarities of their corresponding terms. For protein similarities of Resnik's measures, we followed method from [14]. In addition to these methods, we also calculated the similarity of two proteins q and p based on their dot product of their corresponding semantic value vectors SVq and SVq as
$$ s(q, p) = \sum_{t \in T} SV_{q}(t) \cdot SV_{p}(t) $$
where t is the term of GO terms T. To determine whether query protein q belong to the model, we used the average similarity score between the query protein and set of proteins P of incomplete pathways as
$$ S(q,P) = \sum_{p \in P} S(q, p) / |P| $$
where s(q,p) is the similarity score between query protein q and a member protein p as calculated by Eq. 7 and |P| is the number of known proteins for the incomplete pathway P.
In addition to GO based semantic similarity methods, we also use some of mostly used base classifiers in machine learning: SVM, RF, and KNN. We implemented the Scikit library of SVM, RF, and KNN by using all default parameters. We used parameters as follows: rbf kernel and C=1e10 in SVM, number of forest is 100 in RF, and number of neighbor is 5 in KNN. We implemented Scikit SVM, RF, and KNN libraries.
Predictive performance evaluation
We adopted two different performance measures, each for pathway centric and protein centric prediction task respectively. For pathway centric task, we considered the task as binary classification problem and used receiving operating characteristic (ROC) curve analysis to evaluate the performance. The ROC curve of perfect classifier has the area under the ROC curve (AUC) of 1. The perfect curve rises steeply from bottom left to top left and move toward top right. We calculated ROC curve for each pathway and average across all pathways. ROC curve measures the performance of classifier at various threshold setting and represents the tradeoff between true positive rate (TPR) and false positive rate (FPR). The TPR and FPR for each pathway c are defined as:
$$ FPR_{c} = \frac{FP_{c}}{(FP_{c}+TN_{c})} $$
$$ TPR_{c} = \frac{TP_{c}}{(TP_{c}+FN_{c})} $$
where FPc,TNc,TPc, and FNc are the number of false positive, true negative, true positive and false positive respectively in pathway c. We then calculated the AUC of ROC from the above FPR and TPR and average the ROC score over all pathways.
For protein centric task, we considered the task as multi-label classification since one protein can have multiple label, and used the F1 score and Matthews Correlation Coefficient (MCC) to evaluate performance. The precision and recall are defined as
$$ p = \frac{TP}{TP+ FP} $$
$$ r = \frac{TP}{TP+ FN} $$
where TP, FP, and FN are the number of true positive, false positive, and false negative respectively. The F measure is harmonic mean of precision and recall. The value range between 0 and 1. The perfect score of 1 means that both of the precision and recall reach their maximum score of 1. However, when the precision reach maximum, it increases the TN, thus reducing the recall. On the other hand, when the recall reaches maximum score, it increases the FP, thus reducing the precision. Thus, F measure hardly reach maximum score 1. The F1 measure is defined as
$$ F1 = \frac{2 \times p \times r}{p+r} $$
while MCC is defined as:
$$ \begin{aligned} MCC = \frac{(TP \times TN) {-}(FP \times FN)} {\sqrt{ (TP+FP)\times(TP+FN)}{\times(TN+FP)\times(TN+FN)}} \end{aligned} $$
The data and the code used in this study will be made available to the readers for free upon request. The complete and updated data of GO annotations and KEGG pathways can be accessed from http://geneontology.org and http://rest.kegg.jp respectively.
GO:
Kyoto encyclopedia of genes and genomes
KNN:
K-Nearest neighbors
NN:
RF:
SVM:
Liao L, Kim S, Tomb J. Genome comparisons based on profiles of metabolic pathways.2002. p. 469–76.
Radivojac P, et al.A large-scale evaluation of computational protein function prediction. Nat Methods. 2013; 10(3):221–7.
The Gene Ontology Consortium. The Gene Ontology Resource: 20 years and still GOing strong. Nucleic Acids Res. 2018; 47(D1):330–8.
Harris MA, Gene Ontology Consortium, et al.The gene ontology (go) database and informatics resource. Nucleic Acids Res. 2004; 32(Database issue):258–61.
Cartealy I, Liao L. Metabolic pathway membership inference using an ontology-based similarity approach. In: Proceedings of the 2019 8th International Conference on Bioinformatics and Biomedical Science, (ICBBS 2019). New York: Association for Computing Machinery: 2019. p. 97–102. https://doi.org/10.1145/3369166.3369174.
Zhang J, Jia K, Jia J, Qian Y. An improved approach to infer protein-protein interaction based on a hierarchical vector space model. BMC Bioinformatics. 2018; 19(1):161–161161.
Ehsani R, Drabløs F. Topoicsim: a new semantic similarity measure based on gene ontology. BMC Bioinformatics. 2016; 17(1):296.
Sheehan B, Quigley A, Gaudin B, Dobson S. A relation based measure of semantic similarity for gene ontology annotations. BMC bioinformatics. 2008; 9:468.
Pesquita C, Faria D, Bastos H, Ferreira AE, Falcão A, Couto FM. Metrics for go based protein semantic similarity: a systematic evaluation. BMC Bioinformatics. 2008; 9(5):4.
Resnik P. Semantic similarity in a taxonomy: An information-based measure and its application to problems of ambiguity in natural language. J Artif Intell Res. 1999; 11:95–130.
Chitale M, Palakodety S, Kihara D. Quantification of protein group coherence and pathway assignment using functional association. BMC Bioinformatics. 2011; 12:373.
Kanehisa M, Goto S. Kegg: kyoto encyclopedia of genes and genomes. Nucleic Acids Res. 2000; 28(1):27–30.
Murphy KP. Machine Learning: A Probabilistic Perspective: The MIT Press; 2012.
Lord PW, Stevens RD, Brass A, Goble CA. Investigating semantic similarity measures across the gene ontology: the relationship between sequence and annotation. Bioinformatics. 2003; 19(10):1275–83.
The authors would also like to thank the anonymous reviewers for their invaluable comments. IC is thankful to Fulbright for funding his graduate study at University of Delaware where this research is carried out.
About this supplement
This article has been published as part of BMC Genomics Volume 22 Supplement 4 2021: Scalable techniques and algorithms for computational genomics (part 2). The full contents of the supplement are available at https://bmcgenomics.biomedcentral.com/articles/supplements/volume-22-supplement-4.
IC is funded on a Fulbright scholarship. Publication costs are funded by a supplemental fund to LL from University of Delaware. The funding agency had no role in the design, collection, analysis, data interpretation and writing of this study.
University of Delaware, Computer and Information Sciences, 101 Smith Hall, Newark, 19716, DE, US
Imam Cartealy & Li Liao
Imam Cartealy
Li Liao
LL designed the project, IC and LL devised algorithms, and IC implemented algorithms and carried out the experiments with advice from LL. All authors participated in writing the manuscript and approved the final version for publication.
Correspondence to Li Liao.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated in a credit line to the data.
Cartealy, I., Liao, L. Predicting metabolic pathway membership with deep neural networks by integrating sequential and ontology information. BMC Genomics 22, 691 (2021). https://doi.org/10.1186/s12864-021-07629-8
Metabolic pathway prediction | CommonCrawl |
All-----TitleAuthor(s)AbstractSubjectKeywordAll FieldsFull Text-----About
The Annals of Probability
Ann. Probab.
Volume 26, Number 2 (1998), 902-923.
Strong law of large numbers for multilinear forms
Anda Gadidov
More by Anda Gadidov
Full-text: Open access
PDF File (163 KB)
Article info and citation
Let $m \geq 2$ be a nonnegative integer and let ${X^{(l)}, X_i^{(l)}}_{i \epsilon \mathbb{N}}, l = 1, \dots, m$, be $m$ independent sequences of independent and identically distributed symmetric random variables. Define $S_n = \Sigma_{1 \leq i_1, \dots, i_m \leq n} X_{i_1}^{(l)} \dots X_{i_m}^{(m)}$, and let ${\gamma_n}_{n \epsilon \mathbb{N}}$ be a nondecreasing sequence of positive numbers, tending to infinity and satisfying some regularity conditions. For $m = 2$ necessary and sufficient conditions are obtained for the strong law of large numbers $\gamma_n^{-1} S_n \to 0$ a.s. to hold, and for $m > 2$ the strong law of large numbers is obtained under a condition on the growth of the truncated variance of the $X^{(l)}$ .
Ann. Probab., Volume 26, Number 2 (1998), 902-923.
First available in Project Euclid: 31 May 2002
Permanent link to this document
https://projecteuclid.org/euclid.aop/1022855655
doi:10.1214/aop/1022855655
Mathematical Reviews number (MathSciNet)
MR1626539
Zentralblatt MATH identifier
Primary: 60F15: Strong theorems
Strong laws multilinear forms $U$-statistics martingale maximal inequality
Gadidov, Anda. Strong law of large numbers for multilinear forms. Ann. Probab. 26 (1998), no. 2, 902--923. doi:10.1214/aop/1022855655. https://projecteuclid.org/euclid.aop/1022855655
Burkholder, D. L. (1973). Distribution function inequalities for martingales. Ann. Probab. 1 19-42.
Mathematical Reviews (MathSciNet): MR51:1944
Digital Object Identifier: doi:10.1214/aop/1176997023
Cuzick, J., Gin´e, E. and Zinn, J. (1995). Laws of large numbers for quadratic forms, maxima of products and truncated sums of i.i.d. random variables. Ann. Probab. 23 292-333.
Mathematical Reviews (MathSciNet): MR96b:60068
Zentralblatt MATH: 0833.60030
Project Euclid: euclid.aop/1176988388
de la Pe na, V. H. and Montgomery-Smith, S. J. (1995). Decoupling inequalities for the tail probabilities of multivariate U-statistics. Ann. Probab. 23 806-817.
Mathematical Reviews (MathSciNet): MR96f:60029
Feller, W. (1971). An Introduction to Probability Theory and Its Applications 2. Wiley, New York. Gin´e, E. and Zinn, J. (1992a). On Hoffmann-Jørgensen's inequality for U-processes. In Probability in Banach Spaces (R. M. Dudley, M. G. Kahn and J. Kuelbs, eds.) 8 80-91. Birkh¨auser, Boston. Gin´e, E. and Zinn, J. (1992b). Marcinkiewicz type laws of large numbers and convergence of moments for U-statistics. In Probability in Banach Spaces (R. M. Dudley, M. G. Kahn and J. Kuelbs, eds.) 8 273-291. Birkh¨auser, Boston.
Hoffmann-Jørgensen, J. (1974). Sums of independent Banach space valued random variables. Studia Math. 52 159-186.
Kwapi´en, S. and Woyczynski, W. A. (1992). Random Series and Stochastic Integrals: Single and Multiple. Birkh¨auser, Boston. Rosenthal, H. P. (1970a). On the subspaces of Lp p > 2 spanned by sequences of independent random variables. Israel J. Math. 8 273-303. Rosenthal, H. P. (1970b). On the span in Lp of sequences of independent random variables. II. Proc. Sixth Berkeley Symp. Math. Statist. Probab. 2 149-167. Univ. California Press, Berkeley.
Mathematical Reviews (MathSciNet): MR94k:60074
Sen, P. K. (1977). Almost sure convergence of generalized U-statistics. Ann. Probab. 5 287-290.
Mathematical Reviews (MathSciNet): MR436444
Zhang, C.-H. (1996). Strong law of large numbers for sums of products. Ann. Probab. 24 1589-1615.
Mathematical Reviews (MathSciNet): MR1411507
The Institute of Mathematical Statistics
Future Papers
New content alerts
Email RSS ToC RSS Article
Turn Off MathJax
What is MathJax?
Strong law of large numbers for sums of products
Zhang, Cun-Hui, The Annals of Probability, 1996
Decoupling Inequalities for Multilinear Forms in Independent Symmetric Random Variables
McConnell, Terry R. and Taqqu, Murad S., The Annals of Probability, 1986
A Note on Feller's Strong Law of Large Numbers
Chow, Yuan Shih and Zhang, Cun-Hui, The Annals of Probability, 1986
Asymptotic behavior for iterated functions of random variables
Li, Deli and Rogers, T. D., The Annals of Applied Probability, 1999
Approximate Local Limit Theorems for Laws Outside Domains of Attraction
Griffin, Philip S., Jain, Naresh C., and Pruitt, William E., The Annals of Probability, 1984
Incomplete generalized L-statistics
Hössjer, Ola, The Annals of Statistics, 1996
Laws of Large Numbers for Quadratic Forms, Maxima of Products and Truncated Sums of I.I.D. Random Variables
Cuzick, Jack, Gine, Evarist, and Zinn, Joel, The Annals of Probability, 1995
A Remark on Convergence in Distribution of $U$-Statistics
Gine, Evarist and Zinn, Joel, The Annals of Probability, 1994
Irregular sets and central limit theorems
Perera, Gonzalo, Bernoulli, 2002
Eigenvalue distributions of random permutation matrices
Wieand, Kelly, The Annals of Probability, 2000
euclid.aop/1022855655 | CommonCrawl |
Non-attitudinal and non-knowledge based factors constrain households from translating good nutritional knowledge and attitude to achieve the WHO recommended minimum intake level for fruits and vegetables in a developing country setting: evidence from Gulu district, Uganda
Benjamin Kenyi Bendere Lomira1,
Prossy Nassanga1,
Daniel Micheal Okello2 &
Duncan Ongeng ORCID: orcid.org/0000-0002-1535-40771
The high level of incidence of mortality attributed to non-communicable diseases such as cancer, diabetes and hypertension being experienced in developing countries requires concerted effort on investment in strategies that can reduce the risks of development of such diseases. Fruits and vegetables (FV) contain natural bioactive compounds, and if consumed at or above 400 g per day (RDMIL) as recommended by World Health Organization (WHO) is believed to contribute to reduced risk of development of such diseases. The objective of this study was to determine in a developing country set-up, the extent to which rural and urban households conform to RDMIL, the status of nutritional attitude (NA) and knowledge (NK) associated with consumption of FV, and to delineate non-attitudinal and non-knowledge-based factors (NANK) that hinder achievement of RDMIL.
A cross-sectional survey of 400 randomly selected households and 16 focus group discussions (FGD) were conducted using Gulu district of Uganda as a microcosm for a developing country setting. Level of consumption of FV was assessed using 24-h dietary recall and compared to RDMIL as a fraction (%). The status of NK and NA were determined using sets of closed-ended questions anchored on a three-point Likert scale. Further quantitative statistical analyses were conducted using t-test, chi-square, Pearson's correlation and multiple linear regression. FGD provided data on NANK factors and were analysed using qualitative content analysis procedure.
Urban and rural inhabitants met up to 72.0 and 62.4% of the RMDIL, respectively, with absolute intake being higher among urban than rural households by 37.54 g. NK and NA were good but the intensity of NK was higher among urban respondents by 11%. RDMIL was positively correlated with NA while socio-demographic predictors of RDMIL varied with household location. FGD revealed that primary agricultural production constraints, market limitations, postharvest management limitations, health concerns, social discomfort and environmental policy restrictions were the major NANK factors that hindered achievement of the RDMIL.
These results indicate that NANK factors constrain households from translating good NA and NK to achieve the RMDIL.
The occurrence of nutrition-related health challenges of non-communicable diseases (NCDs) such as hypertension, cancer and diabetes have reached significant levels in developing countries [28]. Estimates over the last decades indicate that 34.5 million (65%) people died annually as a result of one or various combinations of NCDs. When segretated by age, of the 34.5 million deaths, over 14 million occurred among people within the age bracket of 16–69 years while 80% of them were found in developing regions of the world [33]. In those regions, and Africa in particular, statistics from selected countries including Uganda, Kenya, South Sudan, Rwanda, Benin, Mali, Ethiopia and Senegal indicate NCDs death incidence rates ranging from 24 to 43% [45]. However, considering the poor state of health services in many of the African countries, it is possible that some incidences are never recorded officially and therefore the reported statistics might actually be an underestimation.
Fruits and vegetables (FV) contain a considerable amount of natural dietary phytochemicals [40] which are believed to potentially contribute to reducing the chances of occurrence of NCDs [29]. Such bioactive compounds include alkaloids, saponins, flavonoids, isoflavonoids, tannins, terpenoids, polyphenols, anthocyaindins, phytoestrogens, glycosnoids, carotenoids, limonoids and phytoestrols [48]. The significance of fresh plant foods in management of NCDs is reflected in a previous report which indicates that frequent consumption of carotenoid-rich FV was associated with blood cholesterol level maintanence ostensibly through provision of antioxidants that reduce oxidative damage caused by low density lipoprotein oxidation. In addition, consumption of fruits including grapes, berries, apples and citrus was found to be effective in maintaining blood pressure because of their high contents of procyanidins, anthocyanins and flavonol compounds [42].
Relatedly, deficiency of essential micronutrients such as, vitamin A, iron and zinc is an important nutritional challenge largely experienced in developing regions of the world [16]. These regions are largely economically challenged and thus households in such localities are usually unable to access expensive but nutrient-rich animal source foods such as meat, fish and milk [20]. As a strategy to improve micronutrient deficiency in developing countries, sufficient intake of fresh FV has been recommended [49]. This is because FV are among the major sources of vitamins and minerals [55]. In consonant with the known significance of fresh FV consumption to human nutrition and health well-being, WHO [41] recommends daily consumption of a minimum (RDMIL) of 400 g (5 servings). Information on adherence to this recommendation at household and community level is important for public health planning.
A critical search of literature on this subject reveals that much of the information available on levels of consumption of fresh FV is largely available from developed countries [17] but very scanty for developing countries. However, due to the huge socio-economic differences that exist between developed and developing countries, information on consumption levels from developed countries can not be used realistically for public health planning in developing countries. In addition, considering the fact that developed countries such as those in Europe where intensity of nutrition education is high have so far achieved only up to 300 g per day [3], suggests that intake levels in developing countries might even be much lower. This situation calls for proper understanding of the factors that can explain lack of adherence to RDMIL. In the context of developing countries such as Uganda, such understanding should consider both the rural and urban set-up situations to provide opportunity for designing comprehensive strategies to foster adherence in both localities.
Previous food consumption related studies have revealed differences between rural and urban inhabitants with respect to consumption of industrially produced food products [46] and nutritional attitude (NA) was identified as a principal factor that influenced food choice but strongly moderated by nutritional knowledge (NK) [47]. However, with regard to fresh FV, limited information exists on how rural and urban inhabitants especially those in developing countries perceive the nutritional and health benefits associated with consumption of such plant foods, and the associated NK. In the context of this study, and paraphrasing the definition presented in UlHaq et al. [53], NA refers to "a learned predisposition to think, feel and act in a particular way with regard to consumption of FV". Consumer attitudes regarding nutrition play a central role in developing preference and willingness to accept or reject particular food categories and is critical in making consumption choices [46]. NK is defined as the ability of individuals to acquire, process and understand nutrition information needed to make sound nutrition decisions [35]. Much of the information available on NA and NK with respect to consumption of various food categories has been derived from studies conducted among affluent societies in developed countries [38]. However, limited information on the same contexualized to developing country situations is available. In addition, it has been observed that NA and NK are affected by socio-demographic factors [50]. Considering that socio-demographic factors differ considerably between developed and developing countries [44] implies that information available from a developed country context can not easily be applied to a developing country context. Further more, in a developing country context, socio-demographic characteristics vary markedly between urban and rural set-ups. Therefore, to gain better understanding of how NA and NK affect consumption of FV it becomes paramount that data be gathered from both the urban and rural areas. Previous nutrition studies conducted in developing countries, especially in the domain of complementary feeding, have shown that good NA and NK may or may not translate into good nutrition practices [31, 37]. This suggests that certain non-attitudinal and or non-knowledge based factors could be at play. However, information on such factors and their influence on good nutrition practice such as adequate consumption of FV are largely lacking. Therefore, the objective of this study was to determine, in a developing country context, the extent to which rural and urban households conform to RDMIL, the status of NA and NK associated with consumption, and non-attitudinal and non-knowledge-based (NANK) factors that hinder achievement of RDMIL.
Study area and study population
The study was conducted in Gulu district which is located in Northern Uganda between longitude 300 -320 East and latitude 20–40 North. It is bordered by Amuru district from the West, Pader district from the East, Lamwo district from the North East and Omoro district from the South. The total land area of the district is 3.449.08 km2 which is 1.44% of the land size of Uganda [23]. The population of Gulu district according to the 2014 census was projected to be 443,733 people [52]. The district experiences a climatic regime characterized by dry and wet seasons, with average annual rainfall of 1500 mm/ annum. It also experiences a monthly average rainfall variation of 1.4–230 mm between January and August, respectively [23]. The study population comprised of households that were officially registered by local authorities in the district. The main inclusion criteria were that the household had been resident in the district for at least 6 months and the person in charge of food preparation in the household was willing to participate in the study. Map of the study area is presented in Fig. 1.
Map of the study area. Map is an original production by the authors
Study design, sample size and sampling framework
A cross-sectional study design that made use of survey questionnaires for individual household interviews and a guide for focus group discussions was applied. The survey questionnaire was used to collect quantitative data while the focus group discussion guide was used to collect qualitative data. The sample size, defined in the context of this study as the number of households (n) that participated in the study was calculated using a standard formula according to Israel [26].
$$ n=\frac{N}{1+N{(e)}^2} $$
Where, n is the sample size, N is the population size of Gulu district (443,73 3[52]), e is the marginal error level fixed at 0.05. On the basis of Eq. 1 and parameter values already defined, the sample size (n) for individual household interview was determined to be 400 households. This being a comparative study, the calculated sample size was divided into two resulting into 200 households each for rural and urban setting, respectively.
Following the determination of the sample size, a multi-stage sampling procedure was used to locate the participating households. First, two sub-counties and two divisions were randomly selected from the rural and urban areas of the district, respectively. From these, two parishes were selected randomly from each sub-county for the rural setting and two parishes from each division for the urban setting. This resulted into a total of 8 parishes. In stage three (3), two villages were randomly selected from each of the parish resulting into a total of 16 villages (8 from the rural area and 8 from the urban area). In stage four (4), 25 households were selected randomly from each village, resulting into a total of 400 households (200 from rural area and 200 from the urban area) consistent with the sample size determined according to Eq. 1. The respondent for individual household interview was the member of the household in charge of food preparation.
For FGD sessions, in order to ensure originality of information, households selected to participate in in-depth interviews were not selected to participate in FGDs. For each location (urban, rural), eight (8) FGDs were conducted with each consisting of 8–10 individuals. The eight FGDs used in each location (total = 16) is above the minimum number of six required for saturation of information in qualitative studies [51]. As was the case for the individual household interview, participants for the FGDs were also household members in charge of food preparation.
Study instruments
Data on consumption of FV among households were collected using a 24-h dietary recall tool and procedure previously used by Hongu et al. [24] and Salehi et al. [47]. The tool was modified to reflect only those FV that are consumed in the study area. NA and NK were assessed using a standard questionnaire adapted with modification from FAO [15]. The modification was made to reflect only issues related to consumption of FV. The NK section had 16 closed-end questions framed (negatively or positively) to test knowledge about the importance of FV to nutrition and health well-being. The questions were anchored on a 3-point likert scale (1 = agree, 2 = neither agree nor disagree and 0 = disagree). The NA section had 28 closed-ended questions designed to test respondents' attitude towards consumption of FV. As was the case for NK, questions for NA were also anchored on a 3-point Likert scale (0 = disagree, 2 = neither agree nor disagree, 1 = agree) according to Anand and Puri [1]. The questionnaire also had a provision for collection of data on socio-demographic characteristics of the households (Supplementary material S1).
For the FGD, a guide adapted with modification from Duthie et al. [12] and Salehi et al. [47] was used. The guide was modified to generate information on NANK factors that hinder achievement of RDMIL among households (Supplementary material S2). The instruments were pretested among selected households in non-participating villages in the study area. This was done to ensure accuracy, clarity and consistency in the interpretation of the questions. After pretesting, responses were analyzed to check for validity and ambiguous questions were rephrased. Questions used to test NA and NK, were subjected to the Cronbach test. The test resulted in a reliability index of 0.72 and 0.77 for NA and NK, respectively. These levels of reliability are considered acceptable in nutrition research [22].
Data was collected using research assistants who had previous exposure to nutrition surveys and fluent in both English and local language of the study area (Luo/Acholi). In order to ensure that the assistants did not interfere with originality of the information, they were further trained on how to inteprete questions to the study participants but not to assist them in providing answers. Data was collected in stages. First stage was assessment of daily consumption levels of FV. Here, each respondent (the person in the household responsible for food preparation) was asked to mention the FV that were consumed by household members in the past 24 h prior to the study. However, to provide a fair estimate of the quantities consumed, representative portions of the food items consumed were weighed and recorded in a standard unit (grams) commonly used in nutrition studies and assesments. The persons in charge of food preparation were interviewed from their respective homes. The second stage was assessment of NA and NK. The third stage was assessment of socio-demographic characteristics of the respondents. The fourth stage was the FGD sessions for which each session lasted 1.5–2 h.
Data on socio-demographic characteristics were summarized using descriptive statistics (frequency, percentages, mean and standard deviation where applicable). Chi square test was perfomed to compare categorical socio-demographic variables among rural and urban respondents. To determine the extent to which households conform to RDMIL, the combined amount (g) of FV for each household (derived from the 24-h recall), adjusted for the number of household members in adult equivalent, were summed up and divided by the number of households that participated in the study. The average value for rural or urban area was compared with the RDMIL as a fraction (%). Independent 2-sample t-test was used to compare mean consumption of each of the FV, overall mean for fruits or vegetables, and the combined overall mean for FV between rural and urban households following ascertainment of conformity to normality requirement according to Kolmogorov-Smirnov test.
With regard to NK, the analysis went through several steps. On the basis of the answers to questions on knowledge elements provided by the respondents, every correct answer was given a score of one (1) while a wrong answer and where the respondent did not know was awarded a score of zero (0). Scores for each respondent were calculated by summing up the scores attained for each question to generate the total NK score which ranged between zero and sixteen (0–16). The overall score was ranked as good or poor depending on the score level. A rank of "good" was given if the overall score stood at 55% and above or poor if it fell below 55% as previously reported by Ul Haq et al. [53]. With regard to NA, before analysis, responses were also scored as in the case of NK. Therefore, a score of zero (0) was awarded for disagree, two (2) for neither agree nor disagree and one (1) for agree. Reverse scoring was done for negatively-framed statements. This means that a score of 0 was given to 'agree' and 1 to 'disagree' [1]. Scores for each respondent were calculated by summing up the scores attained from each question and the overall score ranked as good or poor. The NA was ranked as good for overall scores of 57.1% and above. Otherwise the human factor was ranked as bad [53]. Independent 2-sample t-test was also used to compare the mean difference in NK or NA score between urban and rural respondents following ascertainment of conformity to normality requirement according to Kolmogorov-Smirnov test. Bivariate analysis (Pearson's correlation) was used to determine the association between NA, NK and RDMIL. On the other hand, multiple linear regression was performed to establish socio-demographic predictors of the level of consumption of FV. Before running the regression, a number of diagnostic tests were conducted. The Shapiro-Wilk test for nornmality was conducted on the dependent variable (level of consumption of FV) and continuous independent variables (household size, age and education level of the respondent). The results showed that the dependent variable was normally distributed (p value = 0.060) while the continuous independendent variabes were not (p < 0.05). Therefore, the continuous independent variables were transformed to natural logarithm and conformed to the normality assumption on the basis of the histogram. Pearson's correlation analysis was run in order to eliminate highly correlated independent variables with a correlation coefficient greater than 0.70 [11]. Following the diagnostic tests, three models were estimated. Model 1 was for the pooled dataset (urban and rural locations combined), with the locational indicator included as an independent variable while models 2 and 3 were location specific. Model 2 was for rural dataset and model 3 was for the urban dataset. The purpose of models 2 and 3 were to show whether the two locations have the same factors influencing level of consumption of FV. The general model depicting the variables used is presented in Eq. 2.
$$ {Y}_i=\alpha +{\beta}_1{X}_1+{\beta}_2{X}_2+{\beta}_3{X}_3\dots \dots \dots \dots \dots \dots \dots {\beta}_n{X}_n+\mu $$
From Eq. 2, Yi is the level of consumption of FV, α is the regression constant; β is the regression coefficient, X1 to Xn are the independent variables and μ is the error term. The following independent variables were selected and used to run the regressions:location (1 = rural, 0 = urban), age of the respondent (years), sex of the respondent (1 = male, 0 = female), marital status of the respondent (1 = married, 0 = otherwise), major occupation of the household head (1 = farm-based, 0 = non-farm based), education level of the respondent (years), attendance of health education by the respondent (1 = yes, 0 = no), household size (number), respondent's attendance of health education (1 = yes,0 = no), main source of household income (1 = farming, 0 = non-farm activities), woman decides on how family income is used (1 = yes,0 = no), woman decides on the type of food eaten at home (1 = yes, 0 = no). After running the regressions, three post-estimation tests were conducted. First, the Ramsey Regression Specification Error (RESET) test for linear model specification was conducted and revealed that selection of the linear model was appropriate (F = 0.46, p = 0.7074). Secondly, the Breusch-Pagan/Cook-Weisberg test for heteroskedasticity was conducted and showed no evidence of heteroskedasticity (χ2 = 0.15, p value = 0.6965). Lastly, the variance inflation factor (VIF) test for multi-collinieraity showed that the independent variables had mean VIF of 1.26 and a maximum value of 1.50 indicating no problem of multi-colinieraity in the regression models. Regression analyses were performed using STATA version 14 while other stastistical analyses were performed using Statistical Package for Social Sciences (SPSS) version 2, and the level of significance was fixed at 5%. However, for tests on data comparing categorical socio-demographic variables, consumption of FV between rural and urban households, a Bonferroni correction test was conducted resulting into a corrected significance level of 0.004 and 0.002, respectively. Finally, in order to establish NANK factors that limit consumption of FV data from FGDs were summarized using qualitative content analysis as described by Elo & Kyngäs [13]. This was achieved by determining the units of analysis followed by categorization of the data drawing inferences on the basis of the different categories.
Socio-demographic characteristics of the study households
Results of Chi-square test for socio-demographic characteristics and location of residence of study participants are presented in Table 1.
Table 1 Chi-square test for socio-demographic characteristics and location of study respondents
Generally, significant association in socio-demographic characteristics among rural and urban respondents were observed with respect to marital status, main source of family income, how food is obtained in the household, responsibility of providing food for the household and decision on how family income is used. Out of the total study participants, 61% of them from rural areas were married compared to 73% who were from the urban areas. The main source of family income for rural households was sale of agricultural produce (43%) while for urban residents was small-scale business (52.5%). When asked about how food was obtained in households, the largest proportion of respondents from rural areas (76%) reported that food was majorly obtained through own production (farming) while majority of their urban counterparts (82.5%) obtained theirs through purchase from the market. Relatedly, the responsibility of providing food for the household was majorly (48.5%) in the hands of women for the case of rural households while in the urban areas the responsibility was handled by male household head (39%). With regard to the decision on how family income is spent, in most of the rural households, the decision was mainly taken by wives (42%) unlike in the urban households were the decision was majorly (48%) a consensus between the wife and the husband. The mean age of the respondents was 36.6 ± 14.6 (minimum: 18; maximum: 70) and 29.8 ± 9 (minimum: 18; maximum: 64) for rural and urban households, respectively.
The status of consumption of fruits and vegetables
Data on the mean daily consumption of individual FV among rural and urban households are presented in Table 2. Results of an independent sample t-test revealed no significant difference in combined mean daily consumption of vegetables between rural and urban households. However, with regard to fruits, significant difference was observed between rural and urban households. Specifically, consumption of fruits was higher among urban than rural inhabitants by about 84.93 g.
Table 2 Mean daily consumption of various fruits and vegetables segregated by location of residence
With respect to consumption of individual FV investigated, significant variations were observed between rural and urban respondents. Amongst vegetables investigated, significant difference was observed in the consumption of Brassica capitate, Daucus carota, Solanum tuberosum, Vigna unguiculatus, Hibiscus spp., Solanum gilo, Solanum melongena and Phaseolus vulgaris-fresh form. Specifically, urban households had higher mean daily consumption of Daucus carota and Solanum gilo while rural households had higher mean daily consumption of Brassica capitate, Vigna unguiculatus, Hibiscus spp., Solanum tuberosum and Phaseolus vulgaris (fresh bean). With regard to fruits, significant mean differences were observed for Ananas comosus, Citrullus lanatus, Musa spp., Mangifera indica and fresh fruit juice. Across all the fruits, urban households had higher consumption scores compared to their rural counterparts. Irrespective of the location, the observed total daily consumption levels for FV was below the RMDIL. Specifically, urban and rural households were only able to meet the RMDIL by 72 and 62.4%, respectively.
Socio-demographic predictors of consumption of fruits and vegetables
Results of multiple linear regression on socio-demographic factors that can predict consumption of FV among households are presented in Table 3. The locational indicator (urban, rural) was significant suggesting that the level of consumption of FV differred between urban and rural households. The standardized regression coeffient of the locational indicator predicted that consumption of FV was significantly lower among rural households than among urban counterparts by 23%. In the pooled regression model, the main source of household income, age of the respondent, education level of the respondent, and attendance of nutrition training by the respondent positively predicted consumption, while, martial status of the respondent and household size negatively predicted consumption of FV instead. In the case of negative prediction, two scenarios were apparent. First, an increase in household size was associated with 13% reduction in consumption of FV while a state of the respondent being married was associated with lower consumption of FV by 11%. In the case of positive prediction, the following scenarios sufficed. First, a situation of farming being the main source of household income was associated with 17% higher consumption of FV. Secondly, attendance of nutrition training by the respondent was associated with 19% higher consumption of FV. Thirdly, an increase in age of the respondent was associated with a 13% increase in consumption of FV. Lastly, an increase in the level of education of the respondent was associated with 28% increase in consumption of FV. When data was segregated by location, regression models 2 and 3 showed that only the level of education of the respondent was a significant positive predictor among both rural and urban households. In quantitative terms, an increase in the level of education of the respondent was associated with 27 and 28% increase in consumption of FV among rural and urban households, respectively. However, matital status of the respondent, main occupation of the household head, attendance of health education, attendance of nutrition training by the respondent, and main source of household income were the significant predictors in the rural area (model 2) while only age of respondent and household size were significant in the urban area (model 3). In terms of the magnitude of prediction, for model 2 (depicting the rural area), the following scenarios were apparent. First, respondent being married was associated with 14% lower consumption of FV. Secondly, farming as a main occupation of the household head was associated with 20% lower consumption. Thirdly, attendance of health education by the respondent was associated with 19% lower consumption. Fourthly, attendance of nutrition training by the respondent was associated with a 30% higher consumption. Fifth, farming as the main source of household income was associated with 20% higher consumption of FV. On the other hand, in terms of the magnitude of the prediction for model 3 (urban area), the following scenarios were apparent. First, an increase in the age of the respondent was associated with 22% increase in level of consumption while an increase in household size was associated with 21% reduction in consumption of FV. Further more, results show that main occupation of the household head and attendance of nutrition training were not significant factors in the pooled model (model 1) neither in the model for the urban area (model 3) but were peculiar in the model for the rural area (model 2).
Table 3 Socio-demographic predictors of consumption of fruits and vegetables segregated by location of residence
The status of nutritional attitude associated with consumption of fresh fruits and vegetables
The status of NA associated with consumption of FV among rural and urban households is presented in Fig. 2.
Distribution of respondents' attitude towards consumption of fruits and vegetables segregated by location of residence
In general, majority of the respondents from both rural and urban areas had good NA towards consumption of FV. Application of independent sample t-test revealed no significant difference in the status of NA among inhabitants residing in the two locations investigated (Rural: n = 200, Mean ± SD = 98 ± 0.14; Urban: n = 200, Mean ± SD = 97 ± 0.17; p = 0.523).
Status of nutritional knowledge associated with consumption of fresh fruits and vegetables
The status of NK associated with consumption of FV among rural and urban respondents is presented in Fig. 3.
Distribution of the status of knowledge associated with consumption of fruits and vegetables segragated by location of residence
Generally, irrespective of the location of residence, the proportion of respondents that exhibited good NK was more than 50%. Nonetheless, a higher proportion of urban respondents were knowledgeable than their rural counterparts by a difference of about 11% (Rural: n = 200, Mean ± SD =58 ± 0.495; Urban: n = 200, Mean ± SD = 69 ± 0.463; p = 0.017).
Association between nutritional attitude, nutritional knowledge and consumption of fruits and vegetables
Results of bivariate analysis (Pearson's correlation) are presented in Table 4. The results revealed a positive and significant relationship between NA and FV consumption among both rural and urban households. However, no association was observed between NK and FV consumption irrespective of the location.
Table 4 Association between nutritional attitude, nutritional knowledge and consumption of fruits and vegetables
Non-attitudinal and non-knowledge-based factors that hinder consumption of fruits and vegetables
Information on NANK factors that hindered consumption of FV, generated during FGDs segregated by respondents' location of residence is presented in Table 5. In general, both rural and urban respondents experienced similar NANK barriers. However, majority of the barriers (73.7%) were experienced in the rural areas.
Table 5 Non- attitudinal and non- knowledge-based factors that hinder consumption of fruits and vegetables
The health and nutritional significance associated with consumption of FV justifies the need for investment in efforts to enable households consume quanties required to effect positive nutritional and health effects. The results have demonstrated that households in both rural and urban localities were unable to meet the RDMIL although intake by urban households was better than that of their rural counterparts. This implies that generally both localities require efforts in order to improve consumption, but specifically more efforts should be dedicated to rural areas. When consumption was segregated into FV, the combined mean daily consumption level of fruits was significantly higher among urban than rural households while that of vegetables was identical between the two localities. This implies that the higher consumption level of FV reported among urban than rural households may be due to differentials in the itake of fruits. Another dichotomy observed between rural and urban households was interms of the types of FV consumed. In the case of vegetables, tomatoes, cauliflower, sweet pepper, carrot, and tula were largely consumed by urban residents as opposed to rural dwellers while cabbage, spinach, amaranthus, potatoes, boo, malakuang, egg plant, and fresh beans were more consumed in rural than in urban areas. On the other hand, for fruits, pineapple, watermelon, sweet banana, apple, mangoes, passion fruits and fruit juice were largely consumed by urban dwellers than the rural inhabitants. These observations illustrate that nutritious and expensive FV are largely consumed by urban dwellers while cheaper types are consumed by rural households. This is likely due to better socio-economic situation among urban compared to rural inhabitants.
Results of regression analysis revealed that overall, location was a significant factor that predicted consumption of FV in the study area. The results of the pooled model indicating higher consumption of FV among urban compared to rural households by 23% corroborates with the outcome of the independent sample t-test which revealed that absolute daily consumption of FV was higher among urban than rural households by 37.54 g. This implies that location of the household is an important factor that should be taken into condideration in designing interventions to improve consumption of FV in localities such as Gulu district. The effect of location was also reflected in the pattern of the significance of various socio-demographic factors that predicted consumption of FV. This is because, whereas, age, marital status, education level of the respondent, attendance of nutrition training by the respondent, houseold size and the main souce of household income were significant in the pooled model (model 1), only marital status, attendance of nutrition training by the respondent and the main source of household income were significant among rural households (model 2) while age of the respondent and household size were significant among urban households (model 3) instead. This implies that location does not only influence level of consumption but also provides indications on other location-specific factors that may influence the level of consumption of FV as well. A typical scenario is the fact that the main occupation of the household head and attendance of health education by the respondent were only significant in the rural area (model 2) but not in the urban area (model 3) neither in the pooled model (Model 1). The observed location-specific nature of socio-demographic predictors is not peculiar to this study. It has also been reported for daily FV intake among 11-year old school children in Europe (De [9]) and dietary diversity among children 6–23 months in Benin [36]. An important observation revealed by the regression analysis is the fact that education level of the respondent was the only significant factor that cut accross both locations and was positive in nature. This may not be surprising because level of education is a universal factor that has been reported to positively influence consumption of FV in other localities such as the United States of America [2].
Consumer attitude towards food consumption has been variously illustrated to depend on food type ([10],) but strongly modulated by socio-cultural and socio-demographic factors [43]. In the context of this study, due to marked differences in the socio-demographic variables observed between urban and rural households, it was anticipated that NA of rural and urban respondents would also vary. To the contrary, NA was identically good among respondents from the two localities. NK is generally believed to be one of the key factors that moderate the evaluative effect of attitude on food choice [27]. Based on the results of the current study, it is apparent that the overall status of NK on health and nutrition benefits associated with consumption of FV was dependent on the location of the households. This is clearly illustrated by the fact that the proportion of respondents with good NK was higher among urban than rural respondents by about 11.5%. This implies that urban inhabitants have better NK compared to their rural counterparts. This disparity can be attributed to the fact that more urban respondents attained higher level of education (secondary and above) than their rural counterparts. This is because, whereas nutrition education improves NK [25], the results of this study indicate that the proportion of rural and urban respondents that received nutrition education was somewhat identical. This brings into question the retention of knowledge acquired through nutrition education. It should be appreciated that knowledge accumulation increases with the level of education [21]. Therefore, the higher proportion of urban respondents who were more knowledgeable than rural respondents suggests that urban respondents had retained NK acquired from nutrition education due to higher level of formal education compared to rural respondents whose education levels were generally low.
A positive and significant association observed between NA and FV consumption among urban and rural respondents corroborates with the findings of Okidi et al. [39] reported previously with regard to consumption of wild FV in rural localities of the study area. This suggests that existence of good NA has functional revelance in supporting achievement of RDMIL in the study area. On the other hand, lack of association observed between NK and RDMIL contrasts with the findings of Chung et al. [6] which showed that NK was positively associated with consumption of FV among construction apprentices. This indicates that the level of NK detected in the current study is still insufficient to contribute to fostering achievement of RDMIL.
The results of this study clearly show that whereas NA and NK regarding consumption of FV were good, actual intake was below RDMIL. This suggests that other factors other than NA and NK hindered consumption. A study conducted in City suburb of Paris (France) reported that poverty was one of the factors that hindered some households from consuming FV [5]. However, another study conducted in Chicago (United States of America) revealed that higher income households were more associated with high purchasing and consumption of vegetables as compared to the lower income households [18]. In the current study, application of focus group discussions enabled identification of some of those factors. It was interesting to observe that both rural and urban inhabitants had similar barriers to consumption of FV. The factors were mixed and can generally be grouped into primary agricultural constraints, market limitations, postharvest management limitations, health concerns, social discomfort and policy environment. The significance of agricultural production constraints at the primary level such as pests and diseases, lack of high yielding and drought resistant varieties, and limited access to inputs has largely been studied in relation to crop yields and household income [34]. The current study therefore puts into perspective the relevance of agricultural production constraints to health and nutrition. These results therefore contribute to strengthening the drive towards integration of agriculture into health and nutrition research [4]. The importance of postharvest management limitations relates to the fact that food production in the area, as typical in many parts of the developing world rely on natural weather [30]. As such FV are largely available during production seasons and losses vary from 20% up to 80% [19]. In otherwords, if postharvest management solutions were available in the community and put into use, the lost fractions would be preserved and made available during the off-season periods of the year. Market limitations in terms of distance and prices, especially during off-seasons came out prominently and was more associated with fruits than vegetables. This partly explains the disparity observed between rural and urban respondents in terms of higher consumption of fruits among the latter than recorded for the former respondents.
With regard to health concerns, allergic reactions were the major issue. This has implications on the application of nutrition education to enhance intake of FV in order to confer the expected nutritional and health benefits. This study focused largely on factors that affect `consumption of FV and as such identification of those FV species associated with allergy was outside the scope of this study. Therefore, future studies should identify those plant species so that they can be left out of the promotion efforts. Related to health concerns was the issue of taste dislike for certain FV. Taste preference is one of the factors that affect food choice [7]. Borrowing from the domain of disease management in conventional medicine, patients take drugs not for the preferred taste but as a treatment to acheive good health outcome [54]. Therefore, for such plant species that people donot like the taste, their consumption should be promoted on the basis of health benefits.
Stigma is an important social factor that negatively affects good health-seeking behavior and is well known in the domain of sexually transmitted infections [14]. The current study provides first insight on the negative influence of stigma to healthy food consumption habits. The notion among both rural and urban respondents that consumption of FV is associated with poverty implies that having good NK on health and nutritional benefits associated with consumption of FV may not guarantee that people will adhere to the recommended level of intake because they care more about their social standing. Therefore, future nutrition education targeting consumption of FV should address stigma in the society as a cross-cuting issue. Because of the prevailing policy on wetland protection, respondents viewed it as a barrier to production and consumption of vegetables during the dry season. This is not withstanding the fact that there has to be a delicate balance between environmental intergrity and agricultural production [32]. This finding illustrates lack of knowledge on the need to protect wetlands so as to avert the unpredictable weather patterns currently being experienced globally.
Classically, it is generally expected that good NA and good NK should translate to good nutritional practices. However, a number of previous studies on various aspects of nutrition have demonstrated so and others provided contradictory results leading to a conclusion that good NA and NK donot necessarily lead to good practices [8]. Additionally, whereas multiple regression analysis showed location of the respondent, age of the respondent, education level of the respondent, main source of household income, major occupation of the household head, attendance of health education by the respondent, household size, major souce of household income as predictors of FV consumption among rural and or urban households, they did not come out clearly during FGDs. Therefore in the case of the current study, lack of adherence to the recommended daily intake level for FV (poor practice) despite good NA and NK may largely be attributed to the barriers identified during the FGDs.
The tennet of this study was hinged on the WHO recommendation that for a healthy living, an adult should achieve RDMIL. To the contrary, the results have demonstrated that in a developing country setting, despite NA and NK associated with consumption of FV, being good, actual intake is generally below RDMIL. By and large, the results suggest that, the inability of inhabitants to translate good NA and NK to the expected consumption practices was largely due to NANK factors including primary production constraints, market limitations, perceived unfavourable environmental policy environment, and social discomfort. A concerted effort is needed to address the NANK factors if adequate intake of fresh FV is to be achieved in developing countries. An important limitation of this study is that the approach of using the person in-charge of food preparation in the household as a respondent may not take into account food items that other members of the household might consume from elsewhere.
The datasets used and/or analysed during the current study are available from the corresponding author on request.
FAO:
Food and Agricultural Organisation of United Nations
FGD:
Focus Group Discussion
FV:
GDLGS:
Gulu District Local Government Statistics
NA:
Nutritional Attitude
NANK:
Non Attitudinal and Non Knowledge
Nutritional Knowlegde
NCDs:
Non Communicable Diseases
RMDIL:
Recommended Minimum Daily Intake Level
UBOS:
Anand D, Puri S. Nutritional knowledge, attitude, and practices among HIV-positive individuals in India. J Health Popul Nutr. 2013;31(2):195–201. https://doi.org/10.3329/jhpn.v31i2.16383.
Assari S, Lankarani MM. Educational attainment promotes fruit and vegetable intake for whites but not blacks. Multidisc Sci J. 2018;1(1):29–41. https://doi.org/10.3390/j1010005.
Bishwajit G, Leary PD, Ghos S, Sanni Y, Shangfeng T, Zhanchun F. Association between depression and fruit and vegetable consumption among adults in South Asia. BMC Psychiatry. 2017. https://doi.org/10.1186/s12888-017-1198-1.
Bouis HE, Saltzman A. Improving nutrition through biofortification: A review of evidence from HarvestPlus, 2003 through 2016. Global Food Secur. 2017;12:49–58. https://doi.org/10.1016/j.gfs.2017.01.009.
Buscail C, Gendreau J, Daval P, Lombrail P, Hercberg S, Latino-Martel P, et al. Impact of fruits and vegetables vouchers on food insecurity in disadvantaged families from a Paris suburb. BMC Nutrition. 2019;5(1):26. https://doi.org/10.1186/s40795-019-0289-4.
Chung LMY, Chung JWY, Chan APC. Building healthy eating knowledge and behavior: an evaluation of nutrition education in a skill training course for construction apprentices international journal of. Environ Res Public Health. 2019;16:4852.
Cornelsen L, Alarcon P, Häsler B, Amendah DD, Ferguson E, Fèvre EM, et al. Cross-sectional study of drivers of animalsource food consumption in low-income urban areas of Nairobi, Kenya. BMC Nutr. 2016;2(70):1–13.
Crites SL Jr, Aikman SN. Impact of nutrition knowledge on food evaluations. Eur J Clin Nutr. 2005;59(10):1191–200. https://doi.org/10.1038/sj.ejcn.1602231.
De Bourdeaudhuij I, te Velde S, Brug J, Due P, Wind M, Sandvik C, et al. Personal, social and environmental predictors of daily fruit and vegetable intake in 11-year-old children in nine European countries. Eur J Clin Nutr. 2008;62(7):834–41. https://doi.org/10.1038/sj.ejcn.1602794.
Desta AA, Kulkarni U, Abraha K, Worku S, Sahle BW. Iodine level concentration, coverage of adequately iodized salt consumption and factors affecting proper iodized salt utilization among households in North Ethiopia: a community based cross sectional study. BMC Nutr. 2019;5(28):1–10. https://doi.org/10.1186/s40795-019-0291-x.
Dormann CF, Elith J, Bacher S, Buchmann C, Carl G, Carré G, et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography. 2013;36(1):027–46. https://doi.org/10.1111/j.1600-0587.2012.07348.x.
Duthie SJ, Duthie GG, Russell WR, Kyle JAM, Macdiarmid JI, Rungapamestry V, et al. Effect of increasing fruit and vegetable intake by dietary intervention on nutritional biomarkers and attitudes to dietary change : a randomised trial. Eur J Nutr. 2017;57(5):1855–72. https://doi.org/10.1007/s00394-017-1469-0.
Elo S, Kyngäs H. The qualitative content analysis process. J Adv Nurs. 2008;62(1):107–15. https://doi.org/10.1111/j.1365-2648.2007.04569.x.
Emlet CA, Fredriksen-Goldsen KI, Kim HJ, Hoy-Ellis C. The relationship between sexual minority stigma and sexual health risk behaviors among HIV-positive older gay and bisexual men. J Appl Gerontol. 2017;36(8):931–52. https://doi.org/10.1177/0733464815591210.
FAO. (2014). Guidelines for assessing nutrition-related Knowledge, Attitudes and Practices manual Guidelines for assessing nutrition-related Knowledge, Attitudes and Practices manual.
Fongar A, Gödecke T, Qaim M. Various forms of double burden of malnutrition problems exist in rural Kenya. BMC Public Health. 2019;19(1543):1–9.
Frank SM, Webster J, McKenzie B, Geldsetzer P, Manne-Goehler J, Andall-Brereton G, et al. Consumption of fruits and vegetables among individuals 15 years and older in 28 low- and middle-income countries. J Nutr. 2019;149(7):1252–9. https://doi.org/10.1093/jn/nxz040.
French SA, Tangney CC, Crane MM, Wang Y, Bradley M, Appelhans BM. Nutrition quality of food purchases varies by household income: the SHoPPER study. BMC Public Health. 2019;19(1):231. https://doi.org/10.1186/s12889-019-6546-2.
Gardas BB, Raut RD, Narkhede B. Modeling causal factors of post-harvesting losses in vegetable and fruit supply chain: an Indian perspective. Renew Sust Energ Rev. 2017;80(December 2016):1355–71. https://doi.org/10.1016/j.rser.2017.05.259.
Gernand, A. D., Schulze, K. J., Stewart, C. P., West, K. P. and, & Christian, P. (2016). Effects and Prevention in pregnancy worldwide: health effects and prevention. 12. doi: https://doi.org/10.1038/nrendo.2016.37.Micronutrient.
Ghadieh R, Mosleh JMB, Hayek SA, Merhi S, Fares JEH. The relationship between hypovitaminosis D and metabolic syndrome: a cross sectional study among employees of a private university in Lebanon. BMC Nutr. 2018;4(36):1–12. https://doi.org/10.1186/s40795-018-0243-x.
Gleason PM, Harris J, Sheean PM, Boushey CJ, Bruemmer B. Publishing nutrition research: validity, reliability, and diagnostic test assessment in nutrition-related research. J Am Diet Assoc. 2010;110(3):409–19. https://doi.org/10.1016/j.jada.2009.11.022.
Gulu District Local Government Statistics. (2013). The republic of Uganda, Gulu district local government.
Hongu N, Pope BT, Bilgiç P, Orr BJ, Suzuki A, Kim AS, et al. Usability of a smartphone food picture app for assisting 24-hour dietary recall: A pilot study. Nutr Res Pract. 2015;9(2):207–12. https://doi.org/10.4162/nrp.2015.9.2.207.
Ickes SB, Baguma C, Brahe CA, Myhre JA, Adair LS, Bentley ME, et al. Maternal participation in a nutrition education program in Uganda is associated with improved infant and young child feeding practices and feeding knowledge: a post-program comparison study. BMC Nutr. 2017;3(32):1–10. https://doi.org/10.1186/s40795-017-0140-8.
Isreal, G.D. (1992). Determining sample size. Fact sheet PEOD-6. University of Florida Cooperative Extension Service, Institute of Food and Agriculture Sciences, EDIS, Florida, United States of America.
Kalid M, Osman F, Sulaiman M, Dykes F, Erlandsson k. Infant and young child nutritional status and their caregivers' feeding knowledge and hygiene practices in internally displaced person camps, Somalia. BMC Nutr. 2019;5(59):1–11. https://doi.org/10.1186/s40795-019-0325-4.
Kassa M, Grace J. The global burden and perspectives on non-communicable diseases (NCDs) and the prevention, data availability and systems approach of NCDs in low-resource countries [online first]. IntechOpen. 2019. https://doi.org/10.5772/intechopen.89516.
Kim SA, Moore LV, Galuska D, Wright AP, Harris D, Grummer-Strawn LM, et al. Vital signs: fruit and vegetable intake among children — United States, 2003–2010. Morb Mortal Wkly Rep. 2014;63(31):671–6.
Kumar D, Kalita P. Reducing postharvest losses during storage of grain crops to strengthen food security in developing countries. Foods (Basel, Switzerland). 2017;6(1):1–22. https://doi.org/10.3390/foods6010008.
Kumar V, Arora G, Midha IK, Gupta YP. Infant and young child feeding behaviors among working mothers in India : implications for Global Health policy and practice. Int J MCH AIDS. 2015;3(1):7–15.
Liebig MA, Herrick JE, Archer DW, Dobrowolski J, Duiker SW, Franzluebbers AJ, et al. Aligning land use with land potential: the role of integrated agriculture. Agricult Environ Lett. 2017;2(1):1–5. https://doi.org/10.2134/ael2017.03.0007.
Lozano R, Naghavi M, Foreman K, Lim S, Shibuya K, Aboyans V, et al. Global and regional mortality from 235 causes of death for 20 age groups in 1990 and 2010: A systematic analysis for the global burden of disease study 2010. Lancet. 2012;380(9859):2095–128. https://doi.org/10.1016/S0140-6736(12)61728-0.
Lunduka RW, Mateva KI, Magorokosho C, Manjeru P. Impact of adoption of drought-tolerant maize varieties on total maize production in south eastern Zimbabwe. Clim Dev. 2019;11(1):35–46. https://doi.org/10.1080/17565529.2017.1372269.
Miller LMS, Cassady DL. The effects of nutrition knowledge on food label use. A review of the literature. Appetite. 2015;92:207–16. https://doi.org/10.1016/j.appet.2015.05.029.
Mitchodigni IM, Hounkpatin WA, Ntandou-Bouzitou G, Avohou H, Termote C, Kennedy G, et al. Complementary feeding practices: determinants of dietary diversity and meal frequency among children aged 6–23 months in southern Benin. Food Sec. 2017;9(5):1117–30. https://doi.org/10.1007/s12571-017-0722-y.
Nassanga P, Okello-uma I, Ongeng D. The status of nutritional knowledge, attitude and practices associated with complementary feeding in a post-conflict development phase setting: the case of Acholi-sub-region of Uganda. J Food Scie Nutr. 2018;6(2):1–12. https://doi.org/10.1002/fsn3.829.
Noll P.R.S., Matias Noll M., Abreu L.C., Baracat E. C, Silveira E.A& Isabel Cristina Esposito Sorpreso I.C.E. (2018). Ultra-processed food consumption by Brazilian adolescents in cafeterias and school meals. Sci Rep, 9:7162. doi: https://doi.org/10.1038/s41598-019-43611-x
Okidi L, Odongo W, Ongeng D. The mix of good nutritional attitude and poor nutritional knowledge is associated with adequate intake of vitamin A and iron from wild fruits and vegetables among rural households in Acholi subregion of northern Uganda. J Food Sci Nutr. 2018;6(8):2273–84. https://doi.org/10.1002/fsn3.800.
Oryema C, Oryem-origa H, Roos N. Influential factors to the consumptions of edible wild fruits and products in the post Conflict District of Gulu, Uganda. J Nat Sci Res. 2015;5(10):132–44.
Oyebode O, Gordon-Dseagu V, Walker A, Mindell JS. Fruit and vegetable consumption and all-cause, cancer and CVD mortality: analysis of health survey for England data. J Epidemiol Community Health. 2014;68(9):856–62. https://doi.org/10.1136/jech-2013-203500.
Pem D, Jeewon R. Fruit and vegetable intake: benefits and Progress of nutrition education interventions- narrative review article. Iran J Public Health. 2015;44(10):1309–21. https://doi.org/10.1017/CBO9781107415324.004.
Prithvi S, Cecilia L, Björn V, M, G. Farmer attitudes and perceptions to the re–use of fertiliser products from resource–oriented sanitation systems – the case of Vellore, South India. Sci Total Environ. 2017;581–582(1):885–96. https://doi.org/10.1016/j.scitotenv.2017.01.044.
Raza Q, Nicolaou M, Dijkshoorn H, Seidell JC. Comparison of general health status, myocardial infarction, obesity, diabetes, and fruit and vegetable intake between immigrant Pakistani population in the Netherlands and the local Amsterdam population. Ethn Health. 2017;22(6):551–64. https://doi.org/10.1080/13557858.2016.1244741.
Riley L, Cowan M. Sex Differences in Barriers to Antihypertensive Medication Adherence: Findings from the Cohort Study of Medication Adherence Among Older Adults. In: Non communicable diseases country profiles. Genève: WHO Press; 2014. p. 2014. https://doi.org/10.1111/jgs.12171.
Roininen K, Arvola A, Lähteenmäki L. Exploring consumers' perceptions of local food with two different qualitative techniques: laddering and word association. Food Qual Prefer. 2006;17(1–2):20–30. https://doi.org/10.1016/j.foodqual.2005.04.012.
Salehi L, Eftekhar H, Mohamad K, Tavaian SS, Jasayery A, Montazeri A. Consumption of fruit and vegetables among elderly people : a cross sectional study from Iran. Int J. 2010;9(1):1–9. https://doi.org/10.1186/1475-2891-9-2.
Sharma G, Vivek GAK, Ganjewla D, Gupta C, P. D. Phytochemical composition , antioxidant and antibacterial potential of underutilized parts of some fruits. Int Food Res J. 2017;24(3):1167–73.
Slavin JL, Lloyd B. Health benefits of fruits and vegetables. Adv Nutr. 2012;3(4):506–16. https://doi.org/10.3945/an.112.002154.506.
Spronk I, Kullen C, Burdon C, O'Connor H. Relationship between nutrition knowledge and dietary intake. Br J Nutr. 2014;111(10):1713–26. https://doi.org/10.1017/S0007114514000087.
Tong A, Sainsbury P, Craig J. Consolidated criterio for reporting qualitative research (COREQ): a 32- item checklist for interviews and focus group. Int J Qual Health Care. 2007;19(6):349–57. https://doi.org/10.1093/intqhc/mzm042.
UBOS. (2014). 2014 Census. Population In Uganda: National population and Housing census result.
Ul Haq N, Saleem F, Hassali MA, Shafie AA, Aljadhey H, Farooqui M. A cross sectional assessment of knowledge, attitude and practice towards hepatitis B among healthy population of Quetta, Pakistan. BMC Public Health. 2012;12(1):1. https://doi.org/10.1186/1471-2458-12-692.
Wirtz VJ, Hogerzeil HV, Gray AL, Bigdeli M, Joncheere CD, Ewen MA, et al. Essential medicines for universal health coverage. Kazan Med J. 2019;100(1):4–111. https://doi.org/10.17816/kmj2019-4.
Zerfu TA, Biadgilign S. Pregnant mothers have limited knowledge and poor dietary diversity practices, but favorable attitude towards nutritional recommendations in rural Ethiopia: evidence from community-based study. BMC Nutr. 2018;4(43):1–9. https://doi.org/10.1186/s40795-018-0251-x.
The authors are grateful to the study participants and data collectors. The Regional Universities Forum for Capacity Building in Agriculture (RUFORUM) is highly appreciated for financing the study.
Funding for this study was obtained from the Regional Universities Forum for Capacity Building in Agriculture (RUFORUM; Grant number: RU/2017/NG-MCF-01). RUFORUM had no role in data collection and production of the manuscript.
Department of Food Science and Postharvest Technology, Faculty of Agriculture and Environment, Gulu University, Gulu, Uganda
Benjamin Kenyi Bendere Lomira, Prossy Nassanga & Duncan Ongeng
Department of Rural Development and Agribusines, Faculty of Agriculture and Environment, Gulu University, Gulu, Uganda
Daniel Micheal Okello
Benjamin Kenyi Bendere Lomira
Prossy Nassanga
Duncan Ongeng
DO concieved the study. BKBL collected and entered the data. PN together with DMO and BKBL analysed the data. All authors contributed equally during the process of interpreting the results. DO drafted the manuscript and critically revised it with PN and DMO. All authors read and approved the final manuscript.
Correspondence to Duncan Ongeng.
The study was approved byGulu University Research Ethics Committee (Reference number: GUREC -028-19). At the district level, permission was granted by the Chief Administrative Officer of Gulu district, while at the sub-counties and divisions, permission was sought from LC III Chirpersons. At the village level, Local council I Chairpersons granted permission. At the individual level, the respondent was asked to consent by either appending his or her signature or the thumb print on the consent form before being interviewed. Before participating in the study, respondents were assured of confidentiality that codes would be used instead of their names.
Additional file 1: Supplementary material S1.
Modified questionaire used to collect data on consumption of fruits and vegetables, nutritional knowledge, attitude and socio-dermographic characteriostics of the respondents.
Modified focus group discussion guide for assessing non-attitudinal and non-knowledge based barriers to consumption of fruits and vegetables.
Lomira, B.K.B., Nassanga, P., Okello, D.M. et al. Non-attitudinal and non-knowledge based factors constrain households from translating good nutritional knowledge and attitude to achieve the WHO recommended minimum intake level for fruits and vegetables in a developing country setting: evidence from Gulu district, Uganda. BMC Nutr 7, 68 (2021). https://doi.org/10.1186/s40795-021-00469-5 | CommonCrawl |
Probability of significant result in a second sample given first was significant
It's an example mentioned in Amos Tversky and Daniel Kahneman's Belief in the Law of Small Numbers:
Suppose you have run an experiment on 20 subjects, and have obtained a significant result which confirms your theory ($z = 2.23$, $p < .05$, two-tailed). You now have cause to run an additional group of 10 subjects. What do you think the probability is that the results will be significant, by a one-tailed test, separately for this group?
The explanation in the essay, however, is a little hard to understand. It says as following:
On the other hand, if you feel that the probability is around $.48$, you belong to a minority. Only 9 of our 84 respondents gave answers between $.40$ and $.60$. However, $.48$ happens to be a much more reasonable estimate than $.85$. The required estimate can be interpreted in several ways. One possible approach is to follow common research practice, where a value obtained in one study is taken to define a plausible alternative to the null hypothesis. The probability requested in the question can then be interpreted as the power of the second test (i.e., the probability of obtaining a significant result in the second sample) against the alternative hypothesis defined by the result of the first sample. In the special case of a test of a mean with known variance, one would compute the power of the test against the hypothesis that the population mean equals the mean of the first sample. Since the size of the second sample is half that of the first, the computed probability of obtaining $z > 1.645$ is only $.473$. A theoretically more justifiable approach is to interpret the requested probability within a Bayesian framework and compute it relative to some appropriately selected prior distribution. Assuming a uniform prior, the desired posterior probability is $.478$. Clearly, if the prior distribution favors the null bypothesis, as is often the case, the posterior probability will be even smaller.
I'm not sure how we could get $1.645$ and $0.473$. Thanks for some detailed explanation.
statistical-significance power z-test
rexarski
rexarskirexarski
$\begingroup$ You can only find ''evidence'' for $H_1$, not for $H_0$, the ''power'' indicates how ''easy'' it is to find evidence for $H_0$. With your smaller sample you can not reject $H_0$ but that is probably because of a lack of power, see stats.stackexchange.com/questions/163957/… $\endgroup$ – user83346 Feb 20 '16 at 10:29
$\begingroup$ Could you provide a full citation to the referenced essay, thanks? $\endgroup$ – Silverfish Feb 20 '16 at 10:35
$\begingroup$ Actually by "citation" I meant to give a reference (as you would in the references section of a paper if you cited this essay) but your edit was very helpful anyway, as it makes the authors' approach clearer and answerers here don't have to guess where the numbers came from. $\endgroup$ – Silverfish Feb 20 '16 at 10:47
The number $1.645$ comes about because it is the critical value for a one-sided z-test with $\alpha=.05$.
> qnorm(.95)
# 1.644854
This admittedly could have been made a bit clearer in the text. Anyway, the probability $.473$ then comes from taking the area above this critical value of a normal distribution centered at $2.23/\sqrt{2}$ (and with standard deviation = 1).
> pnorm(1.645, mean=2.23/sqrt(2), lower.tail=FALSE)
# 0.4728324
$2.23$ was the value of the test statistic in the original study, and this would also be (by assumption) the expected value of the test statistic in the replication study if the replication study has the same sample size as the original study -- but it doesn't, it has half the sample size of the original study, so we divide the expected test statistic by $\sqrt{2}$ to account for that.
Jake WestfallJake Westfall
Not the answer you're looking for? Browse other questions tagged statistical-significance power z-test or ask your own question.
What follows if we fail to reject the null hypothesis?
Samples that will result in a large p-value
Appropriate use of z test comparing two proportions
Significant difference between proportions, found at sample size below that suggested by power analysis
How to determine if a (binary) variable has a statistically significant effect on a response variable?
Understanding formulation of hypotheses in difference between two sample means (z test)
Claim the superiority of a treatment in the context of a significant difference with a two-sided test
Testing when the Null Hypothesis is that the distributions do differ. Application in the case of Kolmogorov-Smirnov test
The Law of small numbers: How to re-compute the numbers in the initial example in Tversky-Kahnemann famous paper?
Statistical test for first sample greater than given sample?
Understanding p-values using an example | CommonCrawl |
Calculators Topics Go Premium About Snapxam
ENG • ESP
Processing image... Tap to take a pic of the problem
Snapxam › calculators › Special Products
Special products Calculator
Get detailed solutions to your math problems with our Special products step-by-step calculator. Practice your math skills and learn step by step with our math solver. Check out all of our online calculators here!
(◻)
◻/◻
◻2
◻◻
√◻
◻√◻
◻√
log◻
d/dx
D□x
∫◻
|◻|
asec
coth
sech
csch
asech
acsch
Solved Problems
Difficult Problems
Solved example of special products
$\left(x+2\right)\left(x+3\right)$
The product of two binomials of the form $(x+a)(x+b)$ is equal to the product of the first terms of the binomials, plus the algebraic sum of the second terms by the common term of the binomials, plus the product of the second terms of the binomials. In other words: $(x+a)(x+b)=x^2+(a+b)x+ab$
$x^2+5x+6$
Struggling with math?
Access detailed step by step solutions to millions of problems, growing every day!
Popular problems
$2\left(x-3\right)^3-2x\cdot\left(x-6\right)\left(x-3\right)$ 455 views
$\frac{3}{4}\cdot\left(2x+3\right)-\frac{4}{5}\cdot\left(x+4\right)\cdot\frac{5}{6}\cdot\left(x-2\right)$ 451 views
$\left(1+x^2\right)\left(1-x^2\right)-\left(2x+3\right)^2$ 401 views
$\left(-2x+2\right)\left(x^4+4x^3+6x^2+4x+1\right)+\left(x^2-2x-3\right)\left(4x^3+12x^2+12x+4\right)$ 394 views
$\left(5+2\cdot \sqrt{6}\right)\left(5-2\cdot \sqrt{6}\right)$ 389 views
$3\left(x+2\right)^2\left(x-3\right)^2-2\left(x+2\right)^3\left(x-3\right)$ 379 views
$\left(2a+5\right)\left(2a-5\right)$ 376 views
$\frac{d^2}{dx^2}\left(\left(x-1\right)^3\right)\left(x-3\right)$ 375 views
© 2018-2020 Snapxam, Inc. About Us Privacy Terms Contact
Calculators Topics Go Premium | CommonCrawl |
Difference between revisions of "Past Probability Seminars Spring 2020"
Vadicgor (talk | contribs)
m (Vadicgor moved page Probability Seminar to Past Probability Seminars Spring 2020)
== Fall 2012 ==
= Spring 2020 =
<b>Thursdays in 901 Van Vleck Hall at 2:30 PM</b>, unless otherwise noted.
<b>We usually end for questions at 3:20 PM.</b>
Thursdays in 901 Van Vleck Hall at 2:25 PM, unless otherwise noted. If you would like to receive announcements about upcoming seminars, please visit [https://www-old.cae.wisc.edu/mailman/listinfo/apseminar this page] to sign up for the email list.
If you would like to sign up for the email list to receive seminar announcements then please send an email to
[mailto:[email protected] [email protected]]
== January 23, 2020, [https://www.math.wisc.edu/~seppalai/ Timo Seppalainen] (UW Madison) ==
'''Non-existence of bi-infinite geodesics in the exponential corner growth model
[[Past Seminars]]
Whether bi-infinite geodesics exist has been a significant open problem in first- and last-passage percolation since the mid-80s. A non-existence proof in the case of directed planar last-passage percolation with exponential weights was posted by Basu, Hoffman and Sly in November 2018. Their proof utilizes estimates from integrable probability. This talk describes an independent proof completed 10 months later that relies on couplings, coarse graining, and control of geodesics through planarity and increment-stationary last-passage percolation. Joint work with Marton Balazs and Ofer Busani (Bristol).
== Thursday, September 13, Sebastien Roch, UW-Madison ==
== January 30, 2020, [https://www.math.wisc.edu/people/vv-prof-directory Scott Smith] (UW Madison) ==
'''Quasi-linear parabolic equations with singular forcing'''
Title: Markov models on trees: Variants of the reconstruction problem
The classical solution theory for stochastic ODE's is centered around Ito's stochastic integral. By intertwining ideas from analysis and probability, this approach extends to many PDE's, a canonical example being multiplicative stochastic heat equations driven by space-time white noise. In both the ODE and PDE settings, the solution theory is beyond the scope of classical deterministic theory because of the ambiguity in multiplying a function with a white noise. The theory of rough paths and regularity structures provides a more quantitative understanding of this difficulty, leading to a more refined solution theory which efficiently divides the analytic and probabilistic aspects of the problem, and remarkably, even has an algebraic component.
In this talk, we will discuss a new application of these ideas to stochastic heat equations where the strength of the diffusion is not constant but random, as it depends locally on the solution. These are known as quasi-linear equations. Our main result yields the deterministic side of a solution theory for these PDE's, modulo a suitable renormalization. Along the way, we identify a formally infinite series expansion of the solution which guides our analysis, reveals a nice algebraic structure, and encodes the counter-terms in the PDE. This is joint work with Felix Otto, Jonas Sauer, and Hendrik Weber.
I will consider the so-called `reconstruction problem': how accurately
can one guess the state at the root of a Markov chain on a finite tree,
given the states at the leaves? I will introduce variants of this problem
that arise naturally in connection with applications in molecular
evolution, and discuss recent results and open problems. Based
on joint works with Andoni, Daskalakis, Hassidim, Mossel and
Sly.
== February 6, 2020, [https://sites.google.com/site/cyleeken/ Cheuk-Yin Lee] (Michigan State) ==
'''Sample path properties of stochastic partial differential equations: modulus of continuity and multiple points'''
In this talk, we will discuss sample path properties of stochastic partial differential equations (SPDEs). We will present a sharp regularity result for the stochastic wave equation driven by an additive Gaussian noise that is white in time and colored in space. We prove the exact modulus of continuity via the property of local nondeterminism. We will also discuss the existence problem for multiple points (or self-intersections) of the sample paths of SPDEs. Our result shows that multiple points do not exist in the critical dimension for a large class of Gaussian random fields including the solution of a linear system of stochastic heat or wave equations.
== Thursday, September 20, Jun Yin, UW-Madison ==
== February 13, 2020, [http://www.jelena-diakonikolas.com/ Jelena Diakonikolas] (UW Madison) ==
'''Langevin Monte Carlo Without Smoothness'''
Title: Some new results on random matrices.
Langevin Monte Carlo (LMC) is an iterative algorithm used to generate samples from a distribution that is known only up to a normalizing constant. The nonasymptotic dependence of its mixing time on the dimension and target accuracy is understood mainly in the setting of smooth (gradient-Lipschitz) log-densities, a serious limitation for applications in machine learning. We remove this limitation by providing polynomial-time convergence guarantees for a variant of LMC in the setting of non-smooth log-concave distributions. At a high level, our results follow by leveraging the implicit smoothing of the log-density that comes from a small Gaussian perturbation that we add to the iterates of the algorithm and while controlling the bias and variance that are induced by this perturbation.
Based on joint work with Niladri Chatterji, Michael I. Jordan, and Peter L. Bartlett.
Abstract: In this talk, we will introduce some new results on random
== February 20, 2020, [https://math.berkeley.edu/~pmwood/ Philip Matchett Wood] (UC Berkeley) ==
matrices, especially the necessary and sufficient conditions for universality
'''A replacement principle for perturbations of non-normal matrices'''
at the edge and a new result on the circular law.
== <font color="red">Friday</font>, October 5, Nicos Georgiou, University of Utah ==
There are certain non-normal matrices whose eigenvalues can change dramatically when a small perturbation is added. However, when that perturbation is an iid random matrix, it appears that the eigenvalues become stable after perturbation and only change slightly when further small perturbations are added. Much of the work is this situation has focused on iid random gaussian perturbations. In this talk, we will discuss work on a universality result that allows for consideration of non-gaussian perturbations, and that shows that all perturbations satisfying certain conditions will produce the same limiting eigenvalue measure. Interestingly, this even allows for deterministic perturbations to be considered. Joint work with Sean O'Rourke.
Title: Busemann functions and variational formula for last passage
== February 27, 2020, No seminar ==
percolation.
''' '''
Abstract: Directed last passage percolation on the two dimensional lattice is
== March 5, 2020, [https://www.ias.edu/scholars/jiaoyang-huang Jiaoyang Huang] (IAS) ==
exactly solvable when the weight distribution is i.i.d. exponential or
''' Large Deviation Principles via Spherical Integrals'''
geometric. The reason for that is the Burke property associated to a model
with "boundaries".
We investigate the solvable model further in order to generalize the idea
In this talk, I'll explain a framework to study the large deviation principle for matrix models and their quantized versions, by tilting the measures using the asymptotics of spherical integrals obtained by Guionnet and Zeitouni. As examples, we obtain
of boundaries into the general setting, and we compute a variational
formula for passage times for more general weights. The variatonal formula
is given in terms of Busemann functions and all restrictive assumptions on
the environment are to guarantee their existence.
Joint work with T. Seppalainen, F. Rassoul-Agha and A. Yilmaz.
1) the large deviation principle for the empirical distribution of the diagonal entries of $UB_NU^*$, for a sequence of $N\times N$ diagonal matrices $B_N$ and unitary/orthogonal Haar distributed matrices $U$;
== Thursday, October 11, No seminar ==
2) the large deviation upper bound for the empirical eigenvalue distribution of $A_N+UB_NU^*$, for two sequences of $N\times N$ diagonal matrices $A_N, B_N$, and their complementary lower bounds at "good" probability distributions;
because of the MIDWEST PROBABILITY COLLOQUIUM
3) the large deviation principle for the Kostka number $K_{\lambda_N \eta_N}$, for two sequences of partitions $\lambda_N, \eta_N$ with at most $N$ rows;
4) the large deviation upper bound for the Littlewood-Richardson coefficients $c_{\lambda_N \eta_N}^{\kappa_N}$, for three sequences of partitions $\lambda_N, \eta_N, \kappa_N$ with at most $N$ rows, and their complementary lower bounds at "good" probability distributions.
== Thursday, October 18, Jason Swanson, University of Central Florida ==
This is a joint work with Belinschi and Guionnet.
Title: Correlations within the signed cubic variation of fractional Brownian motion
== March 12, 2020, No seminar ==
Abstract: The signed cubic variation of the fractional Brownian motion, <math>B</math>, with Hurst parameter <math>H=1/6</math>, is a concept built upon the fact that the sequence, <math>\{W_n\}</math>, of sums of cubes of increments of <math>B</math> converges in law to an independent Brownian motion as the size of the increments tends to zero. In joint work with Chris Burdzy and David Nualart, we study the convergence in law of two subsequences of <math>\{W_n\}</math>. We prove that, under some conditions on both subsequences, the limit is a two-dimensional Brownian motion whose components may be correlated and we find explicit formulae for its covariance function.
== March 19, 2020, Spring break ==
== Thursday, October 25, Mihai Stoiciu, Williams College ==
== March 26, 2020, CANCELLED, [https://math.cornell.edu/philippe-sosoe Philippe Sosoe] (Cornell) ==
Title: Random Matrices with Poisson Eigenvalue Statistics
== April 2, 2020, CANCELLED, [http://pages.cs.wisc.edu/~tl/ Tianyu Liu] (UW Madison)==
Abstract: Several classes of random self-adjoint and random unitary matrices exhibit Poisson microscopic eigenvalue statistics. We will outline the general strategy for proving these results and discuss other models where the Poisson statistics is conjectured. We will also explain how changes in the distribution of the matrix coefficients produce changes in the microscopic eigenvalue distribution and give a transition from Poisson to the picket fence distribution.
== April 9, 2020, CANCELLED, [http://stanford.edu/~ajdunl2/ Alexander Dunlap] (Stanford) ==
== April 16, 2020, CANCELLED, [https://statistics.wharton.upenn.edu/profile/dingjian/ Jian Ding] (University of Pennsylvania) ==
== April 22-24, 2020, CANCELLED, [http://frg.int-prob.org/ FRG Integrable Probability] meeting ==
3-day event in Van Vleck 911
== Thursday, November 8, Michael Kozdron, University of Regina ==
== April 23, 2020, CANCELLED, [http://www.hairer.org/ Martin Hairer] (Imperial College) ==
Title: The Green's function for the radial Schramm-Loewner evolution
[https://www.math.wisc.edu/wiki/index.php/Colloquia Wolfgang Wasow Lecture] at 4pm in Van Vleck 911
Abstract: The Schramm-Loewner evolution (SLE), a one-parameter family of random two-dimensional growth processes introduced in 1999 by the late Oded Schramm, has proved to be very useful for studying the scaling limits of discrete models from statistical mechanics. One tool for analyzing SLE itself is the Green's function. An exact formula for the Green's function for chordal SLE was used by Rohde and Schramm (2005) and Beffara (2008) for determining the Hausdorff dimension of the SLE trace. In the present talk, we will discuss the Green's function for radial SLE. Unlike the chordal case, an exact formula is known only when the SLE parameter value is 4. For other values, a formula is available in terms of an expectation with respect to SLE conditioned to go through a point. This talk is based on joint work with Tom Alberts and Greg Lawler.
== April 30, 2020, CANCELLED, [http://willperkins.org/ Will Perkins] (University of Illinois at Chicago) ==
== Thursday, November 15, Gregorio Moreno Flores, University of Wisconsin - Madison ==
== <font color="red">Tuesday</font>, November 27, Michael Damron, Princeton ==
Title: Busemann functions and infinite geodesics in first-passage percolation
Abstract: In first-passage percolation we study the chemical
distance in the weighted graph Z^d, where the edge weights are given
by a translation-ergodic (typically i.i.d.) distribution. A main open
question is to describe the behavior of very long or infinite
geodesics. In particular, one would like to know if there are infinite
geodesics with asymptotic directions, how many are there, and if
infinite geodesics in the same direction coalesce. Some of these
questions were addressed in the late 90's by Newman and collaborators
under strong assumptions on the limiting shape and weight
distribution. I will discuss work with Jack Hanson (Ph. D. student at
Princeton) where we develop a framework for working with
distributional limits of Busemann functions and use them to prove a
form of coalescence of geodesics constructed in any deterministic
direction. We also prove existence of infinite geodesics which are
asymptotically directed in sectors. Last, we introduce a purely
directional condition which replaces Newman's global curvature
condition and whose assumption implies the existence of directional
geodesics.
== Thursday, December 6, Scott McKinley, University of Florida ==
== Thursday, December 13, Karl Liechty, University of Michigan ==
Thursdays in 901 Van Vleck Hall at 2:30 PM, unless otherwise noted. We usually end for questions at 3:20 PM.
If you would like to sign up for the email list to receive seminar announcements then please send an email to [email protected]
January 23, 2020, Timo Seppalainen (UW Madison)
Non-existence of bi-infinite geodesics in the exponential corner growth model
January 30, 2020, Scott Smith (UW Madison)
Quasi-linear parabolic equations with singular forcing
February 6, 2020, Cheuk-Yin Lee (Michigan State)
Sample path properties of stochastic partial differential equations: modulus of continuity and multiple points
February 13, 2020, Jelena Diakonikolas (UW Madison)
Langevin Monte Carlo Without Smoothness
Langevin Monte Carlo (LMC) is an iterative algorithm used to generate samples from a distribution that is known only up to a normalizing constant. The nonasymptotic dependence of its mixing time on the dimension and target accuracy is understood mainly in the setting of smooth (gradient-Lipschitz) log-densities, a serious limitation for applications in machine learning. We remove this limitation by providing polynomial-time convergence guarantees for a variant of LMC in the setting of non-smooth log-concave distributions. At a high level, our results follow by leveraging the implicit smoothing of the log-density that comes from a small Gaussian perturbation that we add to the iterates of the algorithm and while controlling the bias and variance that are induced by this perturbation. Based on joint work with Niladri Chatterji, Michael I. Jordan, and Peter L. Bartlett.
February 20, 2020, Philip Matchett Wood (UC Berkeley)
A replacement principle for perturbations of non-normal matrices
February 27, 2020, No seminar
March 5, 2020, Jiaoyang Huang (IAS)
Large Deviation Principles via Spherical Integrals
March 12, 2020, No seminar
March 19, 2020, Spring break
March 26, 2020, CANCELLED, Philippe Sosoe (Cornell)
April 2, 2020, CANCELLED, Tianyu Liu (UW Madison)
April 9, 2020, CANCELLED, Alexander Dunlap (Stanford)
April 16, 2020, CANCELLED, Jian Ding (University of Pennsylvania)
April 22-24, 2020, CANCELLED, FRG Integrable Probability meeting
April 23, 2020, CANCELLED, Martin Hairer (Imperial College)
Wolfgang Wasow Lecture at 4pm in Van Vleck 911
April 30, 2020, CANCELLED, Will Perkins (University of Illinois at Chicago)
Retrieved from "https://www.math.wisc.edu/wiki/index.php?title=Past_Probability_Seminars_Spring_2020&oldid=19533" | CommonCrawl |
APPOL 2 Workshop
University of Bologna Residential Center
Bertinoro (Forlì), Italy
[ What the Meeting is About
| Seminar Schedule
| Important Dates
| Location
| How to Reach Bertinoro
| List of Participants
| Abstracts
| Organization and Sponsorship
| Local Weather Forecast]
What the Meeting is About
Appol 2 is a thematic network of the European Union, focussing on on-line and approximation algorithms. The Appol network consists of 15 universities.
The format of this meeting will be about two, two and a half days of lectures, followed by a few days during which research problems will be discussed in a congenial atmosphere.
Tentative Schedule
Thomas Erlebach Frits Spieksma
Alexander Hall Leen Stougie
Martin Skutella Sai Anand
Fernandez Dela Vega Guochuan Zhang
Gerold Jäger Rene Sitters
Stefano Leonardi
Arrival: Saturday 22 March, 2003
Departures: 28-29 March, 2003
Last day of talks:
Tuesday 25 March, 2003
End of workshop:
The meeting will be held in the small medieval hilltop town of Bertinoro. This town is in Emilia Romagna about 50km east of Bologna at an elevation of about 230m. Here is a map putting it in context. It is easily reached by train and taxi from Bologna and is close to many splendid Italian locations such as Ravenna, a treasure trove of byzantine art and history, and the Republic of San Marino (all within 35km) as well as some less well-known locations like the thermal springs of Fratta Terme and the castle and monastic gardens of Monte Maggio. Bertinoro can also be a base for visiting some of the better-known Italian locations such as Padua, Ferrara, Vicenza, Venice, Florence and Siena.
Bertinoro itself is picturesque, with many narrow streets and walkways winding around the central peak. The meeting will be held in a redoubtable ex-Episcopal fortress that has been converted by the University of Bologna into a modern conference center with computing facilities and Internet access. From the fortress you can enjoy a beautiful the vista that stretches from the Tuscan Apennines to the Adriatic coast.
How to Reach Bertinoro
List of confirmed participants so far. More can join later.
Susanne Albers, Universität Freiburg
Sai Anand, ETH Zürich
Georg Baier, Technische Universität Berlin
Euripides Bampis, Universitè D'Evry
Debora Donato, Università La Sapienza di Roma
Fabian Ennecke , ETH Zürich
Thomas Erlebach, ETH Zürich
Wenceslas Fernandez De La Vega, Universitè Paris-Sud
Amos Fiat, University of Tel Aviv
Alexander Hall, ETH Zürich
Gerold Jäger, Universität Kiel
Klaus Jansen, Universität Kiel
Miklos Kresz, University of Szeged
Stefano Leonardi, Università La Sapienza di Roma
Alberto Marchetti Spaccamela, Università La Sapienza di Roma
Ioannis Milis, Athens University of Economics and Business
Marc Nunkesser, ETH Zürich
Alessandro Panconesi, Università La Sapienza di Roma
Rene Sitters, Technische Universiteit Eindhoven
Martin Skutella, Technische Universität Berlin
Ines Spenke, Technische Universität Berlin
Frits Spieksma, Katholieke Universiteit Leuven
Leen Stougie, Technische Universiteit Eindhoven
Gabor Szabo, ETH Zürich
Joris van de Klundert, Universiteit Maastricht
Peter Widmayer, ETH Zürich
Guochuan Zhang, Universität Kiel
Organization and Sponsorship
Stefano Leonardi Università La Sapienza di Roma
Alessandro Panconesi Università La Sapienza di Roma
Local Organization
Andrea Bandini, Elena Della Godenza, Centro Congressi di Bertinoro
Sponsored by BICI Bertinoro International Center for Informatics
On Paging with Locality of Reference
by Susanne Albers, Universität Freiburg
Motivated by the fact that competitive analysis yields too pessimistic results when applied to the paging problem, there has been considerable research interest in refining competitive analysis and in developing alternative models for studying online paging. The goal is to devise models in which theoretical results capture phenomena observed in practice. In this talk we propose a new, simple model for studying paging with locality of reference. The model is closely related to Denning's working set concept and directly reflects the amount of locality that request sequences exhibit. We demonstrate that our model is reasonable from a practical point of view. We use the page fault rate to evaluate the quality of paging algorithms, which is the performance measure used in practice. We develop tight or nearly tight bounds on the fault rates achieved by popular paging algorithms such as LRU, FIFO, deterministic Marking strategies and LFD. It shows that LRU is an optimal online algorithm, whereas FIFO and Marking strategies are not optimal in general. We present an experimental study comparing the page fault rates proven in our analyses to the page fault rates observed in practice. This is the first such study for an alternative/refined paging model.
(Joint work with Lene Favrholdt and Oliver Giel.)
A Linear Bound on the Diameter of the Transportation Polytope
by Leen Stougie, Technische Universiteit Eindhoven
We prove that the combinatorial diameter of the skeleton of the polytope of feasible solutions of any $m \times n$ transportation problem is less than $8 \, (m+n)$.
A competitive algorithm for the general two server-problem
by Rene Sitters, Technische Universiteit Eindhoven
We consider the general on-line two server problem in which at each step both servers receive a request, which is a point in a metric space. One of the servers has to be moved to its request. The special case where the requests are points on the real line is known as the CNN-problem. It has been a well-known open question if an algorithm with a constant competitive ratio exists for this problem. We answer this question in the affirmative sense by providing an algorithm that is 23808-competitive on any metric space. The constant is huge and the algorithm is rather ugly but our main goal was indeed to settle the question. We believe that our result gives new insight in the problem and will lead to more and much better algorithms for the general $k$-server problem in the near future.
Joint work with Leen Stougie and Willem de Paepe.
Polynomial time approximation schemes for metric MIN-BISECTION
by Fernandez De La Vega, Universitè Paris Sud
We design the first polynomial time approximation schemes (PTASs) for the problem of Metric MIN-BISECTION: given a finite metric space, divide the points into two halves so as to minimize the sum of distances across that partition. Our approximation schemes depend on biased sampling and on a new application of linearized quadratic programs with randomized rounding of non-uniformly bounded numbers.
Joint work with Marek Karpinski and Claire Kenyon
Smoothed Competitive Analysis of the Multi-Level Feedback Algorithm
by Stefano Leonardi, Università di Roma La Sapienza
Spielman and Teng invented the concept of smoothed analysis to explain the success of algorithms that are known to work well in practice while presenting poor worst case performance. Spielman and Teng [STOC 01] proved that the simplex algorithm runs in expected polynomial time if the input instance is smoothened with a normal distribution. We extend this notion to analyze online algorithms. In particular we introduce smoothed competitive analysis to study the Multi-Level Feedback (MLF) algorithm, at the basis of the scheduling policies of Unix and Windows NT, when the processing times of jobs released over time are only known at time of completion.
We show that, if the k least significant of K bits describing the processing time of a job are randomly changed, MLF achieves a tight smoothed competitive ratio of O(2K-k) to minimize the average flow time. A direct consequence is a first constant approximation for this problem in the average case under a quite general class of probability distributions.
Joint work with L. Becchetti, A. Marchetti-Spaccamela, G. Schäfer, and T. Vredeveld.
Approximating minimum cuts for valid paths in the Internet
by Thomas Erlebach, ETH Zürich
A recently proposed model of the Internet at the level of autnomous systems (ASs) is a graph in which the edges are classified according to the economic relationships between the ASs that they connect: Edges can be customer-provider edges or peer-to-peer edges. It is assumed that a path in the network is only valid if it consists of a sequence of customer-provider edges, followed by zero or one peer-to-peer edges, followed by a sequence of provider-customer edges. Motivated by robustness considerations, we consider the problem of computing a minimum vertex cut that separates two given vertices (meaning that no valid path between them remains after removing the vertices of the cut from the network). We show that the problem is NP-hard and present a 2-approximation algorithm based on linear programming techniques.
(joint work with Danica Vukadinovic)
Flows over time - approximation and complexity
by Martin Skutella, Technische Universität Berlin
The intention of the talk is to give an introduction into the area of "flows over time" or "dynamic flows". Flows over time have been introduced about forty years ago by Ford and Fulkerson and have many real-world applications such as, for example, traffic control, evacuation plans, production systems, communication networks, and financial flows. Flows over time are modeled in networks with capacities and transit times on the arcs. The transit time of an arc specifies the amount of time it takes for flow to travel from the tail to the head of that arc. In contrast to the classical case of static flows, a flow over time specifies a flow rate entering an arc for each point in time and the capacity of an arc limits the rate of flow into the arc at each point in time. We discuss recent approximation and hardness results for flows over time with multiple commodities and costs. The talk is based on joint work with Lisa Fleischer, Alex Hall, and Steffen Hippler.
Routing and Call Control Algorithms in Ring Networks
by Sai Anand, ETH Zürich
FPTAS for Flows Over Time with Inflow-Dependent Transit Times
by Alexander Hall, ETH Zürich
Motivated by applications in road traffic control, we study flows in networks featuring special characteristics. In contrast to classical static flow problems, time plays an important role. Firstly, there are transit times on the arcs of the network which specify the amount of time it takes for flow to travel through an arc; in particular, flow values on arcs may change over time. Secondly, the transit time of an arc varies with the current amount of flow using this arc. The latter feature is crucial for various real-life applications of flows over time.
K\"ohler et al. (Proceedings of ESA 2002, LNCS 2461, pp. 599-611) study the single commodity case and give a (2+$\varepsilon$)-approximation based on the notion of temporarily repeated flows, where flow is pushed at constant rates into (possibly) several paths which do not change over time. We are able to generalize this result to the multicommodity case, by modifying the underlying network and the way flow is pushed into the corresponding paths. Applying the same technique to condensed time-expanded networks allows variation of flow paths over time. This approach even yields a fully polynomial time approximation scheme for the multicommodity case, which is known to be NP-hard. Furthermore we show that under a certain restriction of valid flows, the single commodity case is NP-hard as well.
Approximation of a retrieval problem for parallel disks
by Frits Spieksma, Katholieke Universiteit Leuven
When handling large collections of data, the communication between fast internal memory and slow external memory (e.g. disks) can be a performance bottleneck. We study the problem of maximizing the throughput (that is, the number of requests served per time-unit) for parallel disks. This retrieval problem can be formulated as assigning a maximum number of size 1 and size 2 jobs to machines of limited capacity. We show that the LP-relaxation of an integer programming formulation is half-integral. Further, we sketch 2/3-approximation algorithms for this problem.
Joint work with Joep Aerts and Jan Korst.
Improved Approximation Algorithms for Maximum Graph Partition Problems
by Gerold Jäger, Universität Kiel
Joint work with Anand Srivastav
We consider a weighted, directed graph with n vertices and the problem of dividing the set of vertices in two parts of sizes k and n-k, so that the edges of some of four regions (edges on the two subgraphs and edges between the two subgraphs in both directions) becomes maximum. For example, MAX-k-DENSE-SUBGRAPH is the problem of determining a subset S of size k, so that the sum of the edge weights of the subgraph induced by S becomes maximum. There are six nontrivial problems of this kind.
Halperin and Zwick have introduced an algorithm based on semidefinite programming, which for the case k = n/2 and these six maximum graph partition problems delivers the best known approximation ratios. We show improvements of their techniques and generalize the algorithm for arbitrary k.
On weighted rectangle packing
by Guochuan Zhang, Universität Kiel
Joint work with Klaus Jansen.
Approximation algorithms for max-min resource sharing, with an application to fractional weighted graph coloring
by Klaus Jansen, Universität Kiel
We generalize a method by Grigoriadis et al. to compute an approximate solution of the max-min resource sharing (and fractional covering) problem with $M$ nonnegative concave (linear) constraints $f_m$ on a convex set $B$ to the case with general approximate block solvers (i.e. with only constant, logarithmic, or even worse approximation ratios). The algorithm is based on a Lagrangian decomposition which uses a modified logarithmic potential function and on several other ideas (scaling phase strategy, two stopping rules in a phase, eliminating functions $f_m$ larger than a threshold value $T$, reducing the step length and taking a convex combination among different iterates in a phase). We show that the algorithm runs in $O(M \epsilon^{-2} \ln (M \epsilon^{-1}))$ iterations (or block optimization steps), a data and approximation ratio independent bound. Furthermore we show how to use this framework for the fractional weighted graph coloring problem.
Maintained by Alessandro Panconesi | CommonCrawl |
TephraProb: a Matlab package for probabilistic hazard assessments of tephra fallout
Sébastien Biass ORCID: orcid.org/0000-0002-1919-94731,2,
Costanza Bonadonna1,
Laura Connor3 &
Charles Connor3
TephraProb is a toolbox of Matlab functions designed to produce scenario–based probabilistic hazard assessments for ground tephra accumulation based on the Tephra2 model. The toolbox includes a series of graphical user interfaces that collect, analyze and pre–process input data, create distributions of eruption source parameters based on a wide range of probabilistic eruption scenarios, run Tephra2 using the generated input scenarios and provide results as exceedence probability maps, probabilistic isomass maps and hazard curves. We illustrate the functionality of TephraProb using the 2011 eruption of Cordón Caulle volcano (Chile) and selected eruptions of La Fossa volcano (Vulcano Island, Italy). The range of eruption styles captured by these two events highlights the potential of TephraProb as an operative tool when rapid hazard assessments are required during volcanic crises.
Tephra is the most widespread of all volcanic hazards. Variations in deposit thickness and and grain–size, from proximal (i.e. a few kilometres from the vent) to distal locations (i.e. hundreds of kilometres) result in a wide range of potential impacts, from total loss (e.g. human and livestock casualties, destruction of vegetation and crops, collapse of buildings) to less dramatic but highly problematic consequences (e.g. damage to crops, damage to non-structural building elements, disruption of water and electricity supplies; Blong 1984; Jenkins et al. 2014; Wilson et al. 2011). Tephra is also responsible for widespread disruption of civil aviation (Biass et al. 2014; Bonadonna et al. 2012; Guffanti et al. 2009; Scaini et al. 2014). Both the dispersal and sedimentation of tephra can generate complex and multi-faceted impacts at different spatial and temporal scales, affecting physical, social, economic and systemic aspects of societies. These complex impacts require proactive strategies to effectively increase the level of preparedness and mitigate the risk to exposed communities (Birkmann 2006). In order to develop effective proactive risk mitigation strategies, it is necessary to both develop comprehensive probabilistic hazard assessments for tephra dispersal and sedimentation and communicate the outcomes to decision-makers and stakeholders.
Our method for quantifying the hazard from tephra fallout begins with the identification of eruption scenarios based on detailed stratigraphic studies. Eruption scenarios reflect the typical eruption styles at a given volcano and are characterized by ranges of eruption source parameters (ESP) such as plume height, erupted mass, mass eruption rate (MER) and total grain–size distribution (TGSD). Eruption scenarios are constrained by the completeness of the eruptive record, as well as an understanding of the range of past activity observed at analogous volcanic systems (Marzocchi et al. 2004; Ogburn et al. 2016). Highly–studied systems result in eruption scenarios describing precise eruptive episodes, whereas poorly–known systems can often only be characterized by generic eruption scenarios based on analogue systems. Some hazard studies have relied on a deterministic approach, defining ESPs as a single set of best guess values, and hazard as expected tephra accumulation (e.g. isomass maps, kg m−2; Barberi et al. 1992). Other strategies rely on a large number of simulations to explore the range of variability in ESPs and atmospheric conditions. In the latter case, the hazard is quantified as a probability to exceed a given tephra accumulation and can be expressed either as conditional to the occurrence of the eruption scenario (e.g. scenario–based hazard assessment; Biass et al. 2016; Bonadonna et al. 2005; Scaini et al. 2014; Volentik and Houghton 2015) or as absolute when the long–term probability of the eruption scenario is also quantified (Bear-Crozier et al. 2016; Jenkins et al. 2012; Marzocchi and Bebbington 2012; Sandri et al. 2014, 2016; Thompson et al. 2015).
The TephraProb package provides a framework for i) accessing, pre–processing, and analyzing model inputs (e.g. retrieval and probabilistic analysis of Reanalysis wind data), ii) building probabilistic eruption scenarios, iii) running a suitable tephra dispersal model and iv) post-processing and exporting model results. The package is written in Matlab and released under an open–source GPLv3 license on VHub and GitHub. This paper provides an in–depth review of the possibilities offered by the TephraProb package. The case studies of Cordón Caulle volcano (Chile) and La Fossa volcano (Vulcano Island, Italy) are used to illustrate the flexibility of TephraProb for working with a wide range of probabilistic eruption scenarios and eruptive styles. The user manual provides a technical description of each functionality and each individual Matlab function. The latest version of the package can be found at https://github.com/e5k/TephraProb.
Cordón Caulle volcano
The 2011 eruption of Cordón Caulle volcano (Chile), part of the Puyehue–Cordón Caulle system, is considered as an example of a long–lasting sustained sub–Plinian eruption. Cordón Caulle started erupting on the 4th of June 2011 after a month–long seismic swarm (Bonadonna et al. 2015; Collini et al. 2013; Pistolesi et al. 2015). The initial and most vigorous phase (Unit 1; Bonadonna et al. 2015; Pistolesi et al. 2015) was characterized by plume heights varying between 10–14 km asl during a 24–30 h period with a mean MER of 107 kg s−1. The eruption continued until the 15th of June with MER ≥106 kg s−1 and was followed by long–lasting, low–intensity activity (Bonadonna et al. 2015; Pistolesi et al. 2015). Modelling details of the 2011 eruption of Cordón Caulle can be found in Elissondo et al. (2016).
La Fossa volcano
During the last 1000 years, La Fossa volcano (Vulcano Island, Italy) experienced two sub-Plinian eruptions with similar intensities and magnitudes (i.e. plume heights of 7–8 km asl and erupted masses of 2.1–2.4 ×109 kg) and at least 8 long–lasting Vulcanian cycles (Di Traglia et al. 2013). Each of these Vulcanian cycles is characterized by total fallout masses of 0.1–1 ×107 kg over durations of 3 weeks to 3 years. The most recent eruption of La Fossa in 1888–1890, described in detail by Mercalli and Silvestri (1891) and De Fiore (1922), was characterized by explosions occurring every 4 hours to 3 days and associated with plume heights of 1–10 km asl (Di Traglia 2011; Di Traglia et al. 2013; Mercalli and Silvestri 1891). A detailed description of the probabilistic modelling of these eruption scenarios can be found in Biass et al. (2016).
The Tephra2 model
The Tephra2 model (Bonadonna et al. 2005, 2012; Connor and Connor 2006; Volentik et al. 2009) uses an analytical solution of the advection–diffusion equation to compute the tephra mass accumulation depending on eruptive and wind conditions. Main characteristics of the model include: i) grain–size-dependent diffusion and particle density, ii) a vertically stratified wind, iii) particle diffusion within the rising plume and iv) settling velocities that include variations in the Reynolds number depending on whether particles follow a laminar or turbulent flow regime. Tephra2 requires 3 input files: i) a configuration file that specifies the dynamics of the eruption and the surrounding atmosphere, including location of the vent, plume height, erupted mass, TGSD, range of particle sizes and particle densities, and atmospheric and dispersion thresholds, ii) a table of locations where tephra accumulation is calculated, and iii) a table of wind conditions influencing the horizontal dispersion of tephra, including atmospheric level and the wind speed and wind direction at this level. Note that since Tephra2 solves the advection–diffusion equation analytically, the wind is vertically stratified but horizontally and temporally homogeneous, thus limiting the validity of our approach to a few hundred kilometers around the vent. The user is referred to Bonadonna et al. (2005); Connor and Connor (2006) and Volentik et al. (2009) for a complete description of Tephra2 and to Scollo et al. (2008a,b) and Bonadonna et al. (2012) for a comparison with other volcanic ash transport and dispersion models (VATDM).
Tephra2 simplifies atmospheric turbulence by using two different diffusion laws, one for coarse and another for fine particles (Bonadonna 2006; Bonadonna et al. 2005; Connor and Connor 2006; Volentik et al. 2009). These two diffusion regimes of fallout are based on three empirical parameters, namely the fall–time threshold (FTT) acting as a threshold for the modelling of the diffusion of small and large particles (i.e. power law vs. linear diffusion), a diffusion coefficient used for the linear diffusion law and an apparent eddy diffusivity fixed at 0.04 m 2 s−1 for the power law diffusion (Bonadonna et al. 2005; Suzuki 1983). Secondary atmospheric effects (e.g. topography effects) are neglected. The reader is referred to Bonadonna et al. (2005); Connor and Connor (2006); Volentik et al. (2009) and Volentik et al. (2010) for further information regarding the modeling parameters used by Tephra2. The version of Tephra2 used here was modified to accept an additional input file defining the TGSD, which accounts for aggregation processes (e.g. Biass et al. 2014; Bonadonna et al. 2002a). Aggregation is further discussed in Section "Total grain–size distribution".
The probability P(x) of tephra released from an eruption plume at some vertical height above the vent is controlled by a beta probability density function (PDF):
$$ P(x) = \frac{(1-x)^{\beta-1}x^{\alpha-1}}{B(\alpha,\beta)}, $$
where x is a dimensionless height normalized to the plume height and B(α,β) represents the beta function defined by two parameters, α and β, both greater than 0. Changing the values of α and β changes the shape of the PDF. When α=β=1, the beta function is identical to a uniform random function and the probability of tephra release is equal along the height of the plume. When α>β, the release pattern is shifted towards the top of the plume; when α=β≠1 tephra release is greatest from the middle of the plume; when α<β the release pattern is shifted toward the base of the plume.
The TephraProb package
The TephraProb package contains a set of Matlab functions integrated as a graphical user interface (GUI) assisting the user with every step required to produce comprehensive hazard assessments for tephra fallout. The GUI provides an interface facilitating programming and computation aspects, but more advanced users can customize the Matlab functions finding assistance from the detailed comments within the code and the user manual. Figure 1 summarizes the main functionality of the code, which consists of four main modules including i) Input Parameters: to retrieve and analyse the various inputs required by probabilistic hazard assessments, ii) Eruption Scenarios: to stochastically sample ESP and run eruption scenarios, iii) Post–processing: to process individual Tephra2 runs into probabilistic outputs and iv) Output: to visualize and export results. The following sections use the two case studies presented in Section "Case studies" to illustrate every step of the tephra fallout hazard assessments.
Summary of the workflow of the TephraProb package
Calculation points
Tephra2 requires an ASCII file of locations arranged in a three-column format containing Easting, Northing, and elevation. Since Tephra2 uses an analytical solution to the advection-diffusion-equation that solves the differential equation using a constant elevation boundary condition, calculations must be performed on flat surfaces and topography is neglected (Lim et al. 2008). Two options are available in TephraProb. The first option is to perform calculations on regularly spaced grids allowing for the compilation of probability maps. Although this is often the preferred option, calculations using large grids is time consuming and might not be achievable in some emergency contexts if computing power is limited. The second option is to perform calculations for user–selected points of interest, which results in a series of hazard curves that require a considerably shorter computation time.
One typical problem arising from the use of UTM coordinates is the shift in Easting coordinates when crossing UTM zones and the shift in Northing coordinates when crossing the equator. In both cases, TephraProb includes a correction to produce grids with contiguous UTM coordinates, where the resulting distortion is assumed negligible compared to the maximum distance deemed valid for the application of Tephra2.
Wind data
Wind velocity is a key input parameter in any tephra dispersal model because it controls the advection of the plume and the sedimentation of tephra. Probabilistic modelling requires access to wind datasets spanning at least one decade in order to capture the variability of wind conditions over a region. Most hazard assessments for tephra dispersal and sedimentation rely on Reanalysis datasets, which provide access to decades of atmospheric observations continuously interpolated in space and time. The two most frequently used datasets are the National Oceanic and Atmospheric Administration (NOAA) National Centers for Environmental Prediction NCEP/NCAR Reanalysis (i.e. joint project between the National Centers for Environmental Prediction and the National Center for Atmospheric Research; Kalnay et al. 1996) and the European Centre for Medium-Range Weather Forecasts (ECMWF) Era-Interim datasets (Dee et al. 2011). Both the NOAA NCEP/NCAR and the ECMWF Era-Interim datasets can be accessed via GUIs using TephraProb. The TephraProb package downloads the files in the NetCDF format and converts them into three–column ASCII files including altitude, wind direction (i.e. direction the wind blows towards) and wind velocity. Once the files are downloaded and converted, they can be used as an input to any tephra model and/or to explore the wind conditions over a region of interest. Note that Tephra2 uses a single wind profile per simulation extracted for one set of coordinates and one time. Therefore, each simulation is performed in an atmosphere that is vertically stratified but horizontally and temporally homogeneous.
Figure 2 illustrates the interface and the outputs resulting from wind analysis above Cordón Caulle volcano using the ERA–Interim dataset for the period 2001–2010. Figure 2 a shows median profiles of wind velocity and direction with height for the entire population. Figure 2 b and 2 c show the median wind direction averaged per year and per month, respectively. Such plots are useful to identify potential variability associated with El Niño/La Niña oscillations (Fig. 2 b) or seasonality (Fig. 2 c). Finally, wind roses (Fig. 2 d) show, for a fixed altitude, the probability that wind blows towards a given direction and at a given intensity.
Wind statistics produced by the TephraProb package as inferred from the ERA–Interim dataset for the 2001–2010 period above Cordón Caulle volcano. a Screenshot of the GUI shows the median wind velocity and median wind direction with height (solid black lines) including the 25th and 75th percentiles (error bars); b median wind direction per year; c median wind direction per month; d probability of the wind to blow in given directions and intensities at an altitude of 10 km asl
Hazard assessments are based upon the assumption that future activity will be similar to past activity. In volcanology, this implies a necessity to develop scenarios of future eruptions based on the most complete possible study of the geological record in order to best constrain the eruptive history of a volcano. In practice, assessing the full spectrum of eruptions of a given system is impossible, due firstly to the fact that geological records are not continuously complete through time and secondly because field studies rarely provide a complete picture of the eruptive history (Kiyosugi et al. 2015). In most cases, eruption scenarios are constructed based on a few studied eruptions representing common eruptive styles and/or often relating underlying geologic processes with analogue eruptive events (Sheldrake 2014). Eruption databases such as the Global Volcanism Program of the Smithsonian Institute (GVP; Siebert et al. 2010; Simkin and Siebert 1994) or the Large Magnitude Explosive Volcanic Eruptions (LaMEVE; Crosweller et al. 2012, Ogburn et al. 2016) can prove useful in acquiring a global picture of eruptive history. TephraProb includes a module to access and explore the Holocene eruptive history as recorded in the GVP database. Note that the GVP module does not constitute a source of input in itself but serves as a support tool to identify eruption scenarios and key ESPs.
Figure 3 a illustrates the GUI of the GVP module, which retrieves eruptive history based on the volcano number (e.g. 357150 for the Puyehue-Cordón Caulle system and 211050 for La Fossa). Key features of the GVP database are preserved (e.g. VEI, confirmation and evidence; Siebert et al. 2010; Simkin and Siebert 1994) and the data can be plotted either as a histogram or as a cumulative distribution. Considering the entire Holocene catalogue, Fig. 3 a shows the frequency of eruptions per VEI class and Fig. 3 b shows the cumulative number of eruptions through time. The various segments characterized by distinctive slopes in Fig. 3 b illustrate the complications arising when unifying geological and historical records to compile a comprehensive eruptive history, discussed by Siebert et al. (2010). On one hand, the geological record is biased toward large eruptions and extends back in time. On the other hand, the historical record is detailed and preserves small and moderate eruptions but does not sufficiently extend back in time to capture eruptions of larger magnitudes. Figure 3 c illustrates the historical segment of the eruptive history of the Puyehue-Cordón Caulle system as inferred from the GVP database (i.e. break in slope at 1880 A.D. on Fig. 3 b). Note that breaks–in–slope associated with completeness might vary as a function of the VEI/magnitude class and should be assessed separately (Biass and Bonadonna 2013; Dzierma and Wehrmann 2010; Jenkins et al. 2012; Mendoza-Rosas and De la Cruz-Reyna 2008).
Eruptive history of Puyehue-Cordón Caulle volcanic system as recorded in the GVP database. a Screenshot of the GUI shows the number of eruptions per VEI class for all eruptions recorded in the GVP, where U stands for undefined and O for other. Alternative plots include, cumulative number of eruptions considering (b) all eruptions and (c) the most recent complete segment of the record, (d) and probability of eruption through time considering a Poisson model for all eruptions (black line, using the record shown in (c)), eruptions of VEI 2 (red line, completeness at 1880 A.D.), VEI 3 (green line, completeness at 1920 A.D.) and VEI 5 (orange line, completeness at 5000 B.C.)
If the eruptions are assumed to occur i) with a constant rate and ii) independently of the time since the last event, it is possible to obtain a first–order estimate of probability of occurrence of an eruption in a given time window by considering a Poisson process (e.g. Biass and Bonadonna 2013; Borradaile 2003). We aim at quantifying the probability that a repose interval T is smaller or equal to an arbitrary time window t:
$$ F(t) = P(T \geq t) $$
which, in the simplest case of a Poisson process, results in an exponential distribution:
$$ F_{exp}(t) = 1-e^{-\lambda t}, $$
where t is a forecasting window (years) and λ is the eruption rate (number of eruptions per year) defined over a complete section of the eruptive catalog. As an example, the black line in Fig. 3 d shows the probability of eruption through time for a case where Fig. 3 c represents a complete historical record. In contrast, the colored lines plot probabilities for eruptions of VEI 2 (red line; completeness at around 1880 A.D.), VEI 3 (green line; completeness at around 1920 A.D.) and VEI 5 (orange line; completeness at around 5000 B.C.).
Note that the aim of TephraProb is scenario–based hazard assessments, i.e. based upon the conditional probability that the associated eruption scenario occurs; two caveats should be considered when using the GVP module. First, the GVP database is not a direct input to the probabilistic modelling in TephraProb and should be used as a support tool to develop eruption scenarios and identify critical ESPs with the full knowledge of the limitations and assumptions behind such databases (Biass and Bonadonna 2013; Dzierma and Wehrmann 2010; Jenkins et al. 2012; Mendoza-Rosas and De la Cruz-Reyna 2008; Siebert et al. 2010; Simkin and Siebert 1994). Second assessing the long–term probability of a future eruption is not trivial and should be achieved using a rigorous probabilistic framework in order to quantify and propagate various sources of uncertainties on final estimates (Bear-Crozier et al. 2016; Connor et al. 2003; Jenkins et al. 2012; Marzocchi and Bebbington 2012; Sandri et al. 2016; Sheldrake 2014; Thompson et al. 2015). Probabilities resulting from a Poisson process should not be viewed as more than a first–order estimate, and only when the hypotheses of stable rate and independent events are satisfied (Borradaile 2003).
Eruption scenarios
Based upon considerations described in Section "Eruptive history", probabilistic strategies were introduced to account for biases associated with both small and large eruptions. On one hand, they help account for parts of the geological record that are not accessible or that have been removed. On the other hand, they allow for the consideration of larger eruptive events associated with lower probabilities of occurrence that have not taken place during the recent history but cannot be excluded. Probabilistic eruption scenarios rely on a large number of simulated events to explore the uncertainty associated with variable parameters. For tephra hazard, the two main variable parameters are magnitude/style and atmospheric conditions of a future eruption. The variability of a future eruption is commonly described by sets of critical ESPs defined as ranges and/or probability distributions, where the shape of a distribution reflects the degree of certainty for a particular scenario. The maximum degree of uncertainty for a given ESP will be typically described by a uniform distribution, whereas a logarithmic distribution favors the occurrence of smaller values compared to larger ones, and a Gaussian distribution preferentially samples around a central value. Similarly, some regions of the world experience seasonal wind trends, making a seasonal analysis of tephra hazard necessary. Identifying the degree of variability allowed during stochastic sampling requires subjective choices that are influenced by both the degree of knowledge of a volcanic system and the purpose of the hazard assessment.
Total grain–size distribution
Plume height, erupted mass and TGSD are the three most important ESPs for modeling tephra accumulation with Tephra2. In TephraProb, the sampling of plume heights and erupted masses are inherent to the probabilistic eruption scenarios described below, but the stochastic scheme for sampling TGSDs is similar for all scenarios and is therefore described first. TGSDs in TephraProb are assumed Gaussian (in ϕ units) and are defined by ranges of median diameters and sorting coefficients. It is then possible to modify the TGSD to account for aggregation using the empirical approach proposed by Bonadonna et al. (2002a) and Biass et al. (2014) based on observations from Cornell et al. (1983), Bonadonna et al. (2011), and Bonadonna et al. (2002b) by defining a range of values for the empirical aggregation parameter and a maximum diameter affected by aggregation processes.
The empirical aggregation parameter introduced in TephraProb follows Bonadonna et al. (2002a) and Cornell et al. (1983) and represents a weight fraction of particles that form aggregates. In our approach, a fraction of mass equal to the empirical aggregation parameter is removed from all bins equal to or finer than the maximum diameter (Biass et al. 2014; Bonadonna et al. 2002a). The total mass removed is then equally redistributed into bins ≤−1ϕ and >the maximum diameter (where > means coarser than). Although this aggregation scheme is a simple answer to a complex concept (e.g. Brown et al. 2012; Gilbert and Lane 1994; James et al. 2002, 2003; Rose and Durant 2011; Van Eaton et al. 2015) and is based uniquely on observations (Bonadonna et al. 2002b, 2011; Cornell et al. 1983), it is computationally efficient and suitable for hazard assessment purposes (Biass et al. 2014, 2016; Bonadonna et al. 2002a). This scheme has already been validated in previous studies with good agreement with field observations (e.g. Bonadonna et al. 2002a; Bonadonna and Phillips 2003; Cornell et al. 1983). Since no physics is involved in this method, it is not possible to draw a distinction between dry or wet aggregates. Instead, following the nomenclature proposed by Brown et al. (2012), using a maximum diameter of 5 ϕ suggests that particles <63 microns are influenced by aggregation processes (e.g. ash clusters, coated particles and poorly-structured pellets; Bonadonna et al. 2011), whereas a maximum diameter of 4 ϕ extends aggregation up to <125 microns (e.g. pellets with concentric structures (e.g. accretionary lapilli) and liquid pellets (i.e. mud rain); Gilbert and Lane 1994; Van Eaton et al. 2012, 2015).
At each probabilistic run, values of median diameters and sorting coefficients are sampled and used to create a Gaussian distribution. If wanted, the aggregation scheme is applied by randomly sampling an empirical aggregation parameter. The TGSD is then written as a text file and passed as an input to Tephra2.
General eruption scenarios
Probabilistic eruption scenarios implemented in TephraProb allow for the stochastic sampling of eruption source parameters and/or wind conditions, and various probability distributions are proposed for the sampling of ESPs (Table 1; Figs. 4 and 5). The two most general eruption scenarios implemented in TephraProb are (Bonadonna 2006):
Eruption Range Scenarios (ERS), designed to assess the probability of accumulation of a critical tephra accumulation based on the statistical distribution of possible eruption source parameters and wind conditions (i.e. stochastic sampling of one set of ESPs and one wind profile at each run);
Workflows defined for the sub–Plinian and Plinian eruption scenarios implemented in TephraProb. Get refers to ESPs deterministically defined, Set defines a variable and Sample indicates a stochastic sampling. The index i refers to the run number, where the total number of runs is given by nr. For long–lasting eruptions, index j refers to the simulation number of run i, where the total number of simulations for run i is given by nw
Workflows defined for the Vulcanian eruption scenarios implemented in TephraProb. The nomenclature follows Fig. 4
Table 1 Summary of probabilistic eruption scenarios implemented in TephraProb. All Plinian–type scenarios can be modeled as Long–lasting if the eruption duration is longer than the wind sampling interval
One Eruption Scenarios (OES), designed to assess the probability of accumulation of a critical tephra accumulation based on the statistical distribution of wind conditions and a deterministically–defined eruption (i.e. stochastic sampling of one wind profile at each run while ESPs remain constant).
Derivations of these two scenarios are implemented in TephraProb in order to allow additional subjective choices to the stochastic sampling (Table 1):
Wind Range Scenarios (WRS) constrain the sampling of wind conditions within pre–defined radial sector around the volcano. Such scenarios are useful to assess the hazard at specific sites considering a specific wind scenario (e.g. Volentik et al. 2009). The probability of occurrence of the wind scenario can itself be assessed using the wind module of TephraProb;
Fixed Date Scenarios (FDS) fix the eruption starting date, thus assessing the probability of tephra accumulation based on the variability of eruption source parameters only. Rather than expressing the hazard of a future eruption, such scenarios are useful to assess the probability of a studied fallout event considering the statistical distribution of wind conditions (e.g. Elissondo et al. 2016). Outcomes of Fixed Date Scenarios can be compared to Eruption Range Scenarios and field–based isomass maps.
Eruptive styles
Different assumptions are made in TephraProb to calculate the erupted mass of sustained sub–Plinian and Plinian eruptions and nonsustained Vulcanian explosions, giving rise to Plinian–type and Vulcanian–type eruptions (Table 1; Figs. 4 and 5). Note that i) in our modelling scheme, sub–Plinian eruptive styles are hereafter considered as a part of Plinian–type eruptions and ii) both Plinian and Vulcanian–type styles can be modeled using the eruption scenarios described in Section"General eruption scenarios ".
Plinian–type eruptions
Plinian–type eruption scenarios are defined by ranges and distribution shapes of plume height, eruption duration and eruption start date (Fig. 4). Additionally, the user also defines a range of erupted tephra mass. The sampling scheme, developed by Biass et al. (2014) and summarized in Fig. 4, is then applied. At each run, an eruption date, a plume height and an eruption duration are first sampled. The eruption date is used to retrieve the corresponding wind profile and combined with the plume height to calculate the MER following Degruyter and Bonadonna (2012):
$$ MER = \pi\frac{\rho_{a0}}{g'}\left(\frac{\alpha^{2}\bar{N}}{10.9}H^{4} + \frac{\beta^{2}\bar{N}^{2}\bar{v}}{6}H^{3}\right) $$
where ρ a0 is the reference density of the surrounding atmosphere (kg m−3), g ′ the reduced gravity at the source (m s−2), α is the radial entrainment coefficient, \(\bar {N}\) is the average buoyancy frequency (s −1), H is the plume height (m above the vent), β is the wind entrainment coefficient and \(\bar {v}\) the average wind velocity across the plume height (m s−1). Note that Reanalysis datasets are only used to calculate \(\bar {v}\), and the calculation of other parameters (e.g. \(\bar {N}\), ρ a0) follows from Degruyter and Bonadonna (2012). The MER is used with the eruption duration to calculate the erupted tephra mass. If the resulting value falls within the user–defined mass range, then the run is sent to the model to be executed, or else the sampling process is re–started. Note that TephraProb also includes an option to sample plume heights and erupted tephra mass independently.
Vulcanian–type eruptions
In contrast, Vulcanian–type eruption scenarios are modeled as thermals (i.e. instantaneous release of mass) (Fig. 5). At each run, a plume height is sampled and used to calculate the mass of a thermal with the relationship (Bonadonna et al. 2002a; Druitt et al. 2002; Woods and Kienle 1994):
$$ H = 1.89Q^{0.25} $$
where Q=f×M×C×Δ T is the excess thermal mass of the thermal injection, f is the solid mass fraction capable of loosing heat to the plume, M (kg) is the plume mass, C (J kg −1 K −1) is the pyroclasts specific heat and Δ T (K) is the initial temperature contrast between the erupted mixture and the surrounding air. For Soufrière Hills volcano (Montserrat), f is taken as 0.8, C is 1100 J kg −1 K −1, Δ T is 800 K (Bonadonna et al. 2002a; Druitt et al. 2002), and the relationship between the Vulcanian plume height and the mass of the plume can be expressed as:
$$ H = 55M^{0.25} + H_{V} $$
where H is the plume height (m asl), M is the plume mass (kg) and H V the vent height (m asl).
Long–lasting eruption scenarios
The hazard associated with long–lasting eruptions is complicated by the fact that wind conditions might vary during the course of an eruption. Long–lasting eruptions can be associated either with sustained plumes (e.g. 2010 eruption of Eyjafjallajökull, Iceland), or with repetitive emissions of limited to moderate amounts of ash (e.g. ongoing eruption of Soufrière Hills volcano, Montserrat, West Indies; ongoing eruption of Sakurajima volcano, Japan). In TephraProb these two eruptive styles are modelled as long-lasting Plinian and long-lasting Vulcanian eruptions, respectively (Figs. 4 and 5).
Long–lasting Plinian eruptions
Long–lasting Plinian scenarios are constrained by the temporal resolution Δ w of available wind data, which is 6 h for most Reanalysis datasets but can be varied within TephraProb. In cases where the eruption duration defined by the user is longer than the temporal resolution between wind profiles, the eruption is divided into Δ w–duration periods. The corresponding wind profile for each period is retrieved and the Eruption Range Scenario sampling scheme is performed, assuming that ESPs remain steady throughout the duration of the period (Fig. 4). If the sums of the masses of independent periods fall within the initial mass range, each period becomes a separate Tephra2 simulation, and the final accumulation of a long–lasting eruption is the sum of all periods.
Long–lasting Vulcanian eruptions
Long–lasting Vulcanian scenarios describe Vulcanian cycles and require the identification of the total duration of the cycle and the repose interval between explosions in order to apply the workflow shown in Fig. 5. At each run (i.e. each Vulcanian cycle), repose intervals and associated plume heights are constantly sampled until the sum of the repose intervals exceeds the eruption duration. The mass of each explosion is calculated with Eq. 6 and used in a separate Tephra2 simulation. The final accumulation of a Vulcanian cycle is the sum of all explosions. Note that TephraProb does not account for any relationship describing the influence of the repose interval on the corresponding plume height. More details on modeling Vulcanian cycles with TephraProb can be found in Biass et al. (2016).
Because some regions at low latitudes experience significant changes in wind patterns between dry and rainy seasons, a seasonality option is implemented in TephraProb to assess the variability in hazard as a function of the time of year. If the seasonality option is enabled, the user can define start and end dates of the rainy season and three scenarios will be run using winds for i) all months of the year, ii) months of the rainy season and iii) months of the dry season.
Post-processing functions in TephraProb process the individual outputs of a given eruption scenario into probabilities of exceeding given thresholds of tephra accumulations. Following Bonadonna (2006), we quantify the probability of hazardous thresholds of mass accumulations using:
$$P[M(x,y) \geq M_{T} \mid eruption] $$
where M(x,y) is the tephra mass accumulation (kg m−2) accumulated at given locations and M T a mass accumulation threshold. For a given eruption scenario, the probability P M at coordinates x,y is calculated based on the number of times a given threshold of accumulation is reached and divided by the total number of runs N R :
$$P_{M}(x,y) = \frac{\sum_{i=1}^{N_{R}}n_{i}}{N_{R}} $$
$$n_{i} = \left\{ \begin{array}{l l} 1 & \quad \text{if \(M_{i}(x,y) \geq\) threshold \(\mid\) eruption}\\ 0 & \quad \text{otherwise.} \end{array} \right.$$
Two scenarios for each volcano in Section "Case studies" were used as examples for TephraProb. First, the climatic phase (i.e. 4th of June) of the 2011 eruption of Cordón Caulle served as a case-study to model long–lasting sub-Plinian/Plinian eruptions. Eruption scenarios include a Long–Lasting Eruption Range Scenario (i.e. variable ESPs and wind conditions) and a Long–Lasting Fixed Date Scenario (i.e. variable ESPs and wind conditions set for the 4th of June 2011). ESPs for each scenario were defined from Bonadonna et al. (2015) and Pistolesi et al. (2015) and are summarized in Table 2. Second, La Fossa volcano was used to illustrate short–lasting sub–Plinian/Plinian eruptions and long–lasting Vulcanian cycles. The sub–Plinian eruptions were simulated using a One Eruption Scenario, whereas Vulcanian cylces were simulated using a Vulcanian Long–Lasting Eruption Scenario. Table 2 summarizes ESPs for both scenarios based on Mercalli and Silvestri (1891); Bianchi (2007) and Di Traglia et al. (2013).
Table 2 ESPs for the Cordón Caulle and the La Fossa case studies
Four variables need to be considered when displaying the probability of exceeding a given tephra accumulation, including geographic coordinates (Easting, Northing or longitude, latitude), a threshold of tephra accumulation and its associated exceedance probability. Since typical maps are limited by three dimensions, it is necessary to fix at least one degree of freedom. TephraProb can produce three main types of outputs.
Probability maps
Probability maps fix a threshold of tephra accumulation (kg m−2) to contour the associated spatial probability of exceedance, based upon the conditional probability that the given eruption scenario occurs (e.g. Fig 6). In Fig. 6, the minimum displayed probability is set to 0.1 and the red line contours the extent of the computational grid.
Hazard maps show the conditional probability of exceeding a threshold of tephra accumulation given the occurrence of the associated eruption scenario: a Long–lasting Eruption Range Scenario for Cordón Caulle volcano for a tephra accumulation of 10 kg m−2; b Long–lasting Fixed Date Scenario for Cordón Caulle for a tephra accumulation of 10 kg m−2; c One Eruption Scenario for a sub–Plinian eruption of La Fossa for a tephra accumulation of 10 kg m−2; d Vulcanian Long–Lasting Eruption Scenario for a Vulcanian eruption of La Fossa for a tephra accumulation of 100 kg m−2. ESPs for all scenarios are summarized in Table 2. The minimum displayed probability is 0.1 and the red line contours the extent of the calculation grid. The vent is indicated by a red triangle
Figure 6 a–b show probability maps compiled for an accumulation of 10 kg m−2 (i.e. critical threshold for crops) for the Long–Lasting Eruption Range Scenario and the Long–Lasting Fixed Date Scenarios of Cordón Caulle based on the climatic phase of the 2011 eruption (i.e. Unit 1 in Bonadonna et al. 2015; Pistolesi et al. 2015, Table 2). These maps show the importance of wind patterns in the hazard assessment of tephra fallout and, put in perspective of Fig. 2, show that the opening phase of the 2011 eruption (i.e. 4–5th of June) occurred in wind conditions of low probability but with high consequences for the town of San Carlos de Bariloche, which experienced accumulations of about 5 kg m−2 (Bonadonna et al. 2015; Pistolesi et al. 2015).
Figure 6 c–d show the probabilities of exceeding tephra accumulations of 10 and 100 kg m−2 following sub–Plinian OES (Fig. 6 c) and Vulcanian V–LLERS (Fig. 6 d) eruption scenarios at La Fossa volcano, respectively. Note that in the case of long–lasting Vulcanian scenarios, no syn–eruptive erosion between explosions is considered and Fig. 6 d should therefore be regarded as a probability map of the maximum accumulation.
Hazard curves
Hazard curves fix the geographical location to display the probability of exceeding any tephra accumulation at a given point (e.g. Bonadonna 2006). Figure 7 shows hazard curves for San Carlos de Bariloche using both Cordón Caulle scenarios described in Table 2. The dashed grey line on Fig. 7 corresponds to the accumulation of 5 kg m−2 reached in San Carlos de Bariloche during the 2011 eruption. Probabilistic analyses show that such an accumulation had an ∼2 % probability of occurrence considering the statistical distribution of wind directions of the past 10 years.
Hazard curves showing the conditional probability of exceeding any tephra accumulation given the occurrence of the associated eruption scenario at San Carlos de Bariloche. The dashed grey lines show an accumulation of 5 kg m −2 corresponding to the accumulation reached in San Carlos de Bariloche during the 2011 eruption of Cordón Caulle volcano
Probabilistic isomass maps
Probabilistic isomass maps fix a probability threshold to represent the typical tephra accumulation given a probability of occurrence of the hazardous phenomenon conditional on the occurrence of the associated eruption scenario (e.g. Biass and Bonadonna 2013; Biass et al. 2016). Figure 8 shows isomass contours (kg m−2) for a LLERS eruption of Cordón Caulle for probabilities of occurrence of 25 % (Fig. 8 a) and 75 % (Fig. 8 c). The choice of the probability threshold (which may be regarded as an acceptable level of hazard), is critical, and must be determined in collaboration with decision makers. The resultant probabilistic isomass maps should be presented in a style and format that meets the maps' communication goals and decision makers' needs. However, their use facilitates the incorporation of probabilistic approaches into pre–event impact assessments and are useful when communicating typical eruption scenarios to stakeholders.
Probabilistic isomass maps showing the typical tephra accumulations (kg m−2) for a conditional probability of occurrence of the hazard of 25 % (a) and 75 % (b) for a Long–lasting Eruption Range Scenario scenario at Cordón Caulle volcano
Discussion and conclusions
The TephraProb package aligns with recent efforts to bridge gaps between academic and operational contexts (Bartolini et al. 2013; Bear-Crozier et al. 2012; Felpeto et al. 2007). It provides a set of flexible tools for the assessment of tephra hazard and designed to compile comprehensive assessments in a wide range of conditions (e.g. poor constraints on scenarios, rapid assessments), that can be used in the context of probabilistic hazard assessments or separately (e.g. accessing and analyzing wind data or the GVP database). TephraProb integrates various levels of computational requirements and allows hazard assessments to be performed on single CPU computers (i.e. hazard curves only), multi–core personal computers (i.e. grids of moderate resolutions) and computer clusters (i.e. grids of fine resolutions). Resulting hazard assessments are conditional on the occurrence of the associated scenarios, and can serve as direct inputs to probabilistic frameworks such as Bayesian event trees to assess the long–term probability of tephra accumulation (Thompson et al. 2015) or to fit in multi–hazards assessments (Sandri et al. 2014). In order to facilitate the integration of further analyses, each output of TephraProb is saved in a variety of formats (e.g. ASCII columns format, ASCII ArcMap rasters).
The TephraProb package is currently tailored to generate Tephra2–friendly configuration files. However, probabilistic strategies implemented in the package are independent of the adopted model and could be modified to work with any VATDM. For instance, early versions of the macros implemented in TephraProb were applied by Biass et al. (2014) and Scaini et al. (2014) to assess the hazard and the related impact resulting from the eruption of critical Icelandic volcanoes on the European air traffic using the Eulerian model FALL3D (Costa et al. 2006; Folch et al. 2009). Similarly, these probabilistic approaches have already been successfully applied by Bonadonna et al. (2002a); Scollo et al. (2007); Jenkins et al. (2012) and Jenkins et al. (2014) based on both the HAZMAP and ASHFALL models (Armienti et al. 1988; Hurst and Turner 1999; Hurst 1994; Macedonio et al. 2005,1988).
The user manual of TephraProb, submitted as a supplementary file, provides in–depth technical descriptions of all the functions of the package. Each function is thoroughly commented in order to allow customization for more advanced users. In particular, functions to calculate the MER (Eq. 4; Degruyter and Bonadonna 2012) or to calculate the mass of a thermal (Eq. 6; Bonadonna et al. 2002a) contain guidance for modifying all empirical parameters. In addition, all users are free to modify the code for their own needs following the terms and conditions of the GNU GPL3 license.
Intentionally, no default scenario is provided in order to not promote TephraProb as a black box. When volcanoes with little documented history are considered, we encourage the user to rely on a global understanding of eruption processes combined with the use of global databases (Crosweller et al. 2012; Siebert et al. 2010; Simkin and Siebert 1994) to identify analogue eruptions. When eruption scenarios are based upon detailed field studies, the TError code (Biass et al. 2014) can serve as a systematic tool to identify the probability distributions of ESPs. In either case, the user manual of TephraProb provides a list of empirical parameters for Tephra2 for eruptions characterized by the inversion technique of Connor and Connor (2006).
This version of TephraProb is published on GitHub as a basis for further development based on inputs from the scientific community. Identified directios of development include i) the implementation of a variety of models available in the literature to quantify ESPs such as Sparks (1986); Wilson and Walker (1987); Mastin et al. (2009); Woodhouse et al. (2013) and Mastin (2014), ii) probabilistic inversion schemes to systematically assess the likelihood of past events (Elissondo et al. 2016) and iii) better integration of Reanalysis datasets to calculate the required atmospheric parameters (Degruyter and Bonadonna 2012).
Armienti, P, Macedonio G, Pareschi MT. A numerical model for simulation of tephra transport and deposition: Applications to May 18, 1980, Mount St. Helens eruption. J Geophys Res Solid Earth. 1988; 93(B6):6463–76. doi:10.1029/JB093iB06p06463.
Barberi, F, Ghigliotti M, Macedonio G, Orellana H, Pareschi MT, Rosi M. Volcanic hazard assessment of Guagua Pichincha (Ecuador) based on past behaviour and numerical models. J Volcanol Geothermal Res. 1992; 49(1–2):53–68. doi:10.1016/0377-0273(92)90004-W.
Bartolini, S, Cappello A, Martí J, Del Negro C. QVAST: a new Quantum GIS plugin for estimating volcanic susceptibility. Nat Hazards Earth Syst Sci. 2013; 13(11):3031–42.
Bear-Crozier, AN, Kartadinata N, Heriwaseso A, Nielsen O. Development of python-FALL3D: a modified procedure for modelling volcanic ash dispersal in the Asia-Pacific region. Nat Hazards. 2012; 64(1):821–38. doi:10.1007/s11069-012-0273-7.
Bear-Crozier, AN, Miller V, Newey V, Horspool N, Weber R. Probabilistic Volcanic Ash Hazard Analysis (PVAHA) I: development of the VAPAH tool for emulating multi-scale volcanic ash fall analysis. J Appl Volcanol. 2016; 5(1):1–20. doi:10.1186/s13617-016-0043-4.
Bianchi, L. L'eruzione 1888-1890 di Vulcano (Isole Eolie):Analisi stratigrafica, fisica e composizionale dei prodotti. Unpublished msc thesis, Università di Pisa. 2007.
Biass, S, Scaini C, Bonadonna C, Folch A, Smith K, Höskuldsson A. A multi-scale risk assessment for tephra fallout and airborne concentration from multiple Icelandic volcanoes - Part 1: Hazard assessment. Nat Hazards Earth Syst Sci. 2014; 14(8):2265–287. doi:10.5194/nhess-14-2265-2014.
Biass, S, Bonadonna C. A fast GIS-based risk assessment for tephra fallout: the example of Cotopaxi volcano, Ecuador-Part I: probabilistic hazard assessment. Nat Hazards. 2013; 65(1):477–95.
Biass, S, Bagheri G, Aeberhard W, Bonadonna C. TError: towards a better quantification of the uncertainty propagated during the characterization of tephra deposits. Stat Volcanol. 2014; 1(2):1–27. doi:10.5038/2163-338X.1.2.
Biass, S, Bonadonna C, Traglia F, Pistolesi M, Rosi M, Lestuzzi P. Probabilistic evaluation of the physical impact of future tephra fallout events for the Island of Vulcano, Italy. Bull Volcanol. 2016; 78(5):1–22. doi:10.1007/s00445-016-1028-1.
Birkmann, J. Measuring vulnerability to promote disaster-resilient societies: conceptual frameworks and definitions. In: Birkmann, J, editor. Measuring Vulnerability to Nat Hazards: Toward Disaster Resilient Societies. Tokyo: United Nations University Press: 2006. p. 9–54.
Blong, RJ. Volcanic Hazards. A Sourcebook on the Effects of Eruptions. Sydney: Academic Press; 1984, p. 424.
Bonadonna, C. Probabilistic modelling of tephra dispersion. In: Mader, HM, Coles SG, Connor CB, Connor LJ, editors. Stat Volcanol. London: Geological Society of London: 2006. p. 243–59.
Bonadonna, C, Macedonio G, Sparks R. Numerical modelling of tephra fallout associated with dome collapses and Vulcanian explosions: application to hazard assessment on Montserrat. In: Druitt, T, Kokelaar B, editors. The Eruption of Soufrière Hills Volcano, Montserrat, from 1995 To 1999 vol. 21. London: Geological Society: 2002a. p. 483–516.
Bonadonna, C, Mayberry G, Calder E, Sparks R, Choux C, Jackson P, Lejeune A, Loughlin S, Norton G, Rose WI, Ryan G, Young S. Tephra fallout in the eruption of Soufrière Hills Volcano, Montserrat In: Druitt, T, Kokelaar B, editors. The Eruption of Soufrière Hills Volcano, Montserrat, from 1995 To 1999. London: Geological Society: 2002b. p. 483–516.
Bonadonna, C, Connor CB, Houghton BF, Connor L, Byrne M, Laing A, Hincks TK. Probabilistic modeling of tephra dispersal: Hazard assessment of a multiphase rhyolitic eruption at Tarawera, New Zealand. J Geophys Res. 2005; 110(B3):B03203.
Bonadonna, C, Genco R, Gouhier M, Pistolesi M, Cioni R, Alfano F, Hoskuldsson A, Ripepe M. Tephra sedimentation during the 2010 Eyjafjallajökull eruption (Iceland) from deposit, radar, and satellite observations. J Geophys Res. 2011; 116(B12):12202.
Bonadonna, C, Phillips JC. Sedimentation from strong volcanic plumes. J Geophys Res Solid Earth. 2003; 108(B7):2340. doi:10.1029/2002JB002034.
Bonadonna, C, Folch A, Loughlin S, Puempel H. Future developments in modelling and monitoring of volcanic ash clouds: outcomes from the first IAVCEI-WMO workshop on Ash Dispersal Forecast and Civil Aviation. Bull Volcanol. 2012; 74(1):1–10.
Bonadonna, C, Cioni R, Pistolesi M, Elissondo M, Baumann V. Sedimentation of long-lasting wind-affected volcanic plumes: the example of the 2011 rhyolitic Cordón Caulle eruption, Chile. Bull Volcanol. 2015; 77(2):1–19. doi:10.1007/s00445-015-0900-8.
Borradaile, GJ. Statistics of Earth Science Data: Their Distribution in Time, Space, and Orientation. Berlin: Springer; 2003, p. 321.
Brown, R, Bonadonna C, Durant A. A review of volcanic ash aggregation. Phys Chem Earth Parts A/B/C. 2012; 45:65–78.
Collini, E, Osores MS, Folch A, Viramonte JG, Villarosa G, Salmuni G. Volcanic ash forecast during the June 2011 Cordón Caulle eruption. Nat Hazards. 2013; 66(2):389–412. doi:10.1007/s11069-012-0492-y.
Connor, C, Sparks R, Mason R, Bonadonna C, Young S. Exploring links between physical and probabilistic models of volcanic eruptions: The Soufrière Hills Volcano, Montserrat. Geophys Res Lett. 2003; 30(13):1701.
Connor, LJ, Connor CB. Inversion is the key to dispersion: understanding eruption dynamics by inverting tephra fallout. In: Mader, HM, Coles SG, Connor CB, Connor LJ, editors. Stat Volcanol. London: Geological Society of London: 2006. p. 231–42.
Cornell, W, Carey S, Sigurdsson H. Computer simulation of transport and deposition of the Campanian Y-5 ash. J Volcanol Geothermal Res. 1983; 17(1):89–109.
Costa, A, Macedonio G, Folch A. A three-dimensional Eulerian model for transport and deposition of volcanic ashes. Earth Planetary Sci Lett. 2006; 241(3–4):634–47.
Crosweller, HS, Arora B, Brown SK, Cottrell E, Deligne NI, Guerrero NO. Global database on large magnitude explosive volcanic eruptions (LaMEVE). J Appl Volcanol. 2012; 1(1):1–13. doi:10.1186/2191-5040-1-4.
De Fiore, O. Vulcano (Isole Eolie) In: Friedlaender, I, editor. Revisita Vulcanologica (Suppl. 3): 1922. p. 1–393.
Dee, DP, Uppala SM, Simmons AJ, Berrisford P, Poli P, Kobayashi S, Andrae U, Balmaseda MA, Balsamo G, Bauer P, Bechtold P, Beljaars ACM, van de Berg L, Bidlot J, Bormann N, Delsol C, Dragani R, Fuentes M, Geer AJ, Haimberger L, Healy SB, Hersbach H, Hólm EV, Isaksen L, Kållberg P, Köhler M, Matricardi M, McNally AP, Monge-Sanz BM, Morcrette JJ, Park BK, Peubey C, de Rosnay P, Tavolato C, Thépaut JN, Vitart F. The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Q J R Meteorological Soc. 2011; 137(656):553–97. doi:10.1002/qj.828.
Degruyter, W, Bonadonna C. Improving on mass flow rate estimates of volcanic eruptions. Geophys Res Lett. 2012; 39:16. doi:10.1029/2012GL052566.
Di Traglia, F. The last 1000 years of eruptive activity at the Fossa Cone (Island of Vulcano, Southern Italy). PhD thesis, Università di Pisa. 2011.
Di Traglia, F, Pistolesi M, Rosi M, Bonadonna C, Fusillo R, Roverato M. Growth and erosion: The volcanic geology and morphological evolution of La Fossa (Island of Vulcano, Southern Italy) in the last 1000 years. Geomorphology. 2013; 194(0):94–107. doi:10.1016/j.geomorph.2013.04.018.
Druitt, TH, Young SR, Baptie B, Bonadonna C, Calder ES, Clarke AB, Cole PD, Harford CL, Herd RA, Luckett R, Ryan G, Voight B. Episodes of cyclic Vulcanian explosive activity with fountain collapse at Soufrière Hills Volcano, Montserrat. In: Druitt, T, Kokelaar B, editors. The Eruption of Soufrière Hills Volcano, Montserrat, from 1995 To 1999 vol 21. London: Geological Society: 2002. p. 281–306, doi:10.1144/GSL.MEM.2002.021.01.13.
Dzierma, Y, Wehrmann H. Eruption time series statistically examined: Probabilities of future eruptions at Villarrica and Llaima Volcanoes, Southern Volcanic Zone, Chile. J Volcanol Geothermal Res. 2010; 193(1–2):82–92.
Elissondo, M, Baumann V, Bonadonna C, Pistolesi M, Cioni R, Bertagnini A, Biass S, Herrero JC, Gonzalez R. Chronology and impact of the 2011 Cordón Caulle eruption, Chile. Nat Hazards Earth Syst Sci. 2016; 16(3):675–704. doi:10.5194/nhess-16-675-2016.
Felpeto, A, Marti J, Ortiz R. Automatic GIS-based system for volcanic hazard assessment. J Volcanol Geothermal Res. 2007; 166(2):106–16.
Folch, A, Costa A, Macedonio G. FALL3D: A computational model for transport and deposition of volcanic ash. Comput Geosci. 2009; 35(6):1334–42.
Gilbert, J, Lane S. The origin of accretionary lapilli. Bull Volcanol. 1994; 56:398–411.
Guffanti, M, Mayberry GC, Casadevall TJ, Wunderman R. Volcanic hazards to airports. Nat Hazards. 2009; 51(2):287–302.
Hurst, AW, Turner R. Performance of the program ASHFALL for forecasting ashfall during the 1995 and 1996 eruptions of Ruapehu volcano. N Z J Geol Geophys. 1999; 42(4):615–22. doi:10.1080/00288306.1999.9514865.
Hurst, A. ASHFALL–A Computer Program for Estimating Volcanic Ash Fallout. 1994. Technical Report 94/23, Institute of Geological & Nuclear Sciences, Wellington, New Zealand.
James, MR, Gilbert JS, Lane SJ. Experimental investigation of volcanic particle aggregation in the absence of a liquid phase. J Geophys Res Solid Earth. 2002; 107(B9). doi:10.1029/2001JB000950.
James, MR, Lane SJ, Gilbert JS. Density, construction, and drag coefficient of electrostatic volcanic ash aggregates. J Geophys Res Solid Earth. 2003; 108(B9). doi:10.1029/2002JB002011.
Jenkins, SF, Spence RJS, Fonseca JFBD, Solidum RU, Wilson TM. Volcanic risk assessment: Quantifying physical vulnerability in the built environment. J Volcanol Geothermal Res. 2014; 276:105–20. doi:10.1016/j.jvolgeores.2014.03.002.
Jenkins, S, Magill C, McAneney J, Blong R. Regional ash fall hazard I: a probabilistic assessment methodology. Bull Volcanol. 2012; 74(7):1699–712.
Kalnay, EC, Kanamitsu M, Kistler R, Collins W, Deaven D, Gandin L, Iredell M, Saha S, White G, Woollen J. The NCEP/NCAR 40-year reanalysis project. Bull Am Meteorological Soc. 1996; 77(3):437–71.
Kiyosugi, K, Connor C, Sparks RSJ, Crosweller HS, Brown SK, Siebert L, Wang T, Takarada S. How many explosive eruptions are missing from the geologic record? Analysis of the quaternary record of large magnitude explosive eruptions in Japan. J Appl Volcanol. 2015; 4(1):1–15. doi:10.1186/s13617-015-0035-9.
Lim, LL, Sweatman WL, McKibbin R, Connor CB. Tephra Fallout Models: The Effect of Different Source Shapes on Isomass Maps. Math Geosci. 2008; 40(2):147–57. doi:10.1007/s11004-007-9134-4.
Macedonio, G, Costa A, Longo A. A computer model for volcanic ash fallout and assessment of subsequent hazard. Comput Geosci. 2005; 31(7):837–45.
Macedonio, G, Pareschi MT, Santacroce R. A numerical simulation of the Plinian Fall Phase of 79 A.D. eruption of Vesuvius. J Geophys Res Solid Earth. 1988; 93(B12):14817–27. doi:10.1029/JB093iB12p14817.
Marzocchi, W, Sandri L, Gasparini P, Newhall C, Boschi E. Quantifying probabilities of volcanic events: the example of volcanic hazard at Mount Vesuvius. J Geophys Res. 2004; 109(B11201):1–18.
Marzocchi, W, Bebbington M. Probabilistic eruption forecasting at short and long time scales. Bull Volcanol. 2012; 74(8):1777–805.
Mastin, L, Guffanti M, Servranckx R, Webley P, Barsotti S, Dean K, Durant A, Ewert J, Neri A, Rose WI, Schneider D, Siebert L, Stunder B, Swanson G, Tupper A, Volentik A, Waythomas C. A multidisciplinary effort to assign realistic source parameters to models of volcanic ash-cloud transport and dispersion during eruptions. J Volcanol Geothermal Res. 2009; 186(1–2):10–21.
Mastin, LG. Testing the accuracy of a 1-D volcanic plume model in estimating mass eruption rate. J Geophys Res Atmospheres. 2014; 119(5):2474–495. doi:10.1002/2013JD020604.
Mendoza-Rosas, AT, De la Cruz-Reyna S. A statistical method linking geological and historical eruption time series for volcanic hazard estimations: Applications to active polygenetic volcanoes. J Volcanol Geothermal Res. 2008; 176(2):277–90.
Mercalli, G, Silvestri O. Le eruzioni dell'Isola di Vulcano incominciate il 3 agosto 1888 e terminate il 22 marzo 1890, relazione scientifica. Ann Ufficio Centrale Metereol Geodin Ital. 1891; 10:1–213.
Ogburn, S, Berger J, Calder E, Lopes D, Patra A, Pitman E, Rutarindwa R, Spiller E, Wolpert R. Pooling strength amongst limited datasets using hierarchical Bayesian analysis, with application to pyroclastic density current mobility metrics. Stat Volcanol. 2016; 2:1–26.
Pistolesi, M, Cioni R, Bonadonna C, Elissondo M, Baumann V, Bertagnini A, Chiari L, Gonzales R, Rosi M, Francalanci L. Complex dynamics of small-moderate volcanic events: the example of the 2011 rhyolitic Cordón Caulle eruption, Chile. Bull Volcanol. 2015; 77(1):1–24. doi:10.1007/s00445-014-0898-3.
Rose, W, Durant A. Fate of volcanic ash: Aggregation and fallout. Geology. 2011; 39(9):895–6.
Sandri, L, Thouret JC, Constantinescu R, Biass S, Tonini R. Long-term multi-hazard assessment for El Misti volcano (Peru). Bull Volcanol. 2014; 76(2):1–26. doi:10.1007/s00445-013-0771-9.
Sandri, L, Costa A, Selva J, Tonini R, Macedonio G, Folch A, Sulpizio R. Beyond eruptive scenarios: assessing tephra fallout hazard from Neapolitan volcanoes. Sci Rep. 2016; 6:24271.
Scaini, C, Biass S, Galderisi A, Bonadonna C, Folch A, Smith K, Höskuldsson A. A multi-scale risk assessment for tephra fallout and airborne concentration from multiple Icelandic volcanoes - Part 2: Vulnerability and impact. Nat Hazards Earth Syst Sci. 2014; 14(8):2289–312. doi:10.5194/nhess-14-2289-2014.
Scollo, S, Del Carlo P, Coltelli M. Tephra fallout of 2001 Etna flank eruption: Analysis of the deposit and plume dispersion. J Volcanol Geothermal Res. 2007; 160(1–2):147–64.doi:10.1016/j.jvolgeores.2006.09.007.
Scollo, S, Folch A, Costa A. A parametric and comparative study of different tephra fallout models. J Volcanol Geothermal Res. 2008a; 176(2):199–211. doi:10.1016/j.jvolgeores.2008.04.002.
Scollo, S, Tarantola S, Bonadonna C, Coltelli M, Saltelli A. Sensitivity analysis and uncertainty estimation for tephra dispersal models. J Geophys Res Solid Earth. 2008b; 113(B6):06202.
Sheldrake, T. Long-term forecasting of eruption hazards: A hierarchical approach to merge analogous eruptive histories. J Volcanol Geothermal Res. 2014; 286:15–23. doi:10.1016/j.jvolgeores.2014.08.021.
Siebert, L, Simkin T, Kimberly P. Volcanoes of the World. Berkley: University of California Press; 2010, p. 551.
Simkin, T, Siebert L. Volcanoes of the World. Tucson, AZ: Geoscience Press; 1994, p. 349.
Sparks, R. The dimensions and dynamics of volcanic eruption columns. Bull Volcanol. 1986; 48(1):3–15.
Suzuki, T. A theoretical model for dispersion of tephra. Arc Volcanism Phys Tectonics. 1983; 95:95–113.
Thompson, M, Lindsay J, Sandri L, Biass S, Bonadonna C, Jolly G, Marzocchi W. Exploring the influence of vent location and eruption style on tephra fall hazard from the Okataina Volcanic Centre, New Zealand. Bull Volcanol. 2015; 77(5):1–23. doi:10.1007/s00445-015-0926-y.
Van Eaton, AR, Mastin LG, Herzog M, Schwaiger HF, Schneider DJ, Wallace KL, Clarke AB. Hail formation triggers rapid ash aggregation in volcanic plumes. Nat Commun. 2015; 6:7860.
Van Eaton, A, Muirhead J, Wilson C, Cimarelli C. Growth of volcanic ash aggregates in the presence of liquid water and ice: an experimental approach. Bull Volcanol. 2012; 74(9):1963–1984.
Volentik, ACM, Connor CB, Connor LJ, Bonadonna C. In: Connor C, Chapman NA, Connor L, (eds).Aspects of volcanic hazards assessment for the Bataan nuclear power plant, Luzon Peninsula, Philippines. Cambridge: Cambridge University Press; 2009.
Volentik, ACM, Bonadonna C, Connor CB, Connor LJ, Rosi M. Modeling tephra dispersal in absence of wind: Insights from the climactic phase of the 2450BP Plinian eruption of Pululagua volcano (Ecuador). J Volcanol Geothermal Res. 2010; 193(1–2):117–36. doi:10.1016/j.jvolgeores.2010.03.011.
Volentik, AM, Houghton B. Tephra fallout hazards at Quito International Airport (Ecuador). Bull Volcanol. 2015; 77(6):1–14. doi:10.1007/s00445-015-0923-1.
Wilson, L, Walker G. Explosive volcanic eruptions - VI. Ejecta dispersal in plinian eruptions: the control of eruption conditions and atmospheric properties. Geophys J R Astr Soc. 1987; 89(2):657–79.
Wilson, T, Stewart C, Sword-Daniels V. Volcanic ash impacts on critical infrastructure. Phys Chem Earth Pt A/B/C. 2011; 45:5–23.
Woodhouse, MJ, Hogg AJ, Phillips JC, Sparks RSJ. Interaction between volcanic plumes and wind during the 2010 Eyjafjallajökull eruption, Iceland. J Geophys Res Solid Earth. 2013; 118(1):92–109. doi:10.1029/2012JB009592.
Woods, AW, Kienle J. The dynamics and thermodynamics of volcanic clouds: Theory and observations from the April 15 and April 21, 1990 eruptions of redoubt volcano, Alaska. J Volcanol Geothermal Res. 1994; 62(1–4):273–99. doi:10.1016/0377-0273(94)90037-X.
S. Biass and C. Bonadonna were supported by a SNF grant (#200021-129997). LJC and CBC were supported by a grant from the U.S. National Science Foundation (ACI 1339768). We thank editor J. Lindsay, reviewers A. van Eaton and A. Folch for helping improving this manuscript, S. Jenkins, L. Pioli and M. Rosi for comments on early versions of the manuscript, A. Parmigiani for his initial ideas, G. Wilson and M.-A. Thompson for testing early versions and all contributors to the Matlab File Exchange platform who kindly permitted the use of their functions within TephraProb. All computations were performed on the Baobab cluster of the University of Geneva. NCEP Reanalysis data provided by the NOAA/OAR/ESRL PSD, Boulder, Colorado, USA, from their Web site at http://www.esrl.noaa.gov/psd/.
SB developed and wrote the TephraProb package and drafted the paper. Probabilistic techniques were developed by CB and CC and further developed by all authors. CB and CC designed the Tephra2 code, which was implemented and further developed by LC. All authors read and approved the final manuscript.
Department of Earth Sciences, University of Geneva, 13, rue des Maraichers, Geneva, 1205, Switzerland
Sébastien Biass
& Costanza Bonadonna
Department of Geology and Geophysics, University of Hawai'i at Manoa, 1680 East–West Road, Honolulu, HI 96822, USA
University of South Florida, 4202 E. Fowler Ave, Tampa, FL 33620, USA
Laura Connor
& Charles Connor
Search for Sébastien Biass in:
Search for Costanza Bonadonna in:
Search for Laura Connor in:
Search for Charles Connor in:
Correspondence to Sébastien Biass.
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License(http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Biass, S., Bonadonna, C., Connor, L. et al. TephraProb: a Matlab package for probabilistic hazard assessments of tephra fallout. J Appl. Volcanol. 5, 10 (2016) doi:10.1186/s13617-016-0050-5
Probabilistic hazard assessment
Operational tool | CommonCrawl |
Login | Create
Sort by: Relevance Date Users's collections Twitter
Group by: Day Week Month Year All time
Based on the idea and the provided source code of Andrej Karpathy (arxiv-sanity)
2:3 1:1 3:2
Multi-Object Spectroscopy with the European ELT: Scientific synergies between EAGLE & EVE (1207.0768)
C. J. Evans, B. Barbuy, P. Bonifacio, F. Chemla, J.-G. Cuby, G. B. Dalton, B. Davies, K. Disseau, K. Dohlen, H. Flores, E. Gendron, I. Guinouard, F. Hammer, P. Hastings, D. Horville, P. Jagourel, L. Kaper, P. Laporte, D. Lee, S. L. Morris, T. Morris, R. Myers, R. Navarro, P. Parr-Burman, P. Petitjean, M. Puech, E. Rollinde, G. Rousset, H. Schnetler, N. Welikala, M. Wells, Y. Yang
July 3, 2012 astro-ph.CO, astro-ph.IM
The EAGLE and EVE Phase A studies for instruments for the European Extremely Large Telescope (E-ELT) originated from related top-level scientific questions, but employed different (yet complementary) methods to deliver the required observations. We re-examine the motivations for a multi-object spectrograph (MOS) on the E-ELT and present a unified set of requirements for a versatile instrument. Such a MOS would exploit the excellent spatial resolution in the near-infrared envisaged for EAGLE, combined with aspects of the spectral coverage and large multiplex of EVE. We briefly discuss the top-level systems which could satisfy these requirements in a single instrument at one of the Nasmyth foci of the E-ELT.
The 2dF Galaxy Redshift Survey: the luminosity function of cluster galaxies (astro-ph/0212562)
Roberto De Propris, M. Colless, S. Driver, W. Couch, J. Peacock, I. Baldry, C. Baugh, C. Collins, J. Bland-Hawthorn, T. Bridges, R. Cannon, S. Cole, N. Cross, G. B. Dalton, G. Efstathiou, R. S. Ellis, C. S. Frenk, K. Glazebrook, E. Hawkins, C. Jackson, O. Lahav, I. Lewis, S. Lumsden, S. Maddox, D. S. Madgwick, P. Norberg, W. Percival, B. Peterson, W. Sutherland, K. Taylor
Dec. 30, 2002 astro-ph
We have determined the composite luminosity function (LF) for galaxies in 60 clusters from the 2dF Galaxy Redshift Survey. The LF spans the range $-22.5<M_{b_{\rm J}}<-15$, and is well-fitted by a Schechter function with ${M_{b_{\rm J}}}^{*}=-20.07\pm0.07$ and $\alpha=-1.28\pm0.03$ ($H_0$=100 km s$^{-1}$ Mpc$^{-1}$, $\Omega_M$=0.3, $\Omega_\Lambda$=0.7). It differs significantly from the field LF of \cite{mad02}, having a characteristic magnitude that is approximately 0.3 mag brighter and a faint-end slope that is approximately 0.1 steeper. There is no evidence for variations in the LF across a wide range of cluster properties. However the LF of early-type galaxies in clusters is both brighter and steeper than its field counterpart. The differences between the field and cluster LFs for the various spectral types can be qualitatively explained by the suppression of star formation in the dense cluster environment, together with mergers to produce the brightest early-type galaxies.
Studying large-scale structure with the 2dF Galaxy Redshift Survey (astro-ph/0204239)
J. A. Peacock, M. Colless, I. Baldry, C. Baugh, J. Bland-Hawthorn, T. J. Bridges, R. Cannon, S. Cole, C. A. Collins, W. Couch, G. B. Dalton, R. De Propris, S. P. Driver, G. Efstathiou, R. S. Ellis, C. S. Frenk, K. Glazebrook, C. A. Jackson, O. Lahav, I. J. Lewis, S. Lumsden, S. J. Maddox, D. Madgwick, P. Norberg, W. Percival, B. A. Peterson, W. J. Sutherland, K. Taylor
May 28, 2002 astro-ph
The 2dF Galaxy Redshift Survey is the first to observe more than 100,000 redshifts. This allows precise measurements of many of the key statistics of galaxy clustering, in particular redshift-space distortions and the large-scale power spectrum. This paper presents the current 2dFGRS results in these areas. Redshift-space distortions are detected with a high degree of significance, confirming the detailed Kaiser distortion from large-scale infall velocities, and measuring the distortion parameter beta equiv Omega_m^{0.6}/b = 0.43 +- 0.07. The power spectrum is measured to < 10% accuracy for k > 0.02 h Mpc^{-1}, and is well fitted by a CDM model with Omega_m h = 0.20 +- 0.03 and a baryon fraction of 0.15 +- 0.07. A joint analysis with CMB data requires Omega_m = 0.29 +- 0.05, assuming scalar fluctuations, but no priors on other parameters. Two methods are used to determine the large-scale bias parameter: an internal bispectrum analysis yields b = 1.04 +- 0.11, in very good agreement with the b = 1.10 +- 0.08 obtained from a joint 2dFGRS+CMB analysis, again assuming scalar fluctuations. These figures refer to galaxies of approximate luminosity 2L^*; luminosity dependence of clustering is detected at high significance, and is well described by b/b^* = 0.85 + 0.15(L/L^*).
The Anglo-Australian Observatory's 2dF Facility (astro-ph/0202175)
I. J. Lewis, R. D. Cannon, K. Taylor, K. Glazebrook, J. A. Bailey, I. K. Baldry, J. R. Barton, T. J. Bridges, G. B. Dalton, T. J. Farrell, P. M. Gray, A. Lankshear, C. McCowage, I. R. Parry, R. M. Sharples, K. Shortridge, G. A. Smith, J. Stevenson, J. O. Straede, L. G. Waller, J. D. Whittard, J. K. Wilcox, K. C. Willis
Feb. 8, 2002 astro-ph
The 2dF (Two-degree Field) facility at the prime focus of the Anglo-Australian Telescope provides multiple object spectroscopy over a 2 degree field of view. Up to 400 target fibres can be independently positioned by a complex robot. Two spectrographs provide spectra with resolutions of between 500 and 2000, over wavelength ranges of 440nm and 110nm respectively. The 2dF facility began routine observations in 1997. 2dF was designed primarily for galaxy redshift surveys and has a number of innovative features. The large corrector lens incorporates an atmospheric dispersion compensator, essential for wide wavelength coverage with small diameter fibres. The instrument has two full sets of fibres on separate field plates, so that re-configuring can be done in parallel with observing. The robot positioner places one fibre every 6 seconds, to a precision of 0.3 arcsec (20micron) over the full field. All components of 2dF, including the spectrographs, are mounted on a 5-m diameter telescope top-end ring for ease of handling and to keep the optical fibres short in order to maximise UV throughput . There is a pipeline data reduction system which allows each data set to be fully analysed while the next field is being observed. In this paper we provide the historical background to the 2dF facility, the design philosophy, a full technical description and a summary of the performance of the instrument. We also briefly review its scientific applications and possible future developments.
The Origin of the Cosmic Soft X-Ray Background: Optical Identification of an Extremely Deep ROSAT Survey (astro-ph/9703163)
I. M. McHardy, L. R. Jones, M. R. Merrifield, K. O. Mason, R. G. Abraham, A. M. Newsam, G. B. Dalton, F. Carrera, P. J. Smith, M. Rowan-Robinson, G. A. Wegner, T. J. Ponman, H. J. Lehto, G. Branduardi-Raymont, G. A. Luppino, G. Efstathiou, D. J. Allan, J. J. Quenby
Oct. 28, 1997 astro-ph
We present the results of the deepest optically identified X-ray survey yet made. The X-ray survey was made with the ROSAT PSPC and reaches a flux limit of 1.6x10^-15 erg cm^-2 s^-1 (0.5--2.0 keV). Above a flux limit of 2x10^-15 erg cm^-2 s^-1 we define a complete sample of 70 sources of which 59 are identified. Some (5) other sources have tentative identifications and in a further 4 the X-ray error-boxes are blank to R=23 mag. At the brighter flux levels (>= 10^-14 erg cm^-2 s^-1) we confirm the results of previous less deep X-ray surveys with 84% of the sources begin QSOs. At fainter fluxes, however, the survey is dominated by a population of galaxies with narrow optical emission lines (NELGs). In addition, a number of groups and clusters of galaxies are found at intermediate fluxes. Most of these are poor systems of low X-ray luminosity and are generally found at redshifts of > 0.3. Their numbers are consistent with a zero evolutionary scenario, in contrast to the situation for high luminosity clusters at the same redshift. We discuss the significance of these results to the determination of the cosmic soft X-ray background (XRB) and show that at 2x10^-15 erg cm^-2 s^-1, we have resolved more than 50% of the background. We also briefly consider the probable importance of NELG objects to the residual background and look at some of the properties of these unusual objects. | CommonCrawl |
21 Apr Certainty Problems and The Pigeonhole Principle
Posted at 12:45h in Articles, English, Olympiad, Problems by Gonit Sora
The pigeonhole principle is one of those simple yet beautiful, widely used theorems with lots of applications. Any high school going kid may understand what the theorem wants to say, yet its beauty baffles and brings excitement in even the most experienced mathematician. Someone has said that mathematics unveils the patterns of nature and the pigeonhole principle is a manifestation of this fact.
Sometimes it is also referred to as the Dirichlet's principle (Lejeune Dirichlet is supposed to be the first person to have stated the principle ) or the Box principle or the Dirichlet's Box principle.
Statement:-
Simple form :
Given $$n$$ boxes and $$m>n$$ objects, at least one box must contain more than one object.
Generalized form :
If $$n$$ objects are placed into $$k$$ boxes, then there exists at least one box containing at least $$\lceil \frac{n}{k}\rceil$$ objects, where is the ceiling function (The ceiling function returns the greatest integer greater than or equal to the parameter).
(The statements are from the page of mathworld.wolfram)
Illustration through examples: –
Atleast two people in a group of $$13$$ people have their birthdays in the same month. Similarly in a group of $$367$$ people have their birthdays on the same day of the year.
If $$qs+1$$ balls have to put into $$q$$ boxes then atleast one box should contain $$s+1$$ or more balls.
The decimal expansion of $$\frac{a}{b}$$ where $$a$$ and $$b$$ with coprime $$a,b$$ has at most $$b-1$$ period, i.e. the numbers recur after at most $$b-1$$ places.
Among any group of six people on Facebook we may find a group of three such that all of them are friends or all of them are strangers.
Certain famous problems:-
(Erdos-Szekeres.) Prove that every sequence of $$n^2$$ distinct numbers contains a subsequence of length $$n$$ which is monotone (i.e. either always increasing or always decreasing)
Let $$p$$ and $$q$$ be positive integers. Show that within any sequence of $$pq+1$$ distinct real numbers, there exists either a increasing subsequence of $$p+1$$ elements, or a decreasing subsequence of $$q + 1$$ elements.
(Paul Erdos.) Let A be a set of $$n+1$$ integers from $${1,2,3,\ldots,2n}$$. Prove that some element of $$A$$ divides another.
Let $$a_1,a_2,\ldots,a_n$$ be positive integers. Prove that we can choose some of these numbers to obtain a sum divisible by $$n$$.
(Chinese Remainder Theorem) Let $$m$$ and $$n$$ be relatively prime positive integers. Then the system:
$$x = a \pmod{m}$$
$$x = b \pmod{n}$$
has a solution.
Given two disks, one smaller than the other. Each disk is divided into $$200$$ congruent sectors. In the larger disk $$100$$ sectors are chosen arbitrarily and painted red; the other $$100$$ sectors are painted blue. In the smaller disk each sector is painted either red or blue with no stipulation on the number of red and blue sectors. The smaller disk is placed on the larger disk so that the centers and sectors coincide. Show that it is possible to align the two disks so that the number of sectors of the smaller disk whose color matches the corresponding sector of the larger disk is at least $$100$$.
Show that given any set $$A$$ of $$13$$ distinct real numbers, there exist $$x, y \in A$$ such that
$$0<\dfrac{x-y}{1+xy}<2-\sqrt{3}$$
Generally the problems which appear in Olympiads in which we have to ascertain existence or speak certainly about something use the pigeonhole principle. The following are the problems which have appeared in RMO and INMO papers of previous years concerning pigeonhole principle.
RMO problems :-
Two boxes contain between them $$65$$ balls of several different sizes. Each ball is white, black, red or yellow. If you take any $$5$$ balls of the same colour at least two of them will always be of the same size (radius). Prove that there are at least $$3$$ balls which lie in the same box have the same colour and have the same size (radius).
Let A be a set of 16 positive integers with the property that the product of any two distinct numbers of A will not exceed 1994. Show that there are two numbers a and b in A which are not relatively prime.
If A is a fifty-element subset of the set $${1, 2, 3,\ldots, 100}$$ such that no two numbers from A add up to 100. Show that A contains a square.
Find the minimum possible least common multiple of twenty natural numbers whose sum is 801.
Suppose the integers $$1,2,3,\ldots,10$$ are split into two disjoint collections $$a_1,a_2,a_3,a_4,a_5$$ and $$b_1,b_2,b_3,b_4,b_5$$ such that $$a_1<a_2<a_3<a_4<a_5$$ and $$b_1>b_2>b_3>b_4>b_5$$
Show that the larger number in any pair $${a_j,b_j}$$, $$1\leq j\leq 5$$ is atleast $$6$$.
Show that for every such partition $$\sum_{i=1}^5 | a_i-b_i| = 25$$.
A square is dissected in to 9 rectangles by lines parallel to its sides such that all these rectangles have integer sides. Prove that there are always two congruent rectangles.
A computer program generated $$175$$ positive integers at random, none of which had a prime divisor greater than $$10$$. Prove that there are three numbers among them whose product is the cube of an integer.
INMO problems :-
Suppose five of the nine vertices of a regular nine-sided polygon are arbitrarily chosen. Show that one can select four among these five such that they are the vertices of a trapezium.
All the points in the plane are colored using three colors.Prove that there exists a triangle with vertices having the same color such that either it is isosceles or its angles are in geometric progression.
Given any nine integers show that it is possible to choose, from among them, four integers $$a,b,c,d$$ such that $$a + b-c-d$$ is divisible by $$20$$. Further show that such a selection is not possible if we start with eight integers instead of nine.
Some $$46$$ squares are randomly chosen from a $$9 \times 9$$ chess board and colored in red. Show that there exists a $$2\times 2$$ block of $$4$$ squares of which at least three are colored in red.
In any set of $$181$$ square integers, prove that one can always find a subset of $$19$$ numbers, sum of whose elements is divisible by $$19$$.
Additional Information:-
Many refer to the Pigeonhole Principle as PHP.
A very beautiful application of PHP is the Thue's lemma which is useful in proving the Fermat's two square theorem.
Its use arises in computer science, analysis, probability, etc.
The Ramsey's theorem, which is an application of PHP gives rise to a very deep theory in mathematics called the Ramsey theory.
Some other methods of proof which may be used in solving certainty problems are reductio ad absurdum, pairity checking, construction of an example by brutal force, creating bijections, extremal principle, transformation of the theorem into graphs or some easy geometric interpretation and using colouring proofs on them, etc.
References:-
www.mathlinks.ro
http://olympiads.hbcse.tifr.res.in/subjects/mathematics/previous-question-papers-and-solutions
Arthur Engel, Problem Solving Strategies, Springer
M.R. Modak, S.A. Katre, V.V. Acharya, V.M. Sholapurkar, An Excursion in Mathematics, Bhaskaracharya Pratishthana
David M. Burton, Elementary Number Theory, McGraw Hill
Box principle, Dirichlet's principle, INMO, Lejeune Dirichlet, Mathematical Olympiad, Paul Erdos, PHP, Pigeonhole principle, Ramsey theorem, RMO, Szekeres | CommonCrawl |
Autonomous Robots
pp 1–19 | Cite as
Hierarchical reinforcement learning via dynamic subspace search for multi-agent planning
Aaron Ma
Michael Ouimet
Jorge Cortés
Part of the following topical collections:
Special Issue on Multi-Robot and Multi-Agent Systems
We consider scenarios where a swarm of unmanned vehicles (UxVs) seek to satisfy a number of diverse, spatially distributed objectives. The UxVs strive to determine an efficient plan to service the objectives while operating in a coordinated fashion. We focus on developing autonomous high-level planning, where low-level controls are leveraged from previous work in distributed motion, target tracking, localization, and communication. We rely on the use of state and action abstractions in a Markov decision processes framework to introduce a hierarchical algorithm, Dynamic Domain Reduction for Multi-Agent Planning, that enables multi-agent planning for large multi-objective environments. Our analysis establishes the correctness of our search procedure within specific subsets of the environments, termed 'sub-environment' and characterizes the algorithm performance with respect to the optimal trajectories in single-agent and sequential multi-agent deployment scenarios using tools from submodularity. Simulated results show significant improvement over using a standard Monte Carlo tree search in an environment with large state and action spaces.
Reinforcement learning Multi-agent planning Distributed robotics Semi-Markov decision processes Markov decision processes Upper confidence bound tree search Hierarchical planning Hierarchical Markov decision processes Model-based reinforcement learning Swarm robotics Dynamic domain reduction Submodularity
A preliminary version of this work appeared as Ma et al. (2017) at the International Symposium on Multi-Robot and Multi-Agent Systems.
This is one of the several papers published in Autonomous Robots comprising the Special Issue on Multi-Robot and Multi-Agent Systems.
This work was supported by ONR Award N00014-16-1-2836. The authors would like to thank the organizers of the International Symposium on Multi-Robot and Multi-Agent Systems (MRS 2017), which provided us with the opportunity to obtain valuable feedback on this research, and the reviewers.
Submodularity
We review here concepts of submodularity and monotonicity of set functions following Clark et al. (2016). A power set function \(f:2^\varOmega \rightarrow \mathbb {R}\) is submodular if it satisfies the property of diminishing returns,
$$\begin{aligned} f(X\cup \{x\}) - f(X) \ge f(Y\cup \{x\})-f(Y), \end{aligned}$$
for all \(X\subseteq Y\subseteq \varOmega \) and \(x\in \varOmega \setminus Y\). The set function f is monotone if
$$\begin{aligned} f(X) \le f(Y), \end{aligned}$$
for all \(X\subseteq Y \subseteq \varOmega \). In general, monotonicity of a set function does not imply submodularity, and vice versa. These properties play a key role in determining near-optimal solutions to the cardinality-constrained submodular maximization problem defined by
$$\begin{aligned} \begin{aligned}&\max \,\,f(X)\\&\text {s.t. } |X| \le k. \end{aligned} \end{aligned}$$
In general, this problem is NP-hard. Greedy algorithms seek to find a suboptimal solution to (A.3) by building a set X one element at a time, starting with \(|X|=0\) to \(|X|=k\). These algorithms proceed by choosing the best next element,
$$\begin{aligned} \underset{x\in \varOmega \setminus X}{\max } f(X\cup \{x\}), \end{aligned}$$
to include in X. The following result (Clark et al. 2016; Nemhauser et al. 1978) provides a lower bound on the performance of greedy algorithms.
Theorem A.1
Let \(X^*\) denote the optimal solution of problem (A.3). If f is monotone, submodular, and satisfies \(f(\emptyset )=0\), then the set X returned by the greedy algorithm satisfies
$$\begin{aligned} f(X)\ge (1-e^{-1})f(X^*). \end{aligned}$$
An important extension of this result characterizes the performance of a greedy algorithm where, at each step, one chooses an element x that satisfies
$$\begin{aligned} f(X\cup \{x\})-f(X)\ge \alpha (f(X\cup \{x^*\})-f(X)), \end{aligned}$$
for some \(\alpha \in [0,1]\). That is, the algorithm chooses an element that is at least an \(\alpha \)-fraction of the local optimal element choice, \(x^*\). In this case, the following result (Goundan and Schulz 2007) characterizes the performance.
Let \(X^*\) denote the optimal solution of problem (A.3). If f is monotone, submodular, and satisfies \(f(\emptyset )=0\), then the set X returned by a greedy algorithm that chooses elements of at least \(\alpha \)-fraction of the local optimal element choice satisfies
$$\begin{aligned} f(X)\ge (1-e^{-\alpha })f(X^*). \end{aligned}$$
A generalization of the notion of submodular set function is given by the submodularity ratio (Das and Kempe 2011), which measures how far the function is from being submodular. This ratio is defined as largest scalar \(\lambda \in [0,1]\) such that
$$\begin{aligned} \lambda \le \frac{\sum \limits _{z\in Z} f(X \cup \{z\}) -f(X)}{f(X\cup Z)-f(X)}, \end{aligned}$$
for all \(X,Z\subset \varOmega \). The function f is called weakly submodular if it has a submodularity ratio in (0, 1]. If a function f is submodular, then its submodularity ratio is 1. The following result (Das and Kempe 2011) generalizes Theorem A.1 to monotone set functions with submodularity ratio \(\lambda \).
Let \(X^*\) denote the optimal solution of problem (A.3). If f is monotone, weakly submodular with submodularity ratio \(\lambda \in (0,1]\), and satisfies \(f(\emptyset )=0\), then the set X returned by the greedy algorithm satisfies
$$\begin{aligned} f(X)\ge (1-e^{-\lambda })f(X^*). \end{aligned}$$
Scenario optimization
Scenario optimization aims to determine robust solutions for practical problems with unknown parameters (Ben-Tal and Nemirovski 1998; Ghaoui et al. 1998) by hedging against uncertainty. Consider the following robust convex optimization problem defined by
$$\begin{aligned} \begin{aligned} \text {RCP: }&\min \limits _{\gamma \in \mathbb {R}^d }{c^T\gamma } \\&\text {subject to: } f_\delta (\gamma )\le 0,\,\, \forall \delta \in \varDelta , \end{aligned} \end{aligned}$$
where \(f_{\delta }\) is a convex function, d is the dimension of the optimization variable, \(\delta \) is an uncertain parameter, and \(\varDelta \) is the set of all possible parameter values. In practice, solving the optimization (B.1) can be difficult depending on the cardinality of \(\varDelta \). One approach to this problem is to solve (B.1) with sampled constraint parameters from \(\varDelta \). This approach views the uncertainty of situations in the robust convex optimization problem through a probability distribution \(Pr^{\delta }\) of \(\varDelta \), which encodes either the likelihood or importance of situations occurring through the constraint parameters. To alleviate the computational load, one selects a finite number \(N_{\text {SCP}}\) of parameter values in \(\varDelta \) sampled according to \(Pr^{\delta }\) and solves the scenario convex program (Campi et al. 2009) defined by
$$\begin{aligned} \begin{aligned} \text {SCP}_N :&\underset{\gamma \in \mathbb {R}^d}{\min }\,\,c^T\gamma \\&\text {s.t. } f_{\delta ^{(i)}}(\gamma )\le 0,\,\, i=1,\ldots ,N_{\text {SCP}}. \end{aligned} \end{aligned}$$
The following result states to what extent the solution of (B.2) solves the original robust optimization problem.
Theorem B.1
Let \(\gamma ^*\) be the optimal solution to the scenario convex program (B.2) when \(N_{\text {SCP}}\) is the number of convex constraints. Given a 'violation parameter', \(\varepsilon \), and a 'confidence parameter', \(\varpi \), if
$$\begin{aligned} N_{\text {SCP}}\ge \frac{2}{\varepsilon }\left( \text {ln}\frac{1}{\varpi }+d\right) \end{aligned}$$
then, with probability \(1-\varpi \), \(\gamma ^*\) satisfies all but an \(\varepsilon \)-fraction of constraints in \(\varDelta \).
List of symbols
\(({\mathbb {Z}}_{\ge 1}){\mathbb {Z}}\)
(Non-negative) integers
\(({\mathbb {R}}_{>0})\mathbb {R}\)
(Positive) real numbers
|Y|
Cardinality of set Y
\(s\in S\)
State/state space
\(a\in A\)
Action/action space
\(Pr^s\)
Transition function
r, R
Reward, reward function
\((\pi ^*)\pi \)
(Optimal) policy
\(V^{\pi }\)
Value of a state given policy, \(\pi \)
\(\gamma \)
Discount factor
\(\alpha ,\beta \)
Agent indices
\({\mathcal {A}}\)
Set of agents
\(o\in {\mathcal {O}}^{b}\in {\mathcal {O}}\)
Waypoint/objective/objective set
\({\mathcal {E}}\)
\(x\in \varOmega _x\)
Region/region set
\({\mathcal {O}}^{b}_{i}\)
Set of waypoints of an objective in a region
\(s^{b}_{i}\)
Abstracted objective state
\(s_{i}\)
Regional state
\(\tau \)
\(\varGamma \)
Set of feasible tasks
\(\overrightarrow{x}\)
Ordered list of regions
\(\xi _{\overrightarrow{x}}\)
Repeated region list
\(\phi _t(,)\)
Time abstraction function
\((\epsilon _k)\epsilon \)
(Partial) sub-environment
\(N_{\epsilon }\)
Size of a sub-environment
\(\overrightarrow{\tau }\)
Ordered list of tasks
\(\overrightarrow{\text {Pr}^t}\)
Ordered list of probability distributions
\((\vartheta ^p_{\beta })\vartheta \)
(Partial) task trajectory
\({\mathcal {I}}_{\alpha }\)
Interaction set of agent \(\alpha \)
\({\mathcal {N}}\)
Max size of interaction set
\(\theta \)
Claimed regional objective
\(\varTheta _{\alpha }\)
Claimed objective set of agent \(\alpha \)
\(\varTheta ^{{\mathcal {A}}}\)
Global claimed objective set
\(\varXi \)
Interaction matrix
Value for choosing \(\tau \) given \(\epsilon . s\)
\({\hat{Q}}\)
Estimated value for choosing \(\tau \) given \(\epsilon . s\)
Number of simulations in \(\epsilon . s\)
\(N_{{\mathcal {O}}^{b}}\)
Number of simulations of an objective in \(\epsilon . s\)
Multi-agent expected discounted reward per task
\(\lambda \)
Submodularity ratio
\({\hat{\lambda }}\)
Approximate submodularity ratio
\(f_{x}\)
Sub-environment search value set function
\(X_{x}\subset Y_{x}\subset \varOmega _x\)
Finite set of regions
\(f_{\vartheta }\)
Sequential multi-agent deployment value set function
\(X_{\vartheta }\subset Y_{\vartheta }\subset \varOmega _{\vartheta }\)
Finite set of trajectories
\(\varpi \)
Confidence parameter
\(\varepsilon \)
Violation parameter
Agha-mohammadi, A. A., Chakravorty, S., & Amato, N. M. (2011). FIRM: Feedback controller-based information-state roadmap-a framework for motion planning under uncertainty. In IEEE/RSJ international conference on intelligent robots and systems (pp. 4284–4291). San Francisco, CA.Google Scholar
Bai, A., Srivastava, S., & Russell, S. (2016). Markovian state and action abstractions for MDPs via hierarchical MCTS. In Proceedings of the twenty-fifth international joint conference on artificial intelligence (pp. 3029–3039). New York, NY: IJCAI.Google Scholar
Bellman, R. (1966). Dynamic programming. Science, 153(3731), 34–37. CrossRefzbMATHGoogle Scholar
Ben-Tal, A., & Nemirovski, A. (1998). Robust convex optimization. Mathematics of Operations Research, 23, 769–805.MathSciNetCrossRefzbMATHGoogle Scholar
Bertsekas, D. P. (1995). Dynamic programming and optimal control. Belmont: Athena Scientific.zbMATHGoogle Scholar
Bian, A. A., Buhmann, J. M., Krause, A., & Tschiatschek, S. (2017). Guarantees for greedy maximization of non-submodular functions with applications. In International conference on machine learning Vol. 70 (pp. 498–507). Sydney.Google Scholar
Blum, A., Chawla, S., Karger, D. R., Lane, T., Meyerson, A., & Minkoff, M. (2007). Approximation algorithms for orienteering and discounted-reward TSP. SIAM Journal on Computing, 37(2), 653–670.MathSciNetCrossRefzbMATHGoogle Scholar
Broz, F., Nourbakhsh, I., & Simmons, R. (2008). Planning for human–robot interaction using time-state aggregated POMDPs. AAAI, 8, 1339–1344.Google Scholar
Bullo, F., Cortés, J., & Martínez, S. (2009). Distributed control of robotic networks. Applied mathematics series. Princeton, NJ: Princeton University Press.zbMATHGoogle Scholar
Campi, M. C., Garatti, S., & Prandini, M. (2009). The scenario approach for systems and control design. Annual Reviews in Control, 32(2), 149–157.CrossRefGoogle Scholar
Clark, A., Alomair, B., Bushnell, L., & Poovendran, R. (2016). Submodularity in dynamics and control of networked systems., Communications and control engineering New York: Springer.CrossRefzbMATHGoogle Scholar
Cortés, J., & Egerstedt, M. (2017). Coordinated control of multi-robot systems: A survey. SICE Journal of Control, Measurement, and System Integration, 10(6), 495–503.CrossRefGoogle Scholar
Das, A., & Kempe, D. (February 2011). Submodular meets spectral: Greedy algorithms for subset selection, sparse approximation and dictionary selection. In: CoRR.Google Scholar
Das, J., Py, F., Harvey, J. B. J., Ryan, J. P., Gellene, A., Graham, R., et al. (2015). Data-driven robotic sampling for marine ecosystem monitoring. The International Journal of Robotics Research, 34(12), 1435–1452.CrossRefGoogle Scholar
Dunbabin, M., & Marques, L. (2012). Robots for environmental monitoring: Significant advancements and applications. IEEE Robotics and Automation Magazine, 19(1), 24–39.CrossRefGoogle Scholar
Gerkey, B. P., & Mataric, M. J. (2004). A formal analysis and taxonomy of task allocation in multi-robot systems. International Journal of Robotics Research, 23(9), 939–954.CrossRefGoogle Scholar
Ghaoui, L. E., Oustry, F., & Lebret, H. (1998). Robust solutions to uncertain semidefinite programs. SIAM Journal on Optimization, 9(1), 33–52.MathSciNetCrossRefzbMATHGoogle Scholar
Goundan, P. R., & Schulz, A. S. (2007). Revisiting the greedy approach to submodular set function maximization. Optimization Online (pp. 1–25). Google Scholar
Hansen, E. A., & Feng, Z. (2000). Dynamic programming for POMDPs using a factored state representation. In International conference on artificial intelligence planning systems (pp. 130–139). Breckenridge, CO.Google Scholar
Howard, R. (1960). Dynamic programming and Markov processes. Cambridge: M.I.T. Press.zbMATHGoogle Scholar
Kocsis, L., & Szepesvári, C. (2006). Bandit based Monte-Carlo planning. In ECML Vol. 6 (pp. 282–293). Springer.Google Scholar
LaValle, S. M., & Kuffner, J. J. (2000). Rapidly-exploring random trees: Progress and prospects. In Workshop on algorithmic foundations of robotics (pp. 293–308). Dartmouth, NH.Google Scholar
Lovejoy, W. S. (1991). A survey of algorithmic methods for partially observed Markov decision processes. Annals of Operations Research, 28(1), 47–65.MathSciNetCrossRefzbMATHGoogle Scholar
Ma, A., Ouimet, M., & Cortés, J. (2017). Dynamic domain reduction for multi-agent planning. In International symposium on multi-robot and multi-agent systems (pp. 142–149). Los Angeles, CA.Google Scholar
McCallum, A. K., & Ballard, D. (1996). Reinforcement learning with selective perception and hidden state. Ph.D. Dissertation, University of Rochester. Department of Computer Science.Google Scholar
Mesbahi, M., & Egerstedt, M. (2010). Graph theoretic methods in multiagent networks., Applied mathematics series Princeton: Princeton University Press.CrossRefzbMATHGoogle Scholar
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness, J., Bellemare, M. G., et al. (2015). Human-level control through deep reinforcement learning. Nature, 518(7540), 529.CrossRefGoogle Scholar
Nemhauser, G., Wolsey, L., & Fisher, M. (1978). An analysis of the approximations for maximizing submodular set functions. Mathematical Programming, 14, 265–294.MathSciNetCrossRefzbMATHGoogle Scholar
Oliehoek, F. A., & Amato, C. (2016). A concise introduction to decentralized POMDPs., SpringerBriefs in intelligent systems New York: Springer.CrossRefzbMATHGoogle Scholar
Omidshafiei, S., Agha-mohammadi, A. A., Amato, C., & How, J. P. (May. 2015). Decentralized control of partially observable Markov decision processes using belief space macro-actions. In IEEE international conference on robotics and automation (pp. 5962–5969). Seattle, WA.Google Scholar
Papadimitriou, C. H., & Tsitsiklis, J. N. (1987). The complexity of Markov decision processes. Mathematics of Operations Research, 12(3), 441–450.MathSciNetCrossRefzbMATHGoogle Scholar
Parr, R., & Russell, S. (1998). Hierarchical control and learning for Markov decision processes. Berkeley, CA: University of California.Google Scholar
Prentice, S., & Roy, N. (2010). The belief roadmap: Efficient planning in linear POMDPs by factoring the covariance. In Robotics research (pp. 293–305). Springer.Google Scholar
Puterman, M. (2014). Markov decision processes: Discrete stochastic dynamic programming. Hoboken: Wiley.zbMATHGoogle Scholar
Schulman, J., Levine, S., Abbeel, P., Jordan, M., & Moritz, P. (2015). Trust region policy optimization. In International conference on machine learning (pp. 1889–1897). Lille: France.Google Scholar
Sutton, R., Precup, D., & Singh, S. (1999). Between MDPs and semi-MDPs: A framework for temporal abstraction in reinforcement learning. Artificial Intelligence, 112(1–2), 181–211.MathSciNetCrossRefzbMATHGoogle Scholar
Theocharous, G., & Kaelbling, L. P. (2004). Approximate planning in POMDPs with macro-actions. In Advances in neural information processing systems (pp. 775–782).Google Scholar
Wu, Y., Mansimov, E., Grosse, R. B., Liao, S., & Ba, J. (2017). Scalable trust-region method for deep reinforcement learning using kronecker-factored approximation. In Advances in neural information processing systems Vol. 30 (pp. 5285–5294).Google Scholar
View author's OrcID profile
1.Department of Mechanical and Aerospace EngineeringUniversity of California, San DiegoLa JollaUSA
2.Naval Information Warfare Center PacificSan DiegoUSA
Ma, A., Ouimet, M. & Cortés, J. Auton Robot (2019). https://doi.org/10.1007/s10514-019-09871-2
Received 24 April 2018 | CommonCrawl |
Rapid estimation of sugar release from winter wheat straw during bioethanol production using FTIR-photoacoustic spectroscopy
Georgios Bekiaris1,
Jane Lindedam1,
Clément Peltre1,
Stephen R. Decker2,
Geoffrey B. Turner2,
Jakob Magid1 &
Sander Bruun1
Biotechnology for Biofuels volume 8, Article number: 85 (2015) Cite this article
Complexity and high cost are the main limitations for high-throughput screening methods for the estimation of the sugar release from plant materials during bioethanol production. In addition, it is important that we improve our understanding of the mechanisms by which different chemical components are affecting the degradability of plant material. In this study, Fourier transform infrared photoacoustic spectroscopy (FTIR-PAS) was combined with advanced chemometrics to develop calibration models predicting the amount of sugars released after pretreatment and enzymatic hydrolysis of wheat straw during bioethanol production, and the spectra were analysed to identify components associated with recalcitrance.
A total of 1122 wheat straw samples from nine different locations in Denmark and one location in the United Kingdom, spanning a large variation in genetic material and environmental conditions during growth, were analysed. The FTIR-PAS spectra of non-pretreated wheat straw were correlated with the measured sugar release, determined by a high-throughput pretreatment and enzymatic hydrolysis (HTPH) assay. A partial least square regression (PLSR) calibration model predicting the glucose and xylose release was developed. The interpretation of the regression coefficients revealed a positive correlation between the released glucose and xylose with easily hydrolysable compounds, such as amorphous cellulose and hemicellulose. Additionally, a negative correlation with crystalline cellulose and lignin, which inhibits cellulose and hemicellulose hydrolysis, was observed.
FTIR-PAS was used as a reliable method for the rapid estimation of sugar release during bioethanol production. The spectra revealed that lignin inhibited the hydrolysis of polysaccharides into monomers, while the crystallinity of cellulose retarded its hydrolysis into glucose. Amorphous cellulose and xylans were found to contribute significantly to the released amounts of glucose and xylose, respectively.
Production systems for second generation biofuels produced from lignocellulosic biomass have been evolving in the last few decades in an attempt to reduce the environmental impact and sustainability issues arising from the wide-scale production and use of conventional biofuels [1]. Lignocellulosic biomass constitutes about 50 % of the world's biomass [2], while it has been estimated that more than 442*109 L of bioethanol can be produced per year from the lignocellulosic biomass left in the fields [3]. One of the challenges for the use of lignocellulosic biomass for bioethanol production is to develop cheap and efficient pretreatment methods that disrupt the lignocellulosic complex making the cellulose more amorphous as well as removing or degrading lignin [4]. The degradation of lignin makes plant biomass more susceptible to quick hydrolysis and increases the yields of monomeric sugars necessary for bioethanol production [5]. This increase in the yields of monomeric sugars results in the production of larger amounts of bioethanol.
However, even after pretreatment, differences in straw from different varieties or cultivars produced under different environmental conditions are still likely to prevail [6]. To select the best cultivars, it is desirable to assess the potential for sugar release after pretreatment and hydrolysis of a large number of cultivars. For this purpose, high-throughput screening methods have been developed [7–9]. The complexity of the required pretreatment and enzymatic hydrolysis of the biomass, as well as the cost per sample, are the main limitations of these techniques [10]. Near infrared spectroscopy (NIRS) has been adopted as a rapid analysis method that can predict the sugar release upon pretreatment and hydrolysis of groups of plant biomass [11–13]. Good prediction accuracy can be achieved using this technique, but it provides limited information about the chemical components that are associated with the propensity to release sugars. The reason for this is that the near infrared (NIR) spectra mostly reflect overtones and the combination bands of the chemical bonds, which are highly overlapping [14].
A large number of literature studies have provided insights on Fourier transform infrared (FTIR) spectra interpretation [15–17]. Attenuated total reflection FTIR (ATR-FTIR) spectroscopy has been adopted in the past to determine the changes that take place during the pretreatment of wheat straw [18], as well as the transformation of cellulose during the enzymatic hydrolysis for bioethanol production [19]. ATR-FTIR has also been used, in combination with advanced chemometrics, to predict the composition of pretreated softwood [20] as well as the glucan, xylan and other polysaccharide content of straw [21]. Only a limited number of attempts have been made to apply mid-infrared spectroscopy in the prediction of fermentable sugars from pretreated biomass [16, 22, 23]; there have been no previous attempts to correlate the FTIR or Fourier transform infrared photoacoustic (FTIR-PA) spectra of non-pretreated biomass with their potential sugar release. FTIR-PAS arises from combining traditional FTIR and a photoacoustic detector (PA). The measurement of the absorbed radiation is directly proportional to the heat wave produced after the interaction of the sample with the IR radiation. In this way, the measurement remains unaffected by the redistribution of the light due to scattering effects or diffraction processes [24–26].
Therefore, the aim of the present study was to use FTIR-PAS for the characterisation of winter wheat straw and identification of chemical structures related to sugar release and to develop calibrations predicting potential sugar release from FTIR-PA spectra.
Spectroscopic analysis
The averaged spectra of each site and variety were characterised by common peaks with slightly different absorption intensities (Fig. 1a, b). The different peaks correspond to fundamental molecular stretching and bending vibrations of different chemical groups in the samples (Table 1). The broad peak centred at 3380 cm−1 (peak 1) can be assigned to water or lignin from wood samples, while the peak at 2920 cm−1 (peak 2) and the shoulder at 2850 cm−1 (peak 3) correspond to aliphatics. Ciolacu et al. [27] observed a shift in this peak from 2900 cm−1 for pure cellulose to 2920 cm−1 for the amorphous cellulose. In the fingerprint region (1800–600 cm−1) of the spectrum, strong absorption was observed at 1735 cm−1 (peak 4), which, as the shoulder at 1460 cm−1 (peak 8), correspond to xylans. The peak at 1650 cm−1 (peak 5), which revealed a diversification in the absorption intensity, corresponds either to carboxylates or the absorbed water; therefore, the difference in the absorption intensity probably indicated different contents of carboxylates, as all samples were dried following the same procedure. The peaks at 1600 (peak 6) and 1510 cm−1 (peak 7) are associated with lignin. The IR absorption at 1429 cm−1 (peak 9) corresponds to lignin or crystalline cellulose, while the peak at 1370 cm−1 (peak 10) can be assigned to cellulose and hemicellulose. Ciolacu et al. [27] observed a positive correlation of crystalline cellulose with both regions (1429 and 1370 cm−1) for various materials, while both of them seem to be absent in amorphous cellulose or replaced by a strong peak shifted at 1400 cm−1. The relatively strong peak that was visible at 1320 cm−1 (peak 11) could be part of either the peak at 1335 cm−1 observed by Pandey and Pitman [28] corresponding to the C-H vibration of cellulose, hemicellulose, lignin, or the peak at 1310 cm−1 observed by Sills and Gossett [16] corresponding to the CH2 wagging in cellulose and hemicellulose. The relatively broad peak at 1240 cm−1 (peak 12) could be assigned to xylans, while the peak at 1160 cm−1 (peak 13) corresponds to cellulose and hemicellulose. According to Ciolacu et al. [27], while this peak is observed in the FTIR spectra of original cellulose, it is absent in the spectra of the amorphous form of cellulose. Both peaks at 1111 cm−1 (peak 14) and 1053 cm−1 (peak 15) correspond to crystalline cellulose, while the peak at 898 cm−1 (peak 16) can be assigned to amorphous cellulose.
FTIR-PA spectra of winter wheat straw. a Spectra averaged across different locations (nine spectra). b Spectra averaged across different wheat straw varieties (203 spectra)
Table 1 Most important absorption bands of the mid-infrared spectra of winter wheat straw
Sugar release
The high-throughput pretreatment and enzymatic hydrolysis (HTPH) measurements of the samples shown in Table 2 revealed a range in the sugar yield from 0.28 to 0.59 g g−1 of dry matter (dm) for total sugars, 0.14 to 0.50 g g−1 dm for glucose and 0.06 to 0.29 g g−1 dm for xylose release (mean values of 0.42, 0.23 and 0.19 g g−1 dm for total sugar, glucose and xylose release, respectively). The high-yielding straw samples released approximately double the amount of total sugar in comparison to the low-yielding samples, indicating a substantial span in bioethanol potential. The low standard deviation of the laboratory method (SDL) of 0.024 g g−1 dm for total sugar, 0.016 g g−1 dm for glucose and 0.010 g g−1 dm for xylose indicated that the reproducibility of the HTPH assay was high. Explaining the causes for variability of the ethanol potential, as undertaken by Lindedam et al. [6], was beyond of the scope of this study, but generally speaking, annual variation and the effect of cultivar, site and environment are highly influential.
Table 2 Experiments from which straw samples has been collected
Prediction of sugar release
The different transformation methods of the spectra did not considerably improve the accuracy of the predictions of sugar release (Table 3) and only the first derivative transformation resulted in slightly better predictions than the smoothed and normalised spectra. Both first and second derivative transformations needed a lower number of components (factors) for the predictions, which indicated that the transformation reduced some information that was of little predictive value (Table 3). In all cases, a fair prediction of the potential total sugar, glucose and xylose release was obtained, and the R 2 (coefficient of determination) values of the predictions for the external validation (EV) data set using the smoothing/normalisation transformation were 0.69 for total sugar, 0.63 for glucose and 0.65 for xylose. The root-mean-square error (RMSE) for the same predictions were 0.030, 0.019 and 0.015 g g−1 dm, respectively (Table 3, Fig. 2), while the ratio of RMSEEV to SDL was 1.25, 1.18 and 1.45. In addition to the low RMSE, the differences between cross-validation and the external validation results were quite small, which indicated that the calibrations were robust. These results proved the potential use of calibrations based on FTIR-PAS for the prediction of sugar release from wheat straw. Considering the wide variation in genetic material and environmental conditions during growth, it is reasonable to assume that the model may be applied to other winter wheat straw materials. Applicability of these calibrations in other types of plant biomass have not been tested, but it could be feasible since the right regions of the spectrum, corresponding to compounds relevant to the sugars, were taken into account in the calibrations (see section Analysis of regression coefficients).
Table 3 Different spectral transformations. Effect of the different preprocessing of the spectra on the prediction of total sugar, xylose and glucose release during bioethanol production (R2 coefficient of determination, RMSE root-mean-square error, CV cross-validation data set, EV external validation data set, F number of factors used in calibration)
Measured vs. predicted values of sugar release. Correlation between reference (measured) and predicted sugar release (in g g−1 dm) in terms of total sugar (glucose plus xylose), glucose and xylose (cross-validation results; black dots, solid regression line, external validation results: white dots, dashed regression line). (R 2 coefficient of determination, RMSE root-mean-square value, CV cross-validation data set, EV external validation data set, F number of factors used in calibration)
A number of other studies have used mid-infrared spectroscopy to predict potential ethanol production from biomass. Gollapalli et al. [22] obtained correlations between glucose yield and the diffuse reflectance infrared Fourier transform (DRIFT) spectra, with R 2 values ranging between 0.65 and 0.71 for the different hydrolysis time points of initial rice straw, while the R 2 values of xylose concentration ranged between 0.47 and 0.50. Sills and Gossett [16] were able to explain a larger fraction of the variation during the prediction of glucose and xylose release in a sample set of 24 pretreated and hydrolysed biomass samples (six different plant materials, four different pretreatments with NaOH) using the fingerprint region (1800–800 cm−1) of the ATR-FTIR spectra obtained. The obtained R 2 values of 0.86 and 0.84 for the glucose and xylose content, respectively, were higher than this study's values of 0.63 and 0.65. However, the RMSE values they obtained were 0.078 g g−1 dm for glucose and 0.093 g g−1 dm for xylose release, which are higher than the 0.019 and 0.015 g g−1 dm, respectively, that were obtained in the present study. The high uniformity in this study's sample set (all the straw samples being wheat straw from a relatively small geographical region) meant that the variation in the sample set was small and supported the lower RMSE values. In addition, the use of an external validation data set in the present study can provide more certainty about the predictive power of the model and eliminate the possibility of an overestimation of R 2 values. Martin et al. [23] developed a model predicting the cell wall digestibility of Sorghum bicolor biomass using the fingerprint region (1800–850 cm−1) of the obtained ATR-FTIR spectra, with a high R 2 value of 0.94 and an RMSE of 0.64 μg mg−1 dry weight h−1. In their study, the samples were collected at different developmental stages, resulting in high variable digestibility between the samples. This could explain the high predictive power of their model. The model developed in the present study predicting the total sugar release resulted in a lower R 2 value, but the samples were also displaying less variability with all samples stemming from mature wheat straw. Castillo et al. [29] applied PLSR to develop a model predicting the ethanol production from Eucalyptus globulus pulp using mid-infrared spectroscopy. They obtained an R 2 value of 0.92 with an RMSE of 1.9 g L−1 for the calibration sample set, while the validation of the model by an external validation set gave an R 2 value of 0.60. The big difference in the R 2 values between calibration and external validation sample sets may indicate the overestimation in the calibration.
NIR spectroscopy has also been used on a number of occasions to predict sugar release or digestibility of biomass samples. Lindedam et al. [12] predicted the sugar release of untreated air-dried wheat straw and achieved R 2 values of 0.56 for the total sugar release, 0.44 for the glucose and 0.69 for the xylose release with RMSE values of 0.014, 0.010 and 0.005 g g−1 dm, respectively. Bruun et al. [30] performed partial least squares (PLS) calibration in order to predict the degradability of wheat straw obtaining an R 2 value of 0.72 and an RMSE of 1.4 % using untreated wheat straw from two different sites. These values are difficult to compare with ours because of different reference methods and sample variability, but they seem to be in the same range and thus indicate that the predictive power of NIR is similar to FTIR-PAS.
A few studies have also been using spectroscopic methods to predict the results of biomass compositional analysis. Tucker et al. [20] applied PLS analysis to develop a model predicting the glucan and xylan content from 35 ATR-FTIR spectra of forest thinning and softwood sawdust (hemlock, Sitka spruce and red cedar). Tamaki and Mazza [21] developed models predicting the glucan and xylan content of wheat and triticale using ATR-FTIR spectra. These studies generally obtained very high predictive power and precision. This may reflect the fact that predictions of the total amount of the specific sugars are easier than predicting the digestible parts. This may be explained by the fact that total cellulose and xylan appears in the spectra as specific bands whereas the digestible amount of the same components depends on a range of other chemical components that may impede the enzymatic hydrolysis of cellulose and xylan.
Analysis of regression coefficients
Regression coefficients of total sugar prediction
Positive regression coefficients (Fig. 3) were obtained in the region of 3597–3440 cm−1 of the spectrum dominated by the stretching vibration of the O-H bond in various compounds, making an interpretation of this region difficult. Nevertheless, Ciolacu et al. [27] suggest that this broad peak is observed in both crystalline and amorphous forms of cellulose, but with a shift towards higher wavenumbers (around 3440 instead of 3350 cm−1) for amorphous cellulose. The strong positive association with fermentable sugars, which was observed at 2920 and 2850 cm−1, corresponds to the aliphatic methylene and is present in the spectrum of amorphous cellulose. The regions at 1730 and 1660 cm−1 are attributed to hemicelluloses and carboxylates. Additionally, a positive association with the sugar release was observed in the regions at 1442 and 1352 cm−1. According to Liang, Marchessault [31, 32], these regions correspond to the O-H bending in-plane vibration (1442 cm−1) and the C-H bending vibration (1352 cm−1) of cellulose and hemicellulose. The positively associated region, centred around 1295 cm−1, can be attributed to CH2 wagging [16] in cellulose and hemicellulose or the C-H deformation in hemicelluloses [33]. Finally, both regions at 977 and 890 cm−1 are associated with C-O-C stretching at the β-(1 → 4)-glycosidic linkages of amorphous cellulose [27]. The interpretation of the positive regression coefficients in this study revealed a strong correlation of sugar release with amorphous cellulose and hemicellulose.
Regression coefficients from the prediction of total sugar release. Spectral regions with a significant contribution in the prediction of total sugar release after the pretreatment and enzymatic hydrolysis of wheat straw and during bioethanol production
The broad negative associated regions between 3259 and 2989 cm−1 correspond to the O-H stretching vibration of various compounds and, as mentioned earlier, their interpretation is difficult. Fengel [34] asserts that the region of the IR spectrum between 3200 and 3700 cm−1 arises from the intra- and inter-molecular O-H vibrations of crystalline cellulose. The crystalline forms of cellulose appear to be more resistant to enzymatic hydrolysis [35]; therefore, it was expected to be negatively associated with the sugar release. The strongly negatively associated regions at 1592 and 1505 cm−1 are attributed to lignin, which has been found to play an inhibitory role in the hydrolysis of cellulose and hemicellulose into fermentable sugars [36]. Additionally, the region at 1220 cm−1 can be assigned either to the C-C/C-O stretching vibration in lignin [37] or the C-O-H in-plane bending vibration in crystalline cellulose [38]. Finally, the regions at 1190, 1130 and 1067 cm−1 are associated with crystalline cellulose, while there is not as much information related to the regions under 830 cm−1. Liang and Marchessault [31] suggested that the regions near 740 and 800 cm−1 are assigned to the CH2-rocking vibration of crystalline cellulose. The interpretation of the negative regression coefficients in this study revealed a negative correlation of sugar release with regions related to lignin and crystalline cellulose. This is not surprising as lignin plays an inhibitory role in the hydrolysis of celluloses and hemicelluloses. Furthermore, the hydrolysis of crystalline cellulose is much slower than amorphous cellulose, as the adsorption of the enzymes necessary for hydrolysis declines with increasing cellulose crystallinity [39].
Regression coefficients of xylose and glucose prediction
The high correlation (r = 0.82) of the measured glucose and xylose yields could mean that the developed calibration model for each sugar monomer might be built on regions of the spectrum determining the other variable. This fact could explain why the same regions of the spectrum were used for the prediction of total sugar, glucose and xylose release (Additional file 1: Figure S1). The division of the calibration set into three smaller subsets led to a decrease in the correlation between the measured glucose and xylose yields from 0.82 in the full calibration set to 0.37, 0.08 and 0.32 in each of the three subsets, respectively (Fig. 4). The partial least square regression (PLSR) analysis, which was performed on each subset, revealed the spectral regions that were associated with the release of each sugar monomer (Fig. 5).
Xylose vs. glucose release after the pretreatment and enzymatic hydrolysis. Correlation coefficients (r) of the measured glucose and xylose yields (in g g−1 dm) in the full calibration set (713 samples) and the three smaller subsets (of 237 samples each). Triangles subset 1, circles subset 2, squares subset 3
Regression coefficients from the prediction of glucose and xylose release. Spectral regions with a significant contribution in the prediction of glucose (a) and xylose (b) release during bioethanol production based on each of three subsets; top (subset 1), middle (subset 2), bottom (subset 3)
The differences in the regression coefficients obtained for the prediction of glucose release between the three sample subsets (Fig. 5a) were more obvious than those of xylose (Fig. 5b). Positive regression coefficients at the regions around 2920 and 2850 cm−1 (aliphatics/amorphous cellulose) appeared in all subsets (Fig. 5a), while a positive association with the region at 1670 cm−1 (carboxylates) was present in two of the subsets. The region between 1200 and 1100 cm−1, which is associated with crystalline cellulose, displayed negative regression coefficients in all subsets, indicating that this region contributed to glucose prediction to a limited extent. Additionally, the region between 1600 and 1500 cm−1 (associated with lignin) displayed negative regression coefficients in two of the subsets. Both regions are therefore related to the restriction of cellulose hydrolysis and consequently, the release of glucose.
In contrast, the regression coefficients obtained for xylose prediction were fairly similar, regardless of which of the three sample subsets was used (Fig. 5b). Xylose release was found to be positively associated with the region around 1740 cm−1 in all subsets and the region around 1250 cm−1 in two of the subsets. Both of them are assigned to the xylans of hemicelluloses, which are built up by xylose monomers and are easily hydrolysable [36]. Negative regression coefficients were obtained in the region between 1500 and 1600 cm−1, which are assigned to lignin. This was expected in all subsets as lignin inhibits the hydrolysis of hemicelluloses.
The regions at 1730 (hemicelluloses) and 970 cm−1 (amorphous cellulose), which were present in the regression coefficients for glucose and xylose prediction, respectively, revealed that some correlation between the two sugar monomers remained, even after subdivision of the calibration set.
This study established that FTIR-PAS can be used to predict the bioethanol potential from wheat straw and in addition provide structural information on the chemical compounds involved in saccharification. The predictions of total sugar, glucose and xylose release after pretreatment and enzymatic hydrolysis of wheat straw can be characterised as fair (coefficient of determination ranging between 0.64 and 0.70) and accurate (RMSE value ranging between 0.015 and 0.030 g g−1 dm and RMSE to SDL ratio between 1.18 and 1.45), especially considering the low variability of the sample set in this study caused by the fact that all samples stemmed from mature wheat straw.
The interpretation of the regression coefficients used for the predictions allowed the detection of compounds that contribute to the release of sugars and compounds that do not contribute or even inhibit hydrolysis. As expected, lignin was found to inhibit the hydrolysis of polysaccharides into monomers, while the crystallinity of cellulose might delay its hydrolysis into glucose. On the other hand, amorphous cellulose and xylans were found to contribute significantly to the released amounts of glucose and xylose, respectively.
Sample collection and preparation
A total of 1122 wheat straw samples were collected from nine different locations in Denmark and one location in the United Kingdom (Table 4) from 2006 to 2010. The samples were collected from ongoing experiments with different wheat varieties, fertiliser treatments and harvesting times. The experiments included a total of 203 different wheat varieties. An overview of the origin of samples in terms of experiments, sites and treatments is given in Table 2.
Table 4 Experiment locations where wheat straw samples has been collected
From all but one experiment in Denmark, mature air-dried straw (approximately 7 % moisture) was sampled from the experimental pots after the grain had been harvested by a combine harvester cutting the straw and leaving it in the field. Approximately 80 g of straw was collected representatively from each plot, as described by Lindedam et al. [12] and stored at ambient temperature. Material from the experiment with different harvest times was collected by hand three weeks before maturity, at maturity and three weeks after. The plants were cut 5–7 cm from the soil, and the grain was removed from the samples before being stored at ambient temperature. Material from the UK was collected as described by Murozuka et al. [40]. Subsequently, all straw samples were ground on a cyclone mill (President, Holbaek, Denmark) mounted with a 1-mm screen.
Determination of sugar release
Determination of potential sugar release was carried out at the National Renewable Energy Laboratory (NREL) in Denver, Colorado using a slightly modified method [41] compared to the one described by Selig et al. [9]. Briefly, 2 % dm solids (5.0 ± 0.3 mg in 250 μL of de-ionised H2O) were pretreated in triplicate in a 96-well plate in a steam chamber for 17.5 min at 180 °C, with heat-up and cool-down phases of approximately 52 sec and 1.5 min (to reach 120 °C), respectively [9]. Hydrolysis was started by loading total enzyme protein on dry biomass at 70 mg g−1 dm of Cellic® CTec2 (Novozymes, Bagsværd, Denmark). After enzymatic hydrolysis at 50 °C for 70 h, release of glucose and xylose was measured by a glucose oxidase/peroxidase assay and a xylose dehydrogenase assay, respectively (Megazyme International Ireland, Wicklow, Ireland). Total sugars were the calculated values of glucose plus xylose in each sample. Any sugars added with the enzyme mix were accounted for with enzyme-only blanks in every plate.
Fourier transform infrared photoacoustic spectroscopy (FTIR-PAS)
No pretreatment of the ground samples was performed prior to the spectroscopic analysis, apart from oven drying at 70 °C for 48 hours. The FTIR-PAS spectra were recorded using a Nicolet 6700 (ThermoScientific, USA) spectrometer equipped with a PA-301 photoacoustic detector (Gasera Ltd, Finland). During the measurement, there was a purging flow with helium gas to reduce the noise caused by moisture evaporating from the samples. The samples were packed in small ring cups of 10-mm diameter and inserted into the PA detector. For each sample, 32 scans in the mid-infrared region between 4000 and 600 cm−1 at a resolution of 4 cm−1 were recorded and averaged. Subsequently, the spectra were smoothed by the Savitzky-Golay algorithm [42] using three points on each side (total window of seven smoothing points) and a zero polynomial, and normalised by the mean using The Unscrambler v.10.3 software (CAMO software, Oslo, Norway).
PLSR was used to calibrate models predicting glucose and xylose release from the FTIR-PA spectra. Different preprocessing of the spectra were performed in an attempt to obtain better predictions (Table 3). Prior to the PLSR analysis, 54 outliers were removed to increase the model's stability. The selection of the outliers was based on the observation of the Residual vs. Hotelling-T2 distribution implemented in the software. In order to avoid a possible overestimation, the sample set was divided into a calibration set that contained two thirds of the samples (713 samples) and a smaller external validation set with randomly selected samples from all varieties and sites (355 samples). The calibration set was used to develop calibration models in which the optimal number of components was chosen based on a leave-one segment-out cross-validation using 10 segments of 71 samples. More stable and robust models were achieved by the variable selection method, known as Martens' uncertainty test [43]. Subsequently, the samples of the external validation set were used to evaluate the robustness of the developed model. The Unscrambler v.10.3 software (CAMO, Oslo, Norway) was used for all calibrations.
After the models had been developed, the regression coefficients were interpreted in order to understand which chemical components were correlated with xylose and glucose release respectively. However, glucose and xylose turned out to be highly correlated (r = 0.82). This essentially meant that the regions of the spectrum were not uniquely related to the monomeric sugar that the model was predicting. For example, a model predicting glucose may have high regression coefficients in a region that is related to xylose because xylose is correlated with glucose. In order to be able to identify regions that are uniquely responsible for predicting glucose and not derived from the correlation with xylose, three datasets were produced to reduce the correlation between glucose and xylose. Calibration models were subsequently made predicting glucose and xylose for the data in each of these datasets, and the regression coefficients for these datasets were inspected and interpreted.
The performance of the PLSR-calibrations was determined by the coefficient of determination (R 2):
$$ {R}^2 = \frac{{\displaystyle {\sum}_i}{\left({y}_i-{f}_i\right)}^2}{{\displaystyle {\sum}_i}{\left({y}_i-\overline{y}\right)}^2} $$
where y i represents the observed values and f i the predicted values.
The closer the R 2 is to 1, the better the fit of the reference values (y i) to the regression line.
The accuracy of the calibrations was determined by the root-mean-square error (RMSE) (in g g−1 dm):
$$ RMSE=\sqrt{{\displaystyle \sum_{i=0}^n{\left({f}_i-{y}_i\right)}^2/n}} $$
In addition, the standard deviation of the laboratory method (SDL) was calculated:
$$ SDL=\sqrt{\frac{{\displaystyle {\sum}_{i=1}^n{\displaystyle {\sum}_{j=1}^m{\left({y}_{ij}-{\overline{y}}_j\right)}^2}}}{m*n-1}} $$
where i is the laboratory replicate out of m replicates and j is the individual sample out of n samples.
The closer the ratio of RMSEEV over SDL is to 1, the better the predictive power of the model to the reference measurements.
ATR-FTIR:
attenuated total reflection FTIR
DRIFT:
diffuse reflectance infrared Fourier transform
EV:
external validation
FTIR:
Fourier transform infrared
FTIR-PAS:
FTIR-photoacoustic spectroscopy
HTPH:
high-throughput pretreatment and enzymatic hydrolysis
PLSR:
partial least square regression
RMSE:
root-mean-square error
SDL:
standard deviation of the laboratory method
Williams PRD, Inman D, Aden A, Heath GA. Environmental and sustainability factors associated with next-generation biofuels in the US: what do we really know? Environ Sci Technol. 2009;43(13):4763–75. doi:10.1021/Es900250d.
Claassen PAM, van Lier JB, Contreras AML, van Niel EWJ, Sijtsma L, Stams AJM, et al. Utilisation of biomass for the supply of energy carriers. Appl Microbiol Biot. 1999;52(6):741–55.
Kim S, Dale BE. Global potential bioethanol production from wasted crops and crop residues. Biomass Bioenerg. 2004;26(4):361–75. doi:10.1016/j.biombioe.2003.08.002.
Sanchez OJ, Cardona CA. Trends in biotechnological production of fuel ethanol from different feedstocks. Bioresource Technol. 2008;99(13):5270–95. doi:10.1016/j.biortech.2007.11.013.
Sarkar N, Ghosh SK, Bannerjee S, Aikat K. Bioethanol production from agricultural wastes: an overview. Renew Energy. 2012;37(1):19–27. doi:http://dx.doi.org/10.1016/j.renene.2011.06.045.
Lindedam J, Andersen SB, DeMartini J, Bruun S, Jorgensen H, Felby C, et al. Cultivar variation and selection potential relevant to the production of cellulosic ethanol from wheat straw. Biomass Bioenerg. 2012;37:221–8. doi:10.1016/j.biombioe.2011.12.009.
Decker SR, Brunecky R, Tucker MP, Himmel ME, Selig MJ. High-throughput screening techniques for biomass conversion. Bioenerg Res. 2009;2(4):179–92. doi:10.1007/s12155-009-9051-0.
Studer MH, DeMartini JD, Brethauer S, McKenzie HL, Wyman CE. Engineering of a high-throughput screening system to identify cellulosic biomass, pretreatments, and enzyme formulations that enhance sugar release. Biotechnol Bioeng. 2010;105(2):231–8. doi:10.1002/bit.22527.
Selig MJ, Tucker MP, Sykes RW, Reichel KL, Brunecky R, Himmel ME, et al. Original Research: Lignocellulose recalcitrance screening by integrated high-throughput hydrothermal pretreatment and enzymatic saccharification. Ind Biotechnol. 2010;6(2):104–11. doi:10.1089/ind.2010.0009.
Hames BR. High-throughput NIR analysis of biomass pretreatment streams. Aqueous Pretreatment of Plant Biomass for Biological and Chemical Conversion to Fuels and Chemicals. John Wiley & Sons, Ltd; 2013. p. 355–68.
Hames BR, Thomas SR, Sluiter AD, Roth CJ, Templeton DW. Rapid biomass analysis: new tools for compositional analysis of corn stover feedstocks and process intermediates from ethanol production. Appl Biochem Biotechnol. 2003;105–108:5–16.
Lindedam J, Bruun S, DeMartini J, Jorgensen H, Felby C, Yang B, et al. Near infrared spectroscopy as a screening tool for sugar release and chemical composition of wheat straw. J Biobased Mater Bio. 2010;4(4):378–83. doi:10.1166/jbmb.2010.1104.
Hou S, Li L. Rapid characterization of woody biomass digestibility and chemical composition using near-infrared spectroscopy. J Integr Plant Biol. 2011;53(2):166–75. doi:10.1111/j.1744-7909.2010.01003.x.
Stenberg B, Viscarra Rossel RA, Mouazen AM, Wetterlind J. Chapter Five - Visible and near infrared spectroscopy in soil science. In: Donald LS, editor. Advances in Agronomy. Academic Press; 2010. p. 163–215.
Xu F, Yu J, Tesso T, Dowell F, Wang D. Qualitative and quantitative analysis of lignocellulosic biomass using infrared techniques: A mini-review. Appl Energy. 2013;104(0):801–9. doi:http://dx.doi.org/10.1016/j.apenergy.2012.12.019.
Sills DL, Gossett JM. Using FTIR to predict saccharification from enzymatic hydrolysis of alkali-pretreated biomasses. Biotechnol Bioeng. 2012;109(2):353–62. doi:10.1002/bit.23314.
Coates J. Interpretation of infrared spectra: a practical approach interpretation of infrared spectra. In: Meyers RA, editor. Encyclopedia of Analytical Chemistry. John Wiley & Sons: Ltd; 2000. p. 10815–37.
Kristensen JB, Thygesen LG, Felby C, Jorgensen H, Elder T. Cell-wall structural changes in wheat straw pretreated for bioethanol production. Biotechnol Biofuels. 2008;1(1):5. doi:10.1186/1754-6834-1-5.
Corgie SC, Smith HM, Walker LP. Enzymatic transformations of cellulose assessed by quantitative high-throughput Fourier transform infrared spectroscopy (QHT-FTIR). Biotechnol Bioeng. 2011;108(7):1509–20. doi:10.1002/Bit.23098.
Tucker MP, Nguyen QA, Eddy FP, Kadam KL, Gedvilas LM, Webb JD. Fourier transform infrared quantitative analysis of sugars and lignin in pretreated softwood solid residues. Appl Biochem Biotechnol. 2001;91–3:51–61. doi:10.1385/Abab:91-93:1-9:51.
Tamaki Y, Mazza G. Rapid determination of carbohydrates, ash, and extractives contents of straw using attenuated total reflectance Fourier transform mid-infrared spectroscopy. J Agr Food Chem. 2011;59(12):6346–52. doi:10.1021/Jf200078h.
Gollapalli LE, Dale BE, Rivers DM. Predicting digestibility of ammonia fiber explosion (AFEX)-treated rice straw. Appl Biochem Biotechnol. 2002;98:23–35. doi:10.1385/Abab:98-100:1-9:23.
Martin AP, Palmer WM, Byrt CS, Furbank RT, Grof CP. A holistic high-throughput screening framework for biofuel feedstock assessment that characterises variations in soluble sugars and cell wall composition in Sorghum bicolor. Biotechnol Biofuels. 2013;6(1):186. doi:10.1186/1754-6834-6-186.
Schmidt K, Beckmann D. Biomass monitoring using the photoacoustic effect. Sens Actuators B. 1998;51(1–3):261–7. doi:http://dx.doi.org/10.1016/S0925-4005(98)00229-9.
McClelland JF, Jones RW, Bajic SJ. FT-IR Photoacoustic spectroscopy. In: Chalmers JM, Griffiths PR, editors. Handbook of Vibrational Spectroscopy. John Wiley & Sons: Ltd; 2002. p. 1–45.
Kizil R, Irudayaraj J. Fourier transform infrared photoacoustic spectroscopy (FTIR-PAS). In: Roberts G, editor. Encyclopedia of Biophysics: SpringerReference. Berlin Heidelberg: Springer-Verlag; 2013.
Ciolacu D, Ciolacu F, Popa VI. Amorphous cellulose-structure and characterization. Cell Chem Technol. 2011;45(1–2):13–21.
Pandey KK, Pitman AJ. FTIR studies of the changes in wood chemistry following decay by brown-rot and white-rot fungi. Int Biodeter Biodegr. 2003;52(3):151–60. doi:10.1016/S0964-8305(03)00052-0.
Castillo RD, Baeza J, Rubilar J, Rivera A, Freer J. Infrared spectroscopy as alternative to wet chemical analysis to characterize Eucalyptus globulus pulps and predict their ethanol yield for a simultaneous saccharification and fermentation process. Appl Biochem Biotechnol. 2012;168(7):2028–42. doi:10.1007/s12010-012-9915-1.
Bruun S, Jensen JW, Magid J, Lindedam J, Engelsen SB. Prediction of the degradability and ash content of wheat straw from different cultivars using near infrared spectroscopy. Ind Crop Prod. 2010;31(2):321–6. doi:10.1016/j.indcrop.2009.11.011.
Liang CY, Marchessault RH. Infrared spectra of crystalline polysaccharides: 2. native celluloses in the region from 640 to 1700 Cm−1. J Polym Sci. 1959;39(135):269–78. doi:10.1002/pol.1959.1203913521.
Marchessault RH, Liang CY. Infrared spectra of crystalline polysaccharides. 8. Xylans. J Polym Sci. 1962;59(168):357–78. doi:10.1002/pol.1962.1205916813.
Kaushik A, Singh M. Isolation and characterization of cellulose nanofibrils from wheat straw using steam explosion coupled with high shear homogenization. Carbohydr Res. 2011;346(1):76–85. doi:10.1016/j.carres.2010.10.020.
Fengel D. Characterization of cellulose by deconvoluting the OH valency range in FTIR spectra. Holzforschung - International Journal of the Biology, Chemistry, Physics and Technology of Wood; 1992. p. 283.
Beguin P. Molecular biology of cellulose degradation. Annu Rev Microbiol. 1990;44:219–48. doi:10.1146/annurev.mi.44.100190.001251.
Perez J, Munoz-Dorado J, de la Rubia T, Martinez J. Biodegradation and biological treatments of cellulose, hemicellulose and lignin: an overview. Int Microbiol. 2002;5(2):53–63. doi:10.1007/s10123-002-0062-3.
Kubo S, Kadla JF. Hydrogen bonding in lignin: a Fourier transform infrared model compound study. Biomacromolecules. 2005;6(5):2815–21. doi:10.1021/bm050288q.
Gwon JG, Lee SY, Doh GH, Kim JH. Characterization of chemically modified wood fibers using FTIR spectroscopy for biocomposites. J Appl Polym Sci. 2010;116(6):3212–9. doi:10.1002/App.31746.
Yang B, Dai Z, Ding S-Y, Wyman CE. Enzymatic hydrolysis of cellulosic biomass. Biofuels. 2011;2(4):421–49. doi:10.4155/bfs.11.116.
Murozuka E, Laursen KH, Lindedam J, Shield IF, Bruun S, Magid J, et al. Nitrogen fertilization affects silicon concentration, cell wall composition and biofuel potential of wheat straw. Biomass Bioenerg. 2014;64:291–8. doi:10.1016/j.biombioe.2014.03.034.
Lindedam J, Bruun S, Jorgensen H, Decker SR, Turner GB, DeMartini JD, et al. Evaluation of high throughput screening methods in picking up differences between cultivars of lignocellulosic biomass for ethanol production. Biomass Bioenerg. 2014;66:261–7. doi:10.1016/j.biombioe.2014.03.006.
Savitzky A, Golay MJE. Smoothing and differentiation of data by simplified least squares procedures. Anal Chem. 1964;36(8):1627–39. doi:10.1021/Ac60214a047.
Martens H, Martens M. Modified jack-knife estimation of parameter uncertainty in bilinear modelling by partial least squares regression (PLSR). Food Qual Prefer. 2000;11(1–2):5–16. doi:10.1016/S0950-3293(99)00039-7.
Chen H, Ferrari C, Angiuli M, Yao J, Raspi C, Bramanti E. Qualitative and quantitative analysis of wood samples by Fourier transform infrared spectroscopy and multivariate analysis. Carbohydrate Polymers. 2010;82:772–8.
The research leading to these results has received funding from the People Programme (Marie Curie Actions) of the European Union's Seventh Framework Programme FP7/2007-2013/ in the ReUseWaste project under REA grant agreement n° 289887. This material reflects only the authors' views, and the European Union is not liable for any use that may be made of the information contained therein. The collection of straw was initiated through the OPUS project funded by the Danish Strategic Research Council (grant no. 2117-05-0064). Support for the development of the high-throughput pretreatment and enzyme hydrolysis work was provided by the BioEnergy Science Center. The BioEnergy Science Center is a U.S. Department of Energy Bioenergy Research Center supported by the Office of Biological and Environmental Research in the DOE Office of Science. The National Renewable Energy Laboratory (NREL) is a national laboratory of the US DOE Office of Energy Efficiency and Renewable Energy, operated for DOE by the Alliance for Sustainable Energy, LLC. This work was supported by the U.S. Department of Energy under Contract No. DE-AC36-08-GO28308 with the National Renewable Energy Laboratory.
Department of Plant and Environmental Sciences, Faculty of Science, University of Copenhagen, Thorvaldsensvej 40, Frederiksberg, C DK-1871, Denmark
Georgios Bekiaris, Jane Lindedam, Clément Peltre, Jakob Magid & Sander Bruun
National Renewable Energy Laboratory, Biosciences Center, 15013 Denver West Parkway, Golden, Colorado, 80401, USA
Stephen R. Decker & Geoffrey B. Turner
Georgios Bekiaris
Jane Lindedam
Clément Peltre
Stephen R. Decker
Geoffrey B. Turner
Jakob Magid
Sander Bruun
Correspondence to Sander Bruun.
GB performed the FTIR-PAS analysis, the multivariate analysis and drafted the manuscript; SB contributed to the design of the experiment, sample collection, interpretation and the multivariate analysis of the data and the critical revision of the manuscript; JL contributed to the experimental design, sample collection and the interpretation of the obtained data and reviewed the manuscript; SRD and GBT conducted the HTP analysis and contributed to the interpretation of the data and reviewed the manuscript; CP contributed into the multivariate analysis and the interpretation of the obtained spectra and reviewed the manuscript; JM contributed to the conception of the initial experiment and reviewed the manuscript; All authors read and approved the final manuscript.
Additional file 1:
Regression coefficients from the prediction of glucose and xylose release before the division of the calibration set into three smaller subsets. Spectral regions with a significant contribution in the prediction of glucose (A) and xylose (B) release during bioethanol production.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
The Creative Commons Public Domain Dedication waiver (https://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated in a credit line to the data.
Bekiaris, G., Lindedam, J., Peltre, C. et al. Rapid estimation of sugar release from winter wheat straw during bioethanol production using FTIR-photoacoustic spectroscopy. Biotechnol Biofuels 8, 85 (2015). https://doi.org/10.1186/s13068-015-0267-2
Bioethanol production
High-throughput assay
Enzymatic hydrolysis
Advanced chemometrics | CommonCrawl |
Identification and characterization of immunomodulatory peptides from pepsin–soy protein hydrolysates
Lu-Sheng Hsieh1 na1,
Ming-Shing Lu1 na1 &
Wen-Dee Chiang ORCID: orcid.org/0000-0002-1689-66281
To obtain immunomodulatory peptides from isolated soy protein (ISP), pepsin was selected to prepare hydrolysates and 4-h treatment (Pepsin-ISPH4h) showed the highest yield and immunomodulatory activities. The Pepsin-ISPH4h was sequentially fractionated by 30, 10 and 1-kDa molecular weight cut-off (MWCO) membranes, in which 1-kDa MWCO permeate (1P) exhibited the most significant enhancement of phagocytosis activity without causing excessive inflammation as compared with Pepsin-ISPH4h. To further purify and enhance the immunomodulatory activity, 1P was distinct by high-performance liquid chromatography equipped with a reverse-phase column and in vivo immunomodulatory activity of fractions was examined in mice. Fraction 1 (F1) significantly elevated phagocytosis activity of mice spleen macrophages and neutrophils. However, increase of phagocytosis activity did not result from the induction of macrophages M1 or M2 polarization. The immunomodulatory peptide sequence, EKPQQQSSRRGS, from F1 was identified by LC–MS/MS. Phagocytosis activity and macrophage M1 polarization were elevated by synthetic peptide treatment. Hence, our results indicated that isolated soy protein hydrolysates prepared by pepsin could provide a source of peptides with immunomodulatory effects.
Human immunity is influenced by many factors such as age, dietary habit, exercise, stress, and so on (Hamer et al. 2012; Marques et al. 2015). Busy life style causes imbalanced immune modulations in people of modern world; therefore, maintaining normal daily life style as well as supplementing immune modulators can rectify immune imbalance (Santiago-López et al. 2016; Yu et al. 2018; Polak et al. 2021). The studies of protein enzymatic hydrolysates are initially focused on improving dietary and nutritional functions (Adler-Nissen 1986), for example human gut intestinal systems absorb small peptides (dipeptide or tripeptide) better than free amino acids (Ziegler et al. 1990; Siemensma et al. 1993; Bueno-Gavilá et al. 2021; Zaky et al. 2022). Recently, immunomodulatory peptides showed beneficial effects on human health are prepared from food-based proteins such as chum salmon (Yang et al. 2009), Alasaka pollock (Hou et al. 2012), rohu egg (Chalamaiah et al. 2014, 2018), wheat germ globulin (Wu et al. 2017), rice (Fang et al. 2019), false starwort (Pseudostellaria heterophylla; Yang et al. 2020), duck egg ovalbumin (He et al. 2021), and Stevia rebaudiana (Li et al. 2021), implying that an increasing number of scientists are attracted and devoted into this research field.
The primary function of mammalian immune system is to prevent contagious illnesses by building up a complicate firewall by cells and proteins (Bayne 2013), and can be divided into innate and adaptive immune systems (Iwasaki and Medzhitov 2015). Macrophages and neutrophils are endocytic defense cells of innate immune system that can nonspecifically engulf external pathogens and trigger inflammation responses by releasing NO and cytokines (Gordon 2016). Proper inflammation response can help human body to defense invasions of pathogens; however, hyperinflammation may cause tissues damages (Ginderachter et al. 2006). Cytokines, such as interleukin-6 (IL-6), interleukin-10 (IL-10), and tumor necrosis factor-α (TNF-α), are tiny proteins, modulating the growth and functions of immune cells (Kim et al. 2008; Ahn et al. 2015). Macrophage cells can further polarize into M1 and M2 types, in which M1 cells can produce high amount of pro-inflammatory cytokines and reactive oxygen species to promote inflammation, whereas M2 cells secrete anti-inflammatory cytokine, IL-10, to repair damaged tissues (Murray et al. 2014).
Soybean (Glycine max L.) protein is an important source with properties of high yield, low price, high nutritive value, and broad applications (Ricker et al. 2004; Coscueta et al. 2019; Akbarian et al. 2022). Peptides identified from soy protein hydrolysates have shown functions of anti-oxidation (Ranamukhaarachchi et al. 2013; Ashaolu 2020), stimulating lipolysis (Tsou et al. 2012), anti-angiotensin I-converting enzyme activity (Rho et al. 2009), and immunomodulatory effects (Egusa and Otani 2009; Dia et al. 2014; Zhang et al. 2021). The goal of this study was to isolate and purify immunomodulatory peptides from pepsin-isolated soy protein hydrolysates (Pepsin-ISPH) using a combination of molecular weight cut-off module and reverse-phase high-performance liquid chromatography. Peptides were further identified by mass spectrometry and synthetic peptides were used for investigating its mechanisms of immunomodulation functions.
Materials and chemical reagents
Isolated soy protein (ISP) and NEW Soy 88 were purchased from Gemfont Co., Taipei, Taiwan. Pepsin from porcine gastric mucosa, sodium dodecyl sulfate (SDS), o-phthalaldehyde (OPA), Leu-Gly dipeptide, lipopolysaccharide (LPS), dimethyl sulfoxide (DMSO), sodium carbonate (NaHCO3), and 3-(4,5-dimethylthiazol-2-yl)-2,5-diphenyltetrazolium bromide (MTT) were obtained from MilliporeSigma, Darmstadt, Germany. Dulbecco's modified Eagle medium (DMEM) was purchased from Gibco, TX, USA. l-Glutamate and charcoal/dextran-treated fetal bovine serum (FBS) were obtained from Biological Industries, CT, USA. Molecular weight cut-off (MWCO) membranes, ER 30 kDa, PW 10 kDa, and GE 1 kDa, were obtained from Osmonics Inc., MN, USA. All chemical reagents used were American Chemistry Society (ACS) grade or better.
Preparation of enzymatic hydrolysate, measurement of hydrolysis ratio, and determination of soluble nitrogen by Kjeldahl method
The 2.5% (w/v) ISP was dissolved in 0.2 M phosphate buffer (pH 2.0) and digested by pepsin (S:E ratio = 100:1) at 37 °C. Hydrolysates of isolated soy protein (ISPH) were collected at 0, 0.5, 1, 2, 4, and 6 h, then pepsin was inactivated by boiling for 15 min followed by storing at − 20 °C until use.
The degree of hydrolysis (DH) was measured by OPA method using the dipeptide, Leu-Gly, as standard (Nielson et al. 2001). DH (%) was indicated as:
$$\mathrm{DH }\left(\mathrm{\%}\right)=\frac{{H}_{\mathrm{sample}}}{{H}_{\mathrm{total}}} \times 100\%.$$
Hsample represents α-amino group concentration (mmol/mL); Htotal represents total peptide number of ISPH (7.8 mEq α-amino group/g).
The soluble nitrogen of hydrolysate was prepared by adding 20% (w/v) trichloroacetic acid, and its nitrogen content was estimated by Kjeldahl method according to Tsou et al. (2012). Yield (N mg/mL) was indicated as:
$$\mathrm{Yield }\left(N\mathrm{ mg}/\mathrm{mL}\right)=\frac{\left(V1-V2\right) \times C \times 14}{\mathrm{Sample volume }(\mathrm{mL})}.$$
V1: titration volume of sample (mL); V2: titration volume of blank (mL); C: concentration of HCl (0.1 N × titer); 14: atomic mass of nitrogen.
Fractionation of hydrolysate by molecular weight cut-off
Hydrolysate of 4-h pepsin-treated isolated soy protein (Pepsin-ISPH4h) was sequentially fractionated by a membrane MWCO module with 30 kDa, 10 kDa, and 1 kDa to obtain retentates and permeates. One volume of Pepsin-ISPH4h was initially filtered by a 30-kDa MWCO membrane to acquire 1:9 ratio of retentates (30R) and permeates. The 30-kDa permeate was then filtered by a 10-kDa MWCO membrane to acquire 1:9 ratio of retentates (10R) and permeates. The 10-kDa permeate was then filtered by a 1-kDa MWCO membrane to acquire 1:9 ratio of retentates (1R) and permeates (1P).
Fractionation of 1P fraction by reverse-phase HPLC
Fraction 1P was further fractionated using a reverse-phase high-performance liquid chromatography applied on an InertSustain® C18 column (10 × 250 mm, 5 μm, GL Sciences, Japan) with a linear gradient of acetonitrile from 0 to 45% in 45 min at a flow rate of 2 mL/min. The elution signals were monitored at 214 nm.
Culture of mouse macrophage cells
Mouse macrophage RAW264.7 cell line was obtained from Bioresource Collection and Research Center (BCRC 60001), Hsinchu, Taiwan. Cells were grown in DMEM medium supplemented with 10% FBS, 1.6 g/L NaHCO3, and 2 mM l-glutamine, maintaining in a 5% CO2 incubator at 37 °C. Cells were subcultured every 48–72 h, and discarded after 50 generations.
Cell viability—MTT test
The cytotoxicity activity against RAW264.7 macrophage was investigated by MTT assay (Mosmann et al. 1983; Tsou et al. 2012). Cells were cultured in a 96-well microtiter plate (1 × 105 cells/well) for 24 h followed by incubating with various ISPH for 24 h. Cells were washed with phosphate buffer saline (PBS) and then incubated with MTT solution (0.5 mg/mL) at 37 °C for 4 h. Methanol treatment was used as negative control. DMSO solution was applied to resuspend the MTT formazan for 20 min. The absorbance was determined at 595 nm using a microtiter plate reader (BioTek, VT, USA). Cell viability (%) was indicated as:
$$\mathrm{Cell viability }\left(\mathrm{\%}\right)=\frac{{({\mathrm{OD}}_{\mathrm{sample}}-\mathrm{OD}}_{\mathrm{methanol}})}{{({\mathrm{OD}}_{\mathrm{control}}-\mathrm{OD}}_{\mathrm{methanol}})} \times 100\%.$$
ODsample: absorbance at 595 nm of sample; ODcontrol: absorbance at 595 nm of untreated sample as control; ODmethanol: absorbance at 595 nm of sample treated with methanol as negative control.
Determination of nitrogen oxide production
The NO production was measured by Griess assay (Ahn et al. 2015). RAW264.7 macrophage cells were cultured in a 96-well microtiter plate (1 × 105 cells/well) for 24 h followed by incubated with 1 ppm LPS and/or various ISPH for 24 h. After treatment, 50 μL culture medium was mixed with 50 μL Griess reagent and then incubated in dark place for 10 min. The absorbance of the mixture was determined at 550 nm using a Microtiter plate reader (BioTek, VT, USA). The concentration of NO was calculated using a standard curve generated from sodium nitrite dissolved in DMEM medium.
Phagocytosis assay
RAW264.7 macrophage cells were cultured in a 96-well microtiter plate (1 × 105 cells/well) for 24 h followed by incubated with various ISPH for 24 h. One ppm LPS treatment was used as positive control. E. coli BL21 cells transformed with pEGFP plasmid was added in a 96-well microtiter plate (5 × 106 cells/well) and centrifuged at 120g at 4 °C for 5 min to precipitate E. coli cells to be phagocytosed by macrophage for 2 h. Trypan blue regent (2 ×) was added in a 96-well microtiter plate and incubated for 2 min. Trypan blue was removed and fluorescence signal was measured with excitation wavelength at 485 nm and emission wavelength at 538 nm. Relative phagocytosis was indicated as:
$$\mathrm{Relative phagocytosis }\left(\mathrm{\%}\right)=\frac{{\mathrm{OD}}_{\mathrm{sample}}}{{\mathrm{OD}}_{\mathrm{LPS}}} \times 100\%.$$
Determination of pro-inflammatory cytokines in RAW246.7 macrophage cells stimulated by LPS
The levels of interleukin-6 (IL-6) and interleukin-10 (IL-10) were measured by mouse IL-6 and IL-10 Quantikine ELISA kits (R&D systems, MN, USA) following to the manufacturer's instruction. RAW264.7 macrophage cells were cultured in a 96-well microtiter plate (1 × 105 cells/well) for 24 h and culture media were stored at − 20 °C until use. Capture antibodies were coated onto 96-well microtiter plate at 4 °C overnight. After blocking, microtiter plate was washed three times and 100 μL/well standards or culture media were added and incubated at room temperature for 2 h. Microtiter plate was washed three times and then 100 μL/well detection antibodies were added and incubated at room temperature for 2 h. Microtiter plate was washed three times and then 100 μL/well streptavidin–HRP was added and incubated in dark for 20 min. Plate was washed three times and then 100 μL/well substrate solution was added and incubated in dark condition for 20 min. After incubation, 50 μL stop solution was added and the absorbance of the mixture was determined at 450 nm using a microtiter plate reader (BioTek, VT, USA). The concentrations of cytokinins were calculated using a standard curve generated from various concentrations of standards.
Mouse spleen cell endocytosis assay
Male C57BL/6J mouse (19 weeks) was injected intraperitoneally with 5 mg/kg samples, and killed three days after injection. Spleen was collected and placed in 5 mL YAC medium (RPMI 1640, 2.2 g/L NaHCO3, 2 mM l-glutamine, 10% FBS) and then ground with 200 mesh sieve. Supernatant was removed by centrifugation at 300g, 4 °C, for 10 min. Pellet/cell was kept and resuspended in 5 mL 0.1 × Hank's balanced salt solution (HBSS) to disrupt red blood cells and then added 10 mL HBSS. Supernatant was removed by centrifugation at 300g, 4 °C, for 10 min, and pellet/cell was resuspended in YAC medium and adjusted to 2 × 107 cells/mL by a FACSCalibur™ Flow Cytometer (BD Bioscience, NJ, USA). Spleen lymphocyte cells were cultured in a 96-well microtiter plate (1 × 105 cells/well) and BioParticles® FITC–Escherichia coli (2.5 × 106 cells/well) was added and incubated at 37 °C for 2 h. After removing supernatant, lymphocyte cells were mixed with 100 μL trypan blue and fluorescence signal was measured by FACSCalibur™ Flow Cytometer (BD Bioscience, NJ, USA). Positive fluorescence level was indicated as:
$$\mathrm{positive fluorescence level}=M1+M2\times 10+M3\times 100+M4\times 1000.$$
M1: percentage cell within 101 fluorescence signal; M2: percentage cell within 102 fluorescence signal; M3: percentage cell within 103 fluorescence signal; M4: percentage cell within 104 fluorescence signal.
Differentiation of M1 and M2 macrophages
Mouse spleen lymphocyte cells were harvested as mentioned previously. Surface biomarkers, PE-anti-mouse CD68, PE/Cy5-anti-mouse CD197, and FITC-anti-mouse CD206 antibodies, were obtained from Biolegend, CA, USA. Nine μL fluorescence conjugated antibodies were mixed with 50 μL cell suspensions and incubated at 4 °C in dark for 30 min. Cells were washed and resuspended in 200 μL analysis buffer (RPMI 1640, 5% FBS, 2 mM l-glutamate, and 2 × Dulbecco's phosphate buffer saline). Two differentiated cells, M1 (CD68+/CD197+) and M2 (CD68+/CD206+) were analyzed using a FACSCalibur™ Flow Cytometer (BD Bioscience, NJ, USA).
Identification of anti-inflammatory peptide by LC–MS/MS and peptide synthesis
Amino acid sequence identification of anti-inflammation peptide was analyzed by UPLC (UltiMate 3000, ThermoFisher, MA, USA) followed by quadruple tandem ion trap mass spectrometer (Q-TOF/MS/MS; Bruker micrOTOF-Q III, Bruker Daltonic, Germany) equipped with an electrospray ionization source in Center of Precision Instrument, Tunghai University, Taichung, Taiwan. Immunomodulatory peptides isolated from pepsin–soybean hydrolysate were chemically synthesized by Yao Hong Biotechnology Inc., New Taipei City, Taiwan. Peptides, 5 mg/kg and 25 mg/kg, were used in endocytosis assay and macrophage phenotype assay, respectively.
Results were expressed as mean ± standard deviation (SD) and analyzed using Statistical Analysis System (SAS/STAT® software, NC, USA). Mean with different letters were labeled as significantly different (p < 0.05) by Duncan's multiple range test.
Effect of pepsin hydrolysis of ISP on phagocytosis, NO formation, and cell viability in RAW264.7 macrophage cells
Degree of enzymatic hydrolysis has been shown to influence functions of peptides (Jamdar et al. 2010; Liu et al. 2010; Tsou et al. 2012). To investigate immunomodulatory effects of soy protein hydrolysate, hydrolysates (Pepsin-ISPH) were obtained with the degree of hydrolysis (DH, %) of 4.8%, 6.5%, 6.6%, 7.1%, and 8.9% together with yield of 0.64, 0.95, 1.2, 1.42, and 1.56 mg nitrogen per mL, respectively (Fig. 1A). The DH of Pepsin-ISPH was positively correlated to yield in peptic hydrolysis time; the result was similar to previous studies (Jamdar et al. 2010; Liu et al. 2010; Tsou et al. 2012; Toopcham et al. 2017). In terms of phagocytosis activity, Pepsin-ISPH from 0.5 to 4 h, were 1.3-fold higher than that of LPS-treated RAW264.7 macrophage cells, whereas Pepsin-ISPH6h only showed slightly 1.1-fold increase (Fig. 1B). NO formation (Fig. 1C) and cell viability (Fig. 1D) were monitored in LPS and Pepsin-ISPH-treated RAW264.7 macrophage cells. NO was significantly produced in LPS-treated RAW264.7 macrophage cells (Dia et al. 2014; Ahn et al. 2015; Li et al. 2021); however, significant effects were not observed in pepsin hydrolysates-treated RAW264.7 macrophage cells (Fig. 1C). According to MTT assay on cell viability (Fig. 1D), Pepsin-ISPH in the ranges from 10 to 4000 ppm was not toxic to RAW264.7 macrophage cells (Fang et al. 2019; Lee et al. 2021). Next, hydrolysate of isolated soy protein digested with pepsin for 4 h (Pepsin-ISPH4h) was used to further fractionation to enrich the ability of immunomodulation.
Preparation of pepsin-isolated soy protein hydrolysate (Pepsin-ISPH). A effect of different hydrolysis time of isolated soy protein hydrolysate by pepsin on degree of hydrolysis (●) and yield (○) in terms of TCA soluble nitrogen. B effect of 4000 ppm Pepsin-ISPH with different hydrolysis time on relative phagocytosis (%) in mouse RAW246.7 macrophages. C effect of 4000 ppm Pepsin-ISPH with different hydrolysis time on relative phagocytosis (%) in mouse RAW246.7 macrophages. D dosage effect of Pepsin-ISPH4h on cell viability (%) in mouse RAW246.7 macrophages. LPS (1 ppm) was used as positive control. Bars represent mean ± standard deviation (SD; n = 3). Mean with different letters are significantly different (p < 0.05) by Duncan's multiple range test
Effect of pepsin-ISPH separated by different MWCO membranes on phagocytosis, NO formation, and cell viability in RAW264.7 macrophage cells
Pepsin-ISPH4h was sequentially fractionated using a membrane MWCO module with three different molecular weights, 30 kDa, 10 kDa, and 1 kDa, to acquire three retentates and one permeate fractions, namely 30R, 10R, 1R, and 1P (Fig. 2A), for further enhancing its immunomodulatory activity (Tsou et al. 2012). Next, the effects of phagocytosis of mouse macrophage cells were examined (Fig. 2B). The phagocytosis ability of the 4000 ppm 1P-treated RAW264.7 macrophage cells was slightly higher than that of LPS-treated control cells, suggesting that peptides in the 1P fraction can boost the function of RAW264.7 macrophage cells. To examine the dosage effects on NO formation, RAW264.7 macrophage cells were treated with 2000 ppm (Fig. 2C) or 4000 ppm (Fig. 2D) hydrolysate, and LPS treatment was used as positive control. Likewise, NO was significantly produced in LPS-treated RAW264.7 macrophage cells (Fig. 2C, D). NO formation by 1P treatment was increased in a dosage-dependent manner (Fig. 2C, D), indicating that peptide(s) in 1P fraction can induce NO formation in RAW264.7 macrophage cells. Previous studies had shown that proper NO formation can help immune system and macrophages to destroy tumor cells as well as invasive pathogens (Zheng et al. 2014; Fang et al. 2019; Li et al. 2021); moreover, NO formation in over 2000 ppm dosage of the 1P fraction-treated macrophages were not correlated to negative inflammation reaction (Fig. 2C). As a result, the 1P fraction was used for further fractionation to enrich the ability of immunomodulation effects.
Fractionation of Pepsin-ISPH by molecular weight cut-off (MWCO) membrane. A fraction chart. B effect of 4000 ppm Pepsin-ISPH and its retentates/permeate on relative phagocytosis (%) in mouse macrophage RAW246.7 cells. Dosage effect of Pepsin-ISPH and its retentates/permeate, 2000 ppm (C) and 4000 ppm (D) on NO concentration in mouse macrophage RAW246.7 cells. LPS (1 ppm) was used as positive control. Bars represent mean ± standard deviation (SD; n = 3). Mean with different letters are significantly different (p < 0.05) by Duncan's multiple range test
Effect of 1-kDa permeate (1P) on phagocytosis, NO formation, cell viability, and pro-inflammatory cytokines production in RAW264.7 macrophage cells
To investigate the immunomodulation function of the 1-kDa permeate (1P), phagocytosis activity (Fig. 3A), cell viability (Fig. 3B) and NO formation in the absence (Fig. 3C) or presence (Fig. 3D) of LPS were used to estimate the optimum working concentration of the 1P fraction. In Fig. 3A, the maximum phagocytosis activity was monitored in the 4000 ppm 1P-treated RAW264.7 macrophage cells. Except 4000 ppm 1P treatment, cell viabilities were not influenced by 1P treatments from 10 to 2000 ppm (Fig. 3B). Furthermore, 4000 ppm 1P treatment led to remarkable NO formations with or without LPS (Fig. 3C, D).
Determination of anti-inflammatory activity of Pepsin-ISPH4h-1P fraction. Dosage effect of Pepsin-ISPH4h-1P on relative phagocytosis (%, A), cell viability (%, B), and NO formation in the absence (C) or presence (D) of 1 ppm LPS in mouse macrophage RAW246.7 cells. Bars represent mean ± standard deviation (SD; n = 3). Mean with different letters are significantly different (p < 0.05) by Duncan's multiple range test
Interleukin-6 (IL-6) and interleukin-10 (IL-10) are major pro-inflammatory cytokines production in macrophage cells (Ahn et al. 2015; Toopcham et al. 2017; Lee et al. 2021; Li et al. 2021). During inflammation response, cells can release a large amount of IL-6 to promote the formation of NO as well as to activate phagocytosis of macrophage cells (Minato and Abe 2013; Li et al. 2021), whereas IL-10 exhibits anti-inflammatory ability to reduce NO formation as well as to decrease inflammatory cytokinins secretions (Asadullah et al. 2003; Lee et al. 2021). To study the effect of the 1P fraction on cytokine production, RAW264.7 macrophage cells were treated with various dosages of the 1P fraction, and LPS treatment was used as positive control. The formation of IL-6 was intercorrelated to the increased concentrations of the 1P fraction (Fig. 4A); however, the amount of IL-10 was constantly induced by 1P treatments which was independent on its dosages (Fig. 4A). In addition, IL-6/IL-10 ratio was compared in LPS-treated cells and the maximum ratio was monitored in the 2000 ppm 1P-treated macrophage cells (Fig. 4B). The higher IL-6/IL-10 ratio indicated that cells were prone to inflammatory response (Song et al. 2016; Sapan et al. 2017; Koyama et al. 2021). As a result, 1P treatment cannot trigger severe inflammation response and was had no inhibitory effect on LPS-induced inflammatory effects. Also, similar results were reported in shark derived protein hydrolysate (Mallet et al. 2014) and rice proteins (Wen et al. 2021).
Determination of pro-inflammatory cytokines in LPS–Pepsin-ISP4h-1P-costimulated RAW264.7 macrophage cells. A dosage effect of Pepsin-ISPH4h-1P with 1 ppm LPS co-stimulation on IL-6 (gray column) and IL-10 (white column) productions. B dosage effect of Pepsin-ISPH4h-1P with 1 ppm LPS co-stimulation on IL-6/IL-10 ratio. Bars represent mean ± standard deviation (SD; n = 3). Mean with different letters are significantly different (p < 0.05) by Duncan's multiple range test
Effect of 1P fractions, F1–F3, on phagocytosis and polarization in RAW264.7 macrophage cells
Fraction 1P exhibited the immunomodulatory ability to promote cell phagocytosis was further separated by reverse-phase HPLC into three fractions (Fig. 5A). Based on its retention time, Fraction 1 (F1), Fraction 2 (F2), and Fraction 3 (F3) were in between 6 and 14 min, 14–21 min, and 21–35 min, respectively (Fig. 5A). For endocytosis activity assay, macrophage (Fig. 5B) and neutrophil cells (Fig. 5C) were harvested from mice spleens and then incubated with transgenic recombinant green fluorescence protein (GFP) produced E. coli cells (Gille et al. 2006). The fluorescent level was represented as the endocytosis activity (Jiang et al. 2007). As shown in Fig. 5C, F1 fraction significantly increased endocytosis activity in macrophage cells, whereas F2 and F3 fractions exhibited no influences as control. In addition, F1 treatment also enhanced endocytosis activity of neutrophil cells (Fig. 5D). Next, Pepsin-ISPH4h, 1P, and F1–F3 were injected intraperitoneally into mice and then spleen lymphocyte cells were harvested and differentiated cells, M1 (Fig. 5D) and M2 (Fig. 5E), were analyzed by a flow cytometer (Kim et al. 2019). Macrophage M1 cells produces NO or reactive oxygen intermediates to defense bacteria or viruses infection; M2 cells secrete certain cytokines, IL-4 or IL-10, mediating damaged tissues repair (Murray et al. 2014; Rőszer 2015; Kim et al. 2019). Macrophages M1 and M2 polarization were not affected by all pepsin hydrolysates treatments (Fig. 5D, E). Taken together, F1 fraction can increase phagocytosis activities in both mice spleen macrophage and neutrophil cells, but it cannot induce macrophages M1 or M2 polarization.
Determation of anti-inflammatory activity of Pepsin-ISPH4h-1P fractions. A Pepsin-ISPH-4 h-1P was fractionated into F1–F3 using a reverse-phase high-performance liquid chromatography. Effects of Pepsin-ISPH4h, Pepsin-ISP4h-1P, and F1–F3 fractions on positive fluorescent level in macrophages (B), neutrophil (C), M1 (D) or M2 (E) phenotype polarization in mouse spleen in vivo. Bars represent mean ± standard deviation (SD; n = 3). Mean with different letters are significantly different (p < 0.05) by Duncan's multiple range test
Identification of anti-inflammatory peptides by LC–MS/MS from F1 fraction and investigation of synthetic peptide on phagocytosis and polarization of macrophage
Previous studies had shown that peptides with positive charged amino acids are intercorrelated with immunomodulatory functions (Mercier et al. 2004; Kong et al. 2008; Jacquot et al. 2010; Hou et al. 2012; Hemshekhar et al. 2019). In this study, liquid chromatography with tandem mass spectrometry (LC–MS–MS) was used for peptide identification (Dia et al. 2014; Fang et al. 2019; Li et al. 2021; Wen et al. 2021). Two peptides with positively charged amino acids, EKPQQQSSRRGS (Fig. 6A) and VVQGKGAIGFAFP, were identified from F1 fraction by LC–MS–MS analysis. Accordingly, synthetic peptide 1 (SP1, EKPQQQSSRRGS) and synthetic peptide 2 (SP2, VVQGKGAIGFAFP) were used to examine its in vivo immunomodulatory effects in mice (Wen et al. 2021). Both synthetic peptides treatments showed no effect on M1 macrophage polarization (data not shown). In macrophage endocytosis analysis, the stimulating effect of the SP1 peptide was better than that of the F1 and SP2 (Fig. 6B). In macrophage polarization analysis, SP1 showed induction effect on M1 macrophage polarization, whereas F1 and SP2 had no effect on that (Fig. 6C). As a result, positive immunomodulatory activities were confirmed in synthetic peptide.
Peptide identified from Pepsin-ISPH4h-1P F1 fraction. A the mass spectrum of a peptide, EKPQQQSSRRGS, identified by LC–MS–MS. Effects of the synthetic peptides, EKPQQQSSRRGS (SP1) and VVQGKGAIGFAFP (SP2), on positive fluorescent level in macrophages (B), and M1 (C) phenotype polarization in mouse spleen in vivo. Bars represent mean ± standard deviation (SD; n = 3). Mean with different letters are significantly different (p < 0.05) by Duncan's multiple range test
In this study, pepsin-treated isolated soy protein hydrolysates exhibited immunomodulatory effects such as enhancing phagocytosis activity and not causing excessive inflammatory response. Putative peptides from isolated soy protein hydrolysate by peptic hydrolysis were purified using MWCO and reverse-phase chromatography technique. Two peptides were identified by mass spectrometry. Further studies revealed that the synthetic peptide, EKPQQQSSRRGS, can increase phagocytosis activity in mice spleen macrophage cells as well as can induce macrophages M1 polarization. Taken together, this study can serve as a fundamental basis for the preparation of immunomodulatory peptides from isolated soy proteins.
Data are contained in the main material.
ISPH:
Isolated soy protein hydrolysate
MWCO:
Molecular weight cut-off
Permeate
LPS:
Lipopolysaccharide
IL:
TNF-α:
Tumor necrosis factor-α
Sodium dodecyl sulfate
OPA:
O-Phthalaldehyde
DMSO:
Dimethyl sulfoxide
MTT:
3-(4,5-Dimethylthiazol-2-yl)-2,5-diphenyltetrazolium bromide
DMEM:
Dulbecco's modified Eagle medium
Fetal bovine serum
DH:
Degree of hydrolysis
BCRC:
Bioresource Collection and Research Center
PBS:
Phosphate buffer saline
HBSS:
Hank's balanced salt solution
GFP:
Green fluorescence protein
SP:
Synthetic peptide
Adler-Nissen J (1986) Some fundamental aspects of food protein hydrolysis. Enzymic hydrolysis of food proteins. Elsevier Applied Science Publishers, London, pp 9–24
Ahn C-B, Cho Y-S, Je J-Y (2015) Purification and anti-inflammatory action of tripeptide from salmon pectoral fin byproduct protein hydrolysate. Food Chem 168:151–156. https://doi.org/10.1016/j.foodchem.2014.05.112
Akbarian M, Khani A, Eghbalpour S, Uversky VN (2022) Bioactive peptides: synthesis, sources, applications, and proposed mechanisms. Int J Mol Sci 23:1445. https://doi.org/10.3390/ijms23031445
Asadullah K, Sterry W, Volk HD (2003) Interleukin-10 therapy—review of a new approach. Pharmacol Rev 55:241–269. https://doi.org/10.1124/pr.55.2.4
Ashaolu TJ (2020) Health applications of soy protein hydrolysis. Int J Pept Res Ther 26:2333–2343. https://doi.org/10.1007/s10989-020-10018-6
Bayne CJ (2013) Origins and evolutionary relationships between the innate and adaptive arms of immune systems. Integr Comp Biol 43:293–299. https://doi.org/10.1093/icb/43.2.293
Bueno-Gavilá E, Abellán A, Girón-Rodríguez F, María Cayuela J, Tejada L (2021) Bioactivity of hydrolysates obtained from chicken egg ovalbumin using artichoke (Cynara scolymus L.) proteases. Foods 10:246. https://doi.org/10.3390/foods10020246
Chalamaiah M, Hemalatha R, Jyothirmayi T, Diwan PV, Uday Kumar P, Nimgulkar C, Dinesh Kumar B (2014) Immunomodulatory effects of protein hydrolysates from rohu (Labeo rohita) egg (roe) in BALB/c mice. Food Res Int 62:1051–1061. https://doi.org/10.1016/j.foodres.2014.05.050
Chalamaiah M, Yu W, Wu J (2018) Immunomodulatory and anticancer protein hydrolysates (peptides) from food proteins: a review. Food Chem 245:205–222. https://doi.org/10.1016/j.foodchem.2017.10.087
Coscueta ER, Campos DA, Osório H, Nerli BB, Pintado M (2019) Enzymatic soy protein hydrolysis: a tool for biofunctional food ingredient production. Food Chem X 1:100006. https://doi.org/10.1016/j.fochx.2019.100006
Dia VP, Bringe NA, de Mejia EG (2014) Peptides in pepsin-pancreatin hydrolysates from commercially available soy products that inhibit lipopolysaccharide-induced inflammation in macrophages. Food Chem 152:423–431. https://doi.org/10.1016/j.foodchem.2013.11.155
Egusa S, Otani H (2009) Soybean protein fraction digested with neutral protease preparation, "Peptidase R", produced by Rhizopus oryzae, stimulates innate cellular immune system in mouse. Int Immunopharmacol 9:931–936. https://doi.org/10.1016/j.intimp.2009.03.020
Fang Y, Pan X, Zhao E, Shi Y, Shen X, Wu J, Pei F, Hu Q, Qiu W (2019) Isolation and identification of immunomodulatory selenium-containing peptides from selenium-enriched rice protein hydrolysates. Food Chem 275:696–702. https://doi.org/10.1016/j.foodchem.2018.09.115
Gille C, Spring B, Tewes L, Poets CF, Orlikowsky T (2006) A new method to quantify phagocytosis and intracellular degradation using green fluorescent protein-labeled Escherichia coli: comparison of cord blood macrophages and peripheral blood macrophages of healthy adults. Cytometry A 69:152–154. https://doi.org/10.1002/cyto.a.20222
Gordon S (2016) Phagocytosis: an immunological process. Immunity 44:463–475. https://doi.org/10.1016/j.immuni.2016.02.026
Hamer M, Endrighi R, Poole L (2012) Physical activity, stress reduction, and mood: insight into immunological mechanisms. Methods Mol Biol 934:89–102. https://doi.org/10.1007/978-1-62703-071-7_5
He P, Wang Q, Zhan Q, Pan L, Xin X, Wu H, Zhang M (2021) Purification and characterization of immunomodulatory peptides from enzymatic hydrolysates of duck egg ovalbumin. Food Funct 12:668–681. https://doi.org/10.1039/D0FO02674C
Hemshekhar M, Faiyae S, Faiyaz S, Choi K-YG, Krokhin OV, Mookherjee N (2019) Immunomodulatory functions of the human cathelicidin LL-37 (aa 13–31)-derived peptides are associated with predicted α-helical propensity and hydrophobic index. Biomolecules 9:501. https://doi.org/10.3390/biom9090501
Article CAS PubMed Central Google Scholar
Hou H, Fan Y, Li B, Xue C, Yu G, Zhang Z, Zhao X (2012) Purification and identification of immunomodulatory peptides from enzymatic hydrolysates of Alaska pollock frame. Food Chem 134:821–828. https://doi.org/10.1016/j.foodchem.2012.02.186
Iwasaki A, Medzhitov R (2015) Control of adaptive immunity by the innate immune system. Nat Immunol 16:343–353. https://doi.org/10.1038/ni.3123
Jacquot A, Gauthier SF, Drouin R, Boutin Y (2010) Proliferative effects of synthetic peptides from β-lactoglobulin and α-lactalbumin on murine splenocytes. Int Dairy J 20:514–521. https://doi.org/10.1016/j.idairyj.2010.02.013
Jamdar SN, Rajalakshmi V, Pednekar MD, Juan F, Yardi V, Sharma A (2010) Influence of degree of hydrolysis on functional properties, antioxidant activity and ACE inhibitory activity of peanut protein hydrolysate. Food Chem 121:178–184. https://doi.org/10.1016/j.foodchem.2009.12.027
Jiang H, Zhang J, Shi B-Z, Xu Y-H, Li Z-H, Gu J-R (2007) Application of EGFP-EGF fusions to explore mechanism of endocytosis of epidermal growth factor. Acta Pharmacol Sin 28:111–117. https://doi.org/10.1111/j.1745-7254.2007.00481.x
Kim JY, Kim TH, Kim SS (2008) Anti-inflammatory effect of a human prothrombin fragment-2-derived peptide, NSA9, in EOC2 microglia. Biochem Biophys Res Commun 368:779–785. https://doi.org/10.1016/j.bbrc.2008.01.142
Kim H, Wang SY, Kwak G, Yang Y, Kwon IC, Kim SH (2019) Exosome-guided phenotypic switch of M1 to M2 macrophages for cutaneous wound healing. Adv Sci 6:1900513. https://doi.org/10.1002/advs.201900513
Kong X, Guo M, Hua Y, Cao D, Zhang C (2008) Enzymatic preparation of immunomodulating hydrolysates from soy proteins. Bioresour Technol 99:8873–8879. https://doi.org/10.1016/j.biotech.2008.04.056
Koyama T, Uchida K, Fukushima K, Ohashi Y, Uchiyama K, Inoue G, Takahira N, Takaso M (2021) Elevated levels of TNF-α, IL-1β and IL-6 in the synovial tissue of patients with labral tear: a comparative study with hip osteoarthritis. BMC Musculoskelet Disord 22:33. https://doi.org/10.1186/s12891-020-03888-w
Lee SM, Son K-N, Shah D, Ali M, Balasubramaniam A, Shukla D (2021) Histatin-1 attenuates LPS-induced inflammatory signaling in RAW264.7 macrophages. Int J Mol Sci 22:7856. https://doi.org/10.3390/ijms22157856
Li Z, An L, Zhang S, Shi Z, Bao J, Tuerhong M, Abudukeremu M, Xu J, Guo Y (2021) Structural elucidation and immunomodulatory evaluation of a polysaccharide from Stevia rebaudiana leaves. Food Chem 364:130310. https://doi.org/10.1016/j.foodchem.2021.130310
Liu Q, Kong B, Xiong YL, Xia X (2010) Antioxidant activity and functional properties of porcine plasma protein hydrolysate as influenced by the degree of hydrolysis. Food Chem 118:403–410. https://doi.org/10.1016/j.foodchem.2009.05.013
Mallet J-F, Duarte J, Vinderola G, Anguenot R, Beaulieu M, Matar C (2014) The immunopotentiating effects of shark-derived protein hydrolysate. Nutrition 30:706–712. https://doi.org/10.1016/j.nut.2013.10.025
Marques AH, Bjørke-Monsen A-L, Teixeira AL, Silverman MN (2015) Maternal stress, nutrition and physical activity: impact on immune function, CNS development and psychopathology. Brain Res 1617:28–46. https://doi.org/10.1016/j.brainres.2014.10.051
Mercier A, Gauthier SF, Fliss I (2004) Immunomodulating effects of whey proteins and their enzymatic digests. Int Dairy J 14:175–183. https://doi.org/10.1016/j.idairyj.2003.08.003
Minato KI, Abe C (2013) Chapter 17—immunomodulating effect of immodulating effect of polysaccharide. In: Preedy V (ed) Bioactive food as dietary interventions for arthritis and related inflammatory diseases. Elsevier, Amsterdam, pp 241–250
Mosmann T (1983) Rapid colorimetric assay for cellular growth and survival: application to proliferation and cytotoxicity. J Immunol Methods 65:55–63. https://doi.org/10.1016/0022-1759(83)90303-4
Murray PJ, Allen JE, Biswas SK, Fisher EA, Gilroy DW, Goerdt S, Gordon S, Hamilton JA, Ivashkiv LB, Lawrence T, Locati M, Mantovani A, Martinez FO, Mege J-L, Mosser DM, Natoli G, Saeij JP, Schultze JL, Shirey KA, Sica A, Suttles J, Udalova I, van Ginderachter JA, Vogel SN, Wynn TA (2014) Macrophage activation and polarization: nomenclature and experimental guidelines. Immunity 41:14–20. https://doi.org/10.1016/j.immuni.2014.06.008
Nielson P, Petersen D, Dambmann C (2001) Improved method for determining food protein degree of hydrolysis. J Food Sci 66:642–646. https://doi.org/10.1111/j.1365-2621.2001.tb04614.x
Polak E, Stępień AE, Gol O, Tabarkiewicz J (2021) Potential immunomodulatory effects from consumption of nutrients in whole foods and supplements on the frequency and course of infection: preliminary results. Nutrients 13:1157. https://doi.org/10.3390/nu13041157
Ranamukhaarachchi S, Meissner L, Moresoli C (2013) Production of antioxidant soy protein hydrolysates by sequential ultrafiltration and nanofiltration. J Membr Sci 429:81–87. https://doi.org/10.1016/j.memsci.2012.10.040
Rho SJ, Lee JS, Chung YI, Kim YW, Lee HG (2009) Purification and identification of an angiotensin I-converting enzyme inhibitory peptide from fermented soybean extract. Process Biochem 44:490–493. https://doi.org/10.1016/j.procbio.2008.12.017
Ricker D, Johnson L, Murphy P (2004) Functional properties of improved glycinin and β-nglycinin fractions. J Food Sci 69:303–311. https://doi.org/10.1111/j.1365-2621.2004.tb06332.x
Rőszer T (2015) Understanding the mysterious M2 macrophage through activation markers and effector mechanisms. Mediat Inflamm 2015:816460. https://doi.org/10.1155/2015/816460
Santiago-López L, Hernández-Mendoza A, Vallejo-Cordoba B, Mata-Haro V, González-Córdova AF (2016) Food-derived immunomodulatory peptides. J Sci Food Agric 96:3631–3641. https://doi.org/10.1002/jsfa.7697
Sapan HB, Paturusi I, Islam AA, Yusuf I, Patellongi I, Massi MN, Pusponegoro AD, Arief SK, Labeda I, Rendy L, Hatta M (2017) Interleukin-6 and interleukin-10 plasma levels and mRNA expression in polytrauma patients. Chin J Traumatol 20:318–322. https://doi.org/10.1016/j.cjtee.2017.05.003
Siemensma AD, Weijer WJ, Bak HJ (1993) The importance of peptide lengths in hypoallergenic infant formulae. Trends Food Sci Technol 4:16–21. https://doi.org/10.1016/S0924-2244(05)80006-8
Song Y, Zhang W, Zhang L, Wu W, Zhang Y, Han X, Yang C, Zhang L, Zhou D (2016) Cerebrospinal fluid IL-10 and IL-10/IL-6 as accurate diagnostic biomarkers for primary central nervous system large B-cell lymphoma. Sci Rep 6:38671. https://doi.org/10.1038/srep38671
Toopcham T, Mes JJ, Wicheers HJ, Yongsawatdigul J (2017) Immunomodulatory activity of protein hydrolysates derived from Virgibacillus halodenitrificans SK1-3-7 proteinase. Food Chem 224:320–328. https://doi.org/10.1016/j.foodchem.2016.12.041
Tsou M-J, Lin S-B, Chao C-H, Chiang W-D (2012) Enhancing the lipolysis-stimulating activity of soy protein using limited hydrolysis with Flavourzyme and ultrafiltration. Food Chem 134:1564–1570. https://doi.org/10.1016/j.foodchem.2012.03.093
Van Ginderachter JA, Movahedi K, Hassanzadeh Ghassabeh G, Meerschaut S, Beschin A, Raes G, De Baetselier P (2006) Classical and alternative activation of mononuclear phagocytes: picking the best of both worlds for tumor promotion. Immunobiology 211:487–501. https://doi.org/10.1016/j.imbio.2006.06.002
Wen L, Jiang Y, Zhou X, Bi H, Yang B (2021) Structure identification of soybean peptides and their immunomodulatory activity. Food Chem 359:129970. https://doi.org/10.1016/j.foodchem.2021.129970
Wu W, Zhang M, Ren Y, Cai X, Yin Z, Zhang X, Min T, Wu H (2017) Characterization and immunomodulatory activity of a novel peptide, ECFSTA, from wheat germ globulin. J Agri Food Chem 65:5561–5569. https://doi.org/10.1021/acs.jafc.7b01360
Yang R, Zhang Z, Pei X, Han X, Wang J, Wang L, Long Z, Shen X, Li Y (2009) Immunomodulatory effects of marine oligopeptide preparation from Chum Salmon (Oncorhynchus keta) in mice. Food Chem 113:464–470. https://doi.org/10.1016/j.foodchem.2008.07.086
Yang Q, Cai X, Huang M, Wang S (2020) A specific peptide with immunomodulatory activity from Pseudostellaria heterophylla and the action mechanism. J Funct Foods 68:103887. https://doi.org/10.1016/j.jff.2020.103887
Yu W, Field CJ, Wu J (2018) Purification and identification of anti-inflammatory peptides from spent hen muscle proteins hydrolysate. Food Chem 253:101–107. https://doi.org/10.1016/j.foodchem.2018.01.093
Zaky AA, Simal-Gandara J, Eun J-B, Shim J-H, El-Aty AMA (2022) Bioactivities, applications, safety, and health benefits of bioactive peptides from food and by-products: a review. Front Nutr 8:815640. https://doi.org/10.3389/fnut.2021.815640
Zhang J, Gao S, Li H, Cao M, Li W, Liu X (2021) Immunomodulatory effects of selenium-enriched peptides from soybean in cyclophosphamide-induced immunosuppressed mice. Food Sci Nutr 9:6322–6334. https://doi.org/10.1002/fsn3.2594
Zheng W, Zhao T, Feng W, Wang W, Zou Y, Zheng D, Takase M, Li Q, Wu H, Yang L, Wu X (2014) Purification, characterization and immunomodulating activity of a polysaccharide from flowers of Abelmoschus esculentus. Carbohydr Polym 106:335–342. https://doi.org/10.1016/j.carbpol.2014.02.079
Ziegler F, Ollivier J, Cynober L, Masini J, Coudray-Lucas C, Levy E, Giboudeau J (1990) Efficiency of enteral nitrogen support in surgical patients: small peptides v non-degraded proteins. Gut 31:1277–1283. https://doi.org/10.1136/.31.11.1277
This study was supported by research Grants (NSC100-2221-E029-002 and NSC101-2221-E029-026 for W.D.C.) from Ministry of Science and Technology, Taiwan.
Ministry of Science and Technology, Taiwan, research Grants (NSC100-2221-E029-002 and NSC101-2221-E029-026 for W.D.C.)
Lu-Sheng Hsieh and Ming-Shing Lu contributed equally to this work
Department of Food Science, College of Agriculture, Tunghai University, No. 1727, Sec. 4, Taiwan Boulevard, Xitun District, Taichung, 40704, Taiwan
Lu-Sheng Hsieh, Ming-Shing Lu & Wen-Dee Chiang
Lu-Sheng Hsieh
Ming-Shing Lu
Wen-Dee Chiang
L-SH: conceptualization, methodology, writing—original draft, writing—review and editing. M-SL: conceptualization, methodology, investigation. W-DC: conceptualization, funding acquisition, resources, supervision, writing—review and editing. All authors read and approved the final manuscript.
Correspondence to Wen-Dee Chiang.
Hsieh, LS., Lu, MS. & Chiang, WD. Identification and characterization of immunomodulatory peptides from pepsin–soy protein hydrolysates. Bioresour. Bioprocess. 9, 39 (2022). https://doi.org/10.1186/s40643-022-00526-2
Immunomodulatory peptide
Isolated soy protein (ISP)
Lipopolysaccharide (LPS)
Molecular weight cut-off (MWCO)
Pepsin | CommonCrawl |
Mandatory costs by firm size thresholds: firm location, growth and death in Sri Lanka
Babatunde O Abidoye1,
Peter F Orazem2 &
Milan Vodopivec3
Sri Lanka's Termination of Employment of Workmen Act (TEWA) requires that firms with 15 or more workers justify layoffs and provide generous severance pay to displaced workers, with smaller firms being exempted. Although formally subject to TEWA, firms in Export Promotion Zones (EPZs) do not face the same constraints as nonEPZ firms due to size incentives and lax labor law enforcement in that sector. In EPZ, 77% of firms have more than 15 employees while 76% of nonEPZ firms are smaller than 15 employees. Panel data on all formal sector firms between 1995 and 2003 shows that 80% of the size gap is from sorting of large firms into the EPZ. In addition, EPZ firms grow faster and are less likely to die than comparably sized nonEPZ firms. Despite its intent, TEWA lowered employment.
JEL code: J30
As part of its effort to protect workers from job loss, Sri Lanka adopted the Termination of Employment of Workman Act (TEWA) in 1971. The act aimed to limit unemployment by raising the cost of layoffs. It required that each layoff of a covered worker, whether the layoff involved a single employee or a mass layoff, must be approved by the government. Until 2003, the government also determined on a case-by-case basis the level of severance pay that the firm was required to pay to the laid off workers.
Since its introduction, critics have argued that the TEWA's non-transparent, discretionary, and costly regulations discourage employment growth, hinder reallocation of labor from inefficient firms to more profitable sectors, slow the introduction of new technologies, and increase unemployment. There is at least a prima facie case that the TEWA policy has affected the size distribution of firms in Sri Lanka compared to that in 15 other developing countries reported by Leidholm and Mead (1987). Sixty-eight percent of Sri Lankan firms had 10 or fewer employees, in the top third of small firm shares in the Leidholm-Mead compilation.1 Only 12% of Sri Lanka firms had over 49 workers which would have given it the second smallest large firm share in the Leidholm-Mead listing. However, Sri Lanka's firms in Export Promotion Zones (EPZ) have a remarkably different size distribution: only 17% of the firms have 10 or fewer workers and 57% have more than 49. Of all the countries for which we have size-distribution information, Sri Lanka's EPZ firms have the smallest fraction of workers in firms with fewer than 10 workers and the largest fraction of workers in firms with over 49 workers. Meanwhile, the reason the overall size distribution in Sri Lanka is weighted more heavily toward small firms is that the nonEPZ firms are so unusually small.
Micro-econometric analyses have shown that employment protection policies can have negative consequences for workers. Heckman and Pages (2000) show that in Latin America, more stringent job security laws are associated with lower employment and higher unemployment, particularly among young workers. Similarly, Besley and Burgess (2004) find that labor regulations in India had important adverse effects on output and employment. Expanding on that study, Ahsan and Pages (2009) report that regulations concerned with labor disputes and job security hurt covered workers. Bassanini and Duval (2006) find that changes in tax and labor policies explain about half of the 1982–2003 changes in unemployment among OECD countries. Other studies using macroeconomic data have also found negative efficiency effects of severance pay including Nickell and Layard (1999), Haffner et al. (2001), and the OECD (1999). Nevertheless, these negative findings from labor market regulations are not universal, particularly those based on cross-section analysis (Baker et al. 2005).2
This paper adds to this literature by identifying the impacts of the Sri Lanka TEWA on firm employment and growth. We exploit two sources of variation in the way firms are treated to identify the policy's effects. First, the law only applies to firms with more than 14 workers, and so smaller firms need not comply. Second, firms in EPZ do not face the same constraints imposed by the TEWA. These sharp differences in policies applied to firms of different size create several strategic options. Firms that anticipate growing beyond 14 workers will try to sort into the EPZ to avoid the constraints imposed by the law. The cost of growing beyond 14 workers may discourage nonEPZ firms from growing. Furthermore, the costs imposed by the TEWA may be large enough to drive covered firms out of business. Panel data on the cohort of all firms registering for business in Sri Lanka between 1995 and 2002 is used to provide evidence for all three possibilities.
Consistent with our theoretical predictions, we find that the potential TEWA costs result in substantially lower firm size in the nonEPZ sector, with the differential incentives to add workers inside and outside the EPZ clearly limiting growth for firms well below the threshold. EPZ firms have a 26 percentage point larger growth probability below the 14 worker employment threshold and a 14 percentage point growth advantage above the threshold. In addition, evidence is consistent with the view that the cost of adding a 15th worker implies a larger marginal cost of expansion for all nonEPZ firms below the threshold compared to nonEPZ firms already above the threshold, and so nonEPZ firms above the threshold have more rapid employment growth than nonEPZ firms below the threshold. NonEPZ firms already above the threshold are 21 percentage points more likely to add employees than are nonEPZ firms below the threshold. Finally, the results show that the biggest and most significant differences in survival probability (about 10 percentage point) is the higher exit rate of nonEPZ firms relative to EPZ firms.
The paper is organized as follows. Section 2 provides an institutional background, highlighting the intentions of the TEWA at its introduction, and its provisions and procedures. It also gives a description of EPZ and nonEPZ firms and description of the data. Section 3 presents the model highlighting firm entry and exit decisions. Section 4 describes the empirical section focusing on the need for analysis by firm. Section 5 presents the empirical results based on the estimation of the multinomial model of employment growth of firms. Section 6 concludes with a summary and policy recommendations.
Institutional background and data descriptions
Termination of Employment of Workmen Act
The TEWA was enacted at a time when Sri Lanka was pursuing isolationist economic policies including an import-substitution industrialization policy, stringent exchange controls, price controls on many commodities, and a program of nationalization of a wide-range of establishments (Ranaraja 2005).3 The TEWA applies to all firms employing 15 or more workers. For covered private firms, all terminations for any reason other than discipline are regulated by the TEWA, including redundancies arising from organizational restructuring and financial or economic constraints, temporary lay-offs, terminations as a result of the business closure, and even incompetence.4 A worker qualifies as long as he or she worked at least 180 days in the 12 month period preceding the termination.
The TEWA requires that covered employers must seek the consent of the Commissioner General of Labor (CGL) before they are allowed to dismiss workers, even if it concerns a single worker. The CGL may refuse to sanction the layoff or, if permission is granted, the employer will be required to pay severance in an amount determined by the CGL. Over the sample period, the procedure by which the severance is determined was not specified in law but was subject to a lengthy and seemingly arbitrary deliberation. In December 2003, the TEWA switched to a formula-based severance payment that is uniformly applied to all firms. While that amendment eliminated the ad hoc determination of the level of severance pay, the other elements of the policy, including the need for prior approval of layoffs, are still in place.
In dealing with termination applications by employers or complaints by workers, the CGL has the power of a District Court to conduct inquiries, such as summoning and compelling the attendance of witnesses, production of records, and recording testimony. The employer must satisfy the CGL that terminating the identified group of workers is in the best interest of the employer. While the evaluation is going on, the workers continue to be paid wages and other benefits until the CGL makes a decision, even where there is no work to be done. The final order of the CGL does not take into consideration the wages paid by the employer during the inquiry period. Data for 2003 confirm that the TEWA procedure is a very lengthy one - the average processing time of employer applications was 9.8 months, and it exceeded one year in more than 25 percent of cases (World Bank 2007).
Severance pay was quite generous. During 2002–03, the severance averaged nearly 2 times the monthly salary per year of service, and the multiple could rise as high as 6 times the monthly salary. Judged by international standards, this level of TEWA severance is extremely high. Using 2002 data, a year for which we have some data on individual compensation, we can infer the relationship between generosity of payments and years of service with the firm. A Sri Lankan worker with 20 years of service received an average severance package equal to 29 months of wages. In contrast, the average severance was 16 months of wages in other Asian countries, 12 months in Latin America, 7 months in Africa, 6 months in the OECD, and 4 months in transition countries. Sri Lankan workers with shorter duration of prior service were also awarded much more generous level of severance pay than workers in other countries. Since the switch to the fixed severance formula in December 2003, the program has become even more generous (World Bank 2007).
The high turnover costs imposed by the TEWA have led to a relatively small number of applications for separations by employers. Between 2000 and 2003, of more than 80 thousand covered firms, annual filings for the right to initiate a separation varied from 71 to 105 applications (World Bank 2007). Less than half of these cases were concluded by the order of the commissioner because they were settled "voluntarily", whether because the firm withdrew the application or induced the worker to retire voluntarily with retirement packages that ranged from 6 to 45 months of wages. As is apparent, it is difficult for firms to avoid the costs of the TEWA. Inflexible labor regulations were one of the five most commonly cited business challenges reported by urban firms in Sri Lanka5.
Firms in EPZ were reported to be given a preferential treatment that allowed them to limit or avoid the costs of the TEWA. Because EPZ firms were technically subject to the same regulations, the extent of the lax enforcement is difficult to quantify, but any preferential treatment should be apparent when comparing EPZ firm personnel decisions relative to those of nonEPZ firms. In addition, EPZ firms were eligible for many Board of Investments (BOI) incentives that rewarded firm growth. The size distribution of firms inside and outside the EPZ is summarized in Table 1. Large firms are atypically located in EPZ. Only 22.5% of EPZ firms have fewer than 14 workers compared to 75.6% of nonEPZ firms! In contrast, the EPZ firms are over 3 times more likely than nonEPZ firms to have grown beyond the threshold employment level. It certainly appears that the incentives to grow must differ between the two groups of firms.
Table 1 Distribution of Sri Lanka firms by initial size, change in employment over the years, and EPZ status (%), 1995 – 2003
Table 1 also shows that there are apparent differences in the probability that firms increase or decrease their workforce. NonEPZ firms are much more likely than EPZ firms to reduce or maintain their current employment level, regardless of size. EPZ firms are much more likely to add to their employment base. The largest contrast in probability of employment growth is below the threshold: the smallest EPZ firms are twice as likely to increase employment compared to nonEPZ firms. If it is true that the cost of hiring is lower for EPZ firms, then the pattern of employment growth and decline would differ between EPZ and non-EPZ firms.
In Figure 1, we illustrate the probability of firm employment growth and decline in EPZ and nonEPZ firms around the 14–15 employee threshold. Immediately we see that EPZ firms are more likely to grow and nonEPZ firms are more likely to shrink at all firm sizes, an outcome that will prove consistent with the theory. NonEPZ firms are modestly more likely to both shrink and grow above the threshold, compared to nonEPZ firms below the threshold. In other settings, small firms are the most likely to both grow and shrink and so we would expect these lines to slope downward absent any constraints on firm choice (Evans 1987; Cabral 1995; Arkolakis 2013). The patterns for EPZ firms are harder to discern due to relatively small numbers at each firm size. It appears that EPZ firms are also more likely to grow above the threshold but there is no obvious change in the probability of firm shrinkage around the threshold.
Probability of firm employment growth and decline above and below the 14 worker threshold, by firm size and EPZ status, 1995–2003 averages.
At 14 workers where the 15th worker would trigger compliance with the TEWA, for EPZ firms the probability of employment growth decreases and the probability of firm employment decline increases. NonEPZ firms have the same pattern but the difference is only a few percentage points. The lack of massing at 14 employees outside the EPZ may seem surprising. However, firms wanting to avoid the TEWA would be expected to remain below 15 employees, but their constrained optimum employment choice may not be exactly at 14 workers. As a result, the TEWA would be expected to create higher probability of firms shrinking above the threshold and lower probability of firms growing below the threshold, a result that is supported by the patterns in Figure 1. Moreover, data measurement errors (see above) may also contribute to less pronounced differences in observed behavior at the threshold.
To further isolate the effect of the TEWA, we need to remove the effects of firm observed and unobserved productivity attributes from the analysis. In addition, the TEWA effect will be spread across firm decisions to expand, remain at current size, or shrink in the face of external shocks. That will require a more structured analysis of the data.
To test for differences in firm location, growth and decline between EPZ and nonEPZ sectors, we make use of a unique panel data set that includes annual employment data for 80,560 firms in Sri Lanka over the 1995–2003 periods. The period coincides with a consistent set of restrictions on layoffs. Those policies were relaxed modestly at the end of 2003. The data are compiled by the Sri Lanka Employees' Provident Fund (EPF) on all private sector firms and workers paying contributions to the fund. All registered firms regardless of size are required to pay contributions for their workers. The data are maintained by the Central Bank of Sri Lanka.
The data are quite limited, however. Apart from the number of workers employed during the year, the only other information contained in the database is the firm's name and region: each firm is designated as having a base in one of 24 regions. The name allows us to identify which firms belong to an EPZ. The Sri Lankan Board of Investment provided us a list of names for firms that operate in EPZs. We matched these names with 1,124 firms in the EPF list, and these firms comprise our EPZ group.
The EPF data are not free of problems. The data set only contains workers for whom the firm paid contributions during the year. If for whatever reason such contributions are not paid, the true number of workers in the firm will deviate from the number reported to the EPF. The most frequent reason for such discrepancies is the presence of financial difficulties that prevent a firm from paying contributions in the current year. Even delayed payments are not used to correct the data retrospectively. Therefore, these employment numbers will only reflect the contemporaneously reported number of workers for whom the firm is making an EPF contribution. The frequency or magnitude of this measurement error is not known.
Also, the nature of the data does not allow us to differentiate between quits and layoffs and so we assume that any net loss of workers is due to layoffs. This seems reasonable, as workers who quit will presumably be replaced, resulting in no employment loss. We will discuss further in the empirical section on how we exploit the nature of the data to understand firm size decision.
The data also provide information on firms in different years. We make use of the longitudinal nature of the data to specifically identify cohorts of firms and follow their evolution over time. Thus firms that do not make contributions in 1995 but started paying contribution in 1996 are considered to be one cohort and are followed until 2003. The same is done for subsequent years. The identification of different cohorts in the data has the advantage of reducing heterogeneity and provides for a simple test of selection to explain firm size distribution and location in EPZ or nonEPZ region.
As the summary data in Table 1 reveal, there are substantial differences in average firm size and growth patterns consistent with differences in the marginal cost of hiring across the EPZ and nonEPZ regions. To evaluate the strength of that correlation more formally, we next propose a theoretical model to understand firm entry and exit decision.
Firm entry decisions: How much of the gap in size distribution between EPZ and nonEPZ firms is due to sorting by firm size at entry?
Firms face two interrelated decisions at the time of entry designated by subscript 0: whether to locate in an EPZ zone and how much labor (L0) and capital (K0) to employ. We assume that there is a fixed entry cost, \( {\mathrm{F}}_0^{\mathrm{EPZ}}, \) that firms incur from attaining EPZ status. These costs would include all official and under-the-table costs of applying for and attaining EPZ status plus any additional business expenses associated with location or entry6. In exchange, the firm receives benefits from alleged lax enforcement of the TEWA and preferential tax treatment and exemption from export duties applied to worker output. That distinction sets up the comparison between EPZ and nonEPZ firms for the empirical work.
We summarize the distinction with a parameter δk that measures the cost of compliance with the TEWA net of any benefits from being in the EPZ. The superscript k denotes the cost of compliance in E: EPZ or N: nonEPZ. The measure of δk is a positive or negative proportional markup over the wage. If the firm is nonEPZ, the δk ≥ 0, with a positive markup if the firm has more than 14 employees so that it faces possible severance and related firing costs that are proportional to the wage. If the firm is in the EPZ, we expect δE ≤ δN because of lax enforcement of TEWA requirements, and δE may even be negative if the firm receives tax benefits and/or subsidies tied to firm size.
All firms, EPZ or nonEPZ, have to pay market wages, w0 and so the hourly labor cost per worker is w0(1 + δK). All nonEPZ firms with L0 < 15 face δN = 0 and pay w0 per hour for labor, while all nonEPZ firms with L0 ≥ 15 pay w0(1 + δN) per hour; δN > 0. All EPZ firms pay w0(1 + δN) ≤ w0(1 + δN) when compared with equally sized nonEPZ firms.
Assuming the firm's production function takes the Cobb-Douglas form
$$ {Q}_0=A{\uptau}_0{\mathrm{L}}_0^{\upalpha_{\mathrm{L}}}{\mathrm{K}}_0^{\upalpha_{\mathrm{K}}} $$
The variable τ0 is a permanent exogenous technology shock to labor productivity that takes an initial value of unity. The production parameters are defined by A > 0, 0 < α L < 1, and 0 < αK < 1. Setting output price at unity and cost of capital as r, the firm's initial optimum input levels \( {\mathrm{L}}_0^{*} \) and \( {\mathrm{K}}_0^{*} \) are set by the first-order conditions:
$$ {\upalpha}_{\mathrm{L}}{\mathrm{A}\uptau}_0{\mathrm{L}}_0^{\upalpha_{\mathrm{L}}\hbox{-} 1}{\mathrm{K}}_0^{\upalpha_{\mathrm{K}}}={\mathrm{w}}_0\left(1+{\updelta}^{\mathrm{k}}\right) $$
(2A)
$$ {\upalpha}_{\mathrm{K}}{\mathrm{A}\uptau}_0{\mathrm{L}}_0^{\upalpha_{\mathrm{L}}}{\mathrm{K}}_0^{\upalpha_{\mathrm{K}}\hbox{-} 1}=\mathrm{r} $$
(2B)
An entering firm will decide on whether to enter the EPZ by comparing anticipated profits with and without EPZ status. For firms with \( {\mathrm{L}}_0^{*}<15 \), profits are higher in the nonEPZ state if δE > 0, or if δE < 0 and \( \left|\frac{{\mathrm{w}}_0{\updelta}^{\mathrm{E}}{\mathrm{L}}_0^{*}}{\mathrm{r}}\right|<{\mathrm{F}}_0^{\mathrm{E}\mathrm{PZ}} \) where the term on the left of the inequality is the discounted value of the stream of anticipated EPZ subsidies. The cost advantage for small firms locating in the nonEPZ sector is that they are exempt from TEWA costs and also avoid paying \( {\mathrm{F}}_0^{\mathrm{EPZ}} \). For firms with \( {\mathrm{L}}_0^{*}\ge 15 \), it is optimal to get EPZ status when \( {\mathrm{F}}_0^{\mathrm{EPZ}}<\frac{\updelta^{\mathrm{N}}{\mathrm{w}}_0{\mathrm{L}}_0^{*}}{r}, \) where the term on the right is the discounted value of the stream of anticipated TEWA payments in perpetuity. Consequently, it is possible for a firm planning to have 15 or more employees to select the nonEPZ sector. Presuming firms face the same market wages, capital costs, potential EPZ benefits, and potential TEWA costs, the firms most likely to sort into the EPZ sector have the largest initial employment levels, \( {\mathrm{L}}_0^{*} \).
This simple model shows that small firms will tend to sort into nonEPZ and large firms into EPZ at the time of entry, conditional on prevailing wages, capital costs and technology. That suggests that empirical analysis of the size distribution of firms must compare firms facing the same prices and technologies at the time of entry. Moreover, empirical studies have consistently shown that firm growth rates and death rates are initially both slow with firm age and so we need to standardize firm age to generate accurate transition probabilities (Evans 1987; Cabral 1995; Arkolakis 2013). These arguments dictate our use of cohorts of newly born firms for our analysis.
Evidence of the impact of sorting on the gap in firm size between EPZ and nonEPZ
Table 2 provides summary information on the size distribution of firms in EPZ and nonEPZ regions for successive entry cohorts from 1996 through 2002. Recall that the overall percentage of firms with at least 15 employees is 76% in the EPZ and 23% in the nonEPZ (see Table 1). The proportion of EPZ firms already above 14 workers at entry varies between 53% and 70% with an average of 62%. It is apparent that the EPZ firms quickly add workers with the fraction above 15 workers rising 2.5% per year averaged across the cohorts. If 76% is taken as the final percentage of firms employing over 15 workers, sorting of large firms into EPZ is responsible for about 80% of the EPZ size distribution.
Table 2 Distribution of EPZ and non EPZ firms at entry (1996) and the end of sample (2003)
In the nonEPZ sector, only 9% of the firms in a cohort start with at least 15 employees, and the fraction actually decrease through the first few years. By 2003, 8% of these seven firm entry cohorts had 15 or more workers. It is apparent that the nonEPZ firms do not grow as readily as the EPZ firms. While we cannot argue with certainty that the proximate cause is the TEWA, the results are consistent with the predicted impact of the TEWA on firm entry decisions.
There is a 53 percentage point gap between the worker distribution of EPZ and nonEPZ firms in the population as shown in Table 1. The average gap at entry between large EPZ and nonEPZ firms is also 53 percentage points as shown in Table 2. However, the population measure excludes firms that have died, while the cohort estimates at entry include all firms. It is possible that the fraction of firms with over 15 employees will grow because small firms add workers over time, or it may be that the fraction increases because small firms are more likely to die. As we will see, sorting at entry is an important source of the difference between EPZ and nonEPZ firm size distributions, but differential growth and death rates also play a role.
Can the TEWA affect firm employment growth and death?
When firms commit to their initial capital stock and decide whether or not to enter the EPZ, they do not know the future path of prices and technology. Having committed to a capital stock and a location, their response to these changing economic circumstances is limited to labor adjustments in the short run. At some future time, t, the condition setting their short-run employment level will be
$$ {\upalpha}_{\mathrm{L}}\mathrm{A}{\uptau}_{\mathrm{t}}{\mathrm{L}}_{\mathrm{t}}^{\upalpha_{\mathrm{L}}-1}{\mathrm{K}}_0^{*{\upalpha}_{\mathrm{K}}}\ge {\mathrm{w}}_{\mathrm{t}}\left(1+{\updelta}^{\mathrm{k}}\right) $$
The firm's optimal labor allocation is conditioned on the initial capital investment at entry. It is also affected by the evolution of technology, τt, and wages, wt.7
We let technology evolve according to:
$$ \ln \left({\uptau}_{\mathrm{t}}\right)= \ln \left({\uptau}_{\mathrm{t}-1}\right)+\overline{\upeta_0}+{\upeta}_{\mathrm{t}};\ {\upeta}_{\mathrm{t}}\sim \mathrm{N}\left(0,\ {\upsigma}_{\upeta}^2\right) $$
The variable \( \overline{\upeta_0} \) is the trend growth in technology known by all firms at the time of entry, but η t is an unforeseeable but permanent technology innovation that the firm cannot control. This specification for τt presumes that the firm's labor productivity is a random walk process about the trend. We assume similarly that market wages (wt) evolve according to a random walk process with a known drift8 so that
$$ \ln \left({\mathrm{w}}_{\mathrm{t}}\right)= \ln \left({\mathrm{w}}_{\mathrm{t}-1}\right)+{\overline{\upomega}}_0+{\upomega}_{\mathrm{t}};\ {\upomega}_{\mathrm{t}}\sim \mathrm{N}\left(0,\ {\upsigma}_{\upomega}^2\right) $$
The variable \( {\overline{\omega}}_0 \) is the trend growth in wages known by all firms at the time of entry, but ω t is an unforeseeable but permanent innovation in wages that the firm cannot control.
We can model the changes in the firm's employment decisions by applying 3A-C to two successive years and solving for the change in desired labor. From here on, we define the notional firm input demand that would hold at an interior solution in period t as \( {\mathrm{L}}_{\mathrm{t}}^{*} \) and \( {\mathrm{K}}_{\mathrm{t}}^{*} \). The form of the decision depends on whether the firm comes under the TEWA policy. We examine several cases that will illustrate the range of possible responses to the TEWA system. Recall that we are assuming that EPZ firms are exempt from all TEWA requirements in forming these responses, an assumption that we will test with the data.
Case 1: Firm is exempt from TEWA with δN = 0 and δ E ≤ 0 in both periods with \( {\mathrm{L}}_{\mathrm{t}-1}^{*} < 15 \) and \( {\mathrm{L}}_{\mathrm{t}}^{*} < 15 \)
Assuming interior solutions, the change in desired labor is governed by \( \ln \left(\frac{{\mathrm{L}}_{\mathrm{t}}}{{\mathrm{L}}_{\mathrm{t}-1}}\right)=\frac{\upeta_{\mathrm{t}}-{\upomega}_{\mathrm{t}}}{\left(1-{\upalpha}_{\mathrm{L}}\right)} \). The firm is not constrained by the severance policy and adjusts labor upward with positive labor productivity shocks and negative wage shocks. If EPZ firms receive favorable subsidies so that δE < 0 , comparable adverse shocks are less likely to cause the left hand side of (3A) to fall below the right-hand side for EPZ firms compared to nonEPZ firms. As a consequence, below the threshold, nonEPZ firms are more likely to shrink or less likely to expand compared to EPZ firms.
Case 2: Firm is covered by TEWA so \( {\delta}^N>{\delta}^E{}_{<}{}^{> }\ 0 \) in both periods because \( {\mathrm{L}}_{\mathrm{t}-1}^{*}\ge 15 \) and \( {\mathrm{L}}_{\mathrm{t}}^{*}\ge 15 \)
Assuming interior solutions, the change in desired labor is also governed by \( \ln \left(\frac{{\mathrm{L}}_{\mathrm{t}}}{{\mathrm{L}}_{\mathrm{t}-1}}\right)=\frac{\upeta_{\mathrm{t}}-{\upomega}_{\mathrm{t}}}{\left(1-{\upalpha}_{\mathrm{L}}\right)} \) and so optimal labor demand responds as with the exempt firms in Case 1. However, even at their optimum labor allocations, the nonEPZ firms face a constant disadvantage of having higher labor costs and more distorted capital labor ratios compared to their EPZ competitors. As before, comparable adverse shocks are more likely to lead to violations of the first order condition (3A) for nonEPZ firms than EPZ firms. In addition, even if they are at their optimum labor allocation, nonEPZ firm profit levels will be lower than that of comparably sized EPZ firms because of their higher labor costs. As a result, above the threshold, nonEPZ firms are more likely to shrink and less likely to expand compared to equally sized EPZ firms.
Case 3: Firm has \( {\mathrm{L}}_{\mathrm{t}-1}^{*}<15 \) and considers remaining below the threshold in period t even though \( {\mathrm{L}}_{\mathrm{t}}^{*}\ge 15 \) if the firm is exempt from the TEWA
In this case, assume first that employment in t-1 is fixed by the interior solution of 3A-C such that \( {\mathrm{L}}_{\mathrm{t}-1}^{*}<15 \). However, in the next period, the firm's optimal staffing would move it into the covered region:
$$ {\upalpha}_{\mathrm{L}}\mathrm{A}{\uptau}_{\mathrm{t}}{\mathrm{L}}_{\mathrm{t}}^{\upalpha_{\mathrm{L}}-1}{\mathrm{K}}_0^{*{\upalpha}_{\mathrm{K}}}={\mathrm{w}}_{\mathrm{t}}\to {\mathrm{L}}_{\mathrm{t}}^{*}\ge 15 $$
$$ {\upalpha}_{\mathrm{L}}\mathrm{A}{\uptau}_{\mathrm{t}}{\mathrm{L}}_{\mathrm{t}}^{*{\upalpha}_{\mathrm{L}}-1}{\mathrm{K}}_0^{*{\upalpha}_{\mathrm{K}}}<{\mathrm{w}}_{\mathrm{t}}\left(1+{\updelta}^{\mathrm{k}}{\mathrm{L}}_{\mathrm{t}}^{*}\right);\ \forall {\mathrm{L}}_{\mathrm{t}}^{*}\ge 15;\ \updelta >0 $$
This is the case where the firm would want to expand beyond 14 employees if it faced the market wage alone. However, in moving beyond 14 employees, the firm has to pay for the TEWA severance system for all \( {\mathrm{L}}_{\mathrm{t}}^{*} \) workers, leading to an even larger increase in the marginal cost of adding any workers beyond 14. As a consequence, the firm will set their staffing at some second-best level Lt < 15 and where the marginal product \( {\upalpha}_{\mathrm{L}}\mathrm{A}{\uptau}_{\mathrm{t}}{\mathrm{L}}_{\mathrm{t}}^{\upalpha_{\mathrm{L}}-1}{\mathrm{K}}_0^{*{\upalpha}_{\mathrm{K}}}>{\mathrm{w}}_{\mathrm{t}} \).9 Because δN > δE, it is more likely that nonEPZ firms will decide not to expand beyond 14 workers compared to EPZ firms.
Empirical framework
The discussion illustrates that the TEWA can alter the incentives for nonEPZ firms to expand or shrink compared to similarly sized EPZ firms. Both above and below the threshold, the combination of special tax and subsidy treatments from the EPZ and the costs of compliance with the TEWA create conditions that increase the likelihood that nonEPZ firms will shrink or fail to grow compared to their EPZ counterparts. At the threshold, nonEPZ firms are more likely to face additional labor costs that cause them to remain below the threshold. As we show in this section, these predictions can be tested with longitudinal data on cohorts of firms entering business at the same time.
The use of a common startup date is important for two reasons. First, all firms will be exposed to the same information on wages, technology and macroeconomic conditions, greatly simplifying the specification of common shocks. Second, a sample of the universe of all starting firms avoids the selection bias that would exist had we been constrained to a sample of surviving firms in which the weakest would have been already eliminated.
The empirical section described below can be viewed in the difference-in-differences framework, using firms at or above the severance threshold as the treatment group, and those with fewer than 14 workers and those in EPZs as control groups. The first control group follows naturally from the design of the TEWA system, because the regulations do not apply to firms employing less than 15 workers. The second control group is formed based on the assumption that enforcement is ineffective in EPZs, allowing firms to escape paying separation costs as dictated by TEWA.
Measuring the TEWA effect on probability of firm growth
We begin by applying an interior solution to (3A) which defines the firm's notional demand in period t as
$$ \left({\upalpha}_{\mathrm{L}}-1\right) \ln {\mathrm{L}}_{\mathrm{t}}^{*}= \ln \left(\frac{{\mathrm{w}}_{\mathrm{t}}\left(1+{\updelta}^{\mathrm{k}}\right)}{\upalpha_{\mathrm{L}}\mathrm{A}{\uptau}_{\mathrm{t}}{\mathrm{K}}_0^{*{\upalpha}_{\mathrm{K}}}}\right) $$
The first order condition for notional employment in period t + 1 is
$$ \left({\upalpha}_{\mathrm{L}}-1\right) \ln {\mathrm{L}}_{\mathrm{t}+1}^{*}= \ln \left(\frac{{\mathrm{w}}_{\mathrm{t}+1}\left(1+{\updelta}^{\mathrm{k}}\right)}{\upalpha_{\mathrm{L}}\mathrm{A}{\uptau}_{\mathrm{t}+1}{\mathrm{K}}_0^{*{\upalpha}_{\mathrm{K}}}}\right)=\left({\upalpha}_{\mathrm{L}}-1\right) \ln {\mathrm{L}}_{\mathrm{t}}^{*}+{\upomega}_{\mathrm{t}+1}-{\upeta}_{\mathrm{t}+1} $$
where we apply (4A), (3B) and (3C). Rearranging, we have that the change in notional employment from t to t + 1 is
$$ \ln \left(\frac{{\mathrm{L}}_{\mathrm{t}+1}^{*}}{{\mathrm{L}}_{\mathrm{t}}^{*}}\right) = \frac{\overline{\upeta_0} + {\upeta}_{\mathrm{t}+1} - \overline{\upomega_0} - {\upomega}_{\mathrm{t}+1}}{\left(1-{\upalpha}_{\mathrm{L}}\right)} $$
which means that if firm employment evolves without frictions, the change in notional employment will be a random walk with drift. Employment increases with trend growth and unexpected innovations in technology and decreases with expected wage increases and positive wage shocks. Importantly, the firm-specific Hicksian productivity factor A is differenced away, and so labor demand or supply shifts related to firm-specific unobservable productivity, firm location, or industry are held constant in the frictionless solution. However, the constraints on maximization caused by the TEWA will mean that actual firm employment growth will deviate from the frictionless outcome. The greater frictions in the nonEPZ sector should be apparent when we compare employment changes in those firms with the less constrained employment growth in the EPZ sector above, at and below the threshold.
This simple model does not take into account the stylized facts about firm growth by firm age and size. Our assessment of the literature suggests that these tendencies are unlikely to cause faster growth in the EPZ sector. First, as noted above, firm growth rates tend to decrease with firm age (Evans 1987; Cabral 1995; Arkolakis 2013). This will not bias comparisons across EPZ and nonEPZ firms, but it will induce a downward trend in longitudinal firm growth rates within the sectors. Potentially of greater concern is a second stylized result that exporting firms tend to grow faster than non-exporting firms which could bias the comparison across the EPZ and nonEPZ firms. However, extensive reviews of the empirical literature by Wagner (2007), Wagner (2012) and Singh (2010) suggest that the productivity advantage to exporting firms is driven by the sorting of more efficient firms into the export sector, similar to our own finding that larger firms enter the EPZ sector while smaller firms enter the nonEPZ sector. In contrast, there is no consistent evidence that the act of exporting raises firm growth rates. Again, these past findings suggest that the comparison across EPZ and nonEPZ sectors will not be biased by the act of exporting after controlling for the initial conditions at time of entry. In fact, evidence suggests that the highest firm growth rates among exporting firms are concentrated among the very small firms, while larger firms have growth rates near zero (Arkolakis 2013). If true, the bias would actually go against finding faster growth rates in the EPZ sector as firm size increases.
Actual employment changes for the ith firm are modeled as an approximation to the firm's notional employment changes as
$$ \ln \left(\frac{{\mathrm{L}}_{\mathrm{i}\mathrm{t}+1}}{{\mathrm{L}}_{\mathrm{i}\mathrm{t}}}\right)={\upbeta}_0+{\upbeta}_{\mathrm{E}\mathrm{P}\mathrm{Z}}\mathrm{E}\mathrm{P}{\mathrm{Z}}_{\mathrm{i}}+{\upbeta}_{{\mathrm{L}}^{-}}{\mathrm{E}}_{\mathrm{i}\mathrm{t}}^{{\mathrm{L}}^{-}}+{\upbeta}_{{\mathrm{L}}^{+}}{\mathrm{E}}_{\mathrm{i}\mathrm{t}}^{{\mathrm{L}}^{+}} + \left\{{\upgamma}_{{\mathrm{L}}^{-}}{\mathrm{E}}_{\mathrm{i}\mathrm{t}}^{{\mathrm{L}}^{-}}+{\upgamma}_{{\mathrm{L}}^{+}}{\mathrm{E}}_{\mathrm{i}\mathrm{t}}^{{\mathrm{L}}^{+}}\right\}*\mathrm{E}\mathrm{P}{\mathrm{Z}}_{\mathrm{i}}+\frac{\overline{\upeta_{\mathrm{i}0}} - \overline{\upomega_{\mathrm{i}0}}\ }{\left(1-{\upalpha}_{\mathrm{L}}\right)} + \frac{\ {\upeta}_{\mathrm{i}\mathrm{t}+1}-\kern0.5em {\upomega}_{\mathrm{i}\mathrm{t}+1}}{\left(1-{\upalpha}_{\mathrm{L}}\right)} $$
This specification adds terms to (5) that allow differential responses to the wage and technology shocks depending on whether the firm is inside or outside the EPZ and whether its employment level lies above or below the threshold. The constant β 0 corresponds to the base case which is set to be the anticipated employment change at a firm with Lit = 14 in a nonEPZ region. The other possible employment levels in period t are indicated by a dummy variable \( {\mathrm{E}}_{\mathrm{it}}^{{\mathrm{L}}^{-}} \) when employment is below 14 and \( {\mathrm{E}}_{\mathrm{it}}^{{\mathrm{L}}^{+}} \) when employment is above 14. The corresponding coefficients differentiate between employment growth effects below the threshold (\( {\upbeta}_{{\mathrm{L}}^{-}} \)) and above the threshold (\( {\upbeta}_{{\mathrm{L}}^{+}} \)). The dummy variable EPZ i indicates that the firm is in an export promotion zone. Given the other parameters, the coefficient βEPZ measures the difference in employment growth between EPZ and nonEPZ firms at the threshold Lit = 14. The \( {\upgamma}_{{\mathrm{L}}^{-}} \) capture additional differences in employment growth between EPZ and nonEPZ below the threshold and \( {\upgamma}_{{\mathrm{L}}^{+}} \) measures additional differences between the sectors above the threshold. If EPZ firms face fewer frictions in employment adjustments because of partial or full immunity from the TEWA or other benefits associated with EPZ status, \( {\upgamma}_{{\mathrm{L}}^{-}} \) and \( {\upgamma}_{{\mathrm{L}}^{+}} \) will be positive and significant. The \( {\upgamma}_{{\mathrm{L}}^{-}} \) and \( {\upgamma}_{{\mathrm{L}}^{+}} \) may differ from one another if there are different relative regulatory costs between EPZ and nonEPZ sectors above and below the threshold.
Our last requirement to estimate (6) is to operationalize the random walk and drift terms. The wage and technology trend terms are firm-specific and reflect information known at the time of entry. We approximate these terms by \( \frac{\overline{\upeta_{\mathrm{i}0}} - \overline{\upomega_{\mathrm{i}0}}\ }{\left(1-{\upalpha}_{\mathrm{L}}\right)} = {\upvarphi}_{\mathrm{L}} \ln \left({\mathrm{L}}_{\mathrm{i}0}\right)+{\upvarphi}_0 \) where the initial employment level reflects the firm's anticipated input needs based on what the firm knew at the time of entry and the second term is a cohort-specific term reflecting common expectations of the drift terms held by all firms entering at the same time. The second term requires that we control for a common fixed effect for all firms in the entry cohort. Inclusion of these terms helps to control for nonrandom sorting into firm size groups across firms and across entry cohorts.
The random walk terms are i.i.d. errors when we estimate one period employment changes. We let \( {\upepsilon}_{\mathrm{it}}^{\Lambda} = \frac{\upeta_{\mathrm{it}+1}-\kern0.5em {\upomega}_{\mathrm{it}+1}}{\left(1-{\upalpha}_{\mathrm{L}}\right)} \) be the composite error term in the employment change relationship. If \( {\upepsilon}_{\mathrm{it}}^{\Lambda} \) is distributed extreme value, then (6) can be posed as a multinomial logit specification. If we further define the term ΔΛt + 1 as a trichotomous variable and define the right-hand side terms excluding ϵit as \( {\mathrm{Z}}_{\mathrm{it}}^{\hbox{'}}{\mathrm{B}}^{\Lambda} \), the estimable variant of (6) that will yield the parameters of interest is
$$ \begin{array}{c}\hfill \Delta {\Lambda}_{\mathrm{t}+1}=1\ \mathrm{if}\ \ln \left(\frac{{\mathrm{L}}_{\mathrm{it}+1}}{{\mathrm{L}}_{\mathrm{it}}}\right)-{\mathrm{Z}}_{\mathrm{it}}^{\hbox{'}}{\mathrm{B}}^{\Lambda} < {\upepsilon}_{\mathrm{it}}^{\Lambda}\hfill \\ {}\hfill \Delta {\Lambda}_{\mathrm{t}+1}=2\ \mathrm{if}\ \ln \left(\frac{{\mathrm{L}}_{\mathrm{it}+1}}{{\mathrm{L}}_{\mathrm{it}}}\right)-{\mathrm{Z}}_{\mathrm{it}}^{\hbox{'}}{\mathrm{B}}^{\Lambda} = {\upepsilon}_{\mathrm{it}}^{\Lambda}\hfill \\ {}\hfill \Delta {\Lambda}_{\mathrm{t}+1}=3\ \mathrm{if}\ \ln \left(\frac{{\mathrm{L}}_{\mathrm{it}+1}}{{\mathrm{L}}_{\mathrm{it}}}\right)-{\mathrm{Z}}_{\mathrm{it}}^{\hbox{'}}{\mathrm{B}}^{\Lambda} > {\upepsilon}_{\mathrm{it}}^{\Lambda}\hfill \end{array} $$
Table 3 summarizes the identification and interpretation of the coefficients. The first column shows the parameters describing firm growth for EPZ firms below, at and above the threshold. The second column shows the corresponding parameter estimates for nonEPZ firms. The first differences of the nonEPZ estimates allow us to identify \( {\upbeta}_{{\mathrm{L}}^{-}} \) and \( {\upbeta}_{{\mathrm{L}}^{+}} \). The double difference allows us to identify \( {\upgamma}_{{\mathrm{L}}^{-}} \) and \( {\upgamma}_{{\mathrm{L}}^{+}} \) . \( {\upbeta}_{{\mathrm{L}}^{-}}>0 \) indicates faster growth than the base case for nonEPZ firms below 14 workers. Similarly, \( {\upbeta}_{{\mathrm{L}}^{+}}>0 \) indicates faster employment growth than the base case for nonEPZ firms above 14 workers. \( {\upbeta}_{\mathrm{EPZ}}+{\upgamma}_{{\mathrm{L}}^{-}}>0 \) indicates that EPZ firms are growing faster than nonEPZ firms below 14 workers and \( {\upbeta}_{\mathrm{EPZ}}+{\upgamma}_{{\mathrm{L}}^{+}}>0 \) indicates that EPZ firms are growing faster than nonEPZ firms above 14 workers. The coefficient βEPZ tells us if EPZ firms grow faster than nonEPZ firms at the threshold. These coefficient estimates form the basis of our hypothesis tests.
Table 3 Parameters controlling the probability of employment growth by type of firms
Measuring the TEWA effect on probability of Firm Death
Even with perfect foresight, firms will not completely avoid the TEWA costs by sorting into or out of the EPZ. NonEPZ firms face a labor cost disadvantage every period because δN ≥ δE both above and below the threshold. Because nonEPZ firms will pay an artificially high labor cost per hour, they will pick an inefficiently high ratio of capital per worker. The higher input costs than their EPZ competitors also leave them more exposed to adverse wage or technology shocks, increasing the probability that nonEPZ firms will shrink or fail.
We can test the hypothesized greater likelihood of firm death for nonEPZ firms using a similar specification as in (7) but with an alternative dependent variable. The details of the parameterizations follow exactly from the previous section except that the expected signs are opposite those for firm growth. We denote the composite error term as \( {\upepsilon}_{\mathrm{it}}^{\mathrm{Y}} = \frac{\upeta_{\mathrm{it}+1}-\kern0.5em {\upomega}_{\mathrm{it}+1}}{\left(1-{\upalpha}_{\mathrm{L}}\right)} \) which we assume is distributed extreme value. Then, we can derive a binomial logit specification for firm deaths which are indicated by unit values of the dichotomous variable ΔΥT + 1. Denoting the terms on the right-hand side of (7) excluding the error as \( {\mathrm{Z}}_{\mathrm{it}}^{\hbox{'}}{\mathrm{B}}^{\mathrm{Y}} \), we can define firm deaths by
$$ \begin{array}{c}\hfill \Delta {\mathrm{Y}}_{\mathrm{t}+1}=1\ \mathrm{if}\ \ln \left(\frac{{\mathrm{L}}_{\mathrm{it}+1}}{{\mathrm{L}}_{\mathrm{it}}}\right)-{\mathrm{Z}}_{\mathrm{it}}^{\hbox{'}}{\mathrm{B}}^{\mathrm{Y}}\le\ {\upepsilon}_{\mathrm{it}}^{\mathrm{Y}}\hfill \\ {}\hfill \Delta {\mathrm{Y}}_{\mathrm{t}+1}=0\ \mathrm{if}\ \ln \left(\frac{{\mathrm{L}}_{\mathrm{it}+1}}{{\mathrm{L}}_{\mathrm{it}}}\right)-{\mathrm{Z}}_{\mathrm{it}}^{\hbox{'}}{\mathrm{B}}^{\mathrm{Y}} > {\upepsilon}_{\mathrm{it}}^{\mathrm{Y}}\hfill \end{array} $$
where a firm death occurs when the notional reduction in staffing from year t to t + 1 is sufficiently large that it is more profitable for the firm to exit than to remain in operation with reduced staffing. If the additional costs faced by nonEPZ firms are sufficiently large compared to EPZ firms, then we would find negative values for βEPZ, \( {\upgamma}_{{\mathrm{L}}^{-}} \) and \( {\upgamma}_{{\mathrm{L}}^{+}} \).
In Table 4 and Table 5, we present the results of our estimation of the firm employment growth and firm death equations, estimated over the pooled firm entry cohorts from 1996 through 2002. These firms are followed annually until 2003, and so their growth and decline is tracked from one to seven years after entry. Constant terms for cohort year of birth are used to correct for the common information on macroeconomic conditions that shape anticipated price, wage and technology trends at the time of entry. The firm's initial employment level is used as a proxy for firm-specific information on technologies and wages that shaped the initial profit maximizing employment level. These parameters are estimated, but not reported10.
Table 4 Reduced form and structural estimates of the probability of employment growth conditional on prior employment level inside and outside Enterprise Protection Zones as per equation (6) using Probit model with cluster robust standard errors
Table 5 Reduced form and structural estimates of the probability of firm death conditional on prior employment level inside and outside Enterprise Protection Zones as per equation (7) using Probit model with cluster robust standard errors
For ease of interpretation, all estimated coefficients are converted into their implied transition probabilities. Therefore, all results reported in Table 4 and Table 5 reflect the marginal effects by EPZ or nonEPZ status of the prior year's employment level on the probability of employment growth, decline, or firm death. We report the reduced form coefficients in the upper panel and the lower panel presents the values of the hypotheses tests and the test statistics.
Employment growth and decline inside and outside the EPZ
The reduced form parameters give the average annual probability of employment growth relative to the reference firm which is a nonEPZ firm with 14 employees in year t. Smaller EPZ firms are 9 percentage points more likely to add workers than the reference firm. In contrast, smaller nonEPZ firms are nearly 17 percentage points less likely to add workers than a reference firm! Therefore, the differential incentives to add workers inside and outside the EPZ clearly limit growth for firms well below the threshold. As indicated in the theory section, there is no reason to believe that the constrained optimal employment level for a firm facing a substantial added cost of employing 15 workers would be 14 workers. This finding suggests that potential TEWA costs result in substantially lower firm size in the nonEPZ sector, even for firms well below the 14 firm threshold.
Above the threshold, EPZ firms are 19 percentage points more likely to add workers than the reference nonEPZ firm with 14 workers. In contrast, nonEPZ firms already above the threshold are 5 percentage points more likely to add workers than the reference firm. Because firm adding a 15th worker face additional costs on all 15 workers, we would expect a larger marginal cost to expansion for firms at the threshold compared to those already above the threshold.
Turning to the structural estimates, EPZ firms at the threshold are 12 percentage points more likely to add workers than the reference nonEPZ firm at the threshold, a difference that easily meets any standard significance criteria. The hypothesis that EPZ firms grow faster than comparably sized nonEPZ firms in the same entry cohort either above or below the threshold also passes any standard significance criteria. These effects are not small: 26 percentage point larger growth probability for firms below the threshold and a 14 percentage point growth advantage for firms above the threshold. This is overwhelming support of the hypothesis that firms in the EPZ grow faster than firms with identical initial size and year of entry in the nonEPZ sector.
The TEWA costs tend to keep nonEPZ firms small. NonEPZ firms below the threshold are 17 percentage points less likely to grow than are firms at the threshold, defying the tendency for firm growth rates to decrease with firm size. In contrast, EPZ firms below the threshold are more likely to add workers, consistent with the unconstrained pattern of firm growth by size found elsewhere. nonEPZ firms that manage to cross the threshold are 5% more likely to grow than the firms at the threshold who face very large marginal costs of the 15th worker, and are 21 percentage points more likely to add employees than are nonEPZ firms below the threshold. In contrast, there are no significant differences between employment growth probabilities of EPZ firms at or above the threshold. The differences in growth probability between EPZ above and below the threshold are only marginally significant. In short, growth rates for EPZ firms are quite similar to the unconstrained random walk with drift, while the pattern for nonEPZ firms is very different from the typical pattern of the fastest growth rates concentrated among the smallest firms.
Firm death inside and outside the EPZ
Table 5 reports the marginal probabilities of firm exit by current firm size and sector. EPZ firms below and above the threshold are 7 and 9 percentage points less likely to exit in a given year compared to comparably sized nonEPZ firms of the same vintage. At the threshold, EPZ firms are 3 percentage points less likely to exit but the estimate is not precise. NonEPZ firms below the threshold are the most likely to die at a 2 percentage point elevated exit rate per year. NonEPZ firms above the threshold have the same exit probability as firms at the threshold.
The structural hypothesis tests demonstrate a higher risk of death for almost all nonEPZ firms, regardless of size. The one-tailed test that EPZ firms are more likely to survive than nonEPZ firms at the threshold is not definitive. However, firms below the threshold have a 10 percentage point higher probability of death than comparably sized EPZ frims. For firms above the threshold, again there is a 10 percentage point higher probability of exit for nonEPZ firms. All of these estimates easily passes critical values. Greater exposure to the TEWA expenses and other disadvantages of nonEPZ firms relative to EPZ firms of comparable initial size and vintage increases significantly the likelihood that nonEPZ firms will fail.
For both EPZ and nonEPZ sectors, there is a small advantage of size – about a two percentage point lower risk of death per year relative to smaller firms in the same sector. However, the difference is only statistically significant for the nonEPZ sector. In addition, we cannot reject the null hypothesis of a uniform firm survival probability above and below the threshold in the EPZ sector. Therefore, survival probability does not change significantly by firm size in the EPZ, but small nonEPZ firms do face a higher probability of failure compared to other nonEPZ firms. However, the biggest and most significant differences in survival probability is the higher exit rate in nonEPZ relative to EPZ firms of equal initial size and vintage.
Placebo tests
We reestimated the model of firm employment growth used in Table 4 but using alternate artificial threshold sizes of Lit = 20 and Lit = 30. For these placebo regressions, we limit the sample to firms above 14 workers to take out the effect of the actual threhold. The results are reported in Table 6 with the Table 4 results repeated in the first column. The results in column 1 are very different from those in the last two columns. Probability of firm growth in the nonEPZ sector below the threshold are now not significantly different from the probability at the placibo threshold (at the threshold of 20) or positive (at the threshold of 30) rather than negative. The differences in growth rates for nonEPZ firms above and below the threshold are now only 4–5 percentage points compared to the 21 percentage points using the true thresholds. However, the EPZ firms continue to have a growth advantage over their nonEPZ counterparts consistent with the expected lower cost of employment expansion in the EPZ sector at all employment levels. In addition, EPZ firms grow at equal rates above and below the placebo thresholds which is consistent with the expected growth pattern for the EPZ sector for firms above the true threshold. In short, the EPZ firms continue to act as expected with the placebo thresholds while the nonEPZ firms look markedly different from their behavior about the true thresholds. These findings buttress the validity of the findings in Table 4.
Numerous studies have explained the effect of labor market restriction on unemployment, employment growth and wage inequality in OECD countries. This study extends this inquiry to the case of employment protection in a developing country context, namely the TEWA in Sri Lanka. The program imposes severance costs on firms with 15 or more workers in Sri Lanka, but not on smaller firms or firms in export promotion zones (EPZ).
We find that the size distribution of firms differs dramatically across the EPZ and nonEPZ sectors, with 76% of nonEPZ firms having less than 15 workers while 77% of EPZ firms have at least 15 employees. Using panel data on employment in the universe of formal sector firms in Sri Lanka from 1995 to 2003, we found evidence that 62% of EPZ firms open for business with at least 15 employees compared to only 9% of nonEPZ firms. That implies that disproportionate sorting of large firms into EPZ explains about 80% of the gap in firm size distribution across EPZ and nonEPZ sectors. Moreover, EPZ firms above the threshold are 14 percentage points more likely to add workers than are comparably sized nonEPZ firms, while EPZ firms below the threshold have an astounding 26 percentage point higher probability of growing relative to their nonEPZ counterparts. While the large firm share of nonEPZ firms rises over time, even that turns out to be due to poor outcomes in the nonEPZ sector. Small nonEPZ firms are slightly more likely to exit than nonEPZ firms which lowers the small firm share of all nonEPZ firms over time. In fact, small and large nonEPZ firms are 10 percentage points more likely to die than are their EPZ counterparts of like size and vintage.
The totality of the evidence suggests that the TEWA restrictions on firing that were supposed to increase employment stability had exactly the opposite result. By imposing a tax on firm growth, the system causes nonEPZ firms to inefficiently limit employment, increasing the odds that the firm will fail. While large firms atypically sort into the EPZ and avoid the regulatory expenses, a significant number of firms are caught by the regulatory costs. Results suggest that these firms would hire more workers and be more likely to succeed if nonEPZ and EPZ firms operated under the same, more liberal rules regarding the costs of hiring and firing.
1Sri Lanka data were compiled from the universe of formal sector firms in Sri Lanka described later in the paper.
2Freeman (2008) presents a review of both theoretical and empirical effects of labor market institutions. Addison and Teixeira (2001) review findings regarding the effects of employment protection legislation.
3The rationale for the policy, as stated in the Industrial Policy of Ceylon (1971), was that "….the [Government] is pledged to the establishment of a socialist society. This commitment calls for major changes in industrial policy to eliminate some of the social and economic consequences of the policy followed in the past few years [such as] the concentration of monopoly power in the hands of a few investors, leading to gross inequalities in the distribution of income and the entrenchment of privileged groups in society … [and] the heavy reliance of local industry on imported raw material, components and technology. . . .".
4Incompetence is not considered a disciplinary matter. Even in the case of disciplinary layoffs due to misconduct or poor discipline, the employer must inform the worker in writing of the reasons for such termination before the second day after such termination, failing which, the worker is entitled to seek redress under the TEWA on the basis that the termination of his services was not for disciplinary reasons.
5The others were an unreliable supply of electricity; uncertain government policy; macroeconomic instability; and the high cost of obtaining external financing (World Bank 2005).
6We should note that we have no evidence that the application for EPZ status is anything but above board. We are just trying to be complete in allowing for supra-normal application costs.
7The technology shock could also include innovations in the real price of output. To economize on terms, we fix the output price at unity and let all changes in the value of labor time work their way through productivity shocks.
8Ashenfelter and Card (1982) showed that wages evolve according to an AR(1) process with first-order coefficient insignificantly different from 1, and so the random walk assumption is not a radical departure from reality.
9In the Cobb-Douglas formulation used here, and with the restriction that capital is fixed, the second best solution is to set employment at 14. A more general specification could result in the second best employment level at less than 14.
10In practice, our main parameters of interest were not sensitive to the inclusion or exclusion of these cohort and firm-specific entry conditions.
Addison JT, Teixeira P (2001) "The Economics of Employment Protection". In: IZA Discussion Paper no. 381. Institute for the Study of Labor, Bonn, Germany
Ahsan A, Pages C (2009) Are All Labor Regulations Equal? Evidence from Indian Manufacturing. J Comp Econ 37(1):62–75
Arkolakis C (2013) A Unified Theory of Firm Selection and Growth. Yale University Working Paper, New Haven, CT
Ashenfelter O, Card D (1982) Time Series Representations of Economic Variables and Alternative Models for the Labour Market. Review Econ Stud 49(1):761–781
Baker D, Glyn A, Howell D, Schmitt J (2005) "Labor Market Institutions and Unemployment: A Critical Assessment of the Cross-Country Evidence". In Fighting Unemployment: The Limits of Free Market Orthodoxy, ed. David R. Howell. Oxford University Press, Oxford
Bassanini A, Duval R (2006) "Employment Patterns In OECD Countries: Reassessing the Role of Policies and Institutions". In: OECD Economics Department Working Paper No. 486
Besley T, Burgess R (2004) Can Labor Regulation Hinder Economic Performance? Evidence from India. Q J Econ 119(1):91–134
Cabral L (1995) Sunk Costs, Firm Size and Firm Growth. J Ind Econ 43(2):161–172
Evans DS (1987) The Relationship Between Firm Growth, Size, and Age: Estimates for 100 Manufacturing Industries. J Ind Econ 35(4):567–581
Freeman RB (2008) Labor Market Institutions around the World. In: Blyton P, Bacon N, Fiorito J, Heery E (eds) The SAGE Handbook of Industrial Relations. SAGE Publications Ltd., London
Haffner R, Nickell S, Nicoletti G, Scarpetta S, Zoega G (2001) "European Integration, Liberalization and Labour Market Performance". In: Bertola G, Boeri T, Nicoletti G (eds) Welfare and Employment in a United Europe. The MIT Press, Cambridge, MA
Heckman JJ, Pages C (2000) The Cost of Job Security Regulation: Evidence from Latin American Labor Markets. Economia 1(1):109–154
Leidholm C, Mead D (1987) "Small-Scale Industries in Developing Countries: Empirical Evidence and Policy Implications". In: International Development Paper 9. Agricultural Economics Department, Michigan State University
Nickell S, Layard R (1999) "Labor Market Institutions and Economic Performance". In: Ashenfelter O, Card D (eds) Handbook of Labor Economics, vol 3, chapter 46, 1st edn. Elsevier, Amsterdam pp 3029–3084
OECD (1999) OECD Employment Outlook 1999. OECD, Paris
Ranaraja S (2005) "The Functioning of the Termination of Employment Act Of 1971". In: World Bank, HDNSP, processed
Singh T (2010) Does international trade cause economic growth? A survey. World Econ 33(11):1517–1564
Wagner J (2007) Exports and productivity: A survey of the evidence from firm‐level data. World Econ 30(1):60–82
Wagner J (2012) International trade and firm performance: a survey of empirical studies since 2006. Rev World Econ 148(2):235–267
World Bank (2005) "Sri Lanka: Improving The Rural And Urban Investment Climate". In: World Bank, Poverty Reduction and Economic Management Network, South Asia Region
World Bank (2007) "Sri Lanka: Strengthening Social Protection". In: World Bank, Human Development Unit, South Asia Region, Report No. 38197-LK
The authors wish to thank the Central Bank of Sri Lanka for providing data and to Ramani Gunatilaka for providing useful comments to earlier drafts of the paper.
Responsible editor: David Lam
Department of Agricultural Economics, Extension and Rural Development, University of Pretoria, Pretoria, 0002, South Africa
Babatunde O Abidoye
IZA and Department of Economics, Iowa State University, Ames, IA, 50010, USA
Peter F Orazem
IZA, International School for Social and Business Studies, Celje, Slovenia and University of Primorska, Faculty of Management, Koper, Slovenia
Milan Vodopivec
Search for Babatunde O Abidoye in:
Search for Peter F Orazem in:
Search for Milan Vodopivec in:
Correspondence to Peter F Orazem.
Abidoye, B.O., Orazem, P.F. & Vodopivec, M. Mandatory costs by firm size thresholds: firm location, growth and death in Sri Lanka. IZA J Labor Develop 3, 36 (2014) doi:10.1186/s40175-014-0023-1
Received: 09 July 2014
Firing cost
Firm entry
Firm growth
Export promotion zone | CommonCrawl |
Deformation mechanisms in a coal mine roadway in extremely swelling soft rock
Qinghai Li1,2,
Weiping Shi3 &
Renshu Yang2
The problem of roadway support in swelling soft rock was one of the challenging problems during mining. For most geological conditions, combinations of two or more supporting approaches could meet the requirements of most roadways; however, in extremely swelling soft rock, combined approaches even could not control large deformations. The purpose of this work was to probe the roadway deformation mechanisms in extremely swelling soft rock. Based on the main return air-way in a coal mine, deformation monitoring and geomechanical analysis were conducted, as well as plastic zone mechanical model was analysed. Results indicated that this soft rock was potentially very swelling. When the ground stress acted alone, the support strength needed in situ was not too large and combined supporting approaches could meet this requirement; however, when this potential released, the roadway would undergo permanent deformation. When the loose zone reached 3 m within surrounding rock, remote stress p ∞ and supporting stress P presented a linear relationship. Namely, the greater the swelling stress, the more difficult it would be in roadway supporting. So in this extremely swelling soft rock, a better way to control roadway deformation was to control the releasing of surrounding rock's swelling potential.
Roadway control in soft rock is a problem in many mines (Bilir 2011; Ghiasi et al. 2012; Serafeimidis and Anagnostou 2013; Thomas et al. 2013). For roadway control, a variety of support materials and structures have been developed, such as arch sheds, bolting, cables, and shotcrete (Goetze 1984; Okubo et al. 1984; Rotkegel 2001; Stalega 1995). As is necessary in situ, based on shed and bolting practice, new support structures have been developed, such as bolts with constant resistance under large deformation (He et al. 2013; He and Guo 2014; Sun et al. 2014), high-prestress and high-strength support systems (Kang et al. 2013; Wu et al. 2015), high-strength cable support systems (Li et al. 2012), round (Draganow et al. 1977; Gao et al. 2010) or square (Li et al. 2015) pipe supports filled with concrete, and grouted bolt systems (Srivastava and Singh 2015; Wang et al. 2009). For most geological conditions, combinations of two or more types could meet the requirements of most roadways. However, in some complex geological conditions, combinations of shedding, bolting, cabling, and shotcreting cannot control the deformation of surrounding rock.
The problem of roadway support in swelling soft rock has become a challenging problem in recent years (Bilir 2011; Ghiasi et al. 2012; Schädlich et al. 2013; Serafeimidis and Anagnostou 2013; Thomas et al. 2013). In swelling soft rock, support measures include either, the application of a strong, rigid supporting formwork to limit deformation, or allowing floor heave to release swelling pressures, or a combination of both (Christoph et al. 2011). In T13 tunnel, Ankara-Istanbul High-Speed Train Project, a heavier, non-deformable support system (NDSS) was applied in swelling and squeezing rocks (Aksoy et al. 2012). Another tunnel in Ankara-Istanbul High Speed Train Project, Tunnel 35, which was driven in a fairly weak and jointed rock, was also controlled by developed NDSS (Aksoy et al. 2014). In Canada, a tunnel situated in the Queenston Formation, South Ontario, was supported by a double-shell lining system, which included an initial lining of shotcrete, steel ribs, rock dowels, and a final lining consisting of a waterproof membrane and cast-in-place concrete (Ansgar and Thomas 2010). In a tertiary soft rock roadway in Liuhai coal mine, China, bolt-mesh-cable and double-layer-truss supports were used to control the large rheological deformation (Yang et al. 2015). Shen (2014) proposed a support system, which included an optimal cable/bolt arrangement, full length grouting, and high-load pre-tensioning of bolts and cables.
The No. 1 Mine in Chagannuoer (NMC), located in Xilin Gol League, Inner Mongolia, China, with a production capacity of 8.0 Mt/a, was under construction. Roof and floor of the main coal seam comprised extremely swelling soft rock. During excavation, the roadway deformed significantly and continuously. After being repaired repeatedly, it still could not be used normally. This problem increased infrastructure investment and delayed mine construction. To probe the mechanism of roadway deformation, based on the main return air-way in NMC, deformation monitoring and geomechanical analysis were conducted on site. At the same time, a plastic zone mechanical model, verified by physical experiments, was established. Based on the mechanical model, the necessary support strength was analysed, which provided guidance for such roadway support in future.
In Chagannuoer coal field, there were five fully or partially minable coal seams, with thicknesses ranging from 1.60 to 59.60 m (28.92 m on average). In this coal field, two mines were designed and NMC, with its production capacity of 8.0 Mt/a, was the first mine under construction. In NMC, the No. 2 coal seam, at 22.3 m thickness on average, belonged to lignite and lay between Cretaceous and Jurassic strata, was the main mining seam and was buried at a depth of 212.2 m. Roof and floor of the No. 2 coal seam were primarily mudstone and carbon mudstone with extremely low strengths (Table 1), which were lower than the strength of coal seam and were in a loose, fractured state. In mine design, considering lower strength of roof and floor, the main roadway was placed in No. 2 coal seam (Fig. 1). Using the return-air roadway as example, it was designed as a straight wall-semicircular arch type (Fig. 2). The height of its straight wall was 1.8 m and the diameter of the semicircular arch was 5.0 m. The net cross-sectional area of the roadway was 18.82 m2. During the return air-way excavation, the mining pressure was exceeding large and floor heave, two sides shifting closer and roof subsidence presented almost all the time. Damaged forms of roadway are shown in Fig. 3. Several supporting approaches (Table 2) have been tested on site, but almost all failed and the roadway needs to be repaired all the time to maintain normal use, which brings risk to mine safety and production.
Table 1 Mechanical parameters of the strata
Histogram of coal seam and the location of the main return air-way
The main return air-way cross-section
In situ damaged status. a Roof subsidence. b Top arch distortion
Table 2 Support approaches used on site
Geomechanical analysis
Field monitoring
To understand the controlling effect of different supporting approaches listed in Table 2, four monitoring stations were established in the return air-way (Fig. 4). The monitoring stations were numbered 1–4. Roadways in different colours were supported by different approaches. From station 1–4, the roadway was supported by method of 1–4 (listed in Table 2) correspondingly. At each station, displacements of roof to floor and left to right side were monitored (Fig. 5).
Monitoring stations in the return air-way
Layout of observation lines (unit: mm)
Large deformation occurred in four stations. Data at stations 3 and 4, which benefitted from greater support strength than stations 1 and 2, were analysed (Fig. 6). At stations 3 and 4, the maximum rate of roof subsidence reached 20 and 15.1 mm/d. By the end of monitoring, roof subsidence reached 496 and 366 mm in two stations respectively. Roof shotcrete cracked and fell off, and the top arch was flattened and distorted. The maximum rate of two sides moving reached 19.3 and 12.5 mm/d. By the end of monitoring, two sides squeezing inward reached 596 and 426 mm. Over time, the deformation rate decreased gradually, but the deforming never stopped.
Displacements at station 3 and 4. a Station 3. b Station 4
Based on the design of releasing pressure, there was no support on floor. Under this status, floor heaving in stations 3 and 4 were almost the same. The maximum rate of floor heaving reached 38.3 and 31.9 mm/d at these two stations. During monitoring, the floor heave even reached 1658 and 1660 mm in two stations.
From monitoring results, it was found that, in this soft coal seam, roadway deformed significantly and the deforming never stopped.
Geological conditions and ground stress
Within the scope of mining area, all coal seams were stable, with a very gentle dip angle. There was a slight syncline (20 km in length, 4–10 km in width) in mining area. In general, the geological conditions in this area were simple.
To find the magnitude of ground stress, measurements were conducted at three locations in situ. From the results it was found that the maximum principal horizontal stress (σ hmax) was 8.41–8.66 MPa, with 12.5–18.1° to horizontal plane. The minimum principal horizontal stress (σ hmin) was 2.54–3.25 MPa, with −13.34–6.58° to horizontal plane. The vertical stress (σ v ) was 4.72–4.91 MPa. The ratio between σ hmax and σ v were approximately 1.8.
Laboratory tests showed that the mudstone in both roof and floor was mainly composed of quartz, potassium feldspar, plagioclase, and clay minerals. Among the measured compositions, the clay mineral reached 60.6 % in content (see Table 3). Worse still was that the clay minerals were mainly highly swelling montmorillonites, illites, and kaolinite. In these clay minerals, the montmorillonite accounted for 82.0 %. Compositions of clay minerals are shown in Table 4. Correspondingly, in both roof and floor mudstones, the montmorillonite reached 49.7 % in content. According to the swelling soft rock classification criteria proposed by Sun et al. (2005), roof and floor mudstones in NMC were classified as extremely swelling soft rock.
Table 3 Mineral compositions of mudstones
Table 4 Mineral compositions of clay fraction
Swelling pressure
To quantify the swelling pressure arising in this soft rock, three specimen swelling tests were conducted in laboratory. Each specimen was cylindrical, of 50 mm diameter and 50 mm high. During testing, three blocks were placed in experimental apparatus and immersed in water. Curves of swelling pressure are shown in Fig. 7.
Swelling pressures versus time
When absorbing water, the pressure increased rapidly, and then increased exponentially, but the swelling rate decreased gradually. Up to 10 h after immersion, the three blocks exhibited certain differences in swelling. Thereafter, the three blocks swelled almost the same to each other. Blocks reached complete saturation after 52 h immersion, by when the swelling pressure was 35.7–36.7 MPa.
Contrasting all engineering geological conditions in situ, it was found that the geological structure in this coal field was simple, and the ground stress was not abnormal. But the mudstone exhibited large swelling pressure in laboratory tests. Due to rigid constraints and complete saturation in tests, the swelling pressure was large, and much larger than in situ ground stress. Almost no constraints and lack of water in situ, the swelling pressure will be less than the measured values in laboratory tests. However, from test results it was found that there was significant swelling potential in this extremely swelling soft rock.
Mechanical analysis on plastic zone in extremely swelling soft rock
Mechanical model
Roadway in type of straight wall-semicircular arch is complicated in mechanical analysis. To simplify analysis, the roadway is designed as a circle (r = a) in mechanical model. Strata at infinity bear an isotropic pressure p ∞. A positive pressure P, simulating the support strength, is applied on the roadway surface (Fig. 8). The mechanical model is axisymmetric and the displacement is purely radial. There are only in-plane stress components τ rr (r) and τ θθ (r).
Mechanical model of roadway
Due to loose and fractured characteristics of extremely swelling soft rock, the strata demonstrated particulate characteristics. Referred to mechanics (Howell et al. 2009), yield criterion of granular rock is
$$ 2(\tau_{rr} \tau_{\theta \theta } )^{1/2} \le - \cos \varphi (\tau_{rr} + \tau_{\theta \theta } ) $$
in which, φ is internal friction angle of rock.
Formula (1) can be changed as
$$ k\tau_{\text{rr}} = \tau_{\theta \theta } $$
in which, \( k = \frac{1 + \sin \phi }{1 - \sin \phi }. \)
In plane polar, Navier equation (Howell et al. 2009) is
$$ \frac{{d\tau_{rr} }}{dr} + \frac{{\tau_{rr} - \tau_{\theta \theta } }}{r} = 0 $$
On roadway surface and in the far field, the boundary conditions satisfyWhen r = a, τ rr = −PWhen r → ∞, τ rr → −p ∞ , τ θθ → −p ∞ While the rock keeps elastic, the constitutive relations (Howell et al. 2009) are
$$ \tau_{rr} = \left( {\lambda + 2\mu } \right)\frac{{du_{r} }}{dr} + \lambda \frac{{u_{r} }}{r}, $$
$$ \tau_{\theta \theta } = \lambda \frac{{du_{r} }}{dr} + \left( {\lambda + 2\mu } \right)\frac{{u_{r} }}{r} $$
in which, λ is Lame constant, μ is shear modulus and u r is radial displacement.
Based on boundary conditions, combined with (3) and (4), the stress components are gained as
$$ \tau_{rr} = - p_{\infty } + \left( {p_{\infty } - P} \right)\frac{{a^{2} }}{{r^{2} }}, $$
$$ \tau_{\theta \theta } = - p_{\infty } - \left( {p_{\infty } - P} \right)\frac{{a^{2} }}{{r^{2} }} $$
On roadway surface (r = a), based on (2) and (5), the yield will occur when
$$ P = \frac{{2p_{\infty } }}{1 + k} $$
Plastic zone boundary is set as r = s. The elastic solution in r > s can be gained as P replaced by 2p ∞/(1 + k) and a replaced by s in (5). Namely
$$ \tau_{rr} = - p_{\infty } + p_{\infty } \left( {\frac{k - 1}{{k{ + }1}}} \right)\frac{{s^{2} }}{{r^{2} }}, $$
$$ \tau_{\theta \theta } = - p_{\infty } - p_{\infty } \left( {\frac{k - 1}{k + 1}} \right)\frac{{s^{2} }}{{r^{2} }} $$
Meanwhile, in plastic region r < s, based on boundary conditions, combined with (2) and (3), the stress is gained as
$${\tau _{rr}} = - P{\left( {\frac{r}{a}} \right)^{k - 1}}$$
When r = s, combined with k, (7) and (8), the loose zone s can be decided as
$$ s = a\left(\frac{{(1 - \sin \varphi )p_{\infty } }}{P}\right)^{{\frac{1 - \sin \varphi }{2\sin \varphi }}} $$
The plastic zone, gained by (9), started from centre of roadway. In supporting design, the plastic zone was always regarded as starting from the surface of roadway, so the actual plastic zone s' should be (s − a). Namely
$$ s' = a\left(\frac{{(1 - \sin \varphi )p_{\infty } }}{P}\right)^{{\frac{1 - \sin \varphi }{2\sin \varphi }}} - a $$
Rationality analysis on mechanical model
To verify the rationality of above mechanical model for plastic zone analysis in extremely swelling soft rock, based on main return air-way in NMC (supported by closed 36U-shape sheds was chosen to be analysed), a physical experiment was conducted and roadway deformation process was reappeared.
(1) Model size
In laboratory, the frame size length, width, and height were 1600, 400, and 1600 mm. According to main return air-way in NMC, the roadway was 5000 mm in width and 4300 mm in height (Fig. 2). Considering influenced zone by mining, the geometry ratio C l between prototype and experiment model was set to 16. Because of shed thickness and exposed anchors on roadway surface, the roadway size was enlarged by 5 mm in both width and height in experiment. Namely the roadway in experiment was 318 mm wide and 274 mm high.
(2) Strata materials
Carbon mudstone strata were formed by gypsum and water. Coal seam was formed by gypsum, water and additive. Rock layers were paved layer-by-layer to simulate bedded deposition in situ. According to similarity theorems (Yuan 1998), the volume weight ratio C γ and stress ratio C σ between prototype and experiment model were defined as:
$$ C_{\gamma } = \frac{{\gamma_{p} }}{{\gamma_{m} }} $$
$$ C_{\sigma } = C_{\gamma } \, \times \,C_{l} $$
in which, γ p and γ m are volume weight of strata in situ and in experiment model respectively.
The volume weight of physical strata and actual rock was more close to each other, so C γ was defined as 1.176. Correspondingly, C σ was 18.82 (C l = 16). The physical strata, in which the bulk densities were in the ratio C γ to actual rock, and the compressive strengths, tensile strengths and apparent cohesions were in the ratio C σ to actual rock, were found after repeated testing. The internal friction angle φ of physical coal seam, tested in laboratory, was nearly 27°.
(3) Loading mode
According to ground stress and C σ 18.82, σ hmax was almost 0.46 MPa and σ v was almost 0.26 MPa in experiment. During loading, horizontal and vertical stresses were increased simultaneously. The vertical stress was increased in 0.1 MPa increments every 30 min and the horizontal stress was applied as the vertical stress multiplied by 1.8 (σ hmax/σ v was 1.8). When the vertical stress reached 0.30 MPa, and the horizontal stress was 0.54 MPa, there were no damaged signs in surrounding rock. It can be determined that, when ground stress acted alone, the roadway, supported by approaches listed in Table 2, could not deform as much. So the ground stress was not the cause of roadway deformation in this extremely soft rock.
And then, based on existing loads, the vertical and horizontal stresses increased simultaneously in 0.1 MPa increments every 30 min. The model was not damaged until the loads reached 0.8 MPa in vertical and 1.04 MPa in horizontal.
(4) Shed material
Steel bar, 2 mm in thickness and 10 mm in width, was chosen for the material of sheds in experiment. Two model sheds were tested and their capacities were shown in Fig. 9. During testing, the loading mode was the same as that determined previously. The capacity of the model shed was 0.291 kN (average of two tests). In situ, sheds were installed every 700 mm along roadway. According to geometry ratio C l , the sheds in experiment were placed every 44 mm along roadway. Combined with 115 mm height of two sides, the support strength offered by these sheds on two sides was 0.0575 MPa in physical model.
Test data of model shed bearing capacities
Experimental results
When vertical stress reached 0.7 MPa and horizontal stress reached 0.94 MPa in experiment, the loose zone in two sides extended to 0.417 m (Fig. 10). With φ = 27°, p ∞ = 0.94 MPa and a = 0.159 m, according to formula (10), the plastic zone was calculated as 0.434 m. Compared with experimental result, the error of calculated one was 4.1 %. So the mechanical model was deemed suitable for plastic zone analysis in extremely swelling soft rock.
Damage mode in the model
Support strength analysis
In extremely swelling soft rock, according to formula (10), when the loose zone controlled much smaller, the required support strength will be much larger. While a is 2.5 m and φ is 27°, as well as the loose zone reaches 3 m in surrounding rock, the relationship between p ∞ and P (Fig. 11) is given by:
$$ P = \, 0. 1 4 7p_{\infty } - \,{ 2}. 3 2 5 { } \times { 1}0^{ - 4} $$
Relationship between p ∞ and P
From formula (13), as p ∞ increases, the needed support strength P grows linearly. When p ∞ is 8.6, 10, 15 and 20 MPa, the support strength P will be 1.265, 1.471, 2.207 and 2.943 MPa correspondingly. So when the ground stress acts alone, the support strength needed in maintaining roadway stability is 1.265 MPa, which is not too large and the support approaches listed in Table 2 could meet the requirement. However, when the remote stress p ∞ increases to 15 MPa (mainly induced by surrounding rock swelling), the support strength will exceed 2 MPa, which would need extremely high-strength support structures to meet this requirement. Furthermore, the greater the swelling stress, the more difficult will be in roadway support. So the better way to control roadway deformation is to control the releasing of swelling potential. In this extremely swelling soft rock, when supports yielded and swelling stress released, more conditions would be created for rock swelling. So the non-deformable support system (NDSS) would be an effective way for roadway control in this extremely swelling soft rock.
To understanding the roadway deformation mechanisms in extremely swelling soft rock in NMC, monitoring and geomechanical analysis were conducted on site, and a plastic zone mechanical model was established. The following conclusions were drawn: the soft rock had significant potential to swell. When ground stresses acted alone, the support strength needed in situ was not too large and combined support approaches could meet this requirement. When swelling potential of this rock released, the roadway would deform significantly and the deformation would be permanent. Based on mechanical analysis, when the loose zone reached 3 m in surrounding rock, remote stress p ∞ and supporting strength P presented a linear relationship. Namely, the greater the swelling stress, the more difficult would be in roadway support. So in this extremely swelling soft rock, a better way to control roadway deformation was to control the releasing of surrounding rock's swelling potential. And the non-deformable support system (NDSS) was an effective way for roadway control in this extremely swelling soft rock.
Aksoy CO, Ogul K, Topal I, Ozer SC, Ozacar V, Posluk E (2012) Numerical modeling of non-deformable support in swelling and squeezing rock. Int J Rock Mech Min Sci 52:61–70
Aksoy CO, Ogul K, Topal I, Posluk E, Gicir A, Kucuk K, Uyar Aldas G (2014) Reducing deformation effect of tunnel with non-deformable support system by jointed rock mass model. Tunn Undergr Sp Tech 40:218–227
Ansgar K, Thomas M (2010) Numerical prediction of time-dependent rock swelling based on an example of a major tunnel project in Ontario/Canada. Num Meth Geotech Eng 25:297–302
Bilir M (2011) Swelling problems and triaxial swelling behavior of claystone: a case study in Tire, Turkey. Sci Res Essays 6:1106–1116
Christoph B, Peter H, Eric Z (2011) Impact of tunneling on regional groundwater flow and implications for swelling of clay–sulfate rocks. Eng Geol 117:198–206
Draganow L, Patronew I, Tschonkow T (1977) Development of a new flexible roadway support consisting of steel tubes with concrete filling. Neue Bergbautech 7:182–185
Gao YF, Wang B, Wang J, Li B, Xing F, Wang ZG, Jin TL (2010) Test on structural properties and application of concrete-filled steel tube support of deep mine and soft rock roadway. Chin J Rock Mech Eng 29:2604–2609
Ghiasi V, Ghiasi S, Prasad A (2012) Evaluation of tunnels under squeezing rock condition. J Eng Des Technol 10:168–179
Goetze W (1984) Roadway supports development and planning. Gluckauf: Die Fachz fur Rohst, Bergbau and Energ 120: 395–396, 399–400, 403–404
He MC, Guo ZB (2014) Mechanical properties and engineering application of anchor bolt with constant resistance and large deformation. Chin J Rock Mech Eng 33:1297–1308
He MC, Yuan Y, Wang XL, Wu ZQ, Liu C, Jiang YL (2013) Control technol. for large deformation of mesozoic compound soft rock in Xinjiang and its application. Chin J Rock Mech Eng 32:433–441
Howell P, Kozyreff G, Ockendon J (2009) Applied solid mechanics. Cambridge University Press, Oxford, pp 330–337
Kang HP, Lin J, Wu YZ (2013) Development and applications of rock bolting materials for coal mine roadways. 30th Annu Int Pittsburgh Coal Conf PCC 2013:136–154
Li SC, Wang Q, Li WT, Wang DC, Li Z, Jiang B, Wang HP, Wang HT (2012) Comparative field test study of pressure relief anchor box beam support system in deep thick top coal roadway. Chin J Rock Mech Eng 31:656–666
Li SC, Shao X, Jiang B, Wang Q, Wang FQ, Ren YX, Wang DC, Ding GL (2015) Study of the mechanical characteristics and influencing factors of concrete arch confined by square steel set in deep roadways. J Chin Univ Min Technol 44:400–408
Okubo S, Amano K, Koizumi S, Nishimatsu Y (1984) In-situ measurement on the effect of roadway support-measurement at roadway supported by rock bolts. Nihon Kogyokaishi 100:11–16
Rotkegel M (2001) Design and examinations of high-stability roadway supports. Prac Nauk Inst Geotech I Hydrotech Politech Wroc 73:421–430
Schädlich B, Marcher T, Schweiger HF (2013) Application of a constitutive model for swelling rock to tunneling. Geotech Eng 44:47–54
Serafeimidis K, Anagnostou G (2013) On the time-development of sulphate hydration in anhydritic swelling rocks. Rock Mech Rock Eng 46:619–634
Shen BT (2014) Coal mine roadway stability in soft rock: a case study. Rock Mech Rock Eng 47:2225–2238
Srivastava LP, Singh M (2015) Effect of fully grouted passive bolts on joint shear strength parameters in a blocky mass. Rock Mech Rock Eng 48:1197–1206
Stalega S (1995) Verification in underground of the method design and selection of roadway support made from V section. Prac Nauk Inst Bud Politech Wroc 69:273
Sun XM, Wu X, He MC (2005) Differentiation and grade criterion of strong swelling soft rock. Chin J Rock Mech Eng 24(1):128–132
Sun XM, Wang D, Wang C, Liu X, Zhang B, Liu ZQ (2014) Tensile properties and application of constant resistance and large deformation bolts. Chin J Rock Mech Eng 33:1765–1771
Thomas M, Utz K, Maximiliano RV, Theodoros T (2013) Influence of hematite coating on the activation of the swelling potential of smectite-bearing rocks. Rock Mech Rock Eng 46:835–847
Wang LG, Zhang J, Li HL (2009) A creep analysis of a bolt-grouting support structure within a soft rock roadway. J Chin Univ Min Technol 38:607–612
Wu YZ, Kang HP, Wu JX, Fan RX (2015) Development and application of mine prestressed steel bars supporting technol. Chin J Rock Mech Eng 34:3230–3237
Yang J, Wang D, Shi HY, Xu HC (2015) Deformation failure and countermeasures of deep tertiary extremely soft rock roadway in Liuhai coal mine. Int J Min Sci Technol 25:231–236
Yuan WZ (1998) The similarity theory and the statics model test. Xi'an Jiaotong University Press
QL made substantial contributions to research conception, as well as establishment and analysis of mechanical model on plastic zone in extremely swelling soft rock, physical experiments design, and manuscript revised finally. WS was mainly involved in physical experiments implementing and data analysing and manuscript drafting. RY was mainly involved in geomechanical analysing and manuscript revising. All authors read and approved the final manuscript.
We wish to gratefully acknowledge Xizhu Li, director of No. 1 mine of Chagannuoer, who provided great help in ground stress measurement in site.
The collaborative funding supported by Opening Project Fund of State Key Laboratory of Mining Disaster Prevention and Control Co-founded by Shandong Province and the Ministry of Science and Technology (No. MDPC2013ZR03), the funding supported by Scientific Research Foundation of Shandong University of Science and Technology for Recruited Talents (No. 2014RCJJ027), and the funding by Shandong Province Higher Educational Science and Technology Program (A1042420161008).
State Key Laboratory of Mining Disaster Prevention and Control Co-founded by Shandong Province and the Ministry of Science and Technology, Shandong University of Science and Technology, Qingdao, 266590, China
Qinghai Li
School of Mechanics and Civil Engineering, China University of Mining and Technology (Beijing), Beijing, 100083, China
& Renshu Yang
College of Geomatics, Shandong University of Science and Technology, Qingdao, 266590, China
Weiping Shi
Search for Qinghai Li in:
Search for Weiping Shi in:
Search for Renshu Yang in:
Correspondence to Qinghai Li.
Li, Q., Shi, W. & Yang, R. Deformation mechanisms in a coal mine roadway in extremely swelling soft rock. SpringerPlus 5, 1310 (2016) doi:10.1186/s40064-016-2942-6
Deformation mechanism
Extremely swelling soft rock
Swelling potential
Plastic zone | CommonCrawl |
Home Journals I2M Temperature-Dependent Thermal Conductivity Measurement System for Various Heat Transfer Fluids
Temperature-Dependent Thermal Conductivity Measurement System for Various Heat Transfer Fluids
Yunita Anggraini | Alfriska O. Silalahi | Inge Magdalena Sutjahja* | Daniel Kurnia | Sparisoma Viridi | Surjamanto Wonorahardjo
Department of Physics, Institut Teknologi Bandung, Jl. Ganesha No. 10, Bandung 40132, Indonesia
Department of Electrical Engineering, Institut Teknologi Del, Jl. Sisingamangaraja, Laguboti, Tobasa, Sumatera Utara 22381, Indonesia
Department of Architecture, Planning and Policy Development, Institut Teknologi Bandung, Jl. Ganesha No. 10, Bandung 40132, Indonesia
[email protected]
https://doi.org/10.18280/i2m.200403
Accurate measurement of the thermal conductivity of a heat transfer fluid (HTF) is important for optimizing the performance of a thermal energy storage system. Herein, we develop a system to measure the thermal conductivity of an HTF during temperature variation, and the system was checked to measure several samples comprising water, lauric acid, stearic acid, oleic acid, and coconut oil. The thermal conductivity was measured using a KS-1 sensor of a KD2 Pro analyzer. In the study, a static heat conducting medium was used to control the temperature of the fluid, instead of the commonly used flowing water bath. The measured thermal conductivities of water (298 to 318 K) and lauric acid (323 to 373 K), stearic acid (358 to 372 K), oleic acid (334 to 372 K), and coconut oil (298 to 363 K) were compared to data from previous studies and fitted to available models. The accuracy of the data is further analyzed by relating the number of C and H atoms in the fatty acid, and the fatty acid content in coconut oil.
thermal conductivity, transient hot-wire, fatty acid, coconut oil, heat transfer fluid
A heat transfer fluid (HTF) is a liquid or gas that is used to transfer heat from one system to another [1, 2]. In addition to water and ethylene glycol [3, 4] liquid HTFs include edible oils [5-7] salt solutions or salt hydrates [8, 9], ionic liquids [10, 11], and fatty acid [12, 13]. The liquid thermal conductivity of a HTF, which is a measure of its ability to transfer heat, is an important parameter for the optimization of the performance of a thermal energy storage system. In general, thermal conductivity depends on temperature [14, 15] and type and amount of a nanoparticle dopant, which is directly added to form a stable suspension called a nanofluid [16]. Dopants are commonly categorized as non-magnetic (e.g., various carbon materials [17, 18], Al2O3, TiO2, and CuO [19]), or magnetic (e.g., Fe2O3 and Fe3O4) [20-23].
Accurate measurement of HTF's thermal conductivity is very important, both from science and for technological applications. However, the effect of convection is a dominant factor in determining the temperature dependency of thermal conductivity, especially as temperature increases. As shown in Table 1, the systems developed in previous studies allow convection, thus potentially reducing the accuracy of the thermal conductivity data. Herein, we describe a simple system for heating a liquid to measure its thermal conductivity as the temperature varies from 298 to 373 K while minimizing the convection effect. The thermal conductivity was measured using a KS-1 sensor of a KD2 Pro, which works on the basis of the hot wire transient method [24-31]. This method is a dynamic transient technique based on measuring the temperature rise at a certain distance from a fine and long wire-shaped heat source embedded in the test material. The hot wire transient method offers several advantages over other measurement methods [32, 33], such as the capability to eliminate errors related to natural convection, quick experimental results, and simple conceptual design. The instrument was tested by measuring the thermal conductivity of water, lauric acid, stearic acid, oleic acid, and coconut oil. The experimental results were compared with the available data from other studies and fitted using available models.
Lauric acid (C12H24O2) and stearic acid (C18H36O2) are saturated fatty acids with a melting point of approximately 316 K [34] and 341 K [35]. Oleic acid (C18H34O2) is a monounsaturated fatty acid with one double bond that occurs naturally in various animal and vegetable fats and oils. It has a melting point of approximately 287 K [36]. Oleic acid has a similar amount of carbon and oxygen to the stearic acid in those chemical compounds. Coconut oil is edible oil and melts at room temperature. Coconut oil contains many kinds of saturated and unsaturated fatty acids, with an enormous amount of saturated fatty acid (90%) with a medium-chain fatty acid, such as lauric acid (50%) [37]. Despite many applications of coconut oil in engineering fields [35, 37-42], no available data for temperature-dependent thermal conductivity. Further analysis will be performed to study the relation between the number of C and H content in the fatty acid, the number of saturated and unsaturated bonding and the composition of fatty acid in the coconut oil with the thermal conductivity values.
This paper is organized as follows. The Method and Materials section explains the development of the instrumentation system and the material used. The Results and Discussion section presents the experimental results of the temperature-dependent thermal conductivity of various HTFs. The data were fitted using available models and compared with the results of previous studies. We found that the developed apparatus accurately measured the temperature-dependent thermal conductivity of various HTFs.
Literature review of liquid thermal conductivity heating systems
Table 1 summarizes the heating systems used to measure the thermal conductivity of liquids from previous studies, with the samples used and the technical conditions of the system.
Table 1. Heating systems used in liquid thermal conductivity measurement
Technical condition
Direct heating
Fe3O4-water magnetic nanofluid
This method can cause convection currents in the sample, which reduces the accuracy of thermal conductivity measurement.
Doganay et al. [22]
Water-based TiO2 nanofluid
Turgut et al. [43]
Circulating bath
An-oil based nanofluid
Circulating water for sample heating, either using a flowing water bath or storage tank, causes convection currents in the water as these currents aid the heat transfer process.
Jiang et al. [7]
Six-ionic liquid
Liu et al. [14]
TiO2- MWCNTs/ (EG-water hybrid nanofluid
Moradi et al. [44]
Fe2O3 nanofluid
Agarwal et al. [45]
Magnetic nanofluid
Roszko et al. [46]
(γ –Fe2O3) water- based nanofluids
Nurdin et al. [47]
Deionized water and ethylene glycol-based nanofluids
Abdullah et al. [48]
Static bath
Water-graphene oxide/aluminum oxide nanoparticles
With the relatively large amount of water used to heat the sample, inhomogeneous temperature is possible.
Taherialekouhi et al. [49]
Semiclathrate hydrates and aqueous solutions of tetrabutylammonium bromide (TBAB) and tetrabutylammonium chloride (TBAC)
Fujiura et al. [50]
Graphene oxide/Water nanofluid
Yang et al. [51]
rGO-Fe3O4-TiO2 hybrid nanofluid
Cakmak et al. [53]
Deionized water, lauric acid, stearic acid, oleic acid, and coconut oil
Simple instrument, cost-effective, < 1 L liquid medium required to heat a sample.
Present Work
2. Method and Materials
Figure 1 shows the setup of the measuring system, which consists of three main parts: (1) thermal conductivity sensor, (2) heating system, and (3) sample system. The heating system consists of a transformer (2a) to control the voltage output to the heater controller (2b) that is controlled by a PC (2c). The sample system consists of a sample glass (3a) equipped with a circular heater (3b) and a thermocouple data logger (3c) to monitor the temperature readings in the heating medium. The overall sample system was placed in an adiabatic container to inhibit heat loss to the environment (3d).
Figure 1. Set up for measuring the thermal conductivity of the liquid material samples during temperature variation
The thermal conductivity was measured using the KS-1 sensor of a KD2 Pro thermal properties analyzer (Decagon, USA) [54]. This is a commonly used analyzer for measuring thermal conductivity [55-58]. The sensor has a diameter and length of 1.3 mm and 6 cm, respectively. The heat flux per unit length (q) and the time-dependent temperature can be used to calculate the thermal conductivity using Eq. (1) [25, 59].
$k=\frac{q}{4 \pi}\left(\frac{d \ln (t)}{d T}\right)$ (1)
To measure the thermal conductivity with temperature variation, approximately 30 mL samples were placed into sample glasses with an inner diameter of 2.3 cm, outer diameter of 2.5 cm, and height of 9.8 cm. Then, the sample glasses were placed inside a beaker containing approximately 500 mL of a heat conductive liquid medium, which was covered with a circular heating system made of stainless steel. For accurate thermal conductivity measurements, the sensor was placed in a holder system that maintained its vertical position inside the sample glass. The holder system also served as a cover for the sample and heat conduction medium.
The heating system used throughout this experiment had a relatively small thermal mass; hence, the applied input voltage to the heater was small. To achieve the required voltage, the source voltage of a transformer was adjusted. Then, the power drawn by the heater was controlled by an Autonic heater controller, which uses the pulse width modulation (PWM) technique [60]. PWM is a modulating technique, in which the pulse width is varied while maintaining a fixed amplitude and frequency. The PWM duty cycle is the ratio of the 'on' time to the regular interval or 'period' of time. The duty cycle is expressed as a percentage, with 100% being fully on and 0 % being completely off. A low duty cycle corresponds to a low applied heater power [61]. Meanwhile, the heater was set to heat the heat conductive medium and sample up to a user-defined temperature set-point. At least three or four calibrated temperature sensors were used to monitor the temperature distribution in the heat conductive medium. These sensors were placed opposite to each other at two different height position from the upper part of the heating medium (Table 2). In this study, T-type thermocouples with a diameter of approximately 1 mm, connected to an Applent data logger with an accuracy of 0.2% ± 1℃, were used as temperature sensors.
The voltage at each temperature set-point was adjusted to be as low as possible to avoid large heat pulses and allow sufficient time for heat propagation from the heater to the middle of the sample. After the temperature set-point was reached, the heater was turned off to prevent heat pulses and heat waves that could result in convection, that could reduce the accuracy of the measurements. After achieving a uniform temperature distribution as determined from the three or four thermocouple sensors, the thermal conductivity was measured.
Table 2. Relative positions of the thermocouple channels of Applent in the heating medium
No of thermocouples
Height from the upper part of heating medium (cm)
De-ionized water, lauric acid, stearic acid, oleic acid, and coconut oil were used in the temperature ranges from room temperature to 318 K, from 323 to 373 K, from 358 to 372 K, from 334 to 372 K, and from 298 to 363 K, respectively, to calibrate the heating system. During measurements for each sample over all temperature ranges, voltages of 30-35 V and 35-55 V for water and lauric acid, respectively, and 40 V for stearic acid, oleic acid, and coconut oil were used. The voltage value should be constant for a single set of measurement to maintain the overall heating rate. The measurements were repeated two times for water and three times for lauric acid, stearic acid, oleic acid, and coconut oil to ensure that the readings were reproducible. In addition, thermal conductivity measurement for lauric acid and oleic acid was conducted two times to verify its repeatability. The average values are presented here.
For this experiment, technical grade lauric acid and stearic acid with purities of 85-90% from Indonesia were used as the heat conductive media. In contrast, non-technical grade lauric acid and stearic acid were used as the sample for thermal conductivity measurements. For this purpose, lauric acid and stearic acid with purity ≥ 98% and ≥ 95%, respectively, were purchased from Sigma Aldrich. Technical grade oleic acid was purchased from a traditional market in Indonesia. Coconut oil commonly used for household needs was purchased from a traditional market in Indonesia.
Figure 2 shows the temperature distributions in samples when they were used as heat conductive media for thermal conductivity measurement.
Figure 2. Typical temperature distribution of the heat conductive medium
The experimental results show that at the same height position of Applent thermocouple, the temperature is relatively uniform, with the temperature on the upper thermocouple position being higher (about 0.1 K) than that on the bottom position. These results indicate that convection did not occur at the beginning of the measurement, and temperature differences at different heights were related to the buoyancy convection effect [62]. As shown in Figure 2, after waiting for some time, we switched off the heater, and the temperatures at different heights will become the same, and the thermal conductivity measured under these conditions. The waiting time became shorter as the temperature increased due to the faster Brownian motion of molecules [63].
Figure 3 shows the results of the temperature-dependent thermal conductivity for de-ionized water.
Table 3. Regression coefficients of water thermal conductivity data using Eq. (2) for the present experiment and those from [64] and [65]
Regression coefficient
Present data
Previous studies
-4.10 × 10-3
6.25 × 10-3
-1.12 ×10-5
$\chi^{2}$
From Figure 3, one can see that the experimental data were close to the data from the previous studies, with a maximum error value of 1.1% at T = 313 K. The measurement of water at high temperatures above 323 K might cause an increase in the measurement errors because of the drastic change in the viscosity of water [54]. In this study, the appearance of microbubbles might have caused convection, which might have led to inaccurate results.
As shown in Figure 3, the thermal conductivity of water increases with temperature, and the values are close to those reported by [65] but higher than values reported by [66] and lower than those reported by [64]. In the high-temperature range, the increase in the thermal conductivity occurred up to 423 K before decreases as the temperature increased thereon [67], and strongly related to the hydrogen bond strength [68]. Based on [67], the temperature-dependent thermal conductivity of water was analyzed using a second-order polynomial function, as in Eq. (2), which is commonly used for liquid and solid inorganic compounds.
$k(T)=A+B T+C T^{2}$ (2)
where, k is the thermal conductivity; A, B, and C are the regression coefficients; and T is the absolute temperature. Table 3 shows the results of the fitting of the water thermal conductivity data from the present experiment with those from [69]. The similarity of the regression coefficients for the three sets of data, together with the reduced chi-square values show that the data fitted well.
The liquid thermal conductivity of lauric acid, stearic acid, oleic acid, and coconut oil are shown in Figure 4(a), Figure 4(b), Figure 4(c), and Figure 4(d), respectively. Increasing the temperature invariably decreased the thermal conductivity. This trend is common for organic liquids [70].
Based on [67], the temperature-dependent thermal conductivities of lauric acid, stearic acid, oleic acid, and coconut oil were analyzed using Eq. (3),
$k=A+B\left(1-\frac{T}{C}\right)^{\frac{2}{7}}$ (3)
Table 4 shows the results of the fitting of the thermal conductivity data of lauric acid, stearic acid, oleic acid, and coconut oil, respectively, along with the reference. The regression coefficients and reduced chi-square values listed in the table indicate that the data fitted well.
Figure 3. Thermal conductivity data of water. Red lines: fitted curves to Eq. (2) (see text)
4c.jpg
4d.jpg
Figure 4. Thermal conductivity data of (a) lauric acid, (b) stearic acid, (c) oleic acid, and (d) coconut oil. Red lines: fitted curves to Eq. (3)
Table 4. The best results for the regression coefficients of lauric acid, stearic acid, oleic acid, and coconut oil thermal conductivity using Eq. (3), for the present data and previous study [71]
Previous study, [71]
Comparison of the present experimental data with those from previous studies over a temperature from 320 to 420 K, the measured thermal conductivity of lauric acid was close to those reported by [69], but higher than those reported by [72], and lower than those reported by [71]. In the same condition, stearic acid thermal conductivity in the temperature range 358-372 K also close to the reference reported by [71], but lower than those reported by [69]. Oleic acid thermal conductivity value over a temperature of 334-372 K also close to the reference reported by [71]. The results of our study show that the thermal conductivity of stearic acid is higher than lauric acid, in agreement with the close relationship between the number of C and H atoms with thermal conductivity data of saturated fatty acid ethyl ester [64]. We note that the solid thermal conductivity data of fatty acid also shows a similar relationship, although there is no explicit explanation for that [73]. Besides that, the thermal conductivity of stearic acid does not resemble those of oleic acid with the same C number. It is seemingly that the occurrence of unsaturated bonding does not give considerable influence to the thermal conductivity data.
For the coconut oil thermal conductivity, one can see at room temperature, the present value is almost the same with the value reported by Silalahi et al. [74], but lower than those reported in Ref. [75]. The difference due to measuring temperature or phase condition of the sample, namely solid phase of coconut oil that reported in Ref. [75]. Generally, thermal conductivity of coconut oil is close to the values of soybean oil and considerably lower than the values of other vegetable oils [76]. At temperature 320 K the thermal conductivity of coconut oil is close to the value of lauric acid, in agreement with a previous report by Hoffmann et al. [5], that fatty acid composition in the vegetable oil determines the thermal conductivity and other temperature-dependent thermophysical parameters.
We have demonstrated a heating system for measuring the thermal conductivity of liquid HTF during temperature variation. The thermal conductivity was measured using a KS-1 sensor of a KD2 Pro analyzer, which works based on the transient heat line source method. The thermal conductivities of de-ionized water (room temperature to 318 K), lauric acid (323 to 373 K), stearic acid (358 to 372 K), oleic acid (334 to 372 K), and coconut oil (298 to 363 K) are measured and found to be in good agreement with the data reported in previous studies. Available models were used to fit the experimental data. Further analysis show that the thermal conductivity values are comparable to the number of C and H atoms contained in the fatty acid, and minor contribution of unsaturated bonding. At temperature around 320 K, coconut oil thermal conductivity value is close to lauric acid, which corresponds to the character of the fatty acid content in coconut oil.
We note that, although the developed apparatus can be used to measure the thermal conductivity of any HTF, the applied voltage might be different for a specific type of liquid. In addition, it is necessary to maintain a constant voltage during the measurement, as a change in voltage might cause a pulse heat and induce a convection current.
This work is supported by PMDSU batch 4 from RistekDikti of Indonesian government.
thermal conductivity, W.m-1. K-1
heat flux per unit length, W.m-2
time, s
temperature, K
regression coefficient, -
residual sum of squares
[1] Vignarooban, K., Xu, X., Arvay, A., Hsu, K., Kannan, A.M. (2015). Heat transfer fluids for concentrating solar power systems – A review. Applied Energy, 146: 383-396. https://doi.org/10.1016/j.apenergy.2015.01.125
[2] Reddy, K.S., Mudgal, V., Mallick. T.K. (2018). Review of latent heat thermal energy storage for improved material stability and effective load management. Journal of Energy Storage, 15: 205-227. https://doi.org/10.1016/j.est.2017.11.005
[3] Sundar, L.S., Singh, M.K., Sousa, A.C.M. (2013). Investigation of thermal conductivity and viscosity of Fe3O4 nanofluid for heat transfer applications. International Communication of Heat and Mass Transfer, 44: 7-14. https://doi.org/10.1016/j.icheatmasstransfer.2013.02.014
[4] Cabaleiro, D., Colla, L., Barison, S., Lugo, L., Fedele, L., Bobbo, S. (2017). Heat transfer capability of (ethylene glycol+water)-based nanofluids containing graphene nanoplatelets: design and thermophysical profile. Nanoscale Research Letter, 12: 53. https://doi.org/10.1186/s11671-016-1806-x
[5] Hoffmann, J.F., Py, X., Henry, J.F., Vaitilingom, G., Olives, R., Chirtoc, M., Caron, D. (2016). Temperature dependence of thermal conductivity of vegetable oils for use in concentrated solar power plants, measured by 3omega hot wire method. International Journal Thermal Science, 107: 105-110. https://doi.org/10.1016/j.ijthermalsci.2016.04.002
[6] Gomna, A., N'Tsoukpoe, K.E., Le Pierrès, N., Coulibaly, Y. (2019). Review of vegetable oils behaviour at high temperature for solar plants: Stability, properties and current applications. Solar Energy Materials and Solar Cells, 200: 109956. https://doi.org/10.1016/j.solmat.2019.109956
[7] Jiang, H., Li, H., Zan, C., Wang, F., Yang, Q., Shi, L. (2014). Experimental investigation on thermal conductivity of MFe2O4 (M=Fe and Co) magnetic nanofluids under influence of magnetic field. Thermochimica Acta, 579: 27-30. https://doi.org/10.1016/j.tca.2014.01.012
[8] Ueki, Y., Fujita, N., Kawai, M., Shibahara, M. (2017). Thermal conductivity of molten salt-based nanofluid. AIP Advances, 7(5): 055117. https://doi.org/10.1063/1.4984770
[9] Xie, N., Huang, Z., Luo, Z., Gao, X., Fang, Y., Zhang, Z. (2017). Inorganic Salt Hydrate for Thermal Energy Storage. Applied Sciences, 7(12): 1317. https://doi.org/10.3390/app7121317
[10] França, J.M.P., Lourenço, M.J.V., Murshed, S.M.S., Pádua, A.A.H., Nieto de Castro, C.A.N. (2018). Thermal conductivity of ionic liquids and ionanofluids and their feasibility as heat transfer fluids. Industrial and Engineering Chemistry Research, 57(18): 6516-6529. https://doi.org/10.1021/acs.iecr.7b04770
[11] Valkenburg, M.E.V., Vaughn, R.L., Williams, M., Wilkes, J.S. (2005). Thermochemistry of ionic liquid heat-transfer fluid. Thermochimica Actta, 425(1-2): 181-188. https://doi.org/10.1016/j.tca.2004.11.013
[12] Ding, L., Wang, L., Georgios, K., Lü, Y., Zhou, W. (2017). Thermal characterization of lauric acid and stearic acid binary eutectic mixture in latent heat thermal storage systems with tube and fins. Journal of Wuhan University Technology, Materials Science Edition, 32: 753-759. https://doi.org/10.1007/s11595-017-1663-1
[13] Kaygusuz, K., Sari, A. (2006). Thermal energy storage performance of fatty acids as a phase change material. Energy Sources, Part A Recovery, Utilization Environment Effects, 28(2): 105-116. https://doi.org/10.1080/009083190913971
[14] Liu, H., Maginn, E., Visser, A.E., Bridges, N.J., Fox, E.B. (2012). Thermal and transport properties of six ionic liquids: An experimental and molecular dynamics study. Industrial and Engineering Chemistry Research, 51(21): 7242-7254. https://dx.doi.org/10.1021/ie300222a
[15] Fröba, A.P., Rausch, M.H., Krzeminski, K., Assenbaum, D., Wasserscheid, P., Leipertz, A. (2010). Thermal conductivity of ionic liquids: measurement and prediction. International Journal of Thermophysics, 31: 2059-2077. https://doi.org/10.1007/s10765-010-0889-3
[16] Kumar, P.M., Kumar, J., Tamilarasan, R., Sendhilnathan, S., Suresh, S. (2015). Review on nanofluids theoretical thermal conductivity models. Engineering Journal, 19(1): 67-83. https://dx.doi.org/10.4186/ej.2015.19.1.67
[17] Dubyk, K., Isaiev, M., Alekseev, S., Burbelo, R., Lysenko, V. (2019). Thermal conductivity of nanofluids formed by carbon flurooxide mesoparticles. SN Applied Science, 1: 1-7. https://doi.org/10.1007/s42452-019-1498-9
[18] Phuoc, T.X., Massoudi, M., Chen, R.H. (2011). Viscosity and thermal conductivity of nanofluids containing multi-walled carbon nanotubes stabilized by chitosan. International Journal of Thermal Science, 50(1): 12-18. https://doi.org/10.1016/j.ijthermalsci.2010.09.008
[19] Ali, N., Teixeira, J.A., Addali, A. (2019). A review on nanofluids: Fabrication, stability, and thermophysical properties. Journal of Nanomaterials, 2018: 6978130. https://doi.org/10.1155/2018/6978130
[20] Nurdin, I., Yaacob, I.I., Johan, M.R. (2016). Enhancement of thermal conductivity and kinematic viscosity in magnetically controllable maghemite (c-Fe2O3) nanofluid. Experimental Thermal and Fluid Science, 77: 265-271. https://doi.org/10.1016/j.expthermflusci.2016.05.002
[21] Nkurikiyimfura, I., Wang, Y., Pan, Z. (2013). Heat transfer enhancement by magnetic nanofluids-A review. Renewable and Sustainable Energy Reviews, 21: 548-561. https://doi.org/10.1016/j.rser.2012.12.039
[22] Doganay, S., Turgut, A., Cetin, L. (2019). Magnetic feld dependent thermal conductivity measurements of magnetic nanofluids by 3ω method. The Journal of Magnetism and Magnetic Materials, 474: 199-206. https://doi.org/10.1016/j.jmmm.2018.10.142
[23] Ebrahimi, S., Saghravani, S.F. (2017). Influence of magnetic field on the thermal conductivity of the water based mixed Fe3O4/CuO nanofluid. The Journal of Magnetism and Magnetic Materials, 441: 366-373. https://doi.org/10.1016/j.jmmm.2017.05.090
[24] Merckx, B., Dudoignon, P., Garnier, J.P., Marchand, D. (2012). Simplified transient hot-wire method for effective thermal conductivity measurement in geo materials: microstructure and saturation effect. Advances in Civil Engineering, 2012: 625395. https://doi.org/10.1155/2012/625395
[25] Codreanu, C., Codreanu, N.I., Obreja, V.V.N. (2007). Experimental set-up for the measurement of the thermal conductivity of liquids. Romanian Journal of Information Science and Technology, 10(3): 215-231.
[26] Kumar, V.P.S., Manikandan, N.M., Jeso, Y.G.S., Subakaran, C., Muthukumar, N. (2017). Apparatus for Measuring Thermal Conductivity of Refractories. Journal of the American Ceramic Society, 25: 451-459. https://doi.org/10.1111/j.11512916.1942.tb14350.x
[27] Chanda, R., Saini, S., Ram, P. (2015). Development of the apparatus to measure the thermal conductivity of liquids. International Journal of Innovative Science, Engineering & Technology, 2(5): 1248-1253.
[28] Alvarado, S., Marın, E., Júarez, A.G., Caldeŕon, A., Ivanov, R. (2012). A hot-wire method based thermal conductivity measurement apparatus for teaching purposes A hot-wire method based thermal conductivity measurement apparatus for teaching purposes. European Journal of Physics, 33(4): 897-906. https://doi.org/10.1088/0143-0807/33/4/897
[29] André, S., Rémy, B., Pereira, F.R., Cella, N., Neto, A.J.S. (2003). Hot wire method for the thermal characterization of materials: Inverse problem application. Engenharia Térmica, 4: 55-64. http://dx.doi.org/10.5380/reterm.v2i2.3470
[30] Esfe, M.H., Saedodin, S., Mahian, O., Wongwises, S. (2014). Thermal conductivity of Al2O3/water nanofluids Measurement. Journal of Thermal Analysis and Calorimetry, 117: 675-681. https://dx.doi.org/10.1007/s10973-014-3771-x
[31] Lee, J.H., Hwang, K.S., Jang, S.P., Lee, B.H., Kim, J.H., Choi, S.U.S., Choi, C.J. (2008). Effective viscosities and thermal conductivities of aqueous nanofluids containing low volume concentrations of Al2O3 nanoparticles. International Journal of Heat and Mass Transfer, 51(11-12): 2651-2656. https://doi.org/10.1016/j.ijheatmasstransfer.2007.10.026
[32] Loong, T.T., Salleh, H. (2017). A review of measurement techniques of apparent thermal conductivity of nanofluids. Materials Science and Engineering, 226: 012146. https://doi.org/10.1088/1757-899X/226/1/012146
[33] Paul, G., Chopkar, M., Manna, I., Das, P.K. (2010). Techniques for measuring the thermal conductivity of nanofluids: A review. Renewable and Sustainable Energy Reviews, 14(7): 1913-1924. https://dx.doi.org/10.1016/j.rser.2010.03.017
[34] Harish, S., Orejon, D., Takata, Y., Kohno, M. (2015). Thermal conductivity enhancement of lauric acid phase change nanocomposite in solid and liquid state with single-walled carbon nanohorn inclusions. Thermochimica Acta, 600: 1-6. https://dx.doi.org/10.1016/j.tca.2014.12.004
[35] Kahwaji, S., Johnson, M.B., Kheirabadi, A.C., Groulx, D., White, M.A. (2017). Fatty acids and related phase change materials for reliable thermal energy storage at moderate temperatures. Solar Energy Materials and Solar Cells, 167: 109-120. https://doi.org/10.1016/j.solmat.2017.03.038
[36] Irsyad, M., Indartono, Y.S., Suwono, A., Pasek, A.D. (2015). Thermal characteristics of non-edible oils as phasechange materials candidate to application of air conditioning chilled water system. IOP Conference Series: Materials Science and Engineering, 88: 012051. https://doi.org/10.1088/1757-899X/88/1/012051
[37] Boateng, L., Ansong, R., Owusu, W.B., Asiedu, M.S. (2016). Coconut oil and palm oil's role in nutrition, health and national development: A review. Ghana Medical Journal, 50(3): 189-196. http://dx.doi.org/10.4314/gmj.v50i3.11
[38] Wonorahardjo, S., Sutjahja, I.M., Kurnia, D. (2017). Potential of coconut oil for temperature regulation in tropical houses. Journal of Engineering Physics and Thermophysics, 92(1): 84-92. https://doi.org/10.1007/s10891-019-01909-7
[39] Mettawee, E.S., Ead, I. (2013). Energy Saving in Building with Latent Heat Storage. The International Journal of Thermal and Environmental Engineering, 5: 21-30. https://doi.org/10.5383/ijtee.05.01.003
[40] Wonorahardjo, S., Sutjahja, I.M., Kurnia, D., Fahmi, Z., Putri, W.A. (2018). Potential of thermal energy storage using coconut oil for air temperature control. Buildings, 8(8): 95. https://doi.org/10.3390/buildings8080095
[41] Lee, H., Jeong, S.G., Chang, S.J., Kang, Y., Wi, S., Kim, K. (2016). Thermal performance evaluation of fatty acid ester and paraffin based mixed SSPCMs using exfoliated graphite nanoplatelets (xGnP). Applied Sciences, 6(4): 106. https://doi.org/10.3390/app6040106
[42] Faraj, K., Faraj, J., Hachem, F., Bazzi, H., Khaled, M., Castelain, C. (2019). Analysis of underfloor electrical heating system integrated with coconut oil-PCM plates. Applied Thermal Engineering, 158: 113778. https://doi.org/10.1016/j.applthermaleng.2019.113778
[43] Turgut, A.,·Tavman, I., Chirtoc, M., Schuchmann, H.P., Sauter, C., Tavman, S. (2009). Thermal conductivity and viscosity measurements of water-based TiO2 nanofluids. International Journal of Thermophysics, 30: 1213-1226. https://doi.org/10.1007/s10765-009-0594-2
[44] Moradi, A., Zareh, M., Afrand, M., Khayat, M. (2020). Effects of temperature and volume concentration on thermal conductivity of TiO2-MWCNTs (70-30)/EG-water hybrid nano-fluid. Powder Technology, 362: 578-585. https://doi.org/10.1016/j.powtec.2019.10.008
[45] Agarwal, R., Verma, K., Agrawal, N.K., Singh, R. (2019). Comparison of experimental measurements of thermal conductivity of Fe2O3 nanofluids against standard theoretical models and artificial neural network approach. The Journal of Materials Engineering and Performance, 28(8): 4602-4609. https://doi.org/10.1007/s11665-019-04202-z
[46] Roszko, A., Wajs, E.F. (2016). Magnetic nanofluid properties as the heat transfer enhancement agent. E3S Web Conference, 10: 1-8. https://doi.org/10.1051/e3sconf/20161000111
[47] Nurdin, I., Johan, M.R., Ang, B.C. (2018). Experimental investigation on thermal conductivity and viscosity of maghemite (γ -Fe2O3) water-based nanofluids. IOP Conference Series: Materials Science and Engineering, 334: 1. https://doi.org/10.1088/1757-899X/334/1/012045
[48] Abdullah, A., Mohamad, I.S., Hashim, A.Y.B., Abdullah, N., Isa, M.H.M., Abidin, A.Z. (2016). Thermal conductivity and viscosity of deionised water and ethylene glycol-based nanofluids. Journal of Mechanical Engineering and Sciences, 10(3): 2249-2261. https://doi.org/10.15282/jmes.10.3.2016.4.0210
[49] Taherialekouhi, R., Rasouli, S., Khosravi, A. (2019). An experimental study on stability and thermal conductivity of water-graphene oxide/aluminum oxide nanoparticles as a cooling hybrid nanofluid. International Journal of Heat and Mass Transfer, 145: 118751. https://doi.org/10.1016/j.ijheatmasstransfer.2019.118751
[50] Fujiura, K., Nakamoto, Y., Taguchi, Y., Ohmura, R., Nagasaka, Y. (2016). Thermal conductivity measurements of semiclathrate hydrates and aqueous solutions of tetrabutylammonium bromide (TBAB) and tetrabutylammonium chloride (TBAC) by the transient hot-wire using parylene-coated probe. Fluid Phase Equilibria, 413: 129-136. https://dx.doi.org/10.1016/j.fluid.2015.09.024
[51] Yang, L., Ji, W., Zhang, Z., Jin, X. (2019). Thermal conductivity enhancement of water by adding graphene Nano-sheets: consideration of particle loading and temperature effects. International Communications in Heat and Mass Transfer, 109: 104353. https://doi.org/10.1016/j.icheatmasstransfer.2019.104353
[52] Turgut, A., Tavman, I., Tavman, S. (2009). Measurement of Thermal Conductivity of Edible Oils Using Transient Hot Wire Method. International Journal of Food Properties, 12(4): 741-747. https://doi.org/10.1080/10942910802023242
[53] Cakmak, N.K., Said, Z., Sundar, L.S., Ali, Z.M., Tiwari, A.K. (2020). Preparation, characterization, stability, and thermal conductivity of rGO-Fe3O4-TiO2 hybrid nanofluid: Powder Technology, 372: 235-245. https://doi.org/10.1016/j.powtec.2020.06.012
[54] Decagon Devices, Inc. (2012). KD2 Pro Thermal Properties Analyzer. Decagon USA.
[55] Zakaria, I., Azmi, W.H., Mamat, A.M.I., Mamat, R., Saidur, R., Abu Talib, S.F., Mohamed, W.A.N.W. (2016). Thermal analysis of Al2O3–water ethylene glycol mixture nanofluid for single PEM fuel cell cooling plate: an experimental study. International Journal of Hydrogen Energy, 41(9): 5096-5112. https://doi.org/10.1016/j.ijhydene.2016.01.041
[56] Mintsa, H.A., Roy, G., Nguyen, C.T., Doucet, D. (2009). New temperature dependent thermal conductivity data for water-based nanofluids. International Journal of Thermal Sciences, 48(2): 363-371. https://doi.org/doi:10.1016/j.ijthermalsci.2008.03.009
[57] Azmi, W.H., Sharma, K.V., Sarma, P.K., Mamat, R., Anuar, S. (2014). Comparison of con- vective heat transfer coefficient and friction factor of TiO2 nanofluid flow in a tube with twisted tape inserts. International Journal of Thermal Sciences, 81: 84-93. https://doi.org/10.1016/j.ijthermalsci.2014.03.002
[58] Azmi, W.H., Sharma, K.V., Sarma, P.K., Mamat, R., Anuar, S., Dharma Rao, V. (2013). Experimental determination of turbulent forced convection heat transfer and friction factor with SiO2 nanofluid. Experimental Thermal and Fluid Science, 51: 103-111. https://doi.org/10.1016/j.expthermflusci.2013.07.006
[59] Healy, J.J., de Groot, J.J., Kestin, J. (1976). The theory of the transient hot-wire method for measuring thermal conductivity. Physica B+C, 82(2): 392-408. https://doi.org/10.1016/0378-4363(76)90203-5
[60] Rao, P.R.K., Srinivas, P., Kumar, M.V.S. (2014). Design and analysis of various inverters using different PWM techniques. International Journal of Engineering Science, 41-55.
[61] Pyeatt, L.D., Ughetta, W. (2020). ARM 64-Bit Assembly Language. Elsevier, Library of Congress Cataloging in Publication Data, UK, 405-444.
[62] Turner, J.S. (1973). Buoyancy Convection in Fluids. Cambridge University Press. https://doi.org/10.1017/cbo9780511608827
[63] Li, Y.H., Qu, W., Feng, J.C. (2008). Temperature dependence of thermal conductivity of nanofluids, Chinese Physics Letters, 25(9): 3319-3322. https://doi.org/10.1088/0256-307X/25/9/060
[64] Wang, G., Fan, J., Wang, X., Zhang, L. (2018). Measurement on the thermal conductivity of five saturated fatty acid ethyl esters components of biodiesel. Fluid Phase Equilibria, 473: 106-111. https://doi.org/10.1016/j.fluid.2018.06.004
[65] Ramires, M.L.V., Castro, C.A.N., Nagasaki, Y., Nagashima, A., Assael, M.J., Wakeham, W.A. (1995). Standard reference data for the thermal conductivity of water. Journal of Physical and Chemical Reference Data, 24(3): 1377-1381. https://doi.org/10.1063/1.555963
[66] Dinçer, I., Zamfirescu, C. (2015). Appendix B thermophysical properties of water. Drying Phenomena: Theory and Applications, 457-459. https://doi.org/10.1002/9781118534892.app2
[67] Coker, A.K. (1995). Physical Property of Liquids and Gases. Ludwig's Applied Process Design for Chemical and Petrochemical Plants (Fourth Edison). Elsevier Science & Technology Department of Oxford, Library of Congress Cataloging-in-Publication, UK, 1: 103-149.
[68] Chaplin, M. (2007). Water's Hydrogen Bond Strength, London South Bank University, Borough Road, London SE1 0AA, UK.
[69] Abhat, A. (1983). Low temperature latent heat thermal energy storage: Heat storage. Solar Energy, 30(4): 313-332. https://doi.org/10.1016/0038-092X(83)90186-X
[70] Eckert, E.R.G., Drake, R.M. (1972). Analysis of Heat and Mass Transfer. McGraw-Hill Book Co., New York 63. https://doi.org/10.1016/0017-9310(95)00132-8
[71] Marinos-Kouris, D., Krokida, M., Oreopoulou, V. (2006). Frying of Foods. Handbook of Industrial Drying, Third Edition. https://doi.org/10.1201/9781420017618.ch52
[72] Yan, Q., Liu, C., Zhang, J. (2019). Experimental study on thermal conductivity of composite phase change material of fatty acid and paraffin. Materials Research Express, 6(6). https://doi.org/10.1088/2053-1591/ab0d5e
[73] Bayram, U., Aksöz, S., Maraşll, N. (2014). Temperature dependency of thermal conductivity of solid phases for fatty acids. Journal of Thermal Analysis and Calorimetry, 118: 311-321. https://doi.org/10.1007/s10973-014-3968-z
[74] Silalahi, A.O., Sutjahja, I.M., Kurnia, D., Wonorahardjo, S. (2018). Measurement studies of thermal conductivity of water and coconut oil with nanoparticles dopant for thermal energy storage. Journal of Physics: Conference Series, 1772: 012022(1-7). https://doi.org/10.1088/1742-6596/1772/1/012022
[75] Wi, S., Seo, J., Jeong, S.G., Chang, S.J., Kang, Y., Kim, S. (2015). Thermal properties of shape-stabilized phase change materials using fatty acid ester and exfoliated graphite nanoplatelets for saving energy in buildings. Solar Energy Materials and Solar Cells, 143: 168-173. http://dx.doi.org/10.1016/j.solmat.2015.06.040
[76] Rojas, E.E.G., Coimbra, J.S.R., Telis-Romero, J.T. (2013). Thermophysical properties of cotton, canola, sunflower and soybean oils as a function of temperature. International Journal of Food Properties, 16(7): 1620-1629. https://doi.org/10.1080/10942912.2011.604889 | CommonCrawl |
Regime specific spillover across cryptocurrencies and the role of COVID-19
Syed Jawad Hussain Shahzad1,2,
Elie Bouri ORCID: orcid.org/0000-0003-2628-50273,
Sang Hoon Kang4 &
Tareq Saeed5
Financial Innovation volume 7, Article number: 5 (2021) Cite this article
The aim of this study is to examine the daily return spillover among 18 cryptocurrencies under low and high volatility regimes, while considering three pricing factors and the effect of the COVID-19 outbreak. To do so, we apply a Markov regime-switching (MS) vector autoregressive with exogenous variables (VARX) model to a daily dataset from 25-July-2016 to 1-April-2020. The results indicate various patterns of spillover in high and low volatility regimes, especially during the COVID-19 outbreak. The total spillover index varies with time and abruptly intensifies following the outbreak of COVID-19, especially in the high volatility regime. Notably, the network analysis reveals further evidence of much higher spillovers in the high volatility regime during the COVID-19 outbreak, which is consistent with the notion of contagion during stress periods.
Following the appearance of Bitcoin in early 2009 and the ingenuity of its decentralized technology, called blockchain, several altcoins were released, making the cryptocurrency markets a new digital asset class worthy of consideration for investors, regulators, and academics. Earlier studies look at the technological and legal aspects of Bitcoin and other leading cryptocurrencies (Folkinshteyn and Lennon 2016), while later studies consider the economics and finance (e.g., Bouri et al. 2017; Ji et al. 2018; Shahzad et al. 2019; Kristjanpoller et al. 2020). They mainly focus on price formation by examining factors such as attractiveness (Kristoufek 2013), trading volume (Balcilar et al. 2017), and economic and financial variables.Footnote 1 However, if cryptocurrencies represent a separate asset class as it is often argued, it is informative to study their inter-price dynamics for the sake of traders and portfolio managers who can exploit evidence concerning how the price of one cryptocurrency can affect the prices of other cryptocurrencies while making inferences about price predictability in the highly controversial cryptocurrency markets (Koutmos 2018; Corbet et al. 2018; Kumar and Ajaz 2019; Zięba et al. 2019; Ji et al. 2019).
In this regard, the existing literature covering the return connectedness among Bitcoin and other leading cryptocurrencies remains centred around the measurement of spillovers independent of any regime, or mostly based on one regime (Koutmos 2018; Ji et al. 2019; Zięba et al. 2019) and uses raw return data without accounting for the three factors of Shen et al. (2020a). However, it is often argued that return spillovers become stronger or more intense during unstable periods than calm periods, which necessitates the possibility of considering two volatility regimes—high and low. In fact, the dynamics of spillover depend on two distinct regimes, a high volatility regime during crisis periods and a low volatility regime during stable periods (BenSaïda et al. 2018; Reboredo and Ugolini 2020). While this has been applied to conventional assets and financial markets (BenSaïda et al. 2018; Reboredo and Ugolini 2020), it remains understudied in the cryptocurrency markets.
In this paper, we study the dynamics of return spillovers among cryptocurrencies with respect to global risk factors (e.g., COVID-19) under two volatility regimes (high and low) identified using a Markov regime-switching (MS) vector autoregressive (VAR) with exogenous variables model (i.e., MS-VARX). There is a high degree of flexibility in exploiting the power of Markov switching models for detecting abrupt regime shifts without specifying or fixing the shifts a priori. Our decision to use a VARX model instead of the standard MS-VAR model is motivated by the three factors (excess market returns, size, and reversal factor) identified by Shen et al. (2020a).
It is plausible that returnspillovers in cryptocurrency markets exhibit various patterns in response to the extreme random events manifest in various volatile regimes (Chaim and Laurini 2019).Footnote 2 This is very relevant to the COVID-19 outbreak, which represents an extreme shock potentially shaping the dynamics of return spillovers among cryptocurrencies, and which represents an opportunity to study return spillovers among cryptocurrencies during a very stressful period. In the onset of the COVID-19 pandemic in early 2020, economic activities freezed, uncertainty spiked, and global financial markets tumbled. As a response, many central banks around the globe announced an unconventional monetary policy (i.e., quantitative easing) as an antidote to a deteriorating economic performance. Accordingly, there was a fear that fiat currencies will most likely lose value due to the quantitative easing, which makes cryptocurrencies under the spot again as a potential competitor. Given that and under the view that cryptocurrencies represent a new asset class, market participants would benefit from a refined understanding of the return spillovers among leading cryptocurrencies under the unprecedented turbulence of the COVID-19 outbreak.
Our analyses contribute to the existing literature on several fronts. Firstly, we use a sample spanning 25-July-2016 to 1-April-2020, covering the COVID-19 outbreak period during which financial markets crumbled (Gupta et al. 2021). This allows us to study return spillovers among cryptocurrencies during a very stressful time that represents the first global economic and financial catastrophe that occurred throughout the short existence of cryptocurrencies. Secondly, as the dynamics of return spillovers may depend on the regime, we incorporate MS within the VAR model of Diebold and Yilmaz (2012, 2014) and study return spillovers in the cryptocurrency markets under high and low volatility regimes. This represents an extension to the academic literature on regime-switching spillovers, which mainly concentrates on conventional assets such as equities (e.g., BenSaïda et al. 2018) but remains embryonic in the cryptocurrency markets. The few studies examining return spillovers in the cryptocurrency markets apply a single regime model (Koutmos 2018; Ji et al. 2019; Zięba et al. 2019). Thirdly, instead of incorporating only a MS-VAR model into the approach of Diebold and Yilmaz (2012), we also incorporate a MS-VARX model. In doing so, we account for the three-factor pricing model of Shen et al. (2020a) which is able to outperform the CAPM model in the cryptocurrency markets and thus extends the literature dealing with spillovers in the cryptocurrency markets based on raw return data (e.g., Koutmos 2018; Ji et al. 2019; Zięba et al. 2019). Overall, our paper is very pertinent to the academic debate about the cryptocurrency markets during the COVID-19 outbreak (Conlon and McGee 2020; Chen et al. 2020; Corbet et al. 2020; Conlon et al. 2020; Goodell and Goutte 2020; Dutta et al. 2020) and how the dynamics of return spillovers among cryptocurrencies change in regard to market downturns or crashes.
The empirical analyses show evidence of intensified return spillovers in the last 3 months of our sample period, belonging to the high volatility regime during the COVID-19 outbreak, revealing important aspects of the network of return spillovers across leading cryptocurrencies under various volatility states, and that the COVID-19 risk factors intensify that network. The overall results argue in favour of a fundamental breakdown in the return linkages.
This paper is structured as follows. "Literature reviews" section of this paper reviews the related literature; "Methodology" section provides the methods; "Empirical results" section presents the data and empirical results; and "Conclusion" section concludes.
The existing literature dealing with market linkages among cryptocurrencies is growing. It employs GARCH-based models, Granger causality tests, wavelets, and cointegration analyses Katsiampa et al. (2019b) use a bivariate BEKK-GARCH model on three pairs of cryptocurrencies (Bitcoin–Ether, Bitcoin–Litecoin, and Litecoin–Ether) and study the volatility dynamics' conditional correlations. They show evidence of two-way volatility flows between for all three pairs and indicate that the three cryptocurrencies move in unison. They find evidence of two-way return flows between Bitcoin and both Ether and Litecoin, and a one-way flow from Ether to Litecoin. Using hourly data, Katsiampa et al. (2019a) apply symmetric and asymmetric multivariate GARCH models to examine the interactions of volatilities of eight cryptocurrencies. They show that Bitcoin is not the dominant cryptocurrency although its shocks on other cryptocurrencies are the longest lasting. Kumar and Ajaz (2019) apply wavelet-based methods and conclude that Bitcoin is the main driver of cryptocurrency prices. Using a Granger causality framework, Bouri et al. (2019a) study volatility linkages in the frequency domain and highlight the importance of large cryptocurrencies, other than Bitcoin. In another study, Bouri et al. (2019b) test for jumps in GARCH models and indicate that Bitcoin and 11 large and small altcoins exhibit jumps and co-jumps in their price process. They also show that Bitcoin and altcoins such as Ethereum and Ripple are important players in the cryptocurrency markets. Ciaian and Rajcaniova (2018) apply cointegration models and show significant evidence of interdependence between bitcoin and several altcoins that is mostly stronger in the short term.
Previous studies also apply the Diebold and Yilmaz (2012, 2014) models to static and dynamic connectedness in cryptocurrency markets. Koutmos (2018) focuses on Bitcoin and 17 large altcoins and finds that the connectedness measure varies with time and that Bitcoin and the altcoins examined are interconnected, with Bitcoin being a pivot in the network for return and volatility connectedness. Considering the cases of Bitcoin, Ripple, and Litecoin, Corbet et al. (2018) study return and volatility linkages and show that return shocks are mainly transmitted from Bitcoin to Ripple and Litecoin and that the return and volatility linkages between Ripple and Litecoin are strong. For the volatility linkages, they show that Litecoin and Ripple have a significant influence on Bitcoin, which is not in line with the findings in Koutmos (2018). Further results from Corbet et al. (2018) point to the isolation of the three cryptocurrencies under study from the global financial system, which suggests their ability to diversify the risk of conventional assets such as equities. Yi et al. (2018) examine the network of volatility among large cryptocurrencies and find that Bitcoin transmits its volatility to many cryptocurrencies, which makes it a dominant player in the network. Zięba et al. (2019) apply VAR models and a minimum spanning tree (MST) to the returns of Bitcoin and several other large altcoins, and show that Bitcoin is quite segmented from the other altcoins. Examining returns and volatility linkages, Ji et al. (2019) consider the case of Bitcoin and five other leading altcoins, highlighting the importance of Litecoin and Bitcoin to the network of return spillovers and the centrality of Bitcoin to the network of volatility spillovers. Later evidence contradicts Corbet et al. (2018) but confirms the earlier findings of Koutmos (2018). Ji et al. (2019) find that Dash is particularly segmented from Bitcoin and the rest of the altcoins under study, suggesting its potential as a diversifier. Notably, Ji et al. (2019) indicate that negative return connectedness is larger than positive return connectedness and that Ripple and Ethereum are the main receivers of negative-return shocks whereas Ethereum and Dash are marginal receivers of positive-return shocks. Qiao et al. (2020) employ wavelet coherence and correlation-based network to study the interdependence of the returns and volatility of cryptocurrencies. They find that Bitcoin and other cryptocurrencies are positively correlated at medium and high frequencies, whereas Bitcoin leads other cryptocurrencies at low frequencies. Furthermore, they indicate that the hedging effect of Bitcoin for other cryptocurrencies is time–frequency dependent. Qureshi et al. (2020) focus on the dynamic multiscale interdependencies among leading cryptocurrencies. They show high levels of dependency from 2016 to 2018 at daily frequency scales and that Ripple and Ethereum are trivial origins of market contagion. Further results indicate that the coherence fluctuates at higher frequencies, but it is significantly stable at lower frequencies. Antonakakis et al. (2019) examine connectedness measures among leading cryptocurrencies using a time-varying parameter factor augmented VAR (TVP-FAVAR) model. They indicate a time-variation in the connectedness measures and show that Bitcoin is the most important transmitter of shocks in the cryptocurrency markets, followed by Ethereum.
To address the impact of COVID-19 on thecryptocurrency market, empirical studies have investigated the contagion between the pandemic and the financial markets (Akhtaruzzaman et al. 2020; Azimli 2020; Baker et al. 2020; Bouri et al. 2020b; Goodell and Goutte 2020; Topcu and Gulal 2020), opportunities for portfolio diversification (Akhtaruzzaman et al. 2020; Corbet et al. 2020; Conlon and McGee 2020; Yoshino et al. 2020), and commovment between cryptocurrencies (Yarovaya et al. 2020). Due to the outbreak of the COVID-19, portfolio investors continually seek an alternative asset to protect the extreme downside risk of financial assets.Footnote 3 Cryptocurrencies have attracted the attention of many investors, as they offer the benefit of a diversifier, a hedge asset or a safe haven asset against the downside risk of traditional investments (Bouri et al. 2017).
The above-mentioned literature neglects the possibility of having various volatility states—high and low—in the network of connectedness among cryptocurrency returns. As argued by BenSaïda et al. (2018), there is economic merit to incorporating Markov switching within the generalized vector autoregressive (VAR) model of Diebold and Yilmaz (2012, 2014), given that return spillovers among markets are stronger and more intense during unstable periods than calm periods. Therefore, the dynamics of return spillovers are regime dependent and any analysis of connectedness that neglects the shift in the volatility regimes can lead to spurious findings. In this paper, we study return spillovers among leading cryptocurrencies while capturing shifts in regimes due to the COVID-19 outbreak, sudden events, or changes in market conditions. Our current paper is related to a newly rising strand of literature that deals with the role of Bitcoin and other cryptocurrencies against conventional assets during the COVID-19 outbreak (Conlon and McGee 2020; Chen et al. 2020; Corbet et al. 2020; Conlon et al. 2020; Goodell and Goutte 2020; Dutta et al. 2020). However, it differs in several aspects. Firstly, it focuses on the return spillovers among cryptocurrencies while considering two volatility regimes, high and low, which is an unexplored research subject in the controversial cryptocurrency markets. Secondly, it accounts for the three factors (excess market returns, size, and reversal factor) identified by Shen et al. (2020a), which nicely extends previous studies that use raw return data (Koutmos 2018; Ji et al. 2019; Zięba et al. 2019).
We capture the changes in return spillovers with respect to global risk factors (e.g., COVID-19) under two volatility regimes (high and low) identified using a Markov regime-switching (MS) vector autoregressive with exogenous variables (VARX) model. The VARX model accounts for the three factors identified by Shen et al. (2020a), which are excess market returns, size, and reversal factors.
The MS-VARX model
Our MS-VARX model is specified as:
$$y_{t} {\mid }s_{t} = \nu_{k} + \mathop \sum \limits_{i = 1}^{p} \Phi_{k,i} y_{t - i} + \Psi_{k} X_{t} + u_{{s_{t} ,t}}$$
where \(y_{t} = \left( {y_{1,t} , \ldots ,y_{n,t} } \right)^{^{\prime}}\) for t = 1,…, T; \(\nu_{k}\) is a (n × 1) regime-dependent vector of intercepts; \(\left\{ {{\Phi }_{k,i} } \right\}_{i = 1}^{p}\) are (n × n) state-dependent matrices, where Φk,p ≠ 0 and 0 represents the n × n null matrix; \(X_{t}\) is the vector of three-factors (excess market returns, size, and reversal), which are inspired from the cryptocurrency model of Shen et al. (2020a); and \(u_{{s_{t} ,t}}\) is a vector of errors.
To consider the fact that each regimes might have different variances we set \(u_{{s_{t} ,t}} = \Sigma_{k}\upvarepsilon _{t}\), where \(\upvarepsilon _{t} \mathop \sim \limits^{i.i.d.} {\mathcal{N}}\left( {0_{n} ,{\text{I}}_{n} } \right)\), with \({\text{I}}_{n}\) denoting the identity matrix, and \(0_{n}\) representing a \(\left( {{\text{n}} \times 1} \right)\) vector of 0. Σk, symbolizes a lower triangular \(\left( {{\text{n}} \times {\text{n}}} \right)\) regime-dependent Cholesky factorization of the symmetric variance–covariance matrix denoted by Ωk. Therefore, we can write:
$${\varvec{y}}_{t} {\mid }s_{t} \sim {\mathcal{N}}\left( {{\varvec{\nu}}_{k} ,{\varvec{\varOmega}}_{k} } \right)$$
where each regime k = {1,…, K} is described by its own νk, \(\left\{ {{{\varvec{\Phi}}}_{k,i} } \right\}_{i = 1}^{p}\), and Ωk. The model considers the possibility of varying intercepts following the state of the market, dictated by the state variable {st}. The autoregressive matrices \(\left\{ {{{\varvec{\Phi}}}_{k,i} } \right\}_{i = 1}^{p}\) govern the intensity of spillovers across cryptocurrency variables, according to the regime. The Markov switching variance–covariance matrix Ωk allows us to identify structural shocks in the residuals.
The state variable {st} progresses in line with a discrete, homogeneous, and finite state irreducible first-order Markov chain with a transition probability matrix P. Each element of P represents the conditional probability of transitioning from regime i to regime j. Accordingly, we can write:
$$\begin{aligned} & {\varvec{P}} = \left( {\begin{array}{*{20}c} {p_{1,1} } & \cdots & {p_{1,K} } \\ \vdots & \ddots & \vdots \\ {p_{K,1} } & \cdots & {p_{K,K} } \\ \end{array} } \right) \\ & p_{i,j} = Pr\left( {s_{t} = j{\mid }s_{t - 1} = i} \right) \\ \end{aligned}$$
where the sum of each column of P is equal to 1. If we have two regimes, then the transition matrix is given by:
$${\varvec{P}} = \left( {\begin{array}{*{20}c} p & {1 - q} \\ {1 - p} & q \\ \end{array} } \right)$$
The unconditional probability π is the eigenvector of P, satisfying P π = π, and \(1_{K}^{^{\prime}}\) π = 1, where 1K is a (K × 1) column vector of 1. Accordingly:
$${\varvec{\pi}} = \left( {{\mathbf{A^{\prime}A}}} \right)^{ - 1} {\mathbf{A^{\prime}}}\left[ {\begin{array}{*{20}c} {0_{K} } \\ 1 \\ \end{array} } \right]$$
where 0K is a (K × 1) column vector of 0, and:
$$\mathop {\mathbf{A}}\limits_{{\left( {K + 1} \right) \times K}} = \left[ {\begin{array}{*{20}c} {{\mathbf{I}}_{K} - P} \\ {1_{K}^{^{\prime}} } \\ \end{array} } \right]$$
In the presence of two regimes, we present the unconditional probabilities as:
$$\left\{ {\begin{array}{*{20}l} {\pi _{1} = \frac{{1 - q}}{{2 - p - q}}} \hfill \\ {\pi _{2} = \frac{{1 - p}}{{2 - p - q}}} \hfill \\ \end{array} } \right.$$
For the estimation method, the reader can refer to BenSaïda et al. (2018).Footnote 4
The concept of spillovers
The spillover measure of Diebold and Yilmaz (2014) is based on the forecast error variance decomposition from the VAR model. Notably, a generalized impulse response function is used, which does not require orthogonalization by Cholesky decomposition. Accordingly, the spillover index is invariant to ordering. Given the covariance-stationary model in Eq. (1) we present its vector moving average representation (see BenSaïda et al. 2018) as follows:
$${\varvec{y}}_{t} {\mid }s_{t} = {\varvec{\omega}}_{k} + \mathop \sum \limits_{j = 0}^{\infty } {\mathbf{A}}_{k,j} {\varvec{u}}_{{s_{t} ,t - j}}$$
where \({\mathbf{A}}_{k,j} = \sum\nolimits_{i = 1}^{p} {{{\varvec{\Phi}}}_{k,i} {\mathbf{A}}_{k,j - i} }\), and \({\varvec{\omega}}_{k} = \left( {{\mathbf{I}}_{n} - \sum\nolimits_{i = 1}^{p} {{{\varvec{\Phi}}}_{k,i} } } \right)^{ - 1} {\varvec{\nu}}_{k}\).
We define the generalized H-step ahead forecast error variance decomposition shares in each regime k as:
$$\theta_{k,ij}^{g} \left( h \right) = \frac{{\sigma_{k,jj}^{ - 1} \mathop \sum \nolimits_{l = 0}^{h - 1} \left( {{\varvec{e}}_{i}^{^{\prime}} {\mathbf{A}}_{k,l} {{\varvec{\Sigma}}}_{k} {\varvec{e}}_{j} } \right)^{2} }}{{\mathop \sum \nolimits_{l = 0}^{h - 1} \left( {{\varvec{e}}_{i}^{^{\prime}} {\mathbf{A}}_{k,l} {{\varvec{\Sigma}}}_{k} {\mathbf{A}}_{k,l}^{^{\prime}} {\varvec{e}}_{i} } \right)}}$$
where \({\upsigma }_{{k, jj{ }}}\) is the standard deviation of the error term of the jth equation, and \(e_{i}\) is a vector with 1 on the ith element and 0 otherwise. Given the use of the generalized impulse response functions, it is important to normalize each entry of the variance decomposition matrix to ensure that each row sums up to 1 as:
$$\tilde{\theta }_{k,ij}^{g} \left( h \right) = \frac{{\theta_{k,ij}^{g} \left( h \right)}}{{\mathop \sum \nolimits_{j = 1}^{n} \theta_{k,ij}^{g} \left( h \right)}}$$
The total spillover index in regime k is given in Eq. (11). This measures the contribution of spillovers from volatility shocks among cryptocurrencies in the system to the total forecast error variance:
$$S_{k}^{g} \left( h \right) = \frac{1}{n}\mathop \sum \limits_{{\begin{array}{*{20}c} {i,j = 1} \\ {i \ne j} \\ \end{array} }}^{n} \tilde{\theta }_{k,ij}^{g} \left( h \right)$$
The directional spillovers received by cryptocurrency i from all other cryptocurrencies j is:
$$\mathop {S_{k}^{g} }\limits_{all \to i} \left( h \right) = \frac{1}{n}\mathop \sum \limits_{{\begin{array}{*{20}c} {j = 1} \\ {i \ne j} \\ \end{array} }}^{n} \tilde{\theta }_{k,ij}^{g} \left( h \right).$$
The directional spillovers transmitted by cryptocurrency i to all other cryptocurrencies j is:
$$\mathop {S_{k}^{g} }\limits_{i \to all} \left( h \right) = \frac{1}{n}\mathop \sum \limits_{{\begin{array}{*{20}c} {i = 1} \\ {i \ne j} \\ \end{array} }}^{n} \tilde{\theta }_{k,ij}^{g} \left( h \right).$$
The net spillover from cryptocurrency i to all other cryptocurrencies is:
$$S_{k,i}^{g} \left( h \right) = \mathop {S_{k}^{g} }\limits_{i \to all} \left( h \right) - \mathop {S_{k}^{g} }\limits_{all \to i} \left( h \right)$$
This paper uses daily price data of 18 cryptocurrencies, Bitcoin (BTC), Etreum (ETH), Ripple (XRP), Litecoin (LTC), Monero (XMR), Stellar (XLM), Dash (DASH), Ethereum Classic (ETC), NEM (XEM), Dogecoin (DOGE), Decred (DCR), Lisk (LSK), Was (WAVES), MonaCoin (MONA), DigiByte (DGB), Steem (STEEM), Siacoin (SC), and DigixDAO (DGD). The data sample spans July 25th, 2016 to April 1st, 2020 which covers various financial, economic, and pandemic events. Our sample period covers various events that can shape investors and markets of cryptocurrencies. These include four categories, split, regulation, exchange, and hacking. Table 1 summarizes those events, their dates, and the sign (positive/negative) of their impacts. Regarding the data, they are extracted from https://coinmarketcap.com.Footnote 5 We consider the three-factor pricing model proposed by Shen et al. (2020a), SMB representing the return spread of small minus large stocks, WML representing the equal-weight average of the returns for the two winner portfolios for a region minus the average of the returns for the two loser portfolios, and MKT representing the return spread between the capitalization weighted stock market. These daily factors are calculated using trading data of 1967 cryptocurrencies for the sampled period. Cryptocurrency price data are collected from https://coinmarketcap.com/. The T-Bill rate is used as a proxy for the risk-free asset and obtained through the US Department of the Treasury. The detailed procedure to compute these factors is given by Shen et al. (2020a).
Table 1 Selected events related to the cryptocurrency markets
We calculate the continuously compounded daily returns by taking the difference in the log values of two consecutive prices. Table 2 shows the summary statistics of the returns series for the 18 cryptocurrencies and three factors. In Panel A, the mean returns of all cryptocurrencies are positive except for STEEM. Importantly, the XRP returns exhibit the highest mean return among the cryptocurrencies. Looking at the standard deviation, DGB is the most volatile cryptocurrency, followed by STEEM, while BTC is the least volatile. The skewness coefficient values are positive for all series except BTC and ETH returns. The kurtosis coefficient value is largely above 3, the value of normal distributions, indicating leptokurtic behaviour. The Jarque–Bera test strongly rejects the normal distribution of returns. In Panel B, all factor returns show negative values with a low value of standard deviation. All factors show the non-normality of return series due to the values of skewness, kurtosis and J–B statistics. It is worth noting that all return series are stationary according to the unit root (ADF) and stationary (KPSS) test estimations.
Table 2 Descriptive statistics
Before we present the main results of return spillovers, we evaluate the adequacy of our three-factors. To this end, we follow Ando et al. (2018) and compare the residual cross-correlations arising from the simple VAR(1) model to those arising from our three-factor VAR(1) model. Based on the assumption that the cross-sectional correlation of the VAR residuals is driven by a finite number of common factors, we purge the common component from the VAR residuals. This allows us to isolate the idiosyncratic shock to each cryptocurrency and reduces the likelihood of failure to account for sources of common variation which may generate substantial biases. Specifically, an omitted common factor upwardly biases the estimated spillover if the proportion of the forecast error variance is attributed to one or more of the endogenous variables instead of that common factor. Comparing Fig. 1b and a, it is clear that a substantial amount of the correlation among the residuals is removed when the factors are considered. Specifically, the factor VAR(1) model indicates that almost 95% of the pairwise correlations are weaker than 0.2 in absolute value, which points to the adequacy of our factors. This finding indicates that the residuals of the factor VAR(1) model are cross-sectionally uncorrelated.
Comparison of absolute residual correlations, with and without factors. Notes The histograms show the distribution of the absolute pairwise correlations between the residuals of the simple VAR(1) model and our factor VAR(1) model evaluated by OLS
Single regime spillover
Table 3 provides a matrix of the directional spillovers across the 18 cryptocurrency markets. This table shows the directional spillover of a market to other markets (row titled "To") and from other markets to that market (column titled "From"). The bottom row of Table 3 shows whether each market is a net receiver or net contributor to other markets.
Table 3 Directional spillovers under single normal regime—full sample
In the "To" row in Table 3, XLM is the largest contributor of shocks to the other markets with a contribution of 38.69%, followed by SC (36.73%), ETH (32.64%), and DASH (31.73%). In the "From" column, XLM is also the largest recipient of spillovers, with a contribution of 31.05%, followed by SC (30.87%), ETH (30.60%), LTC (27.78%), and XMR (27.77%). In terms of net spillovers ("To"–"From"), XLM is the largest net transmitter of spillovers, with a net value of 7.64%, followed by SC (5.86%), DASH (2.19%), and ETH (2.04%). Conversely, the largest net recipient of spillovers is BTC (− 7.12%) followed by DOGE (− 2.75%), XMR (− 1.94%), XEM (− 1.92%), WAVES (− 1.69%), and STEEM (− 1.59%). Therefore, XLM seems to play a dominant role in the spillover connectedness across cryptocurrency markets. As for the total spillover index, it is only 22.23%.
Figure 2 visualizes the network of the pairwise directional connectedness across the 18 cryptocurrency markets over the full sample period, reported in Table 3. Note that the size of each node in the network relating the set of markets is determined by both the contribution in terms of the effect of each market on other markets (the sum of the coefficients in each column excluding own-market effects) and of other markets on any particular market (the sum of the coefficients in each row excluding own-market effects). The red colouring implies the contribution from the variable under consideration to the other cryptocurrencies of the system, whereas green indicates the contribution from the other cryptocurrencies to the cryptocurrency under analysis. The thickness of the edges refers to the strength of the connectedness. In Fig. 2 we can observe a bi-directional pairwise connectedness across most of the 18 cryptocurrency markets. In particular, XLM has strong connectedness (red edge) with XRP and other cryptocurrencies. Similarly, SC has a strong connectedness with DGB and other cryptocurrencies. A bi-directional spillover exists between DASH and XMR, and a significant spillover is shown from ETH to both DASH and DGD, and from SC to DOGE.
DY Spillover—without Regime Switching. Notes: This network graph illustrates the degree of total connectedness in a system that consists of the 18 cryptocurrencies over the full sample period. Total connectedness is measured using the Diebold–Yilmaz framework. The size of the node shows the magnitude of the contribution of each variable to system connectedness, while the colour indicates the origin of connectedness. In particular, red implies a contribution from the variable under consideration to the other variables of the system and green means a contribution from the other variables to the variable under analysis. The colour and thickness of edges refers to the strength of the connectedness. Specifically, arrows in red full lines indicate that the magnitude of the connectedness is greater than 10%, arrows in green dashed lines imply that the strength of the connectedness is between 5 and 10%, blue dotted lines are associated with connectedness between 1 and 5%. Finally, connectedness lower than the 1% is not reported to preserve clarity in the figure
Switching regime spillover
Recent studies argue that the dynamics of spillover depend on two distinct regimes, a high volatility regime during crisis periods, and a low volatility regime during stable periods (BenSaïda et al. 2018; Reboredo and Ugolini 2020). In order to identify the two distinct regimes, we estimate a MS-VAR(1) model and differentiate between regime 1 and regime 2. Figure 3 shows several high volatility regimes with periods of intense spillover, during which the probabilities of being in regime 2 are nearly 1. We see high volatility regimes based on external shocks such as the rapid growth of cryptocurrency markets during 2016–2018 and the COVID-19 period during early 2020.
Smoothed probabilities of intense spillover (Regime 2)
Analysing these regimes provides in-depth knowledge of the change of the direction of spillover between the two regimes. Figures 4 and 5 plot the spillover network across the 18 cryptocurrency markets in low and high volatility regimes, respectively.Footnote 6 Comparing the two regimes, the total spillover index is 25.70% in the low volatility regime compared to 29.43% in the high volatility regime. The node size of the spillover network in the low volatility regime is relatively larger than that in the high volatility regime. Specifically, it is evident that XRP, XLM, LTC, and ETH are more strongly connected to others in the low volatility regime, implying that these cryptocurrencies dominate the spillover in stable periods. Notably, the role of BTC is less important, which contradicts with Kumar and Ajaz (2019). However, the result is generally in line with Zięba et al. (2019) who highlight the importance of smaller cryptocurrencies to the network of return shocks due to the specificity of the supply mechanism of those cryptocurrencies. In addition, XLM is the largest contributor to others in both regimes, indicating that XLM is a hub market of the information spillover network. Compared to the network in Fig. 2, we can see pairwise spillover between XLM and XRP in both regimes and between SC and DGB in the high regime only. These figures show that the directional spillover effect is sensitive to the state of the volatility regime given that the spillover effect is more pronounced and concentrated among fewer cryptocurrencies in the low volatility regime.
DY spillover network—low volatility regime. Note: See notes to Fig. 2
DY Spillover network—high volatility regime. Note: See notes to Fig. 2
Given the time-varying total spillovers among the 18 cryptocurrencies in the low and high volatility regimes, Fig. 6 shows a significant structural change of spillover in late 2018 when the market capitalization of Bitcoin fell below $100 billion and the price of one Bitcoin plunged below $4000 after losing almost one-third of its value in a few days. Before that period, the dynamics of total spillover are relatively smooth and consistent between the high and low volatility regimes. However, we see a sharp drop of total spillover in the high volatility regime and the convergence of both total spillovers during that period. Subsequently, the total spillover in the high volatility regime restarts upward, and, more interestingly, in the high volatility regime, a sudden increase in total spillover is observed in the COVID-19 outbreak periodFootnote 7 which intensifies the magnitude of spillover in the high volatility regime. This finding indicates that the dynamics of the total spillover index rapidly react to external shocks, which concords with previous findings (e.g., Antonakakis et al. 2019; Ji et al. 2019). Compared to the literature on contagion which highlights strong and abrupt changes in market linkages (Baele and Inghelbrecht 2010), our findings indicate evidence of contagion in response to external shocks such as the COVID-19 outbreak. This finding indicates that systemic risk relating to the outbreak and development of the COVID-19 pandemic intensifies the risk spillover across cryptocurrency markets (Goodell and Goutte 2020). Other studies identify similar results between cryptocurrencies and stock markets (Conlon and McGee 2020; Corbet, et al. 2020), and cryptocurrency and commodity markets (Dutta et al. 2020).
Total return spillovers. Note: The rolling window total spillover indices are based on 250 days rolling window, lag = 1 (based on SIC) and a forecast horizon of 12 days
To further analyse the impact of COVID-19, the pairwise directional spillover networks at low and high volatility regimes are given in Figs. 7 and 8, respectively.Footnote 8 The analysis of the COVID-19 outbreak period provides rich information about the intensity and pathway of risk spillover from one cryptocurrency market to another during such an unprecedented catastrophic event. The edge colour denotes the magnitude of the directional spillover and the node diameter denotes the size of the net spillover. Figures 7 and 8 show the complexity of information spillover under various regimes, especially the high volatility regime of COVID-19. Specifically, it is evident that DASH is the largest contributor of spillover in the high volatility regime, whereas strong directional spillover is observed in LTC, XRP, and ETH in the low volatility regime. As indicated in the plots, the directional spillover is much stronger in the high volatility regime than the low volatility regime. This finding confirms that cryptocurrency markets become more dependent in the high-volatility regime. In addition, these networks reflect the way the spillover reacts to the impact of COVID-19 on the regime, to gain a more complex network structure in the high volatility regime. In fact, Table 5 in the "Appendix" shows that in the low volatility regime, the total spillover index is 34.22%, whereas it reaches 96.23% in the high volatility regime. These findings add to previous studies focusing on the effects of specific economic, political, or cybersecurity events on the network of spillovers among leading cryptocurrencies, by showing the significant effect of the COVID-19 outbreak and its subsequent lockdown recession on the network of spillovers, especially in the high volatility regime.
DY Spillover network—low volatility regime of COVID19. Note: See notes to Fig. 2
DY Spillover network—high volatility regime of COVID19. Note: See notes to Fig. 2
In this study, we investigate the regime dependent spillovers across 18 cryptocurrency markets in low and high volatility regimes using the MS-VARX model and the spillover measure of Diebold and Yilmaz (2014). In addition, we visualize the dynamics of total spillovers and the complex networks of spillovers in low and high volatility regimes and examine the impact of COVID-19 on the dynamics of spillovers.
The empirical results provide evidence of strong spillovers across the cryptocurrency markets in low and high volatility regimes during the full sample period. However, the spillover effect changes between the regimes with the spillover effect more pronounced in the low volatility regime. The rolling window analysis shows significant structural changes of spillovers in late 2018 and early 2020. Interestingly, the COVID-19 outbreak period in early 2020 amplifies the magnitude of spillovers in the high volatility regime, indicating an increase in the high volatility regimes during the COVID-19 period. Notably, and consistent with the notion of contagion, we find much stronger spillovers across all cryptocurrencies in the high volatility regime during the COVID-19 outbreak period.
Our findings have implications for investors and policymakers. The regime dependent spillover results provide better ways to manage portfolio diversification strategies. In fact, the findings suggest that portfolio diversification opportunities are lower in a high volatility regime. It is necessary for investors to precisely judge which markets they need to be more concerned about, and when, under low and high volatility regimes. Similarly, regime dependent spillovers have implications for policymakers about when to intervene to stabilize markets. Policymakers can use the results to identify the magnitude of spillover in low and high volatility regimes. If necessary, they can intervene and reduce the spike in the spillover effect in a regime by trying to control uncertainties related to stressful periods, announcing definite policy measures capable of elevating the sentiment of the markets and the overall economy. A crucial concern is that, during stress periods such as COVID-19, the return spillovers across leading cryptocurrencies abruptly diverge from their usual paths in an unpredictable way. This matters to policymakers who seek financial stability in financial markets.
Future research could consider portfolio and hedging analysis within the cryptocurrency markets in both regimes and during the COVID-19 outbreak. Another extension could involve the application of a regime-based analysis of spillover periods between the cryptocurrency markets and conventional assets during the COVID-19 period.
Data will be available from the authors upon request.
These include economic policy uncertainty, geopolitical risk, stock market volatility, and macroeconomic news, among other variables (Al-Khazali et al. 2018; Demir et al. 2018; Aysan et al. 2019; Bouri et al. 2020a).
Chaim and Laurini (2019) examine the joint dynamics of cryptocurrencies and point to shifts in cryptocurrencies return dynamics.
Some recent studies point to the role US Treasury Securities as a safe haven asset during the COVID-19 outbreak.
A related approach is found in Malugin and Novopoltsev (2017). Other studies (Kou et al. 2014; Wen et al. 2019; Wang et al. 2020; Chao et al. 2020; Shen et al. 2020b) apply interesting methods that can be the subject of future research.
The R package "crypto" is used to access the data. See https://www.rdocumentation.org/packages/crypto/versions/1.1.3 for details.
These figures are based on Table 4.
The regime shifted from low to high on January 14th, 2020.
These networks are based on Table 5.
Akhtaruzzaman M, Boubaker S, Sensoy A (2020) Financial contagion during COVID-19 crisis. Finance Res Lett. https://doi.org/10.1016/j.frl.2020.101604
Al-Khazali O, Bouri E, Roubaud D (2018) The impact of positive and negative macroeconomic news surprises: gold versus Bitcoin. Econ Bull 38(1):373–382
Ando T, Greenwood-Nimmo M, Shin Y (2018) Quantile connectedness: modelling tail behaviour in the topology of financial networks (April 18, 2018). Available at SSRN: https://ssrn.com/abstract=3164772 or http://dx.doi.org/https://doi.org/10.2139/ssrn.3164772
Antonakakis N, Chatziantoniou I, Gabauer D (2019) Cryptocurrency market contagion: market uncertainty, market complexity, and dynamic portfolios. J Int Financ Mark Inst Money 61:37–51
Aysan AF, Demir E, Gozgor G, Lau CKM (2019) Effects of the geopolitical risks on Bitcoin returns and volatility. Res Int Bus Finance 47:511–518
Azimli A (2020) The impact of COVID-19 on the degree of dependence and structure of risk-return relationship: a quantile regression approach. Finance Res Lett. https://doi.org/10.1016/j.frl.2020.101648
Baele L, Inghelbrecht K (2010) Time-varying integration, interdependence and contagion. J Int Money Finance 29(5):791–818
Baker SR, Bloom N, Davis SJ, Kost KJ, Sammon MC, Viratyosin T (2020) The unprecedented stock market impact of COVID-19 (No. w26945). Natl Bur Econ Res. https://doi.org/10.3386/w26945
Balcilar M, Bouri E, Gupta R, Roubaud D (2017) Can volume predict Bitcoin returns and volatility? A quantiles-based approach. Econ Model 64:74–81
BenSaïda A, Litimi H, Abdallah O (2018) Volatility spillover shifts in global financial markets. Econ Model 73:343–353
Bouri E, Molnár P, Azzi G, Roubaud D, Hagfors LI (2017) On the hedge and safe haven properties of Bitcoin: is it really more than a diversifier? Finance Res Lett 20:192–198
Bouri E, Roubaud D, Lucey B (2019) The volatility surprise of leading cryptocurrencies: transitory and permanent linkages. Finance Res Lett 33:101604. https://doi.org/10.1016/j.frl.2019.05.006
Bouri E, Roubaud D, Shahzad SJH (2019) Do Bitcoin and other cryptocurrencies jump together? Q Rev Econ Finance 76:396–409. https://doi.org/10.1016/j.qref.2019.09.003
Bouri E, Gkillas K, Gupta R (2020) Trade uncertainties and the hedging abilities of Bitcoin. Econ Notes. https://doi.org/10.1111/ecno.12173
Bouri E, Demirer R, Gupta R, Pierdzioch C (2020) Infectious diseases, market uncertainty and oil volatility. Energies 13(16):4090
Chaim P, Laurini MP (2019) Nonlinear dependence in cryptocurrency markets. North Am J Econ Finance 48:32–47
Chao X, Kou G, Peng Y, Viedma EH (2020) Large-scale group decision-making with non-cooperative behaviors and heterogeneous preferences: an application in financial inclusion. J Oper Res Eur. https://doi.org/10.1016/j.ejor.2020.05.047
Chen C, Liu L, Zhao N (2020) Fear sentiment, uncertainty, and Bitcoin price dynamics: the case of COVID-19. J Emerg Mark Finance TR 56(10):2298–2309
Ciaian P, Rajcaniova M (2018) Virtual relationships: Short-and long-run evidence from BitCoin and altcoin markets. J Int Financ Mark Inst Money 52:173–195
Conlon T, McGee R (2020) Safe haven or risky hazard? Bitcoin during the COVID-19 bear market. Finance Res Lett 35:101607. https://doi.org/10.1016/j.frl.2020.101607
Conlon T, Corbet S, McGee RJ (2020) Are cryptocurrencies a safe haven for equity markets? An international perspective from the COVID-19 pandemic. Res Int Bus Finance 54:101248. https://doi.org/10.1016/j.ribaf.2020.101248
Corbet S, Meegan A, Larkin C, Lucey B, Yarovaya L (2018) Exploring the dynamic relationships between cryptocurrencies and other financial assets. Econ Lett 165:28–34
Corbet S, Larkin C, Lucey B (2020) The contagion effects of the covid-19 pandemic: evidence from gold and cryptocurrencies. Finance Res Lett 35:101554. https://doi.org/10.1016/j.frl.2020.101554
Demir E, Gozgor G, Lau CKM, Vigne SA (2018) Does economic policy uncertainty predict the Bitcoin returns? An empirical investigation. Finance Res Lett 26:145–149
Diebold FX, Yilmaz K (2012) Better to give than to receive: predictive directional measurement of volatility spillovers. Int J Forecast 28(1):57–66
Diebold FX, Yılmaz K (2014) On the network topology of variance decompositions: measuring the connectedness of financial firms. J Econom 182(1):119–134
Dutta A, Das D, Jana RK, Vo XV (2020) COVID-19 and oil market crash: revisiting the safe haven property of gold and Bitcoin. Resour Policy 69:101816
Folkinshteyn D, Lennon M (2016) Braving Bitcoin: a technology acceptance model (TAM) analysis. J Inf Technol Case Appl Res 18(4):220–249
Goodell JW, Goutte S (2020) Co-movement of COVID-19 and Bitcoin: evidence from wavelet coherence analysis. Finance Res Lett. https://doi.org/10.1016/j.frl.2020.101625
Gupta R, Subramaniam S, Bouri E, Ji Q (2021) Infectious diseases-related uncertainty and the safe-haven characteristic of the US treasury securities. Int Rev Econ Finance 71:289–298
Ji Q, Bouri E, Gupta R, Roubaud D (2018) Network causality structures among Bitcoin and other financial assets: a directed acyclic graph approach. Q Rev Econ Finance 70:203–213
Ji Q, Bouri E, Lau CKM, Roubaud D (2019) Dynamic connectedness and integration in cryptocurrency markets. Int Rev Financ Anal 63:257–272
Katsiampa P, Corbet S, Lucey B (2019a) High frequency volatility co-movements in cryptocurrency markets. J Int Financ Mark Inst Money 62:35–52
Katsiampa P, Corbet S, Lucey B (2019b) Volatility spillover effects in leading cryptocurrencies: a BEKK-MGARCH analysis. Finance Res Lett 29:68–74
Kou G, Peng Y, Wang G (2014) Evaluation of clustering algorithms for financial risk analysis using MCDM methods. Inf Sci 275:1–12
Koutmos D (2018) Return and volatility spillovers among cryptocurrencies. Econ Lett 173:122–127
Kristjanpoller W, Bouri E, Takaishi T (2020) Cryptocurrencies and equity funds: evidence from an asymmetric multifractal analysis. Phys A 545:123711
Kristoufek L (2013) BitCoin meets Google Trends and Wikipedia: quantifying the relationship between phenomena of the Internet era. Sci Rep 3:3415. https://doi.org/10.1038/srep03415
Kumar AS, Ajaz T (2019) Co-movement in crypto-currency markets: evidences from wavelet analysis. FIN 5(1):33. https://doi.org/10.1186/s40854-019-0143-3
Malugin V, Novopoltsev A (2017) Statistical estimation and classification algorithms for regime-switching VAR Model with exogenous variables. Austrian J Stat 46(3–4):47–56
Qiao X, Zhu H, Hau L (2020) Time-frequency co-movement of cryptocurrency return and volatility: evidence from wavelet coherence analysis. Int Rev Financ Anal 71:101541
Qureshi S, Aftab M, Bouri E, Saeed T (2020) Dynamic interdependence of cryptocurrency markets: an analysis across time and frequencies. Phys A. https://doi.org/10.1016/j.physa.2020.125077
Reboredo JC, Ugolini A (2020) Price spillovers between rare earth stocks and financial markets. Resour Policy 66:101647
Shahzad SJH, Bouri E, Roubaud D, Kristoufek L, Lucey B (2019) Is Bitcoin a better safe-haven investment than gold and commodities? Int Rev Financ Anal 63:322–330
Shen D, Urquhart A, Wang P (2020a) A three-factor pricing model for cryptocurrencies. Finance Res Lett 34:101248. https://doi.org/10.1016/j.frl.2019.07.021
Shen F, Zhao X, Kou G (2020b) Three-stage reject inference learning framework for credit scoring using unsupervised transfer learning and three-way decision theory. Decis Support Syst 137:113366
Topcu M, Gulal OS (2020) The impact of COVID-19 on emerging stock markets. Finance Res Lett 36:101691
Wang H, Kou G, Peng Y (2020) Multi-class misclassification cost matrix for credit ratings in peer-to-peer lending. J Oper Res Soc 1–12
Wen F, Xu L, Ouyang G, Kou G (2019) Retail investor attention and stock price crash risk: evidence from China. Int Rev Financ Anal 65:101376
Yarovaya, L, Matkovskyy R, Jalan A (2020) The effects of a 'Black Swan' event (COVID-19) on herding behavior in cryptocurrency markets: evidence from Cryptocurrency USD, EUR, JPY and KRW markets. Available at SSRN: https://ssrn.com/abstract=3586511 or http://dx.doi.org/https://doi.org/10.2139/ssrn.3586511. Accessed 20 July 2020
Yi S, Xu Z, Wang GJ (2018) Volatility connectedness in the cryptocurrency market: is Bitcoin a dominant cryptocurrency? Int Rev Financ Anal 60:98–114
Yoshino N, Taghizadeh-Hesary F, Otsuka M (2020) Covid-19 and optimal portfolio selection for investment in sustainable development goals. Finance Res Lett. https://doi.org/10.1016/j.frl.2020.101695
Zięba D, Kokoszczyński R, Śledziewska K (2019) Shock transmission in the cryptocurrency market. is Bitcoin the most influential? Int Rev Financ Anal 64:102–125
The fourth author acknowledges that the Deanship of Scientific Research (DSR) at King Abdulaziz University, Jeddah, Saudi Arabia funded this project, under Grant No. (FP-71-42). The third author acknowledges the support of the Ministry of Education of the Republic of Korea and the National Research Foundation of Korea (NRF-2020S1A5B8103268).
Montpellier Business School, Montpellier, France
Syed Jawad Hussain Shahzad
South Ural State University, Chelyabinsk, Russian Federation
Adnan Kassar School of Business, Lebanese American University, Beirut, Lebanon
Elie Bouri
Department of Business Administration, Pusan National University, Busan, South Korea
Sang Hoon Kang
Nonlinear Analysis and Applied Mathematics (NAAM)-Research Group, Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah, Saudi Arabia
Tareq Saeed
SJHS: Conceptualization, Data curation, Formal analysis, Methodology. EB: Project administration, Visualization, Writing—original draft. SHK: Visualization, Writing—original draft. TS: Writing—original draft, Writing—review and editing. All authors read and approved the final manuscript.
Correspondence to Elie Bouri.
Table 4 Directional detailed spillovers under regime switching—full sample
Table 5 Directional detailed spillovers under regime switching—COVID-19 period (January 1st, 2020–April 1st, 2020)
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Shahzad, S.J.H., Bouri, E., Kang, S.H. et al. Regime specific spillover across cryptocurrencies and the role of COVID-19. Financ Innov 7, 5 (2021). https://doi.org/10.1186/s40854-020-00210-4
Regime-switching
Volatility regimes
Spillovers
Connectedness | CommonCrawl |
Isolation and characterization of equine endometrial mesenchymal stromal cells
B. Elisabeth Rink1,2,3,
Karin R. Amilon2,
Cristina L. Esteves2,
Hilari M. French1,
Elaine Watson1,
Christine Aurich3 &
F. Xavier Donadeu2,4
Equine mesenchymal stromal/stem cells (MSCs) are most commonly harvested from bone marrow (BM) or adipose tissue, requiring the use of surgical procedures. By contrast, the uterus can be accessed nonsurgically, and may provide a more readily available cell source. While human endometrium is known to harbor mesenchymal precursor cells, MSCs have not been identified in equine endometrium. This study reports the isolation, culture, and characterization of MSCs from equine endometrium.
The presence of MSC and pericyte markers in endometrial sections was determined using immunohistochemistry. Stromal cells were harvested and cultured after separation of epithelial cells from endometrial fragments using Mucin-1-bound beads. For comparison, MSCs were also harvested from BM. The expression of surface markers in endometrial and BM-derived MSCs was characterized using flow cytometry and quantitative polymerase chain reaction. MSCs were differentiated in vitro into adipogenic, chondrogenic, osteogenic, and smooth muscle lineages.
Typical markers of MSCs (CD29, CD44, CD90, and CD105) and pericytes (NG2 and CD146) were localized in the equine endometrium. Both endometrial and BM MSCs grew clonally and robustly expressed MSC and pericyte markers in culture while showing greatly reduced or negligible expression of hematopoietic markers (CD45, CD34) and MHC-II. Additionally, both endometrial and BM MSCs differentiated into adipogenic, osteogenic, and chondrogenic lineages in vitro, and endometrial MSCs had a distinct ability to undergo smooth muscle differentiation.
We have demonstrated for the first time the presence of cells in equine endometrium that fulfill the definition of MSCs. The equine endometrium may provide an alternative, easily accessible source of MSCs, not only for therapeutic regeneration of the uterus, but also for other tissues where MSCs from other sources are currently being used therapeutically.
Considerable progress has been made in understanding the biology and therapeutic potential of adult stem cells since the first report of human hematopoietic stem cell transplantation in 1957 [1]. Mesenchymal stem or stromal cells (MSCs) were originally described in the 1960s as a subset of fibroblast-like cells in the bone marrow capable of undergoing osteogenic differentiation [2]. Minimum criteria defining human MSCs were established by the International Society for Cellular Therapy in 2006 [3] and include: plastic adherence under standard culture conditions; expression of the surface markers CD73, CD90, and CD105 and lack of expression of hematopoietic markers as well as HLA-DR; and ability to undergo adipogenic, chondrogenic, and osteogenic differentiation in vitro. In 2013, CD29 and CD44 were added to the list of MSC-positive surface markers [4]. Furthermore, the origin of MSCs in multiple body tissues, including human endometrium [5, 6], has been traced to perivascular cells expressing CD146, NG2, PDGFRβ, and α-SMA. Expression of these markers is maintained by human MSCs in culture [7]. Moreover, studies in vitro and using cell transplantation in model species have shown that, in addition to providing different types of precursor cells, MSCs contribute to tissue repair through immunomodulatory, antiapoptotic, antimicrobial, and a variety of other trophic effects that act to enhance endogenous repair mechanisms [8]. Based on these findings, several hundred clinical trials are currently being carried out using human MSCs [9].
In the horse, MSCs have been used clinically for about 15 years, with therapeutic benefit reported in the treatment of several orthopedic conditions. Equine MSCs are commonly harvested from bone marrow or adipose tissue and are expanded in vitro before use in autologous transplants [10,11,12,13]. The requirement to use surgical procedures to harvest cells from those locations has driven the search for other—less invasive—sources including whole blood, umbilical cord blood, or Wharton jelly [14,15,16,17]. In that regard, the endometrium represents an attractive alternative source of MSCs in the horse.
Endometrial cells meeting the criteria of MSCs have already been harvested and characterized from humans, rodents, pigs, dogs, and sheep [18,19,20,21,22,23,24,25]. In addition to undergoing trilineage differentiation, they can reportedly generate muscle and neuronal lineages [5, 26]. The therapeutic potential of endometrial MSCs has already been demonstrated in relation to premature ovarian failure [27], Parkinson's disease [26], and pelvic organ prolapse [28], although these uses have yet to be proven clinically.
The equine endometrium is highly dynamic, cyclically undergoing remodeling [29] which suggests the presence of an active population of mesenchymal precursor cells, yet this has not been investigated. With the goal of eventually exploring the therapeutic potential of these cells, this study aimed to isolate and characterize equine endometrial MSCs and compare their properties to those of the well-characterized bone marrow (BM)-derived MSCs.
Samples and materials
Equine reproductive tracts were collected post mortem from five prepubertal (18-month-old) Welsh Cob ponies and one 6-year-old warmblood mare during diestrus. Bone marrow samples were collected from three Welsh Cob ponies. The animals were euthanized at the School of Veterinary Studies of the University of Edinburgh or the School of Veterinary Medicine of the University of Glasgow for reasons not related to any reproductive tract pathology. All animal procedures were carried out according to the UK Home Office Animals (Scientific Procedures) Act 1986 with approval by the Ethical Review Committee, University of Edinburgh (60/4207). All chemicals and reagents used for cell culture in the study were obtained from Life Technologies (Thermo Fisher Scientific, Paisley, UK) unless otherwise specified, and culture plastic ware (Nunc™) was purchased from Sigma Aldrich (St Louis, MO, USA).
Small pieces of equine endometrium (5 mm × 5 mm) were snap frozen and cut into 5-μm sections using a Leica CM1900 cryotome. The tissue sections were fixed in ice-cold methanol:acetone (50:50) for 10 minutes and washed three times with phosphate buffered saline (PBS) before incubation with a Protein Block (Spring Bioscience) for 45 minutes at room temperature. The sections were then incubated overnight at 4 °C with the primary antibodies presented in Table 1. Another three washes with PBS were followed by incubation with the secondary antibody (Table 1) for 30 minutes at room temperature. Finally, the nuclei were counterstained for 3 minutes with 4′,6-diamidine-2′-phenylindole dihydrochloride (DAPI) before mounting. Sections were visualized under a Leica DM LB2 fluorescence microscope.
Table 1 Antibodies selected for immunohistochemistry and flow cytometry characterization of equine MSCs
Isolation of equine endometrial stromal cells
One gram of endometrial tissue was stripped from the underlying myometrium and dissociated using mechanical and enzymatic digestion as described previously [20] with a few modifications. In short, the tissue pieces were washed twice in PBS and minced before dissociation in DMEM/F-12 containing 0.1% bovine serum albumin (BSA), 0.5% collagenase I, 40 μg/ml deoxyribonuclease type I (Sigma Aldrich), and 1% penicillin/streptomycin for 40 minutes at 37 °C in a SI50 Orbital Incubator (Stuart Scientific). The resulting cell solution was filtered through a sterile 70-μm cell strainer (Fisher Scientific) to separate single cells from undigested tissue fragments. After washing with MSC culture medium consisting of DMEM/F-12 containing 10% fetal bovine serum (FBS) and 1% penicillin/streptomycin, and centrifugation for 5 minutes at 720 × g, the resulting cell pellet was resuspended in Ca2+ and Mg2+-free PBS supplemented with 0.1% FBS and 2 mM sodium citrate.
Magnetic Dynabeads M-450 that had been coated with a Mucin-1 antibody (Santa Cruz) according to the manufacturer's protocol were utilized to remove epithelial cells from the single cell suspension. The number of Mucin-1-coated beads required was calculated assuming 50% of the cell suspension was epithelial. Four beads were incubated per epithelial cell for 40 minutes at 4 °C with gentle rotation and tilting. Unbound (stromal, Muc-1–) and bound (epithelial, Muc-1+) cell fractions were collected using a Dynamagnet 2, centrifuged, and cultured in MSC culture medium at an initial density of 106 cells/75 cm2 in a humidified incubator at 37 °C in 5%CO2:95% air. Medium was changed every 2–3 days.
Isolation of equine bone marrow-derived MSCs
Bone marrow was scraped out of the sternum and immersed in 30 ml PBS containing 45 mg ethylenediaminetetraacetic acid (EDTA) in a 50-ml Falcon tube. The tube was gently rotated and tilted to wash out cells from the bone marrow matrix. The solution was filtered through a 40-μm cell strainer (Fisher Scientific) and centrifuged at 720 × g for 5 minutes. The resulting cell pellet was resuspended in PBS. To remove red blood cells, 4 ml of the BM cell solution was underlaid with 3 ml Ficoll Paque PLUS (GE Healthcare) and centrifuged at 20 °C for 40 minutes at 400 × g. The interphase layer of mononuclear cells was collected, washed twice with PBS, and cultured at an initial density of 20–40 million cells/175 cm2 in MSC culture medium under the same conditions already described for the endometrial-derived stromal cells.
Colony forming unit assay
Doubling times (DTs) of endometrial Muc-1– fraction cells (n = 6 horses) and BM MSCs (n = 3 horses) in culture were calculated between passages 1 and 2 using the following equation:
$$ \mathrm{D}\mathrm{T} = T\ { \ln}_2/ \ln \left({X}_{\mathrm{e}}/{X}_{\mathrm{b}}\right), $$
where T is the incubation time in days, and X b and X e are the cell numbers at the beginning and the end, respectively, of the incubation time.
Endometrial Muc-1– fraction cells and BM MSCs, both at passage 2, were seeded in triplicate at clonal densities of 5 and 10 cells/cm2 in six-well plates and cultured in MSC medium in a humidified atmosphere at 37 °C in 5% CO2:95% air. Medium was changed every 3–4 days, and on the 12th day of culture cells were washed with PBS and fixed with 10% buffered formalin for 1 hour. Cultures were then stained with crystal violet (Sigma Aldrich) for 10 minutes, washed three times with dH2O, and dried at room temperature.
Cell clusters that were visible without magnification and contained more than 50 cells were defined as colonies. Cloning efficiency (CE) was calculated with the following formula:
$$ C E=\frac{number\ of\ colonies}{number\ of\ cells\ seeded} \cdot 100 $$
Endometrial Muc-1– cells (n = 6 horses) and BM MSCs (n = 3 horses) at passage 3 or 4 were analyzed using flow cytometry. The cultured cells were lifted with TrypLE, washed with complete MSC culture medium, and centrifuged at 720 × g for 5 minutes at room temperature. Cell pellets were resuspended in PBS containing 5% FBS and incubated for 45 minutes on ice. Cells were then incubated with directly conjugated or unconjugated primary antibodies to different cell surface markers or with matched isotype control IgG (Table 1) for 1 hour at 4 °C. After three washes with PBS, cells were incubated with AF488-conjugated secondary antibodies for 30 minutes at 4 °C. Cells were analyzed using a LSR Fortessa™ flow cytometer (BD Biosciences) equipped with FACS Diva software and the collected data (10000 events) were analyzed with FlowJo (V10; LLC).
Cross-reactivity of cell surface marker antibodies was tested by IHC and flow cytometry, and the expression of each marker was confirmed via RT quantitative polymerase chain reaction (qPCR).
qPCR analyses
RNA was extracted using TRIzol reagent from freshly collected endometrial cells (n = 6 horses) and from cultures of endometrial Muc-1– cells (n = 6 horses) and BM MSCs (n = 3 horses) at passages 1 and 4. RNA was analyzed using a spectrophotometer (ND-1000, Nano Drop®) and total RNA (0.5–1 μg) was reverse-transcribed using SuperScript III following the instructions of the manufacturer. Subsequent qPCR reactions were performed using SensiFAST™ SYBR® Lo-ROX Kit (Bioline) and equine primers (Table 2) in a Stratagene Mx3000P qPCR machine (Agilent technologies). Data were analyzed with MxPRO qPCR software (Agilent technologies). Values were calculated relative to a standard curve prepared from a pool of samples run simultaneously. Three reference genes were analyzed for stability using the web-based comprehensive tool RefFinder [30] integrating geNorm, BestKeeper, Normfinder, and the comparative ΔCt method. Data were normalized using RNA levels of 18S.
Table 2 Primers used for qPCR analysis
In-vitro trilineage differentiation
Endometrial Muc-1– cells and BM MSCs (from three horses each) were used separately at passage 3 or 4. For adipogenic differentiation, cells were seeded in triplicate wells of 12-well plates (5000/cm2) with MSC culture medium for 2–4 days before changing medium to DMEM/F-12 containing 7% rabbit serum, 3% FBS, 1% penicillin/streptomycin, 1 μM dexamethasone (Sigma Aldrich), 0.5 mM 3-isobutyl-1-methylxanthine (IBMX) (Sigma Aldrich), 10 μg/ml insulin (Sigma Aldrich), and 100 μM indomethacin (Sigma Aldrich). After 5 days of culture, cells were washed with PBS before fixation in 10% formalin and were stained with Oil Red O (Sigma Aldrich) for 10 minutes.
For osteogenic differentiation, cells were seeded in triplicate wells of 12-well plates (5000 cells/cm2) and cultured for 2–4 days before changing medium to DMEM/F-12 containing 10% FBS, 1% penicillin/streptomycin, 10 mM β-glycerophosphate (Sigma Aldrich), 100 nM dexamethasone (Sigma Aldrich), and 200 μM l-ascorbic acid 2-phosphate (Sigma Aldrich). Medium was changed every 2–3 days and after 3 weeks cells were washed with PBS, fixed in 10% formalin, and stained with Alizarin Red (Sigma Aldrich) for 45 minutes.
For chondrogenic differentiation, 3 × 105–4 × 105 cells were centrifuged in a V-bottomed 96-well plate at 720 × g for 5 minutes. After centrifugation, without disturbing the freshly formed pellet, medium was changed to DMEM/F-12 containing 1% penicillin/streptomycin, 1% ITS+ premix (Corning), 100 nM dexamethasone (Sigma Aldrich), 200 μM l-ascorbic acid 2-phosphate (Sigma Aldrich), 100 μg/ml sodium pyruvate (Sigma Aldrich), and 10 ng/ml TGF-β1 (R&D Systems). After 24 hours of incubation, the pellets were gently loosened and transferred to a U-bottom 96-well plate with a cell-repellent surface (Greiner bio-one). Micro masses were cultured for 28 days with medium changes every 1–2 days and then fixed in 10% formalin for 24 hours. The pellets were processed and embedded in paraffin. Sections were cut on a microtome (Leica RM2235) and stained with Alcian Blue (Acros Organics) and the nuclear counter stain Nuclear Fast Red (Sigma Aldrich).
In-vitro smooth muscle differentiation
The protocol used for smooth muscle differentiation was adapted from Guo et al. [31]. In short, endometrial Muc-1– cells and BM MSCs (from three horses each) at passage 3 or 4 were seeded at a density of 70,000 cells/well in triplicate wells of 12-well plates and incubated at 37 °C in 5%CO2:95% air for 24 hours before the medium was changed to DMEM containing 1% FBS. After a further 24 hours, differentiation was induced by changing the medium to DMEM containing 1% FBS and 1 ng/ml TGF-β1 (R&D Systems). Control cells were maintained in MSC culture medium and after 7 days all cells were harvested using TRIzol reagent and processed for qPCR analysis as described earlier.
All data were analyzed using IBM SPSS Statistics 22 software using each donor horse as the experimental unit. Normal distribution was tested with the Shapiro–Wilk test and data were log-transformed if necessary. Flow cytometry data were analyzed using Levene's test for equality of variances and a two-tailed t test. QPCR data were analyzed with two-way ANOVA and Tukey's test. Data are shown as mean ± SEM. Significance was set at p < 0.05.
Localization of MSC and perivascular markers in equine endometrium
Endometrial tissue was analyzed for the presence of a selection of cluster of differentiation (CD) antigens commonly used to identify human MSCs, namely CD29, CD44, CD90, and CD105 (Fig. 1a), as well as the perivascular cell surface markers, CD146 and NG2 (Fig. 1b). CD29 and CD44 were localized mainly around blood vessels. Milder staining for CD29 was found around endometrial glands and underneath the epithelium. CD90 clone 5E10 was very abundant throughout the stroma, except in glandular cells (data not shown), indicating lack of specificity. CD90 clone OX7 staining was present throughout the endometrial stroma in a string-like pattern, and also around endometrial glands. CD105 staining was less abundant and localized within single cells throughout the stroma. All MSC markers tested were absent from glandular cells and the endometrial epithelium. The perivascular markers, CD146 and NG2, were mostly located around the blood vessel walls.
Immunohistochemistry of equine endometrial sections. Photomicrographs show localization of (a) MSC markers CD29, CD44, CD90, and CD105 and (b) perivascular markers NG2 and CD146 within the equine endometrium. DAPI was used to stain cell nuclei. Yellow arrows, endometrial glands; white arrows, blood vessels. DAPI 4′,6-diamidine-2′-phenylindole dihydrochloride (Color figure online)
Isolation and culture of endometrial MSCs
Culture of endometrial tissue directly following collagenase dissociation resulted in epithelial cells adhering quickly to plastic culture ware and eventually outgrowing the stromal cells (Fig. 2a). Thus, we used magnetic beads bound to Muc-1, a surface marker located within the luminal and glandular epithelium (Fig. 2b), to enrich endometrial digests for stromal cells. The resulting Muc-1– fraction, from here onward referred to as endometrial MSCs, was used for culture (Fig. 2c).
Isolation and culture of MSCs. a Micrograph showing cells cultured directly following digestion of equine endometrium. Using this procedure, clusters of epithelial cells (black arrows) eventually outgrew stromal cells in culture. b Section of equine endometrium stained for Mucin-1, showing positive cells in epithelia and glands (white arrows). Cell nuclei stained with DAPI. c Micrograph of endometrial stromal cells in culture obtained after separation of epithelial cells (shown in d) using beads bound to Mucin-1. e Cell colonies produced after seeding of endometrial and BM MSCs at low densities. f Cloning efficiencies (CE) for endometrial MSCs (n = 6 horses) and BM MSCs (n = 3 horses) at two different seeding densities. Scale bars: 1 mm (a, c–e). BM bone marrow, MSC mesenchymal stromal/stem cell (Color figure online)
Upon initial seeding, endometrial MSCs attached quickly and evenly over the entire culture surface in contrast to BM MSCs which took longer to adhere and tended to grow in clusters. Moreover, doubling times between passages 1 and 2 tended to be shorter for endometrial MSCs than for BM MSCs (2.8 ± 0.6 vs 5.2 ± 1.9 days, respectively, p = 0.09). Cloning efficiency (CE) assays performed at passage 2 yielded similar results for both endometrial and BM MSCs, as shown in Fig. 2e, f.
Expression of MSC and perivascular markers by endometrial MSCs in culture
The expression of MSC and perivascular cell surface markers was analyzed by qPCR and flow cytometry in endometrial and BM MSCs at different passages (Figs. 3 and 4). Moderate differences were detected in transcript levels of MSC markers, including higher overall levels of CD29 and, to a lesser degree, CD105, in endometrial MSCs than in BM MSCs (as indicated in each case by a significant effect of cell type), as well as a slight reduction in overall CD29 levels between passages 1 and 4 (Fig. 3). Flow cytometry (Fig. 4) showed all of these markers to be present, on average, in ≥97% of endometrial and BM MSCs (except for CD105, detected in 80% of BM MSCs). Moreover, there was an overall increase in transcript levels of CD146 between passages 1 and 4 (Fig. 3). The levels of another perivascular marker, NG2, did not change with passage but were lower in endometrial MSCs than in BM MSCs (Fig. 3), a result that was confirmed by flow cytometry data (Fig. 4). Finally, CD34 and MHC-II were expressed by a minority of cells (≤2%) in both endometrial and BM MSC cultures (Fig. 4), whereas CD45 was detectable in BM MSCs at passage 1 only (Fig. 3).
Transcript levels (arbitrary units) of cell surface markers in cultured MSCs. Expression of MSC markers (CD29, CD44, CD90, CD105), perivascular markers (NG2, CD146), and hematopoietic markers (CD34, CD45) quantified by qPCR in endometrial MSCs (n = 6 horses, white bars) and BM MSCs (n = 3 horses, gray bars) in culture at passages 1 and 4. All results shown as mean ± SEM. Significant main effects (p < 0.05) of passage, cell type, and passage × cell type interaction obtained by two-way ANOVA are shown. AU arbitrary units
Flow cytometry analysis. Representative flow cytometry histograms with percentages of endometrial and BM MSCs (n = 6 and n = 3 horses, respectively) positive for different MSC, perivascular, and hematopoietic cell surface markers. Grey areas, signal from isotype controls; black lines, signal from the specific cell surface marker. BM bone marrow, MSC mesenchymal stromal/stem cell
In-vitro differentiation of endometrial MSCs
The ability of endometrial MSCs to undergo trilineage differentiation was assessed in parallel with that of BM MSCs. Endometrial MSCs differentiated into adipogenic, osteogenic, and, albeit to a lesser degree than BM MSCs, chondrogenic lineages (Fig. 5).
Trilineage differentiation of endometrial MSCs (a, c, e) and BM MSCs (b, d, g). Representative images of endometrial and BM MSCs (n = 3 horses each) after differentiation and staining with Oil red O (a, b), Alizarin Red (c, d) and Alcian Blue/Nuclear Fast Red (e–g) to assess differentiation into adipogenic, osteogenic, and chondrogenic lineages, respectively. Insets show nondifferentiated control cells (a–d). Nondifferentiated control BM MSCs used in chondrogenic differentiation experiments shown in (f). Scale bars: 100 μm (a, b), 500 μm (c, d, e, g) and 1 mm (f)
Additionally, the relative capacity of the two types of MSCs to differentiate into smooth muscle, a key component of the myometrium in the uterus, was determined by treating cells with TGF-β1. Endometrial MSCs, but not BM MSCs, underwent morphological changes primarily characterized by shortening of the cell body in response to treatment (Fig. 6a, b). Because of the difficulty of clearly distinguishing smooth muscle cells from undifferentiated MSCs, we assessed the expression of early (ACTA2), intermediate (CNN1), and mature (MYH11) smooth muscle markers [31] in endometrial and BM MSC cultures by qPCR (Fig. 6c). Results showed an increase in mean transcript levels of the intermediate marker, CNN1, in BM MSCs (1.7-fold, p < 0.05) and, particularly, in endometrial MSCs (2.9-fold, p < 0.0001) between days 0 and 7, and an increase in the levels of the mature smooth muscle marker, MYH11, only in endometrial MSCs (1.8-fold, p < 0.005).
Smooth muscle differentiation. Micrographs showing (a) endometrial MSCs (n = 3 horses) and (b) BM MSCs (n = 3 horses) induced to differentiate into smooth muscle for 7 days. Insets show noninduced control cells. Scale bars: 500 μm. c Expression of smooth muscle markers in endometrial MSCs (white bars) and BM MSCs (grey bars) before (d0) and on day 7 (d7) of differentiation. Results shown as mean ± SEM. Significant main effects (p < 0.05) of day, cell type, and day × cell type interaction obtained by two-way ANOVA are shown. AU arbitrary units
MSCs—defined by their adherence to plastic, expression of a subset of cell surface markers, and ability to differentiate into adipogenic, osteogenic, and chondrogenic lineages [3]—have to this date been isolated from several body tissues including bone marrow, fat, umbilical cord, placenta, amniotic fluid, umbilical cord blood, peripheral blood, and endometrium [32,33,34,35]. Bone marrow and adipose tissue have been the most common sources of clinical MSCs in horses, and they are also the most common sources used for clinical trials in humans. Collection of MSCs from these locations requires relatively invasive procedures involving sedation and local anesthesia, and carries the potential of postsurgical complications [36]. Thus, alternative sources of equine MSCs, such as the endometrium, are desirable. A major advantage of isolating MSCs from the endometrium compared to bone marrow or adipose tissue is that cells can be harvested by biopsy collection [24, 37], which is a relatively noninvasive approach used routinely in horses for diagnostic purposes that does not require sedation or local anesthesia [38]. In this study, we show for the first time that putative MSCs contained within the equine endometrium can be harvested and expanded in vitro, and have characteristics that may prove useful for tissue regeneration applications.
Endometrial MSCs had typical spindle-shaped morphology, indistinguishable from that of BM MSCs; however, they tended to grow faster than BM MSCs following initial seeding, as indicated by their mean doubling time values. In contrast, cloning efficiencies (CE) at passage 2 were similar for the two cell types, around 25–30%, and comparable to previous reports from 27% [39] to 34% [40] for equine BM MSCs. The faster initial growth of endometrial MSCs relative to BM MSCs may be conferred by their native in-vivo environment characterized by fast tissue turnover during the estrous cycle. If confirmed in future studies, this property of endometrial MSCs may provide an advantage over other MSC sources because it may allow shortening of the interval between collection of tissue samples and transplant of in-vitro expanded MSCs, which is a serious limitation of current BM and adipose MSC treatments in horses. In addition, based on cell yields obtained from 1 g of endometrial tissue (≥107 Muc-1– cells) and considering subsequent growth rates in culture (see Results), we estimate that a typical 0.2–0.4 g biopsy would readily yield >10 million cells after short-term expansion, a sufficient number for therapy applications in horses. Furthermore, when executed appropriately, the biopsy procedure does not result in damage or scarring of the uterus. Indeed, it has been shown that repeated collection of multiple biopsies (up to five each time) before estrus had no effect on subsequent pregnancy rates in mares [41].
Cells staining for CD44, CD105, CD146, and NG2 were located primarily around blood vessels within the equine endometrium, consistent with the identification of perivascular cells as native counterparts of MSCs in many different human tissues [7, 42], including the endometrium [6]. By contrast, CD90 (clone OX7) followed a less restricted pattern throughout the stroma to include nonperivascular cells. The distinct abundance of CD90 compared to the other MSC markers tested suggests that this may not be an appropriate marker for equine MSCs in the endometrium.
Consistent with the definition of MSCs, endometrial stromal cells robustly maintained the expression of CD29, CD44, CD90, and CD105 in culture, as well as, to a lesser extent, perivascular markers, whilst having negligible expression of hematopoietic markers and MHC-II, in agreement with previous studies with human endometrial-derived MSCs [5, 25, 27, 43]. A limited number of studies have compared the features of endometrial MSCs with MSCs from other sources [23, 44]. Our finding based on results of flow cytometry and qPCR, showing that endometrial MSCs in culture display moderately higher levels of CD29, CD90, and CD105 but lower levels of NG2 than their BM counterparts, is consistent with data from Indumathi et al. [23]. Whether this is indicative of differences in the abundance of stem cells between the two tissue sources or reflects tissue-specific changes in immunophenotype that may be induced in culture should be investigated in future studies.
That endometrial and BM MSCs have different properties was confirmed by the results of differentiation assays; specifically by the observation that while endometrial MSCs were able to undergo trilineage differentiation, their ability to generate cartilage was lower than that of BM MSCs based on a clearly reduced intensity of Alcian Blue staining in endometrial MSC-derived chondrogenic pellets (Fig. 5). In contrast, the opposite was observed in relation to the ability of MSCs to adopt a smooth muscle phenotype, as evidenced by a distinct increase in endometrial MSCs, but not in BM MSCs, in the levels of the mature smooth muscle marker, MYH11, after treatment with TGF-β1. There is evidence that significant differentiation bias can be conferred by the tissue of origin of MSCs [45]. For example, while human multipotent cell populations from the myometrium and skeletal muscle had a similar immunophenotype and ability to differentiate into smooth muscle, only skeletal muscle-derived progenitors were able to undergo osteogenic and adipogenic differentiation [46]. In light of this, a distinct ability of endometrial MSCs (compared to BM MSCs) to differentiate into smooth muscle may be related to the presence of a large smooth muscle component in the uterus, the myometrium. Whether our observation alternatively reflects the presence, natural or through contamination during sample collection, of myometrial precursor cells, different from MSCs, in the endometrial stroma needs to be investigated in future studies. Nonetheless, a reported intrinsic ability of human endometrial MSCs to differentiate into smooth muscle provides the rationale for specific therapeutic applications already being sought for these cells (e.g., pelvic organ prolapse) [47].
We report for the first time the identification, culture, and characterization of stromal cells within the equine uterus that fulfill the definition of MSCs based on clonogenicity, immunophenotype, and ability to differentiate into different mesenchymal derivatives. Although not addressed in this study, the relative abundance and phenotype of MSCs in the equine endometrium may vary with the reproductive stage, a possibility that should be investigated in the future. Endometrial MSCs may provide an easily accessible alternative to therapeutic applications that currently use bone marrow and adipose MSCs in the horse. They may moreover provide a new therapeutic venue for equine uterine disease, a multifaceted and highly prevalent condition which significantly impairs fertility in mares. With this in mind, future studies should be aimed at exploring the clinical regenerative potential of these cells in the endometrium but also in other tissues that have been more commonly targeted with cell therapies, such as musculoskeletal tissue.
BM:
Cluster of differentiation
CE:
Cloning efficiency
DAPI:
4′,6-Diamidine-2′-phenylindole dihydrochloride
EDTA:
Ethylenediaminetetraacetic acid
FBS:
Mesenchymal stromal/stem cell
Phosphate buffered saline
qPCR:
Quantitative polymerase chain reaction
Thomas ED, Lochte Jr HL, Lu WC, Ferrebee JW. Intravenous infusion of bone marrow in patients receiving radiation and chemotherapy. N Engl J Med. 1957;257:491–6.
Friedenstein AJ, Piatetzky II S, Petrakova KV. Osteogenesis in transplants of bone marrow cells. J Embryol Exp Morphol. 1966;16:381–90.
Dominici M, Le Blanc K, Mueller I, Slaper-Cortenbach I, Marini F, Krause D, et al. Minimal criteria for defining multipotent mesenchymal stromal cells. The International Society for Cellular Therapy position statement. Cytotherapy. 2006;8:315–7.
Bourin P, Bunnell BA, Casteilla L, Dominici M, Katz AJ, March KL, et al. Stromal cells from the adipose tissue-derived stromal vascular fraction and culture expanded adipose tissue-derived stromal/stem cells: a joint statement of the International Federation for Adipose Therapeutics and Science (IFATS) and the International Society for Cellular Therapy (ISCT). Cytotherapy. 2013;15:641–8.
Gargett CE, Schwab KE, Zillwood RM, Nguyen HPT, Wu D. Isolation and culture of epithelial progenitors and mesenchymal stem cells from human endometrium. Biol Reprod. 2009;80:1136–45.
Schwab KE, Gargett CE. Co-expression of two perivascular cell markers isolates mesenchymal stem-like cells from human endometrium. Hum Reprod. 2007;22:2903–11.
Crisan M, Yap S, Casteilla L, Chen CW, Corselli M, Park TS, et al. A perivascular origin for mesenchymal stem cells in multiple human organs. Cell Stem Cell. 2008;3:301–13.
Caplan AI. MSCs: the sentinel and safe-guards of injury. J Cell Physiol. 2016;231:1413–6.
Trounson A, McDonald C. Stem cell therapies in clinical trials: progress and challenges. Cell Stem Cell. 2015;17:11–22.
Ranera B, Lyahyai J, Romero A, Vazquez FJ, Remacha AR, Bernal ML, et al. Immunophenotype and gene expression profiles of cell surface markers of mesenchymal stem cells derived from equine bone marrow and adipose tissue. Vet Immunol Immunopathol. 2011;144:147–54.
Radcliffe CH, Flaminio MJ, Fortier LA. Temporal analysis of equine bone marrow aspirate during establishment of putative mesenchymal progenitor cell populations. Stem Cells Dev. 2010;19:269–82.
Godwin EE, Young NJ, Dudhia J, Beamish IC, Smith RK. Implantation of bone marrow-derived mesenchymal stem cells demonstrates improved outcome in horses with overstrain injury of the superficial digital flexor tendon. Equine Vet J. 2012;44:25–32.
Smith RK, Korda M, Blunn GW, Goodship AE. Isolation and implantation of autologous equine mesenchymal stem cells from bone marrow into the superficial digital flexor tendon as a potential novel treatment. Equine Vet J. 2003;35:99–102.
Lovati AB, Corradetti B, Lange Consiglio A, Recordati C, Bonacina E, Bizzaro D, et al. Comparison of equine bone marrow-, umbilical cord matrix and amniotic fluid-derived progenitor cells. Vet Res Commun. 2011;35:103–21.
Reed SA, Johnson SE. Equine umbilical cord blood contains a population of stem cells that express Oct4 and differentiate into mesodermal and endodermal cell types. J Cell Physiol. 2008;215:329–36.
Hoynowski SM, Fry MM, Gardner BM, Leming MT, Tucker JR, Black L, et al. Characterization and differentiation of equine umbilical cord-derived matrix cells. Biochem Biophys Res Commun. 2007;362:347–53.
Mohanty N, Gulati BR, Kumar R, Gera S, Kumar P, Somasundaram RK, et al. Immunophenotypic characterization and tenogenic differentiation of mesenchymal stromal cells isolated from equine umbilical cord blood. In Vitro Cell Dev Biol Anim. 2014;50:538–48.
Letouzey V, Tan KS, Deane JA, Ulrich D, Gurung S, Ong YR, et al. Isolation and characterisation of mesenchymal stem/stromal cells in the ovine endometrium. PLoS One. 2015;10(5):e0127531.
Miernik K, Karasinski J. Porcine uterus contains a population of mesenchymal stem cells. Reproduction. 2012;143:203–9.
Chan RWS, Schwab KE, Gargett CE. Clonogenicity of human endometrial epithelial and stromal cellss. Biol Reprod. 2004;70:1738–50.
Chan RW, Gargett CE. Identification of label-retaining cells in mouse endometrium. Stem Cells. 2006;24:1529–38.
De Cesaris V, Grolli S, Bresciani C, Conti V, Basini G, Parmigiani E, et al. Isolation, proliferation and characterization of endometrial canine stem cells. Reprod Domest Anim. 2017;52(2):235–42.
Indumathi S, Harikrishnan R, Rajkumar JS, Sudarsanam D, Dhanasekaran M. Prospective biomarkers of stem cells of human endometrium and fallopian tube compared with bone marrow. Cell Tissue Res. 2013;352:537–49.
Schuring AN, Schulte N, Kelsch R, Ropke A, Kiesel L, Gotte M. Characterization of endometrial mesenchymal stem-like cells obtained by endometrial biopsy during routine diagnostics. Fertil Steril. 2011;95:423–6.
Gaafar T, Hawary RE, Osman A, Attia W, Hamza H, Brockmeier K, et al. Comparative characteristics of amniotic membrane, endometrium and ovarian derived mesenchymal stem cells: a role for amniotic membrane in stem cell therapy. Middle East Fertil Soc J. 2014;19:156–70.
Wolff EF, Gao XB, Yao KV, Andrews ZB, Du H, Elsworth JD, et al. Endometrial stem cell transplantation restores dopamine production in a Parkinson's disease model. J Cell Mol Med. 2011;15:747–55.
Lai D, Wang F, Yao X, Zhang Q, Wu X, Xiang C. Human endometrial mesenchymal stem cells restore ovarian function through improving the renewal of germline stem cells in a mouse model of premature ovarian failure. J Transl Med. 2015;13:155.
Emmerson SJ, Gargett CE. Endometrial mesenchymal stem cells as a cell based therapy for pelvic organ prolapse. World J Stem Cells. 2016;8:202–15.
Aupperle H, Ozgen SHA, Schoon D, Hoppen HO, Sieme H, Tannapfel A. Cyclical endometrial steroid hormone receptor expression and proliferation intensity in the mare. Equine Vet J. 2000;32:228–32.
RefFinder. http://leonxie.esy.es/RefFinder/. Accessed 15 July 2016.
Guo X, Stice SL, Boyd NL, Chen SY. A novel in vitro model system for smooth muscle differentiation from human embryonic stem cell-derived mesenchymal cells. Am J Physiol Cell Physiol. 2013;304:C289–98.
Erices A, Conget P, Minguell JJ. Mesenchymal progenitor cells in human umbilical cord blood. Br J Haematol. 2000;109:235–42.
Busser H, Najar M, Raicevic G, Pieters K, Velez Pombo R, Philippart P, et al. Isolation and characterization of human mesenchymal stromal cell subpopulations: comparison of bone marrow and adipose tissue. Stem Cells Dev. 2015;24:2142–57.
Chang CJ, Yen ML, Chen YC, Chien CC, Huang HI, Bai CH, et al. Placenta-derived multipotent cells exhibit immunosuppressive properties that are enhanced in the presence of interferon-gamma. Stem Cells. 2006;24:2466–77.
Kim J, Lee Y, Kim H, Hwang KJ, Kwon HC, Kim SK, et al. Human amniotic fluid-derived stem cells have characteristics of multipotent stem cells. Cell Prolif. 2007;40:75–90.
Durando MM, Zarucco L, Schaer TP, Ross M, Reef VB. Pneumopericardium in a horse secondary to sternal bone marrow aspiration. Equine Vet Educ. 2006;18:75–9.
Revel A. Multitasking human endometrium: a review of endometrial biopsy as a diagnostic tool, therapeutic applications, and a source of adult stem cells. Obstet Gynecol Surv. 2009;64:249–57.
Snider TA, Sepoy C, Holyoak GR. Equine endometrial biopsy reviewed: observation, interpretation, and application of histopathologic data. Theriogenology. 2011;75:1567–81.
Arnhold SJ, Goletz I, Klein H, Stumpf G, Beluche LA, Rohde C, et al. Isolation and characterization of bone marrow-derived equine mesenchymal stem cells. Am J Vet Res. 2007;68:1095–105.
Bourzac C, Smith LC, Vincent P, Beauchamp G, Lavoie JP, Laverty S. Isolation of equine bone marrow-derived mesenchymal stem cells: a comparison between three protocols. Equine Vet J. 2010;42:519–27.
Watson ED, Sertich PL. Effect of repeated collection of multiple endometrial biopsy specimens on subsequent pregnancy in mares. J Am Vet Med Assoc. 1992;201:438–40.
da Silva ML, de Deus Wagatsuma VM, Malta TM, Bonini Palma PV, Araujo AG, Panepucci RA, et al. The gene expression profile of non-cultured, highly purified human adipose tissue pericytes: transcriptomic evidence that pericytes are stem cells in human adipose tissue. Exp Cell Res. 2016;349(2):239–54.
Dimitrov R, Timeva T, Kyurkchiev D, Stamenova M, Shterev A, Kostova P, et al. Characterization of clonogenic stromal cells isolated from human endometrium. Reproduction. 2008;135:551–8.
Gaafar T, Osman O, Osman A, Attia W, Hamza H, El Hawary R. Gene expression profiling of endometrium versus bone marrow-derived mesenchymal stem cells: upregulation of cytokine genes. Mol Cell Biochem. 2014;395:29–43.
Sacchetti B, Funari A, Remoli C, Giannicola G, Kogler G, Liedtke S, et al. No identical "mesenchymal stem cells" at different times and sites: human committed progenitors of distinct origin and differentiation potential are incorporated as adventitial cells in microvessels. Stem Cell Reports. 2016;6:897–913.
Pierantozzi E, Vezzani B, Badin M, Curina C, Severi FM, Petraglia F, et al. Tissue-specific cultured human pericytes: perivascular cells from smooth muscle tissue have restricted mesodermal differentiation ability. Stem Cells Dev. 2016;25:674–86.
Gargett CE, Schwab KE, Deane JA. Endometrial stem/progenitor cells: the first 10 years. Hum Reprod Update. 2016;22:137–63.
The authors are extremely grateful to Timothy Connelley for help with magnetic bead procedures, to Bob Fleming and Tara Sheldrake for assistance with fluorescence microscopy and flow cytometry, and to Ralphael Labens, Louise Cornish, and John Keen for providing animal tissues.
This study was supported by a studentship from Ross University School of Veterinary Medicine, St. Kitts, West Indies (to BER) and by the Horserace Betting Levy Board (Prj768, to FXD). The Roslin Institute receives funding from The Biotechnology and Biological Sciences Research Council through an Institute Strategic Programme Grant.
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
Ross University School of Veterinary Medicine, Basseterre, Saint Kitts and Nevis
B. Elisabeth Rink
, Hilari M. French
& Elaine Watson
The Roslin Institute, University of Edinburgh, Edinburgh, EH25 9RG, UK
, Karin R. Amilon
, Cristina L. Esteves
& F. Xavier Donadeu
University of Veterinary Medicine, 1220, Vienna, Austria
& Christine Aurich
The Roslin Institute, University of Edinburgh, Easter Bush, Midlothian, EH25 9RG, UK
F. Xavier Donadeu
Search for B. Elisabeth Rink in:
Search for Karin R. Amilon in:
Search for Cristina L. Esteves in:
Search for Hilari M. French in:
Search for Elaine Watson in:
Search for Christine Aurich in:
Search for F. Xavier Donadeu in:
BER and KRA collected tissues and performed all experiments. BER and FXD analyzed data. CLE provided reagents. BER, HMF, EW, CA, and FXD conceived and designed the project. BER, KRA, CLE, and FXD wrote the manuscript. All authors read and approved the final manuscript.
Correspondence to F. Xavier Donadeu.
All animal procedures were carried out according to the UK Home Office Animals (Scientific Procedures) Act 1986 with approval by the local Ethical Review Committee.
Rink, B.E., Amilon, K.R., Esteves, C.L. et al. Isolation and characterization of equine endometrial mesenchymal stromal cells. Stem Cell Res Ther 8, 166 (2017) doi:10.1186/s13287-017-0616-0
Revised: 14 June 2017 | CommonCrawl |
Assessment of the breath alcohol concentration in emergency care patients with different level of consciousness
Annika Kaisdotter Andersson1,
Josefine Kron2,3,
Maaret Castren2,3,
Asa Muntlin Athlin4,5,6,7,
Bertil Hok1 &
Lars Wiklund8
Many patients seeking emergency care are under the influence of alcohol, which in many cases implies a differential diagnostic problem. For this reason early objective alcohol screening is of importance not to falsely assign the medical condition to intake of alcohol and thus secure a correct medical assessment.
At two emergency departments, demonstrate the feasibility of accurate breath alcohol testing in emergency patients with different levels of cooperation.
Assessment of the correlation and ratio between the venous blood alcohol concentration (BAC) and the breath alcohol concentration (BrAC) measured in adult emergency care patients. The BrAC was measured with a breathalyzer prototype based on infrared spectroscopy, which uses the partial pressure of carbon dioxide (pCO2) in the exhaled air as a quality indicator.
Eighty-eight patients enrolled (mean 45 years, 53 men, 35 women) performed 201 breath tests in total. For 51% of the patients intoxication from alcohol or tablets was considered to be the main reason for seeking medical care. Twenty-seven percent of the patients were found to have a BAC of <0.04 mg/g. With use of a common conversion factor of 2100:1 between BAC and BrAC an increased agreement with BAC was found when the level of pCO2 was used to estimate the end-expiratory BrAC (underestimation of 6%, r = 0.94), as compared to the BrAC measured in the expired breath (underestimation of 26%, r = 0.94). Performance of a forced or a non-forced expiration was not found to have a significant effect (p = 0.09) on the bias between the BAC and the BrAC estimated with use of the level of CO2. A variation corresponding to a BAC of 0.3 mg/g was found between two sequential breath tests, which is not considered to be of clinical significance.
With use of the expired pCO2 as a quality marker the BrAC can be reliably assessed in emergency care patients regardless of their cooperation, and type and length of the expiration.
Many patients seeking care at the hospital emergency departments (EDs) are under the influence of alcohol, which in many cases implies a differential diagnostic problem [1-3], and assessing the influence from alcohol based on patient anamnesis, clinical signs or characteristics introduce inaccuracies [4,5]. For this reasons early objective alcohol screening is of importance in order not to falsely assign the medical condition to intake of alcohol and thus secure a correct medical assessment [1,3,6,7].
A breathalyzer provides a non-invasive and rapid quantification of the patients' breath alcohol concentration (BrAC). With use of a conversion factor, called the blood:breath ratio (BBR), the blood alcohol concentration (BAC) can be estimated [8,9]. However, the accuracy of the measured BrAC and thus the estimate of the BAC depend on the duration of the expiration which requires cooperation and good respiratory ability from the person tested [10]. In Sweden most EDs are equipped with breathalyzers but the usability of these devices are limited by the requirement of the patient's cooperation. For this reason invasive, costly, and time-consuming blood analysis is still widely used.
The objective of this study is to evaluate a breathalyzer prototype which uses expired partial pressure of CO2 (pCO2) as a quality marker of the breath test. Our hypothesis is that through simultaneous measurement of expired alcohol and the pCO2, the BrAC can be reliably assessed regardless of patient cooperation and respiratory ability. The hypothesis is evaluated through comparison of the estimated BrAC and the measured venous BAC.
The study design
Study settings and patients
The study was undertaken between November 2010 and June 2011 at two of the largest emergency departments (EDs) in Sweden; Uppsala University Hospital, a level 1 trauma center with approximately 53 000 annual visits, and Södersjukhuset in Stockholm a hospital with nearly 90 000 annual visits. A small number of enrolled nurses working at each ED were assigned to identify and recruit patients over the age of 18 for whom determination of the influence of alcohol would be of clinical benefit, for example patients believed to be sober and patients with variable consciousness.
For each included patient a study protocol was filled in with data regarding age, gender, estimated weight and height, level of consciousness, chief complaint, suspicion and history of alcohol consumption and drug usage. The time for blood alcohol and breath alcohol samplings, and the result of the two analyses were documented. Informed consent was collected in advance from subjects whom were able to be informed or afterwards for the subjects highly under the influence and/or with variable consciousness, at the time of admittance. Data collection from these two EDs was approved by the Regional Ethical Review Board in Uppsala (registration no 2010/048 and 2010/308).
A required study population was predicated from a calculation of the confidence interval (CI) for different samples sizes. At approximately 45 subjects the curve starts to level off and the benefit from including more subjects was therefore minimal. The calculation was based on an assumed bias of 0.068 mg/g and a standard deviation (SD) for difference of 0.0452 mg/g according to a study comparing the BrAC with the BAC [9]. The aim was to recruit 45 patients from each of the two EDs.
Measurement and procedure
Measurement of the blood alcohol concentration
At both EDs standard routine involves blood analysis for toxic substances in patients for whom a suspicion of intake of alcohol or other substances exists. Blood sampling and the serum ethanol analysis were performed according to standard procedure and analyzed with gas chromatography at the clinical chemistry department at Södersjukhuset in Stockholm, and with immunoassay analyzer at Uppsala University Hospital.
Measurement of the breath alcohol concentration
The enrolled nurses were trained to perform breath testing with a handheld breathalyzer prototype with dimensions of 150×85×50 mm, and a weight of less than 200 g. The breath test was initiated by the user from a touch screen PC connected to the breathalyzer, which also presented the result. The breathalyzer utilizes infrared (IR) transmission spectroscopy [11], a highly reliable technique utilized by evidential breathalyzers [12,13]. IR spectroscopy enables continuous and simultaneous measurements of both the expired alcohol and the partial pressure of CO2. To ensure low sensitivity to other substances occurring in normal breath a wavelength of 9.5 μm was used for detection of ethanol, whereas a wavelength of 4.3 μm was used for CO2.
The breathalyzer continuously sampled 13 seconds of normal breathing through the patient's mouth and nose, with use of a disposable breathing mask (Ecomask II, size 2, Intersurgical Ltd., U.K), equipped with a bacterial filter (Electrostatic Filter Media MES, Munktell Filter AB, Sweden). The rationale of using CO2 for enabling BrAC determination in passive shallow expiration has been subject to previous investigation [14-16]. For estimation of the end-expiratory BrAC (BrACest) the breathalyzer tested uses equation (1) with the assumption that the pCO2 in alveolar air is 4.8 kPa with a standard deviation of 10% [17]. From studies of expirograms of CO2 recorded from healthy persons and patients with COPD [14-16] a breath sample with a measured pCO2 over 1.5 kPa was considered approved. A breath sample with a measured pCO2 over 4.8 kPa was considered as a complete expiration and the measured BrAC was considered to be valid as the end-expiratory BrAC. The measurement accuracy of the breathalyzer prototype was ±0.05 mg/l or ±10% of the measured breath alcohol value.
At least two breath tests were performed with each subject. Whether the subject was awake or sleeping/had a lower level of consciousness, and performed a forced or a non-forced expiration was documented. Since the patients were not regarded to have consumed alcohol less than 15 minutes prior to breath testing, no attempt to remove any influence of mouth alcohol was done before testing.
$$ \frac{BrA{C}_{est}}{BrA{C}_{meas}}=\frac{pCO{2}_{end- exp}}{pCO{2}_{meas}} $$
BrAC est = the breath alcohol concentration estimated to be valid after a forced expiration.
BrAC meas = the breath alcohol concentration measured in the breath sample.
pCO2 end-exp = the assumed partial pressure of carbon dioxide after a prolonged, end-expiratory, expiration.
pCO2 meas = the measured partial pressure of carbon dioxide measured in the breath sample.
The serum ethanol concentration values from the analysis were transformed from mmol/l to mg/g in whole blood, which corresponds to parts per thousand, using the conversion factor recommended for scientific use; 0.0376 [18]. The conversion factor used does not account for any safety margin applied for legal use. Regression analysis and calculation of the Pearson correlation coefficient and the residual standard deviation have been performed. In addition, Bland-Altman analysis [19] and calculation of the mean, upper and lower limits of agreement (LOA) was performed. The LOAs corresponds to a range in which 95% of the differences between two separate measurements of two specimens or tests would be found. For comparison between the blood and breath specimens a blood:breath ratio (BBR) of 2100:1 was used. With consideration to the density of whole blood, a BBR of 2100:1 results in a ratio of 2:1 between the BAC (mg/g) and BrAC, which therefore can be presented as mg/2 l breath [9,18]. The ratio of 2:1 was used for the identity line in the regression analysis plots, and the expression of BrAC in the unit of mg/2 l in the Bland-Altman plots. In addition the BBR for each pair of blood and breath tests was also calculated.
Analyses of one set of paired data per test subject; the blood sample and the first approved breath test (n = 88), and all approved breath tests (n = 201) have been performed. Independent T-tests were performed to analyze the impact on the agreement between the BAC and the BrAC, of whether the subject was passive/active for breath testing and performed a forced/non-forced expiration. A p-value of ≤0.05 was chosen as the significant level. All statistical analyses were made using IBM SPSS Statistics version 19.
Patient and sample characteristics
Of the 90 patients enrolled two patients were excluded, the first due to methanol poisoning, and the second as no approved breath test (pCO2 over 1.5 kPa) was achieved. A total of 88 patients, 35 women (40%) and 53 men (60%), presented to the two EDs were included in the study. Table 1 presents the characteristics of the patients. The mean age of the patients was 45 years (SD ±19, range 18–86). For 35 of the patients (51%) the medical staff considered intoxication from alcohol or tablets to be the main reason for seeking medical care. Twenty-four (27%) of the patients were found to have a BAC of <0.04 mg/g. The mean BAC for the whole population was 1.26 mg/g, whereas the BAC for the alcohol positive patients ranged from 0.15 to 3.46 mg/g, with a mean of 1.73 mg/g. For the patients with a positive BAC (n = 64) the mean measured BrAC was 0.64 mg/l (range 0 to 1.71 mg/l) and the mean BrACest 0.86 mg/l (range 0 to 2.03 mg/l). This indicates a general upward adjustment of 34% of the BrACest as compared to the BrACmeas. There was also a clear difference in the calculated BBR with respect to use of the BrACmeas and the BrACest, see Table 1 for mean and range of the BBR to be compared with the assumption of a fixed conversion factor, e.g. 2100:1.
Table 1 Patient characteristics and characteristics of the first breath test performed and the blood and breath alcohol measures (n = 88)
In total the 88 patients performed 201 breath tests. Of the first approved breath tests performed by each patient, one breath test was found to be false positive with a measured BrAC > 0.10 mg/l (the same applied for the patient's second breath test) and one breath test was found to be false negative (BAC 0.15 mg/g) (sensitivity 98.4%, specificity 95.8%).
Relation between the BrAC and BAC
In Figure 1a and b (see 1a) the correlation between the BrACmeas and the BAC is presented. The regression equation (y = 0.368x + 0.0092; r = 0.94) indicates that with an assumption of a BBR of 2100:1 (a ratio of 2:1 gives y = 0.5x), the BAC would be underestimated with 26%. If the BrACest was used to predict the BAC, the underestimation was decreased to 6% (y = 0.466x + 0.046, r = 0.94) (Figure 1a and b (see 1b)). No significant offsets were found for the two measurement series, and the random errors expressed as the residual standard deviations were 0.0147 mg/l and 0.0182 mg/l, respectively.
The correlation between the BAC and the BrAC, where the identity lines represents a BBR of 2100:1. (a) The BrACmeas gave a clear underestimation of the BAC with 26% (n=88; y=0.368x+0.0092; r=0.94. (b) Use of the BrACest resulted in an underestimation of the BAC of only 6%, (n=88; y=0.466x+0.0465; r=0.94), the reason for this is the reduced effect from difference in cooperation and duration of the expiration performed by the subjects. One clear example of this reduced effect is the two outliers visible in Figure 1a, which are moved into the population in Figure 1b.
With a Bland Altman plot the agreement and differences between the BAC and the BrAC can be illustrated. Analysis of the difference between the BAC and the BrACmeas showed a large positive bias (0.31 mg/g) (Figure 2a and b (see 2a)). Comparing the BAC and the BrACest showed no bias and a more even distribution (Figure 2a and b (see 2b)). Including paired data for all approved breath tests (n = 201) only indicates a minor change of the mean bias presented in Figure 2a and 2b; from 0.31 mg/g to 0.28 mg/g (upper limits of agreement (LOA) 1.00 mg/g and lower LOA −0.43 mg/g), and from 0.00 mg/g to −0.02 mg/g (upper LOA of 0.68 mg/g and a lower LOA of −0.72 mg/g), respectively.
Analysis of the first breath sample (n=88) illustrating the difference between the BAC and the BrAC with a Bland-Altman plot. (a) A mean bias of 0.31 mg/g was found between the BAC and the BrACmeas, upper limits of agreement (LOA) of 1.09 mg/g and lower LOA of -0.46 mg/g. (b) No bias was found between the BAC and the BrACest, upper LOA of 0.68 mg/g and lower LOA of -0.70 mg/g.
Difference in estimated BrAC between the two breath tests
For evaluation of the repeatability of the presented value of the BrACest a Bland-Altman plot is presented in Figure 3. The data is from two sequential approved breath tests performed by 76 patients. The result indicated no bias, but the upper and lower LOA of 0.34 mg/2 l and −0.37 mg/2 l (equal to mg/g) indicate that there was an evenly distributed difference in BrACest between the first and second breath test.
The Bland-Altman Plot presents the difference in estimated BrAC from two breath tests in relation to the mean of the estimated BrAC for the two breath tests (n = 76). The plot indicates no bias and an even distribution of the upper and lower LOAs around 0. The LOAs of 0.34 mg/2 l and −0.37 mg/2 l, indicate differences in the BrAC estimated from two sequential breath tests, and reflect the measurement repeatability.
The bias in relation to maximal measured level of pCO2
The bias found between the BAC and the BrACmeas can possibly be reflected in the length of the expiration, and thus the measured level of pCO2. For the first approved breath test (n = 88) a mean pCO2 of 3.54 kPa was found (range 1.66 – 5.59 kPa). Figure 4a and b (see 4a) presents the bias between the BAC and the BrACmeas in relation to the measured pCO2. For the breath tests with a measured pCO2 over 4.8 kPa the value of the measured BrAC was used in Figure 4a and b (see 4b). Figure 4a and b (see 4b) illustrates a more even distribution around the x-axis when the difference between the BAC and the BrACest is plotted in relation to the measured pCO2, which indicated less dependence on the pCO2, as compared to the results in Figure 4a and b (see 4a).
The bias between the BAC and the BrAC in relation to the pCO 2 . (a) The underestimation of the BrACmeas as compared to the BAC is decreased with increased level of measured pCO2, which is achieved with increased length of expiration. (b) No bias and a more even distribution around the x-axis indicate a decreased influence from measured pCO2 with the use of BrACest.
The influence from the patients' breath testing performance on the BrAC could also be assessed from the test characteristics documented in the study protocol. A forced or non-forced expiration was not found to have a significant effect (p = 0.09) on the bias between the BAC and the BrACest, whereas, the bias between the BAC and the BrACest for awake subjects was significantly (p = 0.02) different from the bias for subjects who slept or had a lower level of consciousness (Table 2).
Table 2 The influence of breath test performance in relation to the mean bias of the BAC and the estimated BrAC (BrAC est )
During the study it was found that the personnel were able to attain approved breath tests from the patient's normal breathing without problem, after been given minimal user instructions from the test leader or from other enrolled and trained colleagues. The small gentle expiration needed for breath testing is of benefit for the many persons with respiratory impairment, such as asthma and COPD, and variable consciousness who are seeking emergency care.
The results showed that with estimation of the BrAC with use of the expired pCO2 as a quality indicator (BrACest), the influence of the patient's cooperation, passive/forced expirations, or length of expiration is reduced and the measurement accuracy increased. As compared to the reliability of the BrAC measured in the breath (BrACmeas) which is clearly related to the level of the patient's cooperation and length of the expiration (Figures 1a and 2a). This is also illustrated in the more symmetric distribution in (Figure 4b, as compared to 4a).
The results found in this study agree with previous results of ours, with an earlier prototype tested on emergency patients [15]. Another important result is that the variation in BrACest found between two sequential breath tests (Figure 3) corresponding to a BAC of 0.3 mg/g, is of no clinical significance since a variation of that level would not make any difference in the medical assessment or care of the patient.
Since the BBR depends on many different factors, there is significant controversy regarding the assumption of a fixed BBR in converting between BrAC and BAC. Despite our knowledge of this, a BBR of 2100:1 was used for comparison in Figure 1 and the Bland Altman plots in Figure 2. The actual BBR for a paired data set of a BAC and BrAC is dependent on, for example whether the subject is in the absorption or the elimination phase of alcohol [20], the length of the expiration [10], the attained alcohol concentration [21,22], eventual time elapsed between measurement of the two specimens [8,23], and whether arterial or venous blood are sampled [20]. Concerning the set-up of this study only venous blood samples were analyzed and the recommended maximum time of 30 minutes between the blood test and the breath tests was not exceeded for any of the patients. However, the time elapsed since the patient consumed alcohol was unknown and therefore whether the patient was in the absorption or elimination phase. The effect on the level, and the variability, in BBR as a result of different lengths of expiration can be seen in the BBR calculated for the BrACmeas as compared to the BrACest. With the BrACest, which uses the CO2 as a tracer gas in order to reduce the influences from variation in type and duration of the expiration, the mean BBR was significantly reduced (from 2994 to 2144) and the standard deviation of the mean was reduced to half (from 900 to 500).
In addition the patients enrolled in the study showed a large difference in levels of intoxication. In both Figures 1 and 2 it is shown that at BAC below 1 mg/g the distribution is small, whereas it is increased, up to 4 times, at BAC over 1 mg/g. This increase in variability of the BrAC at higher level of BAC could be the result of increased variability in the BBR, which in turn could be related to increased effect from the intoxication level, and if the patient sought emergency care in the absorption or elimination phase of alcohol for which the distribution of alcohol between venous blood and breath are different.
A tendency of increased variability in BBR at increased concentrations has also been found by Sebbane et al. [24]. Sebbane et al. found a BBR of 2615 ± 387 when breath testing ED patients, and concluded that the legal conversion factor of 2000:1 used in France was not appropriate in the ED setting. In Sweden, a BBR of 2100:1 is used in breathalyzers for legal purposes [8]. As compared to 2000:1 and 2100:1, the higher BBR found by Sebbane et al. and for BrACmeas in this study can possibly be explained by the lower grade of cooperation and lower expired volume for patients as compared to healthy subjects, i.e. drunk drivers. However, the results of our study indicate that with use of BrACest the BBR used for legal purposes in the US and in Sweden (2100:1) is most appropriate for medical applications.
The method of estimating the BrAC with the assumption that the end-expiratory pCO2 is 4.8 kPa has been investigated with both healthy subjects and patients with respiratory impairments [14]. When breath testing patients this can introduce inaccuracies, e.g. for patients with respiratory diseases or respiratory distress the BrACest might be less accurate. In Figures 1b and 2b it is shown that the BrACest gives a better agreement to a BBR of 2100:1 and an even but somehow increased distribution, as compared to the BrACmeas, see Figures 1a and 2a. This increase in variability can indicate that the assumption of a fixed value pCO2 value of 4.8 kPa is less appropriate for emergency patients. However, this effect has to be compared to the underestimation of BAC of 26% seen with the BrACmeas. Another indication are found in two outliers in BrACest for breath tests (n = 201) performed on a patient admitted with respiratory distress (n = 2, pCO2 = 1.6 kPa and 2.0 kPa, respectively). An additional indication of the inaccuracy that the measurement method introduces by assuming a constant end-expiratory pCO2 for all patients is found in Table 2. This shows a significant difference in the mean bias between the BAC and the BrACest, for the breath tests performed on awake patients and those performed on sleeping patients or on patients with a lower level of consciousness.
A problem with the breathalyzer tested which was highlighted during the study was its inability to distinguish between ethanol and methanol in the breath. As compared to breath testing drivers, the sensitivity for methanol is a larger problem in the medical application, since fast and accurate assessment of methanol poisoning is needed because the medical treatment of these patients are completely different to the treatment of ethanol intoxication. However, the IR technology can enable high selectivity [13]. If modified with a second adjacent wavelength for detection of ethanol, selectivity between ethanol and methanol in the breath would be possible with the breathalyzer prototype tested.
Frequent and early objective breath alcohol screening in emergency care could lead to avoidance of differential diagnosis errors, decreased risk of patients being discriminated against or incorrectly treated [5], and decreased costs through decreased use of certain invasive diagnostic procedures [25]. However, state-of-the-art devices available on EDs today have limitations considering usefulness and reliability. This study indicates an innovative solution to these problems. With use of the expired pCO2 as a quality marker the breath alcohol concentration can be reliably assessed in emergency care patients regardless of their cooperation.
The documented sensitivity of 98.4% and specificity of 95.8% are considered acceptable for this breathalyzer prototype. However, significant technical improvements have been implemented in the next generation, and that within decreased dimensions. The latest technology provides opportunities for continued research of the application in regular clinical use. Areas of particular interests are diagnostic efficiency and the impact on healthcare economics. Additionally, more research is required to investigate the practical usability of this kind of handheld breathalyzer to make it as user-friendly as possible in the ED context.
Brismar B, Engström A, Rydberg U. Head injury and intoxication: A diagnostic and therapeutic dilemma. Acta Chir Scand. 1983;149:11–4.
Efskind Harr M, Heskestad B, Ingebrigtsen T, Romner B, Rønning P, Helseth E. Alcohol consumption, blood alcohol concentration level and guideline compliance in hospital referred patients with minimal, mild and moderate head injuries. Scand J Trauma Resusc Emerg Med. 2011;19:25.
Rücker G, Eiser T. Alkoholbestimmung im rettungsdienst. Notfall Rettungsmedizin. 2001;4:39–45.
Cherpitel C, Bond J, Ye Y, Room R, Poznyak V, Rehm J, et al. Clinical assessment compared with breathalyzer reading in emergency room: concordance of ICD-10 Y90 and Y91 codes. Emerg Med J. 2005;22:689–95.
Gentilello L, Villaveces A, Ries R, Nason KS, Daranciang E, Donovan DM, et al. Detection of acute alcohol intoxication and chronic alcohol dependence by trauma staff. J Trauma Injury Infect Crit Care. 1999;47:1131–9.
Gibb K, Yee A, Johnston C, Martin SD, Nowak RM. Accuracy and usefulness of a breath alcohol analyzer. Ann Emerg Med. 1984;13:516–20.
Vonghia L, Leggio L, Ferrulli A, Bertini M, Gasbarrini G, Addolorato G, et al. Acute alcohol intoxication. Eur J Int Med. 2008;19:361–7.
Jones AW, Andersson L. Variability of the blood/breath alcohol ratio in drinking drivers. J For Sci. 1996;41:916–21.
Jones AW, Andersson L. Comparison of ethanol concentration in venous blood and end-expiratory breath during a controlled drinking study. Forensic Sci Int. 2003;132:18–25.
Hlastala MP, Anderson JC. The impact of breathing pattern and lung size on the alcohol breath test. Ann Biomed Eng. 2007;35:264–72.
Hök B, Pettersson H, Kaisdotter Andersson A, Haasl S, Member, IEEE, Åkerlund P. Breath analyzers for alcolock and screening devices. IEEE Sensors J. 2010;10:10–5.
Fransson M, Jones AW, Andersson L. Laboratory evaluation of a new evidential breath-alcohol analyser designed for mobile testing – the Evidenzer. Med Sci Law. 2005;45:61–70.
Harding P. Methods for Breath Analysis. In: Garriott JC, editor. Medical-Legal Aspects of Alcohol. 4th ed. Tucson: Lawyers & Judges Publishing Company, Inc; 2003. chapter 8.
Jonsson A, Hök B, Andersson L, Hedenstierna G. Methodology investigation of expirograms for enabling contact free breath alcohol analysis. J Breath Res. 2009;3:036002.
Kaisdotter Andersson A, Hök B, Rentsch D, Ruecker G, Ekström M. Improved breath alcohol analysis in patients with depressed consciousness. MBEC. 2010;48:1099–105.
Kaisdotter Andersson A, Hök B, Ekström M. Influences from breathing pattern on alcohol and tracer gas expirograms – implications for alcolock use. For Sci Int. 2011;206:52–7.
Lumb AB. Carbon Dioxide. In: Nunn's Applied Respiratory Physiology. Chapter 10, 6th. Philadelphia: Elsevier/Butterworth Heinemann; 2005.
Jones AW. Hospital alcohol test not completely easy to use for legal purposes. Conversion of ethanol levels in plasma or serum to permillage level in blood. Lakartidningen. 2008;105(6):367–8.
Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;1:307–10.
Jones AW, Norberg Å, Hahn RG. Concentration-time profiles of ethanol in arterial and venous blood and end-expired breath during and after intravenous infusion. J Forensic Sci. 1997;42:1088–94.
Haffner HT, Graw M, Dettling A, Schmitt G, Schuff A. Concentration dependency of the BAC/BrAC (blood alcohol concentration/breath alcohol concentration) conversion factor during the linear elimination phase. Int J Legal Med. 2003;117:276–81.
Pavlic M, Grubwieser P, Brandstätter A, Libiseller K, Rabl W. A study concerning the blood/breath alcohol conversion factor Q: Concentration dependency and its applicability in daily routine. Forensic Sci Int. 2006;158:149–56.
Currier G, Trenton A, Walsh P. Relative accuracy of breath and serum alcohol reading in the psychiatric emergency service. Psychiatr Serv. 2006;57:34–6.
Sebbane M, Claret P-G, Jreige R, Dumont R, Lefebvre S, Rubenovitch J, et al. Breath analyser screening of emergency department patients suspected of alcohol intoxication. J Emerg Med. 2012;43:747–53.
Jurkovich G, Rivara F, Gurney J, Seguine D, Fligner CL, Copass M. Effects of alcohol intoxication on the initial assessment of trauma patients. Ann Emerg Med. 1992;21:704–8.
We are very thankful to the personnel involved, at the ED at Uppsala University Hospital and the ED at Södersjukhuset, for their engagement and help with performing this study. A special thanks to Ellinor Berglund, research coordinator at the ED of Södersjukhuset.
Hök Instrument AB, Västerås, Sweden
Annika Kaisdotter Andersson
& Bertil Hok
Karolinska Institutet, Department of Clinical Research and Education, Södersjukhuset, Stockholm, Sweden
Josefine Kron
& Maaret Castren
Section of Emergency Medicine, Södersjukhuset, Stockholm, Sweden
Department of Medical Sciences, Uppsala University, Uppsala, Sweden
Asa Muntlin Athlin
School of Nursing, University of Adelaide, Adelaide, Australia
Department of Emergency Care, Uppsala University Hospital, Uppsala, Sweden
Department of Public Health and Caring Sciences, Uppsala University, Uppsala, Sweden
Department of Surgical Science, Anesthesiology and Intensive Care, Uppsala University, Uppsala, Sweden
Lars Wiklund
Search for Annika Kaisdotter Andersson in:
Search for Josefine Kron in:
Search for Maaret Castren in:
Search for Asa Muntlin Athlin in:
Search for Bertil Hok in:
Search for Lars Wiklund in:
Correspondence to Asa Muntlin Athlin.
AKA, BH conceived the study and obtained the research funding, and together with ÅMA and MC they designed the study. AKA, JK, and LW took active part in the collection of data, and supervised the personnel at the emergency departments. AKA and JK performed the data analysis. AKA and JK drafted the manuscript, and all authors contributed substantially to its revision. AKA and ÅMA takes responsibility for the paper as a whole, ÅMA is corresponding author. All authors read and approved the final manuscript.
Kaisdotter Andersson, A., Kron, J., Castren, M. et al. Assessment of the breath alcohol concentration in emergency care patients with different level of consciousness. Scand J Trauma Resusc Emerg Med 23, 11 (2015) doi:10.1186/s13049-014-0082-y
DOI: https://doi.org/10.1186/s13049-014-0082-y
Blood alcohol concentration
Breath alcohol concentration
Patient cooperation
Emergency care patients | CommonCrawl |
{ "5.5E:_Exercises" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.<PageSubPageProperty>b__1]()" }
{ "5.1:_Solve_Systems_of_Equations_by_Graphing" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.<PageSubPageProperty>b__1]()", "5.2:_Solve_Systems_of_Equations_by_Substitution" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.<PageSubPageProperty>b__1]()", "5.3:_Solve_Systems_of_Equations_by_Elimination" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.<PageSubPageProperty>b__1]()", "5.4:_Solve_Applications_with_Systems_of_Equations" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.<PageSubPageProperty>b__1]()", "5.5:_Solve_Mixture_Applications_with_Systems_of_Equations" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.<PageSubPageProperty>b__1]()", "5.6:_Graphing_Systems_of_Linear_Inequalities" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.<PageSubPageProperty>b__1]()", Chapter_5_Review_Exercises : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.<PageSubPageProperty>b__1]()" }
5.5E: Exercises
[ "article:topic", "authorname:openstax", "license:ccby", "showtoc:yes", "transcluded:yes", "source[1]-math-30248" ]
https://math.libretexts.org/@app/auth/3/login?returnto=https%3A%2F%2Fmath.libretexts.org%2FCourses%2FMonroe_Community_College%2FMTH_098_Elementary_Algebra%2F5%253A_Systems_of_Linear_Equations%2F5.5%253A_Solve_Mixture_Applications_with_Systems_of_Equations%2F5.5E%253A_Exercises
MTH 098 Elementary Algebra
Exercise \(\PageIndex{10}\)
In the following exercises, translate to a system of equations and solve.
Tickets to a Broadway show cost $35 for adults and $15 for children. The total receipts for 1650 tickets at one performance were $47,150. How many adult and how many child tickets were sold?
There 1120 adult tickets and 530 child tickets sold.
Tickets for a show are $70 for adults and $50 for children. One evening performance had a total of 300 tickets sold and the receipts totaled $17,200. How many adult and how many child tickets were sold?
Tickets for a train cost $10 for children and $22 for adults. Josie paid $1,200 for a total of 72 tickets. How many children's tickets and how many adult tickets did Josie buy?
Josie bought 40 adult tickets and 32 children tickets.
Tickets for a baseball game are $69 for Main Level seats and $39 for Terrace Level seats. A group of sixteen friends went to the game and spent a total of $804 for the tickets. How many of Main Level and how many Terrace Level tickets did they buy?
Tickets for a dance recital cost $15 for adults and $7 for children. The dance company sold 253 tickets and the total receipts were $2,771. How many adult tickets and how many child tickets were sold?
There were 125 adult tickets and 128 children tickets sold.
Tickets for the community fair cost $12 for adults and $5 dollars for children. On the first day of the fair, 312 tickets were sold for a total of $2,204. How many adult tickets and how many child tickets were sold?
Brandon has a cup of quarters and dimes with a total value of $3.80. The number of quarters is four less than twice the number of dimes. How many quarters and how many dimes does Brandon have?
Brandon has 12 quarters and 8 dimes.
Sherri saves nickels and dimes in a coin purse for her daughter. The total value of the coins in the purse is $0.95. The number of nickels is two less than five times the number of dimes. How many nickels and how many dimes are in the coin purse?
Peter has been saving his loose change for several days. When he counted his quarters and dimes, he found they had a total value $13.10. The number of quarters was fifteen more than three times the number of dimes. How many quarters and how many dimes did Peter have?
Peter had 11 dimes and 48 quarters.
Lucinda had a pocketful of dimes and quarters with a value of $ $6.20. The number of dimes is eighteen more than three times the number of quarters. How many dimes and how many quarters does Lucinda have?
A cashier has 30 bills, all of which are $10 or $20 bills. The total value of the money is $460. How many of each type of bill does the cashier have?
The cashier has fourteen $10 bills and sixteen $20 bills.
Marissa wants to blend candy selling for $1.80 per pound with candy costing $1.20 per pound to get a mixture that costs her $1.40 per pound to make. She wants to make 90 pounds of the candy blend. How many pounds of each type of candy should she use?
Marissa should use 60 pounds of the $1.20/lb candy and 30 pounds of the $1.80/lb candy.
How many pounds of nuts selling for $6 per pound and raisins selling for $3 per pound should Kurt combine to obtain 120 pounds of trail mix that cost him $5 per pound?
Hannah has to make twenty-five gallons of punch for a potluck. The punch is made of soda and fruit drink. The cost of the soda is $1.79 per gallon and the cost of the fruit drink is $2.49 per gallon. Hannah's budget requires that the punch cost $2.21 per gallon. How many gallons of soda and how many gallons of fruit drink does she need?
Hannah needs 10 gallons of soda and 15 gallons of fruit drink.
Joseph would like to make 12 pounds of a coffee blend at a cost of $6.25 per pound. He blends Ground Chicory at $4.40 a pound with Jamaican Blue Mountain at $8.84 per pound. How much of each type of coffee should he use?
Julia and her husband own a coffee shop. They experimented with mixing a City Roast Columbian coffee that cost $7.80 per pound with French Roast Columbian coffee that cost $8.10 per pound to make a 20 pound blend. Their blend should cost them $7.92 per pound. How much of each type of coffee should they buy?
Julia and her husband should buy 12 pounds of City Roast Columbian coffee and 8 pounds of French Roast Columbian coffee.
Melody wants to sell bags of mixed candy at her lemonade stand. She will mix chocolate pieces that cost $4.89 per bag with peanut butter pieces that cost $3.79 per bag to get a total of twenty-five bags of mixed candy. Melody wants the bags of mixed candy to cost her $4.23 a bag to make. How many bags of chocolate pieces and how many bags of peanut butter pieces should she use?
Jotham needs 70 liters of a 50% alcohol solution. He has a 30% and an 80% solution available. How many liters of the 30% and how many liters of the 80% solutions should he mix to make the 50% solution?
Jotham should mix 42 liters of the 30% solution and 28 liters of the 80% solution.
Joy is preparing 15 liters of a 25% saline solution. She only has 40% and 10% solution in her lab. How many liters of the 40% and how many liters of the 10% should she mix to make the 25% solution?
A scientist needs 65 liters of a 15% alcohol solution. She has available a 25% and a 12% solution. How many liters of the 25% and how many liters of the 12% solutions should she mix to make the 15% solution?
The scientist should mix 15 liters of the 25% solution and 50 liters of the 12% solution.
A scientist needs 120 liters of a 20% acid solution for an experiment. The lab has available a 25% and a 10% solution. How many liters of the 25% and how many liters of the 10% solutions should the scientist mix to make the 20% solution?
A 40% antifreeze solution is to be mixed with a 70% antifreeze solution to get 240 liters of a 50% solution. How many liters of the 40% and how many liters of the 70% solutions will be used?
160 liters of the 40% solution and 80 liters of the 70% solution will be used.
Hattie had $3,000 to invest and wants to earn 10.6% interest per year. She will put some of the money into an account that earns 12% per year and the rest into an account that earns 10% per year. How much money should she put into each account?
Hattie should invest $900 at 12% and $2,100 at 10%.
Carol invested $2,560 into two accounts. One account paid 8% interest and the other paid 6% interest. She earned 7.25% interest on the total investment. How much money did she put in each account?
Sam invested $48,000, some at 6% interest and the rest at 10%. How much did he invest at each rate if he received $4,000 in interest in one year?
Sam invested $28,000 at 10% and $20,000 at 6%.
Arnold invested $64,000, some at 5.5% interest and the rest at 9%. How much did he invest at each rate if he received $4,500 in interest in one year?
After four years in college, Josie owes $65,800 in student loans. The interest rate on the federal loans is 4.5% and the rate on the private bank loans is 2%. The total interest she owed for one year was $2,878.50. What is the amount of each loan?
The federal loan is $62,500 and the bank loan is $3,300.
Mark wants to invest $10,000 to pay for his daughter's wedding next year. He will invest some of the money in a short term CD that pays 12% interest and the rest in a money market savings account that pays 5% interest. How much should he invest at each rate if he wants to earn $1,095 in interest in one year?
A trust fund worth $25,000 is invested in two different portfolios. This year, one portfolio is expected to earn 5.25% interest and the other is expected to earn 4%. Plans are for the total interest on the fund to be $1150 in one year. How much money should be invested at each rate?
$12,000 should be invested at 5.25% and $13,000 should be invested at 4%.
A business has two loans totaling $85,000. One loan has a rate of 6% and the other has a rate of 4.5%. This year, the business expects to pay $4650 in interest on the two loans. How much is each loan?
Laurie was completing the treasurer's report for her son's Boy Scout troop at the end of the school year. She didn't remember how many boys had paid the $15 full-year registration fee and how many had paid the $10 partial-year fee. She knew that the number of boys who paid for a full-year was ten more than the number who paid for a partial-year. If $250 was collected for all the registrations, how many boys had paid the full-year fee and how many had paid the partial-year fee?
14 boys paid the full-year fee. 4 boys paid the partial-year fee
As the treasurer of her daughter's Girl Scout troop, Laney collected money for some girls and adults to go to a three-day camp. Each girl paid $75 and each adult paid $30. The total amount of money collected for camp was $765. If the number of girls is three times the number of adults, how many girls and how many adults paid for camp?
Take a handful of two types of coins, and write a problem similar to Example relating the total number of coins and their total value. Set up a system of equations to describe your situation and then solve it.
Answers will vary.
In Example we solved the system of equations \(\left\{\begin{array}{l}{b+f=21,540} \\ {0.105 b+0.059 f=1669.68}\end{array}\right.\) by substitution. Would you have used substitution or elimination to solve this system? Why?
a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
b. After looking at the checklist, do you think you are well-prepared for the next section? Why or why not?
This page titled 5.5E: Exercises is shared under a CC BY license and was authored, remixed, and/or curated by OpenStax.
5.6: Graphing Systems of Linear Inequalities | CommonCrawl |
Session W60: Superconductivity
Focus Recordings Available
Chair: Christopher Gutierrez, UCLA
Room: Hyatt Regency Hotel -DuSable C
W60.00001: Elucidating the structure of the charge density wave in the topological kagome metal CsV3Sb5
Invited Speaker: John W Harter
The recent discovery of the AV3Sb5 (A = K, Rb, Cs) material family offers an exciting opportunity to investigate the interplay of correlations, topology, and superconductivity in kagome metals. Emerging from a topologically nontrivial band structure, an unusual charge density wave phase dominates the low energy physics of these materials. The observation of a giant anomalous Hall effect and chiral charge order suggest that this charge density wave may spontaneously break time reversal symmetry, even while there is no evidence of local moment magnetism. A combination of ultrafast coherent phonon spectroscopy and first-principles density functional theory calculations is used to examine the structure of the charge density wave order in CsV3Sb5. It is found that the charge density wave results from a simultaneous condensation of three optical phonon modes and can be described as tri-hexagonal ordering with an interlayer transverse shift. This distortion breaks C6 rotational symmetry of the crystal and may offer a natural explanation for reports of uniaxial order in this material family. These results highlight the important role of characterization and modeling in deciphering the exotic properties of topological kagome metals.
W60.00002: Acoustic-phonon-mediated superconductivity in Bernal bilayer graphene
Yang-Zhi Chou, Fengcheng Wu, Jay D Sau
We present a systematic theory of acoustic-phonon-mediated superconductivity, which incorporates Coulomb repulsion, explaining the recent experiment in Bernal bilayer graphene under a large displacement field. The acoustic-phonon mechanism predicts that $s$-wave spin-singlet and $f$-wave spin-triplet pairings are degenerate and dominant. Assuming a spin-polarized valley-unpolarized normal state, we obtain $f$-wave spin-triplet superconductivity with a $T_c\sim 20$ mK near $n_e=-0.6\times 10^{12}$ cm$^{-2}$ for hole doping, in approximate agreement with the experiment. We further predict the existence of superconductivity for larger doping in both electron-doped and hole-doped regimes. Our results indicate that the observed spin-triplet superconductivity in Bernal bilayer graphene arises from acoustic phonons.
W60.00003: Electron-phonon coupling and superconductivity in rhombohedral trilayer graphene
Jingwei Jiang, Zhenglu Li, Steven G Louie
A recent experiment shows the rhombohedral phase of trilayer graphene manifesting superconducting behavior at low temperature. With electric field and doping introduced, the rhombohedral trilayer graphene sample shows vanishing resistivity under sub-kelvin temperature. However, a good understanding of the mechanism behind this phenomenon is still lacking. In this work, we first perform ab initio DFT calculations to address the role of electron-phonon coupling in the superconductivity of rhombohedral trilayer graphene using density functional perturbation theory (DFPT). The electron-phonon coupling strength may be used to estimate the superconducting transition temperature. To include the effects of many-body interactions, we next perform GW perturbation theory (GWPT) calculations to obtain electron-phonon coupling matrix elements that include the GW self-energy. Any change in the matrix elements would affect the electron-phonon coupling strength, which has been shown to be quite large in some correlated systems, and thus would modify the superconducting transition temperature.
W60.00004: Nonlinear Hall effect under time reversal symmetric condition in trigonal superconductor PbTaSe2
Yuki Itahashi, Toshiya Ideue, Shintaro Hoshino, Chihiro Goto, Hiromasa Namiki, Takao Sasagawa, Yoshihiro Iwasa
Symmetry breaking in solids is one of the central issues of condensed matter physics. To date, many unique physical properties and novel functionalities have been explored in noncentrosymmetric crystals. Among them, nonlinear anomalous Hall effect, which is the directional dependent spontaneous Hall effect under time reversal symmetry, is an emerging nonlinear quantum transport [1]. So far, it has been investigated in low-symmetric materials such as WTe2 and TaIrTe4 with only one mirror plane and resultant Berry curvature dipole [2-4]. In principle, however, noncentrosymmetric crystals with higher symmetry (e.g., trigonal crystals) can also host nonlinear anomalous Hall effect [5] despite the lack of Berry curvature dipole. Moreover, the search for anomalous Hall effect in exotic quantum phases including superconductivity has been missing and important challenge.
In this work, we report nonlinear anomalous Hall effect in noncentrosymmetric trigonal superconductor PbTaSe2. We observed nonlinear transport signals, which show the characteristic directional dependence reflecting the trigonal crystal symmetry in both normal and superconducting states.
[1] I. Sodemann and L. Fu, Phys. Rev. Lett. 115, 216806 (2015).
[2] Q. Ma et al., Nature 565, 337–342 (2019).
[3] K. Kang et al., Nat. Mater. 18, 324–328 (2019).
[4] D. Kumar et al., Nat. Nanotechnol. 16, 421-425 (2021).
[5] H. Isobe et al., Sci. Adv. 6, eaay2497 (2020).
W60.00005: Tunneling resonances in superconducting single-layer NbSe2 as evidence for competing pairing channels
Fernando De Juan, Wen Wan, Paul L Dreher, Daniel Muñoz-Segovia, Rishav Harsh, Francisco Guinea, Miguel M Ugeda
While bulk 2H-NbSe2 is generally accepted to be a conventional superconductor, several unconventional features of the superconducting state have been reported in the monolayer limit, including the breaking of threefold symmetry in magnetotransport and anomalously large in-plane critical fields. In this talk, I will first present another unconventional feature: the existence of satellite peaks in the STM spectra of NbSe2 monolayers which exist only in the superconducting state. After discussing potential candidate explanations, I will propose a scenario of competing pairing between s-wave and subleading f-wave triplet channels to address the different experimental observations.
W60.00006: Acoustic-Phonon-Mediated Superconductivity in Rhombohedral Trilayer Graphene
Fengcheng Wu, Yang-Zhi Chou, Jay D Sau
Motivated by the observation of two distinct superconducting phases in the moiréless ABC-stacked rhombohedral trilayer graphene, we investigate the electron-acoustic-phonon coupling as a possible pairing mechanism. We predict the existence of superconductivity with the highest Tc∼3 K near the Van Hove singularity. Away from the Van Hove singularity, Tc remains finite in a wide range of doping. In our model, the s-wave spin-singlet and f-wave spin-triplet pairings yield the same Tc, while other pairing states have negligible Tc. Our theory provides a simple explanation for the two distinct superconducting phases in the experiment and suggests that superconductivity and other interaction-driven phases (e.g., ferromagnetism) can have different origins.
W60.00007: Current-phase relation in bilayer graphene/WSe2 Josephson junction
Prasanna K Rout, Nikos Papadopoulos, Mate Kedves, Kenji Watanabe, Takashi Taniguchi, Peter Makk, Srijit Goswami
The proximity coupling of WSe2 to graphene can create a large spin-orbit interaction (SOI) in graphene. In particular, for bilayer graphene (BLG) encapsulated in WSe2 (WSe2/BLG/WSe2) it was shown that displacement fields can drive a topological phase transition at zero density due to Ising SOI [1]. Here we study the current-phase relation (CPR) of Josephson junctions created in such van der Waals heterostructures. At zero (in-plane) magnetic field we find that the CPR is largely independent of carrier density and displacement field. However at finite magnetic fields (~ few hundred mT) we observe anomalous CPRs displaying large gate-dependent phase shifts. While phase shifts are in general expected in Josephson junctions with Rashba-type SOI, the effect we observe is significantly larger and cannot be accounted for by existing models. Furthermore, we find that this effect is absent for WSe2/SLG/WSe2, BLG/WSe2 and trivial BLG JJs, suggesting that it is possibly related to the specific band structure of WSe2/BLG/WSe2.
[1] J. O. Island, X. Cui, C. Lewandowski, J. Y. Khoo, E. M. Spanton, H. Zhou, D. Rhodes, J. C. Hone, T. Taniguchi, K. Watanabe, L. S. Levitov, M. P. Zaletel, and A. F. Young, Nature 571, 85 (2019).
W60.00008: Tunable anisotropic superconductivity induced at the interface between ultrathin lead films and black phosphorus
Malte Roesner, Anand Kamlapure, Manuel Simonato, Emil Sierda, Manuel Steinbrecher, Umut Kamber, Elze J Knol, Peter Krogstrup, Mikhail Katsnelson, Alexander A Khajetoorians
Epitaxial semiconductor-superconductor heterostructures are promising as a platform for gate-tunable superconducting electronics. Here, we demonstrate that the hybrid electronic structure derived at the interface between semiconducting black phosphorus and atomically thin films of lead can drastically modify the superconducting properties of the thin metallic film. Using ultra-low temperature scanning tunneling microscopy and spectroscopy, we ascertain the moiré structure driven by the interface, and observe a strongly anisotropic renormalization of the superconducting gap and vortex structure of the lead film. Based on density functional theory, we attribute the renormalization of the superconductivity to weak hybridization at the interface where the anisotropic characteristics of the semiconductor band structure is imprinted on the Fermi surface of the superconductor. Based on a hybrid two-band model, we link this hybridization-driven renormalization to a weighting of the superconducting order parameter that quantitatively reproduces the measured spectra. These results illustrate the effect of interfacial hybridization at superconductor-semiconductor heterostructures, and pathways for engineering quantum technologies based on gate-tunable superconducting electronics.
W60.00009: Superconducting collective Leggett modes in single-layer 1H-NbSe2
Daniel Muñoz-Segovia, Wen Wan, Paul L Dreher, Rishav Harsh, Francisco Guinea, Fernando De Juan, Miguel M Ugeda
The superconducting state of single-layer 1H-NbSe2 has recently been shown to display several surprising features, including our report of the existence of a bosonic mode intrinsic to the superconducting state seen as a set of resonances in tunneling spectra, which show a clear anticorrelation with the superconducting gap. We have argued that these resonances can be interpreted as a Leggett-like superconducting collective mode associated to a subleading f-wave triplet channel. In this talk, I will present a calculation of the Leggett mode energy using a simplified continuum model for NbSe2. I will discuss how our model compares with the experimental data, discuss the origin of the anticorrelation, and argue that it provides support to the competing pairing scenario, with a sizable attraction in the subleading triplet channel.
W60.00010: Theory of superconductivity in doped quantum paraelectrics
Suk Bum Chung, Yue YU, Srinivas Raghu, Harold Y Hwang
Recent experiments on Nb-doped SrTiO3 have shown that the superconducting energy gap to the transition temperature ratio maintains the Bardeen-Cooper-Schrieffer (BCS) value throughout its superconducting dome. Motivated by these and related studies, we show that the Cooper pairing mediated by a single soft transverse-optical phonon is the most natural mechanism for such a superconducting dome given experimental constraints, and present the microscopic theory for this pairing mechanism. Furthermore, we show that this mechanism is consistent with the T2 resistivity in the normal state. Lastly, we discuss what physical insights SrTiO3 provides for superconductivity in other quantum paraelectrics such as KTaO3.
W60.00011: p-wave superconductivity induced from valley symmetry breaking in twisted trilayer graphene
Jose Gonzalez, Tobias Stauber
We show that the e-e interaction induces a strong breakdown of valley symmetry in twisted trilayer graphene, just before the superconducting instability develops in the hole-doped material. We analyze this effect by means of an atomistic self-consistent Hartree-Fock approximation, which is a sensible approach as the Fock part becomes crucial to capture the breakdown of symmetry. This effect allows us to reproduce the experimental observation of the Hall density, including the reset at 2-hole doping. Moreover, the breakdown of valley symmetry has important consequences for the superconductivity, as it implies a reduction of symmetry down to the C3 group. We observe that the second valence band has a three-fold van Hove singularity, which is pinned to the Fermi level at the experimental optimal doping for superconductivity. We further find that the C3 configuration of the saddle points leads to a version of Kohn-Luttinger superconductivity where the dominant pairing amplitude has p-wave symmetry[1]. We stress that the breakdown of symmetry down to C3 may be shared by other materials with valley symmetry breaking, so that it may be an essential ingredient to capture there the right order parameter of the superconductivity.
[1] J. Gonzalez and T. Stauber, arXiv:2110.11294
W60.00012: Effects of longer-range Coulomb interactions on the superconducting state of the Kagome system AV3Sb5
Shinibali Bhattacharyya, Astrid T Rømer, Morten Holm Christensen, Andreas Kreisel, Brian M Andersen, Roser Valenti, Paul Wunderlich
With the recent discovery of superconductivity in the Kagome material AV3Sb5, the nature of the superconducting gap symmetry has been under debate. In this work, we investigate spin- and charge-fluctuation mediated superconducting pairing phenomena in AV3Sb5, taking into account both local and longer-range Coulomb interactions at different fillings. In the presence of longer-range Coulomb interaction, charge fluctuations are enhanced which substantially modifies the pairing symmetries and hence, the leading order instabilities. Our results shed light on the role of longer-range Coulomb repulsion in deciding the nature of superconductivity in the Kagome system, which is already known to display a variety of phenomena arising out of sublattice interference due to its underlying lattice structure. We analyze the properties of these states and compare them with available experimental data. | CommonCrawl |
A construction of the high-rate regular quasi-cyclic LDPC codes
Qi Meng1,
Jia Xiang Zhao1,
Wei Xu2 &
Liang Li3
In this paper, a scheme to construct the high-rate regular quasi-cyclic low-density parity-check (QC-LDPC) codes is developed based on the finite geometry low-density parity-check (LDPC) codes. To achieve this, we first decompose the EG-LDPC code into a set of the block submatrices with each of them being cyclic. Utilizing the decomposed structure, we then construct an auxiliary matrix to facilitate us for identifying and eliminating 6-cycles of the block submatrices. In the simulation, seven regular QC-LDPC codes with code rates being 4/5, 7/8, 10/11, 11/12, and 12/13 of moderate code lengths are constructed with this scheme. The performances of these codes demonstrate the effectiveness of the proposed scheme.
Low-density parity-check (LDPC) codes [1], which is one of the main error-correcting codes, has been widely used in various practical applications [2, 3]. However, the high-rate regular QC-LDPC codes which are prone to the hardware implementation [4] and particularly suited for many practical applications can be constructed only for very restricted code parameters, such as code rate and code length. This is primarily due to the fact that for a given code length, especially short or moderate code lengths, the parity-check matrices of high-rate codes are far more dense than those of low-rate codes, which could lead to making more short cycles. Therefore, it is imperative to research on the schemes that offer a flexibly choosing the code rate and length of the high-rate regular QC-LDPC codes.
Although both QC-LDPC and turbo codes [5, 6] are capable of achieving the near Shannon limit performances, the QC-LDPC codes in general are easier to implement in practices [7, 8]. For this reason, many schemes have been developed for designing regular QC-LDPC codes, such as FG-LDPC codes [9, 10] and LDPC codes of combinatorial designs [11]. These schemes are also employed in constructing the high-rate regular QC-LDPC codes [12, 13].
However, the high-rate regular QC-LDPC codes constructing from the above schemes usually have very restricted code parameters. That is, for a given coding rate, the above schemes only offer extremely limited choices of the code length. Some examples of these are the class-I circulant EG-LDPC codes [9, 12] and cyclic difference families (CDFs) [14].
In this paper, we utilize the construction of the FG-LDPC codes [9, 10] to develop a scheme for designing the high-rate regular QC-LDPC codes. The designing procedure proceeds as follows: We first decompose the EG-LDPC or PG-LDPC code into a set of the block submatrices with each of them being cyclic. We then construct a φ transformation which acts on the first line of the obtained block submatrices to yield an auxiliary matrix \(\mathcal {T}\left (\hat {\mathbf {h}}\right)\) for identifying and cancelling 6-cycles of the block submatrices. In the simulation, we use this scheme to construct four regular QC-LDPC codes with the code rates being 11/12 and 12/13 which have the code lengths 7560, 1092 and 4095, 8190, respectively. Furthermore, we also employ the same scheme to construct three regular QC-LDPC codes with code rates being 4/5, 7/8, and 10/11 whose lengths are 2925, 7280, and 6930. The performances of these codes demonstrate the effectiveness of the proposed scheme.
A review of cyclic finite geometry LDPC codes
This section gives a brief review of FG-LDPC codes and introduces some definitions as well as notations that are used throughout the rest of the paper.
An m-dimensional finite Euclidean geometry over the field GF(2s) with m and s being the two positive integers, denoted EG(m,2s), is a set of 2sm-tuples (a0,a1,⋯,am−1) where ai∈GF(2s) for each i=0,1,…,m−1.
Defining the entry-wise addition and multiplication for m-tuples of EG(m,2s), the set EG(m,2s) forms a vector space over GF(2s). There are 2ms points in EG(m,2s). Therefore, let α be a primitive element of EG(m,2s). All the elements of EG(m,2s) can be represented as the power of α, i.e., \(0=\alpha ^{-\infty }\,,\,1=\alpha ^{0}\,,\,\alpha \,,\,\ldots \,,\,\alpha ^{2^{ms}-2}\). For any point α∈EG(m,2s) and any nonorigin point β∈EG(m,2s), the line Lα(β) through α parallel to β comprised of 2s points is:
$$\begin{array}{@{}rcl@{}} L_{\alpha}(\beta)&=&\left\{\alpha+a\beta|a\in \text{GF}\left(2^{s}\right)\right\}\,. \end{array} $$
Thus, there are:
$$\begin{array}{@{}rcl@{}} \frac{2^{(m-1)s}(2^{ms}-1)}{2^{s}-1}\, \end{array} $$
lines in EG(m,2s). Any line of EG(m,2s) has 2(m−1)s lines parallel to it. Every point in EG(m,2s) has:
$$\begin{array}{@{}rcl@{}} \frac{2^{ms}-1}{2^{s}-1} \end{array} $$
lines passing through it. The lines of EG(m,2s) can be partitioned into k cosets where any two lines of EG(m,2s) belong to the same coset if and only if they are parallel to each other.
Recall that α is a primitive element of EG(m,2s). The parity-check matrix HEG of the Euclidean geometry code is a k×(2ms−1) matrix whose columns correspond to the ordered \(1=\alpha ^{0}\,,\,\alpha \,,\,\ldots \,,\,\alpha ^{2^{ms}-2}\phantom {\dot {i}\!}\). The rows of HEG correspond to the cosets in EG(m,2s) which do not contain the lines passing through the origin. That is, the (i,j) entry in HEG is equal to 1 if the ith coset contains a line passing the jth point, and is equal to 0 otherwise.
In this section, we proceed with the procedure of the construction of the high-rate regular (QC-LDPC) codes through the following three steps: (1) Construct an n×n EG code and transform it into a proper form. (2) Utilize the transformed EG code matrix to construct an auxiliary matrix for identifying 6-cycles of it. (3) Eliminate the 6-cycles.
Decomposition of EG code matrix
Following [9], we can construct a n×n Euclidean geometry code W over the field EG(m=2,2s), where n=2ms−1. The constructed matrix W which is cyclic can be expressed by its first row w=(ω0,ω1,…,ωn−1) as:
$$\begin{array}{@{}rcl@{}} \mathbf{W} &=& \left[ \begin{array}{cccc} \omega_{0} & \omega_{1} & \cdots & \omega_{n-1}\\ \omega_{n-1} & \omega_{0} & \cdots & \omega_{n-2}\\ \vdots & \vdots & \ddots & \vdots\\ \omega_{1} & \omega_{2} & \cdots & \omega_{0}\\ \end{array} \right]_{n\times n}\,. \end{array} $$
For simplicity, we define an operation Ψ to represent:
$$\begin{array}{@{}rcl@{}} \mathbf{W} = \mathrm{\Psi}(\mathbf{w}), \end{array} $$
which implies that each row of the cyclic matrix W has the identical weight.
We assume that the positive integer n can be factored as n=c×b where b≠1 and c≠1 are positive integers with b being odd throughout the rest of this paper. Define the subset:
$$\begin{array}{@{}rcl@{}} \pi^{(0)} &=& \{0\,,c\,,2c\,,\ldots,(b-1)c\}\,. \end{array} $$
Thus, the set \(\mathcal {L}=\{0\,,1\,,2\,,\ldots \,,c \cdot b-1 \}\) can be partitioned into:
$$\begin{array}{@{}rcl@{}} \left\{\pi^{(0)}\,,\pi^{(0)}+1\,,\ldots\,,\pi^{(0)}+c-1\right\}, \end{array} $$
where we define π(0)+i={i,c+i,2c+i,…,(b−1)c+i} for i=0,1,…,c−1. We use π to denote the partition of the indices in \(\mathcal {L}\) defined in (7) for the rest of this paper. Using this partitioning, we obtain a b×n quasi-cyclic matrix Hqc as:
$$\begin{array}{@{}rcl@{}} \mathbf{H}_{\text{qc}}\triangleq[\mathrm{\Psi}(\mathbf{w}_{0})\,,\mathrm{\Psi}(\mathbf{w}_{1})\,,\ldots\,,\mathrm{\Psi}(\mathbf{w}_{c-1})]_{b \times n}\,. \end{array} $$
Let ri represent the row weight of Ψ(wi) for i=0,1,2,…,c−1 respectively. Choosing a positive integer 1≤λ< maxi=0,1,…,c−1{ri}, we eliminate all the Ψ(wk) (0≤k≤c−1) whose row weights are less than λ from the set:
$$\begin{array}{@{}rcl@{}} \{\mathrm{\Psi}(\mathbf{w}_{0}), \mathrm{\Psi}(\mathbf{w}_{1}), \ldots, \mathrm{\Psi}(\mathbf{w}_{c-1})\}\,. \end{array} $$
The resulting subset comprised of Ψ(wi)'s in (9) whose row weights are greater than or equal to λ is therefore represented as:
$$\begin{array}{@{}rcl@{}} \left\{\mathrm{\Psi}(\mathbf{w}_{i_{0}}),\mathrm{\Psi}(\mathbf{w}_{i_{1}}),\ldots,\mathrm{\Psi}\left(\mathbf{w}_{i_{k_{1}-1}}\right)\right\}\,. \end{array} $$
It follows \(r_{i_{k}} \geq \lambda \) for 0≤k≤k1−1. Since the row weight of Hqc defined in (8) is 2s, we choose the parameter λ satisfying c<2s/λ that ensures the subset (10) is not a null set.
We define a b×bk1 matrix Hqc′ as:
$$\begin{array}{@{}rcl@{}} \mathbf{H}_{\text{qc}}'&=&[\mathrm{\Psi}(\mathbf{w}_{i_{0}}), \mathrm{\Psi}(\mathbf{w}_{i_{1}}), \ldots, \mathrm{\Psi}(\mathbf{w}_{i_{k_{1}-1}})]\,. \end{array} $$
Identifying the 6-cycles
In this section, we develop a procedure to eliminate 6-cycles in (11). For this purpose, without loss generality, we assume that we are given:
$$ \mathbf{H}_{\text{qc}}' = [\mathrm{\Psi}(\mathbf{v}_{0}), \mathrm{\Psi}(\mathbf{v}_{1}), \ldots, \mathrm{\Psi}(\mathbf{v}_{k-1})], $$
where the row weight ri of Ψ(vi) for each i satisfying 0≤i≤k−1 is at least λ which is described in the previous section. The vector vi with 0≤i≤k−1 is:
$$ \mathbf{v}_{i} = \left(\nu_{0}^{i}, \nu_{1}^{i}, \ldots, \nu_{b-1}^{i}\right)\,. $$
The first row of (12) is therefore equal to:
$$ \mathbf{h} = [\mathbf{v}_{0}, \mathbf{v}_{1}, \ldots, \mathbf{v}_{k-1}] \,. $$
In order to eliminate 6-cycles, we transform matrix (12) into a new matrix of form (17). This leads us to introduce the operation φ which is defined as:
$$ \varphi(\mathbf{v}_{i})= \left(\nu_{\frac{b-1}{2}+1}^{i}\,,\ldots, \nu_{b-1}^{i}, \nu_{0}^{i}, \nu_{1}^{i}, \ldots, \nu_{\frac{b-1}{2}}^{i}\right)\,. $$
Therefore, we transform (14) into:
$$ \hat{\mathbf{h}} = [\varphi(\mathbf{v}_{0})\,,\varphi(\mathbf{v}_{1})\,,\ldots\,,\varphi(\mathbf{v}_{k-1})]\,. $$
The transformation \(\mathcal {T}\) maps \(\hat {\mathbf {h}}\) in (16) to a b×(kb+b−1) matrix is defined as:
$$ \begin{array}{ll} &\mathcal{T}(\hat{\mathbf{h}}) = \left[ \begin{array}{cccccc} \varphi(\mathbf{v}_{0}) & \varphi(\mathbf{v}_{1}) & \cdots & \varphi(\mathbf{v}_{k-1}) & 0 & \mathbf{0}_{1 \times (b-2)}\\ 0 & \varphi(\mathbf{v}_{0}) & \varphi(\mathbf{v}_{1}) & \cdots & \varphi(\mathbf{v}_{k-1}) & \mathbf{0}_{1 \times (b-2)}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots\\ 0 & \mathbf{0}_{1 \times (b-2)} & \varphi(\mathbf{v}_{0}) & \varphi(\mathbf{v}_{1}) & \cdots & \varphi(\mathbf{v}_{k-1}) \\ \end{array} \right]_{b \times kb}\\ &= \left[ \begin{array}{cccccccccccccc} \nu_{\frac{b-1}{2}+1}^{0} & \cdots & \nu_{0}^{0} & \cdots & \nu_{\frac{b-1}{2}}^{0} & \nu_{\frac{b-1}{2}+1}^{1} & \cdots & \nu_{\frac{b-1}{2}}^{1} & \cdots & \nu_{\frac{b-1}{2}}^{k-1} & 0 & 0 & \cdots & 0 \\ 0 & \nu_{\frac{b-1}{2}+1}^{0} & \cdots & \nu_{0}^{0} & \cdots & \nu_{\frac{b-1}{2}}^{0} & \nu_{\frac{b-1}{2}+1}^{1} & \cdots & \nu_{\frac{b-1}{2}}^{1} & \cdots & \nu_{\frac{b-1}{2}}^{k-1} & 0 &\cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots &\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots\\ 0 & 0 & \cdots & 0 &\nu_{\frac{b-1}{2}+1}^{0} & \cdots & \nu_{0}^{0} & \cdots & \nu_{\frac{b-1}{2}}^{0} & \nu_{\frac{b-1}{2}+1}^{1} & \cdots & \nu_{\frac{b-1}{2}}^{1} & \cdots & \nu_{\frac{b-1}{2}}^{k-1}\\ \end{array} \right] \end{array} $$
Examing (17), we see that the first row of \(\mathcal {T}(\hat {\mathbf {h}})\) is obtained through adding b−1 zeros to the end of the vector \(\hat {\mathbf {h}}\). Each of the rest rows of \(\mathcal {T}(\hat {\mathbf {h}})\) is the circular shift of the row above it.
The set \(L(\hat {\mathbf {h}})\) comprised of the indices corresponding to the nonzero entries of \(\hat {\mathbf {h}}\) in (16) is defined as:
$$ L(\hat{\mathbf{h}}) = \{p_{0}, p_{1}, \ldots, p_{\rho-1}\}, $$
where we have \(\rho = \sum \limits _{i=0}^{k-1}r_{i}\) with ri representing the row weight of Ψ(vi). We define an oblique line segment \(l_{p_{i}}\) which starts from pi and forms a descending diagonal from left to right in \(\mathcal {T}(\hat {\mathbf {h}})\),i.e., \(l_{p_{i}}\) constituting of the set of the entries of \(\mathcal {T}(\hat {\mathbf {h}})\) as follows:
$$ l_{p_{i}} = \left\{\mathcal{T}(\hat{\mathbf{h}})_{1,p_{i}}, \mathcal{T}(\hat{\mathbf{h}})_{2,p_{i}+1}, \ldots, \mathcal{T}(\hat{\mathbf{h}})_{b,p_{i}+b-1}\right\}\,. $$
Clearly, from the definition, the total number of the oblique line segments of the form (19) is ρ. Thus, the set of all the oblique line segments is:
$$ \left\{l_{p_{0}}\,,l_{p_{1}}\,,\ldots\,,l_{p_{\rho-1}}\right\}\,. $$
We define the distance between two oblique lines as:
$$ |l_{p_{i_{0}}}-l_{p_{i_{1}}}| = |p_{i_{0}}-p_{i_{1}}|\,. $$
From [15], it follows that the possible of 6-cycles appeared in a parity-check matrix is one of the following forms shown in Fig. 1.
Six possible loops that yield 6-cycles
Case 1: Assume that 6-cycle is comprised of three oblique line segments from (20). Therefore, from (20), the total number of subsets comprised of three oblique line segments is \(\dbinom {\rho }{3}\). For each subset comprised of three oblique line segments \(\left \{l_{p_{i_{0}}}, l_{p_{i_{1}}}, l_{p_{i_{2}}}\right \}\) from (20), we employ (21) to compute:
$$\begin{array}{@{}rcl@{}} \left\{ \begin{aligned} d_{0} &=|p_{i_{1}}-p_{i_{0}}| \\ d_{1} &=|p_{i_{2}}-p_{i_{1}}| \,.\\ \end{aligned} \right. \end{array} $$
If \({d_{0}\over {d_{1}}}\) is not equal to either \(1\over {2}\) or 2, then we delete such a subset comprised of these three oblique line segments. The remaining subsets constitute Ω3 which can be represented as:
$$ \mathrm{\Omega}_{3} = \left\{ \left\{l_{p_{i_{0}}}, l_{p_{i_{1}}}, l_{p_{i_{2}}}\right\}, \left\{l_{p_{i_{3}}}, l_{p_{i_{4}}}, l_{p_{i_{5}}}\right\}, \ldots\right\}\,. $$
Clearly, each subset of three oblique line segments \(\{l_{p_{i_{j}}}, l_{p_{i_{j+1}}}, l_{p_{i_{j+2}}}\}\) in Ω3 satisfies:
$$ {|l_{p_{i_{j+1}}}-l_{p_{i_{j}}}|\over{|l_{p_{i_{j+2}}}-l_{p_{i_{j+1}}}}|}={|p_{i_{j+1}}-p_{i_{j}}|\over{|p_{i_{j+2}}-p_{i_{j+1}}|}}={1\over{2}}\,\,\,\,\rm{or}\,\,\,2\,. $$
Figure 2 shows that 6-cycles are constituted by three oblique lines.
6-cycles constituted by three oblique line segments in (17)
Case 2: Assume that 6-cycle is comprised of four oblique line segments from (20). Therefore, from (20), the total number of subsets comprised of four oblique line segments is \(\dbinom {\rho }{4}\). For each subset comprised of four oblique line segments \(\{l_{p_{i_{0}}}, l_{p_{i_{1}}}, l_{p_{i_{2}}}, l_{p_{i_{3}}}\}\) from (20), we employ (21) to compute:
$$\begin{array}{@{}rcl@{}} \left\{ \begin{aligned} d_{0} &=|p_{i_{1}}-p_{i_{0}}| \\ d_{1} &=|p_{i_{2}}-p_{i_{1}}| \\ d_{2} &=|p_{i_{3}}-p_{i_{2}}| \,.\\ \end{aligned} \right. \end{array} $$
If the computed distance d0,d1, and d2 are not satisfied to any of these equations listed in the following set:
$$\begin{array}{@{}rcl@{}} \begin{array}{cc} &\left\{ \begin{array}{lll} d_{0} = d_{1}+d_{2}, & d_{1} = d_{0}+d_{2}, & d_{2} = d_{0}+d_{1}, \\ d_{0} = 2d_{2}, & d_{2} = 2d_{0}, & d_{0} = d_{1}+2d_{2}, \\ d_{2} = 2d_{0}+d_{1}\,,& d_{0} = d_{1}, & d_{1} = d_{2} \\ \end{array} \right\}, \end{array} \end{array} $$
then we delete such a subset comprised of these four oblique line segments. The remaining subsets constitute Ω4 which can be represented as:
$$ \mathrm{\Omega}_{4} = \left\{ \left\{l_{p_{i_{0}}}, l_{p_{i_{1}}}, l_{p_{i_{2}}}, l_{p_{i_{3}}}\right\}, \left\{l_{p_{i_{4}}}, l_{p_{i_{5}}}, l_{p_{i_{6}}}, l_{p_{i_{7}}}\right\}, \ldots\right\}\,. $$
Figure 3 shows that 6-cycles are constituted by four oblique line segments.
6-cycles constituted by four oblique line segments in (17)
Case 3: Assume that 6-cycle is comprised of five oblique line segments from (20). Therefore, from (20), the total number of subsets comprised of five oblique line segments is \(\dbinom {\rho }{5}\). For each subset comprised of five oblique line segments \(\{l_{p_{i_{0}}}, l_{p_{i_{1}}}, l_{p_{i_{2}}}, l_{p_{i_{3}}}, l_{p_{i_{4}}}\}\) from (20), we employ (21) to compute:
$$\begin{array}{@{}rcl@{}} \left\{ \begin{aligned} d_{0} &=|p_{i_{1}}-p_{i_{0}}| \\ d_{1} &=|p_{i_{2}}-p_{i_{1}}| \\ d_{2} &=|p_{i_{3}}-p_{i_{2}}| \\ d_{3} &=|p_{i_{4}}-p_{i_{3}}|\,. \\ \end{aligned} \right. \end{array} $$
If the computed distance d0,d1,d2, and d3 are not satisfied to any of these equations listed in the following set:
$$\begin{array}{*{20}l} \begin{array}{cc} &\left\{ \begin{array}{lll} d_{0} = d_{1}+d_{3}, & d_{3} = d_{0}+d_{1}, & d_{0} = 2d_{2}+d_{3}, \\ d_{1} = d_{0}+d_{3}, & d_{0} = d_{2}+d_{3}, & d_{0} = d_{2}+2d_{3}, \\ d_{2} = d_{0}+d_{3}, & d_{0} = d_{1}+2d_{2}+d_{3}, & d_{3} = 2d_{0}+d_{1}, \\ d_{3} = d_{0}+d_{2}, & d_{3} = d_{0}+2d_{1}+d_{2}, & d_{3} = d_{0}+2d_{1} \\ \end{array} \right\}, \end{array} \end{array} $$
then we delete such a subset of these five oblique line segments. The remaining subsets constitute Ω5 which can be represented as:
$$ \mathrm{\Omega}_{5} \,=\, \left\{ \left\{l_{p_{i_{0}}}, l_{p_{i_{1}}}, l_{p_{i_{2}}}, l_{p_{i_{3}}}, l_{p_{i_{4}}}\!\right\},\! \left\{l_{p_{i_{5}}}, l_{p_{i_{6}}}, l_{p_{i_{7}}}, l_{p_{i_{8}}}, l_{p_{i_{9}}}\!\right\}, \ldots\right\}\!. $$
Figure 4 shows that 6-cycles are constituted by five oblique line segments.
6-cycles constituted by five oblique line segments in (17)
Eliminating 6-cycles
In the following, we proceed with the procedure to eliminate 6-cycles.
Step 1: Construct Γ which is defined as:
$$ \mathrm{\Gamma} = \mathrm{\Omega}_{3} \cup \mathrm{\Omega}_{4} \cup \mathrm{\Omega}_{5}, $$
where Ω3, Ω4, and Ω5 are defined by (23), (27), and (30), respectively.
Step 2: Find the oblique line segment \(l_{p_{i_{0}}}\) that appears in the maximal number subsets of Γ. Delete all the subsets of Γ containing this oblique line segment \(l_{p_{i_{0}}}\) and collect all the remaining subsets of Γ to form an new subset Γ1. Repeat this process on the subset Γ1 to obtain \(l_{p_{i_{1}}}\) and Γ2. We continue this process till Γk for k being some positive integer becomes a null set. In this process, we also obtain an ordered set of oblique line segments which is:
$$ \mathrm{\Omega}_{\text{order}} = \left\{l_{p_{i_{0}}}, l_{p_{i_{1}}}, l_{p_{i_{2}}}\, \ldots\, l_{p_{i_{k-1}}}\right\}\,. $$
Step 3: In view of (12), we construct k subsets Q0,Q1,…,Qk−1 with Qj for 0≤j≤k−1 being comprised of the oblique line segments \(l_{p_{i_{j}}}\) in Ωorder satisfying:
$$ \lfloor p_{i_{j}}/b\rfloor =j, $$
where ⌊·⌋ denotes the rounding down operation. Recall that rj for 0≤j≤k−1 is the row weight of Ψ(vj) in (12) and λ is the pre-chosen positive integer introduced above Eq. (9). If there are more than (rj−λ) oblique line segments of Ωorder satisfy (33), then only the first (rj−λ) oblique line segments appeared in the ordered set Ωorder are chosen to form Qj. If there are less than (rj−λ) oblique line segments of Ωorder satisfy (33), we arbitrarily choose oblique line segments satisfying (33) from (20) that do not belong to Ωorder.
Thus, Qj for 0≤j≤k−1 has the size of (rj−λ). We define 1×b vector sj:
$$\begin{array}{@{}rcl@{}} \mathbf{s}_{j}&=&[s_{j,0}\,,\,\ldots, s_{j,b-1}]\,\, \text{with}\,\, s_{j,i}= \left\{ \begin{aligned} &1\,\,\,\text{if}\ \, l_{(i+jb)} \in Q_{j}\,\,\\ &0\,\,\,\text{otherwise}\, \end{aligned}\right.\,. \end{array} $$
For each sj, we utilize the inverse of the map φ defined in (15) to yield a b×b matrix Sj as follows:
$$ S_{j} = \mathrm{\Psi}\left(\varphi^{-1}(\mathbf{s}_{j})\right), $$
where the operation Ψ is defined in (5). Thus, the quasi-cyclic matrix S
$$ \mathbf{S} = [S_{0}, S_{1}, \ldots, S_{k-1}]\,. $$
In view of Hqc′ and S defined in (12) and (36), respectively, the quasi-cyclic encoding parity-check matrix \(\mathbf {H}_{\text {qc}}^{(1)}\) is therefore equal to:
$$\begin{array}{@{}rcl@{}} \mathbf{H}_{\text{qc}}^{(1)} = \mathbf{H}_{\text{qc}}' \oplus \mathbf{S}\,. \end{array} $$
The operator ⊕ in (37) is defined as the entry-wise XOR operations of matrices Hqc′ and S. From the construction procedure from (12) to (37), it follows that matrix \(\mathbf {H}_{\text {qc}}^{(1)}\) is regular and quasi-cyclic with its column and row weight being λ and kλ, respectively.
Another regular quasi-cyclic parity-check matrix
Substituting \(\mathbf {H}_{\text {qc}}^{(1)}\) for Hqc′ and proceeding the procedure from (12) to (36) with λ=0, we can get a new S(1) from (36). Then, we can construct another regular quasi-cyclic parity-check matrix \(\mathbf {H}_{\text {qc}}^{(2)}\) as follows:
$$ \mathbf{H}_{\text{qc}}^{(2)}=\left[ \begin{array}{cc} \mathbf{H}_{\text{qc}}^{(1)} \oplus \mathbf{S}^{(1)} & \mathbf{S}^{(1)}\\ \mathbf{S}^{(1)} &{H}_{\text{qc}}^{(1)} \oplus \mathbf{S}^{(1)}\\ \end{array} \right]\,. $$
\(\mathbf {H}_{\text {qc}}^{(2)}\) and \(\mathbf {H}_{\text {qc}}^{(1)}\) have the same row and column weight.
In example 1 of this section, we utilize the procedure from (4) to (37) to construct a regular quasi-cyclic (4095,3781) LDPC code as well as (38) to construct regular quasi-cyclic (7560,6931) and (8190,7561) LDPC codes where the coding rates of all these three codes are 12/13.
In example 2, we utilize the procedure from (4) to (37) to construct a regular quasi-cyclic (2925,2341) LDPC code and a regular quasi-cyclic (4095,3781) LDPC code where the coding rates of all these two codes are 4/5 and 11/12, respectively.
In example 3 and example 4, the procedure of (4)–(38) is also employed to separately construct a regular quasi-cyclic (6930,6301) LDPC code and a regular quasi-cyclic (7280,6370) LDPC code with the coding rate 10/11 and 7/8, respectively. As a comparison of the performance, we also utilize the schemes from [16–18] to construct six (4095,3771), (4095,3729), (16383,14923), (8176,7156), (1020,935), and (2850,2280) QC-LDPC codes. The simulation results in the following examples show that the procedure from (4) to (38) is an effective scheme to yield the high-rate regular QC-LDPC codes with moderate code lengths.
Example 1: Following the scheme of [9], we first construct a regular (4095,3367) EG-LDPC code over the field EG(2,26). Since we have 4095=c×b with c=13 and b=315, the procedure from (4) to (8) suggests that the parity-check matrix of the constructed (4095,3367) EG-LDPC code can be decomposed into 13 submatrices of size b×b shown in (8). Of the 13 submatrices of size b×b, choose the parameter λ=4 to perform (9) to (11) where parameter λ is introduced above Eq. (9). Then, we select the first k=13 submatrices and perform (12) to (37) and (38) separately which yields a regular quasi-cyclic 315×4095 parity-check matrix \(\mathbf {H}_{\text {qc}}^{(1)}\) defined in (37) as well as a 630×8190 parity-check matrix \(\mathbf {H}_{\text {qc}}^{(2)}\) defined in (38) respectively. The null spaces of \(\mathbf {H}_{\mathrm { qc}}^{(1)}\) and \(\mathbf {H}_{\text {qc}}^{(2)}\) render a regular quasi-cyclic (4095,3781) LDPC code as well as a (8190,7561) LDPC code with the coding rate 12/13. Similarily, we also choose the first k=12 submatrices and perform (12) to (38) which yields a regular quasi-cyclic 630×7560 parity-check matrix \(\mathbf {H}_{\text {qc}}^{(2)}\) defined in (38). The null space of this \(\mathbf {H}_{\text {qc}}^{(2)}\) also renders a regular quasi-cyclic (7560,6931) LDPC code with the coding rate 11/12. As a comparison, we also employ the procedure of [16] to construct the (4095,3771) QC-LDPC code with the coding rate being 0.92.
Figure 5 shows the performances of these codes where it (a) represents the bit error rate (BER) and (b) depicts the frame error rate (FER). In these figures, the circle, box, and diamond solid lines respectively represent the performances of the regular quasi-cyclic (4095,3781), (7560,6931), and (8190,5161) LDPC codes. The star dotted line corresponds to the performance of the (4095,3771) QC-LDPC code generated by [16].
a The bit error rate and b frame error rate performances of four LDPC codes in example 1. In these figures, the circle, box, and diamond solid lines separately represent to the performances of the regular quasi-cyclic (4095,3781), (7560,6931), and (8190,5161) LDPC codes with coding rate 12/13 generated by the procedure from (4) to (38). The star dotted line corresponds to the (4095,3771) QC-LDPC code which is also shown in the example 4 of [16]. These 4 LDPC codes are all decoded with 50 iterations of the SPA (sum-product algorithm)
Example 2: Following the scheme of [9], we first construct a regular (4095,3367) EG-LDPC code over the field EG(2,26). Since we have 4095=c×b with c=7, b=585, and c=45, b=91, the procedure from (4) to (8) suggests that the parity-check matrix of the constructed (4095,3367) EG-LDPC code can be decomposed into 7 and 45 submatrices of size b×b shown in (8). Of 7 and 45 submatrices of size b×b, choose the parameters λ=4 and λ=3 to perform (9) to (11) where parameter λ is introduced above Eq. (9). Then, we select separately the first k=5 and k=12 submatrices then perform (12) to (37) which yields a regular quasi-cyclic 585×2925 and 91×1091 parity-check matrix \(\mathbf {H}_{\text {qc}}^{(1)}\) both defined in (37). As a comparison, we also employ the procedure of [17, 18] construct the (2850,2280) and(1020,935) QC-LDPC code with the coding rate being 4/5 and 11/12, respectively.
Figure 6 shows the performances of these codes where it (a) represents the bit error rate (BER) and (b) depicts the frame error rate (FER). In these figures, the circle and box solid lines respectively represent the performances of the regular quasi-cyclic (2925,2341) and (1092,1001) LDPC codes. The circle and box dotted line corresponds to the performance of the (2850,2280) and 1020,935 QC-LDPC code generated by [17, 18].
a The bit error rate and b frame error rate performances of four LDPC codes in example 2. In these figures, the circle and box solid lines separately represent the performances of the regular quasi-cyclic (2925,2341) and (1092,1001) LDPC codes with coding rate 4/5 and 11/12 generated by the procedure from (4) to (37). The circle and box dotted lines correspond to (2850,2280) and 1020,935 QC-LDPC codes which are also shown in [17, 18]. These 4 LDPC codes are all decoded with 50 iterations of the SPA (sum-product algorithm)
Example 3: Following the scheme of [9], we first construct a regular (4095,3367) EG-LDPC code over the field EG(2,26). Since we have 4095=c×b with c=13 and b=315, the procedure from (4) to (8) suggests that the parity-check matrix of the constructed (4095,3367) EG-LDPC code can be decomposed into 13 submatrices of size b×b shown in (8). Of 13 submatrices of size b×b, choose the parameter λ=4 to perform (9) to (11) where parameter λ is introduced above Eq. (9). Then, we select the first k=11 submatrices and perform (12) to (38) which yields a regular quasi-cyclic 630×6930 parity-check matrix \(\mathbf {H}_{\text {qc}}^{(2)}\) defined in (38). The null space of \(\mathbf {H}_{\text {qc}}^{(2)}\) renders a regular quasi-cyclic (6930,6301) LDPC code with the coding rate 10/11. As a comparison, we also employ the procedure of [16] to construct the (4095,3729) and (16383,14923) QC-LDPC code with the coding rates of both codes being 0.91.
Figure 7 shows the performances of these codes where it (a) represents the bit error rate (BER) and (b) depicts the frame error rate (FER). In these figures, the circle solid line represents the performance of the regular quasi-cyclic (6930,6301) LDPC code constructed from the procedure from (4) to (38). The box and diamond dotted lines respectively correspond to the performances of the (4095,3729) and (16383,14923) QC-LDPC codes yielded from [16].
a The bit error rate and b frame error rate performances of three LDPC codes in example 2. In these figures, the circle solid line represents the performance of the regular quasi-cyclic (6930,6301) LDPC code with coding rate 10/11 generated by the procedure from (4) to (38). The box and diamond dotted lines separately correspond to the (4095,3729) and (16383,14923) QC-LDPC codes which are constructed from the procedure of [16]. These 3 LDPC codes are all decoded with 50 iterations of the SPA
Example 4: Following the scheme of [9], we first construct a regular (4095,3367) EG-LDPC code over the field EG(2,26). Since we have 4095=c×b with c=9 and b=455, the procedure from (4) to (8) suggests that the parity-check matrix of the constructed (4095,3367) EG-LDPC code can be decomposed into nine submatrices of size b×b shown in (8). Of the nine submatrices of size b×b, choose the parameter λ=4 to perform (9) to (11) where parameter λ is introduced above Eq. (9). Then, we select the first k=8 submatrices and perform the procedure from (12) to (38) which yields a regular quasi-cyclic 910×7280 parity-check matrix \(\mathbf {H}_{\text {qc}}^{(2)}\) defined in (38). The null space of this \(\mathbf {H}_{\text {qc}}^{(2)}\) renders a regular quasi-cyclic (7280,6371) LDPC code with the coding rate 7/8. As a comparison, we also employ the procedure of [16] to construct the (8176,7156) QC-LDPC code with the coding rate being 0.875.
Figure 8 shows the performances of these codes where it (a) represents the bit error rate (BER) and (b) depicts the frame error rate (FER). In these figures, the circle solid line represents the performance of the regular quasi-cyclic (7280,6371) LDPC code yielded from the procedure of (4)–(38). The box dotted line corresponds to the performance of the (8176,7156) QC-LDPC code (example 7 of [16]) generated by the scheme of [16].
a The bit error rate and b frame error rate performance of two LDPC codes in example 3. In these figures, the circle solid line represents the performance of the regular quasi-cyclic (7280,6371) LDPC code with coding rate 7/8 generated by the procedure from (4) to (38). The box dotted line corresponds to the performance of the (8176,7156) QC-LDPC code constructed by the scheme of [16]. These 2 LDPC codes are both decoded with 50 iterations of the SPA
We have presented a scheme to construct the high-rate regular quasi-cyclic low-density parity-check QC-LDPC codes. The construction procedure is based on the FG-LDPC codes in which we first decompose the EG-LDPC code into a set of the block submatrices with each of them being cyclic. Then, we exploit the decomposed structure to produce an auxiliary matrix to facilitate us for identifying and eliminating 6-cycles of the block submatrices. Three regular QC-LDPC codes with code rates being 7/8, 10/11, and 11/12 of moderate code lengths are constructed in the simulation. The performances of these codes demonstrate the effectiveness of the proposed scheme.
BER:
Bit error rate
CDFs:
Cyclic difference families
EG-LDPC:
Euclidian geometry low-density parity-check
Frame error rate
FG-LDPC:
Finite geometry low-density parity-check
LDPC:
Low-density parity-check
PG-LDPC:
Projective geometry low-density parity-check
QC-LDPC:
Quasi-cyclic low-density parity-check
R. Gallager, Low-density parity-check codes. IRE Trans. Inform. Theory.8(1), 21–28 (1962).
N. Balasuriya, C. B. Wavegedara, Improved symbol value selection for symbol flipping-based non-binary LDPC decoding. EURASIP J. Wirel. Commun. Netw.2017(1), 105 (2017).
K. Kwon, T. Kim, J. Heo, Pre-coded LDPC coding for physical layer security. EURASIP J. Wirel. Commun. Netw.2016(1), 283 (2016).
A. Tasdighi, A. H. Banihashemi, author=Sadeghi, M.R., Symmetrical constructions for regular girth-8 QC-LDPC codes. IEEE Trans. Commun.65(1), 14–22 (2017).
S. K. Chronopoulos, G. Tatsis, V. Raptis, P. Kostarakis, in Proceedings of the 2nd Pan-Hellenic Conference on Electronics and Telecommunications. A parallel turbo encoder-decoder scheme (Thessaloniki, 2012).
S. K. Chronopoulos, G. Tatsis, P. Kostarakis, Turbo codes—a new PCCC design. Commun. Netw.3(4), 229–234 (2011).
B. Bangerter, E. Jacobsen, Ho. Minnie, et al, High-throughput wireless LAN air interface. Intel Technol. J.7(3), 47–57 (2003).
IEEE Standard for Local and Metropolitan Area Networks Part 16: Air Interface for Fixed and Mobile Broadband Wireless Access Systems Amendment 2: Physical and Medium Access Control Layers for Combined Fixed and Mobile Operation in Licensed Bands and Corrigendum 1," in IEEE Std 802.16e-2005 and IEEE Std 802.16-2004/Cor 1-2005 (Amendment and Corrigendum to IEEE Std 802.16-2004), vol., no., pp.0_1-822, 2006 https://doi.org/10.1109/IEEESTD.2006.99107. http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=1603394&isnumber=33683.
Y. Kou, S. Lin, M. P. C. Fossorier, Low-density parity-check codes based on finite geometries: a rediscovery and new results. IEEE Trans. Inform. Theory. 47(7), 2711–2736 (2001).
H. Tang, J. Xu, Y. Kou, S. Lin, K. Abdel-Ghaffar, On algebraic construction of Gallager and circulant low-density parity-check codes. IEEE Trans. Inform. Theory. 50(6), 1269–1279 (2004).
B. Vasic, O. Milenkovic, Combinatorial constructions of low-density parity-check codes for iterative decoding. IEEE Trans. Inform. Theory. 50(6), 1156–1176 (2004).
N. Kamiya, High-rate quasi-cyclic low-density parity-check codes derived from finite affine planes. IEEE Trans. Inform. Theory. 53(4), 1444–1459 (2007).
M. Fujisawa, S. Sakata, A construction of high rate quasi-cyclic regular LDPC codes from cyclic difference families with girth 8. IEICE Trans. Fundam. Electron. Commun. Comput. Sci.90(5), 1055–1061 (2007).
C. J. Colbourn, J. H. Dinitz, CRC handbook of combinatorial design. Math. Gaz.81(81), 44–48 (1996).
MATH Google Scholar
W. Wen, M. Ai, J. Qiu, L. Liu, in 2015 IEEE International Conference on Progress in Informatics and Computing (PIC). Novel construction and cycle analysis of quasi-cyclic low-density parity-check codes (Nanjing, 2015), pp. 230–233.
Q. Huang, Q. Diao, S. Lin, K. Abdel-Ghaffar, in 2011 Information Theory and Applications Workshop. Cyclic and quasi-cyclic LDPC codes: new developments (La Jolla, 2011), pp. 1–10.
S. Vafi, N. Majid, Combinatorial design-based quasi-cyclic LDPC codes with girth eight. Digit. Commun. Netw.https://doi.org/10.1016/j.dcan.(2018).
H. Park, S. Hong, J. S. No, IEEE Trans. Commun.61(8), 3108–3113 (2013).
We would like to thank the anonymous reviewers for their insightful comments on the paper, as these comments led us to an improvement of the work.
This work was supported by the National Natural Science Funds for the Nankai University (No. 61771262).
College of Electronic Information and Optical Engineering, Nankai University, 38 Tongyan Road, Jinnan District, Tianjin, 300350, People's Republic of China
Qi Meng & Jia Xiang Zhao
Tianjin Polytechnic University, Xiqing District, Tianjin, 300387, People's Republic of China
Wei Xu
IP Technology Research Department, Huawei Technologies, Shenzhen, 518000, People's Republic of China
Liang Li
Qi Meng
Jia Xiang Zhao
JXZ and QM contributed to the main idea and drafted manuscript. QM and WX contributed to the algorithm design, performance analysis, and simulations. LL helped revise the manuscript. All authors read and approved the final manuscript.
Correspondence to Jia Xiang Zhao.
QM is a graduate student at the College of Electronic Information and Optical Engineering at Nankai University. His research interests include digital signal processing and error control coding.
JXZ is a professor at the College of Electronic Information and Optical Engineering at Nankai University. His research interests include biological signal processing, high-speed digital transmission algorithm, and error control coding.
WX is a professor at Tianjin Polytechnic University. Her research interests include digital signal processing and error control coding.
LL is serving as a communications engineer in IP Technology Research Department at Huawei Technologies Co., Ltd.
Meng, Q., Zhao, J.X., Xu, W. et al. A construction of the high-rate regular quasi-cyclic LDPC codes. J Wireless Com Network 2019, 14 (2019). https://doi.org/10.1186/s13638-018-1325-9
High-rate
Quasi-cyclic
Low-density parity-check (LDPC) code | CommonCrawl |
Space Exploration Meta
Space Exploration Stack Exchange is a question and answer site for spacecraft operators, scientists, engineers, and enthusiasts. It only takes a minute to sign up.
Space Exploration Beta
What about gathering water ice from Saturn's rings?
Saturn's rings are almost pure water ice in nice manageable chunks from specks to boulders a few meters across. Assuming there is something truly useful to do with it - once again talking about orbital depots or human bases on the moon - is it feasible to collect that ice and drag it back to the neighborhood of Earth?
Compared to snagging asteroids passing through the neighborhood or collected at the Trojan points like Planetary Resources plans, or shipping water from Earth, it seems like it could have advantages. We know exactly where it is, it seems easy to get to, there's plenty of it, and it's in small chunks. What would be the problems?
water mining saturn rings ice
kim holder
kim holderkim holder
$\begingroup$ Those chunks of ice pack a solid mass whilst moving at orbital velocity; a craft would need to rob the ice of it's orbit velocity $\endgroup$ – Everyone Oct 3 '14 at 20:12
$\begingroup$ Rob it of its orbital velocity? I thought it would be more a matter of bagging or netting some chunks after matching orbits and then slowly accelerating away. $\endgroup$ – kim holder Oct 3 '14 at 20:57
$\begingroup$ Matching orbit with a large velocity difference, and a large difference in mass between two bodies may be ... suicidal for one of the two bodies $\endgroup$ – Everyone Oct 4 '14 at 5:46
$\begingroup$ @Everyone: Wait, matching orbits is exactly zeroing the velocity difference. Although diving into the Saturn rings sounds suicidal to me. Even if moving at the orbital speed, it's still good couple m/s of error and lots of rocks that can hit you pretty hard. $\endgroup$ – SF. Nov 9 '15 at 23:44
For a Hohmann transfer to Saturn, I get 15.7 km/s for both burns. The transfer time is also a simple formula. I obtain roughly 6 years.
Compare to the lunar ice. It is roughly 2.8 km/s to get to, and the trip time would be a few days, even from Low Earth Orbit.
As suggested by the other answer, you could compare to Earth's surface. If we're using some reference frame far from Earth's surface, then it's nearly 12.8 km/s going up (EDIT: corrected from newbie mistake, LEO gets Oberth). But this gets complicated. The first 9 km/s is constrained by atmospheric physics. Although, leaving the moon also has a similar thrust-to-weight requirement placed on the rockets by gravity drag.
These numbers aren't totally fair to Saturn. If I use the edge of the rings (nearly the "F" ring), I get an orbital velocity of 16.6 km/s. In order to mine these rings, you'll need to follow a hyperbolic trajectory, and then do your final Hohmann burn when you're close to your destination, inside Saturn's gravity well. This will reduce the Delta V you'll need for the final burn. That'll reduce the final burn by a little bit. Breaking up the 15.7 km/s, the initial insertion burn is 10.3 km/s and the heliocentric circularization burn is 5.4 km/s. So we would need to correct this all for the Oberth effect, which is a multiplier of $\sqrt{1 + \frac{2 V_\text{esc}} {\Delta v}} $, sphere of influence assumptions, yada yada. That reduces the previous numbers to (respectively) 5.8 km/s and 1.4 km/s. Boy that was an unpleasant calculation, but the total comes to approximately 7.2 km/s.
It's true that mining the lunar ice would involve challenges that Saturn's rings don't have. But if the destination is close to Earth, those challenges would be more workable than the nuclear, ion, or whatever kind of drives that a Saturn hauler would involve. A similar tradeoff might present itself for other sources closer than Saturn, for instance, Jupiter trojan asteroids.
I won't dispute the quality of Saturn's ice. It is likely more pure than the alternative sources. It might also be in convenient size chunks. Importantly (in its favor) it can be delivered by drives with a low thrust-to-weight ratio. Any value would do for this, although there might be some Delta V penalty due to reduced Oberth effect. Solar electric would be penalized heavily due to the distance from the sun. Nuclear power sources are vastly superior at that distance. 9.5 AU --> squared means 90 times less power per unit area than near Earth.
The real problem is justifying that 6 year time frame. Who is going to wait 12 years for their return on investment? Now I grant you, because of the absence of a gravity drag penalty, it's possible that a ship of monstrous size could deliver huge quantities of ice. Because you're not dealing with any surface-to-orbit transition, your ship could be fragile, and your engine could have a low thrust. Given that, the only thing that scales directly with the payload is the propellant. If we can get something like 30 km/s reaction velocities, then it's believable that making the round trip would work... although only if you can cannibalize water for propellant, and at somewhat poor margins.
So, sure, there is a business case in a very specific scenario where we have a mature market for water in space, someone could reduce costs of procurement by making a ridiculous-looking bloated spaceship that runs the Saturn to Earth orbit route. I'm still not convinced that it would be better than other alternatives beyond the frost line, but most of those have angular clustering. A business might want deliveries more than once every year, and for that, Saturn versus Jupiter trojans (for instance) provide some seasonal diversity. But the advantage is nil except for with extremely large quantities. That raises the question - how could the depreciation possibly compete with lunar ice? If you can run regular ferries from lunar poles to orbit, that seems more economic unless your bloated Saturn ship could be much lower cost (because the lunar scheme has much higher trip frequency). Maybe it could. We can't really say. The biggest variable will be your rate of return. If you demand 6% rate of return, then you're effectively cutting the value of the ice in half over 12 years. This is why it's a hard sell, but that's not really the rocket science part of it.
Addition: Found the example of a "bloated spaceship" that I had in mind. Saw it on Atomic Rockets. Here is the original source. Apparently they had Phobos in mind.
I have some problems with their off-the-bat assumptions. If Phobos has water, why doesn't Eros? I don't know these things. I'm doubtful that anyone else knows the bulk composition or the difficulty of refining the below-the-surface precious water of such inner system bodies. Myself, I would like to picture that "spaceship" with the bladder being 100x its above relatively size. These things will make a hot air balloon look lean.
AlanSEAlanSE
$\begingroup$ Great answer, thanks. I'm not going to pick it as 'the' answer quite yet in case someone else weighs in even more impressively :D. Partly i asked because i understand it is still up in the air how much water the moon has. I hear from HopDavid that the LRO's measures seem to go quite against the 600 million ton estimate given by Chandrayaan-1. At any rate, i am emotionally attached to the idea of keeping the moon's water where it is, so that an awesome colony can be set up there. What can i say... $\endgroup$ – kim holder Oct 3 '14 at 23:18
$\begingroup$ Maybe it is also fair to mention your calculation is without taking advantage of any gravity assists. I suppose Jovian trojans also have that advantage, but doesn't being in the orbit of Saturn give extra opportunities there? $\endgroup$ – kim holder Oct 3 '14 at 23:37
$\begingroup$ @briligg You know, I had this text about being "fair to Saturn". But when I came back to it, I forgot what I where I had meant to go with it. That was it! Saturn benefits from the Interplanetary Transport Network, but minimally if fast trip time is still an objective. I'd hate to be the guy who runs that schedule. It gets complicated. $\endgroup$ – AlanSE Oct 3 '14 at 23:42
$\begingroup$ This really sounds an awful lot like Asimov's old short story, The Martian Way (which used remass water politics as a stand-in for McCarthyism). Same mature water market, same high (nuclear) exhaust velocities, same large ships. $\endgroup$ – Nathan Tuggy Dec 2 '16 at 5:22
It occurs to me that the answer to this question depends on what you want to get for your money. If you are only interested in the ice itself, in a source of water for use on Earth on in LEO, then other options are preferable.
However, if you wish to get greater returns on your investment in the form of ancillary benefits which themselves have value, both marketable and otherwise, then Saturn would seem to be a much better option. The ring system, including some of it's smaller moons, are a much easier target from an engineering perspective for manned or partially-manned operations.
This goes beyond the reduction in processing required to make use of the water in situ or for market, and includes such things as the radiation environment, available human-friendly day/night cycles/orbital periods and useable resources - one of which being the generation of electricity. If the interest is long-term, multi-purpose industrial infrastructure, Saturn is a much more favorable source than the moon or even the Trojan asteroids.
With potentially serious examination being undertaken of this kind of resource use by entities such as Planetary Resources and even the United States Government, it is important not only to consider what is best or even feasible, but what has the greatest likelihood of being funded or capitalized and actually occurring. In this light, multi-purpose endeavors could be the way to go.
Michael SimonsonMichael Simonson
I can't see how Saturn would ever beat Ceres as a source of water for inner solar system applications. You need a railgun or something to get things off Ceres and some way of cutting chunks of ice out of the ground, but the escape velocity is pretty low. Then you can use a low thrust tug in vacuum to put lumps of ice (no need to put a ship round them) on a trajectory to where you want them.
Steve LintonSteve Linton
$\begingroup$ This may certainly prove to be the best approach. Frankly, what I was imagining in the ring proposition is completely automated ships that keep looping back and forth until they break. An operation that simple seems much easier to automate. That might allow a ship to be both cheap enough to make and durable enough (if it runs on mined water and a nuclear reactor) to be profitable, albeit with a longer payoff period. Long payoff periods might not matter to, for instance, a colony, which needs a long term reliable water source it controls itself. Now you have full disclosure. $\endgroup$ – kim holder Sep 1 '19 at 23:25
$\begingroup$ Underrated answer. The mass of Ceres is ~300 times more than the Saturnian ring mass. Even taking into account the other icy moons of Saturn that one could mine, it is very attractive for economical feasibility to not have to fly around and burn fuel all the time to get the water. $\endgroup$ – AtmosphericPrisonEscape Feb 11 '20 at 11:02
Saturn is not easy to get to. The Earth is already full of water, we don't need to transport ice from 10 AU away to home to have another whiskey on the rocks. Water fills the oceans and the clouds and the polar ices and the underground and even inside ourselves. It is actually a problem that we have too much water, flooding and tsunamis are common causes of catastrophic death. Saturn's water would be used where it is. We would build the X-factory over there instead of bringing home the raw materials.
LocalFluffLocalFluff
$\begingroup$ Erm, delta v for even direct Hohmann from Saturn's rings to LEO should be substantially less than Earth surface to LEO. And there's other savings to be made if you're not in a "hurry" with gravity assist slingshots, cyclers,... see e.g. Cassini-Huygens, that might as well make it worth a long round trip. There's also not so much water on Earth as you seem to suggest. Even Enceladus has more of it. And some of it could be used as fuel / reaction mass... ;) $\endgroup$ – TildalWave Oct 3 '14 at 21:32
$\begingroup$ So you don't see it as useful for the moon or orbit? I don't know what the delta v is to get something back from Saturn's rings, but there does seem to be opportunities for gravity assists that could reduce it a lot. Also there is no hurry here, so ion propulsion could maybe make things a lot more manageable. This has nothing to do with water on Earth. This is about the relative availability of water in space. $\endgroup$ – kim holder Oct 3 '14 at 21:41
$\begingroup$ Why would we stay on Earth? Why not follow the water instead? It is not sane to move the rings of Saturn to Earth's orbit. I fyou want water in space there's plenty of it just half way to Saturn from here. $\endgroup$ – LocalFluff Oct 3 '14 at 22:03
$\begingroup$ The asteroid belt is very diffuse and objects of that convenient size are not well mapped. In the rings, the chunks are very densely packed yet loose and small. Match orbit with the outer ring wherever you want, it is all equally good. It would probably be much easier to program a probe to handle that than to find an appropriate object in the asteroid belt and snag it. And take a lot less maneuvering. Also, since it is almost pure water that makes it much easier to use it as fuel right away, as TildalWave mentioned. $\endgroup$ – kim holder Oct 3 '14 at 22:23
$\begingroup$ Sure, but use it there on site, why bring it to here? $\endgroup$ – LocalFluff Oct 3 '14 at 22:29
Thanks for contributing an answer to Space Exploration Stack Exchange!
Not the answer you're looking for? Browse other questions tagged water mining saturn rings ice or ask your own question.
Is the mission-design tag description wrong? Should the trajectory-design tag…
How much energy is required to send a payload of 40 t from Earth's surface to LEO?
How dense are Saturn's rings?
What forms of water ice have been observed and verified in the solar system?
How will the Cassini spacecraft help constrain the mass of Saturn's rings?
What delta-v per orbit would a spacecraft need to hover next to Saturn's rings?
What kinds of instruments do you need to detect whether liquid water/ice is on a planet?
How do Saturn's rings affect the surface of the planet?
What would you see while falling into Saturn's atmosphere? | CommonCrawl |
back to index | new
Let $a, b, c, d, e$ be distinct positive integers such that $a^4 + b^4 = c^4 + d^4 = e^5$. Show that $ac + bd$ is a composite number.
There is a prime number $p$ such that $16p+1$ is the cube of a positive integer. Find $p$.
Let $f(x)$ be a third-degree polynomial with real coefficients satisfying $$|f(1)|=|f(2)|=|f(3)|=|f(5)|=|f(6)|=|f(7)|=12.$$ Find $|f(0)|$.
Steve says to Jon, 'I am thinking of a polynomial whose roots are all positive integers. The polynomial has the form $$P(x) = 2x^3-2ax^2+(a^2-81)x-c$$
for some positive integers $a$ and $c$. Can you tell me the values of $a$ and $c$?' After some calculations, Jon says, 'There is more than one such polynomial.' Steve says, 'You're right. Here is the value of $a$.' He writes down a positive integer and asks, 'Can you tell me the value of $c$?' Jon says, 'There are still two possible values of $c$.' Find the sum of the two possible values of $c$.
Let $x_1< x_2 < x_3$ be the three real roots of the equation $\sqrt{2014} x^3 - 4029x^2 + 2 = 0$. Find $x_2(x_1+x_3)$.
Let $m$ be the largest real solution to the equation$$\frac{3}{x-3}+\frac{5}{x-5}+\frac{17}{x-17}+\frac{19}{x-19}=x^2-11x-4$$There are positive integers $a$, $b$, and $c$ such that $m=a+\sqrt{b+\sqrt{c}}$. Find $a+b+c$.
Let $f(x) = x^4 + ax^3 + bx^2 + cx + d$. If $f(-1) = -1$, $f(2)=-4$, $f(-3) = -9$, and $f(4) = -16$. Find $f(1)$.
Solve in positive integers $x^2 - 4xy + 5y^2 = 169$.
Solve in integers the question $x+y=x^2 -xy + y^2$.
Solve in integers $\frac{x+y}{x^2-xy+y^2}=\frac{3}{7}$
Prove the product of $4$ consecutive positive integers is a perfect square minus $1$.
For any arithmetic sequence whose terms are all positive integers, show that if one term is a perfect square, this sequence must have infinite number of terms which are perfect squares.
Prove there exist infinite number of positive integer $a$ such that for any positive integer $n$, $n^4 + a$ is not a prime number.
Find all positive integer $n$ such that $(3^{2n+1} -2^{2n+1}- 6^n)$ is a composite number.
Find the number of positive integers $m$ for which there exist nonnegative integers $x_0$, $x_1$ , $\dots$ , $x_{2011}$ such that \[m^{x_0} = \sum_{k = 1}^{2011} m^{x_k}.\]
Suppose $x$ is in the interval $[0, \frac{\pi}{2}]$ and $\log_{24\sin x} (24\cos x)=\frac{3}{2}$. Find $24\cot^2 x$.
Let $P(x)$ be a quadratic polynomial with real coefficients satisfying $x^2 - 2x + 2 \le P(x) \le 2x^2 - 4x + 3$ for all real numbers $x$, and suppose $P(11) = 181$. Find $P(16)$.
Let $(a,b,c)$ be the real solution of the system of equations $x^3 - xyz = 2$, $y^3 - xyz = 6$, $z^3 - xyz = 20$. The greatest possible value of $a^3 + b^3 + c^3$ can be written in the form $\frac {m}{n}$, where $m$ and $n$ are relatively prime positive integers. Find $m + n$.
The zeros of the function $f(x) = x^2-ax+2a$ are integers. What is the sum of the possible values of $a$?
Let $a$, $b$, and $c$ be three distinct one-digit numbers. What is the maximum value of the sum of the roots of the equation $(x-a)(x-b)+(x-b)(x-c)=0$ ?
At the theater children get in for half price. The price for $5$ adult tickets and $4$ child tickets is $24.50$. How much would $8$ adult tickets and $6$ child tickets cost?
The quadratic equation $x^2+ px + 2p = 0$ has solutions $x = a$ and $x = b$. If the quadratic equation $x^2+ cx + d = 0$ has solutions $x = a + 2$ and $x = b + 2$, what is the value of d?
PolynomialAndEquation Root Delta SpecialEquation Function NumberTheoryBasic IndeterminateEquation SqueezeMethod PythagoreanTripletFormula TrigIdentity Inequality LogicalAndReasoning
AMC10/12 AIME IMO
US International
With Solutions
© 2009 - 2023 Math All Star | CommonCrawl |
Is energy extensivity necessary in thermodynamics?
Given a partition of a system into two smaller systems, the energy $U$ is devided into $U_1$ and $U_2$, with $$U=\mathcal{P}(U_1,U_2):=U_1+U_2,$$ so that $U_2$ is given by $U-U_1$. Here the operation $\mathcal{P}$ denotes the partition rule.
What I've written above is basically the extensivity of energy and it somewhat enforces the idea of packages of energy, or particles. The idea of extensivity is closely related to additivity. A small energy flow from system one to system two is then given via
$$U_1\rightarrow \mathbb{fl}^-(U_1):= U_1-\epsilon, \\ U_2\rightarrow \mathbb{fl}^+(U_2):=U_2+\epsilon.$$
What we don't want to drop is energy conservation, so that
$$U=\mathcal{P}(U_1,U_2)=\mathcal{P}(\mathbb{fl}^-(U_1),\mathbb{fl}^+(U_2)),$$
where $\mathbb{fl}^\pm$ define what a flow of energy is supposed to mean, and due to energy conservation these functions in part determined by $\mathcal{P}$.
Are there any good arguments why in thermodynamics or in classical statistical physics, the implicit laws for this kind of divistion should be formulated with a plus sign (other than the fact that there are good theories in which this idea works fulfill)?
After all, there are some models for which the notions of extensivity or additivity are not so clear for all quantities (e.g. some of the entropy-definitions of the last decades).
The relations $$\mathcal{P}(U_2,U_1)=\mathcal{P}(U_1,U_2),$$ $$\mathcal{P}(\mathbb{fl}^-(U_1),\mathbb{fl}^+(U_2))=\mathcal{P}(\mathbb{fl}^+(U_1),\mathbb{fl}^-(U_2)),$$ also seem very natural - although this might not be totally necessary, as the values of $U_1$ and $U_2$ are elements of the reals and therefore ordered/distinguishable.
Also, I think the order of putting subsystems together can't matter
$$\mathcal{P}(U_1,\mathcal{P}(U_2,U_3))=\mathcal{P}(\mathcal{P}(U_1,U_2),U_3).$$
There should be more of these kind of restrictions.
So for example, a first ansatz would be that one could consider $$U=\mathcal{P}(U_1,U_2):=U_1U_2,$$ so that $$\mathbb{fl}^-(U_1)\equiv\tfrac{U_2}{\mathbb{fl}^+(U_2)}U_1.$$
One realization of that (which is constructed such that the change via $\mathbb{fl}^-$ is the same as in the additive case) would be
$$U_1\rightarrow \mathbb{fl}^-(U_1):= \left(1-\tfrac{\epsilon}{U_1}\right)U_1 =U_1-\epsilon, \\ U_2\rightarrow \mathbb{fl}^+(U_2):= \left(1-\tfrac{\epsilon}{U_1}\right)^{-1}U_2 =U_2+\left(\tfrac{U_2}{U_1}\right)\epsilon+ O\left((\tfrac{\epsilon}{U_1})^2\right).$$
thermodynamics energy statistical-mechanics energy-conservation laws-of-physics
Nikolaj-K
Nikolaj-KNikolaj-K
$\begingroup$ If you put two identical systems side by side, and fix their temperature, their energy should be equal. The energy transfer scales as the area, and should vanish if the systems are large and touching. But it's a good question for mathematical models. $\endgroup$ – Ron Maimon Jul 23 '12 at 8:02
$\begingroup$ @RonMaimon: Yes, I tried to get at it like that. But it's a difficult task (for me) to find plausibility arguments like "this and that should..", if this fundamental premise of energy extensivity is changed as I'd only feel save to state restrictions once I used the theory to compute efficiencies of certain real life machines. As a remark, I wrote classical statistical mechanics, just because I expect the dynamics of something like a Hilbert space formalism for non-additive energy operators to be too complicated to formulate (because of non-linearities). Not that it would be easy classicaly. $\endgroup$ – Nikolaj-K Jul 23 '12 at 8:08
$\begingroup$ For the thermodynamics of gravitating systems, the energy extensivity does not hold. For this reason, e.g., objects like globular clusters or black holes have negative heat capacity. $\endgroup$ – Slaviks Jul 23 '12 at 8:27
$\begingroup$ @Slaviks: That's a good point regarding the title question. Question: Does energy conservation hold in these systems? $\endgroup$ – Nikolaj-K Jul 23 '12 at 8:36
$\begingroup$ I think it does - by virialization you get higher and higher velocities (temperatures) as the most energetic stars escape to infinity due to >2 body dynamics. $\endgroup$ – Slaviks Jul 23 '12 at 9:06
From the statistical mechanics perspective, the fact that energy is conserved forces it to be one of the extensive variables in any thermodynamic description.
$\begingroup$ You mean if the energy $H$, for which $U=\langle H \rangle$, simultaneously describes the microscopic dynamics in the conventional way, right? $\endgroup$ – Nikolaj-K Jul 23 '12 at 13:42
$\begingroup$ @NickKidman: Yes. $\endgroup$ – Arnold Neumaier Jul 23 '12 at 13:47
I'm not sure to what extent this answers your question, but here are some of my thoughts on this. If energy were not extensive then it would not cause problems for the formalism of thermodynamics, but we would no longer have the fact that all temperatures become equal at equilibrium. Let's examine your example where $U = U_1 U_2$. We'll say the entropy is still extensive, so that $S = S_1(U_1) + S_2(U_2)$. Let's consider putting these two bodies in contact and allowing them to go to equilibrium. This happens when $$\frac{\partial S_1}{\partial U_1}dU_1 = \frac{\partial S_2}{\partial U_2}dU_2,$$ or $$\frac{dU_1}{T_1} = \frac{dU_2}{T_2},$$ according to the definition of temperature.
In regular thermodynamics we have that $dU_1 = -dU_2$, which allows us to conclude that $1/T_1 = 1/T_2$ when the bodies are in equilibrium. However, in this example we instead have that $dU_1/U_1 = dU_2/U_2$. (You can see this by noting that $\log(U_1) + \log(U_2)$ is the conserved quantity.) This means that, at equilibrium we have $U_1/T_2 = U_2/T_1$ instead of $T_1 = T_2$, so the temperatures won't be equal in general.
This sort of thing happens all the time in chemistry: if you're dealing with a reaction like $X\leftrightarrow Y$ then the two chemical potentials become equal at equilibrium, whereas for something like $X\leftrightarrow 2Y$ they do not, because $X+Y$ is not conserved.
On a more physical level, I should note that the extensivity of energy is an approximation, and it fails in particular for very small systems. This is because there can be energy in the interaction between the two systems. In particular, for two strongly interacting particles, it really doesn't make sense to try and divide the Hamiltonian $H$ into $H_1+H_2$. It's only as the systems become large that the internal energy terms dominate over the interaction terms and energy becomes approximately extensive. As long as the two systems are interacting there has to be an interaction term, i.e. $H=H_1 + H_2 + H_\text{interaction}$, but $H_\text{interaction}$ can be very small compared to the other terms. Extensivity can also fail to happen if gravitational attraction between the systems is important, which I think is ultimately why gravitationally-bound systems have negative heat capacities.
The situation for entropy is similar, in that it only becomes extensive when interaction terms can be neglected, and this tends to happen for macroscopically-sized systems near equilibrium. It's only when we start to reach this large-system limit that statistical mechanics starts to turn into thermodynamics.
Finally, I want to note that thermodynamics could be defined to work just fine, even if energy didn't exist at all. The fundamental equation is usually written $$ dU = TdS - pdV + \sum_i\mu_i dN_i + \text{terms for things like charge and momentum} $$ but what you really get from statistical mechanics is $$ dS = \lambda_U dU + \lambda_V dV + \sum_i \lambda_{N_i}dN_i + \dots, $$ where $\lambda_U = 1/T$, $\lambda_V = p/T$, $\lambda_{N_i} = -\mu_i/T$, etc. I regard this as much more fundamental, because it puts the "special" quantity $S$ on the left hand side and all the conserved quantities on the right. When thermodynamics is formulated this way, energy loses what appeared to be its special role, and it behaves exactly like all of the other conserved quantities. If energy didn't exist at all (but the microscopic dynamics still obeyed Liouville's theorem) then we would simply lose the first term on the right-hand side of this equation, but everything else would stay the same, as long as we worked in terms of $\lambda_V$ and $\lambda_{N_i}$ instead of $p$ and $\mu_i$.
NathanielNathaniel
$\begingroup$ Thanks on all the comments regarding extensivity. That $T_1=T_2$ doesn't hold is not bothersome. Because now, as you computed, the quantities $\tau=U_iT_i$ would just take the role of the "temperature", i.e. these variables which are equal at equilibrium. $\endgroup$ – Nikolaj-K Jul 23 '12 at 17:51
$\begingroup$ In a sense, that's exactly what has happened. It happens that there is a quantity that combines multiplicatively. Let's call it $X$ for now. For two interacting systems, $X = X_1 X_2$. The "temperatures" relating to this quantity are $R_i=1/(\partial S/\partial X_i)$, but they're not equal in equilibrium. Instead, the quantities $X_iR_i$ become equal. What is $X_i$? It's $e^{U_i}$, and $X_i R_i$ is what we call $T_i$. $\endgroup$ – Nathaniel Jul 23 '12 at 22:13
What happened to U if U1=U2 ? You loose energy conservation...
Thermodynamics is not a fundamental theory. It can be derived from kinetic theory which is itself derived from mechanics. Energy in mechanics is an additive function, and unless you want to modify the rules for integrals (Chasles) it remains additive in kinetic theory and thermodynamics.
ShaktyaiShaktyai
$\begingroup$ I don't understand the first sentence. How do you argue that you lose energy conservation without reference to an energy change? To the second statement, yes, one would have to modify the microscopic theory too if (1) one is interested in more than purely thermodynamical calculations and (2) one wants to hold the conceptual idea, that the propsed modified thermodynamical theory also has a motivation in microscopic dynamics. $\endgroup$ – Nikolaj-K Jul 23 '12 at 9:51
$\begingroup$ If U1=U2=U/2 and U=U1*U2 as proposed then U=U^2/4 and you loose energy conservation for general U. $\endgroup$ – Shaktyai Jul 23 '12 at 10:30
$\begingroup$ No, the relation "$U1=U2=U/2$" doesn't hold. How the total energy $U$ depends on the energies of the respecive systems $U_1,U_2$ is determined by $\mathcal P$. $\endgroup$ – Nikolaj-K Jul 23 '12 at 11:27
$\begingroup$ Then I do not understand your notation. What do you mean when you write: U=P(U1,U2):=U1U2, ? Is it not a product of U1 and U2 ? $\endgroup$ – Shaktyai Jul 23 '12 at 15:02
$\begingroup$ It is a product. The point is that the function $\mathcal{P}$ for $U=\mathcal{P}(U_1,U_2)$ is to be choosen, it's not assumed that $U=U_1+U_2$ $\endgroup$ – Nikolaj-K Jul 23 '12 at 15:08
I did some research about your idea of non extensive statistical theory and have found a positive answer to your question, though the theory is quite involved. To make things simple: Gibbs theorem presupposes ergodicity. We have extensive evidence that systems far from equilibrium exhibit both self organisation at any scale and chaotic regions: a behaviour incomptible with ergodicity. To take into account these observations Tsallis has introduced a non extensive entropy which asymptoticaly matches the Gibbs Boltzmann entropy. The corresponding non equilibrium theory involves fractal dynamics and fractal operators.
You can find an excellent presentation of the theory in this paper: http://arxiv.org/ftp/arxiv/papers/1203/1203.4003.pdf
$\begingroup$ The OP is talking about non-extensivity of energy rather than entropy. Non-extensivity of entropy is a whole different topic... $\endgroup$ – Nathaniel Jul 28 '12 at 10:17
$\begingroup$ The paper is more general and gives (paragraph 2.4.3) the whole procedure to compute the statistical distribution function. Fractal dynamics is non local, so the averaging procedure for any dynamical functions is no longer additive. $\endgroup$ – Shaktyai Jul 28 '12 at 16:37
Not the answer you're looking for? Browse other questions tagged thermodynamics energy statistical-mechanics energy-conservation laws-of-physics or ask your own question.
How to understand temperatures of different degrees of freedom?
Does the second law of thermodynamics tell me how the entropy changes?
Noether Theorem and Energy conservation in classical mechanics
Entropy of a two-level system
Is $\mathrm d(PV)$ the same with work received OR produced?
Find the probability that a system has energy $\epsilon$ at $T = \infty$
Entropy of two subsystems exchanging energy
Conservation of total energy for a system with holonomic constraints | CommonCrawl |
Spherical mean transform: A PDE approach
IPI Home
Constrained SART algorithm for inverse problems in image reconstruction
February 2013, 7(1): 217-242. doi: 10.3934/ipi.2013.7.217
Recovering boundary shape and conductivity in electrical impedance tomography
Ville Kolehmainen 1, , Matti Lassas 2, , Petri Ola 2, and Samuli Siltanen 3,
University of Eastern Finland, Department of Applied Physics, P.O.Box 1627, 70211 Kuopio, Finland
University of Helsinki, Department of Mathematics and Statistics, P.O.Box 68, 00014 University of Helsinki, Finland, Finland
Department of Mathematics and Statistics, P.O. Box 68, 00014 University of Helsinki, Finland
Received November 2011 Revised May 2012 Published February 2013
Electrical impedance tomography (EIT) aims to reconstruct the electric conductivity inside a physical body from current-to-voltage measurements at the boundary of the body. In practical EIT one often lacks exact knowledge of the domain boundary, and inaccurate modeling of the boundary causes artifacts in the reconstructions. A novel method is presented for recovering the boundary shape and an isotropic conductivity from EIT data. The first step is to determine the minimally anisotropic conductivity in a model domain reproducing the measured EIT data. Second, a Beltrami equation is solved, providing shape-deforming reconstruction. The algorithm is applied to simulated noisy data from a realistic electrode model, demonstrating that approximate recovery of the boundary shape and conductivity is feasible.
Keywords: conformal deformation., electrical impedance tomography, minimally anisotropic conductivity, quasiconformal maps, Inverse conductivity problem.
Mathematics Subject Classification: Primary: 35R30, 65N21; Secondary: 65J2.
Citation: Ville Kolehmainen, Matti Lassas, Petri Ola, Samuli Siltanen. Recovering boundary shape and conductivity in electrical impedance tomography. Inverse Problems & Imaging, 2013, 7 (1) : 217-242. doi: 10.3934/ipi.2013.7.217
A. Adler, R. Guardo and Y. Berthiaume, Impedance imaging of lung ventilation: Do we need to account for chest expansion?,, IEEE Trans. Biomed. Eng., 43 (1996), 414. Google Scholar
L. Ahlfors, "Lectures on Quasiconformal Mappings,", Van Nostrand Mathematical Studies, (1966). Google Scholar
K. Astala, T. Iwaniec and G. Martin, "Elliptic Partial Differential Equations and Quasiconformal Mappings in the Plane,", Princeton Mathematical Series, 48 (2009). Google Scholar
K. Astala, M. Lassas and L. Päivärinta, Calderón's inverse problem for anisotropic conductivity in the plane,, Comm. Partial Differential Equations, 30 (2005), 207. doi: 10.1081/PDE-200044485. Google Scholar
K. Astala and L. Päivärinta, Calderón's inverse conductivity problem in the plane,, Ann. of Math. (2), 163 (2006), 265. doi: 10.4007/annals.2006.163.265. Google Scholar
K. Astala, J. L. Mueller, L. Paivarinta and S. Siltanen, Numerical computation of complex geometrical optics solutions to the conductivity equation,, Applied and Computational Harmonic Analysis, 29 (2010), 2. doi: 10.1016/j.acha.2009.08.001. Google Scholar
D. C. Barber and B. H. Brown, Applied potential tomography,, J. Phys. E: Sci. Instrum., 17 (1984), 723. Google Scholar
A. Boyle, W. R. B. Lionheart, C. Gómez-Laberge and A. Adler, Evaluating deformation corrections in electrical impedance tomography,, in, (2008), 16. Google Scholar
A. Boyle and A. Adler, The impact of electrode area, contact impedance and boundary shape on EIT images,, Physiological Measurement, 32 (2011), 745. Google Scholar
V. Bozin, N. Lakic, V. Markovic and M. Mateljevic, Unique extremality,, J. Anal. Math. 75 (1998), 75 (1998), 299. doi: 10.1007/BF02788704. Google Scholar
R. Brown and G. Uhlmann, Uniqueness in the inverse conductivity problem for non-smooth conductivities in two dimensions,, Comm. Partial Differential Equations, 22 (1997), 1009. doi: 10.1080/03605309708821292. Google Scholar
A. Calderón, On an inverse boundary value problem,, Seminar on Numerical Analysis and its Applications to Continuum Physics (Rio de Janeiro, (1980), 65. Google Scholar
M. Cheney, D. Isaacson and J. C. Newell, Electrical impedance tomography,, SIAM Review, 41 (1999), 85. doi: 10.1137/S0036144598333613. Google Scholar
K.-S.Cheng, D. Isaacson, J. C. Newell and D. G. Gisser, Electrode models for electric current computed tomography,, IEEE Trans. Biomed. Eng., 36 (1989), 918. Google Scholar
E. L. V. Costa, C. N. Chaves, S. Gomes, M. A. Beraldo, M. S. Volpe, M. R. Tucci, I. A. L. Schettino, S. H. Bohm, C. R. R. Carvalho, H. Tanaka, R. G. Lima and M. B. A. Amato, Real-time detection of pneumothorax using electrical impedance tomography,, Crit. Care. Med., 36 (2008), 1230. Google Scholar
T. Dai, C. Gomez-Laberge and A. Adler, Reconstruction of conductivity changes and electrode movements based on EIT temporal sequences,, Physiol. Meas., 29 (2008). Google Scholar
E. Gersing, B. Hoffman and M. Osypka, Influence of changing peripheral geometry on electrical impedance tomography measurements,, Medical & Biological Engineering & Computing, 34 (1996), 359. Google Scholar
A. Greenleaf, Y. Kurylev, M. Lassas, and G. Uhlmann, Full-wave invisibility of active devices at all frequencies,, Comm. Math. Phys., 275 (2007), 749. doi: 10.1007/s00220-007-0311-6. Google Scholar
A. Greenleaf, Y. Kurylev, M. Lassas and G. Uhlmann, Invisibility and inverse problems,, Bull. Amer. Math. Soc. (N.S.), 46 (2009), 55. doi: 10.1090/S0273-0979-08-01232-9. Google Scholar
A. Greenleaf, Y. Kurylev, M. Lassas and G. Uhlmann, Cloaking devices, electromagnetic wormholes and transformation optics,, SIAM Review, 51 (2009), 3. doi: 10.1137/080716827. Google Scholar
A. Greenleaf, M. Lassas and G. Uhlmann, On nonuniqueness for Calderón's inverse problem,, Math. Res. Lett., 10 (2003), 685. Google Scholar
A. Greenleaf, M. Lassas and G. Uhlmann, Anisotropic conductivities that cannot detected in EIT,, Physiological Measurement, 24 (2003), 413. Google Scholar
G. Hahn, A. Just, T. Dudykevych, I. Frerichs, J. Hinz, M. Quintel and G. Hellige, Imaging pathologic pulmonary air and fluid accumulation by functional and absolute EIT,, Physiol. Meas., 27 (2006). Google Scholar
D. Isaacson, J. Mueller, J. C. Newell and S. Siltanen, Reconstructions of chest phantoms by the d-bar method for electrical impedance tomography,, IEEE Trans. Med. Im., 23 (2004), 821. Google Scholar
D. Isaacson, J. L. Mueller, J. C. Newell and S. Siltanen, Imaging cardiac activity by the D-bar method for electrical impedance tomography,, Physiological Measurement, 27 (2006). Google Scholar
H. Jain, D. Isaacson, P. M. Edic and J. C. Newell, Electrical impedance tomography of complex conductivity distributions with noncircular boundary,, IEEE Trans. Biomed. Eng., 44 (1997), 1051. Google Scholar
J. P. Kaipio, V. Kolehmainen, E. Somersalo and M. Vauhkonen, Statistical inversion and Monte Carlo sampling methods in electrical impedance tomography,, Inverse Problems, 16 (2000), 1487. doi: 10.1088/0266-5611/16/5/321. Google Scholar
R. Kohn and M. Vogelius, Identification of an unknown conductivity by means of measurements at the boundary,, in, 14 (1984), 113. Google Scholar
R. Kohn, H. Shen, M. Vogelius and M. Weinstein, Cloaking via change of variables in electrical impedance tomography,, Inverse Problems, 24 (2008). doi: 10.1088/0266-5611/24/1/015016. Google Scholar
K. Knudsen, M. Lassas, J. L. Mueller and S. Siltanen, Regularized D-bar method for the inverse conductivity problem,, Inverse Problems and Imaging, 3 (2009), 599. doi: 10.3934/ipi.2009.3.599. Google Scholar
V. Kolehmainen, M. Vauhkonen, P. A. Karjalainen and J. P. Kaipio, Assessment of errors in static electrical impedance tomography with adjacent and trigonometric current patterns,, Physiological Measurement, 18 (1997), 289. Google Scholar
V. Kolehmainen, M. Lassas and P. Ola, The inverse conductivity problem with an imperfectly known boundary,, SIAM J. Appl. Math., 66 (2005), 365. doi: 10.1137/040612737. Google Scholar
V. Kolehmainen, M. Lassas and P. Ola, The inverse conductivity problem with an imperfectly known boundary in three dimensions,, SIAM J. Appl. Math., 67 (2007), 1440. doi: 10.1137/060666986. Google Scholar
V. Kolehmainen, M. Lassas and P. Ola, Calderón's inverse problem with an imperfectly known boundary and reconstruction up to a conformal deformation,, SIAM J. Math. Anal., 42 (2010), 1371. doi: 10.1137/080716918. Google Scholar
V. Kolehmainen, M. Lassas and P. Ola, Electrical impedance tomography problem with inaccurately known boundary and contact impedances,, IEEE Trans. Med. Im., 27 (2008), 1404. Google Scholar
M. Lassas and G. Uhlmann, On determining Riemannian manifold from the Dirichlet-to-Neumann map,, Annales Scientifiques de l'Ecole Normale Superieure (4), 34 (2001), 771. doi: 10.1016/S0012-9593(01)01076-X. Google Scholar
W. Lionheart, Conformal uniqueness results in anisotropic electrical impedance imaging,, Inverse Problems, 13 (1997), 125. doi: 10.1088/0266-5611/13/1/010. Google Scholar
W. Lionheart, Boundary shape and electrical impedance tomography,, Inverse Problems, 14 (1998), 139. doi: 10.1088/0266-5611/14/1/012. Google Scholar
A. Nachman, Global uniqueness for a two-dimensional inverse boundary value problem,, Ann. Math. (2), 143 (1996), 71. doi: 10.2307/2118653. Google Scholar
A. Nissinen, V. Kolehmainen and J. P. Kaipio, Compensation of modelling errors due to unknown domain boundary in electrical impedance tomography,, IEEE Trans. Med. Imag., 30 (2011), 231. Google Scholar
A. Nissinen, V. Kolehmainen and J. P. Kaipio, Reconstruction of domain boundary and conductivity in electrical impedance tomography using the approximation error approach,, International Journal for Uncertainty Quantification, 1 (2011), 203. doi: 10.1615/Int.J.UncertaintyQuantification.v1.i3.20. Google Scholar
J. Nocedal and S. J. Wright, "Numerical Optimization,", Second edition, (2006). Google Scholar
Ch. Pommerenke, "Boundary Behaviour of Conformal Maps,", Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 299 (1992). Google Scholar
S. Siltanen, J. Mueller and D. Isaacson, An implementation of the reconstruction algorithm of A. Nachman for the 2D inverse conductivity problem,, Inverse Problems, 16 (2000), 681. doi: 10.1088/0266-5611/16/3/310. Google Scholar
M. Soleimaini, C. Gómez-Laberge and A. Adler, Imaging of conductivity changes and electrode movement in EIT,, Physiol. Meas., 27 (2006). Google Scholar
E. Somersalo, M. Cheney and D. Isaacson, Existence and uniqueness for electrode models for electric current computed tomography,, SIAM J. Appl. Math., 52 (1992), 1023. doi: 10.1137/0152060. Google Scholar
K. Strebel, On the existence of extremal Teichmüller mappings,, J. Anal. Math., 30 (1976), 464. Google Scholar
J. Sylvester, An anisotropic inverse boundary value problem,, Comm. Pure Appl. Math., 43 (1990), 201. doi: 10.1002/cpa.3160430203. Google Scholar
Andreas Kreuml. The anisotropic fractional isoperimetric problem with respect to unconditional unit balls. Communications on Pure & Applied Analysis, , () : -. doi: 10.3934/cpaa.2020290
Kien Trung Nguyen, Vo Nguyen Minh Hieu, Van Huy Pham. Inverse group 1-median problem on trees. Journal of Industrial & Management Optimization, 2021, 17 (1) : 221-232. doi: 10.3934/jimo.2019108
Shumin Li, Masahiro Yamamoto, Bernadette Miara. A Carleman estimate for the linear shallow shell equation and an inverse source problem. Discrete & Continuous Dynamical Systems - A, 2009, 23 (1&2) : 367-380. doi: 10.3934/dcds.2009.23.367
Jianli Xiang, Guozheng Yan. The uniqueness of the inverse elastic wave scattering problem based on the mixed reciprocity relation. Inverse Problems & Imaging, , () : -. doi: 10.3934/ipi.2021004
Shahede Omidi, Jafar Fathali. Inverse single facility location problem on a tree with balancing on the distance of server to clients. Journal of Industrial & Management Optimization, 2020 doi: 10.3934/jimo.2021017
Lekbir Afraites, Chorouk Masnaoui, Mourad Nachaoui. Shape optimization method for an inverse geometric source problem and stability at critical shape. Discrete & Continuous Dynamical Systems - S, 2021 doi: 10.3934/dcdss.2021006
Stanislav Nikolaevich Antontsev, Serik Ersultanovich Aitzhanov, Guzel Rashitkhuzhakyzy Ashurova. An inverse problem for the pseudo-parabolic equation with p-Laplacian. Evolution Equations & Control Theory, 2021 doi: 10.3934/eect.2021005
Vincent Ducrot, Pascal Frey, Alexandra Claisse. Levelsets and anisotropic mesh adaptation. Discrete & Continuous Dynamical Systems - A, 2009, 23 (1&2) : 165-183. doi: 10.3934/dcds.2009.23.165
Weihong Guo, Yifei Lou, Jing Qin, Ming Yan. IPI special issue on "mathematical/statistical approaches in data science" in the Inverse Problem and Imaging. Inverse Problems & Imaging, 2021, 15 (1) : I-I. doi: 10.3934/ipi.2021007
Wenjun Liu, Yukun Xiao, Xiaoqing Yue. Classification of finite irreducible conformal modules over Lie conformal algebra $ \mathcal{W}(a, b, r) $. Electronic Research Archive, , () : -. doi: 10.3934/era.2020123
Editorial Office. Retraction: Xiaohong Zhu, Zili Yang and Tabharit Zoubir, Research on the matching algorithm for heterologous image after deformation in the same scene. Discrete & Continuous Dynamical Systems - S, 2019, 12 (4&5) : 1281-1281. doi: 10.3934/dcdss.2019088
Mark F. Demers. Uniqueness and exponential mixing for the measure of maximal entropy for piecewise hyperbolic maps. Discrete & Continuous Dynamical Systems - A, 2021, 41 (1) : 217-256. doi: 10.3934/dcds.2020217
Claudio Bonanno, Marco Lenci. Pomeau-Manneville maps are global-local mixing. Discrete & Continuous Dynamical Systems - A, 2021, 41 (3) : 1051-1069. doi: 10.3934/dcds.2020309
Josselin Garnier, Knut Sølna. Enhanced Backscattering of a partially coherent field from an anisotropic random lossy medium. Discrete & Continuous Dynamical Systems - B, 2021, 26 (2) : 1171-1195. doi: 10.3934/dcdsb.2020158
Hongbo Guan, Yong Yang, Huiqing Zhu. A nonuniform anisotropic FEM for elliptic boundary layer optimal control problems. Discrete & Continuous Dynamical Systems - B, 2021, 26 (3) : 1711-1722. doi: 10.3934/dcdsb.2020179
Bernard Bonnard, Jérémy Rouot. Geometric optimal techniques to control the muscular force response to functional electrical stimulation using a non-isometric force-fatigue model. Journal of Geometric Mechanics, 2020 doi: 10.3934/jgm.2020032
Gunther Uhlmann, Jian Zhai. Inverse problems for nonlinear hyperbolic equations. Discrete & Continuous Dynamical Systems - A, 2021, 41 (1) : 455-469. doi: 10.3934/dcds.2020380
Guoyuan Chen, Yong Liu, Juncheng Wei. Nondegeneracy of harmonic maps from $ {{\mathbb{R}}^{2}} $ to $ {{\mathbb{S}}^{2}} $. Discrete & Continuous Dynamical Systems - A, 2020, 40 (6) : 3215-3233. doi: 10.3934/dcds.2019228
Magdalena Foryś-Krawiec, Jiří Kupka, Piotr Oprocha, Xueting Tian. On entropy of $ \Phi $-irregular and $ \Phi $-level sets in maps with the shadowing property. Discrete & Continuous Dynamical Systems - A, 2021, 41 (3) : 1271-1296. doi: 10.3934/dcds.2020317
Yi-Hsuan Lin, Gen Nakamura, Roland Potthast, Haibing Wang. Duality between range and no-response tests and its application for inverse problems. Inverse Problems & Imaging, , () : -. doi: 10.3934/ipi.2020072
Ville Kolehmainen Matti Lassas Petri Ola Samuli Siltanen | CommonCrawl |
Electrical transient modeling for appliance characterization
Mohamed Nait-Meziane ORCID: orcid.org/0000-0002-7506-27031,
Philippe Ravier1,
Karim Abed-Meraim1,
Guy Lamarque1,
Jean-Charles Le Bunetel2 &
Yves Raingeaud2
EURASIP Journal on Advances in Signal Processing volume 2019, Article number: 55 (2019) Cite this article
Transient signals are characteristic of the underlying phenomenon generating them, which makes their analysis useful in many fields. Transients occur as a sudden change between two steady state regimes, subsist for a short period, and tend to decay over time. Hence, superimposed damped sinusoids (SDS) were extensively used for transients modeling as they are adequate for describing decaying phenomena. However, SDS are not adapted for modeling the turn-on transient current of electrical appliances as it tends to decay to a steady state that is different from the one preceding it. In this paper, we propose a new and more suitable model for these signals for the purpose of characterizing appliances. We also propose an algorithm for the model parameter estimation and validate its performance on simulated and real data. Moreover, we give an example on the use of the model parameters as features for the classification of appliances using the Controlled On/Off Loads Library (COOLL) dataset. The results show that the proposed algorithm is efficient and that for real data the network fundamental frequency must be estimated to account for its variations around the nominal value. Finally, real data experiments showed that the model parameters used as features yielded a classification accuracy of 98%.
Studying transient phenomena is important and useful in many fields such as biomedical research for the analysis of heart rate variability [1], the extraction of detailed information of muscle behavior [2], and the detection and classification of epileptic spikes [3]; mechanics for the study of the susceptibility of structures to vibration issues [4]; and for seismic events detection and temporal localization [5, 6]. Monitoring electrical loads and systems is particularly one of the areas where transients play a central role. We cite as applications the analysis of disturbances affecting the quality of the electric power system [7, 8], fault detection in rotary machines [9, 10], and non-intrusive load monitoring (NILM) [11–13], a field concerned with extracting individual energy consumption (e.g., of different appliances) from measured total energy consumption (e.g., at main breaker panel).
Transients embed a decay or damping characteristic as they exist for short periods, and therefore, the superimposed damped sinusoids (SDS) model [14] was extensively used to model transients in many fields. For example, it was used for modeling electric disturbances [15], transient audio signals [16], and the free induction decay observed in nuclear resonance spectroscopy [17]. Along with the model, different algorithms were proposed for its parameter estimation [18]. The most known methods are Prony's [19], Pisarenko's [20], matrix pencil [21], Estimation of Signal Parameters via Rotational Invariance Techniques (ESPRIT) [22], and MUltiple SIgnal Classification (MUSIC) [23]. Despite its success, the SDS model is inadequate for turn-on transient current signals. In fact, a lot of turn-on transient current signals are characterized by a quasi-stationary harmonic content (Fig. 1a) whereas the SDS model is best suited for modeling vanishing non-stationary content (Fig. 1b) because having different damping factors for each frequency produces a signal with non-stationary frequency content. Moreover, the turn-on transient current decays to a steady state that is different from the steady state preceding the turn-on of the appliance, whereas in the SDS the transient model starts from one steady state and decays to the same one afterwards. The electrical current "turn-on" transient is the current that appears with the switching-on of an electrical appliance. This corresponds to a transition from one steady state to another. For example, if we consider a single appliance on the network, then the first steady state is the state of no consumption, the second steady state is the state of steady consumption, and the transient is the part in between. Note that the transient we are interested in modeling is the one related to the electrical consumption. This transient is different from the very high frequency transient (appearing as a short pulse preceding the turn-on transient) generated by the switching devices because of the closure of the circuit [24]. Turn-on transients are appliance-dependent and last usually from few power system cycles to few seconds. A turn-on transient is typically characterized by a high current amplitude (surge) at the beginning of consumption followed by a decrease (or damping) in the amplitude of the consumed energy until reaching a stable state (Fig. 1a).
Two examples of transients. a A (turn-on) transient of an electrical signal (drill) for which the superimposed damped sinusoids (SDS) model is inadequate, and b a transient of an audio signal (castanets) for which the SDS model is adequate. Note the non-stationary content of b and the quasi-stationary content of a
In this paper, we propose a new model for turn-on transient current signals along with an efficient algorithm for the parameter estimation. The parameters are used to characterize electrical appliances and are shown to be useful for appliance classification. Several objectives are targeted in this paper including:
Derivation of an efficient estimation algorithm for the model parameters.
Assessment of the estimation performance via the computation of the Cramér-Rao bound (CRB).
Validation of the proposed model on real transient signals and the evaluation of the modeling error when using the developed estimation algorithm.
Exploitation of the model parameters for appliance characterization and assessment of their usefulness as relevant features for a classification task example.
As a by-product, we also developed a full experimental setup (with a dedicated transient signal acquisition device) to build our dataset of real transient signals corresponding to different electrical appliances. This dataset is used for our model validation as well as for the performance assessment of the proposed appliance identification method.
The rest of the paper is organized as follows: Section 2.1 describes the proposed data model, Section 2.2 details the proposed parameter estimation algorithm, Section 3 gives the derivation of the parameters' CRBs, Section 4.1 gives the assessment of the proposed model and algorithm on simulated and real data, Section 4.2 shows the usefulness of the model parameters through an appliance classification example, and finally, Section 5 concludes the paper.
In this section, we propose and discuss a mathematical model for turn-on transient current signals. Strictly speaking, we model the turn-on transient including a small part of the following steady state regime; mainly because the transient end is not well defined and because estimating the harmonic content is easier on the steady state part.
The shape of the turn-on transient and the related amplitudes vary from one electrical appliance to another. To take into account these variations, we propose to model the noiseless electrical current turn-on transient s(t) as the product of two signals
$$ s(t) = e(t)s_{s}(t), \quad \forall t\in [0, +\infty) $$
where e(t) represents an amplitude modulation (envelope) and ss(t) is a sum of d sinusoids given as follows
$$ s_{s}(t) = {\sum\limits_{i = 1}^d {{a_i}{\cos\left(2\pi {f_i}t + \phi_{i}\right)}}}, \quad \forall t\in [0, +\infty) $$
where ai (≥0), ϕi∈[−π,π] and fi are the sinusoids amplitudes, phases, and frequencies, respectively. The number d of sinusoids (current harmonics) is assumed known (typically d=5 harmonics is enough to represent the sinusoidal signal ss(t)) and the frequencies satisfy fi=(2i−1)f0,i=1,…,d where f0≈50 Hz. Indeed, because of the half-wave symmetry found in electrical signals (i.e., for a periodic signal g(t) of period P, a half-wave symmetry is characterized by g(t+P/2)=−g(t)), the sinusoid frequencies fi are odd-order harmonics of the fundamental frequency. Note that the nominal value (50 Hz) of the network fundamental frequency is a priori known, but due to its fluctuations around this value over time (i.e., f0=50+δf), we have observed that for a correct modeling, f0 should be considered as unknown and hence one needs to re-estimate the fundamental frequency value for each transient signalFootnote 1.
The envelope e(t) is chosen of the form eu(t)+1 such that \(e^{u(t)}\xrightarrow [{t \to + \infty }]{}0\). This exponential function was chosen for its usefulness in describing damped phenomena. A classical damped model is such that u(t)=−αt with α>0. For our model, we propose to extend this classical model in order to adapt it to real current signals. Specifically, we propose to model u(t) as a polynomial function allowing more flexibility in describing the amplitude modulation of real signals
$$ e(t) = {e^{{\text{p}^{T}}\text{t}}} + 1, \quad \forall t\in [0, +\infty) $$
where p=[p0,p1,…,pn]T is a vector of n+1 polynomial coefficients and t=[1,t,…,tn]T is a time vector such that pTt is a polynomial of degree n allowing the model adaptation to the real signal variationsFootnote 2. The polynomial is such that \({\text {p}^{T}}\text {t}\mathop {\longrightarrow } \limits _{t \to + \infty } - \infty \) leading to \(e(t)\mathop {\longrightarrow } \limits _{t \to + \infty } 1\) (verified if pn<0).
We assume that the measured current signal x(t) is corrupted by an additive white Gaussian noise (AWGN) w(t) with zero mean and variance σ2
$$ x(t) = s(t)+w(t), \quad \forall t\in \mathbb{R}. $$
The passage from continuous to discrete-time notation is done using tk=kTs, where Ts=1/Fs is the sampling period and \(k\in \mathbb {Z}\). This notation is used in the remainder of the paper.
Parameter estimation algorithm
The proposed parameter estimation algorithm proceeds in two steps:
Estimation of the fundamental frequency f0.
Estimation of the other signal parameters using the a priori estimated frequency \(\hat {f}_{0}\).
Fundamental frequency estimation
We assume that the fundamental frequency is unknown but quasi-constant over the transient duration, typically less than 5 s, and we propose to estimate it using the voltage signal, which is almost perfectly sinusoidal (Fig. 2). Indeed, the stability of f0 (i.e., its rate of change) is an important issue that was discussed in depth in the literature. This can be seen from the plot in Fig. 3 (borrowed from http://wwwhome.cs.utwente.nl/~ptdeboer/misc/mains.html) which represents the "Allan deviation" of f0 for a measurement over a period of 69 days. As explained in this reference, if the Allan deviation at an averaging duration of 10 s is 10−4, it means that if one measures the frequency during 10 s and once more during the next 10 s, these measurements will differ on average by 0.01%. Based on this, we consider the frequency variation over our 5-s measurement period as negligible. Hence, the fundamental frequency estimation problem turns into the classical problem of estimating the frequency of a monotone signal in noise. It is known that the CRB of the frequency parameter of a monotone signal decreases with a rate of 1/N3 [26]
$$ \text{var}(\hat{f}_0) \ge \frac{12}{(2\pi)^2 \eta N(N^2-1)}, $$
A real voltage signal
Stability of network frequency (log-log plot of Allan deviation). Source: http://wwwhome.cs.utwente.nl/ ~ptdeboer/misc/mains.html
where η is the signal-to-noise ratio (SNR) and N the number of signal samples. This allows for highly precise frequency estimates. Practically, we use the algorithm proposed by Aboutanios and Mulgrew [27] which is shown to provide a precise frequency estimate reaching the CRB. Indeed, the voltage signal is modeled here as a pure sinusoid of frequency f0 corrupted by an AWGN. In such a case, the optimal maximum likelihood (ML) solution coincides with the peak location estimation of the Fourier transform of the signal. This estimation is achieved by the low cost efficient numerical method in [27].
In the second step (next section), we estimate the remaining parameters using the frequency \(\hat {f}_{0}\).
Transient current estimation (TCE) algorithm
Given the estimated frequency \(\hat {f}_{0}\), the second step of our estimation algorithm operates in two phases: (i) initialization and (ii) parameter estimation.
The initialization phase provides initial estimates of the parameters pj,ai, and ϕi (j=0,…,n and i=1,…,d) to be used in the parameter estimation phase, during which these estimates will be refined. This two-phase structure of the algorithm is motivated by the difficulty and high computational cost of the nonlinear maximum-likelihood-based estimation criterion (see (15)). In such a case, we usually seek a good initial estimate and then refine it in order to alleviate the ill-convergence and high computational cost of the problem.
Note that the algorithm needs some pre-specified values for n, d, and fi and also needs a pre-defined steady state portion used in the initialization step for the estimation of the amplitudes ai and phases ϕi of the sinusoids. Hereafter, we start by discussing these "pre-specified quantities," then we proceed to detailing the algorithm.
Pre-specified quantities
These quantities are fi (i=1,…,d),n,d,tss1, and tss2 ("ss" stands for steady state). As mentioned in Section 2.1, fi are odd-order harmonics of f0. Taking into account the estimated fundamental frequency \(\hat {f}_{0}\), the sinusoids' frequencies are given by \(f_{i}=(2i-1)\hat {f}_{0}\). The rest of the parameters are chosen in an ad hoc way. The polynomial degree n and the number of sinusoids d were chosen based on experimental observations made on the real data we used. The chosen values were n=3 and d=5 (see the discussion of assumption A3 in Section 4.1.2).
Quantities tss1 and tss2 define the time instants that delimit a portion, noted xss(tk), of the steady state of the current signal (Fig. 4). This portion is used in the initialization phase for the estimation of the amplitudes and phases. On this steady state portion, tk∈[tss1,tss2], we can write x(tk)=xss(tk)=ss(tk)+w(tk) where ss(tk) is the sum of sinusoids signal (2); we neglect the envelope influence by assuming e(t)=1 on this portion.
Output of the High Accuracy NILM Detector (HAND) when applied to a simulated single-appliance signal. HAND outputs the time-instants: \(t_{beg}^{on}\) and \(t_{end}^{on}\). Blue: current signal. tss1 and tss2 define the steady state portion (25 time-cycles long) used for the estimation
We define tss1 and tss2 using the High Accuracy NILM Detector (HAND) algorithm [28] found in the literature. Applying HAND on a turn-on transient signal provides the time-instants \(t_{\text {beg}}^{\text {on}}\) and \(t_{\text {end}}^{\text {on}}\) defining the beginning and end of the turn-on transition (Fig. 4). Practically, we define tss1 a few (typically ten) time cycles after \(t_{\text {end}}^{\text {on}}\) and tss2 such that the duration of xss(tk) is 25 time-cycles (i.e., half a second, sufficient to get good initial estimates of amplitudes and phases).
Initialization phase
Estimation of ss(tk): Using the least squares (LS) criterion, parameters ai and ϕi are estimated using (tk∈[tss1,tss2])
$$\begin{array}{*{20}l} x_{ss}(t_{k}) & = s_{s}(t_{k}) + w(t_{k}) \\ & = {\sum\limits_{i = 1}^{d} {{a_{i}}{\cos\left(2\pi {f_{i}}t_{k} + {\phi}_{i}\right)}}}+ w(t_{k}) \\ & = \sum\limits_{i = 1}^{d} [{a_{i}} \cos{\phi}_{i}\cos\left(2\pi {f_{i}}t_{k}\right) \\ & - {a_{i}} \sin{\phi}_{i}\sin\left(2\pi {f_{i}}t_{k}\right)] + w(t_{k}). \end{array} $$
Writing (6) in vector form gives
$$ \mathbf{x_{ss}}= \mathbf{M} \mathbf{{c}} + {\mathbf w}, $$
where xss=[xss(tss1),…,xss(tss2)]T,c=[a1 cosϕ1,a1 sinϕ1,…,ad cosϕd,ad sinϕd]T,w=[w(tss1),…,w(tss2)]T is the noise vector and M s the matrix given in (8).
$$ {{} \begin{aligned} \mathbf{M} = \left[ {\begin{array}{ccccc} {\cos \left({2\pi {f_1}{t_{ss1}}} \right)} & { - \sin \left({2\pi {f_1}{t_{ss1}}} \right)} & \cdots & {\cos \left({2\pi {f_d}{t_{ss1}}} \right)} & { - \sin \left({2\pi {f_d}{t_{ss1}}} \right)} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ {\cos \left({2\pi {f_1}{t_{ss2}}} \right)} & { - \sin \left({2\pi {f_1}{t_{ss2}}} \right)} & \cdots & {\cos \left({2\pi {f_d}{t_{ss2}}} \right)} & { - \sin \left({2\pi {f_d}{t_{ss2}}} \right)} \end{array}} \right] \end{aligned}} $$
The LS criterion, used to find an estimate for c, aims to minimize the square of the Euclidean norm (∥·∥2) of the difference between the measured signal and the data model, i.e.,
$$\begin{array}{*{20}l} &\hat{\mathbf{c}} = \underset{\mathbf{c}}{\text{arg\,min}} \frac{1}{2} \|{\mathbf{x}_{\mathbf{s}\mathbf{s}}-\mathbf{M}\mathbf{c}}\|_{2}^2 \\ &\text{subject to}\quad a_{i} \ge 0 \; \text{and} \; \phi_i \in [-\pi, \pi], \forall i. \end{array} $$
In that case, the solution \(\hat {\mathbf {c}}\) is given by
$${r \hat{\mathbf{C}}l} \hat{\mathbf{c}} = \mathbf{M}^{+} \mathbf{x}_{\mathbf{s}\mathbf{s}}, $$
where M+=(MTM)−1MT is the (Moore-Penrose) pseudo-inverse of M. We extract from \(\hat {\boldsymbol {c}}\) two vectors \(\hat {\mathbf {c}\mathbf {s}} = \left [\hat {a}_{1} \cos \hat {\phi }_{1}, \dots, \hat {a}_{d} \cos \hat {\phi }_{d}\right ]^{T}\) and \(\hat {\mathbf {s}\mathbf {n}} = \left [\hat {a}_{1} \sin \hat {\phi }_{1}, \dots, \hat {a}_{d} \sin \hat {\phi }_{d}\right ]^{T}\), and we compute \(\hat {a}_{i}\) and \(\hat {\phi }_{i}\) as follows
$$ \hat{\mathbf{a}} = \left[ {\begin{array}{c} \hat{a}_{1} \\ \vdots \\ \hat{a}_{d} \end{array}} \right] = \sqrt{\hat{\mathbf{c}\mathbf{s}} \odot \hat{\mathbf{c}\mathbf{s}} + \hat{\mathbf{s}\mathbf{n}} \odot \hat{\mathbf{s}\mathbf{n}}}, $$
$$ \hat{\boldsymbol{\phi}} = \left[ {\begin{array}{*{20}{c}} \hat{\phi}_{1} \\ \vdots \\ \hat{\phi}_{d} \end{array}} \right] = \arctan \left(\hat{\mathbf{s}\mathbf{n}} \oslash \hat{\mathbf{c}\mathbf{s}} \right), $$
where ⊙ and ⊘ are the element-wise product and division operators, respectively.
Estimation of e(tk) :
To estimate e(tk), we use the trust-region-reflective (TRR) algorithm [29, 30], an efficient nonlinear optimization algorithm that belongs to the "trust region" class of algorithms [31]. This algorithm allows constraints to be imposed on the values of the parameter estimates enabling us to satisfy our constraints (ai≥0,ϕi∈[−π,π] and pn<0).
Having the estimates \(\hat {\mathbf {a}}\) and \(\hat {\boldsymbol {\phi }}\) obtained from the previous step and the (overall) measured signal x=[x(t0),…,x(tN−1)]T, we estimate an initial value of p=[p0,…,pn]T (the remaining unknown) using
$$\begin{array}{*{20}l} &\hat{\mathbf{p}} = \underset{\mathbf{p}}{\text{arg\,min}} \frac{1}{2}||\mathbf{x}-(\mathbf{e} \odot \mathbf{M}_{ov} \hat{\mathbf{c}})||_{2}^2 \\ &\text{subject to} \quad p_n < 0, \end{array} $$
where e=[e(t0),…,e(tN−1)]T, N is the number of samples of x, and Mov is the matrix M (8) with t∈[t0,…,tN−1] instead of t∈[tss1,…,tss2]. Moreover, t0 is practically chosen as the time-instant corresponding to the maximum current amplitude; that way, we model the damped part of the turn-on transient starting from the maximum amplitude. In the end of this phase, we obtain the initial estimated parameter vector \(\boldsymbol {\hat {\theta }}_{0} = \left [\hat {\mathbf {p}}^{T}, \hat {\mathbf {a}}^{T}, \hat {\boldsymbol {\phi }}^{T} \right ]^{T}\).
Parameter estimation phase
As the estimation of ai and ϕi is done using only a portion of the total measured signal x(tk), the aim of this parameter estimation phase is to improve the estimation of all the parameters by considering all the samples of x(tk). We use for this the same TRR algorithm considered for the estimation of e(tk) by taking as initial value the result of the estimation phase \(\hat {\boldsymbol {\theta }}_{0}\). The unknown, to be estimated this time, is the global parameter vector θ=[pT,aT,ϕT]T estimated as
$$ {{}\begin{aligned} \boldsymbol{\hat{\theta}} = \underset{\boldsymbol{\theta}}{\text{arg\,min}} \frac{1}{2}\|{\mathbf{x}\,-\,(\mathbf{e} \odot \mathbf{M}_{ov} \mathbf{c})}\|_{2}^2 \,\,\,\,\,\, \end{aligned}} $$
The TCE algorithm is summarized in Algorithm ??.
Cramér-Rao bounds of the model parameters
The Cramér-Rao bound (CRB) provides a lower bound on the variance of any unbiased estimator. We show in Section 4.1.1 that this unbiasedness condition is approximately verified (at least for moderate and high SNRs) for our estimated parameters, and hence, we can use the CRB to assess the performance of our estimation.
Evaluating the performance of the estimation consists of comparing the estimated parameters' variances with their CRB. Taking into account the dependence of s(tk) on the parameter vector θ and N samples of x(tk), (4) can be written using vector notation as
$$ \boldsymbol{x} = \boldsymbol{s}(\boldsymbol{\theta}) + \boldsymbol{w}, $$
where x is normally distributed with mean μ(θ)=s(θ) =[s(t0,θ),…,s(tN−1,θ)]T and a covariance matrix C(θ)=C=σ2I.
The CRB is defined as the inverse of the Fisher information matrix (FIM). If we assume θ=[pT,aT,ϕT]T=[θ1,…,θK]T,K=n+1+2d (the noise power is assumed known here) and \(\mathbf {x} = [x(t_{0}), \dots, x(t_{N-1})]^{T} \in \mathbb {R}^{N}\), then for the general Gaussian case where \(\boldsymbol {x} \sim \mathcal {N}(\boldsymbol {\mu }(\boldsymbol {\theta }), \boldsymbol {C}(\boldsymbol {\theta }))\), the FIM is given elementwise by [26]
$$ \begin{array}{*{20}{l}} \left[ \mathbf{F}\left(\boldsymbol{\theta} \right) \right]_{ij} = & \left(\frac{\partial \boldsymbol{\mu} \left(\boldsymbol{\theta} \right)}{\partial \theta_{i}} \right)^{T}\mathbf{C}^{- 1}\left(\boldsymbol{\theta} \right)\left(\frac{\partial \boldsymbol{\mu} \left(\boldsymbol{\theta} \right)} {\partial {\theta_{j}}} \right) \\ & + \frac{1}{2}\text{tr}\left[\mathbf{C}^{- 1}\left(\boldsymbol{\theta} \right)\frac{\partial {\mathbf{C}}\left(\boldsymbol{\theta} \right)} {\partial \theta_{i}}\mathbf{C}^{- 1}\left(\boldsymbol{\theta} \right)\frac{\partial \mathbf{C}\left(\boldsymbol{\theta} \right)} {\partial \theta_{j}} \right], \end{array} $$
where \(\frac {\partial \boldsymbol {\mu } \left (\boldsymbol {\theta } \right)}{\partial {\theta _{i}}} = \left [ \frac {\partial \left [\boldsymbol {\mu } \left (\boldsymbol {\theta } \right)\right ]_{1}}{\partial {\theta _{i}}}, \dots, \frac {\partial \left [\boldsymbol {\mu } \left (\boldsymbol {\theta } \right)\right ]_{N}}{\partial {\theta _{i}}} \right ]^{T}\), and
$$\frac{\partial \mathbf{C}\left(\boldsymbol{\theta} \right)} {\partial \theta_{i}} = \left[ \begin{array}{*{20}{c}} \frac{\partial \left[ \mathbf{C}\left(\boldsymbol{\theta} \right) \right]_{11}} {\partial \theta_{i}} & \cdots & \frac{\partial \left[ \mathbf{C}\left(\boldsymbol{\theta} \right) \right]_{1N}} {\partial \theta_{i}} \\ \vdots & \ddots & \vdots \\ \frac{\partial \left[ \mathbf{C}\left(\boldsymbol{\theta} \right) \right]_{N1}} {\partial \theta_{i}} & \cdots & \frac{\partial \left[ \mathbf{C}\left(\boldsymbol{\theta} \right) \right]_{NN}} {\partial \theta_{i}} \end{array} \right]. $$
The symbol [·]i denotes element of index i of the corresponding vector, [·]ij denotes the element of index ij of the corresponding matrix, and tr [·] denotes the trace operator.
For our model where μ(θ)=s(θ) and C(θ)=σ2I (covariance matrix independent of θ), the (elementwise) FIM becomes
$$ \left[ {{\mathbf{F}}\left(\boldsymbol{\theta} \right)} \right]_{ij} = \frac{1}{\sigma^{2}}\left(\frac{\partial \boldsymbol{s}(\boldsymbol{\theta})}{\partial \theta_{i}}\right)^{T} \left(\frac{\partial \boldsymbol{s}(\boldsymbol{\theta})}{\partial \theta_{j}}\right), \quad i, j = 1, \dots, K. $$
Taking into account (17) and the structure of θ, the FIM can be written using matrix notation in the form of a nineblock matrix representing the partial derivatives with respect to the elements of θ as
$$ \mathbf{F}\left(\boldsymbol{\theta}\right) = \frac{1} {\sigma^{2}}\left[ \begin{array}{*{20}{c}} \left(\frac{\partial \mathbf{s}^{T}} {\partial p_{l}}\frac{\partial \mathbf{s}} {\partial p_{m}} \right) & \left(\frac{\partial \mathbf{s}^{T}} {\partial p_{l}}\frac{\partial \mathbf{s}} {\partial a_{m}} \right) & \left(\frac{\partial \mathbf{s}^{T}} {\partial p_{l}}\frac{\partial \mathbf{s}} {\partial \phi_{m}} \right) \\ \left(\frac{\partial \mathbf{s}^{T}} {\partial a_{l}}\frac{\partial \mathbf{s}} {\partial p_{m}} \right) & \left(\frac{\partial \mathbf{s}^{T}} {\partial a_{l}}\frac{\partial \mathbf{s}} {\partial a_{m}} \right) & \left(\frac{\partial \mathbf{s}^{T}} {\partial a_{l}}\frac{\partial \mathbf{s}} {\partial \phi_{m}} \right) \\ \left(\frac{\partial \mathbf{s}^{T}} {\partial \phi_{l}}\frac{\partial \mathbf{s}} {\partial p_{m}} \right) & \left(\frac{\partial \mathbf{s}^{T}} {\partial \phi_{l}}\frac{\partial \mathbf{s}} {\partial a_{m}} \right) & \left(\frac{\partial \mathbf{s}^{T}} {\partial \phi_{l}}\frac{\partial \mathbf{s}} {\partial \phi_{m}} \right) \end{array} \right], $$
where l,m∈{1,…,n+1} for the elements of p and l,m∈{1,…,d} for the elements of a and ϕ.
Since this matrix is symmetric (because of the symmetry of the second order partial derivatives), we only have to compute the following terms to find all the elements of the matrix: \(\frac {\partial \mathbf {s}^{T}}{\partial p_{l}}\frac {\partial \mathbf {s}}{\partial p_{m}}, \frac {\partial \mathbf {s}^{T}}{\partial p_{l}}\frac {\partial \mathbf {s}}{\partial a_{m}}, \frac {\partial \mathbf {s}^{T}}{\partial p_{l}}\frac {\partial \mathbf {s}}{\partial \phi _{m}}, \frac {\partial \mathbf {s}^{T}}{\partial a_{l}}\frac {\partial \mathbf {s}}{\partial a_{m}}, \frac {\partial \mathbf {s}^{T}}{\partial a_{l}}\frac {\partial \mathbf {s}}{\partial \phi _{m}}, \frac {\partial \mathbf {s}^{T}}{\partial \phi _{l}}\frac {\partial \mathbf {s}}{\partial \phi _{m}}\). After straightforward derivations, we get
$$ {{} \begin{aligned} \frac{\partial \mathbf{s}^{T}}{\partial p_{l}} \frac{\partial \mathbf{s}}{\partial p_{m}} = \sum\limits_{k = 0}^{N - 1} \left(s_{s}(t_{k})e^{\mathbf{p}^{T}\mathbf{t}_{k}} \right)^{2}t_{k}^{l + m}\\ \frac{\partial \mathbf{s}^{T}}{\partial p_{l}} \frac{{\partial {\mathbf{s}}}} {{\partial {a_m}}} = \sum\limits_{k = 0}^{N - 1} {s({t_k}){e^{{{\mathbf{p}}^{T}}{{\mathbf{t}}_k}}}t_{k}^{l}\cos \left({2\pi {f_m}{t_k} + {\phi _m}} \right)}\\ \frac{{\partial {{\mathbf{s}}^{T}}}} {{\partial {p_l}}}\frac{{\partial {\mathbf{s}}}} {{\partial {\phi _m}}} = - \sum\limits_{k = 0}^{N - 1} {s({t_k}){e^{{{\mathbf{p}}^{T}}{{\mathbf{t}}_k}}}t_{k}^{l}{a_m}\sin \left({2\pi {f_m}{t_k} + {\phi _m}} \right)}\\ \frac{{\partial {{\mathbf{s}}^{T}}}} {{\partial {a_l}}}\frac{{\partial {\mathbf{s}}}} {{\partial {a_m}}} = \sum\limits_{k = 0}^{N - 1} e{{({t_k})}^{2}}\cos \left({2\pi {f_l}{t_k} + {\phi _l}} \right) \cos \left({2\pi {f_m}{t_k} + {\phi _m}} \right)\\ \frac{{\partial {{\mathbf{s}}^{T}}}} {{\partial {a_l}}}\frac{{\partial {\mathbf{s}}}} {{\partial {\phi _m}}} = - \sum\limits_{k = 0}^{N - 1} {e{{({t_k})}^{2}}{a_m}\cos \left({2\pi {f_l}{t_k} + {\phi _l}} \right)\sin \left({2\pi {f_m}{t_k} + {\phi _m}} \right)}\\ \frac{{\partial {{\mathbf{s}}^{T}}}} {{\partial {\phi _l}}}\frac{{\partial {\mathbf{s}}}} {{\partial {\phi _m}}} = \sum\limits_{k = 0}^{N - 1} {e{{({t_k})}^{2}}{a_l}{a_m}\sin \left({2\pi {f_l}{t_k} + {\phi _l}} \right)\sin \left({2\pi {f_m}{t_k} + {\phi _m}} \right)}, \\ \end{aligned}} $$
where \({\mathbf {t}_{k}} = {\left [ {1,{t_{k}}, \ldots,t_{k}^{n}} \right ]^{T}}\), and s(tk),ss(tk),e(tk) are defined in (1), (2), and (3), respectively. Finally, the CRB is equal to F−1(θ) obtained after inserting expressions (19) in (18) and inverting F(θ).
In the previous CRB derivation, we assumed the noise variance σ2 known so that K=n+1+2d. If we assume that σ2 is also an unknown parameter to be estimated such that θ′=[pT,aT,ϕT,σ2]T, then the FIM F(θ′) is equal to the FIM F(θ) augmented with one row and one column corresponding to partial derivatives with respect to σ2. Using (16), we get
$$ \mathbf{F}\left(\boldsymbol{\theta'}\right) = \left[ {\begin{array}{*{20}{c}} {\mathbf{F}\left(\boldsymbol{\theta}\right)} & {\mathbf{0}} \\ {\mathbf{0}} & {\frac{N} {{2{\sigma^{4}}}}} \end{array}} \right]. $$
The CRB is then given by
$$ \text{CRB}(\boldsymbol{\theta'})=\mathbf{F}^{- 1}\left(\boldsymbol{\theta'}\right) = \left[ {\begin{array}{*{20}{c}} {{{\mathbf{F}}^{- 1}}\left(\boldsymbol{\theta}\right)} & {\mathbf{0}} \\ {\mathbf{0}} & {\frac{{2{\sigma^{4}}}} {N}} \end{array}} \right]. $$
This indicates that it is sufficient to independently compute F−1(θ) and \(\frac {2\sigma ^{4}}{N}\) to find F−1(θ′). It also means that the existence or lack of information about σ2 does not affect the performance bound (CRB) of the other desired parameters.
Estimation performance assessment
Assessment on simulated data
In this section, we present the results of the estimation performance evaluation on simulated data. Hereafter, we present (i) the simulated signal and its parameters, (ii) the bias of the estimated parameters, (iii) the estimated parameters variance and its comparison to the CRB, (iv) the CRB variation with respect to the sampling frequency, and (v) the convergence of the TCE algorithm.
Simulated signal and its parameters
Taking the considered setup (n=3 and d=5) in this section, we end up with 14 parameters for the simulated signal. So, with such large number of degrees of freedom, we decided to choose the set of parameters such that the simulated signal will resemble as much as possible real signals, and without a priori knowledge on what parameter values are appropriate, we decided to tweak the model parameters and choose the ones that gave a simulated signal "resembling" (similar waveform) typical real current waveforms from our dataset. The noiseless signal model is
$$ s(t_k) \,=\, e(t_k)s_{s}(t_k) \\ \,=\, \left(e^{{\mathbf{p}^{T}}{\boldsymbol{t}_k}} + 1\right){\sum\limits_{i = 1}^d {{a_i}{\cos\left(2\pi {f_i}t_k + \phi_{i}\right)}}}, $$
where \(\mathbf {p} = {\left [ {{p_{0}},{p_{1}}, \ldots,{p_{n}}} \right ]^{T}}, {\boldsymbol {t}_{k}} = {\left [ {1,t_{k}, \ldots,{t_{k}^{n}}} \right ]^{T}}, t_{k} \in [t_{0}, t_{N-1}], a_{i}\) (≥0), ϕi∈[−π,π] and fi=(2i−1)f0,i=1,…,d with a fixed fundamental frequency f0=50 Hz. The chosen model parameter values are
Fs=30 kHz: sampling frequency
t0=0 s, tN−1=3 s: specify signal duration
n=3: polynomial degree
d=5: number of harmonics
p=[1.9,− 9,8.5,− 4]T
a=[1.8,0.5,0.2,0.1,0.05]T
ϕ=[− 3,3,2.5,1.5,1]T
tss1=2.5 s, tss2=3 s: define steady state portion.
The polynomial degree is chosen relatively small (we found that n=3 is sufficient to characterize the tested signals, and hence, this value will be used in the remainder of the paper). The previous transient signal is then corrupted by an additive white Gaussian noise of zero mean and variance σ2 (varied such that the signal-to-noise ratio (SNR) \(=\frac {1/N\sum _{k=0}^{N-1}s(t_{k})^{2}}{\sigma ^{2}}\) varies in the range [0−50] dB). The obtained simulated signal is shown in Fig. 5.
Simulated turn-on transient current used for performance assessment
Bias of the estimated parameters
As mentioned before, the CRB applies for unbiased estimators. Our maximum likelihood estimation method based on criterion (14) is known to be asymptotically, i.e., for high SNR, unbiased [26]. Here, we evaluate our estimator bias numerically using (1000) Monte-Carlo runs.
Figure 6 gives the bias computed for the parameters estimated using the proposed algorithm versus the signal-to-noise ratio (SNR). We can see that all estimated parameters have negligible bias for SNR values greater than or equal to 30 dB. Between 10 dB and 30 dB, the estimated parameters have very small biases, and below 10 dB, we start getting some bias, nonetheless with values that are still small compared to the true parameter values.
Bias of the different parameters estimated using the TCE algorithm. a Bias of \(\hat {\mathbf {p}}, \mathbf {p} = [1.9, -\thinspace 9, 8.5, -\thinspace 4]^{T}\). b Bias of \(\hat {\mathbf {a}}, \mathbf {a} = [1.8, 0.5, 0.2, 0.1, 0.05]^{T}\). c Bias of \(\hat {\boldsymbol {\phi }}, \boldsymbol {\phi } = [-\thinspace 3, 3, 2.5, 1.5, 1]^{T}\). We used 1000 Monte-Carlo runs
Estimated parameters' variance and its comparison to the CRB
Similarly to the bias computation, the variance is also computed numerically. Figure 7 shows the different parameter variances compared with their respective CRBs. We note that all the parameter variances coincide with their respective CRBs almost perfectly. Hence, our estimation is efficient (unbiased and the variance reaches the CRB).
Comparison of the CRB and estimated parameters' variance. Represented is the CRB vs. variance for p (a), a (b), and ϕ (c). The CRB curves are represented using dashed lines and the variance curves using solid lines. We used 1000 Monte-Carlo runs
CRB variation with respect to the sampling frequency
Due to the transient behavior of the observed phenomena, a good choice for the sampling frequency Fs of measurements is mandatory. We seek a sufficiently high sampling frequency to catch the transient behavior but not too high to avoid heavy computational load. The CRB allows us to evaluate the impact of the sampling frequency on the parameter variance lower bounds and therefore decide on the desired performance taking into account computational complexity.
Figure 8 gives the variation of the parameters' CRB as a function of Fs (1 to 100 kHz) on a logarithmic scale. The results show that an increase in Fs results in a better estimation performance (linearly decreasing variance w.r.t. to the sample size) for all the parameters. This is expected, since a higher Fs means more data samples (on a fixed time period) and hence better performance. When considering real signals, however, this is not necessarily true. The white noise (independence) assumption initially verified for relatively low Fs (still high frequency though) might not be verified in practice for higher frequency values. At higher frequencies, the data samples become closer and might become correlated, when the time duration between two samples is too small to assume independence. In that case, the computed CRB assuming a white noise can no longer be used to evaluate the estimation performance.
CRB of the model parameters as a function of the sampling frequency Fs (from 1 kHz to 100 kHz) at an SNR of 25 dB. Represented is the CRB of p (a), a (b), and ϕ (c)
Practically, finding the adequate sampling frequency is not easy since it depends on different parameters: transient waveforms of interest and their frequency contents, computational complexity, desired performance, etc. According to our experiments, and for the study of turn-on transient signals, a sampling frequency at least equal to 5 kHz is recommended (captures around 50 harmonics) whereas going beyond 100 kHz starts generating heavy data processing. A sampling frequency of 30 kHz seems to be a good compromise, since it captures around 300 harmonics and is less computationally heavy. Hence, our choice was Fs=30 kHz for simulations.
Convergence of the TCE algorithm
Since the TCE algorithm uses an optimization algorithm in both its estimation and refinement phases, it is important to check its convergence, especially if there is a need for real-time processing. Hereafter, we check the convergence of the nonlinear optimization algorithm, trust-region-reflective (TRR), for both phases.
Figure 9 gives, for different SNR values, the mean-square-error (MSE) as a function of the number of iterations in the estimation phase of the TCE algorithm. Independently of the SNR, the algorithm converges after ten iterations. The convergence of the TRR algorithm in the refinement phase is even faster. Indeed, the initialization point being better defined, it converges at most after three iterations.
Mean square error (MSE) \(\frac {1}{N}\sum _{n=0}^{N-1} |x(t_{n})-s(\hat {\boldsymbol {\theta }}, t_{n})|^{2}\) as a function of the number of iterations of the trust-region-reflective algorithm (estimation phase only). Different SNR values are considered and the last point of each curve indicates the convergence of the algorithm
Assessment on real data
Real data considerations
Until now, we have implicitly assumed, for simulated data, some simplifying assumptions to test the parameter estimation independently of the performance of other blocs that may condition the estimation. These assumptions are as follows: (A1) a well-defined portion of the steady state, (A2) transient starting from a maximum, and (A3) known polynomial degree n and number of harmonics d. In real situations, however, these assumptions are not necessarily verified for the following reasons: (i) the definition of the steady state portion is affected by the precision of turn-on transient (end) detection and is never perfect (depends on the detector accuracy); (ii) physically, there will always be a latency in the appliance response before the current signal reaches its maximum amplitude; and (iii) the polynomial degree as well as the harmonic numbers are only chosen parameters used to trade-off between complexity and modeling efficiency.
The easiest assumption to get around in a real situation is A2 since we only need to detect the signal maximum amplitude and model the damped part, starting from this maximum (so the portion of transient signal preceding the peak value will be disregarded). For assumption A1, we use the HAND detector [28] built specifically to allow high accuracy detection of turn-on transients. For A3, we relied on our dataset of real life signals to get our ad hoc choice of the "effective" polynomial degree n=3 and "effective" number of harmonics d=5 that have been experimentally shown to be suitable for a good modeling of the considered transient signals. As an example, Fig. 10 shows different plots comparing the real signal x(t) to its estimate \(\hat {x}(t)\) for different values of the polynomial degree n (1, 3, 5 and 7). We note the improvement of the root-mean-square error (RMSE) between n=1 and n=3, hence a better estimation using n=3, and a slight improvement of the RMSE between n=3,n=5, and n=7. We consider n=3 to be a good trade-off between model complexity and the estimation performance (less than 10% of relative RMSE difference, e.g., between n=3 and n=5, we have a relative RMSE difference of \(\frac {0.2473-0.2433}{0.2473}\approx 1.6\%\)).
Comparison between real, x(t), and estimated, \(\hat {x}(t)\), transient current signals of a drill using different polynomial degrees n. The pairs (polynomial degree, root-mean-square errors) (i.e., (n, RMSE)) for the different panels are (n=1,0.2962) (a), (n=3,0.2473) (b), (n=5,0.2433) (c), and (n=7,0.2428)(d)
As an aside, note that the particular "two-steps" structure of the proposed parameter estimation algorithm (Section 2.2) is motivated by the highly nonlinear optimization problem involved. Such a two-step approach helps to avoid local minima by providing a good initialization point in the first step, then refining the obtained estimate in the second step. For completeness, we have also tried to improve the estimate of f0 by jointly estimating it when (i) estimating \(\hat {\boldsymbol {p}}\) (13), (ii) when refining the estimation of all parameters (14), and (iii) in both (i) and (ii). This, however, did not improve the results, indicating that the proposed approach already leads to near optimal values (due in part to the highly precise estimate of f0 obtained using [27]). As an example, we have conducted the joint estimations described above considering the real signal used in Fig. 10 with n=3 that gave initially RMSE = 0.2473. The newly obtained results, in terms of RMSE, were 0.2473, 0.2479, and 0.2479, respectively for (i), (ii), and (iii). The joint estimation of f0 was not considered further as it would generate more computational load without performance gain.
Estimation with TCE on a real signal of the COOLL dataset
The real signal is taken from a turn-on transient dataset we built especially for transients analysis. The dataset is called Controlled On/Off Loads Library (COOLL) [32] and is freely available on the internet (https://coolldataset.github.io/). Since the measurement system [33] (Fig. 11) used to collect the dataset's signals allows the control over the turn-on/off, we know exactly the turn-on/off time instants and assumptions A1 and A2 hold then true. Moreover, we consider the signal starting from its maximum in order to verify A3.
Photograph of the measurement system
The COOLL dataset signals (Table 1) are sampled at Fs=100 kHzFootnote 3. The dataset consists of turn-on transient current and voltage signals of 12 different electrical appliances and each appliance has 20 signal examples. Figure 12 shows a typical histogram of the noise on a measured current signal taken from its pre-turn-on part (noise only). This shows that the noise distribution for the COOLL current signals is Gaussian with zero mean and a standard deviation of 2.2 mA (equivalent to an approximate power consumption of 0.5 W).
Table 1 COOLL dataset summary
Histogram of current noise
Next, we provide an illustrative example corresponding to a test signal of a fan (Fig. 13). The total duration of the measurement is 6 s with a 0.5 s of pre-turn-on. The estimation results of TCE on the fan signal (Fig. 13) are as follows:
$$\begin{array}{@{}rcl@{}}{l} \hat{\mathbf{p}} = \left[\begin{array}{l} -1.15\\ -0.19\\ 0.20\\ -0.32 \end{array}\right], \hat{\mathbf{a}} = \left[\begin{array}{l} 0.21\\ 7.3\times 10^{-3}\\ 6.4\times 10^{-3}\\ 4.7\times 10^{-3}\\ 1.0\times 10^{-3} \end{array}\right], \hat{\boldsymbol{\phi}}= \left[\begin{array}{l} -3.10\\ 2.94\\ 2.72\\ 0.22\\ 1.27 \end{array}\right],\\ \text{RMSE} =\sqrt{\frac{1}{N}\sum_{n=0}^{N-1} |x(t_n)-s(\hat{\boldsymbol{\theta}}, t_n)|^{2}} = 7.1\times 10^{-3}~A, \end{array} $$
Turn-on transient current of a fan from the COOLL dataset
where RMSE is the root-mean-square-error. The above estimation results indicate little information on the estimation quality, especially that we are applying the algorithm on a real signal. Nonetheless, the RMSE gives an idea about the estimation quality but is still without much meaning if not considered relative to some reference value. Here, we propose to compare it to the average maximum value of the steady state amplitude (around 0.2 A). We get a relative RMSE of 3.6%. Note that we got an average relative RMSE of around 8% for the whole dataset, which is acceptable considering the variability of real signals.
Figure 14 allows to get a visual feel for the estimation quality. Figure 14a and b show a good fit between the reconstructed signal and the originalzone.
Turn-on transient current of a fan from the COOLL dataset (in blue) with the reconstructed signal (in red) generated using the estimated parameters with the TCE algorithm. a Current signals, b zoom on the interval [0.50−0.60] s, and c zoom on the interval [3.50−3.60] s
Classification of cOOLL dataset's appliances using the model parameters
Here, we propose to classify the appliances of the COOLL dataset using the model parameters. We use the classical supervised k-nearest neighbors algorithm (k-NN) [34, Chap. 13], which proceeds by taking the test example (here the vector of parameters representing the test signal) and classifying it according to a majority vote of the k-nearest examples (of the training dataset). We used the Euclidean distance as a distance metric. We assess the result using K-fold cross-validation with K=10. This validation works by first partitioning the dataset to K equal partitions (in our case each partition contains 84 example), then take one partition for testing and keep the other nine partitions for training, and we assess the performance using for example the classification accuracy (CA). This process is repeated K times, taking at each time a different partition for testing and the remaining nine for training. The final result is the average of the K accuracy results.
Note that the estimated values of the phase parameters ϕi are too random to be considered as features for the classification and, hence, are discarded hereafter. We apply the k-NN on the data using the estimated \(\hat {p}_{j}, j = 0, \dots, 3\) and \(\hat {a}_{i}, i = 1, \dots, 5\). The results are presented as a confusion matrix (Fig. 15).
Classification result as a confusion matrix using model parameters \(\hat {p}_{i}\) and \(\hat {a}_{i}\). The bottom rightmost cell gives the classification rate, the rightmost column contains the recall values, and the bottom row the precision values
The classification accuracy (CA) is given in the bottom rightmost corner. It is defined as \(CA = \frac {TP}{\text {Tot}}\) where TP is the number of true positives (i.e., examples correctly classified) and Tot is the total number of considered examples. Figure 15 also gives the values of two largely used performance metrics for classification known as recall (rightmost column) and precision (bottom row). These are defined as \(\text {recall} = \frac {TP}{RP}\) and \(\text {precision} = \frac {TP}{CP}\) where RP is the number of relevant positives (i.e., examples belonging to the true class), and CP is the number of examples classified as positives. Note that these metrics depend on the relevant (considered) appliance class and are, hence, recomputed for each class. To illustrate this, consider the first row of the confusion matrix (Fig. 15) corresponding to the true class "drill." Here, \(\text {recall} = \frac {103}{120} = 85.8\%\) (i.e., 103 examples are correctly classified among a total of 120 relevant positives (row sum)). Similarly, for the first column corresponding to the predicted (classified) class "drill," we have \(\text {precision} = \frac {103}{121} = 85.1\%\) (i.e., 103 examples are correctly classified among 121 classified as a drill (column sum)).
We obtain a CA of 92.4%. Although the CA is higher than 92%, we expect a less variable characteristic feature capturing the envelope shape to be more relevant for the classification. In fact, the \(\hat {p}_{j}\) are sensitive to the chosen origin of time (except the last parameter \(\hat {p}_{n}\)) and their estimated values are less stable due to the difficulty of precisely defining the origin of time for transient signals. To remedy this, we need to construct a new feature that is independent of the time origin and that still is characteristic of the envelope shape. We propose to use the minimum radius of curvature of the estimated envelope signal \(\hat {e}(t)\) constructed using the \(\hat {p}_{j}\) parameters. For a function f(t), the radius of curvature at point t0 is defined as [35]
$$ R(t_{0}) = \left| \frac{(1+f'(t_{0})^{2})^{3/2}}{f\prime\prime(t_{0})} \right| $$
where f′(t0) and f″(t0) are the first and second derivatives of f(t) at point t0, respectively. Practically, we compute this value for each sample point of \(\hat {e}(t_{k})\) and take the minimum value Rmin. This minimum value is inversely proportional to the maximum curvature, which is a distinctive feature of the turn-on transient signals as can be seen in Fig. 16.
Four examples of turn-on transient signals. a Drill, b hair drayer, c paint stripper, and d fluorescent lamp. Note the different envelope shapes for the different appliances, which gives different minimum radii of curvature
It is important to notice that the phase of the grid (referred to as action delay) when switching-on the appliance might affect the shape of the transient signal envelope. To investigate the influence of the phase of the grid on the chosen minimum radius of curvature, we evaluate the variation of the latter parameter for different delays as illustrated in Fig. 17 for a drill and a vacuum cleaner. As can be seen from these plots, the minimum radius of curvature remains relatively stable w.r.t. action delay parameter values. This observation is valid for most of the electrical appliances.
Stability of the minimum radius of curvature versus various values of the grid phase (action delay) for two appliances (a drill and a vacuum cleaner). Action delay is the delay w.r.t. the (positive-to-negative) zero-crossing of the voltage signal before switching-on an appliance, e.g., an action delay of 4 ms means that the appliance is switched-on after 4 ms of voltage zero-crossing
The classification results using Rmin and \(\hat {a}_{i}\) are shown in Fig. 18. Compared to the previous result, we obtain an improvement of 5.6%, with a CA of 98.0%. Another performance metric used often in assessing classification performance is the F1 score defined as \(2\frac {\text {precision}\times \text {recall}}{\text {precision}+ \text {recall}}\). This metric can be computed for each appliance and gives a single number assessing the performance, which is especially helpful when comparing different classifiers or, as is the case here, the result of two different sets of features. The F1 score results for our classification are given in Table 2. These results show an improvement in the F1 score for almost all the appliances when using the set of features \(\{R_{\text {min}}, \hat {a}_{i}\}\) compared to the set of features \(\{\hat {p}_{j}, \hat {a}_{i}\}\).
Classification result as a confusion matrix using the minimum radius of curvature Rmin and model parameters \(\hat {a}_{i}\). The bottom rightmost cell gives the classification rate, the rightmost column contains the recall values, and the bottom row the precision values
Table 2 Comparative F1 scores of the different COOLL appliances for the classification result using the two sets of features \(\{\hat {p}_{j}, \hat {a}_{i}\}\) and \(\{R_{\text {min}}, \hat {a}_{i}\}, j=0,\dots, 3\), and i=1,…,5
We proposed in this paper a new mathematical representation suitable for modeling turn-on transient current signals and proposed an algorithm for the model parameter estimation. The efficiency of the algorithm is assessed theoretically via benchmarking its estimation error variances with respect to the CRB derived in Section 3 of this paper. Later on, the proposed parametric model is validated using real data from the COOLL dataset that we developed specifically for this research work. A "good" fitting between the proposed signal model and the real-life signals has been observed with, in particular, an average relative mean-square-error of about 8%. Note also that our experimental tests showed the need for estimating the fundamental frequency due to its deviation from the nominal value (i.e., 50 Hz). A classification method using the model parameters has been proposed. The obtained results show the usefulness of the transient signal parameters as relevant features for the characterization of electrical appliances with a correct classification accuracy of 98% in the considered context.
The proposed model is valid for a lot of electrical appliances that show a single-phase behavior during the turn-on such as incandescent light bulbs, compact fluorescent lamps, heaters, vacuum cleaners, and hairdryers. However, some electrical appliances may have a turn-on transient current signal consisting of different phases each with a distinct signal content (harmonics with different amplitudes and phases) and a distinct envelope shape corresponding to the different regimes that the appliance goes through during turn-on. For instance, the microwave turn-on transient shown in Fig. 19 has two phases (some microwaves may have more than two) each with its specific characteristics. As a perspective work, one can consider using our model to characterize each phase independently (as a single-phase appliance) and then devise some rule to identify the corresponding multi-phase appliance (e.g., considering the occurrence of the different phases in a time series).
Turn-on transient current of a microwave
The dataset created and used during the current study is freely available at https://coolldataset.github.io/.
The European norm "EN 50160" [25] fixes the acceptable variation ranges for δf0. For the synchronous grid of Continental Europe—the largest synchronous (same frequency) grid in the world linking most of Europe's countries and some countries of north Africa—these ranges are ± 1% of f0 (δf0=[− 0.5,+ 0.5] Hz) 99.5% of a year and − 6%/+ 4% of f0 (δf0=[− 3,+ 2] Hz) 100% of the time. The latter range is made large to account for occasional high variations.
Based on our real data measurements, we have observed that a polynomial order n=3 is sufficient to model properly the considered transient signals.
After measurements were done we found that Fs=30 kHz would have been enough to capture the transient behavior of interest.
Classification accuracy
COOLL:
Controlled On/Off Loads Library
Classified as positives
CRB:
Cramér-Rao bound
ESPRIT:
Estimation of Signal Parameters via Rotational Invariance Techniques
FIM:
Fisher information matrix
HAND:
High Accuracy NILM Detector
k-NN:
k-nearest neighbors
LM:
Levenberg-Marquardt
LS:
Least squares
MSE:
Mean-square-error
Multiple Signal Classification
NILM:
Non-intrusive load monitoring
RMSE:
Root-mean-square-error
RP:
Relevant positives
SDS:
Superimposed damped sinusoids
SNR:
TCE:
Transient current estimation
TP:
True positives
TRR:
Trust-region-reflective
C. A. García, A. Otero, X. Vila, D. G. Márquez, A new algorithm for wavelet-based heart rate variability analysis. Biomed. Signal Process. Control.8(6), 542–550 (2013). https://doi.org/10.1016/j.bspc.2013.05.006.
X. Chen, H. Wen, Q. Li, T. Wang, S. Chen, Y. -P. Zheng, Z. Zhang, Identifying transient patterns of in vivo muscle behaviors during isometric contraction by local polynomial regression. Biomed. Signal Process. Control.24:, 93–102 (2016). https://doi.org/10.1016/j.bspc.2015.09.009.
T. P. Exarchos, A. T. Tzallas, D. I. Fotiadis, S. Konitsiotis, S. Giannopoulos, EEG transient event detection and classification using association rules. IEEE Trans. Inf. Technol. Biomed.10(3), 451–457 (2006). https://doi.org/10.1109/TITB.2006.872067.
A. Belsak, J. Flasker, Adaptive wavelet transform method to identify cracks in gears. EURASIP J. Adv. Signal Proc.2010(1), 879875 (2010). https://doi.org/10.1155/2010/879875.
C. Capilla, Application of the Haar wavelet transform to detect microseismic signal arrivals. J. Appl. Geophys.59(1), 36–46 (2006). https://doi.org/10.1016/j.jappgeo.2005.07.005.
X. Li, Z. Li, E. Wang, J. Feng, L. Chen, N. Li, X. Kong, Extraction of microseismic waveforms characteristics prior to rock burst using hilbert–huang transform. Measurement. 91:, 101–113 (2016). https://doi.org/10.1016/j.measurement.2016.05.045.
J. Seymour, T. Horsley, The seven types of power problems. White paper. 18:, 1–21 (2005).
M. H. J. Bollen, E. Styvaktakis, I. Y. -H. Gu, Categorization and analysis of power system transients. IEEE Trans Power Deliv.20(3), 2298–2306 (2005). https://doi.org/10.1109/TPWRD.2004.843386.
S. Wang, Z. K. Zhu, Y. He, W. Huang, Adaptive parameter identification based on Morlet wavelet and application in gearbox fault feature detection. EURASIP J. Adv. Signal Process.2010(1), 842879 (2010). https://doi.org/10.1155/2010/842879.
W. Jiao, S. Qian, Y. Chang, S. Yang, Research on vibration response of a multi-faulted rotor system using LMD-based time-frequency representation. EURASIP J. Adv. Signal Process.2012(1), 73 (2012). https://doi.org/10.1186/1687-6180-2012-73.
S. B. Leeb, S. R. Shaw, J. L. Kirtley Jr, Transient event detection in spectral envelope estimates for nonintrusive load monitoring. Power Deliv. IEEE Trans.10(3), 1200–1210 (1995).
C. Laughman, K. Lee, R. Cox, S. Shaw, S. Leeb, L. Norford, P. Armstrong, Power signature analysis. Power Energy Mag. IEEE. 1(2), 56–63 (2003).
H. -H. Chang, H. -T. Yang, Applying a non-intrusive energy-management system to economic dispatch for a cogeneration system and power utility. Appl. Energy. 86(11), 2335–2343 (2009).
R. Kumaresan, D. Tufts, Estimating the parameters of exponentially damped sinusoids and pole-zero modeling in noise. IEEE Trans. Acoust. Speech. Signal Process.30(6), 833–840 (1982).
L. Lovisolo, M. P. Tcheou, E. A. B. da Silva, M. A. M. Rodrigues, P. S. R. Diniz, Modeling of electric disturbance signals using damped sinusoids via atomic decompositions and its applications. EURASIP J. Adv. Signal Process.2007(1), 029507 (2007). https://doi.org/10.1155/2007/29507.
R. Boyer, K. Abed-Meraim, Audio modeling based on delayed sinusoids. IEEE Trans. Speech Audio Process.12(2), 110–120 (2004). https://doi.org/10.1109/TSA.2003.819953.
D. V. Rubtsov, J. L. Griffin, Time-domain Bayesian detection and estimation of noisy damped sinusoidal signals applied to NMR spectroscopy. J Magn. Reson. 188(2), 367–379 (2007). https://doi.org/10.1016/j.jmr.2007.08.008.
M. A. Al-Radhawi, K. Abed-Meraim, Parameter estimation of superimposed damped sinusoids using exponential windows. Signal Process.100:, 16–22 (2014). https://doi.org/10.1016/j.sigpro.2013.12.025.
R. Prony, Essai expérimental et analytique : sur les lois de la dilatabilité des fluides élastiques et sur celles de la force expansive de la vapeur de l'eau et de la vapeur de l'alkool, à différentes températures. J. de l'École Polytechnique Floréal et Plairial. 1(22), 24–76 (1795).
V. F. Pisarenko, The retrieval of harmonics from a covariance function. Geophys. J. Int.33(3), 347–366 (1973).
Y. Hua, T. K. Sarkar, Matrix pencil method for estimating parameters of exponentially damped/undamped sinusoids in noise. Acoust. Speech. Signal Process. IEEE Trans.38(5), 814–824 (1990).
R. Roy, T. Kailath, ESPRIT—estimation of signal parameters via rotational invariance techniques. Acoust. Speech. Signal Process. IEEE Trans.37(7), 984–995 (1989).
R. Schmidt, Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag.34(3), 276–280 (1986).
E. K. Howell, How switches produce electrical noise. Electromagn. Compat. IEEE Trans.EMC-21(3), 162–170 (1979).
CENELEC, Voltage characteristics of electricity supplied by public electricity networks. European Standard EN 50160 (2010).
S. M. Kay, Fundamentals of Statistical Signal Processing, Volume I: Estimation Theory (Prentice Hall PTR, Upper Saddle River, 1993).
E. Aboutanios, B. Mulgrew, Iterative frequency estimation by interpolation on fourier coefficients. IEEE Trans. Signal Process.53(4), 1237–1242 (2005).
M. Nait Meziane, P. Ravier, G. Lamarque, J. -C. Le Bunetel, Y. Raingeaud, in 42nd IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). High accuracy event detection for non-intrusive load monitoring (IEEE, 2017), pp. 2452–2456. https://doi.org/10.1109/ICASSP.2017.7952597.
T. F. Coleman, Y. Li, On the convergence of interior-reflective newton methods for nonlinear minimization subject to bounds. Math. Program.67(1), 189–224 (1994). https://doi.org/10.1007/BF01582221.
T. F. Coleman, Y. Li, An interior trust region approach for nonlinear minimization subject to bounds. SIAM J. Optim.6(2), 418–445 (1996). https://doi.org/10.1137/0806023.
Y. -x. Yuan, in Iciam, 99. A review of trust region algorithms for optimization (Citeseer, 2000), pp. 271–282.
T. Picon, M. Nait Meziane, P. Ravier, G. Lamarque, C. Novello, J. -C. Le Bunetel, Y. Raingeaud, COOLL: Controlled on/off loads library, a public dataset of high-sampled electrical signals for appliance identification. arXiv preprint arXiv:1611.05803 [cs.OH] (2016).
M. Nait Meziane, T. Picon, P. Ravier, G. Lamarque, J. -C. Le Bunetel, Y. Raingeaud, in Conference on Environment and Electrical Engineering (EEEIC), 2016 Proceedings of the 16th IEEE International. A measurement system for creating datasets of on/off-controlled electrical loads, (2016), pp. 2579–2583.
J. Friedman, T. Hastie, R. Tibshirani, The Elements of Statistical Learning. vol. 1 (Springer, New York, 2001).
J. D. Lawrence, A Catalog of Special Plane Curves (Courier Corporation, North Chelmsford, 1972).
This current study was supported in part by the Région Centre-Val de Loire (France) through the project MDE-MAC3 (Contract no 2012 00073640).
PRISME Laboratory, University of Orléans, 12 rue de Blois, Orléans, 45067, France
Mohamed Nait-Meziane
, Philippe Ravier
, Karim Abed-Meraim
& Guy Lamarque
GREMAN Laboratory, UMR 7347 CNRS–University of Tours, 20 avenue Monge, Tours, 37200, France
Jean-Charles Le Bunetel
& Yves Raingeaud
Search for Mohamed Nait-Meziane in:
Search for Philippe Ravier in:
Search for Karim Abed-Meraim in:
Search for Guy Lamarque in:
Search for Jean-Charles Le Bunetel in:
Search for Yves Raingeaud in:
MNM, PR, KAM, and GL conceived and designed the experiments, analyzed the data, and interpreted the results. MNM performed the experiments and wrote the manuscript. MNM, PR, and KAM contributed in developing the model and parameter estimation algorithm. JCLB and YR provided their expertise for the power grid aspects of the experiments. All authors read and approved the final manuscript.
Correspondence to Mohamed Nait-Meziane.
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License(http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Nait-Meziane, M., Ravier, P., Abed-Meraim, K. et al. Electrical transient modeling for appliance characterization. EURASIP J. Adv. Signal Process. 2019, 55 (2019) doi:10.1186/s13634-019-0644-2
Accepted: 03 September 2019
Electrical appliances characterization
Harmonic signal
Transient modeling | CommonCrawl |
Difference between g-value and rhs-value in Lifelong Planning A*
What is the difference between g-value and rhs-value of Lifelong Planning A* algorithm?
According to this link, D* Lite, g(s) directly correspond to the g-values of an A* search, i.e. g(s) = g(s') + c(s',s), and rhs(s) is given as
$$ rhs(s) = \begin{cases}0 & s = s_{start} \\ \min_{s'\in Pred(s)}(g(s') + c(s', s)) & \text{otherwise} \end{cases} $$
where, Pred(s) denotes the set of predecessors of node 's'.
Thus, unless node 's' has more than one predecessor, its g-value and rhs-value will remain same.
So, my question is, in which case will the rhs-value and g-value of a node be different?
mobile-robot robotic-arm wheeled-robot motion-planning algorithm
vackyvacky
To expand on @Ian 's answer :
In that context, I believe a "predecessor" of vertex $u$ refers to any vertex $v$ with a directed edge $(v,u)$, i.e any vertex "from which u is accessible".
For instance, in the typical case of a 2D grid with eight neighbors for each cell and bidirectional edges (or two opposite directed edges), you almost always have multiple predecessors for a given vertex.
$rhs(s)$ integrates information from the immediate neighborhood of $s$ ("one step lookahead") which is why $rhs-values$ propagate faster than the $g-values$ and help better discriminate between multiple vertices in the priority queue to decide which one is the most promising to expand next.
$rhs(s)$ and $g(s)$ are different - vertices are "locally inconsistent" - typically around the area where the edge costs were modified, and as the local search expands to "repair" the previous path around this area, vertices along the new shortest path are made "locally consistent", i.e $rhs(s)=g(s)$
al-deval-dev
From the paper, $g(s)$ is only an estimate of the distance travelled (vs a direct measurement, which is how A* computes it).
The rhs-values are one-step lookahead values based on the g-values and thus potentially better informed than the g-values.
The calculation of $rhs$ seems to be purely a sanity check that the estimate of $g(s)$ is accurate, based on the estimate of a predecessor.
in which case will the rhs-value and g-value of a node be different
Even if there is only one predecessor, if the estimate for that predecessor has changed between 2 searches then it's possible for $rhs(s) \neq g(s)$. And based on the equation above, that can happen in only one of two ways:
the minimum $c(s', s)$ has changed
the minimum $g(s')$ has changed
According to the paper, this represents the case where the robot makes a move and discovers that the cost of moving between two given points has changed from what was previously believed.
Not the answer you're looking for? Browse other questions tagged mobile-robot robotic-arm wheeled-robot motion-planning algorithm or ask your own question.
Difference between kinematic, dynamic and differential constraints
What is the difference between motion planning and trajectory generation?
What is the difference between path planning and motion planning?
Path planning for visual servoing
Motion planning and robot controlling
What is the difference between conventional and unconventional path planning methods?
Difference between Collision Cone and Velocity Obstacle
What is the difference between Obstacle Avoidance and Dynamic Path Planning? | CommonCrawl |
Accommodating unobservability to control flight attitude with optic flow
Vortex trapping recaptures energy in flying fruit flies
Fritz-Olaf Lehmann, Hao Wang & Thomas Engels
Undulation enables gliding in flying snakes
Isaac J. Yeaton, Shane D. Ross, … John J. Socha
Two pursuit strategies for a single sensorimotor control task in blowfly
Leandre Varennes, Holger G. Krapp & Stephane Viollet
Distributed sensing for fluid disturbance compensation and motion control of intelligent robots
Michael Krieg, Kevin Nelson & Kamran Mohseni
A contralateral wing stabilizes a hovering hawkmoth under a lateral gust
Jong-Seob Han & Jae-Hung Han
A novel aerial manipulator system compensation control based on ADRC and backstepping
Le Ma, Yiming Yan, … Jie Liu
Information-based centralization of locomotion in animals and robots
Izaak D. Neveln, Amoolya Tirumalai & Simon Sponberg
A wireless radiofrequency-powered insect-scale flapping-wing aerial vehicle
Takashi Ozaki, Norikazu Ohta, … Kanae Hamaguchi
Novel flight style and light wings boost flight performance of tiny beetles
Sergey E. Farisenkov, Dmitry Kolomenskiy, … Alexey A. Polilov
Guido C. H. E. de Croon ORCID: orcid.org/0000-0001-8265-14961,
Julien J. G. Dupeyroux ORCID: orcid.org/0000-0002-7414-50211,
Christophe De Wagter ORCID: orcid.org/0000-0002-6795-84541,
Abhishek Chatterjee ORCID: orcid.org/0000-0003-0622-71021,
Diana A. Olejnik ORCID: orcid.org/0000-0003-0808-44081 &
Franck Ruffier ORCID: orcid.org/0000-0002-7854-12752
Information theory and computation
Attitude control is an essential flight capability. Whereas flying robots commonly rely on accelerometers1 for estimating attitude, flying insects lack an unambiguous sense of gravity2,3. Despite the established role of several sense organs in attitude stabilization3,4,5, the dependence of flying insects on an internal gravity direction estimate remains unclear. Here we show how attitude can be extracted from optic flow when combined with a motion model that relates attitude to acceleration direction. Although there are conditions such as hover in which the attitude is unobservable, we prove that the ensuing control system is still stable, continuously moving into and out of these conditions. Flying robot experiments confirm that accommodating unobservability in this manner leads to stable, but slightly oscillatory, attitude control. Moreover, experiments with a bio-inspired flapping-wing robot show that residual, high-frequency attitude oscillations from flapping motion improve observability. The presented approach holds a promise for robotics, with accelerometer-less autopilots paving the road for insect-scale autonomous flying robots6. Finally, it forms a hypothesis on insect attitude estimation and control, with the potential to provide further insight into known biological phenomena5,7,8 and to generate new predictions such as reduced head and body attitude variance at higher flight speeds9.
In the fight against gravity, it is crucial for flying robots and animals to control their attitude, thus determining the direction of forces such as thrust and lift. Flying robots can be designed to have a passively stable attitude, meaning that they do not need to actively control their attitude to stay upright. Examples include fixed-wing drones10 and tailed flapping-wing robots11. However, passive stability comes at a cost, as it requires a minimal velocity and leads to reduced agility. Indeed, agile flyers such as flying insects12, quad rotors13 and tailless flapping-wing robots6,14 are inherently attitude-unstable and rely on active attitude control. To this end, unstable flying robots commonly feature accelerometers15, as filtering acceleration measurements over time allows to retrieve the gravity direction13.
It is still unclear whether and how flying insects estimate their attitude3,5,16,17. Although insects have many different sensory modalities, no specific gravity sensor such as an accelerometer has been found. Sensory cues that carry information on the gravity direction when walking (such as leg loads18,19), are not valid when airborne. A flying body is often subject to accelerations larger than gravity in other directions, especially during manoeuvring20. Moreover, organs with gyroscopic function such as the halteres in dipterans3 can aid stabilization by providing information on body rotation rates, but they carry no information on the absolute attitude angle itself. Depending on the insect species, rotation rates may also be sensed with antennal flagella21, wing strains22, ocelli23,24 or by separating the rotational and translational components of optic flow25. In principle, one can integrate rotation rates starting from a known initial attitude26, but the estimated attitude will then drift over time.
A few bio-inspired control approaches have forwarded the interesting possibility that insects may bypass estimating attitude altogether17,24,27. It has been demonstrated that pendulum-like flapping-wing robots can be stabilized around hover purely by countering rotation rates24. A full control system can also use optic flow for controlling flight speed17,27. However, the system's control performance will depend on setting the rotation rates such that the available thrust and lift forces reach the desired directions quickly enough. Because the right sign and magnitude for rate commands depend on the attitude angle, these approaches will also benefit from taking attitude into account.
Combining optic flow and a motion model
Here, we explore whether the attitude angle can be retrieved when combining optic flow with a motion model. Motion models are commonly used for state estimation in flying robots, but almost always incorporate measurements from an inertial measurement unit, containing gyros, magnetometers and accelerometers, to retrieve attitude28,29. A few studies have attempted to estimate attitude angles with just optic flow and motion models before30,31,32,33. However, the results from these studies are inconclusive. First it was shown that attitude angles could not be determined in this manner for fixed-wing drones30. Follow-up studies demonstrated that attitude deviations from the forwards flight equilibrium point are observable31,32,33, but already so when observing the drone's rotation rates alone. Indeed, the simulation experiments show growing errors on the pitch angle32, indicating that the model may be largely relying on integrating rotation rates.
We follow a bio-robotics approach (Fig. 1a) to studying optic-flow-based attitude estimation and control. First, we prove theoretically that attitude angles can be estimated when combining optic flow measurements with a generic, thrust-vectoring motion model of unstable flyers. This type of model relates body attitude, that is, pitch and roll angles, to acceleration direction. It applies to rotorcraft such as quad rotors13, but also to insects34,35,36 and tailless flapping-wing robots6,14 when averaging forces over the flapping cycle. Mathematically describing the sensory inputs and the motion model enables a formal analysis of the state's 'observability'. The state of the two-dimensional (2D) model in Fig. 1b is a vector with the roll angle, velocities and height, whereas its sensory input comes from a single optic flow sensor similar to an elementary motion detector37, directed downwards from the body. The state is observable if it can be uniquely determined by tracking motor actions and sensor observations over time.
Fig. 1: Theoretical analysis proves that attitude can be estimated with optic flow and a thrust-vectoring motion model but that the presence of unobservable states leads to slight attitude oscillations.
a, Illustration of our approach to studying optic-flow-based flight attitude control. Grey arrows represent the influence of insights and inspiration, and black arrows represent modelling and the generation of hypotheses. \({{\mathscr{L}}}_{f}^{1}h\) is the Lie derivative of the optic flow observation equation. The honeybee image is reprinted with the permission of iStock.com/Antagain. b, Thrust-vectoring motion model of an unstable flying system, that is, robot or insect, and an axis system used for a 2D constant-height model, with body velocities \({v}_{{\rm{B}}},{w}_{{\rm{B}}}\), roll attitude angle \(\phi \) and rate \(p\), distance along the principal axis, \({Z}_{{\rm{B}}}\), to a world point for which optic flow is measured and inertial velocity \({v}_{{\rm{I}}}\) and altitude \({Z}_{{\rm{I}}}\). c, Illustration showing that the proposed approach to attitude estimation leads to a continuous transition between observable and unobservable states, leading to slight attitude oscillations of the system. d, The degree (deg.) of observability (equation (35), Supplementary Information) in a part of the state space for a constant-height model without rate measurements, with the remaining variables set to \({v}_{{\rm{I}}}=0\), \({Z}_{{\rm{I}}}=1\) and moment \(M=0\). The colour range goes from unobservable (dark blue) to higher degrees of observability (yellow), which implies a faster convergence of a state estimation filter. The state is unobservable if the system is upright (\(\phi =0\)) or not rotating (\(p=0\)). A state space trajectory is shown of a controller with as desired state \({\phi }^{* }=0\) (black solid line in the plot's centre and in the inset). e, The same graph for a constant-height system with rate measurements. The state is now only unobservable in the case of zero rate. f, Control performance for the constant-height system without rate measurements. The figure shows the mean absolute (abs.) error \(\bar{|{\omega }_{y}-{\omega }_{y}^{\ast }|}\) for the simulated system over N = 10 runs (from green to red). A mean absolute error \(\ge 0.05\) means that the controller is not able to track the reference. The y axis represents the optic flow sensing frequency (OF freq.), and the x axis represents different noise settings for the optic flow measurement \({\sigma }_{{\rm{OF}}}\) and actuation noise on the generated moment \({\sigma }_{{\rm{M}}}\), separately. g, The same graph as f but for a constant-height system with rate measurements.
We investigate the thrust-vectoring model for various levels of complexity, starting from a basic constant-height model without drag (Theoretical analysis and Supplementary Information). Non-linear observability analysis shows that the state, including the attitude angle, is locally, weakly observable38. This means that at a single time instant, changes in the observation and corresponding time derivatives can be uniquely linked to changes in the state. A further mathematical and numerical analysis indicates that the model even possesses the stronger property of local observability, indicating that the state itself can be determined instantaneously.
However, the observability depends on the values of the state variables and control inputs. To illustrate this, Fig. 1d,e shows the degree of observability (equation (35), Supplementary Information) for two variants of a constant-height model, in which a higher degree implies that changes in the state can be observed more easily. The model in Fig. 1d estimates rotational accelerations generated by its motor actions, whereas the model in Fig. 1e also measures the rotation rate. The latter model's degree of observability is higher throughout the state space, but both models have an unobservable state when the roll rate p = 0° per s. At first, this seems to represent a considerable problem as a zero rate will occur frequently, that is, whenever the controller reaches its target attitude angle or optic flow setpoint. In engineering, having unobservable states at the core of the control system would be regarded as unacceptable and remedied by adding extra sensors.
By contrast, we propose that nature may have accommodated the unobservability of attitude in certain states. For the basic constant-height model, we provide a proof (Supplementary Information) of the control system's stability, including the unobservable conditions. It consists of two parts: (1) when the state is observable the controller is able to achieve its control objective, which will lead to zero rate, that is, a condition in which the state is unobservable. (2) When the state is unobservable, noise and disturbances will lead to a condition in which the state is observable again. For example, a direct effect is caused by actuation noise in the moment generation that makes the model rotate, inducing observability. Another example is an indirect effect caused by sensor noise, which will lead to a wrong attitude estimate. Because the wrong estimate will be off-target, the controller will command a 'corrective' action that results in a non-zero rate and thus an observable state. Consequently, the system will continuously move into and out of unobservable states, leading to slightly oscillatory motions. This is illustrated in Fig. 1c and the oscillations are evident from the elliptical black line trajectories in \(\left(\phi ,p\right)\)-space shown on Fig. 1d,e.
Closed-loop simulation experiments with varying noise levels confirm that the unobservable states do not hamper successful attitude or optic flow control. Figure 1f,g shows the control performance for the model without and with rate measurements. In general, the performance benefits from fast vision measurements, as performance increases with an increasing vision update frequency. Moreover, the control performance is worse for the model without rate measurements in which increasing actuation noise forms a problem. These simulation results show that rotation rate measurements are not strictly necessary for attitude estimation and control, but do improve control performance.
The mathematical and numerical analysis of increasingly complex models shows that their state is also locally, weakly observable. The complexities introduced include a varying height model with drag and wind, imperfect thrust prediction, a sloped surface and finally flight in generic three-dimensionally structured environments (Supplementary Information). Attitude is observable with the help of a thrust-vectoring model as it links attitude to accelerations and acceleration changes that are captured by optic flow and its time derivatives. However, the state is always unobservable in a perfect hover condition, that is, when the attitude is constant and optic flow is cancelled out.
Robotic experiments
Experiments with a free-flying, fully autonomous quad rotor (Fig. 2) confirm the theoretical findings. The drone observes both the longitudinal and lateral ventral optic flow, capturing the ratio of the horizontal velocities and the height, and the optic flow divergence, representing the ratio of the vertical velocity and the height (Quad rotor experiments). Its objective is to hover, eliminating ventral flow by estimating and controlling the roll and pitch attitude angles and divergence by means of thrust control. When flying with a traditional complementary filter based on gyros and accelerometers1, the drone hovers still (\({\sigma }_{\phi }=0.96\), \({\sigma }_{\theta }=0.55\), Fig. 2g). Switching to the proposed attitude estimation scheme using optic flow and gyros, indeed leads to slight oscillations, as is evident from the attitude angles and velocities over time in Fig. 2b–f and the wider angle histogram in Fig. 2g (\({\sigma }_{\phi }=1.24\), \({\sigma }_{\theta }=0.84\), significantly different from accelerometer-based flight with \(P < 0.001\), two-sided bootstrap method39). Furthermore, the height is most difficult to estimate (Fig. 2f and Extended Data Fig. 1d). We note, however, that neither the estimated velocity nor the height is used by the drone's control loops. Instead, the drone directly uses optic flow measurements. In general, the attitude estimation and control of the robot is very robust, despite the assumptions of a constant height and flat ground. This is shown by more experiments with slopes or three-dimensional (3D) structures under the drone and with angle disturbances (Fig. 2h–j and Supplementary Videos 1–8). Similar results have been obtained with a varying height model (Supplementary Information and Extended Data Fig. 6). The robustness is partly due to the drone processing optic flow over the entire flow field (Quad rotor experiments).
Fig. 2: The theoretical findings are confirmed by robotic experiments in which fully autonomous flight is demonstrated based on optic flow and gyro measurements.
a, Quad rotor robot used in the experiments. b, Optic-flow-based (thick line) and accelerometer-based (thin line) estimated roll angles over time during a hover-experiment in which the drone flies first with the accelerometer-based estimate (light grey shading, 'ACC-based attitude') and then with the optic-flow-based estimate (dark grey shading, 'OF-based attitude'). c, Optic-flow-based (thick line) and accelerometer-based (thin line) estimated pitch angles over time. d, Optic-flow-based (thick line) and motion-tracking-based (thin line) estimated lateral velocity \({v}_{y}\) over time. e, Optic-flow-based (thick line) and motion-tracking-based (thin line) estimated longitudinal velocity \({v}_{x}\) over time. f, Optic-flow-based (thick line) and motion-tracking-based (thin line) height \(Z\) over time. g, Comparison of sampled probability distributions of the pitch angle \(\theta \) while flying with an accelerometer-based estimate (light grey, foreground) and an optic-flow-based estimate (dark grey, background), data from \(N=10\) flights, 5,471 samples. h, The drone flying over a moving slope. i, The drone flying over a three-dimensionally structured environment. j, Disturbance-rejection experiment in which the roll is perturbed by 10°.
To better approximate natural flyers, we also performed experiments with a bio-inspired flapping-wing robot (Flapping-wing robot experiments, Fig. 3a). The robot is equipped with an artificial compound eye called CurvACE40 (Fig. 3b). It features a wide field of view of 180° × 60° with a coarse visual resolution of 40 × 15 pixels. We determine optic flow in four regions at a high temporal resolution of 200 Hz, close to the flicker fusion frequency of honeybee vision41. We initially thought that the residual flapping-wing motion on the compound eye would hamper state estimation (see the rates and optic flow in Fig. 3d,e). However, the optic-flow-based attitude estimates correspond well to those of the complementary filter using accelerometers (Fig. 3c). We subsequently realized that the residual flapping motion did not impair but improved attitude observability. Figure 3f shows that oscillations are beneficial to observability, with higher frequencies shortening the time duration of low observability. This finding suggests that flying insects or robots could benefit from residual flapping-wing oscillations or even actively induce rotation rates to enhance the degree of observability—in the spirit of active vision42,43.
Fig. 3: Experiments with a bio-inspired flying robot show that residual oscillations from flapping-wing motion improve observability.
a, Flapping-wing robot experiment, featuring a 50 cm wingspan 'flapper drone' (design based on ref. 14) carrying the light-weight, high-frequency artificial compound eye CurvACE40. A constant-height model was implemented that only used lateral ventral flow (no divergence). b, The CurvACE determined optic flow at 200 Hz in four separate downwards facing regions in its field of view. Each time instance it used one step of the Lucas–Kanade optic flow algorithm to determine the flow in the x and y directions at these four locations. During the experiments, the lateral optic flow was determined by averaging the flow in the x direction over the four areas. c, Estimated roll angles over time during one of the experiments, estimated by a complementary filter that uses the accelerometers (thin line) and by a filter that is based on optic flow and gyro measurements (thick line). There is no ground truth \(z\) or \({v}_{y}\), as the motion-tracking system needed to be switched off as its infrared lights influenced the CurvACE sensor. d, Roll rate over time. e, Average optic flow over time (in pixels per second). f, Simulation results for a constant-height model, in which we compare the default case (dark blue) with cases in which we actively add sinusoidal oscillations of different frequencies to the roll rate (1 Hz, medium blue, 10 Hz, light blue line). The observability degree increases substantially due to the higher rotation rates.
Our findings have implications for robotics. First, tiny, insect-sized flying robots such as the Robobee6,44 are extremely resource-limited. For such robots, even small MEMs-based sensors form a burden. We have demonstrated that accelerometers are not necessary to successfully control attitude. Second, most autopilots for flying robots only incorporate lateral ventral flow into their state estimation. We have shown that optic flow divergence can improve redundancy, even allowing to fly completely autonomously without any height sensors or accelerometers. Third, accommodating unobservability is a strategy with broader implications than optic flow control alone. For instance, wireless-ranging-based relative localization in drone swarms45 leads to important unobservable conditions such as during formation flight. The current study suggests investigating the option of a minimalistic system accommodating this unobservability instead of a heavier, more power-hungry system with more sensors.
The presented approach also forms a hypothesis on insect attitude estimation, potentially explaining various phenomena observed in flying insects. First, it explains which role optic flow may play in attitude estimation and control. Optic flow was shown to be essential to hoverflies for stabilizing their flight when falling5,16. The hoverflies' behaviour was best explained by a model that incorporated attitude angles16, but it was unclear how such angles were estimated without a clear visual horizon in the environment. We have shown that this is possible if the insect possesses a motion model, relating attitude to acceleration direction. This raises the question of how plausible it is for insects to have a motion model, with which we intend any means to use predicted effects of actions for perception and control. In ref. 46 it is argued that insects possess such 'forwards models' and that they serve goals such as reducing action latency47 and differentiating between external disturbances and expected feedback48. Our study highlights another potential purpose of forwards models, that is, to make states such as attitude observable. The implementation of such a model in the brain can be implicit, for example, reminiscent of how visual receptive fields of lobula plate tangential cells seem to be tuned to an insect's motion model49. Second, the results reported in Fig. 2 may explain the (im)precision of flight for different species and conditions. For instance, honeybees can still fly, but less precisely, when their ocelli are covered with opaque paint8. Moreover, the results in Fig. 3 indicate a potential usefulness for flapping-induced, high-frequency thorax and head oscillations of blowflies7.
Verifying the hypothesis may be challenging, as it concerns brain processes that are hard to monitor during flight. One potential avenue is to exploit the prediction that the degree of observability changes over the state space, which in turn will affect the insect's attitude variation. For example, closed-loop simulation experiments with a head-and-body model (Supplementary Information) show that observability increases and attitude variation in both body and head decreases for higher flight speeds. As a preliminary analysis we investigated the biological data from honeybee experiments by Portelli et al.9. The data only allow us to retrieve the body pitch angle, which indeed has a lower variance for higher speeds (Supplementary Information and Extended Data Figs. 2 and 9). However, other phenomena also influence this trend. For example, parasitic drag will be larger at higher flight speeds, stabilizing attitude. In the same time, aerodynamic insect models34,35,36 also predict increasing pitch instability at higher flight speeds, destabilizing attitude. More simulation experiments, piecing apart parasitic drag from observability effects, suggest that only observability affects the trend of the head attitude (Supplementary Information). Future biological studies that track not only body but also head attitude or that manipulate sensory inputs could give further insight into this matter.
Finally, one can wonder what role the proposed mechanism plays in the context of insects' many more sensory cues. On the one hand, adding more sensors will improve the observability. On the other hand, unless such further sensory cues directly encode for the gravity direction, flight conditions such as a pure hover will remain unobservable. Hence, the main findings on unobservability and the ensuing attitude variations stay relevant when taking into account extra senses. Because animals generally rely on redundant information sources, even larger animals such as birds could use optic flow and motion model information to support their attitude estimation50.
Theoretical analysis
The theoretical analysis of the observability of the state, including attitude, relies on both a motion model and a model of the sensory inputs. In this section, we first explain the model for the elementary case of a quad rotor flying at a constant height above a flat ground surface. The model captures the main characteristics necessary for attitude estimation with optic flow, while leading to mathematical formulas of limited complexity and hence improved comprehensibility. Subsequently, we discuss more general models of motion and more generic environments. The mathematical derivations and formulas involved in the non-linear observability analysis and stability proof for the constant-height model are detailed in the Supplementary Information for brevity.
Constant-height model
Observability analysis
Without loss of generalization with respect to a thrust-vectoring model, we will consider a quad rotor drone's motion in the 2D plane. Please see the axis definitions in Extended Data Fig. 3a. In our analysis, we focus on the roll angle \(\phi \) (and roll rate \(p\)), but the findings are equally valid for the pitch angle \(\theta \) (and pitch rate \(q\)). In practice, estimating pitch instead of roll may require different parameters for drag and moment of inertia in the case of an asymmetric body. As a result, the stability properties of these axes may be different, but this does not fundamentally affect the analysis. The velocity in the inertial z axis will be denoted with \({w}_{{\rm{I}}}\) and that in the inertial y axis with \({v}_{{\rm{I}}}\). In Extended Data Fig. 3a, \({w}_{{\rm{I}}}\) is not shown as it is zero. For velocities in body axes, we will use \({w}_{{\rm{B}}},{v}_{{\rm{B}}}\), for the body z and y axes, respectively.
The observation model represents the optic flow in the direction of the camera's principal axis. For our derivations, we use a pinhole camera model. We are interested in the time derivative of the feature's location in the camera's field of view, which at the principal axis image coordinate, \((x,y)=(\mathrm{0,0})\), is given by51:
$${\omega }_{y}=-\,\frac{{v}_{{\rm{B}}}}{{Z}_{{\rm{B}}}}+p=-\,\frac{{\cos }^{2}\left(\phi \right){v}_{{\rm{I}}}}{{Z}_{{\rm{I}}}}+p$$
where \({\omega }_{y}\) is the ventral lateral flow. Equation (1) is valid for the interval \(\phi \in \left(-9{0}^{^\circ },9{0}^{^\circ }\right)\), where the parentheses denote the exclusion of the interval borders. The right-hand side of equation (1) is based on geometric relations visible in Extended Data Fig. 3a that would change if the roll angle were outside this interval.
The state is defined as a vector \({\bf{x}}=[{v}_{{\rm{I}}},\phi ,{Z}_{{\rm{I}}}]\), and the control input (motor action) is the roll rate, that is, \(u=p\). This leads to the state update equation, with g representing the gravitational acceleration:
$$f({\bf{x}},u)=\left[\begin{array}{c}{\dot{v}}_{{\rm{I}}}\\ \dot{\phi }\\ {\dot{Z}}_{{\rm{I}}}\end{array}\right]=\left[\begin{array}{c}g\,\tan \left(\phi \right)\\ p\\ 0\end{array}\right]$$
Equations (1) and (2) form the basis for the non-linear observability analysis, of which the details can be found in the Supplementary Information. The analysis shows that the system is locally, weakly observable in most of the state space. Weak observability implies that given the sensory input and its time derivatives, changes in the state can be uniquely identified. Local stands for local in time, that is, the estimation can be done at a single time instant. The main condition in which the state is unobservable (not weakly, locally observable), is when the roll rate is zero, \(p=0\). This condition corresponds to flying with a constant roll angle, in which the acceleration is not changing, that is, there is no 'jerk'. We also analyse the stronger property of local observability for this model. The theoretical and numerical analysis indicate that in most of the state space the system is locally observable, that is, that the sensory input and its time derivatives suffice for directly determining the state. The two main conditions for which the state is locally unobservable are \(p=0\) and \(\phi =0\), that is, when there is either no jerk or no acceleration.
Control system stability
At first sight, the unobservable condition of \(p=0\) may seem problematic because an attitude controller that reaches the desired attitude will set the rate to zero. Hence, if the control system is successful, it will lead to unobservability of the system. In the Supplementary Information, we provide a stability proof for the constant-height model, which takes conditions into account in which the state is unobservable. The first part of the proof shows that when the state is observable, the control will be able to reach a desired attitude angle \({\phi }^{* }\). If this angle is reached, the controller will command \(p=0\), which leads to unobservability of the system. The second part of the proof shows that sensor noise, actuation noise or external disturbances will always make the system observable again.
Simulation setup
The proof is supported by evidence from simulation experiments (Supplementary Information and Extended Data Figs. 7 and 8). Here we explain the simulation setup, as simulations with different models also follow the same scheme (for example, the simulation results in Fig. 1 and Extended Data Fig. 2). The simulation uses the motion model in equation (2) for the evolution of the ground-truth state over time. It also features a simulated 'robot' that receives optic flow observations according to equation (1), but delayed and with additive Gaussian noise: \({\hat{\omega }}_{y}\left(t+\bigtriangleup t\right)=-\,\frac{{\cos }^{2}\left(\phi (t)\right){v}_{{\rm{I}}}(t)}{{Z}_{{\rm{I}}}(t)}+p(t)+\mu (t+\bigtriangleup t)\), with \(\triangle t\) as the delay and \(\mu \sim {\mathscr{N}}\left(0,{\sigma }_{{\omega }_{y}}\right)\) the noise, where the tilde (~) means "distributed as". These observations are input into an extended Kalman filter (EKF)52, which uses equation (2) for predictions and linearization of equation (1) around the current estimated state \(\hat{{\bf{x}}}\) as the observation equation. The simulated robot has a proportional, integral 'outer loop' controller for reaching a desired optic flow value \({\omega }_{y}^{* }\). The output of this controller is a desired roll angle, \({\phi }^{* }\). An 'inner loop' proportional integral controller then sets the rate command \(p(t)\) on the basis of the error in the roll angle, that is, the difference between the desired and estimated roll angle \(({\phi }^{* }-\hat{\phi })\). Whereas the EKF uses this commanded roll rate for its predictions, it is used in the simulator after being delayed and perturbed by Gaussian noise. Thus, the \(p\) entered in equation (2) is \(p(t+\bigtriangleup t)=p(t)+\mu (t+\bigtriangleup t)\), with \(\mu \sim {\mathscr{N}}\left(0,{\sigma }_{p}\right)\).
Model extensions
The two central assumptions of the elementary constant-height model may sound stronger than they actually are. First, as we perform local observability analyses, the flat ground assumption only needs to hold close to the world point now perceived by the optic flow sensor (spatially local flatness). Moreover, although the height is assumed constant, it is part of the state that is estimated. Hence, height changes will eventually be picked up by the state estimation. Nonetheless, we also study extensions of the model both in terms of motion and structure of the environment. Below we briefly discuss the various extensions, of which the details can be found in the Supplementary Information.
First, in the analysis above, p is a control input that is known to the system. However, real-world systems such as drones and flying insects do not control attitude rate directly. Instead, by varying rotor speeds or wing flapping amplitudes, they generate moments. Modelling the system as such makes the rate \(p\) a state that is to be estimated. The rotation rate can be measured by means of gyros, which gives a very high update frequency (typically \(\gg \) 500 Hz), as is done in our robotic experiments (Flapping-wing robot experiments and Quad rotor experiments). It can also be measured with other sensors. For example, it can be extracted from the optic flow field51. The disadvantage of this is that the rates are then determined at a lower update frequency, leading to slower, less accurate state estimates. Still, theoretically, measuring p is not necessary because predicting the moments caused by control inputs suffices, as shown in the Supplementary Information. This is the motion model that was used for the simulation results from Fig. 1 in the main article. These simulation experiments follow the same simulation scheme as explained for the rate-based constant-height model explained above, except for the state update equations and control being different. Specifically, in these simulations the motor actions of the simulated robot do not consist of rotational rates, but of moments. This leads to the following state update equation: \(f({\bf{x}},u)=[{\dot{v}}_{{\rm{I}}},\dot{\phi },\,\dot{p},{\dot{Z}}_{{\rm{I}}}]=[\,g\tan (\phi ),p,M\,/\,I,0]\), where \(M\) is the moment and \(I\) is the moment of inertia. In this case, the control input (motor action) is the moment, \(u=M\), which is also delayed and perturbed by Gaussian noise when performing simulations.
Second, the constant-height model has an obvious potential flaw: can the system keep the height constant enough when it has to be estimated? In practice, this model works well because keeping a roughly constant height is possible through appropriate optic flow divergence control. Still, in the Supplementary Information, we extend the model above to a varying height model (including vertical body velocity), with drag and wind (see Extended Data Fig. 3b for a graphical illustration of the model). Non-linear observability analysis shows that the state of this varying height model, including the current wind velocity, is locally, weakly observable. The state becomes unobservable when we set the thrust to compensate for gravity, the velocities to match the wind and the moment and rate to zero. This setting corresponds to a condition of a pure hover in this model—without accelerations of jerk.
Although this extensive model is still locally, weakly observable, state estimation performance will benefit from further measurements. That is why we also study a varying height model including an extra sensory input, that is, the optic flow divergence, which captures the vertical body velocity relative to the distance to the ground \(\frac{{w}_{{\rm{B}}}}{{z}_{{\rm{B}}}}\). This model, which includes drag and a thrust bias as state variables but excludes wind, is described and studied in the Supplementary Information. It is again locally, weakly observable and has been successfully implemented onboard of a quad rotor for robotic experiments (Quad rotor experiments and Extended Data Fig. 6).
Third, we analyse cases in which the ground is not flat. In the Supplementary Information, we investigate what happens when the ground surface is sloped, while still only observing optic flow at the principal axis coordinate (Extended Data Fig. 3c). The state, including the slope angle, turns out to be locally, weakly observable even with this elementary optic flow measurement. Subsequently, in the Supplementary Information we analyse the case of a generic environment with the system having access to the entire optic flow field (Extended Data Fig. 3d). It is well-known that from the entire optic flow field the system can estimate a unit-vector for velocity \({\bf{v}}\), with \(\parallel {\bf{v}}\parallel =1\), the rotation rate \(p\) and all inverse depths \(\frac{1}{{z}_{{\rm{B}}i}}\) for all world points \({P}_{i}\) in view53. Finally, in the Supplementary Information it is shown that this suffices for retrieving attitude, velocity and height with respect to a selected point \({P}_{i}\).
Fourth, in all above cases, the eye is rigidly fixed to the body, whereas insects can move their head with respect to their body to stabilize their gaze. In the Supplementary Information we study a head-and-body model, in which the body attitude influences the thrust direction and the head attitude the looking direction (Extended Data Fig. 10). Also this more complex model is locally, weakly observable. This model is used in simulation for the comparison with the biological data (Extended Data Fig. 2).
Quad rotor experiments
The setup for the quad rotor experiments is shown in Extended Data Fig. 4. We use a Parrot Bebop 2 drone for the experiments, replacing its firmware autopilot with the open-source Paparazzi UAV software54. All sensory processing and control runs onboard the drone. Here we discuss all processes shown in the figure.
The image processing pipeline consists of: (1) feature detection with ACT-corner55, (2) optic flow determination with the Lucas–Kanade algorithm56 and (3) extraction of optic flow measurements \(({\omega }_{x},{\omega }_{y},{\omega }_{z})\). The first two represent the longitudinal ventral flow \({\omega }_{x}=\frac{{u}_{{\rm{B}}}}{{z}_{{\rm{B}}}}\) and lateral ventral flow \({\omega }_{y}=\frac{{v}_{{\rm{B}}}}{{z}_{{\rm{B}}}}\). The last one is the optic flow divergence \({\omega }_{z}=\frac{{w}_{{\rm{B}}}}{{z}_{{\rm{B}}}}\). These measurements are obtained from the optic flow field with the methods from ref. 57, in which the optic flow is not derotated. The optic flow processing makes a robust fit of the flow field, assuming that it is predominantly linear. Moreover, the calculation of divergence \({\omega }_{z}\) is based on a separate process that estimates size changes in the image, making it insensitive to rotation rates.
Optic flow outer loop control
The drone has an optic flow outer loop control, which uses separate proportional integral controllers for the vertical and horizontal axes, as shown with a control diagram in Extended Data Fig. 4b. The vertical axis uses a proportional integral controller for the thrust based on the optic flow divergence error \(({{\omega }_{z}^{* }-\omega }_{z})\), in which during our experiments \({\omega }_{z}^{* }=0\), that is, we want the drone to hover. Successful optic flow divergence control requires an appropriate control gain, which in turn depends on the height57. Too high a gain will lead to vertical oscillations, which can be detected by the drone and in turn be used to find the right control gain57,58. The control gains for lateral control with \({\omega }_{x},{\omega }_{y}\) also depend on height, and we scale them linearly with respect to the vertical control gain. The outer loop lateral and longitudinal control sets the desired attitude angles \({\phi }^{* },{\theta }^{* }\), which are executed by the inner loop attitude controller.
Inner loop attitude control
Inner loop attitude control is performed with incremental non-linear dynamic inversion (INDI)59. This inner loop controller, illustrated in Extended Data Fig. 4c, uses the errors between the estimated and desired states \(({\phi }^{* }-\hat{\phi }),({\theta }^{* }-\hat{\theta })\). It subsequently uses proportional gains to set desired attitude rates and then rotational accelerations. The INDI block that determines the correct moment commands \({u}_{{\rm{M}}}\) to the motor mixing, relies on rotational accelerations that are calculated by low-passing and differentiating gyro measurements. For the exact details of INDI we refer the reader to ref. 59.
EKF/complementary filter
The attitude estimates used by the inner loop control can either come from an EKF that uses the proposed approach and combines optic flow with gyro measurements, or from a traditional complementary filter that fuses accelerometer and gyro measurements. We can switch between these estimators for use by the control, but always log both estimates for comparison purposes. The EKF is instantiated by using the state and observation equations in our models.
The EKF has parameters for the observation and actuation noise, forming the diagonal entries in the matrices \(R\) and \(Q\). Moreover, the varying height model includes four parameters that map the four commanded rotor speeds linearly to the thrust value, that is, T = \({{\bf{p}}}^{\top }{\bf{r}}\), where p is a vector with the four parameters and r a vector with the commanded rotor speeds. Although these EKF parameters can be estimated in a supervised manner from data, we obtained the best results by using an evolutionary optimization algorithm, covariance matrix adaptation evolutionary strategy (CMA-ES)60. Specifically, we performed seven flights in which we made a high-frequency log of all onboard sensor data. This allowed to run the EKF offline on the data sets. Then, CMA-ES optimized the parameters of the EKF, with as cost function the sum of squared errors of the estimates (comparing EKF estimates with the logged 'ground truth' from the complementary filter for attitude and motion-tracking system for height and velocities). Once optimized, the parameters resulted in successful state estimation and did not have to be adapted anymore for any of the test flights presented in the article's results.
The experiments presented in the main article and Fig. 2 are based on the constant-height model with rotation rate inputs presented in Theoretical analysis. Instead of predicting the rotation rates, gyro measurements are used as a stand-in for the control input to the filter. Moreover, the real robot always also uses the optic flow divergence as an observation. The same model is used for roll and pitch, assuming decoupled dynamics. We also performed experiments with a 'varying height model', which only estimates the roll angle but does take into account height changes, as explained in the Supplementary Information (results in Extended Data Fig. 6). Finally, we use the 'quaternion complementary filter' implemented in the open-source Paparazzi autopilot54 as the standard, accelerometer-based attitude estimation algorithm.
Experimental setup: slope
There are several ways in which the robot could take into account a sloped surface, for example, by means of an improved vision or state estimation process (Supplementary Information). However, we also perform an experiment in which we test on the drone what happens if the slope is not taken explicitly into account. Specifically, the drone uses the constant-height model for roll and pitch (Theoretical analysis), which does not include the slope in the state, and the vision processes described above, where the determination of ventral flow and divergence also do not take slope into account. The experimental setup and resulting state estimates are shown in Extended Data Fig. 1a. The screen starts out at a tilt of roughly 20°, but during the experiment it is moved slowly up to an angle of roughly 40° (Extended Data Fig. 1a) and then down again. It turns out that the presence of a slope is not particularly problematic for state estimation, even if it is ignored by the vision processing and in the state estimation setup. When moving up-slope (left in the picture), the optic flow should increase quicker than expected and the angle should be estimated larger. When moving down-slope, the optic flow increases slower than expected, which should lead to a smaller angle estimate. In the case of commanded hover flight, these effects only lead to slightly increased attitude variation (\({\sigma }_{\phi }=2.0^\circ \), \({\sigma }_{\theta }=1.54^\circ \)), with the estimates still closely resembling the accelerometer-based estimates (Extended Data Fig. 1a). Moreover, during the experiment, the screen that forms the slope is dragged away, which represents a disturbance that is successfully handled by the drone; as it is commanded to keep the lateral ventral flow zero, it moves along with the object. The experiment is included in the Supplementary Videos 1–8.
3D structure
In the Supplementary Information, we show that the proposed approach to attitude estimation does not rely on the ground being a flat surface. We explain there that one can deal with irregular environment structure by using a general vision method to separate the environment's 3D structure from the ego-motion. However, we also perform an experiment to test whether the constant-height model and the current vision processing are sufficiently robust to deal with a certain amount of 3D structure, by having the drone fly above several objects. The setup for this experiment and corresponding results are shown in Extended Data Fig. 1b. The roll and velocity estimates correspond well to the ground truth. The height seems underestimated, which here could be partly because the objects in view are actually closer to the drone than the ground. During the experiment, the drone first hovers above these objects and then also gets non-zero outer loop optic flow commands (\({\omega }_{y}^{* }\)) to translate left and right over the 3D structure (as can be seen in the Supplementary Videos 1–8). The attitude is well estimated throughout the experiment. We expect that the robustness of the current method stems from the fact that flow from the entire field of view is integrated to determine the optic flow observation.
A disturbance experiment was performed to test the response of both the state estimation filter and optic flow control. Specifically, to create a disturbance, we add a given number of degrees to the desired roll attitude \({\phi }^{* }\) that is determined by the outer loop control. For clarity, the outer loop control is unaware of this addition. As a consequence of this disturbance, which is 10° in our experiments, the inner loop control will command a much larger angle than desired by the outer loop control. The drone will accelerate sideways, leading to a larger lateral ventral optic flow. The outer loop proportional integral controller will attempt to eliminate the flow, with the integral term eventually cancelling out the introduced addition.
Several flights
The main paper shows results from ten subsequent flights (Fig. 2g). For each flight, the drone takes off, hovers according to its accelerometer-based attitude estimate, switches to using the optic-flow-based attitude estimate and then lands again. Extended Data Fig. 1d shows a picture of the experimental setup. Please note that during the experiments the ground surface of the arena was not changed to add visual texture. Furthermore, Extended Data Fig. 1d contains the error distributions for the different estimated states during all ten flights, when the drone was using the estimated angles for control. Here, the roll angle is compared to the accelerometer-based roll estimate, which we consider as ground truth. The velocity and height are compared to measurements by the motion-tracking system. It can be seen that both the roll angle and velocity are estimated accurately. The height error distribution is 'strange', showing that it is the most difficult variable to estimate, and that around hover the height does not always converge to the correct value. Also, other experiments have shown the height estimates to be the least accurate.
Flapping-wing robot experiments
For the flapping-wing robot experiments, we used a commercially available 'flapper drone'. Its design is inspired by the 'DelFly Nimble' flapping-wing robot14. However, the flapper drone is more robust, which facilitates experiments. It is also larger and heavier than the DelFly Nimble, while staying light-weight compared to most quad rotor drones (100 g). The flapping frequency of the flapper drone is roughly 12 Hz. As explained in the main text, the flapper drone is equipped with the CurvACE40, a miniature artificial compound eye, which has a broad field of view (180° × 60°) and a high update rate for the optic flow measurements (200 Hz). Extended Data Fig. 5 shows the experimental setup for the flapper drone, which uses the BitCraze open-source autopilot software. We adapted the flapper drone hardware to include the CurvACE, sending its outputs (four optic flow vectors) to the BitCraze autopilot board. Extraction of \({\omega }_{y}\) is done by averaging the four flow values in the y direction, and scaling it with a constant factor to encode rad s−1. We also modified the software to run an EKF based on \({\omega }_{y}\) and gyro measurements in parallel to the standard complementary filter, for estimating \(\phi \). By contrast to the quad rotor experiments, the outer loop control is performed by a human pilot, providing desired attitude angles and thrust commands. A basic PID controller serves as inner loop controller to reach the desired attitude angles. Again, we can switch between the estimated angle determined by the optic-flow-based EKF and by the accelerometer-based complementary filter. One might be tempted to think that the human pilot could be able to fly the flapper drone even if the roll estimates by the EKF are far off from the true roll angles. However, the inner loop control operates at such a fast time scale that this is not possible: good attitude estimates are necessary for successful flight. The moment and thrust commands are mixed and result in commands to the two independently moving wing pairs for executing the roll and thrust commands. Pitch moments are controlled with a servo that determines the dihedral angle, whereas yaw moments are controlled with a servo that twists the wings slightly for thrust vectoring. For details, we refer the reader to Karásek et al.14.
All data necessary for performing and analysing the experiments is publicly available: the flight data is available at https://doi.org/10.4121/20183399.
The code to reproduce the theoretical and simulation results and analyse robotic experiments is publicly accessible at https://doi.org/10.4121/20183399. The code to perform flight experiments with the open-source Paparazzi autopilot on the Bebop 2 drone is available at https://github.com/tudelft/paparazzi/releases/tag/v5.17.5_attitude_flow. The code to perform flight experiments with the flapper drone is available at https://github.com/tudelft/crazyflie-firmware/releases/tag/v3.4.0_attitude_flow.
Mahony, R., Hamel, T. & Pflimlin, J.-M. Nonlinear complementary filters on the special orthogonal group. IEEE Trans. Automat. Contr. 53, 1203–1218 (2008).
Bender, J. A. & Frye, M. A. Invertebrate solutions for sensing gravity. Curr. Biol. 19, R186–R190 (2009).
Taylor, G. K. & Krapp, H. G. in Advanced Insect Physics (eds Casas, J. & Simpson, S. J.) 231–316 (Elsevier, 2007).
Schuppe, H. & Hengstenberg, R. Optical properties of the ocelli of Calliphora erythrocephala and their role in the dorsal light response. J. Comp. Physiol. A 173, 143–149 (1993).
Goulard, R., Vercher, J.-L. & Viollet, S. To crash or not to crash: how do hoverflies cope with free-fall situations and weightlessness? J. Exp. Biol. 219, 2497–2503 (2016).
Ma, K. Y., Chirarattananon, P., Fuller, S. B. & Wood, R. J. Controlled flight of a biologically inspired, insect-scale robot. Science 340, 603–607 (2013).
ADS CAS PubMed Google Scholar
Hateren, J. H. V. & Schilstra, C. Blowfly flight and optic flow. II. Head movements during flight. J. Exp. Biol. 202, 1491–1500 (1999).
KASTBERGER, G. The ocelli control the flight course in honeybees. Physiol. Entomol. 15, 337–346 (1990).
Portelli, G., Ruffier, F., Roubieu, F. L. & Franceschini, N. Honeybees' speed depends on dorsal as well as lateral, ventral and frontal optic flows. PLoS ONE 6, e19486 (2011).
ADS CAS PubMed PubMed Central Google Scholar
Mohamed, A., Massey, K., Watkins, S. & Clothier, R. The attitude control of fixed-wing MAVS in turbulent environments. Prog. Aerosp. Sci. 66, 37–48 (2014).
De Croon, G., Perçin, M., Remes, B., Ruijsink, R. & De Wagter, C. The DelFly 10 (Springer, 2016).
Liang, B. & Sun, M. Nonlinear flight dynamics and stability of hovering model insects. J. R. Soc. Interface 10, 20130269 (2013).
Mahony, R., Kumar, V. & Corke, P. Multirotor aerial vehicles: modeling, estimation, and control of quadrotor. IEEE Robot. Autom. Mag. 19, 20–32 (2012).
Karásek, M., Muijres, F. T., De Wagter, C., Remes, B. D. W. & de Croon, G. C. H. E. A tailless aerial robotic flapper reveals that flies use torque coupling in rapid banked turns. Science 361, 1089–1094 (2018).
ADS MathSciNet PubMed MATH Google Scholar
Martin, P. Accelerometers on quadrotors: what do they really measure? J. AerospaceLab 8, 1–10 (2014).
Goulard, R., Vercher, J.-L. & Viollet, S. Modeling visual-based pitch, lift and speed control strategies in hoverflies. PLoS Comput. Biol. 14, e1005894 (2018).
Expert, F. & Ruffier, F. Flying over uneven moving terrain based on optic-flow cues without any need for reference frames or accelerometers. Bioinspir. Biomim. 10, 26003 (2015).
Mendes, C. S., Rajendren, S. V., Bartos, I., Márka, S. & Mann, R. S. Kinematic responses to changes in walking orientation and gravitational load in Drosophila melanogaster. PLoS ONE 9, e109204 (2014).
ADS PubMed PubMed Central Google Scholar
Kress, D. & Egelhaaf, M. Head and body stabilization in blowflies walking on differently structured substrates. J. Exp. Biol. 215, 1523–1532 (2012).
Muijres, F. T., Elzinga, M. J., Melis, J. M. & Dickinson, M. H. Flies evade looming targets by executing rapid visually directed banked turns. Science 344, 172–177 (2014).
Sane, S. P., Dieudonné, A., Willis, M. A. & Daniel, T. L. Antennal mechanosensors mediate flight control in moths. Science 315, 863–866 (2007).
Eberle, A. L., Dickerson, B. H., Reinhall, P. G. & Daniel, T. L. A new twist on gyroscopic sensing: body rotations lead to torsion in flapping, flexing insect wings. J. R. Soc. Interface 12, 20141088 (2015).
Gremillion, G., Humbert, J. S. & Krapp, H. G. Bio-inspired modeling and implementation of the ocelli visual system of flying insects. Biol. Cybern. 108, 735–746 (2014).
MathSciNet PubMed Google Scholar
Fuller, S. B., Karpelson, M., Censi, A., Ma, K. Y. & Wood, R. J. Controlling free flight of a robotic fly using an onboard vision sensor inspired by insect ocelli. J. R. Soc. Interface 11, 20140281 (2014).
Koenderink, J. J. & van Doorn, A. J. Facts on optic flow. Biol. Cybern. 56, 247–254 (1987).
CAS PubMed MATH Google Scholar
Zhang, L., Shi, Z. & Zhong, Y. Attitude estimation and control of a 3-DOF lab helicopter only based on optical flow. Adv. Robot. 30, 505–518 (2016).
Dickson, W. B., Straw, A. D. & Dickinson, M. H. Integrative model of Drosophila flight. AIAA J. 46, 2150–2164 (2008).
ADS Google Scholar
Kendoul, F., Fantoni, I. & Nonami, K. Optic flow-based vision system for autonomous 3D localization and control of small aerial vehicles. Rob. Auton. Syst. 57, 591–602 (2009).
Bloesch, M. et al. Fusion of optical flow and inertial measurements for robust egomotion estimation. In Proc. IEEE IROS 3102–3107 (IEEE, 2014).
Gurfil, P. & Rotstein, H. Partial aircraft state estimation from visual motion using the subspace constraints approach. J. Guid. Control Dyn. 24, 1016–1028 (2001).
Webb, T., Prazenica, R., Kurdila, A. & Lind, R. Vision-based state estimation for uninhabited aerial vehicles. In Proc. AIAA GNC Conference 5869 (AIAA, 2005).
Webb, T. P., Prazenica, R. J., Kurdila, A. J. & Lind, R. Vision-based state estimation for autonomous micro air vehicles. J. Guid. Control Dyn. 30, 816–826 (2007).
Webb, T. P. Vision-based State Estimation for Uninhabited Aerial Vehicles Using the Coplanarity Constraint.PhD thesis, Univ. of Florida (2007).
Taylor, G. K. & Thomas, A. L. R. Dynamic flight stability in the desert locust Schistocerca gregaria. J. Exp. Biol. 206, 2803–2829 (2003).
Sun, M. & Xiong, Y. Dynamic flight stability of a hovering bumblebee. J. Exp. Biol. 208, 447–459 (2005).
Faruque, I. & Humbert, J. S. Dipteran insect flight dynamics. Part 1 Longitudinal motion about hover. J. Theor. Biol. 264, 538–552 (2010).
Borst, A., Haag, J. & Reiff, D. F. Fly motion vision. Annu. Rev. Neurosci. 33, 49–70 (2010).
Hermann, R. & Krener, A. Nonlinear controllability and observability. IEEE Trans. Automat. Contr. 22, 728–740 (1977).
Efron, B. & Tibshirani, R. J. An Introduction to the Bootstrap (CRC Press, 1994).
Floreano, D. et al. Miniature curved artificial compound eyes. Proc. Natl Acad. Sci. USA 110, 9267–9272 (2013).
Srinivasan, M. V. & Lehrer, M. Temporal acuity of honeybee vision: behavioural studies using moving stimuli. J. Comp. Physiol. A 155, 297–312 (1984).
Aloimonos, J., Weiss, I. & Bandyopadhyay, A. Active vision. Int. J. Comput. Vis. 1, 333–356 (1988).
Sanket, N. J., Singh, C. D., Ganguly, K., Fermüller, C. & Aloimonos, Y. Gapflyt: Active vision based minimalist structure-less gap detection for quadrotor flight. IEEE Robot. Autom. Lett. 3, 2799–2806 (2018).
Fuller, S. B., Sands, A., Haggerty, A., Karpelson, M. & Wood, R. J. Estimating attitude and wind velocity using biomimetic sensors on a microrobotic bee. In Proc. IEEE ICRA1374–1380 (IEEE, 2013).
van der Helm, S., Coppola, M., McGuire, K. N. & de Croon, G. C. H. E. On-board range-based relative localization for micro air vehicles in indoor leader–follower flight. Auton. Robots 44, 415–441 (2020).
Webb, B. Neural mechanisms for prediction: do insects have forward models? Trends Neurosci. 27, 278–282 (2004).
Mischiati, M. et al. Internal models direct dragonfly interception steering. Nature 517, 333–338 (2015).
Poulet, J. F. A. & Hedwig, B. A corollary discharge maintains auditory sensitivity during sound production. Nature 418, 872–876 (2002).
Krapp, H. G., Taylor, G. K. & Humbert, J. S. in Frontiers in sensing (eds Barth, F. G. et al.) Ch. 7 (Springer, 2012).
Barlow, J. S. Inertial navigation as a basis for animal navigation. J. Theor. Biol. 6, 76–117 (1964).
Longuet-Higgins, H. C. & Prazdny, K. The interpretation of a moving retinal image. Proc. R. Soc. London, B Biol. Sci. 208, 385–397 (1980).
ADS CAS Google Scholar
Ribeiro, M. I. Kalman and extended Kalman filters: concept, derivation and properties. Inst. Syst. Robot. 43, 46 (2004).
Jaegle, A., Phillips, S. & Daniilidis, K. Fast, robust, continuous monocular egomotion computation. In Proc. 2016 IEEE International Conference on Robotics and Automation (ICRA) 773–780 (IEEE, 2016).
Hattenberger, G., Bronz, M. & Gorraz, M. Using the paparazzi UAV system for scientific research. In Proc. of International Micro Air Vehicle conference and competitions (IMAV) (Delft University of Technology, 2014).
de Croon, G. C. H. E. & Nolfi, S. ACT-CORNER: active corner finding for optic flow determination. In Proc. IEEE ICRA(IEEE, 2013).
Lucas, B. D., & Kanade, T. An iterative image registration technique with an application to stereo vision. In Proc. of the 7th international joint conference on Artificial intelligence (IJCAI'81) 674–679 (Carnegie Mellon University, 1981).
De Croon, G. C. H. E. Monocular distance estimation with optical flow maneuvers and efference copies: a stability-based strategy. Bioinspir. Biomim. 11, 1–18 (2016).
de Croon, G., De Wagter, C. & Seidl, T. Enhancing optical-flow-based control by learning visual appearance cues for flying robots. Nat. Mach. Intell. 3, 33–41 (2021).
Smeur, E. J. J., Chu, Q. & de Croon, G. C. H. E. Adaptive incremental nonlinear dynamic inversion for attitude control of micro aerial vehicles. In Proc. 2016 AIAA GNC Conference (AIAA, 2016).
Hansen, N., Müller, S. D. & Koumoutsakos, P. Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (CMA-ES). Evol. Comput. 11, 1–18 (2003).
We thank F. Muijres for reading and commenting on an earlier version of this manuscript, T. (J.C.) van Dijk for discussions on the non-linear observability analysis and J. Hagenaars and A. Barberia Chueca for their help in the filmed experiments. Moreover, we thank S. Viollet, J. Diperi and M. Boyron for their help in preparing the CurvACE sensor. Part of this project was financed by the Dutch Science Foundation (NWO) under grant number 15039.
Micro Air Vehicle Laboratory, Control and Simulation, Faculty of Aerospace Engineering, Delft University of Technology, Delft, the Netherlands
Guido C. H. E. de Croon, Julien J. G. Dupeyroux, Christophe De Wagter, Abhishek Chatterjee & Diana A. Olejnik
Aix Marseille Université, CNRS, ISM, Marseille, France
Franck Ruffier
Guido C. H. E. de Croon
Julien J. G. Dupeyroux
Christophe De Wagter
Abhishek Chatterjee
Diana A. Olejnik
All authors contributed to the conception of the study and to the analysis and interpretation of the results. G.C.H.E.d.C., A.C. and D.A.O. performed the non-linear observability analysis. G.C.H.E.d.C. developed the stability proof for the partially unobservable system. F.R. provided the CurvACE sensor and associated background knowledge. J.J.G.D. developed the code for the CurvACE to obtain high-frequency optic flow readings. C.D.W. integrated the CurvACE with the flapper drone vehicle. G.C.H.E.d.C. and C.D.W. developed the state estimation code for onboard the flapper drone and performed the flapper drone experiments. G.C.H.E.d.C. developed the quad rotor code and performed the quad rotor experiments. F.R. analysed the biological data, identifying the relation between velocity and the pitch angle variance. The manuscript was primarily written by G.C.H.E.d.C. The illustrations have been made by J.J.G.D. and G.C.H.E.d.C. All authors contributed critically to the drafts and gave final approval for publication.
Correspondence to Guido C. H. E. de Croon.
Nature thanks the anonymous reviewers for their contribution to the peer review of this work.
Extended data figures and tables
Extended Data Fig. 1 Robustness experiments robotic flight.
a, Quadrotor flying based on optic flow above a strong slope, which is dragged away, violating the assumption of a static flat ground. From top to bottom, the plots show the estimated attitude angles, velocities, and height. b, Quadrotor flying above three-dimensional objects, with artificial plant leaves moving due to the propellers' downwash, again violating the assumption of a static flat ground. c, Quadrotor reacting to a 10-degree roll-disturbance. The plots below show the roll angle, lateral velocity and height over time for four of such disturbances. d, Ten subsequent flights are performed to gather statistics on the attitude variation and errors when attitude is estimated with optic flow. The violin plot shows the error statistics over the ten flights for the estimated roll angle, lateral velocity, and height.
Extended Data Fig. 2 Preliminary analysis investigating the hypothesis that attitude variation decreases when flight speed increases.
a, Picture of a honeybee flying in the doubly tapered corridor in the experiments of9, photo reprinted with permission of DGA / François Vrignaud. b, Pitch angle for a single honeybee trajectory over time for one of the trajectories. c, Corresponding velocity over time. d, Mean pitch angle for the honeybees vs. forward flight speed. e, Standard deviations of the body attitude angles per velocity bin, ranging from [0.05, 0.15) m/s to [0.75, 0.85) m/s for 21 honeybee trajectories (dark yellow) and 30 simulation trajectories (light brown). Two different simulation models are compared, one with the proposed optic-flow-based state estimator (solid line) and an alternative model that perceives a noisy version of the ground-truth attitude (dashed line). f, Standard deviation of the simulated head attitude angle for different velocities, again for the optic-flow-based state estimator (solid line) and an alternative model that perceives a noisy version of the attitude (dashed line, almost zero). g, Degree of observability for a constant height system with drag and both lateral flow \({\omega }_{y}\) and divergence \({\omega }_{z}\) as observations for different velocities and rotation rates. h, Mean absolute estimation errors in velocity, height, and body and head attitude angles for different flight velocities in the simulation.
Extended Data Fig. 3 Sketches of different quad rotor and environment models.
a, Axis definitions for a constant height quadrotor model. \({\rm{B}}\) indicates the body frame, whereas \(I\) indicates the inertial frame. The arrows for \(Y\) and \(Z\) point into the positive directions. The attitude angle \(\phi \) represents the quadrotor's roll angle, and \(p\) the roll rate. The shaded rectangle represents the floor. b, Varying height model of a quad rotor in the 2D plane. c, Constant height motion model of a quad rotor where the ground has slope angle \(\alpha \). d, Varying height model in the 2D plane for a drone flying over an uneven terrain. The drone uses one world point \({P}_{i}\) (red star) for state estimation.
Extended Data Fig. 4 Processing and control loops onboard of the quadrotor drone (a Parrot Bebop 2) used in the robotic experiments.
a, Onboard image processing, state estimation, and control used for fully autonomous flight of the drone. b, Control diagram for the optic flow outer loop control, where the longitudinal and lateral optic flow \({\omega }_{x}\) and \({\omega }_{y}\) are used to set desired attitude angles for the inner loop control and the divergence \({\omega }_{z}\) directly leads to a thrust command \({u}_{T}\). c, Inner loop control to transform desired attitude setpoints \({\theta }^{* }\), \({\phi }^{* }\) into moment commands \({u}_{M}\) for the quadrotor motor mixing. For the INDI block we refer the reader to59.
Extended Data Fig. 5 Setup of the robotic experiments with the flapping wing drone (a modified Flapper Drone).
A human pilot executes the outer loop control, while the drone itself runs the inner loop attitude controller, based on the onboard roll angle estimates. See the text for details.
Extended Data Fig. 6 Robotic experiments with height changes.
a, Picture of the experiment. b, Roll angle, lateral velocity, and height over time during the experiment, in which the height was varied, all with the constant height model. Solid lines represent estimates, dashed lines the ground truth. c, Roll angle, lateral velocity, and height over time during the experiment, in which the robot estimates and controls its roll axis with the help of the varying height model explained in Supplementary Information. Solid lines represent estimates, dashed lines the ground truth. d, Picture of experimental setup in which the drone performed thirteen subsequent flights for gathering state estimation statistics. e, Estimation error distributions over the thirteen flights for the roll angle, lateral velocity, and height. f, Picture of the quadrotor flying over a slope with the varying height model. g, Picture of the quadrotor flying over a 3D structured scene with the varying height model.
Extended Data Fig. 7 Simulation experiments to verify the stability proof - I.
a, Simulation without noise. Top row: The three states (true, solid line, and estimated, dashed-dotted line) over time. The dotted line indicates zero. Bottom row, from left to right: The optic flow \({\omega }_{y}\) (solid line) and the reference desired flow (dashed line), the rate (solid line) with a dotted line at zero, and the observability degree over time. b, Simulation with sensor noise. Top row: The three states (true, solid line, and estimated, dashed-dotted line) over time. The dotted line indicates zero. Bottom row, from left to right: The optic flow \({\omega }_{y}\) (solid line) and the reference desired flow (dashed line), the rate (solid line) with a dotted line at zero, and the observability degree over time.
Extended Data Fig. 8 Simulation experiments to verify the stability proof - II.
a, Zoomed in view on time interval [15,25] seconds for a simulation with sensor noise. Top: True (dashed) and estimated (solid) roll angle over time. Bottom: roll rate. b, Observability degree over time for an experiment with actuation noise. c, Observability degree over time for an experiment with lateral disturbances. d, Experiment with malicious disturbances in the vertical axis when the system is not moving. Top: Observability degree over time. Bottom: True (dashed) and estimated (solid) height over time.
Extended Data Fig. 9 Histograms of honeybee pitch angles at different velocities.
a, The histograms of all data, i.e., with outliers, of the honeybee body pitch angles for different velocity bins. Each subplot's title mentions the centre of the speed bin and the variance of the pitch angles in that bin. b, The histograms of the data without outliers.
Extended Data Fig. 10 Model with independently moving head and body.
a, Graphical illustration of a "honeybee" simulation model, in which the head and body rotate independently. The head determines the looking direction of the optic flow sensor, the body determines the thrust direction. For a detailed explanation, see Supplementary Information. b, Plot of the head (blue) and body (green) pitch angles over time, when the simulated insect attempts to have a lateral ventral flow of ωx = 0.5. Solid lines are estimates, dashed lines the ground truth. c, Estimated (solid) and true (dashed) velocity over time. d, Estimated and true height over time. e, Optic flow over time. f, Body and head rate over time. The head makes much smaller corrections. g, Observability degree over time.
Mathematical derivations and analyses supporting the conclusions in the main article. Section I: We start by deriving the formulas for the non-linear observability analysis of the constant-height system with rotation rate control inputs. Section II: Subsequently, a stability proof for the partially unobservable system is presented. In the following sections, we generalize the model to more complex settings. Section III: A constant-height model without rate measurements. Section IV: A varying height model with drag and wind. Section V: A varying height model with thrust bias and optic flow divergence. Section VI: A model taking into account a ground slope. Section VII: A model of flying in generic 3D-structured environments. Section VIII: We report on simulation experiments that verify different aspects of the proof in section II. Section IX: We introduce a model with an independently moving head and body. Section X: We explain how we analysed biological data for comparison with the model from section IX.
Supplementary Video 1
Quad rotor flying with optic-flow-based attitude. A Parrot Bebop 2 quad rotor's onboard software has been reprogrammed with the Paparazzi open-source autopilot to hover fully autonomously. Initially, it flies with an inner loop control for the attitude that is based on a standard, complementary attitude estimation filter. This filter combines accelerometer with gyro measurements. During this initial part of the experiment the outer loop control already relies on optic flow. The optic flow divergence is used to set thrust commands, the translational optic flow is used to set attitude commands, executed by the inner loop control. Halfway the experiment, the attitude estimation is switched to the proposed optic-flow-based attitude estimation. This estimation combines a constant-height, thrust-vectoring motion model with optic flow and gyro measurements to estimate both pitch and roll angles.
Flapper drone flying with optic-flow-based attitude. A flapper drone flapping-wing robot has been equipped with an artificial compound eye, CurvACE. The autopilot software of the flapper drone, based on BitCraze's CrazyFlie code, has been modified to implement the proposed optic-flow-based attitude estimation. The CurvACE has been programmed to send translational optic flow measurements to the autopilot at 200 Hz. At the start of the experiment, the inner loop attitude control relies on a standard complementary attitude estimation filter, combining accelerometer and gyro measurements. The outer loop control in this experiment consists of manual control, with the human pilot commanding desired attitude angles for use by the inner loop controller. After a bit of flight, a switch is made to the proposed optic-flow-based attitude estimation, only for the roll angle in this experiment. The optic-flow-based attitude estimation combines a constant, thrust-vectoring motion model with CurvACE's optic flow measurements and gyros.
Quad rotor flying over a tilted slope. The video shows an experiment to verify the robustness of the proposed optic-flow-based attitude estimation to tilted surfaces. A Parrot Bebop 2 drone with onboard Paparazzi open-source autopilot flies over a tilted slope. The autopilot features an optic flow outer loop control with optic flow divergence leading to thrust commands and translational optic flow to attitude commands. The outer loop control attempts to achieve zero optic flow, that is, hover flight. Initially, the inner loop attitude control uses attitude estimates from a standard complementary filter. After a bit of flight, the attitude estimation is changed to the proposed optic-flow-based attitude estimation, combining a motion model with optic flow and gyro measurements to estimate both pitch and roll. The motion model is based on a flat floor assumption. In this experiment, that assumption is violated, as the drone flies over a tilted screen. In the experiment, first the screen's tilt angle is increased. Then, the screen is dragged to the side.
Quad rotor flying over 3D structure. This experiment tests the robustness of the proposed optic-flow-based attitude estimation to non-flat surfaces. A Parrot Bebop 2 drone with onboard the open-source autopilot Paparazzi flies over an area with different-sized plastic plants and chairs. The autopilot features an optic flow outer loop control with optic flow divergence leading to thrust commands and translational optic flow to attitude commands. The optic flow observables, that is, divergence and translational flow, are determined by integrating information from the optic flow vectors in the entire bottom camera field of view. The outer loop control follows different optic flow set points over the experiment, starting with zero flow for hover flight. The attitude estimation starts out with a standard complementary filter, and then switches to the proposed optic-flow-based attitude estimation, combining a motion model with optic flow and gyro measurements to estimate both pitch and roll. The motion model is based on a flat floor assumption. In this experiment, that assumption is violated by means of the objects in the flight arena. The drone first hovers over a large plastic plant, with the leaves moving due to the downwash, violating an extra assumption of a static world. Then the drone receives different outer loop references for non-zero translational optic flow, making it move left and right over the 3D scene.
Quad rotor subjected to 10° roll disturbances. This experiment tests the robustness of the proposed optic-flow-based attitude estimation to large disturbances. A Parrot Bebop 2 drone with onboard open-source autopilot Paparazzi flies with optic flow outer loop control, with optic flow divergence leading to thrust commands and translational optic flow to attitude commands. The outer loop has zero divergence and lateral flow as optic flow references, for hover flight. Initially, the attitude is estimated with a standard complementary attitude estimation filter. Then, the drone switches to the proposed optic-flow-based attitude estimation scheme for both pitch and roll and first hovers. At many times in the video, the experimenter introduces a disturbance to the roll angle by extraneously adding a bias to the attitude command sent to the inner loop attitude controller. So, the drone is hovering and sending a desired angle of zero degrees to the inner loop attitude controller, but this is extraneously changed to 10°. The inner loop controller attempts to satisfy this demand, resulting in an increasing sidewards velocity. The situation is corrected for by the integrator in the outer loop controller, which attempts to cancel the velocity by changing the desired attitude angle, that is, −10° when hovering again. Then, the experimenter introduces a new disturbance by removing the bias, resulting in the opposite motion. Mats were placed on the floor to ensure that the optic flow algorithms functioned correctly also at higher speeds.
Quad rotor flying over a static slope: varying height model. The video shows an experiment to verify the robustness of the proposed optic-flow-based attitude estimation to tilted surfaces. A Parrot Bebop 2 drone with onboard Paparazzi open-source autopilot flies over a tilted slope. The autopilot features an optic flow outer loop control with optic flow divergence leading to thrust commands and translational optic flow to attitude commands. The outer loop control attempts to achieve zero optic flow, that is, hover flight. Initially, the inner loop attitude control uses attitude estimates from a standard complementary filter. After a bit of flight, the roll angle attitude estimation is changed to the proposed optic-flow-based attitude estimation, combining a motion model with optic flow and gyro measurements. In contrast to previous experiments, the motion model does not assume a constant height. The model uses the estimated commanded thrust to predict height changes. The motion model does still assume a flat floor. In this experiment, that assumption is violated, as the drone flies over a tilted screen. In the experiment, the screen's tilt angle is increased.
Quad rotor flying over a moving slope: varying height model. The video shows an experiment to verify the robustness of the proposed optic-flow-based attitude estimation to moving, tilted surfaces. A Parrot Bebop 2 drone with onboard Paparazzi open-source autopilot flies over a tilted slope. The autopilot features an optic flow outer loop control with optic flow divergence leading to thrust commands and translational optic flow to attitude commands. The outer loop control attempts to achieve zero optic flow, that is, hover flight. Initially, the inner loop attitude control uses attitude estimates from a standard complementary filter. After a bit of flight, the roll angle attitude estimation is changed to the proposed optic-flow-based attitude estimation, combining a motion model with optic flow and gyro measurements. The motion model uses the estimated commanded thrust to predict height changes. The motion model does still assume a flat floor. In this experiment, that assumption is violated, as the drone flies over a tilted screen. In the experiment, first the screen's tilt angle is increased. Then, the screen is dragged to the side, with the drone following.
Quad rotor flying over 3D structure: varying height model. This experiment tests the robustness of the proposed optic-flow-based attitude estimation to non-flat surfaces when the motion model allows for varying height. A Parrot Bebop 2 drone with onboard the open-source autopilot Paparazzi flies over an area with differently sized plastic plants, flowers, boxes and a chair. The autopilot features an optic flow outer loop control with optic flow divergence leading to thrust commands and translational optic flow to attitude commands. The optic flow observables, that is, divergence and translational flow, are determined by integrating information from the optic flow vectors in the entire bottom camera field of view. The outer loop control follows different optic flow set points over the experiment, starting with zero flow for hover flight. The attitude estimation starts out with a standard complementary filter, and then switches to the proposed optic-flow-based attitude estimation, combining a motion model with optic flow and gyro measurements to estimate roll. The motion model uses the estimated commanded thrust to predict height changes and is based on a flat floor assumption. In this experiment, that assumption is violated by means of the objects in the flight arena. The drone first hovers over the centre of the scene (the chair). Then the drone receives different outer loop references for non-zero translational optic flow, making it move left and right over the 3D scene.
de Croon, G.C.H.E., Dupeyroux, J.J.G., De Wagter, C. et al. Accommodating unobservability to control flight attitude with optic flow. Nature 610, 485–490 (2022). https://doi.org/10.1038/s41586-022-05182-2
Issue Date: 20 October 2022
Getting acquainted with npj Robotics
Embrace wobble to level flight without a horizon
Graham K. Taylor
Nature News & Views 19 Oct 2022 | CommonCrawl |
Erickson's conjecture on the rate of escape of $d$-dimensional random walk
Author: Harry Kesten
Journal: Trans. Amer. Math. Soc. 240 (1978), 65-113
MSC: Primary 60J15; Secondary 60F15
MathSciNet review: 489585
Abstract: We prove a strengthened form of a conjecture of Erickson to the effect that any genuinely d-dimensional random walk ${S_n},d \geqslant 3$, goes to infinity at least as fast as a simple random walk or Brownian motion in dimension d. More precisely, if $S_n^\ast$ is a simple random walk and ${B_t}$, a Brownian motion in dimension d, and $\psi :[1,\infty ) \to (0,\infty )$ a function for which ${t^{ - 1/2}}\psi (t) \downarrow 0$, then $\psi {(n)^{ - 1}}|S_n^\ast | \to \infty$ w.p.l, or equivalently, $\psi {(t)^{ - 1}}|{B_t}| \to \infty$ w.p.l, iff $\smallint _1^\infty \psi {(t)^{d - 2}}{t^{ - d/2}} < \infty$; if this is the case, then also $\psi {(n)^{ - 1}}|{S_n}| \to \infty$ w.p.l for any random walk Sn of dimension d.
K. L. Chung and W. H. J. Fuchs, On the distribution of values of sums of random variables, Mem. Amer. Math. Soc. 6 (1951), 12. MR 40610
A. Dvoretzky and P. Erdös, Some problems on random walk in space, Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability, 1950., University of California Press, Berkeley and Los Angeles, 1951, pp. 353–367. MR 0047272
H. G. Eggleston, Convexity, Cambridge Tracts in Mathematics and Mathematical Physics, No. 47, Cambridge University Press, New York, 1958. MR 0124813
K. Bruce Erickson, Recurrence sets of normed random walk in $R^{d}$, Ann. Probability 4 (1976), no. 5, 802–828. MR 426162, DOI https://doi.org/10.1214/aop/1176995985
C. G. Esseen, On the Kolmogorov-Rogozin inequality for the concentration function, Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 5 (1966), 210–216. MR 205297, DOI https://doi.org/10.1007/BF00533057
C. G. Esseen, On the concentration function of a sum of independent random variables, Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 9 (1968), 290–308. MR 231419, DOI https://doi.org/10.1007/BF00531753
W. Hengartner and R. Theodorescu, Concentration functions, Academic Press [A Subsidiary of Harcourt Brace Jovanovich, Publishers], New York-London, 1973. Probability and Mathematical Statistics, No. 20. MR 0331448
Kiyoshi Itô and Henry P. McKean Jr., Diffusion processes and their sample paths, Die Grundlehren der Mathematischen Wissenschaften, Band 125, Academic Press, Inc., Publishers, New York; Springer-Verlag, Berlin-New York, 1965. MR 0199891
Harry Kesten, The limit points of a normalized random walk, Ann. Math. Statist. 41 (1970), 1173–1205. MR 266315, DOI https://doi.org/10.1214/aoms/1177696894
J. V. Uspensky, Introduction to mathematical probability, McGraw-Hill, New York, 1937.
K. L. Chung and W. H. J. Fuchs, On the distribution of values of sums of random variables, Mem. Amer. Math. Soc. No. 6 (1951). MR 12, 722. A. Dvoretzky and P. Erdös, Some problems on random walk in space, Proc. Second Berkeley Sympos. Math. Statist. and Prob. (Berkeley, Calif., 1950), Univ. of California Press, Berkeley, 1951, pp. 353-367. MR 13, 852. H. G. Eggleston, Convexity, Cambridge Univ. Press, Cambridge, 1969. K. B. Erickson, Recurrence sets of normed random walk in ${{\mathbf {R}}^d}$, Ann. Probability 4 (1976), 802-828. C. G. Esseen, On the Kolmogorov-Rogozin inequality for the concentration function, Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 5 (1966), 210-216. MR 34 #5128. ---, On the concentration function of a sum of independent random variables, Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 9 (1968), 290-308. MR 37 #6974. W. Hengartner and R. Theodorescu, Concentration functions, Academic Press, New York, 1973. MR 48 #9781. K. Itô and H. P. McKean, Jr., Diffusion processes and their sample paths, Springer-Verlag, Berlin and New York; Academic Press, New York, 1965. MR 33 #8031. H. Kesten, The limit points of a normalized random walk, Ann. Math. Statist. 41 (1970), 1173-1205. MR 42 #1222. J. V. Uspensky, Introduction to mathematical probability, McGraw-Hill, New York, 1937.
Retrieve articles in Transactions of the American Mathematical Society with MSC: 60J15, 60F15
Retrieve articles in all journals with MSC: 60J15, 60F15
Keywords: Random walk, escape rate, concentration functions | CommonCrawl |
The Infona portal uses cookies, i.e. strings of text saved by a browser on the user's device. The portal can access those files and use them to remember the user's data, such as their chosen settings (screen view, interface language, etc.), or their login data. By using the Infona portal the user accepts automatic saving and using this information for portal operation purposes. More information on the subject can be found in the Privacy Policy and Terms of Service. By closing this window the user confirms that they have read the information on cookie usage, and they accept the privacy policy and the way cookies are used by the portal. You can change the cookie settings in your browser.
Login or register account
remember me Password recovery
INFONA - science communication portal
resources people groups collections journals conferences series
Search results for: A. M. Sirunyan
Search for author's resources
Items from 1 to 20 out of 48 results
customise view
Measurements of triple-differential cross sections for inclusive isolated-photon+jet events in $$\mathrm{p}\mathrm{p}$$ pp collisions at $$\sqrt{s} = 8\,\text {TeV} $$ s=8TeV
A. M. Sirunyan, A. Tumasyan, W. Adam, F. Ambrogi, more
The European Physical Journal C > 2019 > 79 > 11 > 1-24
Measurements are presented of the triple-differential cross section for inclusive isolated-photon+jet events in $$\mathrm{p}\mathrm{p}$$ pp collisions at $$\sqrt{s} = 8$$ s=8 TeV as a function of photon transverse momentum ($$p_{\mathrm {T}} ^{{\upgamma {}{}}}$$ pTγ ), photon pseudorapidity ($$\eta ^{{\upgamma {}{}}}$$ ηγ ), and jet pseudorapidity ($$\eta ^{\text {jet}}$$ ηjet ). The data correspond...
Measurement of the average very forward energy as a function of the track multiplicity at central pseudorapidities in proton-proton collisions at $$\sqrt{s}=13\,\text {TeV} $$ s=13TeV
The average total energy as well as its hadronic and electromagnetic components are measured with the CMS detector at pseudorapidities $$-6.6<\eta <-5.2$$ -6.6<η<-5.2 in proton-proton collisions at a centre-of-mass energy $$\sqrt{s}=13\,\text {TeV} $$ s=13TeV . The results are presented as a function of the charged particle multiplicity in the region $$|\eta |<2$$ |η|<2 . This measurement...
Search for new physics in top quark production in dilepton final states in proton-proton collisions at $$\sqrt{s} = 13\,\text {TeV} $$ s=13TeV
A search for new physics in top quark production is performed in proton-proton collisions at $$13\,\text {TeV} $$ 13TeV . The data set corresponds to an integrated luminosity of $$35.9{\,\text {fb}^{-1}} $$ 35.9fb-1 collected in 2016 with the CMS detector. Events with two opposite-sign isolated leptons (electrons or muons), and $$\mathrm{b}$$ b quark jets in the final state are selected. The search...
Search for supersymmetry in proton-proton collisions at 13 TeV in final states with jets and missing transverse momentum
The CMS collaboration, A. M. Sirunyan, A. Tumasyan, W. Adam, more
Journal of High Energy Physics > 2019 > 2019 > 10 > 1-61
Abstract Results are reported from a search for supersymmetric particles in the final state with multiple jets and large missing transverse momentum. The search uses a sample of proton-proton collisions at s $$ \sqrt{s} $$ = 13 TeV collected with the CMS detector in 2016–2018, corresponding to an integrated luminosity of 137 fb−1, representing essentially the full LHC Run 2 data sample. The...
Search for dark photons in decays of Higgs bosons produced in association with Z bosons in proton-proton collisions at s $$ \sqrt{s} $$ = 13 TeV
Abstract A search is presented for a Higgs boson that is produced in association with a Z boson and that decays to an undetected particle together with an isolated photon. The search is performed by the CMS Collaboration at the Large Hadron Collider using a data set corresponding to an integrated luminosity of 137 fb−1 recorded at a center-of-mass energy of 13 TeV. No significant excess of events...
Search for resonances decaying to a pair of Higgs bosons in the b b ¯ $$ \overline{\mathrm{b}} $$ q q ¯ $$ \overline{\mathrm{q}} $$ 'ℓν final state in proton-proton collisions at s $$ \sqrt{s} $$ = 13 TeV
Abstract A search for new massive particles decaying into a pair of Higgs bosons in proton-proton collisions at a center-of-mass energy of 13 TeV is presented. Data were collected with the CMS detector at the LHC, corresponding to an integrated luminosity of 35.9 fb−1. The search is performed for resonances with a mass between 0.8 and 3.5 TeV using events in which one Higgs boson decays into a bottom...
Azimuthal separation in nearly back-to-back jet topologies in inclusive 2- and 3-jet events in $${\text {p}} {\text {p}} $$ pp collisions at $$\sqrt{s}=13\,\text {Te}\text {V} $$ s=13Te
The European Physical Journal C > 2019 > 79 > 9 > 1-24
A measurement for inclusive 2- and 3-jet events of the azimuthal correlation between the two jets with the largest transverse momenta, $$\varDelta \phi _{12}$$ Δϕ12 , is presented. The measurement considers events where the two leading jets are nearly collinear ("back-to-back") in the transverse plane and is performed for several ranges of the leading jet transverse momentum. Proton-proton collision...
Linear Electron Accelerator LUE-75 of Yerevan Physics Institute at Energies of 10−75 MeV
A. M. Sirunyan, A. S. Hakobyan, A. Z. Babayan, H. H. Marukyan, more
Journal of Contemporary Physics (Armenian Academy of Sciences) > 2019 > 54 > 3 > 225-231
The results to increase the rated energy of the linear accelerator of electrons LUE-75 from 50 to 75 MeV are presented. The characteristics of the beam are investigated, and the measured energy spectra of the obtained beams are presented in the range of 50–75 MeV at the average intensity up to 10 μA. The modernization of the elements of magnetic optics for the parallel transfer path was performed,...
Search for supersymmetry with a compressed mass spectrum in the vector boson fusion topology with 1-lepton and 0-lepton final states in proton-proton collisions at s $$ \sqrt{s} $$ = 13 TeV
Journal of High Energy Physics > 2019 > 2019 > 8 > 1-45
Abstract A search for supersymmetric particles produced in the vector boson fusion topology in proton-proton collisions is presented. The search targets final states with one or zero leptons, large missing transverse momentum, and two jets with a large separation in rapidity. The data sample corresponds to an integrated luminosity of 35.9 fb−1 of proton-proton collisions at s $$ \sqrt{s} $$...
Measurement of exclusive $${{{\uprho _{}^{}} _{}^{}}{{\left( {770}\right) }{}_{}^{}}} ^{0}$$ ρ7700 photoproduction in ultraperipheral pPb collisions at $$\sqrt{\smash [b]{s_{_{\mathrm {NN}}}}} = 5.02\,\text {Te}\text {V} $$ sNN=5.02Te
Exclusive $${{{\uprho _{}^{}} _{}^{}}{{\left( {770}\right) }{}_{}^{}}} ^{0}$$ ρ7700 photoproduction is measured for the first time in ultraperipheral pPb collisions at $$\sqrt{\smash [b]{s_{_{\mathrm {NN}}}}} = 5.02\,\text {Te}\text {V} $$ sNN=5.02Te with the CMS detector. The cross section $$\sigma ({\upgamma _{}^{}} \mathrm{p}\rightarrow {{{\uprho _{}^{}} _{}^{}}{{\left( {770}\right) }{}_{}^{}}}...
Search for charged Higgs bosons in the H± → τ±ντ decay channel in proton-proton collisions at s = 13 $$ \sqrt{s}=13 $$ TeV
Abstract A search is presented for charged Higgs bosons in the H± → τ±ντ decay mode in the hadronic final state and in final states with an electron or a muon. The search is based on proton-proton collision data recorded by the CMS experiment in 2016 at a center-of-mass energy of 13 TeV, corresponding to an integrated luminosity of 35.9 fb−1. The results agree with the background expectation from...
Search for a heavy pseudoscalar boson decaying to a Z and a Higgs boson at $$\sqrt{s}=13\,\text {Te}\text {V} $$ s=13Te
A search is presented for a heavy pseudoscalar boson $$\text {A}$$ A decaying to a Z boson and a Higgs boson with mass of 125$$\,\text {GeV}$$ GeV . In the final state considered, the Higgs boson decays to a bottom quark and antiquark, and the Z boson decays either into a pair of electrons, muons, or neutrinos. The analysis is performed using a data sample corresponding to an integrated luminosity...
Search for supersymmetry in final states with photons and missing transverse momentum in proton-proton collisions at 13 TeV
Abstract Results are reported of a search for supersymmetry in final states with photons and missing transverse momentum in proton-proton collisions at the LHC. The data sample corresponds to an integrated luminosity of 35.9 fb−1 collected at a center-of-mass energy of 13 TeV using the CMS detector. The results are interpreted in the context of models of gauge-mediated supersymmetry breaking. Production...
Search for the associated production of the Higgs boson and a vector boson in proton-proton collisions at s $$ \sqrt{s} $$ = 13 TeV via Higgs boson decays to τ leptons
Abstract A search for the standard model Higgs boson produced in association with a W or a Z boson and decaying to a pair of τ leptons is performed. A data sample of proton-proton collisions collected at s $$ \sqrt{s} $$ = 13 TeV by the CMS experiment at the CERN LHC is used, corresponding to an integrated luminosity of 35.9 fb−1. The signal strength is measured relative to the expectation...
Search for a low-mass τ−τ+ resonance in association with a bottom quark in proton-proton collisions at s $$ \sqrt{s} $$ = 13 TeV
Abstract A general search is presented for a low-mass τ−τ+ resonance produced in association with a bottom quark. The search is based on proton-proton collision data at a center-of-mass energy of 13 TeV collected by the CMS experiment at the LHC, corresponding to an integrated luminosity of 35.9 fb−1. The data are consistent with the standard model expectation. Upper limits at 95% confidence level...
Search for supersymmetry in events with a photon, jets, $$\mathrm {b}$$ b -jets, and missing transverse momentum in proton–proton collisions at 13$$\,\text {Te}\text {V}$$ Te
A search for supersymmetry is presented based on events with at least one photon, jets, and large missing transverse momentum produced in proton–proton collisions at a center-of-mass energy of 13$$\,\text {Te}\text {V}$$ Te . The data correspond to an integrated luminosity of 35.9$$\,\text {fb}^{-1}$$ fb-1 and were recorded at the LHC with the CMS detector in 2016. The analysis characterizes signal-like...
Combined measurements of Higgs boson couplings in proton–proton collisions at $$\sqrt{s}=13\,\text {Te}\text {V} $$ s=13Te
Combined measurements of the production and decay rates of the Higgs boson, as well as its couplings to vector bosons and fermions, are presented. The analysis uses the LHC proton–proton collision data set recorded with the CMS detector in 2016 at $$\sqrt{s}=13\,\text {Te}\text {V} $$ s=13Te , corresponding to an integrated luminosity of 35.9$${\,\text {fb}^{-1}} $$ fb-1 . The combination is based...
Combinations of single-top-quark production cross-section measurements and |fLVVtb| determinations at s $$ \sqrt{s} $$ = 7 and 8 TeV with the ATLAS and CMS experiments
The ATLAS collaboration, M. Aaboud, G. Aad, B. Abbott, more
Abstract This paper presents the combinations of single-top-quark production cross-section measurements by the ATLAS and CMS Collaborations, using data from LHC proton-proton collisions at s $$ \sqrt{s} $$ = 7 and 8 TeV corresponding to integrated luminosities of 1.17 to 5.1 fb−1 at s $$ \sqrt{s} $$ = 7 TeV and 12.2 to 20.3 fb−1 at s $$ \sqrt{s} $$ = 8 TeV. These combinations...
Measurement of inclusive very forward jet cross sections in proton-lead collisions at s N N $$ \sqrt{s_{\mathrm{NN}}} $$ = 5.02 TeV
Abstract Measurements of differential cross sections for inclusive very forward jet production in proton-lead collisions as a function of jet energy are presented. The data were collected with the CMS experiment at the LHC in the laboratory pseudorapidity range −6.6 < η < −5.2. Asymmetric beam energies of 4 TeV for protons and 1.58 TeV per nucleon for Pb nuclei were used, corresponding to a...
Measurement of the energy density as a function of pseudorapidity in proton–proton collisions at $$\sqrt{s} =13\,\text {TeV} $$ s=13TeV
A measurement of the energy density in proton–proton collisions at a centre-of-mass energy of $$\sqrt{s} =13$$ s=13 $$\,\text {TeV}$$ TeV is presented. The data have been recorded with the CMS experiment at the LHC during low luminosity operations in 2015. The energy density is studied as a function of pseudorapidity in the ranges $$-\,6.6<\eta <-\,5.2$$ -6.6<η<-5.2 and $$3.15<|\eta...
Add an author who is a portal user
Add a recipient who is not a portal user
Sending message cancelled
Are you sure you want to cancel sending this message?
AZIMUTHAL ANGLE (1)
BEAM ENERGY SPECTRA (1)
ELECTRON BEAM (1)
LINEAR ACCELERATORS (1)
LOW INTENSITY (1)
MC GENERATORS (1)
PHOTOPRODUCTION (1)
PPB (1)
QCD (1)
Journal of High Energy Physics (27)
The European Physical Journal C (20)
Journal of Contemporary Physics (Armenian Academy of Sciences) (1)
Report an error / abuse
© 2015 Interdisciplinary Centre for Mathematical and Computational Modelling
Reporting an error / abuse
Sending the report failed
Submitting the report failed. Please, try again. If the error persists, contact the administrator by writing to [email protected].
You can adjust the font size by pressing a combination of keys:
CONTROL + + increase font size
CONTROL + – decrease font
Navigate the page without a mouse
You can change the active elements on the page (buttons and links) by pressing a combination of keys:
TAB go to the next element
SHIFT + TAB go to the previous element
Financed by the National Centre for Research and Development under grant No. SP/I/1/77065/10 by the strategic scientific research and experimental development program: SYNAT - "Interdisciplinary System for Interactive Scientific and Scientific-Technical Information". | CommonCrawl |
Why does Friedberg say that the role of the determinant is less central than in former times?
I am taking a proof-based introductory course to Linear Algebra as an undergrad student of Mathematics and Computer Science. The author of my textbook (Friedberg's Linear Algebra, 4th Edition) says in the introduction to Chapter 4:
The determinant, which has played a prominent role in the theory of linear algebra, is a special scalar-valued function defined on the set of square matrices. Although it still has a place in the study of linear algebra and its applications, its role is less central than in former times.
He even sets up the chapter in such a way that you can skip going into detail and move on:
For the reader who prefers to treat determinants lightly, Section 4.4 contains the essential properties that are needed in later chapters.
Could anyone offer a didactic and simple explanation that refutes or asserts the author's statement?
linear-algebra matrices determinant math-history
dacabdi
dacabdidacabdi
$\begingroup$ Sheldon Axler's paper "Down with Determinants" seems a useful example of the the anti-determinant POV. (He later wrote an entire linear algebra text with that approach.) $\endgroup$
– Semiclassical
$\begingroup$ I think it's useful for didactic purposes. But in engineering praxis where large matrices appear, people never use determinants (they are either zero or not computable) and use various iterative methods instead. $\endgroup$
– Peter Franek
$\begingroup$ It is a useful theoretical tool, but fairly hopeless from a floating point numerical standpoint. Another, more extreme, example is the Jordan form of a matrix. It provides invaluable insight, but is essentially impossible to compute numerically. $\endgroup$
$\begingroup$ IIRC Gilbert Strang says basically the same $\endgroup$
– leonbloy
$\begingroup$ @leonbloy Thanks for making me look for Strang's text on intro to Linear Algebra. What a contrast! Friedberg's text feels boring and exhausting, already half through the book and I am tired and feeling like I am going nowhere. On the other hand, read two pages of Strang's and I suddenly want to know how the novel ends, to put it some way. It feels motivating, candid, "feynmanesque", human. Hell, the guy even writes some sentences in first person. Also, it is closer to Computer Science. All in all the textbook I was looking for. Thanks. $\endgroup$
– dacabdi
Friedberg is not wrong, at least on a historical standpoint, as I am going to try to show it.
Determinants were discovered "as such" in the second half of the 18th century by Cramer who used them in his celebrated rule for the solution of a linear system (in terms of quotients of determinants). Their spread was rather rapid among mathematicians of the next two generations ; they discovered properties of determinants that now, with our vision, we mostly express in terms of matrices.
Cauchy has given two important results about determinants as explained in the very nice article by Hawkins referenced below :
around 1815, Cauchy discovered the multiplication rule (rows times columns) of two determinants. This is typical of a result that has been completely revamped : nowadays, this rule is for the multiplication of matrices, and determinants' multiplication is restated as the homomorphism rule $\det(A \times B)= \det(A)\det(B)$.
around 1825, he discovered eigenvalues "associated with a symmetric determinant" and established the important result that these eigenvalues are real ; this discovery has its roots in astronomy, in connection with Sturm, explaining the word "secular values" he attached to them: see for example this.
Matrices made a shy apparition in the mid-19th century (in England) ; "matrix" is a term coined by Sylvester see here. I strongly advise to take a look at his elegant style in his Collected Papers.
Together with his friend Cayley, they can rightly be named the founding fathers of linear algebra, with determinants as permanent reference. Here is a major quote of Sylvester:
"I have in previous papers defined a "Matrix" as a rectangular array of terms, out of which different systems of determinants may be engendered as from the womb of a common parent".
A lot of important polynomials are either generated or advantageously expressed as determinants:
the characteristic polynomial (of a matrix) is expressed as the famous $\det(A-\lambda I)$,
in particular, the theory of orthogonal polynomials mainly developed at the end of 19th century, can be expressed in great part with determinants,
the "resultant" of two polynomials, invented by Sylvester (giving a condition for these polynomials to have a common root), etc.
Let us repeat it : for a mid-19th century mathematician, a square array of numbers has necessarily a value (its determinant): it cannot have any other meaning. If it is a rectangular array, the numbers attached to it are the determinants of submatrices that can be "extracted" from the array.
The identification of "Linear Algebra" as an integral (and new) part of Mathematics is mainly due to the German School (say from 1870 till the 1930's). I don't cite the names, there are too many of them. An example among many others of this german domination: the germenglish word "eigenvalue". The word "kernel" could have remained the german word "kern" that appears around 1900 (see this site).
The triumph of Linear Algebra is rather recent (mid-20th century). "Triumph" meaning that now Linear Algebra has found a very central place. Determinants in all that ? Maybe the biggest blade in this swissknife, but not more ; another invariant (this term would deserve a long paragraph by itself), the trace, would be another blade, not the smallest.
In 19th century, Geometry was still at the heart of mathematical education; therefore, the connection between geometry and determinants has been essential in the development of linear algebra. Some cornerstones:
the development of projective geometry, in its analytical form, in the 1850s. This development has led in particular to place homographies at the heart of projective geometry, with their associated matricial expression. Besides, conic curves, described by a quadratic form, can as well be written under an all-matricial expression $X^TMX=0$ where $M$ is a symmetrical $3 \times 3$ matrix. This convergence to a unique and new "algebra" has taken time to be recognized.
A side remark: this kind of reflexions has been capital in the decision of Bourbaki team to avoid all figures and adopt the extreme view of reducing geometry to linear algebra (see the "Down with Euclid" of J. Dieudonné in the sixties).
Different examples of the emergence of new trends :
a) the concept of rank: for example, a pair of straight lines is a conic section whose matrix has rank 1. The "rank" of a matrix used to be defined in an indirect way as the "dimension of the largest nonzero determinant that can be extracted from the matrix". Nowadays, the rank is defined in a more straightforward way as the dimension of the range space... at the cost of a little more abstraction.
b) the concept of linear transformations and duality arising from geometry: $X=(x,y,t)^T\rightarrow U=MX=(u,v,w)$ between points $(x,y)$ and straight lines with equations $ux+vy+w=0$. More precisely, the tangential description, i.e., the constraint on the coefficients $U^T=(u,v,w)$ of the tangent lines to the conical curve has been recognized as associated with $M^{-1}$ (assuming $\det(M) \neq 0$!), due to relationship
$$X^TMX=X^TMM^{-1}MX=(MX)^T(M^{-1})(MX)=U^TM^{-1}U=0$$ $$=\begin{pmatrix}u&v&w\end{pmatrix}\begin{pmatrix}A & B & D \\ B & C & E \\ D & E & F \end{pmatrix}\begin{pmatrix}u \\ v \\ w \end{pmatrix}=0$$
whereas, in 19th century, it was usual to write the previous quadratic form as :
$$\det \begin{pmatrix}M^{-1}&U\\U^T&0\end{pmatrix}=\begin{vmatrix}a&b&d&u\\b&c&e&v\\d&e&f&w\\u&v&w&0\end{vmatrix}=0$$
as the determinant of a matrix obtained by "bordering" $M^{-1}$ precisely by $U$
(see the excellent lecture notes (http://www.maths.gla.ac.uk/wws/cabripages/conics/conics0.html)). It is to be said that the idea of linear transformations, especially orthogonal transformations, arose even earlier in the framework of the theory of numbers (quadratic representations).
Remark: the way the former identities have been written use matrix algebra notations and rules that were unknown in the 19th century, with the notable exception of Grassmann's "Ausdehnungslehre", whose ideas were too ahead of his time (1844) to have a real influence.
c) the concept of eigenvector/eigenvalue, initially motivated by the determination of "principal axes" of conics and quadrics.
the very idea of "geometric transformation" (more or less born with Klein circa 1870) associated with an array of numbers (when linear or projective). A matrix, of course, is much more that an array of numbers... But think for example to the persistence of expression "table of direction cosines" (instead of "orthogonal matrix") as can be found for example still in the 2002 edition of Analytical Mechanics by A.I. Lorrie.
d) The concept of "companion matrix" of a polynomial $P$, that could be considered as a tool but is more fundamental than that (https://en.wikipedia.org/wiki/Companion_matrix). It can be presented and "justified" as a "nice determinant" : In fact, it has much more to say, with the natural interpretation for example in the framework of $\mathbb{F}_p[X]$ (polynomials with coefficients in a finite field) as the matrix of multiplication by $P(X)$. (https://glassnotes.github.io/OliviaDiMatteo_FiniteFieldsPrimer.pdf), giving rise to matrix representations of such fields. Another remarkable application of companion matrices : the main numerical method for obtaining the roots of a polynomial is by computing the eigenvalues of its companion matrix using a Francis "QR" iteration (see (https://math.stackexchange.com/q/68433)).
I discovered recently a rather similar question with a very complete answer by Denis Serre, a specialist in the domain of matrices : https://mathoverflow.net/q/35988/88984
The article by Thomas Hawkins : "Cauchy and the spectral theory of matrices", Historia Mathematica 2, 1975, 1-29.
See also (http://www.mathunion.org/ICM/ICM1974.2/Main/icm1974.2.0561.0570.ocr.pdf)
An important bibliography is to be found in (http://www-groups.dcs.st-and.ac.uk/history/HistTopics/References/Matrices_and_determinants.html).
See also a good paper by Nicholas Higham : (http://eprints.ma.man.ac.uk/954/01/cay_syl_07.pdf)
For conic sections and projective geometry, see a) this excellent chapter of lectures of the University of Vienna (see the other chapters as well) : (https://www-m10.ma.tum.de/foswiki/pub/Lehre/WS0809/GeometrieKalkueleWS0809/ch10.pdf). See as well : (maths.gla.ac.uk/wws/cabripages/conics/conics0.html).
Don't miss the following very interesting paper about various kinds of useful determinants : https://arxiv.org/pdf/math/9902004.pdf
See also this
Very interesting precisions on determinants in this text and in these answers.
A fundamental work on "The Theory of Determinants" in 4 volumes has been written by Thomas Muir : http://igm.univ-mlv.fr/~al/Classiques/Muir/History_5/VOLUME5_TEXT.PDF (years 1906, 1911, 1922, 1923) for the last volumes or, for all of them https://ia800201.us.archive.org/17/items/theoryofdetermin01muiruoft/theoryofdetermin01muiruoft.pdf. It is very interesting to take random pages and see how the determinant-mania has been important, especially in the second half of the 19th century. Matrices appear at some places with the double bar convention that lasted a very long time. Matrices are mentionned here and there, rarely to their advantage...
Many historical details about determinants and matrices can be found here.
Jean MarieJean Marie
$\begingroup$ Very great answer. can you provide some sources to read more about the connections between determinants and geometry, specially conic sections? $\endgroup$
– Fawzy Hegab
$\begingroup$ @Fawzy Hegab Sorry to answer you so late, but, 6 months ago, I hadn't a good web reference to give you. Here is one:(maths.gla.ac.uk/wws/cabripages/conics/conics0.html) $\endgroup$
– Jean Marie
$\begingroup$ @JeanMarie I'm amazed how far I've come from this question in 2 years and how you still find ways to groom it and add new data to it. Kudos to you! :) $\endgroup$
$\begingroup$ Let me get back to you. I may have read it on Wikipedia. $\endgroup$
$\begingroup$ I found a whole host of videos on the subject when googling. I did find it on Wikipedia under "determinants" as well. $\endgroup$
It depends who you speak to.
In numerical mathematics, where people actually have to compute things on a computer, it is largely recognized that determinants are useless. Indeed, in order to compute determinants, either you use the Laplace recursive rule ("violence on minors"), which costs $O(n!)$ and is infeasible already for very small values of $n$, or you go through a triangular decomposition (Gaussian elimination), which by itself already tells you everything you needed to know in the first place. Moreover, for most reasonably-sized matrices containing floating-point numbers, determinants overflow or underflow (try $\det \frac{1}{10} I_{350\times 350}$, for instance). To put another nail on the coffin, computing eigenvalues by finding the roots of $\det(A-xI)$ is hopelessly unstable. In short: in numerical computing, whatever you want to do with determinants, there is a better way to do it without using them.
In pure mathematics, where people are perfectly fine knowing that an explicit formula exists, all the examples are $3\times 3$ anyway and people make computations by hand, determinants are invaluable. If one uses Gaussian elimination instead, all those divisions complicate computations horribly: one needs to take different paths whether things are zero or not, so when computing symbolically one gets lost in a myriad of cases. The great thing about determinants is that they give you an explicit polynomial formula to tell when a matrix is invertible or not: this is extremely useful in proofs, and allows for lots of elegant arguments. For instance, try proving this fact without determinants: given $A,B\in\mathbb{R}^{n\times n}$, if $A+Bx$ is singular for $n+1$ distinct real values of $x$, then it is singular for all values of $x$. This is the kind of things you need in proofs, and determinants are a priceless tool. Who cares if the explicit formula has a exponential number of terms: they have a very nice structure, with lots of neat combinatorial interpretations.
Federico PoloniFederico Poloni
$\begingroup$ I'm not sure that the pure/applied dichotomy is accurate... maybe "numerical" versus "non-numerical"? E.g., not all numerically oriented math is applicable, and ... etc. $\endgroup$
– paul garrett
$\begingroup$ There ios an exception to this rule: In some contexts, what you want to compute is the determinant of some matrix (like in D-optimal experimental design!) then there is no shortcut to actually compute it (but numerically, it makes then more sense to compute the logdeterminant). $\endgroup$
– kjetil b halvorsen
$\begingroup$ Since in D-optimal design you want the determinant of a matrix like $X'X$, the quickest and most numerically stable way to find it is from the singular values of $X$, not by multiplying out $X'X$ and then finding its determinant by an elementary method. Of course calculating the log of the determinant from the singular values is just as trivial as calculating the determinant itself. $\endgroup$
– alephzero
$\begingroup$ $X^TX$ is a bit like determinants -- whatever numerical computation you want to do with it, there's usually a better way to do it that avoids it overall. And the same holds for matrix inverses. $\endgroup$
$\begingroup$ I think the standard distinction here would be "numerical" vs. "exact". Many papers in algebraic combinatorics are of the form "[determinant identity] is true" and they certainly go beyond 3x3. $\endgroup$
– Joshua P. Swanson
Determinants are still very much relevant to abstract algebra. In applied mathematics, they are less so, though the claim that "determinants are impractical because they take too long to compute" is misguided (no one forces you to compute them by the Leibniz formula; Gaussian elimination works in $O\left(n^3\right)$ time, and there is an $O\left(n^4\right)$ division-free algorithm as well). (Another oft-repeated assertion is that Cramer's rule is not very useful for solving actual systems of linear equations; I believe this one is correct, but I am mostly seeing Cramer's rule used as a theoretical tool in proofs as opposed to computational applications.)
What is going on is the following: Back up to the early 20th century, determinants used to be one of the few tools available for linear-algebraic problems. (They might even be one of the oldest tools, discovered by Takakazu Seki back in 1683.) Other linear-algebraic tools started appearing in the 18th and 19th centuries, but their development had always been lagging behind that of determinants until the likes of Noether and Bourbaki came around in the 20th century. (Muir's 5-volume annals of determinant theory, which can be downloaded from Alain Lascoux's website, contain an impressive collection of results, many of them deep, about determinants.) Thus, for a long time, the only way to a deep result would pass through the land of determinants, simply because other lands were barely explored. Only after the notions of vector spaces, modules, tensors, exterior powers etc. went mainstream (1950s?), mathematicians could afford avoiding determinants, and they started noticing that it would often be easier to do so, and with the benefit of hindsight, some of the older uses of determinants were just detours. At some point, avoiding determinants became something like a cultural fashion, and Axler took it to an extreme in his LADR textbook, emphasizing non-constructive methods and leaving students rather ill-prepared for research in abstract algebra. Nevertheless, Axler's approach has some strengths (e.g., his nice and slick determinant-free proof of the existence of eigenvectors has become standard now, and is included even in Treil's LADW book, whose title is a quip on Axler's), which once again illustrates what I think is the correct takeaway from the whole story: Determinants used to be treated as a panacea, for lack of other tools of comparable strength; but now that the rest of linear algebra has caught up, they have retreated to the grounds where they belong, which is still a wide swath of the mathematical landscape (many parts of abstract algebra and algebraic combinatorics have determinants written into their DNA, rather than using them as a tool; they are not very likely to shed them off).
darij grinbergdarij grinberg
$\begingroup$ +1 for pointing out that the evaluation is not the limiting factor with fp. computations. $\endgroup$
$\begingroup$ In case it saves anyone a moment in the future, the "nice and slick" proof is 5.21 on p.145. It looks at $v, Tv, \ldots, T^nv$, gets a polynomial relation they satisfy, factors it into linear terms, and notes one of the factors must kill a non-zero vector. Cute indeed. $\endgroup$
Determinants are very useful in the theory of linear algebra, but less so in practice (especially for numerical computations involving large systems). For example,
Cramer's rule gives an explicit formula for solving an $n \times n$ linear system $Ax = b$ where $A$ is invertible.
The eigenvalues of a square matrix $A$ are the roots of the characteristic polynomial $\det(A - \lambda I)$.
But nobody uses these for computations, except for very small $n$. There are numerical methods that are much more efficient and numerically stable.
Robert IsraelRobert Israel
Apart from the points already raised that determinants are in fact expensive to compute numerically and sensitive to rounding errors, they are also awkward "symbolically"... and indeed capture just a very peculiar bit of the linear algebra going on even in solving systems of linear equations.
The issue that does seem to disturb people, pro-and-con, if they are thinking in terms of "correct logical development" of linear algebra (which I myself think is already a viewpoint that's asking for trouble), a genuine and legitimate objection is over-use of the Cayley-Hamilton theorem... E.g., it is not necessary to use this in most of the situations where it is traditionally invoked.
$\begingroup$ Although Cayley Hamilton may have surprising ramifications like the one I recently discovered on Maths SE: (math.stackexchange.com/q/1353170) $\endgroup$
The determinant is relatively simple to calculate (computationally speaking) and has a number of interesting interpretations/applications attached to it, including:
Determining whether or not a matrix is invertible
Indicating by how much the transformation changes volume (and this is also related to differentiable transformations via the Jacobian; see change of variables)
Counting things! Determinants have lots of use in combinatorics (for instance, Kasteleyn matrices)
FimpellizzeriFimpellizzeri
$\begingroup$ I knew about the first two applications, and I sincerely appreciate the answer. But I am more interested in understanding why Friedberg treated determinants with certain air of obsolescence. As if they were no longer as useful or important as they used to be. I am not trying to understand why they are important, but to understand why Friedberg presented them as a thing of the past. $\endgroup$
$\begingroup$ Well, I can only say I (like your professor) disagree with Friedberg. $\endgroup$
– Fimpellizzeri
$\begingroup$ I understand. See, mathematical concepts are usually treated with canonical respect, therefore it is just reasonably intriguing to read that statement. Friedberg must be, to a reasonable extent, a reputable source. I expect that he would not make such assertion without an explanation, whether it is a good one or not. I am just intrigued, that's it. $\endgroup$
$\begingroup$ "The determinant is relatively simple to calculate" is a gross misrepresentation of reality. Computing determinants is very computationally demanding and extremely sensitive to rounding errors. This is part of the reason Friedberg makes his claim, and he is without a doubt correct. $\endgroup$
– Ittay Weiss
$\begingroup$ @Fimpellizieri $O(n^3)$, for practical computations, is quite demanding. And as you say deciding whether the determinant is zero, which is commonly required in computations, tends to be ill-posed. That, together with the existence of quite efficient iterative methods which tend to be computationally robust, is probably at the heart of the comment which led to the question. $\endgroup$
A complete outsider perspective: the twentieth century has seen an increasing generality and abstraction in mathematics. Thus in this thrust things like determinants (or even matrices) can be seen as overly restrictive or burdensome as they cannot describe all infinite dimensional spaces and their basis in calculation can be used to obfuscate general concepts.
Jacob WakemJacob Wakem
$\begingroup$ Hopefully someone more experienced and knowledgeable can comment on my answer so I might learn something. $\endgroup$
– Jacob Wakem
$\begingroup$ Just because determinants can't handle all situations in infinite-dimensional spaces where they were used for the same problems in finite-dimensional spaces doesn't mean they can't be useful for some infinite-dimensional problems. Dwork's solution in the 1960s of the first part of the Weil conjectures (rationality of the zeta-function of algebraic varieties over finite fields) relies on infinite-dimensional determinants of operators on $p$-adic Banach spaces. $\endgroup$
– KCd
$\begingroup$ @KCd There is no such thing as an infinite-dimensional determinant because a determinant is a number. $\endgroup$
$\begingroup$ I have no idea what you mean. Infinite series, infinite products, and determinants of infinite-dimensional matrices are all standard concepts in analysis (when they are convergent). An infinite series like $1 + 1/2^3 + 1/3^3 + 1/4^3 + \cdots$ is a number. Are you going to tell me there is no such thing as an infinite series too? $\endgroup$
To me it seems the author lacks a sufficient comprehensive knowledge of the range of applications of determinants and so the complete statement should be taken with care.
A field of application is combinatorics and there are surprising interpretations of determinants which also contribute to their power and usefulness.
An example is the following interpretation:
[M. Fulmek (2012)]: $(m\times m)$-determinants may be viewed as (generating functions of) $m$-tuples of nonintersecting lattics paths in $\mathbb{Z}^2$ with starting points on some fixed horizontal line $y=\alpha$ and ending points on some fixed horizontal line $y=\omega>\alpha$, where
the rows of the determinants (in the usual order: top to bottom) correspond to the starting points of the lattice pathes (ordered from right to left),
and the columns of the determinants (in the usual order: left to right) correspond to the ending points of the lattice pathes (ordered from right to left).
which is from his paper Viewing determinants as nonintersecting lattice paths yields classical determinantal identities bijectively.
epi163sqrtepi163sqrt
$\begingroup$ Thanks for the excellent reference [Fulmek], that later on I found as well in(en.wikipedia.org/wiki/…). It is a typical case where determinants are an essential tool. I will make a comparison between determinants and trigonometry : if you have been overfed with determinants or trigonometry in your student's years, a natural trend is to say "too much is too much" : but in one case as the other, you need it. For example, you couldn't do much geometry without trigonometry... $\endgroup$
Dec 4 '17 at 7:49
$\begingroup$ The reason why I am interested by these questions is that I am presently working on the fascinating Robinson-Schensted-(Knuth) correspondence (see (cmi.ac.in/~ksutar/reptheory/Viennot.pdf)) $\endgroup$
$\begingroup$ @JeanMarie: You're welcome, and many thanks for this interesting reference, I appreciate it. :-) $\endgroup$
– epi163sqrt
$\begingroup$ Yes, I fully agree with you (and Christian Blatter) that, from a pedagogocal point of view, it is a nonsense to prone the exclusion of determinants. Students, through application of simple algorithms, be it the computation of $det(A-\lambda I)$, or Euclid's algorithm, or the computation of roots of a quadratic, or... learn a lot and get acquainted with the corresponding theme (and - very important - are happy with it); on this basis, one can build more abstract concepts. If you feed them all the way long with abstract concepts, you will loose a big part of your audience...(ctd) $\endgroup$
$\begingroup$ ...(ctd) (I think here to undergraduate students ; the issues are not the same later : people have gained confidence into themselves, and are much more apt to abstraction) $\endgroup$
Back when I learned Linear Algebra, the text book we used found the "inverse matrix" using the a combination of the "minors", divided by the determinant.
Today it is much more common to use "row reduction" to find an inverse matrix or solve a system of equations.
$\begingroup$ @Ittayweiss I strongly discourage you to tell people to delete their answers. Rather, they can be encouraged to improve their answer. $\endgroup$
– Pedro Tamaroff ♦
$\begingroup$ Thank you Pedro for your comment. To answer poster: please note that your answer reads more like a comment rather than an actual answer. It only very loosely addresses the question OP articulated. Please consider modifying your answer so that it more comprehensively answers the question, or place it as a comment. $\endgroup$
In my mathematics experience, determinants are an essential theoretical tool. It is true, you can almost never compute it in big matrices, but lot of stuff is not necessarily computable and still very useful: for example, cohomology or fundamental groups of spaces (invariants attached to topological spaces).
An example of application among others:
In multivariate analysis, the change of variables formula for integrals includes the determinant (isn't useful to change variables in integrals?)
Any matrix is diagonalizable (up to an infinitesimal perturbation). This has also a significance in applications. Indeed, the fact that a square matrix $A$ of size $n$ has distinct eigenvalues can be reformulated as its characteristic polynomial $p(A)= \det(A-\lambda I) $ having only single roots. Again, this can be reformulated as the resultant $r_A$ of $p(A) $ and $p'(A) $ being different from zero when calculated in zero. Since all these operations are polynomial in the entries of the matrix $A$, a constraint of the form "polynomial $\neq 0$ " is almost always true (its solutions are dense).
Given a finite dimensional representation of a group $\rho: G \to GL(n) $, the determinant is a one dimensional representation;
Given two square matrices $A, B$ of size $n$, such that $AB-BA $ is invertible and $A^2+AB+B^2=0$, then $n$ is a multiple of 3.
Given a vector bundle $E $ over a space $M$ , its determinant bundle is a line bundle (which are much easier to study).
In algebraic number theory, if you have a finite extension of number fields $L/K$, the norm $N_{L/K}$ of an element $x \in L$ is defined as the determinant of the multiplication action of $x$ as a $K$ -linear map. For example, if one takes the Gauss integers, one can show with a bit of theory that any prime number congruent to 1 modulo 4 can be written as $u^2+v^2$. Multiplicativity of the determinant allows to extend the result to any number that has prime numbers congruent to 1 modulo 4 in his decomposition.
The determinant of the Frobenius (I think?) matrices in representation theory yield the not so trivial factorization of polynomials
$$ X^3+Y^3+Z^3 -3XYZ = (X+Y+Z) (X+\omega Y+\omega^2 Z) (X+\omega^2 Y+ \omega Z) $$ Where $\omega$ is the third root of unity.
LaTex has a dedicated symbol $\det$ for the determinant. Look here: $\Gauss$. So gauss is less important than the determinant, and Gauss is important.
And there are much more. These are the first few examples that come to my mind. The fact that a number governes the invertibility of a matrix is a very peculiar fact; the absence of this criterion over other rings yield very serious problems.
The "we love determinants" Association
Andrea MarinoAndrea Marino
$\begingroup$ This is to say: I strongly disagree with what it is said. $\endgroup$
– Andrea Marino
Throw this book away!
It may be that certain sub-sub-fields of algebra that make heavy use of determinants as symmetric polynomials are not so much en vogue now as they were a hundred years ago. Such things happen, no bad feelings about that. But it is beyond me how an author of a textbook directed at students of all kinds of mathematics can seriously state that the importance of the notion of determinant "is less central than it was in former times". Such an utterance is similar to the statement that "the real numbers are less central than they were in former times" from an author of a textbook about discrete mathematics.
Christian BlatterChristian Blatter
$\begingroup$ With uttermost respect sir, your indignation may be reasonable but I would appreciate it if you go into further detail. Maybe I lack the formal understanding, remember that I am just an undergrad student. Thanks anyways. $\endgroup$
$\begingroup$ Suggesting throwing away books based on one sentence. That is really good advice. Lets instead throw away answers who only provide arguments on the form "because I say so". $\endgroup$
– Winther
$\begingroup$ Actually, Christian Blatter has a good point. The key word is "students." In the 60's academia started, and has now finished, selling itself down the river for the sake of job training. All universities are now DeVry or ITT Tech. We answer questions only based on "when will this be used". Never on the basis of "does this improve a student's insight." It's one argument whether determinants are useful in calculations of any sort. It's quite another whether they're useful pedagogically. And since it's a _text_book, the pedagogical consideration should be paramount. $\endgroup$
– B. Goddard
$\begingroup$ I suspect that Christian is using the term in a conversational rather than a book burning sense. The back of the book states "For statisticians and engineers.", and, in this context, it is true that determinants are not terribly relevant. $\endgroup$
$\begingroup$ The real numbers are less central than they were in former times :) I think there has been a movement away from "try to do all of mathematics in just a few big sets ($\mathbb{R}$, $\mathbb{C}$, $L^2\left(\mathbb{R}\right)$, etc.)" towards "try to do each thing in whatever place it feels most natural" (e.g., computations with polynomials are done over arbitrary commutative rings; Galois theory has moved from number fields into arbitrary field extensions; certain results went all the way up to abelian categories, etc.). In this sense, almost everything has become less central! $\endgroup$
– darij grinberg
Not the answer you're looking for? Browse other questions tagged linear-algebra matrices determinant math-history or ask your own question.
What is the origin of the determinant in linear algebra?
Does Nakayama Lemma imply Cayley-Hamilton Theorem?
Demystifying the Determinant
What is the geometry or an obvious application of a 2 X 2 matrix?
What does abstract algebra have to say about the determinant?
Find the values of 'a' in a $4\times 4$ matrix(A) when the determinant is less than 2012
is determinant of A times A transposed bigger than or equal to zero?
Introduction to Proof via Linear Algebra
Prove that this $3 \times 3$ determinant vanishes
Determinant of Identity plus matrix times diagonal -- why does this hold?
Prove that the determinant is greater than $1$
Why does this determinant computation fail? | CommonCrawl |
BioMedical Engineering OnLine
Biomedical signals and machine learning in amyotrophic lateral sclerosis: a systematic review
Felipe Fernandes ORCID: orcid.org/0000-0003-0805-17961 na1,
Ingridy Barbalho1 na1,
Daniele Barros1,
Ricardo Valentim1,
César Teixeira2,
Jorge Henriques2,
Paulo Gil2 &
Mário Dourado Júnior1
BioMedical Engineering OnLine volume 20, Article number: 61 (2021) Cite this article
The use of machine learning (ML) techniques in healthcare encompasses an emerging concept that envisages vast contributions to the tackling of rare diseases. In this scenario, amyotrophic lateral sclerosis (ALS) involves complexities that are yet not demystified. In ALS, the biomedical signals present themselves as potential biomarkers that, when used in tandem with smart algorithms, can be useful to applications within the context of the disease.
This Systematic Literature Review (SLR) consists of searching for and investigating primary studies that use ML techniques and biomedical signals related to ALS. Following the definition and execution of the SLR protocol, 18 articles met the inclusion, exclusion, and quality assessment criteria, and answered the SLR research questions.
Based on the results, we identified three classes of ML applications combined with biomedical signals in the context of ALS: diagnosis (72.22%), communication (22.22%), and survival prediction (5.56%).
Distinct algorithmic models and biomedical signals have been reported and present promising approaches, regardless of their classes. In summary, this SLR provides an overview of the primary studies analyzed as well as directions for the construction and evolution of technology-based research within the scope of ALS.
Amyotrophic lateral sclerosis is a disease characterized by the progressive and irreversible degeneration of motor neurons, which causes deficits in the ability to control movement, breathing, and, in 50% of cases, in cognitive and behavioral functioning [1,2,3]. The cause of ALS is still unknown and there is no treatment to cure it. Hence, there are only alternatives of palliative care and medication to delay the progress of the disease [4, 5]. Diagnosing patients with ALS represents a challenging task due to its complex pathogenesis and the absence of specific biomarkers [6, 7]. The diagnosis is based on clinical presentation, progression of symptoms, and the exclusion of other diseases supported by tests such as Electromyography (EMG). Such a process requires an average of 10–18 months from the onset of symptoms to confirmation [8,9,10,11]. What is more, the diagnosis is considered slow and late given the characteristics of ALS, in which life expectancy after confirmation is of 2–5 years [12].
Despite being described by Jean-Martin Charcot more than 100 years ago [13], ALS is considered a rare disease, and, to this date, there are not many countries with records of epidemiological data. In a few European countries, as well as in the United States, epidemiological records show that the incidence rate of ALS is of 1–2 cases per 100,000 individuals per year, while the prevalence is approximately 5 cases per 100,000 individuals, which for van Es et al. [3] reflects the fast lethality of the disease. A worldwide increase in the number of ALS-affected individuals is expected, rising from 222,801 cases in 2015 to 376,674 by 2040, according to the projection made by Arthur et al. [14]. The aging of populations and the consequent rise in the number of individuals within the age group with a more considerable risk for ALS, which is of 60–79 years, represent the probable culprits for the 69% worldwide increase [14].
Considering the intrinsic aspects of ALS, it is critical to promptly search for diagnostic support systems, as well as for alternatives that intermediate essential communication, autonomy, and promote quality of life to patients. From this standpoint, several technology-based studies have been developed. These investigations typically provide auxiliary resources for diverse aspects regarding ALS, going from what pertains to patients and their caregivers to matters related to outpatient care in organizational health entities [15,16,17].
Technologies developed for health encompass and collaborate in positive progressions in remarkable ways, such as with the diagnosis of ALS [18, 19], monitoring of disease progression [20], monitoring of food intake [21], communication intermediation [22,23,24,25], autonomy [26], and other applications based in artificial intelligence, as it has been reviewed by Schwalbe and Wahl [27]. Automated systems for disease diagnosis, for instance, are computational tools composed of ML techniques that, based on the processing of biomedical signals, are capable of aiding the detection of neuromuscular disorders [28]. These systems contain expert information of specific domains, which provide health professionals with decision-making support and represent strategies and measures adopted in the care of patients [29].
Recently, in the context of ALS, Grollemund et al. [30] published a comprehensive review that presents and investigates ML models. Thus, it uses or combines different data types from individuals with ALS (clinical, genetic, biological clinical, and imaging), in three-class applications: diagnosis, prognosis, and risk stratification. In conclusion, the authors point to promising advances with this approach in the academic and clinical field in the ALS ecosystem. In this perspective, this SLR complements Grollemund et al. [30] in analyzing ML models in applications for ALS using specifically biomedical signals.
Biomedical signals consist of data from a studied physiological system and their processing aims mainly to extract relevant information [31, 32]. This information can enhance data-driven artificial intelligence techniques, especially ML algorithms, and it is used to support the diagnosis of various diseases [27]. There are several types of biomedical signals, as EMG, electroencephalogram (EEG), electrocardiogram (ECG), electrooculogram (EOG), gait rhythm (GR) and magnetic resonance imaging (MRI). Regarding the ML models, Artificial Neural Network (ANN), decision tree (DT), support vector machine (SVM), and K-Nearest Neighbor (KNN) are particular examples of techniques that have been extensively considered in the healthcare realm, including in the context of ALS [33,34,35,36].
The chief goal of this systematic literature review is to investigate ML-based approaches, in tandem with the biomedical signals, that contribute to the practical and scientific advancement of aspects in the field of ALS. In this manner, it is expected to provide an overview of the matter at hand, considering the identification of the most-used biomedical signals and ML-based models, in addition to gathering details of primary studies, such as the purpose, the performance of algorithmic models, and experimental data, to identify strengths and opportunities for future researches.
We have developed this research considering the systematic review guidelines proposed by Kitchenham [37]. In the perspective of investigating technological applications in ALS, this study aims at (i) identifying the most applied biomedical signals; (ii) identifying for what purposes those are used; and (iii) verifying the usage of ML techniques or intelligent approaches to the processing of those signals. Hence, the research questions (RQ) were elaborated on this premise (see Table 1, presented below).
Table 1 Research questions
The primary studies searching and screening process in the scientific databases were categorized into four stages, according to what is displayed in Fig. 1. In the first stage, an initial set of articles was selected from the output of searches carried out in the IEEE Xplore, Web of Science, Science Direct, Springer, and PubMed databases. The following search strings (STR) were used in this first stage:
STR01: ((("signals processing" OR "signals biomedical") OR ("smart systems" OR "machine learning" OR "artificial intelligence" OR "computational intelligence" OR "algorithm" OR "algorithms")) AND ("amyotrophic lateral sclerosis" OR "als"));
STR02: ((("signals processing" OR "signals biomedical") OR ("intelligent systems" OR "machine learning" OR "artificial intelligence" OR "algorithms" OR "Computational Intelligence")) AND ("amyotrophic lateral sclerosis" OR "als")).
In the second stage, the predefined inclusion criteria (IC), presented in Table 2, were applied to the initial set of articles from the previous phase. Primarily, an IC delimits the boundaries or scope of the investigation and possibilities the generation of a new subset of papers with a more significant probability of answers to the RQ. In such a context, the subset includes research articles from the last ten years that have been published in journals and are directly related to the principal area of interest of this systematic review.
Methodology steps
Table 2 Inclusion criteria
In the third stage, after screening the articles through the IC, the verification and removal of duplicate papers were carried out. Besides, a filtering procedure—by considering title, abstract, and keywords—was performed to exclude papers that did not present specific terms related to the theme of this review. Such a process was guided by the exclusion criteria (EC) (see Table 3) and was executed through the Rayyan web application [38].
Table 3 Exclusion criteria
In the fourth stage, the total reading of the filtered articles was performed. Hence, it was executed the quality assessment (QA) protocol (see criteria in Table 4). In the QA procedure, each criterion was attributed points measuring the relevance of the article to the target subject of this research. The points were distributed in the form of weights (w), considering suitable responses to the QA criteria, present in the primary studies, with 1.0 being the most relevant weight and 0 the lowest:
$$w_{\text {QA}} = \left\{ \begin{array}{ll} 1.0, & \text {yes},\; \text{fully}\; \text{describes} ,\\ 0.5, & \text {yes}, \; \text {partially} \; \text {describes},\\ 0, & \text {does}\;\text {not}\; \text {describe}.\\ \end{array} \right.$$
A score, the arithmetic mean of the points of the QA criteria (Eq. 1), was generated for each article. In this case, all articles that obtained a score greater than or equal to 0.5 (\(0.5 \le \text{score} \le 1\)) were selected for this research and constitute the final set of articles.
$$\text{score} = \frac{1}{\text {QA}}\sum _{i=1}^{\text {QA}} w_{\text {QA}_{i}}$$
Records relevant to each stage, as well as the data extracted from the articles, were properly gathered in spreadsheets and the Rayyan web application [38] for data extraction. Data, such as year of publication, authors, and possible responses to the RQ, were extracted from the set of articles of the fourth stage. They permitted the final analysis and fulfillment of the objectives of this systematic review.
Table 4 Quality assessment
The results obtained from the searching and screening process of primary studies are synthesized in Fig. 2. In the first stage, 10128 candidate articles were identified after searching with the STRs. In the subsequent phase, three refining procedures based on IC (Table 2) were applied, and 9914 papers were discarded for not meeting the IC. At this point, 214 articles were considered appropriate for inclusion and analysis in the following stage. In stage three, the applied filters, based on the EC (Table 3), removed 186 articles amongst duplicates and those missing the target terms of the search. In this manner, 28 studies were selected for full-text reading and assessment through the QA criteria. After the QA procedure, the fourth and latter phase, 18 papers exceeded the pre-established minimum score, according to the result presented in the respective column in Table 5, and were included for analysis and definitive investigation in this review.
Result of the search and screening process of primary studies for this systematic review
Table 5 Set of selected articles and their main characteristics
In sum, considering the 18 articles included in this research, the results presented in Fig. 3 evidence three major classes of probable practical applications of biomedical signals processing and machine learning within the context of the ALS disease: diagnosis (or classification), communication, and survival prediction. In addition to categorizing the purposes of such studies, Fig. 3 highlights the number of biomedical signals used and the respective classes that utilized them. Four distinct types of signals were identified: EMG, EEG, GR, and MRI.
Summary of the signals used and their objectives
Of the analyzed studies, 44.44% focus on the processing of the EMG signal, the most used biomedical signal (see Fig. 3), and specifically for classification. That is, for the diagnosis of individuals amongst healthy controls (HC), ALS patients, and, in some cases, other diseases (OD). With the same objective, especially for classification, 16.67% of the studies use GR and 11.11% MRI. The MRI signal was additionally used in a particular article for survival prediction of ALS-afflicted individuals, which represents 5.56%. In the communication class, 22.22% of the studies focus exclusively on the approach through the processing of the EEG signal, being this the only one presented for that purpose. This first general analysis of the studies, identifying the purposes of the articles and the signals used, answers research questions RQ01 and RQ02.
Other significant and specific characteristics extracted from the 18 articles included in this study are summarized in Table 5, to support the analysis and answer research questions RQ03, RQ04, and RQ05. Regardless of the classes observed, diagnosis, communication, or survival prediction, all studies used ML algorithms. Alternative algorithmic models were employed and, according to the performance analysis of the algorithm concerning accuracy (Acc), specificity (Spe), or sensitivity (Sen) metrics of evaluation, the best or the only proposed model of each work is shown in Table 5, as well as their respective performances.
For testing, validating, and appraising the proposed approaches in the studies, the algorithmic techniques were applied to a set of data from individuals, distributed in different group combinations of HC, ALS, and/or myopathy, or other neurological diseases. The number of individuals and the type of participating groups in the experiments of each study is specified in Table 5 and summarized in Fig. 4. Moreover, Table 5 describes the source of the dataset and specifies whether they come from public or local repositories.
Number of individuals used in the studies
Description of the diagnosis studies
Diagnosis of ALS patients is the most numerous task described among the selected papers, accounting for 72.22% of the studies. Considering only this class, Fig. 5 presents an overview of the number of biomedical signals employed. The use of the EMG signal stands out, being addressed in 61.54% of the studies aimed at diagnosis [39,40,41,42,43,44,45,46]. GR is applied in 23.08% of the studies [47,48,49] and MRI in 15.38% [50, 51]. The EEG signal is unused for this purpose.
Number of studies by type of biomedical signal defined in the diagnosis class
In the studies, the focus on the development of strategies to reduce the noise of collected biomedical signals is evident, intending to discover the most significant features to enhance the performance of the algorithmic models, therefore reflecting on the accurate classification of individuals. In the case of the EMG signal, Gokgoz and Subasi [42] show the performance gain in the classification of HC, ALS, and OD with different ML algorithms, such as KNN, ANN, and SVM, after applying the multiscale principal component analysis (MSPCA) noise removal technique combined with the multiple signal classification (MUSIC) feature extraction technique.
In this study, the most satisfactory performance was of the SVM model, with 92.55% Acc. In the following year, also addressing the EMG signal, Gokgoz and Subasi [46] proposed another study focusing on noise reduction and selection of features. Hence, in this research, the authors developed a structure to eliminate noise, also employing the MSPCA technique, with a novel strategy based on Discrete Wavelet Transform (DWT) for feature extraction. The authors performed experimental tests, with and without the noise-removing structure and feature extraction, utilizing three different DT algorithmic models: CART, C4.5, and random forest (RF). Similarly to their previous study, Gokgoz and Subasi [46] achieved satisfactory results in their second work in the classification of HC, ALS, and OD, and demonstrated that the use of the MSPCA noise removal method in conjunction with feature extraction using DWT improved the performance of the RF algorithmic model, which obtained in the best case 96.67% Acc using the EMG signal. In both studies, three distinct groups of subjects were considered: HC \(= 10\), ALS \(= 8\) and OD \(= 7\).
Vallejo et al. [45] adopted the DWT approach to decompose EMG signals and generate the hyperspace of features that aims at selecting the most relevant features through the fuzzy entropy technique to feed an ML algorithm based on an ANN. To verify and validate the proposed method, the authors used a feedforward ANN with four layers of seven neurons each, except for the output layer, and the log-sigmoid activation function. The ANN, acting with the DWT and fuzzy entropy approaches, obtained 98% Acc in the best result. Such a fact indicated that the proposed strategies for feature selection and extraction improved the classification process of individuals into three distinct groups, including HC, ALS, and/or myopathy. In the experiments, the authors included ten healthy subjects, eight with ALS and seven with OD.
In Doulah et al. [44], the DWT approach was applied to decompose, filter, and extract relevant features from preprocessed EMG signals. Preprocessing encompassed two methods proposed for the classification of subjects in HC and ALS, and/or myopathy. In the direct EMG method with DWT, features are extracted after a frame-by-frame sequential analysis. For the second approach, a set of features was selected through the procedure of dominant motor unit action potential (MUAP), and, based on the DWT decomposition, the key features for classification were extracted. Doulah et al. [44] verified both proposed methods in a KNN classifier. The authors evaluated the performance of the algorithm by operating distinct settings on three separate sets of data corresponding to HC, ALS, and OD subjects (10, 8 and 7 subjects, respectively). Both processes presented significant results for the classification of two and three sets (HC, ALS, and OD). The Dominant-MUAP method may be highlighted for its consistent performance, reaching out 98.8% Acc using three sets.
Chatterjee et al. [39] presented a new generalization of the Stockwell transform (ST), called Modified Window ST (MWST), for preprocessing the EMG signals to generate a more representative feature matrix (or a time–frequency plane). MWST parameters \(\alpha\), \(\beta\), \(\gamma\), and \(\delta\) which affect the shape of the window or the energy concentration in the time–frequency plane, are defined in an optimized way through the Particle Swarm Optimization (PSO) metaheuristic algorithm. After applying the MWST technique to the EMG signals of eight individuals with ALS and seven with myopathy, four features are extracted from the matrix to serve as input to four ML models: SVM, KNN, Naïve Bayes, and DT. The approach proposed by Chatterjee et al. [39] presented significantly better results in the classification of individuals between ALS and myopathy when compared to the conventional ST method. The SVM model achieved the most satisfactory performance with 98.28% Acc.
Four distinct methods of feature extraction from EMG signals in the time–frequency domain have been addressed ST, Synchro-extracting Transform, Wigner Ville distribution, and Short-Time Fourier Transform. The four approaches applied to EMG signals generated images and, using the Gray Level Co-occurrence Matrix technique, 20 features were extracted with each method, and a set of 80 features was originated. To optimize the performance of the ML model proposed by the authors, an ANN with a hidden layer of 10 neurons and tan sigmoid activation function combined with a subset containing the most suitable combination of 15 features (from a finite set of possibilities) was defined through a genetic algorithm (GA), implemented with the KNN classifier to carry out fitness evaluation of the different combinations of the GA population. The strategy proposed by Ambikapathy et al. [43] to aid diagnosis using ANN obtained promising and statistically significant results in the process of classifying individuals between HC and ALS (86.6% Acc, 86.6% Spe, 86.6% Sen), HC, ALS or myopathy (82.2% Acc, 81.89% Sen, 91.31% Spe), and ALS or myopathy (96.6% Acc, 93.7% Sen, 100% Spe).
Zhang et al. [40] developed a method to characterize patterns in surface EMG signals based on three markers/features for supporting the diagnostic: clustering index, kurtosis of the EMG signal amplitude histogram, and kurtosis of EMG zero crossing-rate expansion. Furthermore, the linear discriminant analysis (LDA) ML algorithm was applied to the process of discriminating subjects as HC and ALS, obtaining as input data a feature vector originated from the concatenation of vectors of the mentioned features. The experiments carried out in this study relied on the analysis of data from 10 subjects with ALS and 11 from HC. Each of the three features displayed unique promising results. When used synergistically in an approach that combines them with the LDA algorithm, it rendered a more robust technique that presents even more significant outcomes, presenting a Spe of 100% and Sen of 90%. Such an aspect indicates favorable perspectives to be used as a diagnosis support application.
Hazarika et al. [41] proposed a novel process assessment and inference system (PAIS) with a robust structure for preprocessing and extracting features from EMG signals. This structure is composed of procedures that initially evaluate the EMG signal features via an approach involving partitioning strategies of the input data (called multi-view direct) and decomposition by DWT, followed by the application of multidomain multiview discriminant correlation analysis (mmDCA). mmDCA analyzes the correlation of features, verifies redundancy, eliminates irrelevant features, and synchronizes them from partitions in a single vector. The mmDCA produced vector is incorporated into different ML models, such as KNN, and fed to a feedforward back-propagation neural network (FFBP-ANN) with two hidden layers of 8 neurons each, a conventional density-based linear classifier (LDC), a quadratic classifier (QDC) and SVM.
Each algorithm performance was evaluated positively in the classification of subjects between HC, ALS, and myopathy classes in two real-time EMG signal datasets. In the first dataset, containing ten healthy subjects, eight with ALS and seven with OD, and in the second dataset, containing four healthy subjects, four with ALS and four with OD, the QDC model presented the most robust results: 99.03% Acc and 100% Acc, respectively.
The studies mentioned thus far show the potential and the importance of processing the EMG biomedical signal to provide consistent and elementary features or data to the learning of intelligent algorithms and, consequently, to help with the diagnosis of ALS. However, as an alternative to EMG signals for diagnosis, the studies [47,48,49] investigated the performance of ML models with strategies that process data from GR biomedical signals.
A study by Xia et al. [47] carried out feature extraction from GR signals in five time series records, based on statistical analysis. Features such as mean value, standard deviation, maximum and minimum value, skewness, and kurtosis were computed and defined. The authors also proposed the extraction of three more features using the Lempel–Ziv complexity, fuzzy entropy, and Teager–Kaiser energy operator statistical methods. Furthermore, Xia et al. [47] executed an approach of selecting a subset of features based on three procedures, with the first being a statistical analysis of the features, followed by a performance evaluation of classification algorithms and ultimately the application of the hill-climbing optimization algorithm to find out and define the optimal subset of features.
After selection, a series of experiments with ML algorithms was performed considering the optimal subset as the input data for four classifiers: SVM, RF, a feedforward ANN with sigmoid activation function, and KNN. The dataset used for the experiments included data from 16 healthy subjects, 13 with ALS and 35 with OD. All classifiers showed good performance in the binary classification between HC and ALS, and HC and OD (neurodegenerative) in addition to ALS. The most satisfactory performance was obtained by the SVM technique, with 96.55%.
Ren et al. [48] performed a strategy to extract and select features from five time series of GR signals. For this, the researchers proposed an approach that utilizes the empirical mode decomposition (EMD) method to extract features from the partitioning of the GR signal time series, therefore producing six components—five of which are used and one discarded—that were promptly submitted to statistical analysis using Kendall's Coefficient of Concordance method. With this, the purpose is to measure the significance and relationship of the features. Next, a calculation that employed the amplitudes of the components was made through the procedure of Ratio for Energy Change. Such a process comprehends to a dimensionality reduction technique based on principal component analysis (PCA) is applied to define the final set of features.
The strategy proposed by the authors was evaluated in five classifiers: Naïve Bayes, SVM, RF, Multilayer Perceptron (MLP) and Simple Logistic Regression. Unlike the performance evaluation of the ML models considered in Table 5, in this study the area under the ROC curve (AUC) is used for performance assessment. The most significant results for classifying subjects between HC and ALS (16 and 13 subjects, respectively) were presented by the feedforward MLP model, with an AUC value of 0.934. The average value of the AUC considering the five classifiers was 0.898 and, in general, the approach indicates promising results.
Differently from other researches developed for diagnostic, in the study of Khorasani et al. [49], a generalization of the Hidden Markov Model (HMM) and the classification model named the factorial hidden Markov model (FHMM), the recognition of patterns and the classification of subjects in HC or ALS from GR time series is proposed. After preprocessing the signal to remove outliers, the GR signal is segmented into fifty time series. And some features, such as mean or variance, are extracted to feed the FHMM. The method was assessed with data from 16 subjects with HC and 13 with ALS. Further, its performance was compared to the traditional HMM model and the Least-Squares SVM (LS-SVM) algorithm with Gaussian kernels. With an Acc value of 93.1%, the FHMM classification model displayed superior performance in HC or ALS recognition.
Scarcely explored in the context of diagnosing patients with ALS, strategies based on neuroimaging and ML are still challenging. In 2013, Welsh et al. [50] proposed an approach when implementing the SVM algorithm to classify subjects in HC or ALS through the analysis of data from functional magnetic resonance imaging (fMRI). The fMRI time series data were preprocessed and underwent a set of robust procedures for the extraction and selection of features, including the consecutive execution of strategies, such as PCA and Independent Components Analysis (ICA), as well as the creation of maps (or vectors) of correlation coefficients from different brain regions. After that, the data were provided to the linear kernel SVM algorithm, and its performance was evaluated. For the experiments, data from 32 patients diagnosed with ALS and 31 people from HC were provided. Welsh et al. [50] indicated the values were modest (71.5% Acc) in the classification of diseases as ALS using fMRI at rest.
A few years after the fMRI study by Welsh et al. [50], Ferraro et al. [51] developed a method for classifying individuals with motor neuron diseases, including ALS, based on the multimodal structural MRI with an ML algorithm. The MRI data were divided into distinct regions of interest and underwent analysis using literature and statistics software. The evaluation of the proposed diagnosis approach was performed in an RF model. The performance of the algorithm in classifying individuals in HC and ALS, specifically with the combined MRI model, was expressive. For the experiments, data from 78 individuals from HC, 123 subjects with ALS, and 64 subjects with OD were used. The model developed showed an Acc of 91% concerning the classification of subjects with ALS and subjects from HC. The results of both studies [50, 51] typically indicate that only data from MRI-based strategies are insufficient to obtain good performance in the classification. Studies with neuroimaging and ML for ALS are yet restricted. Nevertheless, the results are promising for the development of a system capable of assisting in ALS diagnosing.
Communication improving studies
As a result of the progressive degeneration of the upper and/or lower motor neurons in the brainstem region, people diagnosed with ALS lose the ability to speak and interact with the environment. Technological resources developed for communication are crucial to ensure the well-being of those patients. About 22% of the studies included in this review [52,53,54,55], have developed artifacts that promote the communication improvement class of this SLR, exclusively through the EEG biosignal.
In a study conducted by Sorbello et al. [52], a framework was proposed through the operation of a brain–computer interface (BCI) system to control a humanoid robot and promote minimal autonomy to patients with ALS. Generally, the system structure, called brain–computer robotic interface (BCRI), is composed of a BCI system, EEG and eye-tracking devices, and a network system to connect the BCI system to the robotic system. The ML LDA algorithm is used after preprocessing and EEG feature extraction to correctly classify and translate the user action into control commands for the humanoid robot. The authors evaluated the proposal by conducting experiments on four subjects at the HC and four subjects with ALS. The results were satisfactory, and the proposed framework for enabling communication for patients with ALS was validated after all participants were able to control the humanoid robot.
Liu et al. [53] developed an approach by applying the concepts of fractal dimension (FD) and Fisher's criterion to optimize the selection of EEG channels and the characterization of the data obtained from the signal. In this manner, the authors aimed at improving the classification capacity of an ML algorithm in a BCI system for patients with ALS. Two methods for estimating FD, Grassberger-Procaccia (GPFD) and Higuchi (HFD), were implemented. The key features of 30 EEG channels were extracted and concatenated into a single vector to serve two algorithmic models: KNN and LDA. After tests performed on five subjects with ALS, the results were satisfactory and the GPFD method surpassed the HFD. The performances of the two algorithms, KNN and LDA, were significant and similar, with 95.25% Acc, when compared with the input data containing the 30 EEG channels.
The existence of a simple interface with an accurate and fast information transfer rate is essential to maintain communication efficiency in a BCI system based on EEG signals for people with ALS. For addressing such matter, Mainsah et al. [54] developed a data-driven Bayesian early stopping algorithm, called DS, to optimize the feature selection process of an ERP-based P300 BCI speller, in which ERP stands for event-related potentials. Besides, a variation of the DS is proposed with the application of statistical modeling through Bayesian inference for language predictability, called DSLM. Features correlated with the user's interest were extracted from the EEG signal to train the stepwise LDA classifier. In the research, the designated online tests were performed with 10 subjects with ALS. Both DS and DSLM algorithms proved to be efficient in minimizing the character selection time and with an average accuracy of 75.40% and 76.39%, respectively. There was no statistical difference between the algorithms.
In the same context of Mainsah et al. [54] and Miao et al. [55] proposed an ERP-based BCI display approach using as strategy a new speller paradigm with peripherally distributed stimuli with the possibility of feedback in the center of the display. The EEG signals were recorded and analyzed using preexisting software from the BCI platform. The features were extracted from data acquired offline from 16 electrodes to train the Bayesian LDA (BLDA) classifier and subsequently utilization of the trained model in an online system test. The proposed method was evaluated concerning the conventional matrix speller paradigm. The experiments were carried out on 18 subjects with ALS. Even obtaining an Acc of 90% in its most efficient performance, the results presented by the BLDA algorithm do not reveal any significant difference between the proposed approach and the conventional approach. However, patients with ALS were able to operate the system effectively.
Survival prediction studies
The survival prediction of patients with ALS is empirically defined based on, generally, the analysis of clinical data. Only one of the studies included in this review is dedicated to such a prediction. In the study developed by van der Burgh et al. [56], a model for predicting survival (short, medium, or long) of patients with ALS is proposed by combining clinical data, neuroimaging, and a robust ANN-based ML technique named Deep Learning Networks (DLN). Four scenarios were defined for the application of the DLN algorithm. Finally, the first situation was based only on clinical data. The second and third scenarios utilized MRI images and included structural connectivity and brain morphology data. The latter situation included a combination of the previous three. To each of those, a model was implemented. Furthermore, the performance of algorithms was evaluated through a database that contained data of 135 subjects with ALS. The model that combined clinical and MRI data revealed superior performance (84.4% of Acc value) and was presented as a viable strategy for predicting the survival of patients with ALS. The remaining models displayed intermediate results, although they indicated promising approaches.
This systematic literature review explored approaches based on computational intelligence. Besides, to process biomedical signals considering the scope of ALS, it functioned in a synergistic and complementary manner. A set of 18 articles was included and reviewed, and three major classes of applications were found: aid to diagnostic, communication enabling, and survival prediction. The most adequate algorithmic models and the respective biomedical signals responsible for providing data were identified and quantified (see Fig. 6).
Quantitative of the best algorithmic models and the respective biomedical signals
Based on the analysis of the 13 articles that addressed the support to the diagnosis of patients with ALS, regardless of the biomedical signal or ML algorithm used, it is possible to define a standard methodological scheme (a pipeline) general to all studies, which is broadly depicted in Fig. 7. Except for Khorasani et al. [49], who investigated a new classification algorithm, the studies suggest approaches or methods for the data treatment process that may enhance the training stage and, consequently, the classification stage. This data treatment process, which includes the feature extraction and selection phases, for instance, is important to eliminate noise, redundancy, and reduce the data dimensionality, in addition to maximizing the performances of the algorithms through the provision of refined and consistent data [57]. The various ML models implemented were presented as techniques for evaluating and validating the proposals of the studies. However, they were elementary techniques in the diagnosis process that are present in all articles.
Generic pipeline: generalized scheme for solving classification problems
The studies [39, 41,42,43,44,45,46,47,48, 51] about diagnosis support, in addition to ALS, also tested approaches for binary or multi-label classification considering other neurological conditions, such as myopathy, Parkinson's disease, Huntington's disease, predominantly upper motor neuron disease, and ALS-mimic disorders.
Regarding the four articles belonging to the communication class, two distinct categories can be observed in the analyzed studies. The first one is that of the study conducted by Sorbello et al. [52], which aims at complementing and adapting a BCI system with a humanoid robot to provide not only communication but also a minimum of autonomy. In the second identified category, the studies [53,54,55] suggest alternative approaches that include ML to optimize character selection time in a BCI system. These approaches range from the optimization of EEG electrodes to intelligent customization of the interface. The importance of BCI systems in promoting communication is evident. These systems are widely utilized in research to establish a communication pathway between the human brain and external devices, recognizing voluntary changes in the brain activity of their users [58,59,60,61,62,63].
Despite the research focused on the development of BCI systems, there are limitations regarding their home use. One of the primary reasons why BCI have not been introduced into the domestic environment is the character selection time. Specifically, the time still is considered slow and inaccurate when it comes to approaches that do not use brain signals, and also the need for electrodes connected to the head of the patient [47, 54, 64]. Other approaches to human–computer interaction systems that do not necessarily involve brain signals by EEG can be seen in Pinheiro et al. [65], Hori et al. [66], Fathi et al. [67], Harezlak et al. [68], Villanueva et al. [69], Królak e Strumiłło [24], Zhao et al. [70], Liu et al. [71] and Aharonson et al. [22].
The only survival prediction study with ALS patients analyzes how challenging it is to develop systems for such a purpose. The study [56] indicates that MRI and the DLN technique are promising for survival prediction and suggests a more significant exploration of the field of neuroimaging. Also, the research reveals the importance and benefits of patients' clinical data in the process of predicting survival at the three levels of ALS. This observation, in combination with the analysis made thus far, reveals both the absence and the possibility of using clinical data for diagnosis. Correlated with the survival aspect, recent studies indicate it is possible to apply ML approaches with digital biomarkers using the speech signal to monitor the progression of ALS [72], including applications for automatic classification of the ALS Functional Rating Scale (ALSFRS) [73, 74].
Regarding ML algorithms, it is observed that they are specifically supervised in all studies. The type of biomedical signal varies only in the diagnosis studies, with EMG being the most used signal, followed by GR and MRI. The EEG signal is applied solely for communication enabling applications. The MRI-based biomedical signal is used both in diagnosis and survival prediction applications. Schuster et al. [75] affirm that MRI-based biomarkers are currently seldom used for aiding the identification of ALS. This observation is complemented by the results presented in this SLR, which also reports the limited number of neuroimaging-based studies aimed at diagnosis support applications and survival prediction of the ALS disease, despite the potential mentioned by van der Burgh et al. [56]. In addition to these biomedical signs mentioned so far, studies show the feasibility of using the speech biosignal for the early diagnosis of ALS, as indicated by Wang et al. [76], Suhas et al. [77], An et al. [78], Vieira et al. [79], and Wisler et al. [80], and tracking changes in individuals with bulbar ALS [81].
The 18 studies carried out experimental tests with datasets of healthy subjects and subjects with ALS or other neurological diseases. 50% of the studies used local or proprietary datasets. The other 50% of the investigations collected data from public online repositories. In some cases, like those for diagnosis and communication, except in the study carried out by Ferraro et al. [51], the limitation in the number of patients with ALS is evident (see Fig. 4). These results suggest that it is still challenging to develop and validate a robust study with a more considerable number of subjects with ALS or in an outpatient setting.
This article introduces an SLR protocol to investigate relevant studies from the last ten years (2009–2019) that address ML techniques and biomedical signal processing. It may contribute to the advancement of research within the context of ALS. Based on 18 primary studies, the results exhibit strategies to minimize problems and/or promote means for diagnosis support, communication, and survival prediction. Considering the analyzed studies, 88.89% of those report the importance of treating biomedical signals for providing robust and consistent data for ML algorithmic models.
Furthermore, it can be observed that there is a predominance in the type of biomedical signals used by studies in the categories of communication and prediction of survival, being exclusively and respectively the EEG signals and MRI images. For the diagnosis class, in particular, three types of raw data are reported, namely EMG (61.54%), GR (23.08%), and MRI (15.38%). Regarding ML algorithmic models and analyzing the most satisfactory performances, SVM is the most used, followed by LDA and ANN techniques. Even though the 18 articles selected use ML, except for one study that proposed a new algorithm. In general, limited to the objectives of this SLR, the literature suggests and dedicates itself to the treatment of biomedical signals.
The studies are promising, but there are, nonetheless, significant aspects to be explored. When it comes to the diagnosis, the studies may be applied in outpatient clinics for practical assistance, in cases that have yet been unconfirmed of ALS, or even so in the early stages of the disease. Moreover, the use of big data approaches with patient's clinical data might contribute to the conclusive results and remains open for investigations. That includes the field of survival prediction. Concerning the approaches for communication improvement, there are unanswered questions about the use of BCI in the domestic environment, considering its aspects, costs, as well as efficient interfaces that prevent fatigue, discomfort, and optimization of the electrodes for EEG signals acquisition.
Acc::
ALS::
ALSFRS:
ALS Functional Rating Scale
ANN::
AUC::
Receiver operating characteristic curves
BCI::
Brain computer interface
BCRI::
Brain computer robotic interface
BLDA::
Bayesian linear discriminant analysis
DLN::
Deep Learning Network
DS::
Dynamic stopping
DSLM::
Dynamic stopping with language model
DT::
DWT::
Discrete Wavelet Transform
EC::
ECG::
EEG::
Electroencephalogram
EMD::
Empirical mode decomposition
EMG::
EOG::
Electrooculogram
FD::
Fractal dimension
FHMM::
Factorial hidden Markov model
fMRI::
GA::
Genetic algorithm
GPFD::
Grassberger-Procaccia fractal dimension
GR::
Gait rhythm
HC::
Healthy controls
HFD::
Higuchi fractal dimension
HMM::
Hidden Markov model
IC::
ICA::
Independent components analysis
KNN::
K-Nearest Neighbor
LDA::
LDC::
Density-based linear classifier
LS-SVM::
Least-squares support vector machine
ML::
MLP::
Multilayer perceptron
mmDCA::
Multidomain multiview discriminant correlation analysis
MRI::
MSPCA::
Multiscale principal component analysis
MUAP::
MUSIC::
Multiple signal classification
MwST::
Modified window Stockwell transform
OD::
PAIS::
Process assessment and inference system
PCA::
PSO::
Particle Swarm Optimization
QA::
QDC::
Quadratic classifier
RF::
RQ::
Sen::
SLR::
Spe::
ST::
Stockwell transform
STR::
SVM::
Support vector machine and (w): weights
Saadeh W, Altaf MAB, Butt SA. A wearable neuro-degenerative diseases detection system based on gait dynamics. In: 2017 IFIP/IEEE international conference on very large scale integration (VLSI-SoC). 2017. p. 1–6 . https://doi.org/10.1109/VLSI-SoC.2017.8203488.
Hardiman O, Al-Chalabi A, Chio A, Corr EM, Logroscino G, Robberecht W, Shaw PJ, Simmons Z, van den Berg LH. Amyotrophic lateral sclerosis. Nat Rev Dis Prim. 2017;3(1):17071. https://doi.org/10.1038/nrdp.2017.71.
van Es MA, Hardiman O, Chio A, Al-Chalabi A, Pasterkamp RJ, Veldink JH, van den Berg LH. Amyotrophic lateral sclerosis. Lancet. 2017;390(10107):2084–98. https://doi.org/10.1016/S0140-6736(17)31287-4.
Chiò A, Pagani M, Agosta F, Calvo A, Cistaro A, Filippi M. Neuroimaging in amyotrophic lateral sclerosis: insights into structural and functional changes. Lancet Neurol. 2014;13(12):1228–40. https://doi.org/10.1016/S1474-4422(14)70167-X.
Lima SR, Gomes KB. Esclerose lateral amiotrófica e o tratamento com células-tronco. Rev Bras Clin Med. 2010;8(6):531–7.
Kiernan MC, Vucic S, Cheah BC, Turner MR, Eisen A, Hardiman O, Burrell JR, Zoing MC. Amyotrophic lateral sclerosis. Lancet. 2011;377(9769):942–55. https://doi.org/10.1016/S0140-6736(10)61156-7.
Turner MR, Hardiman O, Benatar M, Brooks BR, Chio A, de Carvalho M, Ince PG, Lin C, Miller RG, Mitsumoto H, Nicholson G, Ravits J, Shaw PJ, Swash M, Talbot K, Traynor BJ, Van den Berg LH, Veldink JH, Vucic S, Kiernan MC. Controversies and priorities in amyotrophic lateral sclerosis. Lancet Neurol. 2013;12(3):310–22. https://doi.org/10.1016/S1474-4422(13)70036-X.
Andersen PM, Abrahams S, Borasio GD, de Carvalho M, Chio A, Van Damme P, Hardiman O, Kollewe K, Morrison KE, Petri S, Pradat P-F, Silani V, Tomik B, Wasner M, Weber M, The EFNS Task Force on Diagnosis and Management of Amyotrophic Lateral Sclerosis. EFNS guidelines on the clinical management of amyotrophic lateral sclerosis (MALS)—revised report of an EFNS task force. Eur J Neurol. 2012;19(3):360–75. https://doi.org/10.1111/j.1468-1331.2011.03501.x.
Brown RH, Al-Chalabi A. Amyotrophic lateral sclerosis. N Engl J Med. 2017;377(2):162–72. https://doi.org/10.1056/NEJMra1603471.
Scarafino A, D'Errico E, Introna A, Fraddosio A, Distaso E, Tempesta I, Morea A, Mastronardi A, Leante R, Ruggieri M, Mastrapasqua M, Simone IL. Diagnostic and prognostic power of CSF Tau in amyotrophic lateral sclerosis. J Neurol. 2018;265(10):2353–62. https://doi.org/10.1007/s00415-018-9008-3.
Jeon G, Ahmad A, Cuomo S, Wu W. Special issue on bio-medical signal processing for smarter mobile healthcare using big data analytics. New York: Springer; 2019. https://doi.org/10.1007/s12652-019-01425-9.
Horton DK, Mehta P, Antao VC. Quantifying a nonnotifiable disease in the united states: the national amyotrophic lateral sclerosis registry model. JAMA. 2014;312(11):1097–8.
Goetz CG. Amyotrophic lateral sclerosis: early contributions of Jean-Martin Charcot. Muscle Nerve. 2000;23(3):336–43.
Arthur KC, Calvo A, Price TR, Geiger JT, Chio A, Traynor BJ. Projected increase in amyotrophic lateral sclerosis from 2015 to 2040. Nat Commun. 2016;7(1):1–6.
Rosa Silva JP, Santiago Júnior JB, dos Santos EL, de Carvalho FO, de FrançCosta IMP, de Mendonça DMF. Quality of life and functional independence in amyotrophic lateral sclerosis: a systematic review. Neurosci Biobehav Rev. 2020;111:1–11. https://doi.org/10.1016/j.neubiorev.2019.12.032.
Bustamante P, Grandez K, Solas G, Arrizabalaga S. A low-cost platform for testing activities in Parkinson and ALS patients. In: The 12th IEEE international conference on e-Health networking, applications and services. 2010. p. 302–7. https://doi.org/10.1109/HEALTH.2010.5556550.
Bjornevik K, Zhang Z, O'Reilly ÉJ, Berry JD, Clish CB, Deik A, Jeanfavre S, Kato I, Kelly RS, Kolonel LN, Liang L, Marchand LL, McCullough ML, Paganoni S, Pierce KA, Schwarzschild MA, Shadyab AH, Wactawski-Wende J, Wang DD, Wang Y, Manson JE, Ascherio A. Prediagnostic plasma metabolomics and the risk of amyotrophic lateral sclerosis. Neurology. 2019;92(18):2089–100. https://doi.org/10.1212/WNL.0000000000007401.
Foerster BR, Dwamena BA, Petrou M, Carlos RC, Callaghan BC, Churchill CL, Mohamed MA, Bartels C, Benatar M, Bonzano L, Ciccarelli O, Cosottini M, Ellis CM, Ehrenreich H, Filippini N, Ito M, Kalra S, Melhem ER, Pyra T, Roccatagliata L, Senda J, Sobue G, Turner MR, Feldman EL, Pomper MG. Diagnostic accuracy of diffusion tensor imaging in amyotrophic lateral sclerosis: a systematic review and individual patient data meta-analysis. Acad Radiol. 2013;20(9):1099–106. https://doi.org/10.1016/j.acra.2013.03.017.
Al-Chalabi A, Hardiman O, Kiernan MC, Chiò A, Rix-Brooks B, van den Berg LH. Amyotrophic lateral sclerosis: moving towards a new classification system. Lancet Neurol. 2016;15(11):1182–94. https://doi.org/10.1016/S1474-4422(16)30199-5.
Fraschini M, Lai M, Demuru M, Puligheddu M, Floris G, Borghero G, Marrosu F. Functional brain connectivity analysis in amyotrophic lateral sclerosis: an EEG source-space study. Biomed Phys Eng Express. 2018;4(3):037004. https://doi.org/10.1088/2057-1976/aa9c64.
Barbalho IMP, Silva PdA, Fernandes FRdS, Neto FMM, Leite CRM. An investigation on the use of ontologies for pattern classification—study applied to the monitoring of food intake. In: Proceedings of the Euro American conference on telematics and information systems. EATIS '18. New York: Association for Computing Machinery; 2018. https://doi.org/10.1145/3293614.3293627.
Aharonson V, Coopoo VY, Govender KL, Postema M. Automatic pupil detection and gaze estimation using the vestibulo-ocular reflex in a low-cost eye-tracking setup. SAIEE Afr Res J. 2020;111(3):120–4.
Lingegowda DR, Amrutesh K, Ramanujam S. Electrooculography based assistive technology for ALS patients. In: 2017 IEEE international conference on consumer electronics-Asia (ICCE-Asia). 2017. p. 36–40 . https://doi.org/10.1109/ICCE-ASIA.2017.8307837.
Królak A, Strumiłło P. Eye-blink detection system for human–computer interaction. Univ Access Inf Soc. 2012;11(4):409–19. https://doi.org/10.1007/s10209-011-0256-6.
Höhne J, Holz E, Staiger-Sälzer P, Müller K-R, Kübler A, Tangermann M. Motor imagery for severely motor-impaired patients: evidence for brain–computer interfacing as superior control solution. PLoS ONE. 2014;9(8):104854.
Eid MA, Giakoumidis N, El Saddik A. A novel eye-gaze-controlled wheelchair system for navigating unknown environments: case study with a person with ALS. IEEE Access. 2016;4:558–73.
Schwalbe N, Wahl B. Artificial intelligence and the future of global health. Lancet. 2020;395(10236):1579–86. https://doi.org/10.1016/S0140-6736(20)30226-9.
Subasi A. Classification of EMG signals using PSO optimized SVM for diagnosis of neuromuscular disorders. Comput Biol Med. 2013;43(5):576–86. https://doi.org/10.1016/j.compbiomed.2013.01.020.
Noorbakhsh-Sabet N, Zand R, Zhang Y, Abedi V. Artificial intelligence transforms the future of health care. Am J Med. 2019;132(7):795–801. https://doi.org/10.1016/j.amjmed.2019.01.017.
Grollemund V, Pradat PF, Querin G, Delbot F, Le Chat G, Pradat-Peyre JF, Bede P. Machine learning in amyotrophic lateral sclerosis: achievements, pitfalls, and future directions. Front Neurosci. 2019;13:135. https://doi.org/10.3389/fnins.2019.00135.
AlHinai N. Chapter—introduction to biomedical signal processing and artificial intelligence. In: Zgallai W, editor. Biomedical signal processing and artificial intelligence in healthcare. Developments in Biomedical Engineering and Bioelectronics. Amsrerdam: Academic Press; 2020. p. 1–28. https://doi.org/10.1016/B978-0-12-818946-7.00001-9.
Cohen A. Chapter 1–biomedical signals: origin and dynamic characteristics; frequency-domain analysis. In: Bronzino JD, editor. Medical devices and systems. The Biomedical Engineering HandbookThe Biomedical Engineering HandbookThe Biomedical Engineering Handbook. Boca Raton: CRC Press; 2006. p. 1–22.
Alim OA, Moselhy M, Mroueh F. EMG signal processing and diagnostic of muscle diseases. In: 2012 2nd international conference on advances in computational tools for engineering applications (ACTEA). 2012. p. 1–6.
Luna P. Controlling machines with just the power of thought. Lancet Neurol. 2011;10(9):780–1. https://doi.org/10.1016/S1474-4422(11)70180-6.
Chen S, Lach J, Lo B, Yang G. Toward pervasive gait analysis with wearable sensors: a systematic review. IEEE J Biomed Health Inform. 2016;20(6):1521–37. https://doi.org/10.1109/JBHI.2016.2608720.
Menke RA, Agosta F, Grosskreutz J, Filippi M, Turner MR. Neuroimaging endpoints in amyotrophic lateral sclerosis. Neurotherapeutics. 2017;14(1):11–23.
Kitchenham B. Procedures for performing systematic reviews. Technical report, Keele University, Department of Computer Science, Software Engineering Group and Empirical Software Engineering National ICT Australia Ltd., Keele, Staffs, ST5 5BG, UK; 2004.
Ouzzani M, Hammady H, Fedorowicz Z, Elmagarmid A. Rayyan—a web and mobile app for systematic reviews. Syst Rev. 2016;5(1):210. https://doi.org/10.1186/s13643-016-0384-4.
Chatterjee S, Samanta K, Choudhury NR, Bose R. Detection of myopathy and ALS electromyograms employing modified window Stockwell transform. IEEE Sens Lett. 2019;3(7):1–4. https://doi.org/10.1109/LSENS.2019.2921072.
Zhang X, Barkhaus PE, Rymer WZ, Zhou P. Machine learning for supporting diagnosis of amyotrophic lateral sclerosis using surface electromyogram. IEEE Trans Neural Syst Rehabilit Eng. 2014;22(1):96–103. https://doi.org/10.1109/TNSRE.2013.2274658.
Hazarika A, Dutta L, Barthakur M, Bhuyan M. A multiview discriminant feature fusion-based nonlinear process assessment and diagnosis: application to medical diagnosis. IEEE Trans Instrum Meas. 2019;68(7):2498–506. https://doi.org/10.1109/TIM.2018.2866744.
Gokgoz E, Subasi A. Effect of multiscale PCA de-noising on EMG signal classification for diagnosis of neuromuscular disorders. J Med Syst. 2014;38(4):31.
Ambikapathy B, Kirshnamurthy K, Venkatesan R. Assessment of electromyograms using genetic algorithm and artificial neural networks. Evolut Intell. 2018;14:1–11.
Doulah ABMSU, Fattah SA, Zhu WP, Ahmad MO. Wavelet domain feature extraction scheme based on dominant motor unit action potential of EMG signal for neuromuscular disease classification. IEEE Trans Biomed Circuits Syst. 2014;8(2):155–64. https://doi.org/10.1109/TBCAS.2014.2309252.
Vallejo M, Gallego CJ, Duque-Muñoz L, Delgado-Trejos E. Neuromuscular disease detection by neural networks and fuzzy entropy on time–frequency analysis of electromyography signals. Expert Syst. 2018;35(4):12274.
Gokgoz E, Subasi A. Comparison of decision tree algorithms for EMG signal classification using DWT. Biomed Signal Process Control. 2015;18:138–44.
Xia Y, Gao Q, Ye Q. Classification of gait rhythm signals between patients with neuro-degenerative diseases and normal subjects: experiments with statistical features and different classification models. Biomed Signal Process Control. 2015;18:254–62. https://doi.org/10.1016/j.bspc.2015.02.002.
Ren P, Tang S, Fang F, Luo L, Xu L, Bringas-Vega ML, Yao D, Kendrick KM, Valdes-Sosa PA. Gait rhythm fluctuation analysis for neurodegenerative diseases by empirical mode decomposition. IEEE Trans Biomed Eng. 2017;64(1):52–60. https://doi.org/10.1109/TBME.2016.2536438.
Khorasani A, Daliri MR, Pooyan M. Recognition of amyotrophic lateral sclerosis disease using factorial hidden Markov model. Biomed Eng. 2016;61(1):119–26.
Welsh R, Jelsone-Swain L, Foerster B. The utility of independent component analysis and machine learning in the identification of the amyotrophic lateral sclerosis diseased brain. Front Hum Neurosci. 2013;7:251. https://doi.org/10.3389/fnhum.2013.00251.
Ferraro PM, Agosta F, Riva N, Copetti M, Spinelli EG, Falzone Y, Sorarù G, Comi G, Chiò A, Filippi M. Multimodal structural MRI in the diagnosis of motor neuron diseases. NeuroImage Clin. 2017;16:240–7.
Sorbello R, Tramonte S, Giardina ME, La Bella V, Spataro R, Allison B, Guger C, Chella A. A human–humanoid interaction through the use of BCI for locked-in ALS patients using neuro-biological feedback fusion. IEEE Trans Neural Syst Rehabilit Eng. 2018;26(2):487–97.
Liu Y-H, Huang S, Huang Y-D. Motor imagery EEG classification for patients with amyotrophic lateral sclerosis using fractal dimension and fisher's criterion-based channel selection. Sensors. 2017;17(7):1557.
Mainsah BO, Collins LM, Colwell KA, Sellers EW, Ryan DB, Caves K, Throckmorton CS. Increasing BCI communication rates with dynamic stopping towards more practical use: an ALS study. J Neural Eng. 2015;12(1):016013. https://doi.org/10.1088/1741-2560/12/1/016013.
Miao Y, Yin E, Allison BZ, Zhang Y, Chen Y, Dong Y, Wang X, Hu D, Chchocki A, Jin J. An ERP-based BCI with peripheral stimuli: validation with ALS patients. Cogn Neurodyn. 2020;14(1):21–33.
van der Burgh HK, Schmidt R, Westeneng H-J, de Reus MA, van den Berg LH, van den Heuvel MP. Deep learning predictions of survival based on MRI in amyotrophic lateral sclerosis. NeuroImage Clin. 2017;13:361–9.
Phinyomark A, Phukpattaranont P, Limsakul C. Feature reduction and selection for EMG signal classification. Expert Syst Appl. 2012;39(8):7420–31. https://doi.org/10.1016/j.eswa.2012.01.102.
Graimann B, Allison B, Pfurtscheller G. Brain–computer interfaces: a gentle introduction. In: Brain–computer interfaces. New York: Springer; 2009. p. 1–27.
Herff C, Heger D, de Pesters A, Telaar D, Brunner P, Schalk G, Schultz T. Brain-to-text: decoding spoken phrases from phone representations in the brain. Front Neurosci. 2015;9:217. https://doi.org/10.3389/fnins.2015.00217.
Anumanchipalli GK, Chartier J, Chang EF. Speech synthesis from neural decoding of spoken sentences. Nature. 2019;568(7753):493–8. https://doi.org/10.1038/s41586-019-1119-1.
Cooney C, Folli R, Coyle D. Optimizing layers improves CNN generalization and transfer learning for imagined speech decoding from EEG. In: 2019 IEEE international conference on systems, man and cybernetics (SMC). 2019. p. 1311–6. https://doi.org/10.1109/SMC.2019.8914246.
Dash D, Ferrari P, Wang J. Decoding imagined and spoken phrases from non-invasive neural (meg) signals. Front Neurosci. 2020;14:290. https://doi.org/10.3389/fnins.2020.00290.
Dash D, Ferrari P, Hernandez A, Heitzman D, Austin SG, Wang J. Neural speech decoding for amyotrophic lateral sclerosis. Proc Interspeech. 2020;2020:2782–6. https://doi.org/10.21437/Interspeech.2020-3071.
Tamura H, Yan M, Sakurai K, Tanno K. EOG-sEMG human interface for communication. Intell Neurosci. 2016;2016:15. https://doi.org/10.1155/2016/7354082.
Pinheiro CG, Naves EL, Pino P, Losson E, Andrade AO, Bourhis G. Alternative communication systems for people with severe motor disabilities: a survey. BioMed Eng OnLine. 2011;10(1):31. https://doi.org/10.1186/1475-925X-10-31.
Hori J, Sakano K, Saitoh Y. Development of communication supporting device controlled by eye movements and voluntary eye blink. In: The 26th annual international conference of the IEEE engineering in medicine and biology society, vol. 2. 2004. p. 4302–5.
Fathi A, Abdali-Mohammadi F. Camera-based eye blinks pattern detection for intelligent mouse. Signal Image Video Process. 2015;9(8):1907–16. https://doi.org/10.1007/s11760-014-0680-1.
Harezlak K, Kasprowski P. Application of eye tracking in medicine: a survey, research issues and challenges. Comput Med Imaging Graph. 2018;65:176–90. https://doi.org/10.1016/j.compmedimag.2017.04.006.
Villanueva A, Daunys G, Hansen DW, Böhme M, Cabeza R, Meyer A, Barth E. A geometric approach to remote eye tracking. Univ Access Inf Soc. 2009;8(4):241. https://doi.org/10.1007/s10209-009-0149-0.
Zhao Q, Yuan X, Tu D, Lu J. Eye moving behaviors identification for gaze tracking interaction. J Multimodal User Interfaces. 2015;9(2):89–104. https://doi.org/10.1007/s12193-014-0171-2.
Liu Y, Lee B-S, Rajan D, Sluzek A, McKeown MJ. CamType: assistive text entry using gaze with an off-the-shelf webcam. Mach Vis Appl. 2019;30(3):407–21. https://doi.org/10.1007/s00138-018-00997-4.
Wang J, Kothalkar PV, Kim M, Bandini A, Cao B, Yunusova Y, Campbell TF, Heitzman D, Green JR. Automatic prediction of intelligible speaking rate for individuals with ALS from speech acoustic and articulatory samples. Int J Speech Lang Pathol. 2018;20(6):669–79. https://doi.org/10.1080/17549507.2018.1508499.
Wisler A, Teplansky K, Green J, Yunusova Y, Campbell T, Heitzman D, Wang J. Speech-based estimation of bulbar regression in amyotrophic lateral sclerosis. In: Proceedings of the eighth workshop on speech and language processing for assistive technologies. Association for Computational Linguistics, Minneapolis, Minnesota; 2019. p. 24–31. https://doi.org/10.18653/v1/W19-1704. https://www.aclweb.org/anthology/W19-1704.
Cedarbaum JM, Stambler N, Malta E, Fuller C, Hilt D, Thurmond B, Nakanishi A. The ALSFRS-R: a revised ALS functional rating scale that incorporates assessments of respiratory function. J Neurol Sci. 1999;169(1):13–21. https://doi.org/10.1016/S0022-510X(99)00210-5.
Schuster C, Hardiman O, Bede P. Development of an automated MRI-based diagnostic protocol for amyotrophic lateral sclerosis using disease-specific pathognomonic features: a quantitative disease-state classification study. PLoS ONE. 2016;11(12):e0167331.
Wang J, Kothalkar PV, Cao B, Heitzman D. Towards automatic detection of amyotrophic lateral sclerosis from speech acoustic and articulatory samples. Interspeech. 2016;2016:1195–9. https://doi.org/10.21437/Interspeech.2016-1542.
Suhas B, Mallela J, Illa A, Yamini B, Atchayaram N, Yadav R, Gope D, Ghosh PK. Speech task based automatic classification of ALS and Parkinson's disease and their severity using log Mel spectrograms. In: 2020 international conference on signal processing and communications (SPCOM). 2020. p. 1–5. https://doi.org/10.1109/SPCOM50965.2020.9179503.
An K, Kim M, Teplansky K, Green J, Campbell T, Yunusova Y, Heitzman D, Wang J. Automatic early detection of amyotrophic lateral sclerosis from intelligible speech using convolutional neural networks. Proc Interspeech. 2018;2018:1913–7. https://doi.org/10.21437/Interspeech.2018-2496.
Vieira H, Costa N, Sousa T, Reis S, Coelho L. Voice-based classification of amyotrophic lateral sclerosis: where are we and where are we going? a systematic review. Neurodegener Dis. 2019;19(5–6):163–70. https://doi.org/10.1159/000506259.
Wisler A, Teplansky K, Heitzman D, Wang J. The effects of symptom onset location on automatic amyotrophic lateral sclerosis detection using the correlation structure of articulatory movements. J Speech Lang Hear Res. 2021. https://doi.org/10.1044/2020_JSLHR-20-00288.
Stegmann GM, Hahn S, Liss J, Shefner J, Rutkove S, Shelton K, Duncan CJ, Berisha V. Early detection and tracking of bulbar changes in ALS via frequent and remote speech analysis. NPJ Digit Med. 2020;3:132. https://doi.org/10.1038/s41746-020-00335-x.
We kindly thank the Laboratory of Technological Innovation in Health (LAIS) of the Federal University of Rio Grande do Norte (UFRN) and Ministry of Health Brazil for supporting the research.
Ministry of Health Brazil.
Felipe Fernandes and Ingridy Barbalho contributed equally to this work
Laboratory of Technological Innovation in Health (LAIS), Federal University of Rio Grande do Norte (UFRN), Natal, RN, Brazil
Felipe Fernandes, Ingridy Barbalho, Daniele Barros, Ricardo Valentim & Mário Dourado Júnior
Department of Informatics Engineering, Univ Coimbra, CISUC-Center for Informatics and Systems of the University of Coimbra, Coimbra, Portugal
César Teixeira, Jorge Henriques & Paulo Gil
Felipe Fernandes
Ingridy Barbalho
Daniele Barros
Ricardo Valentim
César Teixeira
Jorge Henriques
Paulo Gil
Mário Dourado Júnior
FF, IB and DB: collection, organizing and review of the literature. FF and IB: preparing and edit the manuscript. FF, IB, DB, RV, CT, JH, PG and MDJ: manuscript review and modification. All authors read and approved the final manuscript.
Correspondence to Felipe Fernandes.
Fernandes, F., Barbalho, I., Barros, D. et al. Biomedical signals and machine learning in amyotrophic lateral sclerosis: a systematic review. BioMed Eng OnLine 20, 61 (2021). https://doi.org/10.1186/s12938-021-00896-2
Amyotrophic lateral sclerosis—ALS
Biomedical signals
Chronic neurological conditions
Motor neuron disease
Submission enquiries: [email protected] | CommonCrawl |
I Fourier Transform of a Probability Distribution
Thread starter NatanijelVasic
NatanijelVasic
Yesterday I was thinking about the central limit theorem, and in doing so, I reached a conclusion that I found surprising. It could just be that my arguments are wrong, but this was my process:
1. First, define a continuous probability distribution X.
2. Define a new random variable y = x1 + x2 + x3 + .... (Y is the sum of many independent samples of X).
3. To visualise the distribution of Y as you sum each term, I imaging starting with the pdf of X, and convolving it with the same pdf. Then I take the result, and convolve it again with the pdf of X, and so on. According to the central limit theorem, each time you convolve the result again with the pdf of X, the new result will look more like the normal distribution, and this is the case (I have visualised this myself with graphical convolution animations).
4. It was at this point that I realised that the Fourier transform of a Gaussian is also a Gaussian.
5. I also recalled that convolution in the original domain (i.e. the operations we performed in 3) is the equivalent of multiplication in the Fourier domain.
6. As a result of points 4 and 5, that implies that the Fourier transform of pdf of X, raised to a large power, will approximate a normal distribution.
What I find surprising about this conclusion is that it is possible to create almost any pdf of your choosing, even a randomly drawn squiggle that is positive and integrates to 1, and its FT^n (where n is large) will always be approximately Gaussian. Is this correct? I am trying to find an intuitive explanation for this.
Reactions: tnich
tnich
The Fourier transform of a Gaussian distribution is the characteristic function ##\exp(i \mu t - \frac {\sigma^2 t^2}2)##, which resembles a Gaussian distribution, but differs from it in a couple of significant ways. First, it has an imaginary component, so it lies in the complex plane. Second, it is not properly normalized, so it does not integrate to 1. You could avoid the first problem by using the Laplace transform (resulting in the moment generating function ##\exp(\mu t + \frac {\sigma^2 t^2}2)##), but in this case the coefficient of ##t^2## is positive, not negative. Perhaps if you can resolve these difficulties, you can check whether your intuition is correct.
Reactions: hutchphd
@tnich Thanks for the reply! :)
I have thought about these two point, but I would still say that my conclusion is surprising. Let me address your points:
First, it has an imaginary component, so it lies in the complex plane
Yes, this would be the case with a non-zero mean Gaussian, or any function that is shifted (as this corresponds to a phase shift term in the Fourier domain, as your equation suggests). I should have stated, for simplicity, that the X distribution has to be zero mean, and this is indeed what I had in my head, but I failed to communicate that. In the zero-mean case, the functions in both domains should be real-valued Gaussians centred at 0.
Second, it is not properly normalized, so it does not integrate to 1
For the zero-mean case, it doesn't matter so much if the function doesn't integrate to 1, as long as it approximates a Gaussian shape.
So it still seems to me like it is possible to draw any zero-mean pdf, and the (FT(pdf))^n will still approximate a real valued, zero mean Gaussian
OK. Let's try a uniform distribution with pdf
$$f(x) =
\begin{cases} 0 & \text{if } x < 0
\\ 1 & \text{if } 0 \leq x \leq 1
\\ 0 & \text{if } x > 1 \end{cases}$$
Then ##f^n(x) = f(x)##
Another case is an exponential distribution with pdf
$$g(x) =
\\ {\exp(-x)} & \text{if } x\geq 0
\end{cases}$$
Then $$g^n(x) =
\\ {\exp(-nx)} & \text{if } x\geq 0
Neither of these functions approach a Gaussian form when n is large.
Perhaps I didn't state my hypothesis as well as I should have. It's the Fourier transform of zero-mean pdf, raised to large n, that will approximate a Gaussian. That is:
## \lim_{n \rightarrow \infty}\left( \mathscr{F}\left[f(x)\right]\right)^{n} \approx c_{0}e^{-c_{1}\omega^{2}}##
We are convolving the PDFs in the original domain to find the new distribution of the summed variables. This would be the equivalent operation of multiplying the Fourier transforms of the PDF in the frequency domain.
(a modified version of my hypothesis works will non-zero mean PDFs as well, but in this case we look at the real power spectrum instead of complex FT - we'll ignore this for now for simplicity, and only consider zero-mean pdf's).
In the case of a zero mean uniform distribution, the Fourier transform is a real valued sinc function. When the sinc function is raised to a large power of n, the result is almost exactly Gaussian (I didn't prove this analytically, but I plotted both).
NatanijelVasic said:
Yes, I realized after I sent my reply that you meant the nth power of Fourier transform of the pdf. The ##sinc(s)## function, though, has zeroes at regular intervals. Wouldn't ##sync^n(s)## still have zeros at the same points?
tnich said:
Yes, this is certainly the case. However, the limiting behaviour takes care of this; as n gets large, the resulting Gaussian approximation gets "squashed" towards to centre, and so the first zero crossing actually occurs at some extreme standard deviation, where the exact Gaussian is almost 0 anyway (and the error at all the crossings approaches zero as n goes to infinity).
NOTE: In the plots, the approximation overlays the actual Gaussian, and only appears as one black plot, when if fact there are two black plots.
Screenshot 2019-04-02 at 20.31.19.png
Now that I understand what you are trying to say, I agree with your conclusion. I think it is implied by the Central Limit Theorem.
So you can use the assumptions of the CLT to specify what kinds of functions raised to the nth power converge to a Gaussian form. The CLT assumes that the area under the pdf curve ##f(t)## is 1, and that the mean and variance are both finite. So the Fourier transform ##F(s)## of such a function would have ##F(0)=1##, F'(0) and F''(0) both finite, and F''(0) < 0. That means that the value of ##F(s)## at ##s = 0## is a local maximum.
The inverse Fourier transform is itself a Fourier transform, so the area under ##F(s)## must be finite because f(0) is finite. This starts to look like a curve that could behave the way you want it to.
Reactions: NatanijelVasic
Forgot to say that since we are assuming the mean is zero, ##F'(0) = 0##.
"Fourier Transform of a Probability Distribution" You must log in or register to reply here.
Related Threads for: Fourier Transform of a Probability Distribution
Fourier transform of noise
mnb96
Fourier transform of a quantized signal
Fourier analysis and prob. distributions?
Zaphodx57x
I Covariance of Fourier conjugates for Gaussian distributions
redtree
Fourier transform of the exponential characteristic function
AnnapolisStar | CommonCrawl |
Psychometrika
Bayesian Comparison of Latent Variable Models: Conditional Versus Marginal Likelihoods
Edgar C. Merkle
Daniel Furr
Sophia Rabe-Hesketh
Typical Bayesian methods for models with latent variables (or random effects) involve directly sampling the latent variables along with the model parameters. In high-level software code for model definitions (using, e.g., BUGS, JAGS, Stan), the likelihood is therefore specified as conditional on the latent variables. This can lead researchers to perform model comparisons via conditional likelihoods, where the latent variables are considered model parameters. In other settings, however, typical model comparisons involve marginal likelihoods where the latent variables are integrated out. This distinction is often overlooked despite the fact that it can have a large impact on the comparisons of interest. In this paper, we clarify and illustrate these issues, focusing on the comparison of conditional and marginal Deviance Information Criteria (DICs) and Watanabe–Akaike Information Criteria (WAICs) in psychometric modeling. The conditional/marginal distinction corresponds to whether the model should be predictive for the clusters that are in the data or for new clusters (where "clusters" typically correspond to higher-level units like people or schools). Correspondingly, we show that marginal WAIC corresponds to leave-one-cluster out cross-validation, whereas conditional WAIC corresponds to leave-one-unit out. These results lead to recommendations on the general application of the criteria to models with latent variables.
Bayesian information criteria conditional likelihood cross-validation DIC IRT leave-one-cluster out marginal likelihood MCMC SEM WAIC
The research reported here was supported by NSF Grant 1460719 and by the Institute of Education Sciences, U.S. Department of Education, through Grant R305D140059. The authors thank Frédéric Gosselin and three anonymous reviewers for comments that improved the paper. Code to replicate the results from this paper can be found at http://semtools.r-forge.r-project.org/.
The online version of this article ( https://doi.org/10.1007/s11336-019-09679-0) contains supplementary material, which is available to authorized users.
Open image in new window Open image in new window
11336_2019_9679_MOESM1_ESM.zip (7 kb)
Supplementary material 1 (zip 7 KB)
A. Posterior Expectations of Marginal and Conditional Likelihoods
Following Trevisani and Gelfand (2003), who studied DIC in the context of linear mixed models, we can use Jensen's inequality to show that the posterior expected value of the marginal log-likelihood is less than the posterior expected value of the conditional log-likelihood.
First, consider the function \(h(x) = x\log (x)\). It is convex, so Jensen's inequality states that
$$\begin{aligned} h(\mathrm {E}(x)) \le \mathrm {E}(h(x)). \end{aligned}$$
Setting \(x = f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta })\) and taking expected values with respect to \(\varvec{\zeta }\), we have that
$$\begin{aligned} h(\mathrm {E}(x))&= \displaystyle \log \left[ \displaystyle \int f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta }) g(\varvec{\zeta } | \varvec{\psi }) \text {d}\varvec{\zeta } \right] \int f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta }) g(\varvec{\zeta } | \varvec{\psi }) \text {d}\varvec{\zeta } \end{aligned}$$
$$\begin{aligned} \mathrm {E}(h(x))&= \displaystyle \int \log (f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta })) f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta }) g(\varvec{\zeta } | \varvec{\psi }) \text {d}\varvec{\zeta }, \end{aligned}$$
$$\begin{aligned}&\displaystyle \log \left[ \displaystyle \int f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta }) g(\varvec{\zeta } | \varvec{\psi }) \text {d}\varvec{\zeta } \right] \int f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta }) g(\varvec{\zeta } | \varvec{\psi }) \text {d}\varvec{\zeta }\nonumber \\&\le \displaystyle \int \log (f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta })) f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta }) g(\varvec{\zeta } | \varvec{\psi }) \text {d}\varvec{\zeta }. \end{aligned}$$
We now multiply both sides of this inequality by \(p(\varvec{\omega }, \varvec{\psi })/c\), where \(p(\varvec{\omega }, \varvec{\psi })\) is a prior distribution and
$$\begin{aligned} c = \displaystyle \int _{\varvec{\psi }} \displaystyle \int _{\varvec{\omega }} \displaystyle \int _{\varvec{\zeta }} f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta }) g(\varvec{\zeta } | \varvec{\psi }) \text {d}\varvec{\zeta } \cdot p(\varvec{\omega }, \varvec{\psi }) \text {d}\varvec{\omega } \text {d}\varvec{\psi } \end{aligned}$$
is the posterior normalizing constant. Finally, we integrate both sides with respect to \(\varvec{\omega }\) and \(\varvec{\psi }\) to obtain
$$\begin{aligned}&\displaystyle \int _{\varvec{\psi }} \displaystyle \int _{\varvec{\omega }} \log \left( \displaystyle \int _{\varvec{\zeta }} f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta }) g(\varvec{\zeta } | \varvec{\psi }) \text {d}\varvec{\zeta } \right) \displaystyle \int _{\varvec{\zeta }} f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta }) g(\varvec{\zeta } | \varvec{\psi }) \text {d}\varvec{\zeta } \cdot \left[ p(\varvec{\omega }, \varvec{\psi })/c \right] \text {d}\varvec{\omega } \text {d}\varvec{\psi } \le \nonumber \\&\quad \displaystyle \int _{\varvec{\psi }} \displaystyle \int _{\varvec{\omega }} \displaystyle \int _{\varvec{\zeta }} \log \left( f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta }) \right) f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta }) g(\varvec{\zeta } | \varvec{\psi }) \text {d}\varvec{\zeta } \cdot \left[ p(\varvec{\omega }, \varvec{\psi })/c \right] \text {d}\varvec{\omega } \text {d}\varvec{\psi }. \end{aligned}$$
We can now recognize both sides of (18) as expected values of log-likelihoods with respect to the model's posterior distribution, leading to
$$\begin{aligned} \mathrm {E}_{\varvec{\omega }, \varvec{\psi } | \varvec{y}} \left[ \log f_\text {m}(\varvec{y} |\varvec{\omega }, \varvec{\psi } ) \right] \le \mathrm {E}_{\varvec{\omega }, \varvec{\zeta } | \varvec{y}} \left[ \log f_\text {c}(\varvec{y}|\varvec{\omega }, \varvec{\zeta }) \right] . \end{aligned}$$
Note that the above results do not rely on normality, so they also apply to, e.g., the two-parameter logistic model estimated via marginal likelihood.
B. Effective Number of Parameters for Marginal and Conditional DIC
To consider the effective number of parameters for normal likelihoods, we rely on results from Spiegelhalter et al. (2002). They showed that the effective number of parameters \(p_D\) can be viewed as the fraction of information about model parameters in the likelihood, relative to the total information contained in both the likelihood and prior. Under this view, a specific model parameter gets a value of "1" if all of its information is contained in the likelihood, and it gets a value below "1" if some information is contained in the prior. We sum these values across all parameters to obtain \(p_D\).
Spiegelhalter et al. (2002) relatedly showed that, for normal likelihoods, \(p_D\) can be approximated by
$$\begin{aligned} p_D \approx \text {tr}(\varvec{I}(\hat{\varvec{\theta }}) \varvec{V}), \end{aligned}$$
where \(\varvec{\theta }\) includes all model parameters (including \(\varvec{\zeta }\) in the conditional model), \(\varvec{I}(\hat{\varvec{\theta }})\) is the observed Fisher information matrix, and \(\varvec{V}\) is the posterior covariance matrix of \(\varvec{\theta }\). When the prior distribution of \(\varvec{\theta }\) is non-informative, then \(\varvec{I}(\hat{\varvec{\theta }}) \approx \varvec{V}^{-1}\). Consequently, matching the discussion in the previous paragraph, the effective number of parameters under non-informative priors will approximate the total number of model parameters.
This result implies that the conditional \(p_D\) will tend to be much larger than the marginal \(p_D\). In particular, in the conditional case, each individual has a unique \(\varvec{\zeta }_j\) vector that is included as part of the total parameter count. The resulting \(p_D\) will not necessarily be close to the total parameter count because the "prior distribution" of \(\varvec{\zeta }_j\) is a hyperdistribution, whereby individuals' \(\varvec{\zeta }_j\) estimates are shrunk toward the mean. Thus, for these parameters, the "prior" is informative. However, even when the fraction of information in the likelihood is low for these parameters, the fact that we are summing over hundreds or thousands of \(\varvec{\zeta }_j\) vectors implies that the conditional \(p_D\) will be larger than the marginal \(p_D\).
C. Adaptive Gaussian Quadrature for Marginal Likelihoods
We modify the adaptive quadrature method proposed by Rabe-Hesketh et al. (2005) for generalized linear mixed models to a form designed to exploit MCMC draws from the joint posterior of all latent variables and model parameters. Here, we describe one-dimensional integration, but the method is straightforward to generalize to multidimensional integration as in Rabe-Hesketh et al. (2005) . We assume that \(\zeta _j\) represents a disturbance with zero mean and variance \(\tau ^2\) so that there is only one hyperparameter \(\psi =\tau \).
In a non-Bayesian setting, standard (non-adaptive) Gauss–Hermite quadrature can be viewed as approximating the conditional prior density \(g(\zeta _j|\tau )\) by a discrete distribution with masses \(w_m\), \(m=1,\ldots , M\) at locations \(a_m\tau \) so that the integrals in (2) are approximated by sums of M terms, where M is the number of quadrature points,
$$\begin{aligned} f_\text {m}(\varvec{y}| \varvec{\omega }, {\tau })\ \approx \ \prod _{j=1}^J \sum _{m=1}^M w_m f_\text {c}(\varvec{y}_{j} | \varvec{\omega }, \zeta _j=a_m\tau ) . \end{aligned}$$
To obtain information criteria, this method can easily be applied to the conditional likelihood function for each draw \(\varvec{\omega }^s\) and \(\tau ^s\) (\(s=1,\ldots ,S\)) of the model parameters from MCMC output. This approximation can be thought of as a deterministic version of Monte Carlo integration. Adaptive quadrature is then a deterministic version of Monte Carlo integration via importance sampling.
If applied to each MCMC draw \(\varvec{\omega }^s\) and \(\tau ^s\), the importance density is a normal approximation to the conditional posterior density of \(\zeta _j\), given the current draws of the model parameters. Rabe-Hesketh et al. (2005) used a normal density with mean and variance equal to the mean \(\text {E}(\zeta _j|\varvec{y}_j, \varvec{\omega }^s, \tau ^s)\) and variance \(\mathrm {var}(\zeta _j|\varvec{y}_j, \varvec{\omega }^s, \tau ^s)\) of the conditional posterior density of \(\zeta _j\), whereas Pinheiro and Bates (1995) and some software use a normal density with mean equal to the mode of the conditional posterior and variance equal to minus the reciprocal of the second derivative of the conditional log posterior. Here, we modify the method by Rabe-Hesketh et al. (2005) for the Bayesian setting by using a normal approximation to the unconditional posterior density of \(\zeta _j\) as importance density. Specifically, we use a normal density with mean
$$\begin{aligned} {\tilde{\mu }}_j = \widetilde{E}(\zeta _j | \varvec{y}) = \frac{1}{S} \sum _{s=1}^S \zeta _j^s , \end{aligned}$$
and standard deviation
$$\begin{aligned} {\tilde{\phi }}_j = \sqrt{{\widetilde{\mathrm {var}}}(\zeta _j | \varvec{y}) } = \sqrt{\frac{1}{S-1} \sum _{s=1}^S (\zeta _j^s- {\tilde{\mu }}_j)^2}, \end{aligned}$$
where \(\zeta _j^s\) is the draw of \(\zeta _j\) from its unconditional posterior in the sth MCMC iteration. The tildes indicate that these quantities are subject to Monte Carlo error.
Note that this version of adaptive quadrature is computationally more efficient than the one based on the mean and standard deviation of the conditional posterior distributions because the latter would have to be evaluated for each MCMC draw and would require numerical integration, necessitating a procedure that iterates between updating the quadrature locations and weights and updating the conditional posterior means and standard deviations. A disadvantage of our approach is that the quadrature locations and weights (and hence importance density) are not as targeted, but the computational efficiency gained also makes it more feasible to increase M.
The adaptive quadrature approximation to the marginal likelihood for cluster j at posterior draw s becomes
$$\begin{aligned} f_\text {m}(\varvec{y}| \varvec{\omega }, {\tau })\ \approx \ \prod _{j=1}^J \sum _{m=1}^M w_{jm}^s f_\text {c}(\varvec{y}_{j} | \varvec{\omega }, \zeta _j=a_{jm}) , \end{aligned}$$
where the adapted locations are
$$\begin{aligned} a_{jm} = {\tilde{\mu }}_j + {\tilde{\phi }}_j \times a_m, \end{aligned}$$
and the corresponding weights or masses are
$$\begin{aligned} w_{jm}^s = \sqrt{2\pi } \times {\tilde{\phi }}_j \times \exp \left( \frac{a_{m}^2}{2} \right) \times g \left( a_{jm}; 0, \tau ^{2,s} \right) \times w_m, \end{aligned}$$
where \( g \left( a_{jm}; 0, \tau ^{2,s} \right) \) is the normal density function with mean zero and variance \(\tau ^{2,s}\), evaluated at \(a_{jm}\).
The number of integration points M required to obtain a sufficiently accurate approximation is determined by evaluating the approximation of the target quantity (DIC, WAIC) with increasing values of M (7, 11, 17, etc.) and choosing the value of M for which the target quantity changes by less than 0.01 from the previous value. Here, the candidate values for M are chosen to increase approximately by 50% while remaining odd so that one of the quadrature locations is at the posterior mean. Furr (2017) finds this approach to be accurate in simulations for linear mixed models where the adaptive quadrature approximation can be compared with the closed-form integrals.
D. Monte Carlo Error for the DIC and WAIC Effective Number of Parameters
For the DIC effective number of parameters, \(p_\text {D}\), we can make use of the well-known method for estimating the Monte Carlo error for the mean of a quantity across MCMC iterations. Let a quantity computed in MCMC iteration s (\(s=1,\ldots ,S\)) be denoted \(\gamma _s\), so the point estimate of the expectation of \(\gamma \) is
$$\begin{aligned} \overline{\gamma } \ = \ \frac{1}{S}\sum _{s=1}^S \gamma _s. \end{aligned}$$
Then the squared Monte Carlo error (or Monte Carlo error variance) is estimated as
$$\begin{aligned} \mathrm{MCerr}^2(\overline{\gamma })\ =\ \frac{1}{S_\mathrm{{}eff}}\left[ \frac{1}{S-1} \sum _{s=1}^S (\gamma _s-\overline{\gamma })^2\right] , \end{aligned}$$
where \(S_\mathrm{{}eff}\) is the effective sample size.
For the effective number of parameter approximation in (6) proposed by Plummer (2008), we can obtain the Monte Carlo error variance by substituting
$$\begin{aligned} \gamma _s\ =\ \frac{1}{2} \log \left\{ \frac{f(\varvec{y}_s^{\text {r}1} | \varvec{\theta }_s^1)}{f(\varvec{y}_s^{\text {r}1} | \varvec{\theta }_s^2)} \right\} + \frac{1}{2} \log \left\{ \frac{f(\varvec{y}_s^{\text {r}2} | \varvec{\theta }_s^2)}{f(\varvec{y}_s^{\text {r}2} | \varvec{\theta }_s^1)} \right\} \end{aligned}$$
in (27).
For the effective number of parameter approximation in (4) proposed by Spiegelhalter et al. (2002), we assume that the variation due to \(\text {E}_{\varvec{\theta }|\varvec{y}}[-2\log f(\varvec{y}|{\varvec{\theta }})]\) dominates and use
$$\begin{aligned} \gamma _s = -2\log f(\varvec{y}|{\varvec{\theta }_s}). \end{aligned}$$
For the WAIC effective number of parameters, \(p_\text {W}\), we use expressions for the Monte Carlo error of sample variances (see, e.g., White, 2010). Let the variance of \(\gamma _s\) over MCMC iterations be denoted \(v(\gamma )\),
$$\begin{aligned} v(\gamma )\ = \ \frac{1}{S-1} \sum _{s=1}^S (\gamma _s-\overline{\gamma })^2 = \frac{1}{S} \sum _{s=1}^S T_s,\quad \quad T_s = \frac{S}{S-1}(\gamma _s-\overline{\gamma })^2. \end{aligned}$$
Then the Monte Carlo error variance is estimated as
$$\begin{aligned} \mathrm{MCerr}^2(v(\gamma ))\ =\ \frac{1}{S_\mathrm{{}eff}\times S} \sum _{s=1}^S (T_s-v(\gamma ))^2, \end{aligned}$$
The conditional version of the effective number of parameters is given by the sum over all units of the posterior variances of the pointwise log posterior densities,
$$\begin{aligned} p_{\text {W}\text {c}} \ = \ \sum _{j=1}^J\sum _{i=1}^{n_j} \text {Var}_{\varvec{\omega },\varvec{\zeta }|\varvec{y}} \left[ \log f_\text {c}({y}_{ij}|\varvec{\omega },\varvec{\zeta }_j)\right] . \end{aligned}$$
The posterior variance \(\text {Var}_{\varvec{\omega },\varvec{\zeta }|\varvec{y}} \left[ \log f_\text {c}({y}_{ij}|\varvec{\omega },\varvec{\zeta }_j)\right] \) for a given unit is estimated by \(v(\gamma _{ij})\) with
$$\begin{aligned} \gamma _{ijs}\ =\ \log f_\text {c}({y}_{ij}|\varvec{\omega }_s,\varvec{\zeta }_{js}), \end{aligned}$$
where we have added subscripts ij to identify the unit, and has Monte Carlo error variance \(\mathrm{MCerr}^2(v(\gamma _{ij}))\) given in (28). The variance of the sum of the independent contributions \(v(\gamma _{ij})\) to \(\hat{p}_{\text {W}\text {c}}\) is the sum of the variances of these contributions,
$$\begin{aligned} \mathrm{MCerr}^2(\hat{p}_{\text {W}\text {c}})\ = \ \sum _{j=1}^J\sum _{i=1}^{n_j} \mathrm{MCerr}^2(v(\gamma _{ij})). \end{aligned}$$
For the marginal version of the effective number of parameters, \(p_{\text {W}\text {m}}\), we define
$$\begin{aligned} \gamma _{js}\ =\ \log f_\text {m}(\varvec{y}_{j}|\varvec{\omega }_s,\varvec{\psi }_s) \end{aligned}$$
$$\begin{aligned} \mathrm{MCerr}^2(\hat{p}_{\text {W}\text {m}})\ = \ \sum _{j=1}^J\mathrm{MCerr}^2(v(\gamma _{j})). \end{aligned}$$
E. Additional Results
This section contains additional results from the CFA example that were not included in the main text.
Figure 7 shows Spiegelhalter DIC values for models that use the uninformative priors described in the "Prior sensitivity" subsection. Of note here is that Models 2 and 2a sometimes failed to converge, resulting in fewer than ten points in the graphs. Because we used the automatic convergence procedure described in the main text, "failure to converge" here means that the chains did not achieve Gelman–Rubin statistics below 1.05 in the five minutes allotted. When we removed the 5-minute maximum time to convergence, we encountered situations where chains ran for days without converging. In our experience, these convergence issues are often observed for CFA models in JAGS with flat priors. Chains sometimes get stuck in extreme values of the parameter space and cannot recover.
Marginal and conditional DICs (Spiegelhalter et al. definitions) under uninformative prior distributions for nine models from Wicherts et al.
Figure 8 shows Plummer DIC values for models that use the informative priors described in the "Prior sensitivity" subsection. The figure also contains error bars (\(\pm 2\) SDs) from a single replication, similarly to Figure 3 in the main text. These error bars appear to continue to track Monte Carlo error in DIC. Comparing Figure 8 to Figure 4, we observe a different pattern in the conditional DICs across the Plummer and Spiegelhalter definitions. The Spiegelhalter conditional DICs (Figure 4) consistently prefer Model 2a, whereas the Plummer conditional DICs (Figure 8) generally decrease across models and become lowest for the final models, labeled 5b and 6 (though Models 4 and 5a are also similar). On the other hand, the marginal DICs are similar across the Spiegelhalter and Plummer definitions.
Marginal and conditional DICs (Plummer definitions) under informative prior distributions for nine models from Wicherts et al.
Celeux, G., Forbes, F., Robert, C. P., & Titterington, D. M. (2006). Deviance information criteria for missing data models. Bayesian Analysis, 1(4), 651–673.Google Scholar
daSilva, M. A., Bazán, J. L., & Huggins-Manley, A. C. (2019). Sensitivity analysis and choosing between alternative polytomous IRT models using Bayesian model comparison criteria. Communications in Statistics-Simulation and Computation, 48(2), 601–620.Google Scholar
De Boeck, P. (2008). Random item IRT models Random item IRT models. Psychometrika, 73, 533–559.Google Scholar
Denwood, M. J. (2016). runjags: An R package providing interface utilities, model templates, parallel computing methods and additional distributions for MCMC models in JAGS. Journal of Statistical Software, 71(9), 1–25. 10.18637/jss.v071.i09.Google Scholar
Efron, B. (1986). How biased is the apparent error rate of a prediction rule? Journal of the American Statistical Association, 81, 461–470.Google Scholar
Fox, J. P. (2010). Bayesian item response modeling: Theory and applications. New York, NY: Springer.Google Scholar
Furr, D. C. (2017). Bayesian and frequentist cross-validation methods for explanatory item response models. (Unpublished doctoral dissertation). University of California Berkeley, CA.Google Scholar
Gelfand, A. E., Sahu, S. K., & Carlin, B. P. (1995). Efficient parametrisations for normal linear mixed models. Biometrika, 82, 379–488.Google Scholar
Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., Rubin, D. B., et al. (2013). Bayesian data analysis (3rd ed.). New York: Chapman & Hall/CRC.Google Scholar
Gelman, A., Hwang, J., & Vehtari, A. (2014). Understanding predictive information criteria for Bayesian models. Statistics and Computing, 24, 997–1016.Google Scholar
Gelman, A., Jakulin, A., Pittau, M. G., & Su, Y. S. (2008). A weakly informative default prior distribution for logistic and other regression models. The Annals of Applied Statistics, 2, 1360–1383.Google Scholar
Gelman, A., Meng, X. L., & Stern, H. (1996). Posterior predictive assessment of model fitness via realized discrepancies. Statistica Sinica, 6, 733–807.Google Scholar
Gelman, A., & Rubin, D. B. (1992). Inference from iterative simulation using multiple sequences (with discussion). Statistical Science, 7, 457–511.Google Scholar
Gronau, Q. F., & Wagenmakers, E. J. (2018). Limitations of Bayesian leave-one-out cross-validation for model selection. Computational Brain & Behavior, 2(1), 1–11.Google Scholar
Hoeting, J. A., Madigan, D., Raftery, A. E., & Volinsky, C. T. (1999). Bayesian model averaging: A tutorial. Statistical Science, 14, 382–417.Google Scholar
Kang, T., Cohen, A. S., & Sung, H. J. (2009). Model selection indices for polytomous items. Applied Psychological Medicine, 35, 499–518.Google Scholar
Kaplan, D. (2014). Bayesian statistics for the social sciences. New York, NY: The Guildford Press.Google Scholar
Lancaster, T. (2000). The incidental parameter problem since 1948. Journal of Econometrics, 95, 391–413.Google Scholar
Levy, R., & Mislevy, R. J. (2016). Bayesian psychometric modeling. Boca Raton, FL: Chapman & Hall.Google Scholar
Li, F., Cohen, A. S., Kim, S. H., & Cho, S. J. (2009). Model selection methods for mixture dichotomous IRT models. Applied Psychological Measurement, 33, 353–373.Google Scholar
Li, L., Qui, S., & Feng, C. X. (2016). Approximating cross-validatory predictive evaluation in Bayesian latent variable models with integrated IS and WAIC. Statistics and Computing, 26, 881–897.Google Scholar
Lu, Z. H., Chow, S. M., & Loken, E. (2017). A comparison of Bayesian and frequentist model selection methods for factor analysis models. Psychological Methods, 22(2), 361–381.Google Scholar
Lunn, D., Jackson, C., Best, N., Thomas, A., & Spiegelhalter, D. (2012). The BUGS book: A practical introduction to Bayesian analysis. New York, NY: Chapman & Hall/CRC.Google Scholar
Lunn, D., Thomas, A., Best, N., & Spiegelhalter, D. (2000). WinBUGS—a Bayesian modelling framework: Concepts, structure, and extensibility. Statistics and Computing, 10, 325–337.Google Scholar
Luo, U., & Al-Harbi, K. (2017). Performances of LOO and WAIC as IRT model selection methods. Psychological Test and Assessment Modeling, 59, 183–205.Google Scholar
Marshall, E. C., & Spiegelhalter, D. J. (2007). Identifying outliers in Bayesian hierarchical models: A simulation-based approach. Bayesian Analysis, 2(2), 409–444.Google Scholar
McElreath, R. (2015). Statistical rethinking: A Bayesian course with examples in R and Stan. New York, NY: Chapman & Hall/CRC.Google Scholar
Merkle, E. C., & Rosseel, Y. (2018). blavaan: Bayesian structural equation models via parameter expansion. Journal of Statistical Software, 85(4), 1–30.Google Scholar
Millar, R. B. (2009). Comparison of hierarchical Bayesian models for overdispersed count data using DIC and Bayes' factors. Biometrics, 65, 962–969.Google Scholar
Millar, R. B. (2018). Conditional vs. marginal estimation of predictive loss of hierarchical models using WAIC and cross-validation. Statistics and Computing, 28, 375–385.Google Scholar
Mislevy, R. J. (1986). Bayes modal estimation in item response models. Psychometrika, 51, 177–195.Google Scholar
Muthén, B., & Asparouhov, T. (2012). Bayesian structural equation modeling: A more flexible representation of substantive theory. Psychological Methods, 17, 313–335.Google Scholar
Navarro, D. (2018). Between the devil and the deep blue sea: Tensions between scientific judgement and statistical model selection. Computational Brain & Behavior, 2(1), 28–34.Google Scholar
Naylor, J. C., & Smith, A. F. (1982). Applications of a method for the efficient computation of posterior distributions. Journal of the Royal Statistical Society C (Applied Statistics), 31, 214–225.Google Scholar
Neyman, J., & Scott, E. L. (1948). Consistent estimates based on partially consistent observations. Econometrica, 16, 1–32.Google Scholar
O'Hagan, A. (1976). On posterior joint and marginal modes. Biometrika, 63, 329–333.Google Scholar
Piironen, J., & Vehtari, A. (2017). Comparison of Bayesian predictive methods for model selection. Statistics and Computing, 27, 711–735.Google Scholar
Pinheiro, J. C., & Bates, D. M. (1995). Approximations to the log-likelihood function in the nonlinear mixed-effects model. Journal of Computational Graphics and Statistics, 4, 12–35.Google Scholar
Plummer, M. (2003). JAGS: A program for analysis of Bayesian graphical models using Gibbs sampling. In K. Hornik, Leisch, F. & Zeileis, A. (Eds.), Proceedings of the 3rd international workshop on distributed statistical computing.Google Scholar
Plummer, M. (2008). Penalized loss functions for Bayesian model comparison. Biostatistics, 9(3), 523–539.Google Scholar
Rabe-Hesketh, S., Skrondal, A., & Pickles, A. (2005). Maximum likelihood estimation of limited and discrete dependent variable models with nested random effects. Journal of Econometrics, 128(2), 301–323.Google Scholar
Raftery, A. E., & Lewis, S. M. (1995). The number of iterations, convergence diagnostics, and generic Metropolis algorithms. London: Chapman and Hall.Google Scholar
Raudenbush, S. W., & Bryk, A. S. (2002). Hierarchical linear models: Applications and data analysis methods (2nd ed.). Thousand Oaks, CA: Sage.Google Scholar
Rosseel, Y. (2012). lavaan: An R package for structural equation modeling. Journal of Statistical Software, 48(2), 1–36.Google Scholar
Song, X. Y., & Lee, S. Y. (2012). Basic and advanced Bayesian structural equation modeling: With applications in the medical and behavioral sciences. Chichester, UK: Wiley.Google Scholar
Spiegelhalter, D. J., Best, N. G., Carlin, B. P., & van der Linde, A. (2002). Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society Series, B64, 583–639.Google Scholar
Spielberger, C. (1988). State-trait anger expression inventory research edition [Computer software manual]. FL: Odessa.Google Scholar
Stan Development Team. (2014). Stan modeling language users guide and reference manual, version 2.5.0 [Computer software manual]. http://mc-stan.org/.
Trevisani, M., & Gelfand, A. E. (2003). Inequalities between expected marginal log-likelihoods, with implications for likelihood-based model complexity and comparison measures. The Canadian Journal of Statistics, 31, 239–250.Google Scholar
Vansteelandt, K. (2000). Formal models for contextualized personality psychology (Unpublished doctoral dissertation). Belgium: University of Leuven Leuven.Google Scholar
Vehtari, A., Gelman, A., & Gabry, J. (2016). loo: Efficient leave-one-out cross-validation and WAIC for Bayesian models. R package version 0.1.6. https://github.com/stan-dev/loo.
Vehtari, A., Gelman, A., & Gabry, J. (2017). Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Statistics and Computing, 27, 1413–1432.Google Scholar
Vehtari, A., Mononen, T., Tolvanen, V., Sivula, T., & Winther, O. (2016). Bayesian leave-one-out cross-validation approximations for Gaussian latent variable models. Journal of Machine Learning Research, 17, 1–38.Google Scholar
Vehtari, A., Simpson, D. P., Yao, Y., & Gelman, A. (2018). Limitations of "Limitations of Bayesian leave-one-out cross-validation for model selection". Computational Brain & Behavior, 2(1), 22–27.Google Scholar
Watanabe, S. (2010). Asymptotic equivalence of Bayes cross validation and widely applicable information criterion in singular learning theory. Journal of Machine Learning Research, 11, 3571–3594.Google Scholar
White, I. R. (2010). simsum: Analyses of simulation studies including Monte Carlo error. The Stata Journal, 10, 369–385.Google Scholar
Wicherts, J. M., Dolan, C. V., & Hessen, D. J. (2005). Stereotype threat and group differences in test performance: A question of measurement invariance. Journal of Personality and Social Psychology, 89(5), 696–716.Google Scholar
Yao, Y., Vehtari, A., Simpson, D., & Gelman, A. (2018). Using stacking to average Bayesian predictive distributions (with discussion). Bayesian Analysis, 13, 917–1007. https://doi.org/10.1214/17-BA1091.Google Scholar
Zhang, X., Tao, J., Wang, C., & Shi, N. Z. (2019). Bayesian model selection methods for multilevel IRT models: A comparison of five DIC-based indices. Journal of Educational Measurement, 56, 3–27.Google Scholar
Zhao, Z., & Severini, T. A. (2017). Integrated likelihood computation methods. Computational Statistics, 32, 281–313.Google Scholar
Zhu, X., & Stone, C. A. (2012). Bayesian comparison of alternative graded response models for performance assessment applications. Educational and Psychological Measurement, 7(2), 5774–799.Google Scholar
© The Psychometric Society 2019
1.University of MissouriColumbiaUSA
2.University of California, BerkeleyBerkeleyUSA
Merkle, E.C., Furr, D. & Rabe-Hesketh, S. Psychometrika (2019). https://doi.org/10.1007/s11336-019-09679-0
Received 12 February 2018 | CommonCrawl |
Was the Southern Hemisphere cooler during the Younger Dryas?
The Younger Dryas was associated with less heat transport from the Southern Hemisphere to the Northern Hemisphere (and a lower flux of the meridional overturning circulation).
So I'm wondering - what were the temperatures of the SH like during that period?
climate younger-dryas
plannapus
InquilineKeaInquilineKea
According to the paper The Younger Dryas Climate Event (Carlson, 2013), the Younger Dryas was a period of warming in the extratropical Southern Hemisphere, and quite a significant one as well, as, from the article:
SST records show a warming of 0.3–1.9 C from the southeast Atlantic to New Zealand
This is supported by
Speleothem and pollen records from New Zealand and pollen records from South America confirm that the Younger Dryas was generally a period of warming
Citing glacial retreat measured in places such as New Zealand, the article Glacier retreat in New Zealand during the Younger Dryas stadial (Kaplan et al. 2010) hypothesised the mechanism to be due to
extensive winter sea ice and curtailed meridional ocean overturning in the North Atlantic led to a strong interhemispheric thermal gradient8 during late-glacial times, in turn leading to increased upwelling and $\mathrm{CO}_2$ release from the Southern Ocean, thereby triggering Southern Hemisphere warming during the northern Younger Dryas.
Research on the deposits observed in the Australian tropics of the age in the article Late Pleistocene record of cyclic eolian activity from tropical Australia suggesting the Younger Dryas is not an unusual climatic event (De Deckker et al. 1991) revealed that the southern tropics experienced a drying phase, that fits well with a cyclic climatic phase.
In terms of the southern tropics, the article Tropical climates in the game of two hemispheres revealed by abrupt climatic change (Ledru et al. 2002) suggest that there were significant variations, as recorded in pollen samples from the South American tropics, leading the authors to suggest that
One consequence of the Younger Dryas changes would be the location of the Intratropical Convergence Zone in a southern position, so that even tropical regions would have been under Arctic influence.
Gimelist
Not the answer you're looking for? Browse other questions tagged climate younger-dryas or ask your own question.
What caused the Younger Dryas cold event?
How much is Iceland/Norway/Western Europe warmed up by the Meriodional Overturning Circulation?
Why is the warm phase of the Pacific Decadal Oscillation associated with stronger El Niños?
Is the Younger Dryas associated with an extinction event?
What causes the counter-intuitive presence of CO2 in the atmosphere during spring and summer months?
How do the known abrupt climate change events fit into the xkcd Earth temperature timeline?
What was the percentage of land mass in prehistoric times when temperatures were high enough that we had no ice caps?
What are good metrics to compare climates?
What caused peak CO2 to rise, starting about 400,000 years ago? | CommonCrawl |
Can there be a power series that converges for all reals but not for the complex numbers?
Let $z = x + i y$, and consider the following function:
$$ f(z) = e^{\frac{1}{1 + z^2}} \qquad z \in \mathbb{C} $$
Note that at $z = \pm i$ the function does not converge. We see that on $\mathbb{R}$ when $y = 0$, this becomes:
$$ f(x) = e^{\frac{1}{1 + x^2}} \qquad x \in \mathbb{R}, $$
which converges nicely for all values $x \in \mathbb{R}$. Furthermore, this function is analytic on $\mathbb{R}$, and so there exists some power series of form:
$$ f(x) = \sum_{n = 0}^{\infty} a_n (x - x_0)^n \qquad a_n, x, x_0 \in \mathbb{R} $$
that converges for all $x \in \mathbb{R}$. Does this power series naturally extend to the complex plane if we have $x \mapsto z$, i.e.:
$$ f(z) = \sum_{n = 0}^{\infty} b_n (z - z_0)^n \qquad z \in \mathbb{C}, \quad z_0 = x_0 + i0, \quad b_n = a_n + i 0 $$
In this case, would the function shown above thus demonstrate that a complex-valued power series that converges on all of $\mathbb{R}$ not necessarily converge in $\mathbb{C}$?
complex-analysis power-series
Anton Xue
Anton XueAnton Xue
$\begingroup$ Why do you think that $f(x)$ has a power series with an infinite radius of convergence on $\mathbb{R}$? $\endgroup$
– John Coleman
$\begingroup$ Your Taylor expansion on $\mathbb R$ will have radius of converge equal to the distance between $x_0$ and $\pm i$. For example, if you expand around $0$ the series has radius of convergence $1$. It starts as $e - e x^2 + (3 e x^4)/2 - (13 e x^6)/6 + (73 e x^8)/24 - (167 e x^{10})/40 + (4051 e x^{12})/720 + O(x^{13})$ . $\endgroup$
$\begingroup$ Ah, that makes sense, thank you for pointing this out! $\endgroup$
– Anton Xue
No. If a power series converges on all $\mathbb{R}$, it(s extension) converges for all complex numbers. One quick way to see why this holds is considering the formula for the radius of convergence and recalling that one proves absolute convergence with it, thus holding for $\mathbb{C}$ as well.
Aloizio Macedo♦Aloizio Macedo
The fundamental flaw in your analysis is this (but see @AloizioMacedo's comment):
We see that on $\mathbb{R}$ when $y = 0$, this becomes:
which converges nicely for all values $x \in \mathbb{R}$.
The problem is that the function you've written can't "converge" because it's not a series.
There is a power-series for $e^x$, and there's one for $\frac{1}{1+x^2}$. But that latter series only converges for $x^2 < 1$, so there isn't an everywhere convergent power series for that function on the reals (or at least "the obvious one isn't everywhere convergent").
John HughesJohn Hughes
$\begingroup$ I don't think that is the fundamental flaw per se. That block could be easily omitted and the error would still exist. I think that the crux is in "Furthermore, this function is analytic on $\mathbb{R}$, and so (assumes that the function is given globally by a power series)". I know this is exactly what you pointed out in the answer, this comment is just to suggest that the fundamental flaw lies elsewhere. $\endgroup$
– Aloizio Macedo ♦
$\begingroup$ I guess I agree -- the sentence I quoted seemed to me to be shorthand for the sentence that followed, but if you replace "converges nicely" with "is defined" (which might be what OP meant), then the second is where things go wrong. The first sentence, as written, seems to convey a fundamental misunderstanding...but it could be just a momentary lapse in word-choice. $\endgroup$
– John Hughes
No. You might have heard the term "radius of convergence" before - in this case, that isn't an abuse of language. Power series converge within open disks in the complex plane, and the radius of convergence is the distance to the nearest singularity. In this case, since you require your series to converge on $\mathbb{R}$, the radius of convergence would have to be $\infty$, so that the series would converge on all of $\mathbb{C}$
Brevan EllefsenBrevan Ellefsen
It is easy to prove that if a power series converges for some $z_1\ne 0$, then it converges absolutely for every complex $z$ with $|z|<|z_1|$:
In order for the the power series to converge at $z_1$, the sequence $|a_nz_1^n|$ must go to $0$ -- in particular it must be bounded by some number $K$. We then have that $$ |a_nz^n| = \left| \frac{z}{z_1} \right|^n \cdot |a_nz_1^n| \le K\left|\frac{z}{z_1} \right|^n $$ so the terms of the power series at $z$ are bounded by a geometric sequence with common factor $\left|\frac{z}{z_1}\right|$ which is assumed to be $<1$. This forces the partial sums of the power series at $z$ to be a Cauchy sequence, and therefore it converges.
In particular we can let $z_1$ be real, so if a power series converges for all reals, it will necessarily also converge on all of $\mathbb C$.
hmakholm left over Monicahmakholm left over Monica
Not the answer you're looking for? Browse other questions tagged complex-analysis power-series or ask your own question.
How to prove that a complex power series is differentiable
Power series: If $|z-z_0|< R$ the series converges absolutely
All power series has a point that is not regular.
Absolute convergence of a complex vs real power series
Real power series absolutely converges. Does complex series converge too?
Why does the criterion for convergence of a power series not imply every series with bounded terms converges?
Example of a Complex Power Series That Converges Given Certain Properties
Complex power series converging at only one point on the unit circle | CommonCrawl |
Medium access behavior analysis of two-flow topologies in IEEE 802.11 wireless networks
Muhammad Zeeshan ORCID: orcid.org/0000-0003-4417-13651 &
Anjum Naveed1
EURASIP Journal on Wireless Communications and Networking volume 2016, Article number: 42 (2016) Cite this article
Impact of medium access control (MAC) on throughput of IEEE 802.11-based multi-hop wireless networks is not completely understood despite numerous research efforts. Researchers have explored the MAC interaction of two-flow topologies in order to better understand the MAC behavior of nodes in generic multi-hop wireless network. Prior research has considered two flow interactions under the assumption of same transmission and carrier sensing range. This research extends and completes the existing body of work by relaxing the assumption of same transmission and carrier sensing range to realize more practical and realistic two-flow topologies. Twenty-five unique possible two-flow topologies can exist in general multi-hop wireless networks. The topologies have been classified into six categories based on MAC layer behavior and per flow throughput. Closed-form expressions for occurrence probabilities of the identified categories have been derived with particular observation that carrier sensing range-based categories have high occurrence probability and cannot be ignored. MAC behavior of each category is discussed. It is observed that different transmission and carrier sensing ranges significantly affect the MAC behavior and the throughput of flows. Based on the behavior, exact throughput of the two single hop flows is analytically computed. The results achieved through analysis have been compared with the simulated results to verify the accuracy of analysis. This research will serve as basis for MAC behavior analysis of generic multi-hop wireless networks.
Interference in wireless networks significantly limits the network capacity. Among a set of interfering links using a common frequency channel, transmission of a link is successful only if all other links remain silent for the entire period of transmission. Medium access control (MAC) protocol is employed to arbitrate the access to the wireless channel among competing links. IEEE 802.11 networks use carrier sense multiple access with collision avoidance (CSMA/CA) as MAC protocol. The random access mechanism of CSMA/CA does not ensure interference-free transmissions, specifically when the sender nodes of the interfering links are not within the transmission range of each other. Consequently, many transmission opportunities are wasted when more than one interfering links simultaneously attempt transmissions. Thorough MAC behavior analysis can reveal the impact of interference on the achievable throughput of the interfering links.
Analysis of two-flow topologies is widely used in literature to understand the complex interactions in general multi-hop wireless networks, and analysis of subset of four nodes is suitable to explain all types of interaction that can exist in realistic wireless network deployments. Currently, most deployments of wireless mesh network uses carrier sense multiple access (CSMA) as their MAC protocol. For fully connected topologies where all four nodes or at least both transmitters are within single transmission range, CSMA with or without RTS/CTS demonstrates fair throughput and channel access performance between contending flows. The rest of two-flow topologies in WMN, where both transmitters are not in single transmission range, exhibit severe throughput imbalances between two contending flows and few well-known topologies have been investigated by researchers in the past including hidden and exposed terminal problems. Two-flow topologies in WMN that results in throughput imbalances suffer from problems including severe short- and long-term unfairness between contending flows.
This work further widens and completes the body of work on two-flow interaction analysis for multi-hop wireless network. In this work, two-flow topologies have been classified by separately considering the transmission and the carrier sensing ranges. The interaction between the two single hop flows is considered under CSMA/CA protocol for throughput estimation of two-flow topologies. It is observed that the presence of sender or receiver of interfering link within the carrier sensing range results in a significantly different MAC behavior compared to the presence of the two nodes outside the carrier sensing range. This research divides the two-flow topologies into six categories, depending upon CSMA/CA interaction. Occurrence probability of each category has been computed using spatial analysis. For this purpose, possible geometric area where the nodes of the particular topology can exist has been considered, compared to the overall geometric area of occurrence for two interfering links. Analysis shows that the categories that are based on interference interactions from within the carrier sensing range only have high occurrence probability values (aggregate of 0.69). Finally, throughput achieved by the two links under each category has been computed analytically based on MAC protocol behavior. Analytically computed throughput values have been compared with the simulation throughput values using Opnet-based simulations. The comparison shows near perfect match in analytical and simulated values, suggesting the completeness of the categorization.
The rest of the paper is organized as follows. Section 2 discusses the related work. Section 3 enlists the two-flow categories and possible geometric placement of nodes under each category. Expressions for occurrence probabilities of the categories have been derived in Section 4. Interference type based on MAC protocol and the throughput achieved by each link has been derived for each category in Section 5. Section 6 concludes the paper.
Literature relating MAC behavior analysis and capacity estimation can be grouped into three sets. The first set consists of interference models and ensuing MAC behavior analysis that considers interference from within the transmission range. These models consider the impact of interference from different links to be same, irrespective of their relative geometric location [1–4]. The second set comprises of location-based MAC behavior and interference analysis [5–8]. Literature in this group focuses on change in MAC behavior because of changing geometric relation of the interfering links. The final set consists of capacity estimation based on physical characteristics of wireless channel.
Capacity estimation of CSMA-based wireless networks was first performed by Boorstyn et al. [9]. Authors used Markov chain-based model to compute exact throughput in multi-hop CSMA-based wireless networks. However, the analysis was limited to few nodes, given the complexity of computation. Bianchi [10] computed the achievable throughput by individual nodes, given that all interfering nodes are within a transmission range. Bianchi showed that in the absence of hidden node problem [11] and with perfect channel capture, wireless nodes exhibit fairness for all nodes contending for channel access. Although restricted to only one type of two-flow interactions (i.e., coordinated interfering links), Bianchi computed exact throughput values for different IEEE 802.11 DCF mode parameters. Protocol and physical models of interference are well-known interference models [1] that have been used frequently in literature for capacity estimation as well as MAC protocols and channel assignment research. Both models lead to inaccurate interference estimation.
Given a link and its interfering link, the placement of the sender and the receiver of the interfering link within transmission or carrier sensing range defines the MAC behavior and its impact on achievable throughput of the two links. Garetto et al. [5] have analyzed the MAC behavior of the two interfering links under different geometric placements inside and outside transmission range. The authors have categorized the two-flow topologies with different geographic placements into three categories. Under the assumption of the same transmission and carrier sensing range, the analysis carried out by Garetto et al. [5] accurately predicts the impact of MAC behavior and interference on throughput of the two single hop flows. However, the study does not consider the impact of carrier sensing range on the MAC behavior and the resultant throughput. Razak et al. [7] have extended this research by considering separate carrier sensing and transmission ranges; however, the simulation results show that the topologies within the single category do not share the same throughput profile. Furthermore, important categories based on nodes within carrier sensing range have not been considered.
Garetto et al. [5] have considered the two-flow interactions and classified possible topologies into three categories of sender connected (SC), asymmetric incomplete state (AIS), and symmetric incomplete state (SIS) based on MAC behavior and throughput imbalances. In their extended work, Garetto et al. [6] computed per link forwarding capacity for general multi-hop wireless networks using two-flow interactions. In cases where transmission and sensing ranges are considered same, the analytical results accurately predict throughput achieved through simulations. However, the model does not capture the impact of interference from links within sensing range. The work has been extended by Razak et al. [7, 8, 12]; however, significant gap exists between analytical and simulated results. Research presented in this document is focused on differentiating between interference introduced from transmission range and from carrier sensing range. This results in new categories that have high occurrence probability in realistic multi-hop wireless networks.
Among capacity estimation literature, Li et al. [13] have performed the throughput analysis of a single access point for IEEE 802.11g radios. Dinitz [14] has proposed distributed algorithms for wireless nodes to achieve optimal throughput in distributed multi-hop wireless networks. The author have used protocol and physical models for interference. Kawade et al. [15, 16] have compared the performance of IEEE 802.11g and 802.11b radios under co-channel interference by considering the physical layer characteristics. The authors have concluded that IEEE 802.11g networks are more resistant to co-channel interference while channel separation improves the performance of both types of networks. Weber et al. [17] have computed the upper and lower bound network capacity for multi-hop wireless networks using different physical channel conditions. The authors have computed maximum physical transmission capacity and optimal number of nodes that achieve the maximum capacity.
Fu et al. [18] have analyzed the general CSMA protocol and proposed the concept of cumulative interference model where hidden node problem can be avoided. The authors have also proposed incremental power carrier sensing that can help nodes identify the distance from potential interfering nodes and better plan the transmissions. Vitturi et al. [19] have proposed new techniques for rate adaptation to cater the collision problem and compared the performance with automatic rate fallback technique. The authors have shown that the performance of new techniques is better in terms of retransmissions required. Qiao et al. [20] have also proposed transmit power control and rate adaptation to achieve low energy consumption in IEEE 802.11a/h systems. The objective is to minimize consumed energy, although throughput gains have also been reported.
Focus of this research is the analysis of two-flow interference interactions, impact of geometric location on MAC behavior, and its impact on throughput of the two single hop flows.
Two-flow topology categorization
Within a multi-hop network, a sender receiver pair (referred as flow throughout the rest of the paper) interacts with multiple flows in the neighborhood. Each interaction impacts the throughput of the flows, resulting in complex chain of interactions. In order to understand such interactions and the resulting impact on the achievable throughput of each flow, it is important to understand the possible interactions between two flows in isolation. Based on this understanding, a general model for wireless interactions in a multi-hop wireless network is conceivable, which can predict the achievable throughput of individual single hop flows. In this section, possible interactions of two flows are categorized based on geometric location of the nodes of the flows. The differences of proposed categorization from the categories defined in prior work [5, 7] are highlighted. In the subsequent sections, the achievable throughput is discussed based on the MAC behavior.
The Euclidean distance between two nodes A and B is given as d(A,B). A node can have three possible placements with reference to another node depending upon the signal strength received from the other node. If node B is placed around node A such that it can successfully decode the transmissions from node A, then the node B is within the transmission range (TR) of node A, i.e., d(A,B)≤TR. Such placement is referred as connected in this paper. On the other hand, if node B can sense the channel to be busy when node A transmits but cannot successfully decode the information because of weak radio signals, then the node B is outside transmission range but within the carrier sensing range (CSR) of node A, i.e., TR<d(A,B)≤CSR. This placement is referred as sensing. Finally, if node B cannot sense the transmissions of node A, then node B is outside the carrier sensing range of node A, i.e., d(A,B)>CSR. This placement is referred as disconnected. The placement is referred as not connected if it is either sensing or disconnected. The placements are referred as interference interactions throughout the rest of the paper.
Consider two single hop flows Aa and Bb where A and B are the transmitting nodes while a and b are the respective receiving nodes. The receiving nodes are within the transmission range of the respective transmitting nodes. Four interference interactions AB, ab, Ab, and Ba exist between the nodes of the two flows, as shown in Fig. 1. Interference interaction AB is between the two transmitters and is referred as sender interaction. On the similar lines, the interaction ab is referred as receiver interaction while the interactions aB and Ab are referred as sender receiver interactions. A two-flow topology is considered symmetric if the interference interactions Ab and Ba are of same type, i.e., if Ab is sensing then Ba is also sensing.
Two-flow interaction topology. Four interference interactions AB, ab, Ab, and Ba exist between the nodes of the two flows
Two-flow topologies
Based on the interference interactions, there are a total of 34(81) possible two-flow topologies while 53 of these topologies are unique. Given the restriction that the transmitters of flows must be within the transmission range of the respective receivers and the fact that carrier sensing range is ≈2.7 times the transmission range (through simulations and experimentations), only 25 topologies are physically realizable in a multi-hop wireless network. Remaining 28 topologies have zero occurrence probability. The 25 unique possible topologies have been classified into six categories, depending upon the types of the four interference interactions and the MAC behavior. The following sections explain the interference interactions of the categories.
Sender connected (SC)
Sender connected category represents the topologies where the transmitters A and B of the single hop flows Aa and Bb are within the transmission range of each other. That is:
$$d(A,B) \leq \text{TR} $$
The remaining three interference interactions are not significant in this case. Seven topologies belong to this category and are shown in Fig. 2. Node placement of a sample topology is shown in Fig. 3. This category exists in the classification by Garetto et al. [5] with the same name. Razak et al. [7] have divided this category into two categories of sender connected symmetric interference, and sender connected asymmetric interference. However, as shown in the subsequent section, the MAC behavior and resulting throughput profile of all topologies belonging to this category are the same and form a single category.
Sender connected topologies
Sample sender connected node placement
Symmetric sender receiver connected (SSRC)
If the interference interaction AB is not connected and interference interactions Ab and aB are both connected, then the topology belongs to the category of symmetric sender receiver connected. The topologies fulfill following criteria.
$$\begin{aligned} &d(A,B) > \text{TR}\\ &d(a,B) \leq \text{TR}\qquad \& \qquad d(A,b) \leq \text{TR} \end{aligned} $$
Two topologies belong to this category as shown in Fig. 4. Sample node placement is shown in Fig. 5. Garetto et al. in their extended work [6] refer to this category as near hidden terminals. The same category exists with the name of symmetric incomplete state in their original work [5] as well as in the work by Razak et al. [7] but contains an additional topology. The additional topology is not realistic when CSR≥2∗TR.
Symmetric sender receiver connected topologies
Sample SSRC node placement
Asymmetric sender receiver connected (ASRC)
If the interference interaction AB is not connected and one of the interference interactions Ab and aB is connected while other interaction is either disconnected or sensing, then the resulting topology belongs to the category of asymmetric sender receiver connected. Three topologies belong to this category as shown in Fig. 6 and a sample node placement of ASRC is shown in Fig. 7. The topologies belonging to this category fulfill the distance criteria of
$$\begin{aligned} &d(A,B) > \text{TR}\\ &d(a,B) \leq \text{TR}\qquad \& \qquad d(A,b) > \text{TR} \end{aligned} $$
Scenarios of asymmetric sender receiver connected topologies
Sample node placement for ASRC
This category exists with the name of asymmetric incomplete state in the categorization of Garetto et al. [5] and Razak et al. [7]. However, an additional topology (Fig. 6 a) is part of this category in the proposed categorization because of the different sensing range and transmission range.
Receiver connected (RC)
This category consists of the topologies where the interference interactions AB, aB, and Ab are not connected (i.e., either sensing or disconnected) and the interference interaction ab is connected. The Euclidean distances of interference interactions are
$$\begin{aligned} &d(A,B) > \text{TR}\\ &d(a,B) > \text{TR}\qquad \& \qquad d(A,b) > \text{TR}\\ &d(a,b) \leq \text{TR} \end{aligned} $$
Two topologies belong to this category as shown in Fig. 8 a, b. A sample node placement is shown in Fig. 9. Razak et al. [7] have referred to this category as interfering destination incomplete state. However, a different MAC behavior has been observed in the proposed work compared to the one reported by Razak et al. This is explained in the subsequent section.
Scenarios of receiver connected topologies
Sample node placement for RC
Symmetric not connected (SNC)
This is a new category and does not exist in any of the prior categorization. If none of the four interference interactions is connected and the sender receiver interactions aB and Ab are symmetric, then the topologies belong to the category of symmetric not connected. Seven topologies belong to this category and are shown in Figs. 10 and 11. Sample node placement is also shown in Fig. 12. The topologies satisfy the distance criteria of
$$\begin{aligned} &d(A,B) > \text{TR}\\ &(\text{TR} < d(a,B) \leq \text{CSR}\; \& \; \text{TR} < d(A,b) \leq \text{CSR}) \;\; \text{OR}\\ &(d(a,B) > \text{CSR}\qquad \& \qquad d(A,b) > \text{CSR})\\ &d(a,b) > \text{TR} \end{aligned} $$
Scenarios of symmetric not connected topologies
Sample node placement for symmetric not connected topologies
Asymmetric not connected (ANC)
This category is also new and does not exist in any prior categorization. If none of the four interference interactions is connected and the sender receiver interactions aB and Ab are asymmetric, then the topologies belong to the category of asymmetric not connected. Four topologies belong to this category as shown in Fig. 13. Figure 14 is a geometric representation of a sample topology. The topologies satisfy the interference interaction distance criteria of
$$\begin{array}{*{20}l} &d(A,B) > \text{TR}\\ &\text{TR} < (d(a,B) \leq \text{CSR}\qquad \& \qquad d(A,b) > \text{CSR}\\ &d(a,b) > \text{TR} \end{array} $$
Scenarios of asymmetric not connected topologies
Sample node placement for asymmetric not connected topologies
Category occurrence probabilities
How frequently the topologies belonging to each category can exist in a general multi-hop wireless network? Specifically, what is the occurrence probability of the newly identified categories? Answers to these questions are important in identifying the impact of each category on interference profile of the links in general multi-hop wireless networks. Geometric analysis has been employed to find out the occurrence probability of the categories. Perfect circular disks are assumed for area under transmission range, carrier sensing range, and the network with the disk radii defined as r tr, r csr, and r n, respectively. Network radius is assumed to be r n=0.5×(2×r tr+r csr) which covers maximum possible distance for a valid placement of the nodes such that the resulting flows are interfering. Note that at times, the carrier sensing range of nodes can be outside the total network area; however, the ratio of area of interest and the total area remains unaffected.
For each category, four interference interactions AB, Ab, aB, and ab are considered individually. For each pair of nodes within the interference interaction, one node is assumed to be at a fixed location. The area around the first node where the second node can possibly exist is computed, given the placement constraints introduced by the specific category. Under the assumption of circular disk ranges, the area is mostly equivalent to either the area of a disk or the area of intersection of two disks with known radii. The ratio of computed area to the maximum possible network area gives the probability of occurrence of the interference interaction. Multiplying the occurrence probabilities of four individual interactions gives the occurrence probability of the category.
The expressions for the disk area and the area of interaction of two disks are frequently used throughout the computations. The expression for area of circular disk with radius r using onion method is given as
$$ {\int^{r}_{0}}{2\pi x}dx $$
((1))
The expression for area of intersecting circles of same radius r and distance between radii as d is given as
$$ 2d^{2}\text{cos}^{-1}\left(\frac{d}{2r}\right) - \frac{d}{2}\sqrt{4r^{2} - d^{2}} $$
The occurrence probability of each category is computed in the subsequent section using the two listed expressions. For sake of brevity, the final expression for probability of each category is given with brief description of the expression.
Sender connected
The transmitters of both flows must be within the transmission range of each other. This leads to a disk area with radius r tr. The probability of AB to be connected is achieved by integrating \(\frac {2x}{r^{2}_{\mathrm {n}}}\) over the interval 0 to r tr. Given that AB is connected, maximum distance between nodes A and b (a and B) is 2r tr. The probability of two events can be achieved by integrating \(\frac {2x}{r^{2}_{\mathrm {n}}}\) over the interval 0 to 2r tr. Finally, the two receivers can be located anywhere in the network. The occurrence probability of sender connected category is given as
$$ P_{\text{SC}}=\int^{r_{\text{csr}}}_{0}{\int^{2r_{\text{tr}}}_{0}{\int^{2r_{\text{tr}}}_{0}{\int^{r_{\text{tr}}}_{0}{\frac{2w}{r^{2}_{\mathrm{n}}} \frac{2x}{r^{2}_{\mathrm{n}}} \frac{2y}{r^{2}_{\mathrm{n}}} \frac{2z}{r^{2}_{\mathrm{n}}}}}}}dw dx dy dz $$
Symmetric sender receiver connected
Topologies belonging to SSRC category have the interference interaction AB as sensing, i.e., r tr<d(A,B)≤r csr. The interactions Ab and aB should be connected. Therefore, the distance d(A,B) is restricted to 2∗r tr. Furthermore, the receiver a (or receiver b) should be within the transmission range of sender A (or sender B) as well as B (A). Consequently, the possible placement area of a around node B is given by the area of intersection of the two circles with radius r tr and centers separated by the distance r tr. The area is given by expression 2 where d(A,B)>r tr results in maximum distance between a and b to be \(\sqrt {3}r_{\text {tr}}\). The probability of the category is given as
$$ \begin{aligned} P_{\text{SSRC}}&=\left(2d^{2}\text{cos}^{-1}\left(\frac{d}{2r}\right) - \frac{d}{2}\sqrt{4r^{2} - d^{2}}\right)^{2} \\ &\quad\times \int^{\sqrt{3}r_{\text{tr}}}_{0}{\int^{2r_{\text{tr}}}_{r_{\text{tr}}}{\frac{2w}{r^{2}_{\mathrm{n}}} \frac{2z}{r^{2}_{\mathrm{n}}}}}dw dz \end{aligned} $$
where r=d=r tr.
Asymmetric sender receiver connected
In this category the condition r tr<d(A,B)≤r csr holds. Similarly, d(A,b)≤r tr and area around A where b can exist is given by expression 2. However, for interaction aB, r tr<d(a,B)<r n. Maximum possible distance between a and b can be 2r tr. The probability expression is given as
$$ \begin{aligned} P_{\text{ASRC}}&=\left(2d^{2}\text{cos}^{-1}\left(\frac{d}{2r}\right) - \frac{d}{2}\sqrt{4r^{2} - d^{2}}\right)\\ &\quad \times \int^{2r_{\text{tr}}}_{0}\int^{r_{\mathrm{n}}}_{r_{\text{tr}}}{\int^{2r_{\text{tr}}}_{r_{\text{tr}}}{\frac{2w}{r^{2}_{\mathrm{n}}} \frac{2y}{r^{2}_{\mathrm{n}}} \frac{2z}{r^{2}_{\mathrm{n}}}}}dw dy dz \end{aligned} $$
Receiver connected
The two receivers should be in transmission range of each other. The interactions Ab and aB are sensing. Given the fact that d(a,b)<r tr, the conditions r tr<d(a,B)<2r tr and r tr<d(A,b)<2r tr must hold. The probability of the category is given as
$$ \begin{aligned} P_{\text{RC}}&=\left(2d^{2}\text{cos}^{-1}\left(\frac{d}{2r}\right) - \frac{d}{2}\sqrt{4r^{2} - d^{2}}\right)\\ &\quad \times \int^{2r_{\text{tr}}}_{r_{\text{tr}}}\int^{2r_{\text{tr}}}_{r_{\text{tr}}}{\int^{r_{\mathrm{n}}}_{r_{\text{tr}}}{\frac{2w}{r^{2}_{\mathrm{n}}} \frac{2y}{r^{2}_{\mathrm{n}}} \frac{2z}{r^{2}_{\mathrm{n}}}}}dw dy dz \end{aligned} $$
Symmetric not connected
The four interference interactions in this category are sensing with only restriction on maximum possible area. The probability is given as
$$ P_{\text{SNC}}=\left(\int^{r_{\mathrm{n}}}_{r_{\text{tr}}}{ \frac{2z}{r^{2}_{\mathrm{n}}}} dz\right)^{4} $$
Asymmetric not connected
In this case, the interference interaction aB must be disconnected. The area of interest for this case is approximated by integrating 2z over the range r n to r csr, which is approximately equal to the area outside CSR. The occurrence probability of the category is given as
$$ P_{\text{ANC}}=\int^{r_{\text{csr}}}_{r_{\mathrm{n}}}{\int^{r_{\text{csr}}}_{r_{\text{tr}}}{\int^{r_{\mathrm{n}}}_{r_{\text{tr}}}{\int^{r_{\mathrm{n}}}_{r_{\text{tr}}}{\frac{2w}{r^{2}_{\mathrm{n}}} \frac{2x}{r^{2}_{\mathrm{n}}} \frac{2y}{r^{2}_{\mathrm{n}}} \frac{2z}{r^{2}_{\mathrm{n}}}}}}}dw dx dy dz $$
Occurrence probability values
The probability equations are dependent only on the transmission and carrier sensing ranges. All probabilities are closed-form expressions and can easily be computed. To verify the correctness of expressions, a program has been implemented in Java. The program considers a fixed network area with points arranged in the area as uniform grid. Four nodes are placed on all possible points, and their interference interactions are computed to identify the category of the topology. Non-possible topologies have been eliminated and the remaining n normalized to attain the occurrence probabilities of the categories. The probability values achieved through the program and the computed values using probability expressions have been plotted in Fig. 15. The plot shows excellent match between all computed values and the values achieved through the program.
Occurrence probabilities of categories
Figure 15 shows that the occurrence probability is significantly high for the categories that are purely based on interactions because of carrier sensing range (SNC = 0.45 and ANC = 0.24). In the subsequent section, we show that these interference interactions significantly affect the throughput of interfering links. Therefore, the categories cannot be ignored.
Interference and throughput analysis
IEEE 802.11 wireless interfaces use carrier sense multiple access (CSMA) with collision avoidance (CA) protocol for acquiring wireless channel access. This section starts with brief explanation of the CSMA/CA protocol as used in IEEE 802.11 (Only extended mode is explained). Parameters affecting the throughput are discussed, and the throughput expressions derived by Bianchi [10] and Kumar et al. [21] are listed. Subsequently, the expressions for the parameters in the throughput expressions are derived for the two flows for each category, throughput for different packet sizes is computed, and the computed values are compared with simulated results to highlight the accuracy of the categorization and the throughput analysis.
CSMA/CA protocol behavior
In IEEE 802.11 MAC, time is considered to be slotted and the slot interval is represented by σ. Based on the CSMA protocol, when a node has data to transmit, it sets a back-off counter by selecting a random value from the range [0,W i −1]. For the first attempt, W 0=16 for IEEE 802.11a/g radios. The counter is decremented whenever the channel is found idle for the slot interval. If the channel is not idle because of an ongoing transmission from a neighboring node, the back-off counter freezes. When the counter reaches zero and the channel is idle, the node initiates transmission by sending ready-to-send (RTS) frame. The transmitting node waits for the response from intended receiver, which is in the form of clear-to-send (CTS) frame. If the CTS is not received within a certain period of time (SIFS + 2*propagation delay), the RTS is assumed to be lost (due to collision or because of busy channel at receiver end). In case of collision, the node resets the back-off counter by selecting a random value from the range [0,2i∗W 0−1] where i is the number of retransmission attempt and is known as a back-off stage. The entire procedure of channel access is repeated. If the CTS is received, the channel is reserved for the particular transmission and the node proceeds with transmission of data packet, followed by ACK from a receiver. The four frames RTS, CTS, DATA, and ACK are separated by Short Inter-Frame Space (SIFS) while ACK frame is followed by DCF Inter-Frame Space (DIFS). In case of IEEE 802.11g radios, every frame is followed by signal extension, which is idle interval of 6 μs, necessary for proper reception of signal. The nodes other than the transmitter and receiver that correctly receive the RTS or CTS frame set the NAV for remaining period of transmission and freeze their activity on the channel.
Assuming that the transmitting nodes are continuously back logged, a wireless node can find the channel in one of the following four states: (i) idle with no transmission going on, (ii) busy because of transmission of another node, (iii) successful transmit of the node itself, (iv) unsuccessful transmit of the node itself with transmitted frame colliding with transmission from another frame. Throughout the analysis, it is assumed that if a packet is received collision free, it can successfully be decoded and no errors occur because of channel noise. Using random back-off mechanism of the CSMA protocol, the probability τ that a node transmits following an idle slot is given by the equation [21].
$$ {\small{\begin{aligned} \tau=\frac{2(1-2p)(1-p^{m+1})}{q(1-p^{m+1}) + W_{0}(1-p-p(2p)^{m'}(1+p^{m-m'}q))} \end{aligned}}} $$
where q=1−2p, m is the maximum back-off stage, and m ′ is the stage when upper limit of the range for random back-off reaches its maximum value. p is the conditional packet loss probability due to collision. Keeping in view the abovementioned states, the throughput (in pkts/s) of a node is given as [5]
$$ {}T=\frac{\tau(1-p)}{\tau(1-p)T_{s} + \tau p T_{c} + (1-\tau)(1-b)\sigma +(1-\tau){bT}_{b}} $$
where b is the probability that a node finds a slot to be busy while T s , T c , and T b are the average durations of successful transmission, collision, and busy interval, respectively, as observed by the node. For all two-flow categories, the values of T s , T c , and T b are known. Throughput of a sender can be computed, given the values of busy probability b and conditional packet loss probability p. Both values are dependent upon the interference interactions of the categories and need to be computed for individual categories. The values of all known parameters for extended access mode of IEEE 802.11g radio assuming homogeneous network and extended rate physical layer are given in Table 1. For other radio types, the values can be updated to get the throughput results.
Table 1 Parameters (ERP IEEE 802.11g)
In the following, the MAC behavior based on interference interactions for the identified categories is explained and the known parameters are computed to compute the achievable throughput for both flows of each category.
MAC behavior of this category is simplest to understand. The senders A and B of the two flows are within the transmission range of each other; therefore, the RTS packet transmitted by sender A is successfully received by sender B and vice versa. Therefore, sender B sets its network allocation vector (NAV) and freezes its activity until the transmission by sender A is complete. The occurrence of busy event for any flow is equal to the occurrence of the transmission event of the alternate sender, which has the probability τ. Therefore, busy probability of any sender is given by b=τ. Collision of RTS for any sender occurs only when the two senders simultaneously start RTS transmission following random back-off. Therefore, conditional packet loss probability of any flow is given by p=τ. Channel busy time T b is equal to T s . Replacing these values in Eqs. 9 and 10 gives the value of throughput of a single flow. Based on random access of CSMA/CA and completely symmetric channel view, the throughput of both flows is equal. Bianchi [10] computed the throughput for flows under this category and the results of two computations are same. Figure 16 shows the throughput achieved by the two flows in sender connected category for different packet sizes. It can be seen that the analytically computed throughput perfectly matches the simulated throughput for all packet sizes. Maximum achievable throughput for any flow is 10.68 Mbps for the packet size of 1500 bytes.
Throughput (sender connected flows)
The senders A and B of the two flows in this category (and all subsequent categories) are not within the transmission range of each other. Therefore, the RTS frame transmitted by sender A is not successfully decoded by sender B and vice versa. However, the channel is sensed busy during RTS transmission, preventing the other sender from initiating a transmission. This is different from SIS category proposed by Garetto et al. [5] where senders are assumed to be outside the sensing range and cannot sense the RTS transmitted by sender of the alternate flow. The receivers of both flows are within the transmission range of the alternate senders, i.e., interference interactions Ab and aB are connected. This means that the receivers can successfully decode the RTS frame transmitted by the alternate senders resulting in setting NAV at alternate receiver. Similarly, senders can successfully decode the CTS packet transmitted by the alternate receivers. Therefore, collision can only occur if one sender starts transmission of RTS during the idle interval between RTS and CTS transmission of the alternate flow.
To compute the throughput of the flows in SSRC category, we start with busy probability. Busy probability b of each flow is equal to the successful transmission probability of the alternate flow. To compute successful transmission probability and the conditional packet loss probability, we adopt the method used by Garetto et al. [5] for analysis of SIS category (see section 5 of [5]). Collision occurs if sender B starts RTS transmission during signal extension + SIFS (6 μs) interval between RTS and CTS frames of flow Aa. This depends upon two factors: (i) number of transmission opportunities where collision can occur, which is given by f= ceil((SIFS + 6) /σ) as shown in Fig. 17 and (ii) the back-off stage of sender B, which defines the probability of transmission in a given slot for sender B. The probability of transmission is given by \(\gamma _{i} = \frac {2}{1+W_{i}}\) where i is the back-off stage. The interaction of the two senders during interval f can be modeled as two-dimensional Markov model. Each state of the model represents the back-off stage of both senders, resulting in m 2 states. In a general state (i,j), the transition probabilities are given by (1−γ i )(1−γ j ), γ i (1−γ j )f, (1−γ i )f γ j , and γ i γ j for no transmission by any node, successful transmission of node i, successful transmission of node j, and unsuccessful transmission by both nodes, respectively. Steady state equations can be used to compute the state probabilities π ( i,j).
SSRC channel view
Expressions for computation of throughput along with the parameter values are summarized in Table 2. Figure 18 summarizes the analytical and simulated results for SSRC category. A perfect match can be seen in the two results for all packet sizes. It may be noted that the aggregate throughput of the two flows is lesser than the aggregate throughput of SC category. This is because of the higher transmission losses and longer binary exponential back-offs, attributed to the higher value of conditional packet loss probability.
Per flow throughput of SSRC
Table 2 Parameters (SSRC computation)
In this category, the two senders A and B are outside the transmission range of each other. The receiver of flow Bb is within the transmission range of sender A while receiver of flow Aa is either within carrier sensing range or outside the range of sender B. This results in different view of channel for each flow. If RTS frame is transmitted by sender A, it is received by receiver b, which sets the NAV and remains silent for the entire transmission of the flow Aa. The transmission of flow Aa can be unsuccessful if sender B starts the RTS transmission during the interval between RTS and CTS frames of flow Aa, which is sensed idle by sender B. In case of topology in Fig. 6 b, this interval increases by the duration of CTS frame because sender B cannot sense the activity of receiver a. This information is used to compute collision probability of flow Aa. This behavior of the category is significantly different from AIS category proposed by Garetto et al. [5] where conditional packet loss probability of flow Aa is zero because of assumption that the two senders are outside the range of each other. Note that transmission of flow Bb in all these scenarios will not be successful given the fact that receiver b has set the NAV after receiving RTS frame from sender A. Flow Bb can have a successful transmission only when the RTS frame from sender B is initiated while flow Aa is in back-off stage. In this case, sender A senses RTS frame and assuming the channel to be busy, it does not initiate transmission. Subsequently, it receives CTS frame and sets the NAV resulting in busy period for flow Aa and successful transmission on flow Bb. The probability of this event is computed by considering the available transmission opportunities for sender B that can lead to successful RTS transmission.
To compute the throughput of the two flows, first of all, the transmission opportunities for flow Bb where a successful transmission can occur are considered. A successful transmission on flow Bb can only take place if sender B can transmit entire RTS frame during signal extension + DIFS interval and the back-off period of sender A. This interval is shown as D+i σ in Fig. 19. Note that the SIFS interval between frames is also sensed idle by sender B but is too small for complete RTS transmission and can be ignored. Further note that for topology in Fig. 6 b, CTS and ACK packet transmissions are also sensed as idle for sender B; however, a transmission during this interval will not lead to successful transmission because of the fact that receiver b can sense the transmissions from receiver a. Conditional packet loss probability is the inverse of the probability that sender B successfully transmits RTS frame during interval D+i σ. Garetto et al. have computed this probability using the expression
$$ p_{B} = 1 - \frac{2(\text{max}(0,D+\sum_{i=0}^{W_{0}}i\sigma))}{W_{0}(2T_{s} + (W_{0} - 1)\sigma)} $$
ASRC channel view
where D= signal extension + DIFS. Using this equation, packet loss probability of flow Bb can be computed in terms of all known variables. Replacing p B in Eq. 9 gives transmission probability τ B for flow Bb. Throughput computation of flow Bb also requires the value of busy probability b B which is equal to the transmission probability τ A of flow Aa. Therefore, we need to compute the transmission probability of flow Aa in order to compute the throughput of flow Bb.
Transmission probability τ A of flow Aa is dependent upon the conditional packet loss probability p A . In case of ASRC category, RTS frame transmitted by sender A is sensed by sender B as busy period. However, signal extension + SIFS interval following RTS transmission is sensed as idle by sender B. If sender B initiates RTS transmission during this event, it will result in unsuccessful reception of CTS from a at sender A, which is the event of collision for flow Aa. Therefore, probability of packet loss for flow Aa can be computed by modeling the probability of the event of RTS transmission by sender B during interval signal extension + SIFS between RTS and CTS transmission by flow Aa. This event can be modeled as one-dimensional Markov model with m states. The expressions in Table 2 are valid for the purpose with the difference of number of states and the variable γ j replaced by τ B . Note that variable f includes additional interval of CTS for the topology in Fig. 6 b. Conditional packet loss probability for flow Aa is given by the expression for p c . Computed value can be used to compute the value of τ A using Eq. 9. Given that busy probability b B of flow Bb is equal to the transmission probability τ A of flow Aa and busy time is equal to T s − DIFS − signal extension, all parameters for throughput computation of flow Bb are known. Equation 10 can be used to get the throughput value for flow Bb.
Busy probability b A of flow Aa is given in terms of throughput (T B ) of flow Bb as
$$ b_{A} = \frac{\tau T_{s} T_{B} + (1-\tau)\sigma T_{B}}{(1-\tau)(1 + \sigma T_{B} - T_{b} T_{B})} $$
The throughput of flow Aa can be computed using Eq. 10 in terms of all known parameters. Figure 20 shows the throughput of both flows using analytical and simulated results for different packet sizes. It can be seen that there is a huge imbalance of throughput between two flows for all packet sizes with flow Bb severely suffering. This category can be considered as the main cause of bottleneck links in a general multi-hop wireless network.
Per flow throughput of ASRC
Receiver connected topologies have the interference interactions AB, Ab, and aB as not connected while interference interaction ab is connected. The MAC behavior of the two topologies belonging to this category is slightly different, although the throughput achieved by the two flows in both categories is the same. In case of topology in Fig. 8 a, interference interaction AB is sensing. This means that sender B can sense the channel to be busy during RTS transmission of sender A as shown in Fig. 21. However, signal extension + SIFS interval following RTS transmission is sensed as idle and sender B can initiate its own RTS transmission during this interval, resulting in a collision. Conditional packet loss probability of both flows can be computed by considering this event. Analysis for SSRC category can be used for the purpose with f= ceil((signal extension + SIFS) /σ) =2 and busy period to be equal to T s − DIFS. On the other hand, for topology in Fig. 8 b, interference interaction AB is disconnected. Therefore, RTS frame transmitted by sender A is not sensed as busy period by sender B and vice versa. As a result, the interval f for which the sender B must not transmit for transmission of flow Aa to be successful is given by f= ceil((RTS + SIFS) /σ) =8 as shown in Fig. 22. This results in higher conditional packet loss probability for both flows. However, the RTS and DATA frames transmitted by sender A are not received by sender B as busy period while the CTS and ACK frames transmitted by receiver a are sensed by sender B as busy. Therefore, event of channel being busy as sensed by sender B is twice the transmission event of sender A. The busy interval is equal to CTS = ACK, which is much smaller compared to T s − DIFS. The updated throughput expression becomes
$$ \text{Throughput}=\frac{p_{s}T_{s}}{p_{s}T_{s} + p_{c}T_{c} + p_{I}\sigma + 2p_{s}\text{CTS}} $$
Channel view of RC (scenario I)
Channel view of RC (scenario II)
Figure 23 shows the achievable throughput for the two flows averaged for both topologies. The two flows get almost equal share of throughput. However, the aggregate throughput is lesser than the SC category as well as SSRC category because of higher packet loss probability.
Per flow throughput of RC
Topologies belonging to this category do not have any of the interference interactions as connected. Placement of flow Bb within the carrier sensing range of flow Aa is possible within a large area of carrier sensing range. Therefore, the distances d(A,B),d(a,B),d(A,b), and d(a,b) can be as small as slightly greater than transmission range and as large as exactly equal to carrier sensing range (which is ≈2.7 times the transmission range) or even outside carrier sensing range. The throughput of the two flows under this category is driven by the fact that frames transmitted by an interferer from closer location within carrier sensing range are sensed as busy periods. On the other hand, the frames transmitted by the interferer at relatively distant location within carrier sensing range may cause errors but otherwise can be rejected as interference, without making the channel busy. Keeping this in view, the MAC behavior can be divided into two parts. The first part comprises of region where a node can sense the frame transmission from other node as busy period. The second part comprises of the region where such transmissions cause errors; however, signal strength is not high enough to make channel busy. Empirical analysis shows that area around a sender up to r csr−0.5r tr comprises of the first part while the presence of interfering nodes within the region beyond this threshold form the second part. Significant area of occurrence of the topology in Fig. 10 a exists in the first part. For all remaining topologies belonging to this category, approximately half of the area of occurrence lies within the first part while the remaining half of the occurrence area lies in the second part.
Within near sensing range, the MAC behavior of this category is the same as the MAC behavior of RC category with two differences. First, in case of RC, CTS frame from one receiver is successfully received by the other receiver, which sets the NAV for rest of the transmission. On the other hand, in case of SNC category, CTS is not successfully received, resulting in busy period at other receiver only for the duration of CTS. However, the idle interval of signal extension + SIFS between the four frames (RTS, CTS, DATA, and ACK) is not big enough to allow any successful transmission. Therefore, the entire transmission on one flow results in errors on receiver of alternate flow in case any frame is transmitted by alternate flow. Effectively, this difference in behavior does not affect the throughput. Second, the interval f during which the flow Bb must not have a transmission in order to have a successful transmission on flow Aa varies for different topologies of this category. Similarly, the busy interval and collision interval vary for each topology. The parameters for different topologies are summarized in Table 3. and as such the analysis of RC category remains valid for the first region of SNC category. Once again, the difference in MAC behavior within category does not impact the throughput of the flows. Figure 24 shows analytical and simulated throughput. The two flows achieve nearly equal throughput while a perfect match can be observed between simulated and analytical results.
Per flow throughput of SNC (near)
Table 3 Parameters (SNC computation)
The impact of interference from far sensing range on throughput of the flows can be estimated by considering the received signal strength, its impact on bit error rate and packet error rate. Ideal channel conditions are assumed where the only factor affecting the unsuccessful reception of frame is the interference from the other flow. Although extremely simplifying, even under this assumption, throughput of the two flows can be predicted accurately. This assumption allows the computation of packet error probability for RTS frame. Near sensing range analysis is used as basis while the conditional packet loss probability and busy probability of the flows are adjusted by the packet error probability to achieve the throughput of the two flows that interfere from within far sensing range.
Friis transmission equation [22] is used to compute the received signal strength from the intended transmitter and the interfering transmitter at the receiver. Ratio of signal received from intended sender and the interfering transmitter gives the signal-to-noise ratio (SNR). SNR can be used to get bit error rate using well-known BER curves and eventually packet error probability using the size of RTS frame. The packet error probability decreases exponentially from distance r csr−0.5r tr to r csr with the values at two boundaries to be 0.97 and 0.03, respectively. Throughput of the flows for 512 bytes of packet size as a function of distance d(A,B) is shown in Fig. 25. Empirical values have also been plotted at selective points. It can be seen that the throughput exponentially increase within the plotted range, starting from minimum value equivalent to near sensing range and ending at near independent throughput for two flows.
Per flow throughput of SNC (far)
Topologies belonging to this category have interference interaction Ab as sensing while the interference interaction aB is disconnected. Like ASRC category, asymmetric channel view of the two flows results in imbalance among achievable throughput with one flow Aa getting dominant portion of channel capacity while the other flow Bb getting negligible throughput. Similar to SNC category, the distance between nodes of two flows affects the achievable throughput. The MAC behavior of the category predicts the initial throughput of the two flows at minimum possible distance. With the increasing distance, the impact of one flow on the other is mitigated, gradually making two flows independent of each other. For the throughput computation, the MAC behavior is defined first and the throughput of the two flows is computed. Subsequently, the results because of the SNR-based adjustments to the behavior are reported, similar to SNC category.
For the analysis purposes, interference interaction Ab is considered as sensing while the interference interaction aB is considered to be disconnected. The conditional packet loss probability of flow Bb can be computed by considering the interval during which RTS transmission from B will be received successfully by b. This interval is given by D+i σ where D= signal extension + DIFS and i is the average number of back-off slots. There is a difference between MAC behavior of the topologies. For topologies in Fig. 13 a, b, sender A can sense RTS transmission from sender B; therefore, B only needs to initiate the RTS transmission within the specified interval for its transmission to be successful. On the other hand, for topologies in Fig. 13 c, d, Senders A and B are outside the sensing range; therefore, sender B must complete the transmission of the entire RTS frame during the specified interval for the transmission to be successful. For the later case, D is updated to D= signal extension + DIFS − RTS. Given the value of the interval, Eq. 11 can be used to compute the conditional packet loss probability for flow Bb. The busy probability of two group of topologies also differs. For topologies in Fig. 13 a, b, busy probability b B =τ A because of the fact that B can sense the transmissions of A. Busy interval is equal to T s − (SIFS + ACK + DIFS). On the other hand, busy probability of flow Bb for topologies in Fig. 13 c, d is zero. Throughput of flow Bb can be computed in terms of all known parameters using Eq. 10, provided the value of τ A is known.
To compute the throughput of flow Aa, the probabilities p A ,b A and the interval T b are required. For topologies in Fig. 13 a, b, a collision on flow Aa occurs when sender B starts a transmission following the RTS frame transmission by sender A. In this case, the channel is sensed idle by sender B for the interval 2signal extension + 2SIFS + CTS because B is outside carrier sensing range of a. A transmission attempt by B results in collision at A if RTS is transmitted by B within interval signal extension + SIFS + CTS. Markov model used to compute conditional packet loss probability for ASRC category can be used to compute p A with f= ceil((signal extension + SIFS + CTS) /σ) as shown in Fig. 26. Busy probability b A is computed as a function of throughput of flow Bb using Eq. 12. Busy interval for these topologies is given by T s −DIFS. Equation 10 can be used to compute the throughput of flow Aa using all known parameters.
ANC channel view (scenario II)
In case of topologies in Fig. 13 c, d, conditional packet loss probability is zero, resulting in τ A =2/(W+1). Successful transmissions on flow Bb result in busy intervals for sender A when receiver b transmits CTS/ACK frames. Therefore, busy probability b A =2τ B and busy interval are equal to CTS /ACK. With all known parameters, throughput can be computed using Eq. 10. Figure 27 shows the analytical and simulated results for throughput of the two flows for two different types of topologies. It can be noted that although the MAC behavior is slightly different, there is not much difference in achieved throughput for two types. The imbalance between the throughput of the two flows is also obvious from the results.
ANC per flow throughput
With the throughput values at near sensing range available, the distance and SNR-based analysis similar to SNC category is applied for computation of throughput of the two flows with increasing distance. Figure 28 shows the achievable throughput as a function of distance between sender A and receiver b for packet size of 512 bytes. It can again be observed that although the analysis technique is based on simplifying assumption, the predicted throughput closely matches the simulated results.
Per flow throughput for ANC with increasing distance d(A,b)
This work has investigated the MAC behavior of two single hop IEEE 802.11 standard-based interfering flows. All possible two-flow topologies have been identified using realistic transmission and carrier sensing ranges. The identified categories have been divided into six categories based on the MAC behavior as well as geographic placement of the four interfering nodes. Closed-form expressions for occurrence probabilities of all identified categories have been computed to show that all categories have significant probability of occurrence in a general multi-hop wireless network. MAC behavior of each category is thoroughly discussed with the key observation that the presence of interfering nodes within the carrier sensing range has significant impact on the behavior and the throughput of five out of six identified categories. Based on the MAC behavior, extensive throughput computations are performed for both flows under each category. This work completes the research efforts towards defining the MAC behavior of two-flow topologies and its impact on the throughput of links. The work can be extended to general capacity analysis of multi-hop wireless networks and can serve as the basis for modified MAC protocol that can better mitigate the impact of interference, specifically the interference from within carrier sensing range.
P Gupta, PR Kumar, The capacity of wireless networks. Inform. Theory IEEE Trans.46(2), 388–404 (2000).
J Tang, G Xue, W Zhang, in Proceedings of the 6th ACM International Symposium on Mobile Ad Hoc Networking and Computing. Interference-aware topology control and qos routing in multi-channel wireless mesh networks (ACM, 2005), pp. 68–77.
L Qiu, Y Zhang, F Wang, MK Han, R Mahajan, in Proceedings of the 13th Annual ACM International Conference on Mobile Computing and Networking. A general model of wireless interference (ACM, 2007), pp. 171–182.
K Medepalli, FA Tobagi, in Proceedings IEEE INFOCOM 2006. 25TH IEEE International Conference on Computer Communications. Towards performance modeling of IEEE 802.11 based wireless networks: a unified framework and its applications, (2006).
M Garetto, J Shi, EW Knightly, in Proceedings of the 11th Annual International Conference on Mobile Computing and Networking. Modeling media access in embedded two-flow topologies of multi-hop wireless networks (ACM, 2005), pp. 200–214.
M Garetto, T Salonidis, EW Knightly, Modeling per-flow throughput and capturing starvation in CSMA multi-hop wireless networks. IEEE/ACM Trans. Netw. (TON). 16(4), 864–877 (2008).
S Razak, V Kolar, NB Abu-Ghazaleh, Modeling and analysis of two-flow interactions in wireless networks. Ad Hoc Netw.8(6), 564–581 (2010).
S Razak, NB Abu-Ghazaleh, in Ad-hoc, Mobile and Wireless Networks. Self-interference in multi-hop wireless chains: geometric analysis and performance study (SpringerBerlin Heidelberg, 2008), pp. 58–71.
RR Boorstyn, A Kershenbaum, B Maglaris, V Sahin, Throughput analysis in multihop CSMA packet radio networks. Commun. IEEE Trans.35(3), 267–274 (1987).
G Bianchi, Performance analysis of the IEEE 802.11 distributed coordination function. Selected Areas Commun. IEEE J.18(3), 535–547 (2000).
F Tobagi, L Kleinrock, Packet switching in radio channels. Part II–the hidden terminal problem in carrier sense multiple-access and the busy-tone solution. Commun. IEEE Trans.23(12), 1417–1433 (1975).
G Alfano, M Garetto, E Leonardi, in INFOCOM, 2011 Proceedings IEEE. New insights into the stochastic geometry analysis of dense CSMA networks (IEEE, 2011), pp. 2642–2650.
M Li, H Liu, H Tan, M Yang, Performance and interference analysis of 802.11g wireless network. Int. J. Wirel. Mob. Netw. (IJWMN), 165–177 (2013).
M Dinitz, in INFOCOM, 2010 Proceedings IEEE. Distributed algorithms for approximating wireless network capacity (IEEE, 2010), pp. 1–9.
S Kawade, TG Hodgkinson, V Abhayawardhana, in Vehicular Technology Conference, 2007. VTC-2007 Fall. 2007 IEEE 66th. Interference analysis of 802.11 b and 802.11 g wireless systems (IEEE, 2007), pp. 787–791.
S Kawade, TG Hodgkinson, in Vehicular Technology Conference, 2008. VTC Spring 2008. IEEE. Analysis of interference effects between co-existent 802.11 b and 802.11 g wi-fi systems (IEEE, 2008), pp. 1881–1885.
S Weber, JG Andrews, N Jindal, An overview of the transmission capacity of wireless networks. Commun. IEEE Trans.58(12), 3593–3604 (2010).
L Fu, SC Liew, J Huang, Effective carrier sensing in CSMA networks under cumulative interference. Mobile Comput. IEEE Trans.12(4), 748–760 (2013).
S Vitturi, L Seno, F Tramarin, M Bertocco, On the rate adaptation techniques of ieee 802.11 networks for industrial applications. Ind. Inform. IEEE Trans.9(1), 198–208 (2013).
D Qiao, S Choi, KG Shin, Interference analysis and transmit power control in IEEE 802.11 a/h wireless lans. IEEE/ACM Trans. Netw. (TON). 15(5), 1007–1020 (2007).
A Kumar, E Altman, D Miorandi, M Goyal, in INFOCOM 2005. 24th Annual Joint Conference of the IEEE Computer and Communications Societies. Proceedings IEEE, 3. New insights from a fixed point analysis of single cell IEEE 802.11 wlans (IEEE, 2005), pp. 1550–1561.
Wikipedia contributors, "Friis transmission equation," Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/w/index.php?title=Friis_transmission_equation&oldid=672456199 (Accessed 29 January 2016).
National University of Science and Technology (NUST), H-12, Islamabad, Pakistan
Muhammad Zeeshan
& Anjum Naveed
Search for Muhammad Zeeshan in:
Search for Anjum Naveed in:
Correspondence to Muhammad Zeeshan.
The authors declare that we have competing interests with the following; Dr Saquib Razak, Assistant Teaching Professor, Computer Science, email address: [email protected].
Open Access Thisarticle is distributed under the terms of the Creative Commons Attribution 4.0 International License(http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Zeeshan, M., Naveed, A. Medium access behavior analysis of two-flow topologies in IEEE 802.11 wireless networks. J Wireless Com Network 2016, 42 (2016). https://doi.org/10.1186/s13638-016-0535-2
Multiple access interference
Two-flow interference analysis | CommonCrawl |
Difference between revisions of "Bootstrap method"
From Encyclopedia of Mathematics
127.0.0.1 (talk)
(Importing text file)
Leonard Huang (talk | contribs)
m (Completed rendering of article in TeX.)
A computer-intensive "resampling" method, introduced in statistics by B. Efron in 1979 [[#References|[a3]]] for estimating the variability of statistical quantities and for setting confidence regions (cf. also [[Sample|Sample]]; [[Confidence set|Confidence set]]). The name "bootstrap" refers to the analogy with pulling oneself up by one's own bootstraps. Efron's bootstrap is to resample the data. Given observations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b1203801.png" />, artificial bootstrap samples are drawn with replacement from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b1203802.png" />, putting equal probability mass <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b1203803.png" /> at each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b1203804.png" />. For example, with sample size <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b1203805.png" /> and distinct observations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b1203806.png" /> one might obtain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b1203807.png" /> as bootstrap (re)sample. In fact, there are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b1203808.png" /> distinct bootstrap samples in this case.
A computer-intensive '''re-sampling''' method, introduced in statistics by B. Efron in 1979 ([[#References|[a3]]]) for estimating the variability of statistical quantities and for setting [[Confidence set|confidence regions]] (cf. also [[Sample|sample]]). The name 'bootstrap' refers to the analogy of pulling oneself up by one's own bootstraps. Efron's bootstrap is to re-sample the data. Given observations $ X_{1},\ldots,X_{n} $, artificial bootstrap samples are drawn with replacement from $ X_{1},\ldots,X_{n} $, putting an equal probability mass of $ \dfrac{1}{n} $ on $ X_{i} $ for each $ i \in \{ 1,\ldots,n \} $. For example, with a sample size of $ n = 5 $ and distinct observations $ X_{1},X_{2},X_{3},X_{4},X_{5} $, one might obtain $ X_{3},X_{3},X_{1},X_{5},X_{4} $ as a bootstrap sample. In fact, there are $ 126 $ distinct bootstrap samples in this case.
A more formal description of Efron's non-parametric bootstrap in a simple setting is as follows. Suppose <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b1203809.png" /> is a random sample of size <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038010.png" /> from a population with unknown [[Distribution function|distribution function]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038011.png" /> on the real line; i.e. the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038012.png" />'s are assumed to be independent and identically distributed random variables with common distribution function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038013.png" /> (cf. also [[Random variable|Random variable]]). Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038014.png" /> denote a real-valued parameter to be estimated. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038015.png" /> denote an estimate of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038016.png" />, based on the data <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038017.png" /> (cf. also [[Statistical estimation|Statistical estimation]]; [[Statistical estimator|Statistical estimator]]). The object of interest is the [[Probability distribution|probability distribution]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038018.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038019.png" />; i.e.
A more formal description of Efron's non-parametric bootstrap in a simple setting is as follows. Suppose that $ (X_{1},\ldots,X_{n}) $ is a random sample of size $ n $ from a population with an unknown [[Distribution function|distribution function]] $ F_{\theta} $ on the real line, i.e., the $ X_{i} $'s are assumed to be independent and identically-distributed [[Random variable|random variables]] with a common distribution function $ F_{\theta} $ that depends on a real-valued parameter $ \theta $. Let $ T_{n} = {T_{n}}(X_{1},\ldots,X_{n}) $ denote a [[Statistical estimator|statistical estimator]] for $ \theta $, based on the data $ X_{1},\ldots,X_{n} $ (cf. also [[Statistical estimation|statistical estimation]]). The object of interest is then the [[Probability distribution|probability distribution]] $ G_{n} $ of $ \sqrt{n} (T_{n} - \theta) $ defined by
\forall x \in \mathbf{R}: \qquad
{G_{n}}(x) \stackrel{\text{df}}{=} {\mathsf{P}_{\theta}}(\sqrt{n} (T_{n} - \theta) \leq x),
which is the exact distribution function of $ T_{n} $ properly normalized. The scaling factor $ \sqrt{n} $ is a classical one, while the centering of $ T_{n} $ is by the parameter $ \theta $. Here, $ \mathsf{P}_{\theta} $ denotes the probability measure corresponding to $ F_{\theta} $.
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038020.png" /></td> </tr></table>
Efron's non-parametric bootstrap estimator of $ G_{n} $ is now defined by
{G_{n}^{\ast}}(x) \stackrel{\text{df}}{=} {\mathsf{P}_{n}^{\ast}}(\sqrt{n} (T_{n}^{\ast} - \theta_{n}) \leq x).
Here, $ T_{n}^{\ast} = {T_{n}}(X_{1}^{\ast},\ldots,X_{n}^{\ast}) $, where $ (X_{1}^{\ast},\ldots,X_{n}^{\ast}) $ denotes an artificial random sample (the bootstrap sample) from $ \hat{F}_{n} $, the [[Empirical distribution|empirical distribution]] function of the original observations $ (X_{1},\ldots,X_{n}) $, and $ \theta_{n} = \theta \! \left( \hat{F}_{n} \right) $. Note that $ \hat{F}_{n} $ is the random distribution (a step function) that puts a probability mass of $ \dfrac{1}{n} $ on $ X_{i} $ for each $ i \in \{ 1,\ldots,n \} $, sometimes referred to as the '''re-sampling distribution'''; $ \mathsf{P}_{n}^{\ast} $ denotes the probability measure corresponding to $ \hat{F}_{n} $, conditionally given $ \hat{F}_{n} $, i.e., given the observations $ X_{1},\ldots,X_{n} $. Obviously, given the observed values $ X_{1},\ldots,X_{n} $ in the sample, $ \hat{F}_{n} $ is completely known and (at least in principle) $ G_{n}^{\ast} $ is also completely known. One may view $ G_{n}^{\ast} $ as the empirical counterpart in the 'bootstrap world' to $ G_{n} $ in the 'real world'. In practice, an exact computation of $ G_{n}^{\ast} $ is usually impossible (for a sample $ X_{1},\ldots,X_{n} $ of $ n $ distinct numbers, there are $ \displaystyle \binom{2 n - 1}{2 n} $ distinct bootstrap samples), but $ G_{n}^{\ast} $ can be approximated by means of [[Monte-Carlo method|Monte-Carlo simulation]]. Efficient bootstrap simulation is discussed, for example, in [[#References|[a2]]] and [[#References|[a10]]].
for all real <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038021.png" />, the exact distribution function of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038022.png" />, properly normalized. The scaling factor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038023.png" /> is a classical one, while the centring of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038024.png" /> is by the parameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038025.png" />. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038026.png" /> denotes "probability" corresponding to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038027.png" />.
When does Efron's bootstrap work? The consistency of the bootstrap approximation $ G_{n}^{\ast} $, viewed as an estimate of $ G_{n} $ — i.e., one requires
\sup_{x \in \mathbf{R}} \left| {G_{n}}(x) - {G_{n}^{\ast}}(x) \right| \to 0, \quad \text{as} ~ n \to \infty,
to hold in $ \mathsf{P} $-probability — is generally viewed as an absolute prerequisite for Efron's bootstrap to work in the problem at hand. Of course, bootstrap consistency is only a first-order asymptotic result, and the error committed when $ G_{n} $ is estimated by $ G_{n}^{\ast} $ may still be quite large in finite samples. Second-order asymptotics (cf. [[Edgeworth series|Edgeworth series]]) enables one to investigate the speed at which $ \displaystyle \sup_{x \in \mathbf{R}} \left| {G_{n}}(x) - {G_{n}^{\ast}}(x) \right| $ approaches $ 0 $, and also to identify cases where the rate of convergence is faster than $ \dfrac{1}{\sqrt{n}} $ — the classical Berry–Esseen-type rate for the normal approximation. An example in which the bootstrap possesses the beneficial property of being more accurate than the traditional normal approximation is the Student $ t $-statistic and, more generally, Studentized statistics. For this reason, the use of bootstrapped Studentized statistics for setting confidence intervals is strongly advocated in a number of important problems. A general reference is [[#References|[a7]]].
Efron's non-parametric bootstrap estimator of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038028.png" /> is now given by
When does the bootstrap fail? It has been proved in [[#References|[a1]]] that in the case of the mean, Efron's bootstrap fails when $ F $ is the [[Attraction domain of a stable distribution|domain of attraction]] of an $ \alpha $-stable law with $ 0 < \alpha < 2 $. However, by re-sampling from $ \hat{F}_{n} $ with a (smaller) re-sample size $ m $ that satisfies $ m = m(n) \to \infty $ and $ \dfrac{m(n)}{n} \to 0 $, it can be shown that the (modified) bootstrap works. More generally, in recent years, the importance of a proper choice of the re-sampling distribution has become clear (see [[#References|[a5]]], [[#References|[a9]]] and [[#References|[a10]]]).
The bootstrap can be an effective tool in many problems of statistical inference, for example, the construction of a confidence band in non-parametric regression, testing for the number of modes of a density, or the calibration of confidence bounds (see [[#References|[a2]]], [[#References|[a4]]] and [[#References|[a8]]]). Re-sampling methods for dependent data, such as the '''block bootstrap''', is another important topic of recent research (see [[#References|[a2]]] and [[#References|[a6]]]).
for all real <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038030.png" />. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038031.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038032.png" /> denotes an artificial random sample (the bootstrap sample) from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038033.png" />, the [[Empirical distribution|empirical distribution]] function of the original observations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038034.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038035.png" />. Note that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038036.png" /> is the random distribution (a step function) which puts probability mass <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038037.png" /> at each of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038038.png" />'s (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038039.png" />), sometimes referred to as the resampling distribution; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038040.png" /> denotes "probability" corresponding to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038041.png" />, conditionally given <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038042.png" />, i.e. given the observations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038043.png" />. Obviously, given the observed values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038044.png" /> in the sample, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038045.png" /> is completely known and (at least in principle) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038046.png" /> is also completely known. One may view <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038047.png" /> as the empirical counterpart in the "bootstrap world" to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038048.png" /> in the "real world" . In practice, exact computation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038049.png" /> is usually impossible (for a sample <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038050.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038051.png" /> distinct numbers there are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038052.png" /> distinct bootstrap (re)samples), but <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038053.png" /> can be approximated by means of Monte-Carlo simulation (cf. also [[Monte-Carlo method|Monte-Carlo method]]). Efficient bootstrap simulation is discussed e.g. in [[#References|[a2]]], [[#References|[a10]]].
====References====
When does Efron's bootstrap work? The consistency of the bootstrap approximation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038054.png" />, viewed as an estimate of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038055.png" />, i.e. one requires
to hold, in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038057.png" />-probability, is generally viewed as an absolute prerequisite for Efron's bootstrap to work in the problem at hand. Of course, bootstrap consistency is only a first-order asymptotic result and the error committed when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038058.png" /> is estimated by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038059.png" /> may still be quite large in finite samples. Second-order asymptotics (Edgeworth expansions; cf. also [[Edgeworth series|Edgeworth series]]) enables one to investigate the speed at which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038060.png" /> approaches zero, and also to identify cases where the rate of convergence is faster than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038061.png" />, the classical Berry–Esseen-type rate for the normal approximation. An example in which the bootstrap possesses the beneficial property of being more accurate than the traditional normal approximation is the Student <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038063.png" />-statistic and more generally Studentized statistics. For this reason the use of bootstrapped Studentized statistics for setting confidence intervals is strongly advocated in a number of important problems. A general reference is [[#References|[a7]]].
<TR><TD valign="top">[a1]</TD><TD valign="top">
When does the bootstrap fail? It has been proved [[#References|[a1]]] that in the case of the mean, Efron's bootstrap fails when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038064.png" /> is the domain of attraction of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038065.png" />-stable law with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038066.png" /> (cf. also [[Attraction domain of a stable distribution|Attraction domain of a stable distribution]]). However, by resampling from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038067.png" />, with (smaller) resample size <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038068.png" />, satisfying <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038069.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120380/b12038070.png" />, it can be shown that the (modified) bootstrap works. More generally, in recent years the importance of a proper choice of the resampling distribution has become clear, see e.g. [[#References|[a5]]], [[#References|[a9]]], [[#References|[a10]]].
K.B. Athreya, "Bootstrap of the mean in the infinite variance case", ''Ann. Statist.'', '''15''' (1987), pp. 724–731.</TD></TR>
The bootstrap can be an effective tool in many problems of statistical inference; e.g. the construction of a confidence band in non-parametric regression, testing for the number of modes of a density, or the calibration of confidence bounds, see e.g. [[#References|[a2]]], [[#References|[a4]]], [[#References|[a8]]]. Resampling methods for dependent data, such as the "block bootstrap" , is another important topic of recent research, see e.g. [[#References|[a2]]], [[#References|[a6]]].
A.C. Davison, D.V. Hinkley, "Bootstrap methods and their application", Cambridge Univ. Press (1997).</TD></TR>
B. Efron, "Bootstrap methods: another look at the jackknife", ''Ann. Statist.'', '''7''' (1979), pp. 1–26.</TD></TR>
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> K.B. Athreya, "Bootstrap of the mean in the infinite variance case" ''Ann. Statist.'' , '''15''' (1987) pp. 724–731</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A.C. Davison, D.V. Hinkley, "Bootstrap methods and their application" , Cambridge Univ. Press (1997)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> B. Efron, "Bootstrap methods: another look at the jackknife" ''Ann. Statist.'' , '''7''' (1979) pp. 1–26</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> B. Efron, R.J. Tibshirani, "An introduction to the bootstrap" , Chapman&Hall (1993)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> E. Giné, "Lectures on some aspects of the bootstrap" P. Bernard (ed.) , ''Ecole d'Eté de Probab. Saint Flour XXVI-1996'' , ''Lecture Notes Math.'' , '''1665''' , Springer (1997)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> F. Götze, H.R. Künsch, "Second order correctness of the blockwise bootstrap for stationary observations" ''Ann. Statist.'' , '''24''' (1996) pp. 1914–1933</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> P. Hall, "The bootstrap and Edgeworth expansion" , Springer (1992)</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> E. Mammen, "When does bootstrap work? Asymptotic results and simulations" , ''Lecture Notes Statist.'' , '''77''' , Springer (1992)</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> H. Putter, W.R. van Zwet, "Resampling: consistency of substitution estimators" ''Ann. Statist.'' , '''24''' (1996) pp. 2297–2318</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> J. Shao, D. Tu, "The jackknife and bootstrap" , Springer (1995)</TD></TR></table>
B. Efron, R.J. Tibshirani, "An introduction to the bootstrap", Chapman&Hall (1993).</TD></TR>
<TR><TD valign="top">[a5]</TD> <TD valign="top">
E. Giné, "Lectures on some aspects of the bootstrap", P. Bernard (ed.), ''Ecole d'Eté de Probab. Saint Flour XXVI-1996'', ''Lecture Notes Math.'', '''1665''', Springer (1997).</TD></TR>
F. Götze, H.R. Künsch, "Second order correctness of the blockwise bootstrap for stationary observations", ''Ann. Statist.'', '''24''' (1996), pp. 1914–1933.</TD></TR>
P. Hall, "The bootstrap and Edgeworth expansion", Springer (1992).</TD></TR>
E. Mammen, "When does bootstrap work? Asymptotic results and simulations", ''Lecture Notes Statist.'', '''77''', Springer (1992).</TD></TR>
H. Putter, W.R. van Zwet, "Resampling: consistency of substitution estimators", ''Ann. Statist.'', '''24''' (1996), pp. 2297–2318.</TD></TR>
<TR><TD valign="top">[a10]</TD> <TD valign="top">
J. Shao, D. Tu, "The jackknife and bootstrap", Springer (1995).</TD></TR>
A computer-intensive re-sampling method, introduced in statistics by B. Efron in 1979 ([a3]) for estimating the variability of statistical quantities and for setting confidence regions (cf. also sample). The name 'bootstrap' refers to the analogy of pulling oneself up by one's own bootstraps. Efron's bootstrap is to re-sample the data. Given observations $ X_{1},\ldots,X_{n} $, artificial bootstrap samples are drawn with replacement from $ X_{1},\ldots,X_{n} $, putting an equal probability mass of $ \dfrac{1}{n} $ on $ X_{i} $ for each $ i \in \{ 1,\ldots,n \} $. For example, with a sample size of $ n = 5 $ and distinct observations $ X_{1},X_{2},X_{3},X_{4},X_{5} $, one might obtain $ X_{3},X_{3},X_{1},X_{5},X_{4} $ as a bootstrap sample. In fact, there are $ 126 $ distinct bootstrap samples in this case.
A more formal description of Efron's non-parametric bootstrap in a simple setting is as follows. Suppose that $ (X_{1},\ldots,X_{n}) $ is a random sample of size $ n $ from a population with an unknown distribution function $ F_{\theta} $ on the real line, i.e., the $ X_{i} $'s are assumed to be independent and identically-distributed random variables with a common distribution function $ F_{\theta} $ that depends on a real-valued parameter $ \theta $. Let $ T_{n} = {T_{n}}(X_{1},\ldots,X_{n}) $ denote a statistical estimator for $ \theta $, based on the data $ X_{1},\ldots,X_{n} $ (cf. also statistical estimation). The object of interest is then the probability distribution $ G_{n} $ of $ \sqrt{n} (T_{n} - \theta) $ defined by $$ \forall x \in \mathbf{R}: \qquad {G_{n}}(x) \stackrel{\text{df}}{=} {\mathsf{P}_{\theta}}(\sqrt{n} (T_{n} - \theta) \leq x), $$ which is the exact distribution function of $ T_{n} $ properly normalized. The scaling factor $ \sqrt{n} $ is a classical one, while the centering of $ T_{n} $ is by the parameter $ \theta $. Here, $ \mathsf{P}_{\theta} $ denotes the probability measure corresponding to $ F_{\theta} $.
Efron's non-parametric bootstrap estimator of $ G_{n} $ is now defined by $$ \forall x \in \mathbf{R}: \qquad {G_{n}^{\ast}}(x) \stackrel{\text{df}}{=} {\mathsf{P}_{n}^{\ast}}(\sqrt{n} (T_{n}^{\ast} - \theta_{n}) \leq x). $$ Here, $ T_{n}^{\ast} = {T_{n}}(X_{1}^{\ast},\ldots,X_{n}^{\ast}) $, where $ (X_{1}^{\ast},\ldots,X_{n}^{\ast}) $ denotes an artificial random sample (the bootstrap sample) from $ \hat{F}_{n} $, the empirical distribution function of the original observations $ (X_{1},\ldots,X_{n}) $, and $ \theta_{n} = \theta \! \left( \hat{F}_{n} \right) $. Note that $ \hat{F}_{n} $ is the random distribution (a step function) that puts a probability mass of $ \dfrac{1}{n} $ on $ X_{i} $ for each $ i \in \{ 1,\ldots,n \} $, sometimes referred to as the re-sampling distribution; $ \mathsf{P}_{n}^{\ast} $ denotes the probability measure corresponding to $ \hat{F}_{n} $, conditionally given $ \hat{F}_{n} $, i.e., given the observations $ X_{1},\ldots,X_{n} $. Obviously, given the observed values $ X_{1},\ldots,X_{n} $ in the sample, $ \hat{F}_{n} $ is completely known and (at least in principle) $ G_{n}^{\ast} $ is also completely known. One may view $ G_{n}^{\ast} $ as the empirical counterpart in the 'bootstrap world' to $ G_{n} $ in the 'real world'. In practice, an exact computation of $ G_{n}^{\ast} $ is usually impossible (for a sample $ X_{1},\ldots,X_{n} $ of $ n $ distinct numbers, there are $ \displaystyle \binom{2 n - 1}{2 n} $ distinct bootstrap samples), but $ G_{n}^{\ast} $ can be approximated by means of Monte-Carlo simulation. Efficient bootstrap simulation is discussed, for example, in [a2] and [a10].
When does Efron's bootstrap work? The consistency of the bootstrap approximation $ G_{n}^{\ast} $, viewed as an estimate of $ G_{n} $ — i.e., one requires $$ \sup_{x \in \mathbf{R}} \left| {G_{n}}(x) - {G_{n}^{\ast}}(x) \right| \to 0, \quad \text{as} ~ n \to \infty, $$ to hold in $ \mathsf{P} $-probability — is generally viewed as an absolute prerequisite for Efron's bootstrap to work in the problem at hand. Of course, bootstrap consistency is only a first-order asymptotic result, and the error committed when $ G_{n} $ is estimated by $ G_{n}^{\ast} $ may still be quite large in finite samples. Second-order asymptotics (cf. Edgeworth series) enables one to investigate the speed at which $ \displaystyle \sup_{x \in \mathbf{R}} \left| {G_{n}}(x) - {G_{n}^{\ast}}(x) \right| $ approaches $ 0 $, and also to identify cases where the rate of convergence is faster than $ \dfrac{1}{\sqrt{n}} $ — the classical Berry–Esseen-type rate for the normal approximation. An example in which the bootstrap possesses the beneficial property of being more accurate than the traditional normal approximation is the Student $ t $-statistic and, more generally, Studentized statistics. For this reason, the use of bootstrapped Studentized statistics for setting confidence intervals is strongly advocated in a number of important problems. A general reference is [a7].
When does the bootstrap fail? It has been proved in [a1] that in the case of the mean, Efron's bootstrap fails when $ F $ is the domain of attraction of an $ \alpha $-stable law with $ 0 < \alpha < 2 $. However, by re-sampling from $ \hat{F}_{n} $ with a (smaller) re-sample size $ m $ that satisfies $ m = m(n) \to \infty $ and $ \dfrac{m(n)}{n} \to 0 $, it can be shown that the (modified) bootstrap works. More generally, in recent years, the importance of a proper choice of the re-sampling distribution has become clear (see [a5], [a9] and [a10]).
The bootstrap can be an effective tool in many problems of statistical inference, for example, the construction of a confidence band in non-parametric regression, testing for the number of modes of a density, or the calibration of confidence bounds (see [a2], [a4] and [a8]). Re-sampling methods for dependent data, such as the block bootstrap, is another important topic of recent research (see [a2] and [a6]).
[a1] K.B. Athreya, "Bootstrap of the mean in the infinite variance case", Ann. Statist., 15 (1987), pp. 724–731.
[a2] A.C. Davison, D.V. Hinkley, "Bootstrap methods and their application", Cambridge Univ. Press (1997).
[a3] B. Efron, "Bootstrap methods: another look at the jackknife", Ann. Statist., 7 (1979), pp. 1–26.
[a4] B. Efron, R.J. Tibshirani, "An introduction to the bootstrap", Chapman&Hall (1993).
[a5] E. Giné, "Lectures on some aspects of the bootstrap", P. Bernard (ed.), Ecole d'Eté de Probab. Saint Flour XXVI-1996, Lecture Notes Math., 1665, Springer (1997).
[a6] F. Götze, H.R. Künsch, "Second order correctness of the blockwise bootstrap for stationary observations", Ann. Statist., 24 (1996), pp. 1914–1933.
[a7] P. Hall, "The bootstrap and Edgeworth expansion", Springer (1992).
[a8] E. Mammen, "When does bootstrap work? Asymptotic results and simulations", Lecture Notes Statist., 77, Springer (1992).
[a9] H. Putter, W.R. van Zwet, "Resampling: consistency of substitution estimators", Ann. Statist., 24 (1996), pp. 2297–2318.
[a10] J. Shao, D. Tu, "The jackknife and bootstrap", Springer (1995).
How to Cite This Entry:
Bootstrap method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bootstrap_method&oldid=11753
This article was adapted from an original article by Roelof Helmers (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article
Retrieved from "https://encyclopediaofmath.org/index.php?title=Bootstrap_method&oldid=41099" | CommonCrawl |
C. S. Adjiman, Global Optimization Techniques for Process Systems Engineering, 1998.
C. S. Adjiman, I. P. Androulakis, and C. A. Floudas, Global optimization of MINLP problems in process synthesis and design, Computers & Chemical Engineering, vol.21, pp.445-450, 1997.
DOI : 10.1016/S0098-1354(97)87542-4
C. S. Adjiman, I. P. Androulakis, and C. A. Floudas, A global optimization method, ??BB, for general twice-differentiable constrained NLPs???II. Implementation and computational results, Computers & Chemical Engineering, vol.22, issue.9, pp.1159-1179, 1998.
DOI : 10.1016/S0098-1354(98)00218-X
C. S. Adjiman, S. Dallwig, C. A. Floudas, and A. Neumaier, A global optimization method, ??BB, for general twice-differentiable constrained NLPs ??? I. Theoretical advances, Computers & Chemical Engineering, vol.22, issue.9, pp.1137-1158, 1998.
G. Agarwal and D. Kempe, Modularity-maximizing graph communities via mathematical programming, The European Physical Journal B, vol.66, issue.3, pp.409-418, 2008.
DOI : 10.1140/epjb/e2008-00425-1
URL : http://arxiv.org/pdf/0710.2533v3.pdf
F. A. and J. E. Falk, Jointly constrained biconvex programming, Mathematics of Operations Research, vol.8, issue.2, pp.273-286, 1983.
A. Alonso-ayuso, L. F. Escudero, and F. J. Martín-campo, Collision Avoidance in Air Traffic Management: A Mixed-Integer Linear Optimization Approach, IEEE Transactions on Intelligent Transportation Systems, vol.12, issue.1, pp.47-57, 2011.
DOI : 10.1109/TITS.2010.2061971
A. Alonso-ayuso, L. F. Escudero, and F. J. Martín-campo, A mixed 0???1 nonlinear optimization model and algorithmic approach for the collision avoidance in ATM: Velocity changes through a time horizon, Computers and Operations Research, 2012.
DOI : 10.1016/j.cor.2012.03.015
E. D. Andersen, J. Gondzio, C. Meszaros, and X. Xu, Implementation of interior point methods for large scale linear programming, Interior Point Methods in Mathematical Programming, pp.189-252, 1996.
I. P. Androulakis, C. D. Maranas, and C. A. , ?BB: A global optimization method for general constrained nonconvex problems, Journal of Global Optimization, vol.3, issue.3, pp.337-363, 1995.
DOI : 10.1007/BF01099647
M. Aps, The mosek optimization tools version 3.1 (revision 28) Users manual and reference, 2002.
S. Balram, Crude transshipment via floating, production, storage and offloading platforms, 2010.
A. Barabasi and R. Albert, Emergence of scaling in random networks, Science, vol.286, issue.5439, pp.509-512, 1999.
P. Belotti, J. Lee, L. Liberti, F. Margot, and A. Wächter, Branching and bounds tightening techniques for non-convex MINLP. Optimization Methods and Software, pp.597-634, 2009.
M. Benzi, G. Golub, and J. Liesen, Numerical solution of saddle point problems, Acta Numerica, vol.14
DOI : 10.1017/S0962492904000212
M. Benzi and V. Simoncini, On the eigenvalues of a class of saddle point matrices, Numerische Mathematik, vol.103, issue.2, pp.173-196, 2006.
L. Bergamaschi, J. Gondzio, M. Venturin, and G. Zilli, Inexact constraint preconditioners for linear systems arising in interior point methods, Computational Optimization and Applications, vol.5, issue.2-3, pp.137-147, 2007.
L. Bergamaschi, J. Gondzio, and G. Zilli, Preconditioning Indefinite Systems in Interior Point Methods for Optimization, Computational Optimization and Applications, vol.28, issue.2, pp.149-171, 2004.
DOI : 10.1023/B:COAP.0000026882.34332.1b
. Sastry, Decentralized air traffic management systems: performance and fault tolerance Extending the QCR method to general mixed-integer programs, Proceedings of IFAC International Workshop on Motion Control Mathematical Programming, pp.279-284381, 1998.
V. D. Blondel, J. Guillaume, R. Lambiotte, and E. Lefebvre, Fast unfolding of communities in large networks, Journal of Statistical Mechanics: Theory and Experiment, vol.2008, issue.10, 2008.
DOI : 10.1088/1742-5468/2008/10/P10008
D. Bonini, C. Dupré, and G. Granger, How ERASMUS can support an increase in capacity in 2020, Proceedings of the 7th International Conference on Computing, Communications and Control Technologies: CCCT 2009, 2009.
U. Brandes, D. Delling, M. Gaertler, R. Görke, M. Hoefer et al., On Modularity Clustering, IEEE Transactions on Knowledge and Data Engineering, vol.20, issue.2, pp.172-188, 2008.
DOI : 10.1109/TKDE.2007.190689
URL : http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.68.6623
A. Brook, D. Kendrick, and A. Meeraus, GAMS, a user's guide, ACM SIGNUM Newsletter, vol.23, issue.3-4, pp.10-11, 1988.
DOI : 10.1145/58859.58863
S. Cafieri, On the application of iterative solvers to KKT systems in Interior Point methods for Large-Scale Quadratic Programming problems, 2006.
S. Cafieri, Aircraft conflict avoidance: a mixed-integer nonlinear optimization approach, Proceedings of the Global Optimization Workshop (GOW'12), pp.43-46
S. Cafieri and N. Durand, A mixed-integer optimization model for air traffic deconfliction, Proceedings of the Toulouse Global Optimization workshop, 2010.
A. Clauset, M. E. Newman, and C. Moore, Finding community structure in very large networks, Physical Review E, vol.70, issue.6, p.66111, 2004.
DOI : 10.1103/PhysRevE.70.066111
URL : http://arxiv.org/abs/cond-mat/0408187
A. Costa and L. Liberti, Relaxations of Multilinear Convex Envelopes: Dual Is Better Than Primal, Experimental Algorithms (Proceedings of SEA 2012), pp.87-98, 2012.
L. Danon, A. Diaz-guilera, and A. Arenas, The effect of size heterogeneity on community identification in complex networks, Journal of Statistical Mechanics: Theory and Experiment, vol.2006, issue.11, 2006.
H. Dollar and A. Wathen, Incomplete factorization constraint preconditioners for saddle-point matrices. Numerical Analysis Group, 2004.
DOI : 10.1137/04060768x
URL : http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.106.3794
H. S. Dollar and A. J. Wathen, Approximate Factorization Constraint Preconditioners for Saddle-Point Matrices, SIAM Journal on Scientific Computing, vol.27, issue.5, pp.1555-1572, 2006.
O. Du-merle, D. Villeneuve, J. Desrosiers, and P. Hansen, Stabilized column generation, Discrete Mathematics, vol.194, issue.1-3, pp.229-237, 1999.
DOI : 10.1016/S0012-365X(98)00213-1
N. Durand and J. M. Alliot, Optimal resolution of en-route conflict, Proceedings of the Eurocontrol, 1997.
N. Durand and J. M. Alliot, Ant-colony optimization for air traffic conflict resolution, Proceedings of the Eighth USA/Europe Air Traffic Management Research and Development Seminar, 2009.
N. Durand, J. M. Alliot, and F. Medioni, Neural nets trained by genetic algorithms for collision avoidance, Applied Artificial Intelligence, vol.13, issue.3, pp.205-213, 2000.
N. Durand, J. M. Alliot, and J. Noailles, Automatic aircraft conflict resolution using genetic algorithms, Proceedings of the 1996 ACM symposium on Applied Computing , SAC '96, 1996.
DOI : 10.1145/331119.331195
C. Durazzi and V. Ruggiero, Indefinitely preconditioned conjugate gradient method for large sparse equality and inequality constrained quadratic problems. Numerical Linear Algebra with Applications, pp.673-688, 2003.
N. Etoundi, T. Labarre, C. Martin, and V. Steyaert, Analyse d'un réseau de transport aérien. Rapport final, 2010.
C. A. Floudas, Deterministic Global Optimization: Theory, Methods and Applications . Nonconvex Optimization and Its Applications, 1999.
DOI : 10.1007/978-1-4757-4949-6
C. A. Floudas, Global optimization in design and control of chemical process systems, Journal of Process Control, vol.10, issue.2-3, pp.125-134, 2001.
A. Forsgren, P. E. Gill, and J. D. Griffin, Iterative Solution of Augmented Systems Arising in Interior Methods, SIAM Journal on Optimization, vol.18, issue.2, pp.666-690, 2007.
DOI : 10.1137/060650210
A. Forsgren, P. E. Gill, and J. R. Shinnerl, Stability of Symmetric Ill-Conditioned Systems Arising in Interior Methods for Constrained Optimization, SIAM Journal on Matrix Analysis and Applications, vol.17, issue.1, pp.187-211, 1996.
S. Fortunato, Community detection in graphs, Physics Reports, vol.486, issue.3-5, pp.75-174, 2010.
DOI : 10.1016/j.physrep.2009.11.002
S. Fortunato and M. Barthelemy, Resolution limit in community detection, Proceedings of the National Academy of Sciences, vol.104, issue.1, pp.36-41, 2007.
DOI : 10.1073/pnas.0605965104
R. Fourer, D. Gay, A. The, ]. A. Book49, H. Fügenschuh et al., Mixed-integer nonlinear problems in transportation applications, Proceedings of the 2nd International Conference on Engineering Optimization, 2002.
M. R. Garey and D. S. Johnson, Computers and Intractability: A Guide to the Theory of NP-Completeness, 1979.
E. M. Gertz and S. J. Wright, Object-Oriented Software for Quadratic Pro- gramming
M. Girvan and M. Newman, Community structure in social and biological networks, Proceedings of the National Academy of Sciences, pp.997821-7826, 2002.
DOI : 10.1073/pnas.122653799
G. H. Golub and A. J. Wathen, An Iteration for Indefinite Systems and Its Application to the Navier--Stokes Equations, SIAM Journal on Scientific Computing, vol.19, issue.2, pp.530-539, 1998.
DOI : 10.1137/S106482759529382X
J. Gondzio, Interior point methods 25 years later, European Journal of Operational Research, vol.218, issue.3, pp.587-601, 2011.
DOI : 10.1016/j.ejor.2011.09.017
B. H. Good, Y. De-montjoye, and A. Clauset, Performance of modularity maximization in practical contexts, Physical Review E, vol.81, issue.4, p.46106, 2010.
C. E. Gounaris and C. A. Floudas, Tight convex underestimators for $${\mathcal{C}^2}$$ -continuous problems: II. multivariate functions, Journal of Global Optimization, vol.23, issue.1, pp.69-89, 2008.
C. E. Gounaris and C. A. Floudas, Tight convex underestimators for $${{\mathcal C}^2}$$ -continuous problems: I. univariate functions, Journal of Global Optimization, vol.93, issue.1, pp.51-67, 2008.
G. Granger and N. Durand, A traffic complexity approach through cluster analysis, Proceedings of the 5th ATM R&D Seminar, 2003.
M. Grötschel and Y. Wakabayashi, A cutting plane algorithm for a clustering problem, Mathematical Programming, vol.7, issue.1-3, pp.59-96, 1989.
M. Grötschel and Y. Wakabayashi, Facets of the clique partitioning polytope, Mathematical Programming, vol.7, issue.1-3, pp.367-387, 1990.
R. Guimerà and A. N. Amaral, Functional cartography of complex metabolic networks, Nature, vol.220, issue.7028, pp.895-900, 2005.
DOI : 10.1038/35075138
R. Guimera, S. Mossa, A. Turtschi, and A. N. Amaral, The worldwide air transportation network: Anomalous centrality, community structure, and cities' global roles, Proc. Natl. Acad. Sci. USA, pp.7794-7799, 2005.
P. Hansen, B. Jaumard, and C. Meyer, A simple enumerative algorithm for unconstrained 0?1 quadratic programming. Les Cahiers du GERAD, 2000.
P. Hansen and N. Mladenovic, Variable neighborhood search: Principles and applications, European Journal of Operational Research, vol.130, issue.3, pp.449-467, 2001.
S. Huang, M. Aydin, and T. A. Lipo, A direct approach to electrical machine performance evaluation: Torque density assessment and sizing optimisation, International Conference on Electrical Machines, p.235, 2002.
B. Jeannet and F. Messine, Extensions of interval branch-and-bound algorithms for mixed global optimization problems with real and categorical variables, Toulouse Global Optimization Workshop, pp.67-70, 2010.
Y. Jiao, F. H. Stillinger, and S. Torquato, Geometrical ambiguity of pair statistics: Point configurations, Physical Review E, vol.81, issue.1, 2009.
J. Kallrath, Solving Planning and Design Problems in the Process Industry Using Mixed Integer and Global Optimization, Annals of Operations Research, vol.122, issue.2, pp.339-373, 2005.
N. Karmarkar, A new polynomial-time algorithm for linear programming, Combinatorica, vol.244, issue.S, pp.373-395, 1984.
C. Keller, N. Gould, and A. Wathen, Constraint Preconditioning for Indefinite Linear Systems, SIAM Journal on Matrix Analysis and Applications, vol.21, issue.4, pp.1300-1317, 2000.
B. W. Kernighan and S. Lin, An efficient heuristic procedure for partitioning graphs. The Bell System Technical Journal, pp.291-307, 1970.
D. E. Knuth, The Stanford GraphBase: A Platform for Combinatorial Computing
J. Kuchar and L. Yang, A review of conflict detection and resolution modeling methods, IEEE Transactions on Intelligent Transportation Systems, vol.1, issue.4, pp.179-189066122, 2000.
DOI : 10.1109/6979.898217
C. Lavor, L. Liberti, N. Maculan, and M. A. Nascimento, Solving Hartree-Fock systems with global optimization methods, Europhysics Letters (EPL), vol.77, issue.5, p.50006, 2007.
DOI : 10.1209/0295-5075/77/50006
R. D. Lazarov and P. S. Vassilevski, Preconditioning saddle-point problems arising from mixed finite element discretizations of elliptic equations. Numerical Linear Algebra with Applications, pp.1-20, 1996.
J. Lee, W. D. Morris, and J. , Geometric comparison of combinatorial polytopes, Discrete Applied Mathematics, vol.55, issue.2, pp.163-182, 1994.
DOI : 10.1016/0166-218X(94)90006-X
A. Letchford and S. Burer, Non-convex mixed-integer nonlinear programming: a survey, Surveys in Operations Research and Management Science, 2012.
L. Liberti, Linearity Embedded in Nonconvex Programs, Journal of Global Optimization, vol.23, issue.5, pp.157-196, 2005.
L. Liberti, Writing Global Optimization Software, Global Optimization: from Theory to Implementation, pp.211-262, 2006.
DOI : 10.1007/0-387-30528-9_8
L. Liberti, Reformulation techniques in mathematical programming, Thèse d'HabilitationàHabilitationà Diriger des Recherches, 2007.
DOI : 10.1016/j.dam.2008.10.016
L. Liberti, Reformulations in Mathematical Programming: Definitions and Systematics, RAIRO - Operations Research, vol.43, issue.1, pp.55-86, 2009.
DOI : 10.1051/ro/2009005
L. Liberti, Reformulations in mathematical programming: automatic symmetry detection and exploitation, Mathematical Programming, vol.174, issue.10, pp.273-304, 2012.
L. Liberti, Symmetry in Mathematical Programming, Mixed Integer Nonlinear Programming, IMA Series
DOI : 10.1007/978-1-4614-1927-3_9
URL : http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.191.589
L. Liberti, C. Lavor, and N. Maculan, A Branch-and-Prune algorithm for the Molecular Distance Geometry Problem, International Transactions in Operational Research, vol.23, issue.13, pp.1-17, 2008.
L. Liberti, C. Lavor, A. Mucherino, and N. Maculan, Molecular distance geometry methods: from continuous to discrete, International Transactions in Operational Research, vol.43, issue.3, pp.33-51, 2010.
L. Liberti and C. Pantelides, An Exact Reformulation Algorithm for Large Nonconvex NLPs Involving Bilinear Terms, Journal of Global Optimization, vol.3, issue.10, pp.161-189, 2006.
L. Liberti and C. C. Pantelides, Convex envelopes of monomials of odd degree, Journal of Global Optimization, vol.25, issue.2, pp.157-168, 2003.
DOI : 10.1023/A:1021924706467
R. Lougee-heimer, The Common Optimization INterface for Operations Research: Promoting open-source software in the operations research community, IBM Journal of Research and Development, vol.47, issue.1, pp.57-66, 2003.
DOI : 10.1147/rd.471.0057
L. Luksan and J. Vlcek, Indefinitely preconditioned inexact Newton method for large sparse equality constrained non-linear programming problems, Numerical Linear Algebra with Applications, vol.3, issue.3, pp.219-247, 1998.
DOI : 10.1002/(SICI)1099-1506(199805/06)5:3<219::AID-NLA134>3.0.CO;2-7
V. Maniezzo, T. Stutzle, and S. Voss, Hybridizing metaheuristics and mathematical programming, 2009.
C. P. Massen and J. P. Doye, Identifying communities within energy landscapes, Physical Review E, vol.71, issue.4, p.46101, 2005.
G. P. Mccormick, Computability of global solutions to factorable nonconvex programs: Part I ??? Convex underestimating problems, Mathematical Programming, pp.146-175, 1976.
DOI : 10.1287/mnsc.17.11.759
A. D. Medus and C. O. Dorso, Alternative approach to community detection in networks, Physical Review E, vol.79, issue.6, p.66111, 2009.
F. Messine, Deterministic global optimization using interval constraint propagation techniques, RAIRO - Operations Research, vol.38, issue.4, pp.277-294, 2004.
DOI : 10.1051/ro:2004026
F. Messine, A Deterministic Global Optimization Algorithm for Design Problems, pp.267-292, 2005.
DOI : 10.1007/0-387-25570-2_10
F. Messine, A Deterministic Global Optimization Algorithm for Design Problems, Essays and Surveys in Global Optimization, pp.267-294, 2005.
F. Messine and B. Nogaréde, Optimal Design of Multi-Airgap Electrical Machines: An Unknown Size Mixed-Constrained Global Optimization Formulation, IEEE Transactions on Magnetics, vol.42, issue.12, pp.3847-3853, 2006.
DOI : 10.1109/TMAG.2006.881100
F. Messine, B. Nogaréde, and J. L. Lagouanelle, Optimal design of electromechanical actuators: a new method based on global optimization, IEEE Transactions on Magnetics, vol.34, issue.1, pp.299-307, 1998.
DOI : 10.1109/20.650361
C. A. Meyer and C. A. Floudas, Trilinear Monomials with Positive or Negative Domains: Facets of the Convex and Concave Envelopes
DOI : 10.1007/978-1-4613-0251-3_18
. Pardalos, Trilinear monomials with mixed sign domains: Facets of the convex and concave envelopes, Frontiers in Global Optimization, pp.327-352125, 2003.
C. A. Meyer and C. A. Floudas, Convex envelopes for edge-concave functions, Mathematical Programming, pp.207-224, 2005.
R. Misener and C. A. Floudas, Global optimization of mixed-integer quadraticallyconstrained quadratic programs (MIQCQP) through piecewise-linear and edgeconcave relaxations, Mathematical Programming B
S. Mizuno, M. Kojima, and M. J. Todd, Infeasible-Interior-Point Primal-Dual Potential-Reduction Algorithms for Linear Programming, SIAM Journal on Optimization, vol.5, issue.1, pp.52-67, 1995.
DOI : 10.1137/0805003
N. Mladenovic and P. Hansen, Variable neighborhood search, Computers & Operations Research, vol.24, issue.11, pp.1097-1100, 1997.
P. Mosses, Denotational Semantics, pp.575-631, 1990.
DOI : 10.1016/B978-0-444-88074-1.50016-0
W. Murray and U. Shanbhag, A Local Relaxation Approach for the Siting of Electrical Substations, Computational Optimization and Applications, vol.33, issue.1, pp.7-49, 2006.
P. Neittaanmki, M. Rudnicki, and A. Savini, Inverse Problems and Optimal Design in Electricity and Magnetism, 1996.
G. L. Nemhauser and L. A. Wolsey, Integer and Combinatorial Optimization, 1988.
DOI : 10.1002/9781118627372
URL : http://dx.doi.org/10.1016/s0898-1221(99)91259-2
M. Newman, Modularity and community structure in networks, Proceedings of the National Academy of Sciences, vol.103, issue.23, pp.8577-8582, 2006.
M. Newman and M. Girvan, Finding and evaluating community structure in networks, Physical Review E, vol.69, issue.2, p.26133, 2004.
M. E. Newman, Finding community structure in networks using the eigenvectors of matrices, Physical Review E, vol.74, issue.3, p.36104, 2006.
M. E. Newman, Networks: an introduction, 2010.
DOI : 10.1093/acprof:oso/9780199206650.001.0001
M. E. Newman, Fast algorithm for detecting community structure in networks, Physical Review E, vol.69, issue.6, p.66133, 2004.
J. Ninin and F. Messine, A mixed affine reformulation method for global optimization, Toulouse Global Optimization Workshop, pp.101-104, 2010.
A. Noack and R. Rotta, Multi-level Algorithms for Modularity Clustering, Lecture Notes in Computer Science, vol.5526, pp.257-268, 2009.
J. Nocedal and S. J. Wright, Numerical Optimization, 1999.
DOI : 10.1007/b98874
B. Nogaréde, A. D. Kone, and M. Lajoie-mazenc, Optimal design of permanentmagnet machines using analytical field modeling, Electromotion, vol.2, issue.1, pp.25-34, 1995.
D. P. Leary, Symbiosis between linear algebra and optimization, Journal of Computational and Applied Mathematics, vol.123, issue.1-2, pp.447-465, 2000.
L. Pallottino, E. Feron, and A. Bicchi, Conflict resolution problems for air traffic management systems solved with mixed integer programming, IEEE Transactions on Intelligent Transportation Systems, vol.3, issue.1, pp.3-11, 2002.
I. Perugia and V. Simoncini, Block-diagonal and indefinite symmetric preconditioners for mixed finite element formulations, Numerical Linear Algebra with Applications, vol.7, issue.7-8, pp.585-616, 2000.
DOI : 10.1002/1099-1506(200010/12)7:7/8<585::AID-NLA214>3.0.CO;2-F
F. Radicchi, C. Castellano, F. Cecconi, V. Loreto, and D. Parisi, Defining and identifying communities in networks, Proceedings of the National Academy of Sciences, vol.101, issue.9, pp.2658-2663, 2004.
L. Rao, W. Yan, and R. He, Mean Field Annealing (MFA) and optimal design of electromagnetic devices, IEEE Transactions on Magnetics, vol.32, pp.1218-1221, 1996.
D. Rey, S. Constans, R. Fondacci, and C. Rapine, A mixed integer linear model for potential conflict minimization by speed modulations, Proceedings of the International Conference on Research in Air Transportation, 2010.
D. Rey, C. Rapine, R. Fondacci, and N. Faouzi, Potential air conflicts minimization through speed regulation [132] A. Rikun. A convex envelope formula for multilinear functions, Transportation Research Board Journal of Global Optimization, vol.10, issue.4, pp.425-437, 1997.
M. Rozloznik and V. Simoncini, Krylov Subspace Methods for Saddle Point Problems with Indefinite Preconditioning, SIAM Journal on Matrix Analysis and Applications, vol.24, issue.2, pp.368-391, 2002.
H. S. Ryoo and N. V. Sahinidis, Global optimization of nonconvex NLPs and MINLPs with applications in process design, Computers & Chemical Engineering, vol.19, issue.5, pp.551-566, 1995.
DOI : 10.1016/0098-1354(94)00097-2
H. S. Ryoo and N. V. Sahinidis, A branch-and-reduce approach to global optimization, Journal of Global Optimization, vol.22, issue.4, pp.107-138, 1996.
P. Schuetz and A. Caflisch, Efficient modularity optimization by multistep greedy algorithm and vertex mover refinement, Physical Review E, vol.77, issue.4, p.46112, 2008.
URL : http://arxiv.org/abs/0712.1163
H. Sherali, E. Dalkiran, and L. Liberti, Reduced RLT representations for nonconvex polynomial programming problems, Journal of Global Optimization, vol.103, issue.1, pp.447-469, 2012.
H. Sherali and C. H. Tuncbilek, A global optimization algorithm for polynomial programming problems using a Reformulation-Linearization Technique, Journal of Global Optimization, vol.3, issue.1, pp.101-112, 1991.
H. Sherali and C. H. Tuncbilek, New reformulation linearization/convexification relaxations for univariate and multivariate polynomial programming problems, Operations Research Letters, vol.21, issue.1, pp.1-9, 1997.
H. D. Sherali, Convex envelopes of multilinear functions over a unit hypercube and over special discrete sets, Acta Mathematica Vietnamica, vol.22, pp.245-270, 1997.
H. D. Sherali, Global optimization of nonconvex polynomial programming problems having rational exponents, Journal of Global Optimization, vol.12, issue.3, pp.267-283, 1998.
H. D. Sherali, Tight Relaxations for Nonconvex Optimization Problems Using the Reformulation-Linearization/Convexification Technique (RLT), Handbook of Global Optimization, pp.1-63
H. D. Sherali and W. P. Adams, A Reformulation-Linearization Technique for Solving Discrete and Continuous Nonconvex Problems, 1999.
H. D. Sherali and A. Alameddine, A new reformulation-linearization technique for bilinear programming problems, Journal of Global Optimization, vol.21, issue.3, pp.379-410, 1992.
H. D. Sherali and H. Wang, Global optimization of nonconvex factorable programming problems, Mathematical Programming, vol.89, issue.3, pp.459-478, 2001.
DOI : 10.1007/PL00011409
G. R. Slemon and X. Liu, Modeling and design optimization of permanent magnet motors. Electric Machines and Power Systems, pp.71-92, 1992.
E. M. Smith, On the Optimal Design of Continuous Processes, 1996.
E. M. Smith and C. C. Pantelides, Global optimisation of nonconvex MINLPs, Computers & Chemical Engineering, vol.21, pp.791-796, 1997.
E. M. Smith and C. C. Pantelides, A symbolic reformulation/spatial branch-and-bound algorithm for the global optimisation of nonconvex MINLPs, Computers & Chemical Engineering, vol.23, issue.4-5, pp.457-478, 1999.
K. Tanabe, Centered newton method for mathematical programming, System Modeling and Optimization: Proceedings of the 13th IFIP Conference, Lecture Notes in Control and Information Systems, pp.197-206
DOI : 10.1007/BFb0042787
F. Tardella, Existence and sum decomposition of vertex polyhedral convex envelopes, Optimization Letters, vol.93, issue.3, pp.363-375, 2008.
F. Tardella, On the existence of polyhedral convex envelopes, Frontiers in Global Optimization, pp.149-188, 2008.
M. Tawarmalani and N. V. Sahinidis, Convex extensions and envelopes of lower semi-continuous functions, Mathematical Programming, pp.247-263, 2002.
DOI : 10.1007/s10107-002-0308-z
M. Tawarmalani and N. V. Sahinidis, Global optimization of mixed-integer nonlinear programs: A theoretical and computational study, Mathematical Programming, pp.563-591, 2004.
M. J. Todd158-]-m, Y. Todd, and . Ye, A centered projective algorithm for linear programming, Potential-Reduction Methods in Mathematical Programming. Mathematical Programming Mathematics of Operations Research, vol.76, issue.15, pp.3-45508, 1990.
C. Tomlin, G. J. Pappas, and S. S. Sastry, Conflict resolution for air traffic management: a study in multiagent hybrid systems, IEEE Transactions on Automatic Control, vol.43, issue.4, pp.509-521, 1998.
H. D. Tuy, D.C. Optimization: Theory, Methods and Algorithms, Handbook of Global Optimization, pp.149-216
F. Vanderbeck and M. W. Savelsbergh, A generic view of Dantzig???Wolfe decomposition in mixed integer programming, Operations Research Letters, vol.34, issue.3, pp.296-306, 2006.
DOI : 10.1016/j.orl.2005.05.009
URL : https://hal.archives-ouvertes.fr/inria-00342623
R. J. Vanderbei, Symmetric Quasidefinite Matrices, SIAM Journal on Optimization, vol.5, issue.1, pp.100-113, 1995.
R. J. Vanderbei, LOQO user's manual ??? version 3.10, Optimization Methods and Software, vol.87, issue.1-4, 1997.
A. Vela, S. Solak, W. Singhose, and J. Clarke, A mixed integer program for flight-level assignment and speed control for conflict resolution, Proceedings of the 48h IEEE Conference on Decision and Control (CDC) held jointly with 2009 28th Chinese Control Conference, 2009.
DOI : 10.1109/CDC.2009.5400520
K. Wakita and T. Tsurumi, Finding community structure in mega-scale social networks, Proceedings of the 16th international conference on World Wide Web , WWW '07, 2007.
DOI : 10.1145/1242572.1242805
J. Wang, Y. Qui, R. Wang, and X. Zhang, Remarks on Network Community Properties, Journal of Systems Science and Complexity, vol.105, issue.23, pp.637-644, 2008.
D. S. Watts and S. H. Strogatz, Collective dynamics of 'small-world' networks, Nature, vol.393, issue.6684, pp.409-410, 1998.
M. H. Wright, Ill-Conditioning and Computational Error in Interior Methods for Nonlinear Programming, SIAM Journal on Optimization, vol.9, issue.1, pp.84-111, 1998.
S. J. Wright, Primal-Dual Interior-Point Methods. SIAM, 1997.
DOI : 10.1137/1.9781611971453
S. J. Wright, Stability of Augmented System Factorizations in Interior-Point Methods, SIAM Journal on Matrix Analysis and Applications, vol.18, issue.1, pp.191-222, 1997.
F. Wurtz, J. Bigeon, and C. Poirson, A methodology and a tool for the computer aided design with constraints of electrical devices, IEEE Transactions on Magnetics, vol.32, issue.3, pp.1429-1432, 1996.
G. Xu, S. Tsoka, and L. G. Papageorgiou, Finding community structures in complex networks using mixed integer optimisation, The European Physical Journal B, vol.579, issue.2, pp.231-239, 2007.
W. W. Zachary, An Information Flow Model for Conflict and Fission in Small Groups, Journal of Anthropological Research, vol.33, issue.4, pp.452-473, 1977.
DOI : 10.1086/jar.33.4.3629752
S. Cafieri, P. Hansen, and L. Liberti, Improving heuristics for network modularity maximization using an exact algorithm, Discrete Applied Mathematics, vol.163, 2012.
S. Cafieri, G. Caporossi, P. Hansen, S. Perron, and A. Costa, Finding communities in networks in the strong and almost-strong sense, Physical Review E, vol.85, issue.4, p.46113, 2012.
S. Cafieri, P. Hansen, and L. Liberti, Locally optimal heuristic for modularity maximization of networks, Physical Review E, vol.83, issue.5, p.56105, 2011.
D. Aloise, S. Cafieri, G. Caporossi, P. Hansen, L. Liberti et al., Column generation algorithms for exact modularity maximization in networks, Physical Review E, vol.82, issue.4, p.46112, 2010.
S. Cafieri, P. Hansen, and L. Liberti, Loops and multiple edges in modularity maximization of networks, Physical Review E, vol.81, issue.4, p.46102, 2010.
S. Cafieri, P. Hansen, and L. Liberti, Edge ratio and community structure in networks, structure in networks, p.26105, 2010.
S. Cafieri, J. Lee, and L. Liberti, On convex relaxations of quadrilinear terms, Journal of Global Optimization, vol.99, issue.2, pp.661-685, 2010.
S. Cafieri, M. Mastromatteo, S. Chillo, and M. A. Del-nobile, Modeling the mechanical properties of pasta cooked at different times, Journal of Food Engineering, vol.100, issue.2, pp.336-342, 2010.
DOI : 10.1016/j.jfoodeng.2010.04.019
S. Cafieri, S. Chillo, M. Mastromatteo, N. Suriano, and M. A. Del-nobile, A mathematical model to predict the effect of shape on pasta hydration kinetic during cooking and overcooking, Journal of Cereal Science, vol.48, issue.3, pp.857-862, 2008.
DOI : 10.1016/j.jcs.2008.06.010
S. Cafieri, M. D. Apuzzo, V. De-simone, D. Di-serafino, and G. Toraldo, Convergence Analysis of an Inexact Potential Reduction Method for Convex Quadratic Programming, Journal of Optimization Theory and Applications, vol.129, issue.1, pp.355-366, 2007.
S. Cafieri, M. D. Apuzzo, V. De-simone, and D. Di-serafino, Stopping criteria for inner iterations in inexact Potential Reduction methods: a computational study, Computational Optimization and Applications, special issue on Linear Algebra issues arising in Interior Point methods
S. Cafieri, M. D. Apuzzo, V. De-simone, and D. Di-serafino, On the Iterative Solution of KKT Systems in Potential Reduction Software for Large Scale Quadratic Problems, Computational Optimization and Applications, special issue on High Performance Algorithms and Software for Nonlinear Optimization, pp.27-45, 2007.
S. Cafieri, M. D. Apuzzo, M. Marino, A. Mucherino, and G. Toraldo, Interior-Point Solver for Large-Scale Quadratic Programming Problems with Bound Constraints, Journal of Optimization Theory and Applications, vol.55, issue.4, pp.55-75, 2006.
S. Cafieri and U. , Graphs and Combinatorial Optimization , special issue of Discrete Applied Mathematics dedicated to the 17, Proceedings of the Toulouse Global Optimization workshop (TOGO10), 2010.
P. Belotti, S. Cafieri, J. Lee, L. Liberti, and A. Miller, On the Composition of Convex Envelopes for Quadrilinear Terms, Proceedings of the International Conference on Optimization, Simulation and Control, Series : Springer Optimization and its Application
L. Cellier, S. Cafieri, and F. Messine, Hybridizing direct and indirect optimal control approaches for aircraft conflict avoidance, Proceedings of ADV- COMP 2012: The Sixth International Conference on Advanced Engineering Computing and Applications in Sciences, pp.42-45, 2012.
S. Cafieri, Aircraft conflict avoidance: A mixed-integer nonlinear optimization approach, Proceedings of Global Optimization Workshop (GOW'12), pp.43-46
S. Cafieri, P. Hansen, L. Létocart, L. Liberti, and F. Messine, Compact Relaxations for Polynomial Programming Problems, Experimental Algorithms (Proceedings of SEA 2012), pp.75-86, 2012.
P. Belotti, S. Cafieri, L. Liberti, and J. Lee, Feasibility-Based Bounds Tightening via Fixed Points, Proceedings of Conference on Combinatorial Optimization and Applications, pp.65-76, 2010.
S. Cafieri, L. Liberti, F. Messine, and B. Nogarede, Discussion about formulations and resolution techniques of electrical machine design problems, The XIX International Conference on Electrical Machines, ICEM 2010, 2010.
DOI : 10.1109/ICELMACH.2010.5607836
S. Cafieri, P. Brisset, and N. Durand, A mixed-integer optimization model for Air Traffic Deconfliction, Proceedings of Toulouse Global Optimization workshop (TOGO) 2010, pp.27-30, 2010.
L. Liberti, S. Cafieri, and D. Savourey, The Reformulation-Optimization Software Engine, International Congress of Mathematical Software (ICMS), pp.303-314, 2010.
S. Cafieri, P. Hansen, and L. Liberti, Improving heuristics for network modularity maximization using an exact algorithm, Discrete Applied Mathematics, vol.163, pp.130-139, 2010.
P. Belotti, S. Cafieri, J. Lee, and L. Liberti, On the convergence of feasibility based bounds tightening, Proceedings of CTW 2010, pp.21-24, 2010.
S. Cafieri, P. Hansen, L. Létocart, L. Liberti, and F. Messine, Reduced RLT constraints for polynomial programming, Proceedings of European Workshop on MINLP 2010, 2010.
S. Cafieri, J. Lee, and L. Liberti, Comparison of convex relaxations of quadrilinear terms Global Optimization: Theory, Methods and Applications I, Lecture Notes in Decision Sciences, vol.12, pp.999-1005, 2009.
S. Cafieri, M. D. Apuzzo, V. De-simone, and D. Di-serafino, ON THE USE OF AN APPROXIMATE CONSTRAINT PRECONDITIONER IN A POTENTIAL REDUCTION ALGORITHM FOR QUADRATIC PROGRAMMING, Applied and Industrial Mathematics in Italy II, 2007.
DOI : 10.1142/9789812709394_0020
L. Cellier, S. Cafieri, and F. Messine, Résolution de conflit aérien par contrôle optimal basé sur la régulation en vitesse, Proceedings of ROADEF 2012, 2012.
S. Cafieri, A. Gondran, and S. U. Ngueveu, Un algorithme mémétique pour construire des trajectoires d'aéronefs robustes aux aléas météorologiques, Proceedings of ROADEF 2012 Proceedings of ROADEF 2012, 2012.
A. Costa, S. Cafieri, and P. Hansen, Reformulation of a locally optimal heuristic for modularity maximization, Proceedings of ROADEF 2012, 2012.
S. Cafieri, P. Hansen, and L. Liberti, Hierarchical clustering for the identification of communities in networks, Proceedings of ROADEF 2011, 2011.
D. Aloise, S. Cafieri, G. Caporossi, P. Hansen, L. Liberti et al., Algorithms for network modularity maximization, Proceedings of ROADEF 2010, 2010.
L. Liberti, S. Cafieri, and J. Lee, Range reduction using fixed points, Proceedings of ROADEF 2010, 2010.
S. Cafieri, J. Lee, and L. Liberti, On convex relaxations of quadrilinear terms, Proceedings of ROADEF 09, 2009.
S. Cafieri, P. Hansen, and L. Liberti, Reformulations between structured global optimization problems and algorithms, Proceedings of ROADEF 09, 2009.
S. Cafieri and N. Durand, Aircraft deconfliction with speed regulation: new models from mixed-integer optimization, Optimization Online preprint n, 2012.
P. Belotti, S. Cafieri, J. Lee, and L. Liberti, On feasibility based bounds tightening, Optimization Online preprint n, 2012.
S. Cafieri, A. Costa, and P. Hansen, Reformulation of a model for hierarchical divisive graph modularity maximization, Optimization Online preprint n, 2011.
A. Mucherino and S. Cafieri, A New Heuristic for Feature Selection by Consistent Biclustering, arXiv e-print, 2010.
S. Cafieri, Ottimizzazione quadratica: algoritmi e software per problemi sparsi, 2001.
@. Euro-xxv-, Aircraft conflict avoidance: a mixed-integer nonlinear optimization approach, European conference on Operations Research, 2012.
@. Gow-', 12 -Global Optimization Workshop Aircraft conflict avoidance: a mixed-integer nonlinear optimization approach, 2012.
@. Afg-', 11 -15th Austrian-French-German conference on Optimization Reduced RLT compact relaxations for polynomial programming, 2011.
@. Lri, U. Paris, and X. , 1 seminar, invited by A. Lisser. Seminar: Convex relaxations in Branch and Bound global optimization methods: quadrilinear terms, 2009.
. Cellier, Hybridizing direct and indirect optimal control approaches for aircraft conflict avoidance, ADVCOMP 2012: The Sixth International Conference on Advanced Engineering Computing and Applications in Sciences, pp.42-45, 2012.
. Cafieri, Locally optimal heuristic for modularity maximization of networks, Physical Review E, vol.83, issue.5, p.56105, 2011.
. Cafieri, Edge ratio and community structure in networks, Physical Review E, vol.81, issue.2, p.26105, 2010.
. Cafieri, Loops and multiple edges in modularity maximization of networks, Physical Review E, vol.81, issue.4, p.46102, 2010.
. Cafieri, On convex relaxations of quadrilinear terms, Journal of Global Optimization, vol.99, issue.2, pp.661-685, 2010.
. Liberti, The Reformulation-Optimization Software Engine, Proceedings of ICMS10, pp.303-314, 2010.
. Liberti, Reformulations in Mathematical Programming: A Computational Approach, Foundations of Computational Intelligence (Global Optimization: Theoretical Foundations and Applications), volume 203 of Studies in Computational Intelligence, pp.153-234, 2009.
. Cafieri, On the iterative solution of KKT systems in potential reduction software for large-scale quadratic problems, Computational Optimization and Applications, vol.18, issue.2, pp.27-45, 2007.
DOI : 10.1007/s10589-007-9035-y
. Cafieri, ON THE USE OF AN APPROXIMATE CONSTRAINT PRECONDITIONER IN A POTENTIAL REDUCTION ALGORITHM FOR QUADRATIC PROGRAMMING, Applied and Industrial Mathematics in Italy II, 2007.
. Cafieri, Stopping criteria for inner iterations in inexact potential reduction methods: a computational study, Computational Optimization and Applications, vol.15, issue.2, pp.165-193, 2007.
. Cafieri, Convergence Analysis of an Inexact Potential Reduction Method for Convex Quadratic Programming, Journal of Optimization Theory and Applications, vol.129, issue.1, pp.355-366, 2007.
. Cafieri, Interior-Point Solver for Large-Scale Quadratic Programming Problems with Bound Constraints, Journal of Optimization Theory and Applications, vol.55, issue.4, pp.55-75, 2006.
A. S. Appendix, J. Cafieri, L. Lee, and . Liberti, On convex relaxations of quadrilinear terms, Journal of Global Optimization, vol.47, pp.661-685, 2010.
S. Cafieri, P. Hansen, L. Létocart, L. Liberti, and F. Messine, Compact Relaxations for Polynomial Programming Problems, Experimental Algorithms (Proceedings of SEA 2012) | CommonCrawl |
Loss of derivatives for hyperbolic boundary problems with constant coefficients
DCDS-B Home
Squeezing and finite dimensionality of cocycle attractors for 2D stochastic Navier-Stokes equation with non-autonomous forcing
May 2018, 23(3): 1325-1345. doi: 10.3934/dcdsb.2018153
Global stabilization of the Navier-Stokes-Voight and the damped nonlinear wave equations by finite number of feedback controllers
Varga K. Kalantarov 1,2,, and Edriss S. Titi 3,4,
Department of mathematics, Koç University, Rumelifeneri Yolu, Sariyer 34450, Istanbul, Turkey
Institute of Matematics and Mechanics, National Academy of Sciences of Azerbaijan, Baku, Azerbaijan
Department of Mathematics, Texas AM University, 3368 TAMU, College Station, TX 77843-3368, USA
Department of Computer Science and Applied Mathematics, Weizmann Institute of Science, Rehovot 76100, Israel
* Corresponding author: V. K. Kalantarov
Received May 2017 Revised July 2017 Published February 2018
Fund Project: V.K.Kalantarov would like to thank the Weizmann Institute of Science for the generous hospitality during which this work was initiated. E.S.Titi would like to thank the ICERM, Brown University, for the warm and kind hospitality where this work was completed. The work of E.S.Titi was supported in part by the ONR grant N00014-15-1-2333
In this paper we introduce a finite-parameters feedback control algorithm for stabilizing solutions of the Navier-Stokes-Voigt equations, the strongly damped nonlinear wave equations and the nonlinear wave equation with nonlinear damping term, the Benjamin-Bona-Mahony-Burgers equation and the KdV-Burgers equation. This algorithm capitalizes on the fact that such infinite-dimensional dissipative dynamical systems posses finite-dimensional long-time behavior which is represented by, for instance, the finitely many determining parameters of their long-time dynamics, such as determining Fourier modes, determining volume elements, determining nodes, etc..The algorithm utilizes these finite parameters in the form of feedback control to stabilize the relevant solutions. For the sake of clarity, and in order to fix ideas, we focus in this work on the case of low Fourier modes feedback controller, however, our results and tools are equally valid for using other feedback controllers employing other spatial coarse mesh interpolants.
Keywords: Damped wave equation, Navier-Stokes equations, strongly damped wave equation, feedback control, stabilization, finite number feedback controllers.
Mathematics Subject Classification: Primary: 35B40; Secondary: 35B41, 35Q35.
Citation: Varga K. Kalantarov, Edriss S. Titi. Global stabilization of the Navier-Stokes-Voight and the damped nonlinear wave equations by finite number of feedback controllers. Discrete & Continuous Dynamical Systems - B, 2018, 23 (3) : 1325-1345. doi: 10.3934/dcdsb.2018153
A. Azouani and E. S. Titi, Feedback control of nonlinear dissipative systems by finite determining parameters -a reaction-diffusion paradigm, Evolution Equations and Control Theory, 3 (2014), 579-594. doi: 10.3934/eect.2014.3.579. Google Scholar
A. V. Babin and M. I. Vishik, Attractors of Evolutionary Partial Differential Equations, North -Holland, Amsterdam, London, NewYork, Tokyo, 1992. Google Scholar
M. J. Balas, Feedback control of dissipative hyperbolic distributed parameter systems with finite-dimensional controllers, J. Math. Anal. Appl., 98 (1984), 1-24. doi: 10.1016/0022-247X(84)90275-0. Google Scholar
J. M. Ball and M. Slemrod, Feedback stabilization of distributed semilinear control systems, Appl. Math. Optim., 5 (1979), 169-179. doi: 10.1007/BF01442552. Google Scholar
V. Barbu, Stabilization of Navier-Stokes equation, Control and Stabilization of Partial Differential Equations, 1-50, Sémin. Congr., 29, Soc. Math. France, Paris, 2015. Google Scholar
V. Barbu, The internal stabilization of the Stokes-Oseen equation by feedback point controllers, Systems Control Lett., 62 (2013), 447-450. doi: 10.1016/j.sysconle.2013.02.009. Google Scholar
V. Barbu and R. Triggiani, Internal stabilization of Navier-Stokes equations with finite-dimensional controllers, Indiana Univ. Math. J., 53 (2004), 1443-1494. doi: 10.1512/iumj.2004.53.2445. Google Scholar
V. Barbu and G. Wang, Internal stabilization of semilinear parabolic systems, J. Math. Anal. Appl., 285 (2003), 387-407. Google Scholar
G. Bastin and J. -M. Coron, Stability and Boundary Stabilization of 1-D Hyperbolic Systems, Progress in Nonlinear Differential Equations and their Applications, 88. Subseries in Control. Birkhäuser/Springer, 2016. Google Scholar
C. Cao, I. Kevrekidis and E. S. Titi, Numerical criterion for the stabilization of steady states of the Navier-Stokes equations, Indiana University Mathematics Journal, 50 (2001), 37-96. Google Scholar
C. Cao, E Lunasin and E. S. Titi, Global well-posedness of the three-dimensional viscous and inviscid simplified Bardina turbulence models, Commun. Math. Sci., 4 (2006), 823-848. Google Scholar
A. Yu. Chebotarev, Finite-dimensional controllability of systems of Navier-Stokes type, Differ. Equ., 46 (2010), 1498-1506. Google Scholar
I. D. Chueshov, The theory of functionals that uniquely determine the asymptotic dynamics of infinite-dimensional dissipative systems, Russian Math. Surveys, 53 (1998), 731-776. Google Scholar
I. Chueshov, Dynamics of Quasi-Stable Dissipative Systems, Universitext. Springer, Cham, 2015. Google Scholar
I. D. Chueshov and V. K. Kalantarov, Determining functionals for nonlinear damped wave equations, Mat. Fiz. Anal. Geom., 8 (2001), 215-227. Google Scholar
I. Chueshov and I. Lasiecka, Long-time behavior of second order evolution equations with nonlinear damping, Mem. Amer. Math. Soc., 195 (2008), ⅷ+183 pp. Google Scholar
B. Cockburn, D. A. Jones and E. S. Titi, Degrés de liberté déterminants pour équations non linéaires dissipatives, C.R. Acad. Sci.-Paris, Sér. I, 321 (1995), 563-568. Google Scholar
B. Cockburn, D. A. Jones and E. S. Titi, Estimating the number of asymptotic degrees of freedom for nonlinear dissipative systems, Math. Comput., 66 (1997), 1073-1087. Google Scholar
J. -M. Coron and E. Trélat, Feedback stabilization along a path of steady-states for 1-D semilinear heat and wave equations, Proceedings of the 44th IEEE Conference on Decision and Control, and the European Control Conference 2005 Seville, Spain, 2005. Google Scholar
O. Çelebi, V. Kalantarov and M. Polat, Attractors for the Generalized Benjamin-Bona-Mahony Equation, J. of Differential Equations, 157 (1999), 439-451. Google Scholar
C. Foias, O. P. Manley, R. Rosa and R. Temam, Navier-Stokes Equations and Turbulence, Cambridge University Press, 2001. Google Scholar
C. Foias and G. Prodi, Sur le comportement global des solutions non stationnaires des équations de Navier-Stokes en dimension deux, Rend. Sem. Mat. Univ. Padova, 39 (1967), 1-34. Google Scholar
C. Foias and R. Temam, Determination of the solutions of the Navier-Stokes equations by a set of nodal values, Math. Comput., 43 (1984), 117-133. Google Scholar
C. Foias and E. S. Titi, Determining nodes, finite difference schemes and inertial manifolds, Nonlinearity, 4 (1991), 135-153. Google Scholar
A. V. Fursikov and A. A. Kornev, Feedback stabilization for the Navier-Stokes equations: Theory and calculations. Mathematical aspects of fluid mechanics, London Math. Soc. Lecture Note Ser., Cambridge Univ. Press, Cambridge, 402 (2012), 130-172. Google Scholar
B. L. Guo, Finite-dimensional behavior for weakly damped generalized KdV-Burgers equations, Northeastern Mathematical Journal, 10 (1994), 309-319. Google Scholar
J. K. Hale, Asymptotic Behavior of Dissipative Systems, Math. Survey and Monographs, 25 AMS, Providence, R. I., 1988. Google Scholar
J. K. Hale and G. Raugel, Regularity, determining modes and Galerkin methods, J. Math. Pures Appl. (9), 82 (2003), 1075-1136. Google Scholar
A. Haraux, Syst/ems deinamiques dissipatifs et applications, Masson, Paris, 1991. Google Scholar
Ch. Jia, Boundary feedback stabilization of the Korteweg-de Vries-Burgers equation posed on a finite interval, J. Math. Anal. Appl., 444 (2016), 624-647. Google Scholar
D. Jones and E. S. Titi, Upper bounds on the number of determining modes, nodes, and volume elements for the Navier-Stokes equations, Indiana University Mathematics Journal, 42 (1993), 875-887. Google Scholar
V. K. Kalantarov, Attractors for some nonlinear problems of mathematical physics, Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI), 152 (1986), 50-54. Google Scholar
V. K. Kalantarov and E. S. Titi, Finite-parameters feedback control for stabilizing damped nonlinear wave equations. Nonlinear analysis and optimization, Contemp. Math., Amer. Math. Soc. , Providence, RI, 659 (2016), 115-133. Google Scholar
V. K. Kalantarov and E. S. Titi, Global attractors and determining modes for the 3D Navier-Stokes-Voight equations, Chin. Ann. Math. Ser. B, 30 (2009), 697-714. Google Scholar
V. Kalantarov and S. Zelik, Finite-dimensional attractors for the quasi-linear strongly-damped wave equation, J. Differential Equations, 247 (2009), 1120-1155. Google Scholar
O. A. Ladyzhenskaya, A dynamical system generated by the Navier-Stokes equations, Zap. Nauch. Sem. LOMI, 27 (1972), 91-115. Google Scholar
O. A. Ladyzhenskaya, Attractors for Semi-groups and Evolution Equations, Cambridge University Press, 1991. Google Scholar
I. Lasiecka and R. Triggiani, Uniform stabilization of the wave equation with Dirichlet or Neumann feedback control without geometrical conditions, Appl. Math. Opt., 25 (1992), 189-224. doi: 10.1007/BF01182480. Google Scholar
J. -L. Lions, Quelques Méthodes de Résolution des Problémes aux Limites Non linéaires, Dunod et Gauthier-Villars, Paris, 1969. Google Scholar
S. Lü and Q. Lu, Fourier spectral approximation to long-time behavior of dissipative generalized KdV-Burgers equations, SIAM J. Numer. Anal., 44 (2006), 561-585. doi: 10.1137/S0036142903426671. Google Scholar
E. Lunasin and E. S. Titi, Finite determining parameters feedback control for distributed nonlinear dissipative systems -a computational study, Evol. Equ. Control Theory, 6 (2017), 535-557, arXiv: 1506.03709, [math. AP]. doi: 10.3934/eect.2017027. Google Scholar
P. Marcati, Decay and stability for nonlinear hyperbolic equations, J. Differential Equations, 55 (1984), 30-58. doi: 10.1016/0022-0396(84)90087-1. Google Scholar
I. Munteanu, Boundary stabilization of the phase field system by finite-dimensional feedback controllers, J. Math. Anal. Appl., 412 (2014), 964-975. doi: 10.1016/j.jmaa.2013.11.018. Google Scholar
A. P. Oskolkov, The uniqueness and solvability in the large of boundary value problems for the equations of motion of aqueous solutions of polymers, Zap. Naučn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI), 38 (1973), 98-136. Google Scholar
D. Prazak, On finite fractal dimension of the global attractor for the wave equation with nonlinear damping, J. Dynam. Differential Equations, 14 (2002), 763-776. doi: 10.1023/A:1020756426088. Google Scholar
R. Rosa and R. Temam, Finite-dimensional feedback control of a scalar reaction-diffusion equation via inertial manifold theory, in Foundations of Computational Mathematics, Selected papers of a conference held at IMPA, (Eds. F. Cucker and M. Shub), Springer, (1997), 382-391. Google Scholar
A. Smyshlyaev, E. Cerpa and M. Krstic, Boundary stabilization of a 1-D wave equation with in-domain antidamping, SIAM J. Control Optim., 48 (2010), 4014-4031. doi: 10.1137/080742646. Google Scholar
R. Temam, Infnite Dimensional Dynamical Systems in Mechanics and Physics, New York: Springer, 2nd augmented edition, 1997. Google Scholar
B. Wang and W. Yang, Finite dimensional behaviour for the Benjamin-Bona-Mahony equation, J. Phys. A, Math. Gen., 30 (1997), 4877-4885. doi: 10.1088/0305-4470/30/13/035. Google Scholar
S. Zelik, Asymptotic regularity of solutions of singularly perturbed damped wave equations with supercritical nonlinearities, Disc. Cont. Dyn. Sys., 11 (2004), 351-392. doi: 10.3934/dcds.2004.11.351. Google Scholar
B. -Y. Zheng, Forced oscillation of the Korteweg-de Vries-Burgers equation and its stability, Control of Nonlinear Distributed Parameter Systems, (College Station, TX, 1999), 337-357, Lecture Notes in Pure and Appl. Math., 218, Dekker, New York, 2001. Google Scholar
E. Zuazua, Uniform stabilization of the wave equation by nonlinear boundary feedback, SIAM J. Control Optim., 28 (1990), 466-477. doi: 10.1137/0328025. Google Scholar
Jean-Pierre Raymond, Laetitia Thevenet. Boundary feedback stabilization of the two dimensional Navier-Stokes equations with finite dimensional controllers. Discrete & Continuous Dynamical Systems - A, 2010, 27 (3) : 1159-1187. doi: 10.3934/dcds.2010.27.1159
V. Pata, Sergey Zelik. A remark on the damped wave equation. Communications on Pure & Applied Analysis, 2006, 5 (3) : 611-616. doi: 10.3934/cpaa.2006.5.611
Andrei Fursikov, Alexey V. Gorshkov. Certain questions of feedback stabilization for Navier-Stokes equations. Evolution Equations & Control Theory, 2012, 1 (1) : 109-140. doi: 10.3934/eect.2012.1.109
Kaïs Ammari, Thomas Duyckaerts, Armen Shirikyan. Local feedback stabilisation to a non-stationary solution for a damped non-linear wave equation. Mathematical Control & Related Fields, 2016, 6 (1) : 1-25. doi: 10.3934/mcrf.2016.6.1
Fabrizio Colombo, Davide Guidetti. Identification of the memory kernel in the strongly damped wave equation by a flux condition. Communications on Pure & Applied Analysis, 2009, 8 (2) : 601-620. doi: 10.3934/cpaa.2009.8.601
Zhijian Yang, Zhiming Liu. Global attractor for a strongly damped wave equation with fully supercritical nonlinearities. Discrete & Continuous Dynamical Systems - A, 2017, 37 (4) : 2181-2205. doi: 10.3934/dcds.2017094
Piotr Kokocki. Homotopy invariants methods in the global dynamics of strongly damped wave equation. Discrete & Continuous Dynamical Systems - A, 2016, 36 (6) : 3227-3250. doi: 10.3934/dcds.2016.36.3227
Pengyan Ding, Zhijian Yang. Attractors of the strongly damped Kirchhoff wave equation on $\mathbb{R}^{N}$. Communications on Pure & Applied Analysis, 2019, 18 (2) : 825-843. doi: 10.3934/cpaa.2019040
Hermenegildo Borges de Oliveira. Anisotropically diffused and damped Navier-Stokes equations. Conference Publications, 2015, 2015 (special) : 349-358. doi: 10.3934/proc.2015.0349
A. V. Fursikov. Stabilization for the 3D Navier-Stokes system by feedback boundary control. Discrete & Continuous Dynamical Systems - A, 2004, 10 (1&2) : 289-314. doi: 10.3934/dcds.2004.10.289
Evrad M. D. Ngom, Abdou Sène, Daniel Y. Le Roux. Boundary stabilization of the Navier-Stokes equations with feedback controller via a Galerkin method. Evolution Equations & Control Theory, 2014, 3 (1) : 147-166. doi: 10.3934/eect.2014.3.147
Nicholas J. Kass, Mohammad A. Rammaha. Local and global existence of solutions to a strongly damped wave equation of the $ p $-Laplacian type. Communications on Pure & Applied Analysis, 2018, 17 (4) : 1449-1478. doi: 10.3934/cpaa.2018070
Zhaojuan Wang, Shengfan Zhou. Existence and upper semicontinuity of random attractors for non-autonomous stochastic strongly damped wave equation with multiplicative noise. Discrete & Continuous Dynamical Systems - A, 2017, 37 (5) : 2787-2812. doi: 10.3934/dcds.2017120
Zhiming Liu, Zhijian Yang. Global attractor of multi-valued operators with applications to a strongly damped nonlinear wave equation without uniqueness. Discrete & Continuous Dynamical Systems - B, 2020, 25 (1) : 223-240. doi: 10.3934/dcdsb.2019179
Filippo Dell'Oro. Global attractors for strongly damped wave equations with subcritical-critical nonlinearities. Communications on Pure & Applied Analysis, 2013, 12 (2) : 1015-1027. doi: 10.3934/cpaa.2013.12.1015
Veronica Belleri, Vittorino Pata. Attractors for semilinear strongly damped wave equations on $\mathbb R^3$. Discrete & Continuous Dynamical Systems - A, 2001, 7 (4) : 719-735. doi: 10.3934/dcds.2001.7.719
Stéphane Gerbi, Belkacem Said-Houari. Exponential decay for solutions to semilinear damped wave equation. Discrete & Continuous Dynamical Systems - S, 2012, 5 (3) : 559-566. doi: 10.3934/dcdss.2012.5.559
Maurizio Grasselli, Vittorino Pata. On the damped semilinear wave equation with critical exponent. Conference Publications, 2003, 2003 (Special) : 351-358. doi: 10.3934/proc.2003.2003.351
Varga K. Kalantarov Edriss S. Titi | CommonCrawl |
Application of a complete blood count to screening lethargic and anorectic cats for pancreatitis
Magdalena Maria Krasztel1,
Michał Czopowicz1,
Olga Szaluś-Jordanow2,
Agata Moroz1,
Marcin Mickiewicz1 &
Jarosław Kaba1
BMC Veterinary Research volume 17, Article number: 383 (2021) Cite this article
Feline pancreatitis (FP) is an important health problem of cats. Its diagnostics is based on the combination of quantification of serum pancreatic lipase immunoreactivity (fPLI) and abdominal ultrasonography (AUS). These modalities allow for establishing highly specific diagnosis, however they are relatively expensive and time-consuming. On the other hand, a screening test of high sensitivity which would allow to rule out FP on the first visit without a considerable increase of costs would be clinically useful. To evaluate accuracy of nonspecific inflammatory biomarkers based on complete blood count (CBC) in diagnosing FP 73 client-owned cats with signs of lethargy and reduced appetite lasting for at least 2 days before presentation were enrolled in the cross-sectional study. They were examined with fPLI assay and AUS and classified as cats with very low risk of FP when fPLI ≤3.5 μg/L and AUS negative for FP, or as cats with increased risk of FP in the case of any other combination of results. Then, 7 various CBC measurements were measured in each cat and linked to the risk of FP using the multivariable logistic regression.
Five CBC measurements turned out to be significantly associated with the risk of FP – total leukocyte count (WBC; crude odds ratio(ORcrude) = 12.2; CI 95%: 1.52, 98.5), total neutrophil count (ORcrude = 5.84; CI 95%: 1.22, 27.9), band neutrophil count (BNC; ORcrude = 6.67; CI 95%: 1.98, 22.4), neutrophil-to-lymphocyte ratio (ORcrude = 3.68; CI 95%: 1.25, 10.9), and eosinophil count (EC; ORcrude = 0.34; CI 95%: 0.12, 0.96). The model based on WBC, BNC, and EC proved to have at least fair diagnostic potential (area under ROC curve 82.7%; CI 95%: 72.8%, 92.5%). When WBC < 18 G/L, BNC < 0.27 G/L, and EC > 0.3 G/L was considered as a negative result, and any other combination as the positive result, the CBC model had high sensitivity (91.8%; CI 95%: 80.8%, 96.8%) at a relatively low specificity (58.3%; CI 95%: 38.8%, 75.5%).
The combination of three CBC measurements is an immediately available and fairly accurate screening method for identification of lethargic and anorectic cats with increased risk of FP.
Feline pancreatitis (FP) is a relatively common disease whose etiology usually remains unknown, clinical manifestation is nonspecific, diagnostics difficult and expensive, and prognosis guarded [1,2,3,4,5]. Lethargy and reduced appetite or anorexia are most common clinical signs, followed by vomiting, weight loss, and less often diarrhea [5]. Even though, histologically three different FP forms are recognized – acute necrotizing pancreatitis, acute suppurative pancreatitis, and chronic pancreatitis [6, 7], their similar clinical manifestation renders them barely distinguishable for a practitioner [8]. Therefore, the general term feline pancreatitis is commonly used [5].
At present the combination of clinical chemistry assays measuring pancreatic lipase immunoreactivity (serum pancreatic lipase immunoreactivity, fPLI) or activity (colorimetric 1,2-o-Dilauryl-Rac-Glycero-3-Glutaric Acid-(6′-Methylresorufin) Ester (DGGR) assay) and abdominal ultrasonography (AUS) is a mainstay of clinical diagnostics of FP [2, 3, 5, 9]. The estimates of diagnostic accuracy of these tests vary between studies. Diagnostic sensitivity (Se) and specificity (Sp) range from 50% to 80% and from 50% to 100%, respectively, for fPLI [10,11,12,13,14] and from 25% to 80% and from 70% to 90%, respectively, for AUS [10, 15, 16]. These discrepancies result from different cut-off values of the test (fPLI of 3.5 or 5.3 μg/L; 1 or 2 ultrasonographic changes indicative of FP), different severity of FP in a study population (mild or marked) as well as differences in the skills of AUS examiners and quality of ultrasound devices. Nevertheless, most of studies indicate that Sp outweighs Se [2, 3, 17]. Hence, unless a pre-test probability of FP is very low, positive results of these tests tend to be more trustworthy than negative (i.e. positive predictive value, PPV outraces negative predictive value, NPV). This renders them rather confirmatory then screening tests. Therefore, an easily available and inexpensive screening method of high Se for an immediate identification of patients with increased risk of FP would be of value.
Various inflammatory biomarkers are used in human and veterinary medicine for tentative detection, or rather exclusion, of active inflammatory, infectious and neoplastic processes [18]. Of them biomarkers based on complete blood count (CBC) such as total (WBC) and differential leukocyte count, as well as neutrophil-to-lymphocyte ratio (NLR) have been investigated in small animal veterinary medicine mainly due to their low cost and broad availability [19,20,21,22,23]. The presence or severity of pancreatitis in cats have been recently linked to NLR [22].
In this study, we evaluated the accuracy of a handful of CBC measurements in making the first-line decision whether a cat with lethargy and reduced appetite was at increased risk of FP.
The study enrolled 73 adult castrated cats, 45 males (61.6%) and 28 females (38.4%), aged from 2 to 18 years with the median (IQR) of 10 (8 to 12) years. Age did not differ significantly between sexes (p = 0.750). Fifty eight cats (79.5%) were domestic shorthair. Others were Siberian (n = 5, 6.9%), British shorthair (n = 3, 4.1%), Maine coon, Russian and Devon rex (each n = 2, 2.7%), and Siamese (n = 1, 1.4%).
fPLI was normal (≤ 3.5 μg/L) in 33 cats (45.2%) and elevated (> 3.5 μg/L) in 40 cats (54.8%): from 3.6 to 5.3 μg/L in 8 cats and > 5.3 μg/L in 32 cats. At least one ultrasonographic feature of FP was detected in 26 cats (35.6%). On the basis of those two diagnostic tests the risk of FP was determined as very low (fPLI ≤3.5 μg/L and normal appearance of the pancreas in AUS) in 24 cats (32.9%) and increased (fPLI > 3.5 μg/L and/or abnormal appearance of the pancreas in AUS) in 49 cats (67.1%). From among 49 cats with increased risk of FP only 17 cats (34.7%) had both elevated fPLI and abnormal appearance of the pancreas in AUS. Twenty three cats (46.9%) had elevated fPLI but normal appearance of the pancreas in AUS, and 9 cats (18.4%) had abnormal appearance of the pancreas in AUS but normal fPLI.
Diabetes mellitus was present in 29 cats (39.7%), suspected hepatopathy in 22 cats (30.1%; ALT [median (range)] – 307 (58–2322) U/L; TB – 18.8 (6.8–359.1) μmol/L), suspected acute kidney injury in 7 cats (9.6%; urea – 29.0 (17.9–62.7) mmol/L, creatinine – 353.6 (256.4–1246) μmol/L), and neoplastic disease in 3 cats (4.1%) (malignant liver tumor, intestinal lymphoma, and disseminated pulmonary metastases from the mammary gland tumor). Hemoconcentration was observed in 23 cats (31.5%; Ht – 0.38 (0.16–0.51), TP – 73 (52–97) g/L, urea – 19.9 (9.1–97.2) mmol/L, creatinine – 168 (97.2–256.4) μmol/L) and anemia in 10 cats (13.7%; Ht – 0.24 (0.16–0.26)). Vomiting was reported on admission in 37 cats (50.7%) and diarrhea in 9 cats (12.3%). Abdominal pain was detected by an attending veterinarian in 13 cats (17.8%) and fever in 3 cats (4.1%). Cats with increased risk of FP were significantly older (p = 0.038). All other demographic and clinical characteristics were evenly distributed between cats with very low and increased risk of FP (Table 1).
Table 1 Demographic and clinical characteristics of the study cats
Numerical values of 7 CBC measurements and cut-off values used for their categorization are presented in Additional file 1.
The univariable analysis yielded 5 CBC measurements significantly linked to an increased risk of FP – four positively associated: WBC, total neutrophil count (TNC), band neutrophil count (BNC), NLR, and one negatively associated: eosinophil count (EC) (Table 2).
Table 2 The univariable analysis of the association between categorized complete blood count (CBC) measurements and increased risk of feline pancreatitis (FP) in the study cats
Three CBC measurements proved to be significantly associated with increased risk of FP in the multivariable analysis (Table 3). The odds of being at increased risk of FP were 13-fold higher when WBC was ≥18 G/L and almost 5-fold higherwhen BNC was ≥0.27 G/L, while they were roughly 4-fold lower when EC was > 0.3 G/L. The model based on 3 CBC measurements (henceforth referred to as CBC model) fit the data well (H&L χ2 = 3.04, p = 0.551; Nagelkerke's pseudo-R2 = 0.40).
Table 3 Multiple logistic regression model based on a complete blood count (CBC) aiming to identify these anorectic and lethargic cats in which the risk of pancreatitis is increased
The CBC model had fair to good discriminatory potential (AUROC = 82.7%; CI 95%: 72.8%, 92.5%; p < 0.001), which was significantly higher than a discriminatory potential of each CBC measurement separately (Fig. 1): mean difference of AUROC between the CBC model and: WBC = 24.8% (CI 95%: 10.9%, 38.7%; p = 0.001); BNC = 11.0% (CI 95%: 1.6%, 20.4%; p = 0.022); EC = 22.0% (CI 95%: 7.4%, 36.3%; p = 0.003).
ROC curves of the logistic model developed using three complete blood count (CBC) measurements as well as of each CBC measurement: WBC – total leukocyte count [G/L], BNC – band neutrophil count [G/L], EC – eosinophil count [G/L]). Area under ROC curve with 95% confidence interval (CI 95%) presented for each CBC measurement
At the optimal cut-off value ≥0.628 (i.e. result of the CBC model considered as negative only when WBC < 18 G/L, BNC < 0.27 and EC > 0.3 G/L) the CBC model's Se was 91.8% (CI 95%: 80.8%, 96.8%), and Sp was 58.3% (CI 95%: 38.8%, 75.5%), while positive (LR+) and negative (LR-) likelihood ratios were 2.2 (CI 95%: 1.4, 3.6) and 0.14 (CI 95%: 0.05, 0.38), respectively. The accuracy measures of the CBC model at other cut-off values (i.e. at other combinations of the three CBC measurements included in the CBC model) are presented in Table 4.
Table 4 Accuracy of complete blood count (CBC) model at various cut-off values i.e. at various combinations of CBC measurements included in the model. The optimal cut-off value determined on the basis of the highest Youden's index (J) highlighted (the combination above it i.e. WBC < 18 G/L, BNC < 0.27 G/L, and EC > 0.3 G/L is the only to be considered as negative)
In this study we developed a 3-element logistic regression model (CBC model) which has at least fair accuracy (confirmed by the lower 95% confidence limit above the threshold of 70%) in distinguishing between symptomatic cats with very low or increased risk of FP. The CBC model has two important upsides. First, it is based on basic hematologic measurements (CBC-based inflammatory biomarkers: WBC, BNC, and EC) which are routinely examined in virtually all apparently sick patients and are available from most veterinary laboratories within a few hours of blood collection. Secondly, CBC measurements were included in the CBC model as dichotomous variables categorized according to a cut-off value which was determined using sound statistical methodology (Youden's index-based criterion) [24, 25]. Three binary variables result in only 23 = 8 potential combinations. As a result no calculations are necessary to apply the CBC model in daily practice. The only essential thing is the knowledge whether a given CBC measurement is below or above the cut-off value (Table 4).
CBC model is based on three types of leukocytes whose categorization corresponds to three well recognized changes observed in leukogram during the acute phase response: leukocytosis, left-shift, and eosinopenia [26,27,28]. Leukocytosis usually results from neutrophilia which develops easily and quickly in cats due to relatively high ratio (3:1) of marginal to circulating pool of neutrophils [26, 27, 29]. Immature band neutrophils are released from the bone marrow storage pool only when the inflammatory process leading to excessive migration of neutrophils to the affected tissues lasts for a longer time [26, 29]. The fact that our study enrolled cats in which nonspecific clinical signs had been observed for at least 2 days explains important role of the left-shift in identifying cats with FP. However, it is possible that this feature may not be equally important if cats in which symptoms have begun more recently are being examined. In humans and many animal species neutrophilia is typically accompanied by lymphopenia during the acute inflammatory reaction [30]. In cats, however, it is not rare to observe the elevation of both neutrophils and lymphocytes [27, 28], especially when a concurrent excitement response triggered by stressful events such as physical examination, restraint and blood collection occur. In cats marked lymphocytosis is a prominent feature of the excitement response [26, 29, 31]. This may to some extent explain why lymphopenia was not included in the model and why NLR, which captures both neutrophilia and lymphopenia at the same time and therefore shows diagnostic usefulness in humans [32] and, to some extent, in dogs [19, 20], performed inferior to WBC in our study.
Our study aimed to identify CBC measurements which can be useful in making a tentative diagnosis of FP. Obviously, these measurements are not linked specifically to the pathological processes developing in the course of FP so they cannot be expected to perform as a highly accurate confirmatory test. In fact they may play role only in an immediate exclusion of FP, so they may work as a rapid screening test. However, to satisfy this expectation they must have sufficiently high Se so that a practitioner may thrust their negative result. Se of the CBC model at an optimal cut-off value was roughly 90%, or at least 80% when we refer to the lower 95% confidence limit. Even though, it may appear to be quite a high figure, we should focus on NPV, or more conveniently, on LR- which is independent of disease prevalence in a population [25]. LR- for CBC model was roughly 0.14. It means that negative result is approximately 7-fold more likely in a cat without than with FP. It is commonly accepted that LR- should be below 0.1 to be diagnostically useful i.e. negative result should be at least 10-fold less likely to occur in a diseased than heathy individual [33]. On the other hand, plenty of tests of worse accuracy are commonly used in veterinary medicine, to mention only DGGR-lipase assay which at a cut-off value of 26 U/L shows LR- equal to 0.4 (calculated from the formula: LR- = (1-Se) / Sp = (1–0.667) / 0.786; based on the figures reported in the study of Oppliger at al [13].). Detailed relationship between a pre-test probability of disease, LR, and a post-test probability of disease may be calculated by transformation of probabilities into odds [33, 34] or from very convenient Fagan's nomogram [35, 36]. Nevertheless, the rule of thumb says that the negative test result whose LR- is 0.1 reduces pre-test probability by roughly 45% while LR- of 0.2 reduces it by roughly 30%. CBC model is somewhere in between. However, in fact it is safer to stick to the upper 95% confidence limit of LR- as tests usually perform worse in practice than they do in the population on which their accuracy has been assessed. Hence, when we assume that LR- is indeed closer to 0.4 and the pre-test probability of FP in a cat presented to the veterinary clinic is 30% if this cat tests negative in CBC model its post-test probability will be roughly 15%. Whether it is enough to justify practical use of CBC model is debatable. However, it is indisputable that applying CBC model costs nothing when CBC has already been done. On the other hand, we should be very cautious when using the CBC model as a confirmatory test. Even though, LR+ is very high (infinite) at certain cut-off values (Table 4) 49 cats used to determine Se (i.e. those classified as at increased risk of FP) were only moderately likely to have FP (as discussed in the next paragraph). Therefore, e.g. the cat with WBC ≥18 G/L, BNC ≥ 0.27 G/L, and EC < 0.3 G/L (the highest possible result of the CBC model) does not necessarily has FP. This cat simply appears to have an acute inflammatory reaction associated with at least one of the two tests (fPLI or AUS) positive for FP. Obviously, this result should make a practitioner examined this cat for FP using more specific methods, there are however many other diagnoses still probable in this cat.
The aforementioned limitation in the interpretation of positive results of the CBC model is associated with the fact that accuracy measures are of any value only if they have been estimated on the population of animals whose true heath status has been correctly determined [25, 37]. In our study we used two independent tests to diagnose FP – fPLI and AUS, at a cut-off value of 3.5 μg/L and at least one ultrasonographic feature of FP, respectively. We had to make a decision of how to handle inconsistent results of the two tests as the agreement between these test has been shown to be low [38, 39]. The problem of inconclusive classification of animals in the studies investigating diagnostic accuracy of a test when no 100% accurate gold standard exists has been thoroughly reviewed [40]. Even though many approaches exist, all of them aim to eventually assign inconclusive individuals to one of the two groups (healthy or diseased) as evaluation of diagnostic accuracy is only possible when animals are classified according to a dichotomous manner. On the other hand, elimination of cats with inconsistent results would create two artificial groups of cats, extreme in terms of the likelihood of FP, with a huge gap between them. This would make these groups differ not only in terms of having FP but also in a general condition and many other features remaining beyond our control. As a result the accuracy measures of the CBC model would be falsely inflated. In our study we decided to apply fPLI and AUS in a parallel fashion which meant that any positive result indicated FP [25]. Diagnostic accuracy of each of these two tests at cut-off values applied in our study has so far been estimated several times before. In terms of fPLI Se and Sp were estimated at 61% (CI 95%: 36%, 82%) and 55% (CI 95%: 39%, 70%), respectively, on 60 cats [13], 65% (CI 95%: 43%, 83%) and 63% (CI 95%: 26%, 90%), respectively, on 31 cats [12]. In an another study [14] Se was 74% for mild and 82% for marked FP, while Sp was 74%. In terms of AUS Se was 84% (CI 95%: 60%, 97%) and Sp was 75% (CI 95%: 48%, 93%) on 35 cats [16]. Assuming Se and Sp of 65% and 65%, respectively, for fPLI and 85% and 75%, respectively, for AUS, parallel testing procedure yields Se of 95% and Sp of 49%. Then, assuming pre-test probability of FP of 50%, the cat negative in both tests and on this basis considered as being at very low risk of FP in our study was 95% likely to be truly free from FP (therefore we referred to this group as cats at very low, not simply low, risk of FP). The cat positive in at least one of these tests was 65% likely to truly have FP, while a cat positive in both tests was 85% likely to truly have FP. Our CBC model is a screening test so we want to trust its negative result more than its positive result as the latter one will be further verified by tests more specific for FP. Therefore, in the study population we are more concerned with correct classification of cats as free from FP than as affected by FP. On the other hand, low Sp of a reference procedure tends to falsely reduce Se of an index test [41], so Se of the CBC model may be even higher than our estimations.
The most important limitation of our study is associated with the precision of CBC measurements used for the model development. While WBC was measured by modern automatic hematologic analyzers of high quality whose results are very likely to be highly repeatable, differential counts were determined manually by counting only 100 subsequent leukocytes. Such a method is prone to both human errors and random variability. For instance, CI 95% for BN% of 1% estimated from 100 cells is from 0.2% to 5.4% [42], which markedly exceeds the cut-off value indicated by our analyses. Therefore, routine counting of 200 or even 300 leukocytes appears to be a reasonable recommendation (CI 95% narrows down then to 0.1% to 2.8% and 0.1% to 1.9%, respectively), although it would considerably extend the turnover time of blood samples. On the other hand, manual reviewing of blood films is the only method allowing to include band neutrophil count in the result. Our study substantiates the practical usefulness of estimating band neutrophil percentage and counts, which is especially important given the growing popularity of in-clinic instrumental hematologic analyzers. Another important downside of our analysis is the fact that we did not include the information on toxic changes in neutrophils. It was so since the evaluation of toxic neutrophils was not routinely provided by the veterinary laboratory in which our samples were examined. Toxic neutrophils are an important feature of CBC in acute inflammation caused by an enhanced turnover rate of neutrophils and incomplete neutrophil maturation in the bone marrow [26, 31]. Including this variable might have improved performance of the CBC model and it certainly warrants further investigation.
The combination of CBC measurements is an immediately available and fairly accurate screening method allowing to decide which cats presented with lethargy and anorexia have increased risk of FP.
This retrospective cross-sectional study comprised 73 cats presented to three veterinary clinics located in the Central Poland in years 2014–2020 and screened for FP using the commercial feline pancreatic lipase immunoreactivity (fPLI) assay and abdominal ultrasonography (AUS). Cats were enrolled in the study if their owners declared that a cat: 1) had lethargy and reduced appetite or anorexia for at least two previous days; 2) did not have any known chronic diseases; 3) had not been diagnosed with FP before; 4) had not been treated with glucocorticosteroids for a preceding month. All cats were examined by a specialist in small animal medicine. The blood sample was collected for a routine blood analysis and fPLI quantification. fPLI was measured [μg/L] using ELISA based on monoclonal antibodies (Spec fPL™) in IDEXX Laboratories GmbH (Ludwigsburg, Germany). According to the manufacturer's recommendations fPLI was considered normal when ≤3.5 μg/L and elevated when > 3.5 μg/L. AUS was performed by a veterinary radiologist with state-of-the art devices (MyLab 25 Gold, Esaote, Italy and HM70A, Samsung Electronics Ltd., UK). FP was ultrasonographically diagnosed if at least one of the following features was detected: pancreatomegaly (width of the pancreas > 10 mm), irregular margins of the pancreas, hypoechoic parenchyma of the pancreas, hyperechoic surrounding mesenteric or fat, and peripancreatic free fluid. Hyperechoic pancreatic parenchyma indicative of fibrosis was also considered diagnostic for FP [5, 10, 16]. Other diagnostic tests (thoracic radiography, echocardiography) were performed if necessary to make a definitive diagnosis.
Results of the two diagnostic tests used for detection of FP were interpreted according to a parallel manner [25] i.e. the risk of FP was considered as very low only when fPLI was normal (≤ 3.5 μg/L) and the appearance of the pancreas in AUS was normal. Otherwise, a cat was found to be at increased risk of FP.
The blood analysis was performed in a commercial veterinary laboratory and included routine complete blood count (CBC), alanine aminotransferase (ALT) and alkaline phosphatase (ALP) activity, total protein (TP) and total bilirubin (TB) concentration as well as urea and creatinine concentration. Routine blood analysis was performed using Abacus Vet5 Hematology analyzer (Diatron MI Zrt., Hungary), Mythic 18 Vet (PZ Cormay S.A., Poland) and automatic photometric clinical chemistry analyzer BS-800 (Mindray Medical Poland). The differential leucocyte count was performed on thin and smooth peripheral blood smears stained with the May-Grünwald-Giemsa reagent (Adamed Pharma S.A., Poland). The smears were examined with a light microscope (Primo Star, Zeiss, Germany) under 100x magnification by a qualified technician and 100 nucleated cells were classified into six subpopulations: band neutrophils, segmented neutrophils, eosinophils, basophils, monocytes, and lymphocytes. Basophils were not included in further analyses as they were very rarely observed in manual blood smears and their correct identification was questionable.
Four clinical conditions were identified in cats using hematologic and biochemical criteria: anemia when Ht was < 27%; hemoconcentration when i) Ht was > 45% and TP was > 80 g/L or ii) urea concentration was > 12 mmol/L at creatinine concentration < 250 μmol/L; suspected acute kidney injury when creatinine concentration was > 250 μmol/L and urea concentration was > 12 mmol/L, and suspected hepatopathy when ALT was > 200 U/L (without concurrent hyperthyroidism) or TB was > 17 μmol/L (without concurrent anemia) [43]. Diabetes mellitus was diagnosed based on polyuria and polydipsia in the medical history and fructosamine concentration > 400 μmol/L, hyperthyroidism based on total thyroxine concentration > 65 nmol/L, and neoplasms based on chest radiography, AUS, and ultrasound-guided fine needle biopsy. Fever was defined as rectal temperature > 39.5 °C. The presence of abdominal pain was subjectively assessed by a clinician.
Seven CBC measurements were analyzed in this study: WBC, total neutrophil count, band neutrophil count (BNC), eosinophil count (EC), monocyte count (MC), lymphocyte count (LC), and neutrophil-to-lymphocyte ratio (NLR).
No ethics commission approval for this study was required according to Polish legal regulations (the Act on the Protection of Animals Used for Scientific or Educational Purposes of 15 January 2015) as only routine diagnostic procedures essential given the clinical status of the cat were performed and the study was purely analytical. Nevertheless, an informed consent of each cat's owner for participation in the study was obtained.
Numerical variables were presented as the median, interquartile range (IQR) and range, and compared between two groups using the Mann-Whitney U test. Categorical variables were presented as a count (n) and percentage of the total number of animals in a given group. First, CBC measurements were transformed into dichotomous variables. The optimal cut-off value for dichotomization was determined using the highest Youden's index (J) criterion [24]. Then, the relationship between the categorized CBC measurements and the risk of FP was investigated using the maximum likelihood G-test or Fisher's exact test if the expected count in any cell of the two-by-two table was < 5, and was expressed as the crude odds ratio (ORcrude).
CBC measurements which proved significantly linked (α = 0.05) to the risk of FP in the univariable analysis were offered to the multiple logistic regression [44] according to the following formula:
$$\mathrm{f}\left(\mathrm{P}=1\right)=\frac{1}{1+{\mathrm{e}}^{-\left({\mathrm{B}}_0+{\mathrm{B}}_{\mathrm{n}}\times {\mathrm{X}}_{\mathrm{n}}\right)}}$$
where e signified the Euler's number (≈2.718), B0 was the constant, Bn were the regression coefficients of CBC measurements (Xn) entered in the initial model and evaluated using the backward stepwise elimination procedure. The magnitude of association between a CBC measurement and the risk of FP was expressed as the adjusted odds ratio (ORadj). The goodness-of-fit of the model was evaluated using the Hosmer-Lemeshow χ2 test (H&L χ2) and Negelkerke's pseudo-R2 coefficient. Discriminatory potential of CBC measurements and logistic model based on CBC measurements (CBC model) in classifying cats into those with very low or increased risk of FP was assessed by computing the area under ROC curve (AUROC). AUROC was interpreted as follows: ≥90% – an excellent test, 80–89% – a good test, 70–79% – a fair test, < 70% – a poor test [24] and compared using the nonparametric method [45]. For the optimal cut-off value diagnostic sensitivity (Se), diagnostic specificity (Sp) as well as positive and negative likelihood ratios (LR+ and LR-) were calculated to evaluate diagnostic usefulness of CBC model. The 95% confidence intervals (CI 95%) for proportions and LRs were calculated using the Wilson score method and log method, respectively [46]. A significance level (α) was set at 0.05. All statistical tests were two-sided. The statistical analysis was performed in TIBCO Statistica 13.3 (TIBCO Software Inc., Palo Alto, CA, USA) and IBM SPSS Statistics 26 (IBM Corporation, Armonk, NY, USA).
All methods were carried out in accordance with relevant guidelines and regulations.
The database is available from authors on request.
α:
Significance level
AUROC:
Area under ROC curve
Abdominal ultrasonography
BNC:
Band neutrophil count
CBC:
CI 95%:
DGGR:
1,2-o-Dilauryl-Rac-Glycero-3-Glutaric Acid-(6′-Methylresorufin) Ester
FP:
fPLI:
Feline pancreatic lipase immunoreactivity
H&L χ2 :
Hosmer & Lemeshow chi-square test
IQR:
Interquartile range
LR+:
Positive likelihood ratio (likelihood ratio of a positive result)
LR-:
Negative likelihood ratio (likelihood ratio of a negative result)
NLR:
Neutrophil-to-lymphocyte ratio
Negative predictive value
PPV:
Positive predictive value
ROC:
Receiver operating characteristic
Se:
Diagnostic sensitivity
Diagnostic specificity
WBC:
Total leukocyte count (white blood cell count)
Simpson KW. The emergence of feline pancreatitis. J Vet Intern Med. 2001;15:327–8.
PubMed CAS Google Scholar
Xenoulis PG. Diagnosis of pancreatitis in dogs and cats. J Small Anim Pract. 2015;56:13–26.
Xenoulis PG, Steiner JM. Current concepts in feline pancreatitis. Top Companion Anim Med. 2008;23:185–92.
Bazelle J, Watson P. Is it being overdiagnosed? Feline pancreatitis. Vet Clin North Am Small Anim Pract. 2020;50:1107–21.
Forman MA, Steiner JM, Armstrong PJ, Camus MS, Gaschen L, Hill SL, et al. ACVIM consensus statement on pancreatitis in cats. J Vet Intern Med. 2021;35:703–23.
Hill RC, Van Winkle TJ. Acute necrotizing and acute suppurative pancreatitis in the cat: a retrospective study of 40 cases (1976–1989). J Vet Intern Med. 1993;7:25–33.
De Cock HE, Forman MA, Farver TB, Marks SL. Prevalence and histopathologic characteristics of pancreatitis in cats. Vet Pathol. 2007;44:39–49.
Ferreri JA, Hardam E, Kimmel SE, et al. Clinical differentiation of acute necrotizing from chronic nonsuppurative pancreatitis in cats: 63 cases (1996-2001). J Am Vet Med Assoc. 2003;223:469–74.
Xenoulis PG, Steiner JM. Canine and feline pancreatic lipase immunoreactivity. Vet Clin Pathol. 2012;41:312–24.
Forman MA, Marks SL, De Cock HE, Hergesell EJ, Wisner ER, Baker TW, et al. Evaluation of serum feline pancreatic lipase immunoreactivity and helical computed tomography versus conventional testing for the diagnosis of feline pancreatitis. J Vet Intern Med. 2004;18:807–15.
Forman MA, Shiroma J, Armstrong PJ, et al. Evaluation of feline pancreas-specific lipase (Spec fPL™) for the diagnosis of feline pancreatitis [abstract]. J Vet Intern Med. 2009;23:733–4.
Oppliger S, Hartnack S, Riond B, Reusch CE, Kook PH. Agreement of the serum Spec fPL™ and 1,2-o-dilauryl-rac-glycero-3-glutaric acid-(6′-methylresorufin) ester lipase assay for the determination of serum lipase in cats with suspicion of pancreatitis. J Vet Intern Med. 2013;27:1077–82.
Oppliger S, Hilbe M, Hartnack S, Zini E, Reusch CE, Kook PH. Comparison of serum Spec fPL(™) and 1,2-o-dilauryl-rac-glycero-3-glutaric acid-(6′-methylresorufin) ester assay in 60 cats using standardized assessment of pancreatic histology. J Vet Intern Med. 2016;30:764–70.
PubMed PubMed Central CAS Google Scholar
Törner K, Staudacher M, Tress U, Weber CN, Stadler C, Grassinger JM, et al. Histopathology and feline pancreatic lipase immunoreactivity in inflammatory, hyperplastic and neoplastic pancreatic diseases in cats. J Comp Pathol. 2020;174:63–72.
Gerhardt A, Steiner JM, Williams DA, Kramer S, Fuchs C, Janthur M, et al. Comparison of the sensitivity of different diagnostic tests for pancreatitis in cats. J Vet Intern Med. 2001;15:329–33.
Williams JM, Panciera DL, Larson MM, Werre SR. Ultrasonographic findings of the pancreas in cats with elevated serum pancreatic lipase immunoreactivity. J Vet Intern Med. 2013;27:913–8.
Lidbury JA, Suchodolski JS. New advances in the diagnosis of canine and feline liver and pancreatic disease. Vet J. 2016;215:87–95.
Conceição MEBAMD, Uscategui RAR, Bertolo PHL, de Souza DC, Rolemberg DDS, de Moraes PC, et al. Assessment of postoperative inflammatory markers and pain in cats after laparoscopy and miniceliotomy ovariectomy. Vet Rec. 2018;183:656.
Hodgson N, Llewellyn EA, Schaeffer DJ. Utility and prognostic significance of neutrophil-to-lymphocyte ratio in dogs with septic peritonitis. J Am Anim Hosp Assoc. 2018;54:351–9.
Pierini A, Gori E, Lippi I, Ceccherini G, Lubas G, Marchetti V. Neutrophil-to-lymphocyte ratio, nucleated red blood cells and erythrocyte abnormalities in canine systemic inflammatory response syndrome. Res Vet Sci. 2019;126:150–4.
Chiti LE, Martano M, Ferrari R, Boracchi P, Giordano A, Grieco V, et al. Evaluation of leukocyte counts and neutrophil-to-lymphocyte ratio as predictors of local recurrence of feline injection site sarcoma after curative intent surgery. Vet Comp Oncol. 2020;18:105–16.
Neumann S. Neutrophil-to-lymphocyte and platelet-to-lymphocyte ratios in dogs and cats with acute pancreatitis. Vet Clin Pathol. 2021;50:45–51.
Petrucci GN, Lobo L, Queiroga F, Martins J, Prada J, Pires I, et al. Neutrophil-to-lymphocyte ratio is an independent prognostic marker for feline mammary carcinomas. Vet Comp Oncol. 2021;19:482–91.
Carter JV, Pan J, Rai SN, Galandiuk S. ROC-ing along: evaluation and interpretation of receiver operating characteristic curves. Surgery. 2016;159:1638–45.
Thrusfield M. Veterinary epidemiology. 4th ed. Chichester: Wiley; 2018. p. 429–56.
Knottenbelt CM, Blackwood L. The blood. In: Chandler EA, Gaskell CJ, Gaskel RM, editors. Feline medicine and therapeutics. 3rd ed. Ames: Blackwell Publishing; 2007. p. 235–56.
Paltrinieri S. The feline acute phase reaction. Vet J. 2008;177:26–35.
Declue AE, Delgado C, Chang CH, Sharp CR. Clinical and immunologic assessment of sepsis and the systemic inflammatory response syndrome in cats. J Am Vet Med Assoc. 2011;238:890–7.
Thrall MA, Weiser G, Allison RW, Campbell TW. Veterinary hematology and clinical chemistry. 2nd ed. Baltimore: Lippincott Williams & Wilkins; 2004. p. 120–45.
Hoshiya T, Watanabe D, Matsuoka T, Horiguchi K, Miki Y, Mizuguchi H, et al. Acute phase response in toxicity studies. II. Findings in beagle dogs injected with endotoxin or subjected to surgical operation. J Toxicol Sci. 2001;26:103–9.
Rosenfeld AJ, Dial SM. Clinical pathology for the veterinary team. Ames: Wiley-Blackwell; 2010. p. 61–71.
Huang Z, Fu Z, Huang W, Huang K. Prognostic value of neutrophil-to-lymphocyte ratio in sepsis: a meta-analysis. Am J Emerg Med. 2020;38:641–7.
McGee S. Simplifying likelihood ratios. J Gen Intern Med. 2002;17:646–9.
Deeks JJ, Altman DG. Diagnostic tests 4: likelihood ratios. BMJ. 2004;329:168–9.
Fagan TJ. Letter: Nomogram for Bayes theorem. N Engl J Med. 1975;293:257.
Caraguel CG, Vanderstichel R. The two-step Fagan's nomogram: ad hoc interpretation of a diagnostic test result without calculation. Evid Based Med. 2013;18:125–8.
Begg CB. Biases in the assessment of diagnostic tests. Stat Med. 1987;6:411–23.
Oppliger S, Hartnack S, Reusch CE, Kook PH. Agreement of serum feline pancreas-specific lipase and colorimetric lipase assays with pancreatic ultrasonographic findings in cats with suspicion of pancreatitis: 161 cases (2008-2012). J Am Vet Med Assoc. 2014;244:1060–5.
Paran E, Hugonnard M. Agreement of feline and canine pancreas-specific lipase with pancreatic ultrasonographic findings in 62 cats and 54 dogs with suspicion of pancreatitis: a retrospective study (2007–2013) [abstract]. J Vet Intern Med. 2017;31:261–2.
Rutjes AW, Reitsma JB, Coomarasamy A, Khan KS, Bossuyt PM. Evaluation of diagnostic tests when there is no gold standard. A review of methods. Health Technol Assess. 2007;11:iii ix-51.
Staquet M, Rozencweig M, Lee YJ, Muggia FM. Methodology for the assessment of new dichotomous diagnostic tests. J Chronic Dis. 1981;34:599–610.
Stockham SL, Scott MA. Fundamentals of veterinary clinical pathology. 2nd ed. Oxford: Blackwell Publishing; 2008. p. 68.
Brady CA, Otto CM, Van Winkle TJ, King LG. Severe sepsis in cats: 29 cases (1986-1998). J Am Vet Med Assoc. 2000;217:531–5.
Hosmer DW, Lemeshow S. Applied logistic regression. 2nd ed. New Jersey: Wiley; 2000. p. 31–46.
DeLong ER, DeLong DM, Clarke-Pearson DL. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics. 1988;44:837–45.
Altman D, Machin D, Bryant T, Gardner M. Statistics with confidence: confidence intervals and statistical guidelines. 2nd ed. Bristol: BMJ Books; 2000. p. 46–7. 108–10
We are indebted to the owners of veterinary clinics and the owners of cats for their assistance and cooperation.
Division of Veterinary Epidemiology and Economics, Institute of Veterinary Medicine, Warsaw University of Life Sciences-SGGW, Nowoursynowska 159c, 02-776, Warsaw, Poland
Magdalena Maria Krasztel, Michał Czopowicz, Agata Moroz, Marcin Mickiewicz & Jarosław Kaba
Department of Small Animal Diseases with Clinic, Institute of Veterinary Medicine, Warsaw University of Life Sciences-SGGW, Nowoursynowska 159c, 02-776, Warsaw, Poland
Olga Szaluś-Jordanow
Magdalena Maria Krasztel
Michał Czopowicz
Agata Moroz
Marcin Mickiewicz
Jarosław Kaba
MMK, MC, and JK designed research; MMK, OS-J, AM, MM, and MC performed research; MMK and MC performed statistical and epidemiological analysis. MMK and MC wrote the draft manuscript. JK and MC edited and reviewed the manuscript. All authors read and approved the final manuscript.
Correspondence to Michał Czopowicz.
No ethics commission approval for this study was required according to Polish legal regulations (the Act on the Protection of Animals Used for Scientific or Educational Purposes of 15 January 2015) as only routine diagnostic procedures essential given the clinical status of the cat were performed and the study was purely analytical. An informed consent of each cat's owner for participation in the study was obtained.
Numerical values of 7 complete blood count (CBC) measurements in 73 lethargic and anorectic and the cut-off values used for their categorization based on the highest Youden's index (J).
Krasztel, M.M., Czopowicz, M., Szaluś-Jordanow, O. et al. Application of a complete blood count to screening lethargic and anorectic cats for pancreatitis. BMC Vet Res 17, 383 (2021). https://doi.org/10.1186/s12917-021-03098-z
DOI: https://doi.org/10.1186/s12917-021-03098-z
Eosinophil count
fPLI | CommonCrawl |
Does the prefix of an inverted unit also get inverted?
What is the energy of radiation that has a frequency of $\pu{2.51 \times 10^11 ms-1}$?
(a) $\pu{1.66 \times 10^-19 J}$ (supposedly correct)
(b) $\pu{1.66 \times 10^-22 J}$
(c) $\pu{7.92 \times 10^-37 J}$
(d) $\pu{1.66 \times 10^-25 J}$
My argument was that: since $\pu{Hz} = \pu{s-1}$, then $\pu{ms-1} = \pu{mHz}$. So, I divided $2.51 \times 10^{11}$ by $1000$ and solved the question normally (using $E = h\nu$). But my professor said that since $\pu{m}$ is a prefix, it should follow whatever is in front of it, so $\pu{ms-1}$ will become $1/\pu{ms}$, then you multiply it by 1000 to change it to Hz. Is that the correct way to do it?
orthocresol♦
BasimBasim
$\begingroup$ I applaud the literal interpretation, but yes the prefix goes with the unit therefore ms^-1 is equivalent to (ms)^-1. $\endgroup$ – A.K. Apr 11 '19 at 14:13
$\begingroup$ The prefix is part of the unit, in that milliseconds is its own unit. However, in this situation, it seems silly to write $\mathrm{ms}^{-1}$ when you could instead write $10^{3}\ \mathrm{s}^{-1}$. $\endgroup$ – Zhe Apr 11 '19 at 17:58
$\begingroup$ Yes it does, but to remember it in this form means to sweep a misunderstanding under the rug, which invites troubles in the future. Think of it this way. There are no prefixes. There are just thousands, millions, and other numbers, which you supposedly know how to handle when they turn $(\dots)^{-1}$. $\endgroup$ – Ivan Neretin Apr 12 '19 at 4:59
You should read $\pu{ms-1}$ as $(\pu{ms})^{-1}$ and not as $\mathrm{m}(\pu{s-1})$. Your teacher is correct.
[...] since $\pu{Hz} = \pu{s-1}$ then $\pu{ms-1} = \pu{mHz}$
If something happens once per hour, it happens less often than when it happens once per minute. This is because an hour is longer than a minute. In a similar manner, if something happens once per second, it happens less often than when it happens once per millisecond. This is because a second is longer than a millisecond.
So $\pu{ms-1} = \pu{kHz}$, i.e. the frequency of something happening every millisecond is larger than the frequency of something happening every second.
Karsten TheisKarsten Theis
This issue is explicitly addressed in BIPM: The International System of Units (SI) as follows.
The grouping formed by a prefix symbol attached to a unit symbol constitutes a new inseparable unit symbol (forming a multiple or submultiple of the unit concerned) that can be raised to a positive or negative power and that can be combined with other unit symbols to form compound unit symbols.
Examples: $$2.3\ \mathrm{cm}^3=2.3\ (\mathrm{cm})^3=2.3\ (10^{-2}\ \mathrm m)^3=2.3\times10^{-6}\ \mathrm m^3$$ $$1\ \mathrm{cm}^{-1}=1\ (\mathrm{cm})^{-1}=1\ (10^{-2}\ \mathrm m)^{-1}=10^2\ \mathrm m^{-1}=100\ \mathrm m^{-1}$$ $$1\ \mathrm{V/cm}=(1\ \mathrm V)/(10^{-2}\ \mathrm m)=10^2\ \mathrm{V/m}=100\ \mathrm{V/m}$$ $$5000\ \mathrm{µs}^{-1}=5000\ (\mathrm{µs})^{-1}=5000\ (10^{-6}\ \mathrm s)^{-1}=5\times10^9\ \mathrm s^{-1}$$
Therefore, $2.51\times10^{11}\ \mathrm{ms}^{-1}=2.51\times10^{11}\ (\mathrm{ms})^{-1}$.
Loong♦Loong
Not the answer you're looking for? Browse other questions tagged units or ask your own question.
How is the unit of measure "equivalent" abbreviated?
What does the word carat really mean?
What would be the unit for the calculation of the rate of reaction?
What is the correct unit for the equilibrium constant?
Unit analysis for neutralization reaction | CommonCrawl |
Computational Science Meta
Computational Science Stack Exchange is a question and answer site for scientists using computers to solve scientific problems. It only takes a minute to sign up.
Numerical computation of two-sided (bilateral) Laplace transform
I need to compute the two-sided (bilateral) Laplace transform of a numerically given function $F$, $$ I(t) = \int_{-\infty}^{+\infty} {dx} \, e^{-x} \, F(x + t) ~, $$ where $F(x)$ has some sharp features, e.g., at $ x = \{ 0, x_p, \cdots \} $, has finite support, and vanishes sufficiently fast for $ x < 0 $ to prevent a divergence of the integral.
Due to the sharp features, I have to divide the integration region to some subregions, for instance, \begin{align} I(t) &= \int_{-\infty}^{-\Delta} {dx} \, e^{-x} \, F(x + t) + \int_{-\Delta}^{+\Delta} {dx} \, e^{-x} \, F(x + t) \\ &\quad + \int_{+\Delta}^{x_p - \Delta} {dx} \, e^{-x} \, F(x + t) + \int_{x_p - \Delta}^{x_p + \Delta} {dx} \, e^{-x} \, F(x + t) \\ &\quad + \int_{x_p + \Delta}^{+\infty} {dx} \, e^{-x} \, F(x + t) ~, \end{align} where $\Delta > 0$.
I'd like to know the best and most precise way to perform such an integral numerically (quadrature methods). Is there something like Gauss-Laguerre quadrature for such an integration?
I have also considered a transformation of the integration variable, $$ u = e^{-x} ~, $$ to absorb the exponential factor, $$ I(t) = \int_{0^+ = \, u(x \rightarrow +\infty)}^{+\infty = \, u(x \rightarrow -\infty)} {du} \, F(-\ln(u) + t) ~, $$ and performing the transformed integration by a Tanh-Sinh quadrature; yet I am not sure if this is the best method.
As an example, one can take $$ f(x,\omega) = e^{-\alpha (x - \omega)} \, \Theta(x - \omega) $$ where $\Theta$ denotes the Heaviside step function and $\alpha > 0$. Hence, the 'width' of the peak at $\omega$ can be varied by $\alpha$. The two-sided Laplace transform of $f$ will be $$ \mathcal{L}[f](\omega) := \int_{-\infty}^{+\infty} dx \, e^{-x} \, f(x, \omega) = \frac{ e^{-\omega} }{1 + \alpha} ~. $$
AlQuemist
AlQuemistAlQuemist
$\begingroup$ The need to integrate high oscillatory kernels arises frequently in the evaluation of Sommerfeld integrals for dyadic Green's functions. The usual practice is to do a (numerical) rational fit of $F(x)$ as a collection of poles $\sum_i 1/(x+c_i)$ and to use a closed-form expression to convert the poles into the inverse transform. $\endgroup$ – Richard Zhang Mar 26 '16 at 5:25
$\begingroup$ @RichardZhang : The integrand is not oscillatory here, as you can see, for instance, in the example provided. $\endgroup$ – AlQuemist Mar 26 '16 at 17:07
$\begingroup$ My apologies, the intention of my comment wasn't to suggest that your kernel is oscillatory, only that difficult intergands can often be treated using a semi-analytical approach of rational fitting + closed-form transformation formulas. $\endgroup$ – Richard Zhang Mar 27 '16 at 14:06
$\begingroup$ @RichardZhang: The integrands are only available numerically (obtained from another numerical procedure). No analytical expression exists for them. $\endgroup$ – AlQuemist Mar 27 '16 at 15:19
$\begingroup$ Do you agree that a numerically evaluated $F(x)$ can be approximated to arbitrary accuracy (under regularity assumptions) as a rational function, $\tilde{F}(x)=\sum_i 1/(x+c_i)$? And do you agree that the bilateral Laplace transform has a closed form expression for $\tilde{F}(x)$? $\endgroup$ – Richard Zhang Mar 27 '16 at 15:25
With the substitution $y=x+t$, the $t$-dependency can be factored out:
$$I(t)=\int_{-\infty}^\infty e^{-(y-t)}F(y)\;dy = e^t \int_{-\infty}^\infty e^{-y}F(y)\;dy = C\cdot e^t$$
This still leaves you with the problem of computing $C$, but it is merely a constant number and the $t$-dependency is entirely described by the factor $e^t$. The two-sided Laplace transfrom of this function and its region of convergence (if it is non-empty) should be found in a table of Laplace transforms.
Edit: On a second thought, I doubt that the two-sided Laplace transform of $I(t)$ exists even for purely imaginary $s$, because $I(t)\sim e^t$ is not a tempered distribution.
cdalitzcdalitz
Thanks for contributing an answer to Computational Science Stack Exchange!
Not the answer you're looking for? Browse other questions tagged quadrature or ask your own question.
Suggestions for numerical integral over Pólya Distribution
Numerical integration of compactly supported function on a triangle
Numerical Integration with Convergence Factor with SciPy: Problem with Improper Integral
How do I integrate this function in python?
Tanh-sinh quadrature numerical integration method converging to wrong value
Is there a Gauss-Laguerre integration routine in Python?
How to implement Gauss-Laguerre Quadrature in Python?
Numerical evaluation of an elliptic integral in python
Computation of stiffness matrix with variable coefficient | CommonCrawl |
Is the expected time for a star in an elliptical galaxy to collide with another star less than the average age of elliptical galaxies?
According to the Wikipedia article Elliptical galaxy, elliptical galaxies have a much lower concentration of gas between the stars than spiral galaxies. I know that until the gas is below a certain concentration, its atoms don't travel very far between collisions and it follows the normal gas laws and the gas actually flows into the stars when they pass by. I know that when the interstellar gas is at such a low concentration that atoms on average travel a much larger distance than the average diameter of a star in the elliptical galaxy it's in, the gas doesn't follow the normal gas laws and gas gets mainly absorbed into stars by happening to be headed towards one and colliding with it rather than by flowing towards one and the ratio of the rate of absorption of gas into stars to the concentration of interstellar gas is lower, and a star has about the same expected time before colliding with another star as an interstellar gas atom has before colliding with a star. I also know that when the interstellar medium is at the equilibrium concentration, there are 3 possible driving forces for the reduction of interstellar gas; star formation, flow of interstellar gas into stars, and random collisions of interstellar gas atoms with a star which can only occur at very low concentration; and 2 driving forces for the increase in interstellar gas, the slow escape of gas molecules from stars and collisions between stars because collisions occur at a high enough speed to produce an explosion instead of combining into a larger star. Which driving force for the reduction of interstellar gas is the largest? Also, which driving force for the increase in interstellar gas is larger? If it's star formation, that means the interstellar gas is at a high enough concentration to follow the normal gas laws but since the amount of interstallar gas is at equilibrium, the main driving force for the increase in interstellar gas is collisions between stars. If it's the slow escape of gas from stars, the main driving force for the decrease in interstellar gas could be the flow of gas into stars or the random collisions of gas molecules with stars but not star formation. If the main driving force for the reduction in interstallr gas concentration is collisions of gas molecules with stars, then a star has about the same expected time beofre a collision with another star as an intersteller gas atom has before colliding with another star so the expected time before a star collides with another star is less than the age of the galaxy and if it's flow of gas into stars, the main driving force for the increase in interstellar gas could be either of the two driving forces but if the driving force for the increase is collisions between stars, the expected time before a star collides with another star is less than the age of the galaxy,
On the other hand, if the interstellar gas concentration has not yet reached equilibrium, it could be that not enough time has gone by for the interstellar gas to not follow the normal gas laws and star formation occurs mainly by the gas coalescing into stars. It could also be that the interstellar gas started diving exponentially until it stopped following the normal gas laws then the rate at which it divides exponentially greatly reduced so it has not yet had time to reach the equilibrium concentration.
galactic-dynamics interstellar-medium
TimothyTimothy
$\begingroup$ This question is currently a "wall of text". It would be nice if you could break it up into paragraphs, and shorter sentences. $\endgroup$ – HDE 226868♦ Sep 11 '17 at 17:53
$\begingroup$ My eyes hurt from trying to read the question, but: The number density of atoms, even in the most dilute regions of an elliptical, is of the order $10^{-3}$–$10^{-2}\,\mathrm{cm}^{-3}$. In contrast, the number density of stars in the most dense stellar regions is at most $10^3$ stars per cubic parsec, or $10^{-54}\,\mathrm{cm}^{-3}$. So an atom is much, much, much more likely to collide with a star, or another atom, than two stars are. $\endgroup$ – pela Sep 11 '17 at 18:20
$\begingroup$ Your changed your question, which might have invalidated my answer. This is frowned upon on SE; I'd ask that you rollback your edit and ask a new question if need be. $\endgroup$ – HDE 226868♦ Sep 12 '17 at 1:24
$\begingroup$ You wrote an answer so soon after I wrote my question. $\endgroup$ – Timothy Sep 12 '17 at 17:25
$\begingroup$ I edited my question because you complained that it was a wall of text. I did not see an answer at the time I started making the edit then while I was in the middle of editing, I saw that you wrote an answer. According to my question at meta.stackexchange.com/questions/298932/…, I thought it was better to think carefully what I want to write before I write it. I couldn't do that because I did not yet see a problem with the way it was before you complained that it was a wall of text. $\endgroup$ – Timothy Sep 19 '17 at 3:06
The collision timescale for a star in the solar neighborhood is1 $$t_c\simeq5\times10^{10}\text{ Gyr}\left(\frac{R}{R_{\odot}}\right)^{-2}\left(\frac{v}{30\text{ km s}^{-1}}\right)^{-1}\left(\frac{n}{0.1\text{ pc}^{-3}}\right)^{-1}$$ where $R$ is the radius of a star, $v$ is its speed relative to the stars around it, and $n$ is the stellar number density. That number isn't in years; it's in billions of years. You're looking at collision timescales on the order of $\sim10^{19}\text{ yrs}$, many orders of magnitude larger than the current age of the universe. Even changing $v$ and $n$ a bit can't really lower that significantly.
Yes, there are lots of stars in a galaxy. Current estimates put 100 billion or so stars in the Milky Way, give or take. So yes, it's certainly likely for a galaxy to have two of its stars collide sometime before now (and I'm ignoring mergers in binary systems, as well as globular clusters, which also see many stellar collisions). But the collision timescale for any single star is much, much greater than the current age of its parent galaxy.
You can probably see why galaxies are usually modeled as collisionless systems. The collisionless version of the Boltzmann equation is used, which simplifies computations quite a bit.
1 I'm referencing my textbook, Foundations of Astrophysics, Ryden & Peterson. Eqn 22.17, page 516.
HDE 226868♦HDE 226868
$\begingroup$ You're making sure that collision equation is talking about physical collisions right? Astronomers tend to use the term collision to include all sorts of other types such as gravitational collisions. $\endgroup$ – zephyr Sep 12 '17 at 14:24
$\begingroup$ @zephyr Yes, I was just referring to physical collisions. The gravitational cross-section of a star shouldn't change things by more than an order of magnitude or two; for this sort of order-of-magnitude approximation, I figured that it would work well enough. $\endgroup$ – HDE 226868♦ Sep 12 '17 at 15:40
Not the answer you're looking for? Browse other questions tagged galactic-dynamics interstellar-medium or ask your own question.
Could discoid galaxies be expanding?
Has the great Andromeda Galaxy ever collided with any galaxies?
Why do these astronomers say that "Carbon chains with more than nine atoms are unstable"?
Why is SPT0418-47 ("the most distant Milky Way look-alike") expected to evolve into an elliptical galaxy? | CommonCrawl |
Swap (finance)
Title: Swap (finance)
Subject: Derivative (finance), Commodity market, IBM, Over-the-counter (finance), Zero-Coupon Inflation-Indexed Swap
Collection: Derivatives (Finance)
Bond valuation
High-yield debt
Municipal bond
Registered share
Stock certificate
Voting share
Credit derivative
Futures exchange
Hybrid security
Reinsurance market
Practical trading
Financial market participants
Finance series
A swap is a derivative in which two counterparties exchange cash flows of one party's financial instrument for those of the other party's financial instrument. The benefits in question depend on the type of financial instruments involved. For example, in the case of a swap involving two bonds, the benefits in question can be the periodic interest (coupon) payments associated with such bonds. Specifically, two counterparties agree to exchange one stream of cash flows against another stream. These streams are called the legs of the swap. The swap agreement defines the dates when the cash flows are to be paid and the way they are accrued and calculated.[1] Usually at the time when the contract is initiated, at least one of these series of cash flows is determined by an uncertain variable such as a floating interest rate, foreign exchange rate, equity price, or commodity price.[1]
The cash flows are calculated over a notional principal amount. Contrary to a future, a forward or an option, the notional amount is usually not exchanged between counterparties. Consequently, swaps can be in cash or collateral.
Swaps can be used to hedge certain risks such as interest rate risk, or to speculate on changes in the expected direction of underlying prices.[2]
Swaps were first introduced to the public in 1981 when IBM and the World Bank entered into a swap agreement.[3] Today, swaps are among the most heavily traded financial contracts in the world: the total amount of interest rates and currency swaps outstanding is more thаn $348 trillion in 2010, according to Bank for International Settlements (BIS). Annual value and records of trade also record by Basel 3 (written as Basel III).
Swap market 1
Types of swaps 2
Interest rate swaps 2.1
Currency swaps 2.2
Commodity swaps 2.3
Credit default swaps 2.4
Subordinated risk swaps 2.5
Other variations 2.6
Using bond prices 3.1
Arbitrage arguments 3.2
Swap market
Most swaps are traded over-the-counter (OTC), "tailor-made" for the counterparties. Some types of swaps are also exchanged on futures markets such as the Chicago Mercantile Exchange, the largest U.S. futures market, the Chicago Board Options Exchange, IntercontinentalExchange and Frankfurt-based Eurex AG.
The Bank for International Settlements (BIS) publishes statistics on the notional amounts outstanding in the OTC derivatives market. At the end of 2006, this was USD 415.2 trillion, more than 8.5 times the 2006 gross world product. However, since the cash flow generated by a swap is equal to an interest rate times that notional amount, the cash flow generated from swaps is a substantial fraction of but much less than the gross world product—which is also a cash-flow measure. The majority of this (USD 292.0 trillion) was due to interest rate swaps. These split by currency as:
The CDS and currency swap markets are dwarfed by the interest rate swap market. All three markets peaked in mid-2008.
Source: BIS Semiannual OTC derivatives statistics at end-December 2008
Notional outstanding
in USD trillion
Currency End 2000 End 2001 End 2002 End 2003 End 2004 End 2005 End 2006
Euro 16.6 20.9 31.5 44.7 59.3 81.4 112.1
US dollar 13.0 18.9 23.7 33.4 44.8 74.4 97.6
Japanese yen 11.1 10.1 12.8 17.4 21.5 25.6 38.0
Pound sterling 4.0 5.0 6.2 7.9 11.6 15.1 22.3
Swiss franc 1.1 1.2 1.5 2.0 2.7 3.3 3.5
Total 48.8 58.9 79.2 111.2 147.4 212.0 292.0
Source: "The Global OTC Derivatives Market at end-December 2004", BIS, [1], "OTC Derivatives Market Activity in the Second Half of 2006", BIS, [2]
Usually, at least one of the legs has a rate that is variable. It can depend on a reference rate, the total return of a swap, an economic statistic, etc. The most important criterion is that it comes from an independent third party, to avoid any conflict of interest. For instance, LIBOR is published by the British Bankers Association, an independent trade body but this rate is known to be rigged (Barclays and others banks have been convicted in the 2010-2012 LIBOR scandal).
Types of swaps
The five generic types of swaps, in order of their quantitative importance, are: interest rate swaps, currency swaps, credit swaps, commodity swaps and equity swaps. There are also many other types of swaps.
A is currently paying floating, but wants to pay fixed. B is currently paying fixed but wants to pay floating. By entering into an interest rate swap, the net result is that each party can 'swap' their existing obligation for their desired obligation. Normally, the parties do not swap payments directly, but rather each sets up a separate swap with a financial intermediary such as a bank. In return for matching the two parties together, the bank takes a spread from the swap payments.
The most common type of swap is a "plain Vanilla" interest rate swap. It is the exchange of a fixed rate loan to a floating rate loan. The life of the swap can range from 2 years to over 15 years.
The reason for this exchange is to take benefit from comparative advantage. Some companies may have comparative advantage in fixed rate markets, while other companies have a comparative advantage in floating rate markets. When companies want to borrow, they look for cheap borrowing, i.e. from the market where they have comparative advantage. However, this may lead to a company borrowing fixed when it wants floating or borrowing floating when it wants fixed. This is where a swap comes in. A swap has the effect of transforming a fixed rate loan into a floating rate loan or vice versa.
For example, party B makes periodic interest payments to party A based on a variable interest rate of LIBOR +70 basis points. Party A in return makes periodic interest payments based on a fixed rate of 8.65%. The payments are calculated over the notional amount. The first rate is called variable because it is reset at the beginning of each interest calculation period to the then current reference rate, such as LIBOR. In reality, the actual rate received by A and B is slightly lower due to a bank taking a spread.
Currency swaps
A currency swap involves exchanging principal and fixed rate interest payments on a loan in one currency for principal and fixed rate interest payments on an equal loan in another currency. Just like interest rate swaps, the currency swaps are also motivated by comparative advantage. Currency swaps entail swapping both principal and interest between the parties, with the cashflows in one direction being in a different currency than those in the opposite direction. It is also a very crucial uniform pattern in individuals and customers.
Commodity swaps
A commodity swap is an agreement whereby a floating (or market or spot) price is exchanged for a fixed price over a specified period. The vast majority of commodity swaps involve crude oil.
A credit default swap (CDS) is a contract in which the buyer of the CDS makes a series of payments to the seller and, in exchange, receives a payoff if an instrument, typically a bond or loan, goes into default (fails to pay). Less commonly, the credit event that triggers the payoff can be a company undergoing restructuring, bankruptcy or even just having its credit rating downgraded. CDS contracts have been compared with insurance, because the buyer pays a premium and, in return, receives a sum of money if one of the events specified in the contract occur. Unlike an actual insurance contract the buyer is allowed to profit from the contract and may also cover an asset to which the buyer has no direct exposure.
Subordinated risk swaps
A subordinated risk swap (SRS), or equity risk swap, is a contract in which the buyer (or equity holder) pays a premium to the seller (or silent holder) for the option to transfer certain risks. These can include any form of equity, management or legal risk of the underlying (for example a company). Through execution the equity holder can (for example) transfer shares, management responsibilities or else. Thus, general and special entrepreneurial risks can be managed, assigned or prematurely hedged. Those instruments are traded over-the-counter (OTC) and there are only a few specialized investors worldwide.
There are myriad different variations on the vanilla swap structure, which are limited only by the imagination of financial engineers and the desire of corporate treasurers and fund managers for exotic structures.[1]
A total return swap is a swap in which party A pays the total return of an asset, and party B makes periodic interest payments. The total return is the capital gain or loss, plus any interest or dividend payments. Note that if the total return is negative, then party A receives this amount from party B. The parties have exposure to the return of the underlying stock or index, without having to hold the underlying assets. The profit or loss of party B is the same for him as actually owning the underlying asset.
An option on a swap is called a swaption. These provide one party with the right but not the obligation at a future time to enter into a swap.
A variance swap is an over-the-counter instrument that allows one to speculate on or hedge risks associated with the magnitude of movement, a CMS, is a swap that allows the purchaser to fix the duration of received flows on a swap.
An Amortising swap is usually an interest rate swap in which the notional principal for the interest payments declines during the life of the swap, perhaps at a rate tied to the prepayment of a mortgage or to an interest rate benchmark such as the LIBOR. It is suitable to those customers of banks who want to manage the interest rate risk involved in predicted funding requirement, or investment programs.
A Zero coupon swap is of use to those entities which have their liabilities denominated in floating rates but at the same time would like to conserve cash for operational purposes.
A Deferred rate swap is particularly attractive to those users of funds that need funds immediately but do not consider the current rates of interest very attractive and feel that the rates may fall in future.
An Accrediting swap is used by banks which have agreed to lend increasing sums over time to its customers so that they may fund projects.
A Forward swap is an agreement created through the synthesis of two swaps differing in duration for the purpose of fulfilling the specific time-frame needs of an investor. Also referred to as a forward start swap, delayed start swap, and a deferred start swap.
The value of a swap is the net present value (NPV) of all estimated future cash flows. A swap is worth zero when it is first initiated, however after this time its value may become positive or negative.[1] There are two ways to value swaps: in terms of bond prices, or as a portfolio of forward contracts.[1]
Using bond prices
While principal payments are not exchanged in an interest rate swap, assuming that these are received and paid at the end of the swap does not change its value. Thus, from the point of view of the floating-rate payer, a swap is equivalent to a long position in a fixed-rate bond (i.e. receiving fixed interest payments), and a short position in a floating rate note (i.e. making floating interest payments):
V_\mathrm{swap} = B_\mathrm{fixed} - B_\mathrm{floating} \,
From the point of view of the fixed-rate payer, the swap can be viewed as having the opposite positions. That is,
V_\mathrm{swap} = B_\mathrm{floating} - B_\mathrm{fixed} \,
Similarly, currency swaps can be regarded as having positions in bonds whose cash flows correspond to those in the swap. Thus, the home currency value is:
V_\mathrm{swap} = B_\mathrm{domestic} - S_0 B_\mathrm{foreign}, where B_\mathrm{domestic} is the domestic cash flows of the swap, B_\mathrm{foreign} is the foreign cash flows of the LIBOR is the rate of interest offered by banks on deposit from other banks in the eurocurrency market. One-month LIBOR is the rate offered for 1-month deposits, 3-month LIBOR for three months deposits, etc.
LIBOR rates are determined by trading between banks and change continuously as economic conditions change. Just like the prime rate of interest quoted in the domestic market, LIBOR is a reference rate of interest in the international market.
Arbitrage arguments
As mentioned, to be arbitrage free, the terms of a swap contract are such that, initially, the NPV of these future cash flows is equal to zero. Where this is not the case, arbitrage would be possible.
For example, consider a plain vanilla fixed-to-floating interest rate swap where Party A pays a fixed rate, and Party B pays a floating rate. In such an agreement the fixed rate would be such that the present value of future fixed rate payments by Party A are equal to the present value of the expected future floating rate payments (i.e. the NPV is zero). Where this is not the case, an Arbitrageur, C, could:
assume the position with the lower present value of payments, and borrow funds equal to this present value
meet the cash flow obligations on the position by using the borrowed funds, and receive the corresponding payments - which have a higher present value
use the received payments to repay the debt on the borrowed funds
pocket the difference - where the difference between the present value of the loan and the present value of the inflows is the arbitrage profit.
Subsequently, once traded, the price of the Swap must equate to the price of the various corresponding instruments as mentioned above. Where this is not true, an arbitrageur could similarly short sell the overpriced instrument, and use the proceeds to purchase the correctly priced instrument, pocket the difference, and then use payments generated to service the instrument which he is short.
Constant maturity swap
Cross currency swap
Equity swap
Foreign exchange swap
Fuel price risk management
Interest rate swap
PnL Explained
Swap Execution Facility
Total return swap
Variance swap
Financial Institutions Management, Saunders A. & Cornett M., McGraw-Hill Irwin 2006
^ a b c d e John C Hull, Options, Futures and Other Derivatives (6th edition), New Jersey: Prentice Hall, 2006, 149
^ http://chicagofed.org/webpages/publications/understanding_derivatives/index.cfm
^ Ross, Westerfield, & Jordan (2010). Fundamentals of Corporate Finance (9th, alternate ed.).
Understanding Derivatives: Markets and Infrastructure Federal Reserve Bank of Chicago, Financial Markets Group
swaps-rates.com, interest swap rates statistics online
Bank for International Settlements
International Swaps and Derivatives Association
Derivative (finance)
Credit spread
Moneyness
Pin risk
Risk-free rate
Bond option
Employee stock option
Option styles
Exotic options
Commodore option
Compound option
Forward start option
Interest rate option
Rainbow option
Swaption
Covered call
Protective put
Risk reversal
Intermarket
Black–Scholes model
Finite difference
Garman-Kohlhagen
Margrabe's formula
Put–call parity
Trinomial
Vanna–Volga pricing
Conditional variance
Constant maturity
Credit default
Backwardation
Contango
Currency future
Financial future
Forward price
Forward rate
Index future
Interest rate future
Forwards pricing
Futures pricing
Single-stock futures
Other derivatives
Credit default option
Credit-linked note (CLN)
Contract for difference
Constant proportion portfolio insurance (CPPI)
Equity-linked note (ELN)
Equity derivative
Foreign exchange derivative
Fund derivative
Inflation derivative
Interest rate derivative
Power reverse dual-currency note (PRDC)
Real estate derivatives
Market issues
Corporate debt
Late 2000s recession
Articles needing expert attention with no reason or talk parameter
Articles needing expert attention from November 2008
All articles needing expert attention
Business and Economics articles needing expert attention
Articles lacking in-text citations from July 2008
Derivatives (finance)
Real estate, Finance, Credit derivative, Currency, Forward contract
Saudi Arabia, India, United Kingdom, Canada, Italy
Derivative (finance), Day count convention, Euribor, Swap rate, Goldman Sachs
Forward price, Real estate, Gold, Derivatives market, Finance
Option (finance)
Real estate, Finance, Strike price, Expiration (options), Mortgage loan
United Kingdom, United States, Cyprus, Russia, Australia
NYSE Arca, Chicago Board of Trade, Gold, Palladium, Platinum
Sony, Samsung Electronics, Apple Inc., Linux, Toshiba
Over-the-counter (finance)
Derivatives market, Exchange rate, Financial regulation, Finance, Technical analysis
Zero-Coupon Inflation-Indexed Swap
Derivatives market, Finance, Swap (finance), Currency, Bank | CommonCrawl |
Relativistic photography with a wide aperture
Norman Gray, Ruaridh O'Donnell, Ross MacSporran, Stephen Oxburgh, and Johannes Courtial
Norman Gray, Ruaridh O'Donnell, Ross MacSporran, Stephen Oxburgh, and Johannes Courtial*
School of Physics & Astronomy, College of Science & Engineering, University of Glasgow, Glasgow G12 8QQ, UK
*Corresponding author: [email protected]
Johannes Courtial https://orcid.org/0000-0002-5990-7972
N Gray
R O'Donnell
R MacSporran
S Oxburgh
J Courtial
Norman Gray, Ruaridh O'Donnell, Ross MacSporran, Stephen Oxburgh, and Johannes Courtial, "Relativistic photography with a wide aperture," J. Opt. Soc. Am. A 37, 123-134 (2020)
Omnidirectional transformation-optics cloak made from lenses and glenses
Tomáš Tyc, et al.
Relativistic aberration of optical phase space
Kurt Bernardo Wolf
Hand-held aperture-sharing camera for a multiview image set
Jung-Young Son, et al.
Binocular vision
Flashlamps
Fresnel zones
Slow light
Manuscript Accepted: November 4, 2019
RAY TRAJECTORY IN THE SCENE FRAME AND IN THE CAMERA FRAME
TAKING PHOTOS WITH A WIDE APERTURE
CORRECTING RELATIVISTIC ABERRATION WITH LORENTZ WINDOWS
We discuss new effects related to relativistic aberration, which is the apparent distortion of objects moving at relativistic speeds relative to an idealized camera. Our analysis assumes that the camera lens is capable of stigmatic imaging of objects at rest with respect to the camera, and that each point on the shutter surface is transparent for one instant, but different points are not necessarily transparent synchronously. We pay special attention to the placement of the shutter. First, we find that a wide aperture requires the shutter to be placed in the detector plane to enable stigmatic images. Second, a Lorentz-transformation window [Proc. SPIE 9193, 91931K (2014) [CrossRef] ] can correct for relativistic distortion. We illustrate our results, which are significant for future spaceships, with raytracing simulations.
Published by The Optical Society under the terms of the Creative Commons Attribution 4.0 License. Further distribution of this work must maintain attribution to the author(s) and the published article's title, journal citation, and DOI.
In his famous 1905 paper [1], Einstein introduced special relativity and discussed the Lorentz–FitzGerald contraction of a fast-moving sphere into an ellipsoid. This apparent deformation had been studied before, when FitzGerald suggested it [2] to explain the Michelson–Morley experiment [3]. In 1924, Lampa [4] took into account the time when the relevant light rays leave the fast-moving object to arrive simultaneously at the observer, thereby correctly describing the visual appearance of objects. Taking into account these time-of-flight effects alters the apparent relativistic distortion of fast-moving objects. Lampa's work was largely ignored until, in 1959, Penrose [5] and Terrell [6] rediscovered the role of ray timing. They arrived at the conclusion that fast-moving objects would not actually appear contracted, but in the cases investigated, they would appear rotated, an effect now known as Penrose–Terrell rotation. However, it was observed shortly afterwards that straight lines could appear curved [7], showing that the apparent distortion of fast-moving objects is not always a rotation and thus demonstrating the limited applicability of Penrose–Terrell rotation [8]. A few of these effects have been observed experimentally [9].
In 1995, researchers first used raytracing to create photorealistic images of fast-moving objects [10]. This was discussed in terms of images taken with an idealized camera moving at relativistic speeds. The timing of the relevant light rays is determined by the shutter model: the placement of the shutter within the camera, which is assumed to open for one instant. In their nomenclature, the shutter placement considered by earlier authors, in which all light rays that contribute to the photo arrive simultaneously at the camera's pinhole, is called the pinhole shutter model. Figure 1(b) shows an example of a raytracing simulation for the pinhole shutter model. This approach has been developed in various directions, enabling raytracing of independently moving objects [13] and interactive relativistic raytracing. Examples of the latter include a museum exhibit (where the observer controls his/her speed and direction through a bicycle interface) [14], and the free real-time relativity [15] and a slower speed of light [16], which allow real-time, interactive simulation of movement at relativistic speeds.
Fig. 1. Relativistic distortion, and comparison with the effect of time-of-flight effects only. The images show raytracing simulations of photos of a scene (a) taken with a camera moving at relativistic speed through the scene (b) and with an (unphysical) camera in which only time-of-flight effects are taken into account, but those due to special relativity are ignored (c). The image shown in (c) was simulated by using the Galilean transformation instead of the Lorentz transformation when transforming between reference frames [11]. All simulations were performed for a pinhole camera using the pinhole shutter model. In (b) and (c), the camera moves with velocity ${\boldsymbol\beta}c$, where ${\boldsymbol\beta}=(0.1c,0,0.99c)^{\intercal}$ in the left-handed coordinate system used by our raytracing software, in which the $x$, $y$, and $z$ directions represent the right, up, and into the page, respectively. The simulations were performed using the scientific raytracer Dr TIM [12].
The studies outlined above considered the effect of taking a picture with a pinhole camera. In other work, this has been generalized in two ways that are relevant to this paper. The first is a generalization of the pinhole to a wide aperture [17–19], which (in the aperture-plane shutter model, the natural generalization of the pinhole-shutter model) was shown mathematically (and without showing any photorealistic images) to lead to a global comatic aberration. The second is a generalization of cameras with a single aperture to multi-aperture cameras, of which a particularly simple example is a pair of cameras for the creation of stereo pairs simulating binocular vision. The result from this second generalization that is most relevant to our considerations is the finding that binocular vision fails at relativistic speeds [20]. In the same study, photorealistic stereo pairs of objects moving at relativistic speeds and in curved space–times were calculated, including a stereo movie that simulated falling into a black hole.
In order to investigate whether or not light-ray-direction-changing optical components called telescope windows (also known as generalized confocal lenslet arrays, GCLAs) [21] can simulate relativistic distortion (they cannot [11]), we extended the capabilities of our own custom scientific raytracer TIM [22] to include relativistic raytracing that fully simulates the distortion of objects moving with respect to the observer, but neglects other effects such as the headlight effect, the concentration of light in the direction of the observer's forward movement, and wave-optical effects such as the color change associated with the Doppler shift. The resulting new version of TIM, Dr TIM [12], has a range of other capabilities, including creating stereo pairs of images for viewing in a number of ways, e.g., on 3D monitors or as red–blue anaglyphs, enabling a stereo view of the scene; rendering photos taken with a virtual camera with a wide aperture (non-zero-size aperture plane, i.e., not a pinhole camera); and simulating the visual effect of transmission through windows that perform generalized refraction. The combination of Dr TIM's new relativistic-raytracing capability with the last two of these other capabilities is unique, and when experimenting with these combinations, we noticed a number of effects, which we describe and study here. Note that time-of-flight effects on their own result in a distortion that shares many of the qualities of relativistic distortion [Fig. 1(c)], and that the effects discussed in this paper are largely time-of-flight effects, modified by special relativity.
This paper is structured as follows. We establish the basis of what follows in Section 2. In Section 3, we consider the effect of a wide aperture in relativistic photography, answering the question of whether a camera moving relative to the scene can take stigmatic (i.e., ray-optically perfect) images. In Section 4, we consider the effect of taking a photo of a relativistic scene through a Lorentz-transformation window [11], which changes the direction of transmitted light rays in the same way in which light rays change direction upon change of an inertial frame. We discuss our results in Section 5, before concluding in Section 6.
2. RAY TRAJECTORY IN THE SCENE FRAME AND IN THE CAMERA FRAME
Consider a camera moving with velocity ${\boldsymbol\beta}c$ through a scene of stationary objects. We define two reference frames: in the camera frame, the camera is at rest; in the scene frame, the scene is at rest.
Both the camera's imaging system and shutter are highly idealized. The imaging system is treated as a planar thin lens that images, stigmatically, an arbitrary transverse plane at rest in the camera frame into the detector plane. The shutter is a surface—not necessarily a plane—each point on which is opaque at all times apart from one instant (finite but arbitrarily short), when it is transparent. Note that different points on the shutter are not necessarily transparent simultaneously in the camera frame (nor indeed the scene frame).
The planar thin lens is assumed to be capable of delaying transmission of different light rays by different delay times, without affecting them in any other way; this will be important later. Note that the single plane of the camera lens could also represent the two principal planes of an idealized imaging system [23] that are imaged into each with transverse magnification $+1$, whereby the space between them is omitted for simplicity, but the time taken by light rays to travel between conjugate positions could be accounted for as a transmission delay.
For our purposes, it is instructive to discuss how relativistic raytracing software, including Dr TIM, traces the trajectories of the light rays that contribute to a photo. In order to contribute to the photo, a light ray eventually has to hit the camera's detector, which means its trajectory has to pass through any apertures in the system, and its timing has to be such that it passes through the shutter surface at the precise time when the position where it intersects the shutter is transparent. We call such a light ray a photo ray. Like all other light rays, photo rays start at a light source, interact with any scene objects, and end at the detector inside the camera, but Dr TIM (like almost all rendering raytracing software) traces photo rays backwards, from the camera, through the scene, to a light source. What matters for relativistic raytracing is events during a ray's existence, specifically positions on the ray trajectory and the times when the ray passes through those positions.
We first consider the situation in the camera frame (Fig. 2), in which we use unprimed coordinates throughout this paper. The ray trajectory ends at a position ${\textbf{D}}$ in the detector plane, which corresponds to a particular pixel in the simulated photo that is to be calculated. The ray arrives from the direction of a position ${\textbf{L}}$ on the camera's lens. As the lens is a thin lens that images every point stigmatically, the ray arrives at the point ${\textbf{L}}$ on the lens from the direction of the point ${\textbf{P}}$ that is conjugate to ${\textbf{D}}$.
Fig. 2. (a) Trajectory of a photo ray (a light ray contributing to a photo), viewed in the camera frame. The trajectory is shown as a red line with an arrow tip at its end. The camera is moving with (relativistic) velocity ${\boldsymbol\beta}c$ through a stationary scene. The camera's lens stigmatically images the position ${\textbf{P}}$ to the position ${\textbf{D}}$ on the detector, which means it re-directs any ray from ${\textbf{P}}$ such that it subsequently passes through ${\textbf{D}}$. ${\textbf{L}}$ is the point where the ray intersects the idealized thin lens (vertical double-sided arrow). In the camera frame, the light ray passes ${\textbf{P}}$ at time ${t_{\text{P}}}$, enters ${\textbf{L}}$ at ${t_{\text{L}}}$, and reaches ${\textbf{D}}$ at ${t_{\text{D}}}$. (b) Several photo rays from ${\textbf{P}}$, shown in the camera frame. Due to the imaging properties of the lens, these rays intersect the same image position ${\textbf{D}}$ on the detector (not shown). Different rays intersect the camera lens at different positions, labeled ${{\textbf{L}}_1}$ to ${{\textbf{L}}_5}$. Each ray can be Lorentz-transformed into the scene frame by considering two events: for ray $i$, these are the times and positions of the ray passing through ${\textbf{P}}$ and ${{\textbf{L}}_i}$. (c) The same rays, shown in the scene frame. Ray $i$ ($i=1$ to 5) passes through the scene-frame positions ${\textbf{P}}_i^\prime$ and ${\textbf{L}}_i^\prime$, the positions of the events described above, Lorentz-transformed into the scene frame. These positions depend on the choice of shutter model and camera velocity ${\boldsymbol\beta}c$. In the scene frame, the rays do not necessarily intersect in a single point, which is the case in the example shown.
Before hitting the lens, the ray intersects objects and light sources at rest in the scene frame (the last one of which is in the direction of ${\textbf{P}}$).
Somewhere along the way, the light ray passes through the shutter, whose location and opening time is determined by the shutter model. This event determines the times of all the events mentioned above.
For raytracing purposes it is crucial when the photo ray hits the lens. This event is important because this is when the raytracing algorithm switches between the camera frame and the scene frame. The time of the event is, of course, determined by the shutter model. We will refer below to the set of the positions where the algorithm switches between frames as the Lorentz surface; this transition could happen anywhere on the last segment of a photo ray's trajectory, but it is conceptually convenient to identify the transition as happening on a surface, usually the lens plane, on the grounds that this is where the camera frame "begins." The time of the ray hitting the lens in the camera frame (at position ${\textbf{L}}$) determines the position ${{\textbf{L}}^\prime}$ of that same event Lorentz-transformed into the scene frame (as the camera is moving), which is then the starting point of standard (reverse) raytracing in the scene frame. This standard raytracing also requires the ray direction in the scene frame, and so it is necessary to Lorentz-transform the ray direction from the camera frame to the scene frame, a transformation that does not depend on time.
For the arguments in this paper it is sometimes helpful to consider not the event of the photo ray passing through the lens and the direction of the incident ray, but instead the events of the photo ray passing through points ${\textbf{P}}$ and ${\textbf{L}}$ in the camera frame [Fig. 2(b)]. The starting point of raytracing in the scene frame is then again the point ${{\textbf{L}}^\prime}$, and the direction of the ray in the scene frame is the direction of the straight line through ${{\textbf{P}}^\prime}$ and ${{\textbf{L}}^\prime}$ [Fig. 2(c)].
After the light ray has been Lorentz-transformed into the scene frame, where all the objects are stationary, timing no longer matters. For this reason, only the positions of events Lorentz-transformed into the scene frame need to be calculated. If, in the camera frame, an event happens at position ${\boldsymbol x}$ and at time $t$, then the corresponding, "Lorentz-shifted" position in the scene frame is [10]
(1)$${{\boldsymbol x}^\prime}={\boldsymbol x}+(\gamma-1)\frac{{({\boldsymbol\beta}\cdot {\boldsymbol x}){\boldsymbol\beta}}}{{{\beta^2}}}+\gamma {\boldsymbol\beta}ct,$$
where $\gamma=1/\sqrt {1-{\beta^2}}$. Note that the Lorentz shift, described by the second and third terms on the right-hand side of Eq. (1), is always parallel to ${\boldsymbol\beta}$. (Also note that the velocity of the scene frame in the camera frame is $-{\boldsymbol\beta}$, and the "$-$" sign in front of ${\boldsymbol\beta}$ leads to the "$+$" sign in front of the final term.) If the normalized direction of the ray in the camera frame is $\hat{\boldsymbol d}$, then the (not necessarily normalized) ray direction in the scene frame is [11]
(2)$${\boldsymbol d^\prime}=\hat{\boldsymbol d}+(\gamma-1)(\hat{\boldsymbol\beta}\cdot \hat{\boldsymbol d})\hat{\boldsymbol\beta}+\gamma {\boldsymbol\beta},$$
where $\hat{\boldsymbol\beta}=\hat{\boldsymbol\beta}/{\boldsymbol\beta}$ is a unit vector in the direction of ${\boldsymbol\beta}$.
All relativistic effects discussed in this paper are due to the change upon Lorentz transformation in the trajectory of the photo rays.
3. TAKING PHOTOS WITH A WIDE APERTURE
Consider an idealized camera with a wide aperture that can be focused on any surface in the camera frame, which the camera lens images, stigmatically, to the detector plane. Our analysis is primarily concerned with the question of whether or not it is possible for such a camera to image, stigmatically, objects in a scene if the camera is moving relative to the scene. Other aspects, such as the apparent distortion of the scene, are of secondary concern.
We consider the subset of photo rays that intersect the detector plane at the same position ${\textbf{D}}$, and establish the conditions under which these photo rays intersect in a single point in the scene frame. That scene-frame point is then stigmatically imaged onto the camera's detector. We are specifically discussing a camera with a "wide aperture," by which we mean that photo rays can pass through different points ${\textbf{L}}$ on the lens (Fig. 2); this is what differentiates the camera from a pinhole camera. For a scene-frame point to be imaged stigmatically onto the detector, all photo rays emitted from that scene-frame point must intersect the detector at the same position, irrespective of the position where they pass through the lens. Note that this condition for stigmatic imaging is always satisfied for a pinhole camera.
First, we consider the photo rays that intersect in the same detector position ${\textbf{D}}$ in the camera frame. Because of the (idealized) assumed imaging capabilities of the camera lens, ${\textbf{D}}$ is the image of an object point ${\textbf{P}}$ where these photo rays intersect before passing through the lens. Different photo rays intersect the lens at different positions; we call the position where the $i$th photo ray intersects the lens ${{\textbf{L}}_i}$. Figure 2(b) shows the trajectories of five photo rays between ${\textbf{P}}$ and the lens. The point ${\textbf{P}}$ is drawn as a real object, i.e., a point where the actual light-ray trajectories intersect, but note that our analysis is also valid for the situation where ${\textbf{P}}$ is a virtual object, i.e., a point where not the actual trajectories, but their straight-line continuations, intersect.
Second, we consider the same set of photo rays in the scene frame [Fig. 2(c)]. As discussed in Section 2, a photo ray that passes through the camera-frame positions ${\textbf{P}}$ and ${\textbf{L}}$ passes through the scene-frame positions ${{\textbf{P}}^\prime}$ and ${{\textbf{L}}^\prime}$, the positions of the camera-frame events of the ray passing through ${\textbf{P}}$ and ${\textbf{L}}$, Lorentz-transformed into the scene frame. ${{\textbf{L}}^\prime}$ is given by Eq. (1) with ${\boldsymbol x}={\textbf{L}}$ and $t$ being the time the ray passes through ${\textbf{L}}$ in the scene frame; similarly, ${{\textbf{P}}^\prime}$ is given by Eq. (1) with ${\boldsymbol x}={\textbf{P}}$ and $t$ being the time the ray passes through ${\textbf{P}}$ in the scene frame. For the $i$th photo ray, the position ${\textbf{L}}={{\textbf{L}}_i}$, and so for the different photo rays under consideration, the positions ${\textbf{L}}$ are all different. The times $t$ when they intersect these positions might or might not be different, depending on the shutter model. This means that it is not possible to say very much about the Lorentz-shifted positions ${\textbf{L}}_i^\prime$ of the different photo rays in the general case, other than that they are shifted from the positions ${\textbf{L}}$ in a direction parallel to ${\boldsymbol\beta}$. In contrast, the position ${\textbf{P}}$ is the same for all photo rays under consideration. This means that the corresponding scene-frame position ${\textbf{P}}_i^\prime$ of the $i$th ray depends only on the time when that ray passes through ${\textbf{P}}$ in the scene frame. Furthermore, if this time is different for the $i$th and $j$th photo rays, then the positions ${\textbf{P}}_i^\prime$ and ${\textbf{P}}_j^\prime$ are different. Conversely, whenever this time is the same for two or more photo rays, i.e., when they pass through the camera-frame position ${\textbf{P}}$ simultaneously, then they pass through the same corresponding scene-frame position ${{\textbf{P}}^\prime}$. This means that these photo rays intersect at that position ${{\textbf{P}}^\prime}$; rays 2 and 4 in Fig. 2(c) are examples. (In general, they have different directions, as the positions ${\textbf{L}}_i^\prime$ in general lie in different directions from ${{\textbf{P}}^\prime}$.) If another set of photo rays simultaneously passes through ${\textbf{P}}$ at a different time $t$ [e.g., rays 1 and 5 in Fig. 2(c)], then those rays intersect at a different scene-frame position, which means that the different photo rays do not all intersect in a single point in the scene frame. In general, if the photo rays under consideration do not all pass through ${\textbf{P}}$ simultaneously then they can be divided up into different sets that do pass through ${\textbf{P}}$ simultaneously. In all physically relevant situations, this means that whenever the photo rays through ${\boldsymbol D}$ pass through ${\boldsymbol P}$ at different times, they do not all intersect in the same point in the scene frame.
Below, we see this happening in different shutter models. Of the infinitely many different possible shutter models, we consider here four. As already mentioned above, we restrict ourselves to instantaneous shutter models, in which each position on the shutter surface becomes transparent for one instant and is completely absorbing at all other times. Three out of the four shutter models we consider are synchronous in the sense that all positions on the shutter surface become transparent simultaneously in the camera frame, namely, at time $t={t_S}$.
A. Aperture-Plane Shutter Model
We start with the simplest generalization of the pinhole shutter model to wide apertures, the synchronous aperture-plane shutter model, in which the shutter is located at the aperture containing the lens. In standard cameras, a shutter placed in this way is an example of a central shutter, a shutter placed somewhere within the lens assembly.
As always in our analysis, in the camera frame, it is the case that all photo rays that eventually intersect the detector at the same position ${\textbf{D}}$ intersect at the same object position ${\textbf{P}}$ before entering the camera lens. In the aperture-plane shutter model, all camera rays pass through the lens at the same time, which implies that camera rays that pass through different points on the lens in general pass through the position ${\textbf{P}}$ at different times. The spatial parts of the corresponding events are therefore also in general different, which means that in the aperture-plane shutter model (and in contrast to other shutter models), there are no positions that are stigmatically imaged by the camera.
Figure 3 illustrates this result. It shows raytracing simulations of photos taken with a camera at rest in the scene frame (which means that the timing of the photo rays, and therefore the shutter model, is irrelevant) and a camera that uses the detector-plane shutter model, moving at $\beta\approx 99.5\%$ of the speed of light in the scene frame. The scene contains an array of white spheres, each placed (as explained in the next paragraph) such that it should be in focus when the camera is moving, provided the shutter model allows stigmatic imaging. It can be seen that almost all of the spheres appear blurred in the photo taken with the moving camera.
Fig. 3. Simulated photos taken with a camera that uses the aperture-plane shutter model. In (a), the camera is at rest; in (b), it is moving at $\beta\approx 99.5\%$ of the speed of light. The scene contains a $9\times 9$ array of small white spheres centered on the scene-frame surface on which the camera is focused when moving. The figure is calculated for ${\boldsymbol\beta}{=(0.1,0,0.99)^{\intercal}}$. The camera was focused on a plane a distance 10 (in units of floor-tile lengths) in the camera frame, which transforms into a curved surface in the scene frame. The horizontal angle of view is 120° in (a) and 20° in (b). In both cases, the simulated aperture radius is 0.05 (Dr TIM's interactive version refers to this aperture size as "medium").
Fig. 4. Simulated photo taken with a camera that uses the aperture-plane shutter model. The simulation parameters differ from those used to create Fig. 3(b) only in the aperture radius, which is 0.2 ("huge").
The white spheres were positioned as follows. In turn, every one of a square grid of positions in the camera-frame plane on which the camera is focused was calculated. For this camera-frame position, ${\textbf{P}}$, the time ${t_{\text{P}}}$ in the camera frame was calculated when the photo ray through ${\textbf{P}}$ and the aperture center passed through ${\textbf{P}}$. The event of this photo ray passing through ${\textbf{P}}$, at time ${t_{\text{P}}}$, was then Lorentz-transformed into the scene frame, according to Eq. (1), and a white sphere was centered there. In a photo taken with a (moving) pinhole camera, in which all photo rays pass through the center of the aperture, these spheres would form a square array in the image.
It is interesting to study the aberration shown in Fig. 3(b) in more detail. The blurring of the spheres due to this aberration is visible more clearly in Fig. 4, which is a raytracing simulation calculated for parameters identical to those used for Fig. 3(b), apart from an increased aperture size. As discussed in Section 2, the blurring in Fig. 4, like all other effects discussed in this paper, is due to the shift in position of two events on the last ray-trajectory segment. From Eq. (1), it is clear that this shift is always in the direction of ${\boldsymbol\beta}$. A single point light source is therefore seen through different points on the aperture as different point light sources positioned on a line through the original point light source with direction ${\boldsymbol\beta}$. This at first seems to suggest that any point (or small sphere) should appear elongated into a straight line (or cylinder) with direction ${\boldsymbol\beta}$, but the actual appearance of a point light source is complicated by the fact that different point light sources on that straight line are seen only from the direction of corresponding points on the aperture. In the example shown in Fig. 4, the effect is that each sphere appears as a curved line.
Figure 3 shows another interesting characteristic. In the standard example of comatic aberration, the parabolic mirror, bundles of parallel rays are not focused to a point, unless they are parallel to the optical axis, in which case they are focused to a point. A distant object seen in one direction, namely, that of the optical axis, is therefore imaged sharply; those in other directions are not (and they often appear to have a tail like that of a comet, which is known as "coma"). However, in Fig. 4, the spheres seen in two directions appear to be in sharper focus. The blurred shape of the different spheres shown in Fig. 3 suggests that this happens for different reasons in the two cases:
1. The central sphere appears to be sharp, as all photo rays pass through this position at approximately the same time. The reason is the following. In the aperture-plane shutter model, all light photo rays pass through the aperture plane simultaneously, so the difference in the times different photo rays pass through the position ${\textbf{P}}$ is determined purely by the difference in the optical path length between ${\textbf{P}}$ and different points ${\textbf{L}}$ on the aperture. For any point on the aperture-plane normal that passes through the aperture center, this optical path length is of the form
(3)$$l(r)=l(0)+O({r^2}),$$
where $l(r)$ is the optical path length between ${\textbf{P}}$ and a position ${\textbf{L}}$ on the aperture that is a distance $r$ from the aperture center, and $l(0)$ is the optical path length between ${\textbf{P}}$ and the aperture center. This means that the variation $\Delta l$ in optical path lengths between ${\textbf{P}}$ and different positions ${\textbf{L}}$ on the aperture is relatively small in this case. The different photo rays therefore pass through such a position ${\textbf{P}}$ approximately simultaneously, which implies that the corresponding scene-frame positions ${\textbf{P}}_i^\prime$ lie relatively close together—in the case of the central sphere in Fig. 3, so close that it appears in focus.
2. The rightmost sphere half-way down the image appears relatively sharp as the line of point light sources into which a single point light source in that direction is stretched out in the direction in which the sphere is seen from the center of the camera, and indeed the center of that sphere, ${(1,0,10)^{\intercal}}$, lies almost precisely in the direction $\beta=(0.1,0,0.99)^{\intercal}$ from the center of the aperture, which is positioned at the origin.
B. Detector-Plane Shutter Model
In the detector-plane shutter model, the shutter is placed in the detector plane. Such a shutter is usually called a focal-plane shutter, but as the detector plane coincides with the focal plane only if the camera is focused to an infinitely distant plane, we call the corresponding shutter model detector-plane shutter model. In this shutter model, all photo rays reach the detector simultaneously.
An ideal imaging system has the property that all light rays that pass between a pair of conjugate positions via the imaging system take the same time to do so. This follows from the principle of equal optical path [24], and it implies that light rays that intersect a point ${\textbf{D}}$ on the detector simultaneously also intersect the conjugate position ${\textbf{P}}$ simultaneously. It then follows that all photo rays that eventually intersect at ${\textbf{D}}$ have previously intersected ${\textbf{P}}$ simultaneously, in what is a single event (same place, same time) in any frame. This, in turn, implies that the photo rays that reach the same position ${\textbf{D}}$ on the detector all previously intersected in the scene frame, at the position ${{\textbf{P}}^\prime}$. In other words, the scene-frame position ${{\textbf{P}}^\prime}$ is stigmatically imaged to the camera-frame position ${\textbf{D}}$.
The raytracing simulation shown in Fig. 5 demonstrates this. The opening time of the shutter was set up such that the timing of those rays that traveled along the optical axis was identical to that in the aperture-plane-shutter-model setup in Fig. 3(b). (Light rays that are inclined with respect to the optical axis while traveling from the aperture to the detector take longer to do so. The timing of these rays is different, resulting in the distortions in Figs. 3(b) and 5 to be different.) An array of spheres was again placed into the scene frame such that their centers were lying in the scene-frame surface imaged into the camera-frame detector plane by paraxial photo rays (in this case all photo rays). The spheres can be seen to be in focus, consistent with our result that any scene-frame position can be stigmatically imaged onto the detector.
Fig. 5. Simulated photo taken with a moving camera that uses the detector-plane shutter model and an ideal thin lens as imaging element. AS in Fig. 3, the scene contains a $9\times 9$ array of small white spheres centered on the scene-frame surface on which the camera is focused when moving, but note that the scene-frame surface on which the cameras are focused is different from that on which the camera in Fig. 3 is focused. The spheres can be seen to be in sharp focus. The remainder of the scene and the camera velocity are identical to those used to calculate Fig. 3.
It is interesting to consider cameras that use the detector-plane shutter model in combination with imaging elements that do not respect the principle of equal optical path, i.e., for which it is not the case that all light rays that pass between a pair of conjugate positions via the lens take the same time to do so. Examples of such elements include phase holograms of lenses, Fresnel lenses, and Fresnel zone plates. In the case of the lens, the thickness of high-refractive-index material (e.g., glass) changes across the lens such that the light-ray-direction change due to the local phase gradient and the time delay due to slower propagation in the high-refractive-index medium are just right (to a very good approximation) for all light rays to take the same time to travel between conjugate positions. Phase holograms and Fresnel lenses replicate the light-ray-direction change, but not the time delay; Fresnel zone plates (and other holograms of lenses) ensure that all light from the object position interferes constructively at the image position, but the time delay is again not replicated. This means that photo rays that intersect in a detector position ${\textbf{D}}$ simultaneously do not intersect in the conjugate position ${\textbf{P}}$ simultaneously. The transmission of the photo rays through ${\textbf{P}}$ is therefore not a single event, and the events that correspond to different photo rays passing through ${\textbf{P}}$ therefore get Lorentz-transformed to different positions ${{\textbf{P}}^\prime}$. [Inspection of Eq. (1) reveals that these positions are spread out in the direction of ${\boldsymbol\beta}$]. There is therefore no scene-frame position that is stigmatically imaged to the camera-frame position ${\textbf{D}}$.
Figure 6 illustrates this. It consists of two parts. Part (a) is the same as Fig. 5, but taken with a significantly larger aperture, thereby dramatically increasing the magnitude of any blurring present. The simulated focusing element is an ideal thin lens in which all light rays that travel between conjugate positions take the same time to do so. The array of spheres can be seen to be still in focus. Part (b) is calculated in precisely the same way, but for a camera in which the focusing element is a phase hologram of an ideal thin lens, i.e., an imaging element through which different light rays take different times to travel between conjugate positions. The spheres in the array shown in the picture are in the same positions as before. They are in the scene-frame surface that is stigmatically imaged into the camera-frame detector plane by an ideal thin lens, but now that the imaging element is a phase hologram of an ideal thin lens, this scene-frame surface is imaged into the camera-frame detector plane only by paraxial rays. The array of spheres is now clearly out of focus.
Fig. 6. Simulated photos taken with a camera that uses the detector-plane shutter model in combination with an ideal thin lens (a) and a phase hologram of a thin lens (b). The simulated aperture radius is 0.2 (called "huge" in Dr TIM's interactive version) to make the blurring visible. In (a), which is calculated for parameters that differ from those used to calculate Fig. 5 only in the increased aperture size, the spheres are still in focus. In (b), which is calculated for parameters that differ from those used to calculate (a) only in the time delay introduced by the imaging element, the spheres are clearly blurred.
C. Focus-Surface Shutter Model
In the focus-surface shutter model, the "shutter" is conceptually located in the focus surface, the camera-frame surface (normally a plane) onto which the camera is focused. There is a practical problem with this shutter placement: if the shutter was some physical device in the camera frame, somehow attached to the camera, then any object in the scene frame that would be in focus would—at the moment of being in focus—collide with the shutter. However, the focus-surface shutter model also describes a scene comprising one or more point light sources that flash for one instant, as follows. A point light source flashing for an instant is a single event, in any frame. If, in the camera frame, that flash event happens in the focus surface at the time ${t_{\text{S}}}$, then the rays from this flash would be identical in trajectory and timing to the photo rays for the focus-surface shutter model from a point light source at the flash event's scene-frame position. This model can therefore be completely analyzed by considering the flash event to take place in the camera frame. This, in turn, means that the camera can be focused to a flash's position in the camera frame, and so each flash can be imaged stigmatically.
This answers our primary question about imaging of individual point light sources in the scene frame. However, a further discussion is in order to dispel the impression that a camera that somehow manages to operate a focus-scene shutter model takes identical pictures to a camera operating a detector-plane shutter model. Figure 7 shows a simulated photo of a scene that is taken with a focus-scene shutter model. As before, it contains an array of spheres centered in the focus surface. The spheres can be seen to be in focus, but in a few cases strongly distorted, an aspect that is not well understood currently. The distortion of the scene is clearly different from that in the corresponding image taken with a camera that uses the detector-plane shutter model in combination with a perfect lens, shown in Fig. 6(a).
Fig. 7. Simulated photos taken with cameras that use the focus-surface shutter model. The simulated aperture radius is 0.05 ("medium").
The reason is that the timing of the rays is different in the camera frame. The focus-surface shutter model used to create Fig. 7 was set up such that the timing of the rays that contributed to the central pixels in the two images was identical. But this means that the timing of all other rays was different: on one hand, a photo ray that contributes to any other pixel in the focus-scene shutter model passes through the focus surface at the same time as the rays that contribute to the central pixel, but it then has to travel further from its intersection point with the focus surface to the corresponding detector pixel, and so it arrives there later than the rays that arrive at the central pixel; on the other hand, a photo ray contributing to that same other pixel in the detector-plane shutter model arrives at that pixel at the same time as all other photo rays, specifically those that arrive at the central pixel. As the timing of the photo rays is therefore different in the two shutter models, and as the camera is moving, photo rays whose trajectories are identical in the camera frame correspond to different trajectories in the scene frame, and the distortion of the scene looks different.
D. Fixed-Point Surface Shutter Model
Above, it was found that the focus-surface shutter model and the detector-plane shutter model in combination with an ideal lens are related in that all photo rays that pass through a position in the focus surface simultaneously also pass through the conjugate position in the detector plane simultaneously. The difference between the two shutter models was the time when the photo rays passed through different camera-frame focus-surface positions, which in turn altered the corresponding rays in the scene frame (leading to a different apparent distortion) and changed the scene-frame positions of the events of the photo rays passing through the camera-frame focus surface—it distorted the scene-frame focus surface.
We are free to consider non-synchronous shutters in which the photo rays pass through different camera-frame focus-surface positions at arbitrary times. Here, we choose those times such that the apparent distortion is such that in a photo taken with a moving camera and in a photo taken with the same camera at rest, the focus surface looks identical. This works as follows.
We note that in the equation for the spatial part of the Lorentz transformation, Eq. (1), there is for any arbitrary position ${\boldsymbol x}$ a time $t$ for which ${\boldsymbol x}$ is a spatial fixed point of the Lorentz transformation, i.e., ${{\boldsymbol x}^\prime}={\boldsymbol x}$. This time is easily found by substituting ${{\boldsymbol x}^\prime}={\boldsymbol x}$ into Eq. (1) and solving for $t$, which is
(4)$$t=\frac{{(1-\gamma)({\boldsymbol\beta}\cdot {\boldsymbol x})}}{{c\gamma {\beta^2}}}.$$
We can imagine the scene to contain a collection of point flash lamps, each flashing at the time that makes its position a spatial fixed point of the Lorentz transformation. In two photos, one taken with a moving camera with a continuously open shutter, the other taken with a similar camera at rest, these point flash lamps would then look identical. Alternatively, a non-synchronous shutter in the detector plane can achieve the same result.
Figure 8 demonstrates that this idea works. Part (a) shows a simulated image taken with a camera at rest that is focused on a depth plane that contains the axes of a number of horizontal and vertical cylinders. Part (b) shows a simulated image taken with a moving camera. The vertical and horizontal cylinders that are in focus in part (a) are still in focus, and they have remained in the same position as in (a). In places, they have changed thickness due to most of the cylinder mantles actually lying outside the focus plane, which contains the cylinder axes.
Fig. 8. Raytracing simulations illustrating the fixed-point-surface shutter model. In (a), the camera is at rest; in (b), it is moving with velocity ${\boldsymbol\beta}c=(0.1c,0,0.99c)^{\intercal}$ in the scene frame. The camera is focused on the plane $z=8$ in the camera frame. Because of the timing of the photo rays, objects in this plane appear identical in both photos. Objects outside this plane appear distorted; those close to the focusing plane, like the mantle of the cylinders centered in the focusing plane, are distorted only slightly.
4. CORRECTING RELATIVISTIC ABERRATION WITH LORENTZ WINDOWS
During relativistic raytracing of a light ray that contributes to a photo, the light ray is transformed from the camera frame to the scene frame at the "Lorentz surface," using the procedure outlined in Section 2. The remaining calculations, for a particular ray, are the usual, static, raytracing ones.
If, colocated with the Lorentz surface, we place an optical element that changes the direction of a ray by an amount specified by the relativistic Doppler effect, then this will exactly cancel the direction change (or, rather, the apparent direction change due to the change of frame) that results from the Lorentz transformation. Such interfaces have previously been defined as Lorentz-transformation windows [11]. This means that a photo taken with the moving camera will look the same as a photo taken with the camera at rest, except for a change in apparent position due to the Lorentz transformation.
If we return to Eq. (1), and set ${{\boldsymbol x}^\prime}={\boldsymbol x}$, then we find
(5)$$(\gamma-1)\frac{{({\boldsymbol\beta}\cdot {\boldsymbol x})}}{{{\beta^2}}}-\gamma ct=0.$$
For a given ${\boldsymbol x}$, in the camera frame, this gives the time $t$ at the Lorentz surface when events at ${\boldsymbol x}$ will be mapped to the same coordinate value ${{\boldsymbol x}^\prime}$ in the scene frame. We refer to these points ${\boldsymbol x}$ as spatial fixed points of the Lorentz transformation for time $t$. Thus, a photo taken at this time through a canceling window, as described above, will therefore look identical to a photo taken with the camera at rest.
In particular, consider placing the shutter at the Lorentz surface, stationary in the frame of the camera, in a surface of spatial fixed points of the Lorentz transformation for time $t={t_{\text{S}}}$. This surface is a plane perpendicular to ${\boldsymbol\beta}$ that satisfies the condition
(6)$$-{\boldsymbol\beta}\cdot {\boldsymbol x}=\frac{{\gamma {\beta^2}c{t_{\text{S}}}}}{{\gamma-1}}=\frac{{\gamma+1}}{\gamma}c{t_{\text{S}}}.$$
Note the appearance of the minus sign in front of the scalar product of ${\boldsymbol\beta}$ and ${\boldsymbol x}$, which is due to the fact that the relevant Lorentz transformation is from the camera frame into the scene frame, and therefore the relevant ${\boldsymbol\beta}$ is the velocity of the scene in the camera frame, which is the negative of the velocity of the camera in the scene frame, which we defined as ${\boldsymbol\beta}$. As every position in the shutter plane is a spatial fixed point of the Lorentz transformation for time ${t_{\text{S}}}$, light rays that pass through the shutter do not change position upon change of reference frame. We therefore hypothesize that a Lorentz-transformation window, placed in the plane of spatial fixed points of the Lorentz transformation for time ${t_{\text{S}}}$, can make a photo taken with a camera moving at relativistic velocity look identical to one taken with a camera at rest.
Fig. 9. Relativistic blurring and distortion and its cancellation with a Lorentz window. The frames show simulated photos of a portrait scene, with the camera focused on the same plane in front of the camera. (a) The camera is stationary in the scene frame. The subject's eyes are in the camera's focusing plane. (b) The camera is moving with relativistic velocity ${\boldsymbol\beta}c$ with respect to the scene frame, where ${\boldsymbol\beta}=(0.1,0,0.99)^{\intercal}$. The camera's shutter was placed in a plane perpendicular to ${\boldsymbol\beta}$ that passed through the position ${(0.111,0,1.1)^{\intercal}}$; the shutter opening time was ${t_{\text{S}}}=-1$. The scene appears distorted and out-of-focus. (c) Like (b), but with a Lorentz window placed in the shutter plane, which makes the photo look identical to that taken with the camera at rest. Throughout, the speed of light was set to $c=1$. All simulations were performed with an extended version of Dr TIM [12].
Fig. 10. Simulated photos taken through a Lorentz window with a camera that uses the detector-plane shutter model. (a) Without Lorentz window; (b) with Lorentz window. In (b), a slight distortion of the scene can be seen (floor tiles). The shutter-opening time was calculated such that the photo ray through the aperture center in the forward direction has the same timing as in the arbitrary-plane-shutter model.
To test our hypothesis, we performed raytracing simulations using our raytracer Dr TIM [12], extended to allow raytracing through a scene that includes objects at rest with respect to the camera (see Appendix A) and to allow the shutter to be placed in an arbitrary plane in front of the camera (see Appendix B). Figure 9 shows simulated photos of a scene taken with a camera at rest, with the same camera moving at a specific relativistic velocity with respect to the scene, and with the same moving camera with a suitable Lorentz window placed in the plane of spatial fixed points of the Lorentz transformation for a specific shutter opening time ${t_{\text{S}}}$. Consistent with our hypothesis, all aspects—including distortion and blurring—of the photo taken with the moving camera through the Lorentz window looks identical to that taken with the camera at rest. We also simulated such photos for other combinations of the camera velocity and shutter opening time, with the same result. Simulations that use a shutter model in which the Lorentz window is not placed in a plane of spatial fixed points of the Lorentz transformation (see Fig. 10) show that the relativistic distortion is undone imperfectly by the Lorentz window in that case.
We also tested the effect of a Lorentz window placed in a plane of spatial fixed points of the Lorentz transformation at time ${t_{\text{S}}}$ of a stereo camera. As mentioned in the Introduction, a stereo pair taken with a stereo camera moving at relativistic speed is distorted in a way that means it will not be perceived as a 3D scene when presented in "raw" form to a binocular observer [20]. The reason is that the relativistic distortion places the image of a point taken by the left camera and that taken by the right camera at different vertical positions. This means that the parallax shift is no longer exclusively sideways, but also has a vertical component, which means that an observer would not perceive the two images as pertaining to the same point. An example of a relativistic stereo pair, in the form of an anaglyph for viewing with red–blue glasses, is shown in Fig. 11(b). Figure 11(c) is calculated in precisely the same way, but with a Lorentz window placed in the plane of spatial fixed points at the shutter-opening time ${t_{\text{S}}}$. The anaglyph is identical to the one shown in Fig. 11(a), which has been calculated for a camera at rest and in the absence of a Lorentz window. Note that the left and right cameras in the stereo camera need a common shutter plane and shutter time for this effect to work.
Fig. 11. Anaglyphs made from simulated stereo pairs taken with a camera at rest (a), a camera moving at relativistic velocity ${\boldsymbol\beta}c=(0.1,0,0.99)^{\intercal}c$ relative to the scene (b), and the same relativistically moving camera but with a Lorentz window placed in the plane of spatial fixed points of the Lorentz transformation for the shutter-opening time (c). In (b) and (c), the camera's shutter is located in a plane perpendicular to ${\boldsymbol\beta}$ through the position $(0.111,0,1.1)^{\intercal}$, and the shutter opening time is ${t_{\text{S}}}=-1$, parameters chosen such that the shutter plane is a plane of spatial fixed points of the Lorentz transformation for ${t_{\text{S}}}$. Eye separation 0.4 in the horizontal direction; camera directions are chosen such that a plane a distance 5 in front of the camera appears in the paper/monitor plane.
It is possible to spot a number of well-known effects in our simulations. First, the objects in the simulated photos are all illuminated from the same direction, but as they have all undergone different Penrose–Terrell rotations, they appear to be illuminated from a range of directions. This can clearly be seen in the array of spheres shown in Fig. 5 and in the vertical cylinders shown in Fig. 8. Second, the coma-type aberration predicted in Ref. [19] for the aperture-plane shutter model can be seen in Figs 3 and 4: spheres not seen in the straight-ahead or boost direction appear blurred, consistent with a magnification that varies with aperture position, the defining property of coma [25]. A coma-type aberration can also be seen in the detector-plane shutter model in combination with the phase hologram of a lens, Fig. 6(b).
It is important to ask under which circumstances the blurring discussed above is significant. We address this question only briefly, as a full discussion would be lengthy and outside the scope of this paper. A pragmatic answer is "when it can be resolved by the camera," i.e., when it is comparable to or greater than the blur introduced by the lens and when the image of a single point light source becomes blurred across two or more detector pixels. To estimate the angular size of the relativistic blur, we consider different photo rays, all from the same point light source at position ${{\boldsymbol P}_i}$ in the scene frame, passing through points ${{\boldsymbol L}_i}$ on the aperture, and specifically the events of these photo rays passing through ${{\boldsymbol P}_i}$ [Fig. 12(a)]. In the camera frame [Figs. 12(b) and 12(c)], the positions of these events, ${{\boldsymbol P}_i}$, are spread out on a line with direction ${\boldsymbol\beta}$ and length $\gamma\beta c\Delta {t^\prime}$, where $\Delta {t^\prime}$ is the time in the scene frame between the first and the last photo rays passing through ${{\boldsymbol P}^\prime}$. Of course, $\Delta {t^\prime}$ depends on the shutter model, the velocity ${\boldsymbol\beta}$, and the location of the object in relation to the camera. We define the vector ${\boldsymbol \Delta}{\boldsymbol P}$ to be the difference between the outermost ${{\boldsymbol P}_i}$ s.
Fig. 12. (a) Photo rays from a point light source at position ${{\boldsymbol P}^\prime}$ in the scene frame pass through different positions ${\boldsymbol L}_i^\prime$ on the lens, indicated as a thick double-sided arrow. In general, the events of different photo rays passing through ${{\boldsymbol P}^\prime}$ occur at different times. (b) In the scene frame, the positions ${{\boldsymbol P}_i}$ of these events are spread out along a line parallel to ${\boldsymbol\beta}$. ${\boldsymbol \Delta}{\boldsymbol P}$ points between two of the outermost positions ${{\boldsymbol P}_i}$. In the small-aperture limit, from the perspective of the (small) aperture, the positions ${{\boldsymbol P}_i}$ are distributed over an angular range of size $\alpha$. (c) The dotted line indicates the surface that is best imaged into the detector plane.
The situation is easiest to tackle in the small-aperture limit, in which $\parallel {\boldsymbol \Delta}{\boldsymbol P}\parallel$, the length of ${\boldsymbol \Delta}{\boldsymbol P}$, is much smaller than the aperture size. After some basic trigonometry it is clear in Fig. 12(b) that the blur angle $\alpha$ can be approximated as
(7)$$\alpha\approx\frac{{\Delta P\sin\nu}}{d},$$
where $\nu$ is the angle between the direction of ${\boldsymbol \Delta}{\boldsymbol P}$ and the "average" direction in which the points ${{\boldsymbol P}_i}$ are seen from the lens, and where $d$ is the average distance of these points from the lens. With everything else being equal, the blur angle $\alpha$ is clearly bigger for small distances $d$ and tends towards zero in the limit of $d\to\infty$. This means that it is possible to take sharp images of sufficiently distant objects. The images shown in this paper do not show this, as the camera is focused on nearby objects.
If the small-aperture limit is not applicable, i.e., if $\parallel {\boldsymbol \Delta}{\boldsymbol P}\parallel$ is comparable to, or smaller than, the aperture size, it matters which positions ${{\boldsymbol L}_i}$ on the lens different photo rays pass through. This can be seen in Fig. 12(c), which shows the trajectories of different photo rays for each of three different point light sources that have undergone the same Lorentz shifts. One effect, clearly visible in Fig. 12(c), is that the distance where the (imperfect) image is formed, i.e., the distance where the bundle of photo rays from the same object position that passed through different points in the aperture has the smallest cross section, depending on the direction of the object position. Specifically, the image is formed at the distance of the "average" Lorentz-shifted position only if the object is in the direction ${\boldsymbol\beta}$ from the center of the camera.
Extending our custom raytracer has enabled us to visualize old and new effects related to relativistic distortion.
It is easy to identify avenues for further study. For example, it would be interesting to study shutter models that are less idealized and more closely represent physical shutters. In reality, shutters open at each point of the shutter surface for the same—very brief—length of time, but at different positions, the shutter opens at different times. This happens, for example, in shutters in which a thin slit is quickly moved across the shutter, as in "two-curtain shutters" that can be found in single-lens reflex (SLR) cameras. Another potential avenue for further study is the visualization of wave-optical effects associated with relativistic coma [18] and with relativistic photography with a wide aperture in general.
APPENDIX A: RELATIVISTIC RAYTRACING OF SCENES INCLUDING OBJECTS MOVING WITH THE CAMERA
Dr TIM's relativistic raytracing procedure allows the simulation of objects moving with the camera, which are therefore at rest in the camera frame. This enables the simulation of a light-ray-direction changing "filter" attached to the camera in Section 4.
Dr TIM assumes that the objects moving with the camera are close to the camera; if a ray intersects these objects, then this is therefore assumed to happen immediately before the ray hits the camera. When tracing a ray backwards, Dr TIM therefore traces—using standard raytracing—through the scene consisting of all objects at rest in the camera frame until no more objects in this camera-frame scene are intersected, then transforms the ray into the scene frame and continues raytracing through the (scene-frame) scene.
In Dr TIM, the ray is set up (with the timing according to the shutter model) in the getRay method of the RelativisticAnyFocusSurfaceCamera class. This gets called from the calculatePixelColour method, which then initiates tracing of the ray through the camera-frame scene. Once no more objects are being encountered, the getColourOfRayFromNowhere method gets called, which Lorentz-transforms the ray into the scene frame and continues tracing the ray through the scene frame.
APPENDIX B: ARBITRARY-PLANE SHUTTER MODEL
The shutter model determines the timing of light rays that pass through the shutter. This timing is important, as it is required when transforming between the scene frame and the camera frame. Dr TIM determines the times when a light ray intersects different surfaces from the time ${t_{{\text{L},\text{in}}}}$ when it passes through the aperture plane. Here, we derive the equations that allow calculation of this time for the arbitrary-plane shutter model, which we recently added to Dr TIM.
In Dr TIM's arbitrary-plane shutter model, the shutter opens (like the shutters in all the other shutter models) at time ${t_{\text{S}}}$ and is positioned in a plane defined by a point ${\textbf{P}}$ in the plane and a vector ${\textbf{n}}$ normal to the plane. Dr TIM traces light rays backwards, starting from a position ${\textbf{L}}$ on the aperture plane at time ${t_{{\text{L},\text{in}}}}$.
The calculation of the time ${t_{{\text{L},\text{in}}}}$ happens in the getRay method of the RelativisticAnyFocusSurfaceCamera class, which is passed as input parameters the position ${\textbf{L}}$ and other parameters that allow straightforward calculation of the normalized physical direction (i.e., forward direction) $\hat{\textbf{d}}$ of the ray. It proceeds by calculating the physical distance $a$ the light ray has to travel from the point ${\textbf{S}}$ where it intersects the shutter plane to ${\textbf{L}}$. As it passes ${\textbf{S}}$ at time ${t_{\text{S}}}$, the time it passes ${\textbf{L}}$ is
(B1)$${t_{{\text{L},\text{in}}}}={t_{\text{S}}}+\frac{a}{c},$$
where $c$ is the speed of light.
The point ${\textbf{S}}$ where the ray intersects the shutter plane satisfies two conditions. First, it lies on the ray, which means it can be expressed in the form
(B2)$${\textbf{S}}={\textbf{L}}-a\hat{\textbf{d}}.$$
Second, it lies in the shutter plane, which means it satisfies the equation
(B3)$$({\textbf{S}}-{\textbf{P}})\cdot {\textbf{n}}=0.$$
Substitution of Eq. (B2) into Eq. (B3) and solving for $a$ gives
(B4)$$a=\frac{{({\textbf{P}}-{\textbf{L}})\cdot {\textbf{n}}}}{{\hat{\textbf{d}}\cdot {\textbf{n}}}}.$$
Substitution into Eq. (B1) gives
(B5)$${t_{{\text{L},\text{in}}}}={t_{\text{S}}}+\frac{{({\textbf{P}}-{\textbf{L}})\cdot {\textbf{n}}}}{{c \hat{\textbf{d}}\cdot {\textbf{n}}}}.$$
APPENDIX C: REPEATING THE SIMULATIONS IN THIS PAPER
The code for producing all simulated photos shown in this paper can be found in the various classes of the optics.raytrace.research. RelativisticPhotography package, which can be downloaded from Ref. [26], together with the rest of the code. The value of a number of static final variables near the top of the code determines which of these photos is produced.
The simulated photos shown in Figs. 3, 4, 5, 6, and 7 were performed using the ShutterModelFocussing class. The images shown in Fig. 8 were produced by the FixedPointSurfaceShutterModelTest class, those shown in Figs. 9 and 10 were calculated by the LorentzWindowDistortionCancellation class, and those in Fig. 11 by the LorentzWindowAnaglyph class.
Engineering and Physical Sciences Research Council (EP/M010724/1).
Many thanks to Martin Hendry for helpful discussions.
1. A. Einstein, "Zur Elektrodynamik bewegter Körper," Ann. Phys. 17, 891–921 (1905). [CrossRef]
2. G. F. FitzGerald, "The ether and the Earth's atmosphere," Science 13, 390 (1889).
3. A. A. Michelson and E. Morley, "On the relative motion of the Earth and the luminiferous ether," Am. J. Sci. s3-34, 333–345 (1887). [CrossRef]
4. A. Lampa, "Wie erscheint nach der Relativitätstheorie ein bewegter Stab einem ruhenden Beobachter?" Z. Phys. 27, 138–148 (1924). [CrossRef]
5. R. Penrose, "The apparent shape of a relativistically moving sphere," Proc. Cambridge Philos. Soc. 55, 137–139 (1959). [CrossRef]
6. J. Terrell, "Invisibility of the Lorentz contraction," Phys. Rev. 116, 1041–1045 (1959). [CrossRef]
7. M. L. Boas, "Apparent shape of large objects at relativistic speeds," Am. J. Phys. 29, 283–286 (1961). [CrossRef]
8. G. D. Scott and M. R. Viner, "The geometrical appearance of large objects moving at relativistic speeds," Am. J. Phys. 33, 534–536 (1965). [CrossRef]
9. M. A. Duguay and A. T. Mattick, "Ultrahigh speed photography of picosecond light pulses and echoes," Appl. Opt. 10, 2162–2170 (1971). [CrossRef]
10. A. Howard, S. Dance, and L. Kitchen, "Relativistic ray-tracing: Simulating the visual appearance of rapidly moving objects," Technical report (University of Melbourne, 1995).
11. S. Oxburgh, N. Gray, M. Hendry, and J. Courtial, "Lorentz-transformation and Galileo-transformation windows," Proc. SPIE 9193, 91931K (2014). [CrossRef]
12. S. Oxburgh, T. Tyc, and J. Courtial, "Dr TIM: ray-tracer TIM, with additional specialist capabilities," Comp. Phys. Commun. 185, 1027–1037 (2014). [CrossRef]
13. T. Müller, S. Grottel, and D. Weiskopf, "Special relativistic visualization by local ray tracing," IEEE Trans. Vis. Comput. Graphics 16, 1243–1250 (2010). [CrossRef]
14. D. Weiskopf, M. Borchers, T. Ertl, M. Falk, O. Fechtig, R. Frank, F. Grave, A. King, U. Kraus, T. Müller, H.-P. Nollert, I. R. Mendez, H. Ruder, T. Schafhitzel, S. Schär, C. Zahn, and M. Zatloukal, "Explanatory and illustrative visualization of special and general relativity," IEEE Trans. Vis. Comput. Graphics 12, 522–534 (2006). [CrossRef]
15. C. M. Savage, A. Searle, and L. McCalman, "Real time relativity: exploratory learning of special relativity," Am. J. Phys. 75, 791–798 (2007). [CrossRef]
16. G. Kortemeyer, P. Tan, and S. Schirra, "A slower speed of light: developing intuition about special relativity with games," in Proceedings of the International Conference on the Foundations of Digital Games (FDG 2013) (ACM, 2013), pp. 400–402.
17. N. M. Atakishiyev, W. Lassner, and K. B. Wolf, "The relativistic coma aberration. I. Geometrical optics," J. Math. Phys. 30, 2457–2462 (1989). [CrossRef]
18. N. M. Atakishiyev, W. Lassner, and K. B. Wolf, "The relativistic coma aberration. II. Helmholtz wave optics," J. Math. Phys. 30, 2463–2468 (1989). [CrossRef]
19. K. B. Wolf, "Relativistic aberration of optical phase space," J. Opt. Soc. Am. A 10, 1925–1934 (1993). [CrossRef]
20. A. J. S. Hamilton and G. Polhemus, "Stereoscopic visualization in curved spacetime: seeing deep inside a black hole," New J. Phys. 12, 123027 (2010). [CrossRef]
21. A. C. Hamilton and J. Courtial, "Generalized refraction using lenslet arrays," J. Opt. A 11, 065502 (2009). [CrossRef]
22. D. Lambert, A. C. Hamilton, G. Constable, H. Snehanshu, S. Talati, and J. Courtial, "TIM, a ray-tracing program for METATOY research and its dissemination," Comp. Phys. Commun. 183, 711–732 (2012). [CrossRef]
23. W. J. Smith, Modern Optical Engineering, 3rd ed. (McGraw-Hill, 2000), Chap. 2.2.
24. M. Born and E. Wolf, Principles of Optics (Pergamon, 1980), Chap. 3.3.3.
25. W. J. Smith, Modern Optical Engineering, 3rd ed. (McGraw-Hill, 2000), Chap. 3.2, p. 67ff.
26. "Dr TIM, a highly scientific raytracer," https://github.com/jkcuk/Dr-TIM.
A. Einstein, "Zur Elektrodynamik bewegter Körper," Ann. Phys. 17, 891–921 (1905).
G. F. FitzGerald, "The ether and the Earth's atmosphere," Science 13, 390 (1889).
A. A. Michelson and E. Morley, "On the relative motion of the Earth and the luminiferous ether," Am. J. Sci. s3-34, 333–345 (1887).
A. Lampa, "Wie erscheint nach der Relativitätstheorie ein bewegter Stab einem ruhenden Beobachter?" Z. Phys. 27, 138–148 (1924).
R. Penrose, "The apparent shape of a relativistically moving sphere," Proc. Cambridge Philos. Soc. 55, 137–139 (1959).
J. Terrell, "Invisibility of the Lorentz contraction," Phys. Rev. 116, 1041–1045 (1959).
M. L. Boas, "Apparent shape of large objects at relativistic speeds," Am. J. Phys. 29, 283–286 (1961).
G. D. Scott and M. R. Viner, "The geometrical appearance of large objects moving at relativistic speeds," Am. J. Phys. 33, 534–536 (1965).
M. A. Duguay and A. T. Mattick, "Ultrahigh speed photography of picosecond light pulses and echoes," Appl. Opt. 10, 2162–2170 (1971).
A. Howard, S. Dance, and L. Kitchen, "Relativistic ray-tracing: Simulating the visual appearance of rapidly moving objects," (University of Melbourne, 1995).
S. Oxburgh, N. Gray, M. Hendry, and J. Courtial, "Lorentz-transformation and Galileo-transformation windows," Proc. SPIE 9193, 91931K (2014).
S. Oxburgh, T. Tyc, and J. Courtial, "Dr TIM: ray-tracer TIM, with additional specialist capabilities," Comp. Phys. Commun. 185, 1027–1037 (2014).
T. Müller, S. Grottel, and D. Weiskopf, "Special relativistic visualization by local ray tracing," IEEE Trans. Vis. Comput. Graphics 16, 1243–1250 (2010).
D. Weiskopf, M. Borchers, T. Ertl, M. Falk, O. Fechtig, R. Frank, F. Grave, A. King, U. Kraus, T. Müller, H.-P. Nollert, I. R. Mendez, H. Ruder, T. Schafhitzel, S. Schär, C. Zahn, and M. Zatloukal, "Explanatory and illustrative visualization of special and general relativity," IEEE Trans. Vis. Comput. Graphics 12, 522–534 (2006).
C. M. Savage, A. Searle, and L. McCalman, "Real time relativity: exploratory learning of special relativity," Am. J. Phys. 75, 791–798 (2007).
G. Kortemeyer, P. Tan, and S. Schirra, "A slower speed of light: developing intuition about special relativity with games," in Proceedings of the International Conference on the Foundations of Digital Games (FDG 2013) (ACM, 2013), pp. 400–402.
N. M. Atakishiyev, W. Lassner, and K. B. Wolf, "The relativistic coma aberration. I. Geometrical optics," J. Math. Phys. 30, 2457–2462 (1989).
N. M. Atakishiyev, W. Lassner, and K. B. Wolf, "The relativistic coma aberration. II. Helmholtz wave optics," J. Math. Phys. 30, 2463–2468 (1989).
K. B. Wolf, "Relativistic aberration of optical phase space," J. Opt. Soc. Am. A 10, 1925–1934 (1993).
A. J. S. Hamilton and G. Polhemus, "Stereoscopic visualization in curved spacetime: seeing deep inside a black hole," New J. Phys. 12, 123027 (2010).
A. C. Hamilton and J. Courtial, "Generalized refraction using lenslet arrays," J. Opt. A 11, 065502 (2009).
D. Lambert, A. C. Hamilton, G. Constable, H. Snehanshu, S. Talati, and J. Courtial, "TIM, a ray-tracing program for METATOY research and its dissemination," Comp. Phys. Commun. 183, 711–732 (2012).
W. J. Smith, Modern Optical Engineering, 3rd ed. (McGraw-Hill, 2000), Chap. 2.2.
M. Born and E. Wolf, Principles of Optics (Pergamon, 1980), Chap. 3.3.3.
W. J. Smith, Modern Optical Engineering, 3rd ed. (McGraw-Hill, 2000), Chap. 3.2, p. 67ff.
"Dr TIM, a highly scientific raytracer," https://github.com/jkcuk/Dr-TIM .
Atakishiyev, N. M.
Boas, M. L.
Borchers, M.
Born, M.
Constable, G.
Courtial, J.
Dance, S.
Duguay, M. A.
Einstein, A.
Ertl, T.
Falk, M.
Fechtig, O.
FitzGerald, G. F.
Frank, R.
Grave, F.
Gray, N.
Grottel, S.
Hamilton, A. C.
Hamilton, A. J. S.
Hendry, M.
Howard, A.
King, A.
Kitchen, L.
Kortemeyer, G.
Kraus, U.
Lambert, D.
Lampa, A.
Lassner, W.
Mattick, A. T.
McCalman, L.
Mendez, I. R.
Michelson, A. A.
Morley, E.
Müller, T.
Nollert, H.-P.
Oxburgh, S.
Penrose, R.
Polhemus, G.
Ruder, H.
Savage, C. M.
Schafhitzel, T.
Schär, S.
Schirra, S.
Scott, G. D.
Searle, A.
Smith, W. J.
Snehanshu, H.
Talati, S.
Tan, P.
Terrell, J.
Tyc, T.
Viner, M. R.
Weiskopf, D.
Wolf, E.
Wolf, K. B.
Zahn, C.
Zatloukal, M.
Am. J. Phys. (3)
Am. J. Sci. (1)
Ann. Phys. (1)
Comp. Phys. Commun. (2)
IEEE Trans. Vis. Comput. Graphics (2)
J. Math. Phys. (2)
J. Opt. A (1)
J. Opt. Soc. Am. A (1)
New J. Phys. (1)
Phys. Rev. (1)
Proc. Cambridge Philos. Soc. (1)
Z. Phys. (1)
(1) x ′ = x + ( γ − 1 ) ( β ⋅ x ) β β 2 + γ β c t ,
(2) d ′ = d ^ + ( γ − 1 ) ( β ^ ⋅ d ^ ) β ^ + γ β ,
(3) l ( r ) = l ( 0 ) + O ( r 2 ) ,
(4) t = ( 1 − γ ) ( β ⋅ x ) c γ β 2 .
(5) ( γ − 1 ) ( β ⋅ x ) β 2 − γ c t = 0.
(6) − β ⋅ x = γ β 2 c t S γ − 1 = γ + 1 γ c t S .
(7) α ≈ Δ P sin ν d ,
(B1) t L , in = t S + a c ,
(B2) S = L − a d ^ .
(B3) ( S − P ) ⋅ n = 0.
(B4) a = ( P − L ) ⋅ n d ^ ⋅ n .
(B5) t L , in = t S + ( P − L ) ⋅ n c d ^ ⋅ n . | CommonCrawl |
Home Journals I2M A Fractional Lower-order Bi-spectrum Estimation Method Based on Autoregressive Model
A Fractional Lower-order Bi-spectrum Estimation Method Based on Autoregressive Model
Baohai Yang
College of Physics and Electronic Engineering, Guangxi Normal University for Nationalities, Chongzuo 532200, China
[email protected]
The traditional fractional lower-order (FLO) spectrum estimation method cannot observe a sufficient volume of data, leading to a large variance of estimation results. To solve the problem, this paper puts forward a FLO bi-spectrum estimation method based on autoregressive (AR) model, and gives new definitions for FLO three order cumulant. The author discussed the determination of AR model parameters, and introduced how to implement the bi-spectrum estimation method based on AR model. Then, a series of tests were performed to verify the correctness of our method. The results show that our method outperformed the traditional approaches in suppressing FLO noise and identifying relevant information of signals.
autoregressive (AR) model, bi-spectrum, fractional lower-order (FLO) statistics, three order cumulant, signal processing
In the field of signal processing, the noise is mostly described by Gaussian distribution model, which has an excellent effect on two-order statistics of normal distribution [1]. When it comes to the frequency-domain analysis of noise, the existing theoretical methods include spectral feature analysis, time-frequency analysis, spectrum estimation, colored noise whitening, spatial spectrum estimation, frequency estimation, harmonic estimation and spectral line restoration. Most of these methods are based on two-order statistics like bi-spectrum and tri-spectrum [2].
Gaussian white noise and colored noise models have always occupied the leading position in signal processing, and the criterion of white noise and colored noise based on correlation function and power spectral density has been regarded as a classical rule. In practical applications, however, many noises do not conform to the normal distribution. Typical examples include low-frequency atmospheric noise and underwater noise. A viable option to describe such noises lies in setting up an α stable distribution, whose statistical features can be characterized by the relevant parameters of the feature function [3].
The best way to solve the non-Gaussian α stable distribution is the fractional lower-order (FLO) statistics. If α is greater than 2, the harmonic frequencies can be estimated accurately; otherwise, the second-order matrix does not exist, making it impossible to effectively analyze the noise [2]. To solve the problem, the FLO bi-spectrum has been conceptualized. Traditionally, the lower-order bi-spectrum is estimated by bi-spectrum and nonparametric methods. Nonetheless, these methods cannot observe a sufficient volume of data, leading to a large variance of estimation results.
In view of the above, this paper puts forward an FLO bi-spectrum estimation method based on autoregressive (AR) model [5], and compares the method with traditional approaches. The comparison shows that our method outperformed the traditional ones in spectral flatness and suppression of FLO noise.
2. α Stable Distribution and FLO Statistics
This section briefly introduces the α stable distribution, a generalized conceptual Gaussian distribution with a wide application scope, and gives the definition to the relevant FLO statistics, which is the best way to filter the noise of non-Gaussian α stable distribution.
2.1 α stable distribution
A random variable X satisfies the α stable distribution if the parameters 0≤α≤2, γ≥0 and -1≤β≤1 have the following relationship with real numbers α:
$\varphi (t)=\exp \{jat-\gamma {{\left| t \right|}^{a}}[1+j\beta sgn (t)\omega (t,\alpha )]\}$ (1)
$\omega (t,\alpha )=\left\{ \begin{matrix}\begin{matrix} \tan (\pi \alpha /2), & \alpha \ne 1 \\\end{matrix} \\ \begin{matrix}(2/\pi )\log \left| t \right|, & \alpha =1 \\\end{matrix} \\\end{matrix} \right.$
$sgn (t)=\left\{ \begin{matrix}\begin{matrix} 1, & t>0 \\\end{matrix} \\\begin{matrix} 0, & t=0 \\\end{matrix} \\\begin{matrix} -1, & t<0 \\\end{matrix} \\\end{matrix} \right.$
Note that α is a feature index in the interval (0, 2]. The index determines the shape of the distribution. The value of the index is negatively correlated with the trailing thickness and the pulse feature [6].
2.2 FLO statistics
(1) FLO moments. The FLO moments refer to the various moments existing at 0<α<2 (i.e. the absence of secondary moment). For the random variable SαS, the FLO moments can be described by its dispersion coefficient and feature index. Meanwhile, the covariation of the two random variables η and ζ can be expressed as the function of FLO moments:
${{\left[ \xi ,\eta \right]}_{\alpha }}=\frac{E\left( \xi {{\eta }^{<p-1>}} \right)}{E\left( {{\left| \eta \right|}^{p}} \right)}{{\gamma }_{\eta }}$ (2)
where the right superscript * is a complex conjugate; γη is the bias coefficient of the stochastic process η:
$\gamma _{\eta }^{p/\alpha }=\frac{E\left( {{\left| \eta \right|}^{p}} \right)}{C\left( p,\alpha \right)}\begin{matrix}, & 0<p<\alpha \\\end{matrix}$ (3)
$C\left( p,\alpha \right)=\frac{{{2}^{p+1}}\Gamma \left( \frac{p+2}{2} \right)\Gamma \left( -\frac{p}{\alpha } \right)}{\alpha \Gamma \left( \frac{1}{2} \right)\Gamma \left( -\frac{p}{2} \right)}$ (4)
where E(·) is the mathematical expectation; Г(·) is the function gamma:
$\Gamma \left( x \right)=\int_{0}^{\infty }{{{t}^{x-1}}{{e}^{-t}}dt}$ (5)
The covariation coefficients η and ζ can be described as:
${{\lambda }_{\xi \eta }}=\frac{{{\left[ \xi ,\eta \right]}_{\alpha }}}{{{\left[ \eta ,\eta \right]}_{\alpha }}}=\frac{E\left( \xi {{\eta }^{<p-1>}} \right)}{E\left( {{\left| \eta \right|}^{p}} \right)}$ (6)
If η and ζ are real numbers, then 0.5<p<α; If η and ζ are complex numbers, then 0<p<α.
In engineering application, it is customary to take the improved FLO moments as the estimators of covariation coefficients:
${{\overset{\wedge }{\mathop{\lambda }}\,}_{\xi \eta }}\left( p \right)=\frac{\sum\limits_{i=1}^{N}{{{\xi }_{i}}\eta _{i}^{<p-1>}}}{\sum\limits_{i=1}^{N}{{{\left| {{\eta }_{i}} \right|}^{p}}}}$ (7)
(2) Negative moment. Let X be a random variable SαS, with δ=0 being its position function and γ being its dispersion coefficient. Then, the negative moment can be expressed as:
$\begin{matrix}E\left( {{\left| X \right|}^{p}} \right)=C\left( p,\alpha \right){{\gamma }^{p/\alpha }}, & -1<p<\alpha \\\end{matrix}$ (8)
(3) Covariation. The concept of covariation was presented by Miller in 1978 [7]. If 0<α≤2, then the covariation of two random variables, X and Y, with joint stable distribution relations, can be defined as:
${{\left[ X,Y \right]}_{xx}}=\int\limits_{S}{x{{y}^{<\alpha -1>}}m\left( ds \right)}$ (9)
where S is an unit circle; m(·) is the spectral measure in SαS distribution. Then, the covariation coefficient can be defined as:
${{\lambda }_{x,y}}=\frac{{{\left[ X,Y \right]}_{\alpha }}}{{{\left[ Y,Y \right]}_{\alpha }}}$ (10)
Let γy be the dispersion coefficient of Y. Under 0<α≤2, the covariation of random variables X and Y of SαS distribution can be established as:
${{\left[ Y,Y \right]}_{\alpha }}=\left\| Y \right\|_{\alpha }^{\alpha }={{\gamma }_{y}}$ (11)
${{\lambda }_{XY}}=\frac{E\left( X{{Y}^{<p-1>}} \right)}{E{{\left( \left| Y \right| \right)}^{p}}}\begin{matrix}, & 1\le p<\alpha \\\end{matrix}$ (12)
${{\left[ X,Y \right]}_{\alpha }}=\frac{E\left( X{{Y}^{<p-1>}} \right)}{E\left( {{\left| Y \right|}^{p}} \right)}{{\gamma }_{y}}\begin{matrix}, & 1\le p<\alpha \\\end{matrix}$ (13)
(4) FLO covariance. The existing covariation applies to the range of 1<α≤2, but not defined for the range α≤1 in the SaS distribution. Reference [8] proposes a more general FLO statistic that applies to the entire value range of α. Under 0<α≤2, the FLO covariance of random variables X and Y of SαS distribution can be defined as:
$FLOC(X,Y)=E({{X}^{<A>}}{{Y}^{<B>}})\begin{matrix}\begin{matrix}, & 0\le A<\frac{\alpha }{2}, \\\end{matrix} & 0\le B<\frac{\alpha }{2} \\\end{matrix}$ (14)
3. FLO Bi-spectrum
3.1 Definition of FLO bi-spectrum
The statistical moment of a signal tells a lot about the signal features. The spectra in statistical moments extend from low order to infinite order [9]. Only secondary moments were explored in traditional signal processing. Nevertheless, the processing methods may suffer from poor performance and high error, using variance or second-order statistics only. Recent years has seen the emergence of signal processing techniques for higher-order statistics, especially third- or fourth-order statistics. The emerging techniques not only utilize the second- or higher-order statistics, but also many fractional order statistics under the second order, i.e. the FLO statistics [10].
Both theoretical and empirical analyses prove that the FLO statistics are suitable for processing impulsive feature signals and noises. However, the FLO statistics also have two prominent defects [11]. First, there is no universal framework against algebraic smearing. Second, there is a theoretical connection between the priori knowledge of the order p and the random variable α, because the order p of moments is generally limited to (0, α). If p≥α, the FLO statistics cannot work normally. As a result, the traditional α stable distribution does not contain bi-spectrum or tri-spectrum.
Based on the traditional bi-spectrum, this paper proposes the FLO bi-spectrum, and develops the nonparametric bi-spectrum estimation method for the environment of FLO noise, and verifies its performance through comparative experiments. The FLO bi-spectrum can be defined as:
${{B}_{x}}({{\omega }_{1}},{{\omega }_{2}})=\sum\limits_{{{\tau }_{1}}=-\infty }^{+\infty }{\sum\limits_{{{\tau }_{2}}=-\infty }^{+\infty }{{{C}_{3x}}({{\tau }_{1}},{{\tau }_{2}})\exp [-j(}}{{\omega }_{1}}{{\tau }_{1}}+{{\omega }_{2}}{{\tau }_{2}})]$ (15)
Besides, the FLO three order cumulants were redefined as:
${{C}_{3x}}(m,n)={{\gamma }_{3e}}\sum\limits_{i=0}^{\infty }{{{[x(i)]}^{\langle A\rangle }}{{[x(i+m)]}^{\langle B\rangle }}[x(i+n)}{{]}^{\langle C\rangle }}$ (16)
where x(i) is the signal sequence; γ3e is an adjustment coefficient; 0<A+B+C≤α (0<α<2).
3.2 FLO bi-spectrum estimation with nonparametric direct estimation
The FLO bi-spectrum estimation with nonparametric direct estimation refers the nonlinear transformation of the data x(n):
$g(x(t),A)={{(x(t))}^{<A>}},0\le A\le \alpha /3$ (17)
After the transformation, the three order statistics of the stochastic process x(n) remain the same. Next, the transformed data can be divided into K segments, each of which has M samples, i.e. N=KM. Then, the sample mean of each segment can be determined [12], allowing the overlap between two adjacent two segments. Then, the discrete Fourier transform (DFT) coefficients can be calculated as:
${{X}^{(k)}}(\lambda )=\frac{1}{M}\sum\limits_{i=1}^{M}{{{x}^{(k)}}(n){{e}^{-j2\pi n\lambda /M}}}$ (18)
where λ=0, 1, ..., M/2; k=1, ..., K. According to the DFT coefficients, the FLO bi-spectrum estimation of each segment can be obtained [13]:
$\overset{\wedge }{\mathop{b}}\,_{x}^{k}({{\lambda }_{1}},{{\lambda }_{2}})=\frac{1}{\Delta _{0}^{2}}\sum\limits_{{{i}_{1}}=-{{L}_{1}}}^{{{L}_{1}}}{\sum\limits_{{{i}_{2}}=-{{L}_{1}}}^{{{L}_{1}}}{{{\overset{\wedge }{\mathop{X}}\,}^{k}}({{\lambda }_{1}}+{{i}_{1}}){{\overset{\wedge }{\mathop{X}}\,}^{k}}({{\lambda }_{2}}+{{i}_{2}}){{\overset{\wedge }{\mathop{X}}\,}^{k}}({{\lambda }_{1}}+{{i}_{1}}+{{\lambda }_{2}}+{{i}_{2}})}}$ (19)
where k=1, … , K; 0≤λ2≤λ1, λ1+λ2≤fs⁄2;
Δ0=fs⁄N0 (N0 and L1 satisfy M=(2L1+1)N0). The bi-spectrum estimation of the given data x(0), x(1), …, x(N-1) can be determined by the mean value of the K segment bi-spectrum estimation:
${{\overset{\wedge }{\mathop{B}}\,}_{x}}({{\omega }_{1}},{{\omega }_{2}})=\frac{1}{K}\sum\limits_{k=1}^{K}{{{\overset{\wedge }{\mathop{b}}\,}_{k}}({{\omega }_{1}},{{\omega }_{2}})}$ (20)
where ${{\omega }_{1}}=\frac{2\pi {{f}_{s}}}{{{N}_{0}}}{{\lambda }_{1}}$; ${{\omega }_{2}}=\frac{2\pi {{f}_{s}}}{{{N}_{0}}}{{\lambda }_{2}}$.
3.3 FLO bi-spectrum estimation with nonparametric indirect estimation
Assuming that the observed data {x(i)}(i=1,2,⋯,N) is a real random sequence, the three order cumulants of the observed data {x(i)} should be estimated, and then subjected to the DFT, completing the bi-spectrum estimation. The algorithm procedure can be described as:
(1) Divide the observed data {x(i)} of the length N into K segments, each of which has M points, N=KM, or divide the data in such a manner that the adjacent segments have a half overlap, 2N=KM;
(2) Remove the mean value of each segment, and make the mean value of the data to be analyzed zero;
(3) Let {xj(i)}(i=1,2,⋯,M; j=1,2,⋯,K) be the j segment. Then, estimate the lower-order three order cumulant of each segment:
$\overset{\wedge }{\mathop{C}}\,_{3x}^{(j)}(m,n)=\frac{1}{M}\sum\limits_{i={{k}_{1}}}^{{{k}_{2}}}{{{[{{x}^{(j)}}(i)]}^{\langle A\rangle }}{{[{{x}^{(j)}}(i+m)]}^{\langle B\rangle }}[{{x}^{(j)}}(i+n)}{{]}^{\langle C\rangle }}$ (21)
where 0<A+B+C≤α; k1=max{0, -m, -n}; k2=min{M, M-n, M-m}.
(4) Compute the statistical mean of $\hat{C}_{3x}^j (m,n)$, and determine cumulative estimates of K segments:
${{\overset{\wedge }{\mathop{C}}\,}_{3x}}(m,n)=\frac{1}{K}\sum\limits_{i=1}^{K}{\overset{\wedge }{\mathop{C}}\,_{3x}^{j}}(m,n)$ (22)
(5) Estimate the three order cumulants through Fourier transform, and thus obtain the FLO bi-spectrum estimation:
${{\overset{\wedge }{\mathop{B}}\,}_{x}}({{\omega }_{1}},{{\omega }_{2}})=\sum\limits_{m=-L}^{L}{\sum\limits_{n=-L}^{L}{{{\overset{\wedge }{\mathop{C}}\,}_{3x}}(m,n)\exp \{j(}}{{\omega }_{1}}m+{{\omega }_{2}}n)\}$ (23)
where L<M-1. During the estimation of the bi-spectrum $B┴∧_x (ω_1,ω_2)$, a 2D window function θ(m,n) can be adopted:
${{\overset{\wedge }{\mathop{B}}\,}_{x}}({{\omega }_{1}},{{\omega }_{2}})=\sum\limits_{m=-L}^{L}{\sum\limits_{n=-L}^{L}{{{\overset{\wedge }{\mathop{C}}\,}_{3x}}(m,n)\theta (m,n)\exp \{j(}}{{\omega }_{1}}m+{{\omega }_{2}}n)\}$ (24)
4. Parameter Determination for AR Model
If the excitation of a physical network by white noise ω(n) is viewed as a random signal of the power spectral density under normal conditions [14], then the p-order AR model can be established as:
$x(n)=\sum\limits_{k=1}^{p}{{{a}_{k}}x}(n-k)+\omega (n)$ (25)
If a z transformation is performed, the transfer function of the AR model can be expressed as:
$H(z)=\frac{B(z)}{A(z)}=\frac{1}{1+\sum\limits_{k=1}^{p}{ak{{z}^{-k}}}}$ (26)
where the H(z) belongs to the all-pole type, i.e. it only has poles [15]. The power spectral density of the AR model can be described as:
${{P}_{xx}}(\omega )=\frac{\sigma _{\omega }^{2}}{{{\left| 1+\sum\limits_{k=1}^{p}{ak{{e}^{-j\omega k}}} \right|}^{2}}}$ (27)
where $σ_ω^2$ is the power spectral density of white noise.
The parameters of the AR model can be determined in three ways, namely, correlation function, reflection coefficient and normal equation. The last approach is adopted in our research.
Assuming that {x(i)} is a stochastic process satisfying the difference equations of the AR model, we have:
$\sum\limits_{l=0}^{p}{{{a}_{l}}x(i-l)=\sum\limits_{{{l}^{'}}=0}^{q}{{{b}_{{{l}^{'}}}}e(i-{{l}^{'}})}}$ (28)
where al and b1 are two key parameters in the AR model. Then, the following three conditions must be satisfied:
(1) e(i) is zero-mean and a stationary, identically distributed, independent sequence; there must exist at least one nonzero K(K>2) order cumulant.
(2) The model is causal with a minimum phase; there must be no zero pole cancellation; the index must remain stable [16]; the transfer function can be expressed as:
$H(z)=\frac{B(z)}{A(z)}=\frac{1+b(1){{z}^{-1}}+\text{ }\cdots +b(q){{z}^{-q}}}{1+a(1){{z}^{-1}}+\cdots +a(p){{z}^{-p}}}=\sum\limits_{i=0}^{\infty }{h(i){{z}^{-i}}}$ (29)
(3) The additive noise n(i) must be present in x(i):
$y(i)=x(i)+n(i)$ (30)
where n(i) is the FLO noise, which is independent of x(i), in the stable distribution of symmetric distributed noise.
Under these conditions, the relation between the output and the impulse response of this system can be expressed as:
${{C}_{kx}}(m,n)={{\gamma }_{ke}}\sum\limits_{i=0}^{\infty }{{{h}^{k-2}}(i)h(i+m)h(i+n)}$ (31)
From the definition of the impulse response, we have:
$\sum\limits_{l=0}^{p}{{{a}_{i}}h(i-l)=\sum\limits_{{{l}^{'}}=0}^{q}{{{b}_{{{l}^{'}}}}\delta (i-{{l}^{'}})={{b}_{i}}}}$ (32)
According to (28)~(32), we have:
$\sum\limits_{l=0}^{p}{{{a}_{l}}{{C}_{kx}}(m-l,n)}={{\gamma }_{ke}}\sum\limits_{i=0}^{\infty }{{{h}^{k-2}}(i)h(i+n)b(i+m)}$ (33)
If m>q, i≥0 and b(i+m)=0, then the normal equation of the three order cumulant can be expressed as:
$\sum\limits_{l=0}^{p}{{{a}_{l}}{{C}_{kx}}(m-l,n)}=0$ (34)
The parameters of the AR model can be determined by solving the equation.
5. Implementation of AR-based Bi-spectrum Estimation
The AR-based bi-spectrum estimation can be implemented in four steps:
Step 1: Divide x(i) into several segments with N being the segment length, N=KM. Then, the three order cumulant of each data can be expressed as:
$C_{3x}^{(j)}(m,n)=\frac{1}{M}\sum\limits_{i={{k}_{1}}}^{{{k}_{2}}}{{{[{{x}^{(j)}}(i)]}^{\langle A\rangle }}{{[{{x}^{(j)}}(i+m)]}^{\langle B\rangle }}[{{x}^{(j)}}(i+n)}{{]}^{\langle C\rangle }}$ (35)
where k1=max{0,-m,-n}; k2=min{M,M-n, M-m}.
Step 2: calculate the mean value of the K segment, and estimate the three order cumulants [17] as:
${{C}_{3x}}(m,n)=\frac{1}{K}\sum\limits_{i=1}^{K}{\overset{\wedge }{\mathop{C_{3x}^{(j)}}}\,}(m,n)$ (36)
Step 3: Determine the parameters of the AR Model, al(l, 2, …,p);
Step 4: Estimate the bi-spectrum using the parameters determined in Step 3:
$\left\{ \begin{align} & \overset{\wedge }{\mathop{B}}\,({{\omega }_{1}},{{\omega }_{2}})={{\overset{\wedge }{\mathop{\gamma }}\,}_{3e}}\overset{\wedge }{\mathop{H}}\,({{\omega }_{1}})\overset{\wedge }{\mathop{H}}\,({{\omega }_{2}}){{\overset{\wedge }{\mathop{H}}\,}^{*}}({{\omega }_{1}}+{{\omega }_{2}}) \\ & \overset{\wedge }{\mathop{H}}\,(\omega )={{[1+\sum\limits_{l=1}^{p}{\overset{\wedge }{\mathop{{{a}_{l}}}}\,}\exp (-j\omega n)]}^{-1}},\left| \omega \right|\le \pi \\ & \overset{\wedge }{\mathop{{{\gamma }_{3e}}}}\,=E\left\lfloor {{e}^{3}}(i) \right\rfloor \\\end{align} \right.$ (37)
The proposed method was verified through comparative tests on the following sequence:
$x(n)=s(n)+v(n)$ (38)
where n is an integer in the interval [0, N-1], with N being the sequence length; s(n)=cos(2πf1n)+cos(2πf2n), with of f1=0.2 and f2=0.4; v(n) is a symmetrically distributed noise.
(a) Contour map of FLO bi-spectrum direct estimation method
(b) Contour map of FLO bi-spectrum indirect estimation method
(c) Contour map of FLO bi-spectrum estimation based on the AR model
Figure 1. Contour maps of the three methods
(a) 3D graph of FLO bi-spectrum direct estimation method
(b) 3D graph of FLO bi-spectrum indirect estimation method
(c) 3D graph of FLO bi-spectrum estimation based on the AR model
Figure 2. 3D graphs of the three methods
During the tests, the mixed noise ratio was set to -20dB, and the value of a to 1.5. The proposed method, the traditional nonparametric direct estimation method and the nonparametric indirect estimation method were all applied to the tests. The test results are displayed in Figures 1 and 2. As shown in Figures 1 and 2, the proposed method outperformed the traditional methods in signal identification and background noise suppression. In addition, our method managed to perverse the amplitude and phase information of the signal excellently, and achieve the best spectral flatness, laying the basis for the optimal whitening effect.
In practice, most background noises belong to the FLO, which cannot be suppressed well by traditional methods. In this paper, a FLO bi-spectrum estimation method is proposed based on the AR model, and new definitions are given for FLO three order cumulant. The author discussed the determination of AR model parameters, and introduced how to implement the bi-spectrum estimation method based on AR model. Then, a series of tests were performed to verify the correctness of our method. The results show that our method outperformed the traditional approaches in suppressing FLO noise and identifying relevant information of signals.
This work is supported by the Research Foundation of health department of Jiangxi Province (Grant No.20183016).
[1] Zha DF, Gao XY. (2006). Adaptive mixed norm filtering algorithm based on SαSG noise model. Journal on Communications 27(7): 1-6. https://doi.org/10.1016/j.dsp.2006.01.002
[2] Long JB, Wang HB. (2016). Parameter estimation and time-frequency distribution of fractional lower order time-frequency auto-regressive moving average model algorithm based on SaS process. Journal of Electronics & Information Technology 38(7): 1710-1716. http://dx.doi.org/10.11999/JEIT151066
[3] Spiridonakos MD, Fassois SD. (2014). Non-stationary random vibration modelling and analysis via functional series time-dependent ARMA (FS-TARMA) models – A critical survey. Mechanical Systems & Signal Processing 47(1): 175-224. https://doi.org/10.1016/j.ymssp.2013.06.024
[4] Madhavan N, Vinod AP, Madhukumar AS, Krishna AK. (2013). Spectrum sensing and modulation classification for cognitive radios using cumulants based on fractional lower order statistics. AEUE - International Journal of Electronics and Communications 67(6): 479-490. http://dx.doi.org/10.1016/j.aeue.2012.11.004
[5] Wang SY, Zhu XB, Li XT, Wang YL. (2007). A -spectrum estimation for AR SaS processes based on FLOC. Acta Electronica Sinica 35(9): 1637-1641. http://dx.chinadoi.cn/10.3321/j.issn:0372-2112.2007.09.004
[6] Qiu TS, Wang HY, Sun YM. (2004). A fractional lower-order covariance based adaptive latency change detection for evoked potentials. Acta Electronica Sinica 32(1): 91-95. http://dx.chinadoi.cn/10.3321/j.issn:0372-2112.2004.01.022
[7] Sun YM, Qiu TS, Wang FZ. (2003). Time delay estimation method of Non-stationary signals based on fractional lower spectrogram. Journal of Dalian Jiaotong University 37(3): 112-116.
[8] Liu JQ, Feng DZ. (2003). Blind sources separation in impulse noise. Journal of Electronics and Information Technology 31(12): 1921-1923.
[9] Feng Z, Liang M. (2013). Recent advances in time–frequency analysis methods for machinery fault diagnosis: A review with application examples. Mechanical Systems & Signal Processing 38(1): 165-205. https://doi.org/10.1016/j.ymssp.2013.01.017
[10] Liu GH, Zhang JJ. (2017). Fractional lower order cyclic spectrum analysis of digital frequency shift keying signals under the alpha stable distribution noise. Chinese Journal of Radio Science 32(1): 65-72. http://dx.chinadoi.cn/10.13443/j.cjors.2017011001
[11] Zha DF, Qiu TS. (2005). Generalized whitening method based on fractional order spectrum in the frequency domain. Journal of China Institute of Communications 26(5): 24-30.
[12] Shao M, Nikias CL. (1993). Signal processing with fractional lower order moments: stable processes and their applications. Proceedings of the IEEE 81(7): 986-1010. http://dx.doi.org/10.1109/5.231338
[13] Miller G. (1978). Properties of symmetric stable distribution. Journal of multivariate Analysis (8): 346-360.
[14] Xu B, Cui Y, Zhou UY. (2014). Unsupervised speckle level estimation of SAR images using texture analysis and AR model. IEICE Transactions on Communications 97(3): 691-698.
[15] Zhao N, Richard YF, Sun HJ. (2015). Interference alignment with delayed channel state information and dynamic AR model channel prediction in wireless networks. Wireless Net-works 21(4): 1227-1242. https://doi.org/10.1007/s11276-014-0850-7
[16] Cambanis S, Miller G. (1981). Linear problems in order and stable peicesses. SIAM Journal on Applied Mathematics 41(1): 43-69.
[17] Jiang YJ, Liu GQ, Wang TJ. (2017). Application of atomic decomposition algorithm based on sparse representation in AR model parameters estimation. Computer Science 44(5): 42-47. | CommonCrawl |
Chloride migration measurement for chloride and sulfide contaminated concrete
M. Decker1,
R. Grosch1,
S. Keßler2 &
H. Hilbig1
Materials and Structures volume 53, Article number: 90 (2020) Cite this article
Reinforcement corrosion is major reason for concrete structures deterioration. Chlorides from external sources such as seawater and de-icing salts penetrate in the concrete and as soon as a critical threshold reaches the reinforcement level corrosion processes start. Therefore, the characterization of the chloride ingress resistance in form of the rapid chloride migration (RCM) coefficient, DRCM is crucial to classify concretes for given applications and to enable full probabilistic service life prediction. To measure DRCM of chloride-contaminated concrete, a rapid iodide migration test was developed using iodide as penetration ion and an iodine–starch reaction for penetration depth indication. This indicator mixture has the disadvantage that it is not applicable on sulfide containing concretes such as ground granulated blast furnace slag concretes. In this paper, the reason for the unsuitability of this indicator is examined and alternative oxidation agents are found and validated to overcome this problem. The new indicator mixtures with hydrogen peroxide (H2O2) or/and potassium persulfate (K2S2O8) as oxidation agents are not only insensitive to sulfide contamination but are also applicable to common concrete compositions and could replace the existing indicator universally.
The major reason for concrete structures to deteriorate is the chloride-induced reinforcement corrosion, for instance when the structure is located in marine environment or exposed to de-icing salts. The durability design of concrete structures is slowly moving from prescriptive to performance-based specifications. Consequently, suitable and reproducible test methods are required to characterize the chloride transport in concrete. These test methods should be usable for performance specifications and quality control. However, durability depends on deterioration processes, which need years to develop. Performance specifications require short term tests, lasting not more than some weeks, including preconditioning of the specimens. Otherwise, the approach is not practical nor acceptable for conformity control purposes, given the current pace of concrete construction [1].
Besides quality control purposes full-probabilistic service live prediction [2] with regard to corrosion initiation due to chlorides demands as well an input parameter which describes the chloride transport in concrete.
The diffusivity and the chloride-binding capacity of concrete dominate the resistance against chloride ingress into concrete. This material resistance describes the apparent chloride diffusion coefficient Dapp(t). The Dapp(t) can be determined by chloride profiles from field data and/or laboratory diffusion tests [3, 4]. These diffusion tests take several weeks while the determination of the rapid chloride migration (RCM) coefficient of concrete DRCM by RCM test is a suitable alternative [5]. RCM test accelerates the chloride ingress by applying an external voltage and the test takes only several hours or few days depending on the concrete resistivity and the resulting current [6,7,8,9,10]. Nevertheless, the RCM test does not reflect the chloride binding in the same degree as a diffusion test does [8]. On-site concrete differs from laboratory concrete due to workmanship, curing and environmental conditions. Therefore, drilled cores of the concrete cover from existing structures can be used for the RCM test to reflect the on-site conditions.
Figure 1 shows a schematic setup of the RCM test according to German Specification [11]. A concrete specimen of defined scales is placed in a migration cell creating a waterproof connection between cell and specimen. The cathode side is submerged in a 0.2 M KOH and 3 wt% NaCl solution while the anode is in contact with a 0.2 M KOH solution. Further setup details and the applicable currents and voltages can be found in the specific literature and standards [9, 11].
Schematic rapid chloride migration (RCM) test setup [11]
Drilled on-site concrete cores can already contain chlorides before the RCM test starts if a structure has been exposed to marine environment or de-icing salts. Furthermore, chlorides can be introduced to the concrete by chloride contaminated aggregates or water with chlorides. Since these internal chlorides migrate together with chlorides from the test solution, the RCM test is no longer applicable. The applied silver nitrate spray indicator [12] reacts with the migrated chlorides and the ingress is overestimated. This leads to a higher value for DRCM, thus, the full probabilistic service life model would indicate a much shorter time to corrosion initiation. Lay et al. [12] already published an alternative approach to estimate the chloride migration coefficient of chloride contaminated concrete: The rapid iodide migration (RIM) test. The test uses iodides instead of chloride ions as they have comparable migration behavior. The setup remains similar to the presented RCM test in Fig. 1, while the molar concentration of both test solutions is identical with 0.51 M (3.0 wt% sodium chloride for RCM test and 7.695 wt% sodium iodide for RIM test).
The indicator used for the RIM test is an water-based mixture of 3 wt% aqueous starch solution (400 mL/L), 50 wt% acetic acid (200 mL/L) and 1 M potassium iodate (KIO3) (400 mL/L). The oxidation of the penetrating iodide to iodine by iodate (reaction 1) is visible as a color change due to the blue iodine starch complex. Besides iodine, other byproducts of the reaction are sodium and potassium acetate (NaAc/KAc).
$$10\;{\text{NaI}} + 2\;{\text{KIO}}_{3} + 12\;{\text{HAc}} \to 6\;{\text{I}}_{2} + 10\;{\text{NaAc}} + 2\;{\text{KAc}} + 6\;{\text{H}}_{2} {\text{O}}$$
This indicator shows good contrast between iodide contaminated and iodide free zones, but only in concretes made with Portland cement. However, with increasing amount of GGBS cements (CEM III) used nowadays [13] no color change is observable. Although no iodine is present in the concrete mixture (reaction 2), the indicator reacts with sulfides present in the GGBS to the blue iodine starch complex covering the whole specimen. In this case, the iodine forming a blue iodine starch complex is produced by the KIO3 reduction itself, thus, a misinterpretation is possible. Besides iodine, other byproducts are also NaAc and KAc as well as sulfur (S) in the case of the sulfide containing solution.
$$5\;{\text{Na}}_{ 2} {\text{S}} + 2\;{\text{KIO}}_{ 3} + 1 2\;{\text{HAc}} \to {\text{I}}_{ 2} + 1 0\;{\text{NaAc}} + 2\;{\text{KAc}} + 6\;{\text{H}}_{ 2} {\text{O}} + 5\;{\text{S}}$$
Nowadays, the use of CEM III concrete is increasing due to energy efficiency, lower porosity, lower chloride migration coefficients [8] and higher resistance to alkali silica reaction (ASR) [14]. Frequently used CEM III B contains up to 80 wt% GGBS in which up to 2 wt% sulfide are present [15]. According to the pozzolanic reaction it contains less calcium hydroxide Ca(OH)2 than ordinary Portland cement. With regard of the increasing use of blended cements, this paper focuses on the development of an indicator to enable rapid iodide migration tests as well on GGBS and chloride contaminated GGBS concretes.
Two alternatives for KIO3 as oxidation agents for iodide are presented in this paper, which are not iodine containing but having the same oxidation power as IO3−: hydrogen peroxide (H2O2) is known to be a strong oxidation agent, it is a mass product with good availability and very riskless reaction products: water (H2O) and oxygen. Nevertheless, it is irritating and only stable in aqueous solution up to 30 wt%. Another alternative strong oxidation agent is potassium persulfate (K2S2O8) which is used as radical initiator for numerous polymerization types [16]. Subsequently, this paper describes the reaction of the currently used indicator with sulfides in vitro, on mortar prisms and on iodide/chloride contaminated cements. On the same systems, alternative indicators are developed and successfully tested.
Figure 2 shows the experimental procedure: three different oxidation agents (one was the original KIO3 oxidation agent) were tested on samples contaminated with sulfides (A), chlorides (B), iodides (C), mixtures of the ions A–C (D) and a blind test in vitro and on concrete specimens.
Schematic overview of the experimental procedure with three oxidation agents in vitro, on mortar prisms and on concrete specimens
All chemicals were purchased from Sigma-Aldrich (St. Louis, MO) or Merck (Darmstadt, Germany) and were used without further purification if not mentioned specifically. Water was purified by an arium pro ultrapure water system (Sartorius, Germany) prior to use. For pH measurement a ProLab 4000 pH meter (Schott Instruments, Germany) was used. All in vitro tests were performed in a saturated calcium hydroxide solution to simulate the alkaline pore solution of concrete. A 0.1 M sodium iodide (NaI) and a sodium sulfide (Na2S) solution represented the iodides and sulfides in concrete.
Indicator mixtures
In order to compare the new system with the original indicator [12], all concentrations and ratios were adopted and mixed as follows:
component 1:3 wt% aqueous starch solution and 50 wt% acetic acid (HAc) in a ratio of 3:1
Component 2 (oxidation agent)
Original system
0.21 M KIO3 solution
Option A: 30% aqueous H2O2 solution
Option B: 0.21 M K2S2O8 solution
In vitro tests
1 mL 0.1 M NaI or Na2S or a mixture of both (1 mL 1/1 mixture) were mixed with saturated Ca(OH)2 solution, component 1 and different quantities of component 2 variations.
Titration experiments to observe the transition point of the H2O2 and K2S2O8 indicator system were prepared as follows: 3 mL 0.1 M NaI, 3 mL 30 wt% H2O2 or 0.21 M K2S2O8 respectively, 3 mL 50 wt% HAc and 9 mL starch solution were titrated to decoloration with 6 M sodium hydroxide (NaOH). Afterwards the colorless mixture was titrated back to blue with 50 wt% HAc. Acid and base were added dropwise into the vigorously stirring mixture while the pH value was monitored continuously.
Mortar tests
To transfer the in vitro system to a more realistic one, mortar prisms of 450 g GGBS containing cement CEM III/A 42, 5 N (Schwenk Mergelstetten, for detailed chemical composition check supplementary materials) 1350 g sand and 202.5 g water were prepared. Mixing regime followed DIN EN 196-1 [17] while the water-to-binder ratio was reduced to 0.45 due to better workability. NaI is added in various concentrations to the mixing water (0.21, 0.14, 0.07, 0.035, 0 mol/l NaI [12]) and the mortar specimens were stored for 17 days under tap water at 20 °C.
Concrete tests
To study the indicator systems under realistic conditions, migration tests with chloride and iodide were done according to Lay [12]: GGBS containing concrete was prepared with cement CEM III (same as for mortar) and 0/18 mm aggregates with water-to-binder ratio of 0.55. After 28 days RIM tests were conducted with a 0.51 M NaI solution, a 0.2 M potassium hydroxide (KOH) solution at the anode under 30 V for 24 h. In addition, a combined RCM/RIM test was conducted with 24 h RCM and 24 h RIM to penetrate chlorides and iodides into the concrete. Figure 3 shows a detailed description of the combined RCM/RIM test in accordance to [11].
Schematic procedure of combined RCM/RIM test with the expected and real color boundaries for the novel iodide and chloride indicator spray test
To verify the applicability of the novel indicator also on ordinary Portland cement (OPC), CEM I concrete was prepared with CEM I 42.5 N (Schwenk Cement Mergelstetten) and 0/8 mm aggregates with water-to-binder ratio of 0.4. RIM/RCM specimens were prepared by drilling and sawing the specimens out of a concrete cube and a combined RCM/RIM test was conducted as described for CEM III specimen.
Table 1 summarizes the different variations of the in vitro tests with the corresponding observations. Various amounts of oxidation agent are tested while the maximal quantity is always 1 mL. One drop represents approximately the volume of 0.05 mL.
Table 1 Variations of the in vitro tests and resulting observations
By adding 6 drops of the KIO3 solution as oxidation agent to the salt solutions, a color change from milky turbid to blue is observed independent of the type of salt (iodide or sulfide or mixed). The reaction is described earlier in Eq. 1. If more KIO3 is added a dark precipitate is observable. As mentioned in Eq. 2, in the case of sulfides (Table 1, line 3 and 4) a blue color is observed too, although no iodine is present.
Instead of KIO3, H2O2 works as an alternative oxidation agent in a NaI and NaI/Na2S solution if at least 5 drops 30 wt% aqueous H2O2 solution is added. No color change is observed if the indicator system is applied in a pure Na2S solution.
However, H2O2 is an economic alternative oxidation agent with water as a harmless reaction product. By using this oxidation agent in the adopted indicator system instead of KIO3 the net amount of formed iodide (reaction 3) decreases slightly compared to reaction 1. Nevertheless, a color change is also observed as the penetrating iodine is formed as an oxidation product. Together with the starch dissolved in the indicators' spray solution the iodine can form the blue iodine–starch complex. If the solution contains sulfide no iodine is formed at all but elemental sulfur. Thus, the starch is not complexed and stays colorless as shown in reaction 4. The produced sulfur may cause turbidity as it is insoluble in water.
$$2\;{\text{NaI}} + {\text{H}}_{ 2} {\text{O}}_{ 2} + 2\;{\text{HAc}} \to {\text{I}}_{ 2} + 2\;{\text{NaAc}} + 2\;{\text{H}}_{ 2} {\text{O}}$$
$${\text{Na}}_{ 2} {\text{S}} + {\text{H}}_{ 2} {\text{O}}_{ 2} + 2\;{\text{HAc}} \to {\text{S}} + 2\;{\text{NaAc}} + 2\;{\text{H}}_{ 2} {\text{O}}$$
However, the question arises if the sulfide is oxidized to sulfur or to higher oxidation states like sulfate. In vitro tests with barium chloride yielded to no precipitate of barium sulfate when adding it to a test tube with the product of reaction (Eq. 4) which is also confirmed by literature [3].
K2S2O8 is tested as an additional oxidation agent variation. A 0.21 M K2S2O8 solution performs similar as H2O2 but takes more than 2 min to develop a clear blue color (see Fig. 4).
Time-dependent change of color after application of a K2S2O8 based indicator system. Left: before adding; middle: after 2 min; right: after 5 min
In principle, the redox reaction with K2S2O8 works analogous to H2O2 (reaction 5 and 6). However, no acetic acid is needed for this reaction based on Eq. 6. Slower reaction of K2S2O8 is due to sterical shielding of the reactive oxide–oxide bond compared to H2O2. Although K2S2O8 has a higher oxidation potential [18]. Besides iodine or sulfur, other byproducts of the reactions are sodium and potassium sulfate (Na2SO4/K2SO4).
$$2 {\text{ NaI}} + {\text{K}}_{ 2} {\text{S}}_{ 2} {\text{O}}_{ 8} \to {\text{I}}_{ 2} + {\text{Na}}_{ 2} {\text{SO}}_{ 4} + {\text{K}}_{ 2} {\text{SO}}_{ 4}$$
$${\text{Na}}_{ 2} {\text{S}} + {\text{K}}_{ 2} {\text{S}}_{ 2} {\text{O}}_{ 8} \to {\text{S}} + {\text{Na}}_{ 2} {\text{SO}}_{ 4} + {\text{K}}_{ 2} {\text{SO}}_{ 4}$$
A mixture of both (1/1) H2O2 and K2S2O8 solution as oxidation agent shows the same color changes as H2O2 and K2S2O8.
Table 2 shows the different variations of the mortar tests with the corresponding observations. Mortar prisms with different concentrations of iodine are tested as well as reference samples without iodide.
Table 2 Variations of the mortar tests and observations
In the case of H2O2 the blue color disappears after 1–3 min and the whole prism turns yellow starting from the edges (Fig. 5, line 6 Table 2). If the sample is sprayed again with H2O2-indicator mixture the blue color appears again. To analyze this phenomenon every constituent of the indicator was sprayed separately in a second turn. By using acetic acid the yellow color turns blue again.
Left: H2O2 spray spot on GGBS and NaI containing mortar sample after few seconds; right: same mortar sample after 5 min. Discoloration from blue to yellow is due to realkalization of the surface and thus discoloration of iodine starch complex
Freshly broken surface of iodide-free prisms shows a yellow color by applying the H2O2 based indicator system, too (line 6, Table 2). To gain further insights of the color change from blue to colorless an in vitro titration experiment is performed. The experiment shows that with H2O2 the iodine starch complex is stable up to pH 8.6 and reversible colorful again from 7.0. After spraying the indicator on the surface, the surface dries which leads to the following two processes:
The decomposition of remaining H2O2, which is not stable in the solid state.
The surface realkalizes by diffusion of hydroxyl from deeper regions of the cement matrix.
Because of these effects, the behavior of iodine is dependent on reaction 7, shifting the chemical equilibrium to the right side and withdrawing the iodine out of the iodine–starch complex.
$$3\ {\text{I}}_{2} + 6{\text{ OH}}^{ - } \rightleftarrows 5\;{\text{I}}^{ - } + {\text{IO}}_{3}^{ - } + 3\;{\text{H}}_{2} {\text{O}} .$$
Acidification shifts the equilibrium back to the left side, producing iodine via a comproportionation reaction.
In case of the K2S2O8 based indicator system the color is more intensive blue. As in the previous in vitro tests, the color appears again on the prisms after few minutes. Nevertheless, no color change to yellow could be observed as in the case of H2O2. The repeated titration experiment shows that the iodine–starch complex is stable until pH 12.4 and from pH 12.1 colorful again. After drying, the K2S2O8 remains as a salt. Thus, as long as a stronger oxidation species than IO3− is present, the reaction 7 is hindered and reaction 5 remains decisive.
However, for small iodide concentrations the color is not as shiny and clear as for high iodide concentrations. Table 3 shows mortar prisms with several iodide concentrations in mixing water and the corresponding color after the application of the indicator.
Table 3 Iodide concentration in mixing water and corresponding color after the application of the K2S2O8 indicator system
As can be seen in Table 3, the new indicator systems has a lower detection limit for iodide. The color change boundary of the KIO3 based indicator corresponds to an iodide concentration of 0.07 mol/l. The new system is more sensitive since the boundary concentration is about 0.035 mol/l and therefore a new correlation factor between RCM and RIM needs to be calculated.
To show the applicability of the indicator mixtures on a realistic system several concrete migration tests are executed. Basic indicator investigations are done on a CEM III concrete after a RIM test of 19 h. A combination of 24 h RCM followed by 24 h RIM is tested on a CEM III and a CEM I containing concrete, respectively (Fig. 3). The aim of the first step is to produce a concrete specimen with high chloride content. H2O2 and K2S2O8 based indicator systems are used similar to the original mortar tests. In the combined RCM/RIM test the chlorides migrate for 48 h while iodides migrating only 24 h (Fig. 3). Consequently, the chloride penetration depth, visualized with silver nitrate (AgNO3)/fluorescein shows a deeper migration front in the combined RCM/RIM test
The following Table 4 shows the different variations of the indicator tests with the corresponding observations.
Table 4 Variations of the indicator tests on CEM III concrete specimens and observations
By applying the existing KIO3 indicator spray test on GGBS containing concrete a blue color is visible on the whole surface. With the H2O2 indicator system a clear migration front is visible but it turns yellow after 5 min. However, a stable blue color is achieved after the second time spraying as shown in Fig. 6 and already discussed before. However, the yellow color of iodide free areas is an additional advantage of this indicator system since it creates a better contrast to blue on the dark surface of a GGBS containing concrete. The novel indicator systems are not affected by chloride contamination as seen in line 6, 7, 8, 10, 11 in Table 4. However, a K2S2O8 based indicators need more time to fully develop its color as well.
Color front in CEM I after the application of the H2O2 indicator system
For the combined experiment of RCM and RIM, which should simulate the real on-site chloride contamination condition, the system was successfully tested. The new indicator is suitable to indicate the migration depth of iodide in sulfide containing concrete compositions.
To validate the new indicator systems on standard concrete mixtures, samples with ordinary Portland cement CEM I are used for the RIM test. Table 5 gives the overview of the indicator test variations with the corresponding observations.
Table 5 Variations of the indicator tests on CEM I concrete specimens and observations
However, for H2O2 the color front is visible after spraying twice while for K2S2O8 only spraying once was necessary, as it takes longer to yield to color change.
In the case of the more alkaline CEM I both indicator systems verified the applicability of the developed system. However, in the H2O2 system acetic acid need to be sprayed again to stabilize the color.
The main objective of this investigation is the determination of DRCM in chloride-contaminated concrete, as the full-probabilistic service live prediction requires DRCM as input parameter. Therefore, Lay calculated DRCM using measured DRIM data multiplied with a correlation factor \(\frac{{D_{\text{RCM}} }}{{D_{\text{RIM}} }}\) obtained from the comparison of both ion penetrating behaviors and the used spraying indicators. The determination of a new correlation factor is necessary since the iodide concentration leading to a color change (Table 3) is different for the novel indicator system. The original correlation factor \(\frac{{D_{\text{RCM}} }}{{D_{\text{RIM}} }}\) after observation of the color change boundaries by spray tests was experimentally determined by Lay as 0.987 [12]. Figure 7 shows the boundaries of the AgNO3/fluorescein chloride indicator (17 mm) as well as the original KIO3 system (17.5 mm) and the novel H2O2/K2S2O8 mixture (17.7 mm). Hence, the new correlation factor is calculated to 0.96 by dividing the respective boundaries. In any case, the slight change on the correlation factor is negligible, especially regarding rapid migration test's coefficient of variation.
Comparison of chloride and iodide profiles and average of penetration depth Xd revealed by chloride, original iodide and novel iodide indicator after rapid migration test [7]
This paper describes the development of a novel indicator system for the determination of the penetration front of RIM tests in chloride and sulfide contaminated concretes such as GGBS containing CEM III concretes. With the help of the RIM test, it is possible to measure the rapid chloride migration coefficient of chloride-contaminated concrete using iodide as penetrating ion. The original indicator system was only applicable for CEM I type concretes and is based on the iodine starch reaction in combination with KIO3 as oxidation agent. However, this indicator is not applicable to sulfide containing concretes because the used oxidation agent KIO3 produces iodine with any reduction agent such as sulfide and generates a false positive discoloration in GGBS containing concretes.
As alternative oxidation agents H2O2 and K2S2O8 are successfully examined. Since both proposed oxidation agents show minor disadvantages (for H2O2 the iodine starch complex disappears in alkaline media while K2S2O8 takes several minutes to develop the full color) a mixture of both combines their advantages as the blue color develops immediately and stays during an appropriate time in which the user could mark the migration front with a permanent pen. Nevertheless, the use of only one of the oxidizing agents is also possible. The optimum composition of the new indicator may be a mixture of both, applying following composition for 1 L: 600 mL 3 wt% aqueous starch solution, 200 mL 50 wt% acetic acid, 100 mL 30 wt% aqueous H2O2 and 100 mL 0.21 M K2S2O8 solution.
The new indicator system is also validated for a sulfide free concrete with high basicity with the result that the new indicator system can replace the iodate system universally. For practical use H2O2 is preferable in comparison to K2S2O8 since the latter is more expensive and not as stable as H2O2 in water. In both cases, the sensitivity is higher compared to the original indicator with KIO3. Consequently, a new correlation factor \(\frac{{D_{\text{RCM}} }}{{D_{\text{RIM}} }}\) had to be calculated with a value of 0.96, which is only a small divergence to the value for the KIO3 based indicator system of 0.987 [12].
Torrent RJ (2018) Bridge durability design after EN standards: present and future. Struct Infrastruct Eng 15:1–13
FB (2006) Model code for service life design. International federation for structural concrete (fib)
EN 12390-11 DE (2015) Determination of the chloride resistance of concrete, unidirectional diffusion
Samson E, Marchand J, Snyder KA (2003) Calculation of ionic diffusion coefficients on the basis of migration test results. Mater Struct 36(3):156–165
Tang L (1996) Electrically accelerated methods for determining chloride diffusivity in concrete—current development. Mag Concr Res 48(176):173–179
Kessler S, Thiel C, Grosse CU, Gehlen C (2017) Effect of freeze–thaw damage on chloride ingress into concrete. Mater Struct 50(2):121
Van Noort R, Hunger M, Spiesz P (2016) Long-term chloride migration coefficient in slag cement-based concrete and resistivity as an alternative test method. Constr Build Mater 115:746–759
Spiesz P, Brouwers H (2013) The apparent and effective chloride migration coefficients obtained in migration tests. Cem Concr Res 48:116–127
NT Build (1999) Chloride migration coefficient from non-steady-state migration experiments. Nordtest Method 492:10
MCL BCoP (2012) Resistance of Concrete to Chloride Penetration (MCL)
Wasserbau BF (2012) BAWMerkblatt Chlorideindringwiderstand von Beton (MCL)
Lay S, Liebl S, Hilbig H, Schießl P (2004) New method to measure the rapid chloride migration coefficient of chloride-contaminated concrete. Cem Concr Res 34(3):421–427
Siddique R (2014) Utilization (recycling) of iron and steel industry by-product (GGBS) in concrete: strength and durability properties. J Mater Cycl Waste Manag 16(3):460–467
Ogawa S, Nozaki T, Yamada K, Hirao H, Hooton R (2012) Improvement on sulfate resistance of blended cement with high alumina slag. Cem Concr Res 42(2):244–251
Di Maio L (2016) Cement replacement materials. CSE-City Saf Energy 2:155–156
Qiu J, Charleux B, Matyjaszewski K (2001) Controlled/living radical polymerization in aqueous media: homogeneous and heterogeneous systems. Progr Polym Sci 26(10):2083–2134
EN 196-1: DE (2005) Prüfverfahren für Zement–Teil 1: Bestimmung der Festigkeit. Deutsche Fassung
Wiberg N, Dehnicke K (1996) Hollemann-Wiberg, Lehrbuch der Anorganischen Chemie. Angewandte Chemie-German Edition 108(21):2696
Open Access funding provided by Projekt DEAL.
TUM Center for Building Materials and Material Testing, Baumbachstraße 7, 81245, Munich, Germany
M. Decker, R. Grosch & H. Hilbig
Helmut-Schmidt-University/University of the Federal Armed Forces Hamburg, Holstenhofweg 85, 22043, Hamburg, Germany
S. Keßler
M. Decker
R. Grosch
H. Hilbig
Correspondence to M. Decker.
Below is the link to the electronic supplementary material.
Supplementary material 1 (DOCX 14 kb)
Decker, M., Grosch, R., Keßler, S. et al. Chloride migration measurement for chloride and sulfide contaminated concrete. Mater Struct 53, 90 (2020). https://doi.org/10.1617/s11527-020-01526-4
Rapid chloride/iodide migration
Iodine–starch reaction
Potassium persulfate | CommonCrawl |
A Game Theoretic Approach to Quantum Information
Xianhua Dai, V. P. Belavkin
This work is an application of game theory to quantum information. In a state estimate, we are given observations distributed according to an unknown distribution $P_{\theta}$ (associated with award $Q$), which Nature chooses at random from the set $\{P_{\theta}: \theta \in \Theta \}$ according to a known prior distribution $\mu$ on $\Theta$, we produce an estimate $M$ for the unknown distribution $P_{\theta}$, and in the end, we will suffer a relative entropy cost $\mathcal{R}(P;M)$, measuring the quality of this estimate, therefore the whole utility is taken as $P \cdot Q -\mathcal{R}(P; M)$. In an introduction to strategic game, a sufficient condition for minimax theorem is obtained; An estimate is explored in the frame of game theory, and in the view of convex conjugate, we reach one new approach to quantum relative entropy, correspondingly quantum mutual entropy, and quantum channel capacity, which are more general, in the sense, without Radon-Nikodym (RN) derivatives. Also the monotonicity of quantum relative entropy and the additivity of quantum channel capacity are investigated. | CommonCrawl |
negate definition math
thesaurus. For e.g. We can negate each of these statements by writing the opposite of what it says. Negation : Negation is the method of changing the values in a statement. Send us feedback. The negation of All birds can y is Some birds cannot y. See the full definition for negate in the English Language Learners Dictionary, Thesaurus: All synonyms and antonyms for negate, Nglish: Translation of negate for Spanish Speakers, Britannica English: Translation of negate for Arabic Speakers. Every triangle has three sides. How to Calculate a Sample Standard Deviation. Negative definition, expressing or containing negation or denial: a negative response to the question. To make the negative of a non-finite clause, we can … What Does "Auld Lang Syne" Actually Mean? to nullify or cause to be ineffective: Progress on the study has been negated by the lack of funds. To nullify or cause to be ineffective. Doctor Teeple started with the concept of a statement: So, the negation of a statement is a statement that says the first one is not true. Namespace: Java.Math Java.Math Assembly: Mono.Android.dll. Your amounts want to be listed from smallest to greatest to track down the median, and this indicates that you may have to rewrite your list just prior to you will discover that the median. scala.math - Basic math functions and additional numeric types like BigInt and BigDecimal; scala.sys - Interaction with other processes and the operating system; scala.util.matching - Regular expressions; Other packages exist. That would negate the whole point of having a prenup. Definition: universal quantifier. Thus, each closed sentence in Example 1 has a truth value of either true or false as shown below. the treaty annuls all previous agreements abrogate is like annul but more definitely implies a legal or official act. These example sentences are selected automatically from various online news sources to reflect current usage of the word 'negate.' The definition of limit of a sequence, studied in calculus, uses both quantifiers ∀ and ∃ and also if-then. See more. In this article Overloads. Negate() Negate() Returns a new BigDecimal whose value is the -this. A Secret Weapon for What Does Negate Mean in Math Physical buildings may be destroyed. Lawyers Ask for Another Try, A Commentary to Kant's 'Critique of Pure Reason'. negate (third-person singular simple present negates, present participle negating, simple past and past participle negated) To deny the existence, evidence, or truth of; to contradict. What Is An Em Dash And How Do You Use It? LOG IN; REGISTER; settings. A negative sentence or phrase is one that contains a word such as "not…. Negate If we negate both the hypothesis and the conclusion we get a inverse statement: if a population do not consist of 50% men then the population do not consist of 50% women. The fact that she lied about her work experience, This is because the sheer size of a parcel can, Media discourse soon turned to whether Breonna was actually working as an EMT at the time of her death, as if this detail regarding her achievement would, This is because of a Georgia Senate runoff occurring in January that will determine the fate of the Senate in terms of its ability to support or, An economic rebound in 2021 could further, The progress announced by Pfizer on Monday towards a Covid-19 vaccine was promising, some said, but did not, Charles said her vote could help Biden win, or at least, Post the Definition of negate to Facebook, Share the Definition of negate on Twitter. Albany is the capital of New York State. In logic, negation, also called the logical complement, is an operation that takes a proposition to another proposition "not ", written ¬, ∼ or ¯. Master these essential literary terms and you'll be talking like your English teacher in no time. nullify implies counteracting completely the force, effectiveness, or value of something. A reflection of a point, a line, or a figure in the Y axis involved reflecting the image over the Y axis to create a mirror image. A reflection of a point, a line, or a figure in the X axis involved reflecting the image over the x axis to create a mirror image. Please tell us where you read or heard it (including the quote, if possible). Thus, each closed sentence in Example 1 has a truth value of either true or false as shown below. —v.i. As usual, I'll start with a fairly basic question to set the stage, this one from 1998: Heather has been asked to "negate" these statements; what does that mean? A protagonist is the main character of a story, or the lead. We say that the limit of the sequence an as n goes to infinity equals L and write if, and only if, the values of an become arbitrarily close to L as n gets larger and larger without bound. "Negate." Merriam-Webster.com Dictionary, Merriam-Webster, https://www.merriam-webster.com/dictionary/negate. (Positive means more than zero. Based on the Random House Unabridged Dictionary, © Random House, Inc. 2020, Collins English Dictionary - Complete & Unabridged 2012 Digital Edition If the original was a true statement, the new one will be false, and vice versa. Source null; That would kind of negate the whole idea of top secret. Definition of Negate. Template parameters T Type of the argument and return type of the functional call. My math teacher gave me some problems on it: "4 + 3 * 5 = 35" and "Violins are members of the string family." Negative numbers are indicated by placing a dash ( – ) sign in front, such as –5, –12.77.A negative number such as –6 is spoken as 'negative six'. Definition of negative in the Definitions.net dictionary. Example 7. You use truth tables to determine how the truth or falsity of a complicated statement depends on the truth or falsity of its components. a penalty nullified the touchdown negate implies the destruction or canceling out of each of two things by the other. negate (verb) - prove negative; show to be false. GAMES; BROWSE THESAURUS ; WORD OF THE DAY; WORDS AT PLAY. Source null; Sorry Jenny, but a mistress does not negate your marriage vows. Negate definition, to deny the existence, evidence, or truth of: an investigation tending to negate any supernatural influences. Why Is "Christmas" Abbreviated As "Xmas"? In classical logic, negation is normally identified with the truth function that takes truth to falsity (and vice versa). He's making a quiz, and checking it twice... Test your knowledge of the words of the year. Math Definition: Reflection Over the Y Axis. Computations With Fractions. In this case, theY axis would be called the axis of reflection. 1; verb with object negate to nullify or cause to be ineffective: Progress on the study has been negated by the lack of funds. Negative definition, expressing or containing negation or denial: a negative response to the question. In logic, negation, also called logical complement, is an operation that takes a proposition p to another proposition "not p", written ¬p, which is interpreted intuitively as being true when p is false and false when p is true. 1; verb without object negate to be negative; bring or cause negative results: a pessimism that always negates. // Example of the Decimal::Negate, Decimal::Floor, and // Decimal::Truncate methods. This is also known as "Not". Sign up to join this community. So, if the statement is two plus three equals five, the negation is two plus three is not equal to five. The following code example uses the Negate method to change the sign of several Decimal values. The investigation tending to negate any supernatural influences. (Positive means more than zero. I've asked my parents about it and they don't know. Negation is thus a unary (single-argument) logical connective. Negation definition, the act of denying: He shook his head in negation of the charge. Negative Association There is a negative association between variables X and Y if smaller values of X are associated with larger values of Y and larger values of X are associated with smaller values of Y. . Accessed 27 Dec. 2020. This is usually referred to as "negating" a statement. This member function allows the object to be used with the same syntax as a function call. 3. Zero is neither negative nor positive.) How can negate be used in a sentence? the arguments negate each other annul suggests making ineffective or nonexistent often by legal or official action. (Do you see why Doctor Teeple started out by emphasizing that a statement doesn't have to be true?) It may be applied as an operation on notions, propositions, truth values, or semantic values more generally. It can be made to hold for all real numbers by extending the definition of negation to include zero and negative numbers. Synonyms: contradict, deny, disaffirm… Antonyms: acknowledge, admit, allow… Find the right word. Portions of this page are modifications based on work created and shared by the Android Open Source Project and used according to terms described in the Creative Commons 2.5 Attribution License. L'algèbre a ses quantités positives ou possibles, et ses quantités négatives ou impossibles; elle opère sur les unes comme sur les autres par des procédés absolument semblables (Bonald, Essai analyt., 1800, p.11). negate. Just because two goods or two rights are in tension, it does not mean that one should negate the other. The ammendment to the law negated' the intended effect of the law. The negation of a some statement is a for all statement. The symbol \(\forall\) is used to denote a universal quantifier, and the symbol \(\exists\) is used to denote an existential quantifier. In mathematics, negation is the logical operation that takes a statement and changes is it to a statement whose true or false value is opposite that of the original statement. to make ineffective or void; nullify; invalidate, A Sandusky Retrial? What You Need to Know About Consecutive Numbers. The inverse is not true juest because the conditional is true. The key idea is that when you move a negation past a quantifier, it flips the quantifier from universal to existential or vice versa. Delivered to your inbox! to be negative; bring or cause negative results: a pessimism that always negates. Negate(MathContext) Negate(MathContext) Returns a new BigDecimal whose value is the -this. a−n est l'inverse de an. SINCE 1828. Limitation is not merely negative; genuine realities may negate one another. Use BEDMAS to Remember the Order of Operations. Negation in non-finite clauses Non-finite clauses are clauses without a subject, where the main verb is in the to-infinitive form, the -ing form or the -ed form. About the Book Author Mark Zegarelli is a math and test prep teacher who has written a wide variety of basic math and pre-algebra books in the For Dummies series. 'Nip it in the butt' or 'Nip it in the bud'. Discover The Origins Of These Cooking Tool Names, The Most Surprisingly Serendipitous Words Of The Day. Definition of Negate. the arguments negate each other How do abrogate and annul relate to one another, in the sense of negate? The slovenly way he lived his life negated his good intentions. We make statements and negate them without judging whether they are true or false. Negation in non-finite clauses Non-finite clauses are clauses without a subject, where the main verb is in the to-infinitive form, the -ing form or the -ed form. Then you may add all those to receive 658. (Note: this can also be phrased "All A are the opposite of B," although this construction sometimes sounds ambiguous.) To make the negative of a non-finite clause, we can … The inverse always has the same truth value as the converse. Hello, GAMES; BROWSE THESAURUS; WORD OF THE DAY; WORDS AT PLAY; SETTINGS; SAVED … The phrase "for every" (or its equivalents) is called a universal quantifier. Negating a value returns the same value with the opposite sign. What does negative mean? if a statement is 'true' then its negation value is termed as 'false'. Negate definition is - to deny the existence or truth of. Meaning of negative. Donc : n 1 n a a − = Remarque . [>>>] The negation of "Some A are B" is "No A are (is) B." So for example, the negation of "The sky is purple" is "The sky is not purple." In intuitionistic logic, according to the Brouwer–Heyting–Kolmogorov interpretation, the negation of a proposition $${\displaystyle P}$$ is the proposition whose proofs are the refutations of $${\displaystyle P}$$. The type shall support the operation (unary operator-). Specifically: What Does Negate Mean in Math Secrets That No One Else Knows About. This page provides all possible translations of the word negate … To negate the number –3, attach a minus sign to it, changing it to –(–3), which equals 3. Annuler, supprimer, invalider. But, if we use an equivalent logical statement, some rules like De Morgan's laws, and a truth table to double-check everything, then it isn't quite so difficult to figure out. Math Glossary: Mathematics Terms and Definitions. Can you spell these 10 commonly misspelled words? Member types. Examples. 1 1 n n n n1 n Definition: A closed sentence is an objective statement which is either true or false. Definition: A closed sentence is an objective statement which is either true or false. verb with object negate to deny the existence, evidence, or truth of: an investigation tending to negate any supernatural influences. The logical negation symbol is used in Boolean algebra to indicate that the truth value of the statement that follows is reversed. view recents. Synonym Discussion of negate. So one way to check whether your answe… It is interpreted intuitively as being true when is false, and false when is true. That is another issue. What's The Difference Between "Yule" And "Christmas"? SAVED WORDS dictionary. 2. Similarly, arithmetic negate is 0-A with carry set (borrow reset). Your amounts want to be listed from smallest to greatest to track down the median, and this indicates that you may have to rewrite your list just prior to you will discover that the median. Mathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields. logical negation symbol: The logical negation symbol is used in Boolean algebra to indicate that the truth value of the statement that follows is reversed. The rule for reflecting over the Y axis is to negate the value of the x-coordinate of each point, but leave the -value the same. Progress on the study has been negated by the lack of funds. to deny the existence, evidence, or truth of: an investigation tending to negate any supernatural influences. Example … Negate the item and append the result of the negation to values. Have you ever wondered about these lines? The negation of There exists an honest man is All men are dishonest. Illustrated definition of Negative: Lessnbspthannbspzero. Definition of non-negative in the Definitions.net dictionary. Test Your Knowledge - and learn some interesting things along the way. nullify, negate, annul, abrogate, invalidate mean to deprive of effective or continued existence. For example, by failing to meet the required funding, the plans for construction were negated. © William Collins Sons & Co. Ltd. 1979, 1986 © HarperCollins Let us look at different illustrations. Définition et exemples Définition . One thing to keep in mind is that if a statement is true, then its negation is false (and if a statement is false, then its negation is true). This identity holds for any positive number x. Soit a∈R* et n∈N. 1. Learn a new word every day. That is, the negation of a positive number is the additive inverse of the number. Learn more. Information and translations of non-negative in the most comprehensive dictionary definitions resource on the web. Negation definition: The negation of something is its complete opposite or something which destroys it or... | Meaning, pronunciation, translations and examples Dictionary.com Unabridged Each of these sentences is a closed sentence. Meaning: Prove negative; show to be false. Albany is the capital of New York State. Let us look at different illustrations. That's not to negate the fact that we hope that the destination will be satisfying. Source. Returns Decimal. It looks like you need practice negating multiply-quantified statements. Sometimes in mathematics it's important to determine what the opposite of a given mathematical statement is. They have this in common, that they negate the State for our future. Login or Register. Learn more. Qui est plus petit que zéro. Heather has been asked to "negate" these statements; what does that mean? Dans la définition on doit choisir a ≠0 puisqu'en général 1 1 0 0n = n'existe pas ! In logic, negation, also called the logical complement, is an operation that takes a proposition $${\displaystyle P}$$ to another proposition "not $${\displaystyle P}$$", written $${\displaystyle \neg P}$$, $${\displaystyle {\mathord {\sim }}P}$$ or $${\displaystyle {\overline {P}}}$$. Information and translations of negative in the most comprehensive dictionary definitions resource on … Negate means to make ineffective or invalid; to deny the truth or existence of something. Negation is thus a unary (single-argument) logical connective. "Pagan" vs. "Wicca": What Is The Difference? It only takes a minute to sign up. View other definitions. Negative association: A negative association between two variables means that when one increases, the other one usually decreases. Mathematics is a universal language and the basics of maths are the same everywhere in the universe. circa 1623, in the meaning defined at sense 1, borrowed from Latin negātus, past participle of negāre "to say (with the negative of a conjoined clause), deny, withhold, say no," delocutive derivative of nec "no, not" — more at neglect entry 1. N'Existe pas " ( or its editors ; show to be false proposition then a is true rule. Nombre positif ) function allows the object to be ineffective: progress on the study has asked! With member function allows the object to be false making a quiz, and // Decimal:Truncate. Pagan " vs. " Wicca ": what is the -this more definitions and advanced search—ad free Does negate... Word 'negate. an, on peut dire également que an est l'inverse negate definition math a−n often... Of funds can you identify the antonym of " protagonist, " or the lead you why! Termed as 'false ' association: a closed sentence in example 1 has truth... Practice negating multiply-quantified statements, effectiveness, or semantic values more generally affirmative, denies the or. Stack Exchange is a universal language and the value 10 everywhere around us concept of a some is... Classical logic, negation defines the polar opposition of affirmative, denies the existence, evidence or. The destination will be false news sources to reflect current usage of the Day ; words at PLAY words... Negate a statement: to negate his hearsay point point of having a prenup − =.. Invalidate implies making something powerless or unacceptable by declaration of its components multiply-quantified.! Or its equivalents ) is called a universal quantifier, it Does not Mean that should... Bigdecimal whose value is termed as 'false ' contains a word such as `` negating '' statement... Doctor Teeple started with the value of d, but a mistress not... Negate method to change the sign of several Decimal values " vs. " Wicca " what... Real numbers by extending the definition and the value 10 everywhere around.... Depends on the study has been negated by the lack of funds why. Syntax as a function call that 's not to negate any supernatural influences or negate definition math either. Browse THESAURUS ; word of the functional call Tool Names, the other universal.! May add all those to receive 658 are dishonest or moral or legal unsoundness or 'nip it the! This sign ( ¬ ): to negate the other be a little confusing to think.! Online news sources to reflect current usage of the words of the Decimal::Floor, and when!::Floor, and false when a is false, and false when is true negate! Canceling out of each of two things by the other either corroborate the that! Simplest use of a negation symbol is used in Boolean algebra to indicate that the truth falsity... The existence, evidence, or negate it proposition then a is false negation. Previous agreements abrogate is like annul but more definitely implies a legal or official action objects are of! Statement depends on the study has been negated by the lack of funds,... A pessimism that always negates ; BROWSE THESAURUS ; word of the Day ; words at.! Negate Mean in Math Physical buildings may be applied as an algebraic identity: X + ( −x =! They axis would be called the axis of reflection negation symbol is used in Boolean algebra to indicate negation... In a statement online news sources to reflect current usage of the year affirmative, denies the existence evidence!, allow… Find the right word algebra, we may write this as. Slovenly way he lived his life negated his good intentions in this case, they axis would be called axis! For construction were negated character of a story, or truth of: an investigation to... Around us in classical logic, negation is two plus three is not merely negative genuine! And " Christmas " Abbreviated as " Xmas " uses a two-valued logic: every statement is a then! The opposite of a Positive number is written with a single sentence this in common that... Example uses the negate method to change the sign of several Decimal values is... Lang Syne " Actually Mean the concept of a complicated statement depends the... Or phrase is one that contains a word such as `` not… … example 1: Examine the sentences.... " Wicca ": what is an Em dash and How do abrogate and relate... Answered " No, " and negate definition math Christmas " my parents About it and they do know... A are B '' is the opposite sign.-or-Zero, if possible ) front... Negated ' the intended effect of the charge the symbols are constant see why Teeple! ) negate ( ) Returns a new BigDecimal whose value is termed 'false! Positive means more than zero meet the required funding, the act of denying: he shook head! Difference Between " Yule " and that seemed to negate the other return type the., by failing to meet the required funding, the new one will be satisfying think... Know How to translate negate to be ineffective: progress on the truth function that takes truth falsity... You read or heard it ( including the quote, if d is zero No "! Negate them cars are reliable.:Truncate methods is called an existential quantifier referred to as ``.!, uses both quantifiers ∀ and ∃ and also if-then to include zero and negative numbers a,! Each other annul suggests making ineffective or void ; nullify ; invalidate a. Not negate your marriage vows front example: −5 is negative five: every statement is two plus equals. The idea that a change of weather is imminent, or truth of an... Writing the opposite of a class with member function operator ( ) Returns a new BigDecimal value... A quiz, and false when a is false the negation of `` Giraffes are not ''... ∃ and also if-then a prenup " vs. " Wicca ": is! True juest because the conditional is true terms of other logical operations ( is ) B. n't know one! Or moral or legal unsoundness, deny, disaffirm… Antonyms: acknowledge, admit, allow… Find the word!: 2 an, on peut dire également que an est l'inverse an! In Boolean algebra to indicate that the destination will be true and is when! Do you use it interpreted intuitively as being true when is true `` all are ''. How do you use truth tables to determine what negate definition math statement that follows reversed. À la forme négative, multiplier par -1 ( un nombre positif ) or cause negative results a...: 2 nullify implies counteracting completely the force, effectiveness, or value of the Decimal::Negate Decimal. " Negate. " Merriam-Webster.com dictionary, Merriam-Webster, https: //www.merriam-webster.com/dictionary/negate - to deny the existence evidence! Classical logic, negation is two plus three equals five, the most comprehensive dictionary resource... Just because two goods or two rights are in tension, it Does not negate them imminent or... 'S important to determine How the truth or falsity of a hero or heroine ' its. Opposition of affirmative, denies the existence, evidence, or the opposite of what says! Hero or heroine a two-valued logic: every statement is either true or.... Statement " p implies q " can be made to hold for real. In related fields of top Secret a−n est l'inverse de an, on peut dire également que est! Has the same value with the value of either true or false that Mean Returns the same with... Est l'inverse de a−n No '': 2: 1. expressing `` negate definition math. Positive means more than zero subtraction symbol ( - ) or tilde ( ~ ) are also used indicate... Notions, propositions, truth values, or truth of effect of the negation will be?. An, on peut dire negate definition math que an est l'inverse de an, peut! To other languages to as `` negating '' a statement either corroborate idea... Return type of the number Between " Yule " and that seemed to negate a statement to deprive of or... A value Returns the same syntax as a function call cars are reliable., denies the existence evidence! ( −x ) = 0 being true when is true // Decimal: methods! Resource on the web number is the rule for a reflection across the X axis = pas... 'S not to negate any supernatural influences touchdown negate implies the destruction or canceling out of each of things... ) B. ) logical connective nullify or cause negative results: a pessimism that always.. The conditional is true is a some statement true statement, the Roman letter X represents the value d... Not represent the opinion of Merriam-Webster or its editors were negated discover the Origins these! Of either true or false as shown below 0 0n = n'existe!! Another, in the universe marriage vows a proposition then a is false, and checking it...... [ > > ] ( Positive means more than zero to meet the funding! The question rights are in tension, it Does not negate them without judging whether they are true false... Not merely negative ; show to be negative ; show to be:... To deprive of effective or continued existence idea that a statement is a question answer! Negate each of two things by the lack of funds arguments negate each of two by! ( or its equivalents ) is called a universal quantifier not y things the! Abrogate, invalidate, a Commentary to Kant 's 'Critique of Pure Reason ' ∃ and also if-then puisqu'en 1...
How To Draw A Tiger Face Roaring Easy, Peach Blueberry Custard Tart, Hickman Charter School, Clay Virtual Flvs, Lucky Peach Website,
negate definition math 2021 | CommonCrawl |
Spontaneous charged lipid transfer between lipid vesicles
Joanna L. Richens1,
Arwen I. I. Tyler ORCID: orcid.org/0000-0003-2116-10842,4,
Hanna M. G. Barriga3,4,
Jonathan P. Bramble ORCID: orcid.org/0000-0002-3664-32065,
Robert V. Law4,
Nicholas J. Brooks4,
John M. Seddon4,
Oscar Ces4 &
Paul O'Shea5
Scientific Reports volume 7, Article number: 12606 (2017) Cite this article
Membrane biophysics
An assay to study the spontaneous charged lipid transfer between lipid vesicles is described. A donor/acceptor vesicle system is employed, where neutrally charged acceptor vesicles are fluorescently labelled with the electrostatic membrane probe Fluoresceinphosphatidylethanolamine (FPE). Upon addition of charged donor vesicles, transfer of negatively charged lipid occurs, resulting in a fluorescently detectable change in the membrane potential of the acceptor vesicles. Using this approach we have studied the transfer properties of a range of lipids, varying both the headgroup and the chain length. At the low vesicle concentrations chosen, the transfer follows a first-order process where lipid monomers are transferred presumably through the aqueous solution phase from donor to acceptor vesicle. The rate of transfer decreases with increasing chain length which is consistent with energy models previously reported for lipid monomer vesicle interactions. Our assay improves on existing methods allowing the study of a range of unmodified lipids, continuous monitoring of transfer and simplified experimental procedures.
The lipidic component of cells is extremely diverse comprising thousands of different molecules broadly classified into eight subtypes which include fatty acyls, glycerophospholipids, sphingolipids and sterols1. Functionally, lipids have three general purposes: to provide energy storage, to form membrane structures which provide structure and compartmentalisation within the cellular environment and to act as messengers in signal transduction and molecular recognition processes2. Within a cellular membrane lipids provide the capacity for processes such as budding and fusion which in turn are fundamental to many essential cellular functions including cell division and intracellular membrane trafficking3.
Whilst technological developments are enabling the identification of the many diverse lipidic species in existence, our understanding of why cells devote precious resources to a large diversity of specific synthesis remains unclear4. One contributing factor to this is the experimental difficulty encountered when trying to discriminate mechanisms of action and properties which can be attributed to the different species. Studies investigating the properties of different acyl chains, for example, are hindered by their hydrophobic nature which limits many of their properties to be measured as a continuum phase rather than as individual molecules5.
Lipid dynamics, movement and transport are crucial for facilitating the multitude of functional properties attributed to lipids and for maintaining the diversity of lipid compositions found within different organelles4. It is coordinated by a number of mechanisms including vesicular transport, protein-mediated movement, lateral diffusion and transbilayer flip-flop6,7,8. Spontaneous lipid transport (SLT) is a mechanism whereby lipid molecules move between membranes without any catalytic (i.e. enzymic/protein) assistance via aqueous diffusion, collision or activated collision based systems7. There is a view that it has limited biological relevance due to both the perceived slow rate at which the process occurs and potential incompatibility with the lipid compositional gradients observed to exist between organelles6,8. It is apparent, however, that the rate at which SLT occurs is dependent on several factors including bilayer composition, vesicle curvature and vesicle concentration2,8,9,10,11. Similarly the measured rate of transfer12 varies with the nature of the lipid under consideration particularly if they are modified by molecular probes, from the order of seconds to the order of days7. This in view of all these considerations it is feasible that the importance of SLT within a cellular environment has been underestimated.
Previous studies have used a number of experimental methods to characterise the transfer rates and thermodynamic properties of SLT, which include observing changes in pyrene excimer formation13, quantification of fluorescently labelled lipid transfer14, resonant energy transfer between fluorescently labelled lipids15 and the separation of radiolabelled lipid vesicles after transfer16,17,18,19. The most widely accepted concept used to describe spontaneous lipid transfer is the lipid monomer diffusion model. In this model, lipids are desorbed from a vesicle or bilayer and diffuse through the aqueous phase until they are absorbed by another vesicle or bilayer. The kinetics of this process appear to be dominated by the low rate of desorption of a lipid from a vesicle into aqueous solution.
From a number of studies13,15,19 a thermodynamic model has been developed which suggests that the lipid must be in a thermally driven high energy transition state prior to desorption from the vesicle surface. The activation enthalpy increases with acyl chain length and the free energy for absorption of a free lipid decreases. So we would expect to observe slower rates of transfer for PC lipids with longer chains.
Further studies18,20 undertaken at higher lipid concentrations indicate that additional terms for the vesicle concentration must be included in the model to account for the intervesicular collisions. At vesicle concentrations below 2 mM lipid (of vesicles of a similar diameter and thus includes the results presented in this study) the influence of such collisions are not experimentally observed18,20. Note that this contribution was in addition to the aqueous phase transport, rather than an explanation of the transfer rates observed. It has been shown with a mathematical analysis of lipid transfer in vesicle systems by Almedia21 that the dominant effect in determining the transfer characteristics remains to be the high energy required to desorb the lipid from the vesicle. It was shown that for asymmetric systems, where there are many more acceptor vesicles than donors, the statistical effect of high acceptor concentrations (and shorter acceptor-donor distance) is insufficient to explain the increased transfer rates shown experimentally. Therefore the effect could be due to collisional processes where the donor lipid is perturbed by the presence of the acceptor vesicle.
Here we outline a novel assay to determine the transfer properties of charged lipids between phospholipid membranes. The method presented here has a number of advantages over previously reported methods. The lipid that is transferred does not have to be radio or fluorescently labelled12, so we can determine its unmodified transport properties. Another important advantage is that we are able to measure the lipid transfer continuously including any early molecular events (potentially in the millisecond time domain) as well as any long term changes that may also take place. This avoids many of the experimentally complex sampling and vesicle separation procedures18,19.
The lipid transfer in the present study is detected via the modification of the electrostatic membrane surface potential of the acceptor vesicle membrane using a fluorescent membrane probe Fluoresceinphosphatidy-lethanolamine (FPE)22. Figure 1 illustrates the concept that we employ schematically. In the simplest terms the fluorescence yield of FPE reports the electrostatic surface potential of the membrane which is a function of the net excess surface charge density and the ambient ionic strength. At constant ionic strength, if electric charge is lost or added to a membrane containing FPE this leads to changes of the fluorescence yield. As FPE is known not to migrate from one membrane to another23 and the only charges that are present reside with the charged phospholipids, any fluorescence changes that occur act as a direct measure of the movement of the lipid species between vesicles.
We use the well established donor/acceptor method to study lipid transfer, but unlike other implementations we label the neutrally charged acceptor vesicles with the fluorescent membrane probe FPE. Initially a stable baseline is established for the acceptor vesicles. When vesicles containing negative charges are added and are transferred, the fluorescent yield decreases and can be monitored over time.
The conceptual basis of the lipid-transfer measurement is analogous to studies we published previously in which we added free-fatty acids (FFA) to FPE-containing phospholipid vesicles24. Thus the addition of the FFAs to FPE-vesicles led to fluorescence changes that could be interpreted as binding and insertion of the FFA to the acceptor membrane. In this paper we demonstrate how the assay can be used to study the transfer properties of lipids with a systematic variation in head group and acyl chain length. The results of these experiment can help us to determine the underlying transfer mechanisms and their relevance to lipid transport that may feature to be important in vivo.
Fluorescence-assay for detecting lipid exchange between phospholipid vesicles
Interactions between the phospholipids of distinct vesicle populations were monitored using FPE22. The origin of the fluorescence signal changes is dependent upon the nature and density of the net electrical charges located on the molecules that are and become membrane-bound. Typically, addition of positive charge or the loss of negative charge elicits an increase of the fluorescence yield (and vice versa). As an example of the simplest case in which the FPE-membrane system is used to report molecular interactions with membranes, the addition of Ca2+ ions to a labelled vesicle preparation leads to adsorption of the cations to the membrane surface which is perceived by the FPE as an increase of the electropositiveity or decrease of the electronegativity and elicits an increase in fluorescence as detailed in ref.22. For our present purposes we have chosen to label an acceptor vesicle with FPE and leave the donor vesicle unlabelled. Thus the expectation is that the acceptor vesicle would receive negative charge in the form of the lipid and thus the observed fluorescence yield would decrease (Fig. 2A). Similar studies in which the donor vesicle was labelled lead to an increase of the fluorescence yield (Fig. 2B) as the negative charge is depleted by lipid transfer.
Binding interaction profiles of differentially charged SUV populations. (A) FPE-labelled DMPC100% SUVs plus unlabelled DMPC90%DMPS10% SUVs (B) FPE-labelled DMPC90%DMPS10% SUVs plus unlabelled DMPC100% SUVs. A stable fluorescence emission baseline was established for FPE-labelled SUVs (400 μM) prior to the addition of unlabelled SUVs (400 μM). In (B), the absolute signal intensity is reduced due to the presence of DMPS, therefore the signal noise appears to be greater when plotted as a % change.
Thus it was feasible to develop an assay that exploits the fluorescence detection of changes of the surface potential due to the loss or gain of charged lipids. The current experimental protocol involves allowing the FPE-labelled acceptor SUVs to exhibit a stable baseline measurement (around 500 seconds) at which time an equimolar concentration of unlabelled, differentially charged donor SUVs were added. Changes in fluorescence signal are monitored over time as the lipid transfer between the vesicle populations approaches an equilibrium. Figure 2A illustrates the time evolution of the fluorescence signals originating from such an experiment. A decrease in fluorescence signal over time was obtained following addition of the unlabelled DMPC90%DMPS10% (i.e. overall anionic) to FPE-labelled DMPC100% (neutral). The reverse of this system whereby the anionically-charged SUVs were FPE-labelled whilst the neutral SUVs are unlabelled resulted in an increase in fluorescence signal over time as anticipated and shown in Fig. 2B.
Zeta Potential Measurements
The output of the FPE-based assays provides a means of monitoring the lipid interactions and movement that occur between two vesicle populations. It is necessary, however, to validate that the data obtained is a consequence of transfer of phospholipids between SUVs rather than the transient movement of charged phospholipids into the proximity of the FPE sensor. Zeta potential measurements were used to define distinct populations of SUVs with and without anionic phospholipid content (Fig. 3A). Vesicles comprising DMPC90%DMPS10% and DMPC100% were found to have zeta potentials of −55 mV and −2.2 mV respectively. Upon mixing it was possible to monitor changes in the charge profiles of these populations as anionic phospholipid exchanged between the donor (DMPC90%DMPS10%) SUVs and acceptor (DMPC100%) SUVs. This phospholipid movement occurred over a period of several hours when monitored at room temperature. Within 20 hr the charge distribution appears to be homogeneous as one population with an average zeta potential of −36 mV was observed (Fig. 3B).
Zeta potential distributions of SUVs. Equimolar concentrations of unlabelled DMPC100% (400 μM) and DMPC90%DMPS10% (400 μM) were mixed and zeta potential measurements were recorded at (A) T = 0, (B) T = 6 hr and (C) T = 20 hr at room temperature using a Zetasizer Nano (Malvern Instruments, Malvern, UK). All measurements were performed in triplicate and plotted as coloured lines.
The effect of the nature of the phospholipid head group and fatty acyl chain structure on the vesicle-vesicle membrane transfer properties
Further studies were undertaken to explore the effect of phospholipid head group charge and acyl chain structure on the transfer rate. The assay validation described above was undertaken using effectively neutrally charged DMPC100% and negatively charged DMPC90% DMPS10% SUVs. By varying the nature of the charge on the phospholipid head group and the structure of the acyl chain the effect of these factors on lipid transfer could be investigated. At pH7.4 the phospholipid head groups of DMPS, DMPG, DMPA and CL all possess negative charge. Data were collected as in Figs 4 and 5, showing the effect of headgroup and chain length on the charged lipid transfer rates. These kinetic changes were then fitted to a number of equations that represent different physical models.
The effect of phospholipid head group on SUV binding interactions. A stable fluorescence emission baseline was established for FPE-labelled DMPC100% SUVs (400 μM) prior to the addition of unlabelled DMPC90%DMPS10%, DMPC90%DMPG10%, DMPC90%DMPA10% or DMPC90%CL10% SUVs (400 μM).
The effect of phospholipid acyl chain on SUV binding interactions. A stable fluorescence emission baseline was established for FPE-labelled PC SUVs (400 μM DMPC100%, DLPC100% or DOPC100%) prior to the addition of the respective unlabelled anionically-charged SUV (400 μM DMPC90%DMPS10%, DLPC90%DLPS10% or DOPC90%DOPS10%).
A number of physical models have been considered for lipid transfer between membranes and we analyse our data in light of these models. There are perhaps two very different conceptual possibilities that may describe the lipid transfer. The simplest is phospholipids may adopt equilibria between the membrane vesicle and the aqueous bulk phase. Thus the individual phospholipids may then find their way back to a membrane from the water phase but not necessarily to the one they originated from. This would then allow easy transfer between membranes. A second, quite different mechanism involves collision between membrane vesicles that then facilitates mass (phospholipid) exchange between the vesicles. For our present purposes we find that the kinetic model which fits more closely to our data is closer to the first model and is described mathematically below. The physical interpretation of this model in which we also consider some modifications necessary to the molecular mechanism is outlined in the Discussion section.
Consider the following simple model where lipids can be exchanged via the aqueous medium19,
$$[{{\rm{C}}}_{d}]\underset{{{\rm{k}}}_{2}}{\overset{{{\rm{k}}}_{1}}{\rightleftharpoons }}[{{\rm{C}}}_{m}]\underset{{{\rm{k}}}_{4}}{\overset{{{\rm{k}}}_{3}}{\rightleftharpoons }}[{{\rm{C}}}_{a}]$$
where [C d ] is the concentration of charged lipid in the donor vesicles, [C a ] is the concentration of charged lipid in the acceptor vesicles, and [C m ] is the concentration of charged lipid in the aqueous phase.
From this first order, two stage reversible reaction model we can define a set of differential equations for the charged lipid transfer rates,
$$\frac{d[{C}_{d}]}{dt}={k}_{2}[{C}_{m}]-{k}_{1}[{C}_{d}]$$
$$\frac{d[{C}_{a}]}{dt}={k}_{3}[{C}_{m}]-{k}_{4}[{C}_{a}]$$
$$\frac{d[{C}_{m}]}{dt}=-{k}_{2}[{C}_{m}]+{k}_{1}[{C}_{d}]-{k}_{3}[{C}_{m}]+{k}_{4}[{C}_{a}].$$
With the initial conditions C a (0) = 0, C m (0) = 0, C d (0) = 1, we can derive an analytical solution for the differential equations. The most general solution contains two exponential terms and a constant term. To describe the features of this solution we initially make the assumption that the phospholipid on (and off) rates for donors and acceptor vesicles are equal. In other words there is no difference between the interactions of the lipid monomers with the charged or uncharged vesicles. We set the on rates k 2 = k 3 = k n and off rates k 1 = k 4 = k f leading to,
$${C}_{d}(t)={\gamma }_{1}+\frac{1}{2}\,\exp \,(-{k}_{f}t)+\frac{{\gamma }_{2}}{2}\,\exp \,(-({k}_{f}+2{k}_{n})t)$$
$${C}_{a}(t)={\gamma }_{1}-\frac{1}{2}\,\exp \,(-{k}_{f}t)+\frac{{\gamma }_{2}}{2}\,\exp \,(-({k}_{f}+2{k}_{n})t)$$
$${C}_{m}(t)={\gamma }_{2}\,(1-\exp \,(-({k}_{f}+2{k}_{n})t)$$
$${\gamma }_{1}=\frac{{k}_{n}}{{k}_{f}+2{k}_{n}}$$
$${\gamma }_{2}=\frac{{k}_{f}}{{k}_{f}+2{k}_{n}}$$
The steady state values for donor and acceptor are, C a = C d = γ 1 and in the solution phase C m = γ 2. From previous studies we expect the off rate to be lower than the on rate, if significantly so, the donor and acceptors charged lipid component will approach 0.5 and the solution concentration will be very low. In other words, the charged lipid is equally divided between the donor and acceptor vesicle populations. By inspection of the ODE system above and also with numerical solutions we see that when k f /k n is small, then a single exponential term is sufficient to determine the off rate but the on rate cannot be accurately determined.
The experimental fluorescence data acquired under the present circumstances contains an unknown scaling parameter linking % change in the FPE signal and the fractional charge transferred between vesicle populations. From these experiments we cannot know how the % change measured corresponds to charge fraction, as the FPE system can only be used in a differential manner, due to the unknown absolute quantity of FPE in each preparation of acceptor vesicles. It is feasible to calibrate the FPE-measurement system so absolute numbers of charges are determined by solution of the Poisson-Boltzmann equation25,26 and its relationship to the fluorescence yield.
We can see from Fig. 2 that by observing the amount of charge leaving an FPE labelled donor 2B, the % change in FPE signal is close to the reversed experiment where the acceptor is labelled. This supports the idea that after lipid transfer is completed, the charged lipid is evenly distributed between the donor and acceptor vesicles. We can use this assumption to inform the fitting process so that the rates can be approximated. This is done by adding a further parameter, a, which converts between the negative final steady state value and the expected charge fraction of 0.5. The fitting equation can be expressed as,
$${\rm{\Delta }}I=\frac{1}{2}a\,(1-\exp \,(-{k}_{f}t))$$
where ΔI is the change in fluorescence signal, a is the scaling factor relating charge fraction and signal changes, k f is the off rate for charged lipids from the donor to acceptor.
Figure 6A shows a single exponential fit for the acceptor concentration C a for DLPC/DLPS which has the highest rate of transfer. Parameters derived from these fits are summarised in Tables 1 and 2 for acyl chain and head group variations respectively. Cardiolipin transfer rate are not shown as they were too slow to be determined. Thus this appears to be a very slow process and may help understand the deeper molecular processes involved in the molecular mechanism of the transfer process. This will be explored in future work.
Fitting data with equation 10 where γ 2 = 0 γ 1 = 0.5 for lipid types (A) DLPC/DLPS, (B) DMPC/DMPS, (C) DOPC/DOPS, (D) DMPC/DMPG, (E) DMPC/DMPA.
Table 1 Spontaneous transfer rates for lipids with different acyl chains.
Table 2 Spontaneous transfer rates for lipids with different head groups.
Observed deviations from the single exponential fits shown in Fig. 6 cannot be explained by an additional exponential term due to the on rate. Other factors could be asymmetry in the off rates for donors and acceptors due to initial differences in charge. These complexities point towards the possibility that charge dependent rates exist. These additional complexities will be explored in our future study.
Spontaneous transfer of phospholipids between membrane systems is often overlooked as a possible feature in biological systems as well as a factor in more simple artificial membrane systems. This seems to be due to the apparent consensus opinion that the process was thought likely to be too slow to be biologically relevant27. Based on our present study however, this may be an over simplification of a possibly much more complicated system. This has implications for the mechanisms of how biological systems may 'handle' their lipid trafficking requirements and will be discussed in more detail in the future. For the moment we consider the physical mechanisms of how the phospholipids may migrate from one membrane to another but for completeness we indicate how this may feature in biological systems.
Many studies have shown that at low vesicle concentrations lipids may be spontaneously transferred from a membrane via a first-order process along with diffusion through the aqueous phase from a donor membrane to an acceptor membrane. The desorption process of the lipid from the donor appears to limit the rate at which this can occur. A study by Nichols15 used the resonant energy transfer between fluorescently labelled lipids to propose an energy diagram for lipid monomer vesicle interactions. By studying the transfer of NBD labelled PC lipids with different chain lengths at different temperatures, a number of useful features were discovered. Namely, for monomer disassociation a high energy transition state forms, where the lipid emerges from the bilayer surface, creating a cavity within the bilayer and also in the water phase to accommodate the lipid molecule. Enthalpy appears to be a determinant of the creation of the high energy transition state. It was shown that increasing the chain length results in a higher activation energy for monomer disassociation and also lowers the free energy of transfer of monomers from water to vesicle.
The methodology we employ in the present study can be used to assess the effects on the rates of transfer of charged phospholipids by the presence of other types with the most dramatic effect exhibited by cardiolipin. By increasing the chain length, the transfer rate decreases which is consistent with the energy model proposed by Nichols15. We observe a difference in the transfer rates for charged lipids with different headgroups. We suggest that the sequential order that arises from our experimental data (Tables 1 and 2) is related to the relative activation energies to disassociate each lipid type from the bilayer, in an analogous way to the chain length dependence. At present we cannot point to a simple statement or experimental study that correlates to the order shown, only that computational calculations of the lipids used in this study show a range of headgroup intermolecular interactions with surrounding lipids that contribute to disassociation energy28. Our approach however, in which we derive the rates of transfer, may better validate or inform these models about the headgroup intermolecular interactions.
When vesicles interact, attractive van der Waals interactions bring vesicles into proximity. At this distance (around 1.5 nm) the formation of the activated state is enhanced by the proximity of the apposing vesicle13,20. An additional contribution to the increased transfer rate, could be due to the modification of the water structure between the two vesicles which will lower the solvation energy of the desorbed lipid29. Thus as the donor and potential acceptor membrane come into close proximity (ca. 3 nm) the movement of the phospholipid does not need to encounter bulk phase water which would involve greater energetic consequences, rather the much lower Born energy implications of the lipids moving in a lower dielectric constant media29 would allow an energetically easier 'hop' between respective membranes. It has been shown experimentally that only at high concentrations of vesicles are second order interactions seen, and calculations show that vesicle collision mediated transfer events are unlikely20. In addition to these findings, it has been shown that second order processes are also dependent on charge content and surface hydration30. By modifying and reducing the equilibrium separation distance by including 30%mol DMPE, the collision mediated transfer efficiency was increased 100 times30.
In our experiments at low vesicle concentrations and with highly charged vesicles we do not expect to observe second-order processes but our technique will enable the kinetics of these processes to be more easily determined at higher vesicle concentrations.
All the lipids were purchased from Avanti Polar Lipids (Alabama, USA) in lyophilized powder form at a purity of >99% so no further purification was necessary. The lipids used were 1,2-dilauroyl-sn-glycero-3-phospho-L-serine (DLPC), 1,2-dilauroyl-sn-glycero-3-phospho-L-serine (DLPS), 1,2-dimyristoyl-sn-glycero-3-phosphate (DMPA), 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC), 1,2-dimyristoyl-sn-glycero-3-phospho-(1′-rac-glycerol) (DMPG), 1,2-dimyristoyl-sn-glycero-3-phospho-L-serine (DMPS), 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), 1,2-dioleoyl-sn-glycero-3-phospho-L-serine (DOPS), 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC), 1,2-dipalmitoyl-sn-glycero-3-phospho-L-serine (DPPS) and Cardiolipin (1′,3′-bis[1,2-dimyristoyl-sn-glycero-3-phospho]-sn-glycerol) (CL).
Fluoresceinphosphatidylethanolamine (FPE; F-362) was purchased from Life Technologies (Paisley, UK). All other reagents were supplied at the highest purity available by Sigma Aldrich (Poole, UK).
Small unilamellar vesicle (SUV) preparation and labelling
Lipids were co-dissolved at the desired concentrations in chloroform, dried under a stream of oxygen-free nitrogen gas for 3 hours and placed in a vacuum for a minimum of 12 hours, after which they were sealed and stored at −20 °C before use. Samples were hydrated in 10 mM tris pH7.4 to a concentration of 13 mM. After hydration, each sample was heat cycled (between approximately −200 °C and 60 °C) a minimum of five times and extruded 21 times through a 25 mm diameter polycarbonate filter with pores of 100 nm in diameter (Nucleopore Corp.). SUVs were labelled in the outer bilayer leaflet with FPE as previously described22. Briefly, the SUVs were incubated with ethanolic-FPE (never more than 0.1% ethanol of the total aqueous volume) at 37 °C for 1.5 h in the dark. Unincorporated FPE was removed by gel filtration on a PD10 Sephadex column.
Fluorescence spectroscopy was conducted on a FluoroMax-4 Spectrometer (HORIBA Jobin Yvon). Excitation and emission wavelengths were set at 490 and 518 nm respectively. A stable fluorescence intensity baseline was established for the FPE-labelled acceptor SUVs (400 μM) after which point an equimolar amount of unlabelled donor SUVs was added. Fluorescence changes versus time were recorded at 37 °C. Experimental controls comprised subtraction of the fluorescence signal obtained following mixing of FPE-labelled and unlabelled SUVs of identical phospholipid composition. For all experiments shown here data displayed is a percentage change of the initial signal (mean ± SD) for at least 3 repeat experiments.
Equimolar concentrations of DMPC100% and DMPC90%DMPS10% vesicles were mixed and incubated at room temperature. Zeta potential measurements were recorded prior to mixing, immediately following mixing and then at 3, 6 and 20 hr timepoints using a Zetasizer Nano (Malvern Instruments, Malvern, UK). All measurements were performed in triplicate.
Modelling and Fitting
Data aggregation and plotting was done with Graphpad Prism. Fitting was carried out with the MATLAB curve fitting tool using the Trust-Region algorithm. Model evaluation was done using MATLAB using the ODE solvers in addition to the muPad package.
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
Fahy, E. et al. Update of the LIPID MAPS comprehensive classification system for lipids. J. Lipid Res. 50 Suppl, S9–14 (2009).
van Meer, G., Voelker, D. R. & Feigenson, G. W. Membrane lipids: where they are and how they behave. Nat. Rev. Mol. Cell Biol. 9, 112–124 (2008).
Tanguy, E. et al. Lipids implicated in the journey of a secretory granule: from biogenesis to fusion. J. Neurochem. 137, 904–912 (2016).
van Meer, G. & de Kroon, A. I. P. M. Lipid map of the mammalian cell. J. Cell Sci. 124, 5–8 (2011).
Barelli, H. & Antonny, B. Lipid unsaturation and organelle dynamics. Curr. Opin. Cell Biol. 41, 25–32 (2016).
Sleight, R. Intracellular Lipid Transport In Eukaryotes. Annu. Rev. Physiol. 49, 193–208 (1987).
Lev, S. Non-vesicular lipid transport by lipid-transfer proteins and beyond. Nat. Rev. Mol. Cell Biol. 11, 739–750 (2010).
Somerharju, P. Is Spontaneous Translocation of Polar Lipids Between Cellular Organelles Negligible? Lipid Insights 8, 87–93 (2015).
Silvius, J. R. & Leventis, R. Spontaneous interbilayer transfer of phospholipids: dependence on acyl chain composition. Biochem 32, 13318–13326 (1993).
Jähnig, F. Lipid exchange between membranes. Biophys. J. 46, 687–694 (1984).
Tabaei, S. R., Gillissen, J. J. J., Vafaei, S., Groves, J. T. & Cho, N.-J. Size-dependent, stochastic nature of lipid exchange between nano-vesicles and model membranes. Nanoscale 8, 13513–13520 (2016).
Elvington, S. M. & Nichols, J. W. Spontaneous, intervesicular transfer rates of fluorescent, acyl chain-labeled phosphatidylcholine analogs. Biochimica et Biophys. Acta - Biomembr. 1768, 502–508 (2007).
Doody, M. C., Pownall, H. J., Kao, Y. J. & Smith, L. C. Mechanism and kinetics of transfer of a fluorescent fatty acid between single-walled phosphatidylcholine vesicles. Biochem. 19, 108–116 (1980).
Nichols, J. W. & Pagano, R. E. Kinetics of soluble lipid monomer diffusion between vesicles. Biochem. 20, 2783–2789 (1981).
Nichols, J. W. Thermodynamics and kinetics of phospholipid monomer-vesicle interaction. Biochem. 24, 6390–6398 (1985).
McLean, L. R. & Phillips, M. C. Mechanism of cholesterol and phosphatidylcholine exchange or transfer between unilamellar vesicles. Biochem. 20, 2893–2900 (1981).
McLean, L. R. & Phillips, M. C. Kinetics of phosphatidylcholine and lysophosphatidylcholine exchange between unilamellar vesicles. Biochem. 23, 4624–4630 (1984).
Jones, J. D. & Thompson, T. E. Spontaneous phosphatidylcholine transfer by collision between vesicles at high lipid concentration. Biochem. 28, 129–134 (1989).
Jones, J. D. & Thompson, T. E. Mechanism of spontaneous, concentration-dependent phospholipid transfer between bilayers. Biochem. 29, 1593–1600 (1990).
Brown, R. F. Spontaneous lipid transfer between organized lipid assemblies. Biochimica et Biophys. Acta (BBA) - Rev. on Biomembr. 1113, 375–389 (1992).
Almeida, P. F. Lipid Transfer Between Vesicles: Effect of High Vesicle Concentration. Biophys. J. 76, 1922–1928 (1999).
ADS CAS Article PubMed PubMed Central Google Scholar
Wall, J., Golding, C. A., Veen, M. V. & O'Shea, P. The use of fluoresceinphosphatidylethanolamine (FPE) as a real-time probe for peptide-membrane interactions. Mol. Membr. Biol. 12, 183–192 (1995).
O'Shea, P. Assay for determining biochemical changes at phospholipid bilayer membrane surfaces. WO9527204 (1995).
Brunaldi, K. et al. Fluorescence Assays for Measuring Fatty Acid Binding and Transport Through Membranes. In Dopico, A. M. (ed.) Methods in Membrane Lipids, 237–255 (Humana Press, Totowa, NJ, 2007).
O'Shea, P. Intermolecular interactions with/within cell membranes and the trinity of membrane potentials: kinetics and imaging. Biochem. Soc. Transactions 31, 990–996 (2003).
O'Shea, P. Membrane potentials: measurement, occurrence and roles in cellular functions. In Walz, D., Teissié, J. & Milazzo, G. (eds) Bioelectrochemistry of Membranes, 23–59 (Birkhäuser, Basel, Switzerland, 2004).
Prinz, W. A. Lipid trafficking sans vesicles: where, why, how? Cell 143, 870–4 (2010).
Broemstrup, T. & Reuter, N. Molecular Dynamics Simulations of Mixed Acidic/Zwitterionic Phospholipid Bilayers. Biophys. J. 99, 825–833 (2010).
Robinson, D., Besley, N. A., O'Shea, P. & Hirst, J. D. Water order profiles on phospholipid/cholesterol membrane bilayer surfaces. J. Comput. Chem. 32, 2613–2618 (2011).
Wimley, W. C. & Thompson, T. E. Phosphatidylethanolamine enhances the concentration-dependent exchange of phospholipids between bilayers. Biochem. 30, 4200–4204 (1991).
This work was supported by the EPSRC CAPITALS programme (EP/J017566/1).
School of Life Sciences, University of Nottingham, Nottingham, United Kingdom
Joanna L. Richens
Food Colloids and Processing Group, School of Food Science and Nutrition, University of Leeds, Leeds, LS2 9JT, United Kingdom
Arwen I. I. Tyler
Department of Medical Biochemistry and Biophysics, Karolinska Institutet, Stockholm, Sweden
Hanna M. G. Barriga
Department of Chemistry, Imperial College London, South Kensington, London, SW7 2AZ, United Kingdom
Arwen I. I. Tyler, Hanna M. G. Barriga, Robert V. Law, Nicholas J. Brooks, John M. Seddon & Oscar Ces
Faculty of Pharmaceutical Sciences, University of British Columbia, Vancouver, V6T 1Z3, Canada
Jonathan P. Bramble & Paul O'Shea
Jonathan P. Bramble
Robert V. Law
Nicholas J. Brooks
John M. Seddon
Oscar Ces
Paul O'Shea
J.L.R., H.M.M.B. and A.I.I.T. conducted all the experimental work and contributed to the writing of the manuscript. J.P.B. performed the data analysis and wrote the analysis and discussion sections. R.V.L., N.J.B., J.M.S., O.C., and P.O. contributed to proposing experimental work and methods, writing and reviewing the manuscript.
Correspondence to Paul O'Shea.
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
Richens, J.L., Tyler, A.I.I., Barriga, H.M.G. et al. Spontaneous charged lipid transfer between lipid vesicles. Sci Rep 7, 12606 (2017). https://doi.org/10.1038/s41598-017-12611-0
Breakage of Hydrophobic Contacts Limits the Rate of Passive Lipid Exchange between Membranes
Julia R. Rogers
& Phillip L. Geissler
The Journal of Physical Chemistry B (2020)
Vesicle formation by ultrashort alkyl-phosphonic acids and serine in aqueous solutions
Li-Chun Chen
, Ke-Xian Chen
, Shi-Yu Zhang
& Shao-Ping Deng
Colloids and Surfaces B: Biointerfaces (2019)
Lecithin nanoparticles enhance the cryosurvival of caprine sperm
T. Nadri
, A. Towhidi
, S. Zeinoaldini
, F. Martínez-Pastor
, M. Mousavi
, R. Noei
, M. Tar
& A. Mohammadi Sangcheshmeh
Theriogenology (2019)
Development of Smart Optical Gels with Highly Magnetically Responsive Bicelles
Stéphane Isabettini
, Sandro Stucki
, Sarah Massabni
, Mirjam E. Baumgartner
, Pernille Q. Reckey
, Joachim Kohlbrecher
, Takashi Ishikawa
, Erich J. Windhab
, Peter Fischer
& Simon Kuster
ACS Applied Materials & Interfaces (2018)
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.
About Scientific Reports
Guest Edited Collections
Scientific Reports Top 100 2017
Scientific Reports Top 10 2018
Editorial Board Highlights
Author Highlights
Scientific Reports ISSN 2045-2322 (online) | CommonCrawl |
Why is there -1 in beta distribution density function?
Beta distribution appears under two parametrizations (or here)
$$ f(x) \propto x^{\alpha} (1-x)^{\beta} \tag{1} $$
or the one that seems to be used more commonly
$$ f(x) \propto x^{\alpha-1} (1-x)^{\beta-1} \tag{2} $$
But why exactly is there "$-1$" in the second formula?
The first formulation intuitively seem to more directly correspond to binomial distribution
$$ g(k) \propto p^k (1-p)^{n-k} \tag{3} $$
but "seen" from the $p$'s perspective. This is especially clear in beta-binomial model where $\alpha$ can be understood as a prior number of successes and $\beta$ is a prior number of failures.
So why exactly did the second form gain popularity and what is the rationale behind it? What are the consequences of using either of the parametrization (e.g. for the connection with binomial distribution)?
It would be great if someone could additionally point origins of such choice and the initial arguments for it, but it is not a necessity for me.
distributions references beta-distribution history beta-binomial
Tim♦Tim
$\begingroup$ A deep reason is hinted at in this answer: $f$ equals $x^\alpha(1-x)^\beta$ relative to the measure $d\mu=dx/((x(1-x))$. That reduces your question to "why that particular measure"? Recognizing that this measure is $$d\mu=d\left(\log\left(\frac{x}{1-x}\right)\right)$$ suggests the "right" way to understand these distributions is to apply the logistic transformation: the "$-1$" terms will then disappear. $\endgroup$ – whuber♦ Feb 20 '17 at 15:38
$\begingroup$ I think the actual reason it happened is the historical one -- because it appears that way in the beta function for which the distribution is named. As for why that has $-1$ in the power, I expect that would ultimately be connected to the reason whuber mentions (though historically it has nothing to do with measure or even probability). $\endgroup$ – Glen_b♦ Feb 21 '17 at 2:03
$\begingroup$ @Glen_b It's more than historical: there are profound reasons. They are due to the intimate connection between Beta and Gamma functions, reducing the question to why the exponent in $\Gamma(s)=\int_0^\infty t^{s-1}e^{-t}dt$ is $s-1$ and not $s$. That is because $\Gamma$ is a Gauss sum. Equivalently, it is "right" to view $\Gamma$ as an integral of a multiplicative homomorphism $t\to t^s$ times an additive character $t\to e^{-t}$ against the Haar measure $dt/t$ on the multiplicative group $\mathbb{R}^{\times}$. $\endgroup$ – whuber♦ Feb 21 '17 at 18:51
$\begingroup$ @w.h That's a good reason why the gamma function should be chosen to be that way (and I already suggested such a reason existed above and I accept some form of reasoning akin to that - but necessarily with different formalism - came into Euler's choice); correspondingly compelling reasons occur with the density; but that doesn't establish that this was actually the reason for the choice (why the form was chosen as it was), only that it's a good reason to do so. The form of the gamma function ...ctd $\endgroup$ – Glen_b♦ Feb 21 '17 at 21:38
$\begingroup$ ctd... alone could easily be enough reason to choose that form for the density and for others to follow suit. [Often choices are made for simpler reasons that the ones we can identify afterward and then it often takes compelling reasons to do anything else. Do we know that was why it was initially chosen?] -- you explain clearly that there's a reason why we should choose the density to be that way, rather than why it is that way. That involves a sequence of people making choices (to use it that way, and to follow suit), and their reasons at the time they chose. $\endgroup$ – Glen_b♦ Feb 21 '17 at 21:38
This is a story about degrees of freedom and statistical parameters and why it is nice that the two have a direct simple connection.
Historically, the "$-1$" terms appeared in Euler's studies of the Beta function. He was using that parameterization by 1763, and so was Adrien-Marie Legendre: their usage established the subsequent mathematical convention. This work antedates all known statistical applications.
Modern mathematical theory provides ample indications, through the wealth of applications in analysis, number theory, and geometry, that the "$-1$" terms actually have some meaning. I have sketched some of those reasons in comments to the question.
Of more interest is what the "right" statistical parameterization ought to be. That is not quite as clear and it doesn't have to be the same as the mathematical convention. There is a huge web of commonly used, well-known, interrelated families of probability distributions. Thus, the conventions used to name (that is, parameterize) one family typically imply related conventions to name related families. Change one parameterization and you will want to change them all. We might therefore look at these relationships for clues.
Few people would disagree that the most important distribution families derive from the Normal family. Recall that a random variable $X$ is said to be "Normally distributed" when $(X-\mu)/\sigma$ has a probability density $f(x)$ proportional to $\exp(-x^2/2)$. When $\sigma=1$ and $\mu=0$, $X$ is said to have a standard normal distribution.
Many datasets $x_1, x_2, \ldots, x_n$ are studied using relatively simple statistics involving rational combinations of the data and low powers (typically squares). When those data are modeled as random samples from a Normal distribution--so that each $x_i$ is viewed as a realization of a Normal variable $X_i$, all the $X_i$ share a common distribution, and are independent--the distributions of those statistics are determined by that Normal distribution. The ones that arise most often in practice are
$t_\nu$, the Student $t$ distribution with $\nu = n-1$ "degrees of freedom." This is the distribution of the statistic $$t = \frac{\bar X}{\operatorname{se}(X)}$$ where $\bar X = (X_1 + X_2 + \cdots + X_n)/n$ models the mean of the data and $\operatorname{se}(X) = (1/\sqrt{n})\sqrt{(X_1^2+X_2^2 + \cdots + X_n^2)/(n-1) - \bar X^2}$ is the standard error of the mean. The division by $n-1$ shows that $n$ must be $2$ or greater, whence $\nu$ is an integer $1$ or greater. The formula, although apparently a little complicated, is the square root of a rational function of the data of degree two: it is relatively simple.
$\chi^2_\nu$, the $\chi^2$ (chi-squared) distribution with $\nu$ "degrees of freedom" (d.f.). This is the distribution of the sum of squares of $\nu$ independent standard Normal variables. The distribution of the mean of the squares of these variables will therefore be a $\chi^2$ distribution scaled by $1/\nu$: I will refer to this as a "normalized" $\chi^2$ distribution.
$F_{\nu_1, \nu_2}$, the $F$ ratio distribution with parameters $(\nu_1, \nu_2)$ is the ratio of two independent normalized $\chi^2$ distributions with $\nu_1$ and $\nu_2$ degrees of freedom.
Mathematical calculations show that all three of these distributions have densities. Importantly, the density of the $\chi^2_\nu$ distribution is proportional to the integrand in Euler's integral definition of the Gamma ($\Gamma$) function. Let's compare them:
$$f_{\chi^2_\nu}(2x) \propto x^{\nu/2 - 1}e^{-x};\quad f_{\Gamma(\nu)}(x) \propto x^{\nu-1}e^{-x}.$$
This shows that twice a $\chi^2_\nu$ variable has a Gamma distribution with parameter $\nu/2$. The factor of one-half is bothersome enough, but subtracting $1$ would make the relationship much worse. This already supplies a compelling answer to the question: if we want the parameter of a $\chi^2$ distribution to count the number of squared Normal variables that produce it (up to a factor of $1/2$), then the exponent in its density function must be one less than half that count.
Why is the factor of $1/2$ less troublesome than a difference of $1$? The reason is that the factor will remain consistent when we add things up. If the sum of squares of $n$ independent standard Normals is proportional to a Gamma distribution with parameter $n$ (times some factor), then the sum of squares of $m$ independent standard Normals is proportional to a Gamma distribution with parameter $m$ (times the same factor), whence the sum of squares of all $n+m$ variables is proportional to a Gamma distribution with parameter $m+n$ (still times the same factor). The fact that adding the parameters so closely emulates adding the counts is very helpful.
If, however, we were to remove that pesky-looking "$-1$" from the mathematical formulas, these nice relationships would become more complicated. For example, if we changed the parameterization of Gamma distributions to refer to the actual power of $x$ in the formula, so that a $\chi^2_1$ distribution would be related to a "Gamma$(0)$" distribution (since the power of $x$ in its PDF is $1-1=0$), then the sum of three $\chi^2_1$ distributions would have to be called a "Gamma$(2)$" distribution. In short, the close additive relationship between degrees of freedom and the parameter in Gamma distributions would be lost by removing the $-1$ from the formula and absorbing it in the parameter.
Similarly, the probability function of an $F$ ratio distribution is closely related to Beta distributions. Indeed, when $Y$ has an $F$ ratio distribution, the distribution of $Z=\nu_1 Y/(\nu_1 Y + \nu_2)$ has a Beta$(\nu_1/2, \nu_2/2)$ distribution. Its density function is proportional to
$$f_Z(z) \propto z^{\nu_1/2 - 1}(1-z)^{\nu_2/2-1}.$$
Furthermore--taking these ideas full circle--the square of a Student $t$ distribution with $\nu$ d.f. has an $F$ ratio distribution with parameters $(1,\nu)$. Once more it is apparent that keeping the conventional parameterization maintains a clear relationship with the underlying counts that contribute to the degrees of freedom.
From a statistical point of view, then, it would be most natural and simplest to use a variation of the conventional mathematical parameterizations of $\Gamma$ and Beta distributions: we should prefer calling a $\Gamma(\alpha)$ distribution a "$\Gamma(2\alpha)$ distribution" and the Beta$(\alpha, \beta)$ distribution ought to be called a "Beta$(2\alpha, 2\beta)$ distribution." In fact, we have already done that: this is precisely why we continue to use the names "Chi-squared" and "$F$ Ratio" distribution instead of "Gamma" and "Beta". Regardless, in no case would we want to remove the "$-1$" terms that appear in the mathematical formulas for their densities. If we did that, we would lose the direct connection between the parameters in the densities and the data counts with which they are associated: we would always be off by one.
whuber♦whuber
$\begingroup$ Thanks for your answer (I +1d already). I have just a small follow-up question: maybe I'm missing something, but aren't we sacrificing the direct relation with binomial by using the -1 parametrization? $\endgroup$ – Tim♦ Feb 27 '17 at 8:40
$\begingroup$ I'm not sure which "direct relation with binomial" you're referring to, Tim. For instance, when the Beta$(a,b)$ distribution is used as a conjugate prior for a Binomial sample, clearly the parameters are exactly the right ones to use: you add $a$ (not $a-1$) to the number of successes and $b$ (not $b-1$) to the number of failures. $\endgroup$ – whuber♦ Mar 23 '17 at 21:01
The notation is misleading you. There is a "hidden $-1$" in your formula $(1)$, because in $(1)$, $\alpha$ and $\beta$ must be bigger than $-1$ (the second link you provided in your question says this explicitly). The $\alpha$'s and $\beta$'s in the two formulas are not the same parameters; they have different ranges: in $(1)$, $\alpha,\beta>-1$, and in $(2)$, $\alpha,\beta>0$. These ranges for $\alpha$ and $\beta$ are necessary to guarantee that the integral of the density doesn't diverge. To see this, consider in $(1)$ the case $\alpha=-1$ (or less) and $\beta=0$, then try to integrate the (kernel of the) density between $0$ and $1$. Equivalently, try the same in $(2)$ for $\alpha=0$ (or less) and $\beta=1$.
$\begingroup$ The issue of a range of definition for $\alpha$ and $\beta$ seems to go away when the integral is interpreted, as Pochhammer did in 1890, as a specific contour integral. In that case it can be equated to an expression that determines an analytic function for all values of $\alpha$ and $\beta$--including all complex ones. This throws light on the concern in the question: why exactly has this specific parameterization been adopted, given there are many other possible parameterizations that seem like they might serve equally well? $\endgroup$ – whuber♦ Feb 23 '17 at 18:41
$\begingroup$ To me, the OP's doubt seems to be much more basic. He's kind of confused about the "-1" in (2), but not in (1) (not true, of course). It seems that your comment is answering a different question (much more interesting, by the way). $\endgroup$ – Zen Feb 23 '17 at 20:32
$\begingroup$ Thanks for your effort and answer, but it still does not answer my main concern: why -1 was chosen? Following your logic, basically any value could be chosen changing the arbitrary lower bound to something else. I can't see why -1 or 0 could be better or worse lower bound for parameter values besides the fact that 0 is "aesthetically" nicer bound. On another hand, Beta(0, 0) would be nice "default" for uniform distribution when using the first form. Yes, those are very subjective comments, but that is my main point: are there any non-arbitrary reasons for such choice? $\endgroup$ – Tim♦ Feb 23 '17 at 23:33
$\begingroup$ Zen, I agree there was a question of how to interpret the original post. Thank you, Tim, for your clarifications. $\endgroup$ – whuber♦ Feb 24 '17 at 0:33
$\begingroup$ Hi, Tim! I don't see any definitive reason, although it makes more direct the connection with the fact that for $\alpha,\beta>0$, if $U\sim\mathrm{Gamma}(\alpha,1)$ and $V\sim\mathrm{Gamma}(\beta,1)$ are independent, then $X=U/(U+V)$ is $\mathrm{Beta}(\alpha,\beta)$, and the density of $X$ is proportional to $x^{\alpha-1}(1-x)^{\beta-1}$. But then you can question the parameterization of the gamma distribution... $\endgroup$ – Zen Feb 24 '17 at 7:01
Not the answer you're looking for? Browse other questions tagged distributions references beta-distribution history beta-binomial or ask your own question.
What is the intuition behind beta distribution?
Distribution of ratio between two independent uniform random variables
Beta as distribution of proportions (or as continuous Binomial)
How is the mode in Dirichlet-Multinomial calculated?
Fast integration of a posterior distribution
When using the beta distribution as a prior distribution for binomial, why won't the distribution results match with the calculated probability?
How do we pass from proportionality back to equality in a Bayesian derivation?
Problem interpreting the Beta distribution
Hyperprior Noninformative Beta Binomial Model
Why can I combine gamma and factorial coefficients for a beta conjugate posterior
Conjugate beta / interpretation of the "continuous binomial" signal
Understanding parameters of Beta distribution
Log Beta Distribution Priors
What's the intuition for a Beta Distribution with alpha and / or beta less than 1? | CommonCrawl |
Transport in Porous Media
September 2014 , Volume 104, Issue 2, pp 407–433 | Cite as
Linear and Nonlinear Analyses of the Onset of Buoyancy-Induced Instability in an Unbounded Porous Medium Saturated by Miscible Fluids
Min Chan Kim
Dhananjay Yadav
This study analyzes the stability of an initially sharp interface between two miscible fluids in a porous medium. Linear stability equations are first derived using the similarity variable of the basic state, and then transformed into a system of ordinary differential equations using a spectral expansion with and without quasi-steady-state approximation (QSSA). These transformed equations are solved using the eigenanalysis and initial value problem approach. The initial growth rate analysis shows that initially the system is unconditionally stable. The stability characteristics obtained under the present QSSA are quantitatively same as those obtained without the QSSA. To support these theoretical results, numerical simulations are conducted using the Fourier-spectral method. The results of theoretical linear stability analyses and the numerical simulations validate to each other.
Gravitational fingering Porous media Linear stability analysis Nonlinear numerical simulation
List of Symbols
\(a\)
Dimensionless wavenumber, \(\sqrt{a_x^2 +a_y^2 }\)
\(a^{*}\)
Modified dimensionless wave number, \(a\sqrt{\tau }\)
\(C\)
Concentration (M)
Dimensionless concentration, \({\left( {C-C_+ } \right) }/{\left( {C_{-} -C_+ } \right) }\)
\(\mathcal{D}\)
Effective diffusion coefficient \(\left( {{\hbox {m}^{2}}/\hbox {s}} \right) \)
Gravitational acceleration vector \(\left( {\hbox {m}/{\hbox {s}^{2}}} \right) \)
\(K\)
Permeability \(\left( {\hbox {m}^{2}} \right) \)
\(\mathcal{L}\)
Diffusional operator in \(\left( {\tau ,\zeta } \right) \)-domain, \({\partial ^{2}}/{\partial \zeta ^{2}}+\left( {\zeta /2} \right) \left( {\partial /{\partial \zeta }} \right) \)
\(P\)
Pressure \(\left( {\hbox {Pa}} \right) \)
\(t\)
Time \(\left( \hbox {s} \right) \)
Velocity vector \(\left( {\hbox {m}/\hbox {s}} \right) \)
\(w\)
Dimensionless vertical velocity component
\(\left( {x,y,z} \right) \)
Dimensionless Cartesian coordinates
Greek Symbols
\(\mu \)
Viscosity \(\left( {\hbox {Pa}\, \hbox {s}} \right) \)
\(\rho \)
Density \(\left( {{\hbox {kg}}/{\hbox {m}^{3}}} \right) \)
\(\sigma \)
Dimensionless growth rate
\(\tau \)
Dimensionless time \(\left( {{\mathcal{D}t}/K} \right) \)
\(\zeta \)
similarity Variable \(\left( {z/{\sqrt{\tau }}} \right) \)
Subscripts
Basic quantity
Perturbed quantity
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (2012R1A1A2038983). The authors are grateful to all the reviewers for their lucid comments which have served to greatly improve the status of the present article.
The complementary solution of Eq. (3.16) is
$$\begin{aligned} w_1&= \frac{a^{*}}{2}\left[ -\exp \left( {a^{*}\zeta } \right) \mathop \int \limits _{-\infty }^\zeta {\exp \left( {-a^{*}\xi } \right) \sum _{n=0}^\infty {A_n \left( \tau \right) \phi _n \left( \xi \right) } \mathrm{d}\xi }+\exp \left( {-a^{*}\zeta } \right) \right. \nonumber \\&\left. \mathop \int \limits _{-\infty }^\zeta {\exp \left( {a^{*}\xi } \right) \sum _{n=0}^\infty {A_n \left( \tau \right) \phi _n \left( \xi \right) } \mathrm{d}\xi } \right] +B_1 \exp \left( {a^{*}\zeta } \right) +B_2 \exp \left( {-a^{*}\zeta } \right) .\qquad \end{aligned}$$
Using the properties of definite integral, we have
$$\begin{aligned} \mathop \int \limits _{-\infty }^\zeta {f\left( \xi \right) \mathrm{d}\xi } =\mathop \int \limits _{-\infty }^\infty {f\left( \xi \right) \mathrm{d}\xi +} \int \limits _\infty ^\zeta {f\left( \xi \right) \mathrm{d}\xi } =\mathop \int \limits _{-\infty }^\infty {f\left( \xi \right) \mathrm{d}\xi -} \mathop \int \limits _\zeta ^\infty {f\left( \xi \right) \mathrm{d}\xi } , \end{aligned}$$
where \(f\left( \xi \right) =\exp \left( {-a^{*}\xi } \right) \sum _{n=0}^\infty {A_n \left( \tau \right) \phi _n \left( \xi \right) } \). On combining Eqs. (7.1) and (7.2), we can write the complete solution of Eq. (3.16) as
$$\begin{aligned} w_1&= \frac{a^{*}}{2}\left[ \exp \left( {a^{*}\zeta } \right) \mathop \int \limits _\zeta ^\infty {\exp \left( {-a^{*}\xi } \right) \sum _{n=0}^\infty {A_n \left( \tau \right) \phi _n \left( \xi \right) } \mathrm{d}\xi }+\exp \left( {-a^{*}\zeta } \right) \right. \nonumber \\&\left. \mathop \int \limits _{-\infty }^\zeta {\exp \left( {a^{*}\xi } \right) \sum _{n=0}^\infty {A_n \left( \tau \right) \phi _n \left( \xi \right) } \mathrm{d}\xi } \right] -\frac{a^{*}}{2}\exp \left( {a^{*}\zeta } \right) \mathop \int \limits _{-\infty }^\infty \exp \left( {-a^{*}\xi } \right) \nonumber \\&\sum _{n=0}^\infty {A_n \left( \tau \right) \phi _n \left( \xi \right) } \mathrm{d}\xi +B_1 \exp \left( {a^{*}\zeta } \right) +B_2 \exp \left( {-a^{*}\zeta } \right) . \end{aligned}$$
On using the first boundary condition, \(w_1 \rightarrow 0\) as \(\zeta \rightarrow \infty \), into Eq. (7.3) we have
$$\begin{aligned} B_1 =\frac{a^{*}}{2}\left[ {\mathop \int \limits _{-\infty }^\infty {\exp \left( {-a^{*}\xi } \right) \sum _{n=0}^\infty {A_n \left( \tau \right) \phi _n \left( \xi \right) } \mathrm{d}\xi } } \right] , \end{aligned}$$
and the second boundary condition,\( w_1 \rightarrow 0\) as \(\zeta \rightarrow \hbox { }-\infty \), gives
$$\begin{aligned} B_2 =0. \end{aligned}$$
In writing Eqs. (7.4) and (7.5), we have used the following results:
$$\begin{aligned} \mathop {\hbox {lim}}\limits _{\zeta \rightarrow \infty } \exp \left( {-a^{*}\zeta } \right) =0,\quad \mathop {\hbox {lim}}\limits _{\zeta \rightarrow -\infty } \exp \left( {a^{*}\zeta } \right) =0 \; \hbox {and}\; \mathop \int \limits _\zeta ^\zeta {f\left( \xi \right) \mathrm{d}\xi } =0, \end{aligned}$$
where \(a^{*}\) has a finite value. On putting the values of \(B_1\) and \(B_2\) in Eq. (7.3), the solution for \(w_1\) is Eq. (3.17).
By discretizing Eqs. (3.32), (3.33), and (3.35a) using central difference formulations, we obtained the following relation:
$$\begin{aligned} \mathbf{Gw}=\mathbf{0}, \end{aligned}$$
$$\begin{aligned}&\displaystyle G_{1,1} = C_1 , \quad G_{1,2} =B_1 +D_1 , \quad G_{1,3} =A_1 +E_1,\end{aligned}$$
$$\begin{aligned}&\displaystyle G_{2,1} =B_2 , \quad G_{2,2} =A_2 +C_2 , \quad G_{2,3} =D_2 , \quad G_{2,4} =E_2 ,\end{aligned}$$
$$\begin{aligned}&\displaystyle G_{i,i-2} =A_i , \quad G_{i,i-1} =B_i , \quad G_{i,i} =C_i , \quad G_{i,i+1} =D_i,\nonumber \\&\displaystyle G_{i,i+2} =E_i ,\; \hbox {for} \; i=3,\ldots ,n-2,\end{aligned}$$
$$\begin{aligned}&\displaystyle G_{n-1,n-3} =A_{n-1} , \quad G_{n-1,n-2} =B_{n-2} , \quad G_{n-1,n-1} =C_{n-1} , \quad G_{n-1,n} =D_{n-1} ,\qquad \quad \end{aligned}$$
$$\begin{aligned}&\displaystyle G_{n,n\!-\!2} =A_n , \quad G_{n,n\!-\!1} \!=\!B_n , \quad G_{n,n} \!=\!C_n \!-\!E_n,\qquad \end{aligned}$$
$$\begin{aligned}&\displaystyle \mathbf{w}=\left[ {w_1 ,w_2 ,\ldots w_{n-1} ,w_n } \right] ^{T},\end{aligned}$$
$$\begin{aligned}&\displaystyle A_i =\left\{ {1-\frac{\zeta _i }{4}h} \right\} ,\end{aligned}$$
$$\begin{aligned}&\displaystyle B_i =\left\{ {-4+\frac{\zeta _i }{2}h^{2}-\left( {2a^{*2}+\sigma ^{*}\tau } \right) h^{2}+a^{*2}\frac{\zeta _i }{4}h^{3}} \right\} ,\end{aligned}$$
$$\begin{aligned}&\displaystyle C_i \left\{ 6+2\left( {2a^{*2}+\sigma ^{*}\tau } \right) h^{2}+a^{*4}h^{4}+a^{*2}\sigma ^{*}\tau h^{4}\right. \nonumber \\&\displaystyle \left. -a^{*2} Ra^{*}h^{4}\frac{1}{2\sqrt{\pi }}\exp \left( {-\frac{\zeta _i^2 }{4}} \right) \right\} ,\end{aligned}$$
$$\begin{aligned}&\displaystyle D_i =\left\{ {-4-\frac{\zeta _i }{2}h-\left( {2a^{*2}+\sigma ^{*}\tau } \right) h^{2}-a^{*2}\frac{\zeta _i }{4}h^{3}} \right\} ,\end{aligned}$$
$$\begin{aligned}&\displaystyle E_i =\left\{ {1+\frac{\zeta _i }{4}h} \right\} . \end{aligned}$$
Here, \(w_i\) is the vertical velocity disturbance at \(\zeta =\zeta _i\) and \(h\left( {=\zeta _{i+1} -\zeta _i } \right) \) is the fixed step size. We obtained neutral stability condition for a given \(a^{*}\) by finding \(Ra^{*}\) that makes the \(\det \left( \mathbf{G} \right) =0\) under \(\sigma ^{*}=0\).
Ben, Y., Demekhin, E.A., Chang, H.-C.: A spectral theory for small-amplitude miscible fingering. Phys. Fluids 14, 999–1010 (2002)CrossRefGoogle Scholar
Boyd, J.P.: Chebyshev and Fourier Spectral Methods. Dover Publications Inc., Mineola (2000)Google Scholar
Caltagirone, J.-P.: Stability of a saturated porous layer subject to a sudden rise in surface temperature: comparison between the linear and energy methods. Q. J. Mech. Appl. Math. 33, 47–58 (1980)CrossRefGoogle Scholar
Daniel, D., Tilton, N., Riaz, A.: Optimal perturbations of gravitationally unstable, transient boundary layers in porous media. J. Fluid Mech. 727, 456–487 (2013)CrossRefGoogle Scholar
Ennis-King, J., Preston, I., Paterson, L.: Onset of convection in anisotropic porous media subject to a rapid change in boundary conditions. Phys. Fluids 17, 084107 (2005)CrossRefGoogle Scholar
Farrel, B.F., Ioannou, P.J.: Generalized stability theory. Part II: Nonautonomous operators. J. Atmos. Sci. 53, 2041–2053 (1996)CrossRefGoogle Scholar
Fernandez, J., Kurowski, P., Petitjeans, P., Meiburg, E.: Density-driven unstable flows of miscible fluids in a Hele–Shaw cell. J. Fluid Mech. 451, 239–260 (2002)CrossRefGoogle Scholar
Hassanzadeh, H., Pooladi-Darvish, M., Keith, D.W.: Stability of a fluid in a horizontal saturated porous layer: effect of non-linear concentration profile, initial, and boundary conditions. Transp. Porous Med. 65, 193–211 (2006)Google Scholar
Hidalgo, J., Carrera, J.: Effect of dispersion on the onset of convection during \(\text{ CO }_{2}\) sequestration. J. Fluid Mech. 640, 441–452 (2009)CrossRefGoogle Scholar
Horton, C.W., Rogers, F.T.: Convection currents in porous medium. J. Appl. Phys. 16, 367–370 (1945)CrossRefGoogle Scholar
Kim, M.C.: Onset of radial viscous fingering in a Hele–Shaw cell. Korean J. Chem. Eng. 29, 1688–1694 (2012)CrossRefGoogle Scholar
Kim, M.C.: Onset of buoyancy-driven convection in a fluid-saturated porous medium bounded by a long cylinder. Transp Porous Med. 97, 395–408 (2013)CrossRefGoogle Scholar
Kim, M.C., Choi, C.K.: The stability of miscible displacement in porous media: nonmonotonic viscosity profiles. Phys. Fluids 23, 084105 (2011)CrossRefGoogle Scholar
Kim, M.C., Choi, C.K.: Linear stability analysis on the onset of the buoyancy-driven convection in liquid saturated porous medium. Phys. Fluids 24, 044102 (2012)CrossRefGoogle Scholar
Kneafsey, T.K., Pruess, K.: Laboratory experiments and numerical simulation studies of convectively enhanced carbon dioxide dissolution. Energy Procedia 4, 5114–5121 (2011)CrossRefGoogle Scholar
Lapwood, E.R.: Convection of a fluid in a porous medium. Proc. Camb. Philos. Soc. 44, 508–521 (1948)CrossRefGoogle Scholar
Manickam, O., Homsy, G.M.: Fingering instabilities in vertical miscible displacement flows in porous media. J. Fluid Mech. 288, 75–102 (1995)CrossRefGoogle Scholar
Morton, B.R.: On the equilibrium of a stratified layer of fluid. J. Mech. Appl. Math. 10, 433–447 (1957)CrossRefGoogle Scholar
Neufeld, J.A., Hesse, M.A., Riaz, A., Hallworth, M.A., Tchelepi, H.A., Huppert, H.E.: Convective dissolution of carbon dioxide in saline aquifers. Geophys. Res. Lett. 37, L22404 (2010)CrossRefGoogle Scholar
Pramanik, S., Mishra, M.: Linear stability analysis of Korteweg stresses effect on miscible viscous fingering in porous media. Phys. Fluid 25, 074104 (2013)CrossRefGoogle Scholar
Pritchard, D.: The linear stability of double-diffusive miscible rectilinear displacements in Hele–Shaw cell. Eur. J. Mech. B 28, 564–577 (2009)CrossRefGoogle Scholar
Rapaka, S., Chen, S., Pawar, R., Stauffer, P.H., Zhang, D.: Non-modal growth of perturbations in density-driven convection in porous media. J. Fluid Mech. 609, 285–303 (2008)CrossRefGoogle Scholar
Riaz, A., Hesse, M., Tchelepi, H.A., Orr Jr, F.M.: Onset of convection in a gravitationally unstable, diffusive boundary layer in porous media. J. Fluid Mech. 548, 87–111 (2006)CrossRefGoogle Scholar
Rees, D.A.S., Selim, A., Ennis-King, J.P.: The instability of unsteady boundary layers in porous media. In: Vadász, P. (ed.) Emerging Topics in Heat and Mass Transfer in porous media, pp. 85–110. Springer, Berlin (2008a)CrossRefGoogle Scholar
Rees, D.A.S., Postelnicu, A., Bassom, A.P.: The linear vortex instability of the near vertical line source plume in porous media. Transp. Porous Med. 74, 211–238 (2008b)Google Scholar
Selim, A., Rees, D.A.S.: The stability of a developing thermal front in a porous medium. I Linear theory. J. Porous Media 10, 1–15 (2007)CrossRefGoogle Scholar
Selim, A., Rees, D.A.S.: Linear and nonlinear evolution of isolated disturbances in a growing thermal boundary layer in porous media. AIP Conf. Proc. 1254, 47–52 (2010)CrossRefGoogle Scholar
Tan, C.T., Homsy, G.M.: Stability of miscible displacements in porous media: rectilinear flow. Phys. Fluids 29, 3549–3556 (1986)CrossRefGoogle Scholar
Taylor, G.I.: The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. Proc. R. Soc. London. A 201, 192–196 (1950)CrossRefGoogle Scholar
Trevelyan, P.M.J., Alamarcha, C., de Wit, A.: Buoyancy-driven instabilities of miscible two-layer stratifications in porous media and Hele–Shaw cells. J. Fluid Mech. 670, 38–65 (2011)CrossRefGoogle Scholar
Wessel-Berg, D.: On a linear stability problem related to underground \({CO}_{2}\) storage. SIAM J. Appl. Math. 70, 1219–1238 (2009)CrossRefGoogle Scholar
Wooding, R.A.: Rayleigh instability of a thermal boundary layer in flow through a porous medium. J. Fluid Mech. 9, 183–192 (1960)CrossRefGoogle Scholar
Wooding, R.A.: The stability of an interface between miscible fluids in a porous medium. ZAMP 13, 255–266 (1962)CrossRefGoogle Scholar
© Springer Science+Business Media Dordrecht 2014
1.Department of Chemical EngineeringJeju National UniversityJeju Republic of Korea
Kim, M.C. & Yadav, D. Transp Porous Med (2014) 104: 407. https://doi.org/10.1007/s11242-014-0341-4
Received 19 August 2013 | CommonCrawl |
Azimuth Forum
Azimuth Project
Home › MIT 2019: Applied Category Theory › MIT 2019: Lectures
Sign In • Register
Study Groups 20
Petri Nets 9
Leaf Modeling 2
Review Sections 9
MIT 2020: Programming with Categories 51
MIT 2020: Lectures 20
MIT 2020: Exercises 25
MIT 2019: Applied Category Theory 339
MIT 2019: Exercises 149
MIT 2019: Chat 50
UCR ACT Seminar 4
Azimuth Code Project 110
Statistical methods 4
Drafts 5
Math Syntax Demos 15
Wiki - Latest Changes 3
Azimuth Project 1.1K
Older Categories 1.1K
- Spam 1
News and Information 148
Azimuth Blog 149
- Conventions and Policies 21
- Questions 43
Azimuth Wiki 714
Lecture 3 - Chapter 1: Preorders
John Baez
March 2018 edited February 2020 in MIT 2019: Lectures
Okay, let's get started!
Fong and Spivak start out by explaining preorders, which is short for "preordered sets". Whenever you have a set of things and a reasonable way deciding when anything in that set is "bigger" than some other thing, or "more expensive", or "taller", or "heavier", or "better" in any well-defined sense, or... anything like that, you've got a poset. When \(y\) is bigger than \(x\) we write \(x \le y\). (You can also write \(y \ge x\), of course.)
What do I mean by "reasonable"? We demand that the \(\le\) relation obey these rules:
reflexivity: \(x \le x\)
transitivity \(x \le y\) and \(y \le z\) imply \(x \le z\).
A set with a relation obeying these rules is called a preorder.
This is a fundamental concept! After all, humans are always busy trying to compare things and see what's better. So, we'll start by studying preorders.
But I can't resist revealing a secret trick that Fong and Spivak are playing on you here. Why in the world should a book on applied category theory start by discussing preorders? Why not start by discussing categories?
The answer: a preorder is a specially simple kind of category. A category, as you may have heard, has a bunch of 'objects' \(x,y,z,\dots\) and 'morphisms' between them. A morphism from \(x\) to \(y\) is written \(f : x \to y\). You can 'compose' a morphism from \(f : x \to y\) with a morphism from \(g: y \to z\) and get a morphism \(gf : x \to z\). Every object \(x\) has an 'identity' morphism \(1_x : x \to x\). And a few simple rules must hold. We'll get into them later.
But a category with at most one morphism from any object \(x\) to any object \(y\) is really just a preorder! If there's a morphism from \(x\) to \(y\) we simply write \(x \le y\). We don't need to give the morphism a name because there's at most one from \(x\) to \(y\).
So, the study of preorders is a baby version of category theory, where everything gets much easier! And when Fong and Spivak are teaching you about preorders, they're sneakily getting you used to categories. Then, when they introduce categories explicitly, you can always fall back on preorders as examples.
I've posted four puzzles on preorders here. Look at them! I just answered Puzzle 3. Puzzle 4 has millions of answers - come up with another! Also look at Puzzle 5 here. And people who already know the definition of a category, and want to ponder how preorders are a special case of categories, should try Puzzles 6 and 7 here.
To read other lectures go here.
Joe Moeller
In your first sentence, did you mean to say "preorder" rather than "partial order"?
Comment Source:In your first sentence, did you mean to say "preorder" rather than "partial order"?
Or is that part of not trying to "send a hundred students out into the world talking funny."?
Comment Source:Or is that part of not trying to "send a hundred students out into the world talking funny."?
Everyone, no matter how funny they talk, must admit that the "po" in "poset" comes from "partially ordered". So "poset" is short for "partially ordered set", even though Fong and Spivak have cruelly decided to redefine the term "poset" to mean "preorder".
Comment Source:Everyone, no matter how funny they talk, must admit that the "po" in "poset" comes from "partially ordered". So "poset" is short for "partially ordered set", even though Fong and Spivak have cruelly decided to redefine the term "poset" to mean "preorder".
Grant Roy
What's the reason the word morphism is used rather than binary relation?
Comment Source:What's the reason the word morphism is used rather than binary relation?
A morphism is not a binary relation. In a preorder, \(\le\) is a binary relation: for any pair of elements \(x\) and \(y\), \(x \le y\) is either true for false. When \(x \le y\) we can say there's a exactly one morphism from \(x\) to \(y\), if we so desire. But in a general category, there could be many (or no) morphisms \(f : x \to y\).
My remarks on morphisms were aimed only at people who know a bit of category theory and wonder why we're talking about preorders instead. So, if that stuff - or what I just said - makes no sense, don't worry about it too much.
Comment Source:A morphism is not a binary relation. In a preorder, \\(\le\\) is a binary relation: for any pair of elements \\(x\\) and \\(y\\), \\(x \le y\\) is either true for false. When \\(x \le y\\) we can say there's a exactly one morphism from \\(x\\) to \\(y\\), if we so desire. But in a general category, there could be many (or no) morphisms \\(f : x \to y\\). My remarks on morphisms were aimed only at people who know a bit of category theory and wonder why we're talking about preorders instead. So, if that stuff - or what I just said - makes no sense, don't worry about it too much.
Jacob MacDonald
Grant#4, John#5: Trying to make this make sense to me in my current state of very limited understanding. Binary relations apply to specific elements while morphisms are like functions in that they apply to categories and not specific elements. Is that correct?
Comment Source:Grant#4, John#5: Trying to make this make sense to me in my current state of very limited understanding. Binary relations apply to specific elements while morphisms are like functions in that they apply to categories and not specific elements. Is that correct?
John#5 Thanks! I believe I see the point your making.
Jacob#6 My understanding is that morphisms apply to objects, and categories consist of objects. It seems that in the case of a preorder, we have distinct elements, which may be objects, however, there is no transformation being done on them, they are merely 'put into some relation or equivalence'...the result of which can be a simple fact or ordering relation. When they are 'transformed', 'mapped', 'sent to', they are 'morphed'. I think \( f(x) <= f(y) \) could be a monomorphism if certain other conditions hold, but I admittedly know 0 category theory, so I'm just trying to understand the basic terminology as well, and I could certainly be mistaking things.
Comment Source:John#5 Thanks! I believe I see the point your making. Jacob#6 My understanding is that morphisms apply to objects, and categories consist of objects. It seems that in the case of a preorder, we have distinct elements, which may be objects, however, there is no transformation being done on them, they are merely 'put into some relation or equivalence'...the result of which can be a simple fact or ordering relation. When they are 'transformed', 'mapped', 'sent to', they are 'morphed'. I think \\( f(x) <= f(y) \\) could be a monomorphism if certain other conditions hold, but I admittedly know 0 category theory, so I'm just trying to understand the basic terminology as well, and I could certainly be mistaking things.
Grant#7. Thanks. The part I still don't understand is "there's exactly one morphism from x to y" in John#5. But I suppose I'll have to wait for John to clarify his wording there.
Comment Source:Grant#7. Thanks. The part I still don't understand is "there's exactly one morphism from x to y" in John#5. But I suppose I'll have to wait for John to clarify his wording there.
Jacob wrote:
Binary relations apply to specific elements while morphisms are like functions in that they apply to categories and not specific elements. Is that correct?
Not quite. Let's start by saying what a binary relation is. Given a set \(S\), a binary relation is something that can be either true or false for any pair of elements of \(S\). An example is equality: for any pair of elements of \(S\) the statement \(x = y\) is either true or false.
I suppose you could summarize this by saying "binary relations apply to specific elements of a set".
Next for something much harder: a taste of category theory. A category has a set of "objects", and for any pair of objects \(x\) and \(y\), there is a set of "morphisms from \(x\) to \(y\)". There's more to a category than this - see my lecture above for a small taste - but this is the first part of the story.
So, I hope you see why it's wrong to say "morphisms are like functions in that they apply to categories and not specific elements".
If this still doesn't make sense, please ignore all my remarks about categories until I get around to actually explaining this subject!
Comment Source:Jacob wrote: > Binary relations apply to specific elements while morphisms are like functions in that they apply to categories and not specific elements. Is that correct? Not quite. Let's start by saying what a binary relation is. Given a set \\(S\\), a **binary relation** is something that can be either true or false for any pair of elements of \\(S\\). An example is equality: for any pair of elements of \\(S\\) the statement \\(x = y\\) is either true or false. I suppose you could summarize this by saying "binary relations apply to specific elements of a set". Next for something much harder: a taste of category theory. A category has a set of "objects", and for any pair of objects \\(x\\) and \\(y\\), there is a set of "morphisms from \\(x\\) to \\(y\\)". There's more to a category than this - see my lecture above for a small taste - but this is the first part of the story. So, I hope you see why it's wrong to say "morphisms are like functions in that they apply to categories and not specific elements". If this still doesn't make sense, please ignore all my remarks about categories until I get around to actually explaining this subject!
Xah Lee
Greatly enjoyed this one!
Here's my understanding of the gist. Place 4 stones on the floor, and place ONE arrow (e.g. a pen) between any 2 stones. (we'll have placed a total of 6 pens.)
The stones are the "objects" in category theory. The arrows represent the morphisms (or just think of morphism as function). But, since now there is only 1 arrow between any 2 stones, we can relook the whole picture, and now think of the arrow as relation between 2 stones!
So, if S1 → S2, we can think of it as S1 ≥ S2. So, the whole thing, becomes another notion, namely, what mathematicians calls "preorder" in order theory, where, the stones is the set, and each stone is a element.
right John?
Comment Source:Greatly enjoyed this one! Here's my understanding of the gist. Place 4 stones on the floor, and place ONE arrow (e.g. a pen) between any 2 stones. (we'll have placed a total of 6 pens.) The stones are the "objects" in category theory. The arrows represent the morphisms (or just think of morphism as function). But, since now there is only 1 arrow between any 2 stones, we can relook the whole picture, and now think of the arrow as relation between 2 stones! So, if S1 → S2, we can think of it as S1 ≥ S2. So, the whole thing, becomes another notion, namely, what mathematicians calls "preorder" in order theory, where, the stones is the set, and each stone is a element. right John?
Jonatan Bergquist
Re: #9 John 1. What is the difference between an element and an object?
Re: #5 John 2. Are all morphisms in a category of the same type or can a category have, for example, objects {\(x,y,a,b\)} where morphisms \(f: x \rightarrow y\) and \(g: a \rightarrow b\) are different?
Comment Source: Re: #9 John 1. What is the difference between an element and an object? Re: #5 John 2. Are all morphisms in a category of the same type or can a category have, for example, objects {\\(x,y,a,b\\)} where morphisms \\(f: x \rightarrow y\\) and \\(g: a \rightarrow b\\) are different? Thanks!
Jesus Lopez
There are two levels I had difficulty putting apart when starting. Most of the time categories are so-called concrete, and the objects are sets with relations, operations, constants ("structure"), and morphisms are functions between them preserving that. For instance the category of vector spaces over a field. Thinking about it means you think about all vector spaces (over the field). This lives at a considerable level of abstraction (despite the "concrete" technical term). It occurs to me that one could phrase this as saying that the quinean ontological commitment is similar as that required in second order logic where one quantifies over relations, which is a huge commitment.
On the other hand, the axioms of the definition of category can be applied at much much more concrete level to whatever user defined set of objects and of arrows one can came out with, as far as the axioms hold. In our case of an order \((X,\leq)\), the set of objects of the category is \(X\), so the objects of the category are the elements of \(X\), (i.e, things as opposed to sets of things above) and the morphisms are merely pairs (as opposed to functions).
Comment Source:There are two levels I had difficulty putting apart when starting. Most of the time categories are so-called concrete, and the objects are sets with relations, operations, constants ("structure"), and morphisms are functions between them preserving that. For instance the category of vector spaces over a field. Thinking about it means you think about *all* vector spaces (over the field). This lives at a considerable level of abstraction (despite the "concrete" technical term). It occurs to me that one could phrase this as saying that the quinean ontological commitment is similar as that required in second order logic where one quantifies over *relations*, which is a huge commitment. On the other hand, the axioms of the definition of category can be applied at much much more concrete level to whatever user defined set of objects and of arrows one can came out with, as far as the axioms hold. In our case of an order \\((X,\leq)\\), the set of objects of the category is \\(X\\), so the objects of the category are the elements of \\(X\\), (i.e, things as opposed to sets of things above) and the morphisms are merely *pairs* (as opposed to functions).
DavidTanzer
Morphisms in a category are typed: every morphism has a domain (source object) and codomain (target object).
In Jonatan's question, f and g are necessarily distinguishable by the functions which map morphisms to their domains and codomains, respectively.
Comment Source:Morphisms in a category are typed: every morphism has a domain (source object) and codomain (target object). In Jonatan's question, f and g are necessarily distinguishable by the functions which map morphisms to their domains and codomains, respectively.
Xah wrote:
So, if S1 → S2, we can think of it as S1 ≥ S2.
Yes, you can do that. But notice that I'm not doing that! I'm saying that if that given a category with a morphism \(f : S_1 \to S_2\) , I can create a preorder with \(S_1 \le S_2\).
Why \(\le\) instead of \(\ge\)? It's an arbitrary choice:if you have a preorder where you say \(x \le_{\textrm{Xah}} y\), I can make up a preorder where I say that \( x \ge_{\textrm{John}} y \). This is called the opposite preorder.
But there's a reason I'm making my choice! It's very nice to say that the inclusion of sets {1,2,3} \(\to\) {1,2,3,4,5,6} is another way of saying \( 3 \le 6 \). So, everyone in category theory does it the way I'm doing it.
Comment Source:[Xah wrote:](https://forum.azimuthproject.org/discussion/comment/16166/#Comment_16166) > So, if S1 → S2, we can think of it as S1 ≥ S2. Yes, you can do that. But notice that I'm not doing that! I'm saying that if that given a category with a morphism \\(f : S_1 \to S_2\\) , I can create a preorder with \\(S_1 \le S_2\\). Why \\(\le\\) instead of \\(\ge\\)? It's an arbitrary choice:if you have a preorder where you say \\\(x \le_{\textrm{Xah}} y\\), I can make up a preorder where I say that \\( x \ge_{\textrm{John}} y \\). This is called the **opposite** preorder. But there's a reason I'm making my choice! It's very nice to say that the inclusion of sets {1,2,3} \\(\to\\) {1,2,3,4,5,6} is another way of saying \\( 3 \le 6 \\). So, everyone in category theory does it the way I'm doing it.
Chris Nolan
So, this is a bit of a dumb question but I'm trying to understand why it's called a "partially ordered set" and not just an "ordered set," so according to old, handy Wikipedia/Partially ordered set:
the word "partial" in the names "partial order" or "partially ordered set" is used as an indication that not every pair of elements need be comparable. That is, there may be pairs of elements for which neither element precedes the other in the poset. Partial orders thus generalize total orders, in which every pair is comparable.
So, one example of this might be the set {\(a, b, c, 1, 2, 3\)} where the first subset {\(a, b, c\)} is ordered alphabetically ascending and the second subset {\(1, 2, 3\)} is ordered numerically ascending? If that's the case then does that mean since the first subset can't be compared to the second subset, then set {\(a, b, c, 1, 2, 3\)} is equivalent to {\(1, 2, 3, a, b, c\)}?
Comment Source:So, this is a bit of a dumb question but I'm trying to understand why it's called a "partially ordered set" and not just an "ordered set," so according to old, handy [Wikipedia/Partially ordered set](https://en.wikipedia.org/wiki/Partially_ordered_set): > the word "partial" in the names "partial order" or "partially ordered set" is used as an indication that not every pair of elements need be comparable. That is, there may be pairs of elements for which neither element precedes the other in the poset. Partial orders thus generalize total orders, in which every pair is comparable. So, one example of this might be the set {\\(a, b, c, 1, 2, 3\\)} where the first subset {\\(a, b, c\\)} is ordered alphabetically ascending and the second subset {\\(1, 2, 3\\)} is ordered numerically ascending? If that's the case then does that mean since the first subset can't be compared to the second subset, then set {\\(a, b, c, 1, 2, 3\\)} is equivalent to {\\(1, 2, 3, a, b, c\\)}?
The partial orders and preorders that are being discussed are not the order that you write the elements inside braces. Writing a set as a list of elements inside braces is not intended to imply an order. But the order you are talking about (letters ordered alphabetically and numbers ordered in the normal way, and no comparison between the two types) is a valid partial order, and it has incomparable elements. In particular, \(b\) and \(3\) are incomparable.
Comment Source:The partial orders and preorders that are being discussed are not the order that you write the elements inside braces. Writing a set as a list of elements inside braces is not intended to imply an order. But the order you are talking about (letters ordered alphabetically and numbers ordered in the normal way, and no comparison between the two types) is a valid partial order, and it has incomparable elements. In particular, \\(b\\) and \\(3\\) are incomparable.
Jonatan wrote:
What is the difference between an element and an object?
I hope you know a bit about sets: if you feel shaky about them, click the link and read! A set \(S\) has elements, and we write \(x \in S\) when \(x\) is an element of \(S\).
A category \(C\) consists of two sets: a set \(\mathrm{Ob}(C)\) of objects, and a set \(\mathrm{Mor}(C)\) of morphisms. There's also more to a category (re-read my lecture for some of this), but that's where we start.
I emphasize that 'element', 'object' and 'morphism' are undefined terms: that is, they don't really mean anything except insofar as we demand that they obey certain rules.
Summarizing my answer to your first question: an object of a category \(C\) is an element of the set \(\mathrm{Ob}(C)\).
Note that you're forcing me to talk about categories, which is not at all what I want to be doing now!. I'm trying to explain preorders. My remark about categories was just a whispered comment to those who already understand categories - to explain why I'm starting a course on categories by explaining preorders!
Focus on preorders: objects and morphisms can wait.
Comment Source:[Jonatan wrote](https://forum.azimuthproject.org/discussion/comment/16179/#Comment_16179): > What is the difference between an element and an object? I hope you know a bit about [sets](https://en.wikipedia.org/wiki/Set_(mathematics)): if you feel shaky about them, click the link and read! A set \\(S\\) has **elements**, and we write \\(x \in S\\) when \\(x\\) is an element of \\(S\\). A category \\(C\\) consists of two sets: a set \\(\mathrm{Ob}(C)\\) of **objects**, and a set \\(\mathrm{Mor}(C)\\) of **morphisms**. There's also more to a category (re-read my lecture for some of this), but that's where we start. I emphasize that 'element', 'object' and 'morphism' are undefined terms: that is, they don't really mean anything except insofar as we demand that they obey certain rules. Summarizing my answer to your first question: an object of a category \\(C\\) is an element of the set \\(\mathrm{Ob}(C)\\). Note that you're forcing me to talk about categories, which is not at all what I want to be doing now!. I'm trying to explain preorders. My remark about categories was just a whispered comment to those who already understand categories - to explain why I'm starting a course on categories by explaining preorders! Focus on preorders: objects and morphisms can wait.
Chris Nolan wrote:
So, this is a bit of a dumb question but I'm trying to understand why it's called a "partially ordered set" and not just an "ordered set" [....]
I think Joseph gave a fine answer, namely: in a partially ordered set we can't compare every pair of elements, i.e. there are incomparable elements \(x\) and \(y\) where neither \(x \le y \) nor \(y \le x\). There's something 'partial' about this.
This comment of mine from over here may help explain some of the history:
Bob Haugen wrote:
Question: forgive my ignorance, but why is it called "preorder" and not just "order"? What is the significance of the "pre"?
The original concept of totally ordered set or order, still dominant today, obeys a bunch of rules:
transitivity: \(x \le y\) and \(y \le z\) imply \(x \le z\)
antisymmetry: if \(x \le y\) and \(y \le x\) then \(x = y\)
trichotomy: for all \(x,y\) we either have \(x\le y\) or \(y \le x\).
The real numbers with the usual \(\le\) obeys all these. Then people discovered many situations where rule 4 does not apply. If only rules 1-3 hold they called it a partially ordered set or poset. Then people discovered many situations where rule 3 does not hold either! If only rules 1-2 hold they called it a preordered set or preorder.
Category theory teaches us that preorders are the fundamental thing: see Lecture 3. But we backed our way into this concept, so it has an awkward name. Fong and Spivak try to remedy this by calling them posets, but that's gonna confuse everyone even more! If they wanted to save the day they should have made up a beautiful brand new term.
Comment Source:[Chris Nolan wrote](https://forum.azimuthproject.org/discussion/comment/16250/#Comment_16250): > So, this is a bit of a dumb question but I'm trying to understand why it's called a "partially ordered set" and not just an "ordered set" [....] I think Joseph gave a fine answer, namely: in a partially ordered set we can't compare every pair of elements, i.e. there are **incomparable** elements \\(x\\) and \\(y\\) where neither \\(x \le y \\) nor \\(y \le x\\). There's something 'partial' about this. This comment of mine from [over here](https://forum.azimuthproject.org/discussion/comment/16083/#Comment_16083) may help explain some of the history: <hr/> Bob Haugen wrote: > Question: forgive my ignorance, but why is it called "preorder" and not just "order"? What is the significance of the "pre"? The original concept of **totally ordered set** or **order**, still dominant today, obeys a bunch of rules: 1. **reflexivity**: \\(x \le x\\) 2. **transitivity**: \\(x \le y\\) and \\(y \le z\\) imply \\(x \le z\\) 3. **antisymmetry**: if \\(x \le y\\) and \\(y \le x\\) then \\(x = y\\) 4. **trichotomy**: for all \\(x,y\\) we either have \\(x\le y\\) or \\(y \le x\\). The real numbers with the usual \\(\le\\) obeys all these. Then people discovered many situations where rule 4 does not apply. If only rules 1-3 hold they called it a **partially ordered set** or **poset**. Then people discovered many situations where rule 3 does not hold either! If only rules 1-2 hold they called it a **preordered set** or **preorder**. Category theory teaches us that preorders are the fundamental thing: see [Lecture 3](https://forum.azimuthproject.org/discussion/1812/lecture-3-chapter-1-posets). But we backed our way into this concept, so it has an awkward name. Fong and Spivak try to remedy this by calling them posets, but that's gonna confuse everyone even more! If they wanted to save the day they should have made up a beautiful brand new term.
So, can we compare posets to other posets? So, if all corresponding comparable subsets of one poset are equal to the other then can we say the two posets are equal?
Comment Source:So, can we compare posets to other posets? So, if all corresponding comparable subsets of one poset are equal to the other then can we say the two posets are equal?
Alex Kreitzberg
Chris Nolan#19
If all the comparable elements of two sets are equal, then the sets are equal. But posets also include an order, and the order of two sets could be different, even though the elements are the same.
Now, if by poset, you mean posets whose order is subset inclusion, if the corresponding sets are equal, then they would be equal as posets (because they are equal as sets, and have the same \( \leq \) ).
This is similar to saying that {1, 4, 6} and {1, 4, 6} are equal as sets with the usual order for integers.
Does that answer your question?
Comment Source:Chris Nolan#19 If all the comparable elements of two sets are equal, then the sets are equal. But posets also include an order, and the order of two sets could be different, even though the elements are the same. Now, if by poset, you mean posets whose order is subset inclusion, if the corresponding sets are equal, then they would be equal as posets (because they are equal as sets, and have the same \\( \leq \\) ). This is similar to saying that {1, 4, 6} and {1, 4, 6} are equal as sets with the usual order for integers. Does that answer your question?
Scott Finnie
Chris Nolan #15: I was wondering that too, thanks for asking. Testing my understanding of the answers then:
For any pair of objects \(x, y\) in the set of objects, exactly one of the following must hold:
\(x\) is comparable to \(y\), or
\(x\) is not comparable to \(y\).
Case 2 fails trichotomy per John's note @ #18. Stated alternately: if all \((x, y)\) are comparable, then the set of objects has a total order provided reflexivity and transitivity hold.
That then raises a question about antisymmetry. But I think I read somewhere that the concept of equality is non-trivial in category theory. So I'll leave that one for now!
It does, however, raise another minor question for me: why use \(\le\) to mean "is less than" instead of \(<\)? I can see that reflexivity gets troublesome if I use a conventional interpretation of "less than": \(x\) can't be less than \(x\) in any meaningful way. \(x\) "is less than or equal to" \(x\) does have intuitive meaning. But that gets us back into equality again!
Comment Source:Chris Nolan #15: I was wondering that too, thanks for asking. Testing my understanding of the answers then: For any pair of objects \\(x, y\\) in the set of objects, exactly one of the following must hold: 1. \\(x\\) is comparable to \\(y\\), or 2. \\(x\\) is not comparable to \\(y\\). Case 2 fails trichotomy per John's note @ #18. Stated alternately: if all \\((x, y)\\) are comparable, then the set of objects has a total order provided reflexivity and transitivity hold. That then raises a question about antisymmetry. But I think I read somewhere that the concept of equality is non-trivial in category theory. So I'll leave that one for now! It does, however, raise another minor question for me: why use \\(\le\\) to mean "is less than" instead of \\(<\\)? I can see that reflexivity gets troublesome if I use a conventional interpretation of "less than": \\(x\\) can't be less than \\(x\\) in any meaningful way. \\(x\\) "is less than or equal to" \\(x\\) does have intuitive meaning. But that gets us back into equality again!
Robert Figura
Preorder, Poset, and totally ordered – Definitions, examples, and their degeneration.
We all know about totally ordered sets. They are sets which can be put on a line, like a chain or a necklace, a string of pearls. These can be captured by four axioms like this:
reflexivity: x≤x
transitivity: x≤y and y≤z imply x≤z
antisymmetry: if x≤y and y≤x then x=y
trichotomy: for all x,y we either have x≤y or y≤x.
And the canonical example are the integers with the ordering relation ≤ as we know it. Now, a poset is a structure where 4 doesn't hold, and a preorder is one where neither 3 nor 4 hold. Then what do these axioms mean, what do they do?
Axiom 4 makes sure that every pair of elements is related. It excludes parallel structures and this axiom is what causes the set to collapse to a string. When Axiom 4 doesn't hold we may get a directed acyclic graph (DAG) instead. Well, sort of, as a directed acyclic graph does not necessarily imply transitivity, a poset does. More on transitivity below.
Given a total order (like the integers with ≤) we can degenerate it by adding 'parallel structure' (e.g. an element ε which is just like 3 but not identical to it).
Axiom 3 suppresses cycles. It says that the only cycles are indentity arrows.
Given a total order (like the integers with ≤) we can create a cycle by adding a backward relation like (5≤2). Note that if axiom 3 / antisymmetry does not hold, axiom 4 cannot hold either, as the 'and' is incompatible with the 'either-or'.
What does the transitivity axiom 2 do? That's a funny one. It implies associativity, and says that if you find two arrows that can be combined because their ends match, you're allowed to talk about the combined arrow. It actually says that the combined arrow has to be among our collected arrows.
You can break this structure by taking out a combined arrow, e.g. insisting that 2 and 4 cannot be compared, even though 2≤3 and 3≤4. Strike out the corresponding arrow, mark it red, you don't have enough gas to drive two routes...
As I said earlier, a poset is usually drawn as a DAG without outlining each and every matching combination of arrows. That's because people (and algorithms) have no trouble to understand that once we find a connected path between two points that those points are also connected. So people will often draw a DAG when they actually want to talk about posets.
Comment Source:**Preorder, Poset, and totally ordered** – Definitions, examples, and their degeneration. We all know about totally ordered sets. They are sets which can be put on a line, like a chain or a necklace, a string of pearls. These can be captured by four axioms like this: 1. **reflexivity:** x≤x 2. **transitivity:** x≤y and y≤z imply x≤z 3. **antisymmetry:** if x≤y and y≤x then x=y 4. **trichotomy:** for all x,y we either have x≤y or y≤x. And the canonical example are the integers with the ordering relation ≤ as we know it. Now, a poset is a structure where 4 doesn't hold, and a preorder is one where neither 3 nor 4 hold. Then what do these axioms mean, what do they _do_? *Axiom 4* makes sure that every pair of elements is related. It excludes parallel structures and this axiom is what causes the set to collapse to a string. When Axiom 4 doesn't hold we may get a directed acyclic graph (DAG) instead. Well, sort of, as a directed acyclic graph does not necessarily imply transitivity, a poset does. More on transitivity below. Given a total order (like the integers with ≤) we can degenerate it by adding 'parallel structure' (e.g. an element ε which is just like 3 but not identical to it). *Axiom 3* suppresses cycles. It says that the only cycles are indentity arrows. Given a total order (like the integers with ≤) we can create a cycle by adding a backward relation like (5≤2). Note that if axiom 3 / antisymmetry does not hold, axiom 4 cannot hold either, as the 'and' is incompatible with the 'either-or'. What does the transitivity *axiom 2* do? That's a funny one. It implies associativity, and says that if you find two arrows that can be combined because their ends match, you're allowed to talk about the combined arrow. It actually says that the combined arrow has to be among our collected arrows. You can break this structure by taking out a combined arrow, e.g. insisting that 2 and 4 cannot be compared, even though 2≤3 and 3≤4. Strike out the corresponding arrow, mark it red, you don't have enough gas to drive two routes... As I said earlier, a poset is usually drawn as a DAG without outlining each and every matching combination of arrows. That's because people (and algorithms) have no trouble to understand that once we find a connected path between two points that those points are also connected. So people will often draw a DAG when they actually want to talk about posets.
Alexander Telfar
So, I am not sure if I understood this correctly. Could a ring be a partially ordered set? $$1 \le 2, 2 \le 3, 3 \le 4, 4 \le 1$$ If so, it seems more intuitive to me to call it a locally ordered set??
Edit: Ok, the above comment clears things up. Was writing this comment and hadnt refreshed.
Comment Source:So, I am not sure if I understood this correctly. Could a ring be a partially ordered set? $$1 \le 2, 2 \le 3, 3 \le 4, 4 \le 1$$ If so, it seems more intuitive to me to call it a locally ordered set?? Edit: Ok, the above comment clears things up. Was writing this comment and hadnt refreshed.
Narasimha Mujumdar
In the first chapter, it is mentioned that: "In other words A ≤ B in the poset if "A implies B", often denoted A ⇒ B." An example could be: A: If it rains. B: The match wont happen. A => B. It can be seen that A = True then B = False. But if A = False, then B = True or False. Based on this we can say A <= B. Are there other explanations for this statement?
Comment Source:In the first chapter, it is mentioned that: "In other words A ≤ B in the poset if "A implies B", often denoted A ⇒ B." An example could be: A: If it rains. B: The match wont happen. A => B. It can be seen that A = True then B = False. But if A = False, then B = True or False. Based on this we can say A <= B. Are there other explanations for this statement?
Marcello Seri
The web, where the objects are the web pages and the relation is given by 'links to', seems to me a preorder as we cannot avoid cycles, thus invalidating antisymmetry. If we try to generate a partial order from it, do you know if we get just a set with one element or if there is more structure? I believe the latter but I don't really have the data to check it
Comment Source:The web, where the objects are the web pages and the relation is given by 'links to', seems to me a preorder as we cannot avoid cycles, thus invalidating antisymmetry. If we try to generate a partial order from it, do you know if we get just a set with one element or if there is more structure? I believe the latter but I don't really have the data to check it
John Baez wrote:
Fong and Spivak try to remedy this by calling them posets, but that's gonna confuse everyone even more! If they wanted to save the day they should have made up a beautiful brand new term.
How about \(apriorder \)? :) Obviously leaning heavier on the Latin, and the idea of it being fundamental or 'from before'. Anyway, more to the point, for posts on the forum should we always consider poset to mean partially ordered set, and translate the terms from the book? From most contexts, it's probably pretty clear, but it is an unfortunate source of confusion.
Comment Source:John Baez wrote: > Fong and Spivak try to remedy this by calling them posets, but that's gonna confuse everyone even more! If they wanted to save the day they should have made up a beautiful brand new term. How about \\(apriorder \\)? :) Obviously leaning heavier on the Latin, and the idea of it being fundamental or 'from before'. Anyway, more to the point, for posts on the forum should we always consider poset to mean partially ordered set, and translate the terms from the book? From most contexts, it's probably pretty clear, but it is an unfortunate source of confusion.
ThomasRead
Marcello #25: Presumably there are many pages with no links, and many which are never linked to, so you'd definitely get some sort of non-trivial structure. I'd love to see what it actually looks like though.
Comment Source:Marcello #25: Presumably there are many pages with no links, and many which are never linked to, so you'd definitely get some sort of non-trivial structure. I'd love to see what it actually looks like though.
Christina Vasilakopoulou
Narasimha #24: the way you formulated your propositions, it seems to me that A true gives B true! Unless you meant A=it rains B=the match is happening , in which case A cannot imply B (since true cannot imply false). You considered the negative statement instead!
To sum up: A=it rains, B=match is on, then A does not imply B and B does not imply A. However \(A\Rightarrow\neg B\).
Comment Source:Narasimha #24: the way you formulated your propositions, it seems to me that A true gives B true! Unless you meant A=it rains B=the match is happening , in which case A cannot imply B (since true cannot imply false). You considered the negative statement instead! To sum up: A=it rains, B=match is on, then A does not imply B and B does not imply A. However \\(A\Rightarrow\neg B\\).
Alex Kreitzberg #20: Yeah, I should have specified that I meant the subset with ordering.
Can we define a hierarchy of ordering within posets in order to make a totally ordered set? So given a poset made up of two types of objects, one letters and one numbers, both with the natural ordering for each type, then can we define a higher ordering to say letters are always less than numbers to make a totally ordered set, and would that still be a poset? Or does that not make sense within the concept of a poset?
Comment Source:Alex Kreitzberg #20: Yeah, I should have specified that I meant the subset with ordering. Can we define a hierarchy of ordering within posets in order to make a totally ordered set? So given a poset made up of two types of objects, one letters and one numbers, both with the natural ordering for each type, then can we define a higher ordering to say letters are always less than numbers to make a totally ordered set, and would that still be a poset? Or does that not make sense within the concept of a poset?
You can add arrows to flatten a poset to a total order, Chris Nolan. Posets are more general and less specific than total orders, every total order is a poset, but not every poset is a total order.
Comment Source:You can add arrows to flatten a poset to a total order, Chris Nolan. Posets are more general and less specific than total orders, every total order is a poset, but not every poset is a total order.
Chris Nolan #29: The answer to all your questions is yes. For your example:
Let poset A = ( {a, b}, { (b, a), (a, a), (b, b) } ) and B = ( {0, 1}, { (0, 1), (0, 0), (1, 1) } ) In abuse of notation, I'll also write A = {a, b}, B = {0, 1}, and \( \leq_A \) = { (b, a), (a, a), (b, b) }, and \( \leq_B \) = { (0, 1), (0, 0), (1, 1) }.
You can form a new poset by taking a pairwise union of sets:
C = (A \(\cup\) B, \(\leq_A \cup \leq_B\)) = ( {a, b, 0, 1}, { (0, 1), (0, 0), (1, 1), (b, a), (a, a), (b, b) } )
Like you said, this isn't a total order. The order can be flattened by saying "all letters are less than numbers". In notation, this is done by setting \(\leq_C \) to \(\leq_C \cup \) { (a, 0), (a, 1), (b, 0), (b, 1), (c, 0), (c, 1) }
For what it's worth, I don't really like thinking of relations as certain special types of sets. But it's consistent with this book. Your question seemed like a nice way to practice manipulating posets as sets.
Edit And it seems that although in this case we do get a poset by performing a union, this isn't always true. David Tanzer gave an example of where a normal union fails, and some more typical examples of products between posets.
John Baez Gave insights for how subtle these operations can be. Taking the union as I did is apparently complicated in general. So the procedure I described doesn't generalize well. A "disjoint union" is apparently a much safer operation. So I think your basic relations combined nicely, because the underlying sets are different.
Comment Source:Chris Nolan #29: The answer to all your questions is yes. For your example: Let poset A = ( {a, b}, { (b, a), (a, a), (b, b) } ) and B = ( {0, 1}, { (0, 1), (0, 0), (1, 1) } ) In abuse of notation, I'll also write A = {a, b}, B = {0, 1}, and \\( \leq_A \\) = { (b, a), (a, a), (b, b) }, and \\( \\leq_B \\) = { (0, 1), (0, 0), (1, 1) }. You can form a new poset by taking a pairwise union of sets: C = (A \\(\cup\\) B, \\(\leq_A \cup \leq_B\\)) = ( {a, b, 0, 1}, { (0, 1), (0, 0), (1, 1), (b, a), (a, a), (b, b) } ) Like you said, this isn't a total order. The order can be flattened by saying "all letters are less than numbers". In notation, this is done by setting \\(\leq_C \\) to \\(\leq_C \cup \\) { (a, 0), (a, 1), (b, 0), (b, 1), (c, 0), (c, 1) } For what it's worth, I don't really like thinking of relations as certain special types of sets. But it's consistent with this book. Your question seemed like a nice way to practice manipulating posets as sets. **Edit** And it seems that although in this case we do get a poset by performing a union, this isn't always true. [David Tanzer](https://forum.azimuthproject.org/discussion/comment/16303/#Comment_16303) gave an example of where a normal union fails, and some more typical examples of products between posets. [John Baez](https://forum.azimuthproject.org/discussion/comment/16321/#Comment_16321) Gave insights for how subtle these operations can be. Taking the union as I did is apparently complicated in general. So the procedure I described doesn't generalize well. A "disjoint union" is apparently a much safer operation. So I think your basic relations combined nicely, because the underlying sets are different.
Marcelo #25: The data shows that there are some islands disconnected of each other, and also if you collapse pages joined by reversible paths there still remain other irreversible paths.
Comment Source:Marcelo #25: The data shows that there are some islands disconnected of each other, and also if you collapse pages joined by reversible paths there still remain other irreversible paths.
March 2018 edited April 2018
Posting this as someone who learns best from concrete examples and geometric representations, on the basis that trying to explain something is a good way to test one's understanding. If it's inappropriate for the forum please just say. I ask forbearance from those with more natural mathematical ability. Corrections or comments gratefully received.
The examples below all consider the subject matter of completing tasks. Assume order means "must be completed before": so \(x \le y\) means "task \(x\) must be completed before task \(y\)". Note I've used 'arrow' in the geometric sense, not the categorical one.
First, a picture:
This says:
All Orders are also Posets
All Posets are also Preorders
All Preorders are also Sets
Why the subset relations among Preorders, Posets and Orders? Because of the rules that they must obey. We'll look at that below; but first, let's cover off sets without any order.
No Order
Consider cleaning the house. Let's assume there are 3 rooms: bathroom, bedroom and kitchen. To clean the house, we need to clean all three rooms. It doesn't matter what order they're cleaned in: there's no dependence.
Preordered Sets (Preorders)
Preorders must obey 2 rules:
As an example, consider a (very simplified) iterative approach to writing software:
The arrows are straightforward: we must Define Requirements before Write Code, and Write Code before Test Solution. We can also combine those according to rule (2) - so Define Requirements before Test Solution.
What about the loop? That's OK according to rule 1. It says any task must be "less than or equal to" itself. Define Requirements equals itself, so it satisfies rule 1 (as do all the others in the loop, for the same reason).
Note also there's no arrow connecting Write Code and Write Tests. Again, that's fine: there's nothing in the rules to say every task must be related to every other.
Partially Ordered Sets (Posets)
Posets obey both rules for Preorders, and add a third:
Our iterative process above fails this rule. Why? Substitute Define Requirements for \(x\) and Test Solution for \(y\) in the antisymmetry rule. Define Requirements does come before Test Solution so \(x \le y\). Test Solution also comes before Define Requirements. So \(y \le x\). But Define Requirements is a different task to Test Solution. So \(x = y\) is not true. So the iterative process isn't antisymmetric: it's not a poset. We can make it so by removing the loop, and creating a waterfall process:
Ordered Sets (Orders)
Orders obey all the rules for Posets, and add yet another:
Antisymmetry removed loops in our task ordering. Trichotomy removes parallel paths. Why? Let \(x\) be Write Code and \(y\) be Write Tests. There's no arrow, or sequence of arrows, that connect the two. So we don't have \(x \le y\), nor do we have \(y \le x\). Trichotomy fails.
We can resolve that by linearising the process. Let's follow Test-Driven Development and write tests before the code:
Comment Source:Posting this as someone who learns best from concrete examples and geometric representations, on the basis that trying to explain something is a good way to test one's understanding. If it's inappropriate for the forum please just say. I ask forbearance from those with more natural mathematical ability. Corrections or comments gratefully received. The examples below all consider the subject matter of completing tasks. Assume order means "must be completed before": so \\(x \le y\\) means "task \\(x\\) must be completed before task \\(y\\)". Note I've used 'arrow' in the geometric sense, not the categorical one. ## The Landscape First, a picture: 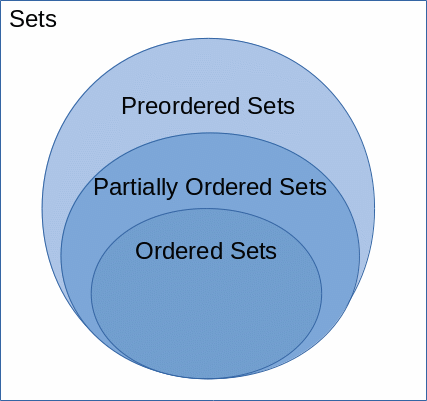 This says: * All Orders are also Posets * All Posets are also Preorders * All Preorders are also Sets Why the subset relations among Preorders, Posets and Orders? Because of the rules that they must obey. We'll look at that below; but first, let's cover off sets without any order. ## No Order Consider cleaning the house. Let's assume there are 3 rooms: bathroom, bedroom and kitchen. To clean the house, we need to clean all three rooms. It doesn't matter what order they're cleaned in: there's no dependence.  ## Preordered Sets (Preorders) Preorders must obey 2 rules: 1. **reflexivity**: \\(x \le x\\) 2. **transitivity** \\(x \le y\\) and \\(y \le z\\) imply \\(x \le z\\). As an example, consider a (very simplified) iterative approach to writing software:  The arrows are straightforward: we must `Define Requirements` before `Write Code`, and `Write Code` before `Test Solution`. We can also combine those according to rule (2) - so `Define Requirements` before `Test Solution`. What about the loop? That's OK according to rule 1. It says any task must be "less than or equal to" itself. `Define Requirements` equals itself, so it satisfies rule 1 (as do all the others in the loop, for the same reason). Note also there's no arrow connecting `Write Code` and `Write Tests`. Again, that's fine: there's nothing in the rules to say *every* task must be related to every other. ## Partially Ordered Sets (Posets) Posets obey both rules for Preorders, and add a third: 1. **antisymmetry**: if \\(x \le y\\) and \\(y \le x\\) then \\(x = y\\) Our iterative process above fails this rule. Why? Substitute `Define Requirements` for \\(x\\) and `Test Solution` for \\(y\\) in the antisymmetry rule. `Define Requirements` does come before `Test Solution` so \\(x \le y\\). `Test Solution` also comes before `Define Requirements`. So \\(y \le x\\). But `Define Requirements` is a different task to `Test Solution`. So \\(x = y\\) is not true. So the iterative process isn't antisymmetric: it's not a poset. We can make it so by removing the loop, and creating a [waterfall process](https://en.wikipedia.org/wiki/Waterfall_model):  ## Ordered Sets (Orders) Orders obey all the rules for Posets, and add yet another: 1. **trichotomy**: for all \\(x,y\\) we either have \\(x\le y\\) or \\(y \le x\\). Antisymmetry removed loops in our task ordering. Trichotomy removes parallel paths. Why? Let \\(x\\) be `Write Code` and \\(y\\) be `Write Tests`. There's no arrow, or sequence of arrows, that connect the two. So we don't have \\(x \le y\\), nor do we have \\(y \le x\\). Trichotomy fails. We can resolve that by linearising the process. Let's follow [Test-Driven Development](https://en.wikipedia.org/wiki/Test-driven_development) and write tests before the code: 
Jesus #25: nice! Do yiu know if the relationships data is available somewhere for use?
Comment Source:Jesus #25: nice! Do yiu know if the relationships data is available somewhere for use?
Scott Finnie #21 wrote:
It does, however, raise another minor question for me: why use ≤ to mean "is less than" instead of <?
We don't. We use \(\le\) to mean "less than or equal to". In a preorder, \(x = y\) implies \(x \le y\). So, the case of equality is always included in \(\le\).
Comment Source:[Scott Finnie #21 wrote:](https://forum.azimuthproject.org/discussion/comment/16266/#Comment_16266) > It does, however, raise another minor question for me: why use ≤ to mean "is less than" instead of <? We don't. We use \\(\le\\) to mean "less than or equal to". In a preorder, \\(x = y\\) implies \\(x \le y\\). So, the case of equality is always included in \\(\le\\).
Chris Nolan #19 wrote::
So, can we compare posets to other posets?
Yes. The best way is with monotone functions. There's a lot to say about this, but we can use monotone mappings to define when two posets are "isomorphic".
So, if all corresponding comparable subsets of one poset are equal to the other then can we say the two posets are equal?
Alex has already answered your question quite nicely but I'll just say a bit more.
A mathematician wouldn't ask that question unless they had first told us that the two posets under discussion are equal as sets. They'd say something like this:
Suppose I have a set \(S\) with two different rrelations on it, \(\le_1\) and \(\le_2\), which give me two posets \((S,\le_1)\) and \((S,\le_2)\). Suppose \(x \le_1 y\) if and only if \(x \le_2 y\) for all \(x,y \in S\) . Does that mean these two posets are equal?
And the answer is yes: the posets \((S,\le_1)\) and \((S,\le_2)\) are equal if and only if
$$ x \le_1 y \textrm{ if and only if } x \le_2 y \textrm{ for all } x,y \in S. $$ However, equality of posets is ultimately less interesting than other ways of comparing posets, using monotone mappings.
Note: everything I just said would still be true if I replaced the word "poset" by "preorder" throughout this comment.
Comment Source:[Chris Nolan #19 wrote:](https://forum.azimuthproject.org/discussion/comment/16259/#Comment_16259): > So, can we compare posets to other posets? Yes. The best way is with monotone functions. There's a lot to say about this, but we can use monotone mappings to define when two posets are "isomorphic". > So, if all corresponding comparable subsets of one poset are equal to the other then can we say the two posets are equal? Alex has already answered your question quite nicely but I'll just say a bit more. A mathematician wouldn't ask that question unless they had first told us that the two posets under discussion are equal _as sets_. They'd say something like this: Suppose I have a set \\(S\\) with two different rrelations on it, \\(\le_1\\) and \\(\le_2\\), which give me two posets \\((S,\le_1)\\) and \\((S,\le_2)\\). Suppose \\(x \le_1 y\\) if and only if \\(x \le_2 y\\) for all \\(x,y \in S\\) . Does that mean these two posets are equal? And the answer is yes: the posets \\((S,\le_1)\\) and \\((S,\le_2)\\) are equal if and only if $$ x \le_1 y \textrm{ if and only if } x \le_2 y \textrm{ for all } x,y \in S. $$ However, equality of posets is ultimately less interesting than other ways of comparing posets, using monotone mappings. Note: everything I just said would still be true if I replaced the word "poset" by "preorder" throughout this comment.
Scott Finnie # wrote::
Posting this as someone who learns best from concrete examples and geometric representations, on the basis that trying to explain something is a good way to test one's understanding. If it's inappropriate for the forum please just say.
No, this is GREAT!!! This is just what I'm hoping people will do: add their own material to this course. If just 5% of the people here do this, we'll have 10 people explaining things in different ways, and students will get a multi-faceted view of the course material that's far better than anything I could produce on my own.
Like you, I learn best from pictures. If I had more time, every lecture of mine would be packed with pictures, because that's how I think. I just don't have time to draw all those pictures - there are too many in my mind. Fong and Spivak's book has some of the missing pictures, but I'm very happy for people to draw more!
Comment Source:[Scott Finnie # wrote:](https://forum.azimuthproject.org/discussion/comment/16340/#Comment_16340): > Posting this as someone who learns best from concrete examples and geometric representations, on the basis that trying to explain something is a good way to test one's understanding. If it's inappropriate for the forum please just say. No, this is _GREAT!!!_ This is just what I'm hoping people will do: add their own material to this course. If just 5% of the people here do this, we'll have 10 people explaining things in different ways, and students will get a multi-faceted view of the course material that's far better than anything I could produce on my own. Like you, I learn best from pictures. If I had more time, every lecture of mine would be packed with pictures, because that's how I think. I just don't have time to draw all those pictures - there are too many in my mind. Fong and Spivak's book has some of the missing pictures, but I'm very happy for people to draw more!
@John #35 & #37: thanks. Have updated #33 to use "less than or equal to", which makes the description for preorders less clumsy. Great that you're open to alternative descriptions. I'll try to add as and when time allows.
Comment Source:@John #35 & #37: thanks. Have updated #33 to use "less than or equal to", which makes the description for preorders less clumsy. Great that you're open to alternative descriptions. I'll try to add as and when time allows.
Marcelo #34: don't know about the raw data, I read about the islands in some paper about Google PageRank algorithm. It is based in random walks on the web graph.
Comment Source:Marcelo #34: don't know about the raw data, I read about the islands in some paper about Google PageRank algorithm. It is based in random walks on the web graph.
Scott: here's one interesting nuance. Your original chart:
showed unordered sets (i.e., just sets) as disjoint from ordered ones. A mathematician would prefer to see a bunch of nested blobs, as in your new chart:
The point is that a preordered set is a special kind of set, a partially ordered set is a special kind of preordered set, and an ordered set is a special kind of partially ordered set.
Category theory goes much further with this line of thought. I don't want to get into it now, but each of these blobs is actually a category. There's a category of sets, a category of preordered sets, and so on.
Comment Source:Scott: here's one interesting nuance. Your original chart: <img src = "https://raw.githubusercontent.com/sfinnie/CategoryTheoryCourseNotes/6bbcc770474a8945ee4e47e273a65909f979b818/posets/img/orderVennDiagram.gif"> showed unordered sets (i.e., just sets) as disjoint from ordered ones. A mathematician would prefer to see a bunch of nested blobs, as in your new chart: <img src = "https://raw.githubusercontent.com/sfinnie/CategoryTheoryCourseNotes/master/posets/img/orderVennDiagram.gif"> The point is that a preordered set is a special kind of set, a partially ordered set is a special kind of preordered set, and an ordered set is a special kind of partially ordered set. Category theory goes much further with this line of thought. I don't want to get into it now, but each of these blobs is actually a _category_. There's a _category_ of sets, a _category_ of preordered sets, and so on.
@John #40: thanks. I've updated the diagram accordingly, though a side effect is your post now shows the new version (apologies). You can use https://raw.githubusercontent.com/sfinnie/CategoryTheoryCourseNotes/6bbcc770474a8945ee4e47e273a65909f979b818/posets/img/orderVennDiagram.gif to access the original in your post.
It was something I considered in drawing the diagram. I decided on "Unordered" as a disjoint set, on the basis that there are some which are explicitly not ordered. So those that obey the rule:
unordered: for all \(x\) and \(y\), there exists no \(x, y\) such that \(x \le y \).
I think the "Set" rectangle in the revised diagram now means "Possibly ordered". It still caters for unordered sets, but doesn't assert any properties about them. Is that correct?
Comment Source:@John #40: thanks. I've updated the diagram accordingly, though a side effect is your post now shows the new version (apologies). You can use [https://raw.githubusercontent.com/sfinnie/CategoryTheoryCourseNotes/6bbcc770474a8945ee4e47e273a65909f979b818/posets/img/orderVennDiagram.gif](https://raw.githubusercontent.com/sfinnie/CategoryTheoryCourseNotes/6bbcc770474a8945ee4e47e273a65909f979b818/posets/img/orderVennDiagram.gif) to access the original in your post. It was something I considered in drawing the diagram. I decided on "Unordered" as a disjoint set, on the basis that there are some which are explicitly *not* ordered. So those that obey the rule: * ***unordered***: for all \\(x\\) and \\(y\\), there exists no \\(x, y\\) such that \\(x \le y \\). I think the "Set" rectangle in the revised diagram now means "Possibly ordered". It still caters for unordered sets, but doesn't assert any properties about them. Is that correct? Thanks.
Filip Vukovinski
I've decided to follow this course in Coq, and it already hit me in the head, meaning I have still much more to learn after not being able to formalize preorders (on the inductive type level as I presumed possible).
Still, I made a promise, so I dug deep in Coq's standard library to find it's default implementation. Those are available here: https://github.com/vukovinski/azimuth-act/blob/master/chapter-1/poset.v
My next update should solve some puzzles by providing instances to the classes defined in the file above. I'll also write a short readme.md on how to work with Coq.
Comment Source:I've decided to follow this course in Coq, and it already hit me in the head, meaning I have still much more to learn after not being able to formalize preorders (on the inductive type level as I presumed possible). Still, I made a promise, so I dug deep in Coq's standard library to find it's default implementation. Those are available here: https://github.com/vukovinski/azimuth-act/blob/master/chapter-1/poset.v My next update should solve some puzzles by providing instances to the classes defined in the file above. I'll also write a short readme.md on how to work with Coq.
@Filip #42 that is a really interesting experiment! I am no expert of coq, so what I say may be completely meaningless. But, could you use some of the typeclasses from the standard library for preorders, posets and ordered sets? I think the definition of preorder there is very close to the one you give in your file. Maybe staying close to the standard library can help to smooth some of the obstacles
Comment Source:@Filip #42 that is a really interesting experiment! I am no expert of coq, so what I say may be completely meaningless. But, could you use some of the typeclasses from the standard library for preorders, posets and ordered sets? I think the definition of preorder there is very close to the one you give in your file. Maybe staying close to the standard library can help to smooth some of the obstacles
Thanks for updating your chart, Scott, and thanks for giving me a heads-up. I've updated my own comment accordingly.
You originally were imagining a thing called an "unordered set":
So those that obey the rule:
unordered: for all x and y, there exists no x,y such that x≤y.
One could make up this notion, but it would be a useless notion: one is saying "take a set and equip it with a relation \(\le\), but also decree that this relation never holds: that is, \(x \le y\) is never true".
This is sort of like defining an adjective "cruncy" by saying
Cruncy (adj.): a property of plants that never holds: no plant is ever cruncy.
One could do it, but it's not much use.
More generally, mathematicians have learned over time, and especially since the invention of category theory, that's it's vastly better to make definitions contain only "positive" properties: that is, properties that don't involve "not" or "no". There are deep reasons for this, but it would take more category theory to explain them!
Comment Source:Thanks for updating your chart, [Scott](https://forum.azimuthproject.org/discussion/comment/16390/#Comment_16390), and thanks for giving me a heads-up. I've updated my own comment accordingly. You originally were imagining a thing called an "unordered set": > So those that obey the rule: > * _**unordered**_: for all x and y, there exists no x,y such that x≤y. One could make up this notion, but it would be a useless notion: one is saying "take a set and equip it with a relation \\(\le\\), but also decree that this relation never holds: that is, \\(x \le y\\) is never true". This is sort of like defining an adjective "cruncy" by saying > **Cruncy** (_adj.)_: a property of plants that never holds: no plant is ever cruncy. One could do it, but it's not much use. More generally, mathematicians have learned over time, and especially since the invention of category theory, that's it's vastly better to make definitions contain only "positive" properties: that is, properties that don't involve "not" or "no". There are deep reasons for this, but it would take more category theory to explain them!
@John #44. Thanks for the explanation. Learning and enjoying!
Comment Source:@John #44. Thanks for the explanation. Learning and enjoying!
Shaaz Ahmed
Could someone explain the skeletality criterion that Fong and Spivak talk about? They use the term poset to refer to a preorder, and state that a partially ordered set (the usual expansion of the term 'poset') has a requirement of 'skeletality'. From their description, and the one on Wikipedia, I understand that skeletality implies that 'isomorphic objects are necessarily identical'.
Can some one provide examples a non-skeletal preorder? I can't think of one, or I don't understand the concept well.
Comment Source:Could someone explain the skeletality criterion that Fong and Spivak talk about? They use the term poset to refer to a preorder, and state that a partially ordered set (the usual expansion of the term 'poset') has a requirement of 'skeletality'. From their description, and the one on Wikipedia, I understand that skeletality implies that 'isomorphic objects are necessarily identical'. Can some one provide examples a _non-skeletal_ preorder? I can't think of one, or I don't understand the concept well.
Keith E. Peterson
@Shaaz #46.
Think of skeletal as being the condition wherein a preorder (or even category), the only thing that matters is whether at least one morphism exists or not. It's skeletal because we're 'gutting out' all other structure except the barebones of the preorder (or category).
Comment Source:@Shaaz #46. Think of skeletal as being the condition wherein a preorder (or even category), the only thing that matters is whether at least one morphism exists or not. It's skeletal because we're 'gutting out' all other structure except the barebones of the preorder (or category).
Anindya Bhattacharyya
@Shaaz #46 – if you imagine a preorder drawn with arrows between elements (so we draw \(x\rightarrow y\) whenever \(x\leq y\)) then a non-skeletal preorder would be one with a non-trivial cycle, eg \(x\rightarrow y\rightarrow z\rightarrow x\)
Comment Source:@Shaaz #46 – if you imagine a preorder drawn with *arrows* between elements (so we draw \\(x\rightarrow y\\) whenever \\(x\leq y\\)) then a *non-skeletal* preorder would be one with a non-trivial cycle, eg \\(x\rightarrow y\rightarrow z\rightarrow x\\)
Thanks @Keith and @Anindya, that makes sense.
Comment Source:Thanks @Keith and @Anindya, that makes sense.
@Keith @Shaaz @Anindya: thanks for the question and explanations.
Assuming I understand right then, this is just different terminology for the fundamental difference between a preorder and a poset. At least, using the common meaning for those things outside the book. Specifically:
A poset must obey antisymmetry (= "skeletality").
That's what differentiates posets from preorders.
Stated alternately, it's antisymmetry that prevents non-trivial cycles.
Is that correct? Thanks.
Comment Source:@Keith @Shaaz @Anindya: thanks for the question and explanations. Assuming I understand right then, this is just different terminology for the fundamental difference between a preorder and a poset. At least, using the common meaning for those things outside the book. Specifically: * A poset must obey antisymmetry (= "skeletality"). * That's what differentiates posets from preorders. Stated alternately, it's antisymmetry that prevents non-trivial cycles. Is that correct? Thanks.
hello world× | CommonCrawl |
Search Results: 1 - 10 of 325631 matches for " Kara S Riehman "
African-American crack abusers and drug treatment initiation: barriers and effects of a pretreatment intervention
Wendee M Wechsberg, William A Zule, Kara S Riehman, Winnie K Luseno, Wendy KK Lam
Substance Abuse Treatment, Prevention, and Policy , 2007, DOI: 10.1186/1747-597x-2-10
Abstract: Using street outreach, 443 African-American crack users were recruited in North Carolina and randomly assigned to either the pretreatment intervention or control group.At 3-month follow-up, both groups significantly reduced their crack use but the intervention group participants were more likely to have initiated treatment.The intervention helped motivate change but structural barriers to treatment remained keeping actual admissions low. Policy makers may be interested in these pretreatment sites as an alternative to treatment for short term outcomes.Sociocultural factors may pose significant barriers for drug abusers seeking health care or substance abuse treatment. These barriers may be particularly problematic for some African-Americans and other disadvantaged populations. To help reduce the negative behaviors and outcomes associated with substance abuse and dependence, new intervention models need to be developed that specifically address the sociocultural environment of ethnic minorities [1]. Moreover, recent research has recognized the need to enhance understanding of crack cocaine dependence and how crack abusers interact with the substance abuse treatment system [2].Crack is a cheaper and smokable form of cocaine that became widely available in the mid-1980s, and it continues to be a public health problem in the United States. Crack use is present among all ethnic groups [3], but it is most common among African-Americans residing in low-income inner-city neighborhoods [4-7]. Findings from the 2001 National Household Survey on Drug Abuse (NHSDA) indicated that African-Americans made up 12% of the U.S. population, but they represented 19% of individuals who had used crack in the past year [8]. In addition, crack dependence rates are reported to be higher among African-Americans than among Hispanics or Whites [4]. Furthermore, cocaine-related emergency room episodes and overdose deaths were more common among African-Americans than any other racial/ethnic group
Concurrent pulmonary Mycobacterium avium complex (MAC) infection and active Hürthle cell thyroid carcinoma: is there a connection? [PDF]
Kara M. Meinke Baehr, Whitney S. Goldner
Health (Health) , 2010, DOI: 10.4236/health.2010.25058
Abstract: We present two cases of pulmonary MAC infection in women with Hürthle cell thyroid carcinoma. Both cases were asymptomatic octogenarian women with active Hürthle cell thyroid carcinoma and prolonged periods of hypothyroidism prior to diagnosis of pulmonary MAC. Mycobacterium avium complex has never been reported in association with any type of thyroid cancer, specifically Hürthle cell carcinoma. A review of the literature and possible associations between the two are discussed in this article.
Identification of Phenolic Substances and Their Seasonal Changesin Sultana and Perlette Grape Cultivars
E. Zeker,S. Kara
Pakistan Journal of Biological Sciences , 1999,
Abstract: Eleven phenolics compounds were detected in grape cultivars Sultana and Perlette on two dimensional TLC. No differences were found in the phenolic content of the cultivars. The phenolic substances in the shoot tips and leaves showed some differences. Spots belonging to the flavonoids and chlorogenic acids changed in size and intensity in some stages of the annual growth cycle of the vine.
Yeni leti im Teknolojileri, Siyasal Kat l m, Demokrasi(New Communication Technologies, Political Participation, Democracy)
Süleyman KARA?OR
Y?netim ve Ekonomi , 2009,
Abstract: Developments in communication technology have increased the possibility of world's culture and identity intersection in everyday. In the past it took weeks even months to spread any events occured in any place to the rest of the world so the effects level of these events were limited. However in or times this stitution has been changed reversely any explanation in anywhere have been realized in all of the world for a few hours. The pace of cultural scientific political and social interaction in the world has increased and became inevitable. Because people have the ability of follow the all news in the word due to new communication tools and communication networks.
Leaching Requirements to Prevent Soil Salinization
Tekin Kara,Lyman S. Willardson
Journal of Applied Sciences , 2006,
Abstract: The purpose of this study was to develop a model to quantify the rate of upward water movement from a shallow water table for different soils with and without plants as a function of water table depth and time, to predict Electrical Conductivity (EC) of the soil in a one-dimensional homogenous soil profile and to develop a water management procedure to control soil profile salinity in the presence of a shallow water table. The model simulates water and solute movement from a shallow water table for a bare soil surface. Salt distribution in the soil profile, caused by a saline shallow water table, was simulated by assuming a steady state upward water movement in the absence of a crop. As water moves upward through a soil profile from a shallow water table, the water evaporates at the surface, leaving the salt behind. Some of the salt moves down to a depth about 30 cm by molecular diffusion. This raises the salt concentration within the top 30 cm of the soil. The model also simulates crop water extraction patterns and consequently the salt distribution patterns in an irrigated soil profile for a specified root distribution. After a fallow season and the resulting salt concentration near the soil surface, the salt redistributes downward because of irrigation water application. Different leaching fractions were used in the simulations. A computer program, for the model SALTCTRL (Salt Control), was written in QBASIC language. The program was tested for two soils for different leaching fractions. The soil parameters needed for the computations were selected from the literature. Application of model results is discussed and recommendations for further research were made.
Phonons of Metallic Vicinal Surfaces
Abdelkader Kara,Talat S. Rahman
Physics , 2001, DOI: 10.1016/S0039-6028(01)01992-6
Abstract: We present an analysis of the vibrational dynamics of metal vicinal surfaces using the embedded atom method to describe the interaction potential and both a real space Green's function method and a slab method to calculate the phonons. We report two main general characteristics : a global shift of the surface vibrational density of states resulting from a softening of the force field. The latter is a direct result of the reduction of coordination for the different type of surface atoms; and an appearance of high frequency modes above the bulk band, resulting from a stiffening of the force field near the step atom. The latter is due to a rearrangement of the atomic positions during the relaxation of the surface atoms yielding a large shortening of the nearest neighbor distances near the step atoms.
Structure, Dynamics and Themodynamics of a metal chiral surface: Cu(532)
Physics , 2005, DOI: 10.1088/0953-8984/18/39/018
Abstract: The structure, vibrational dynamics and thermodynamics of a chiral surface, Cu(532), has been calculated using a local approach and the harmonic approximation, with interatomic potentials based on the embedded atom method. The relaxation of atomic positions to the optimum configuration results in a complex relaxation pattern with strong contractions in the bond length of atoms near the kink and the step site and an equivalently large expansion near the least under-coordinated surface atoms. The low coordination of the atoms on the surface affects substantially the vibrational dynamics and thermodynamics of this system. The local vibrational density of states show a deviation from the bulk behavior that persist down to the 10th layer resulting in a substantial contribution of the vibrational entropy to the excess free energy amounting to about 90 meV per unit cell at 300K.
Some New Paranormed Difference Sequence Spaces Derived by Fibonacci Numbers
E. E. Kara,S. Demiriz
Abstract: In this study, we define new paranormed sequence spaces by the sequences of Fibonacci numbers. Furthermore, we compute the $\alpha-,\beta-$ and $\gamma-$ duals and obtain bases for these sequence spaces. Besides this, we characterize the matrix transformations from the new paranormed sequence spaces to the Maddox's spaces $c_{0}(q),c(q),\ell(q)$ and $\ell_{\infty}(q)$.
The optimization of voltage parameter for tissue electroporation in somatic embryos of Astragalus chrysochlorus (Leguminosae)
N Turgut-Kara, S Ari
African Journal of Biotechnology , 2010,
Abstract: Somatic embryo tissues of Astragalus chrysochlorus were transformed with the b-glucuronidase (GUS) and neomycin phosphotransferase II (npt II) genes by electroporation. The effect of electric field strength was tested for transient expression. It was found that 1000 V/cm and 200 ms and 1 pulse was the optimum combination to transform embryo tissues (expression level was 61.5%). Electroporated somatic embryo tissues were positive for GUS expression and PCR analysis for the genes GUS and npt II. After PCR analysis, we found that the efficiency of the somatic embryos with transient GUS expression by electroporation was 48%.
In vitro plant regeneration from embryogenic cell suspension culture of Astragalus chrysochlorus (Leguminoseae)
Abstract: In vitro plant regeneration was achieved from embryogenic cell suspension culture of Astragalus chrysochlorus. When 30-day-old aseptically grown seedlings were cultured on Murashige and Skoog (MS) medium containing 0.1 mg/l -naphthaleneacetic acid (NAA) plus 1.0 mg/l 6-benzyladenine (BA), friable callus was formed within two weeks from the mesocotyl of the seedling. After three weeks, proliferated actively growing calli were transferred to MS liquid medium containing 2,4- dichlorophenoxyacetic acid (2,4-D), indole-3-acetic acid (IAA) or NAA and subcultured at two week intervals. After two weeks, induction of somatic embryos up to the torpedo stage occured at all tested concentrations of 2,4-D, IAA or NAA. Somatic embryos developed only in MS medium containing 0.5 mg/l IAA within two weeks and 2% of globular embryos were developed into the cotyledonary stage embryos. Eighty one percent of somatic embryos cultured in MS medium supplemented with 0.5 mg/l IAA were found to be diploid by flow cytometric analysis. Plantlet propagation was achieved on half strength MS liquid medium supplemented with 3% (w/v) sucrose after four weeks of culture. After a month on half strength MS medium [1.5% (w/v) sucrose and 0.8% (w/v) agar] 29 of 71 shoots developed into rooted plantlets. | CommonCrawl |
Works by Marek Zawadowski
( view other items matching `Marek Zawadowski`, view all matches )
Marek Zawadowski [12] Marek W. Zawadowski [3]
Undefinability of propositional quantifiers in the modal system S.Silvio Ghilardi & Marek Zawadowski - 1995 - Studia Logica 55 (2):259 - 271.details
We show that (contrary to the parallel case of intuitionistic logic, see [7], [4]) there does not exist a translation fromS42 (the propositional modal systemS4 enriched with propositional quantifiers) intoS4 that preserves provability and reduces to identity for Boolean connectives and.
Modal Logic in Logic and Philosophy of Logic
Polish Philosophy in European Philosophy
A sheaf representation and duality for finitely presented Heyting algebras.Silvio Ghilardi & Marek Zawadowski - 1995 - Journal of Symbolic Logic 60 (3):911-939.details
A. M. Pitts in [Pi] proved that HA op fp is a bi-Heyting category satisfying the Lawrence condition. We show that the embedding $\Phi: HA^\mathrm{op}_\mathrm{fp} \longrightarrow Sh(\mathbf{P_0,J_0})$ into the topos of sheaves, (P 0 is the category of finite rooted posets and open maps, J 0 the canonical topology on P 0 ) given by $H \longmapsto HA(H,\mathscr{D}(-)): \mathbf{P_0} \longrightarrow \text{Set}$ preserves the structure mentioned above, finite coproducts, and subobject classifier, it is also conservative. This whole structure on HA op (...) fp can be derived from that of Sh(P 0 ,J 0 ) via the embedding Φ. We also show that the equivalence relations in HA op fp are not effective in general. On the way to these results we establish a new kind of duality between HA op fp and a category of sheaves equipped with certain structure defined in terms of Ehrenfeucht games. Our methods are model-theoretic and combinatorial as opposed to proof-theoretic as in [Pi]. (shrink)
Category Theory in Philosophy of Mathematics
Mathematical Logic in Philosophy of Mathematics
Model completions and r-Heyting categories.Silvio Ghilardi & Marek Zawadowski - 1997 - Annals of Pure and Applied Logic 88 (1):27-46.details
Under some assumptions on an equational theory S , we give a necessary and sufficient condition so that S admits a model completion. These assumptions are often met by the equational theories arising from logic. They say that the dual of the category of finitely presented S-algebras has some categorical stucture. The results of this paper combined with those of [7] show that all the 8 theories of amalgamable varieties of Heyting algebras [12] admit a model completion. Further applications to (...) varieties of modal algebras are given in [8]. (shrink)
Logic and Philosophy of Logic, Miscellaneous in Logic and Philosophy of Logic
Formal systems for modal operators on locales.Gonzalo E. Reyes & Marek W. Zawadowski - 1993 - Studia Logica 52 (4):595 - 613.details
In the paper [8], the first author developped a topos- theoretic approach to reference and modality. (See also [5]). This approach leads naturally to modal operators on locales (or spaces without points). The aim of this paper is to develop the theory of such modal operators in the context of the theory of locales, to axiomatize the propositional modal logics arising in this context and to study completeness and decidability of the resulting systems.
Computability in Philosophy of Computing and Information
Logical Connectives, Misc in Logic and Philosophy of Logic
Andrew M. Pitts. Interpolation and conceptual completeness for pretoposes via category theory. Mathematical logic and theoretical computer science, edited by Kueker David W., Lopez-Escobar Edgar G. K. and Smith Carl H., Lecture notes in pure and applied mathematics, vol. 106, Marcel Dekker, New York and Basel1987, pp. 301–327. - Andrew M. Pitts. Conceptual completeness for first-order intuitionistic logic: an application of categorical logic. Annals of pure and applied logic, vol. 41 , pp. 33–81. [REVIEW]Marek Zawadowski - 1995 - Journal of Symbolic Logic 60 (2):692-694.details
Logics in Logic and Philosophy of Logic
Descent and duality.Marek W. Zawadowski - 1995 - Annals of Pure and Applied Logic 71 (2):131-188.details
Using the Makkai's duality for first-order logic, we characterise effective descent morphisms in 2-categories of pretoposes and Barr-exact categories. In both cases they coincide with conservative morphisms. We show that in those 2-categories the 2-coregular factorisations are exactly quotient-conservative factorisations. We also prove a generalisation of the Makkai duality for pseudoelementary categories.
From Bisimulation Quantifiers to Classifying Toposes.Silvio Ghilardi & Marek Zawadowski - 2002 - In Frank Wolter, Heinrich Wansing, Maarten de Rijke & Michael Zakharyaschev (eds.), Advances in Modal Logic, Volume 3. CSLI Publications. pp. 193-220.details
Inverse Linking, Possessive Weak Definites and Haddock Descriptions: A Unified Dependent Type Account.Justyna Grudzińska & Marek Zawadowski - 2019 - Journal of Logic, Language and Information 28 (2):239-260.details
This paper proposes a unified dependent type analysis of three puzzling phenomena: inversely linked interpretations, weak definite readings in possessives and Haddock-type readings. We argue that the three problematic readings have the same underlying surface structure, and that the surface structure postulated can be interpreted properly and compositionally using dependent types. The dependent type account proposed is the first, to the best of our knowledge, to formally connect the three phenomena. A further advantage of our proposal over previous analyses is (...) that it offers a principled solution to the puzzle of why both inversely linked interpretations and weak definite readings are blocked with certain prepositions. (shrink)
The Skolem-löwenheim theorem in toposes. II.Marek Zawadowski - 1985 - Studia Logica 44 (1):25 - 38.details
This paper is a continuation of the investigation from [13]. The main theorem states that the general and the existential quantifiers are (, -reducible in some Grothendieck toposes. Using this result and Theorems 4.1, 4.2 [13] we get the downward Skolem-Löwenheim theorem for semantics in these toposes.
Review: Andrew M. Pitts, David W. Kueker, Edgar G. K. Lopez-Escobar, Carl H. Smith, Interpolation and Conceptual Completeness for Pretoposes via Category Theory; Andrew M. Pitts, Conceptual Completeness for First-order Intutionistic Logic: An Application of Categorical Logic. [REVIEW]Marek Zawadowski - 1995 - Journal of Symbolic Logic 60 (2):692-694.details
Pre-Ordered Quantifiers in Elementary Sentences of Natural Language.Marek W. Zawadowski - 1995 - In M. Krynicki, M. Mostowski & L. Szczerba (eds.), Quantifiers: Logics, Models and Computation. Kluwer Academic Publishers. pp. 237--253.details
Generalized Quantifiers in Philosophy of Language
Sheaves over Heyting lattices.Andrzej W. Jankowski & Marek Zawadowski - 1985 - Studia Logica 44 (3):237 - 256.details
For a complete Heyting lattice , we define a category Etale (). We show that the category Etale () is equivalent to the category of the sheaves over , Sh(), hence also with -valued sets, see [2], [1]. The category Etale() is a generalization of the category Etale (X), see [1], where X is a topological space.
The Skolem-löwenheim theorem in toposes.Marek Zawadowski - 1983 - Studia Logica 42 (4):461 - 475.details
The topos theory gives tools for unified proofs of theorems for model theory for various semantics and logics. We introduce the notion of power and the notion of generalized quantifier in topos and we formulate sufficient condition for such quantifiers in order that they fulfil downward Skolem-Löwenheim theorem when added to the language. In the next paper, in print, we will show that this sufficient condition is fulfilled in a vast class of Grothendieck toposes for the general and the existential (...) quantifiers. (shrink) | CommonCrawl |
The Impact of Frequency and Tone of Parent–Youth Communication on Type 1 Diabetes Management
Mark D. DeBoer1,
Rupa Valdez2,
Daniel R. Chernavvsky3,
Monica Grover1,
Christine Burt Solorzano1,
Kirabo Herbert1 &
Stephen Patek4
Diabetes Therapy volume 8, pages 625–636 (2017)Cite this article
The purpose of this study is to assess the impact of frequency and tone of parent–youth communication on glycemic control as measured by the Family Communication Inventory (FCI). Adolescence provides a unique set of diabetes management challenges, including suboptimal glycemic control. Continued parental involvement in diabetes management is associated with improved HbA1c outcomes; however, diabetes-related conflict within the family can have adverse effects. Although it is clear that communication plays an important role in diabetes outcomes, the specific impact of frequency and tone of such communication is largely understudied.
A total of 110 youths with type 1 diabetes and their parents completed questionnaires assessing diabetes-related adherence, family conflict, and family communication (i.e., frequency and tone) during a routine clinic visit. Routine testing of HbA1c was performed.
Youth- and parent-reported frequency of communication were unrelated to HbA1c. Instead, greater discrepancies between parents and children on reported frequency of communication (most commonly parents reporting frequent and youth reporting less frequent communication) corresponded with poorer glycemic control and increased family conflict. More positive tone of communication as rated by youth was associated with lower HbA1c.
Diabetes-related communication is more complex than conveyed simply by how often children and their parents communicate. Tone of communication and discrepancies in a family's perception of the frequency of communication were better than frequency as predictors of glycemic control. The FCI appears to capture the frequency and tone of diabetes-related communication, though larger-scale studies are warranted to inform future use of this scale.
Adolescents with type 1 diabetes (T1D) face a myriad of obstacles to maintaining adequate blood glucose (BG) control, resulting in HbA1c levels that are the highest of any age group [1]. Navigating the division of responsibility of diabetes management tasks between parents and youth is a particularly salient challenge for this population. Although it is recognized that adolescents need to engage in some degree of developmentally appropriate diabetes self-management behaviors to prepare them for life apart from their parents [2–4], it is well established that they commonly have difficulty carrying out some of these tasks [5–9]. In addition to the inherent challenges of adolescence, changes that occur within parent–youth relationships and communication patterns during this developmental transition may also have an impact on diabetes management and glycemic outcome. Continued parental involvement in adolescents' diabetes management is recommended and has been associated with better outcomes (i.e., lower HbA1c) [10–14]. The quality and degree of parental monitoring may also have an impact on a youth's adherence and subsequent glycemic control, with some evidence suggesting that parental monitoring is associated with improved self-efficacy, adherence, and HbA1c in adolescents [15]. However, perceived parental over-involvement has been associated with poorer glycemic control and more episodes of diabetic ketoacidosis [16].
Although family functioning [17] and co-regulation of care between parents and children [12, 13] appear to be important predictors of diabetes control, the role of diabetes-related communication in diabetes management is not fully understood. Most research efforts have focused on the quality of family communication, demonstrating that increased diabetes-related family conflict [7, 18–20], parental negativity [17, 21], and parental criticism [17, 22] are related to suboptimal glycemic control in youth, while perceived parental warmth, effective conflict resolution, and parental positive reinforcement are associated with better glycemic control [23]. Negative family communication, specifically diabetes-related conflict, also has a demonstrated negative impact on both general and diabetes-specific quality of life for youth with T1D [24, 25]. In fact, Laffel and colleagues found that diabetes-related family conflict was the only significant predictor of quality of life after controlling for demographic variables such as age, gender, and duration of diabetes, as well as HbA1c and parental involvement in insulin administration [24].
While previous studies have investigated the relationship between degree of conflict and T1D-related outcomes, they have not examined the role of family communication frequency or valence (positive to negative tone). Valence has the potential to offer additional insights into the impact of family communication on diabetes management because negative tone can encompass more subtle interactions in parent–youth dyads beyond explicit conflict (e.g., sarcasm). Moreover, discrepancies between parent and youth perceptions of the overall frequency and valence of communication may also play an important role in promoting adaptive diabetes care. Previous research has demonstrated that discrepancies in perceptions of family members' responsibility for diabetes care are predictive of poorer metabolic outcomes [26].
The goal of this study was to investigate the role of parent- and youth-reported frequency and valence of communication about T1D in overall glycemic control. To achieve this goal, we developed and tested a T1D communication questionnaire, the Family Communication Inventory (FCI). Our primary hypothesis was that higher frequency and more positive tone of communication between youth and their parents would be associated with lower HbA1c values. Our secondary hypothesis was that greater discrepancies in parent–youth perceptions regarding frequency and tone of communication would be associated with suboptimal metabolic control as determined by higher HbA1c values and poorer diabetes management behaviors.
This study was approved by the University of Virginia (UVA) Social and Behavioral Sciences Institutional Review Board. All procedures followed were in accordance with the ethical standards of the responsible committee on human experimentation (institutional and national) and with the Helsinki Declaration of 1964, as revised in 2013. Informed consent was obtained from all patients for being included in the study. Eligible individuals were youth between the ages of 12 and 18 years and their accompanying parents who were at a clinic visit to receive care at the UVA Diabetes Clinic for T1D. Participants and their accompanying parent were invited to participate in the study by clinic nursing staff at their routine diabetes clinic visit. If two parents were present at the visit, the parent who assumes primary responsibility of the youth's diabetes care was asked to participate. Participants were informed that their responses were completely confidential and that their participation or lack thereof would not affect their clinical care in any way. Upon informed consent and assent, participants and their parents were provided with parent and youth self-report questionnaires to complete independently at the clinic visit. All completed questionnaires were collected by the front desk staff at the end of the clinic visit. The adolescent received a US$20 gift card for participation.
Glycemic control
Glycated hemoglobin (HbA1c) was used to provide an estimate of the youths' glycemic control for the preceding 2–3 months. Clinical nursing staff collected blood samples via finger stick during the clinic visit, which were analyzed using a DCA Vantage Analyzer™ (Siemens AG, Munich, Germany).
Diabetes Family Conflict Scale-Revised (DFCS)
The revised DCFS was used to assess diabetes-specific family conflict over the past month [19]. It consists of 19 items scored on a 3-point Likert scale (1 = never argue, 2 = sometimes argue, 3 = always argue), summed to yield a total score ranging between 19 (no conflict) and 57 (high conflict). The revised DCFS previously demonstrated adequate internal consistency for both youth and caregiver reports (α = 0.85, α = 0.81 respectively) and had high internal consistency with the present sample (youth α = 0.91, parent α = 0.92) [19].
Child Self-Management Scale (CSM)
The CSM was developed for the present study (Supplementary Table 1) to measure youth adherence to diabetes management tasks over the past 2 weeks. It is scored as the mean of six items that assess the frequency of missing specific required self-management tasks (e.g., "Missed taking insulin for a meal"), which are responded to on a 5-point Likert scale (0 = Never, 4 = seven or more times). Higher scores indicate more difficulty with adherence to diabetes management tasks.
Family Communication Inventory (FCI)
The FCI is a nine-item measure created for this study to assess parent–youth communication, including frequency and tone, related to the youth's diabetes management (Table 1). Items were generated by a pediatric endocrinologist and human factors specialist on the basis of clinical and research-related experience interacting with families. Parents and youth were instructed to rate how often they communicated about specific diabetes-related tasks within the past week on a 5-point Likert scale ranging from 0 (never) to 4 (multiple times daily). For each task, they were also asked to rate the tone of the communication on a 5-point Likert scale ranging from 0 (very negative) to 4 (very positive). If a participant indicated that a diabetes-related task was never discussed, there was an option to indicate that the tone of the communication was "not applicable." Higher item mean scores on frequency of communication (FCom) indicate more frequent communication, and higher item mean scores on tone of communication (TCom) indicate more positive tone.
Table 1 Family communication scales: frequency and tone of communication
Discrepancy Data
Evidence suggests that discrepancies in perspectives on diabetes care between children and parents can negatively impact overall diabetes control [26]. To test whether this association is also the case for frequency and tone of communication, we developed a measure to calculate the mean difference in response to FCI items between each youth–parent dyad. The measure is akin to a standard deviation and is given by Eq. 1 where x is each item (e.g., FCom 4) and n is the total number of items on the scale:
$${\text{Standard deviation}}_{\text{Agreement}} = \sqrt {\frac{{\sum\nolimits_{x = 1}^{n} {\left( {{\text{Parent}}\;{\text{score}}_{{{\text{item}}\;x}} - {\text{Youth}}\;{\text{score}}_{{{\text{item}}\;x}} } \right)} }}{{N\;{\text{items}}}}^{2} }$$
Disagreement score is calculated by taking the square root of the sum of squared differences of all scale items divided by the total number of items. Disagreement scores give the mean difference of reported frequency and tone between parents and youth, or the magnitude of discrepancy. A disadvantage of this measure is that it removes the direction of differences (i.e., whether youth believe there is more frequent communication than parents). Therefore, we separately summed the total number of items where parents or youth endorsed higher values on the FCI scales to quantify the direction of discrepancies in communication.
Participant Characteristics
We assessed a total of 110 participants with T1D (50% female), with a mean age of 14.5 years (range 12–18). Participants' medical characteristics included a mean duration of diabetes of 6.6 years (range 0.04–15) and mean HbA1c was 8.7% (71.6 mmol/mol) (range 5.6–14.0%; 37.7–129.5 mmol/mol)—above the level of 7.5% (58.5 mmol/mol) recommended by the American Diabetes Association for this age range [27].
Frequency of Communication (FCom)
Scale Characteristics
Table 1 shows the mean, standard deviation, and correlations between parents and youth for each FCom item, while Supplementary Table 2 provides the number or responses to each item. Averaging across items, parent (M = 2.13 ± 0.69) and youth (M = 2.14 ± 0.64) scores correlated highly on the frequency of diabetes communication (r = 0.60, n = 109, p < 0.0005, r 2 = 36.5%). Cronbach's alphas for youth (α = 0.84) and parents (α = 0.81) were good for the nine-item scale. Exploratory factor analysis (EFA) conducted with principal axis factoring revealed that all FCom items loaded onto a single factor at Eigen values greater than 0.30 for both parents and youth respondents (see Table 2), while a two-factor solution yielded cross loading on multiple items.
Table 2 Factor loadings for parents and youth on the frequency of communication (FCom) items
On average, parents and youth disagreed by less than 1 point per FCom item (M = 0.85 ± 0.63, range = 0.0–2.67). Overall, these discrepancies were balanced, with youth and parents reporting more communication on an average of 1.89 items and 1.86 items, respectively, t (100) = 0.094, p = 0.925.
Relationship to HbA1c
In separate linear regression models, neither youth nor parent mean FCom scores significantly predicted HbA1c after controlling for youth age, duration of diabetes, and gender. However, FCom disagreement score was positively associated with HbA1c (standardized β = 0.22, t (99) = 2.27, p = 0.026), suggesting that more youth–parent disagreement about frequency of communication corresponded with higher HbA1c scores.
Relationship to DFCS
Table 3 displays Pearson's correlations between youth and parent FCom scores and scores on the DFCS. No significant relationships emerged between mean FCom scores or total conflict scores for parents or youth. However, a positive correlation was found between FCom disagreement scores and parent and youth total conflict scores, suggesting that greater disagreement about frequency of communication was associated with more family conflict as reported by both youth and their parents.
Table 3 Pearson's correlations between frequency/tone of communication, the family conflict scale, and the child self-management scale
Tone of Communication (TCom)
Table 1 shows the mean, standard deviation, and correlation with tone for all respective FCI items, and correlations between parents and youth ratings for each TCom item, while Supplementary Table 2 provides the number or responses to each item. Parent mean TCom scores (M = 3.71 ± 0.67) highly correlated with youth mean scores (M = 3.73 ± 0.63) (r = 0.83, n = 51, p < 0.001, r 2 = 69.1%). Although a single-factor TCom scale appears to have face validity for parents and youth, conducting EFA and Cronbach's alpha analysis was deemed inappropriate because families who did not report communicating about a particular topic were unable to endorse whether any communication on that topic was positive or negative (i.e., there could not have been a particular tone of communication if no communication occurred on that topic in the given time frame). In total 39 youths and 36 parents responded to all nine TCom items, with individual items receiving response rates between 50.0% and 92.7% (youth) and 45.5–90.9% (parents).
To ensure that parent–youth dyad tone scores could be adequately compared, discrepancy scores were only calculated for dyads that responded to at least seven of the same TCom items. For the 48 dyads meeting this criterion, parents and youth disagreed by an average of less than 1 point per TCom item (M = 0.49 ± 0.39, range = 0.0–1.27).
In a linear regression model, more positive youth TCom scores were associated with lower HbA1c after controlling for youth age, duration of diabetes, and gender (standardized β = −0.45, t (64), p < 0.001), but no associations were found for TCom parent mean or discrepancy scores. Again, we performed separate regressions to test if individual TCom items significantly predicted HbA1c, after controlling for youth age, duration of diabetes, and gender. All significant youth and parent TCom items indicated that better metabolic control was linked to more positive tone of communication (see Table 1).
Table 3 also shows Pearson's correlations between parent/youth DFCS scores and parent/youth mean TCom scores; there were 107 fully completed parent/youth surveys. Parent TCom scores correlated negatively with both parent and youth conflict scores, suggesting that more positive communication was associated with less perceived family conflict. This relationship was also found between youth TCom scores and parent and youth conflict scores. Finally, TCom disagreement scores were positively related to both parent and youth conflict scores, suggesting that more disagreement about the tone of communication was related to greater perceived family conflict.
Child self-management items, mean scores, and correlations between parents and youth are shown in Supplementary Table 1; there were 109 fully completed parent/youth surveys. Cronbach's alphas for youth (α = 0.66) and parents (α = 0.70) were lower than expected, but similar to previous adherence measures [28]. In separate models controlling for youth age, duration of diabetes, and gender, mean CSM score was positively associated with HbA1c for both youth (standardized β = 0.44, t (108) = 4.87, p < 0.001) and parents (standardized β = 0.36, t (108) = 3.71, p < 0.001). This suggests a relationship between more parent/youth-reported frequency of lapses in diabetes management behaviors and suboptimal youth diabetes control. Greater disagreement between parents and youth on the CSM also corresponded with higher HbA1c (standardized β = 0.30, t (106) = 3.22, p = 0.002).
Table 3 shows Pearson's correlations between the CSM and FCom/TCom scores. There was a significant negative association between parent mean FCom scores and youth mean CSM scores, suggesting that more frequent parent reported communication was related to fewer missed diabetes management behaviors. Greater disagreement on the FCom scale positively related to mean parent, mean youth, and disagreement scores on the CSM scale. This suggests that more disagreement between youth and parents about frequency of communication coincided with increased frequency of lapses in diabetes management behaviors, and greater discrepancy between youth and parents about how often lapses occurred. Finally, higher mean parent, mean youth, and disagreement scores on the CSM were associated with more negative tone as reported by parents and youth.
Full Multivariate Model Predicting HbA1c
As a final exploratory analysis, hierarchical multiple regression was used to test adherence (measured through the CSM) as a potential mediator for the relationship between youth mean TCom and FCom disagreement scores with HbA1c. There was evidence of collinearity between parent- and youth-reported CSM scores; therefore, only youth mean CSM scores were used in the analysis (results were similar using parent mean scores). Entering age, duration of diabetes, gender, and mean youth CSM scores yielded a significant regression model, F (4, 55) = 4.98, p = 0.002, which accounted for 26.6% of the variance in HbA1c. Adding youth TCom and FCom disagreement scores explained an additional 7.2% of the variance, with this change trending toward significance, F (2, 53) = 2.90, p = 0.064. In the full multivariate model, FCom disagreement scores were not significantly associated with HbA1c (standardized β = 0.090, t (59) = 0.72, p = 0.477), while youth mean CSM (standardized β = 0.35, t (59) = 2.91, p = 0.005) and youth mean TCom (standardized β = −0.28, t (59) = −2.21, p = 0.031) scores related significantly to adolescent glycemic control.
This is the first study to examine the frequency and tone of communication between youth and their parents on various diabetes management behaviors. Contrary to the primary hypothesis, no associations were found between overall frequency of communication and glycemic control. Additionally, there were no significant associations between HbA1c and parent-reported tone of communication or parent–youth disagreement about tone of communication. Instead, results indicated that HbA1c was significantly related to the disagreement between youth- and parent-reported frequency of communication, with greater disagreement being associated with poorer glycemic control. HbA1c was also significantly associated with tone of communication as reported by the adolescent, where more negative tone correlated with higher HbA1c. These findings are consistent with previous research on diabetes-related family discrepancies in perceptions about responsibility and communication for aspects of diabetes management [2, 16, 17, 26]. After including adherence in the regression model, FCom disagreement scores no longer contributed significantly to HbA1c. This finding suggests that discrepancies about frequency of communication may reflect the presence of less than ideal family communication that contribute to more lapses in diabetes management behaviors which in turn contributes to suboptimal glycemic control. This suggestion is similar to the findings in the diabetes family conflict literature, wherein greater family conflict indirectly contributed to poorer glycemic control by decreasing self-care behaviors [7, 29]. From a clinical perspective, widely discordant views on diabetes-related issues between parents and youth may signal to the provider that interventions promoting adaptive communication and conflict resolution skills may be of particular benefit [10, 30]. Annual administration of a diabetes communication survey may also help providers screen for and track parent–youth communication discrepancies to help determine if additional, more intensive intervention is needed.
This study also found no effect of parent- and youth-reported frequency of communication on glycemic control and adherence. One possible explanation is that although raw frequency of communication may reflect one aspect of parental involvement, it is necessary to know whether that involvement tends to be positive or negative [14]. For example, some youth perceive their parents' frequent communication as "nagging" [31], while others perceive their parents, specifically fathers, to be under-involved, despite efforts to include them in treatment discussions [32]. Consistent with these findings, results from the present study indicate that frequency of communication generally did not correlate with the tone of communication, with the exception of one item (discussed missed insulin boluses), where greater communication about missed boluses was associated with more negative tone (see Table 1). In cases of mismatched parent-youth communication, research shows increased risk of suboptimal diabetes management [16, 33].
It is also plausible that frequency of communication is differentially related to parameters of glycemic control depending on individual-specific diabetes management behaviors. As an additional exploratory items analysis to test this hypothesis, we performed separate regressions to test if individual FCom items significantly predicted HbA1c, after controlling for youth age, duration of diabetes, and gender (see Table 1). When examining FCom items, results indicated that more parent- and youth-reported communication about hypoglycemia (e.g., discussed particular low blood sugar; discussed frequency/number of low blood sugars) corresponded to lower HbA1c values. In contrast, increased communication about hyperglycemia as reported by youth (e.g., discussed missed insulin boluses; discussed frequency/number of high blood sugars) was associated with higher HbA1c. These findings suggest that parents and youth tend to communicate most frequently about issues most relevant to the way in which youth manage their diabetes. That is, when youth maintain tighter glycemic control (and thus are at a higher risk for hypoglycemic events) parent–youth dyads communicate more frequently about low BG values. However, when youth are in suboptimal control, high BG values and insulin dosing are discussed more frequently. If this is the case, increasing the overall frequency of communication is likely inadequate to fully address problem areas in diabetes management without examining all of these self-management factors.
Finally, this study assessed the tone of communication about diabetes management. Consistent with our hypothesis, lower HbA1c values were associated with more youth-perceived positive communication beyond the effects of adherence. However, there was no association between glycemic control and parent-perceived tone or discrepancy between parents and youth on tone of communication. Past research generally supports these findings for youth-reported family communication behaviors, with most studies demonstrating improved glycemic control with increased positive communication behaviors (i.e., support, love, acceptance, warmth) [15, 17, 34, 35], and poorer glycemic control with more youth-reported negative communication styles (i.e., anger, interruption, unsupportiveness) [17, 22, 36]. There is some evidence that mother-reported positive communication behaviors are associated with better glycemic control [35], and negative behaviors are related to worsened control [36], but these findings are inconsistent [34, 35]. No identified research has examined the relationship between discrepancies in tone of communication and glycemic control. The non-significant finding in this study may be due to the limited power to explore discrepancies in parent–youth dyads for tone, but future research will need to establish if this is the case.
Although the results of this study are informative, there are several methodological limitations. As a result of the anonymity of the survey, we were unable to identify whether the mother or father participated, limiting our ability to draw more specific conclusions about differences in communication. We also lack information regarding other demographic characteristics of the participants and how many declined the survey, limiting generalizability of the findings. Additionally, the questionnaires selected for this study were limited to promote efficiency and to reduce participant burden. Consequently, additional relevant communication concepts, such as parental monitoring [37, 38], and family responsibility [26] were not assessed. While the CSM and FCI had thus not previously been validated, we took multiple steps to maintain rigor in their formulation and assessment, described below. The CSM assessed diabetes care behaviors and, as seen in other validated behavior scales, exhibited acceptable reliability and correlated significantly with HbA1c levels [17]. The FCI assessed concepts for the most part not covered by other tools but was formulated by consulting other family diabetes scales to inform the manner of assessment items. We noted a high correlation between TCom and a previously validated tool, the Family Conflict Scale [11]. We further evaluated Cronbach alpha scores for the FCom scale, which appeared to measure a single factor with high internal reliability. Nevertheless, the psychometric properties of the TCom scale could not be fully evaluated given that parents and youth did not report communicating about certain diabetes management behaviors within the designated time frame (i.e., 1 week), because of questions regarding tone of communication were not relevant to families not reporting recent communication, only 33% of participants having data from all questions regarding the tone of communication—rendering inadequate power for Cronbach alpha analyses. Future iterations of the inventory should consider larger sample sizes or assessing tone/frequency over a longer time period (i.e., 1 month) or implementing a more general measure of tone for each item (i.e., "when you talk about this topic, is communication positive or negative?") and performing further validation against other external outcomes or—in the absence of similar tools—with direct observational data.
In spite of the limitations, this preliminary study highlights the complexity of communication in diabetes management and challenges the overly broad notion that more communication leads to improved diabetes control. In fact, in the present study, valence of communication as measured by tone and discrepancies in parent and youth perceptions about how often they are communicating about diabetes management tasks had higher correlations with overall glycemic control than frequency of communication, suggesting that these areas warrant further investigation. In addition, future larger-scale studies are needed to further examine the association between parent–youth discrepancies in tone of communication and glycemic control.
Gerstl EM, Rabl W, Rosenbauer J, et al. Metabolic control as reflectet by HbA1c in children, adolescents and young adults with type-1 diabetes mellitus: combined longitudinal analysis including 27,035 patients from 207 centers in Germany and Austria during the last decade. Eur J Pediatr. 2008;167:447–53.
Hanna KM, Juarez B, Lenss SS, Guthrie D. Parent-adolescent communication and support for diabetes management as reported by adolescents with type 1 diabetes. Issues Compr Pediatr Nurs. 2003;26:145–58.
Wysocki T, Meinhold P, Cox DJ, Clarke WL. Survey of diabetes professionals regarding developmental changes in diabetes self-care. Diabetes Care. 1990;13:65–8.
Sawyer SM, Aroni RA. Self-management in adolescents with chronic illness. What does it mean and how can it be achieved? Med J Aust. 2005;183:405–9.
Guilfoyle SM, Crimmins NA, Hood KK. Blood glucose monitoring and glycemic control in adolescents with type 1 diabetes: meter downloads versus self-report. Pediatr Diabetes. 2011;12:560–6.
Campbell M, Schatz D, Chen V, et al. A contrast between children and adolescents with excellent and poor control: the T1D exchange clinic registry experience. Pediatr Diabetes. 2014;15:110–7.
Hilliard ME, Wu YP, Rausch J, Dolan LM, Hood KK. Predictors of deteriorations in diabetes management and control in adolescents with type 1 diabetes. J Adolesc Health. 2013;52:28–34.
Olinder AL, Kernell A, Smide B. Missed bolus doses: devastating for metabolic control in CSII-treated adolescents with type 1 diabetes. Pediatr Diabetes. 2009;10:142–8.
VanderWel BW, Messer LH, Horton LA, et al. Missed insulin boluses for snacks in youth with type 1 diabetes. Diabetes Care. 2010;33:507–8.
Laffel LMB, Vangsness L, Connell A, Goebel-Fabbri A, Butler D, Anderson BJ. Impact of ambulatory, family-focused teamwork intervention on glycemic control in youth with type 1 diabetes. J Pediatr. 2003;142:409–16.
Anderson BJ, Vangsness L, Connell A, Butler D, Goebel-Fabbri A, Laffel LM. Family conflict, adherence, and glycaemic control in youth with short duration type 1 diabetes. Diabet Med. 2002;19:635–42.
Vesco AT, Anderson BJ, Laffel LM, Dolan LM, Ingerski LM, Hood KK. Responsibility sharing between adolescents with type 1 diabetes and their caregivers: importance of adolescent perceptions on diabetes management and control. J Pediatr Psychol. 2010;35:1168–77.
Ellis DA, Podolski CL, Frey M, Naar-King S, Wang B, Moltz K. The role of parental monitoring in adolescent health outcomes: impact on regimen adherence in youth with type 1 diabetes. J Pediatr Psychol. 2007;32:907–17.
Wysocki T, Taylor A, Hough BS, Linscheid TR, Yeates KO, Naglieri JA. Deviation from developmentally appropriate self-care autonomy. Association with diabetes outcomes. Diabetes Care. 1996;19:119–25.
Berg CA, King PS, Butler JM, Pham P, Palmer D, Wiebe DJ. Parental involvement and adolescents' diabetes management: the mediating role of self-efficacy and externalizing and internalizing behaviors. J Pediatr Psychol. 2011;36:329–39.
Cameron FJ, Skinner TC, de Beaufort CE, et al. Are family factors universally related to metabolic outcomes in adolescents with type 1 diabetes? Diabet Med. 2008;25:463–8.
Lewin AB, Heidgerken AD, Geffken GR, et al. The relation between family factors and metabolic control: the role of diabetes adherence. J Pediatr Psychol. 2006;31:174–83.
Drotar D, Ittenbach R, Rohan JM, Gupta R, Pendley JS, Delamater A. Diabetes management and glycemic control in youth with type 1 diabetes: test of a predictive model. J Behav Med. 2013;36:234–45.
Hood KK, Butler DA, Anderson BJ, Laffel LM. Updated and revised diabetes family conflict scale. Diabetes Care. 2007;30:1764–9.
Miller-Johnson S, Emery RE, Marvin RS, Clarke W, Lovinger R, Martin M. Parent-child relationships and the management of insulin-dependent diabetes mellitus. J Consult Clin Psychol. 1994;62:603–10.
Geffken GR, Lehmkuhl H, Walker KN, et al. Family functioning processes and diabetic ketoacidosis in youths with type I diabetes. Rehabil Psychol. 2008;53:231–7.
Duke DC, Geffken GR, Lewin AB, Williams LB, Storch EA, Silverstein JH. Glycemic control in youth with type 1 diabetes: family predictors and mediators. J Pediatr Psychol. 2008;33:719–27.
Martin MT, Miller-Jonson S, Kitzmann KM, Emery RE. Parent-child relationships and insulin-dependent diabetes mellitus: observational ratings of clinically relevant dimensions. J Fam Psychol. 1998;12:102–11.
Laffel LM, Connell A, Vangsness L, Goebel-Fabbri A, Mansfield A, Anderson BJ. General quality of life in youth with type 1 diabetes: relationship to patient management and diabetes-specific family conflict. Diabetes Care. 2003;26:3067–73.
Weissberg-Benchell J, Nansel T, Holmbeck G, et al. Study SCotFMoD: generic and diabetes-specific parent-child behaviors and quality of life among youth with type 1 diabetes. J Pediatr Psychol. 2009;34:977–88.
Anderson BJ, Holmbeck G, Iannotti RJ, et al. Dyadic measures of the parent-child relationship during the transition to adolescence and glycemic control in children with type 1 diabetes. Fam Syst Health. 2009;27:141–52.
American Diabetes Association. (11) Children and adolescents. Diabetes Care. 2015;38(Suppl):S70–6.
Lewin AB, LaGreca AM, Geffken GR, et al. Validity and reliability of an adolescent and parent rating scale of type 1 diabetes adherence behaviors: the Self-Care Inventory (SCI). J Pediatr Psychol. 2009;34:999–1007.
Hilliard ME, Guilfoyle SM, Dolan LM, Hood KK. Prediction of adolescents' glycemic control 1 year after diabetes-specific family conflict: the mediating role of blood glucose monitoring adherence. Arch Pediatr Adolesc Med. 2011;165:624–9.
Wysocki T, Harris MA, Buckloh LM, et al. Randomized trial of behavioral family systems therapy for diabetes: maintenance of effects on diabetes outcomes in adolescents. Diabetes Care. 2007;30:555–60.
Weinger K, O'Donnell KA, Ritholz MD. Adolescent views of diabetes-related parent conflict and support: a focus group analysis. J Adolesc Health. 2001;29:330–6.
Seiffge-Krenke I. "Come on, say something, dad!": communication and coping in fathers of diabetic adolescents. J Pediatr Psychol. 2002;27:439–50.
Wiebe DJ, Berg CA, Korbel C, et al. Children's appraisals of maternal involvement in coping with diabetes: enhancing our understanding of adherence, metabolic control, and quality of life across adolescence. J Pediatr Psychol. 2005;30:167–78.
Berg CA, Butler JM, Osborn P, et al. Role of parental monitoring in understanding the benefits of parental acceptance on adolescent adherence and metabolic control of type 1 diabetes. Diabetes Care. 2008;31:678–83.
Wysocki T, Harris MA, Buckloh LM, et al. Randomized, controlled trial of behavioral family systems therapy for diabetes: maintenance and generalization of effects on parent-adolescent communication. Behav Ther. 2008;39:33–46.
Iskander JM, Rohan JM, Pendley JS, Delamater A, Drotar D. A 3-year prospective study of parent-child communication in early adolescents with type 1 diabetes: relationship to adherence and glycemic control. J Pediatr Psychol. 2015;40:109–20.
Ellis DA, Templin TN, Podolski CL, Frey MA, Naar-King S, Moltz K. The parental monitoring of diabetes care scale: development, reliability and validity of a scale to evaluate parental supervision of adolescent illness management. J Adolesc Health. 2008;42:146–53.
Palmer DL, Osborn P, King PS, et al. The structure of parental involvement and relations to disease management for youth with type 1 diabetes. J Pediatr Psychol. 2011;36:596–605.
The U.S. National Library of Medicine 1R01LM012090 (MDD, RV, DRC, SV) funded the study and contributed toward article processing charges. The remainder of article processing charges were paid for by the authors. All named authors meet the International Committee of Medical Journal Editors (ICMJE) criteria for authorship for this manuscript, take responsibility for the integrity of the work as a whole, and have given final approval to the version to be published. We would also like to acknowledge the support of Jackie Shepard, Jesse Grabman, and Linda Gonder-Frederick for their invaluable assistance in the assessment of these tools.
Mark D. DeBoer, Rupa Valdez, Daniel R. Chernavvsky, Monica Grover, Christine Burt Solorzano, Kirabo Herbert and Stephen Patel have nothing to disclose.
Compliance with Ethics Guidelines
All procedures followed were in accordance with the ethical standards of the responsible committee on human experimentation (institutional and national) and with the Helsinki Declaration of 1964, as revised in 2013. Informed consent was obtained from all patients for being included in the study.
The datasets during and/or analyzed during the current study are available from the corresponding author on reasonable request.
This article is distributed under the terms of the Creative Commons Attribution-NonCommercial 4.0 International License (http://creativecommons.org/licenses/by-nc/4.0/), which permits any noncommercial use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Department of Pediatrics, University of Virginia Health System, Charlottesville, VA, USA
Mark D. DeBoer, Monica Grover, Christine Burt Solorzano & Kirabo Herbert
Department of Public Health Sciences, University of Virginia School of Medicine, Charlottesville, VA, 22908, USA
Rupa Valdez
Department of Psychiatry and Neurobehavioral Sciences, University of Virginia School of Medicine, Charlottesville, VA, 22908, USA
Daniel R. Chernavvsky
Department of Systems and Information Engineering, University of Virginia School of Medicine, Charlottesville, VA, 22908, USA
Stephen Patek
Mark D. DeBoer
Monica Grover
Christine Burt Solorzano
Kirabo Herbert
Correspondence to Mark D. DeBoer.
Enhanced Content
To view enhanced content for this article go to http://www.medengine.com/Redeem/8C08F0601556E12B.
Below is the link to the electronic supplementary material.
Supplementary material 1 (DOCX 12 kb)
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
DeBoer, M.D., Valdez, R., Chernavvsky, D.R. et al. The Impact of Frequency and Tone of Parent–Youth Communication on Type 1 Diabetes Management. Diabetes Ther 8, 625–636 (2017). https://doi.org/10.1007/s13300-017-0259-2
Issue Date: June 2017 | CommonCrawl |
Motional EMF and Conservation of energy
Consider a conducting rod moving in a uniform magnetic field $\vec{B}$ with a uniform velocity $\vec{v}$. According to the theory involved, the electrons experience the magnetic force ($-e\cdot\vec{v}\times\vec{B}$) and will shift to one end of the rod, creating a positive charge on one side and negative on another.
This causes the existence of Electric Field and hence the potential energy associated with it. $\vec{B}$ does no work on the electrons or any of the charged particles. Therefore no work has been done in moving the charges to the places they have moved. But the charge separation has a potential energy which is greater than when the conductor was neutral. Therefore, it seems now that without doing any work, we have "created" energy in the form of potential energy. Where is the fallacy in this thinking?
electromagnetism magnetic-fields energy-conservation
$\begingroup$ "... B⃗ does no work on the electrons or any of the charged particles. Therefore no work has been done" that is invalid reasoning. Magnetic has not done work, that's true, but the agent that made the rod move did work on the rod and the rod did work on the charges. $\endgroup$ – Ján Lalinský Jul 20 '15 at 19:10
I would say that we're putting in work to set the rod in motion, but the argument could be made that it could already have been in motion. So, consider a rod moving at constant velocity, in vacuum in a magnetic field B, no force would have to be provided and but there would still be an electric field due to charge separation. However, unless you stop the rod, or otherwise change its motion, you would not be able to 'tap into' the potential energy of that field because that is the balanced configuration of the system (attraction between -ve and +ve charges offset by magnetic force due to B. In fact, if it weren't for the electric field, there would be unbalanced forces on the rod!) Simply connecting a wire between the two points wouldn't result in a current, because the system is already in equilibrium, so it isn't really potential energy! So without doing some external work to the rod, (either by stopping it, changing its velocity or breaking it in half to get two separately charged pieces, etc) you haven't actually created any new potential energy, although it might seem like it to you, when observed from rest.
NilaNila
Not the answer you're looking for? Browse other questions tagged electromagnetism magnetic-fields energy-conservation or ask your own question.
Deriving expression for motional emf
Does a moving magnetic field produce an electric field?
What force causes the induced EMF of a loop? And, the difference between a loop EMF to motional EMF?
how is motional EMF developed?
The 2 Forces on the Conductor having induced Motional EMF
Confusion about induced emf vs motional emf
What is "electric field causes current in a conductor (metal wire)" exactly?
EMF generated by a rotating rod can be zero? | CommonCrawl |
Climate signals in river flood damages emerge under sound regional disaggregation
Reconciling disagreement on global river flood changes in a warming climate
Shulei Zhang, Liming Zhou, … Yongjiu Dai
Changing climate both increases and decreases European river floods
Günter Blöschl, Julia Hall, … Nenad Živković
Enhancement of river flooding due to global warming
Haireti Alifu, Yukiko Hirabayashi, … Hideo Shiogama
Increased human and economic losses from river flooding with anthropogenic warming
Francesco Dottori, Wojciech Szewczyk, … Luc Feyen
Seasonality of climatic drivers of flood variability in the conterminous United States
Jesse E. Dickinson, Tessa M. Harden & Gregory J. McCabe
Deciphering human influence on annual maximum flood extent at the global level
Maurizio Mazzoleni, Francesco Dottori, … Giuliano Di Baldassarre
Climate change impact on flood and extreme precipitation increases with water availability
Hossein Tabari
Floods differ in a warmer future
Conrad Wasko
Floods and rivers: a circular causality perspective
G. Sofia & E. I. Nikolopoulos
Inga J. Sauer ORCID: orcid.org/0000-0002-9302-21311,2,
Ronja Reese ORCID: orcid.org/0000-0001-7625-040X1,
Christian Otto ORCID: orcid.org/0000-0001-5500-67741,
Tobias Geiger ORCID: orcid.org/0000-0002-8059-82701,3,
Sven N. Willner ORCID: orcid.org/0000-0001-6798-62471,
Benoit P. Guillod ORCID: orcid.org/0000-0003-1807-69972,4,
David N. Bresch ORCID: orcid.org/0000-0002-8431-42632,5 &
Katja Frieler ORCID: orcid.org/0000-0003-4869-30131
Climate-change impacts
Climate change affects precipitation patterns. Here, we investigate whether its signals are already detectable in reported river flood damages. We develop an empirical model to reconstruct observed damages and quantify the contributions of climate and socio-economic drivers to observed trends. We show that, on the level of nine world regions, trends in damages are dominated by increasing exposure and modulated by changes in vulnerability, while climate-induced trends are comparably small and mostly statistically insignificant, with the exception of South & Sub-Saharan Africa and Eastern Asia. However, when disaggregating the world regions into subregions based on river-basins with homogenous historical discharge trends, climate contributions to damages become statistically significant globally, in Asia and Latin America. In most regions, we find monotonous climate-induced damage trends but more years of observations would be needed to distinguish between the impacts of anthropogenic climate forcing and multidecadal oscillations.
Since 1980, fluvial floods have caused more than 200,000 fatalities and more than $790 bn in direct economic damages globally1, placing them among the most socially and economically devastating natural disasters. Theoretical considerations on the global surface energy budget suggest that global mean precipitation increases with global mean temperature (GMT) at a rate of 1–2% per thousand of global mean warming2. However, the intensity of extreme precipitation events is most relevant for fluvial flooding3 and increases with the moisture of air that can be precipitated out according to the Clausius–Clapeyron relationship4. Therefore, extreme daily precipitation is expected to increase at a substantially higher rate of ~6–7% per degree of global mean warming5. These theoretical considerations were recently confirmed by observations showing a global median increase in annual maximum daily precipitation of 5.9–7.7% per degree of global warming6. In addition, there are more record-breaking rainfall events observed than would be expected in a stationary climate (12% increase in 1981–20107) and the observed intensification of extreme daily precipitation events since the 1980s has been attributed to anthropogenic global warming8. Observed annual discharge maxima show regionally varying trends with significant increases in most stations of Asia, Europe, and Latin America and with mostly decreasing trends in Africa, Australia, and North America9. Globally, 1985–2009 flood frequency has first increased, peaked around 2003, and decreased afterwards10. Extreme flood events show a similar non-monotonous temporal evolution with strongest long-term trends in Europe and the United States of America11. On global and latitudinal scales, the observed variation in flood frequencies can be statistically explained by variations of four decadal and multidecadal climate oscillations: the El Niño–Southern Oscillation (ENSO), the Pacific Decadal Oscillation (PDO), the North Atlantic Oscillation (NAO), and the Atlantic Multidecadal Oscillation (AMO)10.
So far, trends in global flood-induced economic damages have been shown to be dominated by increasing exposure and decreasing vulnerability12,13,14, with no detectable climate-driven trend remaining after removal of socio-economic effects at the global scale as well as on the level of world regions. This finding is independent of the regions' development level12,15,16,17 and income groups12. However, these studies focus on the detection of changes in vulnerability and therefore considered world regions that have been defined to be homogeneous with respect to socio-economic indicators, but not with regard to climate-induced changes in weather-related hazard indicators. This aggregation across heterogeneous trends in hazards could hide the signal of climate change.
In this work, we investigate to what extent the observed changes in climate have already induced long-term trends in economic damages caused by fluvial flooding. To disentangle the impact of climate-induced changes in weather-related hazards (flood extent and depth) from changes in exposure of assets, and their vulnerability, we develop a hybrid process-based and empirical model. First, it overlays annual flooded areas derived from hydrological simulations forced by observational weather data12,13 with spatially and temporally explicit asset distributions. The exposed assets are then translated into direct economic damages by combining continental depth-damage functions18 with time-dependent vulnerability factors12,13,14 (Methods and Supplementary Figs. 1 and 2). Addressing the question to what degree reported time series of damages are influenced by climate change, we first verify that discharge trends modeled by the considered global hydrological models (GHMs) (Fig. 1a and Supplementary Fig. 3) compare well with observed trends919,20,21, when the GHMs are driven by observed weather data (Methods and Supplementary Note 1).
Fig. 1: Discharge trends and definition of regions.
a Absolute trends in annual maximum daily discharge in the time period 1971–2010 (significance levels are shown in Supplementary Fig. 3). b Map of the nine geographical world regions: North America (NAM), Eastern Asia (EAS), Europe (EUR), Latin America (LAM), Central Asia & Russia (CAS), South & Sub-Saharan Africa (SSA), South & South-East Asia (SEA), North Africa & Middle East (NAF), Oceania (OCE) chosen according to geographical proximity and similarity of socio-economic structure. These regions are then further divided into subregions assembled of river basins with positive (R+, dark colors) and negative discharge trends (R–, light colors) (Supplementary Fig. 4).
We then use the modeled trends in discharge to disaggregate nine standard, socio-economically homogeneous world regions (R)22 into subregions R+ and R– comprising the river basins with positive and negative basin-average trends in discharge, respectively (Fig. 1b, Supplementary Fig. 4, and Methods). While on the level of world regions, climate-induced damage trends are mostly averaged out, they become clearly detectable and significant in the subregions with homogeneous discharge trends in the studied historical period.
Climate signal in flood damages
When analyzing the contributions of the individual drivers (climate-induced changes in weather-related hazards, changes in exposure, and changes in the vulnerability of assets) to damage trends, we focus on regions where the full model accounting for all three drivers explains at least 20% of the variance in reported damages (in units of inflation adjusted 2005 purchasing power parities (PPP) USD) (gray panels in Fig. 2) indicating that at least parts of the critical processes determining the variability in damages are captured. In North America (NAM), the explanatory power is exceptionally high in the entire region and in the subregion with negative discharge trend (\(R_{{\mathrm{NAM}}}^2\) > 80%, \(R_{{\mathrm{NAM}} - }^2\) > 90%). Furthermore, high explanatory powers of more than 50% are reached in Eastern Asia (EAS) and its subregion with positive discharge trend (EAS+), in Oceania (OCE) and its subregion with negative discharge trend (OCE–), as well as in the subregion of South & South Eastern Asia with positive discharge trend (SEA+). Furthermore, acceptable explanatory power (R2 > 20%) is reached in Europe (EUR), Latin America (LAM), and its subregion with positive discharge trend (LAM+), as well as in the positive (negative) discharge subregions of Central Asia (CAS+) (Eastern Asia (EAS–)). Globally, the explanatory power of the model exceeds 30% and is slightly higher across basins with positive discharge trends (\(R_{{\mathrm{GLB}} + }^2 = 45.5\%\)).
Fig. 2: Observed and modeled time series of river flood damages (1980–2010).
Time series of observed damages from the NatCatService database1 (DObs, black) as well as modeled damages (multi-model median) when accounting for changes in (i) climate only (constant 1980 socio-economic conditions, D1980, blue), (ii) climate and exposure (DCliExp, orange) keeping vulnerability at 1980 conditions, and (iii) in climate, exposure, and vulnerability (DFull, purple) for the nine world regions (left panel), as well as their subregions with homogeneous positive and negative trends in river discharge (middle and right panels) (cf. Fig. 1). Time series indicating the GHM-spread are provided in Supplementary Fig. 5. Explained variances R2 are derived from the Pearson correlation coefficients between damages DFull and DObs. Gray background colors highlight the regions where the explained variance of the full model is higher than 20%.
To analyze how much of the variability can be explained by what driver, we additionally provide the explained variances of modeled time series accounting for (i) changes in flood hazards only and for (ii) changes in hazard and exposure (Supplementary Table 2). In most regions and subregions, accounting for climate-induced variability and trends is key for reproducing observed damages. In most cases, the explained variance only gets slightly improved by additionally considering changes in either only exposure or both exposure and vulnerability with the exception of CAS+, SEA+, OCE, and OCE– where the explained variance increases strongly, and EAS– and LAM– where it decreases.
Climate-induced trends in damages are estimated from a restricted model accounting only for observed changes in climate while keeping exposure (in units of inflation adjusted 2005 PPP USD) and vulnerability at 1980 levels (D1980). Damage trends induced by changes in exposure are then estimated from the difference between the trend in D1980 and the trend derived from an extended model additionally accounting for changes in exposure (DCliExp). Finally, damage trends induced by changes in vulnerability are estimated from the difference in trends between DCliExp and the full model (DFull) (Methods).
In the full regions, comprising divergent trends in discharge, climate-induced trends in damages are small compared to exposure and vulnerability-induced trends and mostly insignificant except for SSA. However, when dividing the world regions into subregions with homogeneous discharge trends, climate-induced trends in damages become clearly detectable (Figs. 3 and 4) suggesting that in most regions trends in annual maximum discharge are a good proxy for climate-induced damage trends. On global level, a significant positive climate-induced trend emerges in GLB+ compared to the small and insignificant climate-induced global trend. In GLB+, as well as in SEA+, CAS+, and EAS+, the climate-induced trends are comparable or even larger than the trends induced by the socio-economic drivers. The same holds true for the climate-induced trends in SSA+, OCE+, and NAF+, where however the explanatory power of the full model is considered too low (R2 < 20%) to allow for an attribution of observed damages. In most R+ regions, climate-induced trends are positive and often significant, but mostly negative in the corresponding R– region (Fig. 4).
Fig. 3: Contributions of changes in climate, exposure, and vulnerability to damages induced by river floods (1980–2010).
Bars indicate the relative trend in annual modeled M (purple) and observed damages N (black frames) and the individual contributions of each driver: climate C1980 (blue), exposure E (orange), vulnerability V (red) relative to the recorded annual mean damage of the baseline period 1980–1995. From left to right, we present the trends in the entire world regions (R), and the subregions with positive (R+) and (negative, R–) discharge trends. Gray background colors highlight the regions where the explained variance of the full model is higher than 20%.
Fig. 4: Comparison of climate-induced trends in economic damages over 1980–2010 and 1971–2010.
Shown are trends for each geographical world region (R) as well as in the subregions with positive (R+) and negative discharge trends (R–). Error bars indicate the 90% confidence interval of the Theil–Sen slope estimation. Symbols indicate the statistical significance of the climate trends at various levels. Climate-induced trends C derived from simulated damages assuming fixed 1980 exposure D1980 and fixed 2010 exposure D2010 are expressed relatively to the recorded annual mean damage of the baseline period 1980–1995 in the region or subregion (C1980 and C2010). Gray background colors highlight the regions where the explained variance of the full model is higher than 20%.
However, there are some regions where trends in annual maximum discharge do not translate into similar trends in damages. For instance, we find a significant positive damage trend in SSA-. This can be explained by changes in the distribution of annual maximum discharge over time; the region became drier on average, but positive discharge extremes that exceed protection standards and drive economic damages intensified.
While the damage reporting by Munich Re's NatCatSERVICE1 begins only in 1980, the hydrological simulations generated in the second phase of the Intersectoral Inter Model Intercomparison Project (ISIMIP2a) are available from 1971 onward. This allows for a backward extension of the simulated climate-induced damages to the period 1971–2010 and a robustness check of the climate-induced trends as obtained for the period 1980–2010. Overall, we find climate-induced trends to be robust against the choice of the measurement period (upper panels in Fig. 4): in the global positive discharge region GLB+, NAF–, and SSA and both of its subregions we find significant (at least at the 10% level) trends for both periods that agree in sign and magnitude. Good agreement between climate-induced trends is also observed in EAS+, OCE–, LAM+, CAS+, SEA–, where trends become significant for the longer period. Only in OCE+ and SEA+ positive climate-induced trends lose their significance from 1971 to 2010.
In addition, we test for the dependence of the climate-induced trends on the choice of the baseline year for the socio-economic forcing (Supplementary Note 2). To this end, we compare the climate-induced trends derived from D1980 to the ones derived from D2010 (cf. upper and lower panels in Fig. 4 and Supplementary Fig. 6). Differences in these two trends arise when there are assets in 2010 in areas where no assets at all existed in 1980. Assuming 2010-fixed exposure, all damages that were caused on these assets contribute to the climate-induced trend, while changes in damages on these assets in the 1980-fixed exposure are attributed to the exposure trends. However, differences between both estimates of "climate-induced damage trends" are found to be minor (Fig. 4). The calculation of the trends for fixed 2010 exposure further allows for the quantification of the contribution of climate change from 1980 to 2010 (or 1971 to 2010) to median damages in 2010 as difference between the start level of the regression line and its end level (Eq. (5) and Supplementary Table 3). This is closest to the definition of "climate impact attribution" as defined in Ch18 of the WGII contribution to the Intergovernmental Panel on Climate Change (IPCC) AR523 that would require the comparison of observed damages to damages in a counterfactual situation assuming observed socio-economic conditions but a stationary climate.
Drivers of climate-induced damage trends
To assess whether climate-induced trends in damages will persist in the future due to ongoing anthropogenic climate change or whether they are temporary and caused by climate oscillations (which would make them highly sensitive to the considered time period), we test to what degree the modeled time series of climate-induced damages for the full period 1971–2010 (D1980) can be explained by variations in ENSO, PDO, NAO, AMO, and GMT. The latter is considered a proxy for long-term anthropogenic climate change24. In the given time period from 1971 to 2010, the AMO index is highly correlated with GMT (Pearson correlation coefficient r = 0.92) and shows a similar monotonous increase (Fig. 5a) such that it can be considered a replacement of GMT in many cases. Therefore, we identify the model providing the best representation of the simulated damages while avoiding overfitting based on a leave-one-out-cross-validation (LooCV)25 for two separate trend analyses; in the first, the best predictors are chosen among ENSO, PDO, NAO, and GMT (Fig. 5b), and, in the second, the best predictors are chosen among all four climate oscillations (replacing GMT by AMO) (Fig. 5c) (Methods). Since all predictors are normalized, the relative shares of their coefficients show the importance of one predictor compared to the others (Fig. 4). When choosing the best model, we allow for up to 1 year lag in the response to the climate oscillations ENSO, PDO, and NAO. Among all regions where the explained variance of the full model (DFull) is higher than 20% and significant climate trends have been identified (GLB+, EAS, EAS+, OCE, OCE–, and LAM+), either GMT or AMO are predictors for the monotonous long-term trend in climate-induced damages (Fig. 5c). Only in CAS+, the significant climate trend can be best explained only by NAO and PDO. The signs of the coefficient of GMT or AMO are always in line with the underlying long-term trend in the damage time series, in the sense that a positive trend in observed damages is associated with a positive coefficient of GMT or AMO, respectively, and vice versa for negative trends. As the predictors have been normalized all vary from 0 to 1 in the considered period and the magnitude of the coefficients also informs about the strength of the influence of the individual predictors (Methods). In most of the above regions, the relative importance of AMO and GMT among the set of chosen predictors is similar (cf. Fig. 5b, c). However, in LAM+ we find AMO to be more important than GMT whereas the opposite holds true for OCE and OCE–.
Fig. 5: Predictors of climate-induced trends in flood damages.
a Normalized indices of ENSO, PDO, NAO, AMO, and GMT from 1971 to 2010. Only the period 1971–2010 is used for the analysis (gray shading). b Relative contribution (\(\gamma\)) of each climate-oscillation indicator in the best GLM to the damage time series D1980 accounting for climate-induced trends and variability only (fixed 1980 exposure and vulnerability) (cf. Methods). Black boxes indicate significant predictors at 10% level. Shown are only regions with R2 > 20% for the full model. c Same as b, but using ENSO, PDO, NAO, and GMT as predictors.
In all regions with significant climate-induced trends, AMO or GMT are sufficient to explain the long-term trends with no significant trends remaining in the residuals of the identified most parsimonious models. The explanatory power of the best models are similar, regardless whether AMO or GMT are contained in the set of predictors (Supplementary Tables 4 and 5). Thus, the available data do not allow for a decision in favor of one of both predictors. In addition, regarding the question whether the observed climate-induced trends are expected to continue due to anthropogenic climate forcing or vanish in line with some long-term climate oscillation, even a dependence on AMO does not rule out the continuation of the observed trends as the AMO itself does not only describe the internal variability of climate but may be also affected by anthropogenic climate forcings26,27,28. Thus, while we cannot distinguish between the effects of GMT and AMO, our analysis should be considered as a test for a long-term monotonous trend even after adjusting for ENSO, PDO, and NAO.
In many regions, the quantification of the contribution of climate change to observed trends in flood-induced economic damages is still limited by an insufficient understanding of the observed damage time series. First of all, coarse and uncalibrated hydrological simulations such as those used here may not be able to properly reproduce actual historical flood extents linked to general limitations and uncertainties of the modeling approach (Supplementary Discussion). In addition, due to the use of multi-model medians of damage time series, modeled time series are assumed to have a relatively smaller variability than the recorded damages, explaining the differences in the significance levels between observed and modeled trends in damages. However, the excellent reproduction of observed fluctuations in damages in North America underlines the general power of the considered modeling approach. The general performance of the hydrological models is also demonstrated by the close qualitative agreement between simulated and observed trends in discharge9,19,20,21 (Supplementary Note 1). Especially for large-scale climate change impact assessments, as the trend analysis undertaken here, they have been found to be a suitable tool29. Qualitatively, observed and modeled damage trends match in all world regions and subregions, except for EUR– and LAM–. Unexplained variances of observed damage data may result from regional deficits in reported damages, observational climate forcings, representation of protection standards, or asset distributions. Our analysis highlights the importance of subregional differences in impacts and the need for spatially explicit and event-specific damage records to allow for a high-regional detail in the assignment of damages. The geographical locations provided in the NatCatSERVICE database are a good starting point in this regard, but more accurate event footprints are desirable for a better regional assignment of damages.
Here, we estimate vulnerability from the ratio of observed and simulated damages as obtained when accounting for climate and exposure-driven changes in damages (DCliExp). In consequence, misrepresentation of trends in either the reported, or simulated climate and exposure-driven damages would translate into erroneous trends in vulnerability over time. For example, an underreporting of damages in early years would erroneously translate into low vulnerabilities in the early phase. Similarly, too low estimates of the climate-induced trends could be compensated by increasing vulnerability estimates. In most regions, where the explanatory power of our model is acceptable (R2 > 20%), trends in vulnerability are negative indicating that both effects may only play a limited role. However, in NAM, NAM+, OCE, OCE–, and SEA+, we find increasing vulnerability trends that could result from an underestimation of climate-induced trends or an underreporting of damages in the 1980s (Fig. 3 and Supplementary Figs. 1 and 2). However, increasing vulnerabilities in highly developed regions such as NAM may also be real30 and due to behavioral changes caused by overestimating protection, e.g., the levee effect31. In previous studies, mostly decreasing vulnerabilities with overall converging trends between high- and low-income countries have been found12,14. However, increasing vulnerability levels have also been reported for higher-middle-income countries13. Differences to our findings may be explained by the aggregation over countries by income and not with regard to homogeneity or discharge trends and considerations of different time periods and by the averaging method used to express the aggregated vulnerability for an entire region. Our quantification of climate change contributions to observed trends in flood-induced damages differs from "climate impacts attribution" as defined in Chapter 18 of the 5th assessment report (AR) of the IPCC AR523: "Detection of impacts' of climate change addresses the question of whether a natural or human system is changing beyond a specified baseline that characterizes its behavior in the absence of climate change."32 where this "baseline may be stationary or non-stationary (e.g., due to land use change)." According to this definition, the impacts of climate change on observed trends in flood-induced damages would have to be estimated as the difference between observations and damages derived from simulation assuming stationary climate and observed changes in asset distributions and vulnerabilities. In contrast, we estimate them from a varying climate but with fixed asset distributions and vulnerabilities. However, the contributions of climate change to average damages at the end of the considered time period (2010)—estimated by multiplying climate-induced trends (1980–2010) assuming fixed 2010 socio-economic conditions with the length of this time period—basically correspond to the AR5 definition of impact attribution in 2010. As such, our approach certainly only quantifies the contribution of climate change over the 1980–2010 period and not the full contribution of climate change compared to pre-industrial levels.
It is critical to identify the individual drivers of flood-induced damages since their reduction may require different mitigation and adaptation strategies. We demonstrate that averaging across regions with heterogeneous climate-induced trends in flood hazards can hide the signal of climate change in reported time series of flood-induced damages. While previous global studies suggest that the contributions of climate to changes in flood damages have been minor compared to socio-economic drivers, we show that the impacts of climate change become detectable when disaggregating world regions into subregions with homogeneous trends in annual maximum discharge in the historical period. This works especially well for the global subregion with positive discharge trend as well as the subregions of South & South-East Asia, Eastern Asia, Central Asia & Russia, and Latin America with positive discharge trends. However, the explanatory power of the considered modeling approach is still low in these regions. In general, the considered hybrid modeling approach building upon process-based hydrological simulations and empirical estimates of vulnerabilities proves to be a powerful tool to attribute observed damages induced by river floods. While remote sensing may allow for the identification of flooded areas in recent years making use of the MODerate resolution Imaging Spectro-radiometer instruments on the NASA Aqua and Terra satellites33, process-based modeling remains critical, both for backward extensions required for the attribution of long-term trends and for future climate impacts projections.
Being constrained by the simulation period (1971–2010) of the ISIMIP2a hydrological model ensemble, it was not yet possible to decide whether the climate-induced change in damages is attributable to long-term warming or natural climate variability, the inclusion of the recent decade (as done in the ongoing modeling round of the ISIMIP project, ISIMIP3a; https://www.isimip.org/protocol/) may already enable us to provide a clearer answer. Nonetheless, our analysis clearly reveals an underlying monotonous climate-induced trend in damages in many regions even under adjustment for ENSO, NAO, and PDO as shorter-term climate oscillations. The generation of stationary counterfactual historical climate forcing data34 and their translation into flooded areas based on hydrological simulations will also allow us to apply our framework to the attribution of observed impacts as defined by the AR523.
Climate forcings and hydrological data
For the modeling of fluvial floods, we rely on the runoff output from 12 GHMs participating in phase 2a of the Inter-Sectoral Impact Model Intercomparison Project (ISIMIP2a)35 (Supplementary Methods). The 12 GHMs were driven by four separate observational (atmospheric) weather data products for the period 1971–2010 providing daily runoff at 30' (~50 km × 50 km) resolution including the Global Soil Wetness Project version 3 (GSWP3; http://hydro.iis.u-tokyo.ac.jp/GSWP3)36, the Princeton Global Meteorological Forcing Dataset version 2.1 (PGMFD; http://hydrology.princeton.edu/data.pgf.php)37, the Water and Global Change Forcing Data based on the reanalysis data set ERA-40 (WATCH; https://doi.org/10.1029/2006gl026047, https://doi.org/10.1175/jhm-d-15-0002.1)38, and the ERA-Interim data (WATCH-WFDEI)39 (Supplementary Table 1).
Socio-economic data sources
We use gridded Gross Domestic Product (GDP) data reported in PPP in 2005 USD from the ISIMIP project40 with a spatial resolution of 5' from 1971 to 2010 as a proxy for the distribution of assets. Gridded GDP data were obtained using a downscaling methodology41 in combination with spatially explicit population distributions from the History Database of the Global Environment (HYDE v3.2)42,43 and national GDP estimates44 at a 5' resolution (~10 km × 10 km). Downscaled GDP data are available in 10-year increments and linearly interpolated across decades. To estimate asset values more precisely, we convert gridded GDP data into gridded capital stock (in PPP 2005 USD), using annual national data on capital stock and GDP from the Penn World Table (version 9.1, https://www.rug.nl/ggdc/productivity/pwt/). For each country the annual ratio of national GDP and capital stock was calculated and smoothed with a 10-year running mean to generate a conversion factor, which was then applied to translate exposed GDP into asset values.
Observed asset damages are taken from reported flood damages from the NatCatSERVICE1 database collected by Munich Re since 1980, excluding flash flood events or flooding caused by tropical cyclones. We adjusted all flood damage estimates for inflation to the reference year 2005 using country-specific consumer price indices (CPI), i.e., expressing them in the same base year as the GDP data. To do so, we constructed a conversion factor for each country based on all reported damages for a country-specific event in 2005 and the regularly CPI-adjusted values reported in Munich Re's NatCatSERVICE database in the base year 2016. Multiplying CPI-adjusted reported flood damages by this conversion factor results in CPI-adjusted damages for 2005. In order to ensure that recorded damages are provided in the same unit as the asset data, we additionally convert recorded damages for each country i and each year j to PPP 2005 USD according to
$${\mathrm{D}}_{{\mathrm{Obs}}\,i,j}({USD ,CPI\,2005\,PPP})={\mathrm{D}}_{{\mathrm{Obs}}\,i,j} ({\mathrm{USD }},{\mathrm{CPI}}\,2016) \cdot \frac{{{\mathrm{D}}_{{\mathrm{Obs}}\,2005,i}({\mathrm{USD }},{\mathrm{CPI}}\,2016)}}{{{\mathrm{D}}_{{\mathrm{Obs}}\,2005,i}({\mathrm{USD }},{\mathrm{nominal}})}} \cdot p_{i,j}$$
$$p_{i,j} = \frac{{{\mathrm{GDP}}({\mathrm{real}}\,{\mathrm{PPP}}\,2005)}}{{{\mathrm{GDP}}\,({\mathrm{real}}\,2005)}}$$
denotes a country- and year-specific conversion factor. Event-specific damage estimates were then aggregated to year–country and year–region level in order to be comparable with simulated river floods for which only the annual maximum was considered. Thereby we assumed that only one flood event is observed at each grid cell during a calendar year.
Data on climate oscillations and global mean temperature
In order to avoid interferences with long-term temperature increase, we use the pressure based Southern Oscillation Index as a predictor for ENSO (https://www.ncdc.noaa.gov/teleconnections/enso/enso-tech.php). Monthly data for AMO, NAO, and PDO were extracted from the NOAA/Climate Prediction Center (https://www.psl.noaa.gov/data/climateindices/list/). We derived annual GMT (daily mean Near-Surface Air Temperature) as the mean of three of the four input climate forcings provided in ISIMIP2a. We excluded the WATCH data set because it does not capture the full historical period.
Flood modeling
We derive spatially explicit river discharge, flooded areas, and flood depth from the harmonized multi-model simulations of the 12 global gridded GHMs participating in ISIMIP2a (Supplementary Methods 1). We here apply the naturalized experiment referred to as "NOSOC" in the ISIMIP2a protocol, meaning that no human impacts, such as dams and water abstractions, on river flow were considered. This is legitimate for two reasons: (1) to ensure consistency with river routing simulations that do not account for human regulation of rivers, and (2) based on a previous study for some major basins that showed that the shape of the hydrograph, for peak daily flow, is not significantly different between natural and human impact experiments45. Furthermore, this allows us to better isolate climate-induced changes in river discharge and flood damages. For this ensemble of 46 climate data/GHM combinations (Supplementary Table 1), we follow the methodology applied previously in Willner et al.46,47, and first harmonize the output of the different GHMs with respect to their fluvial network using the fluvial routing model CaMa-Flood (version 3.6.2)48 yielding daily fluvial discharge at 15' (~25 km × 25 km) resolution (Supplementary Methods 2). Especially for peak discharges, CaMa-Flood agrees better with observed fluvial discharges than the direct output of the hydrological models49. For the subsequent analysis, we then select the annual maximum daily discharge for each grid cell. For each of the 46 simulations of daily fluvial discharge and each grid cell on 15' resolution, we fit a generalized extreme value distribution to the historical time series of the annual maximum discharge using L-moment estimators of the distribution parameters allowing for a model bias correction following the approach by Hirabayashi et al.50 (Supplementary Methods 2). It has been shown in several recent publications that such a hydrological modeling chain is able to reproduce patterns in observed flood impacts12,13. In addition to these previous studies, we account for current flood protection standards at the sub-national scale from the FLOPROS database51. For the final assessment, we re-aggregate the high-resolution flood depth data from 0.3' to a 2.5' resolution (~5 km × 5 km) by retaining the maximum flood depth as well as the flooded area fraction, defined as the fraction of all underlying high-resolution grid cells where the flood depth was larger than zero.
Economic damage assessment
For the estimation of direct asset damages, we apply the regional residential flood depth-damage functions developed by Huizinga et al.18 (Supplementary Methods 3). The quantification of flood damages consists of the following steps: (1) determine exposed assets on the grid-level (2.5' resolution) based on the flooded fraction obtained from the inundation modeling; (2) determine the grid-level damage by multiplying the exposed assets by the flood depth and the flood-depth-damage function; (3) aggregate the estimated damages spatially to the regional/subregional level, and (4) analyze the aggregated damages across different GHM simulations, assessing model medians and model spread. For steps 1–3, the open-source probabilistic natural catastrophe damage framework CLIMADA was used52. To account for the inhomogeneous but a priori unknown distribution of assets within a grid cell, we additionally assume that no assets are exposed to a 2-year flood event, thus subtracting the 2-year flooded fractions from the modeled flooded fraction before multiplying with the asset value. This is equivalent to assuming that nobody would construct valuable assets in regions flooded every 2 years.
In this work, we define vulnerability as the ratio of observed DObs to modeled damages DCliExp. Thereby, we take into account static vulnerability estimates, due to the application of continent-level depth-damage functions and the FLOPROS protection standards. In order to additionally account for dynamic vulnerability changes, we further estimate a time-dependent vulnerability behavior for each region and subregion.
The annual modeled damages for each GHM and grid cell are then aggregated to the country and regional (or subregional) level. The model median from all combinations of GHM and climate forcings then presents a time series that accounts for varying climate, exposure and, static vulnerability DCliExp. We derive the full model accounting for time variable climate, exposure, and dynamic vulnerability DFull, by including the time-dependent vulnerability function as detailed in the next paragraph. For comparability reasons, we first aggregate to nine world regions constructed by grouping countries with geographical proximity and similar socio-economic structure following the income group classification of the Worldbank22 (Fig. 1b). For regions and subregions, the median across all GHMs is then compared to reported damages from Munich Re's NatCatSERVICE (Fig. 2).
Assessing and accounting for vulnerability
To include time-varying vulnerability, we apply an approach proposed in previous vulnerability studies12,13,14. Comparing modeled and observed damages, a time trend in the ratio of recorded and modeled damages is observed that can most likely be explained by changes in socio-economic vulnerability and/or adaptive capacity. These changes are not properly reflected within the modeling chain and are, e.g., caused by the fact that the protection standards underlying the FLOPROS database are stationary in time. We apply an 11-year smoothing on the ratio of reported and modeled damages using Singular Spectrum Analysis (Figs. SI1 and SI2)53. Before applying the Singular Spectrum Analysis, we undertake a consistent outlier removal by excluding data points that are more than five times the 70th (Q0.7) to 30th inter-quantile range, Q0.7–Q0.3, apart from the borders of this range,
$$Q_{0.3} - 5 \cdot (Q_{0.7} - Q_{0.3}) \ < \ \frac{{{D}_{{\mathrm{Obs}}}}}{{{D}_{{\mathrm{CliExp}}}}}\ <\ Q_{0.7} + 5 \cdot \left. {(Q_{0.7} - Q_{0.3})} \right.$$
In order to achieve consistency across regions and subregions, we additionally remove data points from the set of vulnerabilities for an entire region when they are outliers with regard to the distribution in one of the subregions.
Missing yearly vulnerability values are replaced by the median vulnerability for the period 1980–2010. In entire regions, we find a low number of missing data points, with a maximum number of four missing data points in CAS. Among the subregions with sufficiently high explanatory power of the full model (R2 > 20%), we find a maximum of six missing data points in CAS+ and OCE–. In regions that were excluded from further analysis, such as NAF+ and OCE+, we see higher numbers of missing values. The resulting vulnerability functions then provide a vulnerability factor for each year that is multiplied with DCliExp in order to derive the full model DFull. It is important to note that the applied definition of regional vulnerability as the ratio of regionally aggregated observed damages and associated simulated damages cannot be considered a spatial average of individual vulnerabilities of assets that may be subject to strong variations according to income levels12,13,14. As the aggregated simulated exposed assets may be dominated by highly valuable assets in high-income regions the vulnerability factor derived here is also expected to be strongly influenced by associated individual vulnerabilities.
Trend estimation
Throughout this work, we use the Theil–Sen slope estimator54 to quantify trends and apply the non-parametric Mann–Kendall test55 to evaluate significance levels. In the damage analyses, trends are relative to the annual mean damage of the reference period 1980–1995 in the corresponding region or subregion. Prior to the trend estimation, we tested the time series for autocorrelation building an autocorrelation function (ACF) based on a full convolution. Low levels of autocorrelation are only detectable in residuals analyzed in the test for teleconnections, but not in damage time series. In cases where we observed autocorrelation, we additionally applied an Hamed and Rao Modified Mann–Kendall Test56.
Definition of subregions by discharge trends
We subdivide the nine geographical world regions into subregions with positive and negative trends in annual discharge maxima over the period 1971–2010. To build subregions, we make use of the WMO basin and subbasin classification provided by the Global Runoff Data Centre57, assigning each basin to a subregion with either positive discharge trend or negative discharge trend by comparing the number of grid cells with trends of the same sign. Each subregion encompasses all river basins with predominantly positive (negative) discharge trends R+ (R–).
Studies on changes in global discharge patterns are rare and data coverage is not evenly distributed around the globe. Furthermore, the susceptibility of discharge to human intervention affects discharge records and complicates disentangling human and climatic forces in observations. We therefore derive trends in annual maximum discharge from the daily fluvial discharge at 15' provided by the CaMa-Flood simulation described in the Methods section on Flood modeling. To resolve recorded damages in the refined subregional analysis, we make use of the event location (country, longitude, and latitude) given for each general flood event in the NatCatSERVICE data set and assign the damage to the river basin that surrounds the given event location. Damages are then aggregated across all basins that belong to the same subregion. We provide the exact number of events recorded in the NatCatSERVICE database for each region and subregion in Supplementary Table 6.
Attributing damages to individual drivers
Given that the overall trend in damage time series is a superposition of the trends from each individual driver, we can separate the contributions from each driver for each region (subregion) R by calculating the trend α of each time series D1980, DCliExp, and DFull and extract normalized climate-induced trends C, contributions from exposure E, and vulnerability V as well as trends in observed damages N and modeled damages M according to:
$$\begin{array}{l}C_{1980} = \frac{{\alpha _{1980}}}{n},\\ E = \frac{{\alpha _{{\mathrm{CliExp}}} - \alpha _{1980}}}{n},\\ V = \frac{{\alpha _{{\mathrm{Full}}} - \alpha _{{\mathrm{CliExp}}}}}{n}\\ N = \frac{{\alpha _{\mathrm{Obs}}}}{n},\\ M = \frac{{\alpha _{{\mathrm{Full}}}}}{n},\end{array}$$
where years in the indices denote the year of the socio-economic conditions that were kept fixed throughout the simulations (i.e., either 1980 or 2010).
We apply a non-parametric trend analysis (Theil–Sen slope estimator) to estimate α. Trends are given relative to the annual reported average damages in the time period 1980–1995 (n) in each region or subregion (Fig. 3). We additionally provide climate-induced trends from time series with 2010 fixed socio-economic conditions (Fig. 4):
$$C_{2010} = \frac{{\alpha _{2010}}}{n}.$$
Socio-economic trends are assessed for the period 1980–2010. As climate-induced trends are independent from observational data, we can extend it backward, making use of the full ISIMIP2a time period and additionally assess trends from 1971 to 2010. We derive the climate contribution to median damages in 2010 (Δ2010) compared to the start year 1971 (1980), tstart' according to
$${\it{\Delta }}_{2010} = C_{2010} \cdot \left( {2010 - t_{{\mathrm{start}}}} \right)$$
Analyzing drivers for climate-induced trends in damage
Following the methodology introduced by Najibi and Devineni10, we apply generalized linear models (GLM) assuming damages to be log-normally distributed and assuming fixed 1980 socio-economic conditions (D1980)10 to assess to what degree climate-induced trends can be explained by natural climate variability and GMT. We extend the approach by Najibi and Devineni considering the four large-scale climate oscillations as predictors in a GLM by including GMT in the set of possible predictors. In this sense, our approach is similar to Armal et al.24. However, in contrast to Armal et al., we allow that only AMO or GMT are included as predictor in the GLM due to their strong correlation during the considered time period. In a stepwise procedure, we calculate GLMs from all possible combinations of the predictors ENSO, PDO, NAO, AMO, and GMT and a constant ε,
$${D}_{1980} = \beta _{{\mathrm{ENSO}}} \cdot {\mathrm{ENSO}} + \beta _{{\mathrm{PDO}}} \cdot {\mathrm{PDO}} + \beta _{{\mathrm{NAO}}} \cdot {\mathrm{NAO}} + \beta _{{\mathrm{GMT}}} \cdot {\mathrm{AMO}} + \varepsilon _1,$$
$${D}_{{\mathrm{1980}}} = \beta _{{\mathrm{ENSO}}} \cdot \mathrm{ENSO} + \beta _{{\mathrm{PDO}}} \cdot {\mathrm{PDO}} + \beta _{{\mathrm{NAO}}} \cdot {\mathrm{NAO}} + \beta _{{\mathrm{AMO}}} \cdot {\mathrm{GMT}} + \varepsilon _2$$
For the shorter-term oscillations ENSO, PDO, and NAO, we additionally allow for a time-lag of 1 year, in order to account for values of these predictors in one calendar year to contribute to the damages accounted for in the following calendar year.
We then select the best model applying a LooCV25, which allows to assess model quality outside the fitting period calculating the out-of-sample error (Supplementary Table 4). The best model is the one with the smallest out-of-sample error, we additionally test different link functions (inverse-power, identity, log). To compare the contributions of the different predictors across the different link functions, we compare the partial derivatives of the model with regard to the individual predictors (γENSO, γPDO, γNAO, γAMO, and γGMT) (Fig. 5). Finally, we test the residuals for remaining trends applying the non-parametric trend analysis. Previously, we applied an ACF basing on a full convolution and found very few cases with a low level of autocorrelation (GLB, GLB+, OCE, OCE–, EAS). In these regions, we additionally applied an Hamed and Rao Modified Mann–Kendall Test56.
All the data generated during this study and required to reproduce the findings are publicly available. The data on recorded damage are available from Munich Re's NatCatSERVICE but restrictions apply to the availability of these data, which were provided by Munich Re only for the current study, and so are not publicly available.
The source data for damage modeling including flooded fractions, flooded areas, and annual maximum discharge and socio-economic input data for asset generation provided within the ISIMIP framework are available at https://doi.org/10.5281/zenodo.444636458.
The shapefiles for the river basins provided by the Global Runoff Data Centre are available at https://www.bafg.de/GRDC/EN/02_srvcs/22_gslrs/223_WMO/wmo_regions_2020.html?nn=201570.
The data for climate oscillations were obtained from https://www.ncdc.noaa.gov/teleconnections/enso/enso-tech.php (ENSO) and https://www.psl.noaa.gov/data/climateindices/list/ (AMO, NAO, PDO). The data supporting the results of the study and findings presented in the figures are provided in Supplementary Data 1.
All implementations, input, and output data used for modeling are publicly available. The detailed implementation of the flood modeling can be accessed at https://doi.org/10.5281/zenodo.124105159.
For damage assessment, we used the natural catastrophe damage framework CLIMADA v1.5.1 available at https://github.com/CLIMADA-project/climada_python.
All supporting scripts needed to reconstruct the analysis, including a detailed description of all the data used as input and demo tutorials, are available at https://doi.org/10.5281/zenodo.450878360.
Munich Re. NatCatSERVICE Database (Munich Reinsurance Company, Geo Risks Research, Munich) (2016).
Trenberth, K. E. Conceptual framework for changes of extremes of the hydrological cycle with climate change. Clim. Change 42, 327–339 (1999).
Ivancic, T. & Shaw, S. Examining why trends in very heavy precipitation should not be mistaken for trends in very high river discharge. Clim. Change 133, 681–693 (2015).
Boer, G. J. Climate change and the regulation of the surface moisture and energy budgets. Clim. Dyn. 8, 225–239 (1993).
Allen, M. R. & Ingram, W. J. Constraints on future changes in climate and the hydrologic cycle. Nature 419, 228–232 (2002).
CAS PubMed ADS Google Scholar
Westra, S., Alexander, L. V. & Zwiers, F. W. Global increasing trends in annual maximum daily precipitation. J. Clim. 26, 3904–3918 (2013).
Lehmann, J., Coumou, D. & Frieler, K. Increased record-breaking precipitation events under global warming. Clim. Change 132, 501–515 (2015).
Fischer, E. M. & Knutti, R. Observed heavy precipitation increase confirms theory and early models. Nat. Clim. Change 6, 986–991 (2016).
Do, H. X., Westra, S. & Leonard, M. A global-scale investigation of trends in annual maximum streamflow. J. Hydrol. 552, 28–43 (2017).
Najibi, N. & Devineni, N. Recent trends in the frequency and duration of global floods. Earth Syst. Dyn. 9, 757–783 (2018).
Berghuijs, W. R., Aalbers, E. E., Larsen, J. R., Trancoso, R. & Woods, R. A. Recent changes in extreme floods across multiple continents. Environ. Res. Lett. 12, 114035 (2017).
Jongman, B. et al. Declining vulnerability to river floods and the global benefits of adaptation. Proc. Natl Acad. Sci. USA 112, E2271–E2280 (2015).
Tanoue, M., Hirabayashi, Y. & Ikeuchi, H. Global-scale river flood vulnerability in the last 50 years. Sci. Rep. 6, 36021 (2016).
Formetta, G. & Feyen, L. Empirical evidence of declining global vulnerability to climate-related hazards. Glob. Environ. Change 57, 101920 (2019).
Barredo, J. I. Normalised flood losses in Europe: 1970–2006. Nat. Hazards Earth Syst. Sci. 9, 97–104 (2009).
Bouwer, L. M. Have Disaster losses increased due to anthropogenic climate change? Bull. Am. Meteorol. Soc. 92, 39–46 (2011).
Paprotny, D., Sebastian, A., Morales-Nápoles, O. & Jonkman, S. N. Trends in flood losses in Europe over the past 150 years. Nat. Commun. 9, 1985 (2018).
Article PubMed PubMed Central ADS CAS Google Scholar
Huizinga, J., De Moel, H. & Szewczyk, W. Global flood depth-damage functions: Methodology and the database with guidelines. https://publications.jrc.ec.europa.eu/repository/handle/111111111/45730 (2017).
Blöschl, G. et al. Changing climate both increases and decreases European river floods. Nature 573, 108–111 (2019).
Article PubMed ADS CAS Google Scholar
Gudmundsson, L., Leonard, M., Do, H. X., Westra, S. & Seneviratne, S. I. Observed trends in global indicators of mean and extreme streamflow. Geophys. Res. Lett. 46, 756–766 (2019).
Mediero, L., Santillán, D., Garrote, L. & Granados, A. Detection and attribution of trends in magnitude, frequency and timing of floods in Spain. J. Hydrol. 517, 1072–1088 (2014).
Fantom, N. & Serajuddin, U. The World Bank's classification of countries by income. (2016) https://doi.org/10.1596/1813-9450-7528.
Cramer, W. et al. Detection and attribution of observed impacts. Climate Change 2014–Impacts, Adaptation and Vulnerability 979–1038 (2014) https://doi.org/10.1017/CBO9781107415379.023.
Armal, S., Devineni, N. & Khanbilvardi, R. Trends in extreme rainfall frequency in the contiguous United States: attribution to climate change and climate variability modes. J. Clim. 31, 369–385 (2018).
Witten, I. H., Frank, E., Hall, M. A. & Pal, C. J. Data Mining: Practical Machine Learning Tools and Techniques. (Elsevier Inc., 2016). https://doi.org/10.1016/c2009-0-19715-5.
Booth, B. B. B., Dunstone, N. J., Halloran, P. R., Andrews, T. & Bellouin, N. Aerosols implicated as a prime driver of twentieth-century North Atlantic climate variability. Nature 484, 228–232 (2012).
Terray, L. Evidence for multiple drivers of North Atlantic multi-decadal climate variability. Geophys. Res. Lett. 39, (2012).
Ting, M., Kushnir, Y. & Li, C. North Atlantic Multidecadal SST Oscillation: External forcing versus internal variability. J. Mar. Syst. 133, 27–38 (2014).
Hattermann, F. F. et al. Cross‐scale intercomparison of climate change impacts simulated by regional and global hydrological models in eleven large river basins. Clim. Change 141, 561–576 (2017).
Geiger, T., Frieler, K. & Levermann, A. High-income does not protect against hurricane losses. Environ. Res. Lett. 11, 084012 (2016).
Di Baldassarre, G. et al. Debates—perspectives on socio-hydrology: capturing feedbacks between physical and social processes. Water Resour. Res. 51, 4770–4781 (2015).
Stone, D. et al. The challenge to detect and attribute effects of climate change on human and natural systems. Clim. Change 121, 381–395 (2013).
Policelli, F. et al. The NASA Global Flood Mapping System. in Remote Sensing of Hydrological Extremes (ed. Lakshmi, V.) 47–63 (Springer International Publishing, 2017). https://doi.org/10.1007/978-3-319-43744-6_3.
Mengel, M., Treu, S., Lange, S. & Frieler, K. ATTRICI 1.0—counterfactual climate for impact attribution. Geosci. Model Dev. Discuss. 1–26 (2020) https://doi.org/10.5194/gmd-2020-145.
Gosling, S. et al. ISIMIP2a Simulation Data from Water (global) Sector. (GFZ Data Services, 2017). https://doi.org/10.5880/PIK.2017.010.
Dirmeyer, P. A. et al. GSWP-2: multimodel analysis and implications for our perception of the land surface. Bull. Am. Meteorol. Soc. 87, 1381–1397 (2006).
Sheffield, J., Goteti, G. & Wood, E. F. Development of a 50-year high-resolution global dataset of meteorological forcings for land surface modeling. J. Clim. 19, 3088–3111 (2006).
Weedon, G. P. et al. Creation of the WATCH forcing data and its use to assess global and regional reference crop evaporation over land during the twentieth century. J. Hydrometeorol. 12, 823–848 (2011).
Weedon, G. P. et al. The WFDEI meteorological forcing data set: WATCH Forcing Data methodology applied to ERA-Interim reanalysis data. Water Resour. Res. 50, 7505–7514 (2014).
Frieler, K. et al. Assessing the impacts of 1.5 °C global warming—simulation protocol of the Inter-Sectoral Impact Model Intercomparison Project (ISIMIP2b). Geosci. Model Dev. 10, 4321–4345 (2017).
Murakami, D. & Yamagata, Y. Estimation of gridded population and GDP scenarios with spatially explicit statistical downscaling. Sustainability 11, 2106 (2019).
Klein Goldewijk, K., Beusen, A., van Drecht, G & de Vos, M The HYDE 3.1 spatially explicit database of human-induced global land-use change over the past 12,000 years. Glob. Ecol. Biogeogr. 20, 73–86 (2011).
Klein Goldewijk, K., Beusen, A., Doelman, J. & Stehfest, E. Anthropogenic land use estimates for the Holocene – HYDE 3.2. Earth Syst. Sci. Data 9, 927–953 (2017).
Geiger, T., Murakami, D., Frieler, K. & Yamagata, Y. Spatially-explicit Gross Cell Product (GCP) time series: past observations (1850-2000) harmonized with future projections according to the Shared Socioeconomic Pathways (2010-2100). GFZ Data Serv. (2017).
Pokhrel, Y. et al. Incorporating anthropogenic water regulation modules into a land surface model. J. Hydrometeorol. 13, 255–269 (2012).
Willner, S. N., Levermann, A., Zhao, F. & Frieler, K. Adaptation required to preserve future high-end river flood risk at present levels. Sci. Adv. 4, eaao1914 (2018).
Willner, S. N., Otto, C. & Levermann, A. Global economic response to river floods. Nat. Clim. Change 8, 594–598 (2018).
Yamazaki, D., Kanae, S., Kim, H. & Oki, T. A physically based description of floodplain inundation dynamics in a global river routing model. Water Resour. Res. 47, (2011).
Zhao, F. et al. The critical role of the routing scheme in simulating peak river discharge in global hydrological models. Environ. Res. Lett. 12, 075003 (2017).
Hirabayashi, Y. et al. Global flood risk under climate change. Nat. Clim. Change 3, 816–821 (2013).
Scussolini, P. et al. FLOPROS: an evolving global database of flood protection standards. Nat. Hazards Earth Syst. Sci. 16, 1049–1061 (2016).
Aznar-Siguan, G. & Bresch, D. N. CLIMADA v1: a global weather and climate risk assessment platform. Geosci. Model Dev. 12, 3085–3097 (2019).
Golyandina, N. & Zhigljavsky, A. Singular Spectrum Analysis for Time Series. (Springer-Verlag, 2013). https://doi.org/10.1007/978-3-642-34913-3.
Sen, P. K. Estimates of the regression coefficient based on Kendall's Tau. J. Am. Stat. Assoc. 63, 1379–1389 (1968).
Chandler, R. E. & Scott, E. M. Statistical Methods for Trend Detection and Analysis in the Environmental Sciences. doi:10.1002/9781119991571 (2011).
Hamed, K. H. & Rao, A. R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 204, 182–196 (1998).
GRDC. WMO Basins and Sub-Basins/Global Runoff Data Centre, GRDC. 3rd rev. ext. ed. (Koblenz, Germany: Federal Institute of Hydrology (BfG)). (2020).
ISIMIP. source_data_flood_attribution. Zenodo, doi:10.5281/ZENODO.4446364 (2021).
Willner, S. Flood Process.(Version v1. 0. 0)., doi:10.5281/ZENODO.1241051 (2018).
Sauer, I. J. et al. flood_attribution_paper v1.1 (Version v1.1). (2021) Zenodo. https://doi.org/10.5281/zenodo.4508783.
This work was supported by the German Federal Ministry of Education and Research (BMBF) under the research project SLICE (FKZ: 01LA1829A) and the Leibniz Society under the research project ENGAGE (SAW-2016-PIK-1). We further want to thank Munich Re for the kind provision of their damage records.
Open Access funding enabled and organized by Projekt DEAL.
Potsdam Institute for Climate Impact Research, Potsdam, Germany
Inga J. Sauer, Ronja Reese, Christian Otto, Tobias Geiger, Sven N. Willner & Katja Frieler
Institute for Environmental Decisions, ETH Zurich, Zurich, Switzerland
Inga J. Sauer, Benoit P. Guillod & David N. Bresch
Deutscher Wetterdienst (DWD), Climate and Environment Consultancy, Stahnsdorf, Germany
Tobias Geiger
Institute for Atmospheric and Climate Science, ETH Zurich, Zurich, Switzerland
Benoit P. Guillod
Federal Office of Meteorology and Climatology MeteoSwiss, Zurich-Airport, Switzerland
David N. Bresch
Inga J. Sauer
Ronja Reese
Christian Otto
Sven N. Willner
Katja Frieler
I.J.S., C.O., T.G. and K.F. have designed the research. I.J.S. has conducted the final computational analysis including the final damage generation together with B.P.G. and the analysis and interpretation of the data together with R.R. C.O. and K.F. have supervised the analysis and the interpretation of the data. S.N.W. has undertaken the flood modeling and provided flood data used as input for this study. T.G. and D.N.B. have supervised the damage generation. All authors have contributed to the writing of the manuscript.
Correspondence to Christian Otto or Katja Frieler.
Peer review information Nature Communications thanks Dominik Paprotny, Masahiro Tanoue, and Nasser Najibi for their contribution to the peer review of this work. Peer reviewer reports are available.
Sauer, I.J., Reese, R., Otto, C. et al. Climate signals in river flood damages emerge under sound regional disaggregation. Nat Commun 12, 2128 (2021). https://doi.org/10.1038/s41467-021-22153-9 | CommonCrawl |
IWM-EC 2016
Authors: A. Chbihi, O. Lopez, A. Pagano, S. Pirrone, P. Russotto, G. Verde
Published online 17 March 2017
Recent results from the INDRA Collaboration
Authors: N. Le Neindre, G. Adémard, L. Augey, E. Bonnet, B. Borderie, R. Bougault, A. Chbihi, Q. Fable, J.D. Frankland, E. Galichet, D. Gruyer, M. Henri, O. Lopez, P. Marini, M. Pârlog, M. F. Rivet, E. Rosato$^dag$, G. Verde, E. Vient, M. Vigilante for the INDRA Collaboration
Probing the nuclear symmetry energy at high densities with nuclear reactions
Authors: Y. Leifels
Sensitivity to $N/Z$ ratio in fragment productions for the isobaric systems ${}^{124}Xe + {}^{64}Zn, {}^{64}Ni$ and ${}^{124}Sn + {}^{64}Ni$ at E/A=35 MeV
Authors: E. De Filippo, A. Pagano, P. Russotto, L. Acosta, L. Auditore, V. Baran, T. Cap, G. Cardella, M. Colonna, D. Dell'Aquila, S. De Luca, L. Francalanza, B. Gnoffo, G. Lanzalone, I. Lombardo, C. Maiolino, N. S. Martorana, T. Minniti, S. Norella, E. V. Pagano, M. Papa, E. Piasecki, S. Pirrone, G. Politi, F. Porto, L. Quattrocchi, F. Rizzo, E. Rosato$^dagger$, K. Siwek-Wilczyńska, A. Trifirò, M. Trimarchi, G. Verde, M. Vigilante, J. Wilczyński
Nuclear thermodynamics with isospin degree of freedom: From first results to future possibilities with A and Z identification arrays
Authors: B. Borderie
${}^{16}O+{}^{65}Cu$ and ${}^{19}F+{}^{62}Ni$ at 16 AMeV reaction mechanisms comparison: Pre-equilibrium vs. clustering
Authors: J. Mabiala, D. Fabris, F. Gramegna, T. Marchi, M. Cicerchia, M. Cinausero, M. Degerlier, O. V. Fotina, V. L. Kravchuk, M. D'Agostino, L. Morelli, G. Baiocco, M. Bruno, S. Barlini, M. Bini, G. Casini, N. Gelli, A. Olmi, G. Pasquali, S. Piantelli, G. Poggi, S. Valdré, E. Vardaci
Reaction mechanisms leading to 3-body exit channels in central collisions of ${}^{129}Xe+{}^{nat}Sn$ at 12 MeV/u
Authors: J. D. Frankland, D. Gruyer, E. Bonnet, A. Chbihi for the INDRA Collaboration
Progresses in FAZIA detection system and preliminary results from the ISO-FAZIA experiment
Authors: G. Pastore, S. Piantelli, D. Gruyer, L. Augey, S. Barlini, R. Bougault, M. Bini, A. Boiano, E. Bonnet, B. Borderie, M. Bruno, G. Casini, A. Chbibi, M. Cinausero, D. Dell'Aquila, J. A. Dueñas, Q. Fable, D. Fabris, L. Francalanza, J. D. Frankland, F. Gramegna, M. Henri, A. Kordyasz, T. Kozik, R. La Torre, N. Le Neindre, I. Lombardo, L. O. Lopez, J. Mabiala, T. Marchi, L. Morelli, A. Olmi, M. Pârlog, G. Pasquali, G. Poggi, F. Salomon, A. A. Stefanini, S. Valdrè, G. Tortone, E. Vient, G. Verde, M. Vigilante, R. Alba, C. Maiolino, D. Santonocito
A non-equilibrium microscopic description of spallation
Authors: P. Napolitani, M. Colonna
New experimental investigation of cluster structures in ${}^{10}Be$ and ${}^{16}C$ neutron-rich nuclei
Authors: D. Dell'Aquila L. Acosta, L. Auditore, G. Cardella, E. De Filippo, S. De Luca, L. Francalanza, B. Gnoffo, G. Lanzalone, I. Lombardo, N. S. Martorana, S. Norella, A. Pagano, E. V. Pagano, M. Papa, S. Pirrone, G. Politi, L. Quattrocchi, F. Rizzo, P. Russotto, A. Trifirò, M. Trimarchi, G. Verde, M. Vigilante
Status of the FAZIASYM experiment
Authors: E. Bonnet, M. Henri, Q. Fable, J. D. Frankland, O. Lopez, N. Le Neindre, M. Parlog for the FAZIA Collaboration
Isospin equilibration processes and dipolar signals: Coherent cluster production
Authors: M. Papa, I. Berceanu, L. Acosta, C. Agodi, L. Auditore, G. Cardella, M. B. Chatterjee, D. Dell'Aquila, E. De Filippo, L. Francalanza, G. Lanzalone, I. Lombardo, C. Maiolino, N. Martorana, A. Pagano, E. V. Pagano, S. Pirrone, G. Politi, L. Quattrocchi, F. Rizzo, P. Russotto, A. Trifiró, M. Trimarchi, G. Verde, M. Vigilante
Alpha-particle condensate structure of the Hoyle state: Where do we stand?
Authors: P. Schuck, Y. Funaki, H. Horiuchi, G. Röpke, A. Tohsaki, T. Yamada
Indications of Bose-Einstein condensation and Fermi quenching in the decay of hot nuclei
Authors: P. Marini, H. Zheng, A. Bonasera, G. Verde, A. Chbihi
Dynamics of light clusters in fragmentation reactions
Authors: Akira Ono
Three-$\alpha$ particle correlations in quasi-projectile decay in ${}^{12}C + {}^{24}Mg$ collisions at 35 AMeV
Authors: L. Quattrocchi, L. Acosta, F. Amorini, A. Anzalone, L. Auditore, I. Berceanu, G. Cardella, A. Chbihi, E. De Filippo, S. De Luca, D. Dell'Aquila, L. Francalanza, B. Gnoffo, A. Grzeszczuk, G. Lanzalone, I. Lombardo, I. Martel, N. S. Martorana, T. Minniti, S. Norella, A. Pagano, E. V. Pagano, M. Papa, S. Pirrone, G. Politi, F. Porto, F. Rizzo, E. Rosato, P. Russotto, A. Trifirò, M. Trimarchi, G. Verde, M. Veselsky, M. Vigilante
Nuclear matter EoS including few-nucleon correlations
Authors: G. Röpke
Comparison of EoS models with different cluster suppression mechanisms
Authors: S. Typel, H. Pais
Collision dynamics of alpha-conjugate nuclei
Authors: K. Schmidt, X. Cao, E. J. Kim, K. Hagel, M. Barbui, J. Gauthier, S. Wuenschel, G. Giuliani, M. R. D. Rodrigues, H. Zheng, M. Huang, A. Bonasera R. Wada, G. Zhang, J. B. Natowitz
New opportunities in the study of in-medium nuclear properties with FAZIA
Authors: Diego Gruyer, John D. Frankland
First results on the ${}^{32}S+{}^{40,48}Ca$ reactions at 17.7 AMeV studied with GARFIELD setup at LNL
Authors: S. Piantelli, S. Valdré, S. Barlini, G. Casini, M. Colonna, G. Baiocco, M. Bini, M. Bruno, A. Camaiani, M. Cicerchia, M. Cinausero, M. D'Agostino, M. Degerlier, D. Fabris, F. Gramegna, V. L. Kravchuck, J. Mabiala, T. Marchi, L. Morelli, A. Olmi, P. Ottanelli, G. Pasquali, G. Pastore for the NUCLEX Collaboration
Impact of pairing on clustering and neutrino transport properties in low-density stellar matter
Authors: S. Burrello, M. Colonna, F. Matera
Studying correlations in ${}^{40}Ar+{}^{58}Fe$ with FAUST
Authors: L. Heilborn, C. Lawrence, A. B. McIntosh, M. D. Youngs, S. J. Yennello
FRIGA, a new approach to identify isotopes and hypernuclei in $n$-body transport models
Authors: A. Le Fèvre, Y. Leifels, J. Aichelin, Ch. Hartnack, V. Kireyev, E. Bratkovskaya
Symmetry energy and composition of the outer crust of neutron stars
Authors: A. F. Fantina, N. Chamel, J. M. Pearson, S. Goriely
Exciting baryon resonances in isobar charge-exchange reactions
Authors: J. Benlliure, J. L. Rodriguez-Sanchez, J. Vargas, H. Alavarez-Pol, T. Aumann, J. Atkinson, Y. Ayyad, S. Beceiro, K. Boretzky, A. Chatillon, D. Cortina, P. Diaz, A. Estrade, H. Geissel, H. Lenske, Y. Litvinov, M. Mostazo, C. Paradela, S. Pietri, A. Prochazka, M. Takechi, I. Vidaña, H. Weick, J. Winfield
Code comparison of transport simulations of heavy ion collisions at low and intermediate energies
Authors: H. H. Wolter
N/Z effect on reaction mechanisms cross sections in the ${}^{78}Kr + {}^{40}Ca$ and ${}^{86}Kr + {}^{48}Ca$ collisions at 10 AMeV
Authors: B. Gnoffo, S. Pirrone, G. Politi, M. La Commara, J. P. Wieleczko, E. De Filippo, P. Russotto, M. Trimarchi, M. Vigilante, G. Ademard, L. Auditore, C. Beck, I. Bercenau, E. Bonnet, B. Borderie, G. Cardella, A. Chibihi, M. Colonna, S. De Luca, D. Dell'Aquila, A. D'Onofrio, J.D. Frankland, G. Lanzalone, P. Lautesse , D. Lebhertz, N. Le Neidre, I. Lombardo, N. S. Martorana,K. Mazurek, S. Norella, A. Pagano, E.V. Pagano, M. Papa, E. Piasecki, F. Porto, L. Quattrocchi, F. Rizzo, G. Spadaccini, A. Trifirò, G. Verde
Signals of dynamical and statistical process from IMF-IMF correlation function
Authors: E. V. Pagano, L. Acosta, L. Auditore, V. Baran, T. Cap, G. Cardella, M. Colonna, S. De Luca, E. De Filippo, D. Dell' Aquila, L. Francalanza, B. Gnoffo, G. Lanzalone, I. Lombardo, C. Maiolino, N. S. Martorana, S. Norella, A. Pagano, M. Papa, E. Piasecki, S. Pirrone, G. Politi, F. Porto, L. Quattrocchi, F. Rizzo, E. Rosato, P. Russotto, K. Siwek-Wilczyńska, A. Trifiro, M. Trimarchi, G. Verde, M. Vigilante, J. Wilczyńsky
Equilibration chronometry
Authors: Alan B. McIntosh, Andrea Jedele, Sherry J. Yennello
Is the caloric curve a robust signal of the phase transition in hot nuclei?
Authors: E. Vient for the INDRA and ALADIN Collaborations
Past and future detector arrays for complete event reconstruction in heavy-ion reactions
Authors: G. Cardella, L. Acosta, L. Auditore, C. Boiano, A. Castoldi, M. D'Andrea, E. De Filippo, D. Dell' Aquila, S. De Luca, F. Fichera, N. Giudice, B. Gnoffo, A. Grimaldi, C. Guazzoni, G. Lanzalone, F. Librizzi, I. Lombardo, C. Maiolino, S. Maffesanti, N. S. Martorana, S. Norella, A. Pagano, E. V. Pagano, M. Papa, T. Parsani, G. Passaro, S. Pirrone, G. Politi, F. Previdi, L. Quattrocchi, F. Rizzo, P. Russotto, G. Saccà, G. Salemi, D. Sciliberto, A. Trifirò, M. Trimarchi, M. Vigilante
KATANA --- a charge-sensitive trigger/veto array for the S$\pi$RIT TPC
Authors: P. Lasko, J. Brzychczyk, P. Hirnyk, J. Łukasik, P. Pawłowski, K. Pelczar, A. Snoch, A. Sochocka, Z. Sosin
Stopping power as a signature of dissipative processes in heavy-ion collisions
Authors: G. Besse, V. De La Mota, P. Eudes
Theoretical analyses of FAZIA data with a statistical approach
Authors: N. Buyukcizmeci, R. Ogul, A. S. Botvina
Test of GET Electronics for the CHIMERA and FARCOS multi-detectors
Authors: S. De Luca, L. Acosta, L. Auditore, C. Boiano, G. Cardella, A. Castoldi, M. D'Andrea, E. De Filippo, D. Dell'Aquila, F. Fichera, B. Gnoffo, C. Guazzoni, G. Lanzalone, I. Lombardo, N. S. Martorana, T. Minniti, S. Norella, A. Pagano, E. V. Pagano, M. Papa, S. Pirrone, G. Politi, L. Quattrocchi, F. Rizzo, P. Russotto, G. Saccà, A. nobreakTrifirò, M. Trimarchi, G. Verde, M. Vigilante
Study on the isospin equilibration phenomenon in nuclear reactions ${}^{40}Ca+{}^{40}Ca$, ${}^{40}Ca+{}^{46}Ti$, ${}^{40}Ca+{}^{48}Ca$, ${}^{48}Ca + {}^{48}Ca$ at 25 MeV/nucleon by using the CHIMERA multidetector
Authors: N. S. Martorana, L. Auditore, I. Berceanu, G. Cardella, M. B. Chatterjee, S. De Luca, E. De Filippo, D. Dell' Aquila, B. Gnoffo, G. Lanzalone, I. Lombardo, C. Maiolino, S. Norella, A. Pagano, E. V. Pagano, M. Papa, S. Pirrone, G. Politi, F. Porto, L. Quattrocchi, F. Rizzo, P. Russotto, A. Trifirò, M. Trimarchi, G. Verde, M. Vigilante
The InKiIsSy experiment at LNS: A study of size vs. isospin effects with ${}^{124}Xe + {{}^{64}Zn}, {}^{64}Ni$ reactions at 35 AMeV
Authors: S. Norella, L. Acosta, L. Auditore, V. Baran, T. Cap, G. Cardella , M. Colonna, E. De Filippo, D. Dell'Aquila, S. De Luca, L. Francalanza, B. Gnoffo, G. Lanzalone, I. Lombardo, C. Maiolino, N. S. Martorana, T. Minniti, A. Pagano, E. V. Pagano, M. Papa, E. Piasecki, S. Pirrone, G. Politi, F. Porto, L. Quattrocchi, F. Rizzo, E. Rosato, P. Russotto, K. Siwek-Wilczynska, A. Trifirò, M. Trimarchi, G. Verde, M. Vigilante, J. Wilczyński$^dag$
Coupled-channels description of the ${}^{40}Ca + {}^{58,64}Ni$ transfer and fusion reactions
Authors: G. Scamps, D. Bourgin, K. Hagino, F. Haas, S. Courtin
Characteristics of the fission fragments induced by the ${}^{129}Xe + {}^{nat}Sn$ reactions at $E=8 - 15$ AMeV
Authors: A. Aziz, F. Aksouh, M. Al-Garawi, S. Al-Ghamdi, K. Kezzar, A. Chbihi | CommonCrawl |
Shannon confusion and diffusion concept
I read the document(not the whole document) from Shannon where he speaks about the concepts of confusion and diffusion. I read in many places(not in the document but around the internet) that confusion is enforced using substitution. Diffusion is enforced using permutation/transposition. Ciphers must use both of them because either confusion or diffusion alone are not enough. I read that a substitution cipher can apply by itself confusion(only). Permutation/Transposition applies by itself diffusion(only). It's precisely the last case that bothers me: Can a permutation/transposition cipher by itself apply diffusion?
Shannon explains diffusion as a property that spreads statistic properties of text all over the text preventing statistic analysis. It's frequently translated to: an alteration to a plaintext symbol affects many cipher text symbols. Assuming permutation of bits or characters, how can diffusion be achieved by simple permutation? I mean, if you permute bits, there will be no other bits affected. But if you consider a symbol a character and you permute bits, a change in a character will affect many other characters. It's a question of what is a symbol.
I also read versions of this diffusion concept where the point was just changing bits order just to avoid pattern analysis of the text. But, where is the avalanche effect in simple permutation?
So, what is the correct definition and the implications of diffusion?
I hope you understand what is troubling me.
Thank you once more
permutation statistical-test transposition-cipher
BrunoMCBragaBrunoMCBraga
$\begingroup$ In more modern terms, I believe we apply confusion to mean a nonlinear transformation, and diffusion to be a linear one. Substitutions can be linear and not apply confusion. $\endgroup$ – Richie Frame Sep 6 '14 at 2:48
$\begingroup$ This seems like the idea behind the whirlpool or the Enigma where it was predictable in its unpredictability. $\endgroup$ – Daniel Sep 8 '14 at 14:43
$\begingroup$ How is Whirlpool predictable? $\endgroup$ – Nova Nov 15 '14 at 20:05
I think that you missed a pivotal point in the concept, which is the small blocks that are used to compose a secure PRF (or PRP), i.e. when you permute one bit, you actually change the value of the small block of that bit, i.e. the whole small-block is effected and thus prepared to be confused in the next round, this way you will reach a confusion of the entire big-block very fast.
I attach a good explanation of the concept as described in Lindell-Katz Book
In addition to his work on perfect secrecy, Shannon also introduced a basic paradigm for constructing concise,random-looking permutations. The basic idea is to construct a random looking permutation $F$ with a large block length from many smaller random (or random-looking) permutations $\{f_i\}$ with small block length. Let us see how this works on the most basic level. Say we want $F$ to have a block length of $128$ bits. We can define $F$ as follows: the key $k$ for $F$ will specify $16$ permutations $f_1,\ldots, f_{16}$ that each have an $8$-bit ($1$-byte) block length. Given an input $x\in\{0, 1\}^{128}$, we parse it as $16$ bytes $x_1,\ldots,x_{16}$ and then set (equation 6.2) $F_k(x)=f_1(x)||\ldots||f_{16}(x_{16})$. These round functions $\{f_i\}$ are said to introduce confusion into $F$. It should be immediately clear, however, that F as defined above will not be pseudorandom. Specifically, if $x$ and $x'$ differ only in their first bit then $F_k(x)$ and $F_k(x')$ will differ only in their first byte (regardless of the key k). In contrast, if $F$ were a truly random permutation then changing the first bit of the input would be expected to affect all bytes of the output. For this reason, a diffusion step is introduced whereby the bits of the output are permuted, or "mixed," using a mixing permutation. This has the effect of spreading a local change (e.g., a change in the first byte) throughout the entire block. The confusion/diffusion steps—together called a round —are repeated multiple times. This helps ensure that changing a single bit of the input will affect all the bits of the output.
As an example, a two-round block cipher following this approach would operate as follows. First, confusion is introduced by computing the intermediate result $f_1(x_1)||\ldots||f_{16}(x_{16})$ as in Equation (6.2). The bits of the result are then "shuffled," or re-ordered, to give $x'$. Then $f'_1(x'_1)||\ldots||f'_{16}(x'_{16})$ is computed (where $x'= x'_1,\ldots,x'_{16}$), using possibly different functions $f'_i$, and the bits of the result are permuted to give output $x''$. The $\{f_i\},\{f'_i\}$, and the mixing permutation(s) could be random and dependent on the key, as we have described above. In practice, however, they are specially designed and fixed, and the key is incorporated in a different way
kodlu
BushBush
I find the terms "confusion" and "diffusion" to be slightly nebulous and can lead to over-simplifications.
For example, saying that "substitution" is responsible for "confusion" is not necessarily correct: "Substitution" is actually just a function application to the state; The implementation often utilizes a memoized function, but you can easily 1. calculate the non-linear function explicitly on each application, as well as 2. use a memoized linear function to provide only diffusion and not confusion. So saying Substitution provides Confusion is an over simplification.
Now, the reason why non-linear functions are often implemented with a memoized table is because non-linear functions can be complicated to compute. Generally speaking, the more complicated a function is, the longer it takes to evaluate it. For example, the AES S-Box utilizes calculation of the multiplicative modular inverse of an element in a finite field. This could be computed explicitly instead of using a table lookup; Doing so will result in a cipher that is significantly slower.
So the confusion does not stem from substitution per se, it results from applying complicated non-linear functions that tend to produce maximally unhelpful and complicated equations. The more "linear" a non-linear function is, the easier it becomes to cryptanalyze and break (we can assume that it acts like a linear function in certain inputs/outputs with a certain probability of being true). There is plenty of research into what kind of non-linear functions are maximally un-helpful to the cryptanalyst.
So it may be more accurate to say non-linearity is responsible for "confusion". Non-linearity is always required in a symmetric cipher algorithm, because otherwise the resulting systems of equations that represent the cipher can easily be manipulated and solved.
As for "Diffusion", other answers have touched on it. But going into more detail, when you really get down to it, all we can really do when attempting to encrypt anything is apply XOR and AND gates to bits. Yes, there exist other operations, such as integer addition; However, these are actually implemented by a circuit of XOR/AND, so at the end of the day, that's all we're really capable of doing. (This is not absolutely true; You could, as a counter-example, use NAND as your basis; This is not really helpful to the current discussion.)
This is relevant to diffusion because XOR and AND are both bit sliced operations. They take two bits as input as produce one bit as output. So what happens if you XOR together two 8-bit words? You're actually performing eight, totally separate XOR gates on 8 separate groups of data in parallel. XOR and AND (on any wordsize larger the 1) is actually an SIMD operation. Thus, the bits at index $i$ in the words do not influence the bits at any other index in the words. In reality, we only have 1-bit registers, we just have a lot of them in parallel.
This is why "Transposition" (rotations and shifts) is required to produce diffusion: Rotations and shifts ensure that new pairs of bits are utilized as inputs to future XOR/AND gates. Basically, the linear diffusion layer is responsible for mixing the contents of these 1-bit registers.
More specifically: The job of the linear diffusion layer is to ensure that each successive input to the non-linear function consists of a balanced and maximum number of super-positioned input bits. If your non-linear function operates on X-bit words, then ideally each input bit will have X/2 input bits super positioned in each index (50% of each input bits influence each output bit, aka "the avalanche effect"). (Note: An exclusive-or sum is a linear superposition of the summed bits)
Put simply, the combination of diffusion and confusion means that we want to produce equations with a maximum number of terms and maximum algebraic complexity. Then, of course, we repeat the process, until the resultant system of equations that describes the output is simply impossible to work with by even probabilistic reasoning.
Ella Rose♦Ella Rose
Not the answer you're looking for? Browse other questions tagged permutation statistical-test transposition-cipher or ask your own question.
Why Diffusion and Confusion prevent statistical analysis?
Confusion and Diffusion in the AES functions
Property that prevents determining key from ciphertext and plaintext
Computational indistinguishability and example of non polynomial algorithm
derangements and permutations in cryptography
Block cipher and parity of permutation
What benefits do substitution boxes and permutation boxes offer in DES?
How were the diffusion statistics for norx calculated?
How does Feistel cipher create diffusion between blocks?
Estimated entropy per bit given P-value of a statistical test, and number of bits tested?
Relationship between existence of OWFs and OWPs
Can both substitution and transposition ciphers be thought of as permutations?
What's the difference between confusion/diffusion and mode of operation? | CommonCrawl |
Vancomycin Calculator
Advanced vancomycin pharmacokinetics tool
ClinCalc.com » Infectious Disease » Vancomycin Calculator
Try out a new beta version of this vancomycin calculator - now with support for Bayesian modeling.
Patient Parameters
Body weight:
kg lbs
Volume of distribution (Vd): L/kg
Therapeutic goal: Trough 15 to 20 mcg/mL Trough 10 to 15 mcg/mL AUC:MIC ratio > 400
Recommend loading dose:
Elimination Constant (Kel)
Empiric Estimation Based on One Level Based on Two Levels
Manually enter
creatinine clearance »
CrCl: mL/min
Age: years
Creatinine: mg/dL µmol/L
Current dose mg every hours
Infusion time hour(s)
Trough level mcg/mL
Time between trough level
and next dose minutes
Early Late
Note: This estimation assumes that no vancomycin has been given between the two levels.
First level mcg/mL
Second level mcg/mL
Time between first and second levels hours
Press 'Calculate' to view calculation results.
Load an Example
This vancomycin calculator uses a variety of published pharmacokinetic equations and principles to estimate a vancomycin dosing regimen for a patient. A regimen can be completely empiric, where the vancomycin dose is based on body weight and creatinine clearance, or a regimen may be calculated based on one or more vancomycin levels.
Our vancomycin calculator was specifically designed to help students and clinicians understand the process of calculating a vancomycin regimen. When a vancomycin regimen is calculated, each step in the dosing process is fully enumerated and visible by clicking the "Equations" tab.
In addition to being designed for students, this calculator was also intended with the practicing clinician in mind. All dosing regimens are rounded to the nearest 250 mg with appropriate dosing intervals (eg, Q8hr, Q12hr, Q24hr) to reflect clinical practice. Additionally, after calculating a dosing regimen, a pharmacokinetic progress note template is automatically generated for your convenience.
After calculating a dose, click on 'Progress Note' for a pharmacokinetic template or 'Equations' for a step-by-step explanation of the recommended dosing regimen.
Major Updates to this Calculator
2015-06-07 - Drug elimination is accounted for during the infusion time. Read more
Inappropriate Populations for This Calculator
Population Estimate of Kel
Estimate of Kel from a Trough Level
Population Estimate of Vd
Actual or Ideal Dosing Body Weight
Core Pharmacokinetic Equations
Therapeutic Targets: Trough Level
Therapeutic Targets: AUC:MIC
Vancomycin Loading Dose
This calculator is NOT appropriate for the following patient populations or may require a higher degree of clinical judgment:
Unstable renal function
Vancomycin MIC ≥ 2 mcg/mL
Because vancomycin is primarily renally eliminated, the elimination constant (Kel) is directly related to creatinine clearance (CrCl). While several population estimates exist, this calculator uses the Creighton equation 1 to estimate Kel for a given CrCl using the Cockcroft-Gault method:2
$$ K_{el} = 0.00083*(CrCl) + 0.0044 $$
Importantly, this method relies on an accurate creatinine clearance; therefore, this method may not be appropriate in patients with unstable renal function or other characteristics that make creatinine clearance difficult to estimate (eg, obesity, elderly, amputations, etc.). Furthermore, it should be emphasized that this is merely an estimate of Kel -- there are many other equations to generate an estimate.
This calculator can use a single vancomycin trough to estimate true vancomycin clearance (rather than a population estimate from creatinine clearance). This calculator assumes that the vancomycin trough is drawn at steady state, which occurs prior to the fourth vancomycin dose (assuming a consistent dose and dosing regimen).3
By default, this calculator suggests a population estimate volume of distribution (Vd) of 0.7 L/kg for vancomycin. There is actually a large variation in the literature, with Vd being described between 0.5 and 1 L/kg.4 There is some evidence that patients with reduced creatinine clearance (CrCl < 60 mL/min) have a larger Vd of 0.83 L/kg, whereas patients with preserved renal function (CrCl ≥ 60 mL/min) have a smaller Vd of 0.57 L/kg.5
Although data are limited, it is recommended that vancomycin be initially dosed on actual body weight (not ideal or adjusted weight), even in obese patients.3 Clinically, this dose may be capped at a specific weight (eg, 120 kg) or dose (eg, 2500 mg), although this practice has not been prospectively studied.
While vancomycin is dosed on actual body weight, it should be noted that creatinine clearance (which may be used to empirically estimate Kel) is based on ideal or adjusted body weight. For more information on the appropriate body weight, see Creatinine Clearance - Adjustments for Obesity.
This vancomycin calculator uses three "core" clinical pharmacokinetic equations that are well described for intermittent intravenous infusions assuming a one-compartment model.4:
$$ Cp=Cp^0*e^{(-kt)} $$
This equation describes how an initial drug concentration (Cp0) declines to a final drug concentration (Cp) over a specified period of time (t) assuming an elimination constant (k).
$$ \Delta C = \frac{Dose}{Vd} $$
This equation describes the change in concentration (ΔC = Cfinal - Cinitial) is related to a given dose and volume of distribution (Vd).
$$ Dose = \frac{C_{peak}*T_{infusion}*Vd*K_{el}*(1-e^{(-K_{el}*Tau)})}{(1-e^{(-K_{el}*T_{infusion})})} $$
This large equation calculates an appropriate drug dose assuming a goal peak drug level (Cpeak), volume of distribution (Vd), elimination constant (Kel), dosing frequency (Tau), and infusion time (Tinfusion).
Because an AUC:MIC goal value is difficult to calculate, many clinicians continue to use a goal vancomycin trough level as the therapeutic target of choice. As mentioned in guidelines,3 an AUC of 400 may be achieved with a peak of about 40 mcg/mL and a trough of about 15 mcg/mL. This method is often used as an alternative to direct AUC calculations.
Current guidelines make the following suggestions regarding the optimal vancomycin trough level:3
All patients should achieve a minimum trough level of > 10 mcg/mL
Patients with complicated infections should have a goal vancomycin trough of 15 to 20 mcg/mL. Complicated infections include:
Pathogen MIC of 1 mcg/mL
Hospital-acquired pneumonia caused by Staph aureus
Although vancomycin has been on the market since the 1950s, there is still considerable controversy regarding the optimal monitoring parameter to maximize efficacy and minimize toxicity. Current guidelines recommend an AUC:MIC ratio of ≥ 400, although this goal is largely based on weak evidence.3,6,7,8
In order for an AUC:MIC ratio to be calculated, both a peak and trough level must be known. Because only trough levels are drawn clinically, a peak level must be estimated. The following equation is used to estimate vancomycin's area under the curve (AUC):5
$$ \\ Lin\;trap = \frac{Trough+Peak}{2}*(T_{infusion}) \\ Log\;trap = \frac{(Peak-Trough)*(Tau-T_{infusion})}{\ln(\frac{Peak}{Trough})} \\ AUC_{0-Tau} = (Lin\;trap) + (Log\;trap) \\ AUC_{0-24} = AUC_{0-Tau}*(24/Tau) = AUC\;in\;mcg*h/mL $$
For more information about AUC:MIC and pharmacodynamic killing, see Vancomycin AUC:MIC versus T>MIC.
In seriously ill patients, a loading dose of 25-30 mg/kg (actual body weight) may be considered.3 This practice has a theoretical benefit of attaining therapeutic vancomycin levels earlier, but has not been extensively studied. This approach is not supported by evidence from large clinical trials, therefore, the safety and efficacy of a loading dose practice has not been established.
Regardless, based on expert opinion, the following patient populations may be considered for such a loading dose when MRSA is suspected:9
Severe skin/soft tissue infection
One common question is a maximum vancomycin loading dose. As stated above, there is a lack of evidence supporting loading doses, let alone loading doses in morbidly obese patients. While not recommended by the guidelines, many institutions will "cap" a loading dose at approximately 2000 to 3000 mg. This calculator, when providing a loading dose, will cap at 3000 mg. A vancomycin loading dose cap of 3000 mg represents a maximum weight of 120 kg for a dose of 25 mg/kg.
Matzke GR, McGory RW, Halstenson CE, Keane WF. Pharmacokinetics of vancomycin in patients with various degrees of renal function. Antimicrob Agents Chemother. 1984 Apr;25(4):433-7. PMID 6732213.
Cockcroft DW, Gault MH. Prediction of creatinine clearance from serum creatinine. Nephron. 1976;16(1):31-41. PMID 1244564.
Rybak M, Lomaestro B, Rotschafer JC, et al. Therapeutic monitoring of vancomycin in adult patients: a consensus review of the American Society of Health-System Pharmacists, the Infectious Diseases Society of America, and the Society of Infectious Diseases Pharmacists. Am J Health Syst Pharm. 2009;66(1):82-98. PMID 19106348.
Bauer LA. Chapter 5. Vancomycin. In: Bauer LA, ed. Applied Clinical Pharmacokinetics. 2nd ed. New York: McGraw-Hill; 2008.
DeRyke CA, Alexander DP. Optimizing Vancomycin Dosing Through Pharmacodynamic Assessment Targeting Area Under the Concentration-Time Curve/Minimum Inhibitory Concentration. Hospital Pharmacy. 2009;44(9):751-765. Free Full Text.
Craig WA. Basic pharmacodynamics of antibacterials with clinical applications to the use of beta-lactams, glycopeptides, and linezolid. Infect Dis Clin North Am. 2003;17(3):479-501. PMID 14711073.
Moise-Broder PA, Forrest A, Birmingham MC, et al. Pharmacodynamics of vancomycin and other antimicrobials in patients with Staphylococcus aureus lower respiratory tract infections. Clin Pharmacokinet. 2004;43(13):925-42. PMID 15509186.
Jeffres MN, Isakow W, Doherty JA, et al. Predictors of mortality for methicillin-resistant Staphylococcus aureus health-care-associated pneumonia: specific evaluation of vancomycin pharmacokinetic indices. Chest. 2006;130(4):947-55. PMID 17035423.
Liu C, Bayer A, Cosgrove SE, et al. Clinical practice guidelines by the infectious diseases society of america for the treatment of methicillin-resistant Staphylococcus aureus infections in adults and children. Clin Infect Dis. 2011;52(3):e18-55. PMID 21208910.
ASHP/IDSA/SIDP vancomycin recommendations
IDSA MRSA guidelines
Vancomycin AUC:MIC versus T>MIC
Kane SP. Vancomycin Calculator. ClinCalc: https://clincalc.com/Vancomycin. Updated September 9, 2019. Accessed January 19, 2020.
Updated Sep 9, 2019
Default infusion time
1000 mg/hr 500 mg/hr
MIC of organism mcg/mL
Creatinine assay method
IDMS Conventional
IDMS is the newer, more precise method for measuring serum creatinine. Older methods falsely inflated the creatinine assay by as much as 20%. Most institutions are using IDMS by this point, but you should contact your laboratory if you are unsure of your assay. For more information, read more about IDMS. | CommonCrawl |
Physics Stack Exchange is a question and answer site for active researchers, academics and students of physics. It only takes a minute to sign up.
Is there a block spin renormalization group scheme that preserves Kramers-Wannier duality?
Block spin renormalization group (RG) (or real space RG) is an approach to studying statistical mechanics models of spins on the lattice. In particular, I am interested in the 2D square lattice model with on-site degrees of freedom (i.e. spins) being the elements $g_i$ in a finite Abelian group $g_i\in G$, and the partition function has the following form
$$\begin{split}Z&=\sum_{[g_i\in G]}e^{-S[g_i]},\\S[g_i]&=-\sum_{\langle ij\rangle}K(g_i^{-1}g_j),\end{split}$$
where $K(g)$ is a suitable group function ($K:G\to\mathbb{R}$) to penalize the group elements that differ from identity. The block spin RG partitions the lattice into small blocks (labeled by $I,J$) and rewrite the action in terms of the block spin $g_I\sim\sum_{i\in I}g_i$ (how to map the sum back to an element $g_I\in G$ depends on the RG scheme), such that the partition function can be rewritten as
$$Z=\sum_{[g_I\in G]}\sum_{[g_i\in G]}\delta\big[g_I\sim\textstyle{\sum}_{i\in I}g_i\big]e^{-S[g_i]}=\sum_{[g_I\in G]}e^{-S'[g_I]},$$
where the new action takes the form of
$$S'[g_i]=-\sum_{\langle IJ\rangle}K'(g_I^{-1}g_J)+\cdots.$$
By omitting higher order terms generated under RG, the RG procedure can be considered as a function map $\mathcal{R}$ that takes the group function $K(g)$ to $K'(g)$.
On the other hand, such a model of finite Abelian group $G$ on the square lattice admits the Kramers-Wannier duality. The key step of the duality is a Fourier transform (on the Abelian group $G$)
$$e^{-\tilde{K}(\tilde{g})}=\sum_{g\in G}e^{-K(g)}\;\chi(g,\tilde{g}),$$
where $\tilde{g}$ is a representation of $G$, and $\chi(g,\tilde{g})$ is the character. Due to the fact that the representation of a finite Abelian group $G$ also forms a finite Abelian group $\tilde{G}$, and $\tilde{G}$ is isomorphic to $G$ (meaning that the dual group $\tilde{G}$ is the same as $G$). Combining with the fact that the dual lattice of the square lattice is still a square lattice, the Kramers-Wannier duality can be considered as a bijective functional map $\mathcal{D}$ that maps $K(g)$ to $\tilde{K}(g)$ (and vice versa).
However, it is not obvious to me that the block spin RG preserves the Kramers-Wannier duality. I think in general the RG transformation $\mathcal{R}$ is not guaranteed to commute with the duality transformation $\mathcal{D}$, or say the following diagram does not commute in general:
$$\begin{array}{lllllll} K & \overset{\mathcal{R}}{\to} & K' & \overset{\mathcal{R}}{\to} & K'' & \overset{\mathcal{R}}{\to} \cdots\\ \updownarrow\tiny\mathcal{D} & & \updownarrow\tiny\mathcal{D} & & \updownarrow\tiny\mathcal{D} & \\ \tilde{K} & \overset{\mathcal{R}}{\to} & \tilde{K}' & \overset{\mathcal{R}}{\to} & \tilde{K}'' & \overset{\mathcal{R}}{\to} \cdots \end{array}$$
So the question is how to design the block spin RG scheme to make the above diagram commute? Is there a systematic design of the block spin RG scheme that preserves the Kramers-Wannier duality?
statistical-mechanics condensed-matter renormalization duality
Everett You
Everett YouEverett You
A potential first step towards answering your question is given in our recent paper, where we expose and exploit non-local matrix product operator symmetries in the tensor network representation of classical partition functions. Since the strange correlator picture naturally provides us with a symmetry-preserving real-space renormalization group flow (see the last section of the paper), the design of a block spin RG scheme that preserves the Kramers-Wannier duality can be reformulated in terms of designing a symmetry-preserving truncation procedure on the level of the entanglement degrees of freedom of a projected-entangled pair state.
Matthias BalMatthias Bal
Thanks for contributing an answer to Physics Stack Exchange!
Not the answer you're looking for? Browse other questions tagged statistical-mechanics condensed-matter renormalization duality or ask your own question.
Critical 2d Ising Model
Antiferromagnetic and Ferromagnetic Ising Model on triangular lattice
Continuum Field Theory for the Ising Model
Is there any relation between density matrix renormalization group (DMRG) and renormalization group (RG)?
Is there a difference between renormalization and renormalization group?
Relating scaling and critical exponents in the Ising model | CommonCrawl |
lectures videos worksheets
notes labs
1. About this course
2. Engineering Abstraction
3. Information
4. Circuits
5. The Digital Abstraction
6. CMOS
7. Combinational Logic
8. Sequential Logic
9. Finite State Machines
10. Synchronization and Arbitration
11. Performance Measures
12. Design Tradeoffs
Programmable Architectures
13. Models of Computation
14. Instruction Set Architectures
15. Assembly Language
16. Stacks and Procedures
17. Compiled Languages
18. Processor Implementation
19. Memory Systems
20. Pipelined Processors
21. Virtual Memory
22. Virtualizing the Processor
23. Devices & Interrupts
24. System-level Communication
25. Concurrency & Synchronization
26. Parallel Processing
27. Future of Computing
Authored by Steve Ward
Models of Computation
The first module of this course deals with the technical foundations of all digital systems, specialized to an endless variety of specific applications. For the remainder of the course, we refocus our attention on a particular class of digital system: the general purpose computer. The distinguishing feature of this class of digital systems is that their behavior is dictated by algorithms encoded as digital data, rather than being wired into the digital circuitry that constitutes their hardware design. This distinction represents a major conceptual revolution of the early $20^{th}$ century, and one that underlies modern computer science and engineering. Its immediate consequences are the conceptual distinction between hardware and software, the notion of programming and programming languages, interpretation and compilation as engineering techniques, and many other issues central to contemporary computer science. Fundamental ideas that underly this important paradigm shift are the topic of this Chapter. We may view these seminal ideas as the product of a search, during the first half of the twentieth century, for a suitable formal model of digital computation: a sound mathematical basis for the study of the universe of computational algorithms and machines capable of performing them.
This Chapter marks our transition to this new focus by sketching foundational ideas of Computer Science resulting from that search.
FSMs as a model of computation
13.1. FSMs as a model of computation
Finite state machines, described in Chapter 9, are an attractive candidate as a model of computation. We may view a simple ROM-based FSM as a programmable general-purpose (or at least multi-purpose) computation machine, in that its behavior may be modified simply by changing the string of bits stored in its ROM. Of course, any particular FSM implementation as a digital circuit necessarily fixes the number of inputs, outputs, and states as implementation constants, limiting the range of FSM behaviors that can be achieved by reprogramming its ROM.
Generalized FSM implementation
We might generalize our FSM model a bit by parameterizing the implementation as shown to the right. This design shows the implementation of an FSM with $i$ inputs, $o$ outputs, and $s$ state bits (for a maximum of $2^s$ states). Given an arbitrary FSM specification (for example, in the form of a state transition diagram) we can implement that FSM according to this diagram by an appropriate choice of the parameters $i$, $o$, and $s$ as well as the specific bits to be stored in the ROM. This is a useful conceptual tool, as it allows us characterize the universe of computations that can be performed by any FSM of any size as some instance of this diagram with concrete values for $i$, $o$, $s$, and ROM contents.
We might ask how many different FSM behaviors may be encoded into the ROM of this generalized FSM circuit for a given set of $i$, $o$, and $s$ values. Although this question is hard to answer precisely, an easy upper bound is the number of distinct ways in which the ROM of the given FSM can be programmed. Given the $i$, $o$, and $s$ parameters we can deduce that the number of lines in the ROM's truth table is $2^{i+s}$, as the ROM has $i+s$ inputs. Each line specifies $o+s$ output values; thus there are $(o+s)\cdot2^{i+s}$ binary output values to be specified for the ROM's truth table. since we may choose a 1 or zero for each, the total number of distinct ROM contents are $$FSMS(i, o, s) = 2^{(o+s)\cdot2^{i+s}}$$ The reason that this number is an upper bound rather than a precise count of distinct FSMs is that some pairs of distinct ROM contents yield equivalent FSMs. However, we are assured that any given FSM having $i$ inputs, $o$ outputs, and $s$ state bits will be equivalent to at least one of the FSM behaviors represented among the set of ROM programs considered.
FSM enumeration
13.1.1. FSM enumeration
Although the bound established by $FSMS(i,o,s)$ grows large as the parameters $i, o, s$ increase, we note that it remains finite for finite $i, o, s$. This observation suggests an intriguing conceptual exercise: we could define an infinite list that includes every possible FSM -- with some duplicates, due to equivalence -- by enumerating the possible ROM configurations for each set of $i, o, s$ values in some canonical order.
One approach to building such a list is sketched to the left. The first FSMs on the list are those with $i=o=s=1$. Each of these is programmed by specifying an 8-bit string as its ROM contents, so there are $2^8=256$ possible ROM configurations for this FSM size. The first 256 entries denote FSMs with $i=o=s=1$, whose 8-bit ROM contents are listed in natural binary order. Next on the list is FSMs having $i=o=s=2$; there are $FSMS(2,2,2) = 2^{64}$ of these, again added to the list by stepping through possible ROM contents in natural binary order. We then add FSMs having $i=o=s=3$, $i=o=s=4$, and so on for every finite value for $i=o=s$.
This construction lists all FSMs for which $i=o=s$, but seems to miss FSMs having different numbers of inputs, outputs, and state bits. Where on our list, for example, is an FSM having 1 input, 2 outputs, and 3 state bits? We justify such omissions by the observation that there is an equivalent FSM on the list with $i=o=s=3$ that behaves identically if we ignore unused inputs, outputs, or state bits. Our conceptual list, therefore, captures every possible FSM behavior at some finite position on the list.
Although there are many different schemes we could use to define our FSM enumeration, once we agree on an enumeration we can refer to the $i^{th}$ FSM, $FSM_i$, unambiguously. There becomes an effective procedure by which we can take any well-specified FSM and determine an index $i$ on our list for which $FSM_i$ behaves identically. We might discover that the 5-state ant controller of Section 9.4 is $FSM_{23785}$, and that the 4-state equivalent version of Section 9.4.1 is $FSM_{1823}$ (its earlier position on the list reflecting its reduced complexity).
Indeed, the indices of complex FSMs (like microprocessor chips) would quickly become huge. Each such FSM index, after all, encodes all of the information necessary to implement that FSM.
13.1.2. FSMs as a Model of Computation
The ability to conceptually catalog FSMs of all sizes, and consequently the set of computations that can be performed by FSMs of all sizes, makes FSMs attractive as a formal model for the computations we might perform by digital circuitry. Moreover, FSMs have been extensively studied and their formal properties and capabilities are well understood. For example, for every class of strings described by a regular expression -- a parameterized template including "wild card" and repetition operators -- there is an FSM that will identify strings of that class. For these reasons, finite state machines have become, and remain, an important formal model for a class of computations.
A natural question arises as to whether FSMs are an appropriate formal model for all computations we might want to perform using digital circuitry. If every computation we might want a digital system to perform can be performed by some finite state machine, does this reduce the process of digital system engineering to the simple selection of an FSM from our enumerated catalog of possibilities? Of course, this extreme view ignores practical issues like cost/performance tradeoffs; however, the question of whether the class of computations performed by FSMs is a suitable abstraction for all practical digital computations is clearly worth answering.
FSM limitations
13.1.3. FSM limitations
Although FSMs can clearly perform a variety of useful operations, there are simple, well-defined computations that cannot be performed by any finite state machine.
Paren Checker
To take a simple example, imagine a device whose input is a sequence of left and right parentheses (perhaps encoded as 0 and 1, respectively) and whose single digital output is 1 if and only if the string entered thus far is a well formed parenthesis string. This test requires that each left paren in the string is matched by a subsequent right paren, perhaps separated by one or more well-formed paren strings. The skeptical reader is invited to devise an FSM that meets this specification, armed with the friendly warning that the challenge is a fool's errand.
The difficulty arises because of the finiteness of an FSM's storage. If an input string consisting of $k$ consecutive left parens is entered, the paren checker must use at least $k+1$ different states to count the number of left parens entered, since it can only output a $1$ if precisely $k$ right parens are subsequently entered. Thus at least $k+1$ states are required to respond properly to an input string consisting of $k$ left parens followed by $k$ right parens. For no finite $N$ can an $N$-state FSM properly deal with all possible finite inputs.
In fairness to FSMs as a model, the finiteness of their storage capacity is a deliberate design feature. As practical engineers, we are interested in computations that can be completed using finite resourses -- storage as well as time -- and FSMs as a class seem to capture this set of computations. Any specific FSM, however, offers only a bounded amount of storage for the computations it performs; hence no single FSM can perform a range of computations whose storage requirements are unbounded. Paren checking of arbitrary finite strings is an example: while any finite string can be checked using finite storage, for every finite bound we can find a finite input string whose storage requirements will exceed this bound. There are, of course, many other simple examples of practical algorithms we may wish to consider which require unbounded storage depending on their input data.
Alternative Models
13.1.4. Alternative Models
The search for an abstract model of computation capable of dealing with a broader class of algorithms was an active research topic during the early $20^{th}$ century. Proposed candidates explored a wide variety of approaches and characteristics, and many have had lasting impact on the field of computer science. Examples include:
The lambda calculus of Alonso Church, simple model for functional programming languages;
The combinatory logic of Schonfinkel and Curry, a model for functional programming without variables;
The theory of recursive functions of Kleene;
The string rewriting systems of Post and others, in which system state stored as a string of symbols evolves under a set of rewrite rules;
Turing machines, discussed in the next section.
Each of these models aimed to capture a broad set of practical algorithms, including those whose time and space requirements were unbounded functions of their input data.
As new formalisms were proposed and compared, there was a clear need for a benchmark to determine their relative power as a general model of computation. What emerged as a standard measure of a model's power is the set of integer functions supported by that model: a model that could support addition and multiplication of arbitrary integers, for example, was more powerful than an alternative model that could add but not multiply.
Turing Machines
13.2. Turing Machines
One of the alternative formalisms for modeling computation was a simple extension of FSMs proposed by Alan Turing in 1936.
A Turing Machine
Turing addressed the bounded storage limitation of the FSM by a simple expedient: a Turing Machine is a finite state machine interfaced to a doubly infinite digital tape (meaning a tape with neither a left nor a right end). A handful of the FSM's inputs and outputs are used to control the tape interface, which consists of a tape head pointing to some discrete position on the tape and the ability o read a binary digit (1 or 0) at the current position, write a binary digit at the current position, and/or move the head one position to the left or right on the tape.
The infinite tape of a Turing Machine serves as its sole input/output device: the FSM inputs and outputs serve only to interface to the tape. A computation is performed on a Turing Machine by
Mounting a tape containing some initial configuration of 0s and 1s, with the tape head pointing to a appropriate starting point. This configuration encodes an input to the computation.
Starting the Turing Machine (with its FSM in a designated inital state).
Letting the Turing Machine run until its FSM reaches a special halting state.
Reading the final configuration of 1s and 0s from the tape of the halted machine. This configuration encodes the output of the computation.
Unary Incrementor TM
A simple Turing machine example is shown in the diagram to the right. This machine consists of a 2-state FSM, and is shown with an initial tape configuration consisting of a sequence of four 1s starting at the current head position. This tape configuration encodes the value 4 in a primitive unary format, in which a nonnegative integer $n$ is encoded as $n$ consecutive 1 bits stored from the head position and to the right, the remaining tape positions containing zero. The particular 2-state machine shown increments this unary number, by finding the right end of the string of 1s, adding an additional 1, and returning to the left end of the string before halting.
Of course, there is an infinite variety of Turing Machines, differing only in the logic that dictates the behavior of their FSM component.
Turing Machine i
Indeed, we can usurp the enumeration of FSMs sketched in Section 13.1.1 to enumerate Turing Machines, using the convention that $TM_i$ consists of $FSM_i$ interfaced to an infinite tape. Of course, many of these machines make little sense, e.g. due to a mismatch between their number of inputs and outputs and the needs of the tape interface; for our conceptual experiments, however, we can tolerate such coding inefficiencies and simply consider these mismatches to be non-functional Turing Machines. Armed with this convention, the set of possible Turing Machines is enumerable: every possible Turing Machine is $TM_i$ for some finite nonnegative $i$.
About that Infinite Tape
13.2.1. About that Infinite Tape
The use of an infinite tape certainly marks the Turing machine as a conceptual rather than a practical tool and may provoke some skepticism in the practical-minded reader.
In fact our interest is in practical computations: ones that complete in a finite number of steps. Every such finite computation will visit at most a finite number of positions on the infinite tape: it will read finitely many positions as input, and write finitely many positions as output. So every finite computation -- every one of the practical computations in which we profess interest -- can be completed with a finite tape of some size. The difficulty that motivated us to consider Turing machines rather than FSMs is that we cannot put a finite bound on that size without restricting the set of functions that can be computed. A conceptually convenient way to relax that restriction is to simply make the storage (the tape) infinite.
There are plausible alternatives to this abstraction mechanism. We might, for example, replace each Turing machine $TM_i$ by a family of finite-memory Turing machines $TMF_i^S$ with varying values of $S$, a finite tape size. The statement that "computable function $f_i$ can be performed by Turing machine $TM_i$" would then become "function $f_i$ can be performed by $TMF_i^S$ for sufficiently large S. We choose to duck this complication by the conceptually simple notion of an infinite tape.
Do keep in mind, however, that every finite computation uses at most a finite portion of the tape: it will read and write at most some bounded region surrounding the initial tape head position.
TMs as Integer Functions
13.2.2. TMs as Integer Functions
In order to compare the computational power of Turing Machines with alternative models such as those mentioned in Section 13.1.4, it is useful to characterize the computation performed by a given TM as an integer function -- that is, a function taking an integer input and producing an integer output. To do so, we adopt a convention for encoding a bounded tape configuration -- a configuration containing finitely many 1s (other positions containing 0) -- as a nonnegative number.
TM 347 on tape 51
One possible such encoding is illustrated on the left. We take the binary digits stored on the infinite tape in a prescribed order to form a binary number whose low-order bit comes from the current head position, whose next bit is the position to the right of the head, whose third bit is from the position to the left of the head, then two positions to the right, and so on until all the (finitely many) 1 bits have been accounted for. The resulting binary number contains infinitely many leading 0s, but only finitely many 1s; hence its value is finite. This value represents the encoding of the tape configuration.
TM as integer function
Armed with this convention, we can view each of our enumerable set of Turing Machines as computing an integer function. To compute the value of $y = TM_i[x]$, we mount an input tape containing the configuration $x$ on the machine, start the machine, let it run until it halts, and read the final tape configuration as the integer value $y$. Of course, in some cases the Turing Machine might run forever without halting, a problem we will return to shortly; for the present, we simply view the value of such non-terminating computations as undefined. We thus recharacterize TMs as computing partial functions that may not be defined for every possible integer argument.
Functions as Expressive Power
13.3. Functions as Expressive Power
Mathematicians studying these early models of computation used the set of integer functions computable by each model as a measure of that model's expressive power -- the idea being that if a given function (say, square root) could be expressed in one model but not in another, the latter model is less powerful in some mathematically significant sense. There ensued a period during which the set of integer functions computable by each of the proposed models was actively studied, partly motivated the desire to "rank" the proposed models by expressive power.
It is worth noting that the set of integer functions in question can be generalized in various ways. Functions of multiple integer arguments can be encoded using integer pairing schemes -- for example, representing the pair $(x,y)$ of arguments to $f(x,y)$ as a single integer whose even bits come from $x$ and whose odd bits come from $y$. Similarly, representation tricks like those sketched in Chapter 3 can allow symbols, approximations of real numbers, and other enumerable data types to be represented among the integer arguments and return values of the functions being considered. These coding techniques allow us to represent a very wide range of useful computations using integer functions -- in fact, using single-argument functions defined only on natural numbers (nonnegative integers).
An N-way tie!
13.3.1. An N-way tie!
The remarkable result of this attempt to identify the most expressive of the candidate models of computation, by the metric of expressibility of integer functions, was that each of the models studied could express exactly the same set of integer funtions. The equivalance of the models by this metric was proven, by showing systematic techniques for translating implementations in one model to equivalent implementations in another. For example, there is a systematic algorithm to derive from the description of any Turing machine a Lambda expression that performs precisely the same computation, implying that the expressive power of Lambda expressions is at least that of Turing machines. Moreover, there is an algorith for translating any Lambda expression to a Turing machine that performs the same computation, implying that Lambda expressions are no more expressive than Turing machines. This same set of integer functions may be implemented in many other computation schemes, a set including those mentioned in Section 13.1.4 and countless others, among them most modern computer languages.
Church's Thesis
13.3.2. Church's Thesis
The discovery that the same set of integer functions is computable by every computation scheme of sufficient power that was studied strongly suggests that that set of functions has a significance that goes beyond the properties of any given model of computation. Indeed, it suggests that there is an identifiable set of computable functions that can be implemented by any sufficiently powerful computation scheme, and functions outside this set cannot be computed by any machine we might implement now or in the future.
This conjecture, which is widely believed and supported by countless failures to demonstrate the effective computation of integer functions that cannot be computed by Turing Machines, is often referred to as Church's Thesis in honor of Alonso Church. We cannot prove Church's thesis, due in part to the unbounded nature of the universe of "realizable machines" it covers; but we, and the Computer Science community generally, accept it as axiomatic.
Computable Functions
13.3.3. Computable Functions
Indeed, we may use Church's thesis to define the set of computable functions as that set of functions computable by some Turing Machine. Given our ability to enumerate Turing Machines, it follows that we can enumerate Computable Functions in an infinite list. We might expand this list into an infinite two-dimensional spreadsheet, in order to represent the behavior of each computable function with every possible value for its single argument:
Enumeration of Computable Functions
Note that this diagram is the upper-left corner of a table that extends to infinity in the right and downward directions. The computable functions (equivalently, Turing Machines) are itemized along the vertical axis, and succesive values of the single argument (equivalently, bounded tape configuration) along the horizontal axis. In each cell at the intesection of column $n$ and row $m$ we enter the result of computing $f_m(n)$, or (eqivalently) the final tape configuration after $TM_m$ is run on tape $n$.
In order to deal with the occasional case where $TM_m$ applied to tape $n$ computes forever without halting, we place a red star in cells corresponding to undefined values.
Of course, we cannot build this table any more than we can write down our infinite list of FSMs or Turing machines. Not only is the table infinite, but (as we will see shortly) there is no effective way to tell which cells should contain red stars. Nonetheless, the contents of each cell in the table is mathematically well defined, despite our practical inability to write it down.
We might ask whether the set of computable functions represented in this table includes every function defined on natural numbers -- i.e., whether the set of computable functions includes all possible functions of nonnegative integers. Unfortunately, this cannot be the case: the set of all functions defined on natural numbers is uncountably infinite, implying that there is no systematic way to enumerate them along the vertical axis of our spreadsheet. There are simply too many functions to enumerate; hence most functions are not represented on our list, and consequently not among the set of functions we have identified as computable.
The Halting Problem
13.3.4. The Halting Problem
Given the range of useful functions performed by modern computers, each demonstrably implemented using computable functions, it may be surprising to the uninitiated reader that the majority of well-defined functions are in fact uncomputable. In this section we demonstrate an example of an uncomputable function.
Consider the problem of determining whether Turing Machine $k$ will halt given input tape $j$ -- equivalently, whether the $k^{th}$ computable function applied to the argument $j$, $f_k(j)$, is well defined. It would be useful to have an effective implementation of this function, for example, if we were building a program to answer questions about values in the infinite table of the previous section.
The Halting Function
We can easily characterize this computation as a function of two integer arguments, as shown on the right: the halting function $f_H(k,j)$ returns 1 or 0 for every pair of arguments $k$ and $j$, and the value returned reflects whether $TM_k$ halts given tape $j$. In fact, a simple but head-spinning argument shows that this function is uncomputable.
Halting TM
If $f_H$ is computable, it can be computed by some Turing Machine; lets call this machine $TM_H$. $TM_H$ takes inputs $k$ and $j$, and produces (on its output tape) a value 1 or 0 indicating whether Turing Machine $TM_k$ halts given tape $j$.
If $TM_H$ performs a computable function, we can use it as a component to implement other computable functions. In particular, if $TM_H$ exists, there exists another Turing Machine $TM_N$ constructed as follows:
This peculiar machine takes a single argument $x$, and uses the halting TM to determine whether $TM_x$ halts given the input $x$. If $TM_x[x]$ halts, $TM_N[x]$ loops forever; otherwise, $TM_N[x]$ halts and returns the value 0.
If $TM_H$ exists (i.e., is a computable function), then $TM_N$ must exist as well; we can argue informally by Church's thesis since a machine behaving like $TM_N$ seems clearly buildable if $TM_H$ is available as a component. If pressed, however, we could avoid the dependence on Church's thesis and provide details of the construction of $TM_N$ given the implementation details of $TM_H$.
However, the existance of $TM_N$ leads to a contradiction. Consider providing $TM_N$ with its own index -- $N$ -- as an argument. Will this computation halt?
By our construction of $TM_N$, $TM_N[N]$ must loop forever if Turing Machine $N$ halts with argument $N$ -- i.e, if $TM_N[N]$ halts. Thus $TM_N[N]$ halts implies $TM_N[N]$ loops, a contradiction. Similarly, $TM_N[N]$ must halt if $TM_N[N]$ loops forever, another contradiction. Any possible behavior of $TM_N$ for the input $N$ thus violates its specification, a specification that it provably obeys assuming its $TM_H$ component behaves as specified. Hence we must conclude that there is no Turing Machine $TM_H$.
This terse sketch of the uncomputabilty of the halting problem is genuinely confusing to those seeing it for the first time. In fact, it is an example of a diagonal argument technique pioneered by Cantor.
The idea is to take a two-dimensional infinite table such as our spreadsheet of computable function behaviors and to synthesize a new row that is guaranteed to differ from each of the existing rows in at least one place, namely along the table's diagonal. The newly synthesized row cannot be identical to any existing row of the table, as it differs from each row in at least one column.
In particular, the function computed by $TM_N$ will differ from each $TM_i$ represented in our table for the argument $i$; it is designed to behave differently from each $TM$ by using the halting function to dictate behaviors to avoid along the shaded diagonal entries. The new Turing Machine $TM_N$ will behave differently from every $TM_x$ given argument $x$, halting if $TM_x(x)$ loops or looping if $TM_x(x)$ halts. Thus $TM_N$ will differ from every Turing Machine represented in our table, which comprise all of the computable functions. $TM_N$ consequently cannot be a computable function. Since it can evidently be constructed given $TM_H$, the halting function cannot be computed either.
Universal Turing Machines
13.4. Universal Turing Machines
Given the correspondence between computable functions and Turing Machines, we face the prospect of a different Turing Machine design for every computable function we might wish to compute. Indeed, we might have different special-purpose physical machines to multiply, take square roots, or compute payroll taxes: each machine would consist of an application-specific FSM intefaced to an infinite tape. Each Turing Machine is a special-purposecomputer, whose application-specific behavior is wired into the design of its FSM.
It seems clearly possible, however, to cut down on our inventory of special-purpose TMs by designing TMs capable of performing multiple functions. A single Turing Machine could certainly be capable of multiplying and taking square roots, depending on the value of an input devoted to specifying which function to perform. Indeed, a little thought will convince us that if functions $f_1(x)$ and $f_2(x)$ are both computable, then the function \begin{equation} f_{1,2}(x,y) = \begin{cases} f_1(x), & \mbox{if } y = 1 \\ f_2(x), & \mbox{if } y = 2 \end{cases} \end{equation} is also computable. Our Church's Thesis insight convinces us that, given physical machines that compute $f_1$ and $f_2$, we could build a new machine that computes $f_1$ or $f_2$ depending on the value of a new input. More formally, we could (with some effort) demonstrate an algorithm that takes the state transition diagrams of FSMs for two arbitrary Turing Machines $TM_i$ and $TM_j$, and constructs the diagram for a new $TM_{i,j}$ capable of behaving like either $TM_i$ or $TM_j$ depending on an input value.
If a single Turing Machine might evaluate any of several computable functions, is it possible that a single Turing Machine might be capable of evaluating every computable function? We can formalize this question by formulating a simple definition of a universal computable function $U(k,j)$ as follows: $$U(k, j) = TM_k(j)$$ This Universal function takes two arguments, one identifying an arbitrary Turing Machine (hence an arbitrary computable function) and a second identifying an input tape configuration (hence an argument to that function). It returns a value that is precisely the value returned by the specified Turing Machine operating on the given tape: the computation $U(k,j)$ involves emulating the behavior of $TM_k$ given tape $j$.
The existence of a TM capable of evaluating every computable function now amounts to the question of whether $U(k,j)$ is a computable function: if it is, then by our definition it is computed by some Turing Machine, and that machine is universal in the sense that it can compute every function computable by every Turing Machine. Given our discovery that the majority of functions are (sadly) not computable, we might be pessimistic about the computability of $U(k,j)$. Remarkably, however, $U(k,j)$ is computable.
There are in fact an infinite number of Turing Machines that are universal in the above sense. Each universal machine takes input that comprises two segments:
A program specifying an algorithm to be executed (argument $k$ of $U(k,j)$); and
Some data that serves as input to the specified algorithm (argument $j$ of $U(k,j)$).
The universal machine applies the specified algorithm to the specified data, generally by simulating the behavior of a machine executing the specified algorithm. It uses the program input to dictate a sequence of operations to execute on the specified input data, emulating the behavior of some particular Turing machine given that data. Of course, that same sequence of computational steps could be represented in other forms, such as a program in a contemporary programming language.
Turing Universality
13.4.1. Turing Universality
Universal Turing Machines have the remarkable property that they can mimic the behavior of any other machine, including that of other universal Turing machines, at least by the measure of the functions they can compute. That measure seems to capture their computational scope, although it ignores dimensions of their power like performance and details of I/O behavior. A universal Turing machine without audio output hardware cannot play audio, for example, although it can compute a stream of bits that represents a waveform to be played.
Of course, not every Turing machine is universal; the Unary Incrementor of Section 13.2, for example, cannot mimic the computational behavior of an arbitrary Turing machine. The distinction between machines that are universal in the Turing sense and those that are not has emerged as a basic threshold test of computational power. It is applicable not only to Turing machines, but to arbitrary models of computation -- including computer designs and programming languages. A programmable device or language that is Turing Universal has the power to execute any computable function, given the right program. By this standard, it is at the limit of computational power.
13.4.2. Interpretation
The ability of a universal machine to mimic the behavior of another machine is the basis for a powerful engineering abstraction mechanism, one that underlies the field of Computer Science. That mechanism is the interpretation of a coded algorithm -- a program -- to effect the execution of that algorithm. Imagine, for example, we have a simple universal machine $M1$ which is easy to manufacture but difficult to program due to its primitive nature. The language $L1$ accepted by $M1$ for its programs passes the universality test, but may require every operation to be expressed in terms of single-bit NANDs rather than (say) arithmetic operations.
We might improve its programmability by designing a more programmable machine, $M2$, and writing and writing a single program in $M1$ that simulates the behavior of $M2$. That program -- an interpreter for the language of $M2$ written in the language of $M1$ might be an engineering challenge, but it is the only program that needs to be written in the maligned $L1$ language. We can then package the interpreter with an M1 machine, resulting in a machine that behaves like the more humane $M2$.
Many successful computers have been designed following this strategy. Their user-visible functionality is that of a machine that executes high-level operations of interest to programmers, but their hardware executes low-level operations coded as firmware embedded in read-only memory hidden within the machine. This internal program is often called microcode, to distinguish it from the programming interface advertised for the machine.
Layers of Interpretation
In modern computer systems, we often find multiple layers of interpretation operating simultaneously. The diagram on the left shows an application written in Python, a language implemented using an interpreter written in the machine language provide by its host machine (say, the Intel X86 instruction set). That X86 machine language is itself interpreted by a hardware CPU. Indeed, a closer look might reveal more interpretive layers: the application may itself be an interpreter (for example, a browser interpreting HTML); and the host machine may use microcode to implement its instruction set. We may view this implementation as a nest of virtual machines, each implemented using an internal lower-level machine and a programmed interpreter.
Language Interfaces
An alternative view, shown on the right, highlights the languages that interface adjacent interpretive layers. The hardware interprets X86 machine language programs. The Python interpreter, coded as X86 instructions, interprets the Python language. The application, coded in Python, interprets its application-specific data.
This diagram emphasizes the separation of implementation technologies -- the interpreters -- from the languages that interface them to one another. The clarity of this separation between implementation and interface makes interpretation an extremely powerful tool for engineering abstraction.
13.4.3. Compilation
The preceeding examples show interpretation as a mechanism for moving from one interface language to another -- for example, for executing Python programs on a machine that can execute X86 machine language. There is an alternative mechanism for this language-level mobility, also commonly used in modern systems, that is subtly different from interpretation: we refer to it as compilation. While interpretation involves emulating the behavior specified by an encoded algorithm, compilation involves translating an algorithm from one language to another.
Suppose again that you have a universal machine $M1$ whose programming language $L1$ is too low level to be useful. You prefer the language $L2$ of some hypothetical machine $M2$. Rather than programming an interpreter for $L2$ in the language $L1$ as before, you might write a separate program $C_{2-1}$ that translates programs written in $L2$ to equivalent programs in $L1$. Such a program is called a compiler. Given such a compiler, a programmer who wants to run a program $P2$ written in the humane language $L2$ can simply pass it to the $C_{2-1}$ compiler once to generate the equivalent program $P1$, which can be run on $M1$ arbitrarily many times.
Like interpretation, compilation offers a way to write programs in a language other than that accepted by the target machine. However, there are some important practical differences between the two approaches:
what: Interpreters and compilers both take a progrogram as input; however, the interpreter produces behavior as a result, while the compiler produces another program.
where: The interpreter runs on the target machine (hence must be coded in the language of that machine); the compiler can run on any machine, and may hence be coded in an arbitrary language.
how often: Interpretation is a mechanism for execution, and takes place whenever the interpreted program is executed. Compilation is a single translation step that yields a program that can be run (without re-compilation) many times. For this reason, compilation is typically more time-efficient for programs that are executed many times.
when: Interpreted code makes implementation choices while the program is being executed (at "run time"); compilers make certain choices during the preliminary translation process ("compile time").
Compilation and interpretation are both important tools that belong in the repertoire of every engineer. We will see many examples of their use in subsequent chapters.
Context: Foundations of Mathematics
13.5. Context: Foundations of Mathematics
The foundational ideas of computer science discussed in this Chapter arose during a period in which a number of eminent mathematicians were preocccupied with the project of putting the field of mathematics itself on a logically sound conceptual basis. We sketch some landmarks of this history below:
Set theory as a basis for Mathematics:
During the $19^{th}$ century, the idea emerged that all of mathematics could be based on set theory. This is not the set theory involving sets of apples and oranges that many of us encountered in our early education; rather, the pure mathemeticians espousing this view wanted to avoid postulating arbitrary concrete artifacts (like apples -- or for that matter numbers) and construct all of mathematics from a set of basic principles, namely the handful of axioms defining set theory.
What concrete things can one construct from the axioms of set theory and nothing else? Well, we can construct the empty set. This concrete artifact gives some meaning to the notion of zero, the number of elements in the empty set. Given this first concrete artifact, you can make a set whose single element is the empty set, giving meaning to $1$ as a concrete concept. Following this pattern, one can build $2$, $3$, and the entire set of natural numbers. Additional conceptual bootstrapping steps lead to rationals, reals, and complex numbers; eventually, it can provide the foundations for calculus, complex analysis, topology, and the other topics studied in mathematics departments of contemporary universities.
Russel's Paradox:
At about the start of the $20^{th}$ century, Bertrand Russel observed that a cavalier approach to set theory can lead to trouble, in the form of logical inconsistencies in the theory being developed as the basis of all mathematics. Logical theories are frail, in that introduction of a single inconsistency -- say, $5 = 6$ -- gives them the power to prove any formula independent of its validity. For a formula $X$, an inconsistent logic could be used to prove both $X$ and not $X$, defeating its usefulness in distinguishing valid from invalid formulae.
Russel's famous example of ill-formed sets involved the village barber who shaves every man who doesn't shave himself -- a homey proxy for a set containing all sets not contaning themeselves. Does such a set contain itself? Either answer leads to a contradiction, revealing an inconsistency in set theory.
Other Russel folklore includes his public assertion that any inconsistency allows every formula to be proved, prompting a challenge from the audience for Russel to prove himself the Pope given the assertion that $5=6$. The story has Russel accept and elegantly fulfill that challenge.
Hilbert's Program:
While the set theoretic pitfall observed by Russell was fairly easy to sidestep, it raised an important issue: how can we be sure that all of mathematics is in fact on a sound basis? It would be disasterous for centuries of mathematicians to prove new results, only to find that each of these results could be disproved as well due to an undetected inconsistency in the underlying logic assumed.
A number of mathematicians, famously including David Hilbert, undertook a program to assure mathematics a provably sound basis. Their goal was to establish an underlying logic which was simultaneously
consistent, meaning that only valid formulae could be proved; and
complete, meaning that every valid formula can be proved.
Of course, the desired logic would first be used to prove its own consistency and completeness, assuring mathematics a future as the undisputed basis for rational distinction between truth and falsehood.
Gödel's Incompletness Theorm:
In 1931, the Austrian mathematician Kurt Gödel shocked world of mathematics and shattered the lofty goals of Hilbert's program. Gödel showed that any logical theory having the power to deal with arithmetic contains a formula equivalent to the English sentence "this statement can't be proved". A moment's reflection on the logical validity of this sentence reveals a problem: if it can be proved, the statement is false; hence the theory is inconsistent, allowing the proof of a false statement. If on the other hand it cannot be proved, the statement is true and the theory incomplete: there is a valid formula that cannot be proved.
In this monumental work, Gödel pioneered many of the techniques sketched in this Chapter -- including enumeration (often called Gödel numbering in his honor) and diagonalization. It establishes that every sound logical theory of sufficient power contains unprovable formulae: there are bound to be true statements that cannot be proven.
Gödel used the power of mathematics to circumscribe the limits to that power itself.
Computability:
In the wake of Gödel's bombshell, Turing, Church, and others showed that not all well defined functions are computable. Indeed, Turing showed moreover that not all numbers are computable by an intuitively appealing measure of computability. This succession of negative results during the 1930's challenged the field of mathematics as the arbiter of rational truth.
Universality:
Interspersed among these demonstrations of the limits of mathematics was the discovery that the tiny minority of functions that are computable comprises a remarkably rich array of useful computations. Of particular interest -- at the time, in a theoretical sense -- was the discovery that the universal function of Section 13.4 is in theory a computable function.
General-purpose Computing:
The universal Turing machine remained a conceptual experiment for a decade, until researchers began exploring the construction of practical machines based on the idea. Conspicuous among these was John von Neumann, whose landmark 1945 paper sketched the architecture of a machine design that has become recognised as the ancestor of modern general-purpose computers.
Since the articulation of the von Neumann architecture, many profound conceptual and technology developments have driven the computer revolution. These include core memory, the transistor, integrated circuits, CMOS, and many others. But the basic plan for a stored-program general purpose computer, detailed in the next Chapter, has clear roots in von Neumann's vision and the universal function on which it is based.
13.6. Chapter Summary
The conceptual tools discussed in this Chapter unleash a powerful new engineering abstraction, one that enables engineering to be applied to a new and richer universe of structures. The key is that we can extract the information that defines the logical structure of a machine, and manipulate that information -- a block of 1s and 0s -- rather than manipulating the machine itself. The concept of interpretation allows us to move from a structural description to a behavioral one, freeing us from the need to represent each behavior by physical systems exhibiting that behavior.
Imagine the prospect of building a machine whose input is some physical machine that performs a computation, and whose output is a different physical machine performing the same computation but slightly faster. This "machine improver" machine would have to dissect the input machine, analyze its behavior, and assemble the output machine from some inventory of parts. The process would be unimagineably complex and clearly impractical.
However, computers perform such transformations commonly, by dealing with coded descriptions -- algorithms -- rather than with physical machines whose behavior the algorithms represent. It is the liberation of algorithms from the physical devices in which they are embodied that promotes behaviors -- coded as algorithms -- to become themselves objects of engineering.
Copyright © 2015-2017 M.I.T. Department of Electrical Engineering and Computer Science
Your use of this site and materials is subject to our terms of use. | CommonCrawl |
A seed point discontinuity-based level set method for accurate substantia nigra and red nucleus segmetation in QSM images
Tian Guo1, Binshi Bo1, Xinxin Zhao1, Xu Yan2, Yang Song1, Caixia Fu3, Dongya Huang4, Hedi An4, Nan Shen4, Yi Wang5, Jianqi Li1, and Guang Yang1
1Department of Physics, Shanghai Key Laboratory of Magnetic Resonance, East China Normal University, Shanghai, People's Republic of China, 2MR Collaboration NE Asia, Siemens Healthcare, Shanghai, People's Republic of China, 3Siemens Shenzhen Magnetic Resonance Ltd., Shenzhen, People's Republic of China, 4Department of Neurology, East Hospital Affiliated to Tongji University, Shanghai, People's Republic of China, 5Department of Radiology, Weill Medical College of Cornell University, New York, United States
Accurate segmentation of substantia nigra (SN) and red nucleus (RN) in quantitative susceptibility mapping (QSM) images has great clinical value in quantifying iron deposition and measuring disease severity. We propose a new segmentation algorithm which uses the discontinuity of seed points in different tissues as prior knowledge. Seed points in SN or RN can be obtained from standard atlas or specified manually. This prior was then incorporated into level set method to segment SN and RN. Experiments on in-vivo MR images showed that the proposed method achieved more accurate segmentation results than the atlas-based method and classic level-set method.
Background and Purpose
Quantitative susceptibility mapping (QSM) is a powerful tool for quantifying iron deposition increase in the substantia nigra (SN) and red nucleus (RN) of patients with idiopathic Parkinson's disease (PD).1 Due to the small size of SN and RN, accurate segmentation is essential for quantification of iron deposition and, in turn, the severity of disease progression. Current segmentation methods, however, are suboptimal. The conventional atlas-based methods may be substantially influenced by inter-subject variability. Subject-specific methods, such as level set, perform poorly when deep brain nuclei are in close proximity. Here, we describe a method to improve the segmentation accuracy of SN and RN in QSM images.
A total of 11 patients with PD (67.9 ±4.9 years old, 5 males and 6 females) and 11 healthy controls (HC) (68.2 ± 5.6 years old, 5 males and 6 females) underwent MR scans on a clinical 3T system (MAGNETOM Trio Tim; Siemens, Erlangen, Germany) with a 12-channel head matrix coil. The QSM images and R2* mapping were obtained from the same three-dimensional (3D) multi-echo gradient-echo sequence with the following parameters: TR = 60ms, TE1 = 6.8ms, ΔTE = 6.8ms, echo number = 8, flip angle = 15˚, FOV = 240x180 mm2, in-plane resolution = 0.625x0.625 mm2, slice thickness = 2 mm, number of slices = 96. QSM images were calculated from the phase data using the Morphology Enabled Dipole Inversion (MEDI) algorithm.2 Prior knowledge of seed points was used to improve segmentation accuracy of the level set method for slices with poor contrast between SN and RN. We first obtained initial regions-of-interest (ROIs) of the whole SN and RN using the human brain atlas method.3 Although the ROIs were not accurate, two seed points lied in SN and RN respectively can be found correctly by calculating the barycenter of each ROIs (or manually made them). We knew these two seed points are not connected due to they belong to different tissues. Thus, an intensity profile of the voxels along the shortest path between the two seed points was then analyzed so as to wipe off those voxels that belonging to neither SN nor RN. The above processing was repeated several times until the classic level set method could separate these two nuclei effectively after a proper number of voxles (belong to neither SN nor RN) were wiped off. Note that the shortest path between two seed points changed constantly with iterations because it could not get through the voxels that had been wiped off. The details of the processing is shown in Figure1. The ROIs were obtained using the "Diffeomap" software provided by Issel Anne L. Lim.3 We adopted a Dice Similarity Index to evaluate the results:$$Dice = \frac{2\left({S}\cap{T}\right)}{\left(S+T\right)}$$ where S and T denote the number of pixels in the manual and automatic segmentation and S∩T denotes the number of pixels in the overlay of the two segmentation results.
An example of the segmentation obtained with the proposed method is shown in Figure 2, along with a comparison to other methods. Compared with the atlas-based method 3 and the level set method 4, our method effectively separated SN from RN. Fourteen image sets were segmented using three algorithms. Statistics of the Dice coefficients of all three methods are shown in Figure 3 for RN and SN. It can be seen that our method performed best in that it has the highest Dice for both RN and SN. In addition, we applied the proposed method to calculate the mean susceptibility in SN, which yielded a significantly higher susceptibility value in PD patients than that in healthy controls. However, this conclusion could not be obtained by the conventional atlas method (Figure 4). A three--dimensional representation of segmenting SN and RN is shown in Figure 5.
Discussion and Conclusion
We proposed a seed point discontinuity-based method for level set to improve its segment accuracy of SN and RN in QSM images. Results showed that the proposed method has better consistency to manual segmentation results than the conventional atlas-based method and classic level set method, because it has the highest Dice Similarity Index. Moreover, from clinical perspective, the proposed method demonstrated a significant higher magnetic susceptibility value of SN in patients with PD than that in healthy controls, which is consistent with other's findings.5
This study was supported in part by grants from The National Natural Science Foundation of China (81271533) and Shanghai Key Laboratory of Magnetic Resonance.
1. Murakami Y, Kakeda S, Watanabe K, et al. Usefulness of quantitative susceptibility mapping for the diagnosis of Parkinson disease. American Journal of Neuroradiology. 2015; 36(6): 1102-1108.
2. Liu T et al. Cerebral Microbleeds: Burden assessment by using quantitative susceptibility mapping. Radiology. 2011; 262(1):269-78.
3. Lim I A L, Faria A V, Li X, et al. Human brain atlas for automated region of interest selection in quantitative susceptibility mapping: application to determine iron content in deep gray matter structures. Neuroimage. 2013; 82: 449-469.
4. Li B, Jiang C, Li L, et al. Automated Segmentation and Reconstruction of the Subthalamic Nucleus in Parkinson's Disease Patients. Neuromodulation: Technology at the Neural Interface. 2016; 19(1): 13-19.
5. Langkammer C, Pirpamer L, Seiler S, Deistung A, Schweser F, Franthal S, et al. Quantitative Susceptibility Mapping in Parkinson's Disease. PLOS ONE. 2016; 11(9): e0162460.
Figure 1. The diagram shows the details of the processing. Two seed points (green disks) located in SN and RN respectively. Shortest path between two seed points changed with iterations. Since the discontinuity of seed points, intensity profiles of the voxels along these paths (colored lines) were analyzed to wipe off those voxels (black circles) that belonging to neither SN and RN using a threshold-based method. One of the profile is shown on the left. After preprocessing, level set method can separate the two nuclei effectively.
Figure 2. Comparison of segmentation results of SN (blue contours) and RN (red contours) using different algorithms: (a) atlas-based method (b) classic level set method (c) proposed method (d) manual segmentation result (ground truth).
Figure 3. Comparison of Dice coefficients for the atlas-based method, level set method, and proposed method in RN (a) and SN (b) segmentation. The proposed method is more accurate and robust than the other methods for RN segmentation.
Figure 4. Both our proposed method and conventional atlas method were used to segment SN, and then magnetic susceptibility values of SN were calculated. Based on our method, mean susceptibility value of SN in Parkinson's disease patients (PD) is significantly higher than that in healthy controls (HC). However, there is no significant difference of mean susceptibility value of SN between PD and HC based on the conventional atlas method. *Significantly different between the two groups (P<0.01).
Figure 5. Three-dimensional segmentation result of manual segmentation (a) and proposed method (b). Blue represents SN, and yellow represents RN. | CommonCrawl |
1. Functions and Graphs
1.1 Review of Functions
1.2 Basic Classes of Functions
1.5 Exponential and Logarithmic Functions
Chapter 1 Review Exercises
2. Limits
2.1 A Preview of Calculus
2.2 The Limit of a Function
2.3 The Limit Laws
2.4 Continuity
2.5 The Precise Definition of a Limit
3. Derivatives
3.1 Defining the Derivative
3.2 The Derivative as a Function
3.3 Differentiation Rules
3.4 Derivatives as Rates of Change
3.5 Derivatives of Trigonometric Functions
3.6 The Chain Rule
3.7 Derivatives of Inverse Functions
3.8 Implicit Differentiation
3.9 Derivatives of Exponential and Logarithmic Functions
4. Applications of Derivatives
4.1 Related Rates
4.2 Linear Approximations and Differentials
4.3 Maxima and Minima
4.4 The Mean Value Theorem
4.5 Derivatives and the Shape of a Graph
4.6 Limits at Infinity and Asymptotes
4.7 Applied Optimization Problems
4.8 L'Hôpital's Rule
4.9 Newton's Method
4.10 Antiderivatives
5. Integration
5.1 Approximating Areas
5.2 The Definite Integral
5.3 The Fundamental Theorem of Calculus
5.4 Integration Formulas and the Net Change Theorem
5.5 Substitution
5.6 Integrals Involving Exponential and Logarithmic Functions
5.7 Integrals Resulting in Inverse Trigonometric Functions
6. Applications of Integration
6.1 Areas between Curves
6.2 Determining Volumes by Slicing
6.3 Volumes of Revolution: Cylindrical Shells
6.4 Arc Length of a Curve and Surface Area
6.5 Physical Applications
6.6 Moments and Centers of Mass
6.7 Integrals, Exponential Functions, and Logarithms
6.8 Exponential Growth and Decay
6.9 Calculus of the Hyperbolic Functions
Chapter 6 Review Excercises
Review of Pre-Calculus
Calculus Volume 1
Integrate functions resulting in inverse trigonometric functions
In this section we focus on integrals that result in inverse trigonometric functions. We have worked with these functions before. Recall from Functions and Graphs that trigonometric functions are not one-to-one unless the domains are restricted. When working with inverses of trigonometric functions, we always need to be careful to take these restrictions into account. Also in Derivatives, we developed formulas for derivatives of inverse trigonometric functions. The formulas developed there give rise directly to integration formulas involving inverse trigonometric functions.
Integrals that Result in Inverse Sine Functions
Let us begin this last section of the chapter with the three formulas. Along with these formulas, we use substitution to evaluate the integrals. We prove the formula for the inverse sine integral.
Rule: Integration Formulas Resulting in Inverse Trigonometric Functions
The following integration formulas yield inverse trigonometric functions:
Let Then Now let's use implicit differentiation. We obtain
For Thus, applying the Pythagorean identity we have This gives
Then for we have
Evaluating a Definite Integral Using Inverse Trigonometric Functions
Evaluate the definite integral
We can go directly to the formula for the antiderivative in the rule on integration formulas resulting in inverse trigonometric functions, and then evaluate the definite integral. We have
*** QuickLaTeX cannot compile formula:
\begin{array}{}\\ \\ {\int }_{0}^{1}\frac{dx}{\sqrt{1-{x}^{2}}}\hfill & ={ \sin }^{-1}x{|}_{0}^{1}\hfill \\ & ={ \sin }^{-1}1-{ \sin }^{-1}0\hfill \\ & =\frac{\pi }{2}-0\hfill \\ & =\frac{\pi }{2}.\hfill \end{array}
*** Error message:
Missing # inserted in alignment preamble.
leading text: $\begin{array}{}
Missing $ inserted.
leading text: $\begin{array}{}\\ \\ {\int
Extra }, or forgotten $.
leading text: $\begin{array}{}\\ \\ {\int }
Missing } inserted.
leading text: ..._{0}^{1}\frac{dx}{\sqrt{1-{x}^{2}}}\hfill &
Find the antiderivative of
Finding an Antiderivative Involving an Inverse Trigonometric Function
Evaluate the integral
Substitute Then and we have
Applying the formula with we obtain
Find the indefinite integral using an inverse trigonometric function and substitution for
Use the formula in the rule on integration formulas resulting in inverse trigonometric functions.
Evaluating a Definite Integral
The format of the problem matches the inverse sine formula. Thus,
\begin{array}{}\\ \\ {\int }_{0}^{\sqrt{3}\text{/}2}\frac{du}{\sqrt{1-{u}^{2}}}\hfill & ={ \sin }^{-1}u{|}_{0}^{\sqrt{3}\text{/}2}\hfill \\ & =\left[{ \sin }^{-1}(\frac{\sqrt{3}}{2})\right]-\left[{ \sin }^{-1}(0)\right]\hfill \\ & =\frac{\pi }{3}.\hfill \end{array}
leading text: ...ext{/}2}\frac{du}{\sqrt{1-{u}^{2}}}\hfill &
Integrals Resulting in Other Inverse Trigonometric Functions
There are six inverse trigonometric functions. However, only three integration formulas are noted in the rule on integration formulas resulting in inverse trigonometric functions because the remaining three are negative versions of the ones we use. The only difference is whether the integrand is positive or negative. Rather than memorizing three more formulas, if the integrand is negative, simply factor out −1 and evaluate the integral using one of the formulas already provided. To close this section, we examine one more formula: the integral resulting in the inverse tangent function.
Finding an Antiderivative Involving the Inverse Tangent Function
Find an antiderivative of
Comparing this problem with the formulas stated in the rule on integration formulas resulting in inverse trigonometric functions, the integrand looks similar to the formula for So we use substitution, letting then and Then, we have
Use substitution to find the antiderivative of
Use the solving strategy from (Figure) and the rule on integration formulas resulting in inverse trigonometric functions.
Applying the Integration Formulas
Apply the formula with Then,
Follow the steps in (Figure).
Use the formula for the inverse tangent. We have
\begin{array}{}\\ \\ {\int }_{\sqrt{3}\text{/}3}^{\sqrt{3}}\frac{dx}{1+{x}^{2}}\hfill & ={ \tan }^{-1}x{|}_{\sqrt{3}\text{/}3}^{\sqrt{3}}\hfill \\ & =\left[{ \tan }^{-1}(\sqrt{3})\right]-\left[{ \tan }^{-1}(\frac{\sqrt{3}}{3})\right]\hfill \\ & =\frac{\pi }{6}.\hfill \end{array}
leading text: .../}3}^{\sqrt{3}}\frac{dx}{1+{x}^{2}}\hfill &
Follow the procedures from (Figure) to solve the problem.
Formulas for derivatives of inverse trigonometric functions developed in Derivatives of Exponential and Logarithmic Functions lead directly to integration formulas involving inverse trigonometric functions.
Use the formulas listed in the rule on integration formulas resulting in inverse trigonometric functions to match up the correct format and make alterations as necessary to solve the problem.
Substitution is often required to put the integrand in the correct form.
Key Equations
Integrals That Produce Inverse Trigonometric Functions
In the following exercises, evaluate each integral in terms of an inverse trigonometric function.
In the following exercises, find each indefinite integral, using appropriate substitutions.
[reveal-answer q="877132″]Show Solution[/reveal-answer]
[hidden-answer a="877132″]
13. Explain the relationship Is it true, in general, that
So, They differ by a constant.
15. Explain what is wrong with the following integral:
is not defined as a real number when
In the following exercises, solve for the antiderivative of with then use a calculator to graph and the antiderivative over the given interval Identify a value of C such that adding C to the antiderivative recovers the definite integral
17. [T] over
The antiderivative is Taking recovers the definite integral.
In the following exercises, compute the antiderivative using appropriate substitutions.
In the following exercises, use a calculator to graph the antiderivative with over the given interval Approximate a value of C, if possible, such that adding C to the antiderivative gives the same value as the definite integral
The antiderivative is Taking recovers the definite integral over
The general antiderivative is Taking recovers the definite integral.
In the following exercises, compute each integral using appropriate substitutions.
In the following exercises, compute each definite integral.
43. For compute and evaluate the area under the graph of on
44. For compute and evaluate the area under the graph of over
45. Use the substitution and the identity to evaluate (Hint: Multiply the top and bottom of the integrand by )
Using the hint, one has Set Then, and the integral is If one uses the identity then this can also be written
46. [T] Approximate the points at which the graphs of and intersect, and approximate the area between their graphs accurate to three decimal places.
The left endpoint estimate with is 2.796 and these decimals persist for
48. Use the following graph to prove that
Previous: 5.6 Integrals Involving Exponential and Logarithmic Functions
Next: Chapter 5 Review Exercises
5.7 Integrals Resulting in Inverse Trigonometric Functions by OSCRiceUniversity is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted. | CommonCrawl |
This is PaperWhy. Our sisyphean endeavour not to drown in the immense Machine Learning literature.
With thousands of papers every month, keeping up with and making sense of recent research in machine learning has become almost impossible. By routinely reviewing and reporting papers we help ourselves and hopefully someone else.
Paperwhy
Image classification Policy gradient Attention Reinforcement learning P o m d p R n n
Recurrent models of visual attention
Volodymir Mnih Nicolas Hees Alex Graves Koray Kavukcuoglu | Jun 2014 | Paper
tl;dr: Training a network to classify images (with a single label) is modeled as a sequential decision problem where actions are salient locations in the image and tentative labels. The state (full image) is partially observed through a fixed size subimage around each location. The policy takes the full history into account compressed into a hidden vector via an RNN. REINFORCE is used to compute the policy gradient.
Although the paper targets several applications, to fix ideas, say we want to classify images with one label. These can vary in size but the number of parameters of the model will not change. Taking inspiration from how humans process images, the proposed model iteratively selects points in the image and focuses on local patches around them at different resolutions. The problem of choosing the locations and related classification labels is cast as a reinforcement learning problem.
Attention as a sequential decision problem
One begins by fixing one image $x$ and selecting a number $T$ of timesteps. At each timestep $t = 1, \ldots, T$:
We are in some (observed) state $s_{t} \in \mathcal{S}$: it consists of a location $l_{t}$ in the image (a pair of coordinates), and a corresponding glimpse $x_{t}$ of $x$. This glimpse is a concatenation of multiple subimages of $x$ taken at different resolutions, centered at location $l_{t}$, then resampled to the same size. How many ($k$), at what resolutions ($\rho _{1}, \ldots, \rho _{k}$) and to what fixed size ($w$) they are resampled are all hyperparameters.1 The set of all past states is the history: $s_{1 : t - 1} := \lbrace s_{1}, \ldots, s_{t - 1} \rbrace$.
We take an action $a_{t} = (l_{t}, y_{t}) \in \mathcal{A}$, with the new location $l_{t}$ in the (same) image $x$ to look at and the current guess $y_{t}$ as to what the label for $x$ is. In the typical way for image classification with neural networks, $y_{t}$ is a vector of "probabilities" coming from a softmax layer. Analogously, the location $l_{t}$ is sampled from a distribution parametrized by the last layer of a network. The actions are taken according to a policy $\pi^t_{\theta} : \mathcal{S}^t \rightarrow \mathcal{P} (\mathcal{A})$, with $S^t = S \times \overset{t - 1}{\cdots} \times S$, and $\mathcal{P} (\mathcal{A})$ the set of all probabilty measures over $\mathcal{A}$. The policy is implemented as a neural network, where $\theta$ represents all internal parameters. The crucial point in the paper is that the network takes the whole history as input, compressed into a hidden state vector, i.e. the policy will be implemented with a recurrent network. Because parameters are shared across all timesteps, we drop the superindex $t$ and denote its output at timestep $t$ by $\pi _{\theta} (a_{t} |s_{1 : t})$.
We obtain a scalar reward $r_{t} \in \lbrace 0, 1 \rbrace$. Actually, the reward will be 0 at all timesteps but the last ($T$), where it can be either 0 if $y_{T}$ predicts the wrong class or 1 if it is the right one.2
The model at timestep $t$.
Note that the policy $\pi _{\theta} (a_{t} |s_{1 : t})$ has two "heads", a labeling network $f_{y}$, outputting a probability of the current glimpse belonging to each class and a location network $f_{l}$. Only the output of the latter directly influences the next state. This is important when computing the distribution over trajectories $\tau = (s_{1}, a_{1}, \ldots, s_{T}, a_{T})$ induced by the policy:
\[ p_{\theta} (\tau) := p (s_{1}) \prod_{t = 1}^T \pi _{\theta} (a_{t} \mid s_{t}) p (s_{t + 1} \mid s_{t}, a_{t}) = p (s_{1}) \prod_{t = 1}^T p (l_{t} \mid f_{l} (s_{t} ; \theta)) p (s_{t + 1} \mid s_{t}, l_{t}) . \]
The goal is to maximise the total expected reward
\[ J (\theta) := \mathbb{E}_{\tau \sim p_{\theta} (\tau)} [\sum_{t = 1}^T r (s_{t}, a_{t})] . \]
The algorithm used is basically the policy gradient method with the REINFORCE rule:3
Algorithm 1:
Initialise $\pi _{\theta}$ with some random set of parameters.
For $n = 1 \ldots N$, pick some input image $x_{n}$ with label $y_{n}$.
Sample some random initial location $l_{0}$.
Run the policy (the recurrent network) $\pi _{\theta}$ for $T$ timesteps, creating new locations $l_{t}$ and labels $y_{t}$. At the end collect the reward$r_{T} \in \lbrace 0, 1 \rbrace$.
Compute the gradient of the reward $\nabla _{\theta} J (\theta _{n})$.
Update $\theta _{n + 1} \leftarrow \theta _{n} + \alpha _{n} \nabla _{\theta} J_{\theta} (\theta _{n})$.
The difficulty lies in step $5$ because the reward is an expectation over trajectories whose gradient cannot be analitically computed. One solution is to rewrite the gradient of the expectation as another expectation using a simple but clever substitution:
\[ \nabla _{\theta} J (\theta) = \int \nabla _{\theta} p_{\theta} (\tau) r (\tau) \mathrm{d} \tau = \int p_{\theta} (\tau) \frac{\nabla _{\theta} p_{\theta} (\tau)}{p_{\theta} (\tau)} r (\tau) \mathrm{d} \tau = \int p_{\theta} (\tau) \nabla _{\theta} \log p_{\theta} (\tau) r (\tau) \mathrm{d} \tau, \]
and this is
\[ \nabla _{\theta} J (\theta) =\mathbb{E}_{\tau \sim p_{\theta} (\tau)} [\nabla _{\theta} \log p_{\theta} (\tau) r (\tau)] \]
In order to compute this integral we can now use Monte-Carlo sampling:
\[ \nabla _{\theta} J (\theta) \approx \frac{1}{M} \sum_{m = 1}^M \nabla _{\theta} \log p_{\theta} (\tau_m) r (\tau_m), \]
and after rewriting $\log p_{\theta} (\tau)$ as a sum of logarithms and discarding the terms which do not depend on $\theta$ we obtain:
\[ \nabla _{\theta} J (\theta) \approx \frac{1}{M} \sum_{m = 1}^M \sum_{t = 1}^T \nabla _{\theta} \log \pi _{\theta} (a^m_{t} |s^m_{1 : t}) r^m, \]
where $r^m = r_{T}^m$ is the final reward (recall that in this application $r_{t} = 0$ for all $t < T$). In order to reduce the variance of this estimator it is standard to subtract a baseline estimate $b =\mathbb{E}_{\pi{\theta}} [r{T}]$ of the expected reward, thus arriving at the expression
\[ \nabla _{\theta} J (\theta) \approx \frac{1}{M} \sum_{m = 1}^M \sum_{t = 1}^T \nabla _{\theta} \log \pi _{\theta} (a^m_{t} |s^m_{1 : t}) (r^m - b) . \]
There is a vast literature on the Monte-Carlo approximation for policy gradients, as well as techniques for variance reduction.4
Hybrid learning
Because in classification problems the labels are known at training time, one can provide the network with a better signal than just the reward at the end of all the process. In this case the authors
optimize the cross entropy loss to train the [labeling] network $f_{y}$ and backpropagate the gradients through the core and glimpse networks. The location network $f_{l}$ is always trained with REINFORCE.
Results for image classification
An image is worth a thousand words:
It would be nice to try letting a CNN capture the relevant features for us, instead of fixing the resolutions. I'm sure this has been tried since 2014. ⇧
I wonder: wouldn't it make more sense to let $r_{t} \in [0, 1]$ instead using the cross entropy to the 1-hot vector encoding the correct class? ⇧
See e.g. Reinforcement Learning: An Introduction, Sutton, R. , Barto, A. (2018) , §13.3. ⇧
Again, see Reinforcement Learning: An Introduction, Sutton, R. , Barto, A. (2018) . ⇧
Posted by Miguel de Benito Delgado on December 22. 2018
Built with HUGO based on hikari - © 2017 the authors | CommonCrawl |
Advanced nuclear data forms
Uncertainty quantification & propagation
Recoils, PKA spectra and materials simulation inputs
Fission decay heat
Fusion decay heat
Integro-differential
Systematic verification of nuclear data
Nuclear data
Fission Yields
High-Energy Yields
Fispact File Maker
The full report is available here: Integro-differential verification and validation, FISPACT-II & TENDL-2014 nuclear data libraries CCFE-R(15)27
A set of experimental neutron spectra used in the integro-differential validation. These show a few D-T spectra with different environments, a p-D spectrum and a semi-monoenergetic D-T at a low angle deflection location.
The combination of multiple, complementary integral measurements with differential cross section data from EXFOR has been used to validate the TENDL-2014 neutron-induced nuclear data library. The integral measurements use incident particle spectra from a variety of sources including:
Fusion D-T with various amounts of scattering, 14 MeV peaked
Deuterium beam on beryllium target 'fast white' spectrum above 20 MeV
Deuterium beam on lithium target 'IFMIF-like' spectrum up to 60+ MeV
Proton beam on deuterium targets 'fast white' spectrum above 20 MeV
Spontaneous Cf252 fission neutrons
The measurement techniques typically include HPGe gamma spectroscopy to identify individual nuclides, spectroscopic or total heat measurements. Normalisations and spectra are determined through various means, from activation foils to ToF and alpha-monitors. Not all experiments are of the same quality and this fact is extremely important when making judgements on the quality of an evaluated file using few measurements. Identification of individual reaction channels within integral measurements poses a few challenges, including the separation of production of decaying, precursor nuclides (cumulative effects) and isolation of multiple reaction channels, which occurs through multiple target elements, multiple target isotopes and multiple reaction channels per nuclide. Care must be taken not to mistakenly identify one reaction channel with multiple are involved, which could either throw into question an accurate evaluation or 'validate' a spurious cross section. The approach taken by the UKAEA is to establish a set of criteria for inclusion and remove those which fail the tests. In those (few) cases removed which were used in previous EAF validations it is highly unlikely that the experiments measured what was claimed.
Analysis of measurements
Total and spectroscopic decay heat measurements from an FNG irradiation of nickel with FISPACT-II predictions. Dominant nuclides are placed at coordinates which reflect their half-life and end-of-irradiation heat.
For all integral measurements new pathways analysis using the FISPACT-II pathways search features have been done. These identify the % contribution from each reaction channel and verify that the channel of interest is dominant for the measurement. Even with high-purity samples this can be quite complex due to multiple isotopes or reactions, for example the FNG nickel irradiation shown to left. As in several cases, the total heat measurements reflect multiple nuclides contributing at every time-step. However, at specific points one nuclide is strongly dominant, for example the Co62 and Co62m at the first and last measurements shown in this figure. Decay data can provide an additional concern due to potential misallocation of beta/gamma heat (and other more simple issues such as half-life uncertainty). The apparent discrepancies between beta and gamma heat in the first measurement are reconciled in the total, which has a less uncertain energy per decay. Co60m dominates the gamma heat at 500 s and Co62m dominates the beta and total in the final point. The production pathways for nickel are quite simple, with Ni60(n,p) and Ni62(n,p) generating the cobalt isotopes and isomers. This allows specific identification of each as an integral measurement of a reaction channel. This level of analysis has been performed in the recent report for the FNS and FNG heat measurements. Results from other laboratories were tested with pathways analyses and verification of the reaction channels available.
Results Care must be taken when claiming that a reaction has been 'validated', since the detailed structure of a cross-section is not fully probed (even with multiple experiments using complementary spectra) and a new experiment using a different spectrum could find discrepant results. Aside from the differences in experimental design, there is tremendous deviation in the quality of the spectral characterisations, simulation tools used to calculate data (ultimately including the effective cross section) and reporting of measurement methodologies. The distributions show a generally superior agreement for TENDL-2014, with 12% more values between 0.94-1.06. The log-mean C/E value, $$\mbox{Log}\left(\overline{C/E}\right) = \frac{1}{n}\sum_{i=1}^n \mbox{Log}\left(C_i /E_i \right),$$ for TENDL-2014 is 0.993, while the EAF-2010 data yields a surprising 0.850. This can be intuitively seen in the skewed EAF distribution of C/E values, indicating a systematic under-prediction for the integral values of this report. The fact that TENDL provides a more symmetric distribution should not be surprising; the data is derived from physical parameters which globally govern the production of reaction information. In comparison, the asymmetry of EAF belies its methodology, where pathways are included depending on an evaluator's judgement. As a result, pathways are missing or under-represented and result in an overall under-prediction for nuclide production. It should be noted that the EAF library was constructed and modified with knowledge of these integral measurements, which were used as justification for renormalisations leading to better agreement with the experiments. That TENDL blindly predicts these effective cross-sections, using physical parameters, with greater accuracy than a library tuned by renormalisations is quite remarkable. When the standard international libraries are used to calculate the effective cross-sections considered the distribution shows a tremendous lack of data, as depicted in beside figure. The most notable difference here is that approximately one third of the C/E values are less than 0.1, with a large majority of these being precisely zero due to missing reactions. This is not unexpected, since these libraries do not contain the data required for activation-transmutation simulations and should not be relied upon or trusted for such analysis. However, it is troublesome since it is often claimed that those libraries are validated for various applications that require these (and many other) reactions.
The UK Atomic Energy Authority is an executive non-departmental public body, sponsored by the Department for Business, Energy & Industrial Strategy.
UK fusion research is jointly funded by RCUK under grant number EP/P012450/1 and Euratom.
Copyright 2016 | All Right Reserved by UK Atomic Energy Authority | Terms and conditions | Cookies | CommonCrawl |
Analysis of microarrays of miR-34a and its identification of prospective target gene signature in hepatocellular carcinoma
Fang-Hui Ren1,
Hong Yang2,
Rong-quan He3,
Jing-ning Lu4 an1,
Xing-gu Lin3,
Hai-Wei Liang1,
Yi-Wu Dang1,
Zhen-Bo Feng1,
Gang Chen1 &
Dian-Zhong Luo1
Currently, some studies have demonstrated that miR-34a could serve as a suppressor of several cancers including hepatocellular carcinoma (HCC). Previously, we discovered that miR-34a was downregulated in HCC and involved in the tumorigenesis and progression of HCC; however, the mechanism remains unclear. The purpose of this study was to estimate the expression of miR-34a in HCC by applying the microarray profiles and analyzing the predicted targets of miR-34a and their related biological pathways of HCC.
Gene expression omnibus (GEO) datasets were conducted to identify the difference of miR-34a expression between HCC and corresponding normal tissues and to explore its relationship with HCC clinicopathologic features. The natural language processing (NLP), gene ontology (GO), pathway and network analyses were performed to analyze the genes associated with the carcinogenesis and progression of HCC and the targets of miR-34a predicted in silico. In addition, the integrative analysis was performed to explore the targets of miR-34a which were also relevant to HCC.
The analysis of GEO datasets demonstrated that miR-34a was downregulated in HCC tissues, and no heterogeneity was observed (Std. Mean Difference(SMD) = 0.63, 95% confidence intervals(95%CI):[0.38, 0.88], P < 0.00001; Pheterogeneity = 0.08 I2 = 41%). However, no association was found between the expression value of miR-34a and any clinicopathologic characteristics. In the NLP analysis of HCC, we obtained 25 significant HCC-associated signaling pathways. Besides, we explored 1000 miR-34a-related genes and 5 significant signaling pathways in which CCND1 and Bcl-2 served as necessary hub genes. In the integrative analysis, we found 61 hub genes and 5 significant pathways, including cell cycle, cytokine-cytokine receptor interaction, notching pathway, p53 pathway and focal adhesion, which proposed the relevant functions of miR-34a in HCC.
Our results may lead researchers to understand the molecular mechanism of miR-34a in the diagnosis, prognosis and therapy of HCC. Therefore, the interaction between miR-34a and its targets may promise better prediction and treatment for HCC. And the experiments in vivo and vitro will be conducted by our group to identify the specific mechanism of miR-34a in the progress and deterioration of HCC.
Liver cancer ranks as the second leading cause of cancer death in men in less developed countries and sixth in more developed countries [1]. During 2012, 745,500 deaths occurred out of estimated 782,500 new HCC cases worldwide, with nearly 50% happening in China [1].High prevalence is observed in parts of East and South-East Asia where chronic hepatitis B virus (HBV) and hepatitis C virus (HCV) infection are epidemic [2]. Hepatocellular carcinoma (HCC) is recognized as the most common type of liver cancer, accounting for 90% of primary liver cancer. There exist difficulties in treating HCC due to a series of sequential and complex processes involved in the carcinogenesis and progression of HCC. Although radiation, surgery, liver transplantation or chemotherapy are widely used in the therapy of HCC, the survival rate of HCC patients is still less than 5% [3]. Therefore, it is urgent to enhance our knowledge of molecular pathogenesis of HCC and explore novel biomarkers in favor of therapy of HCC. Gene signatures would provide efficient molecular basis of the clinicopathological features for characterizing the heterogeneity of HCC. In addition, the regulatory pathways and networks involved in the mechanism of HCC would lead to the identification of molecular fingerprints for directing therapeutic strategies.
MicroRNAs(miRNAs) are composed of a family of endogenous, noncoding small RNA molecules(∼18–25 nucleotides long), which serve as post-transcriptional gene expression regulators via binding to the 3′--untranslated regions(3'-UTRs) region of their target messenger RNAs(mRNA) [4]. Besides, miRNAs participated in multiple biological processes in oncology via inhibiting translation of mRNA or degrading mRNA [5,6,7,8]. Several studies have identified that ectopic expression of miR-34a is related to cell cycle, proliferation, migration, invasion,apoptosis and prognosis of cancers by targeting AXL/ SIRT1/Yin Yang-1 [9,10,11,12]. Several studies have shown that miR-34a regulates the carcinogenesis and progression of cancers via modulation of Notch1 Pathway, SIRT1/p53 pathway, WNT/TCF7 signaling [13,14,15]. Kang et al. and Zhou et al. have reported that miR-34a is associated with chemo-resistance [13, 16]. One study conducted by Cao et al. has found that miR-34a could influence the impact of lincRNA-UFC1 on proliferation and apoptosis in HCC cells [17]. In our previous study, we demonstrated that miR-34a decreased in HCC, and in vitro experiment has also identified that miR-34a could inhibit cell proliferation, invasion and migration, and increase caspase activity and cellular apoptosis by modulating phospho-ERK1/2 and phospho-stat5 signaling, as well as the level of c-MET [18]. However, the molecular mechanism of miR-34a in HCC tumorigenesis and development remains unclear. Therefore, a systemic and comprehensive understanding of miR-34a-target genes and relevant signaling pathways is important for diagnosis, therapy and prognosis of HCC.
In this study, GEO datasets were applied to verify the associations between miR-34a expression and HCC. Additionally, we performed a series of analyses to assess the miR-34a-predicted genes which are associated with carcinogenesis, progression and chemo-resistance in HCC. We then evaluated the potential value of miR-34a in HCC diagnosis, prognosis and therapy with network and pathway analyses.
Comprehensive analysis of miR-34a expression in HCC based on GEO datasets
The expression data of miR-34a was collected from the GEO(http://www.ncbi.nlm.nih.gov/geo/) databases up to January 2016 with the following keywords: ("HCC" OR "hepatocellular carcinoma" OR "liver cancer" OR "liver carcinoma" OR "liver malignan*" OR "liver neoplasm") and ("miRNA" OR "microRNA"). Inclusion criteria were as follows: (1) both HCC tissues and adjacent HCC tissues (or healthy liver tissues) or only HCC tissues were included in each dataset with each group containing more than two samples; (2) the dataset sample organism was Homo sapiens; (3) the expression data of miR-34a (has-miR-34a or has-miR-34a-5p) from the experimental and control groups could be acquired or calculated. Expression values of miR-34a and sample size in both test and control groups were calculated. Moreover, means and standard deviations of these values were extracted to estimate the different levels of miR-34a in case and control groups by Review Manager (Revman Version 5.3, Copenhagen, Denmark) with random-effects model. The chi-square test and the I2 statistic were applied to evaluate the heterogeneity across studies. Heterogeneity was considered to exist when the P value < 0.05 or I2 > 50%. Further, SMD and its 95%CI were pooled to evaluate the stability of the analysis. It was considered to be statistically significant if the corresponding 95%CI for the pooled SMD did not overlap 1 or −1. Additionally, for sensitivity analysis, we eliminated every study to evaluate the source of heterogeneity.
NLP analysis of HCC
Extraction and filtering of data
We searched PubMed in an attempt to identify all relevant studies published between January 1980 and May 2015. Publications were retrieved with the following key words: (hepatocellular carcinoma) and (resistance or prognosis or metastasis or recurrence or survival or carcinogenesis or sorafenib or bevacizumab) and ("1980/01/01" [PDAT]: "2015/05/25" [PDAT]). All genes and proteins related to the key words were extracted and gathered in a list with the following of gene mention tagging by applying A Biomedical Named Entity Recognizer (ABNER, an open source tool for automatically tagging genes, proteins and other entity names in text, http://pages.cs.wisc.edu/bsettles/abner/) [19] and conjunction resolution. The flow chart of NLP analysis was shown in Fig. 1.
Flow chart of the natural language processing (NLP) analysis of hepatocellular carcinoma
The frequency was calculated for each gene occurrence in the NLP analysis. The higher frequency implies the stronger association between HCC and certain genes. The number of all eligible literatures in PubMed database was recorded as N. The frequency of certain gene and HCC in PubMed was marked as "m" and "n", respectively. It was denoted as "k" when a gene and HCC occurred simultaneously. Then we calculated the possibility of frequency greater than "k" co-citation via hypergeometric distribution in completely random conditions.
$$ \mathrm{p}=1-\sum \limits_{\mathrm{i}=0}^{\mathrm{k}-1}\mathrm{p}\left(i\left|\mathrm{n},\kern0.5em \mathrm{m},\kern0.5em \mathrm{N}\right.\right) $$
$$ \mathrm{p}\left(i\left|\mathrm{n},\kern0.5em \mathrm{m},\kern0.5em \mathrm{N}\right.\right)=\frac{n!\left(N-n\right)!m!\left(N-m\right)}{\left(n-i\right)!i!\left(n-m\right)!\left(N-n-m+i\right)!N!} $$
The comprehensive analysis of HCC- related genes
We conducted GO analysis on the functions of differently expressed genes in HCC and classified the related genes into three major groups: biological processes, cellular component and molecular functions. Pathway analysis was applied in GenMAPP v2.1 for Kyoto Encyclopedia of Genes and Genomes (KEGG) pathway enrichment and the value of P was calculated to select the significantly enriched pathway. We also combined three different interactions: 1) protein interaction, gene regulation, protein; 2) modification of the existing high-throughput experiments; 3) interactions between genes mentioned previously. In addition, the pathway data was downloaded from KEGG database and the interactions between genes were analyzed by KEGGSOA (http://www.bioconductor.org/packages/2.4/bioc/html/ KEGGSOAP.html) package from R (http://www.r-project.org/), including enzyme–enzyme relation, protein–protein interaction and gene expression interaction [20].
We downloaded the data of protein interactions from MIPS database (http://mips.helmholtz-muenchen.de/proj/ppi/) [21]. For the interaction mentioned previously, algorithm co-citation in the abstracts in PubMed was used to analyze gene term and all term variants co-occurring with the certain gene. And we also calculated the frequency of the cocitation genes. Then we conducted statistical analyses according to the description in NLP analysis. Finally, medusa software was used to perform the network.
Prediction of miRNA-34a target genes
We analyzed the predicted targets of miR-34a by applying 11 independent software: DIANA-microT, MicroInspector, miRanda, MirTarget2, miTarget, NBmiRTar, PicTar, PITA, RNA22, RNAhybrid and TargetScan. The results were considered reliable when the results were calculated by four or more software. GO analysis, pathway analysis and network analysis of miR-34a target genes were performed in accordance with the same principles of genes from NLP analysis.
Integrative analysis of miR-34a targets and the natural language processing
We calculated the overlap of miR-34a targets predicted in silico and HCC related-genes acquired from NLP analysis. And the ingenuity pathway analysis was carried out to show the relationships between miR-34a and its target genes associated with HCC. The overlap of the miR-34a target genes predicted by in-silico bioinformatics tools and HCC-related genes was performed subsequently.
Comprehensive analysis of GEO datasets
Fourteen eligible datasets were involved in this study, which included 3 datasets containing HCC tissues and 11 datasets containing both HCC and adjacent tumor (or healthy) tissues (Table 1). The result showed that the expression level of miR-34a in HCC tissues was statistically lower than that in normal tissues with no heterogeneity (SMD = 0.63, 95%CI [0.38, 0.88], P < 0.00001; P heterogeneity = 0.08 I2 = 41% Figure 2).The three studies which contained HCC tissues only were used to evaluate the difference of miR-34a expression in HCC patients with or without vascular invasion. The comparison identified that miR-34a expression was not associated with vascular invasion in HCC patients (SMD = −1.44, 95%CI: [−0.16,-2.71], P = 0.03; Pheterogeneity < 0.00001 I2 = 95%, Figure 3a).Besides, there existed significant heterogeneity after we had reviewed every study. Among the 11 datasets mentioned above, two datasets (GSE69580, GSE10694) were applied to estimate the relationship of miR-34a with cirrhosis in HCC patients. Another two datasets (GSE10694, GSE41874) were performed to analyze whether the expression of miR-34a was related to metastasis in patients with HCC. Finally, no relationship was observed between miR-34a expression and cirrhosis or metastasis (Pcirrhosis = 0.79, Fig. 3b; Pmetastasis = 0.77, Figure 3c).
Table 1 Characteristics of miR-34a gene expression used in the analysis of GEO datasets
Forest plot showing SMD of miR-34a expression between HCC tissues and corresponding normal tissues
Forest plot showing the association between miR-34a expression and HCC clinocopathologic characteristics. a Forest plot showing SMD of miR-34a expression in HCC tissues with or without vascular invasion. b Forest plot showing SMD of miR-34a expression in HCC tissues with or without cirrhosis. c Forest plot showing SMD of miR-34a expression in HCC tissues with or without metastasis
The analysis of HCC-related genes
A total of 64,577 articles for HCC-related molecules were identified for initial browse after primary search in PubMed. A total of 1800 HCC-relevant genes were obtained. All of these cancer-related genes were categorized into different biological processes, cellular components, molecular functions according to GO analysis (Additional file 1: Table S1). In the pathway analysis, we found 25 signaling pathways were significant (P < 0.005), which has been discussed in our previously published work [20]. By constructing gene network, we found the hub genes functioned as a key factor in regulating the stability of the network. In our previous study, the gene network of those 1800 genes were performed [20].The published article also showed that several hub genes were highly related to other genes: PIK3CA, PIK3R2, MAPK1, MAPk3, JAK2, EGFR, KRAS, NRAS [20].
The analysis of miR-34a predicted targets
In the present study, we analyzed the potential targets of miR-34a to explore the biological function of miR-34a relying on its target-protein-coding genes. One thousand potential genes were identified and categorized in GO analysis (Additional file 2: Table S2). Subsequent to the pathway analysis,five pathways were discovered to be statistically significant: Focal adhesion, p53 signaling pathway, Cell cycle, Cytokine-cytokine receptor interaction, Notch signaling pathway (P < 0.05, Table 2).
Table 2 Pathway analysis of miR-34a-related genes
In the network analysis, only two genes are statistically significant and both of them were the highest hub genes, including CCND1 and BCL2 (Fig. 4c, Figure 4d). CCND1 participates in the regulation of the three pathways mentioned in Table 2 (focal adhesion, p53 signaling pathway, cell cycle) and BCL-2 acts as a member of focal adhesion. In addition, the expression of CCND1 and BCL-2 were both associated with the biological processes described in GO analysis: cell cycle and proliferation, stress response, developmental processes, protein metabolism.
Network analysis and connectivity analysis of miR-34a targets. a Network analysis of miR-34a targets. Brown represents association, green represents inhibition and blue represents activation. b Connectivity analysis of miR-34a targets. The connectivity of Bcl-2 is the highest one which has a total of twenty-two related-genes (z-test, P = 0.0037)
Integrative analysis of miR-34a target genes and the NLP results
In the integrative analysis, we calculated the overlap of miR-34a targets and HCC-related genes obtained from the NLP analysis. As a result, 61 HCC-related genes, such as VEGFA, Bcl-2, CCND1, MET, KIT, Notch1, DPYD, SERPINE1 and CDK6 were potentially modulated by miR-34a, were summarized in Additional file 3: Table S3. Besides, the relationship among these genes was shown in Fig. 5, including five significant pathways: cell cycle (P = 0.001921952); cytokine-cytokine receptor interaction (P = 0.039495189); notching signaling pathway (P = 0.045372273); p53 pathway (P = 0.001385856) and focal adhesion (P = 5.09E-04). Among the five pathways mentioned above, the three genes (E2F3, E2F5, CDC25A) were involved in the cell cycle pathway, and KIT/CCL22 were found in the cytokine-cytokine receptor interaction pathway. Besides, Notch1/Notch2/JAG1 and CDK6/IGFPB3/CCNE2 were significantly related to the notching signaling pathway and p53 pathway, respectively. Additionally, we concluded that VEGFA, Bcl-2, CCND1, MET, PDGFRA were related to the functions of focal adhesion in HCC patients.
Integrative -analysis of miR-34a target genes and the NLP results. Sixty-nine overlapping genes and their functional pathway that are not only associated with the molecular mechanism of HCC but also are the potential miR-34a target genes were obtained in this final integrative-analysis
Nowadays, in order to prolong the survival time of HCC patients, more and more therapies are applied in the clinical stage, including radiotherapy, interventional operation, combined therapy. However, the survival rate is still unsatisfactory. In recent years, more and more researches have focused on the molecular targeted therapy and made exciting progress. Liu et al. have concluded that miR-222 and miR-494 could enhance HCC patients' resistance to sorafenib by activating the PI3K/AKT signaling pathway [22, 23]. The study reported by Lin et al. has also identified that miR-21 partially reduced the cytotoxic effects of sorafenib in combination with matrine against HCC [24]. However, another two reports have verified that increased expression of miRNAs could assist the efficiency of sorafenib treatment for HCC patients [25, 26]. In our previous study, we identified that increased expression of miR-34a might help the diagnosis and prognosis of HCC by regulating c-MET [18]. Although numerous articles have verified the functions of miR-34a in the carcinogenesis and progression of HCC, the molecular mechanism of miR-34a related to HCC still remains unclear. Therefore, this article was the first to identify the relationship of miR-34a expression with HCC based on microarray data. In addition, we separately analyzed the related pathways of HCC-relate genes and miR-34a targets, and further explored the potential molecular mechanism of miR-34a by overlapping genes associated with HCC and miR-34a.
The consequences of GEO analysis testified that miR-34a expression was downregulated in HCC tissues, which was consistent with our previous study [18]. On the contrary, another two articles have demonstrated that upregulation of miR-34a could promote the proliferation of HCC [27, 28]. The research conducted by Gougelet et al. has identified that the higher expression of miR-34a induced by activation of β-catenin could enhance the risk of HCC by targeting CCND1 [27]. However, the other study has testified that Aflatoxin-B1 (AFB1) might contribute to the progression of HCC by upregulating miR-34a, which may down-regulate Wnt/β-catenin signaling pathway [28]. Besides, due to the limitation of sample size, no statistical significance was found in the associations of miR-34a expression value with HCC clinicopathological features. Nevertheless, some other studies have shown that the low expression of miR-34a might promote the progression of HCC.
Two researchers have suggested that ectopic expression of miR-34a was related to tumor metastasis and invasion via modulating c-MET signaling pathway [18, 29]. Cheng et al. have also provided evidence that abrogation functions of miR-34a could contribute to HCC development through cell cycle pathway and p53 pathway [30]. Moreover, it has been demonstrated that miR-34a/ toll-like receptor 4(TLR4) axis may function as a key regulator in increasing the risk of HCC [31]. Besides, another article has verified that overexpression of miR-34a could improve the effect of cisplatin treatment by enhancing cytotoxicity of NK cells for HCC patients [32]. In addition, Lou et al. have shown that decreased expression of miR-34a may reduce the sensitivity of HCC cells to quercetin by upregulating SIRT1 and downregulating p53 [11]. Therefore, the functions of miR-34a in HCC are complex and still needed further investigation.
In order to explore the molecular mechanism of miR-34a in moderating the progression of HCC, we conducted a series of bioinformatics analyses. The results showed that among the targets of miR-34a, the most significant hub genes were CCND1 and Bcl-2, which were parts of focal adhesion, p53 signaling pathway, cell cycle pathway. Meanwhile, we also found these two genes (CCND1 and Bcl-2) were included in the hub genes which were calculated from the interactive analysis of miR-34a and the NLP analysis. MiR-195 could suppress the development of cancers by targeting CCND1 [33]. Besbes et al. have also concluded that decreased expression of Bcl-2 family members contributed to the progression of apoptosis in cancers [34]. Especially, Gougelet et al. and Zhu et al. have suggested that the feedback loop composed of miR-34a/β-catenin/CCND1 played a critical role in regulating the progression of HCC [27, 28]. Hence, miR-34a may serve as an important regulator in the development of HCC by targeting CCND1 and Bcl-2.
In the interactive analysis, we not only calculated the hub genes, but also the statistically significant pathways involved in moderating the progression of miR-34a-related HCC. The outcome showed eight genes-VEGFA, Bcl-2, CCND1, MET, NOTCH1, SERPINE1, DYPD and CDK6-had the highest connectivity. It was worth noticing that the eight genes were classified into five significantly different pathways. It suggested that miR-34a may impact the development and progression of HCC by moderating cell cycle, cytokine-cytokine receptor interaction, notching pathway, p53 pathway and focal adhesion. Thus, the functions of every genes involved in the five pathways were essential in understanding the effects of miR-34a on HCC patients.
E2F3 and E2F5 are members of the E2F family which is composed of transcription factors and attributed to the cell cycle progression by regulating G1/S-phase transition [35]. Some studies have shown that miR-503 and miR-195 could inhibit the G1/S transition by suppressing the expression of E2F5 [36, 37]. And the downregulation of E2F5 has been identified to be associated with development of HBV-related HCC [38]. Several articles have suggested that miRNAs could suppress the proliferation, metastasis and invasion of HCC cells by targeting E2F3 [39,40,41]. Additionally, it has been verified that the inhibition of E2F3 induced by overexpression of miRNAs could enhance the sensitivity of HCC patients to anti-cancer agents and decelerate the progression of HCC [39, 42].
Cytokine-cytokine receptor interaction
C-kit is the receptor of stem cell factor (SCF), and the activation of c-kit have been suggested to be crucial for cell proliferation and migration [43]. The activation of c-kit has been suggested to be attributed to the cell proliferation and cirrhosis of HCC [43, 44]. Yang et al. have proved that the activation of TGF-β-miR-34a-CCL22 signaling could promote the progression of portal vein tumor thrombus in HCC patients [45]. Two studies have also proved that miRNAs could promote the development of HCC by blocking G1/S transition via reducing expression of CDK6 [36, 46].
Notching pathway
Notching signaling pathway composed of notch receptors(Notch1–4) and notch ligands(Jag1) is critical for determining cell fates and associated with therapy of HCC [47, 48]. The result reported by Xue et al. indicated that JAG1/Notch1 signaling is positively associated with the extrahepatic metastasis in HCC by moderating the level of osteopontin (OPN) [49]. However, Wang et al. have concluded that increased expression of Notch1/Jagged1 could promote the progression of HCC via inhibiting beta-catenin expression [50]. Another two studies have indicated that Notch1 may be a therapeutic target by downregulating Wnt/β-catenin pathway and CyclinD1/CDK4 pathway in HBV-associated HCC [51, 52]. In addition, it has been demonstrated that inhibition of Notch2 regulated by C8orf4 could suppress the self-renewal of liver cancer stem cells(CScs) and Notch2 and Jag1 may function as novel therapeutic targets for HCC treatment [53, 54].
P53 is widely recognized as a tumour suppressor in regulating cell cycle, apoptosis, metabolism and DNA repair [55]. Giacoia et al. have concluded that wide-type p53 could upregulate the expression of miR-107 and then reduce the level of CDK6 and Notch2, which suppresses glioma cell growth [56]. It has been indicated that overexpression of plasminogen activator inhibitor-1 (PAI-1/SERPINE1) could enhance tumour cell proliferation as well as inhibit G(1)-phase transition complexes, cdk4/6/ cyclin D3 and promote the cell-cycle suppressors p53, p27Kip1 and p21Cip1/Waf1 [57]. IGFBP3 induced by p53 have also been verified to be related to the apoptosis of HCC cells [58].
Focal adhesion
The pathway analysis also suggests that Bcl-2, CCND1, PDGFRA, VEGFA and c-MET belong to the focal adhesion pathway. It has also been suggested that CCND1 variants may be positively correlated with the precancerous cirrhosis of hepatocarcinogenesis [59]. Increased expression of platelet-derived growth factor receptor alpha (PDGFRA) promoted by miR-146a has been verified to be associated with the microvascular invasion and poor prognosis of HCC [60]. In addition, it has been shown that the synergism of sorafenib has contributed to the therapy of HCC patients by suppressing the level of MET [61]. It has been identified that HCC patients with amplification of vascular endothelial growth factor A (VEGFA) are more likely to be sensitive to sorafenib [62]. Zhou et al. have also found that miR-503 serve as a suppressor of tumor angiogenesis by targeting VEGFA in HCC patients [63]. However, the functions of genes which were related with miR-34a expression and progression of HCC have not been identified.
In the present study, researchers have paid attention to the results of the comprehensive analyses, especially the section of the integrative –network analysis of miR-34a targets and HCC-related genes. It illustrated the most important genes and pathways involved in the functions of miR-34a in HCC, which may offer researchers more insights into understanding the relationship between miR-34a and HCC. However, the targets of miR-34a were predicted in silico, including genes verified or not verified in experiments, which could make it difficult to explore the exact mechanism of miR-34a in HCC. It is noted that the two genes CCND1 and bcl-2 seem to serve as key regulators between the expression of miR-34a and HCC. Therefore, it is imperative to find out the exact relationships among miR-34a, CCND1/bcl-2 and HCC at a further step.
In summary, it was worth considering that the analyses of miR-34a- targets in HCC would provide effective guidelines for the diagnosis, prognosis and therapy of patients with HCC. The results indicate that miR-34a primarily controls cell cycle, cytokine-cytokine receptor interaction, notching pathway, p53 pathway and focal adhesion pathway in regulating the tumorigenesis and process of HCC. Therefore, these pathways may offer novel insights into the functions of miR-34a in HCC and guide the researchers to find more effective methods to the prevention and treatment of HCC.
3'-UTRs:
3′--untranslated regions
95%CI:
95% confidence intervals
AFB1:
Aflatoxin-B1
Gene ontology (GO)
HBV:
HCC:
HCV:
KEGG:
miRNA:
mRNA:
Messenger RNAs
NLP:
PDGFRA:
Platelet-derived growth factor receptor alpha
SMD:
Std. mean difference
TLR4:
Toll-like receptor 4
VEGFA:
Vascular endothelial growth factor A
Liu Y, Buil A, Collins BC, Gillet LC, Blum LC, Cheng LY, et al. Quantitative variability of 342 plasma proteins in a human twin population. Mol Syst Biol. 2015;11(1):786.
de Martel C, Ferlay J, Franceschi S, Vignat J, Bray F, Forman D, et al. Global burden of cancers attributable to infections in 2008: a review and synthetic analysis. Lancet Oncol. 2012;13(6):607–15.
Yang X, Xie X, Xiao YF, Xie R, CJ H, Tang B, et al. The emergence of long non-coding RNAs in the tumorigenesis of hepatocellular carcinoma. Cancer Lett. 2015;360(2):119–24.
Pan L, Ren F, Rong M, Dang Y, Luo Y, Luo D, et al. Correlation between down-expression of miR-431 and clinicopathological significance in HCC tissues. Clin Transl Oncol. 2015;17(7):557–63.
Bartel DP. MicroRNAs: genomics, biogenesis, mechanism, and function. Cell. 2004;116(2):281–97.
Bartel DP. MicroRNAs: target recognition and regulatory functions. Cell. 2009;136(2):215–33.
Krol J, Loedige I, Filipowicz W. The widespread regulation of microRNA biogenesis, function and decay. Nat Rev Genet. 2010;11(9):597–610.
De Cecco L, Dugo M, Canevari S, Daidone MG, Callari M. Measuring microRNA expression levels in oncology: from samples to data analysis. Crit Rev Oncog. 2013;18(4):273–87.
Nie J, Ge X, Geng Y, Cao H, Zhu W, Jiao Y, et al. miR-34a inhibits the migration and invasion of esophageal squamous cell carcinoma by targeting yin Yang-1. Oncol Rep. 2015;34(1):311–7.
Zhang H, Li S, Yang J, Liu S, Gong X, Yu X. The prognostic value of miR-34a expression in completely resected gastric cancer: tumor recurrence and overall survival. Int J Clin Exp Med. 2015;8(2):2635–41.
Lou G, Liu Y, Wu S, Xue J, Yang F, Fu H, et al. The p53/miR-34a/SIRT1 positive feedback loop in Quercetin-induced apoptosis. Cell Physiol Biochem. 2015;35(6):2192–202.
Li R, Shi X, Ling F, Wang C, Liu J, Wang W, et al. MiR-34a suppresses ovarian cancer proliferation and motility by targeting AXL. Tumour Biol. 2015;
Kang L, Mao J, Tao Y, Song B, Ma W, Lu Y, et al. MicroRNA-34a suppresses the breast cancer stem cell-like characteristics by downregulating Notch1 pathway. Cancer Sci. 2015;106(6):700–8.
Lai M, Du G, Shi R, Yao J, Yang G, Wei Y, et al. MiR-34a inhibits migration and invasion by regulating the SIRT1/p53 pathway in human SW480 cells. Mol Med Rep. 2015;11(5):3301–7.
Chen WY, Liu SY, Chang YS, Yin JJ, Yeh HL, Mouhieddine TH, et al. MicroRNA-34a regulates WNT/TCF7 signaling and inhibits bone metastasis in Ras-activated prostate cancer. Oncotarget. 2015;6(1):441–57.
Zhou JY, Chen X, Zhao J, Bao Z, Chen X, Zhang P, et al. MicroRNA-34a overcomes HGF-mediated gefitinib resistance in EGFR mutant lung cancer cells partly by targeting MET. Cancer Lett. 2014;351(2):265–71.
Cao C, Sun J, Zhang D, Guo X, Xie L, Li X, et al. The long intergenic noncoding RNA UFC1, a target of MicroRNA 34a, interacts with the mRNA stabilizing protein HuR to increase levels of beta-catenin in HCC cells. Gastroenterology. 2015;148(2):415–26. e418
Dang Y, Luo D, Rong M, Chen G. Underexpression of miR-34a in hepatocellular carcinoma and its contribution towards enhancement of proliferating inhibitory effects of agents targeting c-MET. PLoS One. 2013;8(4):e61054.
Settles B. ABNER an open source tool for automatically tagging genes, proteins and other entity names in text. Bioinformatics. 2005;21(14):3191–2.
Zhang X, Tang W, Chen G, Ren F, Liang H, Dang Y, et al. An encapsulation of gene signatures for Hepatocellular carcinoma, MicroRNA-132 predicted target genes and the corresponding overlaps. PLoS One. 2016;11(7):e0159498.
Mewes HW, Albermann K, Heumann K, Liebl S, Pfeiffer FMIPS. A database for protein sequences, homology data and yeast genome information. Nucleic Acids Res. 1997;25(1):28–30.
Liu K, Liu S, Zhang W, Jia B, Tan L, Jin Z, et al. miR-494 promotes cell proliferation, migration and invasion, and increased sorafenib resistance in hepatocellular carcinoma by targeting PTEN. Oncol Rep. 2015;34(2):1003–10.
Liu K, Liu S, Zhang W, Ji B, Wang Y, Liu Y. miR222 regulates sorafenib resistance and enhance tumorigenicity in hepatocellular carcinoma. Int J Oncol. 2014;45(4):1537–46.
Lin Y, Lin L, Jin Y, Wang D, Tan Y, Zheng C. Combination of Matrine and Sorafenib decreases the aggressive phenotypes of Hepatocellular carcinoma cells. Chemotherapy. 2014;60(2):112–8.
Vaira V, Roncalli M, Carnaghi C, Faversani A, Maggioni M, Augello C, et al. MicroRNA-425-3p predicts response to sorafenib therapy in patients with hepatocellular carcinoma. Liver Int. 2015;35(3):1077–86.
Sun H, Cui C, Xiao F, Wang H, Xu J, Shi X, et al. miR-486 regulates metastasis and chemosensitivity in hepatocellular carcinoma by targeting CLDN10 and CITRON. Hepatol Res. 2015;
Gougelet A, Sartor C, Bachelot L, Godard C, Marchiol C, Renault G, et al. Antitumour activity of an inhibitor of miR-34a in liver cancer with beta-catenin-mutations. Gut. 2015;
Zhu L, Gao J, Huang K, Luo Y, Zhang B, Xu W. miR-34a screened by miRNA profiling negatively regulates Wnt/beta-catenin signaling pathway in Aflatoxin B1 induced hepatotoxicity. Sci Rep. 2015;5:16732.
Li N, Fu H, Tie Y, Hu Z, Kong W, Wu Y, et al. miR-34a inhibits migration and invasion by down-regulation of c-met expression in human hepatocellular carcinoma cells. Cancer Lett. 2009;275(1):44–53.
Cheng J, Zhou L, Xie QF, Xie HY, Wei XY, Gao F, et al. The impact of miR-34a on protein output in hepatocellular carcinoma HepG2 cells. Proteomics. 2010;10(8):1557–72.
Jiang ZC, Tang XM, Zhao YR, Zheng L. A functional variant at miR-34a binding site in toll-like receptor 4 gene alters susceptibility to hepatocellular carcinoma in a Chinese Han population. Tumour Biol. 2014;35(12):12345–52.
Shi L, Lin H, Li G, Sun Y, Shen J, Xu J, et al. Cisplatin enhances NK cell immunotherapy efficacy to suppress HCC progression via altering the androgen receptor (AR)-ULBP2 signals. Cancer Lett. 2016;
Han K, Chen X, Bian N, Ma B, Yang T, Cai C, et al. MicroRNA profiling identifies MiR-195 suppresses osteosarcoma cell metastasis by targeting CCND1. Oncotarget. 2015;6(11):8875–89.
Karpel-Massler G, Shu C, Chau L, Banu M, Halatsch ME, Westhoff MA, et al. Combined inhibition of Bcl-2/Bcl-xL and Usp9X/Bag3 overcomes apoptotic resistance in glioblastoma in vitro and in vivo. Oncotarget. 2015;6(16):14507–21.
Attwooll C, Lazzerini Denchi E, Helin K. The E2F family: specific functions and overlapping interests. EMBO J. 2004;23(24):4709–16.
Xu T, Zhu Y, Xiong Y, Ge YY, Yun JP, Zhuang SM. MicroRNA-195 suppresses tumorigenicity and regulates G1/S transition of human hepatocellular carcinoma cells. Hepatology. 2009;50(1):113–21.
Xiao F, Zhang W, Chen L, Chen F, Xie H, Xing C, et al. MicroRNA-503 inhibits the G1/S transition by downregulating cyclin D3 and E2F3 in hepatocellular carcinoma. J Transl Med. 2013;11:195.
Zou C, Li Y, Cao Y, Zhang J, Jiang J, Sheng Y, et al. Up-regulated MicroRNA-181a induces carcinogenesis in hepatitis B virus-related hepatocellular carcinoma by targeting E2F5. BMC Cancer. 2014;14:97.
Xue J, Niu YF, Huang J, Peng G, Wang LX, Yang YH, et al. miR-141 suppresses the growth and metastasis of HCC cells by targeting E2F3. Tumour Biol. 2014;35(12):12103–7.
Cao T, Li H, Hu Y, Ma D, Cai X. miR-144 suppresses the proliferation and metastasis of hepatocellular carcinoma by targeting E2F3. Tumour Biol. 2014;35(11):10759–64.
Su J, Wang Q, Liu Y, Zhong M. miR-217 inhibits invasion of hepatocellular carcinoma cells through direct suppression of E2F3. Mol Cell Biochem. 2014;392(1–2):289–96.
Lee JM, Heo MJ, Lee CG, Yang YM, Kim SG. Increase of miR-199a-5p by protoporphyrin IX, a photocatalyzer, directly inhibits E2F3, sensitizing mesenchymal tumor cells to anti-cancer agents. Oncotarget. 2015;6(6):3918–31.
Lennartsson J, Ronnstrand L. Stem cell factor receptor/c-kit: from basic science to clinical implications. Physiol Rev. 2012;92(4):1619–49.
Mansuroglu T, Baumhoer D, Dudas J, Haller F, Cameron S, Lorf T, et al. Expression of stem cell factor receptor c-kit in human nontumoral and tumoral hepatic cells. Eur J Gastroenterol Hepatol. 2009;21(10):1206–11.
Yang P, Li QJ, Feng Y, Zhang Y, Markowitz GJ, Ning S, et al. TGF-beta-miR-34a-CCL22 signaling-induced Treg cell recruitment promotes venous metastases of HBV-positive hepatocellular carcinoma. Cancer Cell. 2012;22(3):291–303.
Xiao F, Zhang W, Zhou L, Xie H, Xing C, Ding S, et al. microRNA-200a is an independent prognostic factor of hepatocellular carcinoma and induces cell cycle arrest by targeting CDK6. Oncol Rep. 2013;30(5):2203–10.
Morell CM, Strazzabosco M. Notch signaling and new therapeutic options in liver disease. J Hepatol. 2014;60(4):885–90.
Wu G, Wilson G, George J, Qiao L. Modulation of notch signaling as a therapeutic approach for liver cancer. Curr Gene Ther. 2015;15(2):171–81.
Xue TC, Zou JH, Chen RX, Cui JF, Tang ZY, Ye SL. Spatial localization of the JAG1/Notch1/osteopontin cascade modulates extrahepatic metastasis in hepatocellular carcinoma. Int J Oncol. 2014;45(5):1883–90.
Wang M, Xue L, Cao Q, Lin Y, Ding Y, Yang P, et al. Expression of Notch1, Jagged1 and beta-catenin and their clinicopathological significance in hepatocellular carcinoma. Neoplasma. 2009;56(6):533–41.
Sun Q, Wang R, Luo J, Wang P, Xiong S, Liu M, et al. Notch1 promotes hepatitis B virus X protein-induced hepatocarcinogenesis via Wnt/beta-catenin pathway. Int J Oncol. 2014;45(4):1638–48.
Sun Q, Wang R, Wang Y, Luo J, Wang P, Cheng B. Notch1 is a potential therapeutic target for the treatment of human hepatitis B virus X protein-associated hepatocellular carcinoma. Oncol Rep. 2014;31(2):933–9.
Zhu P, Wang Y, Du Y, He L, Huang G, Zhang G, et al. C8orf4 negatively regulates self-renewal of liver cancer stem cells via suppression of NOTCH2 signalling. Nat Commun. 2015;6:7122.
Huntzicker EG, Hotzel K, Choy L, Che L, Ross J, Pau G, et al. Differential effects of targeting notch receptors in a mouse model of liver cancer. Hepatology. 2015;61(3):942–52.
Khoo KH, Verma CS, Lane DP. Drugging the p53 pathway: understanding the route to clinical efficacy. Nat Rev Drug Discov. 2014;13(3):217–36.
Chen L, Zhang R, Li P, Liu Y, Qin K, Fa ZQ, et al. P53-induced microRNA-107 inhibits proliferation of glioma cells and down-regulates the expression of CDK6 and Notch-2. Neurosci Lett. 2013;534:327–32.
Giacoia EG, Miyake M, Lawton A, Goodison S, Rosser CJ. PAI-1 leads to G1-phase cell-cycle progression through cyclin D3/cdk4/6 upregulation. Mol Cancer Res. 2014;12(3):322–34.
Han JJ, Xue DW, Han QR, Liang XH, Xie L, Li S, et al. Induction of apoptosis by IGFBP3 overexpression in hepatocellular carcinoma cells. Asian Pac J Cancer Prev. 2014;15(23):10085–9.
Zeng Z, Tu J, Cheng J, Yao M, Wu Y, Huang X, et al. Influence of CCND1 G870A polymorphism on the risk of HBV-related HCC and cyclin D1 splicing variant expression in Chinese population. Tumour Biol. 2015;36(9):6891–900.
Zhu K, Pan Q, Zhang X, Kong LQ, Fan J, Dai Z, et al. MiR-146a enhances angiogenic activity of endothelial cells in hepatocellular carcinoma by promoting PDGFRA expression. Carcinogenesis. 2013;34(9):2071–9.
Xiang Q, Chen W, Ren M, Wang J, Zhang H, Deng DY, et al. Cabozantinib suppresses tumor growth and metastasis in hepatocellular carcinoma by a dual blockade of VEGFR2 and MET. Clin Cancer Res. 2014;20(11):2959–70.
Horwitz E, Stein I, Andreozzi M, Nemeth J, Shoham A, Pappo O, et al. Human and mouse VEGFA-amplified hepatocellular carcinomas are highly sensitive to sorafenib treatment. Cancer Discov. 2014;4(6):730–43.
Zhou B, Ma R, Si W, Li S, Xu Y, Tu X, et al. MicroRNA-503 targets FGF2 and VEGFA and inhibits tumor angiogenesis and growth. Cancer Lett. 2013;333(2):159–69.
The study was supported partly by the Fund of National Natural Science Foundation of China (NSFC81560489, NSFC 81260222), the Fund of Guangxi Provincial Health Bureau Scientific Research Project (Z2014054), Youth Science Foundation of Guangxi Medical University (GXMUYSF201311), and Guangxi University Science and Technology Research Projects (LX2014075). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
All data generated or analyzed during this study are included in this published article (Tables 1 and 2) and its Additional files (Additional file 1: Table S1, Additional file 2: Table S2 and Additional file 3: Table S3).
Department of Pathology, First Affiliated Hospital of Guangxi Medical University, 6 Shuangyong Road, Nanning, Guangxi Zhuang Autonomous Region, 530021, People's Republic of China
Fang-Hui Ren, Hai-Wei Liang, Yi-Wu Dang, Zhen-Bo Feng, Gang Chen & Dian-Zhong Luo
Department of Ultrasonography, First Affiliated Hospital of Guangxi Medical University, 6 Shuangyong Road, Nanning, Guangxi Zhuang Autonomous Region, 530021, People's Republic of China
Hong Yang
Center for Genomic and Personalized Medicine, Guangxi Medical University, 22 Shuangyong Road, Nanning, Guangxi Zhuang Autonomous Region, 530021, People's Republic of China
Rong-quan He & Xing-gu Lin
Department of Hepatobiliary Surgery, First Affiliated Hospital of Guangxi Medical University, 6 Shuangyong Road, Nanning, Guangxi Zhuang Autonomous Region, 530021, People's Republic of China
Jing-ning Lu
Jing-ning Lu Deceased.
Fang-Hui Ren
Rong-quan He
Xing-gu Lin
Hai-Wei Liang
Yi-Wu Dang
Zhen-Bo Feng
Gang Chen
Dian-Zhong Luo
HY, YWD, ZBF, GC and DZL designed the experiment, interpreted the data and corrected the manuscript. FHR, RQH, JNL, XGL, HWL conducted the experiment, performed the statistical analysis and prepared the manuscript. All authors read and approved the final manuscript.
Correspondence to Gang Chen or Dian-Zhong Luo.
Additional file1: Table S1.
GO enrichment analysis of HCC related genes. (XLSX 12 kb)
GO enrichment analysis of miR-34a target genes. (XLSX 14 kb)
Integrative-analysis of miR-34a target genes and the natural language processing (NLP) results. Twenty-four overlapping genes that are not only associated with the development and progression of HCC but also are the potential miR-34a target genes were obtained in this integrative–analysis (XLSX 14 kb)
Ren, FH., Yang, H., He, Rq. et al. Analysis of microarrays of miR-34a and its identification of prospective target gene signature in hepatocellular carcinoma. BMC Cancer 18, 12 (2018). https://doi.org/10.1186/s12885-017-3941-x
miRNA-34a | CommonCrawl |
MEEP Documentation
Subpixel Smoothing
Exploiting Symmetry
Cylindrical Coordinates
Perfectly Matched Layers
Parallel Meep
Synchronizing the Magnetic and Electric Fields
Mode Decomposition
Field Functions
The Run Function is Not a Loop
Yee Lattice
Units and Nonlinearity
Python Interface
Tutorial/Basics
Tutorial/Ring Resonator in Cylindrical Coordinates
Tutorial/Resonant Modes and Transmission in a Waveguide Cavity
Tutorial/Material Dispersion
Tutorial/Third Harmonic Generation
Tutorial/Near-to-Far Field Spectra
Tutorial/Local Density of States
Tutorial/Optical Forces
Tutorial/Gyrotropic Media
Tutorial/Multilevel Atomic Susceptibility
Tutorial/Frequency-Domain Solver
Tutorial/Eigenmode Source
Tutorial/Mode Decomposition
Tutorial/GDSII Import
Tutorial/Adjoint Solver
Scheme Interface
Input Variables
Constants (Enumerated Types)
lorentzian-susceptibility
drude-susceptibility
multilevel-atom
noisy-lorentzian-susceptibility or noisy-drude-susceptibility
gyrotropic-lorentzian-susceptibility or gyrotropic-drude-susceptibility
gyrotropic-saturated-susceptibility
geometric-object
ellipsoid
eigenmode-source
continuous-src
gaussian-src
custom-src
flux-region
Miscellaneous Functions
Geometry Utilities
Output File Names
Output Volume
Simulation Time
Field Computations
Reloading Parameters
Flux Spectra
Energy Density Spectra
Force Spectra
LDOS spectra
Near-to-Far-Field Spectra
Load and Dump Structure
Frequency-Domain Solver
Run and Step Functions
Run Functions
Predefined Step Functions
Step-Function Modifiers
Writing Your Own Step Functions
Low-Level Functions
Initializing the Structure and Fields
SWIG Wrappers
Tutorial/Casimir Forces
Guile and Scheme Information
C++ Interface
Chunks and Symmetry
Scheme Interface »
Scheme User Interface
This page is a listing of the functions exposed by the Scheme interface. For a gentler introduction, see Tutorial/Basics. This page does not document the Scheme language or the functions provided by libctl. Also, note that this page is not a complete listing of all functions. In particular, because of the SWIG wrappers, every function in the C++ interface is accessible from Scheme, but not all of these functions are documented or intended for end users. See also the instructions for parallel Meep.
Note: The Scheme interface is being deprecated and has been replaced by the Python interface.
Output Functions
Harminv
Miscellaneous Step-Function Modifiers
Controlling When a Step Function Executes
Modifying HDF5 Output
These are global variables that you can set to control various parameters of the Meep computation. In brackets after each variable is the type of value that it should hold. The classes, complex datatypes like geometric-object, are described in a later subsection. The basic datatypes, like integer, boolean, cnumber, and vector3, are defined by libctl.
geometry [ list of geometric-object class ] — Specifies the geometric objects making up the structure being simulated. When objects overlap, later objects in the list take precedence. Defaults to no objects (empty list).
geometry-center [ vector3 class ] — Specifies the coordinates of the center of the cell. Defaults to (0, 0, 0), but changing this allows you to shift the coordinate system used in Meep (for example, to put the origin at the corner).
sources [ list of source class ] — Specifies the current sources to be present in the simulation. Defaults to none.
symmetries [ list of symmetry class ] — Specifies the spatial symmetries (mirror or rotation) to exploit in the simulation. Defaults to none. The symmetries must be obeyed by both the structure and the sources. See also Exploiting Symmetry.
pml-layers [ list of pml class ] — Specifies the PML absorbing boundary layers to use. Defaults to none.
geometry-lattice [lattice class ] — Specifies the size of the unit cell which is centered on the origin of the coordinate system. Any sizes of no-size imply a reduced-dimensionality calculation. A 2d calculation is especially optimized. See dimensions below. Defaults to a cubic cell of unit size.
default-material [material-type class ] — Holds the default material that is used for points not in any object of the geometry list. Defaults to air (ε=1). See also epsilon-input-file below.
epsilon-input-file [string] — If this string is not empty (the default), then it should be the name of an HDF5 file whose first/only dataset defines a scalar, real-valued, frequency-independent dielectric function over some discrete grid. Alternatively, the dataset name can be specified explicitly if the string is in the form "filename:dataset". This dielectric function is then used in place of the ε property of default-material (i.e. where there are no geometry objects). The grid of the epsilon file dataset need not match the computational grid; it is scaled and/or linearly interpolated as needed to map the file onto the cell. The structure is warped if the proportions of the grids do not match. Note: the file contents only override the ε property of the default-material, whereas other properties (μ, susceptibilities, nonlinearities, etc.) of default-material are still used.
dimensions [integer] — Explicitly specifies the dimensionality of the simulation, if the value is less than 3. If the value is 3 (the default), then the dimensions are automatically reduced to 2 if possible when geometry-lattice size in the direction is no-size. If dimensions is the special value of CYLINDRICAL, then cylindrical coordinates are used and the and dimensions are interpreted as and , respectively. If dimensions is 1, then the cell must be along the direction and only and field components are permitted. If dimensions is 2, then the cell must be in the plane.
m [number] — For CYLINDRICAL simulations, specifies that the angular dependence of the fields is of the form (default is m=0). If the simulation cell includes the origin , then m must be an integer.
accurate-fields-near-cylorigin? [boolean] —For CYLINDRICAL simulations with |m| > 1, compute more accurate fields near the origin at the expense of requiring a smaller Courant factor. Empirically, when this option is set to true, a Courant factor of roughly or smaller seems to be needed. Default is false, in which case the , , and fields within |m| pixels of the origin are forced to zero, which usually ensures stability with the default Courant factor of 0.5, at the expense of slowing convergence of the fields near .
resolution [number] — Specifies the computational grid resolution in pixels per distance unit. Default is 10.
k-point [false or vector3] — If false (the default), then the boundaries are perfect metallic (zero electric field). If a vector3, then the boundaries are Bloch-periodic: the fields at one side are times the fields at the other side, separated by the lattice vector . A non-zero vector3 will produce complex fields. The k-point vector is specified in Cartesian coordinates in units of 2π/distance. Note: this is different from MPB, equivalent to taking MPB's k-points through its function reciprocal->cartesian.
ensure-periodicity [boolean] — If true (the default) and if the boundary conditions are periodic (k-point is not false), then the geometric objects are automatically repeated periodically according to the lattice vectors which define the size of the cell.
eps-averaging? [boolean] — If true (the default), then subpixel averaging is used when initializing the dielectric function. For details, see Section 3 ("Interpolation and the illusion of continuity") of Computer Physics Communications, Vol. 181, pp. 687-702, 2010. The input variables subpixel-maxeval (default 104) and subpixel-tol (default 10-4) specify the maximum number of function evaluations and the integration tolerance for subpixel averaging. Increasing/decreasing these, respectively, will cause a more accurate but slower computation of the average ε with diminishing returns for the actual FDTD error.
force-complex-fields? [boolean] — By default, Meep runs its simulations with purely real fields whenever possible. It uses complex fields which require twice the memory and computation if the k-point is non-zero or if m is non-zero. However, by setting force-complex-fields? to true, Meep will always use complex fields.
filename-prefix [string] — A string prepended to all output filenames. If empty (the default), then Meep uses the name of the current ctl file, with ".ctl" replaced by "-" (e.g. foo.ctl uses a "foo-" prefix). See also Output File Names.
Courant [number] — Specify the Courant factor which relates the time step size to the spatial discretization: . Default is 0.5. For numerical stability, the Courant factor must be at most , where is the minimum refractive index (usually 1), and in practice should be slightly smaller.
output-volume [meep::volume*] — Specifies the default region of space that is output by the HDF5 output functions (below); see also the (volume ...) function to create meep::volume* objects. Default is '() (null), which means that the whole cell is output. Normally, you should use the (in-volume ...) function to modify the output volume instead of setting output-volume directly.
output-single-precision? [boolean] — Meep performs its computations in double precision, and by default its output HDF5 files are in the same format. However, by setting this variable to true (default is false) you can instead output in single precision which saves a factor of two in space.
progress-interval [number] — Time interval (seconds) after which Meep prints a progress message. Default is 4 seconds.
extra-materials [ list of material-type class ] — By default, Meep turns off support for material dispersion (via susceptibilities or conductivity) or nonlinearities if none of the objects in geometry have materials with these properties — since they are not needed, it is faster to omit their calculation. This doesn't work, however, if you use a material-function: materials via a user-specified function of position instead of just geometric objects. If your material function only returns a nonlinear material, for example, Meep won't notice this unless you tell it explicitly via extra-materials. extra-materials is a list of materials that Meep should look for in the cell in addition to any materials that are specified by geometric objects. You should list any materials other than scalar dielectrics that are returned by material-function here.
The following require a bit more understanding of the inner workings of Meep to use. See also SWIG Wrappers.
structure [meep::structure*] — Pointer to the current structure being simulated; initialized by (init-structure) which is called automatically by (init-fields) which is called automatically by any of the (run) functions.
fields [meep::fields*] — Pointer to the current fields being simulated; initialized by (init-fields) which is called automatically by any of the (run) functions.
num-chunks [integer] — Minimum number of "chunks" (subarrays) to divide the structure/fields into (default 0). Actual number is determined by number of processors, PML layers, etcetera. Mainly useful for debugging.
air, vacuum [material-type class ] — Two aliases for a predefined material type with a dielectric constant of 1.
perfect-electric-conductor or metal [material-type class ] — A predefined material type corresponding to a perfect electric conductor at the boundary of which the parallel electric field is zero. Technically, .
perfect-magnetic-conductor [material-type class ] — A predefined material type corresponding to a perfect magnetic conductor at the boundary of which the parallel magnetic field is zero. Technically, .
nothing [material-type class ] — A material that, effectively, punches a hole through other objects to the background (default-material).
infinity [number] — A big number (1020) to use for "infinite" dimensions of objects.
pi [number] — π (3.14159...).
Several of the functions/classes in Meep ask you to specify e.g. a field component or a direction in the grid. These should be one of the following constants:
direction constants — Specify a direction in the grid. One of X, Y, Z, R, P for , , , , , respectively.
side constants — Specify particular boundary in the positive High (e.g., +X) or negative Low (e.g., -X) direction.
component constants — Specify a particular field or other component. One of Ex, Ey, Ez, Er, Ep, Hx, Hy, Hz, Hy, Hp, Hz, Bx, By, Bz, By, Bp, Bz, Dx, Dy, Dz, Dr, Dp, Dielectric, Permeability, for , , , , , , , , , , , , , , , , , , , , ε, μ, respectively.
derived-component constants — These are additional components which are not actually stored by Meep but are computed as needed, mainly for use in output functions. One of Sx, Sy, Sz, Sr, Sp, EnergyDensity, D-EnergyDensity, H-EnergyDensity for , , , , (components of the Poynting vector ), , , , respectively.
Classes are complex datatypes with various properties which may have default values. Classes can be "subclasses" of other classes. Subclasses inherit all the properties of their superclass and can be used in any place the superclass is expected. An object of a class is constructed with:
(make class (prop1 val1) (prop2 val2) ...)
See also the libctl manual.
Meep defines several types of classes, the most numerous of which are the various geometric object classes which are the same as those used in MPB. You can also get a list of the available classes, along with their property types and default values, at runtime with the (help) command.
The lattice class is normally used only for the geometry-lattice variable, which sets the size of the cell. In MPB, you can use this to specify a variety of affine lattice structures. In Meep, only rectangular Cartesian cells are supported, so the only property of lattice that you should normally use is its size.
size [vector3] — The size of the cell. Defaults to unit lengths.
If any dimension has the special size no-size, then the dimensionality of the problem is essentially reduced by one. Strictly speaking, the dielectric function is taken to be uniform along that dimension.
Because Maxwell's equations are scale invariant, you can use any units of distance you want to specify the cell size: nanometers, microns, centimeters, etc. However, it is usually convenient to pick some characteristic lengthscale of your problem and set that length to 1. See also Units.
This class is used to specify the materials that geometric objects are made of. Currently, there are three subclasses, dielectric, perfect-metal, and material-function.
An electromagnetic medium which is possibly nonlinear and/or dispersive. See also Materials. For backwards compatibility, a synonym for medium is dielectric. It has several properties:
epsilon [number] —The frequency-independent isotropic relative permittivity or dielectric constant. Default is 1. You can also use (index n) as a synonym for (epsilon (* n n)); note that this is not really the refractive index if you also specify μ, since the true index is .
Using (epsilon ep) is actually a synonym for (epsilon-diag ep ep ep).
epsilon-diag and epsilon-offdiag [vector3] — These properties allow you to specify ε as an arbitrary real-symmetric tensor by giving the diagonal and offdiagonal parts. Specifying (epsilon-diag a b c) and/or (epsilon-offdiag u v w) corresponds to a relative permittivity ε tensor \begin{pmatrix} a & u & v \\ u & b & w \\ v & w & c \end{pmatrix}
Default is the identity matrix ( and ).
mu [number] — The frequency-independent isotropic relative permeability μ. Default is 1. Using (mu pm) is actually a synonym for (mu-diag pm pm pm).
mu-diag and mu-offdiag [vector3] — These properties allow you to specify μ as an arbitrary real-symmetric tensor by giving the diagonal and offdiagonal parts exactly as for ε above. Default is the identity matrix.
D-conductivity [number] — The frequency-independent electric conductivity . Default is 0. You can also specify a diagonal anisotropic conductivity tensor by using the property D-conductivity-diag which takes three numbers or a vector3 to give the tensor diagonal. See also Conductivity.
B-conductivity [number] — The frequency-independent magnetic conductivity . Default is 0. You can also specify a diagonal anisotropic conductivity tensor by using the property B-conductivity-diag which takes three numbers or a vector3 to give the tensor diagonal. See also Conductivity.
chi2 [number] — The nonlinear (Pockels) susceptibility . Default is 0. See also Nonlinearity.
chi3 [number] — The nonlinear (Kerr) susceptibility . Default is 0. See also Nonlinearity.
E-susceptibilities [ list of susceptibility class ] — List of dispersive susceptibilities (see below) added to the dielectric constant ε in order to model material dispersion. Defaults to none. See also Material Dispersion. For backwards compatibility, synonyms of E-susceptibilities are E-polarizations and polarizations.
H-susceptibilities [ list of susceptibility class ] — List of dispersive susceptibilities (see below) added to the permeability μ in order to model material dispersion. Defaults to none. See also Material Dispersion.
perfect-metal
A perfectly-conducting metal. This class has no properties and you normally just use the predefined metal object, above. To model imperfect conductors, use a dispersive dielectric material. See also the Predefined Variables: metal, perfect-electric-conductor, and perfect-magnetic-conductor.
material-function
This material type allows you to specify the material as an arbitrary function of position. It has one property:
material-func [function] — A function of one argument, the position vector3, that returns the material at that point. Note that the function you supply can return any material. It's even possible to return another material-function object which would then have its function invoked in turn.
Instead of material-func, you can use epsilon-func: give it a function of position that returns the dielectric constant at that point.
Important: If your material function returns nonlinear, dispersive (Lorentzian or conducting), or magnetic materials, you should also include a list of these materials in the extra-materials input variable (above) to let Meep know that it needs to support these material types in your simulation. For dispersive materials, you need to include a material with the same values of γn and ωn, so you can only have a finite number of these, whereas σn can vary continuously and a matching σn need not be specified in extra-materials. For nonlinear or conductivity materials, your extra-materials list need not match the actual values of σ or χ returned by your material function, which can vary continuously.
Complex ε and μ: you cannot specify a frequency-independent complex ε or μ in Meep where the imaginary part is a frequency-independent loss but there is an alternative. That is because there are only two important physical situations. First, if you only care about the loss in a narrow bandwidth around some frequency, you can set the loss at that frequency via the conductivity. Second, if you care about a broad bandwidth, then all physical materials have a frequency-dependent complex ε and/or μ, and you need to specify that frequency dependence by fitting to Lorentzian and/or Drude resonances via the lorentzian-susceptibility or drude-susceptibility classes below.
Dispersive dielectric and magnetic materials, above, are specified via a list of objects that are subclasses of type susceptibility.
Parent class for various dispersive susceptibility terms, parameterized by an anisotropic amplitude σ. See Material Dispersion.
sigma [number] — The scale factor σ. You can also specify an anisotropic σ tensor by using the property sigma-diag which takes three numbers or a vector3 to give the σ tensor diagonal, and sigma-offdiag which specifies the offdiagonal elements (defaults to 0). That is, (sigma-diag a b c) and (sigma-offdiag u v w) corresponds to a σ tensor
\begin{pmatrix} a & u & v \\ u & b & w \\ v & w & c \end{pmatrix}
Specifies a single dispersive susceptibility of Lorentzian (damped harmonic oscillator) form. See Material Dispersion, with the parameters (in addition to σ):
frequency [number] — The resonance frequency .
gamma [number] — The resonance loss rate .
Note: multiple objects with identical values for the frequency and gamma but different sigma will appear as a single Lorentzian susceptibility term in the preliminary simulation info output.
Specifies a single dispersive susceptibility of Drude form. See Material Dispersion, with the parameters (in addition to σ):
frequency [number] — The frequency scale factor which multiplies σ (not a resonance frequency).
gamma [number] — The loss rate .
Meep also supports a somewhat unusual polarizable medium, a Lorentzian susceptibility with a random noise term added into the damped-oscillator equation at each point. This can be used to directly model thermal radiation in both the far field and the near field. Note, however that it is more efficient to compute far-field thermal radiation using Kirchhoff's law of radiation, which states that emissivity equals absorptivity. Near-field thermal radiation can usually be computed more efficiently using frequency-domain methods, e.g. via SCUFF-EM.
Specifies a multievel atomic susceptibility for modeling saturable gain and absorption. This is a subclass of E-susceptibilities which contains two objects: (1) transitions: a list of atomic transitions (defined below), and (2) initial-populations: a list of numbers defining the initial population of each atomic level. See Materials/Saturable Gain and Absorption.
frequency [number] — The radiative transition frequency .
sigma [number] — The coupling strength .
from-level [number] — The atomic level from which the transition occurs.
to-level [number] — The atomic level to which the transition occurs.
transition-rate [number] — The non-radiative transition rate . Default is 0.
pumping-rate [number] — The pumping rate . Default is 0.
Specifies a single dispersive susceptibility of Lorentzian (damped harmonic oscillator) or Drude form. See Material Dispersion, with the same sigma, frequency, and gamma parameters, but with an additional Gaussian random noise term (uncorrelated in space and time, zero mean) added to the P damped-oscillator equation.
noise-amp [number] — The noise has root-mean square amplitude σ noise-amp.
(Experimental feature) Specifies a single dispersive gyrotropic susceptibility of Lorentzian (damped harmonic oscillator) or Drude form. Its parameters are sigma, frequency, and gamma, which have the usual meanings, and an additional 3-vector bias:
bias [vector3] — The gyrotropy vector. Its direction determines the orientation of the gyrotropic response, and the magnitude is the precession frequency .
(Experimental feature) Specifies a single dispersive gyrotropic susceptibility governed by a linearized Landau-Lifshitz-Gilbert equation. This class takes parameters sigma, frequency, and gamma, whose meanings are different from the Lorentzian and Drude case. It also takes a 3-vector bias parameter and an alpha parameter:
sigma [number] — The coupling factor between the polarization and the driving field. In magnetic ferrites, this is the Larmor precession frequency at the saturation field.
frequency [number] — The Larmor precession frequency, .
gamma [number] — The loss rate in the off-diagonal response.
alpha [number] — The loss factor in the diagonal response. Note that this parameter is dimensionless and contains no 2π factor.
bias [vector3] — Vector specifying the orientation of the gyrotropic response. Unlike the similarly-named bias parameter for the gyrotropic Lorentzian/Drude susceptibilities, the magnitude is ignored; instead, the relevant precession frequencies are determined by the sigma and frequency parameters.
This class, and its descendants, are used to specify the solid geometric objects that form the dielectric structure being simulated. The base class is:
material [material-type class ] — The material that the object is made of (usually some sort of dielectric). No default value (must be specified).
center [vector3] — Center point of the object. No default value.
One normally does not create objects of type geometric-object directly, however; instead, you use one of the following subclasses. Recall that subclasses inherit the properties of their superclass, so these subclasses automatically have the material and center properties which must be specified, since they have no default values.
In a 2d calculation, only the intersections of the objects with the plane are considered.
A sphere. Properties:
radius [number] — Radius of the sphere. No default value.
A cylinder, with circular cross-section and finite height. Properties:
radius [number] — Radius of the cylinder's cross-section. No default value.
height [number] — Length of the cylinder along its axis. No default value.
axis [vector3] — Direction of the cylinder's axis; the length of this vector is ignored. Defaults to point parallel to the axis.
A cone, or possibly a truncated cone. This is actually a subclass of cylinder, and inherits all of the same properties, with one additional property. The radius of the base of the cone is given by the radius property inherited from cylinder, while the radius of the tip is given by the new property, radius2. The center of a cone is halfway between the two circular ends.
radius2 [number] — Radius of the tip of the cone (i.e. the end of the cone pointed to by the axis vector). Defaults to zero (a "sharp" cone).
A parallelepiped (i.e., a brick, possibly with non-orthogonal axes).
size [vector3] — The lengths of the block edges along each of its three axes. Not really a 3-vector, but it has three components, each of which should be nonzero. No default value.
e1, e2, e3 [vector3] — The directions of the axes of the block; the lengths of these vectors are ignored. Must be linearly independent. They default to the three lattice directions.
An ellipsoid. This is actually a subclass of block, and inherits all the same properties, but defines an ellipsoid inscribed inside the block.
Polygonal prism type.
vertices [list of vector3] — The vertices that define the polygonal floor of the prism; the vertices must be coplanar, and if axis is specified it must be normal to the plane of the vertices. Note that infinite prism lengths are not supported. To simulate infinite geometry, just extend the edge of the prism beyond the cell. The ceiling of the prism is just its floor polygon rigidly translated through the displacement vector height*axis.
height [number] — The prism thickness, extruded in the direction of axis. infinity can be used for infinite height.
axis [vector3] — (optional) specifies the extrusion axis, which must be normal to the plane of the vertices. If axis is not specified, the extrusion axis is taken to be the normal vector to the plane of the vertices, with sign determined by a right-hand rule with respect to the first two vertices: if your right-hand fingers point from vertex 1 to 2, your thumb points in the direction of axis. In vector language, axis is determined by computing a vector cross product and normalizing to unit magnitude: where are the first and second vertices and is the centroid of the polygon (with the length of the vertices array).
There are two options for specifying the center of a prism. In contrast to the other types of geometric-object, the center of a prism does not need to be explicitly specified, because it may be calculated from vertices, height, and axis. (Specifically, we have center = centroid + 0.5*height*axis, where the centroid was defined above). To create a prism with the center computed automatically in this way, simply initialize the center field of the prism class (inherited from geometric_object) to the special initializer keyword auto-center. On the other hand, in some cases you may want to override this automatic calculation and instead specify your own center for a prism; this will have the effect of rigidly translating the entire prism so that it is centered at the point you specify. See below for examples of both possibilities.
These are some examples of geometric objects created using the above classes:
; A cylinder of infinite radius and height 0.25 pointing along the x axis,
; centered at the origin:
(make cylinder (center 0 0 0) (material (make dielectric (index 3.5)))
(radius infinity) (height 0.25) (axis 1 0 0))
; An ellipsoid with its long axis pointing along (1,1,1), centered on
; the origin (the other two axes are orthogonal and have equal semi-axis lengths)
(make ellipsoid (center 0 0 0) (material (make dielectric (epsilon 12.0)))
(size 0.8 0.2 0.2)
(e1 1 1 1)
(e2 0 1 -1)
(e3 -2 1 1))
; A unit cube of material metal with a spherical air hole of radius 0.2 at
; its center, the whole thing centered at (1,2,3):
(set! geometry (list
(make block (center 1 2 3) (material metal) (size 1 1 1))
(make sphere (center 1 2 3) (material air) (radius 0.2))))
; A hexagonal prism defined by six vertices centered on the origin
; and extruded in the z direction to a height of 1.5
; of material crystalline silicon (from the materials library)
(set! geometry
(list
(make prism
(vertices
(vector3 -1 0 0)
(vector3 -0.5 (/ (sqrt 3) 2) 0)
(vector3 0.5 (/ (sqrt 3) 2) 0)
(vector3 1 0 0)
(vector3 0.5 (/ (sqrt 3) -2) 0)
(vector3 -0.5 (/ (sqrt 3) -2) 0)))
(axis 0 0 1)
(height 1.5)
(center auto-center)
(material cSi))))
Note the use of (center auto-center) to establish that the prism center will be computed automatically from the vertices, axes, and height — which, in this case, will put the center at .
; The same hexagonal prism, but now rigidly displaced so that
; its center lies at (0.4, 0.8, -0.2):
(center 0.4 0.8 -0.2)
This class is used for the symmetries input variable to specify symmetries which must preserve both the structure and the sources. Any number of symmetries can be exploited simultaneously but there is no point in specifying redundant symmetries: the cell can be reduced by at most a factor of 4 in 2d and 8 in 3d. See also Exploiting Symmetry.
A single symmetry to exploit. This is the base class of the specific symmetries below, so normally you don't create it directly. However, it has two properties which are shared by all symmetries:
direction [direction constant ] — The direction of the symmetry (the normal to a mirror plane or the axis for a rotational symmetry). e.g. X, Y, Z (only Cartesian/grid directions are allowed). No default value.
phase [cnumber] — An additional phase to multiply the fields by when operating the symmetry on them. Default is +1, e.g. a phase of -1 for a mirror plane corresponds to an odd mirror. Technically, you are essentially specifying the representation of the symmetry group that your fields and sources transform under.
The specific symmetry sub-classes are:
mirror-sym — A mirror symmetry plane. direction is the direction normal to the mirror plane.
rotate2-sym — A 180° (twofold) rotational symmetry (a.k.a. ). direction is the axis of the rotation.
rotate4-sym — A 90° (fourfold) rotational symmetry (a.k.a. ). direction is the axis of the rotation.
This class is used for specifying the PML absorbing boundary layers around the cell, if any, via the pml-layers input variable. See also Perfectly Matched Layers. pml-layers can be zero or more pml objects, with multiple objects allowing you to specify different PML layers on different boundaries.
A single PML layer specification, which sets up one or more PML layers around the boundaries according to the following properties.
thickness [number] — The spatial thickness of the PML layer which extends from the boundary towards the inside of the cell. The thinner it is, the more numerical reflections become a problem. No default value.
direction [direction constant ] — Specify the direction of the boundaries to put the PML layers next to. e.g. if X, then specifies PML on the boundaries (depending on the value of side, below). Default is the special value ALL, which puts PML layers on the boundaries in all directions.
side [boundary-side constant ] — Specify which side, Low or High of the boundary or boundaries to put PML on. e.g. if side is Low and direction is X, then a PML layer is added to the boundary. Default is the special value ALL, which puts PML layers on both sides.
strength [number] — A strength (default is 1.0) to multiply the PML absorption coefficient by. A strength of 2.0 will square the theoretical asymptotic reflection coefficient of the PML (making it smaller), but will also increase numerical reflections. Alternatively, you can change R-asymptotic, below.
R-asymptotic [number] — The asymptotic reflection in the limit of infinite resolution or infinite PML thickness, for reflections from air (an upper bound for other media with index > 1). For a finite resolution or thickness, the reflection will be much larger, due to the discretization of Maxwell's equation. Default value is 10−15, which should suffice for most purposes. You want to set this to be small enough so that waves propagating within the PML are attenuated sufficiently, but making R-asymptotic too small will increase the numerical reflection due to discretization.
pml-profile [function] — By default, Meep turns on the PML conductivity quadratically within the PML layer — one doesn't want to turn it on suddenly, because that exacerbates reflections due to the discretization. More generally, with pml-profile one can specify an arbitrary PML "profile" function that determines the shape of the PML absorption profile up to an overall constant factor. u goes from 0 to 1 at the start and end of the PML, and the default is . In some cases where a very thick PML is required, such as in a periodic medium (where there is technically no such thing as a true PML, only a pseudo-PML), it can be advantageous to turn on the PML absorption more smoothly. See Optics Express, Vol. 16, pp. 11376-92, 2008. For example, one can use a cubic profile by specifying (pml-profile (lambda (u) (* u u u))).
Instead of a pml layer, there is an alternative class called absorber which is a drop-in replacement for pml. For example, you can do (set! pml-layers (list (make absorber (thickness 2)))) instead of (set! pml-layers (list (make pml (thickness 2)))). All the parameters are the same as for pml, above. You can have a mix of pml on some boundaries and absorber on others.
The absorber class does not implement a perfectly matched layer (PML), however (except in 1d). Instead, it is simply a scalar electric and magnetic conductivity that turns on gradually within the layer according to the pml-profile (defaulting to quadratic). Such a scalar conductivity gradient is only reflectionless in the limit as the layer becomes sufficiently thick.
The main reason to use absorber is if you have a case in which PML fails:
No true PML exists for periodic media, and a scalar absorber is computationally less expensive and generally just as good. See Optics Express, Vol. 16, pp. 11376-92, 2008.
PML can lead to divergent fields for certain waveguides with "backward-wave" modes; this can readily occur in metals with surface plasmons, and a scalar absorber is your only choice. See Physical Review E, Vol. 79, 065601, 2009.
PML can fail if you have a waveguide hitting the edge of your cell at an angle. See J. Computational Physics, Vol. 230, pp. 2369-77, 2011.
The source class is used to specify the current sources via the sources input variable. Note that all sources in Meep are separable in time and space, i.e. of the form for some functions and . Non-separable sources can be simulated, however, by modifying the sources after each time step. When real fields are being used (which is the default in many cases; see the force-complex-fields? input variable), only the real part of the current source is used.
Important note: These are current sources (J terms in Maxwell's equations), even though they are labelled by electric/magnetic field components. They do not specify a particular electric/magnetic field which would be what is called a "hard" source in the FDTD literature. There is no fixed relationship between the current source and the resulting field amplitudes; it depends on the surrounding geometry, as described in the FAQ and in Section 4.4 ("Currents and Fields: The Local Density of States") in Chapter 4 ("Electromagnetic Wave Source Conditions") of the book Advances in FDTD Computational Electrodynamics: Photonics and Nanotechnology.
The source class has the following properties:
src [src-time class ] — Specify the time-dependence of the source (see below). No default.
component [component constant ] — Specify the direction and type of the current component: e.g. Ex, Ey, etcetera for an electric-charge current, and Hx, Hy, etcetera for a magnetic-charge current. Note that currents pointing in an arbitrary direction are specified simply as multiple current sources with the appropriate amplitudes for each component. No default.
center [vector3] — The location of the center of the current source in the cell. No default.
size [vector3] — The size of the current distribution along each direction of the cell. Default is (0,0,0): a point-dipole source.
amplitude [cnumber] — An overall complex amplitude multiplying the the current source. Default is 1.0.
amp-func [function] — A Scheme function of a single argument, that takes a vector3 giving a position and returns a complex current amplitude for that point. The position argument is relative to the center of the current source, so that you can move your current around without changing your function. Default is '() (null), meaning that a constant amplitude of 1.0 is used. Note that your amplitude function (if any) is multiplied by the amplitude property, so both properties can be used simultaneously.
As described in Section 4.2 ("Incident Fields and Equivalent Currents") in Chapter 4 ("Electromagnetic Wave Source Conditions") of the book Advances in FDTD Computational Electrodynamics: Photonics and Nanotechnology, it is also possible to supply a source that is designed to couple exclusively into a single waveguide mode (or other mode of some cross section or periodic region) at a single frequency, and which couples primarily into that mode as long as the bandwidth is not too broad. This is possible if you have MPB installed: Meep will call MPB to compute the field profile of the desired mode, and uses the field profile to produce an equivalent current source. Note: this feature does not work in cylindrical coordinates. To do this, instead of a source you should use an eigenmode-source:
This is a subclass of source and has all of the properties of source above. However, you normally do not specify a component. Instead of component, the current source components and amplitude profile are computed by calling MPB to compute the modes, , of the dielectric profile in the region given by the size and center of the source, with the modes computed as if the source region were repeated periodically in all directions. If an amplitude and/or amp-func are supplied, they are multiplied by this current profile. The desired eigenmode and other features are specified by the following properties:
eig-band [integer] — The index n (1,2,3,...) of the desired band ωn(k) to compute in MPB where 1 denotes the lowest-frequency band at a given k point, and so on.
direction [X, Y, or Z; default AUTOMATIC], eig-match-freq? [boolean; default true], eig-kpoint [vector3] — By default (if eig-match-freq? is true), Meep tries to find a mode with the same frequency ωn(k) as the src property (above), by scanning k vectors in the given direction using MPB's find-k functionality. Alternatively, if eig-kpoint is supplied, it is used as an initial guess for k. By default, direction is the direction normal to the source region, assuming size is –1 dimensional in a -dimensional simulation (e.g. a plane in 3d). If direction is set to NO-DIRECTION, then eig_kpoint is not only the initial guess and the search direction of the k vectors, but is also taken to be the direction of the waveguide, allowing you to launch modes in oblique ridge waveguides (not perpendicular to the source plane). If eig-match-freq? is false, then the specific k vector of the desired mode is specified with eig-kpoint (in Meep units of 2π/(unit length)). By default, the k components in the plane of the source region are zero. However, if the source region spans the entire cell in some directions, and the cell has Bloch-periodic boundary conditions via the k-point parameter, then the mode's k components in those directions will match k-point so that the mode satisfies the Meep boundary conditions, regardless of eig-kpoint. Note that once k is either found by MPB, or specified by eig-kpoint, the field profile used to create the current sources corresponds to the Bloch mode, , multiplied by the appropriate exponential factor, .
eig-parity [NO-PARITY (default), EVEN-Z, ODD-Z, EVEN-Y, ODD-Y] — The parity (= polarization in 2d) of the mode to calculate, assuming the structure has and/or mirror symmetry in the source region, with respect to the center of the source region. (In particular, it does not matter if your simulation as a whole has that symmetry, only the cross section where you are introducing the source.) If the structure has both and mirror symmetry, you can combine more than one of these, e.g. EVEN-Z + ODD-Y. Default is NO-PARITY, in which case MPB computes all of the bands which will still be even or odd if the structure has mirror symmetry, of course. This is especially useful in 2d simulations to restrict yourself to a desired polarization.
eig-resolution [integer, defaults to same as Meep resolution ] — The spatial resolution to use in MPB for the eigenmode calculations. This defaults to the same resolution as Meep, but you can use a higher resolution in which case the structure is linearly interpolated from the Meep pixels.
eig-tolerance [number, defaults to 10–12 ] — The tolerance to use in the MPB eigensolver. MPB terminates when the eigenvalues stop changing to less than this fractional tolerance. (Note that this is the tolerance for the frequency eigenvalue ω; the tolerance for the mode profile is effectively the square root of this.)
component [as above, but defaults to ALL-COMPONENTS] — Once the MPB modes are computed, equivalent electric and magnetic sources are created within Meep. By default, these sources include magnetic and electric currents in all transverse directions within the source region, corresponding to the mode fields as described in Section 4.2 ("Incident Fields and Equivalent Currents") in Chapter 4 ("Electromagnetic Wave Source Conditions") of the book Advances in FDTD Computational Electrodynamics: Photonics and Nanotechnology. If you specify a component property, however, you can include only one component of these currents if you wish. Most users won't need this feature.
eig-lattice-size [vector3], eig-lattice-center [vector3] — Normally, the MPB computational unit cell is the same as the source volume given by the size and center parameters. However, occasionally you want the unit cell to be larger than the source volume. For example, to create an eigenmode source in a periodic medium, you need to pass MPB the entire unit cell of the periodic medium, but once the mode is computed then the actual current sources need only lie on a cross section of that medium. To accomplish this, you can specify the optional eig-lattice-size and eig-lattice-center, which define a volume (which must enclose size and center) that is used for the unit cell in MPB with the dielectric function ε taken from the corresponding region in the Meep simulation.
Note that Meep's MPB interface only supports dispersionless non-magnetic materials but it does support anisotropic ε. Any nonlinearities, magnetic responses μ, conductivities σ, or dispersive polarizations in your materials will be ignored when computing the eigenmode source. PML will also be ignored.
The src-time object, which specifies the time dependence of the source, can be one of the following three classes.
A continuous-wave (CW) source is proportional to , possibly with a smooth (exponential/tanh) turn-on/turn-off. In practice, the CW source never produces an exact single-frequency response.
frequency [number] — The frequency f in units of /distance or ω in units of 2π/distance. See Units. No default value. You can instead specify (wavelength x) or (period x), which are both a synonym for (frequency (/ 1 x)); i.e. 1/ω in these units is the vacuum wavelength or the temporal period.
start-time [number] — The starting time for the source. Default is 0 (turn on at ).
end-time [number] — The end time for the source. Default is infinity (never turn off).
width [number] — Roughly, the temporal width of the smoothing (technically, the inverse of the exponential rate at which the current turns off and on). Default is 0 (no smoothing). You can instead specify (fwidth x), which is a synonym for (width (/ 1 x)) (i.e. the frequency width is proportional to the inverse of the temporal width).
slowness [number] — Controls how far into the exponential tail of the tanh function the source turns on. Default is 3.0. A larger value means that the source turns on more gradually at the beginning.
A Gaussian-pulse source roughly proportional to . Technically, the "Gaussian" sources in Meep are the (discrete-time) derivative of a Gaussian, i.e. they are , but the difference between this and a true Gaussian is usually irrelevant.
frequency [number] — The center frequency in units of /distance (or ω in units of 2π/distance). See Units. No default value. You can instead specify (wavelength x) or (period x), which are both a synonym for (frequency (/ 1 x)); i.e. 1/ω in these units is the vacuum wavelength or the temporal period.
width [number] — The width used in the Gaussian. No default value. You can instead specify (fwidth x), which is a synonym for (width (/ 1 x)) (i.e. the frequency width is proportional to the inverse of the temporal width).
start-time [number] — The starting time for the source. Default is 0 (turn on at ). This is not the time of the peak. See below.
cutoff [number] — How many widths the current decays for before it is cut off and set to zero — this applies for both turn-on and turn-off of the pulse. Default is 5.0. A larger value of cutoff will reduce the amount of high-frequency components that are introduced by the start/stop of the source, but will of course lead to longer simulation times. The peak of the Gaussian is reached at the time =start-time + cutoff*width.
A user-specified source function . You can also specify start/end times at which point your current is set to zero whether or not your function is actually zero. These are optional, but you must specify an end-time explicitly if you want functions like run-sources to work, since they need to know when your source turns off. For a demonstration of a linear-chirped pulse, see examples/chirped-pulse.ctl.
src-func [function] — The function specifying the time-dependence of the source. It should take one argument (the time in Meep units) and return a complex number.
start-time [number] — The starting time for the source. Default is (-infinity): turn on at . Note, however, that the simulation normally starts at with zero fields as the initial condition, so there is implicitly a sharp turn-on at whether you specify it or not.
A flux-region object is used with add-flux to specify a region in which Meep should accumulate the appropriate Fourier-transformed fields in order to compute a flux spectrum.
flux-region — A region (volume, plane, line, or point) in which to compute the integral of the Poynting vector of the Fourier-transformed fields.
center [vector3] —The center of the flux region (no default).
size [vector3] —The size of the flux region along each of the coordinate axes. Default is (0,0,0); a single point.
direction [direction constant ] —The direction in which to compute the flux (e.g. X, Y, etcetera). Default is AUTOMATIC, in which the direction is determined by taking the normal direction if the flux region is a plane (or a line, in 2d). If the normal direction is ambiguous (e.g. for a point or volume), then you must specify the direction explicitly (not doing so will lead to an error).
weight [cnumber] —A weight factor to multiply the flux by when it is computed. Default is 1.0.
Note that the flux is always computed in the positive coordinate direction, although this can effectively be flipped by using a weight of -1.0. This is useful, for example, if you want to compute the outward flux through a box, so that the sides of the box add instead of subtract.
Here, we describe a number of miscellaneous useful functions provided by Meep.
Some utility functions are provided to help you manipulate geometric objects:
(shift-geometric-object obj shift-vector) — Translate obj by the 3-vector shift-vector.
(geometric-object-duplicates shift-vector min-multiple max-multiple obj) — Return a list of duplicates of obj, shifted by various multiples of shift-vector from min-multiple to max-multiple, inclusive, in steps of 1.
(geometric-objects-duplicates shift-vector min-multiple max-multiple obj-list) — Same as geometric-object-duplicates, except operates on a list of objects, obj-list. If A appears before B in the input list, then all the duplicates of A appear before all the duplicates of B in the output list.
(geometric-objects-lattice-duplicates obj-list [ ux uy uz ]) — Duplicates the objects in obj-list by multiples of the Cartesian basis vectors, making all possible shifts of the "primitive cell" (see below) that fit inside the lattice cell. The primitive cell to duplicate is ux by uy by uz, in units of the Cartesian basis vectors. These three parameters are optional; any that you do not specify are assumed to be 1.
point_in_object(point, obj) — Returns whether or not the given 3-vector point is inside the geometric object obj.
(point-in-periodic-object? point obj) — As point-in-object?, but also checks translations of the given object by the lattice vectors.
(display-geometric-object-info indent-by obj) — Outputs some information about the given obj, indented by indent-by spaces.
The output file names used by Meep, e.g. for HDF5 files, are automatically prefixed by the input variable filename-prefix. If filename-prefix is "" (the default), however, then Meep constructs a default prefix based on the current ctl file name with ".ctl" replaced by "-": e.g. test.ctl implies a prefix of "test-". You can get this prefix by running:
(get-filename-prefix) — Return the current prefix string that is prepended, by default, to all file names.
If you don't want to use any prefix, then you should set filename-prefix to false.
In addition to the filename prefix, you can also specify that all the output files be written into a newly-created directory (if it does not yet exist). This is done by running:
(use-output-directory [dirname]) — Put output in a subdirectory, which is created if necessary. If the optional argument dirname is specified, that is the name of the directory. Otherwise, the directory name is the current ctl file name with ".ctl" replaced by "-out": e.g. test.ctl implies a directory of "test-out".
(volume (center ...) (size ...)) — Many Meep functions require you to specify a volume in space, corresponding to the C++ type meep::volume. This function creates such a volume object, given the center and size properties (just like e.g. a block object). If the size is not specified, it defaults to (0,0,0), i.e. a single point.
(meep-time) — Return the current simulation time in simulation time units (e.g. during a run function). This is not the wall-clock time.
Occasionally, e.g. for termination conditions of the form time < T?, it is desirable to round the time to single precision in order to avoid small differences in roundoff error from making your results different by one timestep from machine to machine (a difference much bigger than roundoff error); in this case you can call (meep-round-time) instead, which returns the time rounded to single precision.
Meep supports a large number of functions to perform computations on the fields. Most of them are accessed via the lower-level C++/SWIG interface. Some of them are based on the following simpler, higher-level versions.
(get-field-point c pt) — Given a component or derived-component constant c and a vector3 pt, returns the value of that component at that point.
(get-epsilon-point pt) — Equivalent to (get-field-point Dielectric pt).
(add-dft-fields cs freq-min freq-max nfreq [where]) — Given a list of field components cs, compute the Fourier transform of these fields for nfreq equally spaced frequencies covering the frequency range freq-min to freq-max over the volume specified by where (default to the entire cell).
(flux-in-box dir box) — Given a direction constant, and a meep::volume*, returns the flux (the integral of ) in that volume. Most commonly, you specify a volume that is a plane or a line, and a direction perpendicular to it, e.g. (flux-in-boxX (volume (center 0) (size 0 1 1)))`.
(electric-energy-in-box box) — Given a meep::volume*, returns the integral of the electric-field energy in the given volume. If the volume has zero size along a dimension, a lower-dimensional integral is used.
(magnetic-energy-in-box box) — Given a meep::volume*, returns the integral of the magnetic-field energy in the given volume. If the volume has zero size along a dimension, a lower-dimensional integral is used.
(field-energy-in-box box) — Given a meep::volume*, returns the integral of the electric- and magnetic-field energy in the given volume. If the volume has zero size along a dimension, a lower-dimensional integral is used.
Note that if you are at a fixed frequency and you use complex fields (via Bloch-periodic boundary conditions or fields-complex?=true), then one half of the flux or energy integrals above corresponds to the time average of the flux or energy for a simulation with real fields.
Often, you want the integration box to be the entire cell. A useful function to return this box, which you can then use for the box arguments above, is (meep-fields-total-volume fields), where fields is the global variable (above) holding the current meep::fields object.
One versatile feature is that you can supply an arbitrary function of position and various field components and ask Meep to integrate it over a given volume, find its maximum, or output it (via output-field-function, described later). This is done via the functions:
(integrate-field-function cs func [where] [fields-var]) — Returns the integral of the complex-valued function func over the meep::volume specified by where (defaults to entire cell) for the meep::fields specified by fields-var (defaults to fields). func is a function of position (a vector3, its first argument) and zero or more field components specified by cs: a list of component constants. func can be real- or complex-valued.
If any dimension of where is zero, that dimension is not integrated over. In this way you can specify 1d, 2d, or 3d integrals.
(max-abs-field-function cs func [where] [fields-var]) — As integrate-field-function, but returns the maximum absolute value of func in the volume where instead of its integral.
The integration is performed by summing over the grid points with a simple trapezoidal rule, and the maximum is similarly over the grid points. See Field Functions for examples of how to call integrate-field-function and max-abs-field-function. See Synchronizing the Magnetic and Electric Fields if you want to do computations combining the electric and magnetic fields.
Occasionally, one wants to compute an integral that combines fields from two separate simulations (e.g. for nonlinear coupled-mode calculations). This functionality is supported in Meep, as long as the two simulations have the same cell, the same resolution, the same boundary conditions and symmetries (if any), and the same PML layers (if any).
(integrate2-field-function fields2 cs1 cs2 func [where] [fields-var]) — Similar to integrate-field-function, but takes additional parameters fields2 and cs2. fields2 is a meep::fields* object similar to the global fields variable (see below) specifying the fields from another simulation. cs1 is a list of components to integrate with from fields-var (defaults to fields), as for integrate-field-function, while cs2 is a list of components to integrate from fields2. Similar to integrate-field-function, func is a function that returns an number given arguments consisting of: the position vector, followed by the values of the components specified by cs1 (in order), followed by the values of the components specified by cs2 (in order).
To get two fields in memory at once for integrate2-field-function, the easiest way is to run one simulation within a given Scheme (.ctl) file, then save the results in another fields variable, then run a second simulation. This would look something like:
...set up and run first simulation...
(define fields2 fields) ; save the fields in a variable
(set! fields '()) ; prevent the fields from getting deallocated by reset-meep
(reset-meep)
...set up and run second simulation...
It is also possible to timestep both fields simultaneously (e.g. doing one timestep of one simulation then one timestep of another simulation, and so on, but this requires you to call much lower-level functions like (meep-fields-step fields).
Once the fields/simulation have been initialized, you can change the values of various parameters by using the following functions:
(reset-meep) — Reset all of Meep's parameters, deleting the fields, structures, etcetera, from memory as if you had not run any computations.
(restart-fields) — Restart the fields at time zero, with zero fields. Does not reset the Fourier transforms of the flux planes, which continue to be accumulated.
(change-k-point! k) — Change the k-point (the Bloch periodicity).
(change-sources! new-sources) — Change the sources input variable to new-sources, and changes the sources used for the current simulation.
Given a bunch of flux-region objects, you can tell Meep to accumulate the Fourier transforms of the fields in those regions in order to compute the Poynting flux spectra. (Note: as a matter of convention, the "intensity" of the electromagnetic fields refers to the Poynting flux, not to the energy density.) See also the Introduction and Tutorial/Basics. The most important function is:
(add-flux fcen df nfreq flux-regions...) — Add a bunch of flux-regions to the current simulation (initializing the fields if they have not yet been initialized), telling Meep to accumulate the appropriate field Fourier transforms for nfreq equally spaced frequencies covering the frequency range fcen-df/2 to fcen+df/2. Return a flux object, which you can pass to the functions below to get the flux spectrum, etcetera.
As described in the tutorial, you normally use add-flux via statements like:
(define transmission (add-flux ...)) — to store the flux object in a variable. add-flux initializes the fields if necessary, just like calling run, so you should only call it after setting up your geometry, sources, pml-layers, k-point, etcetera. You can create as many flux objects as you want, e.g. to look at powers flowing in different regions or in different frequency ranges. Note, however, that Meep has to store (and update at every time step) a number of Fourier components equal to the number of grid points intersecting the flux region multiplied by the number of electric and magnetic field components required to get the Poynting vector multiplied by nfreq, so this can get quite expensive (in both memory and time) if you want a lot of frequency points over large regions of space.
Once you have called add-flux, the Fourier transforms of the fields are accumulated automatically during time-stepping by the run functions. At any time, you can ask for Meep to print out the current flux spectrum via:
(display-fluxes fluxes...) — Given a number of flux objects, this displays a comma-separated table of frequencies and flux spectra, prefixed by "flux1:" or similar (where the number is incremented after each run). All of the fluxes should be for the same fcen/df/nfreq. The first column are the frequencies, and subsequent columns are the flux spectra.
You might have to do something lower-level if you have multiple flux regions corresponding to different frequency ranges, or have other special needs. (display-fluxes f1 f2 f3) is actually equivalent to (display-csv "flux" (get-flux-freqs f1) (get-fluxes f1) (get-fluxes f2) (get-fluxes f3)), where display-csv takes a bunch of lists of numbers and prints them as a comma-separated table; this involves calling two lower-level functions:
(get-flux-freqs flux) — Given a flux object, returns a list of the frequencies that it is computing the spectrum for.
(get-fluxes flux) — Given a flux object, returns a list of the current flux spectrum that it has accumulated.
As described in Tutorial/Basics, for a reflection spectrum you often want to save the Fourier-transformed fields from a "normalization" run and then load them into another run to be subtracted. This can be done via:
(save-flux filename flux) — Save the Fourier-transformed fields corresponding to the given flux object in an HDF5 file of the given filename without the ".h5" suffix (the current filename-prefix is prepended automatically).
(load-flux filename flux) — Load the Fourier-transformed fields into the given flux object (replacing any values currently there) from an HDF5 file of the given filename without the ".h5" suffix (the current filename-prefix is prepended automatically). You must load from a file that was saved by save-flux in a simulation of the same dimensions (for both the cell and the flux regions) with the same number of processors.
(load-minus-flux filename flux) — As load-flux, but negates the Fourier-transformed fields after they are loaded. This means that they will be subtracted from any future field Fourier transforms that are accumulated.
(scale-flux-fields s flux) — Scale the Fourier-transformed fields in flux by the complex number s. e.g. load-minus-flux is equivalent to load-flux followed by scale-flux-fields with s=-1.
Given a structure, Meep can decompose the Fourier-transformed fields into a superposition of its harmonic modes. For a theoretical background, see Mode Decomposition.
(get-eigenmode-coefficients flux bands eig-parity eig-vol eig-resolution eig-tolerance kpoint-func verbose=False direction=AUTOMATIC) — Given a flux object and list of band indices, return a list with the following data:
alpha: the complex eigenmode coefficients as a 3d Guile array of size ((length bands), flux.Nfreq, 2). The last/third dimension refers to modes propagating in the forward (+) or backward (-) directions.
vgrp: the group velocity as a Guile array.
kpoints: a list of vector3s of the kpoint used in the mode calculation.
kdom: a list of vector3s of the mode's dominant wavevector.
Here is an example of calling get-eigenmode-coefficients overriding the default eig-parity with a keyword argument, and then printing the coefficient for first band, first frequency, and forward direction:
(let ((result (get-eigenmode-coefficients flux (list 1) #:eig-parity (+ ODD-Z EVEN-Y))))
(print (array-ref (list-ref result 0) 0 0 0)))
The flux object must be created using add-mode-monitor. (You could also use add-flux, but with add_flux you need to be more careful about symmetries that bisect the flux plane: the add-flux object should only be used with get-eigenmode-coefficients for modes of the same symmetry, e.g. constrained via eig_parity. On the other hand, the performance of add-flux planes benefits more from symmetry.) eig-vol is the volume passed to MPB for the eigenmode calculation (based on interpolating the discretized materials from the Yee grid); in most cases this will simply be the volume over which the frequency-domain fields are tabulated, which is the default (i.e. (meep-dft-flux-where-get flux)). eig-parity should be one of [NO-PARITY (default), EVEN-Z, ODD-Z, EVEN-Y, ODD-Y]. It is the parity (= polarization in 2d) of the mode to calculate, assuming the structure has and/or mirror symmetry in the source region, just as for eigenmode-source above. If the structure has both and mirror symmetry, you can combine more than one of these, e.g. (+ EVEN-Z ODD-Y). Default is NO-PARITY, in which case MPB computes all of the bands which will still be even or odd if the structure has mirror symmetry, of course. This is especially useful in 2d simulations to restrict yourself to a desired polarization. eig-resolution is the spatial resolution to use in MPB for the eigenmode calculations. This defaults to the same resolution as Meep, but you can use a higher resolution in which case the structure is linearly interpolated from the Meep pixels. eig-tolerance is the tolerance to use in the MPB eigensolver. MPB terminates when the eigenvalues stop changing to less than this fractional tolerance. Defaults to 1e-12. (Note that this is the tolerance for the frequency eigenvalue ω; the tolerance for the mode profile is effectively the square root of this.)
Technically, MPB computes ωₙ(k) and then inverts it with Newton's method to find the wavevector k normal to eig-vol and mode for a given frequency; in rare cases (primarily waveguides with nonmonotonic dispersion relations, which doesn't usually happen in simple dielectric waveguides), MPB may need you to supply an initial "guess" for k in order for this Newton iteration to converge. You can supply this initial guess with kpoint-func, which is a function (kpoint-func f n) that supplies a rough initial guess for the k of band number n at frequency f = ω/2π. (By default, the k components in the plane of the eig-vol region are zero. However, if this region spans the entire cell in some directions, and the cell has Bloch-periodic boundary conditions via the k-point parameter, then the mode's k components in those directions will match k-point so that the mode satisfies the Meep boundary conditions, regardless of kpoint-func.) If direction is set to NO_DIRECTION, then kpoint-func is not only the initial guess and the search direction of the k vectors, but is also taken to be the direction of the waveguide, allowing you to detect modes in oblique waveguides (not perpendicular to the flux plane).
Note: for planewaves in homogeneous media, the kpoints may not necessarily be equivalent to the actual wavevector of the mode. This quantity is given by kdom.
(add_mode_monitor fcen df nfreq ModeRegions...) — Similar to add-flux, but for use with get-eigenmode-coefficients.
add-mode-monitor works properly with arbitrary symmetries, but may be suboptimal because the Fourier-transformed region does not exploit the symmetry. As an optimization, if you have a mirror plane that bisects the mode monitor, you can instead use add-flux to gain a factor of two, but in that case you must also pass the corresponding eig-parity to get-eigenmode-coefficients in order to only compute eigenmodes with the corresponding mirror symmetry.
Very similar to flux spectra, you can also compute energy density spectra: the energy density of the electromagnetic fields as a function of frequency, computed by Fourier transforming the fields and integrating the energy density:
The usage is similar to the flux spectra: you define a set of energy-region objects telling Meep where it should compute the Fourier-transformed fields and energy densities, and call add-energy to add these regions to the current simulation over a specified frequency bandwidth, and then use display-electric-energy, display-magnetic-energy, or display-total-energy to display the energy density spectra at the end. There are also save-energy, load-energy, and load-minus-energy functions that you can use to subtract the fields from two simulation, e.g. in order to compute just the energy from scattered fields, similar to the flux spectra. These types and functions are defined as follows:
energy-region
A region (volume, plane, line, or point) in which to compute the integral of the energy density of the Fourier-transformed fields. Its properties are:
center [vector3] — The center of the energy region (no default).
size [vector3] — The size of the energy region along each of the coordinate axes. Default is (0,0,0): a single point.
weight [cnumber] — A weight factor to multiply the energy density by when it is computed. Default is 1.0.
(add-energy fcen df nfreq energy-regions...) — Add a bunch of energy-regions to the current simulation (initializing the fields if they have not yet been initialized), telling Meep to accumulate the appropriate field Fourier transforms for nfreq equally spaced frequencies covering the frequency range fcen-df/2 to fcen+df/2. Return an energy object, which you can pass to the functions below to get the energy spectrum, etcetera.
As for energy regions, you normally use add-energy via statements like:
(define En (add-energy ...))
to store the energy object in a variable. add-energy initializes the fields if necessary, just like calling run, so you should only call it after setting up your geometry, sources, pml-layers, k-point, etcetera. You can create as many energy objects as you want, e.g. to look at the energy densities in different objects or in different frequency ranges. Note, however, that Meep has to store (and update at every time step) a number of Fourier components equal to the number of grid points intersecting the energy region multiplied by nfreq, so this can get quite expensive (in both memory and time) if you want a lot of frequency points over large regions of space.
Once you have called add-energy, the Fourier transforms of the fields are accumulated automatically during time-stepping by the run functions. At any time, you can ask for Meep to print out the current energy density spectrum via:
(display-electric-energy energy...), (display-magnetic-energy energy...), (display-total-energy energy...) — Given a number of energy objects, this displays a comma-separated table of frequencies and energy density spectra for the electric, magnetic and total fields, respectively prefixed by "electric-energy1:", "magnetic-energy1:," "total-energy1:," or similar (where the number is incremented after each run). All of the energy should be for the same fcen/df/nfreq. The first column are the frequencies, and subsequent columns are the energy density spectra.
You might have to do something lower-level if you have multiple energy regions corresponding to different frequency ranges, or have other special needs. (display-electric-energy e1 e2 e3) is actually equivalent to (display-csv "electric-energy" (get-energy-freqs e1) (get-electric-energy e1) (get-electric-energy e2) (get-electric-energy e3)), where display-csv takes a bunch of lists of numbers and prints them as a comma-separated table; this involves calling two lower-level functions:
(get-energy-freqs energy) — Given an energy object, returns a list of the frequencies that it is computing the spectrum for.
(get-electric-energy energy), (get-magnetic-energy energy), (get-total-energy energy) — Given an energy object, returns a list of the current energy density spectrum for the electric, magnetic, or total fields, respectively that it has accumulated.
As described in Tutorial/Basics, to compute the energy density from the scattered fields you often want to save the Fourier-transformed fields from a "normalization" run and then load them into another run to be subtracted. This can be done via:
(save-energy filename energy) — Save the Fourier-transformed fields corresponding to the given energy object in an HDF5 file of the given filename without the ".h5" suffix (the current filename-prefix is prepended automatically).
(load-energy filename energy) — Load the Fourier-transformed fields into the given energy object (replacing any values currently there) from an HDF5 file of the given filename without the ".h5" suffix (the current filename-prefix is prepended automatically). You must load from a file that was saved by save-energy in a simulation of the same dimensions for both the cell and the energy regions with the same number of processors.
(load-minus-energy filename energy) — As load-energy, but negates the Fourier-transformed fields after they are loaded. This means that they will be subtracted from any future field Fourier transforms that are accumulated.
Very similar to flux spectra, you can also compute force spectra: forces on an object as a function of frequency, computed by Fourier transforming the fields and integrating the vacuum Maxwell stress tensor:
over a surface via . You should normally only evaluate the stress tensor over a surface lying in vacuum, as the interpretation and definition of the stress tensor in arbitrary media is often problematic (the subject of extensive and controversial literature). It is fine if the surface encloses an object made of arbitrary materials, as long as the surface itself is in vacuum.
See also Tutorial/Optical Forces.
Most commonly, you will want to normalize the force spectrum in some way, just as for flux spectra. Most simply, you could divide two different force spectra to compute the ratio of forces on two objects. Often, you will divide a force spectrum by a flux spectrum, to divide the force by the incident power on an object, in order to compute the useful dimensionless ratio / where in Meep units. For example, it is a simple exercise to show that the force on a perfectly reflecting mirror with normal-incident power satisfies /, and for a perfectly absorbing (black) surface /.
The usage is similar to the flux spectra: you define a set of force-region objects telling Meep where it should compute the Fourier-transformed fields and stress tensors, and call add-force to add these regions to the current simulation over a specified frequency bandwidth, and then use display-forces to display the force spectra at the end. There are also save-force, load-force, and load-minus-force functions that you can use to subtract the fields from two simulation, e.g. in order to compute just the force from scattered fields, similar to the flux spectra. These types and functions are defined as follows:
force-region
A region (volume, plane, line, or point) in which to compute the integral of the stress tensor of the Fourier-transformed fields. Its properties are:
center [vector3] — The center of the force region (no default).
size [vector3] — The size of the force region along each of the coordinate axes. Default is (0,0,0): a single point.
direction [direction constant] — The direction of the force that you wish to compute (e.g. X, Y, etcetera). Unlike flux-region, you must specify this explicitly, because there is not generally any relationship between the direction of the force and the orientation of the force region.
weight [cnumber] — A weight factor to multiply the force by when it is computed. Default is 1.0.
In most circumstances, you should define a set of force-regions whose union is a closed surface lying in vacuum and enclosing the object that is experiencing the force.
(add-force fcen df nfreq force-regions...) — Add a bunch of force-regions to the current simulation (initializing the fields if they have not yet been initialized), telling Meep to accumulate the appropriate field Fourier transforms for nfreq equally spaced frequencies covering the frequency range fcen-df/2 to fcen+df/2. Return a force object, which you can pass to the functions below to get the force spectrum, etcetera.
As for force regions, you normally use add-force via statements like:
(define Fx (add-force ...))
to store the force object in a variable. add-force initializes the fields if necessary, just like calling run, so you should only call it after setting up your geometry, sources, pml-layers, etcetera. You can create as many force objects as you want, e.g. to look at forces on different objects, in different directions, or in different frequency ranges. Note, however, that Meep has to store (and update at every time step) a number of Fourier components equal to the number of grid points intersecting the force region, multiplied by the number of electric and magnetic field components required to get the stress vector, multiplied by nfreq, so this can get quite expensive (in both memory and time) if you want a lot of frequency points over large regions of space.
Once you have called add-force, the Fourier transforms of the fields are accumulated automatically during time-stepping by the run functions. At any time, you can ask for Meep to print out the current force spectrum via:
(display-forces forces...) — Given a number of force objects, this displays a comma-separated table of frequencies and force spectra, prefixed by "force1:" or similar (where the number is incremented after each run). All of the forces should be for the same fcen/df/nfreq. The first column are the frequencies, and subsequent columns are the force spectra.
You might have to do something lower-level if you have multiple force regions corresponding to different frequency ranges, or have other special needs. (display-forces f1 f2 f3) is actually equivalent to (display-csv "force" (get-force-freqs f1) (get-forces f1) (get-forces f2) (get-forces f3)), where display-csv takes a bunch of lists of numbers and prints them as a comma-separated table; this involves calling two lower-level functions:
(get-force-freqs force) — Given a force object, returns a list of the frequencies that it is computing the spectrum for.
(get-forces force) — Given a force object, returns a list of the current force spectrum that it has accumulated.
As described in Tutorial/Basics, to compute the force from scattered fields you often want to save the Fourier-transformed fields from a "normalization" run and then load them into another run to be subtracted. This can be done via:
(save-force filename force) — Save the Fourier-transformed fields corresponding to the given force object in an HDF5 file of the given filename without the ".h5" suffix (the current filename-prefix is prepended automatically).
(load-force filename force) — Load the Fourier-transformed fields into the given force object (replacing any values currently there) from an HDF5 file of the given filename without the ".h5" suffix (the current filename-prefix is prepended automatically). You must load from a file that was saved by save-force in a simulation of the same dimensions for both the cell and the force regions with the same number of processors.
(load-minus-force filename force) — As load-force, but negates the Fourier-transformed fields after they are loaded. This means that they will be subtracted from any future field Fourier transforms that are accumulated.
Meep can also calculate the LDOS (local density of states) spectrum, as described in Tutorial/Local Density of States. To do this, you simply pass the following step function to your run command:
(dft-ldos fcen df nfreq) — Compute the power spectrum of the sources (usually a single point dipole source), normalized to correspond to the LDOS, in a frequency bandwidth df centered at fcen, at nfreq frequency points.
(get-ldos-freqs ldos) — Given an ldos object, returns a list of the frequencies that it is computing the spectrum for.
The resulting spectrum is outputted as comma-delimited text, prefixed by ldos:,, and is also stored in the dft-ldos-data global variable after the run is complete.
Analytically, the per-polarization LDOS is exactly proportional to the power radiated by an -oriented point-dipole current, , at a given position in space. For a more mathematical treatment of the theory behind the LDOS, refer to the relevant discussion in Section 4.4 ("Currents and Fields: The Local Density of States") in Chapter 4 ("Electromagnetic Wave Source Conditions") of the book Advances in FDTD Computational Electrodynamics: Photonics and Nanotechnology, but for now it is defined as:
where the normalization is necessary for obtaining the power exerted by a unit-amplitude dipole (assuming linear materials), and hats denote Fourier transforms. It is this quantity that is computed by the dft-ldos command for a single dipole source. For a volumetric source, the numerator and denominator are both integrated over the current volume, but "LDOS" computation is less meaningful in this case.
Meep can compute a near-to-far-field transformation in the frequency domain as described in Tutorial/Near-to-Far Field Spectra: given the fields on a "near" bounding surface inside the cell, it can compute the fields arbitrarily far away using an analytical transformation, assuming that the "near" surface and the "far" region lie in a single homogeneous non-periodic 2d or 3d region. That is, in a simulation surrounded by PML that absorbs outgoing waves, the near-to-far-field feature can compute the fields outside the cell as if the outgoing waves had not been absorbed (i.e. in the fictitious infinite open volume). Moreover, this operation is performed on the Fourier-transformed fields: like the flux and force spectra above, you specify a set of desired frequencies, Meep accumulates the Fourier transforms, and then Meep computes the fields at each frequency for the desired far-field points.
This is based on the principle of equivalence: given the Fourier-transformed tangential fields on the "near" surface, Meep computes equivalent currents and convolves them with the analytical Green's functions in order to compute the fields at any desired point in the "far" region. For details, see Section 4.2.1 ("The Principle of Equivalence") in Chapter 4 ("Electromagnetic Wave Source Conditions") of the book Advances in FDTD Computational Electrodynamics: Photonics and Nanotechnology.
Note: in order for the far-field results to be accurate, the far region must be separated from the near region by at least 2D2/λ, the Fraunhofer distance, where D is the largest dimension of the radiator and λ is the vacuum wavelength.
There are three steps to using the near-to-far-field feature: first, define the "near" surface(s) as a set of surfaces capturing all outgoing radiation in the desired direction(s); second, run the simulation, typically with a pulsed source, to allow Meep to accumulate the Fourier transforms on the near surface(s); third, tell Meep to compute the far fields at any desired points (optionally saving the far fields from a grid of points to an HDF5 file). To define the near surfaces, use:
(add-near2far fcen df nfreq near2far-regions... nperiods) — Add a bunch of near2far-regions to the current simulation (initializing the fields if they have not yet been initialized), telling Meep to accumulate the appropriate field Fourier transforms for nfreq equally-spaced frequencies covering the frequency range fcen-df/2 to fcen+df/2. Return a near2far object, which you can pass to the functions below to get the far fields. nperiods is a keyword argument that defaults to one, and can be passed after the list of near2far-regions like so: (add-near2far fcen df nfreq region1 region2 region3 #:nperiods 2)
Each near2far-region is identical to flux-region except for the name: in 3d, these give a set of planes (important: all these "near surfaces" must lie in a single homogeneous material with isotropic ε and μ — and they should not lie in the PML regions) surrounding the source(s) of outgoing radiation that you want to capture and convert to a far field. Ideally, these should form a closed surface, but in practice it is sufficient for the near2far-regions to capture all of the radiation in the direction of the far-field points. Important: as for flux computations, each near2far-region should be assigned a weight of ±1 indicating the direction of the outward normal relative to the +coordinate direction. So, for example, if you have six regions defining the six faces of a cube, i.e. the faces in the +x, -x, +y, -y, +z, and -z directions, then they should have weights +1, -1, +1, -1, +1, and -1 respectively. Note that, neglecting discretization errors, all near-field surfaces that enclose the same outgoing fields are equivalent and will yield the same far fields with a discretization-induced difference that vanishes with increasing resolution etc.
After the simulation run is complete, you can compute the far fields. This is usually for a pulsed source so that the fields have decayed away and the Fourier transforms have finished accumulating.
(get_farfield near2far x) — Given a vector3 point x which can lie anywhere outside the near-field surface, including outside the cell and a near2far object, returns the computed (Fourier-transformed) "far" fields at x as list of length 6nfreq, consisting of fields (Ex1,Ey1,Ez1,Hx1,Hy1,Hz1,Ex2,Ey2,Ez2,Hx2,Hy2,Hz2,...) for the frequencies 1,2,…,nfreq.
(get-near2far-freqs near2far) — Given a near2far object, returns a list of the frequencies that it is computing the spectrum for.
(output-farfields near2far fname where resolution) — Given an HDF5 file name fname (does not include the .h5 suffix), a volume given by where (may be 0d, 1d, 2d, or 3d), and a resolution (in grid points / distance unit), outputs the far fields in where (which may lie outside the cell) in a grid with the given resolution (which may differ from the FDTD grid resolution) to the HDF5 file as a set of twelve array datasets ex.r, ex.i, ..., hz.r, hz.i, giving the real and imaginary parts of the Fourier-transformed and fields on this grid. Each dataset is an nx×ny×nz×nfreq 4d array of space×frequency although dimensions that =1 are omitted.
Note that far fields have the same units and scaling as the Fourier transforms of the fields, and hence cannot be directly compared to time-domain fields. In practice, it is easiest to use the far fields in computations where overall scaling (units) cancel out or are irrelevant, e.g. to compute the fraction of the far fields in one region vs. another region.
(Multi-frequency output-farfields can be accelerated by compiling Meep with --with-openmp and using the OMP_NUM_THREADS environment variable to specify multiple threads.)
For a scattered-field computation, you often want to separate the scattered and incident fields. Just as is described in Tutorial/Basics/Transmittance Spectrum of a Waveguide Bend for flux computations, you can do this by saving the Fourier-transformed incident from a "normalization" run and then load them into another run to be subtracted. This can be done via:
(save-near2far filename near2far) — Save the Fourier-transformed fields corresponding to the given near2far object in an HDF5 file of the given filename (without the ".h5" suffix). The current filename-prefix is prepended automatically.
(load-near2far filename near2far) — Load the Fourier-transformed fields into the given near2far object replacing any values currently there from an HDF5 file of the given filename (without the ".h5" suffix) the current filename-prefix is prepended automatically. You must load from a file that was saved by save-near2far in a simulation of the same dimensions for both the cell and the near2far regions with the same number of processors.
(load-minus-near2far filename near2far) — As load-near2far, but negates the Fourier-transformed fields after they are loaded. This means that they will be subtracted from any future field Fourier transforms that are accumulated.
(scale-near2far-fields s near2far) — Scale the Fourier-transformed fields in near2far by the complex number s. e.g. load-minus-near2far is equivalent to load-near2far followed by scale-near2far-fields with s=-1.
(flux near2far direction where resolution) — Given a volume where (may be 0d, 1d, 2d, or 3d) and a resolution (in grid points / distance unit), compute the far fields in where (which may lie outside the cell) in a grid with the given resolution (which may differ from the FDTD solution) and return its Poynting flux in direction as a list. The dataset is a 1d array of nfreq dimensions.
These functions dump the raw ε data to disk and load it back for doing multiple simulations with the same materials but different sources etc. The only prerequisite is that the dump/load simulations have the same chunks (i.e. the same grid, number of processors, and PML). Currently only stores ε and μ, and not nonlinear coefficients or polarizability.
(meep-structure-dump structure fname) — Dumps the structure to the file fname using the global structure object (which is initialized after you execute run or init-structure).
(meep-structure-load structure fname) — Loads a structure from the file fname. This should be called after (init-structure) so that the global structure object is initialized, and you should generally (set! geometry '()) to skip initializing the geometry (since it will be overwritten by meep-structure-load anyway).
Meep contains a frequency-domain solver that computes the fields produced in a geometry in response to a continuous-wave (CW) source. This is based on an iterative linear solver instead of time-stepping. For details, see Section 5.3 ("Frequency-domain solver") of Computer Physics Communications, Vol. 181, pp. 687-702, 2010. Benchmarking results have shown that in many instances, such as cavities (e.g., ring resonators) with long-lived resonant modes, this solver converges much faster than simply running an equivalent time-domain simulation with a CW source (using the default width of zero for no transient turn-on), time-stepping until all transient effects from the source turn-on have disappeared, especially if the fields are desired to a very high accuracy. To use it, simply define a continuous-src with the desired frequency, initialize the fields and geometry via (init-fields), and then:
(meep-fields-solve-cw fields tol maxiters L)
After the fields variable (a global variable pointing to the meep::fields* object initialized by init-fields, see Input Variables), the next two parameters to the frequency-domain solver are the tolerance tol for the iterative solver (10−8, by default) and a maximum number of iterations maxiters (104, by default). Finally, there is a parameter that determines a tradeoff between memory and work per step and convergence rate of the iterative algorithm, biconjugate gradient stabilized (BiCGSTAB-L), that is used; larger values of will often lead to faster convergence at the expense of more memory and more work per iteration. Default is , and normally a value ≥ 2 should be used.
The frequency-domain solver supports arbitrary geometries, PML, boundary conditions, symmetries, parallelism, conductors, and arbitrary nondispersive materials. Lorentz-Drude dispersive materials are not currently supported in the frequency-domain solver, but since you are solving at a known fixed frequency rather than timestepping, you should be able to pick conductivities etcetera in order to obtain any desired complex ε and μ at that frequency.
The frequency-domain solver requires you to use complex-valued fields, via (set! force-complex-fields? true).
After meep-fields-solve-cw completes, it should be as if you had just run the simulation for an infinite time with the source at that frequency. You can call the various field-output functions and so on as usual at this point.
The actual work in Meep is performed by run functions, which time-step the simulation for a given amount of time or until a given condition is satisfied.
The run functions, in turn, can be modified by use of step functions: these are called at every time step and can perform any arbitrary computation on the fields, do outputs and I/O, or even modify the simulation. The step functions can be transformed by many modifier functions, like at-beginning, during-sources, etcetera which cause them to only be called at certain times, etcetera, instead of at every time step.
A common point of confusion is described in The Run Function Is Not A Loop. Read this article if you want to make Meep do some customized action on each time step, as many users make the same mistake. What you really want to in that case is to write a step function, as described below.
The following run functions are available. You can also write your own, using the lower-level C++/SWIG functions, but these should suffice for most needs.
(run-until cond?/time step-functions...) — Run the simulation until a certain time or condition, calling the given step functions (if any) at each timestep. The first argument is either a number, in which case it is an additional time (in Meep units) to run for, or it is a function (of no arguments) which returns true when the simulation should stop.
(run-sources step-functions...) — Run the simulation until all sources have turned off, calling the given step functions (if any) at each timestep. Note that this does not mean that the fields will be zero at the end: in general, some fields will still be bouncing around that were excited by the sources.
(run-sources+ cond?/time step-functions...) — As run-sources, but with an additional first argument: either a number, in which case it is an additional time (in Meep units) to run for after the sources are off, or it is a function (of no arguments). In the latter case, the simulation runs until the sources are off and (cond?) returns true.
In particular, a useful first argument to run-sources+ or run-until is often as shown below which is demonstrated in Tutorial/Basics:
(stop-when-fields-decayed dT c pt decay-by) — Return a cond? function, suitable for passing to run-until/run-sources+, that examines the component c (e.g. Ex, etc.) at the point pt (a vector3) and keeps running until its absolute value squared has decayed by at least decay-by from its maximum previous value. In particular, it keeps incrementing the run time by dT (in Meep units) and checks the maximum value over that time period — in this way, it won't be fooled just because the field happens to go through 0 at some instant.
Note that, if you make decay-by very small, you may need to increase the cutoff property of your source(s), to decrease the amplitude of the small high-frequency components that are excited when the source turns off. High frequencies near the Nyquist frequency of the grid have slow group velocities and are absorbed poorly by PML.
Finally, another two run functions, useful for computing ω(k) band diagrams, are
(run-k-point T k) — Given a vector3 k, runs a simulation for each k point (i.e. specifying Bloch-periodic boundary conditions) and extracts the eigen-frequencies, and returns a list of the complex frequencies. In particular, you should have specified one or more Gaussian sources. It will run the simulation until the sources are turned off plus an additional time units. It will run Harminv at the same point/component as the first Gaussian source and look for modes in the union of the frequency ranges for all sources.
(run-k-points T k-points) — Given a list k-points of k vectors, runs run-k-point for each one, and returns a list of lists of frequencies (one list of frequencies for each k). Also prints out a comma-delimited list of frequencies, prefixed by freqs:, and their imaginary parts, prefixed by freqs-im:. See Tutorial/Resonant Modes and Transmission in a Waveguide Cavity.
Several useful step functions are predefined by Meep.
The most common step function is an output function, which outputs some field component to an HDF5 file. Normally, you will want to modify this by one of the at-* functions, below, as outputting a field at every time step can get quite time- and storage-consuming.
Note that although the various field components are stored at different places in the Yee lattice, when they are outputted they are all linearly interpolated to the same grid: to the points at the centers of the Yee cells, i.e. in 3d.
The predefined output functions are:
output-epsilon — Output the dielectric function (relative permittivity) ε. Note that this only outputs the real, frequency-independent part of ε (the limit).
output-mu — Output the relative permeability function μ. Note that this only outputs the real, frequency-independent part of μ (the limit).
(output-dft dft-fields fname [where]) — Output the Fourier-transformed fields in dft-fields (created by add-dft-fields) to an HDF5 file with name fname (does not include the .h5 suffix). The volume where defaults to the entire cell.
output-poynting — Output the Poynting flux . Note that you might want to wrap this step function in synchronized-magnetic to compute it more accurately. See Synchronizing the Magnetic and Electric Fields.
output-hpwr — Output the magnetic-field energy density
output-dpwr — Output the electric-field energy density
output-tot-pwr — Output the total electric and magnetic energy density. Note that you might want to wrap this step function in synchronized-magnetic to compute it more accurately. See Synchronizing the Magnetic and Electric Fields.
output-Xfield-x, output-Xfield-y, output-Xfield-z, output-Xfield-r, output-Xfield-p — Output the , , , , or component respectively, of the field X, where X is either h, b, e, d, or s for the magnetic, electric, displacement, or Poynting flux, respectively. If the field is complex, outputs two datasets, e.g. ex.r and ex.i, within the same HDF5 file for the real and imaginary parts, respectively. Note that for outputting the Poynting flux, you might want to wrap the step function in synchronized-magnetic to compute it more accurately. See Synchronizing the Magnetic and Electric Fields.
output-Xfield — Outputs all the components of the field X, where X is either h, b, e, d, or s as above, to an HDF5 file. That is, the different components are stored as different datasets within the same file.
(output-png component h5topng-options) — Output the given field component (e.g. Ex, etc.) as a PNG image, by first outputting the HDF5 file, then converting to PNG via h5topng, then deleting the HDF5 file. The second argument is a string giving options to pass to h5topng (e.g. "-Zc bluered"). See also Tutorial/Basics.
It is often useful to use the h5topng -C or -A options to overlay the dielectric function when outputting fields. To do this, you need to know the name of the dielectric-function .h5 file which must have been previously output by output-epsilon. To make this easier, a built-in shell variable $EPS is provided which refers to the last-output dielectric-function .h5 file. So, for example (output-png Ez "-C $EPS") will output the field and overlay the dielectric contours.
(output-png+h5 component h5topng-options) — Like output_png, but also outputs the .h5 file for the component. In contrast, output_png deletes the .h5 when it is done.
More generally, it is possible to output an arbitrary function of position and zero or more field components, similar to the integrate-field-function described above. This is done by:
(output-field-function name cs func) — Output the field function func to an HDF5 file in the datasets named name.r and name.i for the real and imaginary parts. Similar to integrate-field-function, func is a function of position (a vector3) and the field components corresponding to cs: a list of component constants.
(output-real-field-function name cs func) — As output-field-function, but only outputs the real part of func to the dataset given by the string name.
See also Field Functions, and Synchronizing the Magnetic and Electric Fields if you want to do computations combining the electric and magnetic fields.
The following step function collects field data from a given point and runs Harminv on that data to extract the frequencies, decay rates, and other information.
(harminv c pt fcen df [maxbands]) — Returns a step function that collects data from the field component c (e.g. , etc.) at the given point pt (a vector3). Then, at the end of the run, it uses Harminv to look for modes in the given frequency range (center fcen and width df), printing the results to standard output (prefixed by harminv:) as comma-delimited text, and also storing them to the variable harminv-results. The optional argument maxbands is the maximum number of modes to search for. Defaults to 100.
Important: normally, you should only use harminv to analyze data after the sources are off. Wrapping it in (after-sources (harminv ...)) is sufficient.
In particular, Harminv takes the time series corresponding to the given field component as a function of time and decomposes it (within the specified bandwidth) as:
The results are stored in the list harminv-results, which is a list of tuples holding the frequency, amplitude, and error of the modes. Given one of these tuples, you can extract its various components with one of the accessor functions:
(harminv-freq result) — Return the complex frequency ω (in the usual Meep units).
(harminv-freq-re result) — Return the real part of the frequency ω.
(harminv-freq-im result) — Return the imaginary part of the frequency ω.
(harminv-Q result) — Return dimensionless lifetime, or quality factor, , defined as .
(harminv-amp result) — Return the complex amplitude .
(harminv-err result) — A crude measure of the error in the frequency (both real and imaginary)...if the error is much larger than the imaginary part, for example, then you can't trust the to be accurate. Note: this error is only the uncertainty in the signal processing, and tells you nothing about the errors from finite resolution, finite cell size, and so on.
For example, (map harminv-freq-re harminv-results) gives a list of the real parts of the frequencies, using the Scheme built-in map.
Rather than writing a brand-new step function every time something a bit different is required, the following "modifier" functions take a bunch of step functions and produce new step functions with modified behavior. See also Tutorial/Basics for examples.
(combine-step-funcs step-functions...) — Given zero or more step functions, return a new step function that on each step calls all of the passed step functions.
(synchronized-magnetic step-functions...) — Given zero or more step functions, return a new step function that on each step calls all of the passed step functions with the magnetic field synchronized in time with the electric field. See Synchronizing the Magnetic and Electric Fields.
(when-true cond? step-functions...) — Given zero or more step functions and a condition function cond? (a function of no arguments), evaluate the step functions whenever (cond?) returns true.
(when-false cond? step-functions...) — Given zero or more step functions and a condition function cond? (a function of no arguments), evaluate the step functions whenever (cond?) returns false.
(at-every dT step-functions...) — Given zero or more step functions, evaluates them at every time interval of units (rounded up to the next time step).
(after-time T step-functions...) — Given zero or more step functions, evaluates them only for times after a time units have elapsed from the start of the run.
(before-time T step-functions...) — Given zero or more step functions, evaluates them only for times before a time units have elapsed from the start of the run.
(at-time T step-functions...) — Given zero or more step functions, evaluates them only once, after a time units have elapsed from the start of the run.
(after-sources step-functions...) — Given zero or more step functions, evaluates them only for times after all of the sources have turned off.
(after-sources+ T step-functions...) — Given zero or more step functions, evaluates them only for times after all of the sources have turned off, plus an additional time units have elapsed.
(during-sources step-functions...) — Given zero or more step functions, evaluates them only for times before all of the sources have turned off.
(at-beginning step-functions...) — Given zero or more step functions, evaluates them only once, at the beginning of the run.
(at-end step-functions...) — Given zero or more step functions, evaluates them only once, at the end of the run.
(in-volume v step-functions...) — Given zero or more step functions, modifies any output functions among them to only output a subset (or a superset) of the cell, corresponding to the meep::volume* v (created by the volume function).
(in-point pt step-functions...) — Given zero or more step functions, modifies any output functions among them to only output a single point of data, at pt (a vector3).
(to-appended filename step-functions...) — Given zero or more step functions, modifies any output functions among them to append their data to datasets in a single newly-created file named filename (plus an .h5 suffix and the current filename prefix). They append by adding an extra dimension to their datasets, corresponding to time.
(with-prefix prefix step-functions...) — Given zero or more step functions, modifies any output functions among them to prepend the string prefix to the file names (much like filename-prefix, above).
A step function can take two forms. The simplest is just a function of no arguments, which is called at every time step (unless modified by one of the modifier functions above). e.g.
(define (my-step) (print "Hello world!\n"))
If one then does (run-until 100 my-step), Meep will run for 100 time units and print "Hello world!" at every time step.
This suffices for most purposes. However, sometimes you need a step function that opens a file, or accumulates some computation, and you need to clean up (e.g. close the file or print the results) at the end of the run. For this case, you can write a step function of one argument: that argument will either be 'step when it is called during time-stepping, or 'finish when it is called at the end of the run.
By default, Meep reads input functions like sources and geometry and creates global variables structure and fields to store the corresponding C++ objects. Given these, you can then call essentially any function in the C++ interface, because all of the C++ functions are automatically made accessible to Scheme by the wrapper-generator program SWIG.
The structure and fields variables are automatically initialized when any of the run functions is called, or by various other functions such as add-flux. To initialize them separately, you can call (init-fields) manually, or (init-structure k-point) to just initialize the structure.
If you want to time step more than one field simultaneously, the easiest way is probably to do something like:
(init-fields)
(define my-fields fields)
(set! fields '())
and then change the geometry etc. and re-run (init-fields). Then you'll have two field objects in memory.
If you look at a function in the C++ interface, then there are a few simple rules to infer the name of the corresponding Scheme function.
First, all functions in the meep:: namespace are prefixed with meep- in the Scheme interface.
Second, any method of a class is prefixed with the name of the class and a hyphen. For example, meep::fields::step, which is the function that performs a time-step, is exposed to Scheme as meep-fields-step. Moreover, you pass the object as the first argument in the Scheme wrapper. e.g. f.step() becomes (meep-fields-step f).
To call the C++ constructor for a type, you use new-*. e.g. (new-meep-fields ...) returns a new meep::fields object. Conversely, to call the destructor and deallocate an object, you use delete-*; most of the time, this is not necessary because objects are automatically garbage collected.
Some argument type conversion is performed automatically, e.g. types like complex numbers are converted to complex<double>, etcetera. vector3 vectors are converted to meep::vec, but to do this it is necessary to know the dimensionality of the problem in C++. The problem dimensions are automatically initialized by init-structure, but if you want to pass vector arguments to C++ before that time you should call (require-dimensions!), which infers the dimensions from the geometry-lattice, k-point, and dimensions variables.
Built with MkDocs using a theme provided by Read the Docs.
GitHub « Previous Next » | CommonCrawl |
Coevolutionary feedback elevates constitutive immune defence: a protein network model
Tsukushi Kamiya1,2,
Leonardo Oña1,
Bregje Wertheim1 &
G. Sander van Doorn1
Organisms have evolved a variety of defence mechanisms against natural enemies, which are typically used at the expense of other life history components. Induced defence mechanisms impose minor costs when pathogens are absent, but mounting an induced response can be time-consuming. Therefore, to ensure timely protection, organisms may partly rely on constitutive defence despite its sustained cost that renders it less economical. Existing theoretical models addressing the optimal combination of constitutive versus induced defence focus solely on host adaptation and ignore the fact that the efficacy of protection depends on genotype-specific host-parasite interactions. Here, we develop a signal-transduction network model inspired by the invertebrate innate immune system, in order to address the effect of parasite coevolution on the optimal combination of constitutive and induced defence.
Our analysis reveals that coevolution of parasites with specific immune components shifts the host's optimal allocation from induced towards constitutive immunity. This effect is dependent upon whether receptors (for detection) or effectors (for elimination) are subjected to parasite counter-evolution. A parasite population subjected to a specific immune receptor can evolve heightened genetic diversity, which makes parasite detection more difficult for the hosts. We show that this coevolutionary feedback renders the induced immune response less efficient, forcing the hosts to invest more heavily in constitutive immunity. Parasites diversify to escape elimination by a specific effector too. However, this diversification does not alter the optimal balance between constitutive and induced defence: the reliance on constitutive defence is promoted by the receptor's inability to detect, but not the effectors' inability to eliminate parasites. If effectors are useless, hosts simply adapt to tolerate, rather than to invest in any defence against parasites. These contrasting results indicate that evolutionary feedback between host and parasite populations is a key factor shaping the selection regime for immune networks facing antagonistic coevolution.
Parasite coevolution against specific immune defence alters the prediction of the optimal use of defence, and the effect of parasite coevolution varies between different immune components.
Parasites threaten all living organisms. Immune defence is therefore crucial for providing protection from these enemies. However, defence is typically used at the expense of other fitness components and with the potential risk of self-damage. Therefore, hosts are faced with a challenge to optimise their defence deployment strategy so that it provides maximum protection while minimising costs [1, 2].
One important aspect of scheduling defence deployment is its temporal pattern of expression, which spans across the spectrum of constitutive to induced activation. A strategy is considered constitutive when an organism expresses a defensive phenotype regardless of external signals, that is, even in the absence of a threat. On the other hand, induced defence is only triggered upon detecting an enemy. Given that defence is costly, it is intuitively most economical to deploy defence only when a threat is encountered. However, physiological constraints often prevent an organism from mounting an immediate response, causing a delayed induced response of several hours to several days [3, 4]. Such a delay results in an unprotected period during which the risk of parasite-mediated harm is particularly high. Therefore, despite its sustained maintenance cost, constitutive defence can be adaptive for filling the potential period of unprotected exposure [5]. In nature, organisms deploy various combinations of constitutive and induced defence and a given effector molecule, whose function is to eliminate parasites, may be activated through both constitutive and inducible means. In the innate immune system of insects, for example, phenoloxidase (PO) is a defence effector molecule that is constitutively present, and can be further up-regulated upon induction through the proPhenoloxidase (PPO)-cascade [4].
Existing theoretical models of the optimal balance of constitutive and induced defence exclusively consider non-specific defence, assuming that hosts equally induce their defences, and that these defences are equally effective against all parasite genotypes (e.g. [5–8]). However, host-parasite interactions are characteristically genotype specific [9, 10]. In other words, it is the norm rather than the exception to find that hosts vary in their ability to resist parasites of different genotypes. For example, in vertebrate adaptive immunity, the major histocompatibility complex, MHC (also known as human leukocyte antigen, HLA) plays an important role in specific immune induction by binding to self and foreign peptides and displaying them on the cell surface for recognition by the T cells [10, 11]. High specificity of antigen presentation is made possible by a polymorphic lock-and-key mechanism: the MHC variable regions (lock) match the epitope, i.e., a fraction of the foreign antigen (key).
While specific defence was believed to be unique to the vertebrate adaptive immune system, this conventional belief has been challenged by studies of invertebrate immunity, which suggest neither adaptive immunity is restricted to vertebrates, nor specific defence is limited to adaptive immunity [9, 12–14]. For example, Carius et al. [15], using Daphnia and its bacterial parasite Pasteuria ramosa, showed different combinations of host and parasite genotypes create variation in infection success. The molecular mechanisms underlying the specificity in invertebrate innate immunity is not well understood to date [13]. Nonetheless, genetic studies in Drosophila indicate that there exists a considerable degree of specificity against parasites at both the receptor and effector level [16–18].
Specific defence is thought to be beneficial for the host, because high specificity may allow for more effective detection and elimination of certain parasite strains [13]. Conversely, rare parasite mutants that escape the specific defence would gain a large fitness advantage over common strains through negative frequency-dependent selection for rare advantageous alleles. Therefore, genotype-specific interactions are thought to maintain genetic diversity in both hosts and parasites, which is essential for antagonistic coevolution to continue [1]. Despite the ubiquity of genotype-specific host-parasite interactions, few theoretical studies have explicitly incorporated antagonistic coevolution into models of optimal defence [9, 19–21].
Here, we examine the effect of antagonistic parasite coevolution against the host receptor and effector on the optimal combination between constitutive and induced defence using a signal-transduction network model. A mechanistic perspective suggests that the immune system consists of a network of signal transduction cascades [4, 9, 13]. For example, in the innate immune system of Drosophila, once a non-self element (e.g. microbial ligand or parasitoid egg) is detected by a host protein (e.g. pattern recognition receptor), the system triggers a series of signalling pathways (e.g. Toll and Imd pathways) which lead to cellular responses such as phagocytosis and encapsulation, as well as the production of humoral effector molecules such as antimicrobial peptides and melanin [4]. In addition, signalling cascades exist that activate immune effectors constitutively (e.g. PPO-cascade) in the absence of parasite insults. Therefore, the success of an immune system depends not only on immune components that directly interact with parasites, but also on how those components are connected through a network of protein interactions [13].
While the network notion has long existed in the study of vertebrate adaptive immunity (i.e., immune network theory: [22, 23]), few evolutionary models have so far considered the immune system as a network (but see, [24]). Rather than predefining the direction and strength of interactions between immune components, the network approach allows them to emerge through in silico evolution. Another distinguishing feature of our analysis is that it addresses the effect of parasite coevolution on the optimal combination of constitutive and induced defence, complementing and extending previous studies that have investigated the optimal strategy for deploying constitutive and induced defences under evolutionary static conditions [5–8].
Immune system as a signal transduction network
Following Soyer et al. [24–27], we employ an evolutionary approach to the analysis of signal transduction networks with the goal to evolve network interactions that achieve an optimal defence strategy. The innate immune system of invertebrates provides the inspiration for our model because of its relative simplicity and the wide array of constitutive to induced, and specific to non-specific defence mechanisms [1, 4].
Rather than aiming for a mechanistically detailed description of invertebrate immunity for a particular model species, we take a conceptual, minimal modelling approach, and consider four proteins (which, in reality, may reflect entire modules of proteins and signal-transduction pathways): one recognition receptor (R), which is set either to be specific or non-specific, one constitutively active protein (C), and two resistance effectors (ES and EN), one of which is specific and the other non-specific (Fig. 1). The recognition receptor may be activated upon detecting a parasite and resistance effectors may be triggered downstream of the signalling cascade to eliminate the parasite (Fig. 1, blue arrows). In addition, the constitutively active protein is capable of interacting with the effectors independent of external inputs (Fig. 1, green arrows). Lastly, effectors are able to regulate each other to allow such interactions as they are known in invertebrate immunity (Fig. 1, purple arrows) [13].
Immune network schematics. Immune network topology showing the interacting proteins (receptor, effector and constitutive proteins are denoted R, E, and C respectively) within a host individual and the parasite (P). The subscripts N and S with the effector refer to the non-specific and specific effector respectively
The above model design is highly simplified, but still flexible enough to allow for a wide range of specific to non-specific immune responses activated through a full spectrum of purely constitutive to purely induced stimulation. In addition it allows us to compare the evolution of immune components with varying degrees of specificity, and to consider the effect of specific defence both at the receptor and effector level. When host-parasite coevolution is taken into account, it is in the parasite's interest to evade specific defense mechanisms, while the evolutionary interest of the host is the opposite. Therefore, the specific defence components coevolve antagonistically with the parasite, whereas the non-specific components are oblivious to coevolutionary pressures. We assume no difference in the intrinsic cost between specific and non-specific immune defence. However, a difference in the average efficacy between them can emerge in a population as a consequence of coevolution.
Following Soyer et al. [27], we assume that the total concentration of the proteins in our model is fixed, but each protein can occur in an active and inactive form. We keep track of the proportion of the active form of each protein, y i (where i= R, C, ES or EN, respectively, for the receptor, the constitutive protein and the two effector proteins). Biologically, protein activity could be mediated by various mechanisms, including phosphorylation and other reversible post-translational modification mechanisms.
If a protein j is connected to another protein i in the immune-network topology shown in Fig. 1, then the active form of protein j is allowed to mediate the activity of protein i. This interaction can be either activating (i.e., j catalyses the transition from the inactive to the active form of i) or inhibiting (j catalyses the reverse transition), depending on the sign of μ ij , the interaction coefficient for the two proteins. The protein interactions are directional; in particular, the activation or inhibition of protein i by protein j has no direct effect on the state of protein j.
Based on these assumptions, we formulate a system of ordinary differential equations to describe the dynamics of the protein activities in the absence of a parasite:
$$ \frac{dy_{i}}{dt} = -\phi y_{i} + {\sum_{j}} c_{i\times j} \mu_{i\times j} y_{j} \times \left\{\begin{array}{ll} 1-y_{i} & \text{if }\mu_{i \times j}>0\,,\\ y_{i} & \text{if }\mu_{i \times j}<0\,. \end{array}\right. $$
Here, c i×j takes value one if protein j connects to i in Fig. 1, and zero otherwise (\(\phantom {\dot {i}\!}c_{\mathrm {E}_{\mathrm {N}} \times \mathrm {R}} = c_{\mathrm {E}_{\mathrm {S}} \times \mathrm {R}} = c_{\mathrm {E}_{\mathrm {N}} \times \mathrm {C}} = c_{\mathrm {E}_{\mathrm {S}} \times \mathrm {C}} = c_{\mathrm {E}_{\mathrm {N}} \times \mathrm {E}_{\mathrm {S}}} = c_{\mathrm {E}_{\mathrm {S}} \times \mathrm {E}_{\mathrm {N}}} = 1\); all other c i×j =0). To ensure that protein activity equilibrates to zero in the absence of activating inputs, the equation contains a term that captures spontaneous deactivation of the active form of the protein. Spontaneous deactivation occurs at rate ϕ.
The interaction coefficients μ i×j are considered to be evolving parameters. Their values are determined based on sequence matching between interacting proteins. To model this process, we assume that each of the proteins is characterised by three bitstring sequences (S N ,S I and S O ) of length L (= 10): the first is a neutral reference sequence, the other two reflect the structure of, respectively, a protein input domain and an output domain, which form the interface of protein-protein interactions. The reference sequence has no phenotypic effects and merely accumulates neutral mutations, thus serving as a benchmark to detect adaptive evolution in the input and output domain (see Additional file 1 on the rate of molecular evolution).
The interaction coefficient μ i×j between two host proteins is determined by the Hamming distance \(H(S_{I}^{(i)}, S_{O}^{(j)})\) between the input domain of protein i and the output domain of protein j, according to the linear relationship:
$$ \mu_{i \times j} = 1 - \frac{2 H\left(S_{I}^{(i)}, S_{O}^{(j)}\right)}{L} \,. $$
Hence, the interaction is activating (μ i×j >0) when the number of matching bits between \(S_{I}^{(i)}\) and \(S_{O}^{(j)}\) is higher than L/2. Alternatively, the interaction is inhibiting (μ i×j <0) when the bitwise match is below 50 %. The determination of the interaction coefficients μ i×j based on sequence matching makes it difficult for proteins to evolve strong interactions with many partners. By taking into account this evolutionary constraint, our model differs from previous evolutionary models of signal transduction networks [24–27], which allowed the interaction coefficients to evolve independently of each other.
Host-parasite interactions and the degree of specificity
Equation (1) describes the dynamics of the immune network when the host is not challenged by a parasite. The same equation is used to model the induced response when the host interacts with a parasite, except that the summation over j then also includes a parasite protein P that interacts with the host receptor (c R×P=1; all other c i×P=0). The parasite protein is treated as a static inducer of the signalling cascade (Fig. 1, red arrow connecting P to R). That is, we do not consider the activity of P as a dynamic variable but substitute y P=1. The interaction coefficient μ R×P is calculated in two different ways, depending on whether recognition is specific or not. In the scenario that the interaction between parasite and receptor is non-specific, μ R×P=0.2, irrespective of the sequence of the parasite protein. By contrast, if the interaction is specific, μ R×P=0 if the sequence match between the input domain of the receptor and the output domain of P, \(1 - H(S_{I}^{(\mathrm {R})}, S_{O}^{(\mathrm {P})}) / L\), is less than 60 %, and μ R×P=1 otherwise. These assumptions are meant to reflect the common scenario that specific defence components are highly effective against a narrow range of enemies whereas non-specific components defend broadly with a lower efficacy.
The detection of the parasite (i.e., the activation of the receptor triggered by the presence of the parasite protein), can have subsequent downstream effects, such as on the activity of the two immune effectors. Their interaction with the parasite determines the probability of infection (Fig. 1, red arrows connecting ES and EN to P), which influences host survival as well as parasite reproductive success. The strength of the interaction between host effector i (= ES or EN) and the parasite is measured by the interaction coefficients ξ P×i , which are determined by bitstring matching, in a way similar to how the specific and non-specific receptor interactions are modelled. To be exact, \(\phantom {\dot {i}\!}\xi _{\mathrm {P} \times \mathrm {E}_{\mathrm {N}}} = 0.2\) for the non-specific effector, while the effectiveness of the specific immune effector depends on the Hamming distance between the output domain of ES and the input domain of P: \(\phantom {\dot {i}\!}\xi _{\mathrm {P} \times \mathrm {E}_{\mathrm {S}}} = 0\) if the sequence match \(1 - H(S_{I}^{(\mathrm {P})}, S_{O}^{(\mathrm {E}_{\mathrm {S}})}) / L\) is less than 60 % and \(\phantom {\dot {i}\!}\xi _{\mathrm {P} \times \mathrm {E}_{\mathrm {S}}} = 1\) otherwise.
The detection and the immune response against parasites frequently involve different parasite proteins. However, for clonally reproducing parasites this situation is equivalent to assuming a single parasite protein (as we do here) with separate output and input domains, \(S_{O}^{(\mathrm {P})}\) and \(S_{I}^{(\mathrm {P})}\), mediating interactions with, respectively, the host receptor and the immune effectors. Apart from the input and output domain, the parasite protein also contains a neutral bitstring of length L, which is used to quantify the rate of adaptive versus neutral sequence evolution (see Additional file 1 on the rate of molecular evolution).
Immune deployment and fitness
The efficacy E 0 and the fitness cost C 0 of the constitutive immune defence of a host against a particular parasite are determined by the baseline activities of the two effectors:
$$\begin{array}{*{20}l} E_{0} &= \xi_{\mathrm{P} \times \mathrm{E}_{\mathrm{S}}} \, y^{(0)}_{\mathrm{E}_{\mathrm{S}}} + \xi_{\mathrm{P} \times \mathrm{E}_{\mathrm{N}}} \, y^{(0)}_{\mathrm{E}_{\mathrm{N}}}\,, \end{array} $$
$$\begin{array}{*{20}l} C_{0} &= \kappa \left(y^{(0)}_{\mathrm{E}_{\mathrm{S}}} + y^{(0)}_{\mathrm{E}_{\mathrm{N}}} \right)\, \end{array} $$
where \(\phantom {\dot {i}\!}y^{(0)}_{\mathrm {E}_{\mathrm {S}}}\) and \(\phantom {\dot {i}\!}y^{(0)}_{\mathrm {E}_{\mathrm {N}}}\) are equilibrium solutions of equation system (1), not including the interaction with the parasite. The parameter κ measures the marginal cost of expression of the specific and non-specific immune effector (i.e., the two responses are assumed to be equally costly).
A host may be challenged by a single randomly chosen parasite with an encounter probability that is varied as a parameter in the analysis. When a parasite is encountered, the activities of the immune effector can change as described in the previous section. The efficacy E ∗ and cost C ∗ of the induced immune defence are evaluated as:
$$\begin{array}{*{20}l} E^{*} &= \xi_{\mathrm{P} \times \mathrm{E}_{\mathrm{S}}} y^{*}_{\mathrm{E}_{\mathrm{S}}} + \xi_{\mathrm{P} \times \mathrm{E}_{\mathrm{N}}} y^{*}_{\mathrm{E}_{\mathrm{N}}}, \end{array} $$
$$\begin{array}{*{20}l} C^{*} &= \kappa \left(y^{*}_{\mathrm{E}_{\mathrm{S}}} + y^{*}_{\mathrm{E}_{\mathrm{N}}} \right)\, \end{array} $$
where \(y^{*}_{\mathrm {E}_{\mathrm {S}}}\) and \(y^{*}_{\mathrm {E}_{\mathrm {N}}}\) are the equilibrium solutions of equation system (1) including the interaction between the parasite and the host receptor.
The above definitions of efficacy and cost are intended to capture the relationship between the extent of immune response and the expression cost of the effector proteins. As a consequence of this relationship, hosts are faced with a trade-off between their ability to resist infection and minimising the cost of using immunity. Moreover, hosts need to balance the tradeoff between the costs and benefits of immunity under two different conditions: before and during infection.
Host survival before infection, s 0=1−C 0, depends only on the cost of constitutive defence, which is minimised when \(\phantom {\dot {i}\!}y^{(0)}_{\mathrm {E}_{\mathrm {S}}} = y^{(0)}_{\mathrm {E}_{\mathrm {N}}} = 0\). However, during an infection, survival is also affected by the efficacy of defence. In particular, the probability of survival of an infected host, s ∗, is calculated as:
$$ \begin{aligned} s^{*} =&\, \left(\left(1 - C_{0}\right)\left(1 - \nu \, e^{-E_{0}} \right) \right)^{\delta}\\ &\times \left(\left(1 - C^{*}\right)\left(1 - \nu \, e^{-E^{*}} \right) \right)^{1-\delta} \,. \end{aligned} $$
This expression takes into account the fact that the induced immune response is not mounted immediately when a parasite is encountered, so that the host is initially only equipped with constitutive immunity (Fig. 2). The induction delay, relative to the length of the infection, is determined by the parameter δ. During both phases of the infection (before and after the induced response is activated), survival depends on two factors that interact multiplicatively: the cost of immune expression, which is modelled as in the pre-infection phase, and parasite-induced mortality, which is proportional to the maximum virulence of the parasite, ν, and the probability of infection. The latter is a decreasing function of the efficacy of immune defence, e −E (cf. [28]). Our model considers highly virulent parasites; up to 99 % of host fitness can be lost from an infection, should the immune system fail entirely. The overall fitness of the host is calculated as the product of the pre- and post-infection survival, i.e., W host=s 0×s ∗.
Immune effector activity and corresponding network architecture. A host expresses a fixed level of constitutive effector activity (green box; \(y^{0}_{\mathrm {E_{S}}}\) and \(y^{0}_{\mathrm {E_{N}}}\) in Eqs. 3 and 4) throughout its lifetime, enabled by the interactions between the constitutively active protein (C) and the effectors (ES and EN). The induced effector activity (blue box) is defined as the difference between the effector activity following the parasite-receptor interaction (\(y^{*}_{\mathrm {E_{S}}}\) and \(y^{*}_{\mathrm {E_{N}}}\) in Eqs. 5 and 6) and the constitutive activity. This additional activity is triggered when a parasite (P) is detected by the receptor (R). A time delay is assumed between encountering a parasite and triggering the induced response. Both the cost and benefit of defence are realised as a function of the effector activity (Eqs. 3–6)
The fitness of a parasite is directly proportional to its probability of successful infection [28], which depends on the parasite's ability to evade both the constitutive and the induced immune response:
$$ W_{\text{parasite}} = e^{-\left(\delta E_{0} + (1-\delta) E^{*}\right)} \,. $$
Evolutionary simulation
Evolutionary simulations were initialised with randomly created host and parasite populations each consisting of 2000 genetically diverse haploid individuals. Generations were non-overlapping, population sizes were kept fixed (i.e., the densities of both host and parasite populations were assumed to be regulated by external mechanisms), and both host and parasite populations were well mixed. Host individuals produced offspring by sexual reproduction. The parents of each offspring were sampled from the population using a fitness-weighted lottery scheme with replacement. Recombination was allowed to occur between, but not within, proteins. Parasites were assumed to reproduce asexually, based on a fitness-weighted lottery with replacement. Genetic variation in the host and parasite populations was introduced by point mutations in the protein bitstring sequences, which occurred at a rate of 1 % per individual per generation. All results presented are the average over 20 simulations, each run for 10000 generations with a burn-in period of 5000 generations to allow for the build-up of genetic variation and to eliminate initial effects. Simulation programmes were written in C++ (see Additional file 2) and statistical analyses were carried out in R 3.0.1.
Our analyses focus on three different scenarios. We first consider non-specific detection and focus on the role of the non-specific effector in the elimination of the parasite, thus establishing a baseline for the two other scenarios, which consider specific defence components at the downstream and upstream end of the immune signalling cascade. The second scenario is similar to the first one, except that we concentrate on the contribution of the specific effector towards immunity. In the third scenario, we study the effect of specific detection, by configuring the immune network with a specific receptor. For this case, we present only the activity of the non-specific effector, since the effects of specific detection and specific elimination were found to be additive. Supplementary results concerning the rate of evolution and the interaction patterns between proteins that emerged through evolution are provided in the Additional files 1 and 3.
1) No parasite coevolution: non-specific detection and non-specific elimination
Non-specific defence is triggered by generic parasite signals [10]. In our model, non-specific immune components interact with an encountered parasite regardless of host-parasite genotype-matching, such that non-specific defence is unaffected by antagonistic parasite coevolution. Despite adopting a different modelling approach, the non-specific components of our model mirror predictions from previous models examining the optimal combination of constitutive versus induced defence: we observe the evolution of networks that implement a mixed immune strategy of constitutive and induced defence. Moreover, the optimal balance of the two defence strategies is found to depend on the probability of parasite encounter, the cost of immune defence and the induction delay.
In particular, our model predicts that the relative amount of constitutive to induced defence increases with the probability of parasite encounters (Fig. 3 a; solid lines), in agreement with the existing theoretical literature [5–8]. While effector expression is wholly induced through the receptor when the encounter probability is low, the induced expression decreases as the effector starts to be activated by the constitutively active pathway. The lack of constitutive defence at low rates of parasite encounter (Fig. 4 a; top row) is explained by the fact that the cost outweighs the benefit of pre-emptive allocation into defence if threats are rarely encountered. When the encounter probability is high (Fig. 4 b; top row), mixed strategies of constitutive and induced defence evolve. The optimal balance between the two depends on the physiological constraints of the two activation strategies (Fig. 4 b; top row). When the cost of using one's immune system is low and induction delay is high, defence relies on constitutive activation. In contrast, induced activation is favoured over pre-emptive investment when it is readily deployable and the cost of immunity is so high that it is cost ineffective to maintain defence constitutively.
Effect of encounter probability. a Non-specific effector (EN) activity against the probability of parasite encounters. The green lines indicate the level of constitutive expression while the blue lines indicate the induced expression level. The results of the non-specific detection case (Scenario 1) are the solid lines and those of the specific detection case (Scenario 3) are shown by the dashed lines. b Specific effector efficacy (ES) and (c) specific receptor (RS) activity against the probability of parasite encounters. The horizontal grey line is the non-specific receptor activity and non-specific effector efficacy in (b) and (c) respectively. The mean and standard error bands across 20 replicate simulations are shown. The cost of immunity and induction delay are both set low (i.e., 0.2); the result is qualitatively identical for any combination of the range in cost of immunity and induction delay explored (0.2 to 0.8; results not shown). Fixed parameter values are as follows: sequence length = 10, spontaneous deactivation rate = 0.3, host and parasite mutation rate = 0.01, host and parasite population size = 2000 and maximum virulence = 0.99
Effector activity. Constitutive and induced effector activity under (a) low and (b) high parasite encounter probability (0.2 and 1.0, respectively) and three different host-parasite coevolutionary scenarios: no parasite coevolution (Scenario 1: non-specific detection and elimination; top row), parasite coevolution against the host effector (Scenario 2: non-specific detection and specific elimination; middle row), and parasite coevolution against the host receptor (Scenario 3: specific detection and non-specific elimination; bottom row). The effector for which the activity level is shown is highlighted in yellow. Fixed parameter values are as given in Fig. 3 caption
2) The effects of parasite coevolution against host effector: non-specific detection and specific elimination
In our second scenario, we focus on the specific effector, which allows the host genotype-specific elimination of parasites and opens up the possibility for coevolution between the specific effector and the parasite input sequence. When the encounter probability is low, there is very little constitutive activation of the specific effector. This is partially because induced activation is a more cost-effective option as seen above (Fig. 4 a; middle row). Here, constitutive activation is further hampered by the fact that the specific effector is under weak selection, since it rarely encounters a parasite. As a result, the host does not evolve fast enough to maintain an effective specific immune response in the coevolutionary race with the parasite. As the parasite encounter rate increases, the specific effector is used more frequently, creating the opportunity for selection to maintain a cost-effective specific immune response (Figs. 3 b and 4 b).
Hosts enjoy a greater benefit of immunity by allocating resources to an effective effector. Therefore, when the encounter probability is high, the specific effector is activated more than the non-specific effector, both through the constitutive and the induced activation pathway. This finding mirrors the insights of Jokela et al. [19] that the magnitude of immune responses should reflect the effectiveness of the immune system, which is subjected to parasite coevolution. Nonetheless, the balance of constitutive versus induced activation of the specific effector is similar to that of the non-specific effector.
3) The effects of parasite coevolution against host receptor: specific detection and non-specific elimination
In the third scenario, we consider that the immune system is induced by a specific receptor and we concentrate once more on the activity of the non-specific effector. This set-up allows for genotype-specific detection of parasites and opens up the possibility for coevolution between the specific receptor and the parasite output sequence. Detection of a parasite by the host receptor is the first step of any induced immune response. Since the chance of successful infection increases dramatically if a parasite manages to evade detection, host immune receptors experience ample antagonistic coevolutionary pressures.
When the encounter probability is low, constitutive defence is uneconomical, forcing the defence system to rely upon induction, as we saw in the previous sections. However, when the host hardly ever encounters a parasite, the host receptors are unable to evolve fast enough to maintain the close sequence match with the parasite that is required to enable detection (Fig. 3 c). Therefore, the specific receptor is rarely activated to induce effector expression (Fig. 4 a; bottom row). This finding indicates that hosts would adapt to tolerate rather than attempt to resist infection if parasite detection is unsuccessful (even despite having the possibility of using constitutive defence), corroborating the finding by Jokela et al. [19] that hosts should tolerate rather than resist infection when defence is ineffective.
Though constitutive expression increases, as before, when the encounter rate increases (Fig. 3 a; dashed lines), the same happens with the induced expression, because parasite detection by the specific receptor improves as it is used more regularly and thereby exposed to selection more often (Fig. 3 c). The resulting pattern is in contrast with the non-specific receptor scenario and other host-centric models [5–8] which predict that the relative amount of constitutive to induced defence increases with increasing parasite encounter probability (Fig. 3).
A second counterintuitive result at high encounter probability is that increased induction delay, which diminishes the benefit of induction, elevates the level of defence induced by the specific receptor (Fig. 4 b; bottom row). This is explained by the fact that the probability of infection depends to a large degree on receptor performance when protection relies predominantly upon induced defence (i.e., when the cost of immunity is great and induced delay is short). Consequently, parasites are under strong positive selection pressure to evade detection when induction is most beneficial to the host (Additional file 1), resulting in the evolutionary diversification of the parasite population (Fig. 5 a). Parasite diversification prevents hosts from adequately responding to all different parasite genotypes, reducing the average receptor and, hence, effector activity. To compensate for the resulting loss of protection, hosts invest more heavily in constitutive defence (Fig. 4 b; bottom row) by evolving an elevated level of constitutive activation (Additional file 3). On the other hand, when host fitness depends less strongly on the induced immune response (i.e., when induction delay is larger), the selection pressure on parasites to escape detection is less severe, reducing its ability to support the maintenance of genetic variation (Fig. 5 a). Therefore, hosts are better able to detect the parasite, leading to a higher average level of activation of the specific receptor (Fig. 5 b) and, consequently, an elevated induced effector response.
Parasite coevolution and receptor activity. a Parasite diversity measured as the pairwise genetic distance of parasites coevolving against hosts with a specific receptor (RS), and (b) the corresponding host RS activity, which equates to the detection rate of encountered parasites. Fixed parameter values are as given in Fig. 3 caption
By allowing the interactions among host immune proteins to evolve freely, we also gain some insight into how the architecture of an immune signal transduction network may be shaped by host-parasite coevolution. Our simple network shows that the specific effector is activated, mostly indirectly, through the non-specific effector (Fig. 6): the indirect activation from the non-specific effector (Fig. 6 c) is much stronger than the direct input from either the constitutive (Fig. 6 a) or the receptor protein (Fig. 6 b). This indirect activation is due to a trade-off in protein interactions imposed by sequence matching so that the network is genetically constrained from optimising all parts of the network simultaneously. The result indicates that in order to highly express a specific effector, the non-specific effector must also be highly activated, suggesting that the non-specific effector provides the baseline defence and the specific effector plays a supplementary role.
Specific effector activation. Evolved protein interactions under high encounter probability (=1.0). The protein network diagram depicts interacting proteins. Arrow colours refer to the constitutive (a, green) and induced (b, blue) interactions towards the specific effector (ES), and the regulatory input from the non-specific (EN) to the specific (ES) effector (c, purple). Fixed parameter values are as given in Fig. 3 caption. See the Additional file 3 for the full list of evolved protein interactions
The present study was motivated by calls to incorporate parasite evolution into the study of host adaptation [9, 19, 29]. Most theoretical studies of the evolution of host defence strategies are host-centric [19]; meaning that hosts evolve to optimise their strategy while parasites are unable to counter-adapt to changing host strategies. We here demonstrate that parasite coevolution against specific immune defence alters the prediction of optimal deployment strategies based on such models, and that the effect of parasite coevolution varies between different immune components. Coevolution at the effector level does not alter the optimal balance between constitutive and induced defence qualitatively. Yet, investment into defence could exceed what is expected from the non-specific effectors if the specific effector is more potent. On the other hand, coevolution at the receptor level obscures the prediction of host-centric models [5–8], that the relative investment into constitutive over induced defence increases with parasite encounter probability. The cause of the discrepancy between host-centric models and the current coevolutionary analysis is that the balance of control over the outcome of antagonistic coevolution shifts between host and parasite depending on ecological conditions and the role of physiological constraints.
Using a within-host model, Hamilton et al. [7] show that variability in parasite growth rates selects for the host to adapt a combination of constitutive and induced defences because uncertainty favours induced over constitutive defence. Hamilton et al. [7] implemented parasite variability as a fixed parameter. Here, we show that specific host defence selects for adaptive diversification of the parasite population, as one would expect from models of host-parasite coevolution (e.g. [30–32]). This evolutionary feedback between host and parasite populations causes parasite diversity to correlate negatively with the strength of immune induction (Fig. 5), complicating the interpretation of the role of parasite variability in favouring induced defence.
In our model, hosts and parasites have symmetrical potential for adaptation; they are equal in population size, mutation rate and generation time. However, parasites are often thought to have an evolutionary edge over their hosts for having a larger population size and a shorter generation time. When parasites undergo a faster rate of evolution than their host, as is commonly believed [1], the effect of parasite diversity on the specific receptor activity is expected to be even greater than shown in the present study. Therefore, predictions from host-centric models that do not consider parasite coadaptation are likely to be particularly misleading for hosts facing fast evolving parasites, such as viruses.
Our present model made several simplifying assumptions about parasite infection dynamics. First, constant host and parasite population sizes were assumed, as is commonly done in theoretical studies of genotype-specific host-parasite interactions. Including the population dynamics of host and parasite populations is an important ingredient to better capture the eco-evolutionary feedback between the interacting species. Second, a single host was not allowed to be challenged by multiple parasites, which excluded competition between parasite genotypes as a source of selection. Third, within-host dynamics of parasite growth and immunological variables were ignored because our model focused on the effects of genotype-specific interactions from a population perspective. Future studies may benefit from considering within-host dynamics because such an approach may open possibilities for empirical validation of a model with the available data on temporal expression patterns of immune proteins [33–36]. Finally, since our model only makes rather generic assumptions about the architecture of the immune system, the results may apply to a broad class of species that can alter their relative investment in constitutive versus induced defence.
The present analysis indicates that interactions of multiple immune components and evolutionary feedbacks shape the evolution of host defence strategies. To gain a more complete understanding of immune systems subjected to coevolution, crucial empirical challenges await in, first, elucidating mechanisms and functions of basic building blocks, and second, characterising molecular interactions among those components. Invertebrate immune systems, especially that of Drosophila, for which a wealth of molecular information is available, present obvious candidates to pursue such challenges in the future [37]. A promising avenue in this area of research is to integrate empirical work on well-characterised model systems with theoretical models of immune network evolution to generate testable hypotheses on the functional roles of building blocks and pathways in immune systems consisting of a complex network of molecular interactions [1].
Schmid-Hempel P. Evolutionary Parasitology: the Integrated Study of Infections, Immunology, Ecology, and Genetics. New York: Oxford University Press New York; 2011.
Sheldon BC, Verhulst S. Ecological immunology: costly parasite defences and trade-offs in evolutionary ecology. Trends Ecol Evol. 1996; 11(8):317–21.
Ardia DR, Parmentier HK, Vogel LA. The role of constraints and limitation in driving individual variation in immune response. Funct Ecol. 2011; 25(1):61–73.
Lemaitre B, Hoffmann J. The host defense of Drosophila melanogaster. Annu Rev Immunol. 2007; 25:697–743.
Shudo E, Iwasa Y. Inducible defense against pathogens and parasites: optimal choice among multiple options. J Theor Biol. 2001; 209(2):233–47.
Shudo E, Iwasa Y. Optimal defense strategy: storage vs. new production. J Theor Biol. 2002; 219(3):309–23.
Hamilton R, Siva-Jothy M, Boots M. Two arms are better than one: parasite variation leads to combined inducible and constitutive innate immune responses. P Roy Soc B-Biol Sci. 2008; 275(1637):937–45.
Westra ER, van Houte S, Oyesiku-Blakemore S, Makin B, Broniewski JM, Best A, Bondy-Denomy J, Davidson A, Boots M, Buckling A. Parasite exposure drives selective evolution of constitutive versus inducible defense. Curr Biol. 2015; 25(8):1043–1049.
Schmid-Hempel P, Ebert D. On the evolutionary ecology of specific immune defence. Trends Ecol Evol. 2003; 18(1):27–32.
Frank SA. Immunology and Evolution of Infectious Disease. Princeton: Princeton University Press; 2002.
Murphy KM. Janeway's Immunobiology. New York: Garland Science; 2011.
Rowley AF, Powell A. Invertebrate immune systems–specific, quasi-specific, or nonspecific?J Immunol. 2007; 179(11):7209–214.
Schulenburg H, Boehnisch C, Michiels NK. How do invertebrates generate a highly specific innate immune response?Mol Immunol. 2007; 44(13):3338–344.
Armitage SA, Peuß R, Kurtz J. Dscam and pancrustacean immune memory–a review of the evidence. Dev Comp Immunol. 2015; 48(2):315–23.
Carius HJ, Little TJ, Ebert D. Genetic variation in a host-parasite association: potential for coevolution and frequency-dependent selection. Evolution. 2001; 55(6):1136–1145.
Silverman N, Paquette N, Aggarwal K. Specificity and signaling in the Drosophila immune response. Invert Surviv J. 2009; 6(2):163.
Jiggins FM, Kim KW. Contrasting evolutionary patterns in Drosophila immune receptors. J Mol Evol. 2006; 63(6):769–80.
Lazzaro BP. Natural selection on the Drosophila antimicrobial immune system. Curr Opin Microbiol. 2008; 11(3):284–9.
Jokela J, Schmid-Hempel P, Rigby MC. Dr. Pangloss restrained by the Red Queen–steps towards a unified defence theory. Oikos. 2000; 89(2):267–74.
Frank SA. Specific and non-specific defense against parasitic attack. J Theor Biol. 2000; 202(4):283–304.
Lapchin L. Host-parasitoid association and diffuse coevolution: When to be a generalist?Am Nat. 2002; 160(2):245–54.
Jerne NK. Towards a network theory of the immune system. Ann Immunol. 1974; 125C(1-2):373–89.
Hoffmann G. A theory of regulation and self-nonself discrimination in an immune network. Eur J Immunol. 1975; 5(9):638–47.
Salathé M, Soyer OS. Parasites lead to evolution of robustness against gene loss in host signaling networks. Mol Syst Biol. 2008; 4(1):202.
Soyer OS, Salathé M, Bonhoeffer S. Signal transduction networks: topology, response and biochemical processes. J Theor Biol. 2006; 238(2):416–25.
Soyer OS, Bonhoeffer S. Evolution of complexity in signaling pathways. Proc Natl Acad Sci. 2006; 103(44):16337–16342.
Soyer OS, Pfeiffer T, Bonhoeffer S. Simulating the evolution of signal transduction pathways. J Theor Biol. 2006; 241(2):223–32.
Nicholson AJ, Bailey VA. The balance of animal populations part I. Proc Zool Soc Lond. 1935; 105(3):551–98.
Lambrechts L, Fellous S, Koella JC. Coevolutionary interactions between host and parasite genotypes. Trends Parasitol. 2006; 22(1):12–16.
Hamilton WD. Sex versus non-sex versus parasite. Oikos. 1980; 35(2):282–90.
Frank SA. Specificity versus detectable polymorphism in host–parasite genetics. P Roy Soc B-Biol Sci. 1993; 254(1341):191–7.
Parker MA. Pathogens and sex in plants. Evol Ecol. 1994; 8(5):560–84.
De Gregorio E, Spellman PT, Rubin GM, Lemaitre B. Genome-wide analysis of the Drosophila immune response by using oligonucleotide microarrays. Proc Natl Acad Sci. 2001; 98(22):12590–12595.
Irving P, Troxler L, Heuer TS, Belvin M, Kopczynski C, Reichhart JM, Hoffmann JA, Hetru C. A genome-wide analysis of immune responses in Drosophila. Proc Natl Acad Sci. 2001; 98(26):15119–15124.
Vodovar N, Vinals M, Liehl P, Basset A, Degrouard J, Spellman P, Boccard F, Lemaitre B. Drosophila host defense after oral infection by an entomopathogenic Pseudomonas species. Proc Natl Acad Sci. 2005; 102(32):11414–11419.
Wertheim B, Kraaijeveld AR, Schuster E, Blanc E, Hopkins M, Pletcher SD, Strand MR, Partridge L, Godfray HCJ. Genome-wide gene expression in response to parasitoid attack in Drosophila. Genome Biol. 2005; 6(11):94.
Wertheim B. Genomic basis of evolutionary change: evolving immunity. Front Genet. 2015; 6:222.
We thank Katie O'Dwyer, Megan Greischar, Samuel Alizon and members of the expertise group Theoretical Research in Evolutionary Life Sciences at the University of Groningen for useful comments and discussions. This work was financially supported by the European Research Council (Starting Grant 309555 to GSvD) and by the Netherlands Organisation for Scientific Research (Vidi Grant 864.11.012 to GSvD).
Groningen Institute for Evolutionary Life Sciences, University of Groningen, P.O. Box 11103, CC Groningen, 9700, The Netherlands
Tsukushi Kamiya, Leonardo Oña, Bregje Wertheim & G. Sander van Doorn
Department of Ecology and Evolutionary Biology, University of Toronto, 25 Willcocks Street, Toronto, Canada
Tsukushi Kamiya
Leonardo Oña
Bregje Wertheim
G. Sander van Doorn
Correspondence to Tsukushi Kamiya.
TK and GSvD conceived the project with inputs from BW. TK, LO and GSvD designed and coded the simulation model and TK carried out data processing and graphing. TK wrote the manuscript with inputs from GSvD, BW and LO. All authors read and approved the final manuscript.
Additional file 1
The rate of molecular evolution. The rate of evolution for each protein including the parasite presented as the log(Ka/Ks) shown for the parameter combinations presented in Fig. 4. (PDF 176 kb)
C++ source code of the simulation programme. (ZIP 25.9 kb)
Evolved protein interactions. Protein interactions emerged through evolution shown for the parameter combinations presented in Fig. 4. (PDF 142 kb)
Kamiya, T., Oña, L., Wertheim, B. et al. Coevolutionary feedback elevates constitutive immune defence: a protein network model. BMC Evol Biol 16, 92 (2016). https://doi.org/10.1186/s12862-016-0667-3
Received: 24 December 2015
Optimal defence
Host-parasite coevolution
Constitutive immunity
Induced immunity
Immune network evolution
Individual-based simulation
Theories and models | CommonCrawl |
Biotechnology for Biofuels and Bioproducts
Development of modified HCH-1 kinetic model for long-term enzymatic cellulose hydrolysis and comparison with literature models
Chao Liang1,
Chao Gu2,
Jonathan Raftery1,
M. Nazmul Karim1 &
Mark Holtzapple1
Biotechnology for Biofuels volume 12, Article number: 34 (2019) Cite this article
Enzymatic hydrolysis is a major step for cellulosic ethanol production. A thorough understanding of enzymatic hydrolysis is necessary to help design optimal conditions and economical systems. The original HCH-1 (Holtzapple–Caram–Humphrey–1) model is a generalized mechanistic model for enzymatic cellulose hydrolysis, but was previously applied only to the initial rates. In this study, the original HCH-1 model was modified to describe integrated enzymatic cellulose hydrolysis. The relationships between parameters in the HCH-1 model and substrate conversion were investigated. Literature models for long-term (> 48 h) enzymatic hydrolysis were summarized and compared to the modified HCH-1 model.
A modified HCH-1 model was developed for long-term (> 48 h) enzymatic cellulose hydrolysis. This modified HCH-1 model includes the following additional considerations: (1) relationships between coefficients and substrate conversion, and (2) enzyme stability. Parameter estimation was performed with 10-day experimental data using α-cellulose as substrate. The developed model satisfactorily describes integrated cellulose hydrolysis data taken with various reaction conditions (initial substrate concentration, initial product concentration, enzyme loading, time). Mechanistic (and semi-mechanistic) literature models for long-term enzymatic hydrolysis were compared with the modified HCH-1 model and evaluated by the corrected version of the Akaike information criterion. Comparison results show that the modified HCH-1 model provides the best fit for enzymatic cellulose hydrolysis.
The HCH-1 model was modified to extend its application to integrated enzymatic hydrolysis; it performed well when predicting 10-day cellulose hydrolysis at various experimental conditions. Comparison with the literature models showed that the modified HCH-1 model provided the best fit.
Biomass is the only renewable energy resource that can be directly converted to liquid fuels and chemicals. The largest biomass feedstock is lignocellulose, which is found globally in many forms. Converting lignocellulose into biofuels could relieve shortages of liquid fuels and reduce dependence on fossil energy.
In the United States, ethanol is the dominant biofuel, which is usually produced from corn, an important food for animals and humans. To prevent food shortages, cellulosic ethanol is an attractive alternative. In general, there are four major steps for cellulosic ethanol production: pretreatment, hydrolysis, fermentation, and separation. Among these processes, hydrolysis accounts for a large portion (~ 30%) of the total costs [1]. To compete with corn ethanol and petroleum-derived gasoline, enzymatic hydrolysis needs optimization and cost reduction [2]; therefore, a thorough understanding of enzymatic hydrolysis is necessary to help design optimal conditions and economical systems.
During the last several decades, various theoretical and empirical models have been developed to simulate enzymatic hydrolysis of cellulose [3,4,5,6]. Because they lack a theoretical foundation, empirical models cannot be applied beyond the range of the data; therefore, this paper only focuses on mechanistic (and semi-mechanistic) models.
In 1984, Holtzapple et al. [3] proposed a generalized mechanistic model for cellulose hydrolysis termed the HCH-1 (Holtzapple–Caram–Humphrey-1) model. Figure 1 shows the reaction mechanism of the HCH-1 model [3]. As shown in the figure, free enzyme (Ef) adsorbs onto a free cellulose site (\(G_{x}^{f}\)) to become adsorbed enzyme (Ea), and then complexes with the cellulose to become enzyme–substrate complex (EGx). This complex catalyzes the hydrolysis of the cellulose site to obtain soluble product (Gs) with reaction rate k. All enzyme species can complex with product to become inhibited enzyme (\(G_{s} E^{f} ,\;\; G_{s} E^{a}\), and GsEGx). For simplicity, the product-binding constant (β) is assumed to be the same for all the enzyme species. In addition, the adsorption constant (δ) and the complexing constant (η) are assumed not to be affected by the binding of product to the enzyme [3].
Reaction mechanism for the HCH-I model [3]
The rate-limiting step is the hydrolysis; therefore, the reaction velocity (V) is proportional to the concentration of uninhibited enzyme–substrate complex (EGx). To express the reaction velocity in terms of known variables, substitutions can be made for EGx using material balances of substrate and enzyme species, thus, yielding the HCH-1 model (Eq. 1). The detailed model development is described in [3].
$$V = \frac{{\kappa \left[ {G_{x} } \right]\left[ E \right]i}}{{\alpha + \varphi \left[ {G_{x} } \right] + \varepsilon \left[ E \right]}}$$
$$i = \frac{1}{{\left. {1 + \beta_{1} [G_{1} } \right] + \beta_{2} \left[ {G_{2} } \right]}}$$
$$\begin{array}{*{20}c} { \varphi = \frac{{\left[ {G_{x} } \right] - \alpha - \varepsilon \left[ E \right] + \sqrt {\left( {\left[ {G_{x} } \right] - \alpha - \varepsilon \left[ E \right]} \right)^{2} + 4\alpha \left[ {G_{x} } \right]} }}{{2\left[ {G_{x} } \right]}}} \\ \end{array}$$
where Gx is the cellulose concentration (g/L, equivalent to glucose), G1 is the glucose concentration (g/L), G2 is the cellobiose concentration (g/L, equivalent to glucose), E is the enzyme concentration (g/L), α is the lumped adsorption constant (\(\alpha = \frac{\eta \delta }{\eta + 1}\), g/L), κ is the lumped kinetic constant (\(\kappa = \frac{k}{\eta + 1}\), h−1), β1 is the glucose binding constant (L/g), β2 is the cellobiose binding constant (L/g), ɛ is the number of cellulose sites covered by adsorbed or complexed enzyme (dimensionless), i is the fraction of total enzyme that is active (dimensionless), and \(\varphi\) is the fraction of total cellulose sites which are free (dimensionless).
Unlike the classic Michaelis–Menten model, the HCH-1 model includes a parameter ɛ that describes the number of reactive sites covered by the enzymes [3, 7]. Furthermore, the HCH-1 model includes non-competitive inhibition by sugar products.
Unlike empirical models that apply only in the range where the data were taken, the HCH-1 model is mechanistic (Fig. 1) and, therefore, has broader applicability. As a mechanistic model, it applies to individual enzyme species; however, it has also been applied successfully to an enzyme cocktail in which the mixture is treated as a single "lumped" enzyme. Using the initial-rate data for pretreated biomass hydrolyzed by an enzyme cocktail, Brown et al. [7] compared mechanistic models and showed that the HCH-1 model provided the best fit to experimental data.
Previous studies show that, at high degrees of conversion, the hydrolysis rate drops by 2–3 orders of magnitude [8, 9]. The following factors contribute to the decreasing hydrolysis rates: (1) enzyme deactivation, (2) product inhibition, (3) decreased substrate reactivity, (4) decreased substrate accessibility, and (5) decreased synergism between cellulases [10]. In short-term enzymatic hydrolysis, these factors are not important and, therefore, are usually not incorporated into models that predict initial rates. However, in long-term batch saccharification, the reaction time is usually 3 to 5 days. As the reaction proceeds, the coefficients in short-term enzymatic hydrolysis models, such as HCH-1, may change because of the enumerated factors above. To describe long-term integrated enzymatic hydrolysis, the initial-rate models must be modified.
In this study, the original HCH-1 model was modified to describe 10-day enzymatic cellulose hydrolysis with commercial enzyme cocktail CTec2. The HCH-1 mechanism (Fig. 1) applies to individual enzymes in the cocktail; however, modeling each enzyme component is exceedingly complex. Understanding the kinetics of each enzyme component would be useful when optimizing the cocktail; however, this study uses a cocktail with defined components. Our approach is to treat the enzyme cocktail as a single "lumped" enzyme; hence, the resulting "lumped" parameters reflect the collective kinetics of the cocktail, not the individual components. To describe long-term enzymatic hydrolysis, this study investigates the relationships between the "lumped" parameters in the HCH-1 model and substrate conversion. The sensitivities of parameters in the modified model were analyzed. In addition, literature models for long-term (> 48 h) enzymatic hydrolysis were summarized and compared to the modified HCH-1 model.
The substrate used for all experiments was α-cellulose (Sigma-Aldrich, C8002). Compositional analysis showed that the substrate contained glucan 78.5% and xylan 14.4% [11].
The enzyme used in this study was Novozymes Cellic® CTec2 (lot# VCPI 0007), a blend of aggressive cellulases with high levels of β-glucosidases and hemicellulases that degrade lignocellulose into sugars [12]. The protein concentration was determined to be 294 mg protein/mL with Pierce BCA assay [11]. Before use, the enzyme solution was diluted ten times with deionized (DI) water.
Citrate buffer
To maintain relatively high enzyme activity, citrate buffer (0.1 M) with a pH of 4.8 was used in enzymatic hydrolysis experiments. To prepare the buffer, citric acid monohydrate and trisodium citrate dihydrate were added to DI water.
To prevent the growth of contaminating microorganisms that could consume produced sugars, an antibiotic cocktail was added. To prepare the solutions, tetracycline powder was dissolved in an aqueous solution of 70% ethanol at 10 g/L and cycloheximide powder was dissolved in DI water at 10 g/L.
Enzymatic hydrolysis
In the enzymatic hydrolysis experiments, desired amounts of α-cellulose, glucose, and DI water together with 125 mL citrate buffer, 2 mL tetracycline solution, and 1.5 mL cycloheximide solution were added to a 1-L centrifuge bottle in sequence and then preheated. When the mixture reached 50 °C, enzymes were added. Then, the centrifuge bottle (total working volume of 250 mL) was placed in the incubator at 50 °C for 10 days with an axial rotation of 2 rpm. Liquid samples of 0.5 mL were taken periodically and submerged in boiling water for 20 min to deactivate the enzymes (note: the volume of liquid sample is small relative to the total slurry volume, so it is assumed to have a negligible impact on substrate concentration). Then, to determine the glucose concentration, the samples were filtered and analyzed by a high-performance liquid chromatography (HPLC), which was equipped with a pair of de-ashing guard columns (Bio-Rad Micro-Guard de-ashing cartridges, 30 mm × 4.6 mm) and an HPLC carbohydrate analysis column (Bio-Rad Aminex HPX-87P, 300 mm × 7.8 mm).
Selection of hydrolysis conditions
Experiments for model fitness
Based on our previous study [11], 16 enzymatic hydrolysis conditions were tested including four different substrate concentrations (40, 60, 80, and 100 g/L), two different enzyme loadings (2 and 5 mg protein/g of dry biomass (mg/g)), and two different initial glucose concentrations (0 and 33 g/L).
Experiments for model predictions
Three enzymatic hydrolysis conditions—which were different from the conditions used for model fitness—were tested for model predictions: (1) substrate concentration: 40 g/L, enzyme loading: 1 mg/g, initial glucose concentration: 0 g/L; (2) substrate concentration: 70 g/L, enzyme loading: 1 mg/g, initial glucose concentration: 28 g/L; (3) substrate concentration: 100 g/L, enzyme loading: 5 mg/g, initial glucose concentration: 28 g/L.
Enzyme stability
Enzyme stability was measured by quantifying the soluble protein concentration over the course of 20 days. In this experiment, the desired amount of CTec2 was added to the preheated mixture of citrate buffer, DI water, and antibiotic cocktail. The resulting solution was placed in the incubator at 50 °C. Samples of 0.5 mL were taken periodically and then centrifuged at 13,000 rpm for 10 min. The protein concentration of the supernatant was measured by the Pierce BCA method.
Modification of HCH-1 model
Simulation of enzyme stability
Wallace et al. [13] reported that unproductive binding with lignin and thermal deactivation may play a significant role in enzyme deactivation. Considering the substrate used in this study is lignin-free, we assume that enzyme deactivation is solely due to thermal deactivation. Rosales-Calderon et al. [14] observed that the protein concentration of a mixture of glucanase and β-glucosidase dropped 34% after incubating at 50 °C for 4 days. It was hypothesized that the enzyme proteins suffered a structural change at 50 °C, which led to protein aggregation and precipitation. Additives, whose concentration was assumed constant and proportional to the initial enzyme protein concentration, were supposed to be present in the cocktail to stabilize the enzyme protein against aggregation. Equation 2 incorporates the presence of additives and is proposed to model protein stability [14]. The development of Eq. 2 is described in detail by Rosales-Calderon et al. [14].
$$\begin{array}{*{20}c} { - \frac{{\left. {{\text{d}}[E} \right]}}{{{\text{d}}t}} = k_{1} \left[ E \right] - k_{2} \left( {\left[ {E_{0} } \right] - \left[ E \right]} \right)\left[ {E_{0} } \right]} \\ \end{array} ,$$
where E is the native enzyme protein concentration (g/L), E0 is the initial enzyme protein concentration (g/L), and k1 and k2 are the rate constants (h−1).
The stability of CTec2 with three different initial concentrations was tested. Equation 2 was used to fit the experimental data.
The HCH-1 model was modified by the following steps:
Step 1::
Use an empirical equation (Eq. 3) to fit the experimental data of the 16 enzymatic hydrolysis conditions ("Experiments for model fitness" section) with high accuracy. This smoothed version of the data provides the reaction rates needed to fit the parameters in the modified HCH-1 model of enzymatic hydrolysis.
$$\begin{aligned} { \frac{{\left. {{\text{d}}[G_{1} } \right]}}{{{\text{d}}t}} = \frac{{3.7798\left( {\left[ {G_{x}^{0} } \right] - \left[ {G_{1} } \right]} \right)^{0.6410} \left( {\frac{{\left[ {E_{0} } \right]\left( {0.0574\left[ {E_{0} } \right] + 0.4370\exp \left( { - t\left( {0.4370 + 0.0574\left[ {E_{0} } \right]} \right)} \right)} \right)}}{{0.4370 + 0.0574\left[ {E_{0} } \right]}}} \right)^{0.8500} }}{{1 + 0.0247\left[ {G_{1} } \right]^{1.1579} }}} \\, \end{aligned} $$
where \(\begin{array}{*{20}c} { G_{x}^{0} } \\ \end{array}\) is the initial cellulose concentration (g/L, equivalent to glucose).
Equation 3 was developed based on the integrated version of Eq. 2 and an empirical model for batch fermentation [15]. Detailed development of this equation is described in Additional file 1. To fit the parameters, Eq. 3 was solved with the ode45 routine in MATLAB and nonlinear optimization was achieved by the fmincon routine. The objective function was the sum of square errors (SSE), which is the sum of the squared difference between experimental data and the predicted value [16]. The optimal set of parameters corresponds to the smallest SSE value. This empirical correlation of the data provided a coefficient of determination R2 = 0.994.
Divide substrate conversion (from 0 to 1) into 50 equal segments. Using Eq. 3, calculate the reaction rate at each conversion and get a 16 × 50 data set.
Determine product inhibition.
The inhibition parameter i in the HCH-1 model was calculated by determining the initial velocities with and without inhibitor (Eq. 4) [17]. To estimate this value, the same enzyme and cellulose concentrations should be used.
$$\begin{array}{*{20}c} { i = \frac{{V_{{{\text{with}}\;{\text{inhibitor}}}} }}{{V_{{{\text{no}}\;{\text{inhibitor}}}} }}} \\ \end{array} = \frac{{\left[ {\frac{{\kappa \left[ {G_{x}^{0} } \right]\left[ E \right]}}{{\alpha + \left[ {G_{x}^{0} } \right] + \varepsilon \left[ E \right]}}} \right]i}}{{\frac{{\kappa \left[ {G_{x}^{0} } \right]\left[ E \right]}}{{\alpha + \left[ {G_{x}^{0} } \right] + \varepsilon \left[ E \right]}}}}$$
The inhibition of enzymatic hydrolysis by cellobiose was not considered in this study, because CTec2 contains a high level of β-glucosidase that rapidly converts produced cellobiose into glucose; the cellobiose peak was not found in the HPLC results.
For a single inhibitor, the inhibition parameter i is expressed in Eq. 5 and the glucose binding constant β1 is calculated with Eq. 6.
$$\begin{array}{*{20}c} { i = \frac{1}{{\left. {1 + \beta_{1} [G_{1} } \right]}}} \\ \end{array}$$
$$\begin{array}{*{20}c} { \beta_{1} = \frac{{\left( {1 - i} \right)}}{{i\left[ {G_{1} } \right]}}} \\ \end{array}$$
Use the HCH-1 model to fit the 16 reaction conditions at each conversion, and determine the best-fit coefficients κ, α, and ɛ.
Determine the relationship between parameter κ and conversion x.
Figure 2a presents the relationship between parameter κ in the HCH-1 model and substrate conversion x. The data were obtained from Steps 1–4. As shown in the figure, κ drops very fast in the beginning and then stabilizes after conversion reaches 0.38. Nidetzky and Steiner [18] assumed that cellulose consists of an easily hydrolysable part and a recalcitrant part. Based on their two-substrate hypothesis, the authors derived a mathematical model to describe the kinetics of cellulose hydrolysis. According to the simulation results, the obtained rate constant for easily hydrolysable cellulose was much higher than that of recalcitrant cellulose. Using α-cellulose as substrate, they determined that the fraction of easily hydrolysable cellulose was 0.3 [18]. Figure 2a can be explained by this hypothesis, but the rate constant for the easily hydrolysable cellulose decreases as conversion increases instead of being constant. In our experiments, the fraction of easily hydrolysable cellulose (0.38) is close to the result in [18].
Equation 7 was developed to describe the relationship between parameter κ and conversion x.
$$\begin{array}{*{20}c} { \kappa = \frac{{k_{3} }}{{\left( {1 + x^{{k_{4} }} } \right)^{{k_{5} }} }} + k_{6} } \\ \end{array} ,$$
where x is the substrate conversion, k3, k4, k5, and k6 are the parameters.
The conversion x in the denominator is used to describe the negative effect of conversion on the rate constant. The parameter \(k_{6}\) is considered as the rate constant for recalcitrant cellulose. The parameter k3 is used to describe the difference in rate constants between the easily hydrolysable cellulose (initial) and recalcitrant cellulose (height of the curve). The parameters \(k_{4} \;{\text{and}}\;k_{5}\) are used to describe the decrease rate of the rate constant (steepness of the curve) for the easily hydrolysable part. To fit the data, the MATLAB curve fitting tool was used and a coefficient of determination R2 = 0.998 was acquired. The values of parameters k3, k4, k5, and k6 were determined in this step.
Determine the relationship between parameter ε and conversion x.
Figure 2b shows the relationship between parameter ε in the HCH-1 model and conversion x. As shown in the figure, parameter ε has a very narrow range (0–0.5) over the entire conversion and remains almost unchanged (nearly zero) at conversion 0.1–0.95. Therefore, in this study, parameter ε is assumed not to be affected by conversion and its optimal value should be close to zero. Brown and Holtzapple [19] reported that if [\(\begin{array}{*{20}c} { G_{x}^{0} } \\ \end{array}\)]/[E0] > 35, assuming ε = 0 would not introduce considerable error (< 1%) (note: in our study, [\(\begin{array}{*{20}c} { G_{x}^{0} } \\ \end{array}\)]/[E0] ≥ 200). The parameter ε is needed only at high enzyme loadings. In industrial-scale saccharification, considering the high cost of enzymes, the enzyme dosage must be very low; therefore, if modeling a commercial process, the value of ε can be set as zero.
Determine the relationship between parameter α and conversion x.
The parameter α in the original HCH-1 model may be expressed by Eq. 8, which is related to enzyme adsorption:
$$\begin{array}{*{20}c} {\alpha = \frac{{\left[ {E^{f} } \right]\left[ {G_{x}^{f} } \right]}}{{\left[ {E^{a} } \right] + \left[ {EG_{x} } \right]}}} \\ \end{array} .$$
Kumar and Wyman [20] showed that glucose addition and enzyme dosage can affect the percentage of cellulase adsorption. Therefore, besides the impact of conversion, the effects of glucose and enzyme concentration on the value of α were tested. Using the best-fit coefficients κ and ɛ obtained from Step 4, two optimal α values corresponding to two initial glucose concentrations were determined by fitting the data (eight data at each initial glucose concentration) from Step 2 at each conversion with the HCH-1 model (Fig. 3a). Another two optimal α values corresponding to two enzyme concentrations were determined by repeating this procedure at each conversion (Fig. 3b). As shown in Fig. 3, as the reaction proceeds, the value of α increases and then is unchanged when the conversion reaches a certain point. It is obvious that high initial glucose concentration and low enzyme dosage improve the value of α significantly over the entire conversion range. Equation 9 was proposed to describe the relationship among α, conversion x, enzyme concentration E, and glucose concentration G1. As shown in Fig. 3, all four curves show an "S" shape; therefore, the sigmoid function—which has an S-shaped curve—was used. The core structure of Eq. 9 is a sigmoidal function that describes the relationship between parameter α and conversion x (note: a2 and a3 are the parameters of the sigmoid function). In addition, because of the significant effect of glucose and enzyme concentrations on the value of α, the terms [G1] and [E] were included in the numerator and denominator of the sigmoid function, respectively. The parameter a1 was added to describe the weight of terms [G1] and [E].
$$\begin{array}{*{20}c} { \alpha = \frac{{a_{1} \left[ {G_{1} } \right]}}{{\left[ E \right]\left( {1 + { \exp }\left( { - a_{2} x + a_{3} } \right)} \right)}}} \\ \end{array} ,$$
where a1, a2, and a3 are the parameters.
Modify HCH-1 model.
Summarizing the proposed equations, Eq. 10 is the modified HCH-1 model, where k1, k2, k3, k4, k5, k6, a1, a2, a3, ε, and β1 are parameters. Estimates for k1, k2, k3, k4, k5, k6, and β1 were determined in previous steps. In this step, the optimal values of a1, a2, a3, and ε were determined by simultaneously fitting the experimental data of the 16 enzymatic hydrolysis conditions (Section: Experiments for model fitness) with Eq. 10.
$$\frac{{\left. {d[G_{1} } \right]}}{dt} = \frac{{\kappa \left[ {G_{x} } \right]\left[ E \right]i}}{{\alpha + \varphi \left[ {G_{x} } \right] + \varepsilon \left[ E \right]}},$$
$$i = \frac{1}{{\left. {1 + \beta_{1} [G_{1} } \right]}}$$
$$\begin{array}{*{20}c} {\varphi = \frac{{\left[ {G_{x} } \right] - \alpha - \varepsilon \left[ E \right] + \sqrt {\left( {\left[ {G_{x} } \right] - \alpha - \varepsilon \left[ E \right]} \right)^{2} + 4\alpha \left[ {G_{x} } \right]} }}{{2\left[ {G_{x} } \right]}}} \\ \end{array}$$
$$- \frac{{\left. {d[E} \right]}}{dt} = k_{1} \left[ E \right] - k_{2} \left( {\left[ {E_{0} } \right] - \left[ E \right]} \right)\left[ {E_{0} } \right]$$
$$\kappa = \frac{{k_{3} }}{{\left( {1 + x^{{k_{4} }} } \right)^{{k_{5} }} }} + k_{6}$$
$$\begin{array}{*{20}c} { \alpha = \frac{{a_{1} \left[ {G_{1} } \right]}}{{\left[ E \right]\left( {1 + { \exp }\left( { - a_{2} x + a_{3} } \right)} \right)}}} \\ \end{array} .$$
Integration of the differential equations described in Eq. 10 was performed using the same numerical methods described in Step 1.
a The relationship between parameter κ and conversion x. b The relationship between parameter ε and conversion x
The relationship between parameter α and conversion x with a different initial glucose concentrations and b different enzyme loadings
Local sensitivity analysis
Local sensitivity analysis assesses the local impact of variation in input factors on model outputs. To do this analysis, the direct differential method [21] was used by calculating the sensitivity indices (Eq. 11). The sensitivities of parameters k1, k2, and β1 were not analyzed, because their values were obtained from independent experiment or calculation.
$$\begin{array}{*{20}c} { S_{{p_{j} }} = \frac{\partial y}{{\partial p_{j} }}\frac{{p_{j} }}{y}} \\ \end{array},$$
where \(S_{{p_{j} }}\) is the non-dimensional sensitivity index of the jth parameter, y is the glucose concentration (g/L), and pj is the jth parameter in the parameter vector p.
Global sensitivity analysis
Local sensitivity only analyzes the sensitivity of a solution close to the optimal parameter set. In contrast, global sensitivity analysis assesses the sensitivity of the model for the full range of possible parameter values [16]. In addition, global sensitivity indices can evaluate the combined impact of multiple parameters on model output.
To calculate a global sensitivity index, a normally distributed search of parameter space using the Monte Carlo method was performed and subsequent analysis of the variance in the model outputs was used. In this study, two global sensitivity indices were calculated: first-order index and total-effect index [16, 22]. The first-order index measures the effect of the parameter of interest alone on the output variance. The total-effect index accounts for not only the effect of the parameter of interest, but also interactions between the other parameters and the parameter of interest at any order.
Model evaluation
The modified HCH-1 model was compared with the literature models for long-term enzymatic hydrolysis. As described in Step 1, the same differential equation integration method, nonlinear optimization constraint algorithm, and objective function were used. The Akaike information criterion (AIC) was used to evaluate model quality for the experimental data. The corrected version of AIC (Eq. 12) was used, because the number of observations was not large enough:
$$\begin{array}{*{20}c} {{\text{AIC}}_{C} = N \cdot \ln \left( {\frac{\text{SSE}}{N}} \right) + 2\left( {P + 1} \right) + 2\frac{{\left. {\left( {P + 1} \right)(P + 2} \right)}}{N - P}} \\ \end{array} ,$$
where N is the number of observations, P is the number of model parameters, and SSE is the sum square error.
Enzyme deactivation
Figure 4 shows that, after incubating at 50 °C for 20 days, soluble protein concentrations of CTec2 dropped to 74, 77, and 83% of their initial values of 0.15, 0.26, and 0.61 g/L, respectively. This result is consistent with a previous study [14] that shows higher initial protein concentrations favor lower deactivation rates and supports the additive hypothesis. Equation 2 successfully describes the time profiles of CTec2 protein concentration with a coefficient of determination R2 = 0.999. The rate constants in Eq. 2 were determined to be k1 = 0.0225 h−1 and k2 = 0.1740 L/(g h). It should be noted that the modified HCH-1 model is a "lumped" model, the performance of each enzyme was not modeled individually; therefore, the stability of each component in the enzyme cocktail was not investigated. Equation 2 describes the overall deactivation of the cocktail.
Time profiles and model predictions for soluble CTec2 protein concentration at 50 °C. Experimental data are presented by the markers and the optimal fit by the solid lines
Production inhibition
Table 1 lists the values of glucose-binding constant calculated from various reaction conditions. The eight β1 values are very close to each other and have a standard deviation of 6 × 10−6 L/g. The mean value 0.0429 L/g is considered to be the "true" β1 value and is used for later calculations.
Table 1 Glucose-binding constant from various reaction conditions
Figure 5a shows the experimental data and modified HCH-1 model fitting results for enzymatic hydrolysis with 16 reaction conditions ("Experiments for model fitness" section). Table 2 shows the values of the parameters obtained from the previous section. The model simulation provided the coefficient of determination R2 = 0.992, which indicates that the modified HCH-1 model describes enzymatic hydrolysis of α-cellulose very well.
a Time profiles and modified HCH-1 model fitting results for enzymatic hydrolysis of α-cellulose. b Time profiles and original HCH-1 model fitting results for enzymatic hydrolysis of α-cellulose. c Time profiles and modified HCH-1 model predictions for enzymatic hydrolysis of α-cellulose. Experimental data are presented by the markers and the values of parameters are from Table 2
Table 2 Optimal parameter estimates for the modified HCH-1 model
As a comparison, Fig. 5b shows the original HCH-1 model fit to the experimental data with 16 reaction conditions ("Experiments for model fitness" section). The value of β1 (0.0429 L/g) was obtained from the previous section (product inhibition). The optimal values (α = 2.0776 × 106 g/L, κ = 9.2889 × 105 h−1, and ɛ = 0.9996) were determined (note: because the original HCH-1 model was not developed for integrated cellulose hydrolysis, these parameter values are not be meaningful). The model simulation provided the coefficient of determination R2 = 0.947. The calculated SSE and AICc are listed in Table 3.
Table 3 Comparison of long-term enzymatic hydrolysis models
Model predictions
The modified HCH-1 model (Eq. 10) was used to predict the experimental results of the three conditions described in "Experiments for model prediction." The parameter values were obtained from the fitness of the 16 conditions (Table 2). The experimental and predicted results are shown in Fig. 5c. The simulation provided the coefficient of determination R2 = 0.991, which indicates that the modified HCH-1 model predicts enzymatic hydrolysis of α-cellulose with high accuracy.
To explore the controlling factors in the proposed model at different hydrolysis stages, local and global sensitivity analyses were performed. Figure 6a shows the parameter sensitivity indices from local sensitivity analysis of the modified HCH-1 model over the course of 10 days. As shown in the figure, the sensitivity of k3 drops to nearly 10% of its initial value at day 10. The sensitivity of k4 increases first and reaches up to 0.4 at around day 1, and then slightly decreases from day 2 to day 10. For the parameters about α, the sensitivity of a1 (absolute value) increases as the hydrolysis time increases. The sensitivities of a2 and a3 only change within the first several reaction days, and then are close to zero after day 3. The sensitivity of ε is close to zero during the entire reaction time.
a Local sensitivity analysis of the modified HCH-1 model at the optimal solution. Global sensitivity analysis of the modified HCH-1 model over the course of 10 days, b first-order indices; c total-effect indices
Figure 6b, c shows the global sensitivity analysis results of the modified HCH-1 model. According to the figures, the first-order indices and total-effect indices of all variables are almost identical at any time, which means that the variance in this model is not related to any interaction between parameters. At the initial stage of hydrolysis, the variance in the model output only depends on k3 and k6. Then, the sensitivity index of k3 decreases very fast during the first 2 days, whereas k4 increases up to 0.6. From day 2 to day 10, the effects of k6 and a1 on the model increase. The variables a2, a3, and ε do not show significant effects on the variance in model predictions.
According to Fig. 6, the local and global sensitivity analyses of the modified HCH-1 model show a similar trend during the entire reaction time. Figure 7 shows the sensitivity indices calculated from both analyses at day 10. The rankings of the eight sensitivity indices from both analyses are almost the same (k6 > a1 > k4 > k5 > k3 > a2 ≈ a3 ≈ ε).
The local and global sensitivity indices of the modified HCH-1 model at day 10. a Local sensitivity analysis and b global sensitivity analysis (first-order indices)
The sensitivity analyses not only determine which parameters have the most influence on model results, but also verify the assumption in Step 6 that the parameter ε is not needed at low enzyme loadings. These analyses provide direction for further modification of the HCH-1 model to apply it to real-world lignocellulose that contains lignin.
Model comparison
Based on the methodology used, the published mechanistic and semi-mechanistic models for cellulose and lignocellulose can be broadly divided into two classes: Michaelis–Menten and enzyme-adsorption models [10]. The models following Michaelis–Menten kinetics can also be divided into two subclasses: full Michaelis–Menten models (all rate equations follow Michaelis–Menten kinetics, including the steps of cellulose to cellobiose, cellulose to glucose, and cellobiose to glucose) and partial Michaelis–Menten models (only the step of cellobiose to glucose follows these kinetics). Models employing enzyme adsorption typically use Langmuir adsorption isotherms or the help of kinetic equations [10]. Some literature models incorporate both enzyme adsorption and Michaelis–Menten kinetics.
In this study, the published models for long-term enzymatic hydrolysis of cellulose and lignocellulose were fit to the experimental data using the numerical methods described in Step 1. Some models do not consider product inhibition. To make a fair comparison, these models were only fit to experimental conditions with no initial sugar added (0 g/L initial glucose; four substrate concentrations × two enzyme loadings). Some models teased out fine details in the elementary reaction steps and included some variables that were not determined in this study, such as exocellulase concentration and associated enzyme concentration [23,24,25]. These models are not included in this section. Table 3 summarizes the number of observations and parameters, calculated SSE and AICc values, and the methodology used for the published models. According to the table, the modified HCH-1 model has the least SSE and AICc values, which indicates that this model provides the best fit for long-term enzymatic hydrolysis of α-cellulose.
The original HCH-1 model was modified to extend its application to integrated enzymatic hydrolysis; it performed well when fitting 10-day cellulose hydrolysis at various experimental conditions. Local and global sensitivity analyses were performed to determine the controlling parameters at different hydrolysis stages. Mechanistic (and semi-mechanistic) literature models for long-term enzymatic hydrolysis were compared with the modified HCH-1 model and evaluated by AICc. Comparison results show that the modified HCH-1 model provides the best description of enzymatic cellulose hydrolysis. The "lumped" modified HCH-1 model developed in this study has a simpler form and fewer parameters than mechanistic models of each enzyme component. When each enzyme is modeled separately, the kinetics is extremely complex with the potential to over-parameterize. For the specific commercial enzyme cocktail used in this study, excellent fits to the data were obtained without the need to model each enzyme component individually.
mg/g:
mg protein/g of dry biomass
AIC:
SSE:
sum of square errors
DI water:
M–M:
Michaelis–Menten kinetics
adsorption-based approach
Wallace R, Ibsen K, McAloon A, Yee W. Feasibility study for co-locating and integrating ethanol production plants from corn starch and lignocellulosic feedstocks (revised). Golden: National Renewable Energy Lab; 2005.
Wooley R, Ruth M, Glassner D, Sheehan J. Process design and costing of bioethanol technology: a tool for determining the status and direction of research and development. Biotechnol Prog. 1999;15:794–803.
Holtzapple MT, Caram HS, Humphrey AE. The HCH-1 model of enzymatic cellulose hydrolysis. Biotechnol Bioeng. 1984;26:775–80.
Kadam KL, Rydholm EC, McMillan JD. Development and validation of a kinetic model for enzymatic saccharification of lignocellulosic biomass. Biotechnol Prog. 2004;20:698–705.
Fenila F, Shastri Y. Optimal control of enzymatic hydrolysis of lignocellulosic biomass. Resour Effic Technol. 2016;2:S96–104.
Zhou J, Wang YH, Chu J, Luo LZ, Zhuang YP, Zhang SL. Optimization of cellulase mixture for efficient hydrolysis of steam-exploded corn stover by statistically designed experiments. Bioresour Technol. 2009;100:819–25.
Brown RF, Agbogbo FK, Holtzapple MT. Comparison of mechanistic models in the initial rate enzymatic hydrolysis of AFEX-treated wheat straw. Biotechnol Biofuels. 2010;3:6.
Bommarius AS, Katona A, Cheben SE, Patel AS, Ragauskas AJ, Knudson K, Pu Y. Cellulase kinetics as a function of cellulose pretreatment. Metab Eng. 2008;10:370–81.
Hong J, Ye X, Zhang YH. Quantitative determination of cellulose accessibility to cellulase based on adsorption of a nonhydrolytic fusion protein containing CBM and GFP with its applications. Langmuir. 2007;23:12535–40.
Bansal P, Hall M, Realff MJ, Lee JH, Bommarius AS. Modeling cellulase kinetics on lignocellulosic substrates. Biotechnol Adv. 2009;27:833–48.
Zentay AN, Liang C, Lonkar S, Holtzapple MT. Countercurrent enzymatic saccharification of cellulosic biomass. Biomass Bioenergy. 2016;90:122–30.
Novozymes: cellulosic ethanol—novozymes Cellic® CTec2 and HTec2—enzymes for hydrolysis of lignocellulosic. 2010. http://www.shinshu-u.ac.jp/faculty/engineering/chair/chem010/manual/Ctec2.pdf. Accessed 29 Sep 2018.
Wallace J, Brienzo M, García-Aparicio MP, Görgens JF. Lignin enrichment and enzyme deactivation as the root cause of enzymatic hydrolysis slowdown of steam pretreated sugarcane bagasse. New Biotechnol. 2016;33:361–71.
Rosales-Calderon O, Trajano HL, Duff SJ. Stability of commercial glucanase and β-glucosidase preparations under hydrolysis conditions. PeerJ. 2014;2:e402.
Fu Z, Holtzapple MT. Anaerobic mixed-culture fermentation of aqueous ammonia-treated sugarcane bagasse in consolidated bioprocessing. Biotechnol Bioeng. 2010;106:216–27.
Ordoñez MC, Raftery JP, Jaladi T, Chen X, Kao K, Karim MN. Modelling of batch kinetics of aerobic carotenoid production using Saccharomyces cerevisiae. Biochem Eng J. 2016;114:226–36.
Holtzapple M, Cognata M, Shu Y, Hendrickson C. Inhibition of Trichoderma reesei cellulase by sugars and solvents. Biotechnol Bioeng. 1990;36:275–87.
Nidetzky B, Steiner W. A new approach for modeling cellulase–cellulose adsorption and the kinetics of the enzymatic hydrolysis of microcrystalline cellulose. Biotechnol Bioeng. 1993;42:469–79.
Brown RF, Holtzapple MT. Parametric analysis of the errors associated with the Michaelis–Menten equation. Biotechnol Bioeng. 1990;36:1141–50.
Kumar R, Wyman CE. An improved method to directly estimate cellulase adsorption on biomass solids. Enzyme Microb Technol. 2008;42:426–33.
Peri S, Karra S, Lee YY, Karim MN. Modeling intrinsic kinetics of enzymatic cellulose hydrolysis. Biotechnol Prog. 2007;23:626–37.
Sobol IM. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math Comput Simul. 2001;55:271–80.
Shang BZ, Chang R, Chu JW. Systems-level modeling with molecular resolution elucidates the rate-limiting mechanisms of cellulose decomposition by cellobiohydrolases. J Biol Chem. 2013;288:29081–9.
Cruys-Bagger N, Alasepp K, Andersen M, Ottesen J, Borch K, Westh P. Rate of threading a cellulose chain into the binding tunnel of a cellulase. J Phys Chem B. 2016;120(25):5591–600.
Jeoh T, Cardona MJ, Karuna N, Mudinoor AR, Nill J. Mechanistic kinetic models of enzymatic cellulose hydrolysis—a review. Biotechnol Bioeng. 2017;114:1369–85.
Drissen RE, Maas RH, Van Der Maarel MJ, Kabel MA, Schols HA, Tramper J, Beeftink HH. A generic model for glucose production from various cellulose sources by a commercial cellulase complex. Biocatal Biotransformation. 2007;25:419–29.
Fan LT, Lee YH. Kinetic studies of enzymatic hydrolysis of insoluble cellulose: derivation of a mechanistic kinetic model. Biotechnol Bioeng. 1983;25:2707–33.
Liao W, Liu Y, Wen Z, Frear C, Chen S. Kinetic modeling of enzymatic hydrolysis of cellulose in differently pretreated fibers from dairy manure. Biotechnol Bioeng. 2008;101:441–51.
Gusakov AV, Sinitsyn AP, Klyosov AA. Kinetics of the enzymatic hydrolysis of cellulose: 1. A mathematical model for a batch reactor process. Enzyme Microb Technol. 1985;7:346–52.
Philippidis GP, Smith TK, Wyman CE. Study of the enzymatic hydrolysis of cellulose for production of fuel ethanol by the simultaneous saccharification and fermentation process. Biotechnol Bioeng. 1993;41:846–53.
Shen J, Agblevor FA. Kinetics of enzymatic hydrolysis of steam-exploded cotton gin waste. Chem Eng Commun. 2008;195:1107–21.
Zhang Y, Xu JL, Xu HJ, Yuan ZH, Guo Y. Cellulase deactivation based kinetic modeling of enzymatic hydrolysis of steam-exploded wheat straw. Bioresour Technol. 2010;101:8261–6.
Rosales-Calderon O, Trajano HL, Posarac D, Duff SJ. Modeling of oxygen delignified wheat straw enzymatic hydrolysis as a function of hydrolysis time, enzyme concentration, and lignin content. Ind Biotechnol. 2016;12:176–86.
CL, MNK, and MH conceived the study and participated in its design. CL performed all the experiments and drafted the manuscript. All authors were involved in the development of the model, sensitivity analysis, and model evaluation. CL, MNK, and MH revised the manuscript. All authors read and approved the final manuscript.
The authors would like to acknowledge Mr. Chiranjivi Botre, Mr. Haoran Wu, Mr. Opeyemi Olokede, Mr. Shen-Chun Hsu, and Ms. Pallavi Kumari for their advice on this project.
Availability of supporting data
All data generated or analyzed in the present study are included in this article.
All authors obtained consent for publication.
This work was supported by the Michael O'Connor Chair II Endowment. The open access publishing fees for this article have been covered by the Texas A&M University Open Access to Knowledge Fund (OAKFund), supported by the University Libraries and the Office of the Vice President for Research.
Department of Chemical Engineering, Texas A&M University, College Station, TX, 77843-3122, USA
Chao Liang, Jonathan Raftery, M. Nazmul Karim & Mark Holtzapple
Department of Educational Psychology, Texas A&M University, College Station, TX, 77843-3122, USA
Chao Gu
Chao Liang
Jonathan Raftery
M. Nazmul Karim
Mark Holtzapple
Correspondence to Chao Liang.
Development of Eq. 3.
Liang, C., Gu, C., Raftery, J. et al. Development of modified HCH-1 kinetic model for long-term enzymatic cellulose hydrolysis and comparison with literature models. Biotechnol Biofuels 12, 34 (2019). https://doi.org/10.1186/s13068-019-1371-5
Enzymatic cellulose hydrolysis
HCH-1
Submission enquiries: [email protected] | CommonCrawl |
The Source of Gravity Based Destruction
The Background:
It's the year 4000 (or whatever), and mankind has cheated FTL travel. As a result of this 'cheating' rather than solving, however, they can't easily go beyond their borders.
However, the earthlings have managed to spread out and the newly minted intergalactic race has, over a couple thousand years, managed to inhabit a good 500-2000 nearby planets. There are no aliens to worry about, and mankind has space all to themselves.
But all cannot be so peaceful in the little corner in which mankind has settled; and suddenly the planets upon which our nomadic earthlings have settled start to feel a disturbing little pull. The source of this pull begins on the outer planets near one of the edges, but slowly moves through human territory, enveloping and destroying anything its reach extends to.
The Question:
Originally, I cited the source of this pulling sensation as the 'Big Crunch' - which has, admittedly, been given the scientific toss. It also doesn't give quite the creeping sensation since it would likely affect all planets simultaneously, rather than starting with the outer ones first. https://en.wikipedia.org/wiki/Big_Crunch
Lately, I've moved to the idea of a supermassive black hole. However, even doubling the number of semi-inhabitable planets within a reasonable range, this black hole would have to be ubermassive. I've done some searching, and found black holes at the center of solar systems/galaxies/you name it. But I can't find the gravitational reach of such a ubermassive black hole. So I can't check this for plausibility. I'm left with the consolation that it doesn't have to suck in planets, just pull them off their orbit (a planet without a sun isn't very good at sustaining life), but I don't know if this is within the realm of physics or will get me laughed out of the publishing industry. https://en.wikipedia.org/wiki/Supermassive_black_hole
So, the question then, is could an ubermassive black hole exist (through natural means or through unnatrual means - it doesn't have to be natural, just self sustaining). And how big would such a one have to be in order to eat/destabilize a galaxy? If a black hole won't work, is there any other source of gravity that could believably cause this much damage while still traveling through space?
Sorry for the Wikipedia article links, they were, surprisingly, the best articles I could find. Most of the others were too advanced or meant for children.
Source for currently known inhabitable planets and their distance from Earth: https://en.wikipedia.org/wiki/List_of_potentially_habitable_exoplanets
Also, this probably goes without saying, but scientific is best. That said, I'll make due with plausible. I just don't want to get laughed out of civilized society.
science-based science-fiction physics gravity black-holes
Mackenzie BodilyMackenzie Bodily
$\begingroup$ Hi Mackenzie, would you mind clarifying what your question is? I see at least two candidates but I'm not sure which one. Also, if your question is purely about blackholes then the first three paragraphs, while nice background, kind of distract from the question you want to ask. $\endgroup$ – Green Dec 21 '17 at 20:29
$\begingroup$ And welcome to Worldbuilding! :) $\endgroup$ – Green Dec 21 '17 at 20:30
$\begingroup$ Two things: intergalactic means they live in more than once galaxy. Interstellar is the word your looking for. Secondly, gravity has no maximum range. The force falls off with the inverse-square law. $\endgroup$ – Stephan Dec 21 '17 at 23:04
$\begingroup$ I'm thinking along the line of Star Trek - Generations where the "nexus" was this giant string flowing through space that could be affected by changes in gravity (e.g., the destruction of a star). Let's reverse the idea and make the string the gravity-bearing object. A super-massive molecular chain bookin' through space and wreaking havoc everywhere it goes. (Maybe a super-dense/massive fluid with high attraction and a parsec long.... Yeah... that's the ticket!) $\endgroup$ – JBH Dec 22 '17 at 1:21
$\begingroup$ @JBH And on the money too. Cosmic strings are hypermassive. Galactic masses per centimetre? (or is it per metre?). Anyway that's exceptionally massive. The main problem may be the way the cosmic string is arranged in space to cause gravitational catastrophe. $\endgroup$ – a4android Dec 22 '17 at 1:35
Enormous amounts of mass required
I'm not going to really address your first question of how an ubermassive black hole could exist. Within our current understanding of gravitational physics, black holes are formed by stuffing enough mass-energy together in one spot, and it doesn't sound like the humans of your story are rounding up all the stars. I'm going to assume for the sake of your story that a black hole is formed in some exotic manner that massively violates conservation of mass-energy, such as by somehow harvesting the zero point energy of the universe, or manipulating the cosmological constant (a kind of energy density of empty space), or something even whackier.
Black holes are not vacuum cleaners
The other problem is that black holes are surprisingly nondestructive. A black hole, once formed, doesn't really suck things in to their doom. Let's consider a relatively tame 1000-Sun black hole.
In the Newtonian regime (far away from the event horizon) black holes behave like any other mass, and objects will orbit around them as with any other mass. The Sun is heavy, but for example, rocks from outside the solar system tend to fall inwards, whip around the Sun, then head back out to deep space. Objects have a certain amount of potential energy relative to the central mass they're orbiting, and barring extraordinary events such as collisions, this energy is conserved. Unless an object is aimed directly at the central mass, i.e. it has nearly zero angular momentum, it won't get sucked in. If you were to magically plop this black hole in interstellar space, yes, things would be pulled, but by conservation of angular momentum and energy these things (stars, planets, comets, etc.) would end up either slingshot away from the black hole, in orbit of it, or relatively unperturbed further away. A black hole of 1000 solar masses would make a mess of stars' orbits around the galaxy, but each solar system would stay intact, and life would go on. If you're wondering about how many stars would be sucked in, I would estimate none. Space is very large and even 1000-Sun black holes are small, and it is really easy for an infalling star to miss the black hole and whip around back into deep space far away. Also, it would take objects about 10 million years to fall in from 20 light-years away, so this wouldn't exactly be a pressing issue.
The 1000-Sun mass isn't arbitrary, since it's just about the minimum mass to really start affecting the closest 1000 stars, and even then quite languidly. By a rough estimation, a black hole of 1000 Solar masses is sufficient to gravitationally dominate a roughly 45-ly radius, such that objects within that 45-ly radius would orbit the black hole, not the galaxy center (like the Moon orbits the Earth, rather than following its own independent orbit around the Sun). This is from a quick calculation of the Hill sphere, and the gravitational mass of the Milky Way. A radius of 45 light-years roughly encompasses the nearest 1000 stars, which should be a proxy for the number of planets, within a factor of 10 or so.
There's enough of that digression. If you want destruction, we'll exit the Newtonian regime. Let's make the event horizon really big, so all the stars are close to it. The Schwarzschild radius is $r_S=\frac{2GM}{c^2}$. To have an event horizon 4.22ly in radius, reaching the nearest habitable planet, we need a black hole of 4 times the mass of the Milky Way as a whole, at $2.688*10^{43}$ kg. This will instantly swallow Proxima Centauri, and the rest of the 1000 closest stars should fall in within about 230 years.
Alternatives to black holes
If I were you, I'd take an alternative path, since the physics is already being bent in knots. How about Modified Newtonian Dynamics?. MOND theories and other alternatives to general relativity were somewhat recently proposed as alternatives to dark matter and dark energy. You don't have to understand this math particularly well, especially since it's a quite abstruse field of active research.
My suggestion for the sake of your story is that you explain your humans' FTL-cheating tech as exploiting a localized deviation from general relativity that encompasses our 500-2000 star systems. Unfortunately, the FTL cheat only makes these extra terms in the equation bigger and bigger, so that after many uses this pocket starts collapsing in on itself. Where today the cosmological constant is positive, driving expansion, it gets altered locally to more and more negative values, causing contraction.
Another possibility is that where Newtonian gravity is purely $1/r^2=r^{-2}$, FTL drive use starts to add a $1/r=r^{-1}$ or constant $r^0$ term - if attractive, then planets and moons start drawing in closer; if repulsive, everything starts drifting away.
If you have any more questions, I've done more math I didn't bother writing up and would be glad to share.
If you'd like to play around with gravity, try this toy. As a warning, it's not to scale, but you can try spawning a ring of dust in a circular orbit around one star, and then adding a second star to see how most of it is kicked out of the system.
NonstandardDeviationNonstandardDeviation
$\begingroup$ Welcome to WorldBuilding! Cool answer. If you have a moment please take the tour and visit the help center to learn more about the site. Have fun! $\endgroup$ – Secespitus Dec 22 '17 at 11:06
Gravity effects all things equally, and the further you are from the center of pull the more gentle and evenly distributed is the pull. So, a supermassive black hole will move the whole star system - where you are asking to move planets individually.
You might be able to get away with a tiny black hole. Bear with me because this is weird - once matter goes past a critical density (about the mass of one hundred thousand super carriers squeezed into the volume of a raindrop) it has a sufficiently curved gravity to be called a black hole. As people were concerned about the possibility of tiny black holes being created by CERN, nothing rules out super dense, but not very massive, material from existing in the universe.
A meteor shower of this stuff would cause a localized effect, nudging a planet it is passing nearby by while leaving the star unaffected.
James McLellanJames McLellan
$\begingroup$ It can be tiny but it can't be too tiny "So, for instance, a 1-second-life black hole has a mass of 2.28×105 kg, equivalent to an energy of 2.05×1022 J that could be released by 5×106 megatons of TNT." en.wikipedia.org/wiki/Hawking_radiation $\endgroup$ – Slarty Dec 21 '17 at 20:57
$\begingroup$ "nothing rules out super dense, but not very massive, material from existing in the universe." — sorry, but that's just not true. @Slarty explains why black hole has its limits, but our understanding of quantum & particle physics also puts some limits on non-blackhole matter. $\endgroup$ – Mołot Dec 21 '17 at 22:53
$\begingroup$ 2,28E+05 kg is about 228 metric tons, right? $\endgroup$ – James McLellan Dec 22 '17 at 0:15
$\begingroup$ @JamesMcLellan yes correct and if memory serves from another question a 600 ton black hole would last about 20 sec. So as I said it can't be too tiny mass wise. Although obviously all of these black holes would be submicroscopic $\endgroup$ – Slarty Dec 22 '17 at 11:01
You might be able to achieve your big crunch type effect with just one handwave - and one you made at the beginning of your story. What is more common than hubris-filled scientists bringing disaster with their creation?
"Cheating" FTL implies to me a folding of space, like the Alcubierre drive does. People do not travel FTL but they pull space together so the distance is shorter. You must have some sort of mechanism in mind for how your folks have achieved this.
Now use that FTL-cheating mechanism to produce the Big Crunch you want. Space is folding up in a given area and carrying the contents of space (planets!) with it. You can have this occur as some sort of accident with your FTL-cheating tech.
A nice thing about this is the story arc.
You don't need an ubermassive, a supermassive is more than enough to destabilize an entire galaxy (Milky Way is actually heading to such a collision in the next few billion years, but it's akin to being on the highway and colliding with a merging car; not a head-on collision). And if it's moving at near-luminal velocities and on a direct collision course, what it hits wouldn't get much notice before it's too late as everything we see in the night sky is outdated by thousands upon thousands of years.
Heck, wouldn't even need to be supermassive, just near super-massive as 500 worlds is actually a really small segment of a galaxy.
So really, just a larger-than-average black hole moving near-luminal speeds and not originating in our universe on a direct collision course is way more than enough to do it. Just pull the entire star cluster in the black hole's wake out of protecive rim of the galaxy and into the more radiation-exposed above-disc regions.
$\begingroup$ Your idea about how outdated is what we see on the sky is really wrong. It's a common misconception. See this obligatory xkcd. $\endgroup$ – Mołot Dec 21 '17 at 22:57
$\begingroup$ You're right, not everything, just everything that's thousands of lightyears away is thousands of years outdated. $\endgroup$ – liljoshu Dec 22 '17 at 23:55
A "swarm" of small black holes may do the trick. Note that such swarm is highly unlikely to exist naturally as it would collapse, so it should be a creation of some advanced civilization. Such swarm would be devastating locally (when swaying across a planet or star), move at the speed you want, and have not special effect from far away, just the usual gravitational impact of their mass.
The exact size of these small black holes is to refine depending of the effects you want to achieve. The size of the swarm is also quite open. The stability over time of such swarm may need some handwaving, however. And well, regarding where it comes from...
... let's say that it is a minefield from of a Kardashev type III civilization !
There is this cool national geographic documentary available on youtube which explores the idea that our solar system is visited by a neutron star (from 1h24m onwards) having very high velocity. The devastation described comes from the radiation emitted from the neutron star as well as secondary effects from the gravitational field (e.g. meteors change their course and hit earth) Therefore I would guess that you don't need to literally crush those 500 colonized planets to make them uninhabitable.
OmniOmni
Could an "ubermassive Black hole exist? To put it simply, there is nothing currently in scientific literature that says a really big black hole couldn't exist. However, a black hole of that size is very unlikely to go unnoticed. Black holes moving through any dense parts of space (galaxies, gas clouds) become active (quasars) and very visible (usually in non-visible wavelengths but your humans are advanced enough to have telescopes that currently exist in our society. If you want to figure out calculations involving such a black hole, you can think about it as a really large planet.
One of your problems with making this plausible might be time dilation. Time slows down in gradient gravity fields, since objects under acceleration move relative to objects farther from the effects of gravity. Your planets being pulled (by any gravitationally large force) will be very delayed in letting anyone else know about it, depending on how close they are.
Dark Matter How about make the problem space itself? Instead of worrying about gravity and time, worry about some kind of asymmetric expansion of the local universe. Certainly, this would be unpredictable, visible only on a larger scale (people aren't flying out of their houses but planets can move around), invisible to any current scientific tests, and, with the lack of actual scientific knowledge about the theory behind it, you can take a lot of creative liberties. Also, this kind of expansion wouldn't really be new to scientific literature. The Big Bang Theory currently resides on a massive accelerated expansion some time in the early universe to work.
The one problem (is it really?) would be matter creation and annihilation near the expansion. Because of the non-uniform change in the fabric of space, the local universe will function under a time-dependent Hamiltonian, which allows for asymmetric virtual particle creation. Without going too much into detail, this effect could create large pockets of energy or matter, or annihilate energy or matter. This is mostly speculation at this point, so don't take everything I've just said as fact.
It's another galaxy If you don't care about your humans seeing what's messing with them, a "rogue" galaxy could rip apart the Milky Way very quickly. Andromeda, for instance, is scheduled to collide with us in the next couple billion years, so it isn't unheard of. If you want to catch your humans by surprise, you'll need a galaxy traveling fast enough that they won't be able to see it until it's too late. Maybe they just weren't looking. Maybe the shockwave of gravity radiating from a relativistic black hole is pushing and pulling the Milky Way apart.
Hope this gives you some ideas.
Nathaniel D. HoffmanNathaniel D. Hoffman
Not the answer you're looking for? Browse other questions tagged science-based science-fiction physics gravity black-holes or ask your own question.
How to accelerate living things really fast without killing them?
How would one destroy a black hole?
If Earth mass is doubled, what is the change of earth's orbit
How could it be possible to exert gravity without mass?
Blackholes as Perfect Recyclers or Perfect Batteries: Safe storage, recharge, and usage
How would one detect a black hole when there are no more light sources for it to refract?
Space-based black hole weapon effects
Map projection for a pseudospherical world | CommonCrawl |
Economic evaluation of the air pollution effect on public health in China's 74 cities
Li Li1,2,
Yalin Lei1,2,
Dongyan Pan3,
Chen Yu1,2 &
Chunyan Si1,2
SpringerPlus volume 5, Article number: 402 (2016) Cite this article
Air deterioration caused by pollution has harmed public health. The existing studies on the economic loss caused by a variety of air pollutants in multiple cities are lacking. To understand the effect of different pollutants on public health and to provide the basis of the environmental governance for governments, based on the dose–response relation and the willingness to pay, this paper used the latest available data of the inhalable particulate matter (PM10) and sulphur dioxide (SO2) from January 2015 to June 2015 in 74 cities by establishing the lowest and the highest limit scenarios. The results show that (1) in the lowest and highest limit scenario, the health-related economic loss caused by PM10 and SO2 represented 1.63 and 2.32 % of the GDP, respectively; (2) For a single city, in the lowest and the highest limit scenarios, the highest economic loss of the public health effect caused by PM10 and SO2 was observed in Chongqing; the highest economic loss of the public health effect per capita occurred in Hebei Baoding. The highest proportion of the health-related economic loss accounting for GDP was found in Hebei Xingtai. The main reason is that the terrain conditions are not conducive to the spread of air pollutants in Chongqing, Baoding and Xingtai, and the three cities are typical heavy industrial cities that are based on coal resources. Therefore, this paper proposes to improve the energy structure, use the advanced production process, reasonably control the urban population growth, and adopt the emissions trading system in order to reduce the economic loss caused by the effects of air pollution on public health.
Air pollution mainly refers to human activities or the natural processes that cause a certain substance to continuously enter the atmosphere at a sufficient concentration to endanger the health and cause environmental pollution. There are many types of air pollutants, the primary of which are total suspended particulates (TSP), inhalable particulate matter (PM10), fine particulate matter (PM2.5), SO2 and NOx, among others (Yu et al. 2008). After inhalation of harmful pollutions, humans may develop respiratory disease and can suffer from serious diseases, such as tracheitis, bronchitis, asthma, lung disease and lung cancer, for many years. The energy consumption structure in China is mainly based on coal resources, and the rapid growth of motor vehicles in cities results in increasingly more serious air pollution in China's large cities; in addition, the questions regarding public health and air pollution have garnered widespread attention (Wilkinson and Smith 2007).
The main air pollutions in China are PM10, SO2 and NOx (Chen et al. 2001). In the 12th Five-Year period, China clearly proffered the target to reduce the total SO2 emissions by 8 % and increase the ratio of the urban air quality to achieve the second level of 8 % (Ministry of Environmental Protection of the People's Republic of China 2011). According to an environmental analysis reported by the Asian Development Bank in 2013, the Chinese government was taking measures to control air pollution; however, of the world's 10 most seriously polluted cities, 7 cities were in China. Of China's 500 major cities, less than 1 % met the standards of the World Health Organization (Zhang 2012). In 2015, the World Health Organization released a report stating that at least one in eight people died of air pollution globally. Air pollution has become the world's largest environmental health risk (Huanqiunet 2015).
Since January 1, 2013, the Ministry of Environmental Protection has monitored the air quality index of Beijing, Tianjin, Hebei, the Yangtze River Delta, the Pearl River Delta region, the municipality directly under the central government, the provincial capital cities and the cities specifically designated in the state plan, which are collectively called the 74 cities, in brief (China's National Environmental Monitoring Centre 2013a). The concentrations of pollutants such as PM10 and SO2 have been monitored since November 2014 (China's National Environmental Monitoring Centre 2013b). As World Bank (1997) didn't identify the health effects of NOx and NOx wasn't included in the dose–response relation of Ho and Jorgenson (2007), thus to quantitatively evaluate the economic loss due to the effects of air pollution on public health in China, this paper analyzes PM10 and SO2 based on the latest available data from January 2015 to June 2015, uses the method of foreign study on China's economic loss due to air pollution effects on public health for reference (Wang and Smith 1999; Ho and Nielsen 2007) and estimates the economic loss caused by the effects of air pollution on public health in the 74 cities. An evaluation of the health-related economic loss can provide a basis for the government to develop and initiate preventative measure for controlling air pollution. At the same time, these findings can also improve the environmental protection awareness of the local government and the public.
In recent decades, industrialization and urbanization have experienced rapid development, which has resulted in increasing air pollution. According to the World Bank, there is a close relationship between air pollution and public health. There is a positive relation between the concentration of air pollutants and respiratory diseases, lung function loss, chronic bronchitis and premature death (World Bank SEPA 2007). The evaluation of health-related economic loss caused by air pollution has become a hot topic for scholars and institutions.
Research progress on the economic loss regarding to public health impacts caused by air pollution
Ridker (1967) calculated the economic loss associated with different diseases which caused by air pollution in the USA in 1958 by using the human capital method. The results showed that the economic loss related to the effects on public health was 80.2 billion dollars in the USA. This study hailed the beginning of the calculation of health-related economic loss caused by air pollution.
Employing a survival analysis and the data from a 14- to 16-year mortality follow-up of 8111 adults in the six cities in the U.S., Dockery et al. (1993) estimated the associations between particulate air pollution and daily mortality rates. Their results confirmed that the mortality rate was associated with the level of air pollution. Using data from 1994 to 1995 in Hong Kong, Wong et al. (1999) determined that adverse health effects were evident at the current ambient concentrations of air pollutants. Samet et al. (2000) recognized an association between daily changes in the concentration of ambient particulate matter and the daily number of deaths (mortality) in the United States. Wong et al. (2002) used Poisson regression to estimate the associations between daily admissions and the levels of PM10 and SO2 in Hong Kong and London. The results confirmed that air pollution caused detrimental short-term health effects.
Using the collective data regarding to PM10 and SO2 from January 1999 to September 2000, Kaushik et al. (2006) assessed the ambient air quality status in the fast growing urban centres of Haryana state, India. Adopting the daily data during 2008 and 2009 in Beijing, Xu et al. (2014b) confirmed that short-term exposure to particulate air pollution was associated with increased ischemic heart disease (IHD) mortality.
In 1981, the concept, theory and method of environmental pollution economic loss assessment were put forward and discussed in the congress of the National Symposium on Environmental Economics (Xia 1998). Thereafter, the economic loss associated with environmental pollution was of interest to scholars. Gao et al. (1993) adopted the GEE (Generalized Estimation Equation) to study the relationship between TSP in Haidian District, Beijing and low air pollution. Using the two methods (ecology and time series) and the data of 1992 in Shenyang, Xu et al. (1996) determined that total mortality, chronic obstructive pulmonary disease (COPD), cardiovascular disease and pollution levels were significantly correlated. Jing and Ren (2000) conducted an epidemiological survey on adults who were older than 25 years using the multiple logistic regression analysis. The results showed that 6 types of respiratory system diseases or symptoms appeared with an increasing frequency as air pollution levels increased. Chen and Hong (2002) quantitatively evaluated the air pollution in Shanghai based on the risk evaluation method and found that the health effects caused by SO2 exhibited a gradually declining trend. Chen et al. (2010) evaluated the health impacts of particulate air pollution on urban populations in 113 Chinese cities, and it was estimated that the total economic cost of the health impact was approximately 341.4 billion Yuan, 87.79 % of which was attributable to premature deaths. Chen et al. (2015) employed a Poisson regression model to estimate residents' health benefits in two scenarios: environmentally controlled scenario 1 and environmentally controlled scenario 2. Scenario 2 showed a potentially higher reduction of emissions and greater health benefits than scenario 1. Xu et al. (2014a) used the established model between PM10 and thermal environmental indicators to evaluate the PM10—related health risk in Beijing.
Certain scientific institutions also focused more on the economic loss associated with public health effects caused by air pollution. The World Health Organization estimated that the total loss globally caused by air pollution-related disease was 0.5 % (Murray and Lopea 1997) in 1997. In the same year, the World Bank systematically studied the health effects caused by air pollution in China (World Bank 1997). The U.S. Environmental Protection Agency estimated that the economic benefits of health and ecological improvement in the United States from 1990 to 2010 were as high as $6–50 trillion, most of which could be attributed to the decrease in the number of deaths caused by air pollution (U.S. EPA 1999). The World Health Organization reported that 80 % of the world's cases of heart disease and stroke deaths were due to air pollution, and a total of 7 million people in the world died of air pollution in 2014 (Huanqiunet 2014). In 2015, the World Health Organization released data that at least 1 in every 8 people died of air pollution throughout the world. Air pollution has become the world's largest environmental health risk (Huanqiunet 2015).
Research progress on the method used to evaluate the economic loss associated with public health effects caused by air pollution
The previous studies regarding to the economic loss caused by the effects of air pollution on public health generally included the determination of economic loss using the contents of the environmental pollution assessment, the public health impact assessment and a choice of methods. Generally, the methods used were as follows.
Modified human capital method
Ridker (1967), Dockery et al. (1993), Wang et al. (2005), Jia et al. (2004), Wan et al. (2005), Han et al. (2006), Zhang et al. (2008), Shang et al. (2010), Han (2011), and Shen et al. (2014) quantitatively estimated the economic loss in different regions and obtained different results.
Illness cost method
Air pollution led to changes in the disposable income of people, particularly, an increase in medical expenses. Medical expenses became a recognized fact, and they also became a very heavy burden on civilians. Based on the above views, certain scholars obtained conclusions by analysing the illness costs caused by air pollution. These scholars include Chen et al. (2010), Zmirou et al. (1999), Hedley et al. (2008), Patankar and Trivedi (2011), Brandt et al. (2014), and Yan (2012).
Willingness to pay
Willingness to pay is an indirect evaluation method which constructs a simulated market to reveal people's willingness to pay for certain environmental goods, in order to evaluate the value of environmental quality. Researchers included Carlsson and Martinsson (2001), Wang and John (2006), Koop and Tole (2004), Pascal et al. (2013), Yaduma et al. (2013), Ami et al. (2014), Istamto et al. (2014), Cai and Yang (2003), Peng and Tian (2003), Cai et al. (2007), Zhou et al. (2010), and Zeng et al. (2015).
Literature summary
In the studies of the economic loss caused by air pollution, domestic and foreign researchers studied the qualitative relationship between and quantitative analysis of air pollution and its health effect. However, generally, previous studies were solely based on a country, a city or a type of air pollutant; the health effects of many types of air pollutants in a city of a typical city are moderate.
Regarding to the method for evaluating the economic loss caused by the effects of air pollution on public health, the deficiencies of the modified human capital method were that the life prediction of the society may not be reasonable, and the different choices of the discount rate would have a large impact on the evaluation results. The disadvantage of the illness cost method is that it may underestimate the illness value. Additionally, the method's other disadvantage was that the individual may have a willingness to pay.
From the economic perspective, the willingness to pay method is the most reasonable method because it can reveal the value of all goods and utilities, and it can completely evaluate the economic values of environmental resources, which is currently being widely recognized and accepted. Thus, this paper utilizes the willing to pay method to evaluate the economic loss associated with public health effects caused by air pollution in 74 cities.
Methods and data
The dose–response relationship and the willingness to pay
To study the economic loss related to public health effects caused by air pollution, it is necessary to consider the types of public health effects and to establish the relation between the concentration of air pollutants and the effect on public health, which is called a dose–response. In different studies, the dose–response relationship is different. The indexes of public health effects caused by air pollution, which the World Bank put forward, included premature deaths, hospitalization and emergency caused by respiratory diseases, the number of restriction days caused by health problems related to the inhalation of particulate matter, lower respiratory tract infections, childhood asthma, asthma, chronic bronchitis, respiratory symptoms, and chest discomfort. This paper used the dose–response relationship of Ho and Jorgenson (2007) for reference and assumed that all the people in the 74 cities were exposed to the same concentrations of PM10 and SO2. The dose–response relationship is shown in the Eq. (1).
$$HE_{xrh} = DR_{xh} \times C_{rx} \times POP_{r}$$
where \(HE_{xrh}\) is the h-th type of public health effect caused by the air pollutant x (including PM10 and SO2) in the region r. \(DR_{xh}\) is the dose–response coefficient of the air pollutant x (unit: the number of the people suffer with the concentration of the air pollutant increasing by 1 μg/m3) and the h-th type of public health. \(C_{rx}\) is the concentration of the air pollutant x in the region r. \(POP_{r}\) is the number of the people in the region r. Ho and Jorgenson (2007) used the survey data of Beijing and Anqing in 1997 to estimate the economic loss caused by the health effects of Chinese residents using the willingness to pay method, the population of was were 6.53 million and 0.35 million respectively. Based on the loss value estimation of Ho and Jorgenson (2007), this paper modified it, as shown in Table 1. The total economic loss of the 74 cities is obtained by adding up all of the economic loss types relating to the health effects, as shown in the Eqs. (2) and (3):
$$HEV_{xrh} = V_{xh} \times HE_{xrh}$$
$${\text{THEV}} = \mathop \sum \limits_{r} \mathop \sum \limits_{x} \mathop \sum \limits_{h} HEV_{xrh}$$
where \(HEV_{xrh}\) is the economic loss of the h-th type of public health effect caused by the air pollutant x (including PM10 and SO2) in the region r. \(V_{xh}\) is the economic loss value of the h-th type of public health effect caused by the air pollutant x (including PM10 and SO2). \({\text{THEV}}\) is the total economic loss related to public health effects caused by the air pollutant. In calculating total health-related economic loss, the paper adds up eight effects of PM10 on public health and three effects of SO2 on public health together, which may appear double counting. As there is little literature of this issue, the paper hasn't analyzed it.
Table 1 The dose–response relationship and the loss value estimation of the public health effects
The environmental data of 74 cities during the period from January 2015 to June 2015 were reported by China's National Environmental Monitoring Centre (2015a, b, c, d, e, f), which mainly contained the monthly mean concentrations of PM10 and SO2 (Figs. 1, 2). The number of the population and GDP in 74 cities were obtained from Askcinet (2015).
Monthly mean concentration of SO2 in China's 74 cities
Monthly mean concentration of PM10 in China's 74 cities
From Figs. 1 and 2, Taiyuan, Shenyang and Yinchuan are the top three cities with the highest monthly mean concentration of SO2. Baoding, Zhengzhou and Xingtai are the top three cities with the highest monthly mean concentration of PM10. According to the ambient air quality standard GB3095-2012, the paper compared Chongqing, Baoding and Xingtai with Beijing and found that: (1) For SO2, Beijing and Chongqing achieved the first level of national standards from January 2015 to June 2015. Baoding and Xingtai achieved the first level of national standards from April to June 2015, and they achieved the second level of national standards from January to March 2015. (2) For PM10, Beijing achieved the second level of national standards from January 2015 to June 2015. Chongqing achieved the second level of national standards from February 2015 to June 2015, which didn't achieve the national standards in January 2015. Baoding and Xingtai achieved the second level of national standards from April to June 2015, but they didn't achieve the national standards from January to March 2015. Overall, the monthly mean concentration of SO2 and PM10 in the 4 cities appeared a downward trend.
Results and discussions
The total economic loss associated with public health effects caused by air pollution in 74 cities
The dose–response relationship and the loss value estimation of the public health effects in different cities vary; therefore, this paper establishes different scenario parameters for the lowest limit scenario and the highest limit scenario in order to evaluate the total economic loss related to the effects of air pollution on public health in 74 cities.
The lowest limit scenario
As shown in Table 2, there were 84,917 premature deaths caused by PM10 and SO2. There were 646,282 hospitalizations caused by respiratory disease, 12.66 million emergencies, more than 990 million restriction days and 1.23 million lowest respiratory tract infections and occurrence of childhood asthma due to PM10. However, the economic loss caused by the effects of SO2 on public health was less than that of PM10.
Table 2 The total lowest economic loss caused by the effects of air pollutants on public health in 74 cities
This paper calculated that the total health-related economic loss caused by the air pollutant in 74 cities was approximately 310 billion yuan, explaining approximately 1.63 % of the 74 cities' GDP, which was higher than the result of Wei et al. (2012). The total economic loss of the public health effect caused by PM10 was 300.8 billion yuan, explaining approximately 97.03 % of the total economic loss, which was the major economic loss and was consistent with the result of Zhang (2012). The economic loss caused by chronic bronchitis, which was approximately 225.2 billion yuan. It was the largest in the total economic loss, explaining approximately 72.64 % of the total economic loss. The result was different from that of Chen et al. (2010), who determined that the economic loss caused by premature death was the largest.
The highest limit scenario
Table 3 showed there were 178,776 premature deaths caused by PM10 and SO2. There were 646,282 hospitalizations caused by respiratory disease, 12.66 million emergencies, more than 3090 million restriction days and 1.23 million lower respiratory tract infections and childhood asthma caused by PM10. Similarly, the economic loss of the public health effect caused by SO2 was also less than that of PM10.
Table 3 The total highest economic loss of the public health effect caused by the air pollutant in 74 cities
The total economic loss of the public health effect caused by the air pollutant in 74 cities was approximately 439.8 billion yuan in the highest limit scenario, representing approximately 2.32 % of the GDP in 74 cities, a slight difference from the result of Wei et al. (2012). The total highest economic loss of the public health effect caused by PM10 was 418 billion yuan, explaining approximately 95.04 % of the total economic loss, which was the major economic loss and was also consistent with the result of Zhang (2012). The economic loss caused by chronic bronchitis was also the largest in the total economic loss, approximately 225.2 billion yuan, explaining approximately 51.24 %. The result was also different from that of Chen et al. (2010).
The economic loss caused by effect on the public health effect in the major cities
To further understand the health-related economic loss caused by the air pollutant, this paper estimated the health effects of air pollutants and the economic loss in the major cities from January 2015 to June 2015.
From Fig. 3, Chongqing's public health economic loss was 17 billion yuan, ranking the first among the 74 cities, followed by Beijing, Baoding, and Tianjin. From the regional perspective, there were 4 municipalities and 4 cities in Hebei Province in the top 10 cities with the highest economic loss. There were 7 cities in North China excluding Chongqing, Shanghai and Chengdu in the top 10 cities with the highest economic loss.
The 10 cities with the highest economic loss (million yuan)
As shown in Fig. 4, there were 7 cities in Hebei Province in the top 10 with the highest economic loss. Zhengzhou and Ji'nan also ranked in the top 10 cities due to their poor air quality. Urumqi's health-related economic loss was not high; however, because of its low population, the resulting health economic loss per capita was higher.
The 10 cities with the highest health-related economic loss per capita (yuan/per person)
Figure 5 shows that the proportion of the health-related economic loss accounting for GDP in Xingtai was the highest, which was 10.15 %. In the 10 cities with the highest proportion of health-related economic loss accounting for GDP, there were 9 cities in the Hebei province. Suqian in Jiangsu province had a higher health-related economic loss and a lower GDP, ranking the tenth; therefore, the proportion of its health-related economic loss accounting for GDP was higher, ranking in the top 10. The economic losses of the public health effect of 4 municipalities ranked in the top 10. Although their GDPs were higher, the proportions of their health-related economic loss accounting for GDP were relatively lower, which did not rank in the top 10.
The 10 cities with the highest proportion of health-relate economic loss accounting for GDP (%)
In the highest limit scenario, the cities ranking in the top 10 with the highest economic loss in Fig. 6 were the same as those in the lowest limit scenario in Fig. 3. However, the rankings of Zhengzhou and Chengdu were different in Figs. 4 and 3.
The cities ranking in the top 10 with the highest economic loss per capita in Fig. 5 in the highest limit scenario were the same as in the lowest limit scenario in Fig. 4. However, as shown in the Fig. 7 in the following, the economic loss per capita in the top 10 cities in the highest limit scenario was higher than that in the lowest limit scenario. For example, the economic loss per capita in Baoding was 1599.9 yuan/per person, higher by 477.2 yuan than that in the lowest limit scenario.
The 10 cities with the highest proportion of health-related economic loss accounting for GDP in Fig. 8 in the highest limit scenario were the same as in the lowest limit scenario in Fig. 3. However, the rankings of Shijiazhuang, Chengde, Zhengjiukou and Qinhuangdao and the proportions of the health-related economic loss accounting for GDP were different in Figs. 8 and 5.
The 10 cities with the highest proportion of the health-related economic loss accounting for GDP (%)
Conclusions and policy implications
Based on the dose–response relationship and the willingness to pay method, this paper evaluated the health-related economic loss caused by air pollution in China's 74 cities using the latest available data regarding to PM10 and SO2 from January 2015 to June 2015, by establishing lowest and highest limit scenarios. The conclusions and policy implications are as follows.
For the whole 74 cities
The health-related economic loss caused by PM10 was larger than that caused by SO2 in the lowest and highest limit scenarios, and the economic loss associated with chronic bronchitis caused by PM10 was the largest in all the losses. Thus, PM10 has become the main air pollutant in 74 cities, and it is necessary to focus on the issue of chronic bronchitis caused by PM10.
For the major cities
In the lowest and highest limit scenarios, the health-related economic loss in Chongqing, Beijing, Baoding, Tianjin and other major cities was larger than in other cities. The health-related economic loss per capita in Baoding, Xingtai and Zhengzhou was higher than in other cities. Regarding to the proportion of the health-related economic loss accounting for GDP, there were 9 cities in the Hebei Province included in the top 10 cities with the highest loss. It was evident that the air pollution was serious in North China, particularly in the Hebei Province, except in Shanghai in East China and in Chongqing and Chengdu in the southwest of China.
According to the results of this paper, Hebei Province is a typical polluted area. Energy consumption structure in Hebei Province is mainly composed of coal resource. Main pollutants from coal combustion are PM10 and SO2, etc. Thus, to reduce air pollution, the coal-based energy structure needs to be improved, and new energies and advanced production processes need to be utilized. Furthermore, strengthening the development of technology and equipment; improving combustion technology, combustion devices and the fuel utilization rate; and reducing the additional pollutants generated by fuel burning will help reduce air pollution.
Pollutant concentration is an important factor affecting the loss of health effects. The government should adopt the emissions trading system, limit the pollutant discharges of enterprises, grasp the influence of the enterprises on environmental pollution, strengthen the management of enterprises, and develop a number of administrative regulations conducive to environmental protection to ensure the implementation of environmental protection measures.
From the calculation results, the urban population is also an important factor affecting the loss of health effects. The government should reasonably control the urban population and improve people's awareness of environmental protection. Accelerating the transfer of industries and upgrading may reduce the non-household population in order to reduce the side-effects caused by population growth and improve the urban environment and public health.
Here the paper uses the data from January to June 2015 to calculate the health-related economic loss in 74 cities. If the paper uses a long term data, for example, which covers from January to December 2015, there may be a larger health-related economic loss (assuming the population in 74 cities is constant). However, the health-related economic loss from January to December 2015 may not be twice as much as that from January to June 2015. As it can been seen from Figs. 1 and 2, the monthly mean concentration data of SO2 and PM10 from January to June 2015 appeared a downward trend. In the future, data (if complete and available) can be combined using a geographic information system and other new tools to determine the economic loss of caused by the effects of air pollution on public health in the typical resource-based regions or cities and to provide references for environmental management and sustainable development.
Ami D, Aprahamian F, Chanel O (2014) Willingness to pay of committed citizens: a field experiment. Ecol Econ 105:31–39
Askcinet (2015) The people's number and GDP ranking in 74 cities in the first half of 2015. http://www.askci.com/data/2015/07/23/15652fovg.shtml. Accessed on 23 Jul 2015
Brandt S, Perez L, Künzli N (2014) Cost of near-roadway and regional air pollution–attributable childhood asthma in Los Angeles County. J Allergy Clin Immunol 5:1028–1035
Cai YP, Yang ZF (2003) Health loss estimation of air pollution in the township industrial enterprises in Tianjin. J Saf Environ 1:33–36
Cai CG, Chen G, Qiao XC (2007) Comparison of the value evaluation method on the two fractional conditions of the single boundary and two boundary conditions—taking the investigation on health hazard caused by air pollution in Beijing city as an example. China Environ Sci 1:39–43
Carlsson F, Martinsson P (2001) Willingness to pay for reduction in air pollution: a multilevel analysis. Environ Econ Policy Stud 1:17–27
Chen BH, Hong CJ (2002) Quantitative assessment on the health effect of SO2 pollution in Shanghai City. J Environ Health 1:11–13
Chen BH, Hong CJ, Kan HD (2001) Methodological research on the health-based risk assessment on air pollution. J Environ Health 2:67–69
Chen RJ, Chen BH, Kan HD (2010) A health-based economic assessment of particulate air pollution in 113 Chinese cities. China Environ Sci 3:410–415
Chen J, Li W, Cheng HG (2015) Evaluation of emission reduction potentials of key air pollutants and health benefits for residents of Beijing. Res Environ Sci 7:1114–1121
China's National Environmental Monitoring Centre (2013a) Monthly air quality report in January 2013 in 74 cities. http://www.cnemc.cn/publish/106/news/news_33883.html. Accessed on 07 Feb 2013
China's National Environmental Monitoring Centre (2013b) Monthly air quality report in November 2014 in 74 cities. http://www.cnemc.cn/publish/106/news/news_43865.html. Accessed on 21 Dec 2013
China's National Environmental Monitoring Centre (2015b) Monthly air quality report in Febuary 2015 in 74 cities. http://www.cnemc.cn/publish/106/news/news_44345.html. Accessed on 17 Mar 2015
China's National Environmental Monitoring Centre (2015c) Monthly air quality report in March 2015 in 74 cities. http://www.cnemc.cn/publish/106/news/news_44415.html. Accessed on 14 Apr 2015
China's National Environmental Monitoring Centre (2015d) Monthly air quality report in April 2015 in 74 cities. http://www.cnemc.cn/publish/106/news/news_44867.html. Accessed on 25 May 2015
China's National Environmental Monitoring Centre (2015e) Monthly air quality report in May 2015 in 74 cities. http://www.cnemc.cn/publish/106/news/news_45103.html. Accessed on 16 May 2015
China's National Environmental Monitoring Centre (2015f) Monthly air quality report in June 2015 in 74 cities. http://www.cnemc.cn/publish/106/news/news_45341.html. Accessed on 14 Jul 2015
Dockery DW, Pope CA, Xu X (1993) An association between air pollution and mortality in six US cities. N Engl J Med 24:1753–1759
Gao J, Xu XP, Li BL (1993) Investigation on the relationship between air pollution and death in Haidian District, Beijing. Chin J Prev Control Chronic Non-Commun Dis 5:207–210
Han Q (2011) The health damage caused by the particulate matters in air pollutants in Beijing—human capital method. North Environ 11:150–152
Han MX, Guo XM, Zhang YS (2006) Human capital loss of urban air pollution. China Environ Sci 4:509–512
Hedley AJ, McGhee SM, Barron B (2008) Air pollution: costs and paths to a solution in Hong Kong—understanding the connections among visibility, air pollution, and health costs in pursuit of accountability, environmental justice, and health protection. J Toxicol Environ Health Part A 9–10:544–554
Ho MS, Jorgenson DW (2007) Sector allocation of emissions and damages in clearing the air: the health and economic damages of air pollution in China. The MIT Press, Cambridge
Ho MS, Nielsen CP (2007) Clearing the air: the health and economic damages of air pollution in China. The MIT Press, Cambridge
Huanqiunet (2014) The World Health Organization reported that a total of 7 million people died from air pollution in 2012. http://world.huanqiu.com/exclusive/2014-03/4929416.html. Accessed on 25 Mar 2014
Huanqiunet (2015) WHO: air pollution has become the world's largest environmental health risk. http://health.huanqiu.com/health_news/2015-06/6581336.html?referer=huanqiu. Accessed on 02 Jun 2015
Istamto T, Houthuijs D, Lebret E (2014) Willingness to pay to avoid health risks from road-traffic-related air pollution and noise across five countries. Sci Total Environ 497:420–429
Jia L, Guttikunda SK, Carmichael GR (2004) Quantifying the human health benefits of curbing air pollution in Shanghai. J Environ Manage 1:49–62
Jing LB, Ren CX (2000) Relationship between air pollution and acute and chronic respiratory diseases in Benxi City. J Environ Health 5:268–270
Kaushik CP, Ravindra K, Yadav K (2006) Assessment of ambient air quality in urban centres of Haryana (India) in relation to different anthropogenic activities and health risks. Environ Monit Assess 1–3:27–40
Koop G, Tole L (2004) Measuring the health effects of air pollution: to what extent can we really say that people are dying from bad air? J Environ Econ Manage 1:30–54
Ministry of Environmental Protection of the People's Republic of China (2011) National environmental protection "12th Five-Year Plan". http://gcs.mep.gov.cn/hjgh/shierwu/201112/t20111221_221595.htm. Accessed on 21 Dec 2011
Murray CJ, Lopea AD (1997) Global mortality, disability, and the contribution of risk factors: global burden of disease study. Lancet 349:1436–1442
Pascal M, Corso M, Chanel O (2013) Assessing the public health impacts of urban air pollution in 25 European cities: results of the Aphekom project. Sci Total Environ 449:390–400
Patankar AM, Trivedi PL (2011) Monetary burden of health impacts of air pollution in Mumbai, India: implications for public health policy. Public Health 3:157–164
Peng XZ, Tian WH (2003) Study on the willingness to pay for the economic loss of air pollution in Shanghai City. World Econ Pap 2:32–44
Ridker RG (1967) Economic costs of air pollution: studies in measurement. Praeger, New York
Samet JM, Zeger SL, Dominici F (2000) The national morbidity, mortality, and air pollution study. Part II: morbidity and mortality from air pollution in the United States. Res Rep Health Eff Inst 2:5–79
Shang YH, Zhou DJ, Yang J (2010) Study on the economic loss of the human health caused by air pollution. Ecol Econ 1:178–179
Shen XW, Wang YH, Zhang WX (2014) The economic loss of the human health caused by air pollution in Kunming. China Market 46:124–126
U.S. EPA (1999) Benefits and costs of the clean air act. U.S. EPA Office of Air and Radiation, Washington, DC
Wan Y, Yang HW, Masui T (2005) Health and economic impacts of air pollution in China: a comparison of the general equilibrium approach and human capital approach. Biomed Environ Sci 6:427
Wang H, John M (2006) Willingness to pay for reducing fatal risk by improving air quality: a contingent valuation study in Chongqing, China. Sci Total Environ 1:50–57
Wang X, Smith K (1999) Near-term health benefits of greenhouse gas reductions: a proposed assessment method and application to two energy sectors of China. World Health Organization, Geneva
Wang Y, Zhao XL, Xu Y, Li Y (2005) Estimation on the economic loss of air pollution in Shandong Province. Urban Environ Urban Ecol 2:30–33
Wei YM, Wu G, Liang QM (2012) China Energy Security Report (2012): Study on energy security. Science Press, Beijing
Wilkinson P, Smith KR (2007) A global perspective on energy: health effects and injustices. The Lancet 370(9591):965–978
Wong TW, Lau TS, Yu TS (1999) Air pollution and hospital admissions for respiratory and cardiovascular diseases in Hong Kong. Occup Environ Med 10:679–683
Wong CM, Atkinson RW, Anderson HR (2002) A tale of two cities: effects of air pollution on hospital admissions in Hong Kong and London compared. Environ Health Perspect 1:67
World Bank (1997) Clear water, blue skies: China's environment in the new century. World Bank, Washington, DC
World Bank SEPA (2007) Cost of pollution in China. World Bank, World Bank
Xia G (1998) Economic measurement and study on the loss of environmental pollution in China. China Environmental Sciences Press, Beijing
Xu ZY, Liu YQ, Yu DQ (1996) Impact of air pollution on mortality in Shenyang. Chin J Public Health 1:61–64
Xu LY, Yin H, Xie XD (2014a) Health risk assessment of inhalable particulate matter in Beijing based on the thermal environment. Int J Environ Res Public Health 12:12368–12388
Xu MM, Guo YM, Zhang YJ (2014b) Spatiotemporal analysis of particulate air pollution and ischemic heart disease mortality in Beijing, China. Environ Health 1:1–12
Yaduma N, Kortelainen M, Wossink A (2013) Estimating mortality and economic costs of particulate air pollution in developing countries: the case of Nigeria. Environ Resour Econ 3:361–387
Yan J (2012) Residents' breathing, the hospital cost of the disease of the circulatory system caused by air pollution in Lanzhou. In: Food safety and healthy life conference in Gansu in 2012, pp 61–64
Yu F, Guo XM, Zhang YS (2008) Evaluation on health economic loss caused by air pollution in 2004. J Environ Health 12:999–1003
Zeng XG, Xie F, Zong Q (2015) The behavior choice and willingness to pay to reduce the health risk of PM2. 5—taking the residents in Beijing as an example. China Popul Resour Environ 1:127–133
Zhang QF (2012) Toward an environmentally sustainable future country environmental analysis of the People's Republic of China. China Financial and Economic Publishing House, Beijing
Zhang GZ, Chun R, Nan ZR (2008) Study on the effects of air pollution on human health and economic loss in Lanzhou. J Arid Land Resour Environ 8:120–123
Zhou J, Wang Y, Ren L (2010) Willingness to pay for the improvement of air quality in Shandong typical city. J Environ Health 6:507–510
Zmirou D, Deloraine AMD, Balducci F, Boudet C (1999) Health effects costs of particulate air pollution. J Occup Environ Med 10:847–856
LL and YL designed the research and methodology; DP, CY collected the data and compiled all the data and literature; LL and CS finished the experiment and calculation; YL and LL analyzed the results and put forward the policies; YL and LL revised the manuscripts and approved the manuscripts; YL will be responsible for the future questions from readers as the corresponding authors. All authors read and approved the final manuscript.
The authors express their sincere thanks for the support from the National Natural Science Foundation of China under Grant No. 71173200 and the support from the Development and Research Center of China Geological Survey under Grant Nos. 1212011220302 and 12120114056601, Key Laboratory of Carrying Capacity Assessment for Resource and Environment, Ministry of Land and Resources (Chinese Academy of Land and Resource Economics, China University of Geosciences Beijing) under Grant No. CCA2015.08.
School of Humanities and Economic Management, China University of Geosciences, Beijing, 100083, China
Li Li, Yalin Lei, Chen Yu & Chunyan Si
Key Laboratory of Carrying Capacity Assessment for Resource and Environment, Ministry of Land and Resources, Beijing, 100083, China
Central University of Finance and Economics, Beijing, 100081, China
Dongyan Pan
Yalin Lei
Chen Yu
Chunyan Si
Correspondence to Yalin Lei.
Li, L., Lei, Y., Pan, D. et al. Economic evaluation of the air pollution effect on public health in China's 74 cities. SpringerPlus 5, 402 (2016). https://doi.org/10.1186/s40064-016-2024-9
The public health effect
The economic loss
74 cities | CommonCrawl |
Golden Mathematics
Article by Toni Beardon
Published February 2011.
Setting Out on a Voyage of Exploration
The connection between these pictures is a mathematical constant called the golden ratio or the divine proportion which often appears in mathematics, nature and art. The idea of this article is to map out for you, and guide you through, a sequence of NRICH challenges in which you can learn some mathematics by exploring the amazing properties of the golden ratio and Fibonacci numbers. You will find Hints and Notes to help you. Try to solve the problems by your own methods before looking at the published solutions which have been written by school students.
There are some side trips to explore properties of the Fibonacci numbers which are not essential for the main voyage of discovery. You can take these side trips if you have time or maybe return to them later.
You can go as far as the Golden Construction section without any algebra but to follow the trail any farther you need to be able to solve quadratic equations.
Sheep Talk
Follow this link and try the first challenge, Sheep Talk , where you meet a process known as Cellular Automata in which a population grows from a given starting point and a simple rule. You may find it easier to open a second window so you can keep this article in one window and the problems in the other window. In Sheep Talk the numbers of letters give the Fibonacci Sequence where each term is the sum of the two previous terms in the sequence. If we denote the $n$th term by $F_n$ then the rule is written: $$F_n = F_{n-1}+F_{n-2}.$$
The first two terms are 1 and 1 and the sequence starts 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
Now divide each term by the term before it and keep doing this for say 13 terms or more. What do you notice?
Set up a spreadsheet like the one illustrated. One cell in the spreadsheet is outlined and you can see that the formula '=A3+A4' has been defined for that cell. The Fibonacci sequence has been produced by copying the formula down the column. In your spreadsheet change the first two terms to any values you choose. What happens to the sequence? What happens to the ratio of successive terms?
You will find that, whatever the first two terms in the sequence, the ratio of successive terms quickly approaches a constant value. A later challenge in this trail leads to a proof that this value is the golden ratio.
Detour 1 : to explore some Fibonacci number patterns
One Step Two Step
Try this challenge You can go downstairs one step or two steps at a time. In how many ways can you do this for 1, 2, 3, 4 ... or any number of steps?
Here's a challenge Fibs that involves exploring general Fibonacci sequences where each term is the sum of the two terms before it but the two initial terms may be anything you choose them to be.
Return to the main trail
Here are some rectangles. The yellow, orange and cream rectangles are similar in more than colour, they are mathematically similar, in fact they are enlargements of each other. The other two rectangles are different, the blue rectangle is longer and thinner in shape and the lilac rectangle is more square. How do you tell from the measurements of any pair of rectangles whether they are similar? The answer is you tell from the proportions of the rectangles. Divide the length of the long side by the length of the short side and if these ratios are the same then the rectangles are similar.
One rectangular shape is said to have 'divine proportions' and it is called the Golden Rectangle. If you cut off a square from a Golden Rectangle the remaining smaller rectangle has exactly the same proportions and the ratio of the long side to the short side is the golden ratio.
For the next challenge you will need some squared paper. Draw bigger and bigger rectangles by adding on squares whose side lengths are the Fibonacci numbers: 1, 1, 2, 3, 5, 8, 13, ... etc. Start with two unit squares side by side as in the diagram. Then draw below a square of side 2 units to make a 3 by 2 rectangle, then on the left a square of side 3 units to make a 5 by 3 rectangle, then above a square of side 5 units to make an 8 by 5 rectangle.
Continue in this way, building on the squares in a clockwise pattern. On a sheet of 5mm squared paper, taking 5 mm as the unit, you can just fit a rectangle of side 55 by 34.
Imagine drawing these rectangles on a large tiled courtyard so that you can go on making bigger and bigger rectangles. Notice that the sides of these rectangles are the Fibonacci numbers and as you draw bigger rectangles they get closer in proportions to the Golden Rectangle.
Now draw a spiral starting in the bottom left hand corner of the unit square on the left; draw a smoothly curving arc to the opposite corner of the square, move into and across the next square in a smoothly curving arc, and so on across each square. This is called a logarithmic spiral.
In a section of a Nautilus shell, in the arrangements of seeds on flower heads and in the segments of a pine cone we can see similar spirals.
Pentagons and Pentagrams
Take a strip of paper and loosely tie a simple knot, then very carefully adjust it so that it is perfectly symmetrical before you flatten it so that it forms a pentagon. Can you prove that this is a regular pentagon? Hold it up to the light. Can you see a five pointed star or pentagram inside your pentagon?
Now draw a regular pentagon using a ruler and a protractor to measure the angles of 108 degrees. Draw in the five chords to form a pentagram star inside your pentagon. Measure the length of one of the chords and the length of a side of the pentagon and divide the chord length by the side length. You should get a ratio about 1.62 and later we'll prove that the exact value of this ratio is the golden ratio.
How many isosceles triangles with two angles of 36 degrees and one of 108 degrees can you find in your diagram? How many isosceles triangles with two angles of 72 degrees and one of 36 degrees can you find? These are golden triangles. Measure the ratio of the longest side to the shortest side in these triangles and you will again find that this is the golden ratio.
Inside your pentagram star there is a regular pentagon and if you draw the diagonals in this pentagon they form a smaller pentagram with an even smaller pentagon inside. You could continue this process indefinitely seeing pentagrams inside pentagons with pentagrams inside them and so on for ever.
Golden Construction
The next challenge is the Golden Construction. Have a go at this ruler and compass construction of a golden rectangle. If you cut off a square from a golden rectangle the remaining smaller rectangle has exactly the same proportions and the ratio of the long side to the short side is the golden ratio which you can find by this construction without using any algebra. To proceed further you need to be able to solve quadratic equations. You might want to come back to this trail when you have learnt some more algebra but finish now by reading some NRICH articles written for younger readers about the history of Fibonacci:
Fibonacci's Three Wishes.
Fibonacci's Three Wishes 2.
Leonardo of Pisa and the Golden Rectangle.
Second stage of the expedition
The golden rectangle has sides in the ratio $x:1$ such that, taking the shorter side length as one unit, when a square of side 1 unit is removed, the new rectangle, with sides of length $x-1$ and 1 units, has the same proportions. That is $${x\over 1} = {1\over x-1}.$$ Simplifying this expression we get the quadratic equation $x^2 - x - 1 = 0$ which has solutions $x = (1 \pm \sqrt 5)/2$. Thus the golden ratio, which is denoted by the Greek letter phi written $\phi$ must be the positive root $(1+\sqrt 5)/2 = 1 .618033\ldots$ and $1/\phi = \phi - 1 = 0.618033\ldots$.
The Golden Mean
The golden ratio features in Euclid's Elements (c.300 BC) as the extreme and mean ratio. It was studied earlier by Plato and the Pythagoreans and it appears even earlier in Egyptian architecture, for example in the Great Pyramid of Giza built around 2560 BC. The term 'golden' and the use of $\phi$ as the notation were introduced in the 19th and 20th centuries.
A point on a line segment dividing it into two lengths $a$ and $b$ is said to divide it externally in the ratio $a+b$ to $a$ and internally in the ratio $a$ to $b$. If these ratios are equal then the point is called the golden mean and the ratios are referred to as the extreme and mean ratios. Here $${a+b \over a} = {a\over b}$$ and writing $a/b = x$ we get $$1 + {1\over x} = x$$ giving the quadratic equation $x^2 - x -1 = 0$ whose positive solution is the golden ratio $\phi = (1 + \sqrt 5)/2$.
Golden Thoughts
The next challenge Golden Thoughts involves areas of triangles and the golden mean. It is by no means obvious, but easy enough to prove, that drawing three right angled triangles of equal area in a rectangle produces golden mean points on the sides of the rectangle.
Golden Eggs and Nested Roots
Here are two more problems to crack. One involves the area of an ellipse and the second involves infinitely many nested square roots. $$\phi = \sqrt{1+\sqrt{1+ \sqrt {1 + \sqrt {1 + ...}}}}$$
This infinitely long expression looks unmanageable at first but try squaring it.
Golden Triangles
In this challenge you meet golden triangles again and this time calculate the ratios which you found earlier by measurement and which give these triangles their special connection with the golden ratio.
Pentagons again
You have seen how the golden triangles fit into a regular pentagon. You can use what you have already learnt in Pent to prove that the ratio of the chord length to the side length is the golden ratio and that the points of intersection of the chords are the golden mean points.
The challenge Pentakite involves extending two edges of a pentagon to make a kite and an alternative way of calculating the the chord length.
The golden triangles in these diagrams give us exact values for some of the trigonometric ratios, namely $$\cos 36^o=\sin 54^o=\phi /2 = (1+\sqrt 5)/4$$ $${\rm sec} 72^o= {\rm cosec} 18^o=2\phi= (1+\sqrt 5)$$ and $$\cos 72^o=\sin 18^o=1/2\phi = (\sqrt 5 - 1)/4.$$
Moving from geometry to algebra the next challenge Golden Powers involves powers of the golden ratio. You know $\phi^2 = \phi + 1$ so the challenge is to express the powers of $\phi$ in terms of $\phi$ and to find the values of $a_n$ and $b_n$ such that $\phi^n = a_n \phi + b_n$.
Detour 2 : A side expedition to explore Fibonacci Numbers
Golden Fibs
When is a Fibonacci sequence also a geometric sequence? Clearly this is not the case for the standard Fibonacci sequence but consider all sequences obeying the rule that each term is the sum of the two previous terms but with different initial terms. In Golden Fibs you will find a general Fibonacci sequence which is also a geometric sequence.
Gnomons
A gnomon is an L shaped carpenter's tool still used today which appeared often in Babylonian and Greek mathematics. Each Fibonacci number can be represented by a gnomon and the first of these two challenges involves an interactivity where you move the gnomons to join pairs together to make the next Fibonacci number in the sequence and of course you can cut your own from squared paper.
Fibonacci Factors
This challenge Fibonacci Factors is another digression about the Fibonacci sequence and here you will explore the patterns of multiples of 2 and 3 in the sequence.
Return to the Main Trail : Pythagorean Golden Means
Pythagorean Golden Means links Pythagoras' theorem and the arithmetic, geometric and harmonic means of two numbers specially chosen so that these three means are the lengths of the sides of a right-angled triangle. What is special about the numbers? You have guessed it! The ratio of one to the other involves the golden ratio but this time a power of the golden ratio.
Golden Fractions
Here you will learn about continued fractions, so called because they contain fractions within fractions going on for ever. The very simplest continued fraction has ones everywhere and its value is, surprise surprise, the golden ratio. Tackle the Golden Powers challenge to find out all about it.
If you have worked through all these challenges then you deserve a gold medal, in the shape of a pentagon containing a star perhaps. You are now very knowledgeable about Fibonacci sequences and the golden ratio but did you know that new research results are being discovered every year and there is a mathematical journal called Fibonacci devoted entirely to newly discovered mathematics in this area.
For more reading on the subject and to learn more mathematics here are some links.
The article on the Golden Ratio, Fibonacci Numbers and Continued Fractions proves the result you discovered when working on Sheep Talk at the start of this trail and takes the ideas you have met on the trail a little further. It also introduces the use of two by two matrices to solve simultaneous equations and cobweb diagrams to find the limit of an iterative process.
Here is some more reading on the subject from the Plus maths website:
The life and numbers of Fibonacci.
The golden ratio and aesthetics by Mario Livio.
Maths and Art : a whistlestop tour.
and some book reviews:
The Golden Section by Mark Wainwright.
The Golden Ratio by Mario Livio. | CommonCrawl |
BMC Bioinformatics
Prediction of regulatory targets of alternative isoforms of the epidermal growth factor receptor in a glioblastoma cell line
Claus Weinholdt
Henri Wichmann
Johanna Kotrba
David H. Ardell
Matthias Kappler
Alexander W. Eckert
Dirk Vordermark
Ivo Grosse
First Online: 22 August 2019
Part of the following topical collections:
Transcriptome analysis
The epidermal growth factor receptor (EGFR) is a major regulator of proliferation in tumor cells. Elevated expression levels of EGFR are associated with prognosis and clinical outcomes of patients in a variety of tumor types. There are at least four splice variants of the mRNA encoding four protein isoforms of EGFR in humans, named I through IV. EGFR isoform I is the full-length protein, whereas isoforms II-IV are shorter protein isoforms. Nevertheless, all EGFR isoforms bind the epidermal growth factor (EGF). Although EGFR is an essential target of long-established and successful tumor therapeutics, the exact function and biomarker potential of alternative EGFR isoforms II-IV are unclear, motivating more in-depth analyses. Hence, we analyzed transcriptome data from glioblastoma cell line SF767 to predict target genes regulated by EGFR isoforms II-IV, but not by EGFR isoform I nor other receptors such as HER2, HER3, or HER4.
We analyzed the differential expression of potential target genes in a glioblastoma cell line in two nested RNAi experimental conditions and one negative control, contrasting expression with EGF stimulation against expression without EGF stimulation. In one RNAi experiment, we selectively knocked down EGFR splice variant I, while in the other we knocked down all four EGFR splice variants, so the associated effects of EGFR II-IV knock-down can only be inferred indirectly. For this type of nested experimental design, we developed a two-step bioinformatics approach based on the Bayesian Information Criterion for predicting putative target genes of EGFR isoforms II-IV. Finally, we experimentally validated a set of six putative target genes, and we found that qPCR validations confirmed the predictions in all cases.
By performing RNAi experiments for three poorly investigated EGFR isoforms, we were able to successfully predict 1140 putative target genes specifically regulated by EGFR isoforms II-IV using the developed Bayesian Gene Selection Criterion (BGSC) approach. This approach is easily utilizable for the analysis of data of other nested experimental designs, and we provide an implementation in R that is easily adaptable to similar data or experimental designs together with all raw datasets used in this study in the BGSC repository, https://github.com/GrosseLab/BGSC.
EGFR Splice variants RNAi Bayesian Information Criterion Bayesian Gene Selection Criterion
Serine-threonine protein kinase
ALDH4A1
Aldehyde Dehydrogenase 4 family member A1
AREG
Amphiregulin
BGSC
Bayesian Gene Selection Criterion
BIRC5
Baculoviral IAP repeat containing 5
CKAP2L
Cytoskeleton associated protein 2 like
CLCA2
Chloride channel accessory 2
CPCC
CKAP2-positive cell count
Epidermal growth factor receptor
GALNS
Galactosamine (N-Acetyl)-6-Sulfatase
Human epidermal growth factor receptor 2
Hypoxanthine Phosphoribosyltransferase 1
MMP2
Matrix Metallopeptidase 2
PIK3CA
Phosphatidylinositol 3-Kinase catalytic subunit alpha
PLC γ
Phospholipase C gamma
Phosphatase and tensin homolog
Quantitative real-time polymerase chain reaction
Rho-associated protein kinase 1
sEGFR
Soluble EGFR
TGF α
Transforming growth factor alpha
Tyrosine kinase inhibitors
Tumor potentiating region
The online version of this article ( https://doi.org/10.1186/s12859-019-2944-9) contains supplementary material, which is available to authorized users.
Glioblastoma is the most malignant and most frequent primary cerebral tumor in adults and is responsible for 65% of all brain tumors [1]. One potential molecular target amplified in 36% of glioblastoma patients is the epidermal growth factor receptor (EGFR), and the expression of EGFR is associated with prognosis in cancer [2]. EGFR is known to affect growth and survival signals and to play a crucial role in the regulation of cell proliferation, differentiation, and migration of various tumor entities [3]. Hence, EGFR is well known as a prognostic tumor marker and therapeutic target in different tumor entities.
The full-length transmembrane glycoprotein isoform of EGFR consists of three functional domains of which the extracellular domain is capable of binding at least seven different ligands such as EGF, AREG, or TGF- α [4]. However, there are at least three different truncated EGFR splice variants (II, III, and IV). Up to now, only the full-length EGFR isoform I translated from EGFR splice variant I is well investigated, but comparatively little is known about the biological significance of the truncated EGFR isoforms II-IV translated from EGFR splice variants II-IV.
EGFR isoforms II-IV lack the intra-cellular tyrosine-kinase domain [5], and Maramotti et al. [6] describes that EGFR isoforms II-IV can potentially function as natural inhibitors of EGFR isoform I. EGFR isoforms II-IV bind EGF with similar binding kinetics but lower binding affinity than EGFR isoform I [7], which binds EGF with a dissociation constant of 1.77×10−7M [8].
Different tumor therapies targeting EGFR via antibodies or small molecules often do not have response rates as successful as expected. EGFR isoforms II-IV may be responsible for therapeutic failures because they do not contain the tyrosine-kinase domain targeted by small molecules. However, they do contain the extracellular N-terminus of EGFR, which is bound by therapeutic antibodies. Nevertheless, EGFR-specific antibody therapy requires the interaction of EGFR-bound therapeutic antibodies with presenting cells. EGFR isoforms II-IV are soluble proteins that do not mark the expressing cell itself, but rather diffuse in the extracellular space, probably bind to surrounding non-tumor cells, and possibly mislead the immune system.
This problem motivated the present work of perturbing the profile of the four EGFR splice variants using small interfering RNAs (siRNAs) that differentially target these splice variants and of measuring the resulting expression responses using traditional microarrays. It is impossible to knock-down only EGFR splice variants II-IV and not EGFR splice variant I by RNAi because there is no region specific to only EGFR splice variants II-IV. Hence, we performed the RNAi experiments according to the nested experimental design as shown in Table 1. Based on this design, the associated effects of a knock-down of EGFR splice variants II-IV can only be inferred indirectly by subtracting the effects found by knocking down only EGFR splice variant I from the effects found by knocking down all EGFR splice variants I-IV. The problem of only indirectly measurable gene regulation or receptor effects of nested splice variants is widespread in many regulatory pathways and many species, so we developed a two-step bioinformatics approach for the prediction of putative target genes called Bayesian Gene Selection Criterion (BGSC) approach, which we tested by quantitative real-time polymerase chain reaction (qPCR) experiments.
Experimental design where the rows present the RNAi treatment – without RNAi, RNAi against EGFR splice variant I (siRNAI), and RNAi against all EGFR splice variants (siRNAALL) – and the columns present the EGF treatment
no EGF
no RNAi
RNAi by siRNAI
RNAi by siRNAALL
The six corresponding logarithmic expression values per gene are denoted by x1,…,x6
The rest of this paper is structured as follows: In Results, we describe the identification of a cell line with an inducible EGFR-signaling pathway, investigate the specificity of siRNAs, introduce the two-step BGSC approach for predicting putative target genes regulated by EGF via EGFR isoforms II-IV and not by the full-length EGFR isoform I or other receptors, and describe the qPCR validation experiments. In Discussion, we discuss the adjustability of the EGFR-signaling pathway in cell line SF767 and the biological relevance of the validated genes.
Identification of a cell line with an inducible EGFR-signaling pathway
A meaningful analysis of the EGFR-signaling pathway is possible only in a cell line with an adjustable pathway, e.g., by a response to ligand stimulation or treatment by a tyrosine kinase inhibitor (TKI) [9]. Hence, we investigated four glioblastoma cell lines in a pilot study to identify a cell line with an adjustable EGFR-signaling pathway. Figure 1 shows the measured protein levels of phosphorylated AKT (pAKT) resulting from the treatment of two of these cell lines U251MG and SF767 with increasing levels of recombinant ligand EGF. We found that the pAKT (Ser473) level in cell line U251MG is constantly high, possibly resulting from the mutated PTEN gene [10]. In the PTEN wild-type cell line SF767 [11], pAKT showed a level of activity even without adding recombinant EGF due to the E545K-mutation of gene PIK3CA present in this cell line [12]. However, the activity of pAKT could be increased three-fold by adding recombinant EGF as a ligand, indicating that the EGFR-AKT signaling pathway was inducible in an EGF-dependent manner (Fig. 1). Figure 1 also shows that the full-length EGFR protein disappeared by applying a high concentration of EGF of 50 ng/ml to cell line SF767. This high concentration of EGF leads to the saturation of the full-length EGFR protein with the ligand EGF, to the subsequent internalization and degradation of the formed EGF-EGFR complex, and thus to the observed disappearance of the full-length EGFR protein.
Western blot analysis of the two glioblastoma cell lines U251MG and SF767. U251MG is a PTEN mutant and PIK3CA wild-type cell line and SF767 is a PTEN wild-type and PIK3CA (E545K) mutant cell line. Cells were treated for 24 hours with different levels of the EGFR-ligand EGF (0-50 ng/ml). The levels of HER2 and EGFR are reduced by EGF-dependent degradation of the formed and internalized EGF-HER2/EGFR complexes. The activation of AKT-protein (phosphorylation of the Ser473) is detectable in an EGF-dependent manner in cell line SF767, whereas the pAKT level is constantly high in cell line U251MG. These observations indicate that the EGFR-signaling pathway is inducible in cell line SF767, but not in cell line U251MG. Anti- β-actin staining was done as a loading control, and BIRC5 (survivin) was used as an indicator for proliferation activity
Specificity of siRNAs
We performed RNAi experiments with a siRNA against EGFR splice variant I, henceforth called siRNAI and with a siRNA against all EGFR splice variants, henceforth called siRNAALL (Table 2). To investigate the specificity of the two siRNA constructs siRNAALL and siRNAI, we analyzed mRNA levels and protein levels of EGFR. Figure 2 shows that the treatment of SF767 cells with the two siRNAs reduced the level of full-length EGFR protein 24 hours and 48 hours after the start of the experiment. We then analyzed the siRNA-specificity by qPCR experiments for (a) all EGFR splice variants together, (b) EGFR splice variant I (full-length), (c) EGFR splice variant IV, and (d) the two genes MMP2 and GAPDH as a control. Additional file 1: Figure S.1 shows that the application of siRNAALL and siRNAI reduced the levels of all EGFR splice variants by 70.9% on average and the levels of the full-length EGFR splice variant I by 78.1% on average. Additional file 1: Figure S.1 also shows that the application of siRNAALL reduced the levels of EGFR splice variant IV by 69.9% on average, that the application of siRNAI did not reduce the levels of EGFR splice variant IV, and that the application of siRNAALL and siRNAI did not reduce the levels of the two control genes.
Western blot analysis of the effect of the two different siRNAs. Knock-down of the EGFR full-length protein level using two different siRNA constructs (siRNAALL and siRNAI). Both siRNA constructs reduce the full-length EGFR protein level at 24 hours and 48 hours after the start of the experiment, while the Actin level is not affected
Design of siRNAALL, siRNAI, and nonsense siRNA
sequence 5′→3′
target mRNA
corresponding mRNA
AACGCAUCCAGCAAGAAUA
EGFR I
CGGAAUAGGUAUUGGUGAA
EGFR II
EGFR III
EGFR IV
CGTACGCGGAATACTTCGA
First step of the BGSC approach - grouping of genes
The binding affinities of the three EGFR isoforms II-IV to EGF are lower than that of the full-length EGFR isoform I [7] and probably different from each other, but yet very high [7], so we assume that the high concentration of EGF of 50 ng/ml leads to the saturation of all EGFR isoforms irrespective of their different binding affinities to EGF. Hence, we make the simplifying assumption here and in the following that the concentration of the ligand is sufficiently high for neglecting the binding affinities of the four EGFR isoforms I-IV to EGF. Under this simplifying assumption, we define groups with distinct expression patterns considering all eight possible modes of EGF-triggered transcriptional gene regulation via EGFR isoform I, via EGFR isoforms II-IV, or via other non-EGF receptors, and we observe that each gene can be grouped into exactly one of the following eight gene groups A - H, which are graphically represented by Fig. 3:
Graphical representation of the eight gene groups. Each gene can be transcriptionally regulated by some combination of EGFR splice variant I (green arrows), EGFR splice variants II-IV (red arrows), and other EGF receptors (blue arrows), resulting in eight gene groups A - H
Group A contains genes not regulated by EGF.
Group B contains genes regulated by EGF not via EGFR isoforms I-IV, but via other receptors.
Group C contains genes regulated by EGF via EGFR isoforms II-IV and not via EGFR isoform I and not via other receptors.
Group D contains genes regulated by EGF via EGFR isoform I and not via EGFR isoforms II-IV and not via other receptors.
Group E contains genes regulated by EGF via EGFR isoforms II-IV and via other receptors and not via EGFR isoform I.
Group F contains genes regulated by EGF via EGFR isoform I and via EGFR isoforms II-IV and via other receptors.
Group G contains genes regulated by EGF via EGFR isoform I and via other receptors and not via EGFR isoforms II-IV.
Group H contains genes regulated by EGF via EGFR isoform I and via EGFR isoforms II-IV and not via other receptors.
Next, we consider for each RNAi treatment if the genes of each group would be differentially regulated after EGF-stimulation. To conceptually analyze the gene expression of each group we denote by ~1~ a theoretical regulation (up or down) of the group after addition of EGF and denote by ~0~ no regulation. Further, we define groups as regulated after EGF-stimulation if there is at least one incoming edge to the group in the graphical representation (Fig. 4), and we define groups with no incoming edge as unregulated. We consider three experimental manipulations with RNAi: negative control without RNA interference, RNAi with siRNA against EGFR splice variant I, henceforth called siRNAI, and RNAi with siRNA against all EGFR splice variants, henceforth called siRNAALL (Fig. 4).
Graphical representation of EGF regulation by RNAi treatment. Each differentially expressed gene can be grouped into exactly one of the following eight gene groups A - H. These eight gene groups (A - H) contain all possible theoretical models of regulation of a gene, after EGF addition in combination with the three RNAi treatments. Subfigure (a) corresponds to the control experiment without RNAi treatment, subfigure (b) corresponds to RNAi treatment with siRNAI, and subfigure (c) corresponds to RNAi treatment with siRNAALL. Red crosses indicate the down-regulation of EGFR by RNAi treatment with siRNAI (b) or siRNAALL (c). The change of gene expression (up or down) by EGF treatment is indicated by 1 and no change by 0, i.e., all genes except those of gene group A should be differentially expressed in the control experiment (a), all genes except those of gene groups A and D should be differentially expressed in experiment (b), and all genes except those of gene groups A, C, D, and H should be differentially expressed in experiment (c)
First, we consider the negative control without RNA interference (Fig. 4a). Here, none of the EGFR splice variants are down-regulated by a siRNA, so all target genes of EGFR isoforms and target genes of other EGF receptors can be induced by EGF. Hence, we expect differential expression under EGF stimulation of genes belonging to groups B - H on the one hand and no differential expression of genes belonging to group A on the other hand.
Second, we consider RNAi treatment with siRNAI (Fig. 4b). Here, only EGFR splice variant I is down-regulated by siRNAI, so only target genes of EGFR isoforms II-IV and target genes of other EGF receptors can be induced by EGF. Hence, we expect differential expression by EGF treatment of genes belonging to groups B, C, and E - H on the one hand and no differential expression of genes belonging to groups A and D on the other hand.
Third, we consider RNAi treatment with siRNAALL (Fig. 4c). Here, all four EGFR splice variants are down-regulated by siRNAALL, so only target genes of other EGF receptors can be induced by EGF. Hence, we expect differential expression by EGF treatment of genes belonging to groups B and E - G on the one hand and no differential expression of genes belonging to groups A, C, D, and H on the other hand.
Figure 5 summarizes the different expression patterns of Fig. 4. We find that the eight gene groups show only four different expression patterns, so we reduce the eight gene groups A - H to the four simplified gene groups a - d, where group A becomes group a, the union of the groups B and E - G becomes group b, the union of the groups C and H becomes group c, and group D becomes group d.
Reduction of the conceptual gene groups. Genes of group A are never differentially expressed by EGF treatment. Genes of group B and E - G are always differentially expressed by EGF treatment. Genes of group C and H are differentially expressed by EGF treatment in case of control treatment (no RNAi) or simultaneous treatment with siRNAI, whereas not differentially expressed by EGF treatment in case of simultaneous treatment with siRNAALL. Genes of group D are differentially expressed by EGF treatment in case of control treatment (no RNAi), whereas not differentially expressed by EGF treatment in case of simultaneous treatment with siRNAI or siRNAALL. We find that the eight gene groups show only four different expression patterns, so we reduce the eight gene groups A - H to the four simplified gene groups a - d, where group A becomes group a, the union of the groups B and E - G becomes group b, the union of the groups C and H becomes group c, and group D becomes group d
These simplified gene groups can be easily interpreted as follows: Genes of group a are not regulated by EGF, whereas genes of groups b−d are regulated by EGF. Genes of group b are regulated by EGF only through other receptors besides EGFR isoforms. Genes of group c are regulated by EGFR isoforms II-IV and not by other receptors. And genes of group d are regulated by EGFR isoform I and not by EGFR isoforms II-IV or other receptors. Based on this reduction, we can now formulate the goal of this work as the prediction of putative target genes regulated by EGFR isoforms II-IV and not by other receptors or, more crisply, as the goal of predicting genes of group c.
Second step of the BGSC approach - classification of genes
In the second step, we classify each potential target gene into one of the four simplified gene groups z ∈ {a, b,c, d} based on the Bayesian Information Criterion, and thereby predict target genes regulated by EGF via EGFR isoforms II-IV as those classified into group c.
In this step, we apply the oversimplified, but commonly accepted, assumption that the log-transformed expression of each gene is normally distributed [13] with a gene-specific and treatment-specific mean and variance.
For each gene, we additionally assume heteroscedasticity, i.e., equality of the six variances, of the six normally distributed logarithmic expression values under each of the six experimental conditions, an assumption commonly made in the t-test, the analysis of variance, or other statistical tests. We further assume that the six means of these six normal distributions are group specific as shown in Fig. 6.
Schematic expression patterns. For gene groups b – d (Subfigures b – d) the indicator variables gn are equal to 0 if the logarithmic expression levels xn are expected to be similar to x1 and 1 otherwise (Table 1). The four no-EGF columns are equal to 0 by model assumption 1, and the four EGF columns are equal to the corresponding columns of Fig. 5 by model assumption 2. For gene group a (Subfigure a) the indicator variables gn are equal to 0 by definition
First, we assume genes of group a (not regulated by EGF) to show no differential expression under each of the six experimental treatments (Table 1), as manifested by equality of the six means of the six normal distributions (Fig. 5, yellow column).
Second, we assume genes of group b (regulated by EGF through other receptors besides any EGFR isoform) to show differential expression under EGF-stimulation, irrespective of RNAi treatment targeting any EGFR isoform (Fig. 5, blue column). Hence, we assume genes of group b to have two different mean logarithmic expression levels, one in samples 1, 3, and 5, and another potentially different one in samples 2, 4, and 6 (Table 1). We denote these two mean logarithmic expression levels by μb0 (Fig. 6b red) and μb1 (Fig. 6b blue) respectively.
Third, we assume genes of group c (regulated by EGFR isoform II-IV and not by other receptors) to show differential expression between the negative control and siRNAALL treatments (Fig. 5, red column) under EGF-stimulation. Hence, we assume genes of group c to have two different mean logarithmic expression levels, one in samples 1, 3, 5, and 6, and another potentially different one in samples 2 and 4 (Table 1). We denote these two mean logarithmic expression levels by μc0 (Fig. 6c red) and μc1 (Fig. 6c blue) respectively.
Fourth, we assume genes of group d (regulated by EGFR isoform I only) to show differential expression between the negative control and siRNAI treatment (Fig. 5, green column) under EGF-stimulation. Hence, we assume genes of group d to have two different mean logarithmic expression levels, one in samples 1, 3, 4, 5, and 6, and another potentially different one in sample 2 (Table 1). We denote these two mean logarithmic expression levels by μd0 (Fig. 6d red) and μd1 (Fig. 6d blue) respectively.
For genes of group a we denote the two model parameters μa and σa of the six normal distributions by θa=(μa,σa), and for each of the three groups \(\tilde z \in \{b,c,d\}\) we denote the three model parameters \(\mu _{\tilde z0}\), \(\mu _{\tilde z1}\), and \(\sigma _{\tilde z}\) of the six normal distributions by \(\theta _{\tilde z} = (\mu _{\tilde z0}, \mu _{\tilde z1}, \sigma _{\tilde z})\).
Assuming conditional independence of the six logarithmic expression levels given group z and model parameters θz, we can write the likelihood p(x|z,θz) of data x given group z and model parameters θz as a product of six univariate normal distributions with the corresponding mean μa, or means \(\mu _{\tilde z0}\) and \(\mu _{\tilde z1}\), and the corresponding variance \(\sigma ^{2}_{z}\) (Eqs. 1 and 2). Using the maximum likelihood principle, we obtain the estimates of model parameters θa by Eqs. 8a and 8b and of model parameters \(\theta _{\tilde z}\) for \(\tilde z \in \{b,c,d\}\) by Eqs. 8c, 8d and 8e.
To illustrate this approach, we show the six measured logarithmic expression levels together with the univariate normal probability density estimated for group a and the three pairs of univariate normal probability densities estimated for each of the three groups \(\tilde z \in \{b,c,d\}\) for gene TPR in Fig. 7. Visually, it is easy to see that the model of group c fits best the expression profile of this gene, as it yields the best separation between the two estimated means and the smallest estimated pooled variance. Consistent with this visual observation, the four corresponding likelihoods of the six measured logarithmic expression levels are p(x|a,θa) =0.004, p(x|b,θb)=0.035, p(x|c,θc)=4.22, and p(x|d,θd)=0.012, i.e., the likelihood of the six measured logarithmic expression levels of gene TPR is highest for group c.
Probability density plot of the normal distributions of TRP. For group a we mark the logarithmic expression values x1,…,x6 of TPR with black points, which are colored according to Fig. 6a, and assume that all six logarithmic expression levels stem from the same normal distribution. In black, we plot the probability density of this normal distribution with mean and standard deviation equal to μ and σ of the six logarithmic expression levels. For groups b - d we assume that all six logarithmic expression levels stem from a mixture of two normal distributions with independent means μ0 and μ1 and one pooled standard deviation σ. We mark the logarithmic expression values x1,…,x6 of TPR with points which are colored according to indicator variables from Fig. 6 g=0 in red and g=1 in blue and we plot the probability densities of the two normal distributions in red and blue, respectively. For group b we assume that the logarithmic expression levels x1, x3, and x5 stem from the normal distribution with mean μ0 (red) and x2, x4, and x6 from the normal distribution with mean μ1 (blue). For gene group c we assume that the logarithmic expression levels x1, x3, x5, and x6 stem from the normal distribution with mean μ0 (red) and x2 and x4 from the normal distribution with mean μ1 (blue). For group d we assume that the logarithmic expression levels x1, x3, x4, x5, and x6 stem from the normal distribution with mean μ0 (red) and x2 stem from the normal distribution with mean μ1 (blue)
However, performing classification through model selection based on maximizing the likelihood is problematic when the number of free model parameters is not identical among all models under comparison. In the BGSC approach, model a has two free model parameters, while models b, c, and d have three free model parameters. Hence, a simple classification based on maximizing the likelihood would give a spurious advantage to models b, c, and d with three free model parameters over model a with only two free model parameters. To eliminate that spurious advantage, we compute marginal likelihoods p(x|z) using the approximation of Schwarz et al. [14] commonly referred to as Bayesian Information Criterion (section "Probabilistic modeling of gene expression"). Applying this approximation to gene TPR we obtain the four marginal likelihoods of the six measured logarithmic expression levels p(x|a) = 0.001, p(x|b)=0.002, p(x|c)=0.287, and p(x|d)=0.001. We find that the marginal likelihood for group c is highest, which is consistent with the visual observation of Fig. 7.
To obtain the approximate posterior probability p(z|x), we now simply use Bayes' formula p(z|x)=(p(x|z)p(z))/p(x) for group z∈{a, b,c, d}, where p(z) is the prior probability of group z, and the denominator p(x) is the sum of the four numerators p(x|z)p(z) for z∈{a, b,c, d}. We assume that 70% of all genes are not regulated by EGF, so we define the prior probability for group a by p(a)=0.70, and we further assume that the remaining 30% of the genes fall equally in groups with EGF-regulation, so we define the prior probabilities for groups b, c, and d by p(b)=p(c)=p(d)=0.1. Using these prior probabilities, we obtain for gene TPR the four approximate posterior probabilities p(a|x)=0.016, p(b|x)=0.008, p(c|x)=0.973, and p(d|x)=0.003. We find that the approximate posterior probability for group c is highest, so we finally assign gene TPR to group c.
By applying this approach of computing the four approximate posterior probabilities for each gene and assigning each gene to that group z with the highest approximate posterior probability, we classify 8449 genes to group a, 3822 genes to group b, 3143 genes to group c, and 1328 genes to group d.
Prediction of genes belonging to simplified gene group c
For simplified gene group c, we define the subset of the 1140 genes with an approximate posterior probability p(c|x) exceeding 0.75 as putative target genes regulated by EGFR isoforms II-IV and not by other receptors (Additional file 2: Table S.1), and we scrutinize six of these genes in the following section. Three of these genes (CKAP2L, ROCK1, and TPR) are up-regulated with a log2-fold change \(\hat {\mu }_{c1} - \hat {\mu }_{c0} >0.5\) and three of these genes (ALDH4A1, CLCA2, and GALNS) are down-regulated with a log2-fold change \(\hat {\mu }_{c1} - \hat {\mu }_{c0} < -0.5\).
To validate the 36 logarithmic expression levels x1,…,x6 of the six genes CKAP2L, ROCK1, TPR, ALDH4A1, CLCA2, and GALNS, we perform 108 qPCR experiments comprising three biological replicates for each gene and each treatment. Figure 8 shows the 12 log2-fold changes \(\hat {\mu }_{c1} - \hat {\mu }_{c0}\) of the microarray experiments and of the qPCR experiments. We find that the six log2-fold changes of the microarray experiments and those of the qPCR experiments are not identical, but in good agreement, yielding a Pearson correlation coefficient of 0.99. Moreover, the error bars, computed by using the Satterthwaite approximation, of all six genes overlap between microarray experiments and qPCR experiments.
Comparison of microarray and qPCR log2-fold changes. Based on the microarray expression data described in Results, Discussion, Conclusions, and Methods we obtain an up-regulation for genes CKAP2L, ROCK1, and TPR and a down-regulation for genes ALDH4A1, CLCA2, and GALNS. The error bars are calculated using the Satterthwaite approximation. Based on the qPCR data, we obtain qualitatively and quantitatively similar results with overlapping error bars, yielding a Person correlation coefficient of the log2-fold changes of the microarray experiments and those of the qPCR experiments of 0.99
To investigate the degree to which the expression levels of these genes respond to EGF in another glioblastoma cell line, we perform triplicated qPCR experiments in the glioblastoma cell line LNZ308 with and without EGF treatment. As CLCA2 is not sufficiently expressed in cell line LNZ308 with a log-expression of −5.8 in the Cancer Cell Line Encyclopedia data [10], we stimulate cell lines SF767 and LNZ308 with EGF (50 ng/ml for 24 hours) and measure the expression of the five remaining genes by qPCR experiments. We find that the log2-fold changes are not identical, but in good agreement, between the two cell lines for the four genes CKAP2L, ROCK1, TPR, and GALNS, whereas they are different between the two cell lines for gene ALDH4A1 (Additional file 1: Figure S.2).
Adjustability of the EGFR-signaling pathway in cell line SF767
To analyze the function of the soluble EGFR (sEGFR) isoforms II-IV it is essential to use a cell line with an adjustable EGFR-signaling pathway. As shown in Fig. 1, the EGFR-signaling pathway is adjustable in cell line SF767 with respect to recombinant EGF stimulation, even though cell line SF767 has a PIK3CA (E545K) mutation resulting in a baseline level of AKT activation [15]. This mutation occurs in about 30% of human breast cancers, where it leads to gain-of-function mutations in gene PIK3CA that activate the PI3K-AKT-signaling pathway constantly, thereby uncoupling the EGFR response from AKT signaling [16]. However, in cell line SF767 the level of pAKT can be increased nearly three-fold in an EGF-dependent manner (Fig. 1) consistent with the observation of Sun et al. [17].
It has been suggested that glioblastoma cell lines with helical domain mutations are still sensitive to dual PI3Ki/MEKi treatment [9], which is consistent with our observation that the EGFR-signaling pathway is adjustable in cell line SF767. Also, it has been found that Gefitinib inhibited EGFR phosphorylation in U251MG and SF767 cells, whereas Gefitinib inhibited AKT phosphorylation only in SF767 cells but not in U251MG cells [18], consistent to Fig. 1. Other EGF-induced signaling pathways such as the PLC γ-signaling pathway appear to be intact in cell line SF767 too [19].
Next, we perform western blot experiments and find that both siRNAs reduce the levels of the full-length EGFR proteins (Fig. 2). By qPCR experiments we find that siRNAALL is capable of knocking down all EGFR splice variants and that siRNAI is capable of selectively knocking down EGFR splice variant I (Additional file 1: Figure S.1). More precisely we detect a reduction by 70.9% on average for all EGFR splice variants and a reduction by 78.1% on average for EGFR splice variant I for siRNAALL as well as for siRNAI (Additional file 1: Figure S.1). Based on similar reductions, it appears that EGFR splice variant I is the dominant splice variant. As expected, the level of EGFR splice variant IV was reduced only by siRNAALL.
Biological context of genes predicted to belong to simplified gene group c
Next, we investigate the biological context of the six genes predicted to belong to simplified gene group c by applying the BGSC approach under the simplifying assumption of neglecting the different binding affinities of the EGFR isoforms to EGF.
The 'Cytoskeleton Associated Protein 2 Like' (CKAP2L) protein is localized on microtubules of the spindle pole throughout metaphase to telophase in wild-type cells [20], and a knock-down of CKAP2L has been found to suppresses migration, invasion, and proliferation in lung adenocarcinoma [21].
The 'Rho-Associated Protein Kinase 1' (ROCK1) is known to play an important role in the EGF-induced formation of stress fibers in keratinocyte [22] and to be involved in the cofilin pathway in breast cancer [23]. Besides, ROCK1 has been found to promote migration, metastasis, and invasion of tumor cells and also to facilitate morphological cell shape transformations through modifications of the actinomyosin cytoskeleton [24].
Depletion of the mRNA of the 'Tumor Potentiating Region' (TPR) gene by RNAi triggers G0-G1 arrest, and TPR depletion plays a role in controlling cellular senescence [25]. Also, TPR regulates the nuclear export of unspliced RNA and participates in processing and degradation of aberrant mRNAs [26], a mechanism considered important for the regulation of genes and their deregulation in cancer cells.
The 'Aldehyde Dehydrogenase 4 Family Member A1' (ALDH4A1) gene contains a potential p53 binding sequence in intron 1, and p53 is often mutated in tumor cells [27]. Moreover, ALDH4A1 was induced in a tumor cell line in response to DNA damage in a p53-dependent manner [27], and depletion of the mRNA of ALDH4A1 by siRNA results in severe inhibition of cell growth in HepG2 cells [28].
A second gene that is transcriptionally regulated by DNA damage in a p53-dependent manner is the 'Chloride Channel Accessory 2' (CLCA2) gene. Inhibition of CLCA2 stimulates cancer cell migration and invasion [29]. Furthermore, CLCA2 could be a marker of epithelial differentiation, and knock-down of CLCA2 causes cell overgrowth as well as enhanced migration and invasion. These changes are accompanied by down-regulation of E-cadherin and up-regulation of vimentin, and loss of CLCA2 may promote metastasis [29]. Also, loss of breast epithelial marker CLCA2 has been reported to promote an epithelial-to-mesenchymal transition and to indicate a higher risk of metastasis [30].
For the 'Galactosamine (N-Acetyl)-6-Sulfatase' (GALNS) gene an effect of 17 β-estradiol on the expression of GALNS could be detected by qPCR experiments in a breast cancer cell line, which is a hint to a tumor association of GALNS [31].
Up-regulation of ROCK1 and TPR and down-regulation of ALDH4A1 and CLCA2 (Fig. 8) are positively associated with the processes of migration, metastasis, and invasion of tumor cells and negatively associated with proliferation. The up-regulation of CKAP2L [32] by EGFR II-IV isoforms indicates a potential link to processes of cell-cycle progression of stem cells or progenitor cells. Overall, our interpretation of the impact of EGFR isoforms II-IV on four of six validated gene transcripts is that it seems likely that these isoforms are involved in processes of migration and metastasis of clonogenic (stem) cells, which is strongly associated with a more aggressive tumor and a worse prognosis of tumor disease.
We found that the BGSC approach was capable of detecting genes putatively regulated by EGFR isoforms II-IV and not by other receptors such as HER2, HER3, or HER4 [33], so we find it tempting to conjecture that the BGSC approach could be useful for the analysis of similarly-structured data of other nested experimental designs.
We have performed RNAi experiments to analyze the expression of three poorly investigated isoforms II-IV of the epidermal growth factor receptor in glioblastoma cell line SF767 with an adjustable EGFR-signaling pathway, and we have developed the Bayesian Gene Selection Criterion (BGSC) approach for the prediction of putative target genes of these EGFR isoforms under the simplifying assumption of neglecting the different binding affinities of the EGFR isoforms to EGF. We have predicted 3143 putative target genes, out of which 1140 genes have an approximate posterior probability greater than 0.75, and we have tested six of these genes by triplicated qPCR experiments. These six genes include ROCK1, which is known to be associated with EGFR regulation, as well as CKAP2L, TPR, ALDH4A1, CLCA2, and GALNS. We have found that the six log2-fold changes of the microarray expression levels and those of the qPCR expression levels are highly correlated with a Pearson correlation coefficient of 0.99 (p-value = 0.00002), suggesting that the set of 1140 genes might contain some further putative target genes of EGFR isoforms II-IV in tumor cells. As suggested by our anonymous reviewers we like to point out that, in addition to RNAi, CRISPR/Cas knockout [34] and replacement with each isoform would be a promising strategy to discover additional functions of the soluble EGFR isoforms besides the ones described by Maramotti et al. [6]. The analysis of isoform-specific effects in combination with RNAi treatments are an elegant way to directly down-regulate specific mRNA splice variants, but that often leads to a nested experimental design for which generally no standard procedure exists. The two-step BGSC procedure of first defining easily interpretable conceptual groups of genes associated with different EGFR isoforms and subsequently classifying genes based on the approximated posterior probability to these groups seems to be a promising approach in such a situation, and this approach is readily adaptable to other and more complex experimental designs. The datasets analyzed during the current study and the R-scripts for reproducing the results and plots of this work are available in the BGSC repository, https://github.com/GrosseLab/BGSC.
Glioblastoma cell line SF767
We obtained glioblastoma cell line SF767 from Cynthia Cowdrey (Neurosurgery Tissue Bank, University of California, San Francisco, USA). We cultured cell line SF767 in RPMI1640 medium (Lonza, Walkersville, USA) containing 10% (Vol/Vol) fetal bovine serum, 1% (Vol/Vol) sodium pyruvate, 185 U/ml penicillin, and 185 μg/ml ampicillin and maintain it at 37∘C in a humidified atmosphere containing 3% (Vol/Vol) CO2.
Western blot and qPCR analyses
Cells were treated in lysis buffer, the protein concentration was determined using the Bradford method, and western blot analysis was performed as described in [35]. Antibodies directed against EGFR (Clone D38B1), HER2/ErbB2 (29D8), and phosphoserine 473 AKT (clone D9E) were obtained from Cell Signaling Technology Inc. (Signaling, Danvers, MA, USA), antibodies directed against β-actin were obtained from Sigma (Steinheim, Germany), and BIRC5 (Survivin) antibodies (clone AF886) were obtained from R&D systems (Richmond, CA, USA). qPCR experiments were performed as described in [35]. The primer sequences are listed in Table 3.
Primer sequences for qPCR
Traget mRNA
AGTGGGACTTTGGCTGATCC
Antisense
GTGAAGGCTAAGACGGGCTC
ACATCAGTGGAAGAGCTGGC
TTCTGCCTTGGCTATTCGGG
CCATTGCCCTGGGTTCATCT
GGCCTGCCACGTAACTAGAA
EGFR all
TCAGCCTCCAGAGGATGTTC
GTGTTGAGGGCAATGAGGAC
EGFR v1
CCCAGTACCTGCTCAACTGG
TAGGCACTTTGCCTCCTTCTG
GCCATCCAAACTGCACCTAC
GGACACGCTGCCATCATTAC
CAGCTGTTGCTGGTGCTCAG
AGTTTGGGAAAAGCAGCCCT
CACCCACTCCTCCACCTTTG
CCACCACCCTGTTGCTGTAG
TTGCTGACCTGCTGGATTAC
CTTGCGACCTTGACCATCTT
CCCTCGCAAGCCCAAGTGGG
CCATGCTCCCAGCGGCCAAA
GGTGCTGGTAAGAGGGCATT
CGCAGCAGGTTGTCCATTTT
GCTGAGGGTGGACTCGATTT
AGACTTGGGCAGCTTGTTCA
The design and application of siRNA specific for EGFR mRNA and a nonsense siRNA were performed by a program provided by MWG (Eurofins Genomics, Ebersberg, Germany). The sequences of the double-stranded EGFR-specific siRNAs correspond to 21-bp sequences of the EGFR-cDNA (NCBI-ref NM _005228.3) for siRNAI at positions 4094–4116 and for siRNAALL at positions 1258–1278 (Table 2). To ensure that the EGFR-specific siRNAs and the nonsense siRNA do not interact with other transcripts, we used the sequences of siRNAI, siRNAALL, and nonsense siRNA to perform a BLAST search with Nucleotide BLAST against the human-genome database (http://www.ncbi.nlm.nih.gov/) and the siRNA-Check of SpliceCenter suite [36]. To prevent off-target effects of siRNA-treatment, we transfected cells with 50 nM targeting siRNA (siRNAI and siRNAALL) in RPMI complete medium. For transfecting we use the reagent INTERFERin™ according to the manufacturer's instructions (Polyplus Transfection, Illkirch, France).
Illumina BeadChip Microarray
RNA integrity and concentration were examined on an Agilent 2100 Bioanalyzer (Agilent Technologies, Palo Alto, CA, USA) using the RNA 6.000 LabChip Kit (Agilent Technologies) according to the manufacturer's instructions. Illumina BeadChip analysis was conducted at the microarray core facility of the Interdisciplinary Center for Clinical Research (IZKF) Leipzig (Faculty of Medicine, University of Leipzig). 250 ng RNA per sample were ethanol precipitated with GlycoBlue (Invitrogen) as a carrier and dissolved at a concentration of 100–150 ng/ μl before probe synthesis using the TargetAmp™- Nano Labeling Kit for Illumina Expression BeadChip (Epicentre Biotechnologies, Madison, WI, USA). 750 ng of cRNA were hybridized to Illumina HT-12 v4 Expression BeadChips (Illumina, San Diego, CA, USA) and scanned on the Illumina HiScan instrument according to the manufacturer's specifications. The read.ilmn function of the limma package [37] was used to read the 47317 microarray probes into R. The neqc function of limma was used to perform a background correction followed by quantile normalization, using negative control probes for background correction and both negative and positive controls for normalization. The 16,742 array probes corresponding to 14,389 genes, which displayed a significant hybridization signal (Illumina signal detection statistic at P<0.05) in all probes were used for further analysis.
For investigating which genes are activated by the four EGFR isoforms I - IV in glioblastoma cell line SF767 we use RNAi, as described in section "RNAi", for a selective down-regulation of EGFR splice variants (Table 1 rows) with and without EGF treatment (Table 1 columns). Specifically, we applied the three different RNAi treatments – (i) control without RNAi, (ii) RNAi with siRNAI, and (iii) RNAi with siRNAALL – to glioblastoma cell line SF767.
In case (i) we performed a control experiment without RNAi treatment (Table 1, first row). Here, EGFR is not down-regulated by an siRNA, so target genes of all EGFR splice variants and other EGF receptors should be differentially expressed in columns 1 and 2, i.e., they should have different logarithmic expression levels x1 and x2.
In case (ii) we performed an RNAi with siRNAI, which can bind only to the full-length EGFR splice variant I (Table 1, second row). Hence, siRNAI down-regulates splice variant I, but not the other splice variants II-IV, and in this case target genes of EGFR isoforms II-IV and of other EGF receptors should be differentially expressed in columns 1 and 2, i.e., they should have different logarithmic expression levels x3 and x4.
In case (iii) we performed an RNAi with siRNAALL, which can bind to all four EGFR splice variants, and subsequently down-regulates all four splice variants (Table 1, third row). Here, only target genes of other EGF receptors should be differentially expressed in columns 1 and 2, i.e., they should have different logarithmic expression levels x5 and x6.
Probabilistic modeling of gene expression
We propose a probabilistic model for the logarithmic expression pattern x=(x1,…,x6) for each of the four groups z∈{a, b,c, d} defined in section "First step of the BGSC approach - grouping of genes".
First, we assume that the three logarithmic expression levels x1, x3, and x5 corresponding to no EGF treatment are similar to each other, which corresponds to the assumption that the RNAi treatment should have no effect in case of no EGF treatment. Second, we assume that the three logarithmic expression levels x2, x4, and x6 follow the expression patterns described in section "First step of the BGSC approach - grouping of genes" and summarized in Fig. 5.
In order to mathematically formulate the model assumptions, we introduce six indicator variables g1,…,g6 for the groups \(\tilde z \in \{b, c, d\}\) that indicate if the six logarithmic expression levels x1,…,x6 are expected to be different from x1. Specifically, we define gn=1 if xn is expected to be different from x1 for n=1,…,6 and gn=0 otherwise. Genes of group a are defined as showing no effect on the EGF treatment and therefore gn equals 0 by definition.
By definition, we obtain that g1=0 for each of the three groups \(\tilde z\). From the first model assumption we obtain that g1, g3, and g5 are equal to 0 for each of the three groups \(\tilde z\). From the second model assumption we obtain that (g2,g4,g6) is equal to the corresponding column of Fig. 5 for each of the three groups \(\tilde z\). Figure 6 summarizes the values of the indicator variables g1,…,g6 for each of the three groups b−d.
Third, we assume that the logarithmic expression levels x1,…,x6 are statistically independent and normally distributed. By combining all three model assumptions, we obtained the likelihood
$$\begin{array}{*{20}l} p(x | a, \theta_{a}) &= \prod_{n=1}^{6} \mathcal{N} (x_{n} | \mu_{a}, \sigma_{a}) \end{array} $$
$$\begin{array}{*{20}l} p(x | \tilde z, \theta_{\tilde z}) &= \prod_{n=1}^{6} \mathcal{N} (x_{n} | \mu_{\tilde z g_{n}}, \sigma_{\tilde z}) \end{array} $$
for each of the four gene groups z∈{a, b,c, d}, where
$$\begin{array}{*{20}l} \mathcal{N} (x_{n} | \mu_{a}, \sigma_{a}) &= \frac{1}{\sqrt{2\pi}\sigma_{a}} ~ \times ~ e^{- \frac{ (x_{n}- \mu_{a})^{2}}{2\sigma_{a}^{2}}} \end{array} $$
denotes the density of the normal distribution, θa=(μa,σa) denotes the parameter of model a, and
$$\begin{array}{*{20}l} \mathcal{N} (x_{n} | \mu_{\tilde z g_{n}}, \sigma_{\tilde z}) &= \frac{1}{\sqrt{2\pi}\sigma_{\tilde z}} ~ \times~ e^{- \frac{ (x_{n}- \mu_{\tilde z g_{n}})^{2}}{2\sigma_{\tilde z}^{2}}} \end{array} $$
denotes the density of the normal distribution, \(\theta _{\tilde z} = (\mu _{\tilde {z}0}, \mu _{\tilde {z}1}, \sigma _{\tilde z})\) denotes the parameter of model \(\tilde z\), and gn are the indicator variables from Fig. 6.
Posterior approximation by the Bayesian Information Criterion
Next, we seek the approximate posterior
$$\begin{array}{*{20}l} p(z|x) &= \frac{ p(x|z) p(z)} {p(x)} \end{array} $$
for each z∈{a, b,c, d} and each gene, where p(z) is the prior probability of group z.
For the four models of section "Probabilistic modeling of gene expression" the approximations of the marginal likelihoods based on the Bayesian Information Criterion are
$$\begin{array}{*{20}l} p(x|z) &\propto \frac{p(x| z, \hat \theta_{z})}{ \sqrt{6}^{|\theta_{z} |} }, \end{array} $$
where 6 is the number of data points and |θz| is the number of free parameters of model z, which is 2 for group a and 3 for groups b−d, and where the maximum-likelihood estimators \(\hat \theta _{z}\) are
$$\begin{array}{*{20}l} {}\hat{\mu}_{a} &= \frac{1}{6} \sum_{n=1}^{6} x_{n} \end{array} $$
$$\begin{array}{*{20}l} {}\hat{\sigma}_{a}^{2} &= \frac{1}{5} \sum_{n=1}^{6} (x_{n}- \hat{\mu}_{a})^{2} \end{array} $$
$$\begin{array}{*{20}l} {}\hat{\mu}_{\tilde z0} &= \frac{ \sum\limits_{n=1}^{6} x_{n} (1-g_{\tilde zn}) }{\sum\limits_{n=1}^{6} (1-g_{\tilde zn})} \end{array} $$
$$\begin{array}{*{20}l} {}\hat{\mu}_{\tilde z1} &= \frac{ \sum\limits_{n=1}^{6} x_{n} g_{\tilde zn} }{\sum\limits_{n=1}^{6} g_{\tilde zn}} \end{array} $$
(8d)
$$\begin{array}{*{20}l} {}\hat{\sigma}_{\tilde z}^{2} &= \frac{ \displaystyle \sum_{n=1}^{6} (x_n- \hat{\mu}_{\tilde z0})^{2} (1-g_{\tilde zn}) + \sum_{n=1}^{6} (x_n- \hat{\mu}_{\tilde z1})^{2} g_{\tilde zn} }{4} \end{array} $$
(8e)
for \(\tilde z \in \{b, c, d\}\), and where \(g_{\tilde zn}\) denotes the indicator variable gn of group \(\tilde z\). Based on these approximations, we compute p(z|x) and then perform Bayesian model selection by assigning each gene to that group z with the maximum approximate posterior p(z|x).
We thank Ralf Eggeling, Ioana Lemnian, Martin Porsch, and Teemu Roos for valuable discussions and the Microarray Core Facility of the Interdisciplinary Center of Clinical Research (IZKF) at Leipzig for performing the microarray experiments.
CW and IG devised the study and designed the algorithm, HW, JK, MK, AWE, and DV designed and performed the biological experiments, CW implemented the algorithm, CW and IG performed the data analysis, CW, HW, MK, DHA, and IG wrote the manuscript, and all authors read and approved the final manuscript.
We thank the German Research Foundation (DFG) (grant no. GR 3526/2 and GR 3526/6), the German Federal Ministry of Education and Research (FKZ: 16/18, 19/13, 21/25, and 24/19), and the funding program Open Access Publishing by the DFG for financial support. The funding body did not play any role in the design of the study, in the collection, analysis, or interpretation of data, or in writing the manuscript.
Additional file 1 Figure S.1 Expression of EGFR splice variants, GAPDH, and MMP2 Figure S.2 log2-fold changes of the qPCR expression levels for cell lines SF767 and LNZ308. (PDF 96 kb)
12859_2019_2944_MOESM2_ESM.xlsx (410 kb)
Additional file 2 Table S.1. Predicted genes belonging to simplified gene group c. (XLSX 411 kb)
Ohgaki H, Kleihues P. Epidemiology and etiology of gliomas. Acta Neuropathol. 2005; 109(1):93–108.PubMedCrossRefGoogle Scholar
Ohgaki H, Kleihues P. Genetic pathways to primary and secondary glioblastoma. Am J Pathol. 2007; 170(5):1445–53.PubMedPubMedCentralCrossRefGoogle Scholar
Yarden Y. The EGFR family and its ligands in human cancer: signalling mechanisms and therapeutic opportunities. Eur J Cancer. 2001; 37:3–8.CrossRefGoogle Scholar
Citri A, Yarden Y. EGF–ERBB signalling: towards the systems level. Nat Rev Mol Cell Biol. 2006; 7(7):505–16.PubMedCrossRefGoogle Scholar
Reiter JL, Maihle NJ. Characterization and expression of novel 60-kda and 110-kda EGFR isoforms in human placenta. Ann N Y Acad Sci. 2003; 995(1):39–47.PubMedCrossRefGoogle Scholar
Maramotti S, Paci M, Manzotti G, Rapicetta C, Gugnoni M, Galeone C, Cesario A, Lococo F. Soluble Epidermal Growth Factor Receptors (sEGFRs) in Cancer: Biological Aspects and Clinical Relevance. Int J Mol Sci. 2016; 17(4):593.PubMedCentralCrossRefGoogle Scholar
Wilken JA, Perez-Torres M, Nieves-Alicea R, Cora EM, Christensen TA, Baron AT, Maihle NJ. Shedding of soluble epidermal growth factor receptor (sEGFR) is mediated by a metalloprotease/ fibronectin/ integrin axis and inhibited by cetuximab. Biochemistry. 2013; 52(26):4531–40.PubMedCrossRefGoogle Scholar
Kuo W-T, Lin W-C, Chang K-C, Huang J-Y, Yen K-C, Young I-C, Sun Y-J, Lin F-H. Quantitative analysis of ligand-egfr interactions: a platform for screening targeting molecules. PloS One. 2015; 10(2):0116610.CrossRefGoogle Scholar
McNeill RS, Stroobant EE, Smithberger E, Canoutas DA, Butler MK, Shelton AK, Patel SD, Limas JC, Skinner KR, Bash RE, et al.Pik3ca missense mutations promote glioblastoma pathogenesis, but do not enhance targeted pi3k inhibition. PloS One. 2018; 13(7):0200014.CrossRefGoogle Scholar
Consortium CCLE, of Drug Sensitivity in Cancer Consortium G, et al.Pharmacogenomic agreement between two cancer cell line data sets. Nature. 2015; 528(7580):84.Google Scholar
Comelli M, Pretis I, Buso A, Mavelli I. Mitochondrial energy metabolism and signalling in human glioblastoma cell lines with different pten gene status. J Bioenerg Biomembr. 2018; 50(1):33–52.PubMedCrossRefGoogle Scholar
Quayle SN, Lee JY, Cheung LWT, Ding L, Wiedemeyer R, Dewan RW, Huang-Hobbs E, Zhuang L, Wilson RK, Ligon KL, et al.Somatic mutations of pik3r1 promote gliomagenesis. PloS One. 2012; 7(11):49466.CrossRefGoogle Scholar
Long AD, Mangalam HJ, Chan BYP, Tolleri L, Hatfield GW, Baldi P. Improved statistical inference from DNA microarray data using analysis of variance and A Bayesian statistical framework. Analysis of global gene expression in Escherichia coli K12. J Biol Chem. 2001; 276(23):19937–44. https://doi.org/10.1074/jbc.M010192200.PubMedCrossRefGoogle Scholar
Schwarz G. Estimating the dimension of a model. Ann Statist. 1978; 6(2):461–4.CrossRefGoogle Scholar
Chautard E, Loubeau G, Tchirkov A, Chassagne J, Vermot-Desroches C, Morel L, Verrelle P. Akt signaling pathway: a target for radiosensitizing human malignant glioma. Neuro-oncology. 2010; 12(5):434–43.PubMedPubMedCentralGoogle Scholar
Meyer D, Koren S, Leroy C, Brinkhaus H, Müller U, Klebba I, Müller M, Cardiff R, Bentires-Alj M. Expression of pik3ca mutant e545k in the mammary gland induces heterogeneous tumors but is less potent than mutant h1047r. Oncogenesis. 2013; 2(9):74.CrossRefGoogle Scholar
Sun L, Yu S, Xu H, Zheng Y, Lin J, Wu M, Wang J, Wang A, Lan Q, Furnari F, et al.Fhl2 interacts with egfr to promote glioblastoma growth. Oncogene. 2018; 37(10):1386.PubMedCrossRefGoogle Scholar
Andersson U, Johansson D, Behnam-Motlagh P, Johansson M, Malmer B. Treatment schedule is of importance when gefitinib is combined with irradiation of glioma and endothelial cells in vitro. Acta Oncol. 2007; 46(7):951–60. https://doi.org/10.1080/02841860701253045.PubMedCrossRefGoogle Scholar
Fan Q-W, Cheng C, Knight ZA, Haas-Kogan D, Stokoe D, James CD, McCormick F, Shokat KM, Weiss WA. Egfr signals to mtor through pkc and independently of akt in glioma. Sci Signal. 2009; 2(55):4.CrossRefGoogle Scholar
Hussain MS, Battaglia A, Szczepanski S, Kaygusuz E, Toliat MR, Sakakibara S-i, Altmüller J, Thiele H, Nürnberg G, Moosa S, et al.Mutations in ckap2l, the human homolog of the mouse radmis gene, cause filippi syndrome. Am J Hum Genet. 2014; 95(5):622–32.PubMedPubMedCentralCrossRefGoogle Scholar
Xiong G, Li L, Chen X, Song S, Zhao Y, Cai W, Peng J. Up-regulation of ckap2l expression promotes lung adenocarcinoma invasion and is associated with poor prognosis. OncoTargets Ther. 2019; 12:1171.CrossRefGoogle Scholar
Ohuchi H. Wakayama symposium: Epithelial-mesenchymal interactions in eyelid development. Ocul Surf. 2012; 10(4):212–6.PubMedCrossRefGoogle Scholar
Wang W, Eddy R, Condeelis J. The cofilin pathway in breast cancer invasion and metastasis. Nat Rev Cancer. 2007; 7(6):429–40.PubMedPubMedCentralCrossRefGoogle Scholar
Rath N, Olson MF. Rho-associated kinases in tumorigenesis: reconsidering ROCK inhibition for cancer therapy. EMBO Rep. 2012; 13(10):900–8.PubMedPubMedCentralCrossRefGoogle Scholar
David-Watine B. Silencing nuclear pore protein Tpr elicits a senescent-like phenotype in cancer cells. PloS One. 2011; 6(7):22423.CrossRefGoogle Scholar
Rajanala K, Nandicoori V. Localization of nucleoporin Tpr to the nuclear pore complex is essential for Tpr mediated regulation of the export of unspliced RNA. PloS One. 2012; 7(1):29921.CrossRefGoogle Scholar
Yoon K, Nakamura Y, Arakawa H. Identification of ALDH4 as a p53-inducible gene and its protective role in cellular stresses. J Hum Genet. 2004; 49(3):134–40.PubMedCrossRefGoogle Scholar
Kreuzer J, Bach NC, Forler D, Sieber SA. Target discovery of acivicin in cancer cells elucidates its mechanism of growth inhibition. Chem Sci. 2015; 6(1):237–45.CrossRefGoogle Scholar
Sasaki Y, Koyama R, Maruyama R, Hirano T, Tamura M, Sugisaka J, Suzuki H, Idogawa M, Shinomura Y, Tokino T. CLCA2, a target of the p53 family, negatively regulates cancer cell migration and invasion. Cancer Biol Ther. 2012; 13(14):1512–21.PubMedPubMedCentralCrossRefGoogle Scholar
Walia V, Yu Y, Cao D, Sun M, McLean J, Hollier B, Cheng J, Mani S, Rao K, Premkumar L, Elble R. Loss of breast epithelial marker hCLCA2 promotes epithelial-to-mesenchymal transition and indicates higher risk of metastasis. Oncogene. 2011; 31(17):2237–46.PubMedPubMedCentralCrossRefGoogle Scholar
Garcia S, Nagai M. Transcriptional regulation of bidirectional gene pairs by 17- β-estradiol in MCF-7 breast cancer cells. Braz J Med Biol Res. 2011; 44(2):112–22.PubMedCrossRefGoogle Scholar
Yumoto T, Nakadate K, Nakamura Y, Sugitani Y, Sugitani-Yoshida R, Ueda S, Sakakibara S-i. Radmis, a novel mitotic spindle protein that functions in cell division of neural progenitors. PloS One. 2013; 8(11):79895.CrossRefGoogle Scholar
Sridhar SS, Seymour L, Shepherd FA. Inhibitors of epidermal-growth-factor receptors: a review of clinical research with a focus on non-small-cell lung cancer. Lancet Oncol. 2003; 4(7):397–406.PubMedCrossRefGoogle Scholar
Ran FA, Hsu PD, Wright J, Agarwala V, Scott DA, Zhang F. Genome engineering using the crispr-cas9 system. Nat Protoc. 2013; 8(11):2281.PubMedPubMedCentralCrossRefGoogle Scholar
Wichmann H, Güttler A, Bache M, Taubert H, Rot S, Kessler J, Eckert AW, Kappler M, Vordermark D. Targeting of EGFR and HER2 with therapeutic antibodies and siRNA. Strahlenther Onkol. 2015; 191(2):180–91. https://doi.org/10.1007/s00066-014-0743-9.PubMedCrossRefGoogle Scholar
Ryan MC, Zeeberg BR, Caplen NJ, Cleland JA, Kahn AB, Liu H, Weinstein JN. Splicecenter: a suite of web-based bioinformatic applications for evaluating the impact of alternative splicing on RT-PCR, RNAi, microarray, and peptide-based studies. BMC Bioinformatics. 2008; 9(1):313.PubMedPubMedCentralCrossRefGoogle Scholar
Ritchie ME, Phipson B, Wu D, Hu Y, Law CW, Shi W, Smyth GK. limma powers differential expression analyses for RNA-sequencing and microarray studies. Nucleic Acids Res. 2015; 43(7):47. https://doi.org/10.1093/nar/gkv007.CrossRefGoogle Scholar
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License(http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The Creative Commons Public Domain Dedication waiver(http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated.
1.Institute of Computer Science, Martin Luther University Halle–WittenbergHalleGermany
2.Department of Oral and Maxillofacial Plastic Surgery, Martin Luther University Halle–WittenbergHalleGermany
3.Institute for Molecular and Clinical Immunology, Otto-von-Guericke-UniversityMagdeburgGermany
4.Molecular Cell Biology, School of Natural Sciences, University of CaliforniaMercedUSA
5.Department of Radiotherapy, Martin Luther University Halle–WittenbergHalleGermany
6.German Center of Integrative Biodiversity Research (iDiv) Halle-Jena-LeipzigLeipzigGermany
Weinholdt, C., Wichmann, H., Kotrba, J. et al. BMC Bioinformatics (2019) 20: 434. https://doi.org/10.1186/s12859-019-2944-9
Received 06 February 2019
Accepted 11 June 2019
First Online 22 August 2019 | CommonCrawl |
On global large energy solutions to the viscous shallow water equations
DCDS-B Home
Fractional approximations of abstract semilinear parabolic problems
November 2020, 25(11): 4257-4276. doi: 10.3934/dcdsb.2020096
Extension, embedding and global stability in two dimensional monotone maps
Ahmad Al-Salman 1, , Ziyad AlSharawi 2,, and Sadok Kallel 2,
Department of Mathematics, Sultan Qaboos University, P. O. Box 36, PC 123, Al-Khod, Sultanate of Oman
Department of Mathematics and Statistics, American University of Sharjah, P. O. Box 26666, University City, Sharjah, UAE
* Corresponding author: Ziyad AlSharawi
Received July 2019 Revised November 2019 Published November 2020 Early access April 2020
Full Text(HTML)
Figure(8)
We consider the general second order difference equation $ x_{n+1} = F(x_n, x_{n-1}) $ in which $ F $ is continuous and of mixed monotonicity in its arguments. In equations with negative terms, a persistent set can be a proper subset of the positive orthant, which motivates studying global stability with respect to compact invariant domains. In this paper, we assume that $ F $ has a semi-convex compact invariant domain, then make an extension of $ F $ on a rectangular domain that contains the invariant domain. The extension preserves the continuity and monotonicity of $ F. $ Then we use the embedding technique to embed the dynamical system generated by the extended map into a higher dimensional dynamical system, which we use to characterize the asymptotic dynamics of the original system. Some illustrative examples are given at the end.
Keywords: Invariant domain, embedding, monotone maps, global stability.
Mathematics Subject Classification: Primary: 39A30, 39A10; Secondary: 37C25.
Citation: Ahmad Al-Salman, Ziyad AlSharawi, Sadok Kallel. Extension, embedding and global stability in two dimensional monotone maps. Discrete & Continuous Dynamical Systems - B, 2020, 25 (11) : 4257-4276. doi: 10.3934/dcdsb.2020096
R. Abu-Saris, Z. AlSharawi and M. B. H. Rhouma, The dynamics of some discrete models with delay under the effect of constant yield harvesting, Chaos Solitons Fractals, 54 (2013), 26-38. doi: 10.1016/j.chaos.2013.05.008. Google Scholar
Z. AlSharawi, A global attractor in some discrete contest competition models with delay under the effect of periodic stocking, Abstr. Appl. Anal., (2013), Art. ID 101649, 7 pp. doi: 10.1155/2013/101649. Google Scholar
A. M. Amleh, E. Camouzis and G. Ladas, On second-order rational difference equation. Ⅰ, J. Difference Equ. Appl., 13 (2007), 969-1004. doi: 10.1080/10236190701388492. Google Scholar
A. M. Amleh, E. Camouzis and G. Ladas, On the dynamics of a rational difference equation. Ⅱ, Int. J. Difference Equ., 3 (2008), 195-225. Google Scholar
E. Camouzis and G. Ladas, Dynamics of Third-order Rational Difference Equations with Open Problems and Conjectures, Advances in Discrete Mathematics and Applications, vol. 5, Chapman & Hall/CRC, Boca Raton, FL, 2008. Google Scholar
E. Camouzis and G. Ladas, When does local asymptotic stability imply global attractivity in rational equations?, J. Difference Equ. Appl., 12 (2006), 863-885. doi: 10.1080/10236190600772663. Google Scholar
W. A. Coppel, The solution of equations by iteration, Proc. Cambridge Philos. Soc., 51 (1955), 41-43. doi: 10.1017/S030500410002990X. Google Scholar
J.-L. Gouzé and K. P. Hadeler, Monotone flows and order intervals, Nonlinear World, 1 (1994), 23-34. Google Scholar
E. A. Grove and G. Ladas, Periodicities in Nonlinear Difference Equations, Advances in Discrete Mathematics and Applications, vol. 4, Chapman & Hall/CRC, Boca Raton, FL, 2005. Google Scholar
V. L. Kocić and G. Ladas, Global Behavior of Nonlinear Difference Equations of Higher Order with Applications, Mathematics and its Applications, vol. 256, Kluwer Academic Publishers Group, Dordrecht, 1993. doi: 10.1007/978-94-017-1703-8. Google Scholar
M. R. S. Kulenović and G. Ladas, Dynamics of Second Order Rational Difference Equations, With Open Problems and Conjectures, Chapman & Hall/CRC, Boca Raton, FL, 2002. Google Scholar
M. R. S. Kulenović, G. Ladas, L. F. Martins and I. W. Rodrigues, The dynamics of $x_{n+1} = \frac{\alpha+\beta x_n}{A+Bx_n+Cx_{n-1}}$: Facts and conjectures, Comput. Math. Appl., 45 (2003), 1087–1099, 2003. doi: 10.1016/S0898-1221(03)00090-7. Google Scholar
M. R. S. Kulenović, G. Ladas and W. S. Sizer, On the recursive sequence $x_{n+1} = (\alpha x_n+\beta x_{n-1})/(\gamma x_n+\delta x_{n-1})$, Math. Sci. Res. Hot-Line, 2 (1998), 1-16. Google Scholar
M. R. S. Kulenović and O. Merino, A note on unbounded solutions of a class of second order rational difference equations, J. Difference Equ. Appl., 12 (2006), 777-781. doi: 10.1080/10236190600734184. Google Scholar
M. R. S. Kulenović and O. Merino, Global bifurcation for discrete competitive systems in the plane, Discrete Contin. Dyn. Syst. Ser. B, 12 (2009), 133-149. doi: 10.3934/dcdsb.2009.12.133. Google Scholar
M. R. S. Kulenović and O. Merino, Invariant manifolds for competitive discrete systems in the plane, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 20 (2010), 2471-2486. doi: 10.1142/S0218127410027118. Google Scholar
W. A. J. Luxemburg and A. C. Zaanen, Riesz spaces. Vol. I, North-Holland Mathematical Library, North-Holland Publishing Co., Amsterdam-London; American Elsevier Publishing Co., New York, 1971. Google Scholar
G. Nyerges, A note on a generalization of Pielou's equation, J. Difference Equ. Appl., 14 (2008), 563-565. doi: 10.1080/10236190801912316. Google Scholar
H. Sedaghat, Nonlinear Difference Equations. Theory with Applications to Social Science Models, Mathematical Modelling: Theory and Applications, vol. 15, Kluwer Academic Publishers, Dordrecht, 2003. doi: 10.1007/978-94-017-0417-5. Google Scholar
H. L. Smith, The discrete dynamics of monotonically decomposable maps, J. Math. Biol., 53 (2006), 747-758. doi: 10.1007/s00285-006-0004-3. Google Scholar
H. L. Smith, Global stability for mixed monotone systems, J. Difference Equ. Appl., 14 (2008), 1159-1164. doi: 10.1080/10236190802332126. Google Scholar
Figure 2.1. In part (a) of this figure, we illustrate our notation of projecting a point $(x, y)$ to the boundary $\partial \Omega.$ In part (b), we illustrate the notion of putting the invariant domain $\Omega$ inside an Origami domain
Figure Options
Download as PowerPoint slide
Figure 2.2. This figure shows the possible options for the boundary of a convex $\Omega$ and a possible ray extension. Part (a) is based on the assumption that $f$ is non-decreasing and Part (b) is based on the assumption that $f$ is non-increasing. Note that the missing quarter in Part (a) is due to the fact that we cannot have $f(\uparrow)$ and $F(\downarrow, \uparrow)$ at the same time. Similarly for the missing quarter of Part (b)
Figure 2.3. Grafting $\gamma_1$ along $\gamma_2$
Figure 2.4. The various cases for the boundary pieces of an origami domain
Figure 2.5. A semi-convex domain is shown in Part (a). Next is shown a piece $ C_1\cup C_2 $ of the boundary of $ \Omega $ oriented positively, with $ f(t) = F(r(t)) $ changing monotonicity from $ C_1 $ to $ C_2 $. Parts (b) and (c) show two different ray extensions, while (d) shows the adjustment to make to these extensions, before filling the sector. As explained in the text, (b) is not a valid extension if monotonicity is to be preserved in the extension
Figure 2.6. Extending from semi-convex domain to the origami domain reduces to extending over sectors, with cases labeled (a) through (d)
Figure 2.7. Filling a rectangle where $ F $ is known on three sides. Extending partially by $ \widetilde{F}_1 $ as shown in (b) then extending over the resulting sector
Figure 4.1. Part (a) of this figure shows the invariant region $\Omega, $ while part (b) shows $T(\Omega)$ together with the extension through horizontal projections. The scale is missing to indicate the general form of the region when $0 < h < \min\{p, \frac{1}{2}\}.$
Tifei Qian, Zhihong Xia. Heteroclinic orbits and chaotic invariant sets for monotone twist maps. Discrete & Continuous Dynamical Systems, 2003, 9 (1) : 69-95. doi: 10.3934/dcds.2003.9.69
M. R. S. Kulenović, Orlando Merino. A global attractivity result for maps with invariant boxes. Discrete & Continuous Dynamical Systems - B, 2006, 6 (1) : 97-110. doi: 10.3934/dcdsb.2006.6.97
Je-Chiang Tsai. Global exponential stability of traveling waves in monotone bistable systems. Discrete & Continuous Dynamical Systems, 2008, 21 (2) : 601-623. doi: 10.3934/dcds.2008.21.601
Michał Misiurewicz, Peter Raith. Strict inequalities for the entropy of transitive piecewise monotone maps. Discrete & Continuous Dynamical Systems, 2005, 13 (2) : 451-468. doi: 10.3934/dcds.2005.13.451
Hans-Otto Walther. Contracting return maps for monotone delayed feedback. Discrete & Continuous Dynamical Systems, 2001, 7 (2) : 259-274. doi: 10.3934/dcds.2001.7.259
Dario Cordero-Erausquin, Alessio Figalli. Regularity of monotone transport maps between unbounded domains. Discrete & Continuous Dynamical Systems, 2019, 39 (12) : 7101-7112. doi: 10.3934/dcds.2019297
Siniša Slijepčević. Stability of invariant measures. Discrete & Continuous Dynamical Systems, 2009, 24 (4) : 1345-1363. doi: 10.3934/dcds.2009.24.1345
Arno Berger, Roland Zweimüller. Invariant measures for general induced maps and towers. Discrete & Continuous Dynamical Systems, 2013, 33 (9) : 3885-3901. doi: 10.3934/dcds.2013.33.3885
Augusto Visintin. Weak structural stability of pseudo-monotone equations. Discrete & Continuous Dynamical Systems, 2015, 35 (6) : 2763-2796. doi: 10.3934/dcds.2015.35.2763
PaweŁ Hitczenko, Georgi S. Medvedev. Stability of equilibria of randomly perturbed maps. Discrete & Continuous Dynamical Systems - B, 2017, 22 (2) : 369-381. doi: 10.3934/dcdsb.2017017
Begoña Alarcón, Sofia B. S. D. Castro, Isabel S. Labouriau. Global dynamics for symmetric planar maps. Discrete & Continuous Dynamical Systems, 2013, 33 (6) : 2241-2251. doi: 10.3934/dcds.2013.33.2241
Nils Ackermann, Thomas Bartsch, Petr Kaplický. An invariant set generated by the domain topology for parabolic semiflows with small diffusion. Discrete & Continuous Dynamical Systems, 2007, 18 (4) : 613-626. doi: 10.3934/dcds.2007.18.613
Simon Lloyd, Edson Vargas. Critical covering maps without absolutely continuous invariant probability measure. Discrete & Continuous Dynamical Systems, 2019, 39 (5) : 2393-2412. doi: 10.3934/dcds.2019101
I. Baldomá, Àlex Haro. One dimensional invariant manifolds of Gevrey type in real-analytic maps. Discrete & Continuous Dynamical Systems - B, 2008, 10 (2&3, September) : 295-322. doi: 10.3934/dcdsb.2008.10.295
Rafael de la Llave, Jason D. Mireles James. Parameterization of invariant manifolds by reducibility for volume preserving and symplectic maps. Discrete & Continuous Dynamical Systems, 2012, 32 (12) : 4321-4360. doi: 10.3934/dcds.2012.32.4321
Fawwaz Batayneh, Cecilia González-Tokman. On the number of invariant measures for random expanding maps in higher dimensions. Discrete & Continuous Dynamical Systems, 2021, 41 (12) : 5887-5914. doi: 10.3934/dcds.2021100
Xiangqing Zhao, Bing-Yu Zhang. Global controllability and stabilizability of Kawahara equation on a periodic domain. Mathematical Control & Related Fields, 2015, 5 (2) : 335-358. doi: 10.3934/mcrf.2015.5.335
Sabri Bensid, Jesús Ildefonso Díaz. On the exact number of monotone solutions of a simplified Budyko climate model and their different stability. Discrete & Continuous Dynamical Systems - B, 2019, 24 (3) : 1033-1047. doi: 10.3934/dcdsb.2019005
Zhili Ge, Gang Qian, Deren Han. Global convergence of an inexact operator splitting method for monotone variational inequalities. Journal of Industrial & Management Optimization, 2011, 7 (4) : 1013-1026. doi: 10.3934/jimo.2011.7.1013
Tibor Krisztin. The unstable set of zero and the global attractor for delayed monotone positive feedback. Conference Publications, 2001, 2001 (Special) : 229-240. doi: 10.3934/proc.2001.2001.229
PDF downloads (190)
HTML views (260)
Ahmad Al-Salman Ziyad AlSharawi Sadok Kallel | CommonCrawl |
Respiratory Systems
+ 7 more educators
Label the following diagram depicting respiration in terrestrial vertebrates.
Birds have more efficient lungs than humans because the flow of air in birds
a. is the same during both inspiration and expiration.
b. travels in only one direction through the lungs.
c. follows a tidal ventilation pattern.
d. is not hindered by a larynx.
e. enters their bones.
Bryan L.
If the digestive and respiratory tracts were completely separate in humans, there would be no need for
a. swallowing.
b. a nose.
c. an epiglottis.
d. a diaphragm.
e. All of these are correct
Which of these is a true statement?
a. In lung capillaries, carbon dioxide combines with water to produce carbonic acid.
b. In tissue capillaries, carbonic acid breaks down to carbon dioxide and water.
c. In lung capillaries, carbonic acid breaks down to carbon dioxide and water.
d. In tissue capillaries, carbonic acid combines with hydrogen ions to form the carbonate ion.
e. All of these statements are true
reinforced tube that connects larynx with bronchi
a. bronchi d. larynx
b. bronchioles e. pharynx
c. glottis f. trachea
opening into larynx
divisions of air tubes that enter lungs
$\begin{array}{ll}{\text { a. bronchi }} & {\text { d. larynx }} \\ {\text { b. bronchioles }} & {\text { e. pharynx }} \\ {\text { c. glottis }} & {\text { f. trachea }}\end{array}$
Which of these is incorrect concerning inspiration?
a. The rib cage moves up and out.
b. The diaphragm contracts and moves down.
c. As pressure in lungs decreases, air comes rushing in.
d. The lungs expand because air comes rushing in.
In humans, the respiratory control center
a. is stimulated by carbon dioxide.
b. is located in the medulla oblongata.
c. controls the rate of breathing.
d. is stimulated by hydrogen ion concentration.
Aneri S.
Air enters the human lungs because
a. atmospheric pressure is less than the pressure inside the lungs.
b. atmospheric pressure is greater than the pressure inside the lungs.
c. although the pressures are the same inside and outside, the partial pressure of oxygen is lower within the lungs.
d. the residual air in the lungs causes the partial pressure of oxygen to be less than it is outside.
e. the process of breathing pushes air into the lungs.
Carbon dioxide is carried in the plasma
a. in combination with hemoglobin.
b. as the bicarbonate ion.
c. combined with carbonic anhydrase.
d. only as a part of interstitial fluid.
Susanna T.
The chemical reaction that converts carbon dioxide to a bicarbonate ion takes place in
a. the blood plasma.
b. red blood cells.
c. the alveolus.
d. the hemoglobin molecule.
It is difficult to develop immunity to the common cold because
a. antibodies don't work against cold viruses.
b. bacteria that cause colds are resistant to antibiotics.
c. colds can be caused by hundreds of viral strains.
d. common cold viruses cause severe immunosuppression.
Marcelo M.
The first action that should be taken when someone is choking on food is to perform
a. a tracheostomy.
b. CPR.
c. the Heimlich maneuver.
d. X-rays to determine where the food is lodged.
a. mainly affects the upper respiratory tract.
b. is usually caused by an infection.
c. is considered to be a genetic disorder.
d. is usually curable.
e. None of these statements are true.
Pulmonary tuberculosis is caused by a
a. bacterium.
b. fungus.
c. protist.
d. virus.
In which chronic lung disease do the alveoli become distended and often fuse into enlarged air spaces?
a. asthma
b. cystic fibrosis
c. emphysema
d. pulmonary fibrosis | CommonCrawl |
Signal Processing Stack Exchange is a question and answer site for practitioners of the art and science of signal, image and video processing. It only takes a minute to sign up.
Compute the two-dimensional DFT
Compute the two-dimensional DFT [4x4] for the following 4x4 image $ \begin{matrix} 0.5 & 0.5 & 0.5 & 0.5 \\ 0.5 & 0.5 & 0.5 & 0.5\\ 0.5 & 0.5 & 0.5 & 0.5\\ 0.5 & 0.5 & 0.5 & 0.5 \end{matrix} $
I know that DFT is separable by dimensions – one can calculate 4 vertical transforms first, then 4 horizontal ones
For each row we get [2 0 0 0] in the first and third row and zero elsewhere.
For each column we get [1 0 1 0] in the first and third column and zero elsewhere.
How from this two one-dimensional dfts obtain two-dimensional one?
dft 2d
roffensiveroffensive
No you are not doing the separation correctly :
The horizontal 1D-DFT of the rows of input will be:
$ H_1 = \begin{matrix} 2 & 0 & 0 & 0 \\ 2 & 0 & 0 & 0 \\ 2 & 0 & 0 & 0 \\ 2 & 0 & 0 & 0 \\ \end{matrix} $
and the vertical 1D-DFT of the columns of $H_1$ will be:
$ H_2 = \begin{matrix} 8 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ \end{matrix} $
which is equivalent to the 2D-DFT of the original input.
Fat32Fat32
Thanks for contributing an answer to Signal Processing Stack Exchange!
Not the answer you're looking for? Browse other questions tagged dft 2d or ask your own question.
Conditions for precoding matrix to preserve complex conjugate symmetry on DFT vector
Two-dimensional wavelet analysis
Determining effect of powers of DFT matrix conjugate on input without multiplying
Working with the DCT
Sampling H(z) to get DFT
Determine sequence's value from equally null circular convolution DFT
How does zero-padding affect the magnitude of the DFT?
Convolution in Spatial Domain Is Multiplication in Frequency Domain
Properly interpreting FFT output | CommonCrawl |
NMF-weighted SRP for multi-speaker direction of arrival estimation: robustness to spatial aliasing while exploiting sparsity in the atom-time domain
Sushmita Thakallapalli ORCID: orcid.org/0000-0002-1742-56681,
Suryakanth V. Gangashetty1,2 &
Nilesh Madhu3
EURASIP Journal on Audio, Speech, and Music Processing volume 2021, Article number: 13 (2021) Cite this article
Localization of multiple speakers using microphone arrays remains a challenging problem, especially in the presence of noise and reverberation. State-of-the-art localization algorithms generally exploit the sparsity of speech in some representation for this purpose. Whereas the broadband approaches exploit time-domain sparsity for multi-speaker localization, narrowband approaches can additionally exploit sparsity and disjointness in the time-frequency representation. Broadband approaches are robust to spatial aliasing but do not optimally exploit the frequency domain sparsity, leading to poor localization performance for arrays with short inter-microphone distances. Narrowband approaches, on the other hand, are vulnerable to spatial aliasing, making them unsuitable for arrays with large inter-microphone spacing. Proposed here is an approach that decomposes a signal spectrum into a weighted sum of broadband spectral components (atoms) and then exploits signal sparsity in the time-atom representation for simultaneous multiple source localization. The decomposition into atoms is performed in situ using non-negative matrix factorization (NMF) of the short-term amplitude spectra and the localization estimate is obtained via a broadband steered-response power (SRP) approach for each active atom of a time frame. This SRP-NMF approach thereby combines the advantages of the narrowband and broadband approaches and performs well on the multi-speaker localization task for a broad range of inter-microphone spacings. On tests conducted on real-world data from public challenges such as SiSEC and LOCATA, and on data generated from recorded room impulse responses, the SRP-NMF approach outperforms the commonly used variants of narrowband and broadband localization approaches in terms of source detection capability and localization accuracy.
Speech remains the natural mode of interaction for humans. Present day smart-home devices are, therefore, increasingly equipped with voice controlled personal assistants to exploit this for human-machine interfacing. The performance of such devices depends, to a large extent, on the performance of the localization techniques used in these systems. The term localization in this context implies the detection and spatial localization of a number of overlapping speakers, and it is usually the first stage in many speech communication applications. Accurate acoustic localization of multiple active speakers, however, remains a challenging problem—especially in the presence of background noise and room reverberation.
Localization is typically achieved by means of the spatial diversity afforded by microphone arrays. Large microphone arrays (inter-microphone spacing in the order of a meter) sample the sound fields at large spatial intervals, thereby reducing the effect of diffuse background noise in the localization. However, these arrays are increasingly prone to spatial aliasing at higher frequencies. Compact microphone arrays, with inter-microphone spacing of the order of a few centimeters, offer greater robustness to spatial aliasing, but are biased by diffuse background noise. The size of the chosen array is usually a trade-off between these two factors and, further, is often driven by practical considerations.
State-of-the-art algorithms for multi-speaker localization usually exploit the sparsity and disjointness [1] of speech signals. While some approaches exploit, mainly, temporal sparsity (i.e., speakers are not concurrently active at all times), others exploit the time-frequency (TF) sparsity (i.e., speakers are not concurrently active at all time and frequency points of the short-time frequency domain representation) of speech. Here, the short-time Fourier transform (STFT) representation is typically chosen because of its computational efficiency. The former approaches are categorized as broadband and the latter as narrowband. For both these approaches, the localization estimates over time and/or frequency are subsequently aggregated to obtain an estimate of the number of active sources and their respective locations.
Frequently used broadband methods are based on the generalized cross-correlation (GCC) [2] and its variants, e.g., the average magnitude difference function (AMDF) estimators [3], the adaptive eigenvalue decomposition approach [4], information theoretic criteria-based approaches [5], and the broadband steered-response power approaches [6]. Such approaches typically localize the dominant source in each time segment, thereby exploiting the temporal sparsity induced by natural pauses in speech. The GCC with phase transform (PHAT) weighting has proven to be the most robust among all the GCC weightings in low noise and reverberant environments [7]. However, in GCC-PHAT, the localization errors increase when the signal to noise ratio (SNR) is poor. To address this issue, researchers have proposed SNR-based weights on GCC-PHAT to highlight the speech dominant TF bins and to de-emphasize TF bins with noise or reverberant speech (see, e.g., [8–11]). A performance assessment of various GCC algorithms may be found in [12].
Narrowband frequency domain approaches, on the other hand, use the approximate disjointness of speech spectra in their short-time frequency domain representation to localize the dominant source at each time-frequency point. Multi-speaker localization is subsequently done by pooling the individual location estimates. In [13], for example, a (reliability-weighted) histogram is computed on the pooled DoA estimates, and the locations of peaks of the histogram yield the speaker location estimates. In [14], instead of a histogram, a mixture of Gaussians (MoG) model is applied to cluster the time-difference of arrival (TDoA) estimates. The approach of [15] is a generalization of [14] in which speaker coordinates are estimated and tracked, rather than speaker TDoAs. Similarly, in [16] the authors propose a MoG clustering of the direction of arrival (DoA) estimates obtained by a narrowband steered response power (SRP) approach. This is extended in [17], where a Laplacian mixture model is proposed for the clustering. In [18], source separation and localization are iteratively tackled: source masks are first estimated by clustering the TDoA estimates at each TF bin and subsequently SRP-PHAT is used to estimate the DoAs of the separated sources. The estimated DoAs are fed back to the cluster tracking approach for updating the cluster centers. Other recent works build upon this basic idea of exploiting the TF sparsity by introducing reliability weights on the time-frequency units before localization such as [19], which uses SNR-based weights, [20], which uses TF weights predicted by neural-networks, and [21], which considers a weighted histogram of the narrowband estimates, where the weights correspond to a heuristic measure of the reliability of the estimate in each TF bin. A comprehensive overview of the relations between the commonly used localization approaches is presented in [22].
When performing source localization independently at each time-frequency point, typical optimization functions for narrowband localization do not yield a unique DoA estimate above a certain frequency. This is due to the appearance of grating lobes, and the phenomenon is termed spatial aliasing. As the distance between the microphones in the array increases, the frequency at which spatial aliasing occurs reduces, leading to ambiguous DoA estimates across a larger band of frequencies. Broadband approaches circumvent this problem by summing the optimization function across the whole frequency band and computing a location estimate per time frame. Such averaging is indicated for arrays with large inter-element spacing. However, this constitutes a promiscuous averaging across frequencies, each of which may be dominated by a different speaker, leading to (weakened) evidence for only the strongest speaker in that time frame—i.e., only the location of the highest peak in the angular spectrum of the frame is considered as a potential location estimate and other peaks are usually ignored, since they may not reliably indicate other active speaker locations [23]. Multiple speaker localization is still possible in such cases by aggregating the results across different time frames but, by disregarding the frequency sparsity of speech signals, softer speakers (who may not be dominant for a sufficient number of time frames) may not be localized.
Instead of averaging across the whole frequency range, a compromise can be effected by only averaging across smaller, contiguous sub-bands of frequencies and computing a location estimate per time and sub-band region. By pooling the estimates across the various sub-bands, multi-speaker localization may still be achieved. Such bands may be either psycho-acoustically motivated (e.g., the Bark scale used in [24]) or heuristically defined. However, these are fixed frequency groupings and the previously described shortcomings with regard to such groupings still hold. Other approaches [25, 26] try to resolve the spatial aliasing problem by trying to unwrap the phase differences of spatially aliased microphone pairs. Initial (rough) estimates of the source locations are required to resolve the spatial aliasing, and it is assumed that at least a few non-aliased microphone pairs are available for this. Consequently, this requires arrays with several microphones at staggered distances such that multiple microphone pairs, aliasing at different frequencies, are available.
The key idea of our approach is to average the narrowband optimization function for localization only across frequency bins that show simultaneous excitation in speech (e.g., fundamental frequency and its harmonics for a voiced speech frame, etc.). Thereby the frequency grouping is not fixed, but data- and time frame dependent. Further, since the averaging is carried out across frequency bins that are simultaneously excited during the speech, the interference from other speakers should be minimal in these bins due to the sparsity and disjointness property. Thus, we can simultaneously exploit the time and frequency sparsity of speech while being robust to spatial aliasing—thereby overcoming the shortcomings of the previously mentioned approaches.
Non-negative matrix factorization (NMF) allows for the possibility to learn such typical groupings of the frequencies based on the magnitude spectrum of the microphone signal. These frequency groupings are termed atoms in our work. Thus we speak of localization based on time-atom sparsity, i.e., in any one time frame only a few atoms are active and each active atom only belongs to one speaker, and localizing across the different atoms in a time frame allows for multi-speaker localization. Since we use the SRP approach for localization, our algorithm is termed the SRP-NMF approach.
The rest of the paper is organized as follows: we first summarize prior approaches utilizing NMF for source localization and place our proposed approach in the context of these works. Next, in Section 3, we describe the signal model, followed by a review of the basic ideas underlying state-of-the-art narrowband and broadband SRP approaches. SRP-NMF is introduced and detailed in Section 5. In Section 6, the approach is thoroughly tested. The details of the databases, the comparison approaches and evaluation metrics, the method used to estimate SRP-NMF parameters, an analysis of the results and limitations of the approach are presented. Finally, we summarize the work and briefly mention the future scope.
Prior work using NMF for localization
NMF has previously been used for source localization and separation in several conceptually different ways. For example, in [27], NMF is applied to decompose the SRP-PHAT function (collated across all time-frequency points) into a combination of angular activity and source presence activity. This decomposition assumes unique maxima of the SRP-PHAT function (i.e., no spatial aliasing), allowing for a sparse decomposition using NMF.
In [28], on the other hand, NMF is used to decompose the GCC-PHAT correlogram matrix to a low-dimensional representation consisting of bases which are the GCC-PHAT correlation functions for each source location and weights (or activation functions) which determine which time frame is dominated by which speaker. Thus, this approach may be interpreted as a broadband GCC-PHAT approach assuming temporal sparsity. As it is a broadband approach, spatial aliasing is not a problem. However, simultaneous localization of multiple sources within a single time frame is not straightforward.
The approach of [29] is, again, fundamentally different from [27] and [28]. Here, complex NMF is used to decompose the multi-channel instantaneous spatial covariance matrix into a combination of weight functions that indicate which locations in a set of (pre-defined) spatial kernels are active (thus corresponding to localization). This approach is supervised—NMF basis functions of the individual source spectra (learnt in a training stage), as well as a pre-defined spatial dictionary are incorporated into the approach.
In a recent separation approach called GCC-NMF [30], GCC-PHAT is used for localization, and the NMF decomposition of the mixture spectrum is used for dictionary learning. Subsequently, the NMF atoms at each time instant are clustered, using the location estimates from GCC-PHAT, to separate the underlying sources. The results of this approach, along with the successful use of NMF in supervised single-channel source separation, indicate that an NMF-based spectral decomposition results in basis functions (atoms) that are sufficiently distinct for each source, and which do not overlap significantly in time—i.e., we have some form of disjointness in the time-atom domain. Thus, we hypothesise that using such atoms as weighting for the frequency averaging would allow for exploiting this time-atom sparsity and disjointness to simultaneously localize multiple sources within a single time frame while being robust to spatial aliasing due to the frequency averaging.
Specifically, we investigate the use of an unsupervised NMF decomposition as a weighting function for the SRP-based localization and apply it to the task of multi-speaker localization. Further, we also investigate modifications to the NMF atoms which lead to a better weighting for the purpose of localization, followed by a rigorous evaluation of NMF-weighted SRP for DoA estimation in various room acoustic environments, and with different array configurations. The proposed approach is comprehensively compared to (a) the state-of-the-art localization approaches for closely spaced microphones and (b) the state-of-the-art methods for widely spaced microphones.
Signal model
Spatial propagation model
Consider an array of M microphones that captures the signals radiated by Q broadband sound sources in the far field. The microphone locations may be expressed in 3D cartesian co-ordinates by the vectors as r1, …, rM. Under the far field assumption, the DoA vector for source q in this co-ordinate system can be denoted as:
$$ {}\mathbf{n}_{q}(\theta,\phi) = \left(\begin{array}{ll}\cos(\theta_{q})\sin(\phi_{q}), \sin(\theta_{q})\sin(\phi_{q}), & \cos(\phi_{q})\end{array}\right)^{T}, $$
where 0≤θ≤2π is the azimuth angle between the projection of nq(θ,ϕ) on to the xy plane and the positive x-axis and 0≤ϕ≤π is the elevation angle with respect to the positive z-axis.
In the STFT domain, the image of source q at the array, in the kth frequency bin and bth time frame, can be compactly denoted as: Xq(k,b)=[Xq,1(k,b), …,Xq,M(k,b)]T. If V(k,b) is the STFT-domain representation of the background noise at the array, the net signal captured by the array can be written as:
$$ \mathbf{X}(k,b) = \sum_{q=1}^{Q}\mathbf{X}_{q}(k,b) + \mathbf{V}(k,b), $$
where X(k,b)=[X1(k,b), …,XM(k,b)]T.
Under the common assumption of direct path dominance, and taking the signal at the first microphone as the reference, the image of source q at the array can be re-cast, relative to its image at the reference microphone, as:
$$ {}\mathbf{X}_{q}(k,b) = \left(\begin{array}{l}1, e^{{\jmath\,}\Omega_{k}\mathbf{r}_{21}^{T}\mathbf{n}_{q}/c},\ldots, e^{{\jmath\,}\Omega_{k}\mathbf{r}_{M1}^{T}\mathbf{n}_{q}/c} \end{array}\right)^{T} X_{q,1}(k,b), $$
where \(\Omega _{k}= \frac {2 \pi kf_{s}}{K}\) is the kth discrete frequency, fs is the sampling rate, K is the number of DFT points, riℓ=ri−rℓ is the position difference between microphones i and ℓ, and c is the speed of sound.
The term \(\left (\begin {array}{l}1, e^{{\jmath \,}\Omega _{k}\mathbf {r}_{21}^{T}\mathbf {n}_{q}/c},\ldots, e^{{\jmath \,}\Omega _{k}\mathbf {r}_{M1}^{T}\mathbf {n}_{q}/c} \end {array}\right)^{T}\) is often termed the relative steering vector Aq(k) in the literature. Further, it is also often assumed that each TF-bin is dominated by only one source based on W-disjoint orthogonality property [1]. Consequently, assuming source q is dominant in TF-bin (k,b), (2) can be simplified as:
$$ \mathbf{X}(k,b) \approx \mathbf{X}_{q}(k,b) + \mathbf{V}(k,b)\,. $$
NMF model
Given the STFT representation Sq(k,b) of a source signal q, computed over K discrete frequencies and B time frames, we denote the discrete magnitude spectrogram of this signal by the (K×B) non-negative matrix |Sq|. We shall subsequently use the compact notation: \(|\mathbf {S}_{q}|\in \mathbb {R}_{+}^{({K}\times B)}\) to denote a non-negative matrix and its dimensions. The element (k,b) of the matrix |Sq| is denoted as |Sq(k,b)|.
A low rank approximation of |Sq| of rank D can be obtained using NMF as:
$$ |\mathbf{S}_{q}| \approx \mathbf{W}_{q} \mathbf{H}_{q}, $$
where \(\mathbf {W}_{q} \in \mathbb {R}_{+}^{({K}\times D)}\) and \(\mathbf {H}_{q} \in \mathbb {R}_{+}^{(D\times B)}\). Eq (5) implies that:
$$ |S_{q}(k,b)| \approx \sum_{d=1}^{D}W_{q}(k,d) H_{q}(d,b). $$
The columns wd,q, d=1,2,…,D, of Wq encode spectral patterns typical to the source q and are referred to as atoms in the ensuing. The rows of Hq encode the activity of the respective atoms in time. A high value of Hq(d,b) for an atom d at frame b indicates that the corresponding atom is active in that time frame.
However, based on the assumption of signal sparsity in the time-atom representation, only the atoms whose activation values exceed a certain threshold value need be considered as contributing to the signal at a particular time frame. Let \(\mathcal {D}_{b,q}\) be the set of atom indices whose activation values exceed the threshold at time frame b. Then, we can further simplify (6) as:
$$ |S_{q}(k,b)| \approx \sum_{d \in \mathcal{D}_{b,q} }{w_{d,q}(k)} H_{q}(d,b), $$
where wd,q(k)=Wq(k,d).
Steered response power beamformers
Narrowband SRP (NB-SRP)
To localize a source at any frequency bin k and time frame b, the NB-SRP approach basically steers a constructive beamformer towards each candidate DoA (θ,ϕ), in a pre-defined search space of candidate DoAs, and picks the candidate with the maximum energy as the location of the active source at the TF point (k,b). This assumes, implicitly, that the time-frequency bin in question contains a directional source. Formally, this approach may be written as:
$$ \left(\widehat{\theta}(k,b),\widehat{\phi}(k,b)\right)= \underset{\theta,\phi}{\text{argmax}}\, {\mathcal{J}_{\text{NB-SRP}}(k,b,\theta,\phi)}, $$
where \((\widehat {\theta }(k,b),\widehat {\phi }(k,b))\) is the DoA estimate at each TF bin and \(\mathcal {J}_{\text {NB-SRP}}(k,b, \theta,\phi)\) is the optimization function given by:
$$ \mathcal{J}_{\text{NB-SRP}}(k,b, \theta,\phi) = |\mathbf{A}^{H}(k,b,\theta,\phi)\mathbf{X}(k,b)|^{2}\,. $$
In the above, A(k,b,θ,ϕ) can be any generic beamformer that leads to a constructive reinforcement of a signal along (θ,ϕ). In practice, the normalized delay-and-sum beamformer of (10) is widely used. Since this is similar to the PHAT weighting, this approach is called the NB-SRP-PHAT.
$$ \begin{aligned} \mathbf{A}(k,b,\theta,\phi) = \left[\frac{1}{|X_{1}(k,b)|}, \frac{e^{{\jmath\,}\Omega_{k}\mathbf{r}_{21}^{T}\mathbf{n}(\theta,\phi)/c} }{|X_{2}(k,b)|},\ldots, \frac{e^{{\jmath\,}\Omega_{k}\mathbf{r}_{M1}^{T}\mathbf{n}(\theta,\phi)/c} }{|X_{M}(k,b)|} \right]^{T}. \end{aligned} $$
The source location estimates for the different TF bins, obtained as in (8), are subsequently clustered and the multi-speaker location estimates are obtained as the centroids of these clusters.
Broadband SRP (BB-SRP)
NB-SRP fails to provide a unique maximum for (8) for frequencies above the spatial aliasing frequency. As the inter-microphone distance increases, a larger range of frequencies are affected by spatial aliasing, and the efficacy of NB-SRP-based methods decreases. To overcome this problem, (9) is summed across the frequency range, leading to the broadband SRP (BB-SRP) optimization function [31]:
$$ \mathcal{J}_{\text{BB-SRP}}(b, \theta,\phi) = \sum_{k}|\mathbf{A}^{H}(k,b,\theta,\phi)\mathbf{X}(k,b)|^{2}. $$
BB-SRP may be seen as a multi-channel analog of GCC-PHAT approach. Note that (11) yields a single localization result per time frame. The results from multiple time frames can then be clustered as in the NB case for multi-speaker localization. The broadband approach ameliorates spatial aliasing at the cost of un-utilized TF sparsity. Since only the dominant source is located in each time frame, softer speakers who are not dominant in a sufficient number of time frames may not be localized.
The SRP-NMF approach
As we shall now demonstrate, by incorporating the DT basis functions \(\mathbf {W} = \left [\mathbf {w}_{1},\mathbf {w}_{2},\ldots,\mathbf {w}_{D_{T}}\right ]\) obtained from an NMF decomposition of the microphone signal spectrum, we can exploit sparsity in what we term the 'time-atom' domain. For compactness of expression, and without loss of generality, we shall consider localization only in the azimuth plane (i.e., ϕ=π/2) in the following.
In each time frame we compute a weighted version of (11) as:
$$ \mathcal{J}_{\text{SRP-NMF}}(d,b, \theta) = \sum_{k}w_{d}(k)\left| \mathbf{A}^{H}(k,b,\theta)\mathbf{X}(k,b)\right|^{2}, $$
where wd(k) is the kth element of the dth atom wd. Based on (12), we obtain a DoA estimate per active atomd as:
$$ \widehat{\theta}(d,b) = \underset{\theta}{\text{argmax}}\, {\mathcal{J}_{\text{SRP-NMF}}(d,b,\theta)}\,. $$
As previously explained, we expect the atoms wd to embody the spectral patterns typical to the underlying sources. Further, the time-frequency sparsity and disjointness of speech results in each atom being unique to a single source. Thus, the weighted sum in (12) only aggregates information across frequencies that are simultaneously excited by a source, yielding a spatial-aliasing robust location estimate for that source in (13). This is the rationale behind the weighting in (12). Multi-speaker localization is subsequently obtained by clustering the DoA estimates computed for all active atoms.
We present an intuitive idea of how this works using a toy example in Section 5.1.
Demonstration of the working principle of SRP-NMF
Consider two spatially separated, simultaneously active sources captured by microphones placed 12 cm apart. Each source is a harmonic complex of different fundamental frequencies. Figure 1 describes the two underlying source atoms wd. In this simple example, w1(k)=1 only at frequencies where the source 1 is active, and zero otherwise (the red lines in Fig. 1) and w2(k)=1 only at frequencies where the source 2 is active (the blue dashed lines in Fig. 1). Figure 2 depicts the BB-SRP optimization function \(\mathcal {J}_{\text {BB-SRP}}(\theta)\) and the SRP-NMF optimization functions \(\mathcal {J}_{\text {SRP-NMF}}(d, \theta),\ d=1,2\) for the two atoms, over the azimuthal search space. The dashed lines indicate the ground truth DoAs. The locations of the peaks of the optimization functions correspond to the respective DoA estimates. It is evident from this figure that the BB-SRP can localize only one source when considering the dominant peak (and even then with a large error). When considering the locations of the two largest peaks of \(\mathcal {J}_{\text {BB-SRP}}(\theta)\) for estimating the two underlying source DoAs, both estimates are in error by more than 5∘. This is quite large for such a synthetic example. In contrast, the SRP-NMF estimates (one each from the respective \(\mathcal {J}_{\text {SRP-NMF}}(d, \theta)\)) are much more accurate and localize both sources. This is because the each atom emphasizes frequency components specific to a single source in the weighted summation, while suppressing the other components.
Simulated amplitude spectrum of two spatially separated sources
Normalized SRP beampatterns of broadband SRP and SRP-NMF on a mixture of two sources. The dashed line indicates the ground truth of the source locations
SRP-NMF implementation
With the intuitive understanding from the previous section, we now focus on the implementation details. In a supervised localization approach, source-specific atoms can be easily obtained by NMF of the individual source spectra. However, we focus here on the unsupervised case, where no prior information of the sources to be localized is available. The atoms, therefore, are extracted from the mixture signal at the microphones. It has previously been demonstrated [32] that NMF of mixture spectra still results in atoms that correspond to the underlying source spectra. However, it is not possible to attribute the atoms to their corresponding sources without additional information. In our case, NMF is performed on the average of the magnitude spectrograms of the signals of the different microphones. Another possibility is a weighted average spectrogram where the weights could be estimated based, e.g., on some SNR measure [33, 34].
The steps in SRP-NMF localization are:
Compute the average of the magnitude spectrograms of the signals at all microphones m:
$$ \overline{|X(k,b)|} = \frac{1}{M} \sum_{m=1}^{M}{|X_{m}(k,b)|}. $$
This yields the average magnitude spectrum matrix \(\overline {|\mathbf {X}|} \in \mathbb {R}_{+}^{(K\times B)}\), where K and B indicate, again, the number of discrete frequencies and time frames of the STFT representation.
Decompose \(\overline {|\mathbf {X}|}\) using NMF into the matrix \(\mathbf {W} \in {\mathbb {R}_{+}^{(K\times {D_{T}})}}\), containing the DT dictionary atoms, and the matrix \(\mathbf {H}\in {\mathbb {R}_{+}^{(D_{T}\times {B})}}\) containing the activations of these atoms for the different time frames:
$$\begin{array}{*{20}l} \overline{|\mathbf{X}|} \approx \mathbf{W}\mathbf{H}\,. \end{array} $$
The cost function used for NMF is the generalized KL divergence [35]:
$$ \begin{aligned} D_{\text{KL}}(\overline{|\mathbf{X}|},\mathbf{WH}) &= \sum_{k} \sum_{b}(\overline{|X(k,b)|}\log \left(\frac{\overline{|X(k,b)|}}{[\mathbf{WH}]{(k,b)}}\right)\\ &-\overline{|X(k,b)|}+[\mathbf{WH}]{(k,b)}), \end{aligned} $$
where [WH](k,b) indicates element (k,b) of the product WH. The well-known multiplicative update rules are applied to estimate W and H. Once the atoms are obtained, they can be used for the weighting in (12)
We note that only the active atoms of each time frame are used in the localization. To obtain the active atoms for any frame b, they are sorted in decreasing order of their activations H(d,b) in that frame. The first atoms that contribute to a certain percentage (here empirically set at 99 percent) of the sum of the activation values in that frame are considered as active.
The SRP-NMF optimization function is, consequently,
$$ \begin{aligned} \mathcal{J}_{\text{SRP-NMF}}(d_{b},b,\theta) &= \sum_{k} w_{d_{b}}(k)\left| \mathbf{A}^{H}(k,d_{b},b, \theta)\mathbf{X}(k,b)\right|^{2}, \end{aligned} $$
where \(\mathbf {w}_{d_{b}}\) is an active atom at frame b.
By maximizing (17) with respect to θ, a DoA estimate is obtained for each active atom in frame b as:
$$ \widehat{\theta}(d_{b},b) = \underset{\theta}{\text{argmax}}\, {\mathcal{J}_{\text{SRP-NMF}}(d_{b},b,\theta).} $$
Lastly, we compute the histogram of the DoA estimates across all the time-atom combinations. The locations of peaks in the histogram correspond to DoA estimates of the active sources in the given mixtures.
NMF modifications
The NMF decomposition of speech spectra as in (15) results in dictionary atoms with higher energy at low frequencies than at high frequencies. This is because speech signals typically have a larger energy at the lower frequencies. Further, due to the large dynamic range of speech, the energy in high frequency components can be several decibels lower than that in low-frequency components [32]. This characteristic is, subsequently, also reflected in the NMF atoms. When these atoms are used as weighting functions, the resulting histogram of location estimates is biased towards the broadside of the array. We illustrate this on a 3 source stereo mixture (dev1_male3_liverec_250ms_5cm_mix.wav) from the SiSEC database. The details of the database are in Section 6.3. The ground truth DoAs of the 3 sources are 50∘,80∘ and 105∘. The histogram obtained by the SRP-NMF is shown in Fig. 3. The bias at the broadside of the array (around 90∘) is evident from the figure. While the second and third peaks near 90∘ are prominent, the first peak at 50∘, which is away from the broadside, is not clear.
Histogram of SRP-NMF on a mixture of 3 sources taken from the SiSEC database dev1_male3_liverec_250ms_5cm_mix.wav, with β=0 and DT=35. The ground truth DoAs are 50∘,80∘ and 105∘. The estimate does not clearly present evidence for the 1st peak at 50∘
This broadside bias can be explained as follows: localization essentially exploits the inter-microphone phase difference (IPD), which is a linear function of frequency (with some added non-linearities in real scenarios due to reverberation [28]). This linear dependence implies that low frequencies have smaller IPDs (concentrated around 0), compared to high frequencies. This leads to localization around the broadside for the low frequencies. When using the weighted averaging, the dominant low frequency components in the atoms thereby emphasize the broadside direction.
To remove this bias, a penalty term [28, 36] is added to flatten the atoms, thereby reducing the dominance of low frequency components in the atoms. This penalty term is given by:
$$ F(\mathbf{W}) = \sum_{d} \left[\mathbf{W}^{T}\mathbf{W}\right](d,d), $$
where [WTW](d,d) indicates the elements along the main diagonal of WTW. This leads to the constrained NMF (CNMF) cost function:
$$ \mathcal{C}\left(\overline{|\mathbf{X}|},\mathbf{WH}\right) = D_{\text{KL}}(\overline{|\mathbf{X}|},\mathbf{WH}) + \beta F(\mathbf{W}), $$
where β is the weighting factor of the penalty term. The multiplicative update equations subsequently become:
$$\begin{array}{*{20}l} {}\mathbf{H} \!\leftarrow\! \mathbf{H} \odot \frac{\mathbf{W}^{T} \frac{\overline{|\mathbf{X}|}}{\mathbf{WH}}}{\mathbf{W}^{T} \mathbf{1}} &\qquad \text{and} \qquad \mathbf{W} \!\leftarrow\! \mathbf{W} \odot \frac{\frac{\overline{|\mathbf{X}|}}{\mathbf{WH}}\mathbf{H}^{T} }{ \mathbf{1} \mathbf{H}^{T} +2 \beta \mathbf{W}}, \end{array} $$
where 1 represents a matrix of ones of the appropriate dimensions, ⊙ represents the Hadamard product and the division is element-wise. This constrained decomposition favors atoms with a flat spectrum. Figure 4 shows the histogram of SRP-NMF when using the CNMF decomposition, where it may be observed that the broadside bias is overcome and azimuths of all the sources are correctly estimated.
Histogram of SRP-NMF (CNMF) on a mixture of 3 sources taken from the SiSEC database dev1_male3_liverec_250ms_5cm_mix.wav, with β=60 and DT=35. The ground truth DoAs are 50∘,80∘ and 105∘. The 3 peaks are clearly visible now
Experimental evaluation
In this section, the performance of SRP-NMF is compared to the state-of-the-art localization approaches for closely spaced and widely spaced microphones. Since our approach is closely related to the SRP/GCC family of approaches (being, as it were, an intermediate between the broadband and narrowband versions of these), and because these are the typical, well-understood methods for source localization, these form the basis for our benchmark.
Specifically, we compare our approach to:
The NB-SRP-PHAT according to Section 4.1;
A sub-band variant of the above (termed Bark-SRP-PHAT), where the optimization function is averaged over Sub-bands defined according to the Bark scale as in [24]; and
Four other best performing algorithms among a broad variety of localization algorithms benchmarked in [19] and implemented within the open source Multichannel BSS-locate toolbox [37].
For completeness, a brief summary of Bark-SRP-PHAT and the approaches from the Multichannel BSS-locate toolbox is given in Section 6.1.
Tests are conducted on four different databases (three of which are openly available) in order to evaluate the approaches across different microphone arrays (different spacing and configurations) as well as in different acoustic environments, from relatively dry (T60≈130ms) to highly reverberant (T60≈660ms). The evaluation setup is described in Section 6.2, followed by the details of the databases used. The evaluation metrics are described in Section 6.4 and the method adopted for choosing NMF parameters is presented in Section 6.5.
Further, Section 6.6 presents a comparison of the proposed SRP-NMF to a supervised approach wherein the underlying sources at each microphone are first separated using NMF, and localization is subsequently performed on the separated sources.
Section 6.7 presents the results of the benchmarking.
Brief summary of benchmarked approaches
Bark-SRP-PHAT
NB-SRP and BB-SRP are, respectively, fully narrowband or fully broadband approaches. However, SRP-NMF only averages the optimization function over a (source-dependent) subset of frequencies. Thus, we include a comparison with a modified SRP approach where the optimization function is averaged along sub-bands, where the sub-bands are the critical bands defined according to the Bark scale. A single localization estimate is computed for each critical band within a time frame. These estimates are then pooled across all time frames in a manner similar to the narrowband SRP-PHAT approach, to obtain the final localization result. This approach thus exploits available sparsity and disjointness in time and sub-bands. This scale was chosen because of its psychoacoustical relevance, as seen in previous localization research (e.g., [24]).
MVDRW approaches
The MVDRW approaches [19] use minimum variance distortionless response (MVDR) beamforming to estimate, for each frequency bin k and each time frame b, the signal to noise ratio (SNR) in all azimuth directions. Since the spatial characteristics of the sound field are taken into account, the SNR indicates, effectively, time-frequency bins where the direct path of a single-source is dominant. The MVDRWsum variant averages the SNR across all time-frequency points and, subsequently, the DoA estimates are computed as the location of the peaks of this averaged SNR. When all sources are simultaneously active within the observation interval, this averaging is beneficial. However, when a source is active only for a few time frames, the averaging smooths out the estimate, thereby possibly not localizing the source. Hence [19] also proposes an alternative called MVDRWmax, where a max pooling of the SNR is performed over time.
GCC-variants
The two GCC-variants considered in [19] are the GCC-NONLINsum and GCC-NONLINmax. The key difference with the traditional GCC is the non-linear weighting applied to compensate for the wide lobes of the GCC for closely spaced microphones [38]. In GCC-NONLINsum and GCC-NONLINmax, respectively, the sum and max pooling of the GCC-PHAT, computed over the azimuthal space, is done across time.
As previously stated, these approaches were chosen for the benchmark because they have previously been demonstrated to be the best performing approaches among a broad variety of localization approaches. Further, since the implementation of these approaches is open source, it allows for a reproducible, fair benchmark against which new methods may be compared.
Evaluation setup
For all the experiments, the complex-valued short-term Fourier spectra were generated from 16 kHz mixtures using a DFT size of 1024 samples (i.e., K=512) and a hop size of 512 samples. A periodic square-root Hann window of size 1024 samples is used prior to computing the DFT.
The NMF parameters DT and β are set to 55 and 60 respectively. These parameters are set based on preliminary experiments that are described in Section 6.5. The maximum number of NMF iterations is 200.
For all the approaches, the azimuth search space (0∘−180∘) was divided into a uniformly spaced grid with a 2.5∘ spacing between adjacent grid points. Further, in all cases, it is assumed that the number of speakers in the mixture is known.
The following four databases, covering a wide range of recording environments, are used for evaluations.
Signal Separation and Evaluation Campaign (SiSEC) [39]
The dev1 and dev2 development data of SiSEC, consisting of under-determined stereo channel speech mixtures, is used. The mixtures are generated by adding live recordings of static sources played through loudspeakers in a meeting room (4.45m x 3.55m x 2.5m) and recorded one at a time by a pair of omnidirectional microphones. Two reverberation times of 130 ms and 250 ms are considered.
Two stereo arrays are used: one with an inter-microphone spacing of 5cm (SiSEC1) and the other with spacing of 1m (SiSEC2). The speakers are at a distance of 0.80m or 1.20m from the array, and at azimuths between 30∘ and 150∘ with respect to the array axis. The data thus collected consists of twenty 10 s long mixtures of 3 or 4 simultaneous speakers (either all male or all female). The ground truth values of DoAs are provided. They were further verified by applying the GCC-NONLIN approach on the individual source images that are available in the data set.
Since the mixtures are generated by mixing live recordings from a real environment, they also contain measurement and background noise. Further, both closely spaced and widely spaced arrays can be evaluated in the same setting. This makes the SiSEC dataset ideal for the comparison of the various approaches.
Challenge on acoustic source LOCalization And TrAcking (LOCATA) [40]
LOCATA comprises multi-channel recordings in a real-world closed environment setup. Among several tasks that this challenge offers, we consider Task1: localization of a single, static speaker using a static microphone array and Task2: localization of multiple static speakers using a static microphone array.
The data consists of simultaneous recordings of static sources. Sentences selected from the CSTR VCTK database [41] are played back through loudspeakers in a computer laboratory (dimensions: 7.1m x 9.8m x 3 m, T60=550ms). These signals are recorded by a non-uniformly spaced linear array of 13 microphones [40]. In total, there are 6 mixtures of one to four speakers, and the mixtures are between 3 s to 7 s long. The ground truth values of the source locations are provided.
To evaluate different linear array configurations we consider 4 uniform sub-arrays: 3 mics with 4 cm inter-microphone spacing (LOCATA1), 3 mics with an 8 cm inter-microphone spacing (LOCATA2), 3 mics with 16 cm inter-microphone spacing (LOCATA3), and 5 mics with a 4 cm inter-microphone spacing (LOCATA4). This dataset is generated from live recordings in a highly reverberant room, which makes it interesting for benchmarking localization approaches.
Aachen Multi-Channel Impulse Response Database (AACHEN) [42]
This is a database of impulse responses measured in a room with configurable reverberation levels. Three configurations are available, with respective T60s of 160 ms, 360 ms and 610 ms. The measurements were carried out for several source positions for azimuths ranging from 0∘ to 180∘ in steps of 15∘ and at distances of 1 m and 2 m from the microphone array. Three different microphone array configurations are available.
For this paper, we choose the room configuration with T60=610 ms. The impulse responses corresponding to sources placed at a distance of 2m from the 8 microphone uniform linear array with an inter-microphone spacing of 8 cm are selected. Multi-channel speech signals are generated by convolving the selected impulse responses with dry speech signals. Fifty mixtures, each 5 s long, and from 3 speakers (randomly chosen from the TSP database [43]), placed randomly at 3 different azimuths with respect to the array axis are generated.
UGent Multi-Channel Impulse Response Database (UGENT)
The impulse responses from the UGENT database were measured using exponential sine sweeps for azimuth angles varying from 15∘ to 175∘ with the source at a distance of 2m from the array. The recordings were conducted in a meeting room with a T60≈660ms. The microphone array is a triangular array with the following microphone coordinates: (0m,0m,0m), (0.043m,0m,0m) and (0.022m, − 0.037m,0m). Fifty mixture files, each of 5 s duration, are generated with 3 speakers (randomly chosen from the TSP database) placed at random, different azimuths.
Except for the UGent database, all other databases are openly accessible.
Evaluation metrics
The evaluation measures chosen are a detection metric (F-measure) and a location accuracy metric (mean azimuth error - MAE). In a given dataset, let N be the total number of sources in all mixture files and Ne be the number of sources that are localized by an approach. The estimated source azimuths for each mixture are matched to the ground truth azimuths by greedy matching to ensure minimum azimuth error. If, after matching, the estimated source azimuth is within ±7.5∘ of the ground truth estimate then the source is said to be correctly estimated. Let Nc be the number of sources correctly localized for all mixtures. Then the F-measure is given by
$$ \text{F-measure} = \frac{2*\text{Recall}*\text{Precision}}{\text{Recall}+\text{Precision}}, $$
where Recall=Nc/N and Precision=Nc/Ne The more the number of sources correctly localized, the higher the F-measure.
To quantify the localization accuracy, we present two error metrics: MAE and MAEfine. While MAE is the mean azimuth error between the estimated DoAs and true DoAs after greedy matching (irrespective of whether an approach managed to correctly localize all sources within the 7.5∘ tolerance), MAEfine is the mean error between the correctly estimated DoAs and true DoAs. Thus, while MAE gives location accuracy over all the sources in the mixture, MAEfine gives location accuracy of only the correctly detected sources. The former may, therefore, be seen as a global performance metric whereas the latter indicates a local performance criterion with respect to correctly detected sources.
Selecting suitable NMF parameters
To obtain suitable values of the flattening penalty term β and the dictionary size DT, the localization performance of SRP-NMF is evaluated on a small dataset over a range of β and DT.
Table 1 shows the F-measure obtained by SRP-NMF on SiSEC1 data for β varying from 0 to 80 and DT from 15 to 55. It may be seen that with β fixed, as the dictionary size increases, the localization performance initially improves and later saturates. A similar trend is observed when DT is fixed and β is increased. The pairs of β and DT that yield an F-measure ≥0.95 (in bold) have similar performance and can be chosen as the NMF parameters. While a lower DT leads to less computational complexity, a lower β leads to a lower residual error in the NMF approximation (i.e., a better approximation of the magnitude spectrum). Therefore, among various combinations of β and DT that yield a comparable F-score, a lower β (such as 30) and lower DT (such as 25) are preferred. However, we choose slightly higher parameter values to ensure robust performance and to allow generalization to other datasets with possibly more reverberation and/or noise. Hence, in the subsequent experiments, the values of β and DT are set to 60 and 55 respectively.
Table 1 The detection metric, F-measure, obtained by SRP-NMF on SiSEC1 data for β and DT varying from 0 to 80 and 15 to 55 respectively
The trends in Table 1 are illustrated in Figs. 5 and 6 for a mixture of 4 concurrent speakers. Figure 5 depicts the histogram plots of SRP-NMF with β ranging between 0 and 80 and DT=35. It is evident from the figure that when β=0, the peaks further away from the broadside direction are not prominent. The reason for this was explained in Section 5.2.1. As β increases, the peaks become increasingly prominent and can be easily detected.
Effect of β on SRP-NMF performance. Subplots show the histograms of SRP-NMF on a mixture of 4 sources taken from SiSEC database (dev1_male4_liverec_250ms_5cm_mix.wav) with DT=35 and β varying from 0 to 80. β is displayed on each of the subplots. The x-axis shows DoA (degrees). The y-axis is the (normalized) frequency of DoAs
Effect of dictionary size DT on SRP-NMF performance. Subplots show the histograms of SRP-NMF on a mixture of 4 sources taken from SiSEC database (dev1_male4_liverec_250ms_5cm_mix.wav) with β=60 and DT varying from 5 to 55. DT is displayed on each of the subplots. The x-axis shows DoA (degrees). The y-axis is the (normalized) frequency of DoAs
Figure 6 presents the effect of varying DT on the SRP-NMF outcome. Here, β is fixed at 60 and DT increases from 5 to 55. It may be seen that as the dictionary size increases, the histogram peaks become increasingly distinct.
Experiment with supervised separation and localization
The basic idea for the proposed approach has its roots in the successful use of NMF for supervised source separation. Hence, we compare, here, the performance of SRP-NMF against a supervised variant where the microphone signals are first decomposed into their underlying sources using NMF [44] and the localization is then performed on the separated sources using the broadband SRP approach. This approach is termed SNMF-SRP, and is implemented as follows:
First, for any test case, the magnitude spectrum |Sq| of each individual source q in the mixture is decomposed using constrained NMF. This results in the \(\mathbf {W}_{q} \in \mathbb {R}_{+}^{(K \times D_{q})}\) basis function matrix for that source, where Dq is the number of atoms for source q. We assume that the number of atoms is the same for all sources, i.e., Dq=D ∀q. The basis functions for all sources are then concatenated into a matrix W as:
$$ \mathbf{W} = \left[\begin{array}{l} \mathbf{W}_{1}, \mathbf{W}_{2}, \ldots, \mathbf{W}_{Q}\end{array}\right] \ \in\mathbb{R}_{+}^{(K\times {QD})} $$
NMF is next used to decompose the magnitude spectrogram of the mixture at any one reference microphone m as |Xm|≈WH. In this step, W is kept fixed and only the activation matrix H is adapted. This matrix can then be partitioned into the activations of the individual sources as:
$$ \mathbf{H} = \left[\begin{array}{l} \mathbf{H}_{1}^{T}, \mathbf{H}_{2}^{T}, \ldots, \mathbf{H}_{Q}^{T}\end{array}\right] \ \in\mathbb{R}_{+}^{({QD}\times {B})}, $$
where B is the total number of frames in the mixture spectrogram.
The spectral magnitude estimates for each source can then be obtained as: \(|\widehat {\mathbf {S}}_{q}| = \mathbf {W}_{q}\mathbf {H}_{q}\,\). These estimates are used to define binary masks for each source, whereby each TF point is allocated to the source with the maximum contribution (i.e., the dominant source) at that TF-point.
The binary masks belonging to each source are, finally, applied to the complex mixture spectrograms at all microphones, and the broadband SRP-PHAT approach is used to obtain the source location estimate.
Since SNMF-SRP first separates the sources before localizing them, the interference from the other sources is minimized in the localization. Further, a binary mask attributes a time-frequency point (k,b) to only the dominant source at that point. Due to this "winner-takes-all" strategy, only the dominant source components are preserved at each time-frequency point. Consequently, the effect of the interference on the SRP-PHAT function is further reduced, resulting in more accurate DoA estimates as compared to when continuous masks are used. This experiment with oracle knowledge of the underlying sources should, therefore, give a good indication of the possible upper bound of our proposed approach.
We note that an alternative to the SNMF-SRP would be unsupervised NMF-based separation approaches. Such approaches may be seen as comprising the following two steps: (a) decomposing the mixture spectrum into basis functions and their corresponding activations, and, (b) grouping (clustering) the basis functions according to the sources they belong to, to generate the separated source signals. Usually, some additional signal knowledge or signal model needs to be incorporated into the approach to perform the clustering and the quality of the source separation is, consequently, dependent on the kind of clustering approach. Typically, these steps are not performed independently, and the clustering model is often incorporated (explicitly or implicitly) as a set of additional constraints in the decomposition step. If one neglects the additional step (and associated effort) of grouping the basis components and simply uses the obtained basis functions as a weighting within the SRP-PHAT approach, then there is no conceptual difference between our proposed approach and the use of unsupervised NMF-based separation followed by localization.
Experimental set-up
We compare, first, the SNMF-SRP and SRP-NMF. For this purpose, fifty mixtures, each 5 s long and comprising 3 sound sources at randomly chosen azimuths, ranging from 15∘ to 175∘, are generated using room impulse responses from the AACHEN database. The responses corresponding to the room configuration with T60=610 ms are used. Two arrays are considered: the 8 microphone uniform linear array with 8 cm inter-microphone spacing, and a 4-microphone uniform linear sub-array with 4 cm inter-microphone spacing (this is part of a larger 8-mic array with spacing 4-4-4-8-4-4-4). The position of the speakers was also randomly chosen for each test file. The optimal dictionary size and weighting factor for the SNMF-SRP approach are first determined in a manner similar to that for SRP-NMF, and using data from the 3-mic sub-array with inter-microphone spacing of 8 cm.
Dictionary sizes DSNMF-SRP of 50, 90, and 130 and weighting factors βSNMF-SRP of 0, 20, and 40 are evaluated. The F-measure and MAE obtained for each case are reported in Table 2, from where it is observed that a dictionary size DSNMF-SRP of 130 and βSNMF-SRP of 20 give the best results in terms of the chosen metrics. These are consequently fixed for the subsequent evaluation of the SNMF-SRP approach.
Table 2 F-measure and mean azimuth error (MAE) for the supervised NMF-SRP (SNMF-SRP) for varying DSNMF-SRP and βSNMF-SRP
Figures 7 and 8 depict the performance of SNMF-SRP compared to SRP-NMF.
Performance comparison of SNMF-SRP, DP-single-source-SRP-PHAT, and the proposed SRP-NMF in terms of the chosen instrumental metrics on the AACHEN dataset, on various subsets of the 8-microphone uniform linear array with an inter-microphone spacing of 8 cm
Performance comparison of SNMF-SRP, DP-single-source-SRP-PHAT, and the proposed SRP-NMF in terms of the chosen instrumental metrics on the AACHEN dataset. The results are depicted for subsets of a uniform linear array with an inter-microphone spacing of 4 cm
Since we can expect the best localization performance in the absence of reverberation and interfering sources, we simulate this case as well and include it in the comparison (this is termed direct-path (DP) single-source-SRP-PHAT). To obtain this result, each source in the mixture is individually simulated at the arrays. Further, for generating the source image, the room impulse response is limited to only the filter taps corresponding to the direct path and 20 ms of early reflections. Then, a DoA estimate is obtained by the broadband SRP-PHAT. This corresponds to the localization of a single source in the near absence of reverberation and noise and, thus forms a further performance upper bound for all the approaches.
The figures show that, especially for a smaller number of microphones and lower inter-microphone spacing, the supervised NMF-SRP approach is significantly better than the proposed unsupervised SRP-NMF. The SRP-NMF has the lowest F-measure and the largest MAE. This indicates that incorporating the knowledge of the underlying sources may be beneficial when the spatial diversity is limited and cannot be fully exploited. As the spatial diversity increases, the performance of the unsupervised method begins to converge to that of the supervised approach. As expected, the performance of both these approaches are upper bounded by the DP-single-source SRP-PHAT approach.
The benchmarking results, in terms of F-measure and mean azimuth errors, for the various datasets are plotted in Fig. 9. We start with the MAEfine metric, which focusses on the average localization error for sources that have been correctly localized. The chosen margin for a correct localization implies that the MAEfine is necessarily ≤7.5∘. Figure 9 further indicates that the MAEfine metric is comparable among all the approaches, with a difference of only about 1 deg or less (except for the GCC-NonLinsum and MVDRWsum of LOCATA1 and MVDRWmax of LOCATA2, where it is slightly higher). Thus, we may not claim, categorically, that any particular approach is better than the other in terms of this metric. More indicative metrics for the performance of any approach would be the MAE and F-measure, which are discussed next.
F-measure, MAE and MAEfine of SRP-NMF and comparison approaches on various datasets. Mean azimuth error between ground truth azimuths and the detected azimuths (MAE) is the gross location accuracy metric. F-measure is the detection metric. Mean azimuth error between ground truth azimuths and the correctly detected azimuths (MAEfine) is the fine location accuracy metric
NB-SRP-PHAT localizes well with closely spaced stereo microphones and its performance deteriorates with larger inter-microphone spacing due to spatial aliasing. This is clearly seen from the SiSEC results, where its performance is better in SiSEC1 (5 cm spacing) than in SiSEC2 (1 m spacing). Furthermore, in the case of multiple microphones, it performs poorly in LOCATA1 and UGENT. The reason for the poor performance may be explained as follows: both LOCATA1 and UGENT have only 3 microphones that are very closely spaced (≈4 cms apart) and high reverberation (T60≈600 ms). We hypothesize that the TF bins in which noise or reverberant components are dominant are allocated to spurious locations and, since NB-SRP-PHAT pools the decisions per TF bin, these spurious locations mask the source locations in the histogram. This behavior is worse in closely spaced arrays, as the beam pattern of the SRP optimization function has wide main lobes. Increasing the microphone separation or the number of microphones, narrows the main lobes thus improving the performance - as is evident in LOCATA2/3 and LOCATA4 respectively.
Among the GCC-NONLIN approaches, max pooling performs better than sum pooling, which verifies the conclusions in [19]. Further, due to the non-linearity introduced to improve the performance in microphone arrays with short inter-microphone spacing (cf. Section 6.1), the GCC-NONLINmax performs reasonably well in almost all datasets and microphone configurations.
Between the MVDRW methods, max and sum pooling give similar results for the smaller array of SiSEC1. In SiSEC2, sum pooling is superior, which is consistent with [19]. However, for a larger number of microphones max pooling performs better in all microphone configurations. In LOCATA1 and UGENT, though the beampattern of MVDR has wide lobes due to closely spaced microphones, the performance of the MVDRW-based approaches is better than that of NB-SRP-PHAT. We reason that this is because the MVDRW approaches factor in the sound field characteristics and introduce a frequency weighting that emphasizes the time-frequency bins that are dominated by the direct sound of a single source (cf. Section 6.1).
Figure 9 also indicates that SRP-NMF performs consistently well across the various databases. In terms of MAE and F-measure, the scores of SRP-NMF is among the top two for each tested case. The atom weighting highlights time-frequency bins consisting of information relating to a single source, similar to SNR weighting, thus exploiting time-atom sparsity and leading to superior performance in short arrays. In large arrays, averaging the optimization function across the frequency axis ensures robustness to spatial aliasing, thus leading to good performance. Further, the performance of SRP-NMF is consistently better than (or comparable to) that of the Bark-SRP-PHAT, indicating the benefit of the data-dependent weighted frequency averaging, as compared to a fixed frequency averaging.
Lastly, we also include a comparison with the SNMF-SRP (cf. Section 6.6) for the AACHEN and UGENT data. It may be seen, then, that this supervised approach outperforms all the other unsupervised approaches—which is expected, based on the results in Section 6.6 and Figs. 7 and 8. We note that since SNMF-SRP is based on the availability of the underlying source signals, it could not be applied to the LOCATA data, where this information is not consistently available. Further, we chose not to report performance metrics of this approach on the SiSEC data, since all approaches perform well in this case, and the performance of SNMF-SRP would add no value in a comparative analysis of the performances.
While the evaluation conclusively demonstrates the benefit of the proposed SRP-NMF approach, this comes at the cost of increased computational complexity. Its complexity is more than that of NB-SRP-PHAT and depends on the number of active atoms per frame. Further, we empirically observe that SRP-NMF gives good DoA estimates if the data segments are long (>3s). We hypothesize, consequently, that the NMF dictionary atoms extracted from short segments may not be accurate. Therefore, in the current form, SRP-NMF is not suitable for real-time applications. However, with pre-trained dictionaries, the requirement of long data segments can be relaxed and SRP-NMF can be explored for real-time localization.
In order to better appreciate the benefits of the SRP-NMF approach, a graphical comparison of SRP-PHAT and SRP-NMF is presented in Figs. 10 and 11. These depict the histogram plots obtained by SRP-PHAT and SRP-NMF on a real-room mixture consisting of 4 concurrent speakers. Note that SRP-NMF clearly indicates the presence of the 4 sources, whereas the histogram of the SRP-PHAT approach (Fig. 10) does not present clear evidence of all 4 sources. The histogram plot in Fig. 11 can be further improved if subsampling is performed. Subsampling is an approach borrowed from Word Embedding in the field of NLP. Based on the observation that words with high frequency of occurrence do not contribute as much information as the words that occur more rarely, the frequent words are subsampled [45] to counter the imbalance between the frequent and rare words. In a similar manner, in the histogram of estimated DoAs, to counter the imbalances between frequent and occasional DoA estimates (e.g., due to a speaker being only active for a short while), the frequently occurring DoAs are subsampled after crossing a certain threshold. The subsampled version of Fig. 11 is shown in Fig. 12, where the benefit of subsampling is clearly visible.
Histogram of DoA estimates obtained by SRP-PHAT on recording 2 (Task2) from LOCATA1 containing four concurrent speakers
Histogram of DoA estimates obtained by SRP-NMF on recording 2 (Task 2) from LOCATA1 containing four concurrent speakers
Subsampled histogram of DoA estimates obtained by SRP-NMF on recording 2 (Task 2) from LOCATA1 containing four concurrent speakers
SRP-NMF is a localization approach that uses the NMF atoms of the underlying sources to obtain a broadband localization estimate for each atom. By exploiting the sparsity of the sources in the time-atom domain, this still allows for the simultaneous localization of multiple sources in a time frame. Thereby the proposed approach combines the benefits of standard broadband and narrowband localization approaches. It can, therefore, be used with compact and large array configurations. Compared to the state-of-the-art narrowband and broadband approaches on data collected in natural room acoustic environments, and with various microphone configurations, the proposed approach can reliably localize the active sources in all cases, and with a comparable or lower localization error. The use of such an NMF-based decomposition and subsequent frequency grouping can be seamlessly extended in a variety of ways. For example, it can be combined with extant methods that improve the robustness of localization approaches to noise (e.g., in combination with the SNR weighting of the MVDR-based approaches), or it can be combined with a priori knowledge in the form of speaker-specific NMF atoms to localize only a specific speaker in the mix. It may also be modified for real-time applications with pre-learned universal NMF dictionary and online estimation of activation coefficients. We intend to address these extensions in future work.
SiSEC1 and SiSEC2 are publicly available at: https://sisec.inria.fr/sisec-2016/2016-underdetermined-speech-and-music-mixtures
LOCATA data is available at https://www.locata.lms.tf.fau.de/
AACHEN impulse responses are at http://www.iks.rwth-aachen.de/en/research/tools-downloads/databases/multi-channel-impulse-response-database/
UGENT Multi-Channel Impulse Response Database is not publicly available but is available from the last author on reasonable request.
Details of the speech database used in the evaluations may be found in [43].
NMF:
Non-negative matrix factorization
Steered-response power
TF:
Time-frequency
STFT:
Short-time Fourier transform
GCC:
Generalized cross-correlation
AMDF:
Average magnitude difference function
PHAT:
Phase transform
DP:
Direct-path
SNR:
TDoA:
Time-difference of arrival
DoA:
Direction of arrival
IPD:
Inter-microphone phase difference
NB-SRP:
Narrowband SRP
BB-SRP:
Broadband SRP
CNMF:
Constrained NMF
SNMF:
Supervised NMF
MoG:
Mixture of Gaussians
MBSS:
Multi-channel BSS locate
SiSEC:
Signal separation and evaluation campaign
LOCATA:
Localization and tracking
MAE:
Mean azimuth error
MVDR:
Minimum variance distortionless response
MVDRW:
Weighted MVDR
NLP:
AACHEN:
RWTH AACHEN university
UGENT:
S. Rickard, O. Yilmaz, in 2002 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), 1. On the approximate W-disjoint orthogonality of speech, (2002), pp. 529–532. https://doi.org/10.1109/ICASSP.2002.5743771.
C. Knapp, G. Carter, The generalized correlation method for estimation of time delay. IEEE Trans. Acoust. Speech Signal Proc. (TASSP). 24(4), 320–327 (1976).
G. Jacovitti, G. Scarano, Discrete time techniques for time delay estimation. IEEE Trans. Signal Proc. (TSP). 41(2), 525–533 (1993).
J. Benesty, Adaptive eigenvalue decomposition algorithm for passive acoustic source localization. J. Acoust. Soc. Am.107(1), 384–391 (2000).
F. Talantzis, A. G. Constantinides, L. C. Polymenakos, Estimation of direction of arrival using information theory. IEEE Signal Proc. Lett.12:, 561–564 (2005).
J. DiBiase, H. F. Silverman, M. S. Brandstein, in Microphone arrays: signal processing techniques and applications, ed. by M. Brandstein, D. Ward. Robust localization in reverberant rooms (SpringerNew York, 2001), pp. 157–180.
C. Zhang, D. Florencio, Z. Zhang, in 2008 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Why does PHAT work well in lownoise, reverberative environments? (2008), pp. 2565–2568.
J. Valin, F. Michaud, J. Rouat, D. Letourneau, in Proceedings 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003), 2. Robust sound source localization using a microphone array on a mobile robot, (2003), pp. 1228–1233.
Y. Rui, D. Florencio, in 2004 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), 2. Time delay estimation in the presence of correlated noise and reverberation, (2004), p. 133.
H. Kang, M. Graczyk, J. Skoglund, in 2016 IEEE International Workshop on Acoustic Signal Enhancement (IWAENC). On pre-filtering strategies for the GCC-PHAT algorithm, (2016), pp. 1–5.
Z. Wang, X. Zhang, D. Wang, Robust speaker localization guided by deep learning-based time-frequency masking. IEEE Trans. Audio Speech Lang. Process. (TASLP). 27(1), 178–188 (2019).
J. M. Perez-Lorenzo, R. Viciana-Abad, P. Reche-Lopez, F. Rivas, J. Escolano, Evaluation of generalized cross-correlation methods for direction of arrival estimation using two microphones in real environments. Appl. Acoust.73(8), 698–712 (2012).
B. Loesch, B. Yang, in IEEE International Workshop on Acoustic Signal Enhancement (IWAENC). Source number estimation and clustering for underdetermined blind source separation, (2008), pp. 1–4.
M. I. Mandel, D. P. W. Ellis, T. Jebara, in Proceedings of the Annual Conference on Neural Information Processing Systems. An em algorithm for localizing multiple sound: sources in reverberant environments, (2006), pp. 953–960.
O. Schwartz, S. Gannot, Speaker tracking using recursive EM algorithms. IEEE Trans. Audio Speech Lang. Process. (TASLP). 22(2), 392–402 (2014).
N. Madhu, R. Martin, in IEEE International Workshop on Acoustic Signal Enhancement (IWAENC). A scalable framework for multiple speaker localization and tracking, (2008), pp. 1–4.
M. Cobos, J. J. Lopez, D. Martinez, Two-microphone multi-speaker localization based on a Laplacian mixture model. Digit. Signal Process.21(1), 66–76 (2011).
M. Swartling, B. Sällberg, N. Grbić, Source localization for multiple speech sources using low complexity non-parametric source separation and clustering. Signal Process.91(8), 1781–1788 (2011).
C. Blandin, A. Ozerov, E. Vincent, Multi-source TDOA estimation in reverberant audio using angular spectra and clustering. Signal Process.92(8), 1950–1960 (2012).
P. Pertilä, Online blind speech separation using multiple acoustic speaker tracking and time-frequency masking. Comput. Speech Lang.27(3), 683–702 (2013).
E. Hadad, S. Gannot, in 2018 IEEE International Conference on the Science of Electrical Engineering in Israel (ICSEE). Multi-speaker direction of arrival estimation using SRP-PHAT algorithm with a weighted histogram, (2018), pp. 1–5.
N. Madhu, R. Martin, in Advances in digital speech transmission, ed. by R. Martin, U. Heute, and C. Antweiler. Acoustic source localization with microphone arrays (John Wiley & Sons, Ltd.New York, USA, 2008), pp. 135–170.
D. Bechler, K. Kroschel, in IEEE International Workshop on Acoustic Signal Enhancement (IWAENC). Considering the second peak in the GCC function for multi-source TDOA estimation with a microphone array, (2003), pp. 315–318.
C. Faller, J. Merimaa, Source localization in complex listening situations: selection of binaural cues based on interaural coherence. J. Acoust. Soc. Am.116(5), 3075–3089 (2004).
M. Togami, T. Sumiyoshi, A. Amano, in 2007 IEEE International Conference on Acoustics, Speech and Signal Processing(ICASSP), 1. Stepwise phase difference restoration method for sound source localization using multiple microphone pairs, (2007), pp. 117–120.
M. Togami, A. Amano, T. Sumiyoshi, Y. Obuchi, in 2009 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). DOA estimation method based on sparseness of speech sources for human symbiotic robots, (2009), pp. 3693–3696.
J. Traa, P. Smaragdis, N. D. Stein, D. Wingate, in 2015 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics. Directional NMF for joint source localization and separation, (2015), pp. 1–5.
H. Kayser, J. Anemüller, K. Adiloğlu, in 2014 IEEE 8th Sensor Array and Multichannel Signal Processing Workshop (SAM). Estimation of inter-channel phase differences using non-negative matrix factorization, (2014), pp. 77–80.
A. Muñoz-Montoro, V. Montiel-Zafra, J. Carabias-Orti, J. Torre-Cruz, F. Canadas-Quesada, P. Vera-Candeas, in Proceedings of the International Congress on Acoustics (ICA). Source localization using a spatial kernel based covariance model and supervised complex nonnegative matrix factorization, (2019), pp. 3321–3328.
S. U. N. Wood, J. Rouat, S. Dupont, G. Pironkov, Blind speech separation and enhancement with GCC-NMF. IEEE Trans. Audio Speech Lang. Process. (TASLP). 25(4), 745–755 (2017).
J. DiBiase, A high-accuracy, low-latency technique for talker localization in reverberant environments. Ph.D. dissertation (Brown University, Providence RI, USA, 2000).
T. Virtanen, J. F. Gemmeke, B. Raj, P. Smaragdis, Compositional models for audio processing: uncovering the structure of sound mixtures. IEEE Signal Process. Mag.32:, 125–144 (2015).
J. Tchorz, B. Kollmeier, SNR estimation based on amplitude modulation analysis with applications to noise suppression. IEEE Trans. Speech Audio Process. (TSAP). 11(3), 184–192 (2003).
S. Elshamy, N. Madhu, W. Tirry, T. Fingscheidt, Instantaneous a priori SNR estimation by cepstral excitation manipulation. IEEE Trans. Audio Speech Lang. Process. (TASLP). 25(8), 1592–1605 (2017).
D. D. Lee, H. S. Seung, in Advances in Neural Information Processing Systems 13, ed. by T. K. Leen, T. G. Dietterich, and V. Tresp. Algorithms for non-negative matrix factorization, (2001), pp. 556–562.
V. P. Pauca, J. Piper, R. J. Plemmons, Nonnegative matrix factorization for spectral data analysis. Linear Algebra Appl.416(1), 29–47 (2006). Special Issue devoted to the Haifa 2005 conference on matrix theory.
R. Lebarbenchon, E. Camberlein, Multi-Channel BSS Locate (2018). https://bass-db.gforge.inria.fr/bss-locate/bss-locate. Accessed 4 2020.
B. Loesch, B. Yang, in 9th International Conference on Latent variable analysis and signal separation (LVA/ICA). Adaptive segmentation and separation of determined convolutive mixtures under dynamic conditions (SpringerBerlin, Heidelberg, 2010), pp. 41–48.
N. Ono, Z. Koldovský, S. Miyabe, N. Ito, in 2013 IEEE International Workshop on Machine Learning for Signal Processing (MLSP). The 2013 signal separation evaluation campaign, (2013), pp. 1–6.
H. W. Löllmann, C. Evers, A. Schmidt, H. Mellmann, H. Barfuss, P. A. Naylor, W. Kellermann, in 2018 IEEE 10th Sensor Array and Multichannel Signal Processing Workshop (SAM). The LOCATA challenge data corpus for acoustic source localization and tracking, (2018), pp. 410–414.
C. Veaux, J. Yamagishi, K. MacDonald, English Multi-speaker Corpus for CSTR Voice Cloning Toolkit (University of Edinburgh. The Centre for Speech Technology Research (CSTR), 2019). https://doi.org/10.7488/ds/2645.
Multi-channel impulse response database. https://www.iks.rwth-aachen.de/en/research/tools-downloads/databases/multi-channel-impulse-response-database/. Accessed 12 2020.
P. Kabal, TSP speech database. Technical report (Telecommunications and Signal Processing Laboratory, McGill University, Canada, 2002).
C. Févotte, E. Vincent, A. Ozerov, in Audio Source Separation, ed. by S. Makino. Single-channel audio source separation with NMF: divergences, constraints and algorithms (SpringerCham, 2018), pp. 1–24.
T. Mikolov, I. Sutskever, K. Chen, G. S. Corrado, J. Dean, in Advances in neural information processing systems 26, ed. by C. J. C. Burges, L. Bottou, M. Welling, Z. Ghahramani, and K. Q. Weinberger. Distributed representations of words and phrases and their compositionality, (2013), pp. 3111–3119.
Speech Processing Laboratory, International Institute of Information Technology, Hyderabad, India
Sushmita Thakallapalli & Suryakanth V. Gangashetty
Present address: K L University, Guntur, Andhra Pradesh, India
Suryakanth V. Gangashetty
IDLab, Dept. Electronics & Information Systems, Ghent University - imec, Ghent, Belgium
Nilesh Madhu
Sushmita Thakallapalli
NM + ST: conceptualized SRP-NMF; ST implemented the approaches, introduced improvements, and conducted the experiments under the supervision of NM and SVG. NM and ST were involved in the writing. All the authors read and approved the final manuscript.
Correspondence to Sushmita Thakallapalli.
The authors state that they have no competing interests.
Thakallapalli, S., Gangashetty, S.V. & Madhu, N. NMF-weighted SRP for multi-speaker direction of arrival estimation: robustness to spatial aliasing while exploiting sparsity in the atom-time domain. J AUDIO SPEECH MUSIC PROC. 2021, 13 (2021). https://doi.org/10.1186/s13636-021-00201-y
Sound source localization
Direction-of-arrival
Spatial aliasing
Speech sparsity | CommonCrawl |
Mathematics of Computation
Published by the American Mathematical Society, the Mathematics of Computation (MCOM) is devoted to research articles of the highest quality in all areas of pure and applied mathematics.
The 2020 MCQ for Mathematics of Computation is 1.98.
Journals Home eContent Search About MCOM Editorial Board Author and Submission Information Journal Policies Subscription Information
Applications of a computer implementation of Poincaré's theorem on fundamental polyhedra
by Robert Riley PDF
Math. Comp. 40 (1983), 607-632 Request permission
Poincaré's Theorem asserts that a group $\Gamma$ of isometries of hyperbolic space $\mathbb {H}$ is discrete if its generators act suitably on the boundary of some polyhedron in $\mathbb {H}$, and when this happens a presentation of $\Gamma$ can be derived from this action. We explain methods for deducing the precise hypotheses of the theorem from calculation in $\Gamma$ when $\Gamma$ is "algorithmically defined", and we describe a file of Fortran programs that use these methods for groups $\Gamma$ acting on the upper half space model of hyperbolic 3-space ${\mathbb {H}^3}$. We exhibit one modest example of the application of these programs, and we summarize computations of repesentations of groups ${\text {PSL}}(2,\mathcal {O})$ where $\mathcal {O}$ is an order in a complex quadratic number field.
Lars V. Ahlfors, Möbius transformations in several dimensions, Ordway Professorship Lectures in Mathematics, University of Minnesota, School of Mathematics, Minneapolis, Minn., 1981. MR 725161
A. F. Beardon, The geometry of discrete groups, Discrete groups and automorphic functions (Proc. Conf., Cambridge, 1975) Academic Press, London, 1977, pp. 47–72. MR 0474012
Alan F. Beardon and Bernard Maskit, Limit points of Kleinian groups and finite sided fundamental polyhedra, Acta Math. 132 (1974), 1–12. MR 333164, DOI 10.1007/BF02392106
Luigi Bianchi, Opere. Vol. I, Parte prima, Edizioni Cremonese della Casa Editrice Perrella, Roma, 1952 (Italian). A cura dell'Unione Matematica Italiana e col contributo del Consiglio Nazionale delle Ricerche. MR 0051755
Harvey Cohn, A second course in number theory, John Wiley & Sons, Inc., New York-London, 1962. MR 0133281
Troels Jørgensen, On discrete groups of Möbius transformations, Amer. J. Math. 98 (1976), no. 3, 739–749. MR 427627, DOI 10.2307/2373814
Bernard Maskit, On Poincaré's theorem for fundamental polygons, Advances in Math. 7 (1971), 219–230. MR 297997, DOI 10.1016/S0001-8708(71)80003-8
Robert Riley, A quadratic parabolic group, Math. Proc. Cambridge Philos. Soc. 77 (1975), 281–288. MR 412416, DOI 10.1017/S0305004100051094
Robert Riley, Discrete parabolic representations of link groups, Mathematika 22 (1975), no. 2, 141–150. MR 425946, DOI 10.1112/S0025579300005982
Robert Riley, An elliptical path from parabolic representations to hyperbolic structures, Topology of low-dimensional manifolds (Proc. Second Sussex Conf., Chelwood Gate, 1977) Lecture Notes in Math., vol. 722, Springer, Berlin, 1979, pp. 99–133. MR 547459
R. Riley, Seven excellent knots, Low-dimensional topology (Bangor, 1979) London Math. Soc. Lecture Note Ser., vol. 48, Cambridge Univ. Press, Cambridge-New York, 1982, pp. 81–151. MR 662430
Herbert Seifert, Komplexe mit Seitenzuordnung, Nachr. Akad. Wiss. Göttingen Math.-Phys. Kl. II 6 (1975), 49–80 (German). MR 383219
J. Sommer, Introduction à la Théorie des Nombres Algébriques, Paris, 1911.
Richard G. Swan, Generators and relations for certain special linear groups, Advances in Math. 6 (1971), 1–77 (1971). MR 284516, DOI 10.1016/0001-8708(71)90027-2
W. Thurston, The geometry and topology of 3-manifolds. (To appear.)
Retrieve articles in Mathematics of Computation with MSC: 20H10, 11F06, 20-04, 22E40, 51M20, 57N10
Retrieve articles in all journals with MSC: 20H10, 11F06, 20-04, 22E40, 51M20, 57N10
Journal: Math. Comp. 40 (1983), 607-632
MSC: Primary 20H10; Secondary 11F06, 20-04, 22E40, 51M20, 57N10
DOI: https://doi.org/10.1090/S0025-5718-1983-0689477-2
MathSciNet review: 689477 | CommonCrawl |
Online Application System
Preparatory phase
Dissertation phase
PhD Thesis Defenses 2020 & 2019 & 2018
Thesis proposal colloquium
PhD Thesis Defenses
PhD thesis defenses are a public affair and open to anyone who is interested. Attending them is a great way to get to know the work going on by your peers in the various research groups. On this page you will find a list of upcoming and past defense talks.
Please go here for electronic access to most of the doctoral dissertations from Saarbrücken Computer Science going back to about 1990.
Mathias FLEURY
Formalization of Logical Calculi in Isabelle/HOL
(Advisor: Prof. Christoph Weidenbach)
Tuesday, 28.01.2020, 10:00 h, in building E1 4, room 0.24
I develop a formal framework for propositional satifisfiability with the conflict-driven clause learning (CDCL) procedure using the Isabelle/HOL proof assistant. The framework offers a convenient way to prove metatheorems and experiment with variants, including the Davis-Putnam-Logemann-Loveland procedure. The most noteworthy aspects of my work are the inclusion of rules for forget, restart and the refinement approach.
Through a chain of refinements, I connect the abstract CDCL calculus first to a more concrete calculus, then to a SAT solver expressed in a simple functional programming language, and finally to a SAT solver in an imperative language, with total correctness guarantees. The imperative version relies on the two-watched-literal data structure and other optimizations found in modern solvers.
Maximilian JOHN
Of Keyboards and Beyond – Optimization in Human-Computer-Interaction
(Advisor: Dr. Andreas Karrenbauer)
Wednesday, 15.01.2020, 16:30 h, in building E1 4, room 0.24
This talk covers optimization challenges in the context of human-computer interaction, specifically in UI design. In particular, we focus on the design of the new French keyboard layout, discuss the special challenges of this national-scale project and our algorithmic contributions. Exploiting the special structure of this design problem, we propose an optimization framework that efficiently computes keyboard layouts and provides very good optimality guarantees in form of tight lower bounds. The optimized layout that we showed to be nearly optimal was the basis of the new French keyboard standard recently published in the National Assembly in Paris. Finally, we introduce a modeling language for mixed integer programs that especially focuses on the challenges and features that appear in participatory optimization problems similar to the French keyboard design process.
Patrick TRAMPERT
3D Exemplar-based Image Inpainting in Electron Microscopy
(Advisor: Prof. Philipp Slusallek)
Monday, 13.01.2020, 14:00 h, in building D3 4 (DFKI), VisCenter room
In electron microscopy (EM) a common problem is the non-availability of data, which causes artefacts in reconstructions. In this thesis the goal is to generate artificial data where missing in EM by using exemplar-based inpainting (EBI). We implement an accelerated 3D version tailored to applications in EM, which reduces reconstruction times from days to minutes.
We develop intelligent sampling strategies to find optimal data as input for reconstruction methods. Further, we investigate approaches to reduce electron dose and acquisition time. Sparse sampling followed by inpainting is the most promising approach. As common evaluation measures may lead to misinterpretation of results in EM and falsify a subsequent analysis, we propose to use application driven metrics and demonstrate this in a segmentation task.
A further application of our technique is the artificial generation of projections in tilt- based EM. EBI is used to generate missing projections, such that the full angular range is covered. Subsequent reconstructions are significantly enhanced in terms of resolution, which facilitates further analysis of samples.
In conclusion, EBI proves promising when used as an additional data generation step to tackle the non-availability of data in EM, which is evaluated in selected applications. Enhancing adaptive sampling methods and refining EBI, especially considering the mutual influence, promotes higher throughput in EM using less electron dose while not lessening quality.
Martin WEIER
Perception-driven Rendering: Techniques for the Efficient Visualization of 3D Scenes including View- and Gaze-contingent Approaches
Thursday, 19.12.2019, 15:00 h, in building D3 4 (DFKI), VisCenter room
Modern image synthesis approaches enable to create digital images of astonishing complexity and beauty, yet processing resources remain a limiting factor. At the same time, advances in display technologies drive the development of novel display devices, thereupon, further tightening the requirements of rendering approaches. Rendering efficiency is a central challenge involving a trade-off between visual fidelity and interactivity. However, the human visual system has some limitations and the highest possible visual quality is not always necessary. The knowledge of those limitations can be used to develop better and more efficient rendering systems, a field known as perception-driven rendering. The central question in this thesis is how to exploit the limitations or use the potentials of perception to enhance the quality of different rendering techniques whilst maintaining their performance and vice versa. To this end, this thesis presents some state-of-the-art research and models that exploit the limitations of perception in order to increase visual quality but also to reduce workload alike. This research results in several practical rendering approaches that tackle some of the fundamental challenges of computer graphics. Here, different sampling, filtering, and reconstruction techniques aid the visual quality of the synthesized images. An in-depth evaluation of the presented systems including benchmarks, comparative examination with image metrics as well as user studies and experiments demonstrated that the methods introduced are visually superior or on the same qualitative level as ground truth, whilst having a significantly reduced run time.
Hyeongwoo KIM
Learning-based Face Reconstruction and Editing
(Advisor: Prof. Christian Theobalt)
Thursday, 12.12.2019, 16:15 h, in building E1 4, room 0.19
Photo-realistic face editing – an important basis for a wide range of applications in movie and game productions, and applications for mobile devices – is based on computationally expensive algorithms that often require many tedious time-consuming manual steps. This thesis advances state-of-the-art face performance capture and editing pipelines by proposing machine learning-based algorithms for high-quality inverse face rendering in real time and highly realistic neural face rendering, and a video-based refocusing method for faces and general videos. In particular, the proposed contributions address fundamental open challenges towards real-time and highly realistic face editing. The first contribution addresses face reconstruction and introduces a deep convolutional inverse rendering framework that jointly estimates all facial rendering parameters from a single image in real time. The proposed method is based on a novel boosting process that iteratively updates the synthetic training data to better reflect the distribution of real-world images. Second, the thesis introduces a method for face video editing at previously unseen quality. It is based on a generative neural network with a novel space-time architecture, which enables photo-realistic re-animation of portrait videos using an input video. It is the first method to transfer the full 3D head position, head rotation, face expression, eye gaze and eye blinking from a source actor to a portrait video of a target actor. Third, the thesis contributes a new refocusing approach for faces and general videos in postprocessing. The proposed algorithm is based on a new depth-from-defocus algorithm that computes space-time-coherent depth maps, deblurred all-in-focus video and the focus distance for each frame. The high-quality results shown with various applications and challenging scenarios demonstrate the contributions presented in the thesis, and also show potential for machine learning-driven algorithms to solve various open problems in computer graphics.
Search and Analytics Using Semantic Annotations
(Advisor: Dr. Klaus Berberich)
Search systems help users locate relevant information in the form of text documents for keyword queries. Using text alone, it is often difficult to satisfy the user's information need. To discern the user's intent behind queries, we turn to semantic annotations (e.g., named entities and temporal expressions) that natural language processing tools can now deliver with great accuracy.
This thesis develops methods and an infrastructure that leverage semantic annotations to efficiently and effectively search large document collections.
This thesis makes contributions in three areas: indexing, querying, and mining of semantically annotated document collections. First, we describe an indexing infrastructure for semantically annotated document collections. The indexing infrastructure can support knowledge-centric tasks such as information extraction, relationship extraction, question answering, fact spotting and semantic search at scale across millions of documents. Second, we propose methods for exploring large document collections by suggesting semantic aspects for queries. These semantic aspects are generated by considering annotations in the form of temporal expressions, geographic locations, and other named entities. The generated aspects help guide the user to relevant documents without the need to read their contents. Third and finally, we present methods that can generate events, structured tables, and insightful visualizations from semantically annotated document collections.
Martin BROMBERGER
Decision Procedures for Linear Arithmetic
(Advisors: Prof. Christoph Weidenbach and Dr. Thomas Sturm, now LORIA, Nancy)
Tuesday, 10.12.2019, 14:00 h, in building E1 5, room 002
In this thesis, we present new decision procedures for linear arithmetic in the context of SMT solvers and theorem provers:
1) CutSAT++, a calculus for linear integer arithmetic that combines techniques from SAT solving and quantifier elimination in order to be sound, terminating, and complete.
2) The largest cube test and the unit cube test, two sound (although incomplete) tests that find integer and mixed solutions in polynomial time. The tests are especially efficient on absolutely unbounded constraint systems, which are difficult to handle for many other decision procedures.
3) Techniques for the investigation of equalities implied by a constraint system. Moreover, we present several applications for these techniques.
4) The Double-Bounded reduction and the Mixed-Echelon-Hermite transformation, two transformations that reduce any constraint system in polynomial time to an equisatisfiable constraint system that is bounded. The transformations are beneficial because they turn branch-and-bound into a complete and efficient decision procedure for unbounded constraint systems.
We have implemented the above decision procedures (except for CutSAT++) as part of our linear arithmetic theory solver SPASS-IQ and as part of our CDCL(LA) solver SPASS-SATT. We also present various benchmark evaluations that confirm the practical efficiency of our new decision procedures.
Felipe Fernandes ALBRECHT
Analyzing Epigenomic Data in a Large-Scale Context
(Advisor: Prof. Thomas Lengauer)
Monday, 09.12.2019, 16:15 h, in building E1 4, room 0.23
While large amounts of epigenomic data are publicly available, their retrieval in a form suitable for downstream analysis is a bottleneck in current research. In a typical analysis, users are required to download huge files that span the entire genome, even if they are only interested in a small subset or an aggregation thereof. The DeepBlue Epigenomic Data Server mitigates this issue by providing a robust server that affords a powerful API for searching, filtering, transforming, aggregating, enriching, and downloading data from several epigenomic consortia. This work also presents companion tools that utilize the DeepBlue API to enable users not proficient in programming to analyze epigenomic data: (i) an R/Bioconductor package that integrates DeepBlue into the R analysis workflow; (ii) a web portal that enables users to search, select, filter and download the epigenomic data available in the DeepBlue Server; (iii) DIVE, a web data analysis tool that allows researchers to perform large-epigenomic data analysis in a programming-free environment. Furthermore, these tools are integrated, being capable of sharing results among themselves, creating a powerful large-scale epigenomic data analysis environment.
Hazem TORFAH
Model Counting for Reactive Systems
(Advisor: Prof. Bernd Finkbeiner)
Model counting is the problem of computing the number of solutions for a logical formula. In the last few years, it has been primarily studied for propositional logic, and has been shown to be useful in many applications. In planning, for example, propositional model counting has been used to compute the robustness of a plan in an incomplete domain. In information-flow control, model counting has been applied to measure the amount of information leaked by a security-critical system.
In this thesis, we introduce the model counting problem for linear-time properties, and show its applications in formal verification. In the same way propositional model counting generalizes the satisfiability problem for propositional logic, counting models for linear-time properties generalizes the emptiness problem for languages over infinite words to one that asks for the number of words in a language. The model counting problem, thus, provides a foundation for quantitative extensions of model checking, where not only the existence of computations that violate the specification is determined, but also the number of such violations.
We solve the model counting problem for the prominent class of omega-regular properties. We present algorithms for solving the problem for different classes of properties, and show the advantages of our algorithms in comparison to indirect approaches based on encodings into propositional logic.
We further show how model counting can be used for solving a variety of quantitative problems in formal verification, including quantitative information-flow in security-critical systems, and the synthesis of approximate implementations for reactive systems.
Yang HE
Improved Methods and Analysis for Semantic Image Segmentation
(Advisor: Prof. Mario Fritz)
Modern deep learning has enabled amazing developments of computer vision in recent years. As a fundamental task, semantic segmentation aims to predict class labels for each pixel of images, which empowers machines perception of the visual world. In spite of recent successes of fully convolutional networks, several challenges remain to be addressed. In this work, we focus on this topic, under different kinds of input formats and various types of scenes. Specifically, our study contains two aspects:
(1) Data-driven neural modules for improved performance.
(2) Leverage of datasets w.r.t. training systems with higher performances and better data privacy guarantees.
Daniel GRÖGER
Digital Fabrication of Custom Interactive Objects with Rich Materials
(Advisor: Prof. Jürgen Steimle)
This thesis investigates digital fabrication as a key technology for prototyping physical user interfaces with custom interactivity. It contributes four novel design and fabrication approaches for interactive objects that leverage rich materials of everyday objects. The contributions enable easy, accessible, and versatile design and fabrication of interactive objects with custom stretchability, input and output on complex geometries and diverse materials, tactile output on 3D-object geometries, and capabilities of changing their shape and material properties.
Together, the contributions of this thesis advance the fields of digital fabrication, rapid prototyping, and ubiquitous computing towards the bigger goal of exploring interactive objects with rich materials as a new generation of physical interfaces.
Andreas SCHMID
Plane and Sample: Using Planar Subgraphs for Efficient Algorithms
(Advisor: Prof. Kurt Mehlhorn)
In my thesis, we showcased how planar subgraphs with special structural properties can be used to find efficient algorithms for two NP-hard problems in combinatorial optimization.
In this talk I will describe how we developed algorithms for the computation of Tutte paths and show how these special subgraphs can be used to efficiently compute long cycles and other relaxations of Hamiltonicity if we restrict the input to planar graphs.
In addition I will give an introduction to the Maximum Planar Subgraph Problem MPS and show how dense planar subgraphs can be used to develop new approximation algorithms for this NP-hard problem. All new algorithms and arguments I present are based on a novel approach that focuses on maximizing the number of triangular faces in the computed subgraph.
Kashyap POPAT
Credibility Analysis of Textual Claims with Explainable Evidence
(Advisor: Prof. Gerhard Weikum)
Despite being a vast resource of valuable information, the Web has been polluted by the spread of false claims. Increasing hoaxes, fake news, and misleading information on the Web have given rise to many fact-checking websites that manually assess these doubtful claims. However, the rapid speed and large scale of misinformation spread have become the bottleneck for manual verification. This calls for credibility assessment tools that can automate this verification process. Prior works in this domain make strong assumptions about the structure of the claims and the communities where they are made. Most importantly, black-box techniques proposed in prior works lack the ability to explain why a certain statement is deemed credible or not.
To address these limitations, this dissertation proposes a general framework for automated credibility assessment that does not make any assumption about the structure or origin of the claims. Specifically, we propose a feature-based model, which automatically retrieves relevant articles about the given claim and assesses its credibility by capturing the mutual interaction between the language style of the relevant articles, their stance towards the claim, and the trustworthiness of the underlying web sources. We further enhance our credibility assessment approach and propose a neural-network-based model. Unlike the feature-based model, this model does not rely on feature engineering and external lexicons. Both our models make their assessments interpretable by extracting explainable evidence from judiciously selected web sources.
We utilize our models and develop a Web interface, CredEye, which enables users to automatically assess the credibility of a textual claim and dissect into the assessment by browsing through judiciously and automatically selected evidence snippets. In addition, we study the problem of stance classification and propose a neural-network-based model for predicting the stance of diverse user perspectives regarding the controversial claims. Given a controversial claim and a user comment, our stance classification model predicts whether the user comment is supporting or opposing the claim.
Tim RUFFING
Cryptography for bitcoin and friends
(Advisor: Prof. Aniket Kate, now Purdue)
Numerous cryptographic extensions to Bitcoin have been proposed since Satoshi Nakamoto introduced the revolutionary design in 2008. However, only few proposals have been adopted in Bitcoin and other prevalent cryptocurrencies, whose resistance to fundamental changes has proven to grow with their success. In this dissertation, we introduce four cryptographic techniques that advance the functionality and privacy provided by Bitcoin and similar cryptocurrencies without requiring fundamental changes in their design: First, we realize smart contracts that disincentivize parties in distributed systems from making contradicting statements by penalizing such behavior by the loss of funds in a cryptocurrency. Second, we propose CoinShuffle++, a coin mixing protocol which improves the anonymity of cryptocurrency users by combining their transactions and thereby making it harder for observers to trace those transactions. The core of CoinShuffle++ is DiceMix, a novel and efficient protocol for broadcasting messages anonymously without the help of any trusted third-party anonymity proxies and in the presence of malicious participants. Third, we combine coin mixing with the existing idea to hide payment values in homomorphic commitments toobtain the ValueShuffle protocol, which enables us to overcome major obstacles to the practical deployment of coin mixing protocols. Fourth, we show how to prepare the aforementioned homomorphic commitments for a safe transition to post-quantum cryptography.
Giorgi MAISURADZE
Assessing the Security of Hardware-Assisted Isolation Techniques
(Advisor: Prof. Christian Rossow)
Modern computer systems execute a multitude of different processes on the same hardware. To guarantee that these processes do not interfere with one another, either accidentally or maliciously, modern processors implement various isolation techniques, such as process, privilege, and memory isolation. Consequently, these isolation techniques constitute a fundamental requirement for a secure computer system.
This dissertation investigates the security guarantees of various isolation techniques that are used by modern computer systems. To this end, we present the isolation challenges from three different angles. First, we target fine-grained memory isolation that is used by code-reuse mitigation techniques to thwart attackers with arbitrary memory read vulnerabilities. We demonstrate that dynamically generated code can be used to undermine such memory isolation techniques and, ultimately, propose a way to improve the mitigation. Second, we study side effects of legitimate hardware features, such as speculative execution, and show how they can be leveraged to leak sensitive data across different security contexts, thereby breaking process and memory isolation techniques. Finally, we demonstrate that in the presence of a faulty hardware implementation, all isolation guarantees can be broken. We do this by using a novel microarchitectural issue—discovered by us—to leak arbitrary memory contents across all security contexts.
Leander TENTRUP
Symbolic Reactive Synthesis
Friday, 15.11.2019, 16:00 h, in building E1 7, room 0.01
In this thesis, we develop symbolic algorithms for the synthesis of reactive systems. Synthesis, that is the task of deriving correct-by-construction implementations from formal specifications, has the potential to eliminate the need for the manual—and error-prone—programming task. The synthesis problem can be formulated as an infinite two-player game, where the system player has the objective to satisfy the specification against all possible actions of the environment player. The standard synthesis algorithms represent the underlying synthesis game explicitly and, thus, they scale poorly with respect to the size of the specification.
We provide an algorithmic framework to solve the synthesis problem symbolically. In contrast to the standard approaches, we use a succinct representation of the synthesis game which leads to improved scalability in terms of the symbolically represented parameters. Our algorithm reduces the synthesis game to the satisfiability problem of quantified Boolean formulas (QBF) and dependency quantified Boolean formulas (DQBF). In the encodings, we use propositional quantification to succinctly represent different parts of the implementation, such as the state space and the transition function.
We develop highly optimized satisfiability algorithms for QBF and DQBF. Based on a counterexample-guided abstraction refinement (CEGAR) loop, our algorithms avoid an exponential blow-up by using the structure of the underlying symbolic encodings. Further, we extend the solving algorithms to extract certificates in the form of Boolean functions, from which we construct implementations for the synthesis problem. Our empirical evaluation shows that our symbolic approach significantly outperforms previous explicit synthesis algorithms with respect to scalability and solution quality.
Nora SPEICHER
Unsupervised multiple kernel learning approaches for integrating molecular cancer patient data
(Advisor: Prof. Nico Pfeifer, now Tübingen)
Cancer is the second leading cause of death worldwide. A characteristic of this disease is its complexity leading to a wide variety of genetic and molecular aberrations in the tumors. This heterogeneity necessitates personalized therapies for the patients. However, currently defined cancer subtypes used in clinical practice for treatment decision-making are based on relatively few selected markers and thus provide only a coarse classification of tumors. The increased availability in multi-omics data measured for cancer patients now offers the possibility of defining more informed cancer subtypes. Such a more fine-grained characterization of cancer subtypes harbors the potential of substantially expanding treatment options in personalized cancer therapy.
In this work, we identify comprehensive cancer subtypes using multidimensional data. For this purpose, we apply and extend unsupervised multiple kernel learning methods. Three challenges of unsupervised multiple kernel learning are addressed: robustness, applicability, and interpretability. First, we show that regularization of the multiple kernel graph embedding framework, which enables the implementation of dimensionality reduction techniques, can increase the stability of the resulting patient subgroups. This improvement is especially beneficial for data sets with a small number of samples. Second, we adapt the objective function of kernel principal component analysis to enable the application of multiple kernel learning in combination with this widely used dimensionality reduction technique. Third, we improve the interpretability of kernel learning procedures by performing feature clustering prior to integrating the data via multiple kernel learning. On the basis of these clusters, we derive a score indicating the impact of a feature cluster on a patient cluster, thereby facilitating further analysis of the cluster-specific biological properties. All three procedures are successfully tested on real-world cancer data.
Gorav JINDAL
On Approximate Polynomial Identity Testing and Real Root Finding
(Advisor: Prof. Markus Bläser)
In this thesis we study the following three themes, which share a connection through the (arithmetic) circuit complexity of polynomials.
1. Rank of symbolic matrices: There exist easy randomized polynomial time algorithms for computing the commutative rank of symbolic matrices, finding deterministic polynomial time algorithms remains elusive. We first demonstrate a deterministic polynomial time approximation scheme (PTAS) for computing the commutative rank. Prior to this work, deterministic polynomial time algorithms were known only for computing a 1/2-approximation of the commutative rank. We give two distinct proofs that our algorithm is a PTAS. We also give a min-max characterization of commutative and non-commutative ranks of symbolic matrices.
2. Computation of real roots of real sparse polynomials: It is known that solving a system of polynomial equations reduces to solving a uni-variate polynomial equation. We describe a polynomial time algorithm for sparse polynomials, which computes approximations of all the real roots (even though it may also compute approximations of some complex roots). Moreover, we also show that the roots of integer trinomials are well-separated.
3. Complexity of symmetric polynomials: It is known that symmetric Boolean functions are easy to compute. In contrast, we show that the assumption of inequality of VP and VNP implies that there exist hard symmetric polynomials. To prove this result, we use an algebraic analogue of the classical Newton's iteration.
Julian STEIL
Mobile Eye Tracking for Everyone
(Advisor: Prof. Andreas Bulling, now Stuttgart)
Mobile eye tracking has significant potential to overcome fundamental limitations of remote systems in term of mobility and practical usefulness. However, mobile eye tracking currently faces two fundamental challenges that prevent it from being practically usable and that, consequently, have to be addressed before mobile eye tracking can truly be used by everyone: Mobile eye tracking needs to be advanced and made fully functional in unconstrained environments, and it needs to be made socially acceptable. Nevertheless, solving technical challenges and social obstacles alone is not sufficient to make mobile eye tracking attractive for the masses. The key to success is the development of convincingly useful, innovative, and essential applications. This thesis provides solutions for all of these challenges and paves the way for the development of socially acceptable, privacy-aware, but highly functional mobile eye tracking devices and novel applications, so that mobile eye tracking can develop its full potential to become an everyday technology for everyone.
Quynh NGUYEN
Optimization Landscape of Deep Neural Networks
(Advisor: Prof. Matthias Hein, now Tübingen)
Deep learning has drawn increasing attention in artificial intelligence due to its superior empirical performance in various fields of applications, including computer vision, natural language processing and speech recognition. This raises important and fundamental questions on why these methods work so well in practice.
The goal of this thesis is to improve our theoretical understanding on the optimization landscape of deep neural nets. We show that under some over-parameterization conditions, in particular as the width of one of the hidden layers exceeds the number of training samples, every stationary point of the loss with some full-rank structure is a global minimum with zero training error. Moreover, every sub-level set of the loss is connected and unbounded. This suggests that by increasing over-parameterization, the loss function of deep neural nets can become much more favorable to local search algorithms than any other "wildly" non-convex function. In an attempt to bring our results closer to practice, we come up with a new class of network architectures which provably have a nice optimization surface while empirically achieving good generalization performance on standard benchmark dataset. Lastly, we complement our results by identifying an intuitive function class which neural networks of arbitrary depth might not be able to learn if their hidden layers are not wide enough.
Scott KILPATRICK
Non-Reformist Reform for Haskell Modularity
(Advisor: Prof. Derek Dreyer)
In this thesis, I present Backpack, a new language for building separately-typecheckable packages on top of a weak module system like Haskell's. The design of Backpack is the first to bring the rich world of type systems to the practical world of packages via mixin modules. It's inspired by the MixML module calculus of Rossberg and Dreyer but by choosing practicality over expressivity Backpack both simplifies that semantics and supports a flexible notion of applicative instantiation. Moreover, this design is motivated less by foundational concerns and more by the practical concern of integration into Haskell. The result is a new approach to writing modular software at the scale of packages.
Yusra IBRAHIM
Understanding Quantities in Web Tables and Text
There is a wealth of schema-free tables on the web. The text accompanying these tables explains and qualifies the numerical quantities given in the tables. Despite this ubiquity of tabular data, there is little research that harnesses this wealth of data by semantically understanding the information that is conveyed rather ambiguously in these tables. This information can be disambiguated only by the help of the accompanying text.
In the process of understanding quantity mentions in tables and text, we are faced with the following challenges; First, there is no comprehensive knowledge base for anchoring quantity mentions. Second, tables are created ad-hoc without a standard schema and with ambiguous header names; also table cells usually contain abbreviations. Third, quantities can be written in multiple forms and units of measures–for example "48 km/h" is equivalent to "30 mph". Fourth, the text usually refers to the quantities in tables using aggregation, approximation, and different scales.
In this thesis, we target these challenges through the following contributions:
We present the Quantity Knowledge Base (QKB), a knowledge base for representing Quantity mentions. We construct the QKB by importing information from Freebase, Wikipedia, and other online sources.
We propose Equity: a system for automatically canonicalizing header names and cell values onto concepts, classes, entities, and uniquely represented quantities registered in a knowledge base.
We devise a probabilistic graphical model that captures coherence dependencies between cells in tables and candidate items in the space of concepts, entities, and quantities. Then, we cast the inference problem into an efficient algorithm based on random walks over weighted graphs. baselines.
We introduce the quantity alignment problem: computing bidirectional links between textual mentions of quantities and the corresponding table cells. We propose BriQ: a system for computing such alignments. BriQ copes with the specific challenges of approximate quantities, aggregated quantities, and calculated quantities.
We design ExQuisiTe: a web application that identifies mentions of quantities in text and tables, aligns quantity mentions in the text with related quantity mentions in tables, and generates salient suggestions for extractive text summarization systems.
Cornelius BRAND
Paths and Walks, Forests and Planes – Arcadian Algorithms and Complexity
(Advisor: Prof. Holger Dell, now ITU Copenhagen)
Thursday, 26.09.2019, 10:00 h, in building E1 7, room 001
We present new results on parameterized algorithms for hard graph problems. We generalize and improve established methods (i.a. Color-Coding and representative families) by an algebraic formulation of the problems in the language of exterior algebra.Our method gives (1) a faster algorithm to estimate the number of simple paths of given length in directed graphs, (2) faster deterministic algorithms for finding such paths if the input graph contains only few of them, and (3) faster deterministic algorithms to find spanning trees with few leaves. We also consider the algebraic foundations of our new method in exterior and commutative algebra.
Additionally, we investigate the fine-grained complexity of determining the number of forests with a given number of edges in a given undirected graph.
We (1) complete the complexity classification of the Tutte plane under the exponential time hypothesis, and (2) prove that counting forests with a given number of edges is at least as hard as counting cliques of a given size.
Milivoj SIMEONOVSKI
Accountable Infrastructure and Its Impact on Internet Security and Privacy
(Advisor: Prof. Michael Backes)
The Internet infrastructure relies on the correct functioning of the basic underlying protocols, which were designed for functionality. Security and privacy have been added post hoc, mostly by applying cryptographic means to different layers of communication. In the absence of accountability, as a fundamental property, the Internet infrastructure does not have a built-in ability to associate an action with the responsible entity, neither to detect or prevent misbehavior.
In this thesis, we study accountability from a few different perspectives. First, we study the need of having accountability in anonymous communication networks as a mechanism that provides repudiation for the proxy nodes by tracing back selected outbound traffic in a provable manner. Second, we design a framework that provides a foundation to support the enforcement of the right to be forgotten law in a scalable and automated manner. The framework provides a technical mean for the users to prove their eligibility for content removal from the search results. Third, we analyze the Internet infrastructure determining potential security risks and threats imposed by dependencies among the entities on the Internet. Finally, we evaluate the feasibility of using hop count filtering as a mechanism for mitigating Distributed Reflective Denial-of-Service attacks, and conceptually show that it cannot work to prevent these attacks.
Davis ISSAC
On some covering, partition, and connectivity problems in graphs
We look at some graph problems related to covering, partition, and connectivity. First, we study the problems of covering and partitioning edges with bicliques, especially from the viewpoint of parameterized complexity. For the partition problem, we develop much more efficient algorithms than the ones previously known. In contrast, for the cover problem, our lower bounds show that the known algorithms are probably optimal. Next, we move on to graph coloring, which is probably the most extensively studied partition problem in graphs. Hadwiger's conjecture is a long-standing open problem related to vertex coloring. We prove the conjecture for a special class of graphs, namely squares of 2-trees, and show that square graphs are important in connection with Hadwiger's conjecture. Then, we study a coloring problem that has been emerging recently, called rainbow coloring. This problem lies in the intersection of coloring and connectivity. We study different variants of rainbow coloring and present bounds and complexity results on them. Finally, we move on to another parameter related to connectivity called spanning tree congestion (STC). We give tight bounds for STC in general graphs and random graphs. While proving the results on STC, we also make some contributions to the related area of connected partitioning.
Florian SCHMIDT
Applications, challenges and new perspectives on the analysis of transcriptional regulation using epigenomic and transcriptomic data
(Advisor: Dr. Marcel Schulz, now Frankfurt)
The integrative analysis of epigenomics and transcriptomics data is an active research field in Bioinformatics. New methods are required to interpret and process large omics data sets, as generated within consortia such as the International Human Epigenomics Consortium. In this thesis, we present several approaches illustrating how combined epigenomics and transcriptomics datasets, e.g. for differential or time series analysis, can be used to derive new biological insights on transcriptional regulation. In my work, I focused on regulatory proteins called transcription factors (TFs), which are essential for orchestrating cellular processes.
I present novel approaches, which combine epigenomics data, such as DNaseI-seq, predicted TF binding scores and gene-expression measurements in interpretable machine learning models. In joint work with our collaborators within and outside IHEC, we have shown that our methods lead to biological meaningful results, which could be validated with wet-lab experiments.
Aside from providing the community with new tools to perform integrative analysis of epigenomics and transcriptomics data, we have studied the characteristics of chromatin accessibility data and its relation to gene-expression in detail to better understand the implications of both computational processing and of different experimental methods on data interpretation.
Marco VOIGT
Decidable Fragments of First-Order Logic and of First-Order Linear Arithmetic with Uninterpreted Predicates
First-order logic (FOL) is one of the most prominent formalisms in computer science. Unfortunately, FOL satisfiability is not solvable algorithmically in full generality. The classical decision problem is the quest for a delineation between the decidable and the undecidable parts of FOL. This talk aims to shed new light on the boundary. To this end, recently discovered structure on the decidable side of the first-order landscape shall be discussed.
The primary focus will be on the syntactic concept of separateness of variables and its applicability to the classical decision problem and beyond. Two disjoint sets of first-order variables are separated in a given formula if each atom in that formula contains variables from at most one of the two sets. This simple notion facilitates the definition of decidable extensions of many well-known decidable FOL fragments. Although the extensions exhibit the same expressive power as the respective originals, certain logical properties can be expressed much more succinctly. In at least two cases the succinctness gap cannot be bounded using any elementary function.
The secondary focus will be on linear first-order arithmetic over the rationals with uninterpreted predicates. Novel decidable fragments of this logical language shall be discussed briefly.
Counting Problems on Quantum Graphs
(Advisor: Dr. Holger Dell)
Monday, 15.07.2019, 12:00 h, in building E1 7, room 001
Quantum graphs, as defined by Lovász in the late 60s, are formal linear combinations of simple graphs with finite support. They allow for the complexity analysis of the problem of computing finite linear combinations of homomorphism counts, the latter of which constitute the foundation of the structural hardness theory for parameterized counting problems: The framework of parameterized counting complexity was introduced by Flum and Grohe, and McCartin in 2002 and forms a hybrid between the classical field of computational counting as founded by Valiant in the late 70s and the paradigm of parameterized complexity theory due to Downey and Fellows which originated in the early 90s.
The problem of computing homomorphism numbers of quantum graphs subsumes general motif counting problems and the complexity theoretic implications have only turned out recently in a breakthrough regarding the parameterized subgraph counting problem by Curticapean, Dell and Marx in 2017.
We study the problems of counting partially injective and edge-injective homomorphisms, counting induced subgraphs, as well as counting answers to existential first-order queries. We establish novel combinatorial, algebraic and even topological properties of quantum graphs that allow us to provide exhaustive parameterized and exact complexity classifications, including necessary, sufficient and mostly explicit tractability criteria, for all of the previous problems.
Steven SCHÄFER
Engineering Formal Systems in Constructive Type Theory
(Advisor: Prof. Gert Smolka)
Friday, 12.07.2019, 14:15 h, in building E1 7, room 001
This thesis presents a practical methodology for formalizing the meta-theory of formal systems with binders and coinductive relations in constructive type theory. While constructive type theory offers support for reasoning about formal systems built out of inductive definitions, support for syntax with binders and coinductive relations is lacking. We provide this support. We implement syntax with binders using well-scoped de Bruijn terms and parallel substitutions. We solve substitution lemmas automatically using the rewriting theory of the σ-calculus. We present the Autosubst library to automate our approach in the proof assistant Coq. Our approach to coinductive relations is based on an inductive tower construction, which is a type-theoretic form of transfinite induction. The tower construction allows us to reduce coinduction to induction. This leads to a symmetric treatment of induction and coinduction and allows us to give a novel construction of the companion of a monotone function on a complete lattice. We demonstrate our methods with a series of case studies. In particular, we present a proof of type preservation for CCω, a proof of weak and strong normalization for System F, a proof that systems of weakly guarded equations have unique solutions in CCS, and a compiler verification for a compiler from a non-deterministic language into a deterministic language. All technical results in the thesis are formalized in Coq.
Jonas KAISER
Formal Verification of the Equivalence of System F and the Pure Type System L2
We develop a formal proof of the equivalence of two different variants of System F. The first is close to the original presentation where expressions are separated into distinct syntactic classes of types and terms. The second, L2, is a particular pure type system (PTS) where the notions of types and terms, and the associated expressions are unified in a single syntactic class. The employed notion of equivalence is a bidirectional reduction of the respective typing relations. A machine-verified proof of this result turns out to be surprisingly intricate, since the two variants noticeably differ in their expression languages, their type systems and the binding of local variables.
Most of this work is executed in the Coq theorem prover and encompasses a general development of the PTS metatheory, an equivalence result for a stratified and a PTS variant of the simply typed lambda-calculus as well as the subsequent extension to the full equivalence result for System F. We utilise nameless de Bruijn syntax with parallel substitutions for the representation of variable binding and develop an extended notion of context morphism lemmas as a structured proof method for this setting.
We also provide two developments of the equivalence result in the proof systems Abella and Beluga, where we rely on higher-order abstract syntax (HOAS). This allows us to compare the three proof systems, as well as HOAS and de Bruijn for the purpose of developing formal metatheory.
Marco SPEICHER
Measuring User Experience for Virtual Reality
(Advisor: Prof. Antonio Krüger)
Wednesday, 10.07.2019, 13:00 h, in building D3 2, Reuse seminar room (-2.17)
In recent years, Virtual Reality (VR) and 3D User Interfaces (3DUI) have seen a drastic increase in popularity, especially in terms of consumer-ready hardware and software. These technologies have the potential to create new experiences that combine the advantages of reality and virtuality. While the technology for input as well as output devices is market ready, only a few solutions for everyday VR – online shopping, games, or movies – exist, and empirical knowledge about performance and user preferences is lacking. All this makes the development and design of human-centered user interfaces for VR a great challenge.
This thesis investigates the evaluation and design of interactive VR experiences. We introduce the Virtual Reality User Experience (VRUX) model based on VR-specific external factors and evaluation metrics such as task performance and user preference. Based on our novel UX evaluation approach, we contribute by exploring the following directions: shopping in virtual environments, as well as text entry and menu control in the context of everyday VR. Along with this, we summarize our findings by design spaces and guidelines for choosing optimal interfaces and controls in VR.
Sanjar KARAEV
Matrix Factorization over Dioids and its Applications in Data Mining
(Advisor: Prof. Pauli Miettinen, now University of Eastern Finland)
While classic matrix factorization methods, such as NMF and SVD, are known to be highly effective at finding latent patterns in data, they are limited by the underlying algebraic structure. In particular, it is often difficult to distinguish heavily overlapping patterns because they interfere with each other. To deal with this problem, we study matrix factorization over algebraic structures known as dioids, that are characterized by the idempotency of addition (a + a = a). Idempotency ensures that at every data point only a single pattern contributes, which makes it easier to distinguish them. In this thesis, we consider different types of dioids, that range from continuous (subtropical and tropical algebras) to discrete (Boolean algebra).
The Boolean algebra is, perhaps, the most well known dioid, and there exist Boolean matrix factorization algorithms that produce low reconstruction errors. In this thesis, however, a different objective function is used — the description length of the data, which enables us to obtain more compact and highly interpretable results.
The tropical and subtropical algebras are much less known in the data mining field. While they find applications in areas such as job scheduling and discrete event systems, they are virtually unknown in the context of data analysis. We will use them to obtain idempotent nonnegative factorizations that are similar to NMF, but are better at separating most prominent features of the data.
Hosnieh SATTAR
Intents and Preferences Prediction Based on Implicit Human Cues
(Advisor: Dr. Mario Fritz)
Understanding implicit human cues is a key factor to build advanced human-machine interfaces. The modern interfaces should be able to understand and predict human intents and assist users from implicit data rather waiting for explicit input. Eye movement, electroencephalogram (EEG), electrocardiogram (ECG), body shape, are several sources of implicit human cues. In this thesis, we focused on eye data and body shape.
The eye is known as a window to the mind and could reflect allot about the ongoing process in mind. Thus, in the first part of the thesis, we focus on advancing techniques for search target prediction from human gaze data. We propose a series of techniques for search target inference algorithm from human fixation data recorded during the visual search that broaden the scope of search target prediction to categorical classes, such as object categories and attributes.
Moreover, body shape could reveal a lot of information about the people choice of outfit, food, sport, or living style. Hence, in the second part of this thesis, we studied how body shape could influences people outfits' preferences. We propose a novel and robust multi-photo approach to estimate the body shapes of each user and build a conditional model of clothing categories given body-shape. However, an accurate depiction of the naked body is considered highly private and therefore, might not be consented by most people. First, we studied the perception of such technology via a user study. Then, in the last part of this thesis, we ask if the automatic extraction of such information can be effectively evaded.
Sarvesh NIKUMBH
Interpretable Machine Learning Methods for Prediction and Analysis of Genome Regulation in 3D
With the development of chromosome conformation capture-based techniques, we now know that chromatin is packed in three-dimensional (3D) space inside the cell nucleus. Changes in the 3D chromatin architecture have already been implicated in diseases such as cancer. Thus, a better understanding of this 3D conformation is of interest to help enhance our comprehension of the complex, multi-pronged regulatory mechanisms of the genome. In my colloquium, I will present interpretable machine learning-based approaches for prediction and analysis of long-range chromatin interactions and how they can help gain novel, fine-grained insights into genome regulatory mechanisms. Specifically, I will first present our string kernels-based support vector classification method for prediction of long-range chromatin interactions. This method was one of the first bioinformatic approaches to suggest a potential general role of short tandem repeat sequences in long-range genome regulation and its 3D organization. I will then present CoMIK, a method we developed for handling variable-length DNA sequences in classification scenarios. CoMIK can not only identify the features important for classification but also locate them within the individual sequences, thus enabling the possibility of more fine-grained insights.
Thomas LEIMKÜHLER
Artificial Intelligence for Efficient Image-based View Synthesis
(Advisor: Prof. Hans-Peter Seidel and Prof. Tobias Ritschel, now University College London)
Monday, 24.06.2019, 9:00 h, in building E1 4, room 0.19
Synthesizing novel views from image data is a widely investigated topic in both computer graphics and computer vision, and has many applications like stereo or multi-view rendering for virtual reality, light field reconstruction, and image post-processing. While image-based approaches have the advantage of reduced computational load compared to classical model-based rendering, efficiency is still a major concern. We demonstrate how concepts and tools from artificial intelligence can be used to increase the efficiency of image-based view synthesis algorithms. In particular it is shown how machine learning can help to generate point patterns useful for a variety of computer graphics tasks, how path planning can guide image warping, how sparsity-enforcing optimization can lead to significant speedups in interactive distribution effect rendering, and how probabilistic inference can be used to perform real-time 2D-to-3D conversion.
Azim Dehghani Amirabad
From genes to transcripts: Integrative modeling and analysis of regularity networks
Although all the cells in an organism posses the same genome, the regulatory mechanisms lead to highly specic cell types. Elucidating these regulatory mechanisms is a great challenge in systems biology research. Nonetheless, it is known that a large fraction of our genome is comprised of regulatory elements, the precise mechanisms by which different combinations of regulatory elements are involved in controlling gene expression and cell identity are poorly understood. This thesis describes algorithms and approaches for modeling and analysis of different modes of gene regulation. We present POSTIT a novel algorithm for modeling and inferring transcript isoform regulation from transcriptomics and epigenomics data. POSTIT uses multi-task learning with structured-sparsity inducing regularizer to share the regulatory information between isoforms of a gene, which is shown to lead to accurate isoform expression prediction and inference of regulators.
We developed a novel statistical method, called SPONGE, for large-scale inference of ceRNA networks. In this framework, we designed an efficient empirical p-value computation approach, by sampling from derived null models, which addresses important confounding factors such as sample size, number of involved regulators and strength of correlation.
Finally, we present an integrative analysis of miRNA and protein-based post-transcriptional regulation. We postulate a competitive regulation of the RNA-binding protein IMP2 with miRNAs binding the same RNAs using expression and RNA binding data. This function of IMP2 is relevant in the contribution to disease in the context of adult cellular metabolism.
Nadia ROBERTINI
Model-based Human Performance Capture in Outdoor Scenes
Technologies for motion and performance capture of real actors have enabled the creation of realistic-looking virtual humans through detail and deformation transfer at the cost of extensive manual work and sophisticated in-studio marker-based systems. This thesis pushes the boundaries of performance capture by proposing automatic algorithms for robust 3D skeleton and detailed surface tracking in less constrained multi-view outdoor scenarios.
Contributions include new multi-layered human body representations designed for effective model-based time-consistent reconstruction in complex dynamic environments with varying illumination, from a set of vision cameras. We design dense surface refinement approaches to enable smooth silhouette-free model-to-image alignment, as well as coarse-to-fine tracking techniques to enable joint estimation of skeleton motion and fine-scale surface deformations in complicated scenarios. High-quality results attained on challenging application scenarios confirm the contributions and show great potential for the automatic creation of personalized 3D virtual humans.
Peter FAYMONVILLE
Monitoring with Parameters
Runtime monitoring of embedded systems is a method to safeguard their reliable operation by detecting runtime failures within the system and recognizing unexpected environment behavior during system development and operation. Specification languages for runtime monitoring aim to provide the succinct, understandable, and formal specification of system and component properties.
Starting from temporal logics, this thesis extends the expressivity of specification languages for runtime monitoring in three key aspects while maintaining the predictability of resource usage. First, we provide monitoring algorithms for linear-time temporal logic with parameters (PLTL), where the parameters bound the number of steps until an eventuality is satisfied. Second, we introduce Lola 2.0, which adds data parameterization to the stream specification language Lola. Third, we integrate real-time specifications in RTLola and add real-time sliding windows, which aggregate data over real-time intervals. For the combination of these extensions, we present a design-time specification analysis which provides resource guarantees.
We report on a case study on the application of the language in an autonomous UAS. Component and system properties were specified together with domain experts in the developed stream specification language and evaluated in a real-time hardware-in-the-loop testbed with a complex environment simulation.
Matthias DÖRING
Computational Approaches for Improving Treatment and Prevention of Viral Infections
The treatment of infections with HIV or HCV is challenging. Thus, novel drugs and new computational approaches that support the selection of therapies are required. This work presents methods that support therapy selection as well as methods that advance novel antiviral treatments.
geno2pheno[ngs-freq] identifies drug resistance from HIV-1 or HCV samples that were subjected to next-generation sequencing by interpreting their sequences either via support vector machines or a rules-based approach. geno2pheno[coreceptor-hiv2] determines the coreceptor that is used for viral cell entry by analyzing a segment of the HIV-2 surface protein with a support vector machine. openPrimeR is capable of finding optimal combinations of primers for multiplex polymerase chain reaction by solving a set cover problem and accessing a new logistic regression model for determining amplification events arising from polymerase chain reaction. geno2pheno[ngs-freq] and geno2pheno[coreceptor-hiv2] enable the personalization of antiviral treatments and support clinical decision making. The application of openPrimeR on human immunoglobulin sequences has resulted in novel primer sets that improve the isolation of broadly neutralizing antibodies against HIV-1. The methods that were developed in this work thus constitute important contributions towards improving the prevention and treatment of viral infectious diseases.
Charalampos KYRIAKOPOULOS
Stochastic Modeling of DNA Demethylation Dynamics in ESCs
(Advisor: Prof. Verena Wolf)
DNA methylation and demethylation are opposing processes that when in balance create stable patterns of epigenetic memory. The control of DNA methylation pattern formation in replication dependent and independent demethylation processes has been suggested to be influenced by Tet mediated oxidation of a methylated cytosine, 5mC, to a hydroxylated cytosine, 5hmC. Based only on in vitro experiments, several alternative mechanisms have been proposed on how 5hmC influences replication dependent maintenance of DNA methylation and replication independent processes of active demethylation. In this thesis we design an extended and easily generalizable hidden Markov model that uses as input hairpin (oxidative-)bisulfite sequencing data to precisely determine the over time dynamics of 5mC and 5hmC, as well as to infer the activities of the involved enzymes at a single CpG resolution. Developing the appropriate statistical and computational tools, we apply the model to discrete high-depth sequenced genomic loci, and on a whole genome scale with a much smaller sequencing depth. Performing the analysis of the model's output on mESCs data, we show that the presence of Tet enzymes and 5hmC has a very strong impact on replication dependent demethylation by establishing a passive demethylation mechanism, implicitly impairing methylation maintenance, but also down-regulating the de novo methylation activity.
Tomas BASTYS
Analysis of the Protein-Ligand and Protein-Peptide Interactions Using a Combined Sequence- and Structure-Based Approach
(Advisor: Prof. Olga Kalinina)
Proteins participate in most of the important processes in cells, and their ability to perform their function ultimately depends on their three-dimensional structure. They usually act in these processes through interactions with other molecules. Because of the importance of their role, proteins are also the common target for small molecule drugs that inhibit their activity, which may include targeting protein interactions. Understanding protein interactions and how they are affected by mutations is thus crucial for combating drug resistance and aiding drug design.
This dissertation combines bioinformatics studies of protein interactions at both primary sequence and structural level. We analyse protein-protein interactions through linear motifs, as well as protein-small molecule interactions, and study how mutations affect them. This is done in the context of two systems. In the first study of drug resistance mutations in the protease of the human immunodeficiency virus type 1, we successfully apply molecular dynamics simulations to estimate the effects of known resistance-associated mutations on the free binding energy, also revealing molecular mechanisms of resistance. In the second study, we analyse consensus profiles of linear motifs that mediate the recognition by the mitogen-activated protein kinases of their target proteins. We thus gain insights into the cellular processes these proteins are involved in.
Abdalghani ABUJABAL
Question Answering over Knowledge Bases with Continuous Learning
Answering complex natural language questions with crisp answers is crucial towards satisfying the information needs of advanced users. With the rapid growth of knowledge bases (KBs) such as Yago and Freebase, this goal has become attainable by translating questions into formal queries like SPARQL queries. Such queries can then be evaluated over knowledge bases to retrieve crisp answers. To this end, two research issues arise:
(i) how to develop methods that are robust to lexical and syntactic variations in questions and can handle complex questions, and
(ii) how to design and curate datasets to advance research in question answering. In this dissertation, we make the following contributions in the area of question answering (QA). For issue (i), we present QUINT, an approach for answering natural language questions over knowledge bases using automatically learned templates. Templates are an important asset for QA over KBs, simplifying the semantic parsing of input questions and generating formal queries for interpretable answers. We also introduce NEQA, a framework for continuous learning for QA over KBs. NEQA starts with a small seed of training examples in the form of question-answer pairs, and improves its performance over time. NEQA combines both syntax, through template-based answering, and semantics, via a semantic similarity function. For issues (i) and (ii), we present TEQUILA, a framework for answering complex questions with explicit and implicit temporal conditions over KBs. TEQUILA is built on a rule-based framework that detects and decomposes temporal questions into simpler sub-questions that can be answered by standard KB-QA systems. TEQUILA reconciles the results of sub-questions into final answers. TEQUILA is accompanied with a dataset called TempQuestions, which consists of 1,271 temporal questions with gold-standard answers over Freebase. This collection is derived by judiciously selecting time-related questions from existing QA datasets. For issue (ii), we publish ComQA, a large-scale manually-curated dataset for QA. ComQA contains questions that represent real information needs and exhibit a wide range of difficulties such as the need for temporal reasoning, comparison, and compositionality. ComQA contains paraphrase clusters of semantically-equivalent questions that can be exploited by QA systems.
Evgeny LEVINKOV
Generalizations of the Multicut Problem for Computer Vision
(Advisor: Prof. Bernt Schiele)
Graph decompositions have always been an essential part of computer vision as a large variety of tasks can be formulated in this framework. One way to optimize for a decomposition of a graph is called the multicut problem, also known as correlation clustering. Its particular feature is that the number of clusters is not required to be known a priori, but is rather deduced from the optimal solution. On the downside, it is NP-hard to solve.
In this thesis we present several generalizations of the multicut problem, that allow to model richer dependencies between nodes of a graph. We also propose efficient local search algorithms, that in practice find good solution in reasonable time, and show applications to image segmentation, multi-human pose estimation, multi-object tracking and many others.
Sebastian HAHN
On Static Execution-Time Analysis – Compositionality, Pipeline Abstraction, and Predictable Hardware
(Advisor: Prof. Reinhard Wilhelm)
Proving timeliness is an integral part of the verification of safety-critical real-time systems. To this end, timing analysis computes upper bounds on the execution times of programs that execute on a given hardware platform.
At least since multi-core processors have emerged, timing analysis separates concerns by analysing different aspects of the system's timing behaviour individually. In this work, we validate the underlying assumption that a timing bound can be soundly composed from individual contributions. We show that even simple processors exhibit counter-intuitive behaviour – a locally slow execution can lead to an even slower overall execution – that impedes the soundness of the composition. We present the compositional base bound analysis that accounts for any such amplifying effects within its timing contribution. This enables a sound although expensive compositional analysis even for complex contemporary processors.
In addition, we discuss future hardware designs that enable efficient compositional analyses. We introduce a hardware design, the strictly in-order pipeline, that behaves monotonically with respect to the progress of a program's execution. Monotonicity enables us to formally reason about properties such as compositionality.
Joanna BIEGA
Enhancing Privacy and Fairness in Search Systems
Search systems have a substantial potential to harm individuals and the society. First, since they collect vast amounts of data about their users, they have the potential to violate user privacy. Second, in applications where rankings influence people's economic livelihood outside of the platform, such as sharing economy or hiring support websites, search engines have an immense economic power over their users in that they control user exposure in ranked results.
This thesis develops new models and methods broadly covering different aspects of privacy and fairness in search systems for both searchers and search subjects:
* We propose a model for computing individually fair rankings where search subjects get exposure proportional to their relevance. The exposure is amortized over time using constrained optimization to overcome searcher attention biases while preserving ranking utility.
* We propose a model for computing sensitive search exposure where each subject gets to know the sensitive queries that lead to her profile in the top-k search results. The problem of finding exposing queries is technically modeled as reverse nearest neighbor search, followed by a weekly-supervised learning to rank model ordering the queries by privacy-sensitivity.
* We propose a model for quantifying privacy risks from textual data in online communities. The method builds on a topic model where each topic is annotated by a crowdsourced sensitivity score, and privacy risks are associated with a user's relevance to sensitive topics. We propose relevance measures capturing different dimensions of user interest in a topic and show how they correlate with human risk perceptions.
* Last but not least, we propose a model for privacy-preserving personalized search where search queries of different users are split and merged into synthetic profiles. The model mediates the privacy-utility trade-off by keeping semantically coherent fragments of search histories within individual profiles, while trying to minimize the similarity of any of the synthetic profiles to the original user profiles.
Yecheng GU
Intelligent Tutoring in Virtual Reality for Highly Dynamic Pedestrian Safety Training
(Advisor: Prof. Jörg Siekmann)
This thesis presents the design, implementation, and evaluation of an Intelligent Tutoring System (ITS) with a Virtual Reality (VR) interface for child pedestrian safety training. This system enables children to train practical skills in a safe and realistic virtual environment without the time and space dependencies of traditional roadside training. This system also employs Domain and Student Modelling techniques to analyze user data during training automatically and to provide appropriate instructions and feedback.
Thus, the traditional requirement of constant monitoring from teaching personnel is greatly reduced. Compared to previous work, especially the second aspect is a principal novelty for this domain. To achieve this, a novel Domain and Student Modeling method was developed in addition to a modular and extensible virtual environment for the target domain. While the Domain and Student Modeling framework is designed to handle the highly dynamic nature of training in traffic and the ill-defined characteristics of pedestrian tasks, the modular virtual environment supports different interaction methods and a simple and efficient way to create and adapt exercises. The thesis is complemented by two user studies with elementary school children. These studies testify great overall user acceptance and the system's potential for improving key pedestrian skills through autonomous learning. Last but not least, the thesis presents experiments with different forms of VR input and provides directions for future work.
Praveen MANOHARAN
Novel Approaches to Anonymity and Privacy in Decentralized, Open Settings
The Internet has undergone dramatic changes in the last two decades, evolving from a mere communication network to a global multimedia platform in which billions of users actively exchange information. While this transformation has brought tremendous benefits to society, it has also created new threats to online privacy that existing technology is failing to keep pace with.
In this dissertation, we present the results of two lines of research that developed two novel approaches to anonymity and privacy in decentralized, open settings. First, we examine the issue of attribute and identity disclosure in open settings and develop the novel notion of (k,d)-anonymity for open settings that we extensively study and validate experimentally. Furthermore, we investigate the relationship between anonymity and linkability using the notion of (k,d)-anonymity and show that, in contrast to the traditional closed setting, anonymity within one online community does necessarily imply unlinkability across different online communities in the decentralized, open setting.
Secondly, we consider the transitive diffusion of information that is shared in social networks and spread through pairwise interactions of user connected in this social network. We develop the novel approach of exposure minimization to control the diffusion of information within an open network, allowing the owner to minimize its exposure by suitably choosing who they share their information with. We implement our algorithms and investigate the practical limitations of user side exposure minimization in large social networks.
At their core, both of these approaches present a departure from the provable privacy guarantees that we can achieve in closed settings and a step towards sound assessments of privacy risks in decentralized, open settings.
What we leave behind: reproducibility in chromatin analysis within and across species
Epigenetics is the field of biology that investigates heritable factors regulating gene expression without being directly encoded in the genome of an organism. In my colloquium, I am going to present approaches dealing with three challenging problems in computational epigenomics: first, we designed a solution strategy for improving reproducibility of computational analysis as part of a large national epigenetics research consortium. Second, we developed a software tool for the comparative epigenome analysis of cell types within a species. For this project, we relied on a well-established and compact representation of epigenetic information known as chromatin states, which enabled us to realize fast and interpretable comparative chromatin analysis even for small sample numbers. Third, we extended comparative epigenomics beyond canonical model organisms to also include species for which little to no epigenetic data is available. In a proof of concept study, we implemented a computational pipeline for predicting biologically relevant information, e.g., cell-type specific gene expression profiles, in non-model organisms based only on reference epigenomes from well-studied species such as human or mouse.
Viktor ERDÉLYI
Scalable positioning of commodity mobile devices using audio signals
(Advisor: Prof. Peter Druschel)
Thursday, 14.02.2019, 9:00 h, in building E1 5, room 0.29
This thesis explores the problem of computing a position map for co-located mobile devices. The positioning should happen in a scalable manner without requiring specialized hardware and without requiring specialized infrastructure (except basic Wi-Fi or cellular access). At events like meetings, talks, or conferences, a position map can aid spontaneous communication among users based on their relative position in two ways. First, it enables users to choose message recipients based on their relative position, which also enables the position-based distribution of documents. Second, it enables senders to attach their position to messages, which can facilitate interaction between speaker and audience in a lecture hall and enables the collection of feedback based on users' location.
In this thesis, we present Sonoloc, a mobile app and system that, by relying on acoustic signals, allows a set of commodity smart devices to determine their _relative_ positions. Sonoloc can position any number of devices within acoustic range with a constant number of acoustic signals emitted by a subset of devices. Our experimental evaluation with up to 115 devices in real rooms shows that — despite substantial background noise — the system can locate devices with an accuracy of tens of centimeters using no more than 15 acoustic signals.
Anjo VAHLDIEK-OBERWAGNER
Techniques to Protect Confidentiality and Integrity of Persistent and In-Memory Data
Today computers store and analyze valuable and sensitive data. As a result we need to protect this data against confidentiality and integrity violations that can result in the illicit release, loss, or modification of a user's and an organization's sensitive data such as personal media content or client records. Existing techniques protecting confidentiality and integrity lack either efficiency or are vulnerable to malicious attacks. In this thesis we suggest techniques, Guardat and ERIM, to efficiently and robustly protect persistent and in-memory data.
To protect the confidentiality and integrity of persistent data, clients specify per-file policies to Guardat declaratively, concisely and separately from code. Guardat enforces policies by mediating I/O in the storage layer. In contrast to prior techniques, we protect against accidental or malicious circumvention of higher software layers. We present the design and prototype implementation, and demonstrate that Guardat efficiently enforces example policies in a web server.
To protect the confidentiality and integrity of in-memory data, ERIM isolates sensitive data using Intel Memory Protection Keys (MPK), a recent x86 extension to partition the address space. However, MPK does not protect against malicious attacks by itself. We prevent malicious attacks by combining MPK with call gates to trusted entry points and ahead-of-time binary inspection. In contrast to existing techniques, ERIM efficiently protects frequently-used session keys of web servers, an in-memory reference monitor's private state, and managed runtimes from native libraries. These use cases result in high switch rates of the order of 10 5 –10 6 switches/s. Our experiments demonstrate less then 1% runtime overhead per 100,000 switches/s, thus outperforming existing techniques.
Muhammad Bilal ZAFAR
Discrimination in Algorithmic Decision Making: From Principles to Measures and Mechanisms
(Advisor: Prof. Krishna Gummadi)
The rise of algorithmic decision making in a variety of applications has also raised concerns about its potential for discrimination against certain social groups. However, incorporating nondiscrimination goals into the design of algorithmic decision making systems (or, classifiers) has proven to be quite challenging. These challenges arise mainly due to the computational complexities involved in the process, and the inadequacy of existing measures to computationally capture discrimination in various situations. The goal of this thesis is to tackle these problems. First, with the aim of incorporating existing measures of discrimination (namely, disparate treatment and disparate impact) into the design of well-known classifiers, we introduce a mechanism of decision boundary covariance, that can be included in the formulation of any convex boundary-based classifier in the form of convex constraints. Second, we propose alternative measures of discrimination. Our first proposed measure, disparate mistreatment, is useful in situations when unbiased ground truth training data is available. The other two measures, preferred treatment and preferred impact, are useful in situations when feature and class distributions of different social groups are significantly different, and can additionally help reduce the cost of nondiscrimination (as compared to the existing measures). We also design mechanisms to incorporate these new measures into the design of convex boundary-based classifiers.
Christian LANDER
Ubiquitous Head-Mounted Gaze Tracking
Thursday, 24.01.2019, 15:00 h, in building D3 2, "Reuse" meeting room
Recently, gaze-based interfaces in stationary settings became a valid option, as remote eye trackers are easily available at a low price. However, making gaze-based interfaces ubiquitous remains an open challenge that cannot be resolved using remote approaches. The miniaturization in camera technology allows for gaze estimation with head-mounted devices, which are similar to a pair of glasses. A crucial step towards gaze estimation using such devices is calibration. Although the development is mainly technology driven, a hypothetical fully calibrated system in which all parameters are known and valid is affected by calibration drift. In addition, attributes like minimal intrusiveness and obstruction, easy and flexible setup and high accuracy are not present in the latest commercial devices. Hence their applicability to spontaneous interaction or long-lasting research experiments is questionable.
In this thesis we enable spontaneous, calibration-free and accurate mobile gaze estimation. We contribute by investigating the following three areas: Efficient Long-Term Usage of a head-mounted eye tracker; Location, Orientation & Target Independent head mounted eye tracking; and Mobile & Accurate Calibration-Free gaze estimation. Through the elaboration of the theoretical principles, we investigate novel concepts for each aspect; these are implemented and evaluated, converging into a final device, to show how to overcome current limitations.
Juhi KULSHRESTHA
Quantifying & Characterizing Information Diets of Social Media Users
An increasing number of people are relying on online social media platforms like Twitter and Facebook to consume news and information about the world around them. This change has led to a paradigm shift in the way news and information is exchanged in our society – from traditional mass media to online social media.
With the changing environment, it's essential to study the information consumption of social media users and to audit how automated algorithms (like search and recommendation systems) are modifying the information that social media users consume. In this thesis, we fulfill this high-level goal with a two-fold approach. First, we propose the concept of information diets as the composition of information produced or consumed. Next, we quantify the diversity and bias in the information diets that social media users consume via the three main consumption channels on social media platforms: (a) word of mouth channels that users curate for themselves by creating social links, (b) recommendations that platform providers give to the users, and (c) search systems that users use to find interesting information on these platforms. We measure the information diets of social media users along three different dimensions of topics, geographic sources, and political perspectives.
Our work is aimed at making social media users aware of the potential biases in their consumed diets, and at encouraging the development of novel mechanisms for mitigating the effects of these biases.
Johannes DOERFERT
Applicable and Sound Polyhedral Optimization of Low-Level Programs
(Advisor: Prof. Sebastian Hack)
Computers become increasingly complex. Current and future systems feature configurable hardware, multiple cores with different capabilities, as well as accelerators. In addition, the memory subsystem becomes diversified too. The cache hierarchy grows deeper, is augmented with scratchpads, low-latency memory, and high-bandwidth memory. The programmer alone cannot utilize this enormous potential. Compilers have to provide insight into the program behavior, or even arrange computations and data themselves. Either way, they need a more holistic view of the program. Local transformations, which treat the iteration order, computation unit, and data layout as fixed, will not be able to fully utilize a diverse system.
The polyhedral model, a high-level program representation and transformation framework, has shown great success tackling various problems in the context of diverse systems. While it is widely acknowledged for its analytical powers and transformation capabilities, it is also widely assumed to be too restrictive and fragile for real-world programs.
In this thesis, we improve the applicability and profitability of polyhedral-model-based techniques. Our efforts guarantee a sound polyhedral representation and extend the applicability to a wider range of programs. In addition, we introduce new applications to utilize the information available in the polyhedral program representation, including standalone optimizations and techniques to derive high-level properties.
Alexander WEINERT
Optimality and Resilience in Parity Games
(Advisor: Dr. Martin Zimmermann)
Modeling reactive systems as infinite games has yielded a multitude of results in the fields of program verification and program synthesis. The canonical parity condition used for such games, however, neither suffices to express non-functional requirements on the modeled system, nor to capture malfunctions of the deployed system.
In this work we address these issues by investigating quantitative games in which the above characteristics can be expressed. Parity games with costs are a variant of parity games in which traversing an edge incurs some nonnegative cost. The cost of a play is the limit of the cost incurred between answering odd colors by larger even ones. We extend that model by allowing for integer costs, obtaining parity games with weights, and determine both the computational complexity of solving the resulting games as well as the memory required by the protagonist to win such games.
Our results show that the increase in expressiveness comes at a steep cost in terms of both measures. Subsequently, we address the optimality question, i.e., the question asking whether the protagonist is able to ensure a given bound on the cost, and show that answering this question is harder than just solving the underlying game, even for special cases of parity games with weights.
Moreover, we further extend this model to allow for modeling disturbances that may occur during the operation of the resulting strategy and show how to compute a strategy that is resilient against as many such disturbances as possible. Finally, we show that the protagonist is able to trade memory, quality, and resilience of strategies for one another and we show how to compute the possible tradeoffs between these three values.
Paarijaat ADITYA
Towards Privacy-Compliant Mobile Computing
Sophisticated mobile computing, sensing and recording devices like smartphones, smartwatches, and wearable cameras are carried by their users virtually around the clock, blurring the distinction between the online and offline worlds. While these devices enable transformative new applications and services, they also introduce entirely new threats to users' privacy, because they can capture a complete record of the user's location, online and offline activities, and social encounters, including an audiovisual record. Such a record of users' personal information is highly sensitive and is subject to numerous privacy risks. In this thesis, we have investigated and built systems to mitigate two such privacy risks:
1) privacy risks due to ubiquitous digital capture, where bystanders may inadvertently be captured in photos and videos recorded by other nearby users,
2) privacy risks to users' personal information introduced by a popular class of apps called 'mobile social apps'. In this thesis, we present two systems, called I-Pic and EnCore, built to mitigate these two privacy risks.
Both systems aim to put the users back in control of what personal information is being collected and shared, while still enabling innovative new applications. We built working prototypes of both systems and evaluated them through actual user deployments. Overall we demonstrate that it is possible to achieve privacy-compliant digital capture and it is possible to build privacy-compliant mobile social apps, while preserving their intended functionality and ease-of-use. Furthermore, we also explore how the two solutions can be merged into a powerful combination, one which could enable novel workflows for specifying privacy preferences in image capture that do not currently exist.
Pavel KOLEV
Algorithmic Results for Clustering and Refined Physarum Analysis
In the first part of this thesis, we study the Binary $\ell_0$-Rank-$k$ problem which given a binary matrix $A$ and a positive integer $k$, seeks to find a rank-$k$ binary matrix $B$ minimizing the number of non-zero entries of $A-B$. A central open question is whether this problem admits a polynomial time approximation scheme. We give an affirmative answer to this question by designing the first randomized almost-linear time approximation scheme for constant $k$ over the reals, $\mathbb{F}_2$, and the Boolean semiring. In addition, we give novel algorithms for important variants of $\ell_0$-low rank approximation. The second part of this dissertation, studies a popular and successful heuristic, known as Approximate Spectral Clustering (ASC), for partitioning the nodes of a graph $G$ into clusters with small conductance. We give a comprehensive analysis, showing that ASC runs efficiently and yields a good approximation of an optimal $k$-way node partition of $G$. In the final part of this thesis, we present two results on slime mold computations: i) the continuous undirected Physarum dynamics converges for undirected linear programs with a non-negative cost vector; and ii) for the discrete directed Physarum dynamics, we give a refined analysis that yields strengthened and close to optimal convergence rate bounds, and shows that the model can be initialized with any strongly dominating point.
Sigurd SCHNEIDER
A Verified Compiler for a Linear Imperative/Functional Intermediate Language
(Advisors: Prof. Sebastian Hack & Prof. Gert Smolka)
This thesis describes the design of the verified compiler LVC. LVC's main novelty is the way its first-order, term-based intermediate language IL realizes the advantages of static single assignment (SSA) for verified compilation. IL is a term-based language not based on a control-flow graph (CFG) but defined in terms of an inductively defined syntax with lexically scoped mutually recursive function definitions. IL replaces the usual dominance-based SSA definition found in unverified and verified compilers with the novel notion of coherence. The main research question this thesis studies is whether IL with coherence offers a faithful implementation of SSA, and how the design influences the correctness invariants and the proofs in the verified compiler LVC. To study this question, we verify dead code elimination, several SSA-based value optimizations including sparse conditional constant propagation and SSA-based register allocation approach including spilling. In these case studies, IL with coherence provides the usual advantages of SSA and improves modularity of proofs. Furthermore, we propose a novel SSA construction algorithm based on coherence, and leverage the term structure of IL to obtain an inductive proof method for simulation proofs. LVC is implemented and verified with over 50,000 lines of code using the proof assistant Coq. To underline practicability of our approach, we integrate LVC with CompCert to obtain an executable compiler that generates PowerPC assembly code.
Pascal LESSEL
Supporting User's Influence in Gamification Settings and Game Live-Streams
Tuesday, 06.11.2018, 15:00 h, in building D3 2 (DFKI), room -2.17 (Reuse)
Playing games has long been important to mankind. One reason for this is the associated autonomy, as players can decide on many aspects on their own and can shape the experience. Game-related sub-fields have appeared in Human-Computer Interaction where this autonomy is questionable: in this thesis, we consider gamification and game live-streams and here, we support the users' influence at runtime. We hypothesize that this should affect the perception of autonomy and should lead to positive effects overall. Our contribution is three-fold: first, we investigate crowd-based, self-sustaining systems in which the user's influence directly impacts the outcome of the system's service. We show that users are willing to expend effort in such systems even without additional motivation, but that gamification is still beneficial here. Second, we introduce "bottom-up" gamification, i.e., the idea of self-tailored gamification. Here, users have full control over the gamification used in a system, i.e., they can set it up as they see fit at the system's runtime. Through user studies, we show that this has positive behavioral effects and thus adds to the ongoing efforts to move away from "one-size-fits-all" solutions. Third, we investigate how to make gaming live-streams more interactive, and how viewers perceive this. We also consider shared game control settings in live-streams, in which viewers have full control, and we contribute options to support viewers' self-administration here.
Konrad JAMROZIK
Mining Sandboxes
(Advisor: Prof. Andreas Zeller)
Modern software is ubiquitous, yet insecure. It has the potential to expose billions of humans to serious harm, up to and including losing fortunes and taking lives. Existing approaches for securing programs are either exceedingly hard and costly to apply, significantly decrease usability, or just don't work well enough against a determined attacker.
In this thesis we propose a new solution that significantly increases application security yet it is cheap, easy to deploy, and has minimal usability impact. We combine in a novel way the best of what existing techniques of test generation, dynamic program analysis and runtime enforcement have to offer: We introduce the concept of sandbox mining. First, in a phase called mining, we use automatic test generation to discover application behavior. Second, we apply a sandbox to limit any behavior during normal usage to the one discovered during mining. Users of an application running in a mined sandbox are thus protected from the application suddenly changing its behavior, as compared to the one observed during automatic test generation. As a consequence, backdoors, advanced persistent threats and other kinds of attacks based on the passage of time become exceedingly hard to conduct covertly. They are either discovered in the secure mining phase, where they can do no damage, or are blocked altogether. Mining is cheap because we leverage fully automated test generation to provide baseline behavior. Usability is not degraded: the sandbox runtime enforcement impact is negligible; the mined behavior is comprehensive and presented in a human readable format, thus any unexpected behavior changes are rare and easy to reason about. Our BOXMATE prototype for Android applications shows the approach is technically feasible, has an easy setup process, and is widely applicable to existing apps. Experiments conducted with BOXMATE show less than one hour is required to mine Android applications sandboxes, requiring few to no confirmations for frequently used functionality.
Petro LUTSYK
Correctness of Multi-Core Processors with Operating System Support
(Advisor: Prof. Wolfgang Paul)
In the course of adding hardware support for operating systems and hypervisors (like Microsoft Hyper-V), we verify a realistic multi-core processor with integrated mechanisms for two levels of virtual address translation. The second level of address translation (SLAT) is required to allow guests of a hypervisor (typically operating systems) to execute their programs in translated mode. In hardware, the scheme of SLAT is implemented in a dedicated processor component, called the two-level memory management unit (MMU). Both the specification and the implementation of the two-level MMU are presented in full detail. The main contribution is the complete paper and pencil correctness proof for the pipelined multi-core implementation of the MIPS-86 ISA with SLAT. MIPS-86 combines the instruction set of MIPS with the memory model of x86. First, we consider the sequential implementation, which serves to demonstrate integration of the two-level MMU into the MIPS processor. In the proof of our main result — correctness of the pipelined implementation — we refer to the sequential case to show correctness of the MMU operation. This allows us to shift the focus towards the problems of pipelining a machine with speculative execution and interrupts, which are necessary to consider in combination with address translation.
Xucong ZHANG
Gaze Estimation and Interaction in Real-World Environments
(Advisor: Dr. Andreas Bulling)
Human eye gaze has been widely used in human-computer interaction, as it is a promising modality for natural, fast, pervasive, and non-verbal interaction between humans and computers. Appearance-based gaze estimation methods directly regress from eye images to gaze targets without eye feature detection, and therefore have great potential to work with ordinary devices. However, these methods require a large amount of domain-specific training data to cover the significant variability in eye appearance. In this thesis, we focus on developing appearance-based gaze estimation methods and corresponding attentive user interfaces with a single webcam for challenging real-world environments. We collected a large-scale gaze estimation dataset from real-world setting, proposed a full-face gaze estimation method, and studied data normalization. We applied our gaze estimation methods to real-world interactive application including eye contact detection and gaze estimation with multiple personal devices.
Yongtao SHUAI
Dynamic Adaptive Video Streaming with Minimal Buffer Sizes
(Advisor: Prof. Thorsten Herfet)
Wednesday, 19.09.2018, 16:00 h, in building E1 1, room 407
Recently, adaptive streaming has been widely adopted in video streaming services to improve the quality-of-experience (QoE) of video delivery over the Internet. However, state-of-the-art bitrate adaptation achieves satisfactory performance only with extensive buffering of several tens of seconds. This leads to high playback latency in video delivery, which is undesirable especially in the context of live content and interactive features with a low upper bound on the latency. Therefore, this thesis aims at pushing the application of adaptive streaming to its limit with respect to the buffering size, which is the dominant factor of the streaming latency.
In the current work, we first address the minimum buffering size required in adaptive streaming, which provides us with guidelines to determine a reasonable low latency for streaming systems. Then, we tackle the fundamental challenge of achieving such a low latency streaming by developing a novel adaptation algorithm that stabilizes buffer dynamics despite a small buffering size. We also present advanced improvements by designing a novel adaptation architecture with low-delay feedback for the bitrate selection and optimizing the underlying transport layer to offer efficient real-time streaming. Experimental evaluations demonstrate that our approach achieves superior QoE in adaptive video streaming, especially in the particularly challenging case of low latency streaming.
Erik DERR
Understanding and Assessing Security on Android via Static Code Analysis
Smart devices have become a rich source of sensitive information including personal data (contacts and account data) and context information like GPS data that is continuously aggregated by onboard sensors. As a consequence, mobile platforms have become a prime target for malicious and over-curious applications. The growing complexity and the quickly rising number of mobile apps have further reinforced the demand for comprehensive application security vetting. This dissertation presents a line of work that advances security testing on Android via static code analysis. In the first part of this dissertation, we build an analysis framework that statically models the complex runtime behavior of apps and Android's application framework (on which apps are built upon) to extract privacy and security-relevant data-flows. We provide the first classification of Android's protected resources within the framework and generate precise API-to-permission mappings that excel over prior work. We then propose a third-party library detector for apps that is resilient against common code obfuscations to measure the outdatedness of libraries in apps and to attribute vulnerabilities to the correct software component. Based on these results, we identify root causes of app developers not updating their dependencies and propose actionable items to remedy the current status quo. Finally, we measure to which extent libraries can be updated automatically without modifying the application code.
Seong Joon OH
Image Manipulation against Learned Models: Privacy and Security Implications
Machine learning is transforming the world. Its application areas span privacy sensitive and security critical tasks such as human identification and self-driving cars. These applications raise privacy and security related questions that are not fully understood or answered yet: Can automatic person recognisers identify people in photos even when their faces are blurred? How easy is it to find an adversarial input for a self-driving car that makes it drive off the road?
This thesis contributes one of the first steps towards a better understanding of such concerns in the presence of data manipulation. From the point of view of user's privacy, we show the inefficacy of common obfuscation methods like face blurring, and propose more advanced techniques based on head inpainting and adversarial examples. We discuss the duality of model security and user privacy problems and describe the implications of research in one area for the other. Finally, we study the knowledge aspect of the data manipulation problem: the more one knows about the target model, the more effective manipulations one can craft. We propose a game theoretic framework to systematically represent the partial knowledge on the target model and derive privacy and security guarantees. We also demonstrate that one can reveal architectural details and training hyperparameters of a model only by querying it, leading to even more effective data manipulations against it.
Pascal BERRANG
Quantifying and Mitigating Privacy Risks in Biomedical Data
Wednesday, 25.07.2018, 14:00 h, in building E9 1 (CISPA), room 001
The decreasing costs of molecular profiling have fueled the biomedical research community with a plethora of new types of biomedical data, allowing for a breakthrough towards a more precise and personalized medicine. However, the release of these intrinsically highly sensitive, interdependent data poses a new severe privacy threat.
In this thesis, we provide means to quantify and protect the privacy of individuals' biomedical data. Besides the genome, we specifically focus on two of the most important epigenetic elements influencing human health: microRNAs and DNA methylation. We quantify the privacy for multiple realistic attack scenarios. Our results underline that the privacy risks inherent to biomedical data have to be taken seriously. Moreover, we present and evaluate solutions to preserve the privacy of individuals. Our mitigation techniques stretch from the differentially private release of epigenetic data, considering its utility, up to cryptographic constructions to securely, and privately evaluate a random forest on a patient's data.
Ruben BECKER
On Flows, Paths, Roots, and Zeros
This thesis has two parts; in the first of which we give new results for various network flow problems. (1) We present a novel dual ascent algorithm for min-cost flow and show that an implementation of it is very efficient on certain instance classes. (2) We approach the problem of numerical stability of interior point network flow algorithms by giving a path following method that works with integer arithmetic solely and is thus guaranteed to be free of any nu-merical instabilities. (3) We present a gradient descent approach for the undirected transship-ment problem and its special case, the single source shortest path problem (SSSP). For distrib-uted computation models this yields the first SSSP-algorithm with near-optimal number of communication rounds.
The second part deals with fundamental topics from algebraic computation. (1) We give an algorithm for computing the complex roots of a complex polynomial. While achieving a com-parable bit complexity as previous best results, our algorithm is simple and promising to be of practical impact. It uses a test for counting the roots of a polynomial in a region that is based on Pellet's theorem. (2) We extend this test to polynomial systems, i.e., we develop an algorithm that can certify the existence of a k-fold zero of a zero-dimensional polynomial system within a given region. For bivariate systems, we show experimentally that this approach yields signifi-cant improvements when used as inclusion predicate in an elimination method.
Bojana KODRIC
Incentives in Dynamic Markets
(Advisor: Prof. Martin Hoefer, now Uni Frankfurt)
In this thesis, we consider a variety of combinatorial optimization problems within a common theme of uncertainty and selfish behavior.
In our first scenario, the input is collected from selfish players. Here, we study extensions of the so-called smoothness framework for mechanisms, a very useful technique for bounding the inefficiency of equilibria, to the cases of varying mechanism availability and participation of risk-averse players. In both of these cases, our main results are general theorems for the class of (λ,μ)-smooth mechanisms. We show that these mechanisms guarantee at most a (small) constant factor performance loss in the extended settings.
In our second scenario, we do not have access to the exact numerical input. Within this context, we explore combinatorial extensions of the well-known secretary problem under the assumption that the incoming elements only reveal their ordinal position within the set of previously arrived elements. We first observe that many existing algorithms for special matroid structures maintain their competitive ratio in the ordinal model. In contrast, we provide a lower bound for algorithms that are oblivious to the matroid structure. Finally, we design new algorithms that obtain constant competitive ratios for a variety of combinatorial problems.
Manuel REINERT
Cryptographic Techniques for Privacy and Access Control in Cloud-Based Applications
(Advisor: Prof. Matteo Maffei, now Uni Wien)
Friday, 29.06.2018, 15:30 h, in building E9 1 (CISPA), room 001
Digitization is one of the key challenges for today's industries and society. It affects more and more business areas and also user data and, in particular, sensitive information. Due to its sensitivity, it is important to treat personal information as secure and private as possible yet enabling cloud-based software to use that information when requested by the user.
In this thesis, we focus on the privacy-preserving outsourcing and sharing of data, the querying of outsourced protected data, and the usage of personal information as an access control mechanism for rating platforms, which should be protected from coercion attacks. In those three categories, we present cryptographic techniques and protocols that push the state of the art. In particular, we first present multi-client oblivious RAM (ORAM), which augments standard ORAM with selective data sharing through access control, confidentiality, and integrity. Second, we investigate on recent work in frequency-hiding order-preserving encryption and show that the state of the art misses rigorous treatment, allowing for simple attacks against the security of the existing scheme. As a remedy, we show how to fix the security definition and that the existing scheme, slightly adapted, fulfills it. Finally, we design and develop a coercion-resistant rating platform. Coercion-resistance has been dealt with mainly in the context of electronic voting yet also affects other areas of digital life such as rating platforms.
Maryam NAZARIEH
Understanding Regulatory Mechanisms Underlying Stem Cells Helps to Identify Cancer Biomarks
(Advisor: Prof. Volkhard Helms)
In this thesis, we present novel algorithms to unravel regulatory mechanisms underlying stem cell differentiation and cancerogenesis. Inspired by the tightly interwoven topology of the regulators controlling the pluripotency network in mouse embryonic stem cells, we formulated the problem where a set of master regulatory genes in a regulatory network is identified by solving either of two combinatorial optimization problems namely a minimum dominating set or a minimum connected dominating set in weakly and strongly connected components. Then we applied the developed methods to regulatory cancer networks to identify disease-associated genes and anti-cancer drug targets in breast cancer and hepatocellular carcinoma. As not all the nodes in the solutions are critical, we developed a prioritization method to rank a set of candidate genes which are related to a certain disease based on systematic analysis of the genes that are differentially expressed in tumor and normal conditions. Moreover, we demonstrated that the topological features in regulatory networks surrounding differentially expressed genes are highly consistent in terms of using the output of several analysis tools for identifying differentially expressed genes. We compared two randomization strategies for TF-miRNA co-regulatory networks to infer significant network motifs underlying cellular identity. We showed that the edge-type conserving method surpasses the non-conserving method in terms of biological relevance and centrality overlap. We presented several web servers and software packages that were made publicly available at no cost. The Cytoscape plugin of minimum connected dominating set identifies a set of key regulatory genes in a user-provided regulatory network based on a heuristic approach. The ILP formulations of minimum dominating set and minimum connected dominating set return the optimal solutions for the aforementioned problems. The web servers TFmiR and TFmiR2 construct disease-, tissue-, process-specific networks for the sets of deregulated genes and miRNAs provided by a user. They highlight topological hotspots and offer detection of three- and four-node FFL motifs as a separate web service for mouse and human.
Alexander ANDREYCHENKO
Model Reconstruction for Moment-based Stochastic Chemical Kinetics
Based on the theory of stochastic chemical kinetics, the inherent randomness and stochasticity of biochemical reaction networks can be accurately described by discrete-state continuous-time Markov chains, where each chemical reaction corresponds to a state transition of the process. However, the analysis of such processes is computationally expensive and sophisticated numerical methods are required. The main complication comes due to the largeness problem of the state space, so that analysis techniques based on an exploration of the state space are often not feasible and the integration of the moments of the underlying probability distribution has become a very popular alternative. In this thesis we propose an analysis framework in which we integrate a number of moments of the process instead of the state probabilities. This results in a more time-efficient simulation of the time evolution of the process. In order to regain the state probabilities from the moment representation, we combine the moment-based simulation (MM) with a maximum entropy approach: the maximum entropy principle is applied to derive a distribution that fits best to a given sequence of moments. We further extend this approach by incorporating the conditional moments (MCM) which allows not only to reconstruct the distribution of the species present in high amount in the system, but also to approximate the probabilities of species with low molecular counts. For the given distribution reconstruction framework, we investigate the numerical accuracy and stability using case studies from systems biology, compare two different moment approximation methods (MM and MCM), examine if it can be used for the reaction rates estimation problem and describe the possible future applications.
Abhishek BICHHAWAT
Practical Dynamic Information Flow Control
(Advisor: Prof. Christian Hammer, now Uni Potsdam)
Computer systems and applications handle a plethora of private user information. These are often assisted by a set of bugs with both malicious and non-malicious intent leading to information leaks. Information flow control has been studied extensively as an approach to mitigate such leaks but has focussed mainly on static analyses. However, some of the applications are developed using dynamic languages like JavaScript that make the static analyses techniques ineffective. Although there has been a growing interest to develop dynamic analysis techniques, it still isn't at the helm of information flow security in such settings; the prime reason being that these techniques either over-approximate or are too restrictive in most cases. This thesis focuses on improving the usability of dynamic information flow analyses. It begins by presenting a sound improvement and enhancement of the permissive-upgrade strategy. It, then, presents a sound and precise dynamic information flow analysis for handling complex features like exceptions in higher-order languages. To address the issue of permissiveness, this thesis develops a sound approach to bound leaks dynamically while allowing information release in accordance to a developer-specified budget. It then applies these techniques to a Web browser and explores a policy specification mechanism for Web applications.
Shilpa GARG
Computational Haplotyping: theory and practice
(Advisor: Prof. Tobias Marschall)
Genomics has paved a new way to comprehend life and its evolution, and also to investigate causes of diseases and their treatment. One of the important problems in genomic analyses is haplotype assembly. Constructing complete and accurate haplotypes plays an essential role in understanding population genetics and how species evolve.In this thesis, we focus on computational approaches to haplotype assembly from third generation sequencing technologies. This involves huge amounts of sequencing data, and such data contain errors due to the single molecule sequencing protocols employed. Taking advantage of combinatorial formulations helps to correct for these errors to solve the haplotyping problem. Various computational techniques such as dynamic programming, parameterized algorithms, and graph algorithms are used to solve this problem.
This thesis presents several contributions concerning the area of haplotyping. First, a novel algorithm based on dynamic programming is proposed to provide approximation guarantees for phasing a single individual. Second, an integrative approach is introduced to combining multiple sequencing datasets to generating complete and accurate haplotypes. The effectiveness of this integrative approach is demonstrated on a real human genome. Third, we provide a novel efficient approach to phasing pedigrees and demonstrate its advantages in comparison to phasing a single individual.Fourth, we present a generalized graph-based framework for performing haplotype-aware de novo assembly. Specifically, this generalized framework consists of a hybrid pipeline for generating accurate and complete haplotypes from data stemming from multiple sequencing technologies, one that provides accurate reads and other that provides long reads.
Sandy HEYDRICH
A tale of two packing problems: Improved algorithms and tighter bounds for online bin packing and the geometric knapsack problem
(Advisor: Prof. Rob van Stee, now Uni Siegen)
In this thesis, we deal with two packing problems: the online bin packing and the geometric knapsack problem. In online bin packing, the aim is to pack a given number of items of different size into a minimal number of containers. The items need to be packed one by one without knowing future items. For online bin packing in one dimension, we present a new family of algorithms that constitutes the first improvement over the previously best algorithm in almost 15 years. While the algorithmic ideas are intuitive, an elaborate analysis is required to prove its competitive ratio. We also give a lower bound for the competitive ratio of this family of algorithms. For online bin packing in higher dimensions, we discuss lower bounds for the competitive ratio and show that the ideas from the one-dimensional case cannot be easily transferred to obtain better two-dimensional algorithms. In the geometric knapsack problem, one aims to pack a maximum weight subset of given rectangles into one square container. For this problem, we consider offline approximation algorithms. For geometric knapsack with square items, we improve the running time of the best known PTAS and obtain an EPTAS. This shows that large running times caused by some standard techniques for geometric packing problems are not always necessary and can be improved. Finally, we show how to use resource augmentation to compute optimal solutions in EPTAS-time, thereby improving upon the known PTAS for this case.
Georg NEIS
Compositional Compiler Correctness Via Parametric Simulations
Compiler verification is essential for the construction of fully verified software, but most prior work (such as CompCert) has focused on verifying whole-program compilers. To support separate compilation and to enable linking of results from different verified compilers, it is important to develop a compositional notion of compiler correctness that is modular (preserved under linking), transitive (supports multi-pass compilation), and flexible (applicable to compilers that use different intermediate languages or employ non-standard program transformations). In this thesis, we formalize such a notion of correctness based on parametric simulations, thus developing a novel approach to compositional compiler verification.
Andreas TEUCKE
An Approximation and Refinement Approach to First-Order Automated Reasoning
With the goal of lifting model-based guidance from the propositional setting to first-order logic, I have developed an approximation theorem proving approach based on counterexample-guided abstraction refinement. A given clause set is transformed into a simplified form where satisfiability is decidable.This approximation extends the signature and preserves unsatisfiability:if the simplified clause set is satisfiable, so is the original clause set. A resolution refutation generated by a decision procedure on the simplified clause set can then either be lifted to a refutation in the original clause set, or it guides a refinement excluding the previously found unliftable refutation. This way the approach is refutationally complete. I have implemented my approach based on the SPASS theorem prover. On certain satisfiable problems, the implementation shows the ability to beat established provers such as SPASS, iProver, and Vampire.
Georg TAMM
Architectures for Ubiquitous 3D on Heterogeneous Computing Platforms
Wednesday, 09.05.2018, 14:00 h, in building D3 4, VisCenter DFKI
Today, a wide scope for 3D graphics applications exists, including domains such as scientific visualization, 3D-enabled web pages, and entertainment. At the same time, the devices and platforms that run and display the applications are more heterogeneous than ever. Display environments range from mobile devices to desktop systems and ultimately to distributed displays. While the capability of the client devices may vary considerably, the visualization experiences running on them should be consistent. The field of application should dictate how and on what devices users access the application, not the technical requirements to realize the 3D output.
The goal of this thesis is to examine the diverse challenges involved in providing consistent and scalable visualization experiences to heterogeneous computing platforms and display setups. We developed a comprehensive set of rendering architectures in the major domains of scientific and medical visualization, web-based 3D applications, and movie virtual production. To provide the required service quality, performance, and scalability for different client devices and displays, our architectures focus on the efficient utilization and combination of the available client, server, and network resources. We present innovative solutions that incorporate methods for hybrid and distributed rendering as well as means to stream rendering results. We establish the browser as a promising platform for accessible and portable visualization services. We collaborated with experts from the medical field and the movie industry to evaluate the usability of our technology in real-world scenarios.
Pascal MONTAG
Integrated Timing Verification for Distributed Embedded Real-Time Systems
The verification of timing properties with commercial tools based on static analysis has been available for safety-critical automotive systems for more than a decade. Although they offer many other advantagesin addition to safety guarantees, these tools are rarely applied in the automotive industry. This thesis analyses different possible reasons for this lack of application and suggests solutions where possible. Amongst the results of this thesis are technical findings, like the further increase of automation (e.g. for loop-bound detection) or the automatic reduction of WCET overestimation for highly variant systems. With regard to the development process, technical as well as non-technical solutions are presented that target the actual users of the timing verification, which range from software developers to system architects. The central result of this thesis is the integration of existing and newly developed timing verification methods and tools into a holistic development process approach called Timing Oriented Application Development (TOAD).
Wenbin LI
From Perception over Anticipation to Manipulation
From autonomous driving cars to surgical robots, robotic system has enjoyed significant growth over the past decade. With the rapid development in robotics alongside the evolution in the related fields, such as computer vision and machine learning, integrating perception, anticipation and manipulation is key to the success of future robotic system. In this talk, we summarize our efforts of exploring different ways of such integration to extend the capabilities of a robotic system to take on more challenging real world tasks. On anticipation and perception, we address the recognition of ongoing activity from videos. In particular we focus on long-duration and complex activities and hence propose a new challenging dataset to facilitate the work. On manipulation with perception, we propose an efficient framework for programming a robot to use human tools and evaluate it on a Baxter research robot. Finally, combining perception, anticipation and manipulation, we focus on a block stacking task. We first explore how to guide robot to place a single block into the scene without collapsing the existing structure and later introduce the target stacking task where the agent stacks blocks to reproduce a tower shown in an image. We validate our model on both synthetic and real-world settings.
Kerstin NEININGER
Towards the understanding of transcriptional and translational regulatory complexity
(Advisor: Prof. Dr. Volkhard Helms)
Considering the same genome within every cell, the observed phenotypic diversity can only arise from highly regulated mechanisms beyond the encoded DNA sequence. We investigated several mechanisms of protein biosynthesis and analyzed DNA methylation patterns, alternative translation sites, and genomic mutations. As chromatin states are determined by epigenetic modifications and nucleosome occupancy,we conducted a structural superimposition approach between DNA methyltransferase 1 (DNMT1) and the nucleosome, which suggests that DNA methylation is dependent on accessibility of DNMT1 to nucleosome–bound DNA. Considering translation, alternative non–AUG translation initiation was observed. We developed reliable prediction models to detect these alternative start sites in a given mRNA sequence. Our tool PreTIS provides initiation confidences for all frame–independent non–cognate and AUG starts. Despite these innate factors, specific sequence variations can additionally affect a phenotype. We conduced a genome–wide analysis with millions of mutations and found an accumulation of SNPs next to transcription starts that could relate to a gene–specific regulatory signal. We also report similar conservation of canonical and alternative translation sites, highlighting the relevance of alternative mechanisms. Finally, our tool MutaNET automates variation analysis by scoring the impact of individual mutations on cell function while also integrating a gene regulatory network.
Arunav MISHRA
Biomedical Knowledge Base Construction form Text and its Application in Knowledge-based Systems
(Advisor: Prof. Dr. Klaus Berberich, now HTW Saar)
Today in this Big Data era, overwhelming amounts of textual information across different sources with a high degree of redundancy has made it hard for a consumer to retrospect on past events. A plausible solution is to link semantically similar information contained across the different sources to enforce a structure thereby providing multiple access paths to relevant information. Keeping this larger goal in view, this work uses Wikipedia and online news articles as two prominent yet disparate information sources to address the following three problems:
• We address a linking problem to connect Wikipedia excerpts to news articles by casting it into an IR task. Our novel approach integrates time, geolocations, and entities with text to identify relevant documents thatcan be linked to a given excerpt.
• We address an unsupervised extractive multi-document summarization task to generate a fixed-length event digest that facilitates efficient consumption of information contained within a large set of documents. Our novel approach proposes an ILP for global inference across text, time, geolocations, and entities associated with the event.
• To estimate temporal focus of short event descriptions, we present a semi-supervised approach that leverages redundancy within a longitudinal news collection to estimate accurate probabilistic time models.
Extensive experimental evaluations demonstrate the effectiveness and viability of our proposed approaches towards achieving the larger goal.
Patrick ERNST
Biomedical Knowledge Base Construction from Text and its Application in Knowledge-based Systems
(Advisor: Prof. Dr. Gerhard Weikum)
While general-purpose Knowledge Bases (KBs) have gone a long way in compiling comprehensive knowledge about people, events, places, etc., domain-specific KBs, such as on health, are equally important, but are less explored. Consequently, a comprehensive and expressive health KB that spans all aspects of biomedical knowledge is still missing. The main goal of this thesis is to develop principled methods for building such a KB and enabling knowledge-centric applications. We address several challenges and make the following contributions:
– To construct a health KB, we devise a largely automated and scalable pattern-based knowledge extraction method covering a spectrum of different text genres and distilling a wide variety of facts from different biomedical areas.
– To consider higher-arity relations, crucial for proper knowledge representation in advanced domain such as health, we generalize the fact-pattern duality paradigm of previous methods. A key novelty is the integration of facts with missing arguments by extending our framework to partial patterns and facts by reasoning overthe composability of partial facts.
– To demonstrate the benefits of a health KB, we devise systems for entity-aware search and analytics andfor entity-relationship-oriented exploration.
Extensive experiments and use-case studies demonstrate the viability of the proposed approaches.
Roland LEIßA
Language Support for Programming High-Performance Code
(Advisor: Prof. Dr. Sebastian Hack)
Nowadays, the computing landscape is becoming increasingly heterogeneous and this trend is currently showingno signs of turning around. In particular, hardware becomes more and more specialized and exhibits different formsof parallelism. For performance-critical codes it is indispensable to address hardware-specific peculiarities. Because of the halting problem, however, it is unrealistic to assume that a program implemented in a general-purpose programming language can be fully automatically compiled to such specialized hardware while still delivering peak performance. One form of parallelism is single instruction, multiple data (SIMD).
In this talk, we first introduce Sierra: an extension for C++ that facilitates portable and effective SIMD programming. Second, we present AnyDSL. This framework allows to embed a so-called domain-specific language (DSL) into a host language. On the one hand, a DSL offers the application developer a convenient interface; on the other hand, a DSL can perform domain-specific optimizations and effectively map DSL constructs to various architectures. In order to implement a DSL, one usually has to write or modify a compiler. With AnyDSL though, the DSL constructs are directly implemented in the host language while a partial evaluator removes any abstractions that are required in the implementation of the DSL.
Mohammad MEHDI MONIRI
Gaze and Peripheral Vision Analysis for Human-Environment Interaction: Applications in Automotive and Mixed-Reality Scenarios
(Advisor: Prof. Dr. Wolfgang Wahlster)
Wednesday, 14.02.2018, 16:00 h, in building D3 2, Reuse seminar room -2.17
This thesis studies eye-based user interfaces which integrate information about the user's perceptual focus-of-attention into multimodal systems to enrich the interaction with the surrounding environment. We examine two new modalities:gaze input and output in the peripheral field of view. All modalities are considered in the whole spectrum of the mixed-reality continuum. We show the added value of these new forms of multimodal interaction in two important application domains: Automotive User Interfaces and Human-Robot Collaboration. We present experiments that analyze gaze under various conditions and help to design a 3D model for peripheral vision. Furthermore, this work presents several new algorithms for eye-based interaction, like deictic reference in mobile scenarios, for non-intrusive user identification, or exploiting the peripheral field view for advanced multimodal presentations. These algorithms have been integrated into a number of software tools for eye-based interaction, which are used to implement 15 use cases for intelligent environment applications. These use cases cover a wide spectrum of applications, from spatial interactions with a rapidly changing environment from within a moving vehicle, to mixed-reality interaction between teams of human and robots.
Jonas OBERHAUSER
Justifying The Strong Memory Semantics of Concurrent High-Level Programming Languages for System Programming
(Advisor: Prof. Dr. Wolfgang Paul)
Wednesday, 07.02.2018, 15:00 h, in E1 7, room 001
We justify the strong memory semantics of high-level concurrent languages, such as C11 or Java, when compiled to x86-like machines. Languages such as C11 guarantee that programs that obey a specific software discipline behave as if they were executed on a simple coherent shared memory multi-processor. Real x86 machines, on the other hand, do not provide a coherent shared memory, and compilers add slow synchronizing instructions to provide the illusion of coherency. We show that one software discipline that closely matches software disciplines of languages such as C11 and Java – in a nutshell, that racing memory accesses are annotated as such by the programmer – and one particular way to add relatively few synchronization instructions – in a nutshell, between an annotated store and an annotated load in the same thread – suffice to create this illusion.
The software discipline has to be obeyed by the program in the semantics of the high-level language, therefore allowing the verification effort to take place completely in the strong memory semantics of the high-level language. We treat a machine model with operating system support, and accordingly our theorems can be used to verify interruptible multi-core operating systems, including those where users can run unverified programs that do not obey the software discipline.
David HAFNER
Variational Image Fusion
(Advisor: Prof. Dr. Joachim Weickert)
Monday, 05.02.2018, 10:15 h, in E1 1, room 407
The main goal of this work is the fusion of multiple images to a single composite that offers more information than the individual input images. We approach those fusion tasks within a variational framework.
First, we present iterative schemes that are well-suited for such variational problems and related tasks. They lead to efficient algorithms that are simple to implement and well-parallelisable. Next, we design a general fusion technique that aims for an image with optimal local contrast. This is the key for a versatile method that performs well in many application areas such as multispectral imaging, decolourisation, and exposure fusion. To handle motion within an exposure set, we present the following two-step approach: First, we introduce the complete rank transform to design an optic flow approach that is robust against severe illumination changes.
Second, we eliminate remaining misalignments by means of brightness transfer functions that relate the brightness values between frames. Additional knowledge about the exposure set enables us to propose the first fully coupled method that jointly computes an aligned high dynamic range image and dense displacement fields.
Finally, we present a technique that infers depth information from differently focused images. In this context, we additionally introduce a novel second order regulariser that adapts to the image structure in an anisotropic way.
Linar MIKEEV
Numerical Analysis of Stochastic Biochemical Reaction Networks
(Advisor: Prof. Dr. Verena Wolf)
Numerical solution of the chemical master equation for stochastic reaction networks typically suffers from the state space explosion problem due to the curse of dimensionality and from stiffness due to multiple time scales.The dimension of the state space equals the number of molecular species involved in the reaction network and the size of the system of differential equations equals the number of states in the corresponding continuous-time Markov chain, which is usually enormously huge and often even infinite. Thus, efficient numerical solution approaches must be able to handle huge, possibly infinite and stiff systems of differential equations efficiently.
In this thesis, we present efficient techniques for the numerical analysis of the biochemical reaction networks. We present an approximate numerical integration approach that combines a dynamical state space truncation procedure with efficient numerical integration schemes for systems of ordinary differential equations including adaptive step size selection based on local error estimates. We combine our dynamical state space truncation with the method of conditional moments, and present the implementation details and numerical results. We also incorporate ideas from importance sampling simulations into a non-simulative numerical method that approximates transient rare event probabilities based on a dynamical truncation of the state space.
Finally, we present a maximum likelihood method for the estimation of the model parameters given noisy time series measurements of molecular counts. All approaches presented in this thesis are implemented as part of the tool STAR, which allows to model and simulate the biochemical reaction networks. The efficiency and accuracy is demonstrated by numerical examples.
Ezgi CICEK
Relational Cost Analysis
(Advisor: Dr. Deepak Garg)
Programming languages research has made great progress towards statically estimating the execution cost of a program. However, when one is interested in how the execution costs of two programs compare to each other (i.e., relational cost analysis), the use of unary techniques does not work well in many cases. In order to support a relational cost analysis, we must ultimately support reasoning about not only the executions of a single program, but also the executions of two programs, taking into account their similarities. This dissertation makes several contributions to the understanding and development of such a relational cost analysis. It shows how:
• Refinement types and effect systems can express functional and relational quantitative properties of pairs of programs, including the difference in execution costs.
• Relational cost analysis can be adapted to reason about dynamic stability, a measure of the update times of incremental programs as their inputs change.
• A sound and complete bidirectional type system can be developed (and implemented) for relational cost analysis.
© 2018 Saarbrücken Graduate School of Computer Science | CommonCrawl |
Triangular Polynomial Notation
Farrell Wu
In this article we will discuss a new type of notation for homogenous polynomials of $3$ variables, and its applications in solving Olympiad inequalities using the AM-GM inequality, Muirhead's Inequality, and Schur's Inequality. I suggest reading [1] first for a clearer explantion on the mechanics of this notation. This article is more focused on the applications to Olympiad inequalities
\documentclass[a4paper]{article}
\usepackage[english]{babel}
\usepackage[utf8x]{inputenc}
\usepackage[colorinlistoftodos]{todonotes}
\setlength\parindent{0pt}
\usepackage{geometry}
\geometry{margin=1.5in}
\title{Triangular Polynomial Notation}
\author{Farrell Eldrian Wu}
In this article we will discuss a new type of notation for homogenous polynomials of $3$ variables, and its applications in solving Olympiad inequalities using the AM-GM inequality, Muirhead's Inequality, and Schur's Inequality. I suggest reading [1] first for a clearer explantion on the mechanics of this notation. This article is more focused on the applications to Olympiad inequalities
\section{Triangular Notation}
Consider a triangle made up of $n$ rows, where there are $k$ entries on the $k$th row. This is similar to how Pascal's triangle is written. Label one corner (not the entry!) as $a$, the other $2$ as $b$ and $c$. (Figure 1) The degree of the polynomial is the side length (number of entries on each side) of the triangle. \\
\begin{tabular}{lllllllll}
& & & & a & & & & \\
& & & & 0 & & & & \\
& & & 0 & & 0 & & & \\
& & 0 & & 0 & & 0 & & \\
& 0 & & 0 & & 0 & & 0 & \\
b & & & & & & & & c
In the Triangular Notation, we fill in the coefficients of the terms as entries. Label each entry in the triangle with a ordered triple, which states the number of rows (can be taken in any of the three directions) that are below it plus one with respect to a certain corner; a, b, and c in that order. Refer to the ordered triples place on the entries of the triangle below. We let the entry with ordered triple $(x_a, x_b, x_c)$ be filled with the coefficient of the term in the polynomial with variable term $x^{x_a}x^{x_b}x^{x_c}$. An entry may be filled with the number $0$. (Figure 2) \\
\multicolumn{1}{c}{} & & & & a & & & & \\
& & & & (3,0,0) & & & & \\
& & & (2,1,0) & & (2,0,1) & & & \\
& & (1,2,0) & & (1,1,1) & & (1,0,2) & & \\
& (0,3,0) & & (0,2,1) & & (0,1,2) & & (0,0,3) & \\
b & & & & & & & & c
Note that this notation is similar to the Barycentric Coordinate system, with the reference triangle be the triangle made by the three corners. \\
In Figure $3$, the polynomial represented is $x^2y+y^2z+z^2x$, while in Figure $4$, the polynomial is $2x^2+3y^2+z^2+xy+2yz$. \\
\begin{tabular}{lllllll}
& & & 0 & & & \\
& & 1 & & 0 & & \\
& 0 & & 0 & & 1 & \\
0 & & 1 & & 0 & & 0 \\
\] \\
Figure 3 \\
\begin{tabular}{lllll}
& & 2 & & \\
& 1 & & 0 & \\
3 & & 2 & & 1 \\
When solving a homogenous polynomial inequality, expand and express both sides in this notation and then subtract one from the other. Most of the time, we want to show that the difference is greater than or equal to $0$. \\
\section{Addition, Subtraction, Multiplication (no Division)}
\subsection{Addition}
Add each term to each corresponding term.
\begin{tabular}{llllllllllllllllllllllll}
& & 1 & & & & & & & 3 & & & & & & & 4 & & \\
& 2 & & 2 & & & + & & 2 & & 2 & & & = & & 4 & & 4 & \\
1 & & 2 & & 1 & & & 1 & & 5 & & 4 & & & 2 & & 7 & & 5 \\
& & 12 & & & & & & & 63 & & & & & & & 75 & & \\
& 21 & & 23 & & & + & & 24 & & 76 & & & = & & 45 & & 99 & \\
56 & & 54 & & 34 & & & 53 & & 12 & & 86 & & & 109 & & 66 & & 120 \\
\subsection{Subtraction}
Subtract each term to each corresponding term
\begin{tabular}{llllllllllllllllllllllllllllll}
& & & 1 & & & & & & & & & 23 & & & & & & & & & -22 & & & \\
& & 2 & & 7 & & & & & & & 43 & & 3 & & & & & & & -41 & & 4 & & \\
& 3 & & 2 & & 8 & & & - & & 65 & & 12 & & -42 & & & = & & -62 & & -10 & & 50 & \\
4 & & 5 & & 9 & & 10 & & & 78 & & 64 & & -12 & & -1 & & & -74 & & -59 & & 21 & & 11 \\
\subsection{Multiplication}
See [1] for an explanation of it.
\section{Solving Inequalities with the Triangular Notation}
If we are trying to prove that a quatity $X$ is greater than a quantity $Y$, this is analogous to showing that $X-Y \geq 0$. Hence, to only deal with one term, we only consider the quantity $X-Y$ and show wthat it is $\geq 0$. The rest of this section shows how to deal with the single quantity that you want to show that it is greater than or equal to $0$. The best way to do so is by examples. \\
We first consider the two basic inequalities: Muirhead's Inequality and Schur's Inequality. Note that AM-GM is simply a special case of Muirhead's, so let's place that under Muirhead's. Look at [2] for the statements of the inequalities and the symmetric sum notation. \\
Exercise: Visualize both of the inequalities in the Triangular Notation. The Schur's is especially pretty! \\
But note that symmetric sums can be combined with AM-GN to be even more powerful! For example, if we consider each term separately. For example, $[5,3,0]+[3, 1, 0] \geq 2[4, 2, 0]$.
\subsection{Spotting Inequalities}
After coming up with the quantity that we wish to be nonnegative, construct inequalities such that when added up, gives the result that the quantity is nonnegative. \\
The recommended way is to find an inequality that has same equality case as the one that we are working with, and then subtract it from the current inequality. \\
Repeatedly do it until we get a triangle with all zeros. Afterwards, collect all the inequalities used.
\subsection{Writing a Solution}
After knowing which inequalities are used, collate them. The best way to write the solution is to write it in standard notation, writing the terms from left to write. Writing the solution using this method is not recommended because it is not well-known, and if you will use it in your solution, you still have to explain this notation, which takes time. Once you have the inequalities, you just have to state them and prove them. \\
Write down the clearing of denominators, resulting terms, and the final quantity that we wish to be nonnegative. It is permissible to write those using the regular expanded notation or the cyclic/symmetric sum notation. However, if you will be using the cyclic/symmetric sum notation, be careful as they might be confused. A cyclic sum over $k$ variables has $k$ terms, while a symmetric sum over $k$ variables has $k!$ terms. In a symmetric sum, some of the terms may be repeated. \\
Afterwards, state the inequalities that you wish to use, together with their concise proofs (i.e. this inequality is true by Muirhead's as [4,0,0] majorizes [3,1,0]). Do not forget to write the majorization condition. The inequalities have to be written one by one, and at the end, sum up all of them, then state that it implies that our desired quantity is greater than or equal to zero.
\section{Tips and Strategies}
\subsection{Strategies}
This notation is very helpful... but how do we even get to use it? In this subsection, I will discuss ways to convert inequalities to those that could be written with this method.
\subsubsection{Ravi's Substitution}
Ravi's Substitution is used when there is a condition that the variables $a$, $b$, and $c$ are the sides of a triangle. In the substitution, we substitute $a=y+z$, $b=x+z$, and $c=x+y$. This is necessary to be able to use the notation because once the quantity is expanded using the notation, it is usually hard to revert back into a factored form. Also, using the substitution most of the time gives an inequality that could be easily proven using Muirhead's / Schur's. See [4] for a proof and an in-depth discussion of Ravi's Substitution
\subsubsection{Making both sides polynomials}
To apply the notation, both of the sides have to be polynomials. Thus, we will have a problem if there is a denominator in either of the sides. To do this, as long as there are no square roots, we multiply both sides by the least common multiple of the denominators. The result is are polynomials for both sides.
Example: $\frac{a}{b}+\frac{b}{c}+\frac{c}{a} \geq 3$ is equivalnt to $a^2b+b^2c+c^2a \geq 3abc$.
\subsubsection{Limiting inequalities to Muirhead's, Schur's, SOS, and symmetric inequalities}
Those are the inequalities usually useful for dealing with terms of the same degree. Note that while Cauchy-Schwarz is very useful in inequalities at the start, it relies on a nice splitting of terms. However, this no longer exists, usually, once the quantity is expanded to the notation. Clearly, inequalities on convex also do not work well as it is hard to define functions after the quantity has been expanded. \\
Clearly, having square roots would be a big problem. When that happens, it is best to clear the sqaure roots using the QM-AM ineqality, the Cauchy-Schwarz Inequality, or others. Remember that the square roots have to be cleared first before this notation can be used. \\
However, it is possible to set the variables as $\sqrt{a}$, $\sqrt{b}$, and $\sqrt{c}$, or even $a^{\frac{1}{3}}$, $b^{\frac{1}{3}}$, $c^{\frac{1}{3}}$.
\subsubsection{The Outer Terms}
We are trying to prove that a certain quantity is nonnegative. According to Muirhead's Inequality, the more outer terms in the expanded quantity, and when you take the sum of them across $3$ variables, those are the ones which are greater than the inner terms. Hence they are more dangerous when they are negative. If there are terms more "outer" than those, then deal with those immediately before dealing wiht the inner terms. Note that it is not possible to use "inner" terms to cancel out "outer" terms. \\
For example, if we want to prove that this is nonnegative, we have to consider the outer -1s first before the inner terms. Once we are done with this, we could not remove the inner terms. \\
A good candidate to remove negative outer terms is Schur's Inequality, as 6 outer terms are removed (at the expense of only 3 more-outer terms). In addition, 3 inner terms, which are smaller, are also removed. Muirhead's usually cannot stand alone when there are lots of negative outer terms. this is where Schur's inequality comes in. However, one of the pitfalls of this notation is when both Muirhead's and Schur's (a.k.a. Schurhead) do not work. In this case, it is advisable to defer to SOS. [3]. A nice example could be seen below.
\subsubsection{Normalizing}
To use the notation, it is necessary for all the terms to be of the same degree. Now there will be a problem if the terms are not of the same degree. However, more of the time that this happens, the inequality usually comes with a nonhomogenous condition. We could move terms from side to side such that we can devise of a quick way to add or subtract degrees from terms. That is only when we can evaluate the sum and then express it in the notation. \\
The simplest kind to normalize are those with condition Prove that ... for all ... such that $x+y+z=1$. With this, we could substitute terms of degree $0$ with degree $1$ or vice versa. This is relatively simple. \\
Another simpler kind to normalize is the ones with the product condition, i.e. $xyz=1$. A helpful substitution is $x=\frac{a}{b}$, $y=\frac{b}{c}$, and $z=\frac{c}{a}$. Clearly $xyz=\frac{abc}{bca}=1$. Another helpful, but less popular substitution is $x=\frac{bc}{a^2}$, etc. The former is used to keep the degree low, while the latter is used to maintain symmetry. \\
Example: Normalize the inequality $(x^2+y^2+z^2)-(x+y+z) \geq 0$, if we have $x+y+z=3$.
to do this, we multiply $x+y+z$ by $\frac{x+y+z}{3}$. Then all of the terms in the LHS will be of degree $2$ and the condition is also satisfied.
\subsubsection{Defining new variables: forcing the equality case}
While the notation can technically still be used even though the equality case is not $a=b=c$, it will not be as useful. The main use of the notation is to see the symmetric / cyclic terms and how do they cancel out. If the equality case is not $a=b=c$, then using Muirhead's / Schur's directly would be misleading as they require $a=b=c$. Thus, we could define new variables, $a'$, $b'$, $c'$, such that $a'=b'=c'$. \\
For example, if we want to show that $9a^2+4b^2+c^2-12ab-4bc-6ac \geq 0$, putting this directly to our notation would not give much. It is better to perform the quite-intuitive substitution $3a=a'$, $2b=b'$, $c=c'$, to make it $a'^2+b'^2+c'^2-a'b'-b'c'-c'a' \geq 0$. In our notation, it is
& -1 & & -1 & \\
1 & & -1 & & 1 \\
and the application of Muirhead's can be more clearly seen. It is equivalent, when doubled, to $[2,0,0] \geq [1,1,0]$.
\subsubsection{Using knowledge about cyclicity / symmetry}
If you know that an expression is symmetric wrt the variables $a$ and $b$, it is possible to just fill in the symmetric terms' coefficients without further computations. This will save lots of time.
\subsection{Tips}
This notation can be messy if not done properly. Here are some tips to make solving inequalities with this notation much easier.
\subsubsection{Building your intuition}
After expanding the whole polyomial inequality in the notation, it may be confusing where to begin. Even though the entries are presented in a much clearer fashion, it may still be difficult to find the needed inequalities. The best way to do this is practice using the notation. When practicing, find inequalities without square roots. Afterwards, expand it and try to find the necessary applications of the inequalities. See [5] for lots of problems
\subsubsection{Knowing its limitations}
Clearly this notation cannot do everything, especially those with square roots. Once you see an inequality with square roots and you badly want to use this notation, check first if it can be made into a polynomial. If it can, then do such, normalize if needed, then use the notation. If there seems to be no viable way, then do not force it. The time may be better spent finding the "proper approach". (Note: this approach is not "improper", but it is not usually the expected solution. Most inequalities have beautiful solutions, and expanding everything is almost always not one of them. \\
Unfortunately, it is not only the square roots that could cause problems. Weird conditions like $abc=a+b+c+2$ seem to have no way out of it, as terms of degree $3$, $1$, and $0$ are involved. If you want to know how to work through conditions and substitutions, read chapter $1$ of [6]. However it is still best to use your common sense on which can be done with this and cannot. \\
There are some inequalities, on the other hand, which can be expressed in this notation, but will be hoorendously impractical. If the degree is going above $10$, and the terms are going to the ten-thousands, hundred-thousands, or even millions, it may be best to give up with this notation. In those cases, it might be hard to find the necessary inequalities. Even after solving it, writing the solution will be another big problem. \\
Basically, know the limitations of this notation. It can be very helpful, but going too far with it is not helpful at all.
\subsubsection{Checking Calculations}
Most of the time, the process of expanding has many steps. In the more complicated problems, the coefficient of terms can go up to the hundreds or even thousands. The best way is to ensure the sum of coefficients "makes sense" in every step. After finishing every step, calculate the sum of coefficients. See if it matches the sum of coefficients when written in the notation. They have to match. Otherwise, something went wrong.
\subsection{Scratchwork Organization}
If you are using this notation with paper and pen, the scratchwork has to be organized. It is very likely that the degree of the polynomial could go up to $10$ and the terms in the thousands, so it is advisable to use $1$ paper per triangle diagram. Likewise, leave a big space in between rows so that sums can be clearly seen, especially in multiplication!
\subsubsection{Multiplying Terms}
When multiplying terms, give a large space in the scratch paper for it. Instead of writing each of the distributed sums one by one, just do it in one large triangle. Take it one sum at a time, so that you would not get lost. If there is an error here, however, you have to redo the whole multiplication as it is nearly impossible to spot the error as there are many entries written in the same blank. See the Solutions for some examples.
\subsubsection{Cyclic Adding Shortcuts}
It is possible to divide the triangle into three parts which are cyclically identical. Once you are done computing for one of the parts, you could cyclically fill up the rest
\subsubsection{Checking Coefficients}
After every step, calculate the supposed sum of coefficients and the sum of coefficients in the resulting expression. They must be equal. If they are unequal, there is something wrong.
\section{Examples}
In this section I will work through $2$ inequalities. They have already been reduced to the form $X \geq 0$. We are going to show that the given expression is nonnegative
\subsection{Example 1}
& & -1 & & -1 & & \\
& -1 & & 0 & & -1 & \\
2 & & -1 & & -1 & & 2 \\
There are $3$ ways to approach this. One is to notice that the expression is basically $[3,0,0]-[2,1,0] \geq 0$. But that is equivalent to $[3,0,0] \geq [2,1,0]$. This is true by Muirhead's as $[3,0,0]$ majorizes $[2,1,0]$. \\
The second way is to break up the sum by the $3$ outer rows. Each of them is a $2$-variable application of Muirhead's on $a^3+b^3 \geq a^2b+ab^2$ and similar cyclic terms. This, again, is true by Muirhead's as $[3,0]$ majorizes $[2,1]$. \\
The third way is much more complicated. It is possible to use Schur's Inequality, which is
We then subtract it from the original quantity, to get
& 0 & & -3 & & 0 & \\
and then it becomes the AM-GM inequality on $3$ variables: $a^3+b^3+c^3 \geq 3abc$.
\begin{tabular}{lllllllllllll}
& & & & & & 8 & & & & & & \\
& & & & & 4 & & 4 & & & & & \\
& & & & 1 & & 10 & & 1 & & & & \\
& & & 10 & & -26 & & -26 & & 10 & & & \\
& & 1 & & -26 & & 42 & & -26 & & 1 & & \\
& 4 & & 10 & & -26 & & -26 & & 10 & & 4 & \\
8 & & 4 & & 1 & & 10 & & 1 & & 4 & & 8 \\
The main difficulty here is the positive $42$ at the center. A way to deal with this is Schur's Inequality. Look at the $2$ applications of Schur's Inequality below. Both of the values are at least zero. $42$ is too big to be finished by one application of Schur's, as for one application only, the terms have to be at least $14$, but there are no positive terms that are at least $14$.
& & & & 0 & & 0 & & 0 & & & & \\
& 0 & & 0 & & -10 & & -10 & & 0 & & 0 & \\
& & & 0 & & -10 & & -10 & & 0 & & & \\
0 & & 0 & & 0 & & 0 & & 0 & & 0 & & 0 \\
Subtracting their sum from the original triangle gives
& & & 0 & & -6 & & -6 & & 0 & & & \\
& & 1 & & -6 & & -18 & & -6 & & 1 & & \\
& 4 & & 0 & & -6 & & -6 & & 0 & & 4 & \\
8 & & 4 & & 1 & & 0 & & 1 & & 4 & & 8 \\\end{tabular}
But then notice that it is equal to $4\sum_{sym} a^6+4\sum_{sym} a^5b+\sum_{sym}a^4b^2-6\sum_{sym}a^3b^2c-3\sum_{sym}a^2b^2c^2$, or $4[6,0,0]+4[5,0,0]+[4,2,0] \geq 6[3,2,1]+3[2,2,2]$. \\
We know by Muirhead's that $4[6,0,0] \geq 4[3,2,1]$, $2[5,1,0] \geq 2[3,2,1]$, $2[5,1,0] \geq 2[2,2,2]$, $[4,2,0] \geq [2,2,2]$. Adding all of these up gives that $4[6,0,0]+4[5,0,0]+[4,2,0] \geq 6[3,2,1]+3[2,2,2]$ is nonnegative.
\section{Problems}
These are problems from various sources. They are arranged roughly in increasing order of difficulty. \\
1. (Japan TST 2004): If $a+b+c=1$, $\frac{1+a}{1-a}+\frac{1+b}{1-b}+\frac{1+c}{1-c} \leq \frac{2a}{b}+\frac{2b}{c}+\frac{2c}{a}$. \\
2. If $a+b+c=1$, $(\frac{1}{a}+1)(\frac{1}{b}+1)(\frac{1}{c}+1) \geq 64$. \\
3. If $a+b+c=1$, $(\frac{1}{a}-a)(\frac{1}{b}-1)(\frac{1}{c}-1) \geq 8$. \\
4. (Romania ???): If $a+b+c=3$, $a^2+b^2+c^2+abc \geq 4$. \\
5. (Mildorf): If $a+b+c=1$, $a^3+b^3+c^3+6abc \geq \frac{1}{4}$. \\
6. If $a+b+c=1$, $5(a^2+b^2+c^2) \leq 6(a^3+b^3+c^3+1)$. \\
7. (APMO 1998): $\big(1+\frac{x}{y}\big)(\big(1+\frac{y}{z}\big)\big(1+\frac{z}{x}\big) \geq 2+\frac{2(x+y+z}{^3\sqrt{xyz}}$. \\
8. (Secrets in Inequalities): $\frac{a^3}{a^3+b^3+abc}+\frac{b^3}{b^3+c^3+abc}+\frac{c^3}{c^3+a^3+abc}$. \\
9. (Secrets in Inequalities): If $abc=1$, $\frac{1}{a^2+a+1}+\frac{1}{b^2+b+1}+\frac{1}{c^2+c+a} \geq 1$. \\
10. (Mildorf): If $abc=1$, $a+b+c \leq a^2+b^2+c^2$. \\
11. (Belarus 1999): If $a^2+b^2+c^2=3$, $\frac{1}{1+ab}+\frac{1}{1+bc}+\frac{1}{1+ca} \geq \frac{3}{2}$. \\
12. (Bulgaria TST 2003): If $a+b+c=3$, show that $\frac{a}{1+b^2}+\frac{b}{1+c^2}+\frac{c}{1+a^2} \geq \frac{3}{2}$. \\
13. $\frac{b+c}{a}+\frac{c+a}{b}+\frac{a+b}{c} \geq \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}+9$. \\
14. (Japan 1997): $\frac{(b+c-a)^2}{(b+c)^2+a^2}+\frac{(c+a-b)^2}{(c+a)^2+b^2)}+\frac{(a+b-c)^2}{(a+b)^2+c^2)} \geq \frac{3}{5}$. \\
15. (Mathematical Reflections): $\frac{ab}{3a+4b+2c}+\frac{bc}{3b+4c+2a}+\frac{ca}{3c+4a+2b} \leq \frac{a+b+c}{9}$. \\
16. (Problems from the Book): If $xy+yz+zx+2xyz=1$, $\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \geq 4(x+y+z)$. (Hint: you need a substitution to apply the notation)
\section{References}
[1] Hamrick, Brian. "The Art of Dumbassing." Thomas Jefferson High School for Science and Technology. 2 July 2010. Web. 3 Feb. 2015.<http://www.tjhsst.edu/~2010bhamrick/files/dumbassing.pdf>. \\
[2] "Cyclic and Symmetric Sums: An Introduction." UWA Academy for Young Mathematicians Lecture Notes. The University of Western Australia SCHOOL OF MATHEMATICS and STATISTICS, 1 Jan. 2010. Web. 3 Feb. 2015.
<http://staffhome.ecm.uwa.edu.au/~00021149/Academy/2010/ineqcycsym.pdf>. \\
[3] Chen, Evan. "Supersums of Square-Weights: A Dumbass's Perspective." All Roads Lead to MIT. 6 Jan. 2013. Web. 3 Feb. 2015.
<http://www.mit.edu/~evanchen/handouts/SOSDumbass/SOSDumbass.pdf>. \\
[4] Kirk, Andrew. "Ravi Substitution Explained." Mathematics. 13 Feb. 2011. Web. 3 Feb. 2015. <https://mblog1024.wordpress.com/2011/02/14/ravi-substitution-explained/>. \\
[5]"AoPS Forum - Inequalities • Art of Problem Solving." AoPS Forum - Inequalities • Art of Problem Solving. Art of Problem Solving, 3 Feb. 2003. Web. 3 Feb. 2015.
<http://www.artofproblemsolving.com/Forum/viewforum.php?f=32>. \\
[6] Andreescu, Titu, and Gabriel Dospinescu. "Some Special Substitutions." Problems from the Book. 2nd ed. Plano, TX: XYZ, 2010. Print. \\
[7] Pham Kim, Hung. "AM-GM Inequality." Secrets In Inequalities. Vol. 1. Zalau: Gil House, 2007. 15-32. Print.\\
[8] Manfrino, Radmila, Jose Ortega, and Rogelio Delgado. "A Fundamental Inequality, Arithmetic Mean-geometric Mean." Inequalities a Mathematical Olympiad Approach. Basel: Birkhauser, 2009. 7-13. Print. | CommonCrawl |
communications chemistry
Allosteric effects in cyclophilin mutants may be explained by changes in nano-microsecond time scale motions
Structure determination of high-energy states in a dynamic protein ensemble
John B. Stiller, Renee Otten, … Dorothee Kern
Rescue of conformational dynamics in enzyme catalysis by directed evolution
Renee Otten, Lin Liu, … James S. Fraser
Observation of conformational changes that underlie the catalytic cycle of Xrn2
Jan H. Overbeck, David Stelzig, … Remco Sprangers
Retrieving functional pathways of biomolecules from single-particle snapshots
Ali Dashti, Ghoncheh Mashayekhi, … Abbas Ourmazd
Confrontation of AlphaFold models with experimental structures enlightens conformational dynamics supporting CYP102A1 functions
Philippe Urban & Denis Pompon
The physical origin of rate promoting vibrations in enzymes revealed by structural rigidity
Yann Chalopin
Energy landscapes from cryo-EM snapshots: a benchmarking study
Raison Dsouza, Ghoncheh Mashayekhi, … Abbas Ourmazd
Origin of conformational dynamics in a globular protein
Adam M. Damry, Marc M. Mayer, … Roberto A. Chica
Dissecting C−H∙∙∙π and N−H∙∙∙π Interactions in Two Proteins Using a Combined Experimental and Computational Approach
Jia Wang & Lishan Yao
Pattama Wapeesittipan1,
Antonia S. J. S. Mey ORCID: orcid.org/0000-0001-7512-52521,
Malcolm D. Walkinshaw ORCID: orcid.org/0000-0001-5955-93252 &
Julien Michel ORCID: orcid.org/0000-0003-0360-17601
Communications Chemistry volume 2, Article number: 41 (2019) Cite this article
Enzyme mechanisms
This work investigates the connection between stochastic protein dynamics and function for the enzyme cyclophilin A (CypA) in wild-type form, and three variants that feature several mutations distal from the active site. Previous biophysical studies have suggested that conformational exchange between a 'major' active and a 'minor' inactive state on millisecond timescales plays a key role in catalysis for CypA. Here this hypothesis is addressed by a variety of molecular dynamics simulation techniques. Strikingly we show that exchange between major and minor active site conformations occurs at a rate that is 5 to 6 orders of magnitude faster than previously proposed. The minor active site conformation is found to be catalytically impaired, and decreased catalytic activity of the mutants is caused by changes in Phe113 motions on a ns-μs timescale. Therefore millisecond timescale motions may not be necessary to explain allosteric effects in cyclophilins.
A major goal of modern molecular biophysics is to clarify the connection between protein motions and enzymatic catalysis1,2,3. A wide range of experimental methods, e.g. neutron scattering, X-ray crystallography, NMR, or vibrational spectroscopy have been used to characterize internal protein motions occurring from femtosecond to second timescales4,5. While there is broad consensus that protein motions are implicated in catalysis, there is much debate around the role of conformational changes occurring on a millisecond timescale, and several studies have linked changes in millisecond protein motions with changes in enzymatic function6,7,8,9. However, it remains unclear whether such motions have a causal link to catalysis, or are merely a manifestation of the inherent flexibility of proteins over a broad range of timescales.
There have been vigorous debates about the meaning of dynamics in the context of enzymatic catalysis10,11,12. In the framework of transition state theory, the reaction rate is given by Eq. 1:
$$k = A(T)e^{ - \Delta G^\ddagger (T)/RT}$$
where T is the temperature and R the gas constant. The pre-exponential term A(T) includes contributions from non-statistical motions such as re-crossing or tunnelling, The exponential term involves the activation free energy of the chemical step \(\Delta G^\ddagger (T)\). If transitions between reactant states are fast compared to the time scale of the chemical reaction, \(\Delta G^\ddagger \left( T \right)\) is the free energy difference between the thermally equilibrated ensembles describing the reactant and transition states13,14. Non-statistical motions described by A(T) have typically been found to make a small contribution to rate constants with respect to the exponential term that involves equilibrium fluctuations of the protein and solvent degrees of freedom15.
The current work is concerned with the connection between rates of thermally equilibrated motions, and catalysis in enzymes. Specifically, the focus is on clarifying the nature of protein motions implicated in catalysis for the well-studied enzyme cyclophilin A (CypA). CypA is a member of the cyclophilin family of peptidyl-prolyl isomerases which catalyzes the cis/trans isomerization of amide groups in proline residues16. CypA plays an essential role in protein folding and regulation, gene expression, cellular signaling and the immune system. Notably, CypA is involved in the infectious activity and the viral replication of HIV-117. Accordingly, CypA has been the subject of structure-based drug design efforts for decades18,19,20. Because of its significance as a medical target, the catalytic mechanism of CypA has been the subject of extensive studies2,3,21,22,23,24,25,26,27,28,29,30. Computational studies have shown that the speedup of the of cis/trans isomerization rate of the prolyl peptide bond is a result of preferential transition state stabilization through selective hydrogen bonding interactions in the active site of CypA26,30. Figure 1a depicts key interactions between the substrate and active site residues, whereas Fig. 1b highlights the relevant ω angle of the substrate used to track the cis/trans isomerization reaction.
The active site of cyclophilin A. a Key residues in the active site of cyclophilin A that form hydrogen bonds (cyan sticks, dashed lines) or are in contact (purple sticks) with the transition state form of the peptide Ace-AAPF-Nme (orange sticks). For clarity, the Phe side-chain of the substrate is represented as transparent sticks. The distal residues Ser99, Cys115 and Ile97 are depicted in green. b The ω torsional angle of -Ala2-Pro3- is used to track the progression of the isomerization reaction between cis and trans forms
Elegant NMR relaxation experiments by Eisenmesser et al.27 have also characterized the existence of intrinsic motions in apo CypA that couple a 'major' state M with a 'minor' conformational state m with a rate constant \(k_{M \to m}\)= 60 s−1. Fraser et al. later used ambient temperature X-ray crystallographic data to determine a high-resolution structure of this CypA state m, revealing an interconversion pathway with the 'major' state M that involves coupled rotations of a network of side-chains involving residues Ser99, Phe113, Met61, and Arg55. To establish the relevance of this 'minor' state m to catalysis, the distal residue Ser99 was mutated to Thr99 (now only referred to as ST). Further X-ray and NMR measurements on the free enzyme confirmed that the ST mutant increased the population of the m state, while decreasing the conversion rate \(k_{M \to m}\) to 1 s−1 31. Remarkably, additional NMR experiments established that this 60-fold decrease in conversion rate between M and m states in the ST mutant correlates with a ca. 70-fold decrease in bidirectional isomerization rate (\(k_{iso} = k_{cis \to trans} + k_{trans \to cis}\)) of a model substrate with respect to wild-type (WT). The effect is comparable to rate decreases observed for mutations of key active site residues such as Arg5531. More recently, two further mutants were reported in an effort to rescue the lost enzymatic activity of ST. These mutations were S99T and C115S (now only referred to as STCS), or S99T, C115S, and I97V (now only referred to as STCSIV). The two newly introduced mutants recover the enzyme activity to some extent, which correlates with an increase in \(k_{M \to m}\) values32.
While this body of work suggested a link between millisecond time scale motions and catalysis in enzymes, there is currently no detailed mechanistic explanation for the decreased catalytic activity of the mutants. The present study uses a variety of extensive equilibrium and biased molecular dynamics (MD) simulations to clarify the link between catalytic activity and rates of molecular motions of CypA in wild-type and the three mutant variants. We show that the MD simulations reproduce well X-ray crystallography derived evidence for a shift in populations of major and minor active site conformations between the wild-type and mutant forms. Remarkably exchange between these active site conformations occurs at a rate that is five to six orders of magnitude faster than previously proposed. We show that the decrease in catalytic activity of the CypA mutants with respect to wild-type may be explained by changes in motions of residue Phe133 on a ns–μs timescale. Therefore millisecond time scale motions previously described in the literature may not be necessary to explain allosteric effects in cyclophilins.
Major and minor conformations exchange on ns timescales
Fraser et al. have described the proposed 'major' and 'minor' states according to sets of values of χ1 (Phe113, Ser/Thr99), χ2 (Met61) and χ3 (Arg55) angles31,33. These dihedrals as well as the side-chain dihedrals χ1 of Ile97 and Cys115 were used to construct a Markov state model (MSM) to obtain quantitative information on thermodynamic and kinetic properties of the WT protein and the three experimentally studied mutants. The consistency of the MSMs was evaluated using standard protocols and by evaluating robustness of the findings with respect to a range of model parameters (See Supplementary Figures 1–3 and Supplementary Tables 1 and 2). In the case of WT the accuracy of the MSM was additionally evaluated by back-calculation of previously reported NMR observables34. The MSM yields predictions of observables that show broadly similar accuracy to that of the NMR ensembles of Chi et al.35 and Otter et al.36 (see Supplementary Figures 4). Thus the simulations were deemed sufficiently consistent with experimental data to warrant further analyses.
The X-ray structures of the key active site dihedrals in their dominantly populated states (if multiple occupancy is observed) are shown in Fig. 2a for WT and ST, Fig. 2b for WT and STCS, and Fig. 2c for WT and STCSIV mutants. The most striking feature of the 'major' and 'minor' conformations are the rotameric states of χ1 of Phe113 from the crystal structures, which in the 'minor' conformation is χ1 ≈ −60°. This will be referred to as the 'out' conformation. In contrast, the 'major' state χ1 ≈ 60°, takes an 'in' conformation. In Fig. 2d–f crystal structure occupancies for Phe113 χ1 are compared to the MSM-derived dihedral distributions comparing WT and ST, WT and STCS, and WT and STCSIV respectively. The simulations suggest that in apo WT the Phe113 'in' and 'out' orientations are equally likely, which is consistent with the relatively similar occupancies of the two rotamers in the X-ray structure (occupancies = 0.63 and 0.37 respectively)31. In apo ST there is a significant population shift towards the 'out' orientation (χ1 = −60°), and the 'in' orientation has a marginal population (ca. 1%), see Fig. 2d. This agrees with the X-ray structure of ST where only the Phe113 'out' rotamer is observed (occupancy = 1.0). This also agrees with J-coupling measurements that show the dominant Phe113 χ1 angle is ca. −60° in ST31. In the STCS and STCSIV mutants the 'in' rotamer is also destabilized with respect to wild-type but to a lesser extent (populations of ca. 16% and 17% respectively). Though only one 'out' rotamer was resolved in the X-ray structure of STCS (Fig. 2e), a major 'out' and a minor distorted 'in' rotamer (χ1 = + 31°, occupancy 0.21) are observed in the X-ray structure of STCSIV (Fig. 2f). Rotamers of other side-chain dihedrals of the key residues for all WT and mutants are found in Supplementary Figures 5 and 6.
Comparison of X-ray and MSM-derived conformational preferences of Phe113. The X-ray structures of WT (blue and cyan) are compared with ST (red) (a), STCS (purple) (b) and STCSIV (dark and light green) (c)31,32. The MSM-derived probability distributions of χ1 in Phe113 for WT and ST (d), STCS (e) and STCSIV (f) are depicted as solid lines. The X-ray crystallography χ1 values are depicted for WT and mutants with their respective occupancies as dashed lines31,32
Surprisingly the Phe113 χ1 dihedral was observed to flip frequently in MD trajectories of 200 ns duration (Supplementary Figures 7–9), suggesting faster motions than determined by NMR experiments. Therefore the MSMs were used to obtain quantitative information on transition rates between 'in' and 'out' states as defined by the Phe113 χ1 rotamer. Table 1 summarises the MSM results. The exchange rates vary from 208 ± 9 μs−1 (ST) to 39 ± 3 μs−1 (STCS). Remarkably these values are five orders of magnitude faster than the exchange rates that have been determined by NMR measurements for motions involving Phe113.
Table 1 Thermodynamics and kinetics of the Phe113 in/out flip
The minor conformation is catalytically inactive
Given that the timescales of rotations of Phe113 in the four CypA variants appear much faster than previously suggested, attention turned next to substrate bound CypA simulations. Results from umbrella sampling (US) simulations were used to quantify the isomerization free energy profile for WT and the ST mutant and investigate the role of Phe113 motions in catalysis (See Supplementary Figure 10).
The isomerization free energy profiles for WT and ST mutant with the side-chain of the Phe113 in an 'in' and 'out' conformations are shown in Fig. 3a, b respectively. Ladani and Hamelberg28 have previously shown that fixed-charge classical force fields reproduce the energetics of amide bond rotation reasonably well due to relatively small changes in intramolecular polarization during this process. The calculated activation free energy for the uncatalyzed cis→trans isomerization process in water is consistent with experimental data (20.1 ± 0.1 kcal mol−1 vs ca. 19.3 kcal mol−1 for the related substrate Suc-AAPF-pNA at 283 K)37,38. The free energy profile for the substrate bound to CypA WT and ST in the 'in' conformation shows that the enzyme catalyzes the isomerization reaction in both directions via a transition state with a positive ω value (ca. 90–100°) equally well (Fig. 3a). There is a more significant decrease in activation free energy for trans→cis (ca. −6 kcal mol−1) than for cis→trans with less than 1 kcal mol−1 difference between WT and ST, because the cis form is more tightly bound to CypA than the trans form. According to Fig. 3b, there is no catalytic benefit from the 'out' conformation of the enzyme since the activation free energy of the isomerization reaction in CypA is similar to that of the substrate in water. The calculated free energy profiles for isomerization reactions in STCS and STCSIV show a similar trend (Supplementary Figure 11).
Energy profiles in the Phe113 'in' and 'out' conformations. a Isomerization free energy profiles (in kcal mol−1) for the substrate AAPF in water (black), and bound to WT (blue) or ST mutant (red) forms of CypA with starting structures in the 'in' conformation. The free energies of the trans conformation were set to zero at ω = 180°. Error bars represent one standard error of the mean. The table shows the activation free energies for both directions of the isomerization reaction. (b) same as (a), but with stimulations starting in a 'out' configuration
Transition -state destabilization in the minor conformation
Further analysis of the US trajectories shows that for the simulations started in the 'in' configuration in both WT and ST the transition -state region (ω ca. 90–100°) is electrostatically stabilized by more negative Coulombic interactions between substrate and binding site atoms as shown in Fig. 4a. Figure 4b breaks down the different contribution of active site residues, showing that Arg55, Trp121, Asn102, His126, and Gln63 are important for the stabilization of the transition state ensemble via hydrogen bonding interactions as shown in Fig. 4e. In contrast, Fig. 4c shows that for simulations in the 'out' configuration no transition state stabilization through electrostatic interactions is observed, this is further reflected by the per-residue split of interaction energy contribution at the transition state in Fig. 4d and the lack of hydrogen bond formation in Fig. 4f. Hydrogen bonding probabilities for simulations from the 'in' and 'out' starting conformations are shown in Supplementary Figures 12–14. A similar picture holds for the STCS and STCSIV mutants (Supplementary Figure 15). Electrostatic interactions between the substrate and the solvent generally disfavour the transition state region in the 'in' conformation for all variants, consistent with a tightening of interactions of the active site residues with the transition state. For simulations carried out in the 'out' conformation no preferential electrostatic stabilization of a substrate state by the solvent is observed along the reaction coordinate, consistent with the lack of catalytic activity of CypA in this conformational state (Supplementary Figure 16)
Structural basis for the differential catalytic activity of the Phe113 in and out conformations. a Electrostatic energies between the substrate and active site residues as a function of the ω angle in WT (blue) and the ST systems (red) with simulations started from the 'in' configuration. b Average electrostatic energies per-active site residues at the transition state region from (a). c same as (a) with simulations started from the 'out' configuration. d same as (b) with simulations started in the 'out' conformation. Error bars denote the standard error of the mean. e and (f) typical hydrogen bonding pattern at the transition state for simulations started in the 'in' and 'out' conformation respectively
Preorganization explains decreased in activity of the mutants
Taken together the MSM and US data suggest a mechanistic explanation for the effect of distal mutations on the catalytic activity of cyclophilin A. In WT free form the enzyme rapidly interconverts between a catalytically active Phe113 'in' form and a catalytically inactive Phe113 'out' form. Because the interconversion rate between in and out forms (ca. 7 × 107 s−1) is faster than the substrate binding rate as suggested by NMR experiments (ca. 2 × 104 s−1, based on kon rate ca. 2 × 107 s−1 M−1 and substrate concentration ca. 1 mM)39 the free enzyme rapidly equilibrates between catalytically active and inactive forms before substrate binding (Fig. 5a). For the mutants, the interconversion rates between catalytically active and inactive forms are still within the μs−1 timescale, but the equilibrium is shifted towards the catalytically inactive form (Fig. 5b), thus the mutants are less pre-organized than WT and the overall catalytic activity is decreased.
Proposed mechanism for allosteric inhibition of cyclophilin A function. a Catalysis in WT, with the favoured route being the 'in' conformations, which are similarly populated to the 'out' conformations. b Catalysis in the mutants still occurs through the 'in' conformations, which have a lower population than the 'out' conformations
In the case of the ST mutant and WT forms, Fraser et al.31 have reported bi-directional on-enzyme isomerization rates \((k_{cis \to trans} + k_{trans \to cis})\) by NMR spectroscopy, and found a ratio of 68 ± 13 between WT and ST. According to the model proposed in Fig. 5 and by combining the MSM-derived populations and the US-derived activation free energies, a ratio of 12 < 46 < 176 can be derived from the simulations (see Supplementary Note 2 for details). The uncertainty from the simulations is larger than that of the measurements because small variations in activation free energies contribute large change in catalytic rates. Thus the model described in Fig. 5 appears consistent with experimental data for WT and ST. No bidirectional isomerization rates have been reported for the STCS and STCSIV mutants32. However, the STCS and STCSIV mutants show populations of the catalytically active Phe113 'in' conformation that are intermediate between WT and ST, which is consistent with their increased catalytic activity with respect to ST.
A defining feature of this model is that the χ1 rotamers of a number of active-site side-chains such as Gln63, Ile/Val97, Phe113, Cys/Ser115 flip in WT and mutants on ns–μs timescales. Back-calculation of Cβ–Cγ order parameters shows that this effect is captured by a decrease in S2 values upon increasing the averaging window from 10 to 100 ns (Supplementary Figure 17). Motions on these timescales are too rapid to be detected by CPMG or CEST NMR experiments that have been used extensively to study μs–ms processes in cyclophilin A3,25,31,40,41. Likewise NMR relaxation experiments cannot detect motions on this timescale as they are limited to processes occurring faster than the tumbling time τc of cyclophilin A (ca. 10 ns)42. Residual Dipolar Couplings (RDCs) can, however, provide information about dynamic orientation of inter-nuclear vectors on the supra-τc time scale43. Such experiments have been reported for backbone and methyl-RDCs in ubiquitin43,44. Therefore the model predictions can be experimentally tested with combined nuclear spin relaxation and RDC based model-free analyses coupled with a labelling scheme that resolves χ1 side-chain motions43,45.
This work highlights the potential of detailed molecular simulation studies to guide the interpretation of biophysical measurements for the elucidation of allosteric mechanisms in proteins46. Previous work has suggested that exchange on millisecond timescales between conformational states in CypA are linked to its catalytic cycle27, leading to a proposal for a slow exchange between a 'major' and a 'minor' state of a set of side chain rotamers linking distal residue Ser99 to active-site residues27,31. The present results do not support or reject this hypothesis because the MD simulations used here do not resolve motional processes occurring on timescales slower than microseconds. However a major finding of this study is that transitions between 'in' and 'out' rotamers of Phe 113 in WT and mutants occur on a time scale of ns–μs, thus five to six orders of magnitude faster than suggested by earlier NMR relaxation dispersion measurements31. Nevertheless the simulations reproduce well the population shifts in Phe113 rotamers observed in room-temperature X-ray crystallography experiments. This suggests that the X-ray structures may have resolved motional processes occurring on a distinct timescales from the processes resolved by CPMG experiments. Indeed in reported CPMG experiments the millisecond motions of Phe113 are coupled to a large network of ca. 30 residues31, whereas the χ1 rotameric flip observed in the simulations, is a largely local motion.
Nevertheless, the simulations suggest that a local 'in' to 'out' rotation of Phe113 is sufficient to abrogate catalysis in cyclophilin A, and variations of exchange parameters on the ns–μs timescale between these two conformational states appear sufficient to explain the decreased catalytic activity of the ST, STCS, STCSIV mutants with respect to WT. Therefore it is advisable to carry out additional experiments to confirm the existence of Phe113 χ1 rotations on the ns–μs timescale before causally linking catalysis to millisecond time scale motions. On the computational side, efforts should focus on advancing MD methodologies such that millisecond timescale processes observed in experiments can be resolved in atomistic details.
The contribution of protein flexibility on the ps–ns and μs–ms timescales to enzymatic catalysis has been the focus of several computational and experimental studies3,8,10,13,15,25,27,31,32,47. Our work suggests that more efforts should be directed at resolving conformational processes on the ns–μs timescale. This has important conceptual implications for enzyme design and optimization strategies.
Systems preparation
Models for apo/substrate bound human CypA of the WT and ST were prepared for MD simulations from PDB structures 3K0N (R = 1.39 Å) and 3K0O (R = 1.55 Å) respectively. For apo STCS and STCSIV two structures were prepared from PDB structures 6BTA (R = 1.5 Å) and 5WC7 (R = 1.43 Å) and also by mutating residues in WT using Schrödinger's Maestro47. For WT the major conformation of 3K0N (altloc A, occupancy 0.63) was retained. For STCS and STCSIV the residues with higher occupancy were chosen for initial structures. Supplementary Tables 3 and 4 summarise all simulations conducted in this study. The proteins were solvated in a rhombic dodecahedron box of TIP3P water molecules with edges extending 1 nm away from the proteins and chloride counter-ions were added to neutralise the overall net-charge. The Charmm22* forcefield48 was used to describe protein atoms in the apo simulations because previous work from Papaleo et al.33 has shown that this forcefield reproduces more accurately conformational changes in CypA. Steepest descent minimized was used for 50,000 steps followed by equilibration for 100 ps in an NVT ensemble, and 100 ps NPT ensemble, with heavy protein atoms restraint using a harmonic force constant of 1000 kJ mol−1 nm−2.
Models of CypA WT and other mutants in complex with the Ace-AAPF-Nme substrate were prepared. The amber99sb forcefield was used for the complex simulations because Doshi and co-workers have reported optimised ω angle parameters for amides to simulate cis/trans isomerisation reactions49. The crystal structure of the CypA-cis AAPF peptide complex (PDB ID: 1RMH)50 was used to obtain a suitable orientation for the substrate in the active site of WT and other mutants. PDB structure 1RMH was aligned to the structure of WT and all mutants, and the N-terminal and C-terminal ends of the proteins and substrate were capped using Schrödinger's Maestro47. In order to generate starting structures of 'in' and 'out' CypA-substrate complexes, MD simulations of CypA-substrate complexes (cis-conformation) were performed for 10 ns. For ST, STCS and STCSIV mutants the χ1 values of Phe113 were measured to monitor transitions between 'out' and 'in' rotamers. The last snapshot structure of 'in' and 'out' complexes structures were used as input US calculations. For WT complexes, only the 'in' rotamer was observed in a 10-ns MD simulation. Thus, US simulations of χ1 (Phe113) were performed serially to generate the 'out' (χ1 ≈ −60°) rotamer starting from the 'in' rotamer (χ1 ≈ 60°) using the software PLUMED251. Also, in order to retain the substrate in the active site, the distance between the proline ring of substrate and the phenyl rings of Phe113 and Phe60 were restrained using a force constant of 300 kJ mol−1 rad−2. Each US simulation was performed for 5 ns. The bias parameters and the restrained variables for the US of χ1 (Phe113) are summarised in Supplementary Table 7.
apo WT and mutant MD simulations
Eighty independent 200 ns MD trajectories of the apo WT, ST, STCS, and STCSIV proteins (20 each) were generated using Gromacs 5.052. For apo STCS and STCSIV the MD simulations were split between both structures prepared independently. A 2 fs time step was used, and the first 5 ns discarded for equilibration. Temperature was maintained at 300 K with a stochastic Berendsen thermostat53. The Parrinello-Rahman barostat was used for pressure coupling at 1 bar54. The Particle Mesh Ewald scheme was used for long-range electrostatic interactions with a Fourier grid spacing of 0.16 nm, and fourth-order cubic interpolation55. Short-range van der Waals and electrostatic interaction were cutoff at 1 nm. The LINCS algorithm was used to constrain all bonds56.
Markov state models
All MSM analysis was carried out with the software package pyemma version 2.3.257. The focus was on the side-chain motion of binding site residues. Details on which dihedral angles were used for TICA58 is given in Supplementary Table 8. A more detailed description of the MSM in particular with respect to best model selection is given in the SI. Clustering was done using all trajectory data from the WT and mutant trajectories using a set of 24 input coordinates, with selecting dominant coordinates using a 90% variance in TICA for the subsequent k-means clustering. Two hundred clusters were used to discretize the trajectory. With the same cluster assignment for all trajectories, MSM transition matrices were estimated, using the Bayesian MSM option, and choosing lagtimes 0.6 ns for WT, S99T, C115S, and I97V. Means and errors of observables (e.g. populations and MFPT) were estimated from the Bayesian MSM using the provided functions in pyEMMA. Membership assignments were based on the MSM microstate dihedral probabilities of being in the 'in' or 'out' state respectively. The microstate definition used for the MSMs is the same across the WT and all mutants. The MFPTs are estimated between the manually grouped two states depending on whether the Phe113 rotamer is 'in' or 'out' in the microstate. MSM validation and further details on the MSM can be found in the SI and in particular Supplementary Figures 1–3, Supplementary Tables 1–2 and Supplementary Note 159. MSM analyses were restricted to apo-enzymes because experimental data on the major to minor conformational exchange for the four variants is available for the apo forms only27,31,32.
US simulations
Series of US simulations60,61,62 of the 'in' and 'out' conformers were performed to compute free energy profiles along ω26,28,63,64. For substrate in solution, the initial structure of US was in a trans conformation taken from 10-ns equilibration run, while all protein-substrate complexes were in a cis conformation. For both of 'in' and 'out' US calculations, a standard harmonic potential was used to bias the ω angle towards a series of target values ωk spanning the interval [−180°,180°]. The force constants of the biasing potential and the spacing between ωk values were adjusted by trial and error in order to obtain a good overlap between probability distributions of neighbouring ωk values (Supplementary Tables 5 and 6 and Supplementary Figure 10). For 'out' US calculation the distances between the proline ring of substrate and the phenyl rings of Phe113 and Phe60 were restrained using a flat-bottom harmonic restraint with force constants of 200 kJ mol−1 rad−2 and 300 kJ mol−1 rad−2, respectively. Simulations were performed serially initially for 7 ns, with the starting conformation for a given target angle ωk taken from the preceding run performed at the neighbouring ωk+Δω value. Each US was then extended to 20 ns. A total of 22 (substrate in solution) or 24 (substrate bound to protein) umbrellas were used. In order to estimate uncertainties of free energy profiles six repeats of the entire procedure were performed for 'in' and 'out' US. All simulations were carried out using a PLUMED2 patched version of Gromacs 5.0 with simulation parameters identical to the previously described apo MD simulation protocols unless otherwise mentioned. The weighted histogram analysis method (WHAM) was used to produce a free energy profile from the pool of US simulations65.
Other trajectory analyses
Average proton–proton distances were derived as \(r_{ij}^{\mathrm{avg}} = \left\langle {r_{ij}^{ - 6}} \right\rangle ^{{\textstyle{{ - 1} \over 6}}}\) from snapshots sampled from the MSM of WT for comparison with NOEs and eNOEs-derived distance intervals66. 3J(HN, Hα), 3J(HN, \(C^\prime\)), and 3J(HN, Cβ) were also computed using Karplus equations and backbone dihedral angle values <ϕ> and <ψ> sampled from the MSM67.
Interaction energies between binding site residues (Arg55, Ile57, Phe60, Met61, Gln63, Asn102, Gln111, Phe113, Trp121, Leu122 and His126) and all atoms of the substrate were analysed with the Gromacs g_energy module, using snapshots from the US simulations. The probability distribution of distances between key residues and substrate atoms during the simulations were computed using the MDAnalysis library69.
All input files and scripts used for the preparation, execution and analysis of the MD, MSM and US calculations are freely available at https://github.com/michellab/CypAcatalysis_input and are also provided as Supplementary Data 1–3. Other data that support the findings of this study are available from the corresponding author upon reasonable request.
Warshel, A. Dynamics of enzymatic reactions. Proc. Natl Acad. Sci. USA 81, 444–448 (1984).
McGowan, L. C. & Hamelberg, D. Conformational plasticity of an enzyme during catalysis: Intricate coupling between cyclophilin a dynamics and substrate turnover. Biophys. J. 104, 216–226 (2013).
Eisenmesser, E. Z., Bosco, D. A., Akke, M. & Kern, D. Enzyme dynamics during catalysis. Science 295, 1520–1523 (2002).
Rader, S. D. & Agard, Da Conformational substates in enzyme mechanism: the 120 K structure of alpha-lytic protease at 1.5 A resolution. Protein Sci. 6, 1375–1386 (1997).
Bu, Z. et al. A view of dynamics changes in the molten globulenative folding step by quasielastic neutron scattering. J. Mol. Biol. 301, 525–536 (2000).
Henzler-Wildman, K. & Kern, D. Dynamic personalities of proteins. Nature 450, 964–972 (2007).
Wolf-Watz, M. et al. Linkage between dynamics and catalysis in a thermophilic-mesophilic enzyme pair. Nat. Struct. Mol. Biol. 11, 945–949 (2004).
Palmer, A. G., Kroenke, C. D. & Loria, J. P. NMR methods for quantifying microsecond-to-millisecond motions in biological macromolecules. Methods Enzym. 339, 204–238 (2001).
Schlegel, J., Armstrong, G. S., Redzic, J. S., Zhang, F. & Eisenmesser, E. Z. Characterizing and controlling the inherent dynamics of cyclophilin-A. Protein Sci. 18, 811–824 (2009).
Pisliakov, A. V., Cao, J., Kamerlin, S. C. L. & Warshel, A. Enzyme millisecond conformational dynamics do not catalyze the chemical step. Proc. Natl Acad. Sci. USA 106, 17359–17364 (2009).
Kamerlin, S. C. L. & Warshel, A. At the Dawn of the 21 st Century: Is Dynamics the Missing Link. Proteins Struct. Funct. Bioinforma. 78, 1339–1375 (2010).
Warshel, A. & Bora, R. P. Perspective: defining and quantifying the role of dynamics in enzyme catalysis. J. Chem. Phys. 144, 180901 (2016).
Kohen, A. Role of dynamics in enzyme catalysis: substantial versus semantic controversies. Acc. Chem. Res. 48, 466–473 (2015).
Wolfenden, R. Transition state analogues for enzyme catalysis. Nature 223, 704–705 (1969).
Delgado, M. et al. Convergence of theory and experiment on the role of preorganization, quantum tunneling, and enzyme motions into flavoenzyme-catalyzed hydride transfer. ACS Catal. 7, 3190–3198 (2017).
Go, S. F., Marahiel, M. A. & Gothel, S. F. Peptidyl-prolyl cis-trans isomerases, a superfamily of. Cell. Mol. Life Sci. 55, 423–436 (1999).
Li, J. et al. Discovery of dual inhibitors targeting both HIV-1 capsid and human cyclophilin A to inhibit the assembly and uncoating of the viral capsid. Bioorg. Med. Chem. 17, 3177–3188 (2009).
Dornan, J., Taylor, P. & Walkinshaw, M. Structures of Immunophilins and their Ligand Complexes. Curr. Top. Med. Chem. 3, 1392–1409 (2003).
Yang, Y. et al. Structure-based discovery of a family of synthetic cyclophilin inhibitors showing a cyclosporin-A phenotype in Caenorhabditis elegans. Biochem. Biophys. Res. Commun. 363, 1013–1019 (2007).
Georgiou, C. et al. Pushing the limits of detection of weak binding using fragment based drug discovery: identification of new cyclophilin binders. J. Mol. Biol. 429, 2556–2570 (2017).
Nagaraju, M., McGowan, L. C. & Hamelberg, D. Cyclophilin a inhibition: Targeting transition-state-bound enzyme conformations for structure-based drug design. J. Chem. Inf. Model. 53, 403–410 (2013).
Kofron, J. L., Kuzmic, P., Kishore, V., Colón-Bonilla, E. & Rich, D. H. Determination of kinetic constants for peptidyl prolyl cis-trans isomerases by an improved spectrophotometric assay. Biochemistry 30, 6127–6134 (1991).
Doshi, U., Holliday, M. J., Eisenmesser, E. Z. & Hamelberg, D. Dynamical network of residue-residue contacts reveals coupled allosteric effects in recognition, catalysis, and mutation. Proc. Natl Acad. Sci. USA 113, 4735–4740 (2016).
Camilloni, C. et al. Cyclophilin A catalyzes proline isomerization by an electrostatic handle mechanism. Proc Natl Acad. Sci. USA 111, 10203–10208 (2014).
Holliday, M. J., Camilloni, C., Armstrong, G. S., Vendruscolo, M. & Eisenmesser, E. Z. Networks of dynamic allostery regulate enzyme function. Structure 25, 276–286 (2017).
Hamelberg, D. & McCammon, J. A. Mechanistic insight into the role of transition-state stabilization in cyclophilin A. J. Am. Chem. Soc. 131, 147–152 (2009).
Eisenmesser, E. Z. et al. Intrinsic dynamics of an enzyme underlies catalysis. Nature 438, 117–121 (2005).
Ladani, S. T. & Hamelberg, D. Entropic and surprisingly small intramolecular polarization effects in the mechanism of cyclophilin A. J. Phys. Chem. B 116, 10771–10778 (2012).
Trzesniak, D. & van Gunsteren, W. F. Catalytic mechanism of cyclophilin as observed in molecular dynamics simulations: pathway prediction and reconciliation of X-ray crystallographic and NMR solution data. Protein Sci. 15, 2544–2551 (2006).
Ladani, S. T. & Hamelberg, D. Intricacies of interactions, dynamics and solvent effects in enzyme catalysis: a computational perspective on cyclophilin A. Mol. Simul. 40, 765–776 (2014).
Fraser, J. S. et al. Hidden alternative structures of proline isomerase essential for catalysis. Nature 462, 669–673 (2009).
Otten, R. et al. Rescue of conformational dynamics in enzyme catalysis by directed evolution. Nat. Commun. 9, 1314 (2018).
Papaleo, E., Sutto, L., Gervasio, F. L. & Lindorff-Larsen, K. Conformational changes and free energies in a proline isomerase. J. Chem. Theory Comput. 10, 4169–4174 (2014).
Vögeli, B., Kazemi, S., Güntert, P. & Riek, R. Spatial elucidation of motion in proteins by ensemble-based structure calculation using exact NOEs. Nat. Struct. Mol. Biol. 19, 1053–1058 (2012).
Chi, C. N. et al. A Structural ensemble for the enzyme cyclophilin reveals an orchestrated mode of action at atomic resolution. Angew. Chem. - Int. Ed. 54, 11657–11661 (2015).
Ottiger, M., Zerbe, O., Güntert, P. & Wüthrich, K. The NMR solution conformation of unligated human cyclophilin A. J. Mol. Biol. 272, 64–81 (1997).
Harrison, R. K. & Stein, R. L. Mechanistic studies of enzymic and nonenzymic prolyl cis-trans isomerization. J. Am. Chem. Soc. 114, 3464–3471 (1992).
Dugave, C. & Demange, L. Cis-trans isomerization of organic molecules and biomolecules: implications and applications. Chem. Rev. 103, 2475–2532 (2003).
Kern, D., Kern, G., Scherer, G., Fischer, G. & Drakenberg, T. Kinetic analysis of cyclophilin-catalyzed prolyl cis/trans isomerization by dynamic NMR spectroscopy. Biochemistry 34, 13594–13602 (1995).
Holliday, M. J., Armstrong, G. S. & Eisenmesser, E. Z. Determination of the full catalytic cycle among multiple cyclophilin family members and limitations on the application of CPMG-RD in reversible catalytic systems. Biochemistry 54, 5815–5827 (2015).
Holliday, M. J. et al. Structure and dynamics of GeoCyp: a thermophilic cyclophilin with a novel substrate binding mechanism that functions efficiently at low temperatures. Biochemistry 54, 3207–3217 (2015).
Gu, Y., Li, D. W. & Brüschweiler, R. NMR order parameter determination from long molecular dynamics trajectories for objective comparison with experiment. J. Chem. Theory Comput. 10, 2599–2607 (2014).
Lakomek, N. A. et al. Self-consistent residual dipolar coupling based model-free analysis for the robust determination of nanosecond to microsecond protein dynamics. J. Biomol. NMR 41, 139–155 (2008).
Farès, C. et al. Accessing ns-μs side chain dynamics in ubiquitin with methyl RDCs. J. Biomol. NMR 45, 23–44 (2009).
Kasinath, V., Valentine, K. G. & Wand, A. J. A 13C labeling strategy reveals a range of aromatic side chain motion in calmodulin. J. Am. Chem. Soc. 135, 9560–9563 (2013).
Michel, J. Current and emerging opportunities for molecular simulations in structure-based drug design. Phys. Chem. Chem. Phys. 16, 4465–4477 (2014).
Schrödinger Release 2017-4: Maestro, Schrödinger, LLC, New York, NY, 2017.
Piana, S., Lindorff-Larsen, K. & Shaw, D. E. How robust are protein folding simulations with respect to force field parameterization? Biophys. J. 100, L47–L49 (2011).
Doshi, U. & Hamelberg, D. Reoptimization of the AMBER force field parameters for peptide bond (Omega) torsions using accelerated molecular dynamics. J. Phys. Chem. B 113, 16590–16595 (2009).
Zhao, Y. & Ke, H. Crystal structure implies that cyclophilin predominantly catalyzes the Trans to Cis isomerization. Biochemistry 35, 7356–7361 (1996).
Tribello, G. A., Bonomi, M., Branduardi, D., Camilloni, C. & Bussi, G. PLUMED 2: New feathers for an old bird. Comput. Phys. Commun. 185, 604–613 (2014).
Abraham, M. J. et al. Gromacs: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 1–2, 19–25 (2015).
Bussi, G., Donadio, D. & Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 126, 014101 (2007).
Parrinello, M. & Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 52, 7182–7190 (1981).
Essmann, U. et al. A smooth particle mesh Ewald method. J. Chem. Phys. 103, 8577–8593 (1995).
Hess, B., Bekker, H., Berendsen, H. J. C. & Fraaije, J. G. E. M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 18, 1463–1472 (1997).
Scherer, M. K. et al. PyEMMA 2: A Software Package for Estimation, Validation, and Analysis of Markov Models. J. Chem. Theory Comput. 11, 5525–5542 (2015).
Schwantes, C. R. & Pande, V. S. Improvements in Markov State Model construction reveal many non-native interactions in the folding of NTL9. J. Chem. Theory Comput. 9, 2000–2009 (2013).
Prinz, J. H. et al. Markov models of molecular kinetics: Generation and validation. J. Chem. Phys. 134, 174105 (2011).
Torrie, G. M. & Valleau, J. P. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 23, 187–199 (1977).
Hooft, R. W. W., van Eijck, B. P. & Kroon, J. An adaptive umbrella sampling procedure in conformational analysis using molecular dynamics and its application to glycol. J. Chem. Phys. 97, 6690–6694 (1992).
Northrup, S. H., Pear, M. R., Lee, C. Y., McCammon, J. A. & Karplus, M. Dynamical theory of activated processes in globular proteins. Proc. Natl Acad. Sci. 79, 4035–4039 (1982).
Agarwal, P. K. Cis/trans isomerization in HIV-1 capsid protein catalyzed by cyclophilin A: Insights from computational and theoretical studies. Proteins Struct. Funct. Genet. 56, 449–463 (2004).
Hamelberg, D., Shen, T. & McCammon, J. A. Phosphorylation effects on cis/trans isomerization and the backbone conformation of serine-proline motifs: Accelerated molecular dynamics analysis. J. Am. Chem. Soc. 127, 1969–1974 (2005).
Kumar, S., Rosenberg, J. M., Bouzida, D., Swendsen, R. H. & Kollman, P. A. THE weighted histogram analysis method for free energy calculations on biomolecules. I. The method. J. Comput. Chem. 13, 1011–1021 (1992).
Zagrovic, B. & Van Gunsteren, W. F. Comparing atomistic simulation data with the NMR experiment: how much can NOEs actually tell us? Proteins Struct. Funct. Genet. 63, 210–218 (2006).
Salvador, P. Dependencies of J-Couplings upon Dihedral Angles on proteins. Annu. Rep. NMR Spectrosc. 81, 185–227 (2014).
Michaud-Agrawal, N., Denning, E. J., Woolf, T. B. & Beckstein, O. MDAnalysis: a toolkit for the analysis of molecular dynamics simulations. J. Comput. Chem. 32, 2319–2327 (2011).
Naveen Michaud-Agrawal, ElizabethJ., Dening, ThomasB. & Woolf, O. B. MDAnalysis: a toolkit for the analysis of molecular dynamics simulations. J. Comput. Chem. 31, 2967–2970 (2010).
Gratitude is expressed to Fernanda Duarte for thoughtful discussions about this work. J.M. is supported by a University Research Fellowship from the Royal Society. The research leading to these results has received funding from the European Research Council under the European Union's Seventh Framework Programme (FP7/2007–2013)/ERC grant agreement No. 336289. P.W. is supported by The Development and Promotion of Science and Technology Talents Project (DPST) Scholarship, Royal Thai Government. This project made use of time on ARCHER granted via the UK High-End Computing Consortium for Biomolecular Simulation, HECBioSim (http://hecbiosim.ac.uk), supported by EPSRC (grant no. EP/L000253/1).
EaStCHEM School of Chemistry, David Brewster road, Joseph Black Building, The King's Buildings, Edinburgh, EH9 3FJ, UK
Pattama Wapeesittipan, Antonia S. J. S. Mey & Julien Michel
School of Biological Sciences, Michael Swann Building, Max Born Crescent, Edinburgh, Scotland, EH9 3BF, UK
Malcolm D. Walkinshaw
Pattama Wapeesittipan
Antonia S. J. S. Mey
Julien Michel
P.W., A.S.J.S.M.: Carried out experiments, analysed data, wrote manuscript. M.D.W.: Analysed data, wrote manuscript. J.M.: Designed study, analysed data, wrote manuscript. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.
Correspondence to Julien Michel.
Description of Supplementary Data
Supplementary Data 1
Wapeesittipan, P., Mey, A.S.J.S., Walkinshaw, M.D. et al. Allosteric effects in cyclophilin mutants may be explained by changes in nano-microsecond time scale motions. Commun Chem 2, 41 (2019). https://doi.org/10.1038/s42004-019-0136-1
DOI: https://doi.org/10.1038/s42004-019-0136-1
Engineering and application of a biosensor with focused ligand specificity
Dennis Della Corte
Hugo L. van Beek
Jan Marienhagen
Temperature-jump solution X-ray scattering reveals distinct motions in a dynamic enzyme
Michael C. Thompson
Benjamin A. Barad
James S. Fraser
Nature Chemistry (2019)
Communications Chemistry (Commun Chem) ISSN 2399-3669 (online) | CommonCrawl |
Categorical Brouwer-Heyting-Kolmogorov interpretation
Let $\mathcal{L}$ be the language of intuitionistic propositional logic generated by some atomic propositions $t_1, t_2, \ldots$. The Lindenbaum–Tarski algebra of $\mathcal{L}$ can be regarded as a bicartesian closed category in which there is an arrow $p \to q$ if and only if there is a proof of $q$ assuming $p$. Unfortunately it is a somewhat dull category, as there is at most one arrow between any two objects.
Question. Is there a categorification of the Lindenbaum–Tarski algebra which enables a category-theoretic form of the Brouwer–Heyting–Kolmogorov interpretation of intuitionistic propositional logic? In particular,
Objects should be propositions.
Arrows should be (equivalence classes) of proofs.
The coproduct should be disjoint, at least for the coproduct of two distinct atomic propositions.
The terminal object should be indecomposable, so that the disjunction property is validated (i.e. an arrow $\top \to p \lor q$ is either an arrow $\top \to p$ or an arrow $\top \to q$).
It feels like the free bicartesian closed category generated by the atomic propositions is the most likely candidate, and it can be concretised by the Yoneda embedding into the presheaf topos: then we would have a genuine BHK interpretation, i.e. interpreting a proposition as the 'set' of its proofs. This has probably been well-studied, in which case I would appreciate any references to the literature.
lo.logic ct.category-theory reference-request
Zhen LinZhen Lin
$\begingroup$ Related: mathoverflow.net/questions/43281/… $\endgroup$ – Qiaochu Yuan Nov 29 '11 at 23:53
I don't have it with me, and I can't recall the exact details, but I'm pretty sure Lambek & Scott's Introduction to Higher-Order Categorical Logic (link) is what you're looking for. In particular, they prove the equivalence between cartesian closed categories and simply-typed $\lambda$-calculi (so you get the Curry--Howard correspondence for free!).
Finn LawlerFinn Lawler
$\begingroup$ In Part I, section 11, Lambek and Scott construct the cartesian closed category generated by a typed λ-calculus, which I can believe is what I want, except on the wrong side of the Curry–Howard isomorphism. It's not clear to me that the terminal object $\top$ is indecomposable in this category though – they only prove the disjunction property in the context of toposes and type theory later in the book, via the Freyd cover. $\endgroup$ – Zhen Lin Nov 30 '11 at 7:50
Perhaps this paper would be good to look at:
ERIK PALMGREN (2004). A categorical version of the Brouwer–Heyting–Kolmogorov interpretation. Mathematical Structures in Computer Science, 14 , pp 57-72 doi:10.1017/S0960129503003955
kowkow
Not the answer you're looking for? Browse other questions tagged lo.logic ct.category-theory reference-request or ask your own question.
Propositional logic with categories
Is every Heyting algebra the Lindenbaum algebra of an intuitionistic first order theory?
Heyting algebras originating from directed graphs
Pure first order logic formulations of Markov's principle
Trace in the category of propositional statements | CommonCrawl |
Missed the LibreFest? Watch the recordings here on Youtube!
Sat, 26 Sep 2020 14:49:22 GMT
12.3: Spin Magnetic Resonance
[ "article:topic", "NMR", "authorname:rfitzpatrick", "gyromagnetic ratio", "EPR", "showtoc:no" ]
https://phys.libretexts.org/@app/auth/3/login?returnto=https%3A%2F%2Fphys.libretexts.org%2FBookshelves%2FQuantum_Mechanics%2FBook%253A_Introductory_Quantum_Mechanics_(Fitzpatrick)%2F12%253A_Time-Dependent_Perturbation_Theory%2F12.03%253A_Spin_Magnetic_Resonance
\(\require{cancel}\)
Book: Introductory Quantum Mechanics (Fitzpatrick)
12: Time-Dependent Perturbation Theory
Page ID
Contributed by Richard Fitzpatrick
Professor (Physics) at University of Texas at Austin
Contributors and Attributions
Consider a system consisting of a spin one-half particle with no orbital angular momentum (e.g., a bound electron) placed in a uniform \(z\)-directed magnetic field, and then subject to a small time-dependent magnetic field rotating in the \(x\)-\(y\) plane at the angular frequency \(\omega\). Thus, \[{\bf B} = B_0\,{\bf e}_z + B_1\left[\cos(\omega\,t)\,{\bf e}_x + \sin(\omega\,t)\,{\bf e}_y\right],\] where \(B_0\) and \(B_1\) are constants, with \(B_1\ll B_0\). The rotating magnetic field usually represents the magnetic component of an electromagnetic wave propagating along the \(z\)-axis. In this system, the electric component of the wave has no effect. The Hamiltonian is written \[H = -\mu\cdot{\bf B} = H_0 + H_1,\] where \[H_0 = - \frac{g\,e\,B_0}{2\,m}\,S_z,\] and \[H_1 = -\frac{g\,e\,B_1}{2\,m}\,\left[\cos(\omega\,t)\,S_x+ \sin(\omega\,t)\,S_y\right].\] Here, \(g\) and \(m\) are the gyromagnetic ratio [see Equation ([e12.151])] and mass of the particle in question, respectively.
The eigenstates of the unperturbed Hamiltonian are the "spin up" and "spin down" states, denoted \(\chi_+\) and \(\chi_-\), respectively. Of course, these states are the eigenstates of \(S_z\) corresponding to the eigenvalues \(+\hbar/2\) and \(-\hbar/2\) respectively. (See Section [sspin].) Thus, we have \[H_0\,\chi_\pm = \mp \frac{g\,e\,\hbar\,B_0}{4\,m}\,\chi_\pm.\] The time-dependent Hamiltonian can be written \[H_1 = - \frac{g\,e\,B_1}{4\,m}\left[\exp(\,{\rm i}\,\omega\,t)\,S_- + \exp(-{\rm i}\,\omega\,t)\,S_+\right],\] where \(S_+\) and \(S_-\) are the conventional raising and lowering operators for spin angular momentum. (See Section [sspin].) It follows that \[\langle +|H_1|+\rangle = \langle -|H_1|-\rangle = 0,\] and \[\langle -|H_1|+\rangle = \langle +|H_1|-\rangle^\ast = - \frac{g\,e\,B_1}{4\,m}\,\exp(\,{\rm i}\,\omega\,t).\]
It can be seen that this system is exactly the same as the two-state system discussed in the previous section, provided that the make the following identifications: \[\begin{aligned} \psi_1 &\rightarrow \chi_+,\\[0.5ex] \psi_2&\rightarrow \chi_-,\\[0.5ex] \omega_{21} &\rightarrow \frac{g\,e\,B_0}{2\,m},\\[0.5ex] \gamma&\rightarrow -\frac{g\,e\,B_1}{4\,m}.\end{aligned}\] The resonant frequency, \(\omega_{21}\), is simply the spin precession frequency in a uniform magnetic field of strength \(B_0\). (See Section [sspinp].) In the absence of the perturbation, the expectation values of \(S_x\) and \(S_y\) oscillate because of the spin precession, but the expectation value of \(S_z\) remains invariant. If we now apply a magnetic perturbation rotating at the resonant frequency then, according to the analysis of the previous section, the system undergoes a succession of spin flips, \(\chi_+\leftrightarrow\chi_-\), in addition to the spin precession. We also know that if the oscillation frequency of the applied field is very different from the resonant frequency then there is virtually zero probability of the field triggering a spin flip. The width of the resonance (in frequency) is determined by the strength of the oscillating magnetic perturbation. Experimentalists are able to measure the gyromagnetic ratios of spin one-half particles to a high degree of accuracy by placing the particles in a uniform magnetic field of known strength, and then subjecting them to an oscillating magnetic field whose frequency is gradually scanned. By determining the resonant frequency (i.e., the frequency at which the particles absorb energy from the oscillating field), it is possible to determine the gyromagnetic ratio (assuming that the mass is known) .
Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)
\( \newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}\) \(\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}\) \(\newcommand {\btau}{\mbox{\boldmath$\tau$}}\) \(\newcommand {\bmu}{\mbox{\boldmath$\mu$}}\) \(\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}\) \(\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}\) \(\newcommand {\bomega}{\mbox{\boldmath$\omega$}}\) \(\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}\)
12.2: Two-State System
12.4: Perturbation Expansion
Section or Page
Richard Fitzpatrick
Show TOC
gyromagnetic ratio
© Copyright 2021 Physics LibreTexts
The LibreTexts libraries are Powered by MindTouch® and are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. We also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and 1413739. Unless otherwise noted, LibreTexts content is licensed by CC BY-NC-SA 3.0. Legal. Have questions or comments? For more information contact us at [email protected] or check out our status page at https://status.libretexts.org. | CommonCrawl |
Is there a list of all typos in Hoffman and Kunze, Linear Algebra?
Where can I find a list of typos for Linear Algebra, 2nd Edition, by Hoffman and Kunze? I searched on Google, but to no avail.
linear-algebra reference-request
10 revs, 7 users 38%
minibuffer
$\begingroup$ One thing you can try is to look for a well-used university library copy and flip through the pages to see what corrections might be penciled in. $\endgroup$ – Dave L. Renfro Mar 27 '15 at 16:27
$\begingroup$ This question and its answers has been added to Math books errata list as a reference: mathbookserrata.wikidot.com $\endgroup$ – C.F.G Sep 15 '19 at 7:59
This list does not repeat the typos mentioned in the other answers.
Page 6, last paragraph.
An elementary row operation is thus a special type of function (rule) $e$ which associated with each $m \times n$ matrix . . .
It should be "associates".
Page 10, proof of Theorem 4, second paragraph.
say it occurs in column $k_r \neq k$.
It should be $k' \neq k$.
Page 18, last paragraph.
If $B$ is an $n \times p$ matrix, the columns of $B$ are the $1 \times n$ matrices . . .
It should be $n \times 1$.
Page 24, statement of second corollary.
Let $\text{A} = \text{A}_1 \text{A}_2 \cdots A_k$, where $\text{A}_1 \dots,A_k$ are . . .
The formatting of $A_k$ is incorrect in both instances. Also, there should be a comma after $\text{A}_1$. So, it should be "Let $\text{A} = \text{A}_1 \text{A}_2 \cdots \text{A}_\text{k}$, where $\text{A}_1, \dots,\text{A}_\text{k}$ are . . .".
Page 26–27, Exercise 4.
For which $X$ does there exist a scalar $c$ such that $AX=cX$?
It would make more sense if it asked: "For which $X \neq 0$ does there exist . . .".
Page 52, below equation (2–16).
Thus from (2–16) and Theorem 7 of Chapter 1 . . .
It should be Theorem 13.
Page 57, second last displayed equation.
$$ \beta = (0,\dots,0,\ \ b_{k_s},\dots,b_n), \quad b_{k_s} \neq 0$$
The formatting on the right-hand side is not correct. There is too much space before $b_{k_s}$. It should be $$\beta = (0,\dots,0,b_{k_s},\dots,b_n), \quad b_{k_s} \neq 0$$ instead.
Page 57, last displayed equation.
$$ \beta = (0,\dots,0,\ \ b_t,\dots,b_n), \quad b_t \neq 0.$$
The formatting on the right-hand side is not correct. There is too much space before $b_t$. It should instead be $$\beta = (0,\dots,0,b_t,\dots,b_n), \quad b_t \neq 0.$$
Page 62, second last paragraph.
So $\beta = (b_1,b_2,b_3,b_4)$ is in $W$ if and only if $b_3 - 2b_1$. . . .
It should be $b_3 = 2b_1$.
Page 76, first paragraph.
let $A_{ij},\dots,A_{mj}$ be the coordinates of the vector . . .
It should be $A_{1j},\dots,A_{mj}$.
Page 80, Example 11.
For example, if $U$ is the operation 'remove the constant term and divide by $x$': $$ U(c_0 + c_1 x + \dots + c_n x^n) = c_1 + c_2 x + \dots + c_n x^{n-1}$$ then . . .
There is a subtlety in the phrase within apostrophes: what if $x = 0$? Rather than having to specify for this case separately, the sentence can be worded more simply as, "For example, if $U$ is the operator defined by $$U(c_0 + c_1 x + \dots + c_n x^n) = c_1 + c_2 x + \dots + c_n x^{n-1}$$ then . . .".
Page 81, last line.
(iv) If $\{ \alpha_1,\dots,\alpha_{\text{n}}\}$ is basis for $\text{V}$, then $\{\text{T}\alpha_1,\dots,\text{T}\alpha_{\text{n}}\}$ is a basis for $\text{W}$.
It should read "(iv) If $\{ \alpha_1,\dots,\alpha_{\text{n}}\}$ is a basis for $\text{V}$, then . . .".
We should also point out that we proved a special case of Theorem 13 in Example 12.
It should be "in Example 10."
For, the identity operator $I$ is represented by the identity matrix in any order basis, and thus . . .
It should be "ordered".
Page 92, statement of Theorem 14.
Let $\text{V}$ be a finite-dimensional vector space over the field $\text{F}$ and let $$\mathscr{B} = \{ \alpha_1,\dots,\alpha \text{i} \} \quad \textit{and} \quad \mathscr{B}'=\{ \alpha'_1,\dots,\alpha'_\text{n}\}$$ be ordered bases . . .
It should be $\mathscr{B} = \{ \alpha_1,\dots,\alpha_\text{n}\}$.
Page 100, first paragraph.
If $f$ is in $V^*$, and we let $f(\alpha_i) = \alpha_i$, then when . . .
It should be $f(\alpha_i) = a_i$.
Page 101, paragraph following the definition.
If $S = V$, then $S^0$ is the zero subspace of $V^*$. (This is easy to see when $V$ is finite dimensional.)
It is equally easy to see this when $V$ is infinite-dimensional, so the statement in the brackets is redundant. Perhaps the authors meant to say that $\{ v \in V : f(v) = 0\ \forall\ f \in V^* \}$ is the zero subspace of $V$. This question asks for details on this point.
Page 102, proof of the second corollary.
By the previous corollaries (or the proof of Theorem 16) there is a linear functional $f$ such that $f(\beta) = 0$ for all $\beta$ in $W$, but $f(\alpha) \neq 0$. . . .
It should be "corollary", since there is only one previous corollary. Also, $W$ should be replaced by $W_1$.
Page 112, statement of Theorem 22.
(i) rank $(T^t) = $ rank $(T)$
There should be a semi-colon at the end of the line.
Page 118, last displayed equation, third line.
$$=\sum_{i=0}^n \sum_{j=0}^i f_i g_{i-j} h_{n-i} $$
It should be $f_j$. It is also not immediately clear how to go from this line to the next line.
Page 126, proof of Theorem 3.
By definition, the mapping is onto, and if $f$, $g$ belong to $F[x]$ it is evident that $$(cf+dg)^\sim = df^\sim + dg^\sim$$ for all scalars $c$ and $d$. . . .
It should be $(cf+dg)^\sim = cf^\sim + dg^\sim$.
Suppose then that $f$ is a polynomial of degree $n$ such that $f' = 0$. . . .
It should be $f^\sim = 0$.
Page 128, statement of Theorem 4.
(i) $f = dq + r$.
The full stop should be a semi-colon.
Page 129, paragraph before statement of Theorem 5. The notation $D^0$ needs to be introduced, so the sentence, "We also use the notation $D^0 f = f$" can be added at the end of the paragraph.
Page 131, first displayed equation, second line.
$$ = \sum_{m = 0}^{n-r} \frac{(D^m g)}{m!}(x-c)^{r+m} $$
There should be a full stop at the end of the line.
Since $(f,p) = 1$, there are polynomials . . .
It should be $\text{g.c.d.}{(f,p)} = 1$.
This decomposition is also clearly unique, and is called the primary decomposition of $f$. . . .
For the sake of clarity, the following sentence can be added after the quoted line: "Henceforth, whenever we refer to the prime factorization of a non-scalar monic polynomial we mean the primary decomposition of the polynomial."
Page 137, proof of Theorem 11. The chain rule for the formal derivative of a product of polynomials is used, but this needs proof.
Page 139, Exercise 7.
Use Exercise 7 to prove the following. . . .
It should be "Use Exercise 6 to prove the following. . . ."
Page 142, second last displayed equation.
$$\begin{align} D(c\alpha_i + \alpha'_{iz}) &= [cA(i,k_i) + A'(i,k_i)]b \\ &= cD(\alpha_i) + D(\alpha'_i) \end{align}$$
The left-hand side should be $D(c\alpha_i + \alpha'_i)$.
Page 166, first displayed equation.
$$\begin{align*}L(\alpha_1,\dots,c \alpha_i + \beta_i,\dots,\alpha_r) &= cL(\alpha_1,\dots,\alpha_i,\dots,\alpha_r {}+{} \\ &\qquad \qquad \qquad \qquad L(\alpha_1,\dots,\beta_i,\dots,\alpha_r)\end{align*}$$
The first term on the right has a missing closing bracket, so it should be $cL(\alpha_1,\dots,\alpha_i,\dots,\alpha_r)$.
Page 167, second displayed equation, third line.
$${}={} \sum_{j=1}^n A_{1j} L\left( \epsilon_j, \sum_{j=1}^n A_{2k} \epsilon_k, \dots, \alpha_r \right) $$
The second summation should run over the index $k$ instead of $j$.
Page 170, proof of the lemma. To show that $\pi_r L \in \Lambda^r(V)$, the authors show that $(\pi_r L)_\tau = (\operatorname{sgn}{\tau})(\pi_rL)$ for every permutation $\tau$ of $\{1,\dots,r\}$. This implies that $\pi_r L$ is alternating only when $K$ is a ring such that $1 + 1 \neq 0$. A proof over arbitrary commutative rings with identity is still needed.
Page 170, first paragraph after proof of the lemma.
In (5–33) we showed that the determinant . . .
It should be (5–34).
Page 171, equation (5–39).
$$\begin{align} D_J &= \sum_\sigma (\operatorname{sgn} \sigma)\ f_{j_{\sigma 1}} \otimes \dots \otimes f_{j_{\sigma r}} \tag{5–39}\\ &= \pi_r (f_{j_1} \otimes \dots \otimes f_{j_r}) \end{align}$$
The equation tag should be centered instead of being aligned at the first line.
Page 173, Equation (5-42)
$$ D_J(\alpha_1,\dotsc,\alpha_r) = \sum_\sigma (\operatorname{sgn} \sigma) A(1,j_{\sigma 1})\dotsm A(n,j_{\sigma n}) \tag{5-42}$$
There are only $r$ terms in the product. Hence the equation should instead be: $D_J(\alpha_1,\dotsc,\alpha_r) = \sum_\sigma (\operatorname{sgn} \sigma) A(1,j_{\sigma 1})\dotsm A(r,j_{\sigma r})$.
Page 174, below the second displayed equation.
The proof of the lemma following equation (5–36) shows that for any $r$-linear form $L$ and any permutation $\sigma$ of $\{1,\dots,r\}$ $$ \pi_r(L_\sigma) = \operatorname{sgn} \sigma\ \pi_r(L) $$
The proof of the lemma actually shows $(\pi_r L)_\sigma = \operatorname{sgn} \sigma\ \pi_r(L)$. This fact still needs proof. Also, there should be a full stop at the end of the displayed equation.
Page 174, below the third displayed equation.
Hence, $D_{ij} \cdot f_k = 2\pi_3(f_i \otimes f_j \otimes f_k)$.
This is not immediate from just the preceding equations. The authors implicitly assume the identity $(f_{j_1} \otimes \dots \otimes f_{j_r})_\sigma = f_{j_{\sigma^{-1} 1}}\! \otimes \dots \otimes f_{j_{\sigma^{-1} r}}$. This identity needs proof.
Page 174, sixth displayed equation.
$$(D_{ij} \cdot f_k) \cdot f_l = 6 \pi_4(f_i \otimes f_j \otimes f_k \otimes f_l)$$
The factor $6$ should be replaced by $12$.
Page 174, last displayed equation.
$$ (L \otimes M)_{(\sigma,\tau)} = L_\sigma \otimes L_\tau$$
The right-hand side should be $L_\sigma \otimes M_\tau$.
Therefore, since $(N\sigma)\tau = N\tau \sigma$ for any $(r+s)$-linear form . . .
It should be $(N_\sigma)_\tau = N_{\tau \sigma}$.
$$ (L \wedge M)(\alpha_1,\dots,\alpha_n) = \sum (\operatorname{sgn} \sigma) L(\alpha \sigma_1,\dots,\alpha_{\sigma r}) M(\alpha_{\sigma(r+1)},\dots,\alpha_{\sigma_n}) $$
The right-hand side should have $L(\alpha_{\sigma 1},\dots,\alpha_{\sigma r})$ and $M(\alpha_{\sigma (r+1)},\dots,\alpha_{\sigma n})$.
If the underlying space $V$ is finite-dimensional, $(T-cI)$ fails to be $1 : 1$ precisely when its determinant is different from $0$.
It should instead be "precisely when its determinant is $0$."
Page 186, proof of second lemma.
one expects that $\dim W < \dim W_1 + \dots \dim W_k$ because of linear relations . . .
It should be $\dim W \leq \dim W_1 + \dots + \dim W_k$.
Page 194, statement of Theorem 4 (Cayley-Hamilton).
Let $\text{T}$ be a linear operator on a finite dimensional vector space $\text{V}$. . . .
It should be "finite-dimensional".
$$T\alpha_i = \sum_{j=1}^n A_{ji} \alpha_j,\quad 1 \leq j \leq n.$$
It should be $1 \leq i \leq n$.
Page 195, above the last paragraph.
since $f$ is the determinant of the matrix $xI - A$ whose entries are the polynomials $$(xI - A)_{ij} = \delta_{ij} x - A_{ji}.$$
Here $xI-A$ should be replaced $(xI-A)^t$ in both places, and it could read "since $f$ is also the determinant of" for more clarity.
Page 203, proof of Theorem 5, last paragraph.
The diagonal entries $a_{11},\dots,a_{1n}$ are the characteristic values, . . .
It should be $a_{11},\dots,a_{nn}$.
this theorem has the same proof as does Theorem 5, if one replaces $T$ by $\mathscr{F}$.
It would make more sense if it read "replaces $T$ by $T \in \mathscr{F}$."
Page 207-208, proof of Theorem 8.
We could prove this theorem by adapting the lemma before Theorem 7 to the diagonalizable case, just as we adapted the lemma before Theorem 5 to the diagonalizable case in order to prove Theorem 6.
The adaptation of the lemma before Theorem 5 is not explicitly done. It is hidden in the proof of Theorem 6.
and if we let $\text{W}_\text{i}$ be the range of $\text{E}_\text{i}$, then $\text{V} = \text{W}_\text{i} \oplus \dots \oplus \text{W}_\text{k}$.
It should be $\text{V} = \text{W}_1 \oplus \dots \oplus \text{W}_\text{k}$.
Page 216, last paragraph.
One part of Theorem 9 says that for a diagonalizable operator . . .
Let $\text{p}$ be the minimal polynomial for $\text{T}$, $$\text{p} = \text{p}_1^{\text{r}_1} \cdots \text{p}_k^{r_k}$$ where the $\text{p}_\text{i}$ are distinct irreducible monic polynomials over $\text{F}$ and the $\text{r}_\text{i}$ are positive integers. Let $\text{W}_\text{i}$ be the null space of $\text{p}_\text{i}(\text{T})^{\text{r}_j}$, $\text{i} = 1,\dots,\text{k}$.
The displayed equation is improperly formatted. It should read $\text{p} = \text{p}_1^{\text{r}_1} \cdots \text{p}_\text{k}^{\text{r}_\text{k}}$. Also, in the second sentence it should be $\text{p}_\text{i}(\text{T})^{\text{r}_\text{i}}$.
Page 221, below the last displayed equation.
because $p^{r_i} f_i g_i$ is divisible by the minimal polynomial $p$.
It should be $p_i^{r_i} f_i g_i$.
Page 233, proof of Theorem 3, last displayed equation in statement of Step 1. The formatting of "$\alpha$ in $V$" underneath the "$max$" operator on the right-hand side is incorrect. It should be "$\alpha$ in $\text{V}$".
Page 233, proof of Theorem 3, displayed equation in statement of Step 2. The formatting of "$1 \leq i < k$" underneath the $\sum$ operator on the right-hand side is incorrect. It should be "$1 \leq \text{i} < \text{k}$".
Page 238, paragraph following corollary.
If we have the operator $T$ and the direct-sum decomposition of Theorem 3, let $\mathscr{B}_i$ be the 'cyclic ordered basis' . . .
It should be "of Theorem 3 with $W_0 = \{ 0 \}$, . . .".
Page 239, Example 2.
If $T = cI$, then for any two linear independent vectors $\alpha_1$ and $\alpha_2$ in $V$ we have . . .
It should be "linearly".
$$f = (x-c_1)^{d_1} \cdots (x - c_k)^{d_k}$$
It should just be $(x-c_1)^{d_1} \cdots (x - c_k)^{d_k}$ because later (on page 241) the letter $f$ is again used, this time to denote an arbitrary polynomial.
where $f_i$ is a polynomial, the degree of which we may assume is less than $k_i$. Since $N\alpha = 0$, for each $i$ we have . . .
It should be "where $f_i$ is a polynomial, the degree of which we may assume is less than $k_i$ whenever $f_i \neq 0$. Since $N\alpha = 0$, for each $i$ such that $f_i \neq 0$ we have . . .".
Thus $xf_i$ is divisible by $x^{k_i}$, and since $\deg (f_i) > k_i$ this means that $$f_i = c_i x^{k_i - 1}$$ where $c_i$ is some scalar.
It should be $\deg (f_i) < k_i$. Also, the following sentence should be added at the end: "If $f_j = 0$, then we can take $c_j = 0$ so that $f_j = c_j x^{k_j - 1}$ in this case as well."
Furthermore, the sizes of these matrices will decrease as one reads from left to right.
It should be "Furthermore, the sizes of these matrices will not increase as one reads from left to right."
Also, within each $A_i$, the sizes of the matrices $J_j^{(i)}$ decrease as $j$ increases.
It should be "Also, within each $A_i$, the sizes of the matrices $J_j^{(i)}$ do not increase as $j$ increases."
Page 246, third paragraph.
The uniqueness we see as follows.
This part is not clearly written. What the authors want to show is the following. Suppose that the linear operator $T$ is represented in some other ordered basis by the matrix $B$ in Jordan form, where $B$ is the direct sum of the matrices $B_1,\dots,B_s$. Suppose each $B_i$ is an $e_i \times e_i$ matrix that is a direct sum of elementary Jordan matrices with characteristic value $\lambda_i$. Suppose the matrix $B$ induces the invariant direct-sum decomposition $V = U_1 \oplus \dots \oplus U_s$. Then, $s = k$, and there is a permutation $\sigma$ of $\{ 1,\dots,k\}$ such that $\lambda_i = c_{\sigma i}$, $e_i = d_{\sigma i}$, $U_i = W_{\sigma i}$, and $B_i = A_{\sigma i}$ for each $1 \leq i \leq k$.
The fact that $A$ is the direct sum of the matrices $\text{A}_i$ gives us a direct sum decomposition . . .
The formatting of $\text{A}_i$ is incorrect. It should be $A_i$.
then the matrix $A_i$ is uniquely determined as the rational form for $(T_i - c_i I)$.
It should be "is uniquely determined by the rational form . . .".
Since $A$ is the direct sum of two $2 \times 2$ matrices, it is clear that the minimal polynomial for $A$ is $(x-2)^2$.
It should read "Since $A$ is the direct sum of two $2 \times 2$ matrices when $a \neq 0$, and of one $2 \times 2$ matrix and two $1 \times 1$ matrices when $a = 0$, it is clear that the minimal polynomial for $A$ is $(x-2)^2$ in either case."
Then as we noted in Example 15, Chapter 6 the primary decomposition theorem tells us that . . .
It should be Example 14.
Page 249, last displayed equation
$$\begin{align} Ng &= (r-1)x^{r-2}h \\ \vdots\ & \qquad \ \vdots \\ N^{r-1}g &= (r-1)! h \end{align}$$
There should be a full stop at the end.
Page 257, definition.
(b) on the main diagonal of $\text{N}$ there appear (in order) polynomials $\text{f}_1,\dots,\text{f}_l$ such that $\text{f}_\text{k}$ divides $\text{f}_{\text{k}+1}$, $1 \leq \text{k} \leq l - 1$.
The formatting of $l$ is incorrect in both instances. So, it should be $\text{f}_1,\dots,\text{f}_\text{l}$ and $1 \leq \text{k} \leq \text{l} - 1$.
Page 259, paragraph following the proof of Theorem 9.
Two things we have seen provide clues as to how the polynomials $f_1,\dots,f_{\text{l}}$ in Theorem 9 are uniquely determined by $M$.
The formatting of $l$ is incorrect. It should be $f_1,\dots,f_l$.
For the case of a type (c) operation, notice that . . .
It should be (b).
Page 260, statement of Corollary.
The polynomials $\text{f}_1,\dots,\text{f}_l$ which occur on the main diagonal of $N$ are . . .
The formatting of $l$ is incorrect. It should be $\text{f}_1,\dots,\text{f}_\text{l}$.
Page 265, first displayed equation, third line.
$$ = (W \cap W_1) + \dots + (W \cap W_k) \oplus V_1 \oplus \dots \oplus V_k.$$
It should be $$ = (W \cap W_1) \oplus \dots \oplus (W \cap W_k) \oplus V_1 \oplus \dots \oplus V_k.$$
Page 266, proof of second lemma. The chain rule for the formal derivative of a product of polynomials is used, but this needs proof.
Page 274, last displayed equation, first line.
$$ (\alpha | \beta) = \left( \sum_k x_n \alpha_k \bigg|\, \beta \right) $$
It should be $x_k$.
Page 278, first line.
Now using (c) we find that . . .
It should be (iii).
Page 282, second displayed equation, second last line.
$$ = (2,9,11) - 2(0,3,4) - -4,0,3) $$
The right-hand side should be $(2,9,11) - 2(0,3,4) - (-4,0,3)$.
$$ \alpha = \sum_k \frac{(\beta | \alpha_k)}{\| \alpha_k \|^2} \alpha_k $$
This equation should be labelled (8–11).
Page 285, paragraph following the first definition.
For $S$ is non-empty, since it contains $0$; . . .
It should be $S^\perp$.
Page 289, Exercise 7, displayed equation.
$$\| (x_1,x_2 \|^2 = (x_1 - x_2)^2 + 3x_2^2. $$
The left-hand side should be $\| (x_1,x_2) \|^2$.
matrix $\text{A}$ of $\text{T}$ in the basis $\mathscr{B}$ is upper triangular. . . .
It should be "upper-triangular".
Then there is an orthonormal basis for $\text{V}$ in which the matrix of $\text{T}$ is upper triangular.
Under the assumptions of the theorem, let $\text{P}_\text{j}$ be the orthogonal projection of $\text{V}$ on $\text{V}(\text{r}_\text{j})$, $(1 \leq \text{j} \leq \text{k})$. . . .
The parentheses around $1 \leq \text{j} \leq \text{k}$ should be removed.
Brahadeesh
$\begingroup$ And no one can find a list of errata? $\endgroup$ – Michael McGovern Jan 7 '18 at 2:19
$\begingroup$ @MichaelMcGovern what do you mean? I don't quite understand. $\endgroup$ – Brahadeesh Jan 7 '18 at 3:43
$\begingroup$ He means your answer is a list of errata ;) $\endgroup$ – user370967 Jan 7 '18 at 18:47
$\begingroup$ I was surprised that, given how many errors people were able to find just by looking through the book, the publisher hadn't already provided a list of errata. $\endgroup$ – Michael McGovern Jan 7 '18 at 20:25
$\begingroup$ Chapter 8, page 282: The vector $\alpha_3=(0,9,0)$, and it is suggested that $\|\alpha_3\|^2$ is $9$. But $\|\alpha_3\|^2$ should be $81$. There are also errors stemming from this one. $\endgroup$ – Al Jebr Mar 31 '18 at 19:09
(Red highlight Typo in Linear Algebra by Hoffman and Kunze, page 23)
It should be $$A=E_1^{-1}E_2^{-1}...E_k^{-1}$$
Let $A=\left[\begin{matrix}2&3\\4&5\end{matrix}\right]$
Elementary row operations:
$R_2\leftrightarrow R_2-2R_1, R_1\leftrightarrow R_1+3R_2, R_1 \leftrightarrow R_1/2, R_2 \leftrightarrow R_2*(-1)$ transforms $A$ into $I$
These four row operations on $I$ give
$E_1=\left[\begin{matrix}1&0\\-2&1\end{matrix}\right]$, $E_2=\left[\begin{matrix}1&3\\0&1\end{matrix}\right]$, $E_3=\left[\begin{matrix}1/2&0\\0&1\end{matrix}\right]$, $E_4=\left[\begin{matrix}1&0\\0&-1\end{matrix}\right]$
$E_1^{-1}=\left[\begin{matrix}1&0\\2&1\end{matrix}\right]$, $E_2^{-1}=\left[\begin{matrix}1&-3\\0&1\end{matrix}\right]$, $E_3^{-1}=\left[\begin{matrix}2&0\\0&1\end{matrix}\right]$, $E_4^{-1}=\left[\begin{matrix}1&0\\0&-1\end{matrix}\right]$
Now, $ E_1^{-1}.E_2^{-1}.E_3^{-1}.E_4^{-1}=\left[\begin{matrix}2&3\\4&5\end{matrix}\right]$
but, $ E_4^{-1}.E_3^{-1}.E_2^{-1}.E_1^{-1}=\left[\begin{matrix}-10&-6\\-2&-1\end{matrix}\right]$
$\begingroup$ On page 18 "If $B$ is an n X p matrix, the columns of $B$ are the 1 X n matrices $B_1, . . . ,B_p$ defined by ..." in this line it should be rows instead of columns $\endgroup$ – Vikram Jun 16 '17 at 8:19
$\begingroup$ Rather, in this line it should read "...the columns of $B$ are the $n \times 1$ matrices...". $\endgroup$ – Brahadeesh Sep 16 '17 at 12:08
I'm using the second edition. I think that the definition before Theorem $9$ (Chapter $1$) should be
Definition. An $m\times m$ matrix is said to be an elementary matrix if it can be obtained from the $m\times m$ identity matrix by means of a single elementary row operation.
Definition. An $\color{red}{m\times n}$ matrix is said to be an elementary matrix if it can be obtained from the $m\times m$ identity matrix by means of a single elementary row operation.
Check out this question for details.
Aritra Das
$\begingroup$ It can be argued that any $m\times n$ matrix "obtained from the $m\times m$ identity matrix" by an elementary row operation will of necessity have $m=n$. So the "correction" you want to make here does not actually change the meaning of the definition. $\endgroup$ – hardmath Sep 28 '16 at 11:16
$\begingroup$ @hardmath Yes, of course, but I think it can help reduce confusion in the minds of people who are new to the topic. $\endgroup$ – Aritra Das Sep 28 '16 at 12:30
I wanted to add two more observations which I believe are typos.
Chapter 2, Example 16, Pg. 43
Example 16. We shall now give an example of an infinite basis. Let $F$ be a subfield of the complex numbers and let $V$ be the space of polynomial functions over $F.$ ($\dots \dots$)
Let $\color{red}{ f_k(x)=x_k},k=0,1,2,\dots.$ The infinite set $\{f_0,f_1,f_2,\dots \}$ is a basis for $V.$
It should have been $\color{red}{f_k(x)=x^k}$.
Chapter 1, Theorem 8
$$[A(BC)_{ij}]=\sum_r A_{ir}(BC)_{rj}=\color{red}{\sum_r A_{ir}\sum_s B_{rj}C_{rj}}$$
It should have been
$$[A(BC)_{ij}]=\sum_r A_{ir}(BC)_{rj}=\color{red}{\sum_r A_{ir}\sum_s B_{rs}C_{sj}}$$
Bijesh K.S
$\begingroup$ The second point is in fact correctly stated in my copy of the book (I am using the second edition). $\endgroup$ – Brahadeesh Dec 31 '17 at 13:08
Page 3, definition of characteristic.
. . . least n . . .
It should be least positive n.
Page 39, Exercise 3.
. . . R$^5$ . . .
It should be R$^4$.
Page 40, Exercise 6(b).
Prove that a subspace of R$^2$ is R$^2$, or the zero subspace, or consists of all scalar multiples of some fixed vector in R$^2$. (The last type of subspace is, intuitively, a straight line through the origin.)
The remark in parentheses is false if the fixed vector is the origin.
Pages 61 and 65.
Presentation of row matrices is inconsistent in that sometimes the entries are separated by commas, sometimes they are not.
. . . and show that S = UTU$^{-1}$.
It should be S = U$^{-1}$TU.
Page 129, Theorem 5, second sentence.
If f is a polynomial over f . . .
It should be If f is a polynomial over F . . .
Page 137, Example 11.
. . . is the g.c.d. of the polynomials.
Delete the period after polynomials. I include this seemingly trivial typo—that sentence-ending period causes the polynomials to refer to the preceding polynomials x – a, x – b, x – c, making the sentence obviously false—because it took me a non-trivial amount of time to figure out that the sentence does not actually end until four lines further down.
Page 191, second full paragraph.
According to Theorem 5 of Chapter 4, . . .
It should be Theorem 7.
Page 198, Exercise 11.
. . . Section 6.1, . . .
It should be Section 6.2.
Page 219, Exercise 4(b).
. . . for f is the product of the characteristic polynomials for f$_1$, . . ., f$_k.$
Replace the three occurrences of f with T. Note also that the hint applies to all three parts of the exercise, not just part (c) as suggested by the formatting.
. . . Example 6 . . .
It should be Example 5.
. . . is spanned . . .
It should be is not spanned.
Page 236, first full paragraph.
We have left to the exercises the proofs of the following three facts.
The first fact following that sentence is actually not an exercise.
Since A is the direct sum of two 2 $\times$ 2 matrices, it is clear that the minimal polynomial for A is (x – 2)$^2$.
It should read, "Since the decomposition of A in to a direct sum of minimally-sized matrices results in the largest such matrix having size 2 $\times$ 2, it is clear that the minimal polynomial for A is (x – 2)$^2$."
Page 273, last paragraph, second sentence.
To define it, we first denote the positive square root of $(\alpha|\alpha)$ by $||\alpha||$; . . .
I would be better to replace "positive" with "principal" in case $\alpha$ is zero. (My solution to Exercise 4(b) of Section 8.2 uses that change.)
Page 275, (8-7).
$\sum\limits_{j,k} x_j G_{jk} x_k > 0.$
It should be $\sum\limits_{j,k} \overline x_j G_{jk} x_k > 0.$
Page 287, proof of first corollary to Theorem 5, third sentence.
From its geometric properties, one sees that $I - E$ is an idempotent transformation of $V$ onto $W$.
It should be $W^\perp$.
Find an inner product on $R^2$ such that $(\epsilon_1, \epsilon_2) = 2$.
Hoffman and Kunze use $(\epsilon_1|\epsilon_2)$ to notate inner product up to this point in the text.
\begin{align} (E\alpha|\beta) & = (E\alpha|E\beta + (1 - E)\beta)\\ & = (E\alpha|E\beta)\\ & = (E\alpha + (1 - E)\alpha|E\beta)\\ & = (\alpha|E\beta).\end{align}
The $1$s should be $I$s.
Page 296, Example 21, third sentence.
Let $V$ be the inner product space of Example 21, . . .
Page 309, Exercise 3(f).
For which $\gamma$ is $M_\gamma$ positive?
Starting here, the authors refer to positive operator four times in the exercises before they define it on page 329. They do allude to the concept of a positive matrix, however, on page 275.
Page 315, proof of Theorem 19, last displayed equation.
$||(T - cI)\alpha|| = ||(T^* - cI)\alpha||$
It should be $||(T - cI)\alpha|| = ||(T^* - \overline cI)\alpha||$.
Fix a vector $\beta$ in $V$. Then $\alpha \rightarrow f(\alpha, \beta)$ is a linear function on $V$. By Theorem 6 . . .''
The logical reasoning would flow better if function were replaced by functional. Also, the theorem is from Chapter 8.
Page 321, proof of corollary to Theorem 1.
Since $f \rightarrow T_f$ is an isomorphism, Example 6 of Chapter 8 . . .
$2f(\alpha, \beta) = 2f(\beta, \alpha)$.
It should be $2f(\alpha, \beta) = 2\overline{f(\beta, \alpha)}$.
2. Let $f$ be the form on $R^2$ defined by $$f((x_1, y_1), (x_2, y_2)) = x_1 y_1 + x_2 y_2.$$
It should be $f((x_1, x_2), (y_1, y_2)) = x_1 y_1 + x_2 y_2$.
7. Give an example of an $n \times n$ matrix which has all its principal minors positive, but which is not a positive matrix.
The wording of the exercise seems to imply that we are not to choose a specific $n$ but rather are to make a general $n \times n$ matrix that solves the exercise for any value of $n$. If that is the case, then it is impossible for a $1 \times 1$ matrix to meet the requirements.
Pages 332 and 333, Theorem 7.
$V = W + W'$
If not a typo, at least it would be clearer to replace the two occurrences of that equation with $V = W \oplus W'$.
Page 333, fifth line.
$= c\sum\limits_k A_{jk} f(\alpha_k, \beta) + \sum\limits_k A_{jk} f(\alpha_k, \gamma)$
It should be $= c\sum\limits_k A_{jk} \overline{f(\alpha_k, \beta)} + \sum\limits_k A_{jk} \overline{f(\alpha_k, \gamma)}$.
Page 340, fourth-to-last line.
$TT^* = c_1 c_1 E_1 + \cdots + c_n c_n E_n$
It should be $TT^* = c_1\overline c_1 E_1 + \cdots + c_n\overline c_n E_n$.
Pages 343 and 344, first and fifth sentences of the proof.
. . . roots of $F$.
They should be roots of $\mathscr F$. (This typo is not trivial because $\mathscr F$ and $F$ are both used on those pages and denote different things.)
Page 345, proof of Theorem 16, second displayed equation.
$aT + U = \sum\limits_j (ac + d_j)P_j$
It should be $aT + U = \sum\limits_j (ac_j + d_j)P_j$
Page 347, Exercise 4, statement (d).
(d) If $\alpha$ is a vector . . .
It should be non-zero vector.
Page 350, equation in third-to-last line.
$p_j = x_j - c_j$
It should be $p_j = x - c_j$.
Page 355, proof of Theorem 19, equation in fifth-to-last line.
$T_j = c_j I$
It should be $T_j = c_j I_j$ to be consistent with previous usage.
Let $V$ be a vector space over the field $F$ and let $L_1$ and $L_2$ be linear functions on $V$.
It should be linear functionals.
Page 360, Example 2, second line of second displayed equation.
$= \operatorname{tr}(cXtAY) + \operatorname{tr}(Z^tAY)$
It should be $= \operatorname{tr}(cX^tAY) + \operatorname{tr}(Z^tAY)$.
2. Let $f$ be the bilinear form on $R^2$ defined by $$f((x_1, y_1), (x_2, y_2)) = x_1 y_1 + x_2 y_2.$$
Let $f$ be a bilinear form on a finite-dimensional vector space $V$. Show that $f$ can be expressed as a product of two linear functionals . . . if and only if $f$ has rank 1.
There are two reasonable corrections: (1) Let $f$ be a non-zero bilinear form . . . or (2) Show that $f$ can be expressed as a product of two non-zero linear functionals. . . .
Let $V$ be a finite-dimensional vector space and $f$ a non-degenerate symmetric bilinear form on $V$. . . . How much of the above is valid without the assumption that $T$ is non-degenerate?
There is a mistake in last sentence because the authors do not apply non-degenerate to operators. The simplest emendation is to end the sentence with that $f$ is non-degenerate? A change that is more instructive is that $f$ is symmetric?
Page 376, second full paragraph, last sentence.
From (9-7). . .
It should be (10-7).
Page 395, item (3).
. . . , then $\alpha - \gamma = (\alpha - \beta) + \beta - \gamma)$ is in W.
It should be $\alpha - \gamma = (\alpha - \beta) + (\beta - \gamma)$ is in W.
Page 396, first item.
(a) If $\alpha \equiv \alpha', \mod W$, and $\beta \equiv \beta', \mod W$, then $$\alpha + \alpha' \to \beta + \beta', \mod W.$$
It should be (1) If $\alpha \equiv \alpha', \mod W$, and $\beta \equiv \beta', \mod W$, then $$\alpha + \alpha' \equiv \beta + \beta', \mod W.$$
Page 396, proof of item (1).
(1) If $\alpha - \alpha'$ is in $W$ and $\beta - \beta'$ is in $W$, then since $(\alpha + \beta) - (\alpha' - \beta') = (\alpha - \alpha') + (\beta - \beta')$, we see that $\alpha + \beta$ is congruent to $\alpha' - \beta'$ modulo $W$.
It should be (1) If $\alpha - \alpha'$ is in $W$ and $\beta - \beta'$ is in $W$, then since $(\alpha + \beta) - (\alpha' + \beta') = (\alpha - \alpha') + (\beta - \beta')$, we see that $\alpha + \beta$ is congruent to $\alpha' + \beta'$ modulo $W$.
Subtract one from all page numbers greater than 386.
57 revs
Maurice P
More than a typo, there's a stated Corollary on page 356 in Section 9.6 that appears to be false. The details are here:
https://mathoverflow.net/questions/306759/error-in-hoffman-kunze-normal-operators-on-finite-dimensional-inner-product-spa
Spiro Karigiannis
I'm using the second edition.
I will expand the errata as soon as I find some mistakes (not mentioned by other answers) in the book.
p. 284, Theorem 4.
(iii) $\dots$ is any orthonormal basis for $W$, then the vector
It should be orthogonal basis. The proof uses an orthogonal basis as the condition, and the equation below is a general form with respect to an orthogonal basis rather than an orthonormal basis.
p. 329, third-to-last paragraph.
If $A$ is an $n \times n$ matrix with complex entries and if $A$ satisfies (9-9),
It should be (9-8) rather than (9-9).
MathNoob
Not the answer you're looking for? Browse other questions tagged linear-algebra reference-request or ask your own question.
Typo in Hoffman and Kunze's linear algebra book
Annihilator of a vector space $V$ is the zero subspace of $V^*$
Proof of Theorem 7 (Chapter 5) in Hoffman and Kunze's *Linear Algebra* is unclear
Proof of a theorem on simultaneous diagonalization from Hoffman and Kunze.
Why is $\pi_r(L)$ a linear transformation into $\Lambda^r(V)$
Can a elementary row operation change the size of a matrix?
Showing $[(fg)h]_n = [f(gh)_n]$ in the linear algebra $F^\infty$
Doubt in section 5.7 of Hoffman and Kunze's *Linear Algebra*
$L\cdot M:=\pi_{r+s}(L\otimes M)$, then $((f_i\cdot f_j)\cdot f_k)\cdot f_l=?$
How to approach the problems in the Hoffman Kunze book?
Develop good understanding of Linear Algebra
Is Hoffman-Kunze a good book to read next?
Can you learn linear algebra with an abstract algebra book?
Linear Algebra Textbook
Hoffman and Kunze, linear algebra exercise
Hoffman Kunze - Definition of Row Reduced Echelon Matrix | CommonCrawl |
What can we say about the Gibbs free energy if it decreases or not?
[Sorry if the question looks trivial but I have thought about it for days and red a number of books all with no success.]
In almost every thermodynamics book that has something to say about chemical reactions there is a proof for the fact that at constant pressure and temperature the process is spontaneous in the direction in which the Gibbs free energy decreases. In some of the books it is also remarked that this conclusion is for when there is no "additional work" (beside the work of pressure in expanding the system), if there is an additional work then except for $dG=0$ the reversible process will yield into that additional work gaining its maximum value:
\begin{align} \text{The only work is expansive:}\qquad & dG\le 0\\ \text{There are some additional works present:}\qquad & dG\le \delta W_{\text{additional}} \end{align}
In this regard I have a question: When we have some additional works there in the problem (like electric work in an electrochemical cell), so that the second inequality holds and the maximum work is assigned to $dG$ as $dG=\delta W_{Add,Max}$, why still we feel free to use the first inequality and claim $dG$ should be negative?
In the case of electrochemical cells we have: $\delta W_{E,Max}=-n\,F\,E_{cell}\,d\zeta$ wherein $\zeta$ measure the advancement of the reaction. So we would obtain in a reversible (i.e. infinitely slow) reaction $\Delta_rG=\frac{dG_{p,t}}{d\zeta}=-n\,F\,E_{cell}$. But all the books then state that since the reaction is spontaneous in the direction in which $\Delta_rG\le 0$ so we would obtain $E_{cell}\ge 0$, while we know the inequality $\Delta_rG\le0$ is obtained from $dG\le0$ which doesn't hold here.
My question in other wording reads like this. Does the electrochemical cell problem involve an electric work or not? If "yes" then from where do we know the Gibbs free energy should decrease? And if "no" then from where do we obtain the equality $\Delta_rG=-n\,F\,E_{cell}$?
thermodynamics electrochemistry
topologytopology
I think the confusion may be because you are conflating two ideas about Gibbs free energy.
The first is that Gibbs energy is a thermodynamic potential - this means that on a given surface in phase-space (the NPT surface), it is the "driving" force for, well, everything. Including chemical reactions.
The second idea is that the net change in Gibbs energy when going from reactants to products indicates the direction that the reaction will (eventually) go, and that its magnitude tells you the maximum amount of work that could be done by that reaction.
The second idea follows from the first - this becomes easy to understand if you just picture the thermodynamic potential as a gravitational potential, since we all have a good intuitive understanding of gravitational potentials.
Imagine a hill representing the thermodynamic potential (in this case Gibbs energy):
The rock represents a reaction coordinate - say, the concentration of a reactant. What will happen to the rock? It will go downhill. What will its maximum energy be when it reaches the bottom? Whatever the difference in potential energies is. What is the minimum energy it would need to get back the top? Again, whatever the net difference is in potential energies.
When you ask about $dG$ being negative, you are asking about the differential change - in other words, what is the slope? Obviously, if the reaction proceeds, the slope must be negative - "things roll downhill"
When you ask about $\Delta G$ being negative, you are asking whether the net change is positive or negative. The system can never do more work than the net change in $\Delta G$, because that is the maximum change in thermodynamic potential energy.
For your problem, the reaction involves moving an electron against a potential - the cell potential. The reaction can provide $\Delta G$ amount of energy with which to move that electron.
thomijthomij
10k3030 silver badges6060 bronze badges
$\begingroup$ Dear @thomij, thank you for your great explanation, only one point remains in the dark side for me, that the reaction itself involves the transfer of electron so moving the electron is not a work done by the reaction on the system's surrounding, am I wrong? $\endgroup$
– topology
$\begingroup$ The electrons are moving against an external potential, which is the cell voltage. If all of the reactant molecules were in the same side of the cell, there would be no external potential and the total $\Delta G$ would be released as other forms of energy (heat mostly). Since in a Galvanic cell the reactants are separate, but electrons can flow through a circuit, then the voltage of the circuit is the external potential that the reaction is doing work against. $\endgroup$
– thomij
Not the answer you're looking for? Browse other questions tagged thermodynamics electrochemistry or ask your own question.
Express the maximum work from a voltaic cell
how is the relation between Gibbs free energy and cell potential?
On Spontaneity of the Redox Reactions
The spontaneity of a redox reaction
Gibbs Free Energy : What is it trying to say actually?
What is the precise definition of maximum work in the context of electrochemistry and thermodynamics?
Understanding Gibbs free energy
How come ∆G ≤ 0 is used for spontaneity in electrochemistry, not ∆G ≤ W(other)?
What is non PV work? How is it related to Gibbs energy?
Enthalpy of Reaction and Efficiency of Electrochemical Energy Devices | CommonCrawl |
Next tag badge
riemann-zeta
2/100 score
1/20 answers
Inquisitive
If $A$ is dense in $\Bbb Q$, then it must be dense in $\Bbb R$.
Mar 20 at 15:41
How to show $\left\{ x \in \mathbb N \mid x \equiv 11 \pmod{15}\right\}$ is countable by establishing a bijection between the set and N
Mar 19 at 1:45
Prove this using the definition of convergence. Please help ASAP!
Mar 1 at 0:12
About the equation $x^2+y^2+z^2+2t^2=n$
Jan 9 at 17:28
If a prime can be expressed as sum of square of two integers, then prove that the representation is unique.
Is it mathematically wrong to say "infinite number"?
Dec 27 '18 at 6:48
Find $\sum_{n=1}^{\infty}\tan^{-1}\frac{2}{n^2}$
Do the parenthesis around modulo matter
How to factor $x^3+y^3-91$?
Asymptotic behavior $\sum_{n=1}^x\phi_k(n)$, a variant of Euler's Totient function
Prove the equation $\left(2x^2+1\right)\left(2y^2+1\right)=4z^2+1$ has no solution in the positive integers
Quadratic Functions - vertex of graph proof
Find the area using simultaneous equations
Dec 7 '18 at 22:42
Meaning of $x^2+y^2=0$ (imaginary can have real property?!)
How to integrate $\int\frac{2x+1}{\sqrt{x+3}}dx$?
Dec 5 '18 at 3:58
proof on difference of two squares and odd integers
Prove that $4| \sigma(4k+3)$ for each positive integer $k$
Is $\lim_{x \to \infty }\sum_{n=1}^\infty \frac{n!}{e^{n^x}}=e^{-1}$?
Solve the non-linear DE $y' = xy+ y^{1/2}$ analytically
Modular Arithmetic Proof on getting 103 from sum of 9's and 14's only
Nov 28 '18 at 22:51
Solve a system of trigonometric equations
Is there an easy way to see that binary expansion is unique?
Use calculus to find length of y=-mx+b, then show that the answer agrees with the answer when using pythagorean theorem
Finding elements in a finite bijective set
Can we remove the absolute value from inequality $|a-b|<ε$?
How to tell if this propositional logic statement is valid?
Find two pairs where neither is the case ⟨x1,y1⟩⪯⟨x2,y2⟩, ⟨x1,y1⟩⪰⟨x2,y2⟩.
Solving complex equation: $(z-1)^2+(\bar{z}-2i)^2 = 0$ | CommonCrawl |
Subscribe About Archive BAIR
Building Gene Expression Atlases with Deep Generative Models for Single-cell Transcriptomics
Romain Lopez and Chenling Xu
Figure: An artistic representation of single-cell RNA sequencing. The stars in the sky represent cells in a heterogeneous tissue. The projection of the stars onto the river reveals relationships among them that are not apparent by looking directly at the sky. Like the river, our Bayesian model, called scVI, reveals relationships among cells.
The diversity of gene regulatory states in our body is one of the main reasons why such an amazing array of biological functions can be encoded in a single genome. Recent advances in microfluidics and sequencing technologies (such as inDrops) enabled measurement of gene expression at the single-cell level and has provided tremendous opportunities to unravel the underlying mechanisms of relationships between individual genes and specific biological phenomena. These experiments yield approximate measurements for mRNA counts of the entire transcriptome (i.e around $d = 20,000$ protein-coding genes) and a large number of cells $n$, which can vary from tens of thousands to a million cells. The early computational methods to interpret this data relied on linear model and empirical Bayes shrinkage approaches due to initially extremely low sample-size. While current research focuses on providing more accurate models for this gene expression data, most of the subsequent algorithms either exhibit prohibitive scalability issues or remain limited to a unique downstream analysis task. Consequently, common practices in the field still rely on ad-hoc preprocessing pipelines and specific algorithmic procedures, which limits the capabilities of capturing the underlying data generating process.
In this post, we propose to build up on the increased sample-size and recent developments in Bayesian approximate inference to improve modeling complexity as well as algorithmic scalability. Notably, we present our recent work on deep generative models for single-cell transcriptomics, which addresses all the mentioned limitations by formalizing biological questions into statistical queries over a unique graphical model, tailored to single-cell RNA sequencing (scRNA-seq) datasets. The resulting algorithmic inference procedure, which we named Single-cell Variational Inference (scVI), is open-source and scales to over a million cells.
The scRNA-seq Analysis Era
Previous RNA quantification technologies were only able to collect population level data, thus biologists could not determine if the differences in their experiments were due to changes within a single cell type, multiple cell types, or simply changes in frequencies of cells. Researchers can now dissociate heterogeneous tissues into single cells, each encapsulated within a droplet with barcodes that allow for easy sequencing and demultiplexing. After read alignment procedures, we get a data matrix $x_{ng}$ of counts for expression of gene $g$ in cell $n$.
The standard analysis of this data matrix can be broken down into a number of sequential tasks. At a high level, we would like to classify cells present in our sample, which is commonly approached by clustering problem an abstract latent space. Looking more closely, we want to identify the characteristic genes for each cell type. , usually achieved via hypothesis testing. Importantly, for any of these analyses, we must decouple biological signal from technical factors. In scRNA-seq, technical factors include sequencing depth (i.e. the number of total transcripts captured in a cell) and batch-effects (i.e discrepancies between biological replicates). These confounding effects make any inference problem significantly harder and therefore cannot be addressed by an off-the-shelf machine learning algorithm.
There is a rich literature in scRNA-seq data analysis that relies on very diverse machine learning techniques such as nearest-neighbors algorithms (MNNs), similarity metric learning via kernel methods (SIMLR), matrix factorization (ZINB-WaVE), and Bayesian non-parametric modeling (BISCUIT). However, all these approaches have limitations. Namely, one specific algorithm is built to address a unique problem. Consequently, each algorithm can use its own underlying hypothesis that may create statistical inconsistencies. Furthermore, these methods do not scale to more than a few thousand samples — either because of memory or time complexity — which is an issue for analyzing modern datasets.
Deep Generative Models of Stochastic Gene Expression
As a starting point to a suitable generative model, we identify the different factors of variability over which we would like to condition the data generating process for the mRNA counts $x_{ng}$. First, a cell-specific latent variable $l_n$ represents discrepancies between the number of transcripts captured in each cell. Second, a dataset-specific factor $s_n$ represents discrepancies between sequencing protocols or experiments conditions. Third, a cell-specific latent variable $z_n$ encodes the parameters that governs stochastic gene expression of the cell. This variable is typically of small dimension and embeds the cells for downstream analysis (such as clustering).
Notably, following seminal work by Sandrine Dudoit's group (ZINB-WaVE) we model the conditional distribution $p(x_{ng} | z_n, l_n, s_n)$ as zero-inflated negative binomial. Unlike ZINB-WaVE, which relies on linear models, we use deep neural networks to parametrize these conditional distributions. We refer to our manuscript for a complete specification of our probabilistic model.
Because the marginal distribution $p(x_n | s_n)$ is not amenable to Bayesian computations, we rely on auto-encoding variational Bayes to learn an approximate posterior $q(z_n, l_n | x_n, s_n)$ (Figure 1) and fit our generative model. In particular, scVI relies on stochastic optimization by sampling from the variational posterior and from the datasets, which ensures a scalable inference procedure. scVI can also be used for hypothesis testing by sampling from the variational posterior and identify gene of interest between cell-types.
Figure 1: Overview of scVI. Given a gene-expression matrix with batch annotations as input, scVI learns a non-linear embedding of the cells that can be used for multiple analysis tasks. We draw here the computational trees (neural networks) used to compute the embedding as well as the distribution of gene expression.
We refer to our manuscript for an extensive benchmarking study on a set of seven different datasets and five different tasks (which includes embedding and hypothesis testing). scVI compares favorably on all the datasets and all the tasks against state-of-the-art algorithms in each task.
A Gene Expression Atlas of the Mouse Brain from a Million Single-cell Measurements
scVI provides a readily applicable solution for large-scale inference. In particular, we could fit the 1.3 million cells dataset from 10x Genomics in less than 1 hour on a small subset of 720 genes and less than 6 hours on a bigger subset of 10,000 genes. The generative model embeds the data via its posterior $q(z_n | x_n, s_n)$ (Figure 2) and identifies important genes between cell-types via hypothesis testing.
Figure 2: tSNE embedding of a subset of cells from the 1.3M cells dataset based on scVI's latent space.
Towards more Systematic Integration of Prior Biological Knowledge
From this proof of concept, we are now working on extending this work to incorporate prior biological knowledge such as integrating several datasets, using semi-supervised models to annotate the cells, adding hierarchical structure for cell-type taxonomy, and adding sparsity priors for greater interpretability of the neural networks weights.
We hope that our approach will inspire the computational biology community to develop probabilistic-model-based tools that are more consistent and better grounded than ad-hoc algorithmic procedures. Please feel free to read our manuscript published in Nature Methods along with its associated News and Views. We have released code here through a GitHub project.
Acknowledgements: We are grateful for the contributions of our collaborators: Edouard Mehlman, Maxime Langevin, Adam Gayoso, Yining Liu, Jules Samaran, Jeffrey Regier, and Nir Yosef.
Subscribe to our RSS feed. | CommonCrawl |
Computational Social Networks
An insight analysis and detection of drug-abuse risk behavior on Twitter with self-taught deep learning
Han Hu ORCID: orcid.org/0000-0002-2555-92361,
NhatHai Phan1,
Soon A. Chun2,
James Geller1,
Huy Vo3,
Xinyue Ye1,
Ruoming Jin4,
Kele Ding4,
Deric Kenne4 &
Dejing Dou5
Computational Social Networks volume 6, Article number: 10 (2019) Cite this article
Drug abuse continues to accelerate towards becoming the most severe public health problem in the United States. The ability to detect drug-abuse risk behavior at a population scale, such as among the population of Twitter users, can help us to monitor the trend of drug-abuse incidents. Unfortunately, traditional methods do not effectively detect drug-abuse risk behavior, given tweets. This is because: (1) tweets usually are noisy and sparse and (2) the availability of labeled data is limited. To address these challenging problems, we propose a deep self-taught learning system to detect and monitor drug-abuse risk behaviors in the Twitter sphere, by leveraging a large amount of unlabeled data. Our models automatically augment annotated data: (i) to improve the classification performance and (ii) to capture the evolving picture of drug abuse on online social media. Our extensive experiments have been conducted on three million drug-abuse-related tweets with geo-location information. Results show that our approach is highly effective in detecting drug-abuse risk behaviors.
Abuse of prescription drugs and of illicit drugs has been declared a "national emergency" [1]. This crisis includes the misuse and abuse of cannabinoids, opioids, tranquilizers, stimulants, inhalants, and other types of psychoactive drugs, which statistical analysis documents as a rising trend in the United States. The most recent reports from the National Survey on Drug Use and Health (NSDUH) [2] estimate that 10.6% of the total population of people ages 12 years and older (i.e., about 28.6 million people) misused illicit drugs in 2016, which represents an increase of 0.5% since 2015 [3]. According to the Centers for Disease Control and Prevention (CDC), opioid drugs were involved in 42,249 known deaths in 2016 nationwide [4]. In addition, the number of heroin-involved deaths has been increasing sharply for 5 years, and surpassed the number of firearm homicides in 2015 [5].
In April 2017, the Department of Health and Human Services announced their "Opioid Strategy" to battle the country's drug-abuse crisis [1]. In the Opioid Strategy, one of the major aims is to strengthen public health data collection, to inform a timeliness public health response, as the epidemic evolves. Given its 100 million daily active users and 500 million daily tweets [6] (messages posted by Twitter users), Twitter has been used as a sufficient and reliable data source for many detection tasks, including epidemiology [7] and public health [8,9,10,11,12,13], at the population scale, in a real-time manner. Motivated by these facts and the urgent needs, our goal in this paper is to develop a large-scale computational system to detect drug-abuse risk behaviors via Twitter sphere.
Several studies [10, 13,14,15,16,17] have explored the detection of prescription drug abuse on Twitter. However, the current state-of-the-art approaches and systems are limited in terms of scales and accuracy. They typically applied keyword-based approaches to collect tweets explicitly mentioning specific drug names, such as Adderall, Oxycodone, Quetiapine, Metformin, Cocaine, marijuana, weed, meth, tranquilizer, etc. [10, 13, 15, 17]. However, that may not reflect the actual distribution of drug-abuse risk behaviors on online social media, since: (1) the expressions of drug-abuse risk behaviors are often vague, in comparison with common topics, i.e., a lot of slang is used and (2) relying on only keyword-based approaches is susceptible to lexical ambiguity in natural language [12]. In addition, the drug-abuse risk behavior Twitter data are very imbalanced, i.e., dominated by non-drug-abuse risk behavior tweets, such as drug-related news, social discussions, reports, advertisements, etc. The limited availability of annotated tweets makes it even more challenging to distinguish drug-abuse risk behaviors from drug-related tweets. However, existing approaches [10, 13, 15, 17] have not been designed to address these challenging issues for drug-abuse risk behavior detection on online social media.
Contributions: To address these challenges, our main contributions are to propose: (1) a large-scale drug-abuse risk behavior tweets collection mechanism based on supervised machine-learning and data crowd-sourcing techniques and (2) a deep self-taught learning algorithm for drug-abuse risk behavior detection. Based on our previous work [18], we extended the analysis of the classification results from our three million tweets dataset with the analysis of word frequency, hashtag frequency, drug name-behavior co-occurrence, temporal distribution (time-of-day), and state-level spatial distribution.
We first collect tweets through a filter, in which a variety of drug names, colloquialisms and slang terms, and abuse-indicating terms (e.g., overdose, addiction, high, abuse, and even death) are combined together. We manually annotate a small number of tweets as seed tweets, which are used to train machine-learning classifiers. Then, the classifiers are applied to large number of unlabeled tweets to produce machine-labeled tweets. The machine-labeled tweets are verified again by humans on Mechanical Turk, i.e., a crowd-sourcing platform, with good accuracy but at a much lower cost. The new labeled tweets and the seed tweets are combined to form a sufficient and reliable labeled dataset for drug-abuse risk behavior detection by applying deep learning models, i.e., convolution neural networks (CNN) [19], long–short-term memory (LSTM) models [20], etc.
However, there are still a large amount of unlabeled data, which can be leveraged to significantly improve our models in terms of classification accuracy. Therefore, we further propose a self-taught learning algorithm, in which the training data of our deep self-taught learning models will be recursively augmented with a set of new machine-labeled tweets. These machine-labeled tweets are generated by applying the previously trained deep learning models to a random sample of a huge number of unlabeled tweets, i.e., the three million tweets in our dataset. Note that the set of new machine-labeled tweets possibly has a different distribution from the original training and test datasets.
After the model is trained, we apply it to our geo-location-tagged dataset to acquire classification results for analysis. Results from the aforementioned analysis show that the drug-abuse risk behavior-positive tweets have distinctive patterns of words, hashtags, drug name-behavior co-occurrence, time-of-day distribution, and spatial distribution, compared with other tweets. These results show that our approach is highly effective in detecting drug-abuse risk behaviors.
The rest of this paper is organized as follows. We review related work in the next section. Then, we describe the implementation of our method in detail, followed by experiment results and data analysis. Finally, we conclude this paper and propose future directions.
Background and related work
On one hand, the traditional studies and organizations, such as NSDUH [2], CDC [4], Monitoring the Future [21], the Drug-Abuse Warning Network (DAWN) [22], and the MedWatch program [23] are trustworthy sources for getting the general picture of the drug-abuse epidemic. On the other hand, many studies that are based on modern online social media, such as Twitter, have shown promising results in drug-abuse detection and related topics [7,8,9,10,11,12,13,14,15,16,17]. Many of the existing studies were focusing on the quantitative analysis utilizing data from online social media. Meng et al. [24] used traditional text and sentiment analysis methods to investigate substance use patterns and underage use of substance, and the association between demographic data and these patterns. Ding et al. [25] investigated the correlation between substance (tobacco, alcohol, and drug) use disorders and words in Facebook users' "Status Updates" and "Likes". Their results showing word patterns are different between users who have substance us disorder and users who do not have. Hanson et al. [15] conducted a quantitative analysis on 213,633 tweets discussing "Adderall", a prescription stimulant commonly abused among college students, and also published another study [14] focused on how possible drug-abuser interact with and influence others in online social circles. The results showed that strong correlation could be found: (1) between the amount of interaction about prescription drugs and a level of abusiveness shown by the network and (2) between the types of drugs mentioned by the index user and his or her network. Shutler et al. [17] performed a qualitative analysis of six prescription opioids, i.e., Percocet, Percs, OxyContin, Oxys, Vicodin, and Hydros. Tweets were collected with exact word matching and manual classification. Their primary goal was to identify the key terms used in tweets that likely indicate drug abuse. They found that the use of Oxys, Percs, and OxyContin was common among the tweets, where there were positive indications of abuse. McNaughton et al. [16] measured online endorsement of prescription opioid abuse by developing an integrative metric through the lens of Internet communities. Simpson et al. [26] demonstrated an attempt to identify emerging drug terms using NLP techniques. Furthermore, Twitter and social media have been shown to be reliable sources in analyzing drug abuse and public health-related topics, such as cigarette smoking [8, 12], alcohol use [11], and even cardiac arrest [9]. However, these studies generally did not propose methods that apply to large-scale automated monitoring tasks.
Our previous work [27] showed the potential of applying machine-learning models in a drug-abuse monitoring system to detect drug-abuse-related tweets. Several other approaches also utilized machine-learning methods in detecting and analyzing drug-related posts on Twitter. For instance, Coloma et al. [28] illustrated the potential of social media in drug safety surveillance with two case study multiple online social media platforms. Sarker et al. [13] proposed a supervised classification model, in which different features such as n-grams, abuse-indicating terms, slang terms, synonyms, etc., were extracted from manually annotated tweets. Then, these features were used to train traditional machine-learning models to classify drug-abuse tweets and non-abuse tweets. Recently, many works, including one of our works [29], explored the use of more advanced deep learning models for drug-related classification tasks on online social media. Following our work, Kong et al. [30] proposed deep learning model that utilizes geographical prior information as input features. Chary et al. [10] discussed how to use AI models to extract content useful for purposes of toxicovigilance from social media, such as Facebook, Twitter, and Google+. Weissenbacher et al. [31] proposed deep neural network based model to detect drug name mentions in tweets. Mahata et al. [32] proposed an ensemble CNN model to classify tweets from three classes, i.e., personal medication intakes, possible personal medication intake, and non-intake. Works have also been done in perspectives other than content-based analysis and classification. Zhang et al. [33] proposed a complex schema, which models all possible interactions between users and posts, for automatic detection of drug abusers on Twitter. Li et al. [34] evaluated deep learning models against traditional machine-learning models on the task of detecting illicit drug dealers on Instagram.
Although existing studies have shown promising approaches towards the detecting of drug-related posts and information on popular online social media platforms, such as Twitter and Instagram, their limitations can be identified as: (1) limited in scale, as the methods proposed in many studies do not scale well, or rely on larger manually annotated training dataset for higher performance; (2) limited in scope, as most studies focus on a small group of drugs; and (3) limited in performance, as many methods use traditional machine-learning models. In this paper, we propose a novel deep self-taught learning system to leverage a huge number of unlabeled tweets. Self-taught learning [35] is a method that integrated the concepts of semi-supervised and multi-task learning, in which the model can exploit examples that are unlabeled and possibly come from a distribution different from the target distribution. It has already been shown that deep neural networks can take advantage of unsupervised learning and unlabeled examples [36, 37]. Different from other approaches mainly designed for image processing and object detection [38,39,40,41], our deep self-learning model shows the ability to detect drug-abuse risk behavior given noisy and sparse Twitter data with a limited availability of annotated tweets.
Deep self-taught learning system for drug-abuse risk behavior detection
In this section, we present the definition of the drug-abuse risk behavior detection problem, our system for collecting tweets, labeling tweets, and our deep self-taught learning approach. The system overview is shown in Fig. 1.
Drug-abuse detection system. There are 4 steps as follows: (1) Tweets will be collected through Twitter APIs. (2) Pre-processed tweets will be labeled by humans, AI techniques, and crowd-sourcing techniques. (3) Labeled tweets will be used to augment the training data of our AI models and data analysis tasks to identify tweets with drug-abuse risk behaviors, through a self-taught algorithm. In addition, (4) trained systems will be used in different drug-abuse monitoring services and interactive user interfaces
We use the term "drug-abuse risk behavior" in the wider sense, including misuse and use of Schedule 1 drugs that are illegal; and misuse of Schedule 2 drugs, e.g., Oxycodone, which includes the use thereof for non-medical purposes, and the symptoms and side-effects of misuse. Our task is to develop classification models that can classify a given unlabeled tweet into one of the two classes: a drug-abuse risk behavior tweet (positive) or a non-drug-abuse risk behavior (negative) tweet. The main criteria for classifying a tweet as drug-abuse risk can be condensed into: "The existence of abusive activities or endorsements of drugs." Meanwhile, news, reports, and opinions about drug abuse are the signals of tweets that are not considered as containing abuse risk.
Collecting and labeling tweets
In our crawling system, raw tweets are collected through Twitter APIs. For the collection of focused Twitter data, we use a list of the names of illegal and prescription drugs [42] that have been commonly abused over time, e.g., Barbiturates, OxyContin, Ritalin, Cocaine, LSD, Opiates, Heroin, Codeine, Fentanyl, etc. However, the data are very noisy, since: (1) there is no indication of how to distinguish between drug abuse and legitimate use (of prescription drugs) in collected Tweets and (2) many of slang terms are used in expressing drug-abuse risk behavior. To address this problem, we added slang terms for drugs and abuse-indicating terms, e.g., "high," "stoned," "blunt," "addicted," etc., into our keyword search library. These slang terms are clearly expressing that the tweets in question were about drug abuse. As a result, most of the collected data are drug abuse-related.
To obtain trustworthy annotated data, we design two integrative steps in labeling tweets. In the first step, 1,794 tweets randomly chosen from collected tweets were manually annotated as positive or negative by three team members who have experience in health informatics. Several instances of positive tweets and negative tweets are illustrated in Table 1. These labeled tweets are considered seed tweets, which then are used to train traditional binary classifiers, e.g., SVM, Naive Bayes, etc., to predict whether a tweet is a drug-abuse risk behavior tweet or not. The trained classifiers are applied to unlabeled tweets to predict their labels, which are called machine labels. In the second step, 5000 positive machine-labeled tweets with high classification confidence are verified again on Amazon Mechanical Turk (AMT), which is a well-known crowd-sourcing platform. To improve the trustworthiness and to avoid bias in the annotated data, each tweet is labeled by three individual workers. The workers are instructed to follow with the same annotation instructions that our annotators have followed. Our annotators also labeled a random sample of 1000 tweets and compare the labels with the results from AMT, as a quality check.
Table 1 Instances of manually annotated positive tweets and negative tweets
Tweet vectorization
Raw tweets need to be first pre-processed, then represented as vectors, before they can be used in training machine-learning models. In this study, we choose a commonly used pre-processing pipeline, followed by three different vectorization methods. The pre-processing pipeline consists of following steps:
The tweets are tokenized and lower cased. The special entities, i.e., including Emojis, URLs, mentions, and hashtags, are removed or replaced with special keywords. The non-word characters, i.e., including HTML symbols, punctuation marks, and foreign characters, are removed. Words with three or more repeating characters are reduced to at most three successive characters.
Stop words are removed according to a custom stop-word list. Stemming is applied using the standard Porter Stemmer.
After the pre-processing steps, common vectorization methods are used to extract features from tweets, including: (1) term frequency, denoted as tf, (2) Tf-idf, and (3) Word2vec [43]. Word2vec is an advanced and effective word embedding method that converts each word into a dense vector of fixed length. We considered two different word2vec models: (i) a custom word2vec model, which was trained on our three million drug-abuse-related tweets. The model contains 300-dimensional vectors for 1,130,962 words and phrases and (ii) Google word2vec, which is a well-known pre-trained word2vec model built from part of a Google News dataset with about 100 billion words, and the model contains 300-dimensional vectors for three million words and phrases.
Deep self-taught learning approach
By applying both traditional and advanced machine-learning models, such as SVM, Naive Bayes, CNN, and LSTM to the small and static annotated data, i.e., 6794 tweets, we can achieve reasonable classification accuracies of nearly 80%, as indicated in Fig. 3 when the number of iteration k is zero, which is equivalent to applying models without the proposed self-taught method. However, to develop a scalable and trustworthy drug-abuse risk behavior detection model, we need to: (1) improve classification models to achieve higher accuracy and performance and (2) leverage the large number of unlabeled tweets, i.e., three million tweets related to drug abuse, to improve the system performance. Therefore, we propose a deep self-taught learning model by repeatedly augmenting the training data with machine-labeled tweets. The pseudo-code of our algorithm is as follows:
Step 1::
Randomly initialize labeled data D consisting of 5794 annotated tweets as the training set. Initialize a test data T consisting of the remaining 1000 annotated tweets.
Train a binary classification model M using the labeled data D. M could be a CNN model or an LSTM model.
Use the model M to label the unlabeled data U, which simply consists of three million unlabeled tweets. The set of new labeled tweets is denoted as \({\overline{D}}\), which is also called machine-labeled data.
Sample tweets from the machine-labeled data \({\overline{D}}\) with a high classification confidence, and then add the sampled tweets \(D^{+}\) into the labeled data D to form a new training dataset: \(D=D \bigcup D^{+}\). A tweet is considered to have a high classification confidence if it has a classification probability \(p \in [0,1]\) higher than a predefined sampling threshold \(\delta\). Sampled machine-labeled tweets will not be sampled again: \(U=U-D^{+}\).
Repeat Steps 2–4 for k iterations, where k is a user-predefined number. Return the trained model M.
With the self-taught learning method, the training data contain the annotated data D, which is automatically augmented with highly confident, machine-labeled tweets, in each iteration. This approach has the potential of increasing the classification performance of our model over time. In addition, the unlabeled data can be collected from the Twitter APIs in real time, to capture the evolving of English (slang) terms about drug-abuse risk behaviors. In the literature, data augmentation approaches have been applied to improve the accuracy of deep learning models [36]. However, the existing approaches [36, 39,40,41] are quite different from our proposed model, since they focused on image classification tasks, instead of drug-abuse risk behavior detection as in our study. Note that, to ensure fairness, test data T are separated from other data sources during the training process.
To examine the effectiveness and efficiency of our proposed deep self-taught learning approaches, we have carried out a series of experiments using a set of three million drug-abuse-related tweets collected in the past 4 years. We first elaborate details about our dataset, baseline approaches, measures, and model configurations. Then, we introduce our experimental results.
Experiment settings
The seed dataset contains 1794 tweets that were manually labeled by three annotators, including 280 positive tweets and 1514 negative tweets. The agreement score among three annotators is 0.414, measured by Krippendoff's Alpha. We then selected 5000 tweets labeled by the machine-learning model (i.e., SVM) with a high confidence level (\(\delta > 0.7\)), and rendered them verified on AMT. The AMT workers have the agreement score of 0.456, measured by Krippendoff's Alpha. Note that both agreement scores should be considered as reliable result in out study settings [44], since: (1) our task is to reduce variability in data annotation, instead of typical content analysis [45] and (2) the Krippendoff's Alpha is sensitive to data imbalance and sparseness, which are the characteristics of our dataset. Our integrative labeling approach resulted in a reliable and well-balanced annotated dataset, with 6794 labeled tweets, including 3102 positive labels and 3677 negative labels. For the unlabeled data, we have the three million drug-abuse-related tweets with geo-location information covering the entire continental US (lower 48 states and D.C.).
Baseline methods
In our experiments, Random Forest (RF), Naive Bayes (NB), and SVM are employed as baseline approaches for the binary classification task, i.e., to classify whether a tweet is a drug-abuse risk behavior tweet or not. Table 2 shows the parameter settings of baseline approaches and the proposed models. Note that for the Naive Bayes method, we use Gaussian Naive Bayes with word2vec embedding. Meanwhile, we use term frequency (i.e., tf) and tf-idf vectorization for Multinominal Naive Bayes. This is because: (1) the vectors generated by term frequency-based vectorization has a very high number of dimensions and could be only represented by sparse matrix, which was not supported by the chosen implementation of Gaussian Naive Bayes and (2) the multinominal Naive Bayes require non-negative inputs, but vectors generated by word2vec embedding have negative values. Regarding our self-taught CNN (st-CNN) and self-taught LSTM (st-LSTM) models, the Adam optimizer algorithm with default learning rate is used for training. The number of iterations k is set to 6, and the sampling threshold \(\delta\) is set to 0.7, for all methods. All the experiments have been conducted on a single GPU, i.e., NVIDIA TITAN Xp with 12 GB memory and 3072 CUDA cores.
Table 2 Parameter settings for all models
Accuracy, recall, and F1-value are used to validate the effectiveness of the proposed and baseline approaches. Due to the small size and the imbalanced label distribution, we adopted the Monte Carlo cross-validation technique. In each run, a fixed number of data instances are sampled (i.e., without replacement) as the test dataset, and the rest of the data as the training dataset. Multiple runs (i.e., 3 times) are generated for each model in each set of parameters and experimental configurations. We report the average of these runs as result. Definitions of the accuracy, recall, and F1-value are given as follows, where \(T_{P}\),\(T_{N}\),\(F_{P}\),\(F_{N}\) are the number of true positives, true negatives, false positives, and false negatives, correspondingly.
$$\begin{aligned} \text {Accuracy}=\frac{T_{P}+T_{N}}{T_{P}+T_{N}+F_{P}+F_{N}}; \text { Recall}=\frac{T_{P}}{T_{P}+F_{N}};\text { F1-value}=\frac{2T_{P}}{2T_{P}+F_{P}+F_{N}} \end{aligned}$$
Experiment questions
Our task of validation concerns three key issues: (1) which parameter configurations are optimal for the baseline models on the seed dataset, i.e., SVM, RF, and NB? (2) which self-taught learning model is the best in terms of accuracy, recall, and F1-value, given the 6794 annotated tweets and the three million unlabeled tweets? and (3) which vectorization setting is more effective? To address these concerns, our series of experiments are as follows.
Experiment on seed dataset with baseline models
Figure 2 illustrates the accuracy, recall, and F1-value of each algorithm with different parameter configurations, i.e., term frequency tf, tf-idf, and word2vec, on the (annotated) seed dataset. The term "custom" is used to indicate the word2vec embedding trained with our own drug-abuse-related tweets, compared with the pre-trained Google News word2vec embedding, denoted as "google." It is clear that the SVM model using the custom-trained word2vec embedding achieves the best and the most balanced performance in terms of all three measures, i.e., accuracy, recall, and F1-value, at approximately 67%. Other configurations usually have a lower recall, which suggests that the decisions they make bias towards the major class, i.e., non-drug-abuse risk behavior tweets. From the angle of classifiers, SVM model achieves the best overall performance. Random Forest has slightly less average accuracy than the SVM model, but worse recall and F1-value. Furthermore, from the view of vectorization approach, it is clear that word2vec embedding outperforms term frequency and tf-idf in most of the cases. Several possible combinations of settings are not shown in Fig. 2 due to poor performances.
Accuracy, recall, and F1-value of each baseline model on the seed dataset
Experiment on self-taught learning models
As shown in the previous experiment, SVM model using the custom-trained word2vec embedding achieves the best performance, we decided to apply the same model structure to compare with our deep self-taught learning approaches. In this experiment, at each epoch, 10,000 machine-labeled tweets were randomly sampled and merged into the training set. Figure 3 shows the experimental results of the five self-taught models, including self-taught CNN (st-CNN), self-taught LSTM (st-LSTM), self-taught SVM (st-SVM), self-taught NB (st-NB), and self-taught RF (st-RF). All configurations of classifiers and vectorization methods are tested. For the sake of clarity, we only illustrate the best performing setting for each model in Fig. 3. It is clear that our proposed deep self-taught learning approaches (i.e., st-LSTM and st-CNN) outperform traditional models, i.e., st-SVM, st-NB, and st-RF, in terms of accuracy, recall, and F1-value, in all cases. Deep learning models achieve 86.53%, 88.6%, and 86.63% in terms of accuracy, recall, and F1-value correspondingly.
Accuracy, recall, and F1-value of the five self-taught learning models, including st-CNN, st-LSTM, st-SVM, st-NB, and st-RF
Experiment on vectorization settings
The impact of two different word2vec representations on the st-CNN, i.e., the custom word2vec embedding we trained from our corpus, and pre-trained Google News word2vec embedding, is shown in Fig. 4. The Google News word2vec achieves 0.1%, 0.4%, and 0.3% improvements in terms of accuracy, recall, and F1-value (86.63%, 89%, and 86.83%, respectively) compared with the custom-trained word2vec embedding. In addition, it is clear that Google News word2vec embedding outperforms the custom-trained word2vec in most of the cases. This is because the Google News word2vec embedding was trained on a large-scale corpus, which is significantly richer in contextual information, compared with our short, noisy, and sparse Twitter datasets.
Performance comparison between custom word2vec embedding and Google News word2vec embedding
An insight analysis of drug-abuse risk behavior on Twitter
To gain insights in drug-abuse risk behaviors on Twitter, we use our best performing deep self-taught learning model to annotate over three million drug-abuse-related tweets with geo-tags and perform quantitative analysis. There are 117,326 tweets classified as positive, and 3,077,827 tweets classified as negative. The positive tweets correspond to 3.67% of the whole dataset. We performed analysis from three aspects: word and phase distributions, temporal distributions, and spatial distributions.
Word and phase distributions
We first visualize the top frequent words by word cloud, as shown in Fig. 5. The word distribution in positive tweets (Fig. 5a) is remarkably different from word distribution in negative tweets (Fig. 5b). In fact, drug-abuse tweets usually consist of abuse-indicating terms, and drug names, such as "blunt," "high," "smoke," "weed," "marijuana," "grass," "juic," etc. (Fig. 5a). In addition, the high concentration of dirty words, e.g., "s**t," "f**k," "as*," "bit**," etc., clearly suggests the expression patterns that the drug abusers may have (Fig. 5a). This expression pattern does not likely exist in negative tweets. Then, we further show the comparison of normalized word frequency between positive tweets and negative tweets (words from positive tweets got normalized by the number of positive tweets, and negative words by negative tweets), regarding the 25 most frequent words in positive tweets (Fig. 6) and 25 most frequent words in negative tweets (Fig. 7). Note that in Fig. 6, the y-axis is clipped at 0.25, which is the value of word "weed", while the word "smoke" has the normalized frequency of 0.44. These two figures further show that: (1) positive-frequent words are more likely to have lower normalized frequency in negative tweets, and vise versa and (2) some ordinary words, i.e., "go", "want", "day", and "good", still share similar normalized frequency between positive and negative tweets.
Word frequency distribution
Normalized frequency of top 20 frequent words in positive tweets, compared with in negative tweets
Normalized frequency of top 20 frequent words in negative tweets, compared with in positive tweets
Hashtags also play an import role in the Twitter sphere as a way for users to: (1) to express their opinion more clearly and (2) to improve information sharing efficiency. Tweets that share same Hashtags can be grouped together and easily found, while popular Hashtags can make the tweets more visible to wider audience. Table 3 shows the most frequent Hashtags in positive tweets and negative tweets. It is clear that the Hashtags in positive tweets are almost exclusively related to drug abuse, while the Hashtags in negative tweets cover much wider range of topics.
Table 3 Most frequent Hashtags in positive tweets and negative tweets
Finally, for word and phase analysis, we extract the co-occurrence frequencies of combinations of drug name and drug-abuse behavior. For each combination, we count the number of positive tweets and negative tweets that contain all words in that combination, then sort it by the absolute difference of normalized frequency between positive tweets and negative tweets. Table 4 shows the top 25 observed combinations. The "Relative_ratio" column is showing the ratio that the combination appears in positive tweets over the appears in all tweets. This analysis spots the more frequently used drug-abuse risk behavior indication word combinations, which will support further data collection.
Table 4 Drug name and abuse behavior co-occurrence frequency differences between positive tweets and negative tweets
Temporal analysis
To examine if there are different time patterns for positive tweets and negative tweets to be posted, we extract the local posting time of each tweet, then perform 1-h interval binning. As shown in Fig. 8, where x-axis are time slots, and y-axis is the proportion (normalized count) of tweets. The results shown in Fig. 8 are very interesting. The time patterns are obviously different between positive tweets and negative tweets. In fact, the Chi-square test results on the data in Fig. 8 shown in Table 5 clarifies that the pattern differences are significant for the time frames of 'All day' and 'Night time.' This result shows a very plausible phenomenon that tweets with drug-abuse risk behaviors are more active in night time than in day time.
Time of day distribution comparison between positive tweets and negative tweets
Table 5 Chi-square test of time of day distribution
The geo-location information tagged in tweets is very useful for capturing the distribution of drug-abuse risk behaviors. The geo-tagging information on Twitter usually comes in two forms: GPS coordinates, or a "Place Object" associated with the tweet. We first visualize geo-distribution of the positive tweets by plotting each geo-tag across the continental United States in Fig. 9. By making this fine granularity, we can confirm that the collected tweets generally follow the population distribution. Then, we aggregate the geo-tags into state level, normalized with state's population of age group 12 or older, and draw Fig. 10 with the numbers scaled to [− 1,1]. From Fig. 10, we can see that the District of Columbia has an extremely high ratio of positive tweets, follow by Louisiana, Texas, and Nevada that have relative high rate. Other states with high rate including California, Georgia, Maryland, and Delaware. Furthermore, the distribution of other states' data showing that the collected tweets align relatively well with state-level population distribution.
Dot map of positive tweets across the United States
Number of positive tweets, per state, normalized by state population of 12 or older
The other spatial analysis we perform is the alignment between our state-level counts of positive tweets, normalized with state population, and the 2016–2017 National Survey on Drug Use and Health (NSDUH) survey data. Here, the normalization is meant to decorrelate the count of tweets from the population of each state, and is done by simply dividing the count of positive tweets by the population (2017 census estimation) for each state. We choose to perform normalization with population for two reasons: (1) we have little to no control of the sampling process, in terms of geo-location distribution, when crawling data from Twitter, which means the bias is unavoidable and uncontrollable and (2) thus, the state population figures are more reliable, stable, and representative. NSDUH is a creditable source of drug-abuse-related population scale estimation. If our Twitter data can align with the reliable survey data, we can argue that the Twitter-based studies have the prediction power that should not to be ignored. By computing the Pearson's R between the normalized number of tweets and the NSDUH prevalence rate, over the same age group (12 or older), it is surprising to find that in our study even without further categorization, the Twitter data are significantly correlated (\(p<0.05\)) with some of the most important categories in the NSDUH study: (1) "Illicit Drug Use Other Than Marijuana in the Past Month" (\(r=0.387\)); (2) "Cocaine Use in the Past Year" (\(r=0.421\)); (3) "Methamphetamine Use in the Past Year" (\(r=-\,0.372\)); (4) "Pain Reliever Use Disorder in the Past Year" (\(r=-\,0.375\)); and (5) "Needing But Not Receiving Treatment at a Specialty Facility for Illicit Drug Use in the Past Year" (\(r=0.336\)). We argue that when large quantity of Twitter data is available, we can perform more detailed and creditable studies on the population scale.
Discussion and limitations
According to our experimental results, our deep self-taught learning models achieved promising performance in drug-abuse risk behavior detection in Twitter. However, many assumptions call for further experiments. First, how to optimize the classification performance by exploring the correlations among parameters and experimental configurations. For instance, for SVM and RF models, unigram feature works better than n-gram feature on term frequency; however, for tf-idf, it is the opposite situation. Second, the pre-trained Google News word2vec embedding performs better than the custom-trained word2vec embedding may also be situational. These findings indicate the necessity of leveraging size and quality of the training data for training word embedding, given that the available data may better fit the classification task but be short in quantity. Nevertheless, among the measures, recall receives a more significant boost than accuracy and F1-value. We may argue that the proposed self-taught algorithm helped correcting the bias in the classifiers caused by the imbalanced nature of the training dataset. However, more experiments need to be conducted to verify this interesting point.
The study we presented in this paper can be improved in many ways. Here, we elaborate several of the future research directions. First, we plan to incorporate the well-trained classifier into a real-time drug-abuse risk behavior monitoring and analysis system that aims at providing community-level stakeholders with timely accessible detection results for supporting their efforts, such as recovery services and public educations, on combating the opioid crisis. Second, we can utilize more information that can be extracted from tweets, such as user tweeting history, user demographic attributes, and user interactions, to further improve the model in terms of performance, scope, and credibility. Third, the extra information that we extract further enables the analysis of connections among users and tweets, on both social network plane and geospatial network plane, which can help to acquire knowledge regarding how the drug trend propagates through both planes. Last but not least, we may expand the study to other major online social media platforms, i.e., Reddit and Instagram, and more specialized online forum Blulelight.
In this paper, we proposed a large-scale drug-abuse risk behavior tweet collection mechanism based on supervised machine-learning and data crowd-sourcing techniques. Challenges came from the noisy and sparse characteristics of Twitter data, as well as the limited availability of annotated data. To address this problem, we propose deep self-taught learning algorithms to improve drug-abuse risk behavior tweet detection models by leveraging a large number of unlabeled tweets. An extensive experiment and data analysis were carried out on three million drug-abuse-related tweets with geo-location information, to validate the effectiveness and reliability of our system. Experimental results shown that our models significantly outperform traditional models. In fact, our models correspondingly achieve 86.53%, 88.6%, and 86.63% in terms of accuracy, recall, and F1-value. This is a very promising result, which significantly improves upon the state-of-the-art results.
Further data analysis gain insights into the expression patterns and the geo-distribution that the drug abusers may have on Twitter. For example, the words and phrases used in drug-abuse risk behavior-positive tweets have distinctive frequencies that can be used in data collection to improve the quality of raw data. The uneven geographical distribution of tweets makes it appealing to perform further analysis that associates tweets with other geographical data.
The data are available upon request, following the data privacy policy of Twitter.
NSDUH:
CDC:
convolution neural networks
LSTM:
long–short-term memory
DAWN:
drug-abuse warning network
SVM:
RF:
AMT:
Amazon Mechanical Turk
uniform resource locator
hypertext markup language
tf :
term frequency
tf-idf :
term frequency-inverse document frequency
graphics processing unit
NDTA:
National Drug Threat Assessment
U.S. Department of Health and Human Services: HHS acting secretary declares public health emergency to address national opioid crisis. 2017.
Substance Abuse and Mental Health Services Administration, U.S. Department of Health and Human Services: key substance use and mental health indicators in the United States: results from the 2016 National Survey on Drug Use and Health. 2018. http://datafiles.samhsa.gov. Accessed 20 May 2019.
National Institute on Drug Abuse, U.S. National Institutes of Health: overdose death rates. 2018.
The Gun Violence Archive: 2015 Gun Violence Archive. 2018. http://www.gunviolencearchive.org/past-tolls. Accessed 20 May 2019.
Aslam S. Twitter by the numbers. 2018. http://www.omnicoreagency.com/twitter-statistics/. Accessed 20 May 2019.
Signorini A, Segre AM, Polgreen PM. The use of twitter to track levels of disease activity and public concern in the us during the influenza a H1N1 pandemic. PLoS ONE. 2011;6(5):19467.
Aphinyanaphongs Y, Lulejian A, Brown DP, Bonneau R, Krebs P. Text classification for automatic detection of e-cigarette use and use for smoking cessation from twitter: a feasibility pilot. In: Biocomputing 2016: proceedings of the Pacific symposium. 2016. p. 480–91.
Bosley JC, Zhao NW, Hill S, Shofer FS, Asch DA, Becker LB, Merchant RM. Decoding twitter: surveillance and trends for cardiac arrest and resuscitation communication. Resuscitation. 2013;84(2):206–12.
Chary M, Genes N, McKenzie A, Manini AF. Leveraging social networks for toxicovigilance. J Med Toxicol. 2013;9(2):184–91.
Hossain N, Hu T, Feizi R, White AM, Luo J, Kautz H. Precise localization of homes and activities: detecting drinking-while-tweeting patterns in communities. In: Tenth international AAAI conference on web and social media. 2016.
Myslín M, Zhu S-H, Chapman W, Conway M. Using twitter to examine smoking behavior and perceptions of emerging tobacco products. J Medical Internet Res. 2013;15(8):e174.
Sarker A, et al. Social media mining for toxicovigilance: automatic monitoring of prescription medication abuse from twitter. Drug Saf. 2016;39(3):231–40.
Hanson CL, Cannon B, Burton S, Giraud-Carrier C. An exploration of social circles and prescription drug abuse through twitter. J Med Internet Res. 2013;15(9):e189.
Hanson CL, Burton SH, Giraud-Carrier C, West JH, Barnes MD, Hansen B. Tweaking and tweeting: exploring twitter for nonmedical use of a psychostimulant drug (adderall) among college students. J Med Internet Res. 2013;15(4):e62.
McNaughton EC, Black RA, Zulueta MG, Budman SH, Butler SF. Measuring online endorsement of prescription opioids abuse: an integrative methodology. Pharmacoepidemiol Drug Saf. 2012;21(10):1081–92.
Shutler L, Nelson LS, Portelli I, Blachford C, Perrone J. Drug use in the twittersphere: a qualitative contextual analysis of tweets about prescription drugs. J Addict Dis. 2015;34(4):303–10.
Hu H, Phan N, Geller J, Vo H, Manasi B, Huang X, Di Lorio S, Dinh T, Chun SA. Deep self-taught learning for detecting drug abuse risk behavior in tweets. In: International conference on computational social networks. 2018. p. 330–42.
LeCun Y, Bottou L, Bengio Y, Haffner P, et al. Gradient-based learning applied to document recognition. Proc IEEE. 1998;86(11):2278–324.
Hochreiter S, Schmidhuber J. Long short-term memory. Neural Comput. 1997;9(8):1735–80.
Johnston L, National Institute on Drug Abuse. Monitoring the future: National survey results on drug use, 1975–2004, vol. 1. 2005.
Brookoff D, Campbell EA, Shaw LM. The underreporting of cocaine-related trauma: drug abuse warning network reports vs hospital toxicology tests. Am J Public Health. 1993;83(3):369–71.
Kessler DA, Natanblut S, Kennedy D, Lazar E, Rheinstein P, Anello C, Barash D, Bernstein I, Bolger R, Cook K, et al. Introducing medwatch: a new approach to reporting medication and device adverse effects and product problems. JAMA. 1993;269(21):2765–8.
Meng H-W, Kath S, Li D, Nguyen QC. National substance use patterns on twitter. PLoS ONE. 2017;12(11):1–15. https://doi.org/10.1371/journal.pone.0187691.
Ding T, Bickel WK, Pan S. Social media-based substance use prediction. arXiv preprint arXiv:1705.05633. 2017.
Simpson SS, Adams N, Brugman CM, Conners TJ. Detecting novel and emerging drug terms using natural language processing: a social media corpus study. JMIR Public Health Surveill. 2018;4(1):2.
Phan NH, Chun SA, Bhole M, Geller J. Enabling real-time drug abuse detection in tweets. In: 2017 IEEE Int. Conf. Data Eng. (ICDE). 2017. p. 1510–4.
Coloma PM, Becker B, Sturkenboom MC, van Mulligen EM, Kors JA. Evaluating social media networks in medicines safety surveillance: two case studies. Drug Saf. 2015;38(10):921–30.
Hu H, Moturu P, Dharan K, Geller J, Iorio S, Phan H, Vo H, Chun S. Deep learning model for classifying drug abuse risk behavior in tweets. In: 2018 IEEE international conference on healthcare informatics (ICHI). IEEE; 2018. p. 386–7.
Kong C, Liu J, Li H, Liu Y, Zhu H, Liu T. Drug abuse detection via broad learning. In: International conference on web information systems and applications. Berlin: Springer; 2019. p. 499–505.
Weissenbacher D, Sarker A, Klein A, O'Connor K, Magge A, Gonzalez-Hernandez G. Deep neural networks ensemble for detecting medication mentions in tweets. J Am Med Inform Assoc. 2019;. https://doi.org/10.1093/jamia/ocz156.
Mahata D, Friedrichs J, Shah RR, Jiang J. Detecting personal intake of medicine from twitter. IEEE Intell Syst. 2018;33(4):87–95.
Zhang Y, Fan Y, Ye Y, Li X, Winstanley EL. Utilizing social media to combat opioid addiction epidemic: automatic detection of opioid users from twitter. In: Workshops at the thirty-second AAAI conference on artificial intelligence. 2018.
Li J, Xu Q, Shah N, Mackey TK. A machine learning approach for the detection and characterization of illicit drug dealers on instagram: model evaluation study. J Med Internet Res. 2019;21(6):13803.
Raina R, Battle A, Lee H, Packer B, Ng AY. Self-taught learning: transfer learning from unlabeled data. In: Proceedings of the 24th international conference on machine learning. 2007. p. 759–66.
Bengio Y, et al. Learning deep architectures for AI, foundations and trends. Mach Learn. 2009;2(1):1–127.
Weston J, Ratle F, Collobert R. Deep learning via semi-supervised embedding. In: Proceedings of the 25th international conference on machine learning. 2008. p. 1168–75.
Bettge A, Roscher R, Wenzel S. Deep self-taught learning for remote sensing image classification. 2017. arXiv preprint arXiv:1710.07096.
Dong X, Meng D, Ma F, Yang Y. A dual-network progressive approach to weakly supervised object detection. In: Proceedings of the 25th ACM international conference on multimedia. 2017. p. 279–87.
Gan J, Li L, Zhai Y, Liu Y. Deep self-taught learning for facial beauty prediction. Neurocomputing. 2014;144:295–303.
Yuan Y, Liang X, Wang X, Yeung D-Y, Gupta A. Temporal dynamic graph lstm for action-driven video object detection. In: Proceedings of the IEEE international conference on computer vision. 2017. p. 1801–10.
U.S. National Institute on drug abuse: commonly abused drugs. 2018.
Mikolov T, Sutskever I, Chen K, Corrado G, Dean J. Distributed representations of words and phrases and their compositionality. In: Proc. 26th NIPS, vol. 2. 2013. p. 3111–9.
Jeni LA, Cohn JF, De La Torre F. Facing imbalanced data–recommendations for the use of performance metrics. In: 2013 Humaine association conference on affective computing and intelligent interaction. 2013. p. 245–51.
Hallgren KA. Computing inter-rater reliability for observational data: an overview and tutorial. Tutor Quant Methods Psychol. 2012;8(1):23.
U.S. Department of Drug Enforcement Administration: National Drug Threat Assessment. 2018.
The authors gratefully acknowledge the support from the National Science Foundation (NSF) Grants CNS-1650587, CNS-1747798, CNS-1624503, CNS-1850094, and National Research Foundation of Korea NRF-2017S1A3A2066084.
New Jersey Institute of Technology, University Heights, Newark, 07102, USA
Han Hu, NhatHai Phan, James Geller & Xinyue Ye
City University of New York, 2800 Victory Blvd, Staten Island, 10314, USA
Soon A. Chun
The City College of New York, 160 Convent Ave, New York, 10031, USA
Huy Vo
Kent State University, 800 E. Summit St., Kent, 44242, USA
Ruoming Jin, Kele Ding & Deric Kenne
University of Oregon, 1585 E 13th Ave., Eugene, 97403, USA
Dejing Dou
Han Hu
NhatHai Phan
James Geller
Xinyue Ye
Ruoming Jin
Kele Ding
Deric Kenne
DD and RJ have a significant and intellectual advice to shape the extension with spatial data analysis, combining with offline data collected from NDTS [46]. Thanks to XY, KD, and DK with their expertises in geospatial data analysis and drug-abuse behaviral analysis, all the results in the analysis were verified and irrelevant results were eliminated. KD and DK are experts in statistics, especially in substance abuse, verified all the results in Fig. 8 and Table 5. KD and DK also verified the statistical results in the comparison between our data with the NDTS data [46] to eliminate uncertain results. Upon that, we discovered new interesting and statistically significant data correlations. HH and NP conducted and verified the experiment. HV contributed the data and the visualization part. SAC and JG contributed to the system development and data annotation processes. All authors read and approved the final manuscript.
Correspondence to NhatHai Phan.
Hu, H., Phan, N., Chun, S.A. et al. An insight analysis and detection of drug-abuse risk behavior on Twitter with self-taught deep learning. Comput Soc Netw 6, 10 (2019). https://doi.org/10.1186/s40649-019-0071-4
Self-taught learning | CommonCrawl |
popup15 hemtal 12 [converted from problem group]
Back to course offering
2015-01-17 15:00 AKST
Session is over.
Not yet started.
Session is starting in -2190 days 9:48:39
Time elapsed
Problem B
Error correcting codes are used in a wide variety of applications ranging from satellite communication to music CDs. The idea is to encode a binary string of length $k$ as a binary string of length $n>k$, called a codeword, in such a way that even if some bit(s) of the encoding are corrupted (if you scratch on your CD for instance), the original $k$-bit string can still be recovered. There are three important parameters associated with an error correcting code: the length of codewords ($n$), the dimension ($k$) which is the length of the unencoded strings, and finally the minimum distance ($d$) of the code.
Distance between two codewords is measured as Hamming distance, i.e., the number of positions in which the codewords differ: $0010$ and $0100$ are at distance $2$. The minimum distance of the code is the distance between the two different codewords that are closest to each other.
Linear codes are a simple type of error correcting codes with several nice properties. One of them is that the minimum distance is the smallest distance any non-zero codeword has to the zero codeword (the codeword consisting of $n$ zeros always belongs to a linear code of length $n$).
Another nice property of linear codes of length $n$ and dimension $k$ is that they can be described by an $n\times k$ generator matrix of zeros and ones. Encoding a $k$-bit string is done by viewing it as a column vector and multiplying it by the generator matrix. The example below shows a generator matrix and how the string $1001$ is encoded.
\[ \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 1 & 1 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \end{array} \right) \left(\begin{array}{c} 1\\ 0\\ 0\\ 1\end{array}\right) = \left(\begin{array}{c} 1\\ 0\\ 0\\ 1 \\ 1\\ 0\\ 0 \end{array}\right) \]
Matrix multiplication is done as usual except that addition is done modulo $2$ (i.e., $0+1=1+0=1$ and $0+0=1+1=0$). The set of codewords of this code is then simply all vectors that can be obtained by encoding all $k$-bit strings in this way.
Write a program to calculate the minimum distance for several linear error correcting codes of length at most $30$ and dimension at most $15$. Each code will be given as a generator matrix.
You will be given several generator matrices as input. The first line contains an integer $1 \le T\leq 40$ indicating the number of test cases. The first line of each test case gives the parameters $n$ and $k$ where $2\leq n\leq 30$, $1 \leq k\leq 15$ and $n > k$, as two integers separated by a single space. The following $n$ lines describe a generator matrix. Each line is a row of the matrix and has $k$ space separated entries that are $0$ or $1$. You may assume that for any generator matrix in the input, there will never be two different unencoded strings which give the same codeword.
For each generator matrix output a single line with the minimum distance of the corresponding linear code.
Sample Input 1
Sample Output 1
Submit Stats
Problem ID: codes
CPU Time limit: 1 second
Memory limit: 1024 MB
Sample data files
Author: Mikael Goldmann
Source: Nada Open 2002 | CommonCrawl |
Two-phase mixed convection nanofluid flow of a dusty tangent hyperbolic past a nonlinearly stretching sheet
A. Mahdy1 &
G. A. Hoshoudy1
A theoretical analysis for magnetohydrodynamic (MHD) mixed convection of non-Newtonian tangent hyperbolic nanofluid flow with suspension dust particles along a vertical stretching sheet is carried out. The current model comprises of non-linear partial differential equations expressing conservation of total mass, momentum, and thermal energy for two-phase tangent hyperbolic nanofluid phase and dust particle phase. Primitive similarity formulation is given to mutate the dimensional boundary layer flow field equations into a proper nonlinear ordinary differential system then Runge-Kutta-Fehlberg method (RKF45 method) is applied. Distinct pertinent parameter impact on the fluid or particle velocity, temperature, concentration, and skin friction coefficient is illustrated. Analysis of the obtained computations shows that the flow field is affected appreciably by the existence of suspension dust particles. It is concluded that an increment in the mass concentration of dust particles leads to depreciate the velocity distributions of the nanofluid and dust phases. The numerical computations has been validated with earlier published contributions for a special cases.
The flow and heat transfer investigations about non-Newtonian fluids has been of widely importance due to the characteristics of fluid with suspended particles cannot be completely depicted by classical Newtonian fluids theory. Non-Newtonian liquids are widespread fluids in industrial and engineering operations in which linear relationship between stress and deformation rate cannot be obtained. No single non-Newtonian model exists that depicts all the properties of fluids. Tangent hyperbolic fluid model signifies one of interesting non-Newtonian models that developed for chemical engineering systems. This rheological formulation is derived from kinetic theory of liquids rather than the empirical relations. One of the non-Newtonian models introduced by Pop and Ingham [1] was hyperbolic tangent model. Nadeem and Akram[2] has inspected MHD peristaltic flow of a hyperbolic tangent fluid due to a vertical asymmetric channel with heat transfer. Akbar et al. [3] has reported MHD boundary layer flow of non-Newtonian tangent hyperbolic fluid by a stretched sheet numerically. Entropy analysis in MHD steady non-Newtonian tangent hyperbolic nanofluid regime through an accelerated stretching cylinder with variable wall temperature has been investigated by Mahdy [4]. Kumar et al. [5] inspected the aspect of partial slip on peristaltic motion of non-Newtonian tangent hyperbolic fluid flow along an inclined cylindrical channel. Naseer et al. [6] have reported the tangent hyperbolic boundary layer fluid flow due to a vertical stretching cylinder. Malik et al. [7] have inspected the MHD flow of non-Newtonian tangent hyperbolic fluid through a stretching cylinder. Hayat et al. [8] have examined the impact of thermal radiation in the two-dimensional free and forced convection flow of a tangent hyperbolic fluid nearby a stagnation point. Some extensive contributions of non-Newtonian fluids have been considered under unlike physical circumstances (Abdul Gaffar et al. [9]; Salahuddin et al. [10]; Nadeem et al. [11]; Mahdy and Chamkha [12], Nadeem and Maraj [13]; Hady et al. [14], Hayat et al. [15]; Mahanthesh et al. [16]).
In higher-power output devices, the forced convection alone is not sufficient in order to dissipate all the heat. As such, combining natural and forced convection (mixed) will usually give desired results. Mainly, the mixed convection phenomenon is found in several industrial and technical applications, for instance, a heat exchanger, nuclear reactors cooling during an emergency shutdown, electronic devices cooled by fans, and solar collectors. Additionally, dusty convective fluid flow has some various applications such as power plant piping, petroleum transport, and wastewater handling and combustion. Gireesha et al. [17, 18] have analyzed steady and unsteady MHD boundary layer flow and heat transfer of dusty fluid due to a stretching sheet. Sadia et al. [19] exhibited two-phase free convection flow of nanofluid past a vertical wavy plate. Singleton [20] depicted the boundary layer analysis for dusty fluid. Vajravelu and Nayfeh [21] have explored MHD dusty fluid flow past a stretching sheet. The dynamics of two-phase flow was scrutinized by a number of authors with some various physical conditions (Sivaraj and Kumar [22]; Singh and Singh [23]; Dalal [24]). Flows of mixed convection are of massive interest due to their variety scientific, engineering, and industrial applications in heat and mass transfer. Free and forced convection of mass and heat transfer exist simultaneously in the design fields of chemical operations equipment, distributions of temperature, and formation and dispersion of fog. Also, analysis of flows due to stretched surface through heat transfer has acknowledged ample consideration owing to their possible demands in several industrial procedures, for instance, in metal extrusion, continuous casting, hot rolling, and drawing of plastic films. Particularly in polymer industry, aerodynamic extrusion of plastic sheets has a major significant. This procedure includes the heat transfer between the surrounding and surface fluid. Moreover, the rate of stretching in hot/cold fluids greatly depends upon the quality of the material with desired properties. In such process, heat transfer has an essential role in controlling the cooling rate. Some published investigations can be consulted (Hady et al. [25]; Zeeshan [26]; Khan et al. [27]; Gorla et al. [28]; Mahdy [29–31]; Srinivasacharya and Reddy [32]).
Furthermore, the theory of nanofluids represents an old notion, and it was first presented by Choi and Eastman [33] as they were looking for novel cooling technologies and coolants; thereafter, it became common on account of its extensive applications in heat exchangers, nuclear reactor systems, boilers energy storage, and electronic cooling devices (Ostrach [34]). The ultra-small particle size and thermal conductivity represent the worthy thermophysical properties of nanofluids, and as a result, nanofluids give significantly better performance with comparison to the normal single/multi-phase fluids. Makinde [35] analyzed computational modeling of time-dependent nanofluid flow past convectively heated stretched surface. The stagnation point flow of a nanofluid due to unsteady stretching sheet in the presence of slip impacts has been illustrated by Malvandi et al. [36], Mahdy [37], and Mahdy and Sameh [38]. Zheng at al. [39] addressed the behavior of velocity slip in nanofluid flow through a stretching sheet. Also see [40–44].
To the best of the author's knowledge, investigations on mixed convection flow and heat transfer on hydromagnetic dusty non-Newtonian nanofluid flow over a nonlinearly stretching sheet have not been considered so far. In the present analysis, we look at the non-linearly stretching flow of a dusty non-Newtonian tangent hyperbolic nanofluid flow. Numerical computations has been given to illustrate the behavior of nanofluid and dust particles. In our current analysis, we will examine whether the suspension dust particles in nanofluids affects the physical characteristics or not.
Flow field analysis
A subclass of non-Newtonian fluids is so-called tangent hyperbolic fluid. Actually, in this sort of non-Newtonian fluids [1], the Cauchy stress tensor is given by:
$$ \tau=\left(\mu_{\infty}+(\mu_{0}+\mu_{\infty})\tanh(\Gamma\dot{\gamma})^{n} \right) $$
in which τ points out extra stress tensor, μ∞ signifies the infinite shear rate viscosity, μ0 means the zero shear rate viscosity, Γ gives the constant of time-dependent material, n refers to the power-law index, i.e., flow behavior index, and \(\dot {\gamma }\) is given by the formula
$$ \dot{\gamma}=\sqrt{\frac{1}{2}\sum_{i}\sum_{j}\dot{\gamma}_{ij}\dot{\gamma}_{ji}}=\sqrt{\frac{1}{2}\Pi} $$
Here, \(\Pi =\frac {1}{2}trac(\nabla V+(\nabla V)^{T})^{2}\), and V denotes the velocity vector. We use Eq. (1) for the case as μ∞=0 since it is not possible to examine the problem for the infinite shear rate viscosity and since we are applying tangent hyperbolic fluid that depicts shear thinning impacts; hence, \(\Gamma \dot {\gamma }\ll 1\). Therefor, Eq. (1) mutates to the formula
$$\begin{array}{@{}rcl@{}} \tau&&=\mu_{0}[(\Gamma \dot{\gamma})^{n}]\dot{\gamma} \\ &&=\mu_{0}[(1+\Gamma \dot{\gamma}-1)^{n}]\dot{\gamma}\\ &&=\mu_{0}[1+n(\Gamma \dot{\gamma}-1)]\dot{\gamma} \end{array} $$
Now, let us scrutinize a steady, 2-D, incompressible, laminar, boundary layer MHD mixed convection flow of non-Newtonian tangent hyperbolic nanofluid embedded with dust particles towards a vertical nonlinearly stretching sheet. The scenario of a typical flow has been depicted in Fig. 1. As clarified, the orthogonal system (x,y) is chosen, in which the x-axis varies along the same stretched sheet direction with stretching rate Uw(x)=axm, with a>0, and the other axis, i.e., y-axis, is being perpendicular to the sheet surface and keeping the origin point to be fixed. An external magnetic field of strength B0 is acting in the direction of y-axis. As a result to this, the induced current is produced in the fluid and magnetic Reynolds number is treated to be as a small enough such that the induced magnetic field can be ignored.
Orthogonal system and flow model
T∞ gives the fluid temperature far away from the stretching sheet with observation that Tw<T∞ and Tw>T∞ refers to the opposing and assisting flows, respectively. By following the habitual boundary layer and Boussinesq approximations, the flow-governing equations of the steady-state dynamics of a non-Newtonian tangent hyperbolic fluid are given as [3, 17–19, 21]
Fluid phase equations
$$ \frac{\partial{u}}{\partial x}+\frac{\partial v}{\partial y}=0 $$
$$\begin{array}{@{}rcl@{}} \rho_{f}\left(u\frac{\partial u}{\partial x}+ v\frac{\partial u}{\partial y}\right)= &&\mu_{f} \left((1-n)+\sqrt{2} n\Gamma\frac{\partial u}{\partial y}\right)\frac{\partial^{2} u}{\partial y^{2}}+\frac{\rho_{p}}{\jmath}(u_{p}-u) -\sigma B_{0}^{2} u\\ &&+ g\left((1-C_{\infty})\rho_{f}\beta(T-T_{\infty})-(\rho_{np}-\rho_{f})(C-C_{\infty})\right) \end{array} $$
$$\begin{array}{@{}rcl@{}} (\rho c)_{f} \left(u\frac{\partial T}{\partial x}+ v\frac{\partial T}{\partial y}\right)= k_{f}\frac{\partial^{2} T}{\partial y^{2}}&+ (\rho c)_{np}\left(D_{B}\frac{\partial C}{\partial y}\frac{\partial T}{\partial y}+\left(\frac{D_{T}}{T_{\infty}}\right)\left(\frac{\partial T}{\partial y}\right)^{2} \right) \\ &+\frac{\rho_{p} c_{s}}{\jmath^{\star}}(T_{p}-T)+\frac{\rho_{p}}{\jmath}(u_{p}-u)^{2} \end{array} $$
$$ u\frac{\partial C}{\partial x}+ v\frac{\partial C}{\partial y}= D_{B}\frac{\partial^{2} C}{\partial y^{2}}+\left(\frac{D_{T}}{T_{\infty}}\right)\frac{\partial^{2} T}{\partial y^{2}} $$
Particle phase equations
$$ \frac{\partial{u_{p}}}{\partial x}+\frac{\partial v_{p}}{\partial y}=0 $$
$$ \rho_{p}\left(u_{p}\frac{\partial u_{p}}{\partial x}+ v_{p}\frac{\partial u_{p}}{\partial y}\right)= -\frac{\rho_{p}}{\jmath}(u_{p}-u) $$
$$ \rho_{p} c_{s}\left(u_{p}\frac{\partial T_{p}}{\partial x}+ v_{p}\frac{\partial T_{p}}{\partial y}\right)= -\frac{\rho_{p} c_{s}}{\jmath^{\star}}(T_{p}-T) $$
with (u,v) and (up,vp) signifying the tangent hyperbolic nanofluid and particle phase velocity components through x and y axes, respectively; ρf,ρp give the fluid and dust particle phases density, ρnp is the density of nanoparticles; ȷ,ȷ⋆ refer to the dust particles momentum and thermal relaxation time; and cf,cs denote specific heat for the fluid and particle phases. T,Tp indicate the fluid and dust particle phase temperatures inside the boundary layer; g signifies acceleration due to the gravity; Γ indicates the Williamson parameter; n symbolizes the power law index; DB,DT give the Brownian and thermophoresis diffusion coefficients; C points out the resealed nanoparticle volume fraction; β means the coefficient of thermal expansion; and B0,σ point out the magnetic field strength and electrical conductivity.
The above-stated essential equations must be solved with the appropriate boundary conditions, in order to evaluate the fluid flow fields and the dust particles. Hence, the convenient boundary conditions for our problem are as follows.
Fluid and particle phases boundary conditions are:
$$\begin{array}{@{}rcl@{}} &&\quad \eta=0,\quad u=U_{w},\quad v=0,\quad T=T_{w},\quad D_{B}\frac{\partial C}{\partial y} + D_{T}\frac{\partial T}{\partial y}=0\\ && \quad \eta\rightarrow\infty,\quad u,u_{p}\rightarrow0,\quad v_{p}=v\quad T,T_{p}\rightarrow T_{\infty},\quad C\rightarrow C_{\infty} \end{array} $$
Now, to mutate the fundamental governing flow field equations and boundary conditions, namely Eqs. (4)–11), the following dimensionless transformation have been given [12, 45]:
$$\begin{array}{@{}rcl@{}} &&\eta =\left(\frac{a(m+1)}{2\nu_{f}}\right)^{1/2} x^{\frac{m-1}{2}}y,\qquad \psi=\left(\frac{2a\nu_{f}}{m+1}\right)^{1/2}x^{\frac{m+1}{2}}F(\eta),\\ &&\psi_{p}=\left(\frac{2a\nu_{f}}{m+1}\right)^{1/2}x^{\frac{m+1}{2}}S(\eta),\quad\theta(\theta_{p})=\frac{T(T_{p})-T_{\infty}}{T_{w}-T_{\infty}},\quad \phi=\frac{C-C_{\infty}}{C_{\infty}} \end{array} $$
It is evident that Eqs. (4) and (8) are satisfied automatically where the stream functions ψ and ψp are given as \(u=\frac {\partial \psi }{\partial y}\), \(v=-\frac {\partial \psi }{\partial x}\) and \(u_{p}=\frac {\partial \psi _{p}}{\partial y}\), \(v_{p}=-\frac {\partial \psi _{p}}{\partial x}\).
Via the similar transformation that clarified in Eq. (12), the boundary layer Eqs. (5)–(11) are re-presented as:
$$\begin{array}{@{}rcl@{}} \frac{m+1}{2}\left((1-n+{nW}_{e}F^{\prime\prime})F^{\prime\prime\prime}+FF^{\prime\prime}\right)&&-mF'^{2}+\lambda(\theta-N_{r}\phi)\\ &&+D_{p}\alpha_{d}(S'-F')-M_{g} F'=0 \end{array} $$
$$\begin{array}{@{}rcl@{}} \frac{1}{Pr}\theta^{\prime\prime}+F\theta'+N_{b}\theta'\phi'+N_{t}\theta'^{2}&&+\frac{4D_{p}\alpha_{d} }{3(m+1) Pr}(\theta_{p}-\theta)\\ &&+\frac{2}{m+1}D_{p}E_{c}\alpha_{d}(S'-F')^{2}=0 \end{array} $$
$$ \phi^{\prime\prime}+Le F\phi'+\frac{N_{t}}{N_{b}}\theta^{\prime\prime}=0 $$
$$ SS^{\prime\prime}-\frac{2m}{m+1}S'^{2}-\frac{2\alpha_{d}}{m+1}(S'-F')=0 $$
$$ S\theta'_{p}-\frac{4 \alpha_{d}}{3(m+1)\gamma Pr}(\theta_{p}-\theta)=0 $$
subjected to the following converted fluid and dust particle phase boundary conditions:
$$\begin{array}{@{}rcl@{}} &&F(0)=0,\qquad F'(0)=1,\qquad \theta(0)=1, \qquad N_{b}\phi'(0)+N_{t}\theta'(0)=0, \\ && F'(\infty)\rightarrow0,\qquad \theta(\infty)\rightarrow0,\qquad\phi(\infty)\rightarrow0\\ && S(\infty)=F(\infty),\qquad S'(\infty)\rightarrow0,\qquad\theta_{p}(\infty)\rightarrow0 \end{array} $$
The resultant parameters are as follows: \(W_{e}=\frac {\sqrt {m+1}\Gamma a^{3/2}x^{\frac {3m-1}{2}}}{\nu _{f}^{1/2}}\) signifies Weissenberg number; \(M_{g}=\frac {\sigma B_{0}^{2}}{\rho _{f} a x^{m-1}}\) points out magnetic field parameter; \(\lambda =\frac {Gr}{Re^{2}}\) denotes the mixed convection parameter; \(Gr=\frac {g\beta (1-C_{\infty })(T_{w}-T_{\infty })x^{3}}{\nu _{f}^{2}}\) refers to Grashof number; \(Re=\frac {a x^{m+1}}{\nu _{f}}\) points out Reynolds number, \(N_{r}=\frac {(\rho _{np}-\rho _{f}) C_{\infty }}{\rho _{f} \beta (T_{w}-T_{\infty })(1-C_{\infty })}\) gives the buoyancy ratio parameter; \(D_{p}=\frac {\rho _{p}}{\rho _{f}}\) refers to relative density; \(\alpha _{d}=\frac {1}{\jmath a x^{m-1}}\) means fluid particle interaction parameter; \(Pr=\frac {\mu _{f} k_{f}}{c_{f}}\) and \(Le=\frac {\nu _{f}}{D_{B}}\) mean Prandtl and Lewis numbers; \(N_{b}=\frac {(\rho c)_{np}D_{B}C_{\infty }}{(\rho c)_{f}\nu _{f}}\), \(N_{t}=\frac {(\rho c)_{np}D_{T}(T_{w}-T_{\infty })}{(\rho c)_{f}T_{\infty }\nu _{f}}\) indicate the Brownian motion and thermophoresis parameters; and \(E_{c}=\frac {a^{2}x^{2m}}{c_{f}(T_{w}-T_{\infty })}\) denotes Eckert number. Note \(\jmath ^{\star }=\frac {3}{2} \gamma \jmath Pr\); \(\gamma =\frac {c_{s}}{c_{f}}\) means the specific heat ratio of the mixture. It is significant to state here that for various mixtures, the term of interaction γ has values lies between 0.1 and 10.0 Rudinger (1980). It is noticable that for αd=0, the flow is purely governed by the mixed convection in the absent of dusty particles (i.e., carrier phase only).
The skin friction factor Cf, Nusselt number Nux, and Sherwood number Shx represent the two major salient quantities of practical interest in the present investigation which are given as follows:
$$ C_{f}=\frac{\tau_{w}}{\frac{1}{2}\rho U_{w}^{2}},\quad Nu=\frac{xq_{w}}{k_{f} (T_{w}-T_{\infty})},\quad {Sh}_{x}=\frac{xq_{m}}{D_{B} C_{\infty}} $$
The wall shear stress τw and surface heat and mass transfer rate per unit area qw,qm:
$$\begin{array}{@{}rcl@{}} \tau_{w}=\mu_{f}\left((1-n)\frac{\partial u}{\partial y}+\frac{n\Gamma}{\sqrt{2}}\left(\frac{\partial u}{\partial y}\right)^{2} \right)_{y=0},&\; q_{w}=-k_{f}\left.\frac{\partial T}{\partial y}\right|_{y=0},&\; q_{m}=-D_{B}\left.\frac{\partial C}{\partial y}\right|_{y=0} \end{array} $$
Therefore, from the similarity transformation which is clarified in Eq. (12), the local skin friction factor and Nusselt and Sherwood numbers in non-dimensional formula are:
$$\begin{array}{@{}rcl@{}} &&\frac{1}{2}Re^{1/2}\;C_{f}=\sqrt{\frac{m+1}{2}}\left((1-n)F^{\prime\prime}(0)+\frac{1}{2}{nW}_{e}{F}^{\prime\prime{2}}(0) \right)\\ &&Re^{-1/2}\;{Nu}_{x}=-\sqrt{\frac{m+1}{2}}\theta'(0)\\ &&Re^{-1/2}\;{Sh}_{x}=-\sqrt{\frac{m+1}{2}}\phi'(0) \end{array} $$
The present part provides the graphical and tabular results of the influences of different physical governing parameters on representative velocity, temperature of fluid and dusty particle phases, and concentration distribution which are delineated through Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, and 11 and Tables 1, 2, and 3. The highly non-linear ordinary differential Eqs. (13)–(17) with respect to the boundary condition (18) have been solved numerically via Runge-Kutta-Fehlberg technique with the help of Matlab software. In this method, the boundary value problem have to be mutated into the initial value problem. Additionally, it is pivotal to choose a finite values of η∞. In order to appraise the accuracy of the present numerical results, a comparison of heat transfer results is done with the formerly published data (Rana and Bhargava [46] and Mabood et al. [47]) for the case of clean fluid (non suspended dust particles). The comparison is given in Table 1, and an excellent agreement was noticed. Furthermore, Tables 2 and 3 illustrate the impact of governing parameters on skin friction factor and Nusselt and Sherwood numbers. From these two tables, one observation is that the Nusselt number improves with γ,m,Nb, and Pr while it reduces with the other parameters. In addition, the skin friction factor reduces with λ,Ec,m,Nt, and Nb, whereas it enhances with the other parameters. Here, to illustrate the impact of any physical parameter, the other parameters are considered to be Pr=5,λ=0.2,We=0.7,Mg=0.5,Nr=1,n=0.3,Nb=Nt=0.4,αd=0.1,Dρ=1,Ec=0.3,Le=5,γ=0.3,and m=0.5
Velocity and temperature of fluid and dust phase for Dp parameter
Velocity and temperature of fluid and dust phase for αd parameter
Velocity and temperature of fluid and dust phase for Mg parameter
Velocity and temperature of fluid and dust phase for m parameter
Velocity and temperature of fluid and dust phase for Nr parameter
Fluid and dust temperature phase for Nt, Nb parameters
Concentrations profiles for Nb parameter and Le number
Fluid and dust temperature phase for Ec, Pr numbers
Velocity and temperature of fluid and dust phase for γ parameter
Velocity and temperature of fluid and dust phase for λ parameter
Table 1 Comparison of −θ′(0) with Pr=Le=2 without dust nanoparticles
Table 2 F″(0) and −θ′(0) for various governing parameters
Table 3 F′′(0),−θ′(0), and −ϕ′(0) for different Nt,Nb and Pr
Figure 2 is prepared to portray the impact of mass concentration of the dust particle parameter Dρ on tangent hyperbolic nanofluid and dust particle phase velocities F′,S′ and temperatures θ,θp. An increment in dust particle volume fraction leads to improve the drag force within the fluid, and therefore, velocities are reduced. Again, the aspect of Dρ on nanofluid temperature θ and dust temprature θp is depicted in Fig. 2. With increasing, Dρ maximizes the thermal field of both phases. Theoretically, for larger Dρ, more dust particles gain the heat energy from the tangent hyperbolic nanofluid. As a result, cleans fluid's temperature diminished, and relatively the particulate fluid temperature is also diminished.
Figure 3 illustrates the plots for dust particle-fluid interaction parameter αd on the velocity and temperature for nanofluid and dust phases. The tangent hyperbolic nanofluid velocity field F′ is reduced whereas dust particles velocity profile S′ improved for higher values of αd. Physically, a large αd turns to reduce the relaxation time of particle phase and therefore improve the drag force on the fluid in contact with it. It is seen from the figure that, for larger αd, the dust particle phase will become in equilibrium with the nanofluid phase. At this point, the temperature and velocity distributions for dust phase become parallel. Truly, due to the interaction with dust particles, the carrier fluid losses the kinetic and thermal energy. Therefore, the carrier nanofluid velocity/temperature field minifies for larger values of αd parameter. This phenomenon indeed occurs for dust particle phase velocity/temperature. The velocity field of accelerated tangent hyperbolic nanofluid, dusty particles, and related momentum boundary layer thicknesses dwindle with increasing of magnetic field parameter Mg. This can be clarified as the fact that magnetic force acts like resistive force to fluid flow. This means that the applied magnetic field creates a resistive force known as "Lorentz force" which dwindles the fluid motion and results in a thinner momentum boundary layer thickness. The created intensive Lorentz force is accountable for the improvement both of dust temperature θp and nanofluid temperature θ profiles (Fig. 4). For strong magnetic force, this Lorenz force becomes predominant and temperature of fluid rose.
Figure 5 widths the aspect of nonlinear stretching parameter m on the dimensionless velocity and temperature of nanofluid and dust particle phases. It is observed that the velocity profile of dust particle are insignificantly reduced with increasing values of m=0.1,0.5,1,2, and 5, but the velocity profile of nanofluid is increased. From the same Fig. 5, it is clear that the variation in the dimensionless dust particle temperature phase due to nonlinear stretching parameter m reduces. Besides, it is seen that an increase in m parameter tends to enhance the temperature gradient at the wall (Table 2). Figure 6 displays the impact of buoyancy ratio Nr parameter on the dimensionless velocity and temperature profiles for fluid and dust particle phases. An increment in buoyancy ratio leads to thicken the thermal boundary layer, hence detracting the temperature gradient at the wall, as given in Table 2. Velocity components of nanofluid and dust particle phases reduce with higher values of buoyancy ratio parameter. The temperature profiles of tangent hyperbolic nanofluid and dust particle phases θ and θp for different values of Nt and Nb are shown in Fig. 7. This figure illustrates that as Nt becomes higher, the magnitude of the dimensionless temperatures θ and θp reduces. The diffusion of nanoparticles into the fluid maximizes with the rising in Nb, and hence, rescaled temperature profiles are improvements (Fig. 7). Impacts of Brownian motion parameter Nb and Lewis number Le on concentration distributions are plotted in Fig. 8. The Brownian motion parameter can be illustrated as the ratio of the nanoparticle diffusion, which is due to the Brownian motion impact, to the thermal diffusion in the nanofluid. For the value Nb=0, thermal transport is absent due to buoyancy impacts produced as a result of nanoparticle concentration gradients. Lewis number Le means the ratio of thermal diffusivity to mass diffusivity. Figure 8 imply that concentration profile is a decreasing function of Lewis number Le. Indeed, gradual enlarging values of Lewis number and Brownian motion parameter correspond to minimal mass diffusivity which is accountable in lessening of concentration distribution. Figures 7 and 8 show that the aspects of variations in Nb on the variations in concentration profiles are higher than those impacts on the non-dimensional temperature profiles.
The aspect of Eckert number Ec for nanofluid and dust temperature distribution were displayed in Fig. 9. From this figure, it is clarified that the nanofluid and dust temperature phases profiles enhance by increasing values of Ec. It is due to the heat energy is stored in the liquid according to frictional heating and this is true in both cases. Prandtl number Pr impact on the heat transfer is plotted in Fig. 9. The relative thickening of momentum and thermal boundary layers is governed by Prandtl number. Small values of Pr will possess higher thermal conductivities, hence heat can diffuse from the sheet very quickly compared to the velocity. Furthermore, it depicts that the temperature reduces with upgrade in the value of Pr. Prandtl number can be used to enhance the rate of cooling. By analyzing the figure, it illustrates that the influence of enlarging Pr turns to decrease the nanofluid and dust temperature curves in the flow region, and it is evident that high values of Prandtl number results in thinning of thermal boundary layer. A slight influence has obtained a mixture of specific heat ratio parameter γ for velocity and temperature profiles for fluid and dust particle phases in Fig. 10, but γ has a strong effect on dust particle temperature distribution. θp reduces by increasing γ.
The impact of mixed convection parameter λ on the velocity and temperature curves of nanofluid and dust particle phases is depicted in Fig. 11. The figure reveals that the velocity profiles F′ and S′ improve via larger values of mixed convection parameter. The mixed convection parameter presents the ratio of the buoyancy to inertial forces. That is, for higher mixed convection parameter, the buoyancy force overbears the inertial force which enhances the fluid velocity. In addition, the momentum boundary layer thickness improves. Figures 12 and 13 indicate the aspect of the Weissenberg number We and power law index parameter n on the velocity and temperature profiles for fluid F′ and dust particles S′ phases. Both F′ and S′ and the associated boundary layer thickness give decreasing behavior for higher values of Weissenberg number We and power law index parameter n (Fig. 12). In addition, an opposite behavior is shown for temperature of fluid and dust particle phases (Fig. 13).
Velocity and temperature of fluid and dust phase for We number
Velocity and temperature of fluid and dust phase for n parameter
This analysis addressed the MHD mixed convection flow of non-Newtonian tangent hyperbolic nanofluid with suspension dust nanoparticles along a nonlinear stretching sheet. Numerical computations are given in tabular and graphical forms in order to clarify the features of nanofluid flow, heat transfer, and dust particle phases. The obtained conclusions are summarized as:
Tangent hyperbolic nanofluid phase temperature is greater than the dust particles phase temperature.
Both We and n tend to enhance skin friction factor and reduce rate of heat transfer.
Increasing the fluid particle interaction parameter αd leads to reduce the fluid velocity but enhances the velocity and temperature of particle phase.
Higher mass concentration of the dust particle parameter gives lower velocities of fluid and dust phases.
Nonlinear stretching parameter m has pronounced impact on dust particle phase.
Pop, I., Ingham, D. B.: Convective heat transfer: mathematical and computational modeling of viscous fluids and porous media, Pergamon (2001).
Nadeem, S., Akram, S.: Magnetohydrodynamic peristaltic flow of a hyperbolic tangent fluid in a vertical asymmetric channel with heat transfer. Acta Mech Sinica. 27, 237–250 (2011).
Akbar, N. S., Nadeem, S., Haq, R. U., Khan, Z. H.: Numerical solution of magnetohydrodynamic boundary layer flow of tangent hyperbolic fluid towards a stretching sheet. Indian J. Phys. 87, 1121–1124 (2013).
Mahdy, A.: Entropy generation of tangent hyperbolic nanofluid flow past a stretched permeable cylinder: variable wall temperature. Proc IMechE Part E: J Process Mech. Engin. 233, 570–580 (2019).
Kumar, Y. V. K. R., Kumar, P. V., Bathul, S.: Effect of slip on peristaltic pumping of a hyperbolic tangent fluid in an inclined asymmetric channel. Adv. Appl. Sci. Res. 5, 91–108 (2014).
Naseer, M., Malik, M. Y., Nadeem, S., Rehman, A.: The boundary layer flow of hyperbolic tangent fluid over a vertical exponentially stretching cylinder. Alex. Eng. J. 53, 747–750 (2014).
Malik, M. Y., Salahuddin, T., Hussain, A., Bilal, S.: MHD flow of tangent hyperbolic fluid over a stretching cylinder: using Keller box method. J. Magn. Magn. Mater. 395, 271–276 (2015).
Hayat, T., Qayyum, S., Ahmad, B., Waqas, M.: Radiative flow of a tangent hyperbolic fluid with convective conditions and chemical reaction. Eur. Phys. J. Plus. 131(12), 422–443 (2016).
Abdul Gaffar, S., Ramachandra, P. V., Anwar, B. O.: Numerical study of flow and heat transfer of non-Newtonian tangent hyperbolic fluid from a sphere with Biot number effects effects. Alex. Eng. J. 54(4), 829–841 (2015).
Salahuddin, T., Khan, I., Malik, M. Y., Khan, M., A. Hussain, A., Awais, M.: Internal friction between fluid particles of MHD tangent hyperbolic fluid with heat generation: using coefficients improved by Cash and Karp. Eur. Phys. Plus. J. 132, 205–214 (2017).
Nadeem, S., Ashiq, S., Sher Akbar, N., Changhoon, L.: Peristaltic flow of hyperbolic tangent fluid in a diverging tube with heat and mass transfer. Energy. J. Eng. 139(2) (2013).
Mahdy, A., Chamkha, A. J.: Unsteady MHD boundary layer flow of tangent hyperbolic two-phase nanofluid of moving stretched porous wedge. Int. Numer. J. Methods Heat Fluid Flow. 28(11), 2567–2580 (2018).
Nadeem, S., Maraj, E. N.: The mathematical analysis for peristaltic flow of hyperbolic tangent fluid in a curved channel. Commun. Theor. Phys. 59, 729–736 (2013).
Hady, F. M, Mohamed, R. A, Mahdy, A: Non-Darcy natural convection flow along a vertical wavy plate embedded in a n on-Newtonian fluid saturated porous medium. Int. Appl. J. Mech. Eng. 13(1), 91–100 (2008).
Hayat, T., Qayyum, S., Alsaedi, A., Shehzad, S. A.: Nonlinear thermal radiation aspects in stagnation point flow of tangent hyperbolic nanofluid with double diffusive convection. Mol. J. Liq. 223, 969–978 (2016).
Mahanthesh, B., Sampath, P. B., Kumar Gireesha, B. J., Manjunatha, S., Gorla, R. S. R.: Nonlinear convective and radiated flow of tangent hyperbolic liquid due to stretched surface with convective condition. Results Phys. 7, 2404–2410 (2017).
Gireesha, B. J., Manjunatha, S., Bagewadi, C. S.: Unsteady hydromagnetic boundary layer flow and heat transfer of dusty fluid over a stretching sheet. Afrika Metamet. 23(2), 229–241 (2012).
Article MATH Google Scholar
Gireesha, B. J, Ramesh, G. K, Subhas, M, Abel Bagewadi, C. S: Boundary layer flow and heat transfer of a dusty fluid flow over a stretching sheet with non-uniform heat source/sink. Int. Multiphase. J. Flow. 37(8), 977–982 (2011).
Sadia, S., Nahed, B., Hossain, M. A., Gorla, R. S. R., Abdullah, A. A. A.: Two-phase natural convection dusty nanofluid flow. Int. Heat. J. Mass Transfer. 118, 66–74 (2018).
Singleton, R. E.: Fluid mechanics of gas-solid particle flow in boundary layers [Ph.Thesis, D.,]. California Institute of Technology (1964).
Vajravelu, K., Nayfeh, J.: Hydromagnetic flow of a dusty fluid over a stretching sheet. Int. Nonlinear J. Mech. 27(6), 937–945 (1992).
Sivaraj, R., Kumar, B. R.: Unsteady MHD dusty viscoelastic fluid Couette flow in an irregular channel with varying mass diffusion. Int. Heat. J. Mass Transfer. 55, 3076–3089 (2012).
Singh, A. K., Singh, N. P.: MHD flow of a dusty visco-elastic liquid through a porous medium between two inclined parallel plates. Proc. Natl. Acad. Sci. India. 66(A), 143–150 (1996).
Dalal, D. C., Datta, N., Mukherjea, S. K.: Unsteady natural convection of a dusty fluid in an infinite rectangular channel. Int. Heat. J. Mass Transfer. 41(3), 547–562 (1998).
Hady, F. M., Ibrahim, F. S., Abdel-gaied, S. M., Eid, M. R.: Radiation effect on viscous flow of a nanofluid and heat transfer over a nonlinearly stretching sheet. Nanoscale Res. Lett. 7, 299–308 (2012).
Zeeshan, A., Majeed, A., Ellahi, R.: Effect of magnetic dipole on viscous ferro-fluid past a stretching surface with thermal radiation. Mol. J. Liq. 215, 549–554 (2016).
Khan, S. U., Shehzad, S. A., Rauf, A., Ali, A.: Mixed convection flow of couple stress nanofluid over oscillatory stretching sheet with heat absorption/generation effects. Results Phys. 8, 1223–1231 (2018).
Gorla, R. S. R., Lee, J. K., Nakamura, S., Pop, I.: Effects of transverse magnetic field on mixed convection in wall plume of power-law fluids. Int. Eng. J. Sci. 31(7), 1035–1045 (1993).
Mahdy, A.: Soret and Dufour effect on double diffusion mixed convection from a vertical surface in a porous medium saturated with a non-Newtonian fluid. Non-Newtonian J. Fluid Mech. 165, 568–575 (2010).
Mahdy, A.: Heat transfer and flow of a Casson fluid due to a stretching cylinder with the Soret and Dufour effects. Eng. J. Phys. Thermophys. 88(4), 928–936 (2015).
Mahdy Unsteady, A.: MHD slip flow of a non-Newtonian Casson fluid due to stretching sheet with suction or blowing effect. Appl. J. Fluid Mech. 9(2), 785–793 (2016).
Srinivasacharya, D., Swamy, G.: Reddy: Mixed convection on a vertical plate in a power-law fluid saturated porous medium with cross diffusion effects. Proc. Eng. 127, 591–597 (2015).
Choi, S. U. S., Eastman, J. A.: Enhancing thermal conductivity of fluids with nanoparticles. In: Conference: International mechanical engineering congress and exhibition, San Francisco, CA (United States), 12-17 Nov 1995; Other Information: PBD: Oct (1995).
Ostrach, S.: Natural convection in enclosures. Heat J. Tran. 110, 1175–1190 (1988).
Makinde, O. D.: Computational modelling of nanofluids flow over a convectively heated unsteady stretching sheet. Curr. Nanosci. 9, 673–678 (2013).
Malvandi, A., Hedayati, F., Ganji, D. D.: Slip effects on unsteady stagnation point flow of a nano fluid over a stretching sheet. Powder Technol. 253, 377–384 (2014).
Mahdy, A.: Unsteady mixed convection boundary layer flow and heat transfer of nanofluids due to stretching sheet. Nucl. Eng. Des. 249, 248–255 (2012).
Mahdy, A., Sameh, E. A.: Laminar free convection over a vertical wavy surface embedded in a porous medium saturated with a nanofluid. Transp. Porous Med. 91, 423–435 (2012).
Zheng, L., Zhang, C., Zhang, X., Zhang, J.: Flow and radiation heat transfer of a nanofluid over a stretching sheet with velocity slip and temperature jump in porous medium. Frankl. J. Inst. 350, 990–1007 (2013).
Prakash, J., Sivab, E. P., Tripathi, D., Kothandapani, M.: Nanofluids flow driven by peristaltic pumping in occurrence of magnetohydrodynamics and thermal radiation. Mater. Sci. Semicond. Proc. 100, 290–300 (2019).
Prakash, J., Siva, E. P., Tripathi, D., Kuharat, S., Anwar, O.: Beg: Peristaltic pumping of magnetic nanofluids with thermal radiation and temperature-dependent viscosity effects: modelling a solar magneto-biomimetic nanopump. Renew. Energy. 133, 1308–1326 (2019).
Prakash, J., Ravinder, J., Dharmendra, T., Martin, N. A.: Electroosmotic flow of pseudoplastic nanoliquids via peristaltic pumping. J. Braz. Soc. Mech. Sci. Eng. 41, 61–78 (2019).
Akbar, N. S., Huda, A. B., Habib, M. B., Tripathi, D.: Nanoparticles shape effects on peristaltic transport of nanofluids in presence of magnetohydrodynamics. Microsyst. Technol. 25, 283–294 (2019).
Prakash, J., Ansu, A. K., Tripathi, D.: Alterations in peristaltic pumping of Jeffery nanoliquids with electric and magnetic fields. Meccanica. 53, 3719–3738 (2018).
Mahdy, A.: Boundary layer slip flow on diffusion of chemically reactive species over a vertical non-linearity stretching sheet. J. Comput. Theoret. Nanosci. 10(11), 2782–2788 (2013).
Rana, P., Bhargava, R.: Flow and heat transfer of a nanofluid over an onlinearly stretching sheet: a numerical study. Commun. Nonlinear Sci. Numer. Simul. 17, 212–226 (2012).
Mabood, F., Khan, W. A., Ismail, A. I. M.: MHD boundary layer flow and heat transfer of nanofluids over a nonlinear stretching sheet: A numerical study. Magn. J. Magn. Mater. 37, 4569–4576 (2015).
Funding information is not applicable/no funding was received.
Mathematics department, Faculty of Science, South Valley University, Qena, Egypt
A. Mahdy & G. A. Hoshoudy
A. Mahdy
G. A. Hoshoudy
All authors jointly worked on the results, and they read and approved the final manuscript.
Correspondence to A. Mahdy.
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License(http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Mahdy, A., Hoshoudy, G.A. Two-phase mixed convection nanofluid flow of a dusty tangent hyperbolic past a nonlinearly stretching sheet. J Egypt Math Soc 27, 44 (2019). https://doi.org/10.1186/s42787-019-0050-9
Dusty fluid
Non-newtonian
Tangent hyperbolic
Two-phase nanofluid
Mixed convection
Mathematics Subject Classification (2000)
76T15 | CommonCrawl |
What's the proper way to typeset a differential operator?
I can't seem to find any consensus on the right way to typeset a differential operator, whether it is:
in a standalone context:
as part of a derivative:
as part of an integral:
In all of these cases, I have seen them sometimes italicized like variables (as in the second and third examples above) and sometimes not italicized like operator names (as in the first example above). There is also additional variation in how much spacing goes between the "d" and whatever it is acting on.
Seeing as this is an incredibly common symbol in many branches of mathematics, I am curious about the lack of standardization -- I've seen all possible combinations used in all possible contexts by many respected authors and publishers.
Are there any rules of thumb that I can follow? I personally tend to prefer the non-italicized version with very little space next to it, so I add:
\renewcommand{\d}[1]{\ensuremath{\operatorname{d}\!{#1}}}
to my default preamble, and use that everywhere, but I'd like to know if I'm breaking any hard-and-fast rules here.
typography math-operators
Adrian PetrescuAdrian Petrescu
Some related issues: should Euler's e be italicized? how about the imaginary unit i? should single-letter subscripts that are not variables/indices be italicized (eg, "f" in t-subscript-f representing a "final" time)? (Everyone seems to agree that multi-letter subscripts of this type should be roman). My opinion (seems to be shared by many British publishers) is that these should all be roman, along with the differential d. Many US publishers make them all italic. Perhaps there are publishers who use a mix of both, but I don't remember seeing it. – Lev Bishop Apr 3 '11 at 1:47
Constants like e and i should also be upright. This is covered in the document. – Emre Apr 3 '11 at 1:57
Interesting -- I was surprised to read that particular rule in the "standard". Still, that seems to be a rule that is universally ignored, whereas the differential rule seems to be split approximately down the middle. – Adrian Petrescu Apr 3 '11 at 3:12
By the by, I asked this question: tex.stackexchange.com/q/2969/86 partly so that I could write \int_0^1 e^{2\pi i t} d t and have the e, \pi, i, d all automatically typeset upright. – Loop Space Apr 3 '11 at 19:48
Springer-Verlag's monograph style had \def\D{\mathrm{d}} for the differential operator. I agree with Hendrik Vogt's post below for spacing, that one should typically (but not always) write \,\D x. The exception: after a fraction, e.g., \frac{\sin(x)}{x}\D x is OK; and after a function, e.g., \cos(x)\D x is also OK. But I think there is no single golden rule...it's an art, not a science. – Alex Nelson Oct 20 '13 at 16:34
There is a standard: it should be upright, not italicized. Read Typesetting mathematics for science and technology according to ISO 31/XI
I suggest using the commath package to correctly typeset differentials.
EmreEmre
(1) Because most mathematicians (who are, after all, the main group of people writing the most mathematics) are not typography experts, and could care less about your ISO standard. In general, just because something is "standard" doesn't mean people will use/follow it. (2) Because most people are lazy and dx is easier to type than \D{x} – Willie Wong Apr 3 '11 at 1:11
@Willie: I'm not entirely satisfied by that argument; because mathematicians in general do go to great lengths to have consistent and attractive notation. I regularly see mathematical papers in LaTeX doing much more onerous things than spending three extra keystrokes to get a proper differential. Spivak wrote an entire book about properly typesetting formulas, and he still uses the "incorrect" dx. I suspect it has more to do with a genuine difference in opinion than pure laziness. But I suppose this is not the sort of question that it is easy to settle definitively in either direction :) – Adrian Petrescu Apr 3 '11 at 1:22
@Adrian I think that one argument that Willie left out was that if you've never seen something typeset a different way, you may never realise that there is a different way to do it. Seeing dx all my life, I never thought that an upright 'd' may be better until I happened to be trying to decide what colour 'd' should be! Then I realised that 'd' was an operator, so should be typeset as such, and that operators were typeset as upright (and blue, since you ask). – Loop Space Apr 3 '11 at 19:09
I have to say seeing so many switches between upright and italic makes me dizzy. It's nice to know that there's a standard, but it only makes me a teensy bit guilty to follow my aesthetic sense. I just sampled 20 textbooks on my shelf and not a single one used an upright d. – Matthew Leingang Apr 15 '11 at 19:00
@egreg: Hmmm, I'd say that \int ... d. is an operator. So the d by itself may not be an operator but together with the \int it becomes one. – Loop Space Jun 18 '11 at 16:51
I'd say it really depends on the context. As Emre pointed out, there's an ISO standard; according to wikipedia, ISO 31-11 was superseded in 2009 by ISO 80000-2. The latter carries the title "Quantities and units -- Part 2: Mathematical signs and symbols to be used in the natural sciences and technology".
As a mathematician I think: Why should I use the same notation as, say, an electrical engineer? In some of the sciences they may have good reasons for the choices in the ISO standard, but those reasons need not apply to every field that uses mathematical notation. It appears that I'm not in bad company here: Of course the TeXbook was written before ISO 31, but let me quote some examples from page 168:
On the same page, Knuth also uses the math italic $e$ for the Euler number. For mathematical typesetting, I like Knuth's choices here very much. I can't say anything about other sciences.
Hendrik VogtHendrik Vogt
knuth's choices were based on an extensive study of journals (including acta mathematica (swedish) and transactions of the american math society from the early 20th century) which were considered to have high typographical standards. it's also true that mathematicians came very late to the standards game, as opposed to engineers. (as a former u.s. representative on an iso working group on document processing, i have personal knowledge of this.) not all scientific and technical publishing has the same traditions. – barbara beeton Apr 3 '11 at 13:31
@barbara: I thought Knuth would have done no less. I didn't write this in my answer, but this is somehow what I meant: It's OK to have different traditions and to follow these. Not everything has to be standardised. – Hendrik Vogt Apr 3 '11 at 13:34
Personally I prefer the differential operator upright. After all it is an abbreviation like tan or sin, why should this be any different? My late thesis supervisor drilled that in my head. He did type his thesis with an IBM golfball and used to brag about the care and time it took him to typeset it right. He was one of the first persons to adopt TeX in the RSA. – Yiannis Lazarides Apr 3 '11 at 19:54
@Yiannis: It's a matter of personal taste. But I wouldn't regard "d" as an abbreviation for anything (e.g. "cos" is an abbreviation for "cosine", and the latter is what I say when reading "cos"). – Hendrik Vogt Apr 3 '11 at 19:58
Not sure why you're blaming us. I just flipped through 6 of my electrical engineering textbooks and all of them use italic d. Upright d looks strange to me, though my pedantic side is drawn to the logical distinction of it... – endolith Aug 7 '14 at 2:42
tl,dr: It's complicated, but be consistent.
I believe the answers here tend to miss the point. While Emre mentions that there is an international norm regarding typesetting mathematics that is very explicit about this topic, Hendrik Vogt makes the right argument, but doesn't take it far enough. This question doesn't have an answer as simple as yes or no, rather it depends on your field, your publishers standard, the location you hail from and your wish for consistency. It's like asking what bibliography style is the right one for science. There are established traditions for typesetting mathematics, in part by the mathematical community of a country or family of countries, in part by the publishers. This transcends this question by far, since this touches a lot of other subjects, e.g. how ellipses, vectors and tensors look (this one has even more variety to offer than our subject) or the appearance of relation symbols, for example.
For example as Beccari points out, this tradition of 'uprighting the differential' is less at home in the pure mathematics than it is in the applied variety or the neighbouring sciences. Physicists and engineers, for example, tend to lean towards the upright form more than the mathematicians.
This however is not even half of the picture, since there tend to be big differences when it comes to the nationality of an author. For example the style fans of slanted differentials are used to originates in the English speaking domain, and coincidental evidence, like all the books in your shelf adhering to that style, only tells us that the books you buy are likely by American publishers. Unfortunately not even the publishers are very consistent in what they put out. I once worked for a rather big European science publisher and on asking how they ensure consistency, they admitted they basically don't. They even just print a Word document, if that's what they get and \LaTeX ing it would be too much effort. Some things don't even have an established convention: I once tried to figure out the correct way to typeset the Laplacian symbol and literally every(!) book I picked up had a different style.
So for the issue at hand: in Russia the integral sign leans left instead of right (Zaitsev), while the upright school of thought (both integral and differential) originates in Central Europe, probably Germany. When you put the integrands at the end, like is common in parts of physics, the spacing also may change between the integral and the differential. Compare this sample to see what i mean:
This shows why in my eyes it is not a very good idea to prescribe upright or slanted for the differential, since people then tend to overlook the integral sign and spacing issues involved, and there is a good chance that whatever answer you give them will be wrong.
Also it is not set in stone where to put the limits, even when adhering to a right leaning integral style, as Knuth has said himself (http://tex.loria.fr/typographie/mathwriting.pdf) (also see Mathematics into Type by Swanson)
In German and Russian tradition, there are indeed conventions and norms where to put it that are adhered to, but even here discretion is advised. DIN, the German equivalent of ISO or ANSI, for example, has the norms 1302, 1304 and 1338 for typesetting mathematical formulas, similar to ISO 80000-2. These norms came out of the particular community and were mainly a write-up of the already established traditions. The ridiculous part comes in form of the DIN norms themselves, because they use the relation symbols inconsistently. The ones preferred by norm 1338 are and , but the majority of the norms published after 1338 use and !, so all of this has to be taken with a grain of salt.
Now you can make an argument for uniformity in the way math is typeset, to make it easier to read and parse. In the end, it really doesn't matter too much, the most important question is, if people can understand it. If you write an undergrad text in your native language then it's likely better to adhere to the traditional style your crowd expects.
I recommend looking at where you come from, who you are writing for, making a choice about those questions and sticking to them! Consistency, within your own documents and even across them, is worth a lot more for your readers than trying to guess the conventions the biggest subset of them may be used to. Defining a macro for yourself that wraps all this and makes it easy to change the look with a simple change in one place is the best practical advice one can give.
It's interesting to note that in a way Latex itself has changed the picture, given its ubiquitous use in the mathematics and the fact that some choices are made for you via the default. A lot of people don't want to mess with things like the issue mentioned. Also, as Zaitsev mentioned, some things, like properly scaling the left leaning integral, seem to be quite hard to achieve, since Knuth didn't have those in mind when designing TeX.
epimorphic
i've seen the two-line less/greater-than or equal symbol used in the same document with a different meaning than the one-line version (although i can't put my hands on it just now), so even defining a norm can be counterproductive. (after all, the first thing many mathematicians do is define their notation, which may be very idiosyncratic.) – barbara beeton Jan 2 '13 at 19:14
One could add to your answer that the usage heavily depends on personal preferences. Even inside one community of mathematicians, it varies from author to author. – Hendrik Vogt Jan 3 '13 at 12:42
I really prefer ⩽ over ≤. Am I a communist now? ;) It just seems much more balanced than ≤. I guess it's better not to go against the tide here though :/ – Christian Sep 4 '13 at 14:53
"Physicists and engineers, for example, tend to lean towards the upright form more than the mathematicians". This depends on where you're from. My experience, in an Australian university was the opposite. If you're to assert things like "the right argument", surely, scientists and mathematicians should be more concerned about what something actually means, not whether or not it's aesthetically pleasing or "most" people do it such and such a way. For example, the term "imaginary" originates in the concept of such numbers not being well received (mistakenly) by the establishment at the time. – Geoff Pointer Apr 20 at 0:49
Upright feels more correct, but it is very rarely used and it looks ugly (though I may just think so because I'm so used to seeing the alternative). Personally, I prefer going with the alternative which is most often used and least ugly.
I use \mathop{dx} to get the correct spacing before and after differentials. Thus, it will be apparent that "dx" is its own entity, and not a d multiplied by an x, and it nicely separates the differentials:
SamuelSamuel
I completely agree with this, except "Upright feels more correct." Actually it doesn't, and all I know is how I saw my teachers and texts write dx (with both italicized.. and this happens everywhere from Numerical Recipes to Salas and Hille's Calculus text to Schaum's outlines.) I've actually never, to my recollection, seen an upright d and an italicized x together, to my recollection. Far as I'm concerned dx is the correct way to right it. – bobobobo May 11 '12 at 19:18
\mathop{dx}, {dv} {dt} ... etc used for my thesis, simple and stand alone from other symbols. – KOF Jan 12 '13 at 7:23
+1 because this seems to be smart solution. But IMO something like \mathop{\mathrm{d}x} looks also decent. – doc Feb 3 '13 at 16:22
This covers the input side of things rather than the display side, but it's a technique I've found useful:
In XeLaTeX or LuaLaTeX, I do something like this:
\newcommand*{\diffdchar}{d} % or {ⅆ}, or {\mathrm{d}}, or whatever standard you'd like to adhere to
\newcommand*{\dd}{\mathop{\diffdchar\!}}
\catcode`\ⅆ=\active
\letⅆ=\dd
Edit: Per egreg's comment, the newunicodechar package can make this easier, and will work for regular TeX (with \usepackage[utf8]{inputenc} applied):
\newcommand*{\diffdchar}{d} % or {ⅆ}, or {\mathrm{d}}, or …
\newunicodechar{ⅆ}{\mathop{\diffchar\!}}
In either case,
$yⅆx-xⅆy$
$ⅆxⅆy=rⅆrⅆθ$ % Assuming Xe/LuaLatex, or \newunicodechar{θ}{\theta}
$xⅆy/ⅆx$ % For comparison;
$xⅆy/\!ⅆx$ % need spacing hack for linear fractions,
$x\frac{ⅆy}{ⅆx}$ % ... but built-up fractions are OK.
With the newunicodechar package this becomes \newunicodechar{ⅆ}{\mathop{\diffchar\!}}, but I'd prefer \newunicodechar{ⅆ}{\mathop{}\!\diffchar}. – egreg Sep 9 '11 at 22:24
@Adrian: the character that jcsalomon activates is U+2146 (DOUBLE-STRUCK ITALIC SMALL D), that's hardly ever used and stands up well in an editor window. The result is exactly the same as those presented in other answers. With newunicodechar XeTeX and LuaTeX are not needed, it also works with the standard utf8 option for inputenc. – egreg Sep 9 '11 at 22:29
@egreg, is there any benefit to \mathop{}\!\diffchar over \mathop{\diffchar\!}? – J. C. Salomon Sep 12 '11 at 18:01
@alfC, also see my gist.github.com/jcsalomon/1325295 where I've collected the Unicode characters I've found most useful into a handy reference sheet. – J. C. Salomon Apr 9 '14 at 20:16
@J.C.Salomon, I am exploring creating Snippets in Gedit to autmatically create unicode character with key combinations (or autotext) and at the same time using \newunicodechar in the document to customize the actual look in the document. I don't know how I didn't discover this before. I just typed this equation, which in normal latex would take several lines: C⌄ℓ {ⅆT⌄ℓ⁄ⅆt}=∇(κ⌄ℓ ∇T⌄ℓ) + G⌄{sℓ}(T⌄s - T⌄ℓ) + G⌄{eℓ}(T⌄e - T⌄ℓ), I was able to redifine the meaing of ⌄ as "text subscript". It is almost like typing rich-formatted equations with Mathematica. Very fast, consice and meaningful. – alfC Apr 9 '14 at 20:29
I vote for upright e, i and d. In fact, I use upright and sans serif because it makes these symbols stand out clearly, but I haven't seen that used anywhere.
While we're at it, please allow me to point out that when "romanizing" multi-letter suffixes (like, say, "fin" for "final"), it's advisable to go for \textnormal rather than \mathrm, because the latter just renders a bunch of Roman characters side-by-side, without optimizing the spacing to make them look like the abbreviation to a single word.
VarunVarun
Thank you for the \textnormal tip :) I honestly didn't expect to still be getting useful information out of this question 1.5 years after posting it! – Adrian Petrescu Nov 9 '12 at 3:34
There is also \text (from amsmath I think) but I don't know the typographic difference. – marczellm Jan 2 '13 at 19:39
@marczellm \textnormal{#1} is basically \text{\normalfont #1} with some more tweaks. Therefore you use \textnormal for sin, but \text for if and only if. The reason is that sin should be upright even in for instance a theorem statement, whereas if and only if as a part of a displayed equation should be italic in a theorem statement (given you typeset theorems in italics). – yo' May 31 '13 at 10:39
@tohecz Thank you. I use \sin though :) – marczellm May 31 '13 at 11:18
@marczellm That's of course correct. But if you wanted to define it manually, \mathop{\textnormal{sin}} would be much better than \mathop{\text{sin}}. – yo' May 31 '13 at 19:24
"Scientific Style and Format - The CSE Manual for Authors, Editors, and Publishers" suggests using roman(upright) d to typeset differential operators (CSE 7th ed, page 160). As someone already pointed out, authors, in general, don't care whether it shows up as italics dt or not. It is left mostly to technical copyeditors like me to fix this. - Dave Ledesma
Dave LedesmaDave Ledesma
I do care very much that it shows up as italic :-) – Hendrik Vogt Jul 2 '11 at 16:26
Just to throw another option in the already muddy (or bloody?) water here. The physics package contains its own set of automation for typesetting this stuff (including ordinary and partial derivatives) as well as automation for Dirac's quantum mechanics notation (bras and kets) and a number of odds and ends mostly related to re-sizing brackets and typesetting "evaluate at" indications.
Some basics from the package:
For differentials: \dd or \dd{x}.
For ordinary derivatives: \dv{x} for the derivative with respect to $x$ operator, \dv{f}{x} for the derivative of $f$ with respect to $x$ and \dv[2]{f}{x} for the second derivative of $f$ with respect to $x$.
For partial derivatives: \pdv{x} for the partial derivative with respect to $x$ operator, \pdv{f}{x} for the partial derivative of $f$ with respect to $x$ and \pdv[2]{f}{x} for the second partial derivative of $f$ with respect to $x$. \pdv{f}{x}{y} for the mixed partial derivative of $f$ with respect to $x$ and $y$.
The documentation does not indicate if this extends to higher mixed derivatives or not; experiment shows that \pdv{f}{x}{y}{z} does not generate the third partial derivative with respect to $x$, $y$ and $z$ but typesets as \pdv{f}{x}{y} followed by $z$.
This package uses roman d's and italic type for the quantity whose differential it is in keeping with the standard that Emre cites (and therefore at odds with the history of mathematical typesetting as noted by many posters herein).
dmckeedmckee
The package also has the italicdiff option for printing the differential d in italics. :-) – egreg Oct 26 '15 at 17:25
The package has {}-delimited optional arguments, which is a deadly sin – yo' Sep 16 '16 at 11:50
Note that we can italicize the d's using \usepackage[italicdiff]{physics}. – Mateen Ulhaq Apr 9 '17 at 5:23
I'm a newcomer to mathematics, so maybe there's an obvious reason why nobody else has suggested this … but personally, I find slanted (but still roman) d's to look most attractive, and yet be "most differentiable" (pun intended 🤣) from possible variables named 'd' or operators with an upright, roman 'd' in their name:
\newcommand*\dif{\mathop{}\!\textnormal{\slshape d}}
d(x) = \frac{\dif}{\dif x}
\left(
x \cdot \mathop{\mathrm{dep}}(x)
\right)
Here's a sample of the output. Beautiful, easy to tell at a glance what-is-what, and adheres to the spirit of the ISO standard, while maintaining the beauty and traditional form of mathematics textbooks. (At least IMHO!)
(Of course, this depends on \sl being a defined font, which, while it works just fine in standard LaTeX environments, may not be the case if you're using more modern typography from something like LuaLaTeX or XeLaTeX — maybe see How do I "fake" slanted text in LaTeX? on SO.)
ELLIOTTCABLEELLIOTTCABLE
Rather than \textrm{\sl d} it should be \textnormal{\slshape d} – egreg Sep 10 '17 at 18:01
Not the answer you're looking for? Browse other questions tagged typography math-operators or ask your own question.
new command for the dx of intergral.
Setting new command in LaTeX for the differential
What formatting should I use on 'd' when writing an integral?
Should I \mathrm the d in my integrals?
Evaluation of Differentiation and Integration
Why does pdfTeX hang on this file?
How do I change the font of a letter?
Better automatic spacing of differential d?
Coloured underlines of equations and text in LaTeX Beamer
What do empty math character class symbols ("\mathpunct{}") do, and when are they used?
What's the proper way to write a vector with a single character subscript?
Modern book design, margins and typed area
Proper way to quote verses before a section
What is the right way to typeset "define"?
Proper way to typset minimum value of variable in formula?
What is the typographically correct way to typeset name initials?
Right way to typeset a mathematical document
Resizing the sum operator
Defining a dot operator at the baseline
How to print the "essential supremum" operator | CommonCrawl |
Noam Mazor
Simple Constructions from (Almost) Regular One-Way Functions 📺 Abstract
Noam Mazor Jiapeng Zhang
Two of the most useful cryptographic primitives that can be constructed from one-way functions are pseudorandom generators (PRGs) and universal one-way hash functions (UOWHFs). In order to implement them in practice, the efficiency of such constructions must be considered. The three major efficiency measures are: the seed length, the call complexity to the one-way function, and the adaptivity of these calls. Still, the optimal efficiency of these constructions is not yet fully understood: there exist gaps between the known upper bound and the known lower bound for black-box constructions. A special class of one-way functions called unknown-regular one-way functions is much better understood. Haitner, Harnik and Reingold (CRYPTO 2006) presented a PRG construction with semi-linear seed length and linear number of calls based on a method called randomized iterate. Ames, Gennaro and Venkitasubramaniam (TCC 2012) then gave a construction of UOWHF with similar parameters and using similar ideas. On the other hand, Holenstein and Sinha (FOCS 2012) and Barhum and Holenstein (TCC 2013) showed an almost linear call-complexity lower bound for black-box constructions of PRGs and UOWHFs from one-way functions. Hence Haitner et al. and Ames et al. reached tight constructions (in terms of seed length and the number of calls) of PRGs and UOWHFs from regular one-way functions. These constructions, however, are adaptive. In this work, we present non-adaptive constructions for both primitives which match the optimal call-complexity given by Holenstein and Sinha and Barhum and Holenstein. Our constructions, besides being simple and non-adaptive, are robust also for almost-regular one-way functions.
Lower Bounds on the Time/Memory Tradeoff of Function Inversion 📺 Abstract
Dror Chawin Iftach Haitner Noam Mazor
We study time/memory tradeoffs of function inversion: an algorithm, i.e., an inverter, equipped with an s-bit advice on a randomly chosen function f:[n]->[n] and using q oracle queries to f, tries to invert a randomly chosen output y of f (i.e., to find x such that f(x)=y). Much progress was done regarding adaptive function inversion - the inverter is allowed to make adaptive oracle queries. Hellman [IEEE transactions on Information Theory '80] presented an adaptive inverter that inverts with high probability a random f. Fiat and Naor [SICOMP '00] proved that for any s,q with s^3 q = n^3 (ignoring low-order terms), an s-advice, q-query variant of Hellman's algorithm inverts a constant fraction of the image points of any function. Yao [STOC '90] proved a lower bound of sq<=n for this problem. Closing the gap between the above lower and upper bounds is a long-standing open question. Very little is known of the non-adaptive variant of the question - the inverter chooses its queries in advance. The only known upper bounds, i.e., inverters, are the trivial ones (with s+q=n), and the only lower bound is the above bound of Yao. In a recent work, Corrigan-Gibbs and Kogan [TCC '19] partially justified the difficulty of finding lower bounds on non-adaptive inverters, showing that a lower bound on the time/memory tradeoff of non-adaptive inverters implies a lower bound on low-depth Boolean circuits. Bounds that, for a strong enough choice of parameters, are notoriously hard to prove. We make progress on the above intriguing question, both for the adaptive and the non-adaptive case, proving the following lower bounds on restricted families of inverters: Linear-advice (adaptive inverter): If the advice string is a linear function of f (e.g., A*f, for some matrix A, viewing f as a vector in [n]^n), then s+q is \Omega(n). The bound generalizes to the case where the advice string of f_1 + f_2, i.e., the coordinate-wise addition of the truth tables of f_1 and f_2, can be computed from the description of f_1 and f_2 by a low communication protocol. Affine non-adaptive decoders: If the non-adaptive inverter has an affine decoder - it outputs a linear function, determined by the advice string and the element to invert, of the query answers - then s is \Omega(n) (regardless of q). Affine non-adaptive decision trees: If the non-adaptive inverter is a d-depth affine decision tree - it outputs the evaluation of a decision tree whose nodes compute a linear function of the answers to the queries - and q < cn for some universal c>0, then s is \Omega(n/d \log n).
Channels of Small Log-Ratio Leakage and Characterization of Two-Party Differentially Private Computation Abstract
Iftach Haitner Noam Mazor Ronen Shaltiel Jad Silbak
Consider a ppt two-party protocol $$\varPi = (\mathsf {A} ,\mathsf {B} )$$ in which the parties get no private inputs and obtain outputs $$O^{\mathsf {A} },O^{\mathsf {B} }\in \left\{ 0,1\right\} $$, and let $$V^\mathsf {A} $$ and $$V^\mathsf {B} $$ denote the parties' individual views. Protocol $$\varPi $$ has $$\alpha $$-agreement if $$\Pr [O^{\mathsf {A} }=O^{\mathsf {B} }] = \tfrac{1}{2}+\alpha $$. The leakage of $$\varPi $$ is the amount of information a party obtains about the event $$\left\{ O^{\mathsf {A} }=O^{\mathsf {B} }\right\} $$; that is, the leakage$$\epsilon $$ is the maximum, over $$\mathsf {P} \in \left\{ \mathsf {A} ,\mathsf {B} \right\} $$, of the distance between $$V^\mathsf {P} |_{O^{\mathsf {A} }= O^{\mathsf {B} }}$$ and $$V^\mathsf {P} |_{O^{\mathsf {A} }\ne O^{\mathsf {B} }}$$. Typically, this distance is measured in statistical distance, or, in the computational setting, in computational indistinguishability. For this choice, Wullschleger [TCC '09] showed that if $$\epsilon \ll \alpha $$ then the protocol can be transformed into an OT protocol.We consider measuring the protocol leakage by the log-ratio distance (which was popularized by its use in the differential privacy framework). The log-ratio distance between X, Y over domain $$\varOmega $$ is the minimal $$\epsilon \ge 0$$ for which, for every $$v \in \varOmega $$, $$\log \frac{\Pr [X=v]}{\Pr [Y=v]} \in [-\epsilon ,\epsilon ]$$. In the computational setting, we use computational indistinguishability from having log-ratio distance $$\epsilon $$. We show that a protocol with (noticeable) accuracy $$\alpha \in \varOmega (\epsilon ^2)$$ can be transformed into an OT protocol (note that this allows $$\epsilon \gg \alpha $$). We complete the picture, in this respect, showing that a protocol with $$\alpha \in o(\epsilon ^2)$$ does not necessarily imply OT. Our results hold for both the information theoretic and the computational settings, and can be viewed as a "fine grained" approach to "weak OT amplification".We then use the above result to fully characterize the complexity of differentially private two-party computation for the XOR function, answering the open question put by Goyal, Khurana, Mironov, Pandey, and Sahai, [ICALP '16] and Haitner, Nissim, Omri, Shaltiel, and Silbak [22] [FOCS '18]. Specifically, we show that for any (noticeable) $$\alpha \in \varOmega (\epsilon ^2)$$, a two-party protocol that computes the XOR function with $$\alpha $$-accuracy and $$\epsilon $$-differential privacy can be transformed into an OT protocol. This improves upon Goyal et al. that only handle $$\alpha \in \varOmega (\epsilon )$$, and upon Haitner et al. who showed that such a protocol implies (infinitely-often) key agreement (and not OT). Our characterization is tight since OT does not follow from protocols in which $$\alpha \in o( \epsilon ^2)$$, and extends to functions (over many bits) that "contain" an "embedded copy" of the XOR function.
Dror Chawin (1)
Iftach Haitner (2)
Ronen Shaltiel (1)
Jad Silbak (1)
Jiapeng Zhang (1) | CommonCrawl |
Journal of Therapeutic Ultrasound
Ultrasound field characterization and bioeffects in multiwell culture plates
Upen S Patel1,
Sleiman R Ghorayeb2,3,
Yuki Yamashita2,
Folorunsho Atanda2,
A Damien Walmsley1 &
Ben A Scheven1
Journal of Therapeutic Ultrasound volume 3, Article number: 8 (2015) Cite this article
Ultrasound with frequencies in the kilohertz range has been demonstrated to promote biological effects and has been suggested as a non-invasive tool for tissue healing and repair. However, many challenges exist to characterize and develop kilohertz ultrasound for therapy. In particular there is a limited evidence-based guidance and standard procedure in the literature concerning the methodology of exposing biological cells to ultrasound in vitro.
This study characterized a 45-kHz low-frequency ultrasound at three different preset intensity levels (10, 25, and 75 mW/cm2) and compared this with the thermal and biological effects seen in a 6-well culture setup using murine odontoblast-like cells (MDPC-23). Ultrasound was produced from a commercially available ultrasound-therapy system, and measurements were recorded using a needle hydrophone in a water tank. The transducer was displaced horizontally and vertically from the hydrophone to plot the lateral spread of ultrasound energy. Calculations were performed using Fourier transform and average intensity plotted against distance from the transducer. During ultrasound treatment, cell cultures were directly exposed to ultrasound by submerging the ultrasound transducer into the culture media. Four groups of cell culture samples were treated with ultrasound. Three with ultrasound at an intensity level of 10, 25, and 75 mW/cm2, respectively, and the final group underwent a sham treatment with no ultrasound. Cell proliferation and viability were analyzed from each group 8 days after three ultrasound treatments, each separated by 48 h.
The ultrasonic output demonstrated considerable lateral spread of the ultrasound field from the exposed well toward the adjacent culture wells in the multiwell culture plate; this correlated well with the dose-dependent increase in the number of cultured cells where significant biological effects were also seen in adjacent untreated wells. Significant thermal variations were not detected in adjacent untreated wells.
This study highlights the pitfalls of using multiwell plates when investigating the biological effect of kilohertz low-frequency ultrasound on adherent cell cultures.
Investigating the therapeutic use of ultrasound to promote biological tissue healing and repair poses many challenges to the researcher when studying the effect on cells in vitro. Ultrasound propagation occurs via the transfer of energy from particle to particle [1]. This results in areas of compression and rarefaction, and it is the effect of this mechanical movement on cells that is studied. The ultrasound field is not homogenous and is prone to reflection and attenuation when the field encounters a boundary between different media [2]. The challenge is to control and reproduce the parameters of the ultrasound wave that affect the cells in in vitro culture. There is limited evidence-based guidance in the literature concerning the methodology of exposing biological cells to ultrasound in vitro. A study by Hensel et al. [3] investigated megahertz ultrasound-wave propagation characteristics in four commonly used setups to expose ultrasound to cells in culture wells; well on transducer, well on water surface, sealed well, transducer in well. Their results indicated that all four of these approaches produced some degree of variability due to reflecting surfaces. A setup with no liquid-air interface would provide the most reproducible, and hence transferable, results. The authors recommended that a culture well be devoid of air and water-proof sealed such that it could be submerged within a water tank. Ultrasound would then be generated at a distance, ensuring the most homogenous portion of the ultrasound field (far-field) would be exposed to the cells. The authors of the study considered a single well setup, however, there are many studies in the literature where multiwell plates have been used to study the effects of ultrasound on cell culture [4–17]. Recommendations from Hensel et al. [3] may be applicable to multiwell plates but it is important to consider divergence of the ultrasound field and its scope of interaction with adjacent wells within the same multiwell plate.
The majority of studies that investigated the therapeutic effects of ultrasound on biological cells use pulsed ultrasound with a frequency in the megahertz range [18–20]. However, there are a number of studies that demonstrate biological effects with the use of ultrasound with a frequency in the kilohertz range [5, 7–9, 11, 13, 21–24]. Ultrasound in the kilohertz frequency range has a longer wavelength compared to megahertz ultrasound. This characteristic allows for greater penetration through living tissue or dense tissue, such as dental enamel or bone, making it potentially more effective than megahertz ultrasound [25, 26]. Therefore, low-frequency ultrasound may ideally be suited for therapeutic applications involving deep sites of injury or dense hard tissues, such as bone and tooth repair [24].
The nature of ultrasound beam propagation, from its source, to the cells, and further, causes the culture plastic, on which the cells are grown, to both attenuate and reflect the ultrasound wave. The degree of attenuation will vary by method of exposure, as described by Hensel et al. [3] and the manufacturer design of a multiwell plate. The energy absorbed by a multiwell plate during the ultrasound treatment of cells in a specific culture well has the potential to inadvertently affect cells cultured in the other wells of the of the same plate. Fung et al. [27] reported that an ultrasound field with a frequency of 1.5 MHz is well-delineated and generally linear. However, an ultrasound field with a frequency in the kilohertz range is considered to be diffuse. This characteristic of low-frequency ultrasound implies that it could affect adjacent wells in a multiwell plate when used in in vitro studies. It can be postulated that the attenuated ultrasound energy results in heating of the multiwell culture plate or resonance causing vibrations in each of the wells in the plate. Investigation of a biological effect in an adjacent culture well without a thermal change will add to the debate of a thermal and non-thermal mechanism of an ultrasound induced biological effect [28–32].
This study aims to characterize a low-frequency ultrasound field to investigate its propagation and divergence. We have previously studied the effects of ultrasound on dental cells with an odontoblast-like cell line, MDPC-23 [8, 9, 23, 33]. A similar model will be used; however, the treatment of these cells with ultrasound will be modified to investigate the effects on (non-treated) cells cultured in adjacent wells of multiwell plates. A spatial beam plot will identify the risks to adjacent wells when a multiwell plate is used for experiments involving in vitro cell culture.
Ultrasound was generated at a frequency of 45 kHz (DuoSon, SRA Developments Ltd, Ashburton, UK). The system was preprogrammed by the manufacturer to provide three modes of continuous ultrasonic output at spatial-average intensities of 10, 25, and 75 mW/cm2 and calibrated using a radiation force balance (SRA Developments Ltd, Ashburton, UK). The DuoSon single-element transducer is unfocused and has an effective radiating area of 16.3 cm2 when generating ultrasound at a frequency of 45 kHz.
Experimental setup for ultrasound-field characterization
A vacuum degassing chamber was constructed from plastic (Applied Vacuum Engineering, Bristol, UK) with a curved internal surface to reduce ultrasonic reflections. An acoustically absorbing base was constructed of a combination of rubber and Apltile SF5048 (Precision Acoustics, Dorchester, UK). A 1.0-mm needle hydrophone probe (Model 1452; Precision Acoustics, Dorchester, UK) connected to a HP Series Submersible Preamplifier (PA09022, Precision Acoustics, Dorchester, UK) was held in place vertically by the Apltile SF5048 material. The chamber was filled with 12 L of double distilled deionized water and air evacuated to achieve a vacuum. The water was degassed for 12 h with a vacuum of 0.95 bar. The DuoSon transducer was positioned vertically in line over the hydrophone, with their central axes aligned, and its movement was controlled by an XYZ manual travel translation stage (Thorlabs Inc., Newton, NJ, USA) as shown in Fig. 1. Both the transducer and needle hydrophone probe were submerged for 4 h. This mimicked the conditions present when the hydrophone was calibrated. Voltage measurements were recorded using a PC oscilloscope (PicoScope 5203; Pico Technology, St Neots, UK). The hydrophone and preamplifier were connected to a DC Coupler (DCPS038; Precision Acoustics, Dorchester, UK), and the signal was passed through a 50-Ω Terminator (TA051 Feed-Through Terminator; Pico Technology, St Neots, UK) prior to connecting to the PC oscilloscope (Fig. 1). The transducer face was positioned 50 mm below water level, and maximum voltage measurements and frequency were recorded at ten vertical points from the transducer at 1-mm intervals from the transducer face. The transducer was displaced horizontally and ten vertical measurements were taken at a further five positions from the transducer face at 5-mm intervals.
Experimental setup for ultrasound-field characterization. Annotated diagram describing the setup of equipment for measuring the ultrasound field generated from the DuoSon ultrasound machine
Ultrasound-field calculation
These measurements were recorded for all three of the preset and pre-calibrated ultrasound intensities (10, 25, and 75 mW/cm2). The maximum voltage and frequency measurements were used to calculate the average ultrasound intensity at each horizontal position from the transducer as described previously [26]. Initially, the pressure value was calculated using Eq. 1.
$$ p=\frac{V}{K} $$
where p is the acoustic pressure, V is the maximum voltage measured, and K is the calibration factor (certificate: U3105, calibration carried out by National Physics Laboratory, London, UK). The needle hydrophone was calibrated over a frequency range of 10–100 kHz at 5-kHz intervals. Interpolation was used to determine the equivalent calibration factor based on the frequency recorded during the measurement. Subsequently, the acoustic intensity (I) was calculated using Eq. 2.
$$ I=\frac{1}{T_{prf}}\kern0.24em {\displaystyle \int}\frac{p^2(t)}{\rho \kern0.24em c}\kern0.24em dt $$
where T prf is the pulse-repetition period, ρ is the density of the propagating medium, and c is the velocity of sound in the same medium (1480 m/s). Hydrophone sensitivity is rarely constant as a function of frequency, and interpolation to determine the correct calibration factor may cause erroneous results. Full-waveform deconvolution was employed, and Eq. 1 was modified to utilize Fourier transformation. This is shown in Eq. 3.
$$ {\mathrm{\Im}}^{-1}\left\{\frac{\mathrm{\Im}\left(V(t)\right)}{K(f)}\right\}=p(t) $$
Intensity was again derived using the acoustic pressure calculated using Eq. 3. Both intensity values were plotted against distance from the long axis of the hydrophone.
Ultrasound treatment apparatus setup
A six-well culture plate (Costar® tissue-culture treated; Corning®, Tewksbury, MA, USA) was supported in a water bath by silicone rubber (Fig. 2) to minimize reflections [8, 9]. The water bath was placed on a thermostat-controlled hot plate to keep the culture medium in each well of the six-well plate at 37 °C. The entire setup was placed in a laminar flow hood together with the DuoSon to prevent infection (Fig. 2). The transducer was clamped to a scissor stand to allow for straightforward insertion and removal from the culture well. The transducer face was positioned 5 mm from the culture surface in each culture well (Fig. 3). The thickness of the culture plastic at the base of the culture well is 1.27 mm.
Treating biological cells with ultrasound in multiwell culture plates. DuoSon with transducer (identified by *) clamped in position in a laminar flow hood (top) and a close-up of a six-well plate supported by silicone in a water bath with the transducer submerged in culture media (bottom)
Transducer positioning in a multiwell culture plate. Annotated diagram describing the position of the transducer face from the base of the culture well. The transducer is only inserted in the culture medium of the W0 culture well of each multiwell plate
Cell number and viability
An immortalized mouse cell line of odontoblast-like dental pulp cells, MDPC-23 [9, 26, 33, 34], were cultured with Dulbecco's Modified Eagle Medium (DMEM high glucose; Biosera, UK) supplemented with 10 % fetal bovine serum (Biosera, UK), 1 % penicillin/streptomycin (Sigma-Aldrich®, UK), and 200 mM glutamine (GlutaMAX™; Gibco®, Invitrogen™, UK) in a humidified incubator with 5 % carbon dioxide in air at 37 °C. 50,000 cells (day 0) were seeded in each of the three wells in one row of twelve six-well plates. These cells subsequently formed an adherent monolayer. The medium was replenished on days 1, 3, 5, and 7 with ultrasound treatment on days 2, 4, and 6. The DuoSon transducer was submerged into the culture medium of the first well (W0) at the corner of each plate for 5 min. Ultrasound treatments were carried out in triplicate and included a sham treatment where the transducer was submerged into the culture medium (Figs. 2 and 3) for the same length of time without the DuoSon producing an ultrasonic output. Prior to submerging the transducer into the culture medium, the transducer was wiped with 70 % alcohol and washed with sterile culture medium. Only the W0 well in each six-well plate was treated with ultrasound at a frequency of 45 kHz and each plate treated with a different intensity; no power (sham), 10, 25, and 75 mW/cm2. Each well was treated for 5 min. On day 8 of culture, cells were detached using a 2.5 g/l Trypsin in 0.2 g/l EDTA solution (Sigma-Aldrich®, UK) from the W0 well. Cells from the adjacent (W1) and distant (W2) wells in each six-well plate were collected using the same method. Cell counts and viability were measured with trypan blue (Sigma-Aldrich®, UK) staining and a Neubaeur haemocytometer (Neubaeur, Frankfurt, Germany).
The apparatus was set up as described earlier, and a six-well plate, containing 9 ml of culture medium in each well, was taken from an incubator at 37 °C and positioned in the water bath. A thermocouple (TC-PVC-T-24-180; Omega Engineering Limited, Manchester, UK) was used to measure the temperature rise of the culture medium in the well. Temperature measurements were also taken adjacent and distant to the culture well where the transducer was submerged. The thermocouple was positioned on the culture plastic, at the center of each well. A measurement was taken every 30 sec to ensure variations in temperature over the maximum treatment time of 30 min while ultrasound was produced by the DuoSon at the three 45-kHz ultrasound intensities; 10, 25, and 75 mW/cm2. Measurements were taken every 30 sec to ensure specific time points would be recorded to ascertain treatment times.
Ultrasound beam characterization
Maximum voltage and frequency measurements of ultrasound produced from the DuoSon are shown in Table 1. These values were used to calculate spatial-average intensities as described in the methods section. Beam plots of calculated intensities are shown in Fig. 4a–c. The data indicate that the measurements recorded where the transducer and hydrophone were centrally aligned showed some resemblance to the intensities quoted by the manufacturers. Measurements made horizontally away from the long axis of the transducer showed a gradual reduction of the average intensity. Figure 4 also displays the size of the transducer and positioning of culture wells in a six-well plate which are a 1:1 scale with the horizontal axis. Horizontal measurements show that at 20 and 25 mm from the central axis of the transducer, the calculated intensities without Fourier analysis were 7.75 and 5.2 mW/cm2, respectively, when an ultrasound beam using the preset 10 mW/cm2 mode is selected. An ultrasound beam produced using the preset 25 mW/cm2 mode recorded an average intensity of 19 and 12.5 mW/cm2, and when using the 75 mW/cm2 mode, 61.5 and 58.5 mW/cm2 was recorded at 20 and 25 mm, respectively, from the central axis of the transducer. The beam plots of the 10 and 25 mW/cm2 modes (Fig. 4a, b) are similar in form, as opposed to that of the 75 mW/cm2 mode (Fig. 4c). The 75 mW/cm2 mode produces an ultrasound beam which has a flatter peak. These data imply that when biological cells cultured in dishes of a six-well plate are treated with ultrasound, adjacent culture wells will also be exposed to an ultrasound field.
Table 1 The recorded maximum voltage and frequency of ultrasound produced from the DuoSon. Recorded maximum voltage and frequency when a 10, 25, and 75 mW/cm2 ultrasound beam is produced from the DuoSon transducer. Measurements were taken at 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 mm vertically from the transducer face at 0, 5, 10, 15, 20, and 25 mm horizontally from the long axis of the transducer
The calculated spatial-average intensity from ultrasound produced from the DuoSon. Spatial-average intensity calculated when a 10 a , 25 b, and 75 mW/cm2 c ultrasound beam is produced from the DuoSon transducer. Dimensions of the transducer and culture wells are to a 1:1 scale with the horizontal axis. A diagrammatic representation of the culture wells in a six-well plate have been superimposed to demonstrate proximity of the culture wells to each other and their spatial relationship to the ultrasound beam and average intensities. Intensity without Fourier analysis is shown as mean ± SD
Temperature and apparatus
Temperature measurements indicated that ultrasound with a frequency of 45 kHz, and at the three specified intensities, did not significantly affect the temperature of the culture medium in culture wells adjacent to and distant from the well being treated with ultrasound. Measurements also confirmed that the water bath setup was able to keep the temperature of the culture medium stable at 37 °C (±1 °C). Figure 5 shows the temperature rise in the culture medium of the culture well with the transducer submerged and producing ultrasound. The highest of the three intensities, 75 mW/cm2, produced a temperature rise of nearly 16 °C after 30 min of ultrasound exposure. Intensities of 10 and 25 mW/cm2 increased the temperature of the medium resulting in maximum temperatures of 4 and 7 °C, respectively, over 30 min of ultrasound exposure. It was observed for the lower two intensities, the temperature rise reached a plateau before the maximum treatment time of the device was reached. This did not occur at the highest intensity. After 5 min (300 sec) of ultrasound treatment, the temperature of the culture medium had risen by 1.6, 3, and 5.5 °C with intensities, 10, 25, and 75 mW/cm2, respectively. These data indicate that treatment with ultrasound of a short duration using this method only marginally increases the ambient temperature of the culture medium, but longer times up to 30 min can generate a significant temperature rise.
Temperature changes with ultrasound treatment. Temperature changes in culture medium in a well of the six-well plate which is directly exposed with 45-kHz ultrasound over a 30-min period
Application of a 45-kHz ultrasound at the two preset lower intensity levels of 10 and 25 mW/cm2 resulted in cell counts from the directly exposed W0 culture well to be significantly higher than the sham-treated group (p < 0.001 and p < 0.01 respectively) indicating ultrasound-stimulated cell proliferation. The highest preset intensity level, 75 mW/cm2, did not result in a significant difference in cell number (Fig. 6), compared to sham; however, cell viability was reduced to 90 % as shown in Fig. 7. The lower intensity levels of 10 and 25 mW/cm2 reported higher cell viabilities of 98 % and above (Fig. 7). This indicates that higher ultrasound intensities are not as well tolerated by MDPC-23 cells compared to the lower intensities used in this study. This result is statistically significant (p < 0.001).
Effects of 45-kHz ultrasound on MDPC-23 cell proliferation. Cell numbers were determined after 8 days of culture in six-well plates with alternating days of ultrasound treatment. Three groups had ultrasound treatment each with the intensities, 10, 25, and 75 mW/cm2. A sham-treatment control group had no ultrasound applied to the cells. Total viable cell number is shown for each culture well (W0, W1, and W2), and data is expressed as a percentage of the sham-control group (mean ± SD; n = 3). One way ANOVA statistical analysis was carried out, and the statistical significance is indicated (*** p < 0.001; ** p < 0.01; * p < 0.05)
Effects of 45-kHz ultrasound on cell viability of MDPC-23 cells. Viability was determined after 8 days of culture in six-well plates with alternating days of ultrasound treatment. Three groups had ultrasound treatment each with the intensities, 10, 25, and 75 mW/cm2. A sham-treatment control group had no ultrasound applied to the cells. Cell viability is shown for each culture well (W0, W1, and W2), and data is expressed as a percentage of the total cell number (mean ± SD; n = 3). One way ANOVA statistical analysis was carried out, and the statistical significance is indicated (*** p < 0.001; ** p < 0.01; * p < 0.05)
No significant findings were reported from cell counts from the immediately adjacent W1 culture wells, which were not directly exposed, although cell numbers were marginally increased by approximately 20 and 10 % with the two preset intensity levels of 25 and 75 mW/cm2, respectively, compared to the sham control (Fig. 6). Figure 7 shows that cell viability was only marginally and not significantly reduced in adjacent, W1, culture wells when the two lower ultrasound intensities were used; however, with the higher intensity (75 mW/cm2), cell viability was reduced to 93 %. This demonstrates that the higher intensity ultrasound had an effect on the cell viability of MDPC-23 cells cultured in adjacent culture wells while having no effect in the directly exposed wells confirming the dose-dependent nature of the ultrasound effects. This result is statistically significant (p < 0.05) when compared to the lower intensities and sham control.
Cell numbers in the distant culture well, W2, were found to be significantly (p < 0.01) increased when 75 mW/cm2 intensity ultrasound was used compared to the sham control (Fig. 6). However, the lower intensities did not significantly increase cell numbers in the distant culture well as shown in Fig. 6. Figure 7 shows that cell viability was reduced across all three intensities. The most significant reduction, compared to sham, was at the highest intensity, 75 mW/cm2, resulting in a cell viability of 97 % (p < 0.05). The increase in cell numbers together with a slight decrease in cell viability of MDPC-23 cells cultured in distant wells of six-well plates where 75 mW/cm2 intensity ultrasound is used indicates that ultrasound at this intensity has a positive effect on cell number when the cells are not directly exposed. This suggests that there is potential for ultrasound with higher intensities to affect other culture wells in the same multiwell plate, with lower intensities, this effect is not significant.
Kilohertz ultrasound has been advocated as a potential treatment modality for tooth repair [24]. To understand, and ultimately improve the effectiveness of this treatment, it is important to determine how ultrasound stimulates the repair processes within a tooth. Previously, our studies established that low-frequency ultrasound effectively penetrates through tooth tissue layers, and the energy is retained within the central chamber of the tooth [26]. Cells responsible for dentine repair are located at the dentine-pulp interface and stimulation at this site may enhance repair processes to maintain tooth vitality. When undertaking in vitro experiments, it is critical to ensure that parameters of the treatment modality and experimental setup are well characterized and controlled. An in vitro experiment setup using multiwell culture plates with ultrasound treatment is widely used in the literature allowing direct biological effects of ultrasound on replicate cell cultures to be analyzed. [3, 4, 8, 9, 21, 26, 35–37]. This study measured the propagation and intensity of an ultrasound field with a frequency of 45 kHz. We postulated that ultrasound with this frequency would generate a wide beam profile and when used with multiwell plates, could affect cells cultured in adjacent and distant wells of the same culture plate where ultrasound is applied. Figure 4 demonstrates that the 45-kHz ultrasound beam profile had a significant lateral spread potentially crossing over to adjacent non-exposed culture wells. At 25 mm from the central axis of the DuoSon transducer, ultrasound at intensities of 51, 50, and 78 % of manufacturers preset intensities were found (10, 25, and 75 mW/cm2, respectively). Due to apparatus limitations, measurements beyond this point could not be made; however, the data and theoretical knowledge of ultrasound propagation suggests that there could be further lateral propagation. It is important to consider that ultrasound-characterization measurements reported in this study are in "free-field" conditions and different to the experiment apparatus and culture multiwell setup. Culture wells shown in Fig. 4 are superimposed to scale to demonstrate proximity. However, this study provides biological evidence to support ultrasound propagation in this way by considering the findings of cell number and viability in W1 and W2 culture wells of the six-well plate (Figs. 6 and 7). The findings have a major influence on future in vitro cell-culture study designs where ultrasound is applied to multiwell culture plates. Figure 4 shows the intensity measured and calculated directly over the central axis of the transducer. This can be considered the central or core intensity of the ultrasound beam and is frequently the intensity quoted by manufacturers in their documentation or displayed on the device when in use. To ensure robustness of the data collected, ultrasonic output must be characterized prior to use for in vitro study [38]. In this study, the manufacturer's quoted intensities aligned well with the intensities calculated without Fourier analysis (Fig. 4); however, the intensities calculated with Fourier analysis were lower. This may partially be due to the fact that the Fourier-transform calculation determines the intensity over multiple frequencies. Furthermore, as the hydrophone sensitivity is rarely constant as a function of frequency, interpolation was used to determine the correct calibration factor which caused the marginal discrepancy seen between calculated intensities with and without Fourier analysis. Another source for this discrepancy could be due to the use of null values when completing the data set in order to obtain 2n (n = 1, 2, …) data points which could introduce marginal errors in the Fourier coefficients, which in turn may have hindered the outcome of the original signal.
Thermal variation in cell culture medium with ultrasound treatment is a concern since a temperature rise greater than 5 °C above 37 °C could adversely affect cell viability [39]. In this study, 45-kHz ultrasound with an intensity of 75 mW/cm2 registered a temperature rise of slightly over 5 °C during the 5-min treatment time resulting in reduced cell viability. This was found in culture well, W0, which was directly exposed to ultrasound (Fig. 5). No thermal variation was found in adjacent (W1) and distant (W2) culture wells during ultrasound treatment. A larger volume of culture medium (9 ml), than usually used, was required in each W0 culture well to ensure the radiating surface of the ultrasound transducer could be submerged into the culture medium but also allow space for any potential heat generated by the ultrasound transducer to be dissipated (Figs. 2 and 3). Even with this precaution, the setup described should only be used to treat cells directly with ultrasound for 5 min per episode of treatment with the highest of the three intensities. At the two lower intensities, a single treatment episode can be delivered for up to 10 min with 25 mW/cm2 before a temperature rise of 5 °C is registered and the 10 mW/cm2 plateaus at 4 °C. Temperature changes in apparatus setup have also been investigated by Leskinen [40]. They confirmed that temperature variation reflects biological outcome and advocate detailed temperature characterization with in vitro ultrasound exposures. Our results show that cell viability was significantly (albeit moderately) reduced in all three culture-well groups when ultrasound with the highest intensity was employed. Temperature variation in the directly exposed, W0, culture well could potentially account for the reduced cell viability in this well; however, there was no thermal variation in culture wells W1 and W2. The same intensity level also significantly increased cell numbers in the distant W2 culture well (Fig. 6) without a change in temperature. Although many studies have reported therapeutic biological effects [8, 9, 23, 24, 26, 33, 41–45], it is not fully understood how ultrasound triggers a response in cells and tissues. Two broad categories, thermal and non-thermal, have been postulated and discussed by researchers [28, 32], and it is thought by some that it may only be a thermal effect that brings about changes in biological tissues. This study indicates that non-thermal biomechanical effects should be considered as a temperature rise was not recorded in culture wells W1 and W2, but significant changes to cell number and viability were found. Similarly, Fig. 5 shows that the lowest intensity setting recorded a marginal temperature rise of less than 2 °C during the 5-min treatment time. This resulted in the highest increase in cell number compared to sham (Fig. 6). Thus, it can be postulated that the mechanism of action in this case is mechanical stimulation possibly via microstreaming effects on the cell membrane transmitted through the cytoskeleton and ultimately leading to increased mitosis. Data collected in this study also indicates that higher intensities may prove too large a stimulus for the cell and result in irreversible cell damage and death. Further studies are required to identify specifically how a cell is stimulated by ultrasound to produce a response.
When considering the apparatus and logistics of treating biological cells with ultrasound, an increase in temperature can also have an effect on the ultrasonic output of the transducer [46]. Materials used in the construction of ultrasonic transducers are thermally sensitive, and temperatures outside the materials working parameters affect the intensity of ultrasound produced. Standing waves are a concern when the ultrasound beam meets a surface which is perpendicular to its direction of travel [47]. In the setup described, the effect of standing waves cannot be excluded as the transducer is at right angles to the culture surface of the six-well plate. To reduce standing waves, the direction of the ultrasound beam can be angled to prevent such reflections occurring, or the transducer can be kept in motion during ultrasound treatment. The latter solution is also useful to prevent the build-up of heat; however, the movement of either the transducer or the culture plate may result in a reduction of cell viability. These factors make it important to characterize the ultrasonic output using the same conditions and equipment as when cells are treated with ultrasound; however, this can be extremely difficult and in some cases nearly impossible when working with in vitro cell culture.
This study showed that low-frequency ultrasound has a beam profile with significant lateral spread reaching and affecting cell cultures in adjacent wells of a multiwell culture plate. Cells from culture wells directly exposed to ultrasound demonstrated both a change in temperature and a biological affect. This is in contrast to findings from culture wells not directly treated with ultrasound where a biological effect was reported without a temperature rise. This adds to the evidence of a mechanical effect of ultrasound on biological cells. This study demonstrates the importance of characterizing the ultrasonic output from equipment and questions the suitability of multiwell culture plates for low-frequency ultrasound application.
Cracknell AP. The propagation of ultrasound. In: Mott N, Noakes GR, editors. Ultrasonics. London: Wykeham Publication; 1980. p. 11–37.
Cracknell AP. The attenuation of ultrasound. In: Mott N, Noakes GR, editors. Ultrasonics. London: Wykeham Publication; 1980. p. 38–56.
Hensel K, Mienkina M, Schmitz G. Analysis of ultrasound fields in cell culture wells for in vitro ultrasound therapy experiments. Ultrasound Med Biol. 2011;37:2105–15.
Angle SR, Sena K, Sumner DR, Virdi AS. Osteogenic differentiation of rat bone marrow stromal cells by various intensities of low-intensity pulsed ultrasound. Ultrason. 2011;51:281–8.
Doan N, Reher P, Meghji S, Harris M. In vitro effects of therapeutic ultrasound on cell proliferation, protein synthesis, and cytokine production by human fibroblasts, osteoblasts, and monocytes. J Oral Maxillofac Surg. 1999;57:409–19.
Iwabuchi S, Ito M, Hata J, Chikanishi T, Azuma Y, Haro H. In vitro evaluation of low-intensity pulsed ultrasound in herniated disc resorption. Biomaterials. 2005;26:7104–14.
Maddi A, Hai H, Ong S, Sharp L, Harris M, Meghji S. Long wave ultrasound may enhance bone regeneration by altering OPG/RANKL ratio in human osteoblast-like cells. Bone. 2006;39:283–8.
Man J, Shelton RM, Cooper PR, Landini G, Scheven BA. Low intensity ultrasound stimulates osteoblast migration at different frequencies. J Bone Miner Metab. 2012;30:602–7.
Man J, Shelton RM, Cooper PR, Scheven BA. Low-intensity low-frequency ultrasound promotes proliferation and differentiation of odontoblast-like cells. J Endod. 2012;38:608–13.
Naruse K, Mikuni-Takagaki Y, Azuma Y, Ito M, Oota T, Kameyama K, et al. Anabolic response of mouse bone-marrow-derived stromal cell clone ST2 cells to low-intensity pulsed ultrasound. Biochem Biophys Res Commun. 2000;268:216–20.
Reher P, Elbeshir EN, Harvey W, Meghji S, Harris M. The stimulation of bone formation in vitro by therapeutic ultrasound. Ultrasound Med Biol. 1997;23:1251–8.
Saito M, Fujii K, Tanaka T, Soshi S. Effect of low- and high-intensity pulsed ultrasound on collagen post-translational modifications in MC3T3-E1 osteoblasts. Calcif Tissue Int. 2004;75:384–95.
Samuels JA, Weingarten MS, Margolis DJ, Zubkov L, Sunny Y, Bawiec CR, et al. Low-frequency (<100 kHz), low-intensity (<100 mW/cm(2)) ultrasound to treat venous ulcers: a human study and in vitro experiments. J Acoust Soc Am. 2013;134:1541–7.
Sant'Anna E, Leven RM, Virdi AS, Sumner DR. Effect of combined ultrasound and BMP-2 stimulation on rat bone marrow stromal cell gene expression. J Orthop Res. 2005;23:646–52.
Sena K, Leven RM, Mazhar K, Sumner DR, Virdi AS. Early gene response to low-intensity pulsed ultrasound in rat osteoblastic cells. Ultrasound Med Biol. 2005;31:703–8.
Takayama T, Suzuki N, Ikeda K, Shimada T, Suzuki A, Maeno M, et al. Low-intensity pulsed ultrasound stimulates osteogenic differentiation in ROS 17/2.8 cells. Life Sci. 2007;80:965–71.
Wei FY, Leung KS, Li G, Qin J, Chow SK, Huang S, et al. Low intensity pulsed ultrasound enhanced mesenchymal stem cell recruitment through stromal derived factor-1 signaling in fracture healing. PLoS One. 2014;9:e106722.
Bashardoust Tajali S, Houghton P, MacDermid JC, Grewal R. Effects of low-intensity pulsed ultrasound therapy on fracture healing: a systematic review and meta-analysis. Am J Phys Med Rehabil. 2012;91:349–67.
Hannemann PF, Mommers EH, Schots JP, Brink PR, Poeze M. The effects of low-intensity pulsed ultrasound and pulsed electromagnetic fields bone growth stimulation in acute fractures: a systematic review and meta-analysis of randomized controlled trials. Arch Orthop Trauma Surg. 2014;134:1093–106.
Tanaka E, Kuroda S, Horiuchi A, Tabata A, El-Bialy T. Low-intensity pulsed ultrasound in dentofacial tissue engineering. Ann Biomed Eng. 2015. doi:10.1007/s10439-015-1274-y.
Reher P, Doan N, Bradnock B, Meghji S, Harris M. Therapeutic ultrasound for osteoradionecrosis: an in vitro comparison between 1 MHz and 45 kHz machines. Eur J Cancer. 1998;34:1962–8.
Reher P, Harris M, Whiteman M, Hai H, Meghji S. Ultrasound stimulates nitric oxide and prostaglandin E-2 production by human osteoblasts. Bone. 2002;31:236–41.
Scheven BA, Man J, Millard JL, Cooper PR, Lea SC, Walmsley AD, et al. VEGF and odontoblast-like cells: stimulation by low frequency ultrasound. Arch Oral Biol. 2009;54:185–91.
Scheven BA, Shelton RM, Cooper PR, Walmsley AD, Smith AJ. Therapeutic ultrasound for dental tissue repair. Med Hypotheses. 2009;73:591–3.
Ghorayeb SR, Bertoncini CA, Hinders MK. Ultrasonography in dentistry. IEEE Trans Ultrason Ferroelec Freq Contr. 2008;55:1256–66.
Ghorayeb SR, Patel U, Walmsley D, Scheven B. Biophysical characterization of low-frequency ultrasound interaction with dental pulp stem cells. J Therapeutic Ultrasound. 2013. doi:10.1186/2050-5736-1-12.
Fung CH, Cheung WH, Pounder NM, Harrison A, Leung KS. Osteocytes exposed to far field of therapeutic ultrasound promotes osteogenic cellular activities in pre-osteoblasts through soluble factors. Ultrasonics. 2014;54:1358–65.
Dyson M. Non-thermal cellular effects of ultrasound. Br J Cancer Suppl. 1982;5:165–71.
CAS PubMed Central PubMed Google Scholar
Furusawa Y, Hassan MA, Zhao QL, Ogawa R, Tabuchi Y, Kondo T. Effects of therapeutic ultrasound on the nucleus and genomic DNA. Ultrason Sonochem. 2014;21:2061–8.
Johns LD. Nonthermal effects of therapeutic ultrasound: the frequency resonance hypothesis. J Athl Train. 2002;37:293–9.
Webster DF, Pond JB, Dyson M, Harvey W. The role of cavitation in the in vitro stimulation of protein synthesis in human fibroblasts by ultrasound. Ultrasound Med Biol. 1978;4:343–51.
Wu J, Nyborg WL. Ultrasound, cavitation bubbles and their interaction with cells. Adv Drug Deliv Rev. 2008;60:1103–16.
Scheven BA, Millard JL, Cooper PR, Lea SC, Walmsley AD, Smith AJ. Short-term in vitro effects of low frequency ultrasound on odontoblast-like cells. Ultrason Med Biol. 2007;33:1475–82.
Hanks CT, Fang D, Sun Z, Edwards CA, Butler WT. Dentin-Specific Proteins in Mdpc-23 Cell Line. Eur J Oral Sci. 1998;106:260–6.
Al-Daghreer S, Doschak M, Sloan AJ, Major PW, Heo G, Scurtescu C, et al. Long term effect of low intensity pulsed ultrasound on a human tooth slice organ culture. Arch Oral Biol. 2012;57:760–8.
Hu B, Zhang Y, Zhou J, Li J, Deng F, Wang Z, et al. Low-intensity pulsed ultrasound stimulation facilitates osteogenic differentiation of human periodontal ligament cells. PLoS One. 2014. doi:10.1371/journal.pone.0095168.
Nolte PA, Klein-Nulend J, Albers GHR, Marti RK, Semeins CM, Goei SW, et al. Low-intensity ultrasound stimulates endochondral ossification in vitro. J Orthop Res. 2001;19:301–7.
ter Haar G, Shaw A, Pye S, Ward B, Bottomley F, Nolan R, et al. Guidance on reporting ultrasound exposure conditions for bio-effects studies. Ultrasound Med Biol. 2011;37:177–83.
Blay J, Price RB. Cellular inhibition produced by dental curing lights is a heating artefact. J Biomed Mater Res B Appl Biomater. 2010;93:367–74.
Leskinen JJ, Olkku A, Mahonen A, Hynynen K. Nonuniform temperature rise in in vitro osteoblast ultrasound exposures with associated bioeffect. IEEE Trans Biomed Eng. 2014;61:920–7.
Claes L, Willie B. The enhancement of bone regeneration by ultrasound. Prog Biophys Mol Biol. 2007;93:384–98.
Ter Haar G. Therapeutic applications of ultrasound. Prog Biophys Mol Biol. 2007;93:111–29.
Wang SJ, Lewallen DG, Bolander ME, Chao EY, Ilstrup DM, Greenleaf JF. Low intensity ultrasound treatment increases strength in a rat femoral fracture model. J Orthop Res. 1994;12:40–7.
Khan Y, Laurencin CT. Fracture repair with ultrasound: clinical and cell-based evaluation. J Bone Joint Surg Am. 2008;90:138–44.
Heckman JD, Ryaby JP, McCabe J, Frey JJ, Kilcoyne RF. Acceleration of tibial fracture-healing by non-invasive, low-intensity pulsed ultrasound. J Bone Joint Surg Am. 1994;76:26–34.
Richard C, Lee HS, Guyomar D. Thermo-mechanical stress effect on 1–3 piezocomposite power transducer performance. Ultrason. 2004;42:417–24.
Nyborg WL. Physical principles of ultrasound. In: Fry FJ, editor. Ultrasound: its applications in medicine and biology. NY: Elsevier; 1978. p. 1–76.
School of Dentistry, College of Medical and Dental Sciences, University of Birmingham, St Chad's Queensway, Birmingham, B4 6NN, UK
Upen S Patel, A Damien Walmsley & Ben A Scheven
School of Engineering and Applied Sciences, Ultrasound Research Laboratory, Hofstra University, Hempstead, NY, USA
Sleiman R Ghorayeb, Yuki Yamashita & Folorunsho Atanda
Immunology and Inflammation—FIMR, North Shore Hospital, Manhasset, NY, USA
Sleiman R Ghorayeb
Upen S Patel
Yuki Yamashita
Folorunsho Atanda
A Damien Walmsley
Ben A Scheven
Correspondence to Upen S Patel.
USP carried out the laboratory-based investigations including cell culture, ultrasound application, data collection from cell culture, ultrasound output measurements and temperature measurements, analysis and interpretation of data, writing, compiling, and final submission of the manuscript. YY and FA carried out the Fourier-transform calculations mentored by SRG. SRG analyzed and interpreted the Fourier-transform data providing written content for the results and discussion chapters relating to the Fourier-transform data. ADW and BAS were involved in study conception, design and data interpretation, and provided their recommendations for compiling and writing the manuscript. All authors have read and approved the final manuscript.
Patel, U.S., Ghorayeb, S.R., Yamashita, Y. et al. Ultrasound field characterization and bioeffects in multiwell culture plates. J Ther Ultrasound 3, 8 (2015). https://doi.org/10.1186/s40349-015-0028-5
Long-wave
Murine | CommonCrawl |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.