| # PyTorch Robot Kinematics | |
| - Parallel and differentiable forward kinematics (FK) and Jacobian calculation | |
| - Load robot description from URDF, SDF, and MJCF formats | |
| # Usage | |
| Clone repository somewhere, then `pip3 install -e .` to install in editable mode. | |
| See `tests` for code samples; some are also shown here. | |
| ## Forward Kinematics (FK) | |
| ```python | |
| import math | |
| import pytorch_kinematics as pk | |
| # load robot description from URDF and specify end effector link | |
| chain = pk.build_serial_chain_from_urdf(open("kuka_iiwa.urdf").read(), "lbr_iiwa_link_7") | |
| # prints out the (nested) tree of links | |
| print(chain) | |
| # prints out list of joint names | |
| print(chain.get_joint_parameter_names()) | |
| # specify joint values (can do so in many forms) | |
| th = [0.0, -math.pi / 4.0, 0.0, math.pi / 2.0, 0.0, math.pi / 4.0, 0.0] | |
| # do forward kinematics and get transform objects; end_only=False gives a dictionary of transforms for all links | |
| ret = chain.forward_kinematics(th, end_only=False) | |
| # look up the transform for a specific link | |
| tg = ret['lbr_iiwa_link_7'] | |
| # get transform matrix (1,4,4), then convert to separate position and unit quaternion | |
| m = tg.get_matrix() | |
| pos = m[:, :3, 3] | |
| rot = pk.matrix_to_quaternion(m[:, :3, :3]) | |
| ``` | |
| We can parallelize FK by passing in 2D joint values, and also use CUDA if available | |
| ```python | |
| import torch | |
| import pytorch_kinematics as pk | |
| d = "cuda" if torch.cuda.is_available() else "cpu" | |
| dtype = torch.float64 | |
| chain = pk.build_serial_chain_from_urdf(open("kuka_iiwa.urdf").read(), "lbr_iiwa_link_7") | |
| chain = chain.to(dtype=dtype, device=d) | |
| N = 1000 | |
| th_batch = torch.rand(N, len(chain.get_joint_parameter_names()), dtype=dtype, device=d) | |
| # order of magnitudes faster when doing FK in parallel | |
| # elapsed 0.008678913116455078s for N=1000 when parallel | |
| # (N,4,4) transform matrix; only the one for the end effector is returned since end_only=True by default | |
| tg_batch = chain.forward_kinematics(th_batch) | |
| # elapsed 8.44686508178711s for N=1000 when serial | |
| for i in range(N): | |
| tg = chain.forward_kinematics(th_batch[i]) | |
| ``` | |
| We can compute gradients through the FK | |
| ```python | |
| import torch | |
| import math | |
| import pytorch_kinematics as pk | |
| chain = pk.build_serial_chain_from_urdf(open("kuka_iiwa.urdf").read(), "lbr_iiwa_link_7") | |
| # require gradient through the input joint values | |
| th = torch.tensor([0.0, -math.pi / 4.0, 0.0, math.pi / 2.0, 0.0, math.pi / 4.0, 0.0], requires_grad=True) | |
| tg = chain.forward_kinematics(th) | |
| m = tg.get_matrix() | |
| pos = m[:, :3, 3] | |
| pos.norm().backward() | |
| # now th.grad is populated | |
| ``` | |
| We can load SDF and MJCF descriptions too, and pass in joint values via a dictionary (unspecified joints get th=0) for non-serial chains | |
| ```python | |
| import math | |
| import torch | |
| import pytorch_kinematics as pk | |
| chain = pk.build_chain_from_sdf(open("simple_arm.sdf").read()) | |
| ret = chain.forward_kinematics({'arm_elbow_pan_joint': math.pi / 2.0, 'arm_wrist_lift_joint': -0.5}) | |
| # recall that we specify joint values and get link transforms | |
| tg = ret['arm_wrist_roll'] | |
| # can also do this in parallel | |
| N = 100 | |
| ret = chain.forward_kinematics({'arm_elbow_pan_joint': torch.rand(N, 1), 'arm_wrist_lift_joint': torch.rand(N, 1)}) | |
| # (N, 4, 4) transform object | |
| tg = ret['arm_wrist_roll'] | |
| # building the robot from a MJCF file | |
| chain = pk.build_chain_from_mjcf(open("ant.xml").read()) | |
| print(chain) | |
| print(chain.get_joint_parameter_names()) | |
| th = {'hip_1': 1.0, 'ankle_1': 1} | |
| ret = chain.forward_kinematics(th) | |
| chain = pk.build_chain_from_mjcf(open("humanoid.xml").read()) | |
| print(chain) | |
| print(chain.get_joint_parameter_names()) | |
| th = {'left_knee': 0.0, 'right_knee': 0.0} | |
| ret = chain.forward_kinematics(th) | |
| ``` | |
| ## Jacobian calculation | |
| The Jacobian (in the kinematics context) is a matrix describing how the end effector changes with respect to joint value changes | |
| (where 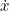 is the twist, or stacked velocity and angular velocity): | |
| 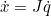 | |
| For `SerialChain` we provide a differentiable and parallelizable method for computing the Jacobian with respect to the base frame. | |
| ```python | |
| import math | |
| import torch | |
| import pytorch_kinematics as pk | |
| # can convert Chain to SerialChain by choosing end effector frame | |
| chain = pk.build_chain_from_sdf(open("simple_arm.sdf").read()) | |
| # print(chain) to see the available links for use as end effector | |
| # note that any link can be chosen; it doesn't have to be a link with no children | |
| chain = pk.SerialChain(chain, "arm_wrist_roll_frame") | |
| chain = pk.build_serial_chain_from_urdf(open("kuka_iiwa.urdf").read(), "lbr_iiwa_link_7") | |
| th = torch.tensor([0.0, -math.pi / 4.0, 0.0, math.pi / 2.0, 0.0, math.pi / 4.0, 0.0]) | |
| # (1,6,7) tensor, with 7 corresponding to the DOF of the robot | |
| J = chain.jacobian(th) | |
| # get Jacobian in parallel and use CUDA if available | |
| N = 1000 | |
| d = "cuda" if torch.cuda.is_available() else "cpu" | |
| dtype = torch.float64 | |
| chain = chain.to(dtype=dtype, device=d) | |
| # Jacobian calculation is differentiable | |
| th = torch.rand(N, 7, dtype=dtype, device=d, requires_grad=True) | |
| # (N,6,7) | |
| J = chain.jacobian(th) | |
| # can get Jacobian at a point offset from the end effector (location is specified in EE link frame) | |
| # by default location is at the origin of the EE frame | |
| loc = torch.rand(N, 3, dtype=dtype, device=d) | |
| J = chain.jacobian(th, locations=loc) | |
| ``` | |
| The Jacobian can be used to do inverse kinematics. See [IK survey](https://www.math.ucsd.edu/~sbuss/ResearchWeb/ikmethods/iksurvey.pdf) | |
| for a survey of ways to do so. Note that IK may be better performed through other means (but doing it through the Jacobian can give an end-to-end differentiable method). | |
| # Credits | |
| - `pytorch_kinematics/transforms` is extracted from [pytorch3d](https://github.com/facebookresearch/pytorch3d) with minor extensions. | |
| This was done instead of including `pytorch3d` as a dependency because it is hard to install and most of its code is unrelated. | |
| An important difference is that we use left hand multiplied transforms as is convention in robotics (T * pt) instead of their | |
| right hand multiplied transforms. | |
| - `pytorch_kinematics/urdf_parser_py`, and `pytorch_kinematics/mjcf_parser` is extracted from [kinpy](https://github.com/neka-nat/kinpy), as well as the FK logic. | |
| This repository ports the logic to pytorch, parallelizes it, and provides some extensions. | |