text
stringlengths 0
3.34M
|
|---|
module CIL.System.Reflection
import public CIL.FFI
import public CIL.FFI.Array
import CIL.Elab.Enums
%language ElabReflection
%default total
%access public export
AppDomainTy : CILTy
AppDomainTy = corlibTy "System.AppDomain"
AppDomain : Type
AppDomain = CIL AppDomainTy
AssemblyTy : CILTy
AssemblyTy = corlibTy "System.Reflection.Assembly"
Assembly : Type
Assembly = CIL AssemblyTy
MethodInfoTy : CILTy
MethodInfoTy = corlibTy "System.Reflection.MethodInfo"
MethodInfo : Type
MethodInfo = CIL MethodInfoTy
MethodInfoArray : Type
MethodInfoArray = TypedArrayOf MethodInfoTy
ParameterInfoTy : CILTy
ParameterInfoTy = corlibTy "System.Reflection.ParameterInfo"
ParameterInfo : Type
ParameterInfo = CIL ParameterInfoTy
ParameterInfoArray : Type
ParameterInfoArray = TypedArrayOf ParameterInfoTy
TypeArray : Type
TypeArray = TypedArrayOf RuntimeTypeTy
implementation IsA Object MethodInfo where {}
implementation IsA Object Assembly where {}
BindingFlagsTy : CILTy
BindingFlagsTy = corlibTyVal "System.Reflection.BindingFlags"
namespace BindingFlags
%runElab
cilEnum BindingFlags BindingFlagsTy Bits32
[ cilField Static 0x08
, cilField Public 0x10
]
namespace Assembly
GetExecutingAssembly : CIL_IO Assembly
GetExecutingAssembly = invokeStatic AssemblyTy "GetExecutingAssembly" (CIL_IO Assembly)
GetType : Assembly -> String -> Bool -> CIL_IO RuntimeType
GetType = invokeInstance "GetType" (Assembly -> String -> Bool -> CIL_IO RuntimeType)
GetExportedTypes : Assembly -> CIL_IO TypeArray
GetExportedTypes = invokeInstance "GetExportedTypes" (Assembly -> CIL_IO TypeArray)
Load : String -> CIL_IO Assembly
Load = invokeStatic AssemblyTy "Load" (String -> CIL_IO Assembly)
ReflectionOnlyLoadFrom : String -> CIL_IO Assembly
ReflectionOnlyLoadFrom = invokeStatic AssemblyTy "ReflectionOnlyLoadFrom" (String -> CIL_IO Assembly)
namespace RuntimeType
get_Name : RuntimeType -> CIL_IO String
get_Name = invokeInstance "get_Name" (RuntimeType -> CIL_IO String)
GetMethod : RuntimeType -> String -> CIL_IO (Maybe MethodInfo)
GetMethod = invokeInstance "GetMethod" (RuntimeType -> String -> CIL_IO (Maybe MethodInfo))
GetMethods : RuntimeType -> BindingFlags -> CIL_IO MethodInfoArray
GetMethods = invokeInstance "GetMethods" (RuntimeType -> BindingFlags -> CIL_IO MethodInfoArray)
namespace MethodInfo
get_Name : MethodInfo -> CIL_IO String
get_Name = invokeInstance "get_Name" (MethodInfo -> CIL_IO String)
GetParameters : MethodInfo -> CIL_IO ParameterInfoArray
GetParameters = invokeInstance "GetParameters" (MethodInfo -> CIL_IO ParameterInfoArray)
get_ReturnType : MethodInfo -> CIL_IO RuntimeType
get_ReturnType = invokeInstance "get_ReturnType" (MethodInfo -> CIL_IO RuntimeType)
Invoke : MethodInfo -> Maybe Object -> Maybe ObjectArray -> CIL_IO Object
Invoke = invokeInstance "Invoke" (MethodInfo -> Maybe Object -> Maybe ObjectArray -> CIL_IO Object)
namespace ParameterInfo
get_Name : ParameterInfo -> CIL_IO String
get_Name = invokeInstance "get_Name" (ParameterInfo -> CIL_IO String)
get_ParameterType : ParameterInfo -> CIL_IO RuntimeType
get_ParameterType = invokeInstance "get_ParameterType" (ParameterInfo -> CIL_IO RuntimeType)
namespace AppDomain
CurrentDomain : CIL_IO AppDomain
CurrentDomain = invokeStatic AppDomainTy "get_CurrentDomain" (CIL_IO AppDomain)
GetAssemblies : AppDomain -> CIL_IO (TypedArrayOf AssemblyTy)
GetAssemblies = invokeInstance "GetAssemblies" (AppDomain -> CIL_IO (TypedArrayOf AssemblyTy))
|
{-# OPTIONS --cubical --no-import-sorts --safe #-}
module Cubical.HITs.Ints.DiffInt where
open import Cubical.HITs.Ints.DiffInt.Base public
open import Cubical.HITs.Ints.DiffInt.Properties public
|
Formal statement is: lemma retract_of_simply_connected: "\<lbrakk>simply_connected T; S retract_of T\<rbrakk> \<Longrightarrow> simply_connected S" Informal statement is: If $S$ is a retract of a simply connected space $T$, then $S$ is simply connected.
|
Formal statement is: lemma contour_integrable_diff: "\<lbrakk>f1 contour_integrable_on g; f2 contour_integrable_on g\<rbrakk> \<Longrightarrow> (\<lambda>x. f1 x - f2 x) contour_integrable_on g" Informal statement is: If $f_1$ and $f_2$ are contour integrable on $g$, then $f_1 - f_2$ is contour integrable on $g$.
|
(*Require Export CatSem.PCF_order_comp.RPCF_syntax.*)
Require Export CatSem.PCF.PCF_RMonad.
Require Export CatSem.PCF_order_comp.RPCF_rep.
Set Implicit Arguments.
Unset Strict Implicit.
Unset Transparent Obligations.
Unset Automatic Introduction.
Program Instance PCFE_rep_struct :
PCFPO_rep_struct PCFEM (fun t => t) := {
app r s := PCFApp r s;
abs r s := PCFAbs r s;
rec t := PCFRec t ;
tttt := PCFconsts ttt ;
ffff := PCFconsts fff;
Succ := PCFconsts succ;
Pred := PCFconsts preds;
CondN := PCFconsts condN;
CondB := PCFconsts condB;
Zero := PCFconsts zero ;
nats m := PCFconsts (Nats m);
bottom t := PCFbottom t
}.
Next Obligation.
Proof.
unfold Rsubst_star_map.
simpl.
apply clos_refl_trans_1n_contains.
apply relorig.
apply app_abs.
Qed.
Next Obligation.
Proof.
apply clos_refl_trans_1n_contains.
apply relorig.
constructor.
Qed.
Next Obligation.
Proof.
apply clos_refl_trans_1n_contains.
apply relorig.
constructor.
Qed.
Next Obligation.
Proof.
apply clos_refl_trans_1n_contains.
apply relorig.
constructor.
Qed.
Next Obligation.
Proof.
apply clos_refl_trans_1n_contains.
apply relorig.
constructor.
Qed.
Next Obligation.
Proof.
apply clos_refl_trans_1n_contains.
apply relorig.
constructor.
Qed.
Next Obligation.
Proof.
apply clos_refl_trans_1n_contains.
apply relorig.
constructor.
Qed.
Next Obligation.
Proof.
apply clos_refl_trans_1n_contains.
apply relorig.
constructor.
Qed.
Next Obligation.
Proof.
apply clos_refl_trans_1n_contains.
apply relorig.
constructor.
Qed.
Next Obligation.
Proof.
apply clos_refl_trans_1n_contains.
apply relorig.
constructor.
Qed.
Next Obligation.
Proof.
apply clos_refl_trans_1n_contains.
apply relorig.
constructor.
Qed.
Definition PCFE_rep : PCFPO_rep := Build_PCFPO_rep PCFE_rep_struct.
|
------------------------------------------------------------------------------
-- Common definitions
------------------------------------------------------------------------------
{-# OPTIONS --exact-split #-}
{-# OPTIONS --no-sized-types #-}
{-# OPTIONS --no-universe-polymorphism #-}
{-# OPTIONS --without-K #-}
module Common.DefinitionsATP where
open import Common.FOL.FOL using ( ¬_ ; D )
open import Common.FOL.Relation.Binary.PropositionalEquality using ( _≡_ )
infix 4 _≢_
------------------------------------------------------------------------------
-- Inequality.
_≢_ : D → D → Set
x ≢ y = ¬ x ≡ y
{-# ATP definition _≢_ #-}
|
#include <stdio.h>
#include <gsl/gsl_errno.h>
#include <gsl/gsl_matrix.h>
#include <gsl/gsl_odeiv2.h>
int
func (double t, const double y[], double f[],
void *params)
{
double mu = *(double *)params;
f[0] = y[1];
f[1] = -y[0] - mu*y[1]*(y[0]*y[0] - 1);
return GSL_SUCCESS;
}
int
jac (double t, const double y[], double *dfdy,
double dfdt[], void *params)
{
double mu = *(double *)params;
gsl_matrix_view dfdy_mat
= gsl_matrix_view_array (dfdy, 2, 2);
gsl_matrix * m = &dfdy_mat.matrix;
gsl_matrix_set (m, 0, 0, 0.0);
gsl_matrix_set (m, 0, 1, 1.0);
gsl_matrix_set (m, 1, 0, -2.0*mu*y[0]*y[1] - 1.0);
gsl_matrix_set (m, 1, 1, -mu*(y[0]*y[0] - 1.0));
dfdt[0] = 0.0;
dfdt[1] = 0.0;
return GSL_SUCCESS;
}
int
main (void)
{
double mu = 10;
gsl_odeiv2_system sys = {func, jac, 2, &mu};
gsl_odeiv2_driver * d =
gsl_odeiv2_driver_alloc_y_new (&sys, gsl_odeiv2_step_rk8pd,
1e-6, 1e-6, 0.0);
int i;
double t = 0.0, t1 = 100.0;
double y[2] = { 1.0, 0.0 };
for (i = 1; i <= 100; i++)
{
double ti = i * t1 / 100.0;
int status = gsl_odeiv2_driver_apply (d, &t, ti, y);
if (status != GSL_SUCCESS)
{
printf ("error, return value=%d\n", status);
break;
}
printf ("%.5e %.5e %.5e\n", t, y[0], y[1]);
}
gsl_odeiv2_driver_free (d);
return 0;
}
|
```python
import sympy as sy
sy.init_printing()
```
```python
M, m, g, l, u, w, z, theta, thetadot = sy.symbols('M,m,g,l,u,w,z,theta, thetadot')
```
```python
Mm = sy.Matrix([[M+m, -m*l*sy.cos(theta)], [-m*l*sy.cos(theta), m*l**2]])
Mm
```
```python
G = sy.Matrix([[m*l*sy.sin(theta)*thetadot**2],[m*g*l*sy.sin(theta)]])
G
```
```python
F = sy.Matrix([[u+w],[l*w]])
F
```
```python
acc = Mm.inv()*(F-G)
sy.simplify(acc.subs({w:0}))
```
```python
sy.simplify(sy.sin(theta+sy.pi))
```
```python
sy.simplify(sy.cos(theta+sy.pi))
```
```python
sy.simplify(sy.cos(-theta))
```
```python
theta2 = -theta+sy.pi
```
```python
sy.simplify(sy.cos(theta2))
```
## With Lagrangian mechanics
```python
from sympy.physics.mechanics import *
q1,q2 = dynamicsymbols('q1,q2') # q1=z, q2=theta
q1d,q2d = dynamicsymbols('q1,q2',1)
zpdot = q1d -l*sy.cos(q2)*q2d
ypdot = l*sy.sin(q2)*q2d
T = 0.5*M*q1d**2 + 0.5*m*(zpdot**2 + ypdot**2)
sy.simplify(sy.expand(T))
```
```python
yp = -l*sy.cos(q2)
U = m*g*yp
L = T-U
L
```
```python
LM=LagrangesMethod(L, [q1,q2])
```
```python
sy.simplify(LM.form_lagranges_equations())
```
```python
sy.simplify(LM.mass_matrix)
```
```python
sy.simplify(LM.forcing)
```
```python
sy.simplify(LM.mass_matrix.inv()*LM.forcing)
```
```python
```
|
#!/usr/bin/env python3
# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
"""
Runs CIFAR10 training on subsets of data.
"""
import argparse
import logging
import os
import shutil
import sys
from datetime import datetime, timedelta
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
import torch.utils.data
import torch.utils.data.distributed
import torch.utils.tensorboard as tensorboard
import torchvision.transforms as transforms
from privacy_lint.dataset import MaskDataset
from torchvision.datasets import CIFAR10
from tqdm import tqdm
def convnet(num_classes):
return nn.Sequential(
nn.Conv2d(3, 32, kernel_size=3, stride=1, padding=1),
nn.ReLU(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(32, 64, kernel_size=3, stride=1, padding=1),
nn.ReLU(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(64, 64, kernel_size=3, stride=1, padding=1),
nn.ReLU(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(64, 128, kernel_size=3, stride=1, padding=1),
nn.ReLU(),
nn.AdaptiveAvgPool2d((1, 1)),
nn.Flatten(start_dim=1, end_dim=-1),
nn.Linear(128, num_classes, bias=True),
)
def save_checkpoint(state, is_best, directory):
torch.save(state, os.path.join(directory, "checkpoint.pth"))
if is_best:
shutil.copyfile(
os.path.join(directory, "checkpoint.pth"),
os.path.join(directory, "model_best.pth"),
)
def accuracy(preds, labels):
return (preds == labels).mean()
def train(args, model, train_loader, optimizer, epoch, device):
start_time = datetime.now()
model.train()
criterion = nn.CrossEntropyLoss()
losses = []
top1_acc = []
for i, (images, target) in enumerate(tqdm(train_loader)):
images = images.to(device)
target = target.to(device)
# compute output
output = model(images)
loss = criterion(output, target)
preds = np.argmax(output.detach().cpu().numpy(), axis=1)
labels = target.detach().cpu().numpy()
# measure accuracy and record loss
acc1 = accuracy(preds, labels)
losses.append(loss.item())
top1_acc.append(acc1)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if i % args.print_freq == 0:
print(
f"\tTrain Epoch: {epoch} \t"
f"Loss: {np.mean(losses):.6f} "
f"Acc@1: {np.mean(top1_acc):.6f} "
)
train_duration = datetime.now() - start_time
return train_duration
@torch.no_grad()
def test(args, model, test_loader, device):
model.eval()
criterion = nn.CrossEntropyLoss()
losses = []
top1_acc = []
for images, target in tqdm(test_loader):
images = images.to(device)
target = target.to(device)
output = model(images)
loss = criterion(output, target)
preds = np.argmax(output.detach().cpu().numpy(), axis=1)
labels = target.detach().cpu().numpy()
acc1 = accuracy(preds, labels)
losses.append(loss.item())
top1_acc.append(acc1)
top1_avg = np.mean(top1_acc)
print(f"\tTest set:" f"Loss: {np.mean(losses):.6f} " f"Acc@1: {top1_avg :.6f} ")
return np.mean(top1_acc)
# flake8: noqa: C901
def main():
args = parse_args()
device = args.device
augmentations = [
transforms.RandomCrop(32, padding=4),
transforms.RandomHorizontalFlip(),
]
normalize = [
transforms.ToTensor(),
transforms.Normalize((0.4914, 0.4822, 0.4465), (0.2023, 0.1994, 0.2010)),
]
train_transform = transforms.Compose(augmentations + normalize)
test_transform = transforms.Compose(normalize)
masks = torch.load(args.mask_path)
mask = masks[args.mask]
train_dataset = MaskDataset(
CIFAR10(
root=args.data_root, train=True, download=True, transform=train_transform
),
mask=mask,
)
train_loader = torch.utils.data.DataLoader(
train_dataset,
batch_size=args.batch_size,
num_workers=args.workers,
pin_memory=True,
)
test_dataset = CIFAR10(
root=args.data_root, train=False, download=True, transform=test_transform
)
test_loader = torch.utils.data.DataLoader(
test_dataset,
batch_size=args.batch_size,
shuffle=False,
num_workers=args.workers,
)
best_acc1 = 0
model = convnet(num_classes=10)
model = model.to(device)
if args.optim == "SGD":
optimizer = optim.SGD(
model.parameters(),
lr=args.lr,
momentum=args.momentum,
weight_decay=args.weight_decay,
)
elif args.optim == "RMSprop":
optimizer = optim.RMSprop(model.parameters(), lr=args.lr)
elif args.optim == "Adam":
optimizer = optim.Adam(model.parameters(), lr=args.lr)
else:
raise NotImplementedError("Optimizer not recognized. Please check spelling")
# Store some logs
accuracy_per_epoch = []
time_per_epoch = []
for epoch in range(args.epochs):
if args.lr_schedule == "cos":
lr = args.lr * 0.5 * (1 + np.cos(np.pi * epoch / (args.epochs + 1)))
for param_group in optimizer.param_groups:
param_group["lr"] = lr
train_duration = train(args, model, train_loader, optimizer, epoch, device)
top1_acc = test(args, model, test_loader, device)
# remember best acc@1 and save checkpoint
is_best = top1_acc > best_acc1
best_acc1 = max(top1_acc, best_acc1)
time_per_epoch.append(train_duration)
accuracy_per_epoch.append(float(top1_acc))
save_checkpoint(
{
"epoch": epoch + 1,
"arch": "Convnet",
"state_dict": model.state_dict(),
"best_acc1": best_acc1,
"optimizer": optimizer.state_dict(),
},
is_best,
directory=args.checkpoint_dir,
)
time_per_epoch_seconds = [t.total_seconds() for t in time_per_epoch]
avg_time_per_epoch = sum(time_per_epoch_seconds) / len(time_per_epoch_seconds)
metrics = {
"accuracy": best_acc1,
"accuracy_per_epoch": accuracy_per_epoch,
"avg_time_per_epoch_str": str(timedelta(seconds=int(avg_time_per_epoch))),
"time_per_epoch": time_per_epoch_seconds,
}
print(metrics)
def parse_args():
parser = argparse.ArgumentParser(description="PyTorch CIFAR10 Training")
parser.add_argument(
"-j",
"--workers",
default=2,
type=int,
metavar="N",
help="number of data loading workers (default: 2)",
)
parser.add_argument(
"--epochs",
default=90,
type=int,
metavar="N",
help="number of total epochs to run",
)
parser.add_argument(
"-b",
"--batch-size",
default=256,
type=int,
help="mini-batch size for test dataset, this is the total "
"batch size of all GPUs on the current node when "
"using Data Parallel or Distributed Data Parallel",
)
parser.add_argument(
"--lr",
"--learning-rate",
default=0.1,
type=float,
metavar="LR",
help="initial learning rate",
dest="lr",
)
parser.add_argument(
"--momentum", default=0.9, type=float, metavar="M", help="SGD momentum"
)
parser.add_argument(
"--wd",
"--weight-decay",
default=0,
type=float,
metavar="W",
help="SGD weight decay",
dest="weight_decay",
)
parser.add_argument(
"-p",
"--print-freq",
default=10,
type=int,
metavar="N",
help="print frequency (default: 10)",
)
parser.add_argument(
"--resume",
default="",
type=str,
metavar="PATH",
help="path to latest checkpoint (default: none)",
)
parser.add_argument(
"-e",
"--evaluate",
dest="evaluate",
action="store_true",
help="evaluate model on validation set",
)
parser.add_argument(
"--seed", default=None, type=int, help="seed for initializing training. "
)
parser.add_argument(
"--delta",
type=float,
default=1e-5,
metavar="D",
help="Target delta (default: 1e-5)",
)
parser.add_argument(
"--checkpoint-dir",
type=str,
default=".",
help="path to save check points",
)
parser.add_argument(
"--data-root",
type=str,
default="../cifar10",
help="Where CIFAR10 is/will be stored",
)
parser.add_argument(
"--log-dir",
type=str,
default="/tmp/stat/tensorboard",
help="Where Tensorboard log will be stored",
)
parser.add_argument(
"--optim",
type=str,
default="SGD",
help="Optimizer to use (Adam, RMSprop, SGD)",
)
parser.add_argument(
"--lr-schedule", type=str, choices=["constant", "cos"], default="cos"
)
parser.add_argument(
"--device",
type=str,
default=("cuda" if torch.cuda.is_available() else "cpu"),
help="Device on which to run the code.",
)
parser.add_argument(
"--mask_path", type=str, required=True, help="Path to masks file"
)
parser.add_argument(
"--mask", type=str, required=True, help="Name of the mask to use on data"
)
return parser.parse_args()
if __name__ == "__main__":
main()
|
State Before: α : Type u_2
β : Type ?u.1445144
ι : Type ?u.1445147
E : Type u_1
F : Type ?u.1445153
𝕜 : Type ?u.1445156
inst✝² : MeasurableSpace α
inst✝¹ : NormedAddCommGroup E
inst✝ : NormedAddCommGroup F
μ : Measure α
p : ℝ≥0∞
hp_pos : p ≠ 0
hp_ne_top : p ≠ ⊤
c : E
hc : c ≠ 0
s : Set α
hs : MeasurableSet s
hcs : Memℒp (↑(piecewise s hs (const α c) (const α 0))) p
⊢ ↑↑μ s < ⊤ State After: α : Type u_2
β : Type ?u.1445144
ι : Type ?u.1445147
E : Type u_1
F : Type ?u.1445153
𝕜 : Type ?u.1445156
inst✝² : MeasurableSpace α
inst✝¹ : NormedAddCommGroup E
inst✝ : NormedAddCommGroup F
μ : Measure α
p : ℝ≥0∞
hp_pos : p ≠ 0
hp_ne_top : p ≠ ⊤
c : E
hc : c ≠ 0
s : Set α
hs : MeasurableSet s
hcs : Memℒp (↑(piecewise s hs (const α c) (const α 0))) p
this : support ↑(const α c) = Set.univ
⊢ ↑↑μ s < ⊤ Tactic: have : Function.support (const α c) = Set.univ := Function.support_const hc State Before: α : Type u_2
β : Type ?u.1445144
ι : Type ?u.1445147
E : Type u_1
F : Type ?u.1445153
𝕜 : Type ?u.1445156
inst✝² : MeasurableSpace α
inst✝¹ : NormedAddCommGroup E
inst✝ : NormedAddCommGroup F
μ : Measure α
p : ℝ≥0∞
hp_pos : p ≠ 0
hp_ne_top : p ≠ ⊤
c : E
hc : c ≠ 0
s : Set α
hs : MeasurableSet s
hcs : Memℒp (↑(piecewise s hs (const α c) (const α 0))) p
this : support ↑(const α c) = Set.univ
⊢ ↑↑μ s < ⊤ State After: no goals Tactic: simpa only [memℒp_iff_finMeasSupp hp_pos hp_ne_top, finMeasSupp_iff_support,
support_indicator, Set.inter_univ, this] using hcs
|
State Before: α : Type u_1
β : Type ?u.104521
m : MeasurableSpace α
μ ν : Measure α
f : ℕ → α → ℝ≥0∞
hf : ∀ (n : ℕ), f n ∈ measurableLE μ ν
n : ℕ
⊢ (fun x => ⨆ (k : ℕ) (_ : k ≤ n), f k x) ∈ measurableLE μ ν State After: case zero
α : Type u_1
β : Type ?u.104521
m : MeasurableSpace α
μ ν : Measure α
f : ℕ → α → ℝ≥0∞
hf : ∀ (n : ℕ), f n ∈ measurableLE μ ν
⊢ (fun x => ⨆ (k : ℕ) (_ : k ≤ Nat.zero), f k x) ∈ measurableLE μ ν
case succ
α : Type u_1
β : Type ?u.104521
m✝ : MeasurableSpace α
μ ν : Measure α
f : ℕ → α → ℝ≥0∞
hf : ∀ (n : ℕ), f n ∈ measurableLE μ ν
m : ℕ
hm : (fun x => ⨆ (k : ℕ) (_ : k ≤ m), f k x) ∈ measurableLE μ ν
⊢ (fun x => ⨆ (k : ℕ) (_ : k ≤ Nat.succ m), f k x) ∈ measurableLE μ ν Tactic: induction' n with m hm State Before: case zero
α : Type u_1
β : Type ?u.104521
m : MeasurableSpace α
μ ν : Measure α
f : ℕ → α → ℝ≥0∞
hf : ∀ (n : ℕ), f n ∈ measurableLE μ ν
⊢ (fun x => ⨆ (k : ℕ) (_ : k ≤ Nat.zero), f k x) ∈ measurableLE μ ν State After: case zero.refine'_1
α : Type u_1
β : Type ?u.104521
m : MeasurableSpace α
μ ν : Measure α
f : ℕ → α → ℝ≥0∞
hf : ∀ (n : ℕ), f n ∈ measurableLE μ ν
⊢ Measurable fun x => ⨆ (k : ℕ) (_ : k ≤ Nat.zero), f k x
case zero.refine'_2
α : Type u_1
β : Type ?u.104521
m : MeasurableSpace α
μ ν : Measure α
f : ℕ → α → ℝ≥0∞
hf : ∀ (n : ℕ), f n ∈ measurableLE μ ν
⊢ ∀ (A : Set α), MeasurableSet A → (∫⁻ (x : α) in A, (fun x => ⨆ (k : ℕ) (_ : k ≤ Nat.zero), f k x) x ∂μ) ≤ ↑↑ν A Tactic: refine' ⟨_, _⟩ State Before: case zero.refine'_1
α : Type u_1
β : Type ?u.104521
m : MeasurableSpace α
μ ν : Measure α
f : ℕ → α → ℝ≥0∞
hf : ∀ (n : ℕ), f n ∈ measurableLE μ ν
⊢ Measurable fun x => ⨆ (k : ℕ) (_ : k ≤ Nat.zero), f k x State After: no goals Tactic: simp [(hf 0).1] State Before: case zero.refine'_2
α : Type u_1
β : Type ?u.104521
m : MeasurableSpace α
μ ν : Measure α
f : ℕ → α → ℝ≥0∞
hf : ∀ (n : ℕ), f n ∈ measurableLE μ ν
⊢ ∀ (A : Set α), MeasurableSet A → (∫⁻ (x : α) in A, (fun x => ⨆ (k : ℕ) (_ : k ≤ Nat.zero), f k x) x ∂μ) ≤ ↑↑ν A State After: case zero.refine'_2
α : Type u_1
β : Type ?u.104521
m : MeasurableSpace α
μ ν : Measure α
f : ℕ → α → ℝ≥0∞
hf : ∀ (n : ℕ), f n ∈ measurableLE μ ν
A : Set α
hA : MeasurableSet A
⊢ (∫⁻ (x : α) in A, (fun x => ⨆ (k : ℕ) (_ : k ≤ Nat.zero), f k x) x ∂μ) ≤ ↑↑ν A Tactic: intro A hA State Before: case zero.refine'_2
α : Type u_1
β : Type ?u.104521
m : MeasurableSpace α
μ ν : Measure α
f : ℕ → α → ℝ≥0∞
hf : ∀ (n : ℕ), f n ∈ measurableLE μ ν
A : Set α
hA : MeasurableSet A
⊢ (∫⁻ (x : α) in A, (fun x => ⨆ (k : ℕ) (_ : k ≤ Nat.zero), f k x) x ∂μ) ≤ ↑↑ν A State After: no goals Tactic: simp [(hf 0).2 A hA] State Before: case succ
α : Type u_1
β : Type ?u.104521
m✝ : MeasurableSpace α
μ ν : Measure α
f : ℕ → α → ℝ≥0∞
hf : ∀ (n : ℕ), f n ∈ measurableLE μ ν
m : ℕ
hm : (fun x => ⨆ (k : ℕ) (_ : k ≤ m), f k x) ∈ measurableLE μ ν
⊢ (fun x => ⨆ (k : ℕ) (_ : k ≤ Nat.succ m), f k x) ∈ measurableLE μ ν State After: case succ
α : Type u_1
β : Type ?u.104521
m✝ : MeasurableSpace α
μ ν : Measure α
f : ℕ → α → ℝ≥0∞
hf : ∀ (n : ℕ), f n ∈ measurableLE μ ν
m : ℕ
hm : (fun x => ⨆ (k : ℕ) (_ : k ≤ m), f k x) ∈ measurableLE μ ν
this : (fun a => ⨆ (k : ℕ) (_ : k ≤ m + 1), f k a) = fun a => f (Nat.succ m) a ⊔ ⨆ (k : ℕ) (_ : k ≤ m), f k a
⊢ (fun x => ⨆ (k : ℕ) (_ : k ≤ Nat.succ m), f k x) ∈ measurableLE μ ν Tactic: have :
(fun a : α => ⨆ (k : ℕ) (_ : k ≤ m + 1), f k a) = fun a =>
f m.succ a ⊔ ⨆ (k : ℕ) (_ : k ≤ m), f k a :=
funext fun _ => iSup_succ_eq_sup _ _ _ State Before: case succ
α : Type u_1
β : Type ?u.104521
m✝ : MeasurableSpace α
μ ν : Measure α
f : ℕ → α → ℝ≥0∞
hf : ∀ (n : ℕ), f n ∈ measurableLE μ ν
m : ℕ
hm : (fun x => ⨆ (k : ℕ) (_ : k ≤ m), f k x) ∈ measurableLE μ ν
this : (fun a => ⨆ (k : ℕ) (_ : k ≤ m + 1), f k a) = fun a => f (Nat.succ m) a ⊔ ⨆ (k : ℕ) (_ : k ≤ m), f k a
⊢ (fun x => ⨆ (k : ℕ) (_ : k ≤ Nat.succ m), f k x) ∈ measurableLE μ ν State After: case succ
α : Type u_1
β : Type ?u.104521
m✝ : MeasurableSpace α
μ ν : Measure α
f : ℕ → α → ℝ≥0∞
hf : ∀ (n : ℕ), f n ∈ measurableLE μ ν
m : ℕ
hm : (fun x => ⨆ (k : ℕ) (_ : k ≤ m), f k x) ∈ measurableLE μ ν
this : (fun a => ⨆ (k : ℕ) (_ : k ≤ m + 1), f k a) = fun a => f (Nat.succ m) a ⊔ ⨆ (k : ℕ) (_ : k ≤ m), f k a
A : Set α
hA : MeasurableSet A
⊢ (∫⁻ (x : α) in A, (fun x => ⨆ (k : ℕ) (_ : k ≤ Nat.succ m), f k x) x ∂μ) ≤ ↑↑ν A Tactic: refine' ⟨measurable_iSup fun n => Measurable.iSup_Prop _ (hf n).1, fun A hA => _⟩ State Before: case succ
α : Type u_1
β : Type ?u.104521
m✝ : MeasurableSpace α
μ ν : Measure α
f : ℕ → α → ℝ≥0∞
hf : ∀ (n : ℕ), f n ∈ measurableLE μ ν
m : ℕ
hm : (fun x => ⨆ (k : ℕ) (_ : k ≤ m), f k x) ∈ measurableLE μ ν
this : (fun a => ⨆ (k : ℕ) (_ : k ≤ m + 1), f k a) = fun a => f (Nat.succ m) a ⊔ ⨆ (k : ℕ) (_ : k ≤ m), f k a
A : Set α
hA : MeasurableSet A
⊢ (∫⁻ (x : α) in A, (fun x => ⨆ (k : ℕ) (_ : k ≤ Nat.succ m), f k x) x ∂μ) ≤ ↑↑ν A State After: case succ
α : Type u_1
β : Type ?u.104521
m✝ : MeasurableSpace α
μ ν : Measure α
f : ℕ → α → ℝ≥0∞
hf : ∀ (n : ℕ), f n ∈ measurableLE μ ν
m : ℕ
hm : (fun x => ⨆ (k : ℕ) (_ : k ≤ m), f k x) ∈ measurableLE μ ν
this : (fun a => ⨆ (k : ℕ) (_ : k ≤ m + 1), f k a) = fun a => f (Nat.succ m) a ⊔ ⨆ (k : ℕ) (_ : k ≤ m), f k a
A : Set α
hA : MeasurableSet A
⊢ (∫⁻ (a : α) in A, f (Nat.succ m) a ⊔ ⨆ (k : ℕ) (_ : k ≤ m), f k a ∂μ) ≤ ↑↑ν A Tactic: rw [this] State Before: case succ
α : Type u_1
β : Type ?u.104521
m✝ : MeasurableSpace α
μ ν : Measure α
f : ℕ → α → ℝ≥0∞
hf : ∀ (n : ℕ), f n ∈ measurableLE μ ν
m : ℕ
hm : (fun x => ⨆ (k : ℕ) (_ : k ≤ m), f k x) ∈ measurableLE μ ν
this : (fun a => ⨆ (k : ℕ) (_ : k ≤ m + 1), f k a) = fun a => f (Nat.succ m) a ⊔ ⨆ (k : ℕ) (_ : k ≤ m), f k a
A : Set α
hA : MeasurableSet A
⊢ (∫⁻ (a : α) in A, f (Nat.succ m) a ⊔ ⨆ (k : ℕ) (_ : k ≤ m), f k a ∂μ) ≤ ↑↑ν A State After: no goals Tactic: exact (sup_mem_measurableLE (hf m.succ) hm).2 A hA
|
[STATEMENT]
lemma (in typed_model) has_all_wt_instances_ofD':
assumes N_wf_trms: "wf\<^sub>t\<^sub>r\<^sub>m\<^sub>s N"
and M_wf_trms: "wf\<^sub>t\<^sub>r\<^sub>m\<^sub>s M"
and N_instance_M: "has_all_wt_instances_of \<Gamma> N M"
and t_in_N: "t \<in> N"
shows "\<exists>\<delta>. wt\<^sub>s\<^sub>u\<^sub>b\<^sub>s\<^sub>t \<delta> \<and> wf\<^sub>t\<^sub>r\<^sub>m\<^sub>s (subst_range \<delta>) \<and> t \<in> M \<cdot>\<^sub>s\<^sub>e\<^sub>t \<delta>"
[PROOF STATE]
proof (prove)
goal (1 subgoal):
1. \<exists>\<delta>. wt\<^sub>s\<^sub>u\<^sub>b\<^sub>s\<^sub>t \<delta> \<and> wf\<^sub>t\<^sub>r\<^sub>m\<^sub>s (subst_range \<delta>) \<and> t \<in> M \<cdot>\<^sub>s\<^sub>e\<^sub>t \<delta>
[PROOF STEP]
using assms is_wt_instance_of_condD'
[PROOF STATE]
proof (prove)
using this:
wf\<^sub>t\<^sub>r\<^sub>m\<^sub>s N
wf\<^sub>t\<^sub>r\<^sub>m\<^sub>s M
has_all_wt_instances_of \<Gamma> N M
t \<in> N
\<lbrakk>wf\<^sub>t\<^sub>r\<^sub>m ?t; wf\<^sub>t\<^sub>r\<^sub>m ?s; is_wt_instance_of_cond \<Gamma> ?t ?s\<rbrakk> \<Longrightarrow> \<exists>\<delta>. wt\<^sub>s\<^sub>u\<^sub>b\<^sub>s\<^sub>t \<delta> \<and> wf\<^sub>t\<^sub>r\<^sub>m\<^sub>s (subst_range \<delta>) \<and> ?t = ?s \<cdot> \<delta>
goal (1 subgoal):
1. \<exists>\<delta>. wt\<^sub>s\<^sub>u\<^sub>b\<^sub>s\<^sub>t \<delta> \<and> wf\<^sub>t\<^sub>r\<^sub>m\<^sub>s (subst_range \<delta>) \<and> t \<in> M \<cdot>\<^sub>s\<^sub>e\<^sub>t \<delta>
[PROOF STEP]
unfolding has_all_wt_instances_of_def
[PROOF STATE]
proof (prove)
using this:
wf\<^sub>t\<^sub>r\<^sub>m\<^sub>s N
wf\<^sub>t\<^sub>r\<^sub>m\<^sub>s M
\<forall>t\<in>N. \<exists>s\<in>M. is_wt_instance_of_cond \<Gamma> t s
t \<in> N
\<lbrakk>wf\<^sub>t\<^sub>r\<^sub>m ?t; wf\<^sub>t\<^sub>r\<^sub>m ?s; is_wt_instance_of_cond \<Gamma> ?t ?s\<rbrakk> \<Longrightarrow> \<exists>\<delta>. wt\<^sub>s\<^sub>u\<^sub>b\<^sub>s\<^sub>t \<delta> \<and> wf\<^sub>t\<^sub>r\<^sub>m\<^sub>s (subst_range \<delta>) \<and> ?t = ?s \<cdot> \<delta>
goal (1 subgoal):
1. \<exists>\<delta>. wt\<^sub>s\<^sub>u\<^sub>b\<^sub>s\<^sub>t \<delta> \<and> wf\<^sub>t\<^sub>r\<^sub>m\<^sub>s (subst_range \<delta>) \<and> t \<in> M \<cdot>\<^sub>s\<^sub>e\<^sub>t \<delta>
[PROOF STEP]
by fast
|
function [ H] = Hmatrix( Ix, Iy, SizeBig, alfa )
%At each pyramid level, this function generates the Hessian matrix for the
%source image
H = zeros([2 2 size(Ix)-SizeBig]);
for i = 1+SizeBig : size(Ix,1)-SizeBig
for j = 1+SizeBig : size(Ix,2)-SizeBig
ix = Ix( i-SizeBig:i+SizeBig, j-SizeBig:j+SizeBig );
iy = Iy( i-SizeBig:i+SizeBig, j-SizeBig:j+SizeBig );
H(1,1,i,j) = alfa+sum(sum( ix.^2 ));
H(2,2,i,j) = alfa+sum(sum( iy.^2 ));
H(1,2,i,j) = sum(sum( ix .* iy ));
H(2,1,i,j) = H(1,2,i,j);
end
end
end
|
INTEGER FUNCTION RANMKT (STDDX,LAVSMT, REGDX,LAVRMT,IMPDX,LAVIMT)
C RANMKT chooses a marker type at random from the three lists of
C available marker types.
INTEGER STDDX,REGDX,IMPDX, WHLIST, RNDINT
INTEGER LAVSMT(*), LAVRMT(*), LAVIMT(*)
100 CONTINUE
WHLIST = RNDINT (1,3)
IF (WHLIST .EQ. 1) THEN
IF (STDDX .LE. 0) GOTO 100
RANMKT = LAVSMT(RNDINT(1,STDDX))
C don't allow marker type 1 (dot)
IF (RANMKT .EQ. 1) GOTO 100
ELSEIF (WHLIST .EQ. 2) THEN
IF (REGDX .LE. 0) GOTO 100
RANMKT = LAVRMT(RNDINT(1,REGDX))
ELSE
IF (IMPDX .LE. 0) GOTO 100
RANMKT = LAVIMT(RNDINT(1,IMPDX))
ENDIF
END
|
@testset "scaledkernel" begin
rng = MersenneTwister(123456)
x = randn(rng)
y = randn(rng)
s = rand(rng) + 1e-3
k = SqExponentialKernel()
ks = ScaledKernel(k, s)
@test ks(x, y) == s * k(x, y)
@test ks(x, y) == (s * k)(x, y)
# Standardised tests.
TestUtils.test_interface(k, Float64)
test_ADs(x -> exp(x[1]) * SqExponentialKernel(), rand(1))
test_params(s * k, (k, [s]))
end
|
[STATEMENT]
lemma brnL_gt_0[simp]: "\<lbrakk>properL cl; 0 < n\<rbrakk> \<Longrightarrow> 0 < brnL cl n"
[PROOF STATE]
proof (prove)
goal (1 subgoal):
1. \<lbrakk>properL cl; 0 < n\<rbrakk> \<Longrightarrow> 0 < brnL cl n
[PROOF STEP]
by (metis properL_def brnL_mono brnL_mono2 le_0_eq length_greater_0_conv nat_le_linear neq0_conv)
|
#include <mtpio/trace_api/cmd_registration.hpp>
#include <iostream>
#include <boost/program_options.hpp>
using namespace mtpio::trace_api;
namespace bpo = boost::program_options;
command_registration* command_registration::_list = nullptr;
namespace {
auto create_command_map() {
auto result = std::map<std::string, command_registration*>();
command_registration* cur = command_registration::_list;
while (cur != nullptr) {
if (result.count(cur->name) > 0) {
std::cerr << "Illformed Program, duplicate subcommand: " << cur->name << "\n";
exit(1);
}
result[cur->name] = cur;
cur = cur->_next;
}
return result;
}
}
int main(int argc, char** argv) {
auto command_map = create_command_map();
bpo::options_description vis_desc("Options");
auto vis_opts = vis_desc.add_options();
vis_opts("help,h", "show usage help message");
bpo::options_description hidden_desc;
auto hidden_opts = hidden_desc.add_options();
hidden_opts("subargs", bpo::value<std::vector<std::string>>(), "args");
bpo::positional_options_description pos_desc;
pos_desc.add("subargs", -1);
bpo::options_description cmdline_options;
cmdline_options.add(vis_desc).add(hidden_desc);
bpo::variables_map vm;
auto parsed_args = bpo::command_line_parser(argc, argv).options(cmdline_options).positional(pos_desc).allow_unregistered().run();
bpo::store(parsed_args, vm);
std::vector<std::string> args = bpo::collect_unrecognized(parsed_args.options, bpo::include_positional);
auto show_help = [&](std::ostream& os) {
os <<
"Usage: trace_api_util <options> command ...\n"
"\n"
"Commands:\n";
for (const auto& e: command_map) {
os << " " << e.second->name << " " << e.second->slug << "\n";
}
os << "\n" << vis_desc << "\n";
};
if (args.size() < 1) {
if (vm.count("help") > 0) {
show_help(std::cout);
return 0;
}
std::cerr << "Error: No command provided\n\n";
show_help(std::cerr);
return 1;
} else if (command_map.count(args.at(0)) == 0) {
std::cerr << "Error: unknown command \"" << args.at(0) << "\"\n\n";
show_help(std::cerr);
return 1;
}
// trim the command name and pass the rest of the args to the defined command
return command_map.at(args.at(0))->func(vm, std::vector<std::string>(args.begin() + 1, args.end()));
}
|
<unk> stains on blood and bone marrow smears are helpful in the distinction of AML from ALL , and in subclassification of AML . The combination of a myeloperoxidase or Sudan black stain and a nonspecific esterase stain will provide the desired information in most cases . The myeloperoxidase or Sudan black reactions are most useful in establishing the identity of AML and distinguishing it from ALL . The nonspecific esterase stain is used to identify a <unk> component in <unk> and to distinguish a poorly differentiated <unk> leukemia from ALL .
|
Formal statement is: lemma has_contour_integral_bound_circlepath: "\<lbrakk>(f has_contour_integral i) (circlepath z r); 0 \<le> B; 0 < r; \<And>x. norm(x - z) = r \<Longrightarrow> norm(f x) \<le> B\<rbrakk> \<Longrightarrow> norm i \<le> B*(2*pi*r)" Informal statement is: If $f$ has a contour integral along a circle of radius $r$ centered at $z$, and $f$ is bounded by $B$ on the circle, then the contour integral is bounded by $B \cdot 2 \pi r$.
|
\documentclass[11pt, fleqn]{article}
\input{../../utils/header.tex}
% \crefname{figure}{Figure}{Figures}
% \crefname{section}{Section}{Sections}
% \crefname{table}{Table}{Tables}
% \crefname{lstlisting}{Listing}{Listings}
\setlength{\parskip}{12pt} % Sets a blank line in between paragraphs
\setlength\parindent{0pt} % Sets the indent for each paragraph to zero
\begin{document}
\title{Machine Learning (41204-01)\\HW \#4}
\author{Will Clark $\vert$ Matthew DeLio \\
\texttt{[email protected]} $\vert$ \texttt{[email protected]} \\
University of Chicago Booth School of Business}
\date{\today}
\maketitle
\section{Cleaning and Partitioning the Dataset}
The dataset available to us has been highly anonymized and not really interpretable in any human-readable form. They only provide numbers and factors that we can feed into our model to predict some event (in our case customer ``churn''). After choosing to predict ``churn'' we took our dataset and went about cleaning it up. To do this we employ the suggested algorithm contained in the assignment:
\begin{itemize}
\item Remove covariates containing all NAs. This brings the number of covariates from 230 to 211\footnote{We considered using a lower threshold here, but were concerned about arbitrarily throwing out interesting covariates. Instead we chose to let the variable selection algorithms perform their task of removing them if they contained no useful data.};
\item Replace remaining NAs of a covariate with its sample mean;
\item Using the relative frequency of levels to collapse and merge factors together using the following rules\footnote{This was applied only to covariates with $>50$ factor levels.}:
\begin{itemize}
\item Levels with $<0.5\%$ (n=$<250$) of observations are set to ``low''
\item Levels with $0.5-1.0\%$ (n=250 to 500) of observations are set to ``medium''
\item Levels with $1.0-2.0\%$ (n=500 to 1,000) of observations are set to ``high''
\item Levels with $>2.0\%$ of observations are left as is.
\end{itemize}
\end{itemize}
Prior to performing variable selection, we partition our dataset up into 3 pieces holding 60\% in the training set and 20\% each in the validation and test sets. The elements are chosen randomly, without replacement, from the cleaned dataset\footnote{We realize that, ideally, we would clean only the training data, applying the same transformations to the validation and test set, but this proves to be too intractable for the homework.}.
\section{Variable Selection}
\subsection{Initial Work}
Our initial work revolved mainly around building a random forest implementation due for both the variable selection and final model (see \cref{sec:init_rf,sec:mod_rf} for subsequent, but similar work) because of the simplicity of getting it working. After completing this work we noticed that model chose to largely ignore the rare event in aggregate, which while maximising the precision of the overall algorithm lead to 100\% mis-prediction for True Positives.
To address this issue we employed an oversampling technique where we take the partitioned training data and even out the occurrence of positive and negative outcomes such that the 7.3\% of positive outcomes becomes 50\%. This results in the reduction in the number of training samples from 30,000 to 4,438.
The subsequent sections (unless otherwise noted) use this oversampled training data to create a fitted model.
\subsection{Random Forest}\label{sec:init_rf}
This tool uses a random forest to fit a relatively small number of tree (500) to our oversampled dataset. After training this model we use the random forest's variable importance output to determine which of the variables are most important. See \cref{fig:rf_var_sel} for a graphical representation of this list. Note that the plot shows the mean decrease in accuracy that would result if the given variable is removed from the model. Using this ranking we select the 30 more important covariates to fit later in \cref{sec:mod_rf}.
\begin{figure}[!htb]
\centering
\caption{Random Forest Important Variables}
\includegraphics[scale=.5]{rf_var_sel.pdf}
\label{fig:rf_var_sel}
\end{figure}
\subsection{The Gamma-Lasso}
Another tool for variable reduction is regression with $L_1$ regularization (i.e. the lasso). The process of estimating a model while penalizing non-zero coefficients is an algorithmic way to reduce the dimensionality of our data set. There are two ways we can add to the dimension reduction process:
\begin{enumerate}
\item Using the Gamma-Lasso in the package \texttt{gamlr} allows us to control the concavity of the penalty function. A more concave penalty function increases the number of variables held out of the model and reduces dimensionality even further.
\item The Gamma-Lasso algorithm gives us a series of models to choose from, each corresponding to a penalty tuning parameter $\lambda$. We can choose $\lambda$ (which determines the variables excluded from the model) according to different information criteria: the Akaike information criterion, the corrected Akaike information criterion, or the Bayes information criterion. In general, the BIC will give us the simplest model (i.e. reduce dimensionality the most), so we will use this criterion to select a model and a set of variables.
\end{enumerate}
By setting $\lambda=10$ (which is a very high concavity tuning parameter) and selecting a model based on the BIC, the Gamma-Lasso chooses a model with only 11 variables.
\subsection{Principal Components Analysis (PCA)}
Another dimension reduction tool is principal components analysis. Here, the goal is to transform our data set into a collection of orthogonal vectors (i.e. principal components). We can order the vectors by the amount of variation in our dependent data that they explain, and choose the first $N$ principal components to represent the data.
The purpose is to reduce the dimensionality of our original data set into a small number of series that together explain a large share of the variation in our dependent variable. There is no obvious way to choose how many principal components to include. We would need to include 53 principal components to capture half of the observed variation in the data. We would need to include only 13, however, to capture one quarter of the observed variation in the data. For the rest of this exercise, we will proceed using the first 13 principal components. This allows us to capture 25 percent of the variation in the data while dropping almost 95 percent of the data series (not even including the series that were dropped as part of the data cleaning process).
\section{Model Selection}
\subsection{Logistic Regression}
The first predictive model we will try is a basic logistic regression model. We will use each of our three sets of reduced variables described above (from the random forest variable importance, the Gamma-Lasso, and PCA). We will simply estimate a linear model and see how well it predicts churn out of sample.
We can see the results in \cref{tab:glm_accuracy}; the rows are labeled according to the dimension reduction algorithm. The logistic regression trained on the random forest and on the gamma-lasso data sets actually performs quite well, with reasonably high accuracy and roughly similar true-positive detection rate (i.e. sensitivitiy). Both models, however, suffer from a fairly high false-positive rate (i.e. specificity) upwards of 60 percent.
\input{glm_accuracy.tex}
\subsection{Random Forest}\label{sec:mod_rf}
Using only the covariates identified in \cref{sec:init_rf} we fit a much larger number of trees to our dataset. The resulting model is then used to fit the non-oversampled validation set which results in the confusion matrix shown below. Note that with this algorithm we have achieved a fairly decent sensitivity of 75\% (true-positive detection rate) at the expense of a relatively low specificity of just 58\% (i.e. we have many false-positives).
\begin{verbatim}
Confusion Matrix and Statistics
Reference
Prediction TRUE FALSE
TRUE 568 3891
FALSE 193 5348
Accuracy : 0.5916
95% CI : (0.5819, 0.6013)
No Information Rate : 0.9239
P-Value [Acc > NIR] : 1
Kappa : 0.1007
Mcnemar's Test P-Value : <2e-16
Sensitivity : 0.7464
Specificity : 0.5789
Pos Pred Value : 0.1274
Neg Pred Value : 0.9652
Prevalence : 0.0761
Detection Rate : 0.0568
Detection Prevalence : 0.4459
Balanced Accuracy : 0.6626
'Positive' Class : TRUE
\end{verbatim}
\subsection{Boosting}
Another possible predictive model is regression tree boosting using the packages \texttt{gbm} and \texttt{caret}. We have three different training data sets available: the data selected by the random forest, the data selected by the Gamma-Lasso, or the principal components discussed above. For each set of training data, we also have the opportunity to tune our boosting tree with the interaction depth, number of trees, and the shrinkage parameter.
To tune the boosting tree algorithm, we use the \texttt{caret} package to perform 5-fold cross-validation on each combination of parameters. We consider values of interaction depth of 1, 5, and 9; we try using 500, 1000, and 1500 trees; and we use shrinkage parameters of 0.01, 0.05, and 0.10. All told, there are 27 different combinations of tuning parameters, for each of three different sets of input variables (depending on the dimension reduction strategy we used).
In \cref{tab:boost_tune} we can see the results of this tuning exercise. For each dimension reduction strategy, we show the optimal set of tuning parameters as well as the out-of-sample accuracy (on a validation data set not used to train the model). We can see that the boosting tree trained on data selected by the Gamma-Lasso is the best (with 67 percent accuracy), followed closely by the variables selected by the random forest (with 65 percent accuracy). The principal components do not fare well, producing out-of-sample accuracy of only 55 percent.
\input{boost_tune.tex}
\subsection{Summary}
Based on the out-of-sample results on our validation data set described above, it looks like the best performing model is the boosting tree trained on the variables selected by the Gamma-Lasso algorithm. We will use this to predict out-of-sample on our last hold-out set of test data.
\section{Out-of-Sample Prediction}
% Feel Free to yank this section if it doesn't make sense, just didn't want you to have to write this up.
Below is the out-of-sample confusion matrix and statistics for the covariates chosen by the Gamma-Lasso algorithm in a boosting tree described above. The model ends up with a very high accuracy (upwards of 93 percent) but performs terribly in terms of specificity. That is, it achieves high accuracy by correctly predicting the non-churn events, but cannot reasonably predict the church events with any accuracy.
\begin{verbatim}
Confusion Matrix and Statistics
Reference
Prediction 0 1
0 9301 684
1 7 8
Accuracy : 0.9309
95% CI : (0.9258, 0.9358)
No Information Rate : 0.9308
P-Value [Acc > NIR] : 0.4944
Kappa : 0.0198
Mcnemar's Test P-Value : <2e-16
Sensitivity : 0.99925
Specificity : 0.01156
Pos Pred Value : 0.93150
Neg Pred Value : 0.53333
Prevalence : 0.93080
Detection Rate : 0.93010
Detection Prevalence : 0.99850
Balanced Accuracy : 0.50540
'Positive' Class : 0
\end{verbatim}
\end{document}
% \input{.tex}
% \begin{figure}
% \centering
% \begin{subfigure}[b]{0.49\textwidth}
% \caption{}
% \includegraphics[width=\textwidth]{.pdf}
% \label{fig:}
% \end{subfigure}
% \hfill
% \begin{subfigure}[b]{0.49\textwidth}
% \caption{}
% \includegraphics[width=\textwidth]{.pdf}
% \label{fig:}
% \end{subfigure}
% \caption{}
% \end{figure}
% \begin{figure}[!htb]
% \centering
% \caption{}
% \includegraphics[scale=.5]{.pdf}
% \label{fig:}
% \end{figure}
|
[STATEMENT]
lemma LIM_const_not_eq[tendsto_intros]: "k \<noteq> L \<Longrightarrow> \<not> (\<lambda>x. k) \<midarrow>a\<rightarrow> L"
for a :: "'a::perfect_space" and k L :: "'b::t2_space"
[PROOF STATE]
proof (prove)
goal (1 subgoal):
1. k \<noteq> L \<Longrightarrow> \<not> (\<lambda>x. k) \<midarrow>a\<rightarrow> L
[PROOF STEP]
by (simp add: tendsto_const_iff)
|
import Data.Vect
createEmpties : Vect n (Vect 0 elem)
createEmpties {n = Z} = []
createEmpties {n = (S k)} = [] :: createEmpties
transposeMat : Vect m (Vect n elem) -> Vect n (Vect m elem)
transposeMat [] = createEmpties
transposeMat (x :: xs) = let xsTrans = transposeMat xs in
zipWith (::) x xsTrans
addMatrix : Num a => Vect n (Vect m a) -> Vect n (Vect m a) -> Vect n (Vect m a)
addMatrix [] [] = []
addMatrix (x :: xs) (y :: ys) = zipWith (+) x y :: addMatrix xs ys
multMatrixHelper : Num t => (xs : Vect n (Vect m t))
-> (ysTrans : Vect p (Vect m t))
-> Vect n (Vect p t)
multMatrixHelper [] ysTrans = []
multMatrixHelper (x :: xs) ysTrans = let topRow = multAll x ysTrans in
topRow :: multMatrixHelper xs ysTrans
where
dotProd : Num t => Vect n t -> Vect n t -> t
dotProd xs ys = sum (zipWith (*) xs ys)
multAll : Num t => Vect n t -> Vect m (Vect n t) -> Vect m t
multAll xs yss = map (dotProd xs) yss
multMatrix : Num t =>
Vect n (Vect m t) -> Vect m (Vect p t) -> Vect n (Vect p t)
multMatrix xs ys = let ysTrans = transposeMat ys in
multMatrixHelper xs ysTrans
|
{-# OPTIONS --type-in-type #-}
open import Data.Unit
open import Data.Product hiding ( curry ; uncurry )
open import Data.List hiding ( concat )
open import Data.String
open import Relation.Binary.PropositionalEquality
module Spire.Examples.PropositionalDesc where
----------------------------------------------------------------------
elimEq : (A : Set) (x : A) (P : (y : A) → x ≡ y → Set)
→ P x refl
→ (y : A) (p : x ≡ y) → P y p
elimEq A .x P prefl x refl = prefl
----------------------------------------------------------------------
Label : Set
Label = String
Enum : Set
Enum = List Label
data Tag : Enum → Set where
here : ∀{l E} → Tag (l ∷ E)
there : ∀{l E} → Tag E → Tag (l ∷ E)
Cases : (E : Enum) (P : Tag E → Set) → Set
Cases [] P = ⊤
Cases (l ∷ E) P = P here × Cases E λ t → P (there t)
case : (E : Enum) (P : Tag E → Set) (cs : Cases E P) (t : Tag E) → P t
case (l ∷ E) P (c , cs) here = c
case (l ∷ E) P (c , cs) (there t) = case E (λ t → P (there t)) cs t
UncurriedCases : (E : Enum) (P : Tag E → Set) (X : Set)
→ Set
UncurriedCases E P X = Cases E P → X
CurriedCases : (E : Enum) (P : Tag E → Set) (X : Set)
→ Set
CurriedCases [] P X = X
CurriedCases (l ∷ E) P X = P here → CurriedCases E (λ t → P (there t)) X
curryCases : (E : Enum) (P : Tag E → Set) (X : Set)
(f : UncurriedCases E P X) → CurriedCases E P X
curryCases [] P X f = f tt
curryCases (l ∷ E) P X f = λ c → curryCases E (λ t → P (there t)) X (λ cs → f (c , cs))
uncurryCases : (E : Enum) (P : Tag E → Set) (X : Set)
(f : CurriedCases E P X) → UncurriedCases E P X
uncurryCases [] P X x tt = x
uncurryCases (l ∷ E) P X f (c , cs) = uncurryCases E (λ t → P (there t)) X (f c) cs
----------------------------------------------------------------------
data Desc (I : Set) : Set₁ where
`End : (i : I) → Desc I
`Rec : (i : I) (D : Desc I) → Desc I
`Arg : (A : Set) (B : A → Desc I) → Desc I
`RecFun : (A : Set) (B : A → I) (D : Desc I) → Desc I
ISet : Set → Set₁
ISet I = I → Set
El : (I : Set) (D : Desc I) (X : ISet I) → ISet I
El I (`End j) X i = j ≡ i
El I (`Rec j D) X i = X j × El I D X i
El I (`Arg A B) X i = Σ A (λ a → El I (B a) X i)
El I (`RecFun A B D) X i = ((a : A) → X (B a)) × El I D X i
Hyps : (I : Set) (D : Desc I) (X : ISet I) (P : (i : I) → X i → Set) (i : I) (xs : El I D X i) → Set
Hyps I (`End j) X P i q = ⊤
Hyps I (`Rec j D) X P i (x , xs) = P j x × Hyps I D X P i xs
Hyps I (`Arg A B) X P i (a , b) = Hyps I (B a) X P i b
Hyps I (`RecFun A B D) X P i (f , xs) = ((a : A) → P (B a) (f a)) × Hyps I D X P i xs
caseD : (E : Enum) (I : Set) (cs : Cases E (λ _ → Desc I)) (t : Tag E) → Desc I
caseD E I cs t = case E (λ _ → Desc I) cs t
----------------------------------------------------------------------
TagDesc : (I : Set) → Set
TagDesc I = Σ Enum (λ E → Cases E (λ _ → Desc I))
toCase : (I : Set) (E,cs : TagDesc I) → Tag (proj₁ E,cs) → Desc I
toCase I (E , cs) = case E (λ _ → Desc I) cs
toDesc : (I : Set) → TagDesc I → Desc I
toDesc I (E , cs) = `Arg (Tag E) (toCase I (E , cs))
----------------------------------------------------------------------
UncurriedEl : (I : Set) (D : Desc I) (X : ISet I) → Set
UncurriedEl I D X = {i : I} → El I D X i → X i
CurriedEl : (I : Set) (D : Desc I) (X : ISet I) → Set
CurriedEl I (`End i) X = X i
CurriedEl I (`Rec j D) X = (x : X j) → CurriedEl I D X
CurriedEl I (`Arg A B) X = (a : A) → CurriedEl I (B a) X
CurriedEl I (`RecFun A B D) X = ((a : A) → X (B a)) → CurriedEl I D X
curryEl : (I : Set) (D : Desc I) (X : ISet I)
(cn : UncurriedEl I D X) → CurriedEl I D X
curryEl I (`End i) X cn = cn refl
curryEl I (`Rec i D) X cn = λ x → curryEl I D X (λ xs → cn (x , xs))
curryEl I (`Arg A B) X cn = λ a → curryEl I (B a) X (λ xs → cn (a , xs))
curryEl I (`RecFun A B D) X cn = λ f → curryEl I D X (λ xs → cn (f , xs))
uncurryEl : (I : Set) (D : Desc I) (X : ISet I)
(cn : CurriedEl I D X) → UncurriedEl I D X
uncurryEl I (`End i) X cn refl = cn
uncurryEl I (`Rec i D) X cn (x , xs) = uncurryEl I D X (cn x) xs
uncurryEl I (`Arg A B) X cn (a , xs) = uncurryEl I (B a) X (cn a) xs
uncurryEl I (`RecFun A B D) X cn (f , xs) = uncurryEl I D X (cn f) xs
data μ (I : Set) (D : Desc I) : I → Set where
con : UncurriedEl I D (μ I D)
con2 : (I : Set) (D : Desc I) → CurriedEl I D (μ I D)
con2 I D = curryEl I D (μ I D) con
----------------------------------------------------------------------
UncurriedHyps : (I : Set) (D : Desc I) (X : ISet I)
(P : (i : I) → X i → Set)
(cn : UncurriedEl I D X)
→ Set
UncurriedHyps I D X P cn =
(i : I) (xs : El I D X i) → Hyps I D X P i xs → P i (cn xs)
CurriedHyps : (I : Set) (D : Desc I) (X : ISet I)
(P : (i : I) → X i → Set)
(cn : UncurriedEl I D X)
→ Set
CurriedHyps I (`End i) X P cn =
P i (cn refl)
CurriedHyps I (`Rec i D) X P cn =
(x : X i) → P i x → CurriedHyps I D X P (λ xs → cn (x , xs))
CurriedHyps I (`Arg A B) X P cn =
(a : A) → CurriedHyps I (B a) X P (λ xs → cn (a , xs))
CurriedHyps I (`RecFun A B D) X P cn =
(f : (a : A) → X (B a)) (ihf : (a : A) → P (B a) (f a)) → CurriedHyps I D X P (λ xs → cn (f , xs))
curryHyps : (I : Set) (D : Desc I) (X : ISet I)
(P : (i : I) → X i → Set)
(cn : UncurriedEl I D X)
(pf : UncurriedHyps I D X P cn)
→ CurriedHyps I D X P cn
curryHyps I (`End i) X P cn pf =
pf i refl tt
curryHyps I (`Rec i D) X P cn pf =
λ x ih → curryHyps I D X P (λ xs → cn (x , xs)) (λ i xs ihs → pf i (x , xs) (ih , ihs))
curryHyps I (`Arg A B) X P cn pf =
λ a → curryHyps I (B a) X P (λ xs → cn (a , xs)) (λ i xs ihs → pf i (a , xs) ihs)
curryHyps I (`RecFun A B D) X P cn pf =
λ f ihf → curryHyps I D X P (λ xs → cn (f , xs)) (λ i xs ihs → pf i (f , xs) (ihf , ihs))
uncurryHyps : (I : Set) (D : Desc I) (X : ISet I)
(P : (i : I) → X i → Set)
(cn : UncurriedEl I D X)
(pf : CurriedHyps I D X P cn)
→ UncurriedHyps I D X P cn
uncurryHyps I (`End .i) X P cn pf i refl tt =
pf
uncurryHyps I (`Rec j D) X P cn pf i (x , xs) (ih , ihs) =
uncurryHyps I D X P (λ ys → cn (x , ys)) (pf x ih) i xs ihs
uncurryHyps I (`Arg A B) X P cn pf i (a , xs) ihs =
uncurryHyps I (B a) X P (λ ys → cn (a , ys)) (pf a) i xs ihs
uncurryHyps I (`RecFun A B D) X P cn pf i (f , xs) (ihf , ihs) =
uncurryHyps I D X P (λ ys → cn (f , ys)) (pf f ihf) i xs ihs
----------------------------------------------------------------------
ind :
(I : Set)
(D : Desc I)
(P : (i : I) → μ I D i → Set)
(pcon : UncurriedHyps I D (μ I D) P con)
(i : I)
(x : μ I D i)
→ P i x
hyps :
(I : Set)
(D₁ : Desc I)
(P : (i : I) → μ I D₁ i → Set)
(pcon : UncurriedHyps I D₁ (μ I D₁) P con)
(D₂ : Desc I)
(i : I)
(xs : El I D₂ (μ I D₁) i)
→ Hyps I D₂ (μ I D₁) P i xs
ind I D P pcon i (con xs) = pcon i xs (hyps I D P pcon D i xs)
hyps I D P pcon (`End j) i q = tt
hyps I D P pcon (`Rec j A) i (x , xs) = ind I D P pcon j x , hyps I D P pcon A i xs
hyps I D P pcon (`Arg A B) i (a , b) = hyps I D P pcon (B a) i b
hyps I D P pcon (`RecFun A B E) i (f , xs) = (λ a → ind I D P pcon (B a) (f a)) , hyps I D P pcon E i xs
----------------------------------------------------------------------
ind2 :
(I : Set)
(D : Desc I)
(P : (i : I) → μ I D i → Set)
(pcon : CurriedHyps I D (μ I D) P con)
(i : I)
(x : μ I D i)
→ P i x
ind2 I D P pcon i x = ind I D P (uncurryHyps I D (μ I D) P con pcon) i x
elim :
(I : Set)
(TD : TagDesc I)
→ let
D = toDesc I TD
E = proj₁ TD
Cs = toCase I TD
in (P : (i : I) → μ I D i → Set)
→ let
Q = λ t → CurriedHyps I (Cs t) (μ I D) P (λ xs → con (t , xs))
X = (i : I) (x : μ I D i) → P i x
in UncurriedCases E Q X
elim I TD P cs i x =
let
D = toDesc I TD
E = proj₁ TD
Cs = toCase I TD
Q = λ t → CurriedHyps I (Cs t) (μ I D) P (λ xs → con (t , xs))
p = case E Q cs
in ind2 I D P p i x
elim2 :
(I : Set)
(TD : TagDesc I)
→ let
D = toDesc I TD
E = proj₁ TD
Cs = toCase I TD
in (P : (i : I) → μ I D i → Set)
→ let
Q = λ t → CurriedHyps I (Cs t) (μ I D) P (λ xs → con (t , xs))
X = (i : I) (x : μ I D i) → P i x
in CurriedCases E Q X
elim2 I TD P =
let
D = toDesc I TD
E = proj₁ TD
Cs = toCase I TD
Q = λ t → CurriedHyps I (Cs t) (μ I D) P (λ xs → con (t , xs))
X = (i : I) (x : μ I D i) → P i x
in curryCases E Q X (elim I TD P)
----------------------------------------------------------------------
module Sugared where
data ℕT : Set where `zero `suc : ℕT
data VecT : Set where `nil `cons : VecT
ℕD : Desc ⊤
ℕD = `Arg ℕT λ
{ `zero → `End tt
; `suc → `Rec tt (`End tt)
}
ℕ : ⊤ → Set
ℕ = μ ⊤ ℕD
zero : ℕ tt
zero = con (`zero , refl)
suc : ℕ tt → ℕ tt
suc n = con (`suc , n , refl)
VecD : (A : Set) → Desc (ℕ tt)
VecD A = `Arg VecT λ
{ `nil → `End zero
; `cons → `Arg (ℕ tt) λ n → `Arg A λ _ → `Rec n (`End (suc n))
}
Vec : (A : Set) (n : ℕ tt) → Set
Vec A n = μ (ℕ tt) (VecD A) n
nil : (A : Set) → Vec A zero
nil A = con (`nil , refl)
cons : (A : Set) (n : ℕ tt) (x : A) (xs : Vec A n) → Vec A (suc n)
cons A n x xs = con (`cons , n , x , xs , refl)
----------------------------------------------------------------------
add : ℕ tt → ℕ tt → ℕ tt
add = ind ⊤ ℕD (λ _ _ → ℕ tt → ℕ tt)
(λ
{ tt (`zero , q) tt n → n
; tt (`suc , m , q) (ih , tt) n → suc (ih n)
}
)
tt
mult : ℕ tt → ℕ tt → ℕ tt
mult = ind ⊤ ℕD (λ _ _ → ℕ tt → ℕ tt)
(λ
{ tt (`zero , q) tt n → zero
; tt (`suc , m , q) (ih , tt) n → add n (ih n)
}
)
tt
append : (A : Set) (m : ℕ tt) (xs : Vec A m) (n : ℕ tt) (ys : Vec A n) → Vec A (add m n)
append A = ind (ℕ tt) (VecD A) (λ m xs → (n : ℕ tt) (ys : Vec A n) → Vec A (add m n))
(λ
{ .(con (`zero , refl)) (`nil , refl) ih n ys → ys
; .(con (`suc , m , refl)) (`cons , m , x , xs , refl) (ih , tt) n ys → cons A (add m n) x (ih n ys)
}
)
concat : (A : Set) (m n : ℕ tt) (xss : Vec (Vec A m) n) → Vec A (mult n m)
concat A m = ind (ℕ tt) (VecD (Vec A m)) (λ n xss → Vec A (mult n m))
(λ
{ .(con (`zero , refl)) (`nil , refl) tt → nil A
; .(con (`suc , n , refl)) (`cons , n , xs , xss , refl) (ih , tt) → append A m xs (mult n m) ih
}
)
----------------------------------------------------------------------
module Desugared where
ℕT : Enum
ℕT = "zero" ∷ "suc" ∷ []
VecT : Enum
VecT = "nil" ∷ "cons" ∷ []
ℕTD : TagDesc ⊤
ℕTD = ℕT
, `End tt
, `Rec tt (`End tt)
, tt
ℕCs : Tag ℕT → Desc ⊤
ℕCs = toCase ⊤ ℕTD
ℕD : Desc ⊤
ℕD = toDesc ⊤ ℕTD
ℕ : ⊤ → Set
ℕ = μ ⊤ ℕD
zero : ℕ tt
zero = con (here , refl)
suc : ℕ tt → ℕ tt
suc n = con (there here , n , refl)
zero2 : ℕ tt
zero2 = con2 ⊤ ℕD here
suc2 : ℕ tt → ℕ tt
suc2 = con2 ⊤ ℕD (there here)
VecTD : (A : Set) → TagDesc (ℕ tt)
VecTD A = VecT
, `End zero
, `Arg (ℕ tt) (λ n → `Arg A λ _ → `Rec n (`End (suc n)))
, tt
VecCs : (A : Set) → Tag VecT → Desc (ℕ tt)
VecCs A = toCase (ℕ tt) (VecTD A)
VecD : (A : Set) → Desc (ℕ tt)
VecD A = toDesc (ℕ tt) (VecTD A)
Vec : (A : Set) (n : ℕ tt) → Set
Vec A n = μ (ℕ tt) (VecD A) n
nil : (A : Set) → Vec A zero
nil A = con (here , refl)
cons : (A : Set) (n : ℕ tt) (x : A) (xs : Vec A n) → Vec A (suc n)
cons A n x xs = con (there here , n , x , xs , refl)
nil2 : (A : Set) → Vec A zero
nil2 A = con2 (ℕ tt) (VecD A) here
cons2 : (A : Set) (n : ℕ tt) (x : A) (xs : Vec A n) → Vec A (suc n)
cons2 A = con2 (ℕ tt) (VecD A) (there here)
----------------------------------------------------------------------
module Induction where
add : ℕ tt → ℕ tt → ℕ tt
add = ind ⊤ ℕD (λ _ _ → ℕ tt → ℕ tt)
(λ u t,c → case ℕT
(λ t → (c : El ⊤ (ℕCs t) ℕ u)
(ih : Hyps ⊤ ℕD ℕ (λ u n → ℕ u → ℕ u) u (t , c))
→ ℕ u → ℕ u
)
( (λ q ih n → n)
, (λ m,q ih,tt n → suc (proj₁ ih,tt n))
, tt
)
(proj₁ t,c)
(proj₂ t,c)
)
tt
mult : ℕ tt → ℕ tt → ℕ tt
mult = ind ⊤ ℕD (λ _ _ → ℕ tt → ℕ tt)
(λ u t,c → case ℕT
(λ t → (c : El ⊤ (ℕCs t) ℕ u)
(ih : Hyps ⊤ ℕD ℕ (λ u n → ℕ u → ℕ u) u (t , c))
→ ℕ u → ℕ u
)
( (λ q ih n → zero)
, (λ m,q ih,tt n → add n (proj₁ ih,tt n))
, tt
)
(proj₁ t,c)
(proj₂ t,c)
)
tt
append : (A : Set) (m : ℕ tt) (xs : Vec A m) (n : ℕ tt) (ys : Vec A n) → Vec A (add m n)
append A = ind (ℕ tt) (VecD A) (λ m xs → (n : ℕ tt) (ys : Vec A n) → Vec A (add m n))
(λ m t,c → case VecT
(λ t → (c : El (ℕ tt) (VecCs A t) (Vec A) m)
(ih : Hyps (ℕ tt) (VecD A) (Vec A) (λ m xs → (n : ℕ tt) (ys : Vec A n) → Vec A (add m n)) m (t , c))
(n : ℕ tt) (ys : Vec A n) → Vec A (add m n)
)
( (λ q ih n ys → subst (λ m → Vec A (add m n)) q ys)
, (λ m',x,xs,q ih,tt n ys →
let m' = proj₁ m',x,xs,q
x = proj₁ (proj₂ m',x,xs,q)
q = proj₂ (proj₂ (proj₂ m',x,xs,q))
ih = proj₁ ih,tt
in
subst (λ m → Vec A (add m n)) q (cons A (add m' n) x (ih n ys))
)
, tt
)
(proj₁ t,c)
(proj₂ t,c)
)
concat : (A : Set) (m n : ℕ tt) (xss : Vec (Vec A m) n) → Vec A (mult n m)
concat A m = ind (ℕ tt) (VecD (Vec A m)) (λ n xss → Vec A (mult n m))
(λ n t,c → case VecT
(λ t → (c : El (ℕ tt) (VecCs (Vec A m) t) (Vec (Vec A m)) n)
(ih : Hyps (ℕ tt) (VecD (Vec A m)) (Vec (Vec A m)) (λ n xss → Vec A (mult n m)) n (t , c))
→ Vec A (mult n m)
)
( (λ q ih → subst (λ n → Vec A (mult n m)) q (nil A))
, (λ n',xs,xss,q ih,tt →
let n' = proj₁ n',xs,xss,q
xs = proj₁ (proj₂ n',xs,xss,q)
q = proj₂ (proj₂ (proj₂ n',xs,xss,q))
ih = proj₁ ih,tt
in
subst (λ n → Vec A (mult n m)) q (append A m xs (mult n' m) ih)
)
, tt
)
(proj₁ t,c)
(proj₂ t,c)
)
----------------------------------------------------------------------
module Eliminator where
elimℕ : (P : (ℕ tt) → Set)
(pzero : P zero)
(psuc : (m : ℕ tt) → P m → P (suc m))
(n : ℕ tt)
→ P n
elimℕ P pzero psuc = ind ⊤ ℕD (λ u n → P n)
(λ u t,c → case ℕT
(λ t → (c : El ⊤ (ℕCs t) ℕ u)
(ih : Hyps ⊤ ℕD ℕ (λ u n → P n) u (t , c))
→ P (con (t , c))
)
( (λ q ih →
elimEq ⊤ tt (λ u q → P (con (here , q)))
pzero
u q
)
, (λ n,q ih,tt →
elimEq ⊤ tt (λ u q → P (con (there here , proj₁ n,q , q)))
(psuc (proj₁ n,q) (proj₁ ih,tt))
u (proj₂ n,q)
)
, tt
)
(proj₁ t,c)
(proj₂ t,c)
)
tt
elimVec : (A : Set) (P : (n : ℕ tt) → Vec A n → Set)
(pnil : P zero (nil A))
(pcons : (n : ℕ tt) (a : A) (xs : Vec A n) → P n xs → P (suc n) (cons A n a xs))
(n : ℕ tt)
(xs : Vec A n)
→ P n xs
elimVec A P pnil pcons = ind (ℕ tt) (VecD A) (λ n xs → P n xs)
(λ n t,c → case VecT
(λ t → (c : El (ℕ tt) (VecCs A t) (Vec A) n)
(ih : Hyps (ℕ tt) (VecD A) (Vec A) (λ n xs → P n xs) n (t , c))
→ P n (con (t , c))
)
( (λ q ih →
elimEq (ℕ tt) zero (λ n q → P n (con (here , q)))
pnil
n q
)
, (λ n',x,xs,q ih,tt →
let n' = proj₁ n',x,xs,q
x = proj₁ (proj₂ n',x,xs,q)
xs = proj₁ (proj₂ (proj₂ n',x,xs,q))
q = proj₂ (proj₂ (proj₂ n',x,xs,q))
ih = proj₁ ih,tt
in
elimEq (ℕ tt) (suc n') (λ n q → P n (con (there here , n' , x , xs , q)))
(pcons n' x xs ih )
n q
)
, tt
)
(proj₁ t,c)
(proj₂ t,c)
)
----------------------------------------------------------------------
add : ℕ tt → ℕ tt → ℕ tt
add = elimℕ (λ _ → ℕ tt → ℕ tt)
(λ n → n)
(λ m ih n → suc (ih n))
mult : ℕ tt → ℕ tt → ℕ tt
mult = elimℕ (λ _ → ℕ tt → ℕ tt)
(λ n → zero)
(λ m ih n → add n (ih n))
append : (A : Set) (m : ℕ tt) (xs : Vec A m) (n : ℕ tt) (ys : Vec A n) → Vec A (add m n)
append A = elimVec A (λ m xs → (n : ℕ tt) (ys : Vec A n) → Vec A (add m n))
(λ n ys → ys)
(λ m x xs ih n ys → cons A (add m n) x (ih n ys))
concat : (A : Set) (m n : ℕ tt) (xss : Vec (Vec A m) n) → Vec A (mult n m)
concat A m = elimVec (Vec A m) (λ n xss → Vec A (mult n m))
(nil A)
(λ n xs xss ih → append A m xs (mult n m) ih)
----------------------------------------------------------------------
module GenericEliminator where
add : ℕ tt → ℕ tt → ℕ tt
add = elim2 ⊤ ℕTD _
(λ n → n)
(λ m ih n → suc (ih n))
tt
mult : ℕ tt → ℕ tt → ℕ tt
mult = elim2 ⊤ ℕTD _
(λ n → zero)
(λ m ih n → add n (ih n))
tt
append : (A : Set) (m : ℕ tt) (xs : Vec A m) (n : ℕ tt) (ys : Vec A n) → Vec A (add m n)
append A = elim2 (ℕ tt) (VecTD A) _
(λ n ys → ys)
(λ m x xs ih n ys → cons A (add m n) x (ih n ys))
concat : (A : Set) (m n : ℕ tt) (xss : Vec (Vec A m) n) → Vec A (mult n m)
concat A m = elim2 (ℕ tt) (VecTD (Vec A m)) _
(nil A)
(λ n xs xss ih → append A m xs (mult n m) ih)
----------------------------------------------------------------------
|
PROGRAM reformat
! Reformat the ensemble-averaged output to the usual WMO TRAN format
! -- sk2out, and to kml -- kmlout, called by sk2out
! File usage:
! fort.31 -- forecast file input
! fort.47 -- seaice_forecast.points
! fort.60 -- output
! fort.61 -- output
! fort.62 -- output
! fort.63 -- output
! fort.64 -- output
! fort.70 -- kml output
! fort.90 -- echo $PDY > fort.90
! fort.91 -- seaice_quote (for tran file construction)
!
! Robert Grumbine original version 2 June 2014
IMPLICIT none
INTEGER npts, tmp, ndays, time
PARAMETER (tmp = 360*180)
PARAMETER (ndays = 16)
INTEGER skpt(tmp)
REAL lat(tmp), lon(tmp), x0(tmp), y0(tmp)
REAL dir(tmp,ndays), dist(tmp,ndays)
INTEGER i, funit2, code
funit2 = 31
OPEN(31, FORM="FORMATTED", STATUS="OLD")
! Read in skiles point locations:
OPEN(47,FILE="seaice_forecast.points",FORM="FORMATTED",
1 STATUS="OLD")
DO i = 1, 207
READ(47, *) skpt(i), y0(i), x0(i)
ENDDO
! Read in forecast and skiles point locations
npts = tmp
CALL getfcst(funit2, x0, y0, dir, dist, code, npts, ndays)
! PRINT *,'getfcst return code = ',code
DO i = 1, npts
skpt(i) = i
ENDDO
! PRINT *,'x0 y0 1 = ',x0(1), y0(1), dir(1,5), dist(1,5)
! Call sk2out day by day, as in original
DO i = 1, ndays !forecast days
!CD PRINT *,'printing out day ',i
time = i*24
CALL sk2out(x0, y0, dir(:,i), dist(:,i), skpt, npts, time)
ENDDO
END
|
from typing import Dict
from typing import List
import javalang
import numpy as np
import pandas as pd
from joblib import Parallel, delayed
from .layout import NewLineBeforeOpenBrace
from .layout import NumEmptyLines
from .layout import NumSpaces
from .layout import NumTabs
from .layout import TabsLeadLines
from .layout import WhiteSpaceRatio
from .lexical import AvgLineLength
from .lexical import AvgParams
from .lexical import NumFunctions
from .lexical import NumKeyword
from .lexical import NumKeywords
from .lexical import NumLiterals
from .lexical import NumTernary
from .lexical import NumTokens
from .lexical import StdDevLineLength
from .lexical import StdDevNumParams
from .lexical import WordUnigramTF
from .syntactic import ASTNodeBigramsTF
from .syntactic import ASTNodeTypesTF
from .syntactic import JavaKeywords
from .syntactic import MaxDepthASTNode
from .utils import build_mapping_to_ids
def calculate_features(path: str) -> Dict:
"""
Calculates a set of features for the given source file.
:param path: path to the file
:return: dictionary with features
"""
with open(path, 'r', errors='ignore') as file:
code = file.read()
file_length = len(code)
tokens = list(javalang.tokenizer.tokenize(code))
tree = javalang.parse.parse(code)
features = {}
# LEXICAL FEATURES
features.update(WordUnigramTF.calculate(tokens))
features.update(NumKeyword.calculate(tokens, file_length))
features.update(NumTokens.calculate(tokens, file_length))
features.update(NumLiterals.calculate(tokens, file_length))
features.update(NumKeywords.calculate(tokens, file_length))
features.update(NumFunctions.calculate(tree, file_length))
features.update(NumFunctions.calculate(tree, file_length))
features.update(NumTernary.calculate(tree, file_length))
features.update(AvgLineLength.calculate(code))
features.update(StdDevLineLength.calculate(code))
features.update(AvgParams.calculate(tree))
features.update(StdDevNumParams.calculate(tree))
# LAYOUT FEATURES
features.update(NumTabs.calculate(code))
features.update(NumSpaces.calculate(code))
features.update(NumEmptyLines.calculate(code))
features.update(WhiteSpaceRatio.calculate(code))
features.update(NewLineBeforeOpenBrace.calculate(code))
features.update(TabsLeadLines.calculate(code))
# SYNTACTIC FEATURES
features.update(MaxDepthASTNode.calculate(tree))
features.update(ASTNodeBigramsTF.calculate(tree))
features.update(ASTNodeTypesTF.calculate(tree))
features.update(JavaKeywords.calculate(tokens))
return features
def calculate_features_for_files(files: List[str], n_jobs: int = 4) -> List[Dict]:
"""
Calculates sets of features for the given source files.
:param files: list of files
:param n_jobs: number of jobs
:return: list with features for each source file
"""
with Parallel(n_jobs=n_jobs) as pool:
features = pool(delayed(calculate_features)(path) for path in files)
return features
def build_sample(sample: Dict, feature_to_id: Dict) -> np.array:
features = np.empty(len(feature_to_id))
features[:] = np.nan
for key, value in sample.items():
index = feature_to_id[key]
features[index] = value
return features
def build_dataset(samples: List[Dict], n_jobs: int = 4) -> pd.DataFrame:
"""
Builds a pandas data frame from the given list of feature sets.
:param samples: list of features
:param n_jobs: number of jobs
:return: data frame with all features
"""
feature_names = set()
for sample in samples:
feature_names |= sample.keys()
feature_names = sorted(feature_names)
feature_to_id = build_mapping_to_ids(feature_names)
with Parallel(n_jobs=n_jobs) as pool:
features = pool(delayed(build_sample)(sample, feature_to_id) for sample in samples)
features = pd.DataFrame(features)
features.columns = feature_names
return features
|
module Proofs.TranslationInvarianceTheory
import Common.Util
import Specifications.TranslationInvariance
import Proofs.GroupTheory
import Proofs.GroupCancelationLemmas
import Symmetry.Opposite
%default total
%access export
infixl 8 #
composeOrder : {(#) : Binop s} -> {(<=) : Binrel s} ->
PartiallyOrderedMagmaSpec (#) (<=) -> (a,b,c,d : s) ->
a <= b -> c <= d -> a # c <= b # d
composeOrder spec a b c d ab cd =
let pp = translationInvariantR spec a b c ab
qq = translationInvariantL spec c d b cd
in transitive (order spec) (a # c) (b # c) (b # d) pp qq
orderInverseL : {(#) : Binop s} -> {(<=) : Binrel s} ->
PartiallyOrderedGroupSpec (#) e inv (<=) -> (a,b,c : s) ->
a # c <= b -> c <= inv a # b
orderInverseL spec a b c given = rewrite sym o2 in o1 where
o1 : inv a # (a # c) <= inv a # b
o1 = translationInvariantL (invariantOrder spec) (a # c) b _ given
o2 : inv a # (a # c) = c
o2 = groupCancel1bis (group spec) a c
orderInverseR : {(#) : Binop s} -> {(<=) : Binrel s} ->
PartiallyOrderedGroupSpec (#) e inv (<=) -> (a,b,c : s) ->
a # c <= b -> a <= b # inv c
orderInverseR spec a b c = orderInverseL (opposite spec) c b a
inverseReversesOrder : {(#) : Binop s} ->
PartiallyOrderedGroupSpec (#) _ inv leq ->
leq a b -> inv b `leq` inv a
inverseReversesOrder spec {a} {b} given = rewriteRelation leq o3 o4 o2 where
o1 : inv a # a `leq` inv a # b
o1 = translationInvariantL (invariantOrder spec) _ _ (inv a) given
o2 : inv a # a # inv b `leq` inv a # b # inv b
o2 = translationInvariantR (invariantOrder spec) (inv a # a) (inv a # b) _ o1
o3 : inv a # a # inv b = inv b
o3 = groupCancel1 (group spec) a _
o4 : inv a # b # inv b = inv a
o4 = groupCancel3bis (group spec) _ b
groupInverseAndOrder : {(#) : Binop s} ->
PartiallyOrderedGroupSpec (#) e inv leq -> (a,b : s) ->
a `leq` b -> a # inv b `leq` e
groupInverseAndOrder spec a b given = rewrite sym o2 in o1 where
o1 : a # inv b `leq` b # inv b
o1 = translationInvariantR (invariantOrder spec) a b _ given
o2 : b # inv b = e
o2 = inverseR (group spec) b
invertNegative : {(<=) : Binrel s} ->
PartiallyOrderedGroupSpec _ zero neg (<=) -> (a : s) ->
a <= zero -> zero <= neg a
invertNegative spec a negative = rewrite sym o2 in o1 where
o1 : neg zero <= neg a
o1 = inverseReversesOrder spec negative
o2 : neg zero = zero
o2 = groupInverseNeutral (group spec)
|
function[box,flag] = getBox2(theta,thetaDot,x,xDot)
theta = wrapTo180(rad2deg(theta));
thetaDot = rad2deg(thetaDot);
flag = 0;
if(theta>=-180&&theta<-150)
thetaBucket = 1;
flag = -1;
elseif(theta>=-150&&theta<-120)
thetaBucket = 2;
flag = -1;
elseif(theta>=-120&&theta<-90)
thetaBucket = 3;
flag = -1;
elseif(theta>=-90&&theta<-60)
thetaBucket = 4;
flag = -1;
elseif(theta>=-60&&theta<-30)
thetaBucket = 5;
flag = -1;
elseif(theta>=-30&&theta<-24)
thetaBucket = 6;
flag = -1;
elseif(theta>=-24&&theta<-18)
thetaBucket = 7;
flag = -1;
elseif(theta>=-18&&theta<-12)
thetaBucket = 8;
flag = -1;
elseif(theta>=-12&&theta<-6)
thetaBucket = 9;
elseif(theta>=-6&&theta<-1)
thetaBucket = 10;
elseif(theta>=-1&&theta<0)
thetaBucket = 11;
elseif(theta>=0&&theta<1)
thetaBucket =12;
elseif(theta>=1&&theta<6)
thetaBucket = 13;
elseif(theta>=6&&theta<12)
thetaBucket = 14;
elseif(theta>=12&&theta<18)
thetaBucket = 15;
flag = -1;
elseif(theta>=18&&theta<24)
thetaBucket = 16;
flag = -1;
elseif(theta>=24&&theta<30)
thetaBucket = 17;
flag = -1;
elseif(theta>=30&&theta<60)
thetaBucket = 18;
flag = -1;
elseif(theta>=60&&theta<90)
thetaBucket = 19;
flag = -1;
elseif(theta>=90&&theta<120)
thetaBucket = 20;
flag = -1;
elseif(theta>=120&&theta<150)
thetaBucket = 21;
flag = -1;
elseif(theta>=150&&theta<=180)
thetaBucket = 22;
flag = -1;
end
if (x < -2.4 || x > 2.4)
flag = -1;
xBucket = 1;
end
if (x<-0.8&&x>=-2.4)
xBucket = 1;
elseif (x<=0.8&&x>=-0.8)
xBucket = 2;
elseif (x<=2.4&&x>0.8)
xBucket = 3;
end
if (xDot<-0.5)
xDotBucket = 1;
elseif (xDot>=-0.5&&xDot<=0.5)
xDotBucket = 2;
else
xDotBucket = 3;
end
if (thetaDot<-50)
thetaDotBucket = 1;
elseif (thetaDot>=-50&&thetaDot<=50)
thetaDotBucket = 2;
else
thetaDotBucket = 3;
end
box = sub2ind([22,3,3,3],thetaBucket,thetaDotBucket,xBucket,xDotBucket);
|
export RunSummary, DataFrame
using TimeZones, DataFrames
struct RunSummary
time::Vector{Float64} # seconds
dist::Vector{Float64}
alt::Vector{Float64}
hr::Vector{Float64}
unit_time::Bool
start_time::ZonedDateTime
function RunSummary(n::Int, time::ZonedDateTime; unit_time::Bool = false)
return new(nan_vec(n), nan_vec(n), nan_vec(n), nan_vec(n), unit_time, time)
end
end
function nan_vec(n::Int)
v = Vector{Float64}(undef, n)
fill!(v, NaN)
return v
end
import Base.length
function length(rs::RunSummary)
return length(rs.time)
end
# function copyrow!(dest::RunSummary, src::RunSummary, ind::Int)
# dest.time[i] = src.time[i]
# dest.dist[i] = src.dist[i]
# dest.hr[i] = src.hr[i]
# dest.alt[i] = src.alt[i]
# end
function unit_run_sum(rs::RunSummary; unit_time = 1.0)
n = Int(round(sum(rs.time)))
unit_rs = RunSummary(n, rs.start_time, unit_time = true)
m = length(rs)
leftover = 0.0
ind = 1
res_time = 0.0
res_dist = 0.0
old_unit_dist = 0.0
old_hr = rs.hr[1]
old_alt = rs.alt[1]
old_unit_Δhr = 0.0
for i = 1:m
t = rs.time[i] + res_time
if t < unit_time
res_time = t
res_dist += rs.dist[i]
continue
end
unit_dist = rs.dist[i] / rs.time[i]
unit_alt = rs.alt[i] / rs.time[i]
unit_Δhr = (rs.hr[i] - old_hr) / rs.time[i]
α = res_time / unit_time
β = unit_time - α
unit_rs.time[ind] = unit_time
unit_rs.dist[ind] = α * old_unit_dist + β * unit_dist
unit_rs.hr[ind] = old_hr + α * old_unit_Δhr + β * unit_Δhr
unit_rs.alt[ind] = α * old_alt + β * unit_alt
ind += 1
t -= unit_time
while t >= 1.0
unit_rs.time[ind] = unit_time
unit_rs.dist[ind] = unit_dist
unit_rs.hr[ind] = unit_rs.hr[ind - 1] + unit_Δhr
unit_rs.alt[ind] = unit_alt
ind += 1
t -= unit_time
end
res_time = t
old_unit_dist = unit_dist
old_hr = unit_rs.hr[ind - 1]
unit_rs.hr[ind - 1]
old_alt = unit_alt
end
return unit_rs
end
function RunMetrics.DataFrame(rs::RunSummary)
df = DataFrames.DataFrame(time = rs.time,
dist = rs.dist,
alt = rs.alt,
hr = rs.hr,
start_time = fill(rs.start_time, length(rs)))
return df
end
|
##############
# Bands
##############
#
# TODO: add extrapolation too (second half of make_bands)
export map_onto_bands, make_1Dglacier, map_back_to_2D, map_back_to_2D!
# used to round (up or down) the binsize to the next decimal place
_binround(binsize::Number) = -floor(Int, log10(abs(binsize)))
_binround(binsize) = 0
"""
make_1Dglacier(dem::Gridded, binsize_or_bins, glaciermask=BitArray([]);
binround=_binround(binsize_or_bins),
window_dem_smooth=0.0,
window_width_smooth=0.0,
alpha_min=deg2rad(0.4),
alpha_max=deg2rad(60.0),
FILL=-9999999.0)
Makes a 1D glacier from a 2D DEM by using Huss' elevation band trick.
Returns:
- bands -- elevation bands. The i-th band is (bands[i], bands[i]+step(bands))
- bandi -- linear index into dem which assigns each cell to a elevation band
- alphas, areas, lengths, widths, x, xmid -- elevation band slope, area, etc
- dem -- the used DEM, a possibly smoothed version of the input DEM
- alpha2d -- slopes at each point of `dem`
"""
function make_1Dglacier(dem::Gridded, binsize_or_bins, glaciermask=trues(size(dem.v));
binround=_binround(binsize_or_bins),
min_bin_number_ends=0,
min_bands=4,
window_dem_smooth=0.0,
window_width_smooth=0.0,
alpha_min=deg2rad(0.4),
alpha_max=deg2rad(60.0),
FILL=-9999999.0,
verbose=true)
dx = step(dem.x)
# Smooth dem to get smooth alpha, smoother bands. This is in
# particular important when there is cross-flow bumpiness, such as
# on Uaar. However, it can also be bad. YMMV, check!
if window_dem_smooth>0
dem = deepcopy(dem)
nofillmask = dem.v.!=FILL
mask = nofillmask .& glaciermask
dem.v[:] = boxcar(dem.v, round(Int,window_dem_smooth/dx), mask, (!).(mask))
dem.v[(!).(nofillmask)] = FILL
end
# no FILL inside glaciermask
@assert !any(dem.v[glaciermask].==FILL)
@assert !any(isnan.(dem.v[glaciermask]))
# 2D slopes
ret_nans = false
alpha2d = absslope(dem, glaciermask, ret_nans)
bands, bandi = bin_grid(dem, binsize_or_bins, glaciermask,
binround=binround, min_bin_number_ends=min_bin_number_ends,
min_bands=min_bands)
@assert length(bands)>=min_bands "Need at least $min_bands elevation bins, only got $(length(bands))"
nb = length(bands)
cellsz = step(dem.x)^2
totalarea = sum(glaciermask)*cellsz
malphas, widths, lengths, areas = (zeros(nb) for i=1:4)
dzs = zeros(nb)
for i=1:nb
ind = bandi[i]
if i!=nb
dzs[i] = abs(bands[i+1]-bands[i])
else
# TODO: a hack. Fix
dzs[i] = abs(bands[i]-bands[i-1])
end
# this is the critical step:
malphas[i] = band_slope!(alpha2d[ind], i, alpha_min, alpha_max)
areas[i] = length(ind)*cellsz
lengths[i] = dzs[i]/tan(malphas[i])
widths[i] = areas[i]/lengths[i]
end
# update missing bands
for i=1:nb
if malphas[i]==-9999
ma1 = malphas[max(1,i-1)]
ma2 = malphas[min(nb,i+1)]
if ma1==-9999 && ma2==-9999
error("Too many consecutive bands for which no slope could be calculated: $(max(1,i-1):min(nb,i+1))")
elseif ma1==-9999
malphas[i] = ma2
elseif ma2==-9999
malphas[i] = ma1
else
malphas[i] = 1/2*(ma1+ma2)
end
lengths[i] = dzs[i]/tan(malphas[i])
widths[i] = areas[i]/lengths[i]
end
end
# Smooth the width:
# Note, this can make the malphas noisy!
if window_width_smooth>0
widths = boxcar(widths, round(Int, window_width_smooth/mean(dzs) ))
for i=1:nb
# make sure length is zero when area is zero
lengths[i] = areas[i]==widths[i]==0 ? zero(lengths[i]) : areas[i]/widths[i]
malphas[i] = atan(dzs[i]/lengths[i])
@assert malphas[i]>=0
end
end
x = vcat(0,cumsum(lengths))
xmid = x[1:end-1] + diff(x)/2
# tests
# if abs(totalarea-sum(areas))>1.0
# error("Something's amiss, sum of area of bands $(sum(areas)) not equal total area $totalarea,")
# end
# check band length against diagonal
tmp = sum(glaciermask,2)
xextent = (findlast(tmp.>0)-findfirst(tmp.>0))*dx
tmp = sum(glaciermask,1)
yextent = (findlast(tmp.>0)-findfirst(tmp.>0))*dx
box_diag = sqrt(xextent^2 + yextent^2)
if verbose && abs(sum(lengths)-box_diag)/box_diag>0.4
warn("Glacier length from might be wrong. Band-length: $(sum(lengths)/1e3)km, bounding-box diag: $(box_diag/1e3)km")
end
return bands, bandi, malphas, areas, lengths, widths, x, xmid, dem, alpha2d
end
"""
band_slope!(alphas, bandnr, alpha_min=deg2rad(0.4), alpha_max=deg2rad(60.0))
Need to calculate a meaningful mean of the slopes in a elevation bin.
*This is tricky but critical!*
One check can be that all the bin-lengths should add up to the total
glacier length.
Input:
- alphas -- slope angles in one band (these are sorted in place, thus the ! in the function name)
- bandnr -- which band those alphas belong to (only used for error message)
- alpha_max, alpha_min -- maximal and minimal allowed slope
"""
function band_slope!(alphas, bandnr, alpha_min, alpha_max)
# parameters
ratio_fac = 2
f_q5 = 0.05
f_q20 = 0.2
f_q80 = 0.8
q_band = (0.55, 0.95)
n = length(alphas)
if n==0
return -9999*one(alpha_min)
# error("Band $bandnr has no elements!")
# return deg2rad(45)
end
# magic slope calculation
sort!(alphas)
# calculate indices of 5th, 20th and 80th percentiles:
iq5 = max(1,round(Int,n*f_q5))
iq20 = max(1,round(Int,n*f_q20))
iq80 = min(n,round(Int,n*f_q80))
# angle of those quantiles:
q5, q20, q80 = [max(rad2deg.(i),eps(alpha_min)) for i in (alphas[iq5], alphas[iq20], alphas[iq80])]
# Now some of Matthias' magic:
a = (q20/q80)*ratio_fac # 2x ratio of angles
a = min(a, q_band[2])
a = max(a, q_band[1]) # scaled to lie [0.55, 0.95]
iq_magic = round(Int,n*a) # set a "new" magic quantile to that value
q_magic = rad2deg(alphas[iq_magic])
# only use indices within those quantiles
ind = q5 .<= rad2deg.(alphas) .< q_magic
out = sum(ind)>1 ? mean(alphas[ind]) : mean(alphas)
# limit alphas
out = max(alpha_min, out)
out = min(alpha_max, out)
return out
end
"""
Bins a gird into bands. Often used to bin a DEM into elevation bands.
- g -- to be binned ::Gridded or ::Matrix
- binsize_or_bins -- bin size or the bins (a Range)
- mask -- specify if not all locations of a gird should be binned.
KW:
- binround -- floor the bin-start using this many digits (see help of floor)
- min_bin_number_ends -- minimum number of elements in the uppermost and lowermost
band. If below, merge those cells into the first viable band.
- min_bands -- minimum number of bands produced (3). Not integrated with min_bin_number_ends!
Return:
- bands -- a range of the bands, e.g. 0.0:10.0:100.0
- bandi -- a Vector{Vector{Int}} of length(bands) with each element
containing the indices of cells in the band
"""
function bin_grid(g::Gridded, binsize_or_bins, mask=BitArray([]);
binround=_binround(binsize_or_bins), min_bin_number_ends=0, min_bands=4)
bin_grid(g.v, binsize_or_bins, mask;
binround=binround, min_bin_number_ends=min_bin_number_ends,
min_bands=min_bands)
end
function bin_grid(v::Matrix, binsize::Number, mask=BitArray([]);
binround=_binround(binsize), min_bin_number_ends=0, min_bands=4)/
if isempty(mask)
v = v
ginds = 1:length(v)
else
@assert size(mask)==size(v)
v = v[mask]
ginds = find(mask[:])
end
nv = length(v)
bins = 1.0:-1
while length(bins)<=min_bands
mi, ma = minimum(v), maximum(v)
if binsize>=0
binstart = floor(mi, binround)
binend = floor(ma, binround) # better: `ceil(ma, binround) - binsize` ?
else
binstart = ceil(ma, binround)
binend = ceil(mi, binround) # better: `ceil(ma, binround) - binsize` ?
end
@assert !isnan(binstart) && !isnan(binend)
bins = binstart:binsize:binend # these are the start of the bins
# decreas binsize for next round
binsize = step(bins)/2
end
return _bin_grid_kernel(bins, nv, v, ginds, min_bin_number_ends)
end
function bin_grid(v::Matrix, bins::AbstractRange, mask=BitArray([]); min_bin_number_ends=0, kw...)
if isempty(mask)
v = v
ginds = 1:length(v)
else
@assert size(mask)==size(v)
v = v[mask]
ginds = find(mask[:])
end
nv = length(v)
_bin_grid_kernel(bins, nv, v, ginds, min_bin_number_ends)
end
@inbounds function _bin_grid_kernel(bins, nv, v, ginds, min_bin_number_ends)
# initialize output
bandi = Vector{Int}[]
for b in bins
ind = Int[]
push!(bandi, ind)
end
# fill it
for j=1:nv
if step(bins)>0
i = searchsortedlast(bins, v[j])
i = i==0 ? 1 : i # if smaller then add to lowest bin
else
# https://github.com/JuliaLang/julia/issues/18653
i = searchsortedlast(collect(bins), v[j], rev=true)
i = i==0 ? 1 : i # if smaller then add to highest bin (i.e. bins[1])
end
push!(bandi[i], ginds[j])
end
# remove top and bottom bins if too few elements
inds2pop = [1,length(bandi)] # remove up to and including these bandi
num = [0,0]
for i = 1:length(bandi)
inds2pop[1] = i
if length(bandi[i])+num[1]>=min_bin_number_ends
break
end
num[1] +=length(bandi[i])
end
for i = length(bandi):-1:1
inds2pop[2] = i
if length(bandi[i])+num[2]>=min_bin_number_ends
break
end
num[2] +=length(bandi[i])
end
# add the dropped cells to the next/previous band
append!(bandi[inds2pop[1]], vcat(bandi[1:inds2pop[1]-1]...))
append!(bandi[inds2pop[2]], vcat(bandi[inds2pop[2]+1:end]...))
return bins[inds2pop[1]:inds2pop[2]], bandi[inds2pop[1]:inds2pop[2]]
end
import Interpolations
"""
Bins a trajectory using a grid
- tr -- trajectory to be binned
- g -- g.v of grid used for binning
- binsize_or_bins -- bin size or the bins (a Range)
- mask -- specify if not all locations of a gird should be binned.]
KW:
- binround -- floor the bin-start using this many digits (see help of floor)
"""
function bin_traj(tr::Traj, g::Gridded, binsize_or_bins, mask=trues(size(g.v)); binround=_binround(binsize_or_bins))
@assert size(mask)==size(g.v)
demi = Interpolations.interpolate((g.x, g.y), g.v, Interpolations.Gridded(Interpolations.Linear()) )
maski = Interpolations.interpolate((g.x, g.y), mask, Interpolations.Gridded(Interpolations.Constant()) ) # returns Int!
v = [demi[x,y] for (x,y) in zip(tr.x,tr.y)]
vm = Bool[maski[x,y] for (x,y) in zip(tr.x,tr.y)]
v = v[vm]
ginds = find(vm)
nv = length(v)
if isa(binsize_or_bins, Number)
mi, ma = minimum(v), maximum(v)
binstart = floor(mi, binround)
binend = floor(ma, binround)
bins = binstart:binsize_or_bins:binend # these are the start of the bins
else
bins = binsize_or_bins
end
_bin_grid_kernel(bins, nv, v, ginds, 0)
end
"""
map_onto_bands(bandi, field, fn=mean)
Map a field onto the (elevation) bands. The field needs to have the
same size as the original binned-grid.
Input:
- bandi -- as returned by bin_grid
- field -- the field, either a Matrix or a Gridded
- fn -- the function to do the reduction with. Default==mean
- fill -- fill value, if set, ignore those points
Output
- the value of the field on the bands. If no values were found in a band,
then return NaN.
"""
function map_onto_bands(bandi, field::Matrix, fn=mean, fill=nothing)
resT = typeof(fn(field[bandi[1]])) # to get result type
out = zeros(resT, length(bandi))
for i in 1:length(bandi)
count = 0
for j=1:length(bandi[i])
val = field[bandi[i][j]]
if val!=fill
# only use the ones which have no fill
out[i] += val
count+=1
end
end
out[i] /=count
end
return out
end
map_onto_bands(bandi, field::Gridded, fn=mean, fill=NaN) = map_onto_bands(bandi, field.v, mean, fill)
"""
map_back_to_2D(dims2d, bandi, field1d)
Maps 1D field back onto 2D. More or less inverse of map_onto_bands.
"""
function map_back_to_2D(dims2d, bandi, field1d)
out = zeros(eltype(field1d), dims2d)
map_back_to_2D!(out, bandi, field1d)
out
end
"""
map_back_to_2D!(out2d, bandi, field1d)
Maps 1D field back onto 2D. More or less inverse of map_onto_bands.
"""
function map_back_to_2D!(out, bandi, field1d)
for (i,is) in enumerate(bandi)
out[is] = field1d[i]
end
nothing
end
"""
bins2matrix(g::Union{Gridded,Matrix}, bands, bandi) -> binmat
Return a matrix which gives the bin-number of each its (i,j) locations.
Locations not binned (i.e. masked) are ==0.
"""
bins2matrix(g::Gridded, bands, bandi) = bins2matrix(g.v, bands, bandi)
function bins2matrix(g::Matrix, bands, bandi)
out = zeros(Int, size(g))
for (n,b) in enumerate(bandi)
for i in b
out[i] = n
end
end
return out
end
"""
bandi_for_other_grid(bands, bandi, g::Gridded,
othergrid::Gridded, othermask=trues(size(othergrid.v))
bandi_for_other_grid(bands, bandi, g::Gridded,
othergrid::Gridded, othermask=trues(size(othergrid.v)))
Returns vector of indices (bandi) to map a different grid (othergird) onto the
bands encoded in `binmat` (or `bands, bandi`) and grid `g`. It only
maps points onto bands which are within the mask applied to generate
the bands. Additionally & optionally, a mask for the othergrid can
also be given. Return:
bandi
"""
function bandi_for_other_grid(bands, bandi::Vector{Vector{Int}}, g::Gridded,
othergrid::Gridded, othermask=trues(size(othergrid.v)))
binmat=bins2matrix(g, bands, bandi)
bandi_for_other_grid(bands, bandi, binmat, g, othergrid, othermask)
end
function bandi_for_other_grid(bands, bandi, binmat::Matrix{Int}, g::Gridded,
othergrid::Gridded, othermask=trues(size(othergrid.v)) )
og = othergrid
@assert size(othergrid)==size(othermask)
if g.x!=og.x || g.y!=og.y
bandi_ = [Int[] for i=1:length(bands)]
s2i = LinearIndices(og.v)
itpm = Interpolations.interpolate((g.x, g.y), binmat,
Interpolations.Gridded(Interpolations.Constant()) );
itpm = Interpolations.extrapolate(itpm, 0);
for j=1:size(og.v,2)
for i=1:size(og.v,1)
if othermask[i,j]
ind = convert(Int, itpm(og.x[i], og.y[j]))
if ind>0
push!(bandi_[ind], s2i[i, j])
end
end
end
end
else
bandi_ = deepcopy(bandi)
end
return bandi_
end
#####################
# Extrapolation of IV
#####################
"""
To specify which edge of a cell is meant. `_noedge` can be used if none
is used.
"""
@enum Loc _noedge=0 left=1 right=2 lower=3 upper=4
"Orientation of a line"
@enum Orientation nohand=0 lefthand=1 righthand=2
"""
One cell-edge of a regular gird of cells. Specified as a cell
and which edge of the four edges of a cell.
TODO:
Arguably not the best datastructure for what is done below.
"""
struct Edge
i::Int # cell ind
j::Int # cell ind
loc::Loc
end
const noedge = Edge(-1,-1,_noedge)
Base.show(io::IO,e::Edge) = println(io, "($(e.i),$(e.j),$(e.loc))")
"""
get_nodes(e::Edge)
Returns the start and end nodes of the edge on the staggered grid.
The nodes are returned such that the cell is on the right of the edge.
"""
function get_nodes(e::Edge)
i,j,loc = e.i, e.j, e.loc
if loc==left
return (i,j), (i,j+1)
elseif loc==right
return (i+1,j+1), (i+1,j)
elseif loc==lower
return (i+1,j), (i,j)
elseif loc==upper
return (i,j+1), (i+1,j+1)
else
error("!")
end
end
"""
orientation(e1::Edge) -> always left
orientation(e1::Edge, e2::Edge)
Return whether the cells are on left, right or both of the two cells.
If not connected throws an error or return `_noedge`, depending on
`throwerror` flag.
"""
function orientation(e1::Edge, e2::Edge, throwerror=true)::Orientation
n1,n2 = get_nodes(e1)
m1,m2 = get_nodes(e2)
if n2==m1
return righthand
elseif n1==m2
return lefthand
elseif n1==m1 || n2==m2
return nohand
elseif throwerror
error("The two edges:\n $e1 $e2 are not connected")
else
return nohand
end
end
orientation(e1::Edge)::Orientation = lefthand
"""
A line made up of a continuous (and sorted) collection of edges. Note
that the edges themselves also have a cell associated with them. So,
a Line also a collection of (possibly repeated) cells.
The line has an orientation: when traversing the Line from 1 to n, all
cells are on the right of their edge.
"""
struct Line
edges::Vector{Edge}
end
#Base.show(io::IO,l::Line) = show(io, l.edges)
Base.getindex(l::Line,i) = l.edges[i]
Base.length(l::Line) = length(l.edges)
"""
orientation(l::Line)
Returns the orientation of a line: `left` means cell is on left of line.
"""
orientation(l::Line)::Orientation = orientation(l.edges)
function orientation(l::Vector)::Orientation
if length(l)==0
error("Line has length 0")
end
if length(l)==1
# println("Line has length $(length(l)). Too short to establish orientation.")
return orientation(l[1]) # returns `left`
end
# establish orientation of first two segments
ori = orientation(l[1],l[2])
for i=3:length(l)
ori2 = orientation(l[i-1],l[i])
if ori2!=ori
println("""
Line changes orientation between edge # $(i-2) and $i from $ori to $ori2.
e0: $(l[i-2])
e1: $(l[i-1])
e2: $(l[i])
""")
return _noedge
end
end
return ori
end
"""
next_edge!(edges::Set{Edge}, edge::Edge, testori::Orientation)
Return an adjacent edge of input edge such that the orientation of the
two edges is equal `testori`. Pops returned edge off `edges`. If no
edge is found, return `Edge(-1,-1,nodege)`.
"""
function next_edge!(edges::Set{Edge}, edge::Edge, testori::Orientation)
edge.loc==_noedge && error("Not a proper edge: $edge")
locs = (left,right,lower,upper)
for i=[0,-1,1],j=[0,-1,1]
for loc in locs
test_edge = Edge(edge.i+i,edge.j+j,loc)
if orientation(edge, test_edge,false)==testori && (test_edge in edges)
return pop!(edges, test_edge)
end
end
end
# nothing found
return noedge
end
"""
get_ux_uy(dem, mask)
The direction and magnitude of steepest descent on each point within the mask.
"""
function get_ux_uy(dem, mask)
ux,uy = (-).(gradient3by3(dem, mask))
return ux, uy
end
"""
get_edges_on_boundary(bands, bandi, binmat, landmask=nothing) -> es
Return a list of sets of cell-edges which are at the boundary.
typeof(es) == Dict{Tuple{Int,Int},Set{Edge}}()
which maps (bandnr,otherbandnr) => Set of edges
"""
function get_cells_on_boundary(bands, bandi, binmat, landmask=nothing)
error("Not updated to Julia 1.0 yet")
dims = size(binmat)
i2s = CartesianIndices(binmat)
if landmask!=nothing
# encode sea cells in binmat
binmat = copy(binmat)
binmat[(landmask.==0) .& (binmat.==0)] = -1
end
# The boundaries of all bands:
# (bandnr,otherbandnr) => Set of edges
edges_at_boundaries = Dict{Tuple{Int,Int},Set{Edge}}()
# Loop to identify all boundary cells of each band and determine
# which cell-edges are on the boundary:
for (ib,bup) in enumerate(bands)
for I in bandi[ib]
i,j = i2s[I].I
loc = 1
# left-right
for ii=-1:2:1
if 1<=i+ii<=dims[1] # skip if outside of binmat
iother = binmat[i+ii,j]
if iother!=ib
push!(get!(edges_at_boundaries, (ib, iother), Set{Edge}()),
Edge(i,j,loc))
end
end
loc+=1
end
# lower-upper
for jj=-1:2:1
if 1<=j+jj<=dims[2] # skip if outside of binmat
iother = binmat[i,j+jj]
if iother!=ib
push!(get!(edges_at_boundaries, (ib, iother), Set{Edge}()),
Edge(i,j,loc))
end
end
loc+=1
end
end
end
return edges_at_boundaries
end
"""
calc_boundaries(bands, bandi, binmat, landmask=nothing)
Calculate interface between bands and also to outside (bandnr==0) and
sea-cells (bandnr==-1).
Returns `boundaries` which is `bandnr => otherbandnr => Vector{Line}`
i.e. the collection of all boundary lines for each
`(bandnr,otherbandnr)`. Each line has the elevation band on its
*left*. For cells outside the glacier `otherbandnr==0` except if
'landmask` is given, then sea-cells have `otherbandnf==-1`.
Of type `Vector{Dict{Int,Vector{Line}}}()`.
"""
function calc_boundaries(bands, bandi, binmat, landmask=nothing)
dims = size(binmat)
if landmask!=nothing
# encode sea cells in binmat
binmat = copy(binmat)
binmat[(landmask.==0) .& (binmat.==0)] = -1
end
# The boundaries of all bands:
# (bandnr,otherbandnr) => Set of edges
edges_at_boundaries = get_cells_on_boundary(bands, bandi, binmat, landmask)
# bandnr => otherbandnr => Vector{Line}
boundaries = [Dict{Int,Vector{Line}}() for i=1:length(bands)]
for ((band,otherband), edges) in edges_at_boundaries
# # delete:
# band, otherband = 2,0
# edges = boundaries[(band,otherband)]
output = Line[]
# Take one starting point and go in both directions until no
# more neighbors found.
while length(edges)>0
firstedge = first(edges)
delete!(edges, firstedge)
out = [Edge[], Edge[]]
for ii=1:2 # first lefthand Orientation(1), then righthand Orientation(2)
curedge = firstedge
while curedge!=noedge
push!(out[ii], curedge)
curedge = next_edge!(edges, curedge, Orientation(ii))
end
end
prepend!(out[2], reverse(out[1][2:end]))
# make sure the elevation band is on the line's left:
ori = orientation(out[2])
if ori == righthand
push!(output, Line(reverse(out[2])))
elseif ori==lefthand
push!(output, Line(out[2]))
elseif ori==nohand
error("""
Constructed line has not a consistent orientation.
Band: $band
Otherband: $otherband
"""
)
end
end
boundaries[band][otherband] = output
end
return boundaries
end
"""
calc_fluxdir(l::Line, ux, uy, window, dx, bands) -> flux,ii,jj,fluxdirx,fluxdiry
Calculated the flux-direction on a Line by taking a running average of (ux,uy)
over some part of it of length window. Also returns the flux to use and the upstream
cell `(ii,jj)`. The flux across the k-th edge is then given by:
flux[k] * h[ii[k],jj[k]] * u[ii[k],jj[k]]
where h is the thickness and u the depth averaged velocity.
The flux across the line is
sum(flux .* h_line .* u_line)
Input:
- l::Line
- ux,uy: unsmoothed velocity field (calculated as fall-line of surface DEM with get_ux_uy)
- window : length of smoothing window (along band) in number of edges
- dx : grid spacing
- bands::AbstractRange : the elevation bands
Output:
- flux : the flux
- ii, jj : indices of upstream cell
- fluxdirx,fluxdiry : flux direction at upstream cell ii, jj
Notes:
- this is not 100% correct but probably close enough.
- now the averaging is over all edges. Arguably it could be done over cells?
"""
function calc_fluxdir(l::Line, ux, uy, window::Int, dx, bands)
edges = l.edges
ne = length(edges)
# flux in x and y-direction on the cell associated with a Line edge:
fluxdirx = zeros(ne)
fluxdiry = zeros(ne)
# the flux which goes with the edge:
flux = zeros(ne)
# indices of upstream cell
ii = zeros(Int,ne)
jj = zeros(Int,ne)
R = CartesianIndices(size(edges))
I1, Iend = first(R), last(R)
for I in R
fx, fy = 0.0, 0.0
for J in CartesianIndices(max(I1, I-I1*window), min(Iend, I+I1*window))
i,j,loc = edges[J].i, edges[J].j, edges[J].loc
# average ux,uy in the two cells
if loc==left
fx += (ux[i-1,j] + ux[i,j])
fy += (uy[i-1,j] + uy[i,j])
elseif loc==right
fx += (ux[i+1,j] + ux[i,j])
fy += (uy[i+1,j] + uy[i,j])
elseif loc==lower
fx += (ux[i,j-1] + ux[i,j])
fy += (uy[i,j-1] + uy[i,j])
elseif loc==upper
fx += (ux[i,j+1] + ux[i,j])
fy += (uy[i,j+1] + uy[i,j])
else
error()
end
end
norm = sqrt(fx^2+fy^2)
fx, fy = fx/norm, fy/norm
fluxdirx[I] = fx
fluxdiry[I] = fy
# figure out upstream cell
i,j,loc = edges[I].i, edges[I].j, edges[I].loc
ii[I],jj[I],flux[I] =
if loc==left
fx<0 ? (i,j,fx*dx) : (i-1,j,fx*dx)
elseif loc==right
fx<0 ? (i+1,j,-fx*dx) : (i,j,-fx*dx)
elseif loc==lower
fy<0 ? (i,j,fy*dx) : (i,j-1,fy*dx)
else #if loc==upper
fy<0 ? (i,j+1,-fy*dx) : (i,j,-fy*dx)
end
end
# for reverse ordered bands, need a sign flip
sig = sign(bands[2]-bands[1])
return sig*flux,ii,jj,fluxdirx,fluxdiry
end
"""
calc_u(q1d, boundaries, u_trial, thick,
ux, uy, dx, mask, bands, bandi, lengths,
flux_dir_window, # in [m]
boxcarM::AbstractMatrix or window_frac,
scale_u=ones(q1d);
plotyes=false,
x=nothing, y=nothing)
Calculates a 2D field of depth averaged ice flow speed `ubar` which has the
same flux across elevation band boundaries as the supplied 1D flux
`q1d`. Only `q1d` is a flow-band variable. The flux across elevation
bands is calculated with `calc_fluxdir`.
Input:
- q1d: 1d flux (m/a) on elevation bands
- boundaries: from calc_boundaries
- u_trial: 2D velocity field which has the right shape (say cross-valley) but not the right magnitude
- thick: ice thickness
- ux,uy: unsmoothed velocity field (calculated as fall-line of surface DEM with get_ux_uy)
- dx: grid size
- mask: true where glacier is
- bands : elevation bands
- bandi
- lengths: length of each elevation band
- flux_dir_window: as used in calc_fluxdir
- boxcarM or window_frac:
- pre-calculated boxcar operator
- window_frac: window over which to smooth as fraction of the maximum(length)
- scale_u (ones(q1d)): if provided scale output by this much -> so make surface speeds
Output:
- ubar2d: the smoothed IV
- ubar: the IV at the elevation-band boundaries
- mask_ubar: true where ubar contains a value
- facs: scaling factor in 1D
Note:
- An assumption about the distribution of the u is needed, which will
be scaled to conform to mass conservation. At the moment a function
`thick[i,j].^u_exp` is used.
"""
function calc_u(q1d, boundaries, u_trial, thick,
ux, uy, dx, mask, bands, bandi, lengths,
flux_dir_window, # in [m]
filter, scale_u=ones(q1d);
plotyes=false,
x=nothing, y=nothing)
u, mask_u, facs = _calc_u(q1d, boundaries, u_trial, thick,
ux, uy, dx, mask, bands,
flux_dir_window, # in [m]
plotyes, x, y, scale_u)
u_ = copy(u)
u_[isnan.(u_)] = 0 # remove NaNs to allow filtering
# type assertion is needed for type-stability
out::Array{eltype(q1d),2} = if filter isa AbstractMatrix
VAWTools.apply_boxcar_matrix(filter, u_)
else
boxcar(u_, Int((filter*maximum(lengths))÷dx)+1, mask_u, (!).(mask) )
end
# Make depth-averaged flow speed into a surface flow speed.
scale_u2d = map_back_to_2D(size(out), bandi, scale_u)
out = out .* scale_u2d
return out, u, mask_u, facs
end
# this helper function is needed for type stability.
function _calc_u(q1d, boundaries, u_trial, thick,
ux, uy, dx, mask, bands,
flux_dir_window,
plotyes,
x, y, scale_u) # these are only needed for plotting
#plotyes && figure()
dims = size(mask)
# calculate the u at all elevation band boundaries:
u2d = zeros(dims)*NaN
facs = Float64[] # scaling factor in 1D
for (ib,bnd) in enumerate(boundaries)
if ib<length(bands)
# Find the receiving band, can be a number further than 1.
ibb = 0
for ib_=ib+1:length(bands)
if haskey(bnd, ib_)
ibb = ib_
break
end
end
ibb==0 && error("No band below band $ib, but $ib is not bottom band! This means that the domain is likely disjoint.")
bb=bnd[ibb]
else # outflow at terminus
# This probably needs updating where several elevation bands contribute (tide-water)
# -> no, only ever the last band does outflow in our 1D model
#
# This errors at times, for example on RGI60-14.11814 (which is not sea-terminating)
bb = get(bnd, -1, bnd[0]) # if sea-terminating use those edges.
end
# loop over segments
ffs = Float64[]
is = Int[]
js = Int[]
for l in bb
#@assert orientation(l)
ff, fi, fj, fx, fy = calc_fluxdir(l, ux, uy, Int(flux_dir_window÷dx), dx, bands)
# if plotyes
# quiver(x[fi],y[fj],fx,fy)
# end
append!(is, fi)
append!(js, fj)
append!(ffs, ff)
end
u_t = [u_trial[i,j] for (i,j) in zip(is,js)]
h_line = [thick[i,j] for (i,j) in zip(is,js)]
q_trial = sum(ffs.*u_t.*h_line)
fac = max(q1d[ib],0)/q_trial
push!(facs, fac)
u = u_t*fac
# m,ij = findmin(u)
#@assert all(u.>=0) "$i, $ij, $(u_trial[ij]), $(ff[ij]), $(q_trial), $(q1d[i]), $(h_line[ij])"
for (n,(i,j)) in enumerate(zip(is,js))
if u[n]<0;
println("Flow speed<0: $(u[n]) at location ($i,$j). This should not happen! Setting to zero.")
u[n]=0
end
# also scale u:
u2d[i,j] = u[n] * scale_u[ib]
end
end
mask_u = mask .& ((!).(isnan.(u2d))) # location of all cells for which `u` was calculated
# if plotyes
# # imshow(binmat',origin="lower", extent=(x[1],x[end],y[1],y[end]), cmap="flag"); colorbar();
# imshow(u',origin="lower", extent=(x[1],x[end],y[1],y[end]),); colorbar(); clim(0,50)
# end
return u2d, mask_u, facs
end
"""
get_iv_boxcar_M(F, dem, mask, bands, bandi, lengths, iv_window_frac)
Precalculate the boxcar operator for the IV calculation (this is the
most expensive part).
"""
function get_iv_boxcar_M(F, dem, mask, bands, bandi, lengths, iv_window_frac)
ux,uy = get_ux_uy(dem, mask)
binmat = bins2matrix(dem, bands, bandi)
boundaries = calc_boundaries(bands,bandi,binmat)
q1d = ones(bands)
u_trial = ones(dem.v)
thick = u_trial
dx = step(dem.x)
flux_dir_window = 2
mask_u = _calc_u(q1d, boundaries, u_trial, thick,
ux, uy, dx, mask,
bands,
flux_dir_window,
false,nothing,nothing,ones(q1d))[2]
return boxcar_matrix(F, Int((iv_window_frac*maximum(lengths))÷dx)+1, mask_u, (!).(mask)),
boundaries, ux, uy
end
#################
# Plotting
################
"""
plot_bands(dem, bands, bandi; bands2plot=1:length(bands))
Plots the bands in 2D. For length(bands2plot)<=16 the default
colorscale will show one color per band.
Needs Plots.jl imported in Main (REPL)
"""
function plot_bands(dem, bands, bandi; bands2plot=1:length(bands))
binmat = Float64.(VAWTools.bins2matrix(dem, bands, bandi))
for i in eachindex(binmat)
if !(binmat[i] in bands2plot)
binmat[i] = NaN
end
end
Main.PyPlot.contourf(dem.x,dem.y,binmat',aspect_ratio=:equal)
end
|
#include "rundeck_opts.h"
SUBROUTINE ATM_DIFFUS(LBASE_MIN,LBASE_MAX,DTIME)
!@sum ATM_DIFFUS(DRYCNV) mixes air caused by dry convection.
!@+ this version checks base layers lbase_min to lbase_max.
!@auth Original Development Team
!@ver 1.0
USE CONSTANT, only : lhe,sha,deltx
USE MODEL_COM
USE GEOM
USE QUSDEF, only : nmom,zmoms,xymoms
USE SOMTQ_COM, only : tmom,qmom
USE DAGCOM, only : ajl,jl_trbhr,jl_damdc,jl_trbdlht
#ifdef TRACERS_ON
USE TRACER_COM, only: TRM,TRMOM,NTM
USE TRACER_DIAG_COM, only: TAJLN,JLNT_TURB
#endif
USE DYNAMICS, only : pk,pdsig,plij,dke
USE PBLCOM, only : dclev,w2gcm,w2_l1
IMPLICIT NONE
integer, intent(in) :: LBASE_MIN,LBASE_MAX
real*8, intent(in) :: dtime ! dummy variable
REAL*8, DIMENSION(IM,JM,LM) :: UT,VT
REAL*8, DIMENSION(LM) :: DP
c COMMON/WORK2/UT,VT,DP ! is this necessary?
INTEGER, DIMENSION(IM) :: IDI,IDJ !@var ID
REAL*8, DIMENSION(IM) :: RA !@var
REAL*8, DIMENSION(IM) :: UMS,VMS !@var
LOGICAL POLE
INTEGER I,J,L,K,IMAX,KMAX,IM1,LMAX,LMIN
C
REAL*8 UKP1(IM,LM), VKP1(IM,LM), UKPJM(IM,LM),VKPJM(IM,LM)
REAL*8 UKM(4,IM,2:JM-1,LM), VKM(4,IM,2:JM-1,LM)
INTEGER LRANG(2,IM,JM)
C
REAL*8, DIMENSION(NMOM) :: TMOMS,QMOMS
REAL*8 DOK,PIJBOT,PIJ,PKMS,THPKMS,QMS
* ,TVMS,THETA,RDP,THM
#ifdef TRACERS_ON
REAL*8, DIMENSION(NMOM,NTM) :: TRMOMS
REAL*8, DIMENSION( NTM) :: TRMS
REAL*8 SDPL,BYSDPL
#endif
if(LBASE_MAX.GE.LM) call stop_model('DRYCNV: LBASE_MAX.GE.LM',255)
! update w2gcm at 1st GCM layer
w2gcm=0.d0
do j=1,jm
do i=1,im
w2gcm(1,i,j)=w2_l1(i,j)
end do
end do
C**** LOAD U,V INTO UT,VT. UT,VT WILL BE FIXED DURING DRY CONVECTION
C**** WHILE U,V WILL BE UPDATED.
UT=U ; VT=V
C**** OUTSIDE LOOPS OVER J AND I
!$OMP PARALLEL DO PRIVATE (I,IM1,IMAX,J,K,KMAX,L,LMIN,LMAX,IDI,IDJ,
!$OMP* DP,PIJ,POLE,PIJBOT,PKMS, QMS,QMOMS, RA,RDP,
#ifdef TRACERS_ON
!$OMP* TRMS,TRMOMS,SDPL,BYSDPL,
#endif
!$OMP* THM,TVMS,THETA,TMOMS,THPKMS, UMS,VMS)
!$OMP* SCHEDULE(DYNAMIC,2)
JLOOP: DO J=1,JM
POLE=.FALSE.
IF (J.EQ.1.OR.J.EQ.JM) POLE=.TRUE.
IMAX=IMAXJ(J)
KMAX=KMAXJ(J)
C****
C**** MAIN LOOP
C****
IM1=IM
ILOOP: DO I=1,IMAX
DO K=1,KMAX
RA(K)=RAVJ(K,J)
IDI(K)=IDIJ(K,I,J)
IDJ(K)=IDJJ(K,J)
END DO
C
LRANG(1,I,J)=-1
LRANG(2,I,J)=-2
C
LMAX=LBASE_MIN-1
lbase_loop: do while(lmax.lt.lbase_max)
LMIN=LMAX+1
LMAX=LMIN
IF (T(I,J,LMIN)*(1.+Q(I,J,LMIN)*deltx).LE.
* T(I,J,LMIN+1)*(1.+Q(I,J,LMIN+1)*deltx)) cycle lbase_loop
C**** MIX HEAT AND MOISTURE THROUGHOUT THE UNSTABLE LAYERS
C**** MIX THROUGH TWO LOWER LAYERS
PIJBOT=PLIJ(LMIN,I,J)
DP(LMIN)=PDSIG(LMIN,I,J)
PIJ=PLIJ(LMIN+1,I,J)
DP(LMIN+1)=PDSIG(LMIN+1,I,J)
PKMS=PK(LMIN,I,J)*DP(LMIN)+PK(LMIN+1,I,J)*DP(LMIN+1)
THPKMS=T(I,J,LMIN)*(PK(LMIN,I,J)*DP(LMIN))
* +T(I,J,LMIN+1)*(PK(LMIN+1,I,J)*DP(LMIN+1))
QMS=Q(I,J,LMIN)*DP(LMIN)+Q(I,J,LMIN+1)*DP(LMIN+1)
C**** sum moments to mix over unstable layers
TMOMS(XYMOMS) =
& TMOM(XYMOMS,I,J,LMIN )*(PK(LMIN ,I,J)*DP(LMIN )) +
& TMOM(XYMOMS,I,J,LMIN+1)*(PK(LMIN+1,I,J)*DP(LMIN+1))
QMOMS(XYMOMS) =
& QMOM(XYMOMS,I,J,LMIN )*(DP(LMIN )) +
& QMOM(XYMOMS,I,J,LMIN+1)*(DP(LMIN+1))
#ifdef TRACERS_ON
TRMS(:) = TRM(I,J,LMIN,:)+TRM(I,J,LMIN+1,:)
TRMOMS(XYMOMS,:) =
& TRMOM(XYMOMS,I,J,LMIN,:)+TRMOM(XYMOMS,I,J,LMIN+1,:)
#endif
IF (LMIN+1.GE.LM) GO TO 150
TVMS=T(I,J,LMIN)*(1.+Q(I,J,LMIN)*deltx)*(PK(LMIN,I,J)*DP(LMIN))
* +T(I,J,LMIN+1)*(1.+Q(I,J,LMIN+1)*deltx)
* *(PK(LMIN+1,I,J)*DP(LMIN+1))
THETA=TVMS/PKMS
C**** MIX THROUGH SUBSEQUENT UNSTABLE LAYERS
DO L=LMIN+2,LM
IF (THETA.LT.T(I,J,L)*(1.+Q(I,J,L)*deltx)) GO TO 160
PIJ=PLIJ(L,I,J)
DP(L)=PDSIG(L,I,J)
PKMS=PKMS+(PK(L,I,J)*DP(L))
THPKMS=THPKMS+T(I,J,L)*(PK(L,I,J)*DP(L))
QMS=QMS+Q(I,J,L)*DP(L)
TVMS=TVMS+T(I,J,L)*(1.+Q(I,J,L)*deltx)*(PK(L,I,J)*DP(L))
TMOMS(XYMOMS) = TMOMS(XYMOMS) +
& TMOM(XYMOMS,I,J,L)*(PK(L,I,J)*DP(L))
QMOMS(XYMOMS) = QMOMS(XYMOMS) +
& QMOM(XYMOMS,I,J,L)*DP(L)
THETA=TVMS/PKMS
#ifdef TRACERS_ON
TRMS(:) = TRMS(:) + TRM(I,J,L,:)
TRMOMS(XYMOMS,:) = TRMOMS(XYMOMS,:) + TRMOM(XYMOMS,I,J,L,:)
#endif
END DO
150 L=LM+1
160 LMAX=L-1
RDP=1./(PIJBOT*SIGE(LMIN)-PIJ*SIGE(LMAX+1))
THM=THPKMS/PKMS
QMS=QMS*RDP
#ifdef TRACERS_ON
SDPL = 0.d0
DO L=LMIN,LMAX
SDPL = SDPL+DP(L)
ENDDO
BYSDPL = 1.D0/SDPL
#endif
DO L=LMIN,LMAX
AJL(J,L,JL_TRBHR)=AJL(J,L,JL_TRBHR)+
& (THM-T(I,J,L))*PK(L,I,J)*PLIJ(L,I,J)
AJL(J,L,JL_TRBDLHT)=AJL(J,L,JL_TRBDLHT)+
& (QMS-Q(I,J,L))*PDSIG(L,I,J)*LHE/SHA
T(I,J,L)=THM
TMOM(XYMOMS,I,J,L)=TMOMS(XYMOMS)/PKMS
TMOM(ZMOMS,I,J,L)=0.
Q(I,J,L)=QMS
QMOM(XYMOMS,I,J,L)=QMOMS(XYMOMS)*RDP
QMOM(ZMOMS,I,J,L)=0.
#ifdef TRACERS_ON
TAJLN(J,L,JLNT_TURB,:)=TAJLN(J,L,JLNT_TURB,:) +
& (TRMS(:)*(DP(L)*BYSDPL)-TRM(I,J,L,:))
TRM(I,J,L,:) = TRMS(:)*(DP(L)*BYSDPL)
TRMOM(XYMOMS,I,J,L,:) = TRMOMS(XYMOMS,:)*(DP(L)*BYSDPL)
TRMOM(ZMOMS,I,J,L,:) = 0.
#endif
END DO
C**** MIX MOMENTUM THROUGHOUT UNSTABLE LAYERS
UMS(1:KMAX)=0.
VMS(1:KMAX)=0.
DO L=LMIN,LMAX
DO K=1,KMAX
UMS(K)=UMS(K)+UT(IDI(K),IDJ(K),L)*DP(L)
VMS(K)=VMS(K)+VT(IDI(K),IDJ(K),L)*DP(L)
ENDDO
ENDDO
UMS(1:KMAX)=UMS(1:KMAX)*RDP
VMS(1:KMAX)=VMS(1:KMAX)*RDP
LRANG(1,I,J)=LMIN
LRANG(2,I,J)=LMAX
c DO L=LMIN,LMAX
c DO K=1,KMAX
c U(IDI(K),IDJ(K),L)=U(IDI(K),IDJ(K),L)
c & +(UMS(K)-UT(IDI(K),IDJ(K),L))*RA(K)
c V(IDI(K),IDJ(K),L)=V(IDI(K),IDJ(K),L)
c & +(VMS(K)-VT(IDI(K),IDJ(K),L))*RA(K)
c AJL(IDJ(K),L,JL_DAMDC)=AJL(IDJ(K),L,JL_DAMDC)
c & +(UMS(K)-UT(IDI(K),IDJ(K),L))*PLIJ(L,I,J)*RA(K)
c ENDDO
c ENDDO
DO L=LMIN,LMAX
IF(J.EQ.1) THEN
DO K=1,KMAX
UKP1(K,L)=(UMS(K)-UT(IDI(K),IDJ(K),L))
VKP1(K,L)=(VMS(K)-VT(IDI(K),IDJ(K),L))
END DO
ELSE IF(J.EQ.JM) THEN
DO K=1,KMAX
UKPJM(K,L)=(UMS(K)-UT(IDI(K),IDJ(K),L))
VKPJM(K,L)=(VMS(K)-VT(IDI(K),IDJ(K),L))
END DO
ELSE
DO K=1,KMAX
UKM(K,I,J,L)=(UMS(K)-UT(IDI(K),IDJ(K),L))
VKM(K,I,J,L)=(VMS(K)-VT(IDI(K),IDJ(K),L))
END DO
END IF
ENDDO
C
enddo lbase_loop
C**** ACCUMULATE BOUNDARY LAYER DIAGNOSTICS
if(lbase_min.eq.1) then ! was called from surfce
DCLEV(I,J)=LMAX
endif
IM1=I
ENDDO ILOOP
ENDDO JLOOP
!$OMP END PARALLEL DO
C
C NOW REALLY UPDATE THE MODEL WINDS
C
J=1
DO K=1,KMAXJ(J)
IDI(K)=IDIJ(K,1,J)
IDJ(K)=IDJJ(K,J)
RA(K) =RAVJ(K,J)
END DO
LMIN=LRANG(1,1,J)
LMAX=LRANG(2,1,J)
DO L=LMIN,LMAX
DO K=1,KMAXJ(J)
U(IDI(K),IDJ(K),L)=U(IDI(K),IDJ(K),L)+UKP1(K,L)*RA(K)
V(IDI(K),IDJ(K),L)=V(IDI(K),IDJ(K),L)+VKP1(K,L)*RA(K)
AJL(IDJ(K),L,JL_DAMDC)=AJL(IDJ(K),L,JL_DAMDC)+
* UKP1(K,L)*PLIJ(L,1,J)*RA(K)
END DO ; END DO
C
DO J=2,JM-1
KMAX=KMAXJ(J)
DO K=1,KMAX
IDJ(K)=IDJJ(K,J)
RA(K) =RAVJ(K,J)
END DO
DO I=1,IM
LMIN=LRANG(1,I,J)
LMAX=LRANG(2,I,J)
DO L=LMIN,LMAX
DO K=1,KMAX
IDI(K)=IDIJ(K,I,J)
U(IDI(K),IDJ(K),L)=U(IDI(K),IDJ(K),L)+UKM(K,I,J,L)*RA(K)
V(IDI(K),IDJ(K),L)=V(IDI(K),IDJ(K),L)+VKM(K,I,J,L)*RA(K)
AJL(IDJ(K),L,JL_DAMDC)=AJL(IDJ(K),L,JL_DAMDC)+
* UKM(K,I,J,L)*PLIJ(L,I,J)*RA(K)
END DO ; END DO
END DO
END DO
C
J=JM
KMAX=KMAXJ(J)
DO K=1,KMAX
IDI(K)=IDIJ(K,1,J)
IDJ(K)=IDJJ(K,J)
RA(K) =RAVJ(K,J)
END DO
LMIN=LRANG(1,1,J)
LMAX=LRANG(2,1,J)
DO L=LMIN,LMAX
DO K=1,KMAX
U(IDI(K),IDJ(K),L)=U(IDI(K),IDJ(K),L)+UKPJM(K,L)*RA(K)
V(IDI(K),IDJ(K),L)=V(IDI(K),IDJ(K),L)+VKPJM(K,L)*RA(K)
AJL(IDJ(K),L,JL_DAMDC)=AJL(IDJ(K),L,JL_DAMDC)+
* UKPJM(K,L)*PLIJ(L,1,J)*RA(K)
END DO ; END DO
C**** Save additional changes in KE for addition as heat later
!$OMP PARALLEL DO PRIVATE (L,I,J)
DO L=1,LM
DO J=2,JM
DO I=1,IM
DKE(I,J,L)=DKE(I,J,L)+0.5*(U(I,J,L)*U(I,J,L)+V(I,J,L)*V(I,J,L)
* -UT(I,J,L)*UT(I,J,L)-VT(I,J,L)*VT(I,J,L))
END DO
END DO
END DO
!$OMP END PARALLEL DO
RETURN
END SUBROUTINE ATM_DIFFUS
subroutine apply_fluxes_to_atm(dt)
!@sum applies earth fluxes to the first layer of the atmosphere
!@auth Original Development Team
!@ver 1.0
USE MODEL_COM, only : im,jm,u,v,t,q,qcheck
USE GEOM, only : imaxj,kmaxj,ravj,idij,idjj,siniv,cosiv,dxyp
USE DYNAMICS, only : byam,am,dke
#ifdef TRACERS_ON
USE TRACER_COM, only : ntm,trm,trmom,trname
#ifdef TRACERS_WATER
* ,trw0,t_qlimit
#endif
USE FLUXES, only : trflux1
#endif
USE FLUXES, only : dth1,dq1,uflux1,vflux1,qflux1
implicit none
REAL*8, PARAMETER :: qmin=1.d-12
integer i,j,k,n
real*8, intent(in) :: dt
real*8 hemi
real*8, dimension(im,jm) :: usave,vsave
do j=1,jm
do i=1,imaxj(j)
t(i,j,1) = t(i,j,1) + dth1(i,j)
q(i,j,1) = q(i,j,1) + dq1(i,j)
end do
end do
#ifdef TRACERS_ON
do n=1,ntm
do j=1,jm
do i=1,imaxj(j)
trm(i,j,1,n) = trm(i,j,1,n) + trflux1(i,j,n)*dt
#ifdef TRACERS_WATER
if (t_qlimit(n).and.trm(i,j,1,n).lt.qmin*trw0(n)*am(1,i,j)
* *dxyp(j)) then
if (qcheck) write(99,*) trname(n),I,J,' TR1:',trm(i,j,1,n)
* ,'->',qmin*trw0(n)*am(1,i,j)*dxyp(j)
trm(i,j,1,n) = qmin*trw0(n)*am(1,i,j)*dxyp(j)
trmom(:,i,j,1,n)=0.
end if
#endif
end do
end do
end do
#endif
c****
c**** add in surface friction to first layer wind
c****
usave=u(:,:,1) ; vsave=v(:,:,1)
c**** polar boxes
do j=1,jm,jm-1
hemi=1.
if(j.le.jm/2) hemi=-1.
do i=1,imaxj(j)
do k=1,kmaxj(j)
u(idij(k,i,j),idjj(k,j),1)=u(idij(k,i,j),idjj(k,j),1) -
* ravj(k,j)*(uflux1(i,j)*cosiv(k)+vflux1(i,j)*siniv(k)*hemi)
* *dt*byam(1,I,J)
v(idij(k,i,j),idjj(k,j),1)=v(idij(k,i,j),idjj(k,j),1) -
* ravj(k,j)*(vflux1(i,j)*cosiv(k)-uflux1(i,j)*siniv(k)*hemi)
* *dt*byam(1,I,J)
end do
end do
end do
c**** non polar boxes
do j=2,jm-1
do i=1,imaxj(j)
do k=1,kmaxj(j)
u(idij(k,i,j),idjj(k,j),1)=u(idij(k,i,j),idjj(k,j),1) -
* ravj(k,j)*uflux1(i,j)*dt*byam(1,I,J)
v(idij(k,i,j),idjj(k,j),1)=v(idij(k,i,j),idjj(k,j),1) -
* ravj(k,j)*vflux1(i,j)*dt*byam(1,I,J)
end do
end do
end do
C**** save change of KE for addition as heat later
do j=2,jm
do i=1,im
dke(i,j,1)=dke(i,j,1)+0.5*(u(i,j,1)*u(i,j,1)+v(i,j,1)*v(i,j,1)
* -usave(i,j)*usave(i,j)-vsave(i,j)*vsave(i,j))
end do
end do
c****
return
end subroutine apply_fluxes_to_atm
|
import game.world10.level15 -- hide
namespace mynat -- hide
/-
# Inequality world.
## Level 16: equivalence of two definitions of `<`
Now let's go the other way.
-/
/- Lemma :
For all naturals $a$ and $b$,
$$
\operatorname{succ}(a)\le b
\implies
a\le b\land\lnot(b\le a).$$
-/
lemma lt_aux_two (a b : mynat) : succ a ≤ b → a ≤ b ∧ ¬ (b ≤ a) :=
begin [nat_num_game]
intro h,
split,
{ apply le_trans a (succ a) b,
exact le_succ_self a,
exact h,
},
intro nh,
apply ne_succ_self a,
apply le_antisymm a (succ a),
exact le_succ_self a,
exact le_trans (succ a) b a h nh,
end
/-
Now for the payoff.
-/
end mynat -- hide
|
@testset "`validate_date`" begin
@test validate_date("6/1/2017") == "6/1/2017"
@test validate_date("06/01/2017") == "6/1/2017"
@test validate_date("6-1-2017") == "6/1/2017" # i guess we'll handle dashes
@test validate_date(Date(2017, 6, 1)) == "6/1/2017"
@test_throws ArgumentError validate_date("5/32/2017") # invalid date rounds to next month
@test_throws ArgumentError validate_date("6/1/17") # full year required
@test_throws ArgumentError validate_date("June 1 2017") # no spelled-out parsing handled
@test_throws ArgumentError validate_date("1 June 2017") # no spelled-out parsing handled
end
@testset "`request_meetings`" begin
meetings = request_meetings("6/1/2020", "6/1/2020")
@test nrow(meetings) == 2
m = first(meetings)
r = Meeting(m) # Just test that this is possible
@test m.name == "Public Health and Public Safety Committee"
@test m.date == DateTime("2020-06-01T18:00:00")
@test isa(m.date, DateTime)
@test isa(m.id, Int)
@test m.link == "http://somervillecityma.iqm2.com/Citizens/Detail_Meeting.aspx?ID=3163"
# Test that current meeting serialization hasn't changed
# If this test _fails_, need to (a) bump `meeting_version` and (b) resave current
# version of cached meeting asset:
test_meeting_path = joinpath(TEST_ASSETS, "v$(SomervilleCouncilParser.meeting_version)",
"meeting.arrow")
# Legolas.write(test_meeting_path, DataFrame(m), SomervilleCouncilParser.meeting_schema) # Uncomment to save new version
@test isfile(test_meeting_path)
previous_mtg = DataFrame(Legolas.read(test_meeting_path))
@test previous_mtg == DataFrame(m)
end
|
theory flash71Rev imports flashPub
begin
section{*Main defintions*}
lemma NI_FAckVsInv71:
(*Rule0VsPInv0*)
shows "invHoldForRule' s (inv71 ) (NI_FAck ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
by( auto)
lemma NI_InvVsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Inv iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_InvAck_1VsInv71:
(*Rule2VsPInv0*)
assumes a1:"iRule1 \<le> N" and a2:"iRule2 \<le> N" and a3:"iRule1~=iRule2 "
shows "invHoldForRule' s (inv71 ) (NI_InvAck_1 iRule1 iRule2 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1 a2 a3,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_InvAck_1_HomeVsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_InvAck_1_Home iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_InvAck_2VsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_InvAck_2 N iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_GetX_GetXVsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Local_GetX_GetX iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_GetX_Nak1VsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Local_GetX_Nak1 iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_GetX_Nak2VsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Local_GetX_Nak2 iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_GetX_Nak3VsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Local_GetX_Nak3 iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_GetX_PutX1VsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Local_GetX_PutX1 N iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_GetX_PutX2VsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Local_GetX_PutX2 N iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_GetX_PutX3VsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Local_GetX_PutX3 N iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_GetX_PutX4VsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Local_GetX_PutX4 N iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_GetX_PutX5VsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Local_GetX_PutX5 N iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_GetX_PutX6VsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Local_GetX_PutX6 N iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_GetX_PutX7VsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Local_GetX_PutX7 N iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_GetX_PutX8VsInv71:
(*Rule2VsPInv0*)
assumes a1:"iRule1 \<le> N" and a2:"iRule2 \<le> N" and a3:"iRule1~=iRule2 "
shows "invHoldForRule' s (inv71 ) (NI_Local_GetX_PutX8 N iRule1 iRule2 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1 a2 a3,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_GetX_PutX8_homeVsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Local_GetX_PutX8_home N iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_GetX_PutX9VsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Local_GetX_PutX9 N iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_GetX_PutX10VsInv71:
(*Rule2VsPInv0*)
assumes a1:"iRule1 \<le> N" and a2:"iRule2 \<le> N" and a3:"iRule1~=iRule2 "
shows "invHoldForRule' s (inv71 ) (NI_Local_GetX_PutX10 N iRule1 iRule2 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1 a2 a3,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_GetX_PutX10_homeVsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Local_GetX_PutX10_home N iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_GetX_PutX11VsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Local_GetX_PutX11 N iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_Get_GetVsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Local_Get_Get iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_Get_Nak1VsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Local_Get_Nak1 iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_Get_Nak2VsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Local_Get_Nak2 iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_Get_Nak3VsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Local_Get_Nak3 iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_Get_Put1VsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Local_Get_Put1 N iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_Get_Put2VsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Local_Get_Put2 iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_Get_Put3VsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Local_Get_Put3 iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Local_PutVsInv71:
(*Rule0VsPInv0*)
shows "invHoldForRule' s (inv71 ) (NI_Local_Put ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P1 s"
apply( auto)
done
then show "?P1 s\<or> ?P2 s\<or> ?P3 s"
by blast
qed
lemma NI_Local_PutXAcksDoneVsInv71:
(*Rule0VsPInv0*)
shows "invHoldForRule' s (inv71 ) (NI_Local_PutXAcksDone ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P1 s"
apply( auto)
done
then show "?P1 s\<or> ?P2 s\<or> ?P3 s"
by blast
qed
lemma NI_NakVsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Nak iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Nak_ClearVsInv71:
(*Rule0VsPInv0*)
shows "invHoldForRule' s (inv71 ) (NI_Nak_Clear ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P1 s"
apply( auto)
done
then show "?P1 s\<or> ?P2 s\<or> ?P3 s"
by blast
qed
lemma NI_Nak_HomeVsInv71:
(*Rule0VsPInv0*)
shows "invHoldForRule' s (inv71 ) (NI_Nak_Home ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P1 s"
apply( auto)
done
then show "?P1 s\<or> ?P2 s\<or> ?P3 s"
by blast
qed
lemma NI_Remote_GetX_NakVsInv71:
(*Rule2VsPInv0*)
assumes a1:"iRule1 \<le> N" and a2:"iRule2 \<le> N" and a3:"iRule1~=iRule2 "
shows "invHoldForRule' s (inv71 ) (NI_Remote_GetX_Nak iRule1 iRule2 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P3 s"
apply( cut_tac a1 a2 a3 , simp)
apply(rule_tac x=" (neg ( andForm ( andForm ( eqn ( IVar ( Para ''UniMsg_Cmd'' iRule1) ) ( Const UNI_GetX )) ( eqn ( IVar ( Para ''UniMsg_Cmd'' Home) ) ( Const UNI_Put )) ) ( eqn ( IVar ( Para ''UniMsg_proc'' iRule1) ) (Const iRule2)) ) ) " in exI,auto)
done
then show "?P1 s\<or> ?P2 s\<or> ?P3 s"
by blast
qed
lemma NI_Remote_GetX_Nak_HomeVsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Remote_GetX_Nak_Home iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P1 s"
apply(cut_tac a1 , auto)
done
then show "?P1 s\<or> ?P2 s\<or> ?P3 s"
by blast
qed
lemma NI_Remote_GetX_PutXVsInv71:
(*Rule2VsPInv0*)
assumes a1:"iRule1 \<le> N" and a2:"iRule2 \<le> N" and a3:"iRule1~=iRule2 "
shows "invHoldForRule' s (inv71 ) (NI_Remote_GetX_PutX iRule1 iRule2 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1 a2 a3,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Remote_GetX_PutX_HomeVsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Remote_GetX_PutX_Home iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P1 s"
apply(cut_tac a1 , auto)
done
then show "?P1 s\<or> ?P2 s\<or> ?P3 s"
by blast
qed
lemma NI_Remote_Get_Nak1VsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Remote_Get_Nak1 iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P1 s"
apply(cut_tac a1 , auto)
done
then show "?P1 s\<or> ?P2 s\<or> ?P3 s"
by blast
qed
lemma NI_Remote_Get_Nak2VsInv71:
(*Rule2VsPInv0*)
assumes a1:"iRule1 \<le> N" and a2:"iRule2 \<le> N" and a3:"iRule1~=iRule2 "
shows "invHoldForRule' s (inv71 ) (NI_Remote_Get_Nak2 iRule1 iRule2 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P3 s"
apply( cut_tac a1 a2 a3 , simp)
apply(rule_tac x=" (neg ( andForm ( andForm ( eqn ( IVar ( Para ''UniMsg_Cmd'' iRule1) ) ( Const UNI_Get )) ( eqn ( IVar ( Para ''UniMsg_Cmd'' Home) ) ( Const UNI_Put )) ) ( eqn ( IVar ( Para ''UniMsg_proc'' iRule1) ) (Const iRule2)) ) ) " in exI,auto)
done
then show "?P1 s\<or> ?P2 s\<or> ?P3 s"
by blast
qed
lemma NI_Remote_Get_Put1VsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Remote_Get_Put1 iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P3 s"
apply( cut_tac a1 , simp)
apply(rule_tac x=" (neg ( andForm ( eqn ( IVar ( Global ''NakcMsg_Cmd'') ) ( Const NAKC_Nakc )) ( eqn ( IVar ( Para ''UniMsg_Cmd'' Home) ) ( Const UNI_Get )) ) ) " in exI,auto)
done
then show "?P1 s\<or> ?P2 s\<or> ?P3 s"
by blast
qed
lemma NI_Remote_Get_Put2VsInv71:
(*Rule2VsPInv0*)
assumes a1:"iRule1 \<le> N" and a2:"iRule2 \<le> N" and a3:"iRule1~=iRule2 "
shows "invHoldForRule' s (inv71 ) (NI_Remote_Get_Put2 iRule1 iRule2 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1 a2 a3,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Remote_PutVsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Remote_Put iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_Remote_PutXVsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Remote_PutX iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_ReplaceVsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_Replace iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_ReplaceHomeVsInv71:
(*Rule0VsPInv0*)
shows "invHoldForRule' s (inv71 ) (NI_ReplaceHome ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
by( auto)
lemma NI_ReplaceHomeShrVldVsInv71:
(*Rule0VsPInv0*)
shows "invHoldForRule' s (inv71 ) (NI_ReplaceHomeShrVld ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
by( auto)
lemma NI_ReplaceShrVldVsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (NI_ReplaceShrVld iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma NI_ShWbVsInv71:
(*Rule0VsPInv0*)
shows "invHoldForRule' s (inv71 ) (NI_ShWb N ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
by( auto)
lemma NI_WbVsInv71:
(*Rule0VsPInv0*)
shows "invHoldForRule' s (inv71 ) (NI_Wb ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
by( auto)
lemma PI_Local_GetX_GetX1VsInv71:
(*Rule0VsPInv0*)
shows "invHoldForRule' s (inv71 ) (PI_Local_GetX_GetX1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P1 s"
apply( auto)
done
then show "?P1 s\<or> ?P2 s\<or> ?P3 s"
by blast
qed
lemma PI_Local_GetX_GetX2VsInv71:
(*Rule0VsPInv0*)
shows "invHoldForRule' s (inv71 ) (PI_Local_GetX_GetX2 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P1 s"
apply( auto)
done
then show "?P1 s\<or> ?P2 s\<or> ?P3 s"
by blast
qed
lemma PI_Local_GetX_PutX1VsInv71:
(*Rule0VsPInv0*)
shows "invHoldForRule' s (inv71 ) (PI_Local_GetX_PutX1 N ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
by( auto)
lemma PI_Local_GetX_PutX2VsInv71:
(*Rule0VsPInv0*)
shows "invHoldForRule' s (inv71 ) (PI_Local_GetX_PutX2 N ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
by( auto)
lemma PI_Local_GetX_PutX3VsInv71:
(*Rule0VsPInv0*)
shows "invHoldForRule' s (inv71 ) (PI_Local_GetX_PutX3 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
by( auto)
lemma PI_Local_GetX_PutX4VsInv71:
(*Rule0VsPInv0*)
shows "invHoldForRule' s (inv71 ) (PI_Local_GetX_PutX4 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
by( auto)
lemma PI_Local_Get_GetVsInv71:
(*Rule0VsPInv0*)
shows "invHoldForRule' s (inv71 ) (PI_Local_Get_Get ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P1 s"
apply( auto)
done
then show "?P1 s\<or> ?P2 s\<or> ?P3 s"
by blast
qed
lemma PI_Local_Get_PutVsInv71:
(*Rule0VsPInv0*)
shows "invHoldForRule' s (inv71 ) (PI_Local_Get_Put ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
by( auto)
lemma PI_Local_PutXVsInv71:
(*Rule0VsPInv0*)
shows "invHoldForRule' s (inv71 ) (PI_Local_PutX ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
by( auto)
lemma PI_Local_ReplaceVsInv71:
(*Rule0VsPInv0*)
shows "invHoldForRule' s (inv71 ) (PI_Local_Replace ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
by( auto)
lemma PI_Remote_GetVsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (PI_Remote_Get iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma PI_Remote_GetXVsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (PI_Remote_GetX iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma PI_Remote_PutXVsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (PI_Remote_PutX iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma PI_Remote_ReplaceVsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (PI_Remote_Replace iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma StoreVsInv71:
(*Rule1VsPInv0*)
assumes a1:"iRule1 \<le> N"
shows "invHoldForRule' s (inv71 ) (Store iRule1 ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
proof -
have "?P2 s"
by (cut_tac a1,auto )
then show "?P1 s\<or>?P2 s\<or>?P3 s"
by auto
qed
lemma StoreHomeVsInv71:
(*Rule0VsPInv0*)
shows "invHoldForRule' s (inv71 ) (StoreHome ) (invariants N)" (is " ?P1 s\<or>?P2 s\<or>?P3 s")
by( auto)
end
|
[STATEMENT]
lemma prWlsAbs_wlsBinp:
assumes "wlsBinp delta binp" and "prWlsAbs gA SEM" and "sWlsVal SEM val"
shows "sWlsBinp SEM delta (lift (\<lambda> A. gA A val) binp)"
[PROOF STATE]
proof (prove)
goal (1 subgoal):
1. sWlsBinp SEM delta (lift (\<lambda>A. gA A val) binp)
[PROOF STEP]
using assms
[PROOF STATE]
proof (prove)
using this:
wlsBinp delta binp
prWlsAbs gA SEM
sWlsVal SEM val
goal (1 subgoal):
1. sWlsBinp SEM delta (lift (\<lambda>A. gA A val) binp)
[PROOF STEP]
unfolding sWlsBinp_def wlsBinp_iff liftAll2_def lift_def prWlsAbs_def
[PROOF STATE]
proof (prove)
using this:
wlsOpS delta \<and> sameDom (barOf delta) binp \<and> (\<forall>i v1 v2. barOf delta i = Some v1 \<and> binp i = Some v2 \<longrightarrow> wlsAbs v1 v2)
\<forall>us s A val. wlsAbs (us, s) A \<and> sWlsVal SEM val \<longrightarrow> sWlsAbs SEM (us, s) (gA A val)
sWlsVal SEM val
goal (1 subgoal):
1. wlsOpS delta \<and> sameDom (barOf delta) (\<lambda>i. case binp i of None \<Rightarrow> None | Some v \<Rightarrow> Some (gA v val)) \<and> (\<forall>i v1 v2. barOf delta i = Some v1 \<and> (case binp i of None \<Rightarrow> None | Some v \<Rightarrow> Some (gA v val)) = Some v2 \<longrightarrow> sWlsAbs SEM v1 v2)
[PROOF STEP]
by (auto simp add: option.case_eq_if sameDom_def)
|
module Goldbach
import Data.DPair
import Data.Nat
public export
data Even : Nat -> Type where
EvZ : Even Z
EvSS : Even n -> Even $ S $ S n
public export
half : (n : Nat) -> {auto ev : Even n} -> Subset Nat (\k => n = k + k) -- like `(k ** n = k + k)` but with compile-time right argument.
half Z = Element Z Refl
half (S $ S k) {ev=EvSS _} = let Element halfK halfKPrf = half k in
Element (S halfK) rewrite sym $ plusSuccRightSucc halfK halfK in
rewrite halfKPrf in
Refl
export
gte1nz : (k : Nat) -> {auto gte : k `GTE` S x} -> Not (k = 0)
gte1nz 0 Refl impossible
gte1nz (S _) Refl impossible
public export
Prime : Nat -> Type
Prime n = (k : Nat) -> {auto gt2 : k `GTE` 2} -> {auto ltn : k `LT` n} -> Not (modNatNZ n k (gte1nz k {x=1}) = 0)
export
goldbach : (x : Nat) -> {auto ev : Even x} -> {auto gt2 : x `GT` 2} -> (y ** z ** (Prime y, Prime z, x = y + z))
|
[STATEMENT]
lemma less_enat_iff: "a < enat i \<longleftrightarrow> (\<exists>j. a = enat j \<and> j < i)"
[PROOF STATE]
proof (prove)
goal (1 subgoal):
1. (a < enat i) = (\<exists>j. a = enat j \<and> j < i)
[PROOF STEP]
by (cases a) auto
|
{-# OPTIONS --safe #-}
module Cubical.Algebra.Polynomials.Multivariate.Base where
open import Cubical.Foundations.Prelude
open import Cubical.Foundations.HLevels
open import Cubical.Data.Nat renaming (_+_ to _+n_)
open import Cubical.Data.Vec
open import Cubical.Algebra.Ring
open import Cubical.Algebra.CommRing
private variable
ℓ ℓ' : Level
module _ (A' : CommRing ℓ) where
private
A = fst A'
open CommRingStr (snd A')
-----------------------------------------------------------------------------
-- Definition
data Poly (n : ℕ) : Type ℓ where
-- elements
0P : Poly n
base : (v : Vec ℕ n) → (a : A) → Poly n
_Poly+_ : (P : Poly n) → (Q : Poly n) → Poly n
-- AbGroup eq
Poly+-assoc : (P Q R : Poly n) → P Poly+ (Q Poly+ R) ≡ (P Poly+ Q) Poly+ R
Poly+-Rid : (P : Poly n) → P Poly+ 0P ≡ P
Poly+-comm : (P Q : Poly n) → P Poly+ Q ≡ Q Poly+ P
-- Base eq
base-0P : (v : Vec ℕ n) → base v 0r ≡ 0P
base-Poly+ : (v : Vec ℕ n) → (a b : A) → (base v a) Poly+ (base v b) ≡ base v (a + b)
-- Set Trunc
trunc : isSet(Poly n)
-----------------------------------------------------------------------------
-- Induction and Recursion
module _ (A' : CommRing ℓ) where
private
A = fst A'
open CommRingStr (snd A')
module Poly-Ind-Set
-- types
(n : ℕ)
(F : (P : Poly A' n) → Type ℓ')
(issd : (P : Poly A' n) → isSet (F P))
-- elements
(0P* : F 0P)
(base* : (v : Vec ℕ n) → (a : A) → F (base v a))
(_Poly+*_ : {P Q : Poly A' n} → (PS : F P) → (QS : F Q) → F (P Poly+ Q))
-- AbGroup eq
(Poly+-assoc* : {P Q R : Poly A' n} → (PS : F P) → (QS : F Q) → (RS : F R)
→ PathP (λ i → F (Poly+-assoc P Q R i)) (PS Poly+* (QS Poly+* RS)) ((PS Poly+* QS) Poly+* RS))
(Poly+-Rid* : {P : Poly A' n} → (PS : F P) →
PathP (λ i → F (Poly+-Rid P i)) (PS Poly+* 0P*) PS)
(Poly+-comm* : {P Q : Poly A' n} → (PS : F P) → (QS : F Q)
→ PathP (λ i → F (Poly+-comm P Q i)) (PS Poly+* QS) (QS Poly+* PS))
-- Base eq
(base-0P* : (v : Vec ℕ n) → PathP (λ i → F (base-0P v i)) (base* v 0r) 0P*)
(base-Poly+* : (v : Vec ℕ n) → (a b : A)
→ PathP (λ i → F (base-Poly+ v a b i)) ((base* v a) Poly+* (base* v b)) (base* v (a + b)))
where
f : (P : Poly A' n) → F P
f 0P = 0P*
f (base v a) = base* v a
f (P Poly+ Q) = (f P) Poly+* (f Q)
f (Poly+-assoc P Q R i) = Poly+-assoc* (f P) (f Q) (f R) i
f (Poly+-Rid P i) = Poly+-Rid* (f P) i
f (Poly+-comm P Q i) = Poly+-comm* (f P) (f Q) i
f (base-0P v i) = base-0P* v i
f (base-Poly+ v a b i) = base-Poly+* v a b i
f (trunc P Q p q i j) = isOfHLevel→isOfHLevelDep 2 issd (f P) (f Q) (cong f p) (cong f q) (trunc P Q p q) i j
module Poly-Rec-Set
-- types
(n : ℕ)
(B : Type ℓ')
(iss : isSet B)
-- elements
(0P* : B)
(base* : (v : Vec ℕ n) → (a : A) → B)
(_Poly+*_ : B → B → B)
-- AbGroup eq
(Poly+-assoc* : (PS QS RS : B) → (PS Poly+* (QS Poly+* RS)) ≡ ((PS Poly+* QS) Poly+* RS))
(Poly+-Rid* : (PS : B) → (PS Poly+* 0P*) ≡ PS)
(Poly+-comm* : (PS QS : B) → (PS Poly+* QS) ≡ (QS Poly+* PS))
-- Base eq
(base-0P* : (v : Vec ℕ n) → (base* v 0r) ≡ 0P*)
(base-Poly+* : (v : Vec ℕ n) → (a b : A) → ((base* v a) Poly+* (base* v b)) ≡ (base* v (a + b)))
where
f : Poly A' n → B
f = Poly-Ind-Set.f n (λ _ → B) (λ _ → iss) 0P* base* _Poly+*_ Poly+-assoc* Poly+-Rid* Poly+-comm* base-0P* base-Poly+*
module Poly-Ind-Prop
-- types
(n : ℕ)
(F : (P : Poly A' n) → Type ℓ')
(ispd : (P : Poly A' n) → isProp (F P))
-- elements
(0P* : F 0P)
(base* : (v : Vec ℕ n) → (a : A) → F (base v a))
(_Poly+*_ : {P Q : Poly A' n} → (PS : F P) → (QS : F Q) → F (P Poly+ Q))
where
f : (P : Poly A' n) → F P
f = Poly-Ind-Set.f n F (λ P → isProp→isSet (ispd P)) 0P* base* _Poly+*_
(λ {P Q R} PS QS RQ → toPathP (ispd _ (transport (λ i → F (Poly+-assoc P Q R i)) _) _))
(λ {P} PS → toPathP (ispd _ (transport (λ i → F (Poly+-Rid P i)) _) _))
(λ {P Q} PS QS → toPathP (ispd _ (transport (λ i → F (Poly+-comm P Q i)) _) _))
(λ v → toPathP (ispd _ (transport (λ i → F (base-0P v i)) _) _))
(λ v a b → toPathP (ispd _ (transport (λ i → F (base-Poly+ v a b i)) _) _))
module Poly-Rec-Prop
-- types
(n : ℕ)
(B : Type ℓ')
(isp : isProp B)
-- elements
(0P* : B)
(base* : (v : Vec ℕ n) → (a : A) → B)
(_Poly+*_ : B → B → B)
where
f : Poly A' n → B
f = Poly-Ind-Prop.f n (λ _ → B) (λ _ → isp) 0P* base* _Poly+*_
|
\chapter{Problem statement}
\label{cha:problemStatement}
Automatic speech recognition is concerned with finding ways to enable computers to recognize spoken language and transcribe it to text. Speech recognition asks the question:
\noindent \textit{What is being said?}
In order to answer this question one must determine, which parts of a recording contain relevant information. These parts should then be decoded and the rest ignored. In order to answer the first question one must ask a second:
\noindent \textit{Which parts are interesting in a recording?}
If interesting parts are found in the recording the system should label them correctly. During the labeling process a sequence of inputs is assigned a sequence of labels. Following this train of thought a sequence to sequence labeling problem must be solved. Speech data consists of frames. Transcription means grouping the interesting frames of the input sequence and assigning labels to these groups. Once input sequence groups are found and matched with a label sequence, the two are considered to be aligned. In order to do the alignment one must know:
\noindent \textit{How can sequence to sequence alignment be established?}
This thesis relies on machine learning methods in its attempt to determine what is being said. Machine learning models typically consist of many unknown weights, which are initially chosen at random. Better values for each weight are determined using a form of gradient descent. The process of using gradient descent to determine good model parameters is often referred to as training. Unfortunately gradient descent does not always lead to an acceptable solution. Only if the training algorithm is run with carefully chosen hyper-parameters on a model complex enough to form an internal representation of the patters it is trained to extract, the optimization process will terminate at a good optimum. Using machine learning methods leads to more important questions:
\noindent \textit{What model architecture is capable of handling the complex patterns found in speech data?}
\textit{Which hyper-parameters should be chosen to train such a model?}
A well known problem of machine learning methods is over-fitting, one must therefore ask:
\noindent \textit{How can a model that generalizes well be trained?}
Working with raw speech data should be possible in principle, in the speech literature researchers often use frequency domain representations of the original speech data. These representations are also called features, which leads to another question:
\noindent \textit{What kind of feature representation of the input signal should be used if any?}
At this point there are a lot of open questions and finding answers might not always be easy, it would therefore be interesting to know:
\noindent \textit{Which methods will allow the solution of any of the questions above?}
Last but not least, this thesis should be useful to others. It's code contributions should benefit future researchers, which leads to one last question:
\noindent \textit{How should software be developed in order to produce useful and maintainable results?}
This thesis is an attempt answer the questions above, trough literature study, coding, and experimentation.
|
Formal statement is: lemma lipschitz_on_cmult_real [lipschitz_intros]: fixes f::"'a::metric_space \<Rightarrow> real" assumes "C-lipschitz_on U f" shows "(abs(a) * C)-lipschitz_on U (\<lambda>x. a * f x)" Informal statement is: If $f$ is $C$-Lipschitz on $U$, then $a f$ is $|a| C$-Lipschitz on $U$.
|
State Before: ι : Type ?u.161852
α : Type u_1
β : Type ?u.161858
inst✝ : HeytingAlgebra α
a✝ b c a : α
⊢ a ≤ ⊤ᶜ ↔ a ≤ ⊥ State After: no goals Tactic: rw [le_compl_iff_disjoint_right, disjoint_top, le_bot_iff]
|
module IdealizedExperiments
using Oceananigans.Units
include("three_layer_constant_fluxes.jl")
two_day_suite_parameters = Dict{Symbol, Any}(
:free_convection => Dict{Symbol, Any}(:momentum_flux => 0.0, :buoyancy_flux => 1.2e-7, :f => 1e-4),
:strong_wind => Dict{Symbol, Any}(:momentum_flux => -1e-3, :buoyancy_flux => 0.0, :f => 1e-4),
:strong_wind_weak_cooling => Dict{Symbol, Any}(:momentum_flux => -7e-4, :buoyancy_flux => 6e-8, :f => 1e-4),
:weak_wind_strong_cooling => Dict{Symbol, Any}(:momentum_flux => -3.3e-4, :buoyancy_flux => 1.1e-7, :f => 1e-4),
:strong_wind_weak_heating => Dict{Symbol, Any}(:momentum_flux => -1e-3, :buoyancy_flux => -4e-8, :f => 1e-4),
:strong_wind_no_rotation => Dict{Symbol, Any}(:momentum_flux => -2e-4, :buoyancy_flux => 0.0, :f => 0.0),
)
for (name, set) in two_day_suite_parameters
set[:name] = string(name)
set[:stop_time] = 2days
end
four_day_suite_parameters = Dict{Symbol, Any}(
:free_convection => Dict{Symbol, Any}(:momentum_flux => 0.0, :buoyancy_flux => 7.0e-8, :f => 1e-4),
:strong_wind => Dict{Symbol, Any}(:momentum_flux => -8e-4, :buoyancy_flux => 0.0, :f => 1e-4),
:strong_wind_weak_cooling => Dict{Symbol, Any}(:momentum_flux => -6.5e-4, :buoyancy_flux => 4e-8, :f => 1e-4),
:weak_wind_strong_cooling => Dict{Symbol, Any}(:momentum_flux => -3e-4, :buoyancy_flux => 7e-8, :f => 1e-4),
:strong_wind_no_rotation => Dict{Symbol, Any}(:momentum_flux => -1e-4, :buoyancy_flux => 0.0, :f => 0.0),
)
for (name, set) in four_day_suite_parameters
set[:name] = string(name)
set[:stop_time] = 4days
end
six_day_suite_parameters = Dict{Symbol, Any}(
:free_convection => Dict{Symbol, Any}(:momentum_flux => 0.0, :buoyancy_flux => 5e-8, :f => 1e-4),
:strong_wind => Dict{Symbol, Any}(:momentum_flux => -7e-4, :buoyancy_flux => 0.0, :f => 1e-4),
:strong_wind_weak_cooling => Dict{Symbol, Any}(:momentum_flux => -5.5e-4, :buoyancy_flux => 3e-8, :f => 1e-4),
:weak_wind_strong_cooling => Dict{Symbol, Any}(:momentum_flux => -2.2e-4, :buoyancy_flux => 5e-8, :f => 1e-4),
:strong_wind_no_rotation => Dict{Symbol, Any}(:momentum_flux => -7e-5, :buoyancy_flux => 0.0, :f => 0.0),
)
for (name, set) in six_day_suite_parameters
set[:name] = string(name)
set[:stop_time] = 6days
end
end # module
|
%===============================================================================
% CVS $Id$
%===============================================================================
\section{Collaboration Environment and Communication}
\subsection{Mailing Lists}
The main ESMF technical mailing list is:
\begin{center}
\htmladdnormallink{esmf\[email protected]}{mailto:esmf\[email protected]}
\end{center}
This list handles telecon announcements, technical questions and
comments, discussions and materials relating to design and code
reviews, planning discussions, project announcements, and any other
items that concern the JST.
The list for active ESMF developers is:
\begin{center}
\htmladdnormallink{esmf\[email protected]}{mailto:esmf\[email protected]}
\end{center}
This list is for people who are developing code and checking
it into the ESMF repository. Mails here may cover coordination
issues relating to check-ins and releases, technical material that
is not yet ready for the JST, and information specific to NCAR
and particular development platforms.
Support questions should be directed to:
\begin{center}
\htmladdnormallink{esmf\[email protected]}{mailto:esmf\[email protected]}
\end{center}
The {\bf Users} tab on the ESMF website describes
how to submit an effective support request and outlines the ESMF support
policy.
People who are interested in occasional high-level project updates
can join the mailing list:
\begin{center}
\htmladdnormallink{esmf\[email protected]}{mailto:esmf\[email protected]}
\end{center}
Subscribers to this list receive more or less quarterly newletters
describing ESMF achievements and events.
To subscribe to any of these lists on-line, see the {\bf Users}
tab on the ESMF website.
\subsection{Meetings and Telecons}
ESMF JST telecons are held as needed, typically on a weekly basis.
Normal telecon times are 1:00pm MT Thursdays, and sometimes Tuesdays.
A calendar of telecon topics is maintained on the home page of
the ESMF website. These telecons are open and are announced to
the esmf\[email protected] list.
The Core Team meets weekly, at 9:30am MT on Wednesdays. The
meeting is also set up as a telecon. Core Team meetings are open
to active developers.
The ESMF project has open community meetings on an annual basis,
usually during late spring.
CRB meetings are held quarterly and are closed. However, prior
to each CRB meeting a JST telecon is devoted to collecting comments,
requirements, and priorities from JST members for consideration by
the CRB.
\subsection{SourceForge Open Source Development Environment}
The ESMF project utilizes the SourceForge open source development
environment. It provides a variety of tools as well as web-browsable
repositories.
\subsubsection{The Main ESMF Site and Repository}
The main ESMF SourceForge site is at:
\begin{center}
\htmladdnormallink{{\bf http://sourceforge.net/projects/esmf}}{http://sourceforge.net/projects/esmf}
\end{center}
This site is accessible from the ESMF website,
via either the {\bf Developers} link or the {\it SourceForge}
logo on the navigation bar. It is used for
\begin{itemize}
\item hosting and browsing the ESMF source code CVS repository;
\item maintaining task lists;
\item archiving mailing lists;
\item providing tarballs of public source code releases (releases
are also made available on the ESMF website);
\item tracking bugs; and
\item tracking support requests.
\end{itemize}
The source code and tools on this site are maintained by the
ESMF Core Team, and contributions and changes cannot be made to
them without coordination with the Core Team.
\begin{sloppypar}
The main ESMF CVS repository is web-accessible at:
\htmladdnormallink{{\bf http://sourceforge.net/cvs/?group\_id=38089}}
{http://sourceforge.net/cvs/?group_id=38089}
\end{sloppypar}
\begin{sloppypar}
The SourceForge site has instructions for checking out code.
Other CVS documentation is available at:
\htmladdnormallink{{\bf http://www.gnu.org/manual/cvs/html\_node/cvs\_toc.html}}{http://www.gnu.org/manual/cvs/html_node/cvs_toc.html}
\end{sloppypar}
All ESMF documents, source code and test and other scripts are stored
in the main repository.
The SourceForge repository contains only the ESMF framework. Components
that use ESMF are stored in repositories at their home institutions.
\subsubsection{The ESMF Contributions Site and Repository}
A second ESMF SourceForge site and repository is at:
\begin{center}
\htmladdnormallink{{\bf http://sourceforge.net/projects/esmfcontrib}}{http://sourceforge.net/projects/esmfcontrib}
\end{center}
Contributors in the broader community can use this site
to archive and share code related to ESMF. Coordination is
not required with the ESMF Core Team in order to check into the
contributions repository.
|
\PassOptionsToPackage{usenames,dvipsnames}{xcolor}
\documentclass[modern]{descnote}
\pdfoutput=1 %for arXiv submission
\usepackage[T1]{fontenc}
\usepackage{ae,aecompl}
\usepackage[utf8]{inputenc}
\usepackage{newtxtext,newtxmath}
\usepackage[english]{babel}
\usepackage{amsmath,amstext}
\usepackage[figure,figure*]{hypcap}
\usepackage[hang]{footmisc}
\setlength{\footnotemargin}{0.8em}
\usepackage{threeparttablex}
\usepackage{longtable}
\usepackage{inconsolata}
% change `finalizecache` to `frozencache` below for arxiv
\usepackage[finalizecache,cachedir=.]{minted}
\definecolor{DESCred}{rgb}{0.63,0.00,0.20}
\hypersetup{colorlinks=true,breaklinks=true,
citecolor=DESCred,filecolor=DESCred,linkcolor=DESCred,urlcolor=DESCred}
%figure path
\graphicspath{{figs/}}
% for \autoref
\renewcommand*\sectionautorefname{Section}
\renewcommand*\subsectionautorefname{Section}
\renewcommand*\subsubsectionautorefname{Section}
%%%%% Custom commands %%%%%%
% For creating hyperlinks
\newcommand*{\https}[1]{\href{https://#1}{\nolinkurl{#1}}}
\newcommand*{\http}[1]{\href{http://#1}{\nolinkurl{#1}}}
% Other useful commands
\DeclareUrlCommand\code{\urlstyle{tt}}
% Commands for editing and revisions
\newcommand{\todo}[1]{{\color{orange} #1}}
\newcommand{\rev}[1]{{\color{blue}\bf #1}}
% Commands for versioning
\newcommand*{\thisversion}{v2}
%%%%% Front Matter %%%%%%
\shorttitle{DESC DC2 Data Release Note}
\shortauthors{LSST~DESC}
\begin{document}
\title{DESC DC2 Data Release Note}
\input{authors}
\begin{abstract}
%\clearpage
% Potential v4
In preparation for cosmological analyses of the Vera C. Rubin Observatory Legacy Survey of Space and Time (LSST), the LSST Dark Energy Science Collaboration (LSST DESC) has created a 300~deg$^2$ simulated survey as part of an effort called Data Challenge 2 (DC2). The DC2 simulated sky survey, in six optical bands with observations following a reference LSST observing cadence, was processed with the LSST Science Pipelines (19.0.0). In this Note, we describe the public data release of the resulting object catalogs for the coadded images of five years of simulated observations along with associated truth catalogs. We include a brief description of the major features of the available data sets. To enable convenient access to the data products, we have developed a web portal connected to Globus data services. We describe how to access the data and provide example Jupyter Notebooks in Python to aid first interactions with the data. We welcome feedback and questions about the data release via a GitHub repository.
\clearpage
\end{abstract}
\tableofcontents
\clearpage
\section{Introduction}
In the next decade, an unprecedented survey of the sky will be carried out using the Vera C. Rubin Observatory, the Legacy Survey of Space and Time \citep{2009arXiv0912.0201L,2019ApJ...873..111I}. One of the major aims of the survey is to unravel the origins of the accelerated expansion of the Universe. The LSST Dark Energy Science Collaboration (DESC)\footnote{\https{lsstdesc.org}} was formed to carry out this exciting endeavor~\citep{Abate:2012za}. In order to prepare for the arrival of data, LSST DESC has undertaken two data challenges (DC1 and DC2) based on sophisticated cosmological and image simulations. The data challenges have been designed to mimic actual data from the Rubin Observatory in small, representative areas of the LSST observing footprint.
Both LSST DESC data challenges are based on realistic simulations of the extragalactic sky and employ an image simulation package, imSim, that provides access to a wide range of features. The resulting synthetic data were processed with Rubin's LSST Science Pipelines~\citep{2017ASPC..512..279J} to generate the final data products. The first data challenge, DC1, covers a $\sim$40 deg$^2$ area and ten years of observations. The image simulations were carried out for $r$-band only. A detailed description and a range of analysis results are provided in~\cite{dc1}. In this data release note, we focus on the second data challenge, DC2. A comprehensive description of the LSST DESC DC2 Simulated Sky Survey can be found in~\cite{2020arXiv201005926L}. DC2 covers $\sim$300 deg$^2$ in the wide-fast-deep (WFD) area to be surveyed by LSST. Within this area, a small 1~deg$^2$ deep-drilling field (DDF), which has a much greater density of observations, has been simulated as well. For the data release described in this note, only data from the WFD campaign and 5 years of observations are provided, corresponding to the planned sixth Rubin data release, DR6. For DC2, all six optical bands $ugrizy$ are included in the image simulations. Both the extragalactic catalog and image simulations include many relevant features expected in LSST data at varying levels of realism, from simpler approximations to more realistic physical models. The choice of how to represent the features depended on the complexity of the actual data and the finite resource availability. The DC2 overview paper \citep{2020arXiv201005926L} provides a comprehensive discussion about the DC2 design choices, which were guided mostly by considerations regarding cosmological probes.
For LSST DESC, the data challenges serve multiple purposes. The advantage of simulated data is that the underlying truth is known. Therefore, even if they are not as complex as observational data or have different systematics, they provide an excellent testbed for DESC analysis pipelines. Given that the data formats closely mimic what is planned for the Rubin data products, they also serve to aid the development and optimization of data access methods. The data challenges also offer the opportunity to exercise the LSST Science Pipelines and investigate their performance, in particular with regard to how systematic effects in the data are handled. By making a first set of the data products publicly available, we hope that other LSST Science Collaborations will be able to carry out useful tests in preparation for arrival of LSST data as well. In addition, the data should be of value for the broader optical astronomy and cosmology communities.
This note is organized as follows. In~\autoref{sec:features} we describe the major features of the DC2 data set. We provide an overview of the data products that are part of this release in~\autoref{sec:products}. We provide instructions for data access, including a set of example Python Jupyter notebooks, in~\autoref{sec:access}. We conclude in~\autoref{sec:outlook} and provide a brief description of possible future data releases.
\section{Major Features of the Data Set}
\label{sec:features}
\subsection{Astrophysical Inputs}
Here we describe the astrophysical inputs for the simulated WFD data set.\footnote{As described in \cite{2020arXiv201005926L}, data that were generated for the DDF region have additional astrophysical components such as strong lenses and an enhanced rate of transients.} The components of this data set are mostly limited to the types of objects needed to support static probes of dark energy science, specifically the galaxies from the cosmoDC2 extragalactic catalog \citep{korytov}. In addition, this data set includes stars from a simulated Milky Way, which are needed for astrometric and photometric calibration by the image processing pipeline, as well as Type Ia supernovae (SNe), which were included throughout the 300~deg$^2$ DC2 region. The center of the WFD region is at R.A.~$= 55^\circ\!\!.064$, Decl.~$= -29^\circ\!\!.783$ (see~\autoref{fig:skymap}), and so the entire simulation region lies well outside of the Ecliptic and Galactic planes.
As noted, the galaxies are from the cosmoDC2 extragalactic catalog\footnote{ \https{portal.nersc.gov/project/lsst/cosmoDC2/}}, which covers 440 deg$^2$ out to a redshift of $z = 3$ and is complete to $m_r <28$. The cosmoDC2 catalog is based on the Outer Rim $N$-body simulation \citep{2019ApJS..245...16H}, and the properties of the galaxies were derived using the Galacticus semi-analytic model \citep{benson_2010b} and painted onto dark matter halos using GalSampler \citep{2020MNRAS.495.5040H}. The derived galaxy properties include stellar mass, morphology, spectral energy distributions, broadband filter magnitudes, host halo information, and weak lensing shears. The bulge and disk components of the galaxies are rendered separately as S\'ersic profiles, and galaxies with $m_i < 27$ have ``knots'' of star formation added in order to model more complex light profiles for the brighter galaxies. The fluxes for these star-forming regions have been re-allocated from the disk component, and the knots have the same spectral energy distribution (SED) as the disk.
The Milky Way stars are simulated using the Galfast model of \citet{2008ApJ...673..864J}, which is based on densities and colors of stars in the Sloan Digital Sky Survey (SDSS). Stellar variability is included for periodic objects (e.g., RR Lyrae and Cepheids) and for non-periodic variables (e.g., CVs, flaring M-dwarfs, etc.). Stars without a definitive variability class are modeled based on the Kepler Q17 data release \citep{2016ksci.rept....3T}. The Galactic reddening is based on the three-dimensional model of \cite{2005AJ....130..659A}.
Finally, Type Ia SNe have been added throughout the DC2 region out to a redshift of $z=1.4$ with a population density that is consistent with observations~(e.g., \citealt{2010ApJ...713.1026D}). The simulated Type Ia SNe light curves were derived from a slightly modified version of the SALT2 model~\citep{2007A&A...466...11G}.
\subsection{Image Simulation Features}
DC2 used the \code{minion_1016} observing cadence\footnote{ \https{docushare.lsst.org/docushare/dsweb/View/Collection-4604}}, which was the Rubin Observatory LSST baseline cadence when production of the DC2 simulations began. This cadence provides the nominal field positions, telescope rotations, and filter selections for each 30-second pointing, as well as predicted seeing and airmass. For the sky background, the LSST sky model is used, which is the ESO sky model with a twilight component added~\citep{2016SPIE.9910E..1AY}. We have added random translational and rotational dithering to the nominal pointings to make the sky coverage more uniform.
The imSim simulation software, which is described in more detail in~\cite{2020arXiv201005926L}, uses the GalSim package \citep{2015A&C....10..121R} to render the astrophysical objects and the night sky. The point-spread functions (PSFs) for each exposure are computed using a set of atmospheric phase screens that are realizations of Gaussian random fields with a Von Karman power spectrum. In addition, the PSF calculation includes an optical model of the telescope based on modeling of the active optics system for Rubin Observatory. After convolution with the PSF, objects are rendered on the LSST CCDs taking into account the instrumental throughput in each band, the object's SED within the bandpass, atmospheric effects such as differential chromatic refraction, and the convergence of the incident beam from the telescope optics. GalSim's sensor model includes the brighter-fatter and tree-ring electrostatic effects that are present in the CCDs used in the LSST Camera (LSSTCam). Finally, electronics readout effects such as bleed trails, CCD segmentation, intra-CCD cross-talk, read noise, etc., are applied. These effects are based on measurements of the actual LSSTCam hardware.
\subsection{Image Processing}
\label{sec:processing}
For the image processing of the DC2 data, we used version 19.0.0 of the LSST Science Pipelines code\footnote{\https{pipelines.lsst.io/v/v19_0_0/index.html}}. The image processing steps are described in detail in \cite{2020arXiv201005926L}, \cite{10.1093/pasj/psx080}, and \cite{2018arXiv181203248B}. Since the simulations lack throughput variation over the focal plane and from visit to visit, we omitted the joint photometric and astrometric calibration across visits, and consequently, the standard passbands for the LSST filters are simply the total throughputs\footnote{\https{github.com/lsst/throughputs/releases/tag/1.4}} used in the simulations and which were derived by the Rubin systems engineering team.
\section{Available Data Sets}
\label{sec:products}
This Data Release (\thisversion{}) provides the data from the WFD campaign for 5 years of observations (corresponding to Rubin's DR6). This data set includes two tables: the Object Table (about 114 million extended sources and 33 million point sources; 118 gigabytes) and the Truth-match Table (about 759 million galaxy entries, 5 million star entries, and half million SN entries; 63 gigabytes). Each is partitioned by sky region (``tract'') into 166 files, as described in detail in ~\autoref{sec:representation}. In addition, two tracts of coadded images are also available. We define each of these data products in the subsections below.
\subsection{Object Table}
\label{sec:object}
The Object Table contains information about static astronomical objects measured on a coadded image. The photometry in the Object Table is measured with the forced photometry method, i.e., it is consistently measured across multiple bands using a fixed position, which is determined from the reference band for each source \citep[Section~3.4 of][]{10.1093/pasj/psx080}.
The generation of the Object Table is described in detail in Section~8 of \cite{2020arXiv201005926L}. In short, after the LSST Science Pipelines (19.0.0) produce the deepCoadd catalogs of multiple bands, we merge these catalogs across bands, and rename and compute certain columns to produce the final Object Table. The columns we rename or compute are meant to produce a science-ready catalog that resembles the Rubin LSST Data Products Definition Document (LSE-163; \https{lse-163.lsst.io}) for the end users.
Each entry (row) in the Object Table corresponds to one measured astronomical object, assigned with a unique ID (\code{objectId}). There are no duplicated entries in the Object Table. For details about the file format and the organization of files for the Object Table, see \autoref{sec:representation}. The full schema for the Object Table can be found in \autoref{app:object-schema}.
\subsection{Truth-match Table}
\label{sec:truth}
The Truth-match Table is a joint representation of both the truth information (i.e., the perfect, noiseless measurement of astronomical objects' positions and fluxes within the standard passbands, used as inputs to the image simulations) and their best matches to the measured objects in the Object Table. The Truth-match Table allows users to examine, for example, the differences between true and measured fluxes and positions, and compare them to the expected levels of photometric and astrometric accuracy and precision.
The generation of the Truth-match Table is described in Section~4.2.1 of \cite{2020arXiv201005926L}. The truth information in the Truth-match Table only includes ``summary'' properties (i.e., static, or infinite-time averaged fluxes) of galaxies, stars, and SNe. Time-varying properties are not included. The match information stored in the Truth-match Table is produced with the following procedure applied for each entry in the Object Table:
\begin{enumerate}
\item Search for all truth entries that are within 1~arcsec and have an $r$-band magnitude difference ($\Delta r$) less than 1~mag. If one or more truth entries satisfying these criteria are found, pick the truth entry with the smallest $|\Delta r|$ as the match, and set \code{is_good_match} to \code{True}.
\item If no truth entry was found in Step (1), pick the truth entry that is the nearest neighbor of the object entry on sky as the match, and set \code{is_good_match} to \code{False}.
\end{enumerate}
Given this procedure, every entry in the Object Table is assigned exactly one match. The majority of object entries have a ``good'' match (i.e., satisfying criteria in Step 1 above), and the rest have a nearest-neighbor match. More than 90\% of the ``good'' matches are not only the closest match in magnitude, but also the nearest neighbor match.
As we will discuss further in \autoref{sec:representation}, the data tables are split by sky regions when stored on disk. The matching procedure described above was applied to each sky region individually; hence, a very tiny fraction ($<0.002\%$) of objects may not have good matches due to being too close to the sky region boundaries.
Because the Object Table was used as the reference catalog for the matching procedure, some truth entries may be chosen as a match more than once, while others may not be chosen at all.
Flags to distinguish these situations are included in the Truth-match Table.
Selecting all entries with \code{match_objectId} $> -1$ from the Truth-match Table would result in a subset of Truth-match entries that have exactly the same row order as the entries in the Object Table (and hence may contain duplicated truth entries). On the other hand, selecting all entries with \code{is_unique_truth_entry} being \code{True} would produce a subset of Truth-match entries that contains all unique truth entries, including truth entries that have not been chosen as a match.
These selections are particularly important for users who wish to access the files directly. For users who use GCRCatalogs (\autoref{sec:gcr}), the reader will automatically select the correct rows depending on whether the user loads the ``Truth'' view (having all truth entries) or the ``Match'' view (having entries that matches to the Object Table). We refer users to the example notebooks we provided (\autoref{sec:notebooks}) for detail.
The file format and the organization of files for the Truth-match Table are described in \autoref{sec:representation}. The full schema for the Truth-match Table can be found in \autoref{app:truth-schema}.
\subsection{Coadded Images}
The coadded images (and the corresponding calibrated exposures, background models, and detected sources; see \autoref{app:coadded-image-files}) for a small sky region (tracts 3828 and 3829; see \autoref{sec:representation} for definition) are available. These images are part of the direct outputs from the image processing using the LSST Science Pipelines (see \autoref{sec:processing}). The coaddition process is described in Sec.~3.3 of \cite{10.1093/pasj/psx080} and Sec.~4.2 of \cite{2018arXiv181203248B}.
The file format and the organization of files for the coadded images are also described in \autoref{sec:representation} and \autoref{app:coadded-image-files}.
\section{Data Access}
\label{sec:access}
\subsection{Data File Format and Organization}
\label{sec:representation}
All data tables in this release are stored in the Apache Parquet\footnote{\https{parquet.apache.org}} format, an efficient columnar storage form, with I/O tools readily available for multiple development systems.
The data files can be easily downloaded to the user's machine via Globus (\autoref{sec:download}), and read with Python packages such as \code{pyarrow} or \code{fastparquet}.\footnote{\code{pyarrow}: \https{arrow.apache.org/docs/python}; \code{fastparquet}: \https{fastparquet.readthedocs.io}}
We additionally provide a Python package, \code{GCRCatalogs}, which contains a high-level user interface to access the data files (see \autoref{sec:gcr}).
\begin{figure}[tbh!]
\centering
\includegraphics[width=0.8\textwidth]{figs/DC2_region_skymap_overlay.png}
\caption{Sky map of the DC2 footprint. The large green trapezoid is the full DC2 footprint. The small red square in the upper right corner is the DDF region that is excluded in this release. Each tract is represented by a rectangle with a number on it showing the tract ID. The light pink region shows the size of the LSSTCam focal plane as a comparison.}
\label{fig:skymap}
\end{figure}
Each data table is further partitioned into several files that correspond to different parts of the sky. The partition is based on the ``tract'' value in the ``Rings sky map'' pixelization of LSST Science Pipelines.\footnote{\https{pipelines.lsst.io/py-api/lsst.skymap.ringsSkyMap.RingsSkyMap.html}} \autoref{fig:skymap} illustrates the partition. The same partition is used for both Object Table and Truth-match Table. No padding is included; i.e., an entry that is near a tract boundary still only appears in the tract it belongs to. Each Parquet file contains only one partition (row group).
The coadded images we provided in this release are parts of the output files from v19.0.0 of the LSST Science Pipelines. These images are stored in the FITS (Flexible Image Transport System) format, and partitioned by filter (passband) and sky region. The sky region partition scheme follows the same ``Rings sky map'' described above. Each tract is further subdivided into ``patches'', and each individual coadded image file corresponds to a single patch. The descriptions of files included in this data set, and the associated filename patterns, can be found in \autoref{app:coadded-image-files}.
\subsection{Downloading Data Files}
\label{sec:download}
The data files are made available via a data portal website\footnote{\https{lsstdesc-portal.nersc.gov}\label{fn:portal}} using Globus\footnote{\https{www.globus.org}} services. Any user can authenticate using their organizational login or with a Globus ID\footnote{\https{www.globusid.org/what}} to initiate transfers of the full or partial data set to another endpoint to which the user has access, whether it be a laptop or a high-performance computing center.
Detailed instructions on data transfers can be found on our data portal website (see Footnote~\ref{fn:portal}).
\subsection{Accessing Data in Python}
\label{sec:gcr}
While the tabular data files are accessible via standard Parquet I/O tools, we provide a high-level Python package, \code{GCRCatalogs}\footnote{\https{github.com/LSSTDESC/gcr-catalogs}}, to assist users to access DC2 data.
The \code{GCRCatalogs} package is installable by package managers \code{pip} and \code{conda}.
Once installed, the package should be configured to recognize the path to which the data files have been downloaded. The DC2 data set will then be readily available in the user's own Python environment.
Detailed instructions can be found in our data portal website (see Footnote~\ref{fn:portal}).
Below we show an example Python code snippet to demonstrate how to use \code{GCRCatalogs} to obtain the R.A. and Decl. columns from three tracts of the Object Table, with a sampling rate of 1\%. The high-level user interface makes the code simple and readable.
\begin{minted}[frame=lines,samepage]{python}
import GCRCatalogs
from GCRCatalogs.helpers.tract_catalogs import tract_filter, sample_filter
obj_cat = GCRCatalogs.load_catalog("desc_dc2_run2.2i_dr6_object")
data = obj_cat.get_quantities(
quantities=['ra', 'dec'], # columns we want to load,
filters=[sample_filter(0.01)], # down sample at 1%
native_filters=[tract_filter([4225, 4226, 4430])], # select 3 tracts
)
\end{minted}
For accessing the coadded images, we recommend using standard FITS I/O tools, such as the \code{fits} module in \code{astropy}.\footnote{\https{docs.astropy.org/en/stable/io/fits/index.html}}
\subsection{Example Python Jupyter Notebook}
\label{sec:notebooks}
\begin{figure}[tbh!]
\centering
\includegraphics[width=\textwidth]{figs/notebook.png}
\caption{Screenshot of the beginning of the Object Table tutorial notebook.}
\label{fig:notebook}
\end{figure}
\begin{figure}[tbh!]
\centering
\includegraphics[width=0.75\textwidth]{figs/number_density.pdf}
\caption{A resulting plot from the example analysis in the tutorial notebook for the Truth-match Table. The plot shows the measured and true galaxy number density as a function of magnitude. The code to generate this plot is included in the notebook.}
\label{fig:number_density}
\end{figure}
We provide two example Python Jupyter Notebooks which further demonstrate how to use \code{GCRCatalogs} to access the tabular data
(currently no example notebook is available for coadded images).
They are designed as tutorials, with clear instructions (see a screenshot in \autoref{fig:notebook}). In addition to demonstrating the access method, these notebooks also explain the data model in detail, and provide a few simple analyses that can be used as starting points for further development (see an example plot from the notebook in \autoref{fig:number_density}).
These notebooks can be found in a GitHub repository\footnote{\https{github.com/LSSTDESC/desc-data-portal/tree/main/notebooks}}.
\section{Summary and Outlook}
\label{sec:outlook}
In this Note we described the first public data release for DC2 carried out by the LSST DESC. We make data available for a simulated WFD survey spanning 300 degree$^2$ and 5 years of Rubin observations, including a subset of the coadd-based catalogs that would be included in Rubin Observatory's DR6. %We provided a brief overview of the major features of the data set in~\autoref{sec:features} and a detailed description of the available products in~\autoref{sec:products}. The data can be accessed via a web portal that offers a convenient interface for data transfers using Globus, and we also released a set of example notebooks to enable first quick experiments, as described in~\autoref{sec:access}.
This data release (\thisversion{}) focuses on a limited set of data products generated with the LSST Science Pipelines. In the future, we plan to extend this data release in several directions. First, LSST DESC is currently working on generating so-called ``add-on'' catalogs. These catalogs provide information obtained from further processing the data. Examples include a photo-$z$ catalog and a cluster catalog. Once these catalogs have been carefully validated and are of sufficient quality to be of broader interest, they will be added to the DC2 Data Release. Second, the processing of the DDF portion of DC2 is still in progress. As explained in more detail in~\cite{2020arXiv201005926L}, the DDF region contains several astrophysical components, e.g.~AGNs, that are not available in the WFD region. As with the add-on catalogs, once careful validation has concluded, we plan to make those data available as well. Finally, for cosmology it is very informative to compare results from different survey data releases to build a better understanding of the impact of the depth of the data on cosmological constraints. Therefore, LSST DESC is currently generating additional coadds and associated catalogs for subsets of the data corresponding to 1- and 2-year depths. Depending on the feedback we receive, these datasets may become part of future public data releases as well.
\section{Conditions of Use}
If you use these data products in a publication, we ask that you cite this Note and the DC2 overview paper~\citep{2020arXiv201005926L}.
If you use \code{GRCCatalogs} to access the data products, please also cite \cite{2018ApJS..234...36M}.
If you would like to serve these data sets on a mirror site, or to ingest and serve them via a different access method (e.g., a database), we ask you to inform LSST~DESC at \href{mailto:[email protected]}{[email protected]} so that we can contact you when future updates are made to these data sets.
We encourage all users to provide feedback and ask questions via the ``Discussions'' feature in the dedicated GitHub repository\footnote{\https{github.com/LSSTDESC/desc-data-portal/discussions}}.
%%%%%% Appendices %%%%%%
\clearpage
\appendix
\section{Changelog}
\input{tables/changelog}
\clearpage
\section{Table Schema}
\subsection{Object Table Schema}
\label{app:object-schema}
\input{tables/schema_object}
\bigskip
\subsection{Truth-match Table Schema}
\label{app:truth-schema}
\input{tables/schema_truth}
\clearpage
\section{Coadded Image File Descriptions}
\label{app:coadded-image-files}
\input{tables/coadded-image-files}
%%%%%% Acknowledgments %%%%%%
\clearpage
\section*{Acknowledgments}
\phantomsection
\addcontentsline{toc}{section}{Acknowledgements}
\input{desc_ack_standard.tex}
% Individual acknowledgments (sorted by author order)
The work of SH, APH, KH, JH, EK, DK, PL, TU and ASV at Argonne National Laboratory was supported under the U.S. DOE contract DE-AC02-06CH11357.
Support for YYM was provided by NASA through the NASA Hubble Fellowship grant no.\ HST-HF2-51441.001 awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Incorporated, under NASA contract NAS5-26555.
% Contribution statements
%% The contributions from the authors are listed below in alphabetical order.
BA investigated variations in the sky model across the focal plane in imSim.
%
HA implemented the dithers and extracted the visit lists for the simulations.
%
YNB worked on the design and implementation of the imSim workflow and developed extensions to Parsl to meet the performance and scalability needs of the imSim workflow.
%
FEB contributed to the development and testing of the AGN model.
%
GB managed the European computational grid work for DC2.
%
RB conceptualized the interaction of Time Domain Science implementations with existing middleware software, compiled scientific desiderata for SN group, developed the implemented the code and the SN population along with their assignment to cosmoDC2 host galaxies, the cadence selection and contributed to the validation of SN, the planning and requirements for strong lensing injection, helped with validation of SN done by JWP, DS, RH, and SJ.
%
JRB contributed to production of the truth catalogs and to the software package GCRCatalogs.
%
DB contributed to the the image processing pipeline configuration, deployment and tuning at CC-IN2P3 and to the validation of the various data products.
%
KC contributed to the simulation and data processing workflows and Globus distribution portal.
%
JC worked on imSim development, image validation, image processing development and debugging, and calibration product generation.
%
JCT was responsible for the definition, implementation, and deployment of the SRS pipeline at CC-IN2P3.
%
AJC led the development of the LSST simulation tools and contributed to the initial definition of the DESC data challenges.
%
ADW developed the LSST DESC exposure checker and organized the DC2 visual inspection effort.
%
RD assisted in organization, planning and obtaining computing resources.
%
SFD helped design and implement the stellar and AGN variability models. He also implemented and maintained the interface between the cosmoDC2 simulations, the GalFast simulations, and ImSim.
%
SWD edited the note text.
%
EG contributed to the field location and dither design.
%
TG worked on the production of certain calibration products, and assisted with management of DESC NERSC resources.
%
SH is the HACC team lead; he contributed to the assessment of image generation computational requirements, co-led the management of DESC NERSC resources.
%
APH helped design and build the model of the galaxy-halo connection used to generate the cosmoDC2 extragalactic catalog.
%
KH was responsible for the overall organization of the DC2 project, was involved in many aspects of the extragalactic catalog production, and contributed to the text of the note.
%
FH implemented the mechanism for making the LSST Science Pipelines available online and usable both at CC-IN2P3 and at NERSC, managed the CC-IN2P3 data processing infrastructure used by the image processing pipeline and was responsible for the prompt data transfer between CC-IN2P3 and NERSC.
%
RH worked on the coordination and testing of simulated SN inside DC2, draft reading and editing.
%
JH was a core member of the extragalactic catalog production team.
%
MJ contributed significant portions of code to both the GalSim and ImSim code bases for the purposes of generating the DC2 images. He also contributed to the simulation design, especially decisions about which features should be included to achieve the desired goals of realism in the galaxy shapes for weak lensing science, while maintaining computational feasibility.
%
JBK was the main developer of the SL Sprinkler that inserted strongly lensed AGN into the instance catalogs and contributed the text of the paper relating to the SL Sprinkler.
%
HMK set up the web portal and managed the DESC software and data resources at NERSC.
%
EK was one of the principal developers of the extragalactic catalog that was used as input to the image simulations and also worked on the validation of the DC2 object catalogs, as described in the DC2 survey paper.
%
DK led the development of the model underlying the extragalactic catalog.
%
KSK contributed to the conceptual design of the simulated survey including determining which electronic effects to simulate and by association which master calibration products to include.
%
FL contributed the model for the knots component included in galaxy light profiles, and the implementation of said model in CatSim and imSim.
%
PL made significant contributions to the development of the cosmoDC2 extragalactic catalog
%
CSL helped develop physical models of the CCD detectors, which allowed physically real simulations of tree rings and the brighter-fatter effect.
%
NL contributed to the generation of strongly lensed host galaxies of multiply lensed AGN and SNIa in the strong lensing systems sprinkled in the DDF.
%
EPL made contributions to the sky model in imSim.
%
RHL contributed to the validation of the final data catalogs and provided support in using the LSST Science Pipelines.
%
RM organized analysis teams and synthesized input that factored into the overall DC2 design and validation, was engaged in the validation efforts, and edited the note text.
%
YYM contributed to the generation, validation, and access of various DC2 data products, the preparation of public release, and text of this note.
%
PJM helped design the survey regions and cadences, provided high-level scientific oversight, and contributed to defining the strong lensing requirements.
%
JEM helped develop and validate the PSF simulation within imSim.
%
JWP contributed to the generation and documentation for the truth tables of strongly lensed SNe and AGN for the full DC2 effort.
%
JP contributes to write notebooks using Apache Spark to access and manipulate the DC2 data.
%
DJP implemented a model for LSST optical effects in imSim, assisted in the development of internal data access tools, and contributed to the visual validation of DC2 images.
%
JP implemented a system for running imSim on the UK computational grid and used it to perform parts of the image simulation runs in Europe.
%
SP contributed to the validation of various DC2 data products, and managed the Apache Spark tools at NERSC.
%
AP contributed to many aspects of the underlying extragalactic catalog and performed initial studies of using imSim in containers.
%
ESR contributed coverage mapping, processing QA for missing tracts, and galaxy color QA.
%
FJS participated in DC2 design phase, and production. Participated in catalog validation and matching between object and truth catalog.
%
SJS wrote the text for the photometric redshifts section.
%
TDU was involved in setting up the initial imSim simulations to scale them up on thousands of nodes of Theta and supporting clusters at Argonne.
%i
ASV was responsible for early generation of instance catalogs, implementing the Parsl workflow for imSim on NERSC and ALCF resources, and helping in initial validation of these outputs.
%
CWW carried out early planning for DC2, worked on development, testing and management of the imSim image simulation program, and tested the released data product format.
%
MPW implemented the code to add lensed host galaxies to the lensed AGN and lensed SNe in the DC2 code.
%
MWV co-led the Data Access Task Force, served as the Data Coordinator, and contributed to validation of the DC2 data products.
%
%%%%%% References %%%%%%
\clearpage
\phantomsection
\addcontentsline{toc}{section}{References}
\bibliographystyle{aasjournal}
\bibliography{ref}
\end{document}
|
corollary isometry_subspaces: fixes S :: "'a::euclidean_space set" and T :: "'b::euclidean_space set" assumes S: "subspace S" and T: "subspace T" and d: "dim S = dim T" obtains f where "linear f" "f ` S = T" "\<And>x. x \<in> S \<Longrightarrow> norm(f x) = norm x"
|
-- ------------------------------------------------------------ [ PaperGRL.idr ]
-- Module : PaperGRL.idr
-- Copyright : (c) Jan de Muijnck-Hughes
-- License : see LICENSE
-- --------------------------------------------------------------------- [ EOH ]
module GRL.Lang.Test.GLang
import GRL.Lang.GLang
paper : GOAL
paper = mkGoal "My First Paper"
abst : GOAL
abst = mkGoal "Abstract"
bib : GOAL
bib = mkGoal "Bibliography"
intr : GOAL
intr = mkGoal "Intro"
meth : GOAL
meth = mkGoal "Methodology"
res : GOAL
res = mkGoal "Results"
disc : GOAL
disc = mkGoal "Discussion"
wabs : TASK
wabs = mkSatTask "Write Abstract" (SATISFIED)
rabs : TASK
rabs = mkSatTask "Review Abstract" (WEAKSATIS)
wbib : TASK
wbib = mkSatTask "Write Bib" (WEAKSATIS)
rbib : TASK
rbib = mkSatTask "Review Bib" (WEAKSATIS)
wIntro : TASK
wIntro = mkSatTask "Write Intro" (DENIED)
rIntro : TASK
rIntro = mkSatTask "Review Intro" (DENIED)
wMeth : TASK
wMeth = mkSatTask "Write Meth" (DENIED)
rMeth : TASK
rMeth = mkSatTask "Review Meth" (DENIED)
wRes : TASK
wRes = mkSatTask "Write Results" (DENIED)
rRes : TASK
rRes = mkSatTask "Review Results" (DENIED)
wDis : TASK
wDis = mkSatTask "Write Discussion" (DENIED)
rDis : TASK
rDis = mkSatTask "Review Discussion" (DENIED)
paperPlan : GModel
paperPlan = emptyModel
\= paper
\= abst \= wabs \= rabs \= bib \= wbib \= rbib
\= intr \= wIntro \= rIntro \= meth \= wMeth \= rMeth
\= res \= wRes \= rRes \= disc \= wDis \= rDis
\= (paper &= [bib,abst,intr,meth,res,disc])
\= (wabs ==> abst | MAKES) \= (rabs ==> abst | MAKES)
\= (wbib ==> bib | MAKES) \= (rbib ==> bib | MAKES)
\= (wIntro ==> intr | MAKES) \= (rIntro ==> intr | MAKES)
\= (wMeth ==> meth | MAKES) \= (rMeth ==> meth | MAKES)
\= (wRes ==> res | MAKES) \= (rRes ==> res | MAKES)
\= (wDis ==> disc | MAKES) \= (rDis ==> disc | MAKES)
-- -------------------------------------------------------------------- [ Test ]
export
runTest : IO ()
runTest = do
putStrLn $ prettyModel paperPlan
-- --------------------------------------------------------------------- [ EOF ]
|
function A=imresize3d(V,scale,tsize,ntype,npad)
% This function resizes a 3D image volume to new dimensions
% Vnew = imresize3d(V,scale,nsize,ntype,npad);
%
% inputs,
% V: The input image volume
% scale: scaling factor, when used set tsize to [];
% nsize: new dimensions, when used set scale to [];
% ntype: Type of interpolation ('nearest', 'linear', or 'cubic')
% npad: Boundary condition ('replicate', 'symmetric', 'circular', 'fill', or 'bound')
%
% outputs,
% Vnew: The resized image volume
%
% example,
% load('mri','D'); D=squeeze(D);
% Dnew = imresize3d(D,[],[80 80 40],'nearest','bound');
%
% This function is written by D.Kroon University of Twente (July 2008)
% Check the inputs
if(exist('ntype', 'var') == 0), ntype='nearest'; end
if(exist('npad', 'var') == 0), npad='bound'; end
if(exist('scale', 'var')&&~isempty(scale)), tsize=round(size(V).*scale); end
if(exist('tsize', 'var')&&~isempty(tsize)), scale=(tsize./size(V)); end
% Make transformation structure
T = makehgtform('scale',scale);
tform = maketform('affine', T);
% Specify resampler
R = makeresampler(ntype, npad);
% Anti-aliasing
if(scale<1)
r=ceil(2.5/scale(1)); H=sinc((-r:r)*scale(1)); H=H./sum(H);
Hx=reshape(H,[length(H) 1 1]);
r=ceil(2.5/scale(2)); H=sinc((-r:r)*scale(2)); H=H./sum(H);
Hy=reshape(H,[1 length(H) 1]);
r=ceil(2.5/scale(3)); H=sinc((-r:r)*scale(3)); H=H./sum(H);
Hz=reshape(H,[1 1 length(H)]);
V=imfilter(imfilter(imfilter(V,Hx, 'same' ,'replicate'),Hy, 'same' ,'replicate'),Hz, 'same' ,'replicate');
end
% Resize the image volueme
A = tformarray(V, tform, R, [1 2 3], [1 2 3], tsize, [], 0);
|
# -*- coding: utf-8 -*-
"""
Created on Mon Jul 20 20:28:35 2020
@author: unique
"""
import tensorflow.compat.v1 as tf
tf.disable_eager_execution() #关闭eager运算
tf.disable_v2_behavior() #禁用TensorFlow 2.x行为
import numpy as np
#训练步数
training_steps = 30000
#构造数据集
'''data=[]
label=[]
for i in range(200):
x1=np.random.uniform(-1,1)
x2=np.random.uniform(0,2)
if x1**2 +x2**2 <= 1:
data.append([np.random.normal(x1,0.1),np.random.normal(x2,0.1)])
label.append(0)
else:
data.append([np.random.normal(x1,0.1),np.random.normal(x2,0.1)])
label.append(1)
#翻转
data = np.hstack(data).reshape(-1,2)
label =np.hstack(label).reshape(-1,1)
#reader = csv.reader(open('f://dos1.csv'))'''
#读取csv文件中的内容
filename_queue1 = tf.train.string_input_producer(["f://spoofing1.csv"])
reader1 = tf.TextLineReader()
key1, value1 = reader1.read(filename_queue1)
filename_queue2 = tf.train.string_input_producer(["f://spoofing2.csv"])
reader2 = tf.TextLineReader()
key2, value2 = reader2.read(filename_queue2)
record_defaults = [[1.0],[1.0],[1.0],[1.0],[1.0],[1.0],[1.0],[1.0],[1.0],[1.0]]
col1,col2,col3,col4,col5,col6,col7,col8,col9,col10= tf.decode_csv(value1, record_defaults=record_defaults)
features = tf.concat([[col1],[col2],[col3],[col4],[col5],[col6],[col7],[col8],[col9]],0)
init_op = tf.global_variables_initializer()
local_init_op = tf.local_variables_initializer()
data=[]
label=[]
with tf.Session() as sess:
coord = tf.train.Coordinator()
threads = tf.train.start_queue_runners(coord=coord)
for i in range(10000):
d,l=sess.run([features,col10])
data.append(d)
label.append(l)
coord.request_stop()
coord.join(threads)
col1,col2,col3,col4,col5,col6,col7,col8,col9,col10= tf.decode_csv(value2, record_defaults=record_defaults)
features = tf.concat([[col1],[col2],[col3],[col4],[col5],[col6],[col7],[col8],[col9]],0)
with tf.Session() as sess:
coord = tf.train.Coordinator()
threads = tf.train.start_queue_runners(coord=coord)
for i in range(10000):
d,l=sess.run([features,col10])
data.append(d)
label.append(l)
coord.request_stop()
coord.join(threads)
data = np.hstack(data).reshape(-1,9)
label =np.hstack(label).reshape(-1,1)
def hidden_layer(input_tensor,weight1,bias1,weight2,bias2,weight3,bias3):
layer1=tf.nn.relu(tf.matmul(input_tensor,weight1)+bias1)
layer2=tf.nn.relu(tf.matmul(layer1,weight2)+bias2)
return tf.matmul(layer2,weight3)+bias3
x = tf.placeholder(tf.float32,shape=(None,9),name="x-input")
y_= tf.placeholder(tf.float32,shape=(None,1),name="y-output")
weight1 = tf.Variable(tf.truncated_normal([9,50],stddev=0.1))
bias1 =tf.Variable(tf.constant(0.1,shape=[50]))
weight2 = tf.Variable(tf.truncated_normal([50,50],stddev=0.1))
bias2 =tf.Variable(tf.constant(0.1,shape=[50]))
weight3 = tf.Variable(tf.truncated_normal([50,1],stddev=0.1))
bias3 =tf.Variable(tf.constant(0.1,shape=[1]))
sample_size = len(data)
#输出y
y = hidden_layer(x,weight1,bias1,weight2,bias2,weight3,bias3)
#损失函数
error_loss = tf.reduce_sum(tf.pow(y_-y,2))/sample_size
tf.add_to_collection("losses",error_loss)
#加入正则化
#regularizer = tf.contrib.layers.l2_regularizer(0.01)
regularizer=tf.keras.regularizers.l2(0.001)
regularization = regularizer(weight1)+regularizer(weight2)+regularizer(weight3)
tf.add_to_collection("losses",regularization)
loss = tf.add_n(tf.get_collection("losses"))
#定义优化器
train_op = tf.train.AdamOptimizer(0.05).minimize(loss)
#train_op = tf.train.GradientDescentOptimizer(0.05).minimize(loss)
#定义准确率
with tf.Session() as sess:
tf.global_variables_initializer().run()
for i in range(training_steps):
sess.run(train_op,feed_dict={x:data,y_:label})
if i%2000 ==0:
loss_value = sess.run(loss,feed_dict={x:data,y_:label})
print("After %d steps, losses:%f" %(i,loss_value))
#验证
#test_accuracy = sess.run(accuracy,feed_dict={x:data1,y_:label1})
#print(test_accuracy*100)
|
module MapLight
import Base.show
using JSON
using HttpCommon
using Requests
export bill_positions,
bill_search,
bill_list,
organization_positions,
organization_search,
authenticate
include("error.jl")
include("endpoint.jl")
include("auth.jl")
include("api.jl")
end
|
{-# OPTIONS --cubical --safe #-}
open import Prelude hiding (A; B)
open import Categories
module Categories.Pushout {ℓ₁ ℓ₂} (C : Category ℓ₁ ℓ₂) where
open Category C
private
variable
A B : Ob
h₁ h₂ j : A ⟶ B
record Pushout (f : X ⟶ Y) (g : X ⟶ Z) : Type (ℓ₁ ℓ⊔ ℓ₂) where
field
{Q} : Ob
i₁ : Y ⟶ Q
i₂ : Z ⟶ Q
commute : i₁ · f ≡ i₂ · g
universal : h₁ · f ≡ h₂ · g → Q ⟶ Codomain h₁
unique : ∀ {eq : h₁ · f ≡ h₂ · g} →
j · i₁ ≡ h₁ → j · i₂ ≡ h₂ →
j ≡ universal eq
universal·i₁≡h₁ : ∀ {eq : h₁ · f ≡ h₂ · g} →
universal eq · i₁ ≡ h₁
universal·i₂≡h₂ : ∀ {eq : h₁ · f ≡ h₂ · g} →
universal eq · i₂ ≡ h₂
HasPushouts : Type (ℓ₁ ℓ⊔ ℓ₂)
HasPushouts = ∀ {X Y Z} → (f : X ⟶ Y) → (g : X ⟶ Z) → Pushout f g
|
Formal statement is: lemma contour_integral_reverse_linepath: "continuous_on (closed_segment a b) f \<Longrightarrow> contour_integral (linepath a b) f = - (contour_integral(linepath b a) f)" Informal statement is: If $f$ is continuous on the closed segment from $a$ to $b$, then the contour integral of $f$ along the line segment from $a$ to $b$ is equal to the negative of the contour integral of $f$ along the line segment from $b$ to $a$.
|
module Main
import Data.Vect
infixr 5 .+.
data Schema = SString | SInt | (.+.) Schema Schema
SchemaType : Schema -> Type
SchemaType SString = String
SchemaType SInt = Int
SchemaType (x .+. y) = (SchemaType x, SchemaType y)
record DataStore (size : Nat) where
constructor MkData
schema : Schema
items : Vect size (SchemaType schema)
setSchema : DataStore 0 -> Schema -> DataStore 0
setSchema (MkData schema []) schema' = MkData schema' []
data Command : Schema -> Type where
SetSchema : Schema -> Command schema
Add : SchemaType schema -> Command schema
Get : Integer -> Command schema
Quit : Command schema
|
\documentclass[a4paper]{article}
\usepackage[utf8]{inputenc}
\usepackage[top=3cm,left=2.5cm,right=2.5cm,bottom=3cm]{geometry}
\usepackage{listings}
\usepackage{hyperref}
\title{\vspace{-5ex}liblat2eps v2.0}
\author{}
\date{\vspace{-5ex}}
\begin{document}
\maketitle
\section{Introduction}
liblat2eps is a small static library providing most of the functionality provided by the lat2eps command to user programs implemented in C or C++. It can be used for exporting lattice graphics in the Encapsulated PostScript (EPS) format directly from the programs, without generating an intermediary data file.
\bigbreak
\section{Installation}
liblat2eps is open source software supplied in source code form. It can be built with the \textit{make} command, which in addition to generating the \texttt{lat2eps} executable will also generate the \texttt{liblat2eps.a} static library. The \textit{gcc} or \textit{clang} compiler must be installed in the system for the build process to succeed. The \texttt{liblat2eps.a} file can be manually copied to a directory where the compiler searches for libraries, like, e.g., \texttt{/usr/local/lib}. The \texttt{lat2eps.h} header file declares the functions provided by the library and can be manually copied to a directory where the compiler searches for header files, like, e.g., \texttt{/usr/local/include}.
\bigbreak
\section{Library functions}
liblat2eps provides the following functions:
\bigbreak\bigbreak
\texttt{int lat2eps\_init(unsigned int width, unsigned int height)}
\bigbreak
The \texttt{lat2eps\_init()} function initializes the resources required by the EPS generation functionality, including allocating memory for holding the lattice state until the EPS output can be generated. This function must be called before any other liblat2eps function is called. The \textit{width} and \textit{height} parameters, which can take values from 1 to 16384, define the maximum dimensions of the lattice. The function returns zero for indicating a failure, or a non-zero value for success.
\bigbreak\bigbreak
\texttt{void lat2eps\_release()}
\bigbreak
The \texttt{lat2eps\_release()} function releases the resources allocated by \texttt{lat2eps\_init()}. It must be called after the EPS output is generated.
\bigbreak\bigbreak
\texttt{void lat2eps\_set\_site(unsigned int x, unsigned int y, int s)}
\bigbreak
The \texttt{lat2eps\_set\_site()} function sets the state of the site with coordinates \textit{x} and \textit{y} to value \textit{s}, within the liblat2eps internal lattice state.
\bigbreak
Typically, programs using liblat2eps should copy their own lattice state to the state held by liblat2eps by calling the \texttt{lat2eps\_set\_site()} function for each lattice site, before calling the \texttt{lat2eps\_gen\_eps()} function to actually generate the EPS output. Programs should avoid calling \texttt{lat2eps\_set\_site()} within their inner simulation loops, as it would likely cause a simulation slowdown. Instead, the programs should perform the copy only when the time for generating a graphic output has arrived, like after a determined number of Monte Carlo steps has been performed. Then the liblat2eps lattice state can be set with a loop like the following:
\bigbreak
\begin{lstlisting}[language=C]
for (y = 0; y < L; ++y) {
for (x = 0; x < L; ++x) {
lat2eps_set_site(x, y, lat[y][x]);
}
}
\end{lstlisting}
\bigbreak
There are 256 different color indexes in liblat2eps, ranging from 0 to 255, which can be used to draw lattice sites of different values. Site values are mapped to color indexes according to a simple rule: $index = value \bmod 256$. Negative values are first converted to unsigned values (e.g., -1 is converted to 255, -2 to 254, and so on). Note: a palette of only 16 different colors is initially defined, repeated over the 256 possible indexes. Thus, if more than 16 colors are needed, they must be redefined through the lat2eps\_set\_color() function.
\bigbreak\bigbreak
\texttt{int lat2eps\_get\_site(unsigned int x, unsigned int y)}
\bigbreak
The \texttt{lat2eps\_get\_site()} function returns the value of the lattice site with coordinates given by \textit{x} and \textit{y}, previously set by a \texttt{lat2eps\_set\_site()} function call, or the default value 0, if no value has been set. This function has been defined for extension purposes and is not required by typical lattice graphic generation.
\bigbreak\bigbreak
\texttt{void lat2eps\_set\_color(unsigned int index, unsigned int pal)}
\bigbreak
The \texttt{lat2eps\_set\_color()} function sets the color index specified by the \textit{index} parameter to a value defined by the \textit{pal} parameter, which should be a numeric value in the 0xRRGGBB format (i.e., an integer composed by three bytes, where the most significant byte defines the red component for the color index, from 0x00 to 0xFF, the middle byte defines the green component, and the least significant byte defines the blue component). It must be called before the \texttt{lat2eps\_gen\_eps()} function.
\bigbreak\bigbreak
\texttt{unsigned int lat2eps\_get\_color(unsigned int index)}
\bigbreak
The \texttt{lat2eps\_get\_color()} function returns the palette definition associated with a color index specified by the \textit{index} parameter. The returned value will be a numeric value in the 0xRRGGBB format.
\bigbreak\bigbreak
\texttt{void lat2eps\_text\_out(float x, float y, float ax, float ay, float angle, unsigned int size, unsigned int color, const char *text)}
\bigbreak
The \texttt{lat2eps\_text\_out()} function generates text entries over the lattice graphic. It can be used to generate text lines to appear in the graphic as they are, or tags that can be later replaced by LaTeX text using PSFrag. It must be called before the \texttt{lat2eps\_gen\_eps()} function. The parameters are the following:
\begin{itemize}
\item \textit{x} is the horizontal coordinate where the text will be positioned. 0 is the leftmost coordinate, while the maximum horizontal coordinate is defined by the lattice width.
\item \textit{y} is the vertical coordinate where the text will be positioned. 0 is the topmost coordinate, while the maximum vertical coordinate is defined by the lattice height.
\item \textit{ax} defines the horizontal alignment. 0 for left-aligning the text relative to the X coordinate, 0.5 for centering it on the X coordinate, 1 for right-aligning it, etc.
\item \textit{ay} defines the vertical alignment. 0 for placing the top of the text on the Y coordinate, 0.5 for centering it on the Y coordinate, 1 for placing the bottom of the text on the Y coordinate, etc.
\item \textit{angle} defines the angle to rotate the text, in degrees (0 for horizontal).
\item \textit{size} defines the font size.
\item \textit{color} defines the color index used to draw the text.
\item \textit{text} is the text to be generated. Parentheses characters in the text must be escaped with backslashes.
\end{itemize}
\bigbreak\bigbreak
\texttt{int lat2eps\_gen\_eps(const char *filename, unsigned int xoff, unsigned int yoff, unsigned int width, unsigned int height, unsigned int border, unsigned int scale)}
\bigbreak
The \texttt{lat2eps\_gen\_eps()} function creates an EPS file containing a graphic representation of the lattice (or a region of the lattice), using the lattice state information previously set through \texttt{lat2eps\_set\_site()} calls, also generating text entries previously defined by \texttt{lat2eps\_text\_out()} calls. This function can be called one or more times, possibly for different regions, before the lattice state is released by a \texttt{lat2eps\_release()} call. The function returns zero for indicating a failure, or a non-zero value for success. The parameters are the following:
\begin{itemize}
\item \textit{filename} defines the name of the EPS file that will be created. If this parameter is \texttt{NULL}, then the EPS data will be written to the standard output.
\item \textit{xoff} defines the first lattice column that will be presented in the graphic.
\item \textit{yoff} defines the first lattice row that will be presented in the graphic.
\item \textit{width} defines the width (in sites) of the sublattice that will be presented in the graphic.
\item \textit{height} defines the height (in sites) of the sublattice that will be presented in the graphic.
\item \textit{border} defines the width of a black border generated around the lattice graphic, or 0 for generating a borderless graphic.
\item \textit{scale} defines the scale used in the conversion of the lattice data to EPS. E.g., when the scale is set to 3, each lattice site will generate a 3x3 pixel square in the EPS output.
\end{itemize}
\bigbreak\bigbreak
\newpage
\section{Sample code}
The source code presented below illustrates a simple usage of the functionality provided by liblat2eps. Providing that the \texttt{lat2eps.h} header and the \texttt{liblat2eps.a} library are installed to standard locations, it could be compiled and linked with the \textit{gcc} compiler through the following command:
\bigbreak
\texttt{gcc sample.c -o sample -lm -llat2eps}
\bigbreak\bigbreak
\begin{lstlisting}[language=C, frame=single]
#include <math.h>
#include <lat2eps.h>
#define L 512
int main(int argc, char *argv[])
{
int x, y;
/* Initializes liblat2eps for a lattice of width L and height L. */
if (!lat2eps_init(L, L)) return -1;
/* Sets color number 9 to red:60 green:70 blue:a0 */
lat2eps_set_color(9, 0x6070a0);
/* Fills the lattice with a circular pattern. */
for (y = 0; y < L; ++y) {
for (x = 0; x < L; ++x) {
lat2eps_set_site(x, y, (int)sqrt(x*x+y*y)/50);
}
}
/* Adds some text. */
lat2eps_text_out(5, 5, 0, 0.5, -45, 15, 1, "Hello");
lat2eps_text_out(5, L-30, 0, 1, 0, 25, 1, "TAG1");
lat2eps_text_out(L-30, 10, 1, 1, 90, 25, 0, "TAG2");
/* Generates an EPS file with the entire lattice, */
/* with border width 1 and scale 1. */
lat2eps_gen_eps("sample.eps", 0, 0, L, L, 1, 1);
/* Releases resources. */
lat2eps_release();
return 0;
}
\end{lstlisting}
\bigbreak\bigbreak
\section{License}
liblat2eps v2.0 is open source software copyrighted by André R. de la Rocha and licensed under the Apache License Version 2.0. A copy of the license can be obtained at: \url{http://www.apache.org/licenses/LICENSE-2.0}
\end{document}
|
/*
Copyright (C) 2017 Quaternion Risk Management Ltd
All rights reserved.
This file is part of ORE, a free-software/open-source library
for transparent pricing and risk analysis - http://opensourcerisk.org
ORE is free software: you can redistribute it and/or modify it
under the terms of the Modified BSD License. You should have received a
copy of the license along with this program.
The license is also available online at <http://opensourcerisk.org>
This program is distributed on the basis that it will form a useful
contribution to risk analytics and model standardisation, but WITHOUT
ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or
FITNESS FOR A PARTICULAR PURPOSE. See the license for more details.
*/
#include <qle/models/cdsoptionhelper.hpp>
#include <qle/pricingengines/blackcdsoptionengine.hpp>
#include <qle/pricingengines/midpointcdsengine.hpp>
#include <ql/exercise.hpp>
#include <ql/quotes/simplequote.hpp>
#include <ql/termstructures/volatility/equityfx/blackconstantvol.hpp>
#include <ql/time/schedule.hpp>
#include <boost/make_shared.hpp>
namespace QuantExt {
CdsOptionHelper::CdsOptionHelper(const Date& exerciseDate, const Handle<Quote>& volatility, const Protection::Side side,
const Schedule& schedule, const BusinessDayConvention paymentConvention,
const DayCounter& dayCounter,
const Handle<DefaultProbabilityTermStructure>& probability, const Real recoveryRate,
const Handle<YieldTermStructure>& termStructure, const Rate spread, const Rate upfront,
const bool settlesAccrual, const bool paysAtDefaultTime, const Date protectionStart,
const Date upfrontDate, const boost::shared_ptr<Claim>& claim,
const BlackCalibrationHelper::CalibrationErrorType errorType)
: BlackCalibrationHelper(volatility, termStructure, errorType), blackVol_(boost::make_shared<SimpleQuote>(0.0)) {
boost::shared_ptr<PricingEngine> cdsEngine =
boost::make_shared<QuantExt::MidPointCdsEngine>(probability, recoveryRate, termStructure);
boost::shared_ptr<CreditDefaultSwap> tmp;
if (upfront == Null<Real>())
tmp = boost::shared_ptr<CreditDefaultSwap>(new CreditDefaultSwap(side, 1.0, 0.02, schedule, paymentConvention,
dayCounter, settlesAccrual, paysAtDefaultTime,
protectionStart, claim));
else
tmp = boost::shared_ptr<CreditDefaultSwap>(
new CreditDefaultSwap(side, 1.0, upfront, 0.02, schedule, paymentConvention, dayCounter, settlesAccrual,
paysAtDefaultTime, protectionStart, upfrontDate, claim));
tmp->setPricingEngine(cdsEngine);
Real strike = spread == Null<Real>() ? tmp->fairSpread() : spread;
if (upfront == Null<Real>())
cds_ = boost::shared_ptr<CreditDefaultSwap>(new CreditDefaultSwap(side, 1.0, strike, schedule,
paymentConvention, dayCounter, settlesAccrual,
paysAtDefaultTime, protectionStart, claim));
else
cds_ = boost::shared_ptr<CreditDefaultSwap>(
new CreditDefaultSwap(side, 1.0, upfront, strike, schedule, paymentConvention, dayCounter, settlesAccrual,
paysAtDefaultTime, protectionStart, upfrontDate, claim));
cds_->setPricingEngine(cdsEngine);
boost::shared_ptr<Exercise> exercise = boost::make_shared<EuropeanExercise>(exerciseDate);
option_ = boost::make_shared<CdsOption>(cds_, exercise, true);
Handle<BlackVolTermStructure> h(
boost::make_shared<BlackConstantVol>(0, NullCalendar(), Handle<Quote>(blackVol_), Actual365Fixed()));
blackEngine_ = boost::make_shared<BlackCdsOptionEngine>(probability, recoveryRate, termStructure, h);
}
Real CdsOptionHelper::modelValue() const {
calculate();
option_->setPricingEngine(engine_);
return option_->NPV();
}
Real CdsOptionHelper::blackPrice(Volatility sigma) const {
calculate();
blackVol_->setValue(sigma);
option_->setPricingEngine(blackEngine_);
Real value = option_->NPV();
option_->setPricingEngine(engine_);
return value;
}
} // namespace QuantExt
|
%%Ex. 2 The meaning of "a = b"
%In Matlab and in any programming language, the statement "a = b" does not mean
%"a equals b". Instead, it prompts the action of replacing the content of a by the
%content of b.
a = 3;
b = a;
b
%Output:3
|
{-# OPTIONS --cubical --no-import-sorts --safe #-}
module Cubical.Algebra.Magma.MorphismProperties where
open import Cubical.Foundations.Prelude
open import Cubical.Foundations.Isomorphism
open import Cubical.Foundations.Equiv
open import Cubical.Foundations.Equiv.HalfAdjoint
open import Cubical.Foundations.HLevels
open import Cubical.Foundations.Univalence
open import Cubical.Foundations.SIP
open import Cubical.Foundations.Function using (_∘_; id)
open import Cubical.Foundations.GroupoidLaws
open import Cubical.Functions.Embedding
open import Cubical.Data.Sigma
open import Cubical.Data.Prod using (isPropProd)
open import Cubical.Algebra
open import Cubical.Algebra.Properties
open import Cubical.Algebra.Magma.Morphism
open import Cubical.Structures.Axioms
open import Cubical.Structures.Auto
open import Cubical.Structures.Record
open import Cubical.Relation.Binary.Reasoning.Equality
open Iso
private
variable
ℓ ℓ′ ℓ′′ : Level
L : Magma ℓ
M : Magma ℓ′
N : Magma ℓ′′
isPropIsMagmaHom : ∀ (M : Magma ℓ) (N : Magma ℓ′) f → isProp (IsMagmaHom M N f)
isPropIsMagmaHom M N f = isPropHomomorphic₂ (Magma.is-set N) f (Magma._•_ M) (Magma._•_ N)
isSetMagmaHom : isSet (M ⟶ᴴ N)
isSetMagmaHom {M = M} {N = N} = isOfHLevelRespectEquiv 2 equiv
(isSetΣ (isSetΠ λ _ → is-set N)
(λ f → isProp→isSet (isPropIsMagmaHom M N f)))
where
open Magma
equiv : (Σ[ g ∈ (⟨ M ⟩ → ⟨ N ⟩) ] IsMagmaHom M N g) ≃ MagmaHom M N
equiv = isoToEquiv (iso (λ (g , m) → magmahom g m)
(λ (magmahom g m) → g , m)
(λ _ → refl) λ _ → refl)
isMagmaHomComp : {f : ⟨ L ⟩ → ⟨ M ⟩} {g : ⟨ M ⟩ → ⟨ N ⟩} →
IsMagmaHom L M f → IsMagmaHom M N g → IsMagmaHom L N (g ∘ f)
isMagmaHomComp {g = g} fHom gHom _ _ = cong g (fHom _ _) ∙ gHom _ _
private
isMagmaHomComp′ : (f : L ⟶ᴴ M) (g : M ⟶ᴴ N) →
IsMagmaHom L N (MagmaHom.fun g ∘ MagmaHom.fun f)
isMagmaHomComp′ (magmahom f fHom) (magmahom g gHom) _ _ = cong g (fHom _ _) ∙ gHom _ _
compMagmaHom : (L ⟶ᴴ M) → (M ⟶ᴴ N) → (L ⟶ᴴ N)
compMagmaHom f g = magmahom _ (isMagmaHomComp′ f g)
compMagmaEquiv : L ≃ᴴ M → M ≃ᴴ N → L ≃ᴴ N
compMagmaEquiv f g = magmaequiv (compEquiv f.eq g.eq) (isMagmaHomComp′ f.hom g.hom)
where
module f = MagmaEquiv f
module g = MagmaEquiv g
isMagmaHomId : (M : Magma ℓ) → IsMagmaHom M M id
isMagmaHomId M _ _ = refl
idMagmaHom : (M : Magma ℓ) → (M ⟶ᴴ M)
idMagmaHom M = record
{ fun = id
; isHom = isMagmaHomId M
}
idMagmaEquiv : (M : Magma ℓ) → M ≃ᴴ M
idMagmaEquiv M = record
{ eq = idEquiv ⟨ M ⟩
; isHom = isMagmaHomId M
}
-- Isomorphism inversion
isMagmaHomInv : (eqv : M ≃ᴴ N) → IsMagmaHom N M (invEq (MagmaEquiv.eq eqv))
isMagmaHomInv {M = M} {N = N} (magmaequiv eq isHom) x y = isInj-f _ _ (
f (f⁻¹ (x •ᴺ y)) ≡⟨ retEq eq _ ⟩
x •ᴺ y ≡˘⟨ cong₂ _•ᴺ_ (retEq eq x) (retEq eq y) ⟩
f (f⁻¹ x) •ᴺ f (f⁻¹ y) ≡˘⟨ isHom (f⁻¹ x) (f⁻¹ y) ⟩
f (f⁻¹ x •ᴹ f⁻¹ y) ∎)
where
_•ᴹ_ = Magma._•_ M
_•ᴺ_ = Magma._•_ N
f = equivFun eq
f⁻¹ = invEq eq
isInj-f : (x y : ⟨ M ⟩) → f x ≡ f y → x ≡ y
isInj-f x y = invEq (_ , isEquiv→isEmbedding (eq .snd) x y)
invMagmaHom : M ≃ᴴ N → (N ⟶ᴴ M)
invMagmaHom eq = record { isHom = isMagmaHomInv eq }
invMagmaEquiv : (M ≃ᴴ N) → (N ≃ᴴ M)
invMagmaEquiv eq = record
{ eq = invEquiv (MagmaEquiv.eq eq)
; isHom = isMagmaHomInv eq
}
magmaHomEq : {f g : M ⟶ᴴ N} → (MagmaHom.fun f ≡ MagmaHom.fun g) → f ≡ g
magmaHomEq {M = M} {N = N} {magmahom f fm} {magmahom g gm} p i = magmahom (p i) (p-hom i)
where
p-hom : PathP (λ i → IsMagmaHom M N (p i)) fm gm
p-hom = toPathP (isPropIsMagmaHom M N _ _ _)
magmaEquivEq : {f g : M ≃ᴴ N} → (MagmaEquiv.eq f ≡ MagmaEquiv.eq g) → f ≡ g
magmaEquivEq {M = M} {N = N} {magmaequiv f fm} {magmaequiv g gm} p i = magmaequiv (p i) (p-hom i)
where
p-hom : PathP (λ i → IsMagmaHom M N (p i .fst)) fm gm
p-hom = toPathP (isPropIsMagmaHom M N _ _ _)
module MagmaΣTheory {ℓ} where
RawMagmaStructure : Type ℓ → Type ℓ
RawMagmaStructure A = A → A → A
RawMagmaEquivStr = AutoEquivStr RawMagmaStructure
rawMagmaUnivalentStr : UnivalentStr _ RawMagmaEquivStr
rawMagmaUnivalentStr = autoUnivalentStr RawMagmaStructure
MagmaAxioms : (A : Type ℓ) → RawMagmaStructure A → Type ℓ
MagmaAxioms A _•_ = isSet A
MagmaStructure : Type ℓ → Type ℓ
MagmaStructure = AxiomsStructure RawMagmaStructure MagmaAxioms
MagmaΣ : Type (ℓ-suc ℓ)
MagmaΣ = TypeWithStr ℓ MagmaStructure
isPropMagmaAxioms : (A : Type ℓ) (_•_ : RawMagmaStructure A)
→ isProp (MagmaAxioms A _•_)
isPropMagmaAxioms _ _ = isPropIsSet
MagmaEquivStr : StrEquiv MagmaStructure ℓ
MagmaEquivStr = AxiomsEquivStr RawMagmaEquivStr MagmaAxioms
MagmaAxiomsIsoIsMagma : {A : Type ℓ} (_•_ : RawMagmaStructure A)
→ Iso (MagmaAxioms A _•_) (IsMagma A _•_)
fun (MagmaAxiomsIsoIsMagma s) x = ismagma x
inv (MagmaAxiomsIsoIsMagma s) (ismagma x) = x
rightInv (MagmaAxiomsIsoIsMagma s) _ = refl
leftInv (MagmaAxiomsIsoIsMagma s) _ = refl
MagmaAxioms≡IsMagma : {A : Type ℓ} (_•_ : RawMagmaStructure A)
→ MagmaAxioms A _•_ ≡ IsMagma A _•_
MagmaAxioms≡IsMagma s = isoToPath (MagmaAxiomsIsoIsMagma s)
Magma→MagmaΣ : Magma ℓ → MagmaΣ
Magma→MagmaΣ (mkmagma A _•_ isMagma) =
A , _•_ , MagmaAxiomsIsoIsMagma _ .inv isMagma
MagmaΣ→Magma : MagmaΣ → Magma ℓ
MagmaΣ→Magma (A , _•_ , isMagma•) =
mkmagma A _•_ (MagmaAxiomsIsoIsMagma _ .fun isMagma•)
MagmaIsoMagmaΣ : Iso (Magma ℓ) MagmaΣ
MagmaIsoMagmaΣ =
iso Magma→MagmaΣ MagmaΣ→Magma (λ _ → refl) (λ _ → refl)
magmaUnivalentStr : UnivalentStr MagmaStructure MagmaEquivStr
magmaUnivalentStr = axiomsUnivalentStr _ isPropMagmaAxioms rawMagmaUnivalentStr
MagmaΣPath : (M N : MagmaΣ) → (M ≃[ MagmaEquivStr ] N) ≃ (M ≡ N)
MagmaΣPath = SIP magmaUnivalentStr
MagmaEquivΣ : (M N : Magma ℓ) → Type ℓ
MagmaEquivΣ M N = Magma→MagmaΣ M ≃[ MagmaEquivStr ] Magma→MagmaΣ N
MagmaIsoΣPath : {M N : Magma ℓ} → Iso (MagmaEquiv M N) (MagmaEquivΣ M N)
fun MagmaIsoΣPath (magmaequiv e h) = (e , h)
inv MagmaIsoΣPath (e , h) = magmaequiv e h
rightInv MagmaIsoΣPath _ = refl
leftInv MagmaIsoΣPath _ = refl
MagmaPath : (M N : Magma ℓ) → (MagmaEquiv M N) ≃ (M ≡ N)
MagmaPath M N =
MagmaEquiv M N ≃⟨ isoToEquiv MagmaIsoΣPath ⟩
MagmaEquivΣ M N ≃⟨ MagmaΣPath _ _ ⟩
Magma→MagmaΣ M ≡ Magma→MagmaΣ N ≃⟨ isoToEquiv (invIso (congIso MagmaIsoMagmaΣ)) ⟩
M ≡ N ■
RawMagmaΣ : Type (ℓ-suc ℓ)
RawMagmaΣ = TypeWithStr ℓ RawMagmaStructure
Magma→RawMagmaΣ : Magma ℓ → RawMagmaΣ
Magma→RawMagmaΣ M = (⟨ M ⟩ , Magma._•_ M)
InducedMagma : (M : Magma ℓ) (N : RawMagmaΣ) (e : ⟨ M ⟩ ≃ ⟨ N ⟩)
→ RawMagmaEquivStr (Magma→RawMagmaΣ M) N e → Magma ℓ
InducedMagma M N e r =
MagmaΣ→Magma (inducedStructure rawMagmaUnivalentStr (Magma→MagmaΣ M) N (e , r))
InducedMagmaPath : (M : Magma ℓ) (N : RawMagmaΣ) (e : ⟨ M ⟩ ≃ ⟨ N ⟩)
(E : RawMagmaEquivStr (Magma→RawMagmaΣ M) N e)
→ M ≡ InducedMagma M N e E
InducedMagmaPath M N e E =
MagmaPath M (InducedMagma M N e E) .fst (magmaequiv e E)
open MagmaΣTheory public using (InducedMagma; InducedMagmaPath)
MagmaPath : (M ≃ᴴ N) ≃ (M ≡ N)
MagmaPath = MagmaΣTheory.MagmaPath _ _
open Magma
uaMagma : M ≃ᴴ N → M ≡ N
uaMagma = equivFun MagmaPath
carac-uaMagma : {M N : Magma ℓ} (f : M ≃ᴴ N) → cong Carrier (uaMagma f) ≡ ua (MagmaEquiv.eq f)
carac-uaMagma (magmaequiv f m) =
(refl ∙∙ ua f ∙∙ refl)
≡˘⟨ rUnit (ua f) ⟩
ua f ∎
Magma≡ : (M N : Magma ℓ) → (
Σ[ p ∈ ⟨ M ⟩ ≡ ⟨ N ⟩ ]
Σ[ q ∈ PathP (λ i → p i → p i → p i) (_•_ M) (_•_ N) ]
PathP (λ i → IsMagma (p i) (q i)) (isMagma M) (isMagma N))
≃ (M ≡ N)
Magma≡ M N = isoToEquiv (iso
(λ (p , q , r) i → mkmagma (p i) (q i) (r i))
(λ p → cong Carrier p , cong _•_ p , cong isMagma p)
(λ _ → refl) (λ _ → refl))
caracMagma≡ : (p q : M ≡ N) → cong Carrier p ≡ cong Carrier q → p ≡ q
caracMagma≡ {M = M} {N = N} p q t = cong (Magma≡ M N .fst) (Σ≡Prop (λ _ →
isPropΣ
(isOfHLevelPathP' 1 (isSetΠ2 λ _ _ → is-set N) _ _) λ _ →
isOfHLevelPathP 1 (λ { (ismagma x) (ismagma y) → cong ismagma (isPropIsSet x y) }) _ _)
t)
uaMagmaId : (M : Magma ℓ) → uaMagma (idMagmaEquiv M) ≡ refl
uaMagmaId M = caracMagma≡ _ _ (carac-uaMagma (idMagmaEquiv M) ∙ uaIdEquiv)
uaCompMagmaEquiv : {L M N : Magma ℓ} (f : L ≃ᴴ M) (g : M ≃ᴴ N)
→ uaMagma (compMagmaEquiv f g) ≡ uaMagma f ∙ uaMagma g
uaCompMagmaEquiv f g = caracMagma≡ _ _ (
cong Carrier (uaMagma (compMagmaEquiv f g))
≡⟨ carac-uaMagma (compMagmaEquiv f g) ⟩
ua (eq (compMagmaEquiv f g))
≡⟨ uaCompEquiv _ _ ⟩
ua (eq f) ∙ ua (eq g)
≡⟨ cong (_∙ ua (eq g)) (sym (carac-uaMagma f)) ⟩
cong Carrier (uaMagma f) ∙ ua (eq g)
≡⟨ cong (cong Carrier (uaMagma f) ∙_) (sym (carac-uaMagma g)) ⟩
cong Carrier (uaMagma f) ∙ cong Carrier (uaMagma g)
≡⟨ sym (cong-∙ Carrier (uaMagma f) (uaMagma g)) ⟩
cong Carrier (uaMagma f ∙ uaMagma g) ∎)
where open MagmaEquiv
|
{-# OPTIONS --without-K #-}
module Pi1Examples where
open import PiU using (U; ONE)
open import PiLevel0 using (_⟷_; _◎_; _⊗_; id⟷;
swap₊; unite⋆l; unite⋆r;
swap⋆; uniti⋆l; uniti⋆r)
open import Pi0Examples using (BOOL)
open import PiLevel1 using (_⇔_; id⇔; trans⇔; _⊡_;
assoc◎l; swapl⋆⇔; assoc◎r; linv◎l; idl◎l; idr◎l; unitil⋆⇔l)
------------------------------------------------------------------------------
-- Better syntax for writing 2paths
infix 2 _▤
infixr 2 _⇔⟨_⟩_
_⇔⟨_⟩_ : {t₁ t₂ : U} (c₁ : t₁ ⟷ t₂) {c₂ : t₁ ⟷ t₂} {c₃ : t₁ ⟷ t₂} →
(c₁ ⇔ c₂) → (c₂ ⇔ c₃) → (c₁ ⇔ c₃)
_ ⇔⟨ α ⟩ β = trans⇔ α β
_▤ : {t₁ t₂ : U} → (c : t₁ ⟷ t₂) → (c ⇔ c)
_▤ c = id⇔
------------------------------------------------------------------------------
-- a nice example of 2 paths
neg₁ neg₂ neg₃ neg₄ neg₅ : BOOL ⟷ BOOL
neg₁ = swap₊
neg₂ = id⟷ ◎ swap₊
neg₃ = swap₊ ◎ swap₊ ◎ swap₊
neg₄ = swap₊ ◎ id⟷
neg₅ = uniti⋆l ◎ swap⋆ ◎ (swap₊ ⊗ id⟷) ◎ swap⋆ ◎ unite⋆l
neg₆ = uniti⋆r ◎ (swap₊ {ONE} {ONE} ⊗ id⟷) ◎ unite⋆r
negEx : neg₅ ⇔ neg₁
negEx = uniti⋆l ◎ (swap⋆ ◎ ((swap₊ ⊗ id⟷) ◎ (swap⋆ ◎ unite⋆l)))
⇔⟨ id⇔ ⊡ assoc◎l ⟩
uniti⋆l ◎ ((swap⋆ ◎ (swap₊ ⊗ id⟷)) ◎ (swap⋆ ◎ unite⋆l))
⇔⟨ id⇔ ⊡ (swapl⋆⇔ ⊡ id⇔) ⟩
uniti⋆l ◎ (((id⟷ ⊗ swap₊) ◎ swap⋆) ◎ (swap⋆ ◎ unite⋆l))
⇔⟨ id⇔ ⊡ assoc◎r ⟩
uniti⋆l ◎ ((id⟷ ⊗ swap₊) ◎ (swap⋆ ◎ (swap⋆ ◎ unite⋆l)))
⇔⟨ id⇔ ⊡ (id⇔ ⊡ assoc◎l) ⟩
uniti⋆l ◎ ((id⟷ ⊗ swap₊) ◎ ((swap⋆ ◎ swap⋆) ◎ unite⋆l))
⇔⟨ id⇔ ⊡ (id⇔ ⊡ (linv◎l ⊡ id⇔)) ⟩
uniti⋆l ◎ ((id⟷ ⊗ swap₊) ◎ (id⟷ ◎ unite⋆l))
⇔⟨ id⇔ ⊡ (id⇔ ⊡ idl◎l) ⟩
uniti⋆l ◎ ((id⟷ ⊗ swap₊) ◎ unite⋆l)
⇔⟨ assoc◎l ⟩
(uniti⋆l ◎ (id⟷ ⊗ swap₊)) ◎ unite⋆l
⇔⟨ unitil⋆⇔l ⊡ id⇔ ⟩
(swap₊ ◎ uniti⋆l) ◎ unite⋆l
⇔⟨ assoc◎r ⟩
swap₊ ◎ (uniti⋆l ◎ unite⋆l)
⇔⟨ id⇔ ⊡ linv◎l ⟩
swap₊ ◎ id⟷
⇔⟨ idr◎l ⟩
swap₊ ▤
------------------------------------------------------------------------------
|
logical function vetow_2gam(p)
implicit none
c--- returns TRUE if the momenta passed into the function
c--- should be vetoed according to the current value of "ipsgen"
include 'constants.f'
include 'ipsgen.f'
include 'masses.f'
include 'part.f'
double precision p(mxpart,4),dot,s345,s346,s3456,xwid
c--- note: parameter "xwid" controls the number of widths away
c--- from the peak to generate according to a BW
parameter(xwid=5d0)
vetow_2gam=.false.
c--- veto for fragmentation contribution
if (part .eq. 'frag') then
if (ipsgen .eq. 1) then
s345=2d0*(dot(p,3,4)+dot(p,3,5)+dot(p,4,5))
if (abs(sqrt(s345)-wmass) .lt. xwid*wwidth) then
vetow_2gam=.true.
endif
endif
return
endif
c--- veto for everything else
if (ipsgen .eq. 1) then
s345=2d0*(dot(p,3,4)+dot(p,3,5)+dot(p,4,5))
if (abs(sqrt(s345)-wmass) .lt. xwid*wwidth) then
vetow_2gam=.true.
return
endif
endif
if ((ipsgen .eq. 1) .or. (ipsgen .eq. 3)) then
s346=2d0*(dot(p,3,4)+dot(p,3,6)+dot(p,4,6))
if (abs(sqrt(s346)-wmass) .lt. xwid*wwidth) then
vetow_2gam=.true.
return
endif
endif
if ((ipsgen .eq. 1) .or. (ipsgen .eq. 3) .or. (ipsgen .eq. 4))then
s3456=2d0*(dot(p,3,4)+dot(p,3,5)+dot(p,3,6)
& +dot(p,4,5)+dot(p,4,6)+dot(p,5,6))
if (abs(sqrt(s3456)-wmass) .lt. xwid*wwidth) then
vetow_2gam=.true.
return
endif
endif
return
end
|
function c = tapas_unitsq_sgm_mu3_config
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% Contains the configuration for the unit square sigmoid observation model for binary responses
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% The unit square sigmoid (ussgm) is the function
%
% f(x) = x^zeta/(x^zeta + (1-x)^zeta) = ustapas_sgm(x; zeta),
%
% where x is in the unit interval, and zeta > 0 is a parameter that determines the shape of the
% sigmoid. Since both its argument and value are always in the unit interval, its graph is
% restricted to the unit square, hence the name unit square sigmoid.
%
% In the application here, the ussgm is the probability of observing a decision y=1 (rather than
% the only alternative y=0) given the current probability mu1hat (or value) of input u=1:
%
% p(y=1|mu1hat) = ustapas_sgm(mu1hat; zeta)
%
% The parameter zeta regulates the steepness of the sigmoid such that it forms the diagonal of
% the unit square for zeta=1 and approaches a step function at 0.5 as zeta approaches infinity.
% Values of 0 < zeta < 1 lead to sigmoids with reverse concavity than usual, but they still
% represent valid observation models.
%
% Zeta can be interpreted as inverse decision noise. To have a shrinkage prior on this, choose a
% high value. It is estimated log-space since it has a natural lower bound at zero.
%
% --------------------------------------------------------------------------------------------------
% Copyright (C) 2012-2013 Christoph Mathys, TNU, UZH & ETHZ
%
% This file is part of the HGF toolbox, which is released under the terms of the GNU General Public
% Licence (GPL), version 3. You can redistribute it and/or modify it under the terms of the GPL
% (either version 3 or, at your option, any later version). For further details, see the file
% COPYING or <http://www.gnu.org/licenses/>.
% Config structure
c = struct;
% Model name
c.model = 'tapas_unitsq_sgm_mu3';
% This model has no free parameters
% Gather prior settings in vectors
c.priormus = [
];
c.priorsas = [
];
% Model filehandle
c.obs_fun = @tapas_unitsq_sgm_mu3;
% Handle to function that transforms observation parameters to their native space
% from the space they are estimated in
c.transp_obs_fun = @tapas_unitsq_sgm_mu3_transp;
return;
|
#include "clic_parser.hpp"
#include <boost/config/warning_disable.hpp>
#include <boost/fusion/adapted/std_pair.hpp>
#include <boost/fusion/include/std_pair.hpp>
#include <boost/iterator/iterator_facade.hpp>
#include <boost/range/iterator_range.hpp>
#include <boost/spirit/include/phoenix_core.hpp>
#include <boost/spirit/include/phoenix_operator.hpp>
#include <boost/spirit/include/phoenix_fusion.hpp>
#include <boost/spirit/include/phoenix_stl.hpp>
#include <boost/spirit/include/qi.hpp>
#include <cassert>
#include <iostream>
namespace spirit = boost::spirit;
namespace ascii = boost::spirit::ascii;
namespace qi = boost::spirit::qi;
namespace phoenix = boost::phoenix;
template <typename Iterator>
struct Grammar : qi::grammar<Iterator, ClicIndexItem ()>
{
Grammar() : Grammar::base_type(line)
{
using qi::_val;
using qi::_1;
using qi::char_;
using qi::lit;
using qi::eps;
using ascii::space;
word = eps[_val = ""] >> (+ (char_ - (lit('\t') | lit('\n')))[_val += _1]);
wordSet = eps[phoenix::clear(_val)] >> (+word[phoenix::insert(_val, _1)] % '\t');
line %= word >> '\t' >> wordSet >> '\n';
}
qi::rule<Iterator, std::string ()> word;
qi::rule<Iterator, std::set<std::string> ()> wordSet;
qi::rule<Iterator, ClicIndexItem ()> line;
};
Grammar<spirit::istream_iterator> grammar;
IndexItemIterator::IndexItemIterator() : i(-1) {}
IndexItemIterator::IndexItemIterator(std::istream& in) :
value(boost::make_shared<ClicIndexItem>()),
i(0),
in(&in),
inputBegin(in)
{
in.unsetf(std::ios::skipws);
}
const ClicIndexItem& IndexItemIterator::dereference() const {
return *value;
}
bool IndexItemIterator::equal(const IndexItemIterator& other) const {
return i == other.i;
}
void IndexItemIterator::increment() {
assert(i != -1);
bool ok = qi::parse(inputBegin, inputEnd, grammar, *value);
if (ok) {
i++;
} else {
i = -1; // reached the end
if (inputBegin != inputEnd) {
std::cerr << "Trailing characters:" << std::endl;
while (!in->eof()) {
char c;
*in >> c;
std::cerr << c;
}
}
}
}
boost::iterator_range<IndexItemIterator> parseIndex(std::istream& in) {
return boost::make_iterator_range(IndexItemIterator(in), IndexItemIterator());
}
|
''' FourRoomMDPClass.py: Contains the FourRoom class. '''
# Python imports.
import math
import os
from collections import defaultdict
import numpy as np
# Other imports
from simple_rl.mdp.MDPClass import MDP
from simple_rl.apmdp.AMDP.CubeMDPClass import CubeMDP
from simple_rl.apmdp.AMDP.RoomCubeStateClass import RoomCubeState
from simple_rl.apmdp.AMDP.CubeStateClass import CubeState
from simple_rl.apmdp.settings.build_cube_env_1 import build_cube_env
from sympy import *
class RoomCubeMDP(CubeMDP):
''' Class for a Cube World with Rooms '''
def __init__(self, len_x=9, len_y=9, len_z=5, init_loc=(1,1,1),
goal_locs=[(9,9,3)], env_file = [],
gamma=0.99, slip_prob=0.00, name="cube_room",
is_goal_terminal=True, rand_init=False,
step_cost=0.0, constraints={'Qg':[],'Qs':[], 'Sg': [], 'Ss': [], 'mode': 'root'}, ap_maps = {}, automata=[],
init_state=[]):
'''
Args:
len_x, len_y, len_z (int)
init_loc (tuple: (int, int,int))
goal_locs (list of tuples: [(int, int,int)...]
env_file: specify environment)
constraints: Q_g and Q_s : goal state in automata and staty state in automata for the reward function
- goal (large positive), stay (zero), otherwise (large negative)
Sg : goal environment state, Ss: stay environment state
Mode: 'root' or 'child', if mode is 'root', reward is determined by automaton state
if mode is 'child', reward is determined by the environment state
ap_maps: dictionary {ap_symbol: (category, state), ...} ex) {a: ('r', [1]), b:('a',west)}
category: floor(f), room(r), lowest level action(a), grid cells (c)
'''
# Load environment file
if len(env_file)==0:
print('Fail to initialize RoomCubeMDP')
else:
cube_env = env_file[0]
len_x = cube_env['len_x']
len_y = cube_env['len_y']
len_z = cube_env['len_z']
walls = cube_env['walls']
self.num_room = cube_env['num_room']
self.num_floor = cube_env['num_floor']
self.room_to_locs = cube_env['room_to_locs']
self.floor_to_rooms = cube_env['floor_to_rooms']
self.floor_to_locs = cube_env['floor_to_locs']
self.room_to_floor = cube_env['room_to_floor']
self.loc_to_room = cube_env['loc_to_room']
CubeMDP.__init__(self, len_x, len_y, len_z, init_loc,
goal_locs=goal_locs, walls=walls,
gamma=gamma, slip_prob=slip_prob, name=name,
is_goal_terminal=is_goal_terminal, rand_init=rand_init, step_cost=step_cost)
self.constraints = constraints # constraints for LTL
self.ap_maps = ap_maps
if self.constraints['mode'] == 'child':
self.constraints['Ss'] = [self.get_room_numbers(init_loc)[0]]
self.automata = automata
# init_state = RoomCubeState(init_loc[0], init_loc[1], init_loc[2], self._transition_q(init_loc, ""))
# if init_state.q != 0:
# init_state.set_terminal(True)
MDP.__init__(self, RoomCubeMDP.ACTIONS, self._transition_func, self._reward_func, init_state=init_state,
gamma=gamma)
def _transition_func(self, state, action):
if state.is_terminal():
return state
next_state_xyz = super()._transition_func(state, action)
evaluated_APs = self._evaluate_APs((next_state_xyz.x, next_state_xyz.y, next_state_xyz.z), action)
next_q = self.automata.transition_func(state.q, evaluated_APs)
if (next_q not in self.constraints['Qg']) and (next_q not in self.constraints['Qs']): # terminal
next_q = -1
next_state = RoomCubeState(next_state_xyz.x, next_state_xyz.y, next_state_xyz.z, next_q)
next_room = self.loc_to_room[(next_state.x, next_state.y, next_state.z)]
if self.constraints['mode'] == 'root':
if next_state.q in self.constraints['Qg'] or next_state.q == -1:
next_state.set_terminal(True)
if self.constraints['mode'] == 'child':
if next_state.q == -1 or next_state.q in self.constraints['Qg']:
next_state.set_terminal(True)
if next_room in self.constraints['Sg']:
next_state.set_terminal(True)
elif next_room not in self.constraints['Ss']:
next_state.set_terminal(True)
return next_state
def is_loc_in_room(self, loc, room_number):
return loc in self.room_to_locs[room_number]
def is_loc_on_floor(self, loc, floor_number):
return loc in self.floor_to_locs[floor_number]
def get_room_numbers(self, loc):
room_numbers = []
for i in range(1, self.num_room+1):
if loc in self.room_to_locs[i]:
room_numbers.append(i)
return room_numbers
def get_floor_numbers(self, loc):
room_number = self.get_room_numbers(loc)[0]
floor_numbers = []
for i in range(1, self.num_floor+1):
if room_number in self.floor_to_rooms[i]:
floor_numbers.append(i)
return floor_numbers
def _reward_func(self, state, action): # TODO: Complete
next_state = self._transition_func(state, action)
if self.constraints['mode'] == 'root':
if next_state.q in self.constraints['Qs']: # stay
reward = -1
elif next_state.q in self.constraints['Qg']: # success
reward = 100
elif next_state.q == -1: # fail
reward = -100
else: # mode child
if next_state.q == -1: # fail
reward = -100
elif self.loc_to_room[(next_state.x, next_state.y, next_state.z)] in self.constraints['Sg']: # goal
reward = 100
else:
reward = -1
return reward
def _evaluate_APs(self, loc, action): # TODO: Complete
evaluated_APs ={}
for ap in self.ap_maps.keys():
if (self.ap_maps[ap][0] == 0) and (self.ap_maps[ap][1] == 'state'): # level 0
evaluated_APs[ap] = (loc[0] == self.ap_maps[ap][2][0]) & (loc[1] == self.ap_maps[ap][2][1]) & (loc[2] == self.ap_maps[ap][2][2])
elif (self.ap_maps[ap][0] == 0 ) and (self.ap_maps[ap][1] == 'action'):
evaluated_APs[ap] = self.ap_maps[ap][2] in action
elif self.ap_maps[ap][0] == 1 and (self.ap_maps[ap][1] == 'state'): # level 1
evaluated_APs[ap] = self.is_loc_in_room(loc, self.ap_maps[ap][2])
elif self.ap_maps[ap][0] == 1 and (self.ap_maps[ap][1] == 'action'): # level 1
evaluated_APs[ap] = self.ap_maps[ap][2] in action
elif self.ap_maps[ap][0] == 2 and (self.ap_maps[ap][1] == 'state'): # level 2
evaluated_APs[ap] = self.is_loc_on_floor(loc, self.ap_maps[ap][2])
elif self.ap_maps[ap][0] == 2 and (self.ap_maps[ap][1] == 'action'): # level 2
evaluated_APs[ap] = self.ap_maps[ap][2] in action
return evaluated_APs
if __name__ == '__main__':
cube_env1 = build_cube_env()
mdp = RoomCubeMDP(env_file=[cube_env1])
|
function phi = correct_azimuth(phi)
%CORRECT_AZIMUTH ensures azimuth angle between -pi and +pi-eps
%
% Usage: phi = correct_azimuth(phi)
%
% Input parameters:
% phi - azimuth / rad. Can be a single value or a matrix.
%
% Output paramteres:
% phi - angle between -pi and +pi-eps / rad
%
% See also: correct_elevation, get_ir
%*****************************************************************************
% The MIT License (MIT) *
% *
% Copyright (c) 2010-2019 SFS Toolbox Developers *
% *
% Permission is hereby granted, free of charge, to any person obtaining a *
% copy of this software and associated documentation files (the "Software"), *
% to deal in the Software without restriction, including without limitation *
% the rights to use, copy, modify, merge, publish, distribute, sublicense, *
% and/or sell copies of the Software, and to permit persons to whom the *
% Software is furnished to do so, subject to the following conditions: *
% *
% The above copyright notice and this permission notice shall be included in *
% all copies or substantial portions of the Software. *
% *
% THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR *
% IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, *
% FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL *
% THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER *
% LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING *
% FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER *
% DEALINGS IN THE SOFTWARE. *
% *
% The SFS Toolbox allows to simulate and investigate sound field synthesis *
% methods like wave field synthesis or higher order ambisonics. *
% *
% https://sfs.readthedocs.io [email protected] *
%*****************************************************************************
%% ===== Checking of input parameters ==================================
nargmin = 1;
nargmax = 1;
narginchk(nargmin,nargmax);
%% ===== Computation ====================================================
% Ensure -2pi <= phi <= 2pi
phi = rem(phi,2*pi);
% Ensure -pi <= phi < pi
phi(phi<-pi) = phi(phi<-pi) + 2*pi;
phi(phi>=pi) = phi(phi>=pi) - 2*pi;
|
import scipy.optimize
import numpy as np
from optimal_gradient_method import *
def getAuxilitaryFunctionResult(f, r, rest_not_eq, x):
x1, x2 = x
H = sum(1/(0.000000001+pow(max(0, -i(x1,x2)),2)) for i in rest_not_eq)
return f(x) + r*H
def barrier(x0, f, r, z, eps, rest_not_eq):
xcur = np.array(x0)
xnew = None
atLeastOnePointFound = False
while not (atLeastOnePointFound and ( ((xcur-xnew)**2).sum() < eps**2 )):
xtemp = optimal_gradient_method(lambda x: getAuxilitaryFunctionResult(f, r, rest_not_eq, x), xcur )
isInside = not any(neq(xtemp[0],xtemp[1]) > eps for neq in rest_not_eq)
if (isInside):
if not atLeastOnePointFound:
atLeastOnePointFound = True
else:
xcur = xnew
xnew = xtemp
r *= z
return xnew
|
{-# LANGUAGE RecordWildCards, BangPatterns #-}
module NeuralNetwork where
import qualified Statistics.Matrix as M
import Control.Monad.Random
-- hyperparameters
data NeuralNetwork =
NeuralNetwork { inputLayerSize :: Int
, outputLayerSize :: Int
, hiddenLayerSize :: Int
, weight1Matrix :: M.Matrix
, weight2Matrix :: M.Matrix
}
initNetwork :: MonadRandom r => Int -> Int -> Int -> r NeuralNetwork
initNetwork inputSize outputSize hiddenSize = do
rs <- getRandomRs (0.0, 1.0)
rs' <- getRandomRs (0.0, 1.0)
return $ NeuralNetwork { inputLayerSize = inputSize
, outputLayerSize = outputSize
, hiddenLayerSize = hiddenSize
, weight1Matrix = M.fromList inputSize hiddenSize $ take (inputSize * hiddenSize) rs
, weight2Matrix = M.fromList hiddenSize outputSize $ take (outputSize * hiddenSize) rs'
}
forwardRs :: NeuralNetwork -> M.Matrix -> (M.Matrix, M.Matrix, M.Matrix, M.Matrix)
forwardRs NeuralNetwork{..} matrix =
let !z2 = matrix * weight1Matrix
!a2 = M.map sigmoid z2
!z3 = a2 * weight2Matrix
in (M.map sigmoid z3, z2, a2, z3)
forward :: NeuralNetwork -> M.Matrix -> M.Matrix
forward nn matrix =
let (r, _, _, _) = forwardRs nn matrix
in r
sigmoid :: Double -> Double
sigmoid z = 1 / (1 + exp (-z))
-- | Derivative of sigmoid function
sigmoidPrime :: Double -> Double
sigmoidPrime z = ez / ((1 + ez) ** 2)
where ez = exp (-z)
costFunction :: NeuralNetwork -> M.Matrix -> M.Matrix -> Double
costFunction nn@NeuralNetwork{..} x y =
let yHat = nn `forward` x
err = sum . map (**2) . M.toList $ y - yHat
in 0.5 * err
costFunctionPrime :: NeuralNetwork -> M.Matrix -> M.Matrix -> (M.Matrix, M.Matrix)
costFunctionPrime nn@NeuralNetwork{..} x y =
let (yHat, z2, a2, z3) = nn `forwardRs` x
!delta3 = (- (y - yHat)) `pointMultiply` (M.map sigmoidPrime z3)
!dJdW2 = (M.transpose a2) * delta3
!delta2 = delta3 * (M.transpose weight2Matrix) * (M.map sigmoidPrime z2)
!dJdW1 = M.transpose x * delta2
in (dJdW1, dJdW2)
pointMultiply :: M.Matrix -> M.Matrix -> M.Matrix
pointMultiply m1 m2 =
let (r, c) = (M.rows m1, M.cols m1)
(l1, l2) = (M.toList m1, M.toList m2)
in M.fromList r c (foldr (\(a,b) xs -> (a * b) : xs) [] (zip l1 l2))
instance Num M.Matrix where
m1 + m2 = let (r, c) = (M.rows m1, M.cols m1)
(l1, l2) = (M.toList m1, M.toList m2)
in M.fromList r c (foldr (\(a,b) xs -> (a + b) : xs) [] (zip l1 l2))
negate m = let (r, c) = (M.rows m, M.cols m)
l = M.toList m
in M.fromList r c (map negate l)
m1 * m2 = m1 `M.multiply` m2
abs m = undefined
signum m = undefined
fromInteger m = undefined
|
"""
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
This project concerns the development of a set of algorithms for solving the fleet
assignment problem under additional constraints:
- Limited capacity of fleets
- Minimum load for fleets
- Discounts
- Stochastic productivity
This problem is completely new in scientific literature and the proposed solutions
are supporteed and validated by a case study based on real data.
Author: Mattia Neroni, Ph.D., Eng.
Contact: [email protected]
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
"""
import pandas as pd
import numpy as np
import functools
import itertools
class Problem:
def __init__(self, avail, demand, costs, maxcap, mincap, discount, prods, stdev):
"""
Initialise.
:param avail: A matrix of available assignments.
:param demand: The demand for each postcode.
:param costs: The costs per hour of fleets.
:param maxcap: The maximum capacities of fleets.
:param mincap: The minimum capacities of fleets.
:param discount: The discount applied to each fleet.
:param prods: The productivity of each vehicle in each postcode expressed in parcels per hour.
:param stdev: Possible deviations calculated on historical delays data.
:attr n_fleets: The number of fleets.
:attr n_postcodes: The number of postcodes.
"""
self.n_postcodes, self.n_fleets = avail.shape
self.avail = avail
self.demand = demand
self.costs = costs
self.maxcap = maxcap
self.mincap = mincap
self.discount = discount
self.prods = prods
self.stdev = stdev
# Some corrections because of the error in numpy library
# to calculate the stochastic productivity with a lognormal
var = stdev * prods
phi = np.sqrt(var + prods**2)
mu = np.log( prods**2 / phi )
sigma = np.sqrt(np.log( phi**2 / prods**2 ))
self.stochastic_prods = functools.partial(np.random.lognormal, mean=mu, sigma=sigma)
# A set of iterators on the fleets that is possible to assign to each postcode
self.avail_assignments = tuple( itertools.cycle(np.where(avail[i] == 1)[0]) for i in range(self.n_postcodes))
def __hash__(self):
return id(self)
def read_problem (path="../data/", max_stdev=0.5):
"""
Mathod used to read the case study problem.
:param path: The directory where all the csv can be found.
:param max_stdev: The maximum standard deviation on stochastic data (i.e., demand and productivity).
"""
avail = pd.read_csv(path + "FleetAreaConstraints.csv", index_col=0).to_numpy().astype("int32")
demand = pd.read_csv(path + "Demand.csv", index_col=0).to_numpy().astype("int32")
fleets_df = pd.read_csv(path + "Fleets.csv", index_col=0)
costs = fleets_df.loc["cost"].to_numpy().astype("float32")
maxcap = fleets_df.loc["maxcapacity"].to_numpy().astype("int32")
mincap = fleets_df.loc["mincapacity"].to_numpy().astype("int32")
discount = fleets_df.loc["greencapacity"].to_numpy().astype("int32")
prods = pd.read_csv(path + "ParcelsPerH.csv", index_col=0).to_numpy().astype("float32")
stdev = pd.read_csv(path + "Delayed.csv", index_col=0).to_numpy().astype("float32") * max_stdev
return Problem(avail, demand, costs, maxcap, mincap, discount, prods, stdev)
|
#pragma once
#include <boost/config/warning_disable.hpp>
#include <boost/spirit/home/x3.hpp>
#include <boost/spirit/home/x3/support/utility/annotate_on_success.hpp>
#include "ast.hpp"
#include "ast_adapted.hpp"
#include "parser_definitions.hpp"
#include "error_handler.hpp"
namespace parser {
using namespace ast;
using boost::fusion::at_c;
using x3::lexeme, x3::lit, x3::alnum, x3::_attr, x3::_val, x3::space,
x3::eol, x3::rule, x3::symbols;
auto const name =
lexeme[!lit('-') >> +(char_ - '?' - '(' - ')' - ':' - space)];
// Rules
rule<class TRequirement, std::vector<Name>> const requirement =
"requirement";
auto const requirement_def = ':' >> name;
BOOST_SPIRIT_DEFINE(requirement);
struct TRequirement : x3::annotate_on_success {};
rule<class TPredicate, Name> const predicate = "predicate";
auto const predicate_def = name;
BOOST_SPIRIT_DEFINE(predicate);
struct TPredicate : x3::annotate_on_success {};
rule<class TRequirements, std::vector<Name>> const requirements =
"requirements";
auto const requirements_def = '(' >> lit(":requirements") >> +requirement >>
')';
BOOST_SPIRIT_DEFINE(requirements);
struct TRequirements : x3::annotate_on_success {};
rule<class TConstant, Constant> const constant = "constant";
auto const constant_def = name;
BOOST_SPIRIT_DEFINE(constant);
struct TConstant : x3::annotate_on_success {};
rule<class TVariable, Variable> const variable = "variable";
auto const variable_def = '?' > name;
BOOST_SPIRIT_DEFINE(variable);
struct TVariable : x3::annotate_on_success {};
rule<class TPrimitiveType, PrimitiveType> const primitive_type =
"primitive_type";
auto const primitive_type_def = name;
BOOST_SPIRIT_DEFINE(primitive_type);
struct TPrimitiveType : x3::annotate_on_success {};
rule<class TEitherType, EitherType> const either_type = "either_type";
auto const either_type_def = '(' >> lit("either") >> +primitive_type >> ')';
BOOST_SPIRIT_DEFINE(either_type);
struct TEitherType : x3::annotate_on_success {};
rule<class TType, Type> const type = "type";
auto const type_def = primitive_type | either_type;
BOOST_SPIRIT_DEFINE(type);
struct TType : x3::annotate_on_success {};
// Typed list of names
rule<class TExplicitlyTypedListNames, ExplicitlyTypedList<Name>> const
explicitly_typed_list_names = "explicitly_typed_list_names";
auto const explicitly_typed_list_names_def = +name >> '-' >> type;
rule<class TImplicitlyTypedListNames, ImplicitlyTypedList<Name>> const
implicitly_typed_list_names = "implicitly_typed_list_names";
auto const implicitly_typed_list_names_def = *name;
rule<class TTypedListNames, TypedList<Name>> const typed_list_names =
"typed_list_names";
auto const typed_list_names_def =
*explicitly_typed_list_names >> -implicitly_typed_list_names;
BOOST_SPIRIT_DEFINE(explicitly_typed_list_names,
implicitly_typed_list_names,
typed_list_names);
struct TExplicitlyTypedListNames : x3::annotate_on_success {};
struct TImplicitlyTypedListNames : x3::annotate_on_success {};
struct TTypedListNames : x3::annotate_on_success {};
// Typed list of variables
rule<class TExplicitlyTypedListVariables,
ExplicitlyTypedList<Variable>> const explicitly_typed_list_variables =
"explicitly_typed_list_variables";
auto const explicitly_typed_list_variables_def = +variable >> '-' >> type;
rule<class TImplicitlyTypedListVariables,
ImplicitlyTypedList<Variable>> const implicitly_typed_list_variables =
"implicitly_typed_list_variables";
auto const implicitly_typed_list_variables_def = *variable;
rule<class TTypedListVariables, TypedList<Variable>> const
typed_list_variables = "typed_list_variables";
auto const typed_list_variables_def =
*explicitly_typed_list_variables >> -implicitly_typed_list_variables;
BOOST_SPIRIT_DEFINE(explicitly_typed_list_variables,
implicitly_typed_list_variables,
typed_list_variables);
struct TExplicitlyTypedListVariables : x3::annotate_on_success {};
struct TImplicitlyTypedListVariables : x3::annotate_on_success {};
struct TTypedListVariables : x3::annotate_on_success {};
// Atomic formula skeleton
rule<class TAtomicFormulaSkeleton, AtomicFormulaSkeleton> const
atomic_formula_skeleton = "atomic_formula_skeleton";
auto const atomic_formula_skeleton_def =
'(' >> name >> typed_list_variables >> ')';
BOOST_SPIRIT_DEFINE(atomic_formula_skeleton);
struct TAtomicFormulaSkeleton : x3::annotate_on_success {};
// Term
rule<class TTerm, Term> const term = "term";
auto const term_def = constant | variable;
BOOST_SPIRIT_DEFINE(term);
struct TTerm : x3::annotate_on_success {};
// Atomic formula of terms
rule<class TAtomicFormulaTerms, AtomicFormula<Term>> const
atomic_formula_terms = "atomic_formula_terms";
auto const atomic_formula_terms_def = '(' >> predicate >> *term >> ')';
BOOST_SPIRIT_DEFINE(atomic_formula_terms);
struct TAtomicFormulaTerms: x3::annotate_on_success {};
// Literals of terms
rule<class TLiteralTerms, Literal<Term>> const literal_terms =
"literal_terms";
auto const literal_terms_def = atomic_formula_terms;
BOOST_SPIRIT_DEFINE(literal_terms);
struct TLiteralTerms: x3::annotate_on_success {};
// Atomic formula of names
rule<class TAtomicFormulaNames, AtomicFormula<Name>> const
atomic_formula_names = "atomic_formula_names";
auto const atomic_formula_names_def = '(' >> predicate >> *name >> ')';
BOOST_SPIRIT_DEFINE(atomic_formula_names);
struct TAtomicFormulaNames: x3::annotate_on_success {};
// Literals of names
rule<class TLiteralNames, Literal<Name>> const literal_names =
"literal_names";
auto const literal_names_def = atomic_formula_names;
BOOST_SPIRIT_DEFINE(literal_names);
struct TLiteralNames: x3::annotate_on_success {};
// Negative literals
auto parse_negative_literal = [](auto& ctx) {
_val(ctx).predicate = _attr(ctx).predicate;
_val(ctx).args = _attr(ctx).args;
_val(ctx).is_negative = true;
};
rule<class TNegativeLiteralTerms, Literal<Term>> const negative_literal_terms = "negative_literal_terms";
auto const negative_literal_terms_def = ('(' >> lit("not") >> literal_terms >> ')')[parse_negative_literal];
BOOST_SPIRIT_DEFINE(negative_literal_terms);
struct TNegativeLiteralTerms: x3::annotate_on_success {};
// Nil
rule<class TNil, Nil> const nil = "nil";
auto const nil_def = '(' >> lit(")");
BOOST_SPIRIT_DEFINE(nil);
struct TNil: x3::annotate_on_success {};
rule<class TSentence, Sentence> sentence = "sentence";
// Connectors (and/or)
struct connector_ : x3::symbols<std::string> {
connector_() {
add
("and", "and")
("or" , "or")
;
}
} connector;
rule<class TConnectedSentence, ConnectedSentence> const connected_sentence =
"connected_sentence";
auto const connected_sentence_def = '('
>> connector
>> *sentence
>> ')';
BOOST_SPIRIT_DEFINE(connected_sentence);
struct TConnectedSentence: x3::annotate_on_success {};
rule<class TNotSentence, NotSentence> const not_sentence =
"not_sentence";
auto const not_sentence_def = '('
>> lit("not")
>> sentence
>> ')';
BOOST_SPIRIT_DEFINE(not_sentence);
struct TNotSentence: x3::annotate_on_success {};
rule<class TImplySentence, ImplySentence> const imply_sentence =
"imply_sentence";
auto const imply_sentence_def = ('(' >> lit("imply"))
> sentence
> sentence
> ')';
BOOST_SPIRIT_DEFINE(imply_sentence);
struct TImplySentence: x3::annotate_on_success {};
// Quantifier (exists/forall)
struct quantifier_ : x3::symbols<std::string> {
quantifier_() {
add
("exists", "exists")
("forall" , "forall")
;
}
} quantifier;
rule<class TQuantifiedSentence, QuantifiedSentence> const quantified_sentence =
"quantified_sentence";
auto const quantified_sentence_def = '('
> quantifier
> '('
> typed_list_variables
> ')'
> sentence
> ')';
BOOST_SPIRIT_DEFINE(quantified_sentence);
struct TQuantifiedSentence: x3::annotate_on_success {};
rule<class TEqualsSentence, EqualsSentence> const equals_sentence =
"equals_sentence";
auto const equals_sentence_def = ('(' >> lit("="))
> term
> term
> ')';
BOOST_SPIRIT_DEFINE(equals_sentence);
struct TEqualsSentence : x3::annotate_on_success {};
rule<class TNotEqualsSentence, NotEqualsSentence> const not_equals_sentence =
"not_equals_sentence";
auto const not_equals_sentence_def = ('('
>> lit("not"))
> equals_sentence
> ')';
BOOST_SPIRIT_DEFINE(not_equals_sentence);
struct TNotEqualsSentence: x3::annotate_on_success {};
auto const sentence_def =
nil
| literal_terms
| connected_sentence
| not_sentence
| imply_sentence
| quantified_sentence
| equals_sentence // Note: HDDL has equals sentences, but PDDL 2.1 does not.
;
BOOST_SPIRIT_DEFINE(sentence);
struct TSentence : x3::annotate_on_success {};
// <p-effect>
rule<class TPEffect, Literal<Term>> const p_effect = "p_effect";
auto const p_effect_def = literal_terms | negative_literal_terms;
BOOST_SPIRIT_DEFINE(p_effect);
struct TPEffect: x3::annotate_on_success {};
// <cond-effect>
rule<class TCondEffect, CondEffect> const cond_effect = "cond_effect";
auto const cond_effect_def = p_effect | '(' >> lit("and") >> *p_effect >> ')';
BOOST_SPIRIT_DEFINE(cond_effect);
struct TCondEffect: x3::annotate_on_success {};
// <effect and <c-effect>
rule<class TEffect, Effect> const effect = "effect";
rule<class TCEffect, CEffect> const c_effect = "c_effect";
rule<class TForallCEffect, ForallCEffect> const forall_c_effect = "forall_c_effect";
auto const forall_c_effect_def = ('(' >> lit("forall")) > '(' >> *variable >> ')' >> effect > ')';
BOOST_SPIRIT_DEFINE(forall_c_effect);
struct TForallCEffect: x3::annotate_on_success {};
rule<class TAndCEffect, AndCEffect> const and_c_effect = "and_c_effect";
auto const and_c_effect_def = ('(' >> lit("and")) > *c_effect > ')';
BOOST_SPIRIT_DEFINE(and_c_effect);
struct TAndCEffect: x3::annotate_on_success {};
rule<class TWhenCEffect, WhenCEffect> const when_c_effect = "when_c_effect";
auto const when_c_effect_def = ('(' >> lit("when")) > sentence > cond_effect >> ')';
BOOST_SPIRIT_DEFINE(when_c_effect);
struct TWhenCEffect: x3::annotate_on_success {};
auto const c_effect_def = forall_c_effect | when_c_effect | p_effect;
auto const effect_def =
nil
| and_c_effect
| c_effect;
BOOST_SPIRIT_DEFINE(c_effect);
BOOST_SPIRIT_DEFINE(effect);
struct TEffect: x3::annotate_on_success {};
struct TCEffect: x3::annotate_on_success {};
// Typed Lists
rule<class TTypes, TypedList<Name>> const types = "types";
auto const types_def = ('(' >> lit(":types"))
> typed_list_names
> ')';
BOOST_SPIRIT_DEFINE(types);
struct TTypes: x3::annotate_on_success {};
rule<class TConstants, TypedList<Name>> const constants = "constants";
auto const constants_def = ('(' >> lit(":constants"))
> typed_list_names
> ')';
BOOST_SPIRIT_DEFINE(constants);
struct TConstants : x3::annotate_on_success {};
rule<class TPredicates, std::vector<AtomicFormulaSkeleton>> const
predicates = "predicates";
auto const predicates_def = ('(' >> lit(":predicates"))
> +atomic_formula_skeleton > ')';
BOOST_SPIRIT_DEFINE(predicates);
struct TPredicates: x3::annotate_on_success {};
rule<class TPrecondition, Sentence> const precondition = "precondition";
auto const precondition_def = lit(":precondition")
> sentence;
BOOST_SPIRIT_DEFINE(precondition);
struct TPrecondition: x3::annotate_on_success {};
rule<class TParameters, TypedList<Variable>> const parameters = "parameters";
auto const parameters_def = lit(":parameters")
> '('
> typed_list_variables
> ')';
BOOST_SPIRIT_DEFINE(parameters);
struct TParameters: x3::annotate_on_success {};
rule<class TTask, Task> const task = "task";
auto const task_def = name >> parameters;
BOOST_SPIRIT_DEFINE(task);
struct TTask: x3::annotate_on_success {};
// Abstract Tasks
rule<class TAbstractTask, Task> const abstract_task = "abstract_task";
auto const abstract_task_def = ('(' >> lit(":task")) > task >> ')';
BOOST_SPIRIT_DEFINE(abstract_task);
struct TAbstractTask: x3::annotate_on_success {};
rule<class TTaskSymbolWithTerms, MTask> const task_symbol_with_terms = "task_symbol_with_terms";
auto const task_symbol_with_terms_def = '(' >> name >> *term >> ')';
BOOST_SPIRIT_DEFINE(task_symbol_with_terms);
struct TTaskSymbolWithTerms: x3::annotate_on_success {};
// Methods used to decompose abstract tasks into primitive actions
// task as defined in Method struct != task defined in task struct
// mtask refers to task definition found within a method:
rule<class TMTask, MTask> const mtask = "mtask";
auto const mtask_def = lit(":task") > task_symbol_with_terms;
BOOST_SPIRIT_DEFINE(mtask);
struct TMTask: x3::annotate_on_success {};
rule<class TSubTaskWithId, SubTaskWithId> const subtask_with_id = "subtask_with_id";
auto const subtask_with_id_def = '(' >> name >> task_symbol_with_terms >> ')';
BOOST_SPIRIT_DEFINE(subtask_with_id);
struct TSubTaskWithId: x3::annotate_on_success {};
rule<class TSubTask, SubTask> const subtask = "subtask";
auto const subtask_def = task_symbol_with_terms | subtask_with_id;
BOOST_SPIRIT_DEFINE(subtask);
struct TSubTask: x3::annotate_on_success {};
rule<class TSubTasks, SubTasks> const subtasks = "subtasks";
auto const subtasks_def = nil | subtask | '(' >> lit("and") >> +subtask >> ')';
BOOST_SPIRIT_DEFINE(subtasks);
struct TSubTasks: x3::annotate_on_success {};
rule<class TOrdering, Ordering> const ordering = "ordering";
auto const ordering_def = '(' >> lit("<") >> name >> name >> ')'; //make sure to use lit("")
BOOST_SPIRIT_DEFINE(ordering);
struct TOrdering: x3::annotate_on_success {};
rule<class TOrderings, Orderings> const orderings = "orderings";
auto const orderings_def = nil | ordering | '(' >> lit("and") >> +ordering >> ')';
BOOST_SPIRIT_DEFINE(orderings);
struct TOrderings: x3::annotate_on_success {};
rule<class TTaskNetworkOrderings, Orderings> const task_network_orderings = "task_network_orderings";
auto const task_network_orderings_def = lit(":ordering") > orderings;
BOOST_SPIRIT_DEFINE(task_network_orderings);
struct TTaskNetworkOrderings: x3::annotate_on_success {};
// Ordering keyword
struct ordering_kw_ : x3::symbols<std::string> {
ordering_kw_() {
add
("tasks", "tasks")
("subtasks" , "subtasks")
("ordered-tasks" , "ordered-tasks")
("ordered-subtasks" , "ordered-subtasks")
;
}
} ordering_kw;
rule<class TMethodSubTasks, MethodSubTasks> const method_subtasks = "method_subtasks";
auto const method_subtasks_def = ':' >> ordering_kw >> subtasks;
BOOST_SPIRIT_DEFINE(method_subtasks);
struct TMethodSubTasks : x3::annotate_on_success {};
rule<class TConstraint, Constraint> const constraint = "constraint";
auto const constraint_def = nil | not_equals_sentence | equals_sentence;
BOOST_SPIRIT_DEFINE(constraint);
struct TConstraint : x3::annotate_on_success {};
rule<class TConstraints, Constraints> const constraints = "constraints";
auto const constraints_def = nil | constraint | '(' >> lit("and") >> +constraint >> ')';
BOOST_SPIRIT_DEFINE(constraints);
struct TConstraints : x3::annotate_on_success {};
rule<class TTaskNetwork, TaskNetwork> const task_network = "task_network";
auto const task_network_def = -method_subtasks
>> -task_network_orderings
>> -(lit(":constraints") > constraints);
BOOST_SPIRIT_DEFINE(task_network);
struct TTaskNetwork: x3::annotate_on_success {};
rule<class TMethod, Method> const method = "method";
auto const method_def = ('(' >> lit(":method"))
> name
> parameters
> mtask // one task
>> -precondition
> task_network
> ')';
BOOST_SPIRIT_DEFINE(method);
struct TMethod: x3::annotate_on_success {};
// Primitive actions
// Note: There is a typo in section 4 of the HDDL paper
// https://arxiv.org/pdf/1911.05499.pdf - in the specification of actions,
// it should be ':effect' instead of ':effects' (line 44 of their listing).
rule<class TAction, Action> const action = "action";
auto const action_def = ('(' >> lit(":action"))
> name
> parameters
>> -precondition
>> -(lit(":effect") >> effect)
> ')';
BOOST_SPIRIT_DEFINE(action);
struct TAction: x3::annotate_on_success {};
// Domain definition
rule<class TDomain, Domain> const domain = "domain";
auto const domain_def = ('(' >> lit("define")) > '('
>> lit("domain")
> name > ')'
> requirements
>> -types
>> -constants
>> -predicates
>> *abstract_task
>> *method
>> *action
> ')';
BOOST_SPIRIT_DEFINE(domain);
struct TDomain : x3::annotate_on_success, ErrorHandlerBase {};
// Problem definition
rule<class TObjects, TypedList<Name>> const objects = "objects";
auto const objects_def = ('(' >> lit(":objects"))
> typed_list_names
> ')';
BOOST_SPIRIT_DEFINE(objects);
struct TObjects: x3::annotate_on_success {};
// <p-init> ::= (:init <init-el>*)
// <init-el> ::= <literal (name)>
rule<class TInit, Init> const init = "init";
auto const init_def = ('(' >> lit(":init"))
>> *literal_names
>> ')';
BOOST_SPIRIT_DEFINE(init);
struct TInit: x3::annotate_on_success {};
rule<class TGoal, Sentence> const goal = "goal";
auto const goal_def = ('(' >> lit(":goal"))
> sentence
> ')';
BOOST_SPIRIT_DEFINE(goal);
struct TGoal: x3::annotate_on_success {};
// Problem class. For the first version of HDDL, only :htn is allowed.
// Later versions might allow different classes to denote problems with
// task insertion, etc.
struct problem_class_ : x3::symbols<std::string> {
problem_class_() {
add
(":htn" , ":htn")
;
}
} problem_class;
rule<class TProblemHTN, ProblemHTN> problem_htn = "problem_htn";
auto const problem_htn_def = ('(' >> problem_class)
> -parameters
> task_network > ')';
BOOST_SPIRIT_DEFINE(problem_htn);
struct TProblemHTN: x3::annotate_on_success {};
rule<class TProblem, Problem> const problem = "problem";
auto const problem_def = ('(' >> lit("define"))
> ('(' >> lit("problem")) > name > ')'
> ('(' >> lit(":domain")) > name > ')'
>> -requirements
>> -objects
>> -problem_htn
> init
>> -goal
> ')';
BOOST_SPIRIT_DEFINE(problem);
struct TProblem: x3::annotate_on_success {};
} // namespace parser
parser::type_type type() { return parser::type; }
parser::literal_terms_type literal_terms() { return parser::literal_terms; }
parser::sentence_type sentence() { return parser::sentence; }
parser::domain_type domain() { return parser::domain; }
parser::problem_type problem() { return parser::problem; }
|
'''Miscellaneous utilities.'''
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import inspect
import six
import numpy as np
def get_class_defining_method(m):
'''
Get the class type that defines `m`, if it is a method. If m is not a
method, returns None. Should work both in python 2 and 3.
Code originated from https://stackoverflow.com/questions/3589311/
'''
if inspect.ismethod(m):
if hasattr(m, 'im_class'):
return m.im_class
for cls in inspect.getmro(m.__self__.__class__):
if cls.__dict__.get(m.__name__) is m:
return cls
m = m.__func__
if inspect.isfunction(m):
try:
cls = getattr(inspect.getmodule(m),
m.__qualname__.split('.<locals>', 1)[0].rsplit('.', 1)[0])
if isinstance(cls, type):
return cls
except AttributeError:
return None
return None
# getargspec(fn)
if six.PY2:
getargspec = inspect.getargspec
def getargspec_allargs(func):
argspec = getargspec(func)
return argspec.args
else: # Python 3
getargspec = inspect.getfullargspec
def getargspec_allargs(func):
argspec = getargspec(func)
return argspec.args + argspec.kwonlyargs
def merge_kwargs(kwargs, kwargs_new):
'''
Merge two kwargs.
One could simply use {**kwargs, **kwargs_new} to merge two kwargs dict,
but we should support old python versions too.
Moreover, values for duplicated key will be overwritten (in favor of kwargs_new).
'''
kwargs = kwargs.copy()
kwargs.update(kwargs_new)
return kwargs
_np_decode = np.vectorize(lambda b: b.decode('utf8'))
def decode_bytes_if_necessary(arg):
"""
Decodes scalar bytes and ndarray of bytes into unicode counterparts.
"""
if isinstance(arg, bytes):
# Regardless of python 2 and 3, return as unicode.
return arg.decode('utf8')
if isinstance(arg, np.ndarray) and arg.dtype == object:
return _np_decode(arg)
else:
return arg
__all__ = (
'get_class_defining_method',
'getargspec',
'merge_kwargs',
'decode_bytes_if_necessary',
)
|
= = Signature sound = =
|
!
! CalculiX - A 3-dimensional finite element program
! Copyright (C) 1998-2019 Guido Dhondt
!
! This program is free software; you can redistribute it and/or
! modify it under the terms of the GNU General Public License as
! published by the Free Software Foundation(version 2);
!
!
! This program is distributed in the hope that it will be useful,
! but WITHOUT ANY WARRANTY; without even the implied warranty of
! MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
! GNU General Public License for more details.
!
! You should have received a copy of the GNU General Public License
! along with this program; if not, write to the Free Software
! Foundation, Inc., 675 Mass Ave, Cambridge, MA 02139, USA.
!
subroutine writeboun(nodeboun,ndirboun,xboun,typeboun,nboun)
!
! writes an MPC to standard output (for debugging purposes)
!
implicit none
!
character*1 typeboun(*)
integer nodeboun(*),ndirboun(*),nboun,i
real*8 xboun(*)
!
write(*,*)
write(*,'(''SPC '')')
do i=1,nboun
write(*,'(i5,1x,i10,1x,i5,1x,e11.4,1x,a1)') i,nodeboun(i),
& ndirboun(i),xboun(i),typeboun(i)
enddo
!
return
end
|
module Selective.Examples.PingPong where
open import Selective.ActorMonad public
open import Prelude
-- An example including three actors: spawner, pinger, ponger
--
-- Spawner is the actor that starts it all.
-- Spawner spawns both pinger and ponger.
-- Then spawner send the reference of ponger to pinger,
-- and the reference of pinger to ponger.
--
-- Pinger is an actor that can receive Bool messages.
-- Pinger counts the number of 'false' messages it receives, until it receives a 'true'
--
-- Ponger is an actor that can receive Nat messages.
-- Ponger keeps sending 'false' until it receives a message containing 10.
Spawnbox : InboxShape
Spawnbox = []
ℕ₁ : Set₁
ℕ₁ = Lift (lsuc lzero) ℕ
Bool₁ : Set₁
Bool₁ = Lift (lsuc lzero) Bool
mutual
PingValues = [ Bool ]ˡ
PongValues = [ ℕ ]ˡ
PingRefs : TypingContext
PingRefs = [ ⊠-of-values PongValues ]ˡ
PongRefs : TypingContext
PongRefs = [ ⊠-of-values PingValues ]ˡ
PongReferenceMessage : MessageType
PongReferenceMessage = [ ReferenceType (⊠-of-values PongValues) ]ˡ
BoolMessage : MessageType
BoolMessage = [ ValueType Bool ]ˡ
Pingbox : InboxShape
Pingbox = BoolMessage ∷ [ PongReferenceMessage ]ˡ
PingReferenceMessage : MessageType
PingReferenceMessage = [ ReferenceType (⊠-of-values PingValues) ]ˡ
NatMessage : MessageType
NatMessage = [ ValueType ℕ ]ˡ
Pongbox : InboxShape
Pongbox = NatMessage ∷ [ PingReferenceMessage ]ˡ
constPingrefs : {A : Set₁} → (A → TypingContext)
constPingrefs _ = PingRefs
pingMainActor : (i : Size) (A : Set₁) → Set₂
pingMainActor i A = ∞ActorM i Pingbox A PingRefs constPingrefs
pinger : ∀ {i} → ∞ActorM (↑ i) Pingbox ⊤₁ [] constPingrefs
pinger .force = waitForPong ∞>> pingMain 0
where
waitForPong : ∀ {i} → ∞ActorM i Pingbox ⊤₁ [] constPingrefs
waitForPong = selective-receive (λ {
(Msg Z _) → false
; (Msg (S Z) _) → true
; (Msg (S (S ())) _)
}) >>= λ {
record { msg = (Msg Z _) ; msg-ok = () }
; record { msg = (Msg (S Z) _) ; msg-ok = refl } → return _
; record { msg = (Msg (S (S ())) x₁) }
}
waitForPingValue : ∀ {i Γ} → ∞ActorM i Pingbox Bool₁ Γ (λ _ → Γ)
waitForPingValue = selective-receive (λ {
(Msg Z _) → true
; (Msg (S Z) _) → false
; (Msg (S (S ())) _)
}) >>= λ {
record { msg = (Msg Z (b ∷ [])) ; msg-ok = refl } → return b
; record { msg = (Msg (S Z) _) ; msg-ok = () }
; record { msg = (Msg (S (S ())) x₁) }
}
pingMain : ∀ {i} → ℕ → pingMainActor i ⊤₁
pingMain n .force = waitForPingValue ∞>>= λ
{ (lift false) → (Z ![t: Z ] ([ lift n ]ᵃ)) >> pingMain (suc n)
; (lift true) → return _}
constPongrefs : {A : Set₁} → (A → TypingContext)
constPongrefs _ = PongRefs
pongMainActor : (i : Size) (A : Set₁) → Set₂
pongMainActor i A = ∞ActorM i Pongbox A PongRefs constPongrefs
ponger : ∀ {i} → ∞ActorM (↑ i) Pongbox ⊤₁ [] constPongrefs
ponger .force = waitForPing ∞>> ((Z ![t: Z ] ([ lift false ]ᵃ)) >> pongMain)
where
waitForPing : ∀ {i} → ∞ActorM i Pongbox ⊤₁ [] constPongrefs
waitForPing = selective-receive (λ {
(Msg Z _) → false
; (Msg (S Z) _) → true
; (Msg (S (S ())) _)
}) >>= λ {
record { msg = (Msg Z _) ; msg-ok = () }
; record { msg = (Msg (S Z) x₁) ; msg-ok = refl } → return _
; record { msg = (Msg (S (S ())) x₁) }
}
waitForPongValue : ∀ {i Γ} → ∞ActorM i Pongbox ℕ₁ Γ (λ _ → Γ)
waitForPongValue = selective-receive (λ {
(Msg Z _) → true
; (Msg (S Z) _) → false
; (Msg (S (S ())) _)
}) >>= λ {
record { msg = (Msg Z (n ∷ [])) ; msg-ok = refl } → return n
; record { msg = (Msg (S Z) x₁) ; msg-ok = () }
; record { msg = (Msg (S (S ())) x₁) }
}
pongMain : ∀ {i} → pongMainActor i ⊤₁
pongMain .force = waitForPongValue ∞>>= λ {
(lift 10) → Z ![t: Z ] [ lift true ]ᵃ
; (lift n) → Z ![t: Z ] [ lift false ]ᵃ >> pongMain
}
spawner : ∀ {i} → ∞ActorM i Spawnbox ⊤₁ [] (λ _ → Pingbox ∷ [ Pongbox ]ˡ)
spawner = do
spawn∞ ponger
spawn∞ pinger
Z ![t: S Z ] [ [ S Z ]>: [ Z ]ᵐ ]ᵃ
S Z ![t: S Z ] [ [ Z ]>: [ Z ]ᵐ ]ᵃ
|
If $S$ is a cone, then the convex hull of $S$ is also a cone.
|
/-
Copyright (c) 2021 Oliver Nash. All rights reserved.
Released under Apache 2.0 license as described in the file LICENSE.
Authors: Oliver Nash
! This file was ported from Lean 3 source module algebra.lie.matrix
! leanprover-community/mathlib commit 55e2dfde0cff928ce5c70926a3f2c7dee3e2dd99
! Please do not edit these lines, except to modify the commit id
! if you have ported upstream changes.
-/
import Mathbin.Algebra.Lie.OfAssociative
import Mathbin.LinearAlgebra.Matrix.Reindex
import Mathbin.LinearAlgebra.Matrix.ToLinearEquiv
/-!
# Lie algebras of matrices
An important class of Lie algebras are those arising from the associative algebra structure on
square matrices over a commutative ring. This file provides some very basic definitions whose
primary value stems from their utility when constructing the classical Lie algebras using matrices.
## Main definitions
* `lie_equiv_matrix'`
* `matrix.lie_conj`
* `matrix.reindex_lie_equiv`
## Tags
lie algebra, matrix
-/
universe u v w w₁ w₂
section Matrices
open Matrix
variable {R : Type u} [CommRing R]
variable {n : Type w} [DecidableEq n] [Fintype n]
/-- The natural equivalence between linear endomorphisms of finite free modules and square matrices
is compatible with the Lie algebra structures. -/
def lieEquivMatrix' : Module.End R (n → R) ≃ₗ⁅R⁆ Matrix n n R :=
{ LinearMap.toMatrix' with
map_lie' := fun T S => by
let f := @LinearMap.toMatrix' R _ n n _ _
change f (T.comp S - S.comp T) = f T * f S - f S * f T
have h : ∀ T S : Module.End R _, f (T.comp S) = f T ⬝ f S := LinearMap.toMatrix'_comp
rw [LinearEquiv.map_sub, h, h, Matrix.mul_eq_mul, Matrix.mul_eq_mul] }
#align lie_equiv_matrix' lieEquivMatrix'
@[simp]
theorem lieEquivMatrix'_apply (f : Module.End R (n → R)) : lieEquivMatrix' f = f.toMatrix' :=
rfl
#align lie_equiv_matrix'_apply lieEquivMatrix'_apply
@[simp]
theorem lieEquivMatrix'_symm_apply (A : Matrix n n R) :
(@lieEquivMatrix' R _ n _ _).symm A = A.toLin' :=
rfl
#align lie_equiv_matrix'_symm_apply lieEquivMatrix'_symm_apply
/-- An invertible matrix induces a Lie algebra equivalence from the space of matrices to itself. -/
def Matrix.lieConj (P : Matrix n n R) (h : Invertible P) : Matrix n n R ≃ₗ⁅R⁆ Matrix n n R :=
((@lieEquivMatrix' R _ n _ _).symm.trans (P.toLinearEquiv' h).lieConj).trans lieEquivMatrix'
#align matrix.lie_conj Matrix.lieConj
@[simp]
theorem Matrix.lieConj_apply (P A : Matrix n n R) (h : Invertible P) :
P.lieConj h A = P ⬝ A ⬝ P⁻¹ := by
simp [LinearEquiv.conj_apply, Matrix.lieConj, LinearMap.toMatrix'_comp,
LinearMap.toMatrix'_toLin']
#align matrix.lie_conj_apply Matrix.lieConj_apply
@[simp]
theorem Matrix.lieConj_symm_apply (P A : Matrix n n R) (h : Invertible P) :
(P.lieConj h).symm A = P⁻¹ ⬝ A ⬝ P := by
simp [LinearEquiv.symm_conj_apply, Matrix.lieConj, LinearMap.toMatrix'_comp,
LinearMap.toMatrix'_toLin']
#align matrix.lie_conj_symm_apply Matrix.lieConj_symm_apply
variable {m : Type w₁} [DecidableEq m] [Fintype m] (e : n ≃ m)
/-- For square matrices, the natural map that reindexes a matrix's rows and columns with equivalent
types, `matrix.reindex`, is an equivalence of Lie algebras. -/
def Matrix.reindexLieEquiv : Matrix n n R ≃ₗ⁅R⁆ Matrix m m R :=
{
Matrix.reindexLinearEquiv R R e
e with
toFun := Matrix.reindex e e
map_lie' := fun M N => by
simp only [LieRing.of_associative_ring_bracket, Matrix.reindex_apply,
Matrix.submatrix_mul_equiv, Matrix.mul_eq_mul, Matrix.submatrix_sub, Pi.sub_apply] }
#align matrix.reindex_lie_equiv Matrix.reindexLieEquiv
@[simp]
theorem Matrix.reindexLieEquiv_apply (M : Matrix n n R) :
Matrix.reindexLieEquiv e M = Matrix.reindex e e M :=
rfl
#align matrix.reindex_lie_equiv_apply Matrix.reindexLieEquiv_apply
@[simp]
theorem Matrix.reindexLieEquiv_symm :
(Matrix.reindexLieEquiv e : _ ≃ₗ⁅R⁆ _).symm = Matrix.reindexLieEquiv e.symm :=
rfl
#align matrix.reindex_lie_equiv_symm Matrix.reindexLieEquiv_symm
end Matrices
|
# GraphHopper Directions API
#
# You use the GraphHopper Directions API to add route planning, navigation and route optimization to your software. E.g. the Routing API has turn instructions and elevation data and the Route Optimization API solves your logistic problems and supports various constraints like time window and capacity restrictions. Also it is possible to get all distances between all locations with our fast Matrix API.
#
# OpenAPI spec version: 1.0.0
#
# Generated by: https://github.com/swagger-api/swagger-codegen.git
#' IsochroneResponsePolygonProperties Class
#'
#' @field bucket
#'
#' @importFrom R6 R6Class
#' @importFrom jsonlite fromJSON toJSON
#' @export
IsochroneResponsePolygonProperties <- R6::R6Class(
'IsochroneResponsePolygonProperties',
public = list(
`bucket` = NULL,
initialize = function(`bucket`){
if (!missing(`bucket`)) {
stopifnot(is.numeric(`bucket`), length(`bucket`) == 1)
self$`bucket` <- `bucket`
}
},
toJSON = function() {
IsochroneResponsePolygonPropertiesObject <- list()
if (!is.null(self$`bucket`)) {
IsochroneResponsePolygonPropertiesObject[['bucket']] <- self$`bucket`
}
IsochroneResponsePolygonPropertiesObject
},
fromJSON = function(IsochroneResponsePolygonPropertiesJson) {
IsochroneResponsePolygonPropertiesObject <- jsonlite::fromJSON(IsochroneResponsePolygonPropertiesJson)
if (!is.null(IsochroneResponsePolygonPropertiesObject$`bucket`)) {
self$`bucket` <- IsochroneResponsePolygonPropertiesObject$`bucket`
}
},
toJSONString = function() {
sprintf(
'{
"bucket": %s
}',
self$`bucket`
)
},
fromJSONString = function(IsochroneResponsePolygonPropertiesJson) {
IsochroneResponsePolygonPropertiesObject <- jsonlite::fromJSON(IsochroneResponsePolygonPropertiesJson)
self$`bucket` <- IsochroneResponsePolygonPropertiesObject$`bucket`
}
)
)
|
# ----------------------------------------------------------------------------
# Copyright (c) 2016-2022, QIIME 2 development team.
#
# Distributed under the terms of the Modified BSD License.
#
# The full license is in the file LICENSE, distributed with this software.
# ----------------------------------------------------------------------------
import unittest
import skbio
import numpy as np
import pandas as pd
from q2_diversity import procrustes_analysis
class PCoATests(unittest.TestCase):
def setUp(self):
axes = ['PC1', 'PC2', 'PC3', 'PC4', 'PC5', 'PC6']
eigvals = pd.Series(np.array([1.5, 0.75, 0.3, 0.15, 0.15, 0.15]),
index=axes)
samples = np.array([[0, 3, 4, 4, 0, 0],
[1, 2, 1, 4, 3, 3],
[2, 3, 1, 0, 0, 1],
[0, 3, 2, 4, 3, 0]])
proportion_explained = pd.Series([0.50, 0.25, 0.10, 0.05, 0.05, 0.05],
index=axes)
samples_df = pd.DataFrame(samples,
index=['A', 'B', 'C', 'D'],
columns=axes)
self.reference = skbio.OrdinationResults(
'PCoA',
'Principal Coordinate Analysis',
eigvals,
samples_df,
proportion_explained=proportion_explained)
samples = np.array([[0.7, 3.7, 4.7, 4.7, 0.7, 0.7],
[1.7, 2.7, 1.7, 4.7, 3.7, 3.7],
[2.7, 3.7, 1.7, 0.7, 0.7, 1.7],
[30, 3.7, 2.7, 4.7, 3.7, 0.7]])
samples_df = pd.DataFrame(samples,
index=['A', 'B', 'C', 'D'],
columns=axes)
self.other = skbio.OrdinationResults(
'PCoA',
'Principal Coordinate Analysis',
eigvals.copy(),
samples_df.copy(),
proportion_explained=proportion_explained.copy())
S = [[-0.1358036, 0.0452679, 0.3621430, 0.1810715, -0.2716072],
[0.0452679, -0.1358036, -0.1810715, 0.1810715, 0.2716072],
[0.2263394, 0.0452679, -0.1810715, -0.5432145, -0.2716072],
[-0.1358036, 0.0452679, 0.0000000, 0.1810715, 0.2716072]]
samples_df = pd.DataFrame(np.array(S),
index=['A', 'B', 'C', 'D'],
columns=axes[:5])
self.expected_ref = skbio.OrdinationResults(
'PCoA',
'Principal Coordinate Analysis',
eigvals[:5].copy(),
samples_df.copy(),
proportion_explained=proportion_explained[:5].copy())
S = [[0.0482731, -0.0324317, 0.0494312, -0.0316828, -0.1584374],
[0.0803620, -0.0718115, -0.0112234, -0.0171011, -0.1101209],
[0.0527554, -0.0042753, -0.0126739, -0.0969602, -0.0964822],
[-0.1813905, 0.1085184, -0.0255339, 0.1457440, 0.3650405]]
samples_df = pd.DataFrame(np.array(S),
index=['A', 'B', 'C', 'D'],
columns=axes[:5])
self.expected_other = skbio.OrdinationResults(
'PCoA',
'Principal Coordinate Analysis',
eigvals[:5].copy(),
samples_df.copy(),
proportion_explained=proportion_explained[:5].copy())
noise = [
[0.04988341, -0.03234447, 0.03177641, -0.03507789, -0.13564394],
[0.09117347, -0.08318546, -0.02249053, -0.01597601, -0.10901541],
[0.05077765, -0.003994, -0.00984688, -0.09356729, -0.09648388],
[-0.19183453, 0.11952393, 0.000561, 0.14462118, 0.34114323]]
samples_df = pd.DataFrame(np.array(noise),
index=['A', 'B', 'C', 'D'],
columns=axes[:5])
self.expected_noise = skbio.OrdinationResults(
'PCoA',
'Principal Coordinate Analysis',
eigvals[:5].copy(),
samples_df.copy(),
proportion_explained=proportion_explained[:5].copy())
self.expected_m2 = 0.72240956
self.expected_p = 0.5
def test_procrustes(self):
ref, other, m2_results = procrustes_analysis(self.reference,
self.other)
true_m2 = m2_results['true M^2 value'][0]
true_p_value = m2_results['p-value for true M^2 value'][0]
skbio.util.assert_ordination_results_equal(ref, self.expected_ref)
skbio.util.assert_ordination_results_equal(other, self.expected_other)
self.assertAlmostEqual(true_m2, self.expected_m2)
self.assertNotAlmostEqual(true_p_value, self.expected_p)
def test_non_zero_p(self):
# generated with np.random.seed(3); np.random.randn(4, 6)
noise = np.array(
[[1.78862847, 0.43650985, 0.09649747, -1.8634927, -0.2773882,
-0.35475898],
[-0.08274148, -0.62700068, -0.04381817, -0.47721803, -1.31386475,
0.88462238],
[0.88131804, 1.70957306, 0.05003364, -0.40467741, -0.54535995,
-1.54647732],
[0.98236743, -1.10106763, -1.18504653, -0.2056499, 1.48614836,
0.23671627]])
self.other.samples += noise
ref, other, m2_results = procrustes_analysis(self.reference,
self.other)
true_m2 = m2_results['true M^2 value'][0]
true_p_value = m2_results['p-value for true M^2 value'][0]
skbio.util.assert_ordination_results_equal(ref, self.expected_ref)
skbio.util.assert_ordination_results_equal(other, self.expected_noise)
# the p value shouldn't be zero even in the presence of noise
self.assertAlmostEqual(true_m2, 0.7388121)
self.assertNotAlmostEqual(true_p_value, 0.001)
def test_zero_permutations_nan_pvalue(self):
ref, other, m2_results = procrustes_analysis(self.reference,
self.other,
permutations='disable')
true_m2 = m2_results['true M^2 value'][0]
true_p_value = m2_results['p-value for true M^2 value'][0]
skbio.util.assert_ordination_results_equal(ref, self.expected_ref)
skbio.util.assert_ordination_results_equal(other, self.expected_other)
self.assertAlmostEqual(true_m2, self.expected_m2)
self.assertTrue(np.isnan(true_p_value))
def test_procrustes_bad_dimensions(self):
self.other.samples = self.other.samples.iloc[:, :4]
self.other.eigvals = self.other.eigvals[:4]
self.other.proportion_explained = self.other.proportion_explained[:4]
with self.assertRaisesRegex(ValueError, 'The matrices cannot be '):
procrustes_analysis(self.reference, self.other)
def test_procrustes_over_dimensions(self):
with self.assertRaisesRegex(ValueError, 'Cannot fit fewer dimensions '
'than available'):
procrustes_analysis(self.reference, self.other, 11)
def test_procrustes_id_mismatch(self):
msg = 'The ordinations represent two different sets of samples'
self.other.samples.index = pd.Index([':L', ':D', ':)', ':('])
with self.assertRaisesRegex(ValueError, msg):
procrustes_analysis(self.reference, self.other)
self.other.samples.index = pd.Index([':L', 'B', 'C', 'D'])
with self.assertRaisesRegex(ValueError, msg):
procrustes_analysis(self.reference, self.other)
self.other.samples.index = pd.Index(['a', 'b', 'c', 'd'])
with self.assertRaisesRegex(ValueError, msg):
procrustes_analysis(self.reference, self.other)
|
module Sessions.Syntax.Values where
open import Prelude hiding (both)
open import Relation.Unary
open import Data.Maybe
open import Data.List.Properties using (++-isMonoid)
import Data.List as List
open import Sessions.Syntax.Types
open import Sessions.Syntax.Expr
open import Relation.Ternary.Separation.Morphisms
data Runtype : Set where
endp : SType → Runtype
chan : SType → SType → Runtype
flipped : Runtype → Runtype
flipped (endp x) = endp x
flipped (chan α β) = chan β α
data Ends : Runtype → Runtype → Runtype → Set where
lr : ∀ {a b} → Ends (endp a) (endp b) (chan a b)
rl : ∀ {a b} → Ends (endp b) (endp a) (chan a b)
instance
≺-raw-sep : RawSep Runtype
RawSep._⊎_≣_ ≺-raw-sep = Ends
≺-has-sep : IsSep ≺-raw-sep
IsSep.⊎-comm ≺-has-sep lr = rl
IsSep.⊎-comm ≺-has-sep rl = lr
IsSep.⊎-assoc ≺-has-sep lr ()
IsSep.⊎-assoc ≺-has-sep rl ()
RCtx = List Runtype
open import Relation.Ternary.Separation.Construct.ListOf Runtype public
End : SType → Runtype → Set
End α τ = [ endp α ] ≤ [ τ ]
ending : ∀ {ys} → Ends (endp γ) ys (chan α β) → End γ (chan α β)
ending lr = -, divide lr ⊎-idˡ
ending rl = -, divide rl ⊎-idˡ
mutual
Env = Allstar Val
data Closure : Type → Type → Pred RCtx 0ℓ where
clos : ∀ {a} → Exp b (a ∷ Γ) → ∀[ Env Γ ⇒ Closure a b ]
Endptr = Just ∘ endp
data Val : Type → Pred RCtx 0ℓ where
tt : ε[ Val unit ]
cref : ∀[ Endptr α ⇒ Val (cref α) ]
pairs : ∀[ Val a ✴ Val b ⇒ Val (prod a b) ]
clos : Exp b (a ∷ Γ) → ∀[ Env Γ ⇒ Val (a ⊸ b) ]
|
= = Awards and honors = =
|
import data.real.basic
#check pow_two_nonneg
variables {x y : ℝ}
-- BEGIN
example (h : y > x^2) : y > 0 ∨ y < -1 :=
begin
left,
linarith [pow_two_nonneg x],
end
example (h : -y > x^2 + 1) : y > 0 ∨ y < -1 :=
begin
right,
linarith [pow_two_nonneg x],
end
--Alternatively
example (h : y > 0) : y > 0 ∨ y < -1 :=
or.inl h
example (h : y < -1) : y > 0 ∨ y < -1 :=
or.inr h
-- END
|
-- Razonamiento ecuacional sobre la inversa de listas unitarias
-- ============================================================
import data.list.basic
open list
variable {α : Type*}
variable x : α
variables (xs : list α)
-- ----------------------------------------------------
-- Ejercicio 1. Definir, por recursión, la función
-- inversa :: list α → list α
-- tal que (inversa xs) es la lista obtenida
-- invirtiendo el orden de los elementos de xs.
-- Por ejemplo,
-- inversa [3,2,5] = [5,2,3]
-- ----------------------------------------------------
def inversa : list α → list α
| [] := []
| (x :: xs) := inversa xs ++ [x]
-- #eval inversa [3,2,5]
-- ----------------------------------------------------
-- Ejercicio 2. Demostrar los siguientes lemas
-- + inversa_nil :
-- inversa ([] : list α) = []
-- + inversa_cons :
-- inversa (x :: xs) = inversa xs ++ [x]
-- ----------------------------------------------------
@[simp]
lemma inversa_nil :
inversa ([] : list α) = [] :=
rfl
@[simp]
lemma inversa_cons :
inversa (x :: xs) = inversa xs ++ [x] :=
rfl
-- ----------------------------------------------------
-- Ejercicio 3. (p. 9) Demostrar que
-- inversa [x] = [x]
-- ----------------------------------------------------
-- 1ª demostración
example : inversa [x] = [x] :=
calc inversa [x]
= inversa ([] : list α) ++ [x] : by rw inversa_cons
... = ([] : list α) ++ [x] : by rw inversa_nil
... = [x] : by rw nil_append
-- 2ª demostración
example : inversa [x] = [x] :=
calc inversa [x]
= inversa ([] : list α) ++ [x] : by simp
... = ([] : list α) ++ [x] : by simp
... = [x] : by simp
-- 3ª demostración
example : inversa [x] = [x] :=
by simp
-- 4ª demostración
example : inversa [x] = [x] :=
begin
rw inversa_cons,
rw inversa_nil,
rw nil_append,
end
-- 5ª demostración
example : inversa [x] = [x] :=
by rw [inversa_cons,
inversa_nil,
nil_append]
-- 6ª demostración
example : inversa [x] = [x] :=
rfl
-- Comentarios sobre la función reverse:
-- + Es equivalente a la función inversa
-- + Para usarla hay que importar la librería
-- data.list.basic y abrir el espacio de nombre
-- list escribiendo al principio del fichero
-- import data.list.basic
-- open list
-- + Se puede evaluar. Por ejemplo,
-- #eval reverse [3,2,5]
-- + Se puede demostrar. Por ejemplo,
-- example : reverse [x] = [x] :=
-- -- by library_search
-- reverse_singleton x
|
(*
* Copyright (c) 2009-2016, Andrew Appel, Robert Dockins,
Aquinas Hobor and Le Xuan Bach
*
*)
Require Import VST.msl.base.
Require Import VST.msl.sepalg.
Require Import VST.msl.psepalg.
Require Import VST.msl.sepalg_generators.
Require Import VST.msl.boolean_alg.
Require Import VST.msl.eq_dec.
Require VST.msl.tree_shares.
Module Share : SHARE_MODEL := tree_shares.Share.
Import Share.
Definition share : Type := Share.t.
Instance pa_share : Perm_alg share := Share.pa.
Instance sa_share : Sep_alg share := Share.sa.
Instance ca_share : Canc_alg share := Share.ca.
Definition emptyshare : share := Share.bot.
Definition fullshare : share := Share.top.
Theorem leq_join_sub : forall s1 s2:Share.t,
s1 <= s2 <-> join_sub s1 s2.
Proof.
split; intros.
pose (s' := glb s2 (comp s1)).
exists s'.
simpl; split.
subst s'.
rewrite glb_commute.
rewrite glb_assoc.
rewrite (glb_commute (comp s1) s1).
rewrite comp2.
apply glb_bot.
subst s'.
rewrite distrib2.
rewrite comp1.
rewrite glb_top.
rewrite <- ord_spec2; auto.
destruct H as [s' H].
destruct H.
rewrite ord_spec2.
rewrite <- H0.
rewrite <- lub_assoc.
rewrite lub_idem; auto.
Qed.
Lemma top_correct' : forall x:t, join_sub x top.
Proof.
intros; rewrite <- leq_join_sub; auto with ba.
Qed.
Lemma bot_identity : identity bot.
Proof.
hnf; intros.
destruct H.
rewrite lub_commute in H0.
rewrite lub_bot in H0.
auto.
Qed.
Hint Resolve bot_identity : core.
Lemma identity_share_bot : forall s,
identity s -> s = bot.
Proof.
intros.
apply identities_unique; auto.
exists s.
apply join_comm.
destruct (top_correct' s).
assert (x = top).
apply H; auto.
subst x; auto.
destruct (top_correct' bot).
assert (x = top).
apply bot_identity; auto.
subst x; auto.
apply join_comm in H1.
destruct (join_assoc H0 H1); intuition.
assert (x = top).
apply H; auto.
subst x.
replace bot with s.
rewrite identity_unit_equiv in H.
trivial.
eapply joins_units_eq; try apply H0. exists top; eauto.
simpl. split. apply glb_bot. apply lub_bot.
Qed.
Lemma factoryOverlap' : forall f1 f2 n1 n2,
isTokenFactory f1 n1 -> isTokenFactory f2 n2 -> joins f1 f2 -> False.
Proof.
intros.
destruct H1.
destruct H1.
apply (factoryOverlap f1 f2 n1 n2 H H0 H1).
Qed.
Lemma identityToken' : forall x, isToken x 0 <-> identity x.
Proof.
intro x; destruct (identityToken x); split; intros.
hnf; intros.
rewrite H in H2; auto.
apply H0.
apply identity_share_bot; auto.
Qed.
Lemma nonidentityToken' : forall x n, (n > 0)%nat -> isToken x n -> nonidentity x.
Proof.
intros.
generalize (nonidentityToken x n H H0).
repeat intro.
apply H1.
apply identity_share_bot; auto.
Qed.
Lemma nonidentityFactory' : forall x n, isTokenFactory x n -> nonidentity x.
Proof.
intros.
generalize (nonidentityFactory x n H); repeat intro.
apply H0.
apply identity_share_bot; auto.
Qed.
Lemma split_join : forall x1 x2 x,
split x = (x1,x2) -> join x1 x2 x.
Proof.
intros; split.
apply split_disjoint with x; auto.
apply split_together; auto.
Qed.
Lemma split_nontrivial' : forall x1 x2 x,
split x = (x1, x2) ->
(identity x1 \/ identity x2) ->
identity x.
Proof.
intros.
rewrite (split_nontrivial x1 x2 x H).
apply bot_identity.
destruct H0.
left; apply identity_share_bot; auto.
right; apply identity_share_bot; auto.
Qed.
Lemma rel_leq : forall a x, join_sub (rel a x) a.
Proof.
intros.
rewrite <- leq_join_sub.
intros.
rewrite ord_spec1.
pattern a at 3.
replace a with (rel a top).
rewrite <- rel_preserves_glb.
rewrite glb_top.
auto.
apply rel_top1.
Qed.
Lemma rel_join : forall a x y z,
join x y z ->
join (rel a x) (rel a y) (rel a z).
Proof.
simpl; intuition. inv H.
constructor.
rewrite <- rel_preserves_glb.
replace bot with (rel a bot).
replace (glb x y) with bot; auto.
apply rel_bot1.
rewrite <- rel_preserves_lub. auto.
Qed.
Lemma rel_join2 : forall a x y s,
nonidentity a ->
join (rel a x) (rel a y) s ->
exists z, s = rel a z /\ join x y z.
Proof.
simpl; intros.
destruct H0.
exists (lub x y).
split.
rewrite <- H1.
symmetry.
apply rel_preserves_lub.
split; auto.
rewrite <- rel_preserves_glb in H0.
replace bot with (rel a bot) in H0.
apply rel_inj_l with a; auto.
hnf; intros; apply H.
subst a; apply bot_identity.
apply rel_bot1.
Qed.
Lemma rel_nontrivial : forall a x,
identity (rel a x) ->
(identity a \/ identity x).
Proof.
intros a x H.
destruct (eq_dec a bot); auto.
subst a.
left. apply bot_identity.
right.
assert (rel a x = bot).
apply identity_share_bot; auto.
assert (x = bot).
replace bot with (rel a bot) in H0.
apply rel_inj_l with a; auto.
apply rel_bot1.
subst x; apply bot_identity.
Qed.
Instance share_cross_split : Cross_alg t.
Proof.
hnf; simpl; intuition. destruct H as [H1 H2]. destruct H0 as [H H3].
exists (glb a c, glb a d, glb b c, glb b d); intuition; constructor.
rewrite (glb_commute a d).
rewrite glb_assoc.
rewrite <- (glb_assoc c d a).
rewrite H.
rewrite (glb_commute bot a).
rewrite glb_bot.
rewrite glb_bot.
auto.
rewrite <- distrib1; rewrite H3; rewrite <- H2; auto with ba.
rewrite (glb_commute b d).
rewrite glb_assoc.
rewrite <- (glb_assoc c d b).
rewrite H.
rewrite (glb_commute bot b).
rewrite glb_bot.
rewrite glb_bot.
auto.
rewrite <- distrib1; rewrite H3; rewrite <- H2; auto with ba.
rewrite (glb_commute a c).
rewrite glb_assoc.
rewrite <- (glb_assoc a b c).
rewrite H1.
rewrite (glb_commute bot c).
rewrite glb_bot.
rewrite glb_bot.
auto.
rewrite (glb_commute a c).
rewrite (glb_commute b c).
rewrite <- distrib1; rewrite H2; rewrite <- H3; auto with ba.
rewrite (glb_commute a d).
rewrite glb_assoc.
rewrite <- (glb_assoc a b d).
rewrite H1.
rewrite (glb_commute bot d).
rewrite glb_bot.
rewrite glb_bot.
auto.
rewrite (glb_commute a d).
rewrite (glb_commute b d).
rewrite <- distrib1; rewrite H2; rewrite <- H3; auto with ba.
Qed.
Lemma bot_correct' : forall x, join_sub bot x.
Proof.
intros s.
destruct (top_correct' s).
exists s.
destruct (top_correct' bot).
assert (x0 = top).
apply bot_identity; auto.
subst x0.
apply join_comm in H0.
destruct (join_assoc H H0); intuition.
apply join_comm in H2.
destruct (join_assoc H1 H2); intuition.
assert (s = x1).
apply bot_identity; auto.
subst x1; auto.
Qed.
Lemma top_share_nonidentity : nonidentity top.
Proof.
hnf; intros.
assert (top = bot).
apply identity_share_bot; auto.
apply nontrivial; auto.
Qed.
Lemma top_share_nonunit: nonunit top.
Proof.
repeat intro. unfold unit_for in H.
destruct H. rewrite glb_commute in H. rewrite glb_top in H. subst.
rewrite lub_bot in H0. apply nontrivial; auto.
Qed.
Lemma bot_join_eq : forall x, join bot x x.
Proof.
intros.
destruct (join_ex_identities x); intuition.
destruct H0.
generalize (H _ _ H0).
intros; subst; auto.
replace bot with x0; auto.
apply identity_share_bot; auto.
Qed.
Lemma join_bot_eq : forall x, join x bot x.
Proof.
intros.
apply join_comm, bot_join_eq.
Qed.
Lemma bot_joins : forall x, joins bot x.
Proof.
intro x; exists x; apply bot_join_eq.
Qed.
Lemma dec_share_identity : forall x:t, { identity x } + { ~identity x }.
Proof.
intro x.
destruct (eq_dec x bot); subst.
left; apply bot_identity.
right; intro; elim n.
apply identity_share_bot; auto.
Qed.
Lemma dec_share_nonunit : forall x:t, { nonunit x } + { ~ nonunit x }.
Proof.
intro x.
destruct (dec_share_identity x) as [H | H]; [right | left].
+ intro; revert H. apply nonunit_nonidentity; auto.
+ apply nonidentity_nonunit; auto.
Qed.
Lemma fullshare_full : full fullshare.
Proof.
unfold full.
intros.
generalize (Share.top_correct);intros.
destruct H as [sigma'' ?].
specialize (H0 sigma'').
rewrite leq_join_sub in H0.
destruct H0.
destruct (join_assoc H H0) as [s [H1 H2]].
apply join_comm in H2. apply unit_identity in H2.
eapply split_identity; eauto.
Qed.
Lemma join_sub_fullshare : forall sh,
join_sub fullshare sh -> sh = fullshare.
Proof.
intros.
generalize fullshare_full; intro.
apply full_maximal in H0.
specialize ( H0 sh H).
auto.
Qed.
Lemma dec_share_full : forall (sh : Share.t),
{full sh} + {~full sh}.
Proof with auto.
intro sh.
destruct (eq_dec sh top); subst.
left. apply fullshare_full.
right. intro. apply n.
generalize (Share.top_correct sh);intro.
apply leq_join_sub in H0.
destruct H0.
specialize ( H x). spec H. exists top...
specialize ( H sh top (join_comm H0))...
Qed.
Lemma rel_congruence : forall a x1 x2,
join_sub x1 x2 ->
join_sub (rel a x1) (rel a x2).
Proof.
intros.
destruct H.
exists (rel a x).
apply rel_join; auto.
Qed.
Lemma share_split_injective:
forall sh1 sh2, Share.split sh1 = Share.split sh2 -> sh1=sh2.
Proof.
intros sh1 sh2;
case_eq (Share.split sh1); case_eq (Share.split sh2); intros.
generalize (split_join _ _ _ H); intro.
generalize (split_join _ _ _ H0); intro.
inv H1.
eapply join_eq; eauto.
Qed.
Lemma share_joins_constructive:
forall sh1 sh2 : t , joins sh1 sh2 -> {sh3 | join sh1 sh2 sh3}.
Proof.
intros.
exists (lub sh1 sh2).
destruct H.
destruct H; split; auto.
Qed.
Lemma share_join_sub_constructive:
forall sh1 sh3 : t , join_sub sh1 sh3 -> {sh2 | join sh1 sh2 sh3}.
Proof.
intros.
exists (glb sh3 (comp sh1)).
destruct H.
destruct H.
split.
rewrite (glb_commute sh3 (comp sh1)).
rewrite <- glb_assoc.
rewrite comp2.
rewrite glb_commute.
rewrite glb_bot.
auto.
rewrite distrib2.
rewrite comp1.
rewrite glb_top.
rewrite <- ord_spec2.
rewrite <- H0.
apply lub_upper1.
Qed.
Lemma triple_join_exists_share : Trip_alg t.
Proof.
repeat intro.
destruct H; destruct H0; destruct H1.
exists (lub a (lub b c)).
split.
rewrite <- H2.
rewrite glb_commute.
rewrite distrib1.
rewrite glb_commute.
rewrite H1.
rewrite glb_commute.
rewrite H0.
rewrite lub_bot; auto.
rewrite <- H2.
apply lub_assoc.
Qed.
Lemma nonemp_split_neq1: forall sh sh1 sh2, nonidentity sh -> split sh = (sh1, sh2) -> sh1 <> sh.
Proof with auto.
intros until sh2; intros H H0.
destruct (dec_share_identity sh2).
generalize (split_nontrivial' _ _ _ H0); intro.
spec H1...
destruct (eq_dec sh1 sh)...
subst sh1.
generalize (split_join _ _ _ H0); intro.
apply join_comm in H1.
apply unit_identity in H1...
Qed.
Lemma nonemp_split_neq2: forall sh sh1 sh2, nonidentity sh -> split sh = (sh1, sh2) -> sh2 <> sh.
Proof with auto.
intros until sh2; intros H H0.
destruct (dec_share_identity sh1).
generalize (split_nontrivial' _ _ _ H0); intro.
spec H1...
destruct (eq_dec sh2 sh)...
subst sh2.
generalize (split_join _ _ _ H0); intro.
apply unit_identity in H1...
Qed.
Lemma bot_unit: forall sh,
join emptyshare sh sh.
Proof.
intro sh.
generalize (bot_joins sh); generalize bot_identity; intros.
destruct H0.
specialize ( H sh x H0). subst.
trivial.
Qed.
Hint Resolve bot_unit : core.
Lemma join_bot: join emptyshare emptyshare emptyshare.
Proof.
apply bot_unit.
Qed.
Lemma share_rel_nonidentity:
forall {sh1 sh2}, nonidentity sh1 -> nonidentity sh2 -> nonidentity (Share.rel sh1 sh2).
Proof.
intros.
unfold nonidentity in *.
generalize (rel_nontrivial sh1 sh2); intro. intuition.
Qed.
Lemma share_rel_nonunit: forall {sh1 sh2: Share.t},
nonunit sh1 -> nonunit sh2 -> nonunit (Share.rel sh1 sh2).
Proof. intros. apply nonidentity_nonunit. apply share_rel_nonidentity.
intro. apply (@identity_unit _ _ _ sh1 Share.bot) in H1. apply H in H1; auto.
apply joins_comm. apply bot_joins.
intro. apply (@identity_unit _ _ _ sh2 Share.bot) in H1. apply H0 in H1; auto.
apply joins_comm. apply bot_joins.
Qed.
Lemma decompose_bijection: forall sh1 sh2,
sh1 = sh2 <-> decompose sh1 = decompose sh2.
Proof.
intros.
split;intros. subst;trivial.
generalize (recompose_decompose sh1);intro.
generalize (recompose_decompose sh2);intro.
congruence.
Qed.
Module ShareMap.
Section SM.
Variable A:Type.
Variable EqDec_A : EqDec A.
Variable B:Type.
Variable JB: Join B.
Variable paB : Perm_alg B.
Variable saB : Sep_alg B.
Definition map := fpm A (lifted Share.Join_ba * B).
Instance Join_map : Join map := Join_fpm _.
Instance pa_map : Perm_alg map := Perm_fpm _ _.
Instance sa_map : Sep_alg map := Sep_fpm _ _.
Instance ca_map {CA: Canc_alg B} : Canc_alg map := Canc_fpm _.
Instance da_map {DA: Disj_alg B} : Disj_alg map := @Disj_fpm _ _ _ _ _ _.
Definition map_share (a:A) (m:map) : share :=
match lookup_fpm m a with
| Some (sh,_) => lifted_obj sh
| None => Share.bot
end.
Definition map_val (a:A) (m:map) : option B :=
match lookup_fpm m a with
| Some (_,b) => Some b
| None => None
end.
Definition empty_map : map := empty_fpm _ _.
Definition map_upd (a:A) (b:B) (m:map) : option map :=
match lookup_fpm m a with
| Some (sh,_) =>
if eq_dec (lifted_obj sh) fullshare
then Some (insert_fpm _ a (sh,b) m)
else None
| None => None
end.
Lemma join_lifted {t} {J: Join t}:
forall (a b c: lifted J), join a b c -> join (lifted_obj a) (lifted_obj b) (lifted_obj c).
Proof. destruct a; destruct b; destruct c; simpl; intros. apply H.
Qed.
Lemma map_join_char : forall m1 m2 m3,
join m1 m2 m3 <->
(forall a,
join (map_share a m1) (map_share a m2) (map_share a m3) /\
join (map_val a m1) (map_val a m2) (map_val a m3)).
Proof with auto.
split; intros.
hnf in H. specialize ( H a).
unfold map_val, map_share, lookup_fpm.
destruct (proj1_sig m1 a) as [[sh1 a1] | ];
destruct (proj1_sig m2 a) as [[sh2 a2] | ];
destruct (proj1_sig m3 a) as [[sh3 a3] | ]; inv H; try solve [inv H0]; simpl; auto.
destruct H3; simpl in *; auto.
split. apply join_lifted; auto. constructor; auto.
split; apply join_unit2; auto.
split; apply join_unit1; auto.
split; apply join_unit1; auto.
split; apply join_unit1; auto.
intro a. specialize ( H a). destruct H.
unfold map_val, map_share, lookup_fpm in *.
destruct (proj1_sig m1 a) as [[sh1 a1] | ];
destruct (proj1_sig m2 a) as [[sh2 a2] | ];
destruct (proj1_sig m3 a) as [[sh3 a3] | ]; inv H0; try solve [inv H1]; auto.
constructor. split; auto.
apply join_unit2_e in H; auto. apply join_unit2; auto.
repeat f_equal. destruct sh1; destruct sh3; simpl in *; subst.
rewrite (proof_irr n n0); auto.
apply join_unit1_e in H; auto. apply join_unit1; auto.
repeat f_equal. destruct sh2; destruct sh3; simpl in *; subst.
rewrite (proof_irr n n0); auto.
constructor. constructor.
Qed.
Lemma empty_map_identity {CAB: Disj_alg B}: identity empty_map.
Proof.
rewrite identity_unit_equiv.
intro x. simpl. auto. constructor.
Qed.
Lemma map_identity_unique {CAB: Disj_alg B}: forall m1 m2:map,
identity m1 -> identity m2 -> m1 = m2.
Proof.
intros.
destruct m1; destruct m2; simpl in *.
cut (x = x0). intros. subst x0.
replace f0 with f; auto.
apply proof_irr; auto.
rewrite identity_unit_equiv in H, H0.
extensionality a.
specialize ( H a); specialize ( H0 a).
apply lower_inv in H.
apply lower_inv in H0.
destruct H; destruct H0; simpl in *.
intuition; congruence.
destruct s0 as [? [? [? [? [? [? ?]]]]]].
rewrite H in H1. inv H1. rewrite H0 in H; inv H.
destruct x3. destruct H2. simpl in *. apply no_units in H. contradiction.
destruct s as [? [? [? [? [? [? ?]]]]]].
rewrite H in H0; inv H0. rewrite H1 in H; inv H.
destruct x2. destruct H2. simpl in *. apply no_units in H. contradiction.
destruct s as [? [? [? [? [? [? ?]]]]]].
rewrite H in H0; inv H0. rewrite H1 in H; inv H.
destruct x2. destruct H2. simpl in *. apply no_units in H. contradiction.
Qed.
Lemma map_identity_is_empty {CAB: Disj_alg B} : forall m,
identity m -> m = empty_map.
Proof.
intros; apply map_identity_unique; auto.
apply empty_map_identity.
Qed.
Lemma empty_map_join {CAB: Disj_alg B} : forall m,
join empty_map m m.
Proof.
intro m. destruct (join_ex_units m).
replace empty_map with x; auto.
apply map_identity_is_empty.
eapply unit_identity; eauto.
Qed.
Lemma map_val_bot : forall a m,
map_val a m = None <-> map_share a m = Share.bot.
Proof.
do 2 intro.
unfold map_val, map_share, lookup_fpm.
destruct (proj1_sig m a); intuition.
disc.
contradiction (no_units a0 a0). destruct a0. simpl in *. subst.
contradiction (n bot). auto.
Qed.
Lemma map_upd_success : forall a v m,
map_share a m = Share.top ->
exists m', map_upd a v m = Some m'.
Proof.
intros.
unfold map_upd. simpl.
unfold map_share, lookup_fpm in*.
destruct (proj1_sig m a).
destruct p.
rewrite H.
unfold fullshare.
destruct (eq_dec top top).
eauto.
elim n; auto.
elim Share.nontrivial; auto.
Qed.
Lemma map_set_share1 : forall a v m m',
map_upd a v m = Some m' ->
map_share a m = Share.top.
Proof.
unfold map_upd, map_share.
intros.
destruct (lookup_fpm m a); disc.
destruct p.
destruct (eq_dec (lifted_obj l) fullshare); disc; auto.
Qed.
Lemma map_set_share2 : forall a v m m',
map_upd a v m = Some m' ->
map_share a m' = Share.top.
Proof.
unfold map_upd, map_share.
intros. destruct (lookup_fpm m a); disc.
destruct p. destruct (eq_dec (lifted_obj l) fullshare); disc.
inv H.
rewrite fpm_gss. auto.
Qed.
Lemma map_set_share3 : forall a v m m',
map_upd a v m = Some m' ->
forall a',
map_share a' m = map_share a' m'.
Proof.
unfold map_upd, map_share.
intros a v m m'.
case_eq (lookup_fpm m a); intros; disc.
destruct p.
destruct (eq_dec (lifted_obj l) fullshare); disc.
inv H0.
destruct (eq_dec a a'). subst.
rewrite H.
rewrite fpm_gss. auto.
rewrite fpm_gso; auto.
Qed.
Lemma map_gss_val: forall a v m m',
map_upd a v m = Some m' ->
map_val a m' = Some v.
Proof.
unfold map_upd, map_val.
intros a v m m'.
case_eq (lookup_fpm m a); intros; disc.
destruct p.
destruct (eq_dec (lifted_obj l) fullshare); disc.
inv H0.
rewrite fpm_gss. auto.
Qed.
Lemma map_gso_val : forall i j v m m',
i <> j ->
map_upd j v m = Some m' ->
map_val i m = map_val i m'.
Proof.
unfold map_upd, map_val.
intros i j v m m'.
case_eq (lookup_fpm m j); intros; disc.
destruct p.
destruct (eq_dec (lifted_obj l) fullshare); disc.
inv H1.
rewrite fpm_gso; auto.
Qed.
Lemma map_gso_share : forall i j v m m',
i <> j ->
map_upd j v m = Some m' ->
map_share i m = map_share i m'.
Proof.
unfold map_upd, map_share.
intros i j v m m'.
case_eq (lookup_fpm m j); intros; disc.
destruct p.
destruct (eq_dec (lifted_obj l) fullshare); disc.
inv H1.
rewrite fpm_gso; auto.
Qed.
Lemma map_upd_join : forall m1 m2 m3 a v m1',
map_upd a v m1 = Some m1' ->
join m1 m2 m3 ->
exists m3', map_upd a v m3 = Some m3' /\
join m1' m2 m3'.
Proof.
intros.
rewrite map_join_char in H0.
destruct (H0 a).
generalize H; intros.
apply map_set_share1 in H.
rewrite H in H1.
destruct H1.
rewrite glb_commute in H1.
rewrite glb_top in H1.
rewrite H1 in H4.
rewrite lub_bot in H4.
symmetry in H4.
destruct (map_upd_success a v _ H4).
exists x; split; auto.
clear H2.
rewrite map_join_char.
intro a'.
destruct (eq_dec a a').
subst a'. split.
apply map_set_share2 in H3. rewrite H3.
apply map_set_share2 in H5. rewrite H5.
rewrite H1. apply join_unit2; auto.
erewrite map_gss_val; eauto.
apply map_val_bot in H1. rewrite H1.
erewrite map_gss_val; eauto. constructor.
destruct (H0 a'). split.
rewrite <- (map_gso_share a' a v m1 m1'); auto.
rewrite <- (map_gso_share a' a v m3 x); auto.
rewrite <- (map_gso_val a' a v m1 m1'); auto.
rewrite <- (map_gso_val a' a v m3 x); auto.
Qed.
Definition build_map (l:list (A * B)) : map :=
fold_right
(fun (ab:A * B) m =>
insert_fpm EqDec_A
(fst ab)
(mk_lifted fullshare top_share_nonunit,snd ab) m)
empty_map l.
Lemma build_map_results : forall (l:list (A*B)) a b,
NoDup (List.map (@fst _ _) l) ->
(In (a,b) l <->
(map_val a (build_map l) = Some b /\
map_share a (build_map l) = Share.top)).
Proof.
induction l; simpl.
split; intros. elim H0.
destruct H0.
unfold build_map in H0. simpl in H0.
unfold map_val in H0.
simpl in H0. discriminate.
intros. split; intros.
destruct H0; subst.
unfold build_map.
simpl fold_right.
split.
unfold map_val.
rewrite fpm_gss. simpl; auto.
unfold map_share.
rewrite fpm_gss. simpl; auto.
generalize H0; intro H1.
rewrite IHl in H0.
inv H.
assert (fst a <> a0).
intro. subst a0.
elim H4.
clear -H1. induction l; simpl in *; intuition; subst; auto.
destruct H0.
unfold build_map. simpl fold_right.
split.
unfold map_val.
rewrite fpm_gso; auto.
unfold map_share.
rewrite fpm_gso; auto.
inv H. auto.
inv H.
destruct H0.
destruct a.
destruct (eq_dec a a0).
subst a0.
left. f_equal.
unfold build_map in H.
unfold map_val in H.
simpl fold_right in H.
rewrite fpm_gss in H.
inv H. auto.
right.
rewrite IHl; auto.
split.
revert H.
unfold build_map, map_val.
simpl fold_right.
rewrite fpm_gso; auto.
revert H0.
unfold build_map, map_share.
simpl fold_right.
rewrite fpm_gso; auto.
Qed.
Lemma build_map_join : forall (l1 l2:list (A * B)),
NoDup (List.map (@fst _ _) (l1++l2)) ->
join (build_map l1)
(build_map l2)
(build_map (l1++l2)).
Proof.
induction l1; intros.
simpl app.
unfold build_map at 1.
simpl fold_right.
apply empty_fpm_join; auto with typeclass_instances.
inv H.
simpl app.
unfold build_map.
simpl fold_right.
apply insert_fpm_join. auto with typeclass_instances.
2: apply (IHl1 l2); auto.
assert (~In (fst a) (List.map (@fst _ _) l2)).
intro.
elim H2.
rewrite map_app.
apply in_or_app.
auto.
clear -H.
induction l2; simpl in *.
auto.
rewrite fpm_gso; auto.
Qed.
End SM.
End ShareMap.
|
{-# OPTIONS --without-K #-}
module hott.core.equality where
open import hott.core.universe
-- | The equality type. In hott we think of the equality type as paths
-- between two points in the space A. To simplify the types we first
-- fix the common parameters.
module common {a : Level}{A : Type a} where
data _≡_ (x : A) : (y : A) → Type a where
refl : x ≡ x
-- Induction principle for ≡ type.
induction≡ : {ℓ : Level}
→ (D : {x y : A} (p : x ≡ y) → Type ℓ)
→ (d : {x : A} → D {x} {x} refl)
→ {x y : A} → (p : x ≡ y) → D p
induction≡ D d refl = d
-- In hott view point, this function takes the inverse of the path
-- from x to y. As a relation you are proving that ≡ is symmetric.
_⁻¹ : ∀{x y}
→ x ≡ y → y ≡ x
refl ⁻¹ = refl
-- The path composition. This means transitivity of the ≡ relation.
_∙_ : ∀ {x y z}
→ x ≡ y → y ≡ z → x ≡ z
refl ∙ refl = refl
infixr 1 _≡_
-- Precedence of multiplication
infixl 70 _∙_
-- Precedence of exponentiation.
infixl 90 _⁻¹
-- Equational reasoning
-- To prove x_0 = x_n by a sequence of proofs
-- x_0 = x_1
-- x_1 = x_2
-- ... you can use the following syntax
--
-- begin x_0 ≅ x_1 by p1
-- ≅ x_2 by p2
-- ....
-- ≅ x_n by pn
-- ∎
--
-- In equational proofs, it is more readable to use by definition
-- than by refl
definition : ∀{x} → x ≡ x
definition = refl
begin_ : (x : A)
→ x ≡ x
begin_ x = refl
_≡_by_ : ∀ {x y : A}
→ x ≡ y
→ (z : A)
→ y ≡ z
→ x ≡ z
p ≡ z by q = p ∙ q
_∎ : ∀{x y : A}
→ (x ≡ y)
→ (x ≡ y)
proof ∎ = proof
infixl 2 begin_
infixl 1 _≡_by_
infixl 0 _∎
-- We now capture path transportation in the following submodule.
module Transport {ℓ : Level} where
-- Path transportation.
transport : ∀ {x y : A}
→ x ≡ y
→ {P : A → Type ℓ}
→ P x → P y
transport refl = λ z → z
-- Another symbol for transport. Use it when you do not want to
-- specify P.
_⋆ : {P : A → Type ℓ}
→ {x y : A}
→ x ≡ y
→ P x → P y
p ⋆ = transport p
open Transport public
open common public
{-# BUILTIN EQUALITY _≡_ #-}
{-# BUILTIN REFL refl #-}
-- The functional congruence, i.e. likes gives likes on application of
-- a function. In the HoTT perspective this says that functions are
-- functors.
ap : ∀ {a b : Level} {A : Type a}{B : Type b} {x y : A}
→ (f : A → B)
→ x ≡ y → (f x) ≡ (f y)
ap f refl = refl
-- The dependent version of ap. This requires transport for its
-- definition.
apd : ∀{a b : Level }{A : Type a}{B : A → Type b}
→ (f : (a : A) → B a)
→ {x y : A}
→ (p : x ≡ y)
→ (p ⋆) (f x) ≡ f y
apd f refl = refl
-- Better syntax fro ap in equational reasoning.
applying_on_ : ∀{ℓ₀ ℓ₁}{A : Type ℓ₀}{B : Type ℓ₁}
→ (f : A → B)
→ {x y : A}
→ (p : x ≡ y)
→ f x ≡ f y
applying_on_ f a = ap f a
-- Better syntax for dependent version of applying on both sides.
transporting_over_ : ∀{ℓ₀ ℓ₁}{A : Type ℓ₀}{B : A → Type ℓ₁}
→ (f : (a : A) → B(a)){x y : A}
→ (p : x ≡ y)
→ (p ⋆) (f x) ≡ f y
transporting f over p = apd f p
infixr 2 applying_on_
infixr 2 transporting_over_
|
program nesthd2
use nesthd2_version_module
implicit none
!----- GPL ---------------------------------------------------------------------
!
! Copyright (C) Stichting Deltares, 2011-2016.
!
! This program is free software: you can redistribute it and/or modify
! it under the terms of the GNU General Public License as published by
! the Free Software Foundation version 3.
!
! This program is distributed in the hope that it will be useful,
! but WITHOUT ANY WARRANTY; without even the implied warranty of
! MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
! GNU General Public License for more details.
!
! You should have received a copy of the GNU General Public License
! along with this program. If not, see <http://www.gnu.org/licenses/>.
!
! contact: [email protected]
! Stichting Deltares
! P.O. Box 177
! 2600 MH Delft, The Netherlands
!
! All indications and logos of, and references to, "Delft3D" and "Deltares"
! are registered trademarks of Stichting Deltares, and remain the property of
! Stichting Deltares. All rights reserved.
!
!-------------------------------------------------------------------------------
! $Id: nesthd2.f90 5717 2016-01-12 11:35:24Z mourits $
! $HeadURL: https://svn.oss.deltares.nl/repos/delft3d/tags/6686/src/tools_gpl/nesthd2/packages/nesthd2/src/nesthd2.f90 $
!***********************************************************************
! Deltares marine and coastal management
!
! program : nesthd2
! version : v1.4
! date : January 1998
! version : 1.50.01 - AVUNDF PC underflow
! SECURE without license check
! programmer : Theo van der Kaaij
!
! function : Determine time series boundary conditions
! for water levels, velocities and/or
! constituents.
! This program uses one real, one integer
! and one character arry to limit memory
! requirements. This main program only
! computes pointers and calls the main
! module.
! notes : 1. Assumed is a layer distribution which is
! equal in both the overall and the detailed
! model.
! 2. Assumed are identical constituents in both
! models
!
! changes v1.3 : Get all the additional information for nesting
! at the beginning of a session
!***********************************************************************
integer lun ( 5 )
integer, dimension(:,:), pointer :: kfs
integer, dimension(:,:), pointer :: mcbsp
integer, dimension(:,:), pointer :: ncbsp
integer, dimension(:,:), pointer :: mnstat
real , dimension(:) , pointer :: thick
real , dimension(:,:) , pointer :: wl
real , dimension(:,:,:) , pointer :: uu
real , dimension(:,:,:,:) , pointer :: vv
real , dimension(:) , pointer :: angle
real , dimension(:,:,:,:,:), pointer :: bndva
character(len= 1), dimension(:), pointer :: typbn
character(len=20), dimension(:), pointer :: nambn
character(len=20), dimension(:), pointer :: namco
character*(256) extnef
character* 63 verid
character* 6 pntnam
logical fout
character*80 CIDENT
integer status
!
integer :: length
integer :: notims, nostat, kmax, lstci, nobnd, mincon
cident = ' '
call getfullversionstring_nesthd2(cident)
!-----------------------------------------------------------------------
!---- 1. Open all files
!-----------------------------------------------------------------------
length = len_trim(cident)
write (* ,'(/, 2a)') ' ', trim(cident)
call opnfl2(lun ,extnef)
write (lun(5),'(/, 2a)') ' ', trim(cident)
write (lun(5),*) ' '
!-----------------------------------------------------------------------
!---- 2. Get dimensions
!-----------------------------------------------------------------------
call getdim(lun(5),lun(1),fout ,extnef,notims,nostat, &
& kmax ,lstci ,nobnd )
if (fout) goto 999
mincon = max(lstci,1)
!-----------------------------------------------------------------------
!---- 3.1 Determine integer pointers
!-----------------------------------------------------------------------
allocate (kfs (nostat, notims))
allocate (mcbsp (nobnd ,2))
allocate (ncbsp (nobnd ,2))
allocate (mnstat(2,nostat))
!-----------------------------------------------------------------------
!---- 3.2 Determine real pointers
!-----------------------------------------------------------------------
allocate (thick(kmax))
allocate (wl (nostat, notims))
allocate (uu (nostat, kmax, notims))
allocate (vv (nostat, kmax, notims, mincon))
allocate (angle(nostat))
allocate (bndva(nobnd, notims, kmax, mincon, 2))
!-----------------------------------------------------------------------
! 3.3 Determine character pointers
!-----------------------------------------------------------------------
allocate (typbn(nobnd))
allocate (nambn(nobnd)) ! each 20 characters long
allocate (namco(lstci+2)) ! each 20 characters long
!-----------------------------------------------------------------------
!---- 4. Call main module
!-----------------------------------------------------------------------
call nest_hd2 (lun , extnef, nostat , notims, kmax , &
lstci , nobnd , mincon , &
thick , wl , uu , vv , angle , &
bndva , &
kfs , mcbsp , ncbsp , mnstat , &
typbn , nambn , namco )
!-----------------------------------------------------------------------
!---- end program
!-----------------------------------------------------------------------
999 continue
call clsfil(lun ,5 )
stop
900 write(lun(5),'(//a)') 'Fatal error detected - Memory problem'
write(lun(5),'( a)') 'Not enough memory for allocating arrays ',pntnam
write(lun(5),'( a)') 'Delft3D-NESTHD2 aborted'
endprogram nesthd2
|
From Test Require Import tactic.
Section FOFProblem.
Variable Universe : Set.
Variable UniverseElement : Universe.
Variable wd_ : Universe -> Universe -> Prop.
Variable col_ : Universe -> Universe -> Universe -> Prop.
Variable col_swap1_1 : (forall A B C : Universe, (col_ A B C -> col_ B A C)).
Variable col_swap2_2 : (forall A B C : Universe, (col_ A B C -> col_ B C A)).
Variable col_triv_3 : (forall A B : Universe, col_ A B B).
Variable wd_swap_4 : (forall A B : Universe, (wd_ A B -> wd_ B A)).
Variable col_trans_5 : (forall P Q A B C : Universe, ((wd_ P Q /\ (col_ P Q A /\ (col_ P Q B /\ col_ P Q C))) -> col_ A B C)).
Theorem pipo_6 : (forall A B C Cprime P Q : Universe, ((wd_ A B /\ (wd_ P Q /\ (wd_ Q C /\ (wd_ P C /\ (wd_ C Cprime /\ (col_ A B C /\ (col_ A B Cprime /\ (col_ P Q A /\ (col_ P Q B /\ col_ P Q Cprime))))))))) -> col_ P A B)).
Proof.
time tac.
Qed.
End FOFProblem.
|
################################################################################
# Rectangular
################################################################################
abstract type AbstractRectangular <: Style end
#####
##### General rectangular methods
#####
boxx(x, width) = [x, x + width, x + width, x, x]
boxy(y, height) = [y, y, y + height, y + height, y]
cartesian(::AbstractRectangular, x, y) = (1.5*x, 1.5*y)
polygon(::AbstractRectangular, x, y) = (boxx(x, 1), boxy(y, 1))
function iorules(style::AbstractRectangular)
offset_skeletons = (
( ( 0, 1), "east", "west"),
( ( 0,-1), "west", "east"),
)
input_rules = squash([
Offset(a, "out[$i]", "$(c)_in[$i]")
for (a,b,c) in offset_skeletons, i in 0:style.io_links-1
])
output_rules = squash([
Offset(a, "$(b)_out[$i]", "in[$i]")
for (a,b,c) in offset_skeletons, i in 0:style.io_links-1
])
return ConnectionRule(
vcat(input_rules, output_rules),
source_filter = filter_io,
dest_filter = filter_io,
)
end
function memory_request_rules(::AbstractRectangular)
# 2 port memories
proc_to_mem2 = ConnectionRule([
Offset((1,0), "memory_out", "in[0]"),
Offset((1,-1), "memory_out", "in[1]")
],
source_filter = filter_memproc,
dest_filter = filter_memory(2),
)
# 1 port memories
proc_to_mem1 = ConnectionRule(
[Offset((1,0), "memory_out", "in[0]")],
source_filter = filter_memproc,
dest_filter = filter_memory(1),
)
return (proc_to_mem1, proc_to_mem2)
end
function memory_return_rules(::AbstractRectangular)
# 2 port memories
mem2_to_proc = ConnectionRule([
Offset((-1,0), "out[0]", "memory_in"),
Offset((-1,1), "out[1]", "memory_in"),
],
source_filter = filter_memory(2),
dest_filter = filter_memproc,
)
# 1 port memories
mem1_to_proc = ConnectionRule(
[Offset((-1,0), "out[0]", "memory_in")],
source_filter = filter_memory(1),
dest_filter = filter_memproc,
)
return (mem2_to_proc, mem1_to_proc)
end
#####
##### Standard Rectangular
#####
struct Rectangular <: AbstractRectangular
# Number of interprocessor links
links :: Int
io_links :: Int
end
directions(::Rectangular) = ("east", "north", "south", "west")
function procrules(style::Rectangular)
offset_skeleton = (
( (-1, 0), "north", "south"),
( ( 1, 0), "south", "north"),
( ( 0, 1), "east", "west"),
( ( 0,-1), "west", "east"),
)
offsets = squash([
Offset(a, "$(b)_out[$i]", "$(c)_in[$i]")
for (a,b,c) in offset_skeleton, i in 0:style.links
])
return ConnectionRule(
offsets,
source_filter = filter_proc,
dest_filter = filter_proc,
)
end
# Port annotations
function port_boundaries(::Rectangular, orientation)
coords = Dict(
"east" => ((1,0), (1,1)),
"south" => ((1,1), (0,1)),
"west" => ((0,0), (0,1)),
"north" => ((1,0), (0,0)),
)
return coords[orientation]
end
function initial_offset(::Rectangular, orientation, direction)
# Select where to start between the start and stop coordinates depending
# on the direction selected
starts = Dict(
( "north", Output ) => 0.55,
( "east" , Output ) => 0.55,
( "south", Input ) => 0.55,
( "west" , Input ) => 0.55,
( "north", Input ) => 0.05,
( "east" , Input ) => 0.05,
( "south", Output ) => 0.05,
( "west" , Output ) => 0.05,
)
return starts[(orientation, direction)]
end
#####
##### 8-4 rectangular
#####
# Neighbors are still in the four cardinal directions, but now there are long distance
# links also that hop over neighbors
struct Rectangular84 <: AbstractRectangular
# Number of interprocessor links
links :: Int
io_links :: Int
end
# Have two types of links in each direction - one for 1 hop links and another for 2 hop links
directions(::Rectangular84) = [
"east",
"east_far",
"north",
"north_far",
"south",
"south_far",
"west",
"west_far",
]
function procrules(style::Rectangular84)
offset_skeleton = (
( (-1, 0), "north", "south"),
( ( 1, 0), "south", "north"),
( ( 0, 1), "east", "west"),
( ( 0,-1), "west", "east"),
( (-2, 0), "north_far", "south_far"),
( ( 2, 0), "south_far", "north_far"),
( ( 0, 2), "east_far", "west_far"),
( ( 0,-2), "west_far", "east_far"),
)
offsets = squash([
Offset(a, "$(b)_out[$i]", "$(c)_in[$i]")
for (a,b,c) in offset_skeleton, i in 0:style.links
])
return ConnectionRule(
offsets,
source_filter = filter_proc,
dest_filter = filter_proc,
)
end
# Port annotations
function port_boundaries(::Rectangular84, orientation)
# Split the near are far links halfway across the border
coords = Dict(
"east" => ((1,0), (1,0.5)),
"east_far" => ((1, 0.5), (1, 1)),
"south" => ((1,1), (0.5, 1)),
"south_far" => ((0.5, 1), (0, 1)),
"west" => ((0,0), (0, 0.5)),
"west_far" => ((0,0.5), (0,1)),
"north" => ((1,0), (0.5,0)),
"north_far" => ((0.5,0), (0,0)),
)
return coords[orientation]
end
function initial_offset(::Rectangular84, orientation, direction)
# Select where to start between the start and stop coordinates depending
# on the direction selected
starts = Dict(
( "north", Output ) => 0.55,
( "east" , Output ) => 0.55,
( "north_far", Output ) => 0.55,
( "east_far" , Output ) => 0.55,
( "south", Input ) => 0.55,
( "west" , Input ) => 0.55,
( "south_far", Input ) => 0.55,
( "west_far" , Input ) => 0.55,
( "north", Input ) => 0.05,
( "east" , Input ) => 0.05,
( "north_far", Input ) => 0.05,
( "east_far" , Input ) => 0.05,
( "south", Output ) => 0.05,
( "west" , Output ) => 0.05,
( "south_far", Output ) => 0.05,
( "west_far" , Output ) => 0.05,
)
return starts[(orientation, direction)]
end
#####
##### 8-8 rectangular
#####
# 8 nearest neighbors
struct Rectangular88 <: AbstractRectangular
# Number of interprocessor links
links :: Int
io_links :: Int
end
# Have two types of links in each direction - one for 1 hop links and another for 2 hop links
directions(::Rectangular88) = [
"east",
"north_east",
"north",
"north_west",
"west",
"south_west",
"south",
"south_east",
]
function procrules(style::Rectangular88)
offset_skeleton = (
( (-1, 0), "north", "south"),
( ( 1, 0), "south", "north"),
( ( 0, 1), "east", "west"),
( ( 0,-1), "west", "east"),
( (-1, 1), "north_east", "south_west"),
( (-1,-1), "north_west", "south_east"),
( ( 1, 1), "south_east", "north_west"),
( ( 1,-1), "south_west", "north_east"),
)
offsets = squash([
Offset(a, "$(b)_out[$i]", "$(c)_in[$i]")
for (a,b,c) in offset_skeleton, i in 0:style.links
])
return ConnectionRule(
offsets,
source_filter = filter_proc,
dest_filter = filter_proc,
)
end
# Port annotations
function port_boundaries(::Rectangular88, orientation)
# Split the near are far links halfway across the border
coords = Dict(
"east" => ((1,0), (1,0.5)),
"south_east" => ((1, 0.5), (1, 1)),
"south" => ((1,1), (0.5, 1)),
"south_west" => ((0.5, 1), (0, 1)),
"north_west" => ((0,0), (0, 0.5)),
"west" => ((0,0.5), (0,1)),
"north_east" => ((1,0), (0.5,0)),
"north" => ((0.5,0), (0,0)),
)
return coords[orientation]
end
function initial_offset(::Rectangular88, orientation, direction)
# Select where to start between the start and stop coordinates depending
# on the direction selected
starts = Dict(
( "north", Output ) => 0.55,
( "east" , Output ) => 0.55,
( "north_east", Output ) => 0.55,
( "south_east" , Output ) => 0.55,
( "south", Input ) => 0.55,
( "west" , Input ) => 0.55,
( "south_west", Input ) => 0.55,
( "north_west" , Input ) => 0.55,
( "north", Input ) => 0.05,
( "east" , Input ) => 0.05,
( "north_east", Input ) => 0.05,
( "south_east" , Input ) => 0.05,
( "south", Output ) => 0.05,
( "west" , Output ) => 0.05,
( "south_west", Output ) => 0.05,
( "north_west" , Output ) => 0.05,
)
return starts[(orientation, direction)]
end
|
From Test Require Import tactic.
Section FOFProblem.
Variable Universe : Set.
Variable UniverseElement : Universe.
Variable wd_ : Universe -> Universe -> Prop.
Variable col_ : Universe -> Universe -> Universe -> Prop.
Variable col_swap1_1 : (forall A B C : Universe, (col_ A B C -> col_ B A C)).
Variable col_swap2_2 : (forall A B C : Universe, (col_ A B C -> col_ B C A)).
Variable col_triv_3 : (forall A B : Universe, col_ A B B).
Variable wd_swap_4 : (forall A B : Universe, (wd_ A B -> wd_ B A)).
Variable col_trans_5 : (forall P Q A B C : Universe, ((wd_ P Q /\ (col_ P Q A /\ (col_ P Q B /\ col_ P Q C))) -> col_ A B C)).
Theorem pipo_6 : (forall A B C M Cprime : Universe, ((wd_ A B /\ (wd_ B C /\ (wd_ A C /\ (wd_ M A /\ (wd_ M B /\ (wd_ M C /\ (wd_ C Cprime /\ (wd_ M Cprime /\ (wd_ B Cprime /\ (wd_ A Cprime /\ (col_ A C Cprime /\ (col_ M A B /\ col_ M C Cprime)))))))))))) -> col_ A B C)).
Proof.
time tac.
Qed.
End FOFProblem.
|
function Y = slmulvec(X, v, d)
%SLMULVEC multiplies a vector to columns or rows of a matrix
%
% $ Syntax $
% - Y = slmulvec(X, v, d)
% - Y = slmulvec(X, v)
%
% $ Arguments $
% - X: The original matrix
% - v: The addend vector
% - d: The dimension along which the vector is to add
% - Y: The resultant matrix
%
% $ Description $
% - Y = slmulvec(X, v, d) selects the most efficienct way to multiple a
% vector v to every column/row of X. If d == 1, then v should be
% a column vector, and is multiplied to each column of X, if d == 2,
% then v should be a row vector, and is multiplied to each row of X.
%
% - Y = slmulvec(X, v) will automatically determine d according to
% the shape of v.
%
% $ Remarks $
% - The implementation simply wraps the mex function vecop_core.
%
% $ History $
% - Created by Dahua Lin, on Sep 10, 2006
%
if nargin < 3
if size(v, 2) == 1
d = 1;
else
d = 2;
end
end
Y = vecop_core(X, v, d, 2); % 2 is the opcode of multiplication in vecop_core
|
The Grammy Award for Best Concept Music Video was an award that was presented to recording artists at the 30th Grammy Awards in 1988 , and the 31st Grammy Awards in 1989 , for quality , concept music videos . The Grammy Awards ( Grammys ) is an annual ceremony that was established in 1958 and was originally called the Gramophone Awards ; awards are presented by the National Academy of Recording Arts and Sciences of the United States to " honor artistic achievement , technical proficiency and overall excellence in the recording industry , without regard to album sales or chart position " .
|
State Before: R : Type u
inst✝⁶ : CommSemiring R
M : Type v
inst✝⁵ : AddCommMonoid M
inst✝⁴ : Module R M
ι : Type w
inst✝³ : DecidableEq ι
inst✝² : Fintype ι
κ : Type u_1
inst✝¹ : DecidableEq κ
inst✝ : Fintype κ
b : Basis ι R M
c : Basis κ R M
f : M →ₗ[R] M
⊢ trace (↑(toMatrix b b) f) = trace (↑(toMatrix b b) (comp (comp id f) id)) State After: no goals Tactic: rw [LinearMap.id_comp, LinearMap.comp_id] State Before: R : Type u
inst✝⁶ : CommSemiring R
M : Type v
inst✝⁵ : AddCommMonoid M
inst✝⁴ : Module R M
ι : Type w
inst✝³ : DecidableEq ι
inst✝² : Fintype ι
κ : Type u_1
inst✝¹ : DecidableEq κ
inst✝ : Fintype κ
b : Basis ι R M
c : Basis κ R M
f : M →ₗ[R] M
⊢ trace (↑(toMatrix b b) (comp (comp id f) id)) = trace (↑(toMatrix c b) id ⬝ ↑(toMatrix c c) f ⬝ ↑(toMatrix b c) id) State After: no goals Tactic: rw [LinearMap.toMatrix_comp _ c, LinearMap.toMatrix_comp _ c] State Before: R : Type u
inst✝⁶ : CommSemiring R
M : Type v
inst✝⁵ : AddCommMonoid M
inst✝⁴ : Module R M
ι : Type w
inst✝³ : DecidableEq ι
inst✝² : Fintype ι
κ : Type u_1
inst✝¹ : DecidableEq κ
inst✝ : Fintype κ
b : Basis ι R M
c : Basis κ R M
f : M →ₗ[R] M
⊢ trace (↑(toMatrix c b) id ⬝ ↑(toMatrix c c) f ⬝ ↑(toMatrix b c) id) =
trace (↑(toMatrix c c) f ⬝ ↑(toMatrix b c) id ⬝ ↑(toMatrix c b) id) State After: no goals Tactic: rw [Matrix.mul_assoc, Matrix.trace_mul_comm] State Before: R : Type u
inst✝⁶ : CommSemiring R
M : Type v
inst✝⁵ : AddCommMonoid M
inst✝⁴ : Module R M
ι : Type w
inst✝³ : DecidableEq ι
inst✝² : Fintype ι
κ : Type u_1
inst✝¹ : DecidableEq κ
inst✝ : Fintype κ
b : Basis ι R M
c : Basis κ R M
f : M →ₗ[R] M
⊢ trace (↑(toMatrix c c) f ⬝ ↑(toMatrix b c) id ⬝ ↑(toMatrix c b) id) = trace (↑(toMatrix c c) (comp (comp f id) id)) State After: no goals Tactic: rw [LinearMap.toMatrix_comp _ b, LinearMap.toMatrix_comp _ c] State Before: R : Type u
inst✝⁶ : CommSemiring R
M : Type v
inst✝⁵ : AddCommMonoid M
inst✝⁴ : Module R M
ι : Type w
inst✝³ : DecidableEq ι
inst✝² : Fintype ι
κ : Type u_1
inst✝¹ : DecidableEq κ
inst✝ : Fintype κ
b : Basis ι R M
c : Basis κ R M
f : M →ₗ[R] M
⊢ trace (↑(toMatrix c c) (comp (comp f id) id)) = trace (↑(toMatrix c c) f) State After: no goals Tactic: rw [LinearMap.comp_id, LinearMap.comp_id]
|
lemma uncountable_convex: fixes a :: "'a::real_normed_vector" assumes "convex S" "a \<in> S" "b \<in> S" "a \<noteq> b" shows "uncountable S"
|
State Before: α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n : ℕ
hin : ¬IsMax ((succ^[n - 1]) i)
⊢ (pred^[n]) ((succ^[n]) i) = i State After: case zero
α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n : ℕ
hin✝ : ¬IsMax ((succ^[n - 1]) i)
hin : ¬IsMax ((succ^[Nat.zero - 1]) i)
⊢ (pred^[Nat.zero]) ((succ^[Nat.zero]) i) = i
case succ
α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n✝ : ℕ
hin✝ : ¬IsMax ((succ^[n✝ - 1]) i)
n : ℕ
hn : ¬IsMax ((succ^[n - 1]) i) → (pred^[n]) ((succ^[n]) i) = i
hin : ¬IsMax ((succ^[Nat.succ n - 1]) i)
⊢ (pred^[Nat.succ n]) ((succ^[Nat.succ n]) i) = i Tactic: induction' n with n hn State Before: case succ
α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n✝ : ℕ
hin✝ : ¬IsMax ((succ^[n✝ - 1]) i)
n : ℕ
hn : ¬IsMax ((succ^[n - 1]) i) → (pred^[n]) ((succ^[n]) i) = i
hin : ¬IsMax ((succ^[Nat.succ n - 1]) i)
⊢ (pred^[Nat.succ n]) ((succ^[Nat.succ n]) i) = i State After: case succ
α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n✝ : ℕ
hin✝ : ¬IsMax ((succ^[n✝ - 1]) i)
n : ℕ
hn : ¬IsMax ((succ^[n - 1]) i) → (pred^[n]) ((succ^[n]) i) = i
hin : ¬IsMax ((succ^[n]) i)
⊢ (pred^[Nat.succ n]) ((succ^[Nat.succ n]) i) = i Tactic: rw [Nat.succ_sub_succ_eq_sub, Nat.sub_zero] at hin State Before: case succ
α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n✝ : ℕ
hin✝ : ¬IsMax ((succ^[n✝ - 1]) i)
n : ℕ
hn : ¬IsMax ((succ^[n - 1]) i) → (pred^[n]) ((succ^[n]) i) = i
hin : ¬IsMax ((succ^[n]) i)
h_not_max : ¬IsMax ((succ^[n - 1]) i)
⊢ (pred^[Nat.succ n]) ((succ^[Nat.succ n]) i) = i State After: case succ
α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n✝ : ℕ
hin✝ : ¬IsMax ((succ^[n✝ - 1]) i)
n : ℕ
hn : ¬IsMax ((succ^[n - 1]) i) → (pred^[n]) ((succ^[n]) i) = i
hin : ¬IsMax ((succ^[n]) i)
h_not_max : ¬IsMax ((succ^[n - 1]) i)
⊢ (pred^[n] ∘ pred) ((succ ∘ succ^[n]) i) = i Tactic: rw [Function.iterate_succ, Function.iterate_succ'] State Before: case succ
α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n✝ : ℕ
hin✝ : ¬IsMax ((succ^[n✝ - 1]) i)
n : ℕ
hn : ¬IsMax ((succ^[n - 1]) i) → (pred^[n]) ((succ^[n]) i) = i
hin : ¬IsMax ((succ^[n]) i)
h_not_max : ¬IsMax ((succ^[n - 1]) i)
⊢ (pred^[n] ∘ pred) ((succ ∘ succ^[n]) i) = i State After: case succ
α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n✝ : ℕ
hin✝ : ¬IsMax ((succ^[n✝ - 1]) i)
n : ℕ
hn : ¬IsMax ((succ^[n - 1]) i) → (pred^[n]) ((succ^[n]) i) = i
hin : ¬IsMax ((succ^[n]) i)
h_not_max : ¬IsMax ((succ^[n - 1]) i)
⊢ (pred^[n]) (pred (succ ((succ^[n]) i))) = i Tactic: simp only [Function.comp_apply] State Before: case succ
α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n✝ : ℕ
hin✝ : ¬IsMax ((succ^[n✝ - 1]) i)
n : ℕ
hn : ¬IsMax ((succ^[n - 1]) i) → (pred^[n]) ((succ^[n]) i) = i
hin : ¬IsMax ((succ^[n]) i)
h_not_max : ¬IsMax ((succ^[n - 1]) i)
⊢ (pred^[n]) (pred (succ ((succ^[n]) i))) = i State After: case succ
α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n✝ : ℕ
hin✝ : ¬IsMax ((succ^[n✝ - 1]) i)
n : ℕ
hn : ¬IsMax ((succ^[n - 1]) i) → (pred^[n]) ((succ^[n]) i) = i
hin : ¬IsMax ((succ^[n]) i)
h_not_max : ¬IsMax ((succ^[n - 1]) i)
⊢ (pred^[n]) ((succ^[n]) i) = i Tactic: rw [pred_succ_of_not_isMax hin] State Before: case succ
α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n✝ : ℕ
hin✝ : ¬IsMax ((succ^[n✝ - 1]) i)
n : ℕ
hn : ¬IsMax ((succ^[n - 1]) i) → (pred^[n]) ((succ^[n]) i) = i
hin : ¬IsMax ((succ^[n]) i)
h_not_max : ¬IsMax ((succ^[n - 1]) i)
⊢ (pred^[n]) ((succ^[n]) i) = i State After: no goals Tactic: exact hn h_not_max State Before: case zero
α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n : ℕ
hin✝ : ¬IsMax ((succ^[n - 1]) i)
hin : ¬IsMax ((succ^[Nat.zero - 1]) i)
⊢ (pred^[Nat.zero]) ((succ^[Nat.zero]) i) = i State After: no goals Tactic: simp only [Nat.zero_eq, Function.iterate_zero, id.def] State Before: α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n✝ : ℕ
hin✝ : ¬IsMax ((succ^[n✝ - 1]) i)
n : ℕ
hn : ¬IsMax ((succ^[n - 1]) i) → (pred^[n]) ((succ^[n]) i) = i
hin : ¬IsMax ((succ^[n]) i)
⊢ ¬IsMax ((succ^[n - 1]) i) State After: case zero
α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n : ℕ
hin✝ : ¬IsMax ((succ^[n - 1]) i)
hn : ¬IsMax ((succ^[Nat.zero - 1]) i) → (pred^[Nat.zero]) ((succ^[Nat.zero]) i) = i
hin : ¬IsMax ((succ^[Nat.zero]) i)
⊢ ¬IsMax ((succ^[Nat.zero - 1]) i)
case succ
α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n✝ : ℕ
hin✝ : ¬IsMax ((succ^[n✝ - 1]) i)
n : ℕ
hn : ¬IsMax ((succ^[Nat.succ n - 1]) i) → (pred^[Nat.succ n]) ((succ^[Nat.succ n]) i) = i
hin : ¬IsMax ((succ^[Nat.succ n]) i)
⊢ ¬IsMax ((succ^[Nat.succ n - 1]) i) Tactic: cases' n with n State Before: case succ
α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n✝ : ℕ
hin✝ : ¬IsMax ((succ^[n✝ - 1]) i)
n : ℕ
hn : ¬IsMax ((succ^[Nat.succ n - 1]) i) → (pred^[Nat.succ n]) ((succ^[Nat.succ n]) i) = i
hin : ¬IsMax ((succ^[Nat.succ n]) i)
⊢ ¬IsMax ((succ^[Nat.succ n - 1]) i) State After: case succ
α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n✝ : ℕ
hin✝ : ¬IsMax ((succ^[n✝ - 1]) i)
n : ℕ
hn : ¬IsMax ((succ^[n]) i) → (pred^[Nat.succ n]) ((succ^[Nat.succ n]) i) = i
hin : ¬IsMax ((succ^[Nat.succ n]) i)
⊢ ¬IsMax ((succ^[n]) i) Tactic: rw [Nat.succ_sub_succ_eq_sub, Nat.sub_zero] at hn⊢ State Before: case succ
α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n✝ : ℕ
hin✝ : ¬IsMax ((succ^[n✝ - 1]) i)
n : ℕ
hn : ¬IsMax ((succ^[n]) i) → (pred^[Nat.succ n]) ((succ^[Nat.succ n]) i) = i
hin : ¬IsMax ((succ^[Nat.succ n]) i)
⊢ ¬IsMax ((succ^[n]) i) State After: case succ
α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n✝ : ℕ
hin✝ : ¬IsMax ((succ^[n✝ - 1]) i)
n : ℕ
hn : ¬IsMax ((succ^[n]) i) → (pred^[Nat.succ n]) ((succ^[Nat.succ n]) i) = i
hin : ¬IsMax ((succ^[Nat.succ n]) i)
h_sub_le : (succ^[n]) i ≤ (succ^[Nat.succ n]) i
⊢ ¬IsMax ((succ^[n]) i) Tactic: have h_sub_le : (succ^[n]) i ≤ (succ^[n.succ]) i := by
rw [Function.iterate_succ']
exact le_succ _ State Before: case succ
α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n✝ : ℕ
hin✝ : ¬IsMax ((succ^[n✝ - 1]) i)
n : ℕ
hn : ¬IsMax ((succ^[n]) i) → (pred^[Nat.succ n]) ((succ^[Nat.succ n]) i) = i
hin : ¬IsMax ((succ^[Nat.succ n]) i)
h_sub_le : (succ^[n]) i ≤ (succ^[Nat.succ n]) i
⊢ ¬IsMax ((succ^[n]) i) State After: case succ
α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n✝ : ℕ
hin✝ : ¬IsMax ((succ^[n✝ - 1]) i)
n : ℕ
hn : ¬IsMax ((succ^[n]) i) → (pred^[Nat.succ n]) ((succ^[Nat.succ n]) i) = i
hin : ¬IsMax ((succ^[Nat.succ n]) i)
h_sub_le : (succ^[n]) i ≤ (succ^[Nat.succ n]) i
h_max : IsMax ((succ^[n]) i)
j : α
hj : (succ^[Nat.succ n]) i ≤ j
⊢ j ≤ (succ^[Nat.succ n]) i Tactic: refine' fun h_max => hin fun j hj => _ State Before: case succ
α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n✝ : ℕ
hin✝ : ¬IsMax ((succ^[n✝ - 1]) i)
n : ℕ
hn : ¬IsMax ((succ^[n]) i) → (pred^[Nat.succ n]) ((succ^[Nat.succ n]) i) = i
hin : ¬IsMax ((succ^[Nat.succ n]) i)
h_sub_le : (succ^[n]) i ≤ (succ^[Nat.succ n]) i
h_max : IsMax ((succ^[n]) i)
j : α
hj : (succ^[Nat.succ n]) i ≤ j
⊢ j ≤ (succ^[Nat.succ n]) i State After: case succ
α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n✝ : ℕ
hin✝ : ¬IsMax ((succ^[n✝ - 1]) i)
n : ℕ
hn : ¬IsMax ((succ^[n]) i) → (pred^[Nat.succ n]) ((succ^[Nat.succ n]) i) = i
hin : ¬IsMax ((succ^[Nat.succ n]) i)
h_sub_le : (succ^[n]) i ≤ (succ^[Nat.succ n]) i
h_max : IsMax ((succ^[n]) i)
j : α
hj : (succ^[Nat.succ n]) i ≤ j
hj_le : j ≤ (succ^[n]) i
⊢ j ≤ (succ^[Nat.succ n]) i Tactic: have hj_le : j ≤ (succ^[n]) i := h_max (h_sub_le.trans hj) State Before: case succ
α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n✝ : ℕ
hin✝ : ¬IsMax ((succ^[n✝ - 1]) i)
n : ℕ
hn : ¬IsMax ((succ^[n]) i) → (pred^[Nat.succ n]) ((succ^[Nat.succ n]) i) = i
hin : ¬IsMax ((succ^[Nat.succ n]) i)
h_sub_le : (succ^[n]) i ≤ (succ^[Nat.succ n]) i
h_max : IsMax ((succ^[n]) i)
j : α
hj : (succ^[Nat.succ n]) i ≤ j
hj_le : j ≤ (succ^[n]) i
⊢ j ≤ (succ^[Nat.succ n]) i State After: no goals Tactic: exact hj_le.trans h_sub_le State Before: case zero
α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n : ℕ
hin✝ : ¬IsMax ((succ^[n - 1]) i)
hn : ¬IsMax ((succ^[Nat.zero - 1]) i) → (pred^[Nat.zero]) ((succ^[Nat.zero]) i) = i
hin : ¬IsMax ((succ^[Nat.zero]) i)
⊢ ¬IsMax ((succ^[Nat.zero - 1]) i) State After: no goals Tactic: simpa using hin State Before: α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n✝ : ℕ
hin✝ : ¬IsMax ((succ^[n✝ - 1]) i)
n : ℕ
hn : ¬IsMax ((succ^[n]) i) → (pred^[Nat.succ n]) ((succ^[Nat.succ n]) i) = i
hin : ¬IsMax ((succ^[Nat.succ n]) i)
⊢ (succ^[n]) i ≤ (succ^[Nat.succ n]) i State After: α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n✝ : ℕ
hin✝ : ¬IsMax ((succ^[n✝ - 1]) i)
n : ℕ
hn : ¬IsMax ((succ^[n]) i) → (pred^[Nat.succ n]) ((succ^[Nat.succ n]) i) = i
hin : ¬IsMax ((succ^[Nat.succ n]) i)
⊢ (succ^[n]) i ≤ (succ ∘ succ^[n]) i Tactic: rw [Function.iterate_succ'] State Before: α : Type u_1
inst✝² : PartialOrder α
inst✝¹ : SuccOrder α
inst✝ : PredOrder α
a b i : α
n✝ : ℕ
hin✝ : ¬IsMax ((succ^[n✝ - 1]) i)
n : ℕ
hn : ¬IsMax ((succ^[n]) i) → (pred^[Nat.succ n]) ((succ^[Nat.succ n]) i) = i
hin : ¬IsMax ((succ^[Nat.succ n]) i)
⊢ (succ^[n]) i ≤ (succ ∘ succ^[n]) i State After: no goals Tactic: exact le_succ _
|
(* The value setup for reviewer confidentiality *)
theory Review_Value_Setup
imports Review_Intro
begin
consts PID :: paperID consts N :: nat
text \<open>\<^term>\<open>(PID,N)\<close> identifies uniquely the review under scrutiny\<close>
subsection \<open>Preliminaries\<close>
declare updates_commute_paper[simp]
text \<open>Auxiliary definitions:\<close>
definition eqExcNth where
"eqExcNth xs ys n \<equiv>
length xs = length ys \<and> (\<forall> i < length xs. i \<noteq> n \<longrightarrow> xs!i = ys!i)"
lemma eqExcNth_eq[simp,intro!]: "eqExcNth xs xs n"
unfolding eqExcNth_def by auto
lemma eqExcNth_sym:
assumes "eqExcNth xs xs1 n"
shows "eqExcNth xs1 xs n"
using assms unfolding eqExcNth_def by auto
lemma eqExcNth_trans:
assumes "eqExcNth xs xs1 n" and "eqExcNth xs1 xs2 n"
shows "eqExcNth xs xs2 n"
using assms unfolding eqExcNth_def by auto
fun eqExcD :: "paper \<Rightarrow> paper \<Rightarrow> bool" where
"eqExcD (Paper name info ct reviews dis decs)
(Paper name1 info1 ct1 reviews1 dis1 decs1) =
(name = name1 \<and> info = info1 \<and> ct = ct1 \<and> dis = dis1 \<and> decs = decs1 \<and>
eqExcNth reviews reviews1 N)"
lemma eqExcD:
"eqExcD pap pap1 =
(titlePaper pap = titlePaper pap1 \<and> abstractPaper pap = abstractPaper pap1 \<and>
contentPaper pap = contentPaper pap1 \<and>
disPaper pap = disPaper pap1 \<and> decsPaper pap = decsPaper pap1 \<and>
eqExcNth (reviewsPaper pap) (reviewsPaper pap1) N)"
by(cases pap, cases pap1, auto)
lemma eqExcD_eq[simp,intro!]: "eqExcD pap pap"
unfolding eqExcD using eqExcNth_eq by auto
lemma eqExcD_sym:
assumes "eqExcD pap pap1"
shows "eqExcD pap1 pap"
using assms unfolding eqExcD using eqExcNth_sym by auto
lemma eqExcD_trans:
assumes "eqExcD pap pap1" and "eqExcD pap1 pap2"
shows "eqExcD pap pap2"
using assms unfolding eqExcD using eqExcNth_trans by auto
definition eeqExcPID_N where
"eeqExcPID_N paps paps1 \<equiv>
\<forall> pid. if pid = PID then eqExcD (paps pid) (paps1 pid) else paps pid = paps1 pid"
lemma eeqExcPID_N_eeq[simp,intro!]: "eeqExcPID_N s s"
unfolding eeqExcPID_N_def by auto
lemma eeqExcPID_N_sym:
assumes "eeqExcPID_N s s1" shows "eeqExcPID_N s1 s"
using assms eqExcD_sym unfolding eeqExcPID_N_def by auto
lemma eeqExcPID_N_trans:
assumes "eeqExcPID_N s s1" and "eeqExcPID_N s1 s2" shows "eeqExcPID_N s s2"
using assms eqExcD_trans unfolding eeqExcPID_N_def by simp blast
lemma eeqExcPID_N_imp:
"eeqExcPID_N paps paps1 \<Longrightarrow> eqExcD (paps PID) (paps1 PID)"
"\<lbrakk>eeqExcPID_N paps paps1; pid \<noteq> PID\<rbrakk> \<Longrightarrow> paps pid = paps1 pid"
unfolding eeqExcPID_N_def by auto
lemma eeqExcPID_N_cong:
assumes "eeqExcPID_N paps paps1"
and "pid = PID \<Longrightarrow> eqExcD uu uu1"
and "pid \<noteq> PID \<Longrightarrow> uu = uu1"
shows "eeqExcPID_N (paps (pid := uu)) (paps1(pid := uu1))"
using assms unfolding eeqExcPID_N_def by auto
lemma eeqExcPID_N_RDD:
"eeqExcPID_N paps paps1 \<Longrightarrow>
titlePaper (paps PID) = titlePaper (paps1 PID) \<and>
abstractPaper (paps PID) = abstractPaper (paps1 PID) \<and>
contentPaper (paps PID) = contentPaper (paps1 PID) \<and>
disPaper (paps PID) = disPaper (paps1 PID) \<and>
decsPaper (paps PID) = decsPaper (paps1 PID)"
using eeqExcPID_N_def unfolding eqExcD by auto
text \<open>The notion of two states being equal everywhere except on the the review \<^term>\<open>(N,PID)\<close>:\<close>
definition eqExcPID_N :: "state \<Rightarrow> state \<Rightarrow> bool" where
"eqExcPID_N s s1 \<equiv>
confIDs s = confIDs s1 \<and> conf s = conf s1 \<and>
userIDs s = userIDs s1 \<and> pass s = pass s1 \<and> user s = user s1 \<and> roles s = roles s1 \<and>
paperIDs s = paperIDs s1
\<and>
eeqExcPID_N (paper s) (paper s1)
\<and>
pref s = pref s1 \<and>
voronkov s = voronkov s1 \<and>
news s = news s1 \<and> phase s = phase s1"
lemma eqExcPID_N_eq[simp,intro!]: "eqExcPID_N s s"
unfolding eqExcPID_N_def by auto
lemma eqExcPID_N_sym:
assumes "eqExcPID_N s s1" shows "eqExcPID_N s1 s"
using assms eeqExcPID_N_sym unfolding eqExcPID_N_def by auto
lemma eqExcPID_N_trans:
assumes "eqExcPID_N s s1" and "eqExcPID_N s1 s2" shows "eqExcPID_N s s2"
using assms eeqExcPID_N_trans unfolding eqExcPID_N_def by auto
text \<open>Implications from \<^term>\<open>eqExcPID_N\<close>, including w.r.t. auxiliary operations:\<close>
lemma eqExcPID_N_imp:
"eqExcPID_N s s1 \<Longrightarrow>
confIDs s = confIDs s1 \<and> conf s = conf s1 \<and>
userIDs s = userIDs s1 \<and> pass s = pass s1 \<and> user s = user s1 \<and> roles s = roles s1 \<and>
paperIDs s = paperIDs s1
\<and>
eeqExcPID_N (paper s) (paper s1)
\<and>
pref s = pref s1 \<and>
voronkov s = voronkov s1 \<and>
news s = news s1 \<and> phase s = phase s1 \<and>
getAllPaperIDs s = getAllPaperIDs s1 \<and>
isRev s cid uid pid = isRev s1 cid uid pid \<and>
getReviewIndex s cid uid pid = getReviewIndex s1 cid uid pid \<and>
getRevRole s cid uid pid = getRevRole s1 cid uid pid \<and>
length (reviewsPaper (paper s pid)) = length (reviewsPaper (paper s1 pid))"
unfolding eqExcPID_N_def getAllPaperIDs_def
unfolding isRev_def getReviewIndex_def getRevRole_def apply auto
unfolding eeqExcPID_N_def eqExcD eqExcNth_def by (cases "pid = PID") auto
lemma eqExcPID_N_imp1:
"eqExcPID_N s s1 \<Longrightarrow> eqExcD (paper s pid) (paper s1 pid)"
"eqExcPID_N s s1 \<Longrightarrow> pid \<noteq> PID \<or> PID \<noteq> pid \<Longrightarrow>
paper s pid = paper s1 pid \<and>
getNthReview s pid n = getNthReview s1 pid n"
unfolding eqExcPID_N_def eeqExcPID_N_def getNthReview_def
apply auto by (metis eqExcD_eq)
lemma eqExcPID_N_imp2:
assumes "eqExcPID_N s s1" and "pid \<noteq> PID \<or> PID \<noteq> pid"
shows "getReviewersReviews s cid pid = getReviewersReviews s1 cid pid"
proof-
have
"(\<lambda>uID. if isRev s cid uID pid then [(uID, getNthReview s pid (getReviewIndex s cid uID pid))] else []) =
(\<lambda>uID. if isRev s1 cid uID pid then [(uID, getNthReview s1 pid (getReviewIndex s1 cid uID pid))] else [])"
apply(rule ext)
using assms by (auto simp: eqExcPID_N_imp eqExcPID_N_imp1)
thus ?thesis unfolding getReviewersReviews_def using assms by (simp add: eqExcPID_N_imp)
qed
lemma eqExcPID_N_imp3:
"eqExcPID_N s s1 \<Longrightarrow> pid \<noteq> PID \<or> PID \<noteq> pid \<or> (n < length (reviewsPaper (paper s PID)) \<and> n \<noteq> N)
\<Longrightarrow>
getNthReview s pid n = getNthReview s1 pid n"
unfolding eqExcPID_N_def
apply auto
apply (metis eeqExcPID_N_imp(2) getNthReview_def)
unfolding eeqExcPID_N_def apply simp unfolding eqExcD eqExcNth_def
by (metis getNthReview_def)
lemma eqExcPID_N_imp3':
assumes s: "reach s"
and "eqExcPID_N s s1" and "pid \<noteq> PID \<or> (isRevNth s cid uid pid n \<and> n \<noteq> N)"
shows "getNthReview s pid n = getNthReview s1 pid n"
proof-
have "isRevNth s cid uid pid n \<Longrightarrow> pid \<noteq> PID \<or> n < length (reviewsPaper (paper s PID))"
using s by (metis isRevNth_less_length)
thus ?thesis using eqExcPID_N_imp3 assms by auto
qed
lemma eqExcPID_N_RDD:
"eqExcPID_N s s1 \<Longrightarrow>
titlePaper (paper s PID) = titlePaper (paper s1 PID) \<and>
abstractPaper (paper s PID) = abstractPaper (paper s1 PID) \<and>
contentPaper (paper s PID) = contentPaper (paper s1 PID) \<and>
disPaper (paper s PID) = disPaper (paper s1 PID) \<and>
decsPaper (paper s PID) = decsPaper (paper s1 PID)"
using eqExcPID_N_imp eeqExcPID_N_RDD by auto
lemma eqExcPID_N_cong[simp, intro]:
"\<And> uu1 uu2. eqExcPID_N s s1 \<Longrightarrow> uu1 = uu2 \<Longrightarrow> eqExcPID_N (s \<lparr>confIDs := uu1\<rparr>) (s1 \<lparr>confIDs := uu2\<rparr>)"
"\<And> uu1 uu2. eqExcPID_N s s1 \<Longrightarrow> uu1 = uu2 \<Longrightarrow> eqExcPID_N (s \<lparr>conf := uu1\<rparr>) (s1 \<lparr>conf := uu2\<rparr>)"
"\<And> uu1 uu2. eqExcPID_N s s1 \<Longrightarrow> uu1 = uu2 \<Longrightarrow> eqExcPID_N (s \<lparr>userIDs := uu1\<rparr>) (s1 \<lparr>userIDs := uu2\<rparr>)"
"\<And> uu1 uu2. eqExcPID_N s s1 \<Longrightarrow> uu1 = uu2 \<Longrightarrow> eqExcPID_N (s \<lparr>pass := uu1\<rparr>) (s1 \<lparr>pass := uu2\<rparr>)"
"\<And> uu1 uu2. eqExcPID_N s s1 \<Longrightarrow> uu1 = uu2 \<Longrightarrow> eqExcPID_N (s \<lparr>user := uu1\<rparr>) (s1 \<lparr>user := uu2\<rparr>)"
"\<And> uu1 uu2. eqExcPID_N s s1 \<Longrightarrow> uu1 = uu2 \<Longrightarrow> eqExcPID_N (s \<lparr>roles := uu1\<rparr>) (s1 \<lparr>roles := uu2\<rparr>)"
"\<And> uu1 uu2. eqExcPID_N s s1 \<Longrightarrow> uu1 = uu2 \<Longrightarrow> eqExcPID_N (s \<lparr>paperIDs := uu1\<rparr>) (s1 \<lparr>paperIDs := uu2\<rparr>)"
"\<And> uu1 uu2. eqExcPID_N s s1 \<Longrightarrow> eeqExcPID_N uu1 uu2 \<Longrightarrow> eqExcPID_N (s \<lparr>paper := uu1\<rparr>) (s1 \<lparr>paper := uu2\<rparr>)"
"\<And> uu1 uu2. eqExcPID_N s s1 \<Longrightarrow> uu1 = uu2 \<Longrightarrow> eqExcPID_N (s \<lparr>pref := uu1\<rparr>) (s1 \<lparr>pref := uu2\<rparr>)"
"\<And> uu1 uu2. eqExcPID_N s s1 \<Longrightarrow> uu1 = uu2 \<Longrightarrow> eqExcPID_N (s \<lparr>voronkov := uu1\<rparr>) (s1 \<lparr>voronkov := uu2\<rparr>)"
"\<And> uu1 uu2. eqExcPID_N s s1 \<Longrightarrow> uu1 = uu2 \<Longrightarrow> eqExcPID_N (s \<lparr>news := uu1\<rparr>) (s1 \<lparr>news := uu2\<rparr>)"
"\<And> uu1 uu2. eqExcPID_N s s1 \<Longrightarrow> uu1 = uu2 \<Longrightarrow> eqExcPID_N (s \<lparr>phase := uu1\<rparr>) (s1 \<lparr>phase := uu2\<rparr>)"
unfolding eqExcPID_N_def by auto
lemma eqExcPID_N_Paper:
assumes s's1': "eqExcPID_N s s1"
and "paper s pid = Paper title abstract content reviews dis decs"
and "paper s1 pid = Paper title1 abstract1 content1 reviews1 dis1 decs1"
shows "title = title1 \<and> abstract = abstract1 \<and> content = content1 \<and> dis = dis1 \<and> decs = decs1"
using assms unfolding eqExcPID_N_def apply (auto simp: eqExcD eeqExcPID_N_def)
by (metis titlePaper.simps abstractPaper.simps contentPaper.simps disPaper.simps decsPaper.simps)+
text \<open>Auxiliary definitions for a slightly weaker equivalence relation defined below:\<close>
definition eqExcNth2 where
"eqExcNth2 rl rl1 n \<equiv>
length rl = length rl1 \<and>
(\<forall> i < length rl. i \<noteq> n \<longrightarrow> rl!i = rl1!i) \<and>
hd (rl!n) = hd (rl1!n)"
lemma eqExcNth2_eq[simp,intro!]: "eqExcNth2 rl rl n"
unfolding eqExcNth2_def by auto
lemma eqExcNth2_sym:
assumes "eqExcNth2 rl rl1 n"
shows "eqExcNth2 rl1 rl n"
using assms unfolding eqExcNth2_def by auto
lemma eqExcNth2_trans:
assumes "eqExcNth2 rl rl1 n" and "eqExcNth2 rl1 rl2 n"
shows "eqExcNth2 rl rl2 n"
using assms unfolding eqExcNth2_def by auto
fun eqExcD2 :: "paper \<Rightarrow> paper \<Rightarrow> bool" where
"eqExcD2 (Paper title abstract ct reviews dis decs)
(Paper title1 abstract1 ct1 reviews1 dis1 decs1) =
(title = title1 \<and> abstract = abstract1 \<and> ct = ct1 \<and> dis = dis1 \<and> decs = decs1 \<and>
eqExcNth2 reviews reviews1 N)"
lemma eqExcD2:
"eqExcD2 pap pap1 =
(titlePaper pap = titlePaper pap1 \<and> abstractPaper pap = abstractPaper pap1 \<and>
contentPaper pap = contentPaper pap1 \<and>
disPaper pap = disPaper pap1 \<and> decsPaper pap = decsPaper pap1 \<and>
eqExcNth2 (reviewsPaper pap) (reviewsPaper pap1) N)"
by(cases pap, cases pap1, auto)
lemma eqExcD2_eq[simp,intro!]: "eqExcD2 pap pap"
unfolding eqExcD2 using eqExcNth2_eq by auto
lemma eqExcD2_sym:
assumes "eqExcD2 pap pap1"
shows "eqExcD2 pap1 pap"
using assms unfolding eqExcD2 using eqExcNth2_sym by auto
lemma eqExcD2_trans:
assumes "eqExcD2 pap pap1" and "eqExcD2 pap1 pap2"
shows "eqExcD2 pap pap2"
using assms unfolding eqExcD2 using eqExcNth2_trans by auto
definition eeqExcPID_N2 where
"eeqExcPID_N2 paps paps1 \<equiv>
\<forall> pid. if pid = PID then eqExcD2 (paps pid) (paps1 pid) else paps pid = paps1 pid"
lemma eeqExcPID_N2_eeq[simp,intro!]: "eeqExcPID_N2 s s"
unfolding eeqExcPID_N2_def by auto
lemma eeqExcPID_N2_sym:
assumes "eeqExcPID_N2 s s1" shows "eeqExcPID_N2 s1 s"
using assms eqExcD2_sym unfolding eeqExcPID_N2_def by auto
lemma eeqExcPID_N2_trans:
assumes "eeqExcPID_N2 s s1" and "eeqExcPID_N2 s1 s2" shows "eeqExcPID_N2 s s2"
using assms eqExcD2_trans unfolding eeqExcPID_N2_def by simp blast
lemma eeqExcPID_N2_imp:
"eeqExcPID_N2 paps paps1 \<Longrightarrow> eqExcD2 (paps PID) (paps1 PID)"
"\<lbrakk>eeqExcPID_N2 paps paps1; pid \<noteq> PID\<rbrakk> \<Longrightarrow> paps pid = paps1 pid"
unfolding eeqExcPID_N2_def by auto
lemma eeqExcPID_N2_cong:
assumes "eeqExcPID_N2 paps paps1"
and "pid = PID \<Longrightarrow> eqExcD2 uu uu1"
and "pid \<noteq> PID \<Longrightarrow> uu = uu1"
shows "eeqExcPID_N2 (paps (pid := uu)) (paps1(pid := uu1))"
using assms unfolding eeqExcPID_N2_def by auto
lemma eeqExcPID_N2_RDD:
"eeqExcPID_N2 paps paps1 \<Longrightarrow>
titlePaper (paps PID) = titlePaper (paps1 PID) \<and>
abstractPaper (paps PID) = abstractPaper (paps1 PID) \<and>
contentPaper (paps PID) = contentPaper (paps1 PID) \<and>
disPaper (paps PID) = disPaper (paps1 PID) \<and>
decsPaper (paps PID) = decsPaper (paps1 PID)"
using eeqExcPID_N2_def unfolding eqExcD2 by auto
text \<open>A weaker state equivalence that allows differences in old versions of the score and comments
of the review \<^term>\<open>(N, PID)\<close>. It is used for the confidentiality property that does not cover
PC members in the discussion phase, when they will learn about scores and comments.\<close>
definition eqExcPID_N2 :: "state \<Rightarrow> state \<Rightarrow> bool" where
"eqExcPID_N2 s s1 \<equiv>
confIDs s = confIDs s1 \<and> conf s = conf s1 \<and>
userIDs s = userIDs s1 \<and> pass s = pass s1 \<and> user s = user s1 \<and> roles s = roles s1 \<and>
paperIDs s = paperIDs s1
\<and>
eeqExcPID_N2 (paper s) (paper s1)
\<and>
pref s = pref s1 \<and>
voronkov s = voronkov s1 \<and>
news s = news s1 \<and> phase s = phase s1"
lemma eqExcPID_N2_eq[simp,intro!]: "eqExcPID_N2 s s"
unfolding eqExcPID_N2_def by auto
lemma eqExcPID_N2_sym:
assumes "eqExcPID_N2 s s1" shows "eqExcPID_N2 s1 s"
using assms eeqExcPID_N2_sym unfolding eqExcPID_N2_def by auto
lemma eqExcPID_N2_trans:
assumes "eqExcPID_N2 s s1" and "eqExcPID_N2 s1 s2" shows "eqExcPID_N2 s s2"
using assms eeqExcPID_N2_trans unfolding eqExcPID_N2_def by auto
text \<open>Implications from \<^term>\<open>eqExcPID_N2\<close>, including w.r.t. auxiliary operations:\<close>
lemma eqExcPID_N2_imp:
"eqExcPID_N2 s s1 \<Longrightarrow>
confIDs s = confIDs s1 \<and> conf s = conf s1 \<and>
userIDs s = userIDs s1 \<and> pass s = pass s1 \<and> user s = user s1 \<and> roles s = roles s1 \<and>
paperIDs s = paperIDs s1
\<and>
eeqExcPID_N2 (paper s) (paper s1)
\<and>
pref s = pref s1 \<and>
voronkov s = voronkov s1 \<and>
news s = news s1 \<and> phase s = phase s1 \<and>
getAllPaperIDs s = getAllPaperIDs s1 \<and>
isRev s cid uid pid = isRev s1 cid uid pid \<and>
getReviewIndex s cid uid pid = getReviewIndex s1 cid uid pid \<and>
getRevRole s cid uid pid = getRevRole s1 cid uid pid \<and>
length (reviewsPaper (paper s pid)) = length (reviewsPaper (paper s1 pid))"
unfolding eqExcPID_N2_def getAllPaperIDs_def
unfolding isRev_def getReviewIndex_def getRevRole_def apply auto
unfolding eeqExcPID_N2_def eqExcD2 eqExcNth2_def by simp metis
lemma eqExcPID_N2_imp1:
"eqExcPID_N2 s s1 \<Longrightarrow> eqExcD2 (paper s pid) (paper s1 pid)"
"eqExcPID_N2 s s1 \<Longrightarrow> pid \<noteq> PID \<or> PID \<noteq> pid \<Longrightarrow>
paper s pid = paper s1 pid \<and>
getNthReview s pid n = getNthReview s1 pid n"
unfolding eqExcPID_N2_def getNthReview_def eeqExcPID_N2_def
apply auto
by (metis eqExcD2_eq)
lemma eqExcPID_N2_imp2:
assumes "eqExcPID_N2 s s1" and "pid \<noteq> PID \<or> PID \<noteq> pid"
shows "getReviewersReviews s cid pid = getReviewersReviews s1 cid pid"
proof-
have
"(\<lambda>uID. if isRev s cid uID pid then [(uID, getNthReview s pid (getReviewIndex s cid uID pid))] else []) =
(\<lambda>uID. if isRev s1 cid uID pid then [(uID, getNthReview s1 pid (getReviewIndex s1 cid uID pid))] else [])"
apply(rule ext)
using assms by (auto simp: eqExcPID_N2_imp eqExcPID_N2_imp1)
thus ?thesis unfolding getReviewersReviews_def using assms by (simp add: eqExcPID_N2_imp)
qed
lemma eqExcPID_N2_eqExcPID_N:
"eqExcPID_N2 s s1 \<Longrightarrow> eqExcPID_N s s1"
unfolding eqExcPID_N_def eqExcPID_N2_def eeqExcPID_N_def eeqExcPID_N2_def eqExcD2 eqExcD
by (auto simp: eqExcNth_def eqExcNth2_def)
lemma eqExcPID_N2_imp3:
"eqExcPID_N2 s s1 \<Longrightarrow> pid \<noteq> PID \<or> PID \<noteq> pid \<or> (n < length (reviewsPaper (paper s PID)) \<and> n \<noteq> N)
\<Longrightarrow>
getNthReview s pid n = getNthReview s1 pid n"
by (metis eqExcPID_N2_eqExcPID_N eqExcPID_N_imp3)
lemma eqExcPID_N2_imp3':
assumes s: "reach s"
and "eqExcPID_N2 s s1" and "pid \<noteq> PID \<or> (isRevNth s cid uid pid n \<and> n \<noteq> N)"
shows "getNthReview s pid n = getNthReview s1 pid n"
by (metis assms eqExcPID_N2_eqExcPID_N eqExcPID_N_imp3')
lemma eqExcPID_N2_imp33:
assumes "eqExcPID_N2 s s1"
shows "hd (getNthReview s pid N) = hd (getNthReview s1 pid N)"
proof(cases "pid = PID")
case False thus ?thesis using eqExcPID_N2_imp3[OF assms] by auto
next
case True thus ?thesis apply simp
using assms unfolding eqExcPID_N2_def eeqExcPID_N2_def eqExcD2 eqExcNth2_def getNthReview_def by auto
qed
lemma eqExcPID_N2_RDD:
"eqExcPID_N2 s s1 \<Longrightarrow>
titlePaper (paper s PID) = titlePaper (paper s1 PID) \<and>
abstractPaper (paper s PID) = abstractPaper (paper s1 PID) \<and>
contentPaper (paper s PID) = contentPaper (paper s1 PID) \<and>
disPaper (paper s PID) = disPaper (paper s1 PID) \<and>
decsPaper (paper s PID) = decsPaper (paper s1 PID)"
using eqExcPID_N2_imp eeqExcPID_N2_RDD by auto
lemma eqExcPID_N2_cong[simp, intro]:
"\<And> uu1 uu2. eqExcPID_N2 s s1 \<Longrightarrow> uu1 = uu2 \<Longrightarrow> eqExcPID_N2 (s \<lparr>confIDs := uu1\<rparr>) (s1 \<lparr>confIDs := uu2\<rparr>)"
"\<And> uu1 uu2. eqExcPID_N2 s s1 \<Longrightarrow> uu1 = uu2 \<Longrightarrow> eqExcPID_N2 (s \<lparr>conf := uu1\<rparr>) (s1 \<lparr>conf := uu2\<rparr>)"
"\<And> uu1 uu2. eqExcPID_N2 s s1 \<Longrightarrow> uu1 = uu2 \<Longrightarrow> eqExcPID_N2 (s \<lparr>userIDs := uu1\<rparr>) (s1 \<lparr>userIDs := uu2\<rparr>)"
"\<And> uu1 uu2. eqExcPID_N2 s s1 \<Longrightarrow> uu1 = uu2 \<Longrightarrow> eqExcPID_N2 (s \<lparr>pass := uu1\<rparr>) (s1 \<lparr>pass := uu2\<rparr>)"
"\<And> uu1 uu2. eqExcPID_N2 s s1 \<Longrightarrow> uu1 = uu2 \<Longrightarrow> eqExcPID_N2 (s \<lparr>user := uu1\<rparr>) (s1 \<lparr>user := uu2\<rparr>)"
"\<And> uu1 uu2. eqExcPID_N2 s s1 \<Longrightarrow> uu1 = uu2 \<Longrightarrow> eqExcPID_N2 (s \<lparr>roles := uu1\<rparr>) (s1 \<lparr>roles := uu2\<rparr>)"
"\<And> uu1 uu2. eqExcPID_N2 s s1 \<Longrightarrow> uu1 = uu2 \<Longrightarrow> eqExcPID_N2 (s \<lparr>paperIDs := uu1\<rparr>) (s1 \<lparr>paperIDs := uu2\<rparr>)"
"\<And> uu1 uu2. eqExcPID_N2 s s1 \<Longrightarrow> eeqExcPID_N2 uu1 uu2 \<Longrightarrow> eqExcPID_N2 (s \<lparr>paper := uu1\<rparr>) (s1 \<lparr>paper := uu2\<rparr>)"
"\<And> uu1 uu2. eqExcPID_N2 s s1 \<Longrightarrow> uu1 = uu2 \<Longrightarrow> eqExcPID_N2 (s \<lparr>pref := uu1\<rparr>) (s1 \<lparr>pref := uu2\<rparr>)"
"\<And> uu1 uu2. eqExcPID_N2 s s1 \<Longrightarrow> uu1 = uu2 \<Longrightarrow> eqExcPID_N2 (s \<lparr>voronkov := uu1\<rparr>) (s1 \<lparr>voronkov := uu2\<rparr>)"
"\<And> uu1 uu2. eqExcPID_N2 s s1 \<Longrightarrow> uu1 = uu2 \<Longrightarrow> eqExcPID_N2 (s \<lparr>news := uu1\<rparr>) (s1 \<lparr>news := uu2\<rparr>)"
"\<And> uu1 uu2. eqExcPID_N2 s s1 \<Longrightarrow> uu1 = uu2 \<Longrightarrow> eqExcPID_N2 (s \<lparr>phase := uu1\<rparr>) (s1 \<lparr>phase := uu2\<rparr>)"
unfolding eqExcPID_N2_def by auto
lemma eqExcPID_N2_Paper:
assumes s's1': "eqExcPID_N2 s s1"
and "paper s pid = Paper title abstract content reviews dis decs"
and "paper s1 pid = Paper title1 abstract1 content1 reviews1 dis1 decs1"
shows "title = title1 \<and> abstract = abstract1 \<and> content = content1 \<and> dis = dis1 \<and> decs = decs1"
using assms unfolding eqExcPID_N2_def apply (auto simp: eqExcD2 eeqExcPID_N2_def)
by (metis titlePaper.simps abstractPaper.simps contentPaper.simps disPaper.simps decsPaper.simps)+
(* major *) lemma eqExcPID_N2_step:
assumes ss1: "eqExcPID_N2 s s1"
and step: "step s a = (ou,s')"
and step1: "step s1 a = (ou1,s1')"
and s: "reach s" and r: "isRevNth s cid uid PID N" (* new *)
shows "eqExcPID_N2 s' s1'"
proof -
note eqs = eqExcPID_N2_imp[OF ss1]
note eqs' = eqExcPID_N2_imp1[OF ss1]
have r: "N < length (reviewsPaper (paper s PID))" using s r by (metis isRevNth_less_length)
have r1: "N < length (reviewsPaper (paper s1 PID))"
using r eqs unfolding eeqExcPID_N2_def eqExcD2 eqExcNth2_def by simp
note simps[simp] = c_defs u_defs uu_defs r_defs l_defs Paper_dest_conv eqExcPID_N2_def eeqExcPID_N2_def eqExcD2 eqExcNth2_def
note * = step step1 eqs eqs' r r1
then show ?thesis
proof (cases a)
case (Cact x1)
with * show ?thesis
proof (cases x1)
case (cReview x81 x82 x83 x84 x85)
with Cact * show ?thesis
by (clarsimp; metis (no_types, lifting) less_SucE nth_append_length right_cons_left)
qed auto
next
case (Uact x2)
with * show ?thesis
proof (cases x2)
case (uReview x71 x72 x73 x74 x75 x76)
with Uact * show ?thesis
by (clarsimp; metis (no_types, lifting) nth_list_update nth_list_update_neq)
qed auto
next
case (UUact x3)
with * show ?thesis
proof (cases x3)
case (uuReview x31 x32 x33 x34 x35 x36)
with UUact * show ?thesis
by (clarsimp; smt list.sel(1) nth_list_update nth_list_update_neq)
qed auto
qed auto
qed
subsection \<open>Value Setup\<close>
fun \<phi> :: "(state,act,out) trans \<Rightarrow> bool" where
"\<phi> (Trans _ (Uact (uReview cid uid p pid n rc)) ou _) =
(pid = PID \<and> n = N \<and> ou = outOK)"
|
"\<phi> (Trans _ (UUact (uuReview cid uid p pid n rc)) ou _) =
(pid = PID \<and> n = N \<and> ou = outOK)"
|
"\<phi> _ = False"
lemma \<phi>_def2:
"\<phi> (Trans s a ou s') =
(ou = outOK \<and>
(\<exists> cid uid p rc.
a = Uact (uReview cid uid p PID N rc)
\<or>
a = UUact (uuReview cid uid p PID N rc)
))"
apply(cases a)
subgoal by simp
subgoal for x2 apply (cases x2, auto) .
subgoal for x3 apply(cases x3, auto) .
by simp_all
lemma uReview_uuReview_step_eqExcPID_N:
assumes a:
"a = Uact (uReview cid uid p PID N rc) \<or>
a = UUact (uuReview cid uid p PID N rc)"
and "step s a = (ou,s')"
shows "eqExcPID_N s s'"
using assms unfolding eqExcPID_N_def eeqExcPID_N_def by (auto simp: u_defs uu_defs eqExcNth_def)
lemma \<phi>_step_eqExcPID_N:
assumes \<phi>: "\<phi> (Trans s a ou s')"
and s: "step s a = (ou,s')"
shows "eqExcPID_N s s'"
using \<phi> uReview_uuReview_step_eqExcPID_N[OF _ s] unfolding \<phi>_def2 by blast
(* major *) lemma eqExcPID_N_step:
assumes s's1': "eqExcPID_N s s1"
and step: "step s a = (ou,s')"
and step1: "step s1 a = (ou1,s1')"
shows "eqExcPID_N s' s1'"
proof -
note eqs = eqExcPID_N_imp[OF s's1']
note eqs' = eqExcPID_N_imp1[OF s's1']
note simps[simp] = c_defs u_defs uu_defs r_defs l_defs Paper_dest_conv eqExcPID_N_def eeqExcPID_N_def eqExcD eqExcNth_def
note * = step step1 eqs eqs'
then show ?thesis
proof (cases a)
case (Cact x1)
with * show ?thesis
proof (cases x1)
case (cReview x81 x82 x83 x84 x85)
with Cact * show ?thesis
by (clarsimp; metis (no_types, lifting) less_SucE nth_append_length right_cons_left)
qed auto
next
case (Uact x2)
with * show ?thesis
proof (cases x2)
case (uReview x71 x72 x73 x74 x75 x76)
with Uact * show ?thesis
by (clarsimp; metis (no_types, lifting) nth_list_update nth_list_update_neq)
qed auto
next
case (UUact x3)
with * show ?thesis
proof (cases x3)
case (uuReview x31 x32 x33 x34 x35 x36)
with UUact * show ?thesis
by (clarsimp; metis (no_types, lifting) nth_list_update nth_list_update_neq)
qed auto
qed auto
qed
lemma eqExcPID_N_step_\<phi>_imp:
assumes ss1: "eqExcPID_N s s1"
and step: "step s a = (ou,s')" and step1: "step s1 a = (ou1,s1')"
and \<phi>: "\<phi> (Trans s a ou s')"
shows "\<phi> (Trans s1 a ou1 s1')"
using assms unfolding \<phi>_def2 by (auto simp add: u_defs uu_defs eqExcPID_N_imp)
lemma eqExcPID_N_step_\<phi>:
assumes s's1': "eqExcPID_N s s1"
and step: "step s a = (ou,s')" and step1: "step s1 a = (ou1,s1')"
shows "\<phi> (Trans s a ou s') = \<phi> (Trans s1 a ou1 s1')"
by (metis eqExcPID_N_step_\<phi>_imp eqExcPID_N_sym assms)
lemma eqExcPID_N2_step_\<phi>_imp:
assumes ss1: "eqExcPID_N2 s s1"
and step: "step s a = (ou,s')" and step1: "step s1 a = (ou1,s1')"
and r: "N < length (reviewsPaper (paper s PID))" (* new *)
and \<phi>: "\<phi> (Trans s a ou s')"
shows "\<phi> (Trans s1 a ou1 s1')"
using assms unfolding \<phi>_def2 by (auto simp add: u_defs uu_defs eqExcPID_N2_imp)
(* More complex, roundabout proof than for other types of documents: *)
lemma eqExcPID_N2_step_\<phi>:
assumes s: "reach s" and s1: "reach s1"
and ss1: "eqExcPID_N2 s s1"
and step: "step s a = (ou,s')" and step1: "step s1 a = (ou1,s1')"
shows "\<phi> (Trans s a ou s') = \<phi> (Trans s1 a ou1 s1')"
proof(cases "\<exists> cid uid. isRevNth s cid uid PID N")
case False
hence "\<not> \<phi> (Trans s a ou s')" unfolding \<phi>_def2 using step
by (auto simp add: u_defs uu_defs) (metis isRev_imp_isRevNth_getReviewIndex)+
moreover have "\<not> \<phi> (Trans s1 a ou1 s1')" using step1 False unfolding \<phi>_def2
by (auto simp add: u_defs uu_defs) (metis eqExcPID_N2_def isRev_imp_isRevNth_getReviewIndex ss1)+
ultimately show ?thesis by auto
next
case True note r = True
note eqs = eqExcPID_N2_imp[OF ss1]
have r: "N < length (reviewsPaper (paper s PID))"
using isRevNth_less_length[OF s] r by auto
have r1: "N < length (reviewsPaper (paper s1 PID))"
using eqs r unfolding eeqExcPID_N2_def eqExcD2 eqExcNth2_def by simp
thus ?thesis by (metis eqExcPID_N2_step_\<phi>_imp eqExcPID_N2_sym assms r)
qed
end
|
### A Pluto.jl notebook ###
# v0.17.1
using Markdown
using InteractiveUtils
# This Pluto notebook uses @bind for interactivity. When running this notebook outside of Pluto, the following 'mock version' of @bind gives bound variables a default value (instead of an error).
macro bind(def, element)
quote
local iv = try Base.loaded_modules[Base.PkgId(Base.UUID("6e696c72-6542-2067-7265-42206c756150"), "AbstractPlutoDingetjes")].Bonds.initial_value catch; b -> missing; end
local el = $(esc(element))
global $(esc(def)) = Core.applicable(Base.get, el) ? Base.get(el) : iv(el)
el
end
end
# ╔═╡ e50f4dc1-99db-439d-9357-fcf523a7f50a
begin
# configuração da página para as cenas do WGLMakie
using WGLMakie, JSServe
Page()
end
# ╔═╡ 9ca215d0-2e8c-11ec-27ae-3bac6ad63ae1
begin
# carregando pacotes necessários
using DrillHoles
using Statistics
using PlutoUI
using DataFrames
using Query
using Plots
# configurações de visualização
theme = WGLMakie.Theme(
resolution = (650,500),
aspect = :data,
colormap=:jet
)
WGLMakie.set_theme!(theme)
end;
# ╔═╡ d380ac0f-28a7-48f4-8463-9dbdf7f66a16
html"""
<p style="background-color:lightgrey" xmlns:cc="http://creativecommons.org/ns#" xmlns:dct="http://purl.org/dc/terms/"><span property="dct:title">  🛠️ <b>Preparação de Amostras</b></span> por <span property="cc:attributionName">Franco Naghetini</span> é licenciado sob <a href="http://creativecommons.org/licenses/by/4.0/?ref=chooser-v1" target="_blank" rel="license noopener noreferrer" style="display:inline-block;">CC BY 4.0<img style="height:22px!important;margin-left:3px;vertical-align:text-bottom;" src="https://mirrors.creativecommons.org/presskit/icons/cc.svg?ref=chooser-v1"><img style="height:22px!important;margin-left:3px;vertical-align:text-bottom;" src="https://mirrors.creativecommons.org/presskit/icons/by.svg?ref=chooser-v1"></a></p>
"""
# ╔═╡ ebaf4b98-9f4a-45bc-ad35-54448f26f90c
PlutoUI.TableOfContents(aside=true, title="Sumário",
indent=true, depth=2)
# ╔═╡ ffdbdfbd-8627-48d9-8e9c-384455b64ed4
md"""

"""
# ╔═╡ b9b5f9a4-431d-40fc-94fe-8d622ba7c5a8
md""" # 🛠️ Preparação de Amostras
Os dados utilizados para a avaliação de um projeto de mineração normalmente apresentam tamanhos e tipos distintos e, portanto, em estado bruto, são inadequados para a condução da estimativa de recursos. Nesse sentido, a **preparação de amostras** é uma etapa que visa realizar um tratamento especial desses dados (*Abzalov, 2016*).
Ainda que uma grande variedade de dados **diretos** (e.g. furos de sondagem, trincheiras) e **indiretos** (e.g. geofísicos) sejam utilizados em empreendimentos minerários, neste módulo, iremos aprender sobre a preparação de **furos de sondagem**, o tipo de dado mais usual na mineração.
"""
# ╔═╡ eedd9f9b-6425-4b8c-ad1f-7bbedc122072
md"""
>##### 📚 Sobre
>- Você pode exportar este notebook como PDF ou HTML estático. Para isso, clique no ícone 🔺🔴, localizado no canto superior direito da pagina. Entretanto, ambos os formatos não são compatíveis com os recursos interativos do notebook.
>- Caso deseje executar alguma célula do notebook, clique no ícone ▶️, localizado no canto inferior direito da célula.
>- Algumas células encontram-se ocultadas (e.g. células que geram os plots). Você pode clicar no ícone 👁️, localizado no canto superior esquerdo da célula, para ocultá-la ou exibí-la.
>- A explicação das células que geram os plots está fora do escopo deste notebook. Entretanto, a sintaxe é bem intuitiva e pode ser facilmente compreendida!
>- Você pode ainda clicar no ícone `...`, no canto superior direito de uma célula, para excluí-la do notebook.
>- Algumas células deste notebook encontram-se encapsuladas pela expressão `md"..."` (e.g. esta célula). Essas são células de texto chamadas de *markdown*. Caso deseje aprender um pouco mais sobre a linguagem *markdown*, clique [aqui](https://docs.pipz.com/central-de-ajuda/learning-center/guia-basico-de-markdown#open).
>- No Pluto, todos os pacotes devem ser importados/baixados na primeira célula do notebook. Clique no ícone 👁️ para exibir essa célula ou consulte a seção *Pacotes utilizados* deste notebook para saber mais informações sobre os pacotes.
>- Utilize a macro ` @which` para verificar a qual pacote uma determinada função pertence.
>- Você pode utilizar este notebook da forma que quiser, basta referenciar [este link](https://github.com/fnaghetini/intro-to-geostats). Consulte a [licença] (https://github.com/fnaghetini/intro-to-geostats/blob/main/LICENSE) para saber mais detalhes.
>- Para mais informações acesse o [README](https://github.com/fnaghetini/intro-to-geostats/blob/main/README.md) do projeto 🚀
"""
# ╔═╡ aa0a8370-7919-41e1-9a05-481df4e48ec7
md"""
## 1. Conceitos básicos
Nesta primeira seção, iremos aprender alguns conceitos teóricos essenciais para compreender o conteúdo deste módulo.
"""
# ╔═╡ 6c867bb6-87d6-420f-8665-fe4581ffd0a9
md"""
### Furos de sondagem
O registro dos **furos de sondagem** é uma das atividades mais comuns e importantes entre geólogos, uma vez que, frequentemente, os furos são a única informação geológica direta sobre as rochas localizadas em subsuperfície. As informações de sondagem, após registradas em um Sistema de Gerenciamento de Banco de Dados, são utilizadas pelos geólogos para gerar interpretações 3D e estimativas de teores de um depósito (*Abzalov, 2016*).
Normalmente, os dados de sondagem são constituídos por um conjunto de tabelas distintas relacionadas entre si por um campo-chave, o identificador dos furos (comumente chamado de `BHID` ou `HOLEID`) (Figura 01).
"""
# ╔═╡ a5bc3c03-856b-4ee2-a71c-8c7e1fe3c641
md"""
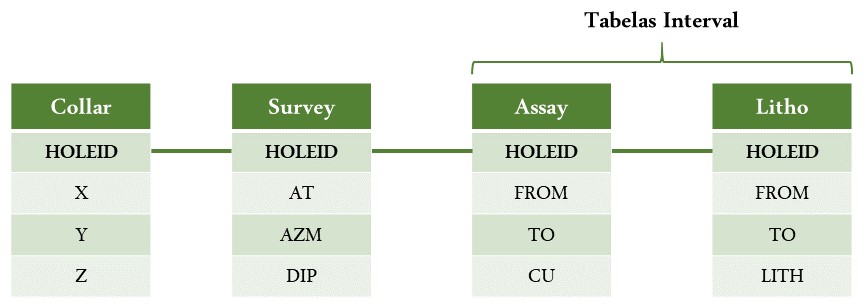
_**Figura 01:** Tabelas Collar, Survey, Assay e Litho relacionadas entre si pelo campo-chave `HOLEID`._
"""
# ╔═╡ ae22a6f0-d857-4229-a003-728d43a50d46
md"""
A tabela **Collar** traz, essencialmente, informações das coordenadas de boca dos furos. Ela pode conter, ainda, informações de profundidade final dos furos, método de aquisição de coordenadas, sistema de referência e data de finalização.
A tabela **Survey** apresenta informações de perfilagem, ou seja, de orientação dos furos (sentido e ângulo de mergulho).
As tabelas do tipo **Interval** são essencialmente constituídas por colunas de início (`FROM`) e final (`TO`) dos intervalos amostrais, bem como por uma característica geológica. A tabela **Assay**, por exemplo, além dos campos que definem o intervalo, contém os campos de teores amostrais analisados em laboratório. Já a tabela **Litho**, por outro lado, traz informações das litologias descritas pelos geólogos.
"""
# ╔═╡ 51199548-4ec2-4034-b955-8d1f97ddd5ee
md""" ### Suporte amostral
Uma característica muito importante dos dados utilizados na mineração é o **suporte amostral**. De forma simples, o suporte está associado ao **tamanho, forma e orientação** das amostras. Os furos de sondagem, por exemplo, são constituídos por diversos intervalos cilíndricos menores (definidos pelos campos `FROM` e `TO`), que podem apresentar tamanhos/comprimentos distintos.
Os exemplos a seguir, extraídos de *Sinclair & Blackwell (2006)*, evidenciam a importância de características geológicas dos depósitos no suporte amostral:
> **Exemplo 1:**. Em depósitos estratiformes, como aqueles de Zn-Pb hospedados em folhelhos, um conjunto de amostras lineares contíguas (e.g. intervalos de testemunhos de sondagem) paralelas ao acamamento são, em média, muito mais similares entre si do que um conjunto de amostras do mesmo tipo, mas perpendiculares ao acamamento. Percebemos aqui a importância da **orientação** das amostras.
> **Exemplo 2:** Em zonas de veios auríferos, amostras perpendiculares à orientação dos veios apresentarão uma grande variabilidade de teores, caso o tamanho do intervalo amostral seja menor do que a distância média entre os veios (algumas amostras podem ter teores nulos!). Por outro lado, amostras perpendiculares aos veios, mas com o tamanho do intervalo amostral superior à distância média entre os veios serão menos erráticas. Percebemos aqui a importância do **tamanho** das amostras.
> ⚠️ Neste módulo, para fins de simplificação, trataremos o conceito de **suporte amostral** como sinônimo do **tamanho/comprimento** dos intervalos amostrais dos furos de sondagem.
"""
# ╔═╡ dd89a21f-ce6b-4a3c-9c22-1f97ac3863a8
md"""
## 2. Geração de furos
Neste módulo, iremos trabalhar com o [Marvin](https://github.com/fnaghetini/intro-to-geostats/tree/main/data/Marvin), um conjunto de dados de um depósito de Cu-Au Pórfiro fictício, mas que apresenta uma série de caracteríticas típicas de depósitos sulfetados (*Whittle et al., 2007*).
> ⚠️ Para fins de simplificação, apenas os teores de `Au` foram mantidos.
Para a importação das tabelas Collar, Survey, Assay e Litho e geração dos furos de sondagem, utilizaremos o pacote [DrillHoles.jl](https://github.com/JuliaEarth/DrillHoles.jl)...
"""
# ╔═╡ 9ce42874-5a58-4e6a-a544-dfea97146cc2
begin
collar = Collar(file = "data/Marvin/collar.csv",
holeid = :HOLEID, x = :X, y = :Y, z = :Z, enddepth=:ENDDEPTH)
survey = Survey(file = "data/Marvin/survey.csv",
holeid = :HOLEID, at = :AT, azm = :AZM, dip = :DIP)
assay = Interval(file = "data/Marvin/assay.csv",
holeid = :HOLEID, from = :FROM, to = :TO)
litho = Interval(file = "data/Marvin/litho.csv",
holeid = :HOLEID, from = :FROM, to = :TO)
end;
# ╔═╡ f9fa9a2f-8099-434e-a76c-4b78160f264a
md"""
Em seguida, podemos utilizar a função `drillhole` para gerar os furos a partir das quatro tabelas importadas...
"""
# ╔═╡ 1e71d41a-5717-462d-81da-8ac35f22c1db
furosdesondagem = drillhole(collar, survey, [assay, litho])
# ╔═╡ 1673eef5-82cf-4eef-8ca2-17d02ecb9b27
md"""
##### Observações
- Uma inconsistência do tipo *overlap* entre as linhas 3 e 4 do arquivo `assay.csv` foi encontrada durante a geração dos furos;
- Esse erro indica que existem amostras duplicadas na tabela de teores;
- Podemos seguir a orientação da mensagem e consultar mais detalhes sobre o erro, utilizando o atributo `warns`...
"""
# ╔═╡ 63ab68f1-b342-4e8c-987d-4fc33166aa3c
furosdesondagem.warns
# ╔═╡ 6e2e4df4-096b-444f-bff3-44c70f3d1dd5
md"""
Se você abrir o arquivo `assay.csv`, perceberá que as linhas 3 e 4, de fato, se referem ao mesmo intervalo (i.e. 5.0 m - 7.5 m). Podemos excluir a linha 4 da tabela de teores, já que ela não possui teor de Au.
Vamos gerar novamente os furos, mas dessa vez importando o arquivo `assay_val.csv` como tabela Assay, ou seja, a tabela de teores já validada...
"""
# ╔═╡ 6b7b4fbe-622e-407c-8ffc-9fe888354ced
begin
# importação da tabela assay validada
assay_val = Interval(file = "data/Marvin/assay_val.csv",
holeid = :HOLEID, from = :FROM, to = :TO)
#
furosvalidados = drillhole(collar, survey, [assay_val, litho])
end
# ╔═╡ f16c8b13-256d-4c1d-a376-4e7d41ecf35d
md"""
##### Observações
- Após a nova geração dos furos, nenhuma inconistência foi relatada;
- Ao final da geração dos furos, são criados quatro objetos: `table`, `trace`, `pars` e `warns` (já discutido).
O objeto `table` contém a própria tabela de furos que será utilizada ao longo deste módulo...
"""
# ╔═╡ 0aed3ddb-b181-4f03-950c-b23e0f153760
furos = furosvalidados.table
# ╔═╡ 10f1c03f-ead5-42c5-a5c5-816d52a15653
md"""
A tabela `furos` é constituída pelas seguintes colunas:
- `HOLEID`: identificador dos furos.
- `FROM` e `TO`: início e final do intervalo amostral em metros.
- `LENGTH`: tamanho do intervalo amostral em metros.
- `AU`: teor de ouro em g/t.
- `DOMAIN`, `ROCKTYPE` e `WEATH`: domínio, tipo de rocha e alteração, respectivamente.
- `X`, `Y` e `Z`: coordenadas geográficas dos centroides dos intervalos.
Já o objeto `trace` contém as informações de perfilagem, ou seja, dados de sentido e ângulo de mergulho dos furos...
"""
# ╔═╡ 9929fafa-2bc5-4fec-83a4-c8f9b1229b0c
furosvalidados.trace
# ╔═╡ b1ec589e-35af-4e34-a663-c72f4b0afe02
md"""
O objeto `pars` contém os nomes das colunas presentes no arquivo de furos e alguns parâmetros sobre a geração dos furos...
"""
# ╔═╡ bfbe894b-a205-4d21-8adf-a26a2052573e
furosvalidados.pars
# ╔═╡ 48e9011a-dfa3-4665-9e23-2aab30e0d294
md"""
## 3. Compositagem
Normalmente, os dados brutos de sondagem (i.e. sem nenhum processamento prévio) apresentam suportes amostrais distintos e precisam ser combinados para produzir amostras de suporte aproximadamente uniforme (*Sinclair & Blackwell, 2006*). Esse procedimento é denominado **compositagem**, e as amostras (combinadas) resultantes são chamadas de **compostas**.
> ⚠️ A compositagem é realizada com o objetivo de combinar intervalos pequenos em intervalos maiores e uniformes. O processo inverso, ou seja, subdividir intervalos maiores em intervalos menores não é uma prática adequada, pois haveria uma suavização da distribuição espacial dos teores que não corresponde à realidade (*Abzalov, 2016*).
Ao compositar as amostras, os teores são recalculados. Segundo *Yamamoto (2001)*, o cálculo do teor composto $t_c$ é realizado pela média dos teores brutos $t_i$ dos intervalos que serão combinados ponderada pelos respectivos tamanhos $e_i$:
```math
t_c = \frac{\sum_{i=1}^{n} t_i e_i}{\sum_{i=1}^{n} e_i}
```
"""
# ╔═╡ 3f55ecbb-8f26-4813-ac3e-97588830d987
md"""
Você pode estar se perguntando sobre o porque devemos uniformizar o suporte amostral. Imagine que queremos calcular o teor médio de Au entre três amostras:
| Amostra | Teor (g/t) | Tamanho (m) |
|:-------:|:----------:|:-----------:|
| AM01 | 2,5 | 2,0 |
| AM02 | 0,5 | 10,0 |
| AM03 | 0,2 | 15,0 |
O teor médio entre essas amostras é de aproximadamente 1 g/t. Repare que, independentemente do tamanho, cada amostra contribui igualmente para o cálculo da média. Entretanto, se fizermos uma análise crítica, perceberemos que uma amostra de 15 metros de comprimento não pode ter o mesmo peso no cálculo do que uma amostra de 2 metros. Se regularizarmos o suporte amostral, no entanto, esse problema será mitigado.
"""
# ╔═╡ c3e6a7e8-c4a2-42ad-9302-cd4be7ee0920
md"""
Segundo *Sinclair & Blackwell (2006)*, a compositagem objetiva:
1. Reduzir o número de amostras e, consequentemente, diminuir o custo computacional;
2. Regularizar o suporte amostral;
3. Reduzir o impacto de valores extremos isolados que podem dificultar a modelagem dos variogramas experimentais ([módulo 4](https://github.com/fnaghetini/intro-to-geostats/blob/main/4-variografia.jl));
4. Adequar o suporte amostral à escala de trabalho.
> ⚠️ A **compositagem por bancadas** busca tornar o suporte amostral igual ou próximo à altura das bancadas, ou seja, à escala de trabalho de minas à céu aberto.
Primeiramente, vamos analisar a distribuição do suporte das amostras. Para isso, utilizaremos o histograma (Figura 02), um gráfico univariado muito útil e que será discutido no [módulo 3](https://github.com/fnaghetini/intro-to-geostats/blob/main/3-analise_exploratoria.jl).
"""
# ╔═╡ 554a5530-e1ca-4261-a1e3-bf27846250fc
histogram(furos[!,:LENGTH], bins=:scott, legend=false,
color=:honeydew2, alpha=0.75, xlims=(0,2.6),
xlabel="Suporte (m)", ylabel="Freq. Absoluta")
# ╔═╡ 4d5eab4d-8510-45ed-97f9-31c6e3af6ab4
md"_**Figura 02:** Distribuição do suporte das amostras brutas._"
# ╔═╡ 99aac39c-f375-42a9-a422-ee1f7ef3a490
md"""
##### Observações
- Existem três grupos de tamanhos de amostras bem definidos: 0.5 m, 1.0 m e 2.5m;
- Como as amostras não estão regularizadas (i.e. mesmo tamanho), iremos compositá-las.
"""
# ╔═╡ e615de83-bcc4-4a84-8e94-140989508805
md"""
Utilizaremos a função `composite`, do pacote [DrillHoles.jl](https://github.com/JuliaEarth/DrillHoles.jl), para realizar a compositagem dos furos brutos. Os parâmetros dessa função são apresentados abaixo:
```julia
composite(dh, interval=1.0, zone=nothing, mode=:equalcomp, mincomp=0.5)
```
- `dh`: objeto de furos de sondagem que será compositado;
- `interval`: comprimento do intervalo das compostas (novo suporte);
- `zone`: coluna de zona. Se considerado, os intervalos só poderão ser combinados caso apresentem o mesmo valor de zona. Podemos utilizar a coluna de litologia `ROCKTYPE`, por exemplo;
- `mode`: método de compositagem;
- `mincomp`: comprimento mínimo do intervalo das compostas. Intervalos menores são descartados.
> ⚠️ Caso você tenha familiaridade com o software Studio RM da [Datamine](https://www.dataminesoftware.com/), perceberá que a função `composite` é muito similar ao processo `COMPDH`.
A seguir, aprenderemos sobre os dois principais métodos de compositagem de furos de sondagem: **comprimento fixo** e **comprimento ótimo**. Como dito anteriormente, o método de compositagem é definido pelo parâmetro `mode`.
"""
# ╔═╡ 29c1aa29-d21f-43c2-b5b4-a2c3443cc983
md"""
### Método do comprimento fixo
O **método do comprimento fixo** visa criar compostas com exatamente o mesmo comprimento `interval`. Além disso, é necessário definir um parâmetro de comprimento mínimo de composta `mincomp` que, por sua vez, é utilizado para decidir se as "bordas" das amostras serão mantidas ou descartadas. Caso as bordas possuam um comprimento inferior a `mincomp`, elas serão descartadas e, caso contrário, serão mantidas.
Perceba que, embora busque gerar compostas de tamanho fixo, a estratégia de comprimento fixo pode levar ao descarte de muitas amostras. Essa é a principal limitação deste método (*Abzalov, 2016*).
Abaixo, realizaremos uma compositagem dos furos pelo método do comprimento fixo, que é representado por `mode=:equalcomp`. O comprimento/suporte das compostas será igual a 10 metros e a coluna `ROCKTYPE` é adotada como campo de zona. O suporte mínimo `mincomp` que uma composta poderá apresentar é de 4 metros. A distribuição do suporte das compostas resultantes é apresesentada pelo histograma da Figura 03.
"""
# ╔═╡ 0bdf2bb0-655c-446a-bb79-91746a380701
begin
# compositagem por comprimento fixo
comps_fixo = composite(furosvalidados, interval=10.0,
zone=:ROCKTYPE, mode=:equalcomp, mincomp=4)
# tabela de compostas
cp_fixo = comps_fixo.table
end;
# ╔═╡ 86161dc5-0980-42e2-8455-6b1b07dddeaf
begin
X̅_fixo = round(mean(cp_fixo.LENGTH), digits=2)
md_fixo = round(median(cp_fixo.LENGTH), digits=2)
histogram(cp_fixo[!,:LENGTH], bins=:scott, legend=:topleft,
color=:honeydew2, alpha=0.75, xlims=(3.5,11),
xlabel="Suporte (m)", ylabel="Freq. Absoluta",
label=false)
vline!([X̅_fixo], color=:red, label="X̅ = $(X̅_fixo) m")
vline!([md_fixo], color=:green, label="md = $(md_fixo) m")
end
# ╔═╡ 66b7f878-c620-4fee-84c0-273bdbc46440
md"_**Figura 03:** Distribuição do suporte das compostas resultantes do método do comprimento fixo._"
# ╔═╡ 7d398c89-f763-4d3b-b196-2949bd91ae9a
md"""
##### Observações
- A grande maioria das compostas agora apresenta suporte igual a 10 metros;
- A distribuição apresenta uma forte assimetria negativa (cauda alongada à esquerda). Esse padrão é típico quando se realiza a compositagem pelo método do comprimento fixo. Os tipos de assimetria que uma distribuição pode apresentar serão discutidos no [módulo 3](https://github.com/fnaghetini/intro-to-geostats/blob/main/3-analise_exploratoria.jl).
"""
# ╔═╡ 62705acb-a304-4bd4-ae30-cca46037c7dd
md"""
### Método do comprimento ótimo
O **método do comprimento ótimo** parte do princípio que as amostras não devem ser descartadas. Essa estratégia faz com que todas as bordas de amostras (maiores que `mincomp`) sejam incluídas em alguma das compostas, de modo que o suporte resultante seja o mais próximo possível do comprimento `interval` definido (*Abzalov, 2016*). O comprimento máximo que uma amostra pode apresentar é igual a `1.5 × interval`.
O fato de essa estratégia ser mais flexível que o método do comprimento fixo faz com que menos amostras sejam descartadas, ainda que as compostas não apresentem um suporte exatamente igual ao `interval` definido.
A seguir, realizaremos uma compositagem dos furos pelo método do comprimento ótimo, que é representado por `mode=:nodiscard`. Para uma posterior comparação entre as estratégias, os demais parâmetros da função `composite` são configurados da mesma forma que o exemplo anterior. A distribuição do suporte das compostas resultantes é apresesentada pelo histograma da Figura 04.
"""
# ╔═╡ ddbeaaf1-a4e4-4a09-a487-9bbdc489c824
begin
# compositagem por comprimento ótimo
comps_otimo = composite(furosvalidados, interval=10.0,
zone=:ROCKTYPE, mode=:nodiscard, mincomp=4)
# tabela de compostas
cp_otimo = comps_otimo.table
end;
# ╔═╡ 59454ea0-138c-4005-9c4b-e2e8667189c2
begin
X̅_otimo = round(mean(cp_otimo.LENGTH), digits=2)
md_otimo = round(median(cp_otimo.LENGTH), digits=2)
histogram(cp_otimo[!,:LENGTH], bins=:scott, legend=:topleft,
color=:honeydew2, alpha=0.75, xlims=(4,14),
xlabel="Suporte (m)", ylabel="Freq. Absoluta",
label=false)
vline!([X̅_otimo], color=:red, label="X̅ = $(X̅_otimo) m")
vline!([md_otimo], color=:green, label="md = $(md_otimo) m")
end
# ╔═╡ 0d9d4d97-e1ff-47a5-9a58-c76788b55468
md"_**Figura 04:** Distribuição do suporte das compostas resultantes do método do comprimento ótimo._"
# ╔═╡ 959927f2-74b6-411d-89f8-034c031d7422
md"""
##### Observações
- A grande maioria das compostas agora apresenta comprimentos entre 9 e 11 metros;
- A distribuição é aproximadamente simétrica. Esse padrão é típico quando se realiza a compositagem pelo método do comprimento ótimo.
"""
# ╔═╡ d50d76db-507e-450e-93a1-e0319edaf98a
md"""
### Comparação entre os algoritmos
Até o momento, já aprendemos que:
> O **método do comprimento fixo**, por ser mais rígido, pode resultar no descarte de muitas amostras. A distribuição do tamanho das compostas é tipicamente assimétrica negativa.
> O **método do comprimento ótimo**, ainda que não gere compostas de suporte fixo, mitiga o descarte de amostras. A distribuição do tamanho das compostas é aproximadamente simétrica.
Ademais, podemos realizar uma comparação estatística entre as amostras brutas e as compostas resultantes de ambos os métodos. Para isso, iremos considerar os seguintes critérios (*Abzalov, 2016*):
1. Metragem total de amostras;
2. Desvio padrão do comprimento das amostras;
3. Média do teor de Au (g/t).
Idealmente, a metragem total das compostas deve coincidir com a das amostras brutas. Para o cálculo da metragem total, utilizaremos a função `sum`.
Como o objetivo da compositagem é regularizar o suporte amostral, a variabilidade (dispersão) do comprimento das amostras `LENGTH` deve ser reduzida. Mediremos essa variabilidade com a função `std`, que representa o desvio padrão.
A compositagem não deve alterar significativamente o teor metalífero médio das amostras. Qualquer mudança superior a 5% deve ser investigada (*Abzalov, 2016*). Para o cálculo do teor médio de Au (g/t), utilizaremos a função `mean`.
Vamos criar uma função `compvalid` que remova eventuais valores faltantes de Au (para o cálculo do teor médio) e retorne um sumário estatístico com essas três informações...
"""
# ╔═╡ 3d52dfab-40d2-4947-9dfe-cc4e6100d75c
function compvalid(amostras::DataFrame, id::String)
s = amostras |> @dropna(:AU) |> DataFrame
report = DataFrame(Amostras = id,
Metragem = sum(amostras.LENGTH),
DP_suporte = std(amostras.LENGTH),
Média_Au = mean(s.AU))
return report
end
# ╔═╡ 98d43ce9-d4a6-4b5f-8777-a0af67eddf9f
md"""
Agora podemos aplicar a função `compvalid` para calcular as estatísticas de cada um dos grupos de amostras (i.e. brutas, compostas fixas e compostas ótimas) e concatenar (verticalmente) as medidas em uma única tabela. Essa concatenação é bastante intuitiva...
"""
# ╔═╡ 58fd4e5b-da58-4cf1-8c99-32892a146bdd
[compvalid(furos, "Brutas")
compvalid(cp_fixo, "Comp. Fixo")
compvalid(cp_otimo, "Comp. Ótimo")]
# ╔═╡ 5431903b-e7b0-47f8-a225-9db66468256e
md"""
##### Observações
- Quando se compara a metragem de amostras brutas com a metragem das compostas, nota-se que, na estratégia do comprimento fixo, mais amostras foram descartadas (185 metros) do que no método do comprimento ótimo (9,5 metros);
- O método do comprimento fixo aumentou a dispersão do comprimento das amostras, enquanto a estratégia do comprimento ótimo reduziu;
- Há uma redução no teor médio de Au após a compositagem pelos dois métodos. Essa redução já era esperada, uma vez que, ao combinar as amostras, há uma diluição dos teores. Entretanto, a mudança na média não foi tão expressiva em ambos os casos (< 3%);
- Pelo menos neste exemplo, o algoritmo do comprimento ótimo mostrou uma melhor performance na compositagem do que a estratégia do comprimento fixo. Ainda sim, sugere-se sempre comparar ambos métodos, se possível.
"""
# ╔═╡ 447e2730-0bd4-4953-ac2e-c6d12cb5e341
md"""
## 4. Visualização dos furos
Agora que realizamos a comparação entre os dois métodos de compositagem e escolhemos as compostas ótimas, podemos visualizá-las interativamente com o pacote [Makie.jl](https://github.com/JuliaPlots/Makie.jl). Esse pacote fornece incríveis recursos interativos de visualização 3D!
Neste notebook, adotaremos o backend [WGLMakie](https://github.com/JuliaPlots/Makie.jl/tree/master/WGLMakie), por ser interativo e compatível com o visualizações no navegador.
> ⚠️ Caso queira aprender como configurar esse backend, clique no ícone 👁️ para exibir o conteúdo das duas primeiras células deste notebook.
Clique na caixa abaixo para visualizar os teores compostos de Au (Figura 05)...
> ⚠️ Ao clicar pela primeira vez, a exibição do plot pode demorar alguns segundos. Entretanto, nos próximos cliques, as compostas serão exibidas instantaneamente! Caso não queira mais visualizá-las, desmarque a caixa para não tornar lenta a execução das demais células.
"""
# ╔═╡ baf8bd0f-07b7-4ce6-8850-4f22c4a20ecf
md"""
Visualizar furos $(@bind viz_furos CheckBox())
"""
# ╔═╡ dbddc346-e9dd-416d-abf5-98d96a95f3ec
begin
if viz_furos
# remoção de valores faltantes
furos_viz = cp_otimo |> @dropna(:AU) |> DataFrame
# visualização dos furos
fig, ax, p = meshscatter(furos_viz.X, furos_viz.Y, furos_viz.Z,
color=furos_viz.AU, markersize=8)
Colorbar(fig[1, 2], p, label="Au (g/t)")
fig
end
end
# ╔═╡ d9cd1583-abec-4dc1-a9db-5bbcf74a48c8
if viz_furos
md"""_**Figura 05:** Visualização dos teores compostos de Au (método do comprimento ótimo)._"""
end
# ╔═╡ 96ae1d18-a0fd-4846-9d4a-843952e14caa
md"""
## Referências
*Abzalov, M. [Applied mining geology](https://www.google.com.br/books/edition/Applied_Mining_Geology/Oy3RDAAAQBAJ?hl=pt-BR&gbpv=0). Switzerland: Springer International Publishing, 2016*
*Sinclair, A. J.; Blackwell, G. H. [Applied mineral inventory estimation](https://www.google.com.br/books/edition/Applied_Mineral_Inventory_Estimation/oo7rCrFQJksC?hl=pt-BR&gbpv=0). New York: Cambridge University Press, 2006.*
*Whittle, G.; Stange, W.; Hanson, N. [Optimising project value and robustness](https://www.whittleconsulting.com.au/wp-content/uploads/2017/03/Optimising-Project-Value-and-Robustness.pdf). In: Project Evaluation Conference, v.1, 2007. 147-155.*
*Yamamoto, J. K. [Avaliação e classificação de reservas minerais](https://www.google.com.br/books/edition/Avalia%C3%A7%C3%A3o_e_classifica%C3%A7%C3%A3o_de_reserva/AkmsTIzmblQC?hl=pt-BR&gbpv=0). São Paulo: Editora da Universidade de São Paulo, 2001*.
"""
# ╔═╡ 0b874268-8410-43fd-9c60-d13e4f2eec0b
md"""
## Recursos adicionais
Um outro tópico importante na fase de preparação de amostras é o *top cut*, comumente chamado de *capping* ou "capeamento". Ainda que esse assunto esteja fora do escopo deste notebook, o podcast abaixo é uma excelente introdução ao tema!
> [Podcast Top Cut - Optiro Mining Industry Consultants](https://open.spotify.com/episode/6Wbho2xFwntNVrU86t32KJ)
"""
# ╔═╡ 6f69c80c-aafc-4db1-bd64-41d5112287fb
md"""
## Pacotes utilizados
Os seguintes pacotes foram utilizados neste notebook:
| Pacote | Descrição |
|:--------------------------------------------------------:|:-----------------------:|
|[JSServe](https://github.com/SimonDanisch/JSServe.jl) | Aplicações interativas |
|[DrillHoles](https://github.com/JuliaEarth/DrillHoles.jl) | Furos de sondagem |
|[Statistics](https://docs.julialang.org/en/v1/) | Cálculo de estatísticas |
|[PlutoUI](https://github.com/fonsp/PlutoUI.jl) | Widgets interativos |
|[DataFrames](https://github.com/JuliaData/DataFrames.jl) | Manipulação de tabelas |
|[Query](https://github.com/queryverse/Query.jl) | Realização de consultas |
|[Plots](https://github.com/JuliaPlots/Plots.jl) | Visualização dos dados |
|[WGLMakie](https://github.com/JuliaPlots/Makie.jl) | Plotagem interativa |
"""
# ╔═╡ 00000000-0000-0000-0000-000000000001
PLUTO_PROJECT_TOML_CONTENTS = """
[deps]
DataFrames = "a93c6f00-e57d-5684-b7b6-d8193f3e46c0"
DrillHoles = "9d36f3b5-8124-4f7e-bcda-df733105c718"
JSServe = "824d6782-a2ef-11e9-3a09-e5662e0c26f9"
Plots = "91a5bcdd-55d7-5caf-9e0b-520d859cae80"
PlutoUI = "7f904dfe-b85e-4ff6-b463-dae2292396a8"
Query = "1a8c2f83-1ff3-5112-b086-8aa67b057ba1"
Statistics = "10745b16-79ce-11e8-11f9-7d13ad32a3b2"
WGLMakie = "276b4fcb-3e11-5398-bf8b-a0c2d153d008"
[compat]
DataFrames = "~1.2.2"
DrillHoles = "~0.1.4"
JSServe = "~1.2.3"
Plots = "~1.22.6"
PlutoUI = "~0.7.16"
Query = "~1.0.0"
WGLMakie = "~0.4.6"
"""
# ╔═╡ 00000000-0000-0000-0000-000000000002
PLUTO_MANIFEST_TOML_CONTENTS = """
# This file is machine-generated - editing it directly is not advised
[[AbstractFFTs]]
deps = ["LinearAlgebra"]
git-tree-sha1 = "485ee0867925449198280d4af84bdb46a2a404d0"
uuid = "621f4979-c628-5d54-868e-fcf4e3e8185c"
version = "1.0.1"
[[AbstractTrees]]
git-tree-sha1 = "03e0550477d86222521d254b741d470ba17ea0b5"
uuid = "1520ce14-60c1-5f80-bbc7-55ef81b5835c"
version = "0.3.4"
[[Adapt]]
deps = ["LinearAlgebra"]
git-tree-sha1 = "84918055d15b3114ede17ac6a7182f68870c16f7"
uuid = "79e6a3ab-5dfb-504d-930d-738a2a938a0e"
version = "3.3.1"
[[Animations]]
deps = ["Colors"]
git-tree-sha1 = "e81c509d2c8e49592413bfb0bb3b08150056c79d"
uuid = "27a7e980-b3e6-11e9-2bcd-0b925532e340"
version = "0.4.1"
[[ArgTools]]
uuid = "0dad84c5-d112-42e6-8d28-ef12dabb789f"
[[ArrayInterface]]
deps = ["Compat", "IfElse", "LinearAlgebra", "Requires", "SparseArrays", "Static"]
git-tree-sha1 = "b8d49c34c3da35f220e7295659cd0bab8e739fed"
uuid = "4fba245c-0d91-5ea0-9b3e-6abc04ee57a9"
version = "3.1.33"
[[Artifacts]]
uuid = "56f22d72-fd6d-98f1-02f0-08ddc0907c33"
[[Automa]]
deps = ["Printf", "ScanByte", "TranscodingStreams"]
git-tree-sha1 = "d50976f217489ce799e366d9561d56a98a30d7fe"
uuid = "67c07d97-cdcb-5c2c-af73-a7f9c32a568b"
version = "0.8.2"
[[AxisAlgorithms]]
deps = ["LinearAlgebra", "Random", "SparseArrays", "WoodburyMatrices"]
git-tree-sha1 = "66771c8d21c8ff5e3a93379480a2307ac36863f7"
uuid = "13072b0f-2c55-5437-9ae7-d433b7a33950"
version = "1.0.1"
[[Base64]]
uuid = "2a0f44e3-6c83-55bd-87e4-b1978d98bd5f"
[[Bzip2_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "19a35467a82e236ff51bc17a3a44b69ef35185a2"
uuid = "6e34b625-4abd-537c-b88f-471c36dfa7a0"
version = "1.0.8+0"
[[CEnum]]
git-tree-sha1 = "215a9aa4a1f23fbd05b92769fdd62559488d70e9"
uuid = "fa961155-64e5-5f13-b03f-caf6b980ea82"
version = "0.4.1"
[[CSV]]
deps = ["Dates", "Mmap", "Parsers", "PooledArrays", "SentinelArrays", "Tables", "Unicode"]
git-tree-sha1 = "b83aa3f513be680454437a0eee21001607e5d983"
uuid = "336ed68f-0bac-5ca0-87d4-7b16caf5d00b"
version = "0.8.5"
[[Cairo_jll]]
deps = ["Artifacts", "Bzip2_jll", "Fontconfig_jll", "FreeType2_jll", "Glib_jll", "JLLWrappers", "LZO_jll", "Libdl", "Pixman_jll", "Pkg", "Xorg_libXext_jll", "Xorg_libXrender_jll", "Zlib_jll", "libpng_jll"]
git-tree-sha1 = "f2202b55d816427cd385a9a4f3ffb226bee80f99"
uuid = "83423d85-b0ee-5818-9007-b63ccbeb887a"
version = "1.16.1+0"
[[ChainRulesCore]]
deps = ["Compat", "LinearAlgebra", "SparseArrays"]
git-tree-sha1 = "2f294fae04aa5069a67964a3366e151e09ea7c09"
uuid = "d360d2e6-b24c-11e9-a2a3-2a2ae2dbcce4"
version = "1.9.0"
[[CodecZlib]]
deps = ["TranscodingStreams", "Zlib_jll"]
git-tree-sha1 = "ded953804d019afa9a3f98981d99b33e3db7b6da"
uuid = "944b1d66-785c-5afd-91f1-9de20f533193"
version = "0.7.0"
[[ColorBrewer]]
deps = ["Colors", "JSON", "Test"]
git-tree-sha1 = "61c5334f33d91e570e1d0c3eb5465835242582c4"
uuid = "a2cac450-b92f-5266-8821-25eda20663c8"
version = "0.4.0"
[[ColorSchemes]]
deps = ["ColorTypes", "Colors", "FixedPointNumbers", "Random"]
git-tree-sha1 = "a851fec56cb73cfdf43762999ec72eff5b86882a"
uuid = "35d6a980-a343-548e-a6ea-1d62b119f2f4"
version = "3.15.0"
[[ColorTypes]]
deps = ["FixedPointNumbers", "Random"]
git-tree-sha1 = "024fe24d83e4a5bf5fc80501a314ce0d1aa35597"
uuid = "3da002f7-5984-5a60-b8a6-cbb66c0b333f"
version = "0.11.0"
[[ColorVectorSpace]]
deps = ["ColorTypes", "FixedPointNumbers", "LinearAlgebra", "SpecialFunctions", "Statistics", "TensorCore"]
git-tree-sha1 = "45efb332df2e86f2cb2e992239b6267d97c9e0b6"
uuid = "c3611d14-8923-5661-9e6a-0046d554d3a4"
version = "0.9.7"
[[Colors]]
deps = ["ColorTypes", "FixedPointNumbers", "Reexport"]
git-tree-sha1 = "417b0ed7b8b838aa6ca0a87aadf1bb9eb111ce40"
uuid = "5ae59095-9a9b-59fe-a467-6f913c188581"
version = "0.12.8"
[[Compat]]
deps = ["Base64", "Dates", "DelimitedFiles", "Distributed", "InteractiveUtils", "LibGit2", "Libdl", "LinearAlgebra", "Markdown", "Mmap", "Pkg", "Printf", "REPL", "Random", "SHA", "Serialization", "SharedArrays", "Sockets", "SparseArrays", "Statistics", "Test", "UUIDs", "Unicode"]
git-tree-sha1 = "31d0151f5716b655421d9d75b7fa74cc4e744df2"
uuid = "34da2185-b29b-5c13-b0c7-acf172513d20"
version = "3.39.0"
[[CompilerSupportLibraries_jll]]
deps = ["Artifacts", "Libdl"]
uuid = "e66e0078-7015-5450-92f7-15fbd957f2ae"
[[Contour]]
deps = ["StaticArrays"]
git-tree-sha1 = "9f02045d934dc030edad45944ea80dbd1f0ebea7"
uuid = "d38c429a-6771-53c6-b99e-75d170b6e991"
version = "0.5.7"
[[Crayons]]
git-tree-sha1 = "3f71217b538d7aaee0b69ab47d9b7724ca8afa0d"
uuid = "a8cc5b0e-0ffa-5ad4-8c14-923d3ee1735f"
version = "4.0.4"
[[DataAPI]]
git-tree-sha1 = "cc70b17275652eb47bc9e5f81635981f13cea5c8"
uuid = "9a962f9c-6df0-11e9-0e5d-c546b8b5ee8a"
version = "1.9.0"
[[DataFrames]]
deps = ["Compat", "DataAPI", "Future", "InvertedIndices", "IteratorInterfaceExtensions", "LinearAlgebra", "Markdown", "Missings", "PooledArrays", "PrettyTables", "Printf", "REPL", "Reexport", "SortingAlgorithms", "Statistics", "TableTraits", "Tables", "Unicode"]
git-tree-sha1 = "d785f42445b63fc86caa08bb9a9351008be9b765"
uuid = "a93c6f00-e57d-5684-b7b6-d8193f3e46c0"
version = "1.2.2"
[[DataStructures]]
deps = ["Compat", "InteractiveUtils", "OrderedCollections"]
git-tree-sha1 = "7d9d316f04214f7efdbb6398d545446e246eff02"
uuid = "864edb3b-99cc-5e75-8d2d-829cb0a9cfe8"
version = "0.18.10"
[[DataValueInterfaces]]
git-tree-sha1 = "bfc1187b79289637fa0ef6d4436ebdfe6905cbd6"
uuid = "e2d170a0-9d28-54be-80f0-106bbe20a464"
version = "1.0.0"
[[DataValues]]
deps = ["DataValueInterfaces", "Dates"]
git-tree-sha1 = "d88a19299eba280a6d062e135a43f00323ae70bf"
uuid = "e7dc6d0d-1eca-5fa6-8ad6-5aecde8b7ea5"
version = "0.4.13"
[[Dates]]
deps = ["Printf"]
uuid = "ade2ca70-3891-5945-98fb-dc099432e06a"
[[DelimitedFiles]]
deps = ["Mmap"]
uuid = "8bb1440f-4735-579b-a4ab-409b98df4dab"
[[Distributed]]
deps = ["Random", "Serialization", "Sockets"]
uuid = "8ba89e20-285c-5b6f-9357-94700520ee1b"
[[Distributions]]
deps = ["ChainRulesCore", "FillArrays", "LinearAlgebra", "PDMats", "Printf", "QuadGK", "Random", "SparseArrays", "SpecialFunctions", "Statistics", "StatsBase", "StatsFuns"]
git-tree-sha1 = "9809cf6871ca006d5a4669136c09e77ba08bf51a"
uuid = "31c24e10-a181-5473-b8eb-7969acd0382f"
version = "0.25.20"
[[DocStringExtensions]]
deps = ["LibGit2"]
git-tree-sha1 = "a32185f5428d3986f47c2ab78b1f216d5e6cc96f"
uuid = "ffbed154-4ef7-542d-bbb7-c09d3a79fcae"
version = "0.8.5"
[[Downloads]]
deps = ["ArgTools", "LibCURL", "NetworkOptions"]
uuid = "f43a241f-c20a-4ad4-852c-f6b1247861c6"
[[DrillHoles]]
deps = ["CSV", "DataFrames", "StatsBase"]
git-tree-sha1 = "b8ad18a7f8f61bebc10da2ded20456a2e2a32de5"
uuid = "9d36f3b5-8124-4f7e-bcda-df733105c718"
version = "0.1.4"
[[EarCut_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "3f3a2501fa7236e9b911e0f7a588c657e822bb6d"
uuid = "5ae413db-bbd1-5e63-b57d-d24a61df00f5"
version = "2.2.3+0"
[[EllipsisNotation]]
deps = ["ArrayInterface"]
git-tree-sha1 = "8041575f021cba5a099a456b4163c9a08b566a02"
uuid = "da5c29d0-fa7d-589e-88eb-ea29b0a81949"
version = "1.1.0"
[[Expat_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "b3bfd02e98aedfa5cf885665493c5598c350cd2f"
uuid = "2e619515-83b5-522b-bb60-26c02a35a201"
version = "2.2.10+0"
[[FFMPEG]]
deps = ["FFMPEG_jll"]
git-tree-sha1 = "b57e3acbe22f8484b4b5ff66a7499717fe1a9cc8"
uuid = "c87230d0-a227-11e9-1b43-d7ebe4e7570a"
version = "0.4.1"
[[FFMPEG_jll]]
deps = ["Artifacts", "Bzip2_jll", "FreeType2_jll", "FriBidi_jll", "JLLWrappers", "LAME_jll", "Libdl", "Ogg_jll", "OpenSSL_jll", "Opus_jll", "Pkg", "Zlib_jll", "libass_jll", "libfdk_aac_jll", "libvorbis_jll", "x264_jll", "x265_jll"]
git-tree-sha1 = "d8a578692e3077ac998b50c0217dfd67f21d1e5f"
uuid = "b22a6f82-2f65-5046-a5b2-351ab43fb4e5"
version = "4.4.0+0"
[[FFTW]]
deps = ["AbstractFFTs", "FFTW_jll", "LinearAlgebra", "MKL_jll", "Preferences", "Reexport"]
git-tree-sha1 = "463cb335fa22c4ebacfd1faba5fde14edb80d96c"
uuid = "7a1cc6ca-52ef-59f5-83cd-3a7055c09341"
version = "1.4.5"
[[FFTW_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "c6033cc3892d0ef5bb9cd29b7f2f0331ea5184ea"
uuid = "f5851436-0d7a-5f13-b9de-f02708fd171a"
version = "3.3.10+0"
[[FileIO]]
deps = ["Pkg", "Requires", "UUIDs"]
git-tree-sha1 = "3c041d2ac0a52a12a27af2782b34900d9c3ee68c"
uuid = "5789e2e9-d7fb-5bc7-8068-2c6fae9b9549"
version = "1.11.1"
[[FillArrays]]
deps = ["LinearAlgebra", "Random", "SparseArrays", "Statistics"]
git-tree-sha1 = "8756f9935b7ccc9064c6eef0bff0ad643df733a3"
uuid = "1a297f60-69ca-5386-bcde-b61e274b549b"
version = "0.12.7"
[[FixedPointNumbers]]
deps = ["Statistics"]
git-tree-sha1 = "335bfdceacc84c5cdf16aadc768aa5ddfc5383cc"
uuid = "53c48c17-4a7d-5ca2-90c5-79b7896eea93"
version = "0.8.4"
[[Fontconfig_jll]]
deps = ["Artifacts", "Bzip2_jll", "Expat_jll", "FreeType2_jll", "JLLWrappers", "Libdl", "Libuuid_jll", "Pkg", "Zlib_jll"]
git-tree-sha1 = "21efd19106a55620a188615da6d3d06cd7f6ee03"
uuid = "a3f928ae-7b40-5064-980b-68af3947d34b"
version = "2.13.93+0"
[[Formatting]]
deps = ["Printf"]
git-tree-sha1 = "8339d61043228fdd3eb658d86c926cb282ae72a8"
uuid = "59287772-0a20-5a39-b81b-1366585eb4c0"
version = "0.4.2"
[[FreeType]]
deps = ["CEnum", "FreeType2_jll"]
git-tree-sha1 = "cabd77ab6a6fdff49bfd24af2ebe76e6e018a2b4"
uuid = "b38be410-82b0-50bf-ab77-7b57e271db43"
version = "4.0.0"
[[FreeType2_jll]]
deps = ["Artifacts", "Bzip2_jll", "JLLWrappers", "Libdl", "Pkg", "Zlib_jll"]
git-tree-sha1 = "87eb71354d8ec1a96d4a7636bd57a7347dde3ef9"
uuid = "d7e528f0-a631-5988-bf34-fe36492bcfd7"
version = "2.10.4+0"
[[FreeTypeAbstraction]]
deps = ["ColorVectorSpace", "Colors", "FreeType", "GeometryBasics", "StaticArrays"]
git-tree-sha1 = "19d0f1e234c13bbfd75258e55c52aa1d876115f5"
uuid = "663a7486-cb36-511b-a19d-713bb74d65c9"
version = "0.9.2"
[[FriBidi_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "aa31987c2ba8704e23c6c8ba8a4f769d5d7e4f91"
uuid = "559328eb-81f9-559d-9380-de523a88c83c"
version = "1.0.10+0"
[[Future]]
deps = ["Random"]
uuid = "9fa8497b-333b-5362-9e8d-4d0656e87820"
[[GLFW_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Libglvnd_jll", "Pkg", "Xorg_libXcursor_jll", "Xorg_libXi_jll", "Xorg_libXinerama_jll", "Xorg_libXrandr_jll"]
git-tree-sha1 = "0c603255764a1fa0b61752d2bec14cfbd18f7fe8"
uuid = "0656b61e-2033-5cc2-a64a-77c0f6c09b89"
version = "3.3.5+1"
[[GR]]
deps = ["Base64", "DelimitedFiles", "GR_jll", "HTTP", "JSON", "Libdl", "LinearAlgebra", "Pkg", "Printf", "Random", "Serialization", "Sockets", "Test", "UUIDs"]
git-tree-sha1 = "d189c6d2004f63fd3c91748c458b09f26de0efaa"
uuid = "28b8d3ca-fb5f-59d9-8090-bfdbd6d07a71"
version = "0.61.0"
[[GR_jll]]
deps = ["Artifacts", "Bzip2_jll", "Cairo_jll", "FFMPEG_jll", "Fontconfig_jll", "GLFW_jll", "JLLWrappers", "JpegTurbo_jll", "Libdl", "Libtiff_jll", "Pixman_jll", "Pkg", "Qt5Base_jll", "Zlib_jll", "libpng_jll"]
git-tree-sha1 = "cafe0823979a5c9bff86224b3b8de29ea5a44b2e"
uuid = "d2c73de3-f751-5644-a686-071e5b155ba9"
version = "0.61.0+0"
[[GeometryBasics]]
deps = ["EarCut_jll", "IterTools", "LinearAlgebra", "StaticArrays", "StructArrays", "Tables"]
git-tree-sha1 = "58bcdf5ebc057b085e58d95c138725628dd7453c"
uuid = "5c1252a2-5f33-56bf-86c9-59e7332b4326"
version = "0.4.1"
[[Gettext_jll]]
deps = ["Artifacts", "CompilerSupportLibraries_jll", "JLLWrappers", "Libdl", "Libiconv_jll", "Pkg", "XML2_jll"]
git-tree-sha1 = "9b02998aba7bf074d14de89f9d37ca24a1a0b046"
uuid = "78b55507-aeef-58d4-861c-77aaff3498b1"
version = "0.21.0+0"
[[Glib_jll]]
deps = ["Artifacts", "Gettext_jll", "JLLWrappers", "Libdl", "Libffi_jll", "Libiconv_jll", "Libmount_jll", "PCRE_jll", "Pkg", "Zlib_jll"]
git-tree-sha1 = "7bf67e9a481712b3dbe9cb3dac852dc4b1162e02"
uuid = "7746bdde-850d-59dc-9ae8-88ece973131d"
version = "2.68.3+0"
[[Graphics]]
deps = ["Colors", "LinearAlgebra", "NaNMath"]
git-tree-sha1 = "1c5a84319923bea76fa145d49e93aa4394c73fc2"
uuid = "a2bd30eb-e257-5431-a919-1863eab51364"
version = "1.1.1"
[[Graphite2_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "344bf40dcab1073aca04aa0df4fb092f920e4011"
uuid = "3b182d85-2403-5c21-9c21-1e1f0cc25472"
version = "1.3.14+0"
[[GridLayoutBase]]
deps = ["GeometryBasics", "InteractiveUtils", "Match", "Observables"]
git-tree-sha1 = "e2f606c87d09d5187bb6069dab8cee0af7c77bdb"
uuid = "3955a311-db13-416c-9275-1d80ed98e5e9"
version = "0.6.1"
[[Grisu]]
git-tree-sha1 = "53bb909d1151e57e2484c3d1b53e19552b887fb2"
uuid = "42e2da0e-8278-4e71-bc24-59509adca0fe"
version = "1.0.2"
[[HTTP]]
deps = ["Base64", "Dates", "IniFile", "Logging", "MbedTLS", "NetworkOptions", "Sockets", "URIs"]
git-tree-sha1 = "14eece7a3308b4d8be910e265c724a6ba51a9798"
uuid = "cd3eb016-35fb-5094-929b-558a96fad6f3"
version = "0.9.16"
[[HarfBuzz_jll]]
deps = ["Artifacts", "Cairo_jll", "Fontconfig_jll", "FreeType2_jll", "Glib_jll", "Graphite2_jll", "JLLWrappers", "Libdl", "Libffi_jll", "Pkg"]
git-tree-sha1 = "8a954fed8ac097d5be04921d595f741115c1b2ad"
uuid = "2e76f6c2-a576-52d4-95c1-20adfe4de566"
version = "2.8.1+0"
[[Hyperscript]]
deps = ["Test"]
git-tree-sha1 = "8d511d5b81240fc8e6802386302675bdf47737b9"
uuid = "47d2ed2b-36de-50cf-bf87-49c2cf4b8b91"
version = "0.0.4"
[[HypertextLiteral]]
git-tree-sha1 = "f6532909bf3d40b308a0f360b6a0e626c0e263a8"
uuid = "ac1192a8-f4b3-4bfe-ba22-af5b92cd3ab2"
version = "0.9.1"
[[IOCapture]]
deps = ["Logging", "Random"]
git-tree-sha1 = "f7be53659ab06ddc986428d3a9dcc95f6fa6705a"
uuid = "b5f81e59-6552-4d32-b1f0-c071b021bf89"
version = "0.2.2"
[[IfElse]]
git-tree-sha1 = "28e837ff3e7a6c3cdb252ce49fb412c8eb3caeef"
uuid = "615f187c-cbe4-4ef1-ba3b-2fcf58d6d173"
version = "0.1.0"
[[ImageCore]]
deps = ["AbstractFFTs", "ColorVectorSpace", "Colors", "FixedPointNumbers", "Graphics", "MappedArrays", "MosaicViews", "OffsetArrays", "PaddedViews", "Reexport"]
git-tree-sha1 = "9a5c62f231e5bba35695a20988fc7cd6de7eeb5a"
uuid = "a09fc81d-aa75-5fe9-8630-4744c3626534"
version = "0.9.3"
[[ImageIO]]
deps = ["FileIO", "Netpbm", "OpenEXR", "PNGFiles", "TiffImages", "UUIDs"]
git-tree-sha1 = "13c826abd23931d909e4c5538643d9691f62a617"
uuid = "82e4d734-157c-48bb-816b-45c225c6df19"
version = "0.5.8"
[[ImageMagick]]
deps = ["FileIO", "ImageCore", "ImageMagick_jll", "InteractiveUtils", "Libdl", "Pkg", "Random"]
git-tree-sha1 = "5bc1cb62e0c5f1005868358db0692c994c3a13c6"
uuid = "6218d12a-5da1-5696-b52f-db25d2ecc6d1"
version = "1.2.1"
[[ImageMagick_jll]]
deps = ["Artifacts", "JLLWrappers", "JpegTurbo_jll", "Libdl", "Libtiff_jll", "Pkg", "Zlib_jll", "libpng_jll"]
git-tree-sha1 = "ea2b6fd947cdfc43c6b8c15cff982533ec1f72cd"
uuid = "c73af94c-d91f-53ed-93a7-00f77d67a9d7"
version = "6.9.12+0"
[[Imath_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "87f7662e03a649cffa2e05bf19c303e168732d3e"
uuid = "905a6f67-0a94-5f89-b386-d35d92009cd1"
version = "3.1.2+0"
[[IndirectArrays]]
git-tree-sha1 = "012e604e1c7458645cb8b436f8fba789a51b257f"
uuid = "9b13fd28-a010-5f03-acff-a1bbcff69959"
version = "1.0.0"
[[Inflate]]
git-tree-sha1 = "f5fc07d4e706b84f72d54eedcc1c13d92fb0871c"
uuid = "d25df0c9-e2be-5dd7-82c8-3ad0b3e990b9"
version = "0.1.2"
[[IniFile]]
deps = ["Test"]
git-tree-sha1 = "098e4d2c533924c921f9f9847274f2ad89e018b8"
uuid = "83e8ac13-25f8-5344-8a64-a9f2b223428f"
version = "0.5.0"
[[IntelOpenMP_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "d979e54b71da82f3a65b62553da4fc3d18c9004c"
uuid = "1d5cc7b8-4909-519e-a0f8-d0f5ad9712d0"
version = "2018.0.3+2"
[[InteractiveUtils]]
deps = ["Markdown"]
uuid = "b77e0a4c-d291-57a0-90e8-8db25a27a240"
[[Interpolations]]
deps = ["AxisAlgorithms", "ChainRulesCore", "LinearAlgebra", "OffsetArrays", "Random", "Ratios", "Requires", "SharedArrays", "SparseArrays", "StaticArrays", "WoodburyMatrices"]
git-tree-sha1 = "61aa005707ea2cebf47c8d780da8dc9bc4e0c512"
uuid = "a98d9a8b-a2ab-59e6-89dd-64a1c18fca59"
version = "0.13.4"
[[IntervalSets]]
deps = ["Dates", "EllipsisNotation", "Statistics"]
git-tree-sha1 = "3cc368af3f110a767ac786560045dceddfc16758"
uuid = "8197267c-284f-5f27-9208-e0e47529a953"
version = "0.5.3"
[[InvertedIndices]]
git-tree-sha1 = "bee5f1ef5bf65df56bdd2e40447590b272a5471f"
uuid = "41ab1584-1d38-5bbf-9106-f11c6c58b48f"
version = "1.1.0"
[[IrrationalConstants]]
git-tree-sha1 = "7fd44fd4ff43fc60815f8e764c0f352b83c49151"
uuid = "92d709cd-6900-40b7-9082-c6be49f344b6"
version = "0.1.1"
[[Isoband]]
deps = ["isoband_jll"]
git-tree-sha1 = "f9b6d97355599074dc867318950adaa6f9946137"
uuid = "f1662d9f-8043-43de-a69a-05efc1cc6ff4"
version = "0.1.1"
[[IterTools]]
git-tree-sha1 = "05110a2ab1fc5f932622ffea2a003221f4782c18"
uuid = "c8e1da08-722c-5040-9ed9-7db0dc04731e"
version = "1.3.0"
[[IterableTables]]
deps = ["DataValues", "IteratorInterfaceExtensions", "Requires", "TableTraits", "TableTraitsUtils"]
git-tree-sha1 = "70300b876b2cebde43ebc0df42bc8c94a144e1b4"
uuid = "1c8ee90f-4401-5389-894e-7a04a3dc0f4d"
version = "1.0.0"
[[IteratorInterfaceExtensions]]
git-tree-sha1 = "a3f24677c21f5bbe9d2a714f95dcd58337fb2856"
uuid = "82899510-4779-5014-852e-03e436cf321d"
version = "1.0.0"
[[JLLWrappers]]
deps = ["Preferences"]
git-tree-sha1 = "642a199af8b68253517b80bd3bfd17eb4e84df6e"
uuid = "692b3bcd-3c85-4b1f-b108-f13ce0eb3210"
version = "1.3.0"
[[JSON]]
deps = ["Dates", "Mmap", "Parsers", "Unicode"]
git-tree-sha1 = "8076680b162ada2a031f707ac7b4953e30667a37"
uuid = "682c06a0-de6a-54ab-a142-c8b1cf79cde6"
version = "0.21.2"
[[JSON3]]
deps = ["Dates", "Mmap", "Parsers", "StructTypes", "UUIDs"]
git-tree-sha1 = "7d58534ffb62cd947950b3aa9b993e63307a6125"
uuid = "0f8b85d8-7281-11e9-16c2-39a750bddbf1"
version = "1.9.2"
[[JSServe]]
deps = ["Base64", "CodecZlib", "Colors", "HTTP", "Hyperscript", "JSON3", "LinearAlgebra", "Markdown", "MsgPack", "Observables", "SHA", "Sockets", "Tables", "Test", "UUIDs", "WebSockets", "WidgetsBase"]
git-tree-sha1 = "91101a4b8ac8eefeed6ca8eb4f663fc660e4d9f9"
uuid = "824d6782-a2ef-11e9-3a09-e5662e0c26f9"
version = "1.2.3"
[[JpegTurbo_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "d735490ac75c5cb9f1b00d8b5509c11984dc6943"
uuid = "aacddb02-875f-59d6-b918-886e6ef4fbf8"
version = "2.1.0+0"
[[KernelDensity]]
deps = ["Distributions", "DocStringExtensions", "FFTW", "Interpolations", "StatsBase"]
git-tree-sha1 = "591e8dc09ad18386189610acafb970032c519707"
uuid = "5ab0869b-81aa-558d-bb23-cbf5423bbe9b"
version = "0.6.3"
[[LAME_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "f6250b16881adf048549549fba48b1161acdac8c"
uuid = "c1c5ebd0-6772-5130-a774-d5fcae4a789d"
version = "3.100.1+0"
[[LZO_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "e5b909bcf985c5e2605737d2ce278ed791b89be6"
uuid = "dd4b983a-f0e5-5f8d-a1b7-129d4a5fb1ac"
version = "2.10.1+0"
[[LaTeXStrings]]
git-tree-sha1 = "c7f1c695e06c01b95a67f0cd1d34994f3e7db104"
uuid = "b964fa9f-0449-5b57-a5c2-d3ea65f4040f"
version = "1.2.1"
[[Latexify]]
deps = ["Formatting", "InteractiveUtils", "LaTeXStrings", "MacroTools", "Markdown", "Printf", "Requires"]
git-tree-sha1 = "95d36f32dde312e694c1de5714821efc4b010815"
uuid = "23fbe1c1-3f47-55db-b15f-69d7ec21a316"
version = "0.15.7"
[[LazyArtifacts]]
deps = ["Artifacts", "Pkg"]
uuid = "4af54fe1-eca0-43a8-85a7-787d91b784e3"
[[LibCURL]]
deps = ["LibCURL_jll", "MozillaCACerts_jll"]
uuid = "b27032c2-a3e7-50c8-80cd-2d36dbcbfd21"
[[LibCURL_jll]]
deps = ["Artifacts", "LibSSH2_jll", "Libdl", "MbedTLS_jll", "Zlib_jll", "nghttp2_jll"]
uuid = "deac9b47-8bc7-5906-a0fe-35ac56dc84c0"
[[LibGit2]]
deps = ["Base64", "NetworkOptions", "Printf", "SHA"]
uuid = "76f85450-5226-5b5a-8eaa-529ad045b433"
[[LibSSH2_jll]]
deps = ["Artifacts", "Libdl", "MbedTLS_jll"]
uuid = "29816b5a-b9ab-546f-933c-edad1886dfa8"
[[Libdl]]
uuid = "8f399da3-3557-5675-b5ff-fb832c97cbdb"
[[Libffi_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "0b4a5d71f3e5200a7dff793393e09dfc2d874290"
uuid = "e9f186c6-92d2-5b65-8a66-fee21dc1b490"
version = "3.2.2+1"
[[Libgcrypt_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Libgpg_error_jll", "Pkg"]
git-tree-sha1 = "64613c82a59c120435c067c2b809fc61cf5166ae"
uuid = "d4300ac3-e22c-5743-9152-c294e39db1e4"
version = "1.8.7+0"
[[Libglvnd_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg", "Xorg_libX11_jll", "Xorg_libXext_jll"]
git-tree-sha1 = "7739f837d6447403596a75d19ed01fd08d6f56bf"
uuid = "7e76a0d4-f3c7-5321-8279-8d96eeed0f29"
version = "1.3.0+3"
[[Libgpg_error_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "c333716e46366857753e273ce6a69ee0945a6db9"
uuid = "7add5ba3-2f88-524e-9cd5-f83b8a55f7b8"
version = "1.42.0+0"
[[Libiconv_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "42b62845d70a619f063a7da093d995ec8e15e778"
uuid = "94ce4f54-9a6c-5748-9c1c-f9c7231a4531"
version = "1.16.1+1"
[[Libmount_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "9c30530bf0effd46e15e0fdcf2b8636e78cbbd73"
uuid = "4b2f31a3-9ecc-558c-b454-b3730dcb73e9"
version = "2.35.0+0"
[[Libtiff_jll]]
deps = ["Artifacts", "JLLWrappers", "JpegTurbo_jll", "Libdl", "Pkg", "Zlib_jll", "Zstd_jll"]
git-tree-sha1 = "340e257aada13f95f98ee352d316c3bed37c8ab9"
uuid = "89763e89-9b03-5906-acba-b20f662cd828"
version = "4.3.0+0"
[[Libuuid_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "7f3efec06033682db852f8b3bc3c1d2b0a0ab066"
uuid = "38a345b3-de98-5d2b-a5d3-14cd9215e700"
version = "2.36.0+0"
[[LinearAlgebra]]
deps = ["Libdl"]
uuid = "37e2e46d-f89d-539d-b4ee-838fcccc9c8e"
[[LogExpFunctions]]
deps = ["ChainRulesCore", "DocStringExtensions", "IrrationalConstants", "LinearAlgebra"]
git-tree-sha1 = "34dc30f868e368f8a17b728a1238f3fcda43931a"
uuid = "2ab3a3ac-af41-5b50-aa03-7779005ae688"
version = "0.3.3"
[[Logging]]
uuid = "56ddb016-857b-54e1-b83d-db4d58db5568"
[[MKL_jll]]
deps = ["Artifacts", "IntelOpenMP_jll", "JLLWrappers", "LazyArtifacts", "Libdl", "Pkg"]
git-tree-sha1 = "5455aef09b40e5020e1520f551fa3135040d4ed0"
uuid = "856f044c-d86e-5d09-b602-aeab76dc8ba7"
version = "2021.1.1+2"
[[MacroTools]]
deps = ["Markdown", "Random"]
git-tree-sha1 = "5a5bc6bf062f0f95e62d0fe0a2d99699fed82dd9"
uuid = "1914dd2f-81c6-5fcd-8719-6d5c9610ff09"
version = "0.5.8"
[[Makie]]
deps = ["Animations", "Base64", "ColorBrewer", "ColorSchemes", "ColorTypes", "Colors", "Contour", "Distributions", "DocStringExtensions", "FFMPEG", "FileIO", "FixedPointNumbers", "Formatting", "FreeType", "FreeTypeAbstraction", "GeometryBasics", "GridLayoutBase", "ImageIO", "IntervalSets", "Isoband", "KernelDensity", "LaTeXStrings", "LinearAlgebra", "MakieCore", "Markdown", "Match", "MathTeXEngine", "Observables", "Packing", "PlotUtils", "PolygonOps", "Printf", "Random", "RelocatableFolders", "Serialization", "Showoff", "SignedDistanceFields", "SparseArrays", "StaticArrays", "Statistics", "StatsBase", "StatsFuns", "StructArrays", "UnicodeFun"]
git-tree-sha1 = "7e49f989e7c7f50fe55bd92d45329c9cf3f2583d"
uuid = "ee78f7c6-11fb-53f2-987a-cfe4a2b5a57a"
version = "0.15.2"
[[MakieCore]]
deps = ["Observables"]
git-tree-sha1 = "7bcc8323fb37523a6a51ade2234eee27a11114c8"
uuid = "20f20a25-4f0e-4fdf-b5d1-57303727442b"
version = "0.1.3"
[[MappedArrays]]
git-tree-sha1 = "e8b359ef06ec72e8c030463fe02efe5527ee5142"
uuid = "dbb5928d-eab1-5f90-85c2-b9b0edb7c900"
version = "0.4.1"
[[Markdown]]
deps = ["Base64"]
uuid = "d6f4376e-aef5-505a-96c1-9c027394607a"
[[Match]]
git-tree-sha1 = "5cf525d97caf86d29307150fcba763a64eaa9cbe"
uuid = "7eb4fadd-790c-5f42-8a69-bfa0b872bfbf"
version = "1.1.0"
[[MathTeXEngine]]
deps = ["AbstractTrees", "Automa", "DataStructures", "FreeTypeAbstraction", "GeometryBasics", "LaTeXStrings", "REPL", "RelocatableFolders", "Test"]
git-tree-sha1 = "70e733037bbf02d691e78f95171a1fa08cdc6332"
uuid = "0a4f8689-d25c-4efe-a92b-7142dfc1aa53"
version = "0.2.1"
[[MbedTLS]]
deps = ["Dates", "MbedTLS_jll", "Random", "Sockets"]
git-tree-sha1 = "1c38e51c3d08ef2278062ebceade0e46cefc96fe"
uuid = "739be429-bea8-5141-9913-cc70e7f3736d"
version = "1.0.3"
[[MbedTLS_jll]]
deps = ["Artifacts", "Libdl"]
uuid = "c8ffd9c3-330d-5841-b78e-0817d7145fa1"
[[Measures]]
git-tree-sha1 = "e498ddeee6f9fdb4551ce855a46f54dbd900245f"
uuid = "442fdcdd-2543-5da2-b0f3-8c86c306513e"
version = "0.3.1"
[[Missings]]
deps = ["DataAPI"]
git-tree-sha1 = "bf210ce90b6c9eed32d25dbcae1ebc565df2687f"
uuid = "e1d29d7a-bbdc-5cf2-9ac0-f12de2c33e28"
version = "1.0.2"
[[Mmap]]
uuid = "a63ad114-7e13-5084-954f-fe012c677804"
[[MosaicViews]]
deps = ["MappedArrays", "OffsetArrays", "PaddedViews", "StackViews"]
git-tree-sha1 = "b34e3bc3ca7c94914418637cb10cc4d1d80d877d"
uuid = "e94cdb99-869f-56ef-bcf0-1ae2bcbe0389"
version = "0.3.3"
[[MozillaCACerts_jll]]
uuid = "14a3606d-f60d-562e-9121-12d972cd8159"
[[MsgPack]]
deps = ["Serialization"]
git-tree-sha1 = "a8cbf066b54d793b9a48c5daa5d586cf2b5bd43d"
uuid = "99f44e22-a591-53d1-9472-aa23ef4bd671"
version = "1.1.0"
[[NaNMath]]
git-tree-sha1 = "bfe47e760d60b82b66b61d2d44128b62e3a369fb"
uuid = "77ba4419-2d1f-58cd-9bb1-8ffee604a2e3"
version = "0.3.5"
[[Netpbm]]
deps = ["FileIO", "ImageCore"]
git-tree-sha1 = "18efc06f6ec36a8b801b23f076e3c6ac7c3bf153"
uuid = "f09324ee-3d7c-5217-9330-fc30815ba969"
version = "1.0.2"
[[NetworkOptions]]
uuid = "ca575930-c2e3-43a9-ace4-1e988b2c1908"
[[Observables]]
git-tree-sha1 = "fe29afdef3d0c4a8286128d4e45cc50621b1e43d"
uuid = "510215fc-4207-5dde-b226-833fc4488ee2"
version = "0.4.0"
[[OffsetArrays]]
deps = ["Adapt"]
git-tree-sha1 = "c0e9e582987d36d5a61e650e6e543b9e44d9914b"
uuid = "6fe1bfb0-de20-5000-8ca7-80f57d26f881"
version = "1.10.7"
[[Ogg_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "7937eda4681660b4d6aeeecc2f7e1c81c8ee4e2f"
uuid = "e7412a2a-1a6e-54c0-be00-318e2571c051"
version = "1.3.5+0"
[[OpenEXR]]
deps = ["Colors", "FileIO", "OpenEXR_jll"]
git-tree-sha1 = "327f53360fdb54df7ecd01e96ef1983536d1e633"
uuid = "52e1d378-f018-4a11-a4be-720524705ac7"
version = "0.3.2"
[[OpenEXR_jll]]
deps = ["Artifacts", "Imath_jll", "JLLWrappers", "Libdl", "Pkg", "Zlib_jll"]
git-tree-sha1 = "923319661e9a22712f24596ce81c54fc0366f304"
uuid = "18a262bb-aa17-5467-a713-aee519bc75cb"
version = "3.1.1+0"
[[OpenLibm_jll]]
deps = ["Artifacts", "Libdl"]
uuid = "05823500-19ac-5b8b-9628-191a04bc5112"
[[OpenSSL_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "15003dcb7d8db3c6c857fda14891a539a8f2705a"
uuid = "458c3c95-2e84-50aa-8efc-19380b2a3a95"
version = "1.1.10+0"
[[OpenSpecFun_jll]]
deps = ["Artifacts", "CompilerSupportLibraries_jll", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "13652491f6856acfd2db29360e1bbcd4565d04f1"
uuid = "efe28fd5-8261-553b-a9e1-b2916fc3738e"
version = "0.5.5+0"
[[Opus_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "51a08fb14ec28da2ec7a927c4337e4332c2a4720"
uuid = "91d4177d-7536-5919-b921-800302f37372"
version = "1.3.2+0"
[[OrderedCollections]]
git-tree-sha1 = "85f8e6578bf1f9ee0d11e7bb1b1456435479d47c"
uuid = "bac558e1-5e72-5ebc-8fee-abe8a469f55d"
version = "1.4.1"
[[PCRE_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "b2a7af664e098055a7529ad1a900ded962bca488"
uuid = "2f80f16e-611a-54ab-bc61-aa92de5b98fc"
version = "8.44.0+0"
[[PDMats]]
deps = ["LinearAlgebra", "SparseArrays", "SuiteSparse"]
git-tree-sha1 = "4dd403333bcf0909341cfe57ec115152f937d7d8"
uuid = "90014a1f-27ba-587c-ab20-58faa44d9150"
version = "0.11.1"
[[PNGFiles]]
deps = ["Base64", "CEnum", "ImageCore", "IndirectArrays", "OffsetArrays", "libpng_jll"]
git-tree-sha1 = "85e3436b18980e47604dd0909e37e2f066f54398"
uuid = "f57f5aa1-a3ce-4bc8-8ab9-96f992907883"
version = "0.3.10"
[[Packing]]
deps = ["GeometryBasics"]
git-tree-sha1 = "1155f6f937fa2b94104162f01fa400e192e4272f"
uuid = "19eb6ba3-879d-56ad-ad62-d5c202156566"
version = "0.4.2"
[[PaddedViews]]
deps = ["OffsetArrays"]
git-tree-sha1 = "646eed6f6a5d8df6708f15ea7e02a7a2c4fe4800"
uuid = "5432bcbf-9aad-5242-b902-cca2824c8663"
version = "0.5.10"
[[Parsers]]
deps = ["Dates"]
git-tree-sha1 = "bfd7d8c7fd87f04543810d9cbd3995972236ba1b"
uuid = "69de0a69-1ddd-5017-9359-2bf0b02dc9f0"
version = "1.1.2"
[[Pixman_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "b4f5d02549a10e20780a24fce72bea96b6329e29"
uuid = "30392449-352a-5448-841d-b1acce4e97dc"
version = "0.40.1+0"
[[Pkg]]
deps = ["Artifacts", "Dates", "Downloads", "LibGit2", "Libdl", "Logging", "Markdown", "Printf", "REPL", "Random", "SHA", "Serialization", "TOML", "Tar", "UUIDs", "p7zip_jll"]
uuid = "44cfe95a-1eb2-52ea-b672-e2afdf69b78f"
[[PkgVersion]]
deps = ["Pkg"]
git-tree-sha1 = "a7a7e1a88853564e551e4eba8650f8c38df79b37"
uuid = "eebad327-c553-4316-9ea0-9fa01ccd7688"
version = "0.1.1"
[[PlotThemes]]
deps = ["PlotUtils", "Requires", "Statistics"]
git-tree-sha1 = "a3a964ce9dc7898193536002a6dd892b1b5a6f1d"
uuid = "ccf2f8ad-2431-5c83-bf29-c5338b663b6a"
version = "2.0.1"
[[PlotUtils]]
deps = ["ColorSchemes", "Colors", "Dates", "Printf", "Random", "Reexport", "Statistics"]
git-tree-sha1 = "b084324b4af5a438cd63619fd006614b3b20b87b"
uuid = "995b91a9-d308-5afd-9ec6-746e21dbc043"
version = "1.0.15"
[[Plots]]
deps = ["Base64", "Contour", "Dates", "Downloads", "FFMPEG", "FixedPointNumbers", "GR", "GeometryBasics", "JSON", "Latexify", "LinearAlgebra", "Measures", "NaNMath", "PlotThemes", "PlotUtils", "Printf", "REPL", "Random", "RecipesBase", "RecipesPipeline", "Reexport", "Requires", "Scratch", "Showoff", "SparseArrays", "Statistics", "StatsBase", "UUIDs"]
git-tree-sha1 = "ba43b248a1f04a9667ca4a9f782321d9211aa68e"
uuid = "91a5bcdd-55d7-5caf-9e0b-520d859cae80"
version = "1.22.6"
[[PlutoUI]]
deps = ["Base64", "Dates", "Hyperscript", "HypertextLiteral", "IOCapture", "InteractiveUtils", "JSON", "Logging", "Markdown", "Random", "Reexport", "UUIDs"]
git-tree-sha1 = "4c8a7d080daca18545c56f1cac28710c362478f3"
uuid = "7f904dfe-b85e-4ff6-b463-dae2292396a8"
version = "0.7.16"
[[PolygonOps]]
git-tree-sha1 = "77b3d3605fc1cd0b42d95eba87dfcd2bf67d5ff6"
uuid = "647866c9-e3ac-4575-94e7-e3d426903924"
version = "0.1.2"
[[PooledArrays]]
deps = ["DataAPI", "Future"]
git-tree-sha1 = "a193d6ad9c45ada72c14b731a318bedd3c2f00cf"
uuid = "2dfb63ee-cc39-5dd5-95bd-886bf059d720"
version = "1.3.0"
[[Preferences]]
deps = ["TOML"]
git-tree-sha1 = "00cfd92944ca9c760982747e9a1d0d5d86ab1e5a"
uuid = "21216c6a-2e73-6563-6e65-726566657250"
version = "1.2.2"
[[PrettyTables]]
deps = ["Crayons", "Formatting", "Markdown", "Reexport", "Tables"]
git-tree-sha1 = "69fd065725ee69950f3f58eceb6d144ce32d627d"
uuid = "08abe8d2-0d0c-5749-adfa-8a2ac140af0d"
version = "1.2.2"
[[Printf]]
deps = ["Unicode"]
uuid = "de0858da-6303-5e67-8744-51eddeeeb8d7"
[[ProgressMeter]]
deps = ["Distributed", "Printf"]
git-tree-sha1 = "afadeba63d90ff223a6a48d2009434ecee2ec9e8"
uuid = "92933f4c-e287-5a05-a399-4b506db050ca"
version = "1.7.1"
[[Qt5Base_jll]]
deps = ["Artifacts", "CompilerSupportLibraries_jll", "Fontconfig_jll", "Glib_jll", "JLLWrappers", "Libdl", "Libglvnd_jll", "OpenSSL_jll", "Pkg", "Xorg_libXext_jll", "Xorg_libxcb_jll", "Xorg_xcb_util_image_jll", "Xorg_xcb_util_keysyms_jll", "Xorg_xcb_util_renderutil_jll", "Xorg_xcb_util_wm_jll", "Zlib_jll", "xkbcommon_jll"]
git-tree-sha1 = "ad368663a5e20dbb8d6dc2fddeefe4dae0781ae8"
uuid = "ea2cea3b-5b76-57ae-a6ef-0a8af62496e1"
version = "5.15.3+0"
[[QuadGK]]
deps = ["DataStructures", "LinearAlgebra"]
git-tree-sha1 = "78aadffb3efd2155af139781b8a8df1ef279ea39"
uuid = "1fd47b50-473d-5c70-9696-f719f8f3bcdc"
version = "2.4.2"
[[Query]]
deps = ["DataValues", "IterableTables", "MacroTools", "QueryOperators", "Statistics"]
git-tree-sha1 = "a66aa7ca6f5c29f0e303ccef5c8bd55067df9bbe"
uuid = "1a8c2f83-1ff3-5112-b086-8aa67b057ba1"
version = "1.0.0"
[[QueryOperators]]
deps = ["DataStructures", "DataValues", "IteratorInterfaceExtensions", "TableShowUtils"]
git-tree-sha1 = "911c64c204e7ecabfd1872eb93c49b4e7c701f02"
uuid = "2aef5ad7-51ca-5a8f-8e88-e75cf067b44b"
version = "0.9.3"
[[REPL]]
deps = ["InteractiveUtils", "Markdown", "Sockets", "Unicode"]
uuid = "3fa0cd96-eef1-5676-8a61-b3b8758bbffb"
[[Random]]
deps = ["Serialization"]
uuid = "9a3f8284-a2c9-5f02-9a11-845980a1fd5c"
[[Ratios]]
deps = ["Requires"]
git-tree-sha1 = "01d341f502250e81f6fec0afe662aa861392a3aa"
uuid = "c84ed2f1-dad5-54f0-aa8e-dbefe2724439"
version = "0.4.2"
[[RecipesBase]]
git-tree-sha1 = "44a75aa7a527910ee3d1751d1f0e4148698add9e"
uuid = "3cdcf5f2-1ef4-517c-9805-6587b60abb01"
version = "1.1.2"
[[RecipesPipeline]]
deps = ["Dates", "NaNMath", "PlotUtils", "RecipesBase"]
git-tree-sha1 = "7ad0dfa8d03b7bcf8c597f59f5292801730c55b8"
uuid = "01d81517-befc-4cb6-b9ec-a95719d0359c"
version = "0.4.1"
[[Reexport]]
git-tree-sha1 = "45e428421666073eab6f2da5c9d310d99bb12f9b"
uuid = "189a3867-3050-52da-a836-e630ba90ab69"
version = "1.2.2"
[[RelocatableFolders]]
deps = ["SHA", "Scratch"]
git-tree-sha1 = "df2be5142a2a3db2da37b21d87c9fa7973486bfd"
uuid = "05181044-ff0b-4ac5-8273-598c1e38db00"
version = "0.1.2"
[[Requires]]
deps = ["UUIDs"]
git-tree-sha1 = "4036a3bd08ac7e968e27c203d45f5fff15020621"
uuid = "ae029012-a4dd-5104-9daa-d747884805df"
version = "1.1.3"
[[Rmath]]
deps = ["Random", "Rmath_jll"]
git-tree-sha1 = "bf3188feca147ce108c76ad82c2792c57abe7b1f"
uuid = "79098fc4-a85e-5d69-aa6a-4863f24498fa"
version = "0.7.0"
[[Rmath_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "68db32dff12bb6127bac73c209881191bf0efbb7"
uuid = "f50d1b31-88e8-58de-be2c-1cc44531875f"
version = "0.3.0+0"
[[SHA]]
uuid = "ea8e919c-243c-51af-8825-aaa63cd721ce"
[[SIMD]]
git-tree-sha1 = "9ba33637b24341aba594a2783a502760aa0bff04"
uuid = "fdea26ae-647d-5447-a871-4b548cad5224"
version = "3.3.1"
[[ScanByte]]
deps = ["Libdl", "SIMD"]
git-tree-sha1 = "9cc2955f2a254b18be655a4ee70bc4031b2b189e"
uuid = "7b38b023-a4d7-4c5e-8d43-3f3097f304eb"
version = "0.3.0"
[[Scratch]]
deps = ["Dates"]
git-tree-sha1 = "0b4b7f1393cff97c33891da2a0bf69c6ed241fda"
uuid = "6c6a2e73-6563-6170-7368-637461726353"
version = "1.1.0"
[[SentinelArrays]]
deps = ["Dates", "Random"]
git-tree-sha1 = "54f37736d8934a12a200edea2f9206b03bdf3159"
uuid = "91c51154-3ec4-41a3-a24f-3f23e20d615c"
version = "1.3.7"
[[Serialization]]
uuid = "9e88b42a-f829-5b0c-bbe9-9e923198166b"
[[ShaderAbstractions]]
deps = ["ColorTypes", "FixedPointNumbers", "GeometryBasics", "LinearAlgebra", "Observables", "StaticArrays", "StructArrays", "Tables"]
git-tree-sha1 = "0d97c895406b552bed78f3a1fe9925248e908ae2"
uuid = "65257c39-d410-5151-9873-9b3e5be5013e"
version = "0.2.8"
[[SharedArrays]]
deps = ["Distributed", "Mmap", "Random", "Serialization"]
uuid = "1a1011a3-84de-559e-8e89-a11a2f7dc383"
[[Showoff]]
deps = ["Dates", "Grisu"]
git-tree-sha1 = "91eddf657aca81df9ae6ceb20b959ae5653ad1de"
uuid = "992d4aef-0814-514b-bc4d-f2e9a6c4116f"
version = "1.0.3"
[[SignedDistanceFields]]
deps = ["Random", "Statistics", "Test"]
git-tree-sha1 = "d263a08ec505853a5ff1c1ebde2070419e3f28e9"
uuid = "73760f76-fbc4-59ce-8f25-708e95d2df96"
version = "0.4.0"
[[Sockets]]
uuid = "6462fe0b-24de-5631-8697-dd941f90decc"
[[SortingAlgorithms]]
deps = ["DataStructures"]
git-tree-sha1 = "b3363d7460f7d098ca0912c69b082f75625d7508"
uuid = "a2af1166-a08f-5f64-846c-94a0d3cef48c"
version = "1.0.1"
[[SparseArrays]]
deps = ["LinearAlgebra", "Random"]
uuid = "2f01184e-e22b-5df5-ae63-d93ebab69eaf"
[[SpecialFunctions]]
deps = ["ChainRulesCore", "IrrationalConstants", "LogExpFunctions", "OpenLibm_jll", "OpenSpecFun_jll"]
git-tree-sha1 = "793793f1df98e3d7d554b65a107e9c9a6399a6ed"
uuid = "276daf66-3868-5448-9aa4-cd146d93841b"
version = "1.7.0"
[[StackViews]]
deps = ["OffsetArrays"]
git-tree-sha1 = "46e589465204cd0c08b4bd97385e4fa79a0c770c"
uuid = "cae243ae-269e-4f55-b966-ac2d0dc13c15"
version = "0.1.1"
[[Static]]
deps = ["IfElse"]
git-tree-sha1 = "a8f30abc7c64a39d389680b74e749cf33f872a70"
uuid = "aedffcd0-7271-4cad-89d0-dc628f76c6d3"
version = "0.3.3"
[[StaticArrays]]
deps = ["LinearAlgebra", "Random", "Statistics"]
git-tree-sha1 = "3c76dde64d03699e074ac02eb2e8ba8254d428da"
uuid = "90137ffa-7385-5640-81b9-e52037218182"
version = "1.2.13"
[[Statistics]]
deps = ["LinearAlgebra", "SparseArrays"]
uuid = "10745b16-79ce-11e8-11f9-7d13ad32a3b2"
[[StatsAPI]]
git-tree-sha1 = "1958272568dc176a1d881acb797beb909c785510"
uuid = "82ae8749-77ed-4fe6-ae5f-f523153014b0"
version = "1.0.0"
[[StatsBase]]
deps = ["DataAPI", "DataStructures", "LinearAlgebra", "LogExpFunctions", "Missings", "Printf", "Random", "SortingAlgorithms", "SparseArrays", "Statistics", "StatsAPI"]
git-tree-sha1 = "65fb73045d0e9aaa39ea9a29a5e7506d9ef6511f"
uuid = "2913bbd2-ae8a-5f71-8c99-4fb6c76f3a91"
version = "0.33.11"
[[StatsFuns]]
deps = ["ChainRulesCore", "IrrationalConstants", "LogExpFunctions", "Reexport", "Rmath", "SpecialFunctions"]
git-tree-sha1 = "95072ef1a22b057b1e80f73c2a89ad238ae4cfff"
uuid = "4c63d2b9-4356-54db-8cca-17b64c39e42c"
version = "0.9.12"
[[StructArrays]]
deps = ["Adapt", "DataAPI", "StaticArrays", "Tables"]
git-tree-sha1 = "2ce41e0d042c60ecd131e9fb7154a3bfadbf50d3"
uuid = "09ab397b-f2b6-538f-b94a-2f83cf4a842a"
version = "0.6.3"
[[StructTypes]]
deps = ["Dates", "UUIDs"]
git-tree-sha1 = "d24a825a95a6d98c385001212dc9020d609f2d4f"
uuid = "856f2bd8-1eba-4b0a-8007-ebc267875bd4"
version = "1.8.1"
[[SuiteSparse]]
deps = ["Libdl", "LinearAlgebra", "Serialization", "SparseArrays"]
uuid = "4607b0f0-06f3-5cda-b6b1-a6196a1729e9"
[[TOML]]
deps = ["Dates"]
uuid = "fa267f1f-6049-4f14-aa54-33bafae1ed76"
[[TableShowUtils]]
deps = ["DataValues", "Dates", "JSON", "Markdown", "Test"]
git-tree-sha1 = "14c54e1e96431fb87f0d2f5983f090f1b9d06457"
uuid = "5e66a065-1f0a-5976-b372-e0b8c017ca10"
version = "0.2.5"
[[TableTraits]]
deps = ["IteratorInterfaceExtensions"]
git-tree-sha1 = "c06b2f539df1c6efa794486abfb6ed2022561a39"
uuid = "3783bdb8-4a98-5b6b-af9a-565f29a5fe9c"
version = "1.0.1"
[[TableTraitsUtils]]
deps = ["DataValues", "IteratorInterfaceExtensions", "Missings", "TableTraits"]
git-tree-sha1 = "78fecfe140d7abb480b53a44f3f85b6aa373c293"
uuid = "382cd787-c1b6-5bf2-a167-d5b971a19bda"
version = "1.0.2"
[[Tables]]
deps = ["DataAPI", "DataValueInterfaces", "IteratorInterfaceExtensions", "LinearAlgebra", "TableTraits", "Test"]
git-tree-sha1 = "fed34d0e71b91734bf0a7e10eb1bb05296ddbcd0"
uuid = "bd369af6-aec1-5ad0-b16a-f7cc5008161c"
version = "1.6.0"
[[Tar]]
deps = ["ArgTools", "SHA"]
uuid = "a4e569a6-e804-4fa4-b0f3-eef7a1d5b13e"
[[TensorCore]]
deps = ["LinearAlgebra"]
git-tree-sha1 = "1feb45f88d133a655e001435632f019a9a1bcdb6"
uuid = "62fd8b95-f654-4bbd-a8a5-9c27f68ccd50"
version = "0.1.1"
[[Test]]
deps = ["InteractiveUtils", "Logging", "Random", "Serialization"]
uuid = "8dfed614-e22c-5e08-85e1-65c5234f0b40"
[[TiffImages]]
deps = ["ColorTypes", "DocStringExtensions", "FileIO", "FixedPointNumbers", "IndirectArrays", "Inflate", "OffsetArrays", "OrderedCollections", "PkgVersion", "ProgressMeter"]
git-tree-sha1 = "945b8d87c5e8d5e34e6207ee15edb9d11ae44716"
uuid = "731e570b-9d59-4bfa-96dc-6df516fadf69"
version = "0.4.3"
[[TranscodingStreams]]
deps = ["Random", "Test"]
git-tree-sha1 = "216b95ea110b5972db65aa90f88d8d89dcb8851c"
uuid = "3bb67fe8-82b1-5028-8e26-92a6c54297fa"
version = "0.9.6"
[[URIs]]
git-tree-sha1 = "97bbe755a53fe859669cd907f2d96aee8d2c1355"
uuid = "5c2747f8-b7ea-4ff2-ba2e-563bfd36b1d4"
version = "1.3.0"
[[UUIDs]]
deps = ["Random", "SHA"]
uuid = "cf7118a7-6976-5b1a-9a39-7adc72f591a4"
[[Unicode]]
uuid = "4ec0a83e-493e-50e2-b9ac-8f72acf5a8f5"
[[UnicodeFun]]
deps = ["REPL"]
git-tree-sha1 = "53915e50200959667e78a92a418594b428dffddf"
uuid = "1cfade01-22cf-5700-b092-accc4b62d6e1"
version = "0.4.1"
[[WGLMakie]]
deps = ["Colors", "FileIO", "FreeTypeAbstraction", "GeometryBasics", "Hyperscript", "ImageMagick", "JSServe", "LinearAlgebra", "Makie", "Observables", "ShaderAbstractions", "StaticArrays"]
git-tree-sha1 = "bafa1c4ab77626f8d8199209b740e097ae03805f"
uuid = "276b4fcb-3e11-5398-bf8b-a0c2d153d008"
version = "0.4.6"
[[Wayland_jll]]
deps = ["Artifacts", "Expat_jll", "JLLWrappers", "Libdl", "Libffi_jll", "Pkg", "XML2_jll"]
git-tree-sha1 = "3e61f0b86f90dacb0bc0e73a0c5a83f6a8636e23"
uuid = "a2964d1f-97da-50d4-b82a-358c7fce9d89"
version = "1.19.0+0"
[[Wayland_protocols_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg", "Wayland_jll"]
git-tree-sha1 = "2839f1c1296940218e35df0bbb220f2a79686670"
uuid = "2381bf8a-dfd0-557d-9999-79630e7b1b91"
version = "1.18.0+4"
[[WebSockets]]
deps = ["Base64", "Dates", "HTTP", "Logging", "Sockets"]
git-tree-sha1 = "f91a602e25fe6b89afc93cf02a4ae18ee9384ce3"
uuid = "104b5d7c-a370-577a-8038-80a2059c5097"
version = "1.5.9"
[[WidgetsBase]]
deps = ["Observables"]
git-tree-sha1 = "c1ef6e02bc457c3b23aafc765b94c3dcd25f174d"
uuid = "eead4739-05f7-45a1-878c-cee36b57321c"
version = "0.1.3"
[[WoodburyMatrices]]
deps = ["LinearAlgebra", "SparseArrays"]
git-tree-sha1 = "9398e8fefd83bde121d5127114bd3b6762c764a6"
uuid = "efce3f68-66dc-5838-9240-27a6d6f5f9b6"
version = "0.5.4"
[[XML2_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Libiconv_jll", "Pkg", "Zlib_jll"]
git-tree-sha1 = "1acf5bdf07aa0907e0a37d3718bb88d4b687b74a"
uuid = "02c8fc9c-b97f-50b9-bbe4-9be30ff0a78a"
version = "2.9.12+0"
[[XSLT_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Libgcrypt_jll", "Libgpg_error_jll", "Libiconv_jll", "Pkg", "XML2_jll", "Zlib_jll"]
git-tree-sha1 = "91844873c4085240b95e795f692c4cec4d805f8a"
uuid = "aed1982a-8fda-507f-9586-7b0439959a61"
version = "1.1.34+0"
[[Xorg_libX11_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg", "Xorg_libxcb_jll", "Xorg_xtrans_jll"]
git-tree-sha1 = "5be649d550f3f4b95308bf0183b82e2582876527"
uuid = "4f6342f7-b3d2-589e-9d20-edeb45f2b2bc"
version = "1.6.9+4"
[[Xorg_libXau_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "4e490d5c960c314f33885790ed410ff3a94ce67e"
uuid = "0c0b7dd1-d40b-584c-a123-a41640f87eec"
version = "1.0.9+4"
[[Xorg_libXcursor_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg", "Xorg_libXfixes_jll", "Xorg_libXrender_jll"]
git-tree-sha1 = "12e0eb3bc634fa2080c1c37fccf56f7c22989afd"
uuid = "935fb764-8cf2-53bf-bb30-45bb1f8bf724"
version = "1.2.0+4"
[[Xorg_libXdmcp_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "4fe47bd2247248125c428978740e18a681372dd4"
uuid = "a3789734-cfe1-5b06-b2d0-1dd0d9d62d05"
version = "1.1.3+4"
[[Xorg_libXext_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg", "Xorg_libX11_jll"]
git-tree-sha1 = "b7c0aa8c376b31e4852b360222848637f481f8c3"
uuid = "1082639a-0dae-5f34-9b06-72781eeb8cb3"
version = "1.3.4+4"
[[Xorg_libXfixes_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg", "Xorg_libX11_jll"]
git-tree-sha1 = "0e0dc7431e7a0587559f9294aeec269471c991a4"
uuid = "d091e8ba-531a-589c-9de9-94069b037ed8"
version = "5.0.3+4"
[[Xorg_libXi_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg", "Xorg_libXext_jll", "Xorg_libXfixes_jll"]
git-tree-sha1 = "89b52bc2160aadc84d707093930ef0bffa641246"
uuid = "a51aa0fd-4e3c-5386-b890-e753decda492"
version = "1.7.10+4"
[[Xorg_libXinerama_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg", "Xorg_libXext_jll"]
git-tree-sha1 = "26be8b1c342929259317d8b9f7b53bf2bb73b123"
uuid = "d1454406-59df-5ea1-beac-c340f2130bc3"
version = "1.1.4+4"
[[Xorg_libXrandr_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg", "Xorg_libXext_jll", "Xorg_libXrender_jll"]
git-tree-sha1 = "34cea83cb726fb58f325887bf0612c6b3fb17631"
uuid = "ec84b674-ba8e-5d96-8ba1-2a689ba10484"
version = "1.5.2+4"
[[Xorg_libXrender_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg", "Xorg_libX11_jll"]
git-tree-sha1 = "19560f30fd49f4d4efbe7002a1037f8c43d43b96"
uuid = "ea2f1a96-1ddc-540d-b46f-429655e07cfa"
version = "0.9.10+4"
[[Xorg_libpthread_stubs_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "6783737e45d3c59a4a4c4091f5f88cdcf0908cbb"
uuid = "14d82f49-176c-5ed1-bb49-ad3f5cbd8c74"
version = "0.1.0+3"
[[Xorg_libxcb_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg", "XSLT_jll", "Xorg_libXau_jll", "Xorg_libXdmcp_jll", "Xorg_libpthread_stubs_jll"]
git-tree-sha1 = "daf17f441228e7a3833846cd048892861cff16d6"
uuid = "c7cfdc94-dc32-55de-ac96-5a1b8d977c5b"
version = "1.13.0+3"
[[Xorg_libxkbfile_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg", "Xorg_libX11_jll"]
git-tree-sha1 = "926af861744212db0eb001d9e40b5d16292080b2"
uuid = "cc61e674-0454-545c-8b26-ed2c68acab7a"
version = "1.1.0+4"
[[Xorg_xcb_util_image_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg", "Xorg_xcb_util_jll"]
git-tree-sha1 = "0fab0a40349ba1cba2c1da699243396ff8e94b97"
uuid = "12413925-8142-5f55-bb0e-6d7ca50bb09b"
version = "0.4.0+1"
[[Xorg_xcb_util_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg", "Xorg_libxcb_jll"]
git-tree-sha1 = "e7fd7b2881fa2eaa72717420894d3938177862d1"
uuid = "2def613f-5ad1-5310-b15b-b15d46f528f5"
version = "0.4.0+1"
[[Xorg_xcb_util_keysyms_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg", "Xorg_xcb_util_jll"]
git-tree-sha1 = "d1151e2c45a544f32441a567d1690e701ec89b00"
uuid = "975044d2-76e6-5fbe-bf08-97ce7c6574c7"
version = "0.4.0+1"
[[Xorg_xcb_util_renderutil_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg", "Xorg_xcb_util_jll"]
git-tree-sha1 = "dfd7a8f38d4613b6a575253b3174dd991ca6183e"
uuid = "0d47668e-0667-5a69-a72c-f761630bfb7e"
version = "0.3.9+1"
[[Xorg_xcb_util_wm_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg", "Xorg_xcb_util_jll"]
git-tree-sha1 = "e78d10aab01a4a154142c5006ed44fd9e8e31b67"
uuid = "c22f9ab0-d5fe-5066-847c-f4bb1cd4e361"
version = "0.4.1+1"
[[Xorg_xkbcomp_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg", "Xorg_libxkbfile_jll"]
git-tree-sha1 = "4bcbf660f6c2e714f87e960a171b119d06ee163b"
uuid = "35661453-b289-5fab-8a00-3d9160c6a3a4"
version = "1.4.2+4"
[[Xorg_xkeyboard_config_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg", "Xorg_xkbcomp_jll"]
git-tree-sha1 = "5c8424f8a67c3f2209646d4425f3d415fee5931d"
uuid = "33bec58e-1273-512f-9401-5d533626f822"
version = "2.27.0+4"
[[Xorg_xtrans_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "79c31e7844f6ecf779705fbc12146eb190b7d845"
uuid = "c5fb5394-a638-5e4d-96e5-b29de1b5cf10"
version = "1.4.0+3"
[[Zlib_jll]]
deps = ["Libdl"]
uuid = "83775a58-1f1d-513f-b197-d71354ab007a"
[[Zstd_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "cc4bf3fdde8b7e3e9fa0351bdeedba1cf3b7f6e6"
uuid = "3161d3a3-bdf6-5164-811a-617609db77b4"
version = "1.5.0+0"
[[isoband_jll]]
deps = ["Libdl", "Pkg"]
git-tree-sha1 = "a1ac99674715995a536bbce674b068ec1b7d893d"
uuid = "9a68df92-36a6-505f-a73e-abb412b6bfb4"
version = "0.2.2+0"
[[libass_jll]]
deps = ["Artifacts", "Bzip2_jll", "FreeType2_jll", "FriBidi_jll", "HarfBuzz_jll", "JLLWrappers", "Libdl", "Pkg", "Zlib_jll"]
git-tree-sha1 = "5982a94fcba20f02f42ace44b9894ee2b140fe47"
uuid = "0ac62f75-1d6f-5e53-bd7c-93b484bb37c0"
version = "0.15.1+0"
[[libfdk_aac_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "daacc84a041563f965be61859a36e17c4e4fcd55"
uuid = "f638f0a6-7fb0-5443-88ba-1cc74229b280"
version = "2.0.2+0"
[[libpng_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg", "Zlib_jll"]
git-tree-sha1 = "94d180a6d2b5e55e447e2d27a29ed04fe79eb30c"
uuid = "b53b4c65-9356-5827-b1ea-8c7a1a84506f"
version = "1.6.38+0"
[[libvorbis_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Ogg_jll", "Pkg"]
git-tree-sha1 = "c45f4e40e7aafe9d086379e5578947ec8b95a8fb"
uuid = "f27f6e37-5d2b-51aa-960f-b287f2bc3b7a"
version = "1.3.7+0"
[[nghttp2_jll]]
deps = ["Artifacts", "Libdl"]
uuid = "8e850ede-7688-5339-a07c-302acd2aaf8d"
[[p7zip_jll]]
deps = ["Artifacts", "Libdl"]
uuid = "3f19e933-33d8-53b3-aaab-bd5110c3b7a0"
[[x264_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "4fea590b89e6ec504593146bf8b988b2c00922b2"
uuid = "1270edf5-f2f9-52d2-97e9-ab00b5d0237a"
version = "2021.5.5+0"
[[x265_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg"]
git-tree-sha1 = "ee567a171cce03570d77ad3a43e90218e38937a9"
uuid = "dfaa095f-4041-5dcd-9319-2fabd8486b76"
version = "3.5.0+0"
[[xkbcommon_jll]]
deps = ["Artifacts", "JLLWrappers", "Libdl", "Pkg", "Wayland_jll", "Wayland_protocols_jll", "Xorg_libxcb_jll", "Xorg_xkeyboard_config_jll"]
git-tree-sha1 = "ece2350174195bb31de1a63bea3a41ae1aa593b6"
uuid = "d8fb68d0-12a3-5cfd-a85a-d49703b185fd"
version = "0.9.1+5"
"""
# ╔═╡ Cell order:
# ╟─e50f4dc1-99db-439d-9357-fcf523a7f50a
# ╟─9ca215d0-2e8c-11ec-27ae-3bac6ad63ae1
# ╟─d380ac0f-28a7-48f4-8463-9dbdf7f66a16
# ╟─ebaf4b98-9f4a-45bc-ad35-54448f26f90c
# ╟─ffdbdfbd-8627-48d9-8e9c-384455b64ed4
# ╟─b9b5f9a4-431d-40fc-94fe-8d622ba7c5a8
# ╟─eedd9f9b-6425-4b8c-ad1f-7bbedc122072
# ╟─aa0a8370-7919-41e1-9a05-481df4e48ec7
# ╟─6c867bb6-87d6-420f-8665-fe4581ffd0a9
# ╟─a5bc3c03-856b-4ee2-a71c-8c7e1fe3c641
# ╟─ae22a6f0-d857-4229-a003-728d43a50d46
# ╟─51199548-4ec2-4034-b955-8d1f97ddd5ee
# ╟─dd89a21f-ce6b-4a3c-9c22-1f97ac3863a8
# ╠═9ce42874-5a58-4e6a-a544-dfea97146cc2
# ╟─f9fa9a2f-8099-434e-a76c-4b78160f264a
# ╠═1e71d41a-5717-462d-81da-8ac35f22c1db
# ╟─1673eef5-82cf-4eef-8ca2-17d02ecb9b27
# ╠═63ab68f1-b342-4e8c-987d-4fc33166aa3c
# ╟─6e2e4df4-096b-444f-bff3-44c70f3d1dd5
# ╠═6b7b4fbe-622e-407c-8ffc-9fe888354ced
# ╟─f16c8b13-256d-4c1d-a376-4e7d41ecf35d
# ╠═0aed3ddb-b181-4f03-950c-b23e0f153760
# ╟─10f1c03f-ead5-42c5-a5c5-816d52a15653
# ╠═9929fafa-2bc5-4fec-83a4-c8f9b1229b0c
# ╟─b1ec589e-35af-4e34-a663-c72f4b0afe02
# ╠═bfbe894b-a205-4d21-8adf-a26a2052573e
# ╟─48e9011a-dfa3-4665-9e23-2aab30e0d294
# ╟─3f55ecbb-8f26-4813-ac3e-97588830d987
# ╟─c3e6a7e8-c4a2-42ad-9302-cd4be7ee0920
# ╟─554a5530-e1ca-4261-a1e3-bf27846250fc
# ╟─4d5eab4d-8510-45ed-97f9-31c6e3af6ab4
# ╟─99aac39c-f375-42a9-a422-ee1f7ef3a490
# ╟─e615de83-bcc4-4a84-8e94-140989508805
# ╟─29c1aa29-d21f-43c2-b5b4-a2c3443cc983
# ╠═0bdf2bb0-655c-446a-bb79-91746a380701
# ╟─86161dc5-0980-42e2-8455-6b1b07dddeaf
# ╟─66b7f878-c620-4fee-84c0-273bdbc46440
# ╟─7d398c89-f763-4d3b-b196-2949bd91ae9a
# ╟─62705acb-a304-4bd4-ae30-cca46037c7dd
# ╠═ddbeaaf1-a4e4-4a09-a487-9bbdc489c824
# ╟─59454ea0-138c-4005-9c4b-e2e8667189c2
# ╟─0d9d4d97-e1ff-47a5-9a58-c76788b55468
# ╟─959927f2-74b6-411d-89f8-034c031d7422
# ╟─d50d76db-507e-450e-93a1-e0319edaf98a
# ╠═3d52dfab-40d2-4947-9dfe-cc4e6100d75c
# ╟─98d43ce9-d4a6-4b5f-8777-a0af67eddf9f
# ╠═58fd4e5b-da58-4cf1-8c99-32892a146bdd
# ╟─5431903b-e7b0-47f8-a225-9db66468256e
# ╟─447e2730-0bd4-4953-ac2e-c6d12cb5e341
# ╟─baf8bd0f-07b7-4ce6-8850-4f22c4a20ecf
# ╟─dbddc346-e9dd-416d-abf5-98d96a95f3ec
# ╟─d9cd1583-abec-4dc1-a9db-5bbcf74a48c8
# ╟─96ae1d18-a0fd-4846-9d4a-843952e14caa
# ╟─0b874268-8410-43fd-9c60-d13e4f2eec0b
# ╟─6f69c80c-aafc-4db1-bd64-41d5112287fb
# ╟─00000000-0000-0000-0000-000000000001
# ╟─00000000-0000-0000-0000-000000000002
|
Government house in Sydney is a beautiful stately building surrounded by just over 12 acres of beautifully landscaped grounds adjoining the Royal Botanic Gardens. It sits just behind the Sydney Opera House overlooking Farm Cove on Sydney Harbour. With its gothic revival architecture and many turrets, it is more like a small castle than a house.
Construction of Government House in Sydney, which replaced the Old Government House in Parramatta, began in 1837. The architect, Edward Blore, was also very much involved in the design of Buckingham Palace in London. In 1845 the first resident, Governor George Gipps, moved in. Except for a period of time between 1996 and 2011 the house has always been the residence of the Governor or Governor-General. Beginning in 1996 the house was managed by the Historic Houses Trust. They continue to manage the property to this day carrying out a rigorous program of restoration and maintenance. In 2011, after much public protest, it was decided that the Governor should once again take up official residence in Government House as it was realized that it was actually costing more to maintain the property without the Governor residing there.
Government House hosts many functions throughout the year, including state functions, concerts, festivals, exhibitions and as many as 250 Vice Regal functions.
Nearby attractions include : Royal Botanic Gardens, Sydney Opera House, Customs House, Justice and Police Museum and the Museum of Sydney.
By Train or Ferry: exit at Circular Quay Station and proceed west on Alfred Street then left on Albert Street and right on Macquarie Street. Enter the park by the horse and rider statue and follow the signs to Government House.
|
State Before: a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
⊢ (∫ (x : ℝ) in a..b, ↑x * (1 + ↑x ^ 2) ^ t) =
(1 + ↑b ^ 2) ^ (t + 1) / (↑2 * (t + 1)) - (1 + ↑a ^ 2) ^ (t + 1) / (2 * (t + 1)) State After: a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
⊢ (∫ (x : ℝ) in a..b, ↑x * (1 + ↑x ^ 2) ^ t) =
(1 + ↑b ^ 2) ^ (t + 1) / (↑2 * (t + 1)) - (1 + ↑a ^ 2) ^ (t + 1) / (2 * (t + 1)) Tactic: have : t + 1 ≠ 0 := by contrapose! ht; rwa [add_eq_zero_iff_eq_neg] at ht State Before: a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
⊢ (∫ (x : ℝ) in a..b, ↑x * (1 + ↑x ^ 2) ^ t) =
(1 + ↑b ^ 2) ^ (t + 1) / (↑2 * (t + 1)) - (1 + ↑a ^ 2) ^ (t + 1) / (2 * (t + 1)) State After: case hderiv
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
⊢ ∀ (x : ℝ), x ∈ [[a, b]] → HasDerivAt (fun {b} => (1 + ↑b ^ 2) ^ (t + 1) / (↑2 * (t + 1))) (↑x * (1 + ↑x ^ 2) ^ t) x
case hint
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
⊢ IntervalIntegrable (fun y => ↑y * (1 + ↑y ^ 2) ^ t) MeasureTheory.volume a b Tactic: apply integral_eq_sub_of_hasDerivAt State Before: a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
⊢ t + 1 ≠ 0 State After: a b : ℝ
n : ℕ
t : ℂ
ht : t + 1 = 0
⊢ t = -1 Tactic: contrapose! ht State Before: a b : ℝ
n : ℕ
t : ℂ
ht : t + 1 = 0
⊢ t = -1 State After: no goals Tactic: rwa [add_eq_zero_iff_eq_neg] at ht State Before: case hderiv
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
⊢ ∀ (x : ℝ), x ∈ [[a, b]] → HasDerivAt (fun {b} => (1 + ↑b ^ 2) ^ (t + 1) / (↑2 * (t + 1))) (↑x * (1 + ↑x ^ 2) ^ t) x State After: case hderiv
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
x : ℝ
a✝ : x ∈ [[a, b]]
⊢ HasDerivAt (fun {b} => (1 + ↑b ^ 2) ^ (t + 1) / (↑2 * (t + 1))) (↑x * (1 + ↑x ^ 2) ^ t) x Tactic: intro x _ State Before: case hderiv
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
x : ℝ
a✝ : x ∈ [[a, b]]
f : HasDerivAt (fun y => ↑1 + y ^ 2) (2 * ↑x) ↑x
⊢ HasDerivAt (fun {b} => (1 + ↑b ^ 2) ^ (t + 1) / (↑2 * (t + 1))) (↑x * (1 + ↑x ^ 2) ^ t) x State After: case hderiv
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
x : ℝ
a✝ : x ∈ [[a, b]]
f : HasDerivAt (fun y => ↑1 + y ^ 2) (2 * ↑x) ↑x
g : ∀ {z : ℂ}, 0 < z.re → HasDerivAt (fun z => z ^ (t + 1) / (2 * (t + 1))) (z ^ t / 2) z
⊢ HasDerivAt (fun {b} => (1 + ↑b ^ 2) ^ (t + 1) / (↑2 * (t + 1))) (↑x * (1 + ↑x ^ 2) ^ t) x Tactic: have g :
∀ {z : ℂ}, 0 < z.re → HasDerivAt (fun z => z ^ (t + 1) / (2 * (t + 1))) (z ^ t / 2) z := by
intro z hz
convert (HasDerivAt.cpow_const (c := t + 1) (hasDerivAt_id _)
(Or.inl hz)).div_const (2 * (t + 1)) using 1
field_simp
ring State Before: case hderiv
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
x : ℝ
a✝ : x ∈ [[a, b]]
f : HasDerivAt (fun y => ↑1 + y ^ 2) (2 * ↑x) ↑x
g : ∀ {z : ℂ}, 0 < z.re → HasDerivAt (fun z => z ^ (t + 1) / (2 * (t + 1))) (z ^ t / 2) z
⊢ HasDerivAt (fun {b} => (1 + ↑b ^ 2) ^ (t + 1) / (↑2 * (t + 1))) (↑x * (1 + ↑x ^ 2) ^ t) x State After: case h.e'_6
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
x : ℝ
a✝ : x ∈ [[a, b]]
f : HasDerivAt (fun y => ↑1 + y ^ 2) (2 * ↑x) ↑x
g : ∀ {z : ℂ}, 0 < z.re → HasDerivAt (fun z => z ^ (t + 1) / (2 * (t + 1))) (z ^ t / 2) z
⊢ (fun {b} => (1 + ↑b ^ 2) ^ (t + 1) / (↑2 * (t + 1))) = fun y =>
((fun z => z ^ (t + 1) / (2 * (t + 1))) ∘ fun y => ↑1 + y ^ 2) ↑y
case h.e'_7
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
x : ℝ
a✝ : x ∈ [[a, b]]
f : HasDerivAt (fun y => ↑1 + y ^ 2) (2 * ↑x) ↑x
g : ∀ {z : ℂ}, 0 < z.re → HasDerivAt (fun z => z ^ (t + 1) / (2 * (t + 1))) (z ^ t / 2) z
⊢ ↑x * (1 + ↑x ^ 2) ^ t = (↑1 + ↑x ^ 2) ^ t / 2 * (2 * ↑x)
case hderiv
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
x : ℝ
a✝ : x ∈ [[a, b]]
f : HasDerivAt (fun y => ↑1 + y ^ 2) (2 * ↑x) ↑x
g : ∀ {z : ℂ}, 0 < z.re → HasDerivAt (fun z => z ^ (t + 1) / (2 * (t + 1))) (z ^ t / 2) z
⊢ 0 < (↑1 + ↑x ^ 2).re Tactic: convert (HasDerivAt.comp (↑x) (g _) f).comp_ofReal using 1 State Before: a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
x : ℝ
a✝ : x ∈ [[a, b]]
⊢ HasDerivAt (fun y => ↑1 + y ^ 2) (2 * ↑x) ↑x State After: case h.e'_6.h.h.e'_5
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
x : ℝ
a✝ : x ∈ [[a, b]]
x✝ : ℂ
⊢ ↑1 = 1
case h.e'_7.h.e'_6
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
x : ℝ
a✝ : x ∈ [[a, b]]
⊢ ↑x = ↑x ^ (2 - 1) Tactic: convert (hasDerivAt_pow 2 (x : ℂ)).const_add 1 State Before: case h.e'_6.h.h.e'_5
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
x : ℝ
a✝ : x ∈ [[a, b]]
x✝ : ℂ
⊢ ↑1 = 1 State After: no goals Tactic: norm_cast State Before: case h.e'_7.h.e'_6
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
x : ℝ
a✝ : x ∈ [[a, b]]
⊢ ↑x = ↑x ^ (2 - 1) State After: no goals Tactic: simp State Before: a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
x : ℝ
a✝ : x ∈ [[a, b]]
f : HasDerivAt (fun y => ↑1 + y ^ 2) (2 * ↑x) ↑x
⊢ ∀ {z : ℂ}, 0 < z.re → HasDerivAt (fun z => z ^ (t + 1) / (2 * (t + 1))) (z ^ t / 2) z State After: a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
x : ℝ
a✝ : x ∈ [[a, b]]
f : HasDerivAt (fun y => ↑1 + y ^ 2) (2 * ↑x) ↑x
z : ℂ
hz : 0 < z.re
⊢ HasDerivAt (fun z => z ^ (t + 1) / (2 * (t + 1))) (z ^ t / 2) z Tactic: intro z hz State Before: a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
x : ℝ
a✝ : x ∈ [[a, b]]
f : HasDerivAt (fun y => ↑1 + y ^ 2) (2 * ↑x) ↑x
z : ℂ
hz : 0 < z.re
⊢ HasDerivAt (fun z => z ^ (t + 1) / (2 * (t + 1))) (z ^ t / 2) z State After: case h.e'_7
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
x : ℝ
a✝ : x ∈ [[a, b]]
f : HasDerivAt (fun y => ↑1 + y ^ 2) (2 * ↑x) ↑x
z : ℂ
hz : 0 < z.re
⊢ z ^ t / 2 = (t + 1) * id z ^ (t + 1 - 1) * 1 / (2 * (t + 1)) Tactic: convert (HasDerivAt.cpow_const (c := t + 1) (hasDerivAt_id _)
(Or.inl hz)).div_const (2 * (t + 1)) using 1 State Before: case h.e'_7
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
x : ℝ
a✝ : x ∈ [[a, b]]
f : HasDerivAt (fun y => ↑1 + y ^ 2) (2 * ↑x) ↑x
z : ℂ
hz : 0 < z.re
⊢ z ^ t / 2 = (t + 1) * id z ^ (t + 1 - 1) * 1 / (2 * (t + 1)) State After: case h.e'_7
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
x : ℝ
a✝ : x ∈ [[a, b]]
f : HasDerivAt (fun y => ↑1 + y ^ 2) (2 * ↑x) ↑x
z : ℂ
hz : 0 < z.re
⊢ z ^ t * (2 * (t + 1)) = (t + 1) * z ^ t * 2 Tactic: field_simp State Before: case h.e'_7
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
x : ℝ
a✝ : x ∈ [[a, b]]
f : HasDerivAt (fun y => ↑1 + y ^ 2) (2 * ↑x) ↑x
z : ℂ
hz : 0 < z.re
⊢ z ^ t * (2 * (t + 1)) = (t + 1) * z ^ t * 2 State After: no goals Tactic: ring State Before: case h.e'_6
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
x : ℝ
a✝ : x ∈ [[a, b]]
f : HasDerivAt (fun y => ↑1 + y ^ 2) (2 * ↑x) ↑x
g : ∀ {z : ℂ}, 0 < z.re → HasDerivAt (fun z => z ^ (t + 1) / (2 * (t + 1))) (z ^ t / 2) z
⊢ (fun {b} => (1 + ↑b ^ 2) ^ (t + 1) / (↑2 * (t + 1))) = fun y =>
((fun z => z ^ (t + 1) / (2 * (t + 1))) ∘ fun y => ↑1 + y ^ 2) ↑y State After: no goals Tactic: simp State Before: case h.e'_7
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
x : ℝ
a✝ : x ∈ [[a, b]]
f : HasDerivAt (fun y => ↑1 + y ^ 2) (2 * ↑x) ↑x
g : ∀ {z : ℂ}, 0 < z.re → HasDerivAt (fun z => z ^ (t + 1) / (2 * (t + 1))) (z ^ t / 2) z
⊢ ↑x * (1 + ↑x ^ 2) ^ t = (↑1 + ↑x ^ 2) ^ t / 2 * (2 * ↑x) State After: case h.e'_7
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
x : ℝ
a✝ : x ∈ [[a, b]]
f : HasDerivAt (fun y => ↑1 + y ^ 2) (2 * ↑x) ↑x
g : ∀ {z : ℂ}, 0 < z.re → HasDerivAt (fun z => z ^ (t + 1) / (2 * (t + 1))) (z ^ t / 2) z
⊢ ↑x * (1 + ↑x ^ 2) ^ t * 2 = (1 + ↑x ^ 2) ^ t * (2 * ↑x) Tactic: field_simp State Before: case h.e'_7
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
x : ℝ
a✝ : x ∈ [[a, b]]
f : HasDerivAt (fun y => ↑1 + y ^ 2) (2 * ↑x) ↑x
g : ∀ {z : ℂ}, 0 < z.re → HasDerivAt (fun z => z ^ (t + 1) / (2 * (t + 1))) (z ^ t / 2) z
⊢ ↑x * (1 + ↑x ^ 2) ^ t * 2 = (1 + ↑x ^ 2) ^ t * (2 * ↑x) State After: no goals Tactic: ring State Before: case hderiv
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
x : ℝ
a✝ : x ∈ [[a, b]]
f : HasDerivAt (fun y => ↑1 + y ^ 2) (2 * ↑x) ↑x
g : ∀ {z : ℂ}, 0 < z.re → HasDerivAt (fun z => z ^ (t + 1) / (2 * (t + 1))) (z ^ t / 2) z
⊢ 0 < (↑1 + ↑x ^ 2).re State After: no goals Tactic: exact_mod_cast add_pos_of_pos_of_nonneg zero_lt_one (sq_nonneg x) State Before: case hint
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
⊢ IntervalIntegrable (fun y => ↑y * (1 + ↑y ^ 2) ^ t) MeasureTheory.volume a b State After: case hint.hu
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
⊢ Continuous fun y => ↑y * (1 + ↑y ^ 2) ^ t Tactic: apply Continuous.intervalIntegrable State Before: case hint.hu
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
⊢ Continuous fun y => ↑y * (1 + ↑y ^ 2) ^ t State After: case hint.hu
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
⊢ Continuous fun y => (1 + ↑y ^ 2) ^ t Tactic: refine' continuous_ofReal.mul _ State Before: case hint.hu
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
⊢ Continuous fun y => (1 + ↑y ^ 2) ^ t State After: case hint.hu.hf
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
⊢ Continuous fun x => 1 + ↑x ^ 2
case hint.hu.hg
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
⊢ Continuous fun x => t
case hint.hu.h0
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
⊢ ∀ (a : ℝ), 0 < (1 + ↑a ^ 2).re ∨ (1 + ↑a ^ 2).im ≠ 0 Tactic: apply Continuous.cpow State Before: case hint.hu.hf
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
⊢ Continuous fun x => 1 + ↑x ^ 2 State After: no goals Tactic: exact continuous_const.add (continuous_ofReal.pow 2) State Before: case hint.hu.hg
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
⊢ Continuous fun x => t State After: no goals Tactic: exact continuous_const State Before: case hint.hu.h0
a b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
⊢ ∀ (a : ℝ), 0 < (1 + ↑a ^ 2).re ∨ (1 + ↑a ^ 2).im ≠ 0 State After: case hint.hu.h0
a✝ b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
a : ℝ
⊢ 0 < (1 + ↑a ^ 2).re ∨ (1 + ↑a ^ 2).im ≠ 0 Tactic: intro a State Before: case hint.hu.h0
a✝ b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
a : ℝ
⊢ 0 < (1 + ↑a ^ 2).re ∨ (1 + ↑a ^ 2).im ≠ 0 State After: case hint.hu.h0
a✝ b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
a : ℝ
⊢ 0 < 1 + a ^ 2 ∨ (1 + ↑(a ^ 2)).im ≠ 0 Tactic: rw [add_re, one_re, ← ofReal_pow, ofReal_re] State Before: case hint.hu.h0
a✝ b : ℝ
n : ℕ
t : ℂ
ht : t ≠ -1
this : t + 1 ≠ 0
a : ℝ
⊢ 0 < 1 + a ^ 2 ∨ (1 + ↑(a ^ 2)).im ≠ 0 State After: no goals Tactic: exact Or.inl (add_pos_of_pos_of_nonneg zero_lt_one (sq_nonneg a))
|
The generalized extreme value distribution (GEV) includes all three
types of extreme value distributions: Type I (Gumbel), type II
(Fr\'{e}chet), and type III (Weibull). Empirically, the scores of some
sequence alignment algorithms appear to follow GEV distributions. The
\eslmod{gev} module is used in estimating the statistical significance
of such scores.
Most local sequence alignment scores follow the Gumbel distribution.
Easel's \eslmod{gumbel} module applies specifically to the Gumbel. The
\eslmod{gev} module is used for Type II or III extreme value
distributions, or for determining which of the three types of
distribution that a dataset best fits.
\subsection{The gev API}
The \eslmod{gev} API consists of the following functions:
\vspace{0.5em}
\begin{center}
\begin{tabular}{ll}\hline
\multicolumn{2}{c}{\textbf{evaluating densities and distributions:}}\\
\ccode{esl\_gev\_pdf()} & Returns the probability density, $P(S=x)$.\\
\ccode{esl\_gev\_logpdf()} & Returns the log of the pdf, $\log P(S=x)$.\\
\ccode{esl\_gev\_cdf()} & Returns the cumulative probability distribution, $P(S \leq x)$.\\
\ccode{esl\_gev\_logcdf()} & Returns the log of the cdf, $\log P(S \leq x)$.\\
\ccode{esl\_gev\_surv()} & Returns right tail mass, 1-cdf, $P(S > x)$\\
\ccode{esl\_gev\_logsurv()} & Returns log of 1-cdf, $\log P(S > x)$.\\
\multicolumn{2}{c}{\textbf{sampling:}}\\
\ccode{esl\_gev\_Sample()} & Returns a GEV-distributed random sample.\\
\multicolumn{2}{c}{\textbf{maximum likelihood parameter fitting:}}\\
\ccode{esl\_gev\_FitComplete()} & Estimates GEV parameters from complete data.\\
\end{tabular}
\end{center}
\vspace{0.5em}
The Gumbel distribution depends on three parameters, $\mu$, $\lambda$,
and $\alpha$. When these parameters are known, the statistical
significance (P-value) of a single score $x$ is $P(S>x)$, obtained by
a call to \ccode{esl\_gev\_surv()}. The E-value for obtaining that
score or better in searching a database of $N$ sequences is just
$NP(S>x)$.
When the parameters are unknown, they can be estimated from scores
obtained from comparisons of simulated random data. The
\ccode{esl\_gev\_FitComplete()} function performs maximum likelihood
parameter fitting \citep{Coles01}.
\subsection{Example of using the gev API}
Below is a code example that samples 10,000 data points from a
Fr\'{e}chet distribution with $\mu=-20$, $\lambda=0.4$, $\alpha=0.1$;
reports the min and max samples, and the probability mass to the left
of the min and to the right of the max (both of which should be about
$\frac{1}{10000}$, since we took 10,000 samples); and then fits those
simulated data to a Gumbel and reports the fitted $\mu$ and $\lambda$:
\input{cexcerpts/gev_example}
\subsection{GEV densities}
The probability density function (pdf) and the cumulative distribution
function (cdf) of the generalized extreme value distribution are
\citep{Coles01}:
\begin{eqnarray}
P(X=x) & = & \lambda \left[ 1 + \alpha \lambda (x - \mu) \right]^{-\frac{\alpha+1}{\alpha}}
\exp \left\{ - \left[ 1 + \alpha \lambda (x - \mu)
\right]^{-\frac{1}{\alpha}} \right\}
\\%
\label{eqn:gev_density}
P(X \geq x) & = & \exp \left\{ - \left[ 1 +
\alpha\lambda(x-\mu) \right]^{-\frac{1}{\alpha}} \right\}
\\%
\label{eqn:gev_distribution}
\end{eqnarray}
The parameters $\mu$, $\lambda$, and $\alpha$ are location, scale, and
shape parameters, respectively, with $-\infty < \mu < \infty$, $0 <
\lambda < \infty$, and $-\infty < \alpha < \infty$.
The Type II (Fr\'{e}chet) distribution corresponds to $\alpha > 0$,
and the Type III (Weibull) distribution corresponds to $\alpha < 0$.
The Type I (Gumbel) distribution arises in the limit $\alpha
\rightarrow 0$. At values $\alpha \simeq 0$, Easel's GEV functions
revert to the Gumbel limit case, as opposed to dividing by zero and
failing.
Technically the GEV is only defined for values of $x$ such that $1 +
\alpha \lambda (x - \mu) > 0$. However, Easel's functions return
sensible values outside this domain, such as 0 for nonexistent
densities.
Generalized extreme value densities for $\mu = 0$ and $\lambda = 1$
are shown below (left) for three settings of $\alpha$; $\alpha = 0$
(Gumbel), $\alpha = 0.1$ (Fr\'{e}chet), and $\alpha = -0.1$
(Weibull). The figure on the right shows the log densities, which more
clearly show how, relative to the exponential right tail of the
Gumbel, the Fr\'{e}chet's tail is longer, and the Weibull's tail is
shorter.
\centerline{
\begin{minipage}{3in}
\includegraphics[width=2.8in]{figures/gev_density}
\end{minipage}
\begin{minipage}{3in}
\includegraphics[width=2.8in]{figures/gev_logdensity}
\end{minipage}
}
For more details, see the excellent description in \citep{Coles01}.
Easel's $\{ \mu, \lambda, \alpha \}$ notation differs from the $\{
\mu, \sigma, \xi \}$ parameterization used by Coles. Use $\lambda =
\frac{1}{\sigma}$ and $\alpha = \xi$ to translate.
\subsection{Fitting GEV distributions to observed data}
Easel fits GEVs by maximum likelihood estimation by numerically
optimizing the log likelihood function, using first derivative
information and conjugate gradient descent. See the \eslmod{gumbel}
chapter for a more general introduction to maximum likelihood fitting.
\subsubsection{Maximum likelihood estimation, complete data}
The function \ccode{esl\_gev\_FitComplete()} uses gradient information
to find parameters that optimize the likelihood function, using the
conjugate gradient descent code in the \eslmod{minimizer} module.
Given $n$ samples $x_1..x_n$, we want to estimate maximum likelihood
parameter estimates $\{ \hat{\mu}, \hat{\lambda}, \hat{\alpha} \}$
that maximize the log likelihood:
\begin{equation}
\log L(\lambda, \mu, \alpha) = n \log \lambda
- \frac{\alpha+1}{\alpha}
\sum_{i=1}^{n} \log\left[1+ \alpha\lambda(x_i - \mu) \right]
- \sum_{i=1}^{n} \left[ 1 + \alpha\lambda (x_i - \mu) \right]^{\frac{1}{\alpha}}
\label{eqn:gev_logL}
\end{equation}
The $\left[ 1 + \alpha\lambda (x_i - \mu) \right]^{\frac{1}{\alpha}}$
term can be rewritten in a more conveniently differentiable form as
$\exp \left\{ \frac{1}{\alpha} \log \left[ 1 + \alpha\lambda (x_i - \mu)
\right] \right\}$.
Since the $\lambda$ parameter is constrained to $\lambda > 0$ but the
numerical optimizer expects unconstrained parameters, we use a change
of variables $\lambda = e^w$ and optimize an unconstrained value $w$.
The gradient of the log likelihood with respect to $\mu$, $w$, and
$\alpha$ is:
%% xref: STL9/118-120
\begin{eqnarray}
\frac{\partial \log L}{\partial \mu} & = &
\sum_{i=1}^n \frac{\lambda (\alpha+1)}{1+\alpha\lambda(x_i-\mu)}
-\sum_{i=1}^n \lambda \exp
\left\{ -\frac{\alpha+1}{\alpha} \log
\left[1+\alpha\lambda(x_i-\mu)\right] \right\}
\\%
\label{eqn:gev_mupartial}
\frac{\partial \log L}{\partial w} & = &
n - \sum_{i=1}^{n} \frac{\lambda (\alpha+1) (x_i - \mu)}
{1 + \alpha \lambda (x_i - \mu)}
+ \sum_{i=1}^n \lambda (x_i - \mu)
\exp \left\{ -\frac{\alpha+1}{\alpha} \log
\left[1+\alpha\lambda(x_i-\mu)\right] \right\}
\\%
\label{eqn:gev_wpartial}
\frac{\partial \log L}{\partial \alpha} & = &
\sum_{i=1}^n \left\{
\begin{array}{l}
- \frac{\alpha+1}{\alpha} \frac{\lambda(x_i-\mu)}
{1 +\alpha\lambda(x_i-\mu)}\\
+ \frac{1}{\alpha^2} \log \left[ 1 + \alpha\lambda(x_i - \mu) \right]\\
+ \frac{1}{\alpha} \frac{\lambda(x_i-\mu)}
{1 +\alpha\lambda(x_i-\mu)}
e^{-\frac{1}{\alpha} \log\left[ 1 + \alpha\lambda(x_i - \mu) \right]}\\
- \frac{1}{\alpha^2} \log \left[ 1 + \alpha\lambda(x_i - \mu) \right]
e^{-\frac{1}{\alpha} \log\left[ 1 + \alpha\lambda(x_i - \mu)
\right]}
\end{array}
\right.
\\%
\label{eqn:gev_alphapartial}
\end{eqnarray}
When $|\alpha\lambda(x_i - \mu)|$ approaches $0$, the GEV approximates
a Gumbel distribution and these equations can be simplified using the
approximation $\log(1+a) \simeq a$.
|
function Mn=dataNorm(M,normOpt)
switch normOpt
case 1 %Using max and min
Mn=double(M);
Mn=Mn-min(Mn(:));
Mn=Mn./max(Mn(:));
case 2 %Using max only and letting M(M<0)= 0
Mn=double(M);
Mn(Mn<0)=0;
Mn=Mn./max(Mn(:));
end
%%
% _*GIBBON footer text*_
%
% License: <https://github.com/gibbonCode/GIBBON/blob/master/LICENSE>
%
% GIBBON: The Geometry and Image-based Bioengineering add-On. A toolbox for
% image segmentation, image-based modeling, meshing, and finite element
% analysis.
%
% Copyright (C) 2006-2022 Kevin Mattheus Moerman and the GIBBON contributors
%
% This program is free software: you can redistribute it and/or modify
% it under the terms of the GNU General Public License as published by
% the Free Software Foundation, either version 3 of the License, or
% (at your option) any later version.
%
% This program is distributed in the hope that it will be useful,
% but WITHOUT ANY WARRANTY; without even the implied warranty of
% MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
% GNU General Public License for more details.
%
% You should have received a copy of the GNU General Public License
% along with this program. If not, see <http://www.gnu.org/licenses/>.
|
[STATEMENT]
lemma LIM_const_not_eq[tendsto_intros]: "k \<noteq> L \<Longrightarrow> \<not> (\<lambda>x. k) \<midarrow>a\<rightarrow> L"
for a :: "'a::perfect_space" and k L :: "'b::t2_space"
[PROOF STATE]
proof (prove)
goal (1 subgoal):
1. k \<noteq> L \<Longrightarrow> \<not> (\<lambda>x. k) \<midarrow>a\<rightarrow> L
[PROOF STEP]
by (simp add: tendsto_const_iff)
|
-- Simple test.
import data.real.basic
section real_tree
inductive real_tree
| Leaf : ℝ → real_tree
| Node : real_tree → real_tree → real_tree
open real_tree
--#print real_tree.rec
--#print real_tree.cases_on
def sum_real_tree : real_tree → ℝ
| (Leaf r) := r
| (Node t1 t2) := (sum_real_tree t1) + (sum_real_tree t2)
end real_tree
-- List construction (Nested inductive).
-- Note: This will change in Lean 4?
section real_branching_tree
inductive real_branching_tree
| Leaf : ℝ → real_branching_tree
| Node : list real_branching_tree → real_branching_tree
open real_branching_tree
--#print real_branching_tree.rec
--#print real_branching_tree.cases_on
@[elab_as_eliminator]
protected def real_branching_tree.cases_on'
: Π {C : real_branching_tree → Sort*} (x : real_branching_tree),
(Π (a : ℝ), C (Leaf a)) →
(Π (l : list real_branching_tree), C (Node l)) →
C x
| C (Leaf a) mL mN := mL a
| C (Node l) mL mN := mN l
def real_branching_tree.lt : real_branching_tree → real_branching_tree → Prop
| t (Node l) := t ∈ l
| t _ := false
instance : has_lt real_branching_tree := ⟨real_branching_tree.lt⟩
@[simp] lemma real_branching_tree.lt_Node
(t : real_branching_tree) (l : list real_branching_tree)
: t < (Node l) ↔ t ∈ l :=
by rw [←real_branching_tree.lt.equations._eqn_2 t l]; refl
lemma real_branching_tree.lt_sizeof (t1 t2 : real_branching_tree)
: t1 < t2 → sizeof t1 < sizeof t2 :=
begin
intro H,
cases t2 with r l,
{ cases H, },
{ change sizeof t1 < real_branching_tree.sizeof (Node l),
rw real_branching_tree.Node.sizeof_spec l,
have H1 := (real_branching_tree.lt_Node t1 l).1 H,
have H2 := list.sizeof_lt_sizeof_of_mem H1,
exact ((nat.one_add (sizeof l)).symm ▸ (nat.lt_succ_of_lt H2)), }
end
lemma real_branching_tree.lt_well_founded : well_founded real_branching_tree.lt :=
(subrelation.wf real_branching_tree.lt_sizeof) (inv_image.wf _ nat.lt_wf)
@[elab_as_eliminator]
protected def real_branching_tree.rec'
: Π {C : real_branching_tree → Sort*},
(Π (a : ℝ), C (Leaf a)) →
(Π (a : list real_branching_tree), C (Node a)) →
Π (x : real_branching_tree), C x :=
begin
intros C m1 m2 x,
apply (well_founded.fix real_branching_tree.lt_well_founded),
intros y Hy,
exact (real_branching_tree.cases_on' y m1 m2),
end
--def real_branching_tree.sum : real_branching_tree → ℝ
--| (Leaf r) := r
--| (Node l) := list.sum (list.map real_branching_tree.sum l)
-- This is still not good enough. Best we can do:
-- mutual inductive foo, list_foo
-- with foo : Type
-- | mk : list_foo -> foo
-- with list_foo : Type
-- | nil : list_foo
-- | cons : foo -> list_foo -> list_foo
end real_branching_tree
|
[STATEMENT]
lemma fv_terms_set_cong: "fv_terms_set ts = fv_terms_set (map (map_term f) ts)"
[PROOF STATE]
proof (prove)
goal (1 subgoal):
1. fv_terms_set ts = fv_terms_set (map (map_term f) ts)
[PROOF STEP]
using fv_term_set_cong
[PROOF STATE]
proof (prove)
using this:
fv_term_set ?t = fv_term_set (map_term ?f ?t)
goal (1 subgoal):
1. fv_terms_set ts = fv_terms_set (map (map_term f) ts)
[PROOF STEP]
by (induction ts) (fastforce simp: fv_terms_set_def)+
|
Require Export ConnectivityGraph.
Require Export Layouts.
Require Export MappingConstraints.
Require Import StandardGateSet.
Import StdList.
(* Alogrithm 3.1 *)
Fixpoint hierarchical_product_permuter_part1 pi permuter_g1g2 (deg_ham : nat) := (* line 2 *)
match deg_ham with
| 0 => pi
| n =>
let r = partial_permutation permuter_g1g2 (* line 1*)
g' = route_v_to_k r permuter_g1g2 (* line 3,4 *)
new_g = route_communicator_v_g1 g' (* line 5,6 *)
in
hierarchical_product_permuter_part1 pi new_g (n-1)
end.
Fixpoint hierarchical_product_permuter_part2 v1 pi permuter_g1g2 := (* line 7 *)
match v1 with
| [] => pi
| (h :: t) =>
let
new_pi = route_v_Vi_to_pi h pi permuter_g1g2 (*line 8 *)
in
hierarchical_product_permuter_part2 t new_pi permuter_g1g2
end,
Definition hierarchical_product_permuter pi permuter_g1g2 deg_ham := (* Algorithm 3.1 *)
let
new_pi = hierarchical_product_permuter_part1 pi permuter_g1g2 deg_ham
v1 = V(new_pi,1)
in
hierarchical_product_permuter_part2 v1 new_pi permuter_g1g2
(* Algorithm 3.2 *)
Fixpoint choose_distinct_sets pi sigma r rowi_V2 :=
match rowi_V2 with
| [] => sigma
| i :: tail => let v = (dom pi) - (dom sigma)
E = (head v, pi_v (v,1), current_v (v, i)) (* line 4 *)
U, V = list_n (num_of (V1 pi)) (* ni = |Vi| *) (* line 6 *)
G = (U, V, E) (* line 6 *)
V_match = v_set (find_minimum_weight G (add_u_v_e G r)) (* line 7~11 *)
new_sigma = app sigma (v_list V_match) (* line 12 *)
in
choose_distinct_sets pi new_sigma (r-1) t
(* Algorithm 3.3 *)
Fixpoint routing_tokens_to_destination pi :=
if (pi == id_dom pi)
then (*return seq of transpositions *)
else
if exists_happy_swap
then routing_tokens_to_destination (do_transposition pi)
else
if (exists_v (dom pi)) and (exists_u (Nu_dom_pi v))
then routing_tokens_to_destination (no_token_swap v u)
else routing_tokens_to_destination (unhappy_swap)
|
function [X_poly] = polyFeatures(X, p)
%POLYFEATURES Maps X (1D vector) into the p-th power
% [X_poly] = POLYFEATURES(X, p) takes a data matrix X (size m x 1) and
% maps each example into its polynomial features where
% X_poly(i, :) = [X(i) X(i).^2 X(i).^3 ... X(i).^p];
%
% You need to return the following variables correctly.
X_poly = zeros(numel(X), p);
% ====================== YOUR CODE HERE ======================
% Instructions: Given a vector X, return a matrix X_poly where the p-th
% column of X contains the values of X to the p-th power.
%
%
for i = 1:p
X_poly(:, i) = (X .^ i)';
end
% =========================================================================
end
|
lemma bounded_connected_Compl_real: fixes S :: "real set" assumes "bounded S" and conn: "connected(- S)" shows "S = {}"
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.