# Perplejidad de los modelos de longitud fija
[[open-in-colab]]
La perplejidad, perplexity en inglés (PPL), es una de las métricas más comunes para evaluar modelos de lenguaje. Antes de sumergirnos, debemos tener en cuenta que esta métrica se aplica específicamente a modelos de lenguaje clásicos (a veces llamados modelos autorregresivos o causales) y no está bien definida para modelos de lenguaje enmascarados como BERT (ver [resumen del modelo](model_summary)).
La perplejidad se define como la media negativa exponenciada del log-likelihood de una secuencia. Si tenemos una secuencia tokenizada \\(X = (x_0, x_1, \dots, x_t)\\), entonces la perplejidad de \\(X\\) es,
$$\text{PPL}(X) = \exp \left\{ {-\frac{1}{t}\sum_i^t \log p_\theta (x_i|x_{
Sin embargo, al trabajar con modelos aproximados, generalmente tenemos una restricción en la cantidad de tokens que el modelo puede procesar. La versión más grande de [GPT-2](model_doc/gpt2), por ejemplo, tiene una longitud fija de 1024 tokens, por lo que no podemos calcular \\(p_\theta(x_t|x_{
Esto es rápido de calcular, ya que la perplejidad de cada segmento se puede calcular en un solo pase hacia adelante, pero sirve como una aproximación pobre de la perplejidad completamente factorizada y generalmente dará como resultado una PPL más alta (peor) porque el modelo tendrá menos contexto en la mayoría de los pasos de predicción.
En cambio, la PPL de modelos de longitud fija debería evaluarse con una estrategia de ventana deslizante. Esto implica deslizar repetidamente la ventana de contexto para que el modelo tenga más contexto al hacer cada predicción.
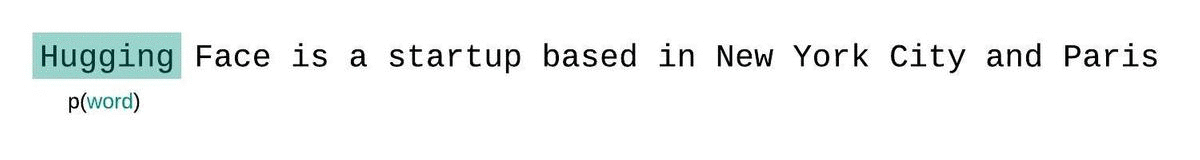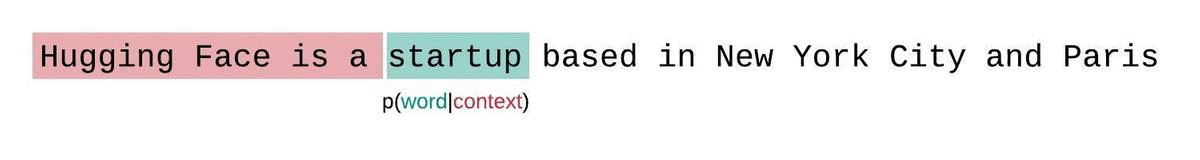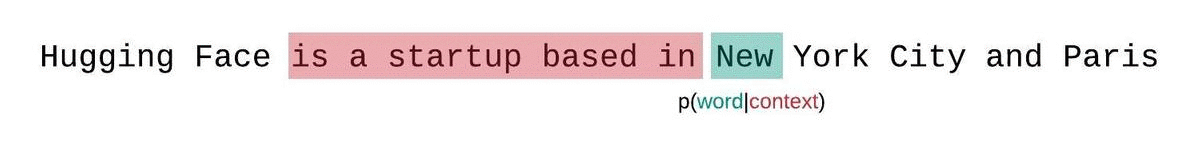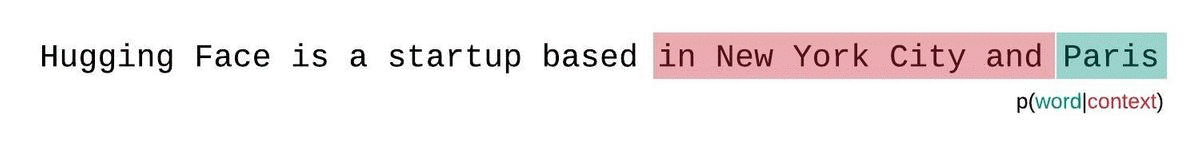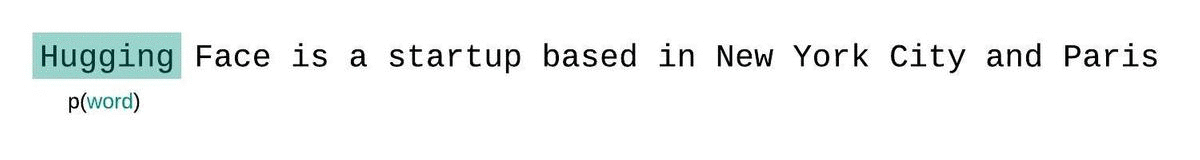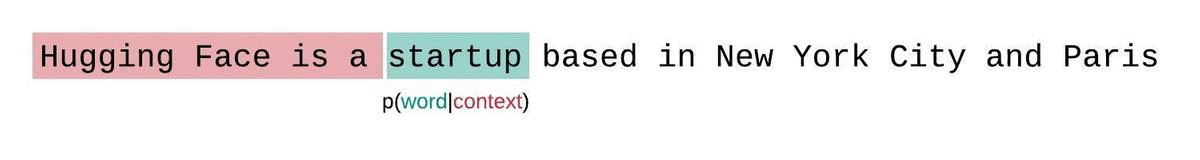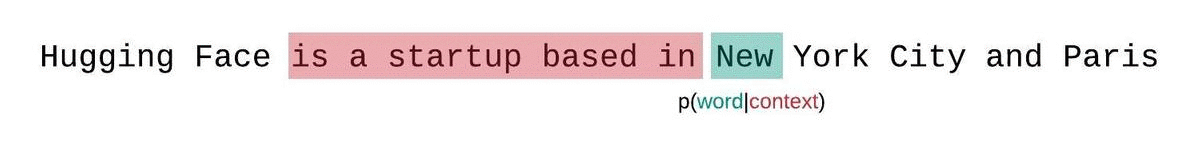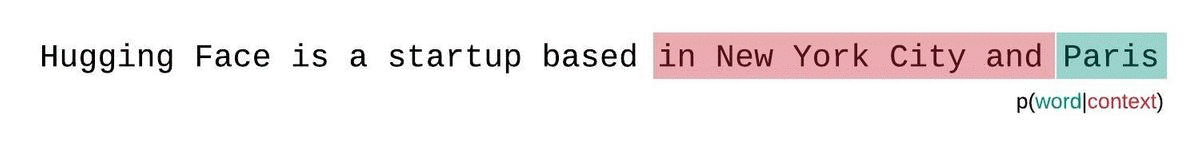Esta es una aproximación más cercana a la verdadera descomposición de la probabilidad de la secuencia y generalmente dará como resultado una puntuación más favorable. La desventaja es que requiere un pase hacia adelante separado para cada token en el corpus. Un buen compromiso práctico es emplear una ventana deslizante estratificada, moviendo el contexto con pasos más grandes en lugar de deslizarse de 1 token a la vez. Esto permite que la computación avance mucho más rápido, mientras le da al modelo un contexto amplio para hacer
predicciones en cada paso.
## Ejemplo: Cálculo de la perplejidad con GPT-2 en 🤗 Transformers
Demostremos este proceso con GPT-2.
```python
from transformers import GPT2LMHeadModel, GPT2TokenizerFast
device = "cuda"
model_id = "openai-community/gpt2-large"
model = GPT2LMHeadModel.from_pretrained(model_id).to(device)
tokenizer = GPT2TokenizerFast.from_pretrained(model_id)
```
Carguemos el conjunto de datos WikiText-2 y evaluemos la perplejidad utilizando algunas estrategias de ventana deslizante diferentes. Dado que este conjunto de datos es pequeño y solo estamos realizando un pase hacia adelante sobre el conjunto, podemos cargar y codificar todo el conjunto de datos en la memoria.
```python
from datasets import load_dataset
test = load_dataset("wikitext", "wikitext-2-raw-v1", split="test")
encodings = tokenizer("\n\n".join(test["text"]), return_tensors="pt")
```
Con 🤗 Transformers, simplemente podemos pasar los `input_ids` como las `labels` a nuestro modelo, y la media negativa del log-likelihood para cada token se devuelve como la pérdida. Sin embargo, con nuestro enfoque de ventana deslizante, hay superposición en los tokens que pasamos al modelo en cada iteración. No queremos que el log-likelihood de los tokens que estamos tratando solo como contexto se incluya en nuestra pérdida, por lo que podemos establecer estos objetivos en `-100` para que se ignoren. El siguiente es un ejemplo de cómo podríamos hacer esto con un paso de `512`. Esto significa que el modelo tendrá al menos `512` tokens como contexto al calcular el log-likelihood condicional de cualquier token (siempre que haya `512` tokens precedentes disponibles para condicionar).
```python
import torch
from tqdm import tqdm
max_length = model.config.n_positions
stride = 512
seq_len = encodings.input_ids.size(1)
nlls = []
prev_end_loc = 0
for begin_loc in tqdm(range(0, seq_len, stride)):
end_loc = min(begin_loc + max_length, seq_len)
trg_len = end_loc - prev_end_loc # puede ser diferente del paso en el último bucle
input_ids = encodings.input_ids[:, begin_loc:end_loc].to(device)
target_ids = input_ids.clone()
target_ids[:, :-trg_len] = -100
with torch.no_grad():
outputs = model(input_ids, labels=target_ids)
# la pérdida se calcula utilizando CrossEntropyLoss, que promedia las etiquetas válidas
# N.B. el modelo solo calcula la pérdida sobre trg_len - 1 etiquetas, porque desplaza las etiqueta internamente
# a la izquierda por 1.
neg_log_likelihood = outputs.loss
nlls.append(neg_log_likelihood)
prev_end_loc = end_loc
if end_loc == seq_len:
break
ppl = torch.exp(torch.stack(nlls).mean())
```
Ejecuta esto con la longitud de paso igual a la longitud máxima de entrada es equivalente a la estrategia sub óptima,
sin ventana deslizante, que discutimos anteriormente. Cuanto menor sea el paso, más contexto tendrá el modelo para
realizar cada predicción y, por lo general, mejor será la perplejidad informada.
Cuando ejecutamos lo anterior con `stride = 1024`, es decir, sin superposición, la PPL resultante es `19.44`, que es
aproximadamente la misma que la `19.93` informada en el artículo de GPT-2. Al utilizar `stride = 512` y, por lo tanto,
emplear nuestra estrategia de ventana deslizante, esto disminuye a `16.45`. Esto no solo es una puntuación más favorable, sino que se calcula de una manera más cercana a la verdadera descomposición autorregresiva de la probabilidad de una secuencia.