problem
stringlengths 18
4.46k
| answer
stringlengths 1
942
| pass_at_n
float64 0.08
0.92
|
|---|---|---|
For a natural number \( N \), if at least five out of the nine natural numbers \( 1 \) through \( 9 \) can divide \( N \) evenly, then \( N \) is called a "Five Sequential Number." What is the smallest "Five Sequential Number" greater than 2000? | 2004 | 0.625 |
Given a natural number \( x = 6^n + 1 \), where \( n \) is an odd natural number. It is known that \( x \) has exactly three distinct prime divisors, one of which is 11. Find \( x \). | 7777 | 0.875 |
In the number \(2 * 0 * 1 * 6 * 07 *\), each of the 5 asterisks needs to be replaced by any of the digits \(0, 2, 4, 5, 6, 7\) (digits can repeat) so that the resulting 11-digit number is divisible by 75. In how many ways can this be done? | 432 | 0.25 |
On the parade ground, 2018 soldiers are lined up in a single row. The commander can order either all soldiers standing in even positions or all soldiers standing in odd positions to leave the formation. After this order, the soldiers remaining in formation close ranks into a single row. In how many ways can the commander issue a series of 8 orders so that there are exactly 7 soldiers left in formation? | 30 | 0.125 |
Mitya is 11 years older than Shura. When Mitya was as old as Shura is now, he was twice as old as she was then. How old is Mitya? | 33 | 0.875 |
Let \( f \) be a function such that
\[
f(x) - \frac{1}{2} f\left(\frac{1}{x}\right) = \log x
\]
for all \( x > 0 \), where \( \log \) denotes the logarithm base 10. Find \( f(1000) \). | 2 | 0.625 |
Given that the complex numbers \( a_{1}, a_{2}, a_{3} \) satisfy
\[
\begin{aligned}
& a_{1}^{2} + a_{2}^{2} + a_{3}^{2} = a_{1}^{3} + a_{2}^{3} + a_{3}^{3} \\
& = a_{1}^{4} + a_{2}^{4} + a_{3}^{4} = 0,
\end{aligned}
\]
find all possible values of \( a_{1} + a_{2} + a_{3} \). | 0 | 0.875 |
A 1962-digit number divisible by 9 is randomly taken. Let the sum of its digits be $a$, the sum of the digits of $a$ be $b$, and the sum of the digits of $b$ be $c$. What is the value of $c$? | 9 | 0.75 |
Let $n$ be a fixed integer such that $n \geq 2$.
(1) Determine the smallest constant $c$ such that the inequality
$$
\sum_{1 \leq i<j \leq n} x_{i} x_{j}\left(x_{i}^{2} + x_{j}^{2}\right) \leq c \cdot \left(\sum_{i=1}^{n} x_{i}\right)^{4}
$$
holds for all non-negative real numbers $x_{1}, x_{2}, \cdots, x_{n}$.
(2) For this constant $c$, determine the necessary and sufficient conditions for equality to hold. | \frac{1}{8} | 0.875 |
Let \( S(n) \) denote the sum of the digits of a natural number \( n \). For example, \( S(123) = 1 + 2 + 3 = 6 \). If two different positive integers \( m \) and \( n \) satisfy the following conditions:
\[
\begin{cases}
m < 100 \\
n < 100 \\
m > n \\
m + S(n) = n + 2S(m)
\end{cases}
\]
then \( m \) and \( n \) form a pair \( \langle m, n \rangle \).
How many such pairs \( \langle m, n \rangle \) are there? | 99 | 0.25 |
Eight strangers are preparing to play bridge. How many ways can they be grouped into two bridge games, meaning into unordered pairs of unordered pairs of people? | 315 | 0.75 |
Given that \( M \) is an arbitrary point on the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1 (a>b>0)\), \( F_{1} \) and \( F_{2} \) are the left and right foci of the ellipse, respectively. The lines \( M F_{1} \) and \( M F_{2} \) intersect the ellipse at points \( A \) and \( B \), respectively. Then \(\frac{b^{2}}{a^{2}}\left(\frac{\left|MF_{1}\right|}{\left|F_{1}A\right|}+\frac{\left|MF_{2}\right|}{\left|F_{2}B\right|}+2\right)=\) ______. | 4 | 0.875 |
All integers are written in sequence starting from one. Determine which digit is in the 206788th position. | 7 | 0.375 |
What is the largest result we can find when we divide a 2-digit number by the sum of its digits? | 10 | 0.375 |
Calculate: \( \arctan \frac{1}{3}+\arctan \frac{1}{5}+\arcsin \frac{1}{\sqrt{50}}+\arcsin \frac{1}{\sqrt{65}} = \). | \frac{\pi}{4} | 0.625 |
Find the 6-digit number beginning and ending in the digit 2 that is the product of three consecutive even integers. | 287232 | 0.875 |
In the right triangle \( KLM \), a circle is constructed on the leg \( KM \) as the diameter, which intersects the hypotenuse \( KL \) at point \( G \). A tangent to the circle is drawn through point \( G \), intersecting the leg \( ML \) at point \( F \). Find the length of \( FL \), given that \( KG = 5 \) and \( LG = 4 \). | 3 | 0.625 |
Let \( \left\{ \frac{1}{(n+1) \sqrt{n} + n \sqrt{n+1}} \right\} \) be a sequence and \( S_n \) be the sum of the first \( n \) terms of this sequence. How many rational numbers are there in the first 2016 terms of the sequence \( \left\{ S_n \right\} \)? | 43 | 0.875 |
A seagull is being fed from a moving boat. A piece of bread is thrown down, the seagull picks it up from the surface of the sea in 3 seconds, and then catches up with the boat in 12 seconds. Upon entering a bay, the boat's speed is halved. How much time will it now take for the seagull to catch up with the boat, after it picks up the piece of bread? | 2 \text{ seconds} | 0.875 |
In a chess tournament, two 7th-grade students and several 8th-grade students participated. Each student played with every other participant once. The two 7th graders together scored 8 points, and all 8th graders scored the same number of points. How many 8th graders participated in the tournament? | 7 | 0.375 |
Rachel and Steven play games of chess. If either wins two consecutive games, they are declared the champion. The probability that Rachel will win any given game is 0.6, the probability that Steven will win any given game is 0.3, and the probability that any given game is drawn is 0.1. Find the value of \(1000P\), where \(P\) is the probability that neither is the champion after at most three games. | 343 | 0.375 |
In front of Vasya, there is a stack of 15 red, 15 blue, and 15 yellow cards. Vasya needs to choose 15 out of all 45 cards to earn the maximum number of points. Points are awarded as follows: for each red card, Vasya earns one point. For each blue card, Vasya earns points equal to twice the number of red cards chosen, and for each yellow card, Vasya earns points equal to three times the number of blue cards chosen. What is the maximum number of points Vasya can earn? | 168 | 0.375 |
For \( x, y \in [1,3] \), find the minimum value of the expression
\[
A = \frac{(3xy + x^{2}) \sqrt{3xy + x - 3y} + (3xy + y^{2}) \sqrt{3xy + y - 3x}}{x^{2} y + y^{2} x}
\] | 4 | 0.875 |
What is the smallest sum that nine consecutive natural numbers can have if this sum ends in 2050306? | 22050306 | 0.375 |
There are 30 people studying in the Slytherin House at Hogwarts. Some of them are friends (friendship is mutual, i.e., if A is friends with B, then B is also friends with A), but no three people are pairwise friends with each other. For New Year, everyone sent postcards to all their friends. What is the maximum number of postcards that could have been sent? | 450 | 0.875 |
Let's draw the diagonals AC and BD of the parallelogram. Let them intersect at point O. Then CO, BN, DM are medians of triangle BCD. Let them intersect at point K. By the property of medians, BK:KN = 2:1. Since DM is perpendicular to AC, triangle CKD is a right triangle. KN is the median drawn to the hypotenuse. Therefore, KN = 1/2 CD. Then BN:CD = 3:2. Thus, BN = 1.5 CD = 9. | 9 | 0.625 |
The instructor of a summer math camp brought several shirts, several pairs of trousers, several pairs of shoes, and two jackets for the entire summer. In each lesson, he wore trousers, a shirt, and shoes, and he wore a jacket only on some lessons. On any two lessons, at least one piece of his clothing or shoes was different. It is known that if he had brought one more shirt, he could have conducted 18 more lessons; if he had brought one more pair of trousers, he could have conducted 63 more lessons; if he had brought one more pair of shoes, he could have conducted 42 more lessons. What is the maximum number of lessons he could conduct under these conditions? | 126 | 0.5 |
In triangle \(ABC\), bisector \(CD\) is drawn from the right angle at \(ACB\); \(DM\) and \(DN\) are the altitudes of triangles \(ADC\) and \(BDC\) respectively.
Find \(AC\), given that \(AM = 4\) and \(BN = 9\). | 10 | 0.875 |
The watermelon seller weighed 20 watermelons (weighing 1 kg, 2 kg, 3 kg, ..., 20 kg) one by one while waiting for customers, balancing a watermelon on one pan of the scale with one or two weights on the other pan (possibly identical). At the same time, the seller noted down which weights he used. What is the minimum number of different numbers that could have appeared in his records if the weight of each weight is an integer number of kilograms? | 6 | 0.125 |
Given a triangle \( \triangle ABC \) with orthocenter \( H \) and circumcenter \( O \). The radius of the circumcircle is 3, and the distance \( OH \) is 1. The side lengths of the triangle are \( |BC| = a \), \( |CA| = b \), and \( |AB| = c \). Find the value of \( a^2 + b^2 + c^2 \). | 80 | 0.875 |
Josh takes a walk on a rectangular grid of \( n \) rows and 3 columns, starting from the bottom left corner. At each step, he can either move one square to the right or simultaneously move one square to the left and one square up. In how many ways can he reach the center square of the topmost row? | 2^{n-1} | 0.5 |
A circle $\omega$ is circumscribed around the triangle $ABC$. A circle $\omega_{1}$ is tangent to the line $AB$ at point $A$ and passes through point $C$, and a circle $\omega_{2}$ is tangent to the line $AC$ at point $A$ and passes through point $B$. A tangent to circle $\omega$ at point $A$ intersects circle $\omega_{1}$ again at point $X$ and intersects circle $\omega_{2}$ again at point $Y$. Find the ratio $\frac{AX}{XY}$. | \frac{1}{2} | 0.125 |
Let \(a\), \(b\), and \(c\) be positive integers, no two of which have a common divisor greater than 1. Show that \(2abc - ab - bc - ca\) is the largest integer which cannot be expressed in the form \(xbc + yca + zab\), where \(x\), \(y\), \(z\) are non-negative integers. | 2abc - ab - bc - ca | 0.875 |
Calculate the double integral
$$
\iint_{D}\left(54 x^{2} y^{2}+150 x^{4} y^{4}\right) d x d y
$$
where the region \(D\) is bounded by the lines \(x=1, y=x^{3}\), and \(y=-\sqrt{x}\). | 11 | 0.625 |
In an angle containing $60^{\circ}$, five circles are inscribed such that each subsequent circle, starting from the second, touches the previous one. By what factor is the sum of the areas of all five circles greater than the area of the smallest circle? | 7381 | 0.5 |
Calculate the indefinite integral:
$$
\int(3x + 4)e^{3x} \, dx
$$ | (x + 1) e^{3x} + C | 0.25 |
Lydia likes a five-digit number if none of its digits are divisible by 3. Find the total sum of the digits of all five-digit numbers that Lydia likes. | 174960 | 0.875 |
Two irreducible fractions have their denominators equal to 600 and 700. Find the minimum value for the denominator of the sum of the fractions. | 168 | 0.375 |
The angle at vertex $C$ is $120^\circ$. A circle with radius $R$ touches the sides of the angle at points $A$ and $B$. Find the length of $AB$. | R | 0.875 |
To which number can the expression
$$
\frac{(a+b)(b+c)(a+c)}{a b c}
$$
be equal if the numbers \( a \), \( b \), and \( c \) satisfy the condition of problem 84? | 8 | 0.25 |
Find the number of natural numbers \( k \), not exceeding 333300, such that \( k^{2} - 2k \) is exactly divisible by 303. | 4400 | 0.125 |
Let \( a \) and \( b \) be two positive integers whose least common multiple is 232848. How many such ordered pairs \( (a, b) \) are there? | 945 | 0.25 |
The base of a triangle is 20; the medians drawn to the lateral sides are 18 and 24. Find the area of the triangle. | 288 | 0.875 |
Study the sequence defined by \(\mathfrak{u}_{0}=0\) and \(\mathfrak{u}_{n+1}=\sqrt{12+\mathfrak{u}_{n}}\) for all \(n \in \mathbb{N}\). | 4 | 0.875 |
How many positive-integer pairs \((x, y)\) are solutions to the equation \(\frac{xy}{x+y} = 1000\)? | 49 | 0.75 |
The integer sequence \(\left\{a_{n}\right\}\) is defined as \(a_{1}=1\), \(a_{2}=2\), and \(a_{n+2}=5a_{n+1}+a_{n}\). Evaluate the expression \(\left[\frac{a_{2}}{a_{1}}\right] \left\{\left[\frac{a_{3}}{a_{2}}\right\} \left\{\frac{a_{4}}{a_{3}}\right\} \cdots \left\{\left[\left\{\frac{a_{2025}}{a_{2024}}\right\}\left[\frac{a_{2024}}{a_{2}}\right]\right.\right.\right.\). | 1 | 0.625 |
The children went to the forest to pick mushrooms. If Anya gives half of her mushrooms to Vitya, all the children will have the same number of mushrooms. But if Anya instead gives all her mushrooms to Sasha, Sasha will have as many mushrooms as all the others combined. How many children went to pick mushrooms? | 6 | 0.625 |
Given \( m > n \geqslant 1 \), find the minimum value of \( m+n \) such that \( 1000 \mid 1978^{m} - 1978^{n} \). | 106 | 0.5 |
Points \( M \) and \( N \) are the midpoints of sides \( BC \) and \( AD \) of quadrilateral \( ABCD \). It is known that \(\angle B = 150^\circ\), \(\angle C = 90^\circ\), and \(AB = CD\). Find the angle between the lines \(MN\) and \(BC\). | 60^\circ | 0.5 |
We brought a cat named Vilda to our intended cottage to catch mice. On Monday, he caught $\frac{1}{2}$ of all the mice, on Tuesday $\frac{1}{3}$ of the remaining mice, on Wednesday $\frac{1}{4}$ of those left after Tuesday's catch, and on Thursday $\frac{1}{5}$ of the rest. On Friday, the remaining mice decided to move away. How many mice were originally at the cottage, given that on Friday, two more mice moved away than Vilda caught on Tuesday? Ensure that each day the number of mice caught was an integer. | 60 | 0.875 |
Let three non-identical complex numbers \( z_1, z_2, z_3 \) satisfy the equation \( 4z_1^2 + 5z_2^2 + 5z_3^2 = 4z_1z_2 + 6z_2z_3 + 4z_3z_1 \). Denote the lengths of the sides of the triangle in the complex plane, with vertices at \( z_1, z_2, z_3 \), from smallest to largest as \( a, b, c \). Find the ratio \( a : b : c \). | 2:\sqrt{5}:\sqrt{5} | 0.875 |
The sequence \(a_{1}, a_{2}, \ldots\) consists of positive numbers and its limit is 0. What is the limit of the following sequence?
$$
b_{n}=\frac{1}{n}\left(\frac{a_{1}}{1+a_{1}}+\ldots+\frac{a_{n}}{1+a_{n}}\right)
$$ | 0 | 0.875 |
The archipelago consists of $N \geqslant 7$ islands. Any two islands are connected by no more than one bridge. It is known that no more than 5 bridges lead from each island and that among any 7 islands, there are always two that are connected by a bridge. What is the maximum possible value of $N$? | 36 | 0.375 |
In a table tennis singles tournament, it was initially planned that each pair of players would play one match. However, 3 players each played 2 matches and then withdrew from the tournament. As a result, 50 matches were played in total. How many matches were played among these 3 players? | 1 | 0.625 |
Vitya and Masha were born in the same year in June. Find the probability that Vitya is at least one day older than Masha. | \frac{29}{60} | 0.875 |
Does there exist a three-digit number whose cube ends in three sevens? | 753 | 0.25 |
In the parallelogram \(ABCD\), the diagonals \(AC = 15\) and \(BD = 9\) are known. The radius of the circumcircle of triangle \(ADC\) is 10. Find the radius of the circumcircle of triangle \(ABD\). | 6 | 0.75 |
Compute the indefinite integral:
$$
\int(1-6 x) e^{2 x} \, dx
$$ | (2 - 3x) e^{2x} + C | 0.25 |
A set of composite numbers from the set $\{1,2,3,4, \ldots, 2016\}$ is called good if any two numbers in this set do not have common divisors (other than 1). What is the maximum number of numbers that a good set can have? | 14 | 0.75 |
A smooth sphere with a radius of 1 cm is dipped in red paint and released between two absolutely smooth concentric spheres with radii of 4 cm and 6 cm respectively (this sphere is outside the smaller sphere but inside the larger one). Upon contact with both spheres, the sphere leaves a red mark. During its movement, the sphere followed a closed path, resulting in a red-bordered area on the smaller sphere with an area of 37 square cm. Find the area of the region bordered by the red contour on the larger sphere. Give your answer in square centimeters, rounded to the nearest hundredth if necessary. | 83.25 | 0.75 |
A table can seat 6 people. Two tables joined together can seat 10 people. Three tables joined together can seat 14 people. Following this pattern, if 10 tables are arranged in two rows with 5 tables in each row, how many people can sit? | 44 | 0.875 |
There are 10 ping pong players participating in a round-robin tournament. The results show that there are no draws, and among any group of 5 players, there is one player who defeats the other 4 and one player who loses to the other 4. How many players have exactly two wins? | 1 | 0.5 |
Given the hyperbola \(\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1\) with the left vertex \(A\) and the right focus \(F\), let \(P\) be an arbitrary point on the hyperbola in the first quadrant. If it is always true that \(\angle PFA = 2 \angle FAP\), find the eccentricity of the hyperbola. | 2 | 0.625 |
By permuting the digits of 20130518, how many different eight-digit positive odd numbers can be formed? | 3600 | 0.625 |
How many ways are there to place three rooks on an \(8 \times 8\) chessboard such that the rooks are in different columns and different rows? | 18816 | 0.625 |
On an island, there are knights who always tell the truth and liars who always lie. One day, 15 natives, among whom there were both knights and liars, formed a circle. Each of them said, "Of the two people standing opposite me, one is a knight and the other is a liar." How many knights are there among them? | 10 | 0.5 |
Expanding the expression \((1+\sqrt{5})^{209}\) using the binomial theorem yields terms of the form \(C_{209}^{k}(\sqrt{5})^{k}\). Find the value of \(k\) for which such a term takes the maximum value. | 145 | 0.875 |
Find all positive integers \( n \) such that \( 2^n + 3 \) is a perfect square. Also, find all positive integers \( n \) such that \( 2^n + 1 \) is a perfect square. | n = 3 | 0.75 |
A boy tells his friend: You can easily remember my phone number the following way. There is an increasing quadruple of natural numbers \(a_{1}, a_{2}, a_{3}, a_{4}\) where both \(a_{2}\) and \(a_{3}\) are the harmonic means of their neighbors, respectively. When you write these numbers next to each other in order, you get a six-digit number. This six-digit number is my phone number. What is it? (The harmonic mean \(a_{2}\) of \(a_{1}\) and \(a_{3}\) is defined as:
$$
\frac{1}{a_{2}}=\frac{1}{2}\left(\frac{1}{a_{1}}+\frac{1}{a_{3}}\right)
$$ | 681224 | 0.375 |
In a certain kingdom, the workforce is composed exclusively of the dwarf clan and the elf clan. Historically in this kingdom, dwarves and elves have always worked separately, and no enterprise ever hired both dwarves and elves simultaneously. The aggregate supply of labor resources for dwarves is represented by the function \( w_{\text{dwar}}^S = 1 + \frac{L}{3} \), and the aggregate supply of labor resources for elves is \( w_{\text{elf}}^S = 3 + L \). Conversely, the inverse function of aggregate demand for dwarf labor is \( w_{\text{dwar}}^D = 10 - \frac{2L}{3} \), and the inverse function of aggregate demand for elf labor is \( w_{\text{elf}}^D = 18 - 2L \).
The newly ascended king is very concerned about the difference in wage rates for his subjects and therefore decrees that the wages of elves and dwarves must be the same, ensuring that workers are not discriminated against based on their clan affiliation. The king believes that wage regulation may negatively impact the kingdom's economy and mandates that all his subjects behave completely competitively. By how many times will the wage of the group of workers, whose wage was lower before the king's intervention, increase if the firms in the kingdom are indifferent to hiring either elves or dwarves? | 1.25 | 0.625 |
Initially, there are three cards in a box, each with numbers $1, 2, 3$. Each time, two cards are drawn from the box, and their sum is written on another blank card, then one card is put back into the box. After performing this operation 5 times, all cards except the last one have been drawn at least once but not more than twice. What is the maximum number on the card in the box at this point? | 28 | 0.125 |
In the figure below, all the small squares on the grid are equal. What is the measure of the angle $\angle A E F$? Justify your answer.
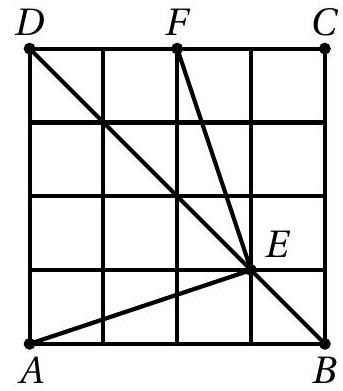 | 90^\circ | 0.125 |
Given two lines \( A_{1} x + B_{1} y = 1 \) and \( A_{2} x + B_{2} y = 1 \) intersect at point \( P(-7, 9) \), find the equation of the line passing through points \( P_{1}\left(A_{1}, B_{1}\right) \) and \( P_{2}\left(A_{2}, B_{2}\right) \). | -7x + 9y = 1 | 0.25 |
Given non-empty sets
$$
\begin{array}{l}
A = \{x \mid m+1 \leqslant x \leqslant 2m-1\}, \\
B = \{x \mid x^2 - 2x - 15 \leqslant 0\},
\end{array}
$$
and \( A \subseteq B \).
Determine the range of the real number \( m \). | [2, 3] | 0.875 |
Find the intersection point of the line and the plane.
\(\frac{x-1}{2}=\frac{y+2}{-5}=\frac{z-3}{-2}\)
\(x + 2y - 5z + 16 = 0\) | (3, -7, 1) | 0.875 |
Let \( M = \{1, 2, 3, \ldots, 1995\} \). Subset \( A \) of \( M \) satisfies the condition: If \( x \in A \), then \( 15x \notin A \). What is the maximum number of elements in \( A \)? | 1870 | 0.375 |
\( w, x, y, z \) are real numbers such that
\[
\begin{aligned}
w+x+y+z & =5 \\
2 w+4 x+8 y+16 z & =7 \\
3 w+9 x+27 y+81 z & =11 \\
4 w+16 x+64 y+256 z & =1
\end{aligned}
\]
What is the value of \( 5w + 25x + 125y + 625z \)? | -60 | 0.5 |
It is known that the only solution to the equation
$$
\pi / 4 = \operatorname{arcctg} 2 + \operatorname{arcctg} 5 + \operatorname{arcctg} 13 + \operatorname{arcctg} 34 + \operatorname{arcctg} 89 + \operatorname{arcctg}(x / 14)
$$
is a natural number. Find it. | 2016 | 0.125 |
A palindromic number is a number that reads the same when the order of its digits is reversed. What is the difference between the largest and smallest five-digit palindromic numbers that are both multiples of 45? | 9090 | 0.875 |
There are five people, \( \mathbf{A} \), \( \mathbf{B} \), \( \mathbf{C} \), \( \mathbf{D} \), and \( \mathbf{E} \), each of whom either always tells the truth or always lies, and they all know each other's behavior. \( \mathrm{A} \) says that \( \mathrm{B} \) is a liar, \( \mathrm{B} \) says that \( \mathrm{C} \) is a liar, \( \mathrm{C} \) says that \( \mathrm{D} \) is a liar, and \( \mathrm{D} \) says that \( \mathbf{E} \) is a liar. How many liars can there be at most among these five people? | 3 | 0.875 |
$n$ mushroom gatherers went into the forest and collectively brought back 450 mushrooms (each one brought home at least one mushroom). A boy named Petya, upon learning this, declared: "There must be at least two of them who brought back the same number of mushrooms!" What is the smallest $n$ for which Petya is certainly correct? Don't forget to justify your answer. | 30 | 0.5 |
In triangle \( T_{0} \), a triangle was formed using its midlines and named \( T_{1} \). In triangle \( T_{1} \), a triangle was formed using its midlines and named \( T_{2} \). Continuing in this manner, triangle \( T_{10} \) was obtained. Find the ratio of the sum of the areas of all these eleven triangles to the area of the last triangle. If the answer is a fractional number, it should be written as a decimal using a dot, for example, \(« 0.15 »\). | 1398101 | 0.625 |
The side $AB$ of triangle $ABC$ is extended beyond vertex $B$ and a point $A_1$ is chosen on the ray $AB$ such that point $B$ is the midpoint of segment $AA_1$. The side $BC$ is extended beyond vertex $C$ and a point $B_1$ is marked on the extension such that $C$ is the midpoint of $BB_1$. Similarly, the side $CA$ is extended beyond vertex $A$ and a point $C_1$ is marked on the extension such that $A$ is the midpoint of $CC_1$. Find the area of triangle $A_1B_1C_1$ if the area of triangle $ABC$ is 1. | 7 | 0.75 |
The distance from $A$ to $B$ is 999 km. Along the road, there are kilometer markers that indicate the distance to $A$ and to $B$ as follows:
$0|999, 1|998, \ldots, 999|0$.
How many of these markers have signs that contain only two different digits? | 40 | 0.5 |
If the sequence \(\left\{a_{n}\right\}\) satisfies \(a_{1}=\frac{1}{2}\) and \(a_{n+1}=\frac{2 a_{n}}{3 a_{n}+2}\) for \(n \in \mathbf{N}_{+}\), then find \(a_{2017}\). | \frac{1}{3026} | 0.875 |
Two individuals undertake a certain task and work for an equal amount of time. $A$ misses 2 days and earns 80 forints in total, while $B$ misses 5 days and earns 63 forints. If $A$ had missed 5 days and $B$ had missed 2 days, then $A$ would earn 2 forints more than $B$. How many days did the work last? | 32 | 0.75 |
Which of the following numbers is closest to \(2.015 \times 510.2\)?
A) 0.1
B) 1
C) 10
D) 100
E) 1000 | 1000 | 0.25 |
For what smallest natural number \( a \) are there exactly 50 perfect squares in the numerical interval \( (a, 3a) \)? | 4486 | 0.125 |
The sequence \(a_{n} = b[\sqrt{n+c}] + d\) is given, where the successive terms are
\[
1, 3, 3, 3, 5, 5, 5, 5, 5, \cdots
\]
In this sequence, each positive odd number \(m\) appears exactly \(m\) times consecutively. The integers \(b\), \(c\), and \(d\) are to be determined. Find the value of \(b+c+d\). | 2 | 0.75 |
Let \( ABC \) be a right triangle with \( \angle A \) being the right angle. Show the equality
\[ BC^{2} = AC^{2} + AB^{2} \]
Hint: Introduce the foot of one of the altitudes. | BC^2 = AC^2 + AB^2 | 0.5 |
How many natural numbers \( \mathrm{N} \) greater than 900 exist such that among the numbers \( 3\mathrm{N}, \mathrm{N} - 900, \mathrm{N} + 15, 2\mathrm{N} \) exactly two are four-digit numbers? | 5069 | 0.125 |
$C$ is a point on the extension of diameter $A B$, $C D$ is a tangent, and the angle $A D C$ is $110^{\circ}$. Find the angular measure of arc $B D$. | 40^\circ | 0.875 |
Determine the two-digit numbers that are 3 less than the sum of the cubes of their digits! | 32 | 0.375 |
Petya cut an 8x8 square along the borders of the cells into parts of equal perimeter. It turned out that not all parts are equal. What is the maximum possible number of parts he could get? | 21 | 0.5 |
Simplify the expression:
\[
\frac{\left(p q^{-1}+1\right)^{2}}{p q^{-1}-p^{-1} q} \cdot \frac{p^{3} q^{-3}-1}{p^{2} q^{-2}+p q^{-1}+1} \div \frac{p^{3} q^{-3}+1}{p q^{-1}+p^{-1} q-1}
\] | 1 | 0.625 |
During breaks, schoolchildren played table tennis. Any two schoolchildren played no more than one game against each other. At the end of the week, it turned out that Petya played half, Kolya - a third, and Vasya - one fifth of the total number of games played during the week. What could be the total number of games played during the week if it is known that at least two games did not involve Vasya, Petya, or Kolya? | 30 | 0.5 |
As shown in the diagram, $E$ is the midpoint of the leg $AB$ of trapezoid $ABCD$. $DF \perp EC$, $DF=10$, and $EC=24$. Find the area of trapezoid $ABCD$. | 240 | 0.125 |
Solve the system:
\[
\begin{aligned}
|x + y| + |1 - x| &= 6, \\
|x + y + 1| + |1 - y| &= 4.
\end{aligned}
\] | (-2, -1) | 0.125 |
Let \( p \) and \( q \) be distinct prime numbers. In how many ways can the fraction \( \frac{1}{pq} \) be decomposed into the sum of the reciprocals of 2 different natural numbers? | 4 | 0.75 |
Find all positive integers \( n \) such that there exist positive integers \( x_{1}, x_{2}, \cdots, x_{2012} \) satisfying
\[ x_{1} < x_{2} < \cdots < x_{2012} \]
and
\[ \frac{1}{x_{1}} + \frac{2}{x_{2}} + \cdots + \frac{2012}{x_{2012}} = n. \] | 1, 2, \ldots, 2012 | 0.125 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.